复数四则运算C语言
复数的四则运算公式

复数的四则运算公式复数是数学中的一个概念,它可以表示为实部与虚部的和。
在复数的四则运算中,包括加法、减法、乘法和除法。
下面将分别介绍这四种运算。
一、复数的加法复数的加法是指将两个复数相加的操作。
假设有两个复数a+bi和c+di,其中a、b、c、d分别为实数部分和虚数部分。
则两个复数的加法可以表示为:(a+bi) + (c+di) = (a+c) + (b+d)i即实部相加,虚部相加。
二、复数的减法复数的减法是指将两个复数相减的操作。
假设有两个复数a+bi和c+di,其中a、b、c、d分别为实数部分和虚数部分。
则两个复数的减法可以表示为:(a+bi) - (c+di) = (a-c) + (b-d)i即实部相减,虚部相减。
三、复数的乘法复数的乘法是指将两个复数相乘的操作。
假设有两个复数a+bi和c+di,其中a、b、c、d分别为实数部分和虚数部分。
则两个复数的乘法可以表示为:(a+bi) × (c+di) = (ac-bd) + (ad+bc)i即实部相乘减虚部相乘,并将结果相加。
四、复数的除法复数的除法是指将两个复数相除的操作。
假设有两个复数a+bi和c+di,其中a、b、c、d分别为实数部分和虚数部分。
则两个复数的除法可以表示为:(a+bi) ÷ (c+di) = [(ac+bd)÷(c^2+d^2)] + [(bc-ad)÷(c^2+d^2)]i即将实部和虚部分别除以除数的实部和虚部的平方和。
通过以上介绍,我们了解了复数的四则运算公式。
在实际应用中,复数的四则运算常常用于电路分析、信号处理等领域。
对于复数的运算要求掌握加减法的运算规则,以及乘法和除法的计算方法。
复数的四则运算在解决实际问题中起到了重要的作用,对于深入理解复数的概念和应用具有重要意义。
因此,掌握复数的四则运算公式对于数学学习和实际应用都是非常重要的。
希望通过本文的介绍,读者能够对复数的四则运算有更深入的了解,并能够熟练运用于实际问题的解决中。
c++语言对复数的四则运算的实现

c++语言对复数的四则运算的实现要求:1.定义复数的结构体2.定义四则运算四种运算函数3.利用函数的调用和参数传递,通过键盘输入(cin的方式)进行运算的两个复数4.结果的输出必须用cout的方式c++语言对复数的四则运算的实现要求:1.定义复数的结构体2.定义四则运算四种运算函数3.利用函数的调用和参数传递,通过键盘输入(cin的方式)进行运算的两个复数4.结果的输出必须用cout的方式#include <iostream.h>struct complex{double real;//复数的实部double image;//复数的虚部};void main(){int i;char calu;complex num1;complex num2;cout<<"请输入第一个复数:"<<endl;cout<<"第一个复数的实部:num1.real=";cin>>num1.real;cout<<"第一个实数的虚部:num1.image=";cin>>num1.image;cout<<"请输入第二个复数:"<<endl;cout<<"第二个实数的实部:num2.real=";cin>>num2.real;cout<<"第二个实数的虚部:num2,image=";cin>>num2.image;loop:cout<<"输入所进行运算的运算符(+,-,*,/):"<<endl;cin>>calu;switch (calu){case'+':double m;double n;m=num1.real+num2.real;n=num1.image+num2.image;cout<<"两个复数的和是:"<<endl;if (n==0)cout<<m<<endl;else if (m==0)cout<<n<<'i'<<endl;else if (n<0)cout<<m<<n<<'i'<<endl;elsecout<<m<<'+'<<n<<'i'<<endl;break;case'-':m=num1.real-num2.real;n=num1.image-num2.image;cout<<"两个复数的差是:"<<endl;if (n==0)cout<<m<<endl;else if (m==0)cout<<n<<'i'<<endl;else if (n<0)cout<<m<<n<<'i'<<endl;elsecout<<m<<'+'<<n<<'i'<<endl;break;case'*':m=(num1.real*num2.real)-(num1.image*num2.image);n=(num1.real*num2.image)+(num2.real*num1.image);cout<<"两个复数的积是:"<<endl;if (n==0)cout<<m<<endl;else if (m==0)cout<<n<<'i'<<endl;else if (n<0)cout<<m<<n<<'i'<<endl;elsecout<<m<<'+'<<n<<'i'<<endl;break;case'/':m=(num1.real*num2.real+num1.image*num2.image)/(num2.real*num2.real+num2.image*num2.image);n=(num1.image*num2.real-num1.real*num2.image)/(num2.real*num2.real+num2.image*nu m2.image);;cout<<"两个复数的商是:"<<endl;if(num2.real==0&&num2.image==0)cout<<"分母为零,不可以进行运算。
复数的四则运算(一)

(a+bi)(c+di)= ac+bci+adi+bdi2
=(ac-bd)+(bc+ad)i
2、复数的乘法满足交换律、
结合律以及乘法对加法的分配律. 即对任何z1, z2, z3 有
z1z2=z2z1; (z1z2)z3=z1(z2z3);
z1(z2+z3)=z1z2+z1z3
例2、 (2 i )( 3 2i )( 1 3i )
一.复数加法的运算法则:
1、运算法则:设复数z1=a+bi, z2=c+di, ( a,b,c,d∈R) 那么:z1+z2=(a+c)+(b+d)i 即:两个复数相加就是实部与实部, 虚部与虚部分别相加.
2、复数的加法满足交换律、结合律,
即对任何 z1, z2, z3∈C,有
z1+z2=z2+z1, (z1+z2)+z3=z1+(z2+z3).
例3、求下列复数的平方根
(1) -4 (2) 2i,3i,-8i
(3) 5+12i
例4:计算
2
(a bi )( a bi ) 解: (a bi )(a bi )
a abi abi b i
2 2
a b
2
2
(a bi )( a bi ) a b
2
2
例5、在复数范围内分解因式 (1) x2 +9 (2) x4 -16
(3) x2+2x+5
再见
二.复数减法的运算法则:
1、运算法则:设复数z1=a+bi, z2=c+di, ( a,b,c,d∈R) 那么:z1-z2=(a-c)+(b-d)i
复数四则运算c语言(加减乘除)

# include "stdio.h"# include "stdlib.h"struct complex{float real;float imaginary;};void InitComplex(complex &c,float r1,float r2){c.real=r1;c.imaginary=r2;}void AddComplex(complex &c,complex c1,complex c2){c.real=c1.real+c2.real;c.imaginary=c1.imaginary+c2.imaginary;}void SubComplex(complex &c,complex c1,complex c2){c.real=c1.real-c2.real;c.imaginary=c1.imaginary-c2.imaginary;}void multiplyComplex (complex &c,complex c1,complex c2){c.real=(c1.real*c2.real)-(c1.imaginary*c2.imaginary);c.imaginary=(c1.real*c2.imaginary)+(c2.real*c1.imaginary);}Void divideComplex(complex &c,complex c1,complex c2){c.real=(c1.real*c2.real+c1.imaginary*c2.imaginary)/(c2.real*c2.real+c2.imaginary*c2.imaginary);c.imaginary=(c1.imaginary*c2.real-c1.real*c2.imaginary)/(c2.real*c2.real+c2.imaginary*c2.imagi nary);}void main(){complex c,c1,c2;float r,r1,r2,r11,r12,r21,r22;int node;printf("qing shu ru xu hao:\n");printf("1:Read complex number;2: Print the complex number;3: Calculates the sum \n");printf("4: Calculates the difference;5: Calculates the product;6: Calculates the division \n");scanf("%d",&node);while(node!=0){switch(node){case 1: printf("please input the real part and the imaginary part \n");scanf("%f%f",&r1,&r2);InitComplex(c,r1,r2);printf("the complex number:c=%f+i%f\n",c.real,c.imaginary);break;case 2: printf("the complex number:c=%f+i%f\n",c.real,c.imaginary);break;case 3: printf("please input the real part and the imaginary part of number 1\n");scanf("%f%f",&r11,&r12);InitComplex(c1,r11,r12);printf("please input the real part and the imaginary part of number 2\n");scanf("%f%f",&r21,&r22);InitComplex(c2,r21,r22);AddComplex(c,c1,c2);printf("Sum:c=%f+i%f\n",c.real,c.imaginary);break;case 4: printf("please input the real part and the imaginary part of number 1\n");scanf("%f%f",&r11,&r12);InitComplex(c1,r11,r12);printf("please input the real part and the imaginary part of number 2\n");scanf("%f%f",&r21,&r22);InitComplex(c2,r21,r22);SubComplex(c,c1,c2);printf("Difference:c=%f+i%f\n",c.real,c.imaginary);break;case 5: printf("please input the real part and the imaginary part of number 1\n");scanf("%f%f",&r11,&r12);InitComplex(c1,r11,r12);printf("please input the real part and the imaginary part of number 2\n");scanf("%f%f",&r21,&r22);InitComplex(c2,r21,r22);multiplyComplex (c,c1,c2);printf("Product:c=%f+i%f\n",c.real,c.imaginary);break;case 6: printf("please input the real part and the imaginary part of number 1\n");scanf("%f%f",&r11,&r12);InitComplex(c1,r11,r12);printf("please input the real part and the imaginary part of number 2\n");scanf("%f%f",&r21,&r22);InitComplex(c2,r21,r22);divideComplex(c,c1,c2);printf("Division:c=%f+i%f\n",c.real,c.imaginary);break;default:printf("Over");}scanf("%d",&node);}}。
复数四则运算

若 z1, z2 是共轭复数,那么
(1)在复平面内,它们所对应的点有怎样的位置关系?
(2) z1 • z2 是一个怎样的数?
关于共轭复数的运算性质
z1 , z2 ∈C , 则
z z z z
得 a 1,b 3
z 1 3i
综上: Z=4,1+ 3i ,1– 3i .
例3 将下列复数表示为 x iy 的形式.
(1)
1 1
i i
7
;
(2) i 1 i . 1i i
解 (1) 1 i (1 i)2 (1 i)2 i, 1 i (1 i)(1 i) 2
(b
4b a2 b2
)i
z 4R
z
b(1
a2
4
b2
)
0
b 0或a2 b2 4 ①
| z 2 | 2得| a bi 2 | 2
(a 2)2 b2 2 ②
将 b=0代入②得 a=4 或 a=0 ∴ Z=4 或 Z=0 (舍)
将 a2 b2 4 代入② (a 2) Nhomakorabea 4 a2 4, 得 a 1
22
22
1
小结: 2 , ( )2 ,
3 1, ( )3 1.
例4:已知z (4 3i)(1 7i) ,求 z 2 i
解:z (4 3i)(1 7i) 2 i
| 4 3i || 1 7i | | 2 i|
5 8 10 6 .
3
3
例5 计算 (1 3i)3 (1 i)6
设 OZ1 及 OZ2 分别与复数 a bi 及复数 c di对应,则 OZ1, (a,b)
C++实现复数四则运算

#include <iostream.h>//using namespace std;class Complex{public:Complex(){real=0;imag=0;}Complex(double r,double i):real(r),imag(i){}friend istream& operator>>(istream&,Complex&);//友元函数,用来输入复数friend ostream& operator<<(ostream&,Complex&);//友元函数,用来输出复数friend Complex operator+(Complex &c1,Complex &c2);//重载加法友元函数声明friend Complex operator-(Complex &c1,Complex &c2);//重载减法友元函数声明friend Complex operator*(Complex &c1,Complex &c2);//重载乘法友元函数声明friend Complex operator/(Complex &c1,Complex &c2);//重载除法友元函数声明private:double real;double imag;};istream & operator>>(istream &input,Complex &c){cout<<"请输入复数的实部:";input>>c.real;cout<<"请输入复数的虚部:";input>>c.imag;return input;}ostream & operator<<(ostream &output,Complex &c){if(c.real==0&&c.imag==0){output<<0;}elseif(c.real==0&&c.imag!=0){output<<c.imag<<"i";}elseif(c.real!=0&&c.imag==0){output<<c.real;}if(c.imag==1){output<<c.real<<"+i";}elseif(c.imag==-1){output<<c.real<<"-i";}elseif(c.imag>0){output<<c.real<<"+"<<c.imag<<"i";}elseif(c.imag<0){output<<c.real<<c.imag<<"i";}return output;}Complex operator +(Complex &c1,Complex &c2){return Complex(c1.real+c2.real,c1.imag+c2.imag);}Complex operator-(Complex &c1,Complex &c2){return Complex(c1.real-c2.real,c1.imag-c2.imag);}Complex operator*(Complex &c1,Complex &c2){return Complex(c1.real*c2.real-c1.imag*c2.imag,c1.real*c2.imag+c1.imag*c2.real);}Complex operator/(Complex &c1,Complex &c2){returnComplex((c1.real*c2.real+c1.imag*c2.imag)/(c2.real*c2.real+c2.imag*c2.imag),(c2.real*c1.imag-c1.real*c2.imag)/(c2.real*c2.real +c2.imag*c2.imag));}void suan(Complex &c1,Complex &c2,Complex &c3){char c;cout<<"菜单:"<<endl;cout<<"1.输入复数1"<<endl;cout<<"2.输入复数2"<<endl;cout<<"+.进行复数相加运算"<<endl;cout<<"-.进行复数相减运算"<<endl;cout<<"*.进行复数相乘运算"<<endl;cout<<"/.进行复数相除运算"<<endl;cout<<"0.退出"<<endl;while(flag){cout<<"请选择操作:"<<endl;cin>>c;switch (c){case '1':cin>>c1;cout<<"您输入的复数是:"<<c1<<endl;break;case '2':cin>>c2;cout<<"您输入的复数是:"<<c2<<endl;break;case '+':c3=c1+c2;cout<<"("<<c1<<")+("<<c2<<")="<<c3<<endl;break;case '-':c3=c1-c2;cout<<"("<<c1<<")-("<<c2<<")="<<c3<<endl;break;case '*':c3=c1*c2;cout<<"("<<c1<<")*("<<c2<<")="<<c3<<endl;break;case '/':c3=c1/c2;cout<<"("<<c1<<")/("<<c2<<")="<<c3<<endl;break;case '0':flag=0;break;default:cout<<"超出范围!"<<endl;}}}int main(){Complex c1,c2,c3;suan(c1,c2,c3);return 0;}。
运用C语言编写复数的四则运算

运用C语言编写复数的四则运算一、需求分析1.设计一个可进行复数运算的演示程序2.实现以下六种基本运算:〔1〕由于输入的实部和虚部生成一个复数;〔2〕两个复数求和;〔3〕两个复数求差;〔4〕两个复数求积;〔5〕从已知复数中别离出虚部。
运算结果一相应的复数或实数的表示形式显示。
3.程序执行的命令包括:4.〔1〕建立一个复数,然后根据提示用户输入两个复数,使得能同时进行两个复数的加.减.乘运算。
(2)输入形式和输入值得范围:分别输入两个复数,其格式为:a+bi用enter结束输入。
(3)输出形式:按程序规定输出其运算值。
如:运算后只有实数时只输出实数虚部部分不表示,反之一样〔1〕0,0;0,0;应输出“0”〔2〕3.1,0;4.22, 8.9; 应输出“7.32+i8.9”(3)-1.33, 2.34; 0.1, -6.5; 应输出“-1.23-i4.16”(4)0, 9.7; -2.1, -9.7;应输出“-2.1”(5)7.7,-8;-7.7,0;应输出“-i8”二.概要分析1.为实现上述程序的功能,需要定义一个表示复数的抽象数据类型。
2.本程序包含的函数:〔1〕主函数main〔〕;(2)构造函数typedef struct〔〕;(3)调用函数Complex createComplex(float a,float b)Complex add(Complex z1,Complex z2)Complex jian(Complex z1,Complex z2)Complex cheng(Complex z1,Complex z2)void printComplex(Complex z);各函数关系如下:(5)主函数伪代码main( ){说明一个构造函数Complex;定义两个实数和虚数分别为z1,z2;提示输入实数和虚数z1,z2;调用子函数;提示输入+ - *;根据输入的符号判断输入的复数做何运算{输入+时,调用加法子函数,打印输出;输入-时,调用加法子函数,打印输出;输入*时,调用加法子函数,打印输出;}}三.详细设计1.主函数及其他函数#include<stdio.h>#include<math.h>typedef struct{float re;float im;} Complex;Complex createComplex(float a,float b) //编写一个函数生成复数// {Complex z;z.re=a;z.im=b;return z;}void printComplex(Complex z) //输出复数并控制其格式// {if(z.re==0&&z.im==0)printf("0\n");else if(z.re!=0&&z.im==0)printf("%.2f\n",z.re);else if(z.re==0&&z.im!=0){if(z.im>0)printf("i%.2f\n",z.im);else if(z.im<0)printf("-i%.2f\n",fabs(z.im));}else{if(z.im>0)printf("%.2f+i%.2f\n",z.re,z.im);elseprintf("%.2f-i%.2f\n",z.re,fabs(z.im));}}Complex add(Complex z1,Complex z2){Complex z;z.re=z1.re+z2.re;z.im=z1.im+z2.im;return z;}Complex jian(Complex z1,Complex z2){Complex z;z.re=z1.re-z2.re;z.im=z1.im-z2.im;return z;}Complex cheng(Complex z1,Complex z2) {Complex z;z.re=z1.re*z2.re-z1.im*z2.im;z.im=z1.re*z2.im+z1.im*z2.re;return z;}main(){float a,b,c,d;Complex z1,z2,c1,c2,c3;printf("请输入元素");scanf("%f%f%f%f",&a,&b,&c,&d); //输入元素并调用函数生成复数z1,z2;并输出//z1=createComplex(a,b);z2=createComplex(c,d);printf("产生的两个复数为:");printComplex(z1);printComplex(z2);c1=add(z1,z2);c2=jian(z1,z2);c3=cheng(z1,z2);printf("这两个复数的和差积:");printComplex(c1);printComplex(c2);printComplex(c3);}四.调试及分析1.由于开始对于结构体使用并不熟悉,使用时语法错误很多,需要多加使用。
复数的四则运算法则公式

复数的四则运算法则公式
我们要探讨复数的四则运算法则。
首先,我们需要了解复数的基本形式和定义。
一个复数可以表示为 a + bi,其中 a 是实部,b 是虚部,i 是虚数单位,满足 i^2 = -1。
接下来,我们将探讨复数的加法、减法、乘法和除法规则。
1. 加法规则:
给定两个复数 a + bi 和 c + di,它们的和是 (a+c) + (b+d)i。
2. 减法规则:
给定两个复数 a + bi 和 c + di,它们的差是 (a-c) + (b-d)i。
3. 乘法规则:
给定两个复数 a + bi 和 c + di,它们的乘积是 (ac - bd) + (ad + bc)i。
4. 除法规则:
给定两个复数 a + bi 和 c + di(其中c ≠ 0),它们的商是 ((ac + bd) / c) + ((bc - ad) / c)i。
加法规则:
给定两个复数 a + bi 和 c + di,它们的和是 (a+c) + (b+d)i。
减法规则:
给定两个复数 a + bi 和 c + di,它们的差是 (a-c) + (b-d)i。
乘法规则:
给定两个复数 a + bi 和 c + di,它们的乘积是 (ac - bd) + (ad + bc)i。
除法规则:
给定两个复数 a + bi 和 c + di(其中c ≠ 0),它们的商是 ((ac + bd) / c) + ((bc - ad) / c)i。
§2 复数的四则运算

()
A.1-2i
B.2-i
C.2+i 答案:D
D.1+2i
5.若x-2+yi和3x-i互为共轭复数,则实数x=______,y=
________.
答案:-1 1
考点一 复数的加减运算 [典例] 计算:(1)(1+2i)+(3-4i)-(5+6i); (2)5i-[(3+4i)-(-1+3i)];
(3)(a+bi)-(2a-3bi)-3i(a,b∈R ). [解] (1)(1+2i)+(3-4i)-(5+6i) =(4-2i)-(5+6i)=-1-8i. (2)5i-[(3+4i)-(-1+3i)]=5i-(4+i)=-4+4i. (3)(a+bi)-(2a-3bi)-3i=(a-2a)+[b-(-3b)-3]i=-a +(4b-3)i.
2+ 2i34+5i (2) 5-4i1-i . 解:(1)(4-i5)(6+2i7)+(7+i11)(4-3i)
=(4-i)(6-2i)+(7-i)(4-3i)
=24-8i-6i-2+28-21i-4i-3
=47-39i.
(2)
25+-42ii31-4+i5i=2
二、基本技能·素养培优
1.判断(正确的打“√”,错误的打“×”)
(1)复数与向量一一对应. (2)复数与复数相加减后结果只能是实数.
(×)Байду номын сангаас(× )
(3)因为虚数不能比较大小,所以虚数的模也不能比较大小.
(× )
(4)两个共轭复数的差为纯虚数.
(√ )
(5)若z1,z2∈C,且z21+z22=0,则z1=z2=0.
4.共轭复数 当两个复数的 实部 相等,虚部 互为相反数时,这样的两个
复数叫做共轭复数 .复数z的共轭复数用 z 来表示,也就是当z= a+bi时, z = a-bi .于是z z =a2+b2= |z|2 .
第五章 §2 复数的四则运算

§2复数的四则运算学习目标1.熟练掌握复数代数形式的加减乘除运算.2.理解复数乘法的交换律、结合律和乘法对加法的分配律.3.理解共轭复数的概念.知识点一复数代数形式的加减法思考类比多项式的加减法运算,想一想复数如何进行加减法运算?答案两个复数相加(减)就是把实部与实部、虚部与虚部分别相加(减),即(a+b i)±(c+d i)=(a±c)+(b±d)i.梳理(1)运算法则设z1=a+b i,z2=c+d i是任意两个复数,那么(a+b i)+(c+d i)=(a+c)+(b+d)i,(a+b i)-(c+d i)=(a-c)+(b-d)i.(2)加法运算律对任意z1,z2,z3∈C,有z1+z2=z2+z1,(z1+z2)+z3=z1+(z2+z3).知识点二复数的乘法及其运算律思考怎样进行复数的乘法运算?答案两个复数相乘,类似于两个多项式相乘,只要把已得结果中的i2换成-1,并且把实部与虚部分别合并即可.梳理(1)复数的乘法法则设z1=a+b i,z2=c+d i是任意两个复数,那么它们的积(a+b i)(c+d i)=(ac-bd)+(ad+bc)i.(2)复数乘法的运算律对于任意z1,z2,z3∈C,有知识点三共轭复数当两个复数的实部相等,虚部互为相反数时,这两个复数叫作互为共轭复数,z的共轭复数用z表示.即当z=a+b i时,z=a-b i.知识点四复数的除法法则设z1=a+b i,z2=c+d i(a,b,c,d∈R,z2≠0),则z1z2=a+b ic+d i=ac+bdc2+d2+bc-adc2+d2i(c+d i≠0).1.在进行复数的加法时,实部与实部相加得实部,虚部与虚部相加得虚部.(√) 2.复数加减乘除的混合运算法则是先乘除,再加减.(√)3.两个共轭复数的和与积是实数.(√)4.若z1,z2∈C,且z21+z22=0,则z1=z2=0.(×)类型一 复数的加法、减法运算例1 (1)若z 1=2+i ,z 2=3+a i(a ∈R ),复数z 1+z 2所对应的点在实轴上,则a =________.(2)已知复数z 满足|z |i +z =1+3i ,则z =________.考点 复数的加减法运算法则题点 复数加减法的综合应用答案 (1)-1 (2)1+43i 解析 (1)z 1+z 2=(2+i)+(3+a i)=5+(a +1)i ,由题意得a +1=0,则a =-1.(2)设z =x +y i(x ,y ∈R ),则|z |=x 2+y 2, ∴|z |i +z =x 2+y 2i +x +y i =x +(x 2+y 2+y )i=1+3i , ∴⎩⎪⎨⎪⎧ x =1,x 2+y 2+y =3,解得⎩⎪⎨⎪⎧x =1,y =43,∴z =1+43i. 反思与感悟 (1)复数的加减运算就是实部与实部相加减,虚部与虚部相加减.(2)当一个等式中同时含有|z |与z 时,一般用待定系数法,设z =x +y i(x ,y ∈R ). 跟踪训练1 (1)若复数z 满足z +i -3=3-i ,则z =________.(2)(a +b i)-(2a -3b i)-3i =________(a ,b ∈R ).(3)已知复数z 满足|z |+z =1+i ,则z =________.考点 复数的加减法运算法则题点 复数加减法的综合应用答案 (1)6-2i (2)-a +(4b -3)i (3)i解析 (1)∵z +i -3=3-i ,∴z =6-2i.(2)(a +b i)-(2a -3b i)-3i=(a -2a )+(b +3b -3)i =-a +(4b -3)i.(3)设z =x +y i(x ,y ∈R ),|z |=x 2+y 2, ∴|z |+z =(x 2+y 2+x )+y i =1+i ,∴⎩⎪⎨⎪⎧ x 2+y 2+x =1,y =1,解得⎩⎪⎨⎪⎧ x =0,y =1, ∴z =i.类型二 复数代数形式的乘除运算例2 计算:(1)⎝⎛⎭⎫-12+32i ⎝⎛⎭⎫32+12i (1+i); (2)(1+2i )2+3(1-i )2+i; (3)(1-4i )(1+i )+2+4i 3+4i. 考点 复数的乘除法运算法则题点 乘除法的运算法则解 (1)⎝⎛⎭⎫-12+32i ⎝⎛⎭⎫32+12i (1+i) =⎣⎡⎦⎤⎝⎛⎭⎫-34-34+⎝⎛⎭⎫34-14i (1+i) =⎝⎛⎭⎫-32+12i (1+i) =⎝⎛⎭⎫-32-12+⎝⎛⎭⎫12-32i =-1+32+1-32i.(2)(1+2i )2+3(1-i )2+i =-3+4i +3-3i 2+i=i 2+i=i (2-i )5=15+25i. (3)(1-4i )(1+i )+2+4i 3+4i =5-3i +2+4i 3+4i=7+i 3+4i =(7+i )(3-4i )(3+4i )(3-4i ) =21-28i +3i +425=25-25i 25=1-i. 反思与感悟 (1)按照复数的乘法法则,三个或三个以上的复数相乘可按从左到右的顺序运算或利用结合律运算,混合运算和实数的运算顺序一致,在计算时,若符合乘法公式,则可直接运用公式计算.(2)根据复数的除法法则,通过分子、分母都乘以分母的共轭复数,使“分母实数化”,这个过程与“分母有理化”类似.跟踪训练2 计算:(1)(4-i)(6+2i)-(7-i)(4+3i);(2)3+2i 2-3i +3-2i 2+3i; (3)(i -2)(i -1)(1+i )(i -1)+i. 考点 复数的乘除法运算法则题点 乘除法的运算法则解 (1)(4-i)(6+2i)-(7-i)(4+3i)=(24+8i -6i +2)-(28+21i -4i +3)=(26+2i)-(31+17i)=-5-15i.(2)3+2i 2-3i +3-2i 2+3i=i (2-3i )2-3i +-i (2+3i )2+3i=i -i =0.(3)(i -2)(i -1)(1+i )(i -1)+i =i 2-i -2i +2i -1+i 2-i +i=1-3i -2+i =(1-3i )(-2-i )(-2+i )(-2-i ) =-2-i +6i +3i 25=-5+5i 5=-1+i. 类型三 i 的运算性质例3 计算:(1)2+2i (1-i )2+⎝ ⎛⎭⎪⎫21+i 2 016; (2)i +i 2+…+i 2 017.考点 虚数单位i 及其性质题点 虚数单位i 的运算性质 解 (1)原式=2(1+i )-2i+⎝⎛⎭⎫22i 1 008=i(1+i)+(-i)1 008 =i +i 2+(-1)1 008·i 1 008=i -1+i 4×252=i -1+1=i.(2)方法一 原式=i (1-i 2 017)1-i =i -i 2 0181-i =i -(i 4)504·i 21-i=i +11-i =(1+i )(1+i )(1-i )(1+i )=2i 2=i. 方法二 因为i n +i n +1+i n +2+i n +3=i n (1+i +i 2+i 3)=0(n ∈N +),所以原式=(i +i 2+i 3+i 4)+(i 5+i 6+i 7+i 8)+…+(i 2 013+i 2 014+i 2 015+i 2 016)+i 2 017=i 2 017=(i 4)504·i =1504·i =i.反思与感悟 (1)等差、等比数列的求和公式在复数集C 中仍适用,i 的周期性要记熟,即i n +i n +1+i n +2+i n +3=0(n ∈N +).(2)记住以下结果,可提高运算速度.①(1+i)2=2i ,(1-i)2=-2i.②1-i 1+i =-i ,1+i 1-i=i.③1i=-i. 跟踪训练3 (1)⎝ ⎛⎭⎪⎫1+i 1-i 2 018=________. 考点 虚数单位i 及其性质题点 虚数单位i 的运算性质答案 -1解析 ⎝ ⎛⎭⎪⎫1+i 1-i 2 018=⎣⎢⎡⎦⎥⎤(1+i )(1+i )(1-i )(1+i ) 2 018=⎝⎛⎭⎫2i 2 2 018 =i 2 018=(i 4)504·i 2=1504·i 2=-1.(2)化简i +2i 2+3i 3+…+100i 100.考点 虚数单位i 及其性质题点 虚数单位i 的运算性质解 设S =i +2i 2+3i 3+…+100i 100,①所以i S =i 2+2i 3+…+99i 100+100i 101,②①-②得(1-i)S =i +i 2+i 3+…+i 100-100i 101=i (1-i 100)1-i -100i 101=0-100i =-100i.所以S =-100i 1-i =-100i (1+i )(1-i )(1+i )=-100(-1+i )2 =50-50i.所以i +2i 2+3i 3+…+100i 100=50-50i.类型四 共轭复数及其应用例4 把复数z 的共轭复数记作z ,已知(1+2i)z =4+3i ,求z .考点 共轭复数的定义与应用题点 利用定义求共轭复数解 设z =a +b i(a ,b ∈R ),则z =a -b i ,由已知得(1+2i)(a -b i)=(a +2b )+(2a -b )i =4+3i ,由复数相等的定义知,⎩⎪⎨⎪⎧ a +2b =4,2a -b =3,得⎩⎪⎨⎪⎧ a =2,b =1, 所以z =2+i.引申探究若将本例条件改为z (z +2)=4+3i ,求z .解 设z =x +y i(x ,y ∈R ).则z =x -y i ,由题意知,(x -y i)(x +y i +2)=4+3i.得⎩⎪⎨⎪⎧x (2+x )+y 2=4,xy -y (x +2)=3, 解得⎩⎨⎧ x =-1-112,y =-32或⎩⎨⎧ x =-1+112,y =-32, 所以z =⎝⎛⎭⎫-1-112-32i 或z =⎝⎛⎭⎫-1+112-32i. 反思与感悟 当已知条件出现复数等式时,常设出复数的代数形式,利用复数相等的充要条件转化为实数问题求解.跟踪训练4 已知复数z 满足|z |=1,且(3+4i)z 是纯虚数,求z 的共轭复数z .考点 共轭复数的定义与应用题点 利用定义求共轭复数解 设z =a +b i(a ,b ∈R ),则|z |=a 2+b 2=1,即a 2+b 2=1.①因为(3+4i)z =(3+4i)(a +b i)=(3a -4b )+(3b +4a )i 是纯虚数,所以3a -4b =0,且3b +4a ≠0.② 由①②联立,解得⎩⎨⎧ a =45,b =35或⎩⎨⎧ a =-45,b =-35.所以z =45-35i 或z =-45+35i.1.设z 1=3-4i ,z 2=-2+3i ,则z 1-z 2在复平面内对应的点位于() A .第一象限 B .第二象限C .第三象限D .第四象限 考点 复数的加减法运算法则题点 复数加减法与点的对应答案 D解析 ∵z 1-z 2=5-7i ,∴z 1-z 2在复平面内对应的点位于第四象限.2.设复数z 满足i z =1,其中i 为虚数单位,则z 等于( )A .-iB .iC .-1D .1考点 复数的乘除法运算法则题点 利用乘除法求复数答案 A解析 z =1i =-i.3.若z =4+3i(i 为虚数单位),则z|z |等于( )A .1B .-1C.45+35iD.45-35i考点 复数的乘除法运算法则题点 乘除法的运算法则答案 D解析z=4+3i,|z|=5,z|z|=45-35i.4.设i 是虚数单位,z 是复数z 的共轭复数,若z =2i 31+i,则z =________. 考点 共轭复数的定义与应用题点 利用定义求共轭复数答案 -1+i解析 z =2i 31+i =-2i (1-i )(1+i )(1-i )=-1-i , 所以z =-1+i.5.已知复数z 满足:z ·z +2z i =8+6i ,求复数z 的实部与虚部的和.考点 共轭复数的定义与应用题点 与共轭复数有关的综合问题解 设z =a +b i(a ,b ∈R ),则z ·z =a 2+b 2,∴a 2+b 2+2i(a +b i)=8+6i ,即a 2+b 2-2b +2a i =8+6i ,∴⎩⎪⎨⎪⎧ a 2+b 2-2b =8,2a =6,解得⎩⎪⎨⎪⎧a =3,b =1, ∴a +b =4,∴复数z 的实部与虚部的和是4.1.复数代数形式的加减法满足交换律、结合律,复数的减法是加法的逆运算.2.复数代数形式的乘除运算(1)复数代数形式的乘法类似于多项式乘以多项式,复数的乘法满足交换律、结合律以及乘法对加法的分配律.(2)在进行复数代数形式的除法运算时,通常先将除法写成分式的形式,再把分子、分母都乘以分母的共轭复数,化简后可得,类似于以前学习的分母有理化.3.复数问题实数化思想复数问题实数化是解决复数问题的基本思想方法,其桥梁是设复数z=a+b i(a,b∈R),利用复数相等的充要条件转化.一、选择题1.若复数z 满足z +(3-4i)=1,则z 的虚部是( )A .-2B .4C .3D .-4考点 复数的加减法运算法则题点 复数加减法的运算法则答案 B解析 ∵z +(3-4i)=1,∴z =-2+4i ,故z 的虚部是4.2.设复数z 满足关系式z +|z |=2+i ,那么z 等于( )A .-34+i B.34-i C .-34-i D.34+i 考点 复数的加减法运算法则题点 复数加减法的运算法则答案 D解析 设z =a +b i(a ,b ∈R ),则z +|z |=(a +a 2+b 2)+b i =2+i , 则⎩⎪⎨⎪⎧ a +a 2+b 2=2,b =1, 解得⎩⎪⎨⎪⎧a =34,b =1, ∴z =34+i.3.已知复数z满足(z-1)i=1+i,则z等于()A.-2-i B.-2+iC.2-i D.2+i考点复数的乘除法运算法则题点利用乘除法求复数答案 C解析由(z-1)i=1+i,两边同乘以-i,则有z-1=1-i,所以z=2-i.4.已知复数z 1=3-b i ,z 2=1-2i ,若z 1z 2是实数,则实数b 等于( )A .6B .-6C .0 D.16考点 复数的乘除法运算法则题点 利用乘除法求复数中的未知数答案 A解析 ∵z 1z 2=3-b i1-2i =(3-b i )(1+2i )(1-2i )(1+2i )=3+2b +(6-b )i 5是实数,∴6-b =0,∴实数b 的值为6,故选A.5.已知i 为虚数单位,图中复平面内的点A 表示复数z ,则表示复数z1+i 的点是()A .MB .NC .PD .Q考点 复数的乘除法运算法则题点 运算结果与点的对应关系答案 D解析 由图可知z =3+i ,所以复数z 1+i =3+i 1+i =(3+i)(1-i )(1+i )(1-i )=4-2i 2=2-i 表示的点是Q (2,-1).故选D.6.设复数z 满足1+z1-z =i ,则|z |等于( )A .1 B. 2 C. 3 D .2考点 复数的乘除法运算法则题点 利用乘除法求复数答案 A解析 由1+z 1-z=i , 得z =-1+i 1+i=(-1+i )(1-i )2=2i 2=i , ∴|z |=|i|=1.7.若z +z =6,z ·z =10,则z 等于( )A .1±3iB .3±iC .3+iD .3-i考点 共轭复数的定义与应用题点 与共轭复数有关的综合问题答案 B解析 设z =a +b i(a ,b ∈R ),则z =a -b i , 所以⎩⎪⎨⎪⎧ 2a =6,a 2+b 2=10,解得⎩⎪⎨⎪⎧ a =3,b =±1,则z =3±i. 8.计算(-1+3i )3(1+i )6+-2+i 1+2i的值是( ) A .0 B .1 C .2i D .i考点 复数四则运算的综合应用题点 复数的混合运算答案 C解析 原式=(-1+3i )3[(1+i )2]3+(-2+i )(1-2i )(1+2i )(1-2i )=(-1+3i )3(2i )3+-2+4i +i +25=⎝⎛⎭⎫-12+32i 3-i +i =1-i +i =i (-i )i+i =2i.二、填空题9.已知a ,b ∈R ,i 是虚数单位,若(1+i)(1-b i)=a ,则a b的值为________. 考点 复数的乘除法运算法则题点 利用乘除法求复数中的未知数答案 2解析 因为(1+i)(1-b i)=1+b +(1-b )i =a ,又a ,b ∈R ,所以1+b =a 且1-b =0,得a =2,b =1,所以a b=2. 10.若复数z 满足(3-4i)z =4+3i(i 是虚数单位),|z |=________.考点 复数的乘除法运算法则题点 利用乘除法求复数答案 1解析 因为(3-4i)z =4+3i ,所以z =4+3i 3-4i =(4+3i )(3+4i )(3-4i )(3+4i )=25i 25=i. 则|z |=1.11.定义一种运算:⎣⎢⎡⎦⎥⎤a b c d =ad -bc .则复数⎣⎢⎡⎦⎥⎤1+i -12 3i 的共轭复数是________.考点 共轭复数的定义与应用题点 利用定义求共轭复数答案 -1-3i解析 ⎣⎢⎡⎦⎥⎤1+i -12 3i =3i(1+i)+2=-1+3i , ∴其共轭复数为-1-3i.三、解答题12.已知z ,ω为复数,(1+3i)z 为纯虚数,ω=z 2+i,且|ω|=52,求ω. 考点 复数的乘除法运算法则题点 乘除法的综合应用解 设z =a +b i(a ,b ∈R ),则(1+3i)z =a -3b +(3a +b )i.由题意得a -3b =0,3a +b ≠0.因为|ω|=⎪⎪⎪⎪⎪⎪z 2+i =52, 所以|z |=a 2+b 2=510,将a =3b 代入,解得a =15,b =5或a =-15,b =-5,故ω=±15+5i 2+i=±(7-i). 13.已知复数z =1+i.(1)设ω=z 2+3z -4,求ω;(2)若z 2+az +b z 2-z +1=1-i ,求实数a ,b 的值. 考点 复数四则运算的综合应用题点 与混合运算有关的未知数求解解 (1)因为z =1+i ,所以ω=z 2+3z -4=(1+i)2+3(1-i)-4=-1-i.(2)因为z =1+i ,所以z 2+az +b z 2-z +1=(1+i )2+a (1+i )+b (1+i )2-(1+i )+1=1-i , 即(a +b )+(a +2)i i=1-i , 所以(a +b )+(a +2)i =(1-i)i =1+i ,所以⎩⎪⎨⎪⎧ a +2=1,a +b =1,解得⎩⎪⎨⎪⎧a =-1,b =2.四、探究与拓展14.投掷两颗骰子,得到其向上的点数分别为m 和n ,则复数(m +n i)(n -m i)为实数的概率为________.考点 复数的乘除法运算法则题点 乘除法的综合应用答案 16解析 易知(m +n i)(n -m i)=mn -m 2i +n 2i +mn =2mn +(n 2-m 2)i. 若复数(m +n i)(n -m i)为实数,则m 2=n 2,即(m ,n )共有(1,1),(2,2),(3,3),(4,4),(5,5),(6,6),6种情况,所以所求概率为636=16. 15.设z 是虚数,ω=z +1z是实数,且-1<ω<2. (1)求|z |的值及z 的实部的取值范围;(2)设μ=1-z 1+z,求证:μ为纯虚数. 考点 复数四则运算的综合应用题点 与四则运算有关的问题(1)解 因为z 是虚数,所以可设z =x +y i(x ,y ∈R ,且y ≠0),则ω=z +1z =(x +y i)+1x +y i =x +y i +x -y i x 2+y 2=⎝⎛⎭⎪⎫x +x x 2+y 2+⎝ ⎛⎭⎪⎫y -y x 2+y 2i. 因为ω是实数,且y ≠0,所以y -y x 2+y 2=0,即x 2+y 2=1. 所以|z |=1,此时ω=2x .又-1<ω<2,所以-1<2x <2.所以-12<x <1, 即z 的实部的取值范围是⎝⎛⎭⎫-12,1. (2)证明 μ=1-z 1+z =1-(x +y i )1+(x +y i )=(1-x -y i )(1+x -y i )(1+x )2+y 2=1-x 2-y 2-2y i 1+2x +x 2+y 2.又x2+y2=1,所以μ=-yi.1+x 因为y≠0,所以μ为纯虚数.。
复 数 的 运 算 法 则

【复数的四则运算(C++)】------------------------------------------------------------------------------------------------------**复数x被定义为二元有序实数对(a,b),记为z=a+bi,这里a和b是实数,i是虚数单位。
**在复数a+bi中,a=Re(z)称为实部,b=Im(z)称为虚部。
当虚部等于零时,这个复数可以视为实数;**当z的虚部不等于零时,实部等于零时,常称z为纯虚数。
**复数的四则运算规定为:**加法法则:(a+bi)+(c+di)=(a+c)+(b+d)i;**减法法则:(a+bi)-(c+di)=(a-c)+(b-d)i;**乘法法则:(a+bi)·(c+di)=(ac-bd)+(bc+ad)i;**除法法则:(a+bi)÷(c+di)=[(ac+bd)-(c2+d2)]+[(bc-ad)-(c2+d2)]i.**当复数的实部和虚部都相等时,两个复数相等**只有当复数的虚部等于零的时候两个复数才可以比较大小------------------------------------------------------------------------------------------------------C++代码:-------------------------------------------头文件-----------------------------------------------------#?ifndef?__COMPLEX_H__?#?define?__COMPLEX_H__#?define?_CRT_SECURE_NO_WARNINGS?1#?include?iostream#?include?stdlib.husing?namespace?std;--声明复数类class?Complexpublic:voidComplex::Print();public:Complex(doublereal,doublep_w_picpath); Complex(constComplexZ);~Complex();boolComplex::operator(constComplexZ); boolComplex::operator(constComplexZ); boolComplex::operator==(constComplexZ); public:ComplexComplexAdd(constComplexZ); ComplexComplexSub(constComplexZ); ComplexComplexMul(constComplexZ); ComplexComplexDiv(constComplexZ);private:double_real;double_p_w_picpath;#?endif?--__COMPLEX_H__----------------------------------------------函数---------------------------------------------------- #?include?"Complex.h"--打印函数void?Complex::Print()if(!this-_p_w_picpath)if(!this-_real)cout0endl;coutthis-_realendl;elseif(!this-_real)coutthis-_p_w_picpath'i'endl;if(this-_p_w_picpath0)coutthis-_realthis-_p_w_picpath'i'endl;coutthis-_real'+'this-_p_w_picpath'i'endl;--构造函数Complex::Complex(double?real,?double?p_w_picpath)_real=real;_p_w_picpath=p_w_picpath;--拷贝构造函数Complex::Complex(const?Complex?Z)_real=Z._real;_p_w_picpath=Z._p_w_picpath;--析构函数Complex::~Complex()--这里的析构函数不需要做任何操作--操作符重载-*小于*-bool?Complex::operator?(const?Complex?Z)if(!this-_p_w_picpath!Z._p_w_picpath)if(this-_realZ._real)returntrue;returnfalse;-*大于*-bool?Complex::operator?(const?Complex?Z)if(!this-_p_w_picpath!Z._p_w_picpath)if(this-_realZ._real)returntrue;returnfalse;-*等于*-bool?Complex::operator==?(const?Complex?Z)if(!this-_p_w_picpath!Z._p_w_picpath)if(this-_real==Z._real)returntrue;elseif(this-_p_w_picpath==Z._p_w_picpath) if(this-_real==Z._real)returntrue;returnfalse;--四则运算-*加法*-Complex?Complex::ComplexAdd(const?Complex?Z) Complextmp(*this);tmp._real?+=?Z._real;tmp._p_w_picpath?+=?Z._p_w_picpath;return?tmp;-*减法*-Complex?Complex::ComplexSub(const?Complex?Z) Complextmp(*this);tmp._real-=Z._real;tmp._p_w_picpath-=Z._p_w_picpath; returntmp;-*乘法*-Complex?Complex::ComplexMul(const?Complex?Z)Complextmp(*this);tmp._real=(this-_real*Z._real)-(this-_p_w_picpath *Z._p_w_picpath);tmp._p_w_picpath=(this-_p_w_picpath*Z._real)+(thi s-_real?*?Z._p_w_picpath);returntmp;-*除法*-Complex?Complex::ComplexDiv(const?Complex?Z)Complextmp(*this);tmp._real=((this-_real*Z._real)+(this-_p_w_picpat h?*?Z._p_w_picpath))?-((Z._real*Z._real)+(Z._p_w_picpath*Z._p_w_picpa th));tmp._p_w_picpath=((this-_p_w_picpath*Z._real)-(th is-_real?*?Z._p_w_picpath))-((Z._real*Z._real)+(Z._p_w_picpath*Z._p_w_picpa th));returntmp;------------------------------------------ 测试用例-------------------------------------------------- #?include?"Complex.h"--测试四则运算-*测试加法*--*ComplexZ1(1,2);ComplexZ2(1,2);Complexret=plexAdd(Z2); ret.Print();*--*测试减法*--*ComplexZ1(-1,2);ComplexZ2(1,1);Complexret=plexSub(Z2); ret.Print();*--*测试乘法*--*ComplexZ1(1,-2);ComplexZ2(1,2);Complexret=pleMul(Z2); ret.Print();*--*测试除法*-ComplexZ1(1,2);ComplexZ2(1,1);Complexret=plexDiv(Z2); ret.Print();*---测试操作符重载boolRET;-*测试“”*---ComplexZ1(1,4); --ComplexZ2(1,4); --RET=Z1Z2;--coutRETendl;--ComplexZ3(1,0); --ComplexZ4(2,0); --RET=Z3Z4;--coutRETendl;-*测试“”*--*ComplexZ1(1,0); ComplexZ2(2,0); RET=Z1Z2; coutRETendl; ComplexZ3(3,0); ComplexZ4(2,0); RET=Z3Z4; coutRETendl;*--*测试“==”*- ComplexZ1(1,4);ComplexZ2(1,4); RET=Z1==Z2; coutRETendl; ComplexZ3(1,1); ComplexZ4(1,3); RET=Z3==Z4; coutRETendl; ComplexZ5(1,0); ComplexZ6(1,0); RET=Z5==Z6; coutRETendl;--测试拷贝构造函数void?Test2() ComplexZ1(1,3); Z1.Print(); ComplexZ2(Z1);Z2.Print();--测试构造函数void?Test1() ComplexZ1(1,3); Z1.Print();int?main()--Test1();--Test2();--Test3();Test4();system("pause");return0;----------------------------------------------------------------------------------------------------- ?C++中的空类,默认产生六个默认成员函数,分别是:构造函数,拷贝(赋值)构造函数,析构函数,赋值操作符重载,取地址操作符重载,const修饰的取地址操作符重载。
数据结构Lab1——复数的四则运算

云南大学软件学院数据结构实验报告指导教师: 2009秋季学期学号:20081120064 姓名:李雪寒【实验题目】实验1. 抽象数据类型.【问题描述】用C或C++语言设计并实现一个可进行复数运算的演示程序。
【基本要求】1.由输入的实部和虚部生成一个复数2.两个复数求和3.两个复数求差4.从已知复数中分离出实部和虚部5.复数及相应运算结果以相应的表现形式显示。
【实现提示】定义复数为由两个相互之间存在次序关系的实数构成的抽象数据类型,则可以利用实数的操作来实现复数的操作。
一、【概要设计】熟悉抽象数据类型的表示和实现方法。
抽象数据类型需借助固有数据类型来表示和实现,即利用处理器中已存在的数据类型来说明新的结构,用已经实现的操作来组合新的操作。
抽象数据类型可以使我们更容易描述现实世界。
例:用线性表描述学生成绩表,用树或图描述遗传关系。
对一个抽象数据类型进行定义时,必须给出它的名字及各运算的运算符名,即函数名,并且规定这些函数的参数性质。
一旦定义了一个抽象数据类型及具体实现,程序设计中就可以像使用基本数据类型那样,十分方便地使用抽象数据类型。
抽象数据类型的描述包括给出抽象数据类型的名称、数据的集合、数据之间的关系和操作的集合等方面的描述。
主程序模块:printf("请输入第一个复数的实部和虚部,中间以空格隔开:");scanf("%f %f",&a,&b);printf("请输入第二个复数的实部和虚部,中间以空格隔开:");scanf("%f %f",&c,&d);/*输入两个复数的实部和虚部*/CreatComplex(c1,a,b);PrintComplex(c1);Printreal(c1);Printimage(c1);CreatComplex(c2,c,d);PrintComplex(c2);Printreal(c2);Printimage(c2);/*通过调用CreatComplex(),PrintComplex(),Printreal(),printimage()函数,用输入的实部和虚部生成复数并输出出来,再从中分离出实部和虚部*/AddComplex(Sum,c1,c2);PrintComplex(Sum);/*求和*/SubComplex(Sub,c1,c2);PrintComplex(Sub);/*求差*/MulComplex(Mul,c1,c2);PrintComplex(Mul);/*求积*/}子程序模块:void CreatComplex(Complex& c,float a,float b){c.real = a;c.image = b;} /*构造复数,包括实部和虚部*/void AddComplex(Complex& sum,Complex c1,Complex c2){sum.real = c1.real + c2.real ;sum.image = c1.image + c2.image ;} /*求和*/void SubComplex(Complex& Sub,Complex c1,Complex c2 ){Sub.real = c1.real -c2.real ;Sub.image = c1.image - c2.image ;}/*求差*/void MulComplex(Complex& Mul,Complex c1,Complex c2 ){Mul.real = c1.real * c2.real - c1.image * c2.image ;Mul.image = c1.real * c2.image + c1.image * c2.real ;}/*求积*/void PrintComplex(Complex c){if (c.image == 0.0)printf("%5.2f\n",c.real );/*所要输出的复数虚部为零时的情况*/else{if(c.real==0.0)printf("%5.2fi\n",c.image); /*所要输出的复数实部为零时的情况*/elseprintf("%5.2f+%5.2fi\n",c.real ,c.image ); /*所要输出的复数实部虚部都不为零时的情况*/}}/*按复数的形式输出复数*/void Printreal(Complex c){printf("该复数的实部是:%5.2f\n",c.real);}/*输出复数的实部*/void Printimage(Complex c){printf("该复数的虚部是:%5.2f\n",c.image);}/*输出复数的虚部*/二、【详细设计】1、分别编写出对两个复数求和、求差、求积以及输出复数和复数的实部虚部的函数,通过在主程序中调用这些函数,来达到实验要求。
复数四则运算C++源程序
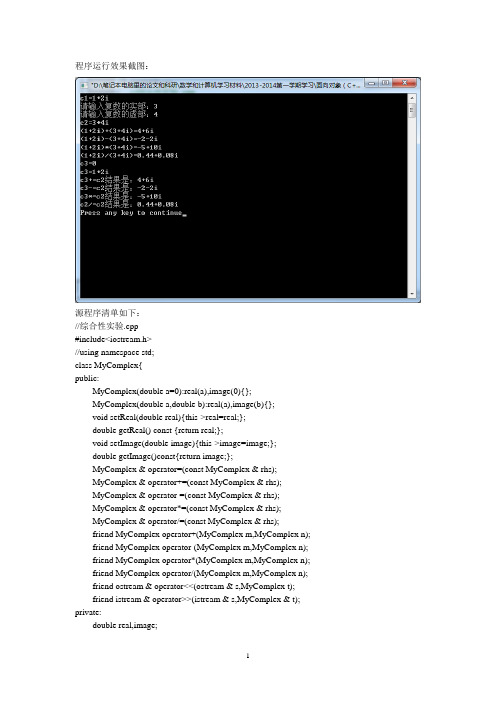
程序运行效果截图:源程序清单如下://综合性实验.cpp#include<iostream.h>//using namespace std;class MyComplex{public:MyComplex(double a=0):real(a),image(0){};MyComplex(double a,double b):real(a),image(b){};void setReal(double real){this->real=real;};double getReal() const {return real;};void setImage(double image){this->image=image;};double getImage()const{return image;};MyComplex & operator=(const MyComplex & rhs);MyComplex & operator+=(const MyComplex & rhs);MyComplex & operator-=(const MyComplex & rhs);MyComplex & operator*=(const MyComplex & rhs);MyComplex & operator/=(const MyComplex & rhs);friend MyComplex operator+(MyComplex m,MyComplex n);friend MyComplex operator-(MyComplex m,MyComplex n);friend MyComplex operator*(MyComplex m,MyComplex n);friend MyComplex operator/(MyComplex m,MyComplex n);friend ostream & operator<<(ostream & s,MyComplex t);friend istream & operator>>(istream & s,MyComplex & t); private:double real,image;};MyComplex & MyComplex::operator=(const MyComplex & rhs){ if(this==&rhs) return *this;this->setReal(rhs.getReal());this->setImage(rhs.getImage());return *this;}MyComplex & MyComplex::operator +=(const MyComplex & rhs){ MyComplex t=(*this)+rhs;this->setReal(t.getReal());this->setImage(t.getImage());return *this;}MyComplex & MyComplex::operator -=(const MyComplex & rhs){ MyComplex t=(*this)-rhs;this->setReal(t.getReal());this->setImage(t.getImage());return *this;}MyComplex & MyComplex::operator *=(const MyComplex & rhs){ MyComplex t=(*this)*rhs;this->setReal(t.getReal());this->setImage(t.getImage());return *this;}MyComplex & MyComplex::operator /=(const MyComplex & rhs){ MyComplex t=(*this)/rhs;this->setReal(t.getReal());this->setImage(t.getImage());return *this;}MyComplex operator+(MyComplex m,MyComplex n){return MyComplex(m.getReal()+n.getReal(),m.getImage()+n.getImage()); }MyComplex operator-(MyComplex m,MyComplex n){return MyComplex(m.getReal()-n.getReal(),m.getImage()-n.getImage());}MyComplex operator*(MyComplex m,MyComplex n){return MyComplex(m.getReal()*n.getReal()-m.getImage()*n.getImage(), m.getImage()*n.getReal()+m.getReal()*n.getImage());}MyComplex operator/(MyComplex m,MyComplex n){double t=n.getReal()*n.getReal()+n.getImage()*n.getImage();return MyComplex((m.getReal()*n.getReal()+m.getImage()*n.getImage())/t,(m.getImage()*n.getReal()-m.getReal()*n.getImage())/t); }ostream & operator<<(ostream & s,MyComplex t){s<<t.getReal();if(t.getImage()>0){s<<"+"<<t.getImage()<<"i";}else if(t.getImage()!=0){s<<t.getImage()<<"i";}return s;}istream & operator>>(istream & s,MyComplex & t){cout<<"请输入复数的实部:";int real=0,image=0;s>>real;cout<<"请输入复数的虚部:";s>>image;t.setReal(real);t.setImage(image);return s;}void main(){MyComplex c1(1,2),c2,c3;cout<<"c1="<<c1<<endl;cin>>c2;cout<<"c2="<<c2<<endl;// c3=c1+c2;cout<<"("<<c1<<")+("<<c2<<")="<<c1+c2<<endl;// c3=c1-c2;cout<<"("<<c1<<")-("<<c2<<")="<<c1-c2<<endl;cout<<"("<<c1<<")*("<<c2<<")="<<c1*c2<<endl;cout<<"("<<c1<<")/("<<c2<<")="<<c1/c2<<endl;// c3=c1/c2;// cout<<c3<<endl;cout<<"c3="<<c3<<endl;c3=c1;cout<<"c3="<<c3<<endl;c3+=c2;cout<<"c3+=c2结果是:"<<c3<<endl;c3=c1;c3-=c2;cout<<"c3-=c2结果是:"<<c3<<endl;c3=c1;c3*=c2;cout<<"c3*=c2结果是:"<<c3<<endl;c3=c1;c3/=c2;cout<<"c2/=c2结果是:"<<c3<<endl;/*int i;cout<<i=2<<endl; //输出运算符不能用赋值表达式,可以加、减、乘、除、乘方、函数等运算符*/}。
用c语言编程计算复数

用c语言编程计算复数一、复数的四则运算二、复数的头文件#include<complex.h>三、一些碎碎念(1)计算方法加法:(a+bi)+(c+di)=(a+c)+(c+d)i【实部与实部相加,虚部与虚步相加】减法:(a+bi)-(c+di)=(a-c)+(c-d)i【实部与实部相减,虚部与虚步相减】乘法:(a+bi)(c+di)=ac+adi+cdi+bdi*i=(ac-bd)+(bc+ad)i【普通的多项式相乘;i^2=-1】除法:(a+bi)/(c+di)=(a+bi)(c-di)/((c+di)(c+di))=((ac+bd)+(bc-ad)i)/(c^2+d^2)【分子分母同时乘以分母的共轭复数,然后上边是乘法,下边也是乘法】(2)例题:本题要求编写程序,计算2个复数的和、差、积、商。
输入在一行中按照a1 b1 a2 b2的格式给出2个复数C1=a1+b1i和C2=a2+b2i的实部和虚部。
题目保证C2不为0。
分别在4行中按照(a1+b1i) 运算符 (a2+b2i) = 结果的格式顺序输出2个复数的和、差、积、商,数字精确到小数点后1位。
如果结果的实部或者虚部为0,则不输出。
如果结果为0,则输出0.0。
(1)C语言中有三个类型可以存储复数float_Complex:实部和虚部都为float类型double_Complex:实部和虚部都为double类型long double_Complex:实部和虚部都为long类型例如:double_Complex x;注:C99对复数的支持,用这种定义方法不需要任何头文件。
(2)加入头文件#include <complex.h>,就可以用complex代替_Complex,这个头文件把虚部定义为'I',所以定义定义这样一个复数可以这样float complex z=a+bI;(3)宏宏名称值complex _Complex_Complex_I 虚数单位,类型为const float_ComplexI _Complex_I这里的I代替Complex_I可以类比bool(#include <stdbool>中的)和Bool一样复数的赋值方法如:doubel complex dc=2.0+3.5*I;(4)几个函数1.double real_part=creal(z);//得到Z的实部2.double imag_part=cimag(z)//得到Z的虚部在处理float和long double类型时,用crealf()和creall(),cimagf()和cimagl()。
§6-2 复数的四则运算

L ( a + c, b + d )
N (c , d )
uuur uuur 复数 c + di 用向量 ON 表示,则 ON = (c, d ) ; uuuu uuur r 所以 OM + ON = (a, b) + (c, d ) = (a + c, b + d ). o
= −20 + 15i
对于任意复数 z = a + bi ,有
z z = ( a + bi )(a − bi ) = a 2 + b 2 即 z z=|z|2 =|z|2 .
13
例2 求证:两个共轭复数之和与积都是一个实数。 证明 : 设z = a + bi, a, b ∈ R, 则 z = a − bi,
所以,当n ∉ N ∗时, 有
i4n+1 = i, i4n+2 = −1, i4n+3 = −i, i4n =1.
规定 : i 0 = 1
12
例1 计算 (1 − 2i )(3 + 4i )(−2 + i ) 解: (1 − 2i )(3 + 4i )(−2 + i ) = (11 − 2i )(−2 + i )
i
4n
= (i
4 n
)
= 1n = 1, i 4 n +1 = i 4 n ⋅ i = i,
i 4 n + 2 = i 4 n ⋅ i 2 = −1, i 4 n +3 = i 4 n ⋅ i 3 = −i。
c语言实现复数运算

在C语言中,我们可以使用结构体(`struct`)来创建复数数据类型。
下面是一个基本的复数运算的示例。
```c#include <stdio.h>// 定义复数结构体typedef struct {double real; // 实部double imag; // 虚部} Complex;// 加法Complex add(Complex a, Complex b) {Complex result;result.real = a.real + b.real;result.imag = a.imag + b.imag;return result;}// 减法Complex subtract(Complex a, Complex b) {Complex result;result.real = a.real - b.real;result.imag = a.imag - b.imag;return result;}// 乘法Complex multiply(Complex a, Complex b) {Complex result;result.real = a.real * b.real - a.imag * b.imag;result.imag = a.real * b.imag + a.imag * b.real;return result;}// 打印复数void printComplex(Complex c) {if (c.imag < 0) {printf("%.2f - %.2fi\n", c.real, fabs(c.imag)); } else {printf("%.2f + %.2fi\n", c.real, c.imag);}}int main() {Complex num1 = {3.0, 2.0}; // 定义复数num1,实部为3.0,虚部为2.0Complex num2 = {1.0, -1.0}; // 定义复数num2,实部为1.0,虚部为-1.0Complex sum = add(num1, num2); // 计算两个复数的和Complex diff = subtract(num1, num2); // 计算两个复数的差Complex prod = multiply(num1, num2); // 计算两个复数的乘积printComplex(sum); // 打印和printComplex(diff); // 打印差printComplex(prod); // 打印乘积return 0;}```这个程序定义了一个复数结构体,并实现了加、减、乘运算。
复数四则运算C语言

#include "stdio.h"
#include "stdlib.h"
typedef struct complex{
float e1;
float e2;
}complex;
complex initcomplex(float x,float y)
{
complex z1;
z1.e1=x;
z1.e2=y;
贺春林掌握c语言的简单编程掌握c语言函数的实现掌握c语言结构体的实现实验原理和内容使用一个结构体来编写代码实现复数的加减乘除结构体
学号:*************姓名:左力专业:通信工程班级:2015级5班
实验项目名称:复数加减乘除
课程名称:数据结构实验指导老师:贺春林
1.实验目的
1、掌握c语言的简单编程
}
void ericomplex(complex &z,complex z1,complex z2)
{float a,b,c,d,e,f,g,h,t;
a=z1.e1*z2.e1;
b=z1.e2*z2.e2;
c=z1.e1*z2.e2;
d=z1.e2*z2.e1;
e=a+b;
f=d-c;
g=z2.e1*z2.e1;
return z1;
}
void addcomplex(complex &z,complex z1,complex z2)
{
z.e1=z1.e1+z2.e1;
z.e2=z1.e2+z2.e2;
}
void minuscomplex(complex &z,complex z1,complex z2)
C语言复数运算(结构体)

C语言复数运算(结构体)为了方便进行复数运算,可以使用结构体来定义一个复数类型。
结构体是C语言中一种自定义的复合数据类型,可以将不同类型的数据组合在一起。
下面是一个用结构体定义的复数类型的示例:```ctypedef structdouble real; // 实数部分double imag; // 虚数部分```对于复数运算,可以通过定义各种操作函数来实现。
下面是常见的复数运算操作的示例代码:```c//复数相加result.real = c1.real + c2.real;result.imag = c1.imag + c2.imag;return result;//复数相减result.real = c1.real - c2.real;result.imag = c1.imag - c2.imag;return result;//复数相乘result.real = c1.real * c2.real - c1.imag * c2.imag;result.imag = c1.real * c2.imag + c1.imag * c2.real;return result;//复数相除double denominator = c2.real * c2.real + c2.imag * c2.imag;result.real = (c1.real * c2.real + c1.imag * c2.imag) / denominator;result.imag = (c1.imag * c2.real - c1.real * c2.imag) / denominator;return result;```在上述代码中,分别定义了复数相加、复数相减、复数相乘和复数相除的函数。
这些函数接受两个复数作为参数,并返回一个复数作为结果。
对于复数相乘和复数相除,需要使用一些复数运算的规则进行计算。
除了上述基本的复数运算操作之外,还可以定义其他的复数运算函数,比如求复数的模、求复数的共轭等。
复数的四则运算

a + bi 记做(a + bi ) ÷ (c + di )或 . c + di
(a + bi) ÷ (c + di) = a + bi ac + bd bc − ad = 2 + 2 i 2 2 c + di c + d c +d
例ห้องสมุดไป่ตู้、计算
1− i (1) 1+ i
13 + 9i (2) 2 (2 + i)
是____________. ____________. 解析:设z=x+yi(x、y∈R),则x2+y2+2x=3表示圆. 答案:以点(-1,0)为圆心,2为半径的圆
【练习】 练习】 1、在复数范围内解方程 、 (1) x2+4=0 (2) z2=2i
2、在复数范围内分解因式 、 (1) x2 + 4 (2) x4 - y4
Cz2-z1 B
z1+z2
2 、 | z 1+ z 2| = | z 1- z 2| 平行四边形OABC OABC是 平行四边形OABC是 矩形
o
z1 A
3、 |z1|= |z2|,| z1+ z2|= | z1- z2| 平行四边形OABC是 平行四边形OABC是 正方形 OABC
三、复数的乘法
o
x
A,说明下列各式所表示的几何意义 例1:已知复数z对应点A,说明下列各式所表示的几何意义. 1:已知复数z对应点A,说明下列各式所表示的几何意义. 已知复数
(1)|z- (1)|z-(1+2i)| (2)|z+(1+2i)| (3)|z- (3)|z-1| (4)|z+2i|
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
if ((z.e2>0)&&(z.e1!=0))
{
printf("%.3f+%.3fi\n",z.e1,z.e2);
};
if ((z.e2<0)&&(z.e1!=0))
{
printf("%.3f%.3fi\n",z.e1,z.e2);
};
if ((z.e2==0)&&(z.e1!=0))
{
printf("%.3f\n",z.e1);
scanf("%f%f",&x,&y);
z1=initcomplex(x,y);
outputcomplex(z1);
printf("请输入第二个复数:");
scanf("%f%f",&x,&y);
z2=initcomplex(x,y);
outputcomplex(z2);
printf("两个复数相加结果");
printf("两个复数相除结果");
ericomplex(z,z1,z2);
outputcomplex(z);
}
学号:*************姓名:左力专业:通信工程班级:2015级5班
实验项目名称:复数加减乘除
课程名称:数据结构实验指导老师:贺春林
1.实验目的
1、掌握c语言的简单编程
2、掌握c语言函数的实现
3、掌握c语言结构体的实现
2.实验原理和内容
使用一个结构体来编写代码,实现复数的加减乘除
结构体:结构体有两个类,即复数的实部和虚部
a=z1.e1*z2.e1;
b=z1.e2*z2.e2;
c=z1.e1*z2.e2;
d=z1.e2*z2.e1;
e=a+b;
f=d-c;
g=z2.e1*z2.e1;
h=z2.e2*z2.e2;
t=g+h;
z.e1=e/t;
z.e2=f/t;
}
void outputcomplex(complex z)
};
if ((z.e1==0)&&(z.e2!=0))
{
printf("%.3fi\n",z.e2);
};
if ((z.e1==0)&&(z.e2==0))
{
printf("0\n");
};
}
void main(){
complex z1,z2,z;
float x,y;
printf("请输入第一个复数:");
复数加减:对应的复数的实部和虚部分别相减
复数乘法:(a+ib)(c+id)=(ac-bd)+i(ad+bc)
复数除法:
3.实验要求
编写代码实现复数的加减乘除
4.实验代码
#include "stdio.h"
#include "stdlib.h"
typedef struct complex{
float e1;
addcomplex(z,z1,z2);
outputcomplex(z);
printf("两个复数相乘结果");
mulcomplex(z,z1,z2);
outputcomplex(z);
printf("两个复数相减结果");
minuscomplex(z,z1,z2);
outputcomplex(z);
{
float a,b,c,d;
a=z1.e1*z2.e1;
b=z1.e2*z2.e2;
c=z1.e1*z2.e2;
d=z1.e2*z2.e1;
z.e1=a-b;
z.e2=c+d;
}
void ericomplex(complex &z,complex z1,complex z2)
{float a,b,c,d,e,f,g,h,t;
float e2;}co源自plex;complex initcomplex(float x,float y)
{
complex z1;
z1.e1=x;
z1.e2=y;
return z1;
}
void addcomplex(complex &z,complex z1,complex z2)
{
z.e1=z1.e1+z2.e1;
z.e2=z1.e2+z2.e2;
}
void minuscomplex(complex &z,complex z1,complex z2)
{
z.e1=z1.e1-z2.e1;
z.e2=z1.e2-z2.e2;
}
void mulcomplex(complex &z,complex z1,complex z2)
