现代测试技术习题解答 第二章 信号的描述与分析 - 副本要点
《测试技术》(第二版)课后习题答案 要点

《测试技术》(第二版)课后习题答案要点《测试技术》(第二版)课后习题答案--要点解决方案:(1)瞬变信号-指数衰减振荡信号,其频谱具有连续性和衰减性。
(2)准周期信号,因为各简谐成分的频率比为无理数,其频谱仍具有离散性别(3)周期信号,因为各简谐成分的频率比为无理数,其频谱具有离散性、调和与收敛。
解:x(t)=sin2?f0t的有效值(均方根值):xrms12t012t01t0?t00x(t)dt?21t0?22岁?f0t dt1(t0?14?f0sin4?f0tt00?t00(1?cos4?f0t)dt?14? f02t0)(t0?sin4?f0t0)?1/2解决方案:周期三角波的时域数学描述如下:x(t)1...-t0/20?t0/2t0?T020? Tt02。
t2a?A.Tt0??2atx(t)??A.t0X (t?NT0)的三角函数展开(1)傅里叶级数:1T0/22t0/221a0??x(t)dt??(1?t)dt??t/20T00T0022t0/2a?nt??t0/2x(t)cosn?0tdt04t0/22??(1?t)cosn?0tdtt00t0?4n?1,3,5,?4?222n??22s in??n?2?n?N2,4,6,?? 20亿美元?2.其中,因为x(T)是一个偶数函数,Sinn?0t是一个奇数函数,X(T)Sinn?0tdtt0?T0/2那么x(T)Sinn?0t也是奇数函数,奇数函数在上下限对称区间上的积分等于0。
所以bn?0。
因此,三角函数展开式如下:14x(t)??22?1cosn?0t?2n?1n?14??22?1sin(n?0t??2)?2n?1n?(n=1,3,5,…)其光谱如下图所示:1a(?)124? (?)? 249? 2.24225? 003050003050单边振幅谱单边相位谱(2)复指数展开式复指数与三角函数展开式之间的关系如下:C0=a0cn=(an-JBN)/2c-n=(an+JBN)/2,因此22222nsinnrecn=an/22n220n1,3,5,n2,4,6,c0a0a0recn=an/2imcn=-bn/21122an?bn?an22icb?n?arctgmn?arctg(?n)recnancn?imcn=-bn/2=0c0?a0?a0?cn?1212112an?bn?an=an222icb?n?arctgmn?arctg(?n)?0recnan2真频谱12229?25? 2recn222?2.29? 222225?- 5.0-3? 0-? 00? 0imcn虚频谱3.05? 0-5?0-3?0-?00?03?05?0?双侧振幅谱212cn229?25? 222? 2.29? 222225?- 5.0-3? 0-? 00? 03? 05? 0n双边相位谱-5?0-3?0-?00?03?05?0?三解:该三角形窗函数是一非周期函数,其时域数学描述如下:x(t)1-t0/20t0/2t2?1.tt?0x(t)1.2t??t0?t0?T02t00?T二用傅里叶变换求频谱。
现代测试技术习题解答 第二章 信号的描述与分析 - 副本

所以
所以x(t+)=y(t++T)
令t1=t++T,代入上式得
x(t1- T)=y(t1),即y(t) =x(t- T)
结果说明了该系统将输入信号不失真地延迟了T时间。
2-12已知信号的自相关函数为Acos,请确定该信号的均方值x2和均方根值xrms。
解:Rx()=Acos
根据以上分析结论,便可由自相关函数图中确定均值(即常值分量)和周期分量的周期及幅值,参见下面的图。例如:如果 ,则 。
所以
解法3:直接按Rxy()定义式计算(参看下图)。
参考上图可以算出图中方波y(t)的自相关函数
2-11某一系统的输人信号为x(t)(见图5-25),若输出y(t)与输入x(t)相同,输入的自相关函数Rx()和输入—输出的互相关函数Rx()之间的关系为Rx()=Rxy(+T),试说明该系统起什么作用?
2- 19假定有一个信号x(t),它由两个频率、相角均不相等的余弦函数叠加而成,其数学表达式为x(t)=A1cos(1t+1)+A2cos(2t+2)求该信号的自相关函数。
解:设x1(t)=A1cos(1t+1);x2(t)=A2cos(2t+2),则
因为12,所以 , 。又因为x1(t)和x2(t)为周期信号,所以
x2=Rx(0)=A
2-13已知某信号的自相关函数,求均方值、和均方根值 。
2-14已知某信号的自相关函数,求信号的均值 、均方根值、功率谱。
2-15已知某信号的自相关函数,求信号的自功率谱。
解:采样序列x(n)
2-18对三个正弦信号x1(t)=cos2t、x2(t)=cos6t、x3(t)=cos10t进行采样,采样频率fs=4Hz,求三个采样输出序列,比较这三个结果,画出x1(t)、x2(t)、x3(t)的波形及采样点位置,并解释频率混叠现象。
现代检测技术智慧树知到课后章节答案2023年下西安交通大学

现代检测技术智慧树知到课后章节答案2023年下西安交通大学西安交通大学第一章测试1.用以标定的仪器,直接的测量出某一待测未知量的量值称为()。
A:直接测量 B:接触式测量 C:间接测量 D:动态测量答案:直接测量2.下列哪项不是闭环控制型现代测试系统的优点()。
A:实时数据采集 B:实时控制 C:实时判断决策 D:远距离传输答案:远距离传输3.下列属于测量过程的是()。
A:测量误差 B:数值和计量单位 C:被测对象 D:测试方法答案:测量误差;数值和计量单位;被测对象;测试方法4.水银温度计测量体温属于直接式测量。
A:错 B:对答案:对5.测试技术与传感技术被称为信息技术系统的()。
A:神经 B:大脑 C:感官答案:感官第二章测试1.下列非线性补偿方法中属于软件补偿的是()。
A:闭环式 B:拟合法 C:差动式 D:开环式答案:拟合法2.A类标准不确定度是用非统计方法得到的不确定度。
A:对 B:错答案:错3.真值在实际测量中是可以确切获知的。
A:对 B:错答案:错4.相对误差是绝对误差与测量仪表量程之比。
A:对 B:错答案:错5.将63.73501四舍五入,保留两位小数为()。
A:63.74 B:63.73 C:64.00 D:63.00答案:63.74第三章测试1.直流电桥可以测量电容的变化。
A:对 B:错答案:错2.全桥接法的灵敏度是半桥双臂接法的几倍()。
A:8 B:1 C:4 D:2答案:23.半导体式应变片比金属丝式应变片的灵敏度高。
A:对 B:错答案:对4.丝式应变片采用栅状结构是为了获得大的电阻变化量。
A:对 B:错答案:对5.下列哪项不是半导体应变片的优点()。
A:易于集成化 B:灵敏度高 C:温度稳定性能好 D:体积小答案:温度稳定性能好第四章测试1.下列哪项是电容式传感器的缺点()。
A:电缆分布电容影响大 B:精度低 C:结构复杂 D:灵敏度低答案:电缆分布电容影响大2.电容式传感器灵敏度最高的是()。
现代测试技术习题解答第二章信号的描述与分析副本
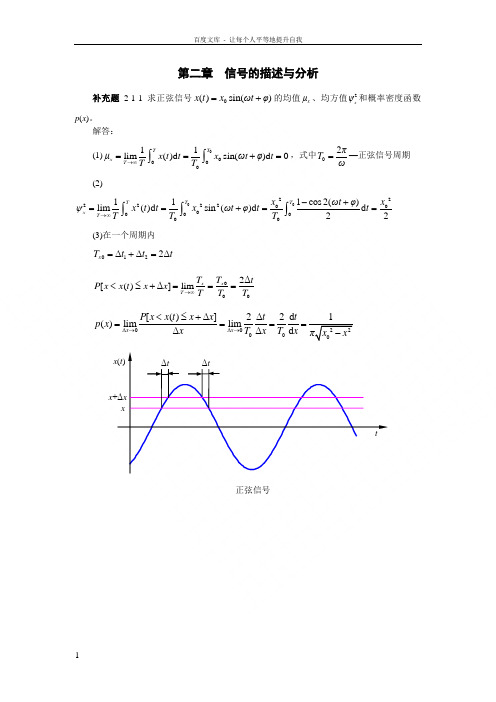
第二章 信号的描述与分析补充题2-1-1 求正弦信号0()sin()x t x ωt φ=+的均值x μ、均方值2x ψ和概率密度函数p (x )。
解答: (1)00011lim ()d sin()d 0TT x T μx t t x ωt φt TT →∞==+=⎰⎰,式中02πT ω=—正弦信号周期(2)2222220000111cos 2()lim()d sin ()d d 22TT T xT x x ωt φψx t t x ωt φt t TT T →∞-+==+==⎰⎰⎰(3)在一个周期内012ΔΔ2Δx T t t t =+=0002Δ[()Δ]limx x T T T tP x x t x x T T T →∞<≤+===22Δ0Δ0000[()Δ]2Δ2d ()limlim ΔΔd x x P x x t x x t t p x x T x T x πx x →→<≤+====-x (t )正弦信号xx +ΔxΔtΔtt2-8 求余弦信号0()sin x t x ωt 的绝对均值x μ和均方根值rms x 。
2-1 求图示所示锯齿波信号的傅里叶级数展开。
2-4周期性三角波信号如图所示,求信号的直流分量、基波有效值、信号有效值及信号的平均功率。
2-1 求图示所示锯齿波信号的傅里叶级数展开。
补充题2-1-2 求周期方波(见图1-4)的傅里叶级数(复指数函数形式),划出|c n|–ω和φn–ω图,并与表1-1对比。
解答:在一个周期的表达式为00 (0)2() (0)2T A t x t T A t ⎧--≤<⎪⎪=⎨⎪≤<⎪⎩积分区间取(-T/2,T/2)00000002202002111()d =d +d =(cos -1) (=0, 1, 2, 3, )T T jn tjn tjn t T T n c x t et Aet Ae tT T T Ajn n n ωωωππ-----=-±±±⎰⎰⎰所以复指数函数形式的傅里叶级数为001()(1cos )jn tjn t n n n Ax t c ejn e n∞∞=-∞=-∞==--∑∑ωωππ,=0, 1, 2, 3, n ±±±。
现代检测技术第二版课后习题

第二章课后习题作业2.1 为什么一般测量均会存在误差?解:由于检测系统不可能绝对精确,测量原理的局限,测量算法得不尽完善,环境因素和外界干扰的存在以及测量过程可能会影响被测对象的原有状态等因素,也使得测量结果不能准确的反映被测量的真值而存在一定误差。
2.2 什么叫系统误差?什么叫随机误差?它们产生的原因有哪些?解:在相同的条件下,多次重复测量同一被测参量时,其测量误差的大小和符号保持不变或在条件改变时,误差按某一确定的规律变化,这种测量误差称为系统误差。
产生系统误差的原因:①测量所用工具本身性能不完善或安装布置调整不当;②在测量过程中因湿度、气压、电磁干扰等环境条件发生变化;③测量方法不完善或测量所依据的理论本省不完善。
在相同条件下多次重复测量同一被测参量时,测量误差的大小与符号的大小均无规律变化,这类误差称为随机误差。
产生随机误差的原因:由于检测仪器或测量过程中某些未知无法控制的随机因素综合作用的结果。
2.3 什么叫绝对误差?什么叫相对误差?什么叫引用误差?解:绝对误差是检测系统的测量值X 与被测量的真值X 0之间的代数差值△x 。
0X -X x =△相对误差是检测系统测量值的绝对误差与被测量的真值的比值δ。
%100X x⨯=△δ 引用误差是检测系统测量值的绝对误差Δx 与系统量程L 之比值γ。
%100Lx⨯=△γ 2.4 工业仪表常用的精度等级是如何定义的?精度等级与测量误差是什么关系?解:工业检测仪器常以最大引用误差作为判断精度等级的尺度,最大引用误差去掉百分号和百分号后的数字表示精度等级。
2.5被测电压范围是0~5V ,现有(满量程)20V 、0.5级和150V 、0.1级两只电压表,应选用那只电表进行测量?解:两种电压表测量所产生的最大绝对误差分别是: |ΔX 1max |=|γ1max | * L 1=0.5% * 20=0.1V |ΔX 2max |=|γ2max | * L 2=0.1% * 150=0.15V 所以|ΔX 1MAX |<|ΔX 2mac | 故选用20、0.5级电压表。
现代测试技术第2章
⑸ 对测试数据进行必要的处理,根据处理结果就可以确定传感器的线 性度、灵敏度、滞后和重复性等静态特性指标。
现代测试技术 第2章 传感器概述
11
返回
上一页
下一页
1.5.2 传感器的动态特性标定
9
返回
上一页
下一页
2. 标定仪器设备精度等级的确定
? 对传感器进行标定,是根据试验数据确定传感 器的各项性能指标,实际上也是确定传感器的 测量精度。
? 标定传感器时,所用的测量仪器的精度至少要 比被标定的传感器的精度高一个等级。这样, 通过标定确定的传感器的静态性能指标才是可 靠的,所确定的精度才是可信的。
第2章 传感器概述
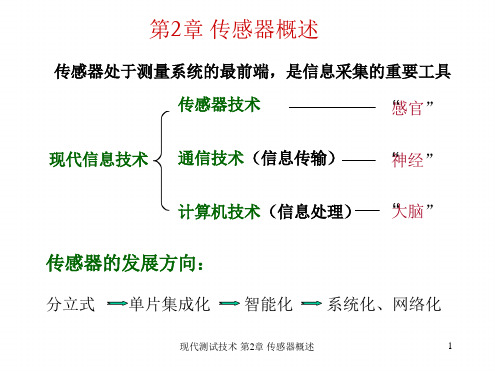
传感器处于测量系统的最前端,是信息采集的重要工具
传感器技术
“感官”
现代信息技术 通信技术(信息传输) “神经”
计算机技术(信息处理) “大脑”
传感器的发展方向:
分立式 单片集成化 智能化
系统化、网络化
现代测试技术 第2章 传感器概述
1
第2章 传感器概述
一、传感器和敏感元件的概念
传感器( Sensor/Transducer )的定义 (GB76615-87 )
1--标准压力表 2—砝码 3—活塞 4—进油阀 5—油杯 6—被标传感器 7—针形阀 8—手轮 9—手摇压力泵
1.5.5 活塞压力计标定压力传感器的示意图
现代测试技术 第2章 传感器概述
13
返回
上一页
下一页
图 1.5.6 压力标定曲线
为了保证压力传感器的测量准确度,需定期检定, 检定周期最长不超过一年。
《测试技术》(第二版)课后习题参考答案

《测试技术》(第二版)课后习题参考答案解:(1) 瞬变信号-指数衰减振荡信号,其频谱具有连续性和衰减性。
(2) 准周期信号,因为各简谐成分的频率比为无理数,其频谱仍具有离散性。
(3) 周期信号,因为各简谐成分的频率比为无理数,其频谱具有离散性、谐波性和收敛性。
解:x(t)=sin2t f 0π的有效值(均方根值):2/1)4sin 41(21)4sin 41(21)4cos 1(212sin 1)(100000000000002020000=-=-=-===⎰⎰⎰T f f T T tf f T T dt t f T dt t f T dt t x T x T T T T rms ππππππ 解:周期三角波的时域数学描述如下:(1)傅里叶级数的三角函数展开:,式中由于x(t)是偶函数,t n 0sin ω是奇函数,则t n t x 0sin )(ω也是奇函数,而奇函数在上下限对称区间上的积分等于0。
故=n b 0。
因此,其三角函数展开式如下:其频谱如下图所示:⎪⎪⎪⎩⎪⎪⎪⎨⎧+≤≤-≤≤-+=)(202022)(0000nT t x T t t T AA t T t T A A t x 21)21(2)(12/0002/2/00000=-==⎰⎰-T T T dt t T T dt t x T a ⎰⎰-==-2/00002/2/00000cos )21(4cos )(2T T T n dt t n t T T dt t n t x T a ωω⎪⎩⎪⎨⎧==== ,6,4,20,5,3,142sin 422222n n n n n πππ⎰-=2/2/0000sin )(2T T n dtt n t x T b ω∑∞=+=1022cos 1421)(n t n nt x ωπ∑∞=++=1022)2sin(1421n t n nπωπ(n =1, 3, 5, …)(2)复指数展开式复指数与三角函数展开式之间的关系如下:)( 21=212121n 22000=-===+====nn n e n m n n n n n a barctg C R C I arctg a A b a C a A C φ A ϕ单边幅频谱 单边相频谱0 ωn φω0 3ω0 5ω0 -ω0 -3ω0 -5ω00 ωI m C nω0 3ω0 5ω0 -ω0 -3ω0 -5ω0虚频谱双边相频谱解:该三角形窗函数是一非周期函数,其时域数学描述如下:用傅里叶变换求频谱。
《测试技术与信号处理》习题答案-华科版

《测试技术与信号处理》习题答案第二章 信号分析基础1、请判断下列信号是功率信号还是能量信号: (1))()(10cos 2∞<<-∞=t e t x t π (2))()(||10∞<<-∞=-t et x t【解】(1)该信号为周期信号,其能量无穷大,但一个周期内的平均功率有限,属功率信号。
(2)信号能量:⎰∞∞-==101)(2dt t x E ,属于能量信号。
2、请判断下列序列是否具有周期性,若是周期性的,请求其周期。
)8()(π-=n j e n x【解】设周期为N ,则有:8)88()()(N jNn j en x e N n x ⋅==+-+π若满足)()(n x N n x =+,则有1)8/sin()8/cos(8/=-=-N j N ejN即:k N π28/=,k N π16=,k = 0,1,2,3,… N 不是有理数,故序列不是周期性的。
3、已知矩形单脉冲信号x 0(t)的频谱为X 0(ω)=A τsinc(ωτ/2) ,试求图示三脉冲信号的频谱。
【解】三脉冲信号的时域表达式为:)()()()(000T t x t x T t x t x -+++=根据Fourier 变换的时移特性和叠加特性,可得其频谱:)]cos(21)[2(sin )()()()(000T c A e X X e X X T j T j ωωττωωωωωω+=++=-4、请求周期性三角波(周期为T ,幅值为0—A )的概率分布函数F(x)与概率密度函数p(x) 。
【解】在一个周期T 内,变量x (t )小于某一特定值x 的时间间隔平均值为:T Ax t i =∆ 取n 个周期计算平均值,当∞→n 时,可有概率分布函数:AxnT t n x F i n =∆=∞→lim)( 概率密度函数:Adx x dF x p 1)()(==5、请求周期性方波的自相关函数。
(设周期为T ,幅值为0—A )t-T【解】对周期函数,可取一个周期求自相关函数,但由于函数的不连续性,必须分段积分,如图:当2/0T ≤≤τ时(图a )])()()()([1)()(1)(222020⎰⎰⎰⎰⎰----⋅-+-⋅-+-⋅+⋅=+=T T T T TT T Tx Adt A dt A A dt A A Adt A T dt t x t x T R ττττττ 即:)41()(2TA R x ττ-=当T T ≤≤τ2/时(图b )])()()()([1)(23232/2/0⎰⎰⎰⎰-----⋅-+⋅-+⋅+-⋅=T T TT T T T x dt A A Adt A Adt A dt A A T R τττττ即:)43()(2TA R x ττ--=第三章 信息论基础知识1、某装置的正常工作温度保持在35—40℃之间。
(完整版)测试技术部分课后习题参考答案

第1章 测试技术基础知识1.4 常用的测量结果的表达方式有哪3种?对某量进行了8次测量,测得值分别为:82.40、82.43、82.50、82.48、82.45、82.38、82.42、82.46。
试用3种表达方式表示其测量结果。
解:常用的测量结果的表达方式有基于极限误差的表达方式、基于t 分布的表达方式和基于不确定度的表达方式等3种1)基于极限误差的表达方式可以表示为0max x x δ=±均值为8118i x x ==∑82.44因为最大测量值为82.50,最小测量值为82.38,所以本次测量的最大误差为0.06。
极限误差max δ取为最大误差的两倍,所以082.4420.0682.440.12x =±⨯=±2)基于t 分布的表达方式可以表示为x t x x ∧±=σβ0标准偏差为s ==0.04样本平均值x 的标准偏差的无偏估计值为ˆx σ==0.014 自由度817ν=-=,置信概率0.95β=,查表得t 分布值 2.365t β=,所以082.44 2.3650.01482.440.033x =±⨯=±3)基于不确定度的表达方式可以表示为0x x x x σ∧=±=±所以082.440.014x =±解题思路:1)给出公式;2)分别计算公式里面的各分项的值;3)将值代入公式,算出结果。
第2章 信号的描述与分析2.2 一个周期信号的傅立叶级数展开为12ππ120ππ()4(cos sin )104304n n n n n y t t t ∞==++∑(t 的单位是秒) 求:1)基频0ω;2)信号的周期;3)信号的均值;4)将傅立叶级数表示成只含有正弦项的形式。
解:基波分量为12ππ120ππ()|cos sin 104304n y t t t ==+ 所以:1)基频0π(/)4rad s ω=2)信号的周期02π8()T s ω==3)信号的均值42a = 4)已知 2π120π,1030n n n n a b ==,所以4.0050n A n π=== 120π30arctan arctan arctan 202π10n n nn bn a ϕ=-=-=-所以有0011()cos()4 4.0050cos(arctan 20)24n n n n a n y t A n t n t πωϕπ∞∞===++=+-∑∑2.3某振荡器的位移以100Hz 的频率在2至5mm 之间变化。
测试技术与信号处理(第三版)课后习题详解
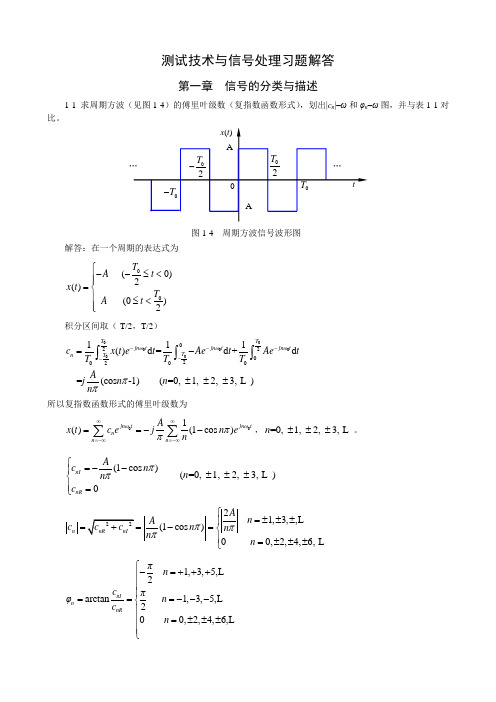
测试技术与信号处理习题解答第一章 信号的分类与描述1-1 求周期方波(见图1-4)的傅里叶级数(复指数函数形式),划出|c n |–ω和φn –ω图,并与表1-1对比。
解答:在一个周期的表达式为00 (0)2() (0)2T A t x t T A t ⎧--≤<⎪⎪=⎨⎪≤<⎪⎩积分区间取(-T/2,T/2)00000002202002111()d =d +d =(cos -1) (=0, 1, 2, 3, )T T jn tjn tjn t T T n c x t et Aet Ae tT T T Ajn n n ωωωππ-----=-±±±⎰⎰⎰所以复指数函数形式的傅里叶级数为001()(1cos )jn tjn tnn n Ax t c ejn en ∞∞=-∞=-∞==--∑∑ωωππ,=0, 1, 2, 3, n ±±±。
(1cos ) (=0, 1, 2, 3, )0nI nR A c n n n c ⎧=--⎪±±±⎨⎪=⎩ππ21,3,,(1cos )00,2,4,6,n An A c n n n n ⎧=±±±⎪==-=⎨⎪=±±±⎩πππ1,3,5,2arctan 1,3,5,200,2,4,6,nI n nR πn c πφn c n ⎧-=+++⎪⎪⎪===---⎨⎪=±±±⎪⎪⎩图1-4 周期方波信号波形图没有偶次谐波。
其频谱图如下图所示。
1-2 求正弦信号0()sin x t x ωt =的绝对均值x μ和均方根值rms x 。
解答:00002200000224211()d sin d sin d cos TTT Tx x x x x μx t t x ωt t ωt t ωt T T T T ωT ωπ====-==⎰⎰⎰rmsx ==== 1-3 求指数函数()(0,0)atx t Ae a t -=>≥的频谱。
测试技术第二章答案

测试技术第二章答案(总8页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--8第二章 习题2-1:典型的测量系统有几个基本环节组成其中哪个环节的繁简程度相差最大典型的测试系统,一般由输入装置、中间变换装置、输出装置三部分组成。
其中输入装置的繁简程度相差最大,这是因为组成输入装置的关键部件是传感器,简单的传感器可能只由一个敏感元件组成,如测量温度的温度计。
而复杂的传感器可能包括敏感元件,变换电路,采集电路。
有些智能传感器还包括微处理器。
2-2:对某线性装置输入简谐信号x(t)=asin(φω+t ),若输出为y(t)=Asin(Φ+Ωt ),请对幅值等各对应量作定性比较,并用不等式等数学语言描述它们之间的关系。
x(t)=asin(φω+t )→y(t)=Asin(Φ+Ωt ), 根据线性装置的输入与输出具有的频率保持特性可知,简谐正弦输入频率与输出频率应相等,既有:Ω=ω,静态灵敏度:K=aA = 常数,相位差:△ϕϕ-Φ== 常数。
2-3:传递函数和频响函数在描述装置特性时,其物理意义有何不同?传递函数定义式:H (s )=)()(s x s y =01110111a s a s a s a b s b s b s b n n n n m m m m ++++++++---- ,其中s=+αj ω称拉氏算子。
H(s)是描述测量装置传输,转换特性的数学模型,是以测量装置本身的参数表示输入与输出之间的关系,与装置或结构的物理特性无关。
频率响应函数定义式:H (ωj )=)()(ωωj x j y =01110111)())()()()(a j a j a j a b j b j b j b n n n n n n n n ++++++++----ωωωωωω 反映了信号频率为ω时输出信号的傅氏变换与输入信号的傅氏变换之比。
频率响应函数H (ωj )是在正弦信号激励下,测量装置达到稳态输出后,输出与输入之间关系的描述。
测试技术章节习题(附答案)

各章节习题<后附答案>第一章信号与其描述〔一〕填空题1、 测试的基本任务是获取有用的信息,而信息总是蕴涵在某些物理量之中,并依靠它们来传输的.这些物理量就是,其中目前应用最广泛的是电信号.2、 信号的时域描述,以为独立变量;而信号的频域描述,以为独立变量.3、 周期信号的频谱具有三个特点:,,.4、 非周期信号包括信号和信号.5、 描述随机信号的时域特征参数有、、.6、 对信号的双边谱而b,实频谱〔幅频谱〕总是对称,虚频谱〔相频谱〕总是对称. 〔二〕判断对错题〔用√或×表示〕1、 各态历经随机过程一定是平稳随机过程.〔 〕2、 信号的时域描述与频域描述包含相同的信息量.〔 〕3、 非周期信号的频谱一定是连续的.〔 〕4、 非周期信号幅频谱与周期信号幅值谱的量纲一样.〔 〕5、 随机信号的频域描述为功率谱.〔 〕〔三〕简答和计算题1、 求正弦信号t x t x ωsin )(0=的绝对均值μ|x|和均方根值x rms .2、 求正弦信号)sin()(0ϕω+=t x t x 的均值x μ,均方值2x ψ,和概率密度函数p<x>.3、 求指数函数)0,0()(≥>=-t a Ae t x at 的频谱.4、 求被截断的余弦函数⎩⎨⎧≥<=T t T t t t x ||0||cos )(0ω的傅立叶变换. 5、 求指数衰减振荡信号)0,0(sin )(0≥>=-t a t e t x at ω的频谱.第二章测试装置的基本特性〔一〕填空题1、 某一阶系统的频率响应函数为121)(+=ωωj j H ,输入信号2sin )(t t x =,则输出信号)(t y 的频率为=ω,幅值=y ,相位=φ. 2、 试求传递函数分别为5.05.35.1+s 和2224.141nn n s s ωωω++的两个环节串联后组成的系统的总灵敏度.3、 为了获得测试信号的频谱,常用的信号分析方法有、和.4、 当测试系统的输出)(t y 与输入)(t x 之间的关系为)()(00t t x A t y -=时,该系统能实现测试.此时,系统的频率特性为=)(ωj H .5、 传感器的灵敏度越高,就意味着传感器所感知的越小.6、 一个理想的测试装置,其输入和输出之间应该具有关系为最佳.〔二〕选择题1、 不属于测试系统的静特性.〔1〕灵敏度〔2〕线性度〔3〕回程误差〔4〕阻尼系数2、 从时域上看,系统的输出是输入与该系统响应的卷积.〔1〕正弦〔2〕阶跃〔3〕脉冲〔4〕斜坡3、 两环节的相频特性各为)(1ωQ 和)(2ωQ ,则两环节串联组成的测试系统,其相频特性为.〔1〕)()(21ωωQ Q 〔2〕)()(21ωωQ Q +〔3〕)()()()(2121ωωωωQ Q Q Q +〔4〕)()(21ωωQ Q - 4、 一阶系统的阶跃响应中,超调量.〔1〕存在,但<5%〔2〕存在,但<1〔3〕在时间常数很小时存在〔4〕不存在5、 忽略质量的单自由度振动系统是系统.〔1〕零阶〔2〕一阶〔3〕二阶〔4〕高阶6、 一阶系统的动态特性参数是.〔1〕固有频率〔2〕线性度 <3>时间常数〔4〕阻尼比7、 用阶跃响应法求一阶装置的动态特性参数,可取输出值达到稳态值倍所经过的时间作为时间常数.〔1〕0.632 〔2〕0.865 〔3〕0.950 〔4〕0.982〔三〕判断对错题〔用√或×表示〕1、 一线性系统不满足"不失真测试〞条件,若用它传输一个1000Hz 的正弦信号,则必然导致输出波形失真.〔〕2、 在线性时不变系统中,当初始条件为零时,系统的输出量与输入量之比的拉氏变换称为传递函数.〔〕3、 当输入信号)(t x 一定时,系统的输出)(t y 将完全取决于传递函数)(s H ,而与该系统的物理模型无关.〔〕4、 传递函数相同的各种装置,其动态特性均相同.〔〕5、 测量装置的灵敏度越高,其测量X 围就越大.〔〕6、 幅频特性是指响应与激励信号的振幅比与频率的关系.〔〕〔四〕简答和计算题1、 什么叫系统的频率响应函数?它和系统的传递函数有何关系?2、 测试装置的静态特性和动态特性各包括那些?3、 测试装置实现不失真测试的条件是什么?4、 某测试装置为一线性时不变系统,其传递函数为1005.01)(+=s s H .求其对周期信号)45100cos(2.010cos 5.0)(︒-+=t t t x 的稳态响应)(t y .5、 将信号t ωcos 输入一个传递函数为ss H τ+=11)(的一阶装置,试求其包括瞬态过程在内的输出)(t y 的表达式.第三章常用传感器〔一〕填空题1、 属于能量控制型的传感器有等,属于能量转换型的传感器有等〔每个至少举例两个〕.2、 金属电阻应变片与半导体应变片的物理基础的区别在于:前者利用引起的电阻变化,后者利用变化引起的电阻变化.3、 为了提高变极距电容式传感器的灵敏度、线性度与减小外部条件变化对测量精度的影响,实际应用时常常采用工作方式.4、 压电式传感器的测量电路〔即前置放大器〕有两种形式:放大器和放大器,后接放大器时,可不受连接电缆长度的限制.5、 涡流式传感器的变换原理是利用了金属导体在交流磁场中的效应.6、 磁电式速度计的灵敏度单位是.7、 压电式传感器是利用某些物质的而工作的.〔二〕选择题1、 电阻应变片的输入为.〔1〕力〔2〕应变〔3〕速度〔4〕加速度2、 结构型传感器是依靠的变化实现信号变换的.〔1〕本身物理性质〔2〕体积大小〔3〕结构参数〔4〕电阻值3、 不能用涡流式传感器进行测量的是.〔1〕位移〔2〕材质鉴别〔3〕探伤〔4〕非金属材料4、 变极距面积型电容传感器的输出与输入,成关系.〔1〕非线性〔2〕线性〔3〕反比〔4〕平方5、 半导体式应变片在外力作用下引起其电阻变化的因素主要是.〔1〕长度〔2〕截面积〔3〕电阻率〔4〕高通6、 压电式传感器输出电缆长度的变化,将会引起传感器的产生变化.〔1〕固有频率〔2〕阻尼比〔3〕灵敏度〔4〕压电常数7、 在测量位移的传感器中,符合非接触测量,而且不受油污等介质影响的是传感器. 〔1〕电容式〔2〕压电式〔3〕电阻式〔4〕电涡流式8、 自感型可变磁阻式传感器,当气隙δ变化时,其灵敏度S 与δ之间的关系是:S =. 〔1〕δ1k 〔2〕δk 〔3〕2-δk 〔4〕2--δk9、 光电倍增管是利用效应制成的器件.〔1〕内光电〔2〕外光电〔3〕光生伏特〔4〕阻挡层〔三〕判断对错题〔用√或×表示〕1、 滑线变阻器式传感器不适于微小位移量测量.〔〕2、 涡流式传感器属于能量控制型传感器〔〕3、 压电加速度计的灵敏度越高,其工作频率越宽.〔〕4、 磁电式速度拾振器的上限工作频率取决于其固有频率.〔〕〔四〕简答和计算题1、 哪些传感器可选作小位移传感器?2、 涡流传感器测量位移与其它位移传感器比较,其主要优点是什么?涡流式传感器能否测量大位移量?为什么?3、 电涡流传感器除了能测量位移外,还能测量哪些非电量?4、 电涡流传感器能否测量塑料物体移动的位移?若能测量理由是什么?不能测量理由是什么?应采取什么措施改进,就可以用电涡流传感器测量了.5、 压电式加速度传感器与压电式力传感器在结构上有何不同,为什么?6、 试用双螺管线圈差动型电感传感器做成一个测力传感器.(1) 用简图说明该传感器的结构并简要说明其作用原理;(2) 两个线圈通常应该接在什么电路中?用图说明如何接法.7、 某电容传感器〔平行极板电容器〕的圆形极板半径)(4mm r =,工作初始极板间距离)(3.00mm =δ,介质为空气.问:(1) 如果极板间距离变化量)(1m μδ±=∆,电容的变化量C ∆是多少?(2) 如果测量电路的灵敏度)(1001pF mV k = ,读数仪表的灵敏度52=k 〔格/mV 〕在)(1m μδ±=∆时,读数仪表的变化量为多少?第四章信号调理、记录和显示〔一〕填空题1、 电桥的作用是把电感、电阻、电容的变化转化为输出的装置.2、 在桥式测量电路中,按照的性质,电桥可分为直流和交流电桥.3、 在桥式测量电路中,根据工作时阻抗参与变化的可将其分为半桥与全桥测量电路.4、 调幅是指一个高频的正〔余〕弦信号与被测信号,使高频信号的幅值随被测信号的而变化.信号调幅波可以看作是载波与调制波的.5、 调频波的解调又称为.6、 调频是利用信号电压的控制一个振荡器,使其输出为等幅波,而与信号电压成正比.7、 常用滤波器的上、下截止频率1c f 、2c f 的定义为,其带宽B =,若为倍频程滤波器1c f 与2c f 的关系为.8、 RC 低通滤波器中RC 值愈,则上截止频率愈低.〔二〕选择题1、 设有一电路,1R 是工作桥臂,2R ,3R ,4R 是固定电阻,且4321R R R R === .工作时1112R R R ∆+→,则电桥输出电压≈y e 〔〕.0e 为电桥的电源电压.〔1〕0114e R R ∆〔2〕0112e R R ∆〔3〕011e R R ∆〔4〕0112e R R ∆ 2、 调幅过程相当于在时域中将调制信号与载波信号.〔1〕相乘〔2〕相除〔3〕相加〔4〕相减3、 电路中鉴频器的作用是.〔1〕使高频电压转变成直流电压〔2〕使电感量转变为电压量〔3〕使频率变化转变为电压变化〔4〕使频率转变为电流4、 一选频装置,其幅—频特性在∞→2f 区间近于平直,在02→f 区间急剧衰减,这叫滤波器.〔1〕低通〔2〕高通〔3〕带通〔4〕带阻5、 一带通滤波器,其中心频率是0f ,-3dB 带宽是B ,则滤波器的品质因数Q 等于. 〔1〕B f +0〔2〕B f -0〔3〕B f 0〔4〕Bf 0〔三〕判断对错题〔用√或×表示〕1、 平衡纯电阻交流电桥须同时调整电阻平衡与电容平衡.〔〕2、 调幅波是载波与调制信号的叠加.〔〕3、 带通滤波器的波形因数λ值越大,其频率选择性越好.〔〕4、 将高通与低通滤波器串联可获得带通或带阻滤波器.〔〕〔四〕简答和计算题1、 何谓电桥平衡?要使直流电桥平衡,桥臂参数应满足什么条件?交流电桥应满足什么条件?2、 调幅波的解调方法有哪几种?3、 抗混滤波器的作用是什么?它选用何种滤波器?其截止频率如何确定?4、 相关滤波器的的基本原理是什么?举例说明其工程应用.5、 以阻值Ω=120R ,灵敏度2=S 的电阻丝应变片与阻值为Ω120的固定电阻组成电桥,供桥电压V V 30=,若其负载电阻为无穷大,应变片的应变μεε2000=.〔1〕求单臂电桥的输出电压与其灵敏度.〔2〕求双臂电桥的输出电压与其灵敏度6、 若)(t x 为调制信号,t f t y 02cos )(π=为载波,)(t x m 为调幅波〔如图所示〕〔1〕利用傅里叶变换性质说明调幅过程的原理.〔2〕画出载波与调幅波的双边频谱图.第五章信号处理初步〔一〕填空题1、 为了识别信号类型,常用的信号分析方法有、和.2、 为了获得测试信号的频谱,常用的信号分析方法有、 和.3、 在数字信号处理中,为避免频率混叠,应使被采样的模拟信号成为,还应使采样频率满足采样定理即.4、 如果一个信号的最高频率为50Hz,为了防止在时域采样过程中出现混叠现象,采样频率应该大于Hz.5、 若x<t>是均值为u x 为零的宽带随机信号其自相关函数τ=0时R x <τ>,τ→∞时R x <τ>.6、 用于评价系统的输出信号和输入信号之间的因果性.7、 若某一信号的自相关函数为)cos(ωτA ,则该信号的均方值为2x ψ ,均方根值为x rms =.8、 最常用的功率谱估计方法为.9、 )(f S x 为信号的沿频率轴的分布,2)(f X 称为.10、 巴塞伐尔定理表示在中计算的信号总能量,等于在中计算的信号总能量. 〔二〕判断对错题〔用√或×表示〕1、 频率分辨力越高,则泄漏误差越小.〔 〕2、 A/D 转换器的位数越多,则量化误差越小.〔 〕3、 对于周期信号,经整周期采样后,可完全避免栅栏效应.〔 〕4、 窗函数频谱的主峰瓣宽度越窄,旁瓣幅度越小,用其截取信号所引起的误差越小.〔 〕5、 互相关函数是偶实函数.〔 〕6、 利用系统输入x<t>与输出y<t>的自功率谱密度函数,可求该系统的频率响应函数.〔 〕7、 若系统是完全线性的,则输入-输出的相干函数一定为1.〔 〕〔三〕简答和计算题1、 已知信号)sin()cos()(2221110ϕωϕω++++=t A t A A t x ,求信号的自相关函数)(τx R ,并画出自功率谱)(ωx S 〔双边幅值谱〕.2、 求频率相同的单位方波和正弦波的互相关函数.3、 相关滤波器的基本原理是什么?举例说明其工程应用.4、 试根据一个信号的自相关函数图形,讨论如何确定该信号中的常值分量和周期成分.5、 某一系统的输入信号为x<t>,若输出y<t>与输入x<t>相同,输入的自相关函数)(τx R 和输入—输出的互相关函数)(τxy R 之间的关系为)()(T R R x x +=ττ ,试说明该系统起什么作用?6、 应用巴塞伐尔定理求⎰∞∞-dt t c )(sin 2的积分值.第六章振动测试〔一〕填空题1、 单自由度系统质量块受力所引起的受迫振动,位移共振频率系统固有频率,速度共振频率系统固有频率,加速度共振频率系统固有频率.2、 单自由度系统质量块受力所引起的受迫振动,在相位共振处位移始终落后于激振力度.3、 单自由度系统基础运动所引起的受迫振动,当激振频率固有频率时,质量块和壳体之间的相对运动和基础振动近于相等.4、 激励方式分为,,.5、 按所测的振动性质可将拾振器分为和.6、 阻抗头的前端是,后面是测量激振点响应的.7、 压电式传感器的测量电路〔即前置放大器〕有两种形式:、和.8、 机械系统的主要振动参数是,和.9、 相对法校准传感器时,经国家计量等部门严格校准过的传感器起着"振动标准传递〞的作用,称为传感器.〔二〕判断对错题〔用√或×表示〕1、 压电式加速度计的灵敏度越高,其工作频率越宽.〔 〕2、 磁电式速度拾振器的上限工作频率取决于其固有频率.〔 〕3、 压电式加速度计手持探针法测振时,加速度计的使用上限频率最低.〔 〕4、 压电式加速度计的重量越轻,使用上限频率越高,灵敏度越低.〔 〕5、 涡流位移传感器属于绝对式拾振器.〔 〕6、 低频激振时,激振器的安装固有频率应比激振频率高3倍以上.〔 〕7、 快速正弦扫描激振属于宽带激振法.〔 〕8、 脉冲锤的锤头越软,则激励的频率X 围越大.〔 〕9、 振动测试中,测得的激励和响应之间的相位差包括了测试系统中所有仪器的相移.〔 〕 〔三〕简答和计算题1、 对单自由度系统质量块受力所引起的受迫振动,分别写出其位移频响函数、速度频响函数、加速度频响函数.2、 对单自由度系统基础位移所引起的受迫振动,分别写出其相对位移频响函数、绝对位移频响函数.3、 对于压电式加速度计,画出其工作原理图,并说明为什么其上限频率取决于固有频率?4、 对于磁电式绝对速度计,画出其工作原理图,并说明为什么其下限频率取决于固有频率?5、 如何用实频曲线估计系统的固有频率和阻尼比?画图说明.参考答案第一章信号与其描述〔一〕1、信号;2、时间〔t 〕,频率〔f 〕;3、离散性,谐波性,收敛性;4、准周期,瞬态非周期;5、均值x μ,均方值2x ψ,方差2x σ;6、偶,奇;〔二〕1、√;2、√;3、╳;4、╳;5、√;〔三〕1、π02x ,20x ;2、0,220x ,)cos(10ϕωπ+t x ;3、f j a A π2+;4、()()T f c T T f c T )2(sin )2(sin 00ωπωπ-++; 5、fa j f a πωπω44202220+--;第二章测试装置的基本特性〔一〕1、1/2,2/1, 45-;2、123;3、傅立叶变换法,滤波器法;4、00t j e A ω-;5、被测量;6、线性;〔二〕〔4〕〔3〕〔2〕〔4〕〔2〕〔3〕〔1〕〔三〕╳ √ √ √ ╳ ╳〔四〕略第三章常用传感器〔一〕1、电阻、电感、电容、涡流;压电、磁电;2、金属丝的几何变形,半导体材料的电阻率变化;3、差动;4、电荷,电压,电荷;5、涡电流;6、mv / <m/s>;7、压电效应. 〔二〕〔2〕〔3〕〔4〕〔2〕〔3〕,〔3〕〔4〕〔4〕〔2〕〔三〕√ √ ╳ ╳〔四〕略第四章信号调理、处理和记录〔一〕1、电压或电流;2、激励电压;3、桥臂数;4、相乘,相乘;5、鉴频;6、幅值,频率;7、幅频特性曲线降为最大值的21倍时对应的频率为截止频率;12c c f f B -=;122c c f f =,8、大;〔二〕〔1〕〔1〕〔3〕〔2〕〔4〕〔三〕√ ╳ ╳ √〔四〕略第五章信号处理初步〔一〕1、概率密度函数,自相关函数;2、带通滤波法,傅立叶变换法;3、有限带宽,h s f f 2>;4、100;5、2x σ,0;6、相干函数;7、A A ,;8、周期图法;9、功率密度,能谱;10、时域,频域;〔二〕1、╳;2、√;3、√;4、√;5、╳;6、╳;7、╳; 〔三〕1、τωτωτ22212120cos 2cos 2)(A A A R x ++=, [][])()(4)()(4)(2222112120ωωδωωδωωδωωδω++-+++-+=A A A S x ; 2、ωτπτsin 2)(=xy R ;3、同频相关、不同频不相关;4、信号的常值分量为其自相关函数均值的开方,周期成分与其自相关函数周期成分的频率相同、幅值成比例关系;5、该系统的作用是使信号幅值不变、相位提前T ;6、⎰⎰-∞∞-==ππππ2/12/1221)(sin df dt t c ;第六章振动的测试〔一〕1、小于,等于,大于;2、90;3、远大于;4、稳态正弦激振,随机激振,瞬态激振;5、相对式,绝对式;6、力传感器,加速度计;7、电荷放大器,电压放大器;8、固有频率,阻尼比,振型;9、参考.〔二〕1、╳;2、╳;3、√;4、√;5、╳;6、√;7、√;8、╳;9、√; 〔三〕略。
《检测技术》作业与自测

《检测技术》作业与自测一、作业及题解第1章 信号及其描述习题答案1.以下信号,哪个是周期信号? 哪个是准周期信号? 哪个是瞬变信号?它们频谱各具有哪些特征? (1)to et f ππ-⋅2cos ;(2)t f t f o o sin 42sin +π;(3)t f t f o o ππ3cos 22cos +答: (1)to et f ππ-⋅2cos 是瞬变信号. 频谱具有连续性和衰减性.(2)t f t f o o sin 42sin +π是准周期信号. 频谱具有离散性,信号中各个频率比不是有理数.(3)t f t f o o ππ3cos 22cos +是周期信号. 频谱具有离散性、谐波性和收敛性。
1 .5 求指数衰减振荡函数t e t x at 0sin )(ω-= (a >0为常数)(题图1.5)的频谱,并作频谱图。
题图1.5解:解法一:直接由定义求:])(1)(1[2][2)(2sin )()(0000000000ωωωωωωωωωωωωωωω-+-++=-=-=⋅==⎰⎰⎰⎰∞+--++-∞---∞--∞∞--j a j a j dt e e j dte e e j e dt e t e dt e t x X t j j a t j j a t j t j t j att j at t j )()(解法二:利用傅里叶变换的频移特性求解。
因为: )(2sin )(000t j t j atate e j e t e t x ωωω-==--- 根据频移特性: )()(00ωωω±⇔X e t x tjωj a eat+⇔-1有: 2)(j X =ω[ )(10ωω++j a - )(10ωω-+j a ]1 .6 已知某信号x(t)的频谱X(f)(题图1.6),求)(2c o s )(00m f f t f t x >>π 的频谱,并作频谱图。
若)(0m f f <,频谱图会出现什么情况?题图1.6解:令t j t j e t f e t f t t f t x 00)(21)(21cos )()(0ωωω+==- 根据傅氏变换的频移性质,有:)(21)(21)(00ωωωωω-++=F F X当ω0<ωm 时,由图可见,00出现混叠,不能通过滤波的方法提取出原信号f (t )的频谱。
现代测试技术习题解答--第二章--信号的描述与分析---副本

现代测试技术习题解答--第二章--信号的描述与分析---副本第二章 信号的描述与分析补充题2-1-1 求正弦信号0()sin()x t x ωt φ=+的均值xμ、均方值2xψ和概率密度函数p (x )。
解答: (1)00011lim()d sin()d 0TT xT μx t t x ωt φt TT →∞==+=⎰⎰,式中02πTω=—正弦信号周期 (2)2222220000111cos 2()lim()d sin ()d d 22TT T xT x x ωt φψx t t x ωt φt t TT T →∞-+==+==⎰⎰⎰(3)在一个周期内12ΔΔ2Δx T t t t =+=0002Δ[()Δ]limx x T T T t P x x t x x T T T →∞<≤+===Δ0Δ000[()Δ]2Δ2d ()limlim ΔΔd x x P x x t x x t t p x x T x T x →→<≤+====正弦信号2-8 求余弦信号0()sin x t x ωt 的绝对均值xμ和均方根值rmsx 。
2-1 求图示2.36所示锯齿波信号的傅里叶级数展开。
2-4周期性三角波信号如图2.37所示,求信号的直流分量、基波有效值、信号有效值及信号的平均功率。
2-1 求图示2.36所示锯齿波信号的傅里叶级数展开。
补充题2-1-2 求周期方波(见图1-4)的傅里叶级数(复指数函数形式),划出|c n |–ω和φn –ω图,并与表1-1对比。
图1-4 周期方波0 tx (T 02-T2T -……A -T 0解答:在一个周期的表达式为00 (0)2() (0)2T A t x t T A t ⎧--≤<⎪⎪=⎨⎪≤<⎪⎩积分区间取(-T/2,T/2)000000002202002111()d =d +d =(cos -1) (=0, 1, 2, 3, )L T T jn tjn tjn t T T n c x t et Aet Ae tT T T Ajn n n ωωωππ-----=-±±±⎰⎰⎰所以复指数函数形式的傅里叶级数为 001()(1cos )jn tjn t n n n Ax t c ejn e n∞∞=-∞=-∞==--∑∑ωωππ,=0, 1, 2, 3, n ±±±L 。
现代测试技术习题解答信号的描述与分析副本

第二章 信号的描述与分析补充题2-1-1 求正弦信号0()sin()x t x ωt φ=+的均值x μ、均方值2x ψ和概率密度函数p (x )。
解答:(1)00011lim ()d sin()d 0TT x T μx t t x ωt φt TT →∞==+=⎰⎰,式中02πT ω=—正弦信号周期(2)2222220000111cos 2()lim()d sin ()d d 22TT T xT x x ωt φψx t t x ωt φt t TT T →∞-+==+==⎰⎰⎰(3)在一个周期内012ΔΔ2Δx T t t t =+=0002Δ[()Δ]limx x T T T tP x x t x x T T T →∞<≤+===Δ0Δ000[()Δ]2Δ2d ()limlim ΔΔd x x P x x t x x t t p x x T x T x →→<≤+====正弦信号x2-8 求余弦信号0()sin x t x ωt 的绝对均值x μ和均方根值rms x 。
2-1 求图示所示锯齿波信号的傅里叶级数展开。
2-4周期性三角波信号如图所示,求信号的直流分量、基波有效值、信号有效值及信号的平均功率。
2-1 求图示所示锯齿波信号的傅里叶级数展开。
补充题2-1-2 求周期方波(见图1-4)的傅里叶级数(复指数函数形式),划出|c n |–ω和φn –ω图,并与表1-1对比。
解答:在一个周期的表达式为图1-4 周期方波信号波形0 tx (tT 02-T020T -……A -AT 000 (0)2() (0)2T A t x t T A t ⎧--≤<⎪⎪=⎨⎪≤<⎪⎩积分区间取(-T/2,T/2)000000002202002111()d =d +d =(cos -1) (=0, 1, 2, 3, )T T jn tjn tjn t T T n c x t et Aet Ae tT T T Ajn n n ωωωππ-----=-±±±⎰⎰⎰所以复指数函数形式的傅里叶级数为001()(1cos )jn tjn t n n n Ax t c ejn e n∞∞=-∞=-∞==--∑∑ωωππ,=0, 1, 2, 3, n ±±±。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 信号的描述与分析补充题2-1-1 求正弦信号0()sin()x t x ωt φ=+的均值x μ、均方值2x ψ和概率密度函数p (x )。
解答: (1)00011lim ()d sin()d 0TT x T μx t t x ωt φt TT →∞==+=⎰⎰,式中02πT ω=—正弦信号周期(2)2222220000111cos 2()lim()d sin ()d d 22TT T xT x x ωt φψx t t x ωt φt t TT T →∞-+==+==⎰⎰⎰(3)在一个周期内012ΔΔ2Δx T t t t =+=0002Δ[()Δ]limx x T T T tP x x t x x T T T →∞<≤+===Δ0Δ000[()Δ]2Δ2d ()limlim ΔΔd x x P x x t x x t t p x x T x T x →→<≤+====正弦信号x2-8 求余弦信号0()sin x t x ωt 的绝对均值x μ和均方根值rms x 。
2-1 求图示2.36所示锯齿波信号的傅里叶级数展开。
2-4周期性三角波信号如图2.37所示,求信号的直流分量、基波有效值、信号有效值及信号的平均功率。
2-1 求图示2.36所示锯齿波信号的傅里叶级数展开。
补充题2-1-2 求周期方波(见图1-4)的傅里叶级数(复指数函数形式),划出|c n|–ω和φn–ω图,并与表1-1对比。
解答:在一个周期的表达式为00 (0)2() (0)2T A t x t T A t ⎧--≤<⎪⎪=⎨⎪≤<⎪⎩积分区间取(-T/2,T/2)00000002202002111()d =d +d =(cos -1) (=0, 1, 2, 3, )T T jn tjn tjn t T T n c x t et Aet Ae tT T T Ajn n n ωωωππ-----=-±±±⎰⎰⎰所以复指数函数形式的傅里叶级数为001()(1cos )jn tjn t n n n Ax t c ejn e n∞∞=-∞=-∞==--∑∑ωωππ,=0, 1, 2, 3, n ±±±。
(1cos ) (=0, 1, 2, 3, )0nInR A c n n n c ⎧=--⎪±±±⎨⎪=⎩ππ21,3,,(1cos )00,2,4,6,n An A c n n n n ⎧=±±±⎪==-=⎨⎪=±±±⎩πππ1,3,5,2arctan1,3,5,200,2,4,6,nI n nRπn c πφn c n ⎧-=+++⎪⎪⎪===---⎨⎪=±±±⎪⎪⎩没有偶次谐波。
其频谱图如下图所示。
图1-4 周期方波信号波形图2-5 求指数函数()(0,0)at x t Ae a t -=>≥的频谱。
解:(2)22022(2)()()(2)2(2)a j f tj f tat j f te A A a jf X f x t edt Ae edt Aa j f a j f a f -+∞∞---∞-∞-=====-+++⎰⎰πππππππ()X f =Im ()2()arctanarctanRe ()X f f f X f a==-πϕ2-6 求被截断的余弦函数0cos ωt (见图1-26)的傅里叶变换。
0cos ()0ωt t T x t t T⎧<⎪=⎨≥⎪⎩解:0()()cos(2)x t w t f t =π w (t )为矩形脉冲信号()2sinc(2)W f T Tf =π()002201cos(2)2j f tj f t f t e e πππ-=+ 所以002211()()()22j f t j f t x t w t e w t e -=+ππ单边指数衰减信号频A /π/-π/2幅频图相频图周期方波复指数函数形式频谱图图1-26 被截断的余弦t ) 0 1-根据频移特性和叠加性得: 000011()()()22sinc[2()]sinc[2()]X f W f f W f f T T f f T T f f =-++=-++ππ 可见被截断余弦函数的频谱等于将矩形脉冲的频谱一分为二,各向左右移动f 0,同时谱线高度减小一半。
也说明,单一频率的简谐信号由于截断导致频谱变得无限宽。
2-6求被截断的余弦函数cos ω0t (题图1-2)的傅立叶变换。
解2-7 求指数衰减信号0()sin at x t e ωt -=的频谱解:()0001sin()2j t j tt e e j-=-ωωω指数衰减信号)f 0-f 0被截断的余弦函数频⎩⎨⎧≥<=T t Tt t t x ;0;cos )(0ω()[]210000222202sin sin 2)(2)(sin 2)(2)(sin 212cos )()(00θθππππππππππ⋅+⋅=⎥⎦⎤⎢⎣⎡--+++=+===--+-+--+∞∞--⎰⎰⎰c c T T f f T f f T f f T f f T dte e e dt tef dt e t x f X ft j t f j t f j T T TTft j ftj所以()001()2j t j tatx t e e e j--=-ωω单边指数衰减信号1()(0,0)at x t e a t -=>≥的频谱密度函数为11221()()j t at j t a j X f x t e dt e e dt a j a ∞∞----∞-====++⎰⎰ωωωωω根据频移特性和叠加性得:[]001010222200222000222222220000()()11()()()22()()[()]2[()][()][()][()]a j a j X X X j j a a a a j a a a a ⎡⎤---+=--+=-⎢⎥+-++⎣⎦--=-+-+++-++ωωωωωωωωωωωωωωωωωωωωωωωωωω2-9 求h (t )的自相关函数。
{(0,0)()0(0)atet a h t t -≥>=< 解:这是一种能量有限的确定性信号,所以()01()()()2at a t a h R h t h t dt e e dt e aττττ∞∞--+--∞=+==⎰⎰ 2-10 求方波和正弦波(见图5-24)的互相关函数。
图5-24 题5-3图指数衰减信号的频谱解法1:按方波分段积分直接计算。
00344304411()()()()()1(1)sin()1sin()(1)sin()2sin()T Txy T TT T T R x t y t dt x t y t dt T T t dt t dt t dt T τττωωτωωτωωτωτπ=+=-⎡⎤=--+-+--⎢⎥⎣⎦=⎰⎰⎰⎰⎰ 解法2:将方波y (t )展开成三角级数,其基波与x (t )同频相关,而三次以上谐波与x (t )不同频不相关,不必计算,所以只需计算y (t )的基波与x (t )的互相关函数即可。
411()cos cos 3cos 535y t t t t ωωωπ⎛⎫=--+- ⎪⎝⎭所以[][]00000114()()()sin()cos()41sin()sin()22sin(2)sin()220sin()sin()T T xy T T T R x t y t dt t t dtT T t t t t dt T t dt dt T T T ττωωωτπωωωτωωωτπωωτωτπωτωτππ⎛⎫=+=-+ ⎪⎝⎭=-+++--⎡⎤=-+-⎢⎥⎣⎦=--=⎰⎰⎰⎰⎰解法3:直接按R xy (τ)定义式计算(参看下图)。
034430441()()()1(1)sin()1sin()(1)sin()2sin()Txy TTT T T R x t y t dt Tt dt t dt t dt T ττττττωωωωτωτπ----=+⎡⎤=-++--⎢⎥⎣⎦=⎰⎰⎰⎰y (参考上图可以算出图中方波y (t )的自相关函数41024()32()0,1,2,y y T T TR TTR nT n ττττττ⎧-≤≤⎪⎪=-≤≤⎨⎪⎪+=±±⎩2-11 某一系统的输人信号为x (t )(见图5-25),若输出y (t )与输入x (t )相同,输入的自相关函数R x (τ)和输入—输出的互相关函数R x (τ)之间的关系为R x (τ)=R xy (τ+T ),试说明该系统起什么作用?解:因为R x (τ)=R xy (τ+T )所以0011lim ()()lim ()()T T T T x t x t dt x t y t T dt TTττ→∞→∞+=++⎰⎰所以x (t +τ)=y (t +τ+T )令t 1 = t +τ+T ,代入上式得x (t 1 - T )=y (t 1),即y (t ) = x (t - T )结果说明了该系统将输入信号不失真地延迟了T 时间。
2-12 已知信号的自相关函数为A cos ωτ,请确定该信号的均方值ψx 2和均方根值x rms 。
解:R x (τ)=Acos ωτ ψx 2= R x (0)=Arms x ==2-13已知某信号的自相关函数,求均方值 、和均方根值rms x 。
2-14已知某信号的自相关函数,求信号的均值x μ、均方根值 、功率谱。
图5-25 题5-4图方波的自相关函数2-15已知某信号的自相关函数,求信号的自功率谱。
解:采样序列x (n )()11111000()()()cos 2()cos ()24N N N s s s n n n n n x n x t t nT nT t nT t πδπδδ---===⎛⎫=-=-=-⎪⎝⎭∑∑∑2-18 对三个正弦信号x 1(t )=cos2πt 、x 2(t )=cos6πt 、x 3(t )=cos10πt 进行采样,采样频率f s =4Hz ,求三个采样输出序列,比较这三个结果,画出x 1(t )、x 2(t )、x 3(t )的波形及采样点位置,并解释频率混叠现象。
采样输出序列为:1,0,-1,0,1,0,-1,0,⋯⋯1203()cos ()24N n n n x n t πδ-=⎛⎫=-⎪⎝⎭∑ 采样输出序列为:1,0,-1,0,1,0,-1,0,⋯⋯1205()cos ()24N n n n x n t πδ-=⎛⎫=-⎪⎝⎭∑ 采样输出序列为:1,0,-1,0,1,0,-1,0,⋯⋯从计算结果和波形图上的采样点可以看出,虽然三个信号频率不同,但采样后输出的三个脉冲序列却是相同的,这三个脉冲序列反映不出三个信号的频率区别,造成了频率混叠。
