约束问题最优化方法共35页文档
合集下载
约束问题最优化方法

* * T * * * T * (1* , 2 ,, m ) 和 * ( 1 , 2 ,, m ) 使 Kuhn-Tucker 条 件 (9-6) 成 立 ,
且 对 满 足 下 述 (9-7) 、(9-8) 、(9-9) 三 条 件 的 任 意 非 零 向 量 z 有 (9-10) 成 立 , 则 x* 是 问 题 (9-1) 的 严 格 局 部 极 小 点 .
第9章
约束问题最优化方法
9.1 约束优化问题的最优牲条件
约束条件下求极小值的非线性规划问题的数学模 型如下:
min f ( x) s.t hi ( x) 0(i 1, 2,, m) g j ( x) 0( j 1, 2,, l )
( 9-1 )
9. 1. 1 基 本 概 念 1. 起 作 用 约 束 设 非 线 性 规 划 问 题 ( 9.1.1 ) 的 可 行 域 为 H
*
9.1.4 二阶充分条件
1. 二 阶 充 分 条 件 对 非 线 性 规 划 问 题 ( 9-1 ) 而 言 , 若 f ( x) 、 gi ( x)( j 1, 2,, l ) 、
hi ( x)(i 1, 2,, m) 二 次 连 续 可 微 , x* 是 可 行 点 , 又 存 在 向 量
2 .正则点
对 于 非 线 性 规 划 问 题 (9-1) , 如 果 可 行 点 x (1) 处 , 各 起 作 用 约 束 的 梯 度 线 性 无 关 , 则 x (1) 是 约 束 条 件 的 一 个 正 则 点,特别地,严格内点也是约束条件的正则点.
3 .可行下降方向的判定条件 在 7.4 节,我们给出了可行下降方向的定义,在这里 我们推导可行下降方向的判定条件. 设x
(1)
且 对 满 足 下 述 (9-7) 、(9-8) 、(9-9) 三 条 件 的 任 意 非 零 向 量 z 有 (9-10) 成 立 , 则 x* 是 问 题 (9-1) 的 严 格 局 部 极 小 点 .
第9章
约束问题最优化方法
9.1 约束优化问题的最优牲条件
约束条件下求极小值的非线性规划问题的数学模 型如下:
min f ( x) s.t hi ( x) 0(i 1, 2,, m) g j ( x) 0( j 1, 2,, l )
( 9-1 )
9. 1. 1 基 本 概 念 1. 起 作 用 约 束 设 非 线 性 规 划 问 题 ( 9.1.1 ) 的 可 行 域 为 H
*
9.1.4 二阶充分条件
1. 二 阶 充 分 条 件 对 非 线 性 规 划 问 题 ( 9-1 ) 而 言 , 若 f ( x) 、 gi ( x)( j 1, 2,, l ) 、
hi ( x)(i 1, 2,, m) 二 次 连 续 可 微 , x* 是 可 行 点 , 又 存 在 向 量
2 .正则点
对 于 非 线 性 规 划 问 题 (9-1) , 如 果 可 行 点 x (1) 处 , 各 起 作 用 约 束 的 梯 度 线 性 无 关 , 则 x (1) 是 约 束 条 件 的 一 个 正 则 点,特别地,严格内点也是约束条件的正则点.
3 .可行下降方向的判定条件 在 7.4 节,我们给出了可行下降方向的定义,在这里 我们推导可行下降方向的判定条件. 设x
(1)
第四章约束问题的最优化方法

当limr(k) 0 k
则(x, r(k) ) f (x) , xk * x *
例: 用内点法求
min
f
(x)
x2 1
x2 2
s.t. g( x) 1 x1 0 的约束最优解。
解:
首先构造内点惩罚函数: (
x,
r)
x2 1
x2 2
rk
ln(x1
1)
用解析法求函数的极小值,运用极值条件:
二. 直接解法:
基本思想:合理选择初始点,确定搜索方向,以迭代公式 x(k+1)= x(k)+α(k)S(k)在可行域中寻优,经过若干次迭代,收敛至最优点。 适用范围:只能求解不等式约束优化问题的最优解。
基本要点:选取初始点、确定搜索方向及适当步长。
搜索原则:每次产生的迭代点必须满足可行性与适用性两个条件。 可行性:迭代点必须在约束条件所限制的可行域内,即满足
1
u1 gu (x)
② .(x, r(k) )
m
f (x) r(k)
1
u1 gu (x)
③ .(x, r (k) )
f (x)
m
r (k) u u 1
1 gu (x)
其中:gu (x) 0,u 1,2,...m
其中:gu (x) 0,u 1,2,...m
gu(x)0, u=1,2,…,p
适用性:当前迭代点的目标函数值较前一点是下降的,即满足 F(xk+1)<F(xk)
收敛条件:
• 边界点的收敛条件应该符合 K-T 条件;
• 内点的收敛条件为: xk1 xk 1
和
约束问题的最优化方法

(k ) (k ) m
1 u 1 g ( x ) u
m
其中:gu ( x) 0, u 1,2,...m
1 u 1 g ( x ) u m 1 (k ) (k ) ③ . ( x, r ) f ( x) ru u 1 g u ( x) m 1 (k ) (k ) ④ .( x, r ) f ( x) r 2 u 1 [ g ( x )] u
min . g k x s.t. x Rn gu x g k x gu x 0
0
0
u 1, 2,..., S 1 u S 1,..., m
以求得的设计点作为新初始点,继续其判断可行性,若仍有不
满足的约束,则重复上述过程,直至初始点可行。
的选择:
要求: ①
② 方法: ①
在可行域内;
不要离约束边界太近。 人工估算,需要校核可行性;
②
计算机随机产生,也需校核可行性。
§5.2 内点惩罚函数法
方法: ③ 搜索方法: 任意给出一个初始点; 判断其可行性,若违反了S个约束,求出不满足约束中的最大值: g k ( x 0 ) max{ gu x 0 } u 1,2,..., S; 应用优化方法减少违反约束:
uI
Z
I为违反约束的集合。
g u x , 当 g u x 0时, maxg u x ,0 { 0 ,当g u x 0时, x, r
(k )
{
f x r k maxg u x ,0 f x
uI
Z
Z一般取2。
k
k
(k )
H [h ( x
1 u 1 g ( x ) u
m
其中:gu ( x) 0, u 1,2,...m
1 u 1 g ( x ) u m 1 (k ) (k ) ③ . ( x, r ) f ( x) ru u 1 g u ( x) m 1 (k ) (k ) ④ .( x, r ) f ( x) r 2 u 1 [ g ( x )] u
min . g k x s.t. x Rn gu x g k x gu x 0
0
0
u 1, 2,..., S 1 u S 1,..., m
以求得的设计点作为新初始点,继续其判断可行性,若仍有不
满足的约束,则重复上述过程,直至初始点可行。
的选择:
要求: ①
② 方法: ①
在可行域内;
不要离约束边界太近。 人工估算,需要校核可行性;
②
计算机随机产生,也需校核可行性。
§5.2 内点惩罚函数法
方法: ③ 搜索方法: 任意给出一个初始点; 判断其可行性,若违反了S个约束,求出不满足约束中的最大值: g k ( x 0 ) max{ gu x 0 } u 1,2,..., S; 应用优化方法减少违反约束:
uI
Z
I为违反约束的集合。
g u x , 当 g u x 0时, maxg u x ,0 { 0 ,当g u x 0时, x, r
(k )
{
f x r k maxg u x ,0 f x
uI
Z
Z一般取2。
k
k
(k )
H [h ( x
第四章 约束最优化方法---最优化方法课件

定理4.1.6 设x*为上述问题的局部最优解且 f(x),ci(x)(1≤i≤m)在x*点可微,则存在非零向量
l*=(l0*,l1*,···,lm*)使得
满足上面的条件的点称为Fritz-John点. 上面的条件仅仅是必要条件.
Fritz-John一阶必要条件
证明概要 设x*处的有效集为
I对显定*=理于然I(结无有x*效论l)=i*可约{=i|0c束以.i(x描,由*)述=于0为c,ii=(存x1),在>20,·l,·若0·及,m定l}.理i(i∈的I结*)论,使成得立,
对于i∈I \ I*,只要令li*=0,即可得到Fritz-John
条件.
例题 (Fritz-John条件)
例4.1.1 min f(x)=(x1-1)2+(x2-1)2 s.t. c1(x1,x2)=(1-x1-x2)3≥0
c2(x)=x1≥0 c3(x)=x2≥0
解:本问题是求点(1,1)T到如图三角形区域的最短 距离.显然唯一最优解为x*=(1/2,1/2)T.
条件下就是原来约束问题的最优解.
点(x*,l*)称为Lagrange函数L(x,l)的驻点.
等式约束问题的二阶充分条件
定理4.1.2 在上面的等式约束问题中,若 (i)f(x)与ci(x)(1≤i≤l)是二阶连续可微函数
(ii)存在x*∈Rn与l*∈Rl使得Lagrange函数的
梯度为零,即 (iii)对于任意非零向量s∈Rn,且
Gordan引理
引理4.1.4 设a1,···,ar是n维向量,则不存在向量 d∈Rn使得
aiTd<0(i=1,···,r) 成立的充要条件是,存在不全为零的非负实数
组l1,···,lr,使
Fritz-John一阶必要条件
l*=(l0*,l1*,···,lm*)使得
满足上面的条件的点称为Fritz-John点. 上面的条件仅仅是必要条件.
Fritz-John一阶必要条件
证明概要 设x*处的有效集为
I对显定*=理于然I(结无有x*效论l)=i*可约{=i|0c束以.i(x描,由*)述=于0为c,ii=(存x1),在>20,·l,·若0·及,m定l}.理i(i∈的I结*)论,使成得立,
对于i∈I \ I*,只要令li*=0,即可得到Fritz-John
条件.
例题 (Fritz-John条件)
例4.1.1 min f(x)=(x1-1)2+(x2-1)2 s.t. c1(x1,x2)=(1-x1-x2)3≥0
c2(x)=x1≥0 c3(x)=x2≥0
解:本问题是求点(1,1)T到如图三角形区域的最短 距离.显然唯一最优解为x*=(1/2,1/2)T.
条件下就是原来约束问题的最优解.
点(x*,l*)称为Lagrange函数L(x,l)的驻点.
等式约束问题的二阶充分条件
定理4.1.2 在上面的等式约束问题中,若 (i)f(x)与ci(x)(1≤i≤l)是二阶连续可微函数
(ii)存在x*∈Rn与l*∈Rl使得Lagrange函数的
梯度为零,即 (iii)对于任意非零向量s∈Rn,且
Gordan引理
引理4.1.4 设a1,···,ar是n维向量,则不存在向量 d∈Rn使得
aiTd<0(i=1,···,r) 成立的充要条件是,存在不全为零的非负实数
组l1,···,lr,使
Fritz-John一阶必要条件
第五节 约束最优化

得到 K-T 条件如下
2( x1 1) 1 2 0 2( xx 2) 1 3 0 2 1 ( 1 x 2 2) 0 2 x1 0 x 0 3 2 1 , 2 , 3 0
作为 K-T 点,还应满足可行性条件:
x1 x 2 2 0 x1 x 2 1 0 x 0, x 0 2 1
定理
hj, j J
4.5.2
对 于 (MP) 问 题 , 若 f , g i , i I ,
在点 x * 处连续可微,可行点 x * 满足(MP)的
2 m in x12 x 2 2 x1 x 2 2 x1 6 x 2 s .t . x1 x 2 4 x1 x 2 2 x , x 0 1 2
取 x (1,1) , 1 0
*
(4.5.8)
其中 i g i ( x ) 0,i I 为互补松紧条件
* *
Kuhn-Tucker条件-例题
• 例4.5.1用K-T条件求解下列问题
m in f ( x1 , x 2 ) ( x1 1) 2 ( x 2 2 ) 2 s .t . g 1 ( x ) x1 x 2 2 0 g 2 ( x ) x1 0 g ( x ) x 0 3 2 h1 ( x ) x1 x 2 1 0
p
Fc ( x ) f ( x ) p c ( x )
k k
其中,
p c ( x ) c k [m ax ( g i ( x ), 0 )]
2
k
ck 2
第五章约束问题的最优化方法

g1 ( x ) x1 x2 4,
g1 ( x) [ 1 , 1 ]T
g2 ( x) x1 ,
g2 ( x) [ 1 , 0 ]T 。
g3 ( x) x2 ,
g3 ( x) [ 0 , 1 ]T 。
18
由K T条件得
x1 3 1 1 0 x 3 1 1 2 0 3 1 0 2
第七讲 约束非线性规划
约束极值及最优性条件
等式约束 不等式约束 一般约束问题
约束极值问题的算法
外点法 内点法 乘子法
1
一 、约束极值问题的最优性条件
1、约束极值问题的表示 min f ( x ) hi ( x ) 0 i 1 , 2 ,, m s .t . g j ( x ) 0 j 1 , 2 , , l
8
2 g3 ( x ) 0。 2
I ( x ) { 1 , 2 }。
x2 g2 ( x ) 0
g3 ( x ) 0
O
g1 ( x ) 0
x
x1
②如何判断一个方向是可行方向?
9
定理1:
给 定 点x Q , 记 点 x 的 积 极 约 束 指 标 集 为 I ( x )。 给 定 向 量 d , 如果对任意的 i I ( x ) 有 gi ( x )T d 0 , 则 d 是 点 x 的 可 行 方 向 。
则 向 量d 是 点 x 处 的 可 行 下 降 方 向 。
证略
③极值点的必要条件: 定理3:
设 x* Q, I ( x*)是其积极约束指标集。
f ( x) 和 gi ( x) (i I ( x*)) 在点x * 处可微,
g1 ( x) [ 1 , 1 ]T
g2 ( x) x1 ,
g2 ( x) [ 1 , 0 ]T 。
g3 ( x) x2 ,
g3 ( x) [ 0 , 1 ]T 。
18
由K T条件得
x1 3 1 1 0 x 3 1 1 2 0 3 1 0 2
第七讲 约束非线性规划
约束极值及最优性条件
等式约束 不等式约束 一般约束问题
约束极值问题的算法
外点法 内点法 乘子法
1
一 、约束极值问题的最优性条件
1、约束极值问题的表示 min f ( x ) hi ( x ) 0 i 1 , 2 ,, m s .t . g j ( x ) 0 j 1 , 2 , , l
8
2 g3 ( x ) 0。 2
I ( x ) { 1 , 2 }。
x2 g2 ( x ) 0
g3 ( x ) 0
O
g1 ( x ) 0
x
x1
②如何判断一个方向是可行方向?
9
定理1:
给 定 点x Q , 记 点 x 的 积 极 约 束 指 标 集 为 I ( x )。 给 定 向 量 d , 如果对任意的 i I ( x ) 有 gi ( x )T d 0 , 则 d 是 点 x 的 可 行 方 向 。
则 向 量d 是 点 x 处 的 可 行 下 降 方 向 。
证略
③极值点的必要条件: 定理3:
设 x* Q, I ( x*)是其积极约束指标集。
f ( x) 和 gi ( x) (i I ( x*)) 在点x * 处可微,
约束问题的最优化方法

3. 优化方法: 选用内点惩罚法,惩罚函数形式为: 6 1 T k k x,r f x r 取 x 0 1,30 , r 0 3 , c 0.7 u 1 g x u 调用 Powell 法求序列无约束优化极值,以逐渐逼近原问 题的极值点。
k 2 x r ( 1 x ) x 1时; x, r k x 1时。 x
4
min.
s.t
f (x) = x
x ∈ R1
g (x) = 1-x ≤ 0
§5.3 外点惩罚函数法
二. 惩罚函数的形式:
①
x, r ( k ) f x r k maxg u x ,0 I u g u x 0 u 1,2,...,m,
(k ) (k ) m
1 u 1 g ( x ) u
m
其中:gu ( x) 0, u 1,2,...m
1 u 1 g ( x ) u m 1 (k ) (k ) ③ . ( x, r ) f ( x) ru u 1 g u ( x) m 1 (k ) (k ) ④ .( x, r ) f ( x) r 2 u 1 [ g ( x )] u
§5.2 内点惩罚函数法
4. 求解过程分析:
§5.3 外点惩罚函数法 (衰减函数法)
一. 基本思想: 外点法将新目标函数
Φ( x , r )
构筑在可行域 D
外,随着惩罚因子 r(k) 的不断 递增,生成一系列新目标函数
Φ(xk ,r(k)),在可行域外逐步
迭代,产生的极值点 xk*(r(k)) 序列从可行域外部趋向原目标 函数的约束最优点 x* 。 例:求下述约束优化问题的最优点。 新目标函数:
第六章约束最优化方法

x1 x2 4 x1 x2 2 1 1
[ 2 , 2 ]T 为K T 点。
二阶充分条件
Page 43
对于一般约束优化问题
min f (x)
s.t. ci ( x) 0 i E ci (x) 0 i I
f ( x) , ci ( x) 二阶连续可微
(ii)
x*
*
为
KT
点,且严格互补松弛条件成立;
证明:令 x' x t d , t 0。则对任意的i I( x),有
ci (x') ci (x) t ci (x)T d o(|| td ||2)
t ci (x)T d o(|| td ||2)
0 x' Q ,即d 为可行方向。
Page 17
可行下降方向:设点 x Q,给定向量d ,如果d 既是点 x 处 的可行方向,又是该点的下降方向,则称d 为点 x 处的可 行下降方向。
有效约束和非有效约束
Page 13
再换句话说,不等式约束问题的在最优解处的某 个小邻域内, 可以看成等式约束问题
例如 考虑由约束
c1( x) 1 x12 x22 0 c2( x) x1 x2 0 c3( x) x1 0 c4( x) x2 0
所确定的可行集,对于点
xA (1,0)T
Page 41
(1) 若 x1 x2 0 :
由1(4 x1 x2 ) 0可得1 0。
1 2 3 2 3 这与2 0矛盾。
(2) 若 x1 0, x2 0:
3 0
x1 1 2 3
x2 1 3 3
1
(4
x1 x2
2 x1 0
)
0
3 x2 0
x1 x2 4
约束优化方法讲解
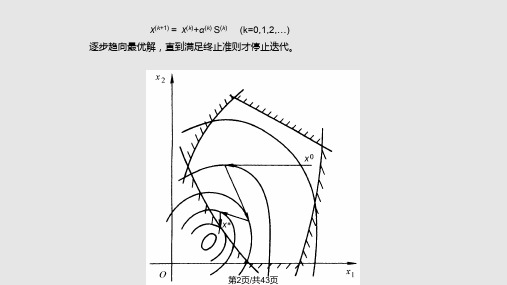
x(k+1)= x(k)+α(k) S(k) (k=0,1,2,…) 逐步趋向最优解,直到满足终止准则才停止迭代。
第2页/共43页
直接解法的原理简单,方法实用,其特点是: 1)由于整个过程在可行域内进行,因此,迭代计算不论 何时终止,都可以获得比初始点好的设计点。 2)若目标函数为凸函数,可行域为凸集,则可获得全域 最优解,否则,可能存在多个局部最优解,当选择的初始 点不同,而搜索到不同的局部最优解。 3)要求可行域有界的非空集。
j 1
k 1
加权转化项
将约束优化问题转换为无约束优化问题。求解无约束 优化问题的极小值,从而得到原约束优化问题的最优 解。
第23页/共43页
惩罚函数法是按一定的法则改变加权因子的值,构 成一系列的无约束优化问题,求一系列无约束最优解, 并不断地逼近原约束优化问题的最优解。因此又称序 列无约束极小化方法。常称SUMT方法。
根据它们在惩罚函数中的作用,分别称障碍项和惩罚 项。
障碍项的作用是当迭代点在可行域内时,在迭代过程 中将阻止迭代点越出可形域。
惩罚项的作用是当迭代点在非可行域或不满足等式约 束条件时,在迭代过程中将迫使迭代点逼近约束边界或 等式约束曲面。
按照惩罚函数在优化过程中迭代点是否可行,分为: 内点法、外点法及混合法。
内点法是将惩罚因数定义于可行域内,而外点法与 内点法不同,是将惩罚项函数定义于可行区域的外部。 序列迭代点从可行域外部逐渐逼近约束边界上的最优 点。
外点法可以用来求解含不等式和等式约束的优化问题。
对于约束优化问题
min f x s.t.g j x 0
hk x 0
第34页/共43页
转化后的外点惩罚函数的形式为:
r 5r
第2页/共43页
直接解法的原理简单,方法实用,其特点是: 1)由于整个过程在可行域内进行,因此,迭代计算不论 何时终止,都可以获得比初始点好的设计点。 2)若目标函数为凸函数,可行域为凸集,则可获得全域 最优解,否则,可能存在多个局部最优解,当选择的初始 点不同,而搜索到不同的局部最优解。 3)要求可行域有界的非空集。
j 1
k 1
加权转化项
将约束优化问题转换为无约束优化问题。求解无约束 优化问题的极小值,从而得到原约束优化问题的最优 解。
第23页/共43页
惩罚函数法是按一定的法则改变加权因子的值,构 成一系列的无约束优化问题,求一系列无约束最优解, 并不断地逼近原约束优化问题的最优解。因此又称序 列无约束极小化方法。常称SUMT方法。
根据它们在惩罚函数中的作用,分别称障碍项和惩罚 项。
障碍项的作用是当迭代点在可行域内时,在迭代过程 中将阻止迭代点越出可形域。
惩罚项的作用是当迭代点在非可行域或不满足等式约 束条件时,在迭代过程中将迫使迭代点逼近约束边界或 等式约束曲面。
按照惩罚函数在优化过程中迭代点是否可行,分为: 内点法、外点法及混合法。
内点法是将惩罚因数定义于可行域内,而外点法与 内点法不同,是将惩罚项函数定义于可行区域的外部。 序列迭代点从可行域外部逐渐逼近约束边界上的最优 点。
外点法可以用来求解含不等式和等式约束的优化问题。
对于约束优化问题
min f x s.t.g j x 0
hk x 0
第34页/共43页
转化后的外点惩罚函数的形式为:
r 5r
约束问题最优化方法PPT共35页

ThankБайду номын сангаасyou
45、法律的制定是为了保证每一个人 自由发 挥自己 的才能 ,而不 是为了 束缚他 的才能 。—— 罗伯斯 庇尔
6、最大的骄傲于最大的自卑都表示心灵的最软弱无力。——斯宾诺莎 7、自知之明是最难得的知识。——西班牙 8、勇气通往天堂,怯懦通往地狱。——塞内加 9、有时候读书是一种巧妙地避开思考的方法。——赫尔普斯 10、阅读一切好书如同和过去最杰出的人谈话。——笛卡儿
约束问题最优化方法
41、实际上,我们想要的不是针对犯 罪的法 律,而 是针对 疯狂的 法律。 ——马 克·吐温 42、法律的力量应当跟随着公民,就 像影子 跟随着 身体一 样。— —贝卡 利亚 43、法律和制度必须跟上人类思想进 步。— —杰弗 逊 44、人类受制于法律,法律受制于情 理。— —托·富 勒
45、法律的制定是为了保证每一个人 自由发 挥自己 的才能 ,而不 是为了 束缚他 的才能 。—— 罗伯斯 庇尔
6、最大的骄傲于最大的自卑都表示心灵的最软弱无力。——斯宾诺莎 7、自知之明是最难得的知识。——西班牙 8、勇气通往天堂,怯懦通往地狱。——塞内加 9、有时候读书是一种巧妙地避开思考的方法。——赫尔普斯 10、阅读一切好书如同和过去最杰出的人谈话。——笛卡儿
约束问题最优化方法
41、实际上,我们想要的不是针对犯 罪的法 律,而 是针对 疯狂的 法律。 ——马 克·吐温 42、法律的力量应当跟随着公民,就 像影子 跟随着 身体一 样。— —贝卡 利亚 43、法律和制度必须跟上人类思想进 步。— —杰弗 逊 44、人类受制于法律,法律受制于情 理。— —托·富 勒
