信号与系统第4章答案
信号与系统自测题(第4章 连续时间信号与系统的复频域分析)含答案

) 。
D
、6
−t
18
( s) s 、线性系统的系统函数 H (s) = Y = ,若其零状态响应 y(t ) = (1 − e F ( s) s + 1
D B
−t
)u (t )
,则系
统的输入信号 f (t ) = (
A
) 。
−t
、 δ (t )
、e
u (t )
C
、e
−2 t
u (t )
D
、 tu(t )
C
2
、s
ω e −2 s + ω2
12
、原函数 e
1 − t a
t f( ) a
的象函数是(
B
B
) 。
C
s 1 F( + ) 、1 a a a 注:原书答案为 D
A
、 aF (as + 1)
、 aF (as + a)
D
、 aF (as + 1 ) a
t f ( ) ↔ aF (as ) a e f (t ) ↔ F ( s + 1)
A
−s s −s s
A
s 、1 F ( )e a a
−s
b a
B
s 、1 F ( )e a a
− sb
C
s 、1 F ( )e a a
t 0
s
b a
D
s 、1 F ( )e a a
sb
、 已知信号 x(t ) 的拉普拉斯变换为 X (s) ,则信号 f (t ) = ∫ λ x(t − λ )d λ 的拉普拉斯变换 为( B ) 。 1 1 1 1 A、 X ( s ) B、 X (s) C、 X ( s) D、 X (s) s s s s 注:原书答案为 C。 f (t ) = ∫ λ x(t − λ )d λ = tu(t ) ∗ x(t )u(t ) tu(t ) ∗ x(t )u(t ) ↔ s1 X (s) 9、函数 f (t ) = ∫ δ ( x)dx 的单边拉普拉斯变换 F ( s ) 等于( D ) 。 1 1 A、 1 B、 C、 e D、 e s s
信号与系统第四章课后习题答案

其拉氏逆变换为: s3 + s 2 + 1 f (t ) = F [ ] = (-e-2t + 2e -4t )U (t ) ( s + 1)( s + 2)
-1
(8)
s+5 s ( s 2 + 2 s + 5) s+5 A B1s + B2 = = + s[( s + 1)2 + 4] s ( s + 1)2 + 4 A= s+5 gs = 1 s[( s + 1) 2 + 4)] s =0
(3) (2 cos t + sin t )U (t ) 查表得: s s + w2 w sin wtU (t ) « 2 s + w2 \ 根据拉氏变换的线性性质: 2s 1 2s + 1 (2 cos t + sin t )U (t ) « 2 + 2 = 2 s +1 s +1 s +1 cos wtU (t ) «
(9) 2d (t - t0 ) + 3d (t ) 根据时移特性:
d (t - t0 ) « e - st0
\ 2d (t - t0 ) + 3d (t ) « 2e - st0 + 3
(10) (t - 1)U (t - 1) 根据复频域微分特性: (-t ) n f (t ) « F ( n ) ( s ) 1 1 -tU (t ) « ( ) ' = - 2 s s 1 \tU (t ) « 2 s 根据时移特性: e- s (t - 1)U (t - 1) « 2 s
\ cos tU (t ) «
(仅供参考)信号与系统第四章习题答案

e −sT
=
−sT
2 − 4e 2
+ 2e −sT
Ts 2
(f) x(t) = sin πt[ε (t)− ε (t − π )]
sin π tε (t ) ↔
π s2 + π 2
L[sin
πtε (t
−π
)]
=
L e jπt
− 2
e− jπt j
ε (t
−π
)
∫ ∫ =
1 2j
∞ π
e
jπt e−st dt
4.3 图 4.2 所示的每一个零极点图,确定满足下述情况的收敛域。
(1) f (t) 的傅里叶变换存在
(2) f (t )e 2t 的傅里叶变换存在
(3) f (t) = 0, t > 0
(4) f (t) = 0, t < 5
【知识点窍】主要考察拉普拉斯变换的零极点分布特性。 【逻辑推理】首先由零极点写出拉普拉斯变换式,再利用反变换求取其原信号,即可求取其收
= cosϕ eω0tj + e−ω0tj − sin ϕ eω0tj − e−ω0tj
2
2j
=
cos 2
ϕ
−
sin 2
ϕ j
e
ω0 t j
+
cosϕ 2
+
sin ϕ 2j
e −ω 0tj
F(s) =
L
cosϕ 2
−
sin ϕ 2j
eω0tj
+
cos 2
ϕ
+
sin ϕ 2j
e
−ω0
t
j
ε
(t
)
∫ ∫ =
信号与系统第四章习题参考答案13

《信号与系统》第四章习题参考答案4-1 解 (1)111()ataL es s a s s a -⎡⎤-=-=⎣⎦++ (2)[]2221221sin 2cos 111s s L t t s s s ++=+++++ (3)()2212tL te s -⎡⎤=⎣⎦+(4)[]21sin(2)4L t s =+,由S 域平移性质,得 ()21s i n (2)14tL e t s -⎡⎤=⎣⎦++ (5)因为1!nn n L t s +⎡⎤=⎣⎦,所以 []2211212s L t s s s++=+= 由S 域平移性质,得 ()()23121ts L t e s -+⎡⎤+=⎣⎦+(6)()2211cos sL at s s a -=-⎡⎤⎣⎦+,由S 域平移性质,得 (){}()2211cos ts L at e s s aβββ-⎡⎤-=-⎣⎦+++ (7)232222L t t s s ⎡⎤+=+⎣⎦ (8)732()327tL t es δ-⎡⎤-=-⎣⎦+ (9)[]22sinh()L t s βββ=-,由S 域平移性质,得()22sinh()atL e t s a βββ-⎡⎤=⎣⎦+-(10)由于()211cos ()cos 222t t Ω=+Ω 所以 222221111c o s ()22424ss L t s s s s ⎛⎫⎡⎤Ω=+∙=+ ⎪⎣⎦+Ω+Ω⎝⎭(11)()()()11111at t L e e a a s a s s a s βββββ--⎡⎤⎛⎫-=-= ⎪⎢⎥--++++⎣⎦⎝⎭ (12)由于()221cos()1ts L e t s ωω-+⎡⎤=⎣⎦++所以 ()()()221cos()1a t a s e L et s ωω--++⎡⎤=⎣⎦++(13)因为(2)(1)(1)(1)(1)(1)t t t te u t e t e e u t ------⎡⎤-=-+-⎣⎦且()(1)(1)2(1)(1)(1)11sst t e e L t eu t L eu t s s ------⎡⎤⎡⎤--=-=⎣⎦⎣⎦++所以 ()(1)(2)2211(2)(1)(1)11s t s s e L teu t e e s s s -----⎡⎤+⎡⎤-=+=⎢⎥⎣⎦+++⎣⎦(14)()(1)tL e f t F s -⎡⎤=+⎣⎦,由尺度变换性质,得(1)ta t L e f aF as a -⎡⎤⎛⎫=+⎢⎥ ⎪⎝⎭⎣⎦(15)()t L f aF as a ⎡⎤⎛⎫=⎪⎢⎥⎝⎭⎣⎦,再由s 域平移性质,得 []2()()at t L e f aF a s a aF as a a -⎡⎤⎛⎫=+=+ ⎪⎢⎥⎝⎭⎣⎦(16)31cos(6)cos (3)cos(3)2t t t -=∙13cos(9)cos(3)44t t =+32213cos (3)48149s s L t s s ⎡⎤=+⎣⎦++由s 域微分性质,得()()22322222213181327cos (3)481494819d s s s s L t t ds s s s s ⎡⎤--⎛⎫⎢⎥⎡⎤=-+=+ ⎪⎣⎦⎢⎥++⎝⎭++⎣⎦(17)[]2cos(2)4sL t s =+,连续两次应用s 域微分性质,有 []()2224cos(2)4s L t t s-=+,()3232224cos(2)4s sL t t s-⎡⎤=⎣⎦+(18)111atL es s a -⎡⎤-=-⎣⎦+,由s 域积分性质,得111111(1)at sL e ds t s s a ∞-⎛⎫⎡⎤-=- ⎪⎢⎥+⎣⎦⎝⎭⎰ln()ln ln s s a s s a ⎛⎫=+-=- ⎪+⎝⎭ (19)351135tt L ee s s --⎡⎤-=-⎣⎦++,由s 域积分性质,得 33111115ln 353t t s e e s L ds t s s s --∞⎛⎫⎡⎤-+⎛⎫=-= ⎪ ⎪⎢⎥+++⎝⎭⎣⎦⎝⎭⎰(20)()22sin aL at s a =⎡⎤⎣⎦+,由s 域积分性质,得()1122211sin 1arctan 21s s at s a s L ds d t s a a a s a π∞∞⎡⎤⎛⎫⎛⎫===-⎢⎥ ⎪ ⎪+⎝⎭⎝⎭⎛⎫⎣⎦+ ⎪⎝⎭⎰⎰ 4-2 解(1)因为()()sin ()2T f t t u t u t ω⎡⎤⎛⎫=--⎪⎢⎥⎝⎭⎣⎦()sin ()sin 22T T t u t t u t ωω⎡⎤⎛⎫⎛⎫=+-- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ 所以可借助延时定理,得()()sin ()sin 22T T L f t L t u t L t u t ωω⎧⎫⎡⎤⎛⎫⎛⎫=+--⎡⎤⎡⎤⎨⎬ ⎪ ⎪⎢⎥⎣⎦⎣⎦⎝⎭⎝⎭⎣⎦⎩⎭222222221sT T s ee S S S ωωωωωω--⎛⎫=+=+ ⎪+++⎝⎭(2)因为()()()sin sin cos cos sin t t t ωϕωϕωϕ+=+ 所以()222222cos sin cos sin sin s s L t s s s ωϕϕωϕϕωϕωωω++=+=⎡⎤⎣⎦+++ 4-3 解此题可巧妙运用延时性质。
信号与系统(第四版)第四章课后答案

第5-10页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
4.1 拉普拉斯变换
四、常见函数的单边拉普拉斯变换
1. (t ) 1, 2.( t) 或1 3. ( t ) s, 4. 指数信号e
1
s
, 0
1 s s0
s0t
(t 2)
f1(t) 1 0 1 f2(t) 1 t
例1:e (t 2) e
-t
2
e
(t 2)
e
2
1 s 1
e
2s
-1 0
第5-17页
■
1
t
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
4.2 拉普拉斯变换性质
1 1e sT
例2: 单边冲激 T(t ) 1 e sT e s 2T 例3: 单边周期信号 fT(t ) (t ) f1(t ) f1(t T ) f1(t 2T ) F1(s )(1 e sT e s 2T )
8 e 2 s
s
f(t ) 1 0 1 y(t ) 2 4 t
二、尺度变换
2s
2
(1 e 2 s 2s e 2 s )
2 e 2 s 2 (1 e 2 s 2s e 2 s ) s
第5-16页
■
0
2
4
t
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
拉氏逆变换的物理意义
f (t )
2 j 1
j
j
F (s)est ds
郑君里《信号与系统》(第3版)(上册)配套题库-章节题库(第4章)【圣才出品】

A.
1 s2
e s
s
B. s 12
es
C. s 12
1 / 167
圣才电子书
1
D. s 12
1
E. s 12
十万种考研考证电子书、题库视频学习平台
【答案】D
【解析】因为
etu(t) 1 s 1
根据拉氏变换的频域微分性质
tet
u
t
1
s
1
1
=
s
1
12
3.信号
d dt
cos tU
t
s2 s2 1
又根据频域微分性质有
t
d dt
cos
tU
t
1
d ds
s2 s2
1
2s s2 1 2
4.信号 f t u t d 的拉普拉斯变换为( )。 0
A.1/s
B.1/(s2)
C.1/(s3)
D.1/(s4)
【答案】C
B.e-αtu(t-T)
C.e-αtu(t-α )
3 / 167
圣才电子书
D.e-αu(t-T)
十万种考研考证电子书、题库视频学习平台
【答案】B
【解析】u(t)的拉氏变换为 1/s,根据时移性,u(t-T)的拉氏变换为 e-sT/s,再
根据频域的时移性,e-αtu(t-T)的拉氏变换为 e-sT/s 的 s 左移α,即 e-sT/s 中的 s 加上
2s 1 2s 1
f(t)中包含Байду номын сангаас激函数 2δ(t),去掉冲激函数以后,根据初值定理
f
(0 )
lim
s
s
3 2s+1
《信号与系统》教与学第四章
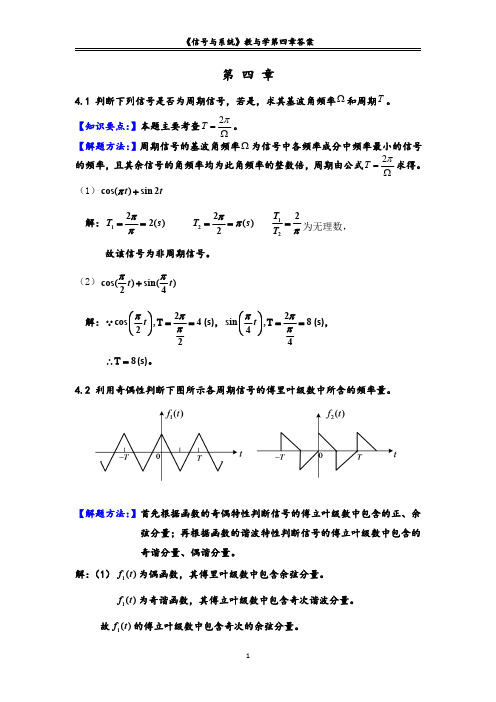
j n e 3
j n
e3
1 n
sin
n 3
,
n
0, 1,
2,
2
《信号与系统》教与学第四章答案
4.4 周期信号 f (t ) 的双边频谱 Fn 如图所示,求其三角函数表达式。
【知识要点:】本题主要考查周期信号的频谱概念,单边谱与双边谱的关系。
(3)计算信号的功率。
【知识要点:】本题主要考查周期信号的频谱概念应用;帕斯瓦尔功率等式应用。
T
2
;
f
t
A0 2
n1
An
cos
nt n
;P
Fn 2 。
n
【解题方法:】利用已知条件观察求出 ,并带入公式计算求出各次谐波分量;
根据单边幅度谱和双边幅度谱的关系、单边相位谱和双边相位谱的关系画出双
边幅度谱和相位谱;最后利用帕斯瓦尔功率等式计算信号的功率。
解:(1)
x
t
16 cos
20
t
4
6
cos
30
t
6
4
cos
40
t
3
10 (rad/s) ,
T
2
2 10
1 (s) , 5
周期信号所含谐波次数为二次,三次,四次;
求得。
(1) cos( t ) sin 2t
解: T1
信号与系统第4章作业解答

s5 sr (0 ) 3r (0 ) r (0 ) 4 3 2 Rzi ( s) 2 s 3s 2 s 3s 2 s 1 s 2
rzi (t ) 4e t 3e 2t
(t 0)
10
2 6 求激励信号和起始状态 为以下二种情况下系统 的完全响应, 并指出其零输入响应、 零状态响应、 自 由响应、 强迫响应各分量 . (2) e(t ) e 3t u (t ), r (0 ) 1, r (0 ) 2.
4
4 5 分别求下列函数的逆变换的初值和终值
s3 (2) ( s 1) 2 ( s 2)
s3 f (0 ) lim sF ( s) lim s 0 2 s s ( s 1) ( s 2)
s3 f () lim sF ( s) lim s 0 2 s 0 s 0 ( s 1) ( s 2)
(1) r (t ) rzi (t ) rzs (t )
d g (t ) g (t ) (t ) 2e t u (t ) dt
2 s 1 sG ( s ) G ( s ) 1 s 1 s 1 1 G(s) g (t ) e t u (t ) s 1
f (t ) (t 2et tet e t e2t )u(t )
7
4 4 求下列函数的拉普拉斯逆变换
e s (19) 4s( s 2 1)
1 A Bs C 2 2 s( s 1) s s 1
A B 0 C 0 A 1
( s 3) E ( s ) e(0 ) Rzs ( s ) s 2 3s 2
1 (2) E ( s ) e( 0 ) 0 s3
郑君里《信号与系统》(第3版)笔记和课后习题(含考研真题)详解(第4章)【圣才出品】

3.全通函数 如果一个系统函数的极点位于左半平面,零点位于右半平面,而且零点与极点对于 jω 轴互为镜像,这种系统函数称为全通函数,此系统则称为全通系统或全通网络。它的幅频特 性是常数。
4.最小相移函数 零点仅位于左半平面或 jω轴的网络函数称为“最小相移函数”,该网络称为“最小相 移网络”。非最小相移函数可以表示为最小相移函数与全通函数的乘积,即非最小相移网络 可以用最小相移网络与全通网络的级联来代替。
(1)部分分式展开法求解
首先将 F(s)展开成部分分式之和的形式,再对各部分分式分别取逆变换后叠加即可
得出 f(t)。
(2)留数定理求解
将拉氏逆变换的积分运算转化为求被积函数 F(s)est 在围线中所有极点的留数之和。
L 1[F (s)] 1 j F (s)estds [F (s)est的留数]
1 s
s2
s 2
,故
7 / 122
圣才电子书 十万种考研考证电子书、题库视频学习平台
L
[1 cos(t)]et
s
1
s (s )2 2
;
(7) L
[t 2
2t]
d2 ds2
1 s
d ds
2 s
2 s3
2 s2
(8) L [2 (t) 3e7t ] 2 3 s7
图 子书、题库视频学习平台
二、系统函数与系统特性 1.系统函数 系统的零状态响应的拉氏变换与激励的拉氏变换之比称为系统函数,即 H(s)=RZS (s)/E(s)。且冲激响应 h(t)↔H(s)。
2.零极点分布
H (s)
(9)e-αtsinh(βt);
(10)cos2(Ωt);
信号与系统 第4章-作业参考答案

题图 4-3-1 解:
11
第四章 傅立叶分析
第 4 章 习题参考答案
4-3-7
1)x(t)是实周期信号,且周期为 6; 3)x(t) = −x(t − 3)
1 3
设某信号x(t)满足下述条件:
2)x(t)的傅里叶系数为ak ,且当k = 0 和 k > 2时,有ak = 0;
1
4) ∫−3 |x(t)|2dt = 6 2 5)a1是正实数。
第四章 傅立叶分析
第 4 章 习题参考答案
第 4 章 习题参考答案
4-1 思考题 答案暂略 4-1 练习题 4-2-2 已知三个离散时间序列分别为 x1 ( n) = cos
2πn 2πn , x3 (n) = e , x 2 (n) = sin 25 10
π x (t ) = sin 4π t + cos 6π t + 时,试求系统输出 y (t ) 的傅立叶级数。 4
解:
3
第四章 傅立叶分析
第 4 章 习题参考答案
4因果系统: y(t) + 4y(t) = x(t)
式中x(t) 为系统输入,y(t)是系统输出。在下面两种输入条件下,求输出y(t)的傅里叶级数 展开: 1)x(t) = cos2πt ;
2
2
= 3 ) f ( t ) Sa (100t ) + Sa
解:
( 60t ) 4)
sin(4π t ) , −∞ < t < ∞ πt
9
第四章 傅立叶分析
第 4 章 习题参考答案
4)T=1/4 4-2-27 设 x(t ) 是一实值信号,在采样频率 ω s = 10000π 时, x(t ) 可用其样本值唯一确定
信号与系统课后习题答案第4章

所示。
➢ 题解图 4.25
按直接形式Ⅰ画出模拟信号流图和 方框图分别如题解图4.25(e)、(f)
所示。
➢ 题解图 4.26
的系统函数H(s)如下,求系统的频
率响应,粗略地画出幅频响应和相 频响应曲线。
H(s)收敛域包含jω轴,故频率响应
(2) 依照系统方框图与信号流 图表示之间的对应关系,分别画出 两系统的信号流图表示,如题解图
2.23(c)、(d)所示。
图分别如题图 4.9(a)、(b)所示,求
系统函数H(s)。
➢ 题图 4.9
4.25 已知线性连续系统的系 统函数如下,用直接形式信号流图 模拟系统,画出系统的方框图。
所示。
点,列出节点电压方程:
h3(t)=ε(t)。
(1) 求系统的冲激响应;
(2) 若输入f(t)=ε(t),求零状
态响应。
➢ 题图 4.6
(1) 求系统的冲激响应;
(2) 若f(t)=tε(t),求零状态响
应。
➢ 题图 4.7
(1) 写出描述系统输入输出关 系的微分方程;
(2) 画出系统的信号流图。
4.4 求题图4.1所示信号的单 ➢ 题图 4.1 边拉氏变换。
(1) f(t)=ε(t)-ε(t-3)。因为
所以
4.7 题图4.2所示为从t=0起始
的周期信号, 求f(t)的单边拉氏变
➢ 题图 4.2
换。
于第一周期信号的象函数与周期因 子的乘积。
(a) 记f(t)中第一周期信号为 相应的象函数为F1(s)。由于
数为F(s),求下列F(s)的原函数f(t) 的初值f(0+)和终值f(∞)。
第4章 北邮信号与系统课后习题解答
(1)抽样后在什么频率上会出现干扰信号?试画出抽样后信号的频谱示意 图。
(2)为了抗干扰,信号在抽样前通过一个抗混淆系统,将干扰信号滤除。 试在题 4-5 图所示的两图中选出合适的抗混淆系统,并画出幅频特性曲线。
(3)为了使有用信号的衰减低于 1dB,混淆信号的衰减高于 15dB,试求所 需的时间参数 RC 的范围。
c
R( j)
H
( j)
E( j)
c 0,
e jt0 ,
c c 其他
设
e2
(t)
sin(ct) ct
,则
F E2 ( j)
e2
(t )
c 0,
,
c c 其他
R2 ( j)
H ( j)
Y j X j
1 e j
2
cos
2
e
j2
可见,虽然该系统具有线性的相频特性,但幅频特性不是常数,因此,该系统不 是无失真传输系统。
4-9 题 4-9 图所示系统中, H1( j) 为理想低通滤波器,其频率特性为
H1
(
j
)
H
i
对
信号
Sa
t 2
是无失真传输的,因此当
Sa
1 2
(t
T
)
Sa(
1 2
t
)
作用时,输出
v2
(t)
Sa
1 2
t
信号与系统(第二版) (曾禹村 著) 北京理工大学出版社 第四章作业参考答案

8 T /2 Asin( 2t / T0 )dt T 0 4A / k , k 1,3,5, x2 (t) A,0 t T / 4
ቤተ መጻሕፍቲ ባይዱ
则 x2 (t)
频谱:
4A
2k 1sin(2k 1) t ,
k 1 0
1
0 10
X ( ) F {sin t ( 1 / 3 ) sin 3 t } 1
X ( ) F { x ( t ) x ( t ) cos 20 t } 6 1 1
X ( ) X ( ) ( 20 ) ( 20 ) / 2 1 1
X ( ) X ( 20 ) / 2 X ( 20 ) / 2 1 1 1
信号与系统第二版曾禹村著北京理工大学出版社第四章作业参考答案由会员分享可在线阅读更多相关信号与系统第二版曾禹村著北京理工大学出版62.
4.2在全波整流电路中,如输入交流电压x(t),则输出电压y(t)=|x(t)|. (a)当 x(t)=cost,概略地画出输出y(t)的波形并求傅里叶系数。 (b)输入信号中直流分量振幅为多少,输出信号中直流分量振幅为多少? 解 : (a) y(t)=| cost |,T=π ,ω =2π /T=2. 1 … 0
9
-9Ω -7Ω -13Ω -11Ω 0
2 Aj /
7 Ω 9Ω
11Ω 13Ω
2 Aj 3
31Ω 33Ω 27Ω 29Ω ω
2 Aj 3
…
2 Aj /
2 Aj 9
1 H1(ω )
-15Ω -5Ω 0 5Ω 15Ω ω
X ( 10 ) 1
2020年智慧树知道网课《信号与系统(宁夏大学)》课后章节测试满分答案

绪论单元测试1【判断题】(1分)信号到的运算中,若a>1,则信号的时间尺度缩小a倍,其结果是将信号的波形沿时间轴放大a倍。
A.错B.对第一章测试1【判断题】(1分)信号到的运算中,若a>1,则信号的时间尺度缩小a倍,其结果是将信号的波形沿时间轴放大a倍。
A.对B.错2【判断题】(1分)如果某连续时间系统同时满足叠加性和齐次性,则称该系统为线性系统。
A.错B.对3【判断题】(1分)直流信号与周期信号都是功率信号。
A.错B.对4【单选题】(1分)将信号变换为()称为对信号的平移或移位。
A.B.C.D.5【单选题】(1分)下列各表达式正确的是()。
A.B.C.D.6【单选题】(1分)积分的结果为()。
A.3B.C.1D.97【单选题】(1分)设输入为、时系统产生的响应分别为、,并设、为任意实常数,若系统具有如下性质:,则系统为()。
A.时不变系统B.因果系统C.非线性系统D.线性系统8【单选题】(1分)()。
A.B.C.D.9【单选题】(1分),该序列是()。
A.非周期序列B.周期C.周期D.周期10【多选题】(1分)连续时间系统系统结构中常用的基本运算有()。
A.微分器B.标量乘法器C.积分器D.加法器11【多选题】(1分)下列等式成立的是()。
A.B.C.D.12【判断题】(1分)一系统,该系统是线性系统。
()A.错B.对第二章测试1【判断题】(1分)强迫响应是零状态响应与部分自由响应之差。
()A.对B.错2【判断题】(1分)连续时间系统的单位阶跃响应是系统在单位阶跃信号作用下的响应。
()A.对B.错3【判断题】(1分)零状态响应是由激励引起的响应。
()A.错B.对4【判断题】(1分)某连续时间系统是二阶的,则其方框图中需要两个积分器。
()A.错B.对5【单选题】(1分)若系统的输入信号为,冲激响应为,则系统的零状态响应是()。
A.B.C.D.6【单选题】(1分)卷积的结果是()。
A.B.C.D.7【单选题】(1分)卷积积分等于()。
信号与系统(段哲民)第三版 第四章答案全解

信号与系统(段哲民)第三版第四章答案全解4.1 选择题答案解析(C)伯努利信号是一个具有有限时间持续性的信号,因此是非因果信号。
解析:伯努利信号只在有限时间内存在,而非因果信号是只存在于负时间的信号。
(D)和三角函数的区别是,余弦函数的相位是0,而不是1。
解析:和三角函数不同,余弦函数的相位是0,表示相位没有滞后。
(B)碰撞行为是随机过程,因此其幅度表示为随机变量是正确的。
解析:碰撞行为是随机过程,其幅度表示为随机变量。
4.2 填空题答案解析1.以下哪个信号不是周期信号?(B)解析:周期信号是指在时间轴上具有循环性质的信号。
正方脉冲信号和方波信号都是周期信号,而冲击信号不是周期信号。
2.正弦信号频率是50Hz,则周期为______。
解析:频率和周期的关系为$f=\\frac{1}{T}$。
根据公式可知,周期$T=\\frac{1}{f}=0.02s$。
3.已知信号$y(t)=3\\sin(2\\pi t + \\frac{\\pi}{6})$,则相位为______。
解析:相位指信号相对于某参考信号的滞后程度。
对于正弦信号,相位为$\\theta = 2\\pi t + \\frac{\\pi}{6}$4.3 解答题答案解析1.请证明复指数函数$e^{j\\theta}$是周期信号。
解析:复指数函数$e^{j\\theta}$可以表示为$e^{j(\\omega_0t+\\phi)}=e^{j\\omega_0t}e^{j\\phi}$,其中$\\omega_0$为角频率。
由于$|\\phi| < \\pi$,所以$e^{j\\phi}$是一个衰减的振荡函数,它是一个周期信号。
2.指出以下信号的类型:(1)冲击信号 (2)阶跃信号 (3)斜坡信号解析:(1) 冲击信号是一个非周期信号;(2) 阶跃信号是一个非周期信号;(3) 斜坡信号是一个非周期信号。
3.已知信号y[y]=2y[y−y],请将该信号分解为若干复指数信号的叠加形式。
信号与系统第四章习题

1 3
s +1 ) ,复频移性质、尺度变换、S 域微分 3
b
b ⎤ 1 s - s ⎡ (4) f (at − b) = f ⎢a(t − )⎥ ↔ F( )e a ,时移性质、尺度变换 a ⎦ a a ⎣
4.7 题图 4.2 所示为从 t=0 起始的周期信号。求 f(t)的单边拉氏变换。
解: (a) f (t ) = f a (t ) *
∑ δ (t − nT )
n =0
∞
- s 1 f a (t ) = ε (t ) − ε (t − T / 2) ↔ (1 - e 2 ) s - s 1 1 1- e 2 1 = = ∴ F(s) = (1 - e 2 ) T -s ⎞ s 1 - e -sT s 1 - e -sT ⎛ ⎜ s ⎜1 + e 2 ⎟ ⎟ ⎝ ⎠ T T - s
2
K1 =
2 jπ / 6 2 − jπ / 6 e , K2 = e 3 3
∴ h(t ) =
π 4 −t 2 −t e cos( 3t + )ε (t ) = e 6 3 3
2
(
3cos 3t - sin 3t ε (t )
)
当 u s (t ) = ε (t ) 时, U( s ) = H ( s) =
−2 t 解:(1) e f (2t ) ↔
1 s+2 F( ) ,复频移性质、尺度变换 2 2 ⎡1 ⎤
2 2 -2s (2) (t − 2) f ( t − 1) = (t − 2) f ⎢ (t − 2)⎥ ↔ 2F′′(2s)e ,时移性质、尺度变换、S 域微分 2 ⎣2 ⎦
1
−t (3) te f (3t ) ↔ − F′(
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第4章拉普拉斯变换与连续系统复频域分析4.6本章习题全解4.1 求下列函数的拉普拉斯变换(注意:为变量,其它参数为常量)。
(1)(2)(3)(4)(5)(6)(7)(8)(9)(10)(11)(12)(13)(14)(15)(16)(17)(18)(19)(20)(21)(22)(23)(24)解:(2)(3)(4)(5)(6)(7)(8)(9)(10)(11)(12)(13)(14)(15)(16)(17)(18) ()(19)(20)(21)(22)(23)(24)4.2 已知,求下列信号的拉普拉斯变换。
(1)(2)(3)(4)(5)解:(1)(2)(3)(4)(5)所以4.3 已知信号的拉普拉斯变换如下,求其逆变换的初值和终值。
(1)(2)(3)(4)解(1)初值:终值:(2)初值:终值:(3)初值:终值:(4)初值:终值:4.4 求题图4.4所示信号的单边拉普拉斯变换。
题图4.4 解(1)所以根据微分性质所以注:该小题也可根据定义求解,可查看(5)小题(2)根据定义(3)根据(1)小题的结果再根据时移性质所以根据微分性质得(4)根据定义注:也可根据分部积分直接求取(5)根据单边拉氏变换的定义,本小题与(1)小题的结果一致。
(6)根据单边拉氏变换的定义,在是,对比(3)小题,可得4.5 已知为因果信号,,求下列信号的拉普拉斯变换。
(1)(2)(3)(4)解:(1)根据尺度性质再根据s域平移性质(2)根据尺度性质根据s域微分性质根据时移性质(3)根据尺度性质再根据s域平移性质(4)根据时移性质再根据尺度性质本小题也可先尺度变化得到,再时移单位,得到结果4.6 求下列函数的拉普拉斯逆变换。
(1)(2)(3)(4)(5)(6)(7)(8)(9)(10)(11)(12)(13)(14)(15)(16)(17)(18)(19)(20)(21)(22)(23)(24)解:(1)(2)(3)(4)(5)(6)(7)(8)(9)(10)(11)(12)(13)(14){} =(15){} =(16){}=(17){}=(18){}=(19){}=(20){}=(21){}=(22){}=(23) {}=(24) ()=4.7 求如题图4.7所示的单边周期信号的拉普拉斯变换。
题图4.7 (1)矩形脉冲信号第一周期的时间信号为:则(2) 第一个周期时间信号为则(3)第一个周期时间信号为:则(4) 一个周期:则4.8 已知线性连续系统的单位冲激响应为。
(1)若系统输入,求系统的零状态响应;(2)若,求系统输入。
解:将系统的单位冲激响应作拉氏变换得系统函数(1)系统输入的拉氏变换为根据系统的S域分析,所以零状态响应的拉氏变换为,所以(2)根据系统的S域分析,所以输入的拉氏变换为求拉氏反变换得4.9 已知系统微分方程为,求下列输入时的零状态响应。
(1);(2);(2)。
解:系统微分方程在零状态下两边做拉氏变换得整理得:(1)输入信号的拉氏变换为所以得做拉氏反变换得零状态响应(2)输入信号的拉氏变换为所以得做拉氏反变换得零状态响应(3)输入信号的拉氏变换为所以得做拉氏反变换得零状态响应4.10 利用拉普拉斯变换求解下列系统的系统函数、零状态响应、零输入响应和全响应。
(1)。
(2)(3);;(4);,,,解:(1)将系统方程两边拉氏变换得:(2)将系统方程两边拉氏变换得:把代入上式,(3)系统函数:(4)4.11 求下列微分方程描述的连续系统的零输入响应。
(1);(2);(3)。
解:(1)考虑输入,将微分方程两边做拉氏变换得代入初始条件,整理得,做拉氏反变换得零输入响应(2)考虑输入,将微分方程两边做拉氏变换得代入初始条件,整理得,做拉氏反变换得零输入响应(3)考虑输入,将微分方程两边做拉氏变换得代入初始条件,整理得,做拉氏反变换得零输入响应4.12 已知连续系统的微分方程为,求在下列输入时的零输入响应、零状态响应和全响应。
(1);(2);解:将系统方程两边拉氏变换得整理得即令状态,得零状态响应的拉氏变换为令,即,得零输入响应的拉氏变换为(1)输入的拉氏变换,和初始状态得对上式求拉氏反变换得,零状态响应零状态响应完全响应(2)输入的拉氏变换,和初始状态得对上式求拉氏反变换得,零状态响应零状态响应完全响应4.13 已知线性连续系统的系统函数和输入信号,求系统的完全响应。
(1);(2)。
解:根据系统得s域分析,系统的零状态响应的拉氏变换为(1)所以根据系统方程可得二阶系统特征方程的系数为1,4,3所以系统的零输入响应的拉氏变换为所以求拉氏反变换得系统的完全响应为(2)所以根据系统方程可得三阶系统特征方程的系数为1,3,2,0所以系统的零输入响应的拉氏变换为所以求拉氏反变换得系统的完全响应为4.14 一线性系统,当输入为时,零状态响应为,求系统的单位冲激响应。
解:输入的拉氏变换为,输出的拉氏变换为求反拉氏变换得系统的单位冲激响应4.15 已知系统的阶跃响应为,为使其零状态响应为,求激励信号。
解:4.16已知线性连续系统在相同的初始状态下,输入为时,完全响应为;输入为时,完全响应为;求在相同的初始状态下,输入为时系统的全响应。
解:根据线性系统的s域分析可知,设系统函数为,零输入响应的拉氏变换为则有(1)(2)其中,,(3),(4)将(3)、(4)代入(1)、(2)联立解得,所以输入为时,系统的全响应为4.17 已知系统函数,试求系统在下列信号激励时的稳态响应。
(1);(2)(1) 系统函数:系统的极点分别是,位于平面的左半平面,所以可得系统的频率响应函数所以系统的正弦稳态响应为(2) 系统函数:系统的极点分别是,位于平面的左半平面,所以可得系统的频率响应函数所以系统的正弦稳态响应为4.18 已知系统函数的零、极点分布如题图 4.18所示,单位冲激响应的初值。
(1)求系统函数;(2)求系统的频率响应函数;(3)求系统的单位冲激响应;(4)求系统在激励下系统的正弦稳态响应。
解:(1)根据题图可知,系统函数的极点为,,零点为根据系统函数的零极点,可写出零极点形式为利用初值定理得所以所以(2)系统的频率响应函数为(3)对求拉氏反变换得(4)所以,所以正弦稳态响应4.19 已知下列各系统函数,画出零、极点图,求单位冲激响应,画出波形,并判断系统是否稳定。
(1);(2);(3);(4)解:(1) 系统零极点图如下:该系统的所有极点都在左半开平面,所以系统稳定。
(2) 系统零级点图如下:该系统的所有极点都在左半开平面,所以系统稳定。
(3) 系统零极点图如下:该系统的所有极点都在左半开平面,所以系统稳定。
(4) 系统零极点图如下:该系统有一个极点位于虚轴上,所以系统不稳定。
4.20 线性系统如题图4.20所示,图中,,。
(1)求系统的系统函数和单位冲激响应;(2)若输入,求系统的零状态响应。
题图4.20解:(1),根据题图可知,求拉氏反变换得单位冲激响应(2),所以求拉氏反变换得系统的零状态响应4.21 线性连续系统如题图4.21所示。
(1)求系统函数;(2)为使系统稳定,求系数的取值围;(3)在临界稳定状态下,求系统单位冲激响应。
题图4.21解:根据题图的系统框图,可得出输入输出关系式整理得,根据劳斯判据准则,要使系统稳定必须满足,这里的分别表示分母的各项系数所以系统稳定得条件为,即(3)在临界稳定状态下,此时,所以求拉氏反变换得系统单位冲激响应4.22某连续系统的分母多项式为:,为使系统稳定,应满足什么条件?解:这是一个三阶系统,三阶系统稳定的充要条件是D(s)中全部系数非零,且同符号,而且还要求满足:所以根据题有:4.23检验以下多项式是否为霍尔维兹多项式。
(1);(2);(3);解:(1) 根据罗斯-霍尔维兹别准,排出罗斯阵列如下:第一行 1 4 4第二行 3 6 0第三行 2 4 0第四行 0 0 0罗斯阵列排列至此,出现一行元素全为0。
可把第3行的一行元素写为辅助多项式,将对求一阶导数,再将辅助多项式导数的系数4,4重新列在第4行,这样得到新的完整的罗斯阵列为第一行 1 4 4第二行 3 6 0第三行 2 4 0第四行 4 4 0第五行 2 0 0罗斯阵列中第1列元素全大于0,所以是霍尔维兹多项式。
(2);根据罗斯-霍尔维兹别准,排出罗斯阵列如下:第一行 1 10 0第二行 25 4 0第三行 0 0第四行 4 0罗斯阵列中第1列元素全大于0,所以是霍尔维兹多项式。
(3);根据罗斯-霍尔维兹别准,排出罗斯阵列如下:第一行 1 2 9第二行 4 3 4第三行 8第四行 -22.6以上阵列的第一列元素不全为正,所以不是霍尔维兹多项式。
4.24已知线性系统的系统函数如下,试判断各系统的稳定性。
(1)(2)(3)解:(1)这是一个二阶系统,其系统(二阶重根系统除外)稳定的充要条件是:分母中全部系数不缺项且同符号,该题目中全部系数分别为 1,5,4.不缺项且全为正,因此该系统稳定。
(2)首先将的特征多项式排列罗斯阵列第一行 1 17 6第二行 7 17 0第三行 6 0第四行 0 0第五行 6 0 0因为系数的罗斯阵列第一列元素全大于零,所以H (s)对应的系统为稳定系统。
(3)H(s)的分母多项式的系数,H (s)分母多项式的系数符号不完全相同,所以H(s)对应的系统为不稳定系统。
4.25已知因果信号的拉氏变换分别如下所示,试问的傅里叶变换是否存在?若存在,写出的表达式。
(1)(2)(3)解:(1)极点:s1=-1+j, s2=-1-j 因为系统所有极点都在左半开平面,所以系统稳定,X (jw)存在 X(jw)=X(s)|s=jw=(2) 极点:s1=0,s2=-1 有一个极点在虚轴上,除了将中的以代换外,还要加一系列冲激函数(3) 极点: s1= -4, s2=1, 所有极点不是都在左半开半面,所以系统不稳定,X(jw)不存在。
第5章连续时间信号的抽样与量化5.6本章习题全解5.1 试证明时域抽样定理。
证明:设抽样脉冲序列是一个周期性冲激序列,它可以表示为由频域卷积定理得到抽样信号的频谱为:式中为原信号的频谱,为单位冲激序列的频谱。
可知抽样后信号的频谱由以为周期进行周期延拓后再与相乘而得到,这意味着如果,抽样后的信号就包含了信号的全部信息。
如果,即抽样间隔,则抽样后信号的频谱在相邻的周期发生混叠,此时不可能无失真地重建原信号。
因此必须要求满足,才能由完全恢复,这就证明了抽样定理。
5.2 确定下列信号的最低抽样频率和奈奎斯特间隔:(1)(2)(3)(4)解:抽样的最大间隔称为奈奎斯特间隔,最低抽样速率称为奈奎斯特速率,最低采样频率称为奈奎斯特频率。
(1),由此知,则,由抽样定理得:最低抽样频率,奈奎斯特间隔。
