信号与系统课后答案第八章作业答案后半部分
信号与系统 陈后金 第二版 课后习题答案(完整版)

(1) f (t) = 3sin 2t + 6 sinπ t
(2) f (t) = (a sin t) 2
(8)
f
(k)
=
cos⎜⎛ ⎝
πk 4
⎟⎞ ⎠
+
sin⎜⎛ ⎝
πk 8
⎟⎞ ⎠
−
2
cos⎜⎛ ⎝
πk 2
⎟⎞ ⎠
解:(1)因为 sin 2t 的周期为π ,而 sin πt 的周期为 2 。
显然,使方程
−∞
0
2-10 已知信号 f (t) 的波形如题 2-10 图所示,绘出下列信号的波形。
f (t)
2
1
−1 0
t 2
题 2-10 图
(3) f (5 − 3t) (7) f ′(t) 解:(3)将 f (t) 表示成如下的数学表达式
(5) f (t)u(1 − t)
由此得
⎧2
f
(t)
=
⎪ ⎨ ⎪ ⎩
f (t)u(1− t) 2
1
0.5
t
−1 0
1
(7)方法 1:几何法。由于 f (t) 的波形在 t = −1处有一个幅度为 2 的正跳变,所以 f ′(t) 在 此处会形成一个强度为 2 的冲激信号。同理,在 t = 0 处 f ′(t) 会形成一个强度为 1 的冲激信 号(方向向下,因为是负跳变),而在 0 < t < 2 的区间内有 f ′(t) = −0.5 (由 f (t) 的表达式可
第 1 页 共 27 页
《信号与系统》(陈后金等编)作业参考解答
(2)显然,该系统为非线性系统。 由于
T{f (t − t0 )}= Kf (t − t0 ) + f 2 (t − t0 ) = y(t − t0 )
数字信号处理学习指导与课后答案第8章

xˆa (t) xa (t) δ(t nT ) n
第8章 上机实验
对上式进行傅里叶变换, 得到
Xˆ a ( j )
[xa (t)
δ(t nT )]e j tdt
n
=
xa
(t
)δ(t
nT
)e
j
t
dt
n
在上式的积分号内只有当t=nT时, 才有非零值, 因此
第8章 上机实验
2. 实验原理与方法
1)
时域采样定理的要点是:
(1) 对模拟信号xa(t)以T进行时域等间隔理想采样, 形成 的采样信号的频谱 Xˆ ( j ) 会以采样角频率Ωs(Ωs=2π/T)为 周期进行周期延拓。 公式为
Xˆ a ( j ) FT[xˆa (t)]
ห้องสมุดไป่ตู้
1 T
X a ( j
第8章 上机实验
8.1 实验一:
8.1.1
1. (1) 掌握求系统响应的方法。 (2) 掌握时域离散系统的时域特性。 (3) 分析、 观察及检验系统的稳定性。
第8章 上机实验
2. 在时域中, 描写系统特性的方法是差分方程和单位脉 冲响应, 在频域可以用系统函数描述系统特性。 已知输入 信号可以由差分方程、 单位脉冲响应或系统函数求出系统对 于该输入信号的响应。 本实验仅在时域求解。 在计算机上 适合用递推法求差分方程的解, 最简单的方法是采用 MATLAB语言的工具箱函数filter函数。 也可以用MATLAB 语言的工具箱函数conv函数计算输入信号和系统的单位脉冲 响应的线性卷积, 求出系统的响应。
第8章 上机实验
8.1.2
信号与系统课后答案8

, ( ( & ( #( "+ #+ % " , , & & % " #( $ +# % # , * ( ( ( ( " #& % # +* ( ** $* $ , ( ( " #& % "+ $
# ( # #& % " +& % #
,%" + , ( ( ( ( #& $ +& % "+ #
"" , ( & ( ( ** $ # % " +& % # ** $ +* (# 1 将式 ( $+ $, 代入式 , / . !整理后得 "" , & & & ( ( ** % # # % " ** % #* $+ (# ! 将式 , & 0 代入式 ( 消去, % # !求得 !!!! "" , & & & ( ( ** % " # % " ** % # +* $+ (# 1 式, 1 $0 ,和, / 即为网络状态方程 !而输出方程为 !!!! !!!! !!!!
#
即 * & & ( # ) *& 1 ## ( " *# $ " , & & & & ** $ ) +& 1 ## ( # *# % " , , 将& ( ( & ) #$ $ # $! 1 #& % 代入上式 !并求解得状态方程 * , & & ( # % #*# %* $ +& ( " +& ( # " , ( ( & $ $ #& % *# $ +# ( " 以( & !! )! 写出题图 !! 0 所示网络的状态方程 " $ 和& % 为状态变量 # " #
信号与系统答案(刘卫东)第八章

8-1对连续非周期信号进行抽样获得离散非周期信号,说明离散非周期信号频谱和连续非周期信号频谱的关系。
解:对非周期信号()a x t 进行冲激抽样,得到的非周期连续信号的傅里叶变换,等于对非周期信号()a x t 进行数值抽样得到的离散非周期信号的离散时间傅里叶变换。
即()()as d X X ωθ=,而冲激抽样信号的傅里叶变换()as X ω是被抽样的非周期连续信号的傅里叶变换()a X ω的周期延拓,延拓周期为2s s T πω=,如果()a x t 频率有限,且抽样过程满则抽样定理,即22s m sT πωω=≥,则延拓过程不产生混叠,()as X ω(即()d X θ)中有完整的()a X ω的波形,在此情况下,截取()as X ω的一个周期,它和()a X ω的关系为:()()(),22s s a s as s d X T X T X ωωωωθω==−<<8-2 已知)()(n u a n x d n d =(1<a ),求)(n x d 的DTFT 。
解:1001()[()]()()()lim 1j k j n n j n n j n j n d d d j k n n n n ae DTFT x n x n e a u n e a e ae ae θθθθθθ−+∞∞∞∞−−−−−→∞=−∞=−∞==−=====−∑∑∑∑ 由于1<a ,所以11()1lim 11j k j j j j k ae e ae ae e aθθθθθ−+−−→∞−==−−−8-3 已知非周期矩形方波信号)2(2()(11T t u T t u t g a a a −−+=,以mT T s 1=的抽样间隔对)(t g a 进行抽样得)(n g d ,计算[])(DTFT )e (n g G d j d =θ,定性画出3=m ,5=m 和7=m 时[])(DTFT )e (n g G d j d =θ的波形,并和)(t g a 的傅立叶变换波形进行比较。
信号与系统课后习题答案

习 题 一 第一章习题解答基本练习题1-1 解 (a) 基频 =0f GCD (15,6)=3 Hz 。
因此,公共周期3110==f T s 。
(b) )30cos 10(cos 5.0)20cos()10cos()(t t t t t f ππππ+==基频 =0f GCD (5, 15)=5 Hz 。
因此,公共周期5110==f T s 。
(c) 由于两个分量的频率1ω=10π rad/s 、1ω=20 rad/s 的比值是无理数,因此无法找出公共周期。
所以是非周期的。
(d) 两个分量是同频率的,基频 =0f 1/π Hz 。
因此,公共周期π==01f T s 。
1-2 解 (a) 波形如图1-2(a)所示。
显然是功率信号。
t d t f TP T TT ⎰-∞→=2)(21lim16163611lim 22110=⎥⎦⎤⎢⎣⎡++=⎰⎰⎰∞→t d t d t d T T T W(b) 波形如图1.2(b)所示。
显然是能量信号。
3716112=⨯+⨯=E J (c) 能量信号 1.0101)(lim101025=-===⎰⎰∞∞---∞→T t ttT e dt edt eE J(d) 功率信号,显然有 1=P W1-3 解 周期T=7 ,一个周期的能量为 5624316=⨯+⨯=E J 信号的功率为 8756===T E P W 1-5 解 (a) )(4)2()23(2t tt δδ=+; (b) )5.2(5.0)5.2(5.0)25(5.733-=-=----t e t e t et tδδδ(c) )2(23)2()3sin()2()32sin(πδπδπππδπ+-=++-=++t t t t 题解图1-2(a) 21题解图1-2(b) 21(d) )3()3()(1)2(-=----t e t t et δδε。
1-6 解 (a) 5)3()94()3()4(2-=+-=+-⎰⎰∞∞-∞∞-dt t dt t t δδ(b) 0)4()4(632=+-⎰-dt t t δ(c) 2)]2(2)4(10[)]42(2)4()[6(63632=+++-=+++-⎰⎰--dt t t dt t t t δδδδ(d)3)3(3)(3sin )(1010=⋅=⎰⎰∞-∞-dt t Sa t dt ttt δδ。
信号与系统王明泉第八章习题解答

第8章 系统分析的状态变量法8.1 学习要求(1)了解状态变量、状态、初始状态、状态空间、状态方程、输出方程、系统方程等概念及内涵;(2)能根据系统结构图、微分方程、差分方程、转移函数、系统框图,正确的选择状态变量,列出系统的状态方程和输出方程,并写成标准矩阵形式;(3)能采用时域方程和变换域方法求解系统状态方程和输出方程; (4)能根据状态方程和输出方程画出系统的框图。
8.2 本章重点(1)连续系统状态方程和输出方程的建立与求解;8.4 本章的内容摘要8.4.1状态方程的建立状态方程是描述系统的状态变量之间及其与激励之间关系的一阶微分方程,而输出方程是用状态变量和激励(有时还可能有激励的某些导数)表示的函数关系式。
(1)连续时间系统状态方程的建立通常,标准形式的状态方程为 )()()(t t t f x x B A +=•系统输出方程的标准形式为 )()()(t t t f x D C y +=式中)(t •x 表示状态变量的一阶导数,)(t f 是与外加信号有关的项,A 、B 、C 和D 为常数矩阵。
直接法:利用系统实际结构及系统所遵循的物理规律直接列出方程的方法。
间接法:根据已知的输入输出方程、系统框图或系统函数列写状态方程的方法。
(2)离散时间系统状态方程的建立对于一个有p 个输入和q 个输出的离散系统,如有k 个状态变量,其状态方程的一般形式为⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+++)()()()()()()1()1()1(212122221112112121222211121121n f n f n f b b b b b b b b b n x n x n x a a a a a a a a a n x n x n x p kp k k p p k kk k k k k k输出方程的一般形式为⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡)()()()()()()()()(212122221112112121222211121121n f n f n f d d d d d d d d d n x n x n x c c c c c c c c c n y n y n y p qp q q p p k qk q q k k q可简写为)()()1(n n n f x x B A +=+ )()()n n n f x D C y(+=式中C B A 、、和D 是常数矩阵。
信号与系统(郑君里)课后答案 第八章习题解答

=
z
z −
1
−
z
z −
2
2
当
z
>
2 时为右边序列 x (n)
=
⎡⎛ 1 ⎞n ⎢⎢⎣⎜⎝ 2 ⎟⎠
−
2n
⎤ ⎥
u
(
n
)
⎥⎦
当
z
<
0.5 时为左边序列
x(n)
=
⎡ ⎢2n ⎢⎣
−
⎛ ⎜⎝
1 2
⎞n ⎟⎠
⎤ ⎥ ⎥⎦
u
(
−n
−
1)
当 0.5 <
z
<
2 时为右边序列 x (n)
=
⎛ ⎜⎝
1 2
⎞ ⎟⎠
n
u
(
n
)
+
2n
u
(
−n
−
1)
8-18 解题过程:
因为 H ( z) =
Z ⎡⎣h (n)⎤⎦
=
z(
z−a
z
> a)
X
(z) =
Z
⎡⎣x (n)⎤⎦
=
z− z −1
( z−N +1
z −1
z
> 1)
Y ( z) = X ( z) H ( z) = z ( ) ⋅ z − z−N+1 z > 1
z − a z −1
(
2
z
)n
⎤ ⎦
∑ = 1−
∞
( 2z )n
n=0
=1− 1 1− 2z
= −2z 1− 2z
=
z
z −
1
⎛ ⎜⎝
z
信号与系统 于敏慧(第二版)第八周作业答案

n=−∞ 3
m=0
1− 3z z − 1
3
3
∑ ∑ ∑ ∑ (6)x[n]是左边序列, X (z) =
∞
x[n]z −n =
0
(1 n)z −n
∞
=−
(1 m)z m = − 1
∞
mz m
n=−∞
n=−∞ 2
m=0 2
2 m=0
∑ 有多种方法可得
∞
mz m =
z −1
,
m=0
(1 − z −1 )2
z
>a
#############################################
第八周作业 2
7.4; 7.9 (2)、(4); 7.11; 7.14 (2); 7.19; 7.20;7.22
7.4 用长除法、留数定理、部分分式法求以下 X(z)的 Z 反变换。
1 − 1 z −1 (1) 2 ,
1 + 1 z −1
2
4
8
16
2
x[n] = {1,− 1 , 1 ,− 1 ,+ 1 − } = (− 1 )n u[n] 2 4 8 16 2
法二:留数定理:
x[n]
=
{Re
s{X
(
z)
z
n−1}
z
=−
1
u[n]
=
{(
z
+
2
1) 2
z ⋅ z n−1
z+
1
} z=−
1
2
= (− 1 )n u[n] 2
(2) z < 0.5 对应的左边序列
x[n] = Z −1{ z − z } = [−0.5n + 2n ]u[−n −1] z − 0.5 z − 2
信号与系统奥本海姆英文版课后答案chapter8

.
Clearly, is just a shifted version of . Therefore,x(t)may be recovered from y(t) simply by multiplying y(t) by . There is no constraint that needs to be placed on to ensure that is recoverable from .
Chapter8 Answers
8.1Using Table 4.1, take the inverse Fourier transform of . This gives .
Therefor Y( ) of y(t) is given by
TheFourier transformof this signal is
.
Thisimplies that is zero for . When is passed through a lowpass fiter with cutoff frequency ,the output will clearly be zero .Therefore =0.
信号系统教材课后习题答案

第6章 系统及系统的时域分析1. 解:由于系统(1)不满足分解性;系统(2)不满足零输入线性;系统(3)不满足零状态线性,故这三个系统都不是线性系统。
对于系统(4),如果直接观察)(n y ~)(n f 关系,似乎系统既不满足齐次性,也不满足叠加性。
但考虑到令)(n f =0时,系统响应为常数b ,若把它看成是由初始状态引起的零输入响应时,系统仍是满足线性系统条件的,故系统(4)是线性系统。
2. 解:(1) 已知)(t f →)](cos[)(t f a t y f =,设 dd t t t t f t f >-=),()(1,则其零状态响应为)](cos[)](cos[)(11d f t t f a t f a t y -==,显然 )()(1d f f t t y t y -=,故该系统是时不变系统。
(2) 已知)(n f →)()(n bf n y f =,设01),()(n n n n f n f >-=,则其零状态响应为)()()(011n n bf n bf n y f -==,显然 )()(01n n y n y f f -=,故该系统是时不变系统。
3. 解:对于(1)~(4),由于任一时刻的零状态响应均与该时刻以后的输入无关,因此都是因果系统。
而对于(5),系统任一时刻的零状态响应都与该时刻以后的激励有关。
响应在先,激励在后,这在物理系统中是不可能的。
因此,该系统是非因果的。
(6)也是非因果的,因为如果0)(=t f ,0t t < 则有 0)3()(==t f t y f ,3t t <可见在区间003t t t <<上0)(≠t y f ,即零状态出现于激励之前,因而该系统是非因果的。
4. 解:(1)显然,无论激励)(n f 是何种形式的序列,只要它是有界的,那么)(n y f 也是有界的,因果该系统是稳定的。
(2)若)()(t u t f =,显然该激励是有界的,但 t x x u t y tf ==⎰∞-d )()(,0≥t它随时间t 无限增长,故该系统是不稳定的。
信号系统(第3版)习题解答

《信号与系统》(第3版)习题解析高等教育目录第1章习题解析 (2)第2章习题解析 (6)第3章习题解析 (16)第4章习题解析 (23)第5章习题解析 (31)第6章习题解析 (41)第7章习题解析 (49)第8章习题解析 (55)第1章习题解析1-1 题1-1图示信号中,哪些是连续信号?哪些是离散信号?哪些是周期信号?哪些是非周期信号?哪些是有始信号?(c) (d)题1-1图解 (a)、(c)、(d)为连续信号;(b)为离散信号;(d)为周期信号;其余为非周期信号;(a)、(b)、(c)为有始(因果)信号。
1-2 给定题1-2图示信号f ( t ),试画出下列信号的波形。
[提示:f ( 2t )表示将f ( t )波形压缩,f (2t)表示将f ( t )波形展宽。
](a) 2 f ( t - 2 ) (b) f ( 2t )(c) f ( 2t)(d) f ( -t +1 )题1-2图解 以上各函数的波形如图p1-2所示。
图p1-21-3 如图1-3图示,R 、L 、C 元件可以看成以电流为输入,电压为响应的简单线性系统S R 、S L 、S C ,试写出各系统响应电压与激励电流函数关系的表达式。
题1-3图解 各系统响应与输入的关系可分别表示为)()(t i R t u R R ⋅= tt i Lt u L L d )(d )(= ⎰∞-=tC C i Ct u ττd )(1)(1-4 如题1-4图示系统由加法器、积分器和放大量为-a 的放大器三个子系统组成,系统属于何种联接形式?试写出该系统的微分方程。
S RS LS C题1-4图解 系统为反馈联接形式。
设加法器的输出为x ( t ),由于)()()()(t y a t f t x -+=且)()(,d )()(t y t x t t x t y '==⎰故有)()()(t ay t f t y -='即)()()(t f t ay t y =+'1-5 已知某系统的输入f ( t )与输出y ( t )的关系为y ( t ) = | f ( t )|,试判定该系统是否为线性时不变系统?解 设T 为系统的运算子,则可以表示为)()]([)(t f t f T t y ==不失一般性,设f ( t ) = f 1( t ) + f 2( t ),则)()()]([111t y t f t f T == )()()]([222t y t f t f T ==故有)()()()]([21t y t f t f t f T =+=显然)()()()(2121t f t f t f t f +≠+即不满足可加性,故为非线性时不变系统。
信号与系统 奥本海姆 中文答案 chapter 8
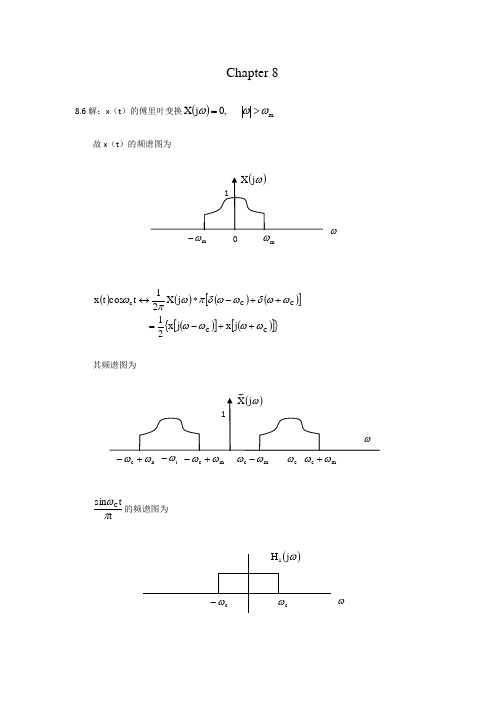
Chapter 88.6解:x (t )的傅里叶变换()m ,0j X ωωω>=故x (t )的频谱图为()()()()[]()[]()[]{}C C C C c j x j x 21j X 21t cos t x ωωωωωωδωωδπωπω++-=++-*↔其频谱图为ttsin C πω的频谱图为故()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛*=t t sin t cos t x -t cos t x t g c c c πωωω的频谱图为故()t cos t g c ω的频谱图为()()()ttAsin t cos t g t x c πωω*=4A =8.9解:(a) 因为1()x t 和2()x t 的截止频率都为c ω,1()x t 经频率为c ω的载波信号调制器经AM —SSB/SC 技术保留下边带后截止频率为c ω。
2()x t 经频率为2c ω的载波信号调制器经AM —SSB/SC 技术保留下边带后有2c c ωωω<<时不为0,其它都为0。
所以,将二者加在一起截止频率为2c ω。
即:2c ωω>时,()0Y j ω=。
(b) 2A =8.12解:2000M ωπ=2c M ωω∴>,即:32220000.510T Tππ->⨯⇒<⨯又410.51010T -∆=⇒∆<⨯8.13解:(a) 11212111()()(1cos)2222j t T j t T T p t P j e d e d πωωπωωωωππ++∞-∞-==+⎰⎰112121111111422sin 1(0)(1cos)()22242T T T p d T T T T ππωππωππ+-∴=+=+=⎰(b) 因为在PAM 中,在1t kT =采样后,来自其它所有脉冲对这个采样值贡献为零,即1()0p t mT -=,m k ≠。
所以,当(0)0p =时,1()0p kT =(1,2,k =±± )8.16解:{}00()(2)(2)j l C e l l jωπδωωπδωωπ+∞=-∞=---+-∑1()()()2j j j Y e X e C e ωωωπ=* 1()()(2)(2)222j j l Y e X e l l j ωωπππδωπδωππ+∞=-∞⎧⎫∴=*---+-⎨⎬⎩⎭∑ 因而在0ωπ≤≤内, 当308ωπ≤≤或38πωπ≤≤时,()0j Y e ω=。
2020年智慧树知道网课《信号与系统(山东联盟-山东师范大学)》课后章节测试满分答案

第一章测试1【判断题】(10分)正弦连续函数一定是周期信号A.对B.错2【判断题】(10分)正弦离散函数一定是周期序列。
A.错B.对3【判断题】(10分)余弦连续函数一定是周期信号。
A.错B.对4【判断题】(10分)余弦离散序列一定是周期的A.对B.错5【判断题】(10分)两个离散周期序列的和一定是周期信号。
A.对B.错6【判断题】(10分)两个连续周期函数的和一定是周期信号。
A.对B.错7【判断题】(10分)两个连续正弦函数的和不一定是周期函数。
A.对B.错8【判断题】(10分)取样信号属于功率信号。
A.对B.错9【判断题】(10分)门信号属于能量信号。
A.错B.对10【判断题】(10分)两个连续余弦函数的和不一定是周期函数。
A.错B.对第二章测试1【判断题】(10分)微分方程的齐次解称为自由响应。
A.对B.错2【判断题】(10分)微分方程的特解称为强迫响应。
A.错B.对3【判断题】(10分)微分方程的零状态响应是稳态响应的一部分A.对B.错4【判断题】(10分)微分方程的零输入响应是稳态响应的一部分A.对B.错5【判断题】(10分)微分方程的零状态响应包含齐次解部分和特解两部分。
A.错B.对6【判断题】(10分)微分方程的零状态响应中的特解部分与微分方程的强迫响应相等。
A.错B.对7【判断题】(10分)对LTI连续系统,当输入信号含有冲激信号及其各阶导数,系统的初始值往往会发生跳变。
A.对B.错8【判断题】(10分)对线性时不变连续系统,当输入信号含有阶跃信号,系统的初始值往往会发生跳变A.对B.错9【判断题】(10分)冲激函数匹配法是用于由零负初始值求解零正初始值。
A.对B.错10【判断题】(10分)LTI连续系统的全响应是单位冲激响应与单位阶跃响应的和。
A.对B.错第三章测试1【判断题】(10分)LTI离散系统的响应等于自由响应加上强迫响应。
A.错B.对2【判断题】(10分)LTI离散系统的响应等于齐次解加上零状态响应的和。
信号与系统课后习题答案第8章

7
第8章 系统的状态空间分析
题图 8.2
8
第8章 系统的状态空间分析
9
第8章 系统的状态空间分析
题解图 8.2
10
第8章 系统的状态空间分析
(2)
11
第8章 系统的状态空间分析
8.3 作为练习,请用MATLAB软件绘制x1(t)、x2(t)波形图 和x(t)的状态轨迹。
8.4 同题8.3。
代入元件值,整理得状态方程:
观察网络,直接写出输出方程:
32
第8章 系统的状态空间分析
题解图 8.10
33
第8章 系统的状态空间分析
34
第8章 系统的状态空间分析
35
第8章 系统的状态空间分析
36
第8章 系统的状态空间分析
37
第8章 系统的状态空间分析
8.11 列出题图 8.9 网络的状态空间方程(以uC、iL为状态变 量;i0、u0为输出)。
144
第8章 系统的状态空间分析
题解图 8.29
145
第8章 系统的状态空间分析
在系统输出端写出输出方程:
整理成矩阵形式,有
146
第8章 系统的状态空间分析
147
第8章 系统的状态空间分析
148
第8章 系统的状态空间分析
149
第8章 系统的状态空间分析
150
第8章 系统的状态空间分析
8.31 已知离散时间系统的模拟框图如题图 8.14 所示,试建 立其状态空间方程,并求出输入为
99
第8章 系统的状态空间分析
100
第8章 系统的状态空间分析
101
第8章 系统的状态空间分析
102
信号与系统课后答案8

故得零状态响应为
1 3 y f (k ) = [2(2)k + (−1) k − (1) k ]U (k ) 2 2
故又得全响应为
1 3 y (k ) = yx (k ) + y f (k ) = [2(2) k − (−1) k ]U (k + 2) + [2(2)k + (−1)k − (1)k ]U (k ) 2 2
第八章 习 题
8.1 求长度为 N 的斜坡序列
k , RN (k ) = 0,
0 ≤ k ≤ N −1 k < 0, k ≥ N
的 z 变换 RN ( z ) ,并求 N = 4 时的 RN ( z ) (见图题 81)。
R N (k )
L
答案
解 方法一
设GN (k ) = U (k ) − U (k − N ), 则 RN (k ) = kGN (k )
答案
解
(1)
F ( z ) = z1 [
z +1 1 3 1 3 ( z − 1)( z − − j )( z − + j ) 2 2 2 2 2z z z = −[ + ] π π j −j z −1 z−e 3 z−e 3
] = z[
2 + z −1
−1 1 3 z− − j 2 2
+
−1 1 3 z− + j 2 2
∞
z <
1 2
(3) F ( z ) =
z z− 1 4
−
z z− 2 3
=
−5 z , 1 2 12( z − )( z − ) 4 3
z >
2 3
1 2 极点P , P2 = ; 零点z1 = 0。 1 = 4 3
信号与系统第1至8章习题参考解答

《信号与系统》第1~8章习题参考解答第一章 (2)第二章 (13)第三章 (22)第四章 (35)第五章 (48)第六章(无) (56)第七章 (57)第八章 (65)第一章1-4 对于例1-1所示信号,由f (t )求f (−3t − 2),但改变运算顺序,先求f (3t )或先求f (−t ),讨论所得结果是否与原例之结果一致。
解:(1). 例1-1的方法: f (t )→ f (t − 2)→ f (3t − 2)→ f (−3t − 2) (2). 方法二:f (t )→ f (3t )→ 2[3()]3f t − →f (−3t − 2) (3). 方法三:f (t )→f (−t ) →[(2)]f t −+ →f (−3t − 2)方法三:1-5 已知()f t ,为求0()f t at −应按下列哪种运算求得正确结果(式中0t ,a 都为正值)?(1)()f at −左移0t (2)()f at 右移0t (3)()f at 左移0t a (4)()f at −右移0ta解:(4)()f at −右移t a:故(4)运算可以得到正确结果。
注:1-4、1-5 题考察信号时域运算:1-4 题说明采用不同的运算次序可以得到一致的结果; 1-5 题提醒所有的运算是针对自变量t 进行的。
如果先进行尺度变换或者反转变换,再进行移位变换,一定要注意移位量和移位的方向。
1-9 粗略绘出下列各函数式的波形图: (1)()(2)()t f t e u t −=− (2)2()(36)()t t f t e e u t −−=+ (3)3()(55)()t t f t e e u t −−=−(4)()cos(10)[(1)(2)]t f t e t u t u t π−=−−− 解:(1)()(2)()tf t e u t −=−(2)2()(36)()ttf t e eu t −−=+(3)3()(55)()ttf t e eu t −−=−(4)()cos(10)[(1)(2)]tf t e t u t u t π−=−−−1-12 绘出下列各时间函数的波形图,注意它们的区别:(1)[()(1)]−−;t u t u t(2)(1)�;t u t−(3)[()(1)](1)−−+−;t u t u t u t(4)(1)(1)−−;t u t(5)(1)[()(1)]−−−−;t u t u t(6)[(2)(3)]−−−;t u t u t(7)(2)[(2)(3)]t u t u t−−−−。
信号与系统课后习题答案

信号与系统课后习题答案信号与系统课后习题答案Company number:【WTUT-WT88Y-W8BBGB-BWYTT-1-1 试分别指出以下波形是属于哪种信号题图1-11-2 试写出题1-1图中信号的函数表达式。
1-3 已知信号)(1t x 与)(2t x 波形如题图1-3中所⽰,试作出下列各信号的波形图,并加以标注。
题图1-3⑴ )2(1-t x ⑵ )1(1t x - ⑶ )22(1+t x⑷ )3(2+t x ⑸ )22(2-tx ⑹ )21(2t x -⑺ )(1t x )(2t x - ⑻ )1(1t x -)1(2-t x ⑼ )22(1tx -)4(2+t x1-4 已知信号)(1n x 与)(2n x 波形如题图1-4中所⽰,试作出下列各信号的波形图,并加以标注。
题图1-4⑴ )12(1+n x ⑵ )4(1n x - ⑶ )2(1nx⑷ )2(2n x - ⑸ )2(2+n x ⑹ )1()2(22--++n x n x ⑺)2(1+n x )21(2n x - ⑻ )1(1n x -)4(2+n x ⑼ )1(1-n x )3(2-n x 1-5 已知信号)25(t x -的波形如题图1-5所⽰,试作出信号)(t x 的波形图,并加以标注。
题图1-51-6 试画出下列信号的波形图:⑴ )8sin()sin()(t t t x ΩΩ= ⑵ )8sin()]sin(211[)(t t t x ΩΩ+=⑶ )8sin()]sin(1[)(t t t x ΩΩ+= ⑷ )2sin(1)(t tt x =1-7 试画出下列信号的波形图:⑴ )(1)(t u e t x t -+= ⑵ )]2()1([10cos )(---=-t u t u t e t x t π⑶ )()2()(t u e t x t --= ⑷ )()()1(t u e t x t --= ⑸ )9()(2-=t u t x ⑹ )4()(2-=t t x δ1-8试求出以下复变函数的模与幅⾓,并画出模与幅⾓的波形图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
频率响应为
H
(e jΩ
)
=
H
(z)
|z = e jΩ
=
4 ⎡⎣ejΩ −1⎤⎦
3
⎡⎢⎣e
jΩ
−
1 3
⎤ ⎥⎦
经计算得极点为 p = 1 ,零点为 z = 1。 3
H(e jΩ)
(Ω)
幅频响应图(横坐标进行了归一化处理)
(c)Yx (z) =
y(−1) + 2 y(−2) + 2 y(−1)z−1 1− z−1 − 2z−2
=
8⋅ z +1⋅ 3 z−2 3
z, z +1
z
>2
其逆
z
变换即零输入响应为
yx
(n)
=
8 3
⋅
2n
u(n)
+
1 3
⋅
(−1)n
u(n)
(d)根据上面计算的零输入和零状态响应可知系统的完全响应为
f (n) = (−1)n u(n) , y(−1) = 0 , y(−2) = 1;
解:(1)将原式两边取单边 Z 变换得,
Y (z) −[z−1Y (z) + y(−1)] − 2[z−2Y (z) + y(−2) + y(−1)z−1] = F (z) + z−1F (z)
整理得:
Y (z)
=
题图 8-23
根据系统框图可得 h(n) = h1(n) ∗[h2 (n) + h3 (n)] ,故 h(n) = δ (n) ∗[h2 (n) + h3(n)] = u(n) + u(n − 2)
根据阶跃响应的定义可得: g(n) = u(n) ∗ h(n) = u(n) ∗[u(n) + u(n − 2)]
H
(z)
=
A⋅
z
+
3 1
3
由于 H (0)
=
A⋅
0−
1 3
=
5 解得
A
=
−5 ,故 H (z)
= (−5)⋅
z
−1 3
,
z
&gz+1
3
3
3
(2)由于收敛域包含单位园,故
H
(e
jΩ
)
=
H
(
z)
|z = e jΩ
=
(
−5)
⋅
⎡⎢⎣e ⎡⎢⎣e
jΩ jΩ
− +
1 3 1 3
⎤ ⎥⎦ ⎤ ⎥⎦
(3)其幅频响应曲线如下图所示
z2 + 4z + 4 z2 + 4z + 4 z +1
故 H(z)
=
Y (z) F(z)
=
z2
z2 + 4z
+
4
,其逆变换即为系统的单位脉冲响应。
H(z) =
z
= k11 + k12
z z2 + 4z + 4 ( z + 2)2 z + 2
其中,
k11
=
(
z
+
2)2
⋅
H (z) z
z = −2
=
−2
131 根据朱里准侧,由于
A(1) = 5 > 0
(−1)2 A(−1) = 0 < 0
a2 >| a0 | 不成立。
所以该系统不是稳定系统。
(2)解: H (z) 的分母为 A(z) = z4 + 2z3 + 2z2 + z +1,对 A(z) 的系数进行朱里排列得:
12211 11221 0 1 0 -1 -1 0 1 0 -1 0 1 1 0 -1
=
−4z
( z + 2)2
+
z↔ z +1
yf
(n)
= (−1)n u(n) + 2n(−2)n u(n)
Yx (z)
=
−4 z 2 (z + 2)2
=
8z (z + 2)2
−
4z z+2
↔
yx
(n)
= 8⋅ n ⋅(−2)n−1 u (n) − 4 ⋅(−2)n
u(n)
完全响应为:
y(n) = yx (n) + y f (n) = 8⋅ n ⋅(−2)n−1 u (n) − 4 ⋅(−2)n u (n) + (−1)n u(n) + 2n(−2)n u(n)
(
z)
=
−4 y (−1) − 4 y (−2) − 4 y
1+ 4z−1 + 4z−2
( −1)
z −1
+
1+
1 4z−1 +
4 z −2
⋅
F
(
z)
代入初始条件及 f (n) = (−1)n u(n) ↔ F ( z ) = z , z > 1得:
z +1
Y ( z ) = −4z2 + z2 ⋅ z
频率响应为:
H
(e jΩ
)
=
H
(z)
|z = e jΩ
=
3 ⎡⎣ejΩ +1⎤⎦
4
⎡⎢⎣e
jΩ
−
1 4
⎤ ⎥⎦
经计算该系统包括一个一阶极点为 p = 1 ,一阶零点为 z = −1,其零极点分布如下图所示: 4
零极点图
H(e jΩ)
(Ω)
幅频响应图(横坐标进行了归一化处理)
ϕ (Ω)
(Ω)
相频响应图(横坐标进行了归一化处理)
y(−1) + 2 y(−2) + 2 y(−1) z−1 1− z−1 − 2z−2
+
1
−
1+ z −1
z −1 −2
z
−2
F (z)
所以,(a) H (z)
=
1
−
1+ z −1
z −1 −2
z
−2
=
z2 + z z2 − z − 2
=
z z−2
,求其逆 Z 变换可得单位脉冲响应为
h(n) = 2n u(n)
-14
-16
H(e jΩ)
-18
-20
-22 0
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
1 (Ω)
幅频响应曲线(横坐标进行了归一化处理)
8-21、已知因果离散系统的差分方程为 y(n) + 1 y(n −1) = f (n) + f (n −1) 3
(1) 求系统函数 H (z) ;
ϕ (Ω)
(Ω )
相频响应图(横坐标进行了归一化处理)
零极点图
8-20、已知因果离散系统的系统函数 H (z) 的零极点分布如题图 8-20 所示,且 H (0) = 5 (1)求系统函数 H (z) ;
(2)求系统的频率响应; (3)粗略画出系统的幅频响应曲线。
题图 8-20
z−1
解:(1)
由零极点图可知:该系统包括一个一阶极点;一个一阶零点,故设
8-19、已知因果离散系统的系统函数如下,试画出该系统的零极点分布图,并求该系统的频
率响应、粗略画出系统的幅频响应和相频响应曲线。
(1) H (z) = 3(z +1) z > 1 ;
4z −1
4
(2) H (z) = 4(z −1) z > 1 。
3z −1
3
解:(1)因为 H (z) 的收敛域为 | z |> 1 ,所以 H (z) 在单位圆上收敛。 4
8-30、已知因果离散系统的系统函数如下,检验各系统是否稳定。
(1) H (z) = 1 ; z2 + 3z +1
(2) H (z)
=
z4
+
z2 +1 2z3 + 2z2
+
z
+1
(1)解: H (z) 的分母为 A(z) = z2 + 3z +1( n = 2 ),对 A(z) 的系数进行朱里排列得
,
k12
=
d dz
⎢⎣⎡( z
+
2)2
⋅
H (z) ⎤ z ⎥⎦
z = −2
= 1,故
H
(z)
=
( −2) ⋅
(
z
z
+ 2)2
+
z
1 +
2
↔
h(n)
=
(−2) ⋅ n ⋅(−2)n−1
u
(n)
+
( −2 )n
u
(n)
= (−2)n u(n) + n(−2)n u(n)
Yf
(z)
=
z3 (z +1)(z + 2)2
(2) 画出 H (z) 的零极点分布图。
解:(1)分别差分方程的两边求单边 z 变换(且 y(n) 的初始状态为零)可得
Y (z) + 1 z−1Y (z) = F (z) + z−1F (z) 3
由此可知: H (z)
=
Y (z) F (z)
=
1+ z−1 1+ 1 z−1
=
z +1 z+ 1
3
由于 u(n) ∗ u(n) = (n +1) u(n) ,根据卷积和的时移特性可得
