2012年数学周报杯模拟试题
2012年中考数学模拟试卷

2012年中考数学模拟试卷一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.计算-2-1的结果是()(A)-1 (B)1 (C)3 (D)-32.如左图,这个几何体的主视图是()A. B. C. D.3.的角平分线AD交BC于点D,,则点D到AB的距离是( )A.1 B.2 C.3 D.44.估计+1的值是()A.在2和3之间 B.在3和4之间C.在4和5之间 D.在5和6之间5.《茂名日报》(2007年5月18日)报道,刚刚投产半年的茂名百万吨乙烯工程传来喜讯,正在创造全国最好的效益,每月为国家创利30 000万元,这个数用科学记数法表示是( )A. B. C. D.6.设一元二次方程的两个根分别是,则下列等式正确的是()A. B.C. D.7.下表是我国部分城市气象台对五月某一天最高温度的预报,当天预报最高温度数据的中位数是()城市北京上海杭州苏州武汉重庆广州东莞珠海深圳最高温26252929313228272829度(℃)A.28 B.28.5 C.29 D.29.58.不等式组的解集是()A. B.C. D.9.如图,一扇形纸片,圆心角为,弦的长为,用它围成一个圆锥的侧面(接缝忽略不计),则该圆锥底面圆的半径为()DD1D2AA1A2A3A4B1B2CC2C1C3C4BA.cm B.cmOBAOC.cm D.cm10.在平行四边形中,点,,,和,,,分别是和的五等分点,点,和,分别是和的三等分点,已知四边形的面积为1,则平行四边形的面积为()A. B. C. D.11.如图,小亮在操场上玩,一段时间内沿的路径匀速散步,能近似刻画小亮到出发点的距离与时间之间关系的函数图象是()A.B.C.D.12.如图,记抛物线的图象与正半轴的交点为,将线段分成等份.设分点分别为,,,,过每个分点作轴的垂线,分别与抛物线交于点,,…,,再记直角三角形,,…的面积分别为,,…,这样就有,,…;记,当越来越大时,你猜想最接近的常数是()P1P2P3P n-11AxyQ1Q2Q3Q n-1O1A. B. C. D.二、填空题(本大题共5个小题,每小题3分,共15分.把答案填在题中横线上)13.分解因式:分解因式:.APO14.如图,PA与半圆O相切于点A,如果∠P=35°,那么∠AOP=_____°.15.如图,把矩形纸片放入平面直角坐标系中,使,分别落在轴,轴上,连结,将纸片沿折叠,使点落在点的位置.若,,则点的坐标为____________.703532285450595616.下图是一组数据的折线统计图,这组数据的极差是 ,平均数是 .FCGDHAEB17.如图,将矩形纸ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=3厘米,EF=4厘米,则边AD的长是___________厘米.三、解答题(本大题共7个小题,共57分.解答应写出文字说明、证明过程或演算步骤)18.(本小题满分7分)(1)计算:先化简,再求值:,其中.(2)解分式方程:解方程:.19.(本小题满分7分)(1)如图,在平行四边形中,,的平分线分别交对边于点,交四边形的对角线于点.求证:.(2)如图,PA,PB是⊙O的切线,点A,B为切点,AC是⊙O的直径,∠ACB=70°.求∠P的度数.20.(本小题满分8分)在一次数学活动中,黑板上画着如图所示的图形,活动前老师在准备的四张纸片上分别写有如下四个等式中的一个等式:①②③④小明同学闭上眼睛从四张纸片中随机抽取一张,再从剩下的纸片中随机抽取另一张.请结合图形解答下列两个问题:(1)当抽得①和②时,用①,②作为条件能判定是等腰三角形吗?说说你的理由;(2)请你用树状图或表格表示抽取两张纸片上的等式所有可能出现的结果(用序号表示),并求以已经抽取的两张纸片上的等式为条件,使不能构成等腰三角形的概率.ADEBC21.(本小题满分8分)今年5月12日,四川汶川发生了里氏8.0级大地震,给当地人民造成了巨大的损失.“一方有难,八方支援”,我市锦华中学全体师生积极捐款,其中九年级的3个班学生的捐款金额如下表:班级(1)班(2)班(3)班金额2000(元)吴老师统计时不小心把墨水滴到了其中两个班级的捐款金额上,但他知道下面三条信息:信息一:这三个班的捐款总金额是7700元;信息二:(2)班的捐款金额比(3)班的捐款金额多300元;信息三:(1)班学生平均每人捐款的金额大于48元,小于51元.请根据以上信息,帮助吴老师解决下列问题:(1)求出(2)班与(3)班的捐款金额各是多少元;(2)求出(1)班的学生人数.22.(本小题满分9分)如图,点A(m,m+1),B(m+3,m-1)都在反比例函数的图象上.(1)求m,k的值;(2)如果M为x轴上一点,N为y轴上一点,xOyAB以点A,B,M,N为顶点的四边形是平行四边形,试求直线MN的函数表达式.23.(本小题满分9分)如图①,在边长为的正方形中,是对角线上的两个动点,它们分别从点,点同时出发,沿对角线以的相同速度运动,过作垂直交的直角边于;过作垂直交的直角边于,连接,.设,,,围成的图形面积为,,,围成的图形面积为(这里规定:线段的面积为).到达到达停止.若的运动时间为,解答下列问题:FEGDCBAH图①BA图②CD(1)当时,直接写出以为(2)顶点的四边形是什么四边形,(3)并求为何值时,.(2)①若是与的和,求与之间的函数关系式.(图②为备用图)②求的最大值.24.(本小题满分9分)如图,已知平面直角坐标系中,有一矩形纸片OABC,O为坐标原点,轴,B(3,),现将纸片按如图折叠,AD,DE为折痕,.折叠后,点O落在点,点C落在点,并且与在同一直线上.CDOABEO1C1xy(1)求折痕AD 所在直线的解析式; (2)求经过三点O,,C的抛物线的解析式; (3)若⊙的半径为,圆心在(2)的抛物线上运动,⊙与两坐标轴都相切时,求⊙半径的值.。
2012年中考数学模拟试题五

2012年全新中考数学模拟试题五*考试时间120分钟 试卷满分150分一、选择题(下列各题的备选答案中,只有一个答案是正确的,将正确答案的序号填在题后的括号内,每小题3分,共24分)1.sin30°的值为( )A .21B .23C .33D .22 2. △ABC 中,∠A =50°,∠B =60°,则∠C =() A .50° B .60° C .70°D .80°3.如图,直线l 1、l 2、l 32x y 来确定点P (x y ,24y x x=-+上的概率为(????) ??????A??11811219167.右图是由几个小立方块搭成的几何体的俯视图,小正方形中的数字表示在该位置的小立方块的个数,那么这个几何体的主视图是( )D . 8.某超级市场失窃,大量的商品在夜间被罪犯用汽车运走。
三个嫌疑犯被警察局传讯,警察局已经掌握了以下事实:(1)罪犯不在A 、B 、C 三人之外;(2)C 作案时总得有A 作从犯;(3)B 不会开车。
在此案中能肯定的作案对象是( )A .嫌疑犯AB .嫌疑犯BC .嫌疑犯CD .嫌疑犯A 和C二、填空题(每小题3分,共24分)9.据中新社报道:2010年我国粮食产量将达到540000000000千克,用科学记数法表示这个粮食产量为______千克.10.用一个半径为6㎝的半圆围成一个圆锥的侧面,则这个圆锥的侧面积为 ㎝2.(结果保留π)11.△ABC 中,AB =6,AC =4,∠A =45°,则△ABC 的面积为 .12.若一次函数的图象经过反比例函数4y x=-图象上的两点(1,m )和(n ,2),则这个一次函数的解析式是 .13. 某品牌的牛奶由于质量问题,在市场上受到严重冲击,该乳业公司为了挽回市场,加大了产品质量的管理力度,并采取2 13了“买二赠一”的促销手段,一袋鲜奶售价1.4元,一箱牛奶18袋,如果要买一箱牛奶,应该付款 元.14.通过平移把点A(2,-3)移到点A ’(4,-2),按同样的平移方式,点B(3,1)移到点B ′, 则点B ′的坐标是 ________15.如图,在甲、乙两地之间修一条笔直的公路,从甲地测得公路的走向是北偏东48°。
2012年新课标数学仿真模拟试卷一(文理合卷)
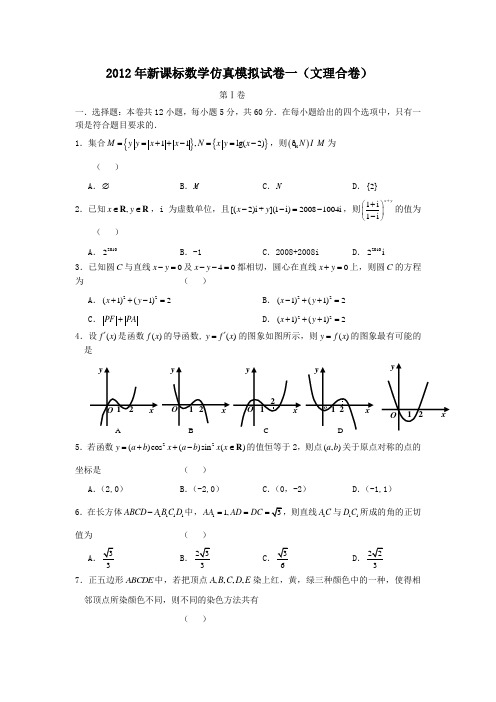
2012年新课标数学仿真模拟试卷一(文理合卷)第Ⅰ卷一.选择题:本卷共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.集合{}{}11,lg(2)M y y x x N x y x ==++-==-,则()N M ðR 为( )A .∅B .MC .ND .{2}2.已知,x y ∈∈R R ,i 为虚数单位,且[(2)i +](1i)20081004i x y --=-,则1i 1i x y++⎛⎫⎪-⎝⎭的值为( )A .20102B .-1C .2008+2008iD .20102i3.已知圆C 与直线0x y -=及40x y --=都相切,圆心在直线0x y +=上,则圆C 的方程为( )A .22(1)(1)2x y ++-=B .22(1)(1)2x y -++=C .PF PA +D .22(1)(1)2x y +++= 4.设()f x '是函数()f x 的导函数,()y f x '=的图象如图所示,则()y f x =的图象最有可能的是5.若函数22()cos ()sin ()y a b x a b x x =++-∈R 的值恒等于2,则点(,)a b 关于原点对称的点的坐标是 ( ) A .(2,0)B .(-2,0)C .(0,-2)D .(-1,1)6.在长方体1111ABCD A B C D -中,11,AA AD DC ===1AC 与11D C 所成的角的正切值为 ( ) ABCD7.正五边形ABCDE 中,若把顶点,,,,A B C D E 染上红,黄,绿三种颜色中的一种,使得相邻顶点所染颜色不同,则不同的染色方法共有( )BA .30种B .27种C .24种D .21种8.已知,,A B C 是平面上不共线的三点,O 为平面ABC 内任一点,动点P 满足等式1[(1)(1)3OP OA OB λλ=-+-(12)](OC λλ++∈ R 且0)λ≠,则P 的轨迹一定通过ABC ∆的( ) A .内心 B .垂心C .重心D .AB 边的中点9.右图所示的算法流程图中,输出的S 表达式为 A .112399++++B .1123100++++C .123.....99++++D .123.....100++++10.(理)定义:若数列{}n a 为任意的正整数n ,都有1(n n a a d d ++=为常数),则称{}n a 为“绝对和数列”,d 叫做“绝对公和” .已知“绝对和数列”{}n a 中,12a =,绝对公和为3,则其前2009项的和2009S 的最小值为A .-2009B .-3010C .-3014(文)已知数列{}n a 的前n 项和是(0n n S a m a =-≠且1)a ≠,那么“数列{}n a 是等比数列”的充要条件是( ) A .1m =B .1m ≥C .1m ≤D .m 为任意实数11.已知12,F F 分别为双曲线22221(0,0)x y a b a b-=>>的左,右焦点,M 为双曲线上除顶点外的任意一点,且12F MF ∆的内切圆交实轴于点N ,则12||||F N NF 的值为( )A .2b B .2a C .2c D 12.函数()f x 的定义域为D ,若对于任意12,x x D ∈,当12x x <时,都有12()()f x f x ≤,则称函数()f x 在D 上为非减函数.设函数()f x 在[0,1]上为非减函数,且满足以下三个条件:①(0)0f = ②1()()32x f f x = ③(1)1()f x f x -=-则11()()38f f +等于 ( )A .34B .12C .1D .23第Ⅱ卷二.填空题:本题共4小题,每小题5分,共20分.把答案填在题中横线上.13.31nx ⎛⎫ ⎪⎝⎭的展开式中第二项与第三项的系数之和等于27,则n 等于 ;系数最大的项是第 项.14.若数列{}n a 满足112,(1)2n n a na n a +=-+=,则数列{}n a 的通项公式n a = . 15.一个多面体的直观图和三视图(正视图、左视图、俯视图)如图所示,则三棱锥C A ABV -的体积为 .16.(理)已知s 表示的区域内存在一个半径为1为 .(文)tan18tan 42tan120tan18tan 42tan 60++三.解答题:本题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分) 设ABC ∆的内角,,A B C 所对的边分别为,,,a b c 且1cos 2a C cb +=.(Ⅰ)求角A 的大小;(Ⅱ)若1a =,求ABC ∆的周长l 的取值范围.18.(本小题满分12分)某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置. 若指针停在A 区域返券60元;停在B 区域返券30元;停在C 区域不返券. 例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.(Ⅰ)若某位顾客消费128元,求返券金额不低于30元的概率;(Ⅱ)若某位顾客恰好消费280元,并按规则参与了活动,他获得返券的金额记为X(元).求随机变量X 的分布列和数学期望.19.(本小题满分12分)如图,三棱柱111ABC A B C -中,侧面11AAC C ⊥底面ABC ,112,AA AC AC AB BC ====, 且AB BC ⊥,O 为AC 中点. (Ⅰ)证明:1AO ⊥平面ABC ; (Ⅱ)求直线1AC 与平面1A AB 所成角的正弦值; (Ⅲ)在1BC 上是否存在一点E ,使得//OE 平面1A AB ,若不存在,说明理由;若存在,确定点E 的位置. 20.(本小题满分12分)如图,设抛物线21:4(0)C y mx m =>的准线与x 轴交于1F ,焦点为2F ;以12,F F 为焦点,离心率12e =的椭圆第18题图1A BCO A 1B 1第19题图第22题图ECADB2C 与抛物线1C 在x 轴上方的交点为P ,延长2PF 交抛物线于点Q ,M 是抛物线1C 上一动点,且M 在P 与Q 之间运动.(Ⅰ)当1m =时,求椭圆2C 的方程; (Ⅱ)当12PF F ∆的边长恰好是三个连续的自然数时,求MPQ ∆面积的最大值.21.(本小题满分12分) 已知函数1ln ()xf x x+=. (Ⅰ)若函数在区间1(,)2a a +(其中0a >)上存在极值,求实数a 的取值范围;(Ⅱ)如果当1x ≥时,不等式()1kf x x ≥+恒成立,求实数k 的取值范围;(Ⅲ)求证[]22(1)(1)()n n n e n -*+>+⋅∈!N .请考生在第(22),(23),(24)三题中任选一题做答,如果多做,则按所做的第一题记分. 22.(本小题满分10分)选修4-1:几何证明选讲如图,在Rt△AB C 中,90C ∠= ,BE 平分∠ABC 交AC 于点E ,点D 在AB 上,DE EB ⊥. (Ⅰ)求证:AC 是△BDE 的外接圆的切线;(Ⅱ)若6AD AE ==,求EC 的长.23.(本小题满分10分)选修4-4:坐标系与参数方程PyxQ第20题图已知曲线C 的极坐标方程是4cos ρθ=.以极点为平面直角 坐标系的原点,极轴为x 轴的正半轴,建立平面直角坐标系,直线l的参数方程是:1x y ⎧=+⎪⎪⎨⎪=⎪⎩,求直线l 与曲线C 相交所成的弦的弦长.24.(本小题满分10分)选修4-5:不等式选讲,,a b c +∈R ,求证:32a b c b c c a a b ++≥+++ 参考答案一:1-5 DBBCB 6-10 BADA (理)B (文)A 11-12 AA 二: 13.【答案】:9 5 14.【答案】:4n -2 15.【答案】:316a ;16.【答案】:(理)2+ (文)-1 三:17.解:(Ⅰ)由1cos 2a C c b +=得1sin cos sin sin 2A C CB += …1分又()sin sin sin cos cos sin B A C A C A C =+=+ …3分 1sin cos sin 2C A C ∴=,sin 0C ≠ ,1cos 2A ∴=, 又0A <<π 3A π∴=…6分(Ⅱ)由正弦定理得:sin sin a B b B A ==,c C =…7分)())1sin sin 1sin sin l a b c B C B A B =++=+=++112cos 2B B ⎫=++⎪⎪⎝⎭12sin 6B π⎛⎫=++ ⎪⎝⎭,3A π=20,,3B π⎛⎫∴∈ ⎪⎝⎭5,666B πππ⎛⎫∴+∈ ⎪⎝⎭1sin ,162B π⎛⎫⎛⎤∴+∈ ⎪ ⎥⎝⎭⎝⎦故ABC ∆的周长l 的取值范围为(]2,3.…12分(Ⅱ)另解:周长l 1a b c b c =++=++ 由(Ⅰ)及余弦定理2222cos a b c bc A =+-221b c bc ∴+=+22()1313()2b c b c bc +∴+=+≤+ 2b c +≤又12b c a l a b c +>=∴=++> 即ABC ∆的周长l 的取值范围为(]2,3.…12分18.解:设指针落在A ,B ,C 区域分别记为事件A ,B ,C . 则111(),(),()632P A P B P C ===.…3分(Ⅰ)若返券金额不低于30元,则指针落在A 或B 区域. 111()()632P P A P B ∴=+=+=…6分即消费128元的顾客,返券金额不低于30元的概率是12.(Ⅱ)由题意得,该顾客可转动转盘2次. 随机变量X 的可能值为0,30,60,90,120.…7分111(0)224P X ==⨯=;111(30)2233P X ==⨯⨯=;11115(60)2263318P X ==⨯⨯+⨯=;111(90)2369P X ==⨯⨯=;111(120)6636P X ==⨯=.…10分所以,随机变量X 的分布列为:其数学期望115110306090120404318936EX =⨯+⨯+⨯+⨯+⨯= . …12分19.解:(Ⅰ)证明:因为11A A AC =,且O 为AC 的中点, 所以1AO AC ⊥.…1分 又由题意可知,平面11AAC C ⊥平面ABC ,交线为AC ,且1AO ⊂平面11AAC C , 所以1AO ⊥平面ABC .…4分(Ⅱ)如图,以O 为原点,1,,OB OC OA 所在直线分别为x ,y ,z 轴建立空间直角坐标系. 由题意可知,112,A A AC AC ===又,AB BC AB BC =⊥; 112OB AC ∴==.所以得:11(0,0,0),(0,1,0),(0,1,0),(1,0,0)O A A C C B -则有:11(0,1,(1,1,0).AC AA AB ===设平面1AA B 的一个法向量为(,,)x y z =n ,则有10000AA y x y AB ⎧⎧⋅==⎪⎪⇔⎨⎨+=⎪⋅=⎪⎩⎩n n ,令1y =,得1,x z =-= 所以(1,1,=-n .…6分111cos ,|||A C A C A C ⋅<>==n n |n因为直线1AC 与平面1A AB 所成角θ和向量n 与1A C所成锐角互余,所以sin θ=.…8分(Ⅲ)设0001(,,),,E x y z BE BC λ==即000(1,,)(x y z λ-=-,得00012x y z λλ⎧=-⎪=⎨⎪=⎩所以(1,2),E λλ=-得(1,2),OE λλ=-…10分令//OE 平面1A AB ,得=0OE ⋅n ,即120,λλλ-++-=得1,2λ=即存在这样的点E ,E 为1BC 的中点.…12分20.解:(Ⅰ)当1m =时, 24y x =,则12(1,0),(1,0)F F -设椭圆方程为22221(0x y a b a b +=>>),则1,c =又12c e a ==,所以22,3a b ==所以椭圆C 2方程为22143x y +=1…4分(Ⅱ)因为c m =,12c e a ==,则2a m =,223b m =,设椭圆方程为2222143x y m m +=由222221434x y m m y mx ⎧+=⎪⎨⎪=⎩,得22316120x mx m +-=…6分即(6)(32)0x m x m +-=,得23P mx =代入抛物线方程得p y =,即2(3m P 212557,24333p m m m PF x m PF a PF m =+==-=-=,12623mF F m ==, 因为12PF F ∆的边长恰好是三个连续的自然数,所以3m =…8分此时抛物线方程为212y x =,(2,P ,直线PQ方程为:3)y x =--.联立23)12y x y x⎧=--⎪⎨=⎪⎩,得2213180x x -+=,即(2)(29)0x x --=,所以92Q x =,代入抛物线方程得Q y =-,即9(,2Q -∴252PQ =. 设2(,)12t M t 到直线PQ 的距离为d,(t ∈-则2752d t ==-…10分当t =max 752d =, 即MPQ ∆面积的最大值为156125216⨯.…12分21.解:(Ⅰ)因为1ln ()xf x x+=,0x > ,则ln ()xf x x'=-, … 1分当01x <<时,()0f x '>;当1x >时,()0f x '<.所以()f x 在(0,1)上单调递增;在(1,)+∞上单调递减,所以函数()f x 在1x =处取得极大值.… 2分因为函数()f x 在区间1(,)2a a +(其中0a >)上存在极值,所以1,112a a <⎧⎪⎨+>⎪⎩ 解得1 1.2a <<… 4分 (Ⅱ)不等式()1kf x x ≥+, 即为(1)(1ln ),x x k x ++≥ 记(1)(1ln )(),x x g x x++=所以22[(1)(1ln )](1)(1ln )ln (),x x x x x x xg x x x '++-++-'==… 6分令()ln ,h x x x =-则1()1h x x'=-,1,()0.x h x '≥∴≥()h x ∴在[1,)+∞上单调递增,min [()](1)10h x h ∴==>, 从而()0g x '>故()g x 在[1,)+∞上也单调递增,min [()](1)2g x g ∴==,所以2k ≤…8分(Ⅲ)由(Ⅱ)知:2()1f x x >+恒成立,即122ln 11,11x x x x x-≥=->-++ 令(1)x n n =+,则2ln[(1)]1(1)n n n n +>-+,所以 2ln(12)1,12⨯>-⨯ 2ln(23)1,23⨯>-⨯ 2ln(34)1,34⨯>-⨯ ………… ……2ln[(1)]1(1)n n n n +>-+.叠加得:22ln[123⨯⨯⨯ (211)(1)]2[1223n n n ⨯+>-++⨯⨯…1](1)n n + 112(1)2211n n n n n =-->-+>-++… 10分则22123⨯⨯⨯…22(1)n n n e -⨯+>,所以[]22(1)(1)()n n n e n -*+>+⋅∈!N …12分22.解(Ⅰ)取BD 的中点O ,连接OE .∵BE 平分∠ABC ,∴∠CBE =∠OBE .又∵OB =OE ,∴∠OBE =∠BEO ,∴∠CBE =∠BEO ,∴BC ∥OE .…3分∵∠C =90°,∴OE ⊥AC ,∴AC 是△BDE 的外接圆的切线.…5分(Ⅱ)设⊙O 的半径为r ,则在△AOE 中,222AE OE OA +=,即2226(r r +=+,解得r =…7分∴OA =2OE ,∴∠A =30°,∠AOE =60°.∴∠CBE =∠OBE =30°.∴EC=1113222BE ==.…10分23.解:曲线C 的极坐标方程是4cos ρθ=化为直角坐标方程为2240x y x +-=,即()2224x y -+=,直线l的参数方程1x y ⎧=+⎪⎪⎨⎪=⎪⎩,化为普通方程为x -y -1=0,…5分曲线C 的圆心(2,0)到直线l,所以直线l 与曲线C 相交所成的弦的弦长.…10分24.解:左端变形111a b c b c c a a b++++++++ 111()()a b c b c c a a b =+++++++, ∴只需证此式92≥即可。
(完整word版)20.2012年全国高中数学联赛模拟卷(十)答案

2012年全国高中数学联赛模拟卷(十)第一试(考试时间:80分钟 满分:120分)姓名:_____________考试号:______________得分:____________一、填空题(共8题,每题8分,64分)1.用区间表示函数1()ln(1)3xf x x -=-+的定义域为 。
( 3.1)-- 2.在△ABC 中。
若1sin cos 3A A +=-,则cos2A =。
93.在数列{}n a 中,1*112,22()n n n a a a n N ++=-=∈,则使10n a >成立的最小正整数n 的值是 。
提示:3,*1112,1()22n n n n a a a n N ++=-=∈ 4.已知()f x 是R 上的奇函数,对任意x R ∈,均有(2)()f x f x +=,且(0,1)x ∈时,2()f x x =,则3()(1)2f f -+= 。
提示:14,(12)(1),(1)0f f f -+=-=5.如图,在四棱锥P ABCD -中,底面ABCD 为正方形,△PAB 为等 边三角形,O 为AB 边的中点,且PO ⊥平面ABCD ,则二面角P AC D --的余弦值为。
6.若正整数m 使得对任意一组满足12341a a a a =的正数1234,,,a a a a 都有123412341111m m m m a a a a a a a a +++≥+++成立,则正整数m 的最小值为 。
提示:3,用排序不等式,右边=234134124123a a a a a a a a a a a a +++不妨设1234a a a a ≥≥≥,列出三组必定成立 7.函数22*()sin cos ,()kk f x x x k N =+∈的最小值为 。
提示:112k -,观察,归纳,证明。
8.将方程33[]40x x -⨯-=([]x 表示不超过x 的最大整数)的实数解从小到大排列成12,,,k x x x L ,则33312k x x x +++=L 。
中国教育学会中学数学教学专业委员会2008--2012年《数学周报杯》竞赛试卷

中国教育学会中学数学教学专业委员会“《数学周报》杯”2008年全国初中数学竞赛试题参考答案答题时注意:1.用圆珠笔或钢笔作答.2.解答书写时不要超过装订线. 3.草稿纸不上交.一、选择题(共5小题,每小题6分,满分30分. 以下每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的. 请将正确选项的代号填入题后的括号里. 不填、多填或错填都得0分)1.已知实数x y ,满足 42424233y y x x -=+=,,则444y x+的值为( ).(A )7 (B ) (C ) (D )5【答】(A )解:因为20x >,2y ≥0,由已知条件得212184x +==, 21122y --==, 所以444y x +=22233y x ++- 2226y x=-+=7. 另解:由已知得:2222222()()30()30x xy y ⎧-+--=⎪⎨⎪+-=⎩,显然222y x -≠,以222,y x -为根的一元二次方程为230t t +-=,所以 222222()1,()3y y x x-+=--⨯=- 故444y x +=22222222[()]2()(1)2(3)7y y x x-+-⨯-⨯=--⨯-= 2.把一枚六个面编号分别为1,2,3,4,5,6的质地均匀的正方体骰子先(第3题)后投掷2次,若两个正面朝上的编号分别为m ,n ,则二次函数2y x mx n =++的图象与x 轴有两个不同交点的概率是( ).(A )512 (B )49 (C )1736 (D )12【答】(C )解:基本事件总数有6×6=36,即可以得到36个二次函数. 由题意知∆=24m n ->0,即2m >4n .通过枚举知,满足条件的m n ,有17对. 故1736P =. 3.有两个同心圆,大圆周上有4个不同的点,小圆周上有2个不同的点,则这6个点可以确定的不同直线最少有( ).(A )6条 (B ) 8条 (C )10条 (D )12条 【答】(B )解:如图,大圆周上有4个不同的点A ,B ,C ,D ,两两连线可以确定6条不同的直线;小圆周上的两个点E ,F 中,至少有一个不是四边形ABCD 的对角线AC 与BD 的交点,则它与A ,B ,C ,D 的连线中,至少有两条不同于A ,B ,C ,D 的两两连线.从而这6个点可以确定的直线不少于8条.当这6个点如图所示放置时,恰好可以确定8条直线. 所以,满足条件的6个点可以确定的直线最少有8条.4.已知AB 是半径为1的圆O 的一条弦,且1AB a =<.以AB 为一边在圆O 内作正△ABC ,点D 为圆O 上不同于点A 的一点,且DB AB a ==,DC 的延长线交圆O 于点E ,则AE 的长为( ).(A)2a (B )1 (C )2(D )a 【答】(B )解:如图,连接OE ,OA ,OB . 设D α∠=,则 120ECA EAC α∠=︒-=∠.又因为()1160180222ABO ABD α∠=∠=︒+︒-120α=︒-,所以ACE △≌ABO △,于是1AE OA ==. 另解:如图,作直径EF ,连结AF ,以点B 为圆心,AB 作⊙B ,因为AB =BC =BD ,则点A ,C ,D 都在⊙B 上,(第4题)由11603022F EDA CBA ∠=∠=∠=⨯︒=︒ 所以2301AE EF sim F sim =⨯∠=⨯︒=5.将1,2,3,4,5这五个数字排成一排,最后一个数是奇数,且使得其中任意连续三个数之和都能被这三个数中的第一个数整除,那么满足要求的排法有( ).(A )2种 (B )3种 (C )4种 (D )5种 【答】(D )解:设12345a a a a a ,,,,是1,2,3,4,5的一个满足要求的排列. 首先,对于1234a a a a ,,,,不能有连续的两个都是偶数,否则,这两个之后都是偶数,与已知条件矛盾.又如果i a (1≤i ≤3)是偶数,1i a +是奇数,则2i a +是奇数,这说明一个偶数后面一定要接两个或两个以上的奇数,除非接的这个奇数是最后一个数.所以12345a a a a a ,,,,只能是:偶,奇,奇,偶,奇,有如下5种情形满足条件:2,1,3,4,5; 2,3,5,4,1; 2,5,1,4,3; 4,3,1,2,5; 4,5,3,2,1. 二、填空题(共5小题,每小题6分,满分30分)6.对于实数u ,v ,定义一种运算“*”为:u v uv v *=+.若关于x 的方程1()4x a x **=-有两个不同的实数根,则满足条件的实数a 的取值范围是 .【答】0a >,或1a <-.解:由1()4x a x **=-,得21(1)(1)04a x a x ++++=,依题意有 210(1)(1)0a a a +≠⎧⎨∆=+-+>⎩,, 解得,0a >,或1a <-.7.小王沿街匀速行走,发现每隔6分钟从背后驶过一辆18路公交车,每隔(第8题)(第9题答案)D 3分钟从迎面驶来一辆18路公交车.假设每辆18路公交车行驶速度相同,而且18路公交车总站每隔固定时间发一辆车,那么发车间隔的时间是 分钟.【答】4.解:设18路公交车的速度是x 米/分,小王行走的速度是y 米/分,同向行驶的相邻两车的间距为s 米.每隔6分钟从背后开过一辆18路公交车,则 s y x =-66. ① 每隔3分钟从迎面驶来一辆18路公交车,则s y x =+33. ② 由①,②可得 x s 4=,所以4=xs. 即18路公交车总站发车间隔的时间是4分钟.8.如图,在△ABC 中,AB =7,AC =11,点M 是BC 的中点, AD 是∠BAC 的平分线,MF ∥AD ,则FC 的长为 . 【答】9.解:如图,设点N 是AC 的中点,连接MN ,则MN ∥AB . 又//MF AD ,所以 FMN BAD DAC MFN ∠=∠=∠=∠,所以 12FN MN AB ==. 因此 1122FC FN NC AB AC =+=+=9.另解:如图,过点C 作AD 的平行线交BA 的延长线为E ,延长MF AE 于点N.则E BAD DAC ACE ∠=∠=∠=∠所以11AE AC ==. 又//FN CE ,所以四边形CENF 是等腰梯形, 即11(711)922CF EN BE ===⨯+=9.△ABC 中,AB =7,BC =8,CA =9,过△ABC 的内切圆圆心I 作DE ∥BC ,分别与AB ,AC 相交于点D ,E ,则DE 的长为 .【答】163. 解:如图,设△ABC 的三边长为a ,b ,c ,内切圆I 的半径为r , BC 边上的高为a h ,则(第8题答案)11()22a ABC ah S abc r ==++△, 所以a r ah a b c=++. 因为△ADE ∽△ABC ,所以它们对应线段成比例,因此a a h r DEh BC-=, 所以 (1)(1)a a a h r r aDE a a a h h a b c-=⋅=-=-++()a b c a b c +=++, 故 879168793DE ⨯+==++().另解:ABC S rp ∆====(这里2a b cp ++=) 所以112r ==,228ABC a S h a ⨯===△由△ADE ∽△ABC ,得23a a h r DE BC h -===, 即21633DE BC === 10.关于x ,y 的方程22208()x y x y +=-的所有正整数解为 .【答】481603232.x x y y ==⎧⎧⎨⎨==⎩⎩,,, 解:因为208是4的倍数,偶数的平方数除以4所得的余数为0,奇数的平方数除以4所得的余数为1,所以x ,y 都是偶数.设2,2x a y b ==,则22104()a b a b +=-,同上可知,a ,b 都是偶数.设2,2a c b d ==,则2252()c d c d +=-,所以,c ,d 都是偶数.设2,2c s d t ==,则2226()s t s t +=-,于是 22(13)(13)s t -++=2213⨯, 其中s ,t 都是偶数.所以222(13)213(13)s t -=⨯-+≤2222131511⨯-<.所以13s -可能为1,3,5,7,9,进而2(13)t +为337,329,313,289,257,故只能是2(13)t +=289,从而13s -=7.于是62044s s t t ==⎧⎧⎨⎨==⎩⎩,,;, 因此 481603232.x x y y ==⎧⎧⎨⎨==⎩⎩,,,另解:因为222(104)(104)2104216x y -++=⨯= 则有2(104)21632,y +≤又y 正整数,所以 143y ≤≤令22|104|,|104|,21632a x b y a b =-=++= 则 因为任何完全平方数的个位数为:1,4,5,6,9由2221632a b +=知22,a b 的个位数只能是1和1或6和6; 当22,a b 的个位数是1和1时,则,a b 的个位数字可以为1或9但个位数为1和9的数的平方数的十位数字为偶数,与22a b +的十位数字为3矛盾。
2012年数学模拟考试试题

A D CB(图1)中等学校招生考试一、选择题:本题12小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.第1~8题每小题选对得3分,第9~12题每小题选对得4分;选错、不选、或选出的答案超过一个,均记零分. 1. 2-的相反数( ) A.2-B.2C.12-D.122. 下列运算中,正确的是( )A . 422x x x =+ B . 222()a b a b -=-C . 4224)2(x x -=- D . 32x x x =⋅3. 如图1,AD ∥BC ,BD 平分∠ABC ,且︒=∠110A ,则D ∠的度数为 ( )A .︒70B .︒35C .︒55D .︒1104. 丽丽买了一张30元的租碟卡,每租一张碟后剩下的余额如表表示,若丽丽租碟25张,则卡中还剩下( ) A.5元 B.10元 C.20元 D.14元211x a x a >-⎧⎨<+⎩无解,则a 5.若不等式组的取值范围是( ) A.2a < B.2a = C.2a > D.2a ≥6. 如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型.若圆的半径为r ,扇形的半径为R ,扇形的圆心角等于120,则r 与R 之间的关系是( ) A.2R r =B.R =C.3R r =D.4R r =7. 若干桶方便面摆放在桌子上,实物图片左边所给的是它的三视图,则这一堆方便面一E共有( ) “摘自网上”A. 5桶B. 6桶C. 9桶D. 12桶 8. 已知函数4y kx =-+与k y x =的图象有两个不同的交点,且112A y ⎛⎫- ⎪⎝⎭,()21B y -,,212C y ⎛⎫⎪⎝⎭,在函数229k y x -=的图象上,则1y ,2y ,3y 的大小关系是( ) A.123y y y <<B.321y y y <<C.312y y y << D.231y y y <<9. 如图,88⨯方格纸上的两条对称轴EF ,MN 相交于中心点O ,对ABC △分别作下列变换:①先以点A 为中心顺时针方向旋转90②先以点O 为中心作中心对称图形,再以点A 90;③先以直线MN 为轴作轴对称图形,再向上平移4方向旋转90.其中,能将ABC △变换成PQR △A.①② B.①③C.②③D.①②③10. 位,再向下平移4个单位,所得图象的函数表达式是()2324y x =+-.类比二次函数的图象的平移,我们对函数12x y x -=-的图象作类似的变换,则( ) A .12x y x -=-的图象可由反比例函数1y x =的图象先向上平移2个单位,再向右平移1个单位得到 B .12x y x -=-的图象可由反比例函数1y x =的图象先向下平移2个单位,再向左平移1个单位得到C .12x y x -=-的图象可由反比例函数1y x =的图象先向左平移2个单位,再向下平移1个单位得到 D .12x y x -=-的图象可由反比例函数1y x =的图象先向右平移2个单位,再向上平移1个单位得到11.如图(a ),在直角梯形ABCD ,90B ∠=,DC AB ∥,动点P 从B 点出发,由B C D A →→→沿边运动,设点P 运动的路程为x ,ABP △的面积为y ,如果关于x 的函数y 的图象如图(b ),则ABC △的面积为( ) A.10B.16C.18D.3212.在平面直角坐标系中,已知点A (-4,0),点B (2,0),若点C 在一次函数122y x =-+的图象上,且△ABC 为等腰三角形,则满足条件的点C 有( ) A. 2个 B. 3个 C. 4个 D. 5第Ⅱ卷(非选择题 共80分)二、填空题:本题共5小题,每小题填对得3分,共15分.只要求填写最后结果.填空题13、上海世博会定于2010年5月1日至10月31日举行,这是继北京奥运会之后我国举办的又一世界盛事,主办机构预计这届世博会将吸引世界各地约69 500 000人次参观.将69 500 000用科学记数法表示(保留两位有效数字)为 14. 已知矩形ABCD 的边AB=5,AD=12,以点A 为圆心半径为5作⊙A ,以点C 为圆心的⊙C 与⊙A 相切,则⊙C 的半径可能是15. 如图,电路图上有四个开关A ,B ,C ,D 和一个小灯泡,闭合开关D 或同时闭合开关A ,B ,C ,都可使小灯泡发光.任意闭合其中两个开关,则小灯泡发光的概率等于____________;16. 如图,正方形ABCD 的边长为2,将长为2的线段QR图(a )的两端放在正方形的相邻的两边上同时滑动.如果Q 点从A 点出发,沿图中所示方向按A→B→C→D→A 滑动到A 止,同时点R 从B 点出发,沿图中所示方向按B→C→D→A→B 滑动到B 止,在这个过程中,线段QR 的中点M 所经过的路线围成的图形的面积为 .17..如图,已知1(10)A ,,2(11)A ,,3(11)A -,,4(11)A --,,5(21)A -,,,则点A 2010的坐标为______________.三、解答题:本题共7小题,共65分.解答时应写出文字说明、证明过程或演算步骤.18、(本题满分8分)某学校九年级有10个班共500名学生,学生小青想了解该年级学生的年龄情况,他随机抽取了一个班级进行统计,得到了下表.(1)请你把表中未填的项目补充完整;(2)从表中可以看出,众数是 ,中位数是 ,平均数是 ; (3)请你根据统计表,在下图中画出该班学生年龄统计直方图(要求标出数字).(4)请你估计该年级年龄15岁的同学大约有多少人?19. (本题满分8分)商场某种新商品每件进价是120元,在试销期间发现,当每件商品售价为130元时,每天可销售70件,当每件商品售价高于130元时,每涨价1元,日销售量就减少1件.据此规律,商14岁 15岁 16岁 年龄 人数品销售正常的情况下,每件商品的销售价定为多少元时,商场日盈利可达到1600元? 20、(本题满分9分) 如图,ABC △中,90ACB =∠,AC BC =,CO 为中线.现将一直角三角板的直角顶点放在点O 上并绕点O 旋转,若三角板的两直角边分别交AC CB ,的延长线于点G H ,.(1)试写出图中除AC BC OA OB OC ===,外其他所有相等的线段; (2)请任选一组你写出的相等线段给予证明. 我选择证明 = .证明:21. (本题满分10分)如图,路边照明灯的灯臂BC 长1.5 m .路灯发出的光线与灯臂垂直,并通过主干道上一点D ,且DA =10 m ,CDA ∠=60°,求灯柱AB 的高.22. (本题满分10分)已知:如图,以ABC △的边AB 为直径的O 交边AC 于点D ,且过点D 的切线DE 平分边BC . (1)BC 与O 是否相切?请说明理由;(2)当ABC △满足什么条件时,以点O ,B ,E ,D 为顶点的四边形是平行四边形?并说明理由. 23、(本题满分10分)如图,足球场上守门员在O 处开出一高球,球从离地面1米的A 处飞出(A 在y 轴上),运动员乙在距O 点6米的B 处发现球在自己头的正上方达到最高点M ,距地面约4米高,球落地后又一次弹起.据实验,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.来源:港中数学网CE BABC OHG(1)求足球开始飞出到第一次落地时,该抛物线的表达式. (2)足球第一次落地点C距守门员多少米?(取7=)(3)运动员乙要抢到第二个落点D,他应再向前跑多少米?(取5=) 24、(本题满分10分)如图,在Rt ABC △中,90C =∠,AC =向点C 以每秒3个单位长的速度运动,动点Q 从点C 出发沿CB 边向点B 以每秒4个单位长的速度运动.P Q ,分别从点A C ,同时出发,当其中一点到达端点时,另一点也随之停止运动.在运动过程中,PCQ △关于直线PQ 对称的图形是PDQ △.设运动时间为t (秒).(1)设四边形PCQD 的面积为y ,求y 与t 的函数关系式; (2)t 为何值时,四边形PQBA 是梯形?(3)是否存在时刻t ,使得PD AB ∥?若存在,求出t 的值;若不存在,请说明理由; (4)通过观察、画图或折纸等方法,猜想是否存在时刻t ,使得PD AB ⊥?若存在,请估计t 的值在括号中的哪个时间段内(01t ≤≤;12t <≤;23t <≤;34t <≤);若不存在,请简要说明理由.P。
(完整word版)不定方程的解法与应用

摘要不定方程是初等数论的一个重要内容,在相关学科和实际生活中也有着广泛的应用.本文首先归纳了整数分离法、系数逐渐减小法和辗转相除法等几种常用的二元一次不定方程的解法;其次进一步讨论了求n元一次不定方程和二次不定方程整数解的方法;最后论述了不定方程在中学数学竞赛题、公务员行测试题和其他学科中的应用,并举例说明.关键词:不定方程;二元一次不定方程;数学竞赛;公务员试题AbstractThe integral solutions of indeterminate equation solving method is an important content of elementary number theory, has been widely used in related disciplines and in real life。
This paper summarizes the integer separation method, coefficient decreases and the Euclidean algorithm and several commonly used two element indefinite equation solution, secondly is further discussed。
For n linear indeterminate equation and the method of two time indefinite equation integer solution, and finally discusses the indeterminate equation applied in secondary school mathematics, civil servants for test and other subjects, and illustrated with examples。
2012-2013学年七年级竞赛模拟数学试题附答案

2012-2013学年七年级竞赛模拟数学试题一、选择题(共8小题,每小题5分,满分40分.以下每小题有且只有一个选项是正确的.请将正确选项的代号填入题后的括号里)1、 计算: (-4)2010×(-0.25)2011=……………………………… ( )A 、-4B 、-1C 、-0.25D 、-20112、设“●,▲,■”分别表示三种不同的物体,如下图所示,前两架天平保持平衡,如果要使第三架天平也平衡,那么“?”处应放“■”的个数为……………………( )A 、5B 、4C 、3D 、23、在高速公路上,从3千米处开始,每隔4千米经过一个限速标志牌;并且从10千米处开始,每隔9千米经过一个速度监控仪。
刚好在19千米处第一次同时经过这两种设施,那么第二次同时经过这两种设施的千米数是…………………………………………( ) A 、55 B 、67 C 、106 D 、1274、如图,正方形ABCD 的边长是3cm ,一个边长为1cm 的小正方形沿着正方形ABCD 的边AB →BC →CD →DA →AB 连续地翻转,那么这个小正方形第一次回到起始位置时,它的方向是…………………………………………………………………………………… ( )A、、、5、如图,把△ABC 绕点C 顺时针旋转25o,得到△A ′B ′C ,A ′B ′交AC 于D ,已知 ∠A ′DC =80o ,若AB 与A ′B ′交与E ,则∠BEA ′的度数是………………… ( )A 、135oB 、 145oC 、155oD 、165o6、适合│2a +7│+│2a -1│=8的整数a 的值的个数有 ………………………………… ( )A 、2B 、4C 、8D 、16●●▲■ ●■ ▲ ●▲ ? (1) (2) (3)(第4题图) D A A 'B ' E (第8题图)7座的人数是听数学的6倍,还剩下一个小组在教室里讨论问题,这一小组是… ( ) A 、第4组 B.、第6组 C 、第7组 D 、第11组8、甲、乙、丙、丁、戊五位同学参加一次节日活动,很幸运的是他们都得到了一件精美的礼品(如图),他们每人只能从其中一串的最下端取一件礼品,直到礼物取完为止,甲第一个取得礼物,然后乙、丙、丁、戊依次取得第2到第5件礼物,他们的取法各种各样.,发现礼物D 最精美,那么取得礼物D 可能性最大的是同学是 ………………… ( )A 、乙B 、丙C 、丁D 、戊二、填空题(每小题5分,共40分)9、定义a*b=ab+a+b,若3*x=27,则x 的值是_____。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012年数学周报杯模拟试题
一、选择题(每题3分,共30分)姓名_________学号自评¬¬¬________
1.若等腰三角形的一个底角为50°,则顶角为()。
A.50°B.100°C.80°D.65°
2、若一组数据1、2、
3、x的极差是6,则x的值为()
A.7
B.8
C.9
D.7或-3
3、要使二次根式有意义,字母必须满足的条件是()
A、≥1
B、>-1
C、≥-1
D、>1
4、若a<1,化简的结果是()
A、a-1
B、-a-1
C、1-a
D、a+1
5.如图,□ABCD的周长是28㎝,△ABC的周长是22㎝,则AC的长为()A.6㎝B.12㎝C.4㎝D.8㎝
6.如图所示,正方形ABCD中,E、F是对角线AC上两点,连接BE、BF、DE、DF,则添加下列哪一个条件不能判定四边形BEDF是菱形()A、∠1=∠2 B、BE=AB C、∠EDA=∠FBC D、AE=CF
7、已知,化简二次根式的正确结果为()
A、B、C、D、
8、已知四边形ABCD中,给出下列四个论断:(1)AB∥CD,(2)AB=CD,(3)AD=BC,(4)AD∥BC.以其中两个论断作为条件,余下两个作为结论,可以构成一些命题.在这些命题中,正确命题的个数有()
A. 2个
B. 3个
C. 4个
D. 6个
9.甲、乙、丙三名射击运动员在某场测试中各射击20次,3人的测试成绩如下表:
甲的成绩
环数7 8 9 10
频数 4 6 6 4
乙的成绩
环数7 8 9 10
频数 6 4 4 6
丙的成绩
环数7 8 9 10
频数 5 5 5 5
则甲、乙、丙3名运动员测试成绩最稳定的是()A.甲B.乙C.丙D.3人成绩稳定情况相同
10、将正方形纸片两次对折,并剪出一个菱形小洞后铺平,得到的图形是()
二、填空(每题3分,共24分)
11、;
12、一组数据库,1,3,2,5,x的平均数为3,那么x= ,这组数据的标准差是______。
13、用两个全等的三角形最多能拼成__________个不同的平行四边形.
14、若梯形的面积为12 ,高为3 ,则此梯形的中位线长为。
15、在菱形ABCD中,已知AC=12,BD=16,那么菱形ABCD的边长为.面积
为。
16、把如图所示的矩形纸片ABCD折叠,B、C两点恰好落在AD边上的点P处,已知
∠MPN=900,PM=6cm,PN=8cm,那么矩形纸片ABCD的面积为___________cm2
17、如图,在正方形ABCD中,点E、F分别在CD、BC上,
且BF=CE,连结BE、AF相交于点G,则下列结论:①BE=AF;
②∠DAF=∠BEC;③∠AFB+∠BEC=900;④AF⊥BE中正确的有
个
18、观察下列各式,,
①猜想5 = 。
=15 。
②试猜想第n个等式为
三、解答题
19、计算或化简(每题4分,共16分)
(1) (212 -313 )×6 (2)(a>0,b>0)
(3)计算:(4) + ( 3 )0 - ( 12 )-2
20、(本题共10分)如图,∠AOB=90°,将三角尺的直角顶点落在∠AOB的平分线OC的任意一点P上,使三角尺的两条直角边与∠AOB的两边分别相交于点E、F。
(1)证明PE=PF;
(2)若OP=10 ,试探索四边形PEOF的面积为定值,并求出这个定值。
21、(10分)如图,在□ABCD中,∠DAB=60°,点E、F分别在CD、AB的延长线上,且AE=AD,CF=CB.(1)求证:四边形AFCE是平行四边形;(2)若去掉已知条件的“∠DAB=60°,上述的结论还成立吗?若成立,请写出证明过程;若不成立,请说明理由.
22.(本题满分10分)如图,在梯形中,两点在边上,且四边形是平行四边形.
(1)与有何等量关系?请说明理由;
(2)当时,求证:四边形是矩形.
23、(10分)某中学开展“八荣八耻”演讲比赛活动,九(1)、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如下图所示。
(1)根据下图,分别求出两班复赛的平均成绩和方差;
(2)根据(1)的计算结果,分析哪个班级的复赛成绩较好?
24、(10分)如图:在正方形ABCD中,点P、Q是CD边上的两点,且DP=CQ,过D作DG⊥AP于H,交AC、BC分别于E,G,AP、EQ的延长线相交于R.
(1)求证:DP=CG;
(2)判断△PQR的形状,请说明理由.
25、(10分)如图:直线y=-x+6与坐标轴分别相交于点A、B,点P是直线AB上的一点,Q是双曲线上的一点,若O、A、P、Q为顶点的四边形是菱形,请在图中找出所有符合条件的点Q,并求出点Q的坐标和写出相应的值。
26.(本题满分10分)
(1)观察与发现
小明将三角形纸片沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展开纸片(如图①);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到(如图②).小明认为是等腰三角形,你同意吗?请说明理由.
(2)实践与运用
将矩形纸片沿过点B的直线折叠,使点A落在BC边上的点F处,折痕为BE(如图③);再沿过点E的直线折叠,使点D落在BE上的点处,折痕为EG(如图④);再展平纸片(如图⑤).求图⑤中的大小.
27、(10分)正方形ABCD与平行四边形EFGH的AB、EF在同一条直线MN上,AB=2㎝, EF=6㎝,BE=2㎝,∠HEF=450,EH=2 ㎝,正方形ABCD以1㎝/s速度向右移动,在移动过程中两图形重叠部分的面积为S㎝2.试探索在不同时间内的面积S(设右移时间为t秒).。
