同时送取货车辆路径问题算法研究综述
配送运输中车辆路径问题研究综述

䝽䘱䘀䗃ѝⲴ䖖䖶䐟 䰞仈⹄ウ㔬䘠㾱˖䝽䘱䘀䗃ѝⲴ䖖䖶䐟 䰞仈аⴤ 䘀ㆩ 亶 Ⲵ⹄ウ✝⛩ѻаDŽ Ҿ䖖䖶䐟 䰞仈Ⲵ ⭘㛼 ˈ 㓣 㔃Ҷ ㊫䰞仈 ≲䀓㇇⌅Ⲵ⹄ウ䘋 ˈ 䎻 ˈѪ 䢤DŽ䭞䇽˖⢙⍱䝽䘱˗䖖䖶䐟 䰞仈˗䙊⭘ ㇇⌅˗㔬䘠DŽThe Current Situation and Development Trends on Vehicle Routing Problems of distribution managementAbstract: Vehicle routing problem is one of the attractive research area in the circles of operations research. In this paper, on the basis of introducing briefly the application background, the research classified the vehicle routing problem, analyzed and summarized the progress of different type of problems and solution algorithms. Furthermore, the research progress of the problems is also discussed. It is expected to provide inference for relevant research work.Key words: distribution management; vehicle routing problem; heuristics; overview.䀶䲿⵰㓿⍾Ⲵ 、 Ⲵ䘋↕ˈ⢙⍱ӗъ䗵䙏 ˈ Ѫ ≁㓿⍾ Ⲵ 㜹 ӗъˈ ≤ 㺑䟿ањ ⧠ԓ 〻 㔬 Ⲵ䟽㾱 ḷDŽкц㓚80 ԓԕ ˈ ⢙⍱ӗъⲴ ˈ⢙⍱ъ Ѫањ⤜・Ⲵӗъ䗵䙏 䎧DŽ❦㘼ˈ ⢙⍱ъӽ Ҿ 㓗䱦⇥ˈо 䗮 ∄䘈 а Ⲵ 䐍ˈ ѝ ケ Ⲵ䰞仈 ⢙⍱ 䖳儈DŽ 㔏䇑[1]ˈ ⢙⍱ 䍩⭘Ѫ7.1зӯ ˈ GDPⲴ∄䟽Ѫ17.8%ˈ㘼 㖾 ㅹ 䗮 ⢙⍱ 㓖 GDPⲴ10%ˈ丙 ㅹѝㅹ 䗮 Ⲵ∄䟽㓖Ѫ15%DŽ䗷儈Ⲵ⢙⍱ Ѫ 㓖 ≁㓿⍾ Ⲵ䟽㾱 ㍐DŽ ↔ˈ 儈⢙⍱ъⲴ、 ㇑⨶≤ ǃ䱽վ⢙⍱ ӏ䴰䀓 Ⲵ 䭞 䰞仈DŽ䘀䗃 ⢙⍱ Ⲵ䟽㾱㓴 䜘 DŽ 䘀䗃 ⢙⍱ 䍩⭘Ⲵ∄ 䖳儈ˈ㓖Ѫ50%[1]DŽ䱽վ䘀䗃 ˈ 儈䘀䗃 ⦷ǃ 䘋⢙⍱ъ 㔝 Ⲵ䟽㾱䙄 DŽѪ⢙⍱䝽䘱ѝⲴ 䭞а⧟ˈ䖖䖶䐟 䰞仈˄Vehicle Routing Problem, VRP˅ 䘀䗃㓴㓷Ո ⲴṨ 䰞仈ѻаDŽ㠚1959 Dantzig Ramser[2]俆⅑ ԕ ˈVRP Ѫ䘀ㆩ 㓴 Ո 亶 Ⲵ ⋯о⹄ウ✝⛩ѻаDŽ⧠ ⭏ӗѝˈ䛞 䘀䗃ǃ 䖖 ⊭䖖䈳 ㅹ䈨 䰞仈䜭 ԕ 䊑ѪVRPDŽ ↔ˈ VRPⲴ␡ ⹄ウˈ ⵰䟽㾱Ⲵ、 ѹ 〻 ⭘ԧ DŽ 㓣 㔃ҶVRP Ⲵ⹄ウ䘋 ˈ ҶVRPⲴ 䎻 ˈѪ 㓿傼 䐟DŽ1. 䖜䖼䐥 䰤从Ⲻ 䘦Ր㔏кˈ 䖖䖶䐟 䰞仈Ⲵа㡜 䘠Ѫ[3, 4]˖ а㌫ 㔉 Ⲵ ˄䘱䍗⛩ 䍗⛩˅ˈ⺞ 䘲 Ⲵ䝽䘱䖖䖶㹼傦䐟㓯ˈ Ӿ䝽䘱ѝ ˈ ⅑ 䇯䰞 њ ⛩ˈ 䘄 䝽䘱ѝ ˈ ┑䏣а Ⲵ㓖 Ԧл˄ 䖖䖶䖭䍗䟿ǃ 䴰≲䟿ǃ 䰤デ䲀 ㅹ˅ˈ 䘀䗃 ˄ ⭘䖖䖶 ǃ䖖䖶㹼傦䐟〻 䰤˅䗮 DŽ 1 ⽪ˈ ѝⲴ Ṷ㺘⽪䖖䖶 ⛩˄ 䖖 䝽䘱ѝ ˅ˈ ⛩㺘⽪䴰㾱䇯䰞Ⲵ ⛩ˈ㓯⇥㺘⽪є⛩ѻ䰤Ⲵ䘎 䐟⇥ˈ ѝ⇿ 㓯⇥ ⵰ањ䍩⭘˄ 䐍 㹼傦 䰤˅DŽ1 䖜䖼䐥 䰤从⽰Fig.1 Schematic figure of VRPⲴ䖖䖶䐟 䰞仈ѫ㾱 ԕлṨ 㾱㍐[5]˖䚃䐟㖁㔌˄Road Network˅ǃ ˄Customer˅ǃ䝽䘱ѝ ˄䖖 ˅˄Distribution Center, Depot˅ǃ䖖䖶˄Vehicle˅ǃ傮傦 ˄Driver˅ǃ䲀 Ԧǃ㹼傦䍩⭘ 㹼傦 䰤ˈԕ Ո ⴞḷ˄Objective˅DŽ њ㾱㍐Ⲵ⢩ 㿱㺘1DŽ㺞1 䖜䖼䐥 䰤从Ⲻ㓺 㾷㍖Tab. 1 Key elements of VRP㓴 㾱㍐⢩䚃䐟㖁㔌1. VRPⲴṨ 㾱㍐ѻа˗2. 䙊 ⭡ 㢲⛩ 㓴 Ⲵ䍻 㺘⽪DŽ 㺘⽪䐟⇥ˈ⛩㺘⽪䚃䐟Ӕ ⛩ǃ䝽䘱ѝ ˗3. ṩ 䐟㖁㚄є⛩䰤Ⲵ䚃䐟⢩ ˈ Ⲵ Ѫ ˗ 䍻Ҹ⇿ 䶎䍏Ⲵ䍩⭘ 䟽ˈ є⛩䰤Ⲵ䘀㹼䐍ˈ䘀㹼 䰤ㅹDŽ1. VRPѝ䖖䖶 Ⲵ 䊑ˈ Ҿ㖁㔌 ѝⲴ ⛩˗2. ⛩Ⲵ ㊫ ˖䘱䍗 ˄Delivery˅ǃ 䍗 ˄Pickup˅ є㘵˗3. ⛩Ⲵ 䴰≲䟿˖а⅑┑䏣ˈ ˄Split˅;4. ⛩Ⲵ 䰤˖䖖䖶 ӔԈ 䍗⢙ 㣡䍩Ⲵ 䰤˗5. ⛩Ⲵ 䰤デ˖ 㾱≲ Ⲵ 䰤 䲀ˈ Ѫ⺜ 䰤デ[6]䖟 䰤デ[7]˗6. ⛩ Ⲵ ⅑ ˖ Ո 㓗˗ ㊫ 亪ˈ 䘱䍗 䍗˗7. ⛩Ⲵ ㌫˖ ḀӋ лˈ ⛩Ⲵ䝽 ㌫ˈ Ӿањ 䍗❦ 䘱 оѻ䝽 Ⲵ⢩ 䘱䍗 ⛩DŽ䝽䘱ѝ 1. ⇿ 䖖䖶䐟㓯Ⲵ䎧⛩ 㓸⛩ˈ Ҿ㖁㔌 ѝⲴ ⛩˗2. 䖖 䟿˖ањ䖖 њ䖖 ˗3. 䖖䖶 䘄 䖖 ˖ VRP[5, 8]ˈ䰝 VRP˗4. 䖖 䰤デ˖ḀӋ лˈ䖖 䲀 ⢩↺㾱≲˄ Ⲵ 䰤 䰤˅˗5. 䖖 ѻ䰤Ⲵ ㌫˖ḀӋ лˈ䖖 䰤 䝽 ㌫ˈ Ӿањ䖖 䛓䟼 Ⲵ䖖䖶 享 оѻ䝽 Ⲵ Ⲵ䖖 DŽ䖖䖶1. 䖖䖶 㠚 䘈 』ˈ ԫ 䘄 ˗2. 䖖䖶㊫ ˖ VRPѝ 䇮䖖䖶Ѫ а㊫ ˈն 䱵䝽䘱㇑⨶ѝˈ䖖䱏 ⭡ н 㻵䖭㜭 ǃн ԕ Ⲵ 䖖䖶㓴 ˗3. 䖖䖶Ⲵ㻵䖭㜭 ˖䖖䖶 Ⲵ䖭䟽䟿 Ⲵ㻵䖭 䟿ㅹ˗4. 䖖䖶 ˖䖖䖶Ⲵ ˈ 䖖䖶䍝㖞䍩⭘ㅹ˗ ⭘ ս 䟼Ⲵ䍩⭘ ս 䰤Ⲵ䍩⭘ 㺑䟿˗5. 䖖䖶Ⲵ 㔝 ˄Duration˅˖䖖䖶 Ⲵ 䇨㹼傦䐍 䰤DŽ傮傦 1. 㔉傮傦 䘱䍗ԫ ˈ 享ㅖ 䰤Ⲵ 㿴 DŽ 傮傦 䲀 Ԧа㡜䜭 Ⲵ䖖䖶䲀 ԦѝDŽ䲀 Ԧ1. 䖖䖶Ⲵ 䍏䖭н㜭䎵䗷䖖䖶Ⲵ㻵䖭㜭 ˗2. 㾱≲䘱䍗ǃ 䍗ǃ 䘱䍗 ˗3. 㾱≲Ⲵ 䰤デ 傮傦 Ⲵ 䰤 ˗4. 䇯䰞 Ⲵ亪 㾱≲DŽ㹼傦䍩⭘㹼傦 䰤1. ⛩о ⛩ѻ䰤ǃ䝽䘱ѝ о ⛩ѻ䰤Ⲵ㹼傦䐍 㹼傦 䰤DŽՈ ⴞḷ1. 䘀䗃 ˈ Ҿ 䴰Ⲵ䖖䖶 ˄ 㓯䐟 ˅ǃ 㹼傦䐍˄ 䰤˅˗2. о Ⲵн ㅹ Ⲵ 㖊 ˗3. 㺑 㓯䐟кⲴ㹼傦 䰤 䖖䖶䖭䟽䟿DŽ2. 䖜䖼䐥 䰤从Ⲻ ㊱䙊䗷 к䘠VRPṨ 㾱㍐䱴 н Ⲵ⢩ 䘲 Ⲵ ˈ 㹽⭏ ⿽н Ⲵ䖖䖶䐟 䰞仈㊫ DŽ ⹄ウ[5, 9, 10]ˈ 㿱ⲴVRP ㊫ 㹽⭏㊫ DŽ VRP㊫ 㻵䖭㜭 ⲴVRPǃ 䐟〻䮯 ⲴVRPǃ 䰤デⲴVRPǃ 〻䘀䗃ⲴVRPˈԕ 䘱䍗ⲴVRP˗ ⁑ Ⲵ кˈ㔃 н Ⲵ㓖 Ԧˈ ҶVRPⲴ㹽⭏㊫ ˈ 䲿 VRPǃ⁑㋺VRPǃ VRPㅹDŽ њ㊫ Ⲵ⢩ 㿱㺘2DŽ㺞2 䖜䖼䐥 䰤从Ⲻ㊱Tab. 2 Types of VRP ㊫ ⢩㻵䖭㜭 ⲴVRP˄Capacitated VRP, CVRP˅1. VRPѝ Ⲵ ˗2. 䜭 Ҿ㾱䘱䍗Ⲵ 㾱 䍗Ⲵˈ 䴰≲䟿 ⸕ˈфн ˗3. 䖖䖶 ㊫ ф䜭 ањ䝽䘱ѝ ˗4. 䖖䖶 㻵䖭㜭 Ⲵ䲀 ˗5. Ո ⴞḷ Ⲵ 䍩⭘ DŽ䐟〻䮯 ⲴVRP˄Distance-Constrained andCapacitated VRP, DCVRP˅1. 䖖䖶㻵䖭㜭 䲀 ˈ 䐟〻䮯 䲀 DŽ䰤デⲴVRP˄VRP with time windows, VRPTW˅1. 䲔Ҷ䖖䖶㻵䖭㜭 Ⲵ㓖 ˈ⇿њ 䜭 ањоѻ㚄㌫Ⲵ㾱≲ Ⲵ 䰤 䰤˗2. Ѫ⺜ 䰤デVRP 䖟 䰤デVRPDŽ⺜ 䰤デ ⇿亩ԫ 享 㾱≲Ⲵ 䰤 ˈ䖟 䰤デ Ḁ亩ԫ н㜭 㾱≲Ⲵ 䰤㤳 ˈ 㔉Ҹа Ⲵ 㖊[11]DŽ〻䘀䗃ⲴVRP˄VRP with backhauls, VRPB˅1. 䳶㻛 2њ 䳶˖㾱≲䘱 а 䟿䍗⢙Ⲵ 〻 ԕ 㾱≲ а 䟿䍗⢙䘀 䝽䘱ѝ Ⲵ 〻 ˗2. 〻 〻 Ⲵ䴰≲ ⸕ф ˗3. 〻 享 Ҿ 〻 DŽ䘱䍗ⲴVRP˄VRP with pickup and delivery˅1. 䖖䖶нӵ 䘱䍗 ˈҏ Ⲵ䍗⢙˗2. ⇿њ ⛩ˈ㿴 㻵DŽ㹽⭏㊫VRP[5]˄Open VRP, OVRP˅1.н㾱≲䖖䖶 ԫ 䘄 ⛩ˈ 㤕㾱≲䘄 ⛩ˈ ⋯ 〻䐟㓯䘄 DŽ䖖 VRP˄Multiple Depots VRP, MDVRP˅1. њ䝽䘱ѝ ˈ䖖䖶 ԕӾԫօањ䝽䘱ѝ ⍮ ˈ ԫ ˈ䖖䖶ҏ ԕ䘄 ԫօањ䝽䘱ѝ ˗2. 䰞仈 Ѫ DŽ䙊 䇮Ḁњ䖖 Ⲵ䖖䖶ӽ䴰䘄 䈕䖖 ˈ≲䀓 ˈ ➗Ḁ⿽㇇⌅ 䝽㔉Ḁњ䖖 ˈ❦ ➗ а䖖 VRP䘋㹼≲䀓[12]DŽ䖖 VRP[13]˄Heterogeneous Fleet VRP,HVRP˅1. 䖖䖶Ⲵ н ˈ䙊 䖖䖶Ⲵ䖭䟽䟿на㠤DŽ䴰≲ ⲴVRP[14]˄VRPwith Split Deliveries˅1. Ⲵ䴰≲ ԕ 㻛 њ䖖䖶 DŽ䲿 VRP˄Stochastic Vehicle Routing Problem, SVRP˅1. Ѫ䲿 VRPǃ䲿 䴰≲VRPǃ䲿 㹼傦 䰤VRP˗2. 䲿 VRP ⢙⍱亶 㓿 ⧠˗3. Ҿ䲿 䴰≲VRPˈ⺞ Ⲵ ⸕ˈն Ⲵ ⺞䴰≲䟿 ⸕ˈ ⟳⋩䝽䘱䰞仈˗4. Ҿ䲿 㹼傦 䰤VRPˈ⹄ウ䖳 ˈ㘼 䲿 㖁㔌 ⸝䐟 䰞仈Ⲵ⹄ウ䖳␡ [15, 16]DŽ⁑㋺VRP˄Fuzzy VRP, FVRP˅1. ḀӋ ˄ 䴰≲ǃ䐍ǃ 䰤デ[3]˅ ⌅ ⺞ 䘠˗2. ⁑㋺ᾲ ⁑ ㇇⌅ 䀓 ↔㊫䰞仈DŽVRP˄Periodic VRP, PVRP˅1. VRPⲴ ˈVRP⹄ウⲴ 䖖䖶Ⲵ ˈ㘼PVRP 䖖䖶Ⲵањ Ⲵ ˈ ањ ˈ⇿њ ┑䏣䴰≲Ⲵ лˈ 㻛 а⅑DŽ䶎 〠㖁㔌VRP˄Asymmetric network VRP, AVRP˅1. ⧠ ѝˈ⭡Ҿ 㹼䚃 ⾱→ 䖜ㅹӔ䙊㇑ ˈ є 䘄Ⲵ䐍 䰤 нㅹ˗2. ⴞ Ⲵ≲䀓㇇⌅䜭 Ҿ䶎 〠TSP䰞仈Ⲵ㇇⌅[17]DŽVRP˄Dynamic VRP, DVRP˅1. 䖖䖶 ˈ䈳 н⺞ 䜘 н⺞ ˗ 䖖䖶 ˈ ⧠ Ⲵ䈳 ˗2. ѹкˈ䲿 VRPˈ⁑㋺VRPˈԕ 㖁㔌VRP䜭 ҾDVRPDŽ↔ ˈ䘈 ԕ 䰤デ㓖 о Ԇ㓖 Ԧ㔃 ˈ 䰤デ㓖 Ⲵ 䘱 ъVRPˈ 䰤デ㓖 Ⲵ 〻䘀䗃VRPㅹDŽ3. 䖜䖼䐥 䰤从Ⲻ≸䀙㇍⌋VRP ⭼ 䇔ⲴNP䳮䰞仈[18]DŽVRP㻛 ˈ ≲䀓㇇⌅Ⲵ 䙐аⴤ ⹄ウⲴ䟽⛩ 䳮⛩DŽⴞ ⿽≲䀓VRPⲴ㇇⌅ˈ 䍘к Ѫ㋮⺞㇇⌅ ㇇⌅є ㊫DŽ㋮⺞㇇⌅ Ҿ ѹ 䇱 ˈ ≲ Ո䀓Ⲵ㇇⌅DŽⴞ ⭘Ҿ≲䀓VRP ԓ㺘 Ⲵ㋮⺞㇇⌅ѫ㾱 ⭼䲀⌅[19]˄Branch and Bound Approach˅ǃ 䶒⌅[20]˄Cutting Planes Approach˅ǃ㖁㔌⍱㇇⌅˄Network Flow Approach˅[21] 㿴 ⌅˄Dynamic Programming Approach˅[22]DŽ⭡ҾVRP NP-䳮䰞仈ˈ Ⲵ㋮⺞㇇⌅Ⲵ䇑㇇䟿а㡜䲿⵰䰞仈㿴⁑Ⲵ 䮯˗ф ⛩䎵䗷50 ˈ㋮⺞㇇⌅ на ≲ 䰞仈Ⲵ Ո䀓[23]DŽ ˈ ⭘䰞仈⢩ ѝㅹ䇑㇇ 䰤 㧧 VRPⲴ⅑Ո䀓 ┑ 䀓Ⲵ ㇇⌅ Ѫ 㘵Ԝ⹄ウⲴ䟽⛩DŽ ㇇⌅ Ѫ㓿 ㇇⌅˄Classical Heuristics˅ 䙊⭘ ㇇⌅˄Metaheuristics˅DŽ3.1 㔅 ㇍⌋˄1˅㢲㓖㇇⌅˄Saving Methods˅⭡Clark WrightҾ1964 俆⅑ [24]ˈ а⿽ Ҿ㢲㓖 Ⲵ䖖䖶䐟㓯䙀↕ 䙐㇇⌅DŽ Ѫ˖ ⇿њ䝽䘱⛩ Ѫа 㓯䐟ˈ 䜘㓯䐟 Ⲵ䳶 Ѫ 䀓DŽ ањ⛩о ањ⛩䘎 а Ⲵ㓯䐟ˈ Ⲵ㓯䐟㜭┑䏣㓖 Ԧˈ 㹼Ⲵˈ Ⲵ㢲㓖 ˄ 䟼〻ǃ䰤ㅹ˅ ѹѪ䘎 䘉є 㓯䐟Ⲵ㢲㓖 DŽӾ 㓯䐟ѝ䘹 㢲㓖 Ⲵ䗩䘋㹼а⅑㓯䐟 ˈ н 㹼ˈ㇇⌅㔃 DŽ䈕㇇⌅ ԕ ┑ 䀓ˈնна 㜭 䇱 Ո䀓DŽ Ո⛩ ⨶ㆰ ф ⧠ˈⴞ Ѫ VRP ㇇⌅ѝӗ⭏ 䀓Ⲵ㇇⌅DŽ䈕㇇⌅ ԕ ˈ 㘵 䘋㇇⌅䘋㹼Ҷ⹄ウˈԕ ≲䀓Ⲵ䍘䟿ˈѫ㾱 ԕл2⿽䙄 ˖а 䙊䗷 Ⲵ 㔃 ㆆ⮕ ⨶㢲㓖 [25, 26]˗Ҽ Ҿ 䝽㇇⌅˄Matching Algorithm˅Ո 䈕㇇⌅ѝⲴ䐟㓯 䗷〻[27, 28]DŽ˄2˅ ㇇⌅˄Sweep Algorithm˅⭡Gillett MillerҾ1974 [29]ˈ ҾĀ 㓴 㓯䐟āⲴ㇇⌅DŽ 䉃Ā 㓴ā ⍮㔉⇿䖶䖖а㓴䝽䘱⛩DŽа⿽ㆰ Ⲵ 㓴 ⌅ ԕ䝽䘱ѝ Ѫ ⛩ˈ ḷ 䶒 Ѫ њ ˈ ↕Ѫ⇿њ Ⲵ⛩ ⍮а䖶䖖DŽ 䉃Ā㓯䐟ā ⇿њ ˈ 䟷⭘ ⌅䘹 䝽⛩ˈ❦ 䟷⭘ ㇇⌅ 㓯䐟DŽ 䘋㹼Ҷа⅑Ā 㓴о㓯䐟āⲴ䐟㓯 䙐 ˈ䘈 䝽⛩ˈ 㔗㔝䘋 Ā 㓴о䐟㓯ā〻 DŽ ↔ ˈⴤ Ⲵ⛩ 䝽 ∅Ѫ→DŽⲴ ㇇⌅а⅑ 㜭ӗ⭏а 䐟㓯ˈ Ѫ ㇇⌅Ⲵ ˈаӋ 㘵⹄ウҶа⅑⭏ 㤕 㹼䖖䖶䐟㓯Ⲵ ⌅ˈ❦ 䙊䗷≲䀓ањ䳶 䰞仈 ⺞ ՈⲴ㓴 ˈ∄䖳 Ⲵ 1-㣡⬓㇇⌅[30, 31] 2-㣡⬓㇇⌅[32]DŽ䴰㾱 Ⲵ ˈ ㇇⌅ 䘲 Ҿ 䶒㔃 ˄Plannar Structure˅ⲴVRPˈ Ҿ䛓Ӌ ḵṬ㺇䚃 ⲴVRPˈ䈕㇇⌅ н䘲⭘DŽ˄3˅䛫 ㇇⌅˄Nearest-Neighbor˅䈕㇇⌅ а⿽ 䙐 䐟㓯⌅ˈ Ӿа ањ䝽䘱⛩Ⲵ㓯䐟 (䙊 䐍䝽䘱ѝ 䘁Ⲵ⛩)ˈӾ 䘹 ⛩ѝㆋ䘹 ⛩ˈ Ӿ ⛩ѝ䘹 ањ⛩ Ѫ 㓯䐟Ⲵ㓸⛩ˈ 㓯䐟Ⲵ DŽԕ↔ 㓯䐟н 䘋㹼 ˈⴤ 㓯䐟⋑ ⛩Ѫ→DŽ ⛩ 䘹 ˈ ㇇⌅㔃 ˗ ˈ ⭏ а Ⲵ 㓯䐟ˈ䟽 䶒Ⲵ㓯䐟 䗷〻ˈⴤ㠣 ⛩䜭 䘹 DŽ˄4˅ ㇇⌅䈕㇇⌅㔃 㢲㓖㇇⌅о䛫 ㇇⌅Ⲵ ˈ 䝽䘱⛩㓣 䐟 ѝԕ 䝽䘱㓯䐟DŽ 〻 о䛫 ㇇⌅լˈ Ӿ 㓯䐟 ˈ 䙐 㓯䐟ˈ ⋑ 㹼 а 㓯䐟DŽ䈕㇇⌅Ⲵ 䭞 䘹 䘲Ⲵ 䝽⛩ 㓯䐟Ⲵ ս㖞䘋㹼 DŽ˄5˅є䱦⇥㇇⌅˄Two-phase Process˅VRPє䱦⇥ ㇇⌅⹄ウѝˈ ԓ㺘 ⲴѪChristofidesㅹӪ[33]ԕ Fisher Jaikumar[34] Ⲵ㇇⌅DŽChistofidesㅹ Ⲵє䱦⇥㇇⌅ѝˈ єњ䱦⇥˖ 䐟㓯 䙐䱦⇥ԕ 㹼䐟㓯 䙐䱦⇥ˈ 䍘 㜭≲䀓ḷ VRPDŽFisher Jaikumarㅹ俆 䙊䗷≲䀓ањ ѹ ⍮䰞仈˄Generalized Assignment ProblemˈGAP˅ ⺞ 㹼Ⲵ亮 ⛩ 㓴ˈ❦ ҾTSP㇇⌅ ⺞ ⇿њ 㓴 Ⲵ䖖䖶䐟㓯DŽGAP ањNP䳮䰞仈ˈ䙊 䙊䗷 Ṭ ㇇⌅ ≲䀓DŽFisher Jaikumar 䲿 Ⲵ⹄ウѝ 㔉 Ҷ亮 ⛩䘹 Ⲵ ⌅ Ṭ ⌅[35, 36]DŽ❦㘼ˈ䈕 ⌅ 䲀 ˖а 䶒ˈ㇇⌅н 㕆〻ˈ 䇑㇇䙏 ⿽ 亮 䘹 ԕ Ṭ 䗷〻 䖳 ˗ а 䶒ˈ㤕䟷⭘Fisher Jaikumar Ⲵ⿽ 亮 ㆋ䘹 ⌅ Ṭ ⌅ˈ ㇇⌅Ⲵ 䖳 ˈа㡜 䳮䗮 㘵 㔉 Ⲵ䇑㇇㔃 [32]DŽ Fisher Jaikumar⹄ウⲴ кˈBramel Simchi-Levi[37]䙊䗷≲䀓ањ㜭 㓖 䘹 䰞仈 ⺞ ⿽ 亮 ⛩ˈՈ ҶFisher Jaikumar ⿽ 亮 ⛩䘹 ⌅ˈն 㘵 㔉 Ҷ 㜭 㓖 VRPк䶒⍻䈅Ⲵ㔃 DŽ ԕⴻ ˈ 䜘 㓿 ㇇⌅ 1960 -1990 䰤 ⲴDŽ 䱵 ⭘ѝˈ ḷ 䀓 䙐 ⌅ 䀓 䘋 ⌅䜭 Ҿ㓿 ㇇⌅DŽа 䶒ˈ 㜭 䀓オ䰤ѝ䘋㹼 䲀 ㍒ˈ 䖳⸝Ⲵ 䰤 ≲ ┑ 䀓˗ а 䶒ˈ䘉㊫㇇⌅㜭 䖳Ѫ ˈԕ 䱵 ⭘ѝ ⻠ Ⲵ䈨 㓖 Ԧˈ ↔ ъ䖟Ԧ ѝ㻛 ⌋ ⭘DŽⴞ ˈ 㓿 ㇇⌅亶 ˈ Ѿ 䘋㹼䟽 䘋Ⲵ DŽ3.2 䙐⭞ ㇍⌋㠚20ц㓚90 ԓˈ䙊䗷⁑ 㠚❦⧠䊑 䗷〻ˈ䇨 㘵 ҶаӋ≲䀓VRPⲴ䙊⭘ ㇇⌅ˈѪ≲䀓 㿴⁑Ⲵ 䝽䘱䰞仈 Ҷ Ⲵ 䐟DŽ䈕㊫ ⌅ 亶 ㍒ ǃ䇠 㔃 ǃԕ 䀓Ⲵ䟽㓴㔃 䎧 ˈ 䈳 オ䰤䘋㹼 ㍒ˈ⢩ Ⲵ 䘋㹼㓥␡䈅 ˈ䘉ṧ 㜭 Ո䀓䳶ѝ ㍒ˈ 㜭 䐣 䜘 ㍒亶 ˈӾ㘼 䇱Ҷ⿽㗔Ⲵ ṧ ˈ䚯 䲧 䜘 Ոˈ 儈Ҷ Ո䀓Ⲵᾲ⦷DŽ䘁 ˈ䙊⭘ ㇇⌅ 䖳 ˈ ⁑ 䘰⚛㇇⌅ǃ⾱ ㍒㇇⌅ǃ䚇Ր㇇⌅ǃ㲱㗔㇇⌅ǃ㋂ 㗔㇇⌅ǃ⾎㓿㖁㔌ǃ ㇇⌅ㅹ䜭 ⭘ ≲䀓VRPDŽ 㢲 ԓ㺘 Ⲵ䙊⭘ ㇇⌅䘋㹼㔬䘠DŽ˄1˅⁑ 䘰⚛㇇⌅˄Simulated Annealing, SA˅1982 ˈKirkpatrickfㅹ փ䘰⚛ 㓴 Ո 亶 ˈ Ҷа⿽≲䀓 㿴⁑VRPⲴ 䘁լ㇇⌅ˈ ⁑ 䘰⚛㇇⌅˄SA˅DŽSAⓀҾ փ䘰⚛䗷〻Ⲵ⁑ ˈ 䍘к а⿽䲿 Ⲵ ㍒ ⌅DŽ ѝˈSA䟷⭘Metropolis ˈ ⭘а㓴〠ѻѪ 䘋 㺘Ⲵ ㇇⌅䘋〻ˈ ㇇⌅ 亩 䰤䟼㔉 ањ䘁լ Ո䀓DŽо㓿 ㇇⌅∄ˈSA 䘠ㆰǃ ⭘⚥⍫ǃ ⭘ ⌋ 䖳 Ԧ䲀 ㅹՈ⛩ˈⴞ 䇨 Ո 䰞仈ѝ ⭘DŽⴞ ҾSAⲴ⹄ウˈ 㔃 ԆՈ ㆆ⮕ ⌅DŽ Tian[38]ㅹӪ 䙐Ҷа⿽ Ҿ Ո ㆆ⮕ⲴSA㇇⌅ ≲䀓VRPˈ ⭘ ㇇⌅ 䙐 䀓ˈ SAо2-opt㔃 ˈ ㇇⌅ѝ ⭘ 䟽 ˈ 䗮 㓸 ˈṩ Ո Ⲵ 䟽 ㊫ ㇇⌅DŽLi[39]ㅹӪ SAо⾱ ㍒㇇⌅㔃 ˈ ⭘TS㇇⌅ѝⲴ〫ս Ӕ ㇇ 㓯䐟 㓯䐟䰤Ⲵ ˈ㘼 SA Ѫ 〻 ˈṩ Ⲵ Ո䀓 䇮 Ⲵ ˈ ㇇⌅䘋㹼 ㍒DŽTavakkoli-Moghaddam[40]ㅹӪ 䛫䘁㇇⌅оSA㔃 ˈԕ⭘ ≲䀓 䖖 VRP 䴰≲ Ⲵ 䖖 VRPDŽ㜑 Տ[41]ㅹ 䲿 䙐VRP 䀓Ⲵ кˈ㔃 ⁑ 䘰⚛㇇⌅ㆆ⮕ˈ䟷⭘䐟 䰤䈳 䐟 Ո ⌅ˈ 䙏 VRP䘋㹼Ҷ≲䀓DŽ⭡ҾSAⲴ 䙏 䖳 ˈфо Ԇ㇇⌅∄ˈSA н㜭 Ⲵ䀓[42]ˈ ↔ⴞ SA VRPѝⲴ ⭘⋑ ⾱ ㍒㇇⌅ 䚇Ր㇇⌅ ⌋DŽ˄2˅⾱ ㍒㇇⌅˄Tabu Search, TS˅1986 Glover Ҷ⾱ ㍒㇇⌅˄TS˅[43]DŽ Ҿ Ӫ㊫ 〻Ⲵа⿽⁑ ˈTS 䜘亶 ㍒Ⲵа⿽ ˈ а⿽ 䙀↕ Ո㇇⌅ˈ ˖㔉 ањ 䀓˄ 䀓˅ 䘹䀓ӗ⭏ ˄亶 㔃 ˅ˈ 䀓Ⲵ亶 ѝ⺞ 㤕 䘹䀓˗㤕 䘹䀓 Ⲵⴞḷ ՈҾ ⴞ Ѫ→ ㍒ Ⲵ³ 䀓´˄Best-so-for˅ˈ 㿶 ⾱ ⢩ ˈ⭘ ԓ 䀓 ³ 䀓´˗㤕н к䘠 䘹䀓ˈ 䘹䀓䳶ѝ䘹 䶎⾱ Ⲵ 䘹䀓Ѫ Ⲵ 䀓ˈ㘼 㿶 о 䀓ⲴՈ ˗к䘠є⿽ л䜭 Ⲵ 䊑 ⾱ 㺘ˈ ⾱ 㺘ѝ 䊑Ⲵԫ ˗ ↔䟽 к䘠䘝ԓ ㍒䗷〻ˈⴤ㠣┑䏣㓸→ DŽ ԕⴻ ˈ亶 㔃 ǃ 䘹䀓䳶ǃ⾱ 䊑ǃ㰀㿶 ǃ㓸→ ㅹ䜭 TS 㜭Ⲵ 䭞DŽˈWillard[44], Pureza Franca[45] TS ⭘ҾVRPˈն䜭 㜭≲ 䖳 Ⲵ㔃 DŽ Osman WassanⲴTS㇇⌅ѝ[46]ˈ ⭘є⿽ 䀓ӗ⭏ ⌅˖ањ 㢲㓖㇇⌅о ⌅㔃 ˈ ањ 㢲㓖㇇⌅о ⍮⌅㔃 ˗ 䛫 㔃 ањє 䐟 䰤Ⲵ њ 㘵єњ䘎㔝Ⲵ ⛩ⲴӔ ˗ ⾱ 䮯 ⭡ањ 〻 ㍒ 䰤䘋㹼 ѹDŽ⍻䈅㔃 ⽪ˈ䘉є⿽TS ⧠ 䜭 Ҷ䖳 Ⲵ㔃 DŽ1994 ˈGendreau[47] Ҷ㓿 ⲴTaburoute㇇⌅ˈ 亶 㔃 ањ亦⛩Ӿ Ⲵ㓯䐟ѝ ˈ а 㓯䐟ѝˈ㘼䘉 㓯䐟 ⭘ԆԜ Ⲵ≲䀓TSPⲴ ѹ ⌅˄GENI˅ ӗ⭏Ⲵpњ 䛫䘁䀓ѻа˗ Ҿ⾱ ˈ Ӿ 䰤[5, 10]ѝ䲿 ањ ˗ ⭘Ҷа⿽ ṧ ㆆ⮕ˈѪ 㘳㲁䛓Ӌ〫 䖳 Ⲵ亦⛩Ⲵ 㜭 ˈ 䛓Ӌ㓿 㻛〫 Ⲵ亦⛩䘋㹼 㖊˗ ⭘՚䎧⛩ˈ⭏ њ䀓 ⇿ањ䜭䘋㹼 䲀Ⲵ ㍒ˈ❦ 䘹 ѝ 㘵Ѫѫ ㍒䗷〻Ⲵ 䀓˗⍻䈅㔃 㺘 ˈ䈕㇇⌅㜭≲ 儈䍘䟿Ⲵ㔃 ˈф ≲ ⴞ Ѫ→Ⲵ 䀓DŽ1995 ˈRochat Taillard[48] Ҷ㠚䘲 䇠 ˄Adaptive Memory˅ᾲ ˈ 䘁 TS亶 ⧠Ⲵ Ⲵ䘋 ѻаDŽ ㍒䗷〻ѝ ⲴՈ䍘䀓 䎧 ˈ❦ 䙊䗷䘉Ӌ䀓Ⲵ㓴 ˈӗ⭏TSⲴ 䀓DŽањ㠚䘲 䇠 а㓴 њ ㍒䗷〻ѝн Ⲵ 䀓DŽ䘉Ӌ䀓ⲴḀӋ ㍐㻛 ˈ 䘋㹼н Ⲵ㓴 ԕӗ⭏ Ⲵ 䀓DŽ VRPѝˈӾ њ䀓ѝ 䘹 Ⲵ䖖䖶㓯䐟 㻛⭘ Ѫањ䎧⛩DŽ䘉њ ⌅ 㓿 ԆԜ 14њḷ VRP⍻䈅䰞仈ѝˈ≲ Ҷєњ ⴞ Ѫ→Ⲵ 䀓DŽ1998 ˈToth Vigo[49] Ҷа⿽ ⌋䘲⭘㤳 Ⲵㆋ㖁⾱ ㍒˄Granular Tabu Search, GTS˅DŽGTSⲴѫ㾱 ⓀҾ˖ањ ѝ䖳䮯Ⲵ䗩㻛 ањ Ո䀓ѝⲴ 㜭 DŽ ↔ˈ䙊䗷⎸ 䮯 䎵䗷ањ䟿 ˄Granularity˅Ⲵ Ⲵ䗩ˈ аӋ⋑ 䙄Ⲵ䀓 ㍒䗷〻ѝ н 㘳㲁DŽ㔃 㺘 ˈ GTS㜭 ⸝Ⲵ 䰤 ≲ Ⲵ䀓DŽ䘁 ˈBrandao[50] 䇮䇑ⲴTSѝˈ䛫 㔃 䘹䀓䳶 ⭡ ˈ ⭘Ҷй⿽〫 ˈ 䐟 䰤 ⛩ ǃ䐟 䰤 ⛩Ӕ ǃ䐟 ⛩Ӕ DŽ⾱ 䮯 ⭡[N/6ˈN/2]ѻ䰤Ⲵ䲿 ˈ ⭘ Ⲵ[N/3] Ѫ⾱ 䮯 䘋㹼 傼⭘ԕ ∄DŽBrandao Eglese[51]䇮䇑Ⲵ≲䀓 䐟 Ⲵ⾱ ㍒㇇⌅ѝˈԕ5⿽ ⌅㧧 䀓ˈ 䘹 ԧ䗩ǃ䘹 䍥䗩ǃ ǃ䘎 䗩 亦⛩(Connected Components)ǃ䐟 (Path Scanning)˗ 䛫 㔃 䗩 ǃ 䗩 є 䐟 кⲴ䗩Ӕ DŽ⭡ҾTS㇇⌅ 䀓 Ⲵ 䎆 ˈ 㘵ԕSolomon ⌅ Ѫ ㇇⌅ˈҏ 䟷⭘ ⌅ǃл ㇇⌅ǃK-tree㇇⌅ӗ⭏ 䀓DŽⴞ ˈTS 䖖VRPǃ 〻䖭䍗VRPǃ 䰤デ㓖 ⲴVRPǃԕ VRP䜭 䟿 ⭘DŽ˄3˅䚇Ր㇇⌅˄Genetic Algorithms, GA˅1975 ˈHolland[52] Ҷ䚇Ր㇇⌅˄GA˅DŽGA а⿽⁑ԯ⭏⢙䘋 䗷〻Ⲵ 䲿 ㍒ ⌅ˈ Ѫ˖ӾՈ 䰞仈Ⲵањ⿽㗔˄а㓴 㹼䀓˅ ˈ ➗䘲㘵⭏ Ո㜌 ⊠Ⲵ ⨶ˈ䙀ԓ˄Generation˅╄ ӗ⭏ 䎺 䎺 Ⲵањ⿽㗔˄а㓴 㹼䀓˅˗ ⇿аԓˈṩ њփ˄ 㹼䀓˅Ⲵ䘲 ˄ⴞḷ ˅ⲴՈ 䘹а䜘 Ո㢟њփ ˄㑱⇆˅ лаԓˈ 䘋㹼Ӕ ˈӗ⭏ ԓ㺘 Ⲵ䀓䳶 Ⲵ⿽㗔DŽ䘉њ䗷〻 㠤⿽㗔 㠚❦䘋 аṧⲴ ԓ⿽㗔∄⡦ԓ 䘲 Ҿ⧟ ˄ 㹼䀓∄ 㹼䀓 䘁䰞仈Ⲵ Ո䀓˅ˈ њ䘋 䗷〻ѝⲴ Ոњփ Ѫ䰞仈Ⲵ 㓸䀓DŽҾн ㊫ Ⲵ䰞仈ˈ օ䇮䇑а⿽ 㖾Ⲵ㕆⸱ Ṹаⴤ GAⲴ ⭘䳮⛩ѻаˈҏ GAⲴањ䟽㾱⹄ウ DŽҼ䘋 㕆⸱ ⌅ GAѝ ⭘Ⲵа⿽㕆⸱ ⌅ˈ❦㘼ˈ Ҿ≲䀓VRP䘉ṧⲴ 䰞仈 ˈҼ㓗 㕆⸱ а Ⲵ㕪䲧DŽ ↔ˈㅖ 㕆⸱ ⌅ ⌋䇔 DŽն ㅖ 㕆⸱ ⌅ ˈ 㔉GA Ҷ Ⲵ䰞仈ˈ㤕䟷 ㆰ Ӕ Պ ԓ㓯䐟ѝ Ӌ亦⛩䟽 ˈ аӋ亦⛩㻛䚇┿ˈ 㠤 㜭 䙽 亦⛩Ⲵ䶎⌅㓯䐟DŽ ↔ˈ 享 у䰘Ⲵ Ҿ亪 ⲴӔ ӗ⭏ Ⲵ ԓ DŽ䘁 㓿 Ҷ л ⌅[5]˖䜘 䝽Ӕ ⌅˄Partially Matched Crossover, PMX˅ǃ亪 Ӕ ⌅˄Order Crossover, OX˅ǃ ⧟Ӕ ⌅˄Cycle Crossover, CX˅ˈԕ 䗩䟽㓴Ӕ ⌅˄Edge Recombination Crossover, ERC˅DŽ Ҿ ˈҏ 㓿 ҶаӋу䰘Ⲵ ⌅ˈ ˄Remove and Reinsert˅ǃ ˄Swap˅ˈԕ 䘶䖜 ˄Inversion˅DŽⴞ ˈ≲䀓VRP OVRPⲴGA ⥞ 䖳 ˈ㘼≲䀓 䰤デⲴVRP ㅹ ⲴGA ⥞ 䖳 DŽ Ⲵ䲀 Ԧˈ⢩ 䰤デⲴ ˈаⴤ ⢥ ⵰ Ⲵ≲䀓 ⌅Ⲵ DŽ䘉㔉GA⭘ Ԉ 䲀 Ԧ 䶒Ⲵ ≲ ㄎҹ Ⲵ㔃 Ҷ ՊDŽ˄4˅㲱㗔㇇⌅˄Ant Colony Optimization, ACO˅㲱㗔㇇⌅ ⭡Dorigo, M., ㅹ[53]Ҿ1991 俆⅑ ⲴDŽACO 㠚❦⭼ѝⵏ 㲱㗔㿵伏㹼ѪⲴ 㘼 Ⲵа⿽⁑ 䘋 ㇇⌅DŽ 伏⢙ ˈ㲲㲱Պ 㓿䗷Ⲵ䐟 䙊䗷 а⿽ ◰㍐˄pheromoneˈ ㇇⌅ѝ〠Ѫ ㍐˅ ḷ䇠ˈ Ⲵ䟿 ṩ 䐟 䮯 伏⢙Ⲵㅹ㓗 DŽ䘉Ӌ ◰㍐Ѫ 㲲㲱 ˈ Ԝ 䘀伏⢙DŽⴞ ˈACO ⭘Ҿ ㊫VRPDŽBullnheimerㅹ[54]䪸 VRP䇮䇑Ҷу䰘Ⲵ㲱㗔䖜〫䘹 ㆆ⮕ˈ 㲱㗔 ㍒ ˈ ⭘2-OptՈ 䐟 ˗Gambardellaㅹ[55] ACO⭘Ҿ≲䀓VRPTWˈ 㘵䟷⭘єњ⿽㗔 Ո 䰞仈ˈањՈ 䖖䖶 ⴞˈањՈ 㓯䐟䮯 ˗Donatiㅹ[56] ACO⭘Ҿ 㖁㔌VRPˈ ㇇⌅ѝ ㍐ ѹѪањ 䰤 䎆䟿ˈ а 〻 к䀓 Ҷ 䰤デⲴ 㖁㔌VRP˗Montemanniㅹ[57]⹄ウҶACO 䖖䖶䐟 䰞仈Ⲵ ⭘ˈ Ҷањ⭡һԦ㇑⨶ǃ㲱㗔㇇⌅ǃ ㍐ ㆆ⮕3њ ㍐㓴 Ⲵ㌫㔏Ṷ ˗Pellegrini ㅹ[58]⹄ウҶн 䖖䖶ǃ 䖖 ǃ 䰤デㅹ㓖 ⲴVRPˈ ⭘2⿽ ⿽ACOՈ ≲䀓˗Gajpal Abad[59]ԕ㋮㤡㲲㲱 䐟 ㆆ⮕Ⲵ㲱㗔㌫㔏≲䀓Ҷ 䘱 ъⲴVRP˗Ugur Aydin[60] ҾACO ҶањӪ ӔӂTSP ⁑ 䖟ԦDŽ˄5˅ ㇇⌅а䙊⭘ ㇇⌅⹄ウ␡ Ⲵ ˈ⹄ウӪ 㓿䖳 ⿽ аⲴ ㇇⌅㔃 䎧 ˈԕ 儈VRPⲴ≲䀓䙏 䀓Ⲵ䍘䟿DŽ1995 ˈGloverㅹ[61] 䈅 GA TS㔃 ˗䛾㤲⾕ 㜑 㔗[62]䙊䗷 䜘 ㍒㜭 Ⲵ⡜ ㇇⌅о ㍒㜭 Ⲵ䚇Ր㇇⌅㔃 ˈ 䙐Ҷ≲䀓⢙⍱䝽䘱䐟 Ո 䰞仈Ⲵ 䚇Ր㇇⌅ˈ 㢟 Ո㔃 ˗䛡 ẵ[63]ˈ[64] ⹄ウҶ㋂ 㗔㇇⌅о Ԇ㇇⌅Ⲵ㔃 VRP 䰞仈кⲴ ⭘˗б⿻䴧[65]ㅹ ⚮ ㇇ 㲱㗔㇇⌅ 䲧 䜘Ո Ⲵ㕪䲧˗Saez[66]ㅹ 䚇Ր㇇⌅о⁑㋺㚊㊫㔃 ˈ ↔ к Ҷа⿽ 㜭䘲 亴 ⌅≲䀓 䖖䖶 䘱 ъVRPDŽ㔬к 䘠ˈ ≲䀓VRPⲴ ⿽䙊⭘ ㇇⌅ ㇇⌅Ⲵ⹄ウ㺘 ˈ Ҿ Ⲯњ Ⲵ ˈ䘉Ӌ ⌅ѝ䜭 ԕ≲ 䶎 Ⲵǃ ⭊㠣 ՈⲴ䀓ˈ㲭❦䘀㇇ 䰤㾱䮯аӋDŽ փ 䈤ˈ ⴞ Ѫ→ˈ⾱ ㍒ ⧠ Ⲵ ⌅˗ Ҿ䚇Ր㇇⌅ ⾎㓿㖁㔌Ⲵ ⌅ 㜭Ո㢟˗㘼 Ҿ⁑ 䘰⚛ 㲱㗔㌫㔏Ⲵ ⌅ㄎҹ н DŽ❦㘼ˈ㘳㲁 ⿽ ⌅ 䙀⅑ ⧠ѝⲴ 㜭 䘋 ˈ ⿽ ㇇⌅ 䳶ѝ ㍒ ṧ ㍒ǃ ㇇⌅≲䀓䍘䟿 䇑㇇ 䰤ѻ䰤㜭㧧 䖳 Ⲵ 㺑ˈ Ⲵ㲱㗔㌫㔏 䚇Ր㇇⌅ 㻛 ˈ о⾱ ㍒㇇⌅ 㖾DŽ4. 㔉 䈣䖖䖶䐟 䰞仈 ㇑⨶ 䘀ㆩ 亶 䱄Ⲵ ⭘ԧ ⹄ウ DŽ䲿⵰⽮ՊⲴ ˈVRPҏ н Ⲵ ˈ 䲿 䴰≲VRPǃ䶎 〠㖁㔌VRPǃԃ -䝽䘱аփ 䐟 䰞仈ㅹ 䘋а↕⹄ウⲴ DŽ 㓣 㔃ҶVRP Ⲵ⹄ウ䘋 䎻 ˈѪ Ⲵ 䢤DŽ㘳 ⥞[1] 䶙 , 㔏䇑 , ѝ ⢙⍱о䟷䍝㚄 Պ. 2010 ⢙⍱䘀㹼 䙊 [M]. ѝ ⢙⍱о䟷䍝㚄 Պ, ѝ ⢙⍱ 䢤2011, Ӝ: ѝ ⢙䍴 ⡸⽮, 2011: 61-62[2] Dantzig, G.B., and Ramser, J.H., The truck dispatching problem [J].Management Science, 1959, 6: 80[3] ⇥仾 . 䖟 䰤デ㓖 Ⲵ 䖖䖶䐟 䰞仈⹄ウ ⭘[D]. 䮯⋉: ѝ , 2009[4] █・ . 䰤デ䖖䖶䐟 䰞仈 ㇇⌅⹄ウ[D]. 䮯⋉: ѝ , 2012[5] ㅖ . 䖖䖶䐟 䰞仈 ⭘⹄ウ[D]. 䮯⋉: ѝ , 2004[6] █・ , ㅖ . ≲䀓 ⺜ 䰤デ䖖䖶䐟 䰞仈Ⲵ ㇇⌅[J]. 䇑㇇ ⭘, 2012, 32(11): 3042-3043, 3070[7] 㛆䳱, ㅖ , 㛢 . 䖟 䰤デⲴ䖖䖶䐟 䰞仈 ⭘ 䇘[C]. 䮯⋉: ѝ 䘀ㆩ ՊㅜӔ⍱Պ, 2000: 634-638[8] ㅖ , 㙲䶆. 䖖䖶䐟 䰞仈 㤕 ⹄ウ䘋 [C]. ␡ : ѝ 䘀ㆩ Պㅜ Ӕ⍱Պ, 2006:395-400[9] Bodin, L.B., Golden, B.L., Assad, A.A., Ball, M.O., Routing and scheduling of vehicles and crews: the state ofthe art [J]. Computer Operation Research, 1983, 10: 163-211[10] Toth, P., Vigo, D. The Vehicle Routing Problem [M]. Society for Industrial and Applied Mathematics,Philadelphia, USA, 2002[11] 㛆 䖹. 䖖䖶䐟 Ո ⥞㔬䘠[J]. ь 㤳 䲒 ˄㠚❦、 ˅, 2010, 2: 31-37[12] Crevier, B., Cordeau, J.F., LaPorte, G., The multi-depot vehicle routing problem with inter-depot routes [J].European Journal of Operational Research, 2007, 176(2): 756-773[13] Golden, B., Assad, A., Levy, L., The fleet size and mix vehicle routing problem [J]. Computer and OperationsResearch, 11(1): 49-66[14] Drorand, M., Trudeau, P. Split delivery routing [J]. Naval Research Logistics, 1990, 37: 383-402[15] 䉒⿹. 䲿 䖖䖶䐟 䰞仈⹄ウ[D]. 䜭: 㾯 Ӕ䙊 , 2003[16] Bent, R.W., and Hentenryck, P.V., Scenario-Based Planning for Partially Dynamic Vehicle Routing withStochastic Customers [J]. Operations Research, 2004, 52(6): 977-987[17] Oppen, J., L okketangen, A., Arc routing in a node routing environment [J]. Computers and OperationsResearch, 2006, 33(4): 1033-1055[18] Lenstra, J.K., and Rinnooy, K., Complexity of vehicle routing and scheduling problem [J]. Network, 1981, 11:221-227[19] . Ҿ ⭼䲀⌅Ⲵ 㹼 ㍒㇇⌅⹄ウ[D]. 㾯 : 㾯 ⭥ 、 , 2011[20] Տ. а⿽ Ҿ䀓 ѝ 䶒Ⲵ ㊫㇇⌅[D]. 䘎: 䘎⨶ , 2009[21] . CVRP 䝽㖁㔌⍱㇇⌅[D]. ⍾ : ь、 , 2003[22] 㕚 㣜, 䛥 . 㿴 ㇇⌅Ⲵ ⨶ ⭘[J]. ѝ 、 , 2005(21): 42-42[23] Golden, B.L., Wasil, E.A., Kelly, J.P., and Chao, I.M., Meatheuristics in vehicle routing [C]. In Crainic, T.G.,and Laporte, G. editors, Fleet Management and Logistics, Kluwer Academic Publishers, London, 1998, 33-56 [24] Clark, G. and Wright, J.R., Scheduling of vehicle routing problem from a central depot to a number ofdelivery points [J]. Operations Research, 1964, 12: 568-581[25] Nelson, M.D., Nygard, K.E., Griffin, J.H., and Shreve, W.E., Implementation techniques for the vehiclerouting problem [J]. Computer and Operations Research, 1985, 12(3): 273-283[26] Paessens, H., The savings algorithm for the vehicle routing problem [J]. European Journal of OperationalResearch, 1988, 34(3): 336-344[27] Altinkemer K., Gavish B., Parallel savings based heuristic for the delivery Problem [J]. Operations Research,1991, 39: 456-469[28] Wark, P., and Holt, J., A repeated matching heuristic for the vehicle routing problem [J]. Journal ofOperational Research Society, 1994, 45: 1156-1167[29] Gillett, B.E., and Miller, L.R., A heuristic algorithm for the vehicle dispatch problem [J]. Operations Research,1974, 22: 340-349[30] Foster, B., and Ryan, D., An integer Programming approach to the vehicle scheduling problem [J]. OperationResearch, 1976, 27: 307-384[31] Ryan, D.M., Hjorring, C., and Glover, F. Extension of the Petal method for vehicle routing [J]. Journal ofOperational Research Society, 1993, 44: 289-296[32] Cordeau, J.F., Gendreau, M., Laporte, G., Potvin, J.Y., and Semet, F., A guide to vehicle routing heuristics [J].Journal of Operational Research Society, 2002, 53(5): 512-522[33] Christofides, N., Mingozzi, A., and Toth, P., The vehicle routing problem [C]. Combinatorial optimization,Chichester, UK: Wiley, 1979: 315-338[34] Fisher, M.L., Jaikumar, R., A generalized assignment heuristic for vehicle routing [J]. Network, 1981, 11:109-124[35] Fisher, M.L., Greenfield, A.J., Jaikumar, R., and Lester, J., A computerized vehicle routing application [J].Interfaces, 1982, 12(4): 42-52[36] Fisher, M.L., Jaikumar, R., and Wassenbove, L.N., Multiplier adjustment method for the generalizedassignment problem [J]. Management Science, 1986, 32: 1095-1103[37] Bramel, J.B., and Simchi-Levi, D., A location based heuristic for general routing problems [J]. OperationsResearch, 1995, 43(4): 649-660[38] Tian, P., Ma, J., and Zhang, D.M., Application of the simulated annealing algorithm to the combinatorialoptimization problem with permutation property: an investigation of generation mechanism [J].European Journal of Operational Research, 1999, 118(1): 81-94[39] Li, H., Lim, A., Huang, J., Local search with annealing-like restarts to solve VRPTW [J]. European Journal ofOperational Research, 2003, 150(1): 115-127[40] Tavakkoli-Moghaddam , R. Safaei, N., Gholipour, Y., A hybrid simulated annealing for capacitated vehiclerouting problems with the independent route length [J]. Applied Mathematics and Computation, 2006, 176(2): 445-454[41] 㜑 Տ, , 㜑 . 䖖䖶䐟 䰞仈Ⲵ⁑ 䘰⚛㇇⌅[J]. ѝ 䐟 , 2006, 19(4): 123-126[42] Breedam, A.V., Improvement heuristics for the vehicle routing problem based on simulated annealing [J].European Journal of Operation Research, 1995, 86(3): 480-490[43] Glover, F. Future paths for integer programming and links to artificial Intelligence [J]. Computers andOperations Research, 1986, 13:533-549[44] Willard, J.A.G., Vehicle routing using r-optimal tabu search [M]. London: The Imperial College, 1989[45] Pureza, V.M., and Franca, P.M., Vehicle routing problems via tabu search metaheuristic [R].Technical ReportCRT-347, Centre for Research on Transportation, Montreal, Canada, 1991[46] OsmanˈI., and Wassan, N., A reactive tabu search metaheuristic for the vehicle routing problem with back-hauls [J]. Journal of Scheduling, 2002, 5(4): 263-285[47] Gendreau, M., Hertz, A., L aporte, G., A tabu search heuristic for the vehicle routing problem [J].Management Science, 1994, 40: 1276-1290[48] Rochat, Y., and Taillard, E.D., Probabilistic diversification and intensification in local search for vehiclerouting [J].Journal of Heuristics, 1995, 1: 147-167[49] Toth, P., and Vigo, D., The granular tabu search and its application to the vehicle routing problem[R].Technical Report OR19819, DEIS, Italy, 1998[50] Brandao, J., A new tabu search algorithm for the vehicle routing problem with backhauls [J]. EuropeanJournal of Operation Research, 2006, 173(2): 540-555[51] Brandao, J., and Eglese, R., A deterministic tabu search algorithm for the capacitated arc routing problem [J].Computers and Operations Research, 2008, 35(4): 1112-1126[52] Holland, J., Adaptation in natural and artificial systems [D]. University of Michigan Wesley, 1975[53] Colorni, A., Dorigo, M., Maniezzo, V., Distributed optimization by ant colonies [J]. In: Proc of the FirstEuropean Conference of Artificial Life. Paris, France Elsevier Publishing, 1991: 134-142[54] Bullnheimer, B., Hartl, R.F., and Strauss, C., Applying ant system algorithm to the vehicle routing problem[A]. Advances and Trends in Local Search Paradigms for Optimizaiton [C], Kluwer Acedenics, 1998: 109-120[55] Gambardella, L.M., Taillard, E., Agazzi, G., MACS-VROTW: a multiple ant colony system for vehiclerouting problems with time window [A]. New ides in optimization [C], London, U.K.: McGraw-Hill, 1999: 63-76[56] Donati, A.V., Montemanni, R., Casagrande, N., Rizzoll, A.E., and Gambardella, L.M., Time dependentvehicle routing problem with a multi ant colony system [R]. Technical Report TR-17-03, IDSIA, Galleria2, Manno, 6928, Switzerland, 2003[57] Montemanni, R., Gambardella, L.M., Rizzoll, A.E., and Donati, A.V., A new algorithm for a dynamic vehiclerouting problem based on ant colony system [R]. Technical Report TR-23-02, IDSIA, Galleria2, Manno, 6928, Switzerland, 2004[58] Pellegrini, P., Favaretto, D., Moretti, E., Multiple ant colony optimization for a rich vehicle routing problem:a case study [J]. Lecture Notes in Computer Science, 2007, 4639: 627-634[59] Gajpal, Y., and Abad, P.L., Multi-ant colony system (MACS) for a vehicle routing problem with backhauls[J]. European Journal of Operation Research, 2009, 196: 102-117[60] Ugur, A., and Aydin, D., An interactive simulation and analysis software for solving TSP using ant colonyoptimization algorithms [J]. Advances in Engineering Software, 2004, 40: 341-349[61] Glover, F., Kelly, J.P., and L aguna, M., Genetic algorithms and tabu search: hybrids for optimization [J].Computers Operation and Research, 1995, 22(1): 111-134[62] 䛾㤲⾕, 㜑 㔗. ⭘ 䚇Ր㇇⌅≲䀓⢙⍱䝽䘱䐟 Ո 䰞仈Ⲵ⹄ウ[J]. ѝ ㇑⨶、 , 2002, 10(5): 51-56[63] 䛡 , ẵ. Ҿ 䘋㋂ 㗔㇇⌅Ⲵ ս-䘀䗃䐟㓯䰞仈⹄ウ[J].ѝ Ỡ 〻, 2006, 17(22):2359-2361[64] . 䖖䖶䐟 䰞仈Ⲵ㋂ 㗔㇇⌅⹄ウо ⭘[D]. ⎉⊏: ⎉⊏ ъ , 2007[65] б⿻䴧, 㜑⾕ , ≨ . ≲䀓 䰤デⲴ䖖䖶䐟 䰞仈Ⲵ 㲱㗔㇇⌅[J]. ㌫㔏 〻⨶䇪о 䐥, 2007,10: 98-104[66] Saez, D., Cortes, C.E., and Nunez, A., Hybrid adaptive predictive control for the multi-vehicle dynamic pick-up and delivery problem based on genetic algorithms and fuzzy clustering. Computers and Operations Research, 2008, 35: 3412-3438。
车辆路径问题及其优化算法研究综述

车辆路径问题及其优化算法研究综述随着科技的进步和电子商务的飞速发展,作为国民经济中一个重要行业的物流产业已成为拉动国家经济发展与提高居民生活水平的重要动力源泉,而物流行业中的车辆路径问题(Vehicle Routing Problem,VRP)是制约物流行业发展的一个关键要素,其研究也受到人们的广泛关注。
车辆路径问题是物流管理与运输组织优化中的核心问题之一,是指在满足一定的约束条件(如时间限制、车载容量限制、交通限制等)下,通过对一系列收货点与发货点客户合理安排行车路线,在客户的需求得到满足的前提下,达到配送车辆最少、配送时间最短、配送成本最低、配送路程最短等目标。
该问题由Dantzig和Ramser于1959年在优化亚特兰大炼油厂的运输路径问题时首次提出,现已成为运筹学中一类经典的组合优化问题,是典型的NP-难题。
通过选取恰当的配送路径,对运输车辆进行优化调度,可以明显提高配送效率,有效减少车辆的空驶率和行驶距离,降低运输成本,加快响应客户的速度从而提高客户服务质量,提高的核心竞争力。
VRP作为物流系统优化环节中关键的一环,其研究成果已经应用到快递和报纸配送连锁商店线路优化以及城市绿化车线路优化等社会实际问题中,因而车辆路径问题的优化研究具有很好的现实意义。
1/ 71 车辆路径问题的分类与基本模型VRP的构成要素通常包括车辆、客户点、货物、配送中心(车场)、道路网络、目标函数和约束条件等,根据侧重点的不同,VRP可以分为不同的类型。
根据运输车辆载货状况分类可分为非满载车辆路径问题和满载车辆路径问题;根据任务特征可分为仅装货、仅卸货和装卸混合的车辆路径问题;根据优化目标的数量可分为单目标车辆路径问题和多目标车辆路径问题;根据配送车辆是否相同可分为同型车辆路径问题和异型车辆路径问题;根据客户对货物接收与发送有无时间窗约束可分为不带时间窗的车辆路径问题和带时间窗的车辆路径问题;根据客户需求是否可拆分可分为需求可拆分车辆路径问题和需求不可拆分车辆路径问题;根据客户是否优先可分为优先约束车辆路径问题和无优先约束车辆路径问题;根据配送与取货完成后车辆是否需要返回出发点可分为开放式车辆路径问题和闭合式车辆路径问题;还可以将上述两个或更多约束条件结合起来,构成一些更复杂的车辆路径问题。
《车辆路径问题求解算法分析2000字》

车辆路径问题求解算法分析综述1.1 算法概述车辆路径问题一般会有多个约束条件叠加,这会增加问题求解的复杂程度,所以此类问题属于NP难题,针对车辆路径问题的求解算法从早期的精确算法逐渐发展到大规模的智能优化算法。
根据目前的研究成果,求解此类问题的方法总体上可分为精确算法和启发式算法,具体如图2-1所示错误!未找到引用源。
图2-1VRP问题的常用求解算法(1)精确算法精确算法可以在有限的计算步骤内求出问题的最优解,但计算时间会随着问题规模的增加以指数速度上升,所以只适用于规模较小的问题。
由于实际问题具有系统性与复杂性,尤其是针对车辆路径问题等NP难题而言,使用精确算法所产生的成本可能是无法接受甚至不现实的,不适合大多数的配送模型。
(2)传统启发式算法为了在可接受的计算成本范围内进行复杂问题的求解,学者引入了启发式算法。
此类方法要求研究人员通过经验总结、实验分析等方式对求解过程进行引导,使得可以在较短时间内找到可接受的满意解。
传统启发式算法需要针对具体问题模型设计相应的算法,通常用来解决组合优化问题,具有计算速度快、程序较为简单等优点。
但是由于搜索范围的局限性,该方法无法保证求得最优解。
同时,传统启发式算法是通过局部搜索技术找到满意解的,容易陷入局部最优。
(3)亚启发式算法亚启发式算法又称元启发式算法,通过全局搜索获取满意解,找到全局最优解的概率更高。
此类算法是以自然界或人类社会中的一些智能现象为基础产生的,例如遗传算法源于自然界中生物的遗传、自然选择等进化规律,蚁群算法源于蚂蚁在觅食过程中的群体行为,粒子群算法源于鸟群的捕食行为,模拟退火算法源于热力学中固体的退火过程。
1.2 遗传算法(1)算法原理遗传算法是一种可以实现全局优化的自适应概率搜索算法,主要启于生物进化中“适者生存”的规律,即自然环境中适应能力越高的群体往往会产生更加优秀的后代。
通过模拟个体交叉和染色体基因突变等现象产生候选解,然后按照一定原则从中选择较优的个体,不断重复上述操作,直至得到达到终止条件的满意解。
物流配送网络中的路径规划与车辆调度算法研究

物流配送网络中的路径规划与车辆调度算法研究路径规划和车辆调度算法在物流配送网络中起着至关重要的作用。
合理的路径规划和车辆调度可以最大程度地提高物流配送网络的效率和经济性。
本文将对路径规划和车辆调度算法在物流配送网络中的研究进行探讨。
一、路径规划算法路径规划是物流配送网络中的核心问题之一。
合理的路径规划可以最大限度地减少运输成本并提高物流配送效率。
在路径规划算法中,最常见的方法是基于图论的算法。
Dijkstra算法是其中一种经典算法,它是一种单源最短路径算法,适用于有向图和带有非负权值的边。
该算法通过不断更新节点到源节点的最短路径长度来找到最短路径。
另外,A*算法是另一种常用的路径规划算法,它在搜索过程中综合考虑了最短路径和启发式信息,具有更高的效率。
除了基于图论的算法,还有一些其他的路径规划算法可以应用于物流配送网络。
例如,遗传算法是一种基于进化规划的算法,它通过模拟生物进化过程来寻找最优解。
遗传算法可以同时考虑多个因素,如时间、成本和容量等,从而得到更优的路径规划结果。
二、车辆调度算法车辆调度是物流配送网络中另一个重要的问题。
良好的车辆调度算法可以提高车辆利用率和运输效率,减少等待时间和行驶里程。
在车辆调度算法中,最常用的方法是基于启发式和优化算法。
其中,最近邻算法是最简单和最常用的启发式算法,它根据车辆的当前位置选择距离最近的订单进行配送。
虽然最近邻算法简单高效,但它不能保证得到全局最优解。
除了基于启发式的算法,还有一些基于优化的车辆调度算法可供选择。
例如,蚁群算法是一种模拟蚂蚁觅食过程的算法,它通过不断地调整车辆路径来优化调度结果。
蚁群算法具有较强的全局搜索能力和自适应性,能够得到较优的车辆调度方案。
另外,遗传算法也可以应用于车辆调度问题。
遗传算法通过模拟生物进化过程,根据适应度函数不断进化种群来寻找最优解。
它可以考虑多个约束条件,如时间窗口、载重限制和行驶距离等,得到最优的车辆调度方案。
物流配送中的路径规划与车辆调度算法研究

物流配送中的路径规划与车辆调度算法研究物流配送是指将货物从生产地点运送到消费者手中的物流过程。
在实际操作中,物流配送中的路径规划与车辆调度是非常重要的环节,对于提高物流效率和降低物流成本具有重要意义。
本文将就路径规划与车辆调度算法在物流配送中的研究进行探讨。
路径规划是指在物流配送过程中确定最优的车辆路径,以保证货物能够按时、高效地送达目的地。
路径规划算法的研究目标是找到在给定时间窗口内,使得车辆行驶距离最短的路径。
经典的路径规划算法包括Dijkstra算法、A*算法和遗传算法等。
这些算法通过不同的计算方式、启发式规则或者遗传优化来寻求最优路径。
Dijkstra算法是一种经典的最短路径算法,它通过构建节点之间的最短路径树来寻找最优路径。
该算法适用于无向图或有向图,能够有效解决单源最短路径问题。
然而,在物流配送中,路网往往具有大规模的节点和边,因此Dijkstra算法的计算复杂度较高,运算时间较长。
A*算法是一种启发式搜索算法,它综合利用了实际代价和预计代价来评估节点的优先级,从而找到最优路径。
A*算法在物流配送中的路径规划中具有较好的效果,其通过引入启发式函数来指导搜索方向,减少了搜索的空间。
然而,A*算法对于路网形状的选择比较敏感,在某些特殊的情况下可能会导致结果不准确。
遗传算法是一种启发式优化算法,通过模拟自然界的生物进化过程来寻找最优解。
在物流配送中,遗传算法可以用于优化车辆路径的选择,以最小化总行驶距离或总成本。
通过不断进化的迭代过程,遗传算法能够找到近似最优解。
然而,遗传算法的计算复杂度较高,运算时间较长。
除了传统的路径规划算法外,近年来,一些基于人工智能的算法也开始应用于物流配送中的路径规划。
例如,深度强化学习算法可以通过学习和优化车辆路径的策略,自动寻找最优解。
这些算法可以根据环境的变化进行实时的决策,适应复杂的物流配送场景。
车辆调度是指在已经确定了最优路径的基础上,对车辆进行合理的分配和调度,以最大限度地利用资源和提高物流运输效率。
具有同时送货和取货特点的单车辆配送路径优化算法

…
・
l ・ 9
具有 同时送 货和取货特点 的单车辆配送路径优化算 法
Optm ia i n g r t i z to Al o ihm fSi l hi l s rbuto Pa h wih t e Cha ac e itc fDe i e y o ng e Ve ce Dit i i n t t h r t rs is o lv r a c p tt m e Ti e nd Pi ku a he Sa m
关 键词 : OV~ P DP 车辆路 径 ; VR S ; 比值 法 ; 值 权
Ke r s y wo d :OV— VRPS DP; e il o t ;ai to we t v h cer ui r tomeh d; i ng
中图分类号 :2 1 F 5
文献标 识码 : A
文 章 编 号 :0 6 4 1 (0 0 3 — 0 9 0 10 — OV— RP D te t a d l u o w r e ai to pi z t n ag r h o h po lm h V S P mah mai l mo e ,p tf r a d a n w rt meh c o d o t ai lo tm f te rb e o OV— RP D ,a d v rf d te mi o i f V S P n ei e h i
王 艳 艳 W a gYa y n n na
( 西安 铁路 职业 技 术学 院 , 西安 7 0 1 1 4) ( i nR i a c t n l T c ncl ntue Xi n7 0 1 , hn X al yVoai a & eh ia si t, ' 0 4 C ia) a w o I t a 1
同时取送货的三维装载约束下车辆路径问题

同时取送货的三维装载约束下车辆路径问题彭碧涛;周世平【摘要】同时取货和送货的三维装载约束下车辆路径问题(3L-VRPSDP)是经典车辆路径问题(VRP)的一个扩展,在3L-VRPSDP中,顾客可能要求同时取货和送货,而且货物装载要考虑其三维大小、先进后出、底面支撑等装载特性。
针对这类问题,提出了基于左底优先和最大接触面优先的装载算法,在装载时要考虑其配送特征;在此基础上,设计了对应的禁忌搜索算法对初始结果进行优化,通过实验验证了算法的有效性。
%The Simultaneous Delivery and Pickup Vehicle Routing Problem with Three-Dimension Loading Constraints (3L-VRPSDP)is a variant of the classical Vehicle Routing Problem(VRP)where clients may require simultaneous pickups and deliveries, at the same time, cargo must consider its three dimensional size, first in last out, bottom support constraints. Considering the distribution characteristics, the loading algorithms based on Left Bottom(LB)and Maximum Contact Area (MCA)are proposed, and the corresponding tabu search algorithms are designed. Experiments are given to prove the validity of the algorithms.【期刊名称】《计算机工程与应用》【年(卷),期】2016(052)006【总页数】6页(P242-247)【关键词】三维装载;车辆路径问题;禁忌搜索;先进后出【作者】彭碧涛;周世平【作者单位】广东外语外贸大学思科信息学院,广州 510006;华南理工大学工商管理学院,广州 510641【正文语种】中文【中图分类】TP39PENG Bitao,ZHOU Shiping.Computer Engineering and Applications,2016,52(6):242-247.同时取货和送货的三维装载约束下车辆路径问题(The Simultaneous Delivery and Pickup Vehicle Routing Problem withThree-DimensionLoadingConstraints,3L-VRPSDP)是经典的车辆路径问题(The Simultaneous Delivery and Pickup Vehicle Routing Problem,VRPSDP)的一个重要的扩展。
车辆路径规划算法在物流配送中的应用研究

车辆路径规划算法在物流配送中的应用研究随着电子商务的快速发展,物流配送成为现代生活中不可或缺的一环。
而在复杂的物流配送网络中,如何高效地规划车辆路径成为了一个关键问题。
车辆路径规划算法的应用在物流配送中具有重要的意义,可以大大提高物流配送的效率,并降低成本。
本篇文章将深入探讨车辆路径规划算法在物流配送中的应用,并分析其优势与挑战。
一、车辆路径规划算法的概述车辆路径规划算法是一个多领域交叉研究的领域,结合了优化理论、图论、运筹学等数学模型和方法。
该算法的目标是通过合理规划车辆的路径,使得配送任务能够在最短的时间内完成,并在满足配送需求的同时降低物流成本。
目前常用的车辆路径规划算法包括:基于规则的方法、启发式方法以及基于模型的优化方法。
二、车辆路径规划算法在物流配送中的应用1. 增加配送效率通过车辆路径规划算法,可以避免车辆在配送过程中的长时间空载或重载状态,合理分配任务,减少配送时间。
例如,可以利用算法根据配送点之间的距离、交通情况等因素,自动规划最佳的路径,减少车辆行驶的里程和时间,从而提高物流配送的效率。
2. 优化车辆调度车辆路径规划算法可以实现车辆的动态调度,根据实时的订单情况和交通信息,及时调整配送路线和车辆数量。
这可以大幅减少等待时间,保证物流服务的时效性和准确性。
同时,通过合理的车辆调度,还可以减少车辆的拥堵现象,降低物流成本。
3. 减少运输成本车辆路径规划算法可以考虑不同路段的拥堵情况、收费情况等因素,从而优化路径,减少燃料消耗和运输成本。
此外,通过合理规划车辆的负载和满载率,还可以减少运输次数和车辆的空载行驶,进一步节约成本。
4. 降低环境污染合理规划车辆路径可以减少车辆的行驶距离和时间,从而减少尾气排放和噪音污染。
通过车辆路径规划算法的应用,可以选择环保的路线和节能的交通工具,对环境保护产生积极影响,推动可持续发展。
三、车辆路径规划算法的优势与挑战1. 优势(1)提高物流配送效率:通过合理规划车辆路径,减少车辆行驶距离和时间,提高物流配送的效率。
物流配送优化中的车辆路径规划算法研究

物流配送优化中的车辆路径规划算法研究随着电商不断崛起,物流配送成为社会不可缺少的一环。
然而,随着交通方式以及消费者购物行为的变化,物流配送环节的复杂度也在不断增加。
为了提高物流配送的效率,减少物流成本,车辆路径规划算法成了当下物流配送中的研究热点。
本文将对物流配送优化中的车辆路径规划算法进行探讨。
一、车辆路径规划算法概述车辆路径规划算法的基本思想是在满足一定约束条件下,针对物流配送问题设计一个有效的配送路径方案。
一般来说,车辆路径规划算法包括以下步骤:建立网格模型、寻找最短路径、优化路径方案。
1.1 建立网格模型为了更好地研究车辆路径规划问题,建立一个清晰的网格模型非常必要。
模型中一般需要考虑的因素包括:交通情况、道路限速、车辆号型、车速等因素。
网格模型建立好之后,就可以进行路径规划算法的优化研究。
1.2 寻找最短路径针对车辆路径规划问题,需要找到最优的路径。
最短路径算法是实现这一目标的重要手段。
最短路径算法包括:Dijkstra算法,Floyd算法,Bellman-Ford算法等。
Dijkstra算法是一种广泛使用的路径规划算法。
它的基本思想是从起点开始,以贪心的策略逐步寻找最短路径。
每次更新邻近节点的距离,不断寻找距离最短的下一个节点,直到找到终点为止。
Floyd算法是另一种经典的路径规划算法。
它是一种迭代算法,通过计算每对节点之间的距离,不断更新路径矩阵中的距离值。
最终,可以得到最短路径的值以及具体路径。
Bellman-Ford算法是一种基于动态规划的路径规划算法。
它的优点是可以处理负权重的边。
1.3 优化路径方案除了寻找最短路径,另一个重要的研究方向是优化路径方案。
常见的路径优化算法包括:遗传算法、模拟退火算法、粒子群算法等。
遗传算法是一种经典的优化算法。
它的基本思想是模拟生物进化的过程,通过基因组合的方式,生成新的路径方案。
遗传算法以粗略的结果为代价,换取时间效率的提高。
模拟退火算法是另一种优化算法。
具有动态客户的同时取送货车辆路径问题优化研究

具有动态客户的同时取送货车辆路径 问题优化研究
随着我国经济转型战略的不断深化与发展,企业对于自身的管理 提出了更高的要求,特别是在占综合成本比例较高的物流管理方 面。从企业角度出发,居高不下的物流成本以及效率低下的配送 方式,大大削弱了企业的竞争力。
因此,配送方式及运输成本作为影响物流成本和效率的主要因素, 成为企业关注的重要问题以及研究的重点。一方面,从资源利用 和节约能源的角度出发,回收利用的逆向物流得到了更多的关注, 越来越多的企业需要实行同时进行取货和送货的配送方式,以此 来避免浪费有效提高资源利用率。
其次,针对具有动态客户的同时取送货车辆路径问题进行了理论 介绍,明确该问题的定义、主要分类,常见的求解算法及其优劣。 文章选取蚁群算法作为解决问题的方法,并对该算法做了详细的 介绍,为后续的方法提出提供了基础。
第三,研究了不带时间窗的具有动态客户的同时取送货车辆路径 问题,针对该问题的特点构建了数学模型。以蚁群优化算法为基 础,结合实时插入方法,提出了符合问题特点的混合蚁群优化算 法ACS-RIM算法,并通过A公司的实例对算法的可行性进行了验证, 合理解决了带有动态客户并且没有时间窗要求的VRPSDP问题。
另一方面,配送过程中出现的各种不确定信息会对既有的配送计 划产生极大影响,这也是企业需要解决的难题。移动通信技术、 定位技术及智能设备的迅猛发展,为具有不确定信息的动态车辆 路径问题提供了解决基础。
因此,对符合现实情况的车辆路径问题进行研究,能够帮助企业 降低成本,提高利润,增强竞争力。本文选取不确定信息中的一 类,即动态客户问题,以更具效率的同时取送货车辆路径问题为 依托展开研究,为企业解决车辆路径问题提供借鉴,论文进行的 主要工作如下:首先,简明扼要的介绍了研究背景及意义,揭示了 该研究的理论意义与现实价值,并对国内外针对该问题的研究做 了总结与分析,阐明了论文的主要研究框架。
带软时间窗的同时取送货车辆路径问题研究

doi: 10.3969/j.issn.1007-7375.2020.05.010带软时间窗的同时取送货车辆路径问题研究李博威1,3,户佐安1,2,贾叶子1,唐诗韵3(西南交通大学 1. 交通运输与物流学院;2.综合交通大数据应用技术国家工程实验室,四川 成都 611756;3.广西交通设计集团有限公司,广西 南宁 530029)摘要: 考虑软时间窗下的车辆路径问题,客户点常伴有同时取送货的双重需求。
针对此类问题,通过对软时间窗、车辆在途前后时间关系及二者融合问题进行刻画,同时将车辆行驶距离、车辆使用数、违反软时间窗总时间、客户满意度等纳入综合考量,构建相应混合整数非线性规划(mixed integer nonlinear programming, MINLP)模型。
设计相应多目标优化求解算法,运用理想点法对目标函数进行转化,将多目标优化问题转化为单目标优化问题。
结合相应算例集,运用LINGO 17.0全局求解程序求得每组算例的全局最优解。
结果表明,针对带软时间窗的同时取送货车辆路径问题(vehicle routing problem with simultaneous pick-up and delivery and soft time windows, VRPSPDSTW),所建模型及算法是有效且可行的。
关键词: 物流工程;车辆路径问题;同时取送货;软时间窗;理想点法中图分类号: U492.2+2 文献标志码: A 文章编号: 1007-7375(2020)05-0075-07A Research on Vehicle Routing Problem with Simultaneous Pick-up andDelivery and Soft Time WindowsLI Bowei1,3, HU Zuoan1,2, JIA Yezi1, TANG Shiyun3(1. School of Transportation and Logistics;2. National Engineering Laboratory of Integrated Transportation Big Data Application Technology,Southwest Jiaotong University, Chengdu 611756, China;3. Guangxi Communications Design Group Co., Ltd., Nanning 530029, China)Abstract: Considering the vehicle routing problem with soft time windows, customer points are often accompanied by dual demands for pick-up and delivery. For these problems, the soft time window, the time relationship of vehicle on the route and the combination between them are described, and a mixed integer nonlinear programming (MINLP) model is built by considering the vehicle travelling distance, vehicle number, total time of the soft time windows being violated and customer satisfaction. The corresponding multi-objective optimization algorithm is designed, and the objective function is transformed by using ideal point method, and the multi-objective optimization problem is transformed into single-objective optimization problem, and combining the set of test problems, each global optimal solution of test problems is solved by the global solver of LINGO 17.0. The results show that the model and algorithm of vehicle routing problem with simultaneous pick-up and delivery and soft time windows (VRPSPDSTW) are effective and feasible.Key words: logistics engineering; vehicle routing problem; simultaneous pick-up and delivery; soft time window; ideal point method随着物流与运输行业的蓬勃发展,基本送达服务已无法满足大众需求,而高品质、高效率的配送服务,更为大众所青睐。
一种新的同时取送货车辆路径问题方法研究
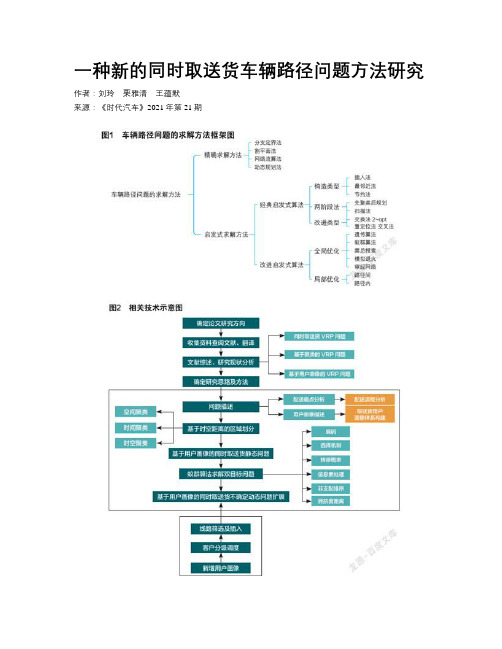
一种新的同时取送货车辆路径问题方法研究作者:刘玲栗雅清王蕴默来源:《时代汽车》2021年第21期摘要:随着国家的富强,社会经济实力的持续增长,我国人民群众的日常生活水平也越来越高,所以人们的网购热情也随之提高。
由此以来,随着人们网购的种类和数量不断增多,网购时的取货和送货问题也浮出水面,成为了一种被广大学者重点研究的问题。
本文针对同时取送货车路径的问题,基于用户画像相关方法建立了双目标模型,随后设计了蚁群算法对静态和动态问题进行相关解析,实验结果可得,该方法在具体问题中的求解速度以及对外界環境不良因素的抗干扰能力较强,为以后的相关研究奠定了理论基础。
关键词:同时取送货车辆路径双目标蚁群算法1 引言同时送货的时效性、客户的满意程度以及各种具有不确定因素的相关问题正随着国家及社会高速发展慢慢的浮出水面[1]。
而如今,随着计算机以及相关技术的快速普及,国家为了应对各场景下精确满足客户需求,完善相关配送规范和配送能力。
末端配送的主要问题是VRPSPD问题,以配送网络为应用场景,结合用户画像理论对取送货问题进行研究,具有现实意义。
当前结合用户画像对同时取送货问题研究的文献相对较少,研究具有高复杂度的NP-hard问题,具有重要学术价值[2-3],研究成果应用于各个领域,车辆路径问题的求解方法框架及技术路线示意如图1-2所示。
2 末端配送概念的相关概述我国末端配送以不同的配送需求主体与配送客体划分,可以将配送服务分为三大类,分别是B2B、B2C、C2C。
3 用户画像流程及方法构架逻辑,其中用户平时在配送服务中的行为数据如:评论参与情况,平台浏览量,进行用户画像。
4 取送货需求用户画像体系构建取送货用户画像标签体系,其中标签获取及处理步骤如下:(1)标签获取,根据相关问卷调查,获得了150份相关数据资料。
对最底层事实标签数据进行定量处理和归一化处理,即可进行下一步数据的收集和分析。
(2)对问卷数据的处理步骤共有三步:①分析各个标签,构建指标评价矩阵Xij。
物流配送中的车辆路径优化算法研究

物流配送中的车辆路径优化算法研究物流配送是供应链管理的重要环节,而车辆路径的优化则直接影响到物流的效率与成本。
为了提高运输效率和降低成本,研究者不断探索并应用各种车辆路径优化算法。
本文将介绍几种常见的算法,并讨论它们在实际物流配送中的应用。
一、贪婪算法贪婪算法是一种简单而高效的车辆路径优化算法,其基本思想是每次选择最优的下一步移动。
在物流配送中,可以将货物的配送点看作节点,通过计算每个节点之间的距离和优先级,然后依次选择下一个距离最近且优先级最高的节点进行配送。
这种算法具有简单易实现的特点,但由于只考虑局部最优解,可能导致整体路径并非最优。
二、遗传算法遗传算法是一种通过模拟自然界生物进化过程的优化算法,它通过不断进化生成并选择合适的解决方案。
在物流配送中,遗传算法可以将每个配送点看作基因,通过随机生成、交叉和变异等操作,在每一代中筛选出适应度较高的解决方案。
这种算法在处理复杂问题时表现优秀,但计算量大,消耗时间较长。
三、模拟退火算法模拟退火算法是一种基于物理退火原理的优化算法,它通过在搜索过程中接受一定概率下降的劣解,以避免陷入局部最优解。
在物流配送中,模拟退火算法可以通过随机选择某个配送点的新位置,在每次迭代中计算路径长度的变化,并根据一定概率接受该变化。
这种算法在避免陷入局部最优解方面表现出色,但也需要适当的参数设置才能达到较好的效果。
四、禁忌搜索算法禁忌搜索算法是一种通过禁忌列表限制搜索过程,避免陷入已探索过的解空间的优化算法。
在物流配送中,禁忌搜索算法可以通过记录已访问过的节点,并设置一定的禁忌期限,来避免重复搜索和陷入局部最优解。
这种算法在处理大规模问题时表现出色,但需要适当的参数设置和启发式函数的设计。
综上所述,物流配送中的车辆路径优化算法有多种选择,每种算法都有其适用的场景和特点。
在实际应用中,可以根据具体需求和条件选择合适的算法进行优化。
同时,为了进一步提高物流配送的效率,还可以结合实时数据和先进的优化模型,不断改进和创新现有的算法,以确保最佳配送路径的确定。
车辆路径安排问题算法研究综述

元启发式算法是一类算法 的总称 , 主要包括遗传算法 、 模拟退火算法、 蚁群算法、 禁忌搜索算法等 。本文根据
求解 V P算法 的分类 , R 概要介绍了 V P R 算法近五年来的研究成果, 并对未来 V P的研 究前景作 了展望 。 R
陈文兰 戴树贵
( 滁州学院 数学Βιβλιοθήκη ,安徽 滁州 290 ) 300
摘
要: 车辆路径安排是决定物沈配送费用的主要 因素。车辆路径安排问题(e ie R u n rbe ,R ) V hc ot g Poll v P是 l i
近 年 来 应 用 数 学 、 算机 科 学 和 物 沈 科 学研 究 的 一个 热 点 问题 , 生 了众 多 的研 究 成 果 。本 文 首先 讨论 了 V P 计 产 R 的 分 类 , 后 基 于 V P算 法 构造 方 法 的 分 类 , 要 介 绍 了近 五年 来 V P算 法 研 究 的 主 要 成果 , 对 研 究方 法 然 R 概 R 并 进 行 了分 析 , 后对 全 文进 行 了总 结 , 探 讨 了该 问题 未 来 的研 究方 法 。 最 并
关键词: 车辆路径安排 问题; 精确算法 ; 启发 式算法 ; 元启发式算法 中图分类号 ;P0 . T316 文献标识码 : A 文章编号: 6 3 1 9 2 0 ) 3 0 1— 7 1 7— 7 4( 0 7 0 — 0 9 0
作者简介: 陈文 兰(9 2 )女 , 17- , 浙江绍兴人 , 士, 硕 滁州学院数 学系。
维普资讯
第 9卷 第 3期
20 0 7年 5 月
滁 州 学 院 学 报
J l A FC 删 伽 U lESr 伽 I Lo 删 N N1 R rY ,
物流配送中车辆路径问题研究

物流配送中车辆路径问题研究物流配送是国民经济正常运转的重要保障,如何实现对其过程的有效管理,降低运营成本,已成为物流企业关注的重点。
如何解决车辆路径问题(Vehicle Routing Problem,VRP)是生成合理物流配送方案的关键,良好的算法能够减少物流车辆配送次数、降低配送车辆的空载率、提高物流配送效率,降低物流配送成本。
VRP是物流配送的核心,也是广大学者的研究热点。
论文结合遗传算法的全局收敛性和蚁群算法信息素的正反馈性,设计了一种可解决单配送中心车辆路径问题的混合算法。
以此为基础,重点研究了基于时间窗约束的多配送中心车辆路径问题。
论文基于MGIS平台,采用插件技术,设计并实现了原型系统,验证了算法的有效性。
主要研究内容和创新点如下:1、研究了车辆路径问题的组成要素、要素特点以及车辆路径问题的分类;探讨了图论在路网表达中的应用,包括基本概念、存储方式及其表达方式;对解决车辆路径问题的不同算法进行分析,奠定了论文的研究基础。
2、对遗传算法与蚁群算法进行研究实现,实验表明,遗传算法具有较快的全局收敛性,蚁群算法具有较快的局部收敛性能,结合两者的特性设计了一种混合算法,建立了一种解决单配送中心车辆路径问题的数学模型,利用混合算法进行求解。
3、对解决多配送中心车辆路径问题的传统方法、整体法以及优化算法进行实现,重点探讨了时间窗约束的多配送中心车辆路径问题,建立了最小运送费用的数学模型;针对该问题,设计了解决时间窗约束的多配送中心车辆路径问题的优化算法;采用该算法对问题进行求解,验证了优化算法在解决时间窗约束的多配送中心车辆路径问题的有效性。
4、采用MGIS应用平台,将单配送中心问题、多配送中心问题以及时间窗约束的多配送中心问题进行系统集成;设计并实现了面向企业物流和军事物流的配送系统。
带同时取货和送货的车辆路径优化问题研究的开题报告

带同时取货和送货的车辆路径优化问题研究的开题报告一、选题背景近年来,随着物流业的飞速发展,越来越多的企业、机构和个人需要及时高效地完成货物的送货和取货任务。
然而,由于路线规划和配送安排等问题的存在,常常导致运输成本高、时间长、效率低等问题。
因此,如何优化带同时取货和送货的车辆路径成为了当前物流领域中需要解决的难题之一。
二、研究内容本课题旨在研究带同时取货和送货的车辆路径优化问题,探索如何通过合理的路线规划和配送安排,较大幅度地降低物流成本,提高配送效率。
具体研究内容包括:1. 对目前常用的车辆路径规划算法进行调研、分析和评价,找出其中的优缺点;2. 设计出适用于同时取货和送货的车辆路径规划模型,并根据实际场景进行建模,考虑各种因素的影响;3. 基于已有算法和模型,对所设计出的车辆路径规划模型进行仿真分析,评估其在不同条件下的优化效果;4. 利用Matlab、Python等计算机编程工具,开发出带同时取货和送货的车辆路径规划系统,实现自动化优化路径规划;5. 结合实际情况,对该系统进行实地应用,通过实际效果的检验和分析,进一步提升系统的优化性能。
三、研究意义本研究对于解决现代物流领域中的车辆路径规划问题具有一定的理论研究与实践应用价值,具体体现在以下几个方面:1. 浅析常见的车辆路径规划算法,找出其优缺点,为后期的模型设计和算法选择提供重要参考;2. 设计适用于同时取货和送货的车辆路径规划模型,考虑实际情况中的复杂性与不确定性,提高模型的适应性和可用性;3. 利用数值仿真等手段对模型进行分析和评估,寻找出较好的路径规划方案,为实际系统开发和使用提供支撑;4. 设计开发出带同时取货和送货的车辆路径规划系统,实现自动化控制和管理,进一步提高物流配送效率和成本控制能力。
综上所述,本研究将对现代物流领域中的车辆路径规划问题作出一定的贡献,有助于提升物流行业的发展和进步。
物流配送中的路径规划算法研究

物流配送中的路径规划算法研究一、引言物流配送在现代社会中起着至关重要的作用。
随着电子商务的蓬勃发展,物流配送的效率和准确性成为了企业竞争力的重要因素之一。
而路径规划算法作为物流配送过程中的核心技术之一,能够提高配送效率、降低成本、增加服务质量。
本文将对物流配送中的路径规划算法进行综述和研究。
二、物流配送中的路径规划算法概述路径规划算法是指根据一定的约束条件,在多个地点之间找到最优路径的方法。
在物流配送中,目标是使得总的运输时间和成本最小化,同时满足各项约束条件,如车辆容量限制、时间窗口限制等。
常见的路径规划算法包括启发式算法、遗传算法、模拟退火算法等。
下面将对这些算法进行详细介绍。
三、启发式算法启发式算法是一种基于经验和直觉的计算方法,通过逐步搜索解空间来寻找较优解的方法。
其中,最著名的启发式算法是迪杰斯特拉算法。
该算法根据节点之间的距离和路径长度,逐步更新各节点的最短路径,并最终找到最短路径。
迪杰斯特拉算法适用于结点数较少和路径长度较短的问题,但对于大规模物流配送问题来说显得力不从心。
四、遗传算法遗传算法是一种基于生物遗传学的优化方法。
该算法通过模拟自然选择、交叉和变异等操作来搜索解空间。
在物流配送中,遗传算法可以通过基因表示路线,并通过对个体的适应度评估和选择来提供更好的解决方案。
遗传算法能够在一定程度上避免陷入局部最优解,但其计算复杂度较高,需要大量的计算资源和时间。
五、模拟退火算法模拟退火算法是一种通过模拟金属冷却过程找到最优解的方法。
该算法通过接受较差解的概率来避免陷入局部最优解,从而提高全局搜索能力。
在物流配送中,模拟退火算法可以通过控制参数的温度和降温速度来在整个解空间中搜索较优解。
然而,模拟退火算法对初始解的依赖性较强,可能陷入局部最优解。
六、综合算法为了充分利用各种算法的优点,研究者们将多种算法进行综合,提出了一系列综合算法。
例如遗传算法和模拟退火算法相结合的遗传模拟退火算法,可以充分利用两种算法的优点,并通过参数调整来平衡两种算法的贡献。
同时送取货的随机旅行时间车辆路径问题研究的开题报告

同时送取货的随机旅行时间车辆路径问题研究的开题报告一、研究背景随着电商和物流产业的快速发展,物流配送的效率和质量成为了越来越被重视的问题。
同时,随机旅行时间车辆路径问题(VRPTW)在物流配送领域中也日益受到关注,该问题的目的是在给定的一组配送地点和时间窗口内,寻找最优的车辆路径来满足配送要求。
在实际操作中,VRPTW 还面临着其他问题,例如货物的拉货和卸货时间以及车辆库存限制等问题。
为了优化物流配送的效率和质量,以及解决VRPTW所面临的种种问题,研究者们提出了各种各样的方法和算法。
但是,很少有研究关注将同步取送货这一要求纳入VRPTW问题中,即一个车辆需要在不同地点同时取货和送货。
因此,本研究旨在利用启发式算法研究同时送取货的VRPTW问题,以优化物流配送效率和质量。
二、研究目的本研究的主要目的是探索同时送取货的VRPTW问题,通过研究和比较不同启发式算法的表现,找到一种有效的优化方法,以提高物流配送的效率和质量。
具体目标如下:1. 提出一种能够同时考虑送货和取货的VRPTW问题的数学模型。
2. 设计和实现不同启发式算法,并对其进行评估和比较。
3. 分析和比较不同算法的优缺点,并提出改进方案。
4. 对问题的求解进行实验验证,以验证算法模型的有效性和可行性,并寻求进一步优化的空间。
三、研究内容本文将分以下几个方面进行研究:1. 同时送取货的VRPTW问题的数学模型在本研究中,我们将采用基于插入的启发式算法(Insertion-Based Heuristics)来解决VRPTW问题。
在这种启发式方法中,需要先将配送点按某种规则插入到路径中,然后逐步调整路径,以寻找最优路径。
为了考虑同时送取货情况,我们需要对现有的VRPTW问题的数学模型进行改进。
2. 算法的设计与实现为了解决此问题,我们将设计和实现多种启发式算法,包括基本的贪心算法、改进的启发式算法和元启发式算法。
我们将使用Python等编程语言实现这些算法,并对其性能和效果进行评估和比较。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
可能会导致不必要 的车辆被使用 , 因此可 以通过将在客户处 的
所不同 的是 , 在
中, 客户
节点 既 具 有 送 货 需 求 (
) , 也 具 有 取 货 需 求
就原材料 的再循环率 、 产 品包装 的 回收, 甚 至产品全部 生命周
期( 包 括义务进 行产 品使用 期结 束后 的 回收 ) , 对 工业 界提 出
一
(
) 。两种需求 的大小都 不超 过车 辆 的容量 , 当
送货和取货两种操作同时进 行来 避免 这种情况 的发生 。另外 ,
受环境保护意识的影响 , 许多实 际问题 中, 顾客具有送货 、 取货
两种需求 , 考虑到操作 的复杂程度 , 他们 可能不会 接受两 种需
求被分开服务 , 而 同时执行 送货 、 取货 两种服务 可 以在很 大程 度上减少这种操作复杂度 , 因此顾客要求 只能被服务一次 。以 上 问题 的解决 归结 为求解 同时送 取货 车辆 路 径 问题 (
第 2期
王科峰 , 等: 同时送取 货车 辆路 径 问题 算 法研 究综述
・ 3 3 5・
而是呈现不规则 变化 。所 以 V R P S D P解 的负 载能力 可行性 控 制是 区别 于 V R P求解 的难 点所 在。 V R P S D P在现 实生 活 中 也广 泛 存 在。例 如 , 在 饮 料 工 业
车辆服务客户 的时候 , 同时执行送 货 、 取货两 种操作从 而保证 每个客户 只被服务一次 。其 目标是最小化总的行驶路径长度 。 正如上文所述 , 中客户节点 具有发货 、 收货两种 需求 , 中那样 单调 变化 ,
) ; 高等 学校 博士 . ) ; 叶春 明( . ),
,
) 。
为 了尽量减少废弃物的排放 , 使用过 的商品在它们生命周 期结束的时候可 以被部分 或全部 回收 、 拆卸、 组装得 以重新使 用 。此外 , 包装 和装载设备也可 以再循环使用 。许多 国家 已经
一
最早是 由
u 在
年提 出的 , 它 是经典
的
个变种 。但是与经典
效 的混合 算法如 量子行 为粒 子群 算法 。 关键 词 :车辆路 径 问题 ;同时送取货 ; 精 确算 法 ; 构造 型启发 式算 法 ; 现代 启发 式算 法 ; 并行 算法
中图分类 号 :
: . .
;
.
.
一 .
文献标 志码 :
. .
文章 编号 :
一
(
) 一
一
一
.
YE
-
。
一
(.
,
,
r
,
&
,
,
; .
&
,
)
:
(
) .
, ‘
:
,
,
,
一
一
,
,
,
,
‘
,
,
,
一
一
_
:
;
;
;
;
;
引言
随着人们对环境问题给予越来越多的关注 , 关于要求私营 企业保护环境的法律条文相继地增加 , 而减少废物 的排放量和 能源的消耗成为相关法律 规定 的两 个主要 内容 。由于能源消
个标准 的车辆路径 问题 (
收稿 日期 :
点 基 金 资 助 项 目(
) 。但是分 开执行正 向、 逆 向操作
一 -
- 一 ;修 回 日期 :
基金项 目:国家教育部人文社会科 学规 划基金 资助 项 目(
)
) ; 河 南 省 自然科 学基 金 资 助 项 目(
系列强制性 的要求 。所有 这些活 动导致 了原材料从 终端 客 如果将正 向和逆 向物 流分开考 虑 , 对 于每一个 方 向, 是一
户 回溯 到 上 游 供 应 链 的流 动 。
并且一辆 车对节点 的服务 只能一次性完成 , 这 就导致 车辆在访 问这些节点 的过程 中的负载并 不是 像
作者简介 : 王科峰 (
度、 智能算法.
- ) , 女, 河南安 阳人 , 博士研究生, 主要研 究方向为车辆路 径优化、 物流 系统优化 (
男, 安徽 宣城人 , 副院长, 教授 , 博导 , 主要研究方向为工业工程 、 供应链 管理 ; 李永林(
- ) , 男, 山东青 岛人 , 博士研 究生, 主要研 究方 向为 生产调
中, 空瓶 必 须 被 回收 ; 在杂货店 , 特 制 的托 盘 或 容 器 可 重 复 使用
采用分支 切割算法求解 问题 效果 的好坏 与割平 面的选取
和加入时机 、 分支策略选择 、 节点选择 、 割池管理等 因素都有很
大 的 关 系 。Mi t c h e l l 求 解
组合优化 问题 的技巧 。L y s g a a r d等人 针对 V R P提 出了一 系 列割平面 的划分算法 , 同时对所采用分支切割算法 的诸要素进 行了讨论 。文献 [ 5 ] 中的割平 面包 括 r o u n d e d c a p a c i t y i n e q u a l i —
昂 .
年
昂 z删
月
丌 井 b肚 川 研 九
●
同时送 取 货 车辆 路径 问题 算 法研 究综 述 术
王科峰 , 叶春明 , 李永林
(. 上海理 工 大学 管理 学院 , 上 海 摘 ;. 河 南理 工 大学 能 源科 学与 工程 学院 , 河 南 焦作 )
要 :针对 同时送 取货 车辆路 径 问题 的研 究算 法进行 了评述 。将该 问题 的求解 方法分 为精 确 算法 、 构 造 型启 算 法研 究在 节点 具有 双重需 求车辆路 径 问题理 论研 究方 面
发式 、 现代 启发 式 以及 并行 算法 四个 大类。从 算法 的原理 、 性能、 适 用环境 , 以及 算 法之 间差异 性 等 方 面对各 类 算 法进 行 了较为 全面 的介绍 。最后 , 说明了
的 意义 , 并提 出未来 算法研 究的 两个发展 方 向 , 即适合 多处理 器上运行 的并 行现代 启发 式算 法 , 以及有
