定积分的应用本科毕业论文开题报告
定积分在几何学上的应用研究报告

8 2a 3
2 sin2 udu
0
0
4 3a 3
8 2a 3
1 2
2
6 3a 3
第六章 定积分的应用
16
说明:Vy 也可按柱壳法求出
Vy
2a 2 xydx 2 2 a t sin t
0
0
a2 1 cost 2 dt
8 a3
2 0
t
sint
sin4 t dt 2
16 a3 2u 0
23
例 13 求阿基米德螺线 a a 0相应于0 2 一段的弧长。
解:
弧长元素为
从而,所求弧长
ds 2 2 d
a 2 2 a 2d a 1 2d
s 2 a 1 2d 0
a
2
1 2
1 2
ln
1
2
2 0
a
2
2
1 4 2
ln
2
1
4 2
第六章 定积分的应用
x t y t
给出时,按顺时针方向规定起点和终点的参数值t1 和t2 。
Y
t 1
对应
x
a
Y a
O
bX
O
a
bX
则曲边梯形面积 A
t2
t1
t t dt
t1 对应x b
第六章 定积分的应用
5
例 求由摆线x a t sint ,y a 1 cost a 0 的一拱与x 轴所围
s b 1 y 2dx b 1 f 2 x dx
a
a
第六章 定积分的应用
20
2.曲线弧由参数方程
x y
t t
t
给出
弧长元素(即弧微分)为ds 2 t 2 t dt ,因此
定积分的应用本科毕业论文开题报告

定积分的应用本科毕业论文开题报告一、选题的性质二、选题的目的和意义选题目的:定积分作为函数的一种特定总和式的极限,是数学知识的重要基础。
通过典型问题,从不同角度,对定积分的特点进行整体把握,探讨定积分在几何学、物理学、以及经济学中的应用,加强对定积分思想的认识,提供用定积分分析解决实际问题的方法。
选题意义:定积分是与应用联系发展起来的,是微积分中的一个重要基本概念,是从实际问题中抽象出来的数学概念,是解决许多实际问题的工具。
在数学方面如求解复杂图形,求数列极限,证明不等式等;而在物理方面,正是由于定积分的产生与发展,才使得物理学中的精确计算成为可能,从而使物理学得到长足的发展,如:气象、弹道的计算,人造卫星轨迹的计算,运动状态的分析等,都要用的到积分;把定积分应用到经济管理学中,可以使一些经济现象更明确,使管理更科学化。
三、与本课题相关的国内外研究现状,预计可能有所创新的方面研究现状:牛顿,莱布尼茨以无穷思想为据,从不同的角度运用了定积分的思想方法创立了微积分,在这新的领域上定积分的思想和方法展现出了勃勃生机,为定积分思想的进一步完善奠定了坚实的基础。
定积分理论的建立,使数学摆脱了许多与无穷有关的悖论和困扰,对于培养人的思维方法,提高分析、解决问题方面有极好的促进作用。
定积分作为微积分的重要组成部分,在几何、物理、经济等方面有着广泛的应用,目前,探究定积分应用的文章非常之多,研究范围也是相当广泛的。
在几何学方面,可以用来计算平面图形面积,立体、旋转体的体积,弧长等;在物理学方面,压力、引力,变力做工,运动轨迹的计算,运动状态分析等也都用到定积分知识;在经济学方面可以用来解决消费过剩,收入流等实际问题。
也正是因为这些应用,推动着积分学的不断发展和完善。
预计创新方面:通过典型例题,从定积分的公式、性质及定积分中值定理出发,来介绍定积分在几何、物理、经济等领域的应用,在前人的基础上对定积分的典型应用进行研究讨论,寻找简单的用定积分解决实际问题的方法。
试论定积分在物理及其他领域的应用

试论定积分在物理及其他领域的应用定积分是微积分中的重要内容,它在物理及其他领域的应用也非常广泛。
在物理学中,定积分被用来描述物体的质量、位置、速度和加速度等物理量。
在工程、经济学和生物学等领域,定积分也有着重要的应用。
本文将重点讨论定积分在物理及其他领域的具体应用。
我们来看一下定积分在物理学中的应用。
在牛顿的运动定律中,质点的位移与质点的速度成正比。
如果我们要求一个质点在某段时间内的位移,我们就需要对质点的速度进行定积分。
即位移等于速度对时间的定积分。
通过定积分,我们可以得到在某段时间内物体的实际位移。
接着,定积分还可以用来求解力的做功。
在物理学中,力对物体做功可表示为力在位移方向上的分量乘以位移。
通过对力在位移方向上的分量进行定积分,我们可以求得力对物体所做的总功。
这在热力学和动力学的研究中非常重要。
定积分还可以用来描述物体的质心位置。
质心是一个物体所有质点的平均位置,其坐标可以通过对物体的质量分布进行定积分来求解。
定积分可以用来计算物体在不同形状和密度分布下的质心位置。
这对于物体的平衡和运动学特性的分析非常重要。
除了物理学,定积分在工程中的应用也非常广泛。
在建筑工程中,定积分可以用来计算墙体的承重能力,来确定弯曲蒙皮板的形状,以及计算电梯的负载能力等。
在土木工程中,定积分可以用来计算建筑物的重力中心位置,来确定建筑物的结构设计。
在电子工程中,定积分可以用来描述电路中的电流、电压和功率等物理量的变化。
通过对电路中电压或电流随时间的变化进行定积分,我们可以得到电路中的能量变化情况。
这对于电路设计和能源管理非常重要。
在计算机科学中,定积分可以用来描述算法的时间复杂度和空间复杂度。
我们可以通过对算法的执行时间随问题规模的变化进行定积分来求解算法的时间复杂度。
这对于选择合适的算法来解决特定的问题非常重要。
在生物学和医学领域,定积分可以用来描述生物体内物质的扩散和传播过程。
在医学影像学中,定积分可以用来对人体组织中的病变进行定量分析,来帮助医生诊断疾病。
本科数学专业论文开题报告完整模板
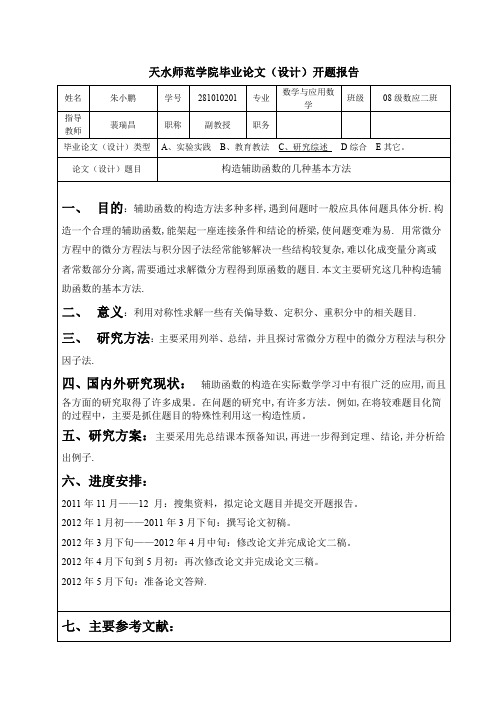
二、 意义:利用对称性求解一些有关偏导数、定积分、重积分中的相关题目. 三、 研究方法:主要采用列举、总结,并且探讨常微分方程中的微分方程法与积分
因子法.
四、国内外研究现状:
辅助函数的构造在实际数学学习中有很广泛的应用,而且
各方面的研究取得了许多成果。在问题的研究中,有许多方法。例如,在将较难题目化简 的过程中,主要是抓住题目的特殊性利用这一构造性质。
五、研究方案:主要采用先总结课本预备知识,再进一步得到定理、结论,并分析给
出例子.
六、进度安排:
天水师范学院本科生毕业论文评定表
作者姓名 二级学院 论文题目 英文名称 论文字数 关 键 词 外文 ordinary differential equation; original function; auxiliary function 本文首先列举出了构造辅助函数的几种较常见的方法,然后重点 介绍了微分方程法与积分因子法构造辅助函数的过程.通过比较 摘 中文 说明用常微分方程中的方法构造辅助函数的可取性和重要性,相 对来说,这是一种具有一定规律可循, 可解决更为一般的命题的方 法. This paper lists several common method of constructing auxiliary function at the first. And then focuses on the process of the differential equation method and the integral factor method of constructing auxiliary functions. By comparison, using the method of ordinary differential equations explained the desirability and importance of constructed the auxiliary function. Relatively speaking, it has some certain rules to follow, and to solve more general propositions.. 指导教师评定 中文 朱小鹏 性别 男 专业 学号 281010201 数学与应用数学
试论定积分在物理及其他领域的应用

试论定积分在物理及其他领域的应用定积分是微积分的一个重要概念,它在物理以及其他领域有着广泛的应用。
在物理学中,定积分可以用来描述物体的质量、速度、加速度、工作以及能量等物理量,同时还可以解决曲线下的面积、体积、质心、惯性矩等问题。
在其他领域,定积分也被广泛应用,如经济学、生物学、工程学等等。
接下来,我们将就定积分在物理及其他领域的应用展开探讨。
我们来看定积分在物理学中的应用。
在物理学中,物体的质量可以通过定积分来描述。
如果一个物体的密度是一个关于空间位置的函数,那么它的质量可以通过对密度函数在整个空间范围内进行定积分来计算。
具体地,如果我们有一个密度函数ρ(x, y, z),那么物体的总质量可以使用以下定积分来表示:\[m = \iiint\limits_{V} \rho(x, y, z) dV\]V表示物体所占据的空间区域,ρ(x, y, z)表示密度函数,dV表示体积元素。
通过对密度函数进行积分,我们可以得到该物体的总质量。
定积分还可以用来描述物体的速度和加速度。
在物理学中,速度可以通过位置函数对时间的导数来描述,而加速度则可以通过速度函数对时间的导数来描述。
在实际问题中,我们有时会遇到需要求解物体在某个时间段内的位移、速度、加速度等问题。
这时,我们可以通过对位置、速度、加速度等函数在给定时间段内进行定积分来求解。
如果我们想要求解一个物体在时间t1到t2内的位移,可以通过对物体的速度函数在这个时间段内进行定积分来求解。
在物理学中,定积分还可以用来描述物体受到的力所做的功。
根据牛顿第二定律,物体所受的合外力等于物体的质量乘以加速度。
当物体受到力的作用而沿着一条曲线运动时,这个力所做的功可以通过对力在位移方向上的投影进行定积分来求解。
具体地,假设物体沿着曲线C从点A移动到点B,力F在C上的投影为f,位移为ds,则力所做的功可以表示为:\[W = \int_C f \cdot ds\]上述是定积分在物理学中的一些应用,下面我们来看定积分在其他领域的应用。
试论定积分在物理及其他领域的应用

试论定积分在物理及其他领域的应用1. 引言1.1 定积分的基本概念定积分是微积分的一个重要概念,它在数学中有着广泛的应用。
定积分的基本概念可以简单地理解为一个函数在一定区间内的累积效果。
在几何学中,定积分可以用来计算曲线下面积,图形的面积和体积等问题。
在数学上,定积分可以看作是不定积分的反运算,通过定积分我们可以求解函数的定积分值。
在实际应用中,定积分被广泛运用于物理、工程、经济等领域。
它的应用使得复杂问题的计算变得简单清晰。
通过定积分,我们可以计算出物体的质量、力的大小、功的大小等物理量。
在力学中,定积分可以用来描述物体的运动规律,计算出物体的位置、速度和加速度等。
在电磁学中,定积分常常用来计算电场强度、磁场强度等问题。
在热力学中,定积分可以用来计算热量、熵等热力学量。
在工程学中,定积分可以帮助工程师计算出工程设计中的各种参数。
在经济学中,定积分在求解供求关系、成本、收益等问题上起着重要作用。
定积分在各个领域中都有着重要的应用价值。
它的基本概念对于理解定积分的应用具有重要意义。
通过深入研究定积分的基本概念,可以更好地理解其在不同领域中的具体应用。
1.2 定积分在物理领域的重要性定积分在物理领域的重要性体现在多个方面,首先在力学中,定积分可以用来描述物体的质量、速度、加速度、力和能量等物理量随时间的变化,从而帮助解决力学中的各种问题。
在电磁学中,定积分可以用来描述电流、电荷、电场、磁场等物理量在空间中的分布和变化规律,从而帮助解决电磁学中的各种问题。
在热力学中,定积分可以用来描述热量、温度、熵等热力学量在空间中的分布和变化规律,从而帮助解决热力学中的各种问题。
在工程学和经济学中,定积分也有着重要的应用,可以用来描述工程和经济系统中的各种物理量的变化规律,从而帮助解决工程和经济学中的各种问题。
定积分在物理领域中的重要性不可忽视,它为我们理解和应用物理定律提供了重要的数学工具和方法。
2. 正文2.1 定积分在力学中的应用在力学中,定积分是一个非常重要的数学工具,它可以用来描述物体在运动过程中的各种性质和运动规律。
定积分的应用

定积分的应用定积分是微积分中的重要内容之一,经常被应用于实际问题的解决中。
本文将从三个方面来论述定积分的应用。
一、定积分在几何中的应用首先,定积分可以用于求曲线下面的面积。
以 y=f(x) 为例,若f(x)>0,则曲线 y=f(x) 与 x 轴的两点 a、b 组成的图形的面积为S=∫baf(x)dx这时,可以将曲线 y=f(x) 分成许多小块,每块宽度为Δx,高度为 f(xi),从而可以得到其面积为ΔS=f(xi)Δx因此,当Δx 趋于 0 时,所有小块的面积之和就等于图形的面积,即∑ΔS→S因此,用定积分就可以求出图形的面积。
其次,定积分还可以用于求旋转体的体积。
以曲线 y=f(x) 在 x 轴上旋转360°为例,其体积为V=π∫baf(x)^2dx这里,π为圆周率。
最后,定积分还可以用于求某些奇特图形的长、面积等等。
二、定积分在物理中的应用物理中也有许多问题可以通过定积分来解决。
比如,运动问题中的速度、加速度,可以通过位移的变化来求得。
若某运动物体的速度为 v(t),则其位移 s(t) 为s(t)=∫v(t)dt同样,若某运动物体的加速度为 a(t),速度为 v(t),则其位移为s(t)=∫v(t)dt=∫a(t)dt最后,定积分还可以用于求密度、质量等物理量。
三、定积分在工程中的应用定积分在工程中的应用也非常广泛。
比如,在流体力学中,对于一条管道中的液体,可以通过惯性和重力等因素,求出其中液体的流量和压力。
而这些流量和压力可以通过定积分计算得出。
在电学中,电量、电荷、电流和电势等都可以通过定积分来求解。
在结构设计中,定积分也常常被用来计算约束力、杠杆比例等。
总之,定积分在几何、物理和工程等领域中都有着广泛应用。
熟练地掌握定积分的方法和应用,对于科学研究和实际问题的解决都有着非常积极的帮助。
定积分的数值计算方法开题报告

毕业论文开题报告信息与计算科学 定积分的数值计算方法一、选题的背景、意义在科学与工程计算中,经常要计算定积分()()().baI f f x dx a b =-∞≤≤≤∞⎰ (1.1)这个积分的计算似乎很简单,只要求出f 的原函数F 就可以得出积分(1.1)的值,即()()().I f F b F a =- (1.2)如果原函数F 非常简单又便于使用,那么式(1.2)就提供了计算起来最快的积分法.但是,积分过程往往将导出新的超越函数,例如,简单积分1dx x ⎰可引出对数函数,它已不是代数函数了;而积分2x edx -⎰,将引出一个无法用有限个代数运算、对数运算或指数运算组合表示的函数.有些积分虽然容易求解,并且原函数仍然是一个初等函数,但可能过于复杂,以致于人们采用(1.2)来计算之前还得三思而行[1].例如2421)11dx C x x =++-⎰ (1.3) 采用式(1.3)这种“精确”表达式时,所需运算次数是个根本问题.由式(1.3)看出,需计算对数和反正切,因此只能计算到一定的近似程度.因此可以看出,这类表面上是“精确”的方法,实际上也是近似的.因此,我们常常需要探讨一些近似计算定积分的数值方法[2].通过人们的研究和发现,得出了很多数值计算的方法,比如利用牛顿-科茨求积公式,复合求积公式,龙贝格积分法,高斯求积公式,切比雪夫求积法等来解决定积分的数值计算问题.构造数值积分公式最通常的方法是用积分区间上的n 次插值多项式代替被积函数,由此导出的求积公式称为插值型求积公式.特别在节点分布等距的情形称为牛顿-柯茨公式,例如梯形公式与抛物线公式就是最基本的近似公式.但它们的精度较差.龙贝格算法是在区间逐次分半过程中,对梯形公式的近似值进行加权平均获得准确程度较高的积分近似值的一种方法,它具有公式简练、计算结果准确、使用方便、稳定性好等优点,因此在等距情形宜采用龙贝格求积公式.当用不等距节点进行计算时,常用高斯型求积公式计算,它在节点数目相同情况下,准确程度较高,稳定性好,而且还可以计算无穷积分[3].二、研究的基本内容与拟解决的主要问题 2.1 牛顿-科茨求积公式[4]2.1.1 公式的一般形式[4]将积分(1.1)中的积分区间[],a b 分成n 等分,其节点k x 为1,()k x a kh h b a n=+=- (0,1,,)k n =.对于给定的函数f ,在节点k x (0,1,,)k n =上的值()k f x 为已知.那么f 在n+1个节点01,,,n x x x 上的n 次代数插值多项式为00()().n nj n k k j k j j k x x p x f x x x ==≠⎡⎤-⎢⎥=⎢⎥-⎢⎥⎣⎦∑∏ 如果记x a th =+,则上式可以写为00()().n nn k k j j k t j p x f x k j ==≠⎡⎤-⎢⎥=⎢⎥-⎢⎥⎣⎦∑∏ (2.1)在积分(1.1)中的被积函数f 用其n+1个节点的代数插值多项式()n p x 来代替,可得 ()()()()bbn n aaI f f x dx I f p x dx =≈=⎰⎰.多项式的积分是容易求出的,因此把上式写为()()()nn n k k I f I f A f x =≈=∑, (2.2)其中 ()00(),n n n k k j j kb a t j A dt b ac n k j=≠--==--∏⎰ (2.3) ()00(1)().!()!n kn n n kj j kct j dt k n k n -=≠-=--∏⎰ (2.4) 公式(2.2)称为牛顿-科茨求积公式或称为等距节点求积公式,k A 称为求积公式系数,()n k c 称为科茨求积系数.2.1.2 梯形公式[5]在牛顿-科茨公式(2.2)中,取n=1时(1)(1)011,2c c ==所以有 []1()()()().2b aI f I f f a f b -≈=+ (2.5) 公式(2.5)称为梯形公式,如果用连接(),()a f a 和(),()b f b 的直线来逼近f ,并对这线性函数进行积分可得到1()I f .再用1()I f 来逼近()I f . 2.1.3 辛普森公式[6]在牛顿-科茨公式(2.2)中,取n=2,则有 220011(1)(2),46c t t dt =--=⎰ 221014(2),26c t t dt =--=⎰222011(1),46c t t dt =-=⎰ 有此得到2()()()4()().32h a b I f I f f a f f b +⎡⎤≈=++⎢⎥⎣⎦(2.6)其中1()2h b a =-.式(2.6)称为辛普森公式.2.2 复化求积公式[7]上面已经给出了计算积分()()baI f f x dx =⎰的3个基本的求积公式:梯形公式,辛普森公式,牛顿-科茨公式,并给出了它们误差的表达式.由这些表达式可知其截断误差依赖于求积区间的长度.若积分区间的长度是小量的话,则这些求积公式的截断误差是该长度的高阶小量.但若积分区间的长度比较大,直接使用这些公式,则精度难以保证.为了提高计算积分的精度,可把积分区间分为若干个小区间,()I f 等于这些小区间上的积分和,然后对每个小区间上的积分应用上述求积公式,并把每个小区间上的结果累加,所得到的求积公式称为复化求积公式.将积分区间[],a b 作n 等分,并记,,0,1,,k b ah x a kh k n n-==+=,于是2.2.1 复化梯形求积公式[8]如果需要求出一个已知函数()f x 在一个很大区间[],a b 上的积分,那么我们可以把区间分成n 个长度为x h ∆=的小区间,对每一个小区间用梯形法则,然后再把这些小区间上的积分值相加.于是就得到了计算定积分的复化梯形公式:1101210()()(222)22n bi i n n ai h hf x dx f f f f f f f -+-=≈+=+++++∑⎰(2.7)11()()k kn x x k I f f x dx +-==∑⎰.2.2.2 复化辛普森求积公式[9]对于积分()baf x dx ⎰,将[],a b 等分,每个小区间长度b ah n-=,节点记为 (0,1,2,,)k x a kh k n =+=,第k 个小区间记为[]1,(1,2,,)k k x x k n -=.记[]1,k k x x -的中点为1121()2k k k xx x --=+,则复化辛普森公式为 1112()()()4()()6n bk k ak k h f x dx S h f x f x f x --=⎡⎤≈=++⎢⎥⎣⎦∑⎰.2.3 龙贝格积分[10]现在要介绍用龙贝格(Romberg )命名的一个算法,龙贝格首先给出了这种算法的递推形式,假设需要积分()baI f x dx =⎰ (2.8)的近似值.在讨论过程中函数()f x 和区间[],a b 将保持不变.2.3.1 递推梯形法则[10]设()T n 表示在长度是()/h b a n =-的n 个子区间上积分I 的梯形法则.根据()''()nbai f x dx h f a ih =≈+∑⎰,我们有 00()()''()''()nn n i i b a b a T h f a ih f a i n n ==--=+=+∑∑, (2.9) 这里求和符号中的两撇表示和式中第一项和最后一项减半. 2.3.2 龙贝格算法[10]在龙贝格算法中使用上述公式.设(,0)R n 表示具有2n个子区间的梯形估计,我们有[]1211(0,0)()()()21(,0)(1,0)((21))2n n n i R b a f a f b R n R n hf a i h -=⎧=-+⎪⎪⎨⎪=-++-⎪⎩∑ , (2.10) 对于一个适度的M 值,计算(0,0),(1,0),(2,0),,(,0)R R R R M ,并且其中没有重复的函数值的计算.在龙贝格算法的其余部分中,还要计算附加值(,)R n m .所有这些都可以被理解为积分I 的估计.计算出(,0)R M 后,不再需要被积函数f 值的计算.根据公式[]1(,)(,1)(,1)(1,1)41mR n m R n m R n m R n m =-+-----, (2.11) 对于1n ≥和1m ≥构造R 阵列的各列.2.4高斯求积[11]前面研究的求积公式都是事先确定了n 个节点,然后按使求积公式阶数达到最大的原 则选取最佳权.由于自由参数为n 个,所以阶数一般为n-1,但如果节点的位置也自由选择,则自由参数的个数将变为2n ,因此求积公式的阶数可达到2n-1.高斯求积公式就是通过选择最佳的节点和权,使求积公式的阶数最大化.一般地,对每个n ,n 点高斯公式都是唯一的,而且阶数为2n-1.因而,对一定的节点个数,高斯求积公式的精度是最高的.但它的求得比牛顿—柯特斯公式要困难得多.虽然它的节点和权也可由待定系数法确定,但得到的方程是非线性的.2.4.1 高斯求积公式[11]为说明高斯求积公式,推导区间[]1,1-上的两点公式1112221()()()()()I f f x dx w f x w f x G f -=≈+=⎰,其中的节点1x 、2x 及权1w 、2w 按使求积公式阶数最大化的原则选取.令公式对前四个单项式精确成立,得力矩方程组112111122112221122113331122112,0,2,30.w w dx w x w x xdx w x w x x dx w x w x x dx ----⎧+==⎪⎪+==⎪⎪⎨⎪+==⎪⎪+==⎪⎩⎰⎰⎰⎰这个非线性方程组的一个解为12121,1,x x w w =-===另一个解可通过改变1x ,2x 的符号而得到.这样,两点高斯求积公式为2()(G f f f =-+,阶数为3.另外,高斯求积公式的节点也可以由正交多项式得到.若p 是n 次多项式,且满足()0,0,,1,bk ap x x dx k n ==-⎰则p 与[],a b 区间上所有次数小于n 的多项式正交,容易证明:1. p 的n 个零点都是实的、单的,且位于开区间(,)a b .2. 区间[],a b 上以p 的零点为节点的n 点插值型求积公式的阶数为2n-1,是唯一的n 点高斯公式.定义2.2[12] 如果1n +个节点的求积公式()()()nbk k ak x f x dx A f x ρ=≈∑⎰(2.14)的代数精度达到21n +,则称式(2.14)为高斯型求积公式,此时称节点k x 为高斯点,系数k A 称为高斯系数.高斯求积公式其最主要的还是研究一些较常用的求积公式,如: 高斯—勒让德(Gauss-Legendre )公式, 高斯—和米特求积公式(Gauss-Hermite ), 高斯—切比雪夫(Gauss-Chebyshev )求积公式.2.5 拟解决的主要问题 1.总结常用的数值积分方法. 2. 区分各种方法的不同点和优缺点.三、研究的方法与技术路线、研究难点,预期达到的目标1.研究方法及技术路线本论文主要以查找资料为主,以现有的知识水平,在前人的研究论述基础上,再进行整理.采取了从阅读已有的数据资料,然后对这些内容进行总结,最后运用相关知识来研究定积分的数值计算方法的技术路线. 2.研究难点(1).关于定积分的数值计算的方法比较多,每种方法的公式很多,要理清和掌握每个公式的用处是一个难点.(2).数值计算的算法很多,每种算法都有其自己的特点,只知其然不知其所以然是一个难点.(3).在前人的基础上,对论题的创新和延伸是一个难点.3.预期达到的目标本次毕业论文通过定积分的数值计算方法的研究,熟悉数值积分的基本思想和原理,能了解数值计算的各种方法,掌握每种方法的原理,熟悉各种计算方法的计算公式及其性质.以及它们的误差估计,同时了解如何借用Matlab对数值计算方法进行编程实现.也掌握参考文献资料查找方法和论文写作的基本要求和方法,培养自己利用所学知识分析和解决问题的能力,从而达到对所学知识融会贯通的能力.四、论文详细工作进度和安排第7学期11周(2010年11月15号)至第7学期12周(2010年11月28号)查阅文献,收集信息、材料并进行加工整理,形成系统材料.第7学期13周(2010年11月29号)至第7学期15周(2010年12月19号)研读文献,完成文献综述、开题报告和外文翻译的初稿.第7学期16周(2010年12月20号)至第7学期17周(2010年12月31号)完成文献综述、开题报告和外文翻译,交指导老师.第7学期18周(2011年1月4号)至第8学期3周(2011年3月11号)完成论文初稿,并通过审核.第8学期4周(2011年3月14号)至第8学期10周(2011年4月29号)1、进入实习单位进行毕业实习,对论文进行修改;2、5月3日前必须返校,完成毕业实习返校,并递交毕业实习报告.第8学期11周(2011年5月3号)至第8学期12周(2011年5月12号)进一步完善直至完成毕业论文,交指导教师.第8学期12周(2011年5月13号)至第8学期13周(2011年5月19号)1、毕业论文评阅,只有通过评审的毕业论文方可参加毕业论文答辩;2、撰写答辩提纲,制作答辩PPT.第8学期14周(2011年5月23号)至第8学期15周(2011年6月3日)完成第一轮论文答辩.第8学期15周(2011年6月4日)至第8学期16周(2011年6月12日)1、6月5日至6月10日第二轮答辩;2、教务处于6月7日至6月12日随机抽取部分毕业论文进行校级答辩.五、主要参考文献:[1] 孙志忠,吴宏伟,袁慰平,闻震初.计算方法与实习(第4版)[M].南京:东南大学出版社,2009,(2): 128~129.[2]Micheal T.Heath.张威,贺华,冷爱萍译.科学计算导论(第2版)[M].北京:清华大学出版社,2005,(10):396~297.[3]李桂成.计算方法[M].北京:电子工业出版社,2005,(10):186.[4] 现代应用数学手册编委会.现代应用数学手册——计算与数值分析卷[M].北京:清华大学出版社,2005,(1): 163~168.[5] 林成森.数值计算方法(上)[M].北京:科学出版社,2004,(5): 220~221.[6]冯康.数值计算方法[M].北京:国防工业出版社,1978,(12): 45~47.[7]孙志忠,袁慰平,闻震初.数值分析(第2版)[M].南京:东南大学出版社,2002,(1): 191~194.[8] (美)柯蒂斯F.杰拉尔德帕特里克O.惠特莱.应用数值分析(第7版)[M].北京:机械工业出版社,2006,(8):222~225.[9]夏爱生,胡宝安,孙利民,夏凌辉.复化Simpson数值求积公式的外推算法[J].军事交通学院学报.2006,第8卷(第1期): 66~68.[10](美)David Kincaid, Ward Cheney .王国荣,俞耀明,徐兆亮译.数值分析(原书第三版)[M].北京:机械工业出版社,2005,(9):400~403.[11]M.T.Heath. Scientific Computing:An Introductory Survey, Sscond Edition[M].清华大学出版社.英文影印版. 2001,(10): 351~355.[12]封建湖,车刚明,聂玉.数值分析原理[M].北京:科学出版社,2001,(9):111~114.。
定积分的意义及其在几何中的应用

定西师范高等专科学校本科毕业论文(设计)题目:定积分的意义及其在几何中的应用学院兰州大学数学与统计学院专业数学应用班级 09数学教育二班学号 **********姓名蔡兴盛指导教师王宾国兰州大学教务处制二O一二年三月定积分的意义及其在几何中应用定积分在大学数学中起着非常重要的作用,是大学数学的基础,在我们的生活中也起着很重要的作用!内容摘要: 一直以来定积分问题就是大学数学学习的重点,也是本科及研究生入学考试重点考察的内容之一,所以本文对定积分的起源、发展以及它在数学、几何学的应用做了重点研究。
幷利用一些例题对这些问题做除了详细解析。
关键词: 定积分 柯西 微分 方程 几何一、定积分的概念 1.1定积分的定义一般地,设函数()f x 在区间[,]a b 上连续,用分点0121i i n a x x x x x x b -=<<<<<<<=将区间[,]a b 等分成n 个小区间,每个小区间长度为x ∆(b ax n-∆=),在每个小区间[]1,i i x x -上取一点()1,2,,i i n ξ=,作和式:11()()n nn i i i i b aS f x f nξξ==-=∆=∑∑如果x ∆无限接近于0(亦即n →+∞)时,上述和式n S 无限趋近于常数S ,那么称该常数S 为函数()f x 在区间[,]a b 上的定积分.记为:()baS f x dx =⎰其中()f x 成为被积函数,x 叫做积分变量,[,]a b 为积分区间,b 积分上限,a 积分下限.说明:(1)定积分()ba f x dx ⎰是一个常数,即n S 无限趋近的常数S (n →+∞时)称为()baf x dx ⎰,而不是n S .(2)用定义求定积分的一般方法是: ①分割:n 等分区间[],a b ; ②近似代替:取点[]1,i i i x x ξ-∈; ③求和:1()ni i b af nξ=-∑; ④取极限:()1()lim nbi an i b af x dx f nξ→∞=-=∑⎰(3)曲边图形面积:()baS f x dx =⎰;变速运动路程21()t t S v t dt =⎰;变力做功 ()baW F r dr =⎰1.2定积分的几何意义如果在区间[,]a b 上函数连续且恒有()0f x ≥,那么定积分()baf x dx ⎰表示由直线,x a x b ==(a b ≠),0y =和曲线()y f x =所围成的曲边梯形的面积.说明:一般情况下,定积分()ba f x dx ⎰的几何意义是介于x 轴、函数()f x 的图形以及直线,x a x b ==之间各部分面积的代数和,在x 轴上方的面积取正号,在x 轴下方的面积去负号.分析:一般的,设被积函数()y f x =,若()y f x =在[,]a b 上可取负值. 考察和式()()()12()i n f x x f x x f x x f x x ∆+∆++∆++∆不妨设1(),(),,()0i i n f x f x f x +<于是和式即为()()()121(){[()][]}i i n f x x f x x f x x f x x f x x -∆+∆++∆--∆++-∆()b af x dx ∴=⎰阴影A 的面积—阴影B 的面积(即x 轴上方面积减x 轴下方的面积)1.3定积分的性质性质1 a b dx ba -=⎰1性质2 ⎰⎰=bab adx x f k dx x kf )()( (其中k 是不为0的常数) (定积分的线性性质)性质3 1212[()()]()()b b baaaf x f x dx f x dx f x dx ±=±⎰⎰⎰ (定积分的线性性质)性质4 ()()()b c baacf x dx f x dx f x dx =+⎰⎰⎰ (其中a<c<b )1.4用定积分求解简单的问题 1.4.1 求立体图形的体积用类似求图形面积的思想我们也可以求一个立体图形的体积,常见的已知几何体的截面积求几何体的体积,另一种是求旋转体的体积,解此类题常用的方法是我们将此物体划分成许多基本的小块,每块的厚度为)(x σ,假设每一个基本的小块横截面积为A (x ),则此小块的体积是A(x))(x σ,将所有的小块加起来,另0)(→x σ,我们可以得到其体积v=lim ∑==bx a x x x A )()(σ其中 a 和 b 分别为计算体积的起始值和终了值. 下面来看几个例题例1 求椭圆面1222222=++cz b y a x 所围立体的体积解:以平面0x x =a x ≤0()截椭球面,得椭圆在YOZ 平面上的正投影1)1()1(22222222=-+-ax c z ax b y所以截面面积函数为)1()(22a x bc x A -=π []a a x ,-∈于是求得椭球体积abc dx ax bc v aa ππ34)1(22=-=⎰-显然当c b a ===r 时,就等于球的体积334r π1.4.2定积分在初等数学里的应用近些年来,定积分还越来越多的被广泛应用到初等数学中的一些问题上来,下面来讨论一下定积分在证明不等式,等式和一些数列的极限的方面的应用一、证明不等式运用积分来证明不等式,一般要利用到积分的如下性质:设)(x f 与)(x g 都在[]b a 上可积且)()(x g x f ≤;则⎰⎰≤babax g dx x f )()(特别的当0)(≡x f 时,有0)(≥⎰badx x g例2 证明贝努利不等式 已知1->x 且N n x ∈≠0且2≥n求证:nx x n +≥+1)1(证明:若01<<-x 或110<+<x 且2≥n 时,1)1(1<+-n x 。
定积分的计算方法研究毕业论文

定积分的计算方法研究毕业论文
一、研究背景
积分作为一种货币形式存在,可以用在零售、旅游、金融、教育等行
业领域,支持企业客户的关系管理和客户价值增长。
企业积分计算方法不
仅可以帮助企业构建客户的长期关系,还可以保持企业的竞争力,并赋予
客户价值。
近年来,各行各业均采用积分计算方法。
随着科技的发展和技
术的进步,企业的积分计算方法也发生了很大的变化,这也体现在企业积
分计算方法的实现上。
企业积分系统的研究有助于提高企业客户关系的管
理效率,提高客户满意度,实现客户管理的长期发展目标。
二、研究内容
1、确定企业积分计算方法的发展状况。
企业积分计算方法是根据客户实际情况确定的,一般包括客户的属性、行为、环境、关系等。
企业可以考虑采用多种计算方法,比如购买、贡献、参与、奖励等;也可以考虑采用多种客户定位方法,如投资能力、消费意
愿等来定位客户,从而确定客户的积分数量。
2、研究企业积分计算方法的实现过程。
企业积分计算方法的实现过程首先要确定企业计算积分的目的,然后
确定企业积分计算的方法,接着确定企业客户的数量和分级客户的积分标准,最后对企业积分计算方法进行评价。
定积分的应用(论文)

定积分的应用中文摘要:本文简要的讨论了定积分在数学、物理学的基本应用。
数学方面包括应用定积分计算平面曲线的弧长、平面图形的面积以及立体图形的体积;物理方面包括应用定积分去求变力对物体所做的功以及求电场的场强。
此外定积分在求数列极限、证明不等式、求和以及因式分解等方面也有广泛的应用;本文在阐述定积分的应用时,充分使用了“微元法”这一基本思路,它是我们解决许多实际问题的核心。
关键词:微元法 定积分 电场强度 数列极限Abstract: This paper discussed the definite integral in mathematics, physics of basic applications. Mathematics including application of definite integral calculation plane curve arc length, the plane figure of the area and volume of three-dimensional graph, Physical aspects including application of definite integral to change to the object force and the work done for electric field. Besides definite integral in the beg sequence limit, proof, inequality summation factoring decomposition and has a wide application in, Based on the expatiation of the definite integral of application, make full use of the "micro element method" the basic idea, it is we solve many practical problems at the core.Key W ords: Micro element method definite integral electric intensity sequence limit引言:恩格斯曾经指出,微积分是变量数学最重要的部分,微积分是数学的一个重要的分支,它是科学技术以及自然科学的各个分支中被广泛应用的最重要的数学工具;如复杂图形的研究,求数列极限,证明不等式等;而在物理方面的应用,可以说是定积分最重要的应用之一,正是由于定积分的产生与发展,才使得物理学中精确的测量计算成为可能,从而使物理学得到了长足的发展,如:气象、弹道的计算,人造卫星轨迹的计算,运动状态的分析等,都要用得到微积分。
定积分法求面积探究毕业论文

定积分法求面积的探究教学系:专业:年级:姓名:学号:导师及职称:摘要定积分是数学中十分重要的工具,其中求图形的面积正是它的运用之一,它的思想就是切割求和,在不同的坐标系下可采用特定的方法求解面积。
本文介绍了几种运用定积分来求面积的方法,其中列举了特殊的例题以及重要的问题解决方法。
如果实际问题中的所求量与某一区间有关且在该区间上具有可加性,我们就可以用函数的定积分来表示这个所求的量,因此我们就可以运用定积分来解决一些实际问题。
同时利用定积分求不规则平面图形的面积,是定积分在几何中的重要应用之一。
如何灵活地运用定积分的定义及有关公式,巧妙地将求不规则图形的面积问题等价转化为求定积分的数值问题就是一大关键,本文结合实例,介绍几种常用的转化方法与求解策略。
从而充分的体现数形结合的数学思想方法。
关键词:定积分;封闭图形;曲面域;对称性Research of square in definite integralABSTRACTA definite integral is very important mathematical tools, for which the graphics area is one of its application, its thought is to cut and, under different coordinate systems can use specific method to find the area. This paper introduces several methods of using the integral area to seek the. Which lists the specific examples and an important method to solve the problem. If practical problems for quantity with a certain interval and in the interval is additive, we can use the definite integral of a function to represent the desired amount. Therefore, we can use the definite integral to solve some practical problems.At the same time, the use of definite integrals for the irregular plane graphics area, is one of the important applications of integral in geometry. How to flexibly use definite integral is defined and the related formulae and skillfully will seek irregular graphic area equivalent transformation to calculate the numerical integral is one of key, the paper with examples, introduces several commonly used transformation method and solution strategy. In order to fully reflect the combination of the mathematical thought and method.Keywords: definite integral; closed graph; surface area; symmetry目录一、引言 (5)二、相关概念 (5)1.1 定积分的定义 (5)1.2 定积分的常用计算方法 (5)1.2.1 直接利用公式及性质计算 (5)1.2.2 利用定积分的区间可加性计算 (6)三、定积分在面积问题中的应用 (6)3.1 直角坐标系下求面积 (6)3.1.1 平面面积 (6)3.1.2 曲面面积 (9)3.2 极坐标 (10)3.3 求旋转曲面的面积 (11)四、常见方法 (10)4.1 巧选积分变量 (14)4.2 巧用对称性 (15)4.3 巧用分割计算 (15)五、结束语 (16)参考文献 (17)致 (13)一、引言积分在自然科学、工程技术、经济管理中有着广泛的应用,比如利用积分求平面图形的面积、变力做功等都是微积分中定积分的应用问题,在数学分析中占据了重要地位。
定积分在物理学中的应用 毕业论文

题目:定积分在物理学中的应用作者姓名:学号:系(院)、专业:数学与统计学院数学与应用数学指导教师姓名:指导教师职称:2012年2月18日摘要定积分是高等数学的重要组成部分,在物理学中也有广泛的应用。
微元法是将物理问题抽象成定积分非常实用的方法。
本文主要通过利用“微元法”的思想求变力做功、水压力、引力和转动惯量等物理问题,说明微元法关键是在局部是建立微元表达式,从而将所求物理问题转化为定积分。
关键词:定积分;物理应用;微元法ABSTRACTThe integral is an important part of higher mathematics, they are widely used in physics. The differential method is a practical method that physical problems are abstracted integral .This paper mainly study the use of differential method, for example, the acting of variable force, water pressure, gravity and so on. It is important that established local and then changed the physical problem into integral.Keywords: integral; physics application; differential method目录1.引言 (1)2.定积分在物理学中的应用举例 (1)2.1变力做功 (1)2.2 抽水做功 (3)2.3液体的压力 (4)2.4引力问题 (6)2.5转动惯量 (7)3.结束语 (10)参考文献 (111)致谢 (11)定积分在物理学中的应用1.引言在物理学中,善于应用定积分解决实际问题是很重要的。
关于定积分的几类数值解法应用 开题报告

3.参考文献∶
[1]李雨. 几类微分方程高阶数值积分法的理论分高考数学导数试题解题研究[D].云南师范大学,2017.
[7]高雪芬. 一元微积分概念教学的设计研究[D].华东师范大学,2013.
[8]代群. 几类分数阶微分方程和方程组解的结构研究[D].吉林大学,2011.
[3]卫蒙. 关于高考中导数与定积分考查内容的研究[D].西北大学,2016.
[4]胡鹏.高数教学中数值积分公式的介绍与应用[J].大学教育,2015(06):69-70.
[5]宋顺利. 两类非线性分数阶微分方程的数值解法[D].哈尔滨工业大学,2014.
[6]刘姣. 基于高职学生职业发展的数学知识技能与相关信息技术研究[D].华东师范大学,2014.
2.选题意义
数学的发展由于定积分的出现得到了极大的促进,但也极大地促进了天文学、力学、物理学、化学、生物学、工程学、经济学等自然科学以及应用科学各个分支的发展。在这些学科中有越来越广泛的应用,特别是计算机的出现更有助于这些学科的发展不断向纵深前进。研究定积分的用法以及最优的数值计算方法对于实际问题具有现实意义,不仅是解决眼前的问题,使复杂的问题变得简单计算,更是对应用问题发展的推动,让科学的思想科学的计算方法不断带领我们取得更长远的进步。在几何意义上,数值计算方法的运用可以将实际的曲线转化成相应的梯形、矩形抛物线进行精确计算求解;在概率意义上,数值计算方法的运用可以以平均值法、“类矩形”Monte-Carlo法以及“类梯形”Monte-Carlo法求得定积分的近似值;在学校教学意义上,数值计算方法的实际教学可以让学生获得良好的教育,掌握定积分解决实际问题的方法,提高自身能力,为将来走向社会打下良好基础;对于学生,可以让学生学有所思,学有所用,用有所长,引导学生用不同的方法解决问题,实现一个有知识储备、能应对复杂问题并解决问题的复合型人才的目标,满足社会经济发展的需要,还有利于学生自我创新意识的发展,在解决实际问题过程中将学习的理论知识应用于现实问题中,在活用数学知识的同时对定积分有更深刻的理解与认识。
定积分不等式开题报告

课题的主要内容:
1 预备知识
2 含定积分的不等式的证明方法
2.1利用定积分的定义来证明定积分不等式
2.2利用定积分的性质来证明定积分不等式
2.3利用积分中值定理和拉格朗日中值定理来证明定积分不等式
文[1]-[2]涉及到利用定积分的定义和性质以及凸函数的性质证明含定积分的不等式证明的内容,文[3]-[10]也涉及到证明含定积分的不等式的各种方法,包括利用定义、利用性质、利用积分中值和拉格朗日中值定理、利用分部积分、构造辅助函数、利用泰勒定理、利用定积分柯西--希瓦茨不等式、利用函数的凹凸性法、利用二重积分,但都比较分散,缺乏系统性,难以找到规律.
[3]任丽萍.定积分不等式的证明方法[J].高等数学研究,2007,10(6):14—16.
[4]杨凡.定积分中不等式的证明[J].天津成人高等学校联合学报,2001,3(3):72—74.
[5]李小平,赵旭波.定积分不等式几种典型证法[J].高等数学研究,2009,12(6):13—17.
[6]崔雅莉.定积分与不等式证明[J].赤峰学院学报(科学教育版),2011,3(8)170—171.
2.4利用分部积分法来证明定积分不等式
2.5构造辅助函数来证明定积分不等式
2.6利用泰勒定理证明定积分不等式
2.7利用定积分柯西---希瓦茨不等式证明定积分不等式
2.8利用函数的凹凸性来证明定积分不等式
2.9利用二重积分证明定积分不等式
研究方法:
研究的方法是文献研究法—根据含定积分的不等式这个课题,通过学习数学分析、常微分方程等教材,在网络上查阅大量关于含定积分的不等式的文章,初步了解含定积分的不等式证明方法和历史背景及现状.在此基础上调查相关文献,请教老师和同学,分析整理材料,从而系统全面地归纳总结出含定积分的不等式的证明方法.
定积分在物理学中的应用论文

摘要:定积分是高等数学的重要组成部分,在物理学中也有广泛的应用。
微元法是将物理学问题抽象成定积分非常实用的方法。
本文主要利用“微元法”的思想求变速直线运动,变力做功等物理问题。
关键词:定积分;物理应用;微元法。
1.引言: 32.定积分定义: 33.定积分在物理学中的应用举例 53.1变速直线运动的路程 53.2变力作功 53.3引力问题 64.结束语:75.参考文献76.致谢71.引言:在物理学中,善于应用定积分解决实际问题是很重要的。
定积分的物理应用关键在于对微元法有一个充分的理解和认识,进而求出变速直线运动,变力作功等物理问题。
2.定积分定义:设函数f(x) 在区间[a,b]上连续,将区间[a,b]分成n个子区间[a,x0],(x0,x1],(x1,x2],…,(xi,b],可知各区间的长度依次是:△x1=X0-a,△x2=X1-x0,…,△xi=b-xi.在每个子区间(xi-1,xi)任取一点ξi(i=1,2,…,n),作和式(见右下图),设λ=max{△x1,△x2,…,△xi}(即λ属于最大的区间长度),则当λ→0时,该和式无限接近于某个常数,这个常数叫做函数f(x) 在区间[a,b]的定积分,记作 badxxf)(。
其中a 与 b叫做积分下限与积分上限,区间[a,b] 叫做积分区间,函数f(x) 叫做被积函数,x 叫做积分变量,f(x)dx 叫做被积式。
3.定积分在物理学中的应用举例3.1变速直线运动的路程设某物体做直线运动,已知速度v=v(t)是时间间隔【1T ,2T 】上t 的连续函数,且v(t)>=0,计算在这段时间内物体经过的路程。
(路程=速度×时间)在时间间隔【1T ,2T 】内任意插入若干个分点2101......T t t t T n =<<<=,把【1T ,2T 】分成n 个小时段],],......[,[],,[12110n n t t t t t t -, 各小时段时间的长依次为Δ011t t t -=,......Δ1--=n n n t t t 。
试论定积分在物理及其他领域的应用

试论定积分在物理及其他领域的应用定积分是微积分中的一个重要概念,它在物理及其他领域中有着广泛的应用。
在物理学中,定积分的应用可以帮助我们解决各种复杂的实际问题,比如计算物体的质心、计算密度分布的质量、计算电场与磁场的功率等。
在其他领域,定积分也被广泛应用于各种领域,比如经济学、生物学和工程学等。
本文将就定积分在物理及其他领域的应用进行更详细的探讨。
一、定积分在物理学中的应用1. 计算物体的质心物理学中,质心是一个非常重要的概念,它表示一个物体整体的平均位置。
利用定积分的方法,我们可以求得任意形状的物体的质心。
一个均匀细杆,利用定积分可以轻松求得其质心位置。
这对于工程设计或者物体平衡问题都具有重要的意义。
2. 计算密度分布的质量在物理学中,经常需要根据密度分布来计算物体的质量。
利用定积分,我们可以求得密度分布在空间中的质量总量。
这在研究天体物理学或者地球物理学等方面有着非常重要的应用。
3. 计算电场与磁场的功率在电磁学中,电场与磁场的功率计算经常需要用到定积分。
当分布的电荷或者电流密度不均匀时,可以利用定积分来计算电场与磁场的功率。
这对于电路设计或者电动机性能分析等方面都具有着非常重要的应用。
二、定积分在其他领域的应用1. 宏观经济学在宏观经济学中,定积分可以用来描述生产总值、就业率、通货膨胀率等经济指标的变化趋势。
通过对这些指标的定积分分析,可以更好地理解宏观经济运行的规律性,并为制定经济政策提供依据。
2. 生物学在生物学领域,定积分可以被应用于描述生物体内各种物质的浓度变化趋势,比如代谢产物在细胞内的扩散过程等。
定积分也可以用来描述生物体的生长规律以及种群数量的动态变化过程。
3. 工程学在工程学中,定积分是一个非常重要的工具,可以用来计算工程设计中各种复杂形状的物体的体积、质量、重心位置等物理量。
在建筑工程中,可以利用定积分来计算建筑结构的重心位置,以便施工和设计过程中的平衡和稳定性分析。
以上只是定积分在物理及其他领域中部分应用的介绍。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选题的性质
二、选题的目的和意义
选题目的:定积分作为函数的一种特定总和式的极限,是数学知识的重要基础。通过典型问题,从不同角度,对定积分的特点进行整体把握,探讨定积分在几何学、物理学、以及经济学中的应用,加强对定积分思想的认识,提供用定积分分析解决实际问题的方法
。
选题意义:定积分是与应用联系发展起来的,是微积分中的一个重要基本概念,是从实际问题中抽象出来的数学概念,是解决许多实际问题的工具。
预计创新方面:通过典型例题,从定积分的公式、性质及定积分中值定理出发,来介绍定积分在几何、物理、经济等领域的应用,在前人的基础上对定积分的典型应用进行研究讨论,寻找简单的用定积分解决实际问题的方法。
四、课题研究的可行性分析
定积分是函数的一种特定总和式的极限,是数学知识的基础,对定积分的一些公式、性质、定积分中值定理已有深刻的理解,通过常见的定积分例题,从不同角度分析、研究定积分的特点,更容易把握和理解。再看近几年的几何、物理,经济等方面的研究,尤其是几何学,定积分在这些研究中扮演着相当重要的角色,而事实也证明定积分的思想确实给相关研究带来很大的方便。所以研究好定积分不单是数学界的问题,更是整个学术界共同的任务。而对其分析研究的结果也必将给以后各方面的课题研究带来意想不到的便捷之处。
五、课题研究的策略、方法和步骤
研究方法:运用文献分析法、文本细读法、比较法、综合分析法等进行研究。
研究的策略和步骤:
首先,了解本论题的研究状况,形成文献综述和开题报告。
其次,进一步搜集阅读资料并研读文本,做好相关记录,形成论题纲要。
第三,深入研究,写成初稿。
最后,反复修改,完成定稿。
六、预期成果形式描述
在数学方面如求解复杂图形,求数列极限,证明不等式等;而在物理方面,正是由于定积分的产生与发展,才使得物理学中的精确计算成为可能,从而使物理学得到长足的发展,如:气象、弹道的计算,人造卫星轨迹的计算,运动状态的分析等,都要用的到积分;把定积分应用到经济管理学中,可以使一些经济现象更明确,使管理更科学化。
通过这次论文撰写深刻认识定积分的重要地位和广泛应用,从不同角度对定积分的特点进行整体把握,对定积分在几何、物理、经济中典型和应用最多的几个方面进行研究分析,并进行总结归纳。
七、指导教师意见
指导教师(签名):
年 月 日
八、学院学位分委员会意见
学院学位分委员会主任(签名或盖章):
年 月 日
