《现代控制理论》试题

合集下载

现代控制理论试卷答案3套

现代控制理论试卷 1一、(10分)判断以下结论，若是正确的，则在括号里打√，反之打×(1)用独立变量描述的系统状态向量的维数是唯一。

（）(2)线性定常系统经过非奇异线性变换后，系统的能观性不变。

（）(3)若一个系统是李雅普诺夫意义下稳定的，则该系统在任意平衡状态处都是稳定的。

（）(4)状态反馈不改变被控系统的能控性和能观测性。

（）(5)通过全维状态观测器引入状态反馈来任意配置系统的闭环极点时，要求系统必须同时能控和能观的。

（）二、（12分）已知系统1001010,(0)00121x x x⎛⎫⎛⎫⎪ ⎪==⎪ ⎪⎪ ⎪⎝⎭⎝⎭，求()x t.三、(12分) 考虑由下式确定的系统：2s+2(s)=43Ws s++，求其状态空间实现的能控标准型和对角线标准型。

四、（9分）已知系统[]210020,011003x x y⎡⎤⎢⎥==⎢⎥⎢⎥-⎣⎦，判定该系统是否完全能观？五、(17分) 判断下列系统的能控性、能观性；叙述李亚普诺夫稳定性的充要条件并分析下面系统的稳定性.[]xy u x x 11103211=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=六、（17分）已知子系统1∑ 111121011x x u -⎡⎤⎡⎤=+⎢⎥⎢⎥-⎣⎦⎣⎦，[]1110y x = 2∑ []22222110,01011x x u y x -⎡⎤⎡⎤=+=⎢⎥⎢⎥-⎣⎦⎣⎦求出串联后系统的状态模型和传递函数.七、（15分）确定使系统2001020240021a x x u b -⎡⎤⎡⎤⎢⎥⎢⎥=-+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦为完全能控时，待定参数的取值范围。

八、（8分）已知非线性系统 ⎩⎨⎧--=+-=2112211sin 2x a x xx x x试求系统的平衡点，并确定出可以保证系统大范围渐近稳定的1a 的范围。

现代控制理论试卷 1参考答案一、(10分)判断以下结论，若是正确的，则在括号里打√，反之打× (1) 用独立变量描述的系统状态向量的维数是唯一。

现代控制理论考试题及答案

答案及评分标准一，填空（3分每空，共15分）1．输出变量 2.变量的个数最少 3.⎥⎦⎤⎢⎣⎡2001 4. 其状态空间最小实现为u x x ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=100001100010 ； u x y 2102121+⎥⎦⎤⎢⎣⎡= 5. 0,021==x x二，选择题（3分每题，共12分） 1.B 2.D 3.B 4.C三，判断题（3分每题，共12分）1.2. √3.4. √四，简答题（共23分）1.（5分）解判定系统11221223x x x x x x =-+⎧⎨=--⎩在原点的稳定性。

解 2114523I A λλλλλ+--==+++，两个特征根均具有负实部，（3分）系统大范围一致渐近稳定。

（2分）无大范围扣一分，无一致渐近扣一分。

2. （5分）11b ab b -⎛⎫⎪--⎝⎭能控性矩阵为（2分）1 rank 211det 1b ab b b ab b -⎛⎫= ⎪--⎝⎭-⎛⎫⇔ ⎪--⎝⎭210b ab =-+-≠ （5分）3.（8分）在零初始条件下进行拉式变换得：)()(2)()()(2)(3)(223S U S SU S U S S Y S SY S Y S S Y S ++=+++12312)()()(232+++++==∴S S S S S S U S Y S G （4分）[]XY U X X 121100321100010.=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=∴ （8分）4.(5分)解：[]B CS G A SI --=1)( （2分）2342+--=S S S （5分）五，计算题1. 1210c u ⎡⎤=⎢⎥⎣⎦，1112201c u -⎡⎤=⎢⎥-⎣⎦能控性矩阵满秩，所以系统能化成能控标准型。

（2分）[][][]1111221122010101c p u -⎡⎤===-⎢⎥-⎣⎦[][]11112122221100p p A ⎡⎤==-=⎢⎥⎣⎦11221112211,11P P --⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦（10分）能控标准型为u x x ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=101010..（12分） 2. 解：11][)(---==A SI L e t At φ (２分)⎥⎦⎤⎢⎣⎡+-+---=-==----------t t tt t t tt Ate e ee e e e e A SI L e t 3232323211326623][)(φ (8分) ∴系统零初态响应为 X(t)=0,34121)(32320)(≥⎥⎦⎤⎢⎣⎡-+-+-=-----⎰t e e e e d Bu et t t t t t A τττ (12分) 3. 解：因为能观性矩阵满秩，所以系统可观，可以设计状态观测器。

现代控制理论考试试题

现代控制理论考试试题现代控制理论考试试题一、简答题1. 什么是反馈控制系统？请简要解释其原理和作用。

反馈控制系统是一种通过测量输出信号并与期望信号进行比较，然后根据比较结果对输入信号进行调整的控制系统。

其原理是通过不断调整输入信号以使输出信号接近期望信号，从而实现对系统的控制。

反馈控制系统的作用是使系统能够自动调整，以适应外部环境的变化和内部扰动，从而提高系统的稳定性和性能。

2. 请简述PID控制器的工作原理和常见应用。

PID控制器是一种基于比例、积分和微分三个控制量的控制器。

其工作原理是根据当前的误差（偏差）信号，分别计算比例项、积分项和微分项，并将它们相加得到最终的控制量。

比例项用于根据当前误差的大小进行调整，积分项用于对累积误差进行调整，微分项用于对误差变化率进行调整。

PID控制器常见应用于工业过程控制、机器人控制、飞行器控制等领域。

3. 请解释什么是系统稳定性？如何判断一个控制系统的稳定性？系统稳定性是指系统在一定的工作条件下，输出信号始终趋于有限的范围内，不会出现无限增长或震荡的现象。

判断一个控制系统的稳定性可以通过判断系统的极点位置。

如果系统的所有极点的实部都小于零，则系统是稳定的；如果存在至少一个极点的实部大于零，则系统是不稳定的。

二、计算题1. 对于一个开环传递函数为G(s)=1/(s^2+2s+1)的系统，请计算其闭环传递函数和稳定裕度。

闭环传递函数可以通过将开环传递函数除以1加上开环传递函数得到，即H(s)=G(s)/(1+G(s))。

代入G(s)的表达式可得H(s)=1/(s^2+3s+2)。

稳定裕度是指系统的相角裕度和增益裕度。

相角裕度可以通过计算闭环传递函数在频率为零时的相位角来得到，即相角裕度=180°+arctan(0)=180°。

增益裕度可以通过计算闭环传递函数在频率为无穷大时的幅值来得到，即增益裕度=1。

2. 对于一个控制系统的状态空间表达式为dx/dt=Ax+Bu，y=Cx+Du，其中A、B、C、D分别为系统的矩阵参数，请计算该系统的传递函数。

现代控制理论试题(详细答案)

现代控制理论试题B 卷及答案一、1 系统[]210,01021x x u y x ⎡⎤⎡⎤=+=⎢⎥⎢⎥-⎣⎦⎣⎦能控的状态变量个数是cvcvx ，能观测的状态变量个数是。

2试从高阶微分方程385y y y u ++=求得系统的状态方程和输出方程（4分/个）解 1．能控的状态变量个数是2，能观测的状态变量个数是1。

状态变量个数是2。

…..（4分）2．选取状态变量1x y =，2x y =，3x y =，可得 …..….…….（1分）12233131835x x x x x x x u y x ===--+= …..….…….（1分）写成010*********x x u ⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦…..….…….（1分）[]100y x = …..….…….（1分）二、1给出线性定常系统(1)()(),()()x k Ax k Bu k y k Cx k +=+=能控的定义。

（3分）2已知系统[]210 020,011003x x y x ⎡⎤⎢⎥==⎢⎥⎢⎥-⎣⎦，判定该系统是否完全能观？(5分)解 1．答：若存在控制向量序列(),(1),,(1)u k u k u k N ++-，时系统从第k 步的状态()x k 开始，在第N 步达到零状态，即()0x N =，其中N 是大于0的有限数，那么就称此系统在第k 步上是能控的。

若对每一个k ，系统的所有状态都是能控的，就称系统是状态完全能控的，简称能控。

…..….…….（3分） 2.[][]320300020012 110-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=CA ………..……….（1分）[][]940300020012 3202=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=CA ……..……….（1分） ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=940320110 2CA CA C U O ………………..……….（1分） rank 2O U n =<，所以该系统不完全能观……..….…….（2分）三、已知系统1、2的传递函数分别为2122211(),()3232s s g s g s s s s s -+==++-+求两系统串联后系统的最小实现。

现代控制理论试卷与答案.docx

、名词解释与简答题(共3题，每小题5分，共15分)U i21 这甲 3!：:l即U['4 _3 111 02 7 ^23 -u 2⑶尖用芷養变换送求取状壽空问表込5t 对賀分产程⑶在零初Ife 条井下取拉氏娈换笹Jv(J)+ ⅛⅛(r)+3⅛ru) + 5K⅛)=5ιt⅛j)+7Γ(i) Γ⅛⅜g√⅛7LF(O =S 7Ti?+JijTS在用传诺两數求系绑的状态空何表达式IL 一定要注咸传递函JS 足百为严搐H 育瑾分SL 即■是百小于札 ⅛ffl =ri WPflTSt 理*U C1R 2 _ U 2U C 21、经典控制理论与现代控制理论的区别2、对偶原理的内容3、李雅普诺夫稳定5、已知系统的微分方程 y - 2y 3y7u。

试列写出状态空间表达式。

6、试将下列状态方程化为对角标准型或者约当标准型。

二、分析与计算题(共8小题，其中4-10小题每题10分，第11小题15分，共 85分)4、电路如图所示，设输入为U 1 ,输出为U 2 ,试自选状态变量并列写出其状态空间表达式。

麻曙秋恋爱■为J l*i ζlX i甘态空闿枝达式为 IHl IitBG 迦睾样机理分箭法，首先帳撼电踣定律则 ^ffl⅛⅛SS ・苒选澤就JS 娈■・求欄粗应的糸筑狀盃空珂舌达式B 也珂以先由电路邀求袴糸址f⅛递函 ≡,再由悟越塑救求潯系臧帝空间表达式采厢机理分护走“设G 两鋼电∣1⅛*ΓP G 两睛的电丘為越小则气 I *+ M TJ C M l⑴j Of ", ⅝+⅞c j i 1口白逐求得条统吠态△■期表込丄(刊 -13」LX3」L5ff It i.IW 1I⅛GV ∙K2 Lu试将下处伏越程化为朋融感P-I-I•-^S∣9U[-3-a 1•u≡IIZ7 4J u..,U.则猖对吊标■壯理l∣⅞^tη=Kn代入求聲公弍轉—⅛l- —<,i*2 f1 丿 1 ,j,1 ⅛'3f,-t i,rt<r-⅛* ft r2 2 2 1-r,(0J- JM(My IM MW-女"C F-3⅛"λf乩* J⅛4f丄■■i⅛,≡≡^Ll J——-一JfJOI-------- ---- X i(O)+βf- Iι7 -.∙Kl⅛ιp TΓl«期于占=-ι¾-I -L d-3 -( -2IJ Il∣2) IK：(IJ液转证追® 求4,j tf-3-3-1-2P llF l aLπIl%二i-3127J如n"Jf Ij= -3^f,A尸U1-12-41■'3 ⅛f,'=H1 -351 -21-I91-S5-21-12I35J7*5-27-Zfl -1I5 3 15J17I27JA_ 2*J22—_屯尸a371-15-27-202716HΛJ-A∣= -J Λs*^⅛r7、已知系统状态空间表达式为X -1-3 y =h:X Iu1 Ix求系统的单位阶跃响应。

现代控制理论试卷及答案-总结

、〔10分,每小题1分〕试判断以下结论的正确性,若结论是正确的, 一〔√〕1. 由一个状态空间模型可以确定惟一一个传递函数.〔√〕2. 若系统的传递函数不存在零极点对消,则其任意的一个实现均为最小实现.〔×〕 3. 对一个给定的状态空间模型,若它是状态能控的,则也一定是输出能控的.〔√〕4. 对线性定常系统x = Ax ,其Lyapunov意义下的渐近稳定性和矩阵A的特征值都具有负实部是一致的.〔√〕5.一个不稳定的系统,若其状态彻底能控,则一定可以通过状态反馈使其稳定.〔×〕 6. 对一个系统,只能选取一组状态变量；〔√〕7. 系统的状态能控性和能观性是系统的结构特性,与系统的输入和输出无关；〔×〕 8. 若传递函数G(s) = C(sI 一A)一1 B 存在零极相消,则对应的状态空间模型描述的系统是不能控且不能观的；〔×〕9. 若一个系统的某个平衡点是李雅普诺夫意义下稳定的,则该系统在任意平衡状态处都是稳定的；〔×〕 10. 状态反馈不改变系统的能控性和能观性.二、已知下图电路,以电源电压 u<t>为输入量,求以电感中的电流和电容中的电压作为状态变量的状态方程,和以电阻 R2 上的电压为输出量的输出方程.〔10 分〕解：〔1〕由电路原理得：二．〔10 分〕图为 R-L-C 电路,设u 为控制量,电感L 上的支路电流和电容 C 上的电压x 为状态变量,电容 C 上的电压x 为输出量,试求：网2 2络的状态方程和输出方程,并绘制状态变量图.解：此电路没有纯电容回路,也没有纯电感电路,因有两个储能元件, 故有独立变量.以电感 L 上的电流和电容两端的电压为状态变量 , 即令：i L = x 1 , u c = x 2,由基尔霍夫电压定律可得电压方程为： • •y y21 =-x x21+ u三、〔每小题 10 分共 40 分〕基础题〔1〕试求 y - 3y - 2y = u + u 的一个对角规 X 型的最小实现.〔10 分〕Y(s) = s 3 + 1 = (s +1)(s 2 - s +1) = s 2 - s +1 = 1+ 1+ -1 …………4 分不妨令X (s)1 = 1 ,X (s)2 = - 1 …………2 分于是有又Y(s)U(s)= 1+ X (s)1U(s)+ X (s)2U(s),所以Y(s) = U (s) + X 1 (s) + X 2 (s) , 即有y = u + x + x …………2 分1 2最终的对角规 X 型实现为则系统的一个最小实现为：=「|2 0 ]+「| 1 ]|u, y = [1 1…………2 分 U (s) s 3 - 3s - 2 (s +1)(s 2 - s - 2) s 2 - s - 2 s - 2 s + 1 L 0 -1-1」U (s) s - 2 U (s) s + 1从上述两式可解出x 1 ,x 2 ,即可得到状态空间表达式如下：〔2〕已知系统 =「| 0 1]| +「|1]|u, y = [1 -2] ,写出其对偶系统,判断该系统的能控性与其对偶系统的能观性.〔10 分〕解答：= 10 3-2+ -12 u…………………………2 分y = [1 2] ……………………………………2 分〔3〕设系统为试求系统输入为单位阶跃信号时的状态响应〔10 分〕 .解(t )=「|e-t 0 ]|L 0 e -2t 」……………………………..…….……..3 分(t) = (t )(0) + j 0t (t )u(t )d τ……….….……….……..3 分=11+ j 0t11d τ ….……..2 分=「| e-t ]| + j t 「| e -(t -t ) ]|d τL e -2t 」 0 |L e -2(t -t )」| .................................................................................... 1 分=(1- e1(1-2= 21 (1 e -2t )………………..1 分〔4〕已知系统 x =01 01x + 11u 试将其化为能控标准型.〔10 分〕「0 1 ]解： u c = 11 02 , u -c 1 =|L 21 - 21 」| ............2 分 p 1= [0 1]u -c1 = [0 1]-121= [21 - 21].…….1 分 p 2= p 1A = [21- 21]01 01= [21 21].……..1 分 L -2 3」 L 2」「 1 - 1 ] 「 1 1]P = |L 212」| ,P -1 = |L -1 1」| ....................2 分能控标准型为x =「|0 1]|x +「|0]|u........ 4 分四、设系统为试对系统进行能控性与能观测性分解,并求系统的传递函数.〔10 分〕解：能控性分解：能观测性分解：传递函数为g(s) ==(2分)五、试用李雅普诺夫第二法,判断系统 x •=「| 0 1 ]| x 的稳定性.〔10分〕方法一：解： x 1= x 2原点 x =0是系统的惟一平衡状态 .选取标准二次型函数为李雅e普诺夫函数,即当x 1 = 0 ,x 2 = 0 时, v(x) = 0 ；当x 1 丰 0 ,x 2 = 0 时,v(x) = 0 ,因此v(x) 为负半定.根据判断,可知该系统在李雅普诺夫意义下是稳定的. 另选一个李雅普诺夫函数,例如：为正定,而为负定的,且当 x ) w ,有V (x)) w .即该系统在原点处是大 X 围渐进稳定. 方法二：• • ••L -1 -1」L 0 1」 L 1」解：或者设P =则由 A T P + PA = -I 得+=可知 P 是正定的.因此系统在原点处是大 X 围渐近稳定的六、〔20 分〕线性定常系统的传函为 Y (s) = s +4U (s) (s + 2)(s +1)〔1〕实现状态反馈,将系统闭环的希翼极点配置为(-4,-3),求反馈阵K .〔5 分〕〔2〕试设计极点为(-10,-10) 全维状态观测器〔5 分〕 . 〔3〕绘制带观测器的状态反馈闭环系统的状态变量图〔4 分〕〔4〕分析闭环先后系统的能控性和能观性〔4 分〕注明：由于实现是不惟一的,本题的答案不惟一！其中一种答案为：解：〔1〕 Y (s) = s + 4 = s + 4U (s) (s + 2)(s +1) s 2 + 3s + 2系统的能控标准型实现为： X =「| 0 1 ]| X +「|0]| u, y = [4 1]X ……1 分系统彻底可控,则可以任意配置极点……1 分令状态反馈增益阵为K = [k k ]……1 分1 2则有A - BK =「| 0 1 ]|,则状态反馈闭环特征多项式为又期望的闭环极点给出的特征多项式为： (s + 4)(s + 3) = s 2+ 7s +12由入2 + (k + 3)入 + (k + 2) = s 2 + 7s +12 可得到K = [4 10]……3 分1 2〔2〕观测器的设计：L -k 2 - 2 -k 1- 3」 L -2 -3」 L 1」由传递函数可知,原系统不存在零极点相消,系统状态彻底能观,可以任意配置观测器的极点.……1 分令E = [e e ]T ……1 分1 2由观测器 = (A - EC)+ Bu + Ey 可得其期望的特征多项式为:f * (s) = f (s) 亭 E = - 311 395T ……4 分〔3〕绘制闭环系统的摹拟结构图第一种绘制方法：……4 分〔注：观测器输出端的加号和减号应去掉！不好意思, 刚发现！！〕第二种绘制方法：〔4〕闭环前系统状态彻底能控且能观,闭环后系统能控但不能观〔因为状态反馈不改变系统的能控性 ,但闭环后存在零极点对消 ,所以系统状体不彻底可观测〕……4 分A 卷-+-41 s32x 21 sx1x14+ + y10++22 - 3+ +1 s 222 - 358 -34 322 - 3 + ++1+ + - s1 4 43v u +-++++一、判断题,判断下例各题的正误,正确的打√ , 错误的打×〔每小题1 分,共10 分〕1、状态方程表达了输入引起状态变化的运动,输出方程则表达了状态引起输出变化的变换过程〔√〕2、对于给定的系统,状态变量个数和选择都不是惟一的〔×〕3、连续系统离散化都没有精确离散化,但近似离散化方法比普通离散化方法的精度高〔×〕4、系统的状态转移矩阵就是矩阵指数〔×〕5、若系统的传递函数存在零极点相消,则系统状态不彻底能控〔×〕6、状态的能空性是系统的一种结构特性,依赖于系统的结构, 与系统的参数和控制变量作用的位置有关〔√〕7、状态能控性与输出能控性之间存在必然的联系〔×〕8、一个传递函数化为状态方程后,系统的能控能观性与所选择状态变量有关〔√ 〕9、系统的内部稳定性是指系统在受到小的外界扰动后,系统状态方程解的收敛性,与输入无关〔√〕10、若不能找到合适的李雅普诺夫函数,那末表明该系统是不稳定的〔×〕二、已知系统的传递函数为试分别用以下方法写出系统的实现：(1) 串联分解(2) 并联分解(3) 直接分解(4) 能观测性规X 型〔20 分〕解：2对于s3 +10s2 + 31s + 30 有(1) 串联分解串联分解有多种,如果不将 2 分解为两个有理数的乘积,如2 = 1 8 ,绘制该系统串联分解的结4构图,然后每一个惯性环节的输出设为状态变量,则可得到系统四种典型的实现为：则对应的状态空间表达式为：需要说明的是, 当交换环节相乘的顺序时,对应地交换对应行之间对角线的元素. . 的实现为：〈0 0一311]XX + u则. .的实现为：〈0一311]XX + u挨次类推！！ (2) 并联分解实现有无数种,若实现为〈X = X + 21u只要满足y = [c L 1 c 2 c 3]2 1〔3〕直接分解〔4〕能观测规 X 型三、给定一个二维连续时间线性定常自治系统 = A , t > 0 .现知,对应于两个不同初态的状态响应分别为试据此定出系统矩阵A.〔10 分〕解： x(t) = e At x(0) 可得四、已知系统的传递函数为〔1〕试确定 a 的取值,使系统成为不能控,或者为不能观测；〔2〕在上述 a 的取值下,写出使系统为能控的状态空间表达式,判断系统的能观测性；〔3〕若a = 3 ,写出系统的一个最小实现.〔15 分〕解：〔1〕因为因此当a = 1 或者a = 2 或者a = 3 时, 浮现零极点对消现象,系统就成为不能控或者不能观测的系统〔2〕可写系统的能控标准形实现为此问答案不惟一存在零极相消,系统不能观〔3〕 a = 3 ,则有G(s) =2 3 一1 3 如例如： s 3 + 10s 2 + 31s +30 = (s + 2) + (s + 3) + (s + 5),则其实现可以为：可写出能控标准形最小实现为此问答案不惟一,可有多种解五、已知系统的状态空间表达式为〔1〕判断系统的能控性与能观测性；〔2〕若不能控,试问能控的状态变量数为多少？〔3〕试将系统按能控性进行分解；〔4〕求系统的传递函数.〔15 分〕解：〔1〕系统的能控性矩阵为U C = [b Ab ]= 10 -20, det U C = 0, rankU C = 1 < 2故系统的状态不能控系统的能观测性矩阵为「 c ] 「 2 5 ]故系统的状态不能观测 4 分〔2〕 rankU = 1 , 因此能控的状态变量数为 1C〔3〕由状态方程式可知是x 能控的, x 是不能控的2 1〔4〕系统的传递函数为1 分2 分G(s) = c (sI - A )-1 b = c (sI - A )-1 b = 5 只与能控子系统有关六、给定系统解李雅普诺夫方程,求使得系统渐近稳定的 a 值 X 围.〔10 分〕七、伺服机电的输入为电枢电压,输出是轴转角,其传递函数为〔1〕设计状态反馈控制器u = -Kx + v ,使得闭环系统的极点为-5 士 j5 ；〔2〕设计全维状态观测器,观测器具有二重极点－15；〔3〕将上述设计的反馈控制器和观测器结合,构成带观测器的反馈控制器,画出闭环系统的状态变量图；〔4〕求整个闭环系统的传递函数.〔20 分〕第二章题 A 卷第一题：判断题,判断下例各题的正误,正确的打√ ,错误的打× 〔每小题 1 分,共 10 分〕 11、状态方程表达了输入引起状态变化的运动,输出方程则表达了状态引起输出变化的变换过程〔 √〕12、对于给定的系统,状态变量个数和选择都不是惟一的〔×〕13、连续系统离散化都没有精确离散化,但近似离散化方法比普通离散化方法的精度高〔×〕3 分2 2 2s + 2U O= |L cA 」| = |L 19 -10」| , det U C = -115 丰 0, rankU O = 214、系统的状态转移矩阵就是矩阵指数〔×〕15、若系统的传递函数存在零极点相消,则系统状态不彻底能控〔×〕16、状态的能空性是系统的一种结构特性 ,依赖于系统的结构, 与系统的参数和控制变量作用的位置有关〔 √〕17、状态能控性与输出能控性之间存在必然的联系〔×〕18、一个传递函数化为状态方程后,系统的能控能观性与所选择状态变量有关〔√〕 19、系统的内部稳定性是指系统在受到小的外界扰动后,系统状态方程解的收敛性,与输入无关〔 √〕20、若不能找到合适的李雅普诺夫函数,那末表明该系统是不稳定的〔×〕第二题：已知系统的传递函数为G(s) == ,试分别用以下方法写出系统的实现：(5) 串联分解〔4 分〕 (6) 并联分解〔4 分〕 (7) 直接分解〔4 分〕 (8) 能观测性规 X 型〔4 分〕(9) 绘制串联分解实现时系统的结构图〔4 分〕解：s对于有s 3 +10s 2 + 31s + 30(3) 串联分解串联分解有三种s = s . 1 . 1 = 1 . s . 1 = 1 . 1 . s s 3 +10s 2 + 31s + 30 (s + 1) (s + 2) (s + 3) (s + 1) (s + 2) (s + 3) (s + 1) (s + 2) (s + 3) = (1)..=.(1).=.(1)对应的状态方程为：(4) 并联分解实现有无数种,其中之三为：〔3〕直接分解〔4〕能观测规 X 型 (10) 结构图第二章题 B 卷第一题：判断题,判断下例各题的正误,正确的打√ ,错误的打× 〔每小题 1 分,共 10 分〕 1、状态空间模型描述了输入-输出之间的行为,而且在任何初始条件下都能揭示系统的内部行为〔 √〕2、状态空间描述是对系统的一种彻底的描述,而传递函数则只是对系统的一种外部描述〔√〕3、任何采样周期下都可以通过近似离散化方法将连续时间系统离散化〔×〕4、对于一个线性系统来说,经过线性非奇妙状态变换后,其状态能控性不变〔 √〕5、系统状态的能控所关心的是系统的任意时刻的运动〔×〕6、能观〔能控〕性问题可以转化为能控〔能观〕性问题来处理〔√〕7、一个系统的传递函数所表示的是该系统既能控又能观的子系统〔√〕8、一个系统的传递函数若有零、极点对消现象,则视状态变量的选择不同,系统或者是不能控的Y(s) s 3 +10s 2 + 31s + 32U (s) (s 2 + 5s + 6)(s + 1)或者是不能观的〔 √〕9、对于一个给定的系统,李雅普诺夫函数是惟一的〔 ×〕 10、若系统对所有有界输入引起的零状态响应的输出是有界的,则称该系统是外部稳定的〔√〕第二题：求以下 RLC 网络系统的状态空间模型, 并绘制其结构图.取电压 e_i 为输入,e_o 为输出.其中 R 1 、R 2 、C 和 L 为常数.第二题图答案:解：〔状态变量可以另取〕定义状态变量： x 1 为电阻两端电压 v,x 2 为通过电感的电流 i.输入 u 为 e_i ,输出 y 为e_o .使用基尔霍夫电流定理列 R 1 和 R 2 间节点的电流方程：使用基尔霍夫电压定理列出包含 C 、R 2 、L 回路的电压方程：最后,输出电压的表达式为：得到状态空间模型：结构图为：第三题：如图所示,系统的输入量为 u 1 和 u 2、输出量为 y 和请选择适当的状态变量,并写出系统的状态空间表达式,根据状态空间表达式求系统的闭环传递函数：第三题图解：状态变量如下图所示〔3 分〕从方框图中可以写出状态方程和输出方程〔4〕状态方程的矩阵向量形式：系统的传递函数为〔3 分〕：. 解：由电路图可知：图1 ：RC 无源网络可得：选,,=所以可以得到：解：运用公式可得：可得传递函数为：解：先求出系统的.可得：令,X<k>+解：计算算式为：所以：解：由于 A 无特定形式,用秩判据简单.因此,不管 a 去何值都不能够联合彻底能控和彻底能观测解：〔1〕选取李雅普若夫函数V<x>,取,可知：V<0>=0,即〔2〕计算基此可知：即：〔3〕判断和出：为正定.并判断其定号性.对取定和系统状态方程,计算得到：为负半定..对此, 只需判断的不为系统状态方程的解.为此,将带入状态方程, 导表明,状态方程的解只为, 不是系统状态方程的解.通过类似分析也可以得证不是系统状态方程的解. 基此, 可知判断.〔4〕综合可知,对于给定非线性时不变系统,可构造李雅普若夫函数判断满足：V<x>为正定, 为负定；对任意,当,有基此,并根据李雅普若夫方法渐近稳定性定理知：系统原点平衡状态为大X 围渐近稳定.解：可知,系统彻底可控,可以用状态反馈进行任意极点配置. 由于状态维数为 3 维.所以设.系统期望的特征多项式为：而令,二者相应系数相等.得：5 3 ]即：验证：A 卷二、基础题〔每题 10 分〕1、给定一个二维连续时间线性定常自治系统 = A , t > 0 .现知,对应于两个不同初态的状态响应分别为试据此定出系统矩阵 A .解： x(t) = e At x(0) 2 分可得e At = 4 4「| 1 (e -t + e 3t )4 分4 e -t + 4 e 3t |「 1 -5 e -t + 3 e 3t |L -1 1 1 ] 21 (e -t + e 3t )」2 ]-1 「| 43 e -t + 41 e 3t -1」| = - 23 e -t + 21e 3t45 e -t + 43e 3t ]|「-1 - 25 e -t + 23e 3t 」 |L 1-2] 1 」| A ==-te3t14-43t =0 = 41 11 2、设线性定常连续时间系统的状态方程为取采样周期T = 1s ,试将该连续系统的状态方程离散化. 解：① 首先计算矩阵指数.采用拉氏变换法：e t = L -1 (s -)-1 = L -1〈-1= L -122)=3 分② 进而计算离散时间系统的系数矩阵.= e T =「|1 0.5 (1- e -2T )] T 「14 分0.4323] 0.1353」|2 分「3 e -t + 1 e 3t |L 0 e -2T 」|| 将T = 1s 代入得 = e = |L 0 - 4 e -t + 4 e 3t| |- 3 e -t + 1 e 3t |L 2 2 = | 2||L -e -t + e 3t2 2 」|=(j T)B =〈(|j T「|10 |l 0 |L00.5(1- e-2t)] )|「0]「0.5T + 0.25e-2T - 0.25]=|L -0.5e-2T + 0.5 」|「1.0789]= | |③故系统离散化状态方程为xx21 = xx21kk+ u (k ) 2 分3、已知系统的传递函数为〔1〕试确定a 的取值,使系统成为不能控,或者为不能观测；〔2〕在上述a 的取值下,写出使系统为能控的状态空间表达式,判断系统的能观测性；〔3〕若a = 3 ,写出系统的一个最小实现.〔10 分〕解：〔1〕因为因此当a = 1 或者a = 2 或者a = 3 时, 浮现零极点对消现象,系统就成为不能控或者不能观测的系统 3 分〔2〕可写系统的能控标准形实现为此问答案不惟一x =-x + u y =[2a 2 0]x3 分存在零极相消,系统不能观 1 分〔3〕a = 3 ,则有G(s) =可写出能控标准形最小实现为此问答案不惟一,可有多种解三、已知系统的状态空间表达式为3 分〔1〕判断系统的能控性与能观测性；〔2〕若不能控,试问能控的状态变量数为多少？〔3〕试将系统按能控性进行分解；〔4〕求系统的传递函数.〔10 分〕解：〔1〕系统的能控性矩阵为UC= [b Ab]=1-2, det UC= 0, rankUC= 1 < 23 分L0.4323」|dt卜||e-2t 」| J|L 1」故系统的状态不能控系统的能观测性矩阵为「 c ] 「 2 5 ] U O= | | = | | ,detU = -115 丰 0, rankU = 2 C O4 分〔2〕 rankU = 1 , 因此能控的状态变量数为 1 1 分 C〔3〕由状态方程式可知是x 能控的, x 是不能控的 2 分3 分B 卷二、基础题〔每题 10 分〕1、给定一个连续时间线性定常系统, 已知状态转移矩阵个(t) 为试据此定出系统矩阵 A .解：A =〈dt d(t) 卜Jt =0=t =0「 0 2 ] = | |2、设线性定常连续时间系统的状态方程为取采样周期T = 1s ,试将该连续系统的状态方程离散化.解：① 首先计算矩阵指数.采用拉氏变换法： ② 进而计算离散时间系统的系数矩阵.「 1 T ] 「1 1]= e T = |L 0 1」|将T = 1s 代入得 = e T = |L 0 1」| ③ 故系统离散化状态方程为 3、已知系统的传递函数为试写出系统的能控标准形实现.〔10 分〕解：系统的能控标准形实现为三、试确定下列系统当 p 与 q 如何取值系统既能控又能观.〔10 分〕解：系统的能控性矩阵为其行列式为 det [b Ab ]= p 2 + p - 12根据判定能控性的定理 , 若系统能控 , 则系统能控性矩阵的秩为 2,亦即行列式值不为2 1〔4〕系统的传递函数为G(s) = c (sI - A )-1 b = c (sI - A )-1 b = 5 只与能控子系统有关2 2 2s + 2L -1 -3」L cA 」 L 19 -10」故系统的状态不能观测[b Ab]= p2+ p - 12 丰00 , det因此当p 丰3,-4 时系统能控系统能观测性矩阵为其行列式为根据判定能观性的定理, 若系统能观, 则系统能观性矩阵的秩为2, 亦即「c ]det | | = 12q2 - q - 1 丰0L cA」1 1因此当q 丰, - 时系统能观3 41 1综上可知, 当p 丰3, -4 , q 丰, - 时系统既能控又能观3 4。

现代控制理论考试试题

现代控制理论考试试题（正文开始）一、选择题1.控制系统的目标是（）。

A. 提高系统的可靠性B. 提高系统的速度C. 提高系统的稳定性D. 提高系统的精度2.在控制系统中，遥感技术主要用于（）。

A. 信号传输B. 参数估计C. 故障检测D. 软件设计3.传感器的作用是（）。

A. 测量和检测B. 控制和调节C. 存储和处理D. 传输和接收4.反馈控制系统的特点是（）。

A. 没有可靠性要求B. 没有精度要求C. 具有稳定性要求D. 具有高速响应要求5.频率响应函数是指（）。

A. 系统的输出响应B. 系统的传输函数C. 系统的幅度特性D. 系统的无穷小响应二、简答题1.请解释什么是控制系统的稳定性，并给出判断系统稳定性的方法。

控制系统的稳定性是指系统在一定刺激下，输出保持有界或有限的范围内，不发生持续增长或不发散的性质。

判断系统稳定性的方法有两种：一种是通过系统的特征方程判断，如果特征方程的所有根的实部都小于零，则系统稳定；另一种是通过系统的频率响应函数判断，如果系统的幅频特性在一定频率范围内有界，则系统稳定。

2.什么是控制系统的鲁棒性？鲁棒性的提高可以通过哪些方法实现？控制系统的鲁棒性是指系统对于参数变化、扰动和不确定性的抵抗能力。

在实际应用中，由于系统中存在参数误差、外部扰动等因素，控制系统往往无法精确满足设计的要求，此时需要考虑鲁棒性。

提高鲁棒性的方法包括：采用更加鲁棒的控制器设计方法，如H∞控制、μ合成控制等；通过系统自适应、鲁棒估计等方法，对系统的参数变化进行实时估计和校正；对系统的扰动进行补偿等。

三、分析题考虑一个反馈控制系统，其开环传递函数为G(s)，闭环传递函数为T(s)，控制器的传递函数为C(s)。

1.给出控制系统的传递函数表达式。

控制系统的传递函数表达式为T(s) = G(s) / (1 + G(s)C(s))。

2.当G(s) = (s+1) / (s^2+3s+2)，C(s) = K，求控制系统的闭环传递函数表达式。

现代控制理论试题与答案

现代控制理论1.经典-现代控制区别:经典控制理论中,对一个线性定常系统,可用常微分方程或传递函数加以描述,可将某个单变量作为输出,直接和输入联系起来;现代控制理论用状态空间法分析系统,系统的动态特性用状态变量构成的一阶微分方程组描述,不再局限于输入量,输出量,误差量,为提高系统性能提供了有力的工具.可以应用于非线性,时变系统,多输入-多输出系统以及随机过程.2.实现-描述由描述系统输入-输出动态关系的运动方程式或传递函数,建立系统的状态空间表达式,这样问题叫实现问题.实现是非唯一的.3.对偶原理系统=∑1(A1,B1,C1)和=∑2(A2,B2,C2)是互为对偶的两个系统,则∑1的能控性等价于∑2的能观性, ∑1的能观性等价于∑2的能控性.或者说,若∑1是状态完全能控的(完全能观的),则∑2是状态完全能观的(完全能控的).对偶系统的传递函数矩阵互为转置4.对线性定常系统∑0=(A,B,C),状态观测器存在的充要条件是的不能观子系统为渐近稳定第一章控制系统的状态空间表达式1.状态方程:由系统状态变量构成的一阶微分方程组2.输出方程:在指定系统输出的情况下,该输出与状态变量间的函数关系式3.状态空间表达式:状态方程和输出方程总合,构成对一个系统完整动态描述4.友矩阵:主对角线上方元素均为1:最后一行元素可取任意值;其余元素均为05.非奇异变换:x=Tz,z=T-1x;z=T-1ATz+T-1Bu,y=CTz+Du.T为任意非奇异阵(变换矩阵),空间表达式非唯一6.同一系统,经非奇异变换后,特征值不变;特征多项式的系数为系统的不变量第二章控制系统状态空间表达式的解1.状态转移矩阵:eAt,记作Φ(t)2.线性定常非齐次方程的解:x(t)=Φ(t)x(0)+∫t0Φ(t-τ)Bu(τ)dτ第三章线性控制系统的能控能观性1.能控:使系统由某一初始状态x(t0),转移到指定的任一终端状态x(tf),称此状态是能控的.若系统的所有状态都是能控的,称系统是状态完全能控2.系统的能控性,取决于状态方程中系统矩阵A和控制矩阵b3.一般系统能控性充要条件:(1)在T-1B中对应于相同特征值的部分,它与每个约旦块最后一行相对应的一行元素没有全为0.(2)T-1B中对于互异特征值部分,它的各行元素没有全为0的4.在系统矩阵为约旦标准型的情况下,系统能观的充要条件是C中对应每个约旦块开头的一列的元素不全为05.约旦标准型对于状态转移矩阵的计算,可控可观性分析方便;状态反馈则化为能控标准型;状态观测器则化为能观标准型6.最小实现问题:根据给定传递函数阵求对应的状态空间表达式,其解无穷多,但其中维数最小的那个状态空间表达式是最常用的.第五章线性定常系统综合1.状态反馈:将系统的每一个状态变量乘以相应的反馈系数,然后反馈到输入端与参考输入相加形成控制律,作为受控系统的控制输入.K为r*n维状态反馈系数阵或状态反馈增益阵2.输出反馈:采用输出矢量y构成线性反馈律H为输出反馈增益阵3.从输出到状态矢量导数x的反馈:A+GC4.线性反馈:不增加新状态变量,系统开环与闭环同维,反馈增益阵都是常矩阵动态补偿器:引入一个动态子系统来改善系统性能5.(1)状态反馈不改变受控系统的能控性(2)输出反馈不改变受控系统的能控性和能观性6.极点配置问题:通过选择反馈增益阵,将闭环系统的极点恰好配置在根平面上所期望的位置,以获得所希望的动态性能(1)采用状态反馈对系统任意配置极点的充要条件是∑0完全能控(2)对完全能控的单输入-单输出系统,通过带动态补偿器的输出反馈实现极点任意配置的充要条件[1]∑0完全能控[2]动态补偿器的阶数为n-1(3)对系统用从输出到x 线性反馈实现闭环极点任意配置充要条件是完全能观 7.传递函数没有零极点对消现象,能控能观8.对完全能控的单输入-单输出系统,不能采用输出线性反馈来实现闭环系统极点的任意配置9.系统镇定:保证稳定是控制系统正常工作的必要前提,对受控系统通过反馈使其极点均具有负实部,保证系统渐近稳定 (1)对系统采用状态反馈能镇定的充要条件是其不能控子系统渐近稳定(2)对系统通过输出反馈能镇定的充要条件是其结构分解中的能控且能观子系统是输出反馈能镇定的,其余子系统是渐近稳定的(3)对系统采用输出到x 反馈实现镇定充要条件是其不能观子系统为渐近稳定10.解耦问题:寻求适当的控制规律,使输入输出相互关联的多变量系统的实现每个输出仅受相应的一个输入所控制,每个输入也仅能控制相应的一个输出11.系统解耦方法:前馈补偿器解耦和状态反馈解耦 12.全维观测器:维数和受控系统维数相同的观测器现代控制理论试题1 ①已知系统u u uy y 222++=+ ，试求其状态空间最小实现。

现代控制理论试题与答案

现代控制理论试题与答案《现代控制理论参考答案》第一章答案1-1试求图1-27系统的模拟结构图，并建立其状态空间表达式。

解：系统的模拟结构图如下：系统的状态方程如下：令，则所以，系统的状态空间表达式及输出方程表达式为1-2有电路如图1-28所示。

以电压为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻上的电压作为输出量的输出方程。

解：由图，令，输出量有电路原理可知：既得写成矢量矩阵形式为：1-4两输入，，两输出，的系统，其模拟结构图如图1-30所示，试求其状态空间表达式和传递函数阵。

解：系统的状态空间表达式如下所示：1-5系统的动态特性由下列微分方程描述列写其相应的状态空间表达式，并画出相应的模拟结构图。

解：令，则有相应的模拟结构图如下：1-6（2）已知系统传递函数,试求出系统的约旦标准型的实现，并画出相应的模拟结构图解：1-7给定下列状态空间表达式‘画出其模拟结构图求系统的传递函数解：（2）1-8求下列矩阵的特征矢量（3）解：A 的特征方程解之得：当时，解得：令得（或令，得）当时，解得：令得（或令，得）当时，解得：令得1-9将下列状态空间表达式化成约旦标准型（并联分解）（2）解：A的特征方程当时，解之得令得当时，解之得令得当时，解之得令得约旦标准型1-10已知两系统的传递函数分别为W1(s)和W2(s)试求两子系统串联联结和并联连接时，系统的传递函数阵，并讨论所得结果解：（1）串联联结（2）并联联结1-11（第3版教材）已知如图1-22所示的系统，其中子系统1、2的传递函数阵分别为求系统的闭环传递函数解：1-11（第2版教材）已知如图1-22所示的系统，其中子系统1、2的传递函数阵分别为求系统的闭环传递函数解：1-12已知差分方程为试将其用离散状态空间表达式表示，并使驱动函数u的系数b(即控制列阵)为（1）解法1：解法2：求T,使得得所以所以，状态空间表达式为第二章习题答案2-4 用三种方法计算以下矩阵指数函数。

现代控制理论试题

现代控制理论试题现代控制理论试题⼀、名词解释（15分）1、能控性2、能观性3、系统的最⼩实现4、渐近稳定性⼆、简答题（15分）1、连续时间线性时不变系统（线性定常连续系统）做线性变换时不改变系统的那些性质？2、如何判断线性定常系统的能控性？如何判断线性定常系统的能观性？3、传递函数矩阵的最⼩实现A、B、C和D的充要条件是什么？4、对于线性定常系统能够任意配置极点的充要条件是什么？5、线性定常连续系统状态观测器的存在条件是什么？三、计算题（70分）1、RC⽆源⽹络如图1所⽰，试列写出其状态⽅程和输出⽅程。

其中，为系统的两端的电压为状态变量,两端的电压为状态变量,电压为为系统的输出输⼊，选y。

23、4、求取下列各连续时间线性时不变系统的状态变量解和5、a的6、判断原点平衡状态即稳定：7、试确定⼀个状态反馈矩阵K，使闭环极点配置为,和。

现代控制理论试题答案⼀、概念题1、何为系统的能控性和能观性？答：（1）对于线性定常连续系统，若存在⼀分段连续控制向量u(t)，能在有限时间区间[t0,t1]内将系统从初始状态x(t0)转移到任意终端状态x(t1)，那么就称此状态是能控的。

（2）对于线性定常系统，在任意给定的输⼊u(t)下，能够根据输出量y(t)在有限时间区间[t0,t1]内的测量值，唯⼀地确定系统在t0时刻的初始状态x(t0 )，就称系统在t0时刻是能观测的。

若在任意初始时刻系统都能观测，则称系统是状态完全能观测的，简称能观测的。

2、何为系统的最⼩实现？答：由传递函数矩阵或相应的脉冲响应来建⽴系统的状态空间表达式的⼯作，称为实现问题。

在所有可能的实现中，维数最⼩的实现称为最⼩实现。

3、何为系统的渐近稳定性？答：若在时刻为李雅普若夫意义下的稳定，且存在不依赖于的实数和任意给定的初始状态，使得时，有，则称为李雅普若夫意义下的渐近稳定⼆、简答题1、连续时间线性时不变系统（线性定常连续系统）做线性变换时不改变系统的那些性质？答：系统做线性变换后，不改变系统的能控性、能观性，系统特征值不变、传递函数不变2、如何判断线性定常系统的能控性？如何判断线性定常系统的能观性？答：⽅法1：对n维线性定常连续系统，则系统的状态完全能控性的充分必要条件为：。

现代控制理论试卷及答案

现代控制理论试卷一、简答题（对或错，10分）（1）描述系统的状态方程不是唯一的。

（2）用独立变量描述的系统状态向量的维数不是唯一的。

（3）对单输入单输出系统，如果1()C sI A B --存在零极点对消，则系统一定不可控或者不可观测。

（4）对多输入多数出系统，如果1()sI A B --存在零极点对消，则系统一定不可控。

（5）李雅普诺夫直接法的四个判定定理中所述的条件都是充分条件。

（6）李雅普诺夫函数是正定函数，李雅普诺夫稳定性是关于系统平衡状态的稳定性。

（8）线性定常系统经过非奇异线性变换后，系统的可控性不变。

（9）用状态反馈进行系统极点配置可能会改变系统的可观测性。

（10）通过全维状态观测器引入状态反馈来任意配置系统的闭环极点时，要求系统必须同时可控和可观测。

对一个线性定常的单输入单输出5阶系统，假定系统可控可观测，通过设计输出至输入的反馈矩阵H 的参数能任意配置系统的闭环极点。

二、试求下述系统的状态转移矩阵()t Φ和系统状态方程的解x 1(t)和x 2(t)。

（15分）1122()()012()()()230x t x t u t x t x t ⎡⎤⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎣⎦12(0)0,(),0(0)1tx u t e t x -⎡⎤⎡⎤==≥⎢⎥⎢⎥⎣⎦⎣⎦ 三、设系统的传递函数为()10()(1)(2)y s u s s s s =++。

试用状态反馈方法，将闭环极点配置在－2，－1＋j ，－1－j 处，并写出闭环系统的动态方程和传递函数。

（15分）四、已知系统传递函数2()2()43Y s s U s s s +=++，试求系统可观标准型和对角标准型，并画出系统可观标准型的状态变量图。

（15分）五、已知系统的动态方程为[]211010a x x uy b x ⎧⎡⎤⎡⎤=+⎪⎢⎥⎢⎥⎨⎣⎦⎣⎦⎪=⎩，试确定a ，b 值，使系统完全可控、完全可观。

现代控制理论基础试题

现代控制理论基础试题一、选择题：1. 什么是现代控制理论的核心概念？A. 反馈原理B. 开环控制C. 传感器D. 控制算法2. 当系统的输出信号与期望的参考信号之间存在差异时，现代控制理论会采取以下哪种策略进行调节？A. 开环控制B. 闭环控制C. 反馈控制D. 前馈控制3. 现代控制系统通常包括哪些基本组成部分？A. 传感器、执行器、控制器B. 输入信号、输出信号、执行器C. 控制器、执行器、参考信号D. 反馈信号、执行器、控制器4. 现代控制理论的主要目标是什么？A. 降低系统效应B. 提高系统稳定性C. 增加系统响应速度D. 最小化系统误差5. 在现代控制系统中，传感器的作用是什么？A. 通过收集系统的反馈信息B. 将输入信号转化为输出信号C. 控制执行器的动作D. 校准控制器的参数二、填空题：6. 现代控制理论中，PID控制器中的比例、积分和微分项分别代表什么？比例项：_______积分项：_______微分项：_______7. 现代控制理论中，系统的稳定性通常通过计算系统的_________来判断。

8. 现代控制理论中，增益裕度是衡量系统稳定性的一个指标，它表示系统输出响应对增益变化的___________。

三、简答题：9. 请简述开环控制和闭环控制的区别。

10. 现代控制系统常用的传感器有哪些？请简要介绍一个传感器的工作原理。

四、分析题：11. 现代控制系统中的反馈环节起到了重要的作用，请你用一个简单的图示来说明反馈控制系统的基本结构。

12. 现代控制理论中，经典PID控制器在某些系统中可能存在不足之处。

请你简要分析当系统存在非线性或时变特性时，经典PID控制器可能出现的问题，并提出解决方案。

结束语：通过本试题，我们回顾了现代控制理论的核心概念、基本组成部分以及控制策略。

掌握现代控制理论对于工程实践具有重要的意义，它可以帮助我们设计和优化各种控制系统，提高系统的性能和稳定性。

希望通过这些试题的训练，您能够对现代控制理论有更深入的理解，并能够在实际应用中灵活运用。

《现代控制理论》期末复习试题4套含答案(大学期末复习试题)

第 1 页共 1 页西安科技大学2004—2005 学年第2 学期期末考试试题（卷）电控院系：班级：姓名：学号：装订线装订线以内不准作任何标记装订线第 2 页共 1 页现代控制理论A 卷答案 1. 解：系统的特征多项式为2221()21(1)1s f s s s s s+-==++=+其特征根为-1（二重），从定理知系统是渐近稳定的。

2 解：Bode 图略解得：开环截止频率：)/(1.2s rad c =ω；相角裕量：)(40rad r ≈3 解：1）系统的传递函数阵为：2231231))((1))()((1][)(du a s a s a s a s a s Du B A sI C s G +⎥⎦⎤⎢⎣⎡-----=+-=-第 3 页共 1 页2）系统的状态结构图，现以图中标记的321,,x x x 为u 2u 14解：1）列写电枢电压u 为输入，以电流i 和旋转速度n 为输出的状态空间表达式。

由于ω.πωn 559260==，可得dtdn J dt d J55.9=ω， 22)2(Dg G mR J ==式中， m 为一个旋转体上的一个质点的质量，质量m 为该质量的重量G 和重力加速度g 之比，R 和D 分别为旋转体的半径和直径，综合上两式可推得dtdn GD dt dn D G dt d J 37548.955.922=⨯⨯⨯=ω 2）从而可得到电机电枢回路电压平衡和电机运动平衡的一组微分方程式第 4 页共 1 页⎪⎪⎩⎪⎪⎨⎧=+=++i C n K dtdn GD u n C Ri dtdiL m b e 3752式中，摩擦系数55.9/B K b =。

选择状态变量n x i x ==21,，则系统得状态空间表达式为u L x x GD K GD C L C L R x x b me ⎥⎥⎦⎤⎢⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎦⎤⎢⎣⎡01375375212221 ⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=211001x x y5 略西安科技大学2004—2005学年第 2 学期 2 期末考试试题（卷）院系：班级：姓名：学号：装订线装订线以内不准作任何标记装订线第 6 页共 1 页现代控制理论B 卷答案：2 解：所给系统为能控标准形，特征多项式为32()det()1f s sI A s s =-=-+ 所希望的闭环系统特征多项式32()(1)(1)(1)342d f s s s j s j s s s =++-++=+++ 从而可得321134,044,121k k k =--=-=-=-=-=-故反馈增益阵k 为[][]123144k k k k ==--- 所求的状态反馈为[]144u kx v x v =+=---+该闭环系统状态方程为()v x v x bk A x +⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=++=342100010对应的结构图如题.2图所示。

现代控制理论试题(详细答案)

现代控制理论试题B 卷及答案2 1cvcvx ，一、 1 系统 x2xu, y 0 1 x 能控的状态变量个数是 0 1能观测的状态变量个数是cvcvx 。

2 试从高阶微分方程 y3y 8 y 5u 求得系统的状态方程和输出方程（4 分/ 个）解 1 ．能控的状态变量个数是 2，能观测的状态变量个数是 1。

状态变量个数是 2。

⋯ .. （4 分）2．选取状态变量 x 1y ， x 2y ， x 3y ，可得⋯ .. ⋯ . ⋯⋯ .（1 分）x 1 x 2x 2 x 3⋯.. ⋯. ⋯⋯ . （1 分）x 3 8x 1 3x 35uy x 1写成 0 1 0 0x0 0 1 x 0 u ⋯.. ⋯. ⋯⋯ . （1 分）8 035y 1 0 0 x ⋯.. ⋯. ⋯⋯ . （1 分）二、 1 给出线性定常系统 x( k 1) Ax( k) Bu( k), y(k) Cx (k) 能控的定义。

（3 分）2 1 0 2 已知系统 x0 2 0 x, y 0 1 1 x ，判定该系统是否完0 03全能观？ (5 分)解 1 ．答：若存在控制向量序列 u (k ), u(k 1), , u(k N 1) ，时系统从第k 步的状态 x(k) 开始，在第 N 步达到零状态，即 x( N ) 0 ，其中 N 是大于0 的有限数，那么就称此系统在第k 步上是能控的。

若对每一个 k ，系统的所有状态都是能控的，就称系统是状态完全能控的，简称能控。

⋯ .. ⋯. ⋯⋯ . （3 分）2.2 1 0CA 0110 2 0 0 2 3⋯⋯⋯.. ⋯⋯⋯.0 0 3（1 分）2 1 0CA20230 2 0 0 4 9 ⋯⋯.. ⋯⋯⋯.（1分）0 0 3C 0 1 1U O CA 0 2 3 ⋯⋯⋯⋯⋯⋯ .. ⋯⋯⋯ . （1 分）CA20 4 9rankU O 2 n ，所以该系统不完全能观⋯⋯ .. ⋯. ⋯⋯ .（2 分）三、已知系统 1、 2 的传递函数分别为g1 (s)s2 1 ,g2s 1 3s 2( s)3s 2 s2s2求两系统串联后系统的最小实现。

(完整版)现代控制理论试卷答案与解析

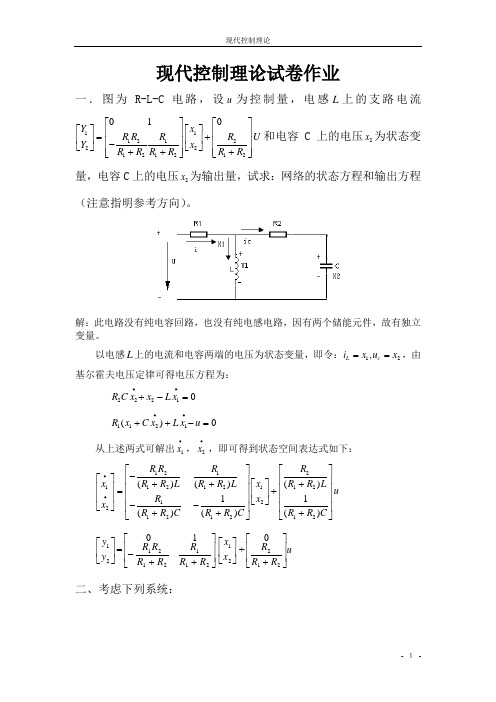
现代控制理论试卷作业一．图为R-L-C电路，设u为控制量，电感L上的支路电流11121222121212010Y xUR R R RY xR R R R R R⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦+++⎢⎥⎢⎥⎣⎦⎣⎦和电容C上的电压2x为状态变量，电容C上的电压2x为输出量，试求：网络的状态方程和输出方程（注意指明参考方向）。

解：此电路没有纯电容回路，也没有纯电感电路，因有两个储能元件，故有独立变量。

以电感L上的电流和电容两端的电压为状态变量，即令：12,L ci x u x==，由基尔霍夫电压定律可得电压方程为：2221R C x x L x••+-=1121()0R x C x L x u••++-=从上述两式可解出1x•，2x•，即可得到状态空间表达式如下：121121212()()R Rx R R LRxR R C••⎡-⎡⎤⎢+⎢⎥⎢=⎢⎥⎢-⎣⎦⎢+⎣121121221212()()11()()R RxR R L R R LuxR R C R R C⎤⎡⎤⎥⎢⎥++⎡⎤⎥⎢⎥+⎢⎥⎥⎢⎥⎣⎦-⎥⎢⎥++⎦⎣⎦⎥⎦⎤⎢⎣⎡21yy=⎥⎥⎦⎤⎢⎢⎣⎡++-21121211RRRRRRR⎥⎦⎤⎢⎣⎡21xx+uRRR⎥⎥⎦⎤⎢⎢⎣⎡+212二、考虑下列系统：（a）给出这个系统状态变量的实现；（b）可以选出参数K（或a）的某个值，使得这个实现或者丧失能控性，或者丧失能观性，或者同时消失。

解：（a）模拟结构图如下：13123312312321332133x u kx xx u kxx x x axy x x•••=--=-=+-=+则可得系统的状态空间表达式：123xxx•••⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦32-⎡⎢⎢⎢⎣112311xkk x ua x-⎡⎤⎤⎡⎤⎢⎥⎥⎢⎥-+⎢⎥⎥⎢⎥⎢⎥⎥⎢⎥-⎦⎣⎦⎣⎦[2y=1]123xxx⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦（b ）因为 3023A -⎡⎢=⎢⎢⎣ 001 k k a -⎤⎥-⎥⎥-⎦ 110b ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦302Ab -⎡⎢=⎢⎢⎣ 0013 k k a -⎤⎥-⎥⎥-⎦131001-⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦ 23023A b -⎡⎢=⎢⎢⎣ 0013 k k a -⎤⎥-⎥⎥-⎦301-⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦92k k a -⎡⎤⎢⎥=-⎢⎥⎢⎥--⎣⎦ [M b = Ab 2110A b ⎡⎢⎤=⎦⎢⎢⎣ 301- 91020k k a -⎤⎡⎥⎢-→⎥⎢⎥⎢--⎦⎣ 010 31k a -⎤⎥-⎥⎥-⎦所以：当1a =时，该系统不能控；当1a ≠时，该系统能控。

现代控制理论试题(详细答案)

现代控制理论试题B卷及答案
一、1 系统能控的状态变量个数是，能观测的状态变量个数是。
2试从高阶微分方程求得系统的状态方程和输出方程（4分/个）
解 1．能控的状态变量个数是2，能观测的状态变量个数是1。状态变量个数是2。…..（4分）
2．选取状态变量，，，可得 …..….…….（1分）
…..….…….（1分）
写成
…..….…….（1分）
…..….…….（1分）
二、1给出线性定常系统能控的定义。（3分）
2已知系统，判定该系统是否完全能观？(5分)
解 1．答：若存在控制向量序列，时系统从第步的状态开始，在第步达到零状态，即，其中是大于0的有限数，那么就称此系统在第步上是能控的。若对每一个，系统的所有状态都是能控的，就称系统是状态完全能控的，简称能控。…..….…….（3分）
设期望的特征多项式为
而能控标准型的特征多项式为
所以，状态反馈控制器增益矩阵是
（3）采用直接法来说明极点配置状态反馈控制器的设计
考虑以下系统
设计一个状态反馈控制器，使闭环系统极点为2−和−3。
该状态空间模型的能控性矩阵为
该能控性矩阵是行满秩的，所以系统能控。
设状态反馈控制器
将其代入系统状态方程中，得到闭环系统状态方程
观测器设计方法：
由于
因此，可以利用极点配置的方法来确定矩阵L，使得具有给定的观测器极点。具体的方法有：直接法、变换法、爱克曼公式。
五、（15分）对于一个连续时间线性定常系统，试叙述Lyapunov稳定性定理，并举一个二阶系统例子说明该定理的应用。
解连续时间线性时不变系统的李雅普诺夫稳定性定理：
线性时不变系统在平衡点处渐近稳定的充分必要条件是：对任意给定的对称正定矩阵Q，李雅普诺夫矩阵方程有惟一的对称正定解P。

现代控制理论期末试题及答案

现代控制理论期末试题及答案一、选择题1. 以下哪项不是现代控制理论的基本特征？A. 多变量控制B. 非线性控制C. 自适应控制D. 单变量控制答案：D. 单变量控制2. PID控制器中，P代表的是什么？A. 比例B. 积分C. 微分D. 参数答案：A. 比例3. 动态系统的状态方程通常是以什么形式表示的？A. 微分方程B. 代数方程C. 积分方程D. 线性方程答案：A. 微分方程4. 控制系统的稳定性可以通过什么分析方法来判断？A. 傅里叶变换B. 拉普拉斯变换C. 巴特沃斯准则D. 极点分布答案：C. 巴特沃斯准则5. 控制系统的性能可以通过什么指标来评估？A. 驰豫时间B. 超调量C. 峰值时间D. 准确度答案：A. 驰豫时间二、问答题1. 说明PID控制器的原理和作用。

答：PID控制器是一种常用的控制器，它由比例环节（P）、积分环节（I）和微分环节（D）组成。

比例环节根据控制误差的大小来产生控制量，积分环节用于累积控制误差并增加控制量，微分环节用于预测控制误差的变化趋势并调整控制量。

PID控制器的作用是通过调整上述三个环节的权重和参数，使得控制系统能够尽可能快速地响应控制信号，并且保持控制精度和稳定性。

2. 什么是状态空间法？简要描述其主要思想。

答：状态空间法是用于描述动态系统的一种方法。

其主要思想是将系统的状态表示为一组变量的集合，通过对这些变量的微分方程建模来描述系统的动态行为。

状态空间模型包括状态方程和输出方程，其中状态方程描述了系统状态的变化规律，输出方程描述了系统输出与状态之间的关系。

通过求解状态方程和输出方程，可以得到系统的状态响应和输出响应，进而对系统进行分析和设计。

三、计算题1. 给定一个具有状态方程和输出方程如下的系统，求解其状态和输出的完整响应。

状态方程：\[\dot{x} = Ax + Bu\]\[y = Cx + Du\]其中，矩阵A为\[A = \begin{bmatrix} -1 & 2 \\ 3 & -4 \end{bmatrix}\]矩阵B为\[B = \begin{bmatrix} 1 \\ 0 \end{bmatrix}\]矩阵C为\[C = \begin{bmatrix} 1 & -1 \end{bmatrix}\]矩阵D为\[D = \begin{bmatrix} 0 \end{bmatrix}\]初值条件为：\[x(0) = \begin{bmatrix} 1 \\ 1 \end{bmatrix}\]输入信号为：\[u(t) = 2 \sin(t)\]答：首先，根据给定的状态方程和初值条件，可以求解出系统的状态响应。

现代控制理论考试题

现代控制理论考试题
1. 简答题（共10小题，每题2分）
1.1 什么是控制理论？
1.2 简述闭环控制系统的基本原理。

1.3 PID控制器中的P、I、D分别代表什么意义？
1.4 什么是系统的稳定性？如何判断一个系统是否稳定？
1.5 什么是系统的可控性和可观测性？
1.6 什么是反馈控制系统？
1.7 请简述Laplace变换的定义和性质。

1.8 什么是传递函数？如何从系统的微分方程中获得传递函数？
1.9 什么是状态空间表示？与传递函数表示有何区别？
1.10 请简述根轨迹法在控制系统设计中的应用。

2. 计算题（共3小题，每题15分）
2.1 给定一个控制系统的传递函数为$G(s)=\frac{10}{s^2+2s}$，请计算系统的阶跃响应。

2.2 如果一个系统的传递函数为$G(s)=\frac{K}{s(s+1)(s+2)}$，试设计一个PID控制器使得系统的阶跃响应的超调量小于5%。

2.3 将以下微分方程转化为状态空间表示：
$$\frac{d^2y}{dt^2}+3\frac{dy}{dt}+2y=u$$
3. 应用题（共2小题，每题20分）
3.1 设计一个控制系统，使得给定系统的开环传递函数为
$G(s)=\frac{K}{s(s+2)}$，并满足以下要求：
- 峰值超调小于10%
- 上升时间小于1秒
- 稳态误差小于0.1
3.2 你了解的现代控制理论中的一种方法（例如状态反馈、最优控制、自适应控制、鲁棒控制等）在工业自动化中的应用。

4. 论述题（共1题，40分）
4.1 以你的理解，简要论述现代控制理论对工业自动化的重要性。

现代控制理论期末试卷青岛大学

现代控制理论期末试卷 | 青岛大学一、简答题（共10题，每题5分，共50分）1.现代控制理论是什么？它的发展历程与意义是什么？2.什么是闭环控制系统？简要描述其基本组成部分。

3.什么是开环控制系统？与闭环控制系统相比，有何优势和劣势？4.什么是传递函数和状态空间方程？它们之间有何联系？5.简述PID控制器的原理和应用场景。

6.什么是校正、补偿和鉴别？分别举例说明。

7.简述模型预测控制（MPC）的基本思想和应用。

8.信号处理在现代控制理论中的作用是什么？举例说明。

9.什么是自适应控制系统？简要说明其工作原理。

10.简述现代控制理论在工业自动化领域的应用。

二、计算题（共5题，每题10分，共50分）1.对于系统的开环传递函数G(s)=K/(s(s+1)(s+2))，计算其闭环传递函数，并将结果化简。

2.一个控制系统的传递函数为G(s) = 1/(s+1)，设计一个合适的PID控制器，使得系统的超调量小于5%、调整时间小于1秒。

3.给定状态空间方程和输出方程如下：x(t+1) = Ax(t) + Bu(t) y(t) = Cx(t)其中，A = [1 1; 0 1]，B = [0; 1]，C = [1 0]。

计算系统的可控性和可观测性。

4.对于一个开环系统，其传递函数为G(s) = (7s + 11)/(s^3 + 5s^2 + 7s+ 3)。

通过根轨迹法判断系统的稳定性，并在实际意义上解释结果。

5.给定一个离散时间系统的状态空间方程如下：x(k+1) = Ax(k) +Bu(k) y(k) = Cx(k)其中，A = [0.8 0.2; -0.2 0.5]，B = [0.1; 0.6]，C = [1 0]。

计算系统的特征值和特征向量。

三、综合题（共2题，每题25分，共50分）1.设计一个控制系统，使得给定开环系统的根轨迹满足以下要求：–当前系统存在一个零点，使得零点与系统极点的虚部之差大于2倍根轨迹的最大角度。