弹性体的应力和应变

合集下载

弹性体的应变与应力特性

弹性体的应变与应力特性弹性体是一种特殊的材料，具有独特的应变和应力特性。

在应用中，了解弹性体的应变和应力特性对于设计和制造具有弹性特性的产品至关重要。

首先，了解什么是应变。

应变是弹性体在受力作用下发生的形变量。

它通常以变形体积与初始体积之比来表示。

当施加外力时，弹性体内的分子或原子之间的相对位置会发生变化，从而引起材料的形变。

应变是弹性体发生的可逆性变形，即当外力消失时，弹性体会恢复到原始形态。

而应力则是弹性体内部由于外界施加力而产生的内部力。

应力和力的大小成正比，与受力点附近的弹性体横截面积成反比。

应力可以分为拉伸应力、压缩应力和剪切应力等。

在材料的应变-应力曲线中，通常可以观察到不同阶段的特征。

首先是线性弹性阶段，这个阶段的特点是应变与应力成正比。

当外力移除时，弹性体会回到原始状态，没有留下永久变形。

接着是屈服点之后的塑性变形阶段。

在这个阶段，应变增加，但材料没有完全失去可逆性。

当外力移除后，材料会部分恢复，但仍然存在永久塑性变形。

最后是断裂阶段，材料无法恢复原状，会发生破裂。

这时，应变和应力之间的关系失去线性关系，也就是材料的断裂点。

弹性体的应变和应力特性对于产品设计和材料选择至关重要。

学习和预测这些特性可以帮助工程师选择恰当的材料，并了解产品在受力时的行为。

例如，汽车制造业中常用的悬挂系统。

这些悬挂系统需要具有弹性特性，以吸收和缓解车辆在不平路面上的震动和冲击。

由于弹性体的应变和应力特性，悬挂系统可以使车辆在行驶过程中保持稳定性和驾驶舒适度。

另一个例子是运动鞋的制造。

在设计运动鞋的缓震系统时，工程师必须考虑弹性体的应变和应力特性。

优秀的缓震系统可以缓解由于跑步等运动产生的震动和冲击，为运动员提供更加舒适和安全的体验。

除了产品设计，了解弹性体的应变和应力特性还有助于研究材料的性能和改进材料的制造工艺。

利用工程分析和模拟方法，可以精确地预测弹性体在不同受力情况下的行为，进而优化产品的设计和生产过程。

弹性力学课后习题及答案

弹性力学课后习题及答案弹性力学课后习题及答案弹性力学是力学的一个重要分支，研究物体在受力作用下的形变和应力分布规律。

在学习弹性力学的过程中，课后习题是巩固所学知识、提高解题能力的重要环节。

本文将为大家提供一些常见的弹性力学课后习题及其答案，希望对大家的学习有所帮助。

一、弹性体的应力与应变1. 一个长为L，截面为A的弹性体，在受力F作用下产生了长度为ΔL的形变。

求该弹性体的应变。

答案：根据胡克定律，应变ε等于形变ΔL与原始长度L的比值，即ε = ΔL / L。

2. 一个弹性体的应变为ε，如果该弹性体的截面积为A，求该弹性体在受力F作用下的应力。

答案：根据胡克定律，应力σ等于受力F与截面积A的比值，即σ = F / A。

二、弹性体的应力分布1. 一个长为L，截面为A的弹性体，在受力F作用下，其应力沿着截面的分布是否均匀？答案：根据胡克定律，应力σ等于受力F与截面积A的比值，即σ = F / A。

由此可知，应力与截面积成反比，即截面积越大，应力越小；截面积越小，应力越大。

因此，弹性体受力作用下的应力分布是不均匀的。

2. 一个长为L，截面为A的弹性体，在受力F作用下，其应力是否与截面的形状有关？答案：根据胡克定律，应力σ等于受力F与截面积A的比值，即σ = F / A。

由此可知，应力与截面积成正比，即截面积越大，应力越小；截面积越小，应力越大。

因此，弹性体受力作用下的应力与截面的形状有关。

三、弹性体的弹性模量1. 一个弹性体的应力为σ，应变为ε，求该弹性体的弹性模量E。

答案：根据胡克定律，应力σ等于弹性模量E与应变ε的乘积，即σ = E * ε。

由此可得，弹性模量E等于应力σ与应变ε的比值，即E = σ / ε。

2. 一个弹性体的弹性模量为E，如果该弹性体的截面积为A，求该弹性体在受力F作用下的形变。

答案：根据胡克定律，形变ΔL等于弹性模量E与受力F的乘积再除以截面积A，即ΔL = (E * F) / A。

弹性体力学中的应变与应力关系

弹性体力学中的应变与应力关系弹性体力学是研究物体在力的作用下变形和恢复原状的力学分支学科，研究的对象主要是固体物质。

在弹性体力学中，应变与应力是两个重要的概念，它们描述了物体的变形和受力状态。

应变和应力之间的关系在弹性体力学中具有重要意义，它们可以通过材料力学模型来描述。

应变是物体在受力作用下发生形变的程度。

一般来说，我们可以将应变分为线性应变和非线性应变。

线性应变是指物体的形变与受力成正比。

例如，当我们拉伸一根弹簧时，弹簧的长度会发生变化，而这种形变与拉力之间是线性相关的。

用数学的语言来表达，线性应变可以用应变量ε表示，其与外力F之间存在着关系ε=ΔL/L，其中ΔL为物体长度的增量，L为物体的原始长度。

非线性应变则是指物体的形变与受力不成比例。

在高强度材料的情况下，非线性应变是不可忽视的。

非线性应变与材料的本构关系有关，常用的本构关系模型包括背应变率本构关系、黏弹性本构关系等。

这些模型可以更准确地描述材料的力学行为，使得我们能够更准确地计算应变。

与应变相对应的是应力。

应力可以看作是物体单位面积的受力情况。

一般来说，应力可以分为正应力和剪应力。

正应力是指垂直于物体内部某一面的力的作用情况。

例如，当我们用一把剪刀剪断一根木棍时，剪刀的受力情况可以被描述为正应力。

剪应力则是指平行于物体内部某一面的力的作用情况。

例如，当我们剪断一个绳索时，绳索的受力情况可以被描述为剪应力。

应变与应力之间的关系又可以通过应力-应变曲线来描述。

应力-应变曲线是弹性体力学研究中的一个重要工具，它可以体现材料的力学性质。

一般来说，应力-应变曲线可以分为弹性阶段、屈服阶段、塑性阶段和断裂阶段。

在弹性阶段，应力与应变成正比。

这个阶段的曲线是一个直线，斜率即为弹性模量，用来描述材料的刚度。

当应力超过一定值时，物体进入屈服阶段。

在屈服阶段，物体的应变不再与应力成正比，而是呈现出非线性关系。

此时物体会发生塑性变形，形成剩余应变。

当应力进一步增加时，物体可能发生断裂。

弹性体的应力与应变

弹性体的应力与应变弹性体是一种在受力作用下可以发生形变，但当受力停止时，能够恢复原来形状和大小的材料。

了解弹性体的应力与应变关系对于工程设计和材料科学具有重要意义。

在本文中，我们将探讨弹性体的应力与应变之间的关系，分析材料的弹性性质以及应力与应变的计算方法。

1. 应力的概念与计算方法应力是指单位面积上作用的力，合理地计算应力是分析弹性体性质的关键。

在计算应力时，常用到两种基本的力学概念：张力和压力。

张力是指沿一维方向的受力情况，通常用F表示，单位为牛顿。

而压力是指在一个平面上均匀分布的力，用P表示，单位是帕斯卡。

应力的计算公式如下：应力 = 受力 / 横截面积2. 应变的概念与计算方法应变是指材料在受力作用下发生的形变，一般用ΔL / L表示。

其中，ΔL是材料长度的变化量，L是材料的初始长度。

应变可以分为线性弹性应变和非线性应变。

线性弹性应变是指材料在受力作用下，形变与受力成正比的状态。

计算线性弹性应变的方法如下：应变 = 形变 / 初始长度而非线性应变则需要更复杂的计算方法来进行分析，涉及到材料的本构关系等。

3. 应力与应变的关系应力与应变之间存在一定的关系，即应力-应变曲线。

弹性体的应力-应变曲线通常可以分为三个阶段：弹性阶段、屈服点和塑性阶段。

在弹性阶段，材料受力时会产生应变，但当受力停止时，材料会完全恢复到原来的状态。

这是因为材料内部的原子或分子只发生了相对位移，而没有发生永久性的结构变化。

当应力超过材料的屈服点时，就进入了屈服点阶段。

在这个阶段中，材料开始发生塑性变形，不再能够完全恢复到原来的状态，具有一定的永久性形变。

塑性阶段是材料的应力与应变不再成正比，继续增加应力会导致更大的应变。

这是由于材料的内部结构发生了永久性的改变，无法恢复原状。

4. 弹性模量和刚度弹性模量是描述材料抵抗形变的能力，可以用来评估材料的刚度。

弹性模量越大，表示材料越难发生形变，具有较高的刚度。

常用的弹性模量有三种：杨氏模量、剪切模量和体积模量。

关于弹性体受力后某一方向的应力与应变关系

弹性力学中应力与应变为线性关系，应力与应变的比例常数E 被称为弹性系数或扬氏模量，不同的材料有其固定的扬氏模量。

虽然无法对应力进行直接的测量但是通过测量由外力影响产生的应变可以计算出应力的大小。

应力是应变的原因，应变是应力的结果。

应力概念解释：物体由于外因(受力、湿度、温度场变化等)而变形时，在物体内各部分之间产生相互作用的内力，以抵抗这种外因的作用，并力图使物体从变形后的位置回复到变形前的位置。

在所考察的截面某一点单位面积上的内力称为应力。

同截面垂直的称为正应力或法向应力，同截面相切的称为剪应力或切应力。

拓展资料
应力会随着外力的增加而增长，对于某一种材料，应力的增长是有限度的，超过这一限度，材料就要破坏。

对某种材
料来说，应力可能达到的这个限度称为该种材料的极限应力。

极限应力值要通过材料的力学试验来测定。

将测定的极限应力作适当降低，规定出材料能安全工作的应力最大值，这就是许用应力。

材料要想安全使用，在使用时其内的应力应低于它的极限应力，否则材料就会在使用时发生破坏。

工程构件，大多数情形下，内力并非均匀分布，通常“破坏”或“失效”往往从内力集度最大处开始，因此，有必要区别并定义应力概念。

弹性力学中的应力与应变关系

弹性力学中的应力与应变关系弹性力学是力学的一个重要分支，研究物体在外力的作用下产生的形变与应力的关系。

在弹性力学理论中，应力与应变关系是最为核心的概念之一。

本文将探讨弹性力学中的应力与应变关系的基本原理，并从不同角度对其进行分析。

一、基本概念在弹性力学中，应力是描述物体内部单位面积受力情况的物理量。

它可以分为正应力和剪应力。

正应力表示物体在垂直于某一平面上的受力情况，剪应力表示物体在平行于某一平面上的受力情况。

应力的大小一般采用希腊字母σ表示。

应变是描述物体形变情况的物理量。

它可以分为线性应变和体积应变。

线性应变表示物体中某一方向上的长度相对变化，体积应变表示物体在各个方向上的体积变化。

应变的大小可以用希腊字母ε表示。

二、胡克定律胡克定律是描述弹性体材料中应力与应变关系最基本的定律。

其数学表达式为σ = Eε，即应力等于弹性模量与应变之积。

其中，弹性模量E是描述物体对应变的抵抗能力的物理量。

根据胡克定律，应力与应变之间的关系是线性的，即若应变增大，则应力也会相应增大。

胡克定律适用范围有限，对于非线性应力-应变关系的材料，需要采用其他力学模型进行描述。

例如，当外力作用超出一定范围时，弹性体会发生塑性变形，此时应力和应变之间的关系就无法再用胡克定律来描述。

三、材料力学模型由于胡克定律的局限性，研究者们提出了各种各样的材料力学模型来描述应力与应变之间的关系。

其中，最常用的有线性弹性模型、非线性弹性模型和本构模型。

线性弹性模型是胡克定律的拓展，它适用于应力与应变关系呈线性关系的情况。

在这种模型中，应力与应变之间的关系是单一的、唯一的。

当外力作用停止后，物体能够完全恢复到初始状态。

非线性弹性模型适用于应力与应变关系不再呈线性关系的情况。

它可以更好地描述材料的实际变形情况。

在这种模型中，应力与应变之间的关系可以是非线性的、曲线状的。

本构模型是一种综合考虑多种因素的力学模型，它可以更全面地描述材料的应力与应变关系。

弹性体的应力和应变

弹性体的应力和应变应力和应变是弹性体力学中重要的概念。

弹性体是指在受力作用下能够发生形变，但在去除力后能够恢复原状的物质。

应力是表示物体内部各点在力作用下的应对程度的物理量，而应变则是表示物体形变程度的物理量。

在本文中，我们将探讨弹性体的应力和应变之间的关系，以及弹性体在不同应力条件下的行为。

首先，我们来介绍应力的概念。

应力是由于外部力作用于物体而引起的内部应力，即单位面积上作用的力。

通常情况下，应力可以分为三种类型：拉应力、压应力和剪应力。

拉应力是指沿物体的长度方向作用的力，压应力则是指作用于物体表面的垂直方向力，而剪应力则是作用于物体表面的平行于其平面的力。

这些应力可以通过数学计算来求得。

对于拉伸或压缩情况下的应力，一般可以通过应力=外力/截面积来计算。

而对于剪切情况下的应力，则可以通过应力=外力/接触面积来计算。

接着，我们来谈谈应变的概念。

应变是指物体由于受到外力作用而产生的形变程度。

同样，应变也可以分为三种类型：线性应变、体积应变和剪切应变。

线性应变是指物体沿作用力方向的长度变化与未受力前的原始长度之比，体积应变则是物体单位体积的变化量与未受力前的原始体积之比，剪切应变是物体平行于受力平面上的平面与未受力前的原始平面之间的夹角变化。

这些应变可以通过数学计算来求得。

通常情况下，线性应变可以通过应变=位移/原始长度来计算，体积应变可以通过应变=体积变化/原始体积来计算，而剪切应变可以通过应变=变形角度/90度来计算。

在了解了应力和应变的概念后，我们可以进一步讨论弹性体在不同应力条件下的行为。

根据背景和材料性质的不同，弹性体在应力作用下会出现不同的应变情况。

当应力作用于弹性体时，弹性体会发生形变，但在去除应力后，弹性体又会恢复到原来的形状。

这种恢复力就是弹性体的回弹力，是由于弹性体内部的分子结构和键的特性所决定的。

此外，弹性体还有一个重要的性质，即背应力。

背应力是指在弹性体内部的不同位置上，由于力的传递产生的相对应力差。

弹性体的应力应变分析

弹性体的应力应变分析弹性体是指在受到外部力的作用下可以发生弹性形变并随着外力的消失而回复原状的物体。

弹性体的应力应变分析研究的是弹性体在受到外力作用下，应力和应变的变化规律，为弹性体结构设计和材料选择提供依据。

弹性体的应力弹性体受到外力作用后，内部会出现应力。

应力是指单位面积内的力，通常用σ表示。

弹性体的应力分为三种：张应力、剪应力和压应力。

张应力是指物体受到拉伸作用时，单位面积内的拉力大小。

例如，拉伸一条钢杆时，钢杆内部会出现张应力。

剪应力是指物体受到剪切作用时，单位面积内的切力大小。

例如，用剪刀剪断一张纸时，纸内部会出现剪应力。

压应力是指物体受到压缩作用时，单位面积内的压力大小。

例如，站在地上时，人体脚底就会受到地面的压力。

弹性体的应变当弹性体受到外力作用后，会产生应变。

应变是指物体形变的程度，通常用ε表示。

弹性体的应变分为三种：拉应变、剪应变和压应变。

拉应变是指物体在受到拉伸作用时，单位长度内的形变量。

例如，拉伸一条钢杆时，钢杆内部会出现拉应变。

剪应变是指物体在受到剪切作用时，单位长度内的形变量。

例如，用剪刀剪断一张纸时，纸内部会出现剪应变。

压应变是指物体在受到压缩作用时，单位长度内的形变量。

例如，站在地上时，人体脚底就会出现压应变。

弹性体的本构关系在弹性体应力应变分析中，需要确定弹性体的本构关系，即应力和应变的关系。

钢材、混凝土和木材等材料的本构关系通过试验方法得到，常用的本构关系有胡克定律、泊松比关系和超弹性本构关系。

胡克定律是最简单的弹性体本构关系，表示应力与应变成比例。

在弱应力下，大部分弹性体本构关系均可以近似用胡克定律描述。

泊松比关系描述了单位体积的物体在沿一个方向受到拉伸作用时，会在垂直于这个方向的平面内发生压缩的程度。

该关系常用于描述石材等非金属材料的弹性体本构关系。

超弹性本构关系是指超过胡克定律描述范围的材料本构关系。

在强应力下，一些弹性体本构关系不再遵循简单的线性关系，超弹性本构关系描述了应力与应变之间的复杂关系。

弹性体与变形弹性体的应力与应变关系

弹性体与变形弹性体的应力与应变关系弹性体是指在外部施加力后能够发生形变，但在去除力后能够恢复原状的物质。

而变形弹性体则是指在外力作用下形变后不能完全恢复原状的物质。

弹性体与变形弹性体在受力时会出现应力与应变的关系，这种关系是研究材料力学性能的重要内容。

一、弹性体的应力与应变关系弹性体在外力作用下，发生形变。

应力是单位面积上的力，定义为单位面积上的力与面积的比值，通常用σ表示，单位为帕斯卡（Pa）。

应变是物体的相对形变，定义为单位长度的变化量与被测长度的比值，通常用ε表示，无单位。

根据弹性体的应力与应变关系，我们可以得到胡克定律，即应力与应变成正比关系。

弹性体的胡克定律可表示为：σ = E * ε其中，E表示弹性体的弹性模量，是反映弹性体变形能力大小的重要参数，单位为帕斯卡（Pa）。

弹性模量越大，代表弹性体越难形变，具有较好的弹性性能。

根据胡克定律，当外力施加于弹性体上时，应力与应变成正比，且两者之间的关系是线性的。

即在弹性极限之内，如果应力增大，应变也会相应增大；如果应力减小，应变也会相应减小。

而且，当外力去除后，弹性体会恢复到原来的形状和大小，应变会回到零。

二、变形弹性体的应力与应变关系变形弹性体与弹性体不同，其在外力作用下形变后不能完全恢复原状。

因此，其应力与应变关系也存在一定的差异。

变形弹性体的应力与应变关系可以用应力-应变曲线来描述。

在应力-应变曲线中，随着应变的逐渐增大，物体的应力并不是线性变化的，而是呈现出一定的非线性特性。

应力-应变曲线通常可以分为弹性阶段、屈服阶段、塑性阶段和断裂阶段。

在弹性阶段，应力与应变基本保持线性关系，符合胡克定律；而在屈服阶段，应力增加的同时，应变开始出现非比例增长。

当应力达到一定程度后，材料会发生塑性变形，进入塑性阶段；在断裂阶段，材料发生破裂。

变形弹性体的应力与应变关系还可以通过一些指标进行描述，如屈服强度、断裂强度、延伸率等。

这些指标是衡量材料变形能力和抗破坏能力的重要参数。

弹性体的应力和应变

5
数学弹性力学的典型问题主要有一般性理论、柱体扭转和弯曲、数学弹性力学的典型问题主要有一般性理论、柱体扭转和弯曲、主要有一般性理论平面问题、变截面轴扭转，回转体轴对称变形等方面平面问题、变截面轴扭转，回转体轴对称变形等方面。等方面。在近代，经典的弹性理论得到了新的发展。例如，在近代，经典的弹性理论得到了新的发展。例如，把切应力的成对性发展为极性物质弹性力学；把协调方程(保证物体变形后连续，各对性发展为极性物质弹性力学；把协调方程(保证物体变形后连续，应变分量必须满足的关系)发展为非协调弹性力学；推广胡克定律，应变分量必须满足的关系)发展为非协调弹性力学；推广胡克定律，除机械运动本身外，还考虑其他运动形式和各种材科的物理方程称为本机械运动本身外，还考虑其他运动形式和各种材科的物理方程称为本构方程。对于弹性体的某一点的本构方程，构方程。对于弹性体的某一点的本构方程，除考虑该点本身外还要考虑弹性体其他点对该点的影响，发展为非局部弹性力学等。虑弹性体其他点对该点的影响，发展为非局部弹性力学等。但是，由于课程所限，但是，由于课程所限，我们在以下几节里仅对弹性体力学作简单的介绍，为振动部分和波动部分作准备。的介绍，为振动部分和波动部分作准备。
6
§8.1 弹性体力学－－弹性体的应力和应变简介弹性体力学－－－－弹性体的应力和应变简介
弹性体有四种形变拉伸压缩、剪切、扭转和弯曲。其实，弹性体有四种形变：拉伸压缩、剪切、扭转和弯曲。其实，最基本的形四种形变：变只有两种拉伸压缩和剪切形变；两种：变只有两种：拉伸压缩和剪切形变；扭转和弯曲可以看作是由两种基本形变的组成。的组成。
Fn ∆l =Y S l0
其中：Y 称为杨氏模量，反映材料对于拉伸或压缩变形的抵抗能力。杨氏模量，其中：称为杨氏模量反映材料对于拉伸或压缩变形的抵抗能力。

弹性力学中的应力和应变

弹性力学中的应力和应变弹性力学是物理学中的一个重要分支，研究物体在外力作用下的变形和应力分布规律。

在弹性力学中，应力和应变是两个关键的概念。

本文将详细介绍弹性力学中的应力和应变，并探讨它们之间的关系和物体在外力作用下的行为。

一、应力的概念与分类在弹性力学中，应力是描述物体内部受力状况的物理量。

它的定义是单位面积上的力，即单位面积上所受的力。

在材料力学中，通常将力的作用面积取无限小，这样就可以得到面积趋于无穷小的情况下的应力。

根据作用方向的不同，应力可以分为三种类型：正应力、剪应力和体应力。

1. 正应力：即垂直于物体截面的力在该截面上单位面积的作用力。

正应力可以分为正拉应力和正压应力，正拉应力是指物体上的拉力，正压应力是指物体上的压力。

2. 剪应力：即平行于物体截面的力在该截面上单位面积的作用力。

剪应力是指物体上的切力，它使得物体相对于截面沿切应变方向发生形变。

3. 体应力：即物体内部体积元素上的力在该体积元素上单位体积的作用力。

体应力是指物体中各个点处的压力或拉力。

二、应变的概念与分类应变是描述物体变形程度的物理量，它是物体的形状改变相对于初始形状的相对变化量。

应变也可以分为三种类型：线性应变、剪应变和体应变。

1. 线性应变：即物体在受力下沿作用力方向产生的长度变化与初始长度的比值。

线性应变通常用拉伸应变表示。

2. 剪应变：即物体在受剪力作用下发生的相对位移与物体初始尺寸的比值。

3. 体应变：即物体受力时体积的相对变化量与初始体积的比值。

三、应力和应变的关系应力和应变之间存在着一定的关系，它们之间通过杨氏模量来联系。

杨氏模量是描述物体在拉伸应力作用下的应变程度的物理量。

弹性体的材料有两个重要的杨氏模量：弹性模量（或称杨氏模量）和剪切模量。

1. 弹性模量（E）：它描述的是物体在正应力作用下的正应变情况。

根据材料的不同，弹性模量也不同。

2. 剪切模量（G）：它描述的是物体在剪应力作用下的剪应变情况。

弹性力学弹性体的应力与应变关系

弹性力学弹性体的应力与应变关系弹性力学是一门研究固体材料在外力作用下的变形和应力分布规律的学科。

其中，弹性体是一类能够在外力作用下发生形变，但恢复力可以将其恢复到原始状态的物质。

弹性体的应力与应变关系是弹性力学中的基本概念和重要理论。

一、什么是应力与应变在力学中，应力是物体受来自外界作用的力引起的单位面积内的力的大小。

它是描述物体受力情况的物理量。

应力可分为正应力和剪应力两种，正应力作用于物体的表面上的垂直方向，而剪应力则作用于物体的表面上的切向方向。

应变是描述材料形变程度的物理量，是物体在受力下发生变形时单位长度的变化。

应变也可分为正应变和剪应变两种，正应变是物体长度在受力作用下产生的相对变化量，而剪应变则是物体形状的变化量与原始尺寸之比。

二、背景知识弹性体的应力与应变关系可以通过背景知识来理解。

弹性体的主要特性是能够在外力的作用下发生形变，但当外力消失时，它能够恢复到原来的形状和尺寸。

这是因为弹性体的分子或原子之间存在着弹性力，当外力作用结束时，弹性力将趋于平衡，使得物体恢复到原来的状态。

三、胡克定律胡克定律是描述弹性体应力与应变关系的基本定律。

根据胡克定律，当外力作用于弹性体时，弹性体内部的应力与应变成正比。

具体数学描述如下：σ = Eε其中，σ代表应力，单位为帕斯卡（Pa），E代表弹性模量，单位为帕斯卡（Pa），ε代表应变，为无单位。

胡克定律适用于弹性体在线性弹性范围内，即应力与应变成正比，并且比例系数恒定。

此时的应力-应变关系为线性关系，称为胡克定律。

超出线性弹性范围后，材料会发生塑性变形。

四、弹性模量弹性模量是表征弹性体抵抗形变的能力大小的物理量。

它是胡克定律中比例系数的倒数，可以用来度量弹性体的刚度。

常见的弹性模量有：1. 杨氏模量（Young's Modulus）：用E表示，描述的是物体在拉伸或压缩时的应变与应力之间的关系。

2. 剪切模量（Shear Modulus）：用G表示，描述的是物体在受剪时的应变与应力之间的关系。

弹性体

1
§8.1 外力、内力、应力
㈠外力与内力
• 外界对弹性体的作用力称为外力；内力就是弹性体内部各部分间的相互作用力 • 为研究内力，必须在弹性体内部取一假想截面 S ，它把弹性体分为两部分，这两部分间的相互作用力叫截面 S 上的内力，内力总是成对出现的 • 在一般情况下，取不同的截面，内力不同；在同一截面的不同点处，内力也不相同
z
τ'
R
r
⒈切应变和切应力的分布规律
从外观看，上端面各半径直线相对下底面转过一个相同的角度φ ，此角称为杆的扭转角；侧面轴向直线倾斜一个相同角度 r ，它就是外层体元的切变角 L r 坐标为r的体元，切变角为： L G r 由胡克定律，切应力 M G L 11
B B'
γ A
C C' D
F
8
§8.4弯曲和扭转
㈠梁的纯弯曲
b h F R F
o' θ
o
y
o x
y dx
x 梁仅在一对等大反向力偶距作用下的弯曲称为纯弯曲,上层被压缩, 下层被拉长，y 轴所在的中间层，既不被压缩，也不被拉长,保持原长，称为中性层,可见纯弯曲形变是由程度不同的拉、压形变组成。
7
㈡剪切形变的胡克定律：
在切应变较小的情况下，切应力与切应变成正比，即 τ=Gγ，G是由材料本身决定的切变弹性模量通过理论推导可知，材料的杨氏模量、切变模量和泊松系数有如下关系： G
E 2(1 )
0 2 Ep 1 G 2
F
㈢剪切形变的势能密度：
0 2 E 与拉、压形变的势能密度 Ep 1 具有相同的形式 2
⒈应变、应力分布规律 • x 处取一厚度为 dx 薄层, 其线应变

弹性体的应力和应变

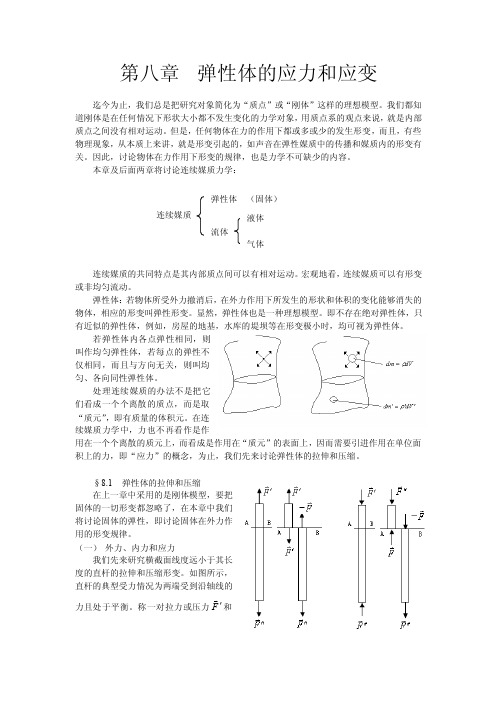
第八章弹性体的应力和应变迄今为止，我们总是把研究对象简化为“质点”或“刚体”这样的理想模型。

我们都知道刚体是在任何情况下形状大小都不发生变化的力学对象，用质点系的观点来说，就是内部质点之间没有相对运动。

但是，任何物体在力的作用下都或多或少的发生形变，而且，有些物理现象，从本质上来讲，就是形变引起的，如声音在弹性媒质中的传播和媒质内的形变有关。

因此，讨论物体在力作用下形变的规律，也是力学不可缺少的内容。

本章及后面两章将讨论连续媒质力学：连续媒质的共同特点是其内部质点间可以有相对运动。

宏观地看，连续媒质可以有形变或非均匀流动。

弹性体：若物体所受外力撤消后，在外力作用下所发生的形状和体积的变化能够消失的物体，相应的形变叫弹性形变。

显然，弹性体也是一种理想模型。

即不存在绝对弹性体，只有近似的弹性体，例如，房屋的地基，水库的堤坝等在形变极小时，均可视为弹性体。

若弹性体内各点弹性相同，则叫作均匀弹性体，若每点的弹性不仅相同，而且与方向无关，则叫均匀、各向同性弹性体。

处理连续媒质的办法不是把它们看成一个个离散的质点，而是取“质元”，即有质量的体积元。

在连续媒质力学中，力也不再看作是作用在一个个离散的质元上，而看成是作用在“质元”的表面上，因而需要引进作用在单位面积上的力，即“应力”的概念，为止，我们先来讨论弹性体的拉伸和压缩。

§8.1 弹性体的拉伸和压缩在上一章中采用的是刚体模型，要把固体的一切形变都忽略了，在本章中我们将讨论固体的弹性，即讨论固体在外力作用的形变规律。

（一）外力、内力和应力我们先来研究横截面线度远小于其长度的直杆的拉伸和压缩形变。

如图所示，直杆的典型受力情况为两端受到沿轴线的力且处于平衡。

称一对拉力或压力F和连续媒质F '' 为外力，一般情况下 |F ' |>>mg(忽略不计)|F '' |>> mg内力：假想截面AB 两侧相互施以向上（下）的拉（压）力：F 和–F 于忽略重力，且处于平衡，故而 |F | = |F ' | = |F ''| （正）应力：s nF =σ其中: s — 横截面积n F — 内力在横截面处法线(即nˆ方向)上的投影拉伸应力 > 0 F 与nˆ同向 σ压缩应力 < 0 F 与nˆ反向σσ的单位: 2m N 称为 “帕斯卡” (国际单位制)σ的量纲：21--MT L(L — 长度 M — 质量 T — 时间)〔例题1〕P333求壁内沿圆周切向的应力(忽略容器自重和大气压力)解：过圆心沿纵向取假想截面,其长度取为一个单位,将一半圆柱形容器和气体作为研究对象,受力情况如下图:按平衡条件:022=+⋅-d R p σ(R p 2⋅-下方气体对上方气体的力 d σ2下方器壁对上方气壁的力)则有: ⇒=d Pp σ器壁内沿圆周的拉伸压力,由此可见：圆柱形容器外部受压而内部压强较小时,刚沿圆周切向有压缩压力。

应力应变计算公式

应力应变计算公式不同材料在受力时会发生应力和应变的变化。

应力是指单位面积受到的力，通常用σ表示，单位是帕斯卡（Pa）或兆帕（MPa）。

而应变是指材料在受到力的作用下发生的变形，通常用ε表示，无单位。

应力和应变之间的关系可以通过应力应变计算公式来描述。

下面将介绍一些常见材料的应力应变计算公式。

1. 弹性体的应力应变计算公式弹性体是指在一定应力范围内，材料会按照一定比例回复到无应力状态的材料。

对于弹性体的应力应变计算公式，一般有两种形式。

第一种是胡克定律，也称为线性弹性模型。

根据胡克定律，应力和应变之间的关系可以表示为：σ = E × ε，其中E是弹性模量，是一个材料的固有属性，单位为帕斯卡（Pa）或兆帕（MPa）。

这个公式适用于线性范围内的应力和应变。

第二种是应力应变曲线，也称为应力应变关系曲线。

这个曲线可以通过实验测定得到。

通常情况下，应力应变曲线是一个非线性的曲线，可以用弹性阶段、屈服阶段、塑性阶段和断裂阶段来描述。

在弹性阶段，应力应变关系遵循胡克定律；在屈服阶段，应力逐渐增加，但应变仍然保持线性；在塑性阶段，应变会逐渐非线性增加；在断裂阶段，材料会发生破裂。

2. 金属的应力应变计算公式金属是一种常见的材料，它具有良好的导电性和导热性，通常用于制造结构件和导线等。

金属的应力应变计算公式可以通过试验得到。

对于金属材料，在应力较小的情况下，它的应力应变关系一般是线性的。

所以可以采用胡克定律来计算金属的应力应变关系。

例如，弹性模量E可以通过拉伸试验或压缩试验来测定。

另外，金属材料还具有屈服点和破断点。

屈服点是指材料开始发生塑性变形的应力值，可以用屈服强度σy来表示。

破断点是指材料发生破裂的应力值，可以用抗拉强度σb来表示。

3. 混凝土的应力应变计算公式混凝土是一种常见的建筑材料，它具有良好的抗压强度和耐久性。

混凝土的应力应变计算公式可以通过试验得到。

对于混凝土材料来说，它的应力应变关系在不同加载方式下会有所不同。

弹性体应力应变关系

σx=f1 εx,εy,εz,γyz,γxz,γxyσy=f2 εx,εy,εz,γyz,γxz,γxyσz=f3 εx,εy,εz,γyz,γxz,γxyτyz=f4 εx,εy,εz,γyz,γxz,γxyτxz=f5 εx,εy,εz,γyz,γxz,γxyτxy=f6 εx,εy,εz,γyz,γxz,γxy或者简写为：σi=f i εj,i,j=1,6满足小变形假设的弹性体，应力可以表示为应变的线性函数：σi=C ijεj,C ij为常数弹性体的应变能可以表示为：Vε=vεdVVvε为应变能密度，可以表示为：vε=1σiεi≥0,i=1,6且满足：σi=ðvεi该式称为格林公式，通过热力学第一定律和第二定律导出。

σ1=ðvεðε1=C11ε1+C12ε2+C13ε3+C14ε4+C15ε5+C16ε6σ5=ðvε5=C51ε1+C52ε2+C53ε3+C54ε4+C55ε5+C56ε6ð2vεðε1ðε5=C15ð2vεðε5ðε1=C51由于偏导的次序可以交换，因此必满足：C15=C51说明C ij是对称的，则对于各向异性体，具有6+30/2=21个独立的弹性常数。

下面考虑材料性能对称问题。

若材料存在对称面，则材料在与该对称面对称的两个方向上具有相同的弹性，称该对称面为弹性对称面，而垂直于弹性对称面的方向称为弹性主方向。

例如：设X轴为材料弹性主方向，则OYZ面为弹性对称面，X轴转动180度后，应力与应变σi′j′=σij n i′i n j′jεi′j′=εij n i′i n j′jσx =C 11εx +C 12εy +C 13εz +C 14γyz +C 15γxz +C 16γxy σy =C 21εx +C 22εy +C 23εz +C 24γyz +C 25γxz +C 26γxy σz =C 31εx +C 32εy +C 33εz +C 34γy′z′+C 35γxz +C 36γxy τyz =C 41εx +C 42εy +C 43εz +C 44γyz +C 45γxz +C 46γxy τxz =C 51εx +C 52εy +C 53εz +C 54γyz +C 55γxz +C 56γxy τxy =C 61εx +C 62εy +C 63εz +C 64γyz +C 65γxz +C 66γxy 坐标变换后应力分量满足以下关系：σx′=σx ,σy′=σy ,σz′=σzτx′y′=−τxy ,τx′z′=−τxz ,τy′z′=τyz 应变分量满足以下关系：εx′=εx ,εy′=εy ,εz′=εzγx′y′=−γxy ,γx′z′=−γxz ,γy′z′=γyz那么，应力——应变关系成为：σx′=C 11εx′+C 12εy′+C 13εz′+C 14γy′z′−C 15γx ′z ′−C 16γx′y′ σy′=C 21εx′+C 22εy′+C 23εz′+C 24γy′z′−C 25γx ′z ′−C 26γx′y′ σz′=C 31εx′+C 32εy′+C 33εz′+C 34γy′z′−C 35γx ′z ′−C 36γx′y′ τy′z′=C 41εx′+C 42εy′+C 43εz′+C 44γy′z′−C 45γx ′z ′−C 46γx′y′ −τx′z′=C 51εx′+C 52εy′+C 53εz′+C 54γy′z′−C 55γx ′z ′−C 56γx′y′ −τx′y′=C 61εx′+C 62εy′+C 63εz′+C 64γy′z′−C 65γx ′z ′−C 66γx′y′ 为了满足坐标变换后应力——应变关系不变，必须满足：C 15=C 16=C 25=C 26=C 35=C 36=C 45=C 46=0则应力——应变关系为：σx =C 11εx +C 12εy +C 13εz +C 14γyz σy =C 21εx +C 22εy +C 23εz +C 24γyz σz =C 31εx +C 32εy +C 33εz +C 34γy′z′ τyz =C 41εx +C 42εy +C 43εz +C 44γyzτxz =C 55γxz +C 56γxy τxy =C 65γxz +C 66γxy 根据对称性，独立的弹性常数为：6+（30-16）/2=13个（21-8=13）。