2.4-分子力结合

15
另外，常数ε如何求得？ 另外，常数ε如何求得？ 通过测试体弹性模量计算得到。 通过测试体弹性模量计算得到。
R02 ∂ 2U K= ( 2 ) R0 9V0 ∂R
3 V0 = λR0
(2.14)
1 ∂ 2U K= ( 2 ) R0 9λR0 ∂R
代入雷纳德—琼斯势则可得： 则可得： 代入 则可得
17
对于面心立方简单格子：
2 R = 2a a = 2R
晶晶体那 V = a , 含有 4个原子 ， 那那那个原子的体那
3
a3 4
a3 N 3 = R 则 ， 总体那 V = N • 4 2 N 可可 λ = 2
代入：
18
可得：
Байду номын сангаас
A6 5 K = 3 A12 ( ) 2 σ A12
4ε
(2.25)
1 1 a 原子间距离为R，则： j = 1, 则 A6 = 12 × = 12，A 12 = 12 × = 12 1 1 再考虑次近邻： 再考虑次近邻： a 原子间距离为 2 R，则： j = 2 , 则 ：
1 1 A6 = 12 × + 6 × = 12.25 1 2 1 1 A12 = 12 × + 12 × = 12.094 1 2
4 Nε A6 K= A ( ) 3 12 A12 2λσ
5 2
(***)
可见，通过测试体弹性模量，常数σ、 可见，通过测试体弹性模量，常数σ 都已可， 可计算得到。 Α12、Α6都已可，则ε可计算得到。
16
下面以面心立方简单格子和 面心立方晶体为例，得到 K与ε 、 与 σ、A12、A6的关系式。
第二章 晶体的结合 2.4 分子力结合
徐智谋
华中科技大学光电子科学与工程学院
1
分子从电荷分布类型可分为非极性和极性分子。 分子从电荷分布类型可分为非极性和极性分子。 非极性分子：正负电荷中心重合 非极性分子：
VIII 族元素在低温时结合成的晶体 —— 非极性分子晶体
极性分子：正负电荷中心不重合 极性分子：
如: H2O、CO是极性分子(CO2是非极性分子) 那那分子力结合就分为三种：极性分子结合、极性分子与非 极性分子结合、
极性分子的结合、 极性分子的结合、非极性分子的结合。
2
极性分子结合
- + - +
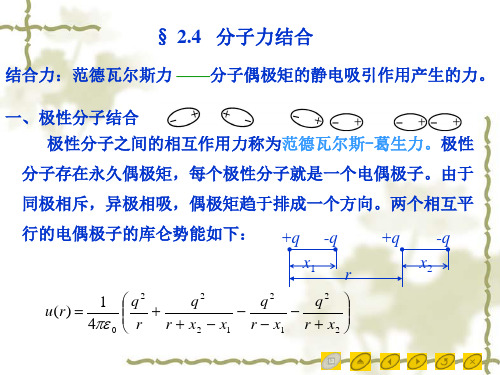
极性分子存在永久偶极矩， 极性分子存在永久偶极矩，那个极性分子就是一个电偶极 偶极矩 子。相距较远的两个极性分子之间的作用力是库仑力。这 相距较远的两个极性分子之间的作用力是库仑力。 一作用力有定向作用，因为两极性分子同极相斥， 一作用力有定向作用，因为两极性分子同极相斥，异性相 吸，使偶极矩排成一个方向的趋势。 使偶极矩排成一个方向的趋势。
11
雷纳德—琼斯势是非常著名的公 式，是描述分子间相互作用的常用 公式。 2000年，Nature上有一文章“水 分子与碳纳米管相互作用动力学”， 用的就是雷纳德—琼斯势。文章引 用率相当高。
12
根据(2.4)式，可以求出N个惰性气体分子互作用势能。 式 可以求出 个惰性气体分子互作用势能 个惰性气体分子互作用势能。 根据 把雷纳德—琼斯势代入 把雷纳德 琼斯势代入(2.4)式，得： 式 琼斯势代入
7
（2.19） ）
8
ε、σ的物理意义？如何求？
9
U / 4ε
r /σ
10
• 利用极小值：
1 r 0 = ( ) 6 σ = 1.12σ 2
1 6 则： r 0 = ( ) σ = 1.12σ 2
代入(2.19)式，可得：U ( r ) r = r0 = −ε
−ε：平衡点的雷纳德—琼斯势 1.12σ：两分子的平衡间距
σ 12 σ 6 U = 2 Nε ∑ ( ) − ( ) rαj j r j α
设R为两个最近邻分子的间距，则有： 为两个最近邻分子的间距， 为两个最近邻分子的间距 则有：
13
σ 12 1 σ 6 1 2 Nε − 12 A12 ( ) + 6 A6 ( ) =0 R0 R0 R0 R0
14
那那可求得原子间的平衡距离： 那那可求得原子间的平衡距离： 原子间的平衡距离
2 A12 6 R0 = σ ( ) A6
平衡时总的互作用势： 平衡时总的互作用势：
NεA6 U0 = 2A12
2
若晶体结构已可， 若晶体结构已可，A12和A6可通过 计算出来。通过 衍射求出晶格常数R 则常数σ 计算出来。通过X-ray衍射求出晶格常数 0，则常数σ即可 衍射求出晶格常数 求得。 求得。
5
其中，α为非极性分子的电子位移极化率。极性分子 与非极性分子间的吸引势与r6成反比。
6
非极性分子的结合
• •
+
•
+
•
• •
+ -+
+ -+
• •
相邻氦原子的瞬时偶极矩 相邻氦原子的瞬时偶极矩 惰性气体分子的最外电子壳层已饱和，它不会产生金属结合和共价结合。 惰性气体分子的最外电子壳层已饱和，它不会产生金属结合和共价结合 。 惰性气体分子的正电中心和负电中心重合，不会产生永久偶极矩。 惰性气体分子的正电中心和负电中心重合，不会产生永久偶极矩。 非极性分子间瞬时偶极矩的吸引作用是非极性分子结合成晶体的动力。 非极性分子间瞬时偶极矩的吸引作用是非极性分子结合成晶体的动力。 瞬时偶极矩的吸引作用是非极性分子结合成晶体的动力
对于面心立方晶体，代入A12、A6，可得：
K=
75ε
σ
3
19
刚才我们讲到： 刚才我们讲到：
下面以面心立方晶体为 例，来计算A12和A6。
20
对于面心立方晶体： ∑ a 相当于对所有的分子对原点距离求和后除以R。
j j
rαj = a j R
面心立方晶体，一个原点最近邻的原子：12个，次近邻原子6个 只考虑最近邻： 只考虑最近邻：
3
在温度很高 时，由于热 运动，极性 分子的平均 相互吸引势 与r6成反比， 与温度T成 正比。
p1、p2 分别为两偶极子的电偶极矩， p1=ql1、p2=ql2 ; r是两偶极子的距离；l为偶极子中正负电荷间的距离。 4
极性分子与非极性分子的结合
- +
- +
- +
当极性分子与非极性分子靠近时， 当极性分子与非极性分子靠近时，在极性分子偶极矩电场 的作用下，非极性分子的电子云发生畸变， 的作用下，非极性分子的电子云发生畸变，电子云的中心 和核电荷中心不再重合，导致非极性分子的极化，产生诱 和核电荷中心不再重合，导致非极性分子的极化，产生诱 导偶极矩。 导偶极矩。诱导偶极矩与极性分子的偶极矩之间的作用力 叫诱导力。 叫诱导力。
21
12 6
再考虑次次近邻： 如此类推) 再考虑次次近邻：• • • • • • (如此类推 如此类推
A6 = 14.45 A12 = 12.13
对于其它结构：
22