三角函数常用积分表
基本积分表

基本积分表 1、⎰+=c kx kdx2、⎰++=+c a x dx x a a 113、⎰+=c x dx xln 1 4、⎰+=+c x dx xarctan 112 5、⎰+=-c x dx x arcsin 1126、⎰+=c x xdx sin cos 7、⎰+-=c x xdx cos sin8、⎰⎰+==c x xdx dx x tan sec cos 1229、⎰⎰+-==c x xdx dx xcot csc sin 122 10、⎰+=c x xdx x sec tan sec11、⎰+-=c x xdx x csc cot csc 12、⎰+=c e dx e x x13、⎰+=c aa dx a x x ln 14、⎰+=c chx shxdx 其中2xx e e shx --=为双曲正弦函数15、⎰+=c shx chxdx 其中2xx e e chx -+=为双曲余弦函数 基本积分表的扩充16、⎰+-=c x xdx cos ln tan17、⎰+=c x xdx sin ln cot18、⎰++=c x x xdx tan sec ln sec 19、c x c x x xdx +=+-=⎰2tan ln cot csc ln csc 20、⎰+=+c a x a dx xa arctan 1122 21、⎰++-=-c a x a x a dx ax ln 21122 22、⎰+-+=-c xa x a a dx x a ln 21122 23、⎰+=-c a x dx x a arcsin 122 24、⎰+++=+c a x x dx a x 2222ln 1 25、⎰+-+=-c a x x dx a x 2222ln 1sin αsin β=-[cos(α+β)-cos(α-β)]/2【注意右式前的负号】 cos αcos β=[cos(α+β)+cos(α-β)]/2sin αcos β=[sin(α+β)+sin(α-β)]/2cos αsin β=[sin(α+β)-sin(α-β)]/2sin α+sin β=2sin[(α+β)/2]·cos[(α-β)/2]sin α-sin β=2cos[(α+β)/2]·sin[(α-β)/2]cos α+cos β=2cos[(α+β)/2]·cos[(α-β)/2]cos α-cos β=-2sin[(α+β)/2]·sin[(α-β)/2] 【注意右式前的负号】三角函数公式大全同角三角函数的基本关系倒数关系: tanα ·cotα=1 sinα ·cscα=1 cosα ·secα=1 商的关系:sinα/cosα=tanα=secα/cscα cosα/sinα=cotα=cscα/secα 平方关系:sin^2(α)+cos^2(α)=1 1+tan^2(α)=sec^2(α) 1+cot^2(α)=csc^2(α)平常针对不同条件的常用的两个公式sin2 α+cos2 α=1 tan α *cot α=1一个特殊公式(sina+sinθ)*(sina+sinθ)=sin(a+θ)*sin(a-θ)证明:(sina+sinθ)*(sina+sinθ)=2 sin[(θ+a)/2] cos[(a-θ)/2] *2 cos[(θ+a)/2] sin[(a-θ)/2] =sin (a+θ)*sin(a-θ)锐角三角函数公式正弦:sin α=∠α的对边/∠α 的斜边余弦:cos α=∠α的邻边/∠α的斜边正切:tan α=∠α的对边/∠α的邻边余切:cot α=∠α的邻边/∠α的对边二倍角公式正弦sin2A=2sinA·cosA 余弦 1.Cos2a=Cos^2(a)-Sin^2(a)=2Cos^2(a)-1 =1-2Sin^2(a) 2.Cos2a=1-2Sin^2(a) 3.Cos2a=2Cos^2(a)-1 正切tan2A=(2tanA)/(1-tan^2(A))三倍角公式sin3α=4sinα·sin(π/3+α)sin(π/3-α) cos3α=4cosα·cos(π/3+α)cos(π/3-α)tan3a = tan a · tan(π/3+a)· tan(π/3-a) 半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA. sin^2(a/2)=(1-cos(a))/2cos^2(a/2)=(1+cos(a))/2 tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))和差化积s inθ+sinφ = 2 sin[(θ+φ)/2] cos[(θ-φ)/2]sinθ-sinφ = 2 cos[(θ+φ)/2] sin[(θ-φ)/2] cosθ+cosφ = 2 cos[(θ+φ)/2]cos[(θ-φ)/2] cosθ-cosφ = -2 sin[(θ+φ)/2] sin[(θ-φ)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB)tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)两角和公式cos(α+β)=cosαcosβ-sinαsinβcos(α-β)=cosαcosβ+sinαsinβsin(α+β)=sinαcosβ+ cosαsinβsin(α-β)=sinαcosβ -cosαsinβ积化和差sinαsinβ = [cos(α-β)-cos(α+β)] /2 cosαcosβ = [cos(α+β)+cos(α-β)]/2sinαcosβ = [sin(α+β)+sin(α-β)]/2 cosαsinβ = [sin(α+β)-sin(α-β)]/2双曲函数sinh(a) = [e^a-e^(-a)]/2 cosh(a) = [e^a+e^(-a)]/2 tanh(a) = sin h(a)/cos h(a) 公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)= sinα cos(2kπ+α)= cosα tan(2kπ+α)= tanα cot (2kπ+α)= cotα 公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)= -sinα cos(π+α)= -cosα tan(π+α)= tanα cot(π+α)= cotα 公式三:任意角α与-α的三角函数值之间的关系:sin(-α)= -sinα cos(-α)= cosα tan(-α)= -tanα cot (-α)= -cotα 公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)= sinα cos(π-α)= -cosα tan(π-α)= -tanα cot(π-α)= -cotα 公式五:利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)= -sinα cos(2π-α)= cosα tan(2π-α)= -tanα cot(2π-α)= -cotα 公式六:π/2±α及3π/2±α与α的三角函数值之间的关系:sin(π/2+α)= cosα cos(π/2+α)= -sinα tan(π/2+α)= -cotα cot(π/2+α)= -tanα sin(π/2-α)= cosα cos(π/2-α)= sinα tan (π/2-α)= cotα cot(π/2-α)= tanα sin(3π/2+α)= -cosα cos(3π/2+α)= sinα tan(3π/2+α)= -cotα cot(3π/2+α)= -tanα sin(3π/2-α)= -cosα cos(3π/2-α)= -sinα tan(3π/2-α)= cotα cot(3π/2-α)= tanα (以上k∈Z) A·sin(ωt+θ)+ B·sin(ωt+φ) = √{(A2 +B2 +2ABcos(θ-φ)} · sin{ ωt + arcsin[ (A·sinθ+B·sinφ) / √{A^2 +B^2; +2ABcos(θ-φ)} } √表示根号,包括{……}中的内容诱导公式sin(-α) = -sinα cos(-α) = cosα tan (-α)=-tanα sin(π/2-α) = cosα cos(π/2-α) = sinα sin(π/2+α) = cosα cos(π/2+α) = -sinα sin(π-α) = sinα cos(π-α) = -cosα sin(π+α) = -sinα cos(π+α) = -cosα tanA= sinA/cosA tan(π/2+α)=-cotα tan(π/2-α)=cotα tan(π-α)=-tanα tan(π+α)=tanα 诱导公式记背诀窍:奇变偶不变,符号看象限万能公式sinα=2tan(α/2)/[1+(tan(α/2))2] cosα=[1-(ta n(α/2))2]/[1+(tan(α/2))2]tanα=2tan(α/2)/[1-(tan(α/2))2]其它公式(1) (sinα)2+(cosα)2=1 (2)1+(tanα)2=(secα)2 (3)1+(cotα)2=(cscα)2 证明下面两式,只需将一式,左右同除(sinα)2,第二个除(cosα)2即可(4)对于任意非直角三角形,总有tanA+tanB+tanC=tanAtanBtanC 证: A+B=π-Ctan(A+B)=t an(π-C) (tanA+tanB)/(1-tanAtanB)=(tanπ-tanC)/(1+tanπtanC)整理可得tanA+tanB+tanC=tanAtanBtanC 得证同样可以得证,当x+y+z=nπ(n∈Z)时,该关系式也成立由tanA+tanB+tanC=tanAtanBtanC可得出以下结论(5)cotAcotB+cotAcotC+cotBcotC=1(6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)cot(C/2) (7)(cosA)2+(cosB)2+(cosC)2=1-2cosAcosBcosC (8)(sinA)2+(sinB)2+(sinC)2=2+2cosAcosBcosC 其他非重点三角函数csc(a) = 1/sin(a) sec(a) = 1/cos(a)编辑本段内容规律三角函数看似很多,很复杂,但只要掌握了三角函数的本质及内部规律就会发现三角函数各个公式之间有强大的联系。
整理高数微积分公式+三角函数公式考研

高数微积分公式三角函数公式考研整理表姓名:职业工种:申请级别:受理机构:填报日期:A4打印/ 修订/ 内容可编辑高等数学公式导数公式:基本积分表:三角函数的有理式积分:一些初等函数:两个重要极限:三角函数公式:·诱导公式:·和差角公式:·和差化积公式:·倍角公式:·半角公式:·正弦定理:·余弦定理:·反三角函数性质:高阶导数公式——莱布尼兹(Leibniz)公式:中值定理与导数应用:曲率:定积分的近似计算:定积分应用相关公式:空间解析几何和向量代数:文件编号:F8-65-23-08-CC 多元函数微分法及应用微分法在几何上的应用:文件编号:F8-65-23-08-CC 方向导数与梯度:多元函数的极值及其求法:重积分及其应用:柱面坐标和球面坐标:曲线积分:曲面积分:高斯公式:斯托克斯公式——曲线积分与曲面积分的关系:常数项级数:级数审敛法:绝对收敛与条件收敛:幂级数:函数展开成幂级数:一些函数展开成幂级数:欧拉公式:三角级数:傅立叶级数:周期为的周期函数的傅立叶级数:微分方程的相关概念:一阶线性微分方程:全微分方程:二阶微分方程:二阶常系数齐次线性微分方程及其解法:二阶常系数非齐次线性微分方程整理丨尼克本文档信息来自于网络,如您发现内容不准确或不完善,欢迎您联系我修正;如您发现内容涉嫌侵权,请与我们联系,我们将按照相关法律规定及时处理。
(完整版)基本积分表

基本积分表1、⎰+=c kx kdx2、⎰++=+c a x dx x a a 113、⎰+=c x dx xln 1 4、⎰+=+c x dx xarctan 112 5、⎰+=-c x dx xarcsin 112 6、⎰+=c x xdx sin cos 7、⎰+-=c x xdx cos sin8、⎰⎰+==c x xdx dx x tan sec cos 1229、⎰⎰+-==c x xdx dx xcot csc sin 122 10、⎰+=c x xdx x sec tan sec11、⎰+-=c x xdx x csc cot csc 12、⎰+=c e dx e x x13、⎰+=c aa dx a x x ln 14、⎰+=c chx shxdx 其中2xx e e shx --=为双曲正弦函数 15、⎰+=c shx chxdx 其中2xx e e chx -+=为双曲余弦函数基本积分表的扩充16、⎰+-=c x xdx cos ln tan17、⎰+=c x xdx sin ln cot18、⎰++=c x x xdx tan sec ln sec 19、c x c x x xdx +=+-=⎰2tan ln cot csc ln csc 20、⎰+=+c a x a dx xa arctan 1122 21、⎰++-=-c a x a x a dx ax ln 21122 22、⎰+-+=-c xa x a a dx x a ln 21122 23、⎰+=-c a x dx x a arcsin 122 24、⎰+++=+c a x x dx a x 2222ln 1 25、⎰+-+=-c a x x dx a x 2222ln 1sinαsinβ=-[cos(α+β)-cos(α-β)]/2【注意右式前的负号】 cosαcosβ=[cos(α+β)+cos(α-β)]/2sinαcosβ=[sin(α+β)+sin(α-β)]/2cosαsinβ=[sin(α+β)-sin(α-β)]/2sin α+sin β=2sin[(α+β)/2]·cos[(α-β)/2]sin α-sin β=2cos[(α+β)/2]·sin[(α-β)/2]cos α+cos β=2cos[(α+β)/2]·cos[(α-β)/2]cos α-cos β=-2sin[(α+β)/2]·sin[(α-β)/2] 【注意右式前的负号】三角函数公式大全同角三角函数的基本关系倒数关系: tanα ·cotα=1 sinα ·cscα=1 cosα ·secα=1 商的关系:sinα/cosα=tanα=secα/cscα cosα/sinα=cotα=cscα/secα 平方关系:sin^2(α)+cos^2(α)=1 1+tan^2(α)=sec^2(α) 1+cot^2(α)=c sc^2(α)平常针对不同条件的常用的两个公式sin² α+cos² α=1 tan α *cot α=1一个特殊公式(sina+sinθ)*(sina+sinθ)=sin(a+θ)*sin(a-θ)证明:(sina+sinθ)*(sina+sinθ)=2 sin[(θ+a)/2] cos[(a-θ)/2] *2 cos[(θ+a)/2] sin[(a-θ)/2] =sin (a+θ)*sin(a-θ)锐角三角函数公式正弦:sin α=∠α的对边/∠α 的斜边余弦:cos α=∠α的邻边/∠α的斜边正切:tan α=∠α的对边/∠α的邻边余切:cot α=∠α的邻边/∠α的对边二倍角公式正弦sin2A=2sinA·cosA 余弦 1.Cos2a=Cos^2(a)-Sin^2(a)=2Cos^2(a)-1 =1-2Sin^2(a) 2.Cos2a=1-2Sin^2(a) 3.Cos2a=2Cos^2(a)-1 正切tan2A=(2tanA)/(1-tan^2(A))三倍角公式sin3α=4sinα·sin(π/3+α)sin(π/3-α) cos3α=4cosα·cos(π/3+α)cos(π/3-α)tan3a = tan a · tan(π/3+a)· tan(π/3-a) 半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA. sin^2(a/2)=(1-cos(a))/2cos^2(a/2)=(1+cos(a))/2 tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))和差化积sinθ+sinφ = 2 sin[(θ+φ)/2] cos[(θ-φ)/2]sinθ-sinφ = 2 cos[(θ+φ)/2] sin[(θ-φ)/2] cosθ+cosφ = 2 cos[(θ+φ)/2]cos[(θ-φ)/2] cosθ-cosφ = -2 sin[(θ+φ)/2] sin[(θ-φ)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB)tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)两角和公式cos(α+β)=cosαcosβ-sinαsinβcos(α-β)=cosαcosβ+sinαsinβsin(α+β)=sinαcosβ+ cosαsinβsin(α-β)=sinαcosβ -cosαsinβ积化和差sinαsinβ = [cos(α-β)-cos(α+β)] /2 cosαcosβ = [cos(α+β)+cos(α-β)]/2sinαcosβ = [sin(α+β)+sin(α-β)]/2 cosαsinβ = [sin(α+β)-sin(α-β)]/2双曲函数sinh(a) = [e^a-e^(-a)]/2 cosh(a) = [e^a+e^(-a)]/2 tanh(a) = sin h(a)/cos h(a) 公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)= sinα cos(2kπ+α)= cosα tan(2kπ+α)= tanα cot (2kπ+α)= cotα 公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)= -sinα cos(π+α)= -cosα tan(π+α)= tanα cot(π+α)= cotα 公式三:任意角α与-α的三角函数值之间的关系:sin(-α)= -sinα cos(-α)= cosα tan(-α)= -tanα cot (-α)= -cotα 公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)= sinα cos(π-α)= -cosα tan(π-α)= -tanα cot(π-α)= -cotα 公式五:利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)= -sinα cos(2π-α)= cosα tan(2π-α)= -tanα cot(2π-α)= -cotα 公式六:π/2±α及3π/2±α与α的三角函数值之间的关系:sin(π/2+α)= cosα cos(π/2+α)= -sinα tan(π/2+α)= -cotα cot(π/2+α)= -tanα sin(π/2-α)= cosα cos(π/2-α)= sinα tan (π/2-α)= cotα cot(π/2-α)= tanα sin(3π/2+α)= -cosα cos(3π/2+α)= sinα tan(3π/2+α)= -cotα cot(3π/2+α)= -tanα sin(3π/2-α)= -cosα cos(3π/2-α)= -sinα tan(3π/2-α)= cotα cot(3π/2-α)= tanα (以上k∈Z) A·sin(ωt+θ)+ B·sin(ωt+φ) = √{(A² +B² +2ABcos(θ-φ)} · sin{ ωt + arcsin[ (A·sinθ+B·sinφ) / √{A^2 +B^2; +2ABcos(θ-φ)} } √表示根号,包括{……}中的内容诱导公式sin(-α) = -sinα cos(-α) = cosαtan (-α)=-tanα sin(π/2-α) = cosα cos(π/2-α) = sinα sin(π/2+α) = cosα cos(π/2+α) = -sinα sin(π-α) = sinα cos(π-α) = -cosα sin(π+α) = -sinα cos(π+α) = -cosα tanA= sinA/cosA tan(π/2+α)=-cotα tan(π/2-α)=cotα tan(π-α)=-tanα tan(π+α)=tanα 诱导公式记背诀窍:奇变偶不变,符号看象限万能公式sinα=2tan(α/2)/[1+(tan(α/2))²] cosα=[1-(tan(α/2))²]/[1+(tan(α/2))²]tanα=2tan(α/2)/[1-(tan(α/2))²]其它公式(1) (sinα)²+(cosα)²=1 (2)1+(tanα)²=(secα)² (3)1+(cotα)²=(cscα)² 证明下面两式,只需将一式,左右同除(sinα)²,第二个除(cosα)²即可(4)对于任意非直角三角形,总有tanA+tanB+tanC=tanAtanBtanC 证: A+B=π-Ctan(A+B)=tan(π-C) (tanA+tanB)/(1-tanAtanB)=(tanπ-tanC)/(1+tanπtanC)整理可得tanA+tanB+tanC=tanAtanBtanC 得证同样可以得证,当x+y+z=nπ(n∈Z)时,该关系式也成立由tanA+tanB+tanC=tanAtanBtanC可得出以下结论(5)cotAcotB+cotAcotC+cotBcotC=1(6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)cot(C/2) (7)(cosA)²+(cosB)²+(cosC)²=1-2cosAcosBcosC (8)(sinA)²+(sinB)²+(sinC)²=2+2cosAcosBcosC 其他非重点三角函数csc(a) = 1/sin(a) sec(a) =1/cos(a)编辑本段内容规律三角函数看似很多,很复杂,但只要掌握了三角函数的本质及内部规律就会发现三角函数各个公式之间有强大的联系。
高等数学公式(定积分微积分三角函数导函数)

高等数学公式基本积分表(1)kdx kx C =+⎰ (k 是常数)(2)1,1x x dx C μμμ+=++⎰ (1)u ≠- (3)1ln ||dx x C x =+⎰(4)2tan 1dxarl x C x =++⎰ (5)arcsin x C =+(6)cos sin xdx x C =+⎰ (7)sin cos xdx x C =-+⎰(8)21tan cos dx x C x =+⎰(9)21cot sin dx x C x =-+⎰(10)sec tan sec x xdx x C =+⎰ (11)csc cot csc x xdx x C =-+⎰ (12)x x e dx e C =+⎰(13)ln xxa a dx C a=+⎰,(0,1)a a >≠且 (14)shxdx chx C =+⎰ (15)chxdx shx C =+⎰(16)2211tan xdx arc C a x a a =++⎰ (17)2211ln ||2x adx C x a a x a -=+-+⎰ (18)sinxarc C a=+(19)ln(x C =++(20)ln |x C =++(21)tan ln |cos |xdx x C =-+⎰ (22)cot ln |sin |xdx x C =+⎰ (23)sec ln |sec tan |xdx x x C =++⎰ (24)csc ln |csc cot |xdx x x C =-+⎰注:1、从导数基本公式可得前15个积分公式,(16)-(24)式后几节证。
2、以上公式把x 换成u 仍成立,u 是以x 为自变量的函数。
3、复习三角函数公式:2222sin cos 1,tan 1sec ,sin 22sin cos ,x x x x x x x +=+==21cos 2cos 2xx +=, 21cos 2sin 2xx -=。
注:由[()]'()[()]()f x x dx f x d x ϕϕϕϕ=⎰⎰,此步为凑微分过程,所以第一类换元法也叫凑微分法。
(完整word版)基本积分表

基本积分表1、⎰+=c kx kdx 2、⎰++=+c a x dx x a a 11 3、⎰+=c x dx xln 1 4、⎰+=+c x dx xarctan 112 5、⎰+=-c x dx xarcsin 112 6、⎰+=c x xdx sin cos 7、⎰+-=c x xdx cos sin8、⎰⎰+==c x xdx dx xtan sec cos 122 9、⎰⎰+-==c x xdx dx xcot csc sin 122 10、⎰+=c x xdx x sec tan sec11、⎰+-=c x xdx x csc cot csc 12、⎰+=c e dx e x x13、⎰+=c aa dx a x x ln 14、⎰+=c chx shxdx 其中2xx e e shx --=为双曲正弦函数 15、⎰+=c shx chxdx 其中2xx e e chx -+=为双曲余弦函数 基本积分表的扩充16、⎰+-=c x xdx cos ln tan 17、⎰+=c x xdx sin ln cot18、⎰++=c x x xdx tan sec ln sec19、c x c x x xdx +=+-=⎰2tan ln cot csc ln csc 20、⎰+=+c a x a dx xa arctan 1122 21、⎰++-=-c a x a x a dx ax ln 21122 22、⎰+-+=-c xa x a a dx x a ln 21122 23、⎰+=-c a x dx x a arcsin 122 24、⎰+++=+c a x x dx a x 2222ln 1 25、⎰+-+=-c a x x dx a x 2222ln 1sinαsinβ=-[cos (α+β)—cos(α—β)]/2【注意右式前的负号】cosαcosβ=[cos (α+β)+cos(α—β)]/2sinαcosβ=[sin(α+β)+sin(α-β)]/2cosαsinβ=[sin (α+β)-sin (α—β)]/2sin α+sin β=2sin [(α+β)/2]·cos[(α-β)/2]sin α—sin β=2cos [(α+β)/2]·sin[(α-β)/2]cos α+cos β=2cos[(α+β)/2]·cos[(α—β)/2]cos α—cos β=-2sin[(α+β)/2]·si n[(α—β)/2] 【注意右式前的负号】三角函数公式大全同角三角函数的基本关系倒数关系:tanα ·cotα=1 sinα ·cscα=1 cosα ·secα=1 商的关系:sinα/cosα=tanα=secα/cscα cosα/sinα=cotα=cscα/secα 平方关系:sin^2(α)+cos^2(α)=1 1+tan^2(α)=sec^2(α)1+cot^2(α)=csc^2(α)平常针对不同条件的常用的两个公式sin² α+cos² α=1 tan α *cot α=1一个特殊公式(sina+sinθ)*(sina+sinθ)=sin(a+θ)*sin(a-θ) 证明:(sina+sinθ)*(sina+sinθ)=2 sin[(θ+a)/2]cos[(a—θ)/2] *2 cos[(θ+a)/2] sin[(a—θ)/2]=sin(a+θ)*sin(a—θ)锐角三角函数公式正弦:sin α=∠α的对边/∠α 的斜边余弦:cos α=∠α的邻边/∠α的斜边正切:tan α=∠α的对边/∠α的邻边余切:cot α=∠α的邻边/∠α的对边二倍角公式正弦sin2A=2sinA·cosA 余弦1。
基本积分表

基本积分表1、⎰+=c kx kdx2、⎰++=+c a x dx x a a 113、⎰+=c x dx xln 1 4、⎰+=+c x dx xarctan 112 5、⎰+=-c x dx xarcsin 112 6、⎰+=c x xdx sin cos 7、⎰+-=c x xdx cos sin8、⎰⎰+==c x xdx dx x tan sec cos 1229、⎰⎰+-==c x xdx dx xcot csc sin 122 10、⎰+=c x xdx x sec tan sec11、⎰+-=c x xdx x csc cot csc 12、⎰+=c e dx e x x13、⎰+=c aa dx a x x ln 14、⎰+=c chx shxdx 其中2xx e e shx --=为双曲正弦函数15、⎰+=c shx chxdx 其中2xx e e chx -+=为双曲余弦函数 基本积分表的扩充16、⎰+-=c x xdx cos ln tan17、⎰+=c x xdx sin ln cot18、⎰++=c x x xdx tan sec ln sec 19、c x c x x xdx +=+-=⎰2tan ln cot csc ln csc 20、⎰+=+c a x a dx xa arctan 1122 21、⎰++-=-c a x a x a dx ax ln 21122 22、⎰+-+=-c xa x a a dx x a ln 21122 23、⎰+=-c a x dx x a arcsin 122 24、⎰+++=+c a x x dx a x 2222ln 1 25、⎰+-+=-c a x x dx a x 2222ln 1sin αsin β=-[cos(α+β)-cos(α-β)]/2【注意右式前的负号】cos αcos β=[cos(α+β)+cos(α-β)]/2sin αcos β=[sin(α+β)+sin(α-β)]/2cos αsin β=[sin(α+β)-sin(α-β)]/2sin α+sin β=2sin[(α+β)/2]·cos[(α-β)/2]sin α-sin β=2cos[(α+β)/2]·sin[(α-β)/2]cos α+cos β=2cos[(α+β)/2]·cos[(α-β)/2]cos α-cos β=-2sin[(α+β)/2]·sin[(α-β)/2] 【注意右式前的负号】三角函数公式大全同角三角函数的基本关系倒数关系: tanα ·cotα=1 sinα ·cscα=1 cosα ·secα=1 商的关系:sinα/cosα=tanα=secα/cscα cosα/sinα=cotα=cscα/secα 平方关系:sin^2(α)+cos^2(α)=1 1+tan^2(α)=sec^2(α) 1+cot^2(α)=csc^2(α)平常针对不同条件的常用的两个公式sin2 α+cos2 α=1 tan α *cot α=1一个特殊公式(sina+sinθ)*(sina+sinθ)=sin(a+θ)*sin(a-θ)证明:(sina+sinθ)*(sina+sinθ)=2 sin[(θ+a)/2] cos[(a-θ)/2] *2 cos[(θ+a)/2] sin[(a-θ)/2] =sin(a+θ)*sin(a-θ)锐角三角函数公式正弦:sin α=∠α的对边/∠α 的斜边余弦:cos α=∠α的邻边/∠α的斜边正切:tan α=∠α的对边/∠α的邻边余切:cot α=∠α的邻边/∠α的对边二倍角公式正弦sin2A=2sinA·cosA 余弦 1.Cos2a=Cos^2(a)-Sin^2(a) =2Cos^2(a)-1=1-2Sin^2(a) 2.Cos2a=1-2Sin^2(a) 3.Cos2a=2Cos^2(a)-1 正切tan2A=(2tanA)/(1-tan^2(A))三倍角公式sin3α=4sinα·sin(π/3+α)sin(π/3-α) cos3α=4cosα·cos(π/3+α)cos(π/3-α) tan3a = tan a · tan(π/3+a)· tan(π/3-a) 半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA); cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA.sin^2(a/2)=(1-cos(a))/2 cos^2(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))和差化积sinθ+sinφ = 2 sin[(θ+φ)/2] cos[(θ-φ)/2]sinθ-sinφ = 2 cos[(θ+φ)/2] sin[(θ-φ)/2] cosθ+cosφ = 2 cos[(θ+φ)/2] cos[(θ-φ)/2]cosθ-cosφ = -2 sin[(θ+φ)/2] sin[(θ-φ)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB)tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)两角和公式cos(α+β)=cosαcosβ-sinαsinβcos(α-β)=cosαcosβ+sinαsinβsin(α+β)=sinαcosβ+cosαsinβsin(α-β)=sinαcosβ -cosαsinβ积化和差sinαsinβ = [cos(α-β)-cos(α+β)] /2 cosαcosβ = [cos(α+β)+cos(α-β)]/2 sinαcosβ = [sin(α+β)+sin(α-β)]/2 cosαsinβ = [sin(α+β)-sin(α-β)]/2双曲函数sinh(a) = [e^a-e^(-a)]/2 cosh(a) = [e^a+e^(-a)]/2 tanh(a) = sin h(a)/cos h(a) 公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)= sinα cos(2kπ+α)= cosα tan(2kπ+α)= tanα cot(2kπ+α)= cotα 公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)= -sinα cos (π+α)= -cosα tan(π+α)= tanα cot(π+α)= cotα 公式三:任意角α与-α的三角函数值之间的关系:sin(-α)= -sinα cos(-α)= cosα tan(-α)= -tanα cot(-α)= -cotα 公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)= sinα cos(π-α)= -co sα tan(π-α)= -tanα cot(π-α)= -cotα 公式五:利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)= -sinα cos(2π-α)= cosα tan(2π-α)= -tanα cot(2π-α)= -cotα 公式六:π/2±α及3π/2±α与α的三角函数值之间的关系:sin(π/2+α)= cosα cos (π/2+α)= -sinα tan(π/2+α)= -cotα cot(π/2+α)= -tanα sin(π/2-α)= cosα cos(π/2-α)= sinα tan(π/2-α)= cotα cot(π/2-α)= tanα sin(3π/2+α)= -cosαcos(3π/2+α)= sinα tan(3π/2+α)= -cotα cot(3π/2+α)= -tanα sin(3π/2-α)= -cosα cos(3π/2-α)= -sinα tan(3π/2-α)= cotα cot(3π/2-α)= tanα (以上k∈Z) A·sin(ωt+θ)+ B·sin(ωt+φ) = √{(A2 +B2 +2ABcos(θ-φ)} · sin{ ωt +arcsin[ (A·sinθ+B·sinφ) / √{A^2 +B^2; +2ABcos(θ-φ)} } √表示根号,包括{……}中的内容诱导公式sin(-α) = -sinα cos(-α) = cosα tan (-α)=-tanα sin(π/2-α) = cosαcos(π/2-α) = sinα sin(π/2+α) = cosα cos(π/2+α) = -sinα sin(π-α) = sinαcos(π-α) = -cosα sin(π+α) = -sinα cos(π+α) = -cosα tanA= sinA/cosA tan (π/2+α)=-cotα tan(π/2-α)=cotα tan(π-α)=-tanα tan(π+α)=tanα 诱导公式记背诀窍:奇变偶不变,符号看象限万能公式sinα=2tan(α/2)/[1+(tan(α/2))2] cosα=[1-(tan(α/2))2]/[1+(tan(α/2))2]tanα=2tan(α/2)/[1-(tan(α/2))2]其它公式(1) (sinα)2+(cosα)2=1 (2)1+(tanα)2=(secα)2 (3)1+(cotα)2=(cscα)2 证明下面两式,只需将一式,左右同除(sinα)2,第二个除(cosα)2即可(4)对于任意非直角三角形,总有tanA+tanB+tanC=tanAtanBtanC 证: A+B=π-C tan(A+B)=tan(π-C)(tanA+tanB)/(1-tanAtanB)=(tanπ-tanC)/(1+tanπtanC) 整理可得tanA+tanB+tanC=tanAtanBtanC 得证同样可以得证,当x+y+z=nπ(n∈Z)时,该关系式也成立由tanA+tanB+tanC=tanAtanBtanC可得出以下结论(5)cotAcotB+cotAcotC+cotBcotC=1(6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)cot(C/2) (7)(cosA)2+(cosB)2+(cosC)2=1-2cosAcosBcosC (8)(sinA)2+(sinB)2+(sinC)2=2+2cosAcosBcosC 其他非重点三角函数csc(a) = 1/sin(a) sec(a) = 1/cos(a)编辑本段内容规律三角函数看似很多,很复杂,但只要掌握了三角函数的本质及内部规律就会发现三角函数各个公式之间有强大的联系。
高等数学公式(定积分 微积分 三角函数 导函数 等等 应有尽有) 值得搜藏
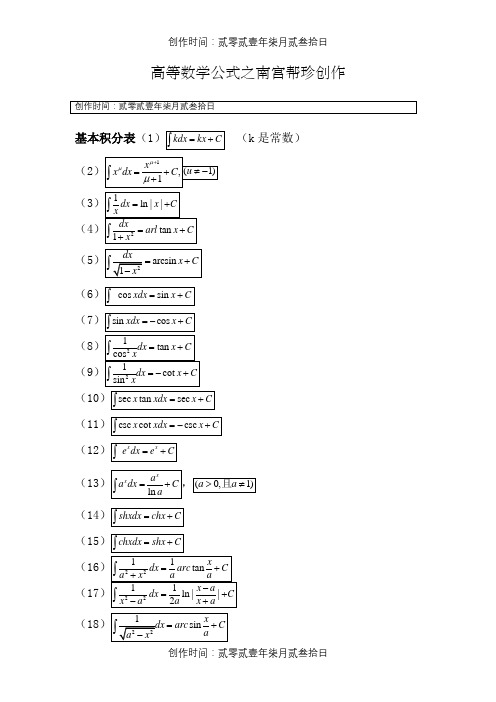
高等数学公式之南宫帮珍创作基本积分表(1(k是常数)(2(3(4(5(6(7(8(9(10(11(12(13(14(15(16(17(18(19(20(21(22(23(24注:1、从导数基本公式可得前15个积分公式,(16)-(24)式后几节证。
23、复习三角函数公式:注一类换元法也叫凑微分法。
此方法是非常重要的一种积分法,要运用自如,务必熟记基本积分表,并掌握罕见的凑微分形式及“凑”的技巧。
小结:1经常使用凑微分公式导数公式: 基本积分表:三角函数的有理式积分:ax x aa a ctgx x x tgx x x x ctgx x tgx a x x ln 1)(log ln )(csc )(csc sec )(sec csc )(sec )(22='='⋅-='⋅='-='='222211)(11)(11)(arccos 11)(arcsin x arcctgx x arctgx x x x x +-='+='--='-='⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰+±+=±+=+=+=+-=⋅+=⋅+-==+==Ca x x a x dx C shx chxdx C chx shxdx Ca a dx a Cx ctgxdx x Cx dx tgx x Cctgx xdx x dx C tgx xdx x dx xx)ln(ln csc csc sec sec csc sin sec cos 22222222C axx a dx C x a xa a x a dx C a x ax a a x dx C a xarctg a x a dx Cctgx x xdx C tgx x xdx Cx ctgxdx C x tgxdx +=-+-+=-++-=-+=++-=++=+=+-=⎰⎰⎰⎰⎰⎰⎰⎰arcsin ln 21ln 211csc ln csc sec ln sec sin ln cos ln 22222222⎰⎰⎰⎰⎰++-=-+-+--=-+++++=+-===-Cax a x a x dx x a Ca x x a a x x dx a x Ca x x a a x x dx a x I nn xdx xdx I n n nn arcsin 22ln 22)ln(221cos sin 2222222222222222222222ππ一些初等函数: 两个重要极限: 三角函数公式: ·诱导公式:·和差角公式: ·和差化积公式: ·倍角公式: ·半角公式: ·正弦定理:·余弦定理:高阶导数公式——莱布尼兹(Leibniz )公式: 中值定理与导数应用: 曲率:2sin2sin 2cos cos 2cos2cos 2cos cos 2sin2cos 2sin sin 2cos2sin2sin sin βαβαβαβαβαβαβαβαβαβαβαβα-+=--+=+-+=--+=+αββαβαβαβαβαβαβαβαβαβαβαctg ctg ctg ctg ctg tg tg tg tg tg ±⋅=±⋅±=±=±±=±1)(1)(sin sin cos cos )cos(sin cos cos sin )sin(定积分的近似计算:定积分应用相关公式:空间解析几何和向量代数:多元函数微分法及应用微分法在几何上的应用:方向导数与梯度:多元函数的极值及其求法:重积分及其应用:柱面坐标和球面坐标:曲线积分:曲面积分:高斯公式:斯托克斯公式——曲线积分与曲面积分的关系:常数项级数:级数审敛法:绝对收敛与条件收敛:幂级数:函数展开成幂级数:一些函数展开成幂级数:欧拉公式:三角级数:傅立叶级数:微分方程的相关概念:一阶线性微分方程:全微分方程:二阶微分方程:二阶常系数齐次线性微分方程及其解法:二阶常系数非齐次线性微分方程。
完整word版,高等数学常用积分公式查询表

导数公式:基本积分表:三角函数的有理式积分:ax x a a a ctgx x x tgx x x x ctgx x tgx a x x ln 1)(log ln )(csc )(csc sec )(sec csc )(sec )(22='='⋅-='⋅='-='='222211)(11)(11)(arccos 11)(arcsin x arcctgx x arctgx x x x x +-='+='--='-='⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰+±+=±+=+=+=+-=⋅+=⋅+-==+==Ca x x a x dx C shx chxdx C chx shxdx Ca a dx a Cx ctgxdx x Cx dx tgx x Cctgx xdx x dx C tgx xdx x dx xx)ln(ln csc csc sec sec csc sin sec cos 22222222C axx a dx C x a xa a x a dx C a x ax a a x dx C a xarctg a x a dx Cctgx x xdx C tgx x xdx Cx ctgxdx C x tgxdx +=-+-+=-++-=-+=++-=++=+=+-=⎰⎰⎰⎰⎰⎰⎰⎰arcsin ln 21ln 211csc ln csc sec ln sec sin ln cos ln 22222222⎰⎰⎰⎰⎰++-=-+-+--=-+++++=+-===-Cax a x a x dx x a Ca x x a a x x dx a x Ca x x a a x x dx a x I nn xdx xdx I n n nn arcsin 22ln 22)ln(221cos sin 2222222222222222222222ππ222212211cos 12sin u dudx x tg u u u x u u x +==+-=+=, , , (一)含有ax b +的积分(0a ≠)1.d x ax b +⎰=1ln ax b C a ++2.()d ax b x μ+⎰=11()(1)ax b C a μμ++++(1μ≠-)3.d x x ax b +⎰=21(ln )ax b b ax b C a +-++4.2d x x ax b +⎰=22311()2()ln 2ax b b ax b b ax b C a ⎡⎤+-++++⎢⎥⎣⎦5.d ()xx ax b +⎰=1ln ax b C b x+-+ 6.2d ()xx ax b +⎰=21ln a ax b C bx b x +-++ 7.2d ()x x ax b +⎰=21(ln )b ax b C a ax b++++ 8.22d ()x x ax b +⎰=231(2ln )b ax b b ax b C a ax b+-+-++ 9.2d ()xx ax b +⎰=211ln ()ax b C b ax b b x +-++的积分10.x C11.x ⎰=22(3215ax b C a -12.x x ⎰=22232(15128105a x abx b C a-+13.x=22(23ax b C a -14.2x=22232(34815a x abx b C a -+ 15.=(0)(0)C b C b ⎧+><16.=2a bx b --⎰17.d x x ⎰=b 18.2d x x ⎰=2a +(三)含有22x a ±的积分19.22d x x a +⎰=1arctan xC a a+ 20.22d ()n x x a +⎰=2221222123d 2(1)()2(1)()n n x n xn a x a n a x a ---+-+-+⎰21.22d xx a -⎰=1ln 2x a C a x a -++(四)含有2(0)ax b a +>的积分22.2d x ax b +⎰=(0)(0)C b C b ⎧+>+<23.2d x x ax b +⎰=21ln 2ax b C a++24.22d x x ax b +⎰=2d x b xa a ax b-+⎰ 25.2d ()x x ax b +⎰=221ln 2x C b ax b++ 26.22d ()x x ax b +⎰=21d a xbx b ax b --+⎰27.32d ()x x ax b +⎰=22221ln 22ax b a C b x bx +-+28.22d ()x ax b +⎰=221d 2()2x xb ax b b ax b+++⎰ (五)含有2ax bx c ++(0)a >的积分29.2d x ax bx c ++⎰=22(4)(4)C b ac Cb ac +<+>30.2d x x ax bx c ++⎰=221d ln 22b x ax bx c a a ax bx c++-++⎰(0)a >的积分31.=1arshxC a +=ln(x C ++ 32.=C +33.x=C34.x=C +35.2x =2ln(2a x C ++36.2x =ln(x C +++37.=1ln aC a x +38.C +39.x 2ln(2a x C ++40.x =2243(25ln(88x x a a x C +++41.x ⎰C +42.x x ⎰=422(2ln(88x a x a x C+++43.d x x ⎰a C +44.x =ln(x C +++(0)a >的积分45.=1arch x xC x a+=ln x C ++ 46.C +47.x =C48.x =C +49.2x 2ln 2a x C ++50.2x =ln x C +++51.=1arccos aC a x +52.2C a x+53.x 2ln 2a x C -++54.x =2243(25ln 88x x a a x C -+++55.x ⎰C +56.x x ⎰=422(2ln 88x a x a x C -++57.x =arccos aa C x -+58.x =ln x C ++(0)a >的积分59.=arcsinxC a + 60.C +61.x =C +62.x =C +63.2x =2arcsin 2a x C a ++ 64.2x arcsinxC a-+65.=1C a +66.2C a x -+67.x 2arcsin 2a x C a++68.x =2243(52arcsin 88x x a x a C a-+69.x ⎰=C70.x x ⎰=422(2arcsin 88x a x x a C a-+71.x ln a a C x +72.x =arcsin xC a-+(0)a >的积分73.2ax b C +++74.x22ax b C +++75.x2ax b C +++76.=C +77.x 2C +78.x =C ++79.x =((x b b a C -+-+80.x =((x b b a C -+-+81.2arcsinC +()a b <82.x 2()4b a C - ()a b <(十一)含有三角函数的积分 83.sin d x x ⎰=cos x C -+84.cos d x x ⎰=sin x C + 85.tan d x x ⎰=ln cos x C -+ 86.cot d x x ⎰=ln sin x C +87.sec d x x ⎰=ln tan()42x C π++=ln sec tan x x C ++ 88.csc d x x ⎰=ln tan 2xC +=ln csc cot x x C -+ 89.2secd x x ⎰=tan x C +90.2csc d x x ⎰=cot x C -+91.sec tan d x x x ⎰=sec x C + 92.csc cot d x x x ⎰=csc x C -+93.2sin d x x ⎰=1sin 224x x C -+ 94.2cos d x x ⎰=1sin 224x x C ++95.sin d n x x ⎰=1211sin cos sin d n n n x x x x n n----+⎰ 96.cos d n x x ⎰=1211cos sin cos d n n n x x x x n n---+⎰ 97.d sin n x x ⎰=121cos 2d 1sin 1sin n n x n x n x n x----⋅+--⎰ 98.d cos n x x ⎰=121sin 2d 1cos 1cos n n x n xn x n x---⋅+--⎰ 99.cos sin d m nx x x ⎰=11211cos sin cos sin d m n m n m x x x x x m n m n-+--+++⎰ =11211cos sin cos sin d m n m n n x x x x x m n m n+----+++⎰ 100.sin cos d ax bx x ⎰=11cos()cos()2()2()a b x a b x C a b a b -+--++-101.sin sin d ax bx x ⎰=11sin()sin()2()2()a b x a b x C a b a b -++-++-102.cos cos d ax bx x ⎰=11sin()sin()2()2()a b x a b x C a b a b ++-++-103.d sin xa b x +⎰tanx a b C ++22()a b >104.d sin xa b x +⎰C+22()a b <105.d cos xa b x +⎰)2x C +22()a b >106.d cos x a b x +⎰C +22()a b <107.2222d cos sin x a x b x +⎰=1arctan(tan )bx C ab a + 108.2222d cos sin xa xb x -⎰=1tan ln 2tan b x a C ab b x a ++-109.sin d x ax x ⎰=211sin cos ax x ax C a a -+ 110.2sin d x ax x ⎰=223122cos sin cos x ax x ax ax C a a a -+++111.cos d x ax x ⎰=211cos sin ax x ax C a a ++112.2cos d x ax x ⎰=223122sin cos sin x ax x ax ax C a a a+-+(十二)含有反三角函数的积分(其中0a >)113.arcsin d x x a ⎰=arcsin x x C a+114.arcsin d x x x a⎰=22()arcsin 24x a x C a -+115.2arcsin d x x x a ⎰=3221arcsin (239x x x a C a +++116.arccos d x x a ⎰=arccos x x C a117.arccos d x x x a⎰=22()arccos 24x a x C a --+118.2arccos d x x x a ⎰=3221arccos (239x x x a C a -++ 119.arctan d x x a ⎰=22arctan ln()2x a x a x C a -++ 120.arctan d x x x a ⎰=221()arctan 22x a a x x C a +-+ 121.2arctan d x x x a ⎰=33222arctan ln()366x x a a x a x C a -+++ (十三)含有指数函数的积分122.d x a x ⎰=1ln x a C a+ 123.e d ax x ⎰=1e ax C a+ 124.e d ax x x ⎰=21(1)e ax ax C a-+ 125.e d n ax x x ⎰=11e e d n ax n ax n x x x a a --⎰ 126.d x xa x ⎰=21ln (ln )x x x a a C a a -+ 127.d n x x a x ⎰=11d ln ln n x n x n x a x a x a a--⎰ 128.e sin d ax bx x ⎰=221e (sin cos )ax a bx b bx C a b-++ 129.e cos d ax bx x ⎰=221e (sin cos )ax b bx a bx C a b +++130.e sin d ax n bx x ⎰=12221e sin (sin cos )ax n bx a bx nb bx a b n--+ 22222(1)e sin d ax n n n b bx x a b n --++⎰131.e cos d ax n bx x ⎰=12221e cos (cos sin )ax n bx a bx nb bx a b n-++ 22222(1)e cos d ax n n n b bx x a b n--++⎰ (十四)含有对数函数的积分132.ln d x x ⎰=ln x x x C -+ 133.d ln x x x ⎰=ln ln x C +134.ln d n x x x ⎰=111(ln )11n x x C n n +-+++ 135.(ln )d n x x ⎰=1(ln )(ln )d n n x x n x x --⎰ 136.(ln )d m n x x x ⎰=111(ln )(ln )d 11m n m n n x x x x x m m +--++⎰ (十五)含有双曲函数的积分137.sh d x x ⎰=ch x C + 138.ch d x x ⎰=sh x C + 139.th d x x ⎰=lnch x C + 140.2sh d x x ⎰=1sh224x x C -++ 141.2ch d x x ⎰=1sh224x x C ++ (十六)定积分142.cos d nx x π-π⎰=sin d nx x π-π⎰=0 143.cos sin d mx nx x π-π⎰=0144.cos cos d mx nx x π-π⎰=0,,m n m n ≠⎧⎨π=⎩145.sin sin d mx nx x π-π⎰=0,,m n m n ≠⎧⎨π=⎩ 146.0sin sin d mx nx x π⎰=0cos cos d mx nx x π⎰=0,,2m n m n ≠⎧⎪⎨π=⎪⎩ 147.n I =20sin d n x x π⎰=20cos d n x x π⎰n I =21n n I n -- 1342253n n n I n n --=⋅⋅⋅⋅- (n 为大于1的正奇数),1I =1 13312422n n n I n n --π=⋅⋅⋅⋅⋅-(n 为正偶数),0I =2π。
反三角函数积分表

反三角函数积分表一、反正弦函数(arcsin x)的积分。
1. ∫arcsin xdx这个积分有点小狡猾呢。
我们用分部积分法来搞定它。
设u = arcsin x,dv=dx。
那么du=(1)/(√(1 x^2))dx,v=x。
根据分部积分公式∫ u dv=uv-∫ v du,就得到∫arcsin xdx=xarcsin x-∫(x)/(√(1 x^2))dx。
对于∫(x)/(√(1 x^2))dx,可以设t = 1 x^2,dt=-2xdx,那么∫(x)/(√(1 x^2))dx=-(1)/(2)∫(dt)/(√(t))=-√(1 x^2)+C。
所以∫arcsin xdx=xarcsin x+√(1 x^2)+C。
二、反余弦函数(arccos x)的积分。
1. ∫arccos xdx同样用分部积分法,设u=arccos x,dv = dx。
则du=-(1)/(√(1 x^2))dx,v=x。
由分部积分公式可得∫arccos xdx=xarccos x+∫(x)/(√(1 x^2))dx。
前面我们算过∫(x)/(√(1 x^2))d x=-√(1 x^2)+C。
所以∫arccos xdx=xarccos x-√(1 x^2)+C。
三、反正切函数(arctan x)的积分。
1. ∫arctan xdx还是分部积分法,设u=arctan x,dv = dx。
于是du=(1)/(1 + x^2)dx,v=x。
根据公式∫ u dv=uv-∫ v du,得到∫arctan xdx=xarctan x-∫(x)/(1 + x^2)dx。
对于∫(x)/(1 + x^2)dx,设t = 1 + x^2,dt = 2xdx,那么∫(x)/(1 +x^2)dx=(1)/(2)∫(dt)/(t)=(1)/(2)ln(1 + x^2)+C。
所以∫arctan xdx=xarctan x-(1)/(2)ln(1 + x^2)+C。
[整理]三角函数积分表.
![[整理]三角函数积分表.](https://img.taocdn.com/s3/m/b04d876fb52acfc789ebc9fc.png)
三角函数积分表
目录:
1. 积分只有 sin的函数
2. 积分只有 cos的函数
3. 积分只有 tan的函数
4. 积分只有 sec的函数
5. 积分只有 csc的函数
6. 积分只有 cot的函数
7. 积分只有 sin和 cos的函数
8. 积分只有 sin和 tan的函数
9. 积分只有 cos和 tan的函数
10. 积分只有 sin和 cot的函数
11. 积分只有 cos和 cot的函数
12. 积分只有 tan和 cot的函数
1. 积分只有sin的函数
其中
其中
(其中是Coversine函数)
其中
其中
其中
其中
2. 积分只有cos的函数
3. 积分只有tan的函数
4. 积分只有sec的函数
5. 积分只有csc
的函数
6. 积分只有
cot的函数
7. 积分只有sin和cos的函数
also:
also:
also:
also:
also:
8. 积分只有sin和tan的函数
9. 积分只有cos和tan的函数
10. 积分只有sin和cot的函数
11. 积分只有cos和cot的函数
12. 积分只有tan和cot的函数。
三角函数不定积分公式表

三角函数不定积分公式表三角函数不定积分公式表————————————在数学中,三角函数是一类重要的函数,可以用来描述物体的角度和距离。
三角函数也可以用来计算不定积分。
掌握三角函数不定积分公式表是很有必要的。
## 一、三角函数不定积分公式表1. $\int \sin x \, dx = -\cos x + C$2. $\int \cos x \, dx = \sin x + C$3. $\int \tan x \, dx = \ln|\sec x| + C$4. $\int \sec x \, dx = \ln|\sec x+\tan x| + C$5. $\int \csc x \, dx = -\ln|\csc x - \cot x| + C$6. $\int \cot x \, dx = \ln|\sin x| + C$7. $\int \sec^2x \, dx = \tan x + C$8. $\int \csc^2x \, dx = -\cot x + C$## 二、如何使用三角函数不定积分公式表1. 确定积分项的形式:在做三角函数不定积分时,首先要确定所要求积分项的形式,即是否是三角函数,是正弦函数还是余弦函数,或者是其他形式。
2. 将积分项写成标准形式:接下来,可以将积分项写成标准形式,即三角函数不定积分公式表中所列出的公式形式。
例如,如果要求积分 $\int 2\sin x\, dx$,可以将其写成 $\int \sin x\, dx$ 的形式。
3. 根据公式表选择合适的公式:根据步骤2的结果,在三角函数不定积分公式表中选择合适的公式。
例如,在上面的例子中,可以选择第一个公式 $\int \sin x\, dx = -\cos x + C$ 。
4. 计算结果并添加常数项:最后,根据所选择的公式计算结果,并添加常数项 $C$ 。
例如,在上面的例子中,可以得到 $2\int \sin x\, dx = -2\cos x + C$ 。
