新人教版八年级下册二次根式与勾股定理月考卷经典

合集下载

新人教版八年级下册二次根式与勾股定理月考卷

二次根式与勾股定理测试卷（满分100）一、选择题（每小题3分，共30分）1. 若x<0，则xx x 2-的结果是（）A ．0B ．—2C ．0或—2D ．2 2.若最简二次根式a a 241-+与是同类二次根式，则a 的值为（）A.43-=aB.34=a C.1=a D.1-=a3.设ab a 1,322=-=，则a 、b 大小关系是( )A.a=bB.a ＞bC.a ＜bD.a ＞-b4. 直角三角形一直角边长为12，另两条边长均为自然数，则其周长为( ). A.30 B.28 C.56 D.不能确定5. 五根小木棒，其长度分别为7，15，20，24，25，现将他们摆成两个直角三角形，其中正确的是（）15242520715202425157252024257202415(A)(B)(C)(D)6. 如图小方格都是边长为1的正方形,则四边形ABCD 的面积是 ( ) A .25 B. 12.5 C. 9 D. 8.5C7.△ABC 是某市在拆除违章建筑后的一块三角形空地.已知∠A=150°，AB=30米，AC=20米，如果要在这块空地上种植草皮，按每平方米草皮a 元计算，那么共需要资金（）A.50a 元B.125a 元C.150a 元D.300a 元8．△ABC 中，AB ＝15，AC ＝13，高AD ＝12，则△ABC 的周长为（）A ．42B ．32C ．42 或 32D ．37 或 339.如图，AB ⊥CD 于B ，△ABD 和△BCE 都是等腰直角三角形，如果CD=17，BE=5，那么AC 的长为（）.A.12B.7C.5D.1310．已知，如图长方形ABCD 中，AB=3cm ，AD=9cm ，将此长方形折叠，使点B 与点D 重合，折痕为EF ，则△ABE 的面积为（）A.3cm 2B.4cm 2C.6cm 2D.12cm 2二、填空题（每小题3分，共21分） 11.若要使xx-2有意义，则x________ 12．若1018222=++x x x x，则x 等于 13．若x ，y 是实数，且2111+-+-<x x y ，那么1|1|--y y 的值是14．一个长方体同一顶点的三条棱长分别是3、4、12，则这个长方体内能容下的最长的木棒为 .15．观察下列一组数：列举：3、4、5，猜想：32＝4+5；列举：5、12、13，猜想：52＝12+13；列举：7、24、25，猜想：72＝24+25；…… ……列举：13、b 、c ，猜想：132＝b +c ；请你分析上述数据的规律，结合相关知识求得b ＝，c = .16.已知如图，△ABC 中，AB=2，∠B=45°，∠C=30°，则BC=17.已知在△ABC 中，∠C=90°，BC 边上的中线AD 长为13，AC 边上中线BE2=331，那么斜边AB 的长为CA B三、计算题与解答题（共49分） 18.计算（每小题5分，共10分） (1) 22(212 +418 －348 )(2) )0()122510(9312>--m mm m m m m19. 若-3≤x ≤2时，试化简│x-2│2(3)x +21025x x -+ ( 7分 )20．如图，四边形ABCD 中，F 为DC 的中点，E 为BC 上一点，且BC=4EC,你能说明∠AFE 是多少度吗?并且证明你的结论。

新人教版八年级数学下册第一次月考二次根式及勾股定理综合测试b4

八年级下二次根式及勾股定理测试卷一、选择题1、已知xy ＞0，化简二次根式2x y x -的正确结果为( )(A)y (B)y - (C)y - (D)y --2．若a ＜0，则||2a a -的值是( )(A)0 (B)－2a (C)2a (D)2a 或－2a 3、下列二次根式中，最简二次根式为( )(A)x 9(B)32-x(C)xy x - (D)b a 234、已知x 、y 为实数，且0)2(312=-+-y x ，则x －y 的值为( )(A)3 (B)－3 (C)1 (D)－15、若最简二次根式b 5与b 23+是同类二次根式，则－b 的值是( )(A)0(B)1(C)－1(D)31 6、下列各式：211,121,27，其中与3是同类二次根式的个数为( ) (A)0个(B)1个(C)2个(D)3个7、当1＜x ＜3时，化简22)3()1(++-x x 的结果正确的是( )(A)4(B)2x ＋2(C)－2x －2(D)－48、不改变根式的大小，把aa --11)1(根号外的因式移入根号内，正确的是( ) (A)a -1 (B)1-a (C)1--a (D)a --19、已知一个Rt △的两边长分别为3和4，则第三边长的平方是（） A ．25B ．14C ．7D ．7或2510、以面积为9 cm 2的正方形对角线为边作正方形，其面积为（）A ．9 cm 2B ．13 cm 2C ．18 cm 2D ．24 cm 2二、填空题 1．函数1-=x xy 的自变量x 的取值范围是______． 2．若实数x 、y 、z 满足0412||22=+-+++-z z z y y x ，则x ＋y ＋z ＝______． 3．长方形的面积为30，若宽为5，则长为______． 4．当x ＝______时，319++x 的值最小，最小值是______5、如图中阴影部分是一个正方形,如果正方形的面积为64厘米2，则X 的长为厘米。

八年级下册数学(人教版)二次根式、勾股定理测试题(最新整理)

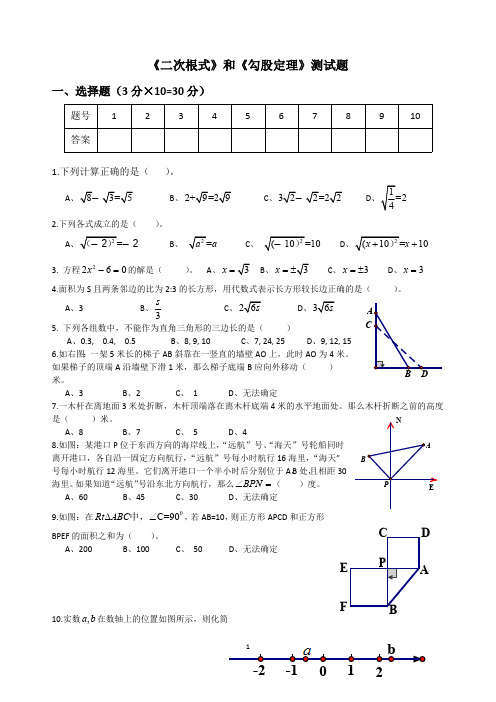
海里。如果知道“远航”号沿东北方向航行，那么 BPN （
A、60
B、45
C、30
D、无法确定
）度。
P
E
9.如图：在 RtABC中，C=900 ，若 AB=10，则正方形 APCD 和正方形
BPEF 的面积之和为（100
C、 50
D、无法确定
E
P
A
10.实数 a, b 在数轴上的位置如图所示，则化简
7.一木杆在离地面 3 米处折断，木杆顶端落在离木杆底端 4 米的水平地面处。那么木杆折断之前的高度
是（）米。
N
A、8
B、7
C、 5
D、4
8.如图：某港口 P 位于东西方向的海岸线上，“远航”号、“海天”号轮船同时
A
离开港口，各自沿一固定方向航行，“远航”号每小时航行 16 海里，“海天” B
号每小时航行 12 海里。它们离开港口一个半小时后分别位于 A，B 处，且相距 30
F
B
1
b
-2 -1 0 1 2
(a 1)2 (a b)2 b 的结果是（）。
A、1
C、 2a
B、b+1
D、1 2a
二、填空题（4 分×5=20 分）
11. 要使 x 1 在实数范围内有意义，则 x 的取值范围是
。
12. 10 2 的整数部分是
，小数部分是
13. 如果一个直角三角形的三条边的长度为 6，8， a .则 a =
3. 方程 2x2 6 0 的解是（）。 A、 x 3 B、 x 3 C、 x 3 D、 x 3
4.面积为 S 且两条邻边的比为 2:3 的长方形，用代数式表示长方形较长边正确的是（）。

新人教版2013-2014学年度八年级下期半期考试题(二次根式勾股定理平行四边形)(经典)

2013-2014学年度2015级八年级下期半期考试数学试题考试时间：120分钟试卷满分：150分（试题范围：二次根式、勾股定理、平行四边形）一、选择题(共12小题，每小题4分，共48分)下面每小题给出的四个选项中, 有且只有一个是正确的, 请把正确选项前的代号填在答卷指定位置．1、计算()24-－ 38 的结果是（）．Ａ.2 Ｂ．±2 Ｃ．-2或0 Ｄ．0． 2、如图，把矩形ABCD 沿EF 对折后使两部分重合，若150∠=，则AEF ∠=（）A ．110°B ．115°C ．120°D ．130° 3、已知Rt △ABC 中,∠C=90°,若a+b=14cm,c=10cm ，则Rt △ABC 的面积是（）A.24cm 2B.36cm 2C.48cm 2D.60cm 2 4、下列各式不是最简二次根式的是（） A.21a + B. 21x + C.24bD.0.1y5、已知：如图,菱形ABCD 中,对角线AC 与BD 相交于点O,OE ∥DC 交BC 于点E,AD=6cm, 则OE 的长为（）. A.6 cm B.4 cm C.3 cm D.2 cm6、给出下列几组数：①6，7，8；②8，15，6；③n 2-1 ，2n ，n 2+1； ④21+，21-，6 ．其中能组成直角三角形三条边长的是（） A ．①③ B ．②④ C ．①② D ．③④7、如图，正方形ABCD 中，以对角线AC 为一边作菱形AEFC ，则∠FAB 等于（）A ．22.5°B ．45°C ．30°D ．135°第2题 CA B1A 0-1-218、若0<x<1,则(x －1x )2+4 －(x+1x)2－4 等于（）A. 2xB. － 2xC. －2xD. 2x9、如图，在平行四边形ABCD 中(AB ≠BC)，直线EF 经过其对角线的交点O,且分别交AD 、BC 于点M 、N ，交BA 、 DC 的延长线于点E 、F ，下列结论： ①AO=BO ；②OE=OF ；③△EAM ≌△CFN ； ④△EAO ≌△CNO ，其中正确的是（）A. ①②B. ②③C. ②④D.③④ 10、小刚准备测量河水的深度,他把一根竹竿插到离岸边1.5m 远的水底,竹竿高出水面0.5m,把竹竿的顶端拉向岸边,竿顶和岸边的水平刚好相齐,河水的深度为( ). A.2m B.2.5cm C.2.25m D.3m11、如图，数轴上的点A 所表示的数为x ，则x 2—10的立方根为（） A ．2-10 B ．-2-10 C ．2 D ．-212、已知：如图，在正方形ABCD 外取一点E ，连接AE 、BE 、DE ．过点A 作AE 的垂线交DE 于点P ．若AE=AP=1，PB=．下列结论： ①△APD ≌△AEB ；②点B 到直线AE 的距离为； ③EB ⊥ED ；④S △APD +S △APB =1+；⑤S 正方形ABCD =4+．其中正确结论的序号是（） A ．①③④ B ．①②⑤ C ．③④⑤ D ．①③⑤ 二、填空题（共6小题，每小题4分，共24分）下列不需要写出解答过程，请将结果直接填写在答卷指定的位置． 13、（－4）2的算术平方根是______，25的平方根是______． 14、函数y=x+2x －1中自变量x 的取值范围是。

人教版八年级下《二次根式》与《勾股定理》综合测试B卷(含答案)

《二次根式》和《勾股定理》综合测试B 一、选择（每小题3分，共36分）1的结果是（）A.12019B. ﹣12019C. 2019D. ﹣20192．下列二次根式中属于最简二次根式的是（）A. B. C. D.3．三角形的三边长a，b，c满足2ab＝（a+b）2﹣c2，则此三角形是（）A. 钝角三角形B. 锐角三角形C. 直角三角形D. 等边三角形4．下列各式计算正确的是（）A. 8﹣2＝6B. 5+5＝10C. 4÷2＝2D. 4×2＝85．有一块边长为24米的正方形绿地，如图所示，在绿地旁边B处有健身器材，由于居住在A处的居民践踏了绿地，小明想在A处树立一个标牌“少走▇米，踏之何忍”请你计算后帮小明在标牌的“▇”填上适当的数字是（）A. 3米B. 4米C. 5米D. 6米6．计算﹣（﹣）﹣的结果是（）A. 3B. 3C. +3D.7．下列满足条件的三角形中，不是直角三角形的是（）A. 三内角之比为1：2：3B. 三边长的平方之比为1：2：3C. 三边长之比为3：4：5D. 三内角之比为3：4：58．如图，在水池的正中央有一根芦苇，池底长10尺，它高出水而1尺，如果把这根芦苇拉向水池一边，它的顶端恰好到达池边的水面则这根芦苇的长度是（）A. 10尺B. 11尺C. 12尺D. 13尺9．若等腰三角形的两边长分别为和，则这个三角形的周长为（）A. B.或 C. D.10．如图，已知1号、4号两个正方形的面积和为7，2号、3号两个正方形的面积和为4，则a，b，c三个正方形的面积和为（）A. 11B. 15C. 10D. 2211．已知，则的值为（）A. B. ±2 C. ± D.12．如图，2×2的方格中，小正方形的边长是1，点A、B、C都在格点上，则AB边上的高长为（）A. B. C. D.二、填空（每小题3分，共18分）13．二次根式是一个整数，那么正整数a最小值是．14．如图，一个电子跳蚤在4×5的网格（网格中小格子均为边长为1的正方形）中，沿A→B→C→A跳了一圈，它跳的总路程是．15．三角形的三边长分别为3、m、5，化简﹣＝．16．如图，是2002年8月北京第24届国际数学家大会会标，由4个全等的直角三角形拼合而成．如果图中大、小正方形的面积分别为52和4，那么一个直角三角形的两直角边的和等于．17．在△ABC中，AB＝13，AC＝15，高AD＝12，则BC的长为．18．读取表格中的信息，解决问题．满足的n可以取得的最小整数是．三、解答（8个小题，共66分）19．（6分）已知三角形的三边分别为a，b，c，且a＝m﹣1，b＝，c＝m+1（m＞1）．（1）请判断这个三角形的形状．（2）试找出一组直角三角形的三边的长，使它的最小边不小于20，另两边的差为2，三边均为正整数．20．（8分）计算：（1）（2﹣1）2﹣（+）（﹣）；（2）．21．（8分）阅读与计算：请阅读以下材料，并完成相应的任务．斐波那契（约1170﹣1250）是意大利数学家，他研究了一列数，这列数非常奇妙，被称为斐波那契数列（按照一定顺序排列着的一列数称为数列）．后来人们在研究它的过程中，发现了许多意想不到的结果，在实际生活中，很多花朵（如梅花、飞燕草、万寿菊等）的瓣数恰是斐波那契数列中的数．斐波那契数列还有很多有趣的性质，在实际生活中也有广泛的应用．斐波那契数列中的第n个数可以用[﹣]表示（其中，n≥1）．这是用无理数表示有理数的一个范例．任务：请根据以上材料，通过计算求出斐波那契数列中的第1个数和第2个数．22．（8分）如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点叫做格点．（1）在图1中以格点为顶点画一个面积为10的正方形；（2）在图2中以格点为顶点画一个三角形，使三角形三边长分别为2、、；（3）如图3，点A、B、C是小正方形的顶点，求∠ABC的度数．23．（8分）若x、y为实数，且y＝，求•的值．24．（9分）如图，在一棵树的10米高B处有两只猴子，其中一只爬下树走向离树20米的池塘C，而另一只爬到树顶D后直扑池塘C，结果两只猴子经过的距离相等，问这棵树有多高？25．（9分）观察下列各式及其验证过程：，验证：．，验证：．（1）按照上述两个等式及其验证过程，猜想的变形结果并进行验证．（2）针对上述各式反映的规律，写出用a（a为任意自然数，且a≥2）表示的等式，并给出验证．（3）针对三次根式及n次根式（n为任意自然数，且n≥2），有无上述类似的变形？如果有，写出用a（a为任意自然数，且a≥2）表示的等式，并给出验证．26．（10分）如图，在四边形ABCD中，AB＝AD，∠DAB＝∠BCD＝90°．设P＝BC+CD，四边形ABCD的面积为S．（1）试探究S与P之间的关系，并说明理由；（2）若四边形ABCD的面积为9，求BC+CD的值．参考答案一、1. C 2.A 3.C 4.D 5.D 6.A 7.D 8.D 9.B 10.B 11.C 12.A二、13. 2 14.7+15.2m﹣10 16.10 17.14或4 18.7三、19. 解：（1）∵（m﹣1）2+（）2＝m2﹣2m+1+4m＝m2+2m+1＝（m+1）2，∴a2+b2＝c2，∴这个三角形是直角三角形；（2）答案不唯一，如：取＝20，∴m ＝100，∴m ﹣1＝99，m+1＝101．此时这三边的长分别为：20、99、101.20.解：（1）原式＝13﹣4﹣（2+2）（﹣）＝13﹣4﹣2＝11﹣4．（2）原式＝4﹣+（﹣1）（+1）＝4﹣+2． 21.解：第1个数，当n ＝1时，[﹣]＝（﹣）＝× ＝1．第2个数，当n ＝2时，[﹣]＝[（）2﹣（）2]＝×（+）（﹣）＝×1× ＝1．22.解：（1）如图1的正方形的边长是，面积是10；（2）如图2的三角形的边长分别为2，，；（3）如图3，连接AC ，由勾股定理得：AC ＝BC ＝＝，AB ∴AC 2+ BC 2＝AB 2，∴∠ACB ＝90°，∴∠ABC＝∠BAC＝45°．23.解：∵y＝，∴x2﹣4≥0，4- x2≥0，x+2≠0，∴x2﹣4＝0，x+2≠0，解得：x＝2，∴y＝，∴•＝×＝×＝．24.解：设BD＝x米，则AD＝（10+x）米，CD＝（30﹣x）米，根据题意，得：（30﹣x）2﹣（x+10）2＝202，解得x＝5．即树的高度是10+5＝15米．25.解：（1）＝4，理由是：＝＝＝4；（2）由（1）中的规律可知3＝22﹣1，8＝32﹣1，15＝42﹣1，∴＝a，验证：＝＝a；正确；（3a（a为任意自然数，且a≥2），＝＝a．26.解：（1）S＝P2，理由如下：连接BD，如图所示：∵∠DAB＝∠BCD＝90°，∴BD2＝AD2+AB2＝DC2+BC2；∵AD＝AB，∴2AD2＝DC2+BC2，∴S＝+＝+＝+＝（DC+BC）2＝P2；（2）根据题意得：P2＝9，∴P2＝36，解得：P＝6，或P＝﹣6（舍去），即BC+CD＝6．。

人教版八年级数学下册《二次根式勾股定理》专题测试-带参考答案

人教版八年级数学下册《二次根式勾股定理》专题测试-带参考答案时间：80分钟总分：120分姓名____________ 得分__________1．（3分）下列判断正确的是( )A ．带根号的式子一定是二次根式B 5aC 21m +D ．二次根式的值必定是无理数2．（338a （）A ．22aB ．342aC ．322aD ．24a3．（3分）已知35a =35b =22a ab b -+ ）A ．26B ．26±C ．24D ．254．（3分）若613x ，小数部分为y ，则(213x y 的值是（）A ．5313-B ．3C ．3135D ．3-5．（3分）若实数a 、b 、c 在数轴上对应点的位置如图，则化简： 222b bc c -+﹣b|=_____．6．（12分）把下列根式化成最简二次根式．（1）512（2）368（3250(0)a b a >（4(0)n mn m n <7．（8分）先化简，再求值：已知322x =+求()221-441x x xx +--的值8. （8分）在一个边长为（35cm 的正方形的内部挖去一个长为（310cm ，宽为65cm 的矩形，求剩余部分图形的面积．9．（9分）计算: 531562 55-31)2; 35235210．（10分）已知11881,2y x x =--22x y x y y x y x+++-11．（9分）把下列根号外的因式移到根号内.(1)1a(2)-xy x y 22-2x xy y xy+x >y >0); (3)11-a ba <b ). 12．（6分）如图,在长方形ABCD 中无重叠放入面积分别为16 cm 2和12 cm 2的两张正方形纸片,求图中空白部分的面积.13.（5分）如图所示，某风景名胜区为了方便游人参观，计划从主峰A 处架设一条缆车线路到另一山峰C处，若在A处测得∠EAC=30°，两山峰的底部BD相距900米，则缆车线路AC的长为多少米？14.（5分）如图，将一根25㎝长的细木棒放入长、宽、高分别为8㎝、6㎝和3求细木棒露在盒外面的最短长度是多少？15.（6分）如图，折叠矩形的一边AD，使点D落在BC边的点F处，已知AB=8cm，BC=10cm，求EC的长16．（8分）如图，某人到岛上去探宝，从A处登陆后先往东走4 km，又往北走1.5 km，遇到障碍后又往西走2 km，再折回向北走到4.5 km处往东一拐，仅走0.5 km就找到宝藏．问登陆点A与宝藏埋藏点B之间的距离是多少？17.（10分）如图，长方体的长为15，宽为10，高为20，点B 离点C 的距离是5，一只蚂蚁如果要沿着长方体的表面从点A 爬到点B ，需要爬行的最短距离是多少？18.（9分）如图，A ，B 两个工厂位于一段直线形河的异侧，A 厂距离河边5km AC =，B 厂距离河边1km BD =，经测量8km CD =，现准备在河边某处(河宽不计)修一个污水处理厂E ．(1)设ED x =，请用x 的代数式表示AE BE +的长；(2)为了使两厂的排污管道最短，污水厂E 的位置应怎样来确定此时需要管道多长？(3)()2291525x x ++-+多少？答案1．C 2．A 3．A 4.【详解】解：3134<<613∴2x = 则小数部分是：6132413=则()(213413413x y = 16133=-=故选：B5.﹣5a+4b﹣3c．6.（1）103（236；（3）52b（4）1mn m7.122-152【详解】分析：用大正方形的面积减去长方形的面积即可求出剩余部分的面积．试题解析：剩余部分的面积为：（352﹣（31065=（15）﹣（215152=（152（cm2）．9.(1)-1；310410.解：1-8x≥0，x≤1 88x-1≥0，x≥1 8∠x=18，y=12∠原式259532--==1 44222．11．（1a（2xy（322-ab a b12.【详解】解:∠两张正方形纸片的面积分别为16 cm2和12 cm2∠16123cm3∠空白部分的面积3-12-3-12-16=(-32.13.314.5cm2268+∠()2 210103+则细木棒露在盒外面的最短长度是25﹣20=5cm.15.【详解】解：∠四边形ABCD 为矩形∠DC =AB =8cm ，AD =BC =10cm ，∠B =∠D =∠C =90°∠折叠矩形的一边AD ，使点D 落在BC 边的点F 处∠AF =AD =10cm ，DE =EF在Rt ∠ABF 中，BF 22221086AF AB (cm)∠FC =BC -BF =4(cm)设EC =x ，则DE =8x -，EF =8x -在Rt ∠EFC 中∠EC 2+FC 2=EF 2∠x 2+42=(8-x )2，解得x =3∠EC 的长为3cm ．16．登陆点A 与宝藏埋藏点B 之间的距离是6.5 km.【详解】解：如图,过点B 作BC ∠AD 于点C则AC ＝4－2＋0.5＝2.5(km),BC ＝4.5＋1.5＝6(km)在Rt∠ABC 中,由勾股定理,得:AB 2＝AC 2＋BC 2＝2.52＋62＝6.52∠AB ＝6.5(km)．答:登陆点A 与宝藏埋藏点B 之间的距离是6.5 km.17. 解：只要把长方体的右侧表面剪开与前面这个侧面所在的平面形成一个长方形，如第1个图：长方体的宽为10，高为20，点B离点C的距离是5AD=10515BD CD BC20在直角三角形ABD中，根据勾股定理得：2222152025∴++；AB BD AD只要把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形，如第2个图：长方体的宽为10，高为20，点B离点C的距离是5AD=BD CD BC1020525在直角三角形ABD中，根据勾股定理得：2222∴++AB BD AD1025529只要把长方体的上表面剪开与后面这个侧面所在的平面形成一个长方形，如第3个图：长方体的宽为10，高为20，点B离点C的距离是5AC CD AD201030在直角三角形ABC中，根据勾股定理得：2222∴++305537AB AC BC<25529537∴蚂蚁爬行的最短距离是25．18.(1)AE BE+22x x=-++(8)251(2)连接AB与CD的交点就是污水处理厂E的位置，此时最少需要管道10km()2291525x x++-+17。

人教版八年级下册二次根式、勾股定理考试测试卷(含word解析)

数学试卷（二次根式、勾股定理）、单选题（共10题；共20分）1 .在下列各式中，一定是二次根式的是（）A. 3 2B. ..Ho c. ,.a 21 D. a a3 .下列变形中，正确的是（ A. （26）2=2 X 3=6 C.匕-♦ 6； - -5 -小 64 .下列组合哪个不是勾股数（A.30,40,50B. 7,24,25BT -D . '"，）「；-4）7二5 .下列二次根式中，与内是同类二次根式的是（）A.B.c.D.6 .一棵大树在一次强台风中于离地面 5 m 处折断倒下，倒下后树顶落在树根部大约12 m 处.这棵大树折断前离度估计为（）7 .如图，a 、b 、c 分别表示直角三角形的三边向外作的正方形的面积,2.若式子运在实数范围内有意义，则 A. x>1B.女1x 的取值范围是（）（X>1D.<1A. 25m B. 18 m C. 17 m D. 13mA. a+b=cB.2+b 2=c 2C.ab=cD.a+b=cC. 5,12,13D. 1,2,3卜列关系正确的是8 .如果最简根式，以二8与是同类二次根式，那么使有意义的x 的取值范围是（）A. x< 10 iB. x> 10C. xv 10 uD. x> 109 .等式，营=不与成立的条件是（）10 .下列根式中，最简二次根式是（）A.差吧.C.、填空题（共6题；共18分）11 .当a= -2时，二次根式 \f2-a 的值是12 .如图，将一根长为 20cm 的筷子置于底面直径为 5cm,高为12cm 的圆柱形水杯中，筷子露在杯子外面的长度为 cm.13 .已知三角形的三边长分别为 ^45 cm, 厢cm, y125 cm ,则这个三角形的周长为 _______ cm.14 .如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形.若正方形 A 、B 、C 、D 的边长分别是3、4、2、3,则最大正方形 E 的面积是15 .若直角三角形的两直角边长为 a 、b,且满足标二五*9-|b —4 = 0则该直角三角形的斜边长为A. xW3'B. x>0 C. x>0且 xw3 D. x>3D.16 .中国数学史上最先完成勾股定理证明的数学家是公元 3世纪三国时期的赵爽，他为了证明勾股定理，创制了一副 "弦图：后人称其为赵爽弦图”（如图1） .图2由弦图变化得到，它是由八个全等的直角三角形拼接而成.将图中正方形MNKT,正方形EFGH 正方形ABCD的面积分别记为 S , S 2 , S 3 , 若S i +&+Q=18,则正方形EFGH 的面积为三、计算题（共2题；共15分）17 .计算：标i-而-1/+ 12x3—1 — 1- I18.计算:⑴廊+杀-屈-旧（2）JI （后行）-中-旧2嘎青六黄41四、解答题(共5题；共47分，19,20,22每题10分，21题5分，23题12分)19.如图，在4ABC 中，AB=13, BC=10, BC边上的中线AD=12.(1)求证：AD^BC;(2)求AC的长.20. (1)已知y/—1 - J-x,求的平方根.(2)当-4<x< 1时，化简，举+&V+16 - 2，d・占+].21.一个25米长的梯子AB,斜靠在一竖直的墙AO上，这时的AO距离为24米，如果梯子的顶端A 沿墙下滑4米，那么梯子底端B也外移4米，对吗？为什么？22.综合题⑴试比较而与后调的大小；（2）你能比较谒二访与向距的大小吗？其中k为正整数.23.如图，B地在A地的正东方向，两地相距28。

人教版八年级数学下册第十七章-勾股定理综合训练练习题(无超纲)

人教版八年级数学下册第十七章-勾股定理综合训练考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、如图，在ABC中，5==，8AB ACBC=，D是线段BC上的动点（不含端点B、C）．若线段AD长为正整数，则点D的个数共有（）A．4个B．3个C．2个D．1个2、如图，在△ABC中，已知AB＝AC＝3，BC＝4，若D，E是边BC的两个“黄金分割”点，则△ADE的面积为（）A．10﹣B． 5 C D．20﹣3、如图，有一个长、宽、高分別为2m、3m、1m的长方体，现一只蚂蚁沿长方体表面从A点爬到B点，那么最短的路径是（）A．3√2m B．√3m C．√2m D．2√5m4、如图，一支铅笔放在圆柱体笔筒中，笔筒的内部底面直径是9cm，内壁高12cm．若这支铅笔长为18cm，则这只铅笔在笔筒外面部分长度不可能的是（）A．3cm B．5cm C．6cm D．8cm5、如图，四边形ABCD是边长为9的正方形纸片，将其沿MN折叠，使点B落在CD边上的点B'处，点B C'=，则AM的长为（）A的对应点为点A'，3A．1.8 B．2 C．2.3 D6、如图，一圆柱高12cm，底面半径为3cm，一只蚂蚁从点A沿圆柱表面爬到点B处吃食物，要爬行的最短路程（π取3）是（）A．15cm B．21cm C．24cm D7、下列是勾股数的一组是（）A．6，8，10 B．2，3，4 C．1，2，3 D．5，7，118、为了测量学校的景观池的长AB，在BA的延长线上取一点C，使得5AC=米，在点C正上方找一点D （即DC BCCDB∠=︒，30⊥），测得60∠=︒，则景观池的长AB为（）ADCA．5米B．6米C．8米D．10米9、下列条件中，能判断△ABC是直角三角形的是（）cA．a：b：c＝3：4：4 B．a＝1，bC．∠A：∠B：∠C＝3：4：5 D．a2：b2：c2＝3：4：510、如图，一只蚂蚁沿着边长为4的正方体表面从点A出发，爬到点B，如果它运动的路径是最短的，则AC的长为（）A．B．4 C．D．第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、如图，在△ABC中，∠ABC＝97.5°，P、Q两点在AC边上，PB＝2，BQ＝，PQ M、N分别在边AB、BC上，∠=_______．（1）PBQ（2）当四边形PQNM的周长最小时，（MP+MN+NQ）2=_______．2、如图，圆柱的底面周长为16，BC＝12，动点P从A点出发，沿着圆柱的侧面移动到BC的中点S，则移动的最短距离为 _____．3、如图，在ABC ∆中，90C ∠=︒，15B ∠=︒，3AC =，AB 的垂直平分线l 交BC 于点D ，连接AD ，则BC 的长为__________．4、如图，一个圆柱形工艺品高为16厘米，底面周长12厘米，现在需要从下底的A 处绕侧面一周，到上底B （A 的正上方）处镶嵌一条金丝，则金丝至少____厘米．5、如图，正方形OABC 的边OC 落在数轴上，OC ＝2，以O 为圆心，OB 长为半径作圆弧与数轴交于点D ，则点D 表示的数是 _______．三、解答题（5小题，每小题10分，共计50分）1、图①，图②均为4×4的正方形网格，每个小正方形的顶点称为格点，且每个小正方形的边长均为1．图中点A ，B ，C 均在格点上，请分别在给定的网格中画出格点M ，使点M 满足相应的要求．（1）在图①中画出格点M ，连结MA ，使MA ＝5．（2）在图②中画出格点M，连结MA，MB，MC，使MA＝MB＝MC．2、在△ABC中，AB、BC、AC这道题时，先画一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），如图1所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．这种方法叫做构图法．（1）△ABC的面积为：；（2）若△DEF1的正方形网格中画出相应的△DEF，并利用构图法求出它的面积；（3）如图2，一个六边形的花坛被分割成7个部分，其中正方形PRBA，RQDC，QPFE的面积分别为13，10，17，且△PQR、△BCR、△DEQ、△AFP的面积相等，求六边形花坛ABCDEF的面积．3、如图，已知线段a，h．（1）尺规作图：作等腰ABC，使底边BC长为a，BC上的高为h．（2）若10a =，12h =，求ABC ∆的周长．4、如图，在△ABC 中，∠ACB ＝90°，AB ＝10cm ，BC ＝6cm ，若点P 从点A 出发，以每秒4厘米的速度沿折线A ﹣C ﹣B ﹣A 运动（运动一周回到点A 时停止运动），设运动时间为t 秒（＞0）．（1）点P 在AC 上运动时，是否存在点P ，使得PA ＝PB ？若存在，求出t 的值；若不存在，说明理由；（2）若点P 运动到BC 上某点时使△ACP 的面积为16cm 2，求此时t 的值．5、（阅读理解）我国古人运用各种方法证明勾股定理，如图①，用四个直角三角形拼成正方形，通过证明可得中间也是一个正方形．其中四个直角三角形直角边长分别为a 、b ，斜边长为c ．图中大正方形的面积可表示为()2a b +，也可表示为2142c ab +⨯，即()22142a b c ab +=+⨯=，所以222+=a b c ．（尝试探究）美国第二十任总统伽菲尔德的“总统证法”如图②所示，用两个全等的直角三角形拼成一个直角梯形BCDE ，其中BCA ADE △△≌，90C D ∠=∠=︒，根据拼图证明勾股定理．（定理应用）在Rt ABC △中，90C ∠=︒，A ∠、B 、C ∠所对的边长分别为a 、b 、c ．求证：222244a c a b c b +=-．---------参考答案-----------一、单选题1、B【分析】首先过A作AE⊥BC，当D与E重合时，AD最短，首先利用等腰三角形的性质可得BE=EC，进而可得BE 的长，利用勾股定理计算出AE长，然后可得AD的取值范围，进而可得答案．【详解】解：如图：过A作AE⊥BC于E，∵在△ABC中，AB=AC=5，BC=8，∴当AE⊥BC，EB=EC=4，∴AE3，∵D是线段BC上的动点(不含端点B，C).若线段AD的长为正整数，∴3⩽AD<5，∴AD=3或AD=4，当AD =4时，在靠近点B 和点C 端各一个，故符合条件的点D 有3点.故选B .【点睛】本题主要考察了等腰三角形的性质，勾股定理的应用，解题的关键是熟练掌握等腰三角形的性质，勾股定理的计算.2、A【分析】过点A 作AF ⊥BC 于点F ，由题意易得2BF CF ==，再根据点D ，E 是边BC 的两个黄金分割点，可得2BE CD ===，根据勾股定理可得AF =28DE DF ==，然后根据三角形的面积计算公式进行求解．【详解】解：过点A 作AF ⊥BC 于点F ，如图所示：∵3AB AC ==，4BC =，∴2BF CF ==，∴在Rt △AFB 中，AF∵点D ，E 是边BC 的两个黄金分割点，∴2BE CD ===，∵4EF BE BF =-=，4DF CD CF =-=，∴DF =EF ，∴28DE DF ==，∴()1181022ADE S DE AF ==-△ 故选：A【点睛】本题主要考查二次根式的运算、勾股定理及等腰三角形的性质与判定，熟练掌握二次根式的运算、勾股定理及等腰三角形的性质与判定是解题的关键．3、A【分析】将图形分三种情况展开，利用勾股定理求出两种情况下斜边的长进行比较，其值最小者即为正确答案．．【详解】解：如图（1），AB =√(2+3)2+12=√26(m )；如图（2），AB =√22+(1+3)2=√20=2√5(m )；如图（3），AB =√32+(2+1)2=3√2(m )，∵3√2<2√5<√26，∴最短的路径是3√2m．故选：A．【点睛】本题主要考查了勾股定理的应用，两点之间线段最短，解题的关键在于能够把长方体展开，利用勾股定理求解．4、D【分析】当铅笔不垂直于底面放置时，利用勾股定理可求得铅笔露出笔筒部分的最小长度；考虑当铅笔垂直于笔筒底面放置时，铅笔在笔筒外面部分的长度是露出的最大长度；从而可确定答案．【详解】=，则铅笔在笔筒外部分的最小长度为：15(cm)18−15=3(cm)；当铅笔垂直于笔筒底面放置时，铅笔在笔筒外面部分的长度为18−12=6（cm），即铅笔在笔筒外面最长不超过6cm，从而铅笔露出笔筒部分的长度不短于3cm，不超过6cm．所以前三项均符合题意，只有D选项不符合题意；故选：D【点睛】本题考查了勾股定理的实际应用，关键是把实际问题抽象成数学问题，分别考虑两种极端情况，问题即解决．5、B【分析】连接BM，MB′，由于CB′=3，则DB′=6，在Rt△ABM和Rt△MDB′中由勾股定理求得AM的值．【详解】解：连接BM，MB′，设AM=x，在Rt△ABM中，AB2+AM2=BM2，在Rt△MDB′中，B′M2=MD2+DB′2，∵折叠，∴MB=MB′，∴AB2+AM2= MD2+DB′2，即92+x2=(9-x)2+(9-3)2，解得x=2，即AM=2，故选：B．【点睛】本题考查了翻折的性质，对应边相等，利用了勾股定理建立方程求解．6、A【分析】根据题意可把立体图形转化为平面图形进行求解，如图，然后根据勾股定理可进行求解．【详解】解：如图，∵圆柱高12cm，底面半径为3cm，∴2312cm,392BC ACππ⨯====，∴在Rt△ACB中，由勾股定理得15cmAB=，∴蚂蚁从点A沿圆柱表面爬到点B处吃食物，要爬行的最短路程为15cm；故选A．【点睛】本题主要考查勾股定理，熟练掌握勾股定理求最短路径问题是解题的关键．7、A【分析】根据勾股数的定义逐项分析即可．【详解】解：A 、∵62+82＝102，∴此选项符合题意；B 、∵22+32≠42，∴此选项不符合题意；C 、∵12+22≠32，∴此选项不符合题意；D 、∵52+72≠112，∴此选项不符合题意．故选：A ．【点睛】此题主要考查了勾股数，解答此题要用到勾股数组的定义，如果a ，b ，c 为正整数，且满足a 2+b 2=c 2，那么，a 、b 、c 叫做一组勾股数．8、D【分析】利用勾股定理求出CD 的长，进而求出BC 的长，AB BC AC =- 即可求解．【详解】解：∵DC BC ⊥，∴90DCB ∠=︒ ，∵30ADC ∠=︒，5AC =，∴210AD AC == ，∴CD =，∵60CDB ∠=︒，∴30B ∠=︒ ，∴2BD CD ==，∴15BC = ，∴15510m AB BC AC =-=-= ，故选：D ．【点睛】本题考查勾股定理的应用，解题关键是掌握勾股定理．9、B【分析】根据勾股定理的逆定理，以及三角形的内角等于180︒逐项判断即可．【详解】A ，设3a x =，4b x ，4=c x ，此时()()()222344x x x +≠，故ABC 不能构成直角三角形，故不符合题意；B ，2221+=，故ABC 能构成直角三角形，故符合题意C ，::3:4:5A B C ∠∠∠=且180A B C ∠+∠+∠=︒，设3A x ∠=，4B x ∠=，5C x ∠=，则有12180x =︒，所以15x =︒，则75C ∠=︒，故ABC 不能构成直角三角形，故不符合题意；D ，设23a x =，24b x =，25c x =，则345x x x +≠，即222a b c +≠，故ABC 不能构成直角三角形，故不符合题意；故选：B【点睛】本题考查了勾股定理的逆定理，和三角形的内角和等知识，能熟记勾股定理的逆定理内容和三角形内角和等于180︒是解题关键．10、C【分析】将正方体展开，右边的正方形与前面正方形放在一个面上，此时AB 最短，根据三角形中位线，求出CN 的长，利用勾股定理求出AC 的长即可．【详解】解：将正方体展开，右边的正方形与前面正方形放在一个面上，展开图如图所示，此时AB 最短， ∵AN ＝MN ，CN ∥BM∴CN ＝12BM ＝2，在Rt △ACN 中，根据勾股定理得：AC故选：C ．．【点睛】本题考查了平面展开-最短路径问题，涉及的知识有：三角形中位线，勾股定理，熟练求出CN 的长是解本题的关键．二、填空题1、45°【分析】作点P 关于AB 的对称点P '，点Q 关于BC 的对称点Q '，连接P Q ''交AB 于M ，交BC 于N ，此时四边形PQNM的周长最小，过点P 作PH BQ ⊥于H ，由勾股定理求出BH =PH BH =45PBQ ∠=︒，再求出150P BQ ∠''=︒，过点Q '作Q K P B '⊥'于K ，在Rt BKQ ∆'中，30KBQ ∠'=︒，BQ BQ '==则KQ '=BK =，在Rt △P Q K ''中，由勾股定理得222P Q ''=+【详解】解：（1）如图，作点P 关于AB 的对称点P '，点Q 关于BC 的对称点Q '，连接P Q ''交AB 于M ，交BC 于N ，此时四边形PQNM 的周长最小，过点P 作PH BQ ⊥于H ，22222PH PB BH PQ HQ ∴=-=-，22222)BH BH ∴-=-，解得：BH =2422PH ∴=-=，PH ∴=PH BH ∴==45PBQ ∴∠=︒，（2）ABP ABP ∠=∠'，CBQ CBQ ∠=∠'，2()2150P BQ ABC PBQ PBQ ABC PBQ ∴∠''=∠-∠+∠=∠-∠=︒，过点Q '作Q K P B '⊥'于K ，在Rt BKQ ∆'中，18015030KBQ ∠'=︒-︒=︒，BQ BQ '==12KQ BQ ∴'='=，BK在Rt △P Q K ''中，2KP BP BK '='+=KQ '=222(222P Q ∴''=+=+22()22MP MN NQ P Q ∴++=''=+【点睛】本题考查轴对称最短问题、勾股定理、含30角的直角三角形的性质、轴对称的性质等知识，解题的关键是学会利用轴对称解决最短问题，学会添加常用辅助线，由直角三角形解决问题．2、10【分析】先把圆柱的侧面展开，连接AS ，利用勾股定理即可得出AS 的长．【详解】解：如图所示，∵AB ＝12×16＝8，BS ＝12BC ＝6，∴AS 10．故答案为：10．【点睛】本题考查的是平面展开一最短路径问题,根据题意画出圆柱的侧面展开图，利用勾股定理求解是解答此题的关键．3、6+【分析】由线段垂直平分线的性质定理得AD=BD，从而有∠DAB=∠B=15゜，由三角形外角性质可得∠ADC=30゜，由含30度角的直角三角形的性质及勾股定理即可求得AD与CD的长，最后可求得BC的长．【详解】∵直线l是线段AB的垂直平分线∴AD=BD∴∠DAB=∠B=15゜∴∠ADC=∠DAB+∠B=30゜∵90AC=∠=︒，3C∴AD=2AC=6∴BD=AD=6由勾股定理得：CD==∴6=+=+BC BD CD故答案为：6+【点睛】本题考查了线段垂直平分线的性质定理，等腰三角形的性质，含30度角的直角三角形的性质及勾股定理，熟练运用这些知识是关键．4、20【分析】将圆柱的侧面展开，得到一个矩形，然后利用两点之间线段最短可得AB'的长即是金丝的最短路线长，然后由勾股定理求解即可．【详解】解：解：沿AB 剪开可得矩形，如图所示：∵圆柱的高为16厘米，底面圆的周长为12厘米，∴A B ''=AB =16厘米，AA '=12厘米，在Rt AA B ''△中，2222121620AB A A A B ''''=+=+=，即金丝的最短路线长是：20厘米．故答案为：20．【点睛】本题考查了平面展开﹣最短路径问题，先根据题意把立体图形展开成平面图形后，再确定两点之间的最短路径．一般情况是两点之间，线段最短．在平面图形上构造直角三角形解决问题．5、﹣【分析】根据勾股定理求出OB 的长，即OD 的长，再根据两点间的距离求出点D 对应的数．【详解】解：由勾股定理知：OB =∴OD ＝∴点D 表示的数为﹣故答案为：﹣【点睛】此题考查了正方形的性质，勾股定理和实数与数轴，得出OD 的长是解题的关键．三、解答题1、（1）见解析；（2）见解析【分析】（1）根据勾股定理解答；（2）连接AB、BC，分别作其垂直平分线，两平分线交点即为所求点M．【详解】解：如图，由勾股定理得5AM=；（2）如图，点M即为所求．【点睛】此题考查了网格中作图，勾股定理的应用，线段垂直平分线的性质，正确理解线段垂直平分线的性质是解题的关键．2、（1）3.5；（2）见解析，3；（3）62【分析】（1）根据网格特点，由长方形的面积减去长方形内除所求三角形以外三个三角形面积即可求解；（2）根据三边的长度，利用勾股定理在网格中画出相应的三角形，利用（1）中方法求解面积即可；（3）先利用正方形的面积求出PR、RQ、PQ，根据构图法求出△PQR的面积，将七个图形面积加起来即可求得该六边形的面积．【详解】解：（1）根据网格，S△ABC=3×3﹣12×2×1﹣12×2×3﹣12×1×3=9﹣1﹣3﹣32=3.5，故答案为：3.5；（22212，∴利用构图法画出相应的△DEF，如图所示，∴S△DEF=2×4﹣12×2×1﹣12×2×2﹣12×1×4=8﹣1﹣2﹣2=3；（3）∵正方形PRBA，RQDC，QPFE的面积分别为13，10，17，∴PRRQ QP构造△PQR，如图所示，∴S△PQR=3×4﹣12×3×1﹣12×2×3﹣12×1×4=12﹣32﹣3﹣2=112，∵△PQR、△BCR、△DEQ、△AFP的面积相等，∴该六边形的面积为13+10+17+4×112=62．【点睛】本题考查网格作图、勾股定理、二次根式的应用、正方形的面积公式、三角形的面积公式、长方形的面积公式，理解构图法的原理，借助网格法和割补法求解图形面积是解答的关键．3、（1）见解析；（2）36．【分析】（1）先在射线BP 上截取BC a =，再作BC 的垂直平分线l 交BC 于D ，然后在直线l 上截取DA h =，则ABC ∆满足条件；（2）先根据等腰三角形的性质得到5BD CD ==，再利用勾股定理计算出13AB =，然后计算ABC ∆的周长．【详解】解：（1）如图，ABC ∆为所作；（2）ABC ∆为等腰三角形，AD BC ⊥，152BD CD BC ∴===，在Rt ABD ∆中，13AB =，ABC ∴∆的周长为：13131036AB AC BC ++=++=．【点睛】本题考查等腰三角形的性质以及勾股定理，掌握等腰三角形的性质是解题的关键．4、（1）2516t =；（2）3t = 【分析】（1）如图所示，连接PB ，则4cm PB PA t ==，先由勾股定理求出8cm AC =，最后在直角△BCP 中利用勾股定理求解即可；（2）根据题意可得()48cm CP t =-，再由21=16cm 2ACP S AC CP =⋅△进行求解求解．【详解】解：（1）假设存在，如图所示，连接PB ，由题意得：4cm PA t =，∴4cm PB PA t ==，∵∠ACB ＝90°，AB ＝10cm ，BC ＝6cm ，∴8cm AC ，∴()84cm PC AC PA t =-=-，∵222PB PC BC =+，∴()()2224846t t =-+，解得2516t =， ∵2584216t =<÷=， ∴2516t =符合题意， ∴当2516t =时，存在点P ，使得PA ＝PB ；（2）由题意得：()48cm CP t =-， ∵21=16cm 2ACP S AC CP =⋅△， ∴()1848=162t ⨯-，∴3t =．【点睛】本题主要考查了勾股定理，解题的关键在于能够熟练掌握勾股定理．5、尝试探究：证明见解析；定理应用：证明见解析【分析】尝试探究：根据全等三角形性质，得BAC AED ∠=∠，结合题意，根据直角三角形两锐角互余的性质，推导得90BAE ∠=︒；结合梯形、三角形面积计算公式，通过计算即可证明222+=a b c ；定理应用：根据提取公因式、平方差公式的性质分析，即可完成222244a c a b c b +=-证明．【详解】尝试探究：∵BCA ADE △△≌，∴BAC AED ∠=∠．∵90D ∠=︒∴90DAE AED ∠+∠=︒．∴90DAE BAC ∠+∠=︒．∵180BAC AED BAE ∠+∠+∠=︒．∴90BAE ∠=︒． ∵直角梯形的面积可以表示为()212a b +，也可以表示为211222ab c ⨯+， ∴()221112222a b ab c +=⨯+，整理，得222+=a b c ．定理应用：在Rt ABC △中，90C ∠=︒，∴222+=a b c ；∵2222a c a b +()222a c b =+．44c b -()()()2222222c b c b a c b =+-=+∴222244a c a b c b +=-．【点睛】本题考查了勾股定理、直角三角形、全等三角形、平方差公式的知识；解题的关键是熟练掌握全等三角形、直角三角形两锐角互余、平方差公式的性质，从而完成求解．。

(完整版)初二数学(人教版)下册二次根式、勾股定理测试题(经典)

金中?二次根式?和?勾股定理?测试题班级姓名学号得分一、选择题〔 32〕题号 1 2 3 4 5 6 7 8答案1.以下计算正确的选项是〔〕。

A 、 8—3=5B 、 2+9=2 9C 、 3 2— 2=22D 、1=242.以下各式成立的是〔〕。

2B 、a 2=aC 、2D 、( x 210A 、〔—2〕 =—2(— 10〕=1010〕 =x3. 方程 2x260 的解是〔〕。

A 、x3 B 、x3C 、x3D 、x 34．化简二次根式 ( 5)23得〔〕A ．53B ．5 3C ．5 3D ． 30AC5.以下几组数中，不能够作为直角三角形三边长度的是〔〕A 、， 2，B 、3，4，5C 、5， 12， 13D 、 20，30， 4BD6.如右图：一架 5 米长的梯子 AB 斜靠在一竖直的墙壁AO 上，此时 AO 为 4 米。

若是梯子的顶端A 沿墙壁下滑 1 米，那么梯子底端B 应向外搬动〔〕米。

A 、 3B 、 2C 、 1D 、无法确定7.一木杆在离地面 3 米处折断，木杆顶端落在离木杆底端 4 米的水平川面处。

那么木杆折断从前的高度是〔〕米。

A 、 8B 、 7C 、 5D 、4C D8.如图：在 Rt ABC 中， C=90 0 ，假设 AB=10，那么正方形 APCD 和正方形BPEF 的面积之和为〔〕。

E PAA 、 200B 、 100C 、 50D 、无法确定FB1二、填空题〔20 分〕9.要使 x 1 在实数范围内有意义，那么x 的取值范围是。

10.10 的整数局部是，小数局部是。

11.若是一个直角三角形的三条边的长度为6，8，a .那么a =。

12.命题“同位角相等，两直线平行〞的抗命题是。

13.在 Rt ABC中， C900, AB 1,那么AB2BC 2AC 2。

三、解答题〔 24 分〕14.计算〔 6 分×4〕〔1〕35210〔2〕(1220) ( 35)〔3〕31〔4〕(253)2( 52)( 52) 21815. 〔 10 分〕在数轴上作出表示的10 点〔不写作法，但必定保存作图印迹〕。