离散数学(王元元)思维导图
离散数学课件14图的基本概念

标定图与非标定图、基图
• 将图的集合定义转化成图形表示之后,常 用ek表示无向边(vi,vj)(或有向边<vi,vj>) ,并称顶点或边用字母标定的图为标定图 ,否则称为非标定图。
• 将有向图各有向边均改成无向边后的无向 图称为原来图的基图。
• 易知标定图与非标定图是可以相互转化的 ,任何无向图G的各边均加上箭头就可以 得到以G为基图的有向图。
称NG(v)∪{v}为v的闭邻域,记做NG(v)。 称{e|e∈E∧e与v相关联}为v的关联集,记做IG(v) 。
• 设有向图D=<V,E>,v∈V, 称{u|u∈V∧<v,u>∈E∧u≠v}为v的后继元集,记做 Г+D(v)。 称{u|u∈V∧<u,v>∈E∧u≠v}为v的先驱元集,记做 Г (v)。 -2020/7/23
2020/7/23
无序积与多重集合
• 设A,B为任意的两个集合,称 {{a,b}|a∈A∧b∈B}为A与B的无序积,记作 A&B。
可将无序积中的无序对{a,b}记为(a,b),并且 允许a=b。
无论a,b是否相等,均有(a,b)=(b,a),因而 A&B=B&A。
• 元素可以重复出现的集合称为多重集合或者 多重集,某元素重复出现的次数称为该元素 的重复度。 2020/7/23
2020/7/23
举例
NG(v1) {v2,v5}
=
NG(v1)
=
{v1,v2,v5}
IG(v1) = {e1,e2,e3}
Г+D(d ) = {c} Г-D(d ) = {a,c} ND(d ) = {a,c} ND(d ) = {a,c,d}
简单图与多重图
离散数学-第11章

图 论
主讲:熊焕亮
图论简介
• 图论(graph theory)是研究节点和边组成的图 形的数学理论和方法,为离散数学的一个重要分 支。图论的基本元素是节点和边(也称线、弧、 枝),用节点表示所研究的对象,用边表示研究 对象之间的某种特定关系。因此,图论可用节点 和边组成的图形及其有关的理论和方法来描述、 分析和解决各种实际问题,已广泛地应用于物理、 化学、运筹学、计算机科学、电子学、信息论、 控制论、网络理论、管理科学、社会科学等几乎 所有学科领域的有关问题。图论与组合数学、线 性规划、群论、矩阵论、概率论、数值分析等数 学分支有密切的关系。
均为偶数,所以 d (v)为偶数,但因中顶点度数为奇数,
vV1
vV1
d (v ) d (v )
vV2
所以 | V1 |必为偶数。
14
11.1.2 简单图、多重图和同构图
V {v1 , v2 ,., vn } 设 G V , E 为一个阶无向图, 称 d (v1 ), d (v2 )d (vn ),为 G 的度数列。对于顶点标定的无向图,它的度数列是唯一的。反之, 对于给定的非负整数列d (d1 , d 2 ,d n ),若存在以 V (v1 , v2 ,, vn ) 为顶点 集的n阶无向图G,使得 d (vi ) d i ,则称d是可图化的。特别地,若所得 的图是简单图,则称d是可简单图化的。 例11.1.2 (1)(3,5,1,4),(1,2,3,4,5)能成为图的度 数列吗?为什么? (2)已知图G 中有15条边,2个度数为4的结点,4个度数为3的结点, 其余结点度数均小于等于2,问G 中至少有多少个结点?为什么? 解 (1)由于给定的两个度数列中奇度顶点个数均为奇数,由上述 推论可知,他们都不能成为图的度数列。 (2)图中边数为15,由握手定理可知,G 中所有结点度数和为30。 除去2个度数为4的结点和4个度数为3的结点,还剩下10度。其余结 点度数小于等于2,假设均为2,则至少要5个结点,所以总共至少要1 1个结点。
_离散数学_课程教学实施方案_屈婉玲

同定位,离散数学知识框架的核心知识单元、推荐知识
单元和可选知识单元是不同的,各知识单元所含知识点
以及知识点的要求也是不同的。
下图给出了面向科学型、工程型、应用型等不同类
型的离散数学知识框架,其中每个方框代表一个知识单
元(组成知识单元的知识点在这里没有给出)。这些知识
才所需离散数学知识结构的角度来描述的,只对相关教
学内容给出了建议,这只是教学实施方案的一部分。教
学实施应该包括更多的内容:教学目标,教学安排(知
识单元和知识点的选择与讲授顺序、学时),各知识点的
教学要求,讲授重点与难点,考核要求与实施办法,教
学环节(课堂教学、作业、实践课题),教学环境与资源
型的计算机科学与技术研究、工程和应用的人才,应该
具有以下几种能力:获取知识的能力、应用知识的能力、
创新能力。通过离散数学的教学,对学生获取知识、应
用知识的能力,对创新思维的培养有着重要的作用。
根据课程的定位,教学实施方案应该体现出离散数
学对其他专业课程的支撑作用,应该强化学科方法的训
练和能力的培养。面向多样性人才的需求,计算机科学
报告提交,在成绩评定上可给予加分鼓励。上机实践对
于理解离散数学中的相关概念和算法有一定作用,考虑
到课程的主要目标是训练正确的逻辑思维方法,提高系
统建模和分析能力,建议上机学时不要挤占课上讲授学
时,可计入总学时。
根据《专业规范》的精神,总结国内部分学校的教
学经验,本文提出了一个面向科学型、工程型和应用型
图
树
基本计数
特殊的图
代数结构
离散数学导论(盘) 教学课件 作者 王元元 张桂芸 第五章演示文稿-支持高清浏览

第五章 关 系5.2 关系
5.2.4 关系特性闭包
定理5.17
设R是集合A上任一二元关系,那么 1 如果R是自反的,那么s(R)和t(R)都是自反的。 2 如果R是对称的,那么r(R)和t(R)都是对称的。 3 如果R是传递的,那么r(R)是传递的。
第五章 关
系2. 关系
4.
关系特性闭包
定理5.18
4 称A为R的前域,B为R的陪域。
第五章 关 系5.2 关系
5.2.2 关系的基本运算
定义5.6
称关系R和S相等,如果R与S有相同的
前域和陪域,并且 x y(xRy xSy)
定义5.7
设R是A到B的关系,R的逆关系或逆 (converse
是B到A的关系,记为R~, 规定为 R~= {<y,x> xRy}
如果R为A上的自反、对称、传递的二元 关系。
第五章 关
系3. 等价关系
1.
等价关系
定义5.12
设R为集合A上的等价关系。对每一a A,
a的等价类(equivalent class),记为[a]R
(或简单地记为[a]),指下列集合
[a]R={x x A∧xRa} a称为[a]R的代表元素。
第五章 关
特性之一,则R1 R2仍有此性质。 2 自反、反自反、对称性对并运算封闭。 3 反自反、对称、反对称性对差运算封闭。 4 对称性对补运算封闭。 5 五大特性对求逆运算均封闭。 6 自反性对合成运算封闭,其他四大特性对合成运算
均不封闭。
第五章 关 系5.2 关系
5.2.4 关系特性闭包
定义5.10
设R是集合A上二元关系,称R "为R的自反闭包 (对称闭包,传递闭包),如果R"满足: (1)R"是自反(对称的,传递的)。 (2)R R"。 (3)对任意A上关系R"" ,若R""满足(1)和(2)
离散数学思维导图第一章
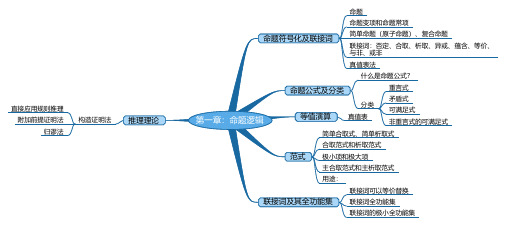
重言式
矛盾式可满足式非重言式的可满足式直接应用规则推理附加前提证明法
归谬法命题
命题变项和命题常项
简单命题(原子命题)、复合命题
联接词:否定、合取、析取、异或、蕴含、等价、与非、或非
什么是命题公式?
分类
真值表简单合取式、简单析取式
合取范式和析取范式
极小项和极大项
用途:
联接词可以等价替换
联接词全功能集
联接词的极小全功能集构造证明法真值表法
主合取范式和主析取范式
命题符号化及联接词命题公式及分类等值演算范式联接词及其全功能集推理理论第一章:命题逻辑。
离散数学第一章

例2: “派小王或小李中的一人去开会” 不能符号化为形式P∨Q ,因为这里的“或”表示 的是排斥或。它表示非此即彼,不可兼得。 运算符 ∨表示可兼或,排斥或以后用另一符号表达。也可
以借助于联结词
或。
┒、∧ 、∨共同来表达这种排斥
课堂练习: 将下列命题符号化: (1) 王东梅学过日语或俄语。 (2) 张小燕生于1977年或1978年。 (3) 小元元只能拿一个苹果或一个梨。
常称为“非”运算,所有可能的运算结果可用下表
(真值表)表示。
P
┒P
T F
F T
例: (a) P: 3是偶数。
则┑P: 3不是偶数。
(b)
的”。 (c) (d)
Q: 4 是质数。
则┑Q: 4 不是质数。或 “说4 是质数是不对 R: 我们都是汉族人。 则┒R: 我们不都是汉族人。 S: 今天下雨并且今天下雪。 则 ┒S:今天不下雨或者今天不下雪。
Q:明天下雨
是两个命题,利用联结词“不”、“并且”、 “或” 等可分别构成新命题: “明天不下雪”; “明天下雪并且明天下雨”; “明天下雪或者明天下雨”等。
即 : “非P”;
“P并且Q”;
“P或Q”等。 在代数式x+3 中, x 、 3 叫运算对象, +叫运 算符,x+3 表示运算结果。在命题演算中, 也用同样术语。 联结词就是命题演算中的运算符,叫逻辑运算符或叫命题联 结词。常用的命题联结主要有 5 个。
2.常用命题联结词 1). 否定词┑ 定义:设P为任一命题。复合命题“非P”(或“P的 否定”)称为P的否定,记作 ┑P,读作“非P”。┒ 为否定联结词。┑P为真当且仅当P为假。 由定义可知, ┑P 的逻辑关系为P不成立,因而P
离散数学的ppt课件

科学中的许多问题。
03
例如,利用图论中的最短路径算法和最小生成树算法
等,可以优化网络通信和数据存储等问题。
运筹学中的应用
01
运筹学是一门应用数学学科, 主要研究如何在有限资源下做 出最优决策,离散数学在运筹 学中有着广泛的应用。
02
利用离散数学中的线性规划、 整数规划和非线性规划等理论 ,可以解决运筹学中的许多问 题。
并集是将两个集合中的所有元素合 并在一起,形成一个新的集合。
详细描述
例如,{1, 2, 3}和{2, 3, 4}的并集是 {1, 2, 3, 4}。
总结词
补集是取一个集合中除了某个子集 以外的所有元素组成的集合。
详细描述
例如,对于集合{1, 2, 3},{1, 2}的 补集是{3}。
集合的基数
总结词
)的数学分支。
离散数学的学科特点
03
离散数学主要研究对象的结构、性质和关系,强调推
理和证明的方法。
离散数学的应用领域
计算机科学
01
离散数学是计重要的工具和方法。
通信工程
02
离散数学在通信工程中广泛应用于编码理论、密码学、信道容
量估计等领域。
集合的基数是指集合中元素的数量。
详细描述
例如,集合{1, 2, 3}的基数是3,即它包含三个元素。
03 图论
图的基本概念
顶点
图中的点称为顶点或节点。
边
连接两个顶点的线段称为边。
无向图
边没有方向,即连接两个顶点的线段可以是双向 的。
有向图
边有方向,即连接两个顶点的线段只能是从一个顶 点指向另一个顶点。
研究模态算子(如necessity、possibility)的语义和语法。
离散数学教程-王元元-第12章 群环域

离散数学 第12章 群、环、域
12.1 半群
12.2.1 群及其基本性质
定义12.3 称代数结构<G,>为群,如果 (1)<G, >为一半群。 (2)<G, >中有幺元e。 (3)<G, >中每一元素都有逆元。 简言之,群是每个元素都可逆的独异点。
群的载体常用字母G表示,G也常用于表示一个群。
离散数学 第12章 群、环、域
12.1 半群
12.1.1 半群及独异点
定理12.3 设<S,>为一半群,那么 (1) 存在<S,>到<SS,◦ >的半群同态h。 (2) <S,>在含有幺元时同构于<h(S),◦>, 后者是<SS,◦ >的一个子代数。 证 证(1):定义函数h:S→SS:对任意aS,h(a)= fa fa:S→S 定义如下: 对任意xS, fa(x)= ax 即将S中的一个元素a影射到一个线性变换fa。现证h为一同态。 对任何元素a,bS , h(ab)=fab (l2-1) 而对任何xS,fab(x)= abx = fa(fb(x))= fa◦fb (x),故fab= fa◦fb ,
由此及式(l2-1)即得 h(ab)= fab = fa◦fb =h(a)◦h(b)
证(2):只需证明a,bS,如果a≠b,则fa≠fb。因为<S,>含有幺元 e,a*e=a≠b*e=b,所以存在xS,fa(x)≠fb(x),定理得证。
离散数学 第12章 群、环、域 12.1 半群
12.1.1 半群及独异点
(4)S由A生成,即S中元素或者为e, 或者为A的成员,或者 为
离散数学王元元习题解答(3)

离散数学王元元习题解答(3)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第二章谓词演算及其形式系统2.1 个体、谓词和量词内容提要谓词演算中把一切讨论对象都称为个体,它们可以是客观世界中的具体客体,也可以是抽象的客体,诸如数字、符号等。
确定的个体常用a,b,c等到小写字母或字母串表示。
a,b,c等称为常元(constants)。
不确定的个体常用字母x,y,z,u,v,w等来表示。
它们被称为变元(variables)。
谓词演算中把讨论对象——个体的全体称为个体域(domain of individuals)),常用字母D表示,并约定任何D都至少含有一个成员。
当讨论对象遍及一切客体时,个体域特称为全总域(universe),用字母U表示。
例如,当初中学生说“所有数的平方非负”时,实数集是个体域;而达尔文在写《物种起源》时,则以全体生物为个体域;也许哲学家更偏爱全总域。
讨论常常会涉及多种类型个体,这时使用全总域也是比较方便的。
当给定个体域时,常元表示该域中的一个确定的成员,而变元则可以取该域中的任何一个成员为其值。
表示D上个体间运算的运算符与常元、变元组成所谓个体项(terms)。
例如,x+y,x2等。
我们把语句中表示个体性质和关系的语言成分(通常是谓语)称为谓词(predicate)。
谓词携有可以放置个体的空位,当空位上填入个体后便产生一个关于这些个体的语句,它断言个体具有谓词所表示的性质和关系。
通常把谓词所携空位的数目称为谓词的元数。
谓词演算中的量词(quantifiers)指数量词“所有”和“有”,分别用符号(All的第一个字母A的倒写) 和(Exist的第一个字母E的反写)来表示。
为了用量词和分别表示个体域中所有个体和有些个体满足一元谓词P,需引入一个变元,同时用作量词的指导变元(放在量词后)和谓词P的命名式变元:xP(x) 读作“所有(任意,每一个)x满足P(x)”。
离散数学课件 离散5.1-5.2节PPT

arj
j=0
= a + ar + ar2
+ . . . + arn
=
arn+1 − a r−1
when
n≠
1
n < 2n for all n > 0
2n < n! for all n ≥ 4
An inequality for harmonic (NÚ) numbers: Let j ≥ 1. Define
To prove that P (n) is true for all n ∈ N, n ≥ n0, where P (n) is a propositional function, we complete two steps:
Basis step: We prove that P (n0) is true. Inductive step: We show that the conditional statement P (k) → P (k + 1) is true for all k ∈ N, k ≥ n0. Here P (k) is called the inductive hypothesis.
离散数学王元元习题解答 (9)

第三篇图论之袁州冬雪创作第八章图8.1 图的基本知识内容提要图的定义及有关术语定义8.1 图(graph)G由三个部分所组成:(1)非空集合V(G),称为图G的结点集,其成员称为结点或顶点(nodes or vertices).(2)集合 E(G),称为图G的边集,其成员称为边(edges). I(3)函数ΨG:E(G)→(V(G),V(G)),称为边与顶点的关联映射(associatve mapping).这里(V(G),V(G))称为VG的偶对集,其成员偶对(pair)形如(u,v),u,v为结点,它们未必分歧.ΨG(e)= (u,v)时称边e关联端点u,v.当(u,v)用作序偶时(V(G),V(G))=V(G)V(G),e称为有向边,e以u为起点,以v为终点,图G称为有向图(directed graph);当(u,v)用作无序偶对时,(u,v)=(v,u),称e为无向边(或边),图G称为无向图(或图).图G常常使用三元序组< V(G),E(G),ΨG>,或< V,E,Ψ>来暗示.显然,图是一种数学布局,由两个集合及其间的一个映射所组成.定义8. 2 设图G为< V,E,Ψ>.(l)当V和E为有限集时,称G为有限图,否则称G 为无限图.本书只讨论有限图.(2)当ΨG为单射时,称G为单图;当ΨG为非单射时,称G为重图,又称知足Ψ(e1) = Ψ(e2)的分歧边e1,e2,为重边,或平行边.(3)当Ψ(e)=(v,v)(或<v,v>)时,称e为环(loops).无环和重边的无向单图称为简单图.当G为有限简单图时,也常常使用(n,m)暗示图G,其中n = V,m = E .(4)Ψ为双射的有向图称为有向完全图;对每(u,v),u v,均有e使Ψ(e)=(u,v)的简单图称为无向完全图,简称完全图,n个顶点的完全图常记作K n.(5)在单图G中,Ψ(e)=(u,v)(或<u,v>)时,也用(u,v)(或<u,v>)暗示边e,这时称u,v邻接e,u,v是e 的端点(或称u为e的起点,v为e的终点);也称e关联合点u , v .不是任何边的端点的结点都称为孤立结点,仅由孤立结点构成的图(E = )称为零图.(6)当给G赋予映射f:V→W,或g:E→W,W为任意集合,常常使用实数集及其子集,此时称G为赋权图,常常使用< V,E,Ψ,f >或< V,E,Ψ,g >或< V,E,Ψ,f,g >暗示之.f(v)称为结点v的权,g(e)称为边e 的权.8.1.2 结点的度定义8.3 在无向图中,结点v 的度(degree )d(v)是v 作为边的端点的数目.在有向图中,结点的度d(v)是v 的出度d +(v)(out-degree )与入度d -(v)(in-degree )的和;v 的出度是v 作为有向边起点的数目,v 的入度是v 作为有向边终点的数目.定理8.1 对任意图G ,设其边数为m, 顶点集为{v 1,v 2,…,v n },那末图的奇数度顶点必为偶数个.定理8.3 自然数序列(a 1,a 2,…,a n )称为一个度序列,如果它是一个图的顶点的度的序列.(a 1,a 2,…,a n )为一度序列,当且仅当∑=n i i a 1为一偶数.定义8.4 一度的顶点称为悬挂点(pendant nodes ). 定义8.6 各顶点的度均相同的图称为正则图(regular graph ).各顶点度均为k 的正则图称为k-正则图.图运算及图同构由于图由结点集、边集及关联映射组成,因此对图可作种种与集合运算相近似的运算.定义8.6 设图G1=<V1,E1,Ψ1>,G2=<V2,E2,Ψ2>,称G1为G2的子图(subgraph ),如果V1V2,E1E2,Ψ1Ψ2.称G1为G2的真子图,如果G1是G2的子图,且G1 G2.称G1为G2的生成子图(spanning subgraph),如果G1是G2的子图,且V1 = V2.定义8.7设图G1=<V1,E1,Ψ1>,G2=<V2,E2,Ψ2>,且Ψ1与Ψ2是相容的,即对任一x,若Ψ1(x)=y1, Ψ2(x)=y2,则y1= y2,从而Ψ1Ψ2为一函数.(1)G1与G2的并,记为G1G2=G3=<V3,E3,Ψ3>,其中V3=V1V2,E3=E1E2,Ψ3= Ψ1Ψ2.(2)G1与G2的交,记为G1G2 =G3 = <V3,E3,Ψ3>,其中V3=V1V2,E3=E1E2,Ψ3= Ψ1Ψ2.(3)若G1为G2的子图,则可定义G2对G1的差,记为G2-G1=G3=<V3,E3,Ψ3>,其中E3 =E2 – E1,V3=V2,Ψ3 = Ψ2E3.(4)G1与G2的环和,记为G1G2,G1G2=(G1G2)-(G1G2)(5)若G为简单图,则可定义G的补,记为G¯,若V(G)= n,则G¯= K n-G定义8.8设图G=<V,E,Ψ >(1)G-e暗示对G作删除边e的运算,G-e = <V,E’,Ψ’ >,其中E’=E-{e},Ψ’= ΨE’.(2)G-v暗示对G作删除顶点v的运算,G-v =<V’,E’,Ψ’ >,其中V’= V-{v},E’=E-{e e 以v为端点},Ψ’=ΨE’.(3)边e切割运算.设G中Ψ(e) = (u,v),对G作边e 切割得G’=<V’,E’,Ψ’ >,其中,V’=V{v’},E’= (E-{e}){e1,e2}, Ψ’= (Ψ-{<e,(u,v)>}){<e1, (u,v’)>,<e2,(v’,v)>}(4)顶点v贯通运算.设G中顶点v恰为边e1,e2的端点,且Ψ (e1) = (u,v),Ψ (e2) = (w,v).对G作顶点v 贯通得G’=<V’,E’,Ψ’ >,其中V’=V-{v}, E’=(E-{e1,e2}){e}, Ψ’=( Ψ-{<e1,(u,v)>,<e2,(w,v)>}){<e, (u,w)>}.切割与贯通是互逆的,二者常被称为同胚运算.定义8.9 设G1=<V1,E1,Ψ1>,G2=<V2,E2,Ψ2>为两个图,称G1与G2同构(isomorphic),如果存在双射f:V1→V2,双射g:E1→E2,使得对每边e E1,Ψ1(e)=(u,v)(或<u,v>)当且仅当Ψ2(g(e)) = (f(u),f(v))(或< f(u),f(v)>)当限于讨论简单图时,可以用顶点的偶对暗示边,即当Ψ(e)=(u,v)时,边e用(u,v)来暗示.这时两图同构的条件可以简化为(u,v)E1当且仅当(f(u),f(v))E2习题解答操练8.11、想一想,一只虫豸是否可以从立方体的一个顶点出发,沿着棱匍匐、它匍匐过每条梭一次且仅一次,而且最终回到原地?为什么?解不成能.可将立方体的一个顶点看做图的一个顶点,把立方体的棱看做图的边,那末该图的四个顶点都是三度的,因此不成能从一个顶点出发,遍历所有的边一次且仅一次,而且最终回到原顶点.2、请设想一张图,它的64个顶点暗示国际象棋棋盘的64个方格,顶点间的边暗示:在这两个顶点暗示的方格之间可以停止“马步”的行走.试指出其顶点有哪几类(依其度分类),每类各有多少个顶点.解其顶点有5类:二度顶点合计4个,三度顶点合计8个,四度顶点,合计20个,六度顶点, 合计16个顶点,八度顶点, 合计16个顶点.3、(l)证明:n个顶点的简单图中不会有多于2)1(nn条边.(2)n个顶点的有向完全图中恰有2n条边.证(l)n个顶点的简单完全图的边数总和为(2)n个顶点的有向完全图的边数总和为4、证明: 在任何n (n≥2)个顶点的简单图G中,至少有两个顶点具有相同的度.证如果G有两个孤立顶点,那末它们即是具有相同的度的两个顶点.如果G恰有一个孤立顶点,那末我们可对有n – 1 个顶点但没有孤立顶点的G’(它由G删除孤立顶点后得到)作下列讨论.无妨设G没有孤立顶点,那末G 的n个顶点的度数应是:1,2,3,…,n–1 这n–1种可以之一,因此必定有两个顶点具有相同的度.5、图8.10是一个迷宫,其中数字暗示通道、和死胡同(包含方针) .请用一个图来暗示这个迷宫(用结点暗示通道、和死胡同(包含方针)),用边暗示它们之间的可直接到达关系.解64手.n是奇数还是偶数.解n顶点度数之和为奇数(奇数个奇数的和),这是不成能的,因此n 是偶数.7、n 个城市间有m 条相互毗连的直达公路.证明:当2)2)(1(-->n n m 时,人们便能通过这些公路在任何两个城市间观光.证 用n 个顶点暗示n 个城市,顶点间的边暗示直达公路,据题意需证这n 个城市的公路网络所构成的图G 是连通的.反设G 不连通,那末可设G 由两个不相关的子图(没有任何边关联分别在两个子图中的顶点)G1,G2组成,分别有n 1,n 2个顶点,从而,n = n 1+n 2,n 1≥1,n 2≥1.由于各子图的边数不超出2)1(-i i n n (),因此G 的边数m 知足: 与已知2)2)(1(-->n n m 抵触,故图G 是连通的. (本题是定理8.8的特例,当然也可以应用这一定理和它的证明方法来解题.)*8、(1)证明:序列(7,6,5,4,3,3, 2),(6,5,5,4,3,2,2)以及(6,6,5,4,3,3,1)都不是简单图的度序列.(2)若自然数序列(d 1,d 2,…,d n )知足d 1>d 2>…>d n ,那末当它为一简单图的度序列时必有(a )∑=ni i d 1为偶数;(b )对任一k ,1≤k ≤n , ∑=k i i d 1≤ k(k-1)+∑+=nk i i d k 1),min(.证(1)由于7个顶点的简单图中不成能有7度的顶点,因此序列(7,6,5,4,3,3, 2)不是简单图的度序列.序列(6,5,5,4,3,2,2)中有三个奇数,因此它不是简单图的度序列.序列(6,6,5,4,3,3,1)中有两个6,若它是简单图的度序列,那末应有两个顶点是6度顶点,于是它们都要与其它所有顶点邻接,该图就不会有一度的顶点,与序列中末尾的1冲突.故(6,6,5,4,3,3,1)也不是简单图的度序列.证(2)∑=ni i d 1为偶数是显然的.思索图中的k 个顶点(k=1,2,…,n ),这k 个顶点的生成子图的度数总和 ≤ k(k-1),而其余n –k 个顶点v k+1,v k+2,…,v n , 可以使 v 1,v 2,…,v k 增加的度数不会超出 因此我们有∑=k i i d 1≤ k(k-1)+∑+=nk i i d k 1),min(.9、画出图8.11中图的补图及它的一个生成子图. 图8.11解 补图 生成子图10、一个简单图,如果同构于它的补,则该图称为自补图.(1)给出一个4个顶点的自补图.(2)给出一个5个顶点的自补图.(3)是否有3个顶点或6个顶点的自补图?(4)证明一个自补图一定有4k 或4k +1个顶点(k 为正整数).解 (1)4个顶点的自补图: (2)5个顶点的自补图:(3)没有.(4)证 设G 为自补图,有n 个顶点.我们已知n 个顶点的完全图有 2)1(-n n 条边,因此G 应恰有4)1(-n n 条边.故或者n 是4的整数倍,或者n –1是4的整数倍,即图G 一定有4k 或4k +1个顶点(k 为正整数).11、(l )证明图 8.12中(a )与(b )同构. (a) (b)图8.12 (2)给出所有分歧构的4个结点的简单图的图示.(l )证在图(a )图(b )间建立双射hvA B D I J C E G H F h(v) α β δ ι η χ φ ϕ κ γ 可逐一验证 (不赘)(u,v)E(a)当且仅当 (h(u),h(v))E(b)(2)所有分歧构的4个结点的简单图的图示有如下11个: A α βD C B χEF δ ε κ φ γGH ηI J ι ϕ*12、K n 暗示n 个顶点的无向完全图.(l )对K 6的各边用红、蓝两色着色,每边仅着一种颜色,红、蓝任选.证明:无论怎样着色,图上总有一个红色边组成的K 3或一个蓝色边组成的K 3.(2)用(l )证明下列事实:任意6个人之间或者有三个人相互认识,或者有3个人相互都不认识.证(l )思索K 6的顶点V ,与之关联的边有5条,其中至少有3条着同一颜色.无妨设均着红色,这三边的另外一个端点分别是u1,u2,u3(如图所示).再思索关联u1,u2,u3的三条边.如果它们中有一条着红色的边,那末我们就已经得到一个红色边组成的K 3,如果它们中没有着红色的边,那末我们就可以够得到一个蓝色边组成的K 3.证(2)用六个顶点暗示6个人,顶点间红色边暗示人员间相互认识,顶点间蓝色边暗示人员间相互不认识,便发生一个边着红、蓝两色的完全图K 6.操纵(1)的结论,可以断定6个人之间或者有三个人相互认识,或者有3个人相互都不认识.8.2 途径、回路及连通性内容提要8.2.1 途径与回路定义8.10 图G 的顶点v 1到顶点v l 的拟途径(pseudo path )是指如下顶点与边的序列:vu2u1u3v1 ,e1 ,v2 ,e2 ,v3 ,… ,v l-1 ,e l-1 ,v l 其中v1 ,v2 ,v3 ,… ,v l-1 ,v l为G的顶点e1 ,e2 ,…,e l-1 为G的边,且e i( i= 1,2,… ,l-1)以v i及v i+1为端点,(对有向图G,e i以v i为起点,以v i+1为终点),拟途径的边数l-1称为该拟途径的长度.当e i( i= 1,2,…, l-1)各不相同时,该拟途径称为途径(walk),又当v i(i = 1,2,… ,l)各不相同时(除v1与v l),则称此途径为通路(Path).v1=v l的途径称为闭途径(closed walk);v1= v l的通路称为回路(circuit).当讨论限于简单图或无平行边的有向图时,上述拟途径、途径、通路等可用顶点序列来暗示,例如用(v1 ,v2 ,v3 ,… ,v l-1 ,v l)代替式v1 ,e1 ,v2 ,e2 ,v3 ,… ,v l-1 ,e l-1 ,v l.定理8.4 在有n个顶点的图G中,如果有从顶点u到v(u v)的拟途径,那末从u到v必有途径,而且必有长度不大于n – 1 的通路.定理8. 5在具有n个顶点的图G中,如果有从v到v的闭途径,那末必定有一条从v到v的长度不大于n的回路.8.2.2 连通性定义8.11称图中顶点u到v是可达的(accesible),如果u = v,或者有一条u到v的途径.定义8.12称无向图G是连通的(connected),如果G的任何两个顶点都是相互可达的.称有向图G是强连通的,如果G的任何两个顶点都是相互可达的;称有向图G是单向连通的,如果G的任何两个顶点中,至少从一个顶点到另外一个顶点是可达的;称有向图G是弱连通的,如果G的有向边被看做无向边时是连通的.图G’称为图G的连通分支(connected components),如果G’是G的子图,G’是连通的,而且不存在G的真子图G’’,使G’’是连通的,且G’’以G’为真子图.定义 8.14 设G’为有向图G的子图,若 G’是强连通的(单向连通的、弱连通的),且G没有真子图G’’使G’为其真子图,而G’’强连通(单向连通、弱连通),那末称G’为G的一个强分图(单向分图、弱分图).定理8. 6 一个图G是不连通的,当且仅当G的顶点集V 可以分成两个不交的非空子集V1和V2,使得任何边都不以V1的一个顶点和V2一个顶点为其两头点.定理8.7 如果图G恰有两个分歧的奇数度的顶点u,v,那末u到v必定是可达的.定理8.8若图G为具有n个顶点、k个连通分支的简单图,那末G至多有2)1)((+--knkn条边.Δ8.2.3 连通度定义 8.15设S为连通图G的顶点集V的子集,称S为G 的点割集(cut-set ofnodes),如果从G中删除S中的所有顶点后得到的图不连通,但S 的任何真子集均无这一特性.当点割集为单元素集合{v }时,v 称为割点(cut-nodes ). 定义8.16χ(G)称为G 的点连通度(node-connectivity ),定义如下:设S 为连通图G 边集E 的子集,称S 为G 的边割集(cut-set of edges ),或割集,如果从G 中删除S 的所有边后所得的图是不连通的,但S 的任何真子集均无这一特性.当割集为单元素集{e }时,称e 为割边(cut-edges ).定义8.18 λ(G)称为图G 的边连通度(edge-connectivity ),定义如下:定理8.9 对任何简单无向图G ,χ(G)≤λ(G)≤δ(G)定理8.10 设G 为n 个顶点、m 条边的简单连通图,那末λ(G)≤nm 2. 习题解答操练8.21、 证明定理8.5.证 设n 个顶点的图G 中,有从v 到v 的闭途径,暗示为 (v,v 1,v 2,…,v k ,v )如果v,v 1,v 2,…,v k 中没有相同顶点(因而未几于n 个),那末它即是一条从v 到v 的长度不大于n 的回路.如果v,v 1,v 2,…,v k 中有相同顶点v i =v j ,例如(v,v1,…, v i,…, v j, v j+1,…,v k,v)那末删除v i到v j的闭途径,得到(v,v1,…, v i, v j+1,…,v k,v)仍然为从v到v的闭途径.如此不竭删除闭途径内相同顶点构成的闭途径,最终必可得到一条从v到v的长度不大于n的回路.2、证明:在简单无向图G中,从结点u到结点v,如果既有奇数长度的通路又有偶数长度的通路,那末G中必有一奇数长度的回路.证设G中,从结点u到结点v的奇数长度的通路为O ,偶数长度的通路为E.对O和E的除结点u和v的相交结点的数目归纳k.k=0,那末O和E恰好构成G的奇数长度的回路.设奇数长度的通路与偶数长度的通路的相交结点的数目少于k时,命题成立.设图G中,从结点u到结点v的奇数长度的通路与偶数长 u 1 2 … k v度的通路有k个相交结点,如图所示:思索结点u到结点k,如果从结点u到结点k,既有奇数长度的通路又有偶数长度的通路,那末据归纳假设,其中有一奇数长度的回路,因而G中必有一奇数长度的回路.如果从结点u到结点k的两条通路均为偶数长度,或均为奇数长度,那末结点k到结点v必定既有奇数长度的通路又有偶数长度的通路,因而构成一奇数长度的回路.3、证明:若简单无向图G是不连通的,那末G¯必定是连通的.证设简单无向图G是不连通的,那末G由两个不相关的子图(没有任何边关联分别在两个子图中的顶点)G1,G2组成,分别有顶点,u1,u2,…,u k 和v1,v2,…,v l.由于边(u i,v j)均不在G中(i=1,2,…,k, j=1,2,…,l)因此(u i ,v j)全部在G¯中,从而G¯是连通的.4、有向图可用于暗示关系,图8.18暗示的二元关系是传递的吗?说说如何由有向图断定关系的传递性.求图8.18暗示的二元关系的传递闭包,说说构作有向图传递闭包的方法.图解从u到v的途径,则必有从u图8.18暗示的二元关系的传递闭包如图8.18(b)所示.构作有向图传递闭包的方法是:对图中任意两个结点u,v,如果有从u 到v 的途径,则添加从u 到v 的边.5、给出图8.19中有向图的强分图,单向分图和弱分图,作出它的凝集图.图8.19 解 图8.19<{v 1,v 2},{<v<{v 3,v 4,v 5},{<v 3,v 5>,<v 4,v 3>,<v 4,v5>,<v 5,v 4>}>,<{v 6},{<v 6,v 6>}> ,<{v 7,v 8,v 9},{<v 7,v 8>,<v 8,v 9>,<v 9,v 7>}>,<{v 10},{}>图8.19中有向图的单向分图有:<{v 1,v 2,v 3,v 4,v 5,v 6},{<v 1,v 2>,<v 2,v 1>,<v 1,v 4>,<v 2,v 3>,<v 4,v 3>,<v 3,v 5>,<v 4,v 5>,<v 5,v 4>,<v 3,v 6>}> ,<{v 7,v 8,v 9,v 10},{<v 7,v 8>,<v 8,v 9>,<v 9,v 7>,<v 7,v 10>}>图8.19 6、有7人a c ,d ,e ,f ,g 分别精晓下列语言,问他们7.a 精晓英语.b 精晓汉语和英语.c 精晓英语、俄语和意大利语.d 精晓日语和英语.e 精晓德语和意大利语.{v 1{v 3,v 4,v 5,v 8,v 9{v 6f 精晓法语、日语和俄语.g 精晓法语和德语.解 下图中7个顶点暗示7个人,关联两个顶点的边暗示两个人同时精晓某一种语言: 由于该图是连通的,因此他们7人是可以自由交谈(需要时借助他人作翻译). 7、证明:一个有向图是单向连通的,当且仅当它有一条颠末每结点的途径.证 充分性是显然的.需要性:设有向图G 是单向连通的,P 是G 中的一条途径,起点为u 1,终点为u k .如下延长这一途径:思索途径外的任意顶点w,若(1)有顶点w 到u 1的途径,则我们如愿.(2)有顶点u k 到w 的途径,则我们如愿.否则,由于有向图是单向连通的,(3)有顶点w 到u k 的途径,和顶点u k-1到w 的途径, 则我们如愿.否则,由于有向图是单向连通的,(4k w的途径, 则我们如愿.否则,(5和顶点u 1到w的途径, 则我们如愿.ab dc e gf u k-1u 1u u 1 u k-2 u k-1如上不竭延长这一途径,直至发生一条颠末每结点的途径.8、称d(u,v)为图G =<V, E, Ψ>中结点u ,v 间的间隔:d 称为图G 的直径,如果d =max{d(u,v)u,v V}.试求图8.20中图的直径,χ(G) ,λ(G),δ(G),并指出一个点割集和一个边割集.图8.20解 d =3 ,χ(G)=3 ,λ(G)=3,δ(G)=3 .9、顶点v 是简单连通图G 的割点,当且仅当G 中存在两个顶点v1,v2,使v1到v2的通路都颠末顶点v .试证明之.证充分性是显然的.需要性:设顶点v 是简单连通图G 的割点,如果不存在两个顶点v1,v2,使v1到v2的通路都颠末顶点v ,那末对任意两个顶点v1,v2,都有一条通路不颠末顶点v ,因而删除顶点v 不克不及使G 不连通,与v 是简单连通图G 的割点抵触.故G 中必存在两个顶点v1,v2,使v1到v2的通路都颠末顶点v .10、边e 是简单连通图G 的割边,当且仅当e 不在G 的任一回路上.试证明之.证 设e 是简单连通图G 的割边,其端点为u,v .删除边 wu …e 后,u,v 应在两个分歧的连通分支中.若e 在G 的一条回路上,那末删除边e 后,u,v 应仍在一条通路上,抵触.故e 不在G 的任一回路上.反之,设e 不在G 的任一回路上,而e 不是简单连通图G 的割边.那末G-{e}仍是连通的,故还有u 到v 的一条通路,从而这条通路连同边e 构成G 中的一条回路,抵触.因此边e 是简单连通图G 的割边11、试用有向图描绘下列问题的解:或人m 带一条狗d ,一只猫c 和一只兔子r 过河.m 每次游过河时只能带一只动物,而没人管理时,狗与兔子不克不及共处,猫和兔子也不克不及共处.问m 怎样把三个动物带过河去?(提示:用结点代表状态,状态用序偶<S1,S2>来暗示,这里S1,S2分别是左岸和右岸的人及动物集合,例如初始状态为< {m,d,c,r} , >.解 描绘上述问题的有向图如下:12、有向图可以刻画一个系统的状态转换,例如用图8.21中的有向图可以描绘识别01010序列的状态转换系统.其中S 为初始状态,在此读入序列,然后依序列中符号转入后续状态(读到0进入S1,读到1进入S2,如此等等).S4暗示读完序列01010应进入的最后状态,S5暗示读完一个非01010序列应进入的最后状态. <{d,r} , {m,c}><{c},{m,d,r}>< {m,c,r},{d} ><{r},{m,c,d}><{m,d,c,r}, ∅><{d,c}, {m,r}><{m,d,c}, {r}> <{m, r},{c,d}><∅,{m,d,c,r}><{d},{m,c,r}><{ m,d,r} , {c}><{r},{m, c,d}><{c,r} , {m,d}>试自行构作识别序列01(10)10的有向图刻画的状态转换系统.(上文中w 暗示空字或重复任意多次w 所得的字.)图8.21解 识别序列01(10)10的有向图刻画的状态转换系统如下:内容提要 8. 3. 1欧拉图与欧拉途径定义8.19 图G 称为欧拉图(Euler graph ),如果图G 上有一条颠末G 的所有顶点、所有边的闭途径.图G 称为欧拉途径(Euler walk ),如果图G 上有一条颠末G 所有顶点、所有边的途径.无向图G 为欧拉图当且仅当G 连通,而且所有顶点的度都是偶数.有向图G 为欧拉图,当且仅当G 是弱连通的,而且每个顶点的出度与入度相等.定理8.12 如果G 为欧拉图,那末G 可分成若干个(一个或几个)回路.定理8.13 无向图G 为欧拉途径(非欧拉图),当且仅当G 连通,而且恰有两个顶点的度是奇数.有向图G 为欧拉途径(非欧拉图),当且仅当G 连通,而且恰有两个顶点的入度与出度不等,它们中一个的出度比入度多1,另外一个入度比出度多l.S 0 S1 1 S2 1 S3 0 S41 0 1S5 S30 1S S1 S2 S4 S50 1 1 0 1 0 1S6.2 哈密顿图及哈密顿通路定义8.20无向图G称为哈密顿图(Hamilton graph),如果G上有一条颠末所有顶点的回路(也称这一回路为哈密顿回路).称无向图有哈密顿通路(非哈密顿图),如果G上有一条颠末所有顶点的通路(非回路).设图G为具有n个顶点的简单无向图,如果G的每对顶点的度数之和都不小于n– 1 ,那末G中有一条哈密顿通路;如果G的每对顶点的度数之和不小于n,且n≥3,那末G为一哈密顿图.定理8.15 当n为不小于3的奇数时,K n上恰有21n条互相均无任何公共边的哈密顿回路.定义8.21图G称为可2-着色(2-chromatic),如果可用两种颜色给G的所有顶点着色,使每个顶点着一种颜色,而同一边的两个分歧端点必须着分歧颜色.定理8.16设图G是可2-着色的.如果G是哈密顿图,那末着两种颜色的顶点数目相等;如果G有哈密顿通路,那末着两种颜色的顶点数目之差至多为一.习题解答操练8. 31、试作出四个图的图示,使第一个既为欧拉图又为哈密顿图;第二个是欧拉图而非哈密顿图;第三个是哈密顿图却非欧拉图;第四个既非欧拉图也非哈密顿图.解(a )既为欧拉图又为哈密顿图;(b )是欧拉图而非哈密顿图;(c )是哈密顿图却非欧拉图;(d )既非欧拉图也非哈密顿图.2、像第一题要求的那样对欧拉途径和哈密顿通路作出四个图.解(a )既有欧拉途径又有哈密顿通路;(b )有欧拉途径而无哈密顿通路;((d )既无欧拉途径也无哈密顿通路3、问n 为何种数值时,K n 既是欧拉图又是哈密顿图.问k 为何值时,k-正则图既是欧拉图又是哈密顿图.解 n 为奇数时,K n 既是欧拉图又是哈密顿图.k 为大于或等于n/2的偶数时,k-正则图既是欧拉图又是哈密顿图.4、证明:恰有两个奇数度顶点u,v 的无向图G 是连通的,当且仅当在G 上添加边(u ,v )后所得的图G*是连通的.证 需要性是显然的.设G*是恰有两个奇数度顶点u,v 的无向图G 添加边(u ,v )后所得,且是连通的,那末图G*是一个欧拉图(每个顶点都是偶数度的连通图),因此G*中删除边(u ,v )后所得的图G 仍是连通的.5、参阅操练8.1第2题.问马能否从某处出发完成所有可以的跳步一次且仅一次后回到原地.解 操练8.1第2题中的图不是欧拉图(它有三个3度的(a ) (b) (c) (d)(a )顶点),因此马不成能从某处出发完成所有可以的跳步一次且仅一次后回到原地.6、参阅操练8.1第2题.问马能否从某处出发跳遍棋盘的所有方格一次且仅一次后回到原地.解马可以从某处出发跳遍棋盘的所有方格一次且仅一次后回到原地.详细跳步如下图所示:幻方中数字n暗示第n个跳步的起点.下图则暗示跳步的图示.幻方7、试计算K n(n≥3)中分歧的哈密顿回路共有多少条.解分歧的哈密顿回路共有2)!1(n条.可以用依次选取每条边来生成哈密顿回路.因为组成回路的第一条边的选择可以是n 种, 组成回路的第二条边的选择可以是n – 1 种, … ,组成回路的第n – 1条边的选择可以是2种,组成回路的第n 条边的选择可以是1种,而每哈密顿回路由此生成两次,因此分歧的哈密顿回路共有2)!1(-n 条.8、十一个学生在一张圆桌旁共进晚餐,要求在每次晚餐上每个学生的邻座都与其它各次晚餐的邻座分歧.问这样共进晚餐能安插多少次.解 每次晚餐上每个学生的邻座都与其它各次晚餐的邻座分歧的安插方式有21-n 种(根据定理8.15.)9、辨别图8.31中各图是否为哈密顿图,若不是,请说明来由,并回答它是否有哈密顿通路.图8.31 解(a ),(b) 是为哈密顿图.(c) 不是哈密顿图,也没有哈密顿通路.在图(c)中增加顶点k ,并对其顶点做二着色,构成图(d)(如下).图(d) 不是哈密顿图,也没有哈密顿通路.因为图中白色顶点比黑色顶点多两个.故(c) 不是哈密顿图,也没有哈密顿通路.否则它的哈密顿回路或哈密顿通路必定颠末顶点k (k 在两个二度顶点之间的边上),从而图(d) 也是哈密顿图,也有哈密顿通路,抵触.10、证明:对哈密顿图G= <V ,E ,Ψ>删除S (V )中的所有顶点后,所得图G ’的连通分支数不大于S.(a ) (b) (c)k(d )证设G1是G 中的哈密顿回路,显然在G1中删除S (V )中的所有顶点后,所得图G 1’的连通分支数k1,不小于在G 中删除S (V )中的所有顶点后,所得图G ’的连通分支数k ,即k ≤k1.由于G1是一条回路,在G1中删除S (V )中的所有顶点后,所得图G 1’的连通分支数k1不大于S 是显然的,即k1≤S.因此 k ≤k1≤S11、设G 为(n ,m )图.证明:如果221+≥-n C m ,那末G 为哈密顿图(提示:运用定理8.14).证设G 中有两个顶点v1和v2的度数之和不大于n – 1 ,那末以v1和v2为端点的边未几于n – 1条.而其余顶点之间的边的数目未几于2)3)(2(--n n 条.故G 的总边数m 知足与221+≥-n C m 抵触,故G 中任意两个顶点的度数之和大于n .根据定理8.14,G 为哈密顿图.12、设有n 个围成一圈跳舞的孩子,每个孩子都至少与其中2n 个是朋友.试证明,总可安插得使每个孩子的双方都是他的朋友.证设n 个孩子为n 个顶点,用边暗示顶点间的朋友关系构成一个图G.由于每个孩子都至少与其中2n 个是朋友,因此G 的每顶点的度数至少是2n ,从而G 的任何两个顶点的度数。
