正弦交流电路电路的功率瞬时功率p
电路原理3章 正弦交流电路的功率

UI cos [1 cos 2t] UI sin sin2t
Q UI sin 单位:乏 (var)
Q UI sin I 2 X
感性电路: Q > 0
容性电路: Q < 0
I
U
+
U X U
UR _
R jX
+ U_ R _+U X
视在功率、无功功率、平均功率关系:
电感在一个周期内吸收的平均功率 为:
P 1
T
pdt
1
T
UI sin 2tdt 0
T0
T0
电感是储能元件,不消耗能量,但是在某一
时间段内,它从外部电路吸收功率。
电感瞬时功率的最大值,定义为电感的无功
功率QL:
电感无功功率:QL UI
I2 XL
U2
XL
单位:乏 (var)
3.7.1.3 电容元件的功率
(1) 视在功率(apparent power)
•
Ii
一端口网络电压有效值与
电流有效值的乘积
Z
S UI 单位:伏安 (VA)
+
•
U
u
-
无 源 网 络
S UI Z I 2
注: SN=UN IN 称为发电机、变压器 等供
电设备的额定视在功率,表示其容量。
(2) 无功功率(reactive power)
并联电容器是电网中用得最多的一种无功功 率补偿设备,目前国内外电力系统中90%的无 功补偿设备是并联电容器。
可以串电容吗?
串联电容器补偿,现在主要应用于超高 压、大容量的输电线路上,例如,山西大同 至北京的500kV输电电线路全长300km,加装 了串联电容补偿后,电网线损降低,电压质 量改善,电网运行的稳定性得到加强,而且 输电能力提高30%以上。
《电工技术》课件 正弦交流电路的功率

P
1 T
0T
pdt
1 T
0TUI[cos
cos(2t
)]dt
UI
cos
P UI cos
单位为瓦(W)
u 与 i 的夹角,即阻抗角
= cos 称为功率 因数,用来衡量对电
源的利用程度。
一、一般计算公式
3.无功功率
Q UI sin 单位为乏(Var)
4.视在功率:电路中总电压与总电流有效值的乘积,表示用电设备的容量。
(3)视在功率: S UI
S
Q
φ
功率三角形
P
S UI 单位为伏安(VA)
注: SN=UN IN 称为发电机、变压器 等供电设备的容量,可用来衡量发电机、变压器可能提供的最大有 功功率。
• 注意 (1)平均功率P、无功功率Q和视在功率S的关系
S2 P2 Q2
(2) P、Q、S 都不是正弦量,不能用相量表示。
S
Q
功率三角形
S PQ P
二、几种特例电路的功率计算
(3) R、 、X L X C
解:
(1)根据电压三角形,求得总电压
U UR2 (UL UC )2 152 (60 80)2 25V
(2)电路中只有电阻是耗能元件,因此电路有功功率就是电阻消耗的功率。
P U R I 151 15W Q QL Q C ULI (UC I ) 20Var S UI 251 25VA
(2)无功功率: Q UI sin
因为电路中只有电感元件和电容元件有无功功率,因此无功功率又可以用公式:
Q QL Q C ULI (UC I )
I2XL I2XC
U
2 L
UC2
XL XC
正弦电路的功率

《电工技术》
知识点:正弦交流电路的功率
1. 瞬时功率
=⋅+ωωϕI U p t t sin sin()m m =-+ϕωϕI U t 2
[cos cos(2)m
m (设电感性电路)
=⋅p i u
2 . 平均功率(有功功率)P
u与i 的相
位差角
总电压总电流
1 UI
pdt ϕ
cos
T
P T =
=⎰
上述公式为有功功率的一般表达式,可推广到任何复杂交流电路,其有功功率等于电阻上消耗的功率。
===2
R R
P P U I I R
功率因数
ϕ
cos
=-=-=L C L C Q I X I X I U U IU 22sin ϕ
)(Q =Q L +(-Q C ) 3 . 无功功率 Q
单位:V A 、kV A
4. 视在功率 S。
电源(发电机、变压器等)可能提供的最大功率(额定电压×额定电流)
ϕ U U R U L -U C S=UI
---功率三角形
5 . 有功功率、无功功率与视在功率间的关系
=S U I
视在功率 =Q U I sin ϕ无功功率
=P U I cos ϕ有功功率
---功率三角形 S
Q P 功率三角形 U R
U
+ U U L C 电压三角形
阻抗
三角
形 R X L -X C ϕ
THE END。
电工基础第66课时.正弦交流电路的功率与功率因数的提高

(1) 电源设备的容量不能充分利用
因为发电设备的额定功率一定
SN UN I N 1000kV A
若用户:cos 1则电源可发出的有功功率为:P ຫໍສະໝຸດ N I Ncos 1000kW
无需提供的无功功率。
cos 0.6 则电源可发出的有功功率为: 若用户:
P U N I Ncos 600kW
或者并联电阻
3.功率因数的提高 (1) 提高功率因数的原则: 必须保证原负载的工作状态不变。即: 加至负载上的电压和负载的有功功率不变。 (2) 提高功率因数的措施:
在感性负载两端适当并电容
I
I C
cos cos I
I
I
U
+
U
R
I L 1
C
I C
1
-
正弦交流电路
若在电路中含有多个不同功率因数的负载,则 每个负载的视在功率分别以S1,S2,S3,……表示, 但总的视在功率: S≠S1+S2+S3+┄。 求总在视在功率时,应先分别求出总有功功率 ΣΡ(各有功功率之和)和总无功功率ΣQ(各无功 功率的代数和),然后根据功率三角形进行合成。 ΣQ=Q1+Q2+Q3+┄。 ΣΡ=P1+P2+P3+┄。 在应用上式时,习惯取感性无功功率为正,容 性无功功率为负。电路总视在功率为:
正弦稳态电路中的功率
瞬时功率 设i= 2 Usinωt u= 2 Isin(ωt+ψ)
画出电压、电流、瞬时功率的波形图。由图可 知瞬时功率有如下特点:
正弦交流电路
(1)、瞬时功率包含有两个分量,一个是恒定 不变的分量UIcosψ,另一个是以2ω角频率交变的 分量UIcos(2ωt+ψ)。
正弦电路的无功功率及视在功率精

平均功率为
P = UI cos±90o)= 0
表明:
正弦稳态中,储能元件电感或电容的平均功率等于 零,不消耗能量,但和电源之间存在能量的交换作用, 即在前半个周期吸收电源的功率并储存起来,后半个 周期又将其全部释放,这种能量交换的速率用另外一 种功率——无功功率来描述。
2、功率因数是正弦电路中一个非常重要的物理量。 其大小表征了电气设备功率的利用率。提高负载的功 率因数是电气工程领域一个非常重要的课题。
本讲作业
1、复习本讲内容; 2、预习下一讲内容——三相电路;
3、书面作业:习题9-2,9-5,9-6。
问题:怎样提高电路的功率因数?
方法: 用电容器与感性负载并联,这样可使电感的磁场 能量与电容的电场能量进行部分交换,从而减少了 电源与负载间能量的交换,即减少了电源提供给负 载的无功功率,也就提高了功率因数。
【例18-2】
下图(a)所示电路表示电压源向一个电感性负载供电的电 路模型,试用并联电容的方法来提高负载的功率因数。
Y G j B 1 3 j4 (0 12 j0 16)S 3 j4 32 42
从上式可见,所并联的电容的复导纳应该为YC = jwC = + j0.16 S,才能使二端网络呈现为纯电阻, 这时电路的导纳等于纯电导,即Y = G = 0.12 S。也 就是说,在端口并联电容值为C = (0.16/w)的电 容后,可以使功率因数提高到1,即效率达到100%。
S S~ UI
功率三角形: 下图所示为RLC串联电路的功率三角形:
正弦交流电路中的功率

六、无源单口网络端口测试
1.无源单口网络端口测试的目的
目的:得到无源电路最简等效电路中的元件参 数值。
2u )
a.电容元件瞬时功率波形如图4-44所示
图4-44 电容元件瞬时功率
Cb..电pC容>的0能,量电容元WC件吸12 C收u功2 率
pC <0,电容元件送出能量
二、平均功率和功率因数
1.平均功率:瞬时功率在一个周期内的平均值用P 表示。
P 1 T
T pdt 1
0
T
T
0 [UI cos UI cos(2t 2u ]dt
(2)电感元件
2
pL
UI
cos(2t
2u
2
)
UI
sin(2t
2u )
a.电感元件瞬时功率波形如图4-43所示
图4-43电感元件瞬时功率
b.电感元件的能量
L
1 2
Li2
C.PL>0,电感元件吸收功率
PL<0,电感元件送出功率
(3)电容元件
2
PC
UI
cos(2t
2u
) 2
UI
sin(2t
(2) 减小, cos 增大,平均功率P增大。
故P与 cos 成正比。
三、无功功率
1.无功功率:表示电路能量交换规模,用Q表示。
Q UI sin
(1)Q>0,无功功率为感性无功功率。
(2)Q<0,无功功率为感性无功功率。
正弦电路的功率(PDF)

今日作业:7-117-137.3 正弦稳态电路中的功率Power in Sinusoidal Steady State一、瞬时功率(Instantaneous Power)----W二、平均功率(Average Power or Active Power)----W 三、无功功率(Reactive Power)----Var 四、视在功率(Apparent Power)----VA 五、功率因数(Power Factor )的提高六、复功率(Complex Power)----VA7.3 正弦稳态电路中的功率Power in Sinusoidal Steady State正弦稳态电路+_ui一、瞬时功率(Instantaneous Power)----WA)cos(2V cos 2ϕωω−==t I i t U u 设:tUI t UI t t UI t UI t t UI ui p ωϕωϕϕϕωϕωϕϕωϕωω2sin sin ]2cos 1[cos ]cos sin 2sin cos 2[cos )cos )2[cos()cos(cos 2⋅++=+⋅+⋅=+−=−⋅==ωti,u,p[cos(2)cos )cos [1cos 2]sin sin 2p UI t UI t UI tωϕϕϕωϕω=−+=++⋅ϕcos UI 不可逆部分可逆部分返回二、平均功率(Average Power or Active Power)----Wϕcos )(10UI dtt p T P T==∫cos ϕ−−功率因数正弦稳态电路+_U I计算平均功率的两种方法ϕcos )()(UI P P P R=∑=21RXtg iu 121−=−=ϕψψϕϕ)()的求解:(返回三、无功功率(Reactive Power)----Var sin Q UI ϕ=计算无功功率的另一种方法XQ Q =∑返回正弦稳态电路+_U I 四、视在功率(Apparent Power)----VA22S P Q UI=+=PQSϕ功率三角形注:在工程上视在功率用来表示电源设备(变压器、发电机等)的容量,也可用来衡量发电机可能提供的最大平均功率(额定电压×额定电流)正弦稳态电路+_U I等于多少?问:此电路的功率因数,另一个负载的,,已知一个负载的)(.cos )(.cos 0850Kw 90070Kw 70222111>==<==ϕϕϕϕP P P 1cos ϕ1P 2cos ϕ21I 2I I+_U解例1问题的提出:日常生活中绝大部分负载为感性cos ϕI当U 、P 一定时,∴五、功率因数(Power Factor )的提高P =P R =UI cos ϕ其消耗的有功功率为:R LR U LU IU +-+-+-1、线路损耗增加;2、终端负载工作电压降低,影响其正常工作;3、电源容量增加。
正弦交流电知识点整理
正选交流电路+三相交流电知识点整理(1)1、正选交流电与直流电的区别所谓正弦交流电路,是指含有正弦电源(激励)而且电路各部分所产生的电压和电流(响应)均按正弦规律变化的电路。
交流发电机中所产生的电动势和正弦信号发生器所输出的信号电压,都是随时间按正弦规律变化的。
它们是常用的正弦电源。
在生产上和日常生活中所用的交流电,一般都是指正弦交流电。
因此,正弦交流电路是电工学中很重要的一个部分。
直流电路:除在换路瞬间,其中的电流和电压的大小与方向(或电压的极性)是不随时间而变化的,如下图所示:正选交流电:正弦电压和电流是按照正弦规律周期性变化的,其波形如下图所示。
正弦电压和电流的方向是周期性变化的。
正弦量:正弦电压和电流等物理量。
正弦量的特征表现在变化的快慢、大小及初始值三个方面,而它们分别由频率(或周期)、幅值(或有效值)和初相位来确定。
所以频率、幅值和初相位就称为确定正弦量的三要素。
2、周期T与频率f周期T:正弦量变化一次所需的时间。
单位:秒(s)频率f:每秒内变化的次数。
单位:赫兹(Hz)两者关系:频率是周期的倒数 f=1/T高频炉的频率是200- 300kHz;中频炉的频率是500-8000Hz;高速电动机的频率是150-2000Hz; 通常收音机中波段的频率是530-1600kHz ,短波段是2.3-23MHz;移动通信的频率是900MHz和1800MHz; 在元线通信中使用的频率可高 300 GHz。
正弦量变化的其他表达方式:角频率正弦量变化的快慢除用周期和频率表示外,还可用角频率ω来表示。
因为一周期内经历了 2π弧度(图 4.1.3) ,所以角频率为:上式表示 T,f,ω三者之间的关系,只要知道其中之一,则其余均可求出。
3、幅值与有效值正弦量在任一瞬间的值称为瞬时值,用小写字母来表示,如 i , U 及 e 分别表示电流、电压及电动势的瞬时值。
瞬时值中最大的值称为幅值或最大值,用带下标 m 的大写字母来表示,如Im, Um 及 Em 分别表示电流、电压及电动势的幅值。
电工学第三章

3-1正弦交流电的基本概念 3-1-1 正弦交流电的三要素 正弦交流电: 大小和方向都随时间按正弦规律作周期性变化 的电量(电压、电流、电动势)。
i
设正弦交流电流:
Im
O
t
T
i I m sin t
初相角:决定正弦量起始位置 角频率:决定正弦量变化快慢 in( t 2 )
I I1 I 2
i i1 i 2
上节复习:
1、写出下列正弦量对应的相量,并作出相量图
i1 4 2 s in ( t 3 0 )
i2 1 0 2 c o s ( t 1 2 0 )
i3 1 4 .1 4 s in ( t 1 5 0 )
相量的模=正弦量的最大值
相量辐角=正弦量的初相角
U
U
u U m sin ( t )
电压的有效值相量
U
U
相量的模=正弦量的最大值
相量辐角=正弦量的初相角
例1:
u 10 sin( 314 t 60 )
写出其相量形式
U 5 2 60
U m 10 60
3-1-3 正弦交流电的参考方向
i
O
i I m sin t
ωt
i 0,实际方向与参考方向相 同
i 0,实际方向与参考方向 相反
3-2正弦交流电的相量表示法
1.正弦量的表示方法 波形图
O
u/i
ωt
瞬时值表达式
u U m sin ( t )
i I m s in
交流电路的功率

2.4 交流电路的功率2.4.1 瞬时功率如图2-30所示,若通过阻抗Z的电流为i=I m sinωt,则Z两端的电压为u=U m sin(ωt+φ),在电流、电压关联参考方向下,瞬时功率为p=ui=U m sin(ωt+φ)×I m sinωt=UI cosφ-UI cos(2ωt+φ)(2-54)图2-30 正弦交流电路在式(2-54)中,第一项为不变的部分,总是大于等于零,是耗能元件上瞬时功率;第二项为变化的部分,是储能元件上瞬时功率。
由此可见,在每一瞬间,电源提供的功率一部分被耗能元件消耗,另一部分与储能元件进行能量交换。
2.4.2 有功功率与功率因数一个周期内瞬时功率的平均值称为平均功率,也称有功功率。
式中,λ=cosφ称为电路的功率因数。
可见,正弦交流电路中的有功功率不但与电压、电流有关,还与电压和电流相位差的余弦值有关。
可见,在正弦交流电路中,电感、电容元件实际不消耗电能,而电阻总是消耗电能的。
有功功率是电路实际消耗的功率,即二端网络中,各电阻所消耗的有功功率之和。
有功功率的单位是瓦特(W)。
2.4.3 无功功率电路中的电感元件与电容元件要与电源之间进行能量交换,根据电感元件、电容元件的无功功率,考虑到与相位相反,于是Q=(U L-U C)I=(X L-X C)I2=UI sinφ(2-56)单个电感元件,Q L=U L I L sinφ=U L I L>0单个电容元件,Q C=U C I C sinφ=-U C I C<0即电感的无功功率取正值,而电容的无功功率取负值,以便区别。
在既有电感又有电容的电路中,总的无功功率为Q L与Q C的代数和,即Q=Q L-Q C无功功率的单位是乏(var)。
2.4.4 视在功率在交流电路中,电压与电流有效值的乘积,只能表示电源可能提供的最大功率,叫视在功率,用字母S表示。
即S=UI=I2|Z| (2-57)视在功率的单位是伏安(V·A),常用来表示电气设备的容量。
正弦交流电路中的R、L、C特性

P UI
1
T
UI(1 cos2 t)dt UI
T0
3-4.2 电感元件的交流电路
基本关系式: u L di dt
i uL
设 i 2 I sin t
则 u L di 2 I L cost
dt
2 I L sin(t 90 )
2 U sin(t 90 )
电感电路中电流、电压的关系
复数形式的欧姆定律
U IR U I( j X L) U I( j XC )
电阻电路
电感电路
电容电路
3.简单正弦交流电路的关系(以R-L电路为例)
* 电压、电流瞬时值的关系符合欧姆定律、克氏
定律。
i
u
R
uR
u uR uL iR L di
L uL
dt
* 电流、电压相量符合相量形式的欧姆定律、克氏
T0
3. 无功功率 Q
瞬时功率达到的最大值(吞吐规模)
p UI sin 2t
Q UI
(电容性无功取负值)
例 求电容电路中的电流
i
u
C
已知: C =1μF
u 70.7 2sin(314 t )
求:I 、i
6
解:X C
1
C
1 314106
3180
电流有效值 I U 70.7 22 . 2 mA X C 3180
p i u 2UI sin t cost UI sin 2t
i uL
p i u UI sin 2t
u
i
t
i
i
i
i
u uuu
p
可逆的 能量转换
过程
+
P <0
演示文稿2 董洁

设计人:董杰
一、正弦交流电路功率的基本概念 二、电阻、电感、电容电路的功率
三、功率因数的提高
一、正弦交流电路功率的基本概念
1.瞬时功率 p
设正弦交流电路的总电压 u 与总电流i的相位差(即阻抗角)为 ,则电压与电 流的瞬时值表达式为
u = Umsin( t ),i = Imsin( t) 瞬时功率为 p = ui = UmImsin( t )sin( t)
P C (tan1 tan 2 ) 2 2fU
其中 1 = arccos1,2 = arccos2,且 1 > 2,1 < 2 。
【例8-6】已知某单相电动机(感性负载)的额定参数是功率 P = 120 W,工频 电压U = 220 V,电流 I = 0.91 A。试求:把电路功率因数 提高到 0.9 时,应使用 一只多大的电容 C 与这台电动机并联?
这样就可以使电感中的磁场能量与电容器的电场能量进行交换,从而减少 电源与负载间能量的互换。在感性负载两端并联一个适当的电容后,对提高电 路的功率因数十分有效。
借助矢量图分析方法容易证明:对于额定电压为 U,额定功率为 P,工作 频率为 f 的感性负载 R-L 来说,将功率因数从 1= cos1提高到 2 = cos2,所 需并联的电容
有功功率 无功功率 视在功率
PR = UI cos = UI = I2R = QR = UI sin = 0
U2 R
S P 2 Q 2 PR
即纯电阻电路消耗功率(能量)。
( 1) 负载的功率因数低,使电源设备的容量不能充分利用。因为电源设备 (发电机、变压器等)是依照它的额定电压与额定电流设计的。
例如一台容量 S = 100 kVA 的变压器,若负载的功率因数 =1时,则此
正弦交流电路的功率

问题与讨论 功率因数补偿到什么程度?理论上可以补偿
成以下三种情况: 成以下三种情况
& IC
ϕ <0
& U
I&
& IC
ϕ =0
& U
& IC
ϕ
ϕ >0
I& U&
I& RL
呈电容性。 呈电容性。
I&
& IRL
呈电感性
I& RL
呈电阻性
cosϕ <1
cosϕ =1
cosϕ < 1
一般情况下很难做到完全补偿 (即: cos 功率因数补偿成感性好,还是容性好? 功率因数补偿成感性好,还是容性好? & & I 'C IC
P = U N I N cos ϕ = 600kW
而需提供的无功功率为: 而需提供的无功功率为
Q = U N I N sinϕ = 800kvar
∴ 提高 cosϕ 可使发电设备的容量得以充分利用
2. 增加线路和发电机绕组的功率损耗 设输电线和发电机绕组的电阻为 r : 要求: 要求 P = U I cosϕ (P、U定值 时 定值)时
* 复功率守恒 , 不等于视在功率守恒
& I
+
.
& U
_
& + U _
1
+
& U2
_
&& & & & S = U I * = (U 1 + U 2 ) I * & & & & = U 1 I * +U 2 I * = S 1 + S 2
07 正弦交流电路的相量法及功率

3.5 正弦交流电路中的电容元件
1 1 I C = jω C U C , U C = IC = −j IC ωC jω C
.
iC
C
uC
+
. _
IC
ψi ψu
IC
.
IC
1 jω C
+
. _
UC
1 IC ωC
相量图: 相量图:
UC
容抗: 容抗:
U C 滞后!
电工学 南京理工大学自动化学院
阻抗和导纳
阻抗Z 阻抗Z和电路性质的关系
R
ϕ > 0 表示 u 领先 i
--电路呈感性 电路呈感性
ϕ < 0 表示 u 落后 i
电工学
--电路呈容性 电路呈容性
电路呈电阻性 ϕ = 0 表示 u 、i同相 --电路呈电阻性
南京理工大学自动化学院
阻抗和导纳
电阻元件的阻抗
电压和电流关联参考方向下: 电压和电流关联参考方向下:
UR
IR
.
IR
R
UR
+
. _
则: R = R = U R Z IR
ψi
ψu
I R与U R 共线
南京理工大学自动化学院 电工学
阻抗和导纳
电感元件的阻抗
电压和电流关联参考方向下: 电压和电流关联参考方向下:
UL
.
IL
jω L
IL
+
UL
. _
ψu
ψi
则 : L = jω L = U L Z IL
电工学
jX L , X L = ω L 感抗
最后根据相量与正弦时间函数的对应关系,写出待求量在 最后根据相量与正弦时间函数的对应关系, 时域中的瞬时值表达式
北航电工电子学第3章正弦交流电路
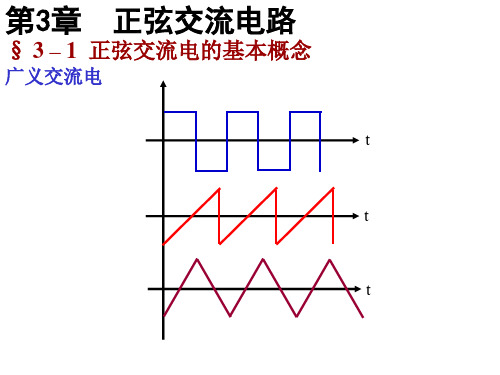
u i ωt
u
u = Ldi/dt, 设 i =ImSin(ωt) , 则 u = Ldi/dt= ωLImCosωt, = UmSin(ωt +π/2)
∴对于电感,有如下结论:
(1) u 、i 同频, 并且 u 超前于 i 90o (2) Um =ωLIm =XLIm , XL=ωL= Um/Im = U/I ——感抗(Ω)
j
A
rejφ ejα –j=1/j= ej–π/2
4。极坐标式 A = r φ 旋转因子的概念
+1
特殊旋转因子 j=ejπ/2,
一、复数与正弦量的关系
i
B
ω t1
A
B
A O φi
φi
ωt1
ωt
二、相量表示法
j 优点: 1。把的正弦量+、-、×、÷ 变为复数的+、-、×、÷ 2。关系简单,一一对应,直接写出 注意:相量仅表示正弦量,不等于正弦量! φ I +1 I
φZ = tg-1 (XL –XC )/R ——阻抗角
阻抗角
φZ = tg-1 (XL –XC )/R——阻抗角 ——决定电路性质 当 XL >XC 时, φZ > 0 , u 超前于 i ——感 性 性
当 XL<XC 时, φZ < 0 , i 超前于 u ——容 当 XL=XC 时, φZ = 0 , u 、i 同相
XC = 1/(2πfC) = 0.159 (Ω) I= U/ XC = 1380 (A) QC = I2XC = 304 (kVar)
四、R、L、C 的 u – i 关系小结
1. 相量表示
电阻元件 电感元件 电容元件
U=RI U = jωL I I = jωC U
电工技术5正弦交流电路的功率

3-7正弦交流电路的功率
一、瞬时功率
i + u N 0
UI cos ϕ
功率因数补偿到什么程度?理论上可以补偿
成以下三种情况: 成以下三种情况
ɺ IC
ϕ <0
ɺ U
Iɺ
ɺ IC
ϕ =0
ɺ U
ɺ IC
ϕ
ϕ >0
Iɺ Uɺ
Iɺ RL
呈电容性。 呈电容性。
Iɺ
Iɺ RL
呈电阻性
ɺ IRL
呈电感性
cosϕ <1
cosϕ =1
cosϕ < 1
一般情况下很难做到完全补偿 (即: cos 功率因数补偿成感性好,还是容性好? 功率因数补偿成感性好,还是容性好?
ɺ I
XL > R、XC > R
3-8 电路中的谐振
谐振概念: 谐振概念:
含有电感和电容的电路, 含有电感和电容的电路,如果无功功率得到完全 补偿,使电路的功率因数等于 , 同相, 补偿,使电路的功率因数等于1,即:u、 i 同相, 便称此电路处于谐振状态。 便称此电路处于谐振状态。 串联谐振: 串联谐振:L 与 C 串联时 并联谐振: 并联谐振:L 与 C 并联时
40W日光灯 日光灯
COSϕ = 0.5
P 40 = = 0.364 A I= U cos ϕ 220× 0.5
供电局一般要求用户的 否则受处罚。 否则受处罚。
COSϕ > 0.9 ,
交流电路-功率详解

Q UI sin
arctan
Q P
R-L-C正弦交流电路中的功率
已知电阻R=30Ω,电感L=328mH,电容C=40µ F,串联后接到 电压
u 220 2 sin(314t 300 )V 的电源上。求电路的P、Q和S。
解:电压相量
220300 V U
P cos UI
功率因数,取决于电路阻抗角。
90,为纯电容或纯电感; 0 ,为纯电阻。
R-L-C正弦交流电路中的功率
3)无功功率(即电容或电感与电源之间交换的功率)
p ui U m sin(t )I m sin t UI cos (1 cos2t ) UI sin sin 2t
PL 0
3)无功功率 为了表示能量交换的规 模大小,将电感瞬时功率的 最大值定义为电感的无功功 率,用QL表示。
QL UI I 2 X L U2 XL
QL的基本单位是乏(var)。
单一参数电路的功率-电容
电容上的电压与电流相位差 90度,相乘后,一部分时间吸收 功率,一部分时间放出功率,平 均功率为零。 1)瞬时功率
单一参数电路的功率-电感
电感上的电压与电流相位差 90度,相乘后,一部分时间吸收 功率,一部分时间放出功率,平 均功率为零。 1)瞬时功率
p pL ui U m sin(t 90) I m sin t 1 U m I m sin 2t UI sin 2t 2
单一参数电路的功率-电感
1)瞬时功率
i I m sin t
u U m sin(t ) p ui U m sin(t )I m sin t UI cos (1 cos2t ) UI sin sin 2t
第6章(3)正弦稳态电路的功率

单位:瓦 (6.5-3)
在正弦稳态情况下,平均功率不仅与电压、电流的有 效值有关,而且与电压、电流的位相差有关。 式中 λ = cos ϕ 称为功率因数(power factor) ϕ = ϕu − ϕi 称功率因数角(power-factor angle) 通常所说的功率,都是指平均功率而言。平均功 率又叫有功功率(active power)。
Q = UI sin ϕ = UI sin ϕ Z
(6.5-27)
②Reactive Power in Terms of Z or Y : 对于不含 独立源的一端口,无功功率也可以 用阻抗或导纳计算。根据式(6.5-6)和(6.5-18), (6.5-18),即 2 * * (6.5-28a) Q = Im(UI ) = Im( ZII ) = I Im( Z ) = I 2 X (ω )
p (t ) = UI cos ϕ + UI cos(2ωt + 2ϕu − ϕ ) = UI cos ϕ + UI cos ϕ cos(2ωt + 2ϕu ) + UI sin ϕ sin(2ωt + 2ϕu )
(6.5-2) 上式中第一项始终大于(或小于、或等于零),它是 瞬时功率中的不可逆部分;第二项是瞬时功率中的 可逆部分,其值正负交替,说明能量在外施电源和 二端网络之间来回交换。
第六章 正弦电路的稳态分析
注: i) 如果一端口只由R、L、C等无源元件组成,则功率 因数角φ=阻抗角φZ,且|φZ|≤900,所以平均功率P≥0, 一端口吸收能量。根据能量守恒可知,P为一端口中电阻 元件所消耗的总功率(∵L、C元件不耗能)。 ii) 如果一端口除无源元件外尚有受控源(亦有功率因 数角φ=阻抗角φZ), |φZ|可能>900。其平均功率P为负 值,说明该一端口对外提供能量。 iii) 如果一端口内含有独立电源,则功率因数角φ为 端口电压与端口电流的位相差。P可能为正,也可能为负 值。即一端口可能吸收能量,也可能对外提供能量。
瞬时功率的计算公式

瞬时功率的计算公式瞬时功率即指在一些时刻t时刻的功率,也就是瞬间的功率。
功率定义为单位时间内传递的能量,可以用公式P=ΔE/Δt来表示,其中P表示功率,ΔE表示单位时间内传递的能量,Δt表示时间间隔。
对于电路系统来说,电功率是电能转化为其他形式能量的速率。
电功率可以表示为电路中电流和电压的乘积,即P=VI,其中P表示电功率,V表示电压,I表示电流。
在直流电路中,电流是常量,所以瞬时功率可以简单地表示为P=IV。
因此,根据欧姆定律,可以将瞬时功率表示为P=I²R,其中R表示电阻。
在交流电路中,电流和电压是随时间变化的,因此瞬时功率的计算稍微复杂一些。
根据欧姆定律,电压和电流之间存在相位差。
假设电压和电流的表达式为V = Vm*sin(ωt + Φv)和I = Im*sin(ωt + Φi),其中Vm和Im分别表示电压和电流的最大值,ω表示角频率,Φv和Φi表示相位差。
根据电功率公式P=VI,将电压和电流的表达式代入,可以得到瞬时功率的计算公式:P = VmIm*sin(ωt + Φv)*sin(ωt + Φi)根据三角函数的和差化简公式,可以将瞬时功率的计算公式进一步简化:P = (1/2)*VmIm*[cos(Φv - Φi) - cos(2ωt + Φv + Φi)]根据此公式,可以通过给定时间t的值来计算瞬时功率。
其中,(Φv - Φi)表示相位差的差异,cos(Φv - Φi)是功率因子,(2ωt + Φv +Φi)表示功率的频率和相位。
在交流电路中,常常用有功功率和无功功率来描述瞬时功率的特征。
有功功率表示电能在电路中真正转化为有用功的能力,而无功功率则表示电能在电路中往返传输的能力。
有功功率可以表示为P = VmIm*cos(Φv- Φi),无功功率可以表示为Q = VmIm*sin(Φv - Φi)。
当相位差(Φv - Φi)为零时,即电压和电流的相位相同时,有功功率最大,此时电能在电路中真正转化为有用功的能力最大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正弦交流电路
§6-4 纯练掌握纯电感电路中电流与电压的相
位关系和数量关系。
2.熟练掌握纯电感电路中的功率关系。
3.掌握电感器在交流电路中的作用。
第六章
正弦交流电路
由电阻很小的电感线圈组成的交流电路,都 可以近似地看成是纯电感电路。
常见电感器
第六章
正弦交流电路
一、电流与电压的关系
第六章
正弦交流电路
【练一练】
把一个电阻可以忽略不计,电感量为10mH的
线圈分别接到频率为5kHz和25kHz的157V交流电 源上,求线圈中的电流大小。
第六章
正弦交流电路
【知识拓展】
利用电感对交流电的阻碍作用可以制成扼流圈。
常见的扼流圈
第六章
正弦交流电路
课堂小结
在纯电感电路中,电压总是超前电流90°。电 流与电压的有效值仍满足欧姆定律,即:
律。但由于电流与电压的相位不同,故电流与电 压的瞬时值不满足欧姆定律。
第六章
正弦交流电路
感抗是用来表示电感线圈对交流电流起阻碍作 用的一个物理量。其计算式为:
X L 2πfL L
感抗的大小,取决于线圈的电感量L和流过它 的电流的频率f。对具有某一固定电感量的线圈而言, f越高则XL越大。在相同电压作用下,线圈中的电 流就会减小。在直流电路中,因频率f=0,故线圈
1.基本关系
i i uL eL ( L ) L t t
即线圈两端的电压大小与电流的变化率成 正比。
第六章
正弦交流电路
2.相位关系
第六章
正弦交流电路
从波形图可清楚看出电 流和电压的相位关系是:电 压总是超前电流90°。 设流过电感的正弦电流的初相为零,则电流、 电压的瞬时值表达式为:
U I XL
Um Im XL
2.在纯电感电路中,电压超前电流90°,这
是否说明先有电压后有电流?
第六章
正弦交流电路
二、电路的功率
1.瞬时功率
pL=uLi=ULmsin(ωt+ )Imsinωt 2
=ULm Imsinωtcosωt
1 = ULm Imsin2ωt 2
=ULIsin2ωt
上式说明,纯电感电路的瞬时功率也是以
正弦交流电路
“无功”的含义是“交换”而不是“消耗”,
它是相对“有功”而言的,绝不能理解为“无用”。
实际中许多含有电感性质的负载,如电动机、
变压器等,都是根据电磁转换原理利用无功功率来
工作的。
第六章
正弦交流电路
[例6—3]
一个0.7H的电感线圈,接在u 220 2 sin(314t 30)V 的交流电源上。试求出通过线圈的电流大小,写出电流的瞬 时值表达式,画出电流、电压的相量图,求出电路的无功功 率。
i I m sin t
π uL U Lm sin(t ) 2
第六章
正弦交流电路
3.数量关系
电感对交流电起阻碍作用
第六章
正弦交流电路
理论和实验都能证明,在纯电感电路中,电
流与电压成正比,与感抗成反比,即: U I XL
这就是纯电感电路的欧姆定律。它说明,纯
电感电路中,电流与电压的有效值仍满足欧姆定
2ω按正弦规律变化的。
第六章
正弦交流电路
1 4 周期内,pL是正值,
在第一和第三个
线圈起着一个负载的
作用。
1 4 周期内,pL是负值,
在第二和第四个
线圈起着一个电源的 作用。
第六章
正弦交流电路
2.平均功率
纯电感线圈接通交流电源后,时而“吞进” 功率,时而“吐出”功率,在一个周期内的平
均功率为零,即PL=0,这表明电感线圈不是
耗能元件,而是储能元件。
第六章
正弦交流电路
3.无功功率 平均功率不能反映线圈与电源之间能量交换 的规模,人们就用瞬时功率的最大值来反映这种
能量交换的规模,并把它叫做电路的无功功率,
用字母QL表示:
UL QL U L I I X L XL
2
2
无功功率的单位为乏尔,简称乏(var)。
第六章
X L 2πfL L
有功功率等于0。
2
UL QL U L I I X L 无功功率: XL
2
的感抗也等于零。由于一般线圈的电阻很小,故电
感线圈可视为短路。
第六章
正弦交流电路
左图所示为线性电感 线圈的感抗随频率变化的 曲线。 可见,电感器在电路 中的作用主要是:通直流, 阻交流。
第六章
正弦交流电路
1.你能看出下列式子中哪些是正确的,哪些 是错误的吗?为什么?
U i XL
u I XL
u i XL
