材料物理-dielectric

合集下载

材料物理化学第三篇习题

Chap 11、Semiconductors11.1 (a) For a semiconductor, show that np product obtained fromEq.(11.27) is proportional to exp(-βE g ) and thus is independent of the position of the chemical potential μ in the bandgap.Eq.(11.27):(b) The law of mass action in semiconductors for reaction creatingpairs of electrons and holes [e.g., Eq.(11.28)] has the form n(T)P(T)∝exp(-βE g ). Explain the significance of this law. (Hint: The law of mass action is described in Section 4.6)Eq.(11.28): (c) Evaluate the np product at T=300K for Si with E g =1.11ev andm eds ﹡=1.05m and m hds ﹡=0.58m.11.2 Using Eq.(11.30) and m eds ﹡=1.05m and m hds ﹡=0.58m for Si,calculate the change in the position of the chemical potential µ in the energy gap of intrinsic Si between T=0 and 300K.Eq.(11.30): 11.3 Calculate the values of N c and N v as defined in Eq.(11.27) for Siat T=300K. The appropriate of density-of-states effective masses for Si are m eds ﹡=1.05m and m hds ﹡=0.58m.11.4 Consider a semiconductor with a bulk energy gap E g =1.5ev andgE v c i i e T N T N T p T n β-=)()()()()()(2/32)()2(2)()(μβμβπ----*===c c E c E B eds i e T N e T k T n T n m )()(2/32)()2(2)()(v v E v E B h ds i e T N e T k T p T p m ----*===μβμβπ **+=eds hdsB g m m T k E T ln 432)(μwith m e﹡=m h﹡=0.1m. Calculate the increase in the energy gap ofthis semiconductor when it is incorporated into the followingstructures:(a) A quantum well (d=2) with L x=10nm.(b) A quantum wire (d=1) with L x=L y=10nm(c) A quantum dot (d=0) with L x=L y=L z=10nm11.5 A Hall effect measurement is carried out on a rectangular barof a semiconductor with dimensions L x=0.04m (the directionof current flow ) and L y=L z=0.002m. When a current I x=5mAflows in the +x direction and a magnetic field B z=0.2T isapplied in the +z direction, the following voltages aremeasured: V x=6V and V y=+0.3mV (i.e., increasing in the +ydirection). Determine the following properties of thesemiconductor bar from these data :(a) The sign of the dominant charge carriers.(b) The concentration of the dominant charge carriers.(c) The electrical conductivity σ.(d) The mobility µ of the dominant charge carriers.11.6Using Eq.(11.59), estimate the increase △n in the electronconcentration in an n-type semiconductor due to the uniformabsorption of light with α=105m-1, I0=1W/m2, and hω=1e V, aquantum efficiency η=1, and a minority-carrier lifetime ηp=10-3s.Eq.(11.59): 11.7 Using the definition of the Hall mobility µH =︱ζR H ︱and theexpression for R H for an intrinsic semiconductor given in Eq.(11.49), show that µH =︱µh -µe ︱.Eq.(11.49): 11.8 Consider the structural transformation of a binary crystal ABfrom the hexagonal wurtzite crystal structure to the cubic zincblende crystal structure in which the density of the atoms remains constant. Find the lattice constant of the resulting cubic crystal if the lattice constants of the initial wurtzite crystal are a =0.3400nm and c =0.5552nm.11.11 List all of the local tetrahedral bonding units, A-B 4, which arepresent in the ternary semiconducting compounds Cu 2SiTe 3, Cu 3PS 4, and CuSi 2P 3. Note that each tetrahedron must contain an average of four bonding electrons per atom.11.13 Derive the expression for the shift △E of the electron energybands from one side of a p-n junction to the other under zero bias as given in Eq.(11.93). Calculate the magnitdde of the built-in electric potential V B =△E/e for Si at T=300K for N d =N a =2×1024m -3. Using these same parameters, calculate the depletion width d and the maximum electric field Q/∈A for a Si p-n junction at T=300 K.ωτηατω pp L I G p n 0)(==∆=∆)(e h eh H ne R μμμμ+-=Eq.(11.93): .Chap 12、Metals and Alloys 12.1 Referring to Section 12.5, show that the condition for the tangencyof the Fermi sphere to the Brillouin zone boundary for the FCC lattice is N =1.36.12.2 Derive Eq.:12.3 Derive Eq.:Chap 13、Ceramics13.1 For the silicon oxynitride compound Si 2N 2O, assume that Si, N,and O atoms have their usual valences (4, 3, and 2) and that the N and O atoms do not form covalent bonds with each other. (a) Given a local bonding unit Si-N x O y for Si with x+y =4,determine x (and y ) for this crystal structure.(b) What are the local bonding units for N and O?13.2 For the Si x N y O z ternary phase diagram, locate the followingcompounds :SiO 2, Si 3N 4, Si 2N 2O, and Si 3N 2O 3.13.3 Find the average number of bridging oxygens, b, and nonbridgingoxygens, n, for the following glasses:(a)CaO•SiO 2, and(b) soda-lime(i.e., 2CaO•3Na 2O•15SiO 2) n ia d B v c a d B g N N T k N N N N T k E E 2ln ln =+=∆)163253(02222∈-=πF F k e m k N U )]1(356[82202ws c ws Coul r r r Nze U --∈=πChap 14、Polymers14.1 A polymer whose viscoelastic properties are described byEq.(14.40) (i.e., the Maxwell model) is subjected to a time-dependent stress σ=σ0exp(-i ωt). Find the steady-state strain. Compare this result to that of a polymer that obeys the Voigt model, given by Eq. (14.37).Eq.(14.40): Eq. (14.37): 14.2 Consider an elastomer consisting of monomers that are opticallyanisotropic [i.e., they have a polarizability α11(ω) for light parallel to the chain axis and α┴(ω) for light polarized perpendicular to the chain axis]. Assume that there are N chains per unit volume. Let )(ωn be the mean index of refraction of the material. The elastomer is stretched with a steching parameter s , as defined in Secti on 14.5. Show that the elastomer will have a birefringence given by)]()()[1()(]2)([452)()()(112211ωαωαωωπωωωδ⊥--⊥--+=-=s s n n N n n nObtain an expression for the stress optical coefficient. C≡δn(ω)/ζ, where ζ is the applied stress.Chap 15、Dielectric and Ferroelectric Materials∙∙=+εησσG ηστεε=+∙15.1 Given the Landau free-energy density for a ferroelectric of the form Where b>c. Let a=a 0(T-T C ) and assume that b and c are constant. Find P z and χ as a function of T for the state of thermal equilibrium. 15.2 Design a piezoelectric actuator that can be used to sweep anSTM head over the surface of a solid. What is the area that can practically be covered?15.3 Adapt Weiss molecular field theory (see Chapter 9) to describe aferroelectric. Assume that there are just two orientations for the electric-dipole moment of a unit cell and that NN cells interact via an exchange interaction. Obtain the hysteresis curve and values for the coercive field E c , saturation polarization P sat , and remanent polarization P rem .15.4 BaTiO 3 is a paraelectric for T>T C =130℃ and has a Curie constantC=76,000K.(a)If the lattice constant for the cubic unit cell of BaTiO 3 is a=0.401nm, calculate the electric-dipole moment µ of this unit cell. (b)What would the corresponding polarization P=µn be at T=0 K?Chap 16、Superconductors16.1 (a) Derive expression for the difference in entropy△S(T)=S n (T)-S s (T) and the difference in specific heatZ y x x z z y z y x o EP P P P P P P c P P P b P a g g -+++++++=)(2)(422222224442△C(T)=C n (T)-C s (T) between the normal and superconducting states in terms of the critical magnetic field H c (T) and its first derivative dH c /dT and second derivative d 2H c /dT 2. [Hint: Use Eq.(16.3) and standard thermodynamic relationships.](b) Evaluate these expressions for △S(T) and △C(T) for the case where H c (T) can be approximated by H c0[1-(T/T c )2] and show that : (ⅰ) △S(T c )=△S(0)=0(ⅱ) △S(T)>0 for 0<T<T c(ⅲ)△C(T c )=-4µ0H c02/T c . Calculate △C(T c ) from this expressionusing T c = 1.175 K and H c0 = 105 Oe = 8360 A/m for Al and compare with the measured result -225 Jm -3K -1 for Al.(ⅳ) △C=0 for T=T c /3 and T=0K.Eq.(16.3): 16.2 (a) Using Eq.(16.5), calculate the condensation energy in J/m 3 and ineV per electron at T=0K for the superconductor Pb for which H c0=6.39×104A/m.(b) Compare your result from part (a) with the expression ε(0)(ε(0)/E F ) where the superconducting energy gap 2ε(0) = 2.6 meV for Pb. Here ε(0)/E F is the fraction of conduction elections whose energies are actually affected by the condensation .Eq.(16.5): 16.3 Consider the London penetration depth λL defined in Eq.(16.10).⎰+=-=H s s s s H T G dH H M T G T H G 02002),0()(),0(),(μμ2)(),0(),0(20T H T G T G c s n μ=-(a) Calculate λL (0K) for the superconducting Al, Pb, and Nb. (b) If a superconductor has a London penetration depth λL (0K)=200nm, what is the concentration n s of superconducting electrons at T=0.5T c .Eq.(16.10): 16.4 When transport current i flows through a superconducting wireof radius R, its path is confined to a region of thickness λ, the penetration depth, just inside the surface of the wire.(a) In this case show that the critical current density J c =i c /A eff is independent of R and can be expressed in terms of the critical field H c by J c =H c /λ. Here A eff is the effective area through which the current flows, with A eff <<πR 2.(b) Calculate J c for superconducting Pb at T=0K. [Note: H c0 = 803 Oe = 63919 A/m and λ(0) = 39 nm](c) Sketch J c (T)/J c (0) from T = 0 K to T c using the temperature dependencies of H c and λ given in Eqs.(16.6) and (16.11), respectively .Eq.(16.6):Eq.(16.11): 16.5 A type Ⅱ superconductor has T c =125k, ΘD =250K, and κ(T c )=50. Onthe basis of standard theories [free-electron model, Debye model, BCS theory, G-L theory, Pauli limit for H c2 given in Eq.(16.33)], 20)()(e T n mT s L μλ=)1()(220c c c T T H T H -=4)/(1)0()(c L L T T T -=λλestimate the following:(a)The superconducting energy gap 2ε(0).(b) The upper critical field H c2(0)=H p .(c)The co herence length ξ(0) and the penetration depth λ(0).(d)The thermodynamic critical field H c0=H c (0).(e)The coefficients γ and A of the electronic and phonon contributions to the specific heat , γT and AT 3, respectively.Eq.(16.33): 16.7 Use Eq.(16.20) to find the limiting values of λ(l ) and ξ(l ) (a) in theclean limit where the electron mean free path l >>ξ0, and (b) in the dirty limit where l <<ξ0.Eq.(16.20): and 16.8 (a) Calculate the density of vortices per unit area B/Φ0 for thefollowing values of B, the average flux density present in the mixed state of a superconductor. Take H c2=1.6MA/m.(i) B = μ0H c2/2. (ii) B ≈ B c2 = μ0H c2.(b)Calculate the average separation d between the vortices from your answers in part (a) and compare your answers with the conherence length ξ. [Hint: You can obtain ξ with the help of Eq.(16.22).]Eq.(16.22): 16.10 Calculate the number of holes N hole per Cu ion in the CuO 2copper-oxygen layers in the superconductor YBa 2Cu 3O 7-x for the Bp T T H μμε0)()(≈l l 11)(10+=ξξll ξλλ+∞=1)()()(2)(2002T T H c ξπμΦ=cases of x = 0, 0.25, and 0.5. Assume the following ionic charge states for the ions in this structure: Y 3+, Ba 2+, Cu 2+, and O 2-.16.11 For the compound with the chemical formula La 1.7Sr 0.3CuO 3.9:(a)what is the total number of electrons per formula unit outside closed shells?(b)How many electrons are contributed by each ion to the CuO 2 layers?(c)what is the average valence of the copper atoms?(d)Assuming that all copper ions have a charge of +2e, what is the number of holes per formula unit?16.12 Derive Eq.(16.33) for the Pauli limiting field H p by settingG n (H)=G s (H) at H=H p and using the Pauli paramagneticsusceptibility χp =µ0µB 2ρ(E F ) of the conduction electrons in thenormal state. [Hint: Use G n (H)-G n (0)=-µ0χp H 2/2, and the BCS resultG n (0)-G s (0)=ρ(E F )ε(0)2/2.]Eq.(16.33):Chap 17、Magnetic Materials17.1 Consider a single-domain uniaxial ferromagnetic particlemagnetized along its easy axis with M=M s in zero applied magnetic field. The magnetic anisotropy energy density is given by E a =K sin 2θ where K >0 and θ is the angle between the B p T T H μμε0)()(≈magnetization M and the easy axis. A magnetic field H is now applied at 90° to the easy axis.(a)Show that the sum of the anisotropy and magnetostatic energy densities for this particle is ｕ(θ)=K sin 2θ-µ0MHsinθ.(b)Find the angle θ be tween M and the easy axis as a function of the magnitude of the field H by minimizing ｕwith respect to θ .(Note that it will be important to check for the stability of the solution by requiring that ∂2ｕ/∂θ2>0.)(c) Show that the resulting magnetization curve (i.e., the plot of thecomponent of M in the direction of H versus the applied field H ) is a straight line (with slop χ=µ0M 2s /2K ) up to H =H k =2k/µ0M s , at which point the magnetization is saturated in the direction of H . Here H k is the effective magnetic anisotropy field in Eq.(17.14).Eq.(17.14): 17.4 Prove that when the shape anisotropy constant K s is <0 (i.e., whenN ⊥<N 11), the magnetization M for a ferromagnetic film will lie in the plane of the film .17.5 Calculate the radius at which a spherical Fe particle behavessuperparamagnetically at T =300K by setting K 1V=K B T , where K 1≈4.2×104J/m 3 is the first-order magnetocrystalline anisotropy coefficient for Fe and V is the volume of the sphere.17.6 Calculate t he increase in temperature ΔT of a magnetic material withsK M KH 02μ=a square magnetization loop, with M s =1370KA/m and H c =1100kA/m, when the loop is traversed once, Assume that the material is thermally-isolated from its surroundings and that its specific heat is 4×106J/m 3K.17.7 For a magnetically isotropic m aterial with magnetostriction λ, provethat B 2(C 11-C 12)=2B 1C 44. Show, in fact, that if the material is also elastically isotropic, then B 1=B 2. (Hint: See Section 10.8)17.8 Show that B (t) and M (t) both lag the applied magnetic fieldH(t )=H 0e -iωt by the same phas e angle δ when µ0H 0<<B 0cosδ. [Hint: Start by substituting the expressions for B (t) and M (t) from Eq.(17.33) into the expression B =µ0(H+M).]Eq.(17.33): andChap 18、Optical Materials18.1 Suppose that a quantum dot has the shape of a two-dimensionalcircular disk. A model that is often used to describe the potential of an electron confined in such a dot is V(r)=m ﹡ω02r 2/2. Suppose a magnetic induction B is imposed perpendicular to the plane of the dot. Show that the electron energy levels are given by the formula where n=0, 1, 2,…………and l=……, -2, -1, 0, 1, 2,……..18.2 Consider a Lorentz oscillator model for an electron moving in )(0)(δω+-=t i e B t B )(0)(φω+-=t i e M t M **-+++=m eB l m eB l n E l n 2)2()()12(220, ωone-dimensional anharmonic potential described by the Toda potential V(x)=Ae -ax +Bx, where A, a and B are constants. The equation of motion isDerive expressions for the linear polarization P , at frequency ω and the nonlinear polarization at frequency 2ω, P (2ω).18.3 Consider a particle of mass m moving in the anharmonicsymmetric potential V(x)=Acosh[a(x-x o )] subject to a damping force –γv and a driving force qE cosωt . Find the Fourier coefficients for the dipole moment at frequencies ω and 3ω. 18.4 Using Vegard′s law , derive an expression for the bandgap energyE g (x,y) of a layer of In 1-x Ga x As y P 1-y which is lattice matched to an InP substrate. Compare your expression with the experimental result given in Eq.(18.15) and comment on any differences.Eq.(18.15): E g =1.35-0.72y+0.12y 2 eVt qE e e aA dtdx dt x d m o ax ax ωγcos )()(22+-=+--。

低介电常数材料研究

低介电常数材料研究低介电常数材料是指具有较低介电常数（dielectric constant）的材料，介电常数是物质在外电场作用下的电极化能力的量度。

低介电常数材料在现代电子器件的设计和制造中起着重要的作用，因为它们能够减少电子设备中的电容效应和信号干扰，提高电子器件的性能和稳定性。

近年来，随着电子器件的不断发展和尺寸的不断缩小，对低介电常数材料的需求也越来越大。

低介电常数材料的研究主要集中在以下几个方面：1. 理论设计与计算：通过理论设计和计算方法，探索具有低介电常数的材料的结构、性质和机理，为低介电常数材料的研制提供理论指导。

采用密度泛函理论（density functional theory，DFT）等计算方法，研究材料的能带结构、电子密度分布和禁带宽度等参数，进而研究材料的介电常数。

通过计算和模拟，可以预测和优化材料的介电性能。

2. 材料的制备和表征：研究低介电常数材料的制备方法以及表征技术，包括薄膜制备、材料结构与成分的表征等。

常用的制备技术包括溶胶-凝胶法、层状堆积法、化学气相沉积等。

通过X射线衍射（X-ray diffraction，XRD）、扫描电子显微镜（scanning electron microscopy，SEM）和透射电子显微镜（transmission electron microscopy，TEM）等表征方法，可以了解材料的晶体结构、形貌和尺寸等。

3.材料性能的优化：为了获得更低的介电常数，可以通过调控材料的结构、成分和形貌等方式进行优化。

例如，可以通过掺杂杂原子、改变晶体结构、调控纳米颗粒的形状和尺寸等方法，来降低材料的介电常数。

此外，还可以通过引入空气微孔、低介电常数填充剂等方式来减低材料的介电常数。

4.材料的应用研究：低介电常数材料在电子器件中的应用是研究的重点之一、例如，低介电常数材料可以用作集成电路中的电介质层，以减少电容效应和信号交叉的干扰。

此外，低介电常数材料还可以应用于微波技术、光子学、传感器等领域，以提高设备的性能。

dielectric

Preparation and characterization of porous silica xerogelﬁlm for lowdielectric applicationJung-Kyun Hong,Hee-Sun Yang,Moon-Ho Jo,Hyung-Ho Park*,Se-Young ChoiDepartment of Ceramic Engineering,Yonsei University,134,Shinchon-dong,Seodaemoon-ku,Seoul120-749,South KoreaAbstractSiO2xerogel thinﬁlm with a low dielectric constant was successfully prepared by a two-step acid-base catalyst procedure and successive surface modiﬁcation with trimethylchlorosilane(TMCS).Only15%porosity could be obtained without surface modiﬁcation but with surface modiﬁcation the porosity increased to50%.These porosity values correspond to measured dielectric constants of3.95and2.45, respectively.The low dielectric constant was revealed to depend mainly on the porous structure of xerogel thinﬁlm obtained with surface modiﬁcation.Fourier transform infrared spectroscopy and X-ray photoelectron spectroscopy analyses were carried out to evaluate the effect of surface modiﬁcation which induces the changes of surface coverage from–OC2H5and–OH to–CH3.Rutherford backscattering spectrometry analysis gave the porosity of SiO2xerogel thinﬁlm as47.5%.The porosity estimation using refractive index obtained from Ellipsometry work was43.2%and agrees well with RBS analysis.The network structure of SiO2xerogel was also evaluated with scanning electron microscopy and transmission electron microscopy.©1997Elsevier Science S.A.Keywords:Silica xerogelﬁlm;Low dielectric constant;Porosity characteristics1.IntroductionThe growth of integrated circuit technology is primarily based on the continued scaling down of devices to ever smaller dimensions.Smaller devices give higher packing density as well as higher operating speeds.However,with higher device speed there is an almost inevitable reduction in the interconnection delay caused by parasitic capacitance between metal layers over the basic gate delay[1].There-fore,low k(i.e.low dielectric constant)materials which substitute for conventional inter-metal dielectric(IMD) have become imperative for the reduction of parasitic capa-citance between multi-metal layers.Sol-gel derived porous SiO2thinﬁlm has great potential as an IMD,because a very low dielectric constant can be achieved from its porosity.It also has a high temperature limit and compatibility with existing microelectronics precursors[2].In particular,one of the porous SiO2gels,aerogels,has extremely high por-osity,up to95%;and its dielectric constant is close to1. With this unique characteristic,SiO2aerogel can be applied to IMD[3–5].In our previous work,we obtained SiO2 aerogel thinﬁlm with good dielectric properties as IMD by a supercritical drying procedure[6].However,this pro-cess is very energy intensive,often dangerous,and not easily adaptable to continuous thinﬁlm forming operations. Therefore,an ambient drying method for the preparation of SiO2aerogelﬁlm was studied and recently reported by Pra-kash et al.[7].This involved using dip coating of reliquiﬁed gels after surface modiﬁcation.In the present work,a novel procedure for the preparation of SiO2xerogel thinﬁlm for application to IMD is proposed. This manuscript contains the results of the fabrication and the characterization as well as the possible application to IMD of SiO2xerogel thinﬁlm.We evaluated material prop-erties by focusing on the surface modiﬁcation and the mea-surements of density and porosity which are directly related to the dielectric property.The dielectric constant of modi-ﬁed SiO2xerogel thinﬁlm was compared with that of SiO2 xerogel thinﬁlm obtained without surface modiﬁcation. 2.ExperimentalSilica sol used in this experiment was prepared using a typical two-step acid/base catalyst procedure.In theﬁrst step,tetraethylorthosilicate(TEOS),ethanol,waterandThin Solid Films308–309(1997)495–5000040-6090/97/$17.00©1997Elsevier Science S.A.All rights reservedPII S0040-6090(97)00486-0*Corresponding author.e-mail:hhpark@bubble.yonsei.ac.krHCl were mixed in the molar ratio 1:4:2:2.0×10−4at room temperature for 4h (stock solution).In the second step,0.725ml of the base-catalyst (0.5M NH 4OH)was added to 10ml of the stock solution.The gelation occurred after 30min at room temperature.The sol with viscosity between 10and 15cp was spun on p-type Si (100)wafer at 3500rev./min for 15s.Since the solvent of sol can be rapidly evapo-rated during the spin deposition,the spin coating was con-ducted in an ethanol atmosphere.The spun-on ﬁlm was aged under an ethanol atmosphere for 10min and the aged ﬁlm was immersed in n -hexane (CH 3(CH 2)4CH 3)in order to wash the ethanol in the gel network structure.After sufﬁ-cient washing,surface modiﬁcation with trimethylchlorosi-lane (TMCS,(CH 3)3SiCl)in n -hexane for 2h at 60°C and successive thermal treatment at 300°C was carried out.The experimental ﬂow is schematically illustrated in Fig.1.The coarse and ﬁne microstructures of the ﬁlms were investigated by scanning electron microscope (SEM;Hita-chi H600)and transmission electron microscope (TEM;Hitachi S2700)observations.The ﬁlm density was comple-mentarily determined using Rutherford backscattering spec-trometry (RBS;NEC6-SDH)with 2.0MeV He 2+ions and cross-sectional SEM.The composition of ﬁlm was also determined using RBS.The refractive index of SiO 2xerogel ﬁlm was measured by Ellipsometer (Gaertner Scientiﬁc;L117C)at its most shallow incident angle of 30°.The ﬁlm density was also calculated using the reported relationship with the refractive index [8]to compare with the measured density value.The chemical species and chemical bonding state were investigated using Fourier transform infrared spectroscopy (FT-IR)and X-ray photoelectron spectro-scopy (XPS).XPS analysis was performed with a V.G.Scientiﬁc ESCALAB 220i-XL spectrometer using Mg k a (1253.6eV)radiation operating at 250W.Narrow scan spectra of all regions of interest were recorded in order to quantify the surface composition and identify the elemental bonding states with pass energy of 20eV and take-off angle of 90°.The dielectric constant was directly measured using an Impedance/Gain-Phase Analyzer (Hewlett Packard;4194A)in MIS structure at 1MHz.The upper and lower electrodes were deposited with Al using a thermal evapora-tor.3.Results and discussionSiO 2xerogel thin ﬁlm was simply prepared after sur-face modiﬁcation with TMCS of spin-coated silica sol.For the preparation of aerogel/xerogel ﬁlms,a dip coating procedure is actually used [9–11].In the present work how-ever,spin coating was conducted for the insurance of good adhesion and planarization of the ﬁlm.The dielectric con-stant was measured as 2.45with MIS structure.This value is much lower than that of conventional SiO 2ﬁlm actually used in the fabrication of integrated circuits (IC).How-ever,unmodiﬁed ﬁlm shows a dielectric constant of 3.95,which is similar to that of conventional SiO 2ﬁlm.Through the surface modiﬁcation,SiO 2xerogel ﬁlm has a unique porous structure,and it shows a very low dielectric con-stant.Table 1summarizes the density,porosity,refractive index and calculated and measured dielectric constants of unmodiﬁed and modiﬁed ﬁlms.The ﬁlm density,r ,can be determined from the measured refractive index (n ),using the relationship,r =(n −1)/0.202for silica xerogel.The dielectric constant (k)and the porosity (P )of the ﬁlms were calculated indirectly from the density.The ﬁlm por-osity was obtained from the relationship,P =1−r /r s where r s (thermally grown conventional SiO 2ﬁlm)=2.27g/cm 3and similarly;the dielectric constant of SiO 2xerogel ﬁlm was determined from the relationship k =1+1.28r ,so k =1+6.33(n −1)[8].The density of unmodiﬁed SiO2Fig.1.Experimental ﬂow of sample preparation.496J.-K.Hong et al./Thin Solid Films 308–309(1997)495–500xerogel ﬁlm (1.93g/cm 3)calculated from the refractive index was not much smaller than that of conventional SiO 2ﬁlm (2.27g/cm 3).However,the density of modiﬁedSiO 2xerogel ﬁlm (1.29g/cm 3)was half the density of con-ventional SiO 2ﬁlm.These density values correspond to the dielectric constants of 2.65and 3.47,respectively.These values are somewhat different from directly measured values (2.45and 3.95),but refractive index can be used for roughly anticipating the physical properties of SiO 2xer-ogel ﬁlm.In some sol-gel derived ﬁlms prepared by dip coating,the porosity of the ﬁlm could be controlled in the approximate range 10–50%without surface modiﬁcation [9–11].In this work however,silica sol was so rapidly spun-on that only a few %of porosity could be achieved without surface modiﬁcation.However,in the surface mod-iﬁed xerogel with TMCS,drying shrinkage is reversible because the hydroxylated surface of SiO 2gel is changed with organosilanes (–Si(CH 3)3)[12].Organosilyl-termi-nated surfaces do not participate in condensation reaction or hydrogen bonding as the gel is collapsed by the capillary tension developed during drying,therefore the shrunkenTable 1Characteristic data of SiO 2xerogelModiﬁed ﬁlmUnmodiﬁed ﬁlm Ellipsometer Density (g/cm 3) 1.29 1.93Refractive index 1.26 1.39Porosity (%)43.215.0Dielectric constant (calculated) 2.65 3.47RBS/SEMDensity (g/cm 3) 1.19 2.17Porosity (%)47.5 4.5Dielectric constant (calculated) 2.52 3.78MIS structureDielectric constant (measured)2.453.95Fig.2.SEM micrographs of SiO 2xerogel ﬁlms;(a)modiﬁed and (b)unmodiﬁed ﬁlms.497J.-K.Hong et al./Thin Solid Films 308–309(1997)495–500elastic network progressively springs back toward its origi-nal porous state [13].The surface morphology and thickness of SiO 2xerogel ﬁlm are clearly shown in SEM micrographs in paring with unmodiﬁed ﬁlm in Fig.2b,the surface morphology of modiﬁed ﬁlm is more porous than that of unmodiﬁed ﬁlm.Unmodiﬁed ﬁlm consists of very small size particles (Ͻ10nm)and appears to form dense SiO 2ﬁlm,but modiﬁed ﬁlm appears to consist of coarse (~40nm)particles and pores.Modiﬁed SiO 2xerogel ﬁlms showed good thickness uniformity,and the average ﬁlm thickness was measured as 550nm.This value is larger than that of unmodiﬁed ﬁlm (420nm)coated under the same conditions.The aging effect in n -hexane during the washing and surface modiﬁcation step induces the particle growth.The formation of nm-scale pores is due to the rever-sible shrinkage which can be achieved through the replace-ment of hydroxylated surface with TMCS [12].To obtain detailed information on network structure,SiO 2xerogel ﬁlm dispersed in ethanol was observed using TEM.The particles shown in Fig.3have sizes between 30and 40nm and build up a 3-dimensional network in SiO 2xerogel ﬁlm.This result is in agreement with the SEM observation.RBS analysis was conducted to determine the porosity of SiO 2xerogel ﬁlm.The density of ﬁlm,which is the most crucial ﬁlm property for low dielectric application,can be determined by integrating the peak area of each elemental range in the RBS spectrum and considering the ﬁlm thick-ness measured using cross-sectional SEM observation.Theporosity of ﬁlm can be directly calculated from density.The RBS spectrum of modiﬁed xerogel ﬁlm is given in Fig.4.In the present work,the density of modiﬁed SiO 2xerogel ﬁlm was determined as l.19g/cm 3.In the case of unmodiﬁed ﬁlm,the ﬁlm density was 2.17g/cm 3.The porosity was calculated under the assumption that the silica framework density is that of thermally grown SiO 2ﬁlm (2.27g/cm 3).The corresponding porosity values were 47.5%and 4.5%for modiﬁed and unmodiﬁed ﬁlms,respectively.With RBS analyses obtained from modiﬁed and unmodi-ﬁed ﬁlms,the composition of ﬁlm,i.e.ratios of O/Si and C/Si,could also be deduced by measuring the yield height of each element.The atomic ratios of Si:O:C were calculated to be 1.0:2.35:0.95and 1.0:2.14:1.21for each sample.In the unmodiﬁed xerogel ﬁlm,O to Si ratio (2.35)is relatively higher than that of conventional SiO 2due to the ethoxy group (–OC 2H 5).In the modiﬁed ﬁlm;the O to Si ratio somewhat decreased but the C to Si ratio increased in com-parison with the unmodiﬁed ﬁlm.From these,it could be deduced that the surface hydroxyl group was replaced by a methyl silyl group during the surface modiﬁcation with TMCS.FT-IR analysis was conducted to obtain information about surface bonding characteristics and evidence of sur-face modiﬁcation.The spectra of as-received unmodiﬁed,thermally treated (at 300°C)unmodiﬁed and modiﬁed ﬁlms are given in Fig.5.In the as-received unmodiﬁed ﬁlm,besides a skeletal Si–O–Si peak,two kinds of C–H stretch-ing peaks and a broad O–H vibration peak centered at 3400cm −1were observed.The peak at 2885cm −1is due to the–Fig.3.TEM micrograph of modiﬁed SiO 2xerogelﬁlm.Fig.4.RBS spectrum of modiﬁed SiO 2xerogel ﬁlm with 2MeV He 2+.498J.-K.Hong et al./Thin Solid Films 308–309(1997)495–500CH 2–of the ethoxy group;and the peak at 2975cm −1is due to the –CH 3of the ethoxy group.This means that the xer-ogel ﬁlm has a lot of ethoxy groups caused by incomplete hydrolysis of TEOS or re-esteriﬁcation [14].These C–H stretching peaks disappeared in thermally treated unmodi-ﬁed ﬁlm at 300°C due to thermal volatility of the ethoxy group.However,the C–H stretching peak due to –CH 3in modiﬁed ﬁlm still appeared at 2965cm −1[7].This means that they have a different chemical environment to each other.The surface of unmodiﬁed xerogel ﬁlm is covered with –OC 2H 5;on the contrary TMCS-modiﬁed xerogel ﬁlm is covered with –CH 3.The C–H stretching peak from TMCS is also found in modiﬁed SiO 2xerogel ﬁlm at 880cm −1due to the Si–C stretching peak vibration [15].The broad O–H peak centered at 3400cm −1is clearly reduced in the modiﬁed ﬁlm due to the replacement of surface hydroxylgroup with methyl silyl group.This result is veriﬁed by RBS analysis.The peak corresponding to absorbed water was observed in as-received unmodiﬁed ﬁlm,but after thermal treatment,the absorbed water was almost removed.In the application of SiO 2xerogel ﬁlm to IMD,the absorbed moisture is very important because it can potentially cause the corrosion of the underlying metal line and also degrade ﬁlm adhesion.In modiﬁed ﬁlm,the absorbed water was also almost removed.A more detailed composition and chemical bonding state of the SiO 2xerogel ﬁlm surface was also examined using XPS.The surface compositions of the above three kinds of SiO 2xerogel ﬁlms are given in Fig.6.The XPS analysis shows that the surface of SiO 2xerogel ﬁlm consists mainly of silicon,oxygen and carbon.The carbon peak is essen-tially composed of C–C/H and C–O bonds,and the silicon peak is mainly composed of Si–O–Si,Si–O–C,Si–O–H and Si–C bonds.The O to Si ratio,3.1,is also much higher than the stoichiometric ratio,2.0.This means that some oxygen has additional bonding states as Si–O–C and Si–O–H bonds.Through the thermal treatment,the surface Si–O–C group was oxidized and changed to Si–O–H.The concentration of carbon is then remarkably reduced but the O to Si ratio is little changed in thermally treated unmo-diﬁed ﬁlm.This result is veriﬁed with the disappearance of the C–H stretching peak and the appearance of the SiO–H peak (3750cm −1)in FT-IR analysis.From the XPS narrow scan analyses in particular,the C 1s spectrum presents the most remarkable change in peak shape of each sample and they are shown in Fig.7.The peak binding energies of 284.7eV,286.4eV and 283.5eV correspond to C–C/H,C–OandFig.5.FT-IR spectra of SiO 2xerogel ﬁlms;(a)as-received unmodiﬁed,(b)thermally-treated unmodiﬁed (300°C),and (c)modiﬁedﬁlms.Fig.6.Atomic compositions of SiO 2xerogel ﬁlms by XPS;(a)as-received unmodiﬁed,(b)thermally treated unmodiﬁed (300°C),and (c)modiﬁed ﬁlms.499J.-K.Hong et al./Thin Solid Films 308–309(1997)495–500C–Si bonds,respectively [16].The decrease of the C–O bond in thermally treated ﬁlm and the appearance of the C–Si bond in modiﬁed ﬁlm with TMCS is clearly seen.These XPS analyses verify that the surface of SiO 2xerogel is modiﬁed with TMCS.4.ConclusionsSurface modiﬁed SiO 2xerogel ﬁlm after spin coating was dried in air and thermally treated at 300°C.It showed about 50%of porosity and a dielectric constant lower than 2.5.On the contrary,only a small percentage of porosity could beachieved with unmodiﬁed sol-gel derived SiO 2ﬁlm.The surface modiﬁcation prevents gel network collapse during the drying process.As a result,the modiﬁed ﬁlm has high porosity and a low dielectric constant.With MIS structure,a dielectric constant of 2.45was directly measured.The dielectric constant of modiﬁed ﬁlm could also be obtained from the refractive index by Ellipsometry and the density by RBS analysis.They were 2.65and 2.52,respectively.These values are much lower than that of conventional SiO 2ﬁlm.The 3-dimensional network of particulate (30–40nm)con-structing porous SiO 2xerogel ﬁlm was clearly observed by TEM work.The surface coverages of modiﬁed and unmo-diﬁed ﬁlms are revealed to be different due to the successful modiﬁcation with TMCS.The spectroscopic work shows that the surface of the modiﬁed ﬁlm was covered with –CH 3,but on the other hand,the surface of the unmodiﬁed ﬁlm was covered with mainly –OC 2H 5and –OH.AcknowledgementsThis work was supported by the Ministry of Education through the Inter-University Semiconductor Research Cen-ter (ISRC 96-E-1063)in Seoul National University.References[1]C.B.Case, A.Kornblit,u and N.H.Hendricks,Proc.ISMIC Conf.,104(1995)116.[2]D.M.Smith,J.Anderson,C.C.Cho,G.P.Johnston and S.P.Jeng,Proc.Mat.Res.Symp.,381(1995)261.[3]L.W.Hrubesh and J.F.Poco,J.Non-Cryst.Solids,188(1995)46.[4]L.W.Hrubesh,L.E.Keene and torre,J.Mater.Res.,8(1993)1736.[5]P.Bru ¨esch,F.Stucki,Th.Baumann,P.Kluge-Weiss,B.Bru ¨hl,L.Niemeyer,R.Stru ¨mpler,B.Ziegier and M.Mielke,Appl.Phys.A.,57(1993)329.[6]M.H.Jo,J.K.Hong,H.H.Park,J.J.Kim and S.H.Hyun,Microelec-tronic Engineering,33(1997)343.[7]S.S.Prakash,C.J.Brinker and A.J.Hurd,J.Non-Cryst.Solids,190(1995)264.[8]S.Henning and L.Svenson,Phys.Scripta,23(1981)697.[9]C.J.Brinker,A.J.Hurd and K.J.Ward,in J.D.Mackanzie and D.R.Ulrich (eds.),Ultrastructure Processing of Advanced Ceramics ,Wiley,New York,1988,p.223.[10]H.Schmidt,G.Rinn,R.Nass and D.Sporn,in C.J.Brinker,D.E.Clark and D.R.Ulich (eds.),Better Ceramics Through Chemistry III ,Material Research Society,Pittsburg,PA,1988,p.743.[11]H.Hirashima and K.Sudoh,J.Non-Cryst.Solids,145(1992)51.[12]S.S.Prakash,C.J.Brinker,A.J.Hurd and S.M.Rao,Nature,374(1995)439.[13]E.P.Plueddemann,Silane Coupling Agents ,Plenum,New York,1991.[14]C.J.Brinker and G.W.Scherer,Sol-Gel Science ,Academic Press,San Diego,1990,Ch.9,p.581.[15]U.Mackens and U.Merkt,Thin Solid Films,97(1982)53.[16]H.H.Park,K.H.Kwon,J.L.Lee,et al.,J.Appl.Phys.76(1994)4596.Fig.7.Changes of C 1s spectra in SiO 2xerogel ﬁlms;(a)as-received unmodiﬁed,(b)thermally treated unmodiﬁed (300°C),and (c)modiﬁed ﬁlms.500J.-K.Hong et al./Thin Solid Films 308–309(1997)495–500。

电介质材料(压电与铁电材料1)

Guangdong Ocean University Xiong Zhengye
Guangdong Ocean University
Xiong Zhengye
当晶体不振动时，可把它看成一个平板电容器称为静电电容C0，它的大小与晶片的几何尺寸、电极面积有关，一般约几个PF到几十PF。当晶体振荡时，机械振动的惯性可用电感L来等效。一般L的值为几十mH到几百mH。晶片的弹性可用电容 C来等效，C的值很小，一般只有0.0002～0.1pF。晶片振动时因摩擦而造成的损耗用R来等效，它的数值约为100Ω。由于晶片的等效电感很大，而C很小，R也小，因此回路的品质因数Q 很大，可达1000～10000。加上晶片本身的谐振频率基本上只与晶片的切割方式、几何形状、尺寸有关，而且可以做得精确，因此利用石英谐振器组成的振荡电路可获得很高的频率稳定度。
Guangdong Ocean University
Xiong Zhengye
从石英晶体谐振器的等效电路可知，它有两个谐振频率，即（1）当L、C、R支路发生串联谐振时，它的等效阻抗最小（等于R）。串联揩振频率用fs表示，石英晶体对于串联揩振频率fs呈纯阻性，（2）当频率高于fs时L、 C、R支路呈感性，可与电容C0发生并联谐振，其并联频率用fd表示。 Guangdong Ocean University Xiong Zhengye
Guangdong Ocean University Xiong Zhengye
（4 ）机械耦合系数：在压电效应中 , 其值等于转换输出能量（如电能）与输入的能量（如机械能）之比的平方根 ; 它是衡量压电材料机电能量转换效率的一个重要参数。
（ 5 ）电阻：压电材料的绝缘电阻将减少电荷泄漏 , 从而改善压电传感器的低频特性。（ 6 ）居里点：压电材料开始丧失压电特性的温度称为居里点。（7）机械品质因数：压电振子在谐振时在一周期内贮存的机械能与损耗的机械能之比。

电介质迷思

陈湘明博客电介质迷思(1): 传输极化两悠悠众所周知，按电性能对物质进行分类时，通常可分为绝缘体、半导体与导体，当然还有超导体。

一般非专业人士很少能想到与半导体同等重要的电介质(dielectric)，也有不少人误以为电介质即等同于绝缘体。

因此，有必要着眼于其基本物理特性及其根源、正确理解电介质。

当人们将物质分类为绝缘体、半导体、导体、以及超导体时，其依据显然是物质的电荷传输特性或曰电荷长程迁移特性。

电荷的传输或曰电荷的长程迁移，作为物质对外电场的响应，其宏观表现即为电流。

根据欧姆定律: J=σE，其中J为电流密度，E电场强度，而σ为电导率张量(二阶对称张量)。

电导率反映了物质的电荷传输特性或曰电荷长程迁移特性。

一般根据电导率数量级大小来划分绝缘体(σ<10-10[Ω.cm]-1)、半导体(10-10[Ω.cm]-1<σ<105[Ω.cm]-1)、以及导体(σ>105[Ω.cm]-1)。

另一方面，物质对外电场的响应除去电荷的传输或曰电荷的长程迁移外、还有电荷短程运动与位移。

这种电荷的短程运动与位移称为极化(Polarization)，其结果是促使正负电荷中心偏移、从而产生电偶极矩。

而以极化方式传递、储存或记录外电场作用和影响的物质就是电介质。

显然，电介质中起主要作用的乃是束缚电荷而非自由电荷。

极化可以来自极性晶体或分子的自发极化、也可以来自电场的诱导作用。

介电响应可用如下方程描述：D=εε0E或P=χε0E，其中，D为电位移、P为极化强度、ε0为真空电容率、ε为相对介电常数、χ为宏观极化率，ε与χ均为二阶对称张量。

由于ε=1+χ，用相对介电常数与宏观极化率描述介电性质是等价的。

介电常数的物理意义可以理解为电介质在极化过程中储存电荷能力之度量。

由于极化过程总伴随着能量损耗，介电常数需要用复数来描述：ε=ε'-jε”。

其中，介电常数的实部ε'反映了电介质极化过程中储存电荷能力之大小，而其虚部ε”则反映了电介质极化过程中的能量损耗，一般用损耗正切(tanδ=ε”/ε')来表征介电损耗(dielectric loss)。

材料物理基础-材料的电学2

南京理工大学化工学院
球状原子模型
该模型把原子核看成一个电量为+q的点电荷，把
核外总电量为-q的所有电子看成是电荷均匀分布的
球状电子云。其球心在原子核，半径为a。球状原子的正负电荷重心重合，其固有偶极矩为零。
电场力通常不足以改变原子核的位置，也不足以改变电子云的形状。球状电子云在电场力F的作用下，一旦离开原来的平衡位置，立即就要受到原子核库仑引力 F ' 的作用，直到两者达到平衡，即
原子或离子中核外电子的分布。
极化强度为单位体积的电矩。极化的大小不仅决定于粒子的感应电矩，而且决定于单位体积的粒子数。因此，凡αe/a3 较大的粒子对极化就有较大的贡献。有些离子，如O2-，C4+， B3+，S2-，Ti4+ 等的 αe/a3具有特别大的值。
南京理工大学化工学院
离子（弹性）位移极化
南京理工大学化工学院
南京理工大学化工学院
3.4 材料的介电性
四个基本参数
介电常数，表示极化介质损耗角正切，表示松弛现象抗电强度，表示击穿现象电导率，表示电导
南京理工大学化工学院
材料的电极化
基本概念
电矩：点电荷q对某一定点(参考点)的电矩定义为qr。r是该
定点至点电荷q所在点的径向量。电矩是个矢量，以μ表示。一个多点电荷系统，相对于某一定点的电矩为： μ=qr qi ri q o
F ' F qEe
南京理工大学化工学院
如果把电子云看成是集中在球心的负点电荷，则根据高斯定理可得，原子核对球中半径介于a与x之间那部分电子云的作用力为零，因为这时闭合面内所包围的电荷总量为零。在半径为x 的小球内的电子云则受原子核库仑引力的作用，因此有

材料物理性能1

Definition of Polarization Vector
P = Npav
pav = the average dipole moment per molecule P = polarization vector, N = number of molecules per unit volume
注意：f0在光频
(a) When a dilectric is placed in an electric field, bound polarization charges appear on the opposite surfaces. (b) The origin of these polarization charges is the polarization of the molecules of the medium. (c) We can represent the whole dielectric in terms of its surface polarization charges +QP and QP.
The electric field inside a polarized dielectric at the atomic scale is not uniform. The local field is the actual field that acts on a molecules. It can be calculated by removing that molecules and evaluating the field at that point from the charges on the plates and the dipoles surrounding the point.

材料物理性能-力热性能@课程2-力学性能资料

介电性能(Dielectric properties)
磁性能（Magnetic properties) —后四部分由赵雷讲授
无机材料物理性能
邓承继博士
3
课程的讲授方法
本科生学习：一方面是知识学习，另外一方面是方法的学习
教师通过知识的讲授，完成这二方面的教学目的；学生这种学习有时比专业知识学习更重要
力学性能：（1）强度耐压抗折（2）韧性（3）刚性
无机材料物理性能
邓承继博士
13
化学性能：（1）抗氧化性能（2）耐腐蚀性能（3）抗渣、抗碱性能
复杂性能（1）复合性能：高温抗折强度、高温蠕变强度等（2）工艺性能：可塑性、流动性等（3）使用性能：耐磨性等
无机材料物理性能
邓承继博士
邓承继博士
16
参考书
除了使用的教材外，在力学和热学部分还有如下参考书：
张清纯，陶瓷材料的力学性能，科学出版社
上硅所译,陶瓷的力学性质,上海科学技术文献出版社
Michel Barsoum, Fundamentals of ceramics, McGrawHill companies, Inc.
无机材料物理性能
邓承继博士
19
应力
应力：单位面积上所受内力，单位是Pa：
F
A
由于材料的面积在外力作用下，可能有变化，A就有变化，有名义应力和实际（真实）应力
由于无机材料的形变小，上面二者差别小
无机材料物理性能
邓承继博士
20
力的分解，见教材第5页的图1.2 注意：力的方向、力的平衡
力的作用：法向应力导致材料的伸长或者缩短，剪切力引起材料的剪切崎变
14
意义

材料物理英语

材料物理英语Material Physics English。

Material physics is a branch of physics that focuses on the study of the physical properties of materials, such as electrical, magnetic, and optical properties, as well as the relationship between the structure and properties of materials. In this document, we will explore some key concepts and terms in material physics, and provide English translations for these terms to help you better understand and communicate about this subject in English.1. Crystal Structure。

Crystal structure refers to the arrangement of atoms or molecules in a crystalline material. The crystal structure of a material determines many of its properties, such as its mechanical, thermal, and electrical behavior. In material physics, crystal structures are often described using terms such as unit cell, lattice, and symmetry operations.2. Band Gap。

dielectric翻译

dielectric翻译【释义】dielectricadj.非传导性的；诱电性的n.电介质；绝缘体【短语】1 dielectric strength介电强度; 绝缘强度; 电介质强度;电介质强度2 dielectric constant电介电常数; 介质常数;电介电常量; 电容率3 gate dielectric闸极介电层; 栅极绝缘层; 栅介质4 Dielectric loss电介电损耗;电介质损耗;电介质损失;电介电损失5 dielectric polarization物电介质极化; 电介质的极化;物介质极化; 介电极化6 dielectric breakdown介电击穿;电子介质击穿; 介质哗; 击穿电压7 Dielectric heating电介质加热;电电介质加热;电介电加热; 高频电流加热8 Dielectric Physics物介质物理学; 电介质9 the dielectric电介质; 电媒质【例句】1 It consists of a transparent dielectric spacer.它由一个透明的电介质隔片构成。

2 It consists of a transparent dielectric spacer.它由一个透明的电介质隔片构成的。

3 A form of coaxial cable which USES air as a dielectric.一种同轴电缆形式，使用空气作为绝缘体。

4 For these reasons, it is preferred that the liquid be dielectric.由于这些原因，是希望得到的液体介质。

5 There are a number of PCB dielectric materials on the market today.在当今的市场上有相当数量的pcb绝缘材料。

6 In the case of dielectric breakdown, a different type of acceleration occurs.在介质击穿的情况下，出现了一种不同类型的加速。

2021年材料物理导论名词解释

As long as you do things with integrity, don't ask about success or failure.通用参考模板（WORD文档/A4打印/可编辑/页眉可删）材料物理导论名词解释Absorption coefficient 吸收常数：垂直于光束方向的水层元内单位厚度的吸收量Acceptor impurity 受主杂质：lll族杂质在Si、Ge中能够接受电子而产生导电空穴并形成负电中心acceptor ionization 受主电离：空穴挣脱受主杂质束缚的过程Antiferromagnetism 反铁磁性：材料中相邻原子或离子的磁矩作反向平行排列使得总磁矩为零的性质。

Birefringence 双折射：光入射到各向异性的晶体分解为两束光而沿不同方向折射的现象 Conduction bands 导带：一部分被电子填充，另一部分能级空着的允带Crystallization 结晶：液态金属转变为固态金属形成晶体的过程Current density 电流密度：描述电路中某点电流强弱和流动方向的物理量currie temperature 居里温度：自发极化急剧消失的温度Diamagnetism 抗磁性：外加磁场使材料中电子轨道运动发生变化，感应出很小的磁矩且该磁矩与外磁场方向相反的性质Dielectric breakdown 介电体击穿：介电体在高电场下电流急剧增大，并在某一电场强度下完全丧失绝缘性能的现象dielectric loss 介电损耗：将电介质在电场作用下，单位时间内消耗的电能Dielectric medium 电介质：能够被电极化的介质Dipolar turning polarization 偶极子转向极化：极性介电体的分子偶极矩在外电场作用下，沿外施电场方向转向而产生宏观偶极矩的极化Disperse phase 分散相：被分散的物质Dispersion of refractive index 折射率的色散：材料的折射率m随入射光频率减小而减小的现象Donor impurity level 施主能级：将被施主杂质束缚的电子能量状态称施主能级Donor impurity 施主杂质：V族杂志在硅、锗中电力时，能够释放电子而产生导电导子并形成整点中心，称其位施主杂质或n型杂志donor ionization 施主电离：施主杂质释放电子的过程Electirical polarization 电子极化：电场作用下，构成原子外围的电子云相对原子核发生位移形成的极化Electrical field 电场：由电荷及变化磁场周围空间里存在的一种特殊物质Electrical resistivity 电阻率：某种材料制成的长1米、横截面积是1平方米的在常温下（20℃时）导线的电阻，叫做这种材料的电阻率。

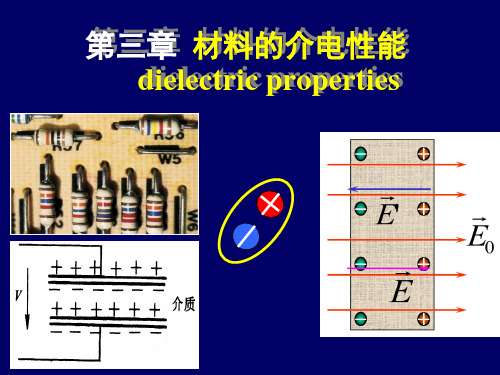
材料物理性能：3-1-1 电介质极化 dielectric polarization

根据上式，可通过测量电介质介电常数求得分子极化率对非极性介质，介电常数与介质的光折射率
n的平方相等
此式联系着介质的电学性能和光学性能。
内电场--电容器 Capacitor
在外电场作用下达到静电平衡时，电介质内部的场强也可以不等于零。类似一个电容器
22
在外电场中电介质形成内电场，同时内电场也影响外电场。
平衡状态，介质温度将越来越高，直至出现永久性破坏。
3) 电击穿强电场作用，电子从电场中获得能量越来越大；大到一定值，导致电离，进入电导状态，发生击穿。
电容器
电介质
3.1.5 偶极子dipole
构成质点的正、负电荷沿电场方向在有限范围内
短程移动，形成一个偶极子。
E
-q
+q
L
电偶极矩：=ql（库仑 ·米）电偶极矩方向：负电荷指向正电荷。与外电场方向一致。
由于极化，电介质表面出现电荷，不能离开，也不能在内部自由移动。称为束缚电荷或极化电荷。它不象导体中的自由电荷能用传导方法将其引走。
14
3.1.3 介电常数 permittivity
平板电容器的电容与施加电压V及极板上产
生的电荷有如下关系：
充满电介质，由于电介质分子极化，极板上产生感应电荷，使极板电荷量增加到
t 120o C
钛酸钡BaTiO3
降温过程结构畸变，对称性下降：
如果在一个轴向发生畸变（如c轴伸长或缩短）
四方晶系
如果在两个轴向发生畸变正交晶系
钛酸钡BaTiO3
如果在[111]轴向发生畸变三方晶系
准同型相界MPB： Morphotropic phase boundary
偶极子 Gd3+-doped PbWO4 [2(GdPb3+).-VPb”]