离散数学试题(1)
最新国家开放大学电大《离散数学》形考任务1试题及答案

最新国家开放大学电大《离散数学》形考任务1试题及答案最新国家开放大学电大《离散数学》形考任务1试题及答.形考任务1(集合论部分概念及性质)单项选择.题目.若集合A=.a, {a}, {1, 2}}, 则下列表述正确的是().选择一项:A.{a, {a}}.B..C.{1, 2..D.{a..题目.设函数f: N→N, f(n)=n+1, 下列表述正确的是.).选择一项: A.f是满射.B.f存在反函.C.f是单射函.D.f是双射.题目.设集合A={1, 2, 3, 4, 5}, 偏序关系是A上的整除关系, 则偏序集<A, >上的元素5是集合A的.).选择一项:A.极小.B.极大.C.最大.D.最小.题目.设A={a, b}, B={1, 2}, C={4, 5}, 从A到B的函数f={<a,1>.<b, 2>}, 从B到C的函数g={<1, 5>.<2, 4>}, 则下列表述正确的是.).选择一项:A.g..={<a, 5>.<b, 4>.B.g..={<5, .>.<4, .>.C.f°.={<5, .>.<4, .>.D.f°.={<a, 5>.<b, 4>.题目.集合A={1.2.3.4}上的关系R={<x, y>|x=y且x.yA}, 则R的性质为.).选择一项:A.传递.B.不是对称.C.反自.D.不是自反.题目.设集合..{1..}, 则P(A...).选择一项:A.{{1}.{a}.{1..}.B.{{1}.{a}.C.{,{1}.{a}.D.{,{1}.{a}.{1..}.题目.若集合A={1, 2}, B={1, 2, {1, 2}},则下列表述正确的是.).选择一项:A.AB, 且A.B.AB, 且A.C.BA, 且A.D.AB, 且A.题目.设集合A={1.2.3}, B={3.4.5}, C={5.6.7},则A∪B–.=.).选择一项:A.{1.2.3.4.B.{4.5.6.7.C.{2.3.4.5.D.{1.2.3.5.题目.设集合..{1.2.3.4.5}上的偏序关系的哈斯图如右图所示, 若A的子集..{3.4.5}, 则元素3为B的.).选择一项:A.最小上.B.下.C.最大下.D.最小.题目1.如果R1和R2是A上的自反关系, 则R1∪R2, R1∩R2, R1-R2中自反关系有.)个.选择一项:A..B..C..D..以下资料为赠送资料:《滴水之中见精神》主题班会教案活动目的: 教育学生懂得“水”这一宝贵资源对于我们来说是极为珍贵的, 每个人都要保护它, 做到节约每一滴水, 造福子孙万代。
离散数学试题与答案试卷一
试卷二答案:
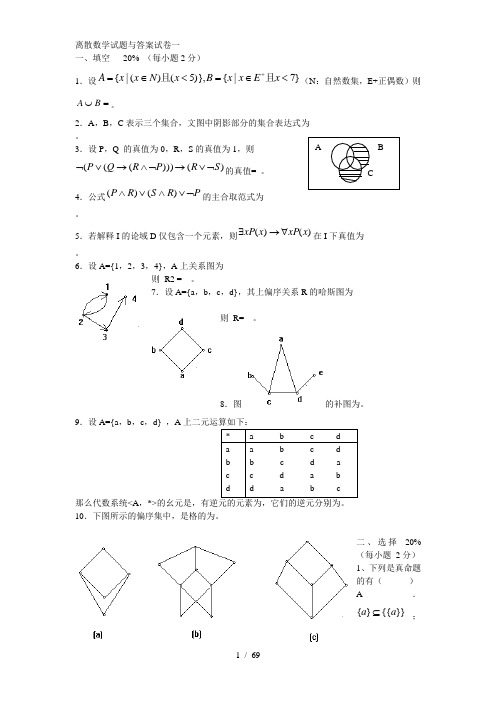
填空20%(每小题2分)
1、 ; 2、T 3、 4、R={<2,2>,<2,3>,<2,4>,<2,5>,<2,6>,<3,2>,<3,3>,<3,4>,<3,5>,<3,6>,<4,5>,<4,6>,<5,2>,<5,3>,<5,4>,<5,5>,<5,6>}; 5、R={<1,2>,<1,3>,<2,1>};R={<1,1>,<2,2>,<3,3>} 6、a;否;有7、Klein四元群;循环群8、B 9、 ;图中无奇度结点且连通10、渗釤呛俨匀谔鱉调硯錦鋇絨钞。
前提: 、 结论: ……3分
① P
② P
③ US②
④ T①I
⑤ T③④I
⑥ T①I
⑦ T⑤⑥I
⑧ EG⑦……11分
3、10分
证明:
。
4、8分
证明:设G中两奇数度结点分别为u和v,若u,v不连通,则G至少有两个连通分支G1、G2,使得u和v分别属于G1和G2,于是G1和G2中各含有1个奇数度结点,这与图论基本定理矛盾,因而u,v一定连通。铙誅卧泻噦圣骋贶頂廡缝勵罴。
选择20%(每小题2分)
题目
1
2
3
4
5
6
7
8
9
10Biblioteka 答案B、DD;DD
B
D
A
离散数学练习题(含答案)

离散数学试题第一部分选择题一、单项选择题1.下列是两个命题变元p,q的小项是( C )A.p∧┐p∧q B.┐p∨qC.┐p∧q D.┐p∨p∨q2.令p:今天下雪了,q:路滑,则命题“虽然今天下雪了,但是路不滑”可符号化为( D )A.p→┐q B.p∨┐qC.p∧q D.p∧┐q3.下列语句中是命题的只有( A )A.1+1=10 B.x+y=10C.sinx+siny<0 D.x mod 3=24.下列等值式不正确的是( C )A.┐(∀x)A⇔(∃x)┐AB.(∀x)(B→A(x))⇔B→(∀x)A(x)C.(∃x)(A(x)∧B(x))⇔(∃x)A(x)∧(∃x)B(x)D.(∀x)(∀y)(A(x)→B(y))⇔(∀x)A(x)→(∀y)B(y)5.谓词公式(∃x)P(x,y)∧(∀x)(Q(x,z)→(∃x)(∀y)R(x,y,z)中量词∀x的辖域是( C )A.(∀x)Q(x,z)→(∃x)(∀y)R(x,y,z))B.Q(x,z)→(∀y)R(x,y,z)C.Q(x,z)→(∃x)(∀y)R(x,y,z)D.Q(x,z)6.设A={a,b,c,d},A上的等价关系R={<a,b>,<b,a>,<c,d>,<d,c>}∪I A,则对应于R的A的划分是( D )A.{{a},{b,c},{d}} B.{{a,b},{c},{d}}C.{{a},{b},{c},{d}} D.{{a,b},{c,d}}7.设A={Ø},B=P(P(A)),以下正确的式子是( A )A.{Ø,{Ø}}∈B B.{{Ø,Ø}}∈BC.{{Ø},{{Ø}}}∈B D.{Ø,{{Ø}}}∈B8.设X,Y,Z是集合,一是集合相对补运算,下列等式不正确的是( A )A.(X-Y)-Z=X-(Y∩Z)B.(X-Y)-Z=(X-Z)-YC.(X-Y)-Z=(X-Z)-(Y-Z)D.(X-Y)-Z=X-(Y∪Z)9.在自然数集N上,下列定义的运算中不可结合的只有( D )A.a*b=min(a,b)B.a*b=a+bC.a*b=GCD(a,b)(a,b的最大公约数)02324# 离散数学试题第1 页共4页02324# 离散数学试题 第 2 页 共4页D .a*b=a(mod b)10.设R 和S 是集合A 上的关系,R ∩S 必为反对称关系的是( A ) A .当R 是偏序关系,S 是等价关系; B .当R 和S 都是自反关系; C .当R 和S 都是等价关系; D .当R 和S 都是传递关系11.设R 是A 上的二元关系,且R ·R ⊆R,可以肯定R 应是( D ) A .对称关系; B .全序关系; C .自反关系; D .传递关系 12.设R 为实数集,函数f :R →R ,f(x)=2x ,则f 是( B ) A .满射函数 B .单射函数 C .双射函数 D .非单射非满射第二部分 非选择题二、填空题1.设论域是{a,b,c},则(∀x)S(x)等价于命题公式 S(a)∧S(b)∧S(c) ;(x ∃)S(x)等价于命题公式 S(a)∨S(b) ∨S(c) 。
离散数学试题及答案1(理工大学)

离散数学试题及答案1(计算机科学与技术)一、单选题(题数:25,共 50.0 分)1不是可满足的公式必永()。
(2.0分)A、假B、真C、负D、正正确答案:A2方法简单但是里面充满了()(2.0分)A、方法论B、推广C、推理D、公式正确答案:A3在联结词的集合Ω中如果一个联结词可以用集合Ω中的其它联结词(),则该联结词在Ω中被称为是冗余的,否则该联结词被称为是独立的。
(2.0分)A、表示B、代言C、规划D、条件正确答案:A4在一阶谓词逻辑的()中,所有命题逻辑的推理规则都要继承下来(2.0分)A、推理B、公式C、检查D、发展正确答案:A5首先求出公式G的无ヨ前束型()(2.0分)A、公式B、实数C、分数D、结构正确答案:A6对()中出现的个体常项,指定一个D中的元素(2.0分)A、AB、FC、GD、V正确答案:A7个体常元:通常用排在前面的小写字毋及其下标()(2.0分)A、表示B、发展C、位置D、幅度正确答案:A8谓词逻辑的任一()A,都可化为和应的ヨ前束范式,并且A是普有效的当且仅当其前東范式是普遍有效的。
(2.0分)A、公式B、检查C、发展D、规划正确答案:A9方法简单但是里面充满了()(2.0分)A、方法论B、推广C、推理D、公式正确答案:A10度为()的顶点称为悬点,与悬点关联的边称为悬边(2.0分)A、1B、2C、3D、4正确答案:A11A,B是命题(),若A→B是永真式,则称A永真蕴含B(2.0分)A、公式B、证明C、发展D、研究正确答案:A12命题公式的主范式包括主()范式和主合取范式两种。
(2.0分)A、析取B、完整C、大众D、发展正确答案:A13在一阶谓词逻辑的()中,所有命题逻辑的推理规则都要继承下来(2.0分)A、推理B、公式C、检查D、发展正确答案:A14如果命题公式A在任意的真值赋值()下的真值都为0,则称A为永假式(或称矛盾式)(2.0分)A、函数B、结果C、大小D、位置正确答案:A15A,B是命题公式,若A→B是(),则称A永真蕴含B(2.0分)A、永真式B、不等式C、法线D、结构式正确答案:A16设公式()和B都是限制性公式(2.0分)A、AB、BC、CD、D正确答案:A17{0,1}上的n元函数f:{0,1}n→{0,1}称为一个n元()函数。
离散数学练习题(含答案)

离散数学练习题(含答案)离散数学试题第一部分选择题1.下列命题变元p,q的小项是(C)。
A。
p∧┐p∧qB。
┐p∨qC。
┐p∧qD。
┐p∨p∨q2.命题“虽然今天下雪了,但是路不滑”可符号化为(D)。
A。
p→┐qB。
p∨┐qC。
p∧qD。
p∧┐q3.只有语句“1+1=10”是命题(A)。
A。
1+1=10B。
x+y=10___<0D。
x mod 3=24.下列等值式不正确的是(C)。
A。
┐(x)A(x)┐AB。
(x)(B→A(x))B→(x)A(x)C。
(x)(A(x)∧B(x))(x)A(x)∧(x)B(x)D。
(x)(y)(A(x)→B(y))(x)A(x)→(y)B(y) 5.量词x的辖域是“Q(x,z)→(x)(y)R(x,y,z)”(C)。
A。
(x)Q(x,z)→(x)(y)R(x,y,z))B。
Q(x,z)→(y)R(x,y,z)C。
Q(x,z)→(x)(y)R(x,y,z)D。
Q(x,z)6.设A={a,b,c,d},A上的等价关系R={。
}∪IA则对应于R的A的划分是(D)。
A。
{{a},{b,c},{d}}B。
{{a,b},{c},{d}}C。
{{a},{b},{c},{d}}D。
{{a,b},{c,d}}7.设A={Ø},B=P(P(A)),以下正确的式子是(A)。
A。
{Ø,{Ø}}∈BB。
{{Ø,Ø}}∈BC。
{{Ø},{{Ø}}}∈BD。
{Ø,{{Ø}}}∈B8.集合相对补运算中,不正确的等式是(A)。
A。
(X-Y)-Z=X-(Y∩Z)B。
(X-Y)-Z=(X-Z)-YC。
(X-Y)-Z=(X-Z)-(Y-Z)D。
(X-Y)-Z=X-(Y∪Z)9.在自然数集N上,不可结合的定义的运算是(D)。
A。
a*b=min(a,b)B。
a*b=a+bC。
a*b=GCD(a,b) (a,b的最大公约数)D。
资料:离散数学试题 (1)

离散数学考试题库(A卷及答案)一、(10分)证明⌝(A∨B)→⌝(P∨Q),P,(B→A)∨⌝P A。
证明:(1)⌝(A∨B)→⌝(P∨Q)P(2)(P∨Q)→(A∨B) T(1),E(3)P P(4)A∨B T(2)(3),I(5)(B→A)∨⌝P P(6)B→A T(3)(5),I(7)A∨⌝B T(6),E(8)(A∨B)∧(A∨⌝B) T(4)(7),I(9)A∧(B∨⌝B) T(8),E(10)A T(9),E二、(10分)甲、乙、丙、丁4个人有且仅有2个人参加围棋优胜比赛。
关于谁参加竞赛,下列4种判断都是正确的:(1)甲和乙只有一人参加;(2)丙参加,丁必参加;(3)乙或丁至多参加一人;(4)丁不参加,甲也不会参加。
请推出哪两个人参加了围棋比赛。
解符号化命题,设A:甲参加了比赛;B:乙参加了比赛;C:丙参加了比赛;D:丁参加了比赛。
依题意有,(1)甲和乙只有一人参加,符号化为A⊕B⇔(⌝A∧B)∨(A∧⌝B);(2)丙参加,丁必参加,符号化为C→D;(3)乙或丁至多参加一人,符号化为⌝(B∧D);(4)丁不参加,甲也不会参加,符号化为⌝D→⌝A。
所以原命题为:(A⊕B)∧(C→D)∧(⌝(B∧D))∧(⌝D→⌝A)⇔((⌝A∧B)∨(A∧⌝B))∧(⌝C∨D)∧(⌝B∨⌝D)∧(D∨⌝A)⇔((⌝A∧B∧⌝C)∨(A∧⌝B∧⌝C)∨(⌝A∧B∧D)∨(A∧⌝B∧D))∧((⌝B∧D)∨(⌝B∧⌝A)∨(⌝D∧⌝A))⇔(A∧⌝B∧⌝C∧D)∨(A∧⌝B∧D)∨(⌝A∧B∧⌝C∧⌝D)⇔T但依据题意条件,有且仅有两人参加竞赛,故⌝A∧B∧⌝C∧⌝D为F。
所以只有:(A∧⌝B∧⌝C∧D)∨(A∧⌝B∧D)⇔T,即甲、丁参加了围棋比赛。
三、(10分)指出下列推理中,在哪些步骤上有错误?为什么?给出正确的推理形式。
(1)∀x(P(x)→Q(x)) P(2)P(y)→Q(y) T(1),US(3)∃xP(x) P(4)P(y) T(3),ES(5)Q(y) T(2)(4),I(6)∃xQ(x) T(5),EG解(4)中ES错,因为对存在量词限制的变元x引用ES规则,只能将x换成某个个体常元c,而不能将其改为自由变元。
离散数学考试题及答案

离散数学考试题及答案一、选择题(每题5分,共20分)1. 下列哪个选项不是离散数学的研究对象?A. 图论B. 组合数学C. 微积分D. 逻辑学答案:C2. 在逻辑学中,下列哪个命题是真命题?A. 如果今天是周一,那么明天是周二。
B. 如果今天是周一,那么明天是周三。
C. 如果今天是周一,那么明天是周四。
D. 如果今天是周一,那么明天是周五。
答案:A3. 在集合论中,下列哪个符号表示集合的并集?A. ∩B. ∪C. ⊆D. ⊂答案:B4. 在图论中,下列哪个术语描述的是图中的顶点集合?A. 边B. 路径C. 子图D. 顶点答案:D二、填空题(每题5分,共20分)1. 如果一个集合A包含5个元素,那么它的子集个数是______。
答案:322. 在逻辑学中,如果命题P和命题Q都是真命题,那么复合命题“P且Q”的真值是______。
答案:真3. 在图论中,如果一个图的顶点数为n,那么它的最大边数是______。
答案:n(n-1)/24. 如果一个二叉树的深度为3,那么它最多包含______个节点。
答案:7三、简答题(每题10分,共30分)1. 请简述什么是图的连通性,并给出一个例子。
答案:图的连通性是指在图中任意两个顶点之间都存在一条路径。
例如,在一个完全图K3中,任意两个顶点之间都可以通过一条边直接连接,因此它是连通的。
2. 解释什么是逻辑蕴含,并给出一个例子。
答案:逻辑蕴含是指如果一个命题P为真,则另一个命题Q也必须为真。
例如,命题P:“如果今天是周一”,命题Q:“明天是周二”。
如果今天是周一,那么根据逻辑蕴含,明天必须是周二。
3. 请描述什么是二叉搜索树,并给出它的一个性质。
答案:二叉搜索树是一种特殊的二叉树,其中每个节点的左子树只包含小于当前节点的数,右子树只包含大于当前节点的数。
它的一个性质是中序遍历可以得到一个有序序列。
四、计算题(每题15分,共30分)1. 给定一个集合A={1, 2, 3, 4, 5},请计算它的幂集,并列出所有元素。
离散数学试题及答案解析

离散数学试题及答案解析一、选择题1. 在集合{1,2,3,4}中,含有3个元素的子集有多少个?A. 4B. 8C. 16D. 32答案:B解析:含有3个元素的子集可以通过组合数公式C(n, k) = n! / [k!(n-k)!]来计算,其中n为集合的元素个数,k为子集中的元素个数。
在本题中,n=4,k=3,所以C(4, 3) = 4! / [3!(4-3)!] = 4。
2. 下列哪个命题是真命题?A. 所有偶数都是整数。
B. 所有整数都是偶数。
C. 所有整数都是奇数。
D. 所有奇数都是整数。
答案:A解析:偶数是指能被2整除的整数,因此所有偶数都是整数,选项A是真命题。
选项B、C和D都是错误的,因为并非所有整数都是偶数或奇数。
二、填空题1. 逻辑运算符“非”(NOT)的真值表是:当输入为真时,输出为______;当输入为假时,输出为真。
答案:假解析:逻辑运算符“非”(NOT)是一元运算符,它将输入的真值取反。
如果输入为真,则输出为假;如果输入为假,则输出为真。
2. 命题逻辑中,合取词“与”(AND)的真值表是:当两个命题都为真时,输出为真;否则输出为______。
答案:假解析:合取词“与”(AND)是二元运算符,只有当两个命题都为真时,输出才为真;如果其中一个或两个命题为假,则输出为假。
三、简答题1. 解释什么是等价关系,并给出一个例子。
答案:等价关系是定义在集合上的一个二元关系,它满足自反性、对称性和传递性。
例如,考虑整数集合上的“同余”关系。
对于任意整数a,b,如果a和b除以同一个正整数n后余数相同,则称a和b模n同余。
这个关系是自反的(a同余a),对称的(如果a同余b,则b同余a),并且是传递的(如果a同余b且b同余c,则a同余c)。
2. 什么是图的连通性?一个图是连通的需要满足什么条件?答案:图的连通性是指在无向图中,任意两个顶点之间都存在一条路径。
一个图是连通的需要满足以下条件:图中的任意两个顶点v和w,都可以通过图中的边相互到达。
离散数学考试试题及答案-1

二、(8分)个体域为{1,2},求∀x∃y(x+y=4)的真值。
解:∀x∃y(x+y=4)⇔∀x((x+1=4)∨(x+2=4))⇔((1+1=4)∨(1+2=4))∧((2+1=4)∨(2+1=4))⇔(0∨0)∧(0∨1)⇔1∧1⇔0四、(10分)已知A={1,2,3,4,5}和R={<1,2>,<2,1>,<2,3>,<3,4>,<5,4>},求r(R)、s(R)和t(R)。
解:r(R)={<1,2>,<2,1>,<2,3>,<3,4>,<5,4>,<1,1>,<2,2>,<3,3>,<4,4>,<5,5>}s(R)={<1,2>,<2,1>,<2,3>,<3,4>,<5,4>,<3,2>,<4,3>,<4,5>}t(R)={<1,2>,<2,1>,<2,3>,<3,4>,<5,4>,<1,1>,<1,3>,<2,2>,<2,4>,<1,4>}五、(10分) 75个儿童到公园游乐场,他们在那里可以骑旋转木马,坐滑行铁道,乘宇宙飞船,已知其中20人这三种东西都乘过,其中55人至少乘坐过其中的两种。
若每样乘坐一次的费用是0.5元,公园游乐场总共收入70元,求有多少儿童没有乘坐过其中任何一种。
解设A、B、C分别表示骑旋转木马、坐滑行铁道、乘宇宙飞船的儿童组成的集合,|A∩B∩C|=20,|A∩B|+|A∩C|+|B∩C|-2|A∩B∩C|=55,|A|+|B|+|C|=70/0.5=140。
由容斥原理,得|A∪B∪C|=|A|+|B|+|C|―|A∩B|―|A∩C|―|B∩C|+|A∩B∩C|所以|A∩B∩C|=75-|A∪B∪C|=75-(|A|+|B|+|C|)+(|A∩B|+|A∩C|+|B∩C|-2|A∩B∩C|)+|A∩B∩C|=75-140+55+20=10没有乘坐过其中任何一种的儿童共10人。
离散数学模拟试题(05年6月)

离散数学模拟试题(一)一、选择题1、由集合运算的定义,下列各式中,正确的是( )。
(A) A ∪E = A; (B) A ∩∅ = A; (C) A ⊕ ∅ = A; (D) A ⊕ A = A.2、设G 如右图:那么G 不是( ). (A)平面图; (B)完全图;(C)欧拉图; (D)哈密顿图.3、设个体域为整数,下列公式中真值为1的是( )。
(A)∀x ∀y(x + y = 1); (B)∀x ∃y(x + y = 1); (C)∃x ∀y(x + y = 1); (D) ⌝ ∃x ∃y(x + y = 1)。
4、下列命题为假的是( )。
(A) {∅}∈ρ(∅); (B) ∅ ⊆ρ({∅});(C) {∅} ⊇ρ(∅); (D)ρ(∅) ∈ρ({∅})。
5、设集合A = {1,2,3,4},A 上的关系R = {(1,1),(2,3),(2,4),(3,4)},则R 具有( ). (A)自反性; (B)传递性; (C)对称性; (D)以上都不是.6、谓词公式)())()((x Q y yR x P x →∃∨∀中量词∀x 的辖域是( )(A) ))()((y yR x P x ∃∨∀ (B) P (x ) (C) )()(y yR x P ∃∨ (D) )(x Q7、谓词公式∃xA (x )∧⌝∃xA (x )的类型是( )(A) 永真式 (B) 矛盾式(C) 非永真式的可满足式 (D) 不属于(A),(B),(C)任何类型8、设L (x ):x 是演员,J (x ):x 是老师,A (x ,y ):x 佩服y. 那么命题“所有演员都佩服某些老师”符号化为( ) (A) ),()(y x A x xL →∀ (B) )),()(()((y x A y J y x L x ∧∃→∀(C) )),()()((y x A y J x L y x ∧∧∃∀ (D) )),()()((y x A y J x L y x →∧∃∀9、设命题公式⌝(P ∧(Q →⌝P )),记作G ,则使G 的真值指派为0的P ,Q 的取值是( ) (A) (0,0) (B) (0,1) (C) (1,0) (D) (1,1) 10、与命题公式P →(Q →R )等值的公式是( )(A) (P ∨Q )→R (B)(P ∧Q )→R (C) (P →Q )→R (D) P →(Q ∨R ) 二、填空题1、命题: ∅ ⊆ {{a }} ⊆ {{a },3,4,1} 的真值 = ____ .2、 设A= {a,b}, B = {x | x 2-(a+b) x+ab = 0}, 则两个集合的关系为:A____B.3、设集合A ={a ,b ,c },B ={a ,b }, 那么 ρ(B )-ρ(A )=______ .4、无孤立点的有限有向图有欧拉路的充分必要条件为: _______________________________________________.5、公式))(),(()),()((x S z y R z y x Q x P x →∃∨→∀的自由变元是 , 约束变元是 .6、设个体域D ={1,2},那么谓词公式)()(y yB x xA ∀∨∃消去量词后的等值式为 .7、设N (x ):x 是自然数,Z (y );y 是整数,则命题“每个自然数都是整数,而有些整数不是自然数”符号化为 8、设G 是n 个结点的简单图,若G 中每对结点的度数之和 ,则G 一定是哈密顿图. 9、设全集合E ={1,2,3,4,5},A ={1,2,3},B ={2,5},~A ⋃~B = .10、设集合A ={a ,b ,c },B ={a ,b },那么P (A )-P (B )= 三、计算题1、求公式 G = (P ∧Q)→R 的主析取范式和主合取范式。
大学《离散数学》期末考试试卷及答案(1)

大学《离散数学》期末考试试卷及答案(1)一、选择题1. 离散数学的主要研究对象是()。
A. 连续的数学结构B. 有限的数学结构C. 数学的综合应用D. 数学的哲学思考2. 命题逻辑是离散数学的一个重要组成部分,它主要研究()。
A. 命题之间的真假关系B. 变量之间的关系C. 函数之间的关系D. 集合之间的关系3. 集合的基本运算包括()。
A. 并、交、差、补B. 加、减、乘、除C. 包含、相等、不等、自反D. 大于、小于、等于、不等于二、填空题1. 若集合A={m|2m-1>3},则A中的元素为______。
2. 有一个集合A={1,2,3},则集合A的幂集为______。
3. 若命题p为真,命题q为假,则复合命题“p∧q”的真值为______。
三、解答题1. 请写出离散数学中常用的数学符号及其含义。
2. 请解释命题逻辑中的充分必要条件及其符号表示,并给出一个例子。
3. 请定义集合的笛卡尔积,并给出两个集合进行笛卡尔积运算的例子。
四、问答题1. 离散数学在计算机科学中有着重要的应用,请列举三个与计算机科学相关的离散数学应用领域并简要介绍。
2. 请简要解释归纳法在离散数学中的作用,并给出一个使用归纳法证明的例子。
3. 什么是有向图?请给出一个有向图的例子,并解释该图中的关系。
参考答案:一、选择题1. B2. A3. A二、填空题1. A={m|2m-1>3}2. {{}, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}}3. 假三、解答题1. 常用数学符号及含义:- ∪:并,表示集合的合并操作。
- ∩:交,表示集合的交集操作。
- ∖:差,表示减去一个集合中的元素。
- ⊆:包含,表示一个集合包含于另一个集合。
- =:相等,表示两个集合具有相同的元素。
2. 充分必要条件是指一个命题的成立与另一个命题的成立互为必要条件,若A是B的充分必要条件,那么当A成立时B一定成立,且当A不成立时B也一定不成立。
离散数学考试试题及答案

离散数学考试试题及答案离散数学考试试题及答案离散数学是计算机科学和数学中的一门重要学科,它研究的是离散的结构和对象。
离散数学的理论和方法在计算机科学、信息科学、通信工程等领域具有广泛的应用。
下面将为大家提供一些离散数学考试试题及答案,希望对大家的学习和复习有所帮助。
1. 集合论题目(1) 设A={1,2,3,4,5},B={3,4,5,6,7},求A∪B的结果。
答案:A∪B={1,2,3,4,5,6,7}(2) 设A={1,2,3,4,5},B={3,4,5,6,7},求A∩B的结果。
答案:A∩B={3,4,5}(3) 设A={1,2,3,4,5},B={3,4,5,6,7},求A-B的结果。
答案:A-B={1,2}2. 图论题目(1) 给定一个无向图G,顶点集为V={A,B,C,D,E},边集为E={(A,B),(A,C),(B,D),(C,D),(D,E)},求该图的邻接矩阵。
答案:邻接矩阵为:A B C D EA 0 1 1 0 0B 1 0 0 1 0C 1 0 0 1 0D 0 1 1 0 1E 0 0 0 1 0(2) 给定一个有向图G,顶点集为V={A,B,C,D,E},边集为E={(A,B),(B,C),(C,D),(D,E),(E,A)},求该图的邻接表。
答案:邻接表为:A ->B ->C ->D ->E -> AB -> CC -> DD -> EE -> A3. 命题逻辑题目(1) 判断以下命题是否为永真式:(p∨q)∧(¬p∨r)∧(¬q∨¬r)。
答案:是永真式。
(2) 给定命题p:如果天晴,那么我去游泳;命题q:我没有去游泳。
请判断以下命题的真假:(¬p∨q)∧(p∨¬q)。
答案:是真命题。
4. 关系代数题目(1) 给定关系R(A,B,C)和S(B,C,D),求R⋈S的结果。
011001[离散数学(1)] 天津大学考试题库及答案
![011001[离散数学(1)] 天津大学考试题库及答案](https://img.taocdn.com/s3/m/063a181ff7ec4afe05a1df57.png)
1 / 6离散数学(1)复习题一、填空题1、集合S={n 100 | n ∈N}的基数为( 0ℵ )。
2、设R 是集合A 上的二元关系,则R 是对称的,当且仅当其关系矩阵( 为对称矩阵 )。
3、集合P={Ф,{a}}的幂集ρ(P)=( {Ф,{Ф},{a}, {Ф,{a}} } )。
4、设A={1,2,7,8},B={i │i ∈N 且i 2<50},则A —B=( {8} )。
5、设(A ,≤)是一个有界格,只要满足( 每个元素均有补元 ),它也是有补格。
6、设S 为非空有限集,代数系统(ρ(S),Y ,I )中,ρ(S)对Y 的零元为( S ),ρ(S)对I 的单位元为( Ф )。
7、重言式的否定式是( 矛盾 )。
8、设A=φ,B={φ,{φ}},则B -A=( {}{}φφ, )。
9、集合A={1,2,…,10}上的关系R={(x ,y )│x+y=10且x 、y ∈A},则R 的性质为( 对称的 )。
10、有界格(P ,∧,∨)对于“∧”运算的零元为( 0 )。
11、设P :张三可以做这件事,Q :李四可以做这件事。
则命题“张三或李四可以做这件事”符号化为( P Q ∨ )。
12、设M={x| f 1(x )=0},N={x| f 2(x )=0},则方程f 1(x )·f 2(x )=0的答案为( M N U )。
13、设 |A|=m ,|B|=n ,则 |ρ(A ×B) | 等于( 2m n ⨯ )。
二、计算与证明题1、设A={0,1},B={a ,b},求:(1)A ×B ;(2)B ×A答:(1)()()()(){}0,,0,,1,,1,A B a b a b ⨯=(2)()()()(){},0,,0,,1,,1B A a b a b ⨯=2、(1)叙述幂集的定义;(2)求集合P={Ф,{a}}的幂集ρ(P).。
《离散数学》试卷及答案精选全文完整版

H(x):x是身体健康的;
S(x):x是科学家
C(x):x是事业获得成功的人
置换规则。
3、设集合|A|=101,S ,且|S|为奇数,则这样的S有2101/2或2100个。
4、设mi是公式G的的主析取范式中的一个极小项,则mi的对偶式不一定是(填“是”/“不是”/“不一定是” ) G的主合取范式中的一个极大项。
5、由3个元素组成的有限集上所有的等价关系有5个
6、给定解释I如下: (1) Di:={2,3}; (2) a=3; (3) 函数f(x)为f(2)=2,f(3)=3; (4) 谓词:F(x)为F(2):=1,F(3):=0;G(x,y)为当i=j时,G(i,j):=1;当i≠j时,G(i,j):=0;其中i,j=2,3;
ac>0并且cu>0
若u>0,则c>0,a>0,因此有ac>0;
若u<0,则c<0,a<0, 也有ac>0;
因此有(a+bi)R(u+vi)
所以R在C*是传递的。所以R是C*上的等价关系。
2、在一阶逻辑自然推理系统F中,构造下面推理的证明。个体域是人的集合。
“每位科学家都是勤奋的,每个勤奋又身体健康的人在事业中都会获得成功。存在着身体健康的科学家。所以,存在着事业获得成功的人。”(15分)
2.设A={1,2,3…10},定义A上的二元关系R={<x,y>|x,y∈A∩x+y=10},试讨论R关于关系的五个方面的性质并说明理由(5分)
解答:R={<1,9>,<9,1>,<2,8>,<8, 2 >,<3,7>,<7,3>,<4,6>,<6, 4 >,<5, 5 >}
离散数学试题及答案解析

离散数学试题及答案解析一、单项选择题(每题2分,共10分)1. 集合A={1,2,3},集合B={2,3,4},则A∩B等于:A. {1,2,3}B. {2,3}C. {1,4}D. {3,4}答案:B2. 以下哪个命题是真命题?A. 所有天鹅都是白色的。
B. 有些天鹅不是白色的。
C. 所有天鹅都不是白色的。
D. 没有天鹅是白色的。
答案:B3. 函数f: A→B的定义域是A,值域是B,那么f是:A. 单射B. 满射C. 双射D. 既不是单射也不是满射答案:D4. 逻辑表达式(p∧q)→r的逆否命题是:A. ¬r→¬(p∧q)B. ¬r→¬p∨¬qC. r→(p∧q)D. ¬r∧¬p∨¬q答案:B5. 有限集合A={a, b, c}的子集个数为:A. 3B. 4C. 7D. 8答案:D二、填空题(每题3分,共15分)1. 如果一个关系R在集合A上是自反的,那么对于A中的每一个元素a,都有___________。
答案:(a, a)∈R2. 命题逻辑中,合取(AND)的逻辑运算符用___________表示。
答案:∧3. 在图论中,一个连通图是指图中任意两个顶点之间都存在___________。
答案:路径4. 集合{1, 2, 3}的幂集包含___________个元素。
答案:85. 如果一个函数f是单射,那么对于任意的x1, x2∈A,如果f(x1)=f(x2),则x1___________x2。
答案:=三、解答题(每题10分,共20分)1. 证明:若p是q的充分条件,q是r的充分条件,则p是r的充分条件。
证明:假设p成立,由于p是q的充分条件,所以q成立。
又因为q是r的充分条件,所以r成立。
因此,p成立可以推出r成立,即p是r的充分条件。
2. 给定一个有向图,其中包含顶点A、B、C、D,边为(A, B),(B, C),(C, D),(D, A),(A, C)。
离散数学经典测试题及答案

离散数学经典测试题及答案第一题: 命题逻辑与真值表根据下列命题符号表示的逻辑表达式,填写真值表。
1. \(p \land q\)2. \((\lnot p \lor q) \land (p \implies q)\)答案1. \(p \land q\)2. \((\lnot p \lor q) \land (p \implies q)\)第二题: 数学归纳法证明使用数学归纳法证明下列等式对于所有\(n \geq 1\)成立。
\(\sum_{i=1}^{n}(2i-1) = n^2\)证明1. 基础步骤:当\(n=1\)时,左边等式为\(1\), 右边等式为\(1^2 = 1\), 成立。
2. 归纳假设:假设当\(n=k\)时等式成立,即\(\sum_{i=1}^{k}(2i-1) = k^2\)。
3. 归纳步骤:考虑\(n=k+1\)的情况,- 左边等式为\(\sum_{i=1}^{k+1}(2i-1) = \sum_{i=1}^{k}(2i-1) + (2(k+1)-1)\)- 右边等式为\((k+1)^2 = k^2 + 2k + 1\)现在我们可以利用归纳假设,将左边等式展开:\(\sum_{i=1}^{k}(2i-1) + (2(k+1)-1) = k^2 + 2k + 1\)然后,化简左边的部分可以得到:\(k^2 + (2k - 1) + (2(k+1) - 1) = k^2 + 2k + 1\)这个等式成立,证明完毕。
第三题: 集合论给定两个集合A和B,证明下列恒等式成立:\(A \cup (B - A) = A \cup B\)证明我们可以使用集合论的定义来证明这个恒等式。
1. 证明\(A \cup (B - A) \subseteq A \cup B\)- 对于任意\(x \in A \cup (B - A)\),有两种情况:- 如果\(x \in A\),则\(x \in A \cup B\),因为\(A \subseteq A \cupB\)。
离散数学考试试题及答案

离散数学考试试题及答案一、选择题(每题2分,共20分)1. 在集合论中,以下哪个选项表示“属于”关系?A. ⊆B. ⊂C. ∈D. ⊇答案:C2. 以下哪个命题是真命题?A. p ∧ ¬pB. p ∨ ¬pC. p → ¬pD. ¬(p → q) → p答案:B3. 以下哪个选项是命题逻辑中的德摩根定律?A. ¬(p ∨ q) = ¬p ∧ ¬qB. ¬(p ∧ q) = ¬p ∨ ¬qC. ¬(p → q) = p ∧ ¬qD. ¬(p ∨ q) = ¬p ∨ ¬q答案:A4. 以下哪个选项是命题逻辑中的蕴含等价?A. p → q ≡ ¬p ∨ qB. p → q ≡ ¬q → ¬pC. p → q ≡ p ∨ ¬qD. p → q ≡ ¬p ∧ q答案:A5. 以下哪个选项是关系的性质?A. 反身性B. 对称性C. 传递性D. 所有选项都是答案:D6. 以下哪个选项是图论中的有向图?A. 无向图中的边没有方向B. 有向图中的边有方向C. 混合图中的边既有方向也有无方向D. 所有选项都是答案:B7. 在图论中,以下哪个选项是树的性质?A. 树是无环的B. 树是连通的C. 树是无向图D. 所有选项都是答案:D8. 以下哪个选项是布尔代数的基本运算?A. 与(AND)B. 或(OR)C. 非(NOT)D. 所有选项都是答案:D9. 以下哪个选项是组合数学中的排列?A. 从n个不同元素中取出m个元素的组合B. 从n个不同元素中取出m个元素的排列C. 从n个相同元素中取出m个元素的组合D. 从n个相同元素中取出m个元素的排列答案:B10. 以下哪个选项是集合论中的幂集?A. 一个集合的所有子集的集合B. 一个集合的所有真子集的集合C. 一个集合的所有超集的集合D. 一个集合的所有子集的个数答案:A二、简答题(每题10分,共30分)1. 简述命题逻辑中的等价命题是什么?答案:等价命题是指两个命题在所有可能的真值赋值下都具有相同真值的命题。
离散数学试题及答案1

离散数学总分:100 考试时间:100分钟一、单项选择题1、一个无向图G是一个二元组〈V,E〉,V代表(正确答案:B,答题答案:)A、边集B、顶点集C、环D、路径2、最佳前缀码可由()算法求出(正确答案:A,答题答案:)A、HuffmanB、PERTC、DijkstraD、Kruskal3、带权为2、3、5、7、8、9的最优树T,权W(T)=()(正确答案:B,答题答案:)A、82B、83C、84D、854、设n阶无向连通图G有m条边,则()(正确答案:A,答题答案:)A、m≥n-1B、m≤n-1C、m=n-1D、m≥n5、经过图中每条边一次且仅一次并且行遍图中每个顶点的通路(回路),称为()(正确答案:A,答题答案:)A、欧拉通路B、简单通路C、初级通路D、哈密尔顿通路6、入度为0的顶点称为()(正确答案:B,答题答案:)A、树根B、树叶C、边D、顶点7、按中序行遍法,其行遍结果为((dce)bf)a(gih),则按后序行遍法其结果为()(正确答案:A,答题答案:)A、a(b(cde) )(igh)fB、a(b(cde) f)(igh)C、((dec)fb)(ghi) aD、(b(cde) f)(igh)a8、设T=〈V,E〉是n阶非平凡树,则T中至少有()片树叶.(正确答案:C,答题答案:)A、1B、2C、3D、49、设有向简单图D的度数列为2,2,3,3,入度列为0,0,2,3,D的出度列为().(正确答案:B,答题答案:)A、2,2,1,0B、2,2,3,3C、0,0,2,3D、2,2,5,610、设G=〈V,E〉是n阶无向简单图,若G中任何顶点都与其余的n-1个顶点相邻,则称G为n阶()(正确答案:A,答题答案:)A、无向图B、无向完全图C、完全图D、有向简单图二、多项选择题1、简单图为()(正确答案:AB,答题答案:)A、不含平行边B、不含环C、不含顶点D、不含单边2、下面给出的符号串集合中,哪些是前缀码?(正确答案:ABD,答题答案:)A、B1={0,10,110,1111}B、B2={1,01,001,000}C、B3={1,11,101,001,0011}D、B4={b,c,aa,ac,aba,abb,abc }3、树的行遍法有()(正确答案:ABC,答题答案:)A、中序B、前序C、后序D、顺序4、无向图G为欧拉图,则()(正确答案:ABC,答题答案:)A、G是连通的B、G中无奇度顶点C、所有顶点的入度等于出度D、奇数个顶点5、无向图G具有欧拉通路,当且仅当G是()(正确答案:AB,答题答案:)A、连通图B、有零个或两个奇度顶点C、回路D、奇数个顶点6、根据边是否有方向,图可分为()(正确答案:CD,答题答案:)A、连通图B、树C、有向图D、无向图7、两图同构,则()(正确答案:ABC,答题答案:)A、顶点个数相同B、边的条数相同C、每个顶点的度相同D、有多重边8、特殊的图有()(正确答案:ABCD,答题答案:)A、二部图B、欧拉图C、哈密尔顿图D、平面图9、下列各组数中,哪些能够成无向图的度数列?(正确答案:ABC,答题答案:)A、1,1,1,2,3B、2,2,2,2,2C、3,3,3,3D、1,2,3,4,510、若图G中任意两个结点u和v,都有从u到v和从v到u的通路,则称G是()(正确答案:A,答题答案:)A、强连通图B、弱连通图C、单向连通图D、连通图三、判断题1、强连通图一定是单向连通图。
大学离散数学复习试题 (1)

离散数学练习题目一、选择题1.设A={{1,2,3},{4,5},{6,7,8}},下列各式中____D______是错的。
A 、A ⊆Φ;B 、{6,7,8}∈A ;C 、{{4,5}}⊂A ;D 、{1,2,3}⊂A 。
2.已知集合A={a,b,c},B={b,c,e},则 A ⊕B=___C___________A.{a,b} B={c} C={a,e} D=φ3.下列语句中,不是命题的是____A_________A.我说的这句话是真话;B. 理发师说“我说的这句话是真话”;C. 如果明天下雨,我就不去旅游;D. 有些煤是白的,所以这些煤不会燃烧;4.下面___D______命题公式是重言式。
A.R Q P ∨→ ;B.)()(Q P R P →∧∨ ;C.)()(R Q Q P ∨↔∨;D 、))()(())((R P Q P R Q P →→→→→→。
5.公式(p ∧q)∨(p ∧~q)的主析取范式是____B_______A.m1∨m2B.m2∨m3C.m0∨m2D. m1∨m36.设L(x):x 是演员,J(x):x 是老师,A(x , y):x 钦佩y ,命题“所有演员都钦佩某些老师”符号化为___D______。
A 、)),()((y x A x L x →∀;B 、))),()(()((y x A y J y x L x ∧∃→∀ ;C 、)),()()((y x A y J x L y x ∧∧∃∀;D 、)),()()((y x A y J x L y x →∧∃∀ 。
7.关于谓词公式(x )(y)(P(x,y)∧Q(y,z))∧(x)p(x,y),下面的描述中错误的是__B_____A .(x )的辖域是(y )(P (x,y )∧Q(y,z))B .z 是该谓词公式的约束变元C .(x )的辖域是P (x,y )D .x 是该谓词公式的约束变元8. 设B A S ⨯⊆,下列各式中____B___________是正确的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
离散数学试题(1)
一、单项选择题(本大题共15小题,每小题1分,共15分)
在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.下列是两个命题变元p,q的小项是()
A.p∧┐p∧q B.┐p∨q
C.┐p∧q D.┐p∨p∨q
2.令p:今天下雪了,q:路滑,则命题“虽然今天下雪了,但是路不滑”可符号化为()A.p→┐q B.p∨┐q
C.p∧q D.p∧┐q
3.下列语句中是命题的只有()
A.1+1=10 B.x+y=10
C.sinx+siny<0 D.x mod 3=2
4.下列等值式不正确的是()
A.┐(∀x)A⇔(∃x)┐A
B.(∀x)(B→A(x))⇔B→(∀x)A(x)
C.(∃x)(A(x)∧B(x))⇔(∃x)A(x)∧(∃x)B(x)
D.(∀x)(∀y)(A(x)→B(y))⇔(∃x)A(x)→(∀y)B(y)
5.谓词公式(∃x)P(x,y)∧(∀x)(Q(x,z)→(∃x)(∀y)R(x,y,z)中量词∀x的辖域是()A.(∀x)Q(x,z)→(∃x)(∀y)R(x,y,z))
B.Q(x,z)→(∀y)R(x,y,z)
C.Q(x,z)→(∃x)(∀y)R(x,y,z)
D.Q(x,z)
6.设R为实数集,函数f:R→R,f(x)=2x,则f是()
A.满射函数B.入射函数
C.双射函数D.非入射非满射
7.设A={a,b,c,d},A上的等价关系R={<a,b>,<b,a>,<c,d>,<d,c>}∪I A,则对应于R的A的划分是()
A.{{a},{b,c},{d}} B.{{a,b},{c},{d}}
C.{{a},{b},{c},{d}} D.{{a,b},{c,d}}
8.设A={Ø},B=P(P(A)),以下正确的式子是()
A.{Ø,{Ø}}∈B B.{{Ø,Ø}}∈B
C.{{Ø},{{Ø}}}∈B D.{Ø,{{Ø}}}∈B
9.设X,Y,Z是集合,一是集合相对补运算,下列等式不正确的是()
A.(X-Y)-Z=X-(Y∩Z)
B.(X-Y)-Z=(X-Z)-Y
C.(X-Y)-Z=(X-Z)-(Y-Z)
D.(X-Y)-Z=X-(Y∪Z)
10.设*是集合A上的二元运算,称Z是A上关于运算*的零元,若()
A.,A
∀有x*Z=Z*x=Z
x∈
B.Z∈A,且A
∀有x*Z=Z*x=Z
x∈
C.Z∈A,且A
∀有x*Z=Z*x=x
x∈
D.Z∈A,且A
∃有x*Z=Z*x=Z
x∈
11.在自然数集N上,下列定义的运算中不可结合的只有()
A.a*b=min(a,b)
B.a*b=a+b
C.a*b=GCD(a,b)(a,b的最大公约数)
D.a*b=a(mod b)
12.设R为实数集,R+={x|x∈R∧x>0},*是数的乘法运算,<R+,*>是一个群,则下列集合关于数的乘法运算构成该群的子群的是()
A.{R+中的有理数} B.{R+中的无理数}
C.{R+中的自然数} D.{1,2,3}
13.设<A,*, >是环,则下列正确的是()
A.<A, >是交换群B.<A,*>是加法群
C. 对*是可分配的D.*对 是可分配的
14.下列各图不是欧拉图的是()
15.设G是连通平面图,G中有6个顶点8条边,则G的面的数目是()
A.2个面B.3个面
C.4个面D.5个面
第二部分非选择题(共85分)
二、填空题(本大题共10小题,每空1分,共20分)
请在每小题的空格中填上正确答案。
错填、不填均无分。
16.一公式为之充分必要条件是其析取范式之每一析取项中均必同时包含一命题变元及其否定;一公式为之充分必要条件是其合取范式之每一合取项中均必同时包含
一命题变元及其否定。
17.前束范式具有形式(Q1V1)(Q2V2)…(Q n V n)A,其中Q i(1≤i≤n)为,A为的谓词公式。
18.设论域是{a,b,c},则(∀x)S(x)等价于命题公式;(x∃)S(x)等价于命题公式。
19.设R为A上的关系,则R的自反闭包r(R)= ,对称闭包s(R)= 。
20.某集合A上的二元关系R具有对称性,反对称性,自反性和传递性,此关系R是,其关系矩阵是。
21.设<S,≤>是一个偏序集,如果S中的任意两个元素都有和,则称S关于≤构成一个格。
22.设Z是整数集,在Z上定义二元运算*为a*b=a+b+a·b,其中+和·是数的加法和乘法,则代数系统<Z,*>的幺元是,零元是。
23.如下平面图有2个面R1和R2,其中deg(R1)= ,deg(R2)= 。
24.无向图G具有一条欧拉回路,当且仅当G是,并且所有结点的度数都是。
25.在下图中,结点v2的度数是,结点v5的度数是。
三、计算题(本大题共6小题,第26—27小题每小题4分,第28、30小题每小题5分,
第29、31小题每小题6分,共30分)
26.(4分)求出从A={1,2}到B={x,y}的所有函数,并指出哪些是双射函数,哪些是满射函数。
27.(4分)如果论域是集合{a,b,c},试消去给定公式中的量词:)0
(=
+
y
∀
∃。
y
x
)(
x
)(
28.(5分)设A={a,b,c },P(A)是A的幂集,⊕是集合对称差运算。
已知<P(A),⊕>是群。
在群<P(A),⊕>中,①找出其幺元。
②找出任一元素的逆元。
③求元素x使满足{a}⊕x={b}。
(p→┐q)的主合取范式
29.(6分)用等值演算法求公式┐(p→q)→
←
30.(5分)画出5个具有5个结点5条边的非同构的无向连通简单图。
31.(6分)在偏序集<Z,≤>中,其中Z={1,2,3,4,6,8,12,14},≤是Z中的整除关系,求集合D={2,3,4,6}的极大元,极小元,最大元,最小元,最小上界和最大下界。
四、证明题(本大题共3小题,第32~33小题每小题6分,第34小题8分,共20分)32.(6分)用等值演算法证明((q∧s)→r)∧(s→(p∨r))⇔(s∧(p→q))→r
33.(6分)设n阶无向树G=<V,E>中有m条边,证明m=n-1。
34.(8分)设P={Ø,{1},{1,2},{1,2,3}},⊆是集合P上的包含关系。
(1)证明:<P,⊆>是偏序集。
(2)在(1)的基础上证明<P,⊆>是全序集
五、应用题(15分)
35.(9分)在谓词逻辑中构造下面推理的证明:每个在学校读书的人都获得知识。
所以如果没有人获得知识就没有人在学校读书。
(个体域:所有人的集合)。
