生产及成本函数分析
经济学的生产和成本理论

经济学的生产和成本理论经济学是一门研究资源配置和决策的科学。
在市场经济中,生产和成本是最基本的概念之一。
生产是指将一定数量的资源转化成一定数量的产品或服务的过程,而成本则是为了生产这些产品或服务必须支出的全部费用。
本文将重点探讨经济学的生产和成本理论。
一、生产函数生产函数是经济学中最基本的生产理论之一。
它描述了一定数量的投入如何转化为一定数量的产出的关系。
生产函数的形式通常为:Y = f(K,L)其中,Y代表产出,K代表资本投入,L代表劳动投入。
生产函数可以用不同的数学形式来表示,比如线性函数、对数函数和指数函数等。
生产函数的图形化描绘可以用等产线来表示。
等产线代表在不同的投入下,可以生产出相同的产出。
图1展示了一个等产线图。
在图中,等产线是曲线,它代表了将劳动和资本的不同组合用于产出时,可以获得相同的产出。
图1:等产线图生产函数的概念也可以用边际产出的概念来解释。
边际产出是指增加一单位投入所带来的额外产出。
边际产出可能随着投入的增加而递减。
这是因为当投入增加到一定程度时,每单位投入会带来较少的额外产出。
二、成本成本是生产中的一个基本概念。
它包括直接成本和间接成本。
直接成本是生产特定产品或服务的直接支出,如劳动力、原材料和设备等。
间接成本是与生产过程相关的费用,但不是直接用于生产特定产品或服务的支出,如场地租金、水电费和管理费用等。
成本还可以分为固定成本和变动成本。
固定成本是指一些不随产量而变化的支出,如场地租金和机器折旧等。
变动成本是指随产量变化而变化的支出,如原材料和劳动力等。
三、成本函数成本函数是将生产函数和成本联系在一起的函数。
它描述了对于不同的生产水平,不同的生产成本。
成本函数的一般形式为:C = f(Y, W)其中,C代表成本,Y代表产出,W代表成本因素。
成本函数也可以用各种数学形式来表示。
一种常见的形式是线性的,如:C = a + bY其中,a代表固定成本,b代表变动成本。
这个线性成本函数的图形化表示如图2所示。
生产函数与成本分析

MC
AC AVC AFC
因為 AFC = TFC/Q,隨著產量 增加,平均每單位產量所分攤 的固定成本愈少,AFC 線必然 不斷下降。
AC 線 在 任 一 點 的 高 度 , 是 AVC、AFC 兩線對應點高度加 總的結果。
隨著產量增加,AFC 線下降的 趨勢先會主導 AC 線下降,但 當產量增加到一定程度後, MC 的上升會帶動 AC 上升, 使 AC 線呈正斜率,因此 AC 線亦可能呈 U 字形。
A
w /r
0
L0
C0
w
Q0
C 1 勞動
w
長期之中,所有的生產要素 數量均可以調整,因此不需 要區分變動成本與固定成本。
長期生產函數 Q = f (L, K) 可 以用等產量線在 L-K 平面上 刻劃;同理,我們可以用等 成本線在 L-K 平面上表現要 素組合與成本間的關係。
等成本線的概念與消費者的 預算線相近;在同一條等成 本線上的任意 L-K 組合,具 有相同的成本水準。
5-15
產量分析-長期分析 (三)
邊際技術替代率的另一種表示法:
MPL :勞動邊際產量。 MPK :資本邊際產量。 邊際技術替代率可以刻劃兩種要素在生產上的替代關係, 如果邊際技術替代率愈高,表示兩種要素在生產上的替 代性愈強。 隨著某種生產要素使用量的增加,用這種生產要素替代 另一種要素的可能性會愈來愈弱,這表示邊際技術替代 率具有遞減的特性。
數量的增加而增加,當勞
動數量增加到一定程度後,
AP
MP 開始遞減,甚或可能
出現負值。
隨著勞動雇用量的增加,勞
MP
動的邊際產量終會出現遞減
圖 5.1 總產量、平均產量與邊際產量的範例 的現象,現象稱為邊際報酬 遞減法則 (law of diminishing
生产与成本函数分析

生产与成本函数分析摘要生产与成本函数分析是管理经济学中一个重要的主题。
通过研究生产函数和成本函数,可以帮助企业决策者了解生产过程中的效率和成本。
本文将对生产函数和成本函数进行详细介绍,并探讨它们之间的关系。
此外,还将介绍生产与成本函数的应用,并讨论它们在管理决策中的重要性。
1. 生产函数生产函数是描述生产过程中输入和输出之间关系的函数。
它表达了生产所需要的输入(劳动、资本等)与输出(产品或服务)的数量之间的关系。
生产函数通常表示为:Y = f(K, L)其中,Y代表产量(输出),K代表资本投入,L代表劳动投入。
函数f(K, L)表示生产函数的具体形式,它可以是线性函数、二次函数、指数函数等等。
生产函数的形式取决于具体的生产过程。
生产函数有几个重要的性质:•递增边际产量:生产函数通常具有递增边际产量的性质。
也就是说,增加一单位的输入(如劳动或资本)会带来更多的产出。
然而,递增边际产量通常在某一点开始递减。
•边际产量递减:随着输入的增加,生产函数的边际产量通常递减。
也就是说,增加一单位的输入会带来递减的额外产出。
了解生产函数对企业决策至关重要。
企业可以通过分析生产函数来确定最优的生产组合,以最大化产出。
2. 成本函数成本函数是描述生产成本与输入数量之间关系的函数。
它表达了生产所需的投入成本与投入数量之间的关系。
成本函数通常表示为:C = g(K, L)其中,C代表成本,K代表资本投入,L代表劳动投入。
函数g(K, L)表示成本函数的具体形式,它可以是线性函数、二次函数等等。
成本函数的形式取决于企业的生产过程和要素价格。
成本函数有几个重要的性质:•递增边际成本:成本函数通常具有递增边际成本的性质。
也就是说,增加一单位的输入会带来递增的额外成本。
然而,递增边际成本通常在某一点开始递减。
•边际成本递减:随着输入的增加,成本函数的边际成本通常递减。
也就是说,增加一单位的输入会带来递减的额外成本。
了解成本函数对企业决策也非常重要。
生产函数和成本函数

生产函数和成本函数:生产函数和成本函数是经济学中两个重要的概念,它们在描述企业的生产行为和成本关系时起着重要的作用。
生产函数表示的是在一定技术条件下,生产要素的投入量与最大可能产出量之间的函数关系。
换句话说,生产函数描述的是企业如何将不同的生产要素(如劳动、资本、土地等)有效地转化为产品或服务。
生产函数的数学表达式通常为Q=f(L,K,N,E),其中Q代表产量,L 代表劳动,K代表资本,N代表土地,E代表企业家才能。
成本函数则描述了在一定的生产技术条件下,生产一定数量的产品所需的最小成本。
成本函数是用来分析企业在生产过程中如何平衡各种生产要素的投入量,以达到最小化成本的目的。
成本函数的数学表达式通常为C=f(Q),其中C代表总成本,Q代表产量。
生产函数和成本函数之间存在密切的关系。
首先,生产函数和成本函数都受到生产要素价格的影响。
当生产要素价格上涨时,企业将面临更高的生产成本,这可能导致企业减少生产要素的投入量,从而降低产量。
其次,生产函数和成本函数在一定条件下可以相互转化。
例如,当企业通过技术创新提高了生产效率时,它可能会在保持产量不变的情况下降低成本,反之亦然。
供给函数,生产函数和成本函数的名词解释

一、供给函数1. 供给函数是指在某一时期内,各种商品或服务的供给数量与商品或服务的价格之间的关系。
它反映了在不同价格水平下的供给情况,通常用数学函数的形式进行表达,其一般形式可以表示为Qs = f(P),其中Qs表示商品或服务的供给数量,P表示商品或服务的价格,f(P)表示价格P下的供给函数。
2. 供给函数可以帮助市场参与者了解和预测供给方面的情况,如在价格上涨时供给数量的增加情况,或在价格下跌时供给数量的减少情况。
供给函数也是市场经济中决定市场平衡价格和数量的重要工具,通过对供给函数的分析可以得出供给曲线,帮助市场参与者做出合理的决策。
3. 供给函数在经济学理论中具有重要意义,它不仅可以用来分析商品或服务的供给情况,还可以用来研究税收政策、补贴政策等对供给数量的影响,是经济学领域中的基础理论之一。
二、生产函数1. 生产函数是指在一定时间内,生产者通过投入一定数量的生产要素(如劳动力、资本、土地等)来生产出一定数量的产品或服务的关系。
它通常用数学函数的形式表示,一般形式可以表示为Q = f(K, L),其中Q表示生产的产量,K表示资本投入,L表示劳动力投入,f(K, L)表示生产函数。
2. 生产函数是生产理论中的一个重要工具,它可以帮助生产者了解和预测生产过程中的产出情况,如在投入增加时产出的增加情况,或在投入减少时产出的减少情况。
生产函数也是确定合理生产要素投入组合、提高生产效率的基础。
3. 生产函数的研究对于生产计划、生产组织、生产管理等方面具有重要意义,通过对生产函数的分析可以帮助生产者优化资源配置,提高生产效率,实现经济增长和社会发展。
三、成本函数1. 成本函数是指在一定时间内,生产者在生产一定数量的产品或服务过程中所用到的各种成本与生产数量之间的关系。
它通常用数学函数的形式表示,一般形式可以表示为C = f(Q),其中C表示生产成本,Q表示生产数量,f(Q)表示成本函数。
2. 成本函数是生产理论中的一个重要工具,它可以帮助生产者了解和预测生产过程中的成本情况,如在产量增加时成本的增加情况,或在产量减少时成本的减少情况。
决策管理-生产与成本决策分析

第三讲生产与成本决策分析企业是一个经济组织,不仅要作出生产多少的决策,还要讲究经济核算,寻求最经济的产品生产方式与方法。
因此,企业在研究市场供求机制、为产量决策提供理论依据的基础上,还要研究生产的经济性问题。
一、生产决策分析(一)生产与生产函数生产是指把投入要素转变为市场需求的产出的过程。
生产决策的首要任务就是要研究如何用最少的投入,实现同样多的产出;或用同样多的投入,实现最大的产出。
企业管理者了解生产函数及优化原则的主要目的,在于为实现生产的经济性奠定必要的理论基础。
生产函数是指在一定的技术条件下,各种生产要素投入量的组合与所能生产的最大产量之间的对应关系。
其一般数学表达式为:Q﹦f(X1,X2,…,X n)式中,Q为产量;X1,X2,…,X n为诸投入要素,如原材料、资金、劳动量等。
需要指出的是,生产函数中的产量指的是最大产量。
这是因为我们假定生产中的所有投入要素都得到了有效的使用,没有丝毫浪费或闲置,所以,这些投入要素所能产生的产量,在给定的技术条件下,是最大可能的产量。
生产决策分析就是通过对生产函数的分析,寻找最优的投入与产出水平,确定最优的要素投入组合,使生产的成本最低或利润最大。
生产函数分为短期生产函数与长期生产函数,这是由投入要素在一定时期内所显示的静态与动态的特性决定的。
在这里,时期的长短不是时间的物理概念,而是相对于具体的生产过程中,投入要素能否发生变化。
所谓短期生产函数,是指企业在此期间内,至少有一种投入要素的数量是不可变的,如厂房、机器设备等;其他投入要素的数量,如劳动力或原材料等可以根据生产情况发生变化。
短期生产函数主要研究产出量与投入的变动要素之间的关系,以确定某一(些)可变要素的最佳投入量。
所谓长期生产函数,是指企业在此期间内,所有投入要素的数量都可以发生变化,不存在固定不变的要素。
长期生产函数研究产出量与所有投入要素之间的数量关系,以确定最适当的生产规模。
(二)单一可变要素最优投入量的确定假定其他要素的投入量不变,只有一种要素的投入量可变,研究这种投入要素的最优使用量,就是短期生产函数要研究的问题。
成本函数分析范文

成本函数分析范文成本函数是描述企业在生产过程中各种成本与产量之间的关系的数学模型。
通过分析成本函数,企业可以了解各种成本对产量的影响,为企业的决策提供有力支持。
本文将从成本函数的定义、类型、分析方法等方面进行详细介绍。
一、成本函数的定义成本函数可以定义为单位生产量所需的成本与产量之间的关系,一般可以表示为C(q),其中C(q)表示产量为q时的成本。
成本函数通常可以分为固定成本与变动成本两个部分,固定成本表示在产量变化时保持不变的成本,如租金、折旧等,而变动成本表示与产量成正比的成本,如原材料、劳动力等。
因此,成本函数一般可以表示为C(q)=FC+VC(q),其中FC 表示固定成本,VC(q)表示变动成本。
二、成本函数的类型根据成本函数的类型,成本函数可以分为线性成本函数、二次成本函数和阶梯成本函数等。
线性成本函数是成本随产量的增加而以固定比率增长的函数。
它的表达式可以表示为C(q)=a+bq,其中a表示固定成本,b表示变动成本的单位成本。
线性成本函数的特点是成本曲线是一条直线,成本随产量的增加而呈线性增长。
二次成本函数是成本随产量的增加而呈二次函数关系的函数。
它的表达式可以表示为C(q)=a+bq+cq^2,其中a表示固定成本,b表示变动成本的一阶系数,c表示变动成本的二阶系数。
二次成本函数的特点是成本曲线呈抛物线形状,成本随产量的增加呈非线性增长。
阶梯成本函数是以不同的产量范围为单位,每个单位范围内的成本函数均为线性或二次函数,而不同单位范围之间的成本函数之间可能存在跳变。
阶梯成本函数的特点是成本曲线是由多段线段构成的,成本随产量的增加表现出明显的跳跃。
三、成本函数的分析方法1.成本函数的平均成本和边际成本分析平均成本表示单位产量的成本,可以通过成本函数求导得到。
边际成本表示单位产量增加一个单位时的增加成本,可以通过成本函数的一阶导数来求得。
通过分析平均成本和边际成本的变化情况,可以找到最优产量和最优成本水平。
成本函数知识点总结

成本函数知识点总结在经济学中,成本函数通常被用来描述生产过程中所用资源的成本与产出之间的关系。
成本函数的一般形式可以表示为:C = f(x1, x2, ..., xn)其中,C 表示成本总额,x1, x2, ..., xn 分别表示不同的资源投入,f 表示生产函数或成本函数的具体形式。
一般来说,成本函数可以分为总成本函数和平均成本函数两种形式。
总成本函数表示的是生产一定数量的产品所需要的总成本,通常表示为:TC = f(x1, x2, ..., xn, Q)其中,TC 表示总成本,Q 表示产出量,x1, x2, ..., xn 表示各种生产要素的投入量。
总成本函数可以帮助生产者了解在不同产出量下所需要的总成本,从而帮助其做出生产规模的决策。
平均成本函数表示的是单位产出所需要的平均成本,通常表示为:AC = TC / Q其中,AC 表示平均成本,TC 表示总成本,Q 表示产出量。
平均成本函数可以帮助生产者了解在不同产出量下单位产品的平均成本,从而帮助其确定最优的产出量和生产规模。
成本函数的知识点总结包括但不限于以下内容:1. 成本函数的分类:总成本函数和平均成本函数2. 成本函数的形式:通常表示为关于生产要素和产出量的函数3. 成本函数的性质:通常具有经济学意义的性质,如递增成本、递减成本等4. 成本函数的应用:帮助生产者了解生产过程中的成本结构,从而帮助其做出合理的决策成本函数的分类成本函数主要可以分为总成本函数和平均成本函数两种形式。
总成本函数表示的是生产一定数量的产品所需要的总成本,通常表示为:TC = f(x1, x2, ..., xn, Q)其中,TC 表示总成本,Q 表示产出量,x1, x2, ..., xn 表示各种生产要素的投入量。
总成本函数可以帮助生产者了解在不同产出量下所需要的总成本,从而帮助其做出生产规模的决策。
平均成本函数表示的是单位产出所需要的平均成本,通常表示为:AC = TC / Q其中,AC 表示平均成本,TC 表示总成本,Q 表示产出量。
第三章生产及成本理论-第三节成本函数和成本曲线

第三节成本函数和成本曲线【本节知识点】1.成本和利润的含义和类型2.成本函数3.成本曲线【本节内容精讲】【知识点】成本和利润的含义【应用举例】假定某一店主每年花费40000元的资金租赁房屋开花店,年终该店主从销售中所获毛利(扣掉了一些直接费用,不包含房屋租赁费)为50000元。
该店主赚了多少钱?【分析】(1)从显成本的角度看,该店主赚了10000元(50000-40000);(2)从隐成本的角度看,该店主可能一点也没赚。
假定市场利率为10%,该店主从事其他职业所能获得的最高收入是20000元(正常利润),则该店主的隐成本是24000元(20000+40000×10%)。
厂商的隐成本和显成本是64000元(24000+40000)。
从机会成本的角度看,该店主不仅没有赚钱,反而赔了钱。
我们也可以说该店主获得的会计利润10000元,但是获得的经济利润是负的14000元(50000—64000)。
【例题:2010年单选题】企业使用自有的资金应计算利息,从成本角度看,这种利息属于()A.固定成本B.显成本C.隐成本D.会计成本【答案】C【解析】考核隐成本的概念。
隐成本是指企业本身所拥有的并且被用于该企业生产过程的那些生产要素的总价格,是企业自己拥有并使用的资源的成本。
【知识点】成本函数1.成本函数的含义和类型成本函数就是表示企业总成本与产量之间关系的公式。
分为短期成本函数和长期成本函数。
(1)短期成本函数可分为固定成本与可变成本C=b+f(q),其中b―――――固定成本f(q)―――可变成本C-----------总成本(2)长期成本函数没有固定成本(从长期看一切生产要素都是可变的)C=f(q)【注】短期成本函数和长期成本函数的区别在于是否含有固定成本。
【例题:2016年多选】关于经济学中成本的说法,正确的有()。
A.生产成本可分为显成本和隐成本两部分B.隐成本实际是一种机会成本C.正常利润不应作为隐成本的一部分计入成本D.成本是企业在生产经营过程中所支付的物质费用和人工费用E.不论从长期还是短期看,成本均可分为固定成本和可变成本【答案】ABD【解析】生产成本包括显成本和隐成本两部分;正常利润属于隐成本中的一部分,C错误;成本是企业在生产经营过程中所支付的物质费用和人工费用。
举例说明生产函数与成本函数的关系

举例说明生产函数与成本函数的关系
生产函数和成本函数之间的关系可以用以下几点来总结:
1. 生产函数反映了企业利用资源生产产品和服务所需要投入的资源类
型和数量,而成本函数表示的是这一投入收回的经济效益方面的曲线;
2. 生产函数描述了企业生产活动耗费的资源,而成本函数反映了企业
通过这一活动获取的经济效益;
3. 生产函数描述的是输入资源及其彼此间的关系,而成本函数则关注
的是企业的投入成本和收回的经济效益;
4. 生产函数表明了输入资源和产出之间的经济关系,而成本函数表明
的是企业的投入成本和输出的经济效益;
5. 生产函数描述的是资源利用的最佳情况,而成本函数则衡量的是企
业的投入成本和收回的经济效率;
6. 生产函数是很多计量经济学建模基础,而成本函数是遵循经济效率
原则进行研究的重要数据。
生产函数与成本函数的关系研究

生产函数与成本函数的关系研究生产函数和成本函数是经济学中重要的概念,是分析经济活动的重要工具。
生产函数是描述生产活动的函数,它表示用不同数量的资源生产出不同数量的产出,它揭示了资源转换成输出的特定规律。
成本函数是描述生产者生产成本的函数,它表示生产不同数量产品所需的总成本。
也就是说,它表明不同数量生产活动所需的成本。
考虑生产函数与成本函数的关系,可以更好地理解生产活动的效率和成本。
一般来说,生产过程可以分为两个阶段生产函数和成本函数。
可以通过这两个阶段,研究生产者如何选择较有效率的生产方式,以及生产过程中成本的变化情况。
生产函数可以帮助生产者更好地掌握生产过程,并选择合理的资源配置方式;而成本函数则可以帮助生产者获取更高的效率,以便更好地控制和降低生产成本。
研究表明,生产函数与成本函数之间存在着一定的关系。
生产效率高的生产过程,其成本将相对较低,反之亦然。
因此,要获得较高的生产效率,生产者应当尽量降低成本。
具体而言,根据不同的生产过程,生产者可以利用机器代替人力资源,以及采用更高效率及更新技术,以降低成本。
另外,生产者还可以利用源多样化等技术,以分散资源使用成本,以此节约成本。
值得一提的是,生产函数与成本函数之间也有一些限制。
生产者往往会被资源和技术条件限制,无法获得更多的输出,或者降低成本。
此外,由于经济发展水平不同,生产函数和成本函数在不同国家及地区也可能存在差异。
因此,生产者应综合考虑本国的特殊经济发展状况,进行合理的生产抉择。
本文就生产函数与成本函数的关系进行了分析和研究,认为它们之间存在着一定的关系,生产者可以利用这种关系,采取适当的措施,以获得更高的生产效率,并降低成本。
另外,要考虑生产过程的特殊情况,针对性地采取措施,以获得更佳的生产效果。
因此,研究和分析生产函数与成本函数之间的关系,对于生产者来说,是一个有意义的经济研究课题。
这可以帮助生产者更好地掌握生产经济学原理,从而推导出更合理的生产方案,实现生产效率的提高和成本的降低。
生产及成本函数分析

等成本线的斜率等于 —w/r MPL/ MPK = w/r
MPL/w = MPK/r
边际实物报酬均等法则(性价比一致)
2019/11/23
生产与成本函数分析
27
两可变投入生产函数
4. 规模报酬与规模经济
当投入的要素变动时,产出也要发生变
动,投入对产出的变动的影响用产出弹性
6 10 24 31 36 40 39
2019/11/23
生产与成本函数分析
17
两可变投入生产函数
Q
45
3450
223050 110505
3 1
1 2 3 4 5 6L
2019/11/23
生产与成本函数分析
K
5
40-45 35-40 30-35 25-30 20-25 15-20 10-15 5-10 0-5
最高点
MP〉0 TP上升 MP〈0 TP下降
MP=0 TP最大
2019/11/23
生产与成本函数分析
12
一可变投入生产函数
3. 边际实物报酬递减法则
一般说来,在一定的技术条件下,只是
一种生产要素的 投入连续增加,而其它
诸要素投入量均保持不变,那末,
当这种要素投入量增加到一定程
度以后,若再继续增加该要素的
由于大规模生产带来明显的规模上的
好处 称规模经济
大规模生产也有不利因素 这称规模
不经济 2019/11/23
生产与成本函数分析
29
两可变投入生产函数
K
K
K
6
6
300
4
200 4
2
100 2
500 6 300 4 100 2
成本函数
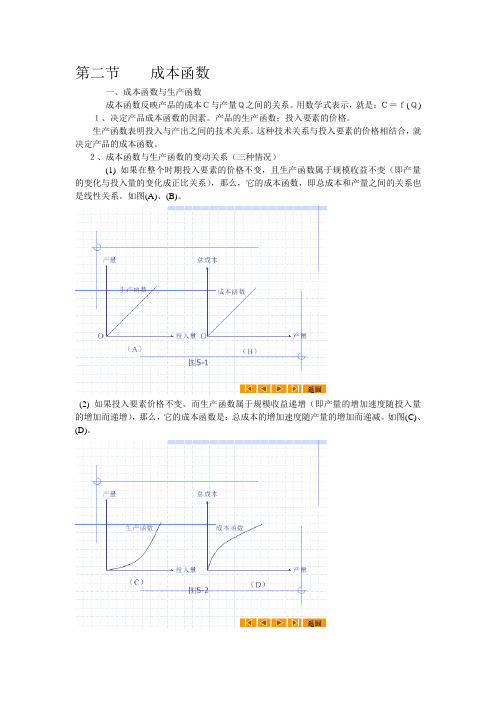
第二节成本函数一、成本函数与生产函数成本函数反映产品的成本C与产量Q之间的关系。
用数学式表示,就是:C=f(Q) 1、决定产品成本函数的因素。
产品的生产函数;投入要素的价格。
生产函数表明投入与产出之间的技术关系。
这种技术关系与投入要素的价格相结合,就决定产品的成本函数。
2、成本函数与生产函数的变动关系(三种情况)(1) 如果在整个时期投入要素的价格不变,且生产函数属于规模收益不变(即产量的变化与投入量的变化成正比关系),那么,它的成本函数,即总成本和产量之间的关系也是线性关系。
如图(A)、(B)。
(2) 如果投入要素价格不变,而生产函数属于规模收益递增(即产量的增加速度随投入量的增加而递增),那么,它的成本函数是:总成本的增加速度随产量的增加而递减。
如图(C)、(D)。
(3) 如果要素价格不变,而生产函数属于规模收益递减(即产量的增长速度随投入量的增加而递减),那么,它的成本函数是:总成本的增加速度随产量的增加而递增。
如图(E)、(F)。
由上可见,成本函数导源于它的生产函数,只要知道某种产品的生产函数,以及投入要素的价格,就可以推导出它的成本函数。
二、总成本、平均成本与边际成本1、总成本(TC):指企业为生产一定量产品所消耗(或支付)的全部成本(费用)。
从短期看,总成本包括:(1) 总固定成本(TFC):即使产量为零也必须支付的费用总额。
(2) 总变动成本(TVC):总成本中随产量增加而增加的费用总额。
即:TC=TFC+TVC。
当然,从长期看,不存在任何固定成本,一切成本都是可变的。
例如,对一家已经建成的钢铁厂来说,无论产量如何变化,厂房和设备总是固定不变的,可变的只是劳力和原材料的数量。
在这种条件下形成的产量和成本之间的关系,就叫做短期成本函数。
其几何表现(或图形)就是短期成本曲线。
显然,在短期成本中,因为有一部分投入要素固定不变,所以,它除了包括变动成本之外,还包括固定成本。
短期成本函数通常用来反映现有企业中产量与成本的关系,所以,它主要用于日常的经营决策。
生产和成本决策分析

二、生产决策分析
(一)生产函数的概念 生产函数是指在一定的技术条件下,
各种生产要素投入量的组合与所能生产 的最大产量之间的对应关系。其一般数 学表达式为:
Q=f(X1,X2,…,Xn) 式中,Q为产量;X1,X2,…,Xn 为诸投
入要素,如原材料、资金、劳动量等。
1、短期生产函数 短期生产函数,是指企业在此期间内,
(四)规模经济性分析
1、规模与收益的关系 ◆规模收益递增(事半功倍) ◆规模收益不变 ◆规模收益递减(事倍功半) 2、促使规模收益递增的原因 ◆工人可以专业化 ◆使用专门化的设备和较先进的技术 ◆大设备单位能力的制造和运转费用通常
比小设备要低 ◆生产要素具有不可分割性
3、促使规模收益递减的原因 主要是管理问题
(管“理”区)(管“条件”区)
AP
O
A
B MP 要素投入量
第一阶段:边际产量>0,边际产量>平均产量 特点:随着投入要素的增加,总产量、平均产量 均呈上升趋势 管理重点:扩大要素投入量
第二阶段: 边际产量>0,边际产量<平均产量 特点:随着投入要素的增加,总产量呈上升趋势, 平均产量呈下降趋势 管理重点:优化要素投入量
生产与成本决策分析
一、对生产的全面理解 二、生产决策分析 三、成本决策分析 四、生产函数与成本函数的应用
问题讨论与交流 1、高投入能否带来高产出?是否投入越多、
产出越大? 2、高产出能否带来高收益?是否产出越多、
效益越好?
一、对生产的全面理解
所谓生产,就是投入与产出之间的转换 关系。 特别强调: ◆任何企业的生产都离不开要素的投入。 ◆任何企业的生产都必须经过相应的转换。 ◆任何企业生产的结果都是产品。
生产函数与成本函数的关系

生产函数与成本函数的关系在经济学中,生产函数和成本函数是两个重要的概念,它们描述了生产过程中的关系和资源利用的效率。
生产函数描述了生产过程中输入与输出的关系,而成本函数则衡量了实现这些输入输出关系所需要的资源费用。
本文将探讨生产函数与成本函数之间的关系,以及它们在经济中的应用。
首先,我们来深入理解生产函数。
生产函数是描述输入和输出之间关系的数学表达式。
它可以用来衡量生产过程中投入要素(如劳动力、资本、原材料等)与产出之间的数量关系。
一般来说,生产函数可以用以下的形式表示:Y = f(K, L)其中,Y代表产出,K代表资本,L代表劳动力。
这种表示方式是最为简单的形式,也称为柯布-道格拉斯生产函数。
其实,生产函数的形式有很多种,可以是线性的、非线性的、具有不同的弹性等。
不同的生产函数反映了不同的生产技术水平和资源利用效率。
然而,生产函数仅仅描述了输入和输出之间的数量关系,并没有考虑到资源的使用成本。
这时候,就需要引入成本函数的概念。
成本函数描述了实现某种生产函数关系所需要的资源费用。
成本函数的形式也有多种,最简单的形式可以表示为:C = wL + rK其中,C代表成本,w代表单位劳动力的价格,L代表劳动力的数量,r代表单位资本的价格,K代表资本的数量。
这种形式的成本函数是线性的,假设劳动力和资本的价格保持不变。
由生产函数和成本函数的定义可知,生产函数和成本函数之间有密切的关系。
实际上,我们可以通过生产函数推导出成本函数,或者根据成本函数推导出生产函数。
利用这种关系,我们可以进行企业生产效率的分析、资源配置和成本优化等经济决策。
例如,假设我们需要分析一家企业的生产效率。
通过观察生产过程中输入与输出的关系,我们可以估算出该企业的生产函数。
再通过观察企业的成本支出情况,可以计算出相应的成本函数。
通过比较生产函数和成本函数,我们就可以评估该企业的资源利用效率。
如果生产函数的斜率(即边际产出)大于成本函数的斜率(即边际成本),那么说明该企业的资源利用相对高效;反之,如果边际产出小于边际成本,说明该企业的资源利用相对低效。
管理经济学的生产决策与成本分析

3、边际产量和平均产量在平均产量曲线 的最高点相交。因为只要边际产量大于 平均产量,不管边际产量是上升还是下 降,平均产量都呈上升趋势。只要边际 产量小于平均产量,平均产量就呈下降 趋势。二者的交点表现为总产量曲线上 的C点。在C点处,总产量曲线的切线与 C点与原点的连线重合。
边际报酬递减规律
内容:对只包含一种生产要素的生产函 数来说,随着生产要素投入量的连续增 加,每增加一单位生产要素所引起的产 量的增加(即边际产量)表现出先上升 最终下降的规律。 成因:在任何产品的生产过程中,可变 生产要素与不变生产要素之间都存在一 个最佳组合比例。是一个经验规律。
K
Q
Q3 =150
Q2 =100
Q1 =50
L
等产量曲线
等产量线的特点
离原点越近的等产量线代表的产量越低, 反之越高。
同一平面上,任意两条等产量线互不相 交。 等产量线凸向原点。
从原点出发的射线代表两种要素投入比 例不变的所有组合方式。
边际技术替代率的定义
边际技术替代率(Marginal Rate of Technical Substitution):
过程中所使用的n种生产要素的投入量, Q表示所能达到的最大产量,则生产函 数可表示如下:
» Q = f ( X1, X2, … X n )
» 若以L表示劳动的投入量;以K表示资本的 投入量,则生产函数可写为 »Q = f ( L , K )
在理解生产函数时必须注意
1、生产函数反映的是一定技术条件下投 入和产出之间的数量关系。技术条件的 改变必然产生新的生产函数。
固定投入比例生产函数的特点
通常假设:投入量L, K都满足最小的要 素投入组合的要求。所以有:
Q = L/U=K/V 进一步有:
成 本 函 数

成本函数
成本函数
一、成本函数的含义 二、边际收益递减规律 三、生产阶段的划分
一、成本函数的含义
(一)成本函数概念 生产函数是表示产出与成本之间的数量关 系 ,如果反过来研究成本与产出之间的关
系,即把成本作为因变量,把产出作为自变量, 那么成本就是产出的函数。反映成本与产出之间 的数量关系的函数即为成本函数。
产
量
生产函
数
总
成
成本函
本
数
O
(a)
要素投入 量
O 产量
(b量增 加的速度大于投入量增加的速度,那么,它的 总成本的增加速度随产量的增加而递减,如图 所示:
产量
成本
生产函数
成本函数
0 (a)
投入量 0
(b)
投入量
一、成本函数的含义
3.若生产函数规模收益递减,即产量增 加的速度入量增加的速度那么,它的总成本的 增加速度随产量的增加而递增。如图所示:
三、长期成本函数
长期成本函数可以表示为以产量为横轴.以成本为 纵轴的坐标图上的长期成本曲线。长期看。企业各 种投入要素都是可变的,因此,在长期中,企业所 有的成本都是可变的。企业的长期成本可分为长期总 成本、长期平均成本、长期边际成本。 1.长期总成本(LTC)
长期总成本是指企业在长期中在每一个产量水平 上通过选择最优的生产规模所能达到的最低总成本。 长期总成本曲线说明在企业可以自由选定投入 要素组合比例的条件下,当企业达到各个最优 规模时可能的最低的总成本。
TC(Q) TFC TVC(Q)
二、短期成本函数
3.总成本 总成本(TC)指短期内生产一定量所付出
的全部成本,是企业总固定成本与总变动成本 之和。由于TVC是产量的函数,因此TC也是产 量的函数。其公式表示为:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020/5/10
a
20
两可变投入生产函数
记作MRTSLK (Marginal rate of technical substitution)
K
MRTSLK = -(K2-K1)/ (L2-L1)
= -ΔK/ΔL
= -dK/ dL
k1
等于等产量线上该点的 k2
q
切线斜率的相反数
O l1 l2
L
2020/5/10
两个可变投入生产函数 (多变量生产函数)
2020/5/10
a
6
一可变投入生产函数
二 一种可变投入的生产函数
技术条件不变 一种可变动投入投入 (劳动) 与固定投入相结合(固定投入通 常是资本) 只生产一种产品,
可能生产的最大产量(Q)与投入要素 之间的关系
通常又称作短期生产函数
2020/5/10
a
7
2020/5/10
a
M PL -
10 20 30 20 15 13 4 0 -4 -8
10
一可变投入生产函数
150 100 50
0 0
30 20 10
0 -100
2020/5/10
2
4
6
8
10 12
AP MP
2
4
6
8
10
a
11
一可变投入生产函数
2.总产量 平均产量 边际产量间的关系
当MP〉AP AP 上升
2020/5/10
a
14
一可变投入生产函数
Q
技术进步引起了总产量 曲线的变动 掩盖了边际 实物报酬递减法则
2020/5/10
L
a
15
两种可变投入生产函数
三 两种可变投入生产函数 只要考察的时间足够长 就不只一种投入在 变动 两种或两种以上的投入可以变动 甚至 所有的投入都可以变动
如投入的劳动和资本都可以变动, 投入和产出之间的关系
MP〈 AP AP 下降
MP = AP AP达到最大值
边际产量曲线必然通过平均产量曲线的
最高点
MP〉0 TP上升 MP〈0 TP下降
MP=0 TP最大
2020/5/10
a
12
一可变投入生产函数
3. 边际实物报酬递减法则
一般说来,在一定的技术条件下,只是
一种生产要素的 投入连续增加,而其它
诸要素投入量均保持不变,那末,
能组合的轨迹
K
等产量线的性质
1.) 斜率为负 2.) 凸向原点 3.) 互不相交
2020/5/10
O
a
q4
q3 q2 q1
L
19
两可变投入生产函数
2. 边际技术替代 1.) 边际技术替代率 不同投入要素之间有一定的技术替代关系 在技术水平不变的条件下,维持同样的
产量,增加一个单位的某投入可以替代另一种 投入的数量 叫作这一种投入要素对 另一种投入要素 的边际技术替代率
一可变投入生产函数
1. 实物产量
可能的最大产量和变动投入之间的关系
可表示为:
TP = Q = f(L)
平均产量 AP ( Average Product)
也随着变动投入的变动而变动
APL = Q / L
2020/5/10
a
8
一可变投入生产函数
在管理经济学中更加关心是边际产量 在一定技术条件下,面其它诸投入要素 都保持不变 每增加一个单位变动投入所引 起的总产量的变动 称边际产量 MP 这 就是贡献
生产与成本函数分析
2020/5/10
a
1
生产函数分析
人类经济活动的四个环节 生产环节起决定性作用
生产力是社会发展的第一杠杆 如何利用资 源最有效的进行生产 从 实物形态研究是生产函数 从 货币形态研究是成本函数
2020/5/10
a
2
生产函数
一 生产函数
在一定的技术条件下,各种生产要投 入量的某一组合与其可能生产的最大产 量之间的关系,称生产函数 即投入和 产出之间的关系 劳动 资本 土地是任何 生产活动的最基本投入
a
21
两可变投入生产函数
两可变投入生产函数 多投入劳动引起的 产量的增加必然等于
少投入资本引起的产量的减少 dL·MPL = -dK·MPK
MRTSLK = MPL/MPK
2020/5/10
a
22
两可变投入生产函数
2.)边际技术替代率递减法则 沿着同一条等产量线 以一种投入要素替 代另一种投入要素 可替代的数量是越来 越少 这称边际技术替代率递减法则 这是边际实物报酬递减法则在多变量分
称原始投入
2020/5/10
a
3
生产函数
生产要素常泛指原始投入和中间投入 可与原始投入相配合而作生产
投入之用称中间投入 生产要素一般分为三类
1.自然资源 2.资本投资 3.劳动 知识与知ቤተ መጻሕፍቲ ባይዱ经济
2020/5/10
a
4
供给
• 完善按劳分配为主、多种分配方式并存的分配 制度。
• 健全劳动、资本、技术、管理等生产要素按贡 献参与分配的制度。
• 逐步提高居民收入在国民收入分配中的比重,提 高劳动报酬在初次分配中的比重。创造条件让 更多群众拥有财产性收入。
• 保护合法收入,调节过高收入,取缔非法收入 。
2020/5/10
a
5
生产函数
投入和产出之间的关系可表示为 Q =f(L,K,···,T) 投入又可分固定投入和变动投入 生产函数分一个可变投入生产函数和
当这种要素投入量增加到一定程
度以后,若再继续增加该要素的
投入,该要素的边际产量会逐步
减少。这就称边际实物报酬递减法
则
2020/5/10
a
13
一可变投入生产函数
这是一个普遍存在的现象 说明三点 1) 是以经验为依据的一般性概括 绝大 多数情况都适用 2). 法则作了技术不变的假定 3). 强调其它投入要素都不变
Q = f ( L, K)
2020/5/10
a
16
两可变投入生产函数
1.等产量线 不同的投入要素组合可以生同样的产量
123456
1 2 8 12 14 14 12
2 7 18 28 30 30 28
3 10 23 33 36 36 28
4 12 28 36 40 40 36
5 12 28 36 40 42 40
6 10 24 31 36 40 39
2020/5/10
a
17
两可变投入生产函数
40-45 35-40
Q
K
30-35
25-30
45
334050
5
1122050505
3 1
1 2 3 4 5 6L
20-25 15-20 10-15 5-10 0-5
2020/5/10
a
18
两可变投入生产函数
等产量线表示具有相同产量的各种要素可
(Marginal Product)
MPL =ΔTP/ΔL = dTP/ dL
2020/5/10
a
9
一可变投入生产函数
L
K
0
10
1
10
2
10
3
10
4
10
5
10
6
10
7
10
8
10
9
10
10
10
Q 0 10 30 60 80 95 108 112 112 108 100
A PL -
10 15 20 20 19 18 16 14 12 10
