复变函数与实变函数的联系与区别
实变函数论与复变函数论的联系与差异

实变函数论与复变函数论的联系与差异实变函数论和复变函数论是数学分析中两个重要的分支,它们都探讨了函数的性质和行为,但是在研究对象和方法上存在一些差异。
下面将详细讨论实变函数论和复变函数论的联系与差异。
一、联系1. 函数的定义:实变函数论和复变函数论都研究函数的性质和行为。
实变函数论研究的是定义在实数域上的函数,而复变函数论研究的是定义在复数域上的函数。
2. 极限:实变函数论和复变函数论都涉及函数的极限概念。
实变函数论中,函数的极限是指函数在某一点处的趋近情况;复变函数论中,函数的极限是指函数在复平面上的趋近情况。
3. 连续性:实变函数论和复变函数论都研究函数的连续性。
实变函数论中,函数在某一点连续意味着在该点的极限存在且等于该点的函数值;复变函数论中,函数在某一点连续意味着在该点的极限存在且与函数值无关。
4. 导数:实变函数论和复变函数论都涉及函数的导数概念。
实变函数论中,导数表示函数在某一点的变化率;复变函数论中,导数表示函数在某一点处的线性逼近。
5. 积分:实变函数论和复变函数论都研究函数的积分。
实变函数论中,积分是通过对函数进行区间分割求和的方式求得;复变函数论中,积分是通过对函数在曲线上进行线积分求得。
二、差异1. 定义域和值域:实变函数论研究的是定义在实数域上的函数,其定义域和值域都是实数集;复变函数论研究的是定义在复数域上的函数,其定义域和值域都是复数集。
2. 解析函数:在复变函数论中,解析函数是指在其定义域上处处可导的函数。
而实变函数论中并没有类似的概念。
3. 复数域的性质:复数域具有复平面的几何结构,而实数域没有这样的结构。
因此,在复变函数论中可以讨论复数函数的奇点、留数等概念,这些在实变函数论中是不存在的。
4. 应用领域:实变函数论主要应用于物理学、经济学等实际问题的建模和分析;复变函数论则主要应用于电磁场、量子力学、流体力学等领域。
总结起来,实变函数论和复变函数论都研究函数的性质和行为,但是在定义域、值域、解析函数概念、复数域的性质和应用领域上存在一些差异。
1.复变函数与实变函数定义区别与联系有哪些
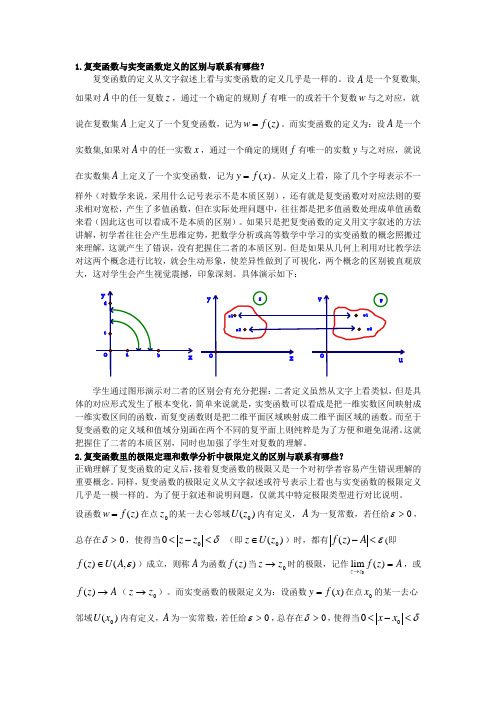
1.复变函数与实变函数定义的区别与联系有哪些?复变函数的定义从文字叙述上看与实变函数的定义几乎是一样的。
设A 是一个复数集,如果对A 中的任一复数z ,通过一个确定的规则f 有唯一的或若干个复数w 与之对应,就说在复数集A 上定义了一个复变函数,记为)(z f w =。
而实变函数的定义为:设A 是一个实数集,如果对A 中的任一实数x ,通过一个确定的规则f 有唯一的实数y 与之对应,就说在实数集A 上定义了一个实变函数,记为)(x f y =。
从定义上看,除了几个字母表示不一样外(对数学来说,采用什么记号表示不是本质区别),还有就是复变函数对对应法则的要求相对宽松,产生了多值函数,但在实际处理问题中,往往都是把多值函数处理成单值函数来看(因此这也可以看成不是本质的区别)。
如果只是把复变函数的定义用文字叙述的方法讲解,初学者往往会产生思维定势,把数学分析或高等数学中学习的实变函数的概念照搬过来理解,这就产生了错误,没有把握住二者的本质区别。
但是如果从几何上利用对比教学法对这两个概念进行比较,就会生动形象,使差异性做到了可视化,两个概念的区别被直观放大,这对学生会产生视觉震撼,印象深刻。
具体演示如下:w1w2z2z1学生通过图形演示对二者的区别会有充分把握:二者定义虽然从文字上看类似,但是具体的对应形式发生了根本变化,简单来说就是,实变函数可以看成是把一维实数区间映射成一维实数区间的函数,而复变函数则是把二维平面区域映射成二维平面区域的函数。
而至于复变函数的定义域和值域分别画在两个不同的复平面上则纯粹是为了方便和避免混淆。
这就把握住了二者的本质区别,同时也加强了学生对复数的理解。
2.复变函数里的极限定理和数学分析中极限定义的区别与联系有哪些?正确理解了复变函数的定义后,接着复变函数的极限又是一个对初学者容易产生错误理解的重要概念。
同样,复变函数的极限定义从文字叙述或符号表示上看也与实变函数的极限定义几乎是一模一样的。
复变函数与留数定理

复变函数与留数定理复变函数在数学中有着重要的地位,它是实变函数的推广和扩展。
复变函数的研究依赖于留数定理,这是复分析中的重要概念。
本文将介绍复变函数以及留数定理的基本概念和应用。
一、复变函数的定义与性质复变函数是定义在复数域上的函数,其定义域和值域都是复数集合。
复变函数可以表示为f(z)=u(x,y)+iv(x,y),其中z=x+iy,u和v是实变函数。
复变函数和实变函数的性质有相似之处,如连续性、可微性和可导性等。
但复变函数的导数是一个复数,具有方向和模的概念。
二、留数定理的基本概念留数是复变函数在孤立奇点处的特殊性质。
留数定理是复变函数理论中的核心内容之一。
对于函数f(z),若z=a是它的孤立奇点,可以通过留数计算沿闭合曲线的积分。
留数定理包括留数定理、柯西公式和狄利克雷问题等。
1. 留数定理留数定理是针对有限孤立奇点的情况。
当f(z)在区域D内有孤立奇点a1,a2,...,an时,针对闭合曲线C内的函数f(z),可以通过求解a1,a2,...,an处的留数来计算C上的积分。
这个定理在复积分计算、曲线积分和求和等问题中有广泛的应用。
2. 柯西公式柯西公式是留数定理的一个重要推论。
柯西公式表明,如果函数f(z)在区域D内解析(即可导),则它在D内的任何闭合曲线C上的积分为零。
这个结论为复变函数的求解和计算提供了方便。
3. 狄利克雷问题狄利克雷问题是留数定理与边值问题相结合的应用,它在电磁学和热传导等领域中起着重要作用。
狄利克雷问题可以通过留数定理求解,将定义在一条封闭曲线上的边值问题转化为计算特定点上的积分问题。
三、复变函数与实变函数的关系复变函数理论是实变函数理论的扩展和推广,两者之间有着密切的联系。
复分析的基本定理和方法可以归结为实分析的特殊情况,同时复分析也为实分析提供了新的解题思路和工具。
1. 复变函数的导数与实变函数的导数复变函数的导数是一个复数,可以表示为f'(z)=u_x+iv_x,其中u_x和v_x是u和v相对于x的偏导数。
实变函数与复变函数之比较_麻桂英

*
收稿日期: 2011 - 07 - 20 作者简介: 麻桂英( 1969 - ) , 女, 内蒙古鄂尔多斯人, 副教授, 研究方向: 函数论。
97
于是 f( x) 在( - ∞ ,+ ∞ ) 上处处可微。 1 ( 2 ) 令 f( x) = 0 可得其全部零点是 0 ,± , π 1 1 ± , …,± , …, 其中 n 为自然数。 nπ 2π 观察这些零点发现, 对于 f( x) 的零点 x = 0 而 1 f( x) 的零点 x = ± , n = 1, 2, 3 …, 言, 以x = 0为 nπ 聚点, 也就是说在点 x = 0 的任意领域内总有异于 x = 0 的 f( x) 的其它零点。 即尽管实变函数 f( x) 不 恒为零且处处可微, 零点 x = 0 却不是孤立零点。
The Comparison Between Real Variable Function and Complex Variable Function
MA Gui - ying, YANG Shang ( Faculty of Mathematics, Baotou Teachers College; Baotou 014030 ) Abstract: This article elaborate the major differences between the real function with one variable and complex function with single variable in three areas. As a result,the intrinsic link between basic course and follow - up course is consolidated and known ,achieving a multiplier effect. Key words: real variable; complex function; analyti达到事半功倍的效果。 关键词: 实变函数; 复变函数; 解析函数 中图分类号: O174. 5 & O174. 1 文献标识码: A 文章编号: 1004 - 1869 ( 2011 ) 03 - 0097 - 02
复变函数与实变函数之异同

数方 面在实 函数 与 复变 函数 中的不 同点 进 行 了分 析 和 比
较.通过 比较我们 可 以发现新 旧知识之 问既存 在 着 区别又 有联 系 ,只有通过 比较分 析才 能够牢 固地 掌握新 旧知识.因
此在教学 与学习的过程 中,一 定要关注二 者的差 异 ,这 样才
能将基础课 与后 继课 紧密结合 ,达 到事 半功倍 的效果.
酶 旗
局
●
。
。
● _ —一 ● ●
变函 寨囊画 乏
◎邓 琴 (杭 州电子科技 大学 理 学院 ,浙 江 杭 州 310018)
【摘要 】本文主要从基本初等 函数方 面阐述 了一元实 变 函数与单变量复 变 函数 问 的重大差 异 ,由此 巩 固和理 解基 础课 与后继课 间的 内在联 系,达 到事半 功倍 的效果.
1
并且 ,等式 lnz =nlnz,In = l (其 中 n为 大于 l的 n
正整数 )不再成立.下 面简单证 明一下.首先 ,上面两个 等式
应理解为两端可能取 的函数值 的全体相 同.现 以 n=2为例 来 说明等式不成立.设 z=re ,则 21nz:21nr+i( +4kqr), 为 整数.又 由 z =/.2e 得 lnz =lnr +i(20+2m盯)=21nr+ i(20+2mlr),m为整数.显然 ,它们的实部相等 ,但虚 部可取 值却不相 同.可用类似 的方法说 明另 一等式也不成立.
对任 意的复数 ,复变函数理论 中定义 正弦 函数 和余 弦
函数分别为sinz=旦_ ,co =生去 .在《数学分析》
中的 sinx,co 是有界 函数 ,即 I sinxI≤1,l COSXI≤1.但 sinz, COSZ在复平面 内不再有界 ,例如
复变函数于是便函数的区别与联系

复变函数与实变函数的联系与区别华中师范大学物理学院2008213421 路丽珍摘要:数的扩展:正数→负数→实数→…在实数范围内:方程当时,没有实根。
→扩大数域,引进复数,由实变函数学习到复变函数,它们有着紧密的联系,也有着巨大的区别。
关键词:复变函数实变函数联系与区别正文:在中学我们主要了解学习了实变函数,与大学期间,我们又更加深入的学习研究了实变函数,与此同时,也开始复变函数的学习。
由此我们看到了:“数的扩展:正数→负数→实数→…在实数范围内:方程当时,没有实根。
→扩大数域,引进复数”。
这样容易给人一种由浅入深、由简入繁、由特殊到一般的感觉,他们有很深的联系,然而事实上,他们有很大的不同,有很大的区别。
下面我们从几个方面来说明实变函数与复变函数的联系与区别。
1.自变量的不同以实数作为自变量的函数就做实变函数;即实数→实变量→实变函数。
以复数作为自变量的函数就叫做复变函数;即复数→复变量→复变函数。
2.实变函数与复变函数的联系区别(1)因为z=x+yi,所以复变函数y=f(z)的实部与虚部都是x,y的函数,即w= f(z)=u(x,y)+iv(x,y),由此可以看成:一个复变函数是两个实变函数的有序组合。
这样,实变函数的许多定义、公式,定理可直接移植到复变函数中。
然而同时,由于复变函数的虚部,实变函数的许多定义、公式,定理也不再是用于复变函数。
(2)对于复变函数与实变函数,我们分别学习了两者的点集、序列、极限、连续性、可微性、积分等性质与应用。
然而同时,由于复变函数的虚部,所要求的点集、序列、极限、连续性、可微性、积分等性质与应用的定义也不尽相同。
实分析(实变函数)与复分析(复变函数)(2010-10-02 13:47:52)/s/blog_4b700c4c0100m95r.html实分析实分析或实数分析是处理实数及实函数的数学分析。
专门研究数列,数列极限,微分,积分及函数序列,以及实函数的连续性,光滑性以及其他相关性质。
复变函数与实变函数的相同与不同联系与区别数学物理方法

精选ppt
1
目录
• 1、复变函数与实变函数特点的比较 • 2、复变函数与实变函数的联系与区别
精选ppt
2
1、复变函数与实变函数特点比较
• 1.1、相同点 • 1.2、不同点
精选ppt
3
一、复变函数与实变函数特点比较
实变函数:以实数作为自变量的函数叫实变 函数,它是微积分学的进一步发展,基础 是点集论(点集论是专门研究点所成的集 合的性质的理论)。当然它与古典数学也 有差别。
• 如此来看,复变函数只是实变函数在微积 分领域的推广与发展,又称复分析。
精选ppt
9
2.1、联系
实变函数有序组合可以这样表示复函: w f(zu ) (yx )i,v(yx),
• 显然,一个复变函数是两个许多定义、公式、定 理可直接移植到复变函数中。
• 举例(文献),以二元实函为例,从连续性、可 导性、可微性、解析性方面说明了两者之间的联 系;以Green公式说明两者的紧密相联;以复变 函数、实变函数的定理巧妙解决相互之间的问题 说明两者联系。
精选ppt
13
谢谢指导!
精选ppt
14
精选ppt
10
2.2、区别
• 重大差别:微分中值定理、解析函数的无穷可微 性(对于单连通区域D内的解析函数来说,具有 无穷可微性, 但对一元实函数而言,这一点是难 以保障的)和零点孤立性。
• 其他方面还有以下几点 1解析函数的值与值之间有紧密联系:柯西积分定理
是解析函数积分的理论基础, 其实质就是一个在 区域内的解析函数是可以用一个积分来表示的, 也就是解析函数在区域内任意处的值总可以用其 在边界上的积分来表示;
• 一些初等函数的值域、周期性、算法(尤 其积分)有很大区别;
复变函数与实变函数微积分理论的比较与应用资料

复变函数与实变函数微积分理论的比较与应用众所周知复变函数论是数学中一个基本的分支学科,它的研究对象是复变数的函数,本学期我们数学专业的学生开始学习这门课程。
复变函数论历史悠久,内容丰富,理论十分完美。
它在数学许多分支、力学以及工程技术科学中有着广泛的应用。
这里先略微简述一下复变函数的历史。
复数起源于求代数方程的根。
复变函数论的全面发展是在十九世纪,就像微积分的直接扩展统治了十八世纪的数学那样,复变函数这个新的分支统治了十九世纪的数学。
当时的数学家公认复变函数论是最丰饶的数学分支,并且称为这个世纪的数学享受,也有人称赞它是抽象科学中最和谐的理论之一。
为复变函数论的创建做了最早期工作的是欧拉、达朗贝尔,法国的拉普拉斯也随后研究过复变函数的积分,他们都是创建这门学科的先驱。
后来为这门学科的发展作了大量奠基工作的要算是柯西、黎曼和德国数学家维尔斯特拉斯。
二十世纪初,复变函数论又有了很大的进展,维尔斯特拉斯的学生,瑞典数学家列夫勒、法国数学家彭加勒、阿达玛等都作了大量的研究工作,开拓了复变函数论更广阔的研究领域,为这门学科的发展做出了贡献。
下面我将对已学的复变函数微积分的相关知识做以总结和归纳。
⒈复变函数的微积分理论㈠复变函数的微分性质我们知道函数的导数是由极限来定义的,所以我先把复变函数的极限理论做以梳理。
①复变函数极限的概念:函数ω=f(z)定义在z0的去心邻域0<│z-z0│<ρ内,如果有一确定的数A存在,对于任给的ε>0,相应的必有一个正数δ(ε)使得当0<│z-z0│<δ(0<δ≤ρ)时,有│f(z) -A│<ε。
即称z→z0是的极限,记为另外复变函数的连续性叙述与实变函数中的叙述是相似的,此处不细表在实变函数时另有说明。
②复变函数导数的概念:设函数ω= f(z)在包含z0的邻域D内有定义,如果极限存在,那么f(z)在z0处可导(或可微)。
该极限成为f(z)在z0的导数,记做f’(z0)=│z=z。
复变函数与实变函数的区别与联系

复变函数与实变函数的区别与联系
复变函数与实变函数的区别主要在于定义域和值域的不同。
1. 定义域:实变函数的定义域是实数集,而复变函数的定义域是复数集。
2. 值域:实变函数的值域也是实数集,而复变函数的值域是复数集。
3. 解析性:复变函数具有解析性,即满足柯西-黎曼方程,因
此可以进行复数的微积分运算,如导数和积分。
而实变函数不一定具有解析性,例如绝对值函数的导数在某些点处是不存在的。
联系:
1. 实变函数是复变函数的一种特殊情况,即定义域和值域都是实数集的复变函数就是实变函数。
2. 复数集可以看作是实数集的扩充,因此复变函数可以看作是实变函数在复数集上的推广。
3. 实变函数与复变函数在函数的取值和性质上有很多相似之处,例如连续性、可微性和可积性等。
总之,复变函数是对实变函数的推广,通过引入复数,可以更加广泛地描述和研究数学问题。
简述复变函数与二元实函数的区别与联系

简述复变函数与二元实函数的区别与联系
一、复变函数与二元实函数的区别
1、定义不同:复变函数是将一个复数集合上的每个复数映射到另一个复数集合上的函数,而二元实函数是将实数集合上的每个实数映射到另一个实数集合上的函数。
2、参数取值不同:复变函数的参数是一个复数,它由实部和虚部两个分量组成,而二元实函数的参数是一个实数;
3、计算结果不同:复变函数的计算结果是一个复数,而二元实函数的计算结果是一个实数;
4、定义域和值域不同:复变函数的定义域和值域都是复数集合,而二元实函数的定义域和值域都是实数集合。
二、复变函数与二元实函数的联系
1、复变函数和二元实函数都属于函数,他们具有映射的性质;
2、复变函数是特殊的二元实函数,可以由二元实函数构造出来,由于复变函数的定义域和值域都是复数集合,因此只需要对二元实函数中的实数值作适当的复数变换,即可得到一个复变函数;
3、复变函数可以用来描述实际问题中的复数变量之间的相互关系,而二元实函数则可以用来描述实际问题中的实数变量之间的相互关系。
- 1 -。
复变函数点解析

复变函数点解析复变函数是数学中的一个重要概念,它是定义在复平面上的函数。
复变函数的研究对于数学的发展和应用具有重要意义,涉及到复数的性质、解析函数的性质以及复积分等内容。
复变函数的定义比实变函数更加复杂,因为它不仅与实数相关,还涉及到虚数。
一个复变函数可以表示为f(z) = u(x,y) + iv(x,y),其中z=x+iy表示复平面上的点,u(x,y)和v(x,y)分别表示x和y 的函数。
复变函数可以看作是将复平面上的点映射到复平面上的点的函数。
解析是复变函数的一个重要概念,如果一个函数在某个区域内处处可导,并且导数也是连续的,那么我们称这个函数在该区域内解析。
解析函数具有很多重要的性质,比如它在该区域内无穷阶可导,可以展开成幂级数等。
复变函数的解析性质使得它在分析数学、物理学、工程学等领域具有广泛的应用。
在分析数学中,复变函数可以用来解决实变函数无法解决的问题,比如复积分、留数定理等。
在物理学中,复变函数可以用来描述电磁场、波动现象等。
在工程学中,复变函数可以用来解决各种工程问题,如电路分析、信号处理等。
复变函数的性质与实变函数有很大的不同。
比如,实变函数的导数可以用极限的方式来定义,而复变函数的导数需要用到复数的性质。
另外,实变函数的导数只有一个值,而复变函数的导数有无穷多个值。
复变函数的导数还有一个重要的性质,即柯西-黎曼条件,它是解析性的充分必要条件。
复变函数还具有一些特殊的函数形式,比如三角函数、指数函数、对数函数等。
这些函数在复平面上具有特殊的性质,比如周期性、分支性等。
复变函数还可以通过复数的极坐标表示形式来进行分析,这对于研究复变函数的性质很有帮助。
复变函数是数学中一个重要而有趣的概念。
它的研究不仅丰富了数学理论,也为其他学科的发展提供了重要的工具和方法。
通过对复变函数的深入研究,我们可以更好地理解数学的美丽和应用的广泛性。
复变函数和实变函数的比较

复变函数和实变函数的比较数域从实数域扩大到复数域后,便产生了复变函数论,复变函数着重讨论解析函数,而解析函数的实部和虚部是相互联系的,这与实变函数有根本的区别。
从某种意义上来说,实函数可以看作复函数的特例。
有关实函数的一些概念,很多都可以推广到复函数上来。
例如:函数的连续性、函数的导数、有(无)界函数、中值定理、泰勒展开式、基本初等函数等。
但是,由于复数域的特殊性,又给这些概念赋予了新的特性。
下面我将选取几个方面粗略地比较实变函数和复变函数的异同。
一、复变函数和实变函数的定义复变函数的定义从文字叙述上看与实变函数的定义几乎是一样的。
复变函数的定义为:设A 是一个复数集,如果对A 中的任一复数z ,通过一个确定的规则f 有唯一的或若干个复数w 与之对应,就说在复数集A 上定义了一个复变函数,记为w =f(z)。
而实变函数的定义为:设A 是一个实数集,如果对A 中的任一实数x ,通过一个确定的规则f 有唯一的实数y 与之对应,就说在实数集A 上定义了一个实变函数,记为y =f(x)。
二者定义虽然从文字上看类似,但是具体的对应形式发生了根本变化,简单来说就是,实变函数可以看成是把一维实数区间映射成一维实数区间的函数,而复变函数则是把二维平面区域映射成二维平面区域的函数,如下图所示。
二、复变函数和实变函数极限过程对比复变函数在某一点的极限定义为:设函数w =f(z)在点z 0的某一去心邻域U(z 0)内有定义,A 为一复常数,若任给ε>0,总存在δ>0,使得当0<|z −z 0|<δ (即z ∈U(z 0))时,都有|f (z )−A |<ε(即f (z )∈U(A,ε))成立,则称A 为函数f (z )当z →z 0时的极限,记作lim z→z 0f (z )=A ,或f (z )→A (z →z 0)。
而实变函数在某一点的极限定义为:w1w2z2z1设函数y =f(x)在点x 0的某一去心邻域U(x 0)内有定义,A 为一实常数,若任给ε>0,总存在δ>0,使得当0<|x −x 0|<δ (即x ∈U(x 0))时,都有|f (x )−A |<ε(即f (x )∈U(A,ε))成立,则称A 为函数f (x )当x →x 时的极限,记作lim x→x 0f (x )=A ,或f (x )→A (x →x 0)。
复变函数论文

复、实变函数的比较与应用作者:阮玲花学号:2专业:数学与应用数学复、实变函数的比较与应用姓名:阮玲花班级:数学132 学号:2数域从实数域扩大到复数域后,便产生了复变函数论,并且深入到了微分方程、拓扑学等数学分支。
复变函数论着重讨论解析函数,而解析函数的实部与虚部就是相互联系的,这与实函数有根本的区别。
有关实函数的一些概念,很多都就是可以推广到复变函数上。
例如:函数的连续性、函数的导数、有(无)界函数、中值定理、泰勒展式、基本初等函数等等。
在中学我们主要了解学习了实变函数,与大学期间我们又更加深入的学习研究了实变函数,与此同时,也开始复变函数的学习。
由此我们瞧到了:“数的扩展:正数→负数→实数→”,在实数范围内:当方程判别式小于0时,没有实根。
→扩大数域,引进复数,这样容易给人一种由浅入深、由简入繁、由特殊到一般的感觉,它们有很深的联系,然而事实上,她们有很大的不同,有很大的区别。
下面我们从几个方面来说明实变函数与复变函数的联系与区别。
(一)实变函数实变函数论即讨论以实数为变量的函数,然而实变与常微分方程等不同,简单地说就就是恰当的改造积分定义使得更多的函数可积。
由于诸如狄利克雷这样的简单函数都不可积,所以原有的积分范围太窄了,进而便产生了Lebesgue创立新积分的原始思路。
Lebesgue积分:(二)复变函数复变函数就是数学分析的继续,复变函数的定义:若在复数平面上存在一个点集E ,对于E 的每一点z,按照一定规律,有一个或多个复数值W 与之相对应,则称W 为z 的函数,记作)(z f W =,z ∈E 邻域:以复数0z 为圆心,以任意小正实数ε为半径做一个圆,则圆内所有点的集合称为0z 的邻域。
把复变函数的)(z f 的实部与虚部分别记作u(x,y)与v(x,y),)(z f =u(x,y)+iv(x,y),所以,复变函数可以归结为一对二元实变函数。
(三) 实变函数及与复变函数比较1.自变量的不同以实数作为自变量的函数就做实变函数;即实数→实变量→实变函数。
实变函数与复变函数的关系

实变函数与复变函数的关系实变函数和复变函数是数学分析中的重要概念。
实变函数是指定义域和值域都是实数的函数,而复变函数是指定义域和值域都是复数的函数。
实变函数与复变函数之间存在一些联系和区别,下面将对它们的关系进行探讨。
一、实变函数的定义与性质实变函数是大家在高中数学中就已经接触到的概念,它是指一个函数的定义域和值域都是实数。
例如,函数f(x)=x²就是一个实变函数。
实变函数有其特定的性质,包括连续性、可导性、积分性等等。
1. 连续性:实变函数在定义域上可以连续或不连续。
连续函数指函数在其定义域上没有间断点,即在任一点x处的极限值等于函数在x处的函数值。
例如,f(x)=sin(x)是一个连续函数。
2. 可导性:实变函数的可导性是指其在定义域上的导数存在。
导数是函数在某一点处的切线斜率,也可用于判断函数的变化趋势。
例如,f(x)=x³是一个可导函数。
3. 积分性:实变函数的积分性是指其在定义域上存在定积分。
定积分是通过确定函数在给定区间上的面积大小来定义的。
例如,f(x)=2x在区间[0, 1]上的定积分为1。
二、复变函数的定义与性质复变函数是指一个函数的定义域和值域都是复数。
复变函数可以分为复平面上的全纯函数和调和函数两类。
全纯函数是指在其定义域上可导的复函数,调和函数是指其实部和虚部都是调和函数的复函数。
1. 全纯函数:全纯函数在复平面上处处可导,且导数连续。
全纯函数的定义和实变函数的可导性类似,但复数的导数计算需满足柯西-黎曼方程。
例如,f(z)=e^z是一个全纯函数。
2. 调和函数:调和函数是指其实部和虚部都是调和函数的复函数。
调和函数在物理、电磁场等领域有重要应用。
例如,f(z)=z+1/z是一个调和函数。
三、实变函数与复变函数的关系实变函数与复变函数之间存在一定的联系和区别。
1. 复变函数包含实变函数:复变函数是实变函数的超集,即实变函数是复变函数的一种特殊情况。
实变函数只考虑实数域上的函数,而复变函数在实数域上也成立。
复变函数的性质与分类

复变函数的性质与分类复变函数是数学中的一个重要概念,它是指定义在复数域上的函数。
与实变函数不同,复变函数具有许多独特的性质和分类方法。
本文将介绍复变函数的性质与分类,并探讨其在数学和物理等领域中的应用。
一、复变函数的性质1. 解析性:复变函数在其定义域内解析,即在该区域内可导无穷次。
这是复变函数与实变函数最大的区别之一。
解析性使得复变函数具有许多重要的性质和应用,如洛朗级数展开和复数积分等。
2. 全纯性:全纯函数是指在其定义域内处处可导的复变函数。
全纯函数是解析函数的一种特殊情况,它在复平面上具有许多重要的性质,如柯西-黎曼方程和柯西积分定理等。
3. 奇点:奇点是指复变函数在某些点上不解析的情况。
奇点分为可去奇点、极点和本性奇点三种类型。
可去奇点是指在该点附近可以通过去除奇点的方式使函数变得解析;极点是指在该点附近函数趋于无穷大;本性奇点是指在该点附近函数既不趋于有限值也不趋于无穷大。
4. 解析延拓:解析延拓是指通过解析性质将函数从定义域延拓到更大的区域。
解析延拓可以使函数在更广泛的区域内具有解析性,从而得到更多的性质和应用。
二、复变函数的分类1. 代数函数:代数函数是指由有限次代数运算和有限次复合运算得到的函数。
代数函数包括多项式函数、有理函数和代数函数的根等。
代数函数在复平面上具有有限个奇点,其性质和行为相对简单。
2. 三角函数:三角函数是指由正弦函数和余弦函数构成的函数。
三角函数在复平面上具有周期性和解析性,其性质和行为与实数域上的三角函数类似。
3. 指数函数和对数函数:指数函数和对数函数是复变函数中的重要类别。
指数函数具有解析性和周期性,对数函数具有多值性和解析性。
指数函数和对数函数在数学和物理等领域中有广泛的应用。
4. 特殊函数:特殊函数是指由特殊函数方程定义的函数,如贝塞尔函数、超几何函数和椭圆函数等。
特殊函数在数学和物理等领域中具有重要的应用,如波动方程、量子力学和电磁场等。
三、复变函数的应用1. 数学分析:复变函数在数学分析中具有广泛的应用,如复数积分、洛朗级数展开和柯西积分定理等。
复变函数积分与实函数积分的区别与联系

复变函数积分与实函数积分的区别与联系作者:潘安香来源:《科学导报·学术》2019年第16期摘要:本文从复变函数的定义出发,讨论了复变函数积分与实函数积分的联系与区别,讨论了彼此的性质以及复变函数解决实函数不能解决的问题,从而进一步弄清他们的区别。
关键词:复变函数;实函数;积分;2.实函数定积分的定义与复变函数定积分的定义的区别与联系我们知道无论是在实函数积分中还是在复变函数积分中,定积分都具有十分重要的意义。
定积分的思想广泛应用于各个领域,我们要深刻理解了定积分的思想,掌握定积分的定义将是非常关键的过程。
下面将会对定积分的定义进行研究。
4.总结数域从实数域拓展到了复数域,实数学分析积分中存在着许多性质。
由于复变函数的积分與实二元线性积分非常类似,因此,实数学分析中的积分的许多性质都可以不加推广的直接运用到复变函数的积分中来,但并不是实数学分析中的积分的性质都可以不加改变的运用到复变函数的积分中来。
复变函数的积分不仅可以解决复变函数中的计算问题,同时也能够解决实函数积分能解决或不能解决的许多问题。
本文通过比较复变函数的积分与是函数积分的区别与联系,一方面让我们进一步明白复变函数与实函数类似的地方。
另一方面又能让我们进一步掌握他们的不同之处,这样我们能够更清楚的弄清复变函数的积分理论,对今后的学习或是生产生活都有很大的帮助。
积分学广泛的应用于其他学科中,只有掌握好了积分学理论才能够很好的把积分学应用于其它学科。
研究复变函数积分与实函数积分的区别与联系,有助于我们更进一步的掌握复变函数和实函数的积分理论。
因此研究复变函数积分与实函数积分的区别与联系具有十分重要的意义。
参考文献:[1] 欧阳光中,朱学炎,金福临,陈传璋.数学分析(第三版)[M].北京:高等教育出版社.1962.[2] 刘玉琏,傅沛仁,刘宁.数学分析讲义(第四版)[M].北京:高等教育出版社.2003.[3] 孙清华,孙昊.复变函数[M].武汉:华中科技大学出版社.2003.(作者单位:叙州区凤仪乡初级中学校)。
实变函数与复变函数的异同

[收稿 日期 ] 2011—12—23 [作者简 介 ] 王艳琴(1982一 ),女,山西阳高人,山西大同煤炭职业技术学院助教,研究方向:基础数学。
2012焦
湖南工业职业技术学院学 报
第 1期
定, 是一有限的复常数.如果仟给s>0,可以找到一个 lim— /(z+W-)-/(z)
( ; )内有定义 ,
为 定数 .若 对 任给 的 s > 0 ,
存 在
找到一个与有关的函数 = (s)>0,使得当 ∈E,并
正 数 (< ) ,
使 得 当 0<l 一 I< 时有
且当0<lz- ̄I< 时,有l/-( 一 I<s;那么,我们
l/( 一 <s 则称函数/当. 趋于 时以 为极限
[摘 要 】 数域从实数域扩 大到复数域后 ,便产生 了复变函数论 ,并且深入 到 了数 学、微 分方程、拓扑 学等数 学分 支。复变 函数论着重讨论解析函数,而解析函数的 实部和虚部是相 互联 系的 ,这与 实函数有根本的 区别。有关实函数 的一些概念 ,很 多都可以推广到复变函数上来.例如 :函数 的连续性、函数的导数 、有(无 )界 函数、中值定理 、泰勒展式 、基本初等 函数等。 [关键词 ] 极限 ;基本初 等函数 ;导数及其几何 意义 ;积分;零点;级数 ;中值定理 [中图分类号 ] TM11 [文章标识码 ] A [文章编号 ] 1671—5004 (2012) 01—0044—05
— ÷
l_3实函数极限与复 函数极限的异 同
(1) 在 实 函 数 中 :
当
时, 是沿着实坐标轴逐渐 向 .to,而使
f A.
.
2.3实 变 函数 与 复变 函数 中导 数 的 不 同 点 (1)实变函数与复变函数 的导数的定义,虽然在 形式上相 同,实质上却有很大 的区别.这是因为实变 函数只沿着实轴逼 近 零 ,而 复变 函数却可 以沿复平面上 的任一 曲线 逼近零 .因 此 ,复 变函数可导的要求 比实变函数可导的要求严格 的多.复 变 函数在一点可 导的定 义与 实一元函数在一点可导的定义看
浅析复函数与实函数地类同与差异

浅析复函数与实函数的类同与差异夏青 数学112班 11101231号摘要复函数与实函数贯穿在我们高中和大学的数学之中,我们通过学习了解了部分实函数和复函数的知识点。
我认为复函数是实函数的后继与延伸,二者在某些概念、结论上既有区别,又有着深刻的联系,因此为了更加清楚、明确二者的概念、结论的相同与相异之处,本文做了一点简单说明。
正文在中学我们主要学习了实函数,大学期间,我们又更加深入地学习研究了实函数,与此同时也进行了复变函数的学习。
在实函数与复函数的学习中中,我发现二者有许多相似之处,并且在许多命题、性质中是可以相互推证,彼此呼应的。
所以在研究复函数中的命题时,会想到从实函数中寻找可以借鉴的东西,但是毕竟二者之间有区别,有时并不能完全照搬照抄,有的甚至有本质的差别。
复变函数论中的柯西—黎曼方程、柯西积分定理、解析函数的幂级数表达式和敛散性、解析函数的泰勒展式与洛朗展式、留数定理等,它们与我们经常使用的实函数有一定的关系,其相关知识点也能运用在实函数的解题上,下面我们将从几个方面来探究其在实函数上的应用。
1.在解决形如cos axe bxdx⎰ sin axe bxdx ⎰ 22(0)a b +≠的实函数的不定积分时,我们往往采用的是分部积分法,其过程往往复杂且容易出错,但是通过我们学习过的复积分能方便的解决这些问题。
我们已知cos sin i ei θθθ=+,我们能不能通过构造一个复积分的问题来解决这个问题。
例1: 计算积分cos axe bxdx ⎰ ,,a b x R Î 此时我们可以添加一个辅助函数 sin ax e bxdx⎰()f x =cos axe bxdx ⎰()g x =sin axe bxdx ⎰()F x =()()()F x f x ig x =+()F x =cos ax e bxdx ⎰+i sin ax e bxdx ⎰=ax ibx e dx+⎰=ax ibxe a ib++12c ic ++=22()(cos sin )ax e a ib bx i bx a b -++ =22[cos sin (sin sin )]axa bxb bx i a bx b bx e a b ++-+此时()f x =22(cos sin )Re ()axa bxb bx F x e a b +=+1c +222(sin sin )()Im ()ax e a bx b bx g x F x c a b -==++由此可以看出复函数积分可以快速解决形如cos ax e bxdx⎰ s i n axe bxdx ⎰ 22(0)a b +≠的问题,但是其解决的问题只是我们常见问题中的很小一部分,我们常见的积分不只是这种情况,更多的是型如:()cos axc dx e bxdx +⎰, ()s i n a xc d x e b x d x +⎰22(0)a b +≠ 我们也可以借助复变的相关知识解决问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
复变函数与实变函数的联系与区别
华中师范大学物理学院 2008213421 路丽珍
摘要: 数的扩展:正数→负数→实数→…在实数范围内:方程当 042<-=∆ac b 时,没有实根。
→扩大数域,引进复数,由实变函数学习到复变函数,它们有着紧密的联系,也有着巨大的区别。
关键词: 复变函数 实变函数 联系与区别
正文:
在中学我们主要了解学习了实变函数,与大学期间,我们又更加深入的学习研究了实变函数,与此同时,也开始复变函数的学习。
由此我们看到了:“数的扩展:正数→负数→实数→…在实数范围内:方程当 042<-=∆ac b 时,没有实根。
→扩大数域,引进复数”。
这样容易给人一种由浅入深、由简入繁、由特殊到一般的感觉,他们有很深的联系,然而事实上,他们有很大的不同,有很大的区别。
下面我们从几个方面来说明实变函数与复变函数的联系与区别。
1. 自变量的不同
以实数作为自变量的函数就做实变函数;即实数→实变量→实变函数。
以复数作为自变量的函数就叫做复变函数;即复数→复变量→复变函数。
2. 实变函数与复变函数的联系区别
(1)因为z=x+yi,所以复变函数y=f(z)的实部与虚部都是x,y 的函数,即w= f(z)=u(x,y)+iv(x,y),由此可以看成:一个复变函数是两个实变函数的有序组合。
这样,实变函数的许多定义、公式,定理可直接移植
到复变函数中。
然而同时,由于复变函数的虚部,实变函数的许多定义、公式,定理也不再是用于复变函数。
(2)对于复变函数与实变函数,我们分别学习了两者的点集、序列、极限、连续性、可微性、积分等性质与应用。
然而同时,由于复变函数的虚部,所要求的点集、序列、极限、连续性、可微性、积分等性质与应用的定义也不尽相同。
