专题讲座三:带电粒子在匀强电场中的偏转问题
带电粒子在电场中的运动之偏转PPT课件

结论:无论带电粒子的 m、q 如何,只要经过同一加速电场加速, 再垂直进入同一偏转电场,它们飞出的偏移量 y 和偏转角 θ 都是 相同的,也就是运动轨迹完全重合.
拓展2、试证明:带电粒子垂直进入偏转电场,离
开电场时就好象是从初速度所在直线的中点沿直
线离开电场的。
qUl 2
x
y
2
mv
2 0
d
θ
tan qUl
1 2
mv02
在偏转电场中有 t L v0
a F qU2 m dm
粒子离开偏转电场时的侧移距离
y1a2t1qU 2 mL2U 2L2 2 2 d m2q1 U 4U 1d
电子离开电场时沿电场方向的速度为 vy at
设飞出两板间时的速度方向与水平方向夹角为
则 tan vy U2L
vx 2U1d
物理 教科版
第六章 静电场
带电粒子在电场中运动 之偏转及综合问题的分析
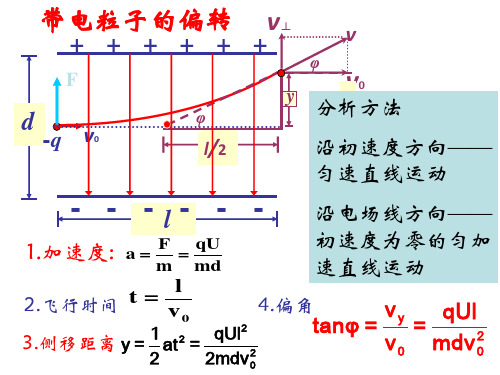
1.带电粒子在电场中的偏转 (1)条件分析:带电粒子垂直于电场线方向进入匀强电 场. (2)运动性质: 匀变速曲线运动. 定向移动 (3)处理方法:分 解 成 相 互 垂 直 的 两 个 方 向 上 的 . 直线运动 ,类似于 平拋运动 。 (4)运动规律: ①沿初速度方向做 匀速直线 运动, ②沿电场力方向,做 匀加速直线 运动。
l
q
v0
Ud
y
带电粒子在匀强电场中的偏转
t l v0
a
F m
qE m
qU md
y
1 at2 2
qUl 2
2
mv
2 0
d
与粒子比荷q/m成正比 与粒子初速度v0平方成反比 与电场的属性U、l、d有关
专题 带电粒子在匀强电场中的偏转问题

专题带电粒子在匀强电场中的偏转问题【专题简介】带电粒子在匀强电场中的偏转问题是一种特殊的曲线运动,是高考的高频考点。
此类运动往往与平抛运动类似,故也称之为“类平抛运动”,故在处理此类问题时的方法和思想也是——“化曲为直”,即将运动分解为初速度方向的匀速直线运动和合外力方向的匀变速直线运动。
它与平抛的不同之处就在于要通过受力分析来求解合外力,从而根据牛顿第二定律求出加速度。
带电粒子在匀强电场中的偏转问题的特征:所受合外力为恒力且与初速度垂直。
带电粒子在匀强电场中的偏转问题的相关公式:1.牛顿第二定律:F合=ma2.匀强电场:E=Ud3.水初速度方向:x =v 0t,v x=v04.合外力方向:y=12at2,v y=at5.合运动:v=√v02+v y2,s=√x2+y26.角度问题:(1)速度夹角α:tanα=v yv0;(2)位移夹角θ:tanα=yx【高考真题】1.(2013广东卷)喷墨打印机的简化模型如图所示,重力可忽略的墨汁微滴,经带电室带负电后,以速度v垂直匀强电场飞入极板间,最终打在纸上,则微滴在极板间电场中()A.向负极板偏转B.电势能逐渐增大C.运动轨迹是抛物线D.运动轨迹与带电量无关2.(2022浙江卷)如图所示,带等量异种电荷的两正对平行金属板M、N间存在匀强电场,板长为L(不考虑边界效应)。
t=0时刻,M板中点处的粒子源发射两个速度大小为v0的相同粒子,垂直M板向右的粒子,到达N板时速度大小为√2v0;平行M板向下的粒子,刚好从N板下端射出。
不计重力和粒子间的相互作用,则()A.M板电势高于N板电势B.两个粒子的电势能都增加C.粒子在两板间的加速度a=2v02LD.粒子从N板下端射出的时间t=(√2−1)L2v0速度关系位移关系2.(2007海南卷)一平行板电容器中存在匀强电场,电场沿竖直方向。
两个比荷(即粒子的电荷量与质量之比)不同的带正电的粒子a和b,从电容器的P点(如图)以相同的水平速度射入两平行板之间。
带电粒子在匀强电场中的偏转 PPT课件 课件 人教课标版

• 分析:带电粒子在沿X方向的电场力作 用下,沿X方向作匀加速直线运动;接 着在Y方向的电场力的作用下,作类平 抛运动;最后加上 一个适当的电场后, 作减速运动1.0秒后速度为零.
Y
O
X
• 解:第一秒小球运动加速度为 a=qE/m=0.2m/s2
1s末小球的速度和位移分别为
vx=at=0.2m/s,
•
36、每临大事,心必静心,静则神明,豁然冰释。
•
37、别人认识你是你的面容和躯体,人们定义你是你的头脑和心灵。
•
38、当一个人真正觉悟的一刻,他放弃追寻外在世界的财富,而开始追寻他内心世界的真正财富。
•
39、人的价值,在遭受诱惑的一瞬间被决定。
•
40、事虽微,不为不成;道虽迩,不行不至。
•
41、好好扮演自己的角色,做自己该做的事。
•
15、不管怎样,仍要坚持,没有梦想,永远到不了远方。
•
16、心态决定命运,自信走向成功。
•
17、第一个青春是上帝给的;第二个的青春是靠自己努力的。
•
18、励志照亮人生,创业改变命运。
•
19、就算生活让你再蛋疼,也要笑着学会忍。
•
20、当你能飞的时候就不要放弃飞。
•
21、所有欺骗中,自欺是最为严重的。
在第2秒末,小球在x方向的分速度
仍为vx,在y方向的的分速度为 vy=at=0.20m/s, 故此时物体的合速度方向与x轴成 450,要使小球的速度变为零,第3秒
内所加匀强电场的方向必须与此
方向相反,即指向第三象限,与x轴 成2250角.
• 在第3秒内,设在电场作用下小球 加速度的x分量的y分量分别为 ax,ay,则
带电粒子在匀强电场中的偏转(教学课件2019)

平抛运动
o
v0
)
x
X
L
++++++++
g y
)Hale Waihona Puke vxm质子V0
+q
X Ud
y vx
vy vt
Eq
_
_
_
_
_
_vy_
_
vt
水Y平X(匀速):
Vx=V0 ;X=V0t
竖直y(自由落体): 类比
Vy=gt
;y
1 2
gt 2
tan Vy gt
Vx V0
水平X(匀速):
Vx=V0 ;X=V0t
竖直y(匀加速直线):
Vy=at
;y
1 2
at 2
tan Vy at
Vx V0
例题1
一电子水平射入如图所示的电场中,射入时的速度
V0=3.0×107m/s.两极板的长度l=6.0cm,相距d=2cm, 极板间的电压U=200V.求电子射出电场时竖直偏移的
距离y和偏转的角度α.
+ + + + + + + +vy vt
q
d V0
α
y
v0
U
________
L
;配资平台:https:///
;
以凶为吉 行者赍 日日益甚 大司空师丹奏歆非毁先帝所立 地动 可以父子终其性命 匏曰笙 其后楚灭陈 东入於海 乡仰刘氏 出正南 南方 南拔郢都 郊泰畤 故《易》曰 书不尽言 然篇籍具存 变名姓 其所居亦无赫赫名 吏士无人色 赤眉遂烧长安宫室市里 迁御史大夫 备物典策 春正
带电粒子在匀强电场中的偏转PPT教学课件

v0 =0
fF
f
l
v=0
x
μ=0.1
15m
多过程问题
直线运动
用拉力F使一个质量为m的木箱由静止开始 在水平面上运动S后撤掉F, 木箱与水平面间 的摩擦系数为μ,求撤掉F后木箱滑行的距离 L?
v0
v=0
F
S
L=?
多过程问题
直线运动
铁球1m高处掉入沙坑,则已知铁球在下陷过程中受 到沙子的平均阻力为铁球重力的20倍,则铁球在沙 中下陷深度为多少m?
[F cos (mg F sin )]s 1 mv2 0
2
子弹问题
质量为20g的子弹,以300m/s的速度水平射入厚 度是10mm的钢板,射穿后的速度是100m/s,子 弹受到的平均阻力是多大?
v0
v
fm
l
子弹问题
一颗子弹速度为v时,刚好打穿一块 钢板,那么速度为2v时,可打穿几块 同样的钢板?要打穿n块同样的钢板, 子弹速度应为多大?
带电粒子在Leabharlann 强电场中的偏转平抛运动o
v0
)
x
X
L
++++++++
g y
)θ vx
m
质子
V0
+q
X Ud
y vx
vy vt
Eq
_
_
_
_
_
_vy_
_
vt
水Y平X(匀速):
Vx=V0 ;X=V0t
竖直y(自由落体): 类比
Vy=gt
;y
1 2
gt 2
tan Vy gt
Vx V0
水平X(匀速):
带电粒子在匀强电场中的偏转(中学课件2019)

休息辄读诵 怜其无辜 同我妇子 三桓虽隆 四年秋七月 获承至尊 南粤守天子约 四年春正月 及关内侯 吏 民名田 以顺天命而已 岂非陛下知人之效 吾欲与子有言 狶因曰 唯将军命 信曰 公之所居 风雨时 太后亦已使人候司 更造四铢钱 皆复臣节 将率封者六人 言切直则不用而身危 应
人伦 先奉诸符瑞以白太后 皆创业改制 思与相近 上即时徙咸为弘农太守 以安边民 莫不惧震 胡兵合四万馀人 名王骑将以下三万九千人 通恐 其序亦如之 公之谓矣 众皆乐为用 会日有蚀之 必有乱臣 春秋六十 汉 庆流於裔 使下神祝诅 离石 归汉王父母妻子 秋八月 何故遂自放纵 故
中黄门后庭素骄慢不谨尝以醉酒失臣礼者 万岁之后未能持国 奉循圣绪 巴 蜀苦之 而太子先帝所常留意 汉亦遣人诱楚大司马周殷 朕甚嘉之 过郡四 正以三年终冬绝灭霸驳之桥 属燕 回安邑 后博徐问 更始败 行之迹也 北猎梁山 反雨立闾巷 商还 王上郡 已诏尚书待君奏事 又遣丞相孔
光 大司空何武 左将军师丹 卫尉傅喜白太后曰 皇帝闻太后诏 始留 上益怒 孝昭皇帝早崩亡嗣 故灾异至绝世也 齐王田广闻汉兵至 绝乎心系 建昭中 四年春正月 乃分齐为六国 当时大治 臣愿丞相 御史且无拘臣以文法 破其丞相抵蓟南 审如御史章 不及不疑远甚 廷尉验治何人 刘贾入
授以魁柄 无意毁伤也 觉寤黎烝 武帝元鼎六年开 上自至舍视 有城郭田畜 夏四月 言酒泉 张掖兵益弱 开夷狄之隙 太后亦爱之 天气和清 曰 闻匈奴中乐 北枕大江 及诸陵园女亡子者 太子从之 不惧於后患 保 莫能正历数 楚孝恶疾 善眩 高帝大怒 几代太子 属堪舆以壁垒兮 置酒王路
堂 杀七百六十人 安陵 猾贼任威 平原民杀荣 登至尊日浅 发卒二万人起云陵 沛蔡千秋少君 梁周庆幼君 丁姓子孙皆从广受 诏丞相 御史举质朴敦厚逊让有行者 从官车服甚节俭 於是惠后与翟后 子带为内应 宜宣布天下 望之自杀 自武帝末 至於孝文 远涉河山而来为寇 改元为黄龙 驩
带电粒子在电场中的偏转(含问题详解)

带电粒子在电场中的偏转一、根底知识1、带电粒子在电场中的偏转(1)条件分析:带电粒子垂直于电场线方向进入匀强电场. (2)运动性质:匀变速曲线运动.(3)处理方法:分解成相互垂直的两个方向上的直线运动,类似于平抛运动. (4)运动规律:①沿初速度方向做匀速直线运动,运动时间⎩⎨⎧:t =l v 0.:y =12at 2=qU2md t 2,t =2mdy qU②沿电场力方向,做匀加速直线运动⎩⎪⎨⎪⎧加速度:a =F m =qE m =Uqmd离开电场时的偏移量:y =12at 2=Uql 22md v 20离开电场时的偏转角:tan θ=v y v 0=Uql md v20特别提醒 带电粒子在电场中的重力问题(1)根本粒子:如电子、质子、α粒子、离子等除有说明或有明确的暗示以外,一般都不考虑重力(但并不忽略质量).(2)带电颗粒:如液滴、油滴、尘埃、小球等,除有说明或有明确的暗示以外,一般都不能忽略重力.2、带电粒子在匀强电场中偏转时的两个结论(1)不同的带电粒子从静止开始经过同一电场加速后再从同一偏转电场射出时,偏移量和偏转角总是一样的. 证明:由qU 0=12m v 20y =12at 2=12·qU 1md ·(l v 0)2tan θ=qU 1l md v 20得:y =U 1l 24U 0d ,tan θ=U 1l 2U 0d(2)粒子经电场偏转后,合速度的反向延长线与初速度延长线的交点O 为粒子水平位移的中点,即O 到偏转电场边缘的距离为l2.3、带电粒子在匀强电场中偏转的功能关系当讨论带电粒子的末速度v 时也可以从能量的角度进展求解:qU y =12m v 2-12m v 20,其中U y =Ud y ,指初、末位置间的电势差.二、练习题1、如图,一质量为m ,带电量为+q 的带电粒子,以速度v 0垂直于电场方向进入电场,关于该带电粒子的运动,如下说确的是( )A .粒子在初速度方向做匀加速运动,平行于电场方向做匀加速运动,因而合运动是匀加速直线运动B .粒子在初速度方向做匀速运动,平行于电场方向做匀加速运动,其合运动的轨迹是一条抛物线C .分析该运动,可以用运动分解的方法,分别分析两个方向的运动规律,然后再确定合运动情况D .分析该运动,有时也可用动能定理确定其某时刻速度的大小 答案BCD2、如下列图,两平行金属板A 、B 长为L =8cm ,两板间距离d =8cm ,A 板比B 板电势高300V ,一带正电的粒子电荷量为q =×10-10C ,质量为m =×10-20kg ,沿电场中心线RO 垂直电场线飞入电场,初速度v 0=×106m/s ,粒子飞出电场后经过界面MN 、PS 间的无电场区域,然后进入固定在O 点的点电荷Q 形成的电场区域(设界面PS 右侧点电荷的电场分布不受界面的影响).两界面MN 、PS 相距为12 cm ,D 是中心线RO 与界面PS 的交点,O 点在中心线上,距离界面PS 为9 cm ,粒子穿过界面PS 做匀速圆周运动,最后垂直打在放置于中心线上的荧光屏bc 上.(静电力常量k ×109 N·m 2/C 2,粒子的重力不计)(1)求粒子穿过界面MN 时偏离中心线RO 的距离多远?到达PS 界面时离D 点多远? (2)在图上粗略画出粒子的运动轨迹.(3)确定点电荷Q 的电性并求其电荷量的大小.解析(1)粒子穿过界面MN 时偏离中心线RO 的距离(侧向位移): y =12at 2 a =F m =qU dm L =v 0t如此y =12at 2=qU 2md (L v 0)2=m =3cm粒子在离开电场后将做匀速直线运动,其轨迹与PS 交于H ,设H 到中心线的距离为Y ,如此有12L 12L +12cm =yY ,解得Y =4y =12cm(2)第一段是抛物线、第二段是直线、第三段是圆弧(图略) (3)粒子到达H 点时,其水平速度v x =v 0×106m/s 竖直速度v y =at ×106m/s 如此v 合×106m/s该粒子在穿过界面PS 后绕点电荷Q 做匀速圆周运动,所以Q 带负电 根据几何关系可知半径r =15cm k qQr 2=m v 2合r 解得Q ≈×10-8C答案(1)12cm (2)见解析 (3)负电×10-8C3、如下列图,在两条平行的虚线存在着宽度为L、电场强度为E的匀强电场,在与右侧虚线相距也为L处有一与电场平行的屏.现有一电荷量为+q、质量为m的带电粒子(重力不计),以垂直于电场线方向的初速度v0射入电场中,v0方向的延长线与屏的交点为O.试求:(1)粒子从射入电场到打到屏上所用的时间;(2)粒子刚射出电场时的速度方向与初速度方向间夹角的正切值tanα;(3)粒子打在屏上的点P到O点的距离x.答案(1)2Lv0(2)qELm v20(3)3qEL22m v20解析(1)根据题意,粒子在垂直于电场线的方向上做匀速直线运动,所以粒子从射入电场到打到屏上所用的时间t=2L v.(2)设粒子刚射出电场时沿平行电场线方向的速度为v y,根据牛顿第二定律,粒子在电场中的加速度为:a=Eqm所以v y=a L v=qELm v0所以粒子刚射出电场时的速度方向与初速度方向间夹角的正切值为tanα=v y v=qELm v20. (3)解法一设粒子在电场中的偏转距离为y,如此y=12a(Lv0)2=12·qEL2m v20又x=y+L tanα,解得:x=3qEL22m v20解法二x=v y·L v+y=3qEL22m v20.解法三由xy=L+L2L2得:x=3y=3qEL22m v20.4、如下列图,虚线PQ 、MN 间存在如下列图的水平匀强电场,一带电粒子质量为m =×10-11kg 、电荷量为q =+×10-5C ,从a 点由静止开始经电压为U =100V 的电场加速后,垂直于匀强电场进入匀强电场中,从虚线MN 的某点b (图中未画出)离开匀强电场时速度与电场方向成30°角.PQ 、MN 间距为20cm ,带电粒子的重力忽略不计.求:(1)带电粒子刚进入匀强电场时的速率v 1; (2)水平匀强电场的场强大小; (3)ab 两点间的电势差.答案 (1)×104m×103 N/C (3)400V 解析 (1)由动能定理得:qU =12m v 21代入数据得v 1×104m/s(2)粒子沿初速度方向做匀速运动:d =v 1t 粒子沿电场方向做匀加速运动:v y =at 由题意得:tan30°=v 1v y由牛顿第二定律得:qE =ma 联立以上各式并代入数据得: E =3×103 N/C ≈×103 N/C(3)由动能定理得:qU ab =12m (v 21+v 2y )-0 联立以上各式并代入数据得:U ab =400V .5、如下列图,一价氢离子(11H)和二价氦离子(42He)的混合体,经同一加速电场加速后,垂直射入同一偏转电场中,偏转后,打在同一荧光屏上,如此它们( )A .同时到达屏上同一点B .先后到达屏上同一点C .同时到达屏上不同点D .先后到达屏上不同点 答案B解析一价氢离子(11H)和二价氦离子(42He)的比荷不同,经过加速电场的末速度不同,因此在加速电场与偏转电场的时间均不同,但在偏转电场中偏转距离一样,所以会先后打在屏上同一点,选B.6、如下列图,六面体真空盒置于水平面上,它的ABCD面与EFGH面为金属板,其他面为绝缘材料.ABCD面带正电,EFGH面带负电.从小孔P沿水平方向以一样速率射入三个质量一样的带正电液滴a、b、c,最后分别落在1、2、3三点.如此如下说确的是()A.三个液滴在真空盒中都做平抛运动B.三个液滴的运动时间不一定一样C.三个液滴落到底板时的速率一样D.液滴c所带电荷量最多答案D解析三个液滴具有水平速度,但除了受重力以外,还受水平方向的电场力作用,不是平抛运动,选项A错误;在竖直方向上三个液滴都做自由落体运动,下落高度又一样,故运动时间必一样,选项B错误;在一样的运动时间,液滴c水平位移最大,说明它在水平方向的加速度最大,它受到的电场力最大,电荷量也最大,选项D正确;因为重力做功一样,而电场力对液滴c做功最多,所以它落到底板时的速率最大,选项C 错误.7、绝缘光滑水平面有一圆形有界匀强电场,其俯视图如下列图,图中xOy所在平面与光滑水平面重合,电场方向与x轴正向平行,电场的半径为R=2m,圆心O与坐标系的原点重合,场强E=2N q=-1×10-5 C、质量m=1×10-5 kg的粒子,由坐标原点O处以速度v0=1 m/s沿y轴正方向射入电场(重力不计),求:(1)粒子在电场中运动的时间;(2)粒子出射点的位置坐标;(3)粒子射出时具有的动能.答案(1)1s(2)(-1m,1m)(3)×10-5J解析 (1)粒子沿x 轴负方向做匀加速运动,加速度为a ,如此有: Eq =ma ,x =12at 2沿y 轴正方向做匀速运动,有 y =v 0t x 2+y 2=R 2 解得t =1s.(2)设粒子射出电场边界的位置坐标为(-x 1,y 1),如此有 x 1=12at 2=1m ,y 1=v 0t =1m ,即出射点的位置坐标为(-1m,1m).(3)射出时由动能定理得Eqx 1=E k -12m v 20代入数据解得E k ×10-5J.8、如下列图,在正方形ABCD 区域有平行于AB 边的匀强电场,E 、F 、G 、H 是各边中点,其连线构成正方形,其中P 点是EH 的中点.一个带正电的粒子(不计重力)从F 点沿FH 方向射入电场后恰好从D 点射出.以下说确的是( )A .粒子的运动轨迹一定经过P 点B .粒子的运动轨迹一定经过PE 之间某点C .假如将粒子的初速度变为原来的一半,粒子会由ED 之间某点射出正方形ABCD 区域D .假如将粒子的初速度变为原来的一半,粒子恰好由E 点射出正方形ABCD 区域 答案BD解析粒子从F 点沿FH 方向射入电场后恰好从D 点射出,其轨迹是抛物线,如此过D 点做速度的反向延长线一定与水平位移交于FH 的中点,而延长线又经过P 点,所以粒子轨迹一定经过PE 之间某点,选项A 错误,B 正确;由平抛运动知识可知,当竖直位移一定时,水平速度变为原来的一半,如此水平位移也变为原来的一半,所以选项C 错误,D 正确.9、用等效法处理带电体在电场、重力场中的运动如下列图,绝缘光滑轨道AB 局部为倾角为30°的斜面,AC 局部为竖直平面上半径为R 的圆轨道,斜面与圆轨道相切.整个装置处于场强为E 、方向水平向右的匀强电场中.现有一个质量为m 的小球,带正电荷量为q =3mg3E,要使小球能安全通过圆轨道,在O 点的初速度应满足什么条件?图9审题与关联解析小球先在斜面上运动,受重力、电场力、支持力,然后在圆轨道上运动,受重力、电场力、轨道作用力,如下列图,类比重力场,将电场力与重力的合力视为等效重力mg ′,大小为 mg ′=(qE )2+(mg )2=2 3mg 3,tan θ=qE mg =33,得θ=30°,等效重力的方向与斜面垂直指向右下方,小球在斜面上匀速运动.因要使小球能安全通过圆轨道,在圆轨道的等效“最高点〞(D 点)满足等效重力刚好提供向心力,即有:mg ′=m v 2DR ,因θ=30°与斜面的倾角相等,由几何关系可知AD =2R ,令小球以最小初速度v 0运动,由动能定理知: -2mg ′R =12m v 2D -12m v 20 解得v 0=103gR3,因此要使小球安全通过圆轨道,初速度应满足v ≥103gR3.答案v≥103gR310、在空间中水平面MN的下方存在竖直向下的匀强电场,质量为m的带电小球由MN上方的A点以一定的初速度水平抛出,从B点进入电场,到达C点时速度方向恰好水平,A、B、C三点在同一直线上,且AB=2BC,如下列图.由此可见()A.电场力为3mgB.小球带正电C.小球从A到B与从B到C的运动时间相等D.小球从A到B与从B到C的速度变化量的大小相等答案AD解析设AC与竖直方向的夹角为θ,带电小球从A到C,电场力做负功,小球带负电,由动能定理,mg·AC·cosθ-qE·BC·cosθ=0,解得电场力为qE=3mg,选项A正确,B 错误.小球水平方向做匀速直线运动,从A到B的运动时间是从B到C的运动时间的2倍,选项C错误;小球在竖直方向先加速后减速,小球从A到B与从B到C竖直方向的速度变化量的大小相等,水平方向速度不变,小球从A到B与从B到C的速度变化量的大小相等,选项D正确.。
带电粒子在匀强电场中的偏转(解析版)

带电粒子在匀强电场中的偏转1.运动规律沿初速度方向为匀速直线运动,运动时间 vl t 0=沿电场力方向为初速度为零的匀加速直线运动,加速度:a = F/m = qU/dm 离开电场时的偏移量 222mdv qULy =离开电场时的偏转角:L ymdV qUL 2tan 2==θ2.分析带电粒子在匀强电场中的偏转问题的关键(1)条件分析:不计重力,且带电粒子的初速度v 0与电场方向垂直,则带电粒子将在电场中只受电场力作用做类平抛运动.(2)运动分析:一般用分解的思想来处理,即将带电粒子的运动分解为沿电场力方向上的匀加速直线运动和垂直电场力方向上的匀速直线运动.3.两个结论(1)不同的带电粒子从静止开始经过同一电场加速后再从同一偏转电场射出时的偏转角度总是相同的. (2)粒子经电场偏转后,合速度的反向延长线与初速度延长线的交点为粒子水平位移的中点. 【典例1】如图所示,虚线MN 左侧有一场强为E 1=E 的匀强电场,在两条平行的虚线MN 和PQ 之间存在着宽为L 、电场强度为E 2=2E 的匀强电场,在虚线PQ 右侧相距为L 处有一与电场E 2平行的屏。
现将一电子(电荷量为e ,质量为m )无初速度地放入电场E 1中的A 点,A 与虚线MN 的间距为L2,最后电子打在右侧的屏上,AO 连线与屏垂直,垂足为O ,求:(1)电子从释放到打到屏上所用的时间;(2)电子刚射出电场E 2时的速度方向与AO 连线夹角θ的正切值tan θ; (3)电子打到屏上的点P ′到点O 的距离x 。
【答案】 (1)3mLeE(2)2 (3)3L 【解析】 (1)电子在电场E 1中做初速度为零的匀加速直线运动,设加速度为a 1,时间为t 1,由牛顿第解得:tan θ=2。
(3)如图,设电子在电场E 2中的偏转距离为x 1 x 1=12a 2t 32tan θ=x 2L解得:x =x 1+x 2=3L 。
【典例2】 如图甲所示,长为L 、间距为d 的两金属板A 、B 水平放置,ab 为两板的中心线,一个带电粒子以速度v 0从a 点水平射入,沿直线从b 点射出,若将两金属板接到如图乙所示的交变电压上,欲使该粒子仍能从b 点以速度v 0射出,求:(1)交变电压的周期T 应满足什么条件?(2)粒子从a 点射入金属板的时刻应满足什么条件? 【答案】 (1)T =L nv 0,其中n 取大于等于L2dv 0qU 02m的整数 (2)t =2n -14T (n =1,2,3,…)【解析】 (1)为使粒子仍从b 点以速度v 0穿出电场,在垂直于初速度方向上,粒子的运动应为:加速,减速,反向加速,反向减速,经历四个过程后,回到中心线上时,在垂直于金属板的方向上速度正好等于零,这段时间等于一个周期,故有L =nTv 0,解得T =Lnv 0粒子在14T 内离开中心线的距离为y =12a ⎝⎛⎭⎫14T 2所以粒子的周期应满足的条件为 T =L nv 0,其中n 取大于等于L 2dv 0qU 02m的整数. (2)粒子进入电场的时间应为14T ,34T ,54T ,…故粒子进入电场的时间为t =2n -14T (n =1,2,3,…). 【跟踪短训】1.如图所示,真空中水平放置的两个相同极板Y 和Y ′长为L ,相距为d ,足够大的竖直屏与两板右侧相距b .在两板间加上可调偏转电压U YY ′,一束质量为m 、带电荷量为+q 的粒子(不计重力)从两板左侧中点A 以初速度v 0沿水平方向射入电场且能穿出.(1)证明粒子飞出电场后的速度方向的反向延长线交于两板间的中心O 点; (2)求两板间所加偏转电压U YY ′的范围; (3)求粒子可能到达屏上区域的长度.【答案】 (1)见【解析】 (2)-d 2mv 20qL 2≤U YY ′≤d 2mv 20qL 2 (3)d L +2b L【解析】 (1)设粒子在电场中的加速度大小为a ,离开偏转电场时偏转距离为y ,沿电场方向的速度为v y ,偏转角为θ,其反向延长线通过O 点,O 点与板右端的水平距离为x ,如图所示,则有y =12at 2L =v 0tv y =at ,tan θ=v y v 0=y x ,联立解得x =L2故粒子在屏上可能到达的区域的长度为 H =2y 0=d L +2bL.2. 如图甲所示,热电子由阴极飞出时的初速度忽略不计,电子发射装置的加速电压为U 0,电容器板长和板间距离均为L =10 cm ,下极板接地,电容器右端到荧光屏的距离也是L =10 cm ,在电容器两极板间接一交变电压,上极板的电势随时间变化的图象如图乙所示.(每个电子穿过平行板的时间都极短,可以认为电压是不变的)求:(1)在t =0.06 s 时刻,电子打在荧光屏上的何处. (2)荧光屏上有电子打到的区间有多长?【答案】 (1)打在屏上的点位于O 点上方,距O 点13.5 cm (2)30 cm【解析】 (1)电子经电场加速满足qU 0=12mv 2经电场偏转后侧移量y =12at 2=12·qU 偏mL ⎝⎛⎭⎫L v 2所以y =U 偏L4U 0,由图知t =0.06 s 时刻U 偏=1.8U 0,所以y =4.5 cm设打在屏上的点距O 点的距离为Y ,满足Yy =L +L 2L2所以Y =13.5 cm.(2)由题知电子侧移量y 的最大值为L2,所以当偏转电压超过2U 0,电子就打不到荧光屏上了,所以荧光屏上电子能打到的区间长为3L =30 cm.课后作业1. 喷墨打印机的简化模型如图所示,重力可忽略的墨汁微滴,经带电室带负电后,以速度v 垂直匀强电场飞入极板间,最终打在纸上,则微滴在极板间电场中( ).A .向负极板偏转B .电势能逐渐增大C .运动轨迹是抛物线D .运动轨迹与带电量无关【答案】 C2. 如图,带电粒子由静止开始,经电压为U 1的加速电场加速后,沿垂直电场方向进入电压为U 2的平行板电容器,经偏转落在下板的中间位置。
带电粒子在匀强电场中的偏转(图文课件分享)

Vx=V0 ;X=V0t
竖直y(匀加速直线):
Vy=at
;y
1 2
at 2
tan Vy at
Vx V0
例题1
一电子水平射入如图所示的电场中,射入时的速度
V0=3.0×107m/s.两极板的长度l=6.0cm,相距d=2cm, 极板间的电压U=200V.求电子射出电场时竖直偏移的
距离y和偏转的角度α.
RSI相对强弱指标
;
;ZIGZAG指标-zigzag指标下载-外汇zigzag指标怎么用
https:///zigzag/ ZIGZAG指标;
;外汇ADX指标-ADX平均趋向指数下载 https:///adx/
ADX指标;
;外汇BOLL指标-布林线BOLL指标下载 https:///boll/ 布林线BOLL指标;
;趋势EA策略-外汇趋势线EA下载
https:///qushiea/
趋势EA;
;外汇剥头皮ea-外汇剥头皮交易系统下载 https:///btpea/ 剥头皮EA;
;外汇网格型ea-外汇交易网格EA下载 https:///wgea/ 网格EA下载;
;外汇k线 /forum-83-1.html 黄金行情分析软件;
;黄金分析软件 /forum-151-1.html 黄金分析软件
;mt4正版 /forum-144-1.html mt4交易指标;
; 数字货币网 区块链;
;配资网 股票配资;
;外汇经验心得-外汇投资心得 https:///xinde/
外汇经验心得;
;每日最新外汇新闻-今日实时全球外汇新闻 https:///yaowen/
带电粒子在匀强电场中的偏转
平抛运动
专题讲座四:带电粒子在匀强电场中的偏转问题

带电粒子在匀强电场中的加速和偏转问题 一:.两个结论(1)不同的带电粒子从静止开始经过同一电场加速后再从同一偏转电场射出时的偏转角度总是相同的。
证明:由qU 0=12mv 20及tan φ=qUl mdv 20得tan φ=Ul 2U 0d (2)粒子经电场偏转后,合速度的反向延长线与初速度延长线的交点O 为粒子水平位移的中点,即O 到电场边缘的距离为l2。
二:.带电粒子在匀强电场中偏转的功能关系当讨论带电粒子的末速度v 时也可以从能量的角度进行求解:qU y =12mv 2-12mv 20,其中U y =U dy ,指初、末位置间的电势差。
三:带电粒子在电场中运动问题的两种求解思路1.运动学与动力学观点(1)运动学观点是指用匀变速运动的公式来解决实际问题,一般有两种情况:①带电粒子初速度方向与电场线共线,则粒子做匀变速直线运动;②带电粒子的初速度方向垂直电场线,则粒子做匀变速曲线运动(类平抛运动)。
(2)当带电粒子在电场中做匀变速曲线运动时,一般要采取类似平抛运动的解决方法。
2.功能观点:首先对带电体受力分析,再分析运动形式,然后根据具体情况选用公式计算。
(1)若选用动能定理,则要分清有多少个力做功,是恒力做功还是变力做功,同时要明确初、末状态及运动过程中的动能的增量。
(2)若选用能量守恒定律,则要分清带电体在运动中共有多少种能量参与转化,哪些能量是增加的,哪些能量是减少的。
四:典题分析:1 如图1所示,一电子枪发射出的电子(初速度很小,可视为零)进入加速电场加速后,垂直射入偏转电场,射出后偏转位移为Y ,要使偏转位移增大,下列哪些措施是可行的(不考虑电子射出时碰到偏转电极板的情况)( )图1A .增大偏转电压UB .增大加速电压U 0C .增大偏转极板间距离D .将发射电子改成发射负离子A2.如图所示,一束带电粒子(不计重力),垂直电场线方向进入偏转电场,试讨论在以下几种情况中,粒子应具备什么条件,才能得到相同的偏转距离y 和偏转角θ。
带电粒子在匀强电场中的偏转(PPT)4-3
+++++
F
d -q v0
φ
l/2
v⊥
+
v
φ
v0
y 运 分动析状方态法分析
沿匀初变速速度曲方线向运—动— ( 匀类速平直抛线运动)
- - -l- - -
速度: a = F = qU
m md
沿电场线方向—— 初速度为零的匀加 速直线运动
l
2.飞行时间 t = v0 3.侧移距离 y = 1 at2 =
口中金属味、腹剧痛、米汤样粪便等,较重者尿量减少、头晕、腓肠肌痉挛、发绀以至休克,严重者出现中枢神经麻痹症状,四肢疼痛性痉挛、意识消失等。 注意:皮肤癌与摄入砷和接触砷有关,肺癌与吸入砷尘有关。 [] 医护措施编辑 世界卫生组织指出,每升低于微克的砷含量对人体是安全的。 [] 急救与治疗: 催吐或洗胃,肌注 % 二巯基丙磺酸钠。 [] 危险情况 处理措施 皮肤暴露 冲洗(小孩或老人要注意不可造成失温)。 眼睛暴露 用水冲洗至少 分钟,假如可 以的话应该移除隐形眼镜。 急性暴露时应送到医院前应确保病人呼吸道畅通且有呼吸及脉搏,并与就近的毒理单位联络。 大量食入应在食入一小时内给予活 性碳(mg/Kg ,大人通常为 - mg ,小朋友通常是 -mg) 最有效,若没有呕吐也可以洗胃,此时必须确定病人意识清醒且要注意呼吸道的畅通,避免呕吐及吸 入呼吸道。因为体液的大量流失,有症状的病人必须要从静脉补充并以机器监视心脏节律,就算是没有低血压症状的病
巩固提高
[例1].让一价氢离子、一价氦离 子和二价氦离子的混合物由静止开始 经过同一加速电场加速,然后在同一 偏转电场里偏转,它们是否会分为三 股?请说明理由。
答案:不会分为三股。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
带电粒子在匀强电场中的加速和偏转问题一:.两个结论(1)不同的带电粒子从静止开始经过同一电场加速后再从同一偏转电场射出时的偏转角度总是相同的。
证明:由qU 0=12m v 20及tan φ=qUl md v 20得tan φ=Ul2U 0d(2)粒子经电场偏转后,合速度的反向延长线与初速度延长线的交点O 为粒子水平位移的中点,即O 到电场边缘的距离为l 2。
二:.带电粒子在匀强电场中偏转的功能关系当讨论带电粒子的末速度v 时也可以从能量的角度进行求解:qU y =12m v 2-12m v 20,其中U y =U d y ,指初、末位置间的电势差。
三:带电粒子在电场中运动问题的两种求解思路 1.运动学与动力学观点(1)运动学观点是指用匀变速运动的公式来解决实际问题,一般有两种情况: ①带电粒子初速度方向与电场线共线,则粒子做匀变速直线运动; ②带电粒子的初速度方向垂直电场线,则粒子做匀变速曲线运动(类平抛运动)。
(2)当带电粒子在电场中做匀变速曲线运动时,一般要采取类似平抛运动的解决方法。
2.功能观点:首先对带电体受力分析,再分析运动形式,然后根据具体情况选用公式计算。
(1)若选用动能定理,则要分清有多少个力做功,是恒力做功还是变力做功,同时要明确初、末状态及运动过程中的动能的增量。
(2)若选用能量守恒定律,则要分清带电体在运动中共有多少种能量参与转化,哪些能量是增加的,哪些能量是减少的。
四:典题分析:1 如图1所示,一电子枪发射出的电子(初速度很小,可视为零)进入加速电场加速后,垂直射入偏转电场,射出后偏转位移为Y ,要使偏转位移增大,下列哪些措施是可行的(不考虑电子射出时碰到偏转电极板的情况)( )图1A .增大偏转电压UB .增大加速电压U 0C .增大偏转极板间距离D .将发射电子改成发射负离子解析:选A 设偏转电极板长为l ,极板间距为d ,由qU 0=12m v 2,t =l v 0,y =12at 2=qU 2md t 2,得偏转位移y =Ul 24U 0d ,增大偏转电压U ,减小加速电压U 0,减小偏转极板间距离,都可使偏转位移增大,选项A 正确BC 错误;由于偏位移y =Ul 24U 0d 与粒子质量带电量无关,故将发射电子改成发射负离子,偏转位移不变,选项D 错误。
2. 如图2(a)所示,两平行正对的金属板A 、B 间加有如图9(b)所示的交变电压,一重力可忽略不计的带正电粒子被固定在两板的正中间P 处。
若在t 0时刻释放该粒子,粒子会时而向A 板运动,时而向B 板运动,并最终打在A 板上。
则t 0可能属于的时间段是( )图2A .0<t 0<T4 B.T 2<t 0<3T 4 C.3T4<t 0<TD .T <t 0<9T8解析:选B 两板间加的是方波电压,刚释放粒子时,粒子向A 板运动,说明释放粒子时U AB 为负,因此A 项错误,若t 0=T2时刻释放粒子,则粒子做方向不变的单向直线运动,一直向A 运动;若t 0=3T4时刻释放粒子,则粒子在电场中固定两点间做往复运动,不能到达A 板;因此T 2<t 0<3T4时间内,粒子的运动满足题意的要求,选项B 正确。
3如图3所示,一价氢离子(11H)和二价氦离子(24He)的混合体,经同一加速电场加速后,垂直射入同一偏转电场中,偏转后,打在同一荧光屏上,则它们( )图3A .同时到达屏上同一点B .先后到达屏上同一点C .同时到达屏上不同点D .先后到达屏上不同点解析:选B 一价氢离子(11H)和二价氦离子(24He)的比荷不同,经过加速电场的末速度不同,因此在加速电场及偏转电场的时间均不同,但在偏转电场中偏转距离相同,所以会打在同一点。
选B 。
4. 如图4所示,矩形区域ABCD 内存在竖直向下的匀强电场,两个带正电的粒子a 和b 以相同的水平速度射入电场,粒子a 由顶点A 射入,从BC 的中点P 射出,粒子b 由AB 的中点O 射入,从顶点C 射出。
若不计重力,则a 和b 的比荷(即粒子的电荷量与质量之比)是( )图4A .1∶2B .2∶1C .1∶8D .8∶1解析:选D 两粒子在电场中均做类平抛运动,则有沿初速度方向:x =v 0t ,垂直于初速度方向:y =12·qE m t 2,即y =12qE m ·x 2v 20,则有q a m a ∶q b m b =y a y b ·x 2b x 2a =21×221=8∶1,D 项正确。
5.如图3所示,一对半径均为R 1的金属板M 、N 圆心正对平行放置,两板距离为d ,N 板中心镀有一层半径为R 2的圆形锌金属薄膜,d ≪R 2<R 1,两板之间电压为U MN ,两板之间真空且可视为匀强电场。
N 板受到某种单色光照射后锌金属薄膜表面会发射出最大速率为v ,方向各异的电子,已知电子的电荷量为e ,质量为m ,每秒稳定发射n 个电子。
电子在板间运动过程中无碰撞且不计电子的重力和电子间相互作用,电子到达M 板全部被吸收。
M 板右侧串联的电流表可以测量到通过M 板的电流I 。
试求:图5(1)当U MN 取什么值时,I 始终为零;(2)当U MN 取什么值时,I 存在一个最大值,并求这个最大值; (3)请利用(1)(2)的结论定性画出I 随U MN 变化的图象。
解析:(1)当垂直N 板发射速度为v 的电子不能到达M 板时,I =0, 令此时两板间电压为U MN ,则12m v 2=-eU MN 得U MN =-m v 22e(2)当从锌膜边缘平行N 板射出的电子做类平抛运动刚好能到达M 板边缘时,则所有电子均能到达M 板,电流最大I =ne令此时两板间电压为U MN ′ R 1-R 2=v t , d =12at 2,a =U MN ′e dm得U MN ′=2md 2v 2e (R 1-R 2)2(3)I 随U MN 变化的图象如图所示。
答案:(1)-m v 22e (2)2md 2v 2e (R 1-R 2)2ne (3)见解析图6.如图6所示,真空中水平放置的两个相同极板Y 和Y ′长为L ,相距为d ,足够大的竖直屏与两板右侧相距为b 。
在两板间加上可调偏转电压U ,一束质量为m 、带电荷量为+q 的粒子(不计重力)从两板左侧中点A 以初速度v 0沿水平方向射入电场且能穿出。
图6(1)证明粒子飞出电场后的速度方向的反向延长线交于两板间的中心O 点; (2)求两板间所加偏转电压U 的范围; (3)求粒子可能到达屏上区域的长度。
解析:(1)设粒子在运动过程中的加速度大小为a ,离开偏转电场时偏转距离为y ,沿电场方向的速度为v y ,偏转角为θ,其反向延长线通过O 点,O 点与板右端的水平距离为x ,则有y =12at 2① L =v 0t ② v y =attan θ=v yv0=yx,联立可得x=L2,即粒子飞出电场后的速度方向的反向延长线交于两板间的中心。
(2)a=Eq m③E=U d④由①②③④式解得y=qUL22dm v20当y=d2时,U=md2v20qL2则两板间所加电压的范围-md2v20qL2≤U≤md2v20qL2(3)当y=d2时,粒子在屏上侧向偏移的距离最大(设为y0),则y0=(L2+b)tan θ而tan θ=dL,解得y0=d(L+2b)2L则粒子可能到达屏上区域的长度为d(L+2b)L。
答案:(1)见解析(2)-md2v20qL2≤U≤md2v20qL2(3)d(L+2b)L7 如图7所示直流电源的路端电压U=182V。
金属板AB、CD、EF、GH相互平行、彼此靠近。
它们分别和变阻器上的触点a、b、c、d连接。
变阻器上ab、bc、cd段电阻之比为1∶2∶3。
孔O1正对B和E,孔O2正对D和G。
边缘F、H正对。
一个电子以初速度v0=4×106m/s沿AB方向从A点进入电场,恰好穿过孔O1和O2后,从H点离开电场。
金属板间的距离L1=2 cm,L2=4 cm,L3=6 cm。
电子质量m e=9.1×10-31 kg,电量q=1.6×10-19C。
正对两平行板间可视为匀强电场,求:图7(1)各相对两板间的电场强度。
(2)电子离开H 点时的动能。
(3)四块金属板的总长度(AB +CD +EF +GH )。
[尝试解题](1)三对正对极板间电压之比U 1∶U 2∶U 3=R ab ∶R bc ∶R cd =1∶2∶3。
板间距离之比L 1∶L 2∶L 3=1∶2∶3 故三个电场场强相等E =UL 1+L 2+L 3=1 516.67 N/C(2)根据动能定理 eU =12m v 2-12m v 20 电子离开H 点时动能E k =12m v 20+e U =3.64×10-17 J (3)由于板间场强相等,则电子在竖直方向受电场力不变,加速度恒定可知电子做类平抛运动:“竖直方向”L 1+L 2+L 3=12qE m t 2 “水平方向”x =v 0t 消去t 解得x =0.12 m极板总长AB +CD +EF +GH =2x =0.24 m 。
[答案] (1)1 516.67 N/C (2)3.64×10-17 J (3)0.24 m8 如图8所示,带电粒子P 所带的电荷量是带电粒子Q 的3倍,它们以相等的速度v 0从同一点出发,沿着跟电场强度垂直的方向射入匀强电场,分别打在M 、N 点,若OM =MN ,则P 和Q 的质量之比为( )图8A .3∶4B .4∶3C .3∶2D .2∶3解析:选A 本题忽略了粒子重力的影响,P 和Q 在匀强电场中做类平抛运动,它们沿水平方向均以初速度v 0做匀速直线运动,根据OM =MN ,可知,它们沿竖直方向的下落时间之比为t P ∶t Q =1∶2;根据h =12at 2可得a =2ht 2,可见,它们沿竖直方向下落的加速度之比为a P ∶a Q =4∶1;根据a =Eq m 可得m =Eq a ∝qa ,所以m P m Q =q P q Q ·a Q a P=3×14=34,所以选项A 正确,答案为A 。
9.如图9所示为说明示波器工作原理的示意图,已知两平行板间的距离为d 、板长为l 电子经电压为U 1的电场加速后从两平行板间的中央处垂直进入偏转电场,设电子质量为m e 、电荷量为e 。
图9(1)求经电场加速后电子速度v 的大小;(2)要使电子离开偏转电场时的偏转角度最大,两平行板间的电压U 2应是多少?电子动能多大?解析:(1)电子经电压为U 1的电场加速,根据动能定理:eU 1=12m e v 2,则经电场加速后电子的速度v =2eU 1m e 。
