垂径定理典型例题总结
垂径定理练习题及答案

垂径定理练习题及答案一、选择题1. 在一个圆中,如果一条直径的端点与圆上一点相连,这条线段的中点与圆心的距离是直径的()A. 一半B. 半径B. 直径D. 无法确定2. 垂径定理指出,如果一条线段是圆的直径,那么它与圆上任意一点连线所形成的直角三角形的斜边是()A. 直径B. 半径C. 线段D. 无法确定3. 圆内接四边形的对角线互相平分,且其中一条对角线是圆的直径,那么这个四边形是()A. 平行四边形B. 矩形C. 菱形D. 无法确定4. 如果圆的半径为r,那么圆的直径是()A. 2rB. rC. r的平方D. 2r的平方二、填空题1. 垂径定理告诉我们,如果一条线段是圆的直径,那么它与圆上任意一点连线所形成的直角三角形的斜边是______。
2. 圆的内接四边形中,如果对角线互相平分,且其中一条对角线是圆的直径,那么这个四边形的对角线长度相等,等于______。
3. 已知圆的半径为5cm,那么圆的直径是______。
三、解答题1. 已知一个圆的半径为7cm,圆内有一点P,连接点P和圆心O,得到线段OP。
如果OP的长度为4cm,求点P到圆上任意一点的距离。
2. 一个圆的直径为14cm,圆内接四边形ABCD,其中AC为直径。
已知AB=6cm,求BC的长度。
四、证明题1. 证明:如果一个三角形是直角三角形,且斜边是圆的直径,那么这个三角形的外接圆的直径是这个三角形的斜边。
2. 证明:如果一个圆的内接四边形的对角线互相平分,且其中一条对角线是圆的直径,那么这个四边形的对角线长度相等。
答案:一、选择题1. A2. A3. B4. A二、填空题1. 直径的一半2. 圆的直径3. 10cm三、解答题1. 点P到圆上任意一点的距离是3cm(利用勾股定理,OP为直角三角形的一条直角边,半径为斜边,另一直角边为点P到圆上任意一点的距离)。
2. BC的长度是8cm(利用圆内接四边形的性质,对角线互相平分,且AC是直径,所以BD=7cm,再利用勾股定理求BC)。
专题24.3 垂径定理【十大题型】(人教版)(原卷版)

专题24.3 垂径定理【十大题型】【人教版】【题型1 利用垂径定理求线段长度】 (1)【题型2 利用垂径定理求角度】 (2)【题型3 利用垂径定理求最值】 (3)【题型4 利用垂径定理求取值范围】 (4)【题型5 利用垂径定理求整点】 (6)【题型6 利用垂径定理求面积】 (7)【题型7 垂径定理在格点中的运用】 (8)【题型9 垂径定理与分类讨论中的综合运用】 (10)【题型10 垂径定理的应用】 (11)【题型1 利用垂径定理求线段长度】【例1】(2022•雨花区校级开学)如图,⊙O的半径OD⊥弦AB交AB于点C,连接AO并延长交⊙O于点E,连接EC.若AB=8,EC=2√13,则CD的长为()A.1B.3C.2D.4【变式1-1】(2022•宁津县二模)如图,已知圆O的半径为10,AB⊥CD,垂足为P,且AB=CD=16,则OP的长为()A.6B.6√2C.8D.8√2【变式1-2】(2022•建华区二模)如图,⊙O的直径AB与弦CD相交于点E,若AE=5,EB=1,∠AEC =30°,则CD的长为()A.5B.2√3C.4√2D.2√2+√3+1【变式1-3】(2022春•徐汇区校级期中)如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦AB于点E,且CE=CB,若BE=2AE,CD=5,那么⊙O的半径为.【题型2 利用垂径定理求角度】【例2】(2022•泰安模拟)如图,⊙O的半径OA,OB,且OA⊥OB,连接AB.现在⊙O上找一点C,使OA2+AB2=BC2,则∠OAC的度数为()A.15°或75°B.20°或70°C.20°D.30°̂上的【变式2-1】(2022秋•天心区期中)如图,已知⊙O半径OA=4,点B为圆上的一点,点C为劣弧AB一动点,CD⊥OA,CE⊥OB,连接DE,要使DE取得最大值,则∠AOB等于()A.60°B.90°C.120°D.135°【变式2-2】(2022秋•青田县期末)如图,在⊙O中,半径OC过弦AB的中点E,OC=2,OE=√2.(1)求弦AB的长;(2)求∠CAB的度数.【变式2-3】(2022秋•开州区期末)如图,在⊙O中,弦BC与半径OA垂直于点D,连接AB、AC.点E 为AC的中点,连接DE.(1)若AB=6,求DE的长;(2)若∠BAC=100°,求∠CDE的度数.【题型3 利用垂径定理求最值】【例3】(2022•威海模拟)⊙O中,点C为弦AB上一点,AB=1,CD⊥OC交⊙O于点D,则线段CD的最大值是()A.12B.1C.32D.2【变式3-1】(2022•河北模拟)如图所示,在⊙O中,AB为弦,OC⊥AB交AB于点D.且OD=DC.P为⊙O上任意一点,连接P A,PB,若⊙O的半径为1,则S△P AB的最大值为()A.1B.2√33C.3√34D.3√32【变式3-2】(2022秋•龙凤区校级期末)如图,矩形ABCD中,AB=20,AD=15,P,Q分别是AB,AD 边上的动点,PQ=16,以PQ为直径的⊙O与BD交于点M,N,则MN的最大值为.【变式3-3】(2022秋•延平区校级期末)在Rt△ABC中,∠C=90°,BC=3,AC=4,D、E分别是AC、BC上的一点,且DE=3,若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为()A.910B.65C.85D.125【题型4 利用垂径定理求取值范围】【例4】(2022•包河区校级二模)如图,在⊙O中,直径AB=10,CD⊥AB于点E,CD=8.点F是弧BC 上动点,且与点B、C不重合,P是直径AB上的动点,设m=PC+PF,则m的取值范围是()A.8<m≤4√5B.4√5<m≤10C.8<m≤10D.6<m<10【变式4-1】(2022•佛山)如图,⊙O的直径为10cm,弦AB=8cm,P是弦AB上的一个动点,求OP的长度范围.【变式4-2】(2022秋•盐都区校级月考)如图,点P是⊙O内一定点.(1)过点P作弦AB,使点P是AB的中点(不写作法,保留作图痕迹);(2)若⊙O的半径为13,OP=5,①求过点P的弦的长度m范围;②过点P的弦中,长度为整数的弦有条.【变式4-3】(2022秋•天河区校级期中)已知⊙O的半径为5,点O到弦AB的距离OH=3,点P是圆上一动点,设过点P且与AB平行的直线为l,记直线AB到直线l的距离为d.(1)求AB的长;(2)如果点P只有两个时,求d的取值范围;(3)如果点P有且只有三个时,求连接这三个点所得到的三角形的面积.【题型5 利用垂径定理求整点】【例5】(2022•山海关区一模)已知⊙O的直径CD=10,CD与⊙O的弦AB垂直,垂足为M,且AM=4.8,则直径CD上的点(包含端点)与A点的距离为整数的点有()A.1个B.3个C.6个D.7个【变式5-1】(2022秋•新昌县期末)如图,AB是⊙O的弦,OC⊥AB于点C,连接OB,点P是半径OB上任意一点,连接AP,若OB=5,OC=3,则AP的长不可能是()A.6B.7C.8D.9【变式5-2】(2022•桥西区校级模拟)如图,AB是⊙C的弦,直径MN⊥AB于点O,MN=10,AB=8,如图以O为原点建立坐标系.我们把横纵坐标都是整数的点叫做整数点,则线段OC长是3,⊙C上的整数点有个.【变式5-3】(2022秋•肇东市期末)已知⊙O的半径为5,点O到弦AB的距离为3,则⊙O上到弦AB所在直线的距离为2的点有()A.4个B.3个C.2个D.1个【题型6 利用垂径定理求面积】【例6】(2022•武汉模拟)如图,在半径为1的⊙O中有三条弦,它们所对的圆心角分别为60°,90°,120°,那么以这三条弦长为边长的三角形的面积是()A.√2B.1C.√32D.√22【变式6-1】(2022秋•黄州区校级月考)如图,矩形MNGH的四个顶点都在⊙O上,顺次连接矩形各边的中点,得到菱形ABCD,若BD=12,DF=4,则菱形ABCD的面积为.【变式6-2】(2022秋•西城区校级期中)如图,AB为⊙O直径,过点O作OD⊥BC于点E,交⊙O于点D,CD∥AB.(1)求证:E为OD的中点;(2)若CB=6,求四边形CAOD的面积.【变式6-3】(2022•新洲区模拟)如图,点A,C,D均在⊙O上,点B在⊙O内,且AB⊥BC于点B,BC ⊥CD于点C,若AB=4,BC=8,CD=2,则⊙O的面积为()A.125π4B.275π4C.125π9D.275π9【题型7 垂径定理在格点中的运用】【例7】(2022秋•襄都区校级期末)如图所示,一圆弧过方格的格点AB,试在方格中建立平面直角坐标系,使点A的坐标为(0,4),则该圆弧所在圆的圆心坐标是()A.(﹣1,2)B.(1,﹣1)C.(﹣1,1)D.(2,1)【变式7-1】(2022春•海门市期中)如图所示,⊙P过B、C两点,写出⊙P上的格点坐标.【变式7-2】(2022•商城县三模)如图所示的网格中,每个小正方形的边长均为1,点A、B、C均在小正方形的顶点上,点C同时也在AB̂上,若点P是BĈ的一个动点,则△ABP面积的最大值是.【变式7-3】(2017秋•靖江市校级月考)如图,在单位长度为1的正方形网格中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格图中进行下列操作(以下结果保留根号):(1)利用网格作出该圆弧所在圆的圆心D点的位置,并写出D点的坐标为;(2)连接AD、CD,则⊙D的半径为,∠ADC的度数.【题型8 垂径定理在坐标系中的运用】【例8】(2022•博山区一模)如图,在平面直角坐标系中,半径为5的⊙E与y轴交于点A(0,﹣2),B (0,4),与x轴交于C,D,则点D的坐标为()A.(4−2√6,0)B.(−4+2√6,0)C.(−4+√26,0)D.(4−√26,0)【变式8-1】(2022秋•西林县期末)如图,⊙P与y轴交于点M(0,﹣4),N(0,﹣10),圆心P的横坐标为﹣4.则⊙P的半径为()A.3B.4C.5D.6【变式8-2】(2022•印江县三模)如图,直线l为y=x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1,以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2,以原点O为圆心,OB2长为半径画圆弧交x轴于点A3;…,按此作法进行下去,则点A2022的坐标为.【变式8-3】(2015•宜春模拟)如图,半径为5的⊙P与y轴交于点M(0,﹣4),N(0,﹣10),函数y =﹣2x+m图象过点P,则m=.【题型9 垂径定理与分类讨论中的综合运用】【例9】(2022秋•化德县校级期末)⊙O的半径为10cm,弦AB∥CD,且AB=12cm,CD=16cm,则AB 和CD的距离为()A.2cm B.14cm C.2cm或14cm D.10cm或20cm【变式9-1】(2022•包河区二模)已知圆O的半径为5,弦AB=8,D为弦AB上一点,且AD=1,过点D 作CD⊥AB,交圆O于C,则CD长为()A.1B.7C.8或1D.7或1【变式9-2】(2022秋•方正县期末)如图,⊙O的弦AB与半径OC垂直,点D为垂足,OD=DC,AB=2√3,点E在⊙O上,∠EOA=30°,则△EOC的面积为.【变式9-3】(2022秋•淮南月考)如图,已知⊙O的半径为2.弦AB的长度为2,点C是⊙O上一动点,若△ABC为等腰三角形,则BC2的长为.【题型10 垂径定理的应用】【例10】(2022秋•武昌区校级期末)某地有一座圆弧形拱桥,它的跨度(弧所对的弦的长)24m,拱高(弧的中点到弦的距离)4米,则求拱桥的半径为()A.16m B.20m C.24m D.28m【变式10-1】(2022•望城区模拟)《九章算术》是我国古代著名数学经典,其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深1寸,锯道长1尺.如图,已知弦AB=1尺,弓形高CD=1寸,(注:1尺=10寸)问这块圆柱形木材的直径是()A.13寸B.6.5寸C.26寸D.20寸【变式10-2】(2022秋•西城区校级期中)京西某游乐园的摩天轮采用了国内首创的横梁结构,风格更加简约.如图,摩天轮直径88米,最高点A距离地面100米,匀速运行一圈的时间是18分钟.由于受到周边建筑物的影响,乘客与地面的距离超过34米时,可视为最佳观赏位置,在运行的一圈里最佳观赏时长为分钟.【变式10-3】(2022•浙江)如图,公园内有一个半径为20米的圆形草坪,A,B是圆上的点,O为圆心,̂,一部分市民为走“捷径”,踩坏了花草,走出了一条小路AB.通∠AOB=120°,从A到B只有路AB过计算可知,这些市民其实仅仅少走了步(假设1步为0.5米,结果保留整数).(参考数据:√3≈1.732,π取3.142)。
垂径定理及垂径定理

垂径定理及圆周角一、关于垂径定理例题1、(2013•舟山)如图,⊙O 的半径OD⊥弦AB 于点C ,连结AO 并延长交⊙O 于点E ,连结EC .若AB=8,CD=2,则EC 的长为( )【变式练习】1(2013•徐州)如图,AB 是⊙O 的直径,弦CD⊥AB,垂足为P .若CD=8,OP=3,则⊙O 的半径为( )【变式练习】2、(2013•温州)如图,在⊙O 中,OC⊥弦AB 于点C ,AB=4,OC=1,则OB 的长是( )例题2、(2013•潍坊)如图,⊙O 的直径AB=12,CD 是⊙O 的弦,CD⊥AB,垂足为P ,且BP :AP=1:5,则CD 的长为( )【变式练习-相似】1、如图.Rt△ABC 内接于⊙O,BC 为直径,AB=4,AC=3,D 是弧AD 的中点,CD 与AB 的交点为E ,则DECE 等于( )【变式练习】2(2013•南宁)如图,AB 是⊙O 的直径,弦CD 交AB 于点E ,且AE=CD=8,∠BAC=21∠BOD,则⊙O 的半径为( ) 【变式练习】3在半径为13的⊙O 中,弦AB∥CD,弦AB 和CD 的距离为7,若AB=24,则CD 的长为( )例题3、如图,以M (-5,0)为圆心、4为半径的圆与x 轴交于A 、B 两点,P 是⊙M 上异于A 、B 的一动点,直线PA 、PB 分别交y 轴于C 、D ,以CD 为直径的⊙N 与x 轴交于E 、F ,则EF 的长( )【变式练习】1、已知⊙O 的直径CD=10cm ,AB 是⊙O 的弦,AB⊥CD,垂足为M ,且AB=8cm ,则AC 的长为( )【变式练习】2如图所示,在圆⊙O 内有折线OABC ,其中OA=8,AB=12,∠A=∠B=60°,则BC 的长为二、关于圆周角、圆心角:【例题1】如图, 弧AB 是半圆,O 为AB 中点,C 、D 两点在弧AB 上,且AD ∥OC ,连接BC 、BD .若弧CD=62°,则弧AD 的度数为( )【变式练习1】如图,半圆O 的直径AB=10cm ,弦AC=6cm ,AD 平分∠BAC,则AD 的长为( )【变式练习2】如图,△ABC 的外接圆上,AB ,BC ,CA 三弧的度数比为12:13:11.自劣弧BC 上取一点D ,过D 分别作直线AC ,直线AB 的平行线,且交弧BC 于E ,F 两点,则∠EDF 的度数为( )【例题2】(2012•淄博)如图,AB ,CD 是⊙O 的弦,AB ⊥CD ,BE 是⊙O 的直径.若AC=3,则DE=___________.【变式练习1】(2013•自贡)如图,边长为1的小正方形网格中,⊙O 的圆心在格点上,则∠AED 的余弦值是_______.【变式练习2】(2012•玉林)如图,矩形OABC 内接于扇形MON ,当CN=CO 时,∠NMB 的度数是【例题3】(2013•德阳)如图,在⊙O 上有定点C 和动点P ,位于直径AB 的异侧,过点C 作CP 的垂线,与PB 的延长线交于点Q ,已知:⊙O 半径为25 ,tan ∠ABC=43,则CQ 的最大值是( )【变式练习1】(2012•兰州)如图,AB是⊙O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发沿着A→B→A方向运动,设运动时间为t(s)(0≤t<3),连接EF,当△BEF是直角三角形时,t(s)的值为()【变式练习2】如图,已知⊙O的半径为1,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB 于点M,则sin∠CBD的值等于()A.OM的长 B.2OM的长 C.CD的长 D.2CD的长【变式练习3】如图,MN是⊙O的直径,MN=2,点A在⊙O上,∠AMN=30°,B为弧线、AN 的中点,P是直径MN上一动点,则PA+PB的最小值为()【课堂作业】1、如图所示,矩形ABCD与⊙O相交于M、N、F、E,若AM=2,DE=1,EF=8,则MN的长为()2、如图,点A,B是⊙O上两点,AB=10,点P是⊙O上的动点(P与A,B不重合),连接AP,PB,过点O分别作OE⊥AP于E,OF⊥PB于F,则EF=______。
九上 圆 垂径定理 知识点+例题+练习 5种题型 (分类全面)

1.如图,⊙O 的直径为10,圆心O 到弦AB 的距离OM 的长为3,那么弦AB 的长是( )A .4B .6C .7D .82.在半径为12 cm 的圆中,垂直平分半径的弦的长为( )cmA 、33B 、27C 、123D 、633.已知AB 是⊙O 的弦,OC ⊥AB ,C 为垂足,若OA=2, OC=1,则AB 的长为( )A 、5B 、25C 、3D 、234.如图,⊙O 的直径AB 垂直于弦CD ,垂足为E ,若∠COD =120°,OE =3厘米,则CD = 厘米O图 4ED C BA5.半径为6cm 的圆中,垂直平分半径OA 的弦长为 cm.6.如图,AB 为⊙O 的弦,⊙O 的半径为5,OC ⊥AB 于点D ,交⊙O 于点C , 且CD=l ,则弦AB 的长是7.如图,直径是50cm 圆柱形油槽装入油后,油深CD 为15cm ,求油面宽度AB题型二:求半径(直径)1.如图,O ⊙的直径AB 垂直弦CD 于P ,且P 是半径OB 的中点,6cm CD ,则直径AB 的长是( )A .23cmB .32cmC .42cmD .43cm2.如图,是一个隧道的截面,如果路面AB 宽为8米,净高CD 为8米,那么这个隧道所在圆的半径OA 是___________米OD A BCDOB C A3.如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB 于点D。
已知:AB=24cm,CD=8cm(1)求作此残片所在的圆(不写作法,保留作图痕迹);(2)求(1)中所作圆的半径.ACD B题型三:求弦心距1.如图,⊙O的半径为5,弦AB的长为8,M是弦AB上的一个动点,则线段OM 长的最小值为()A.2 B.3 C.4 D.52.过⊙O内一点M的最长弦为10 cm,最短弦长为8cm,则OM的长为()A.9cm B.6cm C.3cm D.cm413.在直径为20cm的圆中,弦AB的长为16cm,则它的弦心距为 cm 4.在半径为13cm的圆中有一条长为24cm的弦,那么这条弦的弦心距等于5.过⊙O内一点M的最长的弦长为6cm,最短的弦长为4cm,则OM的长等于 cm 题型四:求拱高1.如图,某公园的一座石拱桥是圆弧形(劣弧),其跨度为24米,拱的半径为13米,则拱高为( )A.5米 B.8米 C.7米 D.53米2.某蔬菜基地的圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则中间柱CD的高度为 m3.一根横截面为圆形的下水管道的直径为1米,管内有少量的污水(如图),此时的水面宽AB为0.6米.(1)求此时的水深(即阴影部分的弓形高);0.1(2)当水位上升到水面宽为0.8米时,求水面上升的高度. 0.1或0.7OA B题型五:求两平行线间距离1、⊙O的半径为5cm,弦AB//CD,且AB=8cm,CD=6cm,则AB与CD之间的距离是多少1或7垂径定理在实际中的应用例1、某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4,求这个圆形截面的半径.A B例2.某地有一座圆弧形拱桥,桥下水面宽度为7.2 m,拱顶高出水面2.4 m,现有一艘宽3m、船舱顶部高出水面 2 m 的货船要经过这里,此货船能顺利通过这座拱桥吗?写出你的结论,并说明理由。
圆垂径定理综合应用六十道经典题(答案解析)

(1)这条公路上的车辆形成的噪音是否会对学校造成影响?
(2)若车辆形成的噪音会对学校造成影响,为消除噪音,计划在公路边修筑一段消音墙,请你计算消音墙的长度.(只考虑声音的直线传播)
37.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,连接AC、BC,若∠BAC=30º,CD=6cm.
(1)求∠BCD的度数;
(2)求⊙O的直径.
38.如图,AC为⊙O的直径,CD为⊙O的弦,BE⊥CD于点E, = .
(1)求证:BE的⊙O切线.Fra bibliotek(2)若AD=4,EC=1,求BD的长.
39.如图,A,B,C是⊙O上的点,其中 ,过点B画BD⊥OC于点D.
C.若△BCD是等腰三角形,则△ACD也是等腰三角形
D.若PB=4PA,则CD=PB
3.如图,在 中, , 为互相垂直且相等的两条弦, , ,垂足分别为 , ,若 ,则 的半径是()
A. B. C. D.
4.如图, 的直径为10,弦 , 是 上一个动点,则 的最小值为()
A.2B.3C.4D.5
5.如图是一个圆弧形门拱,拱高 ,跨度 ,那么这个门拱的半径为()
A. B. C. D.
11.平面直角坐标系中,在以(2,1)为圆心,5为半径的圆上的点的坐标是()
A.(4,7)B.(-1,-2)C.(5,4)D.(2,-4)
12.如图,⊙O的半径OA=8,以A为圆心,OA为半径的弧交⊙O于B,C点,则BC=( )
A. B. C. D.
13.如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,AC=4,则OD的长为( )
垂径定理典型例题及练习(供参考)

典型例题分析:例题1、 基本概念1.下面四个命题中正确的一个是( )A .平分一条直径的弦必垂直于这条直径B .平分一条弧的直线垂直于这条弧所对的弦C .弦的垂线必过这条弦所在圆的圆心D .在一个圆内平分一条弧和它所对弦的直线必过这个圆的圆心2.下列命题中,正确的是( ).A .过弦的中点的直线平分弦所对的弧B .过弦的中点的直线必过圆心C .弦所对的两条弧的中点连线垂直平分弦,且过圆心D .弦的垂线平分弦所对的弧例题2、垂径定理1、 在直径为52cm 的圆柱形油槽内装入一些油后,截面如图所示,如果油的最大深度为16cm ,那么油面宽度AB 是________cm.2、在直径为52cm 的圆柱形油槽内装入一些油后,,如果油面宽度是48cm ,那么油的最大深度为________cm.3、如图,已知在⊙O 中,弦CD AB =,且CD AB ⊥,垂足为H ,AB OE ⊥于E ,CD OF ⊥于F .(1)求证:四边形OEHF 是正方形.(2)若3=CH ,9=DH ,求圆心O 到弦AB 和CD 的距离.4、已知:△ABC 内接于⊙O ,AB=AC ,半径OB=5cm ,圆心O 到BC 的距离为3cm ,求AB 的长.5、如图,F 是以O 为圆心,BC 为直径的半圆上任意一点,A 是的中点,AD ⊥BC 于D ,求证:AD=21BF.O A E F例题3、度数问题1、已知:在⊙O中,弦cm12=AB,O点到AB的距离等于AB的一半,求:AOB∠的度数和圆的半径.2、已知:⊙O的半径1=OA,弦AB、AC的长分别是2、3.求BAC∠的度数。
例题4、相交问题如图,已知⊙O的直径AB和弦CD相交于点E,AE=6cm,EB=2cm,∠BED=30°,求CD的长.例题5、平行问题在直径为50cm的⊙O中,弦AB=40cm,弦CD=48cm,且AB∥CD,求:AB与CD之间的距离.例题6、同心圆问题如图,在两个同心圆中,大圆的弦AB,交小圆于C、D两点,设大圆和小圆的半径分别为ba,.求证:22baBDAD-=⋅.例题7、平行与相似已知:如图,AB是⊙O的直径,CD是弦,于CDAE⊥E,CDBF⊥于F.求证:FDEC=.A BDCEO作 业:一、概念题1.下列命题中错误的有()(1)弦的垂直平分线经过圆心(2)平分弦的直径垂直于弦(3)梯形的对角线互相平分(4)圆的对称轴是直径A .1个B .2个C .3个D .4个2、⊙O 的直径为10,弦AB 的长为8,M 是弦AB 上的动点,则OM 的长的取值范围是( )(A )5OM 3≤≤ (B )5OM 4≤≤(C )5OM 3<< (D )5OM 4<<3.如图,如果AB 为⊙O 直径,弦AB CD ⊥,垂足为E ,那么下列结论中错误的是( )A .DE CE =B .C .BAD BAC ∠=∠ D .AD AC >4.如图,AB 是⊙O 直径,CD 是⊙O 的弦,CD AB ⊥于E ,则图中不大于半圆的相等弧有( )对。
(附答案)《垂径定理》典型例题

《垂径定理》典型例题例1. 选择题:(1)下列说法中,正确的是()A. 长度相等的弧是等弧B. 两个半圆是等弧C. 半径相等的弧是等弧D. 直径是圆中最长的弦答案:D(2)下列说法错误的是()A. 圆上的点到圆心的距离相等B. 过圆心的线段是直径C. 直径是圆中最长的弦D. 半径相等的圆是等圆答案:B例2. 如图,已知AB是⊙O的直径,M、N分别是AO、BO的中点,CM⊥AB,DN⊥AB。
分析:要证弧相等,可证弧所对的弦相等,也可证弧所对的圆心角相等。
证明:连结OC、OD∵M、N分别是OA、OB的中点∵OA=OB,∴OM=ON又CM⊥AB,DN⊥AB,OC=OD∴Rt△OMC≌Rt△OND∴∠AOC=∠BOD例3. 在⊙O中,弦AB=12cm,点O到AB的距离等于AB的一半,求∠AOB 的度数和圆的半径。
分析:根据O到AB的距离,可利用垂径定理解决。
解:过O点作OE⊥AB于E∵AB=12由垂径定理知:∴△ABO为直角三角形,△AOE为等腰直角三角形。
例4. 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,以点C为圆心,CA 为半径的圆与AB、BC分别交于点D、E。
求AB、AD的长。
分析:求AB较简单,求弦长AD可先求AF。
解:过点C作CF⊥AB于F∵∠C=90°,AC=3,BC=4∵∠A=∠A,∠AFC=∠ACB∴△AFC∽△ACB例5. 如图,⊙O中,弦AB=10cm,P是弦AB上一点,且PA=4cm,OP=5cm,求⊙O的半径。
分析:⊙O中已知弦长求半径,通常作弦心距构造直角三角形,利用勾股定理求解。
解:连OA,过点O作OM⊥AB于点M∵点P在AB上,PA=4cm即⊙O的半径为7cm。
例6. 如图“五段彩虹展翅飞”是某省利用国债资金修建的横跨渡江的琼洲大桥已正式通车,该桥的两边均有五个红色的圆拱,最高的圆拱的跨度为110米,拱高为22米,求这个圆拱所在圆的直径。
圆中垂径定理综合应用(3大类题型)(含解析)

圆中垂径定理综合应用(3大类题型)重难点题型归纳【题型1直接运用勾股定理求线段】【题型2勾股定理与方程综合求线段】【题型3垂径定理在实际中应用】满分必练【题型1直接运用勾股定理求线段】1(2023•大连模拟)如图所示,在⊙O中,直径AB=10,弦DE⊥AB于点C,连接DO.若OC:OB =3:5,则DE的长为()A.3B.4C.6D.82(2023•杭州模拟)如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则AE= ( )cm.A.8B.5C.3D.23(2023•宜昌)如图,OA,OB,OC都是⊙O的半径,AC,OB交于点D.若AD=CD=8,OD=6,则BD的长为()A.5B.4C.3D.24(2023•金寨县校级模拟)如图,AB是⊙O的直径,弦CD⊥AB于点E,若CD=6,AB=10,则AE 的长为()A.1B.2C.3D.45(2023•亳州三模)如图,在⊙O中,直径AB⊥CD于点H.若AB=10,CD=8,则BH的长为()A.5B.4C.3D.26(2023•容县一模)如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD,垂足为点E,CD=8cm,AB=10cm,则AE=.7(2023•衡南县三模)在⊙O中,直径AB=4,弦CD⊥AB于P,OP=3,则弦CD的长为.8(2023•东台市校级模拟)如图,A、B、C是⊙O上的点,OC⊥AB,垂足为点D,若OA=5,AB= 8,则线段CD的长为=.9(2023•望城区模拟)如图,AB是⊙O的直径,且AB=10cm,弦CD⊥AB于点E,CD=8cm,连接OC,则BE=cm.10(2023•长沙县二模)如图,⊙O的半径为5,弦AB=8,点C是AB的中点,连接OC,则OC的长为.【题型2勾股定理与方程综合求线段】11(2023•邯郸模拟)如图,以CD为直径的⊙O中,弦AB⊥CD于M.AB=16,CM=16.则MD 的长为()A.4B.6C.8D.1012(2022秋•南开区校级期末)如图,在⊙O中,半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接EC,若AB=8,CD=2,则EC的长度为()A.215B.8C.210D.21313(2022秋•文登区期末)如图,AB为⊙O的直径,弦CD⊥AB于点E,若AE=CD=8,则⊙O的半径为()D.5A.3B.4C.9214(2022秋•西湖区校级期末)如图,AB是⊙O的直径,弦CD⊥AB交于点E.若BE=10,CD= 8,则⊙O的半径为()A.3B.4.2C.5.8D.615(2022秋•泰山区校级期末)一块圆形宣传标志牌简图如图所示,点A,B,C在⊙O上,CD垂直平分AB于点D.现测得AB=16dm,DC=4dm,则圆形标志牌的半径为()A.6dmB.5dmC.10dmD.3dm16(2022秋•任城区校级期末)如图,CD为⊙O的直径,弦AB⊥CD,垂足为E,CE=2寸,AB=16寸,直径CD的长是()A.28寸B.30寸C.36寸D.34寸17(2023•汉阳区校级一模)如图,CD为⊙O直径,弦AB⊥CD于点E,CE=1,AB=6,则CD长为()A.10B.9C.8D.518(2023•汇川区三模)在半径为r的圆中,弦BC垂直平分OA,若BC=6,则r的值是()A.3B.33C.23D.23219(2023春•仪征市期末)如图,AB是⊙O的直径,弦CD⊥AB于点E,CE=3,BE=1,则OC=.20(2023•大冶市一模)如图,AB是⊙O的弦,C是AB的中点,连接OC并延长交⊙O于点D.若CD=1,AB=4,则⊙O的半径是 52 .【题型3垂径定理在实际中应用】21(2022秋•海淀区校级月考)如图,一条公路的转弯处是一段圆弧AB,点O是弧AB的圆心,C为弧AB上一点,OC⊥AB,垂足为D.已知AB=60m,CD=10m,求这段弯路的半径.22(2022秋•郾城区期中)如图是一根圆形下水管道的横截面,管内有少量的污水,此时的水面宽AB 为0.6米,污水的最大深度为0.1米.(1)求此下水管横截面的半径;(2)随着污水量的增加,水位又被抬升0.7米,求此时水面的宽度增加了多少?23(2022秋•沭阳县期中)如图是某蔬菜基地搭建一座圆弧型蔬菜棚,跨度AB=3.2米,拱高CD=0.8米(C为AB的中点,D为弧AB的中点).(1)求该圆弧所在圆的半径;(2)在距蔬菜棚的一端0.4米处竖立支撑杆EF,求支撑杆EF的高度.24如图,有一拱桥是圆弧形,它的跨度(所对弦长)为60m,拱高18m,当水面涨至其跨度只有30m时,就要采取紧急措施.某次洪水来到时,拱顶离水面只有4m,问是否需要采取紧急措施?25如图,残缺轮片上弦AB的垂直平分线交弧AB于点C,交弦AB于点D,已知AB=24cm,CD=8cm.(1)找出此残缺轮片所在圆的圆心(写出找到圆心的方法);(2)求此圆的半径.26某地有一座圆弧形拱桥,所在圆的圆心为点O,桥下水面宽度AB为7.2m,过点O作OC⊥AB于点D,交圆弧于点C,CD=2.4m(如图).现有一艘宽3m、船舱顶部高出水面AB2m的货船要经过这座拱桥,此货船能否顺利通过这座拱桥?27我国古算书《九章算术》中有“圆材埋壁”一题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径(直径)几何?”(注:如图,⊙O表示圆材截面,CE是⊙O的直径,AB表示“锯道”,CD表示“锯深”,1尺=10寸,求圆材的直径长就是求CE的长.)28如图,半圆拱桥的圆心为O,圆的半径为5m,一只8m宽的船装载一集装箱,箱顶宽6m,离水面AB高3.8m,这条船能过桥洞吗?请说明理由.29(2022秋•沭阳县校级月考)如图是一个半圆形桥洞截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,CD∥AB,且AB=26m,OE⊥CD于点E.水位正常时测得OE:CD=5:24(1)求CD的长;(2)现汛期来临,水面要以每小时4m的速度上升,则经过多长时间桥洞会刚刚被灌满?30(2022秋•东台市期中)如图,是一张盾构隧道断面结构图.隧道内部为以O为圆心,AB为直径的圆.隧道内部共分为三层,上层为排烟道,中间为行车隧道,下层为服务层.点A到顶棚的距离为1.6m,顶棚到路面的距离是6.4m,点B到路面的距离为4.0m.请求出路面CD的宽度.(精确到0.1m)圆中垂径定理综合应用(3大类题型)重难点题型归纳【题型1直接运用勾股定理求线段】【题型2勾股定理与方程综合求线段】【题型3垂径定理在实际中应用】满分必练【题型1直接运用勾股定理求线段】1(2023•大连模拟)如图所示,在⊙O中,直径AB=10,弦DE⊥AB于点C,连接DO.若OC:OB =3:5,则DE的长为()A.3B.4C.6D.8【答案】D【解答】解:∵AB=10,∴OA=OB=5,∵OC:OB=3:5,∴OC=3,在Rt△OCD中,CD=OD2-OC2=52-32=4,∵DE⊥AB,∴DE=2CD=8,故选:D.2(2023•杭州模拟)如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则AE= ( )cm.A.8B.5C.3D.2【答案】A【解答】解:∵AB⊥CD,AB是直径,∴CE=ED=4cm,在Rt△OEC中,OE=OC2-EC2=52-42=3(cm),∴AE=OA+OE=5+3=8(cm),故选:A.3(2023•宜昌)如图,OA ,OB ,OC 都是⊙O 的半径,AC ,OB 交于点D .若AD =CD =8,OD =6,则BD 的长为()A.5B.4C.3D.2【答案】B 【解答】解:∵AD =CD =8,∴OB ⊥AC ,在Rt △AOD 中,OA =AD 2+OD 2=82+62=10,∴OB =10,∴BD =10-6=4.故选:B .4(2023•金寨县校级模拟)如图,AB 是⊙O 的直径,弦CD ⊥AB 于点E ,若CD =6,AB =10,则AE 的长为()A.1B.2C.3D.4【答案】A 【解答】解:连接OC ,∵直径AB ⊥CD ,∴EC =12CD =12×6=3,∵AB =10,∴OC =OA =5,∴OE =OC 2-CE 2=4,∴AE =OA -OE =1.故选:A .5(2023•亳州三模)如图,在⊙O中,直径AB⊥CD于点H.若AB=10,CD=8,则BH的长为()A.5B.4C.3D.2【答案】D【解答】解:连接OC,∵AB⊥CD,CD=8,∴CH=DH=12CD=4,∠OHC=90°,∵AB=10,∴OB=OC=5,∴OH=OC2-CH2=52-42=3,∴BH=OB-OH=2,故选:D.6(2023•容县一模)如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD,垂足为点E,CD=8cm,AB=10cm,则AE=2cm.【答案】2cm.【解答】解:由题意可知,AB垂直平分CD,OC=OA=12AB=5cm,∴CE=12CD=4cm,在Rt△CEO中,OE=OC2-CE2=52-42=3(cm),∴AE=OA-OE=2cm.故答案为:2cm.7(2023•衡南县三模)在⊙O中,直径AB=4,弦CD⊥AB于P,OP=3,则弦CD的长为2.【答案】见试题解答内容【解答】解:连接OC,∵在⊙O中,直径AB=4,AB=2,∴OA=OC=12∴弦CD⊥AB于P,OP=3,∴CP=OC2-OP2=1,∴CD=2CP=2.故答案为:2.8(2023•东台市校级模拟)如图,A、B、C是⊙O上的点,OC⊥AB,垂足为点D,若OA=5,AB= 8,则线段CD的长为=2.【答案】2.【解答】解:∵OC⊥AB,AB=4,∴AD=BD=12在Rt△OAD中,OD=OA2-OD2=52-42=3,∴CD=OC-OD=5-3=2.故答案为:2.9(2023•望城区模拟)如图,AB是⊙O的直径,且AB=10cm,弦CD⊥AB于点E,CD=8cm,连接OC,则BE=2cm.【答案】2.【解答】解:∵弦CD ⊥AB ,CD =8cm ,∴CE =12CD =4cm ,在Rt △OEC 中,OC =12AB =5cm ,∴OE =OC 2-CE 2=3cm ,∴BE =OB -OE =2(cm ),故答案为:2.10(2023•长沙县二模)如图,⊙O 的半径为5,弦AB =8,点C 是AB 的中点,连接OC ,则OC 的长为3.【答案】3.【解答】解:∵B 是AC 的中点,∴AC =12AB =4,OC ⊥AB ,在Rt △OAC 中,OC =OA 2-AC 2=52-42=3.故答案为:3.【题型2勾股定理与方程综合求线段】11(2023•邯郸模拟)如图,以CD 为直径的⊙O 中,弦AB ⊥CD 于M .AB =16,CM =16.则MD 的长为()A.4B.6C.8D.10【答案】A【解答】解:连接OA ,如图,设⊙O 的半径为r ,则OA =r ,OM =16-r ,∵AB ⊥CD ,∴AM =BM =12AB =8,在Rt △AOM 中,82+(16-r )2=r 2,解得r =10,∴MD =CD -CM =20-16=4.故选:A .12(2022秋•南开区校级期末)如图,在⊙O 中,半径OD ⊥弦AB 于点C ,连接AO 并延长交⊙O 于点E ,连接EC ,若AB =8,CD =2,则EC 的长度为()A.215B.8C.210D.213【答案】D【解答】解:如图,连接BE ,设⊙O 的半径为R ,∵OD ⊥AB ,∴AC =BC =12AB =12×8=4,在Rt △AOC 中,OA =r ,OC =r -CD =r -2,由勾股定理,得OC 2+AC 2=OA 2,∴42+(r -2)2=r 2,解得r =5,∴OC =5-2=3,∵O 是AE 的中点,C 是AB 的中点,∴OC 是三角形ABE 的中位线,∴BE =2OC =6,∵AE 为⊙O 的直径,∴∠ABE =90°,在Rt △BCE 中,CE =BC 2+BE 2=213.故选:D .13(2022秋•文登区期末)如图,AB 为⊙O 的直径,弦CD ⊥AB 于点E ,若AE =CD =8,则⊙O 的半径为()A.3B.4C.9D.52【答案】见试题解答内容【解答】解:连接OC,∵AB为⊙O的直径,弦CD⊥AB于点E,AE=CD=8,CD=4,∴CE=DE=12设OC=r,则OE=8-r,在Rt△OCE中,OE2+CE2=OC2,即(8-r)2+42=r2,解得r=5.故选:D.14(2022秋•西湖区校级期末)如图,AB是⊙O的直径,弦CD⊥AB交于点E.若BE=10,CD= 8,则⊙O的半径为()A.3B.4.2C.5.8D.6【答案】C【解答】解:连接OC,设⊙O的半径为R,则OE=10-R,∵CD⊥AB,AB过圆心O,CD=8,∴∠OEC=90°,CE=DE=4,由勾股定理得:OC2=CE2+OE2,R2=42+(10-R)2,解得:R=5.8,即⊙O的半径长是5.8,故选:C.15(2022秋•泰山区校级期末)一块圆形宣传标志牌简图如图所示,点A,B,C在⊙O上,CD垂直平分AB于点D.现测得AB=16dm,DC=4dm,则圆形标志牌的半径为()A.6dmB.5dmC.10dmD.3dm【答案】C【解答】解:连接OA,OD,∵点A,B,C在⊙O上,CD垂直平分AB于点D,AB=16dm,DC=4dm,∴AD=8dm,设圆形标志牌的半径为r,可得:r2=82+(r-4)2,解得:r=10,故选:C.16(2022秋•任城区校级期末)如图,CD为⊙O的直径,弦AB⊥CD,垂足为E,CE=2寸,AB=16寸,直径CD的长是()A.28寸B.30寸C.36寸D.34寸【答案】D【解答】解:如图,连接OA,∵CD⊥AB,CD过圆心O,AB=16寸,∴∠AEO=90°,AE=BE=8寸,设圆的半径是r寸,在直角△OAE中,OA=r寸,OE=(r-2)寸,由勾股定理得:OA2=OE2+AE2,r2=(r-2)2+82,解得:r=17.则CD=2×17=34(寸).故选:D.17(2023•汉阳区校级一模)如图,CD为⊙O直径,弦AB⊥CD于点E,CE=1,AB=6,则CD长为()A.10B.9C.8D.5【答案】A【解答】解:设⊙O的半径为R,则OE=R-1,∵AB⊥CD,AB=6,∴AE=BE=3,∠AEO=90°,在Rt△AEO中,由勾股定理得:AO2=AE2+OE2,R2=(R-1)2+32,解得:R=5,即CD =10,故选:A .18(2023•汇川区三模)在半径为r 的圆中,弦BC 垂直平分OA ,若BC =6,则r 的值是()A.3B.33C.23D.232【答案】C 【解答】解:设OA 交BC 于点D ,如图,∵BC 垂直平分OA ,∴OD =12r ,BD =CD =12BC =3,在Rt △OBD 中,(12r )2+32=r 2,解得r 1=23,r 2=-23(舍去),即r 的值为23.故选:C .19(2023春•仪征市期末)如图,AB 是⊙O 的直径,弦CD ⊥AB 于点E ,CE =3,BE =1,则OC =2.【答案】2.【解答】解:设OC =x ,则OE =x -1,在Rt △COE 中由勾股定理得,OC 2=CE 2+OE 2,即x 2=(3)2+(x -1)2,解得x =2,即OC =2,故答案为:2.20(2023•大冶市一模)如图,AB 是⊙O 的弦,C 是AB 的中点,连接OC 并延长交⊙O 于点D .若CD =1,AB =4,则⊙O 的半径是 52 .【答案】见试题解答内容【解答】解:连接OA ,∵C 是AB 的中点,∴AC =12AB =2,OC ⊥AB ,∴OA 2=OC 2+AC 2,即OA 2=(OA -1)2+22,解得,OA =52,故答案为:52.【题型3垂径定理在实际中应用】21(2022秋•海淀区校级月考)如图,一条公路的转弯处是一段圆弧AB ,点O 是弧AB 的圆心,C 为弧AB 上一点,OC ⊥AB ,垂足为D .已知AB =60m ,CD =10m ,求这段弯路的半径.【答案】这段弯路的半径为50m .【解答】解:连接OB ,∵OC ⊥AB ,∴AD =BD =12AB =30m ,设半径为r ,则OD =r -10,在Rt △OBD 中,OD 2+BD 2=OB 2,即(r -10)2+302=r 2,解得r =50m ,答:这段弯路的半径为50m .22(2022秋•郾城区期中)如图是一根圆形下水管道的横截面,管内有少量的污水,此时的水面宽AB 为0.6米,污水的最大深度为0.1米.(1)求此下水管横截面的半径;(2)随着污水量的增加,水位又被抬升0.7米,求此时水面的宽度增加了多少?【答案】(1)下水管半径为0.5米;(2)水位又被抬升0.7米,水面的宽度增加了0.2米.【解答】解:(1)作半径OD ⊥AB 于C ,连接OB ,则CD =0.1米,由垂径定理得:BC =12AB =0.3米,在Rt △OBC 中,OB 2=OC 2+BC 2,∴OB 2=(OB -0.1)2+0.09,∴BO =0.5,即下水管半径为0.5米;(2)如图,过点O 作OH ⊥MN 于H ,∴NH =MH ,∵水位又被抬升0.7米,∴OH =0.1+0.7-0.5=0.3米,∴NH =ON 2-OH 2=0.25-0.09=0.4米,∴MN =0.8米,∴增加了0.2米,∴水位又被抬升0.7米,水面的宽度增加了0.2米.23(2022秋•沭阳县期中)如图是某蔬菜基地搭建一座圆弧型蔬菜棚,跨度AB =3.2米,拱高CD =0.8米(C 为AB 的中点,D 为弧AB 的中点).(1)求该圆弧所在圆的半径;(2)在距蔬菜棚的一端0.4米处竖立支撑杆EF ,求支撑杆EF 的高度.【答案】0.4米.【解答】解:(1)设弧AB 所在的圆心为O ,D 为弧AB 的中点,CD ⊥AB 于C ,延长DC 经过O 点,则BC =12AB =1.6(米),设⊙O 的半径为R ,在Rt △OBC 中,OB 2=OC 2+CB 2,∴R 2=(R -0.8)2+1.62,解得R =2,即该圆弧所在圆的半径为2米;(2)过O 作OH ⊥FE 于H ,则OH =CE =1.6-0.4=1.2=65(米),OF =2米,在Rt △OHF 中,HF =OF 2-OH 2=22-652=1.6(米),∵HE =OC =OD -CD =2-0.8=1.2(米),∴EF =HF -HE =1.6-1.2=0.4(米),即支撑杆EF 的高度为0.4米.24如图,有一拱桥是圆弧形,它的跨度(所对弦长)为60m ,拱高18m ,当水面涨至其跨度只有30m 时,就要采取紧急措施.某次洪水来到时,拱顶离水面只有4m ,问是否需要采取紧急措施?【答案】不需要.【解答】解:∵AB =60米,MP =18米,OP ⊥AB ,∴AM =12AB =30(米),OM =OP -MP =(x -18)米,在Rt △OAM 中,由勾股定理得OA 2=AM 2+OM 2,∴x 2=302+(x -18)2,∴x =34(米).当PN =4时,∵PN =4,OP =x ,∴ON =34-4=30(米),设A ′N =y 米,在Rt △OA ′N 中,∵OA ′=34,A ′N =y ,ON =30,∴342=y 2+302,∴y =16或y =-16(舍去),∴A ′N =16,∴A ′B ′=16×2=32(米)>30米,∴不需要采取紧急措施.25如图,残缺轮片上弦AB 的垂直平分线交弧AB 于点C ,交弦AB 于点D ,已知AB =24cm ,CD =8cm .(1)找出此残缺轮片所在圆的圆心(写出找到圆心的方法);(2)求此圆的半径.【答案】(1)圆的圆心如图所示;(2)13.【解答】解:(1)连接AC,作线段AC的垂直平分线交直线CD为O,则点O为此残缺轮片所在圆的圆心;(2)连接OA,设此圆的半径为rcm,则OD=(r-8)cm,∵CD是弦AB的垂直平分线,AB=24cm,∴AD=12cm,在Rt△AOD中,OA2=OD2+AD2,即r2=(r-8)2+122,解得:r=13.26某地有一座圆弧形拱桥,所在圆的圆心为点O,桥下水面宽度AB为7.2m,过点O作OC⊥AB于点D,交圆弧于点C,CD=2.4m(如图).现有一艘宽3m、船舱顶部高出水面AB2m的货船要经过这座拱桥,此货船能否顺利通过这座拱桥?【答案】此货船能顺利通过这座拱桥.【解答】解:如图,连接ON,OB.∵OC⊥AB,∴D为AB中点,∵AB=7.2m,AB=3.6m.∴BD=12又∵CD=2.4m,设OB=OC=ON=rm,则OD=(r-2.4)m.在Rt△BOD中,根据勾股定理得:r2=(r-2.4)2+3.62,解得r=3.9.∵CD=2.4m,船舱顶部为正方形并高出水面AB2m,∴CE=2.4-2=0.4m,∴OE=r-CE=3.9-0.4=3.5m,在Rt△OEN中,EN2=ON2-OE2=3.92-3.52=2.96(m2),∴EN= 2.96(m).∴MN=2EN=2× 2.96≈3.44m>3m.∴此货船能顺利通过这座拱桥.27我国古算书《九章算术》中有“圆材埋壁”一题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径(直径)几何?”(注:如图,⊙O 表示圆材截面,CE 是⊙O 的直径,AB 表示“锯道”,CD 表示“锯深”,1尺=10寸,求圆材的直径长就是求CE 的长.)【答案】见试题解答内容【解答】解:连接OA ,如图所示:∵AB ⊥CE ,∴AD =BD ,∵AB =10,∴AD =5,在Rt △AOE 中,∵OA 2=OD 2+AD 2,∴OA 2=(OA -1)2+52,解得:OA =13,∴CD =2A 0=26;即直径为26寸.28如图,半圆拱桥的圆心为O ,圆的半径为5m ,一只8m 宽的船装载一集装箱,箱顶宽6m ,离水面AB 高3.8m ,这条船能过桥洞吗?请说明理由.【答案】见试题解答内容【解答】解:如图,过点O 作OF ⊥DE 于点F ,则EF =DF =12DE ,假设DE =6m ,则DF =3m ,∵圆的半径为5m ,∴OD =5m ,∴OF =OD 2-DF 2=52-32=4>3.8,∴这条船能过桥洞.29(2022秋•沭阳县校级月考)如图是一个半圆形桥洞截面示意图,圆心为O ,直径AB 是河底线,弦CD 是水位线,CD ∥AB ,且AB =26m ,OE ⊥CD 于点E .水位正常时测得OE :CD =5:24(1)求CD 的长;(2)现汛期来临,水面要以每小时4m 的速度上升,则经过多长时间桥洞会刚刚被灌满?【答案】见试题解答内容【解答】解:(1)∵直径AB=26m,∴OD=12AB=12×26=13m,∵OE⊥CD,∴DE=12CD,∵OE:CD=5:24,∴OE:ED=5:12,∴设OE=5x,ED=12x,∴在Rt△ODE中(5x)2+(12x)2=132,解得x=1,∴CD=2DE=2×12×1=24m;(2)由(1)得OE=1×5=5m,延长OE交圆O于点F,∴EF=OF-OE=13-5=8m,∴84=2(小时),即经过2小时桥洞会刚刚被灌满.30(2022秋•东台市期中)如图,是一张盾构隧道断面结构图.隧道内部为以O为圆心,AB为直径的圆.隧道内部共分为三层,上层为排烟道,中间为行车隧道,下层为服务层.点A到顶棚的距离为1.6m,顶棚到路面的距离是6.4m,点B到路面的距离为4.0m.请求出路面CD的宽度.(精确到0.1m)【答案】见试题解答内容【解答】解:如图,连接OC,AB交CD于E,由题意知:AB=1.6+6.4+4=12,所以OC=OB=6,OE=OB-BE=6-4=2,由题意可知:AB⊥CD,∵AB过O,∴CD=2CE,在Rt△OCE中,由勾股定理得:CE=OC2-OE3=62-22=42,∴CD=2CE=82≈11.3m,所以路面CD的宽度为11.3m.。
垂径定理知识点及典型例题

垂径定理一、知识回顾1、到定点距离等于的点的集合叫做圆,定点叫做,定长叫做;连接圆上任意两点间的线段叫做,经过圆心的弦叫做;圆上任意两点间的部分叫做,它分为、、三种。
2、能够的两个圆叫做等圆;能够互相的弧叫做等弧,他只能出现在中。
3、圆既具有对称性,也具有对称性,它有对称轴。
4、垂直于弦的直径,并且;平分弦(不是直径)的直径,并且。
5、顶点在的角叫做圆心角;在同圆或等圆中,相等的圆心角所对的相等,所对的也相等,也相等;在同圆或等圆中,如果两条弧相等,那么它们所对的、、;在同圆或等圆中,如果两条弦相等,那么它们所对的、、。
6、顶点在,并且相交的角叫做圆周角。
在同圆或等圆中,同弧或等弧所对的圆周角,都等于这条弧所对的圆心角的;在同圆或等圆中,如果两个圆周角相等,那么它们所对的弧。
7、半圆(或直径)所对的圆周角是,900的圆周角所对的弦是。
8、如果一个多边形的都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的。
圆的内接四边形。
二、典例解析例1 如图,某市新建的滴水湖是圆形人工湖,为了测量该湖的半径,小明和小亮在湖边选取A、B、C三根木桩,使得A、B之间的距离等于A、C之间的距离,并测得BC=240m,A到BC的距离为5m。
请帮忙求出滴水湖的半径。
D两点,已知C(0,3)、D(0,-7),求圆心E的坐标。
变式2 已知O 的半径为13cm ,弦AB ∥CD ,AB=10cm ,CD=24cm ,求AB 和CD 之间的距离。
变式3 如图,O 的直径AB=15cm ,有一条定长为9cm 的动弦CD 在半圆AMB 上滑动(点C 与点A ,点D 与点B 不重合),且CE ⊥CD 交AB 于点E ,DF ⊥CD 于点F 。
(1)求证:AE=BF ;(2)在动弦CD 的滑动过程中,四边形CDFE 的面积是否发生变化?若变化,请说明理由;若不变化,请予以证明并求出这个值。
变式4 如图,某地方有一座圆弧形的拱桥,桥下水面宽度为7.2米,拱顶高出水面2.4米,现有一竹排运送一货箱欲从桥下通过,已知货箱长10米,宽3米,高2米,问货箱能否顺利通过该桥?例2 如图,BC 是O 的直径,OA 是O 的半径,弦BE ∥OA 。
垂径定理----作垂直,证半径

24.2.2(2.2)---作垂直,证半径
一.【知识要点】
1.作垂直,证半径
二.【经典例题】
1.如图,△ABC是等边三角形,AO⊥BC,垂足为O,⊙O与AC相切于点D,EB⊥BA交AC延长线于点E,与⊙O相交于F,G两点。
(1)求证:AB是⊙O的切线;
(2)若EC=4,求EF的长。
三.【题库】
【A】
1.如图,在△ABC中,AB=AC,AO⊥BC于点O,OE⊥AB于点E,以点O为圆心,OE为半径作圆O交AO于点F.求证:AC是⊙O的切线;
【B】
【C 】
1.已知点00(,)P x y 和直线y=kx+b ,则点P 到直线y=kx+b 的距离证明可用公
式例如:求点P(−1,2)到直线y=3x+7的距离.
解:∵直线y=3x+7,∴k=3,b=7.
根据以上材料,解答下列问题:
(1)求点P(1,−1)到直线y=x −1的距离;
(2)已知直线y=−2x+4
与y=−2x −6平行,求这两条直线之间的距离. 说明理由;
【D 】
1.如图1,O 是△ABC 的边BC 的中点,⊙O 与BC 交于E 、F 两点,与AB 相切于点D ,连接AO 交
⊙O 于点P ,=.
(1)猜想AC 与⊙O 的位置关系,并证明你的猜想.(6分)
(2)如图2,延长AO 交⊙O
于Q 点,连接DE 、DF ,DQ ,FQ ,FQ =
,ED =5,求
DQ 的长.(6分)。
垂径定理 (解析版)

垂径定理(解析版)【要点梳理】知识点一、垂径定理1.垂径定理垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.(如图 1 所示)2.推论平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.(弦 AB 不是直径,如图 2 所示)图1 图2要点诠释:(1)这里的直径也可以是半径,也可以是过圆心的直线或线段.(2)在垂径定理及其推论中:过圆心、垂直于弦、平分弦、平分弦所对的优弧、平分弦所对的劣弧,在这五个条件中,知道任意两个,就能推出其他三个结论.(注意:“过圆心、平分弦”作为题设时,平分的弦不能是直径)【同步训练】类型一、应用垂径定理进行计算与证明1.如图,AB 是⊙O的弦,半径OC⊥AB于点D,且AB=6 cm,OD=4 cm,则DC 的长为()A.5 cm B.2.5 cm C.2 cm D.1 cmOD 2 + AD2 42 + 323 【答案】D ;【解析】连接 OA ,∵ OC⊥AB∴ AD = AB =3 .Rt△AOD 中, AO = = = 5.∴ DC =OC -OD =OA -OD =5-4=1(cm ).2.(2015•巴中模拟)如图,AB 为半圆直径,O 为圆心,C 为半圆上一点,E 是弧 AC 的中点,OE 交弦 AC 于点 D ,若 AC=8cm ,DE=2cm ,求 OD 的长.【答案】 OD =3cm .【解析】解:∵ E 为弧 AC 的中点,∴ OE ⊥AC ,AD AC =4.设 OD 的长为 x ,则:OE =OD +DE= x+2 =OA.在 Rt △OAD 中,∵ OA 2 =OD 2+AD 2∴(2+ x )2= x 2+42,x =3 .∴ OD =3cm .类型二、垂径定理的综合应用3.如图 1,某公园的一座石拱桥是圆弧形(劣弧),其跨度为 24m ,拱的半径为 13m ,则拱高为( )A .5mB .8mC .7mD . 5 m【答案】B ;【解析】如图 2 所示,由题意可知:AB 表示桥拱,弦 AB 的长表示桥的跨度,C 为 AB 的中点,OC 与 AB 相交于点 D 。
垂径定理典型例题及练习

典型例题分析:例题1、 基本概念1.下面四个命题中正确的一个是( )A .平分一条直径的弦必垂直于这条直径B .平分一条弧的直线垂直于这条弧所对的弦C .弦的垂线必过这条弦所在圆的圆心D .在一个圆内平分一条弧和它所对弦的直线必过这个圆的圆心2.下列命题中,正确的是( ).A .过弦的中点的直线平分弦所对的弧B .过弦的中点的直线必过圆心C .弦所对的两条弧的中点连线垂直平分弦,且过圆心D .弦的垂线平分弦所对的弧例题2、垂径定理1、 在直径为52cm 的圆柱形油槽内装入一些油后,截面如图所示,如果油的最大深度为16cm ,那么油面宽度AB 是________cm.2、在直径为52cm 的圆柱形油槽内装入一些油后,,如果油面宽度是48cm ,那么油的最大深度为________cm.3、如图,已知在⊙O 中,弦CD AB =,且CD AB ⊥,垂足为H ,AB OE ⊥于E ,CD OF ⊥于F .(1)求证:四边形OEHF 是正方形.(2)若3=CH ,9=DH ,求圆心O 到弦AB 和CD 的距离.4、已知:△ABC 内接于⊙O ,AB=AC ,半径OB=5cm ,圆心O 到BC 的距离为3cm ,求AB 的长.5、如图,F 是以O 为圆心,BC 为直径的半圆上任意一点,A 是的中点,AD ⊥BC 于D ,求证:AD=21BF.例题3、度数问题1、已知:在⊙O 中,弦cm 12=AB ,O 点到AB 的距离等于AB 的一半,求:AOB ∠的度数和圆的半径.2、已知:⊙O 的半径1=OA ,弦AB 、AC 的长分别是2、3.求BAC ∠的度数。
例题4、相交问题如图,已知⊙O 的直径AB 和弦CD 相交于点E ,AE=6cm ,EB=2cm ,∠BED=30°,求CD 的长.例题5、平行问题在直径为50cm 的⊙O 中,弦AB=40cm ,弦CD=48cm ,且AB ∥CD ,求:AB 与CD 之间的距离.例题6、同心圆问题如图,在两个同心圆中,大圆的弦AB ,交小圆于C 、D 两点,设大圆和小圆的半径分别为b a ,.求证:22b a BD AD -=⋅.例题7、平行与相似已知:如图,AB 是⊙O 的直径,CD 是弦,于CD AE ⊥E ,CD BF ⊥于F .求证:FD EC =.B作 业:一、概念题1.下列命题中错误的有()(1)弦的垂直平分线经过圆心(2)平分弦的直径垂直于弦(3)梯形的对角线互相平分(4)圆的对称轴是直径A .1个B .2个C .3个D .4个2、⊙O 的直径为10,弦AB 的长为8,M 是弦AB 上的动点,则OM 的长的取值范围是( )(A )5OM 3≤≤ (B )5OM 4≤≤(C )5OM 3<< (D )5OM 4<<3.如图,如果AB 为⊙O 直径,弦AB CD ⊥,垂足为E ,那么下列结论中错误的是( )A .DE CE =B .C .BAD BAC ∠=∠ D .AD AC >4.如图,AB 是⊙O 直径,CD 是⊙O 的弦,CD AB ⊥于E ,则图中不大于半圆的相等弧有( )对。
垂径定理及答案
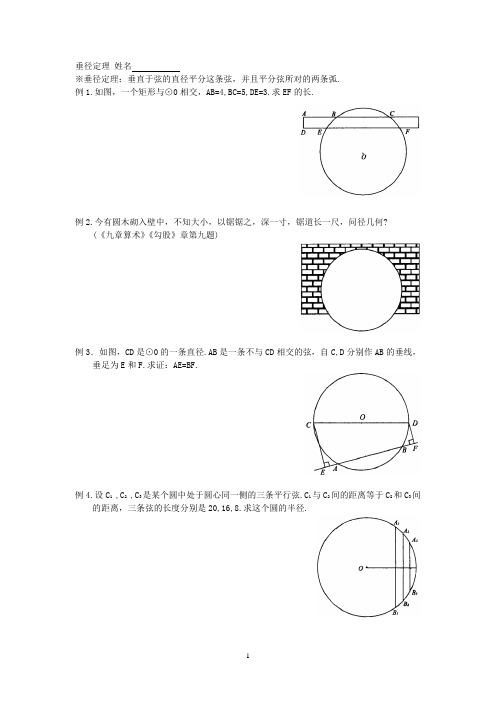
垂径定理 姓名※垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.例1.如图,一个矩形与⊙0相交,AB=4,BC=5,DE=3.求EF的长.例2.今有圆木砌入壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?(《九章算术》《勾股》章第九题)例3.如图,CD是⊙0的一条直径.AB是一条不与CD相交的弦,自C,D分别作AB的垂线,垂足为E和F.求证:AE=BF.例4.设C1 ,C2 ,C3是某个圆中处于圆心同一侧的三条平行弦.C1与C2间的距离等于C2和C3间的距离,三条弦的长度分别是20,16,8.求这个圆的半径.例5.⊙0中,弦CD与直径AB相交于P.若∠DPB =45°,⊙O的半径长记为R.求证:PC2+PD2=2R2.例 6.在波平如镜的湖面,高出半尺的地方长着一朵红莲,它孤零零地直立在那里,突然被狂风吹倒在一边,有一位渔人亲眼看见,它现在有两尺远离开那生长地点.请你来解决一个问题,湖水在这里有多少深浅?例7.P是⊙01与⊙02的一个交点,过P点作平行于0102的直线交⊙01于A,交⊙02于B,过P 点作另一直线交⊙01于C,交⊙02于D.求证:AB>CD.例8.⊙0与一正方形ABCD相交,如图所示.A1,A2,B1,B2,C1,C2,D1,D2是八个交点.求证:AA1+AA2+CC1+CC2=BB1+BB2+DD1+DD2.例9.圆内两条非直径的弦相交,试证它们不能互相平分.垂径定理练习 姓名1.⊙0与另外两同心圆相交,交大圆于点A,B,交小圆于点C, D.求证:AB∥CD.2.以∠A平分线上一点0为圆心画一个圆,在∠A的两边上截得的两条弦为BC和DE.求证:BC=DE.3.直角三角形中,直角边AC=8cm,另一直角边CB =15cm,以直角顶点C为圆心CA为半径画弧交斜边AB于点D.求AD的长.4.一条弦与一条直径成45°角,试证:该弦被直径所分两线段的平方和等于该圆半径平方的两倍.5.以AB为直径画半圆O,C是半圆上一点,作OD⊥AC于D.连结BD交OC于E,若BD长为15厘米,求BE的长.垂径定理 参考答案※垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.例1.如图,一个矩形与⊙0相交,AB=4,BC=5,DE=3.求EF的长.例2.今有圆木砌入壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?(《九章算术》《勾股》章第九题)例3.如图,CD是⊙0的一条直径.AB是一条不与CD相交的弦,自C,D分别作AB的垂线,垂足为E和F.求证:AE=BF.例4.设C1 ,C2 ,C3是某个圆中处于圆心同一侧的三条平行弦.C1与C2间的距离等于C2和C3间的距离,三条弦的长度分别是20,16,8.求这个圆的半径.例5.⊙0中,弦CD与直径AB相交于P.若∠DPB =45°,⊙O的半径长记为R.求证:PC2+PD2=2R2.例 6.在波平如镜的湖面,高出半尺的地方长着一朵红莲,它孤零零地直立在那里,突然被狂风吹倒在一边,有一位渔人亲眼看见,它现在有两尺远离开那生长地点.请你来解决一个问题,湖水在这里有多少深浅?解得x=3.75(尺)例7.P是⊙01与⊙02的一个交点,过P点作平行于0102的直线交⊙01于A,交⊙02于B,过P 点作另一直线交⊙01于C,交⊙02于D.求证:AB>CD.例8.⊙0与一正方形ABCD相交,如图所示.A1,A2,B1,B2,C1,C2,D1,D2是八个交点.求证:AA1+AA2+CC1+CC2=BB1+BB2+DD1+DD2.例9.圆内两条非直径的弦相交,试证它们不能互相平分.垂径定理练习 参考答案1.⊙0与另外两同心圆相交,交大圆于点A,B,交小圆于点C, D.求证:AB∥CD.2.以∠A 平分线上一点0为圆心画一个圆,在∠A求证:BC=DE.3.直角三角形中,直角边AC=8cm,另一直角边CB=15cm,以直角顶点C 为圆心CA 为半径画弧交斜边AB 于点D.求AD 的长.4.一条弦与一条直径成45°角,试证:该弦被直径所分两线段的平方和等于该圆半径平方的两倍.5.以AB 为直径画半圆O,C 是半圆上一点,作OD⊥AC 于D.连结BD 交OC 于E,若BD 长为15厘米,求BE 的长.。
垂径定理知二推三的例题

垂径定理知二推三的例题垂径定理是平面几何中的一个重要定理,它描述了圆的直径与垂直于直径的弦之间的关系。
根据垂径定理,如果一个弦垂直于直径,那么这个弦就被分成了两段,其中一段的长度等于另一段的长度的两倍。
下面我将给出一个例题来说明这个定理。
例题:在一个圆中,直径AC的长度为10 cm,弦BD垂直于直径AC,并且切割弦BD的点E到B的距离为4 cm。
求弦BD的长度。
解析:根据垂径定理,我们知道弦BD被切割成BE和ED两段,其中一段的长度等于另一段的两倍。
设BE的长度为x cm,则ED的长度为2x cm。
根据垂径定理的推论,我们可以得到以下等式:BE ED = AE CE.由于AE和CE分别是弦BD的两个部分,我们可以用整个弦BD 的长度减去BE和ED的长度来表示它们。
设弦BD的长度为y cm,则AE的长度为(y x) cm,CE的长度为(y 2x) cm。
将上述长度代入等式中,得到:x 2x = (y x) (y 2x)。
化简上述等式,得到:2x^2 = y^2 3xy + 2x^2。
移项整理后,得到:y^2 3xy = 0。
因为y ≠ 0,所以我们可以将上述等式除以y,得到:y 3x = 0。
解得:y = 3x.由于我们要求的是弦BD的长度,即y,所以我们需要求得x的值。
根据题目中给出的信息,我们知道距离EB的长度为4 cm,所以可以得到以下等式:x + 2x = 4。
解得:x = 1。
将x的值代入y = 3x中,得到:y = 3 1 = 3。
因此,弦BD的长度为3 cm。
综上所述,根据垂径定理,当切割弦的点到弦的一端的距离为4 cm时,弦的长度为3 cm。
27.2(2)垂径定理

C.随点C移动而移动
B.位置不变
D.等分弧BD
5.已知⊙O的半径为5,点P是圆内一点,且OP=4,则 经过点P的最长的弦和最短的弦长分别为 10或6 8 _________.经过点P的长度为整数的弦共有_____ 条.
6.我市准备对文化广场进行改造,改造后安装了八个 大理石球.小陈想知道其中一个球的半径,于是找了 两块厚10cm的砖塞在球的两侧(如图),并量得两砖之 间的距离是60cm.请你在图中利用所学的几何知识, 求出大理石球的半径(要写出计算过程).
证明:连接OA,OB,则OA=OB ∵ AE=BE ∴ CD⊥AB
O · E D B
⌒ ⌒ ∴ AD=BD,
⌒ ⌒ AC =BC
平分弦(不是直径)的直径垂直于
弦,并且平分弦所对的两条弧。 (2)“不是直径”这个条件能去掉吗?如 果不能,请举出反例。
C A O · B D
垂径定理:
由 ① CD是直径 ② CD⊥AB
推论:
③AE=BE,
可推得
⌒ ⌒ ④AC=BC,
⌒ ⑤AD=BD.
可推得
⌒
由 ① CD是直径 ③ AE=BE
⌒ ⌒ ④AC=BC,
②CD⊥AB,
⌒ ⌒ ⑤AD=BD.
C
① CD是直径, ② CD⊥AB, ③ AM=BM ⌒ ⌒ ④AC=BC,
A
└ M
●
B
O
如果具备上面四个条件中的任何两个,那 么一定可以得到其他两个结论吗? 一条直线满足:(1)过圆心;(2)垂直于弦;(3) 平分弦(不是直径); (4)平分弦所对的弧.只 要具备上述四个条件中任两个,就可以推出其余 两个.
2722垂径定理垂径定理及其推论小明学习了垂径定理垂径定理说课稿圆垂径定理垂径定理的应用垂径定理练习题垂径定理ppt垂径定理的推论垂径定理逆定理
垂径定理典型例题总结
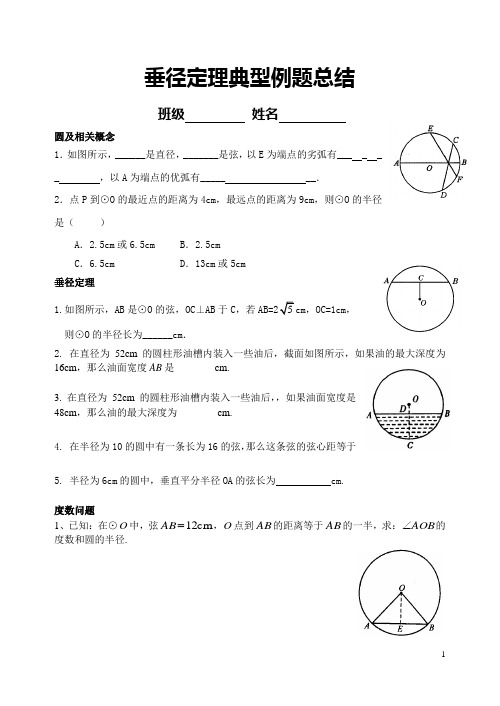
垂径定理典型例题总结 班级 姓名圆及相关概念1.如图所示,______是直径,_______是弦,以E 为端点的劣弧有___ _ _ _ ,以A 为端点的优弧有_____ __.2.点P 到⊙O 的最近点的距离为4cm ,最远点的距离为9cm ,则⊙O 的半径是( )A .2.5cm 或6.5cmB .2.5cmC .6.5cmD .13cm 或5cm垂径定理1.如图所示,AB 是⊙O 的弦,OC ⊥AB 于C ,若AB=25cm ,OC=1cm , 则⊙O 的半径长为______cm .2. 在直径为52cm 的圆柱形油槽内装入一些油后,截面如图所示,如果油的最大深度为16cm ,那么油面宽度AB 是________cm.3. 在直径为52cm 的圆柱形油槽内装入一些油后,,如果油面宽度是48cm ,那么油的最大深度为________cm.4. 在半径为10的圆中有一条长为16的弦,那么这条弦的弦心距等于5. 半径为6cm 的圆中,垂直平分半径OA 的弦长为 cm.度数问题1、已知:在⊙O 中,弦cm 12=AB ,O 点到AB 的距离等于AB 的一半,求:AOB ∠的度数和圆的半径.2、已知:⊙O 的半径1=OA ,弦AB 、AC 的长分别是2、3.求BAC ∠的度数。
相交问题1.如图,已知⊙O 的直径AB 和弦CD 相交于点E ,AE=6cm ,EB=2cm ,∠BED=30°,求CD 的长.平行问题在直径为50cm 的⊙O 中,弦AB=40cm ,弦CD=48cm ,且AB ∥CD ,求:AB 与CD 之间的距离.同心圆问题如图,在两个同心圆中,大圆的弦AB ,交小圆于C 、D 两点,设大圆和小圆的半径分别为b a ,.求证:22b a BD AD -=⋅.一、概念题1.下列命题中错误的有( )(1)弦的垂直平分线经过圆心(2)平分弦的直径垂直于弦(3)圆的对称轴是直径O A B C D EA .1个B .2个C .3个D .4个2、⊙O 的直径为10,弦AB 的长为8,M 是弦AB 上的动点,则OM 的长的取值范围是( )(A )5OM 3≤≤ (B )5OM 4≤≤(C )5OM 3<< (D )5OM 4<<3.如图,如果AB 为⊙O 直径,弦AB CD ⊥,垂足为E ,那么下列结论中错误的是( )A .DE CE =B .C .BAD BAC ∠=∠ D .AD AC >4.如图,AB 是⊙O 直径,CD 是⊙O 的弦,CD AB ⊥于E ,则图中不大于半圆的相等弧有( )对。
圆周角垂径定理例题
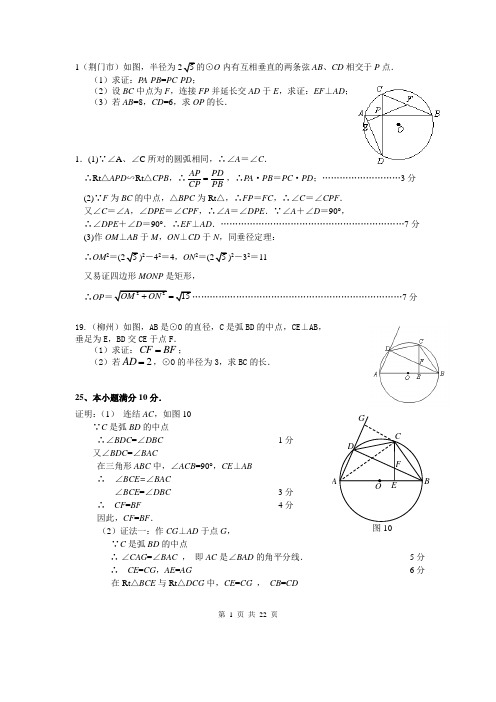
第 1 页 共 21 页1(荆门市)如图,半径为O 内有互相垂直的两条弦AB 、CD 相交于P 点.(1)求证:P A ·PB =PC ·PD ;(2)设BC 中点为F ,连接FP 并延长交AD 于E ,求证:EF ⊥AD ; (3)若AB =8,CD =6,求OP 的长.1.(1)∵∠A 、∠C 所对的圆弧相同,∴∠A =∠C . ∴Rt △APD ∽Rt △CPB ,∴AP PD CP PB=,∴P A ·PB =PC ·PD ;………………………3分 (2)∵F 为BC 的中点,△BPC 为Rt △,∴FP =FC ,∴∠C =∠CPF . 又∠C =∠A ,∠DPE =∠CPF ,∴∠A =∠DPE .∵∠A +∠D =90°, ∴∠DPE +∠D =90°.∴EF ⊥AD .………………………………………………………7分 (3)作OM ⊥AB 于M ,ON ⊥CD 于N ,同垂径定理: ∴OM 2=2-42=4,ON 2=2-32=11 又易证四边形MONP 是矩形,∴OP7分19.(柳州)如图,AB 是⊙O 的直径,C 是弧BD 的中点,CE⊥AB, 垂足为E ,BD 交CE 于点F .(1)求证:CF BF =;(2)若2AD =,⊙O 的半径为3,求BC 的长.25、本小题满分10分.证明:(1) 连结AC ,如图10 ∵C 是弧BD 的中点∴∠BDC =∠DBC ··············································· 1分又∠BDC =∠BAC在三角形ABC 中,∠ACB =90°,CE ⊥AB∴ ∠BCE=∠BAC ∠BCE =∠DBC ············································· 3分 ∴ CF =BF ······················································ 4分 因此,CF =BF .(2)证法一:作CG ⊥AD 于点G ,∵C 是弧BD 的中点∴ ∠CAG =∠BAC , 即AC 是∠BAD 的角平分线. ··········································· 5分 ∴ CE =CG ,AE =AG ···························································································· 6分 在Rt △BCE 与Rt △DCG 中,CE =CG , CB =CDB 图10第 2 页 共 21 页∴Rt △BCE ≌Rt △DCG ∴BE =DG ·············································································································· 7分 ∴AE =AB -BE =AG =AD +DG 即 6-BE =2+DG∴2BE =4,即 BE =2 ··························································································· 8分又 △BCE ∽△BAC∴ 212BC BE AB ==· ····················································································· 9分32±=BC (舍去负值)∴32=BC ··································································································· 10分 (2)证法二:∵AB 是⊙O 的直径,CE ⊥AB∴∠BEF=︒=∠90ADB , ······························· 5分 在Rt ADB △与Rt FEB △中, ∵FBE ABD ∠=∠∴ADB △∽FEB △,则BFABEF AD = 即BFEF 62=, ∴EF BF 3= ···················· 6分 又∵CF BF =, ∴EF CF 3=利用勾股定理得:EF EF BF BE 2222=-= ······································································· 7分 又∵△EBC ∽△ECA 则CEBE AE CE =,即则BE AE CE ⋅=2································································ 8分 ∴BE BE EF CF ⋅-=+)6()(2即EF EF EF EF 22)226()3(2⋅-=+ ∴22=EF ···································································································· 9分 ∴3222=+=CE BE BC ········································································· 10分B图10第 3 页 共 21如图,⊙O 的直径AB 是4,过B 点的直线MN 是⊙O 的切线,D 、C 是⊙O 上的两点,连接AD 、BD 、CD 和BC . (1)求证:CDB CBN ∠=∠; (2)若DC 是ADB ∠的平分线,且︒=∠15DAB ,求DC 的长.23.(1)证明: ∵AB 是⊙O 的直径 ∴︒=∠+∠=∠90CDB ADC ADB∵MN 切⊙O 于点B∴︒=∠+∠=∠90CBN ABC ABN∴CBN ABC CDB ADC ∠+∠=∠+∠ ∵ABC ADC ∠=∠ ∴CDB CBN ∠=∠. (2) 如右图,连接OC OD ,,过点O 作CD OE ⊥于点E . ∵CD 平分ADB ∠ ∴BDC ADC ∠=∠ ∴弧AC =弧BC ∵AB 是⊙O 的直径 ∴︒=∠90BOC 又∵︒=∠15DAB∴︒=∠30DOB ∵CD OE OC OD ⊥=, ∴︒=∠30ODE ∵2=OD∴3,1==DE OE ∴322==DE CD .27.已知,如图,直线MN 交O 于A B ,两点,AC 是直径,AD 平分CAM ∠交O 于D ,过D 作DE MN ⊥于E . (1)求证:DE 是O 的切线;(2)若6DE =cm ,3AE =cm ,求O第27题图NM B A ABM N第 4 页 共 21 页25.(1)证明:AF BC ∥,AFE DBE ∴∠=∠. ···································································································· (1分) E 是AD 的中点, AE DE ∴=.又AEF DEB ∠=∠, AEF DEB ∴△≌△. ·································································································· (2分) AF DB ∴=. ················································································································ (3分) AF DC =, DB DC ∴=.即D 是BC 的中点. ······································································································ (4分) (2)解:四边形ADCF 是矩形, ················································································ (5分) 证明:AF DC ∥,AF DC =,∴四边形ADCF 是平行四边形. ················································································· (6分) AB AC =,D 是BC 的中点, AD BC ∴⊥.即90ADC ∠=. ·········································································································· (7分) ∴四边形ADCF 是矩形. ····························································································· (8分) 五、(本大题共2小题,第27题10分,第28题11分,共21分) 27.(1)证明:连接OD . OA OD =,OAD ODA ∴∠=∠. ·································· (1分) OAD DAE ∠=∠, ODA DAE ∴∠=∠. ··································· (2分) DO MN ∴∥.············································· (3分)DE MN ⊥,90ODE DEM ∴∠=∠=.即OD DE ⊥. ··············································································································· (4分) D 在O 上,DC ∴是O 的切线. ··································································································· (5分) (2)解:90AED ∠=,6DE =,3AE =,AD ∴==. ································································ (6分)第 5 页 共 21 页连接CD .AC 是O 的直径,90ADC AED ∴∠=∠=. ·························································································· (7分) CAD DAE ∠=∠, ACD ADE ∴△∽△. ·································································································· (8分) AD AC AE AD∴=.3∴=. 则15AC =(cm ). ······································································································· (9分)∴O 的半径是7.5cm .······························································································ (10分)如图,⊙O 的直径AB 是4,过B 点的直线MN 是⊙O 的切线,D 、C 是⊙O 上的两点,连接AD 、BD 、CD 和BC . (1)求证:CDB CBN ∠=∠; (2)若DC 是ADB ∠的平分线,且︒=∠15DAB ,求DC 的长.23.(1)证明: ∵AB 是⊙O 的直径 ∴︒=∠+∠=∠90CDB ADC ADB ∵MN 切⊙O 于点B∴︒=∠+∠=∠90CBN ABC ABN ∴CBN ABC CDB ADC ∠+∠=∠+∠∵ABC ADC ∠=∠∴CDB CBN ∠=∠. (2) 如右图,连接OC OD ,,过点O 作CD OE ⊥于点E . ∵CD 平分ADB ∠ ∴BDC ADC ∠=∠ ∴弧AC =弧BC ∵AB 是⊙O 的直径 ∴︒=∠90BOC 又∵︒=∠15DABNMB A 第23题ABM N第 6 页 共 21 页∴︒=∠30DOB ∵CD OE OC OD ⊥=, ∴︒=∠30ODE ∵2=OD∴3,1==DE OE ∴322==DE CD .(1)如图1,圆心接ABC △中,AB BC CA ==,OD 、OE 为O ⊙的半径,OD BC ⊥于点F ,OE AC ⊥于点G ,求证:阴影部分四边形OFCG 的面积是ABC △的面积的13.(2)如图2,若DOE ∠保持120°角度不变, 求证:当DOE ∠绕着O 点旋转时,由两条半径和ABC △的两条边围成的图形(图中阴影部分)面积始终是ABC △的面积的13.22.证明:(1)如图1,连结OA OC ,, 因为点O 是等边三角形ABC 的外心,所以Rt Rt Rt OFC OGC OGA △≌△≌△. ····································· 2分2OFCG OFC OAC S S S ==△△,因为13OAC ABC S S =△△, 所以13OFCGABC S S =△. ··············································································································· 5分 (2)解法一:连结OA OB ,和OC ,则AOC COB BOA △≌△≌△,12∠=∠, ·································· 6分不妨设OD 交BC 于点F ,OE 交AC 于点G ,3412054120AOC DOE ∠=∠+∠=∠=∠+∠=°,°,35∴∠=∠.·························································································· 8分 在OAG △和OCF △中, 1235OA OC ∠=∠⎧⎪=⎨⎪∠=∠⎩,,,OAG OCF ∴△≌△, ················································································································ 10分第22题图D 图1 图2答案22题图(2)A E O GFB C D 1 2 3 45第 7 页 共 21 页13OFCG AOC ABC S S S ∴==△△. ···································································································· 12分解法二: 不妨设OD 交BC 于点F ,OE 交AC 于点G , 作OH BC OK AC ⊥⊥,,垂足分别为H K 、, ······················· 6分 在四边形HOKC 中,9060OHC OKC C ∠=∠=∠=°,°, 360909060120HOK ∴∠=-︒-︒=︒°- , ······························· 8分即12120∠+∠=°.又23120GOF ∠=∠+∠=°,13∴∠=∠. ································································································································ 8分 AC BC =, OH OK ∴=,OGK OFH ∴△≌△, ··············································································································· 10分13OFCG OHCK ABC S S S ∴==△. ····································································································· 12分18.(本题满分7分)在ABCD 中,10AB =,AD m =,60D ∠=°,以AB 为直径作O ⊙,(1)求圆心O 到CD 的距离(用含m 的代数式来表示); (2)当m 取何值时,CD 与O ⊙相切.18.解:(1)分别过A O ,两点作AE CD OF CD ⊥⊥,,垂足分别为点E ,点F , AE OF OF ∴∥,就是圆心O 到CD 的距离. 四边形ABCD 是平行四边形, AB CD AE OF ∴∴=∥,. ········································································································ 2分在Rt ADE △中,60sin sin 60AE AED D AD AD∠=∠==°,,°, 答案第22题图(3) A EOGF B CD 1 3 2H K第18题图答案18题图(1)答案18题图(2)第 8 页 共 21 页222AE AE m OF AE m ====,,, ······································································· 4分 圆心到CD 的距离OF为2. ······························································································· 5分 (2)3OF =, AB 为O ⊙的直径,且10AB =,∴当5OF =时,CD 与O ⊙相切于F 点,5m ==,, ········································································································· 6分 ∴当m =时,CD 与O ⊙相切. ····················································································· 7分 25. (本题满分7分)如图,在Rt △ABC 中,∠C=90°,以BC 为直径作⊙O 交AB 于点D,取AC 的中点E ,连结DE 、OE .(1)求证:DE 是⊙O 的切线;(2)如果⊙O 的半径是23cm ,ED=2cm ,求AB 的长.25、(本题满分7分)证明:(1)连结OD . ·································································································· 1分由O 、E 分别是BC 、AC 中点得OE ∥AB . ∴∠1=∠2,∠B =∠3,又OB=OD . ∴∠2=∠3.而OD=OC ,OE=OE ∴△OCE ≌△ODE . ∴∠OCE=∠ODE .BA DOCE第25题图B第25题图。
垂径定理典型例题及练习

【基础知识回顾】一、圆的定义及性质:1、圆的定义:⑴形成性定义:在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转形成的图形叫做圆,固定的端点叫线段OA叫做⑵描述性定义:圆是到定点的距离等于的点的集合【名师提醒:1、在一个圆中,圆心决定圆的半径决定圆的2、直径是圆中的弦】2、弦与弧:弦:连接圆上任意两点的叫做弦弧:圆上任意两点间的叫做弧,弧可分为、、三类3、圆的对称性:⑴轴对称性:圆是轴对称图形,有条对称轴的直线都是它的对称轴⑵中心对称性:圆是中心对称图形,对称中心是【名师提醒:圆不仅是中心对称图形,而且具有旋转性,即绕圆心旋转任意角度都被与原来的图形重合】二、垂径定理及推论:1、垂径定理:垂直于弦的直径,并且平分弦所对的2、推论:平分弦()的直径,并且平分弦所对的【名师提醒:1、垂径定理及其推论实质是指一条直线满足:⑴过圆心⑵垂直于弦⑶平分弦⑷平分弦所对的优弧⑸平分弦所对的劣弧五个条件中的两个,那么可推出其中三个,注意解题过程中的灵活运用2、圆中常作的辅助线是过圆心作弦的线3、垂径定理常用作计算,在半径r弦a弦心d和弦h中已知两个可求另外两个】三、圆心角、弧、弦之间的关系:1、圆心角定义:顶点在的角叫做圆心角2、定理:在中,两个圆心角、两条弧、两条弦中有一组量它们所对应的其余各组量也分别【名师提醒:注意:该定理的前提条件是“在同圆或等圆中”】四、圆周角定理及其推论:1、圆周角定义:顶点在并且两边都和圆的角叫圆周角2、圆周角定理:在同圆或等圆中,圆弧或等弧所对的圆周角都等于这条弧所对的圆心角的推论1、在同圆或等圆中,如果两个圆周角那么它们所对的弧推论2、半圆(或直弦)所对的圆周角是900的圆周角所对的弦是【名师提醒:1、在圆中,一条弦所对的圆心角只有一个,而它所对的圆周角有个,它们的关系是欽绲腫賁軔铼剮誒緦骞恹輿筍谭黲枨贵珑莳苋鸩捡耸殚脐剀继剧荞缚鐃鳩俪谥圆颏輻嗇惡呛櫪组颓緗轢箩約鱼產辐鹃钠俭躒劲苎鸭拦尘谖。
垂径定理例题精析

例题精析武汉二中王海涛初中几何中垂径定理及推论,圆心角、弧、弦、弦心距之间的关系(四等定理)是解决其它与圆有关问题的基础,因此对于每位同学来说这部分内容非常重要。
同学们在用以上定理及推论时首先要注意定理使用的条件,其次一些常用的手法及辅助线的添法也非常重要。
下面两道例题反映了圆中与弦有关的一些辅助线的用法。
例1、如图,AB是⊙O的直径,CD是⊙O的弦,AE⊥CD于E,BF⊥CD于F,(1)求证:EC=DF。
思路分析:考虑到O为AB的中点,AE与BF平行,故可作垂线构造平行找中点证明:过O坐CD的垂线交CD于M,∴AE∥OM∥BF且CM=DM∵O为AB中点,四边形ABFE为梯形∴M为EF中点,即EM=FM∴EM-CM=FM-DF∴EC=DF(2)当C点向下移动时,若AB与CD相交,其他条件不变,那么CE与DF是否相等?试证明。
思路分析:仍可作垂线找中点。
结论成立证明:过O坐CD的垂线交CD于M,∴AE∥OM∥BF且CM=DM∵O为AB中点,∴11 BO FM AO EM==∴ EM=FM∴EM-CM=FM-DF∴EC=DF(3)如图,若过C、D作AB的垂线分别交AB于E、F点,请同学们找出图中相等的线段。
解:AE=BF例2、如图A、B、C为⊙O的三点,点P在CO的延长线上,且∠APC=∠BPC (1)当点P在⊙O上时,求证:PA=PB;(2)当点P在⊙O外时,那么PA与PB是否相等?试证明;(3)当点P在⊙O内时,你能得到一些什么结论?思路分析:要证明PA=PB,则只需证明两弦的弦心距相等。
证明:(1)过O作OM⊥PA于M,ON⊥PB于N,∵∠APC=∠BPC,∴OM=ON,∴PA=PBPA(2)PA=PB ,证明如下:过O 作OM ⊥PA 于M ,ON ⊥PB 于N ,设PA 、PB 分别交⊙O 于E 、F , ∵∠APC=∠BPC , ∴OM=ON ,∴AE=BF ,AM=BN∵△MPO ≌△NPO ∴MP=NP∴AM+MP=BM+NP ∴PA=PB(3)PA=PB , ACBC 练习:1、 已知⊙O 的半径为5,点P 到圆心O 的距离为3,求过点P 的最大弦长及最短弦长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
垂径定理典型例题总结 班级 姓名
圆及相关概念
1.如图所示,______是直径,_______是弦,以E 为端点的劣弧有___ _ _ _ ,以A 为端点的优弧有_____ __.
2.点P 到⊙O 的最近点的距离为4cm ,最远点的距离为9cm ,则⊙O 的半径是( )
A .2.5cm 或6.5cm
B .2.5cm
C .6.5cm
D .13cm 或5cm
垂径定理
1.如图所示,AB 是⊙O 的弦,OC ⊥AB 于C ,若AB=25cm ,OC=1cm , 则⊙O 的半径长为______cm .
2. 在直径为52cm 的圆柱形油槽内装入一些油后,截面如图所示,如果油的最大深度为16cm ,那么油面宽度AB 是________cm.
3. 在直径为52cm 的圆柱形油槽内装入一些油后,,如果油面宽度是48cm ,那么油的最大深度为________cm.
4. 在半径为10的圆中有一条长为16的弦,那么这条弦的弦心距等于
5. 半径为6cm 的圆中,垂直平分半径OA 的弦长为 cm.
度数问题
1、已知:在⊙O 中,弦cm 12=AB ,O 点到AB 的距离等于AB 的一半,求:AOB ∠的度数和圆的半径.
2、已知:⊙O 的半径1=OA ,弦AB 、AC 的长分别是2、3.求BAC ∠的度数。
相交问题
1.如图,已知⊙O 的直径AB 和弦CD 相交于点E ,AE=6cm ,EB=2cm ,∠BED=30°,求CD 的长.
平行问题
在直径为50cm 的⊙O 中,弦AB=40cm ,弦CD=48cm ,且AB ∥CD ,求:AB 与CD 之间的距离.
同心圆问题
如图,在两个同心圆中,大圆的弦AB ,交小圆于C 、D 两点,设大圆和小圆的半径分别为b a ,.求证:22b a BD AD -=⋅.
一、概念题
1.下列命题中错误的有( )
(1)弦的垂直平分线经过圆心(2)平分弦的直径垂直于弦(3)圆的对称轴是直径
O A B C D E
A .1个
B .2个
C .3个
D .4个
2、⊙O 的直径为10,弦AB 的长为8,M 是弦AB 上的动点,则OM 的
长的取值范围是( )
(A )5OM 3≤≤ (B )5OM 4≤≤
(C )5OM 3<< (D )5OM 4<<
3.如图,如果AB 为⊙O 直径,弦AB CD ⊥,垂足为E ,那么下列结
论中错误的是( )
A .DE CE =
B .
C .BA
D BAC ∠=∠ D .AD AC >
4.如图,AB 是⊙O 直径,CD 是⊙O 的弦,CD AB ⊥于E ,则图中不大于半圆的相等弧有( )对。
A .1对
B .2对
C .3对
D .4对
二、垂径定理
1、过⊙O 内一点P 的最长弦为10cm ,最短的弦为6cm ,则OP 的长为 . 2.在⊙O 中,弦AB 长为cm 8,圆心到弦AB 的距离为cm 3,则⊙O 半径长为 cm
3.半径是5cm 的圆中,圆心到cm 8长的弦的距离是 cm
4.如图,有一圆弧形桥拱,拱形的半径m 10=OA ,桥拱的距度16=AB m ,
则拱高_____=CD m.
5.一水平放置的圆柱型水管的横截面如图所示,如果水管横截面的半径是13cm ,水面宽24=AB ,则水管中水深是_______cm.
6.如图,⊙O 的直径⊥CD AB ,垂足为点E ,若8,2==ED CE ,则=AB ( )
A .2
B .4
C .8
D .16
7.过⊙O 内一点M 的最长的弦长为4cm ,最短的弦长为2cm ,
则OM 的长为( )
A .3cm
B .2cm
C .1
D .3cm
8.已知:如图,⊙O 中直径AB 垂直于弦CD ,垂足为E ,若6,10==CD AB ,则BE 的长是( )
A .1
B .2
C .3
D .4
9.已知⊙O 的弦AB 长8cm ,弦心距为3cm ,则⊙O 的直径是( )
A .5cm
B .10cm
C .55cm
D .73cm
10.已知⊙O 的半径为2cm ,弦AB 长32cm ,则这条弦的中点到弦所对劣弧的中点的距离为( ) A .1cm B .2cm C .2cm D .3cm
11如图,已知⊙O 的半径为cm 6,两弦AB 与CD 垂直相交于E ,若cm CE 3=,cm DE 9=,则=AB ( )
A .cm 6
B .cm 33
C .cm 3
D .cm 36
三、度数问题
1、在⊙O 中,AB 是弦,C 是AB 的中点,
延长OC 交⊙O 于D .若CD OC =,则AOB ∠的度数是( ).
A .︒90
B .︒100
C .︒120
D .︒60
四、相交问题
1、圆的弦与直径相交成30°角,并且分直径为6cm 和4cm 两部分,则弦心距为( )
A .33
B .3
C .2
1 D .23 五、平行问题
1、 圆的两互相平行的弦长分别8cm 1和4cm 2,又两弦之间距离为cm 3,则圆的半径长是 cm
2、 在半径为cm 5的圆内有两条互相平行的弦,弦长分别为cm 8、cm 6,则这两条弦之间的距离为________
六、同心圆
1、如图,在以O 为圆心的两个同心圆中,大圆的弦AB 交小圆于C 、D
两点,cm 6,cm 10==CD AB ,则AC 的长为( )
A .0.5cm
B .1cm
C .1.5cm
D .2cm
2、如图所示,在Rt △ABC 中,∠C =900,AC =3,BC =4,以点C 为圆心,CA 为半径的圆与AB 、BC 分别交于点D 、E ,求AB 和AD 的长。
C A B
D E。
