五年级下册数学试题总复习空间与几何总结与练习北师大版
五年级数学北师大版下册课时练《总复习——图形与几何》(含答案)

答卷时应注意事项1、拿到试卷,要认真仔细的先填好自己的考生信息。
2、拿到试卷不要提笔就写,先大致的浏览一遍,有多少大题,每个大题里有几个小题,有什么题型,哪些容易,哪些难,做到心里有底;3、审题,每个题目都要多读几遍,不仅要读大题,还要读小题,不放过每一个字,遇到暂时弄不懂题意的题目,手指点读,多读几遍题目,就能理解题意了;容易混乱的地方也应该多读几遍,比如从小到大,从左到右这样的题;4、每个题目做完了以后,把自己的手从试卷上完全移开,好好的看看有没有被自己的手臂挡住而遗漏的题;试卷第1页和第2页上下衔接的地方一定要注意,仔细看看有没有遗漏的小题;5、中途遇到真的解决不了的难题,注意安排好时间,先把后面会做的做完,再来重新读题,结合平时课堂上所学的知识,解答难题;一定要镇定,不能因此慌了手脚,影响下面的答题;6、卷面要清洁,字迹要清工整,非常重要;7、做完的试卷要检查,这样可以发现刚才可能留下的错误或是可以检查是否有漏题,检查的时候,用手指点读题目,不要管自己的答案,重新分析题意,所有计算题重新计算,判断题重新判断,填空题重新填空,之后把检查的结果与先前做的结果进行对比分析。
亲爱的小朋友,你们好!经过两个月的学习,你们一定有不小的收获吧,用你的自信和智慧,认真答题,相信你一定会闯关成功。
相信你是最棒的!北师大版五年级数学下册《总复习——图形与几何》课堂作业1.选择题。
(1)下面()不能折成正方体。
(2)一个长方体,长、宽、高分别扩大为原来的2倍、3倍和4倍,则体积扩大了()倍。
A.4B.9C.24(3)在一个长120cm、宽60cm的长方体水箱里,放一块不规则的石块后,水深由原来的40cm上升到42cm,这个石块的体积至少是()dm³。
A.14.4B.14400C.302.4(4)妈妈送两份生日礼物给芳芳(如图),她想将两份礼物放到一个盒子里,放到()盒合适。
2.填空题。
(1)一个长方体的底面是边长为2cm的正方形,高是4dm,这个长方体的棱长总和是()cm,表面积是()cm²,体积是()cm³。
北师大版小学数学五年级下册总复习图形与几何练习题

北师大版小学数学五年级下册总复习图形与几何练习题一、选择题1.超市在学校南偏西30︒的方向上,那么学校在超市的()方向。
A.东偏北30︒B.西偏南30︒C.东偏北60︒2.一个长、宽、高分别是4cm、3cm、2cm长方体与一个棱长是3cm正方体比较,()的体积大。
A.正方体B.长方体C.一样3.下面图形不能围成一个长方体的是()。
A.B.C.二、填空题。
1.(1)用数对表示,秦梨家的位置是( ),书店的位置是( )。
(2)秦梨从(3,3)走到(5,0),她是从( )走到了( )。
(3)秦梨从家到落霞公园的行走路线:从家出发向( )行( )千米到文化广场,再向( )偏( )°行( )千米7.下图是一个正方体的表面展开图,每面都标有数字。
在正方体中,数字“1”对面的数字是“( )”,相交于同一个顶点的三个面上的数字之和最大是( )。
8.有几堆摆好的小方块,从三个不同的方向观察看到的形状如下图,这里至少有( )个小方块.三、判断题。
1.体育馆在学校北偏东30°方向400米处,这是以体育馆为观测点。
( )2.体积单位之间的进率是1000。
( )3.青青家在北偏东45°方向,距离300米。
( )四、解决问题。
1.求下面长方体的体积.(单位:dm)2.下图是一个纸盒的展开图,这个纸盒的表面积是多少平方厘米?3.王华从家往正东方向走600米处到红绿灯处,再往北偏东45°方向走300米到新华书店,最后往北偏西30°方向走150米到学校。
(1)画出王华到学校的路线图。
(2)根据路线示意图,说说王华放学回家时所走的方向和路程。
4.一个长方体的长、宽、高分别是三个连续的奇数。
已知它的体积是315立方米,它的表面积是多少平方米?5.把4个棱长为5dm的正方体纸箱堆在墙角(如下图所示),露在外面的面积有多少平方米?6.说一说从车站怎样走到学校?7.一个长方体形状的蓄水池,长5m,宽4m,高2.5m.(1)蓄水池占地多少平方米?(2)要给池底和四壁抹上水泥,如果每平方米用水泥20.4kg,那么要用水泥多少千克?(3)这个蓄水池最多可以蓄水多少立方米?。
北师大版五年级数学下册总复习空间与图形

• 五年级数学(下)总复习
空间与图形
7.说一说,图一可以通过怎样的变 换得到图二。
• 图一
图二
7.说一说,图一可以通过怎样的变换得到图二。②① ④.o ③知识链接
顺 时针旋 • 1.图形①绕点o___ 90 度得到图形②; 转___ 逆 时针旋 • 2.图形①绕点o___ 90 度得到图形④ ; 转___ 图形① • 3.图形③和_____ 成轴对 称图形;还有吗? (图形②和④ 成轴对称图形)
5、正方体的棱长扩大2倍,它的体积就扩大6倍。( × ) 6、把一个正方体的橡皮泥捏成一个长方体后虽然它的形 状变了,但是它所占的空间大小不变。 (√ )
3.05立方米=(3050 )立方分米 60毫升=( 0.06 )升 450立方厘米=( 0.45 )立方分米 0.8升=( 800 )立方厘米
图形的变换
1.旋转 图形的 变换
2.平移
3.轴对称
如果一个图形沿着一条直线 对折,直线两侧的图形能够完全 重合,这个图形叫轴对称图形。 这条直线叫它的对称轴。
在轴对称图形中,对称轴 两侧相对着的对称点到对称轴 的距离相等,这就是轴对称图 形的性质。 我们可以用这个性质来判断 一个图形是否是一个轴对称图 形,或者作轴对称图形。
有一个长方体游泳池,长50米,宽25米,深3米, (1)这个游泳池占地多少平方米? 50×25=1250(m2 ) (2)要在这个游泳池的四周和底部贴瓷砖,贴瓷砖的面 积是多少平方米?50×25+50×3×2+25×3×2=1700(m2 (2)在离池口1.6米处画一条红色的水位线,按水位线蓄 水,要放入多少立方米水? 50×25×1.4=1750(m3 ) 一块长方体的石头,长是5分米,底面是边长为8厘米的正 方形,每立方分米的石头大约重2.5千克,这块石头重有 多少千克? 8厘米=0.8分米 0.8×0.8×5×2.5=8(kg)
北师版五年级下册数学 期末整理与复习 图形与几何

第4课时 图形与几何
BS 5年级下册
总复习
提示:点击 进入习题
1
2
3
1.填空。
(1)消毒柜的容积大约是220(
)。
dm3
公交车的体积约是60(
)。
(2)1.5 dm3=(
)cm3 m3
3500 cm3=(1500 )mL=(
)L
3500
3.5
(3)一根长36 cm的铁丝正好可以焊成一个长4 cm、 高3 cm的长方体框架,若在这个长方体框架的表 面粘上硬纸板,至少需要( )cm2的硬纸板。
4
(7)如图,少年宫在明明家( 北 )偏( 西 )
(
)°方向上,明明家在少年宫
65 (
)偏(
)(
)°方向上。
南
东
65
2.计算下面图形的表面积和体积。(单位:cm)
表面积:10×10×6+5×5×4 =700(cm2) 体积:10×10×10-5×5×5 =875(cm3)
3.解决问题。 (1)有一块如下图所示的长方形土地,工程队在这块土
(4)一个正方体的底面周长是2452cm,它的表面积是 ( ) cm2,体积是( ) cm3。
216
216
(5)一个长方体长13 cm,宽8 cm,高6 cm,从这个
长方体中切下两个最大且完全相同的正方体后,
剩余部分的体积是(
ห้องสมุดไป่ตู้
)cm3。
(6)一个长方体的体积是129420 dm3,平行于底面的截
面面积是0.06 m2,这个长方体的高是( )m。
地上朝下挖出了一个3 m深的长方体水池。
①如果要在这个水池的四壁及地面贴上瓷砖,贴瓷砖 的面积是多少平方米?
五年级下册数学试题总复习空间与几何总结与练习北师大版
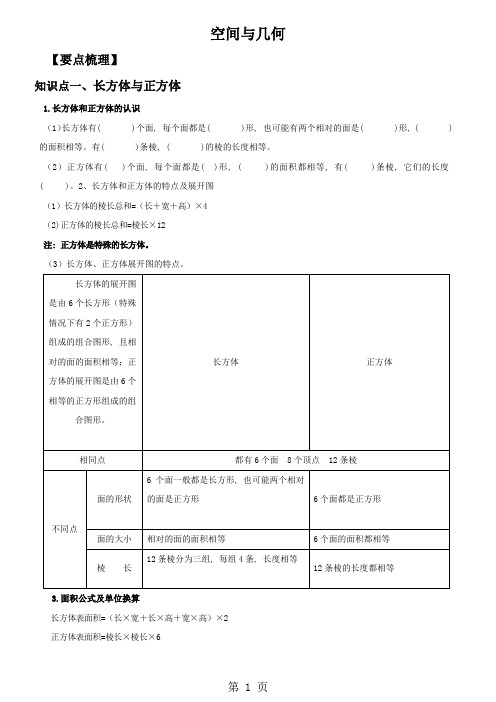
空间与几何【要点梳理】知识点一、长方体与正方体1.长方体和正方体的认识(1)长方体有( )个面, 每个面都是( )形, 也可能有两个相对的面是( )形, ( )的面积相等。
有( )条棱, ( )的棱的长度相等。
(2)正方体有( )个面, 每个面都是( )形, ( )的面积都相等, 有( )条棱, 它们的长度( )。
2、长方体和正方体的特点及展开图(1)长方体的棱长总和=(长+宽+高)×4(2)正方体的棱长总和=棱长×12注: 正方体是特殊的长方体。
(3)长方体、正方体展开图的特点。
3.面积公式及单位换算长方体表面积=(长×宽+长×高+宽×高)×2正方体表面积=棱长×棱长×6无盖长方体表面积=(长×高+宽×高)×2+长×宽面积单位: 1平方米=100平方分米 1公顷=10000平方米1平方分米=100平方厘米 1平方千米=100公顷1平方米=10000平方厘米4.露在外面的面(1)先数出露在外面的面的总个数, 再用一个面的面积乘露在外面的面的总个数。
(2)先观察正方体的摆放特点, 再从中找出露在外面的面的个数间存在规律。
知识点二、体积与容积1.体积与容积的意义①体积: 物体所占空间的大小。
②容积: 容器所能容纳物体的体积。
注:体积是从物体外部量得的, 容积是从容器内部量得的。
2.体积与容积单位常用的体积单位有: 厘米³、分米³、米³。
用字母表示cm³, dm³, m³。
②常用的容积单位有:升和毫升。
用字母表示L , mL 。
牢记:一个手指尖的体积大约是1厘米³, 一个粉笔盒的体积大约是1分米³, 盛1吨水的水箱的体积大约是1米³。
3.长方体、正方体的体积长方体的体积=长×宽×高。
五年级数学下册 专项复习 专项部分 空间与图形 第一组 长方体(一) 北师大版 试题

第一组长方体〔一〕一、填空题。
1.长方体有〔〕个面,〔〕条棱,〔〕个顶点。
相对的棱的长度〔〕,相对的面完全〔〕。
2.一个长方体长5厘米,宽4厘米,高3厘米,它的棱长总和是〔〕厘米。
3.一个正方体的棱长是a,棱长之和是〔〕。
4.一根长48厘米的铁丝扎成一个正方体,这个正方体的棱长是( ) 厘米,它的一个面的面积是〔〕厘米²,它的外表积是〔〕厘米²。
5. 一个长方体的长是8厘米,宽和高都是4厘米,这个长方体有( )个面是正方形,其余各面是( )形,这个长方体的外表积是〔〕厘米²。
6.一个正方体的底面周长是24厘米,正方体的外表积是〔〕厘米²。
7.一个正方体的棱长总和是36厘米,它的外表积是〔〕厘米²。
8.一个正方体的外表积是150厘米2,它的一个面的面积是〔〕厘米2,棱长是〔〕厘米。
9.在一个长方体中,最多有〔〕个面的面积相等,最多有〔〕条棱的长度相等。
10.把一个长6厘米,宽和高都是3厘米的长方体,截成两个小正方体,外表积增加了〔〕厘米²。
11.把两个棱长20分米的正方体摞在一起放在墙角的地面上,那么露在外面的面积应是〔〕。
12.做一个长50厘米,宽40厘米,深1.6分米的抽屉,至少要用( ) 厘米²的木板。
13.用一根96厘米长的铁丝正好制成一个长12厘米、宽8厘米、高〔〕厘米的长方体框架。
14.一个正方体箱子的棱长是4分米,外表积是〔〕分米²。
假设把正方体箱子的上盖取掉,这个正方体箱子的外表积是〔〕分米²。
二、判断题。
1.正方体的每一个面都有4条棱,正方体有6个面,所以正方体有24条棱。
〔〕2.如果长方体有两个相对的面是正方形,那么其余的四个面的面积都相等。
〔〕3.棱长是1分米的正方体纸盒放在桌子上,纸盒所占桌面的面积是1分米²。
〔〕4.把一个长方体木料锯成两个长方体,一共增加了4个面。
〔〕5.有6个面,12条棱,8个顶点的物体都是长方体。
新北师大五年级下册数学空间与图形复习(1)

长方体(一)
空 间 与 图 形
长方体(二)
确定位置 数学好玩
正方体是特殊的长方体。
8个 6个
都是正方 形
8个 6个
都是长方形,或有两个面是正方 形,其余四个面是长方形
每个面都 相等
12条
相对的面 相等
12条
每条棱都 相等
相对的棱 相等
√
√
√
√
√
√
机灵狗沿着正方体的棱剪开得到的展开图为什么是断开的?
间、Z是对面
他们在研究什么数学问题?
他们是怎么解决这个问题的?
怎样计算长方体的表面积,正 方体呢?
长方体的表面积怎样计算?
高 宽 长
长方体的表面积=长×宽× 2+长×高× 2 +高×宽× 2
或
上、下
前、后
左、右
长方体的表面积=(长×宽+长×高 +高×宽)× 2
上(下) 前(后) 左(右)
解法一: 4×3×2+4×2.5×2+3×2.5×2 =24+20+15 =59(平方米)
规律:每增加1个小正方体,露在外面的面就增 加3个。
5 + 3 X(n - 1)
小正方体个数(n) 1 露在外面的面数 5
2 3 4 5 6 9 13 17 21 25
规律:每增加1个小正方体,露在外面的面就增 加4个。
5 + 4 X(n - 1)
小正方体个数(n) 2 露在外面的面数 9
4 6 8 1012 14 19 24 29 34
“一四一”
“一四一”型
“一三二”型
“二二二”型 “三三”型
小结规律:
北师版五年级数学下册复习卷2(总复习——图形与几何)(含答案)
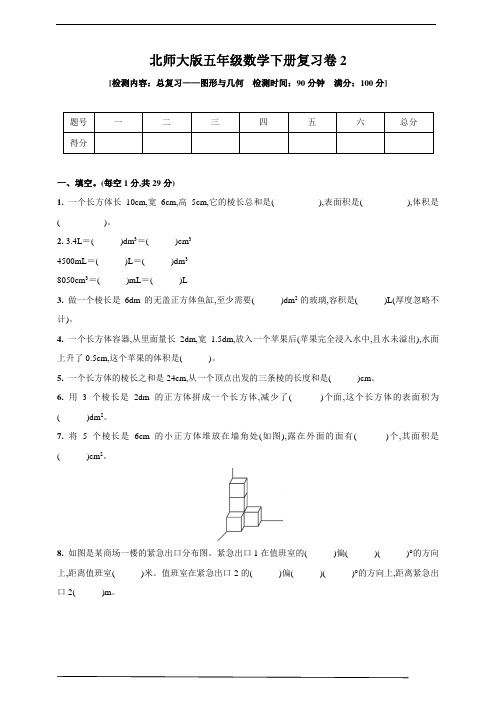
北师大版五年级数学下册复习卷2[检测内容:总复习——图形与几何检测时间:90分钟满分:100分]题号一二三四五六总分得分一、填空。
(每空1分,共29分)1.一个长方体长10cm,宽6cm,高5cm,它的棱长总和是(),表面积是(),体积是()。
2. 3.4L=()dm3=()cm34500mL=()L=()dm38050cm3=()mL=()L3.做一个棱长是6dm的无盖正方体鱼缸,至少需要()dm2的玻璃,容积是()L(厚度忽略不计)。
4.一个长方体容器,从里面量长2dm,宽1.5dm,放入一个苹果后(苹果完全浸入水中,且水未溢出),水面上升了0.5cm,这个苹果的体积是()。
5.一个长方体的棱长之和是24cm,从一个顶点出发的三条棱的长度和是()cm。
6.用3个棱长是2dm的正方体拼成一个长方体,减少了()个面,这个长方体的表面积为()dm2。
7.将5个棱长是6cm的小正方体堆放在墙角处(如图),露在外面的面有()个,其面积是()cm2。
8.如图是某商场一楼的紧急出口分布图。
紧急出口1在值班室的()偏()()°的方向上,距离值班室()米。
值班室在紧急出口2的()偏()()°的方向上,距离紧急出口2()m。
9.把75L的麻油装入容积为500mL的小瓶内,可以装满()瓶。
10.长方体的长、宽、高分别是3cm、3cm、2cm。
在它的外表面全部涂上漆,然后切成1cm3的小正方体。
其中,一面有漆的有()个,两面有漆的有()个,三面有漆的有()个。
二、判断。
(对的画“√”,错的画“×”)(5分)1.一个文具盒的体积大约是120m3。
()2.两个正方体的棱长之和相等,这两个正方体的体积也相等。
()3.两个木箱的体积相等,它们的容积也一定相等。
()4.用8个棱长1cm的小正方体拼成一个长方体或正方体,表面积最小是24cm2。
()5.体积相等的两个长方体表面积也一定相等。
()三、选择。
五年级数学下册 一课一练《总复习—图形与几何》 北师大版(含答案)

《总复习—图形与几何》一、填空题1.有一个长方体玻璃鱼缸,长50分米,宽35分米,高24分米.这个鱼缸前面的玻璃破损,需重配一块平方分米的玻璃;这个鱼缸最多能注升的水.2.长方形邻边互相,对边互相.3.用24块棱长是1厘米的正方体木块堆成一个表面积最小的长方体.这个长方体的表面积是平方厘米.4.把一个长方体的铁块熔铸成一个正方体,它的不变,发生变化;将它分割成两个长方体,它的也不变,增加了.5.一个正方体的棱长为4厘米,它的表面积是平方厘米,体积是立方厘米.二、判断题1.正方形和长方形一定是四边形.()2.长与宽相等的长方形就变成了正方形.()3.长方形和正方形都是平行四边形.()4.棱长是6厘米的立方体,它的表面积和体积相等.()5.长方体和正方体的体积都可以用:V Sh来计算.()6.把一个长方体的长、宽、高都扩大2倍,表面积也扩大2倍.()三、选择题1.求长方体的占地面积就是长方体的()A.表面积B.体积C.底面积D.侧面积2.把一块长方体橡皮泥捏成一个正方体,其中不变的是()A.表面积B.底面积C.体积3.把一块棱长为4cm的正方体橡皮泥,捏成棱长为2cm的正方体,可以捏()块.A.2 B.4 C.84.一个正方体的棱长扩大到原来的3倍,它的体积扩大到原来的()倍.A.3 B.6 C.9 D.275.将一个正方体钢坯锻造成长方体,正方体和长方体()A.体积相等,表面积不相等B.体积和表面积都不相等C.表面积相等,体积不相等D.体积和表面积都相等6.一个正方体的棱长扩大3倍,它的体积扩大()倍.A.27 B.9 C.37.甲、乙两个正方体棱长的比是1:2,那么它们的体积比是()A.1:2B.1:4C.1:6D.1:88.把一个长方体橡皮泥捏成一个正方体,()不变.A.体积B.表面积C.棱长和四、应用题1.一盒饼干长20厘米,宽15厘米,高30厘米,现在要在它的四周贴上商标纸,这张商标纸的面积是多少平方厘米?2.有一个花坛,高0.6米,底面是边长1.2米的正方形.四周用砖砌成,厚度是0.2米,中间填满泥土.花坛所占地有多大?花坛里大约有多少立方米的泥土?3.把一个棱长为5dm的正方体钢块熔铸成一个长10dm、宽20cm的长方体钢块,这个长方体钢块的高是多少?4.一根2.5米长的长方体木料,把它截成3段后,表面积增加了264dm,这根木料的体积是多少立方米?5.一个长方体水箱,从里面量长6dm,宽5dm,高4dm,这个水箱可以装水多少升?6.在一个长、宽、高分别是10厘米、8厘米、5厘米的长方体的8个顶点处,分别截下一个棱长1厘米的正方体后,剩下物体的表面积是多少平方厘米?体积是多少立方厘米?7.看图求苹果的体积.8.一个长方体,表面积是2368cm,底面积是240cm,底面周长是36cm,求这个长方体的体积.9.一件雕塑的底座是用混凝土浇筑成棱长为2.5米长的正方体.(1)这件雕塑占地多少平方米?(2)浇筑这件雕塑的底座需要混凝土多少立方米?(3)给底座四面贴上花岗石,贴花岗石的面积是多少?10.有一间长10米、宽6米、高3米的仓库,现在要给这个仓库的墙壁和屋顶粉刷涂料,除去门窗面积28m.(1)需要粉刷涂料部分的面积是多少?(2)如果每平方米需要0.4千克涂料,那么至少需要购买多少千克涂料?参考答案一、填空题1.1200,42000.2.垂直,平行.3.52.4.体积、表面积、体积、表面积.5.96,64.二、判断题1.√.2.√.3.√.4.⨯5.√.6.⨯.三、选择题1.C.2.C.3.C.4.D.5.A.6.A.7.D.8.A.四、应用题1.解:(20301530)2⨯+⨯⨯(600450)2=+⨯=⨯10502=(平方厘米),2100答:这张商标纸的面积是2100平方厘米.2.解:求花坛的占地面积:⨯=(平方米);1.2 1.2 1.44求花坛的容积:(1.20.22)(1.20.22)0.6-⨯⨯-⨯⨯=⨯⨯0.80.80.6=(立方米);0.384答:花坛所占地有1.44平方米,花坛里大约有0.384立方米的泥土.=分米3.解:20厘米2⨯⨯÷⨯555(102)=÷12520=(分米)6.25答:这个长方体钢块的高是6.25分米.4.解:64平方分米964=平方米,0.644 2.5÷⨯=⨯0.16 2.50.4=(立方米),答:这根木料的体积是0.4立方米.⨯⨯=(立方分米),5.解:654120=升,120立方分米120答:这个水箱可以装水120升.⨯+⨯+⨯⨯6.解:(10810585)2=++⨯(805040)2=⨯1702=(平方厘米);340⨯⨯-⨯⨯⨯10851118=-4008=(立方厘米),392答:剩下物体的表面积是340平方厘米,体积是392立方厘米.-=(厘米)7.解:752⨯⨯=(立方厘米)882128答:苹果的体积是128立方厘米.-⨯÷8.解:高:(368402)36=-÷(36880)36=÷288368=(厘米)⨯=(立方厘米)408320答:这个长方体的体积是320立方厘米.⨯=(平方米)9.解:(1)2.5 2.5 6.25答:这件雕塑的底座占地雕塑6.25平方米.⨯⨯(2)2.5 2.5 2.5=⨯6.25 2.5=(立方米)15.625答:浇注这件雕塑底座需要混凝土雕塑15.625立方米.⨯⨯(3)2.5 2.54=⨯6.254=(平方米)25答:贴花岗石的面积是25平方米.⨯+⨯+⨯⨯-10.解:(1)106(10363)28=+-60968=(平方米)148答:需要粉刷涂料部分的面积是148平方米.⨯=(千克)(2)0.414859.2答:至少需要购买59.2千克涂料.。
2021年-有答案-北师大版五年级(下)期末数学专题复习:图形与几何

2021学年北师大版五年级(下)期末数学专题复习:图形与几何一、填空。
1.2. 填上合适的单位。
一根钢管的长约20________.一间书房地面的面积约是8.5________.一个墨水瓶的容积约是52________.一瓶止咳糖浆的容积约是200________.一间仓库的容积约是2700________.一个文具盒的体积约是78________.3. 下面图形能围成一个长方体的是()A. B.C. D.下面的长方体都是用棱长1cm的小正方体摆成的。
算出它们的体积。
一个长方体,长4m,宽3m,高2.4m,它的占地面积是多少平方米?表面积和体积呢?以灯塔为观察点:A岛在________偏________的方向上,距离是________千米;B岛在________偏________的方向上,距离是________千米。
一个正方体油箱,从里面量棱长是3dm,这个油箱的容积是多少升?如果每升油重0.82kg,那么这个油箱最多能装油多少千克?有一块棱长是80厘米的正方体的铁块,现在要把它溶铸成一个横截面积是20平方厘米的长方体,这个长方体的长是多少厘米?学校要修长50m、宽40m的长方形操场。
先铺10cm厚的三合土,再铺5cm厚的煤渣。
需要三合土和煤渣各多少立方米?求图中大圆球的体积。
参考答案与试题解析2021学年北师大版五年级(下)期末数学专题复习:图形与几何一、填空。
1.【答案】0.078,4500,8040,12000,0.613,1250(00)【考点】体积、容积进率及单位换算【解析】(1)低级单位立方分米化高级单位立方米除以进率10(00)(2)高级单位升化低级单位毫升乘进率10(00)(3)高级单位立方分米化低级单位毫升乘进率10(00)(4)高级单位立方分米化低级单位立方厘米乘进率10(00)(5)低级单位毫升化高级单位升除以进率10(00)(6)高级单位立方米化低级单位立方厘米乘进率10000(00)故答案为:0.078,4500,8040,12000,0.613,1250(00)2.【答案】分米,平方米,ml,ml,平方米,立方厘米【考点】根据情景选择合适的计量单位【解析】根据情景根据生活经验,对长度单位、面积单位和体积(容积)单位和数据大小的认识,可知计量一根钢管的长用“分米”做单位;可知计量一间书房地面的面积用“平方米”做单位;可知计量一个墨水瓶的容积用“ml”做单位;可知计量一瓶止咳糖浆的容积的容积用“ml”做单位;可知计量一间仓库的容积用“平方米”做单位;可知计量一个文具盒的体积用“立方厘米”做单位;据此得解。
五年级数学下册 专项复习 专项部分 空间与图形 第二组 长方体(二) 北师大版

第二组长方体(二)一、填空题。
1.物体所占()叫做物体的体积。
常用的体积单位()、()、()。
计算液体容量时要用()、()。
2.在下面的括号里填上合适的单位。
一块橡皮的体积约是12();一台洗衣机的体积约是600();一个集装箱所占空间约是60();汽车的油箱大约能盛汽油50()。
3.一个正方体的棱长扩大到原来的3倍,它的表面积扩大到原来的()倍,体积扩大到原来的()倍。
4.一个正方体的棱长是a厘米,这个正方体棱长之和是( )厘米,它的表面积是( )厘米²,体积是( )厘米³。
5.用棱长2厘米的正方体切成棱长1厘米的小正方体,可以切成()块。
6.一个长方体长5米,宽3米,高4米,它的体积是()米³。
7.3.5米³=()分米³ 470厘米³=()分米³0.8米³=()厘米³ 60分米³=()米³4300毫升=()升 35分米³=()升1200厘米²=()分米²=()米²8.25米³=()分米³=()升4.8升=()分米³=()厘米³8.一个长方体从它的一个顶点引出三条棱的长度分别是:10厘米、6厘米、5厘米。
这个长方体的体积是()分米³。
9.一个长方体铁皮水桶高是6分米,底面是边长3分米的正方形,这个水桶的容积是( )升。
10.一个长方体的长是5厘米,宽是4厘米,高是3厘米,它的底面积是()厘米²。
11.一个正方体纸盒的表面积是5.1平方分米,它的占地面积是( )分米²。
12.有药水2.5升,如果将药水全部倒入一个容积是10毫升的瓶子里,可以装满()瓶。
13.一个正方体的棱长是3厘米,用三个这样的正方体拼成一个长方体,这个长方体的表面积是( ) 厘米²,体积是( ) 厘米³。
北师大版数学五年级下册 整理与复习

高1.5分米的水的体积是苹果的体积与原来水的体积之和。
V = abh =2×2×1.5 = 6(dm³)= 6(L) 6 -5.6 = 0.4(L)= 0.4(dm³)
V = a³ =1.8³ =5.832(dm³)
V = abh =15×15×30 =6750(cm³)
返回
整理与复习(1)
把一个棱长为30厘米的正方体钢坯重新锻造
成高5厘米、宽4厘米的长方体钢材,锻造后
的钢材长多少米?
锻造前后的体积是不变的。所以V长方体 = V正方体。
V正方体 = a³ = 30³
1 和7互为倒数
7
0.25×4=1 0.25和4互为倒数
还学习分数和小数的互化,能口头说一说吗?
返回
整理与复习(2)
综合运用
1.解方程。
x-
3 4
=
2 5
解:x=
2 5
3 4
x=280
15 20
x=
23 20
x+
1=4 37
解:x=
4 7
1 3
x=1221
7 21
x=
5 21
返回
整理与复习(2)
a = V长方体÷b÷h = 27000÷5÷4
=27000(cm³)
= 1350(cm)
答:锻造后的钢材长13.5米。 = 13.5(m)
返回
整理与复习(1)
如图,一个长方体的长是12厘米,宽是4厘米、
高是3厘米,把它裁成一个最大的正方体,正
五年级数学下册重难点题型训练《总复习—图形与几何》常考题集锦(原卷版)(北师大版)

2020年北师大版数学五年级下册重难点题型同步训练《总复习—图形与几何》常考题集锦一.选择题1.(2019秋•龙州县期末)求长方体的占地面积就是长方体的()A.表面积B.体积C.底面积D.侧面积2.(2019•株洲模拟)把一块长方体橡皮泥捏成一个正方体,其中不变的是()A.表面积B.底面积C.体积3.(2019•湘潭模拟)把一块棱长为4cm的正方体橡皮泥,捏成棱长为2cm的正方体,可以捏()块.A.2 B.4 C.84.(2019•防城港模拟)一个正方体的棱长扩大到原来的3倍,它的体积扩大到原来的()倍.A.3 B.6 C.9 D.275.(2019•岳阳模拟)将一个正方体钢坯锻造成长方体,正方体和长方体()A.体积相等,表面积不相等B.体积和表面积都不相等C.表面积相等,体积不相等D.体积和表面积都相等6.(2019•永州模拟)一个正方体的棱长扩大3倍,它的体积扩大()倍.A.27 B.9 C.37.(2018秋•江都区校级期末)甲、乙两个正方体棱长的比是1:2,那么它们的体积比是() A.1:2B.1:4C.1:6D.1:88.(2019•株洲模拟)把一个长方体橡皮泥捏成一个正方体,()不变.A.体积B.表面积C.棱长和二.填空题9.(2019秋•张家港市校级期末)有一个长方体玻璃鱼缸,长50分米,宽35分米,高24分米.这个鱼缸前面的玻璃破损,需重配一块平方分米的玻璃;这个鱼缸最多能注升的水.10.(2019秋•洛川县期末)长方形邻边互相,对边互相.11.(2019•郴州模拟)用24块棱长是1厘米的正方体木块堆成一个表面积最小的长方体.这个长方体的表面积是平方厘米.12.(2019•郴州模拟)把一个长方体的铁块熔铸成一个正方体,它的不变,发生变化;将它分割成两个长方体,它的也不变,增加了.13.(2019春•成武县期末)一个正方体的棱长为4厘米,它的表面积是平方厘米,体积是立方厘米.三.判断题14.(2019秋•焦作期末)正方形和长方形一定是四边形..(判断对错)15.(2019•保定模拟)长与宽相等的长方形就变成了正方形..(判断对错)16.(2018秋•海口期末)长方形和正方形都是平行四边形.(判断对错)17.(2019春•成武县期中)棱长是6厘米的立方体,它的表面积和体积相等..(判断对错)18.(2019春•成武县期末)长方体和正方体的体积都可以用:V Sh来计算..(判断对错)19.(2019春•卢龙县期中)把一个长方体的长、宽、高都扩大2倍,表面积也扩大2倍.(判断对错)四.应用题20.(2019秋•市中区期末)一盒饼干长20厘米,宽15厘米,高30厘米,现在要在它的四周贴上商标纸,这张商标纸的面积是多少平方厘米?21.(2019秋•市中区期末)有一个花坛,高0.6米,底面是边长1.2米的正方形.四周用砖砌成,厚度是0.2米,中间填满泥土.花坛所占地有多大?花坛里大约有多少立方米的泥土?22.(2019•株洲模拟)把一个棱长为5dm的正方体钢块熔铸成一个长10dm、宽20cm的长方体钢块,这个长方体钢块的高是多少?五.操作题23.(2019•重庆模拟)下面立体图形从上面、正面和左面看的形状分别是什么?画一画六.解答题64dm,这根木24.(2019春•蒙城县期末)一根2.5米长的长方体木料,把它截成3段后,表面积增加了2料的体积是多少立方米?25.(2019春•通榆县期末)一个长方体水箱,从里面量长6dm,宽5dm,高4dm,这个水箱可以装水多少升?26.(2019春•武汉月考)在一个长、宽、高分别是10厘米、8厘米、5厘米的长方体的8个顶点处,分别截下一个棱长1厘米的正方体后,剩下物体的表面积是多少平方厘米?体积是多少立方厘米?27.(2019•天津模拟)看图求苹果的体积.28.(2019•郴州模拟)一个长方体,表面积是240cm,底面周长是36cm,求这个长方体368cm,底面积是2的体积.29.(2018秋•浦口区期末)一件雕塑的底座是用混凝土浇筑成棱长为2.5米长的正方体.(1)这件雕塑占地多少平方米?(2)浇筑这件雕塑的底座需要混凝土多少立方米?(3)给底座四面贴上花岗石,贴花岗石的面积是多少?30.(2019春•甘州区校级期中)有一间长10米、宽6米、高3米的仓库,现在要给这个仓库的墙壁和屋顶粉刷涂料,除去门窗面积28m.(1)需要粉刷涂料部分的面积是多少?(2)如果每平方米需要0.4千克涂料,那么至少需要购买多少千克涂料?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
空间与几何【要点梳理】知识点一、长方体与正方体1、长方体和正方体的认识(1)长方体有()个面,每个面都是()形,也可能有两个相对的面是()形,()的面积相等。
有()条棱,()的棱的长度相等。
(2)正方体有()个面,每个面都是()形,()的面积都相等,有()条棱,它们的长度()。
2、长方体和正方体的特点及展开图(1)长方体的棱长总和=(长+宽+高)×4(2)正方体的棱长总和=棱长×12注:正方体是特殊的长方体。
(3)长方体、正方体展开图的特点。
长方体的展开图是由6个长方形(特殊情况下有2个正方形)组成的组合图形,且相对的面的面积相等;正方体的展开图是由6个相等的正方形组成的组合图形。
长方体正方体相同点都有6个面8个顶点12条棱不同点面的形状6个面一般都是长方形,也可能两个相对的面是正方形6个面都是正方形面的大小相对的面的面积相等6个面的面积都相等棱长12条棱分为三组,每组4条,长度相等12条棱的长度都相等3、面积公式及单位换算长方体表面积=(长×宽+长×高+宽×高)×2正方体表面积=棱长×棱长×6无盖长方体表面积=(长×高+宽×高)×2+长×宽面积单位:1平方米=100平方分米1公顷=10000平方米1平方分米=100平方厘米1平方千米=100公顷1平方米=10000平方厘米4、露在外面的面(1)先数出露在外面的面的总个数,再用一个面的面积乘露在外面的面的总个数。
(2)先观察正方体的摆放特点,再从中找出露在外面的面的个数间存在规律。
知识点二、体积与容积1、体积与容积的意义①体积:物体所占空间的大小。
②容积:容器所能容纳物体的体积。
注:体积是从物体外部量得的,容积是从容器内部量得的。
2、体积与容积单位①常用的体积单位有:厘米³、分米³、米³。
用字母表示cm³,dm³,m³。
②常用的容积单位有:升和毫升。
用字母表示L ,mL 。
牢记:一个手指尖的体积大约是1厘米³,一个粉笔盒的体积大约是1分米³,盛1吨水的水箱的体积大约是1米³。
3、长方体、正方体的体积长方体的体积=长×宽×高。
用字母表示是V=abh正方体的体积=棱长×棱长×棱长。
用字母表示是V=a³长方体(正方体)的体积=底面积×高。
用字母表示是V=sh4、体积与容积单位的换算①体积单位间的进率:1米³=1000分米³(1 m³=1000dm³)1分米³=1000厘米³(1 dm³=1000cm³)②容积单位间的进率:1升=1000毫升(1 L=1000mL)③体积单位与容积单位间的关系:1分米³=1升(1 dm³=1 L)1厘米³=1毫升(1cm³=1mL)④高级单位×进率低级单位低级单位÷进率高级单位1、根据方向和距离确定位置的方法:(1)确定好方向,并用量角器测量出被测物体的方位角度;(2)用直尺测量出被测物体和观测点之间的图上距离,结合单位长度计算出实际距离;(3)根据方向(角度)和距离准确判断或描述被测物体的位置。
2、描述路线图时,要先按行走路线确定每一个观测点,然后以每一个观测点为参照物,描述到下一个目标所行走的方向和路程。
知识点四、数据的表示和分析1、条形统计图、折线统计图、的特点、作用2、复式条形统计图(1)、复式条形统计图的制作方法:与单式条形统计图的制作方法基本相同,只是在魅族中有两个数据,需要两种不同颜色(或底纹)的直条来表示,同时要注明图例。
(2)、读复式条形统计图的方法:可以用横向、纵向、综合、对比等不同的方法观察,从中获取尽可能多的信息。
3、复式折线统计图(1)、复式折线统计图的特点:能表示两组数据数量的多少和数量的增减变化情况,还能反映两组数据的变化趋势。
(2)、复式条形统计图的制作方法:与单式折线统计图的制作方法基本相同,只是需要用不同的图例表示不同的数据。
4、平均数的再认识(1)、平均数的意义:一组数据中所有数据之和再除以数据的个数。
它是反映数据集中趋势的一种指标,具有代表性。
(2)、平均数的特点:平均数是一个良好的集中量数,反映灵敏,易受极端数据的影响,每个数据或大或小的变化都会影响到最终结果。
(3)、求平均数的方法:总数量÷总份量=平均数。
【典型例题】类型一、长方体与正方体的表面积与体积例1、1、长方体的表面积公式是,正方体的表面积公式是。
2、长方体的体积公式是,正方体的体积公式是。
3、常用的体积单位有,常用的容积单位有。
4、相邻面积单位之间的进率是,相邻体积单位之间的进率是。
例2、(1)分别求出下面图形的表面积和体积。
(2)某仓库粉刷墙壁,仓库长为50米,宽40米,高5米,门窗面积约为50平方米,这个仓库需粉刷的墙壁面积约为多少?在无损耗的情况下,每平方米用涂料0.8升,在实际粉刷时有18的损耗,粉刷仓库实际需要多少升?(3)算出右边图形的表面积。
(4)下面的图形分别是上面哪个盒子的展开图?想一想,连一连。
(5)下面哪些图形沿虚线折叠后能围成正方体吗?举一反三:长宽高表面积体积5cm 4cm 3cm8dm 6cm 240cm³5m 8m 200m³3、一个长方体形状蓄水池,长5米,宽4米,高2.5米①蓄水池的占地多少平方米?②要给池底和四壁抹上水泥,如果每平方米用水泥7.5千克,一共要多少水泥?这个蓄水池可以蓄水多少立方米?3、新建的篮球馆要铺设木质地板,已知该馆的长36米,宽20米,铺设它用了21.6立方米的木材,那么铺设的地板有多少厘米厚度?例3、一个长方体玻璃缸,从里面量长40cm,宽30cm,缸里装有水(为装满),把一个小铁球完全浸入水中,这时水面升高了0.8cm。
这个小铁球的体积是多少立方厘米?“教书先生”恐怕是市井百姓最为熟悉的一种称呼,从最初的门馆、私塾到晚清的学堂,“教书先生”那一行当怎么说也算是让国人景仰甚或敬畏的一种社会职业。
只是更早的“先生”概念并非源于教书,最初出现的“先生”一词也并非有传授知识那般的含义。
《孟子》中的“先生何为出此言也?”;《论语》中的“有酒食,先生馔”;《国策》中的“先生坐,何至于此?”等等,均指“先生”为父兄或有学问、有德行的长辈。
其实《国策》中本身就有“先生长者,有德之称”的说法。
可见“先生”之原意非真正的“教师”之意,倒是与当今“先生”的称呼更接近。
看来,“先生”之本源含义在于礼貌和尊称,并非具学问者的专称。
称“老师”为“先生”的记载,首见于《礼记?曲礼》,有“从于先生,不越礼而与人言”,其中之“先生”意为“年长、资深之传授知识者”,与教师、老师之意基本一致。
举一反三:3、一个体积为20dm³的铁块沉入一个从里面量长为5dm,宽为2dm的长方体容器中(水没有溢出)水面会上升多少分米?类型三、确定位置例4、1、看图判断对的打“√,错的打×。
(1)笑笑家住在红红家的北面。
( )(2)东东家在笑笑家的西边。
( )(3)红红家离超市最近。
( )(4)医院在红红家的左边。
( )(5)邮局在笑笑家的东北方向。
( )(6)红红家距医院最远。
( )(7)笑笑家在医院的东南方向。
( )(8)笑笑家住的位置最佳。
( )2、按照图上所示的位置填空。
(1)游泳馆在小文家的北偏( ) ( ) °方向,距离是 ( )米;(2)电影院在小文家东偏( ) ( ) °方向,距离 ( )米;(3)图书馆在小文家的 ( )偏 ( ) ( ) °方向,距离是 ( )米;(4)百货超市在小文家的 ( )偏 ( ) ( )°方向,距离是 ( ) 米;举一反三:4、填空。
(1)淘气从家向( )走( )米,再向( )走( )米到学校。
(2)从体育馆向( )走( )米,再向( )走( )米,再向( )走( )米,再向( )走( )米到商店。
(3)亮亮从学校向北走300米,再向西走200米到家,用“○”标出亮亮家的位置。
(4)军军从淘气家向南走100米,再向西走800米才到家,用“☆”标出军军家的位置。
(5)军军从家向( )走( )米,再向( )走( )米到商店。
(6)学校离( )家最近,是( )米。
(淘气、军军、亮亮)。
5、找到每个建筑物的位置。
(1)体育馆在钟楼北偏( ) ( )°方向,距离是( )米;(2)新华书店在钟楼( )偏( ) ( ) °方向,距离是( )米;(3)怡心公园在钟楼( )偏( ) ( )°方向,距离( )米;(4)百货大楼在钟楼( )偏( ) ( )°方向,距离是( )米;类型四、数据的表示和分析例5、两种统计图的特点以及它们的区别1、条形统计图的特点是,折线统计图的特点是。
2、某工厂要反映四、五、六月份产量的增长变化情况,应绘制统计图;要表示水果超市各种水果的销售数量,应绘制统计图。
举一反三:5、东风电视机场2019年各季度生产电视机的台数统计图如下:(1)平均每个季度产()台,全年平均每月产()台。
(2)第四季度比第一季度增产()%,第二季度比第四季度少()%.(3)下半年占全年台数的()%.【巩固练习】观察内容的选择,我本着先静后动,由近及远的原则,有目的、有计划的先安排与幼儿生活接近的,能理解的观察内容。
随机观察也是不可少的,是相当有趣的,如蜻蜓、蚯蚓、毛毛虫等,孩子一边观察,一边提问,兴趣很浓。
我提供的观察对象,注意形象逼真,色彩鲜明,大小适中,引导幼儿多角度多层面地进行观察,保证每个幼儿看得到,看得清。
看得清才能说得正确。
在观察过程中指导。
我注意帮助幼儿学习正确的观察方法,即按顺序观察和抓住事物的不同特征重点观察,观察与说话相结合,在观察中积累词汇,理解词汇,如一次我抓住时机,引导幼儿观察雷雨,雷雨前天空急剧变化,乌云密布,我问幼儿乌云是什么样子的,有的孩子说:乌云像大海的波浪。
有的孩子说“乌云跑得飞快。
”我加以肯定说“这是乌云滚滚。
”当幼儿看到闪电时,我告诉他“这叫电光闪闪。
”接着幼儿听到雷声惊叫起来,我抓住时机说:“这就是雷声隆隆。
”一会儿下起了大雨,我问:“雨下得怎样?”幼儿说大极了,我就舀一盆水往下一倒,作比较观察,让幼儿掌握“倾盆大雨”这个词。
雨后,我又带幼儿观察晴朗的天空,朗诵自编的一首儿歌:“蓝天高,白云飘,鸟儿飞,树儿摇,太阳公公咪咪笑。
”这样抓住特征见景生情,幼儿不仅印象深刻,对雷雨前后气象变化的词语学得快,记得牢,而且会应用。
