高鸿业微观经济学业第七版课后答案消费者选择
高鸿微观经济学业第七版课后答案第二章 需求、供给和均衡价格

第二章需求、供给和均衡价格第一部分教材配套习题本习题详解一、简答题1. 下列事件对x商品的需求有何影响?(1)x商品的生产厂商投入大量资金做广告宣传。
(2)生产x商品的工人的工资增加了。
(3)y商品是x商品的替代品,y商品的价格下降了。
(4)消费者的收入增加了。
解答:(1)x 商品的生产厂商投入大量资金做广告宣传,提高商品的知名度和消费者对商品的偏好,导致在每一价格下,消费者对商品需求量增加,使需求曲线向右移动。
(2)生产x 商品的工人的工资增加了。
对x商品的需求没有直接影响,需求曲线不变,但是工人的工资增加,增加了生产成本,使供给曲线向左上移动,需求不变供给减少,导致均衡价格上升,均衡数量减少。
(3)y 商品是x 商品的替代品,y 商品的价格下降了,x 商品相对贵了,消费者用y商品替代x商品,导致在每一价格下,消费者对商品需求量减少,使需求曲线向左移动。
(4)若消费者消费的是正常商品,消费者的收入增加了,在每一价格下,消费者对商品需求量增加,使需求曲线向右移动;若消费者消费的是劣商品(抵挡商品),导致在每一价格下,消费者对商品需求量减少,使需求曲线向左移动。
2. 下列事件对棉花供给有何影响?(1)气候恶劣导致棉花歉收。
(2)种植棉花所需的化肥的价格上升。
(3)政府对种植棉花的农户实施优惠政策。
(4)棉花价格上升。
下列事件对棉花供给有何影响?(1)气候恶劣导致棉花歉收。
解答:(1)棉花的供给曲线会左移。
因为恶劣气候导致的棉花歉收, 在棉花价格不变的情况下,会使棉花的供给数量减少,棉花的供给曲线会左移。
(2)棉花的供给曲线会左移。
因为化肥价格上升使得棉花的生产成本上升、利润下降,在任一价格水平下,农户都会缩小棉花种植面积,导致棉花供给数量下降, 棉花的供给曲线会左移。
(3)棉花的供给曲线会右移。
因为政府对种植棉花农户的优政策将激励农户的生产积极性,在任价格水平下,户都会大棉花种面积,导致棉花供给数量増加,棉花的供给曲线会右移。
(完整word版)高鸿业微观经济学业第七版课后答案18第三章消费者选择

第三章消费者选择第一部分 教材配套习题本习题详解1.已知一件衬衫的价格为80元,一份肯德基快餐的价格为20元,在某 消费者关于这两种商品的效用最大化的均衡点上,一份肯德基快餐对衬衫的边 际替代率MRS是多少?解答:用 X 表示肯德基快餐的份数;Y 表示衬衫的件数;MRSXY 表示在 维持效用水平不变的前提下,消费者增加一份肯德基快餐消费时所需要放弃的衬衫的消费数量。
在该消费者实现关于这两种商品的效用最大化时,在均衡点上有边际替代率等于价格比,则有:201804X XY YP Y MRS X P ∆=-===∆它表明,在效用最大化的均衡点上,该消费者关于一份肯德基快餐对衬衫 的边际替代率MRS为0.25。
2.假设某消费者的均衡如图3—1所示。
其中,横轴OX1和纵轴OX2分别 表示商品1和商品2的数量,线段AB为消费者的预算线,曲线U 为消费者的无差异曲线,E点为效用最大化的均衡点。
已知商品1的价格P1=2元。
求:(1)求消费者的收入; (2)求商品2的价格P2; (3)写出预算线方程; (4)求预算线的斜率;(5)求E点的MRS12的值。
图3—1 某消费者的均衡解答:(1)横轴截距表示消费者的收入全部购买商品1的数量为30单位,且已知P1=2元,所以,消费者的收入 M=2×30=60元。
(2)图3—1中纵轴截距表示消费者的收入全部购买商品2的数量为20单位,且由(1)已知收入 M=60元,所以,商品2的价格P 2=M 20=6020=3(元)。
(3)由于预算线方程的一般形式为 P 1X 1+P 2X 2=M,所以本题预算线方程具体写为:2X 1+3X 2=60。
(4)(4)将(3)中的预算线方程进一步整理为X 2=-23X 1+20。
所以,预算线的斜率为-23。
(5)在消费者效用最大化的均衡点E 上,有211212X PMRS X P ∆=-=∆,即无差异曲线斜率的绝对值即MRS 等于预算线斜率的绝对值P 1P 2。
高鸿业微观经济学业第七版课后答案18第三章消费者选择

第三章消费者选择第一部分教材配套习题本习题详解1.已知一件衬衫的价格为80元,一份肯德基快餐的价格为20元,在某消费者关于这两种商品的效用最大化的均衡点上,一份肯德基快餐对衬衫的边际替代率MRS是多少?解答:用X表示肯德基快餐的份数;Y表示衬衫的件数;MRSXY表示在维持效用水平不变的前提下,消费者增加一份肯德基快餐消费时所需要放弃的衬衫的消费数量。
在该消费者实现关于这两种商品的效用最大化时,在均衡点上有边际替代率等于价格比,则有:MRSXY YPXXPY201804它表明,在效用最大化的均衡点上,该消费者关于一份肯德基快餐对衬衫的边际替代率MRS为0.25。
2.假设某消费者的均衡如图3—1所示。
其中,横轴OX1和纵轴OX2分别表示商品1和商品2的数量,线段AB为消费者的预算线,曲线U为消费者的无差异曲线,E点为效用最大化的均衡点。
已知商品1的价格P1=2元。
求:(1)求消费者的收入;(2)求商品2的价格P2;(3)写出预算线方程;(4)求预算线的斜率;(5)求E点的MRS12的值。
图3—1某消费者的均衡解答:(1)横轴截距表示消费者的收入全部购买商品1的数量为30单位,且已知P1=2元,所以,消费者的收入M=2×30=60元。
(2)图3—1中纵轴截距表示消费者的收入全部购买商品2的数量为20M 单位,且由(1)已知收入M=60元,所以,商品2的价格P2=20=60 20=3(元)。
(3)由于预算线方程的一般形式为P1X1+P2X2=M,所以本题预算线方程具体写为:2X1+3X2=60。
(4)(4)将(3)中的预算线方程进一步整理为X2=-23X1+20。
所以,预算线的斜率为2 -。
3(5)在消费者效用最大化的均衡点E上,有MRS12 X P21XP12,即无差异曲线斜率的绝对值即MRS等于预算线斜率的绝对值P1。
因此,MRS12=P2P1=P22。
33.对消费者实行补助有两种方法:一种是发给消费者一定数量的实物补助,另一种是发给消费者一笔现金补助,这笔现金额等于按实物补助折算的货币量。
高鸿业《西方经济学(微观部分)》(第7版)笔记和课后习题复习备考资料答案

高鸿业《西方经济学(微观部分)》(第7版)笔记和课后习题(含考研真题)详解完整版>精研学习网>免费在线试用20%资料全国547所院校视频及题库资料考研全套>视频资料>课后答案>往年真题>职称考试目录隐藏第1章引论1.1复习笔记1.2课后习题详解1.3名校考研真题详解第2章需求、供给和均衡价格2.1复习笔记2.2课后习题详解2.3名校考研真题详解第3章消费者选择3.1复习笔记3.2课后习题详解3.3名校考研真题详解第4章生产技术4.1复习笔记4.2课后习题详解4.3名校考研真题详解第5章成本5.1复习笔记5.2课后习题详解5.3名校考研真题详解第6章完全竞争市场6.1复习笔记6.2课后习题详解6.3名校考研真题详解第7章不完全竞争市场7.1复习笔记7.2课后习题详解7.3名校考研真题详解第8章生产要素价格的决定8.1复习笔记8.2课后习题详解8.3名校考研真题详解第9章一般均衡论和福利经济学9.1复习笔记9.2课后习题详解9.3名校考研真题详解第10章博弈论初步10.1复习笔记10.2课后习题详解10.3名校考研真题详解第11章市场失灵和微观经济政策11.1复习笔记11.2课后习题详解11.3名校考研真题详解内容简介隐藏本书是高鸿业《西方经济学(微观部分)》(第7版)教材的学习辅导书,严格按照高鸿业《西方经济学(微观部分)》(第7版)教材内容进行编写,共分11章,主要包括以下内容:(1)整理名校笔记,浓缩内容精华。
每章的复习笔记以高鸿业主编的《西方经济学(微观部分)》(第7版)为主,并结合国内外其他微观经济学经典教材对各章的重难点进行了整理,因此,本书的内容几乎浓缩了经典教材的知识精华。
(2)解析课后习题,提供详尽答案。
本书参考大量相关辅导资料对高鸿业主编的《西方经济学(微观部分)》(第7版)的所有课后习题进行了详细的分析和解答,并对相关重要知识点进行了延伸和归纳。
高鸿微观经济学业第七版课后答案第二章 需求、供给和均衡价格

第二章需求、供给和均衡价格第一部分教材配套习题本习题详解一、简答题1. 下列事件对x商品的需求有何影响?(1)x商品的生产厂商投入大量资金做广告宣传。
(2)生产x商品的工人的工资增加了。
(3)y商品是x商品的替代品,y商品的价格下降了。
(4)消费者的收入增加了。
解答:(1)x 商品的生产厂商投入大量资金做广告宣传,提高商品的知名度和消费者对商品的偏好,导致在每一价格下,消费者对商品需求量增加,使需求曲线向右移动。
(2)生产x 商品的工人的工资增加了。
对x商品的需求没有直接影响,需求曲线不变,但是工人的工资增加,增加了生产成本,使供给曲线向左上移动,需求不变供给减少,导致均衡价格上升,均衡数量减少。
(3)y 商品是x 商品的替代品,y 商品的价格下降了,x 商品相对贵了,消费者用y商品替代x商品,导致在每一价格下,消费者对商品需求量减少,使需求曲线向左移动。
(4)若消费者消费的是正常商品,消费者的收入增加了,在每一价格下,消费者对商品需求量增加,使需求曲线向右移动;若消费者消费的是劣商品(抵挡商品),导致在每一价格下,消费者对商品需求量减少,使需求曲线向左移动。
2. 下列事件对棉花供给有何影响?(1)气候恶劣导致棉花歉收。
(2)种植棉花所需的化肥的价格上升。
(3)政府对种植棉花的农户实施优惠政策。
(4)棉花价格上升。
下列事件对棉花供给有何影响?(1)气候恶劣导致棉花歉收。
解答:(1)棉花的供给曲线会左移。
因为恶劣气候导致的棉花歉收, 在棉花价格不变的情况下,会使棉花的供给数量减少,棉花的供给曲线会左移。
(2)棉花的供给曲线会左移。
因为化肥价格上升使得棉花的生产成本上升、利润下降,在任一价格水平下,农户都会缩小棉花种植面积,导致棉花供给数量下降, 棉花的供给曲线会左移。
(3)棉花的供给曲线会右移。
因为政府对种植棉花农户的优政策将激励农户的生产积极性,在任价格水平下,户都会大棉花种面积,导致棉花供给数量増加,棉花的供给曲线会右移。
高鸿业微观经济学业第七版课后答案18第三章消费者选择

第三章消费者选择第一部分教材配套习题本习题详解1.已知一件衬衫的价格为80元,一份肯德基快餐的价格为20元,在某消费者关于这两种商品的效用最大化的均衡点上,一份肯德基快餐对衬衫的边际替代率MRS是多少?解答:用X表示肯德基快餐的份数;Y表示衬衫的件数;MRSXY表示在维持效用水平不变的前提下,消费者增加一份肯德基快餐消费时所需要放弃的衬衫的消费数量。
在该消费者实现关于这两种商品的效用最大化时,在均衡点上有边际替代率等于价格比,则有:Y P X20 1MRS XYX P Y80 4它表明,在效用最大化的均衡点上,该消费者关于一份肯德基快餐对衬衫的边际替代率MRS为0.25。
2.假设某消费者的均衡如图3—1所示。
其中,横轴OX1和纵轴OX2分别表示商品1和商品2的数量,线段AB为消费者的预算线,曲线U为消费者的无差异曲线,E点为效用最大化的均衡点。
已知商品1的价格P1=2元。
求:(1)求消费者的收入;(2)求商品2的价格P2;(3)写出预算线方程;(4)求预算线的斜率;(5)求E点的MRS12的值。
图3—1某消费者的均衡解答:(1)横轴截距表示消费者的收入全部购买商品1的数量为30单位,且已知P1=2元,所以,消费者的收入M=2×30=60元。
(2)图3—1中纵轴截距表示消费者的收入全部购买商品2的数量为20M 60 单位,且由(1)已知收入M=60元,所以,商品2的价格P2=20=20=3(元)。
(3)由于预算线方程的一般形式为P1X1+P2X2=M,所以本题预算线方程具体写为:2X1+3X2=60。
2(4)(4)将(3)中的预算线方程进一步整理为X2=-X1+20。
所以,预算线的斜率为-2。
3(5)在消费者效用最大化的均衡点E上,有MRS12X2P1,即无差异曲线斜率X1P2的绝对值即MRS等于预算线斜率的绝对值P1。
因此,MRS=P1=2。
P2 12P2 33.对消费者实行补助有两种方法:一种是发给消费者一定数量的实物补助,另一种是发给消费者一笔现金补助,这笔现金额等于按实物补助折算的货币量。
高鸿业微观经济学业第七版课后答案18第三章消费者选择

精心整理第三章消费者选择第一部分教材配套习题本习题详解1.已知一件衬衫的价格为80元,一份肯德基快餐的价格为20元,在某消费者关于这两种商品的效用最大化的均衡点上,一份肯德基快餐对衬衫的边际替代率MRS是多少?解答:用X表示肯德基快餐的份数;Y表示衬衫的件数;MRSXY表示在维持效用水平不变的前提下,消费者增加一份肯德基快餐消费时所需要放弃的衬衫的消费数量。
在该消费者实现关于这两种商品的效用最大化时,在22X 1+3(4)(4)将(3)中的预算线方程进一步整理为X 2=-X 1+20。
所以,预算线的斜率为-。
(5)在消费者效用最大化的均衡点E 上,有211212X PMRS X P ∆=-=∆,即无差异曲线斜率的绝对值即MRS 等于预算线斜率的绝对值。
因此,MRS 12==。
3.对消费者实行补助有两种方法:一种是发给消费者一定数量的实物补助,另一种是发给消费者一笔现金补助,这笔现金额等于按实物补助折算的货币量。
试用无差异曲线分析法,说明哪一种补助方法能给消费者带来更大的效用。
解答:一般说来,发给消费者现金补助会使消费者获得更大的效用。
其原因在于:在现金补助的情况下,消费者可以按照自己的偏好来购买商品,以获得尽可能大的效用。
如图3—3所示。
图3—3实物补贴和货币补贴在图中,AB是按实物补助折算的货币量等于现金补助情况下的预算线。
在现金补助的预算线AB上,消费者根据自己的偏好选择商品1和商品2的购买量分别为*1X 和*2X ,从而实现了最大的效用水平U2,即在图3—3中表现为预算线AB和无差异曲线U2相切的均衡点E。
在实物补助的情况下,则通常不会达到最大的效用水平U2。
因为,譬如,当实物补助两商品数量分别为x11、x21的F点,或者为两商品数量分别为x12和x22的G点时,则消费者获得无差异曲线U1所表示的效用水平,显然,U1<U2。
4.假设某商品市场上只有A 、B 两个消费者,他们的需求函数各自为Q =20-4P 和Q =30-5P 。
最新高鸿业微观经济学业第七版课后答案18第三章消费者选择资料

第三章消费者选择第一部分 教材配套习题本习题详解1.已知一件衬衫的价格为80元,一份肯德基快餐的价格为20元,在某 消费者关于这两种商品的效用最大化的均衡点上,一份肯德基快餐对衬衫的边 际替代率MRS是多少?解答:用 X 表示肯德基快餐的份数;Y 表示衬衫的件数;MRSXY 表示在 维持效用水平不变的前提下,消费者增加一份肯德基快餐消费时所需要放弃的衬衫的消费数量。
在该消费者实现关于这两种商品的效用最大化时,在均衡点上有边际替代率等于价格比,则有:201804X XY YP Y MRS X P ∆=-===∆它表明,在效用最大化的均衡点上,该消费者关于一份肯德基快餐对衬衫 的边际替代率MRS为0.25。
2.假设某消费者的均衡如图3—1所示。
其中,横轴OX1和纵轴OX2分别 表示商品1和商品2的数量,线段AB为消费者的预算线,曲线U 为消费者的无差异曲线,E点为效用最大化的均衡点。
已知商品1的价格P1=2元。
求:(1)求消费者的收入; (2)求商品2的价格P2; (3)写出预算线方程; (4)求预算线的斜率;(5)求E点的MRS12的值。
图3—1 某消费者的均衡解答:(1)横轴截距表示消费者的收入全部购买商品1的数量为30单位,且已知P1=2元,所以,消费者的收入 M=2×30=60元。
(2)图3—1中纵轴截距表示消费者的收入全部购买商品2的数量为20单位,且由(1)已知收入 M=60元,所以,商品2的价格P 2=M 20=6020=3(元)。
(3)由于预算线方程的一般形式为 P 1X 1+P 2X 2=M,所以本题预算线方程具体写为:2X 1+3X 2=60。
(4)(4)将(3)中的预算线方程进一步整理为X 2=-23X 1+20。
所以,预算线的斜率为-23。
(5)在消费者效用最大化的均衡点E 上,有211212X PMRS X P ∆=-=∆,即无差异曲线斜率的绝对值即MRS 等于预算线斜率的绝对值P 1P 2。
高鸿业微观第七版第,,章习题参考答案
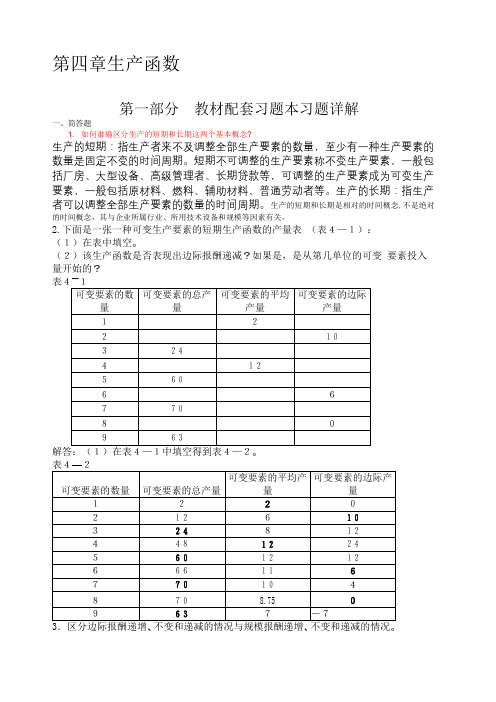
第四章生产函数第一部分教材配套习题本习题详解一、简答题1. 如何准确区分生产的短期和长期这两个基本概念?生产的短期:指生产者来不及调整全部生产要素的数量,至少有一种生产要素的数量是固定不变的时间周期。
短期不可调整的生产要素称不变生产要素,一般包括厂房、大型设备、高级管理者、长期贷款等,可调整的生产要素成为可变生产要素,一般包括原材料、燃料、辅助材料、普通劳动者等。
生产的长期:指生产者可以调整全部生产要素的数量的时间周期。
生产的短期和长期是相对的时间概念,不是绝对的时间概念,其与企业所属行业、所用技术设备和规模等因素有关。
2.下面是一张一种可变生产要素的短期生产函数的产量表(表4—1):(1)在表中填空。
(2)该生产函数是否表现出边际报酬递减?如果是,是从第几单位的可变要素投入量开始的?—解答:边际报酬变化是指在生产过程中一种可变要素投入量每增加一个单位时所引起的总产量的变化量,即边际产量的变化,而其他生产要素均为固定生产要素,固定要素的投入数量是保持不变的。
边际报酬变化一般包括边际报酬递增、不变和递减三个阶段。
很显然,边际报酬分析可视为短期生产分析。
规模报酬分析方法是描述在生产过程中全部生产要素的投入数量均同比例变化时所引起的产量变化特征,当产量的变化比例分别大于、等于、小于全部生产要素投入量变化比例时,则分别为规模报酬递增、不变、递减。
很显然,规模报酬分析可视为长期生产的分析视角。
区别:①前提条件不同,边际报酬变化生产要素分为不变和可变生产要素,生产要素比例发生变化;规模报酬分析研究生产要素同比例变动。
②考察时间长短不同。
边际报酬变化分析的是短期生产规律;规模报酬研究长期生产规律。
③指导意义不同。
边际报酬变化指出要按比例配置生产要素;规模报酬指出要保持企业的适度规模。
④由于前提条件不同,两规律独立发挥作用,不存在互为前提,互为影响关系。
联系:随着投入要素增加,产量一般都经历递增、不变和递减三个阶段。
高鸿业微观第七版第2章习题参考答案

第二章需求、供给和均衡价格一、简答题1.【答案】(1)广告宣传会增加消费者对x的偏好,使得对x的需求增加,需求曲线右移。
(2)生产x商品的工人工资增加提高了x的生产成本,使得x的供给减少,但需求不会变。
(3)替代品y的价格下降,使得消费者更多购买y了,使得对x的需求减少,需求曲线左移。
(4)消费者收入增加后,对所有正常品的需求都增加,如果x是正常品,则会增加对x的需求,需求曲线右移;但如果x是劣等品,则会减少对x的需求,需求曲线左移。
2.【答案】(1)棉花歉收导致供给减少,供给曲线左移。
(2)化肥涨价导致生产成本上升,使得棉花供给减少,供给曲线左移。
(3)政府的优惠政策导致生产成本下降,使得棉花供给增加,供给曲线右移。
(4)棉花价格上升使得棉花本期供给量增加,但供给不变,即供给曲线不移动。
如果生产者会据此认为棉花上升的价格能持续,则,下一期会增加棉花种植,导致下一期棉花供给增加,供给曲线右移;但如果生产者不认为棉花上升的价格能持续,则不会增加下一期棉花种植,下一期棉花供给也不变。
3.【答案】(1)P e=6,Q e=20。
图略。
(2)P e=7,Q e=25。
图略。
(3)P e=5.5,Q e=22.5。
图略。
(4)静态分析与比较静态分析的联系:变量的调整时间被假设为零。
在(1)、(2)和(3)中,所有外生变量或内生变量都属于同一个时期。
而且,在分析由外生变量变化所引起的内生变量变化的过程中,也假定这种调整时间为零。
两者的区别:静态分析是根据既定的外生变量数值求内生变量值的分析方法。
比较静态分析是研究外生变量变化对内生变量的影响方式,以及分析比较不同数值的外生变量下内生变量的不同数值。
(5)需求变动对均衡值的影响:由(1)可知当需求函数为Q d=50-5P、供给函数为Q s =-10+5P时,均衡价格P e=6、均衡数量Q e=20;当需求增加,如变为(2)中的Q d=60-5P时,得出均衡价格P e=7、均衡数量Q e=25。
高鸿业,微观经济学,第七版,课后答案,西方经济学18第八章生产要素价格地决定

第八章生产要素价格的决定第一部分教材配套习题本习题详解一、简答题说明生产要素理论在微观经济学中的地位。
1.解答:第一,从商品的角度分析,微观经济学可以分为“产品”的理论和“要素”的理论两个部分,前者讨论产品的价格和数量的决定,后者讨论要素的价格和数量的决定。
第二,产品的理论和要素的理论是相互联系的。
特别是,产品理论离不开要素理论,否则就不完全。
这是因为,首先,在推导产品需求曲线时,假定消费者的收入水平为既定,但并未说明收入水平是如何决定的;其次,在推导产品供给曲线时,假定生产要素的价格为既定,但并未说明要素价格是如何决定的。
上述两点不完全性可以概括为缺乏对要素价格和使用量决定的解释。
为了弥补这个不足,需要研究生产要素市场。
因此,要素理论可以看成是产品理论的自然延伸和发展。
第三,在西方经济学中,产品的理论通常被看成是“价值”理论,要素理论通常被看成是“分配”理论。
产品理论加上要素理论,或者,价值理论加上分配理论,这样才构成了整个微观经济学的一个相对完整的体系。
2.试述完全竞争厂商及市场在存在和不存在行业调整情况下的要素需求曲线。
解答:第一,在完全竞争条件下,厂商对要素的需求曲线向右下方倾斜,即随着要素价格的下降,厂商对要素的需求量将增加。
第二,在完全竞争市场,如果不考虑某厂商所在行业中其他厂商的调整,则该厂商的要素需求曲线就恰好与其边际产品价值曲线重合。
这是一条向右下方倾斜的曲线。
随着要素价格的下降,各厂商对要素的需求量将增加。
由于不存在行业调整,完全竞争厂商的要素需求曲线与边际产品价值曲线重合,市场的要素需求曲线就是市场上所有要素的边际产品价值曲线的简单加总。
第三,完全竞争市场厂商要素需求若存在行业调整,那么,要素价格的变化引起所有其他厂商的要素需求量和要素使用量及产量的变动。
在完全竞争条件下,单个厂商产量变化不会影响产品价格,但全体厂商的产量变动将改变产品的市场价格。
产品价格使厂商n的边际产品价值曲线发生改变,从而厂商n的要素需求曲线也不再等于其边际产品价值曲线。
高鸿业微观经济学业第七版课后答案18第三章消费者选择

第三章消费者选择第一部分教材配套习题本习题详解1.已知一件衬衫的价格为80元,一份肯德基快餐的价格为20元,在某消费者关于这两种商品的效用最大化的均衡点上,一份肯德基快餐对衬衫的边际替代率MRS是多少?解答:用X表示肯德基快餐的份数;Y表示衬衫的件数;MRSXY表示在维持效用水平不变的前提下,消费者增加一份肯德基快餐消费时所需要放弃的衬衫的消费数量。
在该消费者实现关于这两种商品的效用最大化时,在均衡点上有边际替代率等于价格比,则有:Y P X201MRS XYX P Y804它表明,在效用最大化的均衡点上,该消费者关于一份肯德基快餐对衬衫的边际替代率MRS为 0.25 。
2.假设某消费者的均衡如图3—1所示。
其中,横轴OX1和纵轴OX2分别表示商品1和商品2的数量,线段AB为消费者的预算线,曲线U为消费者的无差异曲线,E点为效用最大化的均衡点。
已知商品1的价格P1=2元。
求:(1)求消费者的收入;(2)求商品2的价格P2;(3)写出预算线方程;(4)求预算线的斜率;(5)求E点的MRS12的值。
图3—1某消费者的均衡解答:(1)横轴截距表示消费者的收入全部购买商品1的数量为30单位,且已知P1=2元,所以,消费者的收入M=2×30=60元。
(2)图3—1中纵轴截距表示消费者的收入全部购买商品2的数量为20M 60单位,且由(1)已知收入M=60元,所以,商品2的价格P2=20=20=3(元)。
(3)由于预算线方程的一般形式为P1 X1+P2X2= M, 所以本题预算线方程具体写为:2X1+ 3X2= 60。
2(4)(4) 将 (3) 中的预算线方程进一步整理为X2=-X1+ 20。
所以,预算线的斜率为-2。
3(5)在消费者效用最大化的均衡点E上,有 MRS12X 2P1,即无差异曲线斜率X1P2的绝对值即 MRS 等于预算线斜率的绝对值P1。
因此, MRS =P1=2。
P212P233.对消费者实行补助有两种方法:一种是发给消费者一定数量的实物补助,另一种是发给消费者一笔现金补助,这笔现金额等于按实物补助折算的货币量。
高鸿业-微观经济学-第七版-课后答案18第四章生产函数
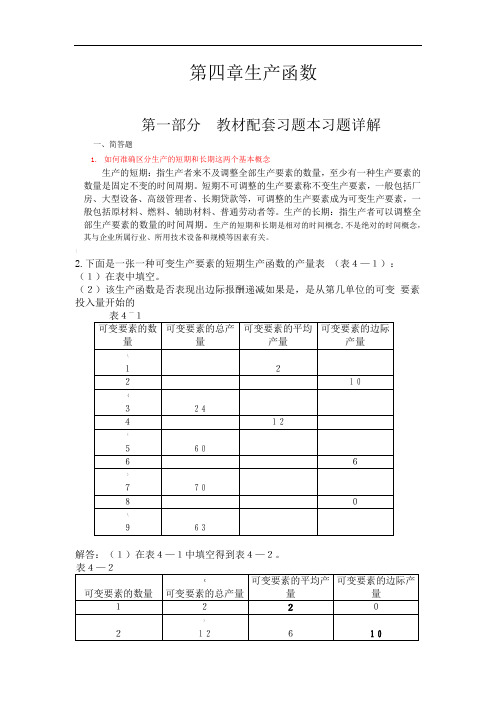
第四章生产函数第一部分教材配套习题本习题详解一、简答题1.如何准确区分生产的短期和长期这两个基本概念生产的短期:指生产者来不及调整全部生产要素的数量,至少有一种生产要素的数量是固定不变的时间周期。
短期不可调整的生产要素称不变生产要素,一般包括厂房、大型设备、高级管理者、长期贷款等,可调整的生产要素成为可变生产要素,一般包括原材料、燃料、辅助材料、普通劳动者等。
生产的长期:指生产者可以调整全部生产要素的数量的时间周期。
生产的短期和长期是相对的时间概念,不是绝对的时间概念,其与企业所属行业、所用技术设备和规模等因素有关。
|2.下面是一张一种可变生产要素的短期生产函数的产量表(表4—1):(1)在表中填空。
(2)该生产函数是否表现出边际报酬递减如果是,是从第几单位的可变要素投入量开始的—解答:(1)在表4—1中填空得到表4—2。
·3.区分边际报酬递增、不变和递减的情况与规模报酬递增、不变和递减的情况。
解答:边际报酬变化是指在生产过程中一种可变要素投入量每增加一个单位时所引起的总产量的变化量,即边际产量的变化,而其他生产要素均为固定生产要素,固定要素的投入数量是保持不变的。
边际报酬变化一般包括边际报酬递增、不变和递减三个阶段。
很显然,边际报酬分析可视为短期生产分析。
规模报酬分析方法是描述在生产过程中全部生产要素的投入数量均同比例变化时所引起的产量变化特征,当产量的变化比例分别大于、等于、小于全部生产要素投入量变化比例时,则分别为规模报酬递增、不变、递减。
很显然,规模报酬分析可视为长期生产的分析视角。
区别:①前提条件不同,边际报酬变化生产要素分为不变和可变生产要素,生产要素比例发生变化;规模报酬分析研究生产要素同比例变动。
②考察时间长短不同。
边际报酬变化分析的是短期生产规律;规模报酬研究长期生产规律。
③指导意义不同。
边际报酬变化指出要按比例配置生产要素;规模报酬指出要保持企业的适度规模。
④由于前提条件不同,两规律独立发挥作用,不存在互为前提,互为影响关系。
高鸿业微观经济学业第七版课后答案消费者选择

(3)6= xy ,XY=36;若 x=4,y=9
MRS XY
=
Y X
= 9 =2.25
4
(4)当 x=3 时, MRSXY =4;当 x=4 时, MRSXY =2.25,所以该无差异曲线的边际替
代率是递减的。
5.已知某消费者每年用于商品 1 和商品 2 的收入为 540 元,两商
品的价格分别为 P1=20 元和 P2=30 元,该消费者的效用函数为
5.某消费者是一个风险回避者,他面临是否参与一场赌博的选择:如果他参与这场赌博, 他将以 5%的概率获得 10000 元,以 95%的概率获得 10 元;如果他不参与这场赌博,他将 拥有 509.5 元。那么,他会参与这场赌博吗?为什么?
解答:该风险回避的消费者不会参与这场赌博<U2。
4.假设某商品市场上只有 A、B 两个消费者,他们的需求函数各自为 Q=20-4P 和 Q= 30-5P。
(1)列出这两个消费者的需求表和市场需求表。
(2)根据(1),画出这两个消费者的需求曲线和市场需求曲线。
解答:(1)由消费者 A 和 B 的需求函数可编制消费 A 和 B 的需求表。至于市场的需求 表的编制可以使用两种方法,一种方法是利用已得到消费者 A、B 的需求表,将每一价格水 平上两个消费者的需求数量加总来编制市场需求表;另一种方法是先将消费者 A 和 B 的需 求函数加总求得市场需求函数,即市场需求函数 Qd=Q+Q=(20-4P)+(30-5P)=50-9P, 然后运用所得到的市场需求函数 Qd=50-9P 来编制市场需求表。按以上方法编制的需求表 如下所示。
, 3
8
5
X
8 1
X
5
8 2
MU 2
高鸿业微观第七版第 章习题参考答案

第四章生产函数第一部分教材配套习题本习题详解一、简答题1. 如何准确区分生产的短期和长期这两个基本概念?生产的短期:指生产者来不及调整全部生产要素的数量,至少有一种生产要素的数量是固定不变的时间周期。
短期不可调整的生产要素称不变生产要素,一般包括厂房、大型设备、高级管理者、长期贷款等,可调整的生产要素成为可变生产要素,一般包括原材料、燃料、辅助材料、普通劳动者等。
生产的长期:指生产者可以调整全部生产要素的数量的时间周期。
生产的短期和长期是相对的时间概念,不是绝对的时间概念,其与企业所属行业、所用技术设备和规模等因素有关。
2.下面是一张一种可变生产要素的短期生产函数的产量表(表4—1):(1)在表中填空。
(2)该生产函数是否表现出边际报酬递减?如果是,是从第几单位的可变要素投入量开始的?—解答:边际报酬变化是指在生产过程中一种可变要素投入量每增加一个单位时所引起的总产量的变化量,即边际产量的变化,而其他生产要素均为固定生产要素,固定要素的投入数量是保持不变的。
边际报酬变化一般包括边际报酬递增、不变和递减三个阶段。
很显然,边际报酬分析可视为短期生产分析。
规模报酬分析方法是描述在生产过程中全部生产要素的投入数量均同比例变化时所引起的产量变化特征,当产量的变化比例分别大于、等于、小于全部生产要素投入量变化比例时,则分别为规模报酬递增、不变、递减。
很显然,规模报酬分析可视为长期生产的分析视角。
区别:①前提条件不同,边际报酬变化生产要素分为不变和可变生产要素,生产要素比例发生变化;规模报酬分析研究生产要素同比例变动。
②考察时间长短不同。
边际报酬变化分析的是短期生产规律;规模报酬研究长期生产规律。
③指导意义不同。
边际报酬变化指出要按比例配置生产要素;规模报酬指出要保持企业的适度规模。
④由于前提条件不同,两规律独立发挥作用,不存在互为前提,互为影响关系。
联系:随着投入要素增加,产量一般都经历递增、不变和递减三个阶段。
高鸿业微观经济学业第七版课后答案第三章消费者选择

第三章消费者选择第一部分教材配套习题本习题详解1.已知一件衬衫的价格为80元,一份肯德基快餐的价格为20元,在某消费者关于这两种商品的效用最大化的均衡点上,一份肯德基快餐对衬衫的边际替代率MRS是多少?解答:用X表示肯德基快餐的份数;Y表示衬衫的件数;MRSXY表示在维持效用水平不变的前提下,消费者增加一份肯德基快餐消费时所需要放弃的衬衫的消费数量。
在该消费者实现关于这两种商品的效用最大化时,在均衡点上有边际替代率等于价格比,则有:它表明,在效用最大化的均衡点上,该消费者关于一份肯德基快餐对衬衫的边际替代率MRS为0.25。
2.假设某消费者的均衡如图3—1所示。
其中,横轴OX1和纵轴OX分别表示商品1和商品2的数量,线段AB为消费者的预算线,曲线U为2消费者的无差异曲线,E点为效用最大化的均衡点。
已知商品1的价格P1=2元。
求:(1)求消费者的收入;(2)求商品2的价格P2;(3)写出预算线方程;(4)求预算线的斜率;(5)求E点的M的值。
RS12图3—1某消费者的均衡解答:(1)横轴截距表示消费者的收入全部购买商品1的数量为30单位,且已知P1=2元,所以,消费者的收入M=2×30=60元。
(2)图3—1中纵轴截距表示消费者的收入全部购买商品2的数量为20单位,且由(1)已知收入M=60元,所以,商品2的价格P2===3(元)。
(3)由于预算线方程的一般形式为P1X1+P2X2=M,所以本题预算线方程具体写为:2X1+3X2=60。
(4)(4)将(3)中的预算线方程进一步整理为X2=-X1+20。
所以,预算线的斜率为-。
(5)在消费者效用最大化的均衡点E 上,有211212X PMRS X P ∆=-=∆,即无差异曲线斜率的绝对值即MRS 等于预算线斜率的绝对值。
因此,MRS 12==。
3.对消费者实行补助有两种方法:一种是发给消费者一定数量的实物补助,另一种是发给消费者一笔现金补助,这笔现金额等于按实物补助折算的货币量。
高鸿业微观第七版第章习题参考答案
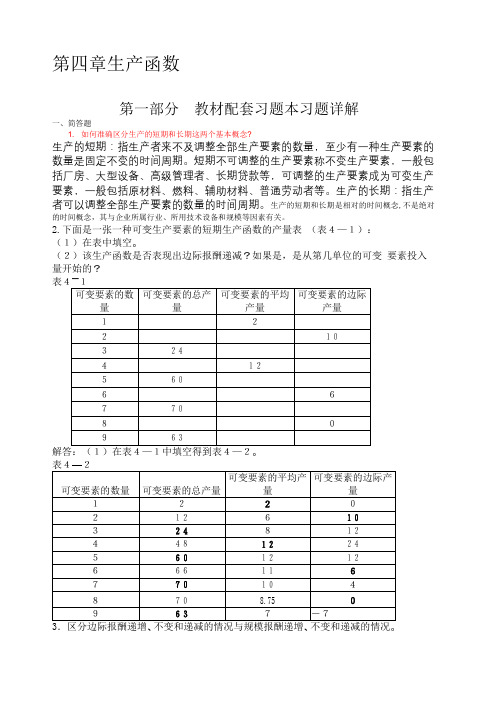
第四章生产函数第一部分教材配套习题本习题详解一、简答题1. 如何准确区分生产的短期和长期这两个基本概念?生产的短期:指生产者来不及调整全部生产要素的数量,至少有一种生产要素的数量是固定不变的时间周期。
短期不可调整的生产要素称不变生产要素,一般包括厂房、大型设备、高级管理者、长期贷款等,可调整的生产要素成为可变生产要素,一般包括原材料、燃料、辅助材料、普通劳动者等。
生产的长期:指生产者可以调整全部生产要素的数量的时间周期。
生产的短期和长期是相对的时间概念,不是绝对的时间概念,其与企业所属行业、所用技术设备和规模等因素有关。
2.下面是一张一种可变生产要素的短期生产函数的产量表(表4—1):(1)在表中填空。
(2)该生产函数是否表现出边际报酬递减?如果是,是从第几单位的可变要素投入量开始的?—解答:边际报酬变化是指在生产过程中一种可变要素投入量每增加一个单位时所引起的总产量的变化量,即边际产量的变化,而其他生产要素均为固定生产要素,固定要素的投入数量是保持不变的。
边际报酬变化一般包括边际报酬递增、不变和递减三个阶段。
很显然,边际报酬分析可视为短期生产分析。
规模报酬分析方法是描述在生产过程中全部生产要素的投入数量均同比例变化时所引起的产量变化特征,当产量的变化比例分别大于、等于、小于全部生产要素投入量变化比例时,则分别为规模报酬递增、不变、递减。
很显然,规模报酬分析可视为长期生产的分析视角。
区别:①前提条件不同,边际报酬变化生产要素分为不变和可变生产要素,生产要素比例发生变化;规模报酬分析研究生产要素同比例变动。
②考察时间长短不同。
边际报酬变化分析的是短期生产规律;规模报酬研究长期生产规律。
③指导意义不同。
边际报酬变化指出要按比例配置生产要素;规模报酬指出要保持企业的适度规模。
④由于前提条件不同,两规律独立发挥作用,不存在互为前提,互为影响关系。
联系:随着投入要素增加,产量一般都经历递增、不变和递减三个阶段。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
M
解得: X1
3M 8P1
,代入(1)式得 X 2
5M 8P2
所以,该消费者关于两商品的需求函数为 X1
3M 8P1
,X2
5M 8P2
4.假定某消费者的效用函数为U q0.5 3M ,其中,q 为某商品的
消费量,M 为收入。求:(1)该消费者的需求函数;
(2)该消费者的反需求函数;
(3)当 p 1 , q 4 时的消费者剩余。
P
A 的需求量 Q
A 的需求量 Q
市场需求量 Q+Q
0
20
30
50
1
16
25
41
2
12
20
32
3
8
15
23
4
4
10
14
5
0
5
5
6
0
0
(2)由(1)中的需求表,所画出的消费者 A 和 B 各自的需求曲线 以及市场的需求曲线如图 3—4 所示。
图 3-4 消费者 A 和 B 各自的需求曲线以及市场的需求曲线 在此,需要特别指出的是,市场需求曲线有一个折点,该点发生 在价格 P=5 和需求量 Qd=5 的坐标点位置。关于市场需求曲线的这 一特征解释如下:市场需求曲线是市场上单个消费者需求曲线的水平 加总,即在 P≤5 的范围,市场需求曲线由两个消费者需求曲线水平 加总得到,在 P≤5 的范围,市场需求函数 Qd=Q+Q=(20-4P)+(30 -5P)=50-9P 成立;;而当 P>5 时,消费者 A 的需求量为 0,只有 消费者 B 的需求曲线发生作用,所以,P>5 时,B 的需求曲线就是市 场需求曲线。当 P>6 时,只有消费者 B 的需求也为 0。 市场需求函数是:
P1=20
元和
P2=30
元,该消费者的效用函数为
U=3X1X
2 2
,
该消费者每年购买这两种商品的数量各应是多少?每年从中获得总
效用是多少?
解答:
把已知条件和
MU1,MU
2
值带入下面均衡条件
MU1 P1
MU 2 P2
P1X1 P2 X 2 M
得方程组:
3
X
2 2
20
6 X1 X 2 30
20X1 30X2 540
3PX
=
2M 3
PX 1
可得肉肠的需求价格弹性为:edx= (
2M 3
PX 2
PX ) 1
2M 3
PX1
面包对肉肠的需求交叉弹性为:
eyx= Y
PX
PX Y
( 2M 3
PX
2
PX
2M 3
PX1
) 1
7.已知某消费者的效用函数为 U=X1X2,两商品的价格分别为 P1
=4,P2=2,消费者的收入是 M=80。现在假定商品 1 的价格下降为
dPX
PX X
( M 2
PX 2
PX ) 1
M 2
PX1
(2)面包对肉肠的需求交叉弹性为:
exy= dY
dX
PX Y
(
M 2
PX
2
PX
M 2
PX1
) 1
(3)maxU(X,Y)=min(X,Y)
s.t.PxX+PYY=M
如果
Px=2PY,X=Y,解上述方程有:X=Y=
M PX PY
2M =
(1)求消费者的 收入; (2)求商品2的 价格P2; (3)写出预算线 方程; (4)求预算线的 斜率; (5)求E点的M RS12的值。
图3—1某消费者的均衡 解答:(1)横轴截距表示消费者的收入全部购买商品1的数量为30单位, 且已知P1=2元,所以,消费者的收入M=2×30=60元。 (2)图3—1中纵轴截距表示消费者的收入全部购买商品2的数量为20
解方程得,X1=9,X2=12,U=3X1X=
3888
35
3.假定某消费者的效用函数为U
X
8 1
X
8 2
,两商品的价格分别为
P1,
P2,消费者的收入为 M。分别求该消费者关于商品 1 和商品 2 的需求
函数。
解:根据消费者效用最大化的均衡条件: MU1 P11 ,其中,由已
MU 2 P2
知的效用函数U
MU x
此时消费者效用最大化的均衡条件为
MUy
Байду номын сангаас
PX Py
,由于 0 ,
Px x Py y M
MU x
故该方程组化为
MUy
PX Py
,显然,当商品 x 和商品 y 的价格以及
Px
x
Py
y
M
消费者的收入同时变动一个比例时,消费者对两商品的需求关系维持
不变。
(3)由消费者的需求函数可得: Px x , Py y ,式中参数 为商
解答:一般说来,发给消费者现金补助会使消费者获得更大的效用。其原因
在于:在现金补助的情况下,消费者可以按照自己的偏好来购买商品,以获
得尽可能大的效用。如图3—3所示。
图3—3实物补贴和货币补贴 在图中,AB是按实物补助折算的货币量等于现金补助情况下的预算线。在
现金补助的预算线AB上,消费者根据自己的偏好选择商品1和商品2的购买量
U1<U2。
4.假设某商品市场上只有 A、B 两个消费者,他们的需求函数各
自为 Q=20-4P 和 Q=30-5P。
(1)列出这两个消费者的需求表和市场需求表。
(2)根据(1),画出这两个消费者的需求曲线和市场需求曲线。
解答:(1)由消费者 A 和 B 的需求函数可编制消费 A 和 B 的需求
表。至于市场的需求表的编制可以使用两种方法,一种方法是利用已
P1=2。求:
(1)由商品 1 的价格 P1 下降所导致的总效应,使得该消费者对商品
根据消费者效用最大化的均衡条件
MUy
PX Py
,代入已知条件,解
Px x Py y M
方程组得消费者关于商品 x 和商品 y 的需求函数分别为:
x= aM , y= M
PX
Py
(2)商品 x 和商品 y 的价格以及消费者的收入同时变动一个比例,
相当于消费者的预算线变为 Px x Py y M ,其中 为一非零常数。
一个比例时,消费者对两商品的需求量维持不变。
(3)证明消费者效用函数中的参数 和 分别为商品 x 和商品 y
的消费支出占消费者收入的份额。
解:(1)由消费者的效用函数U
x
MU x
y ,解得:
U x
x 1 y
MUy U x y 1
y
消费者的预算约束方程为 PX x Py y M
MU x
第三章消费者选择
第一部分教材配套习题本习题详解
1.已知一件衬衫的价格为80元,一份肯德基快餐的价格为20元, 在某消费者关于这两种商品的效用最大化的均衡点上,一份肯德基快餐对衬 衫的边际替代率MRS是多少?
解答:用X表示肯德基快餐的份数;Y表示衬衫的件数;MRSXY表示 在维持效用水平不变的前提下,消费者增加一份肯德基快餐消费时所需要放 弃的衬衫的消费数量。在该消费者实现关于这两种商品的效用最大化时,在 均衡点上有边际替代率等于价格比,则有:
分别为
X
* 1
和
X
* 2
,从而实现了最大的效用水平U2,即在图3—3中表现为预算
线AB和无差异曲线U2相切的均衡点E。
在实物补助的情况下,则通常不会达到最大的效用水平U2。因为,譬如,
当实物补助两商品数量分别为x11、x21的F点,或者为两商品数量分别为x
12和x22的G点时,则消费者获得无差异曲线U1所表示的效用水平,显然,
单位,且由(1)已知收入M=60元,所以,商品2的价格 P2===3 (元)。 (3)由于预算线方程的一般形式为 P1X1+P2X2=M,所以本题 预算线方程具体写为:2X1+3X2=60。 (4)(4)将(3)中的预算线方程进一步整理为 X2=-X1+20。所以, 预算线的斜率为-。
(5)在消费者效用最大化的均衡点
得到消费者 A、B 的需求表,将每一价格水平上两个消费者的需求数
量加总来编制市场需求表;另一种方法是先将消费者 A 和 B 的需求
函数加总求得市场需求函数,即市场需求函数 Qd=Q+Q=(20-4P)
+(30-5P)=50-9P,然后运用所得到的市场需求函数 Qd=50-9P
来编制市场需求表。按以上方法编制的需求表如下所示。
它表明,在效用最大化的均衡点上,该消费者关于一份肯德基快餐对衬 衫的边际替代率MRS为 0.25。
2.假设某消费者的均衡如图3—1所示。其中,横轴OX1和纵轴OX 2分别表示商品1和商品2的数量,线段AB为消费者的预算线,曲线U为 消费者的无差异曲线,E点为效用最大化的均衡点。已知商品1的价格P1 =2元。求:
解:(1)令肉肠的需求为 X,面包卷的需求为 Y,相应的价格为
Px、PY,且有 Px=PY 该题目的效用论最大化问题可以写为:
maxU(X,Y)=min(X,Y)
s.t.PxX+PYY=M
解上述方程有:X=Y=
M PX PY
=
M 2PX
=
M 2
PX 1
由此可得肉肠的需求的价格弹性为:
edx=- dX
(4)该无差异曲线的边际替代率是递减的吗
解答:(1)
MU X
=U'(X)=
1 2
X
1
2Y
1 2
,
MUY
=U'(Y)=
1 2
X
1
2Y
1 2
MRS XY
Y X
