2021届高三高考数学模拟测试卷(六)【含答案】

合集下载

2021年高考数学模拟试卷(6)理(含解析)

2021年高考数学模拟试卷（6）理（含解析）一、选择题：（每小题5分，共60分）1．已知集合A={x|﹣1≤x≤3}，集合B={x|＜0}，则A∪B=（） A． {x|﹣1＜x＜0} B． {x|﹣1≤x＜0} C． {x|x＜0} D． {x|x≤3}2．若各项均为正数的等比数列{an }满足a2=1，a3a7﹣a5=56，其前n项的和为Sn，则S5=（）A． 31 B． C． D．以上都不对3．“a=﹣2”是“直线l1：ax﹣y+3=0与l2：2x﹣（a+1）y+4=0互相平行”的（）A．充分不必要条件 B．必要不充分条件C．充分必要条件 D．既不充分也不必要条件4．抛物线y=ax2的准线方程是y=2，则a的值为（）A． B． C． 8 D．﹣85．若定义在R上的偶函数y=f（x）是[0，+∞）上的递增函数，则不等式f（log2x）＜f（﹣1）的解集是（）A．（，2） B．（﹣∞，﹣2）∪（2，+∞） C． R D．（﹣2，2）6．计算（1﹣cosx）dx=（）A．π+2 B．π﹣2 C．π D．﹣27．某几何体的三视图如图所示，则该几何体的体积是（）A． B． C． D．8．将函数y=f（x）的图象按向量=（﹣，2）平移后，得到函数g（x）=sin（2x+）+2的图象，则函数f（x）的解析式为（）A． y=sin2x B． y=sin（2x+） C． y=sin（2x+） D． y=sin（2x﹣）9．已知不等式组表示的平面区域恰好被圆C：（x﹣3）2+（y﹣3）2=r2所覆盖，则实数k的值是（）A． 3 B． 4 C． 5 D． 610．直线l：y=k（x﹣）与曲线x2﹣y2=1（x＞0）相交于A、B两点，则直线l倾斜角的取值范围是（）A． {0，π） B．（，）∪（，） C． [0，）∪（，π） D．（，）11．设f（x）=|lg（x﹣1）|，若0＜a＜b，且f（a）=f（b），则ab的取值范围是（） A． [1，2] B．（1，2） C．（4，+∞） D．（2，+∞）12．已知函数f（x）=，若关于x的方程f（f（x））=0有且仅有一个实数解，则实数a的取值范围是（）A．（﹣∞，0） B．（﹣∞，0）∪（0，1） C．（0，1） D．（0，1）∪（1，+∞）二、填空题（每小题5分，共计20分）13．函数f（x）=xe x在点（1，f（1））处的切线的斜率是．14．数列{}（n∈N*）的前n项的和S n= ．15．在下列给出的命题中，所有正确命题的序号为．①函数y=2x3﹣3x+1的图象关于点（0，1）成中心对称；②对∀x，y∈R，若x+y≠0，则x≠1，或y≠﹣1；③若实数x，y满足x2+y2=1，则的最大值为；④若△ABC为钝角三角形，则sinA＜cosB．16．在△ABC中，AC=6，BC=7，，O是△ABC的内心，若，其中0≤x≤1，0≤y≤1，则动点P 的轨迹所覆盖的面积为．三、解答题（17题10分，其它各题均为12分，共计70分）17．已知函数f（x）=（sinx+cosx）2+2cos2x．（1）求f（）的值；（2）求f（x）的递减区间．18．在△ABC中，角A、B、C的对边分别为a，b，c，且a=3，b=4，B=+A．（1）求cosB的值；（2）求sin2A+sinC的值．19．已知数列．（1）求a2，a3；（2）若存在一个常数λ，使得数列为等差数列，求λ值；（3）求数列{a n}通项公式．20．如图，在四棱锥P﹣ABCD中，底面ABCD是边长为2的菱形，∠ABC=60°，E、F分别是PB、CD的中点，且PB=PC=PD=4．（1）求证：PA⊥平面ABCD；（2）求证：EF∥平面PAD；（3）求二面角A﹣PB﹣C的余弦值．21．已知椭圆的两个焦点坐标分别是（﹣，0），（，0），并且经过点（，）．（1）求椭圆的标准方程；（2）若斜率为k的直线l经过点（0，﹣2），且与椭圆交于不同的两点A、B，求△OAB面积的最大值．22．设函数f（x）=x2+x+aln（x+1），其中a≠0．（1）若a=﹣6，求f（x）在[0，3]上的最值；（2）若f（x）在定义域内既有极大值又有极小值，求实数a的取值范围；（3）求证：不等式（n∈N*）恒成立．xx年河北省保定一中高考数学模拟试卷（理科）（6）参考答案与试题解析一、选择题：（每小题5分，共60分）1．已知集合A={x|﹣1≤x≤3}，集合B={x|＜0}，则A∪B=（）A． {x|﹣1＜x＜0} B． {x|﹣1≤x＜0} C． {x|x＜0} D． {x|x≤3}考点：并集及其运算．专题：集合．分析：利用并集的性质求解．解答：解：∵集合A={x|﹣1≤x≤3}，集合B={x|＜0}={x|x＜0}，∴A∪B={x|x≤3}．故选：D．点评：本题考查并集的求法，解题时要认真审题，是基础题．2．若各项均为正数的等比数列{a n}满足a2=1，a3a7﹣a5=56，其前n项的和为S n，则S5=（） A． 31 B． C． D．以上都不对考点：等比数列的前n项和．专题：等差数列与等比数列．分析：由题意和等比数列的性质可得a5=8，进而可得公比q，代入求和公式可得．解答：解：由等比数列的性质可得a3a7=a52，∵a3a7﹣a5=56，∴a52﹣a5=56，结合等比数列{a n}的各项均为正数可解得a5=8，∴公比q满足q3==8，∴q=2，∴a1=，∴S5===，故选：C点评：本题考查等比数列的前n项和，求出数列的公比是解决问题的关键，属基础题．3．“a=﹣2”是“直线l1：ax﹣y+3=0与l2：2x﹣（a+1）y+4=0互相平行”的（）A．充分不必要条件 B．必要不充分条件C．充分必要条件 D．既不充分也不必要条件考点：必要条件、充分条件与充要条件的判断．专题：简易逻辑．分析：根据充分必要条件的定义结合两直线平行的性质及判定得出答案．解答：解：当a=﹣2时，l1：2x+y﹣3=0，l2：2x+y+4=0，两直线平行，是充分条件；若直线l1：ax﹣y+3=0与l2：2x﹣（a+1）y+4=0互相平行，则a（a+1）=2，解得：a=﹣2，或a=1，不是必要条件，故选：A．点评：本题考查了充分必要条件，考查了两直线平行的性质及判定，是一道基础题．4．抛物线y=ax2的准线方程是y=2，则a的值为（）A． B． C． 8 D．﹣8考点：抛物线的定义．分析：首先把抛物线方程转化为标准方程x2=my的形式，再根据其准线方程为y=﹣即可求之．解答：解：抛物线y=ax2的标准方程是x2=y，则其准线方程为y=﹣=2，所以a=﹣．故选B．点评：本题考查抛物线在标准方程下的准线方程形式．5．若定义在R上的偶函数y=f（x）是[0，+∞）上的递增函数，则不等式f（log2x）＜f （﹣1）的解集是（）A．（，2） B．（﹣∞，﹣2）∪（2，+∞） C． R D．（﹣2，2）考点：对数函数的单调性与特殊点；函数奇偶性的性质．专题：函数的性质及应用．分析：因为y=f（x）是定义在R上的偶函数，所以在[0，+∞）上单调递增，则在对称区间（﹣∞，0）上单调递减．所以f（﹣1）=f（1），所以讨论log2x在区间[0，+∞）和（﹣∞，0）两种情况，所以log2x≥0即x≥1时，为了用上函数y=f（x）在[0，+∞）上单调递增的条件，将原不等式变成，f（log2x）＜f（1），根据单调性，所以得到log2x＜1，x ＜2，所以1≤x＜2，同样的办法，求出log2x＜0时的原不等式的解，这两种情况所得的解求并集即可．解答：解：根据已知条件知：y=f（x）在（﹣∞，0）是减函数，f（﹣1）=f（1）；∴①若log2x≥0，即x≥1，由原不等式得：f（log2x）＜f（1）；∴log2x＜1，x＜2；∴1≤x＜2；②若log2x＜0，即0＜x＜1，f（log2x）＜f（﹣1）；∴log2x＞﹣1，x；∴；综上得原不等式的解集为．故选A．点评：考查偶函数的概念，偶函数在对称区间上的单调性的特点，以及对数函数的单调性．6．计算（1﹣cosx）dx=（）A．π+2 B．π﹣2 C．π D．﹣2考点：定积分．专题：计算题；导数的概念及应用．分析：求出原函数，即可求得定积分．解答：解：（1﹣cosx）dx=（x﹣sinx）=（﹣sin）﹣[﹣﹣sin（﹣）]=π﹣2，故选：B．点评：本题考查定积分，考查学生的计算能力，比较基础．7．某几何体的三视图如图所示，则该几何体的体积是（）A． B． C． D．考点：由三视图求面积、体积．专题：空间位置关系与距离．分析：由已知的三视图可得：该几何体是一个以主视图为底面的四棱锥，分别求出棱锥的底面面积和高，代入棱锥体积公式，可得答案．解答：解：由已知的三视图可得：该几何体是一个以主视图为底面的四棱锥，其底面面积S=2×2=4，高h=2×=，故该几何体的体积V=Sh=×4×=，故选：D点评：根据三视图判断空间几何体的形状，进而求几何的表（侧/底）面积或体积，是高考必考内容，处理的关键是准确判断空间几何体的形状，一般规律是这样的：如果三视图均为三角形，则该几何体必为三棱锥；如果三视图中有两个三角形和一个多边形，则该几何体为N棱锥（N值由另外一个视图的边数确定）；如果三视图中有两个为矩形和一个多边形，则该几何体为N棱柱（N值由另外一个视图的边数确定）；如果三视图中有两个为梯形和一个多边形，则该几何体为N棱柱（N值由另外一个视图的边数确定）；如果三视图中有两个三角形和一个圆，则几何体为圆锥．如果三视图中有两个矩形和一个圆，则几何体为圆柱．如果三视图中有两个梯形和一个圆，则几何体为圆台．8．将函数y=f（x）的图象按向量=（﹣，2）平移后，得到函数g（x）=sin（2x+）+2的图象，则函数f（x）的解析式为（）A． y=sin2x B． y=sin（2x+） C． y=sin（2x+） D． y=sin（2x﹣）考点：函数y=Asin（ωx+φ）的图象变换．专题：三角函数的图像与性质．分析：先求出向量的相反向量﹣，然后将函数y=sin（x+）+2按照﹣的方向进行平移整理，即可得到答案．解答：解：∵=（﹣，2），∴﹣=（，﹣2），将y=sin（2x+）+2按照向量﹣平移后得到，y=sin[2（x﹣）+]=sin2x的图象，故选：A．点评：本题主要考查三角函数按向量的方向进行平移．属基础题．9．已知不等式组表示的平面区域恰好被圆C：（x﹣3）2+（y﹣3）2=r2所覆盖，则实数k的值是（）A． 3 B． 4 C． 5 D． 6考点：简单线性规划．专题：计算题；作图题；不等式的解法及应用．分析：由题意作出其平面区域，则可知，（0，﹣6）关于（3，3）的对称点（6，12）在x ﹣y+k=0上，从而解出k．解答：解：由题意作出其平面区域，由平面区域恰好被圆C：（x﹣3）2+（y﹣3）2=r2所覆盖可知，平面区域所构成的三角形的三个顶点都在圆上，又∵三角形为直角三角形，∴（0，﹣6）关于（3，3）的对称点（6，12）在x﹣y+k=0上，解得k=6，故选D．点评：本题考查了简单线性规划，作图要细致认真，属于中档题．10．直线l：y=k（x﹣）与曲线x2﹣y2=1（x＞0）相交于A、B两点，则直线l倾斜角的取值范围是（）A． {0，π） B．（，）∪（，） C． [0，）∪（，π） D．（，）考点：双曲线的简单性质．专题：圆锥曲线中的最值与范围问题．分析：首先根据题意直线l：y=k（x﹣）与曲线x2﹣y2=1（x＞0）相交于A、B两点，进一步判断直线的斜率和渐近线的斜率的关系求出结果．解答：解：曲线x2﹣y2=1（x＞0）的渐近线方程为：y=±x直线l：y=k（x﹣）与相交于A、B两点所以：直线的斜率k＞1或k＜﹣1由于直线的斜率存在：倾斜角故选：B点评：本题考查的知识要点：直线与双曲线的关系，直线的斜率和渐近线的斜率的关系．11．设f（x）=|lg（x﹣1）|，若0＜a＜b，且f（a）=f（b），则ab的取值范围是（） A． [1，2] B．（1，2） C．（4，+∞） D．（2，+∞）考点：基本不等式在最值问题中的应用；对数函数的图像与性质．专题：函数的性质及应用．分析： f（x）是含有绝对值的函数，结合函数的图象或通过去绝对值考查f（x）的单调性，找出a和b的关系，结合基本不等式求范围即可．解答：解：先画出函数f（x）=|lg（x﹣1）|的图象，如图：∵0＜a＜b，且f（a）=f（b），∴1＜a＜2，b＞2，∴﹣lg（a﹣1）=lg（b﹣1），∴=b﹣1，∴a=1+，∴ab=b+=b+=b﹣1++2＞2=4，∴ab的取值范围是（4，+∞），故选：C点评：本题考查函数的性质、基本不等式等，去绝对值是解决本题的关键，综合性强．12．已知函数f（x）=，若关于x的方程f（f（x））=0有且仅有一个实数解，则实数a的取值范围是（）A．（﹣∞，0） B．（﹣∞，0）∪（0，1） C．（0，1） D．（0，1）∪（1，+∞）考点：分段函数的应用．专题：函数的性质及应用．分析：利用换元法设t=f（x），则方程等价为f（t）=0，作出函数f（x）的图象，利用数形结合即可得出此题的关键是a•2x取不到1和0．解答：解：设t=f（x），则f（t）=0，若a＜0时，当x≤0，f（x）=a•2x＜0．由f（t）=0，即，此时t=1，当t=1得f（x）=1，此时x=有唯一解，此时满足条件．若a=0，此时当x≤0，f（x）=a•2x=0，此时函数有无穷多个点，不满足条件．若a＞0，当x≤0，f（x）=a•2x∈（0，a]．此时f（x）的最大值为a，要使若关于x的方程f（f（x））=0有且仅有一个实数解，则a＜1，此时0＜a＜1，综上实数a的取值范围是（﹣∞，0）∪（0，1）故选：B点评：本题主要考查函数方程根的个数的应用，利用换元法，结合数形结合是解决本题的关键．二、填空题（每小题5分，共计20分）13．函数f（x）=xe x在点（1，f（1））处的切线的斜率是2e ．考点：利用导数研究曲线上某点切线方程．专题：导数的综合应用．分析：求出原函数的导函数，在导函数解析式中取x=1得答案．解答：解：∵f（x）=xe x，∴f′（x）=e x+xe x，则f′（1）=2e．故答案为：2e．点评：本题考查学生会利用导数求曲线上过某点切线方程的斜率，考查了基本初等函数的导数公式，是基础题．14．数列{}（n∈N*）的前n项的和S n= ．考点：数列的求和．专题：等差数列与等比数列．分析： a n==，利用“裂项求和”即可得出．解答：解：a n==，∴S n=…+==．故答案为：．点评：本题考查了“裂项求和”求数列的前n项和，属于基础题．15．在下列给出的命题中，所有正确命题的序号为①②③．①函数y=2x3﹣3x+1的图象关于点（0，1）成中心对称；②对∀x，y∈R，若x+y≠0，则x≠1，或y≠﹣1；③若实数x，y满足x2+y2=1，则的最大值为；④若△ABC为钝角三角形，则sinA＜cosB．考点：命题的真假判断与应用．专题：函数的性质及应用．分析：本题考查的知识点是判断命题真假，比较综合的考查了函数的性质，我们可以根据对称性等函数的性质对四个结论逐一进行判断，可以得到正确的结论．解答：解：①函数y=2x3﹣3x+1=的图象关于点（0，1）成中心对称，假设点（x0，y0）在函数图象上，则其关于①点（0，1）的对称点为（﹣x0，2﹣y0）也满足函数的解析式，则①正确；②对∀x，y∈R，若x+y≠0，对应的是直线y=﹣x以外的点，则x≠1，或y≠﹣1，②正确；③若实数x，y满足x2+y2=1，则=，可以看作是圆x2+y2=1上的点与点（﹣2，0）连线的斜率，其最大值为，③正确；④若△ABC为钝角三角形，若A为锐角，B为钝角，则sinA＞cosB，④错误．故答案为：①②③点评：③的判断中使用了数形结合的思想，是数学中的常见思想，要加深体会．16．在△ABC中，AC=6，BC=7，，O是△ABC的内心，若，其中0≤x≤1，0≤y≤1，则动点P 的轨迹所覆盖的面积为．考点：平面向量的综合题．专题：平面向量及应用．分析：根据，其中0≤x≤1，0≤y≤1，可得动点P的轨迹所覆盖的面积是以OA，OB为邻边的平行四边形，S=AB×r，r为△ABC的内切圆的半径，计算AB及r，即可得到结论．解答：解：∵，其中0≤x≤1，0≤y≤1，∴动点P的轨迹所覆盖的面积是以OA，OB为邻边的平行四边形∴S=AB×r，其中r为△ABC的内切圆的半径在△ABC中，由余弦定理可得cosA=∴5AB2﹣12AB﹣65=0∴AB=5∴∵O是△ABC的内心，∴O到△ABC各边的距离均为r，∴∴r=∴S=AB×r==．故答案为：．点评：本题考查向量知识的运用，考查余弦定理，考查三角形面积的计算，属于中档题．三、解答题（17题10分，其它各题均为12分，共计70分）17．已知函数f（x）=（sinx+cosx）2+2cos2x．（1）求f（）的值；（2）求f（x）的递减区间．考点：三角函数中的恒等变换应用．专题：三角函数的图像与性质．分析：（1）首先利用三角关系式的恒等变换变形成正弦型函数，进一步求出函数的值．（2）根据（1）的结论，利用整体思想求单调区间．解答：解：（1）f（x）=1+2sinxcosx+2cos2x=sin2x+cos2x+2=所以：+2=（2）令：（k∈Z）（k∈Z）所以f（x）的单调减区间是点评：本题考查的知识要点：三角关系式的恒等变换变形成正弦型函数，进一步求出函数的值，利用整体思想求单调区间．18．在△ABC中，角A、B、C的对边分别为a，b，c，且a=3，b=4，B=+A．（1）求cosB的值；（2）求sin2A+sinC的值．考点：正弦定理；余弦定理．专题：计算题；三角函数的求值；解三角形．分析：（1）运用正弦定理和诱导公式、以及同角公式，即可得到cosB；（2）由二倍角的正弦和余弦公式，以及诱导公式，化简计算即可得到．解答：解（1）∵，∴cosB=cos（+A）=﹣sinA，又a=3，b=4，所以由正弦定理得，所以=，所以﹣3sinB=4cosB，两边平方得9sin2B=16cos2B，又sin2B+cos2B=1，所以，而，所以．（2）∵，∴，∵，∴2A=2B﹣π，∴sin2A=sin（2B﹣π）=﹣sin2B=又A+B+C=π，∴，∴sinC=﹣cos2B=1﹣2cos2B=．∴．点评：本题考查正弦定理和运用，考查三角函数的化简和求值，注意运用二倍角公式和诱导公式，以及同角三角函数的基本关系式，属于中档题．19．已知数列．（1）求a2，a3；（2）若存在一个常数λ，使得数列为等差数列，求λ值；（3）求数列{a n}通项公式．考点：等差关系的确定；数列的函数特性．专题：计算题．分析：（1）直接根据递推关系，以及a1=0，可求出a2，a3；（2）先假设数列为等差数列，取前三项，根据等差中项可求出λ的值，然后根据等差数列的定义证明即可；（3）根据（2）可求出数列的通项公式，从而求出数列{a n}通项公式．解答：解：（1）由．…（4分）（2）由数列为等差数列知∴解得λ=1=∴为等差数列．…（9分）（3）由（2）可知：∴∴…（13分）点评：本题主要考查了等差数列的判定，以及通项公式的求解，属于中档题．20．如图，在四棱锥P﹣ABCD中，底面ABCD是边长为2的菱形，∠ABC=60°，E、F分别是PB、CD的中点，且PB=PC=PD=4．（1）求证：PA⊥平面ABCD；（2）求证：EF∥平面PAD；（3）求二面角A﹣PB﹣C的余弦值．考点：与二面角有关的立体几何综合题；直线与平面平行的判定；直线与平面垂直的判定．专题：空间位置关系与距离；空间角．分析：（1）取BC的中点M，连结AM，PM，由已知条件推导出PA⊥BC，PA⊥CD，由此能证明PA⊥平面ABCD．（2）取PA的中点N，连结EN，ND，由已知得四边形ENDF是平行四边形，由此能证明EF∥平面PAD．（3）取AB的中点G，过G作GH⊥PB于点H，连结HC，GC，由已知得∠GHC是二面角A﹣PB ﹣C的平面角，由此能求出二面角A﹣PB﹣C的余弦值．解答：（1）证明：取BC的中点M，连结AM，PM．∵AB=BC，∠ABC=60°，∴△ABC为正三角形，∴AM⊥BC．又PB=PC，∴PM⊥BC，AM∩PM=M，∴BC⊥平面PAM，PA⊂平面PAM，∴PA⊥BC，同理可证PA⊥CD，又BC∩CD=C，∴PA⊥平面ABCD．…（4分）．（2）证明：取PA的中点N，连结EN，ND．∵PE=EB，PN=NA，∴EN∥AB，且．又FD∥AB，且，∴，∴四边形ENDF是平行四边形，∴EF∥ND，而EF⊄平面PAD，ND⊂平面PAD，∴EF∥平面PAD．…（8分）（3）解：取AB的中点G，过G作GH⊥PB于点H，连结HC，GC．则CG⊥AB，又CG⊥PA，PA∩AB=A，∴CG⊥平面PAB．∴HC⊥PB，∴∠GHC是二面角A﹣PB﹣C的平面角．在Rt△PAB中，AB=2，PB=4，∴．又Rt△BHG∽Rt△BAP，∴，∴．在Rt△HGC中，可求得，∴，∴，故二面角A﹣PB﹣C的余弦值为．…（12分）．点评：本题考查PA⊥平面ABCD的证明，考查EF∥平面PAD的证明，考查二面角A﹣PB﹣C 的余弦值的求法，解题时要注意空间思维能力的培养．21．已知椭圆的两个焦点坐标分别是（﹣，0），（，0），并且经过点（，）．（1）求椭圆的标准方程；（2）若斜率为k的直线l经过点（0，﹣2），且与椭圆交于不同的两点A、B，求△OAB面积的最大值．考点：椭圆的简单性质．专题：计算题；圆锥曲线的定义、性质与方程．分析：（1）利用待定系数法求椭圆的标准方程，在求a时利用椭圆的定义比较简单；（2）利用弦长公式先求出|AB|，然后利用面积公式构建关于斜率k的函数，通过换元法利用基本不等求△OAB面积的最大值．解答：解：（1）设椭圆的标准方程为，由椭圆的定义可得．∴，又，∴b=1，故椭圆的标准方程为．（2）设直线l的方程为y=kx﹣2，由，得（1+3k2）x2﹣12kx+9=0，依题意△=36k2﹣36＞0，∴k2＞1（*）设A（x1，y1），B（x2，y2），则，∴，由点到直线的距离公式得，∴．设，∴，当且仅当时，上式取等号，所以，△OAB面积的最大值为．点评：第（1）问用待定系数法求椭圆的方程时，也可以把点代入方程求解，但这种方法计算量大；第（2）问得到的面积表达式比较复杂，当函数表达式比较复杂时，考虑用换元法转化成简单函数，但要注意转化后函数的定义域．22．设函数f（x）=x2+x+aln（x+1），其中a≠0．（1）若a=﹣6，求f（x）在[0，3]上的最值；（2）若f（x）在定义域内既有极大值又有极小值，求实数a的取值范围；（3）求证：不等式（n∈N*）恒成立．考点：利用导数求闭区间上函数的最值；函数在某点取得极值的条件；导数在最大值、最小值问题中的应用．专题：导数的综合应用．分析：（1）当a=﹣6时，由f′（x）=0得x=2，可判断出当x∈（0，1）时，f（x）单调递减；当x∈（1，3]时，f（x）单调递增，从而得到f（x）在[0，3]上的最值．（2）要使f（x）在定义域内既有极大值又有极小值，即f（x）在定义域内与X轴有三个不同的交点，即使f′（x）=0在（﹣1，+∞）有两个不等实根，即2x2+3x+1+a=0在（﹣1，+∞）有两个不等实根，可以利用一元二次函数根的分布，即可求a的范围．（3）先构造函数h（x）=x3﹣x2+ln（x+1），然后研究h（x）在 [0，+∞）上的单调性，求出函数h（x）的最小值，从而得到ln（x+1）＞x2﹣x3，最后令x=，即可证得结论．解答：解：（1）由题意知，f（x）的定义域为（﹣1，+∞），a=﹣6时，由f'（x）=2x+1﹣==0，得x=1（x=﹣舍去），当x∈（0，1）时，f′（x）＜0，当x∈（1，3]时，f′（x）＞0，所以当x∈（0，1）时，f（x）单调递减；当x∈（1，3]时，f（x）单调递增，所以f（x）min=f（1）=2﹣6ln2，f（x）max=f（3）=12﹣12ln2，（2）由题意f'（x）=2x+1+==0在（﹣1，+∞）有两个不等实根，即2x2+3x+1+a=0在（﹣1，+∞）有两个不等实根，设g（x）=2x2+3x+1+a，则，解之得0＜a＜；（3）对于函数g（x）=x2﹣ln（x+1），令函数h（x）=x3﹣g（x）=x3﹣x2+ln（x+1）则h′（x）=3x2﹣2x+=，∴当x∈[0，+∞）时，h′（x）＞0所以函数h（x）在[0，+∞）上单调递增，又h（0）=0，∴x∈（0，+∞）时，恒有h（x）＞h（0）=0即x2＜x3+ln（x+1）恒成立．取x=∈（0，+∞），则有ln（ +1）＞﹣恒成立．即不等式（n∈N*）恒成立点评：本题以函数为载体，考查函数的最值，考查函数的单调性．第一问判断f（x）在定义域的单调性即可求出最小值．第二问将f（x）在定义域内既有极大值又有极小值问题转化为f（x）在定义域内与X轴有三个不同的交点是解题的关键，第三问的关键是构造新函数，利用导数证明不等式．"23430 5B86 宆34424 8678 虸22006 55F6 嗶20305 4F51 佑39251 9953 饓33446 82A6 芦38358 95D6 闖wER eM。

专题35 空间中线线角、线面角,二面角的求法-

专题35 空间中线线角、线面角、二面角的求法【高考地位】立体几何是高考数学命题的一个重点，空间中线线角、线面角的考查更是重中之重. 其求解的策略主要有两种方法：其一是一般方法，即按照“作——证——解”的顺序进行；其一是空间向量法，即建立直角坐标系进行求解. 在高考中常常以解答题出现，其试题难度属中高档题.类型一空间中线线角的求法方法一平移法例1正四面体ABCD 中， E F ，分别为棱AD BC ，的中点，则异面直线EF 与CD 所成的角为 A.6π B. 4π C. 3π D. 2π 【变式演练1】【2021届全国著名重点中学新高考冲刺】如图，正方体1111ABCD A B C D -，的棱长为6，点F 是棱1AA 的中点，AC 与BD 的交点为O ，点M 在棱BC 上，且2BM MC =，动点T （不同于点M ）在四边形ABCD 内部及其边界上运动，且TM OF ⊥，则直线1B F 与TM 所成角的余弦值为（）A B C D ．79【变式演练2】【江苏省南通市2020-2021学年高三上学期9月月考模拟测试】当动点P 在正方体1111ABCD A B C D -的棱DC 上运动时，异面直线1D P 与1BC 所成角的取值范围（）A ．,64ππ⎡⎤⎢⎥⎣⎦B ．,63ππ⎡⎤⎢⎥⎣⎦C ．,43ππ⎡⎤⎢⎥⎣⎦D ．,32ππ⎡⎫⎪⎢⎣⎭【变式演练3】【甘肃省白银市靖远县2020届高三高考数学（文科）第四次联考】在四面体ABCD 中，2BD AC ==，AB BC CD DA ====E ，F 分别为AD ，BC 的中点，则异面直线EF 与AC 所成的角为（）A ．π6B ．π4C ．π3D ．π2【变式演练4】【2020年浙江省名校高考押题预测卷】如图，在三棱锥S ABC -中，SA ⊥平面ABC ，4AB BC ==，90ABC ∠=︒，侧棱SB 与平面ABC 所成的角为45︒，M 为AC 的中点，N 是侧棱SC上一动点，当BMN △的面积最小时，异面直线SB 与MN 所成角的余弦值为（）A ．16B ．3C D ．6方法二空间向量法例2、【重庆市第三十七中学校2020-2021学年高三上学期10月月考】在长方体1111ABCD A B C D -中，E ，F ，G 分别为棱1AA ，11C D ，1DD 的中点，12AB AA AD ==，则异面直线EF 与BG 所成角的大小为（） A ．30B ．60︒C ．90︒D ．120︒例3、【四川省泸县第四中学2020-2021学年高三上学期第一次月考】在长方体1111ABCD A B C D -中，2BC =，14AB BB ==，E ，F 分别是11A D ，CD 的中点，则异面直线1A F 与1B E 所成角的余弦值为（）A ．34B ．34-C D ．6【变式演练5】【2021届全国著名重点中学新高考冲刺】《九章算术》是古代中国乃至东方的第一部自成体系的数学专著，书中记载了一种名为“刍甍”的五面体（如图），其中四边形ABCD 为矩形，//EF AB ，若3AB EF =，ADE 和BCF △都是正三角形，且2AD EF =，则异面直线AE 与CF 所成角的大小为（）A ．6π B ．4π C ．3π D ．2π 【变式演练6】【云南省云天化中学、下关一中2021届高三复习备考联合质量检测卷】如图所示，在正方体1111ABCD A B C D -中，点E 为线段AB 的中点，点F 在线段AD 上移动，异面直线1B C 与EF 所成角最小时，其余弦值为（）A ．0B ．12C D ．1116类型二空间中线面角的求法方法一垂线法第一步首先根据题意找出直线上的点到平面的射影点；第二步然后连接其射影点与直线和平面的交点即可得出线面角；第三步得出结论.例3如图，四边形ABCD是矩形，1,AB AD ==E 是AD 的中点，BE 与AC 交于点F ，GF ⊥平面ABCD .（Ⅰ）求证：AF ⊥面BEG ；（Ⅰ）若AF FG =，求直线EG 与平面ABG 所成角的正弦值.【变式演练7】已知三棱柱111ABC A B C -的侧棱与底面边长都相等,1A 在底面ABC 内的射影为ABC 的中心,则1AB 与底面ABC 所成角的正弦值为（）A ．13 B． C．3 D ．23【变式演练8】【北京市朝阳区2020届高三年级下学期二模】如图，在五面体ABCDEF 中，面ABCD 是正方形，AD DE ⊥，4=AD ，2DE EF ==，且π3EDC ∠=．（1）求证：AD ⊥平面CDEF ；（2）求直线BD 与平面ADE 所成角的正弦值；GFEDCBA（3）设M 是CF 的中点，棱AB 上是否存在点G ，使得//MG 平面ADE ？若存在，求线段AG 的长；若不存在，说明理由．方法二空间向量法第一步首先建立适当的直角坐标系并写出相应点的空间直角坐标；第二步然后求出所求异面直线的空间直角坐标以及平面的法向量坐标；第三步再利用a bsin a bθ→→→→⋅=即可得出结论.例4 【内蒙古赤峰市2020届高三（5月份）高考数学（理科）模拟】在四棱锥P ABCD -中，底面ABCD 为等腰梯形，//BC AD ，222AD BC CD ===，O 是AD 的中点，PO ⊥平面ABCD ，过AB 的平面交棱PC 于点E （异于点C ，P 两点），交PO 于F .（1）求证：//EF 平面ABCD ；（2）若F 是PO 中点，且平面EFD 与平面ABCD 求PC 与底面ABCD 所成角的正切值.【变式演练9】【2020年浙江省名校高考仿真训练】已知三棱台111ABC A B C -的下底面ABC 是边长为2的正三角形，上地面111A B C △是边长为1的正三角形.1A 在下底面的射影为ABC 的重心，且11A B A C ⊥.（1）证明：1A B ⊥平面11ACC A ；（2）求直线1CB 与平面11ACC A 所成角的正弦值.类型三空间二面角的求解例4【江西省部分省级示范性重点中学教科研协作体2021届高三统一联合考试】三棱锥S ABC -中，2SA BC ==，SC AB ==，SB AC ==记BC 中点为M ，SA 中点为N（1）求异面直线AM 与CN 的距离；（2）求二面角A SM C --的余弦值.【变式演练10】【2021年届国著名重点中学新高考冲刺】如图，四边形MABC 中，ABC 是等腰直角三角形，90ACB ∠=︒，MAC △是边长为2的正三角形，以AC 为折痕，将MAC △向上折叠到DAC △的位置，使D 点在平面ABC 内的射影在AB 上，再将MAC △向下折叠到EAC 的位置，使平面EAC ⊥平面ABC ，形成几何体DABCE .（1）点F 在BC 上，若//DF 平面EAC ，求点F 的位置；（2）求二面角D BC E --的余弦值. 【高考再现】1．【2020年高考山东卷4】日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时间．把地球看成一个球（球心记为O ），地球上一点A 的纬度是指OA 与地球赤道所在平面所成角，点A 处的水平面是指过点A 且与OA 垂直的平面．在点A 处放置一个日晷，若晷面与赤道所在平面平行，点A 处的纬度为北纬40︒，则晷针与点A 处的水平面所成角为（）A ．20︒B ．40︒C ．50︒D ．90︒2. 【2017课标II ，理10】已知直三棱柱111C C AB -A B 中，C 120∠AB =，2AB =，1C CC 1B ==，则异面直线1AB 与1C B 所成角的余弦值为（）A B C D 3．【2020年高考全国Ⅰ卷理数16】如图，在三棱锥P ABC -的平面展开图中，1,3,,,30AC AB AD AB AC AB AD CAE ===⊥⊥∠=︒，则cos FCB ∠=_____________．4.【2020年高考全国Ⅱ卷理数20】如图，已知三棱柱111ABC A B C -的底面是正三角形，侧面11BB C C 是矩形，,M N 分别为11,BC B C 的中点，P 为AM 上一点．过11B C 和P 的平面交AB 于E ，交AC 于F ．（1）证明：1AA //MN ，且平面1A AMN ⊥平面11EB C F ；（2）设O 为Ⅰ111C B A 的中心，若F C EB AO 11平面∥，且AB AO =，求直线E B 1与平面AMN A 1所成角的正弦值．5.【2020年高考江苏卷24】在三棱锥A —BCD 中，已知CB =CD BD =2，O 为BD 的中点，AO Ⅰ平面BCD ，AO =2，E 为AC 的中点．（1）求直线AB与DE所成角的余弦值；（2）若点F在BC上，满足BF=14BC，设二面角F—DE—C的大小为θ，求sinθ的值．6．【2020年高考浙江卷19】如图，三棱台DEF—ABC中，面ADFC⊥面ABC，∠ACB=∠ACD=45°，DC =2BC．（I）证明：EF⊥DB；（II）求DF与面DBC所成角的正弦值．7．【2020年高考山东卷20】如图，四棱锥P ABCD-的底面为正方形，PD⊥底面ABCD，设平面PAD与平面PBC的交线为l．（1）证明：l⊥平面PDC；（2）已知1PD AD==，Q为l上的点，求PB与平面QCD所成角的正弦值的最大值．【反馈练习】1．【江西省乐平市第一中学2021届高三上学期联考理科】已知正方体1111ABCD A B C D -中，点E ，F 分别是线段BC ，1BB 的中点，则异面直线DE 与1D F 所成角的余弦值为（）A B C ．35 D ．452．【湖南省永州市宁远、道县、东安、江华、蓝山、新田2020届高三下学期六月联考】某四棱锥的三视图如图所示，点E 在棱BC 上，且2BE EC =，则异面直线PB 与DE 所成的角的余弦值为（）A ．BCD ．153．【2020届河北省衡水中学高三下学期第一次模拟】如图，在棱长为3的正方体1111ABCD A B C D -中，点P 是平面11A BC 内一个动点，且满足12DP PB +=1B P 与直线1AD 所成角的余弦值的取值范围为（）A ．10,2⎡⎤⎢⎥⎣⎦B ．10,3⎡⎤⎢⎥⎣⎦C ．12⎡⎢⎣⎦D ．1,22⎡⎢⎣⎦4．【广西玉林市2021届高三11月教学质量监测理科】如图，在正方体ABCD ﹣A 1B 1C 1D 1中，点E ，F 分别是棱AD ，CC 1的中点，则异面直线A 1E 与BF 所成角的大小为（）A ．6πB ．4πC ．3πD ．2π 5．【山东省泰安市2020届高三第四轮模拟复习质量】如图，在三棱锥A —BCD 中，AB =AC =BD =CD =3，AD =BC =2，点M ，N 分别为AD ，BC 的中点，则异面直线AN ，CM 所成的角的余弦值是（）A ．58B ．8C ．78D ．86．【福建省厦门市2020届高三毕业班（6月）第二次质量检查（文科）】如图，圆柱1OO 中，12OO =，1OA =，1OA O B ⊥，则AB 与下底面所成角的正切值为( )A ．2BC ．2D ．127．【内蒙古赤峰市2020届高三（5月份）高考数学（理科）】若正方体1AC 的棱长为1，点P 是面11AA D D 的中心，点Q 是面1111D C B A 的对角线11B D 上一点，且//PQ 面11AA B B ，则异面直线PQ 与1CC 所成角的正弦值为__.8．【吉林省示范高中（四平一中、梅河口五中、白城一中等）2020届高三第五次模拟联考】如图，已知直三棱柱ADF BCE -，AD DF ⊥，2AD DF CD ===，M 为AB 上一点，四棱锥F AMCD -的体积与该直三棱柱的体积之比为512，则异面直线AF 与CM 所成角的余弦值为________.9．【湖北省华中师大附中2020届高三下学期高考预测联考文科】如图，AB 是圆O 的直径，点C 是圆O 上一点，PA ⊥平面ABC ，E 、F 分别是PC 、PB 边上的中点，点M 是线段AB 上任意一点，若2AP AC BC ===.（1）求异面直线AE 与BC 所成的角：（2）若三棱锥M AEF -的体积等于19，求AM BM10．【广东省湛江市2021届高三上学期高中毕业班调研测试】如图，三棱柱111ABC A B C -中，底面ABC 是边长为2的等边三角形，侧面11BCC B 为菱形，且平面11BCC B ⊥平面ABC ，160CBB ∠=︒，D 为棱1AA 的中点．（1）证明：1BC ⊥平面1DCB ；（2）求二面角11B DC C --的余弦值．11．【河南省焦作市2020—2021学年高三年级第一次模拟考试数学（理）】如图，四边形ABCD 为菱形，120ABC ∠=︒，四边形BDFE 为矩形，平面BDFE ⊥平面ABCD ，点P 在AD 上，EP BC ⊥.（1）证明：AD ⊥平面BEP ；（2）若EP 与平面ABCD 所成角为60°，求二面角C PE B --的余弦值.12．【广西南宁三中2020届高三数学（理科）考试】如图1，在直角ABC 中，90ABC ∠=︒，AC =AB =D ，E 分别为AC ，BD 的中点，连结AE 并延长交BC 于点F ，将ABD △沿BD 折起，使平面ABD ⊥平面BCD ，如图2所示.（1）求证：AE CD ⊥；（2）求平面AEF 与平面ADC 所成锐二面角的余弦值.13．【广西柳州市2020届高三第二次模拟考试理科】已知三棱锥P ABC -的展开图如图二，其中四边形ABCD ABE △和BCF △均为正三角形，在三棱锥P ABC -中：（1）证明：平面PAC ⊥平面ABC ；（2）若M 是PA 的中点，求二面角P BC M --的余弦值．14．【浙江省“山水联盟”2020届高三下学期高考模拟】四棱锥P ABCD -，底面ABCD 为菱形，侧面PBC 为正三角形，平面PBC ⊥平面ABCD ，3ABC π∠=，点M 为AD 中点.；（1）求证：CM PB（2）若点N是线段PA上的中点，求直线MN与平面PCM所成角的正弦值.。

2021-2022年高三下学期第六次模拟考试数学(理)试题含答案

2021年高三下学期第六次模拟考试数学（理）试题含答案一、选择题（本大题包括12小题，每小题5分，共60分，） 1．集合，，则（）A 、B 、C 、D 、 2．若复数，其中是虚数单位，则复数的模为 A ． B ．C ．D ．23．某学生在一门功课的22次考试中，所得分数如下茎叶图所示，则此学生该门功课考试分数的极差与中位数之和为A ．117B ．118C ．118．5D ．119．5 4．已知，函数在上单调递减.则的取值范围是（） A. B. C. D. 5．数列的前n 项和为，若，则( ) A. B. C.D.6．若程序框图如图所示,则该程序运行后输出的值是 A ．B ．C ．D ．7．设函数()log (01)a f x x a =<<的定义域为,值域为,若的最小值为,则实数a 的值为 A ．B ．或C ．D ．或8．设x ∈R ，向量a ＝（2，x ），b ＝（3，－2），且a ⊥b ，则｜a －b ｜＝A ．5B ．C ．2D ．6 9．二项式展开式中的系数是( )A ．-14B ．14C ．-28D ．28 10．在△ABC 中，若,，则b=（） A ．3 B ．4 C.5 D .611．设函数11,(,2)()1(2),[2,)2x x f x f x x ⎧--∈-∞⎪=⎨-∈+∞⎪⎩，则函数的零点的个数为开始否 n ＝3n +1n 为偶数k ＝k ＋1 结束n ＝5，k ＝0 是输出k n 否是A ．4B ．5C ．6D ．712．已知双曲线上一点，过双曲线中心的直线交双曲线于两点，记直线的斜率分别为，当最小时，双曲线离心率为( ) A ． B ． C D二、填空题(本大题包括4小题，每小题5分，共20分)． 13．—个几何体的三视图如图所示(单位:m )则该几何体的体积为___．14．若整数．．满足0700y x x y x -≥⎧⎪+-≤⎨⎪≥⎩,则的最大值为． 15．向平面区域}10,20|),{(≤≤≤≤y x y x .内随机投入一点，则该点落在曲线⎪⎩⎪⎨⎧≤<-≤≤=)21(2)10(23x x x x y 下方的概率等于_______．16．若一个棱锥的底面是正多边形，并且顶点在底面的射影是底面的中心，这样的棱锥叫做正棱锥．已知一个正六棱锥的各个顶点都在半径为3的球面上，则该正六棱锥的体积的最大值为_____．三、解答题（本大题包括6小题，共70分，解答应写出文字说明，证明过程或演算步骤）． 17．（本小题满分12分）已知二次函数的图像经过坐标原点，其导函数为，数列的前项和为，点均在函数的图像上．（Ⅰ）求数列的通项公式；（Ⅱ）设是数列的前项和，求使得对所有都成立的最小正整数18．（本小题满分12分） A 、B 两个投资项目的利润率分别为随机变量X 1和X 2．根据市场分析，X 1和X 2的分布列分别为X 1 5％ 10％ P0.80.2X 2 2％ 8％ 12％ P0.20.50.3（Ⅰ）在两个项目上各投资100万元，Y 1和Y 2分别表示投资项目A 和B 所获得的利润，求方差DY 1，DY 2；（Ⅱ）将万元投资A 项目，万元投资B 项目，表示投资A 项目所得利润的方差与投资B 项目所得利润的方差的和．求的最小值，并指C 1B 1A 1出x 为何值时，取到最小值．（注：）19．（本小题满分12分）如图，在三棱柱中，侧面底面，，，，为中点．（Ⅰ）证明：平面；（Ⅱ）求直线与平面所成角的正弦值；（Ⅲ）在上是否存在一点，使得平面?若存在，确定点的位置；若不存在，说明理由 20．（本小题满分12分）已知两定点，和定直线l ：，动点在直线上的射影为，且．（Ⅰ）求动点的轨迹的方程并画草图；（Ⅱ）是否存在过点的直线，使得直线与曲线相交于，两点，且△的面积等于？如果存在，请求出直线的方程；如果不存在，请说明理由 21．（本小题满分12分）已知函数，且.（Ⅰ）若曲线在点处的切线垂直于轴，求实数的值；（Ⅱ）当时，求函数的最小值；（Ⅲ）在（Ⅰ）的条件下，若与的图像存在三个交点，求的取值范围请考生在第22、23、24题中任选一．．．题．作答，如果多做，按所做第1题计分。

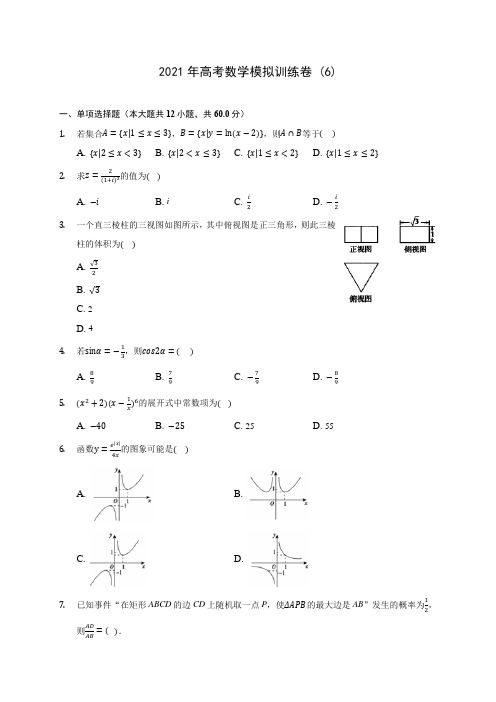
2021届高考数学一轮复习第二章函数、导数及其应用考点测试6函数的单调性(含解析)人教版B版

考点测试6 函数的单调性高考概览本考点是高考的常考知识点，常与函数的奇偶性、周期性相结合综合考查．题型为选择题、填空题，分值5分，难度为低、中、高各种档次考纲研读 1.理解函数的单调性、最大值、最小值及其几何意义 2．会运用基本初等函数的图象分析函数的单调性一、基础小题1．下列函数中，在区间(0,1)上是增函数的是( ) A ．y ＝|x | B ．y ＝3－x C ．y ＝1xD ．y ＝－x 2＋4答案 A解析函数y ＝3－x ，y ＝1x，y ＝－x 2＋4在(0,1)上均为减函数，y ＝|x |在(0,1)上为增函数，故选A.2．函数y ＝x 2－6x ＋10在区间(2,4)上( ) A ．递减 B ．递增 C ．先递减后递增 D ．先递增后递减答案 C解析由函数y ＝x 2－6x ＋10的图象开口向上，对称轴为直线x ＝3，知y ＝x 2－6x ＋10在(2,4)上先递减后递增，故选C.3．若函数f (x )＝(2a －1)x ＋b 是R 上的减函数，则实数a 的取值范围为( )A.⎣⎢⎡⎭⎪⎫12，＋∞ B ．⎝ ⎛⎦⎥⎤－∞，12C.⎝ ⎛⎭⎪⎫12，＋∞ D ．⎝⎛⎭⎪⎫－∞，12 答案 D解析当2a －1<0，即a <12时，该函数是R 上的减函数．故选D.4．已知函数y ＝f (x )在R 上单调递增，且f (m 2＋1)>f (－m ＋1)，则实数m 的取值范围是( )A ．(－∞，－1)B ．(0，＋∞)C ．(－1,0)D ．(－∞，－1)∪(0，＋∞)答案 D解析由题意得m 2＋1>－m ＋1，故m 2＋m >0，解得m <－1或m >0.故选D. 5．函数f (x )＝－x ＋1x 在⎣⎢⎡⎦⎥⎤－2，－13上的最大值是( )A.32 B ．－83C ．－2D ．2答案 A解析因为f (x )＝－x ＋1x 在⎣⎢⎡⎦⎥⎤－2，－13上为减函数，所以当x ＝－2时，f (x )取得最大值，且为2－12＝32.故选A.6．函数f (x )＝⎩⎪⎨⎪⎧x ＋cx ≥0，x －1x <0是增函数，则实数c 的取值范围是( )A ．[－1，＋∞)B ．(－1，＋∞)C ．(－∞，－1)D ．(－∞，－1]答案 A解析 ∵f (x )在R 上单调递增，∴c ≥－1，即实数c 的取值范围是[－1，＋∞)．故选A.7．设函数f (x )在R 上为增函数，则下列结论一定正确的是( ) A ．y ＝1f x在R 上为减函数B ．y ＝|f (x )|在R 上为增函数C ．y ＝－1f x在R 上为增函数D ．y ＝－f (x )在R 上为减函数答案 D解析 A 错误，如y ＝x 3，y ＝1f x在R 上无单调性；B 错误，如y ＝x 3，y ＝|f (x )|在R 上无单调性； C 错误，如y ＝x 3，y ＝－1f x在R 上无单调性；故选D.8．若函数f (x )＝x 2＋a |x |＋2，x ∈R 在区间[3，＋∞)和[－2，－1]上均为增函数，则实数a 的取值范围是( )A.⎣⎢⎡⎦⎥⎤－113，－3 B ．[－6，－4] C ．[－3，－22] D ．[－4，－3]答案 B解析由于f (x )为R 上的偶函数，因此只需考虑函数f (x )在(0，＋∞)上的单调性即可．由题意知f (x )在[3，＋∞)上为增函数，在[1,2]上为减函数，故－a2∈[2,3]，即a ∈[－6，－4]．9．若f (x )＝－x 2＋2ax 与g (x )＝ax ＋1在区间[1,2]上都是减函数，则a 的取值范围是( )A ．(－1,0)∪(0,1]B ．(－1,0)∪(0,1)C ．(0,1)D ．(0,1]答案 D解析 f (x )＝－(x －a )2＋a 2，当a ≤1时，f (x )在[1,2]上是减函数；g (x )＝ax ＋1，当a >0时，g (x )在[1,2]上是减函数，则a 的取值范围是0<a ≤1.故选D.10．已知函数f (x )的图象关于直线x ＝1对称，当x 2>x 1>1时，[f (x 2)－f (x 1)]·(x 2－x 1)<0恒成立，设a ＝f ⎝ ⎛⎭⎪⎫－12，b ＝f (2)，c ＝f (e)，则a ，b ，c 的大小关系为( )A ．c >a >bB ．c >b >aC ．a >c >bD ．b >a >c答案 D解析因为f (x )的图象关于直线x ＝1对称，所以f ⎝ ⎛⎭⎪⎫－12＝f ⎝ ⎛⎭⎪⎫52.由x 2>x 1>1时，[f (x 2)－f (x 1)]·(x 2－x 1)<0恒成立，知f (x )在(1，＋∞)上单调递减．因为1<2<52<e ，所以f (2)>f ⎝ ⎛⎭⎪⎫52>f (e)，所以b >a >c .11．设函数f (x )＝⎩⎪⎨⎪⎧－x 2＋4x ，x ≤4，log 2x ，x >4.若函数y ＝f (x )在区间(a ，a ＋1)上单调递增，则实数a 的取值范围是________．答案 (－∞，1]∪[4，＋∞)解析作出函数f (x )的图象如图所示，由图象可知f (x )在(a ，a ＋1)上单调递增，需满足a ≥4或a ＋1≤2，即a ≤1或a ≥4.12．已知f (x )＝ax ＋1x ＋2，若对任意x 1，x 2∈(－2，＋∞)，有(x 1－x 2)[f (x 1)－f (x 2)]>0，则a 的取值范围是________．答案 ⎝ ⎛⎭⎪⎫12，＋∞ 解析由f (x )＝ax ＋1x ＋2＝a ＋1－2ax ＋2，且y ＝f (x )在(－2，＋∞)上是增函数，得1－2a <0，即a >12.二、高考小题13．(2019·全国卷Ⅲ)设f (x )是定义域为R 的偶函数，且在(0，＋∞)单调递减，则( )答案 C解析因为f (x )是定义域为R 的偶函数，所以f ⎝ ⎛⎭⎪⎫log 314＝f (－log 34)＝f (log 34)．又因为log 34>1>>0，且函数f (x )在(0，＋∞)单调递减，所以f (log 34)< ．故选C.14．(2019·全国卷Ⅱ)下列函数中，以π2为周期且在区间⎝ ⎛⎭⎪⎫π4，π2单调递增的是( )A ．f (x )＝|cos2x |B ．f (x )＝|sin2x |C ．f (x )＝cos|x |D ．f (x )＝sin|x |答案 A解析作出函数f (x )＝|cos2x |的图象，如图．由图象可知f (x )＝|cos2x |的周期为π2，在区间⎝⎛⎭⎪⎫π4，π2上单调递增．同理可得f (x )＝|sin2x |的周期为π2，在区间⎝ ⎛⎭⎪⎫π4，π2上单调递减，f (x )＝cos|x |的周期为2π.f (x )＝sin|x |不是周期函数．故选A.15．(2017·全国卷Ⅱ)函数f (x )＝ln (x 2－2x －8)的单调递增区间是( ) A ．(－∞，－2) B ．(－∞，1) C ．(1，＋∞) D ．(4，＋∞)答案 D解析由x 2－2x －8>0可得x >4或x <－2，所以x ∈(－∞，－2)∪(4，＋∞)，令u ＝x2－2x －8，则其在x ∈(－∞，－2)上单调递减，在x ∈(4，＋∞)上单调递增．又因为y ＝ln u 在u ∈(0，＋∞)上单调递增，所以f (x )＝ln (x 2－2x －8)在x ∈(4，＋∞)上单调递增．故选D.16．(2017·北京高考)已知函数f (x )＝3x－⎝ ⎛⎭⎪⎫13x ，则f (x )( )A ．是奇函数，且在R 上是增函数B ．是偶函数，且在R 上是增函数C ．是奇函数，且在R 上是减函数D ．是偶函数，且在R 上是减函数答案 A解析 ∵函数f (x )的定义域为R ，f (－x )＝3－x－⎝ ⎛⎭⎪⎫13－x ＝⎝ ⎛⎭⎪⎫13x －3x ＝－f (x )，∴函数f (x )是奇函数．∵函数y ＝⎝ ⎛⎭⎪⎫13x 在R 上是减函数，∴函数y ＝－⎝ ⎛⎭⎪⎫13x 在R 上是增函数．又y ＝3x在R上是增函数，∴函数f (x )＝3x－⎝ ⎛⎭⎪⎫13x 在R 上是增函数．故选A.17．(2016·北京高考)下列函数中，在区间(－1,1)上为减函数的是( ) A ．y ＝11－xB ．y ＝cos xC ．y ＝ln (x ＋1)D ．y ＝2－x答案 D解析 A 中，y ＝11－x ＝1－x －1的图象是将y ＝－1x的图象向右平移1个单位得到的，故y ＝11－x在(－1,1)上为增函数，不符合题意；B 中，y ＝cos x 在(－1,0)上为增函数，在(0,1)上为减函数，不符合题意；C 中，y ＝ln (x ＋1)的图象是将y ＝ln x 的图象向左平移1个单位得到的，故y ＝ln (x ＋1)在(－1,1)上为增函数，不符合题意；D 中，y ＝2－x＝⎝ ⎛⎭⎪⎫12x 在(－1,1)上为减函数，所以D 符合题意．18．(2016·天津高考)已知f (x )是定义在R 上的偶函数，且在区间(－∞，0)上单调递增．若实数a 满足f (2|a －1|)>f (－2)，则a 的取值范围是________．答案 ⎝ ⎛⎭⎪⎫12，32 解析由题意知函数f (x )在(0，＋∞)上单调递减．因为f (2|a －1|)>f (－2)，且f (－2)＝f (2)，所以f (2|a －1|)>f (2)，所以2|a －1|<，解得12<a <32.三、模拟小题19．(2019·武汉模拟)若函数f (x )＝2|x －a |＋3在区间[1，＋∞)上不单调，则a 的取值范围是( )A ．[1，＋∞)B ．(1，＋∞)C ．(－∞，1)D ．(－∞，1]答案 B解析因为函数f (x )＝2|x －a |＋3＝⎩⎪⎨⎪⎧2x －2a ＋3，x ≥a ，－2x ＋2a ＋3，x <a ，因为函数f (x )＝2|x －a |＋3在区间[1，＋∞)上不单调，所以a >1，所以a 的取值范围是(1，＋∞)．故选B.20．(2019·郑州模拟)函数y ＝x －5x －a －2在(－1，＋∞)上单调递增，则a 的取值范围是( )A ．a ＝－3B ．a <3C ．a ≤－3D ．a ≥－3答案 C 解析 y ＝x －a －2＋a －3x －a －2＝1＋a －3x －a －2＝1＋a －3x －a ＋2，由题意知⎩⎪⎨⎪⎧a －3<0，a ＋2≤－1，得a ≤－3.所以a 的取值范围是a ≤－3.21．(2019·重庆模拟)定义新运算“⊕”：当a ≥b 时，a ⊕b ＝a ；当a <b 时，a ⊕b ＝b 2，则函数f (x )＝(1⊕x )x －(2⊕x )，x ∈[－2,2]的最大值等于( )A ．－1B ．1C ．6D ．12答案 C解析由已知得，当－2≤x ≤1时，f (x )＝x －2；当1<x ≤2时，f (x )＝x 3－2.因为f (x )＝x －2，f (x )＝x 3－2在定义域内都为增函数，所以f (x )的最大值为f (2)＝23－2＝6.22．(2019·漳州模拟)已知函数f (x )＝⎩⎪⎨⎪⎧x 3，x ≤0，ln x ＋1，x >0，若f (2－x 2)>f (x )，则实数x 的取值范围是( )A ．(－∞，－1)∪(2，＋∞)B ．(－∞，－2)∪(1，＋∞)C ．(－1,2)D ．(－2,1)答案 D解析因为当x ＝0时，两个表达式对应的函数值都为零，所以函数的图象是一条连续的曲线．因为当x ≤0时，函数f (x )＝x 3为增函数，当x >0时，f (x )＝ln (x ＋1)也是增函数，所以函数f (x )是定义在R 上的增函数．因此，不等式f (2－x 2)>f (x )等价于2－x 2>x ，即x 2＋x －2<0，解得－2<x <1.23．(2020·沈阳市高三摸底)如果函数y ＝f (x )在区间I 上是增函数，且函数y ＝f xx在区间I 上是减函数，那么称函数y ＝f (x )是区间I 上的“缓增函数”，区间I 叫做“缓增区间”．若函数f (x )＝12x 2－x ＋32是区间I 上的“缓增函数”，则“缓增区间”I 为( )A ．[1，＋∞)B ．[0，3]C ．[0,1]D ．[1，3]答案 D解析因为函数f (x )＝12x 2－x ＋32的对称轴为直线x ＝1，所以函数y ＝f (x )在区间[1，＋∞)上是增函数，又当x ≥1时，f x x ＝12x －1＋32x ，令g (x )＝12x －1＋32x(x ≥1)，则g ′(x )＝12－32x 2＝x 2－32x 2，由g ′(x )≤0得1≤x ≤ 3，即函数f x x ＝12x －1＋32x 在区间[1，3]上单调递减，故“缓增区间”I 为[1，3]．24．(2019·广东名校联考)设函数f (x )＝⎩⎪⎨⎪⎧1，x >0，0，x ＝0，－1，x <0，g (x )＝x 2f (x －1)，则函数g (x )的单调递减区间是________．答案 [0,1)解析由题意知g (x )＝⎩⎪⎨⎪⎧x 2，x >1，0，x ＝1，－x 2，x <1.函数图象如图所示，其单调递减区间是[0,1)．一、高考大题本考点在近三年高考中未涉及此题型．二、模拟大题1．(2019·福建泉州高三阶段测试)已知定义在R 上的函数f (x )满足：①f (x ＋y )＝f (x )＋f (y )＋1；②当x >0时，f (x )>－1.(1)求f (0)的值，并证明f (x )在R 上是单调增函数； (2)若f (1)＝1，解关于x 的不等式f (x 2＋2x )＋f (1－x )>4. 解 (1)令x ＝y ＝0得f (0)＝－1. 在R 上任取x 1>x 2，则x 1－x 2>0，f (x 1－x 2)>－1.又f (x 1)＝f ((x 1－x 2)＋x 2)＝f (x 1－x 2)＋f (x 2)＋1>f (x 2)，所以f (x )在R 上是单调增函数． (2)由f (1)＝1，得f (2)＝3，f (3)＝5.由f (x 2＋2x )＋f (1－x )>4得f (x 2＋x ＋1)>f (3)，又因为f (x )在R 上是增函数，故x 2＋x ＋1>3，解得x <－2或x >1，故原不等式的解集为{x |x <－2或x >1}．2．(2019·安徽肥东高级中学调研)函数f (x )＝2x －ax的定义域为(0,1]． (1)当a ＝－1时，求函数f (x )的值域；(2)若f (x )在定义域上是减函数，求a 的取值范围．解 (1)因为a ＝－1，所以函数f (x )＝2x ＋1x ≥22⎝ ⎛⎭⎪⎫当且仅当x ＝22时，等号成立，所以函数f (x )的值域为[22，＋∞)．(2)若函数f (x )在定义域上是减函数，则任取x 1，x 2∈(0,1]且x 1<x 2都有f (x 1)>f (x 2)成立，即f (x 1)－f (x 2)＝(x 1－x 2)⎝⎛⎭⎪⎫a ＋2x 1x 2x 1x 2>0，只要a <－2x 1x 2即可，由x 1，x 2∈(0,1]，得－2x 1x 2∈(－2,0)，所以a ≤－2，故a 的取值范围是(－∞，－2]．3．(2019·湖南永州模拟)已知二次函数f (x )＝ax 2＋bx ＋1(a >0)，F (x )＝⎩⎪⎨⎪⎧f x ，x >0，－fx ，x <0.若f (－1)＝0，且对任意实数x 均有f (x )≥0成立．(1)求F (x )的表达式；(2)当x ∈[－2,2]时，g (x )＝f (x )－kx 是单调函数，求实数k 的取值范围．解 (1)因为f (－1)＝0，所以a －b ＋1＝0，所以b ＝a ＋1，所以f (x )＝ax 2＋(a ＋1)x ＋1. 因为对任意实数x 均有f (x )≥0恒成立，所以⎩⎪⎨⎪⎧a >0，Δ＝a ＋12－4a ≤0，所以⎩⎪⎨⎪⎧a >0，a －12≤0.所以a ＝1，从而b ＝2，所以f (x )＝x 2＋2x ＋1，所以F (x )＝⎩⎪⎨⎪⎧x 2＋2x ＋1，x >0，－x 2－2x －1，x <0.(2)g (x )＝x 2＋2x ＋1－kx ＝x 2＋(2－k )x ＋1. 因为g (x )在[－2,2]上是单调函数，所以k －22≤－2或k －22≥2，解得k ≤－2或k ≥6.故实数k 的取值范围是(－∞，－2]∪[6，＋∞)．4．(2019·陕西西安长安区大联考)已知定义在区间(0，＋∞)上的函数f (x )满足f (x 1·x 2)＝f (x 1)＋f (x 2)，且当x >1时，f (x )>0.(1)求f (1)的值；(2)证明：f (x )为单调增函数；(3)若f ⎝ ⎛⎭⎪⎫15＝－1，求f (x )在⎣⎢⎡⎦⎥⎤125，125上的最值．解 (1)因为函数f (x )满足f (x 1·x 2)＝f (x 1)＋f (x 2)，令x 1＝x 2＝1，则f (1)＝f (1)＋f (1)，解得f (1)＝0. (2)证明：设x 1，x 2∈(0，＋∞)，且x 1>x 2，则x 1x 2>1，所以f ⎝ ⎛⎭⎪⎫x 1x2>0，所以f (x 1)－f (x 2)＝f ⎝⎛⎭⎪⎫x 2·x 1x2－f (x 2)＝f (x 2)＋f ⎝ ⎛⎭⎪⎫x 1x 2－f (x 2)＝f ⎝ ⎛⎭⎪⎫x 1x 2>0，所以f (x 1)>f (x 2)，所以f (x )在(0，＋∞)上是增函数． (3)因为f (x )在(0，＋∞)上是增函数．若f ⎝ ⎛⎭⎪⎫15＝－1，则f ⎝ ⎛⎭⎪⎫15＋f ⎝ ⎛⎭⎪⎫15＝f ⎝ ⎛⎭⎪⎫125＝－2，因为f ⎝ ⎛⎭⎪⎫15×5＝f (1)＝f ⎝ ⎛⎭⎪⎫15＋f (5)＝0，所以f (5)＝1，则f (5)＋f (5)＝f (25)＝2，f (5)＋f (25)＝f (125)＝3，即f (x )在⎣⎢⎡⎦⎥⎤125，125上的最小值为－2，最大值为3.。

2021年高考数学模拟训练卷 (6)(含答案解析)

2021年高考数学模拟训练卷 (6)一、单项选择题（本大题共12小题，共60.0分）1.若集合A={x|1≤x≤3}，B={x|y=ln(x−2)}，则A∩B等于()A. {x|2≤x<3}B. {x|2<x≤3}C. {x|1≤x<2}D. {x|1≤x≤2}2.求z=2(1+i)2的值为()A. −iB. iC. i2D. −i23.一个直三棱柱的三视图如图所示，其中俯视图是正三角形，则此三棱柱的体积为()A. √32B. √3C. 2D. 44.若sinα=−13，则cos2α=()A. 89B. 79C. −79D. −895.(x2+2)(x−1x)6的展开式中常数项为()A. −40B. −25C. 25D. 556.函数y=e|x|4x的图象可能是()A. B.C. D.7.已知事件“在矩形ABCD的边CD上随机取一点P，使ΔAPB的最大边是AB”发生的概率为12，则ADAB=()．A. 12B. 14C. √32D. √748. 圆x 2+y 2+4x −4y =0和圆x 2+y 2+2x −8=0相交于M ，N 两点，则|MN|= ( )A. 4B. 3√55C. 12√55D. 6√559. 在△ABC 中，内角A ，B ，C 的对边长分别为a ，b ，c ，已知a 2−c 2=b ，且sin(A −C)=2cosAsinC ，则b =( )A. 6B. 4C. 2D. 110. 已知直三棱柱ABC −A 1B 1C 1的顶点都在球O 上，且AB =4，AA 1=6，∠ACB =30°，则此直三棱柱的外接球O 的表面积是( )A. 25πB. 50πC. 100πD.500π311. 己知A 、F 分别为双曲线C 的左顶点和右焦点，点D 在C 上，△AFD 是等腰直角三角形，且∠AFD =90°，则C 的离心率为( )A. √2B. √3C. 2D. √2+112. 已知函数f(x)=(x −m)2+(ae x −3m)2(m ∈R)的最小值为910，则正实数a =( )A. 3B. 3e −2C. 3e 2D. 3或3e −2二、填空题（本大题共4小题，共20.0分）13. 设PA ⃗⃗⃗⃗⃗ =(k , 12)，PB ⃗⃗⃗⃗⃗ =(4 , 5)，PC ⃗⃗⃗⃗⃗ =(10 , k)，则k = ______ 时，点A ，B ，C 共线． 14. 若x ，y 满足{x ≥1y ≥−1x +y ≥3，则z =x +2y 的最小值为______．15. 函数f(x)=Asin(ωx +φ)(其中A >0，ω>0，|φ|<π2)的图象如图所示，则，f(0)=______．16. 已知直线y =x +b(b ≠0)与抛物线y =12x 2交于A ，B 两点，O 为抛物线的顶点．若OA ⊥OB ，则实数b 的值为________．三、解答题（本大题共7小题，共84.0分）17.已知数列{a n}的前n项和为S n，a1=2，且满足a n+1=S n+2n+1(n∈N∗).}为等差数列；(Ⅰ)证明数列{S n2n(Ⅱ)求S1+S2+⋯+S n．18.某水产品经销商销售某种鲜鱼，售价为每千克20元，成本为每千克15元，销售宗旨是当天进货当天销售，如果当天卖不完，那么未售出的部分全部处理，平均每千克损失3元．根据以往的市场调查，将市场日需求量(单位：千克)按[50,150)，[150,250)，[250,350)，[350,450)，[450,550)进行分组，得到如图的频率分布直方图．(Ⅰ)未来连续三天内，连续两天该种鲜鱼的日需求量不低于350千克，而另一天的日需求量低于350千克的概率；(Ⅱ)在频率分布直方图的日需求量分组中，以各组区间的中点值代表该组的各个值，并以日需求量落入该区间的频率作为日需求量取该区间中点值的概率．若经销商每日进货400千克，记经销商每日利润为X(单位：元)，求X的分布列和数学期望．19. 如图，在四棱锥P −ABCD 中，侧面PAD ⊥底面ABCD ，侧棱PA =PD =√2，底面ABCD 为直角梯形，其中BC//AD ，AB ⊥AD ，AD =2AB =2BC =2，O 为AD 中点．(1)求证：PO ⊥平面ABCD ；(2)求异面直线PB 与CD 所成角的余弦值.20. 已知椭圆C ：x 2a 2+y 2b 2=1(a >b >0)的离心率为12，设A(0,b)，B(a,0)，F 1，F 2，分别是椭圆的左右焦点，且S △ABF 2=√32(1)求椭圆C 的方程；(2)过F 1的直线与以F 2为焦点，顶点在坐标原点的抛物线交于P ，Q 两点，设F 1P ⃗⃗⃗⃗⃗⃗⃗ =λF 1Q ⃗⃗⃗⃗⃗⃗⃗ ，若λ∈[2,3]，求△F 2PQ 面积的取值范围．21.已知函数f(x)=13x3−x2+ax(其中a为常数)．(1)若x=−1是f(x)的极值点，求函数f(x)的减区间；(2)若f(x)在(−2,+∞)上是增函数，求a的取值范围．22.在平面直角坐标系中，曲线C的参数方程为{x=3+5cosθy=−4+5sinθ(θ为参数)，以平面直角坐标系的原点O为极点，x轴正半轴为极轴建立极坐标系．(1)求曲线C的极坐标方程；(2)过点P(2,0)，倾斜角为π4的直线l与曲线C相交于M，N两点，求1|PM|+1|PN|的值．23.已知函数f(x)=|2x−a|+|2x+3|，g(x)=|3x−2|．(1)解不等式g(x)<|2x+1|；(2)若对任意的x1∈R，任意的x2∈[0,1]，使得f(x1)≥g(x2)成立，求实数a的取值范围．【答案与解析】1.答案：B解析：解：∵B={x|y=ln(x−2)}={x|x−2>0}={x|x>2}，∴A∩B={x|2<x≤3}，故选：B根据集合的交集运算进行求解．本题主要考查集合的基本运算，比较基础．2.答案：A解析：解：z=2(1+i)2=22i=1i=−i−i2=−i，则z的值为：−i．故选：A．利用复数代数形式的乘除运算化简复数z，则答案可求．本题考查了复数代数形式的乘除运算，是基础题．3.答案：B解析：解：由三视图还原原几何体如图，原几何体是正三棱柱，底面边长为2，高为1．∴底面积为S=√3，体积V=√3×1=√3．故选：B．由三视图还原原几何体，可知原几何体是正三棱柱，底面边长为2，高为1，然后由棱柱体积公式求解．本题考查由三视图求面积、体积，关键是由三视图还原原几何体，是中档题．4.答案：B解析：本题考查了二倍角公式的应用，利用公式可以将所求cos2α应用已知的sinα表示，属于基础题型．解：sinα=−13,cos2α=1−2sin2α=1−2×(−13)2=79.故选B．5.答案：B解析：本题考查了二项式定理的应用，考查了推理能力与计算能力，属于基础题．利用展开式的通项公式即可得出．解：因为(x−1x )6的展开式的通项公式为：T r+1=C6r x6−r(−1x)r=(−1)r C6r x6−2r，所以(x2+2)(x−1x)6的展开式中常数项为：x2(−1)4C64x−2+2×(−1)3C63x0=15−40=−25．故选B．6.答案：C解析：解：函数为奇函数，图象关于原点对称，排除B，当x=1时，y=e4<1，排除A；当x→+∞时，e|x|4x→+∞，排除D．故选：C．判断函数的奇偶性和对称性，利用特殊值和极限思想进行排除．本题主要考查函数图象的识别和判断，判断函数的奇偶性以及利用排除法是解决本题的关键．7.答案：D解析：如图所示，设CD上的P1，P2两点刚好满足P1B=P2A=AB，那么，当P在P1P2之间时，就满足“ΔAPB的最大边是AB”，根据几何概型P1P2=12CD，DP1=14CD，设CD=4，AD=x，则DP2=3⇒AP 2=√7=AB ，故选D ．8.答案：C解析：本题考查直线与圆、圆与圆的位置关系，涉及直线与圆相交的性质以及弦长的计算，属于中档题．首先求出直线MN ，根据弦心距和半径和弦长之间的关系求出|MN |解：∵两圆的方程分别为x 2+y 2+4x −4y =0，x 2+y 2+2x −8=0，两式相减可得x −2y +4=0， ∴两圆的公共弦所在直线的方程是x −2y +4=0．∵圆x 2+y 2+4x −4y =0的圆心坐标为(−2,2)，半径为2√2， ∴圆心到公共弦的距离，∴|MN|=2√(2√2)2−(2√55)2=12√55，故选C ．9.答案：C解析：本题主要考查正弦定理和余弦定理的应用，属于基础题．由条件利用正弦定理和余弦定理求得2(a 2−c 2)=b 2，再根据已知条件，求得b 的值．解：在△ABC 中，∵sin(A −C)=sinAcosC −cosAsinC =2cosAsinC ， ∴sinAcosC =3cosAsinC ， ∴a ⋅a 2+b 2−c 22ab=3c ⋅b 2+c 2−a 22bc，∴2(a 2−c 2)=b 2．又已知a 2−c 2=b ，∴b =2，故选：C ．10.答案：C解析：本题考查球的表面积公式，利用正弦定理求三角形外接圆半径，属于基础题．首先利用三棱柱和球的关系求出球的半径，进一步利用球的表面积公式求出结果．解：根据直三棱柱ABC−A1B1C1的顶点都在球O上，且AB=4，AA1=6，∠ACB=30°，在△ABC中，ABsin30∘=8=d(d为△ABC外接圆的直径)，设外接球的半径为R，所以R=√(d2)2+(AA12)2=5，所以S球=4π⋅52=100π，故选：C．11.答案：C解析：解：由题意，|AF|=|DF|∴c+a=b2a，∴e2−e−2=0，∵e>1，∴e=2，故选：C．由题意，|AF|=|DF|，可得c+a=b2a，即可求出C的离心率．本题考查双曲线C的离心率，考查学生的计算能力，比较基础．12.答案：A解析：解：(x−m)2+(ae x−3m)2表示点A(x,ae x)与点B(m,3m)的距离的平方，点A在曲线y=ae x上，点B在曲线y=3x上，如图，可得a>0，设与y=3x平行的直线与曲线y=ae x相切于点P(x0,ae x0).∵y′=ae x，∴ae x0=3，…①。

2020-2021学年上海市华东师范大学第二附属中学高三下学期5月高考模拟测试数学试卷含详解

上海市华东师范大学第二附属中学2020-2021年高三下学期5月高考模拟测试数学试卷（最后一卷）2021.5.31一、填空题（本大题共12题，满分54分，第1-6题每题4分，第7-12题每题5分）1.若集合{}12,A x x x R =-<∈，则A Z = _________.2.方程33log 1log (2)x x =-+的解集为_________.3.已知a R ∈，复数()(1)a i i z i-+=，若z 的虚部为1，则a =_________.4.已知cos 5cos(2),sin 32θππθθθ=-<，则sin 2θ=_________.5.若二项式21()n x x-的展开式共有6项，则此展开式中含4x 的项的系数是_________.6.若抛物线228x y =上一点00(,)x y 到焦点的距离是该点到x 轴距离的3倍，则0y =______.7.袋中有大小相同的黑球和白球各1个，每次从袋中抽取1个，有放回的随机抽取3次，则至少抽到1个黑球的概率是_________.8.设等比数列{}n a 的前n 项和为n S ，若396,,S S S 成等差数列，若254a a +=，则8a 的值为_________.9.已知球O 的半径是1，,,A B C 三点都在球面上，若A 和B 的球面距离、A 和C 的球面距离都是4π，B 和C 的球面距离是3π，则二面角B OA C --的大小是_________.10.已知实数,x y 满足不等式组2040250x y x y x y -+≥⎧⎪+-≥⎨⎪--≤⎩，若目标函数(10)z y ax a =+-<<最大值为8，则a 的值为_________.11.在平面直角坐标系xOy 中，已知点(2,2)A ，,E F 为圆22:(1)(1)4C x y -+-=上的两动点，且EF =，若圆C 上存在点P ，使得,0AE AF mCP m +=>，则m 的取值范围为_________.12.已知0,0a b ≠>，若222()2f x b ax b a x b b =+-+-有两零点12,x x ，且120x x +<，则ab的取值范围上_________.二、选择题（本大题共有4小题，满分20分，每题5分）13.关于“若4a b +=，则,a b 至少有一个等于2”及其逆命题的说法正确的是（）A.原命题为真，逆命题为假B.原命题为假，逆命题为真C.原命题为真，逆命题为真D.原命题为假，逆命题为假14.设34:02x xp x-≤，22:(21)0q x m x m m -+++≤，若p 是q 的必要不充分条件，则实数m 的取值范围为（）A.[]2,1- B.[]31-， C.[)(]2,00,1- D.[)(]2,10,1-- 15.甲、乙两人在相同的条件下各打靶6次，每次打靶的情况如图所示（虚线为甲的折线图），则以下说法错误的是（）A.甲、乙两人打靶的平均环数相等B.甲的环数的中位数比乙的大C.甲的环数的众数比乙的大D.甲打靶的成绩比乙的更稳定16.已知梯形CEPD 如图(1)所示，其中8,6PD CE ==，A 为线段PD 的中点，四边形ABCD 为正方形，现沿AB 进行折叠，使得平面PABE ⊥平面ABCD ，得到如图(2)所示的几何体．已知当AB 上一点F 满足(01)AF AB λλ=<<时，平面DEF ⊥平面PCE ，则λ的值为（）A.12B.23C.35D.45三、解答题（本题共5小题，满分76分）17.（7分+7分）已知关于x 得二次方程：2(2)4(2)0(,)x i x ab a b i a b R ++++-=∈.（1）当方程有实数根时，求点(,)a b 的轨迹方程；（2）求方程实数根的取值范围.18.（7分+7分）已知函数23()sin 3sin cos (,,0)2f x a x a x x a b a b a =+-+<,（1）若当0,2x π⎡⎤∈⎢⎥⎣⎦时，函数()f x 的值域为[]5,1-，求实数,a b 的值；（2）在（1）条件下，求函数()f x 图像的对称中心和单调区间.19.（3分+4分+7分）近来，国内多个城市纷纷加码布局“夜经济”，以满足不同层次的多元消费，并拉动就业、带动创业，进而提升区域经济发展活力.某夜市的一位工艺品售卖者，通过对每天销售情况的调查发现：该工艺品在过去的一个月内（按30天计），每件的销售价格()P x (单位：元)与时间x （单位：天）（130,x x N *≤≤∈）的函数关系满足()10kP x x=+（k 为常数，且>0k ），日销售量()Q x （单位：件）与时间x 的部分数据如下表所示：x15202530()Q x 55605550设该工艺品的日销售收入为()f x （单位：元），且第20天的日销售收入为603元.（1）求k 的值；（2）给出以下四种函数模型：①()Q x ax b =+；②()||Q x a x m b =-+；③()xQ x ab =；④()log b Q x a x =.请你根据上表中的数据，从中选择你认为最合适的一种函数模型来描述日销售量()Q x 与时间x 的变化关系，并求出该函数的解析式；（3）利用问题（2）中的函数()Q x ，求()f x 的最小值.20.（4分+6分+6分）如图，已知双曲线C 的方程为22221x y a b-=（0a b >>），两条渐近线的夹角为3arccos5，焦点到渐近线的距离为1．M 、N 两动点在双曲线C 的两条渐近线上，且分别位于第一象限和第四象限，P 是直线MN 与双曲线右支的一个公共点，MP PN λ= .（1）求双曲线C 的方程；（2）当=1λ时，求PM PN ⋅的取值范围；（3）试用λ表示MON △的面积S ，设双曲线C 上的点到其焦点的距离的取值范围为集合Ω，若5λ∈Ω，求S 的取值范围.21.已知数列{}n a ：1，2-，2-，3，3，3，4-，4-，4-，4-，⋅⋅⋅，11(1),,(1)k k k k k ---⋅⋅⋅-个，即当1)(122k k k k n -+<≤（）（*k ∈N ）时，1(1)k n a k -=-，记12n n S a a a =++⋅⋅⋅+（*n ∈N ）.（1）求2020S 的值；（2）求当(1)(1)(2)22k k k k n +++<≤（*k ∈N ），试用n 、k 的代数式表示n S （*n ∈N ）；（3）对于*t ∈N ，定义集合{|t n P n S =是n a 的整数倍，*n ∈N ，且1}n t ≤≤，求集合2020P 中元素的个数.上海市华东师范大学第二附属中学2020-2021年高三下学期5月高考模拟测试数学试卷（最后一卷）2021.5.31一、填空题（本大题共12题，满分54分，第1-6题每题4分，第7-12题每题5分）1.若集合{}12,A x x x R =-<∈，则A Z = _________.【答案】{0,1,2}【解析】:13A x -<<，{}0,1,2A Z ∴= 。

2021年浙江省新高考测评卷数学(第六模拟)

2021年浙江省新高考测评卷数学（第六模拟）学校:___________姓名：___________班级：___________考号：___________一、单选题1．已知集合{}24A x x =-<<，{}2B x x =≥，{}3C x x =<，则A B C ⋂⋂=（）A ．{}24x x -<< B ．{}24x x ≤<C ．{}23x x -<<D ．{}23x x ≤<2．复数z =）A ．1B ．79C ．59D ．133．若实数x ，y 满足约束条件1,31,1,x y x y x y +≤⎧⎪-≥⎨⎪-≤⎩则2020z x y =-的最大值为（）A ．2020-B ．2020C ．4039D ．40404．5x ⎛ ⎝的展开式中2x 的系数是（）A ．60B ．80C ．90D ．1205．已知p ：2x a +<，q ：x a ≥，且p 是q 的充分不必要条件，则实数a 的取值范围是（） A ．(],1-∞- B ．(),1-∞-C ．[)1,+∞D ．()1,+∞6．若12ln 2a =，b =，4log 3c =，则（） A ．c b a >> B ．c a b >>C ．a c b >>D ．a b c >>7．设1x ，2x ，{}31,0,1,2x ∈-，那么满足32212308x x x ≤++≤的所有有序数组()123,,x x x 的组数为（）A ．45B ．46C ．47D ．488．已知椭圆22221x y a b+=（0a b >>）的左、右焦点分别是1F ，2F ，点P 在椭圆上，O 是坐标原点，12123F PF FOP π∠=∠=，则椭圆的离心率是（）A．32- BC．2D．29．在ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，若22b a bc -=，则sin sin 2A B +=（）A ．0B ．12C．2D ．13-10．已知函数()()()()22673,log 113,x x x f x x x ⎧-+-≥⎪=⎨+-<<⎪⎩若关于x 的方程()()220f x mf x m +++=⎡⎤⎣⎦有6个根，则m 的取值范围为（）A．(,2-∞- B．(2,2--C ．()2,-+∞D．2,2--⎡⎣二、填空题11．已知三倍角公式()()sin34sin sin 60sin 60αααα=+-°°，则sin 20sin60sin100sin140=°°°°______．12．某几何体的三视图如图所示，则该几何体的体积为______．13．已知向量a ，b 满足23a b a b +≥-，则ba在a 方向上的投影的最小值是______．三、双空题14．已知等差数列{}n a 的前n 项和为n S ，公差为d ．若17102S =，1112a =，则d =______，20S =______．15．已知随机变量X 的分布列为()()()12aP X n n n ==++（1,2,3n =），其中a 为16．已知双曲线C 的右焦点为()2,0F ，且C 经过点(A ，则双曲线C 的标准方程为______；若直线AF 与y 轴交于点B ，点(),P x y 是C 右支上一动点，且(y ∈-，直线AP 与以AB 为直径的圆相交于另一点D ，则PA PD ⋅的最大值是______．17．如图，直四棱柱1111ABCD A B C D -的底面是边长为2的正方形，13AA =，E ，F 分别是AB ，BC 的中点，过点1D ，E ，F 的平面记为α，则平面α截直四棱柱1111ABCD A B C D -所得截面的面积为______，平面α与平面11BB C C 所成角的余弦值为______．四、解答题18．已知函数()227cos 24cos 32πx f ωx ωx ⎛⎫=-+- ⎪⎝⎭（0>ω）的图象与x 轴的两个相邻交点间的最短距离为6π．（1）求()0f ；（2）求函数()f x 在[]0,π上的单调递增区间．19．如图，在四棱锥P ABCD -中，底面ABCD 为直角梯形，//AD BC ，90ADC ∠=︒，二面角P AD C --的余弦值为13，M 是棱PC 的中点，2PA PD AD ===，1BC =，CD =．（1）求证：AD PB ⊥；（2）求直线MA 与平面PAD 所成角的正弦值．20．已知数列{}n a 满足113a =，11113n n na a +++=．（1）证明：数列1134n na +⎧⎫-⎨⎬⎩⎭为等比数列，并求数列{}n a 的通项公式；（2）求证：1235n a a a ++⋅⋅⋅+<． 21．设O 为坐标原点，M 是x 轴上一点，过点M 的直线交抛物线C ：24y x =于点A ，B ，且4OA OB ⋅=-．（1）求点M 的坐标；（2）求232BM AM-的最大值．22．已知函数()e 1xx a f x =-+（a ∈R ）．（1）讨论函数()f x 的单调性；（2）当1a =时，令()()ln g x f x =，若函数()g x 的图象与直线y kx m =+相交于不同的两点A ，B ，设1x ，2x （12x x <）分别为点A ，B 的横坐标，求证：21111k x x <+<．参考答案1．D 【分析】根据交集的概念运算可得结果. 【详解】{}24A B x x ⋂=≤<，{}23A B C x x ⋂⋂=≤<，故选：D ． 2．A 【分析】利用复数的四则运算以及复数的概念即可求解. 【详解】3i 11i3z +===，所以z 的虚部为13，实部为3-，故z 的虚部和实部的平方和是221133⎛⎫⎛⎫+-= ⎪ ⎪ ⎪⎝⎭⎝⎭．故选：A 3．B 【分析】作出可行域，将目标函数进行变形，根据目标函数的几何意义并数形结合可得最优解，得到目标函数的最值．【详解】根据题意作出可行域如图中阴影部分所示，由2020z x y =-得1120202020y x z =-，数形结合可知当直线2020z x y =-经过点()0,1-时，z 取得最大值，为2020．故选：B 4．C 【分析】利用通项公式35215C 3r rr r T x-+=⋅，得2r，可得系数【详解】5x⎛+ ⎝的展开式的通项公式为3552155C C 3rr r r r r r T x x --+==⋅，令3522r -=，得2r ，则2x 的系数为225C 390⨯=．故选：C 【点睛】求二项式展开式指定项的系数，利用通项公式1C r n r rr n T a b -+=和x 的幂指数相等可求．5．A 【分析】首先求出p ，记为A ，再求出q ，记为B ，依题意可得A B ，即可得到不等式，解得即可；【详解】解：因为p ：2x a +<，所以:22p a x a --<<-+，记为{}|22A x a x a =--<<-+；:q x a ≥，记为{}|B x x a =≥．因为p 是q 的充分不必要条件，所以AB所以2a a ≤--，解得1a ≤-．故选：A 6．B 【分析】由已知可得2log e 2a =，ln 22b =，2log 32c =，利用对数式的单调性可得答案. 【详解】2log e 12ln 22a ==，ln 22b ==，24log 3log 32c ==，由于22log 3log e 1>>，0ln 21<<，∴c a b >>．故选：B. 7．C 【分析】对1x 的取值进行分类讨论，结合已知分析2x 和3x 的取值情况，然后利用排列组合知识求解即可．【详解】①当12x =时，22230x x +=，则230x x ==，共1组；②当11x =时，222317x x -≤+≤，则2x ，3x 不同时为2，共1124414115C C ⋅-=-=组； ③当10x =时，222308x x ≤+≤，则2x ，3x 为1,0,1,2中任一元素，共11244416C C ⋅==组；④当11x =-时，222319x x ≤+≤，则2x ，3x 不同时为0，共1124414115C C ⋅-=-=组．故满足题意的有序数组共有47组．故选：C. 8．D 【分析】利用12123F PF FOP π∠=∠=，得到121PFO F F P ∽△△，利用11121PF F O F F PF =，求得1PF =，利用定义得到22PF a =，再利用余弦定理得解. 【详解】根据12123F PF FOP π∠=∠=以及121PF F OF P ∠=∠，得121PFO F F P ∽△△，于是11121PF F O F F PF =，所以1PF =，又122PF PF a +=，所以22PF a =．在21F F P △中，由余弦定理，得)()()22214222()2c a a =+-⨯-，即2220c a -=，所以220e -=，因为01e <<，所以椭圆的离心率e = 故选D 【点睛】本题以椭圆为载体，考查三角形相似、余弦定理以及椭圆的定义与性质．利用三角形相似、椭圆定义得到焦半径是解题关键. 9．A 【分析】由余弦定理得2cos b A b c =+，再由正弦定理得2sin cos B Asin sin cos sin cos B A B B A =++，化简可得()sin sin B B A =-，结合三角函数的性质得2B πA =+可得答案.【详解】由22b a bc -=得2222b c a bc c +-=+，由余弦定理得2cos b A b c =+，再由正弦定理得()2sin cos sin sin sin sin B A B C B A B =+=++sin sin cos sin cos B A B B A =++，即sin cos sin sin cos B A B A B =+，得()sin sin B B A =-，由于()0,B π∈，(),B A ππ-∈-，所以B A B -=（舍去）或B A B π-+=，故2B πA =+，于是()sin 2sin sin B πA A =+=-，所以sin sin 20A B +=．故选：A. 10．B 【分析】作出函数()f x 的图象,令()t f x =，则原方程可化为220t mt m +++=在()0,2上有2个不相等的实根，再数形结合得解. 【详解】作出函数()f x 的图象如图所示．令()t f x =，则()()220f x mf x m +++=⎡⎤⎣⎦可化为220t mt m +++=，要使关于x 的方程()()220f x mf x m +++=⎡⎤⎣⎦有6个根，数形结合知需方程220t mt m +++=在()0,2上有2个不相等的实根1t ，2t ，不妨设1220t t <<<，()22t m t m g t =+++，则()()()2420,02,2020,24220m m m g m g m m ⎧-+>⎪⎪<-<⎪⎨⎪=+>⎪=+++>⎪⎩解得22m -<<-，故m 的取值范围为(2,2--，故选B ．【点睛】形如()y g f x =⎡⎤⎣⎦的函数的零点问题与函数图象结合较为紧密，处理问题的基础和关键是作出()f x ，()g x 的图象．若已知零点个数求参数的范围，通常的做法是令()t f x =，先估计关于t 的方程()0g t =的解的个数，再根据()f x 的图象特点，观察直线y t =与()y f x =图象的交点个数，进而确定参数的范围．11．316【分析】根据三倍角公式，诱导公式及40α=︒，代入求值即可．【详解】因为sin 20sin100sin140sin 20sin100sin 40=°°°°°°()()sin 40sin 6040sin 6040+-=°°°°°1sin1204==°，所以3sin 20sin 60sin100sin14016==°°°°．故答案为：31612．133【分析】根据三视图确定空间几何体的形状，运用体积公式进行求解即可. 【详解】由该几何体的三视图可知，该几何体为一个长方体与一个三棱锥的组合体，24=，三棱锥的体积为：111211323⨯⨯⨯⨯=，故该几何体的体积为113433+=．故答案为：13313．12【分析】对已知不等式两边平方并化简，利用平面向量数量积的定义和投影的概念，可得最小值．【详解】由23a b a b +≥-得2223a b a b +≥-，得22224496a a b b a a b b +⋅+≥-⋅+，所以22a b a ⋅≥．设a ，b 的夹角为θ，则22cos a b θa ⋅≥，所以cos 12b θa≥，即b a 在a方向上的投影的最小值是12．故答案为：1214．3 210 【分析】利用等差数列的通项公式与前n 项和公式求出1a ，d ，再利用等差数列的前n 项和公式求出20S . 【详解】由已知及等差数列的通项公式与求和公式可得1111012a a d =+=①，1711716171022S a d ⨯=+=②，由①②得118a =-，3d =， ∴()202019201832102S ⨯=⨯-+⨯=．故答案为:3；210 15．103296【分析】利用分布列的性质求得103a =，进而求得()1P X =，()2P X =，()3P X =，得到()E X ，最后利用数学期望的相关公式求解即可．【详解】()()()1212P X aa a n n n n n ==-+=+++，由()()()1231P X P X P X =+=+==，即125a a -=，得103a =，则()519P X ==，()5218P X ==，()136P X ==，∴()55129123918618E X =⨯+⨯+⨯=，即()()2929338316E X E X =⨯==．故答案为：103，296. 16．2213y x -=48【分析】设双曲线C 的标准方程为()222210,0x y a b a b-=>>，利用待定系数法可求得双曲线C 的标准方程，利用平面向量数量积的运算法则可得出249PA PD PF ⋅=-，求出PF 的最小值，即可得解. 【详解】由题意可设双曲线C 的标准方程是()222210,0x y a b a b-=>>，则22222416451a b c a b⎧+==⎪⎨-=⎪⎩，解得2213a b ⎧=⎨=⎩，所以，双曲线C 的标准方程为2213y x -=.直线AF的斜率为422AF k ==-，直线AF的方程为)22y x =-，在直线AF 的方程中，令0x =，可得y =-，即点(0,B -，因为2A B F x x x +=，2A BF y y y +=，所以，点F 为线段AB 的中点，故以AB 为直径的圆的圆心为F ，且半径为7AF =，如图，连接PB 、PF 、BD ，由于点D 是以AB 为直径的圆上异于A 、B 的一点，则BD AD ⊥，由双曲线的几何性质可知min 1PF c a =-=，PA PF FA =+，PB PF FB PF FA =+=-，()PA PD PA PD PA PB BD PA PB BD PA PA PB ⋅=-⋅=-⋅+=-⋅-⋅=-⋅ ()()222224949148PF FA PF FA AF PF AF PF PF =-+⋅-=-=-=-≤-=.故答案为：2213y x -=；48.【点睛】关键点点睛：解决本题的关键是会转化，会根据向量数量积的几何意义把PA PD ⋅转化为PA PB -⋅，再根据平面向量的知识求解.173【分析】设直线EF 分别与DA ，DC 的延长线交于点P ，Q ，连接1D P ，交1AA 于点M ，连接1D Q ，交1CC 于点N ，得到截面，再利用直四棱柱的棱长和结构特征得到截面的各边长，利用分割法求得截面面积；取FN 的中点G ，连接QG ，CG ，结合平面与平面所成角的定义得到QGC ∠为平面α与平面11BB C C 所成的角或其补角，最后利用余弦定理求解即可．【详解】设直线EF 分别与DA ，DC 的延长线交于点P ，Q ，连接1D P ，交1AA 于点M ，连接1D Q ，交1CC 于点N ，连接ME ，FN ，∴平面α截直四棱柱1111ABCD A B C D -的截面为五边形1D MEFN ．由平行线分线段成比例知：1AP BF ==，故13DP DD ==，故△1DD P 为等腰直角三角形，∴1AM AP ==，故12A M =，则11D M D N ==ME EF FN ==MN ，易知MN =∴五边形1D MEFN 可以分成等边三角形1D MN 和等腰梯形MEFN 两部分，等腰梯形MEFN 的高h ==MEFN 的面积为=．又(12D MNS ==∴五边形1D MEFN 的面积为=．易知1CF CQ CN ===，则由勾股定理得FN NQ FQ ===取FN 的中点G ，连接CG ，QG ，则CG FN ⊥，QG FN ⊥，且CG =，QG =，故QGC ∠为平面α与平面11BB C C 所成角或其补角．在△QGC中，由余弦定理得222131cos 23CG QG QC QGC CG QG +-+-∠===⋅，∴平面α与平面11BB C C，3. 【点睛】关键点点睛：根据直棱柱的性质，应用平面的延展性补全截面，得到面α截1111ABCD A B C D -的截面为五边形1D MEFN ，求各边长度，进而求面积；根据二面角定义，找到其对应的平面角并求其余弦值. 18．（1）0；（2）单调递增区间为0,12π⎡⎤⎢⎥⎣⎦，7,12ππ⎡⎤⎢⎥⎣⎦．【分析】（1）将0x =代入函数()f x 的解析式，直接求值即可；（2）先由三角恒等变换得到()3232πx x f ω⎛⎫=+- ⎪⎝⎭，令()0f x =，解出方程的根，结合()f x 的图象与x 轴的两个相邻交点间的最短距离为6π，求出1ω=，即可得到()f x 的解析式，然后利用正弦函数的图象与性质求解即可．【详解】（1）()22717cos 4cos 04003222f π⎛⎫=-+-=-+-= ⎪⎝⎭．（2）()11cos 272cos 24222ωx ωx ωx f x +=-+⨯-332cos 222ωx ωx =+- 3232πωx ⎛⎫=+- ⎪⎝⎭．令()0f x =，则sin 232πωx ⎛⎫+= ⎪⎝⎭，所以2233ππωx k π+=+或22233ππωx k π+=+，k ∈Z ，故k x πω=或6πk πx ωω=+，k ∈Z ，所以()f x 的图象与x 轴的两个相邻交点间的最短距离为66ππω=，故1ω=，()3232πf x x ⎛⎫=+- ⎪⎝⎭．当[]0,x π∈时，72,333x πππ⎡⎤+∈⎢⎥⎣⎦，当2,332πππx ⎡⎤+∈⎢⎥⎣⎦，即[0,]12x π∈或372,323πππx ⎡⎤+∈⎢⎥⎣⎦，即7[,]12x ππ∈时，()f x 单调递增，故()f x 的单调递增区间为0,12π⎡⎤⎢⎥⎣⎦，7,12ππ⎡⎤⎢⎥⎣⎦．【点睛】关键点点睛：熟练掌握三角恒等变换公式以及三角函数的图象和性质是解题关键.19．（1）证明见解析；（2）51．【分析】（1）取AD 的中点Q ，连接PQ ，BQ ，可知AD ⊥平面PBQ ，从而可证明.（2）先证明平面PBQ ⊥平面ABCD ，过点P 作PG BQ ⊥于点G ，则PG ⊥平面ABCD ，故以G 为原点，以GB ，GP 所在直线分别为y ，z 轴，过点G 且与AD 平行的直线为x 轴，建立如图所示的空间直角坐标系，利用向量法求解线面角. 【详解】（1）、证明：取AD 的中点Q ，连接PQ ，BQ ，因为PA PD =，所以PQ AD ⊥．由题意知//BC AD ，12BC AD =，又12DQ AD =，所以//BC DQ ，BC DQ =，所以四边形BCDQ 为平行四边形，所以//DC BQ ，因为90ADC ∠=︒，所以DC AD ⊥，所以BQ AD ⊥．又PQ ，BQ ⊂平面PBQ ，PQ BQ Q =，所以AD ⊥平面PBQ ，又PB ⊂平面PBQ ，所以AD PB ⊥．（2）由AD ⊥平面PBQ ，AD ⊂平面ABCD ，得平面PBQ ⊥平面ABCD ，过点P 作PG BQ ⊥于点G ，则PG ⊥平面ABCD ，故以G 为原点，以GB ，GP 所在直线分别为y ，z 轴，过点G 且与AD 平行的直线为x 轴，建立如图所示的空间直角坐标系．易知PQB ∠为二面角P AD C --的平面角，所以1cos 3PQB ∠=．在Rt PQG △中，PQ =1cos 3PQG ∠=，得QG =PG =，则13QG BQ =，1,,03A ⎛⎫- ⎪ ⎪⎝⎭，1,3D ⎛⎫-- ⎪ ⎪⎝⎭，1,3C ⎛⎫- ⎪ ⎪⎝⎭，0,0,3P ⎛ ⎝⎭，1,,233M ⎛- ⎝⎭，所以1,,33PA ⎛⎫=-- ⎪ ⎪⎝⎭，1,33PD ⎛=--- ⎝⎭，3,233AM ⎛=- ⎝⎭．设平面PAD 的法向量为(),,n x y z =，则0,0n PA n PD ⎧⋅=⎨⋅=⎩即0,0,x y z x y z ⎧--=⎪⎪⎨⎪-=⎪⎩则0x =，令y =1z =-，故()0,22,1n =-为平面PAD 的一个法向量．设直线MA 与平面PAD 所成的角为θ，则sin cos ,θn AM ===，即直线MA 与平面PAD ．【点睛】方法点睛：向量法求解空间几何问题的步骤：建、设、求、算、取1、建：建立空间直角坐标系，以三条互相垂直的直线的交点为原点，没有三条垂线时需做辅助线；建立右手直角坐标系，尽可能的使得较多的关键点落在坐标轴或坐标平面内.2、设：设出所需的点的坐标，得出所需的向量坐标.3、求：求出所需平面的法向量4、算：运用向量的数量积运算，验证平行、垂直，利用线面角公式求线面角，或求出两个平面的法向量的夹角的余弦值5、取：根据题意，或二面角的范围，得出答案.20．（1）证明见解析；()14331nn n a -=⎡⎤+-⎣⎦；（2）证明见解析．【分析】（1）由题得211131344n n n n a a +++⎛⎫-=-- ⎪⎝⎭，即得数列1134n na +⎧⎫-⎨⎬⎩⎭为等比数列，再求数列{}n a 的通项公式；（2）对n 分类讨论利用放缩法求证. 【详解】（1）因为11113n n na a +++=，所以2211111313131334444n n n n n n n n n a a a a ++++++⎛⎫-=--=-+=-- ⎪⎝⎭，又119933444a -=-=，所以数列1134n na +⎧⎫-⎨⎬⎩⎭是以34为首项，1-为公比的等比数列，所以()11133144n n n a +--=⋅-，即()113314n n n a -⎡⎤=+-⎣⎦，故()14331nn n a -=⎡⎤+-⎣⎦．（2）由113a =，216a =，得121325a a +=<，当4n ≥且n 为偶数时，11111141143341133131333231333n nn n n n n n n n n a a ------+⎛⎫⎛⎫+=+=⋅<+ ⎪⎪+-⋅+⋅-⎝⎭⎝⎭，所以1234111411113633333n n n a a a -⎛⎫++⋅⋅⋅+<++⨯++⋅⋅⋅++ ⎪⎝⎭114123132712322754513+⨯=+=<<-；当3n ≥且n 为奇数时，1n +为偶数，则12135n n a a a a +++⋅⋅⋅++<，由于0n a >，则1235n a a a ++⋅⋅⋅+<．综上，1235n a a a ++⋅⋅⋅+<．【点睛】方法点睛：方法技巧若数列的通项公式中含有()1n-，则在求数列的前n 项和时，常需要对n 分奇偶分别求解．21．（1）()2,0；（2）2．【分析】（1）设211,4y A y ⎛⎫ ⎪⎝⎭，222,4y B y ⎛⎫ ⎪⎝⎭，(),0M m ，由4OA OB ⋅=-得到128y y =-，设直线:AB x ty m =+与抛物线方程联立，由根与系数的关系得到2m =，即可得到点M 的坐标；（2）由题意及弦长公式得到AM ，BM ，利用根与系数的关系得到221114AM BM +=，进而得232BM AM-的表达式，然后构造函数，利用函数的单调性求函数的最大值，即可得到232BM AM -的最大值．【详解】（1）设211,4y A y ⎛⎫ ⎪⎝⎭，222,4y B y ⎛⎫ ⎪⎝⎭，(),0M m ，则222212121212,,44416y y y y OA OB y y y y ⎛⎫⎛⎫⋅=⋅=+=- ⎪ ⎪⎝⎭⎝⎭，解得128y y =-，设直线:AB x ty m =+，联立方程，得2,4,x ty m y x =+⎧⎨=⎩得2440y ty m --=，由根与系数的关系知，1248m y y -==-，所以2m =，故点M 的坐标为()2,0．（2）由（1）知，124y y t +=，128y y =-．易知1AM y =，2M B =，所以()()22222212111111t y t y AM BM +=+++()()222122222121616141641y y t t y y t ++===++，则222321132||3284BM BM BM AM BM BM ⎛⎫-= -⎪-=-- ⎪⎝⎭．令()2328u f u u =--，2u >，则()3641f u u='-，所以()f u 在()2,4上单调递增，在()4,+∞上单调递减，所以()()min 42f u f ==，即232BM AM -的最大值是2，当且仅当4BM =时取等号．【点睛】方法技巧：圆锥曲线中的最值问题是高考中的热点问题，常涉及不等式、函数的值域问题，综合性比较强，解法灵活多样，但主要有两种方法：一是几何方法，即利用圆锥曲线的定义、几何性质以及平面几何中的定理、性质等进行求解；二是代数方法，即把要求最值的几何量或代数式表示为某个（些）参数的函数，然后利用函数、不等式的知识等进行求解． 22．（1）当0a ≤时，()f x 在(),-∞+∞上单调递增；当0a >时，()f x 在(),ln a -∞-上单调递增，在()ln ,a -+∞上单调递减．；（2）证明见解析．【分析】（1）求导后，分类讨论a ，利用导数的符号可得函数()f x 的单调性；（2）求出()g x 的解析式，利用斜率公式求出2121ln ln 1x x k x x -+=-，将所证不等式化为11ln 1t t t-<<-（1t >），再构造两个函数，利用导数可证结论成立. 【详解】（1）()f x 的定义域为(),-∞+∞，且()1e xf x a ='-．当0a ≤时，()0f x '>，则()f x 在(),-∞+∞上单调递增．当0a >时，若(),ln x a ∈-∞-，则()0f x '>，()f x 在(),ln a -∞-上单调递增；若()ln ,x a ∈-+∞，则()0f x '<，()f x 在()ln ,a -+∞上单调递减．综上所述，当0a ≤时，()f x 在(),-∞+∞上单调递增；当0a >时，()f x 在(),ln a -∞-上单调递增，在()ln ,a -+∞上单调递减．（2）当1a =时，()e 1xx x f =-+，所以()()ln ln 1g x f x x x =-+=，所以()()21221121212121ln ln ln ln 1g x g x x x x x x x k x x x x x x ---+-===----，所以2121ln ln 1x x k x x -+=-．要证21111k x x <+<，即证212211ln 1ln 1x x x x x x -<<-．因为210x x >>，所以210x x ->，即证21221211ln x x x x x x x x --<<．令21x t x =，则1t >，即证11ln 1t t t-<<-（1t >）．令()ln 1t t φt =-+（1t >），则()1110φt t t t-=='-<，所以()t ϕ在()1,+∞上单调递减，所以()0t ϕ<，即ln 10t t -+<，ln 1t t <-（1t >）．①令()1ln 1h t t t =+-（1t >），则()221110t h t t t t'-=-=>，所以()h t 在()1,+∞上单调递增，则()0h t >，即1ln 1t t >-（1t >）．②综合①②得11ln 1t t t-<<-（1t >），所以21111k x x <+<. 【点睛】关键点点睛：将所证不等式化为11ln 1t t t-<<-（1t >），再构造两个函数，利用导数证明不等式成立是解题关键.。

2021届高三高考数学模拟测试卷(五)【含答案】

2021届高三高考数学模拟测试卷（五）【含答案】第Ⅰ卷（选择题)一、单选题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．设集合{0,1}M =，{|01}N x x =<≤，则M N ⋃=（） A ．[0,1] B ．(0,1] C ．[0,1) D ．(,1]-∞【答案】A 【解析】【分析】利用并集的定义求解即可．【详解】∵集合{0,1}M =，集合{|01}N x x =<≤，∴{|01}M N x x ⋃=≤≤，即M N ⋃=[0,1]. 故选：A 【点睛】本题考查了并集的定义与计算问题，属于基础题． 2．命题:p x ∀∈R ，220x x ->的否定为（）． A ．x ∀∈R ，220x x -≤ B ．x ∀∈R ，220x x -< C ．x ∃∈R ，220x x -> D ．x ∃∈R ，220x x -≤【答案】D 【解析】命题p 的否定，将“x ∀∈R ”变成“x ∃∈R ”，将“220x x ->” 变成“220x x -≤”．故选D ．点睛：(1)对全称(存在性)命题进行否定的两步操作：①找到命题所含的量词，没有量词的要结合命题的含义加上量词，再进行否定；②对原命题的结论进行否定.(2)判定全称命题“,()x M p x ∀∈”是真命题，需要对集合M 中的每个元素x ，证明()p x 成立；要判定一个全称命题是假命题，只要举出集合M 中的一个特殊值0x ，使0()p x 不成立即可.要判断存在性命题是真命题，只要在限定集合内至少能找到一个0x x =，使0()p x 成立即可，否则就是假命题. 3．若复数34sin cos 55z i θθ⎛⎫=-+- ⎪⎝⎭是纯虚数，则tan()θ-π的值为( ) A ．34±B ．43C ．34-D ．43-【答案】C 【解析】【分析】根据所给的虚数是一个纯虚数，得到虚数的实部等于0，而虚部不等于0，得到角的正弦和余弦值，根据同角三角函数之间的关系，得到结果. 【详解】若复数34sin (cos )55z i θθ=-+-是纯虚数，则3sin 05θ-=且4cos 05θ-≠，所以3sin 5θ=，4cos 5θ=-，所以3tan 4θ=-，故tan()θ-π=3tan 4θ=-．故选C ．【点睛】本题主要考查了复数的基本概念，属于基础题．纯虚数是一个易错概念，不能只关注实部为零的要求，而忽略了虚部不能为零的限制，属于易错题.4．已知变量x ，y 满足{2x −y ≤0x −2y +3≥0x ≥0 ，则z =log 4(2x +y +4)的最大值为（）A ．2B ．32C ．23D ．1【答案】B 【解析】试题分析：根据题中所给的约束条件，画出相应的可行域，可以求得2x +y +4在点(1,2)处取得最大值8，所以z 的最大值为log 48=32，故选B ．考点：线性规划．5．设0a >，0b >，2lg 4a 与lg 2b 的等差中项，则21a b+的最小值为（） A ．22B ．3 C ．4D ．9【答案】D 【解析】∵2lg4a 与lg2b 的等差中项， ∴2lg 4lg 2a b =+，即2lg 2lg 42lg 2aba b+=⋅=，∴21a b +=．所以212122()(2)55249b a a b a b a b a b+=++=++≥+= 当且仅当22b a a b =即13a b ==时取等号， ∴21a b+的最小值为9． 6．《中国好歌曲》的五位评委给一位歌手给出的评分分别是：118x =，219x =，320x =，421x =，522x =，现将这五个数据依次输入如图程序框进行计算，则输出的S 值及其统计意义分别是( )A ．2S =，即5个数据的方差为2B ．2S =，即5个数据的标准差为2C ．10S =，即5个数据的方差为10D ．10S =，即5个数据的标准差为10【答案】A 【解析】【分析】算法的功能是求()()()22212202020i S x x x =-+-+⋯+-的值，根据条件确定跳出循环的i 值，计算输出S 的值．【详解】由程序框图知：算法的功能是求()()()22212202020i S x x x =-+-+⋯+-的值， ∵跳出循环的i 值为5， ∴输出S =()()()2221[1820192020205⨯-+-+- ()()2221202220]+-+-= ()14101425⨯++++=.故选A. 【点睛】本题考查了循环结构的程序框图，根据框图的流程判断算法的功能是关键，属于基础题． 7．十九世纪末，法国学者贝特朗在研究几何概型时提出了“贝特朗悖论”，即“在一个圆内任意选一条弦，这条弦的弦长长于这个圆的内接等边三角形边长的概率是多少？”贝特朗用“随机半径”、“随机端点”、“随机中点”三个合理的求解方法，但结果都不相同．该悖论的矛头直击概率概念本身，强烈地刺激了概率论基础的严格化．已知“随机端点”的方法如下：设A 为圆O 上一个定点，在圆周上随机取一点B ，连接AB ，所得弦长AB 大于圆O 的内接等边三角形边长的概率．则由“随机端点”求法所求得的概率为（） A ．15B ．14C ．13D ．12【答案】C 【解析】【分析】由题意画出图形，求出满足条件的B 的位置，再由测度比是弧长比得答案．【详解】解：设“弦AB 的长超过圆内接正三角形边长”为事件M ，以点A 为一顶点，在圆中作一圆内接正三角形ACD ，则要满足题意点B 只能落在劣弧CD 上，又圆内接正三角形ACD 恰好将圆周3等分，故1()3P M =故选：C ．【点睛】本题考查几何概型的意义，关键是要找出满足条件弦AB 的长度超过圆内接正三角形边长的图形测度，再代入几何概型计算公式求解，是基础题．8．椭圆221169x y +=的两个焦点为1F ，2F ，过2F 的直线交椭圆于A 、B 两点，若6AB =，则11AF BF +的值为( )A ．10B ．8C ．16D ．12【答案】A 【解析】【分析】由椭圆的定义可得：12122AF AF BF BF a +=+=，即可得出．【详解】由椭圆的定义可得：121228AF AF BF BF a +=+==，()()1122221616610AF BF a AF a BF AB ∴+=-+-=-=-=，故选A ．【点睛】本题考查了椭圆的定义及其标准方程，考查了推理能力与计算能力，属于中档题．9．如图是一个几何体的三视图，根据图中的数据（单位：cm ），可知此几何体的体积是（）A ．324cmB ．364cm 3C ．3(62522)cm +D ．3(248582)cm +【答案】B 【解析】由三视图可知，该几何体是如下图所示的四棱锥，故体积为16444433⨯⨯⨯=3cm .故选B.10．已知函数()sin f x x =，将()f x 的图象上的所有点的横坐标缩短到原来的12，纵坐标扩大为原来的3倍，再把图象上所有的点向上平移1个单位长度，得到函数()y g x =的图象，则函数()g x 的周期可以为（） A ．2πB ．πC ．32π D ．2π【答案】B 【解析】【分析】先利用三角函数图象变换规律得出函数()y g x =的解析式，然后由绝对值变换可得出函数()y g x =的最小正周期.【详解】()sin f x x =，将函数()y f x =的图象上的所有点的横坐示缩短到原来的12，可得到函数sin 2y x =的图象，再将所得函数图象上所有点的纵坐标扩大为原来的3倍，得到函数3sin 2y x=的图象，再把所得图象向上平移1个単位长度，得到()3sin 21g x x =+，由绝对值变换可知，函数()y g x =的最小正周期为22T ππ==，故选：B. 【点睛】本题考查三角函数变换，同时也考查三角函数周期的求解，解题的关键就是根据图象变换的每一步写出所得函数的解析式，考查推理能力，属于中等题.11．过曲线22122:1(0,0)x y C a b a b-=>>的左焦点1F 作曲线2222:C x y a +=的切线，设切点为,M 延长1F M 交曲线23:2(0)C y px p =>于点,N 其中13,C C 有一个共同的焦点，若10,MF MN +=则曲线1C 的离心率为（）． A 51+ B 5C 21+ D 2【答案】A 【解析】【分析】设双曲线的右焦点的坐标为()2,0F c ，利用O 为12F F 的中点，M 为1F N 的中点，可得OM 为12NF F 的中位线，从而可求1NF ，再设()x,y N ，过点1F 作x 轴的垂线，由勾股定理得出关于,a c 的关系式，最后即可求得离心率．【详解】设双曲线的右焦点为2F ，则2F 的坐标为(),0c ．因为曲线1C 与3C 有一个共同的焦点，所以曲线3C 的方程为24y cx =．因为10MF MN +=，所以1MF MN NM =-=，所以M 为1F N 的中点，因为O 为12F F 的中点，所以OM 为12NF F 的中位线，所以OM ∥2NF ．因为|OM |=a ，所以22NF a =．又21NF NF ⊥，122F F c =，所以()()221222NF c a b =-=．设N (x ,y )，则由抛物线的定义可得2x c a +=，所以2x a c =-．过点F 1作x 轴的垂线，点N 到该垂线的距离为2a ，在1RtF PN 中，由勾股定理得22211||+||||F P PN F N =，即22244y a b +=，所以2224(2)44()c a c a c a -+=-，整理得210e e --=，解得512e =．故选A ．【点睛】解答本题时注意以下几点：（1）求双曲线的离心率时，可根据题中给出的条件得到关于,,a b c 的关系式，再结合222a b c +=得到,a c 间的关系或关于离心率e 的方程（或不等式），由此可得离心率的取值（或范围）．（2）本题中涉及的知识较多，解题时注意将题中给出的关系进行转化，同时要注意圆锥曲线定义在解题中的应用．12．函数()f x 满足()()1,,2x e f x f x x x ⎡⎫=+∈+∞⎢⎣'⎪⎭， ()1f e =-，若存在[]2,1a ∈-，使得31232f a a e m ⎛⎫-≤--- ⎪⎝⎭成立，则m 的取值（）A ．2,13⎡⎤⎢⎥⎣⎦B ．2,3⎡⎫+∞⎪⎢⎣⎭C ．[)1,+∞ D ．12,23⎡⎤⎢⎥⎣⎦【答案】A 【解析】由题意设()()x f x g x e =，则()()1()xf x f xg x e x-'='=，所以()ln g x x c =+（c 为常数）．∵()1f e =-，∴(1)(1)1f g c e==-=，∴()()(1ln )x x f x g x e e x =⋅=-+， ∴1()(ln 1)xf x e x x =+-'．令1()ln 1h x x x =+-，则22111()x h x x x x-=-=，故当112x <<时，()0,()h x h x '<单调递减；当1x >时，()0,()h x h x '>单调递增．∴()(1)0h x h ≥=，从而当1,2x ⎡⎫∈+∞⎪⎢⎣⎭时，()0f x '≥，∴()f x 在区间1,2⎡⎫+∞⎪⎢⎣⎭上单调递增．设[]3()32,2,1a a a e a ϕ=---∈-，则2()333(1)(1)a a a a ϕ'=-=+-，故()a ϕ在(2,1)--上单调递增，在(1,1)-上单调递减，所以max ()(1)a e ϕϕ=-=-． ∴不等式31232f a a e m ⎛⎫-≤--- ⎪⎝⎭等价于12(1)f e f m ⎛⎫-≤-= ⎪⎝⎭，∴1211122m m ⎧-≤⎪⎪⎨⎪-≥⎪⎩，解得213m ≤≤，故m 的取值范围为2[,1]3．选A ．点睛：本题考查用函数的单调性解不等式，在解答过程中首先要根据含有导函数的条件构造函数()()x f x g x e =，并进一步求得函数()f x 的解析式，从而得到函数()f x 在区间1,2⎡⎫+∞⎪⎢⎣⎭上的单调性．然后再根据条件中的能成立将原不等式转化为12(1)f f m ⎛⎫-≤ ⎪⎝⎭，最后根据函数的单调性将函数不等式化为一般不等式求解即可．第Ⅱ卷（非选择题)二、填空题：本大题共4小题，每小题5分，共20分。

2021年新高考数学模拟试卷全国卷(附参考答案和详解)

绝密★启用前2021年普通高等学校招生模拟考试（3）数学（适用新高考地区）总分：150分考试时间：120分钟★祝考试顺利★注意事项：1、本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分。

答卷前，考生务必将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证条形码粘贴在答题卡的指定位置。

用2B 铅笔将答题卡上试卷类型A 后的方框涂黑。

2、选择题的作答：选出每小题答案后，用2B 铅笔将答题卡上对应题目的答案标号涂黑。

写在试题卷、草稿纸、答题卡上的非答题区域均无效。

3、填空题和解答题的作答：用签字笔直接答在答题卡上对应的答题区域内，写在试题卷、草稿纸、答题卡上的非答题区域均无效。

4、考试结束后，将本试卷和答题卡一并上交。

第I 卷一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1.i 是虚数单位，复数3i1i+=-（）A.12i +B.24i +C.12i --D.2i -2.设常数a ∈R ，集合{|(1)()0}A x x x a =--≥，{|1}B x x a =≥-，若A B =R ，则a 的取值范围为（）A.(,2)-∞B.(,2]-∞C.(2,)+∞D.[2,)+∞3.已知函数()f x 为奇函数，且当0x >时，21()f x x x=+，则(1)f -=（）A.2B.1C.0D.2-4.设向量=a (1,cos )θ与b (1,2cos )θ=-垂直，则cos2θ等于（）A.2 B.12C.0D.1-5.直线:1l y kx =+与圆22:1O x y +=相交于,A B 两点，则“1k =”是“OAB 的面积为12”的（） A.充分而不必要条件 B.必要而不充分条件C.充分必要条件D.既不充分又不必要条件6.设三棱柱的侧棱垂直于底面，所有棱长都为a ，顶点都在一个球面上，则该球的表面积为（）A.2πa B.27π3a C.211π3a D.25πa7.已知命题122121:,,(()())()0p x x f x f x x x ∀∈--≥R ，则p ⌝是（） A.122121,,(()())()0x x f x f x x x ∃∈--≤R B.122121,,(()())()0x x f x f x x x ∀∈--≤R C.122121,,(()())()0x x f x f x x x ∃∈--<RD.122121,,(()())()0x x f x f x x x ∀∈--<R8.函数()2ln f x x =的图像与函数2()45g x x x =-+的图像的交点个数为（） A.3B.2C.1D.0二、多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得3分，有选错的得0分.9.现行普通高中学生在高一升高二时面临着选文理科的问题，学校抽取了部分男、女学生意愿的一份样本，制作出如下两个等高堆积条形图．根据这两幅图中的信息，下列统计结论中正确的有（）A.样本中的女生数量等于男生数量B.样本中有理科意愿的学生数量多于有文科意愿的学生数量C.样本中的男生偏爱理科D.样本中的女生偏爱文科10.已知两定点(1,0)A -，(1,0)B ，若直线l 上存在点M ，使得||||3MA MB +=，则称直线l 为“M 型直线”．则下列给出的直线中，是“M 型直线”的有（）A.2x =B.3y x =+C.21y x =--D.23y x =+11.如图，在正方体1111-ABCD A B C D 中，M ，N 分别是1BC ，1CD 的中点，则下列判断正确的为（）A.MN 与1CC 垂直B.MN 与AC 垂直C.MN 与BD 平行D.MN 与11A B 平行12.下列结论中正确的有（） A.命题：”(0,2)x ∀∈，33x x >“的否定是“(0,2)x ∃∈，33x x ≤” B.若直线l 上有无数个点不在平面α内，则l αC.若随机变量ξ服从正态分布2(1,)N σ，且(2)0.8P ξ<=，则(01)0.2P ξ<<=D.等差数列{}n a 的前n 项和为n S ，若43a =，则721S =第Ⅱ卷本卷包括填空题和解答题两部分，共90分. 三、填空题：本题共4小题，每小题5分。

2021年高三数学下学期六模考试理(含解析)

2021年高三数学下学期六模考试理（含解析）一、选择题：（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．定义集合运算：A⊙B=｛z ︳z= xy（x+y），x∈A，y∈B｝，设集合A=｛0，1｝，B=｛2，3｝，则集合A⊙B的所有元素之和为A．0 B．6 C．12 D．18【答案】D【解析】因为A⊙B=｛z ︳z= xy（x+y），x∈A，y∈B｝，所以当集合A=｛0，1｝，B=｛2，3｝，集合A⊙B= ，所以其所有元素之和为18.2．已知M（-2，7），N（10，-2），点P是线段MN上的点且则P点的坐标是（）A．（-14,-16）B．（22,-11）C．（6,1）D．(2, 4)【答案】D【解析】设，因为，所以，所以P点的坐标是(2, 4)。

3．若,则直线=1必不经过 ( )A．第一象限 B．第二象限 C．第三象限 D．第四象限【答案】B【解析】因为，所以，所以直线=1必不经过第二象限。

4．样本a1，a2，a3，…，a10的平均数为，样本b1，b2，…，b10的平均数为，那么样本a1，b1，a2，b2，a3，b3，…，a10，b10的平均数是（）A．+ B．(+) C．2(+) D．(+)【答案】B【解析】因为样本a1，a2，a3，…，a10的平均数为，样本b1，b2，…，b10的平均数为，所以样本a1，b1，a2，b2，a3，b3，…，a10，b10的平均数是(+)。

5．已知函数f (x)=x2 - 4x + 3,集合M={（x, y) | f (x)+f (y)≤0},集合N={（x, y) | f (x) - f (y)≥0},则集合M∩N的面积是（）A． B． C．π D．2π【答案】C【解析】集合M={（x, y) | f (x)+f (y)≤0}{}{}2222|43430|(2)(2)2x x x y y x x y =-++-+≤=-+-≤，表示以（2,2）为圆心，为半径的圆的内部；集合N ={（x , y ) | f (x ) - f (y )≥0}(){}{}22|43430|()(4)0x x x y y x x y x y =-+--+≥=-+-≥，所以集合M ∩N 的面积是π。

2021年高三第三次高考模拟考试数学文含答案

2021年高三第三次高考模拟考试数学文含答案考试说明：本试卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分，考试时间120分钟．（1）答题前，考生先将自己的姓名、准考证号码填写清楚；（2）选择题必须使用2B铅笔填涂，非选择题必须使用0.5毫米黑色字迹的签字笔书写，字体工整，字迹清楚；（3）请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效，在草稿纸、试题卷上答题无效；（4）保持卡面清洁，不得折叠、不要弄破、弄皱，不准使用涂改液、刮纸刀．第I卷（选择题，共60分）一、选择题(本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．)1.已知全集，集合，，那么集合（A）（B）（C）（D）2.复数等于（A）（B）（C）（D）3.已知，，，则（A）（B）（C）（D）4.已知直线和平面，则的一个必要条件是（A），（B），（C），（D）与成等角5.已知与之间的一组数据：已求得关于与的线性回归方程为＝2.1＋0.85，则的值为（A ）（B ）（C ）（D ） 6. 在数列中，已知，则等于（A ）（B ）（C ）（D ） 7. 执行如图所示的程序框图，若输出，则框图中①处可以填入（A ）（B ）（C ）（D ）8. 已知，其中实数满足，且的最大值是最小值的4倍，则的值是（A ）（B ）（C ）4 （D ）9. 已知双曲线的右焦点为，过的直线交双曲线的渐近线于A , B 两点，且与其中一条渐近线垂直，若，则该双曲线的离心率是（A ）（B ）（C ）（D ）10. 已知函数，则下列结论正确的是（A ）若，则（B ）函数的图象与的图象相同（C ）函数的图象关于对称（D ）函数在区间上是增函数11. 已知一个正四面体的俯视图如图所示，其中四边形是边长为的正方形，则该正四面体的内切球的表面积为（A ）（B ）（C ）（D ）12. 定义在上的函数满足下列两个条件：（1零点，则实数的取值范围是（A）（B）（C）（D）xx年哈尔滨市第三中学第三次高考模拟考试数学试卷（文史类）第Ⅱ卷（非选择题，共90分）二、填空题（本大题共4小题，每小题5分，共20分，将答案填在答题卡相应的位置上．）13.从1,2,3,4,5,6这六个数中，随机抽取2个不同的数，则这2个数的和为偶数的概率是 .14.若等边的边长为，平面内一点满足，则 .15.已知，则 .16.若在由正整数构成的无穷数列中，对任意的正整数，都有，且对任意的正整数，该数列中恰有个，则= .三、解答题（本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤．）17.（本小题满分12分）设的内角的对边分别为，满足)32(sin2(2-=．-+sin)cbCBca sinAb3（Ⅰ）求角的大小；（Ⅱ）若，，求的面积．18.（本小题满分12分）某校从参加某次知识竞赛的同学中，选取名同学将其成绩(百分制，均为整数)分成，，，，，六组后，得到部分频率分布直方图（如图），观察图形中的信息，回答下列问题.（Ⅰ）求分数在内的频率，并补全这个频率分布直方图；（Ⅱ）从频率分布直方图中，估计本次考试成绩的中位数；（Ⅲ）若从第1组和第6组两组学生中，随机抽取2人，求所抽取2人成绩之差的绝对值大于10的概率.19.（本小题满分12分）如图，在三棱柱中，，，为的中点，．A（Ⅰ）求证：平面平面；（Ⅱ）求三棱锥的体积．20. （本小题满分12分）已知椭圆（）的左，右焦点分别为，上顶点为．为抛物线的焦点，且，0．（Ⅰ）求椭圆的标准方程；（Ⅱ）过定点的直线与椭圆交于两点（在之间），设直线的斜率为（），在轴上是否存在点，使得以为邻边的平行四边形为菱形？若存在，求出实数的取值范围；若不存在，请说明理由．21. （本小题满分12分）已知函数（）.（Ⅰ）求函数的最大值；（Ⅱ）若，且关于的方程在上恰有两个不等的实根，求实数的取值范围；（Ⅲ）设各项为正数的数列满足，（），求证：.请考生在第22，23，24三题中任选一题作答，如果多做，则按所做的第一题记分． 22. （本小题满分10分）选修4－1如图，是⊙的一条切线，切点为，都是⊙的割线，．（Ⅰ）证明：；（Ⅱ）证明：．23.（本小题满分10分）选修4－4：坐标系与参数方程在直角坐标平面内，以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程是，直线的参数方程是（为参数）.（Ⅰ）过极点作直线的垂线，垂足为点，求点的极坐标；（Ⅱ）若点分别为曲线和直线上的动点，求的最小值.24.（本小题满分10分）选修4—5：不等式选讲已知函数.（Ⅰ）若关于的不等式的解集为，求实数的值；（Ⅱ）若对于任意的恒成立，求实数的取值范围.xx年哈尔滨市第三中学第三次高考模拟考试数学答案（文史类）选择题:1B 2A 3A 4D 5D 6D 7B 8B 9D 10D 11A 12D填空题:13．14. 15. 16.45解答题:17.解：（Ⅰ）由已知及正弦定理可得，整理得，…………………………2分所以．…………………………4分又，故．…………………………5分（Ⅱ）由正弦定理可知，又，，，所以．…………………………6分又，故或．………………………… 8分若，则，于是；………………………… 10分若，则，于是．………………………… 12分18.解：（Ⅰ）………………………………2分（Ⅱ）………………………………6分（Ⅲ）第1组：人（设为1，2，3，4，5，6）第6组：人（设为A，B，C）共有36个基本事件，满足条件的有18个，所以概率为…………12分19.解：（Ⅰ）取中点为，连接，．因为，所以．又，，所以平面，因为平面，所以．…3分由已知，，又，所以，因为，所以平面．又平面，所以平面平面． (6)分（Ⅱ）三棱锥的体积=三棱锥的体积由（Ⅰ）知，平面平面,平面平面, , 平面所以,即,即点到的距离, …………………………9分 ………………………… 11分所以 ………………………… 12分 20. 解：（Ⅰ）由已知，，，所以． ……… 1分在中，为线段的中点，故，所以．……… 2分于是椭圆的标准方程为．…4分（Ⅱ）设（），，取的中点为．，，又，所以． ………………………… 6分因为，所以，． ……… 8分因为，所以，即，整理得． ………………………… 10分因为时，，，所以． ……… 12分21.解：（Ⅰ）函数的定义域为，，当时，取最大值 ……………………………………4分（Ⅱ），由得在上有两个不同的实根，设，时，，时，，O02ln 21312ln 232)4()1(<-=+-=-g g ，得则 ……………………………………8分（Ⅲ）由（1）知当时，。

2021年普通高等学校招生全国统一考试理科数学模拟卷六(附带答案及详细解析)

绝密★启用前2021年普通高等学校招生全国统一考试理科数学（模拟卷六）本试卷共5页，23题(含选考题)。

全卷满分150分。

考试用时120 分钟。

★祝考试顺利★注意事项:1.答题前，先将白己的姓名、准考证号填写在试卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2. 选择题的作答:每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。

写在试卷、草稿纸和答题卡上的非答题区域均无效。

3. 非选择题的作答:用黑色签字笔直接答在答题卡.上对应的答题区域内。

写在试卷、草稿纸和答题卡，上的非答题区域均无效。

4.选考题的作答: 先把所选题目的题号在答题卡上指定的位置用2B铅笔涂黑。

答案写在答题卡.上对应的答题区域内，写在试卷、草稿纸和答题卡.上的非答题区域均无效。

.5.考试结束后，请将本试卷和答题卡-并上交。

一、单选题1.已知集合A={x|√x<2}，B={x||x−1|<2}，则A∩B=（）A. {x|0<x<3}B. {x|−1<x<3}C. {x|0≤x<3}D. {x|−1<x<2}2.若复数z满足(3−4i)z=11+2i，其中i为虚数单位，则z的虚部为（）A. −2B. 2C. −2iD. 2i3.已知△ABC内接于单位圆，则长为sinA、sinB、sinC的三条线段（）A. 能构成一个三角形，其面积大于△ABC面积的14B. 能构成一个三角形，其面积等于△ABC面积的14C. 能构成一个三角形，其面积小于△ABC面积的14D. 不一定能构成三角形4.已知 α,β 是平面， m,n 是直线，则下列命题中不正确的是（） A. 若 m ∥ n,m ⊥α ，则 n ⊥α B. 若 m ∥ α,α∩β=n ，则 m ∥nC. 若 m ⊥ α,m ⊥β ，则 α ∥ βD. 若 m ⊥ α,m ⊂β ，则 α⊥ β 5.执行如图所示的程序框图，若输入 a,b,c 的值分别是 1,2,3 ，则输出 a,b,c 的值依次为（）A. 2,3,3B. 2,3,1C. 3,2,1D. 1,3,3 6.设函数 y =x sin x +cos x 的图象在点 (t,f(t)) 处切线的斜率为 k ,则函数 k =g(t) 的部分图象为（）A. B. C. D.7.设 f(x)=||x −1|−1| ，关于 x 的方程 [f(x)]2+k ⋅f(x)+1=0 ，给出下列四个命题，其中假命题的个数是（）①存在实数k ，使得方程恰有3个不同的实根；②存在实数k ，使得方程恰有4个不同的实根；③存在实数k ，使得方程恰有5个不同的实根；④存在实数k ，使得方程恰有6个不同的实根.A. 0B. 1C. 2D. 38.已知等比数列{a n }的公比q=2，则 2a 1+a 22a 3+a 4的值为（）A. 14B. 12C. 18D. 19.一个由半球和四棱锥组成的几何体，其三视图如图所示．则该几何体的体积为（）A. 13 + 23 πB. 13 + √23π C. 13 + √26π D. 1+ √26π10.已知函数y=log a （ax 2﹣x ）在区间[2，4]上是增函数，则实数a 的取值范围是（） A. （ 14，1 ）∪（1，+∞） B. （1，+∞） C. (14，1) D. （0， 18 ） 11.在椭圆x 2a 2+y 2b 2=1(a >b >0)中，F 1,F 2分别是其左右焦点，若椭圆上存在一点P 使得|PF 1|=2|PF 2| ，则该椭圆离心率的取值范围是( )A. (13,1) B. [13,1) C. (0,13) D. (0,13]12.函数 f(x)=sin(ωx +φ)(x ∈R)(ω>0,|φ|<π2) 的部分图象如图所示，如果 x 1,x 2∈(π6,2π3) ，且 f(x 1)=f(x 2) ，则 f(x 1+x 2)= （）A. −√32B. −12C. 12 D. √32二、填空题13.(1+x −x 2)6 的展开式中，含 x 10 项的系数是________14.已知向量序列 a 1⃗⃗⃗⃗ ,a 2⃗⃗⃗⃗ ,a 3⃗⃗⃗⃗ ⋅⋅⋅a n ⃗⃗⃗⃗ ⋅⋅⋅ ，满足如下条件： |a 1|=2 ， |d |=√24 ， 2a 1⃗⃗⃗⃗ ⋅d =−1 ，且 a n ⃗⃗⃗⃗ −a n−1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =d (n ≥2) ，若 a 1⃗⃗⃗⃗ ⋅a k ⃗⃗⃗⃗ =0 ，则 k = ________. 15.已知双曲线 C ：x 2a 2−y 2b 2=1(a >0,b >0) 的一条渐近线方程为 y =√52x ,且与椭圆x 212+y 23=1 有公共焦点．则曲线C 的方程为________．16.△ABC 中，角 A,B,C 的对边分别为 a,b,c ，重心为 G ，若 a ⋅GA ⃗⃗⃗⃗⃗ +b ⋅GB ⃗⃗⃗⃗⃗ +√33c ⋅GC ⃗⃗⃗⃗⃗ =0⃗ , 则 A = ________. 三、解答题17.在 ΔABC 中， a 、 b 、 c 分别是角 A 、 B 、 C 的对边，且 acosA ,ccosB ,bcosB成等差数列.（1）求角 A 的大小；（2）若 a =√3 ，求 ΔABC 周长的取值范围.18.若关于x 的方程22x ＋2x a ＋a ＋1＝0有实根，求实数a 的取值范围．19.在四棱锥AB中，底面ABCD为平行四边形，平面PAD⊥平面ABCD，ΔPAD是边长为4的等边三角形，BC⊥PB，E是AD的中点.（1）求证：BE⊥PD；（2）若直线AB与平面PAD所成角的正弦值为√15，求平面PAD与平面PBC所成的4锐二面角的余弦值.20.已知函数f（x）=xlnx，g（x）= x．e x（1）证明方程f（x）=g（x）在区间（1，2）内有且仅有唯一实根；（2）记max{a，b}表示a，b两个数中的较大者，方程f（x）=g（x）在区间（1，2）内的实数根为x0，m（x）=max{f（x），g（x）}，若m（x）=n（n∈R）在（1，+∞）内有两个不等的实根x1，x2（x1＜x2），判断x1+x2与2x0的大小，并说明理由．21.椭圆x2a2+y2b2=1(a>b>0)的离心率为√32，长轴长为12，直线y=kx﹣4与椭圆交于A，B，弦AB的长为√10，求此直线的斜率．22.在直角坐标系xOy中，以原点O为极点，x轴的正半轴为极轴建立极坐标系．已知曲线C1的极坐标方程为ρ2= 31+2cos x ，直线l的极坐标方程为ρ= 4sinθ+cosθ．（I）写出曲线C1与直线l的直角坐标方程；（II）设Q为曲线C1上一动点，求点Q到直线l距离的最小值．23.设函数f(x)=|x+2|.（1）求不等式f(x)+f(−x)≥6的解集；（2）若不等式f(x−4)−f(x+1)>kx+m的解集为(−∞,+∞)，求k+m的取值范围.答案解析部分一、单选题1.【答案】C【考点】交集及其运算【解析】【解答】解不等式√x<2，可得0≤x<4；解不等式|x−1|<2，即−2< x−1<2，解得−1<x<3.所以，A={x|0≤x<4}，B={x|−1<x<3}，因此，A∩B={x|0≤x<3}.故答案为：C.【分析】求出集合A，B，利用交集的定义即可得到答案。

广东省佛山市石门中学2021届高三下学期5月高考模拟数学试题含答案

2021届高三高考模拟数学试题一、单选题：本题共8小题，每小题5分，共40分。

四个选项中，只有一项是符合要求的。

1.【黄志平】已知U =R ,函数()ln 1y x =-的定义域为M ,集合{}220N x x x =->,则=)(N C M U （）A. (],0-∞ B. ()0,1 C. [)1,2 D. [)2,+∞2.设()()1i i 2x y +-=，其中x ，y 是实数，i 是虚数单位，则x y +=A ．1BCD ．23.【刘振龙】在一个抛硬币的游戏里，抛出的前2个硬币都是正面朝上，则在抛第3个硬币时，正面朝上的概率为（）A.18 B.14 C.12 D.384.若,l m 是两条不同的直线，m 垂直于平面α，则“l m ⊥”是“//l α”的（） A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件5.【付强】如图，圆柱1OO 的轴截面11ABB A 是正方形，,D E 分别是1AA 和1BB 的中点，C 是弧AB 的中点，则经过C D E 、、的平面与圆柱1OO 侧面相交所得到的的曲线的离心率是（）C. 2D. 6. 【黄志平】已知,a b 是单位向量，且()1,1a b +=-，若向量c a b =-，则a 与c 的夹角为（） A ．π6 B ．π4 C ．π3 D ．2π37.【马安华】 (x 2+2a x- a)5的展开式中各项的系数和为1024,则a 的值为（）A 、1B 、2C 、3D 、48.【罗建中】已知两点()()1,3,2,3,M N --在曲线上存在点P 满足|MP |=|NP |的曲线方程是（）A ．2410x y +-= B. 22125x y +=C. 2212y x += D. 2212y x -= 二、多选题：本题共4小题，每小题5分，共20分。

在每小题给出的选项中，有多项符合题目要求。

全部选对的得5分，部分选对的得2分，有选错得0分。

2021年高三第三次高考模拟考试理数试题含答案

2021年高三第三次高考模拟考试理数试题含答案一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.设集合{}{}2|13,|680A x x B x x x =-≤≤=-+<，则等于（）A ．B ．C ．D ．2.设是虚数单位，若为纯虚数，则实数的值为（）A ．2B ．-2C ．D ．3.函数与在上都是递减的，实数的取值范围是（）A ．B ．C ．D ．4.甲、乙两人从4门课程中各选修2门，则甲、乙所选的课程中恰有1门相同的概率是（）A ．B ．C ．D ．5.在如图所示的算法流程图中，输出的值为（）A ．11B ．12C ．13D ．156.下列双曲线中，与双曲线的离心率和渐近线都相同的是（）A ．B ．C ．D ．7.如图，网格纸上小正方形的边长为1，粗线画出的是某多面体的三视图，该多面体的体积是（）A ．32B ．16C ．D ．8.在约束条件0024x y y x t y x ≥⎧⎪≥⎪⎨+≤⎪⎪+≤⎩下，当时，其所表示的平面区域的面积为，与之间的函数关系用下列图像表示，正确的应该是（）A ．B ．C ．D ．9.函数的最小正周期为，给出下列四个命题：（1）的最大值为3；（2）将的图像向左平移后所得的函数是偶函数；（3）在区间上单调递增；（4）的图象关于直线对称．其中正确说法的序号是（）A ．（2）（3）B ．（1）（4）C ．（1）（2）（4）D ．（1）（3）（4）10.已知()()()()4241220126243111x x a a x a x a x ++=+++++++，则的值为：（） A ． B ． C ． D ．11.已知定义在的函数，若仅有一个零点，则实数的取值范围是（） A ． B ． C ． D ．12.将半径都为1的4个彼此相切的钢球完全装入形状为正三棱台的容器里，该正三棱台的高的最小值为（）A ．B ．C ．D ．第Ⅱ卷二、填空题:本大题共四小题，每题5分，满分20分．13.已知向量与的夹角为120°，，则等于___________．14.数列满足1120212112n n n n n a a a a a +⎧⎛⎫≤< ⎪⎪⎪⎝⎭=⎨⎛⎫⎪-≤< ⎪⎪⎝⎭⎩，若，则___________． 15.已知是抛物线上的一条动弦，且的中点横坐标为2，则的最大值为___________．16. 的三个内角的对边分别是，其面积．若，则边上的中线长的取值范围是__________．三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17.（本小题满分12分）已知各项均为正数的数列的前项和，且．（1）求的通项公式；（2）若数列满足，求的前项和．18.（本小题满分12分）某中学对男女学生是否喜爱古典音乐进行了一个调查，调查者学校高三年级随机抽取了100名学生，调查结果如下表：喜爱不喜爱总计男学生60 80女学生总计70 30（1）完成上表，并根据表中数据，判断是否有95%的把握认为“男学生和女学生喜欢古典音乐的程度有差异”；（2）从以上被调查的学生中以性别为依据采用分层抽样的方式抽取10名学生，再从这10名学生中随机抽取5名学生去某古典音乐会的现场观看演出，求正好有个男生去观看演出的分布列及期望．附：0.100 0.050 0.0102.7063.841 6.63519.（本小题满分12分）如图，四棱锥的侧面是正三角形，底面为菱形，点为的中点，若．（1）求证：；（2）若，求二面角的余弦值．20.（本小题满分12分）已知直线与椭圆相交于不同的两点，且线段的中点的坐标为．（1）求椭圆的离心率；（2）设为坐标原点，且，求椭圆的方程．21.（本小题满分12分）已知函数()()()()()()2231,ln 134x f x x e g x a x x a x a a R =+=+++-+∈．（1）若，求函数的单调区间；（2）若恒成立，求的取值范围．请考生在22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分.22.（本小题满分10分）选修4-1：几何证明选讲如图，是的一条切线，切点为，直线都是的割线，已知．（1）若，求的值；（2）求证：．23. （本小题满分10分）选修4-4：坐标系与参数方程已知直角坐标系中，以坐标原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为，两点极坐标分别为．（1）求曲线的参数方程；（2）在曲线上取一点，求的最值．24. （本小题满分10分）选修4-5：不等式选讲设函数．（1）若，求不等式的解集；（2）若不等式的解集为，求的值．参考答案一、选择题CAAC BCDA DBBC二、填空题13. 4 14. 15. 6 16.三、解答题17.（本小题12分）解：（1）由，解得，由假设，因此，故的通项为．．．．．．．．．．．．．．．．．．．．．．6分（2）由1323133132nb n nn n==+--++．．．．．．．．．．．．．．．．．．．．．．．．．．．．8分得前项和1111323132233n nii ib i i n===+-=+∑∑．．．．．．．．．．．．．．．．12分18．（本小题12分）解：（1）喜爱不喜爱总计男学生60 20 80女学生10 10 20总计 70 30100将表中的数据代入公式计算，得()2210060102010100 4.7627030802021K ⨯⨯-⨯==≈⨯⨯⨯，由于，所以有95%的把握认为“男学生和女学生喜欢古典音乐的程度有差异”．．．．．．．．．．．．．．．5分（2）由题意知：这10名学生中有8名男生和2名女生，故可取值3，4，5．．．．．．．．．．6分()()()32415082828255510101056214055623,4,5252925292529C C C C C C P X P X P X C C C ============．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．8分故其分布列为：3 4 5．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．10分该分布满足超几何分布，故其期望．．．．．．．．．．．．．．．．．．．．．12分19.（本小题12分）（1）证明：由得，从而，且，又∵，∴平面，而平面，得，又∵，∴．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．6分（2）解：如图建立直角坐标系，其中为坐标原点，轴平行于，的中点坐标，连结，又知，由此得到：()333331,,,0,,,2,0,04422GA PB BC ⎛⎫⎛⎫=--=-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，有， ∴，∵的夹角为等于所求二面角的平面角，20.（本小题12分）解：（1）设，代入椭圆，两式相减：()()()()22121212120b x x x x a y y y y -++-+=，由题意可知：代入上式得，∵，∴，从而所求离心率．．．．．．．．．．．．．．．．．．．．．．．．5分（2）由（1）得椭圆的方程为：，与直线联立方程组并化简得：，从而，得，且，．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．7分∵，∴，有得：，解得：（满足）．故所求的椭圆的方程为．．．．．．．．．．．．．．．．．．．．．．．．．．．．12分21．（本小题12分）解：（1）当，，得，或，得．故所求增区间为和，减区间为………………………………4分（2）由，有()()()2231ln 134xx e a x x a x a +≥+++-+，令()()()()2231ln 134x h x x e a x x a x a =+-+----， ①当时，()()()2323312x a h x x e x a x '=+--+-+， 1°当时，()()()23233012x a h x x e x a x '=+--+-=+， 2°当时，()()()2323312x a h x x e x a x '=+--+-+ ()()()()22123232311011x x a x e x a x e a x x ⎛⎫<+--+-=+-+-< ⎪++⎝⎭， 3°当时，()()()2323312x a h x x e x a x '=+--+-+ ()()()()22123232311011x x a x e x a x e a x x ⎛⎫>+--+-=+-+-> ⎪++⎝⎭，在递减，在递增，∴，②当时，在时，，即，而对于函数，不妨令，有()()()()4223ln 13ln 123ln 112314a a g x a x x a x a a x a a e a -⎛⎫=+++-+>++-=-+++-= ⎪⎝⎭，故在内存在，使得不恒成立，综上：的取值范围是．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．12分22．（本小题满分10分）（1）证明:由题意可得：四点共圆，∴，∴，∴，又∵．．．．．．．．．．．．．．．．．．．．．．4分（2）∵为切线，为割线，∴，又∵，∴，∴，又∵，∴，∴，又∵，∴∴．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．10分23．（本小题满分10分）解：（1）由，得，即，故所求参数方程为：（为参数）．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．4分（2）由已知条件知两点直角坐标分别为，令，()()()()222222cos 12sin cos 12sin 8sin 12AP BP t t t t t +=++++-++=+，故当，有最小值4，，有最大值20．．．．．．．．．．．．．．．．．．．．．．．．．．．．10分24．（本小题满分10分）解：（1）时，由得，当时，有，得；时，有，解集为空集；时，有，得，综上，所求解集为．．．．．．．．．．．．．．．．．．．．．．．．．．．4分（2）法一：由的解集为知：是方程一个根，得而当时，由解得，合题意；当时，由解得，合题意．综上：．．．．．．．．．．．．．．．．．．．．．．．．．．10分法二：不等式可化为：，分别作出及的图象由图可知若的解集为，则有：，解得：．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．10分•f8 31109 7985 禅f=N36467 8E73 蹳 &23880 5D48 嵈K 36298 8DCA 跊。

2021届高三毕业班摸底测试数学试题 (6)(含答案解析)

2021届高三毕业班摸底测试数学试题 (6)一、单选题1．已知直线l 过点(),0A a 且斜率为1，若圆224x y +=上恰有3个点到l 的距离为1，则a 的值为（）A ．B ．±C ．2±D ．2．已知△ABC 内角A 、B 、C 所对的边分别为a 、b 、c ，若a=3，b=2，A=60°，则cosB=（）A B ．±C D ． 3．复数()1z i i =-，则z =（）A ．1BC ．2D ．44．已知数列{}n a 为等比数列，472a a +=，224720a a +=，则110a a 的值为（）A ．16B ．8C ．-8D ．-165．已知函数()()8sin 03f x x πωω⎛⎫=-> ⎪⎝⎭的最小正周期为π,若()f x 在,243m π⎡⎤-⎢⎥⎣⎦上单调递增,在223m π⎡⎤⎢⎥⎣⎦上单调递减,则实数m 的取值范围是( ) A ．3,2ππ⎡⎤⎢⎥⎣⎦B ．55,64ππ⎡⎤⎢⎥⎣⎦C ．,32ππ⎡⎤⎢⎥⎣⎦D ．4,83ππ⎡⎤-⎢⎥⎣⎦ 6．函数y =e |x|−4cosx(e 为自然对数的底数)的图象可能是( )A ．B ．C ．D ． 7．如图放置的边长为1的正方形PABC 沿x 轴顺时针滚动一周，设顶点P 的运动轨迹与x 轴所围区域为M ，若在平面区域{04,(,)|02x N x y y ≤≤⎧⎫=⎨⎬≤≤⎩⎭内任意取一点Q ，则所取的点Q 恰好落在区域M 内部的概率为A ．16πB ．8πC ．18π+D ．28π+8．函数()ln x f x x=，则（） A ．e x =为函数()f x 的极大值点B ．e x =为函数()f x 的极小值点C ．1ex =为函数()f x 的极大值点 D ．1e x =为函数()f x 的极小值点 9．设集合{}2,3,4,5M =，集合{}2,4,6N =，则M N ⋂是（）A ．{}2,3,4,5B ．{}2,4C ．{}2,3,4,5,6D ．{}2,4,610．已知正方体1111-ABCD A B C D 的棱长为2，E 为11A B 的中点，下列说法中正确的是（） A ．1ED 与1B C 所成的角大于60B ．点E 到平面11ABCD 的距离为1C ．三棱锥1E ABC -D ．直线CE 与平面1ADB 所成的角为4π 11．下列说法正确的是（）A ．若1a <1,则a>1B ．若y=x+1x,则y 的最小值为2 C ．y=3sin(x+1)是周期函数 D ．平面非零的向量,,a b c ，满足a b a c ⋅=⋅，则b c =12．设奇函数()f x 的定义域为[5,5]-，若当[0,5]x ∈时，()f x 的图象如图所示，则不等式()0f x <的解集是（）A ．(2,5)B ．(5,2)(2,5)--⋃C ．(2,0)(2,5)-⋃D ．(5,0)(2,5)-⋃二、填空题 13．三棱锥A BCD -的各顶点都在球O 的球面上，AB BC ⊥，CD ⊥平面ABC ，4BC =，5BD =，球O 的表面积为169π，则A BCD -的表面积为_______．14．如图是一个三角形数阵，满足第n 行首尾两数均为n ，(),A i j 表示第()2i i ≥行第j 个数，则()100,2A 的值为__________．15．下表是某厂1～4月份用水量(单位：百吨)的一组数据：由散点图可知，用水量y 与月份x 之间有较好的线性相关关系，其线性回归直线方程是0.7y x a =-+，则a 等于___16．已知x,y 满足条件{2x +y ≥4x −y ≥1x −2y ≤2，则z =x +2y 的最小值为三、解答题17．已知实数满足.（1）若，求实数的取值范围；（2）求的最小值.18．在△ABC 中,角A 、B 、C 所对的边分别为a,b,c ，已知1cos 24C =-(I)求sinC 的值；(Ⅱ)当a=2，2sinA=sinC 时，求b 及c 的长． 19．已知函数()()()1ln 1f x x x m n =++++⎡⎤⎣⎦，曲线()y f x =在点()()0,0f 处的切线方程为21y x =+.（1）求m ，n 的值和()f x 的单调区间；（2）若对任意的[)0,x ∈+∞，()f x kx >恒成立，求整数k 的最大值.20．三棱锥A BCD -中，平面ABD ⊥平面BCD ，AB AD ⊥，E ，F 分别为BD ，AD 的中点.（1）求证：EF 平面ABC ；（2）若CB CD =，求证：AD ⊥平面CEF .21．已知曲线C 的极坐标方程是=1，以极点为原点，极轴为轴的正半轴建立平面直角坐标系，直线的参数方程为为参数）．（1）写出直线与曲线C 的直角坐标方程；（2）设曲线C 经过伸缩变换得到曲线，设曲线上任一点为，求的最小值． 22．已知椭圆()2222:10x y C a b a b+=>>的左右焦点分别为12,F F ，抛物线24y x =与椭圆C 有相同的焦点，且椭圆C过点3 1,2⎛⎫ ⎪⎝⎭．（I）求椭圆C的标准方程；（Ⅱ）若椭圆C的右顶点为A，直线l交椭圆C于,E F两点（,E F与A点不重合），且满足AE AF⊥，若点P为EF中点，求直线AP斜率的最大值．23．袋中有20个大小相同的球,其中记上0号的有10个,记上n号的有n个(n=1,2,3,4).现从袋中任取一个球,ξ表示所取球的标号.(1)求ξ的分布列、期望和方差;(2)若η=aξ+b,E(η)=1,D(η)=11,试求a,b的值.参考答案1．D根据直线l 过点(),0A a 且斜率为1，写出直线方程，再根据圆224x y +=上恰有3个点到l 的距离为1，结合半径，则由圆心到直线的距离为1求解.因为直线l 过点(),0A a 且斜率为1，所以直线方程为y x a =-，即0x y a --=，因为圆224x y +=上恰有3个点到l 的距离为1，所以圆心到直线的距离为：1，1=，解得a =故选：D本题主要考查直线与圆的位置关系，还考查了运算求解的能力，属于基础题.2．C试题分析：由正弦定理sin sin a b A B =，得sin 3B =，∴cos 3B =±，又∵a b >，∴A B >，∴B 为锐角，∴cos 3=B ．考点：正弦定理．3．B分析：先化简复数z,再求复数z 的模得解.详解：由题得1,z i =+所以z ==故答案为：B 点睛：（1）本题主要考查复数的运算和复数的模，意在考查复数的基础知识.(2)复数(,),z x yi x y R z =+∈=4．C由472a a +=，224720a a +=，可得()24747202a a a a =+-，可得11047a a a a =．∵472a a +=，224720a a +=，∴()24747202a a a a =+-，解得478a a =-，∴110478a a a a ==-，故选：C ．本题考查了等比数列的通项公式及其性质，考查了推理能力与计算能力，属于中档题 5．B由函数()f x 的最小正周期为π可得2ω=，求出()8sin 23f x x π⎛⎫=- ⎪⎝⎭的增区间与减区间，分别令,243m π⎡⎤-⎢⎥⎣⎦与223m π⎡⎤⎢⎥⎣⎦是其子集即可. 由题意可得2ππω=，求得2ω=，令222232k x k πππππ-≤-≤+，求得5,1212k x k k Z ππππ-≤≤+∈，由3222232k x k πππππ+≤-≤+，求得511,1212k x k k Z ππππ+≤≤+∈，因为()f x 在,243m π⎡⎤-⎢⎥⎣⎦上单调递增,在223m π⎡⎤⎢⎥⎣⎦上单调递减, 所以555312564212m m m ππππ⎧≤⎪⎪⇒≤≤⎨⎪≥⎪⎩，所以实数m 的取值范围是55,64ππ⎡⎤⎢⎥⎣⎦，故选B. 函数sin()y A x ωϕ=+的单调区间的求法：(1) 代换法：①若0,0A ω>>,把x ωϕ+看作是一个整体，由22k x ππωϕ+≤+≤()322k k Z ππ+∈求得函数的减区间，2222k x k πππωϕπ-+≤+≤+求得增区间；②若0,0A ω><,则利用诱导公式先将ω的符号化为正，再利用①的方法，或根据复合函数的单调性规律进行求解；(2) 图象法：画出三角函数图象，。

2021年高考模拟试卷(6)参考答案

高考模拟试卷(6)参考答案南通市数学学科基地命题第Ⅰ卷（必做题，共160分）一、填空题1．4．因为A ∩B ={4}，所以4∈A ，故x ＝4．2．2+i ．由z 1·－z 2＝5，得－z 2＝52+i＝2－i ，所以z 1＝2+i ． 3．1115．用枚举法.从6，7，8，9，10，11六个任取两个数有15种不同的取法，其中两个数互质有(6,7)，(6,11)，(7,8)，(7,9)，(7,10)，(7,11)，(8,9)，(8,11)，(9,10)，(9,11)，(10,11)共11组，故其概率为1115．4. 32．由x 1，x 2，…，x 100的方差是2，则3x 1，3x 2，…，3x 100的方差是18，所标准差为32．5．126．由程序框可知：S ＝2＋22＋…＋2n ＝2 n +1－2＞100，则最的n 值为6，所以输出的S =27－2＝126．6. 3．正四棱柱的表面积为14，两个底面积之和为2，故侧面积为12，⇒AA 1＝3．7. 6．作出如图所示的平面区域，得面积S =12×(42－22)＝6．8. ［74π，254π)．区间［0,1］至少包含218个周期而不到318个周期，故178×2πω≤1＜258×2πω，解之得74π≤ω＜254π． 9．217．由(a ＋b )⊥(a －2b )，得(a ＋2b )·(a －2b )＝0，⇒|a |2－4|b |2＝0，则|a |＝2|b |， cos 〈a ＋b ，a －b 〉＝(a ＋b )·(a －b ) |a ＋b || a －b |＝a 2－b 2 a 2+2a ·b +b 2 a 2－2a ·b +b 2＝3b 2 21b 2＝217．10. (－∞，0)∪［1，+∞)．若t ＜0，令x ＝1t ，则f (1t )＝e 1/t －1－1＜1e －1＜0；若t ＝0，f (x )＝e x -1＞0，不合题意；若t ＞0，只需f (x )min ≤0，求导数，得f ′(x )＝e x -1－t ，令f ′(x )＝0，解得x ＝ln t +1．当x ＜ln t +1时，f ′(x )＜0，f (x )在区间(－∞，ln t +1)上是减函数；当x ＞ln t +1时，f ′(x )＞0，f (x )在区间(ln t +1，＋∞)上是增函数．故f (x )在x ＝ln t +1处取得最小值f (ln t +1)＝t －t (ln t +1)＝－t ln t ．所以－t ln t ≤0，由t ＞0，得ln t ≥0，所以t ≥1．11. 34．设数列{a n }的公差为d ，则a 2＝a 1+d ，a 5＝a 1+4d ，a 9＝a 1+8d ．由a 2、a 5、a 9依次成比数列得 a 2 a 9＝a 52，即(a 1+d )(a 1+8d )＝(a 1+4d )2，化简上式得 a 1d ＝8d 2，又d ＞0，所以a 1＝8d ．a 1+a 2+…+a k a 1＝a 1k +k (k +1)2 a 1＝k ＋k (k －1)16＞100，解得k min ＝34．12. 2＋1．抛物线方程为y 2＝8x ，且a 2+b 2＝4，设B (x 0，y 0)、C (x 0，－y 0) (x 0＞0，y 0＞0)．则可知∠BF 1C 为直角，△BCF 1是等腰直角三角形，故y 0＝x 0+2，y 02＝8x 0，解得x 0＝2，y 0＝4，将其代入双曲线得 4a 2－16b 2＝1．再由a 2+b 2＝4解得a ＝22－2，所以e ＝222－2＝2＋1．13.110．由题意可设 tan A ＝2k ，tan B ＝3k ，tan C ＝6k ，k ＞0，而在△ABC 中，tan A ＋tan B ＋tan C ＝tan A tan B tan C ，于是k ＝116，从而cos A cos B cos C ＝3 20×2 15×1 12＝110． 14. 12. 法一当x ＝0时，原式值为0；当x ≠0时，由2x 3+7x 2+6x x 2+4x ＋3＝，令t ＝2x +7+6x，由x ∈(0,4］得t ∈［2＋ 3，+∞)，f (x )＝g (t )＝2t t 2+1＝2t +1t ．而t ＋1t≥4，当且仅当t ＝2＋3时，取得等号，此时x ＝3，所以f (x )≤12．即f (x )的最大值为12．法二 f (x )＝2x (x 2+4x +3)－x 2x 2+4x ＋3＝2x x 2+4x ＋3－(x x 2+4x ＋3)2，于是令t ＝x x 2+4x ＋3，所求的代数式为 2t －t 2．当x ＝0时，t ＝0；当x ≠0时，有t ＝1x +4+3x ≤123+4＝2－32，所以t ∈［0，2－32］，当t ＝2－32， 2t －t 2有最大值12，此时x ＝3．二、解答题15. 法一：联立⎩⎪⎨⎪⎧sin(α＋π3)＝6－24，sin 2α＋cos 2α＝1．⇒4sin 2α－( 6－ 2)sin α－(1＋3)＝0，解之得sin α＝6＋24，和sin α＝－22，因为α∈(0，π)，所以sin α＝6＋24，且α∈(π2，π)，所以cos α＝2－64．(1) sin(α－π4)＝sin αcos π4－cos αsin π4＝6＋24×22－2－64×22＝62×22＝32．m (N)(2)sin2α＝2sin αcos α＝2×6＋24×2－64＝－12，cos2α＝1－2sin 2α＝－32． cos(2α－π3)＝cos2αcos π3－sin2αsin π3＝－32．法二：因为α∈(0，π)，sin(α＋π3)＝6－24＜12，所以α＋π3＞5π6，所以α＋π3＝11π12，所以α＝7π12．(1) sin(α－π4)＝sin(7π12－π4)＝sin π3＝32．(2) cos(2α－π3)＝sin(2×7π12－π3)＝cos 5π6＝－32．16．（1）证法一：取B 1C 1的中点为N ，连O 1N ，BN ．因为O 1，N 分别是△A 1B 1C 1边A 1C 1与B 1C 1的中点，所以O 1N ∥A 1B 1，且O 1N ＝12A 1B 1，又MB ＝12AB ＝12A 1B 1，且MB ∥A 1B 1，所以O 1N ∥MB ，且O 1N ＝MB ，所以四边形BMO 1N 为平行四边形，所以O 1M ∥NB ，NB ⊂平面BB 1C 1C ，O 1M ⊄平面BB 1C 1C ，所以O 1M ∥平面BB 1C 1C ．（2）连AC 与BD ，因为ABCD 是菱形，所以AC ⊥BD ；又因为平面AA 1C 1C ⊥平面ABCD ，平面AA 1C 1C ∩平面ABCD ＝AC ，所以BD ⊥平面AA 1C 1C ，因为AA 1⊂平面AA 1C 1C ，所以BD ⊥AA 1，BB 1∥AA 1，BD ⊥BB 1，所以平行四边形BB 1D 1D 是矩形．17. 如图所示，系统受力的水平分量和与竖直分量和都为零，得⎩⎨⎧2sin α－3sin β＝0，2cos α＋3cos β＝m ，(1)因为∠AOB ＝120°，即α＋β＝120°，由⎩⎨⎧2sin α－3sin β＝0 (1)，2cos α＋3cos β＝m (1)2+(2)2得4＋9＋12cos(α＋β)＝m 2，故m ＝7N ．(2)由⎩⎨⎧2sin α－3sin β＝0，2cos α＋3cos β＝m ，得⎩⎨⎧2sin α＝3sin β (3)，2cos α＝m －3cos β (4) ，(3)2+(4)2得4＝9－6m cos β＋m 2，即m 2－6m cos β＋5＝0．解得m ＝3cos β± 9cos 2β－5．因为α是锐角，由(2)得m －3cos β＞0，即m ＞3cos β，从而m ＝3cos β＋ 9cos 2β－5，且9cos 2β－5＞0，又因为β为锐角，得到1＞cos β＞53．因此5＜m ＜5．答：(1)当∠AOB ＝120°，m 的值为 7N ；(2)系统处于平衡状态时，m 的取值范围是(5，5)． 18. （1）记点P (x 0，y 0)．则3x 02+4y 02＝12．由l PA ：y ＝(x ＋2)y 0x 0+2，得M (3，5y 0x 0+2)；由l PA ：y ＝(x －2)×y 0x 0－2，得N (3，y 0x 0－2)，而F (1，0)得FM →·FN →＝(2，5y 0x 0+2)·(2，y 0x 0－2)＝4＋5y 02x 02－4＝4－154＝14．(2)记点Q 为(s ，t )，直线BQ 、AQ 分别与直线x =3交于点M ′(3，t s －2)，N ′ (3，5ts ＋2)．由题意，点M ′即为点M ，故t s －2＝5y 0x 0+2，再由t s －2·5t s ＋2＝－154＝5y 0x 0+2·y 0x 0－2，得5t s ＋2＝y 0x 0－2．即N ′与N 点重合．于是A 、Q 、N 三点共线．19.（1）设数列{}n a 公差为d ，则111123(1)2(2)n n n a a a n d a nd dn a d +-=+=+-++=+-对n *∀∈N 成立，所以12223d a d =⎧⎨-=-⎩，，故1d =，11a =-．（2）由123n n a a n ++=-，知{(2)}n a n --为等比数列，公比1q =-，所以1(2)(1)(1)n n a n a ---=+-，故1(2)(1)(1)n n a n a -=-++-．① 当n 为不小于3的奇数时，由22113n n n n a a a a ++++≥，得22(1)(2)323n a n a n -++---≥，化简得22(3)2a a n +--+≥恒成立，所以22a a +≥，解得a ≥1． ② n 为不小于2的偶数时，同理有223(3)a a n +--≥恒成立，因为0a >，显然恒成立．所以0a >．由①②得1a ≥，故a 的最小值为1．20. (1)因为f (x )≥g (x )对任意实数x 恒成立，所以，ax 2≥a 2x 2对任意实数x 恒成立，所以，2a a -≤0，解得0≤a ≤1．又由题意可得a ≠0，所以实数a 的取值范围为0＜a ≤1．(2)(i)因函数g (x )的图象开口向上，且其零点为x 3，x 4，故g (x )＜0⇔x ∈(x 3，x 4)．因x 1，x 2是f (x )的两个不同零点，故f (x 1)=f (x 2)=0．因x 3＜x 1＜x 4，故g (x 1)＜0=f (x 1)，于是221()a a x -＜0．注意到x 1≠0，故20a a -<．因g (x 2)-f (x 2)=222()a a x -＜0，故g (x 2)＜f (x 2)=0，从而x 2∈(x 3，x 4)，于是x 3＜x 2＜x 4．(ii)记x 1=x 3=t ，故f (t )=at 2+bt +1=0，g (t )=a 2t 2+bt +1=0，于是(a -a 2)t 2=0．因a ≠0，且t ≠0，故a =1．所以，f (x )=g (x )且其图象开口向上．所以，对x ∀∈1(,)x -∞，f (x )递减，()f x '递增且()f x '＜0，g (x )递减且g (x )＞0．若m ＞n ，则()f n '＜()f m '＜0，于是1()g n ＞1()g p ＞0，从而g (p )＞g (n )＞0，故n ＞p ．同上，当n ＞p 时，可推得p ＞m ．所以，p ＞m ＞n ＞p ，矛盾．所以，m ＞n 不成立．同理，n ＞m 亦不成立．所以，m =n ．同理，n =p ．所以，m =n =p ．第Ⅱ卷（附加题，共40分）21. A. 连AD ，因为AB 为直径，所以AD ⊥BD ，CDM又DE ⊥AB ，所以∠ABD ＝∠ADE ．另一方面，D 是弧AC 的中点，所以∠DAC ＝∠ABD ，所以∠ADE ＝∠DAC ．所以△AMD 为等腰三角形，所以AM ＝DM ．B ．设a b M c d ⎡⎤=⎢⎥⎣⎦，由条件有，11311a b c d ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦，且19215a b c d -⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦， 3329215a b c d a b c d +=⎧⎪+=⎪∴⎨-+=⎪⎪-+=⎩，解得1436a b c d =-⎧⎪=⎪∴⎨=-⎪⎪=⎩，1436M -⎡⎤∴=⎢⎥-⎣⎦． C. 由4cos ρθ=，得24cos ρρθ=，224x y x ∴+=，即圆C 的方程为()2224x y -+=，又由,2,x m y ⎧=+⎪⎪⎨⎪⎪⎩消t ，得0x y m --=，直线l 与圆C相切，2=，2m ∴=±D. ()|1||2|.b b f x a a≥+--设,()|1||2|[3,3].bt g t t t a ==+--∈- |1||1| 3.x x ∴-++≥3(1)123.2x x x ≥≥∴≥当时，(2)123,.x <<≥当-1时，无解3(3)123.2x x x ≤-≥∴≤-当时，-综上，33.22x x ≤-≥或22. 作AP ⊥CD 于点P ，分别以AB 、AP 、AO 所在直线为x 、y 、z 轴建立坐标系，则A (0，0，0)，B (1，0，0)，P (0，22，0)，D (－22，22，0)，O (0，0，2)，M (0，0，1)．（1）AB ＝(1，0，0)，MD ＝(－22，22，－1)，则cos ＜AB ，MD ＞＝－12，故AB 与MD 所成角为π3．（2）OP ＝(0，22，－2)，OD ＝(－22，22，－2)，设平面OCD 法向量n ＝(x ，y ，z )，则n ·OP ＝0，n ·OD ＝0，即⎩⎨⎧22y －2z ＝0－22x ＋22y －2z ＝0，取z ＝2，则n ＝(0，4，2)．易得平面OAB 的一个法向量为m ＝(0，1，0)，cos ＜n ，m ＞＝223，故平面OAB 与平面OCD 所成二面角的平面角余弦值为223．23．先用数学归纳法证明1[a 0，a 1]＋1[a 1，a 2]＋…＋1[a n －1，a n ]≤1a 0(1－12n )．当n ＝1时，1[a 0，a 1]≤12a 0＝1a 0(1－12)成立．假设n ＝k 时命题成立则当n ＝k ＋1时1[a 0，a 1]＋1[a 1，a 2]＋…＋1[a k ，a k ＋1]≤1[a 0，a 1]＋1a 1(1－12n )，因此，只需证辅助命题“1[a 0，a 1]＋1a 1(1－12k )≤1a 0(1－12k ＋1)”．设(a 0，a 1)＝d ，则a 0＝xd ，a 1＝yd (x ，y ∈N *，y ＞x ≥1，(x ，y )＝1) 所以1[a 0，a 1]＋1a 1(1－12k )－1a 0(1－12k ＋1)＝1xyd ＋1yd (1－12k )－1xd (1－12k ＋1)＝1xyd [1＋x (1－12k )－y (1－12k ＋1)]＝1xyd [1－(y －x )(1－12k ＋1)－x2k ＋1] ≤1xyd [1－1·(1－12k ＋1)－12k ＋1]＝0．从而1[a 0，a 1]＋1a 1(1－12k )≤1a 0(1－12k ＋1)．即n ＝k ＋1时命题成立．由上可知，对一切n ∈N *，命题都成立．而1a 0(1－12n )≤1－12n ，故1[a 0，a 1]＋1[a 1，a 2]＋…＋1[a n －1，a n ]≤1－12n ．。