南邮信与系统课后答案

合集下载

南邮信号与系统课后答案精选精品PPT课件

如图所示，试求该系统的零状态响应。
xk
hk
4
3 2
4
2 1
-2 -1 0 1 2 3 k
-2
-1 0 1 2 3 4 k
-1
解： xk 4, 2,3,2 hk 4,,1,2,1
4 2 3 2 4 1 2 1
4 2 3 2 8 4 6 4 4 2 3 2 16 8 12 8 16 12 22 5 2 7 2
k
1
uk
4 3
1k 1
8 3
0.5k 1 u k
2 3
1k 2
4 3
0.5k 2
k 1
k 1
2 3
1k
2
4 3
0.5k 2
4 3
1k
1
8 3
0.5k 1
uk
2 3
1k
1 3
0.5k
4 3
1k
4 3
0.5k
uk
21k 0.5k uk
2-25 计算下列卷积
2 2 e3tut
hh00
1 0 2 1
c1c1 0.02.55cc22
0 1
c1
c2
2
3 4
3
h0
k
2 3
1k
4 3
0.5k
uk
1
hk h0 k 2 2h0 k 1
2 3
1k 2
4 3
0.5k 2
uk
1
2
2 3
1k 1
4 3
0.5k 1 u k
2 3
1k 2
4 3
0.5k 2
第二章信号与系统的时域分析
作业
1

信与系统课后习题答案—第资料章

第1章习题答案1－1 题1－1图所示信号中，哪些是连续信号？哪些是离散信号？哪些是周期信号？哪些是非周期信号？哪些是有始信号？解： ① 连续信号：图（a ）、（c ）、（d ）； ② 离散信号：图（b ）； ③ 周期信号：图（d ）； ④ 非周期信号：图（a ）、（b ）、（c ）； ⑤有始信号：图（a ）、（b ）、（c ）。

1－2 已知某系统的输入f(t)与输出y(t)的关系为y(t)=|f(t)|，试判定该系统是否为线性时不变系统。

解：设T 为此系统的运算子，由已知条件可知： y(t)=T[f(t)]=|f(t)|，以下分别判定此系统的线性和时不变性。

① 线性 1）可加性不失一般性，设f(t)=f 1(t)+f 2(t)，则y 1(t)=T[f 1(t)]=|f 1(t)|，y 2(t)=T[f 2(t)]=|f 2(t)|，y(t)=T[f(t)]=T[f 1(t)+f 2(t)]=|f 1(t)+f 2(t)|，而|f 1(t)|＋|f 2(t)|≠|f 1(t)+f 2(t)|即在f 1(t)→y 1(t)、f 2(t)→y 2(t)前提下，不存在f 1(t)＋f 2(t)→y 1(t)＋y 2(t)，因此系统不具备可加性。

由此，即足以判定此系统为一非线性系统，而不需在判定系统是否具备齐次性特性。

2）齐次性由已知条件，y(t)=T[f(t)]=|f(t)|，则T[af(t)]=|af(t)|≠a|f(t)|=ay(t) （其中a 为任一常数）即在f(t)→y(t)前提下，不存在af(t)→ay(t),此系统不具备齐次性，由此亦可判定此系统为一非线性系统。

② 时不变特性由已知条件y(t)=T[f(t)]=|f(t)|，则y(t-t 0)=T[f(t-t 0)]=|f(t-t 0)|，即由f(t)→y(t)，可推出f(t-t 0)→y(t-t 0)，因此，此系统具备时不变特性。

南邮信号与系统答案第6章

∞
信号与系统 · 习题解答
⎧ 1 k = 0,1,2,3 ⎪ *（3） f (k ) = ⎨− 1 k = 4,5,6,7 ⎪0 其它 ⎩
第5页
解法一：f (k ) = δ (k ) + δ (k − 1) + δ (k − 2) + δ (k − 3)
− δ (k − 4) − δ (k − 5) − δ (k − 6) − δ (k − 7) ↔ 1 + z −1 + z − 2 + z −3 − z − 4 − z −5 − z −6 − z −7 1 − ( z −1 ) 4 1 − ( z −1 ) 4 (1 − z − 4 ) 2 z z 4 −1 2 = − z −4 = = [ 4 ] −1 −1 −1 z −1 z 1− z 1− z 1− z
信号与系统 ·Z变换式，试求f(0)，f(1)，f(2)和f(∞)。 z 2 − 2z (1) F ( z ) = 2 ( z − 1)( z + 0.5)
解：由初值定理：f (0) = lim F ( z ) = 0 z →∞
f (1) = lim z[ F ( z ) − f (0)] = 1
1
L
1 2
3
0
4
k
f (k ) = δ (k ) + δ (k − 2) + δ (k − 4) + L + δ (k − 2m) + L ↔ 1+ z
−2 ∞
+z
−4
+L+ z
− 2m
+L
2
1 m 1 z = ∑( 2 ) = = 2 1 z −1 m=0 z 1− 2 z 解法二： 1 1 1 z 1 z z2 k f (k ) = ε (k ) + (−1) ε (k ) ↔ + = 2 2 2 2 z −1 2 z +1 z −1

信号与系统课后答案第三章作业答案

初始为 0， C2 -4
y f (t) -4e3tu(t) 4e2tu(t)
全响应= yx (t)+y f (t) 4e2tu(t)-2e3tu(t)
3-2 描述某 LTI 系统的微分方程为
d2 y(t) dt 2

3dy(t) dt来自2y(t)

df (t) dt

6
1
1
(2e1 e1 et ) u(t)
e1(2 et ) u(t)
（2）
f
(t)

a[u(t
s) 2

u(t
2)]
h(t) b[u(t 2) u(t 3)]
f
(t)

h(t)

ab[(t

1 2
)
u(t
1 2
)

(t

1 2
)
u(t
1) 2

tu(t)

1 4
(et

e3t
)u(t)

1 2
t
e3tu(t)

[
1 4
et

(
1 2
t

1 4
)e3t
]u
(t)
3-19 一个 LTI 系统，初始状态不祥。当激励为 f (t) 时其全响应为
(2e3t sin 2t)u(t) ；当激励为 2 f (t) 时其全响应为 (e3t 2sin 2t)u(t) 。求
（1）初始状态不变，当激励为 f (t 1) 时的全响应，并求出零输入相应、
零状态响应；（2）初始状态是原来的两倍、激励为 2 f (t) 时系统的全响应。

南邮信号与系统答案第5章

信号与系统 · 习题解答
第11页
5-8 试用单位阶跃序列表示图示离散信号。 (b) f (k)
2
3
2
1 −2 −1 0 1 2 3
4 5
6
−1
k
解：f 2 (k ) = ε (k + 2) + ε (k ) + ε (k − 2) − 4ε (k − 4) + ε (k − 6)
信号与系统 · 习题解答
10 5
k<0 k =0 k ≥1
∴ f1 (k − 1) + f 2 (k + 1) 0 k <0 ⎧ ⎪ =⎨ 1 k =0 ⎪2 k + k − 1 k ≥ 1 ⎩
2
1
−1 0 1 2
L
3 k
信号与系统 · 习题解答
第5页
*（4） f1 (k − 1) ⋅ f 2 (k + 1) 解：
f1 (k − 1) ⋅ f 2 (k + 1) ⎧ 0 ⎪ =⎨ 0 ⎪2 k (k − 1) ⎩ ⎧ 0 =⎨ k ⎩2 (k − 1) k <0 k =0 k ≥1 k <1 k ≥1
⎧C1 = 0 解得 C1 = 0 ， ⎪ 2 ⎨ 2 2 C2 = ⎪2[C1 cos 3 π + C2 sin 3 π ] = 2 3 ⎩
2 2 sin kπ 所以 yzi (k ) = 2 ⋅ 3 3
k
k ≥0
信号与系统 · 习题解答
第19页
5-15 试求下列差分方程的单位函数响应（1） y (k + 2) + 3 y (k + 1) + 2 y (k ) = x(k + 1) + x(k )

南邮计算机通信与网络习题答案

南邮计算机通信与网络习题答案计算机通信与网络习题答案1.1什么是计算机网络？答：我们可以把计算机网络定义为：把分布在不同地点且具有独立功能的多个计算机，通过通信设备和线路连接起来，在功能完善的网络软件运行下，以实现网络中资源共享为目标的系统。

1.3计算机网络的拓扑结构种类有哪些？各自的特点是什么？答：网络的拓扑（T opology ）结构是指网络中各节点的互连构形，也就是连接布线的方式。

网络拓扑结构主要有五种：星形、树形、总线形、环形和网络形，如图1.1所示。

图1.1星形结构的特点是存在一个中心节点，其他计算机与中心节点互连，系统的连通性与中心节点的可靠性有很大的关系。

树形结构的特点是从根节点到叶子节点呈现层次性。

总线形结构的特点是存在一条主干线，所有的计算机连接到主干线上。

环形结构是将所有计算机连接到一个环形的线路，每两个计算机之间有两条线路相连。

网络型是一种不规则的连接，事实上，目前的因特网就是这种拓扑结构。

1.5由n 个结点构成的一星型拓扑结构的网络中，共有多少个直接的连接？对由n 个结点构成的环状拓扑结构的网络中呢？对由n 个结点构成的全连接网络中呢？答：在由n 个结点构成的一星型拓扑结构的网络中有（n-1）个直接连接。

在由n 个结点构成的环状拓扑结构的网络中有（n ）个直接连接。

在由n 个结点构成的全连接拓扑结构的网络有（n －1）n/2个直接连接。

1.6在广播式网络中，当多个节点试图同时访问通信通道时，信道将会产生冲突，所有节点都无法发送数据，形成信道容量的浪费。

假设可以把时间分割成时间片，n 个节点中每个节点在每个时间片试图使用信道的概率为p ，试计算由于冲突而浪费的时间片的百分比。

答：每个时间片只有一个节点访问的概率为：p(1-p)n-1+ p(1-p)n-1+….+ p(1-p)n-1=n* p(1-p)n-1 从而每个时间片冲突的概率为：1- n* p(1-p)n-1即位由于冲突而浪费的时间片百分比。

南京邮电大学信号与系统-信号与系统4

《信号与系统》SIGNALS AND SYSTEMS ZB
7. 单边双曲正弦信号 sinht(t)
sinht1(et et)
2
sinht(t)s22
8. 单边双曲余弦信号 cosht(t)
c osth1(et et)
2
cosht(t)s2s2
《信号与系统》SIGNALS AND SYSTEMS ZB

0
(4) 任何可以进行拉氏变换的信号，其拉氏变换 F(s) 中一
定《没信有号冲与激系函统数》。SIGNALS AND SYSTEMS ZB
4.1.3 （单边）拉氏变换的收敛域
信号 f (t) 乘以收敛因子后，有可能满足绝对可积的
条件。是否一定满足，还要看 f (t) 的性质与的相对关系。通常把使 f (t)e- t 满足绝对可积条件的值的范围
称为衰减因子； e- t 为收敛因子。《信号与系统》SIGNALS AND SYSTEMS ZB
取 f(t)e- t 的傅里叶变换：
F[f(t)et] f(t)etejtdt f(t)e(j)tdt

它是 j的函数，可以表示成

Fj f(t)e(j)tdt
例如增长的指数信号： et(t) (0)
2. 0 0：拉氏变换、傅氏变换都存在，且 F(s)F()sj
例如衰减的指数信号：et(t) (0)
F() 1 j
F(s) 1
s
3. 0 0：拉氏变换、傅氏变换都存在，但傅氏变换中
含有冲激函数
P185 表4-1
作业《信号与系统》SIGNALS AND SYSTEMS ZB 返回
连续信号与系统的复频域分析概述
傅里叶变换（频域）分析法

信号与系统课后习题答案第7章

143
第7章离散信号与系统的Z域分析 144
第7章离散信号与系统的Z域分析
题图 7.7
145
第7章离散信号与系统的Z域分析 146
第7章离散信号与系统的Z域分析
题解图 7.31
147
第7章离散信号与系统的Z域分析
(2) 由H(z)写出系统传输算子: 对应算子方程和差分方程为
148
7.25 已知一阶、二阶因果离散系统的系统函数分别如下，求离散系统的差分方程。
111
第7章离散信号与系统的Z域分析 112
第7章离散信号与系统的Z域分析 113
第7章离散信号与系统的Z域分析 114
第7章离散信号与系统的Z域分析
7.26 已知离散系统如题图7.5所示。 (1) 画出系统的信号流图； (2) 用梅森公式求系统函数H(z)； (3) 写出系统的差分方程。
① 或者
② 容易验证式①、②表示同一序列。
57
第7章离散信号与系统的Z域分析 58
第7章离散信号与系统的Z域分析 59
第7章离散信号与系统的Z域分析 60
第7章离散信号与系统的Z域分析 61
第7章离散信号与系统的Z域分析
也可以将Yzs(z)表示为
再取Z逆变换，得 ②
自然，式①、②为同一序列。
44
第7章离散信号与系统的Z域分析 45
第7章离散信号与系统的Z域分析 46
第7章离散信号与系统的Z域分析
7.10 已知因果序列f(k)满足的方程如下，求f(k)。
47
第7章离散信号与系统的Z域分析 48
第7章离散信号与系统的Z域分析
(2) 已知K域方程为
49

南京邮电大学《信号与系统》信号与系统3

2
2
2 5cos(3t 36.9) 2cos(6t 60) cos(9t 30)
单边幅度频谱：
An
5
2 1
0
3
单边相位频谱：
n
36.9
6
9 n0
30 0
3
6 9 n0
《信号与系统》SIG 6N0ALS AND SYSTEMS ZB
(2) 双边频谱
f (t) 2 5cos(3t 36.9) 2cos(6t 60) cos(9t 30)
例：试将图示周期矩形脉冲
f (t)
A
信号 f (t)展开为(1)三角型和
(2)指数型傅里叶级数。
解：(1) f (t)是偶函数，故只含有常
数项和余弦T项。 2
2
T
t
a0
1 T
2
f (t)dt 2 T
2 Adt A
0
T
2
an
2 T
2
f (t) cosn0tdt
4 T
2 Acosn0tdt
0
2
4 A sin( n0 ) 2 A sin( n0 )
n0T
2
n
2
《f 信(t) 号 A与T 系统n1》n2ASIsGinN(nA2L0S)AcoNsnD0StYSTEMS ZB
(2) 指数型傅立叶级数
T
Fn
1 T
2 f (t)e jn0tdt 1
T
T
2 Ae jn0tdt
2
2
2 2.5[e j(3t36.9 ) e j(3t36.9 ) ]
当 f (t)是实奇函数时，则 Fn是虚奇函数。
（利《用信号Fn与的系计统算》公S式IG可N以A证LS明AN）D SYSTEMS ZB

1998-2010南京邮电大学通信原理参考答案答案

2000年试题参考答案一、填空 1、)(log 2i x p -∑∞=-12)(l o g )(i i i x p x p p(x i )=n1i=1,2,3…2、)2)(exp(21)(22σσπa x x f --=ak 0(a H t E ∙=)0()]([ξ) π2020hw n k (输出噪声功率谱密度H o w w k n w p ≤=200)()3、恒参信道随参信道恒参信道4、接收信号中除当前码元以外的所有码元在抽样时刻的总和si s sT w T T i w H ππ22)4(≤=+∑+∞-∞= 部分响应系统滚降系统（均衡？）5、相位连续幅度恒定（能量集中）带宽最小6、2，17、hc c w w w w H w w H ≤=-++常数)()( 相干二、1、信息熵H=－p(x 1)2log p(x 1)－p(x 0)2log p(x 0)=0.97 bit/符号信息速率Rb=1000×0.97bit/s=970 bit/s2、接收端收到0的概率p(0)=0.4×0.97+0.02×0.6=0.4(全概率公式) 接收端收到1的概率p(1)=1－p(0)=0.6 平均丢失信息量H(x/y)= －p(0)[p(0/0)2log p(0/0)－p(1)2logp(1/0)] －p(1)[p(0/1)2logp(0/1)－p(1)2logp(1/1)]=0.4[0.972log 0.97－0.022log 0.02]－0.6[0.032log 0.03－0.982log 0.98]=0.16 bit/符号信息传输速率R=1000(H －H(x/y))bit/s=810 bit/s三、1、mm f f w A k m =11022/1044=⨯===f m m f m radw v A srad k ππ2、)]102sin(102cos[)(46t t A t m s ⨯+⨯=ππ3、khz B mkhz f m f B ff 40110)1(2===+=4、调制制度增益6)1(32=+=f fm m G 接收机输出信噪比3106161⨯==oo ii N S N S噪声功率w k B n Ni7120108401010222--⨯=⨯⨯⨯=⨯⨯=接收机输入信号功率w N S i i 4310341061-⨯=⨯⨯=平均发射功率w S Si 3400106=⨯=四、1、等效带宽0041221ττππ=⨯=B 奈奎斯特传输速率baudR B 0max 21412ττ=⨯=2、系统实际带宽002121ττππ=⨯=B 最高频带利用率hz baud B R B /10max ==η3、s bit R R B b /238log 02max τ=⨯=4、s bit R s bit R b b /23/340max 0ττ=<=但由于,2,1230=≠k kR b τ因此存在码间干扰（无码间干扰传输要求⋅⋅⋅==,2,1,max n nR R B B ）五、发送”1”错判为”0”的概率2)1()1()(21011-=-+=-=⎰⎰+-+-A dV A V dV A V f Pe AA发送”0”错判为”1”的概率2)1()1()(210100-=--=-=⎰⎰--A dV A V dV A V f Pe AA系统误码率2)1(2121201-=+=A Pe Pe Pe （对双极性信号，最佳判决门限为Vd *=0）六、1、用π相位表示”1”，用0相位表示 ”0”，2PSK 波形如图1 1 0 0 1 1 0 02、baudk R sbit k R B b 2048/2048== 信号频率khz f s 2048=带宽khz f B s 40962== 频带利用率hz baud BR B /5.0==η3、框图如下图 (反向抽判)各点波形如下图参考”0” 1 1 0 0 1 1 0 0abcd七、1、输出信噪比No Mq S 222==，由题意7,102,10,40lg10424≥≥≥≥N qS qS No o 即2、抽样频率m 2f f s ≥，码元周期s T s μ2=，码元速率MbaudT R sB 5.01==，时分复用时，hz f R f m B s 3571,710≤≤⨯⨯3、为保证不过载，要求m s m s m m f f A f f A πσπ200,01.02≥=≤∙ 八、1、1),()(=-=k t T ks t h 一般情况2、3、最佳判决时刻取20T t =，02max 2max 2A ,41,2n T r T A E n E r ===故九、1、当输入为时，)(t δ系统冲激响应为)2()()(s T t t t h --=δδ，wTs j e w H 21)(--=2、易知该系统为第Ⅳ类部分响应系统，因此12-=r C r2001年试题参考答案一、填空 1、M2logMsT 2l o g 1sT 2M2log212、R (∞) R(0) R(0)-R (∞)3、接收信号中除当前码元以外的所有码元在抽样时刻的总和si ssT w T T i w H ππ≤=+∑+∞-∞=)2( 部分响应系统滚降系统（均衡？）4、552khz 96khz （为余数为最大整数，，k n kB nB f nk B f h s 22),1(2+=+=）5、最大似然比准则 -1 2psk6、最大输出信噪比准则 )()(*d jwt t t kS e W kS d--二、1、22/105.0)()()(322B f f B f hzw k f H f P f P c c i o +≤≤-⨯==-w B k df k df f P N Bf B f o o c c 32223210105.02)(-+--∞+∞-⨯=⨯⨯==⎰⎰（系数2是由于双边功率谱密度）2、）310)(5.0)(-⨯=τδτi R (注：）（频域，时域频域）（（时域w t πδδ211↔↔))]()([105.0)(32c B c B o f f g f f g k f P ++-⨯=-（选用f 作变量时，无系数2π）tf j c B tf j c B c c eBt BSa f f g eBt BSa f f g ππππ22)()(,)()(-↔+↔-（频域平移，c c f w π2=）32223210)2cos()(])()([105.0)(---⨯=+⨯=τπτπππτππc tf j tf j o f B BSa k eBt BSa e Bt BSa k R c c 三、 1、5=mm f W A k rad w v A v rad km m f33102,10,/10⨯===ππ,)102sin(10)(3t t m ⨯=π2、5==mm f f W A k m3、khz m f B f 126102)1(23=⨯⨯=+=,载频hz f c 610=4、输入信号功率w v S i 50002)100(2==输入噪声功率w B f Pn N i 4.2)(2==调制制度增益450)1(32=+=f fm m G 310375.94.25000450⨯=⨯=oo N S四、信息码 1 0 1 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 差分码0 1 1 0 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 HDB3 +1 0 -1 0 +1 -1 +1 -1 +1 -1 0 0 0 –V +B 0 0 +V 0 0 五、1、抽样频率khz f s 8= 编码位数38log 2==N 带宽khz khz B 2408310=⨯⨯=2、khz B B 480)1('=+=α 六、发送”1”错判为”0”的概率=--=-=⎰⎰∞-∞-dx A x dx A x f Pe Vdnn Vd]2)(exp[21)(221σσπ发送”0”错判为”1”的概率dx A x dx A x f Pe VdnnVd⎰⎰∞-+-=+=]2)(exp[21)(220σσπ系统误码率为dxA x p dx A x p Pe p Pe p Pe VdnnVdnn⎰⎰∞-∞-+-+--=+=]2)(exp[21)0(]2)(exp[21)1()0()1(222201σσπσσπ最佳判决门限设为*d V ，应使系统误码率最小。

(完整版)南邮计算机通信与网络习题答案

计算机通信与网络习题答案1.1什么是计算机网络？答：我们可以把计算机网络定义为：把分布在不同地点且具有独立功能的多个计算机，通过通信设备和线路连接起来，在功能完善的网络软件运行下，以实现网络中资源共享为目标的系统。

1.3计算机网络的拓扑结构种类有哪些？各自的特点是什么？答：网络的拓扑（Topology）结构是指网络中各节点的互连构形，也就是连接布线的方式。

网络拓扑结构主要有五种：星形、树形、总线形、环形和网络形，如图1.1所示。

星型结构树型结构总线型结构环型结构网络型结构图1.1星形结构的特点是存在一个中心节点，其他计算机与中心节点互连，系统的连通性与中心节点的可靠性有很大的关系。

树形结构的特点是从根节点到叶子节点呈现层次性。

总线形结构的特点是存在一条主干线，所有的计算机连接到主干线上。

环形结构是将所有计算机连接到一个环形的线路，每两个计算机之间有两条线路相连。

网络型是一种不规则的连接，事实上，目前的因特网就是这种拓扑结构。

1.5由n个结点构成的一星型拓扑结构的网络中，共有多少个直接的连接？对由n个结点构成的环状拓扑结构的网络中呢？对由n个结点构成的全连接网络中呢？答：在由n个结点构成的一星型拓扑结构的网络中有（n-1）个直接连接。

在由n个结点构成的环状拓扑结构的网络中有（n）个直接连接。

在由n个结点构成的全连接拓扑结构的网络有（n－1）n/2个直接连接。

1.6在广播式网络中，当多个节点试图同时访问通信通道时，信道将会产生冲突，所有节点都无法发送数据，形成信道容量的浪费。

假设可以把时间分割成时间片，n个节点中每个节点在每个时间片试图使用信道的概率为p，试计算由于冲突而浪费的时间片的百分比。

答：每个时间片只有一个节点访问的概率为：p(1-p)n-1+ p(1-p)n-1+….+ p(1-p)n-1=n* p(1-p)n-1从而每个时间片冲突的概率为：1- n* p(1-p)n-1即位由于冲突而浪费的时间片百分比。

信号与系统课后答案（ＰＤＦ）

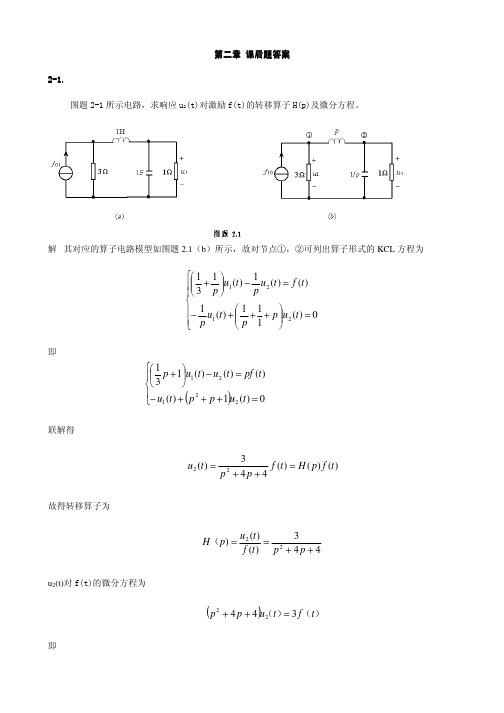
第二章第二章课后题答案课后题答案2-1.1.图题2-1所示电路，求响应u 2(t)对激励f(t)的转移算子H(p)及微分方程。

解其对应的算子电路模型如图题2.1（b ）所示，故对节点①，②可列出算子形式的KCL 方程为= +++−=−+0)(111)(1)()(1)(1312121t u p p t u p t f t u p t u p即()=+++−=−+0)(1)()()()(13122121t u p p t u t pf t u t u p联解得)()()(443)(22t f p H t f p p t u =++=故得转移算子为443)()()22++==p p t f t u p H （u 2(t)对f(t)的微分方程为()）（）（t f t u p p 34422=++即）（t f t u t u dt d t u dt d 3)(4)(4)(22222=++2-2图题2-2所示电路，求响应i(t)对激励f(t)的转移算子H(p)及微分方程。

解其对应的算子电路模型如图2.2（b）所示。

故得）（）（t f p p p p pp t f t i 3011101022221.01)(2+++=+×++=故得转移算子为30111010)()()(2+++==p p p t f t i p Hi(t)对f(t)的微分方程为)()1010()()3011(2t f p t i p p +=++即)(10)(10)(30)(11)(22t f t f dt d t i t i dt d t i dt d +=++2-3图题2-3所示电路，已知u C (0-)=1 V, i(0-)=2 A。

求t>0时的零输入响应i(t)和u C (t)。

解其对应的算子电路模型如图题2.3（b）所示。

故对节点N 可列写出算子形式的KCL 方程为0)(2312= ++t u p p C又有uc(t)=pi(t)，代入上式化简，即得电路的微分方程为=====++−+−+1)0()0(2)0()0(0)()23(2c cu u i i t i p p电路的特征方程为0232=++p p故得特征根（即电路的自然频率）为p 1=-1，p 2=-2。

南邮信号与系统课后答案第一章

所以为非能非功信号
1-7 判断下列信号是能量信号，还是功率信号或者都不是。
(1)
பைடு நூலகம்
1
k
解：显然该信号为离散周期信号，因此是功率信号
1-8 判断下列系统是否为线性系统，是否为时不变系统，并简单说明理由。其中y(t)、y(k)为系统的完全响应， q(0)为系统的初始状态，x(t)、x(k) 为系统的激励。
1-6 判断下列信号是能量信号，还是功率信号或者都不是。
(3) 2e3t
解：E lim 2e
T T T
3t
dt lim
2
T
T T
4e 6t dt
2 lime 6T e6T 3 T
2 1 T 1 1 6T 3t P lim 2e dt lim e e 6T T 2T T 3 T T 由罗必塔法则 2 lim e 6T T
第一章信号与系统的基本概念
作
业
南京邮电大学通信与信息工程学院信息工程系
1-1 判断下面的信号是否为周期信号，如果是，确定其基本周期。
2
4 sin 2t ut 4
解：因为t 0时，ut 0，所以为非周期信号
4
cos2t 2 cos5t
(4)
yt 3q0x3t
解：不满足分解性，因此为非线性系统。
当x1 t xt td 时，y1 t 3q0x3t td yt td 3q0x3t td 所以为时变系统
1-10 判断下列系统是否为因果系统，并简单说明理由。
(5) yk 2 2 yk 1 yk xk 1 3xk

信号与系统第二版课后答案

解(1)
(2)
3-6对于如题3-6图所示的三角波信号，试证明其频谱函数为
题3-6图
证因为
0，|t| >
则
3-7试求信号f(t) = 1 + 2cost+ 3cos3t的傅里叶变换。
解因为
12()
2cost2[(1)+(+ 1)]
3cos3t3[(3)+(+ 3)]
故有
F() = 2[() +(1)+(+ 1)]+3[(3)+(+ 3)]
(t)s(t)，(t)s(t)
故有
y1(t)=yzi(t)+s(t)= 3e3t(t)
y2(t)=yzi(t)s(t)= e3t(t)
从而有
y1(t)y2(t)= 2s(t)= 2e3t(t)
即
s(t)= e3t(t)
故冲激响应
h(t)=s(t)=(t)3e3t(t)
2-16若系统的零状态响应
y(t)=f(t)*h(t)
试证明：
(1)
(2)利用(1)的结果，证明阶跃响应
证（1）因为
y(t)=f(t)h(t)
由微分性质，有
y(t)=f(t)h(t)
再由积分性质，有
（2）因为
s(t)=(t)h(t)
由（1）的结果，得
3-1求题3-1图所示周期信号的三角形式的傅里叶级数表示式。
题3-1图
解对于周期锯齿波信号，在周期( 0，T)内可表示为
图p2-6
2-7如题2-7图一阶系统，对(a)求冲激响应i和uL，对(b)求冲激响应uC和iC，并画出它们的波形。
题2-7图
解由图(a)有

南京邮电大学信号与系统习题3

A f (t)
A 2
−τ τ 0 − 2
τ τ
2
t
解：信号 f (t)可以分解为：可以分解为：
《信号与系统》SIGNALS AND SYSTEMS
A A f (t) = gτ (t) + g2τ (t) 2 2 Aτ ωτ ↔ Sa( ) + AτSa(ωτ) 2 2
ZB
3-26 已知
f (t) = f1(t) + f2(t)的频谱密度函数 F(ω) = 4Sa(ω) − j
−20 0
20
ZB
f2(t) 3-34 已知图所示锯齿脉冲 f (t)的傅 f (t) 已知图(a)所示锯齿脉冲 1 1 1 jω jω 里叶变换 F(ω) = (e − jωe −1)， −1 0 t 0 1 2t ω2 (a) (c) 利用傅里叶变换的性质，求图(c) 利用傅里叶变换的性质，求图、(f) 所示信号的傅里叶变换。所示信号的傅里叶变换。解:(c) f2(t) = f (t −1) + f (−t +1) = f (t −1) + f [−(t −1)] ↔ F(ω)e− jω + F(−ω)e− jω = [F(ω) + F(−ω)]e− jω
ZB
3-33 试应用调制定理，求题示信号试应用调制定理，的傅里叶变换，并画出频谱图。的傅里叶变换，并画出频谱图。解： (t) = ε (t + π ) −ε (t − π )cos20t f

π − 5 5 5 π π 2π π Sa( ω) Qε (t + ) −ε (t − ) ↔ 5 5 5 5
双边相位频谱：双边相位频谱：
2π 2π θn 2π 5 1 5 −8 3 3 1 3 0 2π 8 nω0 8 nω0 2π −5 −1 2π − − − 《信号与系统》SIGNALS AND SYSTEMS ZB 3 3 3

南邮信号与系统课后答案第三章

3-14
如题图 3 14 所示信号 f t F ，在不求出前提下，求
1
F 的
f t
(1) F 0 F 0
-1
0
1
t
解： F 0 F 0

f t e
j t
dt
0

f t dt
f 1 t
1
(a)
2 5
0
-1
2 5
t
2 2 解： f 1 t cos 10 t u t u t cos 10 tg 4 t 5 5 5 2 f t g 4 t Sa F 5 5 5 4 f 1 t 1 2
y 1 t
H 2
cos 2 t
4 5
sin 2 t cos 2 t 127
4 5 Ae
j

另解：
1 j2 1 j2
j
e
j 127

y t A cos 2 t cos 2 t 127

1 10
g 10 t Sa 5 1 10 5
1 10 , A 10
Sa 5 t 2
g 10
对称性
u 5 u 5

g 10

5
3-8
已知 f t F ，求下列函数的傅里叶
2 j
F e
2 j
t ( 6 ) t 2 f 2

南京邮电大学信号与系统习题2

2
t
t

( c ) 当 2 t 3时, y (t ) （ 2)d 2
1
2 1
0 1 2
2
( d ) 当 3 t 4时,
t 2
2 1 0 1 2
(e) 当 t 4时, y (t ) 0
ZB

《信号与系统》SIGNALS AND SYSTEMS
t
2 1 0 1 2

(b) 当 1 t 2时, y (t ) （ 2)d 2
1

t
x( ) h( ) (t ) x( ) h( ) (t ) x( ) h( ) (t ) x x x
2 2 2 t 2 1
0 1 2
2

2 1
0
2

(a ) 当 t 1时, y (t ) 0
(b) 当 1 t 2时, y ( t ) （ 2 t ) d 2
h(t ) x( ) h( ) 2 t
2 1
0
t 1
h(t ) x( ) h( ) 2 t
2
h(t ) x( ) h( ) 2 t
e e

(5) et (t ) * cost (t )
2t t
e e

2 ( t )
d e
2t

t
t
e 2t (e t 0) e
t
e d

t
e(t ) cosd (t ) et
t
0

e cosd (t )
《信号与系统》SIGNALS AND SYSTEMS 3