史上最详细的平面曲线的弧长公式计算(微积分)
弧长的计算公式

弧长的计算公式
弧长的计算公式
弧长计算公式是一个数学公式,为L=n×π×r/180,L=α×r。
其中n是圆心角度数(角度制),r是半径,L是圆心角弧长,α是圆心角度数(弧度制)。
曲线的弧长也称曲线的长度,是曲线的特征之一。
不是所有的曲线都能定义长度,能够定义长度的曲线称为可求长曲线。
扇形面积公式
一条弧和经过这条弧两端的两条半径所围成的图形叫扇形(半圆与直径的组合也是扇形),它是由圆周的一部分与它所对应的圆心角围成。
S扇=LR/2(L为扇形弧长,R为半径)或π(R^2)*N/360(即扇形的度数)
扇形是与圆形有关的一种重要图形,其面积与圆心角(顶角)、圆半径相关,圆心角为n°,半径为r的扇形面积为n/360*πr^2.
如果其顶角采用弧度单位,则可简化为1/2×弧长×(半径)。
扇形还与三角形有相似之处,上述简化的面积公式亦可看成:1/2×弧长×(半径),与三角形面积:1/2×底×高相似。
高等数学 6-4平面弧长的积分

积分变量为 x ,在 [ a, b] 上任取小区间 [ x, x + dx ] ,以对应小切线段的长代替小弧 段的长
y
} dy
o
a
x
x + dx
2
b
2
x
小切线段的长 ( dx ) + ( dy ) 弧长元素 ds = 1 + y′ dx
2
= 1 + y′2 dx
弧长 s =
∫
b
a
1 + y′2 dx.
π
0
1 + a 2 cos 2 x dx,
设椭圆的周长为 s2 四、极坐标情形 曲线弧为 r = r (θ ) (α ≤ θ ≤ β ) ,其中 ϕ (θ ) 在 [α , β ] 上具有连续导数.
x = r (θ ) cos θ Q (α ≤ θ ≤ β ) y = r (θ ) sin θ
解:Q r ′ = a,
4
∴ s=∫
=
β
a 2π 1 + 4π 2 + ln(2π + 1 + 4π 2 ) . 2
[
α
r 2 (θ ) + r ′2 (θ )dθ = ∫
2π
0
]
a 2θ 2 + a 2 dθ = a ∫
2π
0
θ 2 + 1dθ
五、小结 平面曲线弧长的概念 弧微分的概念 求弧长的公式:直角坐标系下;参数方程情形下;极坐标系下
a
b
x n
例 2 计算曲线 y = 解: y′ = n sin
∫
0
n sin θ dθ 的弧长 (0 ≤ x ≤ nπ ) .
10.3平面曲线的弧长

O
C( x0 , 0) x
图中 x 轴 ( x 0)表示直线轨道,AB是半径为R的
圆弧轨道,OA为缓冲轨道. 缓冲曲线常采用三次 曲线
y x3 , 6Rl
其中 l 是 OA 的弧长.对此曲线用曲率公式求得: K 8R2l2x .
4R2l 2 x4 3 2
当 x 从 0 变为 x0 时,曲率 K 从 0 连续地变为
K
(a2 sin2 t
ab b2 cos2 t )3 2
(a 2
ab b2 )sin2 t
b2 3 2
.
当 a b 0 时, 在 t 0, π 处曲率最大,在 t π , 2
3π 处曲率最小,
2
Kmax
a b2
, Kmin
b a2
.
由例1可得,若
a
b
R,
n
记 || T || max{ P0 P1 , P1P2 , , Pn1Pn }, sT Pi1Pi i 1
分别表示最长弦的长度和折线的总长度.
定义1 对于曲线C的无论怎样的分割T,如果存在有限极限
lim
|T || 0
sT
s.
则称曲线C是可求长的,并把极限s定义为曲线C的弧长.
定理10.1 设曲线C由参数方程(1)给出.若C为一光滑曲线,
则C是可求长的,且弧长为
S=
x2 t y2 t dt
(2)
证: 1. 对C作任意分割T={P0,P1,…,Pn},并设P0与Pn
分别对应 t= 与t= ,且
Pi ( xi, yi )= ( x ( t i ), y ( t i ) ), i=1,2,…,n-1.
高等数学(上)02-62.2 平面曲线的弧长

定义:若在弧痂上任意作内接折线,当折线段的最大 边
长人一0时,折线的长度趋向于一个确定的极限,则称 此极限为曲线弧分的弧长,即
n
"姓財Ml
i=l
并称此曲线弧为可求长的.
/ B=Mn A=Mo
定理:任意光滑曲线孤都是可求长的. (证明略)
若 (p(t), 屮 Q) 连 续
可导,且[。'(。]2+ [“0)]2。0, 则曲线C : {二*)E["]为光滑 曲线; 当/(X)连续可2
因此所求弧长
S=
(6>) + /2(6>) 60
例7.求连续曲线段 "L应如d,的孤长. 解:
•/ cosx> 0, /. s=E
2
<x<^
‘2 dx
二2』2 + (Vcosx)2 dx
例8.计算摆线
x = a(t-smt)(口>0)一 拱(0M〈2m) y = a(l- cos t)
的弧长.
y\
rr2(6>) d<9
= ^a1O2+a1
=oJl + "2 dO :.s = a[2\ll + 02d0 (P349 公式 39)
Jo?Jl + din<9 + Jl + 屮 I2来自22/rI
0
=。兀』1 + 4兀2 + ;m(27T + J]+ 4/ )
(1)曲线弧由直角坐标方程给出:
y = f(x) {a<x<b)
孤长元素(弧微分):
ds = J(dx)2 +(dy)2
y
高数弧长公式积分

高数弧长公式积分
在微积分中,弧长是指曲线上的一段长度。
对于一条曲线
y=f(x),如果想要求出其在区间[a,b]上的弧长,可以利用高数弧长公式。
高数弧长公式为:
L = ∫a^b √(1+(dy/dx)) dx
其中,dy/dx表示曲线的斜率,也就是导数。
求出dy/dx,再将其平方加一,开根号后与dx相乘,再对x从a到b积分,即可得到该曲线在[a,b]上的弧长。
需要注意的是,对于参数方程x=x(t),y=y(t),其弧长公式为:
L = ∫a^b √(dx/dt)+(dy/dt) dt
这里的dx/dt和dy/dt分别表示x和y对t的导数。
在实际应用中,高数弧长公式常常用于计算曲线的弧长、曲线的曲率半径等。
掌握好该公式的使用方法,可以大大提高微积分的解题效率。
- 1 -。
平面曲线的弧长

由弧长公式得
s
2 0
x '2 ( t ) y '2 ( t )dt
2
0
2a (1 cos t )dt
2
2 0
2a
t sin dt 8a . 2
例 1 求摆线 x a( t sin t ), y a(1 cos t )(a 0) 一拱 的弧长.
求长的, 且弧长为
s
x '2 ( t ) y '2 ( t )dt .
证明
如前所述, 对C 作任意分割T { P0 , P1 ,
Pn },
并设 P0 与 Pn 分别对应 t 与 t ,且
Pi ( xi , yi ) ( x( t i ), y( t i )), i 1,2..., n 1 .
i 1
t
i 1 i
n
i
i t i .
i 1
n
从而公式成立.
例 1 求摆线 x a( t sin t ), y a(1 cos t )(a 0) 一拱 的弧长.
解
x (t ) a(1 cos t ), y (t ) a sin t ,
x'2 ( i ) y'2 ( i )
i
,
x'2 ( i ) y'2 (i )
则有
sT [ x '2 ( i ) y '2 ( i ) i ]t i .
i 1 n
利用三角不等式容易证明
i y' (i ) y' ( i ) y ' (i ) y ' ( i ) ,
《微积分》第八节 平面曲线的弧长
小结
平面曲线弧长的概念
弧微分的概念
直角坐标系下
求弧长的公式
参数方程情形下
极坐标系下
思考题
闭区间[a, b]上的连续曲线 y f ( x)
是否一定可求长?
思考题解答
不一定.仅仅有曲线连续还不够,必须保证 曲线光滑才可求长.
作业
P236习题3_8 1(单),2(2),3,4(2), 5,7(1、4),8,10(单)
三、平面曲线的弧长
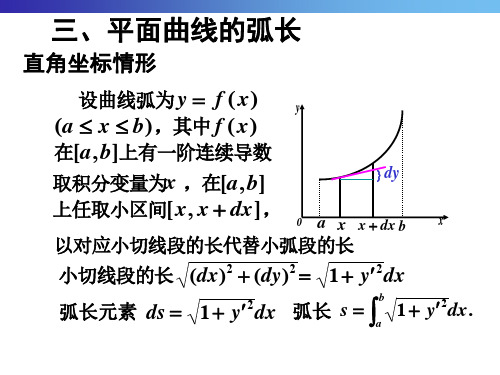
直角坐标情形
设曲线弧为 y f ( x) y (a x b),其中 f ( x)
在[a, b]上有一阶连续导数
取积分变量为x ,在[a, b]
dy
上任取小区间[ x, x dx],
o a x x dx b x
以对应小切线段的长代替小弧段的长
小切线段的长 (dx)2 (dy)2 1 y2dx
曲线弧为 ( ) ( )
其中 ( ) 在[ , ]上具有连续导数.
x y
( (
)cos )sin
( )
dx [()cos ()sin]d,
dy [()sin ()cos]d,
ds (dx)2 (dy)2 2( ) 2( )d,
弧长
s
2( ) 2( )d .
例5
求极坐标系下曲线r
a
sin
3
3
的长.
(a 0) (0 3)
解
r
3a
sin
3
2
cos
3
1 3
a sin
2
cos
,
3 3
s
r 2( ) r2( )d
3 0
a2
sin
3
利用微积分计算曲线弧长

利用微积分计算曲线弧长微积分是一门用来研究数学变化的学科,涵盖了微分和积分两个重要内容。
其中积分在曲线的弧长计算中扮演着重要的角色。
曲线的弧长是指一条曲线从起点到终点的路径长度。
在计算曲线弧长时,我们需要使用微积分的方法。
一、直线的弧长计算我们先来看最简单的情况,也就是在直线上计算弧长。
在数学中,直线可以用 y = kx + b 的形式进行表示。
假设在一个坐标系中有两点 (x1, y1) 和 (x2, y2),它们连成的直线方程为 y = kx + b。
为了计算这段直线对应的弧长,我们需要先求出直线的斜率 k,然后将斜率代入勾股定理得到斜率的系数。
假设直线上的斜率为 k,则斜率系数为√(1 + k^2)。
最后,我们只需要求出两点之间的距离 d 即可。
计算公式如下:弧长= √(1 + k^2) × d二、折线的弧长计算对于一条折线,我们可以将其分解成多个线段,每个线段的长度为√((x2 - x1)^2 + (y2 - y1)^2)。
然后将所有线段的长度相加就得到了折线的总弧长。
三、曲线的弧长计算曲线是一条连续的线,可以用函数 y = f(x) 描述。
为了简化计算,我们可以将曲线分成微小的线段,每个线段与 x 轴平行,并用勾股定理计算它们的长度。
接着,我们使用微积分的方法将这些小线段加起来,就得到了整条曲线的弧长。
具体来说,我们需要将曲线函数 y = f(x) 关于 x 轴旋转 360 度,从而形成一个旋转曲面。
随着旋转角度的增加,曲线的轨迹形成了一个圆周。
因此,曲线的弧长可以表示为:弧长= ∫[a,b]√(1 + f'(x)^2)dx其中 [a,b] 是曲线所覆盖的区间。
f'(x) 表示曲线的导数,也就是f(x) 的斜率。
这个式子看起来比较复杂,但实际上用微积分的方法很容易推导出来。
需要注意的是,曲线的弧长计算与曲线方程的形式无关,只需要知道曲线在坐标系中的函数形式即可。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 r 3a sin cos a sin cos 3 3 3 3 3
2
10
2
7.4 平面曲线的弧长
例 求阿基米德螺线 r a (a 0)上相应于
从 0到2 π的弧长.
解
o
2π
2πa
x
s
r 2 ( ) r 2 ( )d
a a d a 0
2 2 2
2π
0
2 1d
a [2 π 1 4 π 2 ln( 2 π 1 4 π 2 )]. 2
x x a dx 2
2 2
a x a ln | x x 2 a 2 | C 2
2 2
11
2
7.4 平面曲线的弧长
s
r 2 ( ) r 2 ( )d
3
解 s
r 2 ( ) r 2 ( )d
6 4 2 2
2 a sin a sin cos d 0 3 3 3 2 3π 3 a sin d πa . 0 2 3
s1 2
s2 2
π
π
0
2 2 2 1 a cos xdx 1 y dx 0
2
π
设椭圆的周长为s2
2
0 π
2 2 2 ( x) ( y) dt 20 (sin t ) (1 a )(cos t ) dt
2
2
π
2
0 π
1 a cos tdt
2 2
0
1 a cos xdx s1 .
2 2
8
7.4 平面曲线的弧长
四、极坐标情形
曲线弧为 r r ( ) ( )
其中r ( )在[ , ]上 具有连续导数.
现在计算这曲线弧的长度. 由直角坐标与极坐标的关系:
为参数的 x r cos x r ( ) cos ( ) 参数方程 y r ( ) sin y r sin
四、小结
平面曲线弧长的概念
直角坐标系下 参数方程情形下 求弧长的公式 极坐标系下
12
7.4 平面曲线的弧长
思考题
闭区间[a, b]上的连续曲线 y = f (x)是否 一定可求长?
解答
不一定. 仅仅有曲线连续还不够,
必须保证曲线光滑才可求长.
13
( dx ) 2 ( dy ) 2 1 y 2 dx
dx
弧长元素 ds 1 y dx , 弧长 s 1 y 2 dx . a (弧微分)
2
3
b
7.4 平面曲线的弧长
(chx ) shx
chxdx shx C
s
b
a
2 1 y dx
2 2 r ( ) r ( )d 弧长元素为 ds (dx ) (dy )
2
2
弧长 s
r 2 ( ) r 2 ( )d .
9
7.4 平面曲a sin 的长. 3 ( a 0) (0 3 π )
a xa x x a 例 悬链线方程 y (e e ) ach 2 a 计算介于 x b与x b 之间一段弧长度. x x y 解 y ach , y sh a a a
x ch x 1 ( y ) 1 sh a a 所求弧长为
现在计算这曲线弧的长度. 取参数t为积分变量, 其变化区间为 [ , ]. 对应于 [ , ] 上任一小区间 [t , t dt ]的小弧段的 长度的近似值, 即弧长元素为
2 2 ds (dx ) (dy ) ( t ) ( t )dt
2
2
弧长 s
7.4 平面曲线的弧长
7.4 平面曲线的弧长
弧长的概念 直角坐标情形
参数方程情形
极坐标情形 小结 思考题 作业
7.4 平面曲线的弧长
一、平面曲线弧长的概念
Mi
设A、B是曲线 y 弧上的两个端点, 在
M2
M1
M n1
B Mn 弧上插入分点 A M 0 , A M0 M1 ,, M i , , M n1 , M n B, 依次用弦将 O x 相邻两点联结起来, 得到一条内接折线. 记每条弦
光滑曲线弧是可求长.
2
7.4 平面曲线的弧长
二、直角坐标情形
y
设曲线弧为y = f (x)
(a x b), 其中f (x)在
y f ( x)
[a, b]上有一阶连续导数.
dy
现在计算这曲线弧的长度. o a x x dx b x 取积分变量为x, 在[a, b]上 任取小区间 [ x, x dx], 以对应小切线段的长代替小 弧段的长, 小切线段的长为:
s 4s1
4
0
第一象限部分的弧长
2 2 ( x ) ( y ) dt
π 2
a a
O
a
x
4 3a sin t cos tdt
6a .
π 2 0
a
7
7.4 平面曲线的弧长
例 证明正弦线 y a sin x (0 x 2π) 的弧长
x cos t 等于椭圆 (0 t 2π) 的周长. 2 y 1 a sin t 证 设正弦线的弧长等于s1 对称性
2 ( t ) 2 ( t )dt .
6
7.4 平面曲线的弧长
s
2 ( t ) 2 ( t )dt
例 求星形线 x 2 3 y 2 3 a 2 3 ( a 0) 的全长.
x a cos 3 t (0 t 2π) 解 星形线的参数方程为 3 y a sin t 对称性 y
n
π
0
π
t t t t sin cos 2 sin cos dt 2 2 2 2
2
2
t t n sin cos dt 4n. 0 2 2
5
7.4 平面曲线的弧长
三、参数方程情形
x ( t ), 曲线弧为 ( t ) y (t ) 其中 ( t ), ( t ) 在[a, b]上具有连续导数.
的长度为 | M i 1 M i |, i 1,2,, n, 令 max | M i 1 M i | . 如果当分点无限增加, 且 0时, 折线长度的极限
lim | M i 1 M i | 存在, 则称此极限为曲线弧 AB的
0
n i 1
1 i n
弧长(长度).
2
2
b
O
bx
b x b x x s ch dx 2 ch dx 2ash 2ash . 0 a0 a b a a
b
b
4
7.4 平面曲线的弧长
x n
s
b
a
1 y 2 dx
例 计算曲线 y 0 n sin d 的弧长 (0 x nπ ).
x 1 x 解 y n sin sin , n n n π nπ x π x nt 0 0 n π s 1 sin dx 1 sint ndt 0 n dx ndt 0
