静力学方程的应用1
流体静力学方程的应用

二. 液位测量 (1)近距离液位测量装置 压差计读数R反映出容器 内的液面高度。
ρ0 − ρ h= R ρ
液面越高,h越小,压差计读数R越小;当液 面达到最高时,h为零,R亦为零。
(2)远距离液位测量装置 管道中充满氮气, 其密度较小,近似 认为 而
p A ≈ pB
p A = p a + ρБайду номын сангаасh
流体静力学基本方程式的应用 三、液位测量
近距离液位测量装置
远距离液位测量装置
ρ0 − ρ h= R ρ
ρ0 h= R ρ
1-4 流体静力学基本方程式的应用
被测流体是气体
p1 − p 2 ≈ Rgρ 0
一端与被测点连接 , 另一端与大气相通, 另一端与大气相通,则 测得的是表压或真空度。 测得的是表压或真空度。 图中R 问:图中R表示表压还是 真空度? 真空度?
流体静力学基本方程式的应用
例2 如附图所示, 如附图所示 , 水在管道中
流动。 为测得a 两点的压力差, 流动 。 为测得 a、b 两点的压力差 , 在管路上方安装一U 形压差计, 在管路上方安装一 U 形压差计 , 指示液为汞。 指示液为汞 。 已知压差计的读数 R=100mm, 试计算 a 、 b 截面的 100mm, 试计算a mm 压力差。 压力差 。 已知水与汞的密度分别 为1000kg/m3和13600 kg/m3。 1000kg/m
流体静力学基本方程式的应用
解:取等压面1-1′,2-2′ 取等压面1
p1 = p1'
p 2 = p 2'
p1' = pa − ρgx
p1 = p2 + ρ0 gR = p2' + ρ0 gR = pb − ρg ( x + R) + ρ0 gR
流体静力学方程的应用条件

流体静力学方程的应用条件流体静力学是流体力学的一个分支,研究的是静止流体的力学性质和行为。
在实际应用中,流体静力学方程经常用于解决各种与静止流体相关的问题。
下面将介绍流体静力学方程的应用条件及其在不同领域的具体应用。
流体静力学方程适用于稳定的静止流体系统,即系统中的流体没有运动。
这意味着流体的速度、加速度等都为零,只存在压力和重力。
当流体系统处于平衡状态时,流体静力学方程可以用来描述和分析流体的力学性质。
在建筑工程领域,流体静力学方程被广泛应用于水压力计算。
例如,在水坝工程中,需要计算水坝底部受到的压力,以确保水坝的稳定性。
通过应用流体静力学方程,可以计算出水坝底部受到的水压力,并据此设计水坝的结构和厚度,确保其能够承受水压力的作用。
在航空航天领域,流体静力学方程的应用条件也得到了充分利用。
例如,在航空器的燃油系统中,需要保证燃油能够平稳地供给到发动机。
通过应用流体静力学方程,可以计算出燃油供给系统中的压力分布,并据此设计和优化燃油管道的布局和尺寸,以确保燃油能够稳定地输送到发动机。
在地质学领域,流体静力学方程被用于地下水的流动分析。
地下水是地球内部的一种重要水资源,对于地下水的合理开发和利用具有重要意义。
通过应用流体静力学方程,可以计算地下水的压力分布和流速,进而预测地下水的流动方向和速率。
这对于地下水资源的管理和保护具有重要的参考意义。
除了以上几个领域,流体静力学方程还被广泛应用于液压系统、水污染控制、海洋工程等领域。
在液压系统中,流体静力学方程被用于计算液压缸中的压力和力的分布,以实现液压系统的运动控制。
在水污染控制中,流体静力学方程被用于计算污水处理设备中的压力和流速,以实现污水的处理和净化。
在海洋工程中,流体静力学方程被用于计算海洋结构物受到的水压力和力的分布,以确保结构物的安全性和稳定性。
流体静力学方程在各个领域都有着广泛的应用。
通过应用流体静力学方程,可以计算出流体系统中的压力分布和力的分布,进而实现对流体系统的分析和设计。
流体静力学基本方程式的应用

ρρAC、:ρ9B
:指示液的密度 流体的密度
9
第一节 流体静力学基本方程式
(3)斜管压差计 ❖ 当被测量的流体的压差更小时,可采用斜管压差计。
R'=R/sinα
10
10
第一节 流体静力学基本方程式
2.液位的测量
h =(ρ0-ρ)R/ρ
11
11
5
5
第一节 流体静力学基本方程式
三、流体静力学基本方程式
p = p0 + g h
(1)液体内静压强随液体的深度的增大而增大, 等深处形成等压面。
(2)当液面上方的压力p0有改变时,液体内部各
点的压力p也发生同样大小的改变,称为帕斯卡原
理。
6
第一节 流体静力学基本方程式
四、流体静力学基本方程式的应用 ❖ 1.压力与压力差的测量
第一章 流体流动
目录
第一节 流体静力学基本方程式 第二节 流体流动的基本方程式 第三节 流体在管内的流动 第四节 流速和流量的测量
第一节 流体静力学基本方程式
一、流体的密度
❖ 1.混合液体的密度
1 xwA xwB xwn
m A B
n
❖ 2.混合气体的密度
3
m AxVA A xVB AxVn
(1)U形管压差计 (2)微差压差计 ❖ 2.液位的测量
7
7
图1-3 U型管压差计
第一节 流体静力学基本方程式
(1)U形管压差计
p1- p2=(ρA-ρ)gR
ρA:指示液的密度 ρ: 流体的密度
8
8
第一节 流体静力学基本方程式
(2)微差压差计 ❖ 若所测的压力差很小,可采用微差压差计。
流体静力方程应用
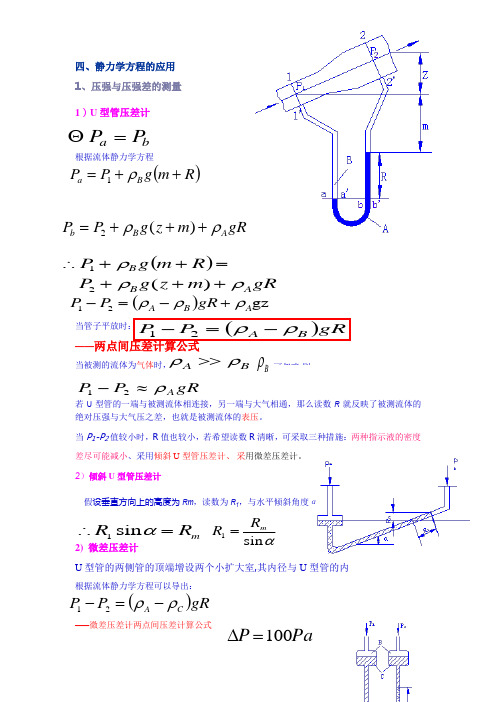
四、静力学方程的应用 1、压强与压强差的测量 1)U 型管压差计根据流体静力学方程当管子平放时: ——两点间压差计算公式当被测的流体为气体时, 若U 型管的一端与被测流体相连接,另一端与大气相通,那么读数R 就反映了被测流体的绝对压强与大气压之差,也就是被测流体的表压。
当P 1-P 2值较小时,R 值也较小,若希望读数R 清晰,可采取三种措施:两种指示液的密度差尽可能减小、采用倾斜U 型管压差计、 采用微差压差计。
2)倾斜U 型管压差计假设垂直方向上的高度为Rm ,读数为R 1,与水平倾斜角度α2) 微差压差计 U 型管的两侧管的顶端增设两个小扩大室,其内径与U 型管的内根据流体静力学方程可以导出: ——微差压差计两点间压差计算公式 ba P P =Θ()R m g P P B a ++=ρ1gRm z g P P A B b ρρ+++=)(2())( 21gR m z g P R m g PA B B ρρρ+++=++∴()gz 21A B A gR P P ρρρ+-=-可忽略,则 B ρB A ρρ>>, gRP P A ρ≈-21()gRP P B A ρρ-=-21m R R =∴αsin 1αsin 1m R R =()gRP P C A ρρ-=-21PaP 100=∆例:用3种压差计测量气体的微小压差试问:1)用普通压差计,以苯为指示液,其读数R 为多少?2)用倾斜U 型管压差计,θ=30°,指示液为苯,其读数R’为多少?3)若用微差压差计,其中加入苯和水两种指示液,扩大 室截面积远远大于U 型管截面积,此时读数R 〃为多少? R 〃为R 的多少倍? 已知:苯的密度 水的密度计算时可忽略气体密度的影响。
解:1)普通管U 型管压差计U 型管的两侧管 3/879m kg c=ρg P RC ρ∆=807.9879100⨯=m 0116.0=。
流体静力学方程的应用条件(一)

流体静力学方程的应用条件(一)流体静力学方程的应用条件1. 理论背景在研究流体行为时,流体静力学是其中的一个重要方面。
流体静力学是研究流体在静止状态下的行为和力学性质的学科。
通过应用流体静力学方程,我们可以分析和解决许多与流体静停止状态有关的问题。
2. 流体静力学方程的概述流体的静平衡在流体静力学中,我们考虑的是流体处于静止状态,并且没有流动的情况。
这意味着流体内部的每一点都保持静止,并且没有速度梯度存在。
流体静力学方程流体静力学方程是描述流体静力学行为的基本方程,它包括了质量守恒、动量守恒和能量守恒定律。
流体静力学方程可以用来计算流体内的压力分布、压力力学、力的传递以及其他与流体在静止状态下相关的物理量。
3. 流体静力学方程的应用条件根据流体静力学方程的性质和适用范围,我们可以得出以下应用条件:•流体应为牛顿流体:流体力学方程适用于牛顿流体,即粘度随剪切速率保持恒定。
如果流体具有非牛顿性质,例如塑性流体或非牛顿粘性流体,流体静力学方程将不再适用。
•流体应为静止状态:流体静力学方程适用于流体处于静止状态下的情况。
如果流体具有流动或速度梯度,流体动力学方程将更适用于分析此类情况。
•流体应为恒定密度流体:流体静力学方程假设流体具有恒定的密度。
如果流体的密度随位置或时间变化,流体静力学方程将不再适用。
•流体应为亚音速流体:流体静力学方程适用于亚音速流体,即流体的速度小于声速。
如果流体处于超音速流动状态,流体动力学方程将更适合分析。
4. 结论流体静力学方程是解决与流体在静态条件下相关问题的基本工具。
然而,我们必须注意应用流体静力学方程的条件,以确保结果的准确性和可靠性。
只有在满足适用条件的情况下,我们才能有效地利用流体静力学方程解决实际问题。
以上是流体静力学方程的应用条件的简要介绍。
通过理解并应用这些条件,我们可以更好地利用流体静力学方程分析和解决与静态流体行为有关的问题。
5. 应用举例下面列举几个典型的应用例子,展示在何种情况下可以应用流体静力学方程:•管道内的压力分布:当液体在管道内静止时,可以使用流体静力学方程来计算管道内的压力分布。
4-第一节 流体静力学方程应用

2、学会应用方程式的步骤并计算简单问题
3、静力学基本方程式的解题思路、方法及应用
教学难点
静力学基本方程式的解题思路、方法及应用
教学方法
习题法
使用教具
多媒体教学平台
板书设计
主要教学内容及步骤
复习:
1、静止流体的特性
2、流体静力学基本方程式的推导及意义
3、应用公式进行计算的方法及简单应用
若U管一端与设备或管道某一截面连接,另一端与大气相通,这时读数R所反映的是管道中某截面处的绝对压强与大气压强之差,即为表压强或真空度,从而可求得该截面的绝压。
二、液面测定:
液柱压差计是于容器底部器壁及液面上方器壁处各开一小孔,用玻璃管将两孔相连接。玻璃管内所示的液面高度即为容器内的液面高度。这种构造(图1-7所示)易于破损,而且不便于远距离观测。
备课时间
授课时间
授课课时
2
授课形式
讲授
授课章节
名称
第一章第一节
四、静力学基本方程式的应用举例
静力学基本方程式的应用
教学目的
1、熟悉静力学基本方程式
2、学会应用方程式的步骤并计算简单问题
3、知道液柱压强计、液面测定的基本原理及
4、通过例题的讲解,进一步熟悉静力学基本方程式的解题思路、方法及应用
教学重点
根据静力学基本方程:PC=P1+(H+R)ρg
PC,=p2+Hρg+RρAg
因C-C,是等压面,PC= PC,
P1+(H+R)ρg = P2+Hρg+RρAg
2、压强的测定:
选1-1,为等压面,P1=P1,
P1= PP1,= Pa + RgρA
第二讲流体静力学基本方程及其应用

第二讲流体静力学基本方程及其应用【学习要求】1.理解流体静力学方程的意义;2.掌握流体静力学方程的应用。
【预习内容】1.在均质流体中,流体所具有的与其所占有的之比称为。
任何流体的密度都随它的和而变化,但对液体的密度影响很小,可忽略,故常称液体为的流体。
2.流体静压力的两个重要特性分别是:(1);(2)。
3.1atm = mmHg = Pa = mH2O【学习内容】一、流体静力学基本方程式1.流体静力学基本方程式的形式p2 = p1+ ρ ( z1—z2 )g 或p2 = p1+ hρg流体静力学方程表明:在重力作用下静止液体内部的变化规律。
即在液体内部任一点的流体静压力等于。
2.流体静力学基本方程式的意义流体静力学方程表明:(1)当作用于流体面上方的压强有变化时;(2)当流体面上方的压强一定时,静止流体内部任一点压强的大小与流体本身的和有关,因此在的的同一液体处,处在都相等。
二、流体静力学基本方程式的应用1.流体进压强的测量(1)U形管压差计①U形管压差计由、及管内指示液组成。
②指示液要与被测流体不,不起,其密度要,通常采用的指示液有、、及等。
③U形管压差计可用来测量压强差,也可以用来测量或。
【典型例题】例1用U形管测量管道中1、2两点的压强差。
已知管内流体是水,指示液是密度为1595 kg/m3的CCl4,压差计读数为40cm,求压强差(p1– p2)。
若管道中的流体是密度为2.5kg/m3的气体,指示液仍为CCl4,U形管读数仍为40cm,则管道中1、2两点的压强差是多少Pa?【例2】某蒸汽锅炉用本题附图中串联的汞-水U形管压差计以测量液面上方的蒸气压。
已知汞液面与基准面的垂直距离分别为h1 = 2.3 m,h2 = 1.2 m,h3 = 2.5 m,h4 = 1.4m,两U形管间的连接管内充满了水。
锅炉中水面与基准面的垂直距离h5 = 3.0m,大气压强p a = 99kPa。
试求锅炉上方水蒸汽的压强p0为若干(Pa)?【随堂练习】1.大气压强为750mmHg时,水面下20m深处水的绝对压强为多少Pa?2.水平导管上的两点接一盛有水银的U形管压差计(如图所示),压差计读数为26mmHg。
流体静力学方程的应用

液面测定
生产中经常需要了解容器内液体的贮存量,或需 要控制设备里液体的液面,因此要对液面进行测定。
有些液面测定方法,是以静力学基本方程为依据的。
确定液封高度
液封的目的:防治气体泄漏、倒流或有毒气体 溢出;有时则是防止压力过高而起到泄压作用, 以保护设备。
安全水封:当设备内压力超过规定值时,气体就 会从水封管排出,以确保设备操作安全。
水封管插入液面下的深度:
h P1
水g
切断水封:正常操作时,水封不灌水,气体可以绕过 隔板出入储罐,需要切断时,向水封内注入一定高度的水, 使隔板进入水的深度大于两侧可能的压差即可。
溢流水封 用水洗涤的气体设备,通常设备内还有气体,洗
涤液在不断流进的同时还会不断地流出,同时还要 保证设备的气体不外泄。
2.斜管压差计
当被测量的流体压力或压差不大时,读数H很小, 为得到精确读数,可采用斜管压差计,此时:
H H
sin
斜管压差计
注意:倾斜角越小,其值越小,则H值放大为H’的倍数越大。
3.微差压差计
由静力学方程可知:
P1 P2 P ( A B )gH
双液柱微差计
对于一定的压差,密度差越小则H越大,所以应该选 择两种密度接近的指示液。
流体静力学方程的应用
㈠ 压力测量
1.U形管液柱压差计
P2
P1
P2
P1
Hale Waihona Puke L HP1=P2两边液面相等
P1>P2
两边液面不等
P2
P1
L ba H
P1>P2
两边液面不等
Pa P1 g(L H ) Pb P2 gL 0 gH
Pa Pb
P1 P2 (0 )gH 0
3 流体静力学基本方程式的应用

p p1 p2 (A C )gR RC g
式中 ΔR=R(d/D)2为小室的液面差,d为U管内径,D为小室内径。
结构:如图示。于容器底部器
壁及液面上方器壁处各开一
小孔,用玻璃管将两孔相连
接。玻璃管内所示的液面高
H
度即为容器内的液面高度。
缺点:易于破损,而且不便于 远距离观测。
(2)液柱压差计:压差法测量液位
结构:于容器或设备外边设一个称为平衡器的小室,用一装有
指示液的U管压差计将容器与平
衡器连通起来,小室内装的液体
与容器内的相同,其液面的高度
维持在容器液面允许到达的最大
高度处。 由: pA' pA
则: g(m h) g(m R) AgR
h A R
m A A’
由此可见,容器内液面越高,h越小,压差计读数R越小;
当容器内的液面达到最大高度时,h为零,压差计读数R亦为零。
(3)鼓泡式液柱测量装置:若容器离操作室较远或埋在地下,
⑤ 复式U形管压差计 应用:适用于压差较大,而测量空间高度有限,这样, 通过串联方式可以在有限高度空间范围内拓宽测量范围。 A(顺置)
指示液ρ0>被测流体ρ,则:
Pa
p0=p4-ρg(h5-h4)
3 1
p4=p3+ρ0g(h3-h4) p3=p2-ρg(h3-h2)
1.2.3 流体静力学基本方程式的应用
流体静力学原理应用非常广泛,它是连通器和液柱压差计 工作原理的基础,还用于容器内液位的测量,液封装置等。解 题的基本要领是正确确定等压面。 1、压强或压强差的测量
流体静力学方程的适用条件(一)

流体静力学方程的适用条件(一)流体静力学方程的适用条件引言流体静力学是研究流体在静力平衡状态下的行为规律的学科,描述了流体静力学方程的适用条件对于理解和解决流体的静态问题非常重要。
适用条件在研究流体静力学方程的适用条件时,需要考虑以下几个方面:1.静态平衡条件–流体必须处于静力平衡状态,即没有加速度和剪切力的存在。
–流体内部各点之间的压强相等,即存在等压面。
这要求流体没有外力或外压作用。
2.宏观尺度–流体静力学方程适用于宏观尺度,即适用于大尺度上对流体进行整体平均的情况。
–该方程不适用于涉及微观尺度或有明显界面效应的情况。
3.不可压缩性–流体静力学方程假设流体是不可压缩的,即流体密度在空间和时间上保持不变。
–在某些特殊情况下,对于可压缩流体,可以通过适当的近似方法将其视为不可压缩流体进行处理。
4.没有动力学效应–流体静力学方程适用于没有动力学效应的情况,即流体中没有涡旋运动或渗透流存在。
总结流体静力学方程的适用条件主要包括静态平衡、宏观尺度、不可压缩性和没有动力学效应等。
在理解和应用流体静力学方程时,我们必须考虑这些条件,并根据具体情况进行适当的近似和简化。
这些适用条件是我们研究和解决流体静态问题的基础。
以上是针对流体静力学方程的适用条件的相关介绍,希望能对读者有所帮助。
应用范围流体静力学方程的适用条件在很多领域都有广泛的应用,包括但不限于以下几个方面:1.工程液压学–在液压系统中,通过流体静力学方程可以计算液压系统中的压力分布、液体高度等参数。
–这有助于优化液压系统的设计和运行,提高系统的效率和安全性。
2.建筑水力学–在水资源工程中,流体静力学方程可用于计算大坝、堤坝和水闸等结构的承压能力。
–这可以帮助工程师评估工程结构的稳定性,并制定相应的安全措施。
3.管道输送–在管道系统中,流体静力学方程可用于计算流体在管道中的流速和压力分布。
–这对于优化管道输送系统的设计和运行非常重要,能够提高流体的输送效率和节约能源。
静力学平衡方程

静力学平衡方程静力学平衡方程静力学平衡方程是物理学中一个重要的概念,是力学中用于描述物体所受外力作用下的静止状态的基本定理。
在数学上,这个方程被表达为:ΣF = 0其中ΣF表示作用在物体上的所有力的矢量和,等于零表示物体处于静止状态。
这个方程包含了牛顿第一定律,即一个物体如果受到的合力为零,则其将保持静止或匀速直线运动。
在工程学和物理学中,这个方程被广泛应用于杠杆、支撑结构、桥梁等工程中。
工程师通过运用这个方程来计算物体能否保持平衡,以及所需要的支撑结构大小和材料强度等参数。
杠杆原理杠杆原理是静力学平衡方程中应用最为广泛的应用之一,特别是在机械和结构工程中。
杠杆按位置分为一类,二类和三类。
在一类杠杆中,力和支点的位置关系导致了杠杆的刚性比较小,所以在外力相等的情况下,较小力的杆杆就可以产生比较大的力矩,从而达到平衡的效果。
例如,一个人试图从一个杆子上旋起一个沉重的箱子。
这个箱子对于人来说可能是太重了,但当他用一个搬运杆来支撑这个箱子时,他只需要用比箱子重的更小的力来旋转搬运杆,从而达到平衡的效果。
支撑结构另一个重要的应用是支撑结构。
在物理学和工程学中,支撑结构是指支撑物体并通过承受一定负载来保持稳定平衡的任何物体。
举个例子,一个高楼需要一定的支撑结构来承受地心引力以及风力等对建筑的作用力。
支撑结构必须满足静力学平衡方程,使支撑物体的重力和其他作用力等于零。
通过分析材料的强度和平衡方程,工程师可以计算出所需的支撑结构大小和材料强度,从而设计出完美的支撑结构。
桥梁桥梁结构也需要应用静力学平衡方程来保持稳定。
桥梁通常是由高低不平的地面或水体中跨过而设计的。
在设计桥梁时,需要考虑桥梁的重量、材料强度和内部支撑结构,以确保桥梁稳定平衡。
在桥梁支撑结构的设计中,静力学平衡方程是一个重要的工具。
通过计算桥墩、悬挂和支撑结构对于承受负载所产生的力和力矩,工程师可以确定支撑结构的安全度,从而设计桥梁的内部结构。
总结在物理学和工程学中,静力学平衡方程是至关重要的一个概念。
静力学方程

p1 = p0
等于液面 压强加上
z1
–
z2
=
h液面到该
点液柱产
h - 距液生面的深压度强 o
则: p2 = p0 + gh (2)p1 Fra bibliotek0z1
GG
z2 p2
h
o
基准面
SHANDONG UNIVERSITY
Yang Yanzhao
二、结论
因流体仅处 于重力场中
1. p0一定,p2与ρ、h 有关;
p0
p1 h
G
z1 z2 p2
下端面:p2A ↑
o
o
基准面
重 力:ρgA( z1- z2 )↓ A — 流体柱横截面积
Yang Yanzhao
SHANDONG UNIVERSITY
静止:∑F⊥ = 0
即: p2 = p1+ g ( z1 – z2 ) (1)
静止流体
上端面 → 液面内部任意
点的压强,
B A
R2
A R
(a)
(b)
2. 图(b)中 R 值表示什么?
SHANDONG UNIVERSITY
(2) 倒U型压差计(a)
R
Yang Yanzhao
p1 p2
B
R
(a)
(3) 微差压差计(b)
A
(b)
p1- p2 = R ( A - B ) g
2. 液位测量(a)
Yang Yanzhao
SHANDONG UNIVERSITY
气柜
p大
h1
h2
h
AB
(a)
(b)
3. 液封(b) 若要 p ≦ p规,h实___h计
静力学基本方程及其应用

p FN A
液体静压力特性: (1)液体静压力的方向总是沿着作用面的内法线方向。 (2)静止液体中任何一点所受到各个方向压力都相等。
二、 液体静力学基本方程
方 取研究对象:微圆柱体
程
推 受力分析:pA p0A ghA
导
A
静力学基本方程: p p0 gh
静止液体中任意点的静压力是液体表面上的压力和
三、帕斯卡原理
容器内的液 体各点压力为
PW F A2 A1
在密闭容器内,施加于静止液体上的压力将以 等值同时传到液体内部所有各点。
【例2】 图所示为相互连通的两个 F
G
液压缸,已知大缸内径D = 100mm
,小缸内径d = 20mm,大活塞上放
一质量为5 000kg的物体。试求在小 d
D
活塞上所加的力F有多大才能使大活
106 N/m2
根据静力学基本方程,深度为h处的液体压力为
p P0 gh 106 900 9.8 0.5
1.004 4 106 (N/m2 ) 106 (Pa)
结论:液体在受外界压力作用的情况下,液体自重所形成的那 部分压力ρgh相对很小,在液压系统中常可忽略不计。 因而可近似认为整个液体内部的压力是相等的。
【例1】 如图所示,容器内盛有油液。已 知油的密度ρ = 900kg/m3,活塞上的作用 力F = 1 000N,活塞的面积A = 1×10−3m2 ,假设活塞的重量忽略不计。问活塞下方深 度为h = 0.5m处的压力等于多少?
解:活塞与液体接触面上的压力均匀分布,有
P0
F A
1 000N 1103 m2
液体静力学
研究内容:研究液体处于静止状态的力学规律和这 些规律的实际应用。
静力学方程表达式

静力学方程表达式静力学方程是描述物体静止或平衡状态的力学方程。
它是根据牛顿第二定律和物体平衡的条件推导出来的。
在静力学中,我们将物体看作一个质点,忽略其大小和形状,只考虑物体所受的力和力的作用点。
静力学方程的表达式为力的合力等于零。
静力学方程的表达式可以写作ΣF = 0,其中ΣF表示力的合力。
这个方程表明,在物体处于静止或平衡状态时,所有作用在物体上的力的合力等于零。
这意味着所有作用在物体上的力相互抵消,物体不会发生加速度或者改变其状态。
静力学方程的应用非常广泛。
在工程学中,我们可以利用静力学方程来解决各种物体平衡的问题。
例如,当我们需要计算一个悬挂在天花板上的吊灯所受的力时,我们可以利用静力学方程来分析吊灯所受的重力和悬挂绳所施加的力,从而确定吊灯是否处于平衡状态。
静力学方程也可以用来解决斜面上物体的平衡问题。
当一个物体放置在斜面上时,我们可以利用静力学方程来分析物体所受的重力和斜面对物体的支持力,从而确定物体是否会滑动或者停留在斜面上。
静力学方程还可以应用于桥梁和建筑物的设计中。
在设计桥梁或者建筑物时,我们需要确保结构的平衡,以防止其倒塌或者发生变形。
通过应用静力学方程,我们可以计算出各个支撑点所受的力,并且合理安排结构的材料和支撑方式,以确保结构的稳定性和安全性。
静力学方程的应用不仅仅局限于实际问题的求解,它还在物理学的理论研究中发挥着重要作用。
在物理学中,我们可以利用静力学方程来推导出其他重要的物理定律和方程。
例如,牛顿第三定律可以通过静力学方程来推导。
根据牛顿第三定律,当两个物体相互作用时,它们所受的力大小相等、方向相反。
通过应用静力学方程,我们可以推导出这个定律,并且解释为什么两个相互作用的物体会有相等大小、方向相反的力。
静力学方程是力学中一个非常基础且重要的方程。
通过应用静力学方程,我们可以解决各种与物体平衡相关的问题,并且推导出更多的物理定律和方程。
因此,掌握和理解静力学方程对于力学和物理学的学习非常关键。
3、静力学例子

因为r2与r1相差不大,所以(r2-r1)很小,这样,即使(p1-p2)很小,读数R也可能较大。
例1-2 当被测压差较小时,为使压
差计读数较大,以减小测量中人为因 素造成的相对误差,也常采用倾斜式 压差计,其结构如图1-9所示。试求 若被测流体压力p1=1.014′105Pa (绝压),p2端通大气,大气压为 1.013′105Pa,管的倾斜角a=10°, 指示液为酒精溶液,其密度 r0=810kg/m3,则读数R¢为多少cm? 若将右管垂直放置,读数又为多少 cm?
(2)双液柱压差计
双液柱压差计又称微差压差计。由式1-13可见,若所测广 义压力头之差很小,则U形压差计的读数R可能很小,读数的相 对误差就会很大,这时若采用如图1-8所示的双液柱压差计将 会使读数放大几倍或更多。该压差计的特点是在U形管两侧增 设两个小室,使小室的横截面积远大于管横截面积,且在小室 和U形管中分别装入两种互不相溶而密度又相差不大的指示 液,设其密度分别为r1、r2,且r1略小于r2。 将双液柱压差计与两测压点相连,在被测压差作用下,两侧指 示液显示出高度差。因为小室截面积足够大,故小室内液面高 度变化可忽略不计。由静力学原理可推知:
解 (1)由静力学原理可知:
将p1=1.014′105Pa, p2=1.013′105Pa,r0=810kg/m3,a=10°代入得:
=0.073m=7.3cm (2)若管垂直放置,则读数
=0.013m=1.3cm 可见,倾斜角为10°时,读数放大了7.3/1.3=5.6倍。
上一页 化工原理网络教程
如图1-6所示,U形管一端通大气,另一端与 被测压力容器A相通。在U形管中注入某种指 示液,指示液密度须大于容器A中被测流体 的密度,且与被测流体不互溶、不发生化学 反应。 设U形管中指示液液面高度差为R,指示液密 度为r0,被测流体密度为r,则由静力学方 程可得:
流体静力学基本方程式的适用条件是

流体静力学基本方程式的适用条件流体静力学是研究静止的流体力学现象的学科,主要研究流体静力学基本方程式的解法和应用。
流体静力学基本方程式包括质量守恒方程、动量守恒方程和能量守恒方程。
这些方程式适用于静止的流体,即不受外力而处于平衡状态的流体。
下面我们将详细介绍流体静力学基本方程式的适用条件。
一、质量守恒方程质量守恒方程是研究流体静力学的基本方程式之一,它描述了流体内质量的守恒。
质量守恒方程的适用条件如下:1. 流体是静止的,即流体的速度为零。
2. 流体是连续的,即流体是连续的物质,不存在空隙。
3. 流体是不可压缩的,即流体的密度不随时间和位置的变化而变化。
4. 流体是单相的,即流体内的物理和化学性质是均匀的。
二、动量守恒方程动量守恒方程是研究流体静力学的基本方程式之一,它描述了流体内动量的守恒。
动量守恒方程的适用条件如下:1. 流体是静止的,即流体的速度为零。
2. 流体是连续的,即流体是连续的物质,不存在空隙。
3. 流体是不可压缩的,即流体的密度不随时间和位置的变化而变化。
4. 流体是单相的,即流体内的物理和化学性质是均匀的。
5. 流体是粘性的,即流体内存在摩擦力。
三、能量守恒方程能量守恒方程是研究流体静力学的基本方程式之一,它描述了流体内能量的守恒。
能量守恒方程的适用条件如下:1. 流体是静止的,即流体的速度为零。
2. 流体是连续的,即流体是连续的物质,不存在空隙。
3. 流体是不可压缩的,即流体的密度不随时间和位置的变化而变化。
4. 流体是单相的,即流体内的物理和化学性质是均匀的。
5. 流体是绝热的,即流体内不存在热传导。
以上是流体静力学基本方程式的适用条件,下面我们将通过实例来进一步说明。
实例:一艘船停泊在湖面上,船底面积为10平方米,船重为50吨,水的密度为1000千克/立方米。
求船底受到的水的压力。
解析:根据质量守恒方程可知,流体在静止状态下,密度不随位置和时间的变化而变化,因此可以将水的密度视为恒定值1000千克/立方米。
工程流体力学2.4流体静力学基本方程的应用
第四节 流体静力学基本方程的应用
一、测压管 适用范围
测压管适用于测量较小的压强,但不适合测真空。 一般不超过9800Pa,相当于1mH2O。
如果被测压强较高,则需加长测压管的长度,使用 就很不方便。
测压管中的工作介质就是被测容器中的流体,所以 测压管只能用于测量液体的压强。
第四节 流体静力学基本方程的应用
M点的绝对压强为
p pa gh
M点的计示压强为 pe p pa gh
用测得的液柱高度h,可得到容器中液体的计示压强 及绝对压强。
第第四四节节 流流体体静静力力学学基基本本方方程程的的应应用用
一、测压管
测量容器中的真空
pV pa p gh
pv
h
pa
一、测压管
1.结构 测压管是一种最简单的液柱式测压计,是以液柱高度 为表征测量点压强的连通管。一端与被测点容器壁的孔口 相连,另一端直接和大气相通的直管。
为了减少毛细现象所造成的误差,采用一根内径为 10mm左右的直玻璃管。
图(2-9)测压管
第四节 流体静力学基本方程的应用
一、测压管 2.测量原理
n 1
sin
当Θ=300时
h2 Lsin30
1 2
L
压强差的液柱读数放大了两倍;
当Θ=100时
n 1/ sin10 5.75 倾斜微压计可使读数更精确。
但若Θ过小(如小于50)时,倾斜玻璃管内的液体将 产生较大的波动,位置不易确定。
应用静力学基本方程式的步骤:
(1)选择正确的等压面
当A、s和ρ 一定时,K仅是倾斜角Θ 的函数。改变 Θ 的大小,可得到不同的K值,即将被测压强差的L值 放大了不同的倍数。倾斜微压计的放大倍数
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
表压强=绝对压强-大气压强 真空度=大气压强-绝对压强=-表压
3)真空度: 真空表的读数
绝对压强、真空度、表压强的关系为
A 表
压
强 大气压强线
真空度
绝 对
B
压
绝对压强
强
绝对零压线
当用表压或真空度来表示压强时,应分别注明。
如:4×103Pa(真空度)、200KPa(表压)。
(mmH2O,mmHg等)。
换算关系为: 1atm 1.033kgf / cm2 760mmHg 10.33mH2O 1.0133105 Pa
1工程大气压 1kgf / cm2 735.6mmHg 10mH2O 9.807104 Pa
2、压强的表示方法
1)绝对压强(绝压): 流体体系的真实压强称为绝对压强。
流体的特征是分子之间的内聚力极小,几乎有无 限的流动性,而且可以几乎毫无阻力地将其形状改变 。当流速低于声速时,气体和液体的流动具有相同的 规律。
一般说来,液体的形状与容器相同,具有一定的 自由表面,其体积几乎不随压强和温度而改变。与之 相反,气体的形状与容器完全相同,完全充满整个容 器,其体积随压强和温度的变化而有明显改变。流体 的体积随压强和温度而变的这个性质,称为流体的压 缩性。
第一章 流体流动
第 一 节 流体静止的基本方程
概述
流体是指具有流动性的物体,包括液体和气体。 研究流体平衡和运动宏观规律的科学称为流体力学。 流体力学分为流体静力学和流体动力学。
化工生产中所处理的原料、中间体和产品,大多 数是流体。按生产工艺要求,制造产品时往往把它们 依次输送到各设备内,进行药物反应或物理变化,制 成的产品又常需要输送到贮罐内贮存。过程进行的好 坏、动力消耗及设备的投资都与流体的流动状态密切 相关。
4 C水
4C水 1000kg / m3
例题分析
1、下列叙述正确的是( ) A.单元操作一定是物理性操作 B.单元操作作用于不同化工产品生产过程时,基本原理不相同。 C.物系在自然变化时,如任其发展,未必能达到平衡状态. D.向某过程输入的能量等于向某过程输出的能量
例题分析
2、O2 在300K和5Mpa时的密度为多少?
3。 在标准大气压下下列四个压强,绝对压强最高的是( )
A)10kPa(表); B)10kPa(真); C)10kPa;
D)100kPa。
4、已知某地大气压为标准大气压,某生产设备上真空表读数
10mmHg,则以下正确的是( )
A 10.2米水柱
B、绝对压力750mmHg
C、绝对压力1.02*105
D、表压750mmHg
当混合物气体可视为理想气体时, ——气体混合物密度计算式
m
PM m RT
——理想气体混合物密度计算式
5.与密度相关的几个物理量
1)比容:单位质量的流体所具有的体积,用υ表示,单位
为m3/kg。
在数值上:
1
2)比重(相对密度):某物质的密度与4℃下的水的密度的比
值,用 d合气在270C和150KPa时的密度。 混合气中乙烯的体积分数 40% 。
二、流体的静压强
1、压强的定义
流体的单位表面积上所受的压力,称为流体的静压强,简 称压强。
p P A
SI制单位:N/m2,即Pa。 其它常用单位有: atm(标准大气压)、工程大气压kgf/cm2;流体柱高度
一、流体的密度
1. 密度定义
单位体积的流体所具有的质量,ρ;
m
V
2. 影响ρ的主要因素
SI单位kg/m3。
任何流体的密度,都随它的温度和压强变化。但压强对液体的密度 影响很小,可忽略不计,故常称液体为不可压缩的流体。
3.气体密度的计算
理想气体在标况下的密度为:
0
M 22.4
例如:标况下的空气,
例题分析
1、某设备A处表压30KPa,B处真空度70Pa,A,B两处相比( )
A 处绝压低40KPa
B处绝压低40Kpa
C.处绝压高100Kpa
D.处绝压高100KPa
2.某设备上真空表读数为0.09MPa,若当地大气压强为0.1MPa,
则设备内绝对压强为___。
A)101.33kPa; B)10kPa; C)0.91kPa; D)90kPa。
0
M 22.4
29 22.4
1.29kg
/
m3
一定温度、压强下的密度:
0
p p0
T0 T
PV nRT m nM PVM PM
V V RTV RT
4.混合物的密度
1)液体混合物的密度ρm
取1kg液体,令液体混合物中各组分的质量分率分别为:
xwA、xwB、、xwn ,
其中xwi
mi m总
当m总 1kg时,xwi mi
假设混合后总体积不变,
V总
xwA
1
xwB
2
xwn
n
m总
m
1 xwA xwB xwn ——液体混合物密度计算式
m 1 2
n
2)气体混合物的密度
取1m3 的气体为基准,令各组分的体积分率为:xvA,xvB,…,xVn,
三、流体静力学方程
1、方程的推导
在1-1’截面受到垂直向下的压力 在2-2’ 截面受到垂直向上的压力: 小液柱本身所受的重力:
F1 p1A
F2 p2 A
W mg Vg Az1 z2 g
因为小液柱处于静止状态,
F 0
F2 F1 Az1 z1 g 0
其中:
xVi
Vi V总
i =1, 2, …., n
当V总=1m3时,
由 m 知,
V
混合物中各组分的质量为: 1xVA , 2xVB ,......, n xVn
若混合前后,气体的质量不变,m总 1x1 2x2 ....... nxn mV总
当V总=1m3时,
m 1x1 2x2 ...... n xn
两边同时除A
F2 A
F1 A
gz1
z2
0
p2 p1 gz1 z2 0
p2 p1 gz1 z2
令 z1 z2 h 则得: p2 p1 gh
若取液柱的上底面在液面上,并设液面上方的压强为P0,
取下底面在距离液面h处,作用在它上面的压强为P
