origin拟合准一年级准二年级动力学方程详解
origin拟合准一级准二级动力学方程详解8050
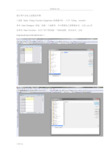
建立用户自定义函数的步骤:1.选择Tools: Fitting Function Organizer (快捷键F9) ,打开Fitting function单击New Category 按钮,创建一个函数类,可以根据自己需要重命名,比如yxz.然后单击New Function,在这个类下面创建一个新的函数,然后命名,比如thepseudosecondorderkinetic 1:2. 对该函数进行简短的描述,Brief Description栏输入:To used for the pseudo second order kinetic fitting,定义函数所需参数,ParameterNames:a,k;输入函数方程。
Function 栏输入需编写的方程:y=((a^2)*k*x)/(1+a*k*x) 这个方程的逻辑关系一定要对!3.然后进行点击Function 右侧的按钮4.编译正确是前提是:方程正确,方程中的相关参数在方程之前进行了创建,参数声明和方程建立完成之后,单击进入编译界面,单击Compile5.当出现上图红框中文字是,证明公式定义成功,否则失败!须重新定义。
6.在file中单击save,然后单击return to dialog,再单击OK。
7.至此,用户自定义函数的建立已经完成。
二、自定义拟合函数的使用:1先建立原文件图用点格式绘图2.完成后点击工具栏里的Analysis----Fitting----3. 选择刚建立的yxz 下的thepseudosecondorderkinetic 1 公式。
4. 点击Parameters5.在参数栏中分别设置a和k 的初始值(可以根据经验任意设置),设置数值是只需在value 这一栏双击鼠标,就可以输入数据!6.随后点击单击一次拟合之后,得到以下结果:7.拟合并不很理想,然后直接拟合到收敛,可以看到拟合结果满意,单击OK:拟合到收敛8 拟合完成结果如图9.拟合曲线数据点,点击上图中Fit NLCURvel 输出10.可以根据上述拟合数据作图。
origin拟合一级动力学方程

origin拟合一级动力学方程
本文介绍了使用Origin软件对一级动力学方程进行拟合的方法和步骤。
首先介绍了一级动力学方程的基本形式和含义,然后详细讲解了如何在Origin中建立数据表格、绘制曲线、选择合适的拟合函数、设置拟合参数和条件、进行拟合优度检验等步骤。
最后,以实例演示了如何利用Origin进行一级动力学方程的拟合,并给出了结果分析和讨论。
本文旨在帮助读者更好地掌握使用Origin进行数据拟合的方法和技巧,以及应用一级动力学方程进行数据处理和分析的基本原理和应用场景。
- 1 -。
origin拟合准一级准二级动力学方程详解

建立用户自定义函数得步骤:1、选择Tools: Fitting Function Organizer(快捷键F9) ,打开Fittingfunctionorganizer、单击New Category按钮,创建一个函数类,可以根据自己需要重命名,比如yxz、然后单击New Function,在这个类下面创建一个新得函数,然后命名,比如thepseudosecondorderkinetic 1:2、对该函数进行简短得描述,Brief Description栏输入:To used for the pseudo secondorder kineticfitting,定义函数所需参数,ParameterNames:a,k;输入函数方程。
Function 栏输入需编写得方程:y=((a^2)*k*x)/(1+a*k*x)这个方程得逻辑关系一定要对!3、然后进行点击Function右侧得按钮4、编译正确就是前提就是:方程正确,方程中得相关参数在方程之前进行了创建,参数声明与方程建立完成之后,单击进入编译界面,单击pile5、当出现上图红框中文字就是,证明公式定义成功,否则失败!须重新定义。
6、在file中单击save,然后单击return to dialog,再单击OK.7、至此,用户自定义函数得建立已经完成.二、自定义拟合函数得使用:1先建立原文件图用点格式绘图2、完成后点击工具栏里得Analysis-———Fitting---—3、选择刚建立得yxz下得thepseudosecondorderkinetic 1 公式.4、点击Parameters5、在参数栏中分别设置a与k得初始值(可以根据经验任意设置),设置数值就是只需在value 这一栏双击鼠标,就可以输入数据!6、随后点击单击一次拟合之后,得到以下结果:7、拟合并不很理想,然后直接拟合到收敛,可以瞧到拟合结果满意,单击OK:拟合到收敛8拟合完成结果如图Array 9、拟合曲线数据点,点击上图中Fit NLCURvel输出10、可以根据上述拟合数据作图。
origin拟合准一级准二级动力学方程详解之欧阳数创编

建立用户自定义函数的步骤:时间:2021.03.02 创作:欧阳数1.选择 Tools: Fitting Function Organizer (快捷键F9) ,打开 Fitting function organizer. 单击 New Category 按钮,创建一个函数类,可以根据自己需要重命名,比如 yxz.然后单击 New Function,在这个类下面创建一个新的函数,然后命名,比如thepseudosecondorderkinetic 1:2. 对该函数进行简短的描述,Brief Description栏输入:To used for the pseudo second order kinetic fitting,定义函数所需参数,ParameterNames:a,k;输入函数方程。
Function 栏输入需编写的方程:y=((a^2)*k*x)/(1+a*k*x) 这个方程的逻辑关系一定要对!3.然后进行点击 Function 右侧的按钮4.编译正确是前提是:方程正确,方程中的相关参数在方程之前进行了创建,参数声明和方程建立完成之后,单击进入编译界面,单击Compile5.当出现上图红框中文字是,证明公式定义成功,否则失败!须重新定义。
6.在file中单击 save,然后单击return to dialog,再单击OK。
7.至此,用户自定义函数的建立已经完成。
二、自定义拟合函数的使用:1先建立原文件图用点格式绘图2. 完成后点击工具栏里的AnalysisFitting3. 选择刚建立的yxz 下的thepseudosecondorderkinetic 1 公式。
4. 点击 Parameters5.在参数栏中分别设置 a和k 的初始值(可以根据经验任意设置),设置数值是只需在 value 这一栏双击鼠标,就可以输入数据!6.随后点击单击一次拟合之后,得到以下结果:7.拟合并不很理想,然后直接拟合到收敛,可以看到拟合结果满意,单击OK:拟合到收敛8 拟合完成结果如图9.拟合曲线数据点,点击上图中 Fit NLCURvel 输出10.可以根据上述拟合数据作图。
origin拟合一级动力学方程

origin拟合一级动力学方程
本文将介绍使用Origin软件拟合一级动力学方程的方法。
动力学方程通常用于描述化学反应的速率与反应物浓度的关系。
一级动力学方程是其中一种常见的形式,它表达了反应速率与反应物浓度的线性关系,可表示为:
r = k[A]
其中,r为反应速率,k为速率常数,[A]为反应物A的浓度。
首先,我们需要准备实验数据。
可以在实验室内进行一系列反应实验,记录反应物浓度与时间的变化,然后根据反应速率公式计算出每个实验点的反应速率。
将这些数据输入到Origin软件中,并绘制出反应速率与[A]之间的关系图。
接下来,我们可以使用Origin软件中的Nonlinear Curve Fit 功能来拟合一级动力学方程。
选择Function Fitting窗口中的
'Nonlinear Curve Fit'选项卡,然后选择一级动力学方程作为拟合的函数形式。
根据实验数据的单位和量级,设定参数初值和边界条件,然后点击Fit按钮进行拟合。
Origin软件会自动计算出最优拟合结果,并绘制出拟合曲线和残差图。
最后,我们可以根据拟合结果来分析反应速率与反应物浓度之间的关系、预测反应速率的变化趋势,以及评估实验数据的可靠性和精度。
总之,使用Origin软件拟合一级动力学方程是一种简单、直观、有效的方法,可用于研究化学反应的速率与反应物浓度的关系,为化
学反应动力学研究提供了有力的工具。
origin一级和二级动力学方程

origin一级和二级动力学方程动力学方程是描述物体在运动状态下受到的外力、运动状态和时间的关系的数学方程。
通常,动力学方程可以分为一级和二级两类。
一级动力学方程描述的是物体的速度与外力之间的关系。
对于质量为m的物体而言,其速度v可以通过牛顿第二定律来描述,即F = ma。
其中F表示物体所受的合外力,a表示物体的加速度。
根据速度的定义v = ds/dt,其中s表示物体在某一时刻的位移,t表示时间,将速度表示为对位移s对时间t的导数,可以得到:dv/dt = d^2s/dt^2 = a这就是一级动力学方程,也叫牛顿第二定律的微分形式。
它表示了加速度与外力之间的关系。
一级动力学方程的求解方法有多种,最常用的是将其转化为一维的运动方程进行求解。
例如,对于一个弹簧振子来说,其一级动力学方程可以表示为:m(d^2x/dt^2) = -kx其中m表示质量,k表示劲度系数,x表示振子的位移。
该方程可以通过求解二阶常微分方程来得到振子的运动规律。
除了一级动力学方程,还存在二级动力学方程。
二级动力学方程描述的是物体的位移与外力之间的关系。
对于质量为m的物体而言,其位移x可以通过牛顿第二定律来描述,即F = ma。
将位移表示为对速度v对时间t的积分,可以得到:dx/dt = v再将速度表示为对加速度a对时间t的积分,可以得到:d^2x/dt^2 = a这就是二级动力学方程,也叫牛顿第二定律的积分形式。
它表示了位移与外力之间的关系。
二级动力学方程的求解方法与一级动力学方程类似,可以将其转化为一维的运动方程进行求解。
例如,对于一个自由下落的物体来说,其二级动力学方程可以表示为:d^2y/dt^2 = -g其中g表示重力加速度,y表示物体的垂直位移。
该方程可以通过求解二阶常微分方程来得到物体的下落规律。
总之,一级动力学方程描述的是速度与外力之间的关系,而二级动力学方程描述的是位移与外力之间的关系。
这两类方程在物体运动的研究中具有广泛的应用,通过求解它们可以得到物体的运动规律,为科学研究和工程实践提供重要的理论基础。
origin拟合准一次方程

origin拟合准一次方程在数学学习中,我们会遇到很多需要拟合的问题,比如拟合一个折线图、散点图等等。
其中,中学数学课程中涉及到比较多的是拟合一次函数(即直线)。
今天我们就来介绍一种拟合一次函数的方法——“origin拟合准一次方程”。
所谓“origin”就是一款数据分析和绘图软件,也是一款统计分析软件。
在该软件中,有一个很方便的拟合准一次方程的功能。
通过这个功能,我们可以轻松地将给定数据拟合成一条直线,并得出斜率和截距。
以下是具体的步骤:第一步:准备数据首先,我们需要准备一组数据,这组数据可以是统计年报上的数据,也可以是我们个人或者团队某一个领域的调研所得数据。
不同的数据需要使用不同的方法来处理。
比如,对于折线图,我们需要比较平滑地处理数据,对于散点图,我们需要将散点图上的各点进行线性拟合之后,得出拟合一次函数。
总之,所有的数据需要先经过处理,得到符合拟合条件的数据。
第二步:导入数据将处理好的数据导入到“origin”软件中。
导入方式有多种,可以在软件中新建一页,使用“导入”的方式将数据导入。
也可以将数据保存在Excel、txt等文件中,再在软件中打开这个文件。
第三步:可视化数据将数据进行可视化处理,可以画散点图、折线图、柱形图等等。
也可以根据自己的需要,选择不同的图形进行可视化展示。
第四步:进行拟合点击菜单栏中的“分析”选项,再选择“拟合”选项。
如果想要进行一次函数的拟合,需要在拟合选项中选择“线性拟合”,设置拟合的类型为“一次函数”。
这时,我们就可以得出拟合的直线方程。
第五步:检验拟合效果通过R方值检验拟合效果。
R方值表示实际数据与拟合直线之间的差异程度。
若R方值越大,则说明实际数据与拟合直线之间的差异越小,拟合效果越好。
一般来说,R方值大于0.8或0.9就可以认为拟合效果很好了。
以上就是利用“origin拟合准一次方程”的一般流程。
总之,该方法操作简单,效率高,是一种非常实用的拟合方式。
准二级动力学origin拟合

准二级动力学origin拟合
动力学方程是描述物理系统随时间演化规律的数学模型,它在物
理学和工程学等领域中具有广泛的应用。
而动力学origin拟合则是针
对动力学方程的一种特殊拟合方法,它可以实现基于实验数据拟合模
型参数的目的,从而为实验研究提供有力的支持。
动力学origin拟合分为一级和二级两种,其中二级动力学
origin拟合则是在一级动力学origin拟合的基础上,引入了更多的参数用于描述系统的复杂动态行为。
与一级动力学origin拟合相比,二级动力学origin拟合可以更
加准确地刻画系统的行为特征,如反应速率、反应机理和反应动力学等。
同时,它还可以对多个过程进行拟合,包括物质的转化、反应和
传输等。
这些拟合结果可以帮助研究者更好地理解实验数据和实际过
程中所涉及的物理和化学机制。
在进行二级动力学origin拟合时,通常需要选择适当的动力学
方程作为拟合模型,并考虑系统中各种参数之间的相互关系。
此外,
还需要对实验数据进行分析和处理,以便更好地反映系统的真实状态。
总之,二级动力学origin拟合是一种非常有价值的研究方法,
它可以帮助研究者更好地理解复杂系统的行为特征。
未来,随着数据
科学和计算力的进一步发展,这种拟合方法的应用将会越来越广泛,
为各个领域的研究带来更多的突破和进展。
准二级动力学方程origin拟合

准二级动力学方程origin拟合准二级动力学方程拟合是数据分析和统计学中非常重要的一种方法,它通常用来描述一些复杂的物理、化学和生物过程。
在很多实际应用中,该方法常常被用来预测某些数据集的行为模式和趋势性。
下文将围绕准二级动力学方程拟合,分步骤阐述其原理和拟合过程。
一、准二级动力学方程的定义准二级方程通常被定义为一个解析式,其中包含参数a、b、c和d,形式如下:y(t) = a/(b+t)^c + d其中y(t)代表某个物理量在时刻t的值,a、b、c和d都是未知参数,需要通过数据拟合获得。
二、拟合过程在实际应用中,我们通常会将若干个数据点代入准二级方程中,使用最小二乘法或其他拟合技巧来计算出参数a、b、c和d的值。
这个过程可以简单分为以下几个步骤:1. 数据预处理:对于任何数据分析任务,数据预处理都是至关重要的一步。
在进行准二级方程拟合时,我们需要先将数据进行预处理,如去除噪声,平滑数据等。
2. 数据建模:在进行准二级方程拟合之前,我们需要先将数据转化为可供分析的形式。
通常,我们需要将所有的自变量和因变量转化为对数形式,这样才能做到线性拟合。
3. 拟合过程:在得到数据模型后,我们需要使用拟合算法来确定模型的参数值。
对于准二级方程,我们通常采用非线性最小二乘算法来进行拟合。
这个过程中,我们需要指定初始值并确保算法能够顺利找到拟合值域。
4. 参数评价:在进行准二级方程拟合时,我们需要使用各种评价指标来衡量该模型的准确性和可信度。
这些指标通常包括拟合误差、均方根误差、决定系数等等。
5. 结果解读:最后,我们需要对拟合结果进行解读,确定该模型是否具有实用性和可靠性。
如果需要,我们还可以利用该模型进行预测和优化。
三、应用领域准二级动力学方程拟合在众多领域中都有广泛应用。
其中包括:1. 化学动力学:准二级方程可以被用来描述各种化学反应的速率与浓度之间的关系,帮助化学家优化反应过程和预测反应行为。
2. 生物学:准二级方程也被广泛用于分析细菌生长、细胞增殖等生命科学问题,帮助生物学家了解生物过程的动力学本质。
origin拟合准二级动力学方程

origin拟合准二级动力学方程
Origin是一款科学绘图软件,可以用于数据分析和拟合。
准二级动力学方程是描述快速反应动力学的方程之一,其形式为:
d[A]/dt = k([A]0 - [A])^2
其中,[A]是反应物的浓度,t是时间,k是反应速率常数,[A]0是反应物的初始浓度。
在Origin中,拟合准二级动力学方程可以通过以下步骤完成:
1. 打开Origin软件,并导入数据文件。
2. 选择数据,并打开拟合窗口。
3. 在拟合窗口中选择“非线性拟合”选项。
4. 在拟合函数列表中选择准二级动力学方程。
5. 进行参数设置,包括起始参数、参数界限等。
6. 进行拟合,并查看拟合结果和拟合曲线。
7. 分析拟合结果,包括参数值、相关系数、拟合优度等。
需要注意的是,拟合准二级动力学方程需要有足够的数据点和反应速率常数的估计值,否则拟合结果可能不准确。
同时,拟合结果也需要进行统计分析和验证,
以确保其可靠性和可重复性。
origin准一级动力学方程拟合

origin准一级动力学方程拟合以origin准一级动力学方程拟合为标题的文章:原始准一级动力学方程是动力学中的基本方程之一,用于描述物体或系统的运动状态和变化。
它是基于牛顿第二定律推导而来的,能够准确地描述物体在受力作用下的运动规律。
动力学是研究物体运动的学科,通过建立数学模型,用方程式来描述物体的运动。
原始准一级动力学方程是其中的一个重要方程。
它的形式可以表示为:F = ma,其中F为物体所受的合力,m为物体的质量,a为物体的加速度。
这个方程的物理意义非常明确。
它表明物体所受的合力与物体的质量和加速度成正比。
当物体的质量增加时,所受的合力也会增加;当物体的加速度增加时,所受的合力也会增加。
因此,通过测量物体的质量和加速度,我们可以计算出物体所受的合力。
原始准一级动力学方程在物理学中有着广泛的应用。
例如,在机械工程中,我们可以利用这个方程来计算物体所受的力,并设计出合适的机械结构。
在天体物理学中,我们可以利用这个方程来研究行星的运动规律。
在生物学中,我们可以利用这个方程来研究动物的运动方式。
除了原始准一级动力学方程,还有其他几个重要的动力学方程,如牛顿第一定律、牛顿第三定律等。
这些方程共同构成了动力学的基础理论。
它们不仅在科学研究中起着重要作用,也在工程技术和日常生活中有着广泛的应用。
准一级动力学方程的拟合是指通过实验数据来确定物体所受的合力。
通常情况下,我们无法直接测量物体所受的合力,但可以通过测量物体的质量和加速度来间接确定。
为了获得更精确的结果,我们可以进行多次测量,并利用拟合方法来求解最优的合力值。
在拟合过程中,我们通常会利用计算机软件或数学工具来进行计算。
通过输入实验数据和初始参数,软件会自动进行计算,并给出最佳拟合结果。
拟合的过程可以分为线性拟合和非线性拟合两种情况。
对于准一级动力学方程来说,通常属于非线性拟合问题。
通过准一级动力学方程的拟合,我们可以得到物体所受的合力,并进一步分析物体的运动规律。
准二级动力学方程origin拟合

准二级动力学方程origin拟合动力学方程是描绘物体在运动中的状态和变化的数学描述,是现代物理学的基础之一。
其中,准二级动力学方程是一种应用广泛的动力学方程类型,可以很好地描述物体的运动状态。
本文将主要介绍准二级动力学方程的定义、特点以及如何进行Origin拟合。
准二级动力学方程定义准二级动力学方程是指物体在运动中受到二级阻尼力影响时的运动方程。
这种运动方程的特点是,临界阻尼值(即阻尼系数和共振频率相等时的阻尼系数)一定存在,当阻尼系数小于临界阻尼值时,运动状态为过阻尼(overdamped);当阻尼系数等于临界阻尼值时,运动状态为临界阻尼(critical damping);当阻尼系数大于临界阻尼值时,运动状态为欠阻尼(underdamped)。
准二级动力学方程特点有几个显著的特点值得我们注意:一、准二级动力学方程与振幅振动非常相关。
Am即振幅,当摩擦不会导致振幅衰减,就会发生振幅振动。
二、在临界阻尼条件下,准二级动力学方程达到极值点后的变化速度恰好为0。
三、在欠阻尼情况下,振幅随时间变化的规律呈幅度衰减,频率保持不变。
振幅随时间呈指数函数下降,随时间的平方函数振荡。
四、另一个显著的特点,它可以应用于各种物理现象的研究,例如自然界中的自由振动、电路中的振荡现象、化学反应的动力学问题等等。
如何进行Origin拟合进行准二级动力学方程的Origin拟合需要注意以下几点:一、确定数据根据实验测量得到的数据,包括时间与振荡振幅的关系。
二、创建分析模型打开Origin软件,创建一个新工作簿,输入数据。
然后选择Plot > New Plot,将数据绘制在图表中。
接下来,选择Analysis > Nonlinear Curve Fit > Peak: Ad-hoc with Fixed Half Width 这个选项。
三、设置曲线拟合在设置曲线拟合之前,需要先定义模型函数,即准二级动力学方程。
origin一级和二级动力学方程

origin一级和二级动力学方程
Origin是一款数据分析和绘图软件,其中的一级和二级动力学方程没有固定的表达形式,需要根据具体的反应过程和实验数据来确定。
以下是一般情况下的拟合步骤:
1. 选择【Tools】菜单下的【Fitting Function Organizer】命令(快捷键F9),打开【Fitting function organizer】对话框。
2. 单击【New Category】按钮,创建一个函数类,可以根据需要重命名为“yxz”。
然后单击【New Function】,在该类下创建一个新的函数,并命名为“thepseudosecondorderkinetic 1”。
3. 在【Brief Description】栏中输入“To used for the pseudo second order kinetic fitting”,定义函数所需的参数,即“ParameterNames:a,k”。
4. 输入函数方程“y=((a^2)*k*x)/(1+a*k*x)”,确保方程的逻辑关系正确。
5. 点击【Function】右侧的按钮。
6. 在【File】菜单中单击【Save】,然后单击【Return to dialog】,再单击【OK】。
至此,用户自定义函数建立完成,可以在Origin中使用该函数进行拟合操作。
请注意,具体的动力学方程可能会因反应过程和实验条件的不同而有所变化,建议在进行数据分析之前,仔细阅读相关的文献资料,确保方程的准确性和适用性。
origin拟合准一级准二级动力学方程详解

建立用户自定义函数的步骤:1、选择Tools: Fitting Function Organizer (快捷键F9) ,打开Fitting function organizer、单击New Category 按钮,创建一个函数类,可以根据自己需要重命名,比如yxz、然后单击New Function,在这个类下面创建一个新的函数,然后命名,比如thepseudosecondorderkinetic 1:2、对该函数进行简短的描述,Brief Description栏输入:To used for the pseudo second order kinetic fitting,定义函数所需参数,ParameterNames:a,k;输入函数方程。
Function 栏输入需编写的方程:y=((a^2)*k*x)/(1+a*k*x) 这个方程的逻辑关系一定要对!3、然后进行点击Function 右侧的按钮4、编译正确就是前提就是:方程正确,方程中的相关参数在方程之前进行了创建,参数声明与方程建立完成之后,单击进入编译界面,单击Compile5、当出现上图红框中文字就是,证明公式定义成功,否则失败!须重新定义。
6、在file中单击save,然后单击return to dialog,再单击OK。
7、至此,用户自定义函数的建立已经完成。
二、自定义拟合函数的使用:1先建立原文件图用点格式绘图2、完成后点击工具栏里的Analysis----Fitting----3、选择刚建立的yxz 下的thepseudosecondorderkinetic 1 公式。
4、点击Parameters5、在参数栏中分别设置a与k 的初始值(可以根据经验任意设置),设置数值就是只需在value 这一栏双击鼠标,就可以输入数据!6、随后点击单击一次拟合之后,得到以下结果:7、拟合并不很理想,然后直接拟合到收敛,可以瞧到拟合结果满意,单击OK:拟合到收敛8 拟合完成结果如图9、拟合曲线数据点,点击上图中Fit NLCURvel 输出10、可以根据上述拟合数据作图。
origin拟合准二级动力学方程

Origin拟合准二级动力学方程概述准二级动力学方程是一种常见的动力学模型,用于描述化学反应、生物动力学、环境系统等领域中的动态过程。
在实际研究中,根据实验数据来拟合准二级动力学方程是非常重要的,可以帮助我们深入理解和预测系统的行为。
理论基础准二级动力学方程可以表示为:r = k * (A - B * t) / (1 + C * t)其中,r是反应速率,k是速率常数,A和B是反应物的浓度,t是反应时间,C是另一个常数。
Origin软件Origin是一款功能强大的数据分析和可视化软件,可以广泛应用于物理、化学、生物等领域的科研工作。
Origin提供了许多工具和功能,可以方便地进行数据拟合和分析。
准备数据在使用Origin进行准二级动力学方程的拟合之前,我们首先需要获得一组实验数据。
这些数据应包括反应时间和对应的反应速率。
数据导入1.打开Origin软件并创建一个新项目。
2.在工作表中输入实验数据,第一列为时间,第二列为速率。
拟合准二级动力学方程1.在工作表中选择要拟合的数据。
2.点击菜单栏中的Analysis,选择Fitting,再选择Nonlinear Curve Fit。
3.在弹出的对话框中,选择User-defined Function作为拟合函数类型。
4.在拟合函数中输入准二级动力学方程的表达式。
5.定义拟合参数和初始值。
6.点击Fit按钮进行拟合。
7.查看拟合结果和拟合图像,评估拟合质量。
拟合结果分析拟合结果中的参数值和拟合曲线可以帮助我们理解实验数据和了解反应过程。
下面是一些拟合结果的分析方法:1.检查拟合参数的物理意义和单位。
2.计算拟合曲线和实验数据之间的残差。
3.计算拟合函数的相关系数,评估拟合曲线和实验数据的拟合程度。
4.进行统计分析,例如计算拟合参数的置信区间和假设检验。
5.根据拟合曲线对反应过程进行预测和优化。
结论使用Origin软件拟合准二级动力学方程可以帮助我们深入理解系统的动力学行为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
o r i g i n拟合准一年级准二年级动力学方程详解内部编号:(YUUT-TBBY-MMUT-URRUY-UOOY-DBUYI-0128)
建立用户自定义函数的步骤:1.选择 Tools: Fitting Function Organizer (快捷键F9) ,打开 Fitting function organizer. 单击 New Category 按钮,创建一个函数类,可以根据自
己需要重命名,比如 yxz.然后单击 New Function,在这个类下面创建一个新的
函数,然后命名,比如 thepseudosecondorderkinetic 1:
2. 对该函数进行简短的描述,Brief Description栏输入:To used for the pseudo second order kinetic fitting,定义函数所需参数,ParameterNames:
a,k;输入函数方程。
Function 栏输入需编写的方程:y=((a^2)*k*x)/(1+a*k*x) 这个方程的逻辑关系一定要对!
3.然后进行点击Function 右侧的按钮
4.编译正确是前提是:方程正确,方程中的相关参数在方程之前进行了创建,参
数声明和方程建立完成之后,单击进入编译界面,单击Compile
5.当出现上图红框中文字是,证明公式定义成功,否则失败!须重新定义。
6.在file中单击 save,然后单击return to dialog,再单击OK。
7.至此,用户自定义函数的建立已经完成。
二、自定义拟合函数的使用:
1先建立原文件图用点格式绘图
2. 完成后点击工具栏里的Analysis----Fitting----
3. 选择刚建立的yxz 下的thepseudosecondorderkinetic 1 公式。
4. 点击 Parameters
5.在参数栏中分别设置 a和k 的初始值(可以根据经验任意设置),设置数值是只需在 value 这一栏双击鼠标,就可以输入数据!
6.随后点击单击一次拟合之后,得到以下结果:
7.拟合并不很理想,然后直接拟合到收敛,可以看到拟合结果满意,单击OK:
拟合到收
8 拟合完成结果如图
9.拟合曲线数据点,点击上图中 Fit NLCURvel 输出
10.可以根据上述拟合数据作图。
