振动习题86610
大学物理17振动学习题ppt课件

(a) 合振动的频率与分振动的频率相同
(b)合振动的振幅 A A12 A22 2A1 A2 cos(2 1 )
(c)合振动的初相 tg A1 sin1 A2 sin2
2. 合振动加强、减弱的条件A1 cos1 A2 cos 2
(1) 2k (k 0,1,2,)
2
1
A A1 A2 合振动加强,并与分振动同相
相对于其平衡位置的正位移处回到平衡位置时,第二个质点正在
最大正位移处.则第二个质点的振动方程为
(A)
x2
Acos(t
a
1 2
π).
(B)
x2
Acos(t
a
1 2
π)
.
(C)
x2
Acos(t
a
3 2
π) .
(D)
x2 Acos(t a π)
.
2
解:由图看出,振动2比振动1位相落后90度
a
1
2
B
2
19
16、如图所示的是两个简谐振动 的振动曲线,它们合成的余弦振 动的初相为 __________________. 解: 由图知二者同振动方向、
同频率,且位相相反。
x
A
O
1 2
A
2
x1 t (s) 4 x2
合振动位相与振幅大者相 同,由矢量图可知初相为
(或 3 )
2
2
20
17、两个同方向同频率的简谐振动
o
t
6
6
6
6
解:
t
设x Acos(t
M sin(t )
0时 , 0
1 2
M
) M
M
cos
振动波动作业习题及解答

Ch.10.振动、Ch.11波动作业习题及解答AωOXt =0图2A图1ωt =0OX=010-1. 一小球与轻弹簧组成的谐振动系统,振动规律为0.05cos(8π3),x =t +π(t 的单位为秒, x 的单位为米)。
求: (1) 振动的角频率、周期、振幅、初相、速度和加速度的最大值; (2) t =1s 、t =2s 、t =10s 时刻的相位; (3) 分别画出位移、速度和加速度与时间的关系曲线。
解(1): 将小球的运动方程0.05cos(8π3),x =t +π与谐振动的表达式0cos()x A t ωϕ=+比较知,系统的角频率、周期、振幅和初相分别为:108π(s );=2(4)s ;0.05(m );3;T A πωπωπϕ-====系统振动速度、加速度的表式分别为02220sin(4sin(8π3)(m s);cos( 3.2cos(8π3)(m s )v =dx /dt =-A t t +πa =dv /dt =-A t t +πωωϕπωωϕπ+)=-0.+)=-速度和加速度的最大值为:12220.4π 1.26(m s );=3.2π31.6(m s )m m v A a A ωω--==≈=≈ 解(2): 由相位表达式0()8/3t t t ϕωϕππ=+=+知, t =1s 、t =2s 、t =10s 时刻振子的相位分别为:2549241333333(1s )8π(2s )16(10s )80t +t t +ππππππϕϕπϕπ=====+====;; 解(3): x (t ), v (t ), a (t )曲线如下图所示。
10-2.(选作题)某个与轻弹簧相连的小球,沿X 轴作振幅为A 的简谐振动,周期为T 。
其振动表达式用余旋函数表示。
若t =0时小球的运动状态分别为:(1) 0x A =-; (2) 过平衡位置向X正向运动; (3) 过x =0.5A 向X 负向运动; (4) 过x =X 正向运动。
大学物理振动波动例题习题

振动波动一、例题(一)振动1.证明单摆是简谐振动,给出振动周期及圆频率。
2. 一质点沿x 轴作简谐运动,振幅为12cm ,周期为2s 。
当t = 0时, 位移为6cm ,且向x 轴正方向运动。
求: (1) 振动表达式;(2) t = 0.5s 时,质点的位置、速度和加速度;(3)如果在某时刻质点位于x =-0.6cm ,且向x 轴负方向运动,求从该位置回到平衡位置所需要的时间。
3. 已知两同方向,同频率的简谐振动的方程分别为:x 1= 0.05cos (10 t + 0.75π) 20.06cos(100.25)(SI)x t π=+求:(1)合振动的初相及振幅.(2)若有另一同方向、同频率的简谐振动x 3 = 0.07cos (10 t +ϕ 3 ), 则当ϕ 3为多少时 x 1 + x 3 的振幅最大?又ϕ 3为多少时 x 2 + x 3的振幅最小?(二)波动1. 平面简谐波沿x 轴正方向传播,振幅为2 cm ,频率为 50 Hz ,波速为 200 m/s 。
在t = 0时,x = 0处的质点正在平衡位置向y 轴正方向运动,求:(1)波动方程(2)x = 4 m 处媒质质点振动的表达式及该点在t = 2 s 时的振动速度。
2. 一平面简谐波以速度m/s 8.0=u 沿x 轴负方向传播。
已知原点的振动曲线如图所示。
求:(1)原点的振动表达式;(2)波动表达式;(3)同一时刻相距m 1的两点之间的位相差。
3. 两相干波源S 1和S 2的振动方程分别是1cos y A t ω=和2cos(/2)y A t ωπ=+。
S 1距P 点3个波长,S 2距P 点21/4个波长。
求:两波在P 点引起的合振动振幅。
4.沿X 轴传播的平面简谐波方程为:310cos[200(t )]200x y π-=- ,隔开两种媒质的反射界面A 与坐标原点O 相距2.25m ,反射波振幅无变化,反射处为固定端,求反射波的方程。
机械振动习题及答案

第一章概述1.一简谐振动,振幅为0.20cm ,周期为0.15s ,求最大速度和加速度。
解:2.一加速度计指示结构谐振在80HZ 时具有最大加速度50g ,求振动的振幅。
(g=10m/s2)mga θθ+sin mga θ+6.请画出同一方向的两个运动:1()2sin(4)x t t π=,2()4sin(4)x t t π=合成的的振动波形7.请画出互相垂直的两个运动:1()2sin(4)x t t π=,2()2sin(4)x t t π=合成的结果。
如果是1()2sin(4/2)x t t ππ=+,2()2sin(4)x t t π=第二章单自由度系统1., 0.05m, 0.1m 0.2m/s 0.08m/s 一物体作简谐振动当它通过距平衡位置为处时的速度分别为和。
求其振动周期、振幅和最大速度。
5N/m 时,123k k k 分析表明:和并联,之后与串联1212eq k k k k k =+和并联后的等效刚度:5钢索的刚度为绕过定滑轮吊着质量为的物体以匀速下降,410N/m, 100kg0.5m/s 若钢索突然卡住,求钢索内的最大张力。
33 10kg =0.01m 20 6.410m .610m 20m c δ--=⨯⨯s 一单自由度阻尼系统,时,弹簧静伸长。
自由振动个循环后,振幅从降至1。
求阻尼系数及个循环内阻尼力所消耗的能量。
0 ()52.5sin(1030)N f t t =-初始条件下被简谐力激发的响应。
系统的运动方程:0()()sin()mu t ku t f t ωϕ+=-特解为:()sin()d u t B t ωϕ=-*20/()0.01d B f k m ω=-=响应:奇次方程通解:12()cos sin n n u t a t a tωω=+12()cos sin 0.01sin()n n u t a t a t t ωωωϕ=++-43 100kg 910N/m 2.410Ns/m ()90sin N (1) ; (2) ; (3) max()n d d k c f t t B B ωωωω=⨯=⨯=质量为的机器安装在刚度和阻尼系数的隔振器上,受到铅垂方向激振力作用而上下振动。
大学物理振动习题含答案

大学物理振动习题含答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN一、选择题:1.3001:把单摆摆球从平衡位置向位移正方向拉开,使摆线与竖直方向成一微小角度 ,然后由静止放手任其振动,从放手时开始计时。
若用余弦函数表示其运动方程,则该单摆振动的初相为 (A) (B) /2 (C) 0 (D) [ ]2.3002:两个质点各自作简谐振动,它们的振幅相同、周期相同。
第一个质点的振动方程为x 1 = A cos(t + )。
当第一个质点从相对于其平衡位置的正位移处回到平衡位置时,第二个质点正在最大正位移处。
则第二个质点的振动方程为: (A))π21cos(2++=αωt A x (B) )π21cos(2-+=αωt A x (C))π23cos(2-+=αωt A x (D) )cos(2π++=αωt A x [ ] 3.3007:一质量为m 的物体挂在劲度系数为k 的轻弹簧下面,振动角频率为。
若把此弹簧分割成二等份,将物体m 挂在分割后的一根弹簧上,则振动角频率是(A) 2 (B) ω2 (C) 2/ω (D) /2 [ ]4.3396:一质点作简谐振动。
其运动速度与时间的曲线如图所示。
若质点的振动规律用余弦函数描述,则其初相应为 (A) π/6 (B) 5π/6 (C) -5π/6 (D) -π/6 (E) -2π/3 [ ]5.3552:一个弹簧振子和一个单摆(只考虑小幅度摆动),在地面上的固有振动周期分别为T 1和T 2。
将它们拿到月球上去,相应的周期分别为1T '和2T '。
则有 (A) 11T T >'且22T T >' (B) 11T T <'且22T T <'(C) 11T T ='且22T T =' (D) 11T T ='且22T T >' [ ]6.5178:一质点沿x 轴作简谐振动,振动方程为)312cos(1042π+π⨯=-t x (SI)。
大学物理题库-振动与波动【精选文档】

振动与波动题库一、选择题(每题3分)1、当质点以频率ν 作简谐振动时,它的动能的变化频率为( )(A ) 2v(B )v (C )v 2 (D )v 42、一质点沿x 轴作简谐振动,振幅为cm 12,周期为s 2.当0=t 时, 位移为cm 6,且向x 轴正方向运动。
则振动表达式为( )(A))(3cos 12.0ππ-=t x (B ))(3cos 12.0ππ+=t x(C ))(32cos 12.0ππ-=t x (D ))(32cos 12.0ππ+=t x3、 有一弹簧振子,总能量为E,如果简谐振动的振幅增加为原来的两倍,重物的质量增加为原来的四倍,则它的总能量变为 ( )(A )2E (B)4E (C)E /2 (D )E /4 4、机械波的表达式为()()m π06.0π6cos 05.0x t y +=,则 ( ) (A) 波长为100 m (B) 波速为10 m·s-1(C) 周期为1/3 s (D) 波沿x 轴正方向传播 5、两分振动方程分别为x 1=3cos (50πt+π/4) ㎝ 和x 2=4cos (50πt+3π/4)㎝,则它们的合振动的振幅为( )(A) 1㎝ (B )3㎝ (C )5 ㎝ (D )7 ㎝ 6、一平面简谐波,波速为μ=5 cm/s ,设t= 3 s 时刻的波形如图所示,则x=0处的质点的振动方程为 ( )(A ) y=2×10-2cos (πt/2-π/2) (m )(B) y=2×10-2cos (πt + π) (m )(C) y=2×10-2cos (πt/2+π/2) (m )(D ) y=2×10-2cos (πt -3π/2) (m)7、一平面简谐波,沿X 轴负方向 传播。
x=0处的质点的振动曲线如图所示,若波函数用余弦函数表示,则该波的初位相为( ) (A )0 (B )π(C ) π /2 (D) - π /28、有一单摆,摆长m 0.1=l ,小球质量g 100=m 。
机械振动试题(含答案)(2)

机械振动试题(含答案)(2)一、机械振动 选择题1.下列说法中正确的有( )A .简谐运动的回复力是按效果命名的力B .振动图像描述的是振动质点的轨迹C .当驱动力的频率等于受迫振动系统的固有频率时,受迫振动的振幅最大D .两个简谐运动:x 1=4sin (100πt +3π) cm 和x 2=5sin (100πt +6π) cm ,它们的相位差恒定2.如图所示,质量为A m 的物块A 用不可伸长的细绳吊着,在A 的下方用弹簧连着质量为B m 的物块B ,开始时静止不动。
现在B 上施加一个竖直向下的力F ,缓慢拉动B 使之向下运动一段距离后静止,弹簧始终在弹性限度内,希望撤去力F 后,B 向上运动并能顶起A ,则力F 的最小值是( )A .(A m +B m )gB .(A m +2B m )gC .2(A m +B m )gD .(2A m +B m )g3.如图所示的单摆,摆球a 向右摆动到最低点时,恰好与一沿水平方向向左运动的粘性小球b 发生碰撞,并粘在一起,且摆动平面不便.已知碰撞前a 球摆动的最高点与最低点的高度差为h ,摆动的周期为T ,a 球质量是b 球质量的5倍,碰撞前a 球在最低点的速度是b 球速度的一半.则碰撞后A 56T B 65T C .摆球最高点与最低点的高度差为0.3hD .摆球最高点与最低点的高度差为0.25h4.如图所示,固定的光滑圆弧形轨道半径R =0.2m ,B 是轨道的最低点,在轨道上的A 点(弧AB 所对的圆心角小于10°)和轨道的圆心O 处各有一可视为质点的静止小球,若将它们同时由静止开始释放,则( )A .两小球同时到达B 点B .A 点释放的小球先到达B 点C .O 点释放的小球先到达B 点D .不能确定5.如图甲所示,一个单摆做小角度摆动,从某次摆球由左向右通过平衡位置时开始计时,相对平衡位置的位移x 随时间t 变化的图象如图乙所示.不计空气阻力,g 取10m/s 2.对于这个单摆的振动过程,下列说法中不正确的是( )A .单摆的位移x 随时间t 变化的关系式为8sin(π)cm x t =B .单摆的摆长约为1.0mC .从 2.5s t =到 3.0s t =的过程中,摆球的重力势能逐渐增大D .从 2.5s t =到 3.0s t =的过程中,摆球所受回复力逐渐减小6.图(甲)所示为以O 点为平衡位置、在A 、B 两点间做简谐运动的弹簧振子,图(乙)为这个弹簧振子的振动图象,由图可知下列说法中正确的是( )A .在t =0.2s 时,弹簧振子可能运动到B 位置B .在t =0.1s 与t =0.3s 两个时刻,弹簧振子的速度相同C .从t =0到t =0.2s 的时间内,弹簧振子的动能持续地增加D .在t =0.2s 与t =0.6s 两个时刻,弹簧振子的加速度相同7.如图所示,物块M 与m 叠放在一起,以O 为平衡位置,在ab 之间做简谐振动,两者始终保持相对静止,取向右为正方向,其振动的位移x 随时间t 的变化图像如图,则下列说法正确的是( )A .在1~2T t 时间内,物块m 的速度和所受摩擦力都沿负方向,且都在增大 B .从1t 时刻开始计时,接下来4T 内,两物块通过的路程为A C .在某段时间内,两物块速度增大时,加速度可能增大,也可能减小D .两物块运动到最大位移处时,若轻轻取走m ,则M 的振幅不变 8.装有一定量液体的玻璃管竖直漂浮在水中,水面足够大,如图甲所示。
机械振动考题及答案
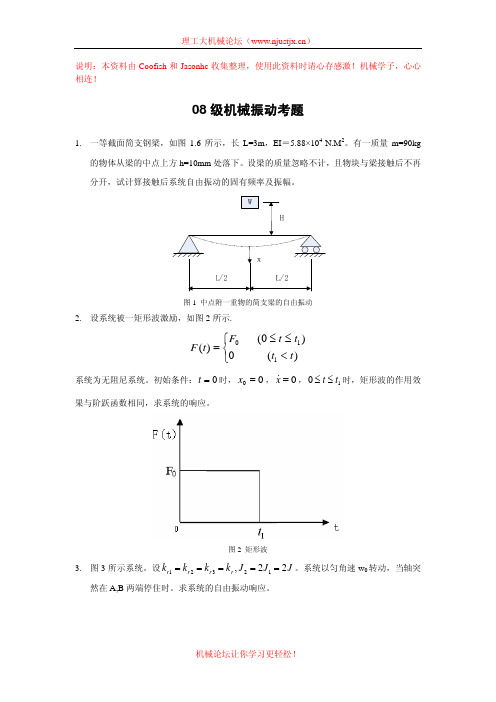
⎛
M
M
M ⎞
T
将 ω2 = ω3 =
k 代回主振型的线性方程组,得: m
M ⎛ ⎜3− m ⎜ ⎜ −1 ⎜ −1 ⎜ ⎜ −1 ⎝
⎞ −1 −1 −1⎟ ⎛ φ1i ⎞ ⎛ 0 ⎞ ⎟ ⎜φ ⎟ ⎜ 0 ⎟ 0 0 0 ⎟ ⎜ 2i ⎟ = ⎜ ⎟ , ( i = 2,3) ⎜φ ⎟ ⎜ 0 ⎟ 0 0 0 ⎟ ⎜ 3i ⎟ ⎜ ⎟ ⎟ φ ⎝ 4i ⎠ ⎝ 0 ⎠ 0 0 0⎟ ⎠
x ( t ) = x ( t1 ) cos ωn ( t − t1 ) +
x ( t1 )+ 0
•
ωn
sin ωn ( t − t1 )
机械论坛让你学习更轻松!
欢迎光临机械论坛(南京理工大学)
=
F0 F 1 − cos ωn t1 ) cos ωn ( t − t1 ) + 0 2 sin ωn t1 sin ωn ( t − t1 ) 2 ( mωn mωn F0 ⎡ cos ωn ( t − t1 ) − cos ωn t ⎤ ⎦ mωn 2 ⎣
⎛M ⎜ T 由于 φ2 M φ3 = ( 0 1 1 −2 ) ⎜ ⎜ ⎜ ⎝ ⎞⎛ 0 ⎞ ⎟⎜ ⎟ m ⎟ ⎜ 1 ⎟ = 3m ≠ 0 ⎟⎜ 0 ⎟ m ⎟⎜ ⎟ m ⎠ ⎝ −1 ⎠
T
T
′ = φ2 + cφ3 = ( 0 1 + c 1 −2 − c ) 强迫 φ3′ 与 φ2 正交。 取 φ3 ⎛M ⎜ T ′ = ( 0 1 1 −2 ) ⎜ 即: φ2 M φ3 ⎜ ⎜ ⎝ ∴ c = −2 ⎞⎛ 0 ⎞ ⎟⎜ ⎟ m ⎟ ⎜ 1 + c ⎟ = 3m ( c + 2 ) = 0 ⎟⎜ 1 ⎟ m ⎟⎜ ⎟ m ⎠ ⎝ −2 − c ⎠
《振动力学》习题集(附答案解析)
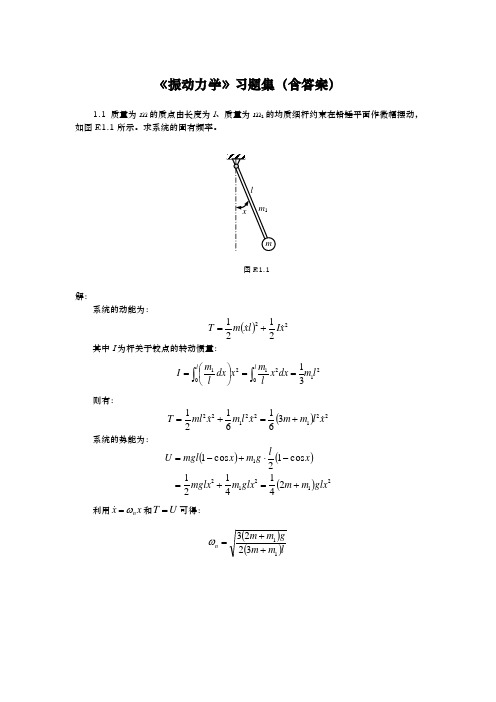
代入各单元状态变量的第一元素,即:
得到模态:
,
5.10在图E5.10所示系统中,已知GIpi(i= 1 , 2),li(i= 1 , 2)和Ji(i= 1 , 2)。用传递矩阵法计算系统的固有频率和模态。
图E5.10
解:
两自由端的边界条件为: , 。
其中: , 。
由自由端边界条件得频率方程:
,
代入各单元状态变量的第一元素,即:
图 T 2-26答案图 T 2-25
解:
受力如答案图T 2-26。对O点取力矩平衡,有:
4.7 两质量均为m的质点系于具有力F的弦上,如图E4.7所示。忽略振动过程中弦力的变化写出柔度矩阵,建立频率方程。求系统的固有频率和模态,并计算主质量、主刚度、简正模态,确定主坐标和简正坐标。
图E4.7答案图E4.7(1)
(3)
故:
由(3)得:
2.5在图E2.3所示系统中,已知m,c,k, 和 ,且t=0时, , ,求系统响应。验证系统响应为对初值的响应和零初值下对激励力响应的叠加。
图E2.3
解:
,
求出C,D后,代入上面第一个方程即可得。
2.7 由一对带偏心质量的等速反向旋转齿轮构成的振动机械安装在弹簧和阻尼器构成的支承上,如图E2.7所示。当齿轮转动角速度为 时,偏心质量惯性力在垂直方向大小为 。已知偏心重W= 125.5N,偏心距e=15.0cm,支承弹簧总刚度系数k= 967.7N/cm,测得垂直方向共振振幅 ,远离共振时垂直振幅趋近常值 。求支承阻尼器的阻尼比及在 运行时机器的垂直振幅。
故频率方程为:
5.1质量m、长l、抗弯刚度EI的均匀悬臂梁基频为3.515(EI/ml3)1/2,在梁自由端放置集中质量m1。用邓克利法计算横向振动的基频。
(完整word版)振动与波复习题及答案

第九章振动复习题1. 一轻弹簧,上端固定,下端挂有质量为m 的重物,其自由振动的周期为T .今已知振子离开平衡位置为x 时,其振动速度为v ,加速度为a .则下列计算该振子劲度系数的公式中,错误的是:(A) 2max 2max /x m k v =. (B) x mg k /=.(C) 22/4T m k π=. (D) x ma k /=. [ B ] 2. 一长为l 的均匀细棒悬于通过其一端的光滑水平固定轴上,(如图所示),作成一复摆.已知细棒绕通过其一端的轴的转动惯量231ml J =,此摆作微小振动的周期为(A) g l π2. (B) gl22π.(C) g l 322π. (D) gl 3π. [ C ] 3. 把单摆摆球从平衡位置向位移正方向拉开,使摆线与竖直方向成一微小角度θ ,然后由静止放手任其振动,从放手时开始计时.若用余弦函数表示其运动方程,则该单摆振动的初相为(A) π. (B) π/2. (C) 0 . (D) θ. [ C ]4. 两个质点各自作简谐振动,它们的振幅相同、周期相同.第一个质点的振动方程为x 1 = A cos(ωt + α).当第一个质点从相对于其平衡位置的正位移处回到平衡位置时,第二个质点正在最大正位移处.则第二个质点的振动方程为(A) )π21cos(2++=αωt A x . (B) )π21cos(2-+=αωt A x .(C) )π23cos(2-+=αωt A x . (D) )cos(2π++=αωt A x . [ B ][ ]6. 一质点作简谐振动.其运动速度与时间的曲线如图所示.若质点的振动规律用余弦函数描述,则其初相应为(A) π/6. (B) 5π/6. (C) -5π/6. (D) -π/6. (E) -2π/3. [ ]7. 一个弹簧振子和一个单摆(只考虑小幅度摆动),在地面上的固有振动周期分别为T 1和T 2.将它们拿到月球上去,相应的周期分别为1T '和2T '.则有(A) 11T T >'且22T T >'. (B) 11T T <'且22T T <'.(C) 11T T ='且22T T ='. (D) 11T T ='且22T T >'. [ D ] 8. 一弹簧振子,重物的质量为m ,弹簧的劲度系数为k ,该振子作振幅为A 的简谐振动.当重物通过平衡位置且向规定的正方向运动时,开始计时.则其振动方程为: (A) )21/(cos π+=t m k A x (B) )21/cos(π-=t m k A x(C) )π21/(cos +=t k m A x (D) )21/cos(π-=t k m A xv 21(E) t m /k A x cos = [ B ] 9. 一质点在x 轴上作简谐振动,振辐A = 4 cm ,周期T = 2 s ,其平衡位置取作坐标原点.若t = 0时刻质点第一次通过x = -2 cm 处,且向x 轴负方向运动,则质点第二次通过x = -2 cm 处的时刻为(A) 1 s . (B) (2/3) s .(C) (4/3) s . (D) 2 s . [ B ]10.一物体作简谐振动,振动方程为)41cos(π+=t A x ω.在 t = T /4(T 为周期)时刻,物体的加速度为(A) 2221ωA -. (B) 2221ωA . (C) 2321ωA -. (D)2321ωA . [ B ] 11. 两个同周期简谐振动曲线如图所示.x 1的相位比x 2的相位(A) 落后π/2. (B) 超前π/2. (C) 落后π . (D) 超前π.[ B ]12. 一个质点作简谐振动,振幅为A ,在起始时刻质点的位移为A 21,且向x 轴的正方向运动,代表此简谐振动的旋转矢量图为[ B ]13. 一简谐振动曲线如图所示.则振动周期是(A) 2.62 s . (B) 2.40 s .(C) 2.20 s .(D) 2.00 s . [ B ]A21-A21-A21 21A21 AA21-A21-2115. 用余弦函数描述一简谐振子的振动.若其速度~时间(v ~t )关系曲线如图所示,则振动的初相位为(A) π/6. (B) π/3.(C) π/2. (D) 2π/3. (E) 5π/6.[ A ]17. 一弹簧振子作简谐振动,总能量为E 1,如果简谐振动振幅增加为原来的两倍,重物的质量增为原来的四倍,则它的总能量E 2变为 (A) E 1/4. (B) E 1/2.(C) 2E 1. (D) 4 E 1 . [ D ]18 弹簧振子在光滑水平面上作简谐振动时,弹性力在半个周期内所作的功为(A) kA 2. (B)221kA . (C) (1/4)kA 2. (D) 0. [ D ]19. 一物体作简谐振动,振动方程为)21cos(π+=t A x ω.则该物体在t = 0时刻的动能与t = T /8(T 为振动周期)时刻的动能之比为:(A) 1:4. (B) 1:2. (C) 1:1.(D) 2:1. (E) 4:1. [ D ]20.动的初相为 (A) π23. (B) π.(C) π21. (D) 0. [ B ] 二. 填空题21. 在t = 0时,周期为T 、振幅为A 的单摆分别处于图(a)、(b)、(c)三种状态.若选单摆的平衡位置为坐标的原点,坐标指向正右方,则单摆作小角度摆动的振动表达式(用余弦函数表示)分别为 (a) ______________________________;(b) ______________________________;(c) ______________________________.23. 在两个相同的弹簧下各悬一物体,两物体的质量比为4∶1,则二者作简谐振 动的周期之比为___2:1___.24. 一质点作简谐振动,速度最大值v m = 5 cm/s ,振幅A = 2 cm .若令速度具有 正最大值的那一时刻为t = 0,则振动表达式为_____50.02cos()22x t π=-___.25. 一物体作余弦振动,振幅为15×10-2m ,角频率为6π s -1,初相为0.5 π,则21--(c)A/ -A 2cos()2x A t T ππ=+2cos()2x A t T ππ=+2cos()x A t T ππ=+振动方程为 __0.15cos(6)2x t ππ=+(SI).27. 一简谐振动的表达式为)3cos(φ+=t A x ,已知 t = 0时的初位移为0.04 m ,初速度为0.09 m/s ,则振幅A =____0.05m_________ ,初相φ =____3arcsin 5-____________.30. 已知两个简谐振动的振动曲线如图所示.两简谐振动的最大速率之比为_______1:1__________.31.则此简谐振动的三个特征量为A =_____0.1m________;ω =_____/6rad s π_____;φ =_____3π__________. .34. 已知三个简谐振动曲线如图所示,则振动方程分别为:x 1 =10cos t π______________________, x 2 =10cos()2t ππ- _____________________,x 3 =10cos()t ππ+_______________________.37.一简谐振动的旋转矢量图如图所示,振幅矢量长2cm ,则该简谐振动的初相为_____4π_______.振动方程为__0.02cos()4x t ππ=+____________.41. 一作简谐振动的振动系统,振子质量为2 kg ,系统振动频率为1000 Hz ,振 幅为0.5 cm ,则其振动能量为______1002πJ________.43. 一弹簧振子系统具有1.0 J 的振动能量,0.10 m 的振幅和1.0 m/s 的最大速率,t x (cm)则弹簧的劲度系数为____200N/m_______,振子的振动频率为_5πHZ________. 44.两个同方向的简谐振动曲线如图所示.合振动的振幅 为______21A A -___________,合振动的振动方程 为_____212()cos()2x A A t T ππ=-+______. 50. 一个质点同时参与两个在同一直线上的简谐振动,其表达式分别为)612cos(10421π+⨯=-t x , )652cos(10322π-⨯=-t x (SI)则其合成振动的振幅为___0.01m________,初相为____6π_____.第十章波复习题一、选择题1. 在下面几种说法中,正确的说法是: (A) 波源不动时,波源的振动周期与波动的周期在数值上是不同的. (B) 波源振动的速度与波速相同.(C) 在波传播方向上的任一质点振动相位总是比波源的相位滞后(按差值不大于π计). (D) 在波传播方向上的任一质点的振动相位总是比波源的相位超前.(按差值不大于π计)[ C ]2. 机械波的表达式为y = 0.03cos6π(t + 0.01x ) (SI) ,则 (A) 其振幅为3 m . (B) 其周期为s 31. (C) 其波速为10 m/s . (D) 波沿x 轴正向传播. [ B ] 3.一平面简谐波沿Ox 正方向传播,波动表达式为]2)42(2cos[10.0π+-π=x t y (SI),该波在t = 0.5s 时刻的波形图是 [ A ]·---4. 横波以波速u 沿x 轴负方向传播.t 时刻波形曲线如图.则该时刻 [ D ](A) A 点振动速度大于零. (B) B 点静止不动. (C) C 点向下运动. (D) D 点振动速度小于零.5. 把一根十分长的绳子拉成水平,用手握其一端.维持拉力恒定,使绳端在垂直于绳子的方向上作简谐振动,则(A) 振动频率越高,波长越长. (B) 振动频率越低,波长越长.(C) 振动频率越高,波速越大. (D) 振动频率越低,波速越大.[ B ] 6. 一平面余弦波在t = 0时刻的波形曲线如图所示,则O 点的振动初相φ 为: (A) 0. (B)π21(C) π (D)π23(或π-21) [ B ]7. 如图所示,有一平面简谐波沿x 轴负方向传播,坐标原点O 的振动规律为)cos(0φω+=t A y ),则B 点的振动方程为(A) ])/(cos[0φω+-=u x t A y .(B) )]/([cos u x t A y +=ω.(C) })]/([cos{0φω+-=u x t A y . (D)})]/([cos{0φω++=u x t A y . [ C ]8.如图所示为一平面简谐波在t = 0 时刻的波形图,该波的波速u = 200 m/s ,则P 处质点的振动曲线为[ C ]9. 一平面简谐波沿x 轴正方向传播,t = 0 时刻的波形图如图所示,则P 处质点的振动在t = 0时刻的旋转矢量图是 [ A ]xy Ouy(m)ωSA ϖO ′ωSA ϖO′ωϖO ′ωSAϖO ′(A)(B)(C)(D)S10. 一平面简谐波沿Ox 轴正方向传播,t = 0 时刻的波形图如图所示,则P 处介质质点的振动方程是(A))314cos(10.0π+π=t y P (SI).(B) )314cos(10.0π-π=t y P (SI). (C) )312cos(10.0π+π=t y P (SI).(D) )612cos(10.0π+π=t y P (SI). [ A ]11. 图示一简谐波在t = 0时刻的波形图,波速 u = 200 m/s ,则P 处质点的振动速度表达式为 [ C ](A))2cos(2.0π-ππ-=t v (SI). (B) )cos(2.0π-ππ-=t v (SI). (C) )2/2cos(2.0π-ππ=t v (SI).(D) )2/3cos(2.0π-ππ=t v (SI).12.在同一媒质中两列相干的平面简谐波的强度之比是I 1 / I 2 = 4,则两列波的振幅之比是(A) A 1 / A 2 = 16. (B)A 1 / A 2 = 4.(C) A 1 / A 2 = 2.(D) A 1 / A 2 = 1 /4. [ C ] 13. 一列机械横波在t 时刻的波形曲线如图所示,则该时刻能量为最大值的媒质质元的位置是:(A) o ',b ,d ,f . (B) a ,c ,e ,g .(C) o ',d . (D) b ,f . [ B ]14. 一平面简谐波在弹性媒质中传播,在某一瞬时,媒质中某质元正处于平衡位置,此时它的能量是 (A) 动能为零,势能最大. (B) 动能为零,势能为零.(C) 动能最大,势能最大. (D) 动能最大,势能为零. [C ] 15. 一平面简谐波在弹性媒质中传播,在媒质质元从最大位移处回到平衡位置的过程中(A) 它的势能转换成动能. (B) 它的动能转换成势能. (C) 它从相邻的一段媒质质元获得能量,其能量逐渐增加.(D) 它把自己的能量传给相邻的一段媒质质元,其能量逐渐减小.[ C ] 16. 如图所示,S 1和S 2为两相干波源,它们的振动方向均垂直于图面,发出波长为λ 的简谐波,P 点是两列波相遇区域中的一点,已知λ21=P S ,λ2.22=P S ,两列波在P 点发生相消干涉.若S 1的振动方程为)212cos(1π+π=t A y ,则S 2的振动方程为(A) )212cos(2π-π=t A y . (B) )2cos(2π-π=t A y .(C) )212cos(2π+π=t A y . (D) )1.02cos(22π-π=t A y . [ D ]S17. 两相干波源S 1和S 2相距λ /4,(λ 为波长),S 1的相位比S 2的相位超前π21,在S 1,S 2的连线上,S 1外侧各点(例如P 点)两波引起的两谐振动的相位差是:(A) 0. (B)π21. (C) π. (D) π23. [ C ] 18. S 1和S 2是波长均为λ 的两个相干波的波源,相距3λ /4,S 1的相位比S 2超前π21.若两波单独传播时,在过S 1和S 2的直线上各点的强度相同,不随距离变化,且两波的强度都是I 0,则在S 1、S 2连线上S 1外侧和S 2外侧各点,合成波的强度分别是(A) 4I 0,4I 0. (B) 0,0.(C) 0,4I 0 . (D) 4I 0,0. [ A ] 19 在驻波中,两个相邻波节间各质点的振动 (A) 振幅相同,相位相同. (B) 振幅不同,相位相同.(C) 振幅相同,相位不同. (D) 振幅不同,相位不同. [ B ] 20 在波长为λ 的驻波中,两个相邻波腹之间的距离为 (A) λ /4. (B) λ /2.(C) 3λ /4. (D) λ . [ B ] 21.沿着相反方向传播的两列相干波,其表达式为)/(2cos 1λνx t A y -π= 和 )/(2cos 2λνx t A y +π=.在叠加后形成的驻波中,各处简谐振动的振幅是 (A) A . (B) 2A .(C))/2cos(2λx A π. (D) |)/2cos(2|λx A π. [ D ]二、填空题22.一个余弦横波以速度u 沿x 轴正向传播,t 时刻波形曲线如图所示.试分别指出图中A ,B ,C 各质点在 该时刻的运动方向.A _____________;B_____________ ;C ______________ . 23. 一平面简谐波的表达式为)37.0125cos(025.0x t y -= (SI),其角频率ω =__________________________,波速u =______________________,波长λ = _________________.24. 频率为100 Hz 的波,其波速为250 m/s .在同一条波线上,相距为0.5 m 的两点的相位差为________________.25. 图为t = T / 4 时一平面简谐波的波形曲线,则其波的表达式为 ______________________________________________.26、一平面简谐波沿Ox 轴正方向传播,波长为λ.若如图P 1点处质点的振动方程为)2cos(1φν+π=t A y ,则P 2点处质点的振动方程为_________________________________;与P 1点处质点振动状态相同的那些点的位置是___________________________.S 1S 2Pλ/4-xOP 1P 227、一简谐波沿x 轴正方向传播.x 1和x 2两点处的振动曲线分别如图(a)和(b)所示.已知x 2 .> x 1且x 2 - x 1 < λ(λ为波长),则x 2点的相位比x 1点的相位滞后___________________.28、已知某平面简谐波的波源的振动方程为t y π=21sin 06.0(SI),波速为2 m/s .则在波传播前方离波源 5 m 处质点的振动方程为_-______________________.29、(1)一列波长为λ 的平面简谐波沿x 轴正方向传播.已知在λ21=x处振动的方程为y = A cos ω t ,则该平面简谐波的表达式为______________________________________. (2) 如果在上述波的波线上x = L (λ21>L)处放一如图所示的反射面,且假设反射波的振幅为A ',则反射波的表达式为 _______________________________________ (x ≤L ).30、一平面简谐波沿x 轴负方向传播.已知 x = -1 m 处质点的振动方程为)cos(φω+=t A y ,若波速为u ,则此波的表达式为 _________________________________________________________. 31、一个波源位于O 点,以O 为圆心作两个同心球面,它们的半径分别为R 1和R 2,在两个球面上分别取相等的面积∆S 1和∆S 2,则通过它们的平均能流之比=21P /P ___________________.32、一点波源发出均匀球面波,发射功率为4 W .不计媒质对波的吸收,则距离 波源为2 m 处的强度是__________________.33、如图所示,波源S 1和S 2发出的波在P 点相遇,P 点距波源S 1和S 2的距离分别为 3λ 和10 λ / 3 ,λ 为两列波在介质中的波长,若P 点的合振幅总是极大值,则两波在P 点的振动频率___________,波源S 1 的相位比S 2 的相位领 先_________________.34、如图所示,S 1和S 2为同相位的两相干波源,相距为L ,P 点距S 1为r ;波源S 1在P 点引起的振动振幅为A 1,波源S 2在P 点引起的振动振幅为A 2,两波波长都是λ ,则P 点振幅A =_________________________________________________________. 35、两相干波源S 1和S 2的振动方程分别是tA y ωcos 1=和)21cos(2π+=t A y ω.S 1距P 点3个波长,S 2距P 点21/4个波长.两波在P 点引起的两个振动的相位差是____________.36、 S 1,S 2为振动频率、振动方向均相同的两个点波源,振动方向垂直纸面,两者相距λ23(λ为波长)如图.已知S 1的初相为π21. (1) 若使射线S 2C 上各点由两列波引起的振动均干涉相消,则S 2的初相应为________________________.(2) 若使S 1 S 2连线的中垂线MN 上各点由两列波引起的 振动均干涉相消,则S 2的初位相应为_______________________.(a)(b)PS S1237、 两列波在一根很长的弦线上传播,其表达式为 y 1 = 6.0×10-2cos π(x - 40t ) /2 (SI) y 2 = 6.0×10-2cos π(x + 40t ) /2 (SI)则合成波的表达式为__________________________________________________; 在x = 0至x = 10.0 m 内波节的位置是_____________________________________ __________________________________;波腹的位置是________________________________________________________. 38、设入射波的表达式为)(2cos 1λνxt A y +π=.波在x = 0处发生反射,反射点为固定端,则形成的驻波表达式为____________________________________. 39、 一驻波表达式为t x A y ππ=100cos 2cos .位于x 1 = 3 /8 m 的质元P 1与位于x 2 = 5 /8 m 处的质元P 2的振动相位差为_____________________________. 40、 在弦线上有一驻波,其表达式为 )2cos()/2cos(2t x A y νλππ=, 两个相邻波节之间的距离是_______________.。
机械振动习题及答案

一.选择题(共10个小题,每题4分,共40分。
在下列各题中,有的小题只有一个选项正确,有的小题有多个选项正确。
全部选对的得4分,漏选的得2分,错选、不选的得0分)1.关于简谐振动的加速度,下列说法正确的是()A.大小与位移成正比,方向一周期变化一次B.大小不变,方向始终指向平衡位置C.大小与位移成正比,方向始终指向平衡位置D.大小变化是均匀的,方向一周期变化一次2.一单摆摆长为l,若将摆长增加1m,则周期变为原来的1.5倍,可以肯定l长为()A.2mB.1.5mC.0.8mD.0.5m3.甲、乙两个单摆的摆长相等,将两上摆的摆球由平衡位置拉起,使摆角θ乙>θ<5°,由静止开始释放,则()甲A.甲先摆到平衡位置B.乙先摆到平衡位置C.甲、乙两摆同时到达平衡位置D.无法判断4.对单摆的振动,以下说法中正确的是()A.单摆摆动时,摆球受到的向心力大小处处相等B.单摆运动的回复力是摆球所受合力C.摆球经过平衡位置时所受回复力为零D.摆球经过平衡位置时所受合外力为零5.如图5-27是某振子作简谐振动的图象,以下说法中正确的是()A.因为振动图象可由实验直接得到,所以图象就是振子实际运动的轨迹B.由图象可以直观地看出周期、振幅,还能知道速度、加速度、回复力与能量随时间的变化情况C.振子在B位置的位移就是曲线的长度D.振子运动到B点时的速度方向即为该点的切线方向6、B两个弹簧振子,A的固有频率为f,B的固有频率为4f,若它们均在频率为3f的策动力作用下作受迫振动,则()A.振子A的振幅较大,振动频率为FB.振子B的振幅较大,振动频率为3fC.振子A的振幅较大,振动频率为3FD.振子B的振幅较大,振动频率为4f7.如图5-28所示为质点作简谐振动的图象,从图象可看出()A.质点振动的频率为2.5B.质点振动的振幅为4时刻质点的加速度方向沿x轴正方向1时刻质点的速度方向沿x轴正方向18.图5-29为一物体作简谐振动的图象,根据图象判定下列哪个时刻物体的加速度为零,而速度最大,方向沿x轴反方向()A.1s末B.2s末C.3s末D.4s末9.如图5-30所示,一根水平细钢丝两边固定,它下面悬挂三个摆长为1.00m,0.50m,0.25m的单摆,三个摆球相同,现用周期变化的外力作用于细钢丝上,下述判断正确的是()A.外力的频率为0.5时,B球振幅最大B.外力的频率为1时,A 球振幅最大 C.外力的频率为1时,C 球振幅最大 D. 外力的频率为2时,A 球振幅最大10.以下振动现象中表现为共振现象的是( )A.钱塘江大桥上正通过一列火车时的振动 B.挑水的人由于行走,使扁担和水桶上下振动,结果水桶中的水溢出 C.工厂中机器开动引起厂房的振动 D. 快艇上的机关炮正连续向敌人射击时的振动二.填空题(每空5分,共30分)11.如图所示,一个偏心轮的圆心为O ,重心为C ,它们所组成的系统在竖直方向上发生自由振动的频率为f .如果偏心轮以角速度ω绕O轴匀速转动,则当ω 时振动最为剧烈,这个现象称为 . 12.在“用单摆测重力加速度”的实验中,可供选择的器材是A 、20长细线B 、1m 长细线C 、1m 长粗线D 、小铁球(带小孔)E 、塑料球(带小孔)F 、毫米刻度尺G 、厘米刻度尺H 、秒表I 、时钟J 、铁架台K 、游标卡尺。
大学物理振动习题含答案

一、选择题:1.3001:把单摆摆球从平衡位置向位移正方向拉开,使摆线与竖直方向成一微小角度? ,然后由静止放手任其振动,从放手时开始计时。
若用余弦函数表示其运动方程,则该单摆振动的初相为(A) ? (B) ?/2 (C) 0 (D) ??[ ]2.3002:两个质点各自作简谐振动,它们的振幅相同、周期相同。
第一个质点的振动方程为x 1 = A cos(?t + ?)。
当第一个质点从相对于其平衡位置的正位移处回到平衡位置时,第二个质点正在最大正位移处。
则第二个质点的振动方程为:(A))π21cos(2++=αωt A x (B) )π21cos(2-+=αωt A x (C))π23cos(2-+=αωt A x (D) )cos(2π++=αωt A x [ ]3.3007:一质量为m 的物体挂在劲度系数为k 的轻弹簧下面,振动角频率为?。
若把此弹簧分割成二等份,将物体m 挂在分割后的一根弹簧上,则振动角频率是(A) 2?? (B) ω2 (C) 2/ω (D) ? /2[ ]4.3396:一质点作简谐振动。
其运动速度与时间的曲线如图所示。
若质点的振动规律用余弦函数描述,则其初相应为 (A) ?/6 (B) 5?/6 (C) -5?/6 (D) -?/6(E) -2?/3 [5.3552:一个弹簧振子和一个单摆(只考虑小幅度摆动),在地面上的固有振动周期分别为T 1和T 2。
将它们拿到月球上去,相应的周期分别为1T '和2T '。
则有(A) 11T T >'且22T T >' (B) 11T T <'且22T T <'(C) 11T T ='且22T T =' (D) 11T T ='且22T T >'[ ]6.5178:一质点沿x 轴作简谐振动,振动方程为)312cos(1042π+π⨯=-t x (SI)。
《振动力学》习题集[含答案解析]
![《振动力学》习题集[含答案解析]](https://img.taocdn.com/s3/m/e240f1182379168884868762caaedd3383c4b5ca.png)
考虑到 的影响,则叠加后的 为:
2.1一弹簧质量系统沿光滑斜面作自由振动,如图T 2-1所示。已知, ,m=1 kg,k= 49 N/cm,开始运动时弹簧无伸长,速度为零,求系统的运动规律。
图T 2-1答案图T 2-1
解:
, cm
rad/s
cm
2.2如图T 2-2所示,重物 悬挂在刚度为k的弹簧上并处于静平衡位置,另一重物 从高度为h处自由下落到 上而无弹跳。求 下降的最大距离和两物体碰撞后的运动规律。
,
代入各单元状态变量的第一元素,即:
得到模态:
,
5.10在图E5.10所示系统中,已知GIpi(i= 1 , 2),li(i= 1 , 2)和Ji(i= 1 , 2)。用传递矩阵法计算系统的固有频率和模态。
图E5.10
解:
两自由端的边界条件为: , 。
其中: , 。
由自由端边界条件得频率方程:
,
代入各单元状态变量的第一元素,即:
得到模态:
,
5.11在图E5.11所示系统中悬臂梁质量不计,m、l和EI已知。用传递矩阵法计算系统的固有频率。
图E5.11
解:
引入无量纲量:
, , ,
定义无量纲的状态变量:
边界条件:
左端固结: ,右端自由:
根据传递矩阵法,有:
其中点传递矩阵和场传递矩阵分别为:
,
得:
利用此齐次线性代数方程的非零解条件导出本征方程:
解:
, ,
根据 和 的自由体动力平衡关系,有:
故:
当 = 时,令:
, ,
代入矩阵方程,有:
,
根据 得:
,
第一振型第二振型
答案图E4.7(2)
机械振动基础习题
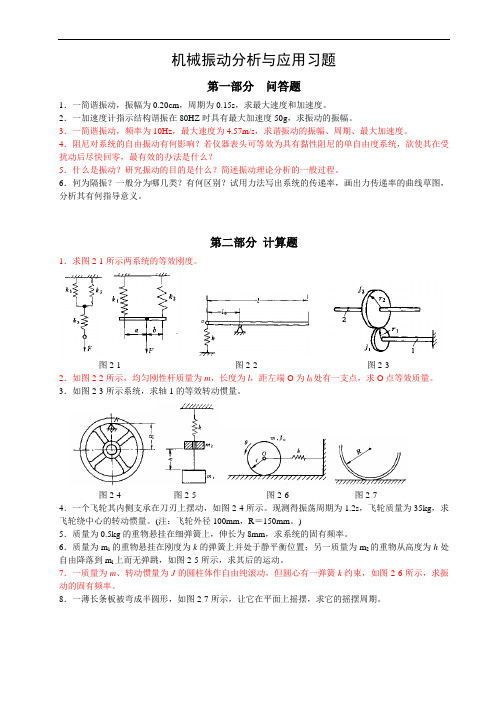
机械振动分析与应用习题第一部分问答题1.一简谐振动,振幅为0.20cm,周期为0.15s,求最大速度和加速度。
2.一加速度计指示结构谐振在80HZ时具有最大加速度50g,求振动的振幅。
3.一简谐振动,频率为10Hz,最大速度为4.57m/s,求谐振动的振幅、周期、最大加速度。
4.阻尼对系统的自由振动有何影响?若仪器表头可等效为具有黏性阻尼的单自由度系统,欲使其在受扰动后尽快回零,最有效的办法是什么?5.什么是振动?研究振动的目的是什么?简述振动理论分析的一般过程。
6.何为隔振?一般分为哪几类?有何区别?试用力法写出系统的传递率,画出力传递率的曲线草图,分析其有何指导意义。
第二部分计算题1.求图2-1所示两系统的等效刚度。
图2-1 图2-2 图2-32.如图2-2所示,均匀刚性杆质量为m,长度为l,距左端O为l0处有一支点,求O点等效质量。
3.如图2-3所示系统,求轴1的等效转动惯量。
图2-4 图2-5 图2-6 图2-74.一个飞轮其内侧支承在刀刃上摆动,如图2-4所示。
现测得振荡周期为1.2s,飞轮质量为35kg,求飞轮绕中心的转动惯量。
(注:飞轮外径100mm,R=150mm。
)5.质量为0.5kg的重物悬挂在细弹簧上,伸长为8mm,求系统的固有频率。
6.质量为m1的重物悬挂在刚度为k的弹簧上并处于静平衡位置;另一质量为m2的重物从高度为h处自由降落到m l上而无弹跳,如图2-5所示,求其后的运动。
7.一质量为m、转动惯量为J的圆柱体作自由纯滚动,但圆心有一弹簧k约束,如图2-6所示,求振动的固有频率。
8.一薄长条板被弯成半圆形,如图2-7所示,让它在平面上摇摆,求它的摇摆周期。
图2-8 图2-99.长度为L 、重量为W 的均匀杆对称地支承在两根细绳上,如图2-8所示。
试建立杆相对于铅垂轴线o-o 的微角度振动方程并确定它的周期。
10.求图2-9所示系统的等效刚度和固有频率。
11.用能量法求图2-10所示均质圆柱体振荡的固有频率。
《振动习题》课件

认真听讲,做好笔记
学习建议
课后复习,巩固知识
遇到问题,及时请教老师或同学
定期进行习题练习,提高解题能力
展望未来
课件在振动工程领域的应用 前景
课件在教育领域的推广和应 用
振动习题PPT课件的未来发 展趋势
课件在振动工程领域的创新 和突破
汇报人:
动态图表应用:数据分析、 报告展示、教学演示等
公式推导
振动方程:描述 振动系统的运动 规律
振动频率:描述 振动系统的振动 频率
振动幅值:描述 振动系统的振动 幅度
振动相位:描述 振动系统的振动 相位
实例解析
实例1:单自由度振动系统 实例2:多自由度振动系统 实例3:振动系统的响应分析 实例4:振动系统的控制与优化
振动分类
自由振动:物体在无外力作用下的振动
共振:物体在特定频率下产生的振动
受迫振动:物体在外力作用下的振动
自激振动:物体在自身激励作用下的振 动
阻尼振动:物体在阻尼作用下的振动
非线性振动:物体在非线性作用下的振 动
振动方程建立
建立方法:根据牛顿第二定 律和胡克定律推导
振动方程的解:包括自由振 动和受迫振动
动画演示
动画类型:包括 文字、图片、视 频等
动画效果:包括 缩放、旋转、平 移等
动画时间:根据 内容需要调整动 画时间
动画顺序:按照 逻辑顺序进行动 画演示
动态图表
动态图表类型:折线图、柱 状图、饼图、散点图等
动态图表制作:使用Excel、 PowerPoint等软件制作
动态图表:可以展示数据随 时间变化的趋势和规律
,
汇报人:
目录
课件背景
振动习题PPT课件是为了帮助学生更好地理解和掌握振动原理而设计的 课件内容涵盖了振动的基本概念、振动方程、振动分析方法等 课件采用了丰富的多媒体元素,如动画、视频、音频等,以提高学生的学习兴趣和效果 课件还提供了大量的习题和案例分析,帮助学生巩固所学知识,提高解决问题的能力
完整word版振动与波复习题及答案

第九章振动复习题1. 一轻弹簧,上端固定,下端挂有质量为 m 的重物,其自由振动的周期为 T .今已知 振子离开平衡位置为 x 时,其振动速度为 v ,加速度为a .则下列计算该振子劲度系数的公 式中,错误的是: (A) k 2 . 2mvmax / xmax . (B) k mg / x . (C) k 2 24 m/T . (D) k ma/x . 2. 一长为 作成一复摆. I 的均匀细棒悬于通过其一端的光滑水平固定轴上, 1 2J -ml 2,此摆作微小振 3 已知细棒绕通过其一端的轴的转动惯量 动的周期为 (A) 2 (C) 2 fir忖(B) 2 1—()Vgrrfe .(D ) (如图所示), 3.把单摆摆球从平衡位置向位移正方向拉开,使摆线与竖直方向成一微小角度 后由静止放手任其振动, 的初相为 从放手时开始计时.若用余弦函数表示其运动方程, O ,然 则该单摆振动 (A). (C) 0 . 4.两个质点各自作简谐振动,它们的振幅相同、周期相同.第一个质点的振动方程为 X 1 = Acos( t + ).当第一个质点从相对于其平衡位置的正位移处回到平衡位置时,第二个 质点正在最大正位移处.则第二个质点的振动方程为 1 2n ).2n. (B) /2. (D). (A ) (C )X 2X 2Acos( tAcos( t(B) x 2Acos((D) x 2 A cos(:6. 一质点作简谐振动.其运动速度与时间的曲线如图所 示.若质点的振动规律用余弦函数描述,则其初相应为 (A) /6 . (B) 5/6 . (C) -5/6 .(D) - /6 . (E) -2 /3 . : : 7. 一个弹簧振子和一个单摆(只考虑小幅度摆动),在地 面上的固有振动周期分别为 T 1和T 2 .将它们拿到月球上去,有 (A) T 1 T 1 且 T 2 T2 . (C) T 1 T 1 且 T 2 T2 .(B) T 1 T 1 且 T 2(D)T 1T1 且 T21-n).F )V mh m O V(m/s) h 相应的周期分别为T i 和T 2 .则T 2 . T 2 .8. 一弹簧振子,重物的质量为 m,弹簧的劲度系数为 k,该振子作振幅为 重物通过平衡位置且向规定的正方向运动时, (A) x Acos(J k/ m t 2 ) (C) x Acos(Jm/k t 1 n开始计时.则其振动方程为: (B) x Acos(Jk/m t (D) x Acos(Jm/k t:D :A 的简谐振动.当(C)尹A 2(B) \^A 22(D)^T SA 22(E) X Acos J k / m t: B :9. 一质点在X 轴上作简谐振动,振辐A = 4 cm ,周期T = 2 s ,其平衡位置取作坐标原点. t = 0时刻质点第一次通过 处的时刻为 (A) 1 s . (C) (4⑶ s . 若 X = - 2 cm 处,且向X 轴负方向运动,则质点第二次通过 X = -2 cm (B) (2/3) s .(D) 2 s . 10. 一物体作简谐振动, 振动方程为x Acos( t1 ) •在t = T/4( T 为周期)时刻, 411. (A ) (C ) 两个同周期简谐振动曲线如图所示. 落后/2. (B)超前 落后. (D)超前.: X 1的相位比 12. 一个质点作简谐振动,振幅为 A , 1 刻质点的位移为 一A ,且向X 轴的正方向运动,代表 2 简谐振动的旋 B : 在起始时 X 2的相位(A)(C)t(D ®XX■>13. (A )(D) 2.00 s .(C ): 2.20 s . B :物体的加速度为(A)护A 215.用余弦函数描述一简谐振子的振动.若其速度〜时间( 动的初相位为(A) (C) /6. /2. (B) /3. (D) 2 /3.(E) 5 16. v17. 物的质量增为原来的四倍,则它的总能量 (A) E 1/4. (B) E 1/2. (C) 2E 1. (D) 4 E 1 . 一弹簧振子作简谐振动,总能量为 E 1,如果简谐振动振幅增加为原来的两倍,重 E2变为 18 弹簧振子在光滑水平面上作简谐振动时, 丄尿. 2 0. (A) kA 2• (B ) 弹性力在半个周期内所作的功为 (C) (1/4) kA 2. (D ) 19. 一物体作简谐振动, 振动方程为 X Acos( t 1 ).则该物体在t = 0时刻的动能与 t = T/8 (T 为振动周期)时刻的动能之比为: (A) 1:4. (B) 1:2. (C) 1:1 . (D) 2:1 . (E) 4:1. 20.图中所画的是两个简谐振动的振动曲线.若这两个简谐振动可叠加,则合成勺余弦振 动的初相为 (A) 3 . (C) 1 . 二.填空题 21.在 t = 0 时, (B) (D) 0. X 2 A/2 O X 1 -A 周期为T 、振幅为A 的单摆分别处于图(a)、(b)、 (c)三种状态.若选单摆的平衡位置为坐标的原点,坐标指向正右 方, 为 则单摆作小角度摆动的振动表达式(用余弦函数表示)分别(a) 2 X A cos(—t —) T 2 V o (a)(b ) (b ) 2X A cos(—t —)'T 2 (c ) X Acos(2—t 23. 动的周期之比为在两个相同的弹簧下各悬一物体,两物体的质量比为 2:1 . 4 : 1,则二者作简谐振24. 一质点作简谐振动,速度最大值 v m = 5 cm/s ,振幅 正最大值的那一时刻为 t = 0,则振动表达式为 A = 2 cm .若令速度具有50.02cos(—t —).2 2 —25. 一物体作余弦振动,振幅为 15 X 10-2 m ,角频率为6 s 1,初相为0.5 ,则 V 0 0I (c )振动方程为 _x 0.15cos(6 t y) (SI).27. 一简谐振动的表达式为X Acos(3t ),已知t = 0时的初位移为0.04 m ,初速度43. 一弹簧振子系统具有 1.0 J 的振动能量,为 0.09 m/s ,则振幅 A = _________________________ 0.05m . ,初相.3arcsi n- 530.已知两个简谐振动的振动曲线如图所示.两简谐振动的最大速率之比为 31. 一简谐振动用余弦函数表示,其振动曲线如图所示, 则此简谐振动的三个特征量为 A = 0.1m — rad /s 6 34.已知三个简谐振动曲线如图所示,则振动方程分别为: X 1 = 10cos X 2 = 10cos(t2) x 3 = 10cos( 37.—简谐振动的旋转矢量图如图所示,振幅矢量长 2cm ,则该简谐振动的初相为 为_x 0.02cos( t —) — 4 41. 一作简谐振动的振动系统,振子质量为 2 kg ,系统振动频率为 1000 Hz ,振幅为0.5 cm ,则其振动能量为100 2J0.10 m 的振幅和1.0 m/s 的最大速率,则弹簧的劲度系数为200N/m,振子的振动频率为 -HZ44.两个同方向的简谐振动曲线如图所示.合振动的振幅 A A i,合振动的振动方程 A 护 A 1x (A 2 A)cos(*t -) __________ . 50. 一个质点同时参与两个在同一直线上的简谐振动,其表达式分 别为 2 X 1 4 10 cos(2t1 ) , X23 10 2cos(2t I (SI )则其合成振动的振幅为 0.01m ,初相为第十章波复习题一、选择题 1.:2. (A) (B) (C) (D) C 在下面几种说法中,正确的说法是: 波源不动时,波源的振动周期与波动的周期在数值上是不同的. 波源振动的速度与波速相同. 在波传播方向上的任一质点振动相位总是比波源的相位滞后(按差值不大于 在波传播方向上的任一质点的振动相位总是比波源的相位超前. :计).(按差值不大于计) 机械波的表达式为 y = 0.03cos6 (t + 0.01X )(SI) ,_则1 (B)其周期为一 s . 3 (D)波沿X 轴正向传播. (A) 其振幅为 (C)其波速为 3. 一平面简谐波沿 s 时刻的波形图是 3 m .10 m/s . Ox 正方向传播, :B 波动表达式为y 0.10COS[2 (£ :A: X -)- 4 2 ](SI),该波在 t = 0.5横波以波速 u 沿x 轴负方向传播.t 时刻波形曲线如图•则该时刻 (A ) (C ): A 点振动速度大于零. C 点向下运动. (B) B 点静止不动. (D) D 点振动速度小于零. u 5. 振动,则 把一根十分长的绳子拉成水平,用手握其一端•维持拉力恒定,使绳端在垂直于绳子的方向上作简谐 (A)振动频率越高,波长越长. (B)振动频率越低,波长越长. (C) 振动频率越高,波速越大. 6. 一平面余弦波在t = 0时刻的波形曲线如图所示,则为: (D)振动频率越低,波速越大. O 点的振动初相 B :(B) 1 (D) 3 如图所示,有一平面简谐波沿 Acos( t 0)),则 (A)0. (C ) 7. 规律为y 1 ) : B : 2 x 轴负方向传播,坐标原点B 点的振动方程为 (或 O 的振动(A ) (B ) (C ) y Acos[ t (x/ u) Acos [t (x/u)]. Acos{ [t Acos{ [t (x/u)] 0]. (D) 8如图所示为一平面简谐波在 0}. 0}. (x/u)] t = 0时刻的波形图, 该波的波速 u =200m/s ,贝U P 处质点的振动曲线为 y (m) A 0.1...0.1y p (m)Iy p (m)A0.1&窖(m)2(A)y p (m)i\t (s) 0―xLz(B) ^-^.5t (s)0.10.2(C)y p (m)A0.1& — t (s) 0(D) t (s)9. 一平面简谐波沿x 轴正方向传播,t = 0时刻的波形图如图所示,则t =0时刻的旋转矢量图是 [A质点的振动在(A ) A S (C)A Q ,>S(B) 0 --- ・ A A SO ,A(D)尸於(A) A 1 / A 2 = 16 .(B) A 1 / A 2 = 4 .(C) A 1 / A 2 =2 .(D) A 1 / A 2 = 1 /4 .(A)动能为零,势能最大.(B)动能为零,势能为零.10. 一平面简谐波沿 Ox 轴正方向传播,t = 0时刻的波形图如 图所示,贝U P 处介质质点的振动方程是 (A ) 0.10cos(4 (B ) y P 0.10cos(4 t(C) 0.10cos(2 3) 1) 1 (SI). (SI). (SI). (D) y P 0.10cos(2 t 6 )(SI). 图示一简谐波在t = 0时刻的波形图, 波速u (A) v 0.2 cos(2 t ) (SI). (B) v0.2 cos( t ) (SI). (C) v 0.2 cos(2 t /2) (SI). (D ) v 0.2 cos( t 3 /2) (SI).11. 0. 0.05y (m) u =20 m/s =200 m/s ,则P 处质点的振动速度表达式为 12 .在同一媒质中两列相干的平面简谐波的强度之比是4,则两列波的振幅之比是U (m)I 1 / I 2 =13. 一列机械横波在大值的媒质质元的位置是: 时刻的波形曲线如图所示,则该时刻能量为最(A) 0/, b , d , f . (C) 0/, d . 14.一平面简谐波在弹性媒质中传播,在某一瞬时,媒质中某质元 正处于平衡位置,此时它的能量是(B) a ,c ,e ,g . (D) b , f . : B : (C)动能最大,势能最大. (D)动能最大,势能为零.15 . 一平面简谐波在弹性媒质中传播,在媒质质元从最大位移处回到平衡位置的过程中 它的势能转换成动能. 它的动能转换成势能.它从相邻的一段媒质质元获得能量,其能量逐渐增加. [C (A ) (B) (C ) 它把自己的能量传给相邻的一段媒质质元,其能量逐渐减小. [ 16 .如图所示,S 和S 2为两相干波源,它们的振动方向均垂直于图面,发出 波长为的简谐波,P 点是两列波相遇区域中的一点,已知 S 1P 2 , (D) S 2P 2.2 ,两列波在P 点发生相消干涉.若S 1的振动方程为 y i Acos(2 t 1 ),则S 2的振动方程为 2 )(A)y 2Acos(2 t(C)y 2A cos(2 t1).12 ).(B )(D )y 2 Acos(2 t y 2 2Acos(2 t 0.117.两相干波源S i 和S 2相距/4,(为波长),S i 的相位比S 2的相位超前1一,在S i , S 2的连线上,S i 外侧各点(例如P 点)两波引起的两谐振动的相2位差是:/4 K>1 SiS2(A) 0- 1(B)—2(C) (D)-218 .&和S 2是波长均为的两个相干波的波源,相距 3 /4, S i 的相位比播时,在过S i 和S 2的直线上各点的强度相同,不随距离变化,且两波的强度都是 S i 外侧和S 2外侧各点,合成波的强度分别是(A) 4I 0,4I 0. (B) 0,0. (C) 0,4I 0 . (D) 4I 0,0.19 在驻波中,两个相邻波节间各质点的振动(A) 振幅相同,相位相同. (B)振幅不同, (C)振幅相同,相位不同.(D)振幅不同,20 在波长为的驻波中,两个相邻波腹之间的距离为1&超前一-2则在 若两波单独传I o , S i 、S 2连线上相位相同.相位不同.(A)/4.(B) /2.(C) 3 /4.(D).21.沿着相反方向传播的两列相干波,其表达式为y 1 Acos2 ( t x/ )和 y在叠加后形成的驻波中,各处简谐振动的振幅是(A) A .(B) 2A .(C) 2Acos(2 X/ ).(D)12Acos(2 x/ 二、填空题Acos2 X/)122.一个余弦横波以速度 u 沿x 轴正向传播,t 时刻波形曲线如图所示. 分别指出图中A ,B ,C 各质点在该时刻的运动方向.A _______________ ; B_____________ ; C ____________23. 一平面简谐波的表达式为y 其角频率0.025cos(125t 0.37x) (SI),波速u =长 = ____________________ .24.频率为100 Hz 的波,其波速为250 m/s .在同一条波线上,相距为 两点的相位差为25.图为t = T / 4时一平面简谐波的波形曲线,则其波的表达式为 26、一平面简谐波沿 Ox 轴正方向传播,波长为.若如图P i 点处质点的振动方程为y rAcos(2 t ),则P 2点处质点的振动方程为 ____________________________________ ; 与卩1点处质点振动状态相同的那些点的位 0.5 m 的P i OP 2 x2I35、两相干波源 S i 和S 2的振动方程分别是y i Acos t 和1一 ).S i 距P 点3个波长,S 2距P 点2I/4个波长.两波在2位差 是如图.已知S i 的初相为丄 27、一简谐波沿x 轴正方向传播.X i 和x 2两点处的振动曲线分别如图 (a)和 (b)所示.已知X 2 .> X i 且X 2 - X i < (为波长),则X 2点的相位比 X i 点的相位滞后28、已知某平面简谐波的波源的振动方程为 iy 0.06叫(SI),波速为 2 m/s._KU在波传播前方离波源5 m 处质点的振动方程为(b)29、( i ) 一列波长为 的平面简谐波沿X 轴正方向传播.已知在 X振动的方程为y = Acos t ,则该平面简谐波 波疏的表达式为媒质 夕波密纟媒质h t反射面1(2)如果在上述波的波线上 X = L ( L -)处放一如图所示的反射2面,且假设反射波的振幅为 A/,则反射波的表达式为_______________________________________ (X < L).30、一平面简谐波沿 X 轴负方向传播•已知 X = -i m 处质点的振动方程为速为u 则此波的表达式为______________________________________y Acos( t ),若波相等的面积 S l 和S 2,则通过它们的平均能流之比P i /p 232、一点波源发出均匀球面波,发射功率为 4 W . 波源为2 m 处的强度是 ____________________ .不计媒质对波的吸收,则距离33、如图所示,波源 S i 和S 2发出的波在P 点相遇,P 点距波源S i 和S 的距离 分别为3和I0 3,为两列波在介质中的波长, 若P 点的合振幅总是极大 值,则两波在P 点的振动频率 _____________________________ ,波源S i 的相位比S 2的相位领 先 __________________ .S i34、如图所示,S i 和S 2为同相位的两相干波源,相距为 L ,P 点距 源S i在P 点引起的振动振幅为 A i ,波源S 2在P 点引起的振动振幅为 波 长 都 是,贝U P 点 振 幅S i 为r ;波A 2,两波i0 3L Si r PS 2y A cos( t p 点引起的两个振动的相36、 S i ,S 2为振动频率、振动方向均相同的两个点波源,振动方向垂直纸面,两者相距3-(为波长)2jM3(i)若使射线S2C上各点由两列波引起的振动均干涉相消,则S2的初相应为 .(2)若使S i S2连线的中垂线MN上各点由两列波引起的振动均干涉相消,则S2的初位相应为______________________________________________ S i j S2 CIN2I 11两列波在一根很长的弦线上传播, y i = 6.0 X 10 2cos (x - 40t) /2 y 2 = 6.0 X 10 2cos (x + 40t) /2 则合成波的表达式为 ________________ 在x = 0至x = 10.0 m 内波节的位置是 37、 其表达式为 (SI ) (SI ) ;波腹的位置是 38、设入射波的表达式为 % Acos2 ( t ―) •波在x = 0处发生反射,反射点 为固定端,则形成的驻波表达式为 39、 一驻波表达式为 y A cos2 x cos100 t .位于x 1 = 3 /8 m 的质元 元P 2的振动相位差为 ___________________________________ . P i 与位于X 2 = 5 /8 m 处的质 40、在弦线上有一驻波,其表达式为 y 2Acos(2 x/ )cos(2 t),两个相邻波节之间的距离是。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机械振动习题集同济大学机械设计研究所2004.91_简谐运动及其运算1-1求下列简谐函数的单边复振幅和双边复振幅 (1))3sin(2πω+=t x (2))410cos(4ππ+=t x (3))452cos(3︒+=t x π1-2通过简谐函数的复数表示,求下列简谐函数之和。
(1))3sin(21πω+=t x )32sin(32πω+=t x (2)t x π10sin 51=)410cos(42ππ+=t x(3))302sin(41︒+=t x π )602sin(52︒+=t x π)452cos(33︒+=t x π)382cos(74︒+=t x π )722cos(25︒+=t x π答案:(1))6.6cos(359.412︒+=t x ω (2))52.4710cos(566.312︒-=t x π (3))22.92cos(776.1412345︒+=t x π1-3试计算题1中)(t x 的一阶对数和二阶导数对应的复振幅,并给出它们的时间历程。
1-4设)(t x 、)(t f 为同频简谐函数,并且满足)(t f cx x b xa =++ 。
试计算下列问题 (1)已知)3712sin(10)(,25,6,5.1 +====πt x cb a ,求)(t f (2)已知)647sin(25)(,30,7,3 +====πt fc b a ,求)(t x 1-5简述同向异频简谐振动在不同频率和幅值下合成的不同特点。
1-6利用“振动计算实用工具”,通过变换频率和相位总结垂直方向振动合成的特点。
2_单自由度系统振动2-1请解释有阻尼衰减振动时的固有圆频率d ω为什么总比自由振动时的固有圆频率n ω小?答案:因为n d ωξω21-=,ξ<12-2在欠阻尼自由振动中,把ξ改成0.9的时候,有人说曲线不过X 轴了,这种说法正确么,请说明理由?答案:ξ<1为小阻尼的衰减振动,当然过X 轴2-3在单自由度自由振动时候,给定自由振动时的固有圆频率n ω,阻尼系数ξ,初始位移0x ,以及初始速度0v ,答案:如n ω2-4 如图2-1答案:T 2=2-5 以角速度ω答案:22ωω-=mn2-6 如图2-3所示,具有与竖直线成一微小角β的旋转轴的重摆,假设球的重量集中于其质心C 处,略去轴承中的摩擦阻力,试确定仅考虑球的重量W 时,重摆微小振动的频率。
答案:n ω=2-7 图2-4所示,竖直杆的顶端带有质量kg m 1=时,测得振动频率为Hz 5.1。
当带有质量kg m 2=时,测得振动频率为Hz 75.0。
略去杆的质量,试求出使该系统成为不稳定平衡状态时顶端质量s m 为多少?图2-4答案:m s =2-8 确定图2-5答案:n =ω2-9 确定图2-6系统的固有频率,滑轮质量为M 。
2-10 确定图2-7答案:()r R gn -=32ω2-11 一个粘性阻尼单自由度系统,在振动时测出周期为1.8s ,相邻两振幅之比为4.2:1。
求此系统的无阻尼固有频率。
答案:πω14.1=n2-12 一个龙门起重机,要求其水平振动在25s 内振幅衰减到最大振幅的5%。
起重机可简化成图2-8系统。
等效质量m 10.0=,问起重机水平方向的刚度k 至少应达何值。
2-13 某洗衣机重14700N ,用四个弹簧对称支承,每个弹簧的弹簧常数为m N k /80360=。
a) 计算此系统的临界阻尼系数c c ;b) 在系统上安装四个阻尼器,每一个阻尼系数为m s N c /4.1646⋅=。
这时,系统自由振动经过多少时间后,振幅衰减到10%;c)衰减振动的周期为多少?与不安装阻尼器时的振动周期作比较。
答案:a) m s N c c /43914⋅=; b) s t 137.0=;c) s T d 434.0= 而s T n 429.0=2-14 一个集中质量为m2-9所答案:δ=2-15 一质量c 相撞后一起作自由振动,如图m 在相撞后多少答案:t =2-16自由振动时的固有圆频率为1rad/s, 阻尼系数为1, 初始位移和速度均为0, 外界激励频率为0.5rad/s, x"u=0.1, q"°=30,利用所给计算工具画出简谐振动以及受Duhamel 积分激励的系统(m=40)的瞬态响应与稳态响应的叠加图 答案:简谐振动:受Duhamel 积分激励:2-17 一个有阻尼弹簧-质量系统,受到简谐激励力的作用。
试证明:发生位移共振的频率比221/ζωω-==n r ; 发生速度共振的频率比1=r ;发生加速度共振的频率比221/1ζ+=r 。
2-18 一个电动机安装在一个工作台的中部。
电动机和工作台的总重量为356N ,转动部分的重量89N ,偏心为1cm 。
观察到:当电动机装到工作台上时,其变形为3.2cm 。
在自由振动时,1cm 的位移在1s 内将减小1/32cm 。
电动机的转速为900r/min 。
假定阻尼时粘性的,计算运动的最大幅值。
答案:0.235cm2-19 一个车轮以速度v 等速沿波形面移动,如图2-11所示。
确定重为W 的质量块在垂直方向运动的振幅。
假定在W 的作用下弹簧的静位移为s m v cm st /2.18,7.9==δ,波形面可表为cm l cm a l x a y 92,5.2,/sin ===π。
答案:2-20 图2-12系统的上支承,作振幅为1.2cm ,频率为系统无阻尼固有频率的简谐运动。
假定c m N k 6.262,/6958==值。
答案:F N F d s 4.29,89==2-21 在图2-13t F ωsin 。
试求质量块m 的振幅。
答案:()()t k k m x n ωωωsin 222122-+=2-22 一机器重4410N ,支承在弹簧隔振器上,弹簧的静变形为0.5cm 。
机器有一偏心重,产生偏心激励力N gF 254.2ω=,ω为激励频率,g 为重力加速度,不计阻尼。
求:a) 机器转速为1200r/min 时,传入地基的力;b) 机器的振幅。
答案:a) N F 7.514max =;b) cm X 0584.0=2-23 一位移传感器,其固有频率为4.75Hz ,阻尼比为0.65,确定测量误差分别小于:a) 1%;b) 2%的最低测试频率。
2-24 如果加速度计的固有频率是所测试运动频率的4倍,该加速度计的读数误差是多少?答案:6.66%3_二自由度系统振动3-1如图,已知m 2=2×m 1=m ,k 3=2k 1=2k 2=2k ,x 10=1.2,x 20=10x =20x =0,试求系统的固有频率,主振型以及相应。
答案:利用程序,易得 固有频率:ωn 1=3.162277rad/s ,ωn 2=5 rad/s主振型:系统相应:t x 5cos 8.03.1622777t cos 4.01+= t x 5cos 4.03.1622777t cos 4.02-=3-2已知:⎥⎦⎤⎢⎣⎡=11009][m ,[c ]= ⎥⎦⎤⎢⎣⎡--11.01.01,][k =⎥⎦⎤⎢⎣⎡--905050110,)}({t f =⎭⎬⎫⎩⎨⎧21,激振力频率ω=3rad/s,试求系统的稳态响应。
答案:利用给定程序,输入给定数据,即获得系统的稳态响应。
3-3如图所示,已知质量比μ=0.1,固有频率比δ=0.909,放大系数r =1.55, ζ=0.1846,m1=11,k1=100,根据程序求动力吸振器弹簧的刚度及其质量答案:m 2= 1.1 k 2=3-4 。
答案:1n ω {}u 13-5 2J ,它们答案:1n ω 2n ω {}TTJ J u u 2121/1;11-==3-6 试确定图3-3所示皮带传动系统的固有频率和特征向量。
两皮带轮的转动惯量分别为1J 和2J ,直径分别为1d 和2d 。
答案:{n u 2111,0=ωn 2=ω3-7 写出图3-40θ答案:⎭⎬⎫⎩⎨⎧⎬⎨⎥⎢⎬⎨⎢⎢⎣⎡000321l m ; 4-ωn3-8 解定图题答案:22.1n ω式中222221,mr rmb mr rma +=+=3-9 试确定图3-6系统的固有频率,略去滑轮重量。
答案:022212122212114=+⎥⎦⎤⎢⎣⎡---m m k k m k m k m k n nωω3-10 如图3-7所示的行车,梁的弯曲截面矩45110cm I =,2/210m GN E =,m L 45=。
小车2m 重11760N ,m N k /343000=,答案:;65.20;75.321==n n ωω 22.5;798.021-==r r3-11 一重块2W 自高h 处自由落下,然后与弹簧-质量系统112k gW k --一起作自由振动,如图3-8所示,试求其响应。
已知k W h k k k W W W /100,,2121=====。
答案:)]sin(913.3)sin(3.10[/22111φωφω+++=t t k W x n n , )]sin(418.2)sin(67.16[/22112φωφω+-+=t t k W x n n ;n 1ω1φ3-12 v 驰来的另一辆车m 答案:1x = n ω3-13 如图3-10所示,一刚性跳板,质量为3m ,长l ,左端以铰链支承于地面,右端通过支架支承于浮船上,支架的弹簧常数为k ,阻尼系数为c ,浮船质量为m 。
如果水浪引起一t F F ωsin 0=的激励力作用于浮船上。
试求跳板的最大摆动角度max Θ。
3-15图3-324 多自由度系统振动4-1对指定的广义坐标1θ,2θ,3θ,求图示三级摆,当第一、二两质量上作用有简谐激振力t F ωsin 2时的稳态响应,其中0F 是常数,lg 522=ω。
答案:t mg F ωθθθsin 654450321⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛4-2图示一无质量均质简支梁,弯曲刚性常数为EJ ,上有集中质量m 1=m2=m3=m ,在第一个质量上作用有激振力t P ωcos 。
假设各阶主阵型阻尼比01.0=i ζ(i =1,2,3)。
已知激振频率37688.1ml EJ=ω,求各质量的稳态响应。
4-3在图示系统中,各质量只能沿铅垂方向运动。
在质量4m 上作用有铅垂激振力t P ωcos 0,求系统的无阻尼强迫振动的稳态响应。
又若考虑到各弹性元件中的阻尼,假设振型阻尼比02.0=i ζ(i =1,2,3),mk25.12=ω,求系统的稳态响应。
4-5如图所示的汽车在mab I c =的情形下的固有频率,设a =2.3m ,b =0.94m ,Kg m 3104.5⨯=,m 1=m 2=650Kg ,m KN K K /3521==,前后轮的轮胎刚度均为K =1200KN/m 。
