在裂纹尖端引入奇异单元的偶应力有限元法
应用三维有限单元法计算应力强度因子

应用三维有限单元法计算应力强度因子应用三维有限单元法计算应力强度因子摘要描述了两种基于有限单元计算面形裂纹应力强度因子的方法,建议了一种创造三维有限单元网格的途径。
计算方法的精度通过和其它解析解或数值解的比较得到了说明。
关键词应力强度因子有限元损伤容限设计断裂评定无论在损伤容限设计还是在缺陷评定阶段,工程师们需要知道正在分析的构件中裂纹的应力强度因子,因为判断含裂纹构件的断裂,或者计算剩余疲劳寿命大多依赖于这一参量。
因此,在断裂力学发展中,如何求取应力强度因子一直是一个重要的课题。
当前已有许多方法可用来计算应力强度因子,较为典型的有解析法、边界配位法、有限单元法、边界元素法、体力法、权函数法和线弹簧模型。
利用这些方法,大量的应力强度因子解已经获得,已出版的应力强度手册[1]中收编了许多典型的解。
尽管如此,工程师们仍然会感到自己所需要的应力强度因子解很难找到,这是因为要解决的工程问题往往是一些受复杂载荷的构件,包含的裂纹也往往是一些不规则裂纹。
本文简单介绍了两种基于三维有限单元法计算面形裂纹应力强度因子的方法。
有限单元法已经成为工程设计分析领域中一个强有力的计算工具,它能模拟非常复杂的构件。
基于有限元的应力强度因子计算方法,自然也将具有卓越的工程能力。
除了计算方法的介绍以外,还将简单描述一种简化网格的生成方法。
最后提供了一些所得到的典型应力强度因子解,并和大家熟知的解进行了比较,以说明本文所描述的方法的可靠性。
1 计算方法简介图1表示了笔者[2,3]建议的裂纹尖端网格形图1 裂纹前沿单元网格式。
网格由3个半环共12个20节点三维等参单元组成,每个半环有4个单元,其中第一个半环单元的中节点被移至1/4点位置,以模拟裂纹尖端应力和应变场的奇异性[4,5]。
根据线弹性断裂理论[6~8],裂纹尖端的位移场可表示为u t=0 (3)式中,n和t分别为裂纹前沿的法线方向和切线方向;z为垂直于裂纹平面方向(见图2);μ为材料剪切模量。
孔边应力集中和裂纹尖端应力强度因子的有限元分析

$ 圆孔板孔边裂纹应力中分析
误差为 @%DQT% 同上应用 &’()(算得该模型双向受力时孔
边裂纹的应力强度因子为 $JD%,=%通 过查表 可得
U%* 计算模型
其 对 应 的 因 子 R0 1%QJG<H>#代 入 式 9D.计 算 得 OP
如图 =-.所示#在边长为 ,11EE#厚为 =EE 0 $Q,%,J#&’()(计 算 所 得 的 值 的 相 对 误 差 为
* *$*
武 汉 理 工 大 学 学 报 8交 通 科 学 与 工 程 版 (
0$$0年 第 07卷
!"#$% " 比较圆孔平板单向受力和双向受力的应力强
度因子可以看出当圆孔平板受到等值的单向受力 和 双 向 受 力 时 &其 单 向 受 力 的 应 力 强 度 因 子 大 于
’( 问题描述
)( 裂纹尖端网格图
OP0 R/LSF
9D.
式中#对于图 D所示的中心裂纹#因子 R0,#故由
上 式 可 计 算 得 O,0 $QH%$$#&’()(计 算 所 得 的
OP值的相对误差为 ,%H$T%
0,1EE#弹性模量为 @%1G1$HI,1=23-#泊松 比为 1%@JJ#承受单向均布正应力#其大小 /0,11 23-#在 与 /作 用 线 垂 直 的 直 径 两 端 的 孔 边 有 裂 纹#裂纹长度为 FA60$EE%
图 * 圆孔板孔边裂纹问题及其网格划分
及 中 心 裂 纹 K圆 孔 孔 边 裂 纹 的 应 力 强 度 因 子 L并 与 理论解进行了比较@
S@S 单向受力圆孔平板的应力分布 S@S@S 计算模型 如图 #,&所示L正 方形平 板中 心 有一 圆 孔L圆 孔 半 径 TU !VVL正 方 形 边 长 为 #$$VVL厚度为 OVVL弹性模量为 !W#$OXY,L 泊 松 比 为 $@G@在 正 方 形 左 右 两 边 加 一 Z方 向 均 布拉力L其集度为 [U#$$XY,@
Ⅰ型裂纹尖端圆弧对应力强度因子影响的数值研究

Ⅰ型裂纹尖端圆弧对应力强度因子影响的数值研究赵春风;李晓杰;闫鸿浩;王美芹【期刊名称】《科学技术与工程》【年(卷),期】2010(010)004【摘要】应力强度因子表征了裂纹尖端奇异应力场的强度,它是研究裂纹扩展规律和带裂纹构件强度的基础.采用有限元法,对受均布荷载作用存在边缘Ⅰ型裂纹的平面板进行了数值分析.研究了裂纹尖端圆弧对应力强度因子的影响,分别计算了具有不同裂尖圆弧r0的Ⅰ型裂纹的应力强度因子.采用应力法计算不同半径处的表观应力强度因子,插值到裂尖圆弧而得.根据计算结果,绘制KI-r0曲线,利用最小二乘法拟合至尖裂纹(r0=0)即得理想尖裂纹的应力强度因子,与解析解相差仅0.7%.该曲线为带圆弧裂纹的应力强度因子测试和带圆弧裂纹构件强度计算提供了依据.【总页数】5页(P961-965)【作者】赵春风;李晓杰;闫鸿浩;王美芹【作者单位】工业装备国家重点实验室大连理工大学运载学部工程力学系,大连,116024;工业装备国家重点实验室大连理工大学运载学部工程力学系,大连,116024;工业装备国家重点实验室大连理工大学运载学部工程力学系,大连,116024;合肥工业大学土木与水利工程学院,合肥,230009【正文语种】中文【中图分类】O346.1【相关文献】1.裂纹尖端解析解与周边数值解联合求解应力强度因子 [J], 苏海东;祁勇峰;龚亚琦2.厚壁筒双轴向表面裂纹尖端应力强度因子影响因素的研究 [J], 秦晓峰;谢里阳;何雪浤;钱文学;马园园3.管道表面焊缝裂纹尖端应力强度因子的数值模拟研究 [J], 曹先凡;秦延龙4.焊接裂纹尖端应力强度因子数值计算 [J], 高季明;王晓春5.预制V型裂纹尖端应力强度因子的研究 [J], 王成端因版权原因,仅展示原文概要,查看原文内容请购买。
三维裂纹前缘应力强度因子数值计算方法

0 引 言
船舶与海洋工程结构在建造和营运过程中不可避 免地存在一些裂纹,这些裂纹在交变载荷作用下将会 发生扩展,最终可能会导致结构发生断裂失效,严重 影响结构的安全使用。采用数值方法预报含裂纹结构 裂纹扩展形貌及扩展寿命具有重要的工程应用价值, 可为结构裂纹检测周期的确定、疲劳寿命评估及抗疲 劳设计提供支撑。结构裂纹前缘应力强度因子(SIF) 是含裂纹结构疲劳裂纹扩展形貌及寿命数值预报方法
· 10 ·
舰船科学技术
第 41 卷
型应力强度因子的计算方法。采用平板表面裂纹研究 三维裂纹整个裂纹前缘各个位置应力强度因子随裂纹 网格划分参数变化情况,通过整个裂纹前缘应力强度 因子数值计算结果与 Newman-Raju 解析公式[6]计算结果 的对比分析,验证了数值计算方法的准确性,最终提 出裂纹网格划分参数取值范围。为了验证文中提出的 数值计算方法计算其他类型裂纹前缘应力强度因子的 准确性,采用数值计算方法计算分析了疲劳裂纹扩展 三点弯曲试样裂纹扩展过程中裂纹前缘应力强度因 子,并与解析解进行对比分析,验证了数值计算方法 计算穿透性裂纹前缘应力强度因子的准确性。
文中基于 20 节点奇异单元 1/4 节点位移法,提出 三维裂纹网格划分方法及裂纹前缘不同位置、不同类
收稿日期: 2018 – 06 – 30 基金项目: 国防预研项目资助项目 (3020503010101) 作者简介: 黄如旭 (1987 – ),男,工程师,研究方向为船舶与海洋工程结构疲劳与断裂理论、实验及数值模拟。
中的关键参数,一些学者提出了采用奇异单元求解裂 纹尖端应力强度因子的有限元模型,并以裂纹最深点 及裂纹端点处的应力强度因子作为计算参量模拟简单 焊接接头裂纹面内扩展形貌[1 – 5]。然而,由于工程结构 承受载荷复杂性及结构中裂纹分布随机性致使结构最 大主应力与裂纹平面并不垂直,裂纹扩展形貌将不再 保持平面。结构三维裂纹前缘各个位置处应力强度因 子准确计算将是模拟真实裂纹扩展形貌的前提。
应力奇异概念

应力奇异概念
"应力奇异"通常用于描述在材料或结构中某些区域产生无穷大
或趋近于无穷大的应力值的现象。
这种情况通常发生在材料中存在缺陷、尖锐边缘或集中载荷的地方。
应力奇异性是材料力学和结构分析中的一个重要概念。
在一个结构或材料中,如果存在一个几何尖锐的角点、裂纹尖端、孔洞边缘等地方,应力场可能在这些区域内增大,导致应力奇异。
在这些区域内,传统的弹性理论和公式可能不再适用,需要采用更为复杂的理论和方法,例如弹塑性理论或断裂力学。
一些常见的应力奇异问题包括:
1.尖端应力问题(Stress Concentration):在结构中存在几何尖锐或
不连续的地方,如孔洞、缺口、裂纹等,导致应力场在这些区域内增大。
2.裂纹尖端问题(Crack Tip Singularity):当裂纹的尖端附近,应力
场可能呈现出奇异性,这在断裂力学中是一个重要的研究对象。
应对应力奇异性问题,工程师和研究人员可能使用一些修正方法,如引入应力集中系数、使用奇异积分等。
这有助于更准确地预测和分
析结构在奇异区域内的应力分布。
应变梯度理论的新进展_一_偶应力理论和SG理论

第21卷第2期机 械 强 度V o l.21N o.2 1999年6月JOU RNAL O F M ECHAN I CAL STR EN GTH June1999应变梯度理论的新进展(一)Ξ——偶应力理论和SG理论RECENT AD VANCES IN STRA IN GRAD IENT PLAST I C IT Y-——Couple stress theory and SG theory黄克智ΞΞ 邱信明 姜汉卿(清华大学工程力学系,北京100084)Hw a ng Ke hchih Q iu X inm ing J ia ng Ha nq ing(D ep a rt m en t of E ng ineering M echan ics,T sing hua U n iversity,B eij ing100084,Ch ina) 摘要 介绍两种应变梯度塑性本构模型:CS应变梯度塑性理论——偶应力理论、SG应变梯度塑性理论。
并对它们在断裂力学中的应用进行了评述。
给出一种考虑可压缩性的方法,并根据这种模型用薄梁弯曲的例子给出了可压缩性的影响。
本文的讨论虽限制在形变理论范围内,但按照相应的方法也可以得到流动理论的形式。
关键词 应变梯度 塑性 偶应力 高阶应力 断裂中图分类号 O344Abstract In the paper tw o k inds of fram ew o rk of strain gradien t p lasticity recen tly developed and their app licati on s are review ed:strain gradien t p lasticity fo r CS so lid——the coup le stress2theo ry,strain gradien t p lasticity fo r SG so lid.T he app licati on s are m ain ly focu ssed on the fractu re p rob lem s.O ne w ay of accoun ting fo r m aterial comp ressib ility is suggested.T he review is confined to the defo rm ati on theo ry versi on,though the flow theo ry versi on can be parallelly con structed.Key words stra i n grad ien t,pla stic ity,couple stress,h igher-order stress,fracture1 引言新近的试验表明,当非均匀塑性变形特征长度在微米量级时,材料具有很强的尺度效应。
基于奇异元计算分析裂纹尖端应力强度因子

文 中 以 ANS YS软件 为基 础 ,分别采用 2 0节 点和 1 2节点奇 异单元 建立 了含表 面裂纹 的平板 的两
种 有 限元模 型 。对 有 限元 网格技 术及 裂纹 体网格 剖分 的要求 作 了深入 研究 ,评估 了两 种有 限元模 型计 算 的应 力强 度 因子 对 网格 的敏感程 度 ,进而 判 断出哪种 有 限元模 型计算 的应 力 强度 因子更 稳定可靠 ,
对 图 2所 示的含 半椭 圆表面 裂纹 的平板 模型 进行有 限元 计算 和分析 ,在 有 限元模型 中考虑 了裂 纹 前缘周 围 区域 网格 的变 化对 应力 强度 因子的 影响 ,分 析不 同奇异 单元 所建 的有 限元 模型计 算 结果 的稳
定性。
含有表 面裂 纹 的有 限平 板示 于 图 2 ,图 中的各个 参数列 于表 1 。在平 板长度 两端 受到垂 直裂 纹面方
法 、混 合法 、权 函数法 和线 弹簧法 等 。利用 这些 方法 , 已经 获得 许 多裂纹 体模 型的应 力强度 因子 的大
小 ,应 力强 度 因子手 册 中收编 了许 多种 典型 裂纹 体模 型应力 强度 因子的解 ,但 由于裂纹 体几 何形 式 J 及 所受载 荷 的复杂 性 ,很多情 况 下应力 强度 因子 的解难 以从现 有 手册查 到 。而有 限元 方法不 受裂纹 体 几何及载 荷形 式的 限制 ,因而在 断裂力 学 中得 到 了非 常广泛 的应用 。
o1 / 点 4节
0 中间 节 点 ・ 角 节 点 ● 裂 纹 尖 端
( )2 点 的 奇 异 元 a 0节
( ) 1 点 的奇 异 元 b 2节 ( )2 节 点奇 异 元 围绕 裂 尖 形 式 c 0 图 1 奇 异 单元 类 型 及 其 围绕 裂 尖 形 式
U形管周向表面椭圆裂纹应力强度因子分析
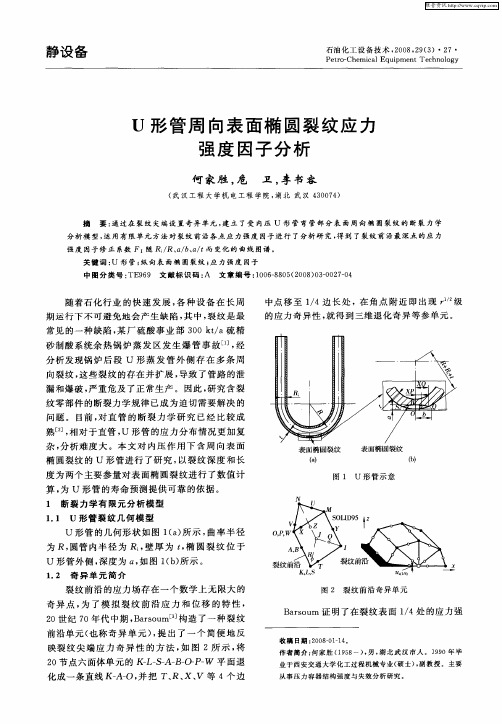
B ro m 证 明了在 裂纹 表 面 1 4处 的应力 强 as u /
收 稿 日期 :0 80 —4 2 0— 11 。
作 者 简 介 : 家 胜 ( 9 8 ) 男 , 北 武 汉 市 人 。 19 何 15 一 , 湖 9 0年 毕 业 于西 安 交通 大学 化 工 过 程 机 械 专 业 ( 士 ) 副 教 授 。主 要 硕 ,
随 着石 化行 业 的快 速 发 展 , 种 设 备 在 长 周 各
期 运行 下不 可避 免地 会产 生缺 陷 , 中 , 纹是 最 其 裂
中点移 至 1 4边长 处 ,在 角点 附近 即出 现 r 。 / 级 的应力 奇 异性 , 就得 到 三维退 化奇 异等 参单 元 。
常见 的一种 缺陷 , 厂硫 酸事 业 部 3 0k / 某 0 ta硫 精
1 断裂 力学有 限元 分析 模型
图 1 U 形 管 示 意
1 1 U 形管裂 纹 几何模 型 .
U 形 管 的几何 形状 如 图 1 a 所 示 , () 曲率 半 径
为 R, 圆管 内半 径 为 Ri壁 厚 为 t椭 圆 裂 纹 位 于 , ,
U 形管 外侧 , 深度 为 a 如 图 1 b 所示 。 , ()
从 事 压 力 容器 结 构强 度 与失 效 分 析 研 究 。
2 0节点六 面体单 元 的 K- — — B O- — 平 面退 L SA— — P W
化成 一条 直线 K— 0, 把 T、 X、 等 4个 边 A一 并 R、
维普资讯
工程硕士第六章有限单元法解平面裂纹问题2006

第六有限单元法解平面裂纹问题应力强度因子第1节 有限元素法简介 1. 基本步骤(1)结构离散化, 将作为分析对象的弹性体离散化为有限个单元;(2)元素分析,对每个单元, 形成连接结点位移和结点载荷的刚度矩阵; (3)全结构平衡,建立总刚度矩阵及全结构刚度方程; (4)边界条件处理;(5)求解刚度方程, 确定结点位移; (6)求解应变、应力。
2. 基本公式将连续体离散化后,根据收敛准则给定收敛的位移函数,各元素的内位移为:{}[]{}αQ u = (6-1-1){}Q 为基底函数矩阵,{}α为广义位移列阵。
位移函数可以多种函数形式, 最常用的是多项式。
例如:(1) 杆元:x a a x u 21)(+=即:{}[]⎭⎬⎫⎩⎨⎧=21,1a a x u(2) 平面四结点矩形板元:xya y a x a a y x v xya y a x a a y x u 87654321),(),(+++=+++=即:{}⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧⎥⎦⎤⎢⎣⎡=⎭⎬⎫⎩⎨⎧=82111),(),(a a a xy yxxyy x y x v y x u u 由位移边界条件:{}[]{}αδC e = (6-1-2){}e δ为元素在局部坐标系中位移列阵。
C 为位移变换矩阵。
例如: 图6-1-1所示杆元lxu i u j i j图6-1-1 局部坐标系中的杆元素边界条件为:0=x , i u u =)0( l x =, j u l u =)(即:{}[]{}αδc a a l u u j i e =⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡=⎭⎬⎫⎩⎨⎧=21101 于是:{}[][]{}[]{}ee N C Q u δδ==-1 (6-1-3)N 为形状函数,可用广义坐标法求得:[][][]1-=C Q N (6-1-4)N 也可由结点插值求得。
例如上述杆元:(1)广义坐标法求解:[]⎥⎥⎦⎤⎢⎢⎣⎡-=-l l c 11011 [][][]⎥⎥⎦⎤⎢⎢⎣⎡-==l lx N N N j i 1101,1,=⎥⎦⎤⎢⎣⎡-l x l x ,1(2)插值法求解:由Lagrange 插值公式:lx l x x x x x N lxl l x x x x x N i j i j ji j i =--=--=-=--=--=0010根据几何关系可得:{}[]{}[][]{}[]{}ee B N u δδ∂∂ε=== (6-1-5){}ε为应变矩阵, B 为几何矩阵。
基于奇异元计算分析裂纹尖端应力强度因子

基于奇异元计算分析裂纹尖端应力强度因子裂纹是材料中常见的缺陷,会导致材料的断裂和失效。
裂纹尖端应力强度因子是衡量裂纹尖端应力集中程度的重要参数,可以帮助工程师设计出更加安全可靠的工程结构。
在裂纹尖端附近的应力场通常具有奇异性,对于常见的模型,如平面应力问题中直角裂纹和边缘裂纹,可以通过奇异元分析来获得裂纹尖端应力强度因子。
奇异元分析是将问题的解表示为具有奇异性质的特解和非奇异性质的次解的组合。
在裂纹尖端附近,应力场通常会呈现出1/r^(1/2)或ln(r)/r等奇异性质,其中r为距离裂纹尖端的距离。
通过合适的奇异元,可以很好地模拟裂纹尖端附近的应力场,并计算出裂纹尖端应力强度因子。
裂纹尖端应力强度因子K是描述裂纹尖端应力场的一个参数,它通常包括模式I、模式II和模式III三种模式。
模式I是裂纹正向拉伸的模式,模式II是横向剪切的模式,模式III是法向剪切的模式。
裂纹尖端应力强度因子K_I、K_II和K_III分别对应着这三种模式。
裂纹尖端应力强度因子可以通过J积分或Williams级数展开等方法进行计算,而奇异元方法是一种更加直观和直接的计算裂纹尖端应力强度因子的方法。
奇异元方法的基本思想是利用奇异元函数来表示裂纹尖端附近的应力场,通过求解边界条件来确定奇异元函数中的待定系数,最终得到裂纹尖端应力强度因子。
在奇异元方法中,通常选择合适的奇异元函数作为基函数,如1/r^(1/2)、ln(r)/r等,并将该基函数展开成一组线性独立的函数,再通过变分原理或加权残差法来求解出待定系数,从而得到裂纹尖端应力强度因子。
奇异元方法的优点在于能够直接针对裂纹尖端附近的奇异性质进行建模,并且能够在裂纹尖端附近自动适应网格密度,计算结果更加精确。
此外,奇异元方法还可以方便地对不同裂纹形状和加载条件进行分析,并能够有效地处理多裂纹和非线性问题。
总的来说,奇异元方法是一种有效的计算裂纹尖端应力强度因子的方法,能够帮助工程师更好地理解裂纹尖端附近的应力场分布,设计出更加安全可靠的工程结构。
有限单元法 裂缝宽度

有限单元法裂缝宽度
有限单元法(Finite Element Method,简称FEM)是一种数值分析方法,用于解决工程问题中的连续介质力学问题。
在使用有限单元法进行裂缝宽度计算时,可以采用以下步骤:将结构划分为有限数量的离散单元或网格。
这些单元可以是一维、二维或三维的,并且通常是简单的几何形状,如线段、三角形或四边形。
在每个单元上建立适当的数学模型,包括材料特性、载荷和边界条件等。
这些模型可以根据具体情况选择,如线弹性模型、弹塑性模型等。
利用合适的数值方法,如有限元法中的加权残差法或变分法,对每个单元进行力学计算,得到单元内部的应力和应变分布。
根据裂纹的力学性质,如应力强度因子等,计算裂纹尖端处的应力场。
根据应力场的结果,可以使用一些经验公式或裂纹力学理论来计算裂纹的宽度。
根据裂纹宽度的计算结果,可以评估结构的可靠性和安全性,并采取相应的修复或加固措施。
需要注意的是,裂纹宽度的计算不仅涉及力学模型和数值方法的选择,还需要准确的材料参数和边界条件输入。
同时,裂纹宽度的计算结果只能作为参考,需要结合实际情况进行综合评估和判断。
木材裂纹尖端应力场的有限元分析和开裂方向预测

Ab ta t T kn E a lso pu e ( ie se t ) frisa c ,tef i lme t ot ae o B U a sr c : a igS B smpe fsrc P ca ap r a o n tn e h nt ee n f r fA AQ S w s a i e s w
第 4 6卷 第 1 O期
20l0年 l 月 0
林
业
科
学
V0 . 1 46. . 0 No 1 Oc ., t 2 0 10
SCI ENTI A
SI VAE L
S NI I CAE
木 材裂 纹 尖 端应 力 场 的有 限元 分 析 和 开 裂 方 向预 测
t e c a k T e r s ls s o d t e d r c i n o h x mu Mie te s o o r s mp e s a o g t e g a n o h o h r c . hs f f u a l s wa l n h r i f t e wo d o wh n d a n a i lp a e c n e e r u d t e c a k tp t s a s h wn t a h a i ft e t n ie sr s e p n i u a e r wi g a r d a l n e t r d a o n h r c i .I lo s o h t e r t o h e sl t sp r e d c l r i t o e
6 0。,3 ,0。r s e tv l 0。 e p c i e y,“ a g n i ln r lsr s n e s t a t rr t r e i n wa p l d t r ditt e d r c i n o t n e ta o ma t s i t n i f c o a i c i ro ” e y o t s a p i o p e c h ie t f e o
局部解情况下的裂纹尖端单元划分

局部解情况下的裂纹尖端单元划分[摘要]在弹塑性情况下,通过比较在无限大板情况下,裂纹尖端的单元采用无钝化的奇异单元和有钝化的非奇异单元有限元计算结果同Prandtl场的解析解进行对照,结果表明采用有钝化的非奇异单元在裂纹尖端区域的计算结果是正确的。
[关键词]断裂力学;有限元法;单元剖分在弹塑性情况下,含裂纹的无限大板,在两端载荷的作用下,在裂纹尖端附近范围内,材料会发生强烈的非线性变形,这一非线性的塑性区内随着,应力场的奇异性凸显。
在有限元中,为了计算时裂纹尖端的塑性区的应力场,就需要对裂纹尖端进行单独的单元划分。
由于裂纹尖端的奇异性,因此对裂纹尖端的小范围区域内单元的划分有很高的要求,不同的划分形式使得有限元计算结果有着显著的差异。
一、裂纹尖端局部解析解假设理想塑性材料,并且不可压缩,对于平面应变问题,有:则可以采用塑性力学中平面滑移线理论。
含裂纹平面应变问题的滑移线(图1)各分区的应力解为:A区:A区的裂纹表面为自由,故为均匀应力区。
B区:该区有直线边为X轴,其上故也为均匀应力区。
C区(扇形区):这个由A,B,C三个区域构成的场,称为Prandtl场。
其应力应变场如图2所示二、有限元计算模型和单元总体划分对一近似无限大板的裂纹尖端进行有限元程序的计算,对该无限大板采用下图形式进行划分。
计算模型参数如下:长L=150宽W=50裂纹长度b=25非裂纹长度a=25屈服极限杨氏模量E=222.5GPa波松比V=0.3由于裂纹尖端应力场的计算需要较高的网格精度,所以把整个模型分为两组单元,第一组为围绕裂纹尖端的第一圈单元,其余为第二组单元。
第一组单元半径三、裂纹尖端不同单元划分形式的比较由于裂纹尖端对单元的划分具有极高的敏感度,采用不同的单元划分形式会对计算结果有不同的影响,甚至左右计算结果的正确性,所以,采用一种合适的单元划分形式会使有限元计算结果和真实的解析解十分吻合。
现对无限大板采用不同的划分形式进行比较1.裂纹尖端不考虑钝化。
有限元分析中应力奇异问题的处理

F K, 9 , F Y, 一1 0 0 0 1在 关 键 点 9处 施 加 ~1 0 0 0 N 的 载 荷 F K, 1 0 , F Y, 一1 0 0 0 1在 关 键 点 1 0处 施 加 一 1 0 0 0 N 的 载荷
网格 密 度
O . 0 5 0 . 0 2 5 0 . 0 1
行 参数 化 处理 , 并 采用 自底 向 上 的方 式 建 立 L型 箱 型 结构 , 在 箱 型 构 件 长 臂 端 部 4个 关 键 点 施 加 大 小 为 1 0 0 0 N 的连 续 载 荷 , 然 后 在 箱 型 构 件 短 臂 端 部 4个 关 键点 施 加全 约束 ( 即 限制 了所 选 关 键 点 在 6个 方 向 的所有 自由度 ) 。L型 构件 的参 数 化模 型见 图 1 , 相 关
敛, 而约 束处 产生 的最 大应 力逐 渐发 散 , 因此结 构 的约
收 稿 日期 :2 0 1 3 — 1 0 — 1 6 ;修 回 E t 期 :2 0 1 3 — 1 2 — 3 0
作 者 简 介 :王 鑫 ( 1 9 8 1 一 ) ,女 ,山 西 j 台 人 ,讲 师 ,在 读 硕 士 研 究 生 ,研 究 方 向 :机 械 设 计 及 理 论 。
又具有 膜 力 , 可 以 承 受 平 面 内荷 载 和 法 向荷 载[ 3 的 作 用 。采 用参 数 化 设 计 语 言 AP DL的 方 式 对 模 型 进
对 所建 模 型进行 参 数 设 置 及 计算 , 逐 步对 模 型 进
行 网格 细 化 , 分别 设 置 网格 密 度 为 0 . 0 5 , 0 . 0 2 5 , 0 . 0 1
力奇异 , 但 是 并不 能很 好地 解决 这 个 问题 。 ( 2 )模 型 连 接 处 的 尖 角 是 产 生 应 力 奇 异 性 的 关 键, 因此 , 用平 滑 的过 渡 曲线连 接两 个构 件 可 以很好 地 解 决应 力奇 异 性 问题 。 ’
利用有限元线法奇异线映射技巧计算应力强度因子

利用有限元线法奇异线映射技巧计算应力强度因子
徐永君;袁驷
【期刊名称】《工程力学》
【年(卷),期】1999(1)a01
【摘要】本文讨论了有限元线法的奇异线映射技巧在具有任意切口,任意切口边界条件的多材料反平面断裂问题和平面断裂问题的应用,不仅使得计算速度和计算精度有显著提高,同时使得位移的导数项易于较精确地给出。
【总页数】7页(P85-91)
【关键词】有限元线法;奇异线映射;应力强度因子
【作者】徐永君;袁驷
【作者单位】中国科学院力学研究所;清华大学土华系
【正文语种】中文
【中图分类】O346.1
【相关文献】
1.分域边界元法双映射奇异元计算应力强度因子 [J], 欧贵宝;陈建兵;赵东杨
2.用奇异有限元法计算正交各向异性复合材料平面断裂的应力强度因子 [J], 刘云忠
3.利用线弹簧模型计算含表面裂纹的板壳结构的复合型应力强度因子 [J], 卫欣;杨卫;余寿文
4.用杂交/混合奇异有限元法计算应力强度因子 [J], 孟广伟;张理苏
5.在奇异项上叠加有限元法计算动应力强度因子 [J], 张宁生;赵学仁
因版权原因,仅展示原文概要,查看原文内容请购买。
裂纹尖端应力强度因子的有限元计算方法分析_刘明尧_百度.

第 33 卷第 6 期刘明尧 , 柯孟龙 , 周祖德 , 等 : 裂纹尖端应力强度因子的有限元计算方法分析 121 20 mm 的平板为例 , 采用 ANSYS 命令流的方法 , 得出外推法和虚拟裂纹闭合法所需的暂存空间分别为 2. 172 M B 、0 . 873 M B , 所需的总计算时间分别为 7 . 33 s 、3 . 55 s , 虚拟裂纹闭合法的效率更高。
综上所述 , 虚拟裂纹闭合法能达到解析法、 1/ 4 节点法和位移外推法的计算精度 , 且由于其对裂纹尖端单元性质要求低 , 计算简单易行、效率更高 , 适合各种单元类型和结构的计算 , 是计算裂纹尖端应力强度因子很好的选择。
4结论 a. 采用逐节点建模和实体建模相结合方法建立了含裂纹板有限元模型 , 说明了该方法的可行性。
b. 分析了 1/ 4 节点法、位移外推法、虚拟裂纹闭合法的特点 , 1/ 4 节点法精度高但难以进行数值模拟 , 位移外推法相比于 1/ 4 节点法更节约计算资源 , 虚拟裂纹闭合法间接求解应力强度因子且不受裂纹尖端单元性质的影响。
根据有限元计算的节点位移和节点力 , 分别用 1/ 4 节点法、位移外推法、虚拟裂纹闭合法计算应力强度因子并与手册值比较 , 3 种方法都能达到较高的精度。
计算的过程表明 , 虚拟裂纹闭合法的效率最高 , 1/ 4 节点法最低。
c. 研究了裂纹长度、平板几何尺寸对裂纹尖端应力强度因子 K I 的影响。
K I 与平板受的载荷成线性关系; 当平板宽度和高度分别满足 a/W >0 . 2 、a/ H > 0. 1 时 , K I 受 W 、H 的影响较大 ; 当a/W < 0. 2 或 a/ H < 0. 1 时 , K I 值分别随 W 、H 而趋于σ πa 。
d. 通过 1/ 4 节点法、位移外推法、虚拟裂纹闭合法 3 种方法的比较分析 , 可知虚拟裂纹闭合法更具优势 , 这对选择合适的裂纹尖端应力强度因子计算方法具有指导意义。
在裂纹尖端引入奇异单元的偶应力有限元法

在裂纹尖端引入奇异单元的偶应力有限元法
周晓敏;温庆阳
【期刊名称】《计算机辅助工程》
【年(卷),期】2016(25)3
【摘要】针对在微观状态下结构力学行为会受尺度效应影响的问题,在偶应力理论中考虑微观结构的旋转梯度可以较好解释结构的尺度效应.建立基于一般偶应力理论的有限元法的基本方程,并在裂纹尖端引入奇异单元,计算受单向拉伸的中心斜裂纹板裂纹尖端场的应力强度因子(StressIntensity Factor,SIF),分析特征长度变化对SIF的影响,对比偶应力理论下的结果与经典理论下的结果.结果表明:在裂纹尖端引入奇异单元可以提高计算精度和稳定性;偶应力使得裂纹尖端SIF比经典理论下的值小,并且SIF随着特征长度增大而减小.
【总页数】6页(P13-18)
【作者】周晓敏;温庆阳
【作者单位】江西理工大学建筑与测绘工程学院,江西赣州361000;江西理工大学建筑与测绘工程学院,江西赣州361000
【正文语种】中文
【中图分类】TU452;O344.3
【相关文献】
1.基于有限元法对裂纹尖端应力强度因子的计算分析 [J], 袁浩;李菁;谢禹钧;侯汶雨
2.基于奇异元计算分析裂纹尖端应力强度因子 [J], 陈景杰;黄一;刘刚
3.表面涂层材料终止于界面裂纹尖端弹塑性奇异应力场 [J], 李一全;杨英歌
4.基于有限元法对裂纹尖端应力强度因子的计算 [J], 杨巍;张宁;许良
5.基于有限元法对裂纹尖端应力强度因子的计算 [J], 杨巍;张宁;许良;
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在裂纹尖端引入奇异单元的偶应力有限
元法
在微观状态下,结构的特征尺寸与材料的特征长度处于相近数量级,材料缺陷(微裂纹)处不同点之间的相互作用不可忽略,因此结构将出现传统连续介质理论无法解释的尺度效应现象.此时,建立基于连续介质框架、考虑尺度效应的本构模型就成为联系经典连续介质力学和微观力学之间的桥梁.偶应力理论就是在此背景下发展起来的应变梯度理论的一种.*****T兄弟提出一般偶应力理论,将材料的特征长度和第二切变模量引入结构的本构关系中,系统建立考虑偶应力影响时的本构模型,解释材料的尺度效应现象.基于偶应力理论的力学问题只有极少数问题有解析解,一般采用有限元法及扩展有限元法(Extended Finite Element Method,XFEM)研究.赵勇等和齐磊等采用有限元法研究考虑偶应力影响下的小孔应力集中问题.王胜军基于有限元法给出一般偶应力理论与转动约束偶应力理论的异同.张敦福等和吴延峰等采用有限元法分析考虑偶应力理论情况下的岩石剪切带等问题.赵冰等采用有限元法分析微梁弯曲的尺度效应.徐慧等和侯日立等采用有限元法研究单向拉伸裂纹板.茹忠亮等给出扩展有限元法在断裂力学问题上的应用.吴圣川等对断裂力学问题及其
CAE软件的现状和发展给出系统的综述,并且基于成熟的扩展有限元法和自主研发的虚节点法推出具有完全自主知识产权的三维疲劳裂纹扩展分析软件ALOF.霍金东等采用Abaqus的XFEM 功能对折弯片的断裂问题进行仿真.陈星文运用XFEM分析三维高压管道中的裂纹扩展问题.
由于裂纹尖端应力场具有奇异性,计算结果受网格划分影响较大.*****提出奇异单元,并应用于断裂力学中裂纹尖端应力场的求解,提高有限元法计算断裂问题的精度和稳定性,避免裂纹尖端区域网格划分困难.沈辉等研究奇异单元有限元法计算精度受网格划分的影响情况.李尧臣等提出引入位移协调奇异单元的有限元法.林广平等构造三维奇异单元.段庆全等采用奇异单元分析裂纹扩展问题.
本文研究裂纹尖端应力强度因子(Stress Intensity Factor,SIF)的尺度效应现象,将一般偶应力理论与有限元法相结合,并在裂纹尖端引入奇异单元,分别分析含边裂纹的三点受力梁和受单向拉伸的中心斜裂纹板的裂纹尖端SIF,给出偶应力和奇异单元对SIF的影响,并分析特征长度与裂纹长度比值变化对SIF的影响规律.
1分析方法
基于一般偶应力理论的平面应力单元(见图1),微元上作用的单位面积力和单位面积力偶的直角分量分别为(σx,σy,τxy,
τyx)和(μx,μy).
图1考虑偶应力的微元体
Fig.1Microelement considering couple stress
分析考虑偶应力影响的平面弹性问题时,切应力不再具有互等性,需在每个平面微元中增加2个偶应力项,因此偶应力理论下的平衡方程需要在传统弹性力学的基础上进行相应修改,即为σxx+τyxy=0
τxyx+σyy=0
μxx+μyy+τxy-τyx=0 (1)剪切应变εyx和εx y示意见图2.在微元体中,由于偶应力的存在,微元体会有微转动出现,产生弯曲效应,并引发微转角ωz.
a)εyxb)εxy图2剪切应变εyx和εxy
Fig.2Shear strains εyx and εxy
弯曲效应所产生的曲率使εxy≠εyx,剪应力互等定理不再成立.微元几何方程为εx
式中:E为弹性模量;v为泊松比;G为剪切模量;Gc为第二剪切模量;l为材料的特征长度,是为平衡一般偶应力理论中应变和应变梯度的量纲而引入的材料常数.l具有长度的量纲,是一种依赖于材料微观结构形态的特征常数,其大小取决于材料的微结构,不受外界约束或载荷影响.
力边界条件为fx
fy
=[nm]σxτxyμx
τyxσyμy (4)式中:n和m为边界的外法线方向余弦;fx和fy为边界上已知的面力;为边界上已知的面力偶.
位移边界条件为u=
ωz=z (5)式中:和z分别为边界上已知的位移和转角.
为更好地描述裂纹尖端处应力场的奇异性,在裂纹尖端引入奇异单元.裂纹尖端划分的等参奇异三角形单元见图3,坐标原点设于裂纹尖端点,采用极坐标(r,θ)表示,将单元中与裂纹尖端相连边界上的节点移至边长的1/4处.a)奇异单元节点分布b)裂纹尖端坐标系及节点布置
三角形奇异单元的形函数可以由划线法得到.形函数为N1=(4ξ+4η-1)(ξ+η-1)
2数值算例
2.1含边裂纹的3点受力梁
含边裂纹3点受力梁模型见图4,其中:梁长L=8 m,梁高h=1 m,截面为正方形;在梁的中心沿高度方向有一长度为a=0.5 m的单边裂纹,在裂纹延长线与上表面的交点处作用有大小为F=10 kN的集中载荷.材料的弹性模量E=200 GPa,切变模量G=E/2(1+v),泊松比v=0.3,第二切变模量取Gc=G,特征长度与梁高比l/h=0.001.
图4含边裂纹的3点受力梁模型
Fig.4Model of threepoints bending beam with edge crack
经典理论解、传统有限元解以及考虑奇异单元和偶应力下计算得到的含边裂纹三点受力梁模型SIF的结果比较见表1.由此可以看出:相对于未考虑奇异单元法的结果,采用奇异单元法得到的SIF更接近理论解;考虑一般偶应力理论后,裂纹尖端SIF要小于未考虑偶应力的值.
表1不同方法得到应力强度因子
Tab.1Results of SIF obtained by different methods
kPa/m2求解方法SIF经典理论213.0传统有限元191.8奇异单元211.8偶应力有限元177.5偶应力奇异单元201.3
2.2单向受拉中心斜裂纹板
两端受大小为σ=10 kPa均布力拉伸的中心斜裂纹板见图5,其中:板宽w=2 m,高h=2.5 m,裂纹长2a=0.2 m,与水平面夹角α=45°.图5单向受拉中心斜裂纹板模型
Fig.5Model of plate with incline center crack in
uniaxial tension
裂纹尖端附近单元有限元网格划分见图 6.材料的弹性模量E=200 GPa,泊松比v=0.3,取特征长度与裂纹半长的比值l/a=1,第二切变模量与切变模量比值Gc/G=0.5;KI=KI/K0,KII=KII/K0分别为无量纲化I型和II型SIF,其中K0=σπa.
图6裂纹尖端附近单元有限元网格划分
Fig.6Finite element mesh around crack tip
在不考虑偶应力影响的条件下,采用解析法得到的经典理论解见表2.整体采用8节点四边形单元划分得到的8节点等参元解,整体采用8节点四边形单元划分后在裂纹尖端采用奇异单元划分得到奇异单元解.由表2可见:在相同网格划分密度下,采用奇异单元求得的复合型裂纹的I型和II型SIF相对于仅采用8节点等参元得到的结果具有更高的精度.
表2I型和II型SIF
Tab.2SIF of type I and II求解方法KIKII经典理论0.5000.5008节点等参元0.4140.416奇异单元0.4830.500
考虑偶应力影响的情况下不同特征长度对I型和II型SIF的影响见表3.由此可知:在不同的特征长度下,考虑偶应力影响计算得到的I型和II型SIF会随着特征长度与裂纹长度之比的增加而减小;当特征长度与结构尺寸处于相近数量级时,尺度效应明显;当特征长度远小于结构尺寸时,偶应力对计算结果的影响较小.
3结论
本文将奇异单元、偶应力理论和有限元法相结合,给出在裂纹尖端使用奇异单元的一般偶应力理论有限元法,得出如下主要结论.
(1)在同等网格划分密度下,采用奇异单元法得到的裂纹尖端SIF相对于仅采用8节点四边形单元得到的结果更接近理论解.
(2)考虑一般偶应力理论后会减小裂纹尖端SIF的值;随着特征长度的减小,SIF减小;在特征长度与裂纹半宽处于相近数量级时,SIF受特征长度影响明显;当特征长度远大于裂纹半宽时,SIF受特征长度改变影响较小.。
