协调的尺度相关连续偶应力理论简介
李同林 弹塑性力学 第2章 应力理论 应变理论

§2—4 最大(最小)剪应力、空间应力圆、 应力椭球
1、最大(最小)剪应力
由2-25及
2 2 2 l1 l 2 l3 1 求出:
2 2 xy xy (cos2 sin 2 ) ( y x ) sin cos
x y
x y
cos 2 xy sin 2
x y
2
sin 2 xy cos 2
xz 0
2 2 n Px2 Py2 Pz2 n
2 2 ( 1l1 ) 2 ( 2l2 ) 2 ( 3l3 ) 2 ( 1l12 2l2 3l3 )
( )l ( )l ( 1 3 )l ( 2 3 )l 3
(2—28)
2 3 2 2
12
1 2
2
2.空间应力圆 · 应力椭球
一点应力状态 用解析法研究 用几何法研究 (1)空间应力圆
若三个坐标轴的方向都恰取为应力主方向,则由 式(2—24)或(2—15)可求出用,外法线为n的斜截面 2 2 n、 n、 1、 2和 3表示的l12、l2 和l3 , 上的正应力 其表达式为:
3 2 n I1 n I 2 n I 3 0
(2—13)
(2—18)
理论上可证明:当一点的应力状态确定时,由式2-18 必可求出三个实根,即为主应力,且 1 2 3 。 主应力彼此正交。
I1 x y z ii 1 2 2 2 I 2 x y y z z x xy yz zx ( ii jj ij ji ) 2 x xy xz
正交各向异性功能梯度微板弯曲行为尺度效应

第51卷第4期2020年4月中南大学学报(自然科学版)Journal of Central South University (Science and Technology)V ol.51No.4Apr.2020正交各向异性功能梯度微板弯曲行为尺度效应康泽天,张岩,周博,薛世峰(中国石油大学(华东)储运与建筑工程学院,山东青岛,266580)摘要:为了研究材料参数沿微板厚度方向呈连续梯度变化的正交各向异性功能梯度微板弯曲行为的尺度效应,基于新修正偶应力理论和Kirchhoff 弹性板理论,引入2个正交方向的材料特征尺度参数,将正交各向异性功能梯度微板的应力、偶应力、应变和曲率等基本变量描述为位移分量偏导数的表达式,并根据最小势能原理推导微板的平衡方程和边界条件。
利用建立的模型,以材料弹性模量、剪切模量和材料特征尺度参数均沿微板厚度方向呈正弦梯度变化的四边简支微板为例,研究微板在双向正弦分布载荷作用下的弯曲行为,分析材料特征尺度参数与板厚比、材料各向异性和功能梯度参数对微板挠度、正应力和偶应力尺度效应的影响,定量标定考虑尺度效应时正交各向异性功能梯度微板结构的临界几何尺寸参数。
研究结果表明:应用本文模型求解的微板挠度和正应力总是小于经典弹性Kirchhoff 板模型解;板厚与材料尺度参数比值越小,微板挠度和正应力的尺度效应越明显;功能梯度参数对微板挠度、正应力和偶应力的尺度效应有一定影响;沿2个正交方向的特征尺度参数对微板挠度、正应力和偶应力的尺度效应影响程度不同。
关键词:正交各向异性;功能梯度;尺度效应;平衡方程;微机电系统中图分类号:TB34文献标志码:A开放科学(资源服务)标识码(OSID)文章编号:1672-7207(2020)04-0902-10Size-dependent bending behaviors of orthotropic functionallygraded microplatesKANG Zetian,ZHANG Yan,ZHOU Bo,XUE Shifeng(College of Pipeline and Civil Engineering,China University of Petroleum,Qingdao 266580,China)Abstract:Based on the new modified couple stress theory and Kirchhoff elastic plate theory,the size-dependent bending behaviors of orthotropic functionally graded microplates with material parameters varying continuously along the thickness direction were studied.The basic variables of orthotropic functionally graded microplates,such as stress,couple stress,strain and curvature,were described as the function of partial derivative of displacement component by introducing different material length-scale parameters in two orthogonal directions.The equilibrium equation and boundary conditions of the microplate were derived according to the principle of minimum potential energy.Employing the presented model,the bending behavior of a four-sided simply supported microplate under bidirectional sinusoidal distributed loads with the materials parameters was studied,such as elastic modulus,shear modulus and material length-scale parameters,varying with the thickness in a sinusoidal gradient function.TheDOI:10.11817/j.issn.1672-7207.2020.04.005收稿日期:2019−07−04;修回日期:2019−09−15基金项目(Foundation item):国家重点研发计划项目(2017YFC0307604)(Project(2017YFC0307604)supported by the National KeyResearch and Development Program of China)通信作者:周博,教授,从事智能材料与结构力学、微尺度材料力学和油气井工程力学等研究;E-mail:**************.cn第4期康泽天,等:正交各向异性功能梯度微板弯曲行为尺度效应effects of the ratio of length scale parameters to the plate thickness,material anisotropy and functional graded parameters on the size effects of deflection,normal stress and couple stress were analyzed.The critical geometric dimension parameters of orthotropic functionally graded microplates with consideration of the size effect were quantitatively calibrated.The results show that the solutions of the deflection and normal stress of the microplates are always smaller than those of the classical elastic Kirchhoff plate model.The smaller the ratio of plate thickness to material length scale parameters,the more obvious the size effects of the deflection and normal stress.The size effects of deflection,normal stress and couple stress of the microplate are influenced by the functionally graded parameter.The length-scale parameters in two orthogonal directions have different effects on the scale effects of deflection,normal stress and couple stress of the microplate.Key words:orthotropic;functionally graded;size effect;equilibrium equation;micro electro-mechanical systems (MEMS)功能梯度材料是材料组分或几何尺寸沿结构特定方向成连续梯度变化的一种新型材料,具有消除应力集中、减小残余应力、增强连接强度和减小裂纹驱动力等许多普通均质材料不具备的优异性能,广泛应用于航空航天、人工智能和微机电系统等领域[1−3]。
基于Cosserat理论的平面等参元

第19卷第1期2010年3月计算机辅助工程Co m puter A ided Eng i n eeri n gV o.l19N o.1M ar.2010工程数值仿真与CAE算法Num erica l Si m u lati o n of Eng ineeri n g and C AE A l g orithm文章编号:1006-0871(2010)01 0012 05基于Cosserat理论的平面等参元齐 磊, 张若京(同济大学航空航天与力学学院,上海 200092)摘 要:为解释材料在微尺度下的尺度效应,基于C osserat理论,从势能泛函驻值条件出发提出构造8节点Serendipity平面等参元,并建立平面有限元法.每个节点拥有3个独立节点自由度,分别为2个方向的线位移和1个逆时针方向的角位移.用该方法分析含中心小孔的无限平板在单轴拉伸情况下的应力集中问题.数值计算结果与Cosserat理论的解析解非常符合,表明应力集中因数k 受泊松比 ,常数c及a/l值的影响很大;由于偶应力的存在,小孔周围的应力分布明显小于经典弹性力学理论的预测.通过对材料常数c的调节可以将该方法推广应用于基于M i n d li n偶应力理论的数值分析中.关键词:Cosserat理论;偶应力;平面有限元法;等参元;尺度效应;应力集中中图分类号:O241.82 文献标志码:APlane isopara metric ele m ent based on Cosserat theoryQ I Le,i Z HANG Ruo ji n g(Co lleg e of A erospace Eng.&M echanics,TongjiU n i v.,Shanghai200092,China)Abst ract:To expla i n the sca le effect o f m aterials under the m icroscale,based on Cossera t theory and deduced fro m the stationary conditi o n o f potential energy functiona,l an eight node Serendipity p lane isopara m etric e le m ent is proposed and a fi n ite ele m ent m ethod for p lane is developed.There are threei n dependent node freedo m s at each node,i n clud i n g li n ear displace m ent in t w o d irecti o ns andcounterc l o ckw ise angular d isp lace m en.t The stress concentration prob le m o f a i n fi n ite flat p late w ith a centra l s m all hole is ana l y zed by t h e m ethod i n the case of un iax ial tensi o n.The num erical calculation resu lts are i n good agree m en t w ith the analytica l so lution based on Cosserat theory,wh ich i n d icate tha t the stress concen trati o n factor k is strong l y infl u enced by Po i s son rati o ,constant c and the value o f a/l;the stress d istribution ar ound the little ho le is sign ificantly less than the prediction of classical elastic ity theory due to the ex istence o f couple stress.The m ethod can be applied to the num erica l ana l y sis based on M indlin couple stress theory by t h e regu lation o f constant c.K ey w ords:Cosserat theory;couple stress;finite ele m ent m ethod for p lane;isopara m etetric ele m en;tsca le effec;t stress concen trati o n收稿日期:2009 07 20 修回日期:2009 10 10基金项目:国家自然科学基金(10772136);教育部博士点基金(20060247016);上海市重点学科建设项目(B302)作者简介:齐 磊(1983 ),男,河北廊坊人,硕士研究生,研究方向为有限元数值分析和计算,(E m ail)fayak@163.co m;张若京(1946 ),男,北京人,教授,博导,博士,研究方向为固体力学,(E ma il)zhangr@j t ongj.i 0 引 言经典的连续介质力学理论已被广泛应用于许多工程领域,如航空航天、车船、机械和土木等.事实证明,这种理论适合应用于具有宏观结构力学性能的分析.在微尺度下,由于尺度效应的影响,材料的部分力学性能不同于经典连续介质力学理论的预测.近年来的大量实验研究也表明,当金属试件的尺寸在微米或亚微米量级时,材料具有很强的尺度效应.如在细铜丝扭转实验中,FLECK等[1]发现,当铜丝直径从170 m下降到12 m时,无量纲的扭转硬化增加至3倍;在N i材质的薄梁弯曲试验中, STOLKEN等[2]观察到当梁的厚度从100 m下降到12.5 m时,无量纲的弯曲硬化显著增加,而在单轴拉伸情况下这种尺度效应不存在.在微米量级尺度下,微观硬度试验与颗粒增强金属基复合材料中也观察到尺度效应.当压痕深度从10 m减至1 m时,金属硬度增加1倍[3 6];对于以碳化硅颗粒加强的A l Si基复合材料,LLOYD[7]等观察到当保持颗粒体积比为15%的条件下,将颗粒直径从16 m减为7.5 m时,复合材料的强度显著增加.以上这些实验现象用经典弹性力学理论都无法解释,因为在其本构模型中不存在任何尺度参数,无法预测材料的尺度效应.因此,很多学者致力于建立考虑包含尺度影响的连续介质模型,并取得丰硕成果,这其中,COSSERAT两兄弟[8]于1909年提出Cosserat理论.TOUPI N[9],M I N DLI N[10]和KO I TER[11]等对Cosserat理论加以简化又提出各自的偶应力理论.1 Cosserat理论和M i nd li n偶应力理论简介在Cosserat理论中(见图1),由于材料点处有偶应力m 的存在,使得Cauchy应力t 为非对称,图1 偶应力微元体因此将不对称的Cauchy应力t 分解为对称的! 和反对称∀ 的两部分:!=(t +t )/2∀ =(t -t )/2(1)以p 表示体力,q表示体力偶,则平衡方程可表示为! , +∀ , +p =0(2)m , +∀12-∀21+q=0(3)以s 表示应变,则几何变形方程为s11=u1,1, s12=u2,1-#, s22=u2,2s21=u1,2+#, ∃1=#,1, ∃2=#,2(4)式中:u=[u,v]T为线位移向量;#为微元体的微转动;∃1和∃2分别为与m1和m2相对应的形变,称为曲率.在Cosserat理论中,#为与线位移u和v相互独立的自由度,因此应变张量与应力张量一样都是非对称的.将应变张量分解为对称的% 和反对称的& 2部分:% =(s +s )/2& =(s -s )/2(5)式中:% 和& 是分别与对称应力! 和反对称应力∀ 相对应的形变.本构方程为! =D s &∋%&∋∀ =D a &∋&&∋, m =E ∃(6)对于平面应力问题D s &∋=2G∋ &∋∋+1-∋ ∋&∋(7)D a &∋=2cG∋ &∋∋,E =4G l2∋ (8)式中:G为剪切模量; 为泊松比;∋为K ronecker符号;l为表征材料尺度效应的特征长度;c为无量纲的常数.对于平面应变问题,则可令泊松比为 / (1- ).边界条件可以表示为u =u- , #=#-(9)T- =t n=(! +∀ )nM-=m n(10)式中:u- 和#-分别为边界线位移和角位移;T- 和M-分别为作用于边界上的面力和面力偶;n为边界上的单位外法线矢量.势能泛函为((u ,#)=12!A(! % +∀ & +m ∃ )d A-!A(u p +#q)d A-13第1期齐 磊,等:基于Cosserat理论的平面等参元!)(u T - +#M -)d )(11)在M i n dli n 的偶应力理论[12]中,微转动被约束,从而导致应变张量对称.又因为曲率∃包含线位移的2阶导数,这就要求位移形函数必须满足C 1连续,这无疑给单元构造带来很大困难.另外,在M i n dli n 的偶应力理论中,应力张量是非对称的,应变张量是对称的,因此本构方程无法确定所有应力分量与应变分量的关系.本文采用Cosserat 理论,避免C 1连续的要求,通过对材料常数c 的调节可以把Cosserat 理论的数值方法推广应用于M i n dli n 的偶应力理论中.[13]2 有限元法将上述表达式写成列阵形式:!={!x ,!y ,!xy }T∀={∀xy }, m ={m x ,m y }T(12)其中!x =!11, !y =!22, !xy =!12∀xy =∀12, m x =m 1, m y =m 2%={%x ,%y ,%xy }T&={&xy }, ∃={∃x ,∃y }T(13)其中%x =%11, %y =%22, %xy =2%12&xy =2∃12, ∃x =∃1, ∃y =∃2对于平面应力问题D s=G 21- 21-2 1- 21- 0001D a=c G [1], E =4Gl200l2(14)对于平面应变问题,可令泊松比为 /(1- ),则本构关系为!=D s%∀=D a &, m =E ∃(15)势能泛函为(=12!A(%TD s%+&TD a&+∃TE ∃)d A -!A(u Tp+#q )d A -!)(u TT -+#M -)d )(16)如图2所示,采用8节点Serend i p ity 单元,节点自由度分别为2个方向的线位移和1个逆时针方向的角位移U ={u,v,#}T(17)图2 8节点Serend i p ity 单元应力应变列向量分别为!*={!x ,!y ,!xy ,∀xy ,m x ,m y }T%*={%x ,%y ,%xy ,&xy ,∃x ,∃y }T(18)对位移进行差值U e=N e r e=[N 1I 3,N 2I 3,N 3I 3,N 4I 3,N 5I 3,N 6I 3,N 7I 3,N 8I 3]re(19)式中:I 3为3阶单位矩阵;N i 为Serendipity 单元双二次函数;r e为单元位移向量r e={u 1,v 1,#1,u 2,v 2,#2,∀,u 8,v 8,#8}T(20)将几何方程式(4)代入式(19)得单元应变列向量%*=LU e=x0 y -y 00y x x 000-2xyTu v #(21)将式(19)~(21)代入式(16),并令∋(=0得K e r e=Pe(22)其中K e=!A eB TDB d A (23)B =LNe(24)D =D s3#3DaE 2#26#6(25)P e=P eA +P e)=!A eN T {p x,p y,q }Td A +!)eN T{T -x ,T -y ,M -}Td )(26)3 数值算例考虑无限大弹性平板的平面应变问题.圆孔半径为a,远处作用x 方向的均匀分布力为p 0.由于问题的对称性,取1/4平板进行分析,见图3.取计算域为30a,平板厚度取单位长度1,共划分单元54414计 算 机 辅 助 工 程 2010年个,节点1743个(含边中节点).由于关注的是小孔周围的应力集中情况,故在小孔周围局部进行网格细化,以得到更好的结果,见图4.图3 有限元计算网格 图4 小孔周围局部网格细化计算结果见图5和表1,可知由于有偶应力影响,小孔周围的应力集中因数k与经典弹性力学理论解相比有所降低,且k的大小受泊松比 影响较大. 越大,k就越大.本文解与文献[14]中基于Cosserat理论的解析解非常符合,误差不足千分之一.需要说明的是,对于平面应变问题,将不得不面对不可压问题( 接近极限值0.5时).本文所采取的措施是将式(16)中体积分的第1项应变能拆分成斜偏应变能和体积应变能两部分,并分别进行精确积分和2#2减缩积分,以保证在不可压状态下体积应变能所产生的单刚奇异性及整个单刚的非奇异.表1括号内数据均为采用精确积分的结果.图5 应力集中因数k随 变化曲线表1 应力集中因数k随 变化(常数c=0.5,材料特征长度l=a)00.10.20.30.40.490.4990.49990.49999解析解[14] 2.3055 2.35252.40302.4573 2.51612.57322.57912.57982.5798本文解 2.3074 2.35432.40472.4591 2.51782.57482.5819(2.5845)2.5867(2.6819)2.5947(4.6269)误差/%0.080.080.070.070.070.060.110.270.58为便于观察,将应力结果数据转化为极坐标形式.其中,经典解是指基于经典弹性力学理论的解析解!∗/p0沿∗=90∃的r方向分布,见表2和图6.表2 !∗/p沿∗=90∃的r方向分布(常数c=0.5,材料特征长度l=a,泊松比 =0.3) r/a1 1.03 1.051.081.12 1.15 1.181.221.251.331.40经典解3.000 2.803 2.6312.4812.3492.232 2.129 2.0181.9221.7651.642解析解[12]2.457 2.341 2.2382.1462.0641.990 1.924 1.8521.7881.6801.592本文解2.459 2.239 2.1522.3492.0661.996 1.926 1.8561.7871.6871.587误差/%0.080.340.040.280.100.300.100.22-0.050.42-0.31注:经典解是指基于经典弹性理论的解析解.图6 !∗/p沿∗=90∃的r方向分布从表2及图6可知,在∗=90∃时,!∗/p0的值沿r方向逐渐减小,当半径在1.4a处时,!∗/p0的偶应力解(包括Cosserat理论的解析解[14]和本文的数值解)已经与经典解十分接近,偶应力影响已经非常小.因此,在进行网格细化时,只对r<1.4a的单元进行细化.图6中还有2条数据是对不可压问题的计算结果,可以看出平均误差在0.5%以内,表明此单元完全能够用于不可压材料的计算.表2中第2,4,6,8和10这5列数据的本文解都是边中节点数据,且9,10和11这3个节点为单元网格加密过程中过渡单元中的节点,因此误差略微偏大.从图7可以发现,k随着c的增大而减小.当c在0到10变化时,其对k的影响较大.c越接近0,小孔周围的应力分布情况越接近于经典弹性理论的解析解;c值越大,结果越接近于M indlin偶应力理论的解析解,这与文献[13]中的结论一致.当c>15第1期齐 磊,等:基于Cosserat理论的平面等参元100时,其结果可认为是M i n d li n 偶应力理论的数值解.从能量泛函中也不难找到其理论依据:在M i n dli n 偶应力理论中宏观转动与微转动相等,即#=(u 2,1-u 1,2)/2.将此式化为u 2,1-u 1,2-2#=0并将罚函数的方法引入到位能泛函中,修改后的位能泛函与式(11)完全一致,式中体积分第2项即为引入的约束条件.其中,& =u , -u , -2#e ,∀ =G c & ,c 即可认为是罚参数.因此,当c %&时,Cosserat 理论的解即为M indli n 偶应力理论的解,而一般情况下c 并不会取得很大,因此在式(21)中的&xy 项虽然出现形函数N i 及其1阶导数耦合的情况,但不会产生类似剪切锁死现象.然而,为了使此单元同时也能应用于M i n d li n 偶应力理论的数值计算,c 的取值很大,这将会遇到剪切锁死.如前面所述,可将此积分项认为是引入的罚函数积分项,在进行计算时可将其单独提出来进行2#2减缩积分,以保证所计算出来的单刚为奇异,与讨论不可压时对体积应变能的积分处理方法相同,而本文的实际计算过程是将斜偏应变能项与弯曲应变能项合并、体积应变能项与反剪切应变能项合并,分别以精确积分和2#2减缩积分计算单刚,最后再相加形成完整单刚.图7 !∗/p 0沿∗=90∃的r 方向分布从表3及图8发现,应力集中因数k 受a /l 的影响较大.当a /l 值小于6时,k 的值随a /l 值的增大而迅速增大;当a /l 值大于6时,k 的值受a /l 值的影响渐渐减小;当a /l 值大于25时,可近似认为应力k 已经不受偶应力的影响.表3 应力集中因数k 随a /l 变化(常数c =0.5,泊松比 =0.3)a /l 0.112346810152025解析解[14]2.366 2.457 2.5792.6792.7522.844 2.895 2.9252.9622.9772.985本文解2.366 2.459 2.5822.6812.7552.847 2.898 2.9282.9652.9802.988误差/%0.020.080.120.070.110.110.100.100.100.100.10图8 k 随a /l 变化曲线4 结 论基于Cosserat 理论,构造出性能较好的8节点Serendipity 单元,数值计算精度较高,能够很好地反映出偶应力在作用域中的应力分布.通过对带中心小孔受单轴拉伸的无限平板进行分析,发现应力集中因数k 受泊松比 ,常数c 及a /l 值的影响规律,得到小孔周围应力分布情况,能与基于Cosserat 理论的解析解很好符合,同时也可以应用于M i n d li n 偶应力理论的求解.参考文献:[1] FLECK N A ,MULLER G M,AS H BY M F .S trai n grad ient p l asti city :theory and exp eri m en t[J].Act a M etall u rgicaM ateriali a ,1994,42(2):475 487.[2] STOLKEN J S ,EVANS A G .A m i crobend test m et hod for m eas uri ng t he plas tici ty lengt h scale[J].A cta M at eri ali a ,1998,46(14):51095115.[3] NI X W D .M ec h an i ca l prop erties of t h i n fil m s[J].M etall u rgical&M ateri als T ran s A,1989,20(11):2217 2245.[4] STEL M AS H ENKO N A,W ALLS M G,BRO W N L M ,et a l .M icro i ndentations on W and M o oriented s i ngle crystals :an ST M st udy[J].ActaM et all urg i ca M ateri alia ,1993,41(10):2855 2865.[5] M A Q i ng ,CLARKE D R .S i ze depend ent h ardness of silver s i ngle crystals[J ].J M ater Res ,1995,10(4):853 863.[6] POOLE W J ,ASHBY M F ,FLECK N A .M i cro hardnes s of anneal ed and w ork h arden ed copper pol ycrystals [J ].S cri p t a M etall u rgicaM at eri ali a ,1996,34(4):559 564.(下转第26页)参考文献:[1] BEL IS J,DEP AUW J,CALLEWAERT D,et a l.Fail u re m echanis m s and residua l capacit y of annealed gl ass/SGP la m i nat ed bea m s at roo mte mp erature[J].E ng Fail ure An a,l2009,16(6):1866 1875.[2] 张其林.玻璃幕墙结构设计[M].上海:同济大学出版社,2007:57 58.[3] 马眷荣,臧曙光,丁丽梅.夹层玻璃力学模型的探讨[J].航空材料学报,1998,18(3):57 60.[4] J G J102 2003 玻璃幕墙工程技术规范[S].北京:中国建筑工业出版社,2003:22 33.[5] 贺瑞丽,郑百林,武秀根,等.用APDL对悬索桥结构进行有限元分析[J].计算机辅助工程,2008,17(2):30 33.[6] VALLABHAN C V G,DAS Y C,RA M ASAMUDRA M an j un atha.Properti es of PVB i n terlayer u sed i n la m i n ated gl ass[J].J M at C i vil E ng,1992,4(1):71 76.(编辑 廖粤新)(上接第16页)[7] LLOYD D J.Particl e rei n f orced al um i nu m and m agnesi um matri x co m posites[J].IntM at er Rev i e w s,1994,39(1):1 23.[8] COSSERAT E,COSSERAT F.Theorie de corp def or m ab l es[M].E diti ons A H er m ann,Pari s:1909.[9] TOUPI N R A.E l astic m ateri als w it h couple stresses[J].A rch Rati onalM ech&An a,l1962,11(1):385 414.[10] M I NDLI N R D.M i cro s tr u cture i n li near el asti city[J].A rch Rati onalM ech&An a,l1964,16(1):51 78.[11] KOI TER W T.C oup l e stresses i n the t heory of elasti city,I and II[C]//P roc K N ed Ak ad W et B,1964:17 44[12] M I NDLI N R D.In fl u ence of coup le stress on stress con cen trati ons[J].E xp M ech,1962,3(1):1 7.[13] 李雷,吴长春.基于Coss erat理论的应变梯度非协调数值研究[J].工程力学,2004,21(5):166 171.[14] 刘俊,黄铭,葛修润.考虑偶应力影响的应力集中问题求解[J].上海交通大学学报,2001,35(10):1481 1485.(编辑 廖粤新)(上接第21页)参考文献:[1] 王瑞,陈海霞,王广峰.ANSYS有限元网格划分浅析[J].天津工业大学学报,2002,21(4):8 11.[2] 江雄心,万平荣.整体规划技术在三维有限元网格生成中的应用[J].锻压技术,2006:119 122.[3] 吴淑芳,付沛福,李运兴,等.平面区域四边形网格自动生成技术[J].计算结构力学及其应用,1996,13(2):208 216.[4] 李华,李笑牛,程耿东,等.1种全四边形网格生成方法 改进模板法[J].计算力学学报,2002,19(1):16 191.[5] 严蔚敏,吴伟民.数据结构(C语言版)[M].北京:清华大学出版社,2002:216 222.[6] 李华,程耿东,顾元宪.1种新的全四边形网格快速生成方法 模板法[J].计算结构力学及其应用,1996,13(1):25 39.[7] 金晶,吴新跃.有限元网格划分相关问题分析研究[J].计算机辅助工程,2005,14(2):75 78.(编辑 廖粤新)。
应变梯度理论

应变梯度理论应变梯度理论是近解释材料在微米尺度下的尺寸效应现象而发展起来的一种新理论。
Fleek 等[6]于1994年在细铜丝的扭转实验中观测到微尺度下应变梯度的硬化,其中直径12m μ的无量纲扭转硬化约为直径170m μ的三倍。
通过对12.5m μ、25m μ和50m μ三种厚度纯镍薄片的弯曲测试,Stolken 和Evanslv[7]于 1998年发现镍的无量纲弯曲硬化随着薄片厚度的减小而明显增大,然而在拉伸试验中并未发现这种微尺度现象。
Chong 和Lam[8]于 1999年通过压痕实验观察到热固性环氧树脂和热塑性聚碳酸酷的无量纲硬化与应变梯度有关,材料的塑性具有微尺度效应。
McFarland 和Colton[9J 于2005年通过对不同厚度聚丙烯悬臂微梁的弯曲测试,同样观测到无量纲弯曲刚度随梁厚减小而增大。
与宏观尺度相比,微尺度下结构的力学特性及行为研究主要考虑到以下两个方面(1)尺度效应。
材料不是无限可分。
因此材料颗粒的固有属性将影响到微结构的力学特性。
(2)表面和界面效应。
一些在宏观尺度下常被忽略的力和现象,在微尺度下起着重要的作用;而一些在宏观领域作用显着的力和现象,在微尺度下作用微小,甚至可以忽略。
例如,微尺度下,与特征尺寸L 的高次方成比例的惯性力、电磁力(L3)等的作用相对减小,而与尺寸的低次方成比例的粘性力、弹性力(L2)、表面张力(Ll)、静电力(L0)等的作用相对增大。
随着尺寸的减小,表面积(L2)与体积(L3)之比相对增大,表面力学和物理效应将起主导作用。
理论模型建立(1)偶应力理论早在一个多世纪前,voigt[12]便提出了体力偶和面力偶的概念,并建议构建考虑作用在材料微粒表面或边界上的力偶的连续模型。
随后Cosserat 兄弟[14]根据的假设建立了相关的Cosserat 理论,对应的运动方程中出现了偶应力。
直到20世纪60年代左右,一些学者才开始尝试Cosserat 理论的改进扩展工作,他们对Cosserat 连续体物质点的旋转施加一定约束,并逐渐发展了一种更为普遍的理论—偶应力理论。
偶应力理论层合梁的稳定性及尺度效应

为 了解释 这一 现 象 , 之发 展 的细 观 理 论 主 为
要有 偶应 力理论 和应 变梯 度理论 。
收 稿 日期 : 0 2—0 21 6—2 0
基金项 目:国家 自然科学基 金资助项 目 ( 目编号 :17 16 项 10 2 5 ) 作者简介 : 陈万吉( 9 1 14 一), , 宁鞍 山人 , 男 辽 教授 , 博士生导师 , 主要研究方 向: 飞机轻 质复合材料结构 高阶强论有限元软体研 发 非线性力学中数学规划法 , 细观偶压力/ 应变梯 度理论 和有 限元 。
1
材 料细 观材料 参数 。偶应 力 理论是 在 细观尺 度上 增 加绕 夹杂 的转 动 平衡 条 件 , 即在 平 衡 方程 中添 加 转动平 衡条 件 ( 即绕 细 观夹 杂 的转 动 平 衡 ) 这 , 是偶应 力理 论 的基 础 , 1 示在 ( , 面 内绕纤 表 Z) 维转 动细观 参数 , 纤维 断面 与基体 相互 作用 , 纤维 被看成 是 影 响 转 动 平 衡 的 夹 杂 。1 示在 ( 2表 Y, Z) 内基 体 内绕 夹 杂 的转 动细 观 参 数 。这 与经 面 典 的偶 应力 理论 引入材 料细 观参数 的方法是 一致
明显增大, 这种现象被称为尺度效应。传统 的弹 性力 学理 论不 考 虑材 料 的 微 观结 构 , 以无 法 对 所
这种 尺度 效应 给 出解 释 。
长度 参数 )N ue ( 4个 细观 材 料 长度 参 , ebr H 含
数 ) 。近 期 有 FekH t isn 等 l — uc no 【 ( 1个 细 c h 等 含 观材 料 长 度 参 数 ) 出 的 偶 应 力 理 论 和 Y g 提 n a 等 _ 提 出的修 正 对称 偶应 力 理论 ( 1个 细观 材 8 含 料长 度参 数 ) 。
微细观尺度下欧拉梁的力学模型及有限元分析

微细观尺度下欧拉梁的力学模型及有限元分析贺丹;陈博;杨万里【摘要】A model of micro Euler beam containing only one internal material length scale parameter and ap-plieing to arbitrary boundary conditions was proposed based on the modified couple stress theory. Equilibri-um differential equation of micro Euler beam was deduced using the Hamiltonˊs principle,of which the form was similar to the classical model. The only difference was an additional term in bending rigidity associated with material length scale parameter. The equation could be used directly to analyze and explain multi-scale problems. Therefore,a strategy reducing modulus was proposed to solve the problems such as bending,vibra-tion and buckling of micro beams by classical beam elements. The numerical results show that the bending rigidity of the Euler beam in a micro scale is higher than that in a macro scale,indicating that model presen-ted in this paper can capture the scale effects. It is found that the geometric size is a significant factor of the scale effects.%基于修正偶应力理论建立了仅含一个尺度参数且适用于各种边界条件的微尺度欧拉梁模型。
clausius-duhem 推导应力定义

clausius-duhem 推导应力定义克劳修斯-迪亨定理(Clausius-Duhem theorem)是热力学中一个重要的理论结果,它描述了连续介质力学中的守恒定律和热力学第一定律之间的关系。
为了推导克劳修斯-迪亨定理,我们首先需要介绍一下什么是连续介质力学。
连续介质力学是一种处理物质的宏观力学性质的理论框架,它假设物质可以连续地分布在空间中,并且力学性质在空间上是连续变化的。
通过连续介质力学,我们可以研究材料的形变、流动等宏观现象。
在连续介质力学中,我们可以描述物质的宏观性质,比如速度、密度、温度等。
为了描述物质的运动,我们需要引入一个称为连续介质的基本方程——守恒定律。
守恒定律指出在任何一个物质体积V内的某个宏观性质Q的变化率与它的流出和流入有关。
守恒定律的一般形式可以写成如下的微分方程:∂Q/∂t + ∇·(ρvQ) = S其中,∂Q/∂t表示时间t的变化率,∇·表示散度运算,ρ表示密度,v表示速度,Q表示宏观性质的值,S表示宏观性质的源项。
守恒定律的一个重要应用是质量守恒定律。
对于质量守恒定律来说,宏观性质Q表示物质的质量,即Q=ρ,密度的变化率∂ρ/∂t与质量的流出和流入有关。
接下来,我们需要引入热力学第一定律,它描述了能量的转化和守恒。
热力学第一定律可以写成如下的微分方程:∂(ρE)/∂t + ∇·(ρvE + q) = W + Q其中,ρE表示单位体积内的总能量,∇·表示散度运算,v表示速度,q表示传热通量,W表示单位体积内的功率,Q表示宏观性质的源项。
根据热力学第一定律和质量守恒定律,我们可以得到能量方程的两个重要等价形式:∂(ρE)/∂t + ∇·(ρvE + q) = W + Q∂(ρE)/∂t + ∇·(ρvE) = W + Q当传热通量q为零时,第一个等式化简为第二个等式。
这是因为在某些情况下,传热可以忽略不计,比如在绝热流动过程中。
考虑尺度依赖的平面正交各向异性功能梯度Mindlin板静弯曲模型

考虑尺度依赖的平面正交各向异性功能梯度Mindlin板静弯曲模型贺丹;杨子豪【摘要】基于各向异性修正偶应力理论建立了能够考虑尺度依赖的平面正交各向异性功能梯度板静弯曲模型.模型中引入两个正交材料尺度参数,因此能够分别描述正交方向上不同程度的尺度效应.基于虚功原理推导了平衡方程和边界条件,并以受双向正弦载荷作用的简支板为例分析了尺度效应对板弯曲挠度产生的影响.算例结果表明:基于模型得到的板弯曲挠度总是小于传统一阶剪切板理论给出的结果,即捕捉到了尺度效应;尺度效应在尺度参数与几何尺寸接近时显著,而在几何尺寸远大于尺度参数时消失;此外,功能梯度变化指数和板跨厚比也会对尺度效应产生一定影响.【期刊名称】《沈阳航空航天大学学报》【年(卷),期】2017(034)004【总页数】7页(P41-47)【关键词】修正偶应力理论;功能梯度材料;正交各向异性;尺度效应;材料尺度参数【作者】贺丹;杨子豪【作者单位】沈阳航空航天大学辽宁省飞行器复合材料结构分析与仿真重点实验室,沈阳110136;沈阳航空航天大学辽宁省飞行器复合材料结构分析与仿真重点实验室,沈阳110136【正文语种】中文【中图分类】TB330.1功能梯度材料是由两种或两种以上组份材料混合制备的先进复合材料。
与传统复合材料层合结构相比,功能梯度材料因其具有沿梯度方向连续变化的力学性能有效避免了传统层合结构中由层间应力不连续导致的结构脱层失效,从而被广泛应用到实际工程领域,其中就包括微米/纳米量级的装置和系统,如:薄膜[1-2]、原子力显微镜[3]、微机电系统(MEMS)[4]、纳机电系统(NEMS)[5]以及生物传感装置[6]。
当材料进入到微尺度领域,其力学性能往往表现出较宏观状态更高的刚度,这种现象被称为材料力学行为的尺度效应[7-8]。
传统的连续介质理论由于缺乏描述微观结构特性的方法而无法对尺度效应做出合理的解释。
非传统广义连续介质理论,如:应变梯度理论[9]和偶应力理论[10-11]则通过引入材料尺度参数(MLSPs)而具备了这种能够描述尺度效应的能力。
偶应力介质结构的最优强度拓扑优化

偶应力介质结构的最优强度拓扑优化苏文政【摘要】在等应变能密度分布的意义下给出了偶应力介质结构最优强度的拓扑优化设计方法.优化模型的设计变量为单元的密度,约束函数为许用材料的体积用量,目标函数通过等应变能密度准则隐式地给出.该方法的优点在于将强度约束/目标的显式应力形式进行转化,避免了应力函数优化问题中的奇异性、强非线性及约束的局部性等困难.数值算例表明,基于优化模型,偶应力介质的最优结果依赖于结构的最小局部尺寸与偶应力介质特征长度的比值.当宏观结构的尺寸远大于特征长度时,偶应力介质的结果趋于经典连续介质的相应结果.【期刊名称】《科学技术与工程》【年(卷),期】2014(014)035【总页数】3页(P157-159)【关键词】偶应力;强度;拓扑优化;准则法【作者】苏文政【作者单位】大连交通大学土木与安全工程学院,大连116028【正文语种】中文【中图分类】O342偶应力连续介质理论[1]由于包含了反映材料自身微结构尺度特征的材料特征长度参数,能够解释由于材料的微结构和宏观结构的尺寸相近而产生的尺寸效应,近年来广泛应用于超轻多孔固体以及多相复合材料的等效性能表征[2, 3]。
基于偶应力等效连续介质模型的结构分析和设计,需要新的实现方法。
同经典连续介质相比,偶应力连续介质具有高阶特点,如偶应力介质认为材料质点既具有平动自由度也具有转动自由度,质点之间既能够传递力也能够传递力偶。
这种高阶特点使得偶应力介质结构的分析和设计方法更为复杂。
目前,对于经典连续介质,结构拓扑优化已经成为结构设计领域的重要方法之一。
在结构的初始设计阶段,拓扑优化能够提供具有革命性的概念设计产品。
20世纪80年代,程耿东、Kikuchi、Bendsøe等人通过引入微结构的概念,最终创立了当代拓扑优化的主流方法——微结构法[4—7]。
此后,该领域也相继出现了一些其他的方法,如ESO方法[8]、ICM方法[9]以及水平集方法[10]等。
(完整版)格里菲斯理论

4.3.6 格里菲思(Griffith)理论以上各种理论都把材料看作连续的均匀介质,格里菲思理论则有所不同。
格里菲思认为:材料内部存在着许多细微裂隙,在力的作用下,这些细微裂隙的周围,特别是缝端,可以产生应力集中现象。
材料的破坏往往从缝端开始,裂缝扩展,最后导致材料的完全破坏。
下面我们较详细地导出格里菲思破坏准则。
设岩石中含有大量的方向杂乱的细微裂隙,其中有一系列如图4-22所示,它们的长轴方向与大主应力1σ成β角。
按照格里菲思概念,假定这些裂隙是张开的,并且形状类似于椭圆。
研究证明,即使在压应力情况下,只要裂隙的方位合适,则裂隙的边壁上也出现很高的拉应力。
一旦这种拉应力超过材料的局部抗拉强度,在这张开裂隙的边壁上开始破裂。
图4-22 细微裂隙受力示意图 图4-23 椭圆裂隙周围材料上的应力为了确定张开的椭圆裂隙边壁周围的应力,作了如下简化假定:1)这椭圆可以作为半无限弹性介质中的单个孔洞处理,即:假定相邻的裂隙之间不相互影响,并忽略材料特性的局部变化;2)椭圆及作用于其周围材料上的应力系统可作为二维问题处理,即把裂缝的三维空间形状和裂缝平面内的应力z σ的影响忽略不计。
这些假定所引起的误差将小于±10%。
在分析中,按岩石力学中的习惯规定,应力以压为正,以拉为负,以及321σσσ>>。
取x 轴沿着裂隙的方向(椭圆长轴方向),y 轴正交于裂隙面方向(椭圆短轴方向)。
椭圆裂隙的参数方程式如下(见图4-23):αcos a x =;αsin b y = (4-45)式中,a 和b ——椭圆的长半轴和短半轴(mm);α—对x 轴的偏心角(º)。
椭圆的轴比用下式表示:ab m =椭圆裂隙周壁上偏心角为α的任意点的切向应力b σ可用弹性力学中的英格里斯(1nglis)公式表示:(){}(){}(){}ααααταασασσ22222222sin cos cos sin 12cos sin 21cos 2+++-+++=m m m m m m xy x y b(4-46)因为在岩石内的裂隙很狭,即轴比m 很小,形状扁平,所以最大的拉应力显然发生在靠近椭圆裂隙的端点处,也就是说,发生在α角很小的地方。
【国家自然科学基金】_cosserat理论_基金支持热词逐年推荐_【万方软件创新助手】_20140803
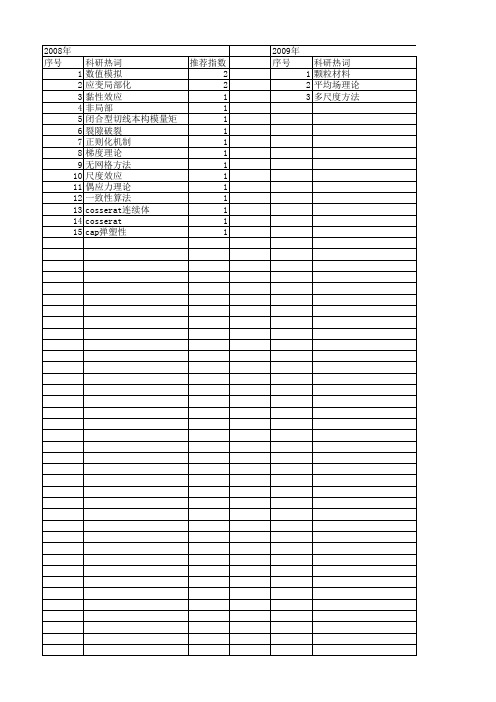
科研热词 推荐指数 数值模拟 2 应变局部化 2 黏性效应 1 非局部 1 闭合型切线本构模量矩阵 1 裂隙破裂 1 正则化机制 1 梯度理论 1 无网格方法 1 尺度效应 1 偶应力理论 1 一致性算法 1 cosserat连续体 1 cosserat 1 cap弹塑性 1
2009年 序号
科研热词 1 颗粒材料 2 平均场理论10年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
科研热词 cosserat理论 尺度效应 偶应力 节理岩体 等效模型 有限元分析 微梁 刚柔耦合系统 非均质材料 耦合变形量 等参元 离散 渐近均匀化方法 欧拉方程 有效性能 应力集中 平面有限元法 头发建模 固有频率 动力学
推荐指数 3 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2013年 序号 1 2 3 4 5 6 7 8 9
科研热词 平均场理论 平均偶应力定义 尺寸效应 多尺度模拟 三维有限元 hill定理 cosserat连续体模型 cosserat连续体 abaqus
推荐指数 5 3 3 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
2011年 科研热词 推荐指数 cosserat理论 2 颗粒材料 1 非均匀材料 1 离散颗粒集合体 1 离散单元法 1 直接均匀化方法 1 梯度增强cosserat连续体 1 有效弹性模量 1 微-方向模型 1 广义协调等参元 1 广义协调条件 1 平均场理论 1 守恒量 1 双自变量 1 动力学普遍定理 1 rve边界条件 1 hill定理 1 hill-mandel条件 1 cosserat连续体 1 cosserat弹性杆 1
Cosserat弹塑性模型在ABAQUS中的数值实施

Cosserat弹塑性模型在ABAQUS中的数值实施彭从文;董龙彬;吴群【摘要】The subroutine UEL embedded in commercial FEM software ABAQUS is utilized to develop a user element based on the material of pressure-dependent elasto-plastic Cosserat continuum model. The user element adopt plane eight-node isoparametric unit which include three degree of freedom (two translation and one rotation) at each node. The Drucker-Prager material model with associate flow rule is used, and the stress integration algorithm is four-order Runge-Kutta method. The user element is used to analyze the influence of mesh density and the material characteristic length in the material localization problem. The results show that the thickness of shear band and the equivalent plastic strain are independent of mesh density, with the increase of the material characteristic length, the thickness of shear band and the equivalent plastic strain decrease constantly.%利用大型有限元软件ABAQUS提供的接口程序UEL,开发了压力相关弹塑性Cosserat连续体材料的用户单元.采用平面八节点等参单元,包括平动与转动三个自由度,考虑相关联流动的Drycjer-Prager材料模型,应力计算采用四阶龙格-库塔法.利用该单元分析了材料局部化问题中网格密度与材料特征长度的影响.结果表明,网格密度对材料剪切带厚度与等效塑性应影响很小;随着特征长度增大,剪切带厚度增大,等效塑性应变峰值减小.【期刊名称】《武汉工程大学学报》【年(卷),期】2011(033)006【总页数】5页(P102-106)【关键词】Cosserat模型;FEM;ABAQUS;UEL;局部化【作者】彭从文;董龙彬;吴群【作者单位】长江大学城市建设学院,湖北荆州434023;荆州市城市规划设计研究院,湖北荆州434000;深圳中广核工程设计有限公司,广东深圳518031【正文语种】中文【中图分类】TB120 引言偶应力理论是微极理论的一个特例,Cosserat兄弟最先提出了完整的偶应力理论[1],Toupin[2],Mindlin等[3]对该理论作了进一步的发展和完善.Cosserat理论引入了旋转自由度和相应的微曲率,引入了与微曲率能量共轭的偶应力、以及具有“特征长度”意义的尺度参数.该理论可以较好地处理网格敏感性和控制方程失去椭圆性的问题,近年来,由于细观力学、非均质力学的发展,Cosserat理论重新受到关注,逐渐成为研究热点之一.数值方法是重要的研究手段之一,为了提高计算精度与效率,基于大型通用数值计算平台的二次开发方法得到了广泛的应用.目前,许多数值计算平台没有内嵌Cosserat计算模型,关于Cosserat模型的二次开发还不多见[4-6]. ABAQUS是目前最流行、功能最强的商用有限元软件之一,该软件可以进行结构静、动力分析,具有强大的非线性计算能力、丰富的材料库及良好的扩充功能,自1997年进入我国以来,越来越多的国内企业和研究机构采用ABAQUS作为产品研发和科学研究的工具.本文采用ABAQUS的用户接口程序,研究压力相关弹塑性Cosserat连续体模型的用户子程序UEL实施方法.1 Cosserat连续体模型考虑Cosserat连续体平面问题,每个材料点有三个自由度.u=应力、应变分别定义为:S=E=几何方程为:ui,j=uj,i-eijkωk(1)κij=ωj,i(2)静力平衡方程为:σij,j+fi=0(3)mij,i+eijkσik+qj=0(4)式(1)~(4)中,fi、qj分别为体积力与体积力偶;eijk为排列算子;ux,uy,ωz分别是平面内平移与转动自由度;mxz,myz偶应力;κxz,κyz为微曲率.对于弹性材料,其本构关系为[7]S=DeE(5)式(5)中,G,v,a,l分别是材料的剪切模量、泊松比、COSSERAT材料参数及特征长度.对于弹塑性Cosserat材料,采用基于Drucker-Prager屈服准则的弹塑性Cosserate连续体模型,其屈服函数与流动势函数分别为[8](6)(7)式(7)中,其中,α,β,A,B为材料参数,σ,s分别为应力与偏应力张量.Cosserat连续体弹塑性本构关系推导方法同经典连续介质力学,应力应变增量关系为(8)式(8)中,内变量采用等效塑性应变,为硬化项定义为2 UEL实现方法及计算流程2.1 子程序编写注意事项(1)ABAQUS提拱了两类单元自定义方法.一类是线性单元,可以通过结果文件或INP文件直接给出,不需要编写UEL;另一类就是通用单元,通过UEL子程序定义;(2)UEL子程序中更新变量与分析问题类别有关.同一个模型中可能遇到不同的分析步,如地应力平衡、静力分析、摄动步分析等,因此,编写UEL时要区别处理;(3)UEL允许自定义荷载.包括集中荷载、均布荷载及弯矩等.其中,对于均布荷载,须定义荷载标志号;(4)自定义单元在ABAQUS/CAE中不可见.若想在ABAQUS/CAE中显示自定义单元变形图,可以将ABAQUS标准单元与自定义单元绑定,同时将标准单元材料参数设为小值.UEL子程序中所有输出变量均通过SDV写入结果文件(.fil、.dat),其分量在ABAQUS/CAE中不可见.2.2 AMATRX与RHS计算UEL界面与ABAQUS内核主要通过AMATRX与RHS等变量进行数值传递.本文采用八节点等参单元,设单元节点位移、插值函数与位移应变转换矩阵分别为d、N与B,单元内任一点位移u及应变ε为u=∑Nidi=Nd(9)ε=Bd(10)式(9~10)中,B=将式(9)、(10)代入Cosserat介质虚功方程(11)进行方程离散.(11)式(11)中,f=,t=对于线性问题,结合材料本构关系,得到式(12).(12)式(12)中,将式(12)简记为Kd=f′(13)对于非线性问题,采用Newton-Raphson方法,将式(13)改写为ψ(d)=K(d)d-f′(14)设ψ(d)为具有一阶导数的连续导数,初始近似值为d(0),第i次迭代的近似值为d(i).将函数ψ(d)在d(i)处展开,保留线性项,忽略高阶项得:(15)d(i+1)=d(i)+Δd(i)(16)式(15)中,与Ψ(d)分别为UEL中需更新变量AMATRX与RHS.2.3 计算流程计算流程如图1所示.图1 UEL流程图Fig.1 Flow of UEL3 性状分析3.1 有限元模型模型几何尺寸10×5 m2,采用三种不同网格密度,单元数分别是15×30、20×40、25×50.边界条件为底端竖向固定,左侧水平向固定.材料弹性模量25 GPa,泊松比0.3,内摩擦角35°,粘聚力1.5 MPa,软化模量15 MPa.采用相关联流动法则.顶部采用位移加载方式,加载量为20 mm,加载方向向下.为了触发局剪切带,对左下角单元弱化处理.采用高斯完全积分,四阶龙格-库塔显式应力积分方法.3.2 计算结果计算模型分析了不同网格密度及特征长度的影响,计算结果如图2~6所示.(1)局部化带的客观性.图2为经典连续介质理论得到的等效塑性应变云图,图3与图4分别是采用Cosserat理论计算得到的等效塑性应变云图与应力应变曲线.由图可知,采用Cosserat理论计算时,随着网格密度增加,剪切带厚度与等效塑性应变峰值基本不变.当采用经典连续介质理论计算时,计算结果有明显的网格依赖性,随着网格密度增加,软化带逐渐变窄,等效塑性应变峰值也不断增大,计算收敛趋于弱化.图2 不同网格密度等效塑性应变云图Fig.2 Contour of equivalent plastic strain with different mesh density注:(a)15×30, (b)20×40,(c)25×50图3 不同网格密度等效塑性应变云图(特征长度0.15)Fig.3 Contour of equivalent plastic strain with different mesh density (characteristic length:0.15)注:(a)15×30, (b)20×40,(c)25×50图4 不同网格密度下应力位移曲线Fig.4 Stress-displacement curve with different mesh density(2)特征长度的影响.Cosserat理论引入特征长度作为正则化机制,特征长度决定Cosserat连续体模型模拟应变局部化问题的能力并影响局部化剪切带宽度大小.图5与图6分别为不同特征长度下采用Cosserat理论计算得到的等效塑性应变云图和应力位移曲线.由图2~6可知,随着特征长度增大,剪切带厚度增大,等效塑性应变峰值减小,材料软化模量降低.图5 不同特征长度下等效塑性应变云图(网格20×40)Fig.5 contour of equivalent plastic strain with different characteristic length (mesh density: 20×40)注:(a)0.2 (b)0.15 (c)0.05图6 不同特征长度的影响Fig.6 Effect of different characteristic length4 结语基于ABAQUS接口程序UEL,开发了压力相关弹塑性Cosserat连续体材料的用户单元,并采用该单元分析了有限元网格密度及材料特征长度对材料局部化的影响.结果表明,采用Cosserat理论计算时网格密度对材料剪切带厚度、等效塑性应变影响很小,这也在一定程度上说明本文方法的正确性.要特别说明的是,基于ABAQUS平台进行二次开发能有效地利用现有程序代码,减小开发工作量,缩短有限元程序开发周期,极大地提高科研工作效率.参考文献:[1] Cosserat E, Cosserat F. Theorie des Corps Deformables [M].Paris: Herman et Files, 1909.[2] Toupin R A. Elastic materials with couple stresses [J].Archive Rational Mechanics and analysis, 1962(11): 385-414.[3] Mindlin R D, Tiersten H F. Effects of couple stresses in linear elasticity [J]. Archive Rational Mechanics and analysis, 1962(11): 415-448.[4] 杨乐, 吴德伦, 许年春. 偶应力理论的层状岩体洞室数值模拟[J]. 重庆建筑大学学报, 2008, 30(3):73-77.[5] 尹雪英, 杨春和, 李银平. 层状盐岩体三维Cosserat介质扩展本构模型的程序实现[J]. 岩土力学, 2007,28(7):1415-1420,1426.[6] 朱珍德, 秦天昊, 王士宏, 等. 基于Cosserat理论的柱状节理岩体各向异性本构模型研究[J]. 岩石力学与工程学报,2010,29(增2): 4068-4076.[7] Sharbati E, Naghdabadi R. computational aspects of the cosserat finite element analysis of localization phenomenon[J]. Computational materials science,2006(38):303-315.[8] HAYDAR ARSLAN. Localization analysis of granular materials in cosserat elastoplasticity -formulation and finite element Implementation [D]. Colorado: University of Colorado, 2006, 85-88.。
考虑偶应力的弹性力学问题

1、 平衡方程
图 1 偶应力理论中的微元体iii
如图,������������������ 代表应力,������������������ 代表偶应力。它们应满足静力平衡方程: ∑ ������������ =0, ∑ ������������ =0, ∑ ������������ =0 ∑ ������������ =0, ∑ ������������ =0, ∑ ������������ =0 由∑ ������������ =0,得 (������������������ +
+ +
������������������������ ������������ ������������������������
+ ������������������ − ������������������ + ������������ = 0 + ������������������ − ������������������ + ������������ = 0 (1-3)
������������−������������������ ) ������������������������
������������������������ ������������
− (������������������ +
������������) ������������������������������������ +
考虑偶应力的弹性力学问题
摘要:传统弹性力学不考虑偶应力在材料中的作用,而当考虑这一点时,弹性力学的基本方 程就会发生变化,从而使应力张量与应变张量发生变化,变得不再对称,还需要引入新的共 轭张量和弹性常数,即与偶应力功共轭的曲率张量和表征材料微结构的材料特征长度。 关键词:偶应力 曲率张量 基本方程 ∁1 类理论 传统连续介质并没有考虑偶应力在材料中的作用,这在其运用于宏观结构的力学分析, 诸如航空航天、机械、土木等工程时,发挥了巨大的作用。而近年来,随着其应用范围扩大 到微观尺度,出现了明显的不适用。例如薄膜(其厚度为 1μm量级或更小) ; 微传感器, 微致 动器, 及微电子机械系统(MEMS, 整个系统的尺寸小于 10μm) ; 微电子封装与微电子装置(其 器件小于 10μm ), 颗粒或纤维尺寸为 10μm量级的先进的复合材料以及微加工.这些新的应 用具有的共同特点是部件或变形所涉及的特征长度尺寸很小, 典型地为(0.1~ 10 ) μm。i在这 种情况下,材料的性质会发生显著变化,如强度随尺寸减小而增强。因为此时材料的微结构 和微缺陷已经必须要考虑了。 偶应力理论正是解决该类问题的一种比较简单的方法, 引入了偶应力张量与旋转梯度这 一对功共轭张量。旋转梯度与曲率具有相同的量纲,对于微结构的转动,其旋转半径与该结 构的特征长度有关, 从而将材料特征长度与旋转梯度联系起来。 而为了平衡转动梯度和应变 之间的量纲, 本构中出现一个具有长度量纲的新材料长度参数。 该材料长度参数依赖于材料 的微结构和微缺陷,从而将材料微结构微缺陷的影响引入连续介质力学理论。ii 该理论基本可分为两大类: 一类认为质点旋转矢量独立于位移矢量, 也称之为∁0类理论; 另一种认为旋转矢量依赖于位移矢量,也称之为∁1 类理论。本文主要介绍∁1 类理论,即有: 1 ������������ = ������������������������ ������������,������ 2 这是一阶应变梯度理论的一种特殊情况。同时本文也建立在小变形的基础上。
协调的尺度相关连续偶应力理论简介

协调的尺度相关连续偶应力理论简介令狐烈1摘要:经典的小变形弹性力学理论比如柯西弹性力学理论忽略了偶应力,在宏观尺度的时候适用的很好,但是随着材料的尺寸越做越小,特别是在纳米技术以及微电子技术的发展,对弹性力学提出了新的要求,要求我们不得不考虑到偶应力的情况。
本文简单回顾偶应力理论的发展,并详细介绍一种偶应力理论:尺度相关协调连续偶应力理论。
除了客观地介绍该理论的原理,文中还加入了本人自己的理解,着重介绍与其物理本质相关的一般性结论。
关键词:微观尺度,偶应力,协调的尺度相关连续理论。
1.引言经典的连续介质力学基于连续性假设,认为物体是有无数多的没有体积的空间点组成,这些点没有体积,但是有确定的空间和物理特征,比如位置,质量与运动。
这样的假设就必然导致力偶被忽略,因为组成物质的基本单元是没有体积的点,这样的模型只考虑到平移改变平移特征承受力矢,不能有考虑到转动与改变转动特征的力偶。
这样得到的理论在宏观的时候适用的很好,但是随着材料的尺度发展的越来越小,比如计算机的电路集成;在处理这些微观问题的时候却出现了问题。
丢弃了连续性假设的偶应力理论的分析和计算都异常复杂,因此后来发展了尺度相关连续介质力学,把微观尺度考虑进去,但同时也能够退化为宏观尺度的连续介质力学。
这样的理论需要使用尺度相关的变形度量,比如曲率张量,结果便需要考虑到偶应力。
Toupin等人[1]使用宏观转动真实的转动得到了一种偶应力理论,他们使用转动向量的梯度来作为曲率张量。
可惜的是他们的理论遇到一些麻烦,其中最主要的是偶应力张量的球形部分和体力偶在应力张量本构关系中的表现形式无法确定。
这些不协调的偶应力理论被称为模糊偶应力理论。
另外有一个分支被称为微极理论(micropolar theories)[2, 3],该理论使用微转动,结果却引入了额外的只有度。
还有一种第二梯度理论[4](second gradient theories)引入应变梯度,1浙江大学航空航天学院工程力学系转动和其他的一些组合。
多段微梁固有振动特性的尺寸效应分析

多段微梁固有振动特性的尺寸效应分析
陈大双;郝淑英;张昆鹏;张琪昌
【期刊名称】《天津理工大学学报》
【年(卷),期】2022(38)6
【摘要】尺寸效应将影响多段微梁的固有振动特性。
针对微机电系统中一种三段式微梁,基于哈密顿原理建立了多段微梁的无阻尼自由振动方程,并求出微梁的固有频率和模态,将不同角度下的理论结果与有限元仿真进行对比验证。
采用修正偶应力理论推导考虑材料尺度参数的多段微梁变形能表达式,并进行多段微梁固有频率和模态的尺寸效应分析。
结果表明:随着材料尺度参数与特征尺寸比值的增大,多段微梁的固有频率逐渐增加。
微梁各段间的角度越大,尺寸效应对1阶固有频率的影响越显著,而尺寸效应对微梁的模态几乎没有影响。
【总页数】7页(P1-7)
【作者】陈大双;郝淑英;张昆鹏;张琪昌
【作者单位】天津理工大学天津市先进机电系统设计与控制重点实验室;天津理工大学机电工程国家级实验教学示范中心;天津大学天津市非线性动力学与控制重点实验室
【正文语种】中文
【中图分类】O321
【相关文献】
1.城轨U梁与箱梁桥上无缝线路受力及桥梁固有振动特性分析
2.悬臂微梁固有频率和模态的尺寸效应
3.深海实尺寸顶张力立管固有振动特性分析
4.Bernoulli-Euler微梁振动特性的尺寸效应
5.基于广义弹性理论的微梁固有频率及模态的尺寸效应
因版权原因,仅展示原文概要,查看原文内容请购买。
连续体力学发展史

连续体力学发展史全文共四篇示例,供读者参考第一篇示例:连续体力学发展史连续体力学是力学的一个重要分支,研究的是连续介质的力学行为。
在物质世界中,几乎所有的物质都是连续的,因此研究其性质和行为对于我们理解自然和科学发展至关重要。
本文将对连续体力学的发展历史进行详细的介绍,希望能够带给读者更深入的了解。
古希腊时期,人们对物质的本质和性质进行了探讨,开始了对连续介质的研究。
亚里士多德认为物质是连续的,对空间的无限分割并不符合物质的本质。
他的连续体观念对后来的科学发展产生了重要的影响,奠定了连续体力学的基础。
随着科学技术的发展,人们对连续介质的研究逐渐深入。
十七世纪,牛顿提出了著名的牛顿力学,建立了刚体力学的基础。
但是刚体并不是自然界中所有物体的真实状态,连续介质的研究需求越来越迫切。
在十八世纪中期,拉普拉斯提出了流体动力学的基本方程,奠定了连续体力学的理论基础。
从此,连续体力学逐渐成为力学领域的一个重要分支。
随着科学技术的不断进步,连续体力学的研究也得到了长足的发展。
十九世纪末,爱因斯坦提出了广义相对论,重新诠释了引力的本质,并对连续介质的理论进行了重要的拓展。
在二十世纪,量子力学的发展对连续介质的研究提出了新的挑战,人们开始探讨微观尺度和宏观尺度之间的联系和转换。
各种新的理论和模型相继诞生,为连续体力学的研究提供了新的思路和方法。
近年来,随着计算机技术和数值模拟的不断发展,连续体力学的研究取得了更加深入和广泛的成果。
人们利用数值模拟和计算机模拟手段,对连续介质的力学行为进行了详细的研究和分析,取得了一系列重要的科学成果。
实验技术的不断进步也为连续体力学提供了更加直接和准确的验证手段,使得理论和实验相互印证,相互促进,推动了该领域的快速发展。
未来,随着科学技术的不断发展和进步,连续体力学的研究将会更加深入和广泛。
人们将不断拓展研究领域,深化理论模型,提出新的问题和挑战,探索更广阔的科学领域。
人们将继续加强理论研究和实验验证的结合,促进理论和实践的相互促进,推动连续体力学的不断发展和完善。
正则化方法求解偶应力反问题

正则化方法求解偶应力反问题姚宇新;薛齐文【摘要】Tikhonov's regularization approach has been used to identify parameters for the inverse couple-stress problem based on Bregman distances and weighted Bregman distances in the construction of regularization terms for the Tikhonov's function. The inverse problem is formulated implicitly as an optimization problem with the cost functional of squared residues between calculated and measured quantities. A FE model is given, taking account of inhomogeneity and facilitating to sensitivity analysis for direct and inverse problems. Satisfactory numerical validation is given including a preliminary investigation of effect of noise data on the results and the computational efficiency for different regularization terms. Results show that the proposed method can identify parameters for the inverse couple-stress problem with high computational precision/efficiiency and the ability of anti-noisy data. It could improve computational efficiency for the weighted Bregman distances function as regularization terms.%引入Bregman函数及其加权函数作为正则项,应用Tikhonov正则化方法,对偶应力反问题相关参数进行识别.利用相关测量信息和计算信息构造最小二乘函数.在考虑材料非均质的同时,建立了便于敏度分析的偶应力正/反问题数值求解模型.给出了相关的数值算例,并对信息误差以及不同正则项的计算效率作了探讨.数值结果表明所提的求解策略不仅能够对相关的材料参数进行有效识别,而且具有较高的计算精度、较好的稳定性和一定的抗噪性.采用加权的Bregman距离函数作正则项可以提高计算效率.【期刊名称】《科学技术与工程》【年(卷),期】2011(011)033【总页数】4页(P8131-8134)【关键词】Bregman函数;偶应力;反问题;正则化【作者】姚宇新;薛齐文【作者单位】大连交通大学土木与安全工程学院,大连116028;大连交通大学土木与安全工程学院,大连116028;工业装备结构分析国家重点实验室,大连116023【正文语种】中文【中图分类】O343.1偶应力理论是研究具有微结构、一定特征尺度介质力学行为的重要工具之一。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
协调的尺度相关连续偶应力理论简介令狐烈1摘要:经典的小变形弹性力学理论比如柯西弹性力学理论忽略了偶应力,在宏观尺度的时候适用的很好,但是随着材料的尺寸越做越小,特别是在纳米技术以及微电子技术的发展,对弹性力学提出了新的要求,要求我们不得不考虑到偶应力的情况。
本文简单回顾偶应力理论的发展,并详细介绍一种偶应力理论:尺度相关协调连续偶应力理论。
除了客观地介绍该理论的原理,文中还加入了本人自己的理解,着重介绍与其物理本质相关的一般性结论。
关键词:微观尺度,偶应力,协调的尺度相关连续理论。
1.引言经典的连续介质力学基于连续性假设,认为物体是有无数多的没有体积的空间点组成,这些点没有体积,但是有确定的空间和物理特征,比如位置,质量与运动。
这样的假设就必然导致力偶被忽略,因为组成物质的基本单元是没有体积的点,这样的模型只考虑到平移改变平移特征承受力矢,不能有考虑到转动与改变转动特征的力偶。
这样得到的理论在宏观的时候适用的很好,但是随着材料的尺度发展的越来越小,比如计算机的电路集成;在处理这些微观问题的时候却出现了问题。
丢弃了连续性假设的偶应力理论的分析和计算都异常复杂,因此后来发展了尺度相关连续介质力学,把微观尺度考虑进去,但同时也能够退化为宏观尺度的连续介质力学。
这样的理论需要使用尺度相关的变形度量,比如曲率张量,结果便需要考虑到偶应力。
Toupin等人[1]使用宏观转动真实的转动得到了一种偶应力理论,他们使用转动向量的梯度来作为曲率张量。
可惜的是他们的理论遇到一些麻烦,其中最主要的是偶应力张量的球形部分和体力偶在应力张量本构关系中的表现形式无法确定。
这些不协调的偶应力理论被称为模糊偶应力理论。
另外有一个分支被称为微极理论(micropolar theories)[2, 3],该理论使用微转动,结果却引入了额外的只有度。
还有一种第二梯度理论[4](second gradient theories)引入应变梯度,1浙江大学航空航天学院工程力学系转动和其他的一些组合。
尽管这些理论使用真实的连续体来描述变形,但是其公式却不能够和变价条件以及虚功原理的能量对偶性保持一致。
这里要介绍的是一种协调的尺度相关连续偶应力理论(a consistent size-dependent continuum mechanics theory for couple-stress)[5]。
该理论考虑真实的连续体的运动位移与转动,结合边界条件,虚功原理,得到了不依赖与附加自由度的偶应力理论,发现偶应力张量的反对称性以及转动张量梯度的反对称部分是协调的曲率张量,它们两者之间满足虚功原理的对偶关系,而且发现应变梯度并非变形的基本度量。
除了客观地介绍该理论的原理,文中还加入了本人自己的理解。
这里着重介绍与其物理本质相关的一般性结论,相关算例还请参考原文。
2.平衡方程考虑一个体积为V,边界为S的连续体。
在该连续体中的两个有限体之间的相互作用通过二者的接触表面dS上的作用力()t nidS与作用力偶()m nidS和传递,其中()t ni是力牵引向量(force--traction vectors),()m ni是力偶牵引向量(moment-traction vectors)。
表面力和表面力偶通常使用非对称的应力张量ij σ和偶应力张量ij μ来表示:()t (1)n i ij j n σ=----- ()m (2)n i ij j n μ=-----而应力张量和偶应力张量可以进行加法分解,写为对称与反对称部分的和: ij ij ij (3)S A μμμ=+-----ij ij ij (4)S A σσσ=+-----这里的上标S 表示对称部分(symmetric ),A 表示反对称部分(antisymmetric ),与原文中的圆括弧下标表示对称,方括弧下标表示反对称有所不同,但是这只是一个记号,并没有太大的影响。
现在考虑有限体积(可以是微元体积,也可以是整个体积)的平衡,设其体积为a V ,表面为Sa 。
连续介质力学的原则是质量平衡,线动量就,角动量与能量的平衡,其一般形式为:(*)t Vsvddv d dv d =•+-----⎰⎰⎰Q F A S其中,Q 表示研究的物理量,F 表示表面作用项,S 表示源。
在准静态情形下,该部分体积的线动量和角动量平衡的方程为:()at0(5)t n j jj V savadV dv dS F dv d =+=----⎰⎰⎰()()ax t +m t x 0(6)n n i ijk j k i V Sa ijk j k i Vad dv dS d F C dv εε⎡⎤Ω=⎣⎦⎡⎤++=-----⎣⎦⎰⎰⎰这里的Fi 和Ci 分别表示单位提及的体积力和体力偶。
ijk ε是置换符号。
使用方程(1)和(2),以及散度定理,并注意体积的任意性可以得到一般偶应力理论平衡方程的微分形式:ji,i 0(7)i F σ+=-----ji,ijk +0(8)j jk i C μεσ+=-----在经典连续介质力学中,没有考虑到偶应力与体力偶,也就是 μji = 0 和Ci = 0。
因此角动量平衡方程(8)表明应力张量是对称的,这就意味着应力张量有6个独立量,这里有3个平衡方程,另外的三个方程为本构方程,这就是经典的弹性理论比如柯西理论的情形。
而在偶应力理论中,应力张量和偶应力张量一共有18个未知量,但是平衡方程只有6个,似乎另外的12个方程都要去本构方程中找。
这也正是2发展偶应力理论的麻烦之处。
本文介绍协调的尺度相关连续偶应力理论希望通过探究边界条件,虚功原理和一些运动学知识来发现变量之间的关系,减少独立未知变量的个数。
3.运动学(几何方程)这里仅仅考虑微小变形的运动学(几何方程)。
在笛卡尔坐标系中,定义u i 为连续介质的位移场。
考虑连续体重相邻的两点P 和Q ,它们在参考构型中的位置分别为xi 和 xi + dxi ,两点之间的相对位移为:d (10)i i j ij u u dx =-----,其中,u i ,j 是P 点的位移梯度张量。
事实上, 位移梯度张量本身并不适合于度量变形,因此对位移梯度张量进行加法分解为对称与反对称部分:,u (11)i j ij ij e ω=+-----,,1=u u )(12)2ij i j j i e +-----(,,1=u -u )(13)2ij i j j i ω-----(这里的张量e ij 和 ωij 分别是小变形的应变张量(strain tensor )和转动张量(rotation tensor )。
转动张量对应的转动向量(rotation vector )ωi 定义为:,11=(14a)22i ijk kj ijk k j u ωεωε=-----其向量形式为:1=(14b)2u ω∇⨯-----相应地,该转动向量与转动张量的关系为j =(15)i ijk k ωεω-----其分量形式为:123213312=-==-(16a )c ωωωωωω-,,因此,相对位移可以分解为:12d d +d (17)i i i u u u =-----()()1d e d (18)i ij j u x =-----() 2d d (19)i ij j u x ω=-----()ωij 被视为为微元线段dxi 相对于P 点产生的类似刚体转动,转动导致的相对位移与微元段垂直:2d d d d 0(20)i i ij i j u x x x ω==-----()由于ωij 对于微元线段d i x 的伸长和收缩没有影响,它就不可能出现在度量材料伸缩的张量中。
因此,在经典的弹性理论,比如柯西理论中,使用对称部分应变张量用来描述微小变形的是合理的。
在偶应力理论,需要另外一个张量来度量任意微元线段的曲率。
为了找到该张量,考察转动向量ωi 。
相邻两点P ,Q 之间的相对转动为:,d =(21)i i j j dx ωω-----其中,张量ωi,j 是P 点的转动向量的梯度。
其分量ω1,1,ω2,2 和 ω3,3 表征微元线段的沿着坐标轴的扭转,第一个下标表示作用面,第二个下标表示微元线段的方向。
非对角线的元素表示微元线段的扭曲曲率,第一个下标表示观察平面,第二个下标表示观察的微元段。
综上所述,在微小变形中,连续体P 点临近点Q 点的移动总结起来有:随着P 点的平动,相对P 点的伸缩,相对P 点转动和微元线段PQ 的扭转与弯曲整个过程中,微元段dxi 就好像一根弹性纤维,后面就把它叫做微元纤维以突出扭曲变形特征。
整个过程如图1所示:曲率的适当度量方式必须是可以度量任意一个微元线段dxi 的纯曲率的张量。
因此,在曲率张量中,对角线元素ω 1,1,ω 2,2 和ω3,3不能够出现。
但是不能够把他们简单的删除。
通过把张量ωi,j 分解为对称和反对称两个部分,可以得到:i j ij (22)ij ωχκ=+-----,()ij ,,1(23)2i j j i χωω=+----- ()ij ,,1-(24)2i j j i κωω=-----对称张量χij 可以通过对转动张量使用应力算子(strain operator )得到,而反对称张量κij 为P 点的转动向量的旋度。
从(23)可以得到:111,1222,2333,3,(25a )c χωχωχω===------()23322,33,21==+(26)2χχωω----- ()13311,33,11==+(27)2χχωω-----图1:弹性体中任意一个微元段弹性纤维的变化情况示意图()12211,22,11==+(28)2χχωω----- (25)对角线元素χ11 , χ22 和χ33代表微元纤维沿着X1,x1,x3方向的纯扭转,如上面提到的那样。
另一方面,观察(26)卡以看到,χ23 , χ13 和 χ12 来度量平行于X2X3,X1X3,和X1X2平面变形后与球度(sphericity )的偏离[6]。
进一步,我们可以看到对称张量χij 一定存在主值,代表沿着主轴方向的纯扭转。
因此,可以把χij 称为扭转张量(torsion tensor )并且希望这个张量在连续介质材料中对于变形的基本度量没有影响。
相反,这里猜测基本的曲率张量是转动张量κij 的反对称的旋度。
下面通过考虑偶应力的虚功原理来证明。
注意到d ωi 中只有垂直于dxi 的那部分才会产生纯弯曲。
因此,通过把d ωi 进行分解:()()12d d +d (27)i i i ωωω=-----()2d (28)i ij j dx ωχ=-----()2d (29)i ij j dx ωκ=-----注意到:()()2i d 030i i ij j dx dx dx ωκ==-----这表明d ωi (2)是d ωi 中垂于dxi 的分量。
