(完整版)Excel在长期投资决策中的应用
长期投资决策中EXCEL财务函数的应用

摘要:以EXCEL财务函数为切入点,通过对典型实例的研讨,关注如何及时、迅速、高效地进行投资决策分析,从而提高工作质量与效率,提升决策的准确性,这对提高企业竞争力,使企业立于不败之地,有非常重要的现实意义。
关键词:投资;决策;EXCEL;财务函数随着市场经济的日益活跃,企业面临的经济环境也在发生变化。
为维持自身竞争力,企业总是会投放一定的财力用于对内或对外的投资活动,而其中又以长期投资更为重大。
长期投资数额大,周期长,项目多跨年建设、多年受益,风险也较大,存在诸多不确定因素,对企业影响深远。
因此,在投资范畴和投资行为日益多元化的今天,根据市场竞争的需要,或为扩大现有的经营规模,或为丰富自身经营的厚度和广度,或以各种证券投资的形式获利等目的,企业管理团队如何充分利用所有者赋予的投资决策权,及时、迅速、高效地进行各种投资决策,就显得尤为重要。
进行投资决策,要坚决杜绝在缺乏调查研究和缜密分析的情况下轻率拍板的现象,需要对相关项目的投资支出、投资收入进行对比分析,选出对企业来说最为适合,或者说经济效益最佳的投资项目或方案。
在这一过程中,正确的计算和评价投资项目的经济效益是投资决策的核心问题。
在手工条件下,由于建立模型本身的困难和计算的复杂性,财务人员往往不能精确、高效地进行定量分析,很多时候凭感觉决策、靠估计定夺,使决策失准,造成了许多不良后果。
随着计算机技术的日益普及,财务管理人员可以借助常用的计算机软件工具有效地建立投资模型、运用计算公式进行相对准确的定量分析,EXCEL财务函数就是一种重要的财务决策辅助工具。
总体来说,EXCEL中可供利用的常用投资函数众多,主要包括价值型指标和效率型指标,诸如:FV———某项投资的未来值、NPV———某项投资的净现值、PMT———贷款分期偿还额、PV———某项投资的现值、IRR———现金流的内部收益率等。
此外,在进行长期投资时我们往往通过构架相关的决策模型,测算投资成本和收益,确定投资效益,使之即使在条件发生变化时也能随机应变、应付自如。
EXCEL在长期投资决策中的应用

EXCEL在长期投资决策中的应用长期投资具有投金额大、投资回收期长、投资风险大等特点,因此任何企业在进行长期投资时都应该十分谨慎的对待,在进行长期投资之前必须对项目进行可行性分析。
正是由于长期投资决策涉及的时间会比较长,因此进行项目可行性分析时,通常都要考虑资金的时间价值,而资金时间价值的计算具有理论抽象、计算复杂等特点,特别是对计算能力的要求比较高。
财务人员如果能够正确、灵活地使用Excel 进行财务函数的计算,可使原本复杂的计算变得非常简单,并能大大减轻日常工作中有关指标计算的工作量。
在现行的财务评价理论中大部分都是根据项目产生的现金净流量进行的,因此下面将从EXCEL在现金净流量计算中的应用及EXCEL在长期投资评价指标计算中的应用这两个方面就有关问题作进一步的探讨。
一EXCEL在现金净流量计算中的应用长期投资决策中,重点研究的是现金净流量,而把利润的研究放在次要的地位,主要是处于以下几个原因:首先,由于整个投资有效年限内,利润总计与现金净流量总计是相等的,所以现金净流量可以取代利润作为评价净收益的指标;其次,利润在各年的分布要受折旧方法、会计政策选择等人为因素的影响,而现金净流量的分布不受这些人为因素的影响,可以保证评价的客观性;再次,一般来讲,有利润的年份不一定有多余的现金,而一个项目能否维持下去,不取决于一定期间是否盈利,取决于有没有现金用于各种支付,因此在投资分析中,现金流动状况分析比盈亏分析更重要。
基于上述原因,在长期投资决策时首先就必须要分析、计算项目各年产生的现金净流量。
目前常用于计算项目现金净流量的方法主要有以下三种:一是,现金净流量=营业收入-付现成本-所得税。
在使用这个公式计算现金净流量时必须首先预计出项目的税前利润,否则就没有办法知道项目应缴的所得税额。
二是,现金净流量=净利润+折旧。
使用这种方法计算现金净流量时,也必须先计算项目的利润。
为了简便计算,常有的计算现金净流量的方法是,现金净流量=收入×(1-所得税率)-付现成本×(1-所得税率)+折旧×所得税率。
excel在投资管理决策中的应用

excel在投资管理决策中的应用Excel是一种广泛应用于投资管理决策的工具,主要应用于数据分析、建立模型、预测和计算等方面。
下面,将从以下3个方面详细解释Excel在投资管理决策中的应用。
1.数据分析
在投资管理过程中,为了做出正确的决策,需要进行大量数据分析。
利用Excel可以收集、组织和分析大量数据,比如公司业绩、经济数据、市场调查数据等,以了解市场趋势,分析风险和机会。
Excel 中的数据透视表和筛选器可以轻松帮助投资者快速实现对数据的理解和分析。
2.建立模型
利用Excel可以建立各种模型,包括投资组合选择、资产评估和风险模型等,以便更好地理解市场,确定投资策略,制定计划和决策。
为了建立准确的模型,需要准确的数据输入和合理的假设,以及适用的公式和函数。
利用Excel的目标搜索、求解器、含键值的查找和分类函数等工具帮助投资者设计和优化模型,提高决策的准确性。
3.预测与计算
投资决策需要进行各种预测和计算,包括股票预测、资产评估、风险计算等。
Excel包含了各种算术、统计和财务函数,方便进行计算。
此外,Excel还包括图表、图像和其他视觉工具,以帮助投资者理
解数据、趋势和模式。
这些工具可以帮助投资者表达和展示自己的想法和计划,增加与其他投资者的沟通和合作的效率。
综上所述,Excel在投资管理决策中的应用广泛,可以帮助投资者进行数据分析、建立模型、预测和计算,以更好地理解市场,确定投资策略,制定计划和决策。
Excel在股票与投资分析中的应用

Excel在股票与投资分析中的应用在现代金融领域中,股票与投资分析起着至关重要的作用。
投资者需要准确地分析市场数据,作出明智的投资决策。
在这个过程中,Excel作为一种功能强大的电子表格软件,提供了广泛的工具和函数,可以帮助投资者进行股票与投资分析。
本文将探讨Excel在股票与投资分析中的应用,包括数据处理、数据可视化、技术分析和风险管理等方面。
1. 数据处理在股票与投资分析中,数据处理是非常重要的一步。
投资者需要收集、整理和分析大量的市场数据,以便做出准确的投资判断。
Excel提供了各种数据处理功能,比如数据筛选、排序、计算以及数据透视表等。
使用这些功能,投资者可以轻松地对市场数据进行有效的处理和分析。
2. 数据可视化数据可视化是帮助投资者更好地理解和分析数据的关键。
Excel提供了丰富的图表工具,可以将数据以直观的方式进行展示。
投资者可以使用折线图、柱状图、饼图等各种图表类型,将市场数据可视化地呈现出来。
这种可视化的方式可以帮助投资者更好地观察数据的趋势和规律,从而作出更明智的投资决策。
3. 技术分析技术分析是股票与投资分析中常用的一种方法。
投资者根据历史数据和图表模式,预测未来市场走势。
Excel提供了各种函数和工具,可以帮助投资者进行技术分析。
比如,投资者可以使用移动平均线函数计算不同时间段内的平均价格。
另外,投资者还可以使用条件格式化功能,将不同的技术指标以不同的颜色显示,以便更好地观察图表模式和趋势。
4. 风险管理在投资过程中,风险管理是非常重要的一环。
Excel提供了各种功能,帮助投资者评估和管理投资风险。
比如,投资者可以使用内置的函数计算股票的波动率和标准差,以评估股票的风险水平。
此外,通过建立投资组合模型和使用Excel的求解器工具,投资者还可以进行资产配置和风险分散,以降低投资风险。
总结起来,Excel在股票与投资分析中具有广泛的应用。
它可以用于数据处理、数据可视化、技术分析和风险管理等方面,帮助投资者进行股票与投资的决策。
EXCEL在财务中应用投资项目决策

EXCEL在财务中应⽤投资项⽬决策
利⽤excel中的内置函数进⾏投资决策分析。
项⽬投资决策⼀般是通过⽐较投资决策指标进⾏的,投资决策指标⼀般包括⾮贴现指标和贴现指标。
⾮贴现指标包括投资回收期、会计收益率等,贴现指标包括净现值、内涵报酬率和现在指数等。
下⾯通过⼀个案例,了解⼀下使⽤excel⼯具进⾏投资决策⽅案分析。
假设某公司有A、B两个投资项⽬,A项⽬需要投⼊资⾦20万元,B项⽬需要投⼊资⾦5万元,该公司资⾦成本率为10%,两个项⽬经营期各年现⾦流量如下:
投资项⽬第1年第2年第3年第4年
A项⽬60,00060,00060,00060,000
B项⽬10,00020,00030,00015,000
分别计算两个投资项⽬的净现值、内涵报酬率、投资回收期,并⽐较选择投资项⽬。
解析:根据题意设计表格
具体计算结果及公式设计如下:
其中净现值NPV、内涵报酬率IRR的计算考虑了货币的时间价值,投资回收期计算没有考虑货币时间价值,求得是静态
的投资回收期。
excel在投资决策中的应用

excel在投资决策中的应用Excel是一款广泛应用于投资决策的电子表格软件,它可以帮助投资者更好地分析数据,作出更明智的决策。
以下是Excel在投资决策中的应用:1. 数据收集与整理在投资决策过程中,要收集和整理大量的数据,Excel可以帮助投资者快速地进行数据输入和排序。
还可以使用数据分析工具来解读数据,如图表、图形、过滤器等。
2. 交易模型构建建立交易模型是投资决策的重要环节,Excel可以快速建立各种投资模型。
例如,根据某只股票的历史价格数据,可以使用Excel的趋势线工具来预测该股票的未来价格走势;根据企业的财务报表,可以用Excel建立财务模型用于预测公司的未来业绩等。
3. 风险分析投资决策的一个关键要素是风险管理。
Excel可以用于风险分析,帮助投资者识别和管理风险。
例如,可以通过建立风险矩阵来评估项目的风险,或者通过基于蒙特卡罗模拟的风险分析来评估股票投资的风险。
4. 投资组合管理投资者通常会持有多种不同的资产类型和证券,这需要投资者建立投资组合,Excel可以帮助投资者定量评估投资组合的风险和回报,以此在投资组合中进行优化调整。
可以使用Excel制作投资组合回报率的图像,模拟并优化投资组合的分配。
资金管理是投资决策中一个重要的方面。
Excel可以用于跟踪和记录资金流动,包括资产和负债的记录,以及现金流分析。
这样,投资者可以更好地管理自己的资金,减少战略风险和市场波动所带来的负面影响。
总之,Excel在投资决策中的应用极为实用且广泛。
通过使用Excel的数据分析、模型构建、风险分析、投资组合管理和资金管理等工具,投资者可以更加精确地进行投资决策,并且更好地管理投资组合,从而达到更高的回报并降低风险。
长期投资决策中EXCEL财务函数的应用

摘要:以EXCEL财务函数为切入点,通过对典型实例的研讨,关注如何及时、迅速、高效地进行投资决策分析,从而提高工作质量与效率,提升决策的准确性,这对提高企业竞争力,使企业立于不败之地,有非常重要的现实意义。
关键词:投资;决策;EXCEL;财务函数随着市场经济的日益活跃,企业面临的经济环境也在发生变化。
为维持自身竞争力,企业总是会投放一定的财力用于对内或对外的投资活动,而其中又以长期投资更为重大。
长期投资数额大,周期长,项目多跨年建设、多年受益,风险也较大,存在诸多不确定因素,对企业影响深远。
因此,在投资范畴和投资行为日益多元化的今天,根据市场竞争的需要,或为扩大现有的经营规模,或为丰富自身经营的厚度和广度,或以各种证券投资的形式获利等目的,企业管理团队如何充分利用所有者赋予的投资决策权,及时、迅速、高效地进行各种投资决策,就显得尤为重要。
进行投资决策,要坚决杜绝在缺乏调查研究和缜密分析的情况下轻率拍板的现象,需要对相关项目的投资支出、投资收入进行对比分析,选出对企业来说最为适合,或者说经济效益最佳的投资项目或方案。
在这一过程中,正确的计算和评价投资项目的经济效益是投资决策的核心问题。
在手工条件下,由于建立模型本身的困难和计算的复杂性,财务人员往往不能精确、高效地进行定量分析,很多时候凭感觉决策、靠估计定夺,使决策失准,造成了许多不良后果。
随着计算机技术的日益普及,财务管理人员可以借助常用的计算机软件工具有效地建立投资模型、运用计算公式进行相对准确的定量分析,EXCEL财务函数就是一种重要的财务决策辅助工具。
总体来说,EXCEL中可供利用的常用投资函数众多,主要包括价值型指标和效率型指标,诸如:FV———某项投资的未来值、NPV———某项投资的净现值、PMT———贷款分期偿还额、PV———某项投资的现值、IRR———现金流的内部收益率等。
此外,在进行长期投资时我们往往通过构架相关的决策模型,测算投资成本和收益,确定投资效益,使之即使在条件发生变化时也能随机应变、应付自如。
第五章 Excel在项目投资决策中的应用

例题
元的卡车, 例:假设购买了一辆价值80000元的卡车, 假设购买了一辆价值 元的卡车 其折旧年限为10年 残值为 其折旧年限为 年,残值为4000元,则第 元 一年和第十年的折旧分别为: 一年和第十年的折旧分别为: SYD(80000,4000,10,1)=13818.18 SYD(80000,4000,10,10)=1381.82
⑶ 计算方法
⑴
NCFt ∑ (1 + )t r t =1
n
C =0
NCFt:第t年的现金净流量; r:内涵报酬率; n:预计使用年限; C:初始投资额。 ② 通用公式:
n Ot It ∑ (1 + )t = ∑ (1 + )t r r t =1 t =1 n
2 项目投资决策中常用的几个 项目投资决策中常用的几个Excel函 函 数
①
NCF t NPV = ∑ -C t 1 t =1 ( + K)
n
NCFt:第t年的净现金流量 K:贴现率(资本成本或企业要求的报酬 率)。 n :预计使用年限 C:初始投资额 适用于初始投资一次性支出的情况。
1.2.1 净现值
② 通用式
NPV = ∑
n
t =1
NCFt t (1 + K)
n——开始投资至项目终结时的年数; NCFt ——第t年的现金流量; K——贴现率(资本成本或企业要求的报 酬率)。 ③ 定义式: n n O
NCF AR = R ×100% C
非年金式
1.2 贴现现金流量评价指标
1.2.1 净现值 ⑴ 含义:通过计算净现值评价比较投资项 目优劣的一种方法。 ⑵净现值(Net Present Value , NPV) 特定投资项目未来现金流入的现值与未来 现金流出的现值之间的差额。 ⑶ 计算公式
Excel在财务与投资决策中的最佳应用方法

Excel在财务与投资决策中的最佳应用方法在如今的商业环境中,财务和投资决策对于企业的成功至关重要。
而在这一过程中,Excel作为一款强大的电子表格工具,具备了许多强大的功能,可以帮助财务专业人员和投资者进行数据分析、预测和决策。
本文将探讨Excel在财务与投资决策中的最佳应用方法。
一、数据的收集与整理Excel在财务与投资决策中的第一个重要应用是数据的收集与整理。
财务专业人员需要准确的数据来进行分析和决策。
在Excel中,可以通过创建数据表格、列表或数据库来输入和收集各种数据。
使用Excel的筛选和排序功能,可以轻松地对数据进行分类和整理,以便更好地进行分析。
二、财务分析与报表生成Excel在财务分析和报表生成方面的应用也是非常广泛的。
财务专业人员可以使用Excel的公式和函数来进行各种财务分析,如财务比率计算、趋势分析和比较分析等。
通过利用Excel的图表工具,可以直观地呈现财务数据,帮助用户更好地理解和解释数据。
此外,Excel还可以自动生成各种财务报表,如资产负债表、损益表和现金流量表等。
三、预测与预算在财务与投资决策中,预测和预算是至关重要的环节。
Excel具备了许多强大的功能,可以帮助财务专业人员和投资者进行预测和预算工作。
通过使用Excel的趋势分析和回归分析功能,可以根据历史数据预测未来的趋势和发展方向。
此外,Excel的“数据表”功能也可以帮助用户进行预算,进而制定出合理的财务和投资计划。
四、投资组合分析在投资领域,Excel被广泛应用于投资组合分析。
通过利用Excel的函数和工具,可以对各种投资组合进行风险和回报分析。
可以通过Excel的排序、筛选和图表功能,直观地展示各种投资组合的表现,并根据不同的投资目标和风险承受能力做出最佳的投资决策。
五、模拟与决策树分析Excel对于模拟和决策树分析也提供了强大的支持。
对于投资者而言,模拟分析可以帮助他们了解不同投资决策的潜在结果和风险。
Excel在财务中的应用第06章Excel在投资决策分析中的应用

谢谢观看
对于独立项目,现值指数大于1或等于1,表明项目未来现金流入现值超过或等于现金 流出现值,则项目可行,否则为不可行项目。对于互斥项目,在投资规模相同情况下,应 选择现值指数高的项目;对于投资规模不同的项目,则要视资金是否受限制而定。
现值指数是一个标志投资项目获利能力的相对指标,使不同的投资项目具有可比性, 因此,现值指数在投资决策分析中具有广泛的适用性。
Excel在财务中的应用
第6章 Excel在投资决策分析中的应用
本章学习目标
学习 目标
本章主要介绍投资决策的内容和方法。通过本章的学习, 读者应该掌握回收期法、年平均报酬率法、净现值法、 现值指数法、内含报酬率法等投资决策分析方法,熟练 运用Excel 2010进行固定资产折旧方法对比、固定资产 更新成本分析、固定资产更新决策分析。
相比回收期法,年平均报酬率法考虑了投资方案的寿命期,更为全面,但是使用“利 润”概念,受折旧方法影响,且忽略了利润实现的时间性。因此,年平均报酬率法通常作 为项目初步评价的手段,而不是最终的依据。
6.1.2 年平均报酬率法
年平均报酬率=年均税后利润/投资总额 进行投资决策时,应将投资方案的年平均报酬率与投资者主观上既定的期望年平均报 酬率相比较: 投资方案年平均报酬率>期望年均报酬率,则接受该投资方案; 投资方案年平均报酬率<期望年均报酬率,则拒绝该投资方案。 当有两个或两个以上投资方案可供选择时,则应该选择年平均报酬率高的投资方案。
6.1.1 回收期法
当经营期各年现金净流量相等时,其公式为: 回收期=原始投资额/每年现金净流入
当经营期各年现金净流量不相等时,回收期应按累计现金流入量计算。在这种方法下, 累计现金流入量与原始投资额达到相等所需的时间,即为回收期。其公式为:
Excel在项目投资决策中的应用

2. 折现评价指标和方法
(1)净现值
n
NPV
NCFt
t0 (1i)t
(2)净现值率 NPV NR P V n NC t F n It IP t0(1i)t t0(1i)t
(3)获利指数
经营期净现金流量现之值和 PI 原始投资的现值合计
(4)内部收益率
n
NPV
NCtF 0
t0(1IR)Rt
整理ppt
按工作小时计算: 年折 每 旧 工 额 作 年 小 工 时 固 作 总 折 定 小
年折 每 旧 工 额 作 年 小 工 时 固 作 总 折 定 小 预 工 旧 资 时 计 作 额 产 年 净 小 原 工 残 时 值 作 值
整理ppt
9
6.2.1 固定资产折旧方法
3.定率余额递减法
某年折旧 该额 年初固定 资 固产 定净 折值 旧率
j1
替换设备的费用现值
N t
P1 V (N t)C I1 S 1 (N t)PV i,N tIF C 1jPV i,jIPF V i,t I
j 1
任务期内两台设备的总费用现值
PVNC PV0tC 1PV1(N C t)
【例6-19】
整理ppt
25
6.6.5 设备现代化改造的决策
【例6-20】
【例6-17】
整理ppt
23
6.6.3 设备经济寿命的计算
设备使用t年的年均费用
AtC I0St PV i,t IF jt1CjPV i,jIF P1 Vi,tIFA
【例6-18.4 设备更新时机的选择
使用设备的费用现值
t
PV 0t CI0S0tPVi,tIF C0jPVi,jIF
整理ppt
【推荐下载】EXCEL在长期投资决策中的应用

EXCEL在长期投资决策中的应用论文频道一路陪伴考生编写大小论文,其中有开心也有失落。
在此,小编又为朋友编辑了“EXCEL在长期投资决策中的应用”,希望朋友们可以用得着! 长期投资具有投金额大、投资回收期长、投资风险大等特点,因此任何企业在进行长期投资时都应该十分谨慎的对待,在进行长期投资之前必须对项目进行可行性分析。
正是由于长期投资决策涉及的时间会比较长,因此进行项目可行性分析时,通常都要考虑资金的时间价值,而资金时间价值的计算具有理论抽象、计算复杂等特点,特别是对计算能力的要求比较高。
财务人员如果能够正确、灵活地使用Excel进行财务函数的计算,可使原本复杂的计算变得非常简单,并能大大减轻日常工作中有关指标计算的工作量。
在现行的财务评价理论中大部分都是根据项目产生的现金净流量进行的,因此下面将从EXCEL在现金净流量计算中的应用及EXCEL在长期投资评价指标计算中的应用这两个方面就有关问题作进一步的探讨。
一EXCEL在现金净流量计算中的应用 长期投资决策中,重点研究的是现金净流量,而把利润的研究放在次要的地位,主要是处于以下几个原因:首先,由于整个投资有效年限内,利润总计与现金净流量总计是相等的,所以现金净流量可以取代利润作为评价净收益的指标;其次,利润在各年的分布要受折旧方法、会计政策选择等人为因素的影响,而现金净流量的分布不受这些人为因素的影响,可以保证评价的客观性;再次,一般来讲,有利润的年份不一定有多余的现金,而一个项目能否维持下去,不取决于一定期间是否盈利,取决于有没有现金用于各种支付,因此在投资分析中,现金流动状况分析比盈亏分析更重要。
基于上述原因,在长期投资决策时首先就必须要分析、计算项目各年产生的现金净流量。
目前常用于计算项目现金净流量的方法主要有以下三种:一是,现金净流量=营业收入-付现成本-所得税。
在使用这个公式计算现金净流量时必须首先预计出项目的税前利润,否则就没有办法知道项目应缴的所得税额。
(完整版)Excel在长期投资决策中的应用

课程论文首页Excel在长期投资决策中的应用XXX中文摘要:长期投资项目在现代公司发展中发挥着日益重要的作用,其决策指标的研究意义也逐渐增强。
本文首先将长期投资项目分为三种类型,继而针对不同情况,在Excel中建立不同类型的决策指标,从而验证了Excel在解决企业长期投资问题上的有效性,为企业快速实现项目投资决策提供了一种切实可行的方法。
关键词:长期投资Excel 决策指标随着市场经济的日益活跃, 企业面临的经济环境也在发生变化。
为维持自身竞争力, 企业总是会投放一定的财力用于对内或对外的投资活动, 而其中又以长期投资更为重大。
长期投资数额大, 周期长, 项目多跨年建设、多年受益, 风险也较大, 存在诸多不确定因素, 对企业影响深远。
因此, 在投资范畴和投资行为日益多元化的今天, 根据市场竞争的需要, 或为扩大现有的经营规模, 或为丰富自身经营的厚度和广度, 或以各种证券投资的形式获利等目的,企业管理团队如何充分利用所有者赋予的投资决策权, 及时、迅速、高效地进行各种投资决策, 就显得尤为重要。
长期投资方案的决策指标一般分为静态指标和动态指标两类。
由于长期投资决策时间跨度比较大,决定了这类投资决策势必要考虑货币的时间价值。
而静态投资指标是在站在现时的角度对未来的投资进行的分析,没有考虑倾向的时间价值,必然影响了投资决策的科学性,已经逐渐被动态投资指标所取代,在企业投资决策模型中占据了主导地位。
最常见的动态投资指标主要有净现值、现值指数、内部报酬率等几种指标,企业可以根据不同的情况,采用不同的投资决策指标。
本文将长期投资方案分为三类:独立投资方案、互斥投资方案和最优组合投资方案。
分别对这三种不同类型的投资方案进行分析,第一部分主要介绍独立投资方案在某些指标不确定的情况下所进行的方案取舍,第二部分主要介绍用增量收益分析法所进行的多个互斥方案的选优,第三部分主要介绍用线性规划模型所进行的多个方案优化组合。
EXCEL在投资决策中应用

设备来代替旧设备,以减少成本,
量,如图 8-7 所示。在单元格 B17
增加收益。新旧设备有关资料如图
中输入公式“=SLN(B3,B6,B4)” ,
8-6 所示,银行年利率为 10%。计
计算旧设备年折旧额;在单元格
算分析并决策。具体的操作步骤如
B18 中输入公式“=B15-B16-B17” ,
下:
计算利润总额;在单元格 B19 中输
tm1 (1 IRR)t
m t 0
(1
It IRR)t
0
12
2021年8月16日10时26分
内含报酬率决策规则
• 对于独立项目,只要内含报酬率大于或等于项目的必要报酬
1
率,投资项目就可行;反之,则项目不可行。
2
• 对于互斥项目,应选择内含报酬率较高的项目。
210321年8月16日10时26分
内含报酬率法的评价
n NCFt
PI t1 (1 r )t I0
n NCFt
PI tm1 (1 r)t m
It
t0 (1 r)t
10
2021年8月16日10时26分
现值指数决策规则
• 对于独立项目,现值指数大于 1,表明项目未来现金流入现
1
值超过现金流出现值,项目可行;反之,则项目不可行。
• 对于互斥项目,在投资规模相同情况下,应选择现值指数高
▪ 第三步:在单元格 B7 中输入公式 “=(NPV(B2,C4:H4)NPV(B2,C4))/(-NPV(B2,C4)-B4)” , 计算投资项目现值指数。
22
2021年8月16日10时26分
8.2.2 净现值、现值指数和内含报酬率分析
例8-2
▪ 某企业有一个投资项目, 初始投资 1 500万元, 其中第0年和第1年分 别投入1 000万元和 500万元,预计 第 2~6 年每年的现金流如图 8-2 所示,资本成本率为 10%,问该项 目是否可行?具体的操作步骤如下:
利用Excel进行风险管理和投资决策

利用Excel进行风险管理和投资决策在进行风险管理和投资决策时,利用Excel可以帮助我们进行数据分析、建模和预测,从而更好地评估风险、制定投资策略和做出决策。
在本文中,我们将介绍如何利用Excel进行风险管理和投资决策,并且探讨一些常用的工具和技巧。
一、数据收集与整理在进行风险管理和投资决策之前,我们首先需要收集相关的数据,并且对数据进行整理和准备。
Excel提供了丰富的数据处理功能,可以帮助我们进行数据导入、清洗、格式化和排序。
1. 数据导入:我们可以利用Excel中的“数据导入”功能将外部数据文件(如CSV、文本文件等)导入到Excel中进行处理与分析。
2. 数据清洗:Excel提供了各种数据清洗工具,如删除重复数据、去除空值、修改数据类型等,帮助我们清理和整理数据。
3. 数据格式化:在进行数据分析之前,我们需要对数据进行适当的格式化,如设定日期格式、数字格式、百分比格式等,使得数据更易读和理解。
4. 数据排序:Excel的排序功能可以帮助我们对数据进行排序,如按照日期、数值大小等排序,以便更好地观察和分析数据。
二、数据分析与建模在数据准备好之后,我们可以开始进行数据分析和建模,以便更好地评估风险和进行投资决策。
下面是一些常用的Excel分析工具和技巧。
1. 图表分析:Excel提供了丰富的图表功能,如折线图、柱状图、饼图等,在数据可视化方面非常有帮助。
通过图表,我们可以更直观地观察数据的趋势和变化,帮助我们做出决策。
2. 数据透视表:Excel中的数据透视表功能可以帮助我们对大量数据进行汇总和分析。
我们可以根据需要选择汇总字段、行字段和列字段,生成多维度的数据分析报表,以便更好地了解数据和发现规律。
3. 数据函数:Excel中内置了众多的数据函数,可以帮助我们进行各种计算和分析。
如求和函数、平均值函数、标准差函数等,可以帮助我们计算数据的统计指标。
4. 数据建模:Excel的数据建模功能可以帮助我们建立各种模型和预测。
Excel进行投资决策案例
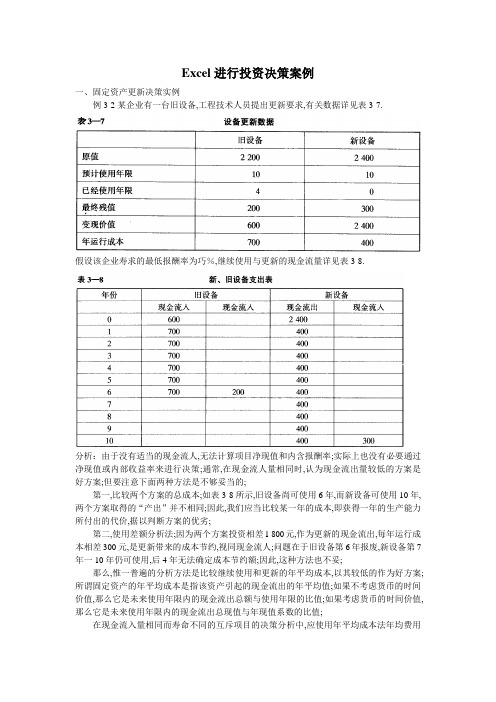
Excel进行投资决策案例一、固定资产更新决策实例例3-2某企业有一台旧设备,工程技术人员提出更新要求,有关数据详见表3-7.假设该企业寿求的最低报酬率为巧%,继续使用与更新的现金流量详见表3-8.分析:由于没有适当的现金流人,无法计算项目净现值和内含报酬率;实际上也没有必要通过净现值或内部收益率来进行决策;通常,在现金流人量相同时,认为现金流出量较低的方案是好方案;但要注意下面两种方法是不够妥当的;第一,比较两个方案的总成本;如表3-8所示,旧设备尚可使用6年,而新设备可使用10年,两个方案取得的“产出”并不相同;因此,我们应当比较某一年的成本,即获得一年的生产能力所付出的代价,据以判断方案的优劣;第二,使用差额分析法;因为两个方案投资相差1 800元,作为更新的现金流出,每年运行成本相差300元,是更新带来的成本节约,视同现金流人;问题在于旧设备第6年报废,新设备第7年一10年仍可使用,后4年无法确定成本节约额;因此,这种方法也不妥;那么,惟一普遍的分析方法是比较继续使用和更新的年平均成本,以其较低的作为好方案;所谓固定资产的年平均成本是指该资产引起的现金流出的年平均值;如果不考虑货币的时间价值,那么它是未来使用年限内的现金流出总额与使用年限的比值;如果考虑货币的时间价值,那么它是未来使用年限内的现金流出总现值与年现值系数的比值;在现金流入量相同而寿命不同的互斥项目的决策分析中,应使用年平均成本法年均费用o固定资产的年平均成本模本设吧口下:1.打开工作簿“投资决策”,创建新工作表“年平均成本”;2.在工作表“年平均成本”中设计表格,设计好后的表格详见表3-100 3.按表3-9所示在工作表“年平均成本”中输人公式;表3-9 工作表“年平均成本”中公式这样便创建了一个固定资产的年平均成本法比较模本,详见表3-10.表3-10 年平均成本分析表模本4.在相应单元格中输人数据;5.输人数据家毕后,并可看到计算结果详见表3-1106.保存工作表“年平均成本”;表3-11 年平均成本分析表计算结果表3-11中计算结果表明:在不考虑货币的时间价值时,旧设备的年平均成本为767元,高于新设备的年平均成本610元;而考虑货币的时间价值时,在最低报酬率为15%的条件下,旧设备的年平均成本为836元,低于新设备的年平均成本863元;一般进行投资决策分析时,需要考虑货币的时间价值,因此,继续使用旧设备应优先考虑;二、固定资产的经济寿命决策案例例3-31设某资产原值为1 400元,运行成本逐年增加,折余价值逐年下降,有关数据详见表3-12;分析:为计算固定资产经济寿命,必须计算不同使用年限下的总成本,然后进行比较便可得到固定资产的经济寿命;因此,固定资产经济寿命计算模型就是用于计算不同使用年限下的总成本;1.打开工作簿“投资决策”,创建新工作表“经济寿命”;2.在工作表“经济寿命”中设计表格,详见表3-14;3.按表3-13所示在工作表“经济寿命”中输人公式;表3-13 单元格中公式①将单元格H2中的公式复制到单元格区域H2: H9中的步骤为:·选择单元格H2;·单击“编辑”菜单,单击“复制”;·选择单元格区域H2: H9;·单击“编辑”菜单,单击“粘贴”;其他复制类似上述过程;这样便创建了固定资产的经济寿命计算模本,详见表3-14.表3-14 经济寿命分析表模本续前表4.在相应单元格中输人数据;5.输人数据完毕后,并可看到计算结果,详见表3-15;6.保存工作表“经济寿命”;表3-15 经济寿命分析表计算结果三、所得税和折旧对投资影响的案例例3-4某公司有一台设备,购于两年前,现考虑是否更新;该公司所得税率为4096,其他有关资料详见表3-16;此外假定两设备的生产能力相同,并且未来可使用年限相同,公司期望的最低报酬率为10%.表3-16 某公司新、旧设备有关数据续前表1.打开工作簿“投资决策”,创建新工作表“投资决策”;2.在工作表“投资决策”中设计表格,设计好后的表格详见表3-18;3.按表3-17所示在工作表“投资决策”中输入公式;表3-17 单元格中公式表3-18 投资决策分析表模本4.在相应单元格输人数据;5.输人数据完毕后,并可看到计算结果,气见表3-19;6.保存工作表“投资决策”;表3-19 投资决策分析表计算结果表3-19中计算结果表明:更换新设备的现金流出总现值为39 107.8元,比继续使用旧设备的现金流出总现值35 973元要多出3 134.80元;因此,继续使用旧设备较好;值得指出的是,如果未来的尚可使用年限不同,则需要将总现值转换成年平均成本,然后进行比较;四、风险调整贴现率法案例下面将用Excel来求解例3-1.1.打开工作餐“投资决策”,创建新工作表“风险调整”;2.在工作表“风险调整”中设计表格,设计好后的表格详见表3-21.3.按表3-20所示在工作表“风险调整”中输人公式;表3-20 工作表中公式NPVA no _ risk, has _ risk, factor, nyear, init _ cost, flowin, possible其中,no_risk为无风险的最低报酬率数值单元格;has_risk为有风险的最低报酬率数值单元格;nyear 为总投资年数数值单元格;factor为项目变化系数数值单元格;init_cost为原始成本数值单元格;flowin 为营业现金流人数值单元格区域,必须为列区域,单元格区域中的值必须为数值型;possible为取得营业现金的概率数值单元格区域,必须为列区域,单元格区域中的值必须为数值型;这样创建了一个固定资产投资的风险调整贴现率法模本,详见表3-210表3-21 工作表“风险调整”计算模本4;按例3-1中提供的数据在表3-21中的产元格区域B3: G12和单元格A15: D15中输人数据后便可得到计算结果,详见表3-22;5.保存工作表“风险调整”;表3-22 工作表“风险调整”计算结果表3-22中的计算结果表明:C投资机会所产生的净现值最大,A投资机会次之,B投资机会做所产生的净现值最少;因此,三个投资机会的优先顺序为:C>A>B.五、综合案例1997年1月,ABC飞机制造公司打算建立一条生产线生产小型减震系统;为珍,公司要花费1 000万元购买设备,另外还要支付50万元的安装费,该设备的经济寿命为5年,属于加速成本回收系统中回收年限为5年的资产类别此案例所用的折旧率依次为20%, 34%, 20%, 14%, 14%,此折旧系国外企业使用,对国内企业只需使用相应折旧方法就算出折旧率;该项目要求公司增加营运资本,增加部分主要用于原材料及备用零件储存;但是,预计的原材料采购额也会增加公司的应付账款,其结果是需增加5万元净营运资本;1996年,该公司曾请咨询公司为该项目进行了一次论证,咨询费共计5万元;咨询公司认为,如果不实施该项目,这个仓库只有被卖掉;研究表明,除去各项费用和税金后,这个仓库能净卖20万元;尽管该项目投资大部分于1997年间支出,公司原则上假定所有投资引起的现金流量都发生在年末,而且假定每年的经营现金流量也发生在年末;新生产线于1998年初可安装完毕并投人生产;不包括折旧费在内的固定成本每年为100万元,变动成本为销售收人的60%;公司适用40%的所得税;具有平均风险的投资项目的资本成本为10%05年后,公司计划拆除生产线和厂房,将地皮捐赠给某市作为公园用地;因公司的公益贡献,公司可免缴一部分税款;免缴额与清理费用大致相等;如果不捐赠,生产设备可以卖掉,其残值收人取决于经济状况;残值在经济不景气、经济状况一般和高涨时分别为50万元、100万元和200万元;工程技术人员和成本分析专家认为以上数据真实可靠;另外销售量取决于经济状况;如果经济保持目前增长水平,1998年的销售收人可达1 000万元销售量为1 000套,单价1万元;;5年中,预计销售量稳定不变;但是销售收人预计随通货膨胀而增长,预计每年通货膨胀率为5%;如果1998年经济不景气,销售量只有900套;反之,经济高涨,销售量可达1 100套;5年内各年销售量依据各种经济状况下的1998年的销售水平进行估计;该公司管理人员对经济状况的估计为:不景气可能性为25%,状况一般的可能性为50%,状况高涨可能性为25%;间题如下:1.假设该项目风险水平与公司一般项目风险水平相同,依据销售量和残值的期望值,请计算该项目的净现值;该项目在1999年发生亏损,请说明负所得税的意义,这种处理对只有一条生产线的新公司是否合适咨询费是否应包含在项目分析中2.计算不同经济状况下该项目的净现值,并将他们用各自经济状况的概率加权求得期望净现值,并同第1个间题比较说明是否一致;3.试讨论对一个大公司中的许多小项目进行的概率分析的作用与对一个小公司的一个大项目进行的概率分析的作用是否相同;4.假设公司具有平均风险的项目的净现值变异系数为0.5-1.0;关于项目的资本成本,公司的处理原则是:高于平均风险碑目的资本成本为在平均风险项目的资本成本基础上增加2%,低于平均风险项目的,则降低1%;请根据第1个问题所得的净现值重新评价项目的风险水平;是否应该接受该项目5.如果经济不景气,项目可在1999年末下马不能在第一年末下马,因为项目一旦上马,公司必须履行合同规定的责任和义务;由于设备磨损不大,可卖得800万元;建筑物含厂房及地皮出售可得税后收人15万元;5万元的营运资本也可回收;请计算净现值,并说明这个假设对项目预计收益和风险产生的影响;6.在投资项目分析时,存在两种风险:总风险和市场风险用a表示;请说明本案例评估的是哪一种风险,并讨论这两种风险及它们与投资决策的相关性;7.假设销售量和残值在销售量1 000套、残值113.5万元的基础上发生士10%,士20,士30%的变动;当销售量变化时,残值不变;反之亦然;做现值对销售量和残值的敏感性,并说明计算结果;一根据案例提供的信息建立计算净现值的模本1.创建一个名为“净现值分析表”的工作表;2.在所创建的工作表中设计一个表格,详见表3-24.3.创建模本;按照表3-23所示在工作表“净现值分析表”中输人公式;表3-23单元格公式①将单元格C8中的公式复制到单元格区域C8: F8中的步骤为:.选择单元格C8;.单击“编辑”菜单,单击“复制”;.选择单元格区域C8: F8;.单击“编辑”菜单,单击“粘贴”;其他复制类似上述过程;这样便创建了一个模本,详见表3-240表3-24 计算净现值的模本①这些单元格需要输人数据;4.保存工作表“净现值分析表”;二计算期望净现值和各种经济状况下的净现值在上述模本中数据输人单元格中输人不同组数据,便可计算得到期望净现值和各种经济状况下的净现值,计算结果详见表3-25、表3-26、表3-27和表3-28;表3-25 期望净现值计算结果表①此行的贴现系数为四舍五人后保留两位小数的结果,故与第21行现值的结果有些出入;表3-25~表3-28,表3-31和表3-33均存在此问题;表3-26 经济不景气下期望净现值计算结果表表3-27 经济一般期望净现值计算结果表续前表表3-28 经济商涨期望净现值计算结果表续前表三回答第1-5个问题1.表3-22的计算结果表明,净现值为697 688.60元;这是期望净现值,是在给定了不同经济状况下现金流量的估计值和每种经济状况发生概率的条件下,并假设该项目具有平均风险的情况下得出的数值;如果公司有其他盈利项目,那么2000年末发生的亏损额被其他项目的利润额抵偿,公司应税收益总额会降低,减税额即负所得税;如果公司只有这样一个亏损项目而没有有利可图的项目半抵偿这部分亏损,那么预计现金流量是不准确的;在这种情况下,公司只有等到赚取了可纳税的收人后才能提供纳税收益,由于这种收益不能立即成为现实,那么该项目的价值就降低了;咨询费是沉没成本,与投资决策无关,不应包含在决策分析之中;2.从表3-26、表3-27和表3-28中可以看出,经济不景气下净现值为一531 299元,经济状况一般情况下净现值为651 119.50元,经济高涨情况下净现值为2019814元;期望净现值为697 688.62元0.25 x一531 298.78+0.5 x 651 119.52+0.25 x 2 019 814.221;该结果与表3-25的计算结果相同;3.在现实生活中,经济状况可能在估计范围内任意变动,销售量和残值不可能只表现为三种估计值的一种;因此,依据离散数值计算出来的净现值不可能是真正有用的信息;具有众多小型项目的大公司和只有一个大型项目的小公司相比较,概率分析对后者显得更为重要;在大公司,某个项目中高估了现金流量可能被另一个项目低估的现金流量抵销,此外,对某个小型项目现金流量的错误估计不可能像对大型项目现金流量的错误估计那样而导致破产;尽管概率分析对小型项目来说比较适用,但花费的成本可能要大于收益;4.使用Excel计算变异系数;表3-29是计算变异系数的模本;表3-29 计算变异系数的模本表3-30 变异系数的计算结果根据表3-30所示模本计算得到变异系数为1.29;该系数要比公司一般项目的变异系数0.5~1.0要大,该项目风险水平高于平均风险,资本成本应增加2%,用以贴现该项目的每年现金净流量;根据表3-24所给的模本计算风险调整后的净现值贴现率为12%,详见表3-31;表3-31 风险调整后期望净现值计算结果表从上表可知净现值为119889-60元,应该接受该项目;5.计算经济不景气情况下1999年该项目下孕时的净现值;利用类似表3-24所示的计算净现值的模本,设计计算贴现率为10%时经济不景气情况下1999年该项目下马时的计算净现值的模本,详见表3-32.表3-32 经济不景气情况下1999年下马时期望净现值计算模本表3-33 经济不景气情况下1999年下马时期望净现值计算结果表该项目上马时的损失-531299元要刁a因此,经济不景气时该项目下马有利;。
第四章Excel在投资决策中的应用

该公式表示,先对A方案求内含报酬率,再用该方案的内含报酬率作为贴现率计算净现值,则净现值必定为0。
【例4-5】 假设某企业投资决策,有关数据如图5-2所示,内含报酬率的计算公式定义如下: 在工作表中A方案的内含报酬率,即B10单元公式为: =IRR(B4:B7,10%) 即guess为10%,B4:B7为参考地址。 =IRR(B4: B7) 即guess为缺省。 B方案的内含报酬率,即C10单元公式为: =IRR(C4: C7) C方案的内含报酬率,即D10单元公式为: =IRR(D4: D7) 由图4-1可知,A,B方案的内含报酬率大于资金成本率,可以接受;C方案的内含报酬率小于资金成本率,应 该放弃。 在工作表中,由于内含报酬率与投资额、每期的现金流量等基本数据之间建立了链接关系,当投资方案改变 时,财务人员只需改变方案中的基本数据,新方案的内含报酬率将自动计算出来。在投资决策模型中运用IRR() 函数,大大简化了内含报酬率的计算工作。
4. MIRR()修正内含报酬率函数 内含报酬率虽然考虑了时间价值,但是未考虑现金流入的再投资机会。根据再投资的假设,已经有学者提出 修正内含报酬率法,以此来弥补内含报酬率法忽略再投资机会成本的缺点。 语法:MIRR(values, finance—rate, reinvest一rate) 功能:返回某连续期间现金流量(values)的修正内含报酬率。MIRR函数同时考虑了投入资金的成本 (finance—rate)及各期收入的再投资报酬率(reinvest—rate)。 参数: values必须是个含有数值的数组或参考地址。这些数值分别代表各期的支出(负数)及收入(正数)数额。 values参数中至少必须含有一个正数及一个负数,否则MIRR函数会返回错误值#DIV/0 1。MIRR函数根据values的 顺序来解释现金流量的顺序,参数中的正文、逻辑值或空白单元,都会被忽略不计。 finance—rate代表资金成本或必要报酬率。 reinvest—rate代表再投资资金机会成本或再投资报酬率。
Excel在投资决策中的应用

Excel在投资决策中的应用①主要概念净现值——按一定的折现率,将投资方案未来所产生的所有现金流入现值减去现金流出现值后的差额即为净现值。
在投资项目评估中,净现值大于零表示该项目可行。
内部报酬率——又称内含报酬率,是指能够使未来现金流入量现值等于未来现金流出量现值的折现率,或者说是使投资方案净现值为零的折现率。
当计算出来的内部报酬率高于投资项目的资本成本或要求的最低投资报酬率则项目可行。
修正的内部报酬率——又称内部修正率法、修正的内含报酬率、修正内部收益率、改进内部收益率,是在一定的贴现率条件下,将投资项目未来的现金流入量按照预定的贴现率计算至最后一年的终值,使现金流入量的终值与投资项目的现金流出量达到价值平衡的贴现率。
修正的内部报酬同时考虑了投资的成本和现金再投资的收益率。
现值指数——是指投资方案未来现金流入现值与现金流出现值的比率,又称现值比率、获利指数、折现后收益-成本比率。
利用现值指数法进行投资决策,现值指数大于1,方案可行,且现值指数越大方案越优。
现值指数法的主要优点是可以进行独立投资机会获利能力的比较。
现金流量——是指投资项目在其计算期内因资金循环而引起的现金流入和现金流出增加的数量。
这里的“现金”概念是广义的,包括各种货币资金及与投资项目有关的非货币资产的变现价值。
②知识拓展拓展1:用Excel计量投资风险价值由于市场波动,投资者会不可避免地面临风险的威胁,对风险进行合理计量和控制是财务管理的重要内容。
方差、标准差、协方差、相关系数和β系数等作为测算风险程度的数量指标已得到广泛应用。
所谓风险价值,是指在正常的市场条件下和给定的置信度内,由于市场波动而导致某项资产或投资组合在既定时期内可能遭受的最大价值损失。
例如,某项投资在95%的置信水平下的日风险价值为100万元,则表明在正常的市场条件下以95%的概率来保证该投资在未来1日内的平均损失不会超过100万元;或者说,就是该项投资每天损失超过100万元的可能性为5%(1-95%);也可以理解为,20日内,只存在1日损失超过100万元的可能性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课程论文首页Excel在长期投资决策中的应用XXX中文摘要:长期投资项目在现代公司发展中发挥着日益重要的作用,其决策指标的研究意义也逐渐增强。
本文首先将长期投资项目分为三种类型,继而针对不同情况,在Excel中建立不同类型的决策指标,从而验证了Excel在解决企业长期投资问题上的有效性,为企业快速实现项目投资决策提供了一种切实可行的方法。
关键词:长期投资Excel 决策指标随着市场经济的日益活跃, 企业面临的经济环境也在发生变化。
为维持自身竞争力, 企业总是会投放一定的财力用于对内或对外的投资活动, 而其中又以长期投资更为重大。
长期投资数额大, 周期长, 项目多跨年建设、多年受益, 风险也较大, 存在诸多不确定因素, 对企业影响深远。
因此, 在投资范畴和投资行为日益多元化的今天, 根据市场竞争的需要, 或为扩大现有的经营规模, 或为丰富自身经营的厚度和广度, 或以各种证券投资的形式获利等目的,企业管理团队如何充分利用所有者赋予的投资决策权, 及时、迅速、高效地进行各种投资决策, 就显得尤为重要。
长期投资方案的决策指标一般分为静态指标和动态指标两类。
由于长期投资决策时间跨度比较大,决定了这类投资决策势必要考虑货币的时间价值。
而静态投资指标是在站在现时的角度对未来的投资进行的分析,没有考虑倾向的时间价值,必然影响了投资决策的科学性,已经逐渐被动态投资指标所取代,在企业投资决策模型中占据了主导地位。
最常见的动态投资指标主要有净现值、现值指数、内部报酬率等几种指标,企业可以根据不同的情况,采用不同的投资决策指标。
本文将长期投资方案分为三类:独立投资方案、互斥投资方案和最优组合投资方案。
分别对这三种不同类型的投资方案进行分析,第一部分主要介绍独立投资方案在某些指标不确定的情况下所进行的方案取舍,第二部分主要介绍用增量收益分析法所进行的多个互斥方案的选优,第三部分主要介绍用线性规划模型所进行的多个方案优化组合。
因为企业的项目投资资金一般都是有限的,所以就以上三种情况,笔者在在资金有限的情况下,利用Excel分别进行方案的对比选优,并且都加以案例解析以助于理解(以下案例均假设某企业资金限额为180万元,项目贴现率为12% ,每期现金流量均发生在期末)。
一、独立投资方案独立投资方案是指两个投资方案相互独立的、互不影响,一个方案的取舍与另一个方案无关,这种类型的投资一般是企业对不同用途的项目的投资,因此只需对项目自身的可盈利性进行判断。
在进行投资方案的选择时,可以用净现值、内部投资报酬率、现值指数等多种动态投资指标进行判断,这几种指标计算得出的结果是一致的。
当方案中的某些指标无法定量确定时,这时就要从概率角度来进行决策分析,就要用到蒙特卡洛模拟方法。
蒙特卡罗模拟以数理统计理论为基础,按照一定的概率分布来产生随机数,模拟可能出现的各种随机现象,所以也称作随机模拟。
下面就净现值法并加以蒙特卡洛模拟来进行独立投资方案的评估。
例1:假设企业现有一独立投资方案,项目寿命周期不确定,经专家评估,项目寿命周期可能性为3-6年,年净现金流量出现的可能性在53-60万元之间,出现的概率均服从均匀分布。
具体计算步骤如下:1. 建立Excel表格,保存并并命为[独立投资方案.xls]。
2. 用蒙特卡洛模拟方法进行模拟。
对于寿命期固定或未来净现金流量确定的独立方案,在进行决策时可以直接用Excel里面的财务函数NPV 进行计算。
但是对于项目寿命期和净现金流量都不确定的方案,就要进行方案概率的分析。
模拟过程如下,因为项目寿命期和净现金流量都服从均匀分布,所以在A3中输入“=3+(6-3)*rand()”,在B4中输入“=53+(60-53)*rand()”,得出两个参数的一组随机变量,在净现值一栏C3中输入“=-180+B3*(POW ER(1+12% ,A3)-1)/(12% *POW ER(1+12% ,A3))”,(power函数是幂函数),得出两个随机变量所对应的净现值。
用右下角的填充柄往下拉,模拟5000次,可得到5000组随机值。
3. 计算净现值为负的概率,在D3中输入“=COUNTIF(C3:C5003, “<0”)/5000”,可得到净现值为负的概率,因模拟图太大,故截取一部分如下图所示,(单位:万元)从上例可以看出,在寿命周期、净现金流量等参数无法确定,不能用NPV或PV函数进行决策时,就需要用蒙特卡洛模拟方法,对可能出现的各种情况进行随机模拟。
运用蒙特卡洛模拟法,通过对项目未来可能为企业带来的收益及损失的概率估计,以此为重要指标,再结合企业自身经济实力以及管理者对风险的喜恶程度、对项目未来前景的估计等指标综合考虑,对项目进行最终评估。
二、互斥投资方案对于互斥方案,用内部报酬率法和净现值法计算得到的结果可能存在矛盾,因为内部报酬率在项目寿命周期中是按照项目各自的内部报酬率进行再投资而形成的增值,并且不能体现投资方案对财务的绝对贡献额,因此净现值法与内部报酬率所得结果可能不一致。
下面通过实例来说明在净现值法与内部报酬率不一致时,企业如何进行方案的选优。
例2:假设企业有如下4种投资方案可供选择,只能从如下方案中选择其中的一种,各年净现金流量如表1所示:方案第0年第1年第2年第3年A -55 12 28 32B -70 24 45 38C -85 46 76D -100 55 88E -120 63 77 40在Excel表格中解决以上互斥投资问题具体步骤如下:1.建立Excel表格,保存并命名为[互斥投资方案选优.xls]。
2. 将以上投资方案数据输入Excel表格,[B3:E7] 表示各个方案的净现金流量,[F3:F7]为各个方案的净现值,B8 为基准收益率。
在F3中输入“=NPV(C3:E3)+B3”,得出方案A 的净现值,同理可得各个投资项目的净现值,在B9中输入“=INDEX(FI3:F7,M ATCH (M AX(F3:F7),F3:F7,O))”得到净现值最大的方案E。
用IRR函数,可以得到四种方案各自的内部报酬率,在B10中输入“=INDEX(G3:G7,M ATCH (M AX(G3:G7),G3:G7,0))”得内部报酬率最大的方案C 。
两种指标所得结论不一致。
此时,要用增量收益分析法来进行分析。
先求得增量方案“E-C ”各年的现金流量,通过各年现金流量可得“E-C ”的净现值及内部报酬率。
在B12中输入“=IF(F11﹥0, “可行”,“不可行”)”,可得出是否接受“E-C ”。
只要净现值大于 0 或者内部报酬率大于 12% ,即可接受“E-C ”。
表明在对 C 方案进行投资后,还可以继续接受“E-C ”,即选择项目应为C+(E-C )=E ,如果“E-C ”不可行,则说明“E-C ”不被接受,故选择方案C ,如下图如示从上例可知,在对互斥方案进行选择时,可以在考虑它的增量收益的基础上,来巧妙地解决现净值及内部报酬率不一致时,所应做出的方案取舍问题。
使企业在面对两种方法所得结论不一致,管理层有争议的情况下,更具说服力。
同独立投资项目一样,如果项目未来的净现金流量及周期不确定,仍可通过蒙特卡洛模拟方法来进行概率分析。
三、最优组合投资方案第三种常见的长期投资方案是在多个可供选择的投资项目中,将其进行组合,找出能使投资项目盈利最大化的最优组合方案。
在进行方案最优组合时,可以将其转化为整数线性规划问题。
整数线性规划问题的基本原理如下:假设有 j 种投资方案,jNPV 为每项方案的净现值,A 表示资金限额,jF 表示每种方案的初始投资额,jX 表示此方案是否被选中,jX =0表示此方案未被选中,jX =1表示此方案被选中。
根据以上条件,可以得到如下的整数线性规划问题:目标函数:max{NPV} =jnj jNPV x*1∑=;约束条件:0≤nj =jnj jF x*1∑=≤A ;jX =0 或 1;下面根据整数线性规划原理,通过一个实例在 Excel 中实现方案的最优组合。
例3:假设例2中的五个项目为非互斥项目,企业可以进行最优组合。
现在我们在满足资金限额的条件下,从这五个项目中选取最优的投资组合。
具体步骤如下:1. 运行Excel 表格,建立工作薄并保存为[投资项目最优组合.xls]。
2. 在有关区域中输入投资项目的数据,[F3:F7]表示各个投资项目的净现值,[G3:G7]为各个项目的变量,选择此项目则用1 表示,放弃此项目则用 0 表示。
各项目的净现值可以通过财务函数NPV来求解,在F3里面输入“=NPV(D8,C3:E3)+B3”,依次类推,在单元格F3—F7中分别进行拖动填充,可以得出各个项目的净现值。
在B9中输入“=-SUM PRODUCT(B3:B7,G3:G7)”,在B10中输入“=SUM PRODUCT(F3:F7,G3:G7)”。
3. 利用规划求解工具进行方案的最优组合。
在[工具]栏中选择[加载宏]选项,选择里面的[规划求解]对话框,单击确定安装[规划求解]选项。
“设置目标单元格”项目设置为单元格B10;“等于”设置为“最大值”;“可变单元格”设置为G3:G7;在[约束]中添加4 个约束条件:-(B3*G3+B4*G4+B5*G5+B6*G6+B7*G7)≦B8,$B$9≦$B$8,$G$3:$G$7≦1,$G$3:$G$7≧0,$G$3:$G$7=整数。
4. 最后,单击【求解】按纽,则Excel自动运算结果显示在G3—G7 中。
应选择方案B和D,如下图所示:通过Excel里的一些工具,可以帮助企业快速进行方案的最优组合,使企业能够充分利用有限的资金进行有效的投资。
四、结论综合以上可以看出,根据投资方案的类型不同,通过Excel可以用不同的方法进行投资项目决策,使企业在遇到不同类型的投资决策时,可以针对具体情况,快速有效地运用不同方法进行方案的选择,以求得最佳结果。
参考文献:[1]程莉莉.项目投资决策不确定性评价方法缺陷与蒙特卡罗模拟的改进[J].现代财经.2008.[2]向寿生,尚宇梅.Excel在投资项目概率分析中的应用[J].商业研究.2008.[3]肖淑芳,吴仁群.Excel财务量化分析.北京:中国人民大学出版社[M ].2003.[4]韩良智.Excel在财务管理与分析中的应用.北京:中国水利水电出版社[M ].2008.。
