北京市海淀区2012年中考二模数学试题及答案
2012年北京市海淀区高三数学理科二模试卷及答案(WORD版)

北京市海淀区2012高三二模数 学(理科)2012.05一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.(1)若sin cos 0θθ<,则角θ是 (A )第一或第二象限角 (B )第二或第三象限角 (C )第三或第四象限角 (D )第二或第四象限角 (2)已知命题p :0x ∃∈R ,021x =.则p ⌝是 (A )0x ∀∈R ,021x ≠ (B )0x ∀∉R ,021x ≠ (C )0x ∃∈R ,021x ≠(D )0x ∃∉R ,021x ≠(3)直线11x ty t =+⎧⎨=-⎩(t 为参数)的倾斜角的大小为(A )4-π (B )4π (C )2π(D )34π(4)若整数,x y 满足1,1,3,2x y x y y ìïïï-?ïïï+?íïïïï£ïïî则2x y +的最大值是 (A )1(B )5(C )2 (D )3(5)已知点12,F F 是椭圆2222x y +=的两个焦点,点P 是该椭圆上的一个动点,那么12PF PF +u u u r u u u u r的最小值是(A )0 (B )1 (C )2 (D)(6)为了得到函数2log y =2log y x =的图象上所有的点的(A )纵坐标缩短到原来的12倍,横坐标不变,再向右平移1个单位长度 (B )纵坐标缩短到原来的12倍,横坐标不变,再向左平移1个单位长度(C )横坐标伸长到原来的2倍,纵坐标不变,再向左平移1个单位长度(D )横坐标伸长到原来的2倍,纵坐标不变,再向右平移1个单位长度(7)某几何体的主视图与俯视图如图所示,左视图与主视图相同,且图中的四边形都是边长为2的正方形,两条虚线互相垂直,则该几何体的体积是(A )203(B )43(C )6 (D )4(8)点(,)P x y 是曲线1:(0)C y x x=>上的一个动点,曲线C 在点P 处的切线与x 轴、y 轴分别交于,A B 两点,点O 是坐标原点. 给出三个命题:①PA PB =;②OAB ∆的周长有最小值4+;③曲线C 上存在两点,M N ,使得OMN ∆为等腰直角三角形.其中真命题的个数是(A )1 (B )2 (C )3 (D )0二、填空题:本大题共6小题,每小题5分,共30分,把答案填在题中横线上. (9)在面积为1的正方形ABCD 内部随机取一点P ,则PAB ∆的面积大于等于14的概率是_________. (10)已知1021012311(1)x a a x a x a x +=++++L . 若数列123,,,,(111,)k a a a a k k #?Z L 是一个单调递增数列,则k 的最大值是 . (11)在ABC ∆中,若120A ??,5c =,ABC ∆的面积为,则a = .(12)如图,O e 的直径AB 与弦CD 交于点P ,7, 5, 15CP PD AP ===,则DCB Ð=______.(13)某同学为研究函数()1)f x x =#的性质,构造了如图所示的两个边长为1的正方形ABCD 和BEFC ,点P 是边BC 上的一个动点,设CP x =,则()AP PF f x +=. 请你参考这些信息,推知函数()f x 的图象的对称轴是 ;函数()4()9g x f x =-的零点的个数是 .俯视图主视图BEFAB C DP(14)曲线C 是平面内到定点(1,0)A 的距离与到定直线1x =-的距离之和为3的动点P 的轨迹. 则曲线C 与y 轴交点的坐标是 ;又已知点(,1)B a (a 为常数),那么PB PA +的最小值()d a = . 三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. (15)(本小题满分13分)已知公差不为0的等差数列{}n a 的前n 项和为n S ,346S a =+,且1413,,a a a 成等比数列. (Ⅰ)求数列{}n a 的通项公式; (Ⅱ)求数列1{}nS 的前n 项和公式. (16)(本小题满分14分)如图所示,PA ^平面ABC ,点C 在以AB 为直径的⊙O 上,30CBA??,2PA AB ==,点E 为线段PB 的中点,点M 在»AB 上,且OM ∥AC . (Ⅰ)求证:平面MOE ∥平面P AC ;(Ⅱ)求证:平面P AC ^平面PCB ;(Ⅲ)设二面角M BP C --的大小为θ,求cos θ的值.(17)(本小题满分13分)某公司准备将100万元资金投入代理销售业务,现有A ,B 两个项目可供选择: (1)投资A 项目一年后获得的利润X且X 1的数学期望E (X 1)=12;(2)投资B 项目一年后获得的利润X 2(万元)与B 项目产品价格的调整有关, B 项目产品价格根据销售情况在4月和8月决定是否需要调整,两次调整相互独立且在4月和8月进行价格调整的概率分别为p (0< p <1)和1-p . 经专家测算评估:B 项目产品价格一年内调整次数X (次)与X 2的关系如下表所示:(Ⅱ)求X 2的分布列;(Ⅲ)若E (X 1)< E (X 2),则选择投资B 项目,求此时 p 的取值范围.(18)(本小题满分13分)ME BOCAP已知椭圆C :22221(0)x y a b a b+=>>的右焦点为(1,0)F ,且点(1,2-在椭圆C 上. (Ⅰ)求椭圆C 的标准方程;(Ⅱ)已知动直线l 过点F ,且与椭圆C 交于A ,B 两点.试问x 轴上是否存在定点Q ,使得716QA QB ⋅=-u u u r u u u r 恒成立?若存在,求出点Q 的坐标;若不存在,请说明理由.(19)(本小题满分14分)已知函数21()ln()(0)2f x a x a x x a =--+<. (Ⅰ)求()f x 的单调区间;(Ⅱ)若12(ln 21)a -<<-,求证:函数()f x 只有一个零点0x ,且012a x a +<<+; (Ⅲ)当45a =-时,记函数()f x 的零点为0x ,若对任意120,[0,]x x x ∈且211,x x -=都有21()()f x f x m -≥成立,求实数m 的最大值.(本题可参考数据:99ln 20.7,ln 0.8,ln 0.5945≈≈≈)(20)(本小题满分13分)将一个正整数n 表示为12(*)p a a a p +++?N L 的形式,其中*i a ÎN ,1,2,,i p =L ,且p a a a ≤≤≤Λ21,记所有这样的表示法的种数为)(n f (如4=4,4=1+3,4=2+2,4=1+1+2,4=1+1+1+1,故5)4(=f ).(Ⅰ)写出)5(),3(f f 的值,并说明理由;(Ⅱ)对任意正整数n ,比较)1(+n f 与)]2()([21++n f n f 的大小,并给出证明; (Ⅲ)当正整数6≥n 时,求证:134)(-≥n n f .海淀区高三年级第二学期期末练习数 学(理科)参考答案及评分标准 2012.05一. 选择题:本大题共8小题,每小题5分,共40分.最新整理二.填空题:本大题共6小题,每小题5分,共30分.(9)12(10)6(11(12)45°(13)12x=;2(14)(0,±;1.41,4, 1.41,2,1 1.a aa aa aìï??ïïï+-<?íïï--<<ïïïî或注:(13)、(14)题第一空3分;第二空2分.三.解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. (15)(本小题满分13分)解:(Ⅰ)设等差数列{}n a的公差为0d¹.因为346S a=+,所以11323362da a d创+=++. ①……………………………………3分因为1413,,a a a成等比数列,所以2111(12)(3)a a d a d+=+. ②……………………………………5分由①,②可得:13,2a d==. ……………………………………6分所以21na n=+.……………………………………7分(Ⅱ)由21na n=+可知:2(321)22nn nS n n++?==+.……………………………………9分所以11111()(2)22nS n n n n==-++. ……………………………………11分所以123111111n nS S S S S-+++++L11111111111()2132435112n n n n=-+-+-++-+--++L21111135()212124(1)(2)n nn n n n+=+--=++++.所以数列1{}nS的前n项和为2354(1)(2)n nn n+++.最新整理……………………………………13分(16)(本小题满分14分)(Ⅰ)证明:因为点E 为线段PB 的中点,点O 为线段AB 的中点,所以 OE ∥PA . ……………………………………1分 因为 PA Ì平面PAC ,OE Ë平面PAC ,所以 OE ∥平面P AC . ……………………………………2分因为 OM ∥AC , 因为 AC Ì平面PAC ,OM Ë平面PAC ,所以 OM ∥平面P AC . ……………………………………3分因为 OE Ì平面MOE ,OM Ì平面MOE ,OE OM O =I ,所以 平面MOE ∥平面P AC . ………………………………………5分(Ⅱ)证明:因为 点C 在以AB 为直径的⊙O 上,所以 90ACB??,即BC AC ⊥.因为 PA ^平面ABC ,BC Ì平面ABC , 所以PA BC ⊥. ……………………………………7分因为 AC Ì平面PAC ,PA Ì平面PAC ,PA AC A =I ,所以 BC ^平面PAC . 因为 BC Ì平面PBC ,所以 平面P AC ^平面PCB . ……………………………………9分(Ⅲ)解:如图,以C 为原点,CA 所在的直线为x 轴,CB 所在的直线为y 轴,建立空间直角坐标系C xyz -. 因为 30CBA??,2PA AB ==,所以2cos30CB =?1AC =.延长MO 交CB 于点D . 因为 OM ∥AC ,所以131, 1,2222MD CB MD CD CB ^=+===.最新整理所以 (1,0,2)P ,(0,0,0)C,B,3(,,0)22M . 所以 (1,0,2)CP =u u u r,CB =u u u r.设平面PCB 的法向量(,,)=x y z m .因为 0,0.CP CBìï?ïíï?ïîu u u r u u u r m m所以(,,)(1,0,2)0,(,,)0,x y z x y z ì?ïïíï?ïî即20,0.x z ì+=ïïíï=ïî令1z =,则2,0x y =-=.所以 (2,0,1)=-m . ……………………………………12分 同理可求平面PMB 的一个法向量n ()=.……………………………………13分 所以 1cos ,5⋅==-⋅m n m n m n . 所以 1cos 5θ=. ………………………………………14分 (17)(本小题满分13分) 解:(Ⅰ)由题意得:0.41,11120.41712.a b a b ++=⎧⎨+⨯+=⎩解得:0.5,0.1a b ==. ……………………………………3分 (Ⅱ)X 2 的可能取值为4.12,11.76,20.40.()[]2 4.12(1)1(1)(1)P X p p p p ==---=-,()[]22211.761(1)(1)(1)(1)P X p p p p p p ==--+--=+-,()220.40(1)P X p p ==-.所以X 2的分布列为:(Ⅲ)由(Ⅱ)可得:()2224.12(1)11.76(1)20.40(1)E Xp p p p p p ⎡⎤=-++-+-⎣⎦211.76p p =-++. ……………………………………11分因为E (X 1)< E (X 2),所以21211.76p p <-++.最新整理所以0.40.6p <<.当选择投资B 项目时,p 的取值范围是()0.4,0.6.……………………………………13分(18)(本小题满分13分) 解:(Ⅰ)由题意知:1c =.根据椭圆的定义得:22a =,即a = ……………………………………3分 所以 2211b =-=.所以 椭圆C 的标准方程为2212x y +=. ……………………………………4分 (Ⅱ)假设在x 轴上存在点(,0)Q m ,使得716QA QB ⋅=-u u u r u u u r 恒成立.当直线l 的斜率为0时,(A B .则7,0)(,0)16m m ?=-. 解得 54m =?. ……………………………………6分 当直线l的斜率不存在时,(1,(1,22A B -.由于557(1,(1,424216+?-?,所以54m ?. 下面证明54m =时,716QA QB ⋅=-u u u r u u u r 恒成立.……………………………………8分显然 直线l 的斜率为0时,716QA QB ⋅=-u u u r u u u r .当直线l 的斜率不为0时,设直线l 的方程为:1x ty =+,()()1122,,,A x y B x y .由221,21x y x ty ìïï+=ïíïï=+ïî可得:22(2)210t y ty ++-=. 显然0∆>.1221222,21.2t y y t y y t ìïï+=-ïï+ïíïï=-ïï+ïî……………………………………10分最新整理因为 111x ty =+,221x ty =+,所以 112212125511(,)(,)()()4444x y x y ty ty y y -?=--+ 2121211(1)()416t y y t y y =+-++2221121(1)24216t t t t t =-+++++ 22222172(2)1616t t t --+=+=-+.综上所述:在x 轴上存在点5(,0)4Q ,使得716QA QB ⋅=-u u u r u u u r恒成立. ……………………………………13分 (19)(本小题满分14分)(Ⅰ)解:()f x 的定义域为(,)a +∞.2(1)'()1a x a xf x x x a x a-++=-+=--. ……………………………………1分令'()0f x =,0x =或+1x a =.当10a -<<时,+10a >,函数()f x 与'()f x 随x 的变化情况如下表:所以,函数()f x 的单调递增区间是(0,1)a +,单调递减区间是(,0)a 和(1,)a ++?.……………………………………3分当1a =-时,2'()01x f x x -=≤+. 所以,函数()f x 的单调递减区间是(1,)-+?. ……………………………………4分 当1a <-时,+10a <,函数()f x 与'()f x 随x 的变化情况如下表:所以,函数()f x 的单调递增区间是(1,0)a +,单调递减区间是(,1)a a +和(0,)+?.最新整理……………………………………5分(Ⅱ)证明:当12(ln21)0a -<<-<时,由(Ⅰ)知,()f x 的极小值为(0)f ,极大值为(1)f a +.因为(0)ln()0f a a =->,2211(1)(1)(1)(1)022f a a a a +=-+++=->,且()f x 在(1,)a ++?上是减函数,所以()f x 至多有一个零点. ……………………………………7分 又因为211(2)ln 2[2(ln 21)]022f a a a a a a +=--=---<, 所以 函数()f x 只有一个零点0x ,且012a x a +<<+.……………………………………9分(Ⅲ)解:因为412(ln 21)5-<-<-, 所以 对任意120,[0,]x x x ∈且211,x x -=由(Ⅱ)可知:1[0,1)x a ∈+,20(1,]x a x ∈+,且21x ≥. ……………………………………10分因为 函数()f x 在[0,1)a +上是增函数,在(1,)a ++?上是减函数,所以 1()f x (0)f ≥,2()f x (1)f ≤. ……………………………………11分 所以 12()()(0)(1)f x f x f f -?.当45a =-时,1(0)(1)ln()12a f f a a -=--=491ln 542->0. 所以 12()()(0)(1)0f x f x f f -?>. ……………………………………13分所以 21()()f x f x -的最小值为491(0)(1)ln 542f f -=-. 所以 使得21()()f x f x m -≥恒成立的m 的最大值为491ln 542-.……………………………………14分(20)(本小题满分13分)(Ⅰ)解:因为3=3,3=1+2,3=1+1+1,所以3)3(=f .因为5=5,5=2+3,5=1+4,5=1+1+3,5=1+2+2,5=1+1+1+2,5=1+1+1+1+1, 所以7)5(=f . ……………………………………3分 (Ⅱ)结论是)1(+n f )]2()([21++≤n f n f . 证明如下:由结论知,只需证).1()2()()1(+-+≤-+n f n f n f n f最新整理. 因为21≥+n ,把1+n 的一个表示法中11a =的1a 去掉,就可得到一个n 的表示法;反之,在n 的一个表示法前面添加一个“1+”,就得到一个1n +的表示法,即1+n 的表示法中11a =的表示法种数等于n 的表示法种数,所以)()1(n f n f -+表示的是1+n 的表示法中11a ¹的表示法数,)1()2(+-+n f n f 是2n +的表示法中11a ¹的表示法数.同样,把一个11a ¹的1+n 的表示法中的p a 加上1, 就可得到一个11a ¹的2n +的表示法,这样就构造了从11a ¹的1+n 的表示法到11a ¹的2+n 的表示法的一个对应.所以有).1()2()()1(+-+≤-+n f n f n f n f ……………………………………9分 (Ⅲ)由第(Ⅱ)问可知:当正整数6m ³时,()(1)(1)(2)(6)(5)f m f m f m f m f f --?--吵-L . 又,7)5(,11)6(==f f 所以 ()(1)4f m f m --?. *对于*式,分别取m 为n ,,7,6Λ,将所得等式相加得)5(4)5()(-≥-n f n f .即134)(-≥n n f . ……………………………………13分。
北京海淀区中考数学二模试题及答案

海淀区九年级第二学期期末练习数学1.6 的绝对值是()A.6B. 61D.1C.662. 以下运算正确的选项是()A. a a 2a 2B. a 2 a 3a 6 C. a 3 a 3 D. ( a) 3 a 33. 如图, RtABC 中, ACB90 ,过点 C 的直线 DF 与BAC 的均分线 AE 平行,若 B 50,则 BCF ()A.100B.80 C. 70 D. 50D CFEAB4. 已知关于 x 的一元二次方程 x 2x1 m 1 0 有实数根,则 m 的取值范围是()4A. m 2B. m 5C. m 2D. m 55. 在 6 张完整同样的卡片上分别画有线段、等边三角形、直角梯形、正方形、正五边形和圆各一个图形。
从这 6 张卡片随机地抽取一张卡片, 则这张卡片上的图形是中心对称图形的概率是()11 C.1 2A.B.D.36 326. 两个半径不等的圆相切,圆心距为 6cm ,且大圆半径是小圆半径的2 倍,则小圆的半径为()A. 3B. 4C.2或4 D. 2 或 67. 农科所连续四年在两块环境同样的实验田里种植甲、 乙两种不一样品种的小麦。
亩产量(单位:公斤)统计以下表。
设甲、乙品种四年亩产量的均匀数挨次为x 甲 , x 乙 ,四年亩产量的方差挨次为 S 2 甲,S 2 乙 ,则以下关系中完整正确的选项是()品种 年份20072008 2009 201022甲454457462459,甲乙S 甲S 乙A. x x乙454459465458B. x甲x乙, S2甲S2乙C. x甲x乙, S2甲S2乙D. x甲x乙, S2甲S2乙8. 一个不透明的小方体的的 6 个面上分别写有数学1, 2, 3, 4,5, 6,任意两对面上所写的两个数字之和为7。
将这样的几个小方体依据相接触的两个面上的数字之和为8 摆放成一个几何体,这个几何体的三视图如右图所示,已知图中所注明的是部分面上所见的数字,则★所代表的数是()A.1B.2C.3D.49.一个正 n 边形的每个内角都是108 ,则n_______.10.将抛物线 y x2向左平移 3 个单位,再向下平移 2 个单位后,所得抛物线的分析式为___________.11.如图,在扇形 OAB 中,AOB 90 ,C 为 OA 的中点,点 D 在AB上,且CD OB ,则ABD ______.ACDO B 12. 某种数字化的信息传输中,先将信息转变为数学0 和1 构成的数字串,并对数字串进行了加密后再传输。
北京市中考数学二模试题汇编 人教新课标版

目录丰台区2012年初三统一练习 石景山2012年初三统一练习 顺义区2012年初三统一练习 大兴区2012年初三统一练习 通州区2012年初三统一练习 门头沟2012年初三统一练习 房山区2012年初三统一练习 延庆县2012年初三统一练习 密云县2012年初三统一练习 海淀区2012年初三统一练习丰台区2012年初三统一练习(二)数 学 试 卷学校 姓名 准考证号 考生须知 1.本试卷共6页,共五道大题,25道小题,满分120分.考试时间120分钟. 2.在试卷和答题卡上准确填写学校名称、姓名和准考证号. 3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效.4.在答题卡上,选择题、作图题用2B 铅笔作答,其他试题用黑色字迹签字笔作答. 5.考试结束,将本试卷、答题卡和草稿纸一并交回.一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个..是符合题意的. 1.2-的绝对值是A .12-B .12 C .2 D .2-2.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,2.5微米等于0.000 002 5米,把0.000 002 5用科学记数法表示为A .62.510⨯ B .50.2510-⨯ C . 62.510-⨯ D .72510-⨯ 3.如图,在△ABC 中, DE ∥BC ,如果AD =1, BD =2,那么DEBC的值为 ED AA.12B.13C.14D.194.在4张完全相同的卡片上分别画有等边三角形、矩形、菱形和圆,在看不见图形的情况下随机抽取1张,卡片上的图形是中心对称图形的概率是A.14B.12C.34D.15.若230x y++-=则y x的值为A.-8 B.-6 C.6 D.86.下列运算正确的是A.222()a b a b+=+ B.235a b ab+=C.632a a a÷= D.325a a a⋅=7.小张每天骑自行车或步行上学,他上学的路程为2 800米,骑自行车的平均速度是步行的平均速度的4倍,骑自行车上学比步行上学少用30分钟.设步行的平均速度为x米/分.根据题意,下面列出的方程正确的是A.30428002800=-xxB.30280042800=-xxC.30528002800=-xxD.30280052800=-xx8.如图1是一个小正方体的侧面展开图,小正方体从图2所示的位置依次翻到第1格、第2格、第3格、第4格,这时小正方体朝上..一面的字是A.北 B.京 C.精 D.神二、填空题(本题共16分,每小题4分)91x-x的取值范围是.10.分解因式:=+-babba25102.11.如图, ⊙O的半径为2,点A为⊙O上一点,OD⊥弦BC于点D,如果1OD=,那么BAC∠=________︒.DOCBA12.符号“f ”表示一种运算,它对一些数的运算如下:2(1)11f =+,2(2)12f =+,2(3)13f =+,2(4)14f =+,…,利用以上运算的规律写出()f n = (n 为正整数) ;(1)(2)(3)(100)f f f f ⋅⋅⋅= .三、解答题(本题共30分,每小题5分)13.计算: ()︒⎪⎭⎫ ⎝⎛+45sin 4-211-3-272-03 .14.已知2230a a --=,求代数式2(1)(2)(2)a a a a --+-的值.15.解分式方程:21124x x x -=--.16.如图,在△ABC 与△ABD 中, BC 与AD 相交于点O ,∠1=∠2,CO = DO .求证:∠C =∠D .17.已知:如图,在平面直角坐标系xOy 中,一次函数y =-x 的图象与反比例函数ky x=的图象交于A 、B 两点. (1)求k 的值;(2)如果点P 在y 轴上,且满足以点A 、B 、P 为顶点的三角形是直角三角形,直接写出点P 的坐标.18.为了增强居民的节约用电意识,某市拟出台居民阶梯电价政策:每户每月用电量不超过230千瓦时的部分为第一档,按每千瓦时0.49元收费;超过230千瓦时且不超过400千瓦时的部分为第二档,超过的部分按每千瓦时0.54元收费;超过400千瓦时的部分为第三档,超过的部分按每千瓦时0.79元收费.(1 4月份总用电量/千瓦时电费/元 小刚 200 小丽30021DOCBA(2)设一户家庭某月用电量为x 千瓦时,写出该户此月应缴电费y (元)与用电量x (千瓦时)之间的函数关系式.四、解答题(本题共20分,每小题5分)19.已知:如图,菱形ABCD 中,过AD 的中点E 作AC 的垂线EF ,交AB 于点M ,交CB 的延长线于点F .如果FB 的长是2,求菱形ABCD 的周长.20.已知:如图,点A 、B 在⊙O 上,直线AC 是⊙O 的切线,联结AB 交O C 于点D ,AC =CD . (1)求证:OC ⊥OB ;(2)如果OD =1,tan∠OCA =52,求AC 的长.21.某课外小组为了解本校八年级700名学生每学期参加社会实践活动的时间,随机对该年级50名学生进行了调查,根据收集的数据绘制了如下的频数分布表和频数分布直方图(各组数据包括最小值,不包括最大值). (1)补全下面的频数分布表和频数分布直方图:(2)可以估计这所学校八年级的学生中,每学期参加社会实践活动的时间不少于8小时的学生大约有多少人?分组/时 频数 频率 6~8 2 0.04 8~10 0.12 10~12 12~14 18 14~16 10 0.20 合 计501.00OD CBAMFEBCDA22.小杰遇到这样一个问题:如图1,在□ABCD 中,AE ⊥BC 于点E ,AF ⊥CD 于点F ,连结EF ,△AEF的三条高线交于点H ,如果AC =4,EF =3,求AH 的长.小杰是这样思考的:要想解决这个问题,应想办法将题目中的已知线段与所求线段尽可能集中到同一个三角形中.他先后尝试了翻折、旋转、平移的方法,发现可以通过将△AEH 平移至△GCF 的位置(如图2),可以解决这个问题.请你参考小杰同学的思路回答: (1)图2中AH 的长等于 .(2)如果AC =a ,EF =b ,那么AH 的长等于 .BA D CEFHG HFECDA B图1 图2五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23.已知关于x 的一元二次方程242(1)0x x k -+-=有两个不相等的实数根. (1)求k 的取值范围;(2)如果抛物线242(1)y x x k =-+-与x 轴的两个交点的横坐标为整数,求正整数k 的值;(3)直线y =x 与(2)中的抛物线在第一象限内的交点为点C ,点P 是射线OC 上的一个动点(点P 不与点O 、点C 重合),过点P 作垂直于x 轴的直线,交抛物线于点M ,点Q 在直线PC 上,距离点P 为2个单位长度,设点P 的横坐标为t ,△PMQ 的面积为S ,求出S 与t 之间的函数关系式.24.在△ABC 中,D 为BC 边的中点,在三角形内部取一点P ,使得∠ABP =∠ACP .过点P 作PE ⊥AC 于点E ,PF ⊥AB 于点F .12345–1–2–3–412345–1–2xy O(1)如图1,当AB =AC 时,判断的DE 与DF 的数量关系,直接写出你的结论;(2)如图2,当AB ≠AC ,其它条件不变时,(1)中的结论是否发生改变?请说明理由.图1 图225.如图,将矩形OABC 置于平面直角坐标系xOy 中,A (32,0),C (0,2). (1) 抛物线2y x bx c =-++经过点B 、C ,求该抛物线的解析式;(2)将矩形OABC 绕原点顺时针旋转一个角度α(0°<α<90°),在旋转过程中,当矩形的顶点落在(1)中的抛物线的对称轴上时,求此时这个顶点的坐标; (3)如图(2),将矩形OABC 绕原点顺时针旋转一个角度θ(0°<θ<180°),将得到矩形OA’B’C’,设A’C’的中点为点E ,联结CE ,当θ= °时,线段CE 的长度最大,最大值为 .AEFPD CE BAD F P北京市丰台区2011_2012学年第二学期初三综合练习(二)参考答案题号 1 2 3 4 5 6 7 8 答案 CCBCADAA题号 91011 12答案x ≥12)5(-a b 60°21n+;5151 13.解:原式=3-1+4-422⨯……4分 =6-22….5分14.解:2(1)(2)(2)a a a a --+-=22224a a a --+……1分. =224a a -+. ……2分2230a a --=, ∴223a a -=.…3分∴原式=224347a a -+=+=.….….5分 15.21124x x x -=-- 解:2(2)(4)1x x x +--=.……1分 22241x x x +-+=.……2分23x =-.…… 3分32x =-.…….4分 检验:经检验,32x =-是原方程的解.∴原方程的解是32x =-.……5分16.证明:∠1=∠2, ∴OA=OB .…1分在△COA 和△DOB 中 ,OA=OB ,∠AOC =∠BOD ,CO=DO .∴△COA ≌△DOB .……….4分∴∠C =∠D . …………….5分 17.解: (1)反比例函数ky x=的图象经过点A (-1,1) , ∴-11-1k =⨯=.…………1分 (2)P 1(0,2)、 P 2(0,-2)、P 3(0,2)、 P 4(0,-2) ……5分18.解:(1)……2分4月份总用电量/千瓦时电费/元 小刚 200 98 小丽300150.5(2)当0230x ≤≤时,0.49y x =;……3分 当230400x <≤时,0.54-11.5y x =;……4分当400x >时,0.79-111.5y x =.……5分 四、解答题(本题共20分,每小题5分) 19.解:联结BD . ∵在菱形ABCD 中,∴AD ∥BC ,AC ⊥BD .……1分 又∵EF ⊥AC , ∴BD ∥EF .∴四边形EFBD 为平行四边形.……2分 ∴FB = ED =2.……3分 ∵E 是AD 的中点. ∴AD =2ED =4.……4分 ∴菱形ABCD 的周长为4416⨯=.……5分20.(1)证明:∵OA =OB , ∴∠B =∠4. ∵CD =AC , ∴∠1=∠2.∵∠3=∠2,∴∠3=∠1. ∵AC 是⊙O 的切线, ∴OA ⊥AC .……1分∴∠OAC =90°.∴∠1+∠4=90°. ∴∠3+∠B =90°. ∴OC ⊥OB .……2分(2)在Rt △OAC 中 ,∠OAC =90°, ∵tan∠OCA =52, ∴52OA AC =.……3分 ∴设AC =2x ,则AO =5x .由勾股定理得,OC =3x .∵AC =CD , ∴AC =CD =2x . ∵OD =1, ∴OC =2x +1.∴2x +1=3x .……4分∴x =1. ∴AC =21⨯=2.……5分21.解: (1)……3分(注:错一空扣1分,最多扣3分)…4分(2)700⨯(1-0.04)=672.……5分答:这所学校每学期参加社会实践活动的时间不少于8小时的学生大约有672人.22.解:(1)7;……3分(2)22a b -.……5分 分组/时 频数 频率 6~8 2 0.04 8~10 6 0.1210~12 14 0.28 12~14 18 0.36 14~16 10 0.20合 计 50 1.0023.解:(1)由题意得△>0. ∴△=2(4)4[2(1)]8240k k ---=-+>.……1分 ∴解得3<k .……2分(2)∵3<k 且k 为正整数,∴1=k 或2.……3分当1=k 时,x x y 42-=,与x 轴交于点(0,0)、(4,0),符合题意; 当2=k 时,242+-=x x y ,与x 轴的交点不是整数点,故舍去. 综上所述,1=k .……4分(3)∵2,4y x y x x =⎧⎨=-⎩,∴点C 的坐标是(5,5).∴OC 与x 轴的夹角为45°.过点Q 作QN ⊥PM 于点N ,(注:点Q 在射线PC 上时,结果一样,所以只写一种情况432ABCD O1即可)∴∠NQP =45°,NQ PM S ⋅=21.∵PQ ,∴NQ =1.∵P (t t ,),则M (t t t 4,2-),∴PM =t t t t t 5)4(22+-=--.……5分 ∴t t S 5212+-=. ∴当50<<t 时,t t S 25212+-=;……6分 当5>t 时,t t S 25212-=.……7分24.解:(1)DE =DF .……1分(2)DE =DF 不发生改变.……2分理由如下:分别取BP 、CP 的中点M 、N ,联结EM 、DM 、FN 、DN .∵D 为BC 的中点,∴BP DN BP DN //,21=.……3分∵,AB PE ⊥∴BP BM EM 21==.∴21,∠=∠=EM DN .∴12213∠=∠+∠=∠.…4分同理,524,//DM FN MD PC =∠=∠. ∴四边形MDNP 为平行四边形.……5分∴67∠=∠.∵,41∠=∠∴35∠=∠. ∴EMD DNF ∠=∠.……6分 ∴△EMD ≌△DNF . ∴DE =DF .……7分25.解:(1)∵矩形OABC ,A (32,0),C (0,2),∴B (32,2).∴抛物线的对称轴为x =3.∴b =3.……1分∴二次函数的解析式为:2232y x x =-++.……2分(2)①当顶点A 落在对称轴上时,设点A 的对应点为点A ’,联结OA ’,设对称轴x =3与x 轴交于点D ,∴OD =3. ∴OA ’ = OA =32.在Rt △OA ’D 中,根据勾股定理A ’D =3. ∴A ’(3,-3) . ……4分 ②当顶点落C 对称轴上时(图略),设点C 的对应点为点C ’,联结OC ’, 在Rt △OC ’D 中,根据勾股定理C ’D =1. ∴C ’(3,1).……6分 (3) 120°,4.……8分石景山区2012年初三第二次统一练习数 学 试 卷7654321NMCD BPFEACA B yxB'C'DA'O考 生 须 知 1.本试卷共10页.第10页为草稿纸,全卷共五道大题,25道小题. 2.本试卷满分120分,考试时间120分钟.3.在试卷密封线内准确填写区(县)名称、毕业学校、姓名和准考证号. 4.考试结束后,将试卷和答题纸一并交回.题号 一 二 三 四五 总分 分数第Ⅰ卷(共32分)一、选择题(本题共32分,每小题4分)在每个小题给出的四个备选答案中,只有一个是正确的,请将所选答案前的字母填在题后的括号内.1.2的算术平方根是( ) A .21B .2C .2-D .2±2.2012年2月,国务院同意发布新修订的《环境空气质量标准》增加了PM2.5监测指标.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如果1微米=0.000 001 米,那么数据0.000 002 5用科学记数法可以表示为( ) A .6105.2-⨯ B .5105.2-⨯ C .5105.2⨯- D .6105.2-⨯-3.如图,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个钝角为120︒ 的菱形,剪口与折痕所成的角α 的度数应为( )A .15︒或30︒B .30︒或45︒C .45︒或60︒D .30︒或60︒ 4年星级饭店客房出租率(%)的情况如下表:年份 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 出租率62625265626160524956A .61、62B .62、62C .61.5、62D .60.5、625.如图,有6张形状、大小、质地均相同的卡片,正面分别印有北京精神——“爱国、创新、包容、厚德”的字样.背面完全相同,现将这6张卡片洗匀后正面向下放在桌子上,从中随机抽取一张,抽出的卡片恰好是“创新”的概率是( ) A .31 B .32 C .61 D .41 6.若一个多边形的内角和是900°,则这个多边形的边数是( )第3题图爱国创新包容厚德爱国创新A .5B .6C .7D .87.将二次函数2x y =的图象如何平移可得到342++=x x y 的图象( ) A .向右平移2个单位,向上平移一个单位 B .向右平移2个单位,向下平移一个单位 C .向左平移2个单位,向下平移一个单位 D .向左平移2个单位,向上平移一个单位8.已知正方形纸片的边长为18,若将它按下图所示方法折成一个正方体纸盒,则纸盒的边(棱)长是( ) A .6B .23C .29D .32第Ⅱ卷(共88分)二、填空题(本题共16分,每小题4分) 9.分式3-x x有意义的条件为 . 10.分解因式:=-339ab b a ______ ________. 11.已知:如图是斜边为10的一个等腰直角三角形与两个半径为5的扇形的重叠情形,其中等腰直角三角形顶角平分线与两扇形相切,则图中阴影部分面积的和是 .12.如图所示,圆圈内分别标有1,2,…,12,这12个数字,电子跳蚤每跳一步,可以从一个圆圈逆时针跳到相邻的圆圈,若电子跳蚤所在圆圈的数字为n ,则电子跳蚤连续跳(2-3n )步作为一次跳跃,例如:电子跳蚤从标有数字1的圆圈需跳12-13=⨯步到标有数字2的圆圈内,完成一次跳跃,第二次则要连续跳42-23=⨯步到达标有数字6的圆圈,…依此规律,若电子跳蚤从①开始,那么第3次能跳到的圆圈内所标的数字为 ;第2012次电子跳蚤能跳到的圆圈内所标的数字为 .三、解答题(本题共30分,每小题5分)第8题图 第11题图111210987654321第12题图13.()22145cos 314.38-⎪⎭⎫⎝⎛+︒---π.解:14.解分式方程123482---=-xxx .解:15.已知,如图,点D 在边BC 上,点E 在△ABC 外部,DE 交AC 于F ,若AD =AB ,∠1=∠2=∠3. 求证:BC=DE . 证明:16.已知:0162=-+x x ,求代数式()()()()3312122+-+--+x x x x x 的值.解:17.已知一次函数y kx b =+的图象与直线3y x =-平行且经过点()3,2-,与x 轴、y轴分别交于 A 、 B 两点. (1)求此一次函数的解析式;(2)点C 是坐标轴上一点,若△ABC 是底角为︒30的等腰三角形,求点C 的坐标. 解:18.列方程(组)解应用题:如图是一块长、宽分别为60 m 、50 m 的矩形草坪,草坪中有宽度均为x m 的一横两纵的甬道.(1)用含x 的代数式表示草坪的总面积S ;yx O 321FEABC D(2)当甬道总面积为矩形总面积的4.10%时,求甬道的宽. 解:四、解答题(本题共20分,每小题5分)19.如图,梯形纸片ABCD 中,AD //BC ,∠B =30º.折叠纸片使BC 经过点A ,点B 落在点B’处,EF 是折痕,且BE =EF =4,AF ∥CD . (1)求∠BAF 的度数; (2)当梯形的上底AD 多长时,线段DF 恰为该梯形的高? 解:20.以下是根据全国 2011年国民经济和社会发展统计公报中的相关数据,绘制的统计图的一部分. 请根据以上信息,解答下列问题:(产量相关数据精确到1万吨)(1)请补全扇形统计图;(2)通过计算说明全国的粮食产量与上一年相比,增长最多的是 年; (3)2011年早稻的产量为 万吨;(4)2008-2011这三年间,比上一年增长的粮食产量的平均数为多少万吨,若按此平均数增长,请你估计2012年的粮食产量为多少万吨.(结果保留到整数位) 解:21.已知:如图,M 是⊙O 的直径AB 上任意一点,过点M 作AB 的垂线MP ,D 是MPA BDEC B 'F 6%22%%早稻夏粮秋粮2011年各类粮食占全体 粮食的百分比分组统计图的延长线上一点,联结AD 交⊙O 于点C ,且PC PD =. (1)判断直线PC 与⊙O 的位置关系,并证明你的结论; (2)若22tan =D ,3=OA ,过点A 作PC 的平行线AN 交⊙O 于点N .求弦AN 的长.解:22.阅读下面材料:小阳遇到这样一个问题:如图(1),O 为等边△ABC 内部一点,且3:2:1::=OC OB OA ,求AOB ∠的度数.小阳是这样思考的:图(1)中有一个等边三角形,若将图形中一部分绕着等边三角形的某个顶点旋转60°,会得到新的等边三角形,且能达到转移线段的目的.他的作法是:如图(2),把△CO A 绕点A 逆时针旋转60°,使点C 与点B 重合,得到△O AB ',连结O O '. 则△O AO '是等边三角形,故OA O O =',至此,通过旋转将线段OA 、OB 、OC 转移到同一个三角形B O O '中. (1)请你回答:︒=∠AOB . (2)参考小阳思考问题的方法,解决下列问题: 已知:如图(3),四边形ABCD 中,AB=AD ,∠DAB =60°,∠DCB =30°,AC =5,CD =4.求四边形ABCD 的面积. 解:五、解答题(本题满分22分,第23题7分,第24题7分,第25题8分) 23.已知:直线122y x =+分别与 x 轴、y 轴交于点A 、点B ,点P (a ,b )在直线AB 上,点P 关于y 轴的对称点P ′ 在反比例函数xky =图象上.(1) 当a =1时,求反比例函数xky =的解析式;DCBAM CODPB图⑴ 图⑵ 图⑶(C )OCBAOCB A(2) 设直线AB 与线段P'O 的交点为C .当P'C =2CO 时,求b 的值;(3) 过点A 作AD //y 轴交反比例函数图象于点D ,若AD =2b,求△P ’DO 的面积.解:24.在△ABC 中,AC AB =,D 是底边BC 上一点,E 是线段AD 上一点,且∠BAC CED BED ∠=∠=2.(1) 如图1,若∠︒=90BAC ,猜想DB 与DC 的数量关系为 ; (2) 如图2,若∠︒=60BAC ,猜想DB 与DC 的数量关系,并证明你的结论; (3)若∠︒=αBAC ,请直接写出DB 与DC 的数量关系.A B C D E AE B C D图1 图2y x O 备用图解:25.已知:抛物线y=-x2+2x+m-2交y轴于点A(0,2m-7).与直线y=2x交于点B、C(B在右、C在左).(1)求抛物线的解析式;∠=∠,(2)设抛物线的顶点为E,在抛物线的对称轴上是否存在一点F,使得BFE CFE 若存在,求出点F的坐标,若不存在,说明理由;(3)射线OC上有两个动点P、Q同时从原点出发,分别以每秒5个单位长度、每秒25个单位长度的速度沿射线OC运动,以PQ为斜边在直线BC的上方作直角三角形PMQ (直角边分别平行于坐标轴),设运动时间为t秒,若△PMQ与抛物线y=-x2+2x+m-2有公共点,求t的取值范围.解:yOx备用图草稿纸石景山区2012初三第二次统一练习数学参考答案阅卷须知:1.一律用红钢笔或红圆珠笔批阅.2.为了阅卷方便,解答题中的推导步骤写得较为详细,考生只要写明主要过程即可.若考生的解法与本解法不同,正确者可参照评分参考给分,解答右端所注分数,表示考生正确做到这一步应得的累加分数.一、选择题(本题共8道小题,每小题4分,共32分)题 号 12345678答 案B A D D A C C B二、填空题(本题共4道小题,每小题4分,共16分) 9.3≠x ; 10.()()b a b a ab 33-+; 11.225-225π; 12.10;6. 三、解答题(本题共6道小题,每小题5分,共30分)13.解:()22145cos 3--14.38-⎪⎭⎫⎝⎛+︒-π=4223122+⨯-- ……………………………4分 =322+…………………………………………………5分 14. 123482---=-xxx解:()()123228---=-+x x x x ……………………………1分 ()()()42382--+-=x x x ……………………………3分46822+---=x x x ……………………………4分∴10-=x经检验:10-=x 是原方程的根.………………………5分15.证明:∵∠1=∠2=∠3∴DAE BAC ∠=∠…………………………… 1分 又∵AFE DFC ∠=∠∴E C ∠=∠ …………………………… 2分 在△ABC 和△ADE 中⎪⎩⎪⎨⎧=∠=∠∠=∠AD AB EC DAE BAC …………………………… 3分 ∴△ABC ≌△ADE ……………………………………………………… 4分∴BC=DE . ……………………………………………………… 5分 16.解:原式222922144x x x x x -++-++= …………………………………2分1062++=x x ………………………………… 3分当0162=-+x x 时,162=+x x ………………………………… 4分 原式11=. …………………………………5分17.解:(1)∵一次函数y kx b =+的图象与直线3y x =-平行且经过点()3,2-∴⎩⎨⎧-=+-=323b k k 解得⎩⎨⎧=-=33b k∴一次函数解析式为33+-=x y …………………………………1分(2)令0=y ,则1=x ;令0=x 则3=y∴()()3,0,0,1B A∵1=OA ,3=OB …………………………2分 ∴2=AB ∴︒=∠30ABO若AC AB =,可求得点C 的坐标为()0,31C 或()3,02-C ………………………4分 若CA CB =如图︒=︒-︒=∠3030603OAC ,3330tan 3=︒=OA OC ∴⎪⎪⎭⎫ ⎝⎛33,03C …………………………………………5分 ∴()0,31C ,()3,02-C ,⎪⎪⎭⎫ ⎝⎛33,03C 18.解:(1)S = 6050⨯-(60 x + 2×50 x -2×x 2 )=3000 + 2x 2-160x .………2分(2)由题意得:-2x 2+160x =60501000104⨯⨯, ………………3分 解得 x = 2 或 x = 78. …………………………………4分 又0<x <50,所以x = 2,答:甬道的宽是2米. ……………………………………5分 19. 解:(1)∵BE =EF ∴∠EFB =∠B ,由题意,△EF B '≌△BEF∴∠EFB ’ =∠EFB =∠B=30° ∴△BFA 中,︒=︒-︒-︒-︒=∠90303030180BAF ……………………………………2分 (2)联结DF ,∵AD //BC ,AF ∥CD∴四边形AFCD 是平行四边形 ……………………………………3分 ∴∠C =∠A FB =60°∴CD =AF =3230cos =︒EF ……………………………………4分 若BC DF ⊥,则360cos =︒=CD FC此时3=AD . ……………………………………5分 20.(1)72%;(2)2011;(3)3427; ……………………每空1分,共3分(4)(57121-52871)÷3≈=1417 ………………………………………4分57121+1417=58538. ………………………………………5分21.(1)联结CO , … …………………………………1分∵DM ⊥AB∴∠D+∠A=90° ∵PC PD = ∴∠D=∠PCD ∵OC=OA∴∠A=∠OCA∴∠OCA+∠PCD=90° ∴PC ⊥OC∴直线PC 是⊙O 的切线 …………………………………2分 (2)过点A 作PC 的平行线AN 交⊙O 于点N . ∴∠NAC=∠PCD=∠D, AN ⊥OC,设垂足是Q ∴Rt △CQA 中 ∴22tanD QAC tan ==∠ ∴设CQ=x ,AQ=x 2 ∴OQ=x -3∵222AQ OQ OA +=∴222)3()2(3x x -+=解得2=x …………………………………4分 ∴22=AQ∴242==AQ AN …………………………………5分22. 解:(1)150° ………………………1分(2) 如图,将△ADC 绕点A 顺时针旋转60°,使点D 与点B 重合,………2分 得到△O AB ',连结O C '. 则△O AC '是等边三角形,可知4,5'===='DC BO CA O C ,ADC ABO ∠=∠'……………………3分在四边形ABCD 中,︒=∠-∠-︒=∠+∠270360DCB DAB ABC ADC ,)(360''ABO ABC BC O ∠+∠-︒=∠∴︒=︒-︒=90270360. ……………………4分34522=-=∴BC 6432543215432''-=⨯⨯-⨯=-=∴∆∆BCO ACO ABCD S S S 四边形.………………5分23.(1)∵点P 在直线AB 上, 1=a 时,2121+⨯=b =25………………………1分 ∴)25,1(P ,∴)25,1(-'P ,代入x k y = 得25-=k , ∴x y 25-= …………………………2分 (2)联结'PP∵点P 和点P '关于y 轴对称 ∴'PP ∥x 轴P 'Pxy ODC BA O 'DCBA∴OCA C PP ∽△△'∴'PP ∶=OA C P '∶CO …………3分 ∵CO C P 2'= ∴'PP =OA 2∵221+=x y 与x 轴交于点A 、点B ∴)0,4(-A ,)2,0(B 可得4=OA∴8'=PP ∴a =4∴42421=+⨯=b ………………………5分 (3)当点P 在第一象限时:∵点P 和点P '关于y 轴对称且),(b a P∴),('b a P -∵y AD ∥∴)24-(b D , ∵D P 、点点'在xk y =上 ∴b a b⨯-=⨯-24 ∴2=a∴32221=+⨯=b ∵),23,4(-D )3,2('-P∴29'=DO P S △ …………6分当点P 在第二象限时:)24-(bD -,∴b a b⨯-=-⨯-24∴2-=a∴12)2(21=+-⨯=b∵),21,4(--D )1,2('P∴23'=DO P S △ …………7分24.解:(1)DC DB 2= (2) DC DB 2=证明:过点C 作CF ∥BE 交AD 的延长线于点F , 在 AD 上取点G 使得CF CG =A∴76∠=∠=∠F∵︒=∠=∠=∠602BAC CED BED ∴︒=∠=∠606F ,︒=∠30CED ∴41205∠=︒=∠∵︒=∠+∠=∠=∠+∠6021713 ∴23∠=∠ ∵AC AB = ∴△ABE ≌△CAG ∴AG BE AE CG ==, ∵︒=∠-∠=∠306CED GCE ∴EG CG =∴BE AG CG CF 2121===由△DBE ∽△DCF 得2==FCBEDC BD∴DC DB 2=(3) 结论:DC DB 2=.25.解:(1)点A (0,2m -7)代入y =-x 2+2x +m -2,得m =5∴抛物线的解析式为y =-x 2+2x +3 ………………………2分(2)由⎩⎨⎧=++-=x y x x y 2322得⎪⎩⎪⎨⎧==323y x ,⎪⎩⎪⎨⎧=-=323y x∴B (32,3),C (32,3--)B (32,3)关于抛物线对称轴1=x 的对称点为)32,32('-B可得直线C B '的解析式为32632-+=x y , 由⎩⎨⎧=-+=132632y x y ,可得⎩⎨⎧==61y x∴)6,1(F ………………………5分(3)当)2,2(t t M --在抛物线上时,可得03242=-+t t ,4131±-=t , 当)2,(t t P --在抛物线上时,可得32=t ,3±=t ,舍去负值,所以t 的取值范围是34131≤≤+-t .………………8分87654321E D AGF图(2)F E B AO 顺义区2012届初三第二次统一练习考生须知1.本试卷共5页,共五道大题,25道小题,满分120分.考试时间120分钟. 2.在试卷和答题卡上准确填写学校名称、姓名和准考证号. 3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效.4.在答题卡上,选择题、作图题用2B 铅笔作答,其他试题用黑色字迹签字笔作答. 5.考试结束,将本试卷、答题卡和草稿纸一并交回.一、选择题(本题共32分,每小题4分) 下面各题均有四个选项,其中只有一个..是符合题意的. 1.9的平方根是A .3B .-3C .3±D .132.据人民网报道,“十一五”我国铁路营业里程达9.1万公里.请把9.1万用科学记数法表示应为A .59.110⨯B .49.110⨯C .49110⨯D . 39.110⨯ 3.如图,下列选项中不是..正六棱柱三视图的是( )A B C D4.把2416a b b -分解因式,结果正确的是A .2(24)b a - B . (22)(22)b a a +-C .24(2)b a -D .4(2)(2)b a a +-5.北京是严重缺水的城市,市政府号召居民节约用水,为了解居民用水情况,小敏在某小区随机抽查了10户家庭的5月份用水量,结果如下(单位:立方米):5,6,6,2,5,6,7,10,7,6,则关于这10户家庭的5月份用水量,下列说法错误的是 A.众数是6 B.极差是8C.平均数是6D.方差是46.如图,小华同学设计了一个圆直径的测量器,把标有刻度的尺子OA 、OB 在O 点钉在一起,并使它们保持互相垂直.在测直径时,把O 点靠在圆周上,读得刻度OE=4个单位, OF=3个单位,则圆的直径为A .7个单位B .6个单位C .5个单位D .4个单位7.从1,-2, 3,-4四个数中,随机抽取两个数相乘,积是正数的概率是A .14 B .13 C .12D .238.将一正方形纸片按下列顺序折叠,然后将最后折叠的纸片沿虚线剪去右上方的小三角形.将纸片展开,得到的图形是DCBA二、填空题(本题共16分,每小题4分)9.若分式261xx--的值为0,则x的值等于.10.如图,□ABCD中,E是边BC上一点,AE交BD于F,若2BE=,3EC=,则BFDF的值为.11.将方程2410x x--=化为2()x m n-=的形式,其中m,n是常数,则m n+=.12.如图,△ABC中,AB=AC=2 ,若P为BC的中点,则2AP BP PC+的值为;若BC边上有100个不同的点1P,2P,…,100P,记i i i im AP BP PC=+(1i=,2,…,100),则12m m++…100m+的值为.三、解答题(本题共30分,每小题5分)13.计算:101()322sin45(32)4---+︒-.14.解不等式2(2)x+≤4(1)6x-+,并把它的解集在数轴上表示出来.15.已知:如图,E,F在BC上,且AE∥DF,AB∥CD ,AB=CD.FEDCBAP i P CBAFBA求证:BF = CE .16.解分式方程:32322x x x -=+-.17.已知2x -3=0,求代数式5(2)(2)(4)1x x x x ---++的值.18.某市实施“限塑令”后,2008年大约减少塑料消耗约4万吨.调查分析结果显示,从2008年开始,五年内该市因实施“限塑令”而减少的塑料消耗量y (万吨)随着时间x (年)逐年成直线上升,y 与x 之间的关系如图所示.(1)求y 与x 之间的关系式;(2)请你估计,该市2011年因实施“限塑令”而减少的塑料消耗量为多少?四、解答题(本题共20分,每小题5分) 19.如图,在矩形ABCD 中,E 是边CB 延长线上的点,且EB=AB ,DE 与AB 相交于点F ,AD=2,CD=1,求AE 及DF 的长.20.已知:如图,P 是⊙O 外一点,PA 切⊙O 于点A ,AB 是⊙O 的直径,BC ∥OP 交⊙O 于点C .(1)判断直线PC 与⊙O 的位置关系,并证明你的结论; (2)若BC=2,11sin23APC ∠=,求PC 的长及点C 到PA 的距离.21.阅读对人成长的影响是巨大的,一本好书往往能改变人的一生,每年的4月23日被联合国教科文组织确定为“世界读书日”.某校倡导学生读书,下面的表格是学生阅读课FEDC B AOCBAP外书籍情况统计表,图1是该校初中三个年级学生人数分布的扇形统计图,其中八年级学生人数为204人,请你根据图表中提供的信息,解答下列问题:图书种类 频数 频率科普常识 840 b名人传记 8160.34 中外名著 a0.25 其他1440.06(1)求该校八年级学生的人数占全校学生总人数的百分比; (2)求表中a ,b 的值;(3)求该校学生平均每人读多少本课外书?22.阅读下列材料:问题:如图1,P 为正方形ABCD 内一点,且PA ∶PB ∶PC =1∶2∶3,求∠APB 的度数.小娜同学的想法是:不妨设PA=1, PB=2,PC=3,设法把PA 、PB 、PC 相对集中,于是他将△BCP 绕点B 顺时针旋转90°得到△BAE (如图2),然后连结PE ,问题得以解决.请你回答:图2中∠APB 的度数为 . 请你参考小娜同学的思路,解决下列问题:如图3,P 是等边三角形ABC 内一点,已知∠APB=115°,∠BPC=125°.(1)在图3中画出并指明以PA 、PB 、PC 的长度为三边长的一个三角形(保留画图痕迹);(2)求出以PA 、PB 、PC 的长度为三边长的三角形的各内角的度数分别等于 .EDDPPPCCCBBBAAA图1 图2 图3五、解答题(本题共22分,第23题7分,第24题7分,第25题8分)23.如图,直线AB 经过第一象限,分别与x 轴、y 轴交于A 、B 两点,P为线段AB 上任意一点(不与A 、B 重合),过点P 分别向x 轴、y 轴PyB D作垂线,垂足分别为C 、D .设OC=x ,四边形OCPD 的面积为S . (1)若已知A (4,0),B (0,6),求S 与x 之间的函数关系式; (2)若已知A (a ,0),B (0,b ),且当x=34时,S 有最大值98,求直线AB 的解析式; (3)在(2)的条件下,在直线AB 上有一点M ,且点M 到x 轴、y 轴的距离相等,点N在过M 点的反比例函数图象上,且△OAN 是直角三角形,求点N 的坐标. 24.已知:如图,D 为线段AB 上一点(不与点A 、B 重合),CD ⊥AB ,且CD=AB ,AE ⊥AB ,BF ⊥AB ,且AE=BD ,BF=AD .(1)如图1,当点D 恰是AB 的中点时,请你猜想并证明∠ACE 与∠BCF 的数量关系; (2)如图2,当点D 不是AB 的中点时,你在(1)中所得的结论是否发生变化,写出你的猜想并证明;(3)若∠ACB=α,直接写出∠ECF 的度数(用含α的式子表示).图1 图225.如图,在平面直角坐标系xOy 中,二次函数212y x bx c =++的图象经过点A (-3,6),并与x 轴交于点B (-1,0)和点C ,顶点为P .(1)求二次函数的解析式;(2)设D 为线段OC 上的一点,若DPC BAC ∠=∠,求点D 的FED CBAFE D C B A坐标;(3)在(2)的条件下,若点M 在抛物线212y x bx c =++上,点N 在y 轴上,要使以M 、N 、B 、D 为顶点的四边形是平行四边形,这样的点M 、N 是否存在,若存在,求出所有满足条件的点M 的坐标;若不存在,说明理由.顺义区2012届初三第二次统一练习 数学学科参考答案及评分细则二、填空题(本题共16分,每小题4分,)9.3; 10.25; 11.7; 12.4,400. 三、解答题(本题共30分,每小题5分)13.解:101()322sin 45(32)4---+︒--2432212=-+⨯- …………………………………………………… 4分 322=- …………………………………………………………………… 5分 14.解:去括号,得 24x +≤446x -+.…………………………………………… 1分移项,得 24x x -≤464-+-.…………………………………………… 2分 合并,得 2x -≤-2 . ………………………………………… 3分 系数化为1,得 x ≥1 . ……………………………………………… 4分 不等式的解集在数轴上表示如下:……………………………………… 5分15.证明:∵ AE ∥DF ,∴∠1=∠2. ………………………… 1分 ∵ AB ∥CD , ∴ ∠B =∠C .………………………… 2分在△ABE 和 △DCF 中, 12,,,B C AB DC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴ △ABE ≌△DCF .…………………………………………………… 4分 ∴ BE =CF . ∴BE -EF =CF -EF .即BF =CE .……………………………………………………………… 5分16.解:去分母,得 3(2)2(2)3(2)(2)x x x x x --+=+-.…………………… 1分去括号,得 223624312x x x x ---=-. ………………………… 2分 整理,得 88x -=-.…………………………………………………… 3分解得 1x =. ……………………………………………………………… 4分 经检验,1x =是原方程的解.……………………………………………… 5分 ∴ 原方程的解是1x =.17.解:5(2)(2)(4)1x x x x ---++22510(28)1x x x x =--+-+ ……………………………………………… 2分22510281x x x x =---++24129x x =-+ ………………………………………………………………… 3分(23)(23)x x =+- …………………………………………………………… 4分当2x -3=0时,原式(23)(23)0x x =+-=.………………………………… 5分18.解:(1)设y 与x 之间的关系式为y=kx+b .……………………………………… 1分21F EDC B A由题意,得20084,2010 6.k b k b +=⎧⎨+=⎩ 解得1,2004.k b =⎧⎨=-⎩ …………………… 3分∴y 与x 之间的关系式为y =x -2004(2008≤x ≤2012). …………… 4分(2)当x =2012时,y =2012-2004=8.∴该市2012年因“限塑令”而减少的塑料消耗量约为8万吨.……… 5分19.解:∵四边形ABCD 是矩形,且AD=2,CD=1,∴BC=AD=2,AB=CD=1,∠ABC =∠C= 90°,AB ∥DC .∴EB=AB=1. ………………………………………………………………… 1分 在Rt △ABE 中,222AE AB BE =+=.………………………………… 2分在Rt △DCE 中,22221310DE DC CE =+=+=.………………… 3分∵AB ∥DC ,∴12EF EB DF BC ==. …………………………………………………………… 4分 设EF x =,则2DF x =.∵EF DF DE +=, ∴210x x +=. ∴10x =. ∴22103DF x ==5分 20.解:(1)直线PC 与⊙O 相切.证明:连结OC ,∵BC ∥OP ,∴∠1 =∠2,∠3=∠4. ∵OB=OC , ∴∠1=∠3.∴∠2=∠4.又∵OC=OA ,OP=OP ,∴△POC ≌△POA . ……………………………………………… 1分 ∴∠PCO =∠PAO . ∵PA 切⊙O 于点A , ∴∠PAO =90°. ∴∠PCO =90°.∴PC 与⊙O 相切. ……………………………………………… 2分(2)解:∵△POC ≌△POA ,∴∠5=∠6=12APC ∠. ∴11sin 5sin 23APC ∠=∠=.∵∠PCO =90°,∴∠2+∠5=90°. ∴1cos 2sin 53∠=∠=. 4321O C B AP图3MPCBAD85674321O CBAP∵∠3=∠1 =∠2, ∴1cos 33∠=. 连结AC ,∵AB 是⊙O 的直径, ∴∠ACB =90°.∴261cos 33BC AB ===∠.………………………………………… 3分∴OA=OB=OC=3,2242AC AB BC =-=.∴在Rt △POC 中,9sin 5OCOP ==∠.∴2262PC OP OC =-=.…………………………………… 4分 过点C 作CD ⊥PA 于D , ∵∠ACB =∠PAO =90°,∴∠3+∠7 =90°,∠7+∠8 =90°. ∴∠3=∠8.∴1cos 8cos 33∠=∠=.在Rt △CAD 中,14cos 842233AD AC =∠=⨯=. ∴22163CD AC AD =-=.……………………………………… 5分 21.解:(1)∵1-28%-38%=34%.∴该校八年级学生的人数占全校学生总人数的百分比为34%.……… 1分(2)∵1440.062400÷=,∴24000.25600a =⨯=, ……………………………………………… 2分84024000.35b =÷=. ……………………………………………… 3分(3)∵八年级学生人数为204人,占全校学生总人数的百分比为34%,∴全校学生总人数为20434%600÷=. ……………………………… 4分 ∴该校学生平均每人读课外书:24006004÷=.答:该校学生平均每人读4本课外书. ………………………………… 5分22.解:图2中∠APB 的度数为 135° .……………… 1分 (1)如图3,以PA 、PB 、PC 的长度为三边长的一个三角形是 △APM .(含画图)………… 2分 (2)以PA 、PB 、PC 的长度为三边长的三角形的各内角的度数分别等于60°、65°、55° .……………… 5分23.解:(1)设直线AB 的解析式为y kx b =+,由A (4,0),B (0,6),得40,6.k b b +=⎧⎨=⎩ 解得3,26.k b ⎧=-⎪⎨⎪=⎩ ∴直线AB 的解析式为362y x =-+.……………………………… 1分 ∵OC=x ,∴3(,6)2P x x -+. ∴3(6)2S x x =-+. 即2362S x x =-+(0< x <4). …………………………………… 2分 (2)设直线AB 的解析式为y mx n =+,∵OC=x ,∴(,)P x mx n +.∴2S mx nx =+.∵当x=34时,S 有最大值98,∴3,24939.1648n m m n ⎧-=⎪⎪⎨⎪+=⎪⎩ 解得2,3.m n =-⎧⎨=⎩∴直线AB 的解析式为23y x =-+.………………………………… 3分∴A (32,0),B (0,3). 即32a =,3b =.……………………………………………………… 5分(3)设点M 的坐标为(M x ,M y ),由点M 在(2)中的直线AB 上, ∴23M M y x =-+.∵点M 到x 轴、y 轴的距离相等, ∴M M x y =或M M x y =-.当M M x y =时,M 点的坐标为(1,1). 过M 点的反比例函数的解析式为1y x=. ∵点N 在1y x=的图象上,OA 在x 轴上,且△OAN 是直角三角形, ∴点N 的坐标为32,23⎛⎫⎪⎝⎭.……………………………………………… 6分 当M M x y =-时,M 点的坐标为(3,-3),BD C FEA 过M 点的反比例函数的解析式为9y x=-. ∵点N 在9y x=-的图象上,OA 在x 轴上,且△OAN 是直角三角形, ∴点N 的坐标为3,62⎛⎫-⎪⎝⎭.……………………………………………… 7分 综上,点N 的坐标为32,23⎛⎫⎪⎝⎭或3,62⎛⎫- ⎪⎝⎭.24.解:(1)猜想:∠ACE=∠BCF .证明:∵D 是AB 中点,∴AD=BD ,又∵AE=BD ,BF=AD , ∴AE=BF . ∵CD ⊥AB ,AD=BD , ∴CA=CB .∴∠1 =∠2. ∵AE ⊥AB ,BF ⊥AB , ∴∠3 =∠4=90°.∴∠1+∠3 =∠2+∠4.即∠CAE=∠CBF . ∴△CAE ≌△CBF .∴∠ACE=∠BCF .……………………………………………… 2分(2)∠ACE=∠BCF 仍然成立.证明:连结BE 、AF .∵CD ⊥AB ,AE ⊥AB , ∴∠CDB=∠BAE=90°. 又∵BD = AE ,CD = AB ,△CDB ≌△BAE .……………… 3分∴CB=BE ,∠BCD=∠EBA .在Rt △CDB 中,∵∠CDB =90°,∴∠BCD+∠CBD =90°. ∴∠EBA+∠CBD =90°.即∠CBE =90°.∴△BCE 是等腰直角三角形.∴∠BCE=45°. ……………………………………………… 4分 同理可证:△ACF 是等腰直角三角形.∴∠ACF=45°. ……………………………………………… 5分 ∴∠ACF=∠BCE .∴∠ACF -∠ECF =∠BCE -∠ECF .即∠ACE=∠BCF .……………………………………………… 6分(3)∠ECF 的度数为90°-α.……………………………………………… 7分4321F E DCB A。
2012年北京各区县二模试题分类几何综合解析版

2012年北京各区县二模试题分类几何综合解析版2012年北京市中考数学二模分类汇编——几何综合与中点有关的问题1.(昌平24) 如图,D 是△ABC 中AB 边的中点,△BCE 和△ACF 都是等边三角形,M 、N 别是CE 、CF 的中点. (1)求证:△DMN 是等边三角形; (2)连接EF ,Q 是EF 中点,CP ⊥EF 于点P .求证:DP =DQ . 同学们,如果你觉得解决本题有困难,可以阅读下面两位同学的解题思路作为参考:小聪同学发现此题条件中有较多的中点,因此考虑构造三角形的中位线,添加出了一些辅助线;小慧同学想到要证明线段相等,可通过证明三角形全等,如何构造出相应的三角形呢?她考虑将△NCM 绕顶点旋转到要证的对应线段的位置,由此猜想到了所需构造的三角形的位置.24. 证明:(1)取AC 的中点G ,连接NG 、DG .NME F C∴DG =21BC ,DG ∥BC ;△NGC 是等边三角形.∴NG = NC CM . …………………2分 ∵∠1 + ∠2 = 180º,∴∠NGD + ∠2 = 240º.∵∠2 + ∠3 = 240º,∴∠NGD =∠3.∴△NGD≌△NCM . ……………………3分 ∴ND = NM ,∠GND =∠CNM .∴∠DNM =∠GNC = 60º.∴△DMN 是等边三角形.………………………………4分(2)连接QN 、PM .∴QN=21CE= PM . ……………………5分Rt △CPE 中,PM =EM ,∴∠4= ∠5.∵MN ∥EF ,∴∠5= ∠6,∠7=∠8.67854P Q N M E C C 321G NM E F∵NQ ∥CE ,∴∠7= ∠4.∴∠6= ∠8.∴∠QND = ∠PMD . ………………………6分∴△QND ≌△PMD .∴DQ = DP . ……………………7分2.(丰台24)在△ABC 中,D 为BC 边的中点,在三角形内部取一点P ,使得∠ABP =∠ACP .过点P 作PE ⊥AC 于点E ,PF ⊥AB 于点F . (1)如图1,当AB =AC 时,判断的DE 与DF 的数量关系,直接写出你的结论; (2)如图2,当AB AC ,其它条件不变时,(1)中的结论是否发生改变?请说明理由.图1图224.解:(1)DE =DF .……1分A E F PB DC E B A DF P(2)DE =DF 不发生改变. (2)分理由如下:分别取BP 、CP 的中点M 、N ,联结EM 、DM 、FN 、DN .∵D 为BC 的中点,∴BP DN BP DN //,21=.……3分∵,AB PE ⊥∴BP BM EM 21==. ∴21,∠=∠=EM DN .∴12213∠=∠+∠=∠.…4分 同理,524,//DM FN MD PC =∠=∠.∴四边形MDNP 为平行四边形.……5分∴67∠=∠ ∵,41∠=∠∴35∠=∠. ∴EMD DNF ∠=∠.……6分∴△EMD ≌△DNF . ∴DE =DF .……7分3.(海淀25.)在矩形ABCD 中, 点F 在AD 延长线上,且DF = DC , M 为AB 边上一点, N 为MD 的中点, 点E 在直线CF 上(点E 、C 不重合).(1)如图1, 若AB =BC , 点M 、A 重合, E为CF 的中点,试探究BN 与NE 的位置关系及BM CE 的值, 并证明你的结论;(2)如图2,且若AB =BC , 点M 、A 不重合,7654321N M C D B P F E ABN =NE ,你在(1)中得到的两个结论是否成立,若成立,加以证明; 若不成立, 请说明理由;(3)如图3,若点M 、A 不重合,BN =NE ,你在(1)中得到的结论两个是否成立, 请直接写出你的结论.图 1 图 2 图325. 解:(1)BN 与NE 的位置关系是BN ⊥NE ;CE BM 2 证明:如图,过点E 作EG ⊥AF 于G , 则∠EGN =90°.∵ 矩形ABCD 中, AB =BC ,∴ 矩形ABCD 为正方形.∴ AB =AD =CD , ∠A =∠ADC =∠DCB =90°.∴ EG//CD , ∠EGN =∠A , ∠CDF =90°.……………1分∵ E 为CF , F A ( M ) D N D A C E N M B F E C BF N M E C B∴ GF =DG =11.22DF CD = ∴ 1.2GE CD = ∵ N 为MD (AD )的中点,∴ AN =ND =11.22AD CD = ∴ GE =AN ,NG=ND+DG=ND+AN=AD=AB . ………2分∴ △NGE ≌△BAN .∴ ∠1=∠2.∵ ∠2+∠3=90°,∴ ∠1+∠3=90°.∴ ∠BNE =90°.∴ BN ⊥NE . ……………………………3分∵ ∠CDF =90°, CD =DF ,可得 ∠F =∠FCD =45°, 2.CF CD =. 于是122CF CE CE CE BM BA CD CD ==== …………4分(2)在(1)中得到的两个结论均成立.证明:如图,延长BN 交CD 的延长线于点G ,连结BE 、GE ,过E 作EH ⊥CE ,交CD 于点H .H B C E M∵四边形ABCD是矩形,∴AB∥CG.∴∠MBN=∠DGN,∠BMN=∠GDN.∵N为MD的中点,∴MN=DN.∴△BMN≌△GDN.∴MB=DG,BN=GN.∵BN=NE,∴BN=NE=GN.∴∠BEG=90°. (5)分∵EH⊥CE,∴∠CEH =90°.∴∠BEG=∠CEH.∴∠BEC=∠GEH.由(1)得∠DCF =45°.∴∠CHE=∠HCE =45°.∴EC=EH,∠EHG =135°.∵∠ECB=∠DCB+∠HCE =135°,∴∠ECB =∠EHG.∴△ECB≌△EHG.∴EB=EG,CB=HG.∵BN=NG,∴BN⊥NE. ……………………6分∵BM =DG= HG-HD= BC-HD =CD-2CE,∴2. ……………………7分CEBM不一定等于(3)BN⊥NE;CEBM2. ……………………8分密云25.已知菱形ABCD的边长为1,60ADC∠=o,等边△AEF两边分别交DC、CB于点E、F.(1)特殊发现:如图1,若点E、F分别是边DC、CB的中点,求证:菱形ABCD对角线AC、BD的交点O即为等边△AEF的外心;(2)若点E、F始终分别在边DC、CB上移动,记等边△AEF的外心为P.①猜想验证:如图2,猜想△AEF的外心P落在哪一直线上,并加以证明;②拓展运用:如图3,当E 、F 分别是边DC 、CB 的中点时,过点P 任作一直线,分别交DA 边于点M ,BC 边于点G ,DC 边的延长线于点N ,请你直接写出11DM DN+的值.25.(本小题满分8分)证明:(1)如图1:分别连结OE 、OF .∵四边形ABCD 是菱形,∴AD DC CB ==,AC BD ⊥,DO BO =, 且112302ADC ∠=∠=∠=o . ∴在Rt △AOD 中,有12AO AD =. 又 E 、F 分别是边DC 、CB 的中点,∴1122EO CB DC OF ===.∴AO EO FO ==.∴点O 即为等边△AEF 的外心. ------------------------- 3分(2)①猜想:△AEF 的外心P 落在对角线DB 所在的直线上.证明:如图2:分别连结PE 、PA ,作PQ DC ⊥于Q ,PH AD⊥于H .则90PQE PHD ∠=∠=o∵60ADC ∠=o, ∴在四边形QDHP 中,120QPH ∠=o.又 ∵点P 是等边△AEF 的外心,60EFA ∠=o,∴PE PA =,2260120EPA EFA ∠=∠=⨯=oo. ∴αβ∠=∠.∴△PQE ≌△PHA (AAS ).∴PQ=PH . ∴点P 在ADC ∠的角平分线上.∵菱形ABCD 的对角线DB 平分ADC ∠, ∴ 点P 落在对角线DB 所在直线上--- 6分 ②112DM DN+=. ---------------------- 8分 旋转变换在几何证明应用延庆24. (1)如图1:在△ABC 中,AB=AC ,当∠ABD =∠ACD=60°时,猜想AB 与BD+CD 数量关系,请直接写出结果 ;(2)如图2:在△ABC 中,AB=AC ,当∠ABD =∠ACD=45°时,猜想AB 与BD+CD 数量关系并证明你的结论; (3)如图3:在△ABC 中,AB=AC ,当∠ABD =∠ACD=β(20°≤β≤70°)时,直接写出AB 与BD+CD 数量关系(用含β的式子表示)。
2012北京中考二模海淀区数学试题(word无水印版含答案)

海淀区九年级第二学期期末练习数学试卷答案及评分参考 2012. 6说明: 与参考答案不同, 但解答正确相应给分. 一、选择题(本题共32分,每小题4分)1. B2. C3. A4. C5. B6. D7. D8. C 二、填空题(本题共16分,每小题4分)9.23x ≥10. 5 11. 12 12.8; 21n n +- (每空各 2分)三、解答题(本题共30分,每小题5分) 13115()3tan 604---+︒=54-+…………………………………………………4分=1. …………………………………………………5分14.解:去分母,得 ()()()()63223x x x x x ++-=-+. ………………………………2分2261826x x x x x ++-=+-. ……………………………………………………3分整理,得 324x =-.解得 8x =-. ………………………………………………………………4分 经检验,8x =-是原方程的解.所以原方程的解是8x =-. ……………………………………………………5分15.证明:∵ AC //EG ,∴ C C PG ∠=∠. …………1分 ∵ BC //EF ,∴ C P G F E G ∠=∠.∴ C F E G ∠=∠. …………………………………………2分在△ABC 和△GFE 中,,,,AC G E C FEG BC FE =⎧⎪∠=∠⎨=⎪⎩∴ △ABC ≌△GFE . …………………………………………………4分∴A G ∠=∠. …………………………………………………5分 16. 解:原式=()()()21111111a a a a a +-⋅-+-- ……………………………………………2分=()21111a a a +--- …………………………………………………3分=22.(1)a -- …………………………………………………4分由2220a a --=,得 2(1)3a -=.∴ 原式=23-. …………………………………………………5分17.解:(1)依题意设一次函数解析式为2y kx =+. …………………………………1分∵ 点A (2,0-)在一次函数图象上,GFE DCAP∴022k =-+.∴ k =1. ……………………………………………………2分 ∴ 一次函数的解析式为2y x =+. …………………………………3分 (2)A B C ∠的度数为15︒或105︒. (每解各1分) ……………………5分18.解: ∵∠ADB =∠CBD =90︒,∴ DE ∥CB . ∵ BE ∥CD , ∴ 四边形BEDC 是平行四边形. ………1分 ∴ BC=DE . 在Rt △ABD 中,由勾股定理得8AD ===. ………2分设D E x =,则8EA x =-. ∴8EB EA x ==-.在Rt △BDE 中,由勾股定理得 222D E B D E B +=.∴ 22248x x +=-(). ……………………………………………………3分∴ 3x =.∴ 3BC D E ==. ……………………………………………………4分 ∴1116622.22ABD BD C ABCD S S S BD AD BD BC ∆∆=+=⋅+⋅=+=四边形 ………… 5分四、解答题(本题共20分,第19题、第20题各5分,第21题6分, 第22题4分) 19.解:(1)甲图文社收费s (元)与印制数t (张)的函数关系式为0.11s t =. ……1分(2)设在甲、乙两家图文社各印制了x 张、y 张宣传单, 依题意得 {1500,0.110.13179.x y x y +=+= ………………………………………… 2分解得800,700.x y =⎧⎨=⎩ ……………………………………………… 3分答:在甲、乙两家图文社各印制了800张、700张宣传单. ………………4分(3) 乙 . ……………………………………………………… 5分20.(1)证明:连结OC .∴ ∠DOC =2∠A . …………1分∵∠D = 90°2A -∠, ∴∠D +∠DOC =90°.∴ ∠OCD =90°.∵ OC 是⊙O 的半径,∴ 直线CD 是⊙O 的切线. ………………………………………………2分 (2)解: 过点O 作OE ⊥BC 于E , 则∠OEC =90︒.∵ BC =4,∴ CE =12BC =2.∵ BC //AO ,∴ ∠OCE =∠DOC .∵∠COE +∠OCE =90︒, ∠D +∠DOC =90︒,∴ ∠COE =∠D . ……………………………………………………3分 ∵tan D =12,D EBA∴tan C O E ∠=12.∵∠OEC =90︒, CE =2, ∴4tan CE O E CO E==∠.在Rt △OEC 中, 由勾股定理可得O C ==在Rt △ODC 中, 由1tan 2O C D CD==,得CD =, ……………………4分由勾股定理可得10.O D =∴10.AD OA OD OC OD =+=+= …………………………………5分 21.解:(1)(64)50%20+÷=. 所以李老师一共调查了20名学生. …………………1分(2)C 类女生有 3 名,D 类男生有 1 名;补充条形统计图略.说明:其中每空1分,条形统计图1分. ……………………………………4分 (3)解法一:由题意画树形图如下:………………………5分从树形图看出,所有可能出现的结果共有6种,且每种结果出现的可能性相等,所选 两位同学恰好是一位男同学和一位女同学的结果共有3种. 所以P (所选两位同学恰好是一位男同学和一位女同学)=3162=. ………………6分 解法二:由题意列表如下:………………………5分由上表得出,所有可能出现的结果共有6种,且每种结果出现的可能性相等,所选 两位同学恰好是一位男同学和一位女同学的结果共有3种. 所以P (所选两位同学恰好是一位男同学和一位女同学)=3162=. ………………6分22.解:(1)画图如下:(答案不唯一) …………………………………2分图3(2)图3中△FGH 的面积为7a . …………………………………4分五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23. 解:(1)∵ 抛物线2(1)(2)1y m x m x =-+--与x 轴交于A 、B 两点,从D 类中选取从A 类中选取女女男男女女男女男∴210,(2)4(1)0.m m m ì- ïïíïD =-+->ïî由①得1m ¹, 由②得0m ¹,∴ m 的取值范围是0m ¹且1m ¹.……………………………………………2分 (2)∵ 点A 、B 是抛物线2(1)(2)1y m x m x =-+--与x 轴的交点,∴ 令0y =,即 2(1)(2)10m x m x -+--=. 解得 11x =-,211x m =-.∵1m >, ∴10 1.1m >>--∵ 点A 在点B 左侧,∴ 点A 的坐标为(1,0)-,点B 的坐标为1(,0)1m -. …………………………3分∴ OA=1,OB =11m -.∵ OA : OB =1 : 3, ∴131m =-.∴ 43m =.∴ 抛物线的解析式为212133y x x =--. ………………………………………4分(3)∵ 点C 是抛物线212133y x x =--与y 轴的交点,∴ 点C 的坐标为(0,1)-.依题意翻折后的图象如图所示. 令7y =,即 2121733x x --=.解得16x =, 24x =-.∴ 新图象经过点D (6,7). 当直线13y x b =+经过D 点时,可得5b =. 当直线13y x b =+经过C 点时,可得1b=-.当直线1(1)3y x b b =+<-与函数2121(0)33y x x x =-->的图象仅有一个公共点P (x 0, y 0)时,得20001121333x b x x +=--.整理得 203330.x x b ---= ①② …………………………………………1分由2(3)4(33)12210b b D =----=+=,得74b =-.结合图象可知,符合题意的b 的取值范围为15b -<≤或74b <-. ……………7分说明:15b -<≤ (2分),每边不等式正确各1分;74b <- (1分)24.解:(1)∵22222221212112()()4422y x x x m x m m x m m mmm m=-=-+-⋅=--,∴抛物线的顶点B 的坐标为11(,)22m m -. ……………………………1分(2)令2220x x m-=,解得10x =, 2x m =.∵ 抛物线xx my 222-=与x 轴负半轴交于点A ,∴ A (m , 0), 且m <0. …………………………………………………2分 过点D 作DF ⊥x 轴于F .由 D 为BO 中点,DF //BC , 可得CF =FO =1.2C O∴ DF =1.2BC由抛物线的对称性得 AC = OC . ∴ AF : AO =3 : 4. ∵ DF //EO ,∴ △AFD ∽△AOE . ∴.FD AF O EAO=由E (0, 2),B 11(,)22m m -,得OE =2, DF =14-∴134.24m -=∴ m = -6.∴ 抛物线的解析式为2123y x x =--. ………………………………………3分(3)依题意,得A (-6,0)、B (-3, 3)、C (-3, 0).可得直线OB 的解析式为x y -=,直线BC 为3x =-. 作点C 关于直线BO 的对称点C '(0,3),连接AC 于M ,则M 即为所求.由A (-6,0),C ' (0, 3),可得 直线AC '的解析式为321+=x y .由13,2y x y x⎧=+⎪⎨⎪=-⎩解得2,2.x y =-⎧⎨=⎩ ∴ 点M 的坐标为(-2, 2). ……………4分由点P 在抛物线2123y x x =--上,设P (t ,2123t t --).(ⅰ)当AM 为所求平行四边形的一边时. 如右图,过M 作MG ⊥ x 轴于G , 过P 1作P 1H ⊥ BC 于H , 则x G = x M =-2, x H = x B =-3. 由四边形AM P 1Q 1为平行四边形, 可证△AMG ≌△P 1Q 1H . 可得P 1H = AG =4. ∴ t -(-3)=4. ∴ t =1.∴17(1,)3P -. ……………………5分如右图,同 方法可得 P 2H=AG =4. ∴ -3- t =4. ∴ t =-7.∴27(7,3P --. ……………………6分(ⅱ)当AM 为所求平行四边形的对角线时, 如右图,过M 作MH ⊥BC 于H , 过P 3作P 3G ⊥ x 轴于G , 则x H = x B =-3,x G =3P x =t .由四边形AP 3MQ 3为平行四边形, 可证△A P 3G ≌△MQ 3H . 可得AG = MH =1. ∴ t -(-6)=1. ∴ t =-5. ∴35(5,)3P -. ……………………………………………………7分综上,点P 的坐标为17(1,)3P -、27(7,3P --、35(5,3P -.25. 解:(1)BN 与NE 的位置关系是BN ⊥NE ;C E B M2证明:如图,过点E 作EG ⊥AF 于G , 则∠EGN =90°.∵ 矩形ABCD 中, AB =BC ,∴ 矩形ABCD 为正方形.∴ AB =AD =CD , ∠A =∠ADC =∠DCB =90°.∴ EG//CD , ∠EGN =∠A , ∠CDF =90°. ………………………………1分 ∵ E 为CF 的中点,EG//CD , ∴ GF =DG =11.22DF CD =∴ 1.2G E CD =∵ N 为MD (AD )的中点, ∴ AN =ND =11.22AD CD =321FEA (M )CDB∴GE=AN, NG=ND+DG=ND+AN=AD=AB. ……………………………2分∴△NGE≌△BAN.∴∠1=∠2.∵∠2+∠3=90°,∴∠1+∠3=90°.∴∠BNE =90°.∴BN⊥NE.……………………………………………………………3分∵∠CDF =90°, CD=DF,可得∠F =∠FCD =45°,CFCD= .于是122CFCE CE CEBM BA CD CD====……………………………………4分(2)在(1)中得到的两个结论均成立.证明:如图,延长BN交CD的延长线于点G,连结BE、GE,过E作EH⊥CE,交CD于点H.∵四边形ABCD是矩形,∴AB∥CG.∴∠MBN=∠DGN,∠BMN=∠GDN.∵N为MD的中点,∴MN=DN.∴△BMN≌△GDN.∴MB=DG,BN=GN.∵BN=NE,∴BN=NE=GN.∴∠BEG=90°.……………………………………………5分∵EH⊥CE,∴∠CEH =90°.∴∠BEG=∠CEH.∴∠BEC=∠GEH.由(1)得∠DCF =45°.∴∠CHE=∠HCE =45°.∴EC=EH, ∠EHG =135°.∵∠ECB =∠DCB +∠HCE =135°,∴∠ECB =∠EHG.∴△ECB≌△EHG.∴EB=EG,CB=HG.∵BN=NG,∴BN⊥NE. ……………………………………………6分∵BM =DG= HG-HD= BC-HD =CD-CE,∴CEBM2. ……………………………………………7分(3)BN⊥NE;CEBM2.………………………………………………8分HGAB CDEMNF。
2012年北京市各区二模试题分类解析【数学理】(10):平面向量.pdf

课题使用人编号07课型新授课课时1主备人石伟锋 备课 时间教 学 目 标(一)情感、态度、价值观:树立正确的资源环境意识和对自然环境的忧患意识。
以保护环境为荣,以破坏环境为耻,树立人与自然和谐共处的人生价值。
有意识的控制人对自然的破坏行为。
(二)能力:能从自我做起,珍爱和保护大自然的一切生命。
提高保护自然、保护环境的能力。
(三)知识:了解人与大自然的不和谐之音的表现,懂得人与大自然和谐相处的重要性。
重点 难点 教学难点:自然景观遭到人为的破坏教具多媒体 电子白板教法学法 讨论、欣赏、感悟、体验历年考点 展示 交流 自然物种在减少 自然景观遭到人为破坏 教师引导,PPT出示材料,阅读思考、讨论: 大自然物种不断减少、甚至灭绝的原因是什么? 如何保护物种,我们能做些什么? 教师引导,PPT出示材料, 这些自然景观为什么遭到人为破坏? 如何去改变这种状况? 教师引导归纳总结 结合本地实际,探讨如何保护自然景观 学生先阅读课本和PPT材料 ⑴、思考讨论,学生畅所欲言 ⑵讨论:如何保护物种,我们能做些什么? 分小组交流: 结合本地实际,探讨如何保护自然景观 15教 学 过 程环节知识点教师活动学生活动估时合作 探究 展示 交流3、环境状况 不容乐观教师:PPT出示,环境的一些恶化状况的图片, 然后让学生谈谈所知道的情况 在观察的基础上, 让学生总结,什么是环境问题?有什么危害? 并初步探讨如何解决这些问题? 老师对一些有创意的观点和看法做法及时鼓励和表扬,激发学生探究和参与环保的热情,进行有效的情感教育和升华。
积极思考 结合实际 总结归纳 建言献策 11强化 应用 形成 能力巩固训练投放课堂练习 限时规范训练 巩固学习成果 规范答题 反馈补偿12 构建 网络知识结构1、先由学生谈谈观点、收获、体会。
2、老师总结2教后反思 初中学习网,资料共分享!我们负责传递知识! 含义:是指人类不合理地开发利用自然资源所造成的环境污染与破坏。
2012年北京各区县二模试题分实验操作题解析版
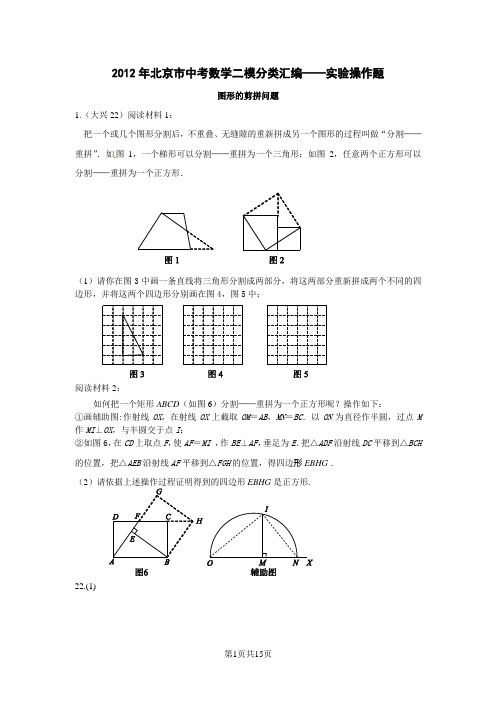
2012年北京市中考数学二模分类汇编——实验操作题图形的剪拼问题1.(大兴22)阅读材料1:把一个或几个图形分割后,不重叠、无缝隙的重新拼成另一个图形的过程叫做“分割——重拼”.如图1,一个梯形可以分割——重拼为一个三角形;如图2,任意两个正方形可以分割——重拼为一个正方形.(1)请你在图3中画一条直线将三角形分割成两部分,将这两部分重新拼成两个不同的四边形,并将这两个四边形分别画在图4,图5中;阅读材料2:如何把一个矩形ABCD(如图6)分割——重拼为一个正方形呢?操作如下:①画辅助图:作射线OX,在射线OX上截取OM=AB,MN=BC.以ON为直径作半圆,过点M 作MI⊥OX,与半圆交于点I;②如图6,在CD上取点F,使AF=MI,作BE⊥AF,垂足为E.把△ADF沿射线DC平移到△BCH 的位置,把△AEB沿射线AF平移到△FGH的位置,得四边形EBHG.(2EBHG是正方形.22.(1)2分 (2)证明:在辅助图中,连接∵ON 是所作半圆的直径,∴∠OIN =90°.∵M I ⊥ON , ∴∠OMI =∠IMN =90°且∠∴△OIM ∽△INM .∴OM IM =IM NM .即IM 2=OM ·NM .………………3分 ∵OM=AB ,MN=BC ∴IM 2 = AB ·BC∵AF=IM ∴AF 2=AB ·BC=AB ·AD .∵四边形ABCD 是矩形,BE ⊥AF ,∴DC ∥AB ,∠ADF =∠BEA =90°. ∴∠DFA =∠EAB .∴△DFA ∽△EAB . ∴AD BE =AFAB .即AF ·BE =AB ·AD=AF 2.∴AF =BE .……………………4分∵AF=BH ∴BH =BE . 由操作方法知BE ∥GH ,BE =GH .∴四边形EBHG 是平行四边形. ∵∠GEB =90°,∴四边形EBHG 是正方形.………………………5分2.(怀柔22)阅读下面材料:在数学课上,李老师给同学们提出两个问题:①“谁能将下面的任意三角形分割后,再拼成一个矩形”;②“谁能将下面的任意四边形分割后,再拼成一个平行四边形”.图⑤ 图⑥图⑦图⑧ 图⑨图① 图② 图③ 图④. 经过小组同学动手合作,第3案,如图1和图2所示;请你参考小亮同学的做法,解决下列问题:(1)“请你将图3再设计一种分割方法,沿分割线剪开后所得的几块图形恰好也能拼成一个矩形”;(2)“请你设计一种方法,将图4分割后,再拼成一个矩形”.22.答案:(说明:本题分割方法不唯一)(1)…………………2分方法一、方法二、方法三、方法四、(2)……5分方法一、方法二、图形的面积问题3.(房山22)⑴阅读下面材料并完成问题:已知:直线AD与△ABC的边BC交于点D,①如图1,当BD=DC时,则S△ABD________S△ADC.(填“=”或“<”或“>”)图3图4DBCADBCABCAD图1 图2 图3②如图2,当BD =21DC 时,则=∆ABD S A D C S ∆ .③如图3,若AD ∥BC ,则有S ∆DBC S ∆ .(填“=”或“<”或“>”)⑵请你根据上述材料提供的信息,解决下列问题:过四边形ABCD 的一个顶点画一条直线,把四边形ABCD 的面积分成1︰2的两部分.(保留画图痕迹)22.①=--------------------------------------1分②21--------------------------------------2分③=--------------------------------------3分⑵BDE ∥AC 交BC 延长线于点E F 为BE 三等分点 过E 作F G ∥BD 交DC 于点E ,BC 于G 则直线AF 为所求 则直线DG 为所求 --------------------------------------5分BCADlN4.(西城区22) 阅读下列材料小华在学习中发现如下结论:如图1,点A ,A 1,A 2在直线l 上,当直线l ∥BC 时,BCABC A ABC S S S 21∆∆∆==.请你参考小华的学习经验画图(保留画图痕迹):(1)如图2,已知△ABC ,画出一个..等腰△DBC ,使其面积与△ABC 面积相等; (2)如图3,已知△ABC ,画出两个..Rt △DBC ,使其面积与△ABC 面积相等(要求:所画的两个三角形不全等...); (3)如图4,已知等腰△ABC 中,AB=AC ,画出一个..四边形ABDE ,使其面积与△ABC 面积相等,且一组对边DE=AB ,另一组对边BD ≠AE ,对角∠E =∠B .图2 图3 图422.解:(1) 如图所示,答案不唯一. 画出△D 1BC ,△D 2BC ,△D 3BC ,△D 4BC ,△D 5BC 中的一个即可.(将BC 的平行线l 画在直线BC 下方对称位置所画出的三角形亦可)﹍﹍ 2分符合要求的点,或将BC 的平行线画在直线BC 下方对称位置所画出的三角形亦可) ﹍﹍﹍﹍﹍﹍﹍﹍﹍4分(3) 如图所示(答案不唯一).﹍﹍﹍ 5分如上图所示的四边形ABDE 的画法说明:(1)在线段BC 上任取一点D (D 不为BC 的中点),连结AD ;(2)画出线段AD 的垂直平分线MN ;(3)画出点C 关于直线MN 的对称点E ,连结DE ,AE . 则四边形ABDE 即为所求.B5.(平谷22)在数学活动课上,老师请同学们在一张长为18cm ,宽为14cm 的长方形纸上剪下一个腰为12cm 的等腰三角形(要求等腰三角形的一个顶点与长方形的一个顶点重合,其余两个顶点在长方形的边上).小明同学按老师要求画出了如图(1)的设计方案示意图,请你画出与小明的设计方案不同的所有满足老师要求的示意图,并通过计算说明哪种情况下剪下的等腰三角形的面积最小(含小明的设计方案示意图).22.正确画出图形2分图(1)272AEF S cm ∆=;..........................................................3分图(2)2AEF S ∆=;..................................................4分 图(3)2AEF S ∆=.比较上述计算结果可知,图(3)剪下的三角形面积最小. ...............5分图形变换操作题6.(延庆22)阅读下面材料:阅读下面材料:小伟遇到这样一个问题:如图1,在△ABC (其中∠BAC 是一个可以变化的角)中,AB=2,AC=4,以BC 为边在BC 的下方作等边△PBC ,求AP 的最大值。
2012年北京海淀区中考二模数学试卷

2012年北京海淀中考二模数 学2012年6月一、选择题(本题共 32 分,每小题 4 分)下面各题均有四个选项,其中只有一个是符合题意的 1.-5的倒数是A .15B .15C .5D .52.2012年4月22日是第43个世界地球日,中国国土资源报社联合腾讯网发起“世界地球日”微话题,共有18 891 511人次参与了这次活动,将18 891 511用科学记数法表示(保留三个有效数字)约为A. 18.9 106B. 0.189 108C. 1.89 107D. 18.8 1063.把2x 2 − 4x + 2分解因式,结果正确的是A .2(x − 1)2B .2x (x − 2)C .2(x 2 − 2x + 1)D .(2x −2)24.右图是由七个相同的小正方体堆砌而成的几何体,则这个几何体的俯视图是A B C D5.从1, -2, 3这三个数中,随机抽取两个数相乘,积为正数的概率是A .0B .13C .23D .16.如图,在△ABC 中,∠C =90°,BC =3,D ,E 分别在 AB 、AC 上,将△ADE 沿DE翻折后,点A 落在点A ′处,若A ′为CE 的中点,则折痕DE 的长为C. 中位数是51.5D. 众数是588.如图,在梯形ABCD 中,AD //BC ,∠ABC =60°,AB = DC =2, AD =1,R 、P 分别是BC 、CD 边上的动点(点R 、B 不重合, 点P 、C 不 重合),E 、F 分别是AP 、RP 的中点,设BR=x ,EF=y ,则下列 图象中,能表示y 与x 的函数关系的图象大致是A B C D二、填空题(本题共16分,每小题4分) 9.若二次根式23 x 有意义,则 x 的取值范围是.10.若一个多边形的内角和等于540 ,则这个多边形的边数是.11.如图,在平面直角坐标系xOy 中,已知点A 、B 、C 在双曲线xy 6上,BD x 轴于D , CE y 轴于E ,点F 在x 轴上,且AO =AF , 则图中阴影部分的 面积之和为 .12.小东玩一种“挪珠子”游戏,根据挪动珠子的难度不同而得分不同,规定每次挪动珠子的颗数与所得分数的对应关系如下表所示:按表中规律,当所得分数为71分时,则挪动的珠子数为颗; 当挪动n 颗珠子时(n 为大于1的整数), 所得分数为 (用含n 的代数式表示).三、解答题(本题共30分,每小题5分)1311|5|()3tan604. F E P B CD A 班级14.解方程:6123x x x . 15.如图,AC //EG , BC //EF , 直线GE 分别交BC 、BA 于P 、D ,且AC=GE , BC=FE .求证: A = G .16.已知2220a a ,求代数式221111121a a a a a 的值.17.如图,一次函数的图象与x 轴、y 轴分别交于点A (-2, 0)、B (0, 2).(1)求一次函数的解析式; (2)若点C 在x 轴上,且OC =23, 请直接写出 ABC 的度数.18.如图,在四边形ABCD 中, ADB = CBD =90 ,BE//CD 交AD 于E , 且EA=EB .若AB=54,DB =4, 求四边形ABCD 的面积.GFED C A PEDCA四、解答题(本题共20分,每小题5分)19.某街道办事处需印制主题为“做文明有礼的北京人,垃圾减量垃圾分类从我做起”的宣传单. 街道办事处附近的甲、乙两家图文社印制此种宣传单的收费标准如下:甲图文社收费s (元)与印制数t (张)的函数关系如下表:乙图文社的收费方式为:印制2 000张以内(含2 000张),按每张0.13元收费;超过 2 000张,均按每张0.09元收费.(1)根据表中给出的对应规律,写出甲图文社收费s (元)与印制数t (张)的函数关系式; (2)由于马上要用宣传单,街道办事处同时在甲、乙两家图文社共印制了1 500张宣传单,印制费共179元,问街道办事处在甲、乙两家图文社各印制了多少张宣传单?(3)若在下周的宣传活动中,街道办事处还需要加印5 000张宣传单,在甲、乙两家图文社中选择 图文社更省钱.20.如图,AC 、BC 是⊙O 的弦, BC //AO , AO 的延长线与过点C 的射线交于点D , 且D =90 -2 A .(1)求证:直线CD 是⊙O 的切线;(2)若BC=4,1tan 2D ,求CD 和AD 的长.21.李老师为了了解所教班级学生完成数学课前预习的具体情况,对本班部分学生进行了为期半个月的跟踪调查,他将调查结果分为四类,A :很好;B :较好;C :一般;D :较差.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:(1)李老师一共调查了多少名同学?(2)C 类女生有 名,D 类男生有 名,将上面条形统计图补充完整; (3)为了共同进步,李老师想从被调查的A 类和D 类学生中各随机选取一位同学进行 “一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位 男同学和一位女同学的概率.22.阅读下面材料:小明遇到这样一个问题:我们定义: 如果一个图形绕着某定点旋转一定的角度 (0 < <360 ) 后所得的图形与原图形重合,则称此图形是旋转对称图形. 如等边三角形就是一个旋转角为120 的旋转对称图形. 如图1,点O 是等边三角形△ABC 的中心, D 、E 、F 分别为AB 、BC 、 CA 的中点, 请你将△ABC 分割并拼补成一个与△ABC.图1 图2小明利用旋转解决了这个问题,图2中阴影部分所示的图形即是与△ABC 面积相等的新的旋转对称图形.请你参考小明同学解决问题的方法,利用图形变换解决下列问题: 如图3,在等边△ABC 中, E 1、E 2、E 3分别为AB 、 BC 、CA 的中点,P 1、P 2, M 1、M 2, N1、N 2分别为 AB 、BC 、CA 的三等分点.(1)在图3中画出一个和△ABC 面积相等的新的旋转 对称图形,并用阴影表示(保留画图痕迹); (2)若△ABC 的面积为a ,则图3中△FGH 的面积为 .E 3E 1 2 P 1P 2N 1N 2B A 图3GFH 类别50%25%15%D C B A五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23.已知抛物线 2(1)(2)1y m x m x 与x 轴交于A 、B 两点.(1)求m 的取值范围;(2)若m >1, 且点A 在点B 的左侧,OA : OB =1 : 3, 试确定抛物线的解析式;(3)设(2)中抛物线与y 轴的交点为C ,过点C 作直线l //x 轴, 将抛物线在y 轴左侧的部分沿直线 l 翻折, 抛物线的其余部分保持不变,得到一个新图象. 请你结合新图象回答: 当直线13y x b 与新图象只有一个公共点P (x 0, y 0)且 y 07时, 求b 的取值范围.24.如图, 在平面直角坐标系xOy 中,抛物线x x my 222与x 轴负半轴交于点A , 顶点为B , 且对称轴与x 轴交于点C .(1)求点B 的坐标 (用含m 的代数式表示);(2)D 为BO 中点,直线AD 交y 轴于E ,若点E 的坐标为(0, 2), 求抛物线的解析式;(3)在(2)的条件下,点M 在直线BO 上,且使得△AMC 的周长最小,P 在抛物线上,Q 在直线 BC 上,若以A 、M 、P 、Q 为顶点的四边形是平行四边形,求点P 的坐 标.备用图25.在矩形ABCD 中, 点F 在AD 延长线上,且DF = DC , M 为AB 边上一点, N 为MD 的中点, 点E 在直线CF 上(点E 、C 不重合).(1)如图1, 若AB =BC , 点M 、A 重合, E 为CF 的中点,试探究BN 与NE 的位置关系及BMCE的值, 并证明你的结论; (2)如图2,且若AB =BC , 点M 、A 不重合, BN =NE ,你在(1)中得到的两个结论是否成立, 若成立,加以证明; 若不成立, 请说明理由;(3)如图3,若点M 、A 不重合,BN =NE ,你在(1)中得到的结论两个是否成立, 请直接写出你的结论.图1 图2 图3FA ( M) DNDCENM B FECBFNMECB A数学试卷答案及评分参考阅卷须知:1.为便于阅卷,本试卷答案中有关解答题的推导步骤写得较为详细,阅卷时,只要考生将主要过程正确写出即可.2.若考生的解法与给出的解法不同,正确者可参照评分参考相应给分. 3.评分参考中所注分数,表示考生正确做到此步应得的累加分数. 一、选择题(本题共32分,每小题4分) 1.B 2.C 3.A 4.C 5.B 6.D 7.D 8.C二、填空题(本题共16分,每小题4分) 9.23x10.511.1212.8; 21n n (每空各 2分)三、解答题(本题共30分,每小题5分)13115()3tan604=54 …………………………………………………4分=1.…………………………………………………5分14.解:去分母,得 63223x x x x x . ………………………………2分2261826x x x x x . ……………………………………………………3分 整理,得 324x .解得 8x .………………………………………………………………4分 经检验,8x 是原方程的解. 所以原方程的解是8x . ……………………………………………………5分15.证明:∵ AC //EG ,∴ C CPG . …………1分∵ BC //EF ,∴ CPG FEG . ∴ C FEG . …………………………………………2分在△ABC 和△GFE 中,,,,AC GE C FEG BC FE ∴ △ABC ≌△GFE . …………………………………………………4分 ∴A G .…………………………………………………5分GFEDC BAP16.解:原式= 21111111a a a a a……………………………………………2分 =21111a a a…………………………………………………3分 =22.(1)a …………………………………………………4分由2220a a ,得 2(1)3a .∴ 原式=23.…………………………………………………5分17.解:(1)依题意设一次函数解析式为2y kx .…………………………………1分∵ 点A (2,0)在一次函数图象上, ∴022k .∴ k =1. ……………………………………………………2分 ∴ 一次函数的解析式为2y x .…………………………………3分 (2)ABC 的度数为15 或105 . (每解各1分) ……………………5分 18.解: ∵ ADB = CBD =90 ,∴ DE ∥CB . ∵ BE ∥CD ,∴ 四边形BEDC 是平行四边形. ………1分 ∴ BC=DE .在Rt △ABD 中,由勾股定理得8AD . ………2分 设DE x ,则8EA x . ∴8EB EA x .在Rt △BDE 中,由勾股定理得 222DE BD EB . ∴ 22248x x ().……………………………………………………3分∴ 3x .∴ 3BC DE .……………………………………………………4分∴1116622.22ABD BDC ABCD S S S BD AD BD BC 四边形………… 5分四、解答题(本题共20分,第19题、第20题各5分,第21题6分, 第22题4分)19.解:(1)甲图文社收费s (元)与印制数t (张)的函数关系式为0.11s t . ……1分(2)设在甲、乙两家图文社各印制了x 张、y 张宣传单, 依题意得1500,0.110.13179.x y x y ………………………………………… 2分解得800,700.x y……………………………………………… 3分答:在甲、乙两家图文社各印制了800张、700张宣传单. ………………4分 (3) 乙 . ……………………………………………………… 5分DEC20.(1)证明:连结OC .∴ ∠DOC =2∠A . …………1分 ∵∠D = 90°2A , ∴∠D +∠DOC =90°. ∴ ∠OCD =90°.∵ OC 是⊙O 的半径,∴ 直线CD 是⊙O 的切线. ………………………………………………2分 (2)解: 过点O 作OE ⊥BC 于E , 则∠OEC =90 .∵ BC =4,∴ CE =12BC =2.∵ BC //AO , ∴ ∠OCE =∠DOC .∵∠COE +∠OCE =90 , ∠D +∠DOC =90 , ∴ ∠COE =∠D . ……………………………………………………3分∵tan D =12,∴tan COE 12.∵∠OEC =90 , CE =2,∴4tan CEOE COE.在Rt △OEC 中, 由勾股定理可得OC 在Rt △ODC 中, 由1tan 2OC D CD,得CD ……………………4分由勾股定理可得 10.OD∴10.AD OA OD OC OD …………………………………5分21.解:(1)(64)50%20 . 所以李老师一共调查了20名学生. …………………1分(2)C 类女生有 3 名,D 类男生有 1 名;补充条形统计图略.说明:其中每空1分,条形统计图1分. ……………………………………4分 (3)解法一:由题意画树形图如下:………………………5分从树形图看出,所有可能出现的结果共有6种,且每种结果出现的可能性相等,所选 两位同学恰好是一位男同学和一位女同学的结果共有3种. 所以P (所选两位同学恰好是一位男同学和一位女同学)=3162. ………………6分 解法二:由题意列表如下:从D 类中选取从A 类中选取女女男男女女男女男5分由上表得出,所有可能出现的结果共有6种,且每种结果出现的可能性相等,所选 两位同学恰好是一位男同学和一位女同学的结果共有3种. 所以P (所选两位同学恰好是一位男同学和一位女同学)=3162. ………………6分22.解:(1)画图如下:(答案不唯一)…………………………………2分图3(2)图3中△FGH 的面积为7a . …………………………………4分五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23.解:(1)∵ 抛物线2(1)(2)1y m x m x 与x 轴交于A 、B 两点,∴210,(2)4(1)0.m m m 由①得1m ,由②得0m ,∴ m 的取值范围是0m且1m . ……………………………………………2分(2)∵ 点A 、B 是抛物线2(1)(2)1y m x m x 与x 轴的交点,∴ 令0y ,即 2(1)(2)10m x m x .解得 11x ,211x m .∵1m ,∴10 1.1m ∵ 点A 在点B 左侧,∴ 点A 的坐标为(1,0) ,点B 的坐标为1(,0)1m . …………………………3分 ∴ OA=1,OB =11m .∵ OA : OB =1 : 3,∴131m . ①②…………………………………………1分∴ 3m.∴ 抛物线的解析式为212133y x x . ………………………………………4分(3)∵ 点C 是抛物线212133y x x 与y 轴的交点,∴ 点C 的坐标为(0,1).依题意翻折后的图象如图所示. 令7y ,即2121733x x . 解得16x , 24x .∴ 新图象经过点D (6,7).当直线13y x b 经过D 点时,可得5b .当直线13y x b 经过C 点时,可得1b .当直线1(1)3y x b b 与函数2121(33y x x x 的图象仅有一个公共点P (x 0, y 0)时,得20001121333x b x x . 整理得203330.x x b 由2(3)4(33)12210b b ,得74b 结合图象可知,符合题意的b 的取值范围为15b 或4b. ……………7分 24.解:(1)∵22222221212112()()4422y x x x mx m m x m m m m m m , ∴抛物线的顶点B 的坐标为11(,)22m m . ……………………………1分(2)令2220x x m,解得10x ,2x m .∵ 抛物线x x my 222 与x 轴负半轴交于点A ,∴ A (m , 0), 且m <0. …………………………………………………2分过点D 作DF x 轴于F .由 D 为BO 中点,DF //BC , 可得CF =FO =1.2CO ∴ DF =1.2BC由抛物线的对称性得 AC = OC . ∴ AF : AO =3 : 4.∵ DF //EO ,∴ △AFD ∽△AOE . ∴.FD AFOE AO由E (0, 2),B 11(,)22m m ,得OE =2, DF =14m .∴134.24m∴ m = -6.∴ 抛物线的解析式为2123y x x . ………………………………………3分(3)依题意,得A (-6,0)、B (-3, 3)、C (-3, 0).可得直线OB 的解析式为x y,直线BC 为3x . 作点C 关于直线BO 的对称点C (0,3),连接AC 交BO 于M ,则M 即为所求. 由A (-6,0),C (0, 3),可得 直线AC 的解析式为321x y .由13,2y x y x解得2,2.x y ∴ 点M 的坐标为(-2, 2).……………4分由点P 在抛物线2123y x x 上,设P (t ,213t (ⅰ)当AM 为所求平行四边形的一边时.如右图,过M 作MG x 轴于G , 过P 1作P 1H BC 于H ,则x G = x M =-2, x H = x B =-3.由四边形AM P 1Q 1为平行四边形, 可证△AMG ≌△P 1Q 1H . 可得P 1H = AG =4. ∴ t -(-3)=4. ∴ t =1.∴17(1,)3P . ……………………5分 如右图,同 方法可得 P 2H=AG =4. ∴ -3- t =4. ∴ t =-7.∴27(7,)3P . ……………………6分(ⅱ)当AM 为所求平行四边形的对角线时, 如右图,过M 作MH BC 于H , 过P 3作P 3G x 轴于G ,则x H = x B =-3,x G =3P x =t .由四边形AP 3MQ 3为平行四边形, 可证△A P 3G ≌△MQ 3H . 可得AG = MH =1. ∴ t -(-6)=1. ∴ t =-5. ∴35(5,)3P . (7)综上,点P 的坐标为17(1,)3P 、27(7,)3P 、3(5,)3P . 25.解:(1)BN 与NE 的位置关系是BN ⊥NE ;CEBM 证明:如图,过点E 作EG ⊥AF 于G , 则∠EGN =90°.∵ 矩形ABCD 中, AB =BC , ∴ 矩形ABCD 为正方形.∴ AB =AD =CD , ∠A =∠ADC =∠DCB =90°.∴ EG//CD , ∠EGN =∠A , ∠CDF =90°. ………………………………1分 ∵ E 为CF 的中点,EG//CD ,∴ GF =DG =11.22DF CD∴ 1.2GE CD∵ N 为MD (AD )的中点, ∴ AN =ND =11.22AD CD ∴ GE =AN , NG=ND+DG=ND+AN=AD=AB . ……………………………2分∴ △NGE ≌△BAN . ∴ ∠1=∠2.∵ ∠2+∠3=90°, ∴ ∠1+∠3=90°. ∴ ∠BNE =90°. ∴ BN ⊥NE . ……………………………………………………………3分 ∵ ∠CDF =90°, CD =DF , 可得 ∠F =∠FCD =45°,2.CF CD .于是122.CF CE CE CE BM BA CD CD……………………………………4分(2)在(1)中得到的两个结论均成立.证明:如图,延长BN 交CD 的延长线于点G ,连结BE 、GE ,过E 作EH ⊥CE ,交CD 于点H .∵ 四边形ABCD 是矩形, ∴ AB ∥CG .321FEA (CNB∴∠MBN=∠DGN,∠BMN=∠GDN.∵N为MD的中点,∴MN=DN.∴△BMN≌△GDN.∴MB=DG,BN=GN.∵BN=NE,∴BN=NE=GN.∴∠BEG=90°.………………………5分∵EH⊥CE,∴∠CEH =90°.∴∠BEG=∠CEH.∴∠BEC=∠GEH.由(1)得∠DCF =45°.∴∠CHE=∠HCE =45°.∴EC=EH,∠EHG =135°.∵∠ECB =∠DCB +∠HCE =135°,∴∠ECB =∠EHG.∴△ECB≌△EHG.∴EB=EG,CB=HG.∵BN=NG,∴BN⊥NE. ……………………………………………6分∵BM =DG= HG-HD= BC-HD =CD-CE,∴CEBM. ……………………………………………7分(3)BN⊥NE;CEBM.………………………………………………8分HGAB CDEMNF。
2012年北京市东城区、西城区、海淀区初三数学二模试题及答案
北京市东城区 2011--2012 学年第二学期初三综合练习(二)一、选择题(本题共 32 分,每小题 4 分) 下面各题均有四个选项,其中只有一个是符合题意的. 1. 1 2的绝对值是1 2A.B. 1 2C. 2D.-22. 下列运算中,正确的是 A. a a a B. a a a C. a a a D. 4 a a 3 a 3.一个不透明的袋中装有除颜色外均相同的 5 个红球和 3 个黄球,从中随机摸出一个,摸到黄球的概率 是2 3 5 3 4 12632A.1 8B.1 3C.3 8D.3 54.下列图形中,既是轴对称图形又是中心对称图形的是 .. ..D B C A 5. 若一个正多边形的一个内角等于 150° ,则这个正多边形的边数是 A.9 B.10 C.11 D.12 6. 在“我为震灾献爱心”的捐赠活动中,某班 40 位同学捐款金额统计如下: 金额(元) 学生数(人) 20 3 30 7 35 5 50 15 100 10 D.15,502 2y则在这次活动中,该班同学捐款金额的众数和中位数是 A.30,35 B.50,35 C.50,50 7.已知反比例函数 y A.没有实根 C.有两个相等实根k2 xOx的图象如图所示,则一元二次方程 x ( 2 k 1) x k 1 0 根的情况是 B. 有两个不等实根 D.无法确定2 28.用 min{a,b}表示 a,b 两数中的最小数,若函数 y min{ x 1, 1 x } ,则 y 的图象为y1 1 xy1y1y1 1 x -1-1 0-1 01 x-1 001 xA B 二、填空题(本题共 16 分,每小题 4 分)CD9. 反比例函数 y k x的图象经过点(-2,1) ,则 k 的值为_______. .主视图 俯视图 左视图10. 已知一个几何体的三视图如图所示,则该几何体是 11. 如图,将三角板的直角顶点放置在直线 AB 上的点 O 处. 使斜边 CD∥AB,则∠a 的余弦值为__________.12. 如图, R t △ A B C 中, A C B 9 0 , C A B 3 0 , B C 2 ,O, H 分别为边 A B, A C 的中点,将 △ A B C 绕点 B 顺时针旋A1转 1 2 0 到 △ A1 B C 1 的位置,则整个旋转过程中线段 O H 所扫过 部分的面积(即阴影部分面积)为 三、解答题(本题共 30 分,每小题 5 分)2 13. 先化简,再求值: (2 x 1) ( x 2)( x 2) 4 x ( x 1) ,其中 x H A OC B.O1H1 C13 3 2.14. 解分式方程:x 1 x 21 2 x 3.15. 如图, A、 、 的坐标分别为 点 B C (3, 、 3) (2, 、 1) (5, , 1) 将△ABC 先向下平移 4 个单位, 得△A1B1C1; 再将△A1B1C1 沿 y 轴翻折,得△A2B2C2. (1)画出△A1B1C1 和△A2B2C2; A (2)求线段 B2C 长. B O C x y16. 如图,点 D 在 A B 上, D F 交 A C 于点 E , C F ∥ A B , A E E C . 求证: A D C F . A D B E FC17. 列方程或方程组解应用题 为了配合学校开展的“爱护地球母亲”主题活动,初三(1)班提出“我骑车我快乐”的口号. “五一”之后小 明不用父母开车送,坚持自己骑车上学. 五月底他对自己家的用车情况进行了统计,5 月份所走的总路程 比 4 月份的4 5还少 100 千米,且这两个月共消耗 93 号汽油 260 升. 若小明家的汽车平均油耗为 0.1 升/千米,求他家 4、5 两月各行驶了多少千米.18.如图,矩形 ABCD 的边 AB 在 x 轴上,AB 的中点与原点 O 重合,AB=2,AD=1,点 Q 的坐标为(0,2). (1)求直线 QC 的解析式; (2)点 P(a,0)在边 AB 上运动,若过点 P、Q 的直线将矩形 ABCD 的周长分成 3∶1 两部分,求出此时 a 的值.四、解答题(本题共 20 分,每小题 5 分) 19. 如图,在梯形 ABCD 中,AD//BC,BD 是∠ABC 的平分线. (1)求证:AB=AD;A D(2)若∠ABC=60° ,BC=3AB,求∠C 的度数BC20. 如图,四边形 ABCD 是平行四边形,以 AB 为直径的⊙O 经过点 D,E 是⊙O 上一点,且AED=45. (1) 试判断 CD 与⊙O 的位置关系,并证明你的结论; (2) 若⊙O 的半径为 3,sinADE=5 6,求 AE 的值.21.某商店在四个月的试销期内,只销售 A,B 两个品牌的电视机,共售出 400 台.试销结束后,将决定 经销其中的一个品牌.为作出决定,经销人员正在绘制两幅统计图,如图 l 和图 2. (1)第四个月销量占总销量的百分比是_______; (2)在图 2 中补全表示 B 品牌电视机月销量的折线图; (3)经计算,两个品牌电视机月销量的平均水平相同,请你结合折线的走势进行简要分析,判断该商店 应经销哪个品牌的电视机.图1图222. 如图 1 是一个三棱柱包装盒, 它的底面是边长为 10cm 的正三角形, 三个侧面都是矩形. 现将宽为 15cm 的彩色矩形纸带 AMCN 裁剪成一个平行四边形 ABCD(如图 2) ,然后用这条平行四边形纸带按如图 3 的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分) ,纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.在图 3 中,将三棱柱沿过点 A 的侧棱剪开,得到如图 4 的 侧面展开图.为了得到裁剪的角度,我们可以根据展开图拼接出符合条件的平行四边形进行研究. (1)请在图 4 中画出拼接后符合条件的平行四边形; (2)请在图 2 中,计算裁剪的角度(即∠ABM 的度数).A MDNB图2C图1D F A图4C E B五、解答题(本题共 22 分,第 23 题 7 分,第 24 题 7 分,第 25 题 8 分) 23. 已知关于 x 的一元二次方程 x 2 ax b 0 , a 0 , b 0 .2 2(1)若方程有实数根,试确定 a,b 之间的大小关系;(2)若 a∶b=2∶ 3 ,且 2 x1 x 2 2 ,求 a,b 的值; (3)在(2)的条件下,二次函数 y x 2 a x b 的图象与 x 轴的交点为 A、C(点 A 在点 C 的左侧) ,2 2与 y 轴的交点为 B,顶点为 D.若点 P(x,y)是四边形 ABCD 边上的点,试求 3x-y 的最大值.24. 如图 1,在△ ABC 中,AB=BC=5,AC=6. △ ECD 是△ ABC 沿 CB 方向平移得到的,连结 AE,AC 和 BE 相交于点 O. (1)判断四边形 ABCE 是怎样的四边形,并证明你的结论; (2) 如图 2, 是线段 BC 上一动点 P (不与点 B、C 重合) 连接 PO 并延长交线段 AE 于点 Q, , QR⊥BD, 垂足为点 R.①四边形 PQED 的面积是否随点 P 的运动而发生变化?若变化,请说明理由;若不变,求出四边 形 PQED 的面积; ②当线段 BP 的长为何值时,以点 P、Q、R 为顶点的三角形与△ BOC 相似?E Q AEAOODC 图1BDC R 图2PB25. 如图,已知在平面直角坐标系 xOy 中,直角梯形 OABC 的边 OA 在 y 轴的正半轴上,OC 在 x 轴的正半 轴上,OA=AB=2,OC=3,过点 B 作 BD⊥BC,交 OA 于点 D.将∠DBC 绕点 B 按顺时针方向旋转, 角的两边分别交 y 轴的正半轴、x 轴的正半轴于点 E 和 F. (1)求经过 A、B、C 三点的抛物线的解析式; (2)当 BE 经过(1)中抛物线的顶点时,求 CF 的长; (3)在抛物线的对称轴上取两点 P、Q(点 Q 在点 P 的上方) ,且 PQ=1,要使四边形 BCPQ 的周长最 小,求出 P、Q 两点的坐标. y E A D O F C x B北京市东城区 2010--2011 学年第二学期初三综合练习(二) 数学试卷参考答案一、选择题(本题共 32 分,每小题 4 分)题 号 答 案 题 号 答 案1 A 9 -22 D3 C 10 圆柱4 B5 D 111 26 C7 A 12 π8 A二、填空题(本题共 16 分,每小题 4 分)三、解答题: (本题共 30 分,每小题 5 分) 13. (本小题满分 5 分) 解: 原式 4 x 4 x 1 x 4 4 x 4 x2 2 2„„„„„„3 分 „„„„„„4 分 x 3 .2当x 3 3 2时 , 27 15 3 . 3 4 4 23 3 原式 2 „„„„„„5 分14. (本小题满分 5 分) 解:x 1 x2 1 x2 3„„„„„„1 分去分母得 x-1+1=3(x-2) 解得 x=3. 经检验:x=3 是原方程的根. 所以原方程的根为 x=3.„„„„„„4 分 „„„„„„5 分15. (本小题满分 5 分) 解: (1)A1 点的坐标为(3,-1) 1 点的坐标为(2,-3) 1 点的坐标为(5,-3) ,B ,C ; A2 点的坐标为(-3,-1) 2 点的坐标为(-2,-3) ,B , C2 点的坐标为(-5,-3). 图略,每正确画出一个三角形给 2 分. (2)利用勾股定理可求 B2C= 16. (本小题满分 5 分) 证明:∵ C F ∥ A B , ∴ ∠A=∠ACF, ∠ADE=∠CFE. 在△ADE 和△CFE 中, ∠A=∠ACF, ∠ADE=∠CFE, AE EC , ∴ △ADE≌△CFE. ∴ AD CF . -------2 分 A D --------4 分 ------5 分 B E F65 .„„„„„„5 分C17. (本小题满分 5 分) 解:设小刚家 4、5 两月各行驶了 x、y 千米.--------------------------1 分4 y x 100 , 依题意,得 5 0 . 1 x 0 . 1 y 260 . ----------------------------3 分解得, x 1 5 0 0 . y 1100-------------------------------4 分答:小刚家 4 月份行驶 1500 千米,5 月份行驶了 1100 千米. -----------5 分18. (本小题满分 5 分) 解: (1)由题意可知 点 C 的坐标为(1,1) . „„„„„„„„„„„„„1 分 设直线 QC 的解析式为 y kx b . ∵ 点 Q 的坐标为(0,2), ∴ 可求直线 QC 的解析式为 y x 2 .„„„„„„„„„„„„„2 分 (2)如图,当点 P 在 OB 上时,设 PQ 交 CD 于点 E,可求点 E 的坐标为( 则 AP AD DE 2 由题意可得 2 5 2 5 2 a 3(3 3 2 a) . a ,CE BC BP 3 3 2 a.a 2,1) .∴ a 1. „„„„„„„„„„„„„4 分 由对称性可求当点 P 在 OA 上时, a 1 ∴ 满足题意的 a 的值为 1 或-1. „„„„„„„„„„„„„5 分四、解答题(本题共 20 分,每小题 5 分) 19.(本小题满分 5 分) 解: (1)证明:∵BD 是∠ABC 的平分线, ∴ ∠1=∠2. ∵ AD//BC,∴∠2=∠3. ∴ ∠1=∠3. ∴AB=AD. ---------------------2 分1AD3B2EFC(2)作 AE⊥BC 于 E,DF⊥BC 于 F. ∴ EF=AD=AB. ∵ ∠ABC=60° ,BC=3AB, ∴ ∠BAE=30° . ∴ BE=1 2AB.BA∴ BF =23AB=21BC .∴ BD=DC . ∴ ∠C =∠2.∵ BD 是∠ABD 的平分线, ∴ ∠1=∠2=30°.∴ ∠C =30°. -------------------------5分20.(本小题满分5分)解:(1)CD 与圆O 相切. …………………1分 证明:连接OD ,则∠AOD =2∠AED =2⨯45︒=90︒. …………………2分 ∵四边形ABCD 是平行四边形,∴AB //DC .∴∠CDO =∠AOD =90︒.∴OD ⊥CD . …………………3分 ∴CD 与圆O 相切.(2)连接BE ,则∠ADE =∠ABE .∴sin ∠ADE =sin ∠ABE =65. …………………4分∵AB 是圆O 的直径,∴∠AEB =90︒,AB =2⨯3=6. 在Rt △ABE 中,sin ∠ABE =ABAE =65.∴AE =5 .21.(本小题满分5分)解:(1)30%; ……………………2分 (2)如图所示. ……………………4分(3)由于月销量的平均水平相同,从折线的走势看,A 品牌的月销量呈下降趋势,而B 品牌的月销量呈上升趋势.所以该商店应经销B 品牌电视机. …………………5分 22.(本小题满分5分)解:(1)将图4中的△ABE 向左平移30cm ,△CDF 向右平移30cm ,拼成如图下中的平行四边形,此平行四边形即为图2中的□ABCD .…………………2分(2)由图2的包贴方法知:AB 的长等于三棱柱的底边周长,∴AB =30.∵ 纸带宽为15,∴ sin ∠ABM =151302A M A B==.∴∠AMB =30°. …………………5分五、解答题:(本题共22分,第23题7分,第24题7分,第25题8分)23.(本小题满分7分) 解:(1) ∵ 关于x 的一元二次方程2220x ax b ++=有实数根,∴ Δ=,04)2(22≥-b a 有a 2-b 2≥0,(a+b )(a-b )≥0. ∵ 0,0>>b a , ∴ a+b >0,a-b ≥0.∴ b a ≥. …………………………2分(2) ∵ a ∶b =2,∴ 设2,a k b ==.解关于x 的一元二次方程22430x kx k ++=,得 -3x k k =-或.当12,= -3x k x k =-时,由1222x x -=得2k =. 当123,= -x k x k =-时,由1222x x -=得25k =-(不合题意,舍去).∴ 4,a b ==. …………………………5分(3) 当4,a b ==时,二次函数2812y x x =++与x 轴的交点为、C 的交点坐标分别为A (-6,0)、(-2,0),与y 轴交点坐标为(0,12),顶点坐标D 为(-4,-4). 设z =3x -y ,则3y x z =-.画出函数2812y x x =++和3y x =的图象,若直线3y x =平行移动时,可以发现当直线经过点C 时符合题意,此时最大z 的值等于-6 ……………7分 24. (本小题满分7分)解:(1)四边形ABCE 是菱形.证明:∵ △ECD 是△ABC 沿BC 方向平移得到的,∴ EC ∥AB ,EC =AB .∴ 四边形ABCE 是平行四边形. 又∵ AB =BC ,∴四边形ABCE 是菱形. ……………2分(2)①四边形PQED 的面积不发生变化,理由如下: 由菱形的对称性知,△PBO ≌△QEO , ∴ S △PBO = S △QEO321GRQPOEDC BA∵ △ECD 是由△ABC 平移得到的, ∴ ED ∥AC ,ED =AC =6. 又∵ BE ⊥AC , ∴BE ⊥ED∴S 四边形PQED =S △QEO +S 四边形POED =S △PBO +S 四边形POED =S △BED=12×BE ×ED =12×8×6=24. ……………4分②如图,当点P 在BC 上运动,使以点P 、Q 、R 为顶点的三角形与△COB 相似. ∵∠2是△OBP 的外角, ∴∠2>∠3.∴∠2不与∠3对应 . ∴∠2与∠1对应 .即∠2=∠1,∴OP =OC =3 .过O 作OG ⊥BC 于G ,则G 为PC 的中点 . 可证 △OGC ∽△BOC . ∴ CG :CO =CO :BC . 即 CG :3=3:5 . ∴ CG =95.∴ PB =BC -PC =BC -2CG =5-2×95=75 .∴ BD =PB +PR +RF +DF =x +185+x +185=10.∴ x =75∴ BP =75. ……………7分25.(本小题满分8分) 解:(1)由题意得A (0,2)、B (2,2)、C (3,0).设经过A ,B ,C 三点的抛物线的解析式为y=ax 2+bx +2. 则⎩⎨⎧=++=++02390224b a b a解得 ⎪⎪⎩⎪⎪⎨⎧=-=3432b aH∴ 224233y x x =-++.……………2分(2)由224233y x x =-++=228(1)33x --+.∴ 顶点坐标为G (1,83).过G 作GH ⊥AB ,垂足为H . 则AH =BH =1,GH =83-2=23.∵ EA ⊥AB ,GH ⊥AB ,∴ EA ∥GH .∴GH 是△BEA 的中位线 . ∴EA =3GH =43.过B 作BM ⊥OC ,垂足为M . 则MB =OA =AB .∵ ∠EBF =∠ABM =90°,∴ ∠EBA =∠FBM =90°-∠ABF . ∴ R t △EBA ≌R t △FBM . ∴ FM =EA =43.∵ CM =OC -OM =3-2=1, ∴ CF =FM +CM =73.……………5分(3)要使四边形BCGH 的周长最小,可将点C 向上 平移一个单位,再做关于对称轴对称的对称点C 1,得点C 1的坐标为(-1,1). 可求出直线BC 1的解析式为1433y x =+.直线1433y x =+与对称轴x =1的交点即为点H ,坐标为(1,53).点G 的坐标为(1,23).……………8分海淀区九年级第二学期期末练习数 学 2012. 6一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个..是符合题意的. 1. -5的倒数是A .15B .15- C .5- D .52. 2012年4月22日是第43个世界地球日,中国国土资源报社联合腾讯网发起“世界地球日”微话题,共有18 891 511人次参与了这次活动,将18 891 511用科学记数法表示(保 留三个有效数字)约为A. 18.9⨯106B. 0.189⨯108C. 1.89⨯107D. 18.8⨯106 3. 把2x 2− 4x + 2分解因式,结果正确的是A .2(x − 1)2B .2x (x − 2)C .2(x 2− 2x + 1) D .(2x −2)24. 右图是由七个相同的小正方体堆砌而成的几何体, 则这个几何体的俯视图是A BCD 5.从1, -2, 3这三个数中,随机抽取两个数相乘,积为正数的概率是A .0B .13C.23D .16. 如图,在△ABC 中,∠C =90°,BC =3,D ,E 分别在 AB 、AC 上,将△ADE 沿DE翻折后,点A 落在点A ′处,若A ′为CE 的中点,则折痕DE 的长为 A.21 B. 3C. 2D. 1A'EDABCA. 极差是40B. 平均数是60C. 中位数是51.5D. 众数是588.如图,在梯形ABCD 中,AD //BC ,∠ABC =60°,AB = DC =2, AD =1, R 、P 分别是BC 、CD 边上的动点(点R 、B 不重合, 点P 、C 不重合),E 、F 分别是AP 、RP 的中点,设BR=x ,EF=y ,则下列 图象中,能表示y 与x 的函数关系的图象大致是A B C D二、填空题(本题共16分,每小题4分)9. 若二次根式23-x 有意义,则 x 的取值范围是 .10.若一个多边形的内角和等于540︒,则这个多边形的边数是 .11. 如图,在平面直角坐标系xOy 中,已知点A 、B 、C 在双曲线xy 6=上,BD ⊥x 轴于D , CE ⊥ y 轴于E ,点F 在x 轴上,且AO =AF , 则图中阴影部分的面积之和为 .12.小东玩一种“挪珠子”游戏,根据挪动珠子的难度不同而得分不同,规定每次挪动珠子的颗数与所得分数的对应关系如下表所示:按表中规律,当所得分数为71分时,则挪动的珠子数为 颗; 当挪动n 颗 珠子时(n 为大于1的整数), 所得分数为 (用含n 的代数式表示).三、解答题(本题共30分,每小题5分) 1311|5|()3tan 604---+︒.14.解方程:6123x x x +=-+.15. 如图,AC //EG , BC //EF , 直线GE 分别交BC 、BA 于P 、D ,且AC=GE , BC=FE . 求证:∠A =∠G .FE R P B C DA GF E D CBAP16.已知2220a a --=,求代数式221111121a a a a a --÷--++的值.17. 如图,一次函数的图象与x 轴、y 轴分别交于点A (-2, 0)、B (0, 2). (1)求一次函数的解析式; (2)若点C 在x 轴上,且OC =23, 请直接写出∠ABC 的度数.18. 如图,在四边形ABCD 中,∠ADB =∠CBD =90︒,BE//CD 交AD 于E , 且EA=EB .若AB=54,DB =4,求四边形ABCD 的面积.四、解答题(本题共20分,第19题、第20题各5分,第21题6分,第22题4分) 19. 某街道办事处需印制主题为“做文明有礼的北京人,垃圾减量垃圾分类从我做起”的宣传单. 街道办事处附近的甲、乙两家图文社印制此种宣传单的收费标准如下: 甲图文社收费s (元)与印制数t (张)的函数关系如下表:乙图文社的收费方式为:印制2 000张以内(含2 000张),按每张0.13元收费;超过 2 000张,均按每张0.09元收费.(1)根据表中给出的对应规律,写出甲图文社收费s (元)与印制数t (张)的函数关系式; (2)由于马上要用宣传单,街道办事处同时在甲、乙两家图文社共印制了1 500张宣传单,印制费共179元,问街道办事处在甲、乙两家图文社各印制了多少张宣传单? (3)若在下周的宣传活动中,街道办事处还需要加印5 000张宣传单,在甲、乙两家EDA图文社中选择 图文社更省钱.20.如图,AC 、BC 是⊙O 的弦, BC //AO , AO 的延长线与过点C 的射线交于点D , 且∠D =90︒-2∠A .(1)求证:直线CD 是⊙O 的切线;(2)若BC=4,1tan 2D =,求CD 和AD 的长.21. 李老师为了了解所教班级学生完成数学课前预习的具体情况,对本班部分学生进行了 为期半个月的跟踪调查,他将调查结果分为四类,A :很好;B :较好;C :一般;D : 较差.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:(1)李老师一共调查了多少名同学?(2)C 类女生有 名,D 类男生有 名,将上面条形统计图补充完整; (3)为了共同进步,李老师想从被调查的A 类和D 类学生中各随机选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.22.阅读下面材料:小明遇到这样一个问题:我们定义: 如果一个图形绕着某定点旋转一定的角度α (0︒ <α <360︒) 后所得的图形与原图形重合,则称此图形是旋转对称图形. 如等边三角形就是一个旋转角为120︒的旋转对称图形. 如图1,点O 是等边三角形△ABC 的中心, D 、E 、F 分别为AB 、BC 、 CA 的中点, 请你将△ABC 分割并拼补成一个与△ABC .图1 图2小明利用旋转解决了这个问题,图2中阴影部分所示的图形即是与△ABC 面积相等的新的旋转对E 3 E 1P 1 P 2 N 1N 2 AFH 类别50%25%15%D C B A称图形.请你参考小明同学解决问题的方法,利用图形变换解决下列问题: 如图3,在等边△ABC 中, E 1、E 2、E 3分别为AB 、 BC 、CA 的中点,P 1、P 2, M 1、M 2, N 1、N 2分别为 AB 、BC 、CA 的三等分点.(1)在图3中画出一个和△ABC 面积相等的新的旋转 对称图形,并用阴影表示(保留画图痕迹);(2)若△ABC 的面积为a ,则图3中△FGH 的面积为 .五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23.已知抛物线 2(1)(2)1y m x m x =-+--与x 轴交于A 、B 两点.(1)求m 的取值范围;(2)若m >1, 且点A 在点B 的左侧,OA : OB =1 : 3, 试确定抛物线的解析式;(3)设(2)中抛物线与y 轴的交点为C ,过点C 作直线l //x 轴, 将抛物线在y 轴左侧的部分沿直线 l翻折, 抛物线的其余部分保持不变,得到一个新图象. 请你结合新图象回答: 当直线13y x b=+与新图象只有一个公共点P (x 0, y 0)且 y 0≤7时, 求b 的取值范围.24. 如图, 在平面直角坐标系xOy 中,抛物线xx m y 222-=与x 轴负半轴交于点A , 顶点为B , 且对称轴与x 轴交于点C .(1)求点B 的坐标 (用含m 的代数式表示);(2)D 为BO 中点,直线AD 交y 轴于E ,若点E 的坐标为(0, 2), 求抛物线的解析式; (3)在(2)的条件下,点M 在直线BO 上,且使得△AMC 的周长最小,P 在抛物线上,Q 在直线 BC 上,若以A 、M 、P 、Q 为顶点的四边形是平行四边形,求点P 的坐 标.备用图25. 在矩形ABCD 中, 点F 在AD 延长线上,且DF = DC , M 为AB 边上一点, N 为MD 的中点, 点E 在直线CF 上(点E 、C 不重合).(1)如图1, 若AB =BC , 点M 、A 重合, E 为CF 的中点,试探究BN 与NE 的位置关系及BMCE 的值, 并证明你的结论;(2)如图2,且若AB =BC , 点M 、A 不重合, BN =NE ,你在(1)中得到的两个结论是否成立, 若成立,加以证明; 若不成立, 请说明理由;(3)如图3,若点M 、A 不重合,BN =NE ,你在(1)中得到的结论两个是否成立, 请直接写出你的结论.图1 图2 图3海淀区九年级第二学期期末练习数学试卷答案及评分参考 2012. 6说明: 与参考答案不同, 但解答正确相应给分. 一、选择题(本题共32分,每小题4分)1. B2. C3. A4. C5. B6. D7. D8. C 二、填空题(本题共16分,每小题4分)9.23x ≥10. 5 11. 12 12.8; 21n n +- (每空各 2分)三、解答题(本题共30分,每小题5分) 13115()3tan 604---+︒=54-+ …………………………………………………4分=1. …………………………………………………5分14.解:去分母,得 ()()()()63223x x x x x ++-=-+. ………………………………2分2261826x x x x x ++-=+-. ……………………………………………………3分整理,得 324x =-.解得 8x =-. ………………………………………………………………4分F A ( M ) D N D C E N M B F E C B F NM E C B A经检验,8x =-是原方程的解.所以原方程的解是8x =-. ……………………………………………………5分15.证明:∵ AC //EG ,∴ C C PG ∠=∠. …………1分 ∵ BC //EF ,∴ C P G F E G ∠=∠.∴ C F E G ∠=∠. …………………………………………2分在△ABC 和△GFE 中,,,,AC G E C FEG BC FE =⎧⎪∠=∠⎨=⎪⎩∴ △ABC ≌△GFE . …………………………………………………4分∴A G ∠=∠. …………………………………………………5分 16. 解:原式=()()()21111111a a a a a +-⋅-+-- ……………………………………………2分=()21111a a a +--- …………………………………………………3分=22.(1)a -- …………………………………………………4分由2220a a --=,得 2(1)3a -=.∴ 原式=23-. …………………………………………………5分17.解:(1)依题意设一次函数解析式为2y kx =+. …………………………………1分 ∵ 点A (2,0-)在一次函数图象上, ∴022k =-+.∴ k =1. ……………………………………………………2分 ∴ 一次函数的解析式为2y x =+. …………………………………3分 (2)A B C ∠的度数为15︒或105︒. (每解各1分) ……………………5分 18.解: ∵∠ADB =∠CBD =90︒, ∴ DE ∥CB . ∵ BE ∥CD ,∴ 四边形BEDC 是平行四边形. ………1分 ∴ BC=DE . 在Rt △ABD 中,由勾股定理得8AD ===. ………2分设D E x =,则8EA x =-. ∴8EB EA x ==-.在Rt △BDE 中,由勾股定理得 222D E B D E B +=.∴ 22248x x +=-(). ……………………………………………………3分 ∴ 3x =.∴ 3BC D E ==. ……………………………………………………4分 ∴1116622.22ABD BD C ABCD S S S BD AD BD BC ∆∆=+=⋅+⋅=+=四边形 ………… 5分四、解答题(本题共20分,第19题、第20题各5分,第21题6分, 第22题4分) 19.解:(1)甲图文社收费s (元)与印制数t (张)的函数关系式为0.11s t =. ……1分GFE DCB AP D ECA(2)设在甲、乙两家图文社各印制了x 张、y 张宣传单, 依题意得{1500,0.110.13179.x y x y +=+= ………………………………………… 2分解得800,700.x y =⎧⎨=⎩ ……………………………………………… 3分答:在甲、乙两家图文社各印制了800张、700张宣传单. ………………4分 (3) 乙 . ……………………………………………………… 5分20.(1)证明:连结OC .∴ ∠DOC =2∠A . …………1分∵∠D = 90°2A -∠, ∴∠D +∠DOC =90°. ∴ ∠OCD =90°. ∵ OC 是⊙O 的半径,∴ 直线CD 是⊙O 的切线. ………………………………………………2分(2)解: 过点O 作OE ⊥BC 于E , 则∠OEC =90︒.∵ BC =4,∴ CE =12BC =2.∵ BC //AO , ∴ ∠OCE =∠DOC .∵∠COE +∠OCE =90︒, ∠D +∠DOC =90︒,∴ ∠COE =∠D . ……………………………………………………3分 ∵tan D =12,∴tan C O E ∠=12.∵∠OEC =90︒, CE =2, ∴4tan CE O E CO E==∠.在Rt △OEC 中, 由勾股定理可得O C ==在Rt △ODC 中, 由1tan 2O C D CD==,得CD =, ……………………4分由勾股定理可得10.O D =∴10.AD OA OD OC OD =+=+= …………………………………5分 21.解:(1)(64)50%20+÷=. 所以李老师一共调查了20名学生. …………………1分(2)C 类女生有 3 名,D 类男生有 1 名;补充条形统计图略.说明:其中每空1分,条形统计图1分. ……………………………………4分(3)解法一:由题意画树形图如下:………………………5分从树形图看出,所有可能出现的结果共有6种,且每种结果出现的可能性相等,所选 两位同学恰好是一位男同学和一位女同学的结果共有3种.从D 类中选取从A 类中选取女女男男女女男女男所以P (所选两位同学恰好是一位男同学和一位女同学)=3162=. ………………6分解法二:由题意列表如下:………………………5分由上表得出,所有可能出现的结果共有6种,且每种结果出现的可能性相等,所选 两位同学恰好是一位男同学和一位女同学的结果共有3种. 所以P (所选两位同学恰好是一位男同学和一位女同学)=3162=. ………………6分22.解:(1)画图如下:(答案不唯一) …………………………………2分图3(2)图3中△FGH 的面积为7a. …………………………………4分五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23. 解:(1)∵ 抛物线2(1)(2)1y m x m x =-+--与x 轴交于A 、B 两点,∴210,(2)4(1)0.m m m ì- ïïíïD =-+->ïî由①得1m¹, 由②得0m ¹,∴ m 的取值范围是0m ¹且1m ¹. ……………………………………………2分 (2)∵ 点A 、B 是抛物线2(1)(2)1y m x m x =-+--与x 轴的交点,∴ 令0y =,即 2(1)(2)10m x m x -+--=. 解得 11x =-,211x m =-.∵1m >, ∴10 1.1m >>--∵ 点A 在点B 左侧,∴ 点A 的坐标为(1,0)-,点B 的坐标为1(,0)1m -. …………………………3分∴ OA=1,OB =11m -.∵ OA : OB =1 : 3,①② …………………………………………1分∴131m =-.∴ 43m =.∴ 抛物线的解析式为212133y x x =--. ………………………………………4分(3)∵ 点C 是抛物线212133y x x =--与y 轴的交点,∴ 点C 的坐标为(0,1)-.依题意翻折后的图象如图所示. 令7y =,即2121733x x --=.解得16x =, 24x =-.∴ 新图象经过点D (6,7). 当直线13y x b =+经过D 点时,可得5b =. 当直线13y x b =+经过C 点时,可得1b =-. 当直线1(1)3y x b b =+<-与函数2121(33y x x x =-->的图象仅有一个公共点P (x 0, y 0)时,得20001121333x b x x +=--.整理得 2003330.x x b ---=由2(3)4(33)12210b b D =----=+=,得74b =-结合图象可知,符合题意的b 的取值范围为15b -<≤或4b <-. ……………7分24.解:(1)∵22222221212112()()4422y x x x m x m m x m m mmm m=-=-+-⋅=--,∴抛物线的顶点B 的坐标为11(,)22m m -. ……………………………1分(2)令2220x x m-=,解得10x =, 2x m =.∵ 抛物线xx m y 222-=与x 轴负半轴交于点A ,∴ A (m , 0), 且m <0. …………………………………………………2分 过点D 作DF ⊥x 轴于F .由 D 为BO 中点,DF //BC , 可得CF =FO =1.2C O ∴ DF =1.2BC由抛物线的对称性得 AC = OC .∴ AF : AO =3 : 4. ∵ DF //EO ,∴ △AFD ∽△AOE . ∴.FD AF O EAO=由E (0, 2),B 11(,)22m m -,得OE =2, DF =14m -.∴134.24m -=∴ m = -6.∴ 抛物线的解析式为2123y x x =--. ………………………………………3分(3)依题意,得A (-6,0)、B (-3, 3)、C (-3, 0).可得直线OB 的解析式为x y -=,直线BC 为3x =-. 作点C 关于直线BO 的对称点C '(0,3),连接AC '交BO 于M ,则M 即为所求. 由A (-6,0),C ' (0, 3),可得 直线AC '的解析式为321+=x y .由13,2y x y x⎧=+⎪⎨⎪=-⎩解得2,2.x y =-⎧⎨=⎩ ∴ 点M 的坐标为(-2, 2). ……………4分由点P 在抛物线2123y x x =--上,设P (t ,213t - (ⅰ)当AM 为所求平行四边形的一边时. 如右图,过M 作MG ⊥ x 轴于G , 过P 1作P1H ⊥ BC 于H , 则x G = x M =-2, x H = x B =-3.由四边形AM P 1Q 1为平行四边形, 可证△AMG ≌△P 1Q 1H . 可得P 1H = AG =4. ∴ t -(-3)=4. ∴ t =1.∴17(1,)3P -. ……………………5分如右图,同 方法可得 P 2H=AG =4. ∴ -3- t =4. ∴ t =-7.∴27(7,)3P --. ……………………6分(ⅱ)当AM 为所求平行四边形的对角线时, 如右图,过M 作MH ⊥BC 于H , 过P 3作P 3G ⊥ x 轴于G , 则x H = x B =-3,x G =3P x =t .由四边形AP 3MQ 3为平行四边形, 可证△A P 3G ≌△MQ 3H . 可得AG = MH =1. ∴ t -(-6)=1. ∴ t =-5. ∴35(5,)3P -. ……………………………………………………7分综上,点P 的坐标为17(1,)3P -、27(7,)3P --、35(5,)3P -.25. 解:(1)BN 与NE 的位置关系是BN ⊥NE ;C E B M2证明:如图,过点E 作EG ⊥AF 于G , 则∠EGN =90°.∵ 矩形ABCD 中, AB =BC ,∴ 矩形ABCD 为正方形.∴ AB =AD =CD , ∠A =∠ADC =∠DCB =90°.∴ EG//CD , ∠EGN =∠A , ∠CDF =90°. ………………………………1分 ∵ E 为CF 的中点,EG//CD , ∴ GF =DG =11.22DF CD =∴ 1.2G E CD =∵ N 为MD (AD )的中点, ∴ AN =ND =11.22AD CD =∴ GE =AN , NG=ND+DG=ND+AN=AD=AB . ……………………………2分 ∴ △NGE ≌△BAN . ∴ ∠1=∠2. ∵ ∠2+∠3=90°, ∴ ∠1+∠3=90°. ∴ ∠BNE =90°.∴ BN ⊥NE . ……………………………………………………………3分 ∵ ∠CDF =90°, CD =DF , 可得 ∠F =∠FCD =45°,CF CD=.于是122CFCECECEBM BA CD CD ====……………………………………4分(2)在(1)中得到的两个结论均成立.证明:如图,延长BN 交CD 的延长线于点G ,连结BE 、GE ,过E 作EH ⊥CE ,交CD 于点H .∵ 四边形ABCD 是矩形, ∴ AB ∥CG .∴ ∠MBN =∠DGN ,∠BMN =∠GDN . ∵ N 为MD 的中点, ∴ MN =DN .∴ △BMN ≌△GDN . ∴ MB =DG ,BN =GN .HGABCDEMNF321GFEA (M )CDNB∵ BN =NE ,∴ BN =NE =GN .∴ ∠BEG =90°. ……………………………………………5分 ∵ EH ⊥CE , ∴ ∠CEH =90°. ∴ ∠BEG =∠CEH . ∴ ∠BEC =∠GEH . 由(1)得∠DCF =45°. ∴ ∠CHE =∠HCE =45°. ∴ EC=EH , ∠EHG =135°. ∵∠ECB =∠DCB +∠HCE =135°, ∴ ∠ECB =∠EHG . ∴ △ECB ≌△EHG . ∴ EB =EG ,CB =HG . ∵ BN =NG ,∴ BN ⊥NE. ……………………………………………6分∵ BM =DG= HG -HD= BC -HD =CD -HD =CH=CE ,∴CE BM=2……………………………………………7分(3)BN ⊥NE ;CE BM2.………………………………………………8分北京市西城区2012年初三二模试卷数 学 2011. 6一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个..是符合题意的. 1.3-的倒数是A .3B .13-C .3-D .132.2010年,我国国内生产总值(GDP )为58 786亿美元,超过日本,成为世界第二大经济体.58 786用科学记数法表示为 A .45.878610⨯ B .55.878610⨯ C .358.78610⨯ D .50.5878610⨯ 3.⊙O 1的半径为3cm ,⊙O 2的半径为5cm ,若圆心距O 1O 2=2 cm ,则这两圆的位置关系是A .内含B .外切C .相交D .内切 4.若一个多边形的内角和是它的外角和的2倍,则这个多边形是A .四边形B .五边形C .六边形D .八边形 5.某鞋店试销一种新款女鞋,销售情况如下表所示:鞋店经理最关心的是哪种型号的鞋销量最大.对他来说,下列统计量中最重要的是A .平均数B .众数C .中位数D .方差6.小明的爷爷每天坚持体育锻炼,一天他步行到离家较远的公园,打了一会儿太极拳后跑步回家.下面的四个函数图象中,能大致反映当天小明的爷爷离家的距离y 与时间x 的函数关系的是7.下图的长方体是由A ,B ,C ,D 四个选项中所示的四个几何体拼接而成的,而且这四个几何体都是由4个同样大小的小正方体组成的,那么长方体中,第四部分所对应的几何体应是8.在平面直角坐标系xOy 中,点P 在由直线3+-=x y,直线4y =和直线1x =所围成的区域内或其边界上,点Q 在x 轴上,若点R 的坐标为(2,2)R ,则QP QR +的最小值为A .B .25+C .D .4 二、填空题(本题共16分,每小题4分) 9.分解因式 m 3 – 4m = . 10.函数21-=x y 中,自变量x 的取值范围是 .11.如图,两同心圆的圆心为O ,大圆的弦AB 与小圆相切,切点为P .若两圆的半径分别为2和1,则弦长AB =;若用阴影部分围成一个圆锥(OA 与OB 重合),则该圆锥的底面半径长为 . 12.对于每个正整数n ,抛物线2211(1)(1)n n n n n yx x +++=-+与x 轴交于A n ,B n 两点,若n n A B 表示这两点间的距离,则n n A B = (用含n 的代数式表示);11222011A B A B A B +++ 的值为 .三、解答题(本题共30分,每小题5分) 13.计算:2273181---⎪⎭⎫ ⎝⎛--- .14.已知:如图,直线AB 同侧两点C ,D 满足CAD DBC ∠=∠, AC =BD ,BC 与AD 相交于点E .求证:AE =BE .15.已知:关于x 的一元二次方程2420x x k ++=有两个不相等的实数根. (1)求k 的取值范围;(2)当k 取最大整数值时,用公式法求该方程的解.16.已知 122=+xy x ,215xy y +=,求代数式()22()x y y x y +-+的值.17.如图,一次函数y kx b =+()0≠k 的图象与反比例函数m y x=()0≠m 的图象交于(3,1)A -,(2,)B n 两点.(1)求反比例函数和一次函数的解析式;(2)求△AOB 的面积.18.今年3月12日,某校九年级部分学生参加植树节活动,以下是根据本次植树活动的有关数据制作的统计图的一部分.请根据统计图所提供的有关信息,完成下列问题:(1)参加植树的学生共有 人; (2)请将该条形统计图补充完整;(3)参加植树的学生平均每人植树 棵.(保留整数)四、解答题(本题共20分,每小题5分)19.某汽车运输公司根据实际需要计划购买大、中型两种客车共20辆,已知大型客车每辆62万元,中型客车每辆40万元,设购买大型客车x(辆),购车总费用为y(万元).(1)求y与x的函数关系式(不要求写出自变量x的取值范围);(2)若购买中型客车的数量少于大型客车的数量,请你给出一种费用最省的方案,并求出该方案所需费用.20.如图,在梯形ABC D中,AB∥D C,5AB=,4C D=,连结并延长BD到E,使==,10AD BC=,作EF AB⊥,交BA的延长线于点F.DE BD(1)求tan ABD∠的值;(2)求AF的长.21.已知:如图,BD为⊙O的直径,点A是劣弧BC的中点,AD交BC于点E,连结AB.(1)求证:2=⋅;A B A E A D(2)过点D作⊙O的切线,与BC的延长线交于点F,若AE=2,ED=4,求EF的长.22.如图1,若将△AOB绕点O逆时针旋转180°得到△COD,则△AOB≌△COD.此时,我们称△AOB 与△COD为“8字全等型”.借助“8字全等型”我们可以解决一些图形的分割与拼接问题.例如:图2中,△ABC是锐角三角形且AC>AB,E为AC的中点,F为BC上一点且BF≠FC(F不与B,C 重合),沿EF将其剪开,得到的两块图形恰能拼成一个梯形.请分别按下列要求用直线将图2中的△ABC重新进行分割,画出分割线及拼接后的图形.(1)在图3中将△ABC沿分割线剪开,使得到的两块图形恰能拼成一个平行四边形;(2)在图4中将△ABC沿分割线剪开,使得到的三块图形恰能拼成一个矩形,且其中的两块为直角三角形;(3)在图5中将△ABC沿分割线剪开,使得到的三块图形恰能拼成一个矩形,且其中的一块为钝角三角形.五、解答题(本题共22分,第23题7分,第24题7分,第25题8分)23.阅读下列材料:若关于x 的一元二次方程20ax bx c ++=()0≠a 的两个实数根分别为x 1,x 2,则12b x x a+=-,12c x x a⋅=.解决下列问题:已知:a ,b ,c 均为非零实数,且a >b >c ,关于x 的一元二次方程20ax bx c ++=有两个实数根,其中一根为2.(1)填空:42a b c ++ 0,a 0,c 0;(填“>”,“<”或“=”)(2)利用阅读材料中的结论直接写出方程20ax bx c ++=的另一个实数根(用含a ,c 的代数式表示); (3)若实数m 使代数式2am bm c ++的值小于0,问:当x =5m +时,代数式2ax bx c ++的值是否为正数?写出你的结论并说明理由.。
2012北京中考数学二模全等分类
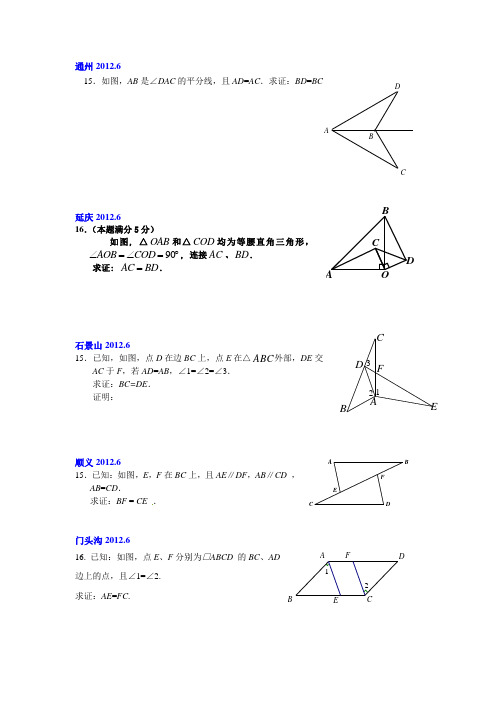
DABC 15.如图,AB是∠DAC的平分线,且AD=AC.求证:BD=BC延庆2012.616.(本题满分5分)如图, △OAB和△COD均为等腰直角三角形,90AOB COD∠=∠=︒, 连接AC、BD.求证: AC BD=.石景山2012.615.已知,如图,点D在边BC上,点E在△ABC外部,DE交AC于F,若AD=AB,∠1=∠2=∠3.求证:BC=DE.证明:顺义2012.615.已知:如图,E,F在BC上,且AE∥DF,AB∥CD ,AB=CD.求证:BF = CE .门头沟2012.616.已知:如图,点E、F分别为□ABCD的BC、AD边上的点,且∠1=∠2.求证:AE=FC.F EDCB A21FEDCBA16.如图,在△ABC 与△ABD 中, BC 与AD 相交于点O ,∠1=∠2,CO = DO .求证:∠C =∠D .密云2012.615.已知:如图,∠C =∠CAF =90°,点E 在AC 上,且AE =BC ,EF ⊥AB 于点D .求证:AB =FE . ,请直接写出△AOB 的面积.朝阳2012.616.已知:如图,点D 、E 分别在AB 、AC 上,BE 与CD 相交于点F ,BD=CE ,∠B =∠C .求证:BE =CD .昌平2012.616.如图:已知在等边三角形ABC 中,点D 、E 分别是AB 、BC 延长线上的点,且BD =CE .求证:DC =EA .西城2012.615.如图,点F ,G 分别在△ADE 的AD ,DE 边上,C ,B 依次21DOCBAA DCEB为GF 延长线上两点,AB=AD ,∠BAF =∠CAE ,∠B=∠D . (1)求证:BC=DE ;(2)若∠B=35°,∠AFB =78°,直接写出∠DGB 的度数.大兴2012.615.已知:如图,∠ABC=90°,DC ⊥BC ,E ,F 为BC 上两点,且BE CF =,AB DC =. 求证:ABF DCE △≌△;燕山2012.615. 已知:如图, P 是线段AB 的中点,线段MN 经过 点P ,MA ⊥AB ,NB ⊥AB .求证:AM=BN.东城2012.615. 已知:如图,∠ABC =∠DCB ,BD 、CA 分别是∠ABC 、∠DCB的平分线. 求证:AB =DC ..平谷2012.6 16.如图,BE ⊥CE 于E ,AD ⊥ED 于D ,∠ACB =90°,AC =BC . 求证:AD =CE .房山2012.616.如图,在△ABC 中,AD 是中线,分别过点B 、C 作AD 及其延长线的垂线BE 、CF ,垂足分别为点E 、F .求证:BE =CF . 证明:ABPMN。
2012北京海淀区高三二模数学参考答案文科

海淀区高三年级第二学期期末练习数 学(文科)参考答案及评分标准 2012.05一.选择题:本大题共8小题,每小题5分,共40分.二.填空题:本大题共6小题,每小题5分,共30分.(9 (11) (12)12(13)12;1] (14)1或13;Æ 注:(13)、(14)题第一空3分;第二空2分.三.解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. (15)(本小题满分13分) 解:(Ⅰ)因为5346S a =+,所以115454(2)62da a d 创+=++. ①……………………………………3分 因为139,,a a a 成等比数列,所以2111(8)(2)a a d a d +=+. ② ……………………………………5分 由①,②及0d ¹可得:12,2a d ==.……………………………………6分 所以2n a n =. ……………………………………7分 (Ⅱ)由2n a n =可知:2(22)2n n nS n n +?==+.……………………………………9分所以1111(1)1n S n n n n ==-++. ……………………………………11分 所以1211111n nS S S S -++++211111111122311n n n n =-+-++-+--+1111n n n =-=++. ……………………………………13分 所以 数列1{}nS 的前n 项和为1n n +. (16)(本小题满分13分)解:由题意可知,甲、乙两位同学分别从四道题中随机抽取一题,所有可能的结果有16个,它们是:11(,)A A ,12(,)A A ,1(,)A B ,1(,)A C ,21(,)A A ,22(,)A A ,2(,)A B ,2(,)A C ,1(,)B A ,2(,)B A ,(,)B B ,(,)B C ,1(,)C A ,2(,)C A ,(,)C B ,(,)C C . ……………………………………3分(Ⅰ)用M 表示事件“甲、乙两位同学所选的题目难度相同”,则M 包含的基本事件有:11(,)A A ,12(,)A A ,21(,)A A ,22(,)A A ,(,)B B ,(,)C C . 所以63()=168P M =. ……………………………………8分 (Ⅱ)用N 表示事件“甲所选题目的难度大于乙所选题目的难度”,则N 包含的基本事件有:1(,)B A ,2(,)B A ,1(,)C A ,2(,)C A ,(,)C B . 所以5()16P N =. ……………………………………13分 (17)(本小题满分14分)(Ⅰ)证明:连接'BC .在正方体''''ABCD A B C D -中,''AB C D =,AB ∥''C D . 所以 四边形''ABC D 是平行四边形. 所以 'AD ∥'BC .因为 ,F G 分别是',''BB B C 的中点,所以 FG ∥'BC .所以 FG ∥'AD . ……………………………………2分因为 ,'EF AD 是异面直线, 所以 'AD Ë平面EFG .因为 FG Ì平面EFG ,数学参考答案第3页,共6页所以 'AD ∥平面EFG .………………………………………4分(Ⅱ)证明:连接'B C .在正方体''''ABCD A B C D -中,''A B ^平面''BCC B ,'BC Ì平面''BCC B , 所以 '''A B BC ⊥.在正方形''BCC B 中,''B C BC ⊥,因为 ''A B Ì平面''A B C ,'B C Ì平面''A B C ,''''A B B C B =,所以'BC ⊥平面''A B C . ……………………………………6分因为 'A C Ì平面''A B C , 所以''BC A C ⊥. ……………………………………7分 因为 FG ∥'BC , 所以 'A C FG ⊥.同理可证:'A C EF ⊥.因为 EF Ì平面EFG ,FG Ì平面EFG ,EFFG F =,所以 'A C ^平面EFG . ……………………………………9分 (Ⅲ)点,',,A D H F 不共面. 理由如下: ……………………………………10分 假设,',,A D H F 共面. 连接',,C F AF HF .由(Ⅰ)知,'AD ∥'BC , 因为 'BC Ì平面''BCC B ,'AD Ë平面''BCC B .所以 'AD ∥平面''BCC B .……………………………………12分 因为 ''C D H Î,所以 平面'AD HF 平面'''BCC B C F =. 因为 'AD Ì平面'AD HF , 所以 'AD ∥'C F .所以 'C F ∥'BC ,而'C F 与'BC 相交,矛盾.所以 点,',,A D H F 不共面. ……………………………………14分 (18)(本小题满分13分) 解:222()(3)'()(3)x a x a f x x a --+=+. HG FED'C'B'A'D C BAHG FED'C'B'A'D C BA4令'()0f x =,解得x a =或3x a =-. ……………………………………2分 (Ⅰ)当0a >时,'()f x ,()f x 随着x 的变化如下表函数()f x 的单调递增区间是(3,)a a -,函数()f x 的单调递减区间是(,3)a -∞-,(,)a +∞. ……………………………………4分当0a <时,'()f x ,()f x 随着x 的变化如下表函数()f x 的单调递增区间是(,3)a a -,函数()f x 的单调递减区间是(,)a -∞,(3,)a -+∞. ……………………………………6分(Ⅱ)当1a =时,由(Ⅰ)得()f x 是(3,1)-上的增函数,是(1,)+∞上的减函数.又当1x >时,21()03x f x x +=>+. ……………………………………8分 所以 ()f x 在[3,)-+∞上的最小值为1(3)6f -=-,最大值为1(1)2f =.……………………………………10分 所以 对任意12,[3,)x x ∈-+∞,122()()(1)(3)3f x f x f f -≤--=. 所以 对任意12,[3,)x x ∈-+∞,使12()()f x f x m -≤恒成立的实数m 的最小值为23. ……………………………………13分数学参考答案第5页,共6页(Ⅰ)解:由题意知:1c =.根据椭圆的定义得:2a =a = ……………………………………3分 所以 2211b =-=.所以 椭圆C 的标准方程为2212x y +=. ……………………………………4分 (Ⅱ)证明:当直线l 的斜率为0时,(A B . 则557(2,0)(,0)4416QA QB ⋅=⋅=-. ……………………………………6分当直线l 的斜率不为0时,设直线l 的方程为:1x ty =+,()()1122,,,A x y B x y .由221,21x y x ty ìïï+=ïíïï=+ïî可得:22(2)210t y ty ++-=.显然0∆>.1221222,21.2t y y t y y t ìïï+=-ïï+ïíïï=-ïï+ïî……………………………………9分 因为 111x ty =+,221x ty =+,所以 112212125511(,)(,)()()4444x y x y ty ty y y -?=--+ 2121211(1)()416t y y t y y =+-++2221121(1)24216t t t t t =-+++++ 22222172(2)1616t t t --+=+=-+. 即 716QA QB ⋅=-. ……………………………………13分6(Ⅰ)解:因为3=3,3=1+2,3=1+1+1,所以3)3(=f .因为5=5,5=2+3,5=1+4,5=1+1+3,5=1+2+2,5=1+1+1+2,5=1+1+1+1+1, 所以7)5(=f . ……………………………………3分 (Ⅱ)证明:因为21≥+n ,把1+n 的一个表示法中11a =的1a 去掉,就可得到一个n 的表示法;反之,在n 的一个表示法前面添加一个“1+”,就得到一个1n +的表示法,即1+n 的表示法中11a =的表示法种数等于n 的表示法种数,所以 )()1(n f n f -+表示的是1+n 的表示法中11a ¹的表示法数.即 (1)()1f n f n +-?. ……………………………………8分 (Ⅲ)结论是)1(+n f )]2()([21++≤n f n f . 证明如下:由结论知,只需证 ).1()2()()1(+-+≤-+n f n f n f n f由(Ⅱ)知:)()1(n f n f -+表示的是1+n 的表示法中11a ¹的表示法数,)1()2(+-+n f n f 是2+n 的表示法中11a ¹的表示法数.考虑到21≥+n ,把一个11a ¹的1+n 的表示法中的p a 加上1,就可变为一个11a ¹的2+n 的表示法,这样就构造了从11a ¹的1+n 的表示法到11a ¹的2+n 的表示法的一个对应,所以有).1()2()()1(+-+≤-+n f n f n f n f ……………………………………14分。
2012年北京市海淀区高三数学理科二模试卷及答案(WORD版)

北京市海淀区2012高三二模数 学(理科)2012.05一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.(1)若sin cos 0θθ<,则角θ是 (A )第一或第二象限角 (B )第二或第三象限角 (C )第三或第四象限角 (D )第二或第四象限角 (2)已知命题p :0x ∃∈R ,021x =.则p ⌝是 (A )0x ∀∈R ,021x ≠ (B )0x ∀∉R ,021x ≠ (C )0x ∃∈R ,021x ≠(D )0x ∃∉R ,021x ≠(3)直线11x ty t =+⎧⎨=-⎩(t 为参数)的倾斜角的大小为(A )4-π (B )4π (C )2π(D )34π(4)若整数,x y 满足1,1,3,2x y x y y ìïïï-?ïïï+?íïïïï£ïïî则2x y +的最大值是 (A )1(B )5(C )2 (D )3(5)已知点12,F F 是椭圆2222x y +=的两个焦点,点P 是该椭圆上的一个动点,那么12PF PF +u u u r u u u u r的最小值是(A )0 (B )1 (C )2 (D)(6)为了得到函数2log y =2log y x =的图象上所有的点的(A )纵坐标缩短到原来的12倍,横坐标不变,再向右平移1个单位长度 (B )纵坐标缩短到原来的12倍,横坐标不变,再向左平移1个单位长度(C )横坐标伸长到原来的2倍,纵坐标不变,再向左平移1个单位长度(D )横坐标伸长到原来的2倍,纵坐标不变,再向右平移1个单位长度(7)某几何体的主视图与俯视图如图所示,左视图与主视图相同,且图中的四边形都是边长为2的正方形,两条虚线互相垂直,则该几何体的体积是(A )203(B )43(C )6 (D )4(8)点(,)P x y 是曲线1:(0)C y x x=>上的一个动点,曲线C 在点P 处的切线与x 轴、y 轴分别交于,A B 两点,点O 是坐标原点. 给出三个命题:①PA PB =;②OAB ∆的周长有最小值4+;③曲线C 上存在两点,M N ,使得OMN ∆为等腰直角三角形.其中真命题的个数是(A )1 (B )2 (C )3 (D )0二、填空题:本大题共6小题,每小题5分,共30分,把答案填在题中横线上. (9)在面积为1的正方形ABCD 内部随机取一点P ,则PAB ∆的面积大于等于14的概率是_________. (10)已知1021012311(1)x a a x a x a x +=++++L . 若数列123,,,,(111,)k a a a a k k #?Z L 是一个单调递增数列,则k 的最大值是 . (11)在ABC ∆中,若120A ??,5c =,ABC ∆的面积为,则a = .(12)如图,O e 的直径AB 与弦CD 交于点P ,7, 5, 15CP PD AP ===,则DCB Ð=______.(13)某同学为研究函数()1)f x x =#的性质,构造了如图所示的两个边长为1的正方形ABCD 和BEFC ,点P 是边BC 上的一个动点,设CP x =,则()AP PF f x +=. 请你参考这些信息,推知函数()f x 的图象的对称轴是 ;函数()4()9g x f x =-的零点的个数是 .俯视图主视图BEFAB C DP(14)曲线C 是平面内到定点(1,0)A 的距离与到定直线1x =-的距离之和为3的动点P 的轨迹. 则曲线C 与y 轴交点的坐标是 ;又已知点(,1)B a (a 为常数),那么PB PA +的最小值()d a = . 三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. (15)(本小题满分13分)已知公差不为0的等差数列{}n a 的前n 项和为n S ,346S a =+,且1413,,a a a 成等比数列. (Ⅰ)求数列{}n a 的通项公式; (Ⅱ)求数列1{}nS 的前n 项和公式. (16)(本小题满分14分)如图所示,PA ^平面ABC ,点C 在以AB 为直径的⊙O 上,30CBA??,2PA AB ==,点E 为线段PB 的中点,点M 在»AB 上,且OM ∥AC . (Ⅰ)求证:平面MOE ∥平面P AC ;(Ⅱ)求证:平面P AC ^平面PCB ;(Ⅲ)设二面角M BP C --的大小为θ,求cos θ的值.(17)(本小题满分13分)某公司准备将100万元资金投入代理销售业务,现有A ,B 两个项目可供选择: (1)投资A 项目一年后获得的利润X且X 1的数学期望E (X 1)=12;(2)投资B 项目一年后获得的利润X 2(万元)与B 项目产品价格的调整有关, B 项目产品价格根据销售情况在4月和8月决定是否需要调整,两次调整相互独立且在4月和8月进行价格调整的概率分别为p (0< p <1)和1-p . 经专家测算评估:B 项目产品价格一年内调整次数X (次)与X 2的关系如下表所示:(Ⅱ)求X 2的分布列;(Ⅲ)若E (X 1)< E (X 2),则选择投资B 项目,求此时 p 的取值范围.(18)(本小题满分13分)ME BOCAP已知椭圆C :22221(0)x y a b a b+=>>的右焦点为(1,0)F ,且点(1,2-在椭圆C 上. (Ⅰ)求椭圆C 的标准方程;(Ⅱ)已知动直线l 过点F ,且与椭圆C 交于A ,B 两点.试问x 轴上是否存在定点Q ,使得716QA QB ⋅=-u u u r u u u r 恒成立?若存在,求出点Q 的坐标;若不存在,请说明理由.(19)(本小题满分14分)已知函数21()ln()(0)2f x a x a x x a =--+<. (Ⅰ)求()f x 的单调区间;(Ⅱ)若12(ln 21)a -<<-,求证:函数()f x 只有一个零点0x ,且012a x a +<<+; (Ⅲ)当45a =-时,记函数()f x 的零点为0x ,若对任意120,[0,]x x x ∈且211,x x -=都有21()()f x f x m -≥成立,求实数m 的最大值.(本题可参考数据:99ln 20.7,ln 0.8,ln 0.5945≈≈≈)(20)(本小题满分13分)将一个正整数n 表示为12(*)p a a a p +++?N L 的形式,其中*i a ÎN ,1,2,,i p =L ,且p a a a ≤≤≤Λ21,记所有这样的表示法的种数为)(n f (如4=4,4=1+3,4=2+2,4=1+1+2,4=1+1+1+1,故5)4(=f ).(Ⅰ)写出)5(),3(f f 的值,并说明理由;(Ⅱ)对任意正整数n ,比较)1(+n f 与)]2()([21++n f n f 的大小,并给出证明; (Ⅲ)当正整数6≥n 时,求证:134)(-≥n n f .海淀区高三年级第二学期期末练习数 学(理科)参考答案及评分标准 2012.05一. 选择题:本大题共8小题,每小题5分,共40分.最新整理二.填空题:本大题共6小题,每小题5分,共30分.(9)12(10)6(11(12)45°(13)12x=;2(14)(0,±;1.41,4, 1.41,2,1 1.a aa aa aìï??ïïï+-<?íïï--<<ïïïî或注:(13)、(14)题第一空3分;第二空2分.三.解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. (15)(本小题满分13分)解:(Ⅰ)设等差数列{}n a的公差为0d¹.因为346S a=+,所以11323362da a d创+=++. ①……………………………………3分因为1413,,a a a成等比数列,所以2111(12)(3)a a d a d+=+. ②……………………………………5分由①,②可得:13,2a d==. ……………………………………6分所以21na n=+.……………………………………7分(Ⅱ)由21na n=+可知:2(321)22nn nS n n++?==+.……………………………………9分所以11111()(2)22nS n n n n==-++. ……………………………………11分所以123111111n nS S S S S-+++++L11111111111()2132435112n n n n=-+-+-++-+--++L21111135()212124(1)(2)n nn n n n+=+--=++++.所以数列1{}nS的前n项和为2354(1)(2)n nn n+++.最新整理……………………………………13分(16)(本小题满分14分)(Ⅰ)证明:因为点E 为线段PB 的中点,点O 为线段AB 的中点,所以 OE ∥PA . ……………………………………1分 因为 PA Ì平面PAC ,OE Ë平面PAC ,所以 OE ∥平面P AC . ……………………………………2分因为 OM ∥AC , 因为 AC Ì平面PAC ,OM Ë平面PAC ,所以 OM ∥平面P AC . ……………………………………3分因为 OE Ì平面MOE ,OM Ì平面MOE ,OE OM O =I ,所以 平面MOE ∥平面P AC . ………………………………………5分(Ⅱ)证明:因为 点C 在以AB 为直径的⊙O 上,所以 90ACB??,即BC AC ⊥.因为 PA ^平面ABC ,BC Ì平面ABC , 所以PA BC ⊥. ……………………………………7分因为 AC Ì平面PAC ,PA Ì平面PAC ,PA AC A =I ,所以 BC ^平面PAC . 因为 BC Ì平面PBC ,所以 平面P AC ^平面PCB . ……………………………………9分(Ⅲ)解:如图,以C 为原点,CA 所在的直线为x 轴,CB 所在的直线为y 轴,建立空间直角坐标系C xyz -. 因为 30CBA??,2PA AB ==,所以2cos30CB =?1AC =.延长MO 交CB 于点D . 因为 OM ∥AC ,所以131, 1,2222MD CB MD CD CB ^=+===.最新整理所以 (1,0,2)P ,(0,0,0)C,B,3(,,0)22M . 所以 (1,0,2)CP =u u u r,CB =u u u r.设平面PCB 的法向量(,,)=x y z m .因为 0,0.CP CBìï?ïíï?ïîu u u r u u u r m m所以(,,)(1,0,2)0,(,,)0,x y z x y z ì?ïïíï?ïî即20,0.x z ì+=ïïíï=ïî令1z =,则2,0x y =-=.所以 (2,0,1)=-m . ……………………………………12分 同理可求平面PMB 的一个法向量n ()=.……………………………………13分 所以 1cos ,5⋅==-⋅m n m n m n . 所以 1cos 5θ=. ………………………………………14分 (17)(本小题满分13分) 解:(Ⅰ)由题意得:0.41,11120.41712.a b a b ++=⎧⎨+⨯+=⎩解得:0.5,0.1a b ==. ……………………………………3分 (Ⅱ)X 2 的可能取值为4.12,11.76,20.40.()[]2 4.12(1)1(1)(1)P X p p p p ==---=-,()[]22211.761(1)(1)(1)(1)P X p p p p p p ==--+--=+-,()220.40(1)P X p p ==-.所以X 2的分布列为:(Ⅲ)由(Ⅱ)可得:()2224.12(1)11.76(1)20.40(1)E Xp p p p p p ⎡⎤=-++-+-⎣⎦211.76p p =-++. ……………………………………11分因为E (X 1)< E (X 2),所以21211.76p p <-++.最新整理所以0.40.6p <<.当选择投资B 项目时,p 的取值范围是()0.4,0.6.……………………………………13分(18)(本小题满分13分) 解:(Ⅰ)由题意知:1c =.根据椭圆的定义得:22a =,即a = ……………………………………3分 所以 2211b =-=.所以 椭圆C 的标准方程为2212x y +=. ……………………………………4分 (Ⅱ)假设在x 轴上存在点(,0)Q m ,使得716QA QB ⋅=-u u u r u u u r 恒成立.当直线l 的斜率为0时,(A B .则7,0)(,0)16m m ?=-. 解得 54m =?. ……………………………………6分 当直线l的斜率不存在时,(1,(1,22A B -.由于557(1,(1,424216+?-?,所以54m ?. 下面证明54m =时,716QA QB ⋅=-u u u r u u u r 恒成立.……………………………………8分显然 直线l 的斜率为0时,716QA QB ⋅=-u u u r u u u r .当直线l 的斜率不为0时,设直线l 的方程为:1x ty =+,()()1122,,,A x y B x y .由221,21x y x ty ìïï+=ïíïï=+ïî可得:22(2)210t y ty ++-=. 显然0∆>.1221222,21.2t y y t y y t ìïï+=-ïï+ïíïï=-ïï+ïî……………………………………10分最新整理因为 111x ty =+,221x ty =+,所以 112212125511(,)(,)()()4444x y x y ty ty y y -?=--+ 2121211(1)()416t y y t y y =+-++2221121(1)24216t t t t t =-+++++ 22222172(2)1616t t t --+=+=-+.综上所述:在x 轴上存在点5(,0)4Q ,使得716QA QB ⋅=-u u u r u u u r恒成立. ……………………………………13分 (19)(本小题满分14分)(Ⅰ)解:()f x 的定义域为(,)a +∞.2(1)'()1a x a xf x x x a x a-++=-+=--. ……………………………………1分令'()0f x =,0x =或+1x a =.当10a -<<时,+10a >,函数()f x 与'()f x 随x 的变化情况如下表:所以,函数()f x 的单调递增区间是(0,1)a +,单调递减区间是(,0)a 和(1,)a ++?.……………………………………3分当1a =-时,2'()01x f x x -=≤+. 所以,函数()f x 的单调递减区间是(1,)-+?. ……………………………………4分 当1a <-时,+10a <,函数()f x 与'()f x 随x 的变化情况如下表:所以,函数()f x 的单调递增区间是(1,0)a +,单调递减区间是(,1)a a +和(0,)+?.最新整理……………………………………5分(Ⅱ)证明:当12(ln21)0a -<<-<时,由(Ⅰ)知,()f x 的极小值为(0)f ,极大值为(1)f a +.因为(0)ln()0f a a =->,2211(1)(1)(1)(1)022f a a a a +=-+++=->,且()f x 在(1,)a ++?上是减函数,所以()f x 至多有一个零点. ……………………………………7分 又因为211(2)ln 2[2(ln 21)]022f a a a a a a +=--=---<, 所以 函数()f x 只有一个零点0x ,且012a x a +<<+.……………………………………9分(Ⅲ)解:因为412(ln 21)5-<-<-, 所以 对任意120,[0,]x x x ∈且211,x x -=由(Ⅱ)可知:1[0,1)x a ∈+,20(1,]x a x ∈+,且21x ≥. ……………………………………10分因为 函数()f x 在[0,1)a +上是增函数,在(1,)a ++?上是减函数,所以 1()f x (0)f ≥,2()f x (1)f ≤. ……………………………………11分 所以 12()()(0)(1)f x f x f f -?.当45a =-时,1(0)(1)ln()12a f f a a -=--=491ln 542->0. 所以 12()()(0)(1)0f x f x f f -?>. ……………………………………13分所以 21()()f x f x -的最小值为491(0)(1)ln 542f f -=-. 所以 使得21()()f x f x m -≥恒成立的m 的最大值为491ln 542-.……………………………………14分(20)(本小题满分13分)(Ⅰ)解:因为3=3,3=1+2,3=1+1+1,所以3)3(=f .因为5=5,5=2+3,5=1+4,5=1+1+3,5=1+2+2,5=1+1+1+2,5=1+1+1+1+1, 所以7)5(=f . ……………………………………3分 (Ⅱ)结论是)1(+n f )]2()([21++≤n f n f . 证明如下:由结论知,只需证).1()2()()1(+-+≤-+n f n f n f n f最新整理. 因为21≥+n ,把1+n 的一个表示法中11a =的1a 去掉,就可得到一个n 的表示法;反之,在n 的一个表示法前面添加一个“1+”,就得到一个1n +的表示法,即1+n 的表示法中11a =的表示法种数等于n 的表示法种数,所以)()1(n f n f -+表示的是1+n 的表示法中11a ¹的表示法数,)1()2(+-+n f n f 是2n +的表示法中11a ¹的表示法数.同样,把一个11a ¹的1+n 的表示法中的p a 加上1, 就可得到一个11a ¹的2n +的表示法,这样就构造了从11a ¹的1+n 的表示法到11a ¹的2+n 的表示法的一个对应.所以有).1()2()()1(+-+≤-+n f n f n f n f ……………………………………9分 (Ⅲ)由第(Ⅱ)问可知:当正整数6m ³时,()(1)(1)(2)(6)(5)f m f m f m f m f f --?--吵-L . 又,7)5(,11)6(==f f 所以 ()(1)4f m f m --?. *对于*式,分别取m 为n ,,7,6Λ,将所得等式相加得)5(4)5()(-≥-n f n f .即134)(-≥n n f . ……………………………………13分。
2012年北京市各区二模试题分类解析【数学理】(6):数列.pdf

情感态度与价值观 :正确认识发展与环保的矛盾,树立科学的发展观。
【教学重点】 1.了解那树的生命历程,把握树的价值、品格及其命运,理解作者的思想情感。
2.掌握托物寓意的表现手法,体会比喻、拟人等修辞的表达效果。
【教学难点】 1.揣摩关键语句,体味作者痛苦、悲悯、愤激的情感,感受老树命运的悲剧色彩。
2.正确理解蚂蚁王国的事情,体会作者的用意。
【教具准备】多媒体课件【教学方法】 1.朗读法 2.讨论点拨法 3.品读法 4.延伸拓展法 【课时安排】一课时 【教学过程】 【教学目标】资料助读;朗读课文,整体感知;理清行文思路,把握树的生命历程;感知树的形象,体会作者的情感。
一、导语设计 :大地上最悦目的颜色是绿色,大地上站立的最大的生命群体是森林,但是在今天,许多地方的绿色正逐渐被吞噬,他们在疾速奔驰的人类文明的车轮的碾压下,成片成片地消失了。
这不,就连街头那棵老树也未能幸免,就让我们一起拜读王鼎钧先生为那树写的“悼词”吧。
二、资料助读 1.关于作者王鼎钧,台湾著名的散文家。
主要的散文作品有《人生三书》(《开放的人生》《人生试金石》《我们现代人》)《人生观察》《长短调》《世事与棋》《情人眼》《碎玻璃》《灵感》等。
2.多媒体播放反映人类生存困境的若干画面,如水土流失、土壤沙化、沙漠蔓延、洪水肆虐、森林面积锐减、资源严重枯竭…… 三、朗读课文,整体感知 1.学生默读课文,积累生字生词,并交流。
多媒体显示; 佝偻(gōu lóu):脊背向前弯曲,文中指老树枝干弯曲。
倒坍(tān):倒塌。
萌庇(yìn bì):大树枝叶遮蔽阳光,宜于人们休息。
引颈受戮:伸长脖子接受杀戮。
踝骨(huái):指树干靠近根的部位。
虬须(qiú):卷曲的胡子。
这里指树根。
周道如砥(dī)这里形容公路的平坦,畅通无阻。
2.选朗读水平较高的学生范读课文,教师提醒学生注意把握感情分寸,应深沉,不宜强烈奔放。
2012年北京市各区二模试题分类解析【数学理】(1):集合.pdf

1、认识生态环境破坏对我们将来生活的影响并提高环保意识。
2、学习报告文学写作手法的运用;并以此写作倡导书。
教学难点: 1、真正意义上认识到环保的重要性。
2、认识到环保是我们每个公民的职责;并制止环境破坏者的行为。
过程和方法: 朗读课文后揣摩文章字里行间充盈的感情和中心的关系,体味文中所设置的悬念。
教学方法: 诵读法与讨论法 教学过程: 一、导入: 当我们眼见一个广阔、美丽、充满生机的地方变为荒漠;原本牛马成群,绿林环绕,河流清澈的生命绿洲,现在却是一片死寂,寸草不生,不见飞鸟,令人恐怖;我们会深思,这种生态的巨变,就发生在我们的身边,这就是我们今天要认识的一个地方——罗布泊。
二、初读课文:1、正确识读、理解文中生字: 萧瑟(sè)和煦(xù)干涸(hé)吞噬(shì)裸露(luǒ)戈壁(gē)荡漾(yàng)娱乐(yú) 2、词语释义: 萧瑟:①形容风吹树木的声音;②形容冷落,凄凉。
和煦:温暖,多指阳光、风等。
干涸:(河道、池塘等)没有水了。
吞噬:蚕食、并吞。
裸露:没有东西遮盖。
戈壁滩:蒙古或新疆人称沙漠地区,这种地区尽是沙子和石块,地面缺水,植物稀少。
沧海桑田:大海变成农田,农田变成大海。
比喻世事变化很大。
也说桑田沧海。
3、内容提要: 要比较具体地把握课文内容,可以做一份内容提要,就下面几个问题画出要点:①今日罗布泊是怎样的一个地方?关键词是“沙漠”“神秘”。
②过去罗布泊是怎样的一个地方?关键词是“绿洲”“仙湖”。
③罗布泊为什么会消亡?关键词是“改道”“四盲”。
④同样的悲剧还有哪些?关键词是“青海湖”“月牙泉”。
全文充满了痛惜之情,为罗布泊生态环境的破坏而痛惜,为人们的盲目性造成的悲剧而痛惜。
生态意识,环保意识,可持续发展意识,是课文的基本理念。
课文又涉及西部大开发战略问题,用历史的教训,说明生态环境保护的重要。
北京市2012年中考数学二模试题分类 代数综合(教师版)

2012年市中考数学二模分类汇编——代数综合题整数根、系数是整数问题1.(昌平23.)已知m 为整数,方程221x mx +-=0的两个根都大于-1且小于32,当方程的两个根均为有理数时,求m 的值.23.解: 设221y x mx =+-. ………………………………1分 ∵2210x mx +-=的两根都在1-和32之间,∴ 当1x =-时,0y >,即:210m --> .…………2分当32x =时,0y >,即:931022m +->. ……………3分∴1213m -<<.…………………4分∵m 为整数,∴210m =--,,. …………………………5分 ① 当2m =-时,方程222104812x x --=∆=+=,, ∴ 此时方程的根为无理数,不合题意.② 当1m =-时,方程212121012x x x x --==-=,,,符合题意.③ 当0m =时,方程2210x -=,x =综合①②③可知,1m =-.…………………… 6分2.(房山)23.)已知:关于x 的方程mx2-3(m -1)x +2m -3=0. ⑴当m 取何整数值时,关于x 的方程mx2-3(m -1)x +2m -3=0的根都是整数;⑵若抛物线32)1(32-+--=m x m mx y 向左平移一个单位后,过反比例函数)0(≠=k x ky 上的一点(-1,3),①求抛物线32)1(32-+--=m x m mx y 的解析式; ②利用函数图象求不等式0>-kx x k的解集.解:⑴ ⑵① ②23.解:⑴当m=0时,x=1----------------------------1分当m ≠0,可解得x1=1,x2=m mm 3232-=------------------2分 ∴31±±=,m 时,x 均有整数根--------------------------------------3分综上可得310±±=,,m 时,x 均有整数根⑵①抛物线向左平移一个单位后得到3-------------4分 过点(-1,3)代入解得m=3∴抛物线解析式为y= 3x2-6x +②k=-1×3=-3-----------------------6∴x>1或-1<x<0-----------------------73.(平谷23)已知抛物线22y x mx m =-+-. (1)求证此抛物线与x 轴有两个不同的交点;(2)若m 是整数,抛物线22y x mx m =-+-与x 轴交于整数点,求m 的值;(3)在(2)的条件下,设抛物线顶点为A ,抛物线与x 轴的两个交点中右侧交点为B .若M 为坐标轴上一点,且MA MB =,求点M 的坐标. 23.解:(1)证明:令0y =,则220x mx m -+-=.因为248m m ∆=-+2(2)40m =-+>, 1分 所以此抛物线与x 轴有两个不同的交点. 2分(2)因为关于x 的方程220x mx m -+-=的根为2(2)4m m x ±-+=,由m 为整数,当2(2)4m -+为完全平方数时,此抛物线与x 轴才有可能交于整数点.设22(2)4m n -+=(其中n 为整数), 3分所以 [(2)][(2)]4n m n m +---=. 因为 (2)n m +-与(2)n m --的奇偶性相同,所以2222n m n m +-=⎧⎨-+=⎩,;或222 2.n m n m +-=-⎧⎨-+=-⎩,解得 2m =.经检验,当2m =时,关于x 的方程220x mx m -+-=有整数根. 所以 2m =...................................5分 (3) 当2m =时,此二次函数解析式为222(1)1y x x x =-=--,则顶点A 的坐标为(11-,).抛物线与x 轴的交点为(0)O ,0、(20)B ,. 设抛物线的对称轴与x 轴交于1M ,则1(10)M ,.在直角三角形1AM O中,由勾股定理,得2AO =,由抛物线的对称性可得,2AB AO ==.又2222+=, 即 222OA AB OB +=.所以 △ABO 为等腰直角三角形.且11M A M B =.所以1(1)M ,0为所求的点. 6分若满足条件的点2M 在y 轴上时,设2M 坐标为(0)y ,.过A 作AN y ⊥轴于N ,连结2AM 、2BM .则22M A M B =.由勾股定理,有22222M A M N AN =+;22222M B M O OB =+.即 2222(1)12y y ++=+. 解得 1y =. 所以2(0)M ,1为所求的点.7分综上所述满足条件的M 点的坐标为(10,)或(01,).4.(门头沟23) 已知抛物线y =ax2+x +2. (1)当a =-1时,求此抛物线的顶点坐标和对称轴; (2)若代数式-x2+x +2的值为正整数,求x 的值;(3)若a 是负数时,当a =a1时,抛物线y =ax2+x +2与x 轴的正半轴相交于点M(m ,0);当a =a2时,抛物线y =ax2+x +2与x点N(n ,0). 若点M 在点N 的左边,试比较a1与a223. 当a=-1时,y=-x2+x+2,∴a=-1,b=1,c=2.∴抛物线的顶点坐标为(21,49),对称轴为直线x=21(2)∵代数式-x2+x+2的值为正整数,∴函数y=-x2+x+2的值为正整数.又因为函数的最大值为49,∴y 的正整数值只能为1或2.当y=1时,-x2+x+2=1,解得2511+=x ,2512-=x (3)分当y=2时,-x2+x+2=2,解得x3=0,x4=1.……………4分∴x 的值为2511+=x ,2512-=x ,0或1.(3) 当a <0时,即a1<0,a2<0.经过点M 的抛物线y=a1x2+x+2的对称轴为121a x -=,经过点N 的抛物线y=a2x2+x+2的对称轴为221a x -=.…………5分∵点M 在点N 的左边,且抛物线经过点(0,2)∴直线121a x -=在直线221a x -=的左侧……………6分∴121a -<221a -.∴a1<a2.…………………………………7分 5.(怀柔23)已知抛物线22(21)1y x m x m =+-+- (m 为常数) . (1)若抛物线22(21)1y x m x m =+-+-与x 轴交于两个不同的整数点,求m 的整数值;(2)在(1)问条件下,若抛物线顶点在第三象限,试确定抛物线的解析式;(3)若点M(x1,y1)与点N(x1+k ,y2)在(2)中抛物线上 (点M 、N 不重合), 且y1=y2. 求代数式21116+6+5-+1x x k k ⋅的值.23.解:(1)由题意可知,△=()222-1-4(-1)m m =5-4m >0,.…………………1分又抛物线与x 轴交于两个不同的整数点, ∴5-4m 为平方数,设k2 =5-4m ,则满足要求的m 值为1,-1,-5,-11,-19…… ∴满足题意的m 整数值的代数式为2-++1n n (n 为正整数). …………………………3分 (2)∵抛物线顶点在第三象限, ∴只有m=1符合题意,抛物线的解析式为2=+y x x .…………………4分(3)∵点M ()11,x y 与N ()12,x k y +在抛物线2=+y x x 上, ∴2111=+y x x ,2211=(+)++y x k x k ∵,21y y = ∴()221111+=+++.x x x k x k整理,得()12++1=0k x k∵点M 、N 不重合,∴k ≠0.∴2x1 =-k -1.……………………………………6分∴21116+6+5-+1x x kk ⋅=()2+116-3(k+1)+5-4+1k k k ⋅=6.………7分6.在平面直角坐标系xOy 中,抛物线21124y x =+的顶点为M ,直线2y x =,点()0P n ,为x 轴上的一个动点,过点P 作x 轴的垂线分别交抛物线21124y x =+和直线2y x =于点A ,点B.⑴直接写出A ,B 两点的坐标(用含n 的代数式表示);⑵设线段AB 的长为d ,求d 关于n 的函数关系式及d 的最小值,并直接写出此时线段OB 与线段PM 的位置关系和数量关系;(3)已知二次函数2y ax bx c =++(a ,b ,c 为整数且0a ≠),对一切实数x 恒有x ≤y ≤2124x +,求a ,b ,c 的值.25.解:(1)21(2)4A n n +,,()B n n ,.﹍﹍﹍﹍﹍﹍﹍﹍﹍2分 (2) d =AB=A B y y -=2124n n -+. ∴d =2112()48n -+=2112()48n -+.﹍﹍3分 ∴ 当14n =时,d 取得最小值18. ﹍﹍ 4分当d 取最小值时,线段OB 与线段PM 的位置 关系和数量关系是OB ⊥PM 且OB=PM. (如图10) ﹍﹍﹍﹍﹍ 5分(3) ∵ 对一切实数x 恒有 x ≤y ≤2124x +,∴ 对一切实数x ,x ≤2ax bx c ++≤2124x +都成立. (0a ≠) ①当0x =时,①式化为 0≤c ≤14.∴ 整数c 的值为0.﹍﹍﹍﹍﹍ 6分此时,对一切实数x ,x ≤2ax bx +≤2124x +都成立.(0a ≠)即 222,12.4x ax bx ax bx x ⎧≤+⎪⎨+≤+⎪⎩对一切实数x 均成立. 由②得()21ax b x+-≥0 (0a ≠) 对一切实数x 均成立.∴()210,10.a b >⎧⎪⎨∆=-≤⎪⎩由⑤得整数b此时由③式得,2ax x +≤2124x +对一切实数x 均成立. (0a ≠)即21(2)4a x x --+≥0对一切实数x 均成立. (0a ≠)当a=2时,此不等式化为14x -+≥0,不满足对一切实数x 均成立.当a≠2时,∵21(2)4a x x --+≥0对一切实数x 均成立,(0a ≠)∴2220,1(1)4(2)0.4a a ->⎧⎪⎨∆=--⨯-⨯≤⎪⎩④② ⑥∴ 由④,⑥,⑦得 0 <a ≤1.∴ 整数a 的值为1. ﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍8分 ∴ 整数a ,b ,c 的值分别为1a =,1b =,0c =. 利用数形结合研究交点、方程的根1.(东城23.) 已知关于x 的方程2(1)(4)30m x m x -+-+=. (1) 若方程有两个不相等的实数根,求m 的取值X 围;(2)若正整数m 满足822m ->,设二次函数2(1)(4)3y m x m x =-+-+的图象与x 轴交于A B 、两点,将此图象在x 轴下方的部分沿x 轴翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象回答:当直线3y kx =+与此图象恰好有三个公共点时,求出k 的值(只需要求出两个满足题意的k 值即可).23.解:(1)2(4)12(1)m m ∆=--- 2(2)m =+.……2分由题意得,2(2)m +>0且10m -≠ .∴ 符合题意的m 的取值X 围是 21m m ≠-≠且的 一切实数. ……3分 (2)∵ 正整数m 满足822m ->, ∴ m 可取的值为1和2 .又∵ 二次函数2(1)(4)3y m x m x =-+-+, ∴ m =2.……4分∴ 二次函数为2-23y x x =++. ∴ A 点、B 点的坐标分别为(-1,0)、(3,0). 依题意翻折后的图象如图所示.由图象可知符合题意的直线3y kx =+经过点A 、B . 可求出此时k 的值分别为3或-1.……7分注:若学生利用直线与抛物线相切求出k=2也是符合题意的答案.2.(海淀23)已知抛物线 2(1)(2)1y m x m x =-+--与x 轴交于A 、B 两点.(1)求m 的取值X 围;(2)若m>1, 且点A 在点B 的左侧,OA : OB=1 : 3, 试确定抛物线的解析式;(3)设(2)中抛物线与y 轴的交点为C ,过点C 作直线l //x 轴, 将抛物线在y 轴左侧的部分沿直线 l 翻折, 抛物线的其余部分保持不变,得到一个新图象. 请你结合新图象回答: 当直线y =公共点P(x0, y0)且 y0≤7时, 求b 的取值X 围23.解:(1)∵抛物线2(1)(2)1y m x m x =-+--与x 轴交于A 、B 两点, ∴210,(2)4(1)0.m m m由①得1m , 由②得0m,∴m 的取值X 围是0m且1m. …………2分(2)∵点A 、B 是抛物线2(1)(2)1y m x m x =-+--与x 轴的交点, ∴令0y =,即2(1)(2)10m x m x -+--=. 解得11x =-,211x m =-.∵1m >,∴10 1.1m >>--∵点A 在点B 左侧,∴点A 的坐标为(1,0)-,点B 的坐标为1(,0)1m -. …………………………3分∴OA=1,OB=11m -.①②………………………1分∵OA : OB=1 : 3,∴131m =-. ∴43m.∴抛物线的解析式为212133y x x =--. ………………………………………4分 (3)∵点C 是抛物线212133y x x =--与y 轴的交点,∴ 点C 的坐标为(0,1).依题意翻折后的图象如图所示.令7y =,即2121733x x --=.解得16x =, 24x =-. ∴ 新图象经过点D (6,7).当直线13y x b=+经过D 点时,可得5b =. 当直线13y x b=+经过C 点时,可得1b =-.当直线1(1)3y x b b =+<-与函数2121(0)33y x x x =-->的图象仅有一个公共点P(x0, y0)时,得20001121333x b x x +=--.整理得 2003330.x x b ---=由2(3)4(33)12210b b ,得74b =-. 结合图象可知,符合题意的b 的取值X 围为15b -<≤或74b.……………7分通州22.已知关于x 的方程2(31)220mx m x m --+-= (1)求证:无论m 取任何实数时,方程恒有实数根.(2)若关于x 的二次函数2(31)22y mx m x m =--+-的图象经过坐标原点(0,0),求抛物线的解析式.(3)在直角坐标系xoy 中,画出(2)中的函数图象,结合图象回答问题:当直线y x b =+ 与(2)中的函数图象只有两个交点时,求b 的取值X 围. 22..解:(1)分两种情况讨论. 当0m =时,方程为x 20-=2=∴x ,方程有实数根,………………………………………….(1分)②当0m ≠,则一元二次方程的根的判别式()()2222314229618821m m m m m m m m m ∆=----=-+-+=++⎡⎤⎣⎦=()21m +≥0不论m 为何实数,∆≥0成立,∴方程恒有实数根 ………………………………………….(2分)综合①、②可知m 取任何实数, 方程()231220mx m x m --+-=恒有实数根………………….(3分)(2) 二次函数2(31)22y mx m x m =--+-的图象与经过(0,0)∴022=-m∴1=m ………………………………………….(4分)∴二次函数解析式为:x x y 22-=………………………….(5分) (3)在(2)条件下,直线y x b =+与二次函数图象只有两个交点,结合图象可知212y x xy x b ⎧=-⎨=+⎩当1y y =时,得230x x b --= 由940b ∆=+=得94b =-………………………….(6分)综上所述可知:当49->b 时,直线y x b =+与(2)中的图象有两个交点. ………….(7分)23.(延庆) 已知:关于x 的一元二次方程01-m x 2m 2-mx 2=++)((1)若此方程有实根,求m 的取值X 围;(3)解:如图所示:①当直线l 经过原点O 时与半圆P 有两个交点,即b=0………5分②当直线l 与半圆P 相切于D 点时有一个交点,如图由题意可得Rt △EDP 、Rt △ECO 是等腰直角三角形,∵DP=2 ∴EP=22………….6分 ∴OC=2-22 即b=2-22∴当0≤b <2-22时,直线l 与半圆P 只有两个交点。
2012年北京中考二模数学试题分类汇编——代数综合题试题与答案

新世纪教育网精选资料 版权全部 @新世纪教育网2012 年北京市中考数学二模分类汇编——代数综合题整数根、系数是整数1.(昌平23.)已知 m 整数,方程 2x2mx 1 =0 的两个根都大于 -1 且小于3,当方程2的两个根均 有理数 ,求m 的 .23.解:y2 x 2 mx1.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分∵ 2x2mx 1 0 的两根都在 1和3之 ,2∴ 当 x1 , y0 ,即: 2 m 1 0 .⋯⋯⋯⋯ 2 分当 x3 , y0 ,即: 9 3 m 1 0 .⋯⋯⋯⋯⋯ 3 分2212 2∴m 1.⋯⋯⋯⋯⋯⋯⋯4 分3∵ m 整数,∴ m2, 1,0 .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分① 当 m2 ,方程 2x 22x1 0,48 12 ,∴ 此 方程的根 无理数,不合 意.② 当 m1 ,方程 2x2x 10, x 11, x 21,切合 意.2③ 当 m0 ,方程 2x 2 10 , x2 ,不切合 意.2合①②③可知,m1.⋯⋯⋯⋯⋯⋯⋯⋯6 分2.(房山) 23.)已知:对于2x 的方程 mx - 3( m - 1) x +2m -3=0.⑴当 m 取何整数 ,对于 x 的方程 mx 2- 3( m -1) x + 2m - 3=0 的根都是整数;⑵若抛物ymx 23( m 1)xm 3 向左平移一个 位后, 反比率函数2yk(k 0) 上的一点( -1,3 ),x①求抛物 ymx 2 3(m 1) x 2m 3 的分析式;②利用函数 象求不等式k kx 0的解集 .xy 解:⑴43 ⑵①2- 4②23.解:⑴当 m=0 时, x=1---------------------------- 1 分当 m ≠ 0,可解得 x 1=1, x 2=2m323-----------------2 分m m∴ m 1, 3 时, x 均有整数根 --------------------------------------3分综上可得 m 0, 1, 3 时, x 均有整数根⑵①抛物线向左平移一个单位后获得 y= m( x + 1) 2- 3( m - 1)( x + 1) + 2m - 3 -------------4 分 过点( -1,3 )代入解得 m= 3y∴抛物线分析式为2----------5 分4y= 3x - 6x + 3②k=- 1× 3=- 3-----------------------6 分3 ∴x>1 或- 1<x<0----------------------- 7分21x-4-3-2 -1O1234- 1- 2 - 3 - 43.(平谷 23)已知抛物线 y x 2 mx m 2 .(1)求证此抛物线与 x 轴有两个不一样的交点;(2)若m 是整数, 抛物线 yx2mx m 2 与 x轴交于整数点, 求 m3 2的值;( )在( )的条件下,设抛物线极点为 A ,抛物线与 x 轴的两个交点中右边交点为B .若 M 为坐标轴上一点,且 MAMB ,求点 M 的坐标.23.解:( 1)证明:令 y0,则 x 2 mx m 2 0 .由于m 2 4m 8 ( m 2)2 4 0 , ·············1 分因此此抛物线与x 轴有两个不一样的交点.··············2 分( 2)由于对于 x 的方程 x 2 mxm 20 的根为 x m( m 2)24 ,由 m 为整数,当 (m 2)2 4 为完整平方数时,此抛物线与2x 轴才有可能交于整数点.设 (m2) 2 4 n 2 (此中 n 为整数), ··························3 分因此 [ n (m 2)][ n ( m 2)] 4 .由于n (m 2) 与 n (m 2) 的奇偶性同样,n m 2 ,n m 2,因此2 或2;解得 m 2 .,当 m 2 ,关于x的方程x2mx m 20 有整数根.所以m 2 ...................................5分(3)当m 2,此二次函数分析式y x2 2 x(x 1)21,点 A 的坐(1,1).抛物与 x 的交点O(0, 0)、 B(2,0).抛物的称与x 交于M1,M 1(10),.在直角三角形AM 1O 中,由勾股定理,得AO 2 ,由抛物的称性可得,AB AO2.又( 2)2( 2)222222,即OAAB O B.因此△ ABO 等腰直角三角形.且M 1A M1B .因此M1(1,0) 所求的点.····························6分若足条件的点M 2在y上, M 2坐(0,y).A 作 AN ⊥ y 于 N ,AM2、BM2.M2A M2B.由勾股定理,有M2A2M 2N2AN 2; M2B2M 2O2OB2.即( y 1)2 12y 222.解得y 1.因此 M 2 (0,1) 所求的点.·······················7 分上所述足条件的M 点的坐( 1,0)或(0,1).4.(沟 23)已知抛物y= ax2+ x+ 2.(1)当 a=-1 ,求此抛物的点坐和称;(2) 若代数式- x2+ x+2 的正整数,求x 的;(3) 若 a 是数,当 a= a1,抛物 y=ax2+ x+ 2 与 x 的正半订交于点M(m ,0);当a= a2,抛物 y= ax2+x+ 2 与 x 的正半订交于点N(n, 0). 若点 M 在点 N 的左,比 a1与 a2的大小 .y 4 3 2 123. 当 a=-1 , y=-x 2+x+2 ,∴ a=-1,b=1,c=2.-4-3-2-1O 1 2 3 4 x-1-2( 1 , 9),称直 x=1-3∴抛物的点坐. ⋯⋯2分2 42-4 (2) ∵代数式 -x2+x+2 的正整数,∴函数y=-x 2+x+2的正整数 .又因函数的最大9,∴ y 的正整数只好1或2. 4当 y=1 , -x2+x+2 =1,解得x115, x215⋯⋯⋯⋯3 分22当 y=2 , -x 2+x+2 =2,解得 x 3=0,x 4=1. ⋯⋯⋯⋯⋯4 分1515∴ x 的 x 1, x 2,0或 1.22(3)当 a < 0 ,即 a 1< 0, a 2< 0.点 M 的抛物 y=a 1x 2+x+2 的 称 x1 ,2a 1点 N 的抛物 y=a 2x 2+x+2 的 称 x1 . ⋯⋯⋯⋯5分2a 2∵点 M 在点 N 的左 ,且抛物 点 (0,2)1 在直 x1 ∴直 x的左 ⋯⋯⋯⋯⋯6 分2a 1 2a 21 1∴<. ∴ a 1< a 2. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7 分2a 12a 25.( 柔 23)已知抛物yx 2(2m 1)x m 2 1 (m 常数 ) .( 1)若抛物y x2(2m 1)x m 2 1 x交于两个不一样的整数点, 求 m 的整数 ;与 ( 2)在( 1) 条件下,若抛物 点在第三象限, 确立抛物 的分析式;( 3)若点 M(x 1,y 1)与点 N(x 1+k ,y 2)在( 2)中抛物 上 (点 M 、N 不重合 ), 且 y 1=y 2. 求代数式 x 1216+6 x 1 +5-k 的 .k+1223.解:( 1)由 意可知, △ = 2m-1-4( m 2 -1)=5 - 4m > 0, . ⋯⋯⋯⋯⋯⋯⋯ 1 分又抛物 与 x 交于两个不一样的整数点,∴ 5- 4m 平方数,k 2 =5 - 4m , 足要求的 m1,- 1,- 5,- 11,- 19⋯⋯ ∴ 足 意的 m 整数 的代数式 -n 2 +n+1 (n 正整数 ). ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 3 分( 2)∵抛物 点在第三象限,∴只有 m=1 切合 意,抛物 的分析式y=x 2 +x . ⋯⋯⋯⋯⋯⋯⋯4 分( 3)∵点 Mx 1,y 1 与 N x 1 k,y 2 在抛物 y=x 2 +x 上,∴ y 1 =x 12 +x 1 , y 2 =(x 1 +k)2 +x 1 +k ∵ y 1y 2 ,∴ x 12 2+x 1 = x 1 +k +x 1 +k.整理,得 k 2 x 1 +k +1 =0∵点 M 、 N 不重合,∴ k ≠ 0.∴ 2x 1 =- k - 1. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 6 分2∴ x 1216+6 x 1 +5-k =k +116-3(k+1)+5-k =6. ⋯⋯⋯ 7 分4k +1k +16 .在平面直角坐 系xOy中,抛物 21的 点 M ,直y 2x ,点 P n ,04x 上的一个 点, 点P 作 x 的垂 分 交抛物 y 1 2x21和直 y 2x 于点4A ,点 B.⑴直接写出 A , B 两点的坐 (用含n 的代数式表示);⑵ 段 AB 的 d ,求 d 对于 n 的函数关系式及 d 的最小 ,并直接写出此 段OB 与 段 PM 的地点关系和数目关系;(3) 已知二次函数 y ax 2bxc ( a , b , c 整数且 a0 ), 全部 数x 恒有x ≤y ≤2x21,求 a , b , c 的 .425.解: (1) A(n ,2n 21) , B( n ,n) .﹍﹍﹍﹍﹍﹍﹍﹍﹍2 分4(2) d =AB= y Ay B = 2n 2n 1 .y41∴ d = 2(n1 )2 1 = 2( n 1 )2 1.﹍﹍3 分4 8 4 8 A∴ 当 n 1, d 获得最小1.﹍﹍ 4分M B481 O P1x当 d 取最小 , 段 OB 与 段 PM 的地点10关系和数目关系是 OB ⊥PM 且 OB=PM. (如 10)﹍﹍﹍﹍﹍ 5 分(3) ∵ 全部 数 x 恒有x ≤ y ≤ 2x 2 1 ,4∴ 全部 数 x , x ≤ ax2bxc ≤ 2x 21都建立 . ( a0 )①4 当 x0 ,①式化0≤ c ≤1.4∴整 数 c的0.﹍﹍﹍﹍﹍6分此 , 全部 数 x , x ≤ ax2bx ≤ 2x21都建立 .( a0 )4x ax 2bx,②即bx 2 x21 . ③对一确实数x 均建立 .ax24由②得 ax 2b 1 x ≥ 0( a 0 ) 对一确实数 x 均建立 . a 0,④ ∴b20.⑤11由⑤得整数 b 的值为 1.﹍﹍﹍﹍﹍﹍﹍﹍﹍ 7 分此时由③式得, ax2x ≤ 2x21对一确实数 x 均建立 . ( a 0 )4即 (2 a)x2x1≥ 0 对一确实数 x 均建立 . ( a0 )4当 a=2 时,此不等式化为x1≥ 0,不知足对一确实数x 均建立 .4当 a ≠2时,∵ (2 a) x2x1≥ 0 对一确实数 x 均建立, ( a0 )42 a 0,⑥ ∴( 1)24 (2 a)1 ⑦20.4∴ 由④,⑥,⑦得 0 < a ≤1.∴ 整数 a 的值为 1.﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍8 分∴ 整数 a , b , c 的值分别为 a 1 , b 1, c0 .利用数形联合研究交点、方程的根1.(东城 23.) 已知对于 x 的方程 (1m) x 2 (4 m) x3 0 .(1) 若方程有两个不相等的实数根,求m 的取值范围;( 2)若正整数 m 知足 8 2m 2,设二次函数 y (1 m) x 2(4 m) x 3 的图象与 x 轴交于 A 、B 两点,将此图象在 x 轴下方的部分沿x 轴翻折, 图象的其他部分保持不变, 获得一个新的图象.请你联合这个新的图象回答:当直线 y kx3 与此图象恰巧有三个公共点时,求出 k 的值(只要要求出两个知足题意的k 值即可).23.解:( 1)(4 m) 212(1m)(m 2分2 ).⋯⋯2由意得, (m2)2>0且1 m 0.∴符合意的m的取范是m2且 m 1的全部数.⋯⋯ 3分(2)∵ 正整数m足8 2m 2,∴ m 可取的 1 和 2 .又∵ 二次函数 y (1 m) x2(4 m) x 3 ,∴m =2.⋯⋯4分∴二次函数y - x22x 3.∴ A 点、 B 点的坐分( -1,0)、( 3,0).依意翻折后的象如所示.由象可知切合意的直y kx 3 点A、B.可求出此k 的分 3 或 -1.⋯⋯ 7 分注:若学生利用直与抛物相切求出k=2 也是切合意的答案.2.(海淀23)已知抛物y (m1)x2(m2) x 1 与x交于A、 B 两点.(1)求 m 的取范;(2)若 m>1, 且点 A 在点 B 的左, OA : OB=1 : 3, 确立抛物的分析式;(3)( 2)中抛物与y 的交点C,点 C 作直 l //x ,将抛物在y 左的部分沿直l 翻折 , 抛物的其他部分保持不,获得一个新象. 你合新象回答: 1b 与新象只有一个公共点P( x0, y0)且 y07 ,求 b 的取范 .当直yx3y87654321-4 -3 -2 -1 O 1 2 3 4 5 6 7 8 x23. 解:( 1)∵ 抛物y(m1)x 2( m2) x1 与x交于A、B两点,ì①?m - 1 ? 0,?⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分∴ í2②??D = ( m - 2) + 4( m- 1) > 0.由①得 m 11 ,由②得 m 10 ,∴ m 的取范是m 10且 m 1 1 .⋯⋯⋯⋯ 2 分( 2)∵ 点 A、 B 是抛物y(m1)x2(m2) x 1 与x的交点,∴令 y 0 ,即 (m 1)x2( m 2) x 1 0 .解得x1 1 , x21.m 1∵ m1,∴10 1. m 1∵点 A在点 B左,∴点 A的坐(1,0) .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3分1,0) ,点B的坐 (m1∴ OA= 1,OB=1.m 1∵OA : OB=1 : 3,∴1 3 .m1∴m= 4 .3∴ 抛物的分析式y1x22x 1 .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4 分33( 3)∵ 点 C 是抛物y 1 x2 2 x 1 与y的交点,3 3∴点 C 的坐(0,- 1).依意翻折后的象如所示.令 y 7 ,即1x22x 1 7 .33解得 x1 6 , x24.∴新象点 D(6,7) .当直y1 D 点,可得 b 5 .x b3当直 y1x b C 点,可得 b1y.837D1 x 1 x2 2 x6当直y b(b1)与函数 y1(x0)533343的象有一个公共点P(x0, y0),得21121B2Axb 1 .-4 -3 -2 -1O 1 234567x0x0x0-1C l 333-2整理得 x023x03b30.-3-4 -5由D=(-3)2- 4(- 3b - 3) = 12b+ 21 = 07-6,得 b-7.4-8合象可知,切合意的 b 的取范1b 5或b < -7.⋯⋯⋯⋯⋯7 分4通州 22.已知对于x的方程mx2(3m 1)x2m 20( 1)求:无m取任何数,方程恒有数根.( 2)若对于x的二次函数y mx2(3m 1)x2m 2 的象坐原点(0,0),求抛物的分析式 .( 3)在直角坐系xoy 中,画出(2)中的函数象,合象回答:当直 y x b 与( 2)中的函数象只有两个交点,求 b 的取范.22. .解:( 1)分两种状况 .①当 m0 ,方程x20x 2 ,方程有数根,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯.(1 分)②当 m0 ,一元二次方程的根的判式3m 129m26m 18m28m m22m 1 4m 2m 2= m2≥ 0 不m何数,≥ 01建立,方程恒有数根⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯.(2 分)合①、②可知m 取任何数,方程 mx23m 1 x2m20 恒有数根⋯⋯⋯⋯⋯⋯⋯.(3 分)(2)二次函数y mx2(3m1)x2m 2的象与( 0,0)2m20m1⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯.(4 分)二次函数分析式:y x22x ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯.(5 分)(3)在( 2)条件下,直y x b 与二次函数象只有两个交点,合象可知y x22x1当 y1y ,y x b得 x2 3x b 0由9 4b 0得 b 9⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ .(6 分) 49上所述可知:当b,4直 y x b 与(2)中的象有两个交点. ⋯⋯⋯⋯ .(7 分 )23. (延)已知 :对于 x 的一元二次方程mx2 - 2m 2 x m - 1 0()(1)若此方程有根 ,求 m 的取范 ;(2)在 (1)的条件下 ,且 m 取最小的整数 ,求此方程的两个根 ;(3) 在 (2)的前提下 ,二次函数y mx2(-2m2)x m - 1 与x有两个交点,接两点的段 ,并以条段直径在x 的上方作半P,直l的分析式y=x+b,若直l 与半 P 只有两个交点 ,求出 b 的取范 .23. ( 1)解:∵对于 x 的一元二次方程有根∴ m≠ 0,且△≥ 0⋯..1 分∴△ =( 2m+2)2-4m( m-1)=12m+4≥ 0解得 m≥-132D1∴当 m≥-,且 m≠ 0 此方程有根 ,⋯⋯ ..2 分C3E( 2)解:∵在 (1)的条件下 ,当 m 取最小的整数 ,AO P5∴ m=1⋯⋯⋯⋯ ..3 分∴原方程化: x2-4x=0x( x-4 ) =0x1=0,x2=4 ⋯⋯⋯⋯ .. ⋯⋯⋯⋯ ..4 分2( 3)解:如所示:①当直l 原点O与半P有两个交点,即b=0 ⋯⋯⋯ 5 分②当直 l 与半P相切于D点有一个交点,如由意可得Rt △ EDP、Rt △ ECO是等腰直角三角形,4∵DP=2∴EP= 2 2 ⋯⋯⋯⋯.6分∴OC= 2 2-2即 b= 2 2 - 2∴当 0≤ b<2 2 - 2 ,直l与半P只有两个交点。
2012年北京市各区二模试题分类解析【数学理】(13):排列、组合及二项式定理.pdf

4、背诵课文。
二、能力目标 1、复述课文,掌握作者求学的主要经历,理清行文思路,提高诵读能力。
2、理解本文对比手法的运用,体会其独特的表达效果。
三、情感目标 学习作者克服困难、勤心求学的精神和意志,树立正确的苦乐观,珍惜现有的优越条件,努力学习,早日成才。
四、教学重点 1、翻译课文,背诵课文,理解本文作者执著的求学之志和殷殷劝勉之情。
2、把握寓理于事的写作方法和对比的表现手法,学习形象说理的技巧。
五、教学难点 引导学生运用现代观念重新审视作品,理解文中作者的求学态度。
六、教学方法 诵读法 讨论点拨法 复述法 品读法 延伸拓展法 教学时间:二教时。
第一教时 一、导入新课 方法一:常言道:“自古雄才多磨难,从来纨绔少伟男。
”孟子也说:“夫天将降大任于斯人也,必先苦其心志,劳其筋骨,饿其体肤,空乏其身,行拂乱其所为。
” 这些都说明了苦难并非全是坏事。
只要我们善于化苦难为动力,则苦难就会成为成功的垫脚石。
今天我们来学习宋濂的《送东阳马生序》。
(板书课文标题) 方法二:同学们,在五单元前面几篇课文里,我们学习了几种古代不同体裁的文章,如吴均的书信体山水小品文——《与朱元思书》、陶渊明的自传体文章——《五柳先生传》、韩愈的议论性文章——《马说》,今天我们一起来学习一篇体裁为赠序的文章——《送东阳马生序》,看看作者是怎样用自己的切身体会勉励马生勤奋学习的。
二、作者简介: 宋濂,明初文学家。
字景濂,号潜溪,浦江人(现渐江义乌人)。
他年少时受业于元末古文大家吴莱、柳贯、黄等。
元朝至正九年,召他为翰林院编修,因为身老不仕,隐居龙门山著书。
明初,征他作江南儒学提举,让他为太子讲经,修《元史》,官至翰林学士承旨、知制诰,朝廷的重要文书,大都由他参与撰写。
年老辞官,后因长孙宋慎犯罪,被流放到四川,途中病死。
他与刘基、高启为明初诗文三大家。
朱无璋称他为:开国文臣之首。
刘基称赞他为:当今文章第一。
四方学者称他为:太史公。
