材料科学基础第二章
材料科学基础_第2章_固体材料的结构

4
共价键
原子间不产生电子的转移,借共用电子对产生的力结合, 如金刚石,单质硅,SiC 特点: 1.饱和性:电子必须由(8-N)个邻近原子共有;
2.具有方向性:氧化硅四面体中硅氧键为109°
3. 脆性:外力作用,原子间发生相对位移,键将被 破坏
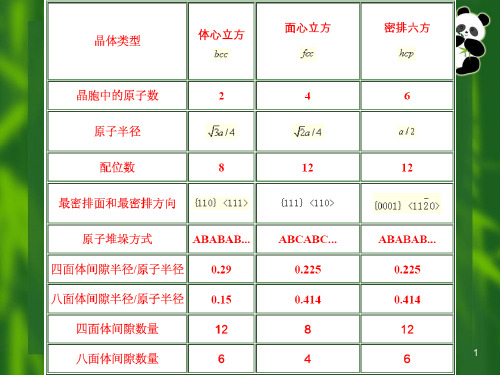
配位数与致密度 配位数 CN=12 致密度 k=0.74
25
体心立方结构(特征)
体心立方晶格密排面
26
ቤተ መጻሕፍቲ ባይዱ
体心立方晶格(间隙及堆垛方式)
间隙: 也是两种,为八面体和四面体间隙, 八面体间隙位于晶胞六面体每个面的中心和每个棱的 中心由一个面上四个角和相邻两个晶胞体心共6个原围成, 即数量为6。大小为rB=0.154R(在<100>) 或rB=0.633R (在<110>) 。
配位数: CN=8 致密度: k=0.68
31
密排六方晶格原子位置
32
密排六方晶格晶胞原子数
33
密排六方晶格密排面
34
密排六方晶格原子配位数
35
密排六方晶格(间隙及堆垛方式)
• 间隙: 较为复杂,如图2.34 八面体间隙rB=0.414R 有 6 个 四面体间隙rB=0.225R 有 12 个
图1 Cl和Na离子保持r0的距离
图2 NaCl 晶体
9
•
分子键(范德华力)
以若静电吸引的方式使分子或原子团连接在一起的。
特点:除高分子外,键的结合不如化学键牢固,无饱和性, 无方向性。
氢键: 分子间特殊作用力
表达为:X—H—Y 特点:具有饱和性和方 向性,可存在于分子内 或分子间。氢键主要存 在于高分子材料内。
材料科学基础第2章
可编辑ppt
10
2.3.1 固溶体
固溶体(solid solution) :
合金组元通过溶解形成一种成分和性能均匀的、 且结构与组元之一相同的固相称为固溶体。
➢ 固溶体的最大特点是保持溶剂的晶体结构。
➢ 与固溶体晶格相同的组元为溶剂,一般在合金中 含量较多;另一组元为溶质,含量较少。
✓ 各向异性:由于在不同方向上的原子排列的紧密程 度不同使晶体在不同方向上的物理、化学和力学性 能不同。而一般整个晶体不显示各向异性,称为伪 等向性。
✓ 晶粒:组成晶体的结晶颗粒。 ✓ 多晶体:凡由两颗以上晶粒组成的晶体一般金属都
是多晶体。。
可编辑ppt
4
晶粒
可编辑ppt
5
Байду номын сангаас
多相合金
可编辑ppt
6
可编辑ppt
12
(3)按溶质原子在溶剂中的分布特点分类 无序固溶体:溶质原子在溶剂中任意分布, 无规律性。
有序固溶体:溶质原子按一定比例和有规 律分布在溶剂晶格的点阵或间隙里。
(4)按基体类型分类: 一次固溶体:以纯金属为基形成的固溶体。
二次固溶体:以化合物为基形成的固溶体。
可编辑ppt
13
固溶体的两种类型(置换和间隙)
中间相可以用分子式来大致表示其组成。
合金相的性质由以下三个因素控制: (1)电化学因素(电负性或化学亲和力因素)
电负性—化学亲和力越大越容易形成化合物,电负性 相近的元素容易形成固溶体。
(2)原子尺寸因素 △r=(rA-rB)/rA △r越大,越易形 成中间相。 △r越小,越易形成固溶体
(3)原子价因素(电子浓度因素): C电子=[A(100-x) +Bx]/100 C越大,越易形成
材料科学基础 第二章 固体材料的结构

第二章固体材料的结构固体材料的各种性质主要取决于它的晶体结构。
原子之间的作用结合键与晶体结构密切相关。
通过研究固体材料的结构可以最直接、最有效地确定结合键的类型和特征。
固体材料主要包括:金属、合金、非金属、离子晶体、陶瓷研究方法:X光、电子、中子衍射——最重要、应用最多§2-1 结合键结合键——原子结合成分子或固体的结合键决定了物质的物理、化学、力学性质。
一切原子之间的结合力都起源于原子核与电子间的静电交互作用(库仑力)。
不同的结合键代表了实现结构)的不同方式。
一、离子键典型的金属与典型的非金属元素就是通过离子键而化合的。
从而形成离子化合物或离子晶体由共价键方向性特点决定了的SiO2四面体晶体结构极性共价键非极性共价键五、氢键含有氢的分子都是通过极性共价键结合,极性分子之间结合成晶体时,通过氢键结合。
例如:H 2O ,HF ,NH 3等固态冰液态水§2-2 金属原子间的结合能一、原子作用模型固态金属相邻二个原子之间存在两种相互作用:a) 相互吸引——自由电子吸引金属正离子,长程力;b) 相互排斥——金属正离子之间的相互排斥,短程力。
平衡时这二个力相互抵消,原子受力为0,原子处于能量最低状态。
此时原子间的距离为r0。
§2-3 合金相结构基本概念♦合金——由两种或两种以上的金属或金属非金属元素通过化学键结合而组成的具有金属特性的材料。
♦组元、元——组成合金的元素。
♦相——具有相同的成分或连续变化、结构和性能的区域。
♦组织——合金发生转变(反应)的结果,可以包含若干个不同的相,一般只有一到二个相。
♦合金成分表示法:(1) 重量(质量)百分数A-B二元合金为例m B——元素B的重量(质量m A——元素A的重量(质量合金中的相分为:固溶体,化合物两大类。
固溶体金属晶体(溶剂)中溶入了其它元素(溶质)后,就称为固溶体。
一、固溶体的分类:♦按溶质原子在溶剂中的位置分为:置换固溶体,间隙固溶体♦按溶解度分为:有限固溶体,无限固溶体♦按溶质原子在溶剂中的分布规律分为:有序固溶体,无序固溶体置换固溶体:溶质原子置换了溶剂点阵中部分溶剂原子。
材料科学基础_第二章-合金的相结构

(2) TCP相 TCP相(topologically close-packed phase)的特点: ①由配位数为12、14、15、16的配位多面体堆垛而成;②呈层状 结构。
TCP相类型:①Lavs相 AB2型 镁合金、不锈钢中出现
②σ相 AB型或AxBx型 有害相
b.间隙化合物 间隙化合物的晶体结构比较复杂。其表达式有如下类型: M3C、M7C3、M23C6、M6C。间隙化合物中金属元素M常被其 它金属元素所代替形成化合物为基的固溶体(二次固溶体)。
在H、N、C、B等非金属元素中,由于H和N的原子半径很小,与所 有过渡族金属都满足rX/rM<0.59,所以过渡族金属的氢化物、氮化物 都为间隙相;而硼原子半径rB/rM>0.59较大, rB/rM>0.59,硼化物 均为间隙化合物;而碳原子半径处于中间,某些碳化物为间隙相,某些 为间隙化合物。
4.超结构—有序固溶体
超结构(super structure/lattice)类型: 有序化条件:异类原子之间的相互吸引大于同类原 子间 有序化影响因素:温度、冷却速度和合金成分
5.金属间化合物的性质及应用(P56) (1)——(7)
CuAu有序固溶体的晶体结构
2.4 离子晶体
离子晶体有关概念 1.离子晶体(ionic crystal) :由正、负离子通过离子键按
相分类:固溶体和中间相(金属间化合物)
固溶体——
中间相——
中间相可以用分子式来大致表示其组成。
合金相的性质由以下三个因素控制:
(1)电化学因素(电负性或化学亲和力因素)
电负性——
(2)原子尺寸因素 △r=(rA-rB)/rA 中间相。 △r越小,越易形成固溶体
材料科学基础-第二章-材料的凝固

制备材料的典型工艺过程:
金属材料:凝固 陶瓷材料:烧结 聚合物:反应合成
凝固与结晶:
凝固(Solidification) 物质从液态转变为固态的过程。
自由能大于体积自由能,即阻力大于驱动力,
那么尺寸在rK~ r0 范围的晶核能够成为稳定的 晶核吗?
当r = rK 时,G 有极大值GK
GK
4 3
2σ
GV
3 GV
4
2σ
GV
2 σ
1 3
4
2σ
GV
2
σ
1 3
4rK2σ
1 3
SKσ
结论:
晶核半径与G的关系
当形成临界晶核时,体积自由能的降低只补偿了表面自由能的2/3,还有 1/3的表面自由能需要另外供给,即需要对形核做功。称GK为形核功。
③形核率(Nucleation Rate)
单位时间、单位体积液相中形成的晶核数目,即晶核形成的速率,记
作
•
N
,单位为cm-3·s-1。
影响形核率的因素:
形核功
随过冷度的增加,即随温度的降低,形核 功减小,形核率增大。
原子扩散能力
随过冷度的增加, 即随温度的降低, 原子
扩散能力下降, 形核困难, 形核率减小。
当 r>rK时,随 r 的增加,体系自由能减 小,晶胚转变为晶核;
当 r=rK时,晶胚处于亚稳状态,即可能消 失,也可能长大成为晶核;
把半径为rK的晶胚称为临界晶核,rK称为临 界晶核半径。
材料科学基础第2章
晶胞示意图
晶胞大小和形状表示方法
晶胞大小和形状表示方法为:
晶胞的棱边长度a、b、c(称为点阵常数、晶格常 数(lattice constants/parameters)); 棱边的夹角为α、β、γ(称为晶轴间夹角)。 选取晶胞的原则: 1、应反映出点阵的高度对称性 2、棱和角相等的数目最多 3、棱边夹角为直角时,直角数目最多 4、晶胞体积最小
晶面指数(hkil)其中i=-(h+k)
晶向指数 [uvtw] 其中t=-(u+v)
六方晶系按两种晶轴系所得的晶面指数和晶向 指数可相互转化:
六方晶系的晶向(面)指数示意图
六方晶系的一些晶向(面)指数
4.晶带
晶带——所有平行或相交于同一直线的晶面构成一个 晶带,此直线称为晶带轴。属此晶带的晶面称为共 带面。 晶带定理:同一晶带上晶带轴[uvw]和晶带面(hkl) 之间存在以下关系:hu+kv+lw=0 通过晶带定理可以求晶向指数或晶面指数。 a) 求两不平行的晶面(h1k1l1)和(h2k2l2)的晶 带轴。 b) 求两个不平行的晶向[u1v1w1]和[u2v2w2]所决定 的晶面。
面心立方八面体间隙面心立方Biblioteka 面体间隙面心立方四面体间隙
面心立方四面体间隙
面心立方原子堆垛顺序
面心立方晶体的 ABCABC 顺序密堆结构
2.体心立方晶格(特征)
原子排列:晶胞八个顶角和晶胞体心各有一个原子 点阵参数:a=b=c,α=β=γ=90º 晶胞中原子数:n=8×1/8+1=2个 3 原子半径: 4R 3a, R a
三种典型金属晶体结构刚球模型
三种典型金属晶体结构晶胞原子数
原子半径与晶格常数
三种典型金属晶格密排面的堆垛方式
上海交大-材料科学基础-第二章-1

晶面的位向
h : k : l cos : cos : cos
cos2 cos2 cos2 1 立方晶系
晶面间距
dhkl
a h
cos
b h
cos
c h
cos
d
2hkl [(
h a
)2
( h )2 b
( h )2 ] c
cos2
cos2
cos2
式中h、k、l为晶面指数(hkl),a、b、c为 点阵常数,α、β、γ为晶面法线方向与晶轴夹角。
每个原子周围的情况完全相同,则这种原子所组成的
网格称为简单晶格。
复式晶格:如果晶体由两种或两种以上原子组成,同 种原子各构成和格点相同的网格,网格的相对位移而 形成复式晶格。
cc
金刚石结构
2.1.2 晶向指数和晶面指数
晶列:布拉菲格子的格点可以看成是分布在一系列相 互平行的直线上,而无遗漏,这样直线称为晶列;
uvw 放入方括号内,写成[uvw],即为待标定晶向的晶 向指数。若为负值,则在指数上加一负号。(化整数, 列括号)
xa : yb : zc u :v : w abc
立方晶系中一些常用的晶向指数
例:如图在立方体中, a i , b j , c k
方法2
D是BC的中点,求BE,AD的晶列指数
第二章 固体结构
本章主要内容
❖ 2.1晶体学基础 ❖ 2.2金属的晶体结构 ❖ 2.3合金相结构 ❖ 2.4离子晶体结构 ❖ 2.5共价晶体结构
概述
❖ 物质按聚集状态分类: 气态、液态和固态; ❖ 按原子(或分子)排列特征分类:晶体和非晶体。
绝大部分陶瓷、少数高分子材料、金属及合金是晶体; 多数高分子材料、玻璃及结构复杂材料是非晶体。
材料科学基础第二章

y
[111]
x
[111]
例:画出晶向
[112 ]
2.立方晶系晶面指数
晶面指数的确定方法
(a)建立坐标系,结点为原点, 三棱为方向,点阵常数为单位 (原点在标定面以外,可以采 用平移法); (b)晶面在三个坐标上的截距a1 a2 a3 ; (c)计算其倒数 b1 b2 b3 ; (d)化成最小、整数比h:k:l ; 放在圆方括号(hkl),不加逗号, 负号记在上方 。
3.六方晶系晶面和晶向指数
三指数表示六方晶系晶面和晶向的缺点:晶体学上等价的 晶面和晶向不具有类似的指数。 例:
晶面指数
(11 0)
(100)
[010] [100]
从晶面指数上不能明确表示等同晶面,为了克服这一缺点, 采用a1、a2、a3及c四个晶轴, a1、a2、a3之间的夹角均 为120º ,晶面指数以(hkil)表示。 根据立体几何,在三维空间中独立的坐标轴不会超过三 个可证明 : i= - (h+k) 或 h+k+i=0
六方晶系
d hkl
h k l a b c
2 2 2
d hkl
a h2 k 2 l 2
1 l c
2
4 h 2 hk k 2 3 a2
注:以上公式是针对简单晶胞而言的,如为复杂晶胞, 例如体心、面心,在计算时应考虑晶面层数增加的影 响,如体心立方、面心立方、上下底(001)之间还有 一层同类型晶面,实际
[1 00 ]
[0 1 0]
[010]
[1 00]
y
[100]
x
[00 1]
材料科学基础第二章

• 2.2.3.1 简单间隙化合物:金属原子形成与 其本身晶格类型不同的一种新结构,非金 属原子处于该晶格的间隙之中。例如:V单 晶为面心立 • 方晶格, 而VC晶体 • 中V原子构成面心立 • 方晶格,C原子占据 • 所有八面体间隙而形 • 成NaCl型结构。
• 简单间隙化合物的分子式通常为MX,M2X, MX2,M4X等,但实际成分有出入,这与间 隙的填充程度相关。有些结构简单的间隙 化合物甚至可以相互熔解,形成连续固熔 体,如TiC-ZrC, TiC-VC, TiC-NbC等。但 是当两种间隙相中的金属原子的半径差 >15%时,即使两种固熔体的结构相同,相 互间的熔解度也是很小的。 • 表2-4为钢中常见间隙相。
• 2.1.5 固熔体的性能:固熔体的硬度和强度 通常高于各单一元素,而塑性较低,这种 现象叫固熔强化。其规律为: • 1) 间隙式原子的强化效果高于置换式原子, 熔质与熔剂原子的尺寸相差越大效果越明显。 原因是间隙式原子往往择优分布于位错线 上,形成间隙原子“气团”,造成位错钉 扎而强化。
• 2) 某些具有无序-有序转变的固熔体,其有 序态强度高于无序态强度。这种现象叫有 序强化。其原因为:有序态中相邻原子为 异种原子,A-B键强于A-A键。 • 熔质原子的引入还会引起固熔体某些物理 性能发生变化。如熔质原子增加会引起材 料电阻率升高,且电阻值与温度关系不大。 Fe-Cr-Al和Cr-Ni电阻丝皆为固熔体合金。
第二章 固体中的相结构
• 在任一给定的物质系统中,具有同一化学 成分、同一原子聚集状态和性质的均匀连 续组成部分称为相phase。 • 从结构上可以将相分为固熔体、化合物、 陶瓷晶体相、玻璃及分子相五类。
• 2.1 固熔体Solid solution • 固熔体是固态下一种组元(熔质)熔解于另一 种组元(熔剂)中而形成的新相,特点是固熔 体具有熔剂组元的点阵类型。熔质原子在 熔剂中的最大含量叫极限熔解度或固熔度, 通常用摩尔分数表示。 • 按熔质原子在点阵中的位置分为置换固熔 体和间隙固熔体;按熔解度大小分为无限 固熔体和有限固熔体;按各组元原子在点 阵中的排列秩序性分为无序固熔体和有序 固熔体。
材料科学基础第2章

菱方 Rhombohedral a=b=c, α=β=γ≠90º
四方(正方)Tetragonal a=b≠c, α=β=γ=90º
立方 Cubic a=b=c, α=β=γ=90º
简单菱方
简单四方 体心四方
简单立方 体心立方 面心立方
简单三斜
简单单斜
底心单斜
简单正交
体心正交
底心正交
面心正交
简单六方
回转对称轴(n)1,2,3,4,6
宏观对称性 元素 对称面(m)
对称中心(i) 回转 — 反演轴 1,2,3,4,6
微观对称性
元素
滑动面 螺旋轴
a,b,c,n,d 21;31,32;41,43,42;61,65,62,64,63
点群(point group)—晶体中所有点对称元素的集合 根据晶体外形对称性,共有32种点群 空间群(space group)—晶体中原子组合所有可能方式 根据宏观、微观对称元素在三维空间的组合,可能存在 230种空间群(分属于32种点群)
原子半径(atomic radius) R
配位数(coordination number)
致密度(Efficiency of space filling)
N
K
nv
n 4 R3
3
VV
轴比(axial ratio) c/a
堆垛(Stacking) 密排结构(close-packed crystal structure) 最密排面(close-packed plane of atoms) fcc {1 1 1} ABCABCABC······ hcp{0 0 0 1} ABABABAB······
晶系
三斜Triclinic a≠b≠c ,α≠β≠γ
材料科学基础-第2章

a b c,
90o
13
14种Bravais点阵
3. 正交Orthorhombic: 简单正交 (4) 底心正交 (5) 体心正交 (6) 面心正交 (7)
a b c,
90
o
14
14种Bravais点阵
4. 六方Hexagonal:
简单六方(8)
a x
O
b
y
点阵矢量
ruvw ua vb wc
11
7种晶系,14种布拉菲Bravais点阵
晶系 Crystal systems 点阵参数 Lattice parameters 布拉维点阵类型 Types of Bravais lattice 简单三斜(1) 简单单斜(2) 底心单斜(3) 简单正交(4) 底心正交(5) 体心正交(6) 面心正交(7) 简单六方(8) 实例 Instances K2CrO7 -S CaSO4•H2O Fe3C Ga -S Mg, Zn Cd, Ni, As As, Sb, Bi -Sn, TiO2 Fe, Cr, Cu, Ag, Ni,V
abc
90
abc
90%以上 的金属具 有立方晶 系和六方 晶系
12
90
14种Bravais点阵
1. 三斜Triclinic :简单三斜(1)
a b c,
90
o
2. 单斜Monoclinic : 简单单斜(2) 底心单斜(3)
(321)取倒数为 0.333,0.5 ,1
Z
(321)
Y
X
(200)、(333)等是否存在? 具有公因子的晶面不存在
材料科学基础-2

[ 1 11]
[1 1 1]
[1 1 1]
[11 1 ]
[1 1 1]
[1 1 1]
[1 1 1]
例:在一个面心立方晶胞中画出[012]、[123] 晶向。
晶面:通过空间点阵中任一组阵点的平面代表晶 体中的原子平面,称为晶面 晶面指数:表示晶体中点阵平面的指数,由晶面 与三个坐标轴的截距值所决定。 晶面指数的标定步骤: 建坐标:所定晶面不应通过原点; 求截距:求出待定晶面在三个坐标轴上的截距, 如果该晶面与某坐标轴平行,则其截距为∞; 取倒数:取三个截距值的倒数; 化整并加圆括号:将三个截距的倒数化为最小 整数h、k、l,并加圆括号,即(hkl),如果截距 为负值,则在负号标注在相应指数的上方。
正交
三、晶向指数与晶面指数(Miller指数)
晶向:空间点阵中各阵点列的方向代表晶体中原子排列的 方向,称为晶向,即空间点阵中任意两阵点的连接矢量。 晶向指数:表示晶体中点阵方向的指数。 晶向指数的确定步骤:
z
[ 1 11]
[112] • 建立坐标系; • 确定坐标值:在待定晶向上确定 [1 1 1] [1 1 0] 距原点最近的一个阵点的三个坐标值; • 化整并加方括号:将三个坐标值化为最小 [001] [111] 整数u、v、w,并加方括号。如有负值,在 [010] o 该数值上方标负号。 [100] [110]
• 在立方晶系中,具有相同指数的晶面和晶向 必定相互垂直。不适合其它晶系。 如: [121] (121) 即:晶向 [121] 为晶面 (121)的法向量。 ★ 因此,晶面指数可作为向量进行运算。
例:在一个面心立方晶胞中画出(102)、 (223) 晶面。
六方晶系的晶向指数和晶面指数
材料科学基础2-1

晶体结构=空间点阵+结构基元
实际晶体——质点体积忽略——空间点阵——阵点连线——晶格(空间格子)
2.晶胞----具有代表性的基本单元(最小平行六面体)作为点 阵的组成单元,称为晶胞
u1 u2 u3 v1 v2 v3 w1 w 2 =0,则三个晶轴同在一个晶面上 w3
h1 h2 h3
k1
l1
则三个晶面同属一个晶带 k 2 l2 =0,则三个晶轴同属一个晶带 k3 l3
• 若已知两个不平行的晶面(h1k1l1)和( h2k2l2 ),则其 晶带轴[uvw]可以用下式求得
或者写成
第三个问题:晶体的性质由什么决定?
决定 化学组成 结构 晶体性质
晶体结构 = 结构基元 + 空间点阵
结晶化学
晶体结构学
化学组成也会影响晶体结构!
2.2 金属的晶体结构
金属在固态下一般都是晶体。决定晶体结构的内在因素 是原子,离子,分子间键合的类型及键的强弱。金属晶体是 以金属键结合,其晶体结构比较简单,常见的有: 心立方结构A1或fcc(face—centered cubic)立方晶系
图2.2表示在二维点阵选取不同的晶胞
• 晶胞参数:
•
平行六面体的三根棱长a、b、c及其夹角α 、β 、γ 是表 示它本身的形状、大小的一组参数,称为点阵参数(晶胞 参数)
根据平行六面体中结点的分布情况,又可以分为四种格 子类型:简单格子(P)、底心格子(C)、体心格子(I) 和面心格子(F)。
5. 晶面间距
一般是晶面指数数值越小,其面间距较大,并且其阵点密度 较大
材料科学基础课件第二章--晶体结构

小结
1. 晶体结构是指晶体中原子或分子的排列情况,由空间点阵 与结构基元构成,晶体结构的形式是无限多的。
2. 空间点阵是把晶体结构中原子或分子等结构基元抽象为周
围环境相同的阵点之后,描述晶体结构的周期性和对称性的
图像。
17
2.1.2 晶向指数和晶面指数
(1) 晶向指数 晶向(crystal directions)—通 过晶体中任意两个原子中心连 成直线来表示晶体结构的空间 的各个方向。
些晶向可归为一个晶向族,用〈uvw〉表示。如
〈111〉 晶 向 族 包 括 [111] 、 [T11] 、 [1T1] 、 [11T] 、 [TT1]、[1TT]、[T1T]、[TTT];〈100〉晶向族包括 [100]、[010]、[001]、[T00]、[0T0]、[00T] 。
(4)同一晶向族中晶向上原子排列因对称关系而等同。
范德华键的特点及典型的分子晶体的性质:
范德华键(分子键)是通过“分子力”而产生的键合。分子力 包括三种力:葛生力(Keesen force)──极性分子中的固有 偶极矩产生的力,德拜力(Debye force)──感应偶极矩产生 的力,即极性分子和非极性分子之间的作用力,伦敦力 (London force)──非极性分子中的瞬时偶极矩产生的力。 当分子力不是唯一的作用力时,它们可以忽略不计。
2 晶体结构
晶体:物质是由原子、分子或离子按一定的空间 结构排列所组成的固体,其质点在空间的分布具 有周期性和对称性,因而晶体具有规则的外形。
1
晶体的宏观特征
石英
硫
2
钠长石 Na[AlSi3O8]
绿柱石 Be3Al2(SiO3)6
3
祖母绿Be3Al2[Si6O18]
材料科学基础(东北大学)第二章ppt课件

大得多,电子运动的速度比离子实快得多,在 讨论传导电子运动时,可以认为离子是固定在 瞬时位置上。这样多粒子的多体问题就简化为 多电子的问题。
• 单电子近似 通常利用哈特里-福克自洽场方法,
每个电子是在固定的离子势场和其它电子的平均 势场中运动,多电子问题就简化为单电子问题。 单电子近似也称为哈特里-福克近似或自洽场近 似。更精确的单电子理论是密度泛函理论。
ipxiEt
iEt
(x,t)Aee (x)e
定态波函数
对x取二阶导数
d22mE0
dx2 2
d22m(EU)0
dx2 2
p2 2mE
p2 2m(EU)
定态薛定谔方程 22m(EU)0
2
薛定谔方程可以这样理解:
• 一质量为m并在势能为U(x,y,z)的势场中运动的微观
粒子,其运动的稳定状态必然与波函数φ(x,y,z)相联 系。
Hψ(r)[-2h2 2Vr)(ψ ] =Eψ
晶格周期性势场: V(r)V(rRl)
——周期性势场中运动的电子通常称为布洛赫电子。
如果假定在晶体中势场V(r)处处相等,即V(r)=常数, 还可使薛定谔方程进一步简化。在这种情况下,电子在均 匀恒定的势场中运动,就好像自由电子一样,故这种近似 成为自由电子近似。选择势能零点,使V(r)=0,方程变为
该理论成功地计算出金属电导率(欧姆定律)以及电导
率和热导率的关系。
欧姆定律
电导率:
IU R
j E
ne2l ne2 t
mv m
j nev
经典自由电子理论的局限性
经典电子论模型成功地说明了欧姆定律,导电与导 热的正比关系。但在说明以下问题遇到困难:
材料科学基础第二章材料的凝固

液体
晶核 新的晶核 晶核长大 晶粒相互接触 液体消失,结晶完成
液体
形核
长大
晶粒, 构成多晶体
长大
晶体
结晶的一般过程——形核和长大
第二章 材料的凝固-§2.3 金属结晶的原理
第三节 金属结晶的原理
一、结晶的热力学条件
金属结晶为什么需要过冷?
第三章 材料制备的基本过程-§3.1 金属的结晶
σ LB σ αB σ αL cosθ
L
式中:
-晶核与基底的接触角(润湿角);
L-晶核与液相之间的表面能; B -晶核与基底之间的表面能;
LB
LB - 液相与基底之间的表面能。
液相L
S1
晶核
B
r
基底B S2
非均匀形核示意图
在基底B上形成晶核时总的自由能
变化G :
G VGV GS
GS σ L S1 σ BS2 σ LBS2 σ L S1 (σ B σ LB )S2
第二章 材料的凝固-§2.3 金属结晶的原理
讨论:
当T >Tm 时,G=Gs-GL>0, 结晶不能进行。
当T =Tm 时,G=Gs-GL=0, 液、固两相处于动态平衡,
既能结晶,也会熔化。
当T <Tm 时,G=Gs-GL<0, 结晶能够进行。
G
T
Gs
GL
T T1 Tm T2
液、固两相自由能随温度 变化的关系曲线
第二章 材料的凝固-§2.3 金属结晶的原理
二、结晶的结构条件
有序原子团-晶到Tm以下时,一些尺寸较大的有序原子 团就会稳定下来,成为晶核的胚芽,即晶胚 (Embyro),晶胚在一定的条件下能够转变为晶 核。因此,结构起伏是结晶不可缺少的条件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.AB2型化合物的结构 以荧石(CaF2)为代表,具有 面心立方结构
3.A2B3 型化合物的结构
刚玉是典型代表 ,简单六方 点阵
33
4. ABO3型化合物的结构 钙钛矿(CaTiO3)为为ABO3型化合物的典型 。
34
5. AB2O4型结构 以尖晶石(MgAl2O4)为典型。
晶格特征:面心立方点阵
24
表1-6 间隙相的化学式及晶格类型
化学式类 型 钢中可能遇到的间隙相化学 式 晶格类型
M4 X
M2 X
Fe4 N ,Nb4 C, Mn4 C
Fe2 N,Cr2N,W2C,Mo2C TaC,TiC,ZrC,VC TiN,ZrN,VN MoN,CrN,WC VC2,CeC2,ZrH2,TiH2, LaC2
22
晶格类型:取决于电子浓度。
电子浓度为3/2时,呈体心立方结构,相;
电子浓度为21/13时,具有复杂立方晶格, 相 ; 电子浓度为21/12时,则为密排六方晶格, 相 。 性能特点:电子化合物以金属键为主,具有明 显的金属特性,其强度、硬度高
23
三、间隙化合物
由过渡族元素与碳、氮、氢、硼等原子半 径较小的非金属元素形成的化合物称为间隙化 合物。 1.间隙相 当非金属原子半径与金属原子半径 之比小于0.59时,形成具有简单晶格的间隙化 合物,称为间隙相。一些间隙相及晶格类型见 表1-6。间隙相具有金属特性,有极高的熔点 及硬度,非常稳定。
6
2.影响置换固溶体溶解度的因素 1) 原子尺寸因素
原子尺寸差越小,越易形成置换固溶体,且溶 解度越大。 原因:两组元的原子尺寸差别愈大,畸变能的 增加也愈大。在畸变能增加到一定程度后,晶 体就变得不稳定。
△r=(rA-rB)/rA 当△r<15%时,有利于大量互溶
7
2)晶体结构因素 形成无限固溶体的必要条件:溶质与溶剂的晶 体结构类型相同。 只有满足这个条件,溶质原子才有可能连续不 断地置换固溶晶格中的原子,而仍能保持固溶 体原来的晶格类型。 溶剂晶格间隙的形状大小不同,溶解度不同。 一般情况下面心立方中的溶解度大于体心立方 中的溶解度。
30
按结构可分为:氧化物陶瓷,硅酸盐陶瓷。 陶瓷的特点:
结合键主要是离子键,或含有一定比例的共
价键;
有确定的成分,可以用准确的分子式表示;
具有典型的非金属性质等。
31
一、氧化物结构陶瓷 氧化物陶瓷是典型的离子化合物。 有AB,AB2,A2B3,ABO3,AB2O4等结构。 1.AB型结构
32
AB2型:CaF2型,Ca2+离子构成了面心立方结 构。8个F-离子位于面心立方的四面体间隙当 中,其离子数比为1:2。
21
二、电子化合物(电子相)
电子化合物是由ⅠB族或过渡族金属元素与ⅡB, ⅢA,ⅣA族元素形成的金属化合物。 键型:金属键(金属-金属),有明显的金属 特性 组成:电子浓度对应晶体结构,可用化学式表 示,但其成分可在一定范围内变化,故可认为 电子化合物是以化合物为基的固熔体。 特点:不遵守化合价规律,而是按照一定电子 浓度值形成的化合物。
42
三、玻璃结构
无规网络学认为,玻璃态结构与晶体结构相似, 是由离子多面体组成的空间网络。在玻璃态的 网络结构中,多面体的排列无规律。
43
44
第五节
分子相
分子相:是指固体中分子的聚集状态,它决定 了分子固体的微观结构。 高分子:相对分子质量特别大的有机化合物的 总称,称为聚合物或高聚物。
45
聚合物分类: 从聚合物分子结构上可分为线型聚合物和三维 网型聚合物;2)从聚合物受热时的行为上, 可分为热塑性聚合物和热固性聚合物。 一、大分子及其构成 1.高分子化合物:由一种或多种化合物聚合而 成的相对分子质量很大的化合物。又称聚合物 或高聚物。
46
2.分类 按相对分子质量:分为低分子聚合物(<5000) 和高分子聚合物(>5000)。 按组成物质:分为有机聚合物和无机聚合物。
组成高分子的低分子化合物称为单体。
47
高分子化合物的分子很大,主要呈长链型,故 常称大分子链或分子链。大分子链由许多结构 相同的基本单元重复连接构成的。 链节:组成大分子链的这种特定结构单元。 高分子化合物的大分子链由链节连成,链节的 重复次数称为聚合度。
简单间隙化合物的分子 式通常为MX,M2X,MX2, M4X等,但实际成分常 常包括一定范围,这与 间隙的填充程序有关。
26
2复杂间隙化合物 复杂间隙化合物主要是铬、锰、铁、钴的碳化 物以及铁的硼化物等。在合金钢中常见的有M3C 型(如Fe3C)、M7C3型(如Cr7C3)、M23C6型(如 Cr23C6)和M6C型(如Fe3W3C)等。 特点:晶体结构都很复杂
8
3)电负性因素 负电性(电负性):从其他原子夺取电子而变为 负离子的能力。 电负性差不大时:随着电负性差值的增加,越 易形成固溶体,溶解度越大。 溶质原子与溶剂原子的负电性相差很大,即两 者之间化学亲和力很大,则它们往往容易形成 比较稳定的化合物。(不再是固溶体)
9
4) 电子浓度因素 电子浓度:两个组元的价电子总数(e)和两组 元的原子总数(a)之比
面心立方
密排六方 面心立方 体心立方 简单六方 面心立方
MX
MX2
25
钢中常见间隙化合物的硬度及熔点 类型 化学式 硬度HV 熔点/℃ TiC 2850 3080 ZrC 2840 3472±20 简单结构间隙化合物 VC 2010 2650 NbC 2050 3680±50 TaC 1550 3980 WC 1730 2785 ±5 MoC 1480 2527 复杂结构间隙化合物 Cr23 C6 1650 1577 Fe3 C ~800 1227
⑶按溶质原子在固溶体内分布是否有规则,固 溶体分为有序固溶体和无序固溶体。
合金的组织
4
一、置换固溶体 置换固溶体:溶质原子位于晶格点阵位置的固 溶体。 固溶度:固溶体中溶质原子在固溶体中的浓度。
5
1.影响固溶度的Hume-Rothery经验规律
1)如果形成合金的元素其原子半径之差对溶剂 原子半径的比(取绝对值)超过14%~15%,则 固溶度(摩尔分数)极为有限; 2)溶剂和溶质的电化学性质相近; 3)两个给定元素的相互固溶度(摩尔分数)是 与它们各自的原子价有关;
合金组元相互作用形成的晶格类型和特性完全 不同于任一组元的新相即为金属化合物 ——中间相。其性能特点是熔点一般较高,硬 度高,脆性大。金属化合物是许多合金的重要 组成相(常作为强化相)。
17
一、正常价化合物 正常价化合物就是符合原子价规则的化合物。 组元间电负性相差较大,且形成的化合物严格 遵守化合价规律,此类化合物称为正常价化 合物。例如: Mg2Si、 Cu2Se、ZnS、AlP等。
35
二、硅酸盐结构的特点及分类
硅酸盐是一种廉价的陶瓷材料。
1 硅酸盐结构的特点
基本结构——SiO4四面体
36
2.硅酸盐结构分类
将硅酸盐分成岛状、链状、 层状、骨架状四类。 1)含有有限硅氧团的硅酸盐 (也称岛状硅酸盐) 含孤立有限硅氧团的硅酸盐 单个硅氧四面体为-4价。孤 立的含义:硅氧四面体彼此 之间不能直接通过了离子键 或共价键连接。
第二章 固体中的相结构
合金:两种或两种以上的金属,或金属与非金 属经一定方法合成的具有金属特性的物质。 组元:组成合金最基本的独立的物质。(如一 元、二元、三元合金〕,可以是元素,也可以 是化合物。
合金系:给定合金以不同的比例而合成的一系 列不同成分合金的总称。如Fe-C,Fe-Cr等。
1
“相”——是指在任一给定的物质系统中,具 有同一化学成分、同一原子聚集状态和性质的 均匀连续组成部分。当由金属和其他一种或多 种元素通过化学键合而形成合金材料时,一定 成分的合金可以由若干不同的相组成。 虽然固体中有各种不同的相,但从结构上可将 其分为固溶体、化合物、陶瓷晶体相、玻璃相 及分子相等五类。
c
e xv (100 x)u a 100
10
二、间隙固溶体 间隙固熔体是由那些原子半径小于0.1nm的非 金属元素,如氢(0.046nm)、氮(0.071nm)、 碳(0.077nm)、硼(0.097nm)及氧 (0.060nm)熔入到熔剂金属晶体点阵的间隙 中所形成的固熔体。
特点:溶解度一般都很小,只形成有限固溶体
18
正常价化合物具有比较简单、不同于其组成元 素的晶体结构。其分子式一般有AB,A2B(AB2) 两种类型。
性能:熔点、硬度及脆性均较高
19
AB型:NaCl结构,双面心立方穿插而成。 ZnS(闪锌矿)每个原子具有4个相邻的 异类原子,是由两种原子各自的面心立方点阵 穿插而成。
20
ZnS(硫锌矿)型,每个原子周围有4个异类原 子构成,两种类型的原子各自组成自己的HCP。
11
三、有序固溶体
1.原子微观分布特征
近年来的研究表明,所谓无序固熔体只是宏观 上的一种近似说法。从微观尺度看,它们并不 均匀,可能出现偏聚、部分有序和完全有序。 同类原子间的结合能大于异类原子间的结合能 时,呈现偏聚。 同类原子间的结合能小于异类原子间的结合能 时,形成有序分布。
12
完全无序
偏聚
39
双链结构
基本单元是4个硅氧团(2+4),分子式为 [Si4O11]6-。 3)层状硅酸盐
40
4)骨架状硅酸盐
骨架状硅酸盐也称为网 络状硅酸盐,它是由硅 氧四面体在空间组成的 三维网络结构。 硅石(SiO2)
41
第四节Biblioteka 玻璃相玻璃:一般是指从液态凝固下来的、结构与液 态连续的非晶态固体。形成玻璃的内部条件是 黏度,外部条件是冷却速度。 一、黏度 黏度增大,达到一定温度时,即固化成玻璃。 二、 冷却速度 冷却速度很快时也可以得到非晶态结构。
