高考数学一轮复习专题训练立体几何
高三数学一轮复习【立体几何】练习题

高三数学一轮复习【立体几何】练习题1.空间中,用a,b,c表示三条不同的直线,γ表示平面,则下列说法正确的有()A.若a∥b,b∥c,则a∥cB.若a⊥γ,b⊥γ,则a∥bC.若a∥γ,b∥γ,则a∥bD.若a⊥b,b⊥c,则a⊥c答案AB解析根据空间平行直线的传递性可知A正确;由直线与平面垂直的性质定理知B正确;若a∥γ,b∥γ,则a,b可能平行、相交或异面,故C错误;若a⊥b,b⊥c,则a,c可能相交、平行或异面,故D错误.2.对于两条不同直线m,n和两个不同平面α,β,下列选项正确的为()A.若m⊥α,n⊥β,α⊥β,则m⊥nB.若m∥α,n∥β,α⊥β,则m⊥n或m∥nC.若m∥α,α∥β,则m∥β或m⊂βD.若m⊥α,m⊥n,则n∥α或n⊂α答案ACD解析对A,令m,n分别为直线m,n的方向向量,因为m⊥α,n⊥β,所以m⊥α,n⊥β,又α⊥β,所以m⊥n,即m⊥n,所以选项A正确;对B,如图所示,在正方体ABCD-A1B1C1D1中,令平面ABCD为平面α,平面ABB1A1为平面β,直线A1C1为m,直线C1D为n,满足α⊥β,m∥α,n∥β,但m与n既不平行也不垂直,所以选项B错误;对C,若m⊄β,过m作一平面γ分别与平面α和平面β相交,且交线分别为a,b,则m∥a,a∥b,所以m∥b,所以m∥β;若m⊂β,符合题意,所以选项C 正确;对D,若n⊂α,符合题意;若n⊄α,过直线n作一平面β与平面α相交,设交线为b,因为b⊂α,m⊥α,所以m⊥b,又m⊥n,且n,b在同一平面内,所以n∥b,所以n∥α,所以选项D正确.综上,选ACD.3.如图是一个正方体的平面展开图,则在该正方体中()A.AE∥CDB.CH∥BEC.DG⊥BHD.BG⊥DE答案BCD解析由正方体的平面展开图还原正方体如图,连接AH,DE,BG,BH,DG,HC.由图形可知,AE⊥CD,故A错误;因为HE∥BC,HE=BC,所以四边形BCHE为平行四边形,所以CH∥BE,故B正确;因为DG⊥HC,DG⊥BC,HC∩BC=C,HC,BC⊂平面BHC,所以DG⊥平面BHC,又BH⊂平面BHC,所以DG⊥BH,故C正确;因为BG∥AH,而DE⊥AH,所以BG⊥DE,故D正确.故选BCD.4.用一个平面截正方体,所得的截面不可能是()A.锐角三角形B.直角梯形C.有一个内角为75°的菱形D.正五边形答案BCD解析对于A,如图1,截面的形状可能是正三角形,故A可能;图1图2对于B,首先考虑平面截正方体得到的截面为梯形,且QR与AA1不平行,如图2所示,不妨假设PQ⊥QR,因为AA1⊥平面A1B1C1D1,PQ⊂平面A1B1C1D1,所以AA1⊥PQ,从而有PQ⊥平面A1ABB1,这是不可能的,故B不可能;对于C,当平面截正方体得到的截面为菱形(非正方形)时,只有如下情形,如图3,其中P,R为所在棱的中点,易知当菱形为PBRD1时,菱形中的锐角取得最小值,即∠PD1R最小.设正方体的棱长为2,则PD1=RD1=5,PR=22,则由余弦定理,得cos∠PD1R=PD21+RD21-PR22PD1·RD1=5+5-82×5×5=15<6-24=cos 75°,所以∠PD1R>75°,故C不可能;图3对于D,假设截面是正五边形,则截面中的截线必然分别在5个面内,由于正方体有6个面,分成两两平行的三对,故必然有一对平行面中有两条截线,而根据面面平行的性质可知这两条截线互相平行,但正五边形的边中是不可能有平行的边的,故截面的形状不可能是正五边形,故D不可能.综上所述,选BCD.5.已知正方体ABCD-A1B1C1D1的棱长为2,M为AA1的中点,平面α过点D1且与CM垂直,则()A.CM⊥BDB.BD∥平面αC.平面C1BD∥平面αD.平面α截正方体所得的截面图形的面积为9 2答案ABD解析如图,连接AC,则BD⊥AC.因为BD⊥AM,AM∩AC=A,AM,AC⊂平面AMC,所以BD⊥平面AMC,又CM⊂平面AMC,所以BD⊥CM,故A正确;取AD的中点E,连接D1E,DM,由平面几何知识可得D1E⊥DM,又CD⊥D1E,DM∩CD=D,DM,CD⊂平面CDM,所以D1E⊥平面CDM,又CM⊂平面CDM,所以D1E⊥CM.连接B1D1,过点E作EF∥BD,交AB于F,连接B1F,所以CM⊥EF,又D1E∩EF=E,D1E,EF⊂平面D1EFB1,所以CM⊥平面D1EFB1,所以平面α截正方体所得的截面图形即梯形D1EFB1.由EF∥BD,BD⊄平面α,EF⊂平面α,得BD∥平面α,故B正确;连接AB1,AD1,易知平面AB1D1∥平面C1BD,而平面AB1D1∩平面α=B1D1,所以平面C1BD与平面α不平行,故C不正确;截面图形为等腰梯形D1EFB1,EF=2,B1D1=22,D1E=B1F=5,所以截面图形的面积S=12×(2+22)×(5)2-⎝⎛⎭⎪⎫22-222=92,故D正确.6.在正方体ABCD-A1B1C1D1中,N为底面ABCD的中心,P为线段A1D1上的动点(不包括两个端点),M为线段AP的中点,则()A.CM与PN是异面直线B.CM>PNC.平面PAN⊥平面BDD1B1D.过P,A,C三点的正方体的截面一定是等腰梯形答案BCD解析对于选项A,如图,连接NC,PC,则A,N,C三点共线.又M为AP的中点,N为AC的中点,所以CM与PN共面,故A错误;对于选项B,因为P为线段A1D1上的动点(不包括两个端点),所以AC>AP.在△MAC中,CM2=AC2+AM2-2AC·AM cos∠MAC=AC2+14AP2-AC·AP·cos∠MAC.在△PAN中,PN2=AP2+AN2-2AP·AN cos∠PAN=AP2+1 4AC 2-AP ·AC cos ∠PAN ,则CM 2-PN 2=34(AC 2-AP 2)>0,所以CM >PN ,故B 正确;对于选项C ,在正方体ABCD-A 1B 1C 1D 1中,易知AC ⊥平面BDD 1B 1,即AN ⊥平面BDD 1B 1,又AN ⊂平面PAN ,所以平面PAN ⊥平面BDD 1B 1,故C 正确; 对于选项D ,连接A 1C 1,在平面A 1B 1C 1D 1内作PK ∥A 1C 1,交C 1D 1于K ,连接KC .在正方体中,A 1C 1∥AC ,所以PK ∥AC ,PK ,AC 共面,所以四边形PKCA 就是过P ,A ,C 三点的正方体的截面,AA 1=CC 1,A 1P =C 1K ,所以AP =CK ,即梯形PKCA 为等腰梯形,故D 正确.故选BCD.7.如图,在正四棱柱ABCD-A 1B 1C 1D 1中,AA 1=2AB =2,点P 为线段AD 1上一动点,则下列说法正确的是( )A.直线PB 1∥平面BC 1DB.三棱锥P-BC 1D 的体积为13C.三棱锥D 1-BC 1D 外接球的表面积为3π2D.直线PB 1与平面BCC 1B 1所成角的正弦值的最大值为53 答案 ABD解析 对于A 选项,连接B 1D 1,AB 1,根据正四棱柱的性质可知AD 1∥BC 1,BD ∥B 1D 1,因为BC 1⊄平面AB 1D 1,AD 1⊂平面AB 1D 1,所以BC 1∥平面AB 1D 1,同理得BD ∥平面AB 1D 1,又BC 1∩BD =B ,所以平面AB 1D 1∥平面BC 1D ,又PB 1⊂平面AB 1D 1,所以PB 1∥平面BC 1D ,所以A 选项正确;对于B 选项,易知AD 1∥平面BC 1D ,所以V P-BC 1D =V A-BC 1D =V C 1-ABD =13×12×1×1×2=13,所以B 选项正确;对于C 选项,三棱锥D 1-BC 1D 的外接球即正四棱柱ABCD-A 1B 1C 1D 1的外接球.设外接球的半径为R ,则4R 2=12+12+22=6,所以外接球的表面积为4πR 2=6π,所以C 选项错误;对于D 选项,过P 作PE ∥AB ,交BC 1于点E ,则PE ⊥平面BCC 1B 1,连接B 1E ,则∠PB 1E 即直线PB 1与平面BCC 1B 1所成的角,当B 1E 最小时,∠PB 1E 最大,此时B 1E ⊥BC 1,由等面积法得S △BB 1C 1=12BC 1·B 1E =12BB 1·B 1C 1,解得B 1E =25,在Rt △PB 1E 中,PE =AB =1,所以PB 1=12+⎝ ⎛⎭⎪⎫252=35,所以∠PB 1E 的正弦值的最大值为PE PB 1=53,所以D 选项正确.故选ABD.8.如图,已知正方体ABCD-A 1B 1C 1D 1的棱长为2,E ,F ,G 分别为BC ,CC 1,BB 1的中点,则( )A.直线D1D与直线AF垂直B.直线A1G与平面AEF平行C.平面AEF截正方体ABCD-A1B1C1D1所得的截面的面积为9 2D.点A1和点D到平面AEF的距离相等答案BCD解析对于选项A,假设AF与D1D垂直,又D1D⊥AE,AE∩AF=A,AE,AF⊂平面AEF,所以D1D⊥平面AEF.因为EF⊂平面AEF,所以D1D⊥EF,这显然是错误的,所以假设不成立,故A错误;图1对于选项B,取B1C1的中点N,连接A1N,GN,如图1所示,易知A1N∥AE,又AE⊂平面AEF,A1N⊄平面AEF,所以A1N∥平面AEF.因为GN∥EF,EF⊂平面AEF,GN⊄平面AEF,所以GN∥平面AEF.又A1N,GN⊂平面A1GN,A1N∩GN=N,所以平面A1GN∥平面AEF.因为A1G⊂平面A1GN,所以A1G∥平面AEF,故B正确;对于选项C,连接AD1,FD1,如图2所示,因为AD1∥EF,所以四边形AD1FE 为平面AEF截正方体ABCD-A1B1C1D1所得的截面,又AD1=22+22=22,图2EF =12+12=2,D 1F =AE =12+22=5,所以四边形AD 1FE 为等腰梯形, 高为(5)2-⎝ ⎛⎭⎪⎫222=322,则S 梯形AD 1FE =12×(2+22)×322=92,故C 正确;对于选项D ,连接A 1D ,如图2所示,由选项C 可知A 1D 与平面AEF 相交且交点为A 1D 的中点,所以点A 1和点D 到平面AEF 的距离相等,故D 正确.综上,选BCD.9.已知棱长为a 的正方体ABCD-A 1B 1C 1D 1中,M 是B 1C 1的中点,点P 在正方体的表面上运动,且总满足MP ⊥MC ,则下列结论中正确的是( ) A.点P 的轨迹中包含AA 1的中点B.点P 在侧面AA 1D 1D 内的轨迹的长为5a4 C.MP 长度的最大值为21a4D.直线CC 1与直线MP 所成角的余弦值的最大值为55 答案 BCD解析 如图,取A 1D 1的中点E ,分别取A 1A ,B 1B 上靠近A 1,B 1的四等分点F ,G ,连接EM ,EF ,FG ,MG ,易知EM ∥FG 且EM =FG ,所以E ,M ,F ,G 四点共面.连接GC ,因为MG 2=⎝ ⎛⎭⎪⎫a 22+⎝ ⎛⎭⎪⎫a 42=5a 216,MC 2=⎝ ⎛⎭⎪⎫a 22+a 2=5a 24,GC 2=⎝ ⎛⎭⎪⎫3a 42+a 2=25a 216,因此MG 2+MC 2=GC 2,所以MG ⊥MC ,易知ME ⊥MC ,又MG ∩ME =M ,MG ,ME ⊂平面MEFG ,所以MC ⊥平面MEFG ,即点P 的轨迹为四边形MEFG (不含点M ),易知点P 在侧面AA 1D 1D 内的轨迹为EF ,且EF =MG =5a4,所以A 选项错误,B 选项正确;根据点P 的轨迹可知,当P 与F 重合时,MP 最长,易知FG ⊥平面BB 1C 1C ,则FG ⊥MG ,连接MF ,所以MF =a 2+5a 216=21a4,故C 选项正确;由于点P 的轨迹为四边形MEFG (不含点M ),所以直线CC 1与直线MP 所成的最小角就是直线CC 1与平面MEFG 所成的角,又向量CC 1→与平面MEFG 的法向量CM →的夹角等于∠C 1CM ,且sin ∠C 1CM =a25a 2=55,所以直线CC 1与平面MEFG 所成角的余弦值为55,即直线CC 1与直线MP 所成角的余弦值的最大值等于55,故D 选项正确.10.如图,长方体ABCD-A 1B 1C 1D 1中,AB =BC =1,AA 1=2,M 为AA 1的中点,过B 1M 作长方体的截面α交棱CC 1于N ,则( )A.截面α可能为六边形B.存在点N,使得BN⊥截面αC.若截面α为平行四边形,则1≤CN≤2D.当N与C重合时,截面图形的面积为36 4答案CD解析设N0为棱CC1的中点,当N从C1移动到C时,其过程中存在以下几种情况,如图1,当点N在线段C1N0上时,截面α为平行四边形;当点N在线段N0C上(不包括点N0,C)时,截面α为五边形;当点N与点C重合时,截面α为梯形.图1图2由以上分析可知,对于A,截面α不可能为六边形,所以A错误;对于B,假设BN⊥截面α,因为B1M⊂α,所以BN⊥B1M,所以必有点N,C重合,而BC与平面B1CQM不垂直,所以B错误;对于C,当截面α为平行四边形时,点N在线段C1N0上,则1≤CN≤2,所以C 正确;对于D,当点N与点C重合时,截面α为梯形,如图2,过M作MM′⊥B1C,垂足为M′.设梯形的高为h,B1M′=x,则在Rt△B1MM′中,由勾股定理,得h2=(2)2-x2,①同理h 2=⎝ ⎛⎭⎪⎫522-⎝ ⎛⎭⎪⎫52-x 2,② 由①②,解得x =255,h =65,所以截面α的面积等于12×⎝⎛⎭⎪⎫5+52·h =12×352×65=364,所以D 正确. 综上可知,选CD.。
高考一轮复习-立体几何练习题

高考一轮复习练习卷立体几何初步一、选择题:本大题共4小题,每小题4分,共16分。
在每小题给出的四个选项中只有一项是符合题目要求。
1. 一个直角三角形绕斜边旋转360°形成的空间几何体为( )A.一个圆锥B.一个圆锥和一个圆柱C.两个圆锥D.一个圆锥和一个圆台2.如图,在长方体ABCD −A 1B 1C 1D 1中,AA 1=3,AD =4,AB =5,由A 在表面到达C 1的最短行程为( )A.12B.√74C.√80D.3√103.设三棱柱的侧棱垂直于底面,所有棱长都为a ,顶点都在一个球面上,则该球的表面积为( )A.πa 2B.73πa 2C.113πa 2 D.5πa 2 4.已知三棱锥S −ABC 中,底面ABC 为边长2的等边三角形,SA 垂直于底面ABC ,SA =3,AB 与面SBC 所成角的正弦值为( )A.√34B.√54C.√74D.34 二、选择题:本大题共2小题,每小题4分,共8分。
在每小题给出的四个选项中有多项是符合题目要求。
全部选对得7分,部分选对得DC 1B 1BD 1A3人,有选错的得0分。
5.已知已知m,n是两条不同直线,α,β是两个平面,则下列命题正确的是()A.α,β垂直于同一平面,则α与β平行B.m,n垂直于同一平面,则m与n平行C.α,β不平行,则α内不存在与β平行的直线D.m,n不平行,则m与n不可能垂直于同一平面6.设四面体的六条棱的长分别为1,1,1,1,√2,a,且长为a的棱与长为√2的棱异面,则a的取值可以是()A.32B.2 C.1 D.75三、填空题:本大题共4小题,每小题5分,共20分。
7.一个棱柱有10个顶点,且所有侧棱张之和为100,则其侧棱长为8.四面体S−ABC中,各个侧面都是边长为a的正三角形,E,F分别是SC和AB的中点,则异面直线EF与SA所成角等于9.设m,n是不同的直线,α,β,γ是不同的平面,有以下四个命题:(1)α∥βα∥γ}⇒β∥γ;(2)α⊥βm∥α}⇒m∥β;(3)m⊥αm∥β}⇒α⊥β;(4)m∥nn⊂α}⇒α⊥β;其中假命题有10.如图所示为一个水平放置的正方形ABCO,在直角坐标系xOy中,点B的坐标为(2,2),则在用斜二测画法画出的正方形的直观图中,顶点B '到x'轴的距离为,该直观图的面积为四、解答题:本大题共2小题,共16分。
2024届高考数学一轮复习学案第七章立体几何与空间向量7.9空间距离及立体几何中的探索问题新人教A版

§7.9 空间距离及立体几何中的探索问题 考试要求 1.会求空间中点到直线以及点到平面的距离.2.以空间向量为工具,探究空间几何体中线、面的位置关系或空间角存在的条件. 知识梳理1.点到直线的距离如图,已知直线l 的单位方向向量为u ,A 是直线l 上的定点,P 是直线l 外一点,设AP →=a ,则向量AP →在直线l 上的投影向量AQ →=(a·u )u ,在Rt△APQ 中,由勾股定理,得PQ =|AP →|2-|AQ →|2 =________________.2.点到平面的距离如图,已知平面α的法向量为n ,A 是平面α内的定点,P 是平面α外一点.过点P 作平面α的垂线l ,交平面α于点Q ,则n 是直线l 的方向向量,且点P 到平面α的距离就是AP →在直线l 上的投影向量QP →的长度,因此PQ =⎪⎪⎪⎪⎪⎪AP →·n |n |=⎪⎪⎪⎪⎪⎪AP →·n |n |=__________.思考辨析判断下列结论是否正确(请在括号中打“√”或“×”)(1)平面α上不共线的三点到平面β的距离相等,则α∥β.( )(2)点到直线的距离也就是该点与直线上任一点连线的长度.( )(3)直线l 平行于平面α,则直线l 上各点到平面α的距离相等.( )(4)直线l 上两点到平面α的距离相等,则l 平行于平面α.( )教材改编题1.正方体ABCD -A 1B 1C 1D 1的棱长为2,则A 1A 到平面B 1D 1DB 的距离为( )A. 2 B .2 C.22 D.3222.已知直线l 经过点A (2,3,1)且向量n =⎝ ⎛⎭⎪⎫22,0,22为l 的一个单位方向向量,则点P (4,3,2)到l 的距离为________.3.设正方体ABCD -A 1B 1C 1D 1的棱长为2,则点D 1到平面A 1BD 的距离是________.题型一 空间距离例1 (1)(2023·长沙模拟)空间中有三点P (1,-2,-2),M (2,-3,1),N (3,-2,2),则点P 到直线MN 的距离为( )A .2 2B .2 3C .3D .2 5听课记录:______________________________________________________________ ________________________________________________________________________(2)(2022·济宁模拟)如图,在三棱柱ABC -A 1B 1C 1中,AB ⊥平面BCC 1B 1,BC =12AB =12AA 1=2,BC 1=23,M 为线段AB 上的动点.①证明:BC 1⊥CM ;②若E 为A 1C 1的中点,求点A 1到平面BCE 的距离.________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ 思维升华 (1)点到直线的距离.①设过点P 的直线l 的单位方向向量为n ,A 为直线l 外一点,点A 到直线l 的距离d =|PA →|2-PA →·n 2;②若能求出点在直线上的射影坐标,可以直接利用两点间距离公式求距离.(2)求点面距一般有以下三种方法.①作点到面的垂线,求点到垂足的距离;②等体积法;③向量法.跟踪训练1 (1)(2023·枣庄模拟)在长方体ABCD -A 1B 1C 1D 1中,AA 1=AB =2,AD =1,点F ,G分别是AB ,CC 1的中点,则△D 1GF 的面积为________.(2)如图所示,在长方体ABCD -A 1B 1C 1D 1中,AD =AA 1=1,AB =2,点E 在棱AB 上移动.①证明:D 1E ⊥A 1D ;②当E 为AB 的中点时,求点E 到平面ACD 1的距离.________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ 题型二 立体几何中的探索性问题例2 (2022·常德模拟)如图,三棱柱ABC -A 1B 1C 1的底面是等边三角形,平面ABB 1A 1⊥平面ABC ,A 1B ⊥AB ,AC =2,∠A 1AB =60°,O 为AC 的中点.(1)求证:AC ⊥平面A 1BO ;(2)试问线段CC 1上是否存在点P ,使得平面POB 与平面A 1OB 夹角的余弦值为277,若存在,请计算CP CC 1的值;若不存在,请说明理由. ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________思维升华 (1)对于存在判断型问题的求解,应先假设存在,把要成立的结论当作条件,据此列方程或方程组,把“是否存在”问题转化为“点的坐标是否有解,是否有规定范围内的解”等.(2)对于位置探究型问题,通常借助向量,引进参数,综合已知和结论列出等式,解出参数. 跟踪训练2 如图,四棱锥S -ABCD 的底面是正方形,每条侧棱的长都是底面边长的2倍,P 为侧棱SD 上的点.(1)求证:AC⊥SD;(2)若SD⊥平面PAC,求平面PAC与平面DAC夹角的大小;(3)在(2)的条件下,侧棱SC上是否存在一点E,使得BE∥平面PAC.若存在,求SE∶EC的值;若不存在,请说明理由.________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________。
立体几何 大题-2023届高三数学一轮复习
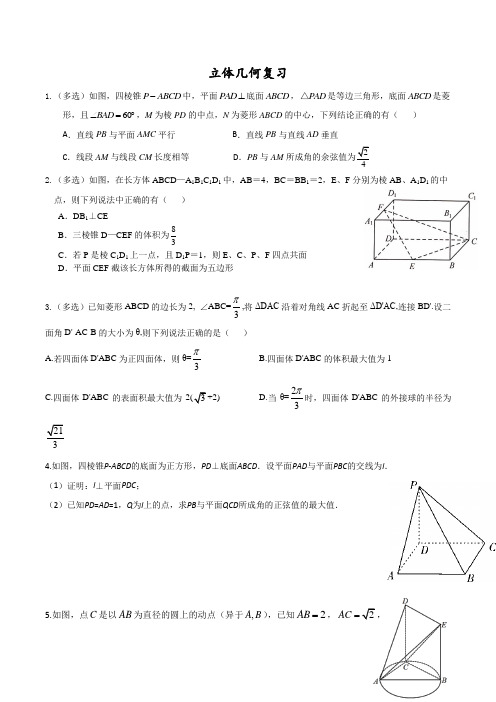
立体几何复习1.(多选)如图,四棱锥P ABCD -中,平面PAD ⊥底面ABCD ,PAD △是等边三角形,底面ABCD 是菱形,且60BAD ∠=︒,M 为棱PD 的中点,N 为菱形ABCD 的中心,下列结论正确的有( ) A .直线PB 与平面AMC 平行 B .直线PB 与直线AD 垂直C .线段AM 与线段CM 长度相等D .PB 与AM 所成角的余弦值为24 2.(多选)如图,在长方体ABCD —A 1B 1C 1D 1中,AB =4,BC =BB 1=2,E 、F 分别为棱AB 、A 1D 1的中点,则下列说法中正确的有( )A .DB 1⊥CEB .三棱锥D —CEF 的体积为83C .若P 是棱C 1D 1上一点,且D 1P =1,则E 、C 、P 、F 四点共面D .平面CEF 截该长方体所得的截面为五边形3.(多选)已知菱形ABCD 的边长为2, ∠ABC=3π,将ΔDAC 沿着对角线AC 折起至ΔD'AC,连接BD'.设二面角D'-AC-B 的大小为θ,则下列说法正确的是( )A.若四面体D'ABC 为正四面体,则θ=3π B.四面体D'ABC 的体积最大值为1 C.四面体D'ABC 的表面积最大值为2(3+2) D.当θ=23π时,四面体D'ABC 的外接球的半径为2134.如图,四棱锥P -ABCD 的底面为正方形,PD ⊥底面ABCD .设平面PAD 与平面PBC 的交线为l . (1)证明:l ⊥平面PDC ;(2)已知PD =AD =1,Q 为l 上的点,求PB 与平面QCD 所成角的正弦值的最大值.5.如图,点C 是以AB 为直径的圆上的动点(异于,A B ),已知2AB =,2AC =,AE =BEDC 为矩形,平面ABC ⊥平面BEDC .设平面EAD 与平面ABC 的交线为l .(1)证明:l BC ;(2)求平面ADE 与平面ABC 所成的锐二面角的余弦值.6.7. 在如图所示的几何体中,四边形ABCD 为正方形,PA ⊥平面ABCD ,//PA BE ,2BE =,4AB PA ==.(1)求证://CE 平面PAD ;(2)在棱AB 上是否存在一点F ,使得二面角E PC F --的大小为60︒?如果存在,确定点F 的位置;如果不存在,说明理由.8.如图,四棱锥P -ABCD 中,底面ABCD 是直角梯形,AB ∥DC ,∠BAD =90°,PD =DC =BC =2PA =2AB =2,PD ⊥DC .(1)求证:PA ⊥平面ABCD ;(2)设BM =BD λ(0<λ<1),当二面角A-PM-B 的余弦值为77时,求λ的值.9.如图,四棱锥P ABCD -中,四边形ABCD 是菱形,PA PC =,BD PA ⊥,E 是BC 上一点,且3EC BE =,设AC BD O =.(1)证明:PO ⊥平面ABCD ;(2)若60BAD ∠=︒,PA PE ⊥,求二面角A PE C --的余弦值.10.如图,在四棱锥P ABCD -中,底面ABCD 是菱形,PA ⊥平面ABCD .(1)求证:平面PAC ⊥平面PBD ;(2)若2AP AB ==,60BAD ∠=︒,求二面角A PB D --的余弦值.11.如图,在三棱柱ABC-A 1B 1C 1中,ΔABC 是边长为2的等边三角形,平面ABC ⊥平面AA 1B 1B,A 1A=A 1B,∠A 1AB=60°,O 为AB 的中点,M 为A 1C 1的中点. (1)求证:OM//平面BB 1C 1C;(2)求二面角C 1-BA 1-C 的正弦值.12.如图,在五面体ABCDEF 中,四边形ABEF 为正方形,平面ABEF ⊥平面CDFE ,CD ∥EF ,DF ⊥EF , EF =2CD =2.(1)若DF =2,求二面角A -CE -F 的正弦值;(2)若平面ACF ⊥平面BCE ,求DF 的长.13.如图,在斜三棱柱111ABC A B C -中,底面是边长为3的等边三角形,12A A =,点1A 在下底面上的射影是ABC ∆的中心O .(1)求证:平面1A AO ⊥平面11BCC B ;(2)求二面角1C AB C --的余弦值.14.如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,AD CD ⊥,//AD BC ,2PA AD CD ===,3BC =.E为PD的中点,点F在PC上,且13 PFPC=.(Ⅰ)求证:CD⊥平面PAD;(Ⅱ)求二面角F AE P--的余弦值;(Ⅲ)设点G在PB上,且23PGPB=.判断直线AG是否在平面AEF内,说明理由.15.如图,在三棱锥A-BCD中,△ABD与△BCD都为等边三角形,平面ABD⊥平面BCD,M,O分别为AB,BD 的中点,AO∩DM=G,N在棱CD上且满足2CN=ND,连接MC,GN.(1)证明:GN∥平面ABC;(2)求直线AC和平面GND所成角的正弦值.16.在多面体ABCDE中,平面ACDE⊥平面ABC,四边形ACDE为直角梯形,CD∥AE,AC⊥AE,AB⊥BC,CD=1,AE=AC=2,F为DE的中点,且点E满足EB4EG=.(1)证明:GF∥平面ABC;(2)当多面体ABCDE的体积最大时,求二面角A—BE—D的余弦值.17一副标准的三角板(图1)中,∠ABC为直角,∠A=60°,∠DEF为直角,DE=EF,BC=DF.把BC与DF重合,拼成一个三棱锥(图2)。设M是AC的中点,N是BC的中点。(1)求证:平面ABC⊥平面EMN;(2)若AC=4,二面角E-BC-A为直二面角,求直线EM与平面ABE所成的正弦18.如图四边形ABCD为梯形,AD∥BC,BM⊥AD于M,CN⊥AD于N,∠A=45°,AD=4BC=4,AB=2,现沿CN将△CDN折起,使△ADN为正三角形,且平面AND⊥平面ABCN,过BM的平面与线段DN、DC分别交于E、F.(1)求证:EF⊥DA;(2)在棱DN上(不含端点)是否存在点E,使得直线DB与平面BMEF所成角的正弦值为34,若存在,请确定E点的位置;若不存在,说明理由.19.如图,在四棱锥P—ABCD中,底面ABCD为正方形,PD⊥底面ABCD,M为线段PC的中点,PD=AD,N为线段BC上的动点.(1)证明:平面MND⊥平面PBC;(2)当点N在线段BC的何位置时,平面MND与平面PAB所成锐二面角的大小为30°?指出点N的位置,并说明理由.。
考点7 空间向量与立体几何—高考数学一轮复习考点创新题训练(含解析)

考点7 空间向量与立体几何—高考数学一轮复习考点创新题训练1.坡屋顶是我国传统建筑造型之一,蕴含着丰富的数学元素.安装灯带可以勾勒出建筑轮廓,展现造型之美.如图,某坡屋顶可视为一个五面体,其中两个面是全等的等腰梯形,两个面是全等的等腰三角形.若,,且等腰梯形所在的平面、等腰三角形所在的平面与平面ABCD 的夹角的正切值均为,则该五面体的所有棱长之和为( )A. B. C. D.2.中和殿是故宫外朝三大殿之一,位于紫禁城太和殿与保和殿之间,中和殿建筑的亮点是屋顶为单檐四角攒(cuán )尖顶,体现天圆地方的理念,其屋顶部分的轮廓可近似看作一个正四棱锥.已知此正四棱锥的侧棱长为,这个角接近30°,若取,则下列结论正确的是( )A.正四棱锥的底面边长为48mB.正四棱锥的高为4mC.正四棱锥的体积为D.正四棱锥的侧面积为3.两个相交平面构成四个二面角,其中较小的二面角称为这两个相交平面的夹角.由正方体的四个顶点所确定的平面统称为该正方体的“表截面”.则在正方体中,两个不重合的“表截面”的夹角大小不可能为( )A. B. C. D.25m AB =10m BC AD ==102m 112m 117m 125m30θ=︒2230︒45︒60︒90︒4.海口钟楼的历史悠久,最早是为适应对外通商而建立,已成为海口的最重要的标志性与象征性建筑物之一,如图所示,海口钟楼的主体结构可以看成一个长方体,四个侧面各有一个大钟,则从8:00到10:00这段时间内,相邻两面钟的分针所成角为的次数为( )A.2B.4C.6D.85.在空间直角坐标系Oxyz 中,,,若直线AB 与平面xOy 交于点,( )6.在空间直角坐标系中,经过点且一个法向量为的平面的方程为,经过点P 且一个方向向量为的直的方程为的距离为( )7.阅读材料:空间直角坐标系中,过点且一个法向量为的平面的方程为,阅读上面材料,解决下面问题:已知平面的方程为,点,则点Q 到平面距离为( )8.《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1000多年.在《九章算术》60︒()1,,2A m (),0,1B n (),,0P x y 2y +=O xyz -()000,,P x y z (),,m a b c = α()()()0000a x x b y y c z z -+-+-=()(),,0n v v μωμω=≠ 0y y v -==3541x y z -++=5y ==O xyz -()000,,P x y z (),,n a b c = α()()()0000a x x b y y c z z -+-+-=α21x y z -+=()3,1,1Q -α中,将底面为矩形且一侧棱垂直于底面的四棱锥称为阳马.如图是阳马,平面,,,.则该阳马的外接球的表面积为( )C.9.(多选)如图所示的空间几何体是由高度相等的半个圆柱和直三棱柱组合而成,,,G 是上的动点.则( )A.平面平面B.G 为的中点时,C.存在点G ,使得直线与的距离为D.存在点G ,使得直线与平面所成的角为10.(多选)布达佩斯的伊帕姆维泽蒂博物馆收藏的达芬奇方砖是在正六边形上画了具有视觉效果的正方体图案(如图1)把三片这样的达芬奇方砖拼成图2的组合,这个组合再转换成图3所示的几何体.若图3中每个正方体的棱长为1,则( )P ABCD -PA ⊥ABCD 5PA =3AB =4BC =π100ABF DCE -AB AF ⊥4AB AD AF ===»CDADG ⊥BCG»CD//BF DG EF AG CF BCG 60︒··A.B.异面直线与C.点P 到直线D.M 为线段上的一个动点,则的最大值为311.有很多立体图形都体现了数学的对称美,其中半正多面体是由两种或两种以上的正多边形围成的多面体,半正多面体因其最早由阿基米德研究发现,故也被称作阿基米德体.如图,这是一个棱数为24,棱长都相等的半正多面体,它的所有顶点都在同一个正方体的表面上,可以看成是由一个正方体截去八个一样的四面体所得.已知点为线段上一点且,,则______.12.如图,在棱长为8的正方体中,E 是棱上的一个动点,给出下列三个结论:①若F 为上的动点,则EF 的最小值为到平面③M 为BC 的中点,P 为空间中一点,且与平面ABCD 所成的角为,PM 与平面ABCD122QC AD AB AA =++ CQ AD CQ ME MC ⋅ E BC BE BC λ= λ=1111ABCD A B C D -1AA 1BD D BED PD 30︒所成的角为,则P 在平面ABCD 上射影的轨迹长度为,其中所有正确结论的序号是___________.13.六氟化硫,化学式为,在常压下是一种无色、无臭、无毒、不燃的稳定气体,有良好的绝缘性,在电器工业方面具有广泛用途.六氟化硫结构为正八面体结构(正八面体每个面都是正三角形,可以看作是将两个棱长均相等的正四棱锥将底面粘接在一起的几何体),如图所示,硫原子位于正八面体的中心,6个氟原子分别位于正八面体的6个顶点,若相邻两个氟原子之①该八面体的表面积为③若点P 为棱上一动点,存在点P ,使得;④若点P 为棱上的动点,则三棱锥的体积为定值..若为空间向量与232323a ab bc c =123231312321213132a b c a b c a b c a b c a b c a b c ++---1122a b x y x j i y ⨯= b ⨯ a 60︒6SF EC AP BE ⊥EC F ABP -b的叉乘,其中,,为单位正交基底.以O 为坐标原点,分别以的方向为x 轴,y 轴,z 轴的正方向建立空间直角坐标系,已知A ,B 是空间直角坐标系中异于O 的不同两点.(1)①若,求;②证明:.(2)记的面积为,证明:(3)问:的几何意义表示以15.在①,②这三个条件中任选一个,补充在下面的横线中,并完成问题.问题:如图,在正方体中,以D 为坐标原点,建立空间直角坐标系.已知点的坐标为,E 为棱上的动点,F 为棱上的动点,_________,试问是否存在点E ,F 满足?若存在,求出的值;若不存在,请说明理由.()()DE CF DE CF +⊥- ||DE = cos ,1EF DB <〈〉< 1111ABCD A B C D -D xyz -1D (0,0,2)11D C 11B C 1EF A C ⊥AE BF ⋅ ()111111,,a x y z x y i j k z =++∈R ()222222,,b x i y j z k x y z =++∈R {},,i j k ,,i j k ()()0,2,1,1,3,2A B -OA OB ⨯ 0OA OB OB OA ⨯+⨯= AOB △AOB S △12AOB S OA =⨯ △2()OA OB ⨯ △⨯答案以及解析1.答案:C解析:如图,过E 作平面ABCD ,垂足为O ,过E 分别作,,垂足分别为G ,M ,连接OG ,OM ,由题意得等腰梯形所在的平面、等腰三角形所在的平面与底面夹角分别为和,所以.因为平面,平面ABCD ,所以.因为,,平面,,所以平面EOG .因为平面EOG ,所以.同理,.又,故四边形OMBG 是正方形,所以由得,所以,所以,所以在直角三角形EOG 中,,在直角三角形EBG 中,,,又因为,所有棱长之和为.故选C.2.答案:C解析:如图,在正四棱锥中,O为正方形的中心,,则H为的中点,连接,,,则平面,,则为侧面与底面所成的锐二面角,EO ⊥EG BC⊥EM AB ⊥EMO ∠EGO∠tan tan EMO EGO ∠=∠=MO CO =EO ⊥ABCD BC ⊂EO BC ⊥EG BC ⊥EO EG ⊂EOG EO EG E = BC ⊥OG ⊂BC OG ⊥OM BM ⊥BM BG ⊥10BC =5OM =EO =5OG =EG ===5BG OM ==8EB ===55255515EF AB =--=--=2252101548117(m)⨯+⨯++⨯=S ABCD -ABCD SH AB ⊥AB SO OH AO SO ⊥ABCD OH AB ⊥SHO ∠设底面边长为.正四棱谁的则面与底两所成的䌼二面但为,这个角接近,取,,则,,.在中,,解得,故底面边长为,正四棱锥的高为,侧面积为,体积.故选C 3.答案:A 解析:在正方体中,平面ABCD 和平面的夹角为,D 选项错误.平面和平面的夹角为,B 选项错误.设正方体的棱长为1,建立如图所示的空间直角坐标系,则,,,,,,,设平面的法向量为,则令,可得.设平面的法向量为,则令,可得,设平面与平面的夹角为,则由于,所以,所以C 选项错误.平面ABCD 与平面的夹角为.由图可知两个不重合的“表截面”的夹角的大小不可能为.故选A.2a θ30︒30θ=︒30SHO ∴∠=︒OH a =OS =SH =Rt SAH △222a ⎫+=⎪⎪⎭12a =24()m 12=21424122S =⨯⨯=3124243V =⨯⨯⨯=1111ABCD A B C D -11ADD A 90︒11BDD B 11ADD A 45︒1111ABCD A B C D -(1,0,0)A (1,1,0)B 1(0,0,1)D (0,1,0)C (0,1,0)AB ∴= 1(1,1,1)BD =-- (1,0,0)CB = 11ABC D 111,)(,x y z =m 111110,0,AB y BD x y z ⎧⋅==⎪⎨⋅=--+=⎪⎩ m m 11x =(1,0,1)=m 11A BCD 222,)(,x y z =n 212220,0,CB x BD x y z ⎧⋅==⎪⎨⋅=--+=⎪⎩ n n 21y =(0,1,1)=n 11ABC D 11A BCD θcos ||||θ⋅===m n m n 090θ︒≤≤︒60θ=︒1111A B C D 0︒30︒4.答案:D 解析:在长方体中,以点A 为原点,,,所在直线分别为x 轴、y 轴、z 轴建立如图所示的空间直角坐标系.设矩形的对角线的交点为E ,矩形的对角线的交点为F ,分针长为a .考查到这个时间段,设t 时刻,侧面和侧面内的钟的分针的位置分别为M ,N ,,其中,则,所以.由题意得.因为,所以的取值为,,,,即在到这个时间段,相邻两面钟的分针所成角为的次数为4,因此,从到这段时间内,相邻两面钟的分针所成角为的次数为8.故选D.5.答案:B解析:依题意,,显然,解得,即,6.答案:C解析:由题可知点在直线l 上,取平面内一点根据题设材料可知平面一个法向量为,所以的距离为11AA B B 11AA D D 8:009:0011AA B B 11AA D D (sin ,0,cos )EM a a θθ= 3600θ-︒≤≤︒(0,sin ,cos )FN a a θθ=- EM FN ⋅=22cos a θ2|||cos ,|cos ||||EM FN EM FN EM FN θ⋅〈〉=== θ=3600θ-︒≤≤︒1111ABCD A B C D -AB AD 1AA θ45-︒135-︒225-︒315-︒8:009:0060︒8:0010:0060︒(1,,1),(,,1)BA n m BP x n y =-=-- //BP 11y m -==2x n y m=-⎧⎨=-⎩2()1m -=22(1)1n m -+==(0,0,0)O α(0,0,P α()3,5,4m =- (0,0,OP = cos ,OP m OP m OP m ⋅<>===7.答案:A解析:平面的法向量,在平面上任取一点,则,8.答案:B解析:因,平面,平面,则,,又因四边形为矩形,则.则阳马的外接球与以,,为长宽高的长方体的外接球相同.又,,.则外接球的直径为长方体体对角线,故外接球半径为:.故选:B 9.答案:AB解析:对于选项A ,由题意知,,平面,因为平面,所以,又,、平面,所以平面,因为平面,所以平面平面,即选项A 正确;对于选项B ,当G 为的中点时,取的中点H ,连接,,则,,所以四边形是平行四边形,所以,因为和都是等腰直角三角形,所以,所以,所以,即选项B 正确;对于选项C ,因为,且平面,平面,所以平面,所以直线与的距离等价于直线到平面的距离,也等价于点F 到平面的距离,以A 为坐标原点,,,所在直线分别为x ,y ,z 轴建立如图所示的空间直角坐标系,则 ,,,设点,其中,,由射影定理知,,即,所以,,,1cos ,4OP OP m <>== α()1,1,2n =- α()1,0,1A -()4,1,0QA =- QA n d n⋅=== PA ABCD ⊥平面AB ⊂ABCD AD ⊂ABCD PA AB ⊥PA AD ⊥ABCD AB AD ⊥PA AB AD 5PA =3AB =4AD BC ==R ===2504π4π50π4S R ==⋅=DG CG ⊥AD ⊥CDG CG ⊂CDG AD CG ⊥DG AD D = DG AD ⊂ADG CG ⊥ADG CG ⊂BCG ADG ⊥BCG »CD »AB AH GH //AD GH AD GH =ADGH //DG AH ABF △ABH △45ABF HAB ∠=∠=︒//AH BF //BF DG //EF AD EF ⊂/ADG AD ⊂ADG //EF ADG EF AG EF ADG ADG AF AB AD ()4,0,0F ()0,0,0A ()0,0,4D (),,4G m n -04m <≤04n <≤2(4)m n n =-224m n n +=()4,0,0AF = ()0,0,4AD = (),,4AG m n =-设平面的法向量为,则,取,则,,所以,若直线与的距离为到平面的距离为而点F 到平面的距离G ,使得直线与的距离为对于选项D ,,,所以,,,设平面的法向量为,则,取,则,,所以,若直线与平面所成的角为,则由,知,此方程无解,所以不存在点G ,使得直线与平面所成的角为,即选项D 错误.故选:AB.10.答案:BD解析:如图建立空间直角坐标系:ADG (),,n x y z = 4040n AD z n AG mx ny z ⎧⋅==⎪⎨⋅=-++=⎪⎩ x n =y m =0z =(),,0n n m = EF AG F ADG ADG 4AF n d n ⋅====≤=< EF AG ()0,4,4C ()0,4,0B ()0,0,4BC = (),4,0CG m n =-- ()4,4,4CF =-- BCG (),,m a b c = 40(4)0m BC c m CG ma n b ⎧⋅==⎪⎨⋅=-+-=⎪⎩ b m =4a n =-0c =()4,,0m n m =- CF BCG 60︒sin 60cos ,CF m CF m CF m ⋅︒====⋅ ()24m n n =-4n -=2850m m n n ⎛⎫⋅-⋅+= ⎪⎝⎭CF BCG 60︒则,,,,,,,,故,,,,,,,,对于A ,所以,A 错误;对于C ,记同向的单位向量为,则点P 到直线的距离,故C 错误;对于D ,设点,使,,,,,则,故,则因,则时,即点M 与点Q 重合时,取得最大值3,故D 项正确.故选:BD.122,,333||QC a QC ⎛⎫==-- ⎪⎝⎭ d ==QM tQC = (1,0,2)Q (0,2,0)C (1,2,22)M t t t -+-+(1,2,22)(1,22,22)ME MC t t t t t t ⋅=+--⋅--- 2229123913t t t ⎛⎫=-+=-- ⎪⎝⎭01t ≤≤0t =ME MC ⋅ (1,0,2)Q (0,2,0)C (1,1,0)A (1,2,0)B (0,1,0)D 1(1,1,1)A 1(0,1,1)D (2,0,1)P (1,2,2)QC =-- (1,0,0)AD =- (0,1,0)AB = 1(0,0,1)AA = (0,2,2)BC =- (1,1,0)BD =-- (1,0,1)QP =- 1(1,0,1)AD =- 122(1,0,0)2(0,1,0)2(0,0,1)(1,2,2)AD AB AA QC ++=-++=-≠ (1,2,2)QC =-- CQ (,,)M x y z 01t ≤≤(2,0,0)E (1,,2)(1,2,2)x y z t --=--解析:将半正多面体补成正方体,建立如图所示的空间直角坐标系.,,,,,,,所以,,则,.设直线DE 与直线AF 所成角为,则即,解得12.答案:①②③解析:①平面,EF 取最小值即为E到平面的距离,为分别为,的中点.故①正确.②由①知,三角形到平面的距离为,③建立如图所示的空间直角坐标系,()2,1,0A ()2,2,1F ()1,0,2B ()0,1,2C ()1,2,2D ()0,1,1AF = ()1,1,0BC =- (),,0BE BC λλλ==- []0,1λ∈()1,,2E λλ-(),2,0DE λλ=-- θcos cos ,AF DE AF DE AF DE θ⋅==== 2610λλ+-=λ==1//AA 11BB D D 11BB D D 1AA 1BD BED =1BED h 18883h =⨯⨯⨯=则,作平面ABCD 于点H ,由题意及几何关系得,设点,则,即点H 的轨迹方程为迹长度为.故③正确.13.答案:①③④八面体的表面积为②连接,相交于点O ,连接,在八面体中,平面是正方形,且平面,,在中,,所以该八面体的体积为③若点P 为棱上一动点,当点P 与点重合时,因为在正方形中,,且平面,平面,所以,又因为,是平面内两条相交直线,所以平面,平面可得,③正确;④在正八面体中,,平面,平面所以平面,若点P 为棱上的动点,则点P 到平面的距离与直线到平面的距离相等且是一个定值,三棱锥的体积为是定值,④正确;14.答案:(1)①;()4,8,0M PH ⊥3DH MH =(),y,0H x 22229(4)(8)x y x y ⎡⎤+=-+-⎣⎦229(9)2x y ⎛⎫-+-= ⎪⎝⎭2π=182⨯=AC BD OE ABCD OE ⊥ABCD 2AC BD ==DBE △1OE ===1213⨯=EC C ABCD AC BD ⊥EO ⊥ABCD AC ⊂ABCD AC EO ⊥BD EO BED AC ⊥BED BE ⊂BED AP BE ⊥//EC AF EC ⊄ABF AF ⊂ABF //EC ABF EC ABF EC ABF F ABP -13FAB F ABP P ABF V V S h --==⨯⨯△()1,1,2-②证明见解析(2)证明见解析(3)6解析:(1)①因为,,则.②证明:设,,则,与互换,与互换,与互换,可得,故.(2)证明:因为故.由(1),,,()0,2,1A ()1,3,2B -()021*******,1,2132i j k OA OB i j k i i j k ⨯==-++--=-+=-- ()111,,A x y z ()222,,B x y z 121212212121OA OB y z i z x j x y k x y k z x j y z i⨯=++---()122112211221,,y z y z z x z x x y x y =---2x 1x 2y 1y 2z 1z ()211221122112,,OB OA y z y z z x z x x y x y ⨯=--- ()0,0,00OA OB OB OA ⨯+⨯== sin AOB ∠===1sin 2AOB S OA OB AOB =⋅∠= △AOB ⨯2222()OB OA OB OA OB ⨯-⋅= ()111,,OA x y z = ()222,,OB x y z =()122112211221,,OA OB y z y z z x z x x y x y ⨯=--- ()()()2222122112211221OB y z y z z x z x x y x y ⨯=-+-+-,成立,故,故的几何意义表示:以15.答案:选择①:存在点,,满足;选择②:存在点,,满足;选择③:不存在点E ,F 满足,理由见解析解析:由题意知,正方体的棱长为2,则,,,,,设,,则,,,,所以,.选择①:因为,所以,即,得,若,则,则,故存在点,,满足,142()EF AC a b ⋅=-+ 82AE BF b ⋅=- ()()DE CF DE CF +⊥- ()()0DE CF DE CF +⋅-= 22DE CF = a b =10EF AC ⋅= 42()0a b -+=1a b ==(0,1,2)E 22111x y z ++222222x y z ++()22121212()OA OB x x y y z z ⋅=++2()OA OB ⋅ ⨯1222AOB OA OB OA OB S OA =⨯⋅⨯=⋅⨯ △21()63AOB OA OB S OA OB ⨯=⋅⨯⨯ △2()OA OB ⨯ △⨯(0,1,2)E (1,2,2)F 1EF A C ⊥6AE BF ⋅= 10,,22E ⎛⎫ ⎪⎝⎭3,2,22F ⎛⎫ ⎪⎝⎭1EF A C ⊥5AE BF ⋅= 1EF A C ⊥1111ABCD A B C D -(2,0,0)A (2,2,0)B 1(2,0,2)A (0,0,0)D (0,2,0)C (0,,2)(02)E a a ≤≤(,2,2)(02)F b b ≤≤(,2,0)EF b a =- 1(2,2,2)AC =-- (2,,2)AE a =- (2,0,2)BF b =- (1,2,2)F 1EF A C ⊥此时.选择②:因为,若,则,得故存在点,,满足,此时.选择③:因为,所以与不共线,又,所以,即,则,故不存在点E ,F 满足.826AE BF b ⋅=-= ||DE = (0,,2)DE a = ==10EF AC ⋅= 42()0a b -+=b =10,,22E ⎛⎫ ⎪⎝⎭3,2,22F ⎛⎫ ⎪⎝⎭1EF A C ⊥825AE BF b ⋅=-= 0cos ,1EF DB <〈〉< EF DB (2,2,0)DB = 2b a ≠-2a b +≠142()0EF AC a b ⋅=-+≠ 1EF A C ⊥。
2023年高考数学一轮复习第七章立体几何与空间向量6空间向量的概念与运算练习含解析

空间向量的概念与运算考试要求 1.了解空间向量的概念,了解空间向量的基本定理及其意义,掌握空间向量的正交分解及其坐标表示.2.掌握空间向量的线性运算及其坐标表示,掌握空间向量的数量积及其坐标表示,能用向量的数量积判断向量的共线和垂直.3.理解直线的方向向量及平面的法向量,能用向量方法证明立体几何中有关线面位置关系的一些简单定理.知识梳理1.空间向量的有关概念名称定义空间向量在空间中,具有大小和方向的量相等向量方向相同且模相等的向量相反向量方向相反且模相等的向量共线向量表示若干空间向量的有向线段所在的直线互相平行或重合的向量(或平行向量)共面向量平行于同一个平面的向量2.空间向量的有关定理(1)共线向量定理:对任意两个空间向量a,b(b≠0),a∥b的充要条件是存在实数λ,使a =λb.(2)共面向量定理:如果两个向量a,b不共线,那么向量p与向量a,b共面的充要条件是存在唯一的有序实数对(x,y),使p=x a+y b.(3)空间向量基本定理如果三个向量a,b,c不共面,那么对任意一个空间向量p,存在唯一的有序实数组(x,y,z),使得p=x a+y b+z c,{a,b,c}叫做空间的一个基底.3.空间向量的数量积及运算律(1)数量积非零向量a,b的数量积a·b=|a||b|cos〈a,b〉.(2)空间向量的坐标表示及其应用设a=(a1,a2,a3),b=(b1,b2,b3).向量表示坐标表示数量积a·b a1b1+a2b2+a3b3共线a =λb(b ≠0,λ∈R )a 1=λb 1,a 2=λb 2,a 3=λb 3 垂直 a ·b =0(a ≠0,b ≠0)a 1b 1+a 2b 2+a 3b 3=0模 |a |a 21+a 22+a 23夹角余弦值 cos 〈a ,b 〉=a ·b|a ||b |(a ≠0,b ≠0)cos 〈a ,b 〉=a 1b 1+a 2b 2+a 3b 3a 21+a 22+a 23·b 21+b 22+b 234.空间位置关系的向量表示(1)直线的方向向量:如果表示非零向量a 的有向线段所在直线与直线l 平行或重合,则称此向量a 为直线l 的方向向量.(2)平面的法向量:直线l ⊥α,取直线l 的方向向量a ,则向量a 为平面α的法向量. (3)空间位置关系的向量表示位置关系向量表示直线l 1,l 2的方向向量分别为n 1,n 2 l 1∥l 2 n 1∥n 2⇔n 1=λn 2(λ∈R ) l 1⊥l 2 n 1⊥n 2⇔n 1·n 2=0 直线l 的方向向量为n ,平面α的法向量为m ,l ⊄αl ∥α n ⊥m ⇔n ·m =0 l ⊥α n ∥m ⇔n =λm (λ∈R ) 平面α,β的法向量分别为n ,mα∥β n ∥m ⇔n =λm (λ∈R )α⊥βn ⊥m ⇔n ·m =0常用结论1.在平面中,A ,B ,C 三点共线的充要条件是:OA →=xOB →+yOC →(其中x +y =1),O 为平面内任意一点.2.在空间中,P ,A ,B ,C 四点共面的充要条件是:OP →=xOA →+yOB →+zOC →(其中x +y +z =1),O 为空间中任意一点.思考辨析判断下列结论是否正确(请在括号中打“√”或“×”) (1)直线的方向向量是唯一确定的.( × )(2)若直线a 的方向向量和平面α的法向量平行,则a ∥α.( × )(3)在空间直角坐标系中,在Oyz 平面上的点的坐标一定是(0,b ,c ).( √ ) (4)若a ·b <0,则〈a ,b 〉是钝角.( × ) 教材改编题1.若{a ,b ,c }为空间向量的一个基底,则下列各项中,能构成空间向量的一个基底的是( ) A .{a ,a +b ,a -b } B .{b ,a +b ,a -b } C .{c ,a +b ,a -b } D .{a +b ,a -b ,a +2b } 答案 C解析 ∵λa +μb (λ,μ∈R )与a ,b 共面. ∴A,B ,D 不正确.2.如图,在平行六面体ABCD -A 1B 1C 1D 1中,M 为A 1C 1与B 1D 1的交点.若AB →=a ,AD →=b ,AA 1—→=c ,则下列向量中与BM →相等的向量是( )A .-12a +12b +cB.12a +12b +c C .-12a -12b +cD.12a -12b +c 答案 A解析 由题意,根据向量运算的几何运算法则, BM →=BB 1—→+B 1M —→=AA 1—→+12(AD →-AB →)=c +12(b -a )=-12a +12b +c .3.设直线l 1,l 2的方向向量分别为a =(-2,2,1),b =(3,-2,m ),若l 1⊥l 2,则m =________. 答案 10解析 ∵l 1⊥l 2,∴a ⊥b , ∴a ·b =-6-4+m =0,∴m =10.题型一 空间向量的线性运算例1 如图所示,在平行六面体ABCD -A 1B 1C 1D 1中,设AA 1—→=a ,AB →=b ,AD →=c ,M ,N ,P 分别是AA 1,BC ,C 1D 1的中点,试用a ,b ,c 表示以下各向量:(1)AP →;(2)A 1N —→;(3)MP →+NC 1—→. 解 (1)∵P 是C 1D 1的中点, ∴AP →=AA 1—→+A 1P —→=AA 1—→+A 1D 1—→+D 1P —→ =AA 1—→+AD →+12DC →=a +c +12AB →=a +c +12b .(2)∵N 是BC 的中点, ∴A 1N —→=A 1A —→+AB →+BN → =-a +b +12BC →=-a +b +12AD →=-a +b +12c .(3)∵M 是AA 1的中点, ∴MP →=MA →+AP →=12A 1A —→+AP →=-12a +(a +c +12b )=12a +12b +c . 又NC 1—→=NC →+CC 1—→=12BC →+AA 1—→=12AD →+AA 1—→=12c +a .∴MP →+NC 1—→=⎝ ⎛⎭⎪⎫12a +12b +c +⎝ ⎛⎭⎪⎫12c +a =32a +12b +32c . 教师备选如图,在三棱锥O -ABC 中,M ,N 分别是OA ,BC 的中点,G 是△ABC 的重心,用基向量OA →,OB →,OC →表示OG →,则下列表示正确的是( )A.14OA →+12OB →+13OC →B.12OA →+12OB →+12OC → C .-16OA →+13OB →+13OC →D.13OA →+13OB →+13OC → 答案 D解析 MG →=MA →+AG →=12OA →+23AN →=12OA →+23(ON →-OA →)=12OA →+23⎣⎢⎡⎦⎥⎤12OB →+OC →-OA → =-16OA →+13OB →+13OC →.OG →=OM →+MG →=12OA →-16OA →+13OB →+13OC →=13OA →+13OB →+13OC →.思维升华 用基向量表示指定向量的方法 (1)结合已知向量和所求向量观察图形.(2)将已知向量和所求向量转化到三角形或平行四边形中.(3)利用三角形法则或平行四边形法则把所求向量用已知基向量表示出来.跟踪训练1 (1)(2022·宁波模拟)如图,在三棱锥O -ABC 中,点P ,Q 分别是OA ,BC 的中点,点D 为线段PQ 上一点,且PD →=2DQ →,若记OA →=a ,OB →=b ,OC →=c ,则OD →等于( )A.16a +13b +13cB.13a +13b +13cC.13a +16b +13cD.13a +13b +16c 答案 A解析 OD →=OP →+PD →=12OA →+23PQ →=12OA →+23(OQ →-OP →) =12OA →+23OQ →-23OP → =12OA →+23×12(OB →+OC →)-23×12OA → =16OA →+13OB →+13OC → =16a +13b +13c . (2)在正方体ABCD -A 1B 1C 1D 1中,点F 是侧面CDD 1C 1的中心,若AF →=xAD →+yAB →+z AA 1—→,则x -y +z 等于( )A.12B .1C.32D .2 答案 B解析 AF →=AD →+DF →=AD →+12(DD 1—→+D 1C 1—→)=AD →+12(AA 1—→+A 1B 1—→)=AD →+12(AA 1—→+AB →)=AD →+12AB →+12AA 1—→,则x =1,y =12,z =12,则x -y +z =1.题型二 空间向量基本定理及其应用例2 已知A ,B ,C 三点不共线,对平面ABC 外的任一点O ,若点M 满足OM →=13(OA →+OB →+OC →).(1)判断MA →,MB →,MC →三个向量是否共面; (2)判断点M 是否在平面ABC 内. 解 (1)由题知OA →+OB →+OC →=3OM →, 所以OA →-OM →=(OM →-OB →)+(OM →-OC →), 即MA →=BM →+CM →=-MB →-MC →, 所以MA →,MB →,MC →共面.(2)方法一 由(1)知,MA →,MB →,MC →共面且基线过同一点M , 所以M ,A ,B ,C 四点共面,从而点M 在平面ABC 内. 方法二 因为OM →=13(OA →+OB →+OC →)=13OA →+13OB →+13OC →, 又因为13+13+13=1,所以M ,A ,B ,C 四点共面,从而M 在平面ABC 内. 教师备选如图所示,已知斜三棱柱ABC -A 1B 1C 1,点M ,N 分别在AC 1和BC 上,且满足AM →=k AC 1—→,BN →=kBC →(0≤k ≤1).判断向量MN →是否与向量AB →,AA 1—→共面.解 因为AM →=k AC 1—→,BN →=kBC →, 所以MN →=MA →+AB →+BN → =k C 1A —→+AB →+kBC →=k (C 1A —→+BC →)+AB →=k (C 1A —→+B 1C 1—→)+AB → =k B 1A —→+AB →=AB →-k AB 1—→=AB →-k (AA 1—→+AB →) =(1-k )AB →-k AA 1—→,所以由共面向量定理知向量MN →与向量AB →,AA 1—→共面. 思维升华 证明空间四点P ,M ,A ,B 共面的方法 (1)MP →=xMA →+yMB →;(2)对空间任一点O ,OP →=OM →+xMA →+yMB →;(3)对空间任一点O ,OP →=xOM →+yOA →+zOB →(x +y +z =1); (4)PM →∥AB →(或PA →∥MB →或PB →∥AM →).跟踪训练2 (1)(多选)(2022·武汉质检)下列说法中正确的是( ) A .|a |-|b |=|a +b |是a ,b 共线的充要条件 B .若AB →,CD →共线,则AB ∥CDC .A ,B ,C 三点不共线,对空间任意一点O ,若OP →=34OA →+18OB →+18OC →,则P ,A ,B ,C 四点共面D .若P ,A ,B ,C 为空间四点,且有PA →=λPB →+μPC →(PB →,PC →不共线),则λ+μ=1是A ,B ,C 三点共线的充要条件答案 CD解析 由|a |-|b |=|a +b |,可得向量a ,b 的方向相反,此时向量a ,b 共线,反之,当向量a ,b 同向时,不能得到|a |-|b |=|a +b |,所以A 不正确; 若AB →,CD →共线,则AB ∥CD 或A ,B ,C ,D 四点共线,所以B 不正确; 由A ,B ,C 三点不共线,对空间任意一点O , 若OP →=34OA →+18OB →+18OC →,因为34+18+18=1,可得P ,A ,B ,C 四点共面,故C 正确; 若P ,A ,B ,C 为空间四点,且有PA →=λPB →+μPC →(PB →,PC →不共线), 当λ+μ=1时,即μ=1-λ,可得PA →-PC →=λ(PB →+CP →), 即CA →=λCB →,所以A ,B ,C 三点共线,反之也成立,即λ+μ=1是A ,B ,C 三点共线的充要条件,所以D 正确.(2)已知A ,B ,C 三点不共线,点O 为平面ABC 外任意一点,若点M 满足OM →=15OA →+45OB →+25BC →,则点M ________(填“属于”或“不属于”)平面ABC . 答案 属于解析 ∵OM →=15OA →+45OB →+25BC →=15OA →+45OB →+25(OC →-OB →)=15OA →+25OB →+25OC →,∵15+25+25=1, ∴M ,A ,B ,C 四点共面. 即点M ∈平面ABC .题型三 空间向量数量积及其应用例3 如图所示,已知空间四边形ABCD 的每条边和对角线长都等于1,点E ,F ,G 分别是AB ,AD ,CD 的中点,计算:(1)EF →·BA →.(2)求异面直线AG 和CE 所成角的余弦值. 解 设AB →=a ,AC →=b ,AD →=c . 则|a |=|b |=|c |=1,〈a ,b 〉=〈b ,c 〉=〈c ,a 〉=60°, (1)EF →=12BD →=12c -12a ,BA →=-a ,EF →·BA →=⎝ ⎛⎭⎪⎫12c -12a ·(-a )=12a 2-12a ·c =14. (2)AG →=12(AC →+AD →)=12b +12c ,CE →=CA →+AE →=-b +12a ,cos 〈AG →,CE →〉=AG →·CE →|AG →||CE →|=⎝ ⎛⎭⎪⎫12b +12c ·⎝⎛⎭⎪⎫-b +12a ⎝ ⎛⎭⎪⎫12b +12c 2·⎝ ⎛⎭⎪⎫12a -b 2=-1232×32=-23,由于异面直线所成角的范围是⎝⎛⎦⎥⎤0,π2,所以异面直线AG 与CE 所成角的余弦值为23.教师备选已知MN 是正方体内切球的一条直径,点P 在正方体表面上运动,正方体的棱长是2,则PM →·PN →的取值范围为( )A.[]0,4B.[]0,2C.[]1,4D.[]1,2 答案 B解析 设正方体内切球的球心为O , 则OM =ON =1,PM →·PN →=()PO →+OM →·()PO →+ON →=PO →2+PO →·()OM →+ON →+OM →·ON →, ∵MN 为球O 的直径, ∴OM →+ON →=0,OM →·ON →=-1, ∴PM →·PN →=PO →2-1, 又P 在正方体表面上移动,∴当P 为正方体顶点时,||PO →最大,最大值为3;当P 为内切球与正方体的切点时,||PO →最小,最小值为1, ∴PO →2-1∈[]0,2,即PM →·PN →的取值范围为[]0,2.思维升华 由向量数量积的定义知,要求a 与b 的数量积,需已知|a |,|b |和〈a ,b 〉,a 与b 的夹角与方向有关,一定要根据方向正确判定夹角的大小,才能使a·b 计算准确.跟踪训练3如图所示,在四棱柱ABCDA 1B 1C 1D 1中,底面为平行四边形,以顶点A 为端点的三条棱长都为1,且两两夹角为60°.(1)求AC 1的长; (2)求证:AC 1⊥BD ;(3)求BD 1与AC 夹角的余弦值. (1)解 记AB →=a ,AD →=b ,AA 1—→=c , 则|a |=|b |=|c |=1,〈a ,b 〉=〈b ,c 〉=〈c ,a 〉=60°, ∴a ·b =b ·c =c ·a =12.|AC 1—→|2=(a +b +c )2=a 2+b 2+c 2+2(a ·b +b ·c +c ·a )=1+1+1+2×⎝ ⎛⎭⎪⎫12+12+12=6, ∴|AC 1—→|=6,即AC 1的长为 6. (2)证明 ∵AC 1—→=a +b +c ,BD →=b -a , ∴AC 1—→·BD →=(a +b +c )·(b -a )=a ·b +|b |2+b ·c -|a |2-a ·b -a ·c =0. ∴AC 1—→⊥BD →,∴AC 1⊥BD .(3)解 BD 1—→=b +c -a ,AC →=a +b , ∴|BD 1—→|=2,|AC →|=3, BD 1—→·AC →=(b +c -a )·(a +b ) =b 2-a 2+a ·c +b ·c =1.∴cos〈BD 1—→,AC →〉=BD 1—→·AC →|BD 1—→||AC →|=66.∴AC 与BD 1夹角的余弦值为66.题型四 向量法证明平行、垂直例4 如图,在四棱锥P -ABCD 中,PA ⊥底面ABCD ,AD ⊥AB ,AB ∥DC ,AD =DC =AP =2,AB =1,点E 为棱PC 的中点.证明:(1)BE ⊥DC ; (2)BE ∥平面PAD ; (3)平面PCD ⊥平面PAD .证明 依题意,以点A 为坐标原点建立空间直角坐标系(如图),可得B (1,0,0),C (2,2,0),D (0,2,0),P (0,0,2).由E 为棱PC 的中点,得E (1,1,1).(1)BE →=(0,1,1), DC →=(2,0,0),故BE →·DC →=0, 所以BE ⊥DC .(2)因为AB ⊥AD ,又PA ⊥平面ABCD ,AB ⊂平面ABCD ,所以AB ⊥PA ,PA ∩AD =A ,PA ,AD ⊂平面PAD , 所以AB ⊥平面PAD ,所以AB →=(1,0,0)为平面PAD 的一个法向量, 而BE →·AB →=(0,1,1)·(1,0,0)=0, 所以BE ⊥AB , 又BE ⊄平面PAD , 所以BE ∥平面PAD .(3)由(2)知平面PAD 的法向量AB →=(1,0,0), PD →=(0,2,-2), DC →=(2,0,0),设平面PCD 的一个法向量为n =(x ,y ,z ), 则⎩⎪⎨⎪⎧n ·PD →=0,n ·DC →=0,即⎩⎪⎨⎪⎧2y -2z =0,2x =0,令y =1,可得n =(0,1,1)为平面PCD 的一个法向量. 且n ·AB →=(0,1,1)·(1,0,0)=0, 所以n ⊥AB →.所以平面PAD ⊥平面PCD . 教师备选如图,已知AA 1⊥平面ABC ,BB 1∥AA 1,AB =AC =3,BC =25,AA 1=7,BB 1=27,点E 和F 分别为BC 和A 1C 的中点.(1)求证:EF ∥平面A 1B 1BA ; (2)求证:平面AEA 1⊥平面BCB 1.证明 因为AB =AC ,E 为BC 的中点,所以AE ⊥BC . 因为AA 1⊥平面ABC ,AA 1∥BB 1,所以以过E 作平行于BB 1的垂线为z 轴,EC ,EA 所在直线分别为x 轴、y 轴, 建立如图所示的空间直角坐标系.因为AB =3,BE =5, 所以AE =2,所以E (0,0,0),C (5,0,0),A (0,2,0),B (-5,0,0),B 1(-5,0,27). A 1(0,2,7),则F ⎝⎛⎭⎪⎫52,1,72.(1)EF →=⎝ ⎛⎭⎪⎫52,1,72,AB →=(-5,-2,0),AA 1→=(0,0,7).设平面AA 1B 1B 的一个法向量为n =(x ,y ,z ), 则⎩⎪⎨⎪⎧n ·AB →=0,n ·AA 1—→=0,所以⎩⎨⎧-5x -2y =0,7z =0,取⎩⎨⎧x =-2,y =5,z =0,所以n =(-2,5,0).因为EF →·n =52×(-2)+1×5+72×0=0,所以EF →⊥n . 又EF ⊄平面A 1B 1BA , 所以EF ∥平面A 1B 1BA . (2)因为EC ⊥平面AEA 1,所以EC →=(5,0,0)为平面AEA 1的一个法向量. 又EA ⊥平面BCB 1,所以EA →=(0,2,0)为平面BCB 1的一个法向量. 因为EC →·EA →=0,所以EC →⊥EA →, 故平面AEA 1⊥平面BCB 1.思维升华 (1)利用向量法证明平行、垂直关系,关键是建立恰当的坐标系(尽可能利用垂直条件,准确写出相关点的坐标,进而用向量表示涉及到直线、平面的要素).(2)向量证明的核心是利用向量的数量积或数乘向量,但向量证明仍然离不开立体几何的有关定理.跟踪训练4 如图,在四棱锥P -ABCD 中,底面ABCD 是边长为a 的正方形,侧面PAD ⊥底面ABCD ,且PA =PD =22AD ,设E ,F 分别为PC ,BD 的中点.求证:(1)EF ∥平面PAD ; (2)平面PAB ⊥平面PDC .证明 (1)如图,取AD 的中点O ,连接OP ,OF .因为PA =PD ,所以PO ⊥AD .又侧面PAD ⊥底面ABCD ,平面PAD ∩平面ABCD =AD ,PO ⊂平面PAD , 所以PO ⊥平面ABCD .又O ,F 分别为AD ,BD 的中点, 所以OF ∥AB .又四边形ABCD 是正方形, 所以OF ⊥AD . 因为PA =PD =22AD , 所以PA ⊥PD ,OP =OA =a2.如图,以O 为坐标原点,OA ,OF ,OP 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系,则A ⎝ ⎛⎭⎪⎫a 2,0,0,F ⎝ ⎛⎭⎪⎫0,a2,0,D ⎝ ⎛⎭⎪⎫-a 2,0,0,P ⎝ ⎛⎭⎪⎫0,0,a 2,B ⎝ ⎛⎭⎪⎫a 2,a ,0,C ⎝ ⎛⎭⎪⎫-a 2,a ,0.因为E 为PC 的中点,所以E ⎝ ⎛⎭⎪⎫-a 4,a 2,a4. 易知平面PAD 的一个法向量为 OF →=⎝⎛⎭⎪⎫0,a 2,0,因为EF →=⎝ ⎛⎭⎪⎫a4,0,-a 4,OF →·EF →=⎝ ⎛⎭⎪⎫0,a 2,0·⎝ ⎛⎭⎪⎫a 4,0,-a 4=0.且EF ⊄平面PAD ,所以EF ∥平面PAD .(2)因为PA →=⎝ ⎛⎭⎪⎫a2,0,-a 2,CD →=(0,-a ,0),所以PA →·CD →=⎝ ⎛⎭⎪⎫a2,0,-a 2·(0,-a ,0)=0,所以PA →⊥CD →, 所以PA ⊥CD .又PA ⊥PD ,PD ∩CD =D ,PD ,CD ⊂平面PDC ,所以PA ⊥平面PDC .又PA ⊂平面PAB ,所以平面PAB ⊥平面PDC .课时精练1.已知a =(2,1,-3),b =(0,-3,2),c =(-2,1,2),则a ·(b +c )等于( ) A .18B .-18C .32D .-3 2 答案 B解析 因为b +c =(-2,-2,4), 所以a ·(b +c )=-4-2-12=-18.2.已知空间任意一点O 和不共线的三点A ,B ,C ,若OP →=xOA →+yOB →+zOC →(x ,y ,z ∈R ),则“x =2,y =-3,z =2”是“P ,A ,B ,C 四点共面”的( ) A .必要不充分条件 B .充分不必要条件 C .充要条件D .既不充分也不必要条件 答案 B解析 由x +y +z =1,得P ,A ,B ,C 四点共面,当P ,A ,B ,C 四点共面时,x +y +z =1,显然不止2,-3,2.故“x =2,y =-3,z =2”是“P ,A ,B ,C 四点共面”的充分不必要条件.3.已知空间向量a =(1,0,1),b =(1,1,n ),且a·b =3,则向量a 与b 的夹角为( ) A.π6B.π3C.2π3D.5π6答案 A解析 由题意,a ·b =1+0+n =3, 解得n =2,又|a |=1+0+1=2,|b |=1+1+4=6,所以cos 〈a ,b 〉=a·b |a ||b |=32×6=32,又〈a ,b 〉∈[0,π], 所以a 与b 的夹角为π6.4.直线l 的一个方向向量为(2,1,1),平面α的一个法向量为(4,2,2),则( ) A .l ∥α B .l ⊥α C .l ∥α或l ⊂αD .l 与α的位置关系不能判断 答案 B解析 直线l 的一个方向向量为(2,1,1),平面α的一个法向量为(4,2,2), 显然它们共线,所以l ⊥α.5.(多选)已知空间三点A (1,0,3),B (-1,1,4),C (2,-1,3),若AP →∥BC →,且|AP →|=14,则点P 的坐标为( ) A .(4,-2,2) B .(-2,2,4) C .(-4,2,-2) D .(2,-2,4)答案 AB解析 因为B (-1,1,4),C (2,-1,3), 所以BC →=(3,-2,-1), 因为AP →∥BC →,所以可设AP →=λBC →=(3λ,-2λ,-λ), 因为|AP →|=3λ2+-2λ2+-λ2=14,解得λ=±1,所以AP →=(3,-2,-1)或AP →=(-3,2,1), 设点P (x ,y ,z ),则AP →=(x -1,y ,z -3),所以⎩⎪⎨⎪⎧ x -1=3,y =-2,z -3=-1或⎩⎪⎨⎪⎧ x -1=-3,y =2,z -3=1,解得⎩⎪⎨⎪⎧x =4,y =-2,z =2或⎩⎪⎨⎪⎧x =-2,y =2,z =4.所以点P 的坐标为(4,-2,2)或(-2,2,4).6.(多选)已知空间中三点A (0,1,0),B (2,2,0),C (-1,3,1),则下列结论正确的有( ) A.AB →与AC →是共线向量B .与AB →共线的单位向量是(1,1,0) C.AB →与BC →夹角的余弦值是-5511D .平面ABC 的一个法向量是(1,-2,5) 答案 CD解析 对于A ,AB →=(2,1,0),AC →=(-1,2,1),不存在实数λ,使得AB →=λAC →, 所以AB →与AC →不是共线向量,所以A 错误;对于B ,因为AB →=(2,1,0),所以与AB →共线的单位向量为⎝ ⎛⎭⎪⎫255,55,0或⎝ ⎛⎭⎪⎫-255,-55,0,所以B 错误;对于C ,向量AB →=(2,1,0),BC →=(-3,1,1), 所以cos 〈AB →,BC →〉=AB →·BC →|AB →||BC →|=-5511,所以C 正确;对于D ,设平面ABC 的法向量是n =(x ,y ,z ), 因为AB →=(2,1,0),AC →=(-1,2,1), 所以⎩⎪⎨⎪⎧n ·AB →=0,n ·AC →=0,即⎩⎪⎨⎪⎧2x +y =0,-x +2y +z =0.令x =1,则n =(1,-2,5),所以D 正确.7.已知a =(x ,1,1),b =(-2,2,y ),a ·b =0,则2x -y =________. 答案 2解析 因为a =(x ,1,1),b =(-2,2,y ),a ·b =0,所以-2x +2+y =0,2x -y =2.8.已知点A (-1,1,0),B (1,2,0),C (-2,-1,0),D (3,4,0),则AB →在CD →上的投影向量为________.答案 ⎝ ⎛⎭⎪⎫32,32,0 解析 由已知得AB →=(2,1,0),CD →=(5,5,0), ∴AB →·CD →=2×5+1×5+0=15, 又|CD →|=52,∴AB →在CD →上的投影向量为AB →·CD →|CD →|·CD →|CD →|=1552×CD →52=310CD →=⎝ ⎛⎭⎪⎫32,32,0. 9.如图所示,在直三棱柱ABC -A 1B 1C 1中,CA =CB =1,∠BCA =90°,棱AA 1=2,M ,N 分别是A 1B 1,A 1A 的中点.(1)求BN →的长;(2)求cos 〈BA 1—→,CB 1—→〉的值; (3)求证:A 1B ⊥C 1M .(1)解 以C 为坐标原点,CA ,CB ,CC 1所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系,如图.B (0,1,0),N (1,0,1),∴BN →=(1,-1,1), ∴|BN →|=12+-12+12= 3.(2)解 ∵A 1(1,0,2),B (0,1,0),C (0,0,0),B 1(0,1,2),∴BA 1—→=(1,-1,2),CB 1—→=(0,1,2),∴BA 1—→·CB 1—→=3,|BA 1—→|=6,|CB 1—→|= 5. ∴cos〈BA 1—→,CB 1—→〉=BA 1—→·CB 1—→|BA 1—→||CB 1—→|=3010.(3)证明 ∵C 1(0,0,2),M ⎝ ⎛⎭⎪⎫12,12,2, ∴A 1B —→=(-1,1,-2),C 1M —→=⎝ ⎛⎭⎪⎫12,12,0,∴A 1B —→·C 1M —→=-12+12+0=0.∴A 1B —→⊥C 1M —→, ∴A 1B ⊥C 1M .10.如图,在四棱锥P -ABCD 中,PD ⊥底面ABCD ,底面ABCD 为正方形,PD =DC ,E ,F 分别是AB ,PB 的中点.(1)求证:EF ⊥CD ;(2)在平面PAD 内求一点G ,使GF ⊥平面PCB .(1)证明 如图,以D 为坐标原点,分别以DA ,DC ,DP 所在直线为x 轴、y 轴、z 轴建立空间直角坐标系,设AD =a ,则D (0,0,0),A (a ,0,0),B (a ,a ,0),C (0,a ,0),E ⎝⎛⎭⎪⎫a ,a 2,0,P (0,0,a ), F ⎝ ⎛⎭⎪⎫a 2,a 2,a 2. EF →=⎝ ⎛⎭⎪⎫-a2,0,a 2,DC →=(0,a ,0).因为EF →·DC →=0,所以EF →⊥DC →,即EF ⊥CD .(2)解 设G (x ,0,z ),则FG →=⎝ ⎛⎭⎪⎫x -a 2,-a 2,z -a2,CB →=(a ,0,0),CP →=(0,-a ,a ),若使GF ⊥平面PCB ,则需FG →·CB →=0,且FG →·CP →=0,由FG →·CB →=⎝ ⎛⎭⎪⎫x -a 2,-a 2,z -a2·(a ,0,0)=a ⎝ ⎛⎭⎪⎫x -a2=0,得x =a2,由FG →·CP →=⎝ ⎛⎭⎪⎫x -a 2,-a 2,z -a2·(0,-a ,a ) =a 22+a ⎝ ⎛⎭⎪⎫z -a2=0,得z =0.所以G 点坐标为⎝ ⎛⎭⎪⎫a2,0,0,即G 为AD 的中点时,GF ⊥平面PCB .11.(多选)(2022·山东百师联盟大联考)下面四个结论正确的是( )A .向量a ,b (a ≠0,b ≠0),若a⊥b ,则a·b =0B .若空间四个点P ,A ,B ,C ,PC →=14PA →+34PB →,则A ,B ,C 三点共线C .已知向量a =(1,1,x ),b =(-3,x ,9),若x <310,则〈a ,b 〉为钝角D .任意向量a ,b ,c 满足(a·b )·c =a·(b·c )答案 AB解析 由向量垂直的充要条件可得A 正确;∵PC →=14PA →+34PB →,∴14PC →-14PA →=34PB →-34PC →,即AC →=3CB →,∴A ,B ,C 三点共线,故B 正确;当x =-3时,两个向量共线,夹角为π,故C 错误;由于向量的数量积运算不满足结合律,故D 错误.12.(多选)(2022·重庆市第七中学月考)给出下列命题,其中为假命题的是( )A .已知n 为平面α的一个法向量,m 为直线l 的一个方向向量,若n ⊥m ,则l ∥αB .已知n 为平面α的一个法向量,m 为直线l 的一个方向向量,若〈n ,m 〉=2π3,则l 与α所成角为π6C .若两个不同的平面α,β的法向量分别为u ,v ,且u =(1,2,-2),v =(-2,-4,4),则α∥βD .已知空间的三个向量a ,b ,c ,则对于空间的任意一个向量p ,总存在实数x ,y ,z 使得p =x a +y b +z c答案 AD解析 对于A ,由题意可得l ∥α或l ⊂α,故A 错误;对于B ,由图象可得,∠CAD =2π3,则∠DAB =π3,所以∠ADB =π6, 根据线面角的定义可得,l 与α所成角为π6,故B 正确; 对于C ,因为u =-12v =-12(-2,-4,4) =(1,2,-2),所以u ∥v ,故α∥β,故C 正确;对于D ,当空间的三个向量a ,b ,c 不共面时,对于空间的任意一个向量p ,总存在实数x ,y ,z 使得p =x a +y b +z c ,故D 错误.13.(2022·杭州模拟)在棱长为1的正方体ABCD -A 1B 1C 1D 1中,E ,F 分别为A 1D 1,BB 1的中点,则cos∠EAF =________;EF =________.答案 25 62 解析 如图,以A 为坐标原点,AB ,AD ,AA 1所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系,∵正方体棱长为1,则E ⎝ ⎛⎭⎪⎫0,12,1,F ⎝⎛⎭⎪⎫1,0,12, ∴AE →=⎝ ⎛⎭⎪⎫0,12,1,AF →=⎝⎛⎭⎪⎫1,0,12, EF →=⎝ ⎛⎭⎪⎫1,-12,-12, cos 〈AE →,AF →〉=AE →·AF →|AE →||AF →|=1252×52=25, ∴cos∠EAF =25, EF =|EF →|=12+⎝ ⎛⎭⎪⎫-122+⎝ ⎛⎭⎪⎫-122=62. 14.如图,已知四棱柱ABCD -A 1B 1C 1D 1的底面A 1B 1C 1D 1为平行四边形,E 为棱AB 的中点,AF →=13AD →,AG →=2GA 1—→,AC 1与平面EFG 交于点M ,则AM AC 1=________.答案 213解析 由题图知,设AM →=λAC 1—→(0<λ<1),由已知AC 1—→=AB →+AD →+AA 1—→=2AE →+3AF →+32AG →,所以AM →=2λAE →+3λAF →+3λ2AG →,因为M ,E ,F ,G 四点共面,所以2λ+3λ+3λ2=1, 解得λ=213.15.已知O 点为空间直角坐标系的原点,向量OA →=(1,2,3),OB →=(2,1,2),OP →=(1,1,2),且点Q 在直线OP 上运动,当QA →·QB →取得最小值时,OQ →的坐标是______.答案 ⎝ ⎛⎭⎪⎫43,43,83 解析 因为点Q 在直线OP 上,所以设点Q (λ,λ,2λ),则QA →=(1-λ,2-λ,3-2λ),QB →=(2-λ,1-λ,2-2λ),QA →·QB →=(1-λ)(2-λ)+(2-λ)(1-λ)+(3-2λ)·(2-2λ)=6λ2-16λ+10=6⎝⎛⎭⎪⎫λ-432-23. 即当λ=43时,QA →·QB →取得最小值-23, 此时OQ →=⎝ ⎛⎭⎪⎫43,43,83. 16.(2022·株州模拟)如图,棱柱ABCD -A 1B 1C 1D 1的所有棱长都等于2,∠ABC 和∠A 1AC 均为60°,平面AA 1C 1C ⊥平面ABCD .(1)求证:BD ⊥AA 1;(2)在直线CC 1上是否存在点P ,使BP ∥平面DA 1C 1,若存在,求出点P 的位置,若不存在,请说明理由.(1)证明 设BD 与AC 交于点O ,则BD ⊥AC ,连接A 1O ,在△AA 1O 中,AA 1=2,AO =1,∠A 1AO =60°,所以A 1O 2=AA 21+AO 2-2AA 1·AO cos60°=3,所以AO 2+A 1O 2=AA 21,所以A 1O ⊥AO .由于平面AA 1C 1C ⊥平面ABCD ,且平面AA 1C 1C ∩平面ABCD =AC ,A 1O ⊂平面AA 1C 1C ,所以A 1O ⊥平面ABCD .以O 为坐标原点,OB ,OC ,OA 1所在直线分别为x 轴、y 轴、z 轴,建立如图所示的空间直角坐标系,则A (0,-1,0),B (3,0,0),C (0,1,0),D (-3,0,0),A 1(0,0,3),C 1(0,2,3).由于BD →=(-23,0,0),AA 1—→=(0,1,3),AA 1—→·BD →=0×(-23)+1×0+3×0=0,所以BD →⊥AA 1—→,即BD ⊥AA 1.(2)解 假设在直线CC 1上存在点P ,使BP ∥平面DA 1C 1,设CP →=λCC 1—→,P (x ,y ,z ),则(x ,y -1,z )=λ(0,1,3).从而有P (0,1+λ,3λ),BP →=(-3,1+λ,3λ). 设平面DA 1C 1的一个法向量为n 1=(x 1,y 1,z 1), 则⎩⎪⎨⎪⎧n 1·A 1C 1—→=0,n 1·DA 1—→=0, 又A 1C 1—→=(0,2,0),DA 1—→=(3,0,3),则⎩⎨⎧ 2y 1=0,3x 1+3z 1=0,取n 1=(1,0,-1),因为BP ∥平面DA 1C 1,所以n 1⊥BP →,即n 1·BP →=-3-3λ=0,解得λ=-1,即点P 在C 1C 的延长线上,且|CP →|=|CC 1—→|.。
立体几何专题检测——江苏省2023届高三数学一轮总复习

江苏省2023届高三数学一轮总复习专题检测立体几何一、选择题:本题共8小题,每小题5分共40分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1、下列命题正确的是A 、正方形的直观图是正方形B 、用一个平面去截棱锥,底面和截面之间的部分组成的几何体是棱台C 、各个面都是三角形的几何体是三棱锥D 、圆锥有无数条母线2、设,αβ是两个不同的平面,,m n 是两条不同的直线,则下列结论中正确的是A 、 若m α⊥,m n ⊥,则 n α∥B 、 若αβ⊥,m α⊥,n β⊥,则m n ⊥C 、若n α∥,m n ⊥,则m α⊥D 、若αβ∥,m ⊂α,n ⊂β,则m n ∥3、已知圆锥的高为6,其侧面展开图为一个半圆,则该圆锥的母线长为A .2 2B .2 3C .2 6D .4 24、正多面体共有5种,统称为柏拉图体,它们分别是正四面体、正六面体(即正方体)、正八面体、正十二面体、正二十面体.连接正方体中相邻面的中心,可以得到另一个柏拉图体.已知该柏拉图体的体积为323,则生成它的正方体的棱长为( ) A. 2 B. 322 C. 324 D. 45、南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某水库.已知该水库水位为海拔1485m .时,相应水面的面积为21400km .;水位为海拔1575m .时,相应水面的面积为21800km .,将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔1485m .上升到1575m .7 2.65≈)( ) A. 931.010m ⨯B. 931.210m ⨯C. 931.410m ⨯D.931.610m ⨯6、在平行六面体1111ABCD A B C D -中,底面ABCD 是边长为 1 的正方形,侧棱1113,60AA A AD A AB ︒=∠=∠=,则1AC =( ).A 22 .B 10 .C 3 .D 177、如图,正方体1111ABCD A B C D -的棱长为1,,,,E F G H 分别是所在棱上的动点,且满足1DH BG AE CF +=+=,则以下四个结论正确的是( )A .,,,E G F H 四点一定不共面B .若四边形EGFH 为矩形,则DH CF =C .若四边形EGFH 为菱形,则,E F 一定为所在棱的中点D .若四边形EGFH 为菱形,则四边形EFGH 周长的取值范围为[4,25]8. 足球运动成为当今世界上开展最广、影响最大、最具魅力、拥有球迷数最多的体育项目之一,2022年卡塔尔世界杯是第22届世界杯足球赛.比赛于2022年11月21日至12月18日在卡塔尔境内7座城市中的12座球场举行.已知某足球的表面上有四个点A ,B ,C ,D 满足2dm AB BC AD BD CD =====,二面角A BD C --的大小为23π,则该足球的体积为( ) A.342dm 27πB.3352dm 27πC.314dm 27πD.32dm 27π二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得 5分,有选错的得0分,部分选对的得2分. 9、已知直线l 与平面α相交于点P ,则( ) A .α内不存在直线与l 平行 B .α内有无数条直线与l 垂直C .α内所有直线与l 是异面直线D .至少存在一个过l 且与α垂直的平面 10、已知正方体1111ABCD A B C D -,则( ) A. 直线1BC 与1DA 所成的角为90︒ B. 直线1BC 与1CA 所成的角为90︒ C. 直线1BC 与平面11BB D D 所成的角为45︒D. 直线1BC 与平面ABCD 所成的角为45︒11、在一个圆锥中,D 为圆锥的顶点,O 为圆锥底面圆的圆心,P 为线段DO 的中点,AE 为底面圆的直径,△ABC 是底面圆的内接正三角形,AB =AD =3,则下列说法正确的是 A .BE ∥平面PACB .PA ⊥平面PBCC .在圆锥侧面上,点A 到DB 中点的最短距离为32D .记直线DO 与过点P 的平面α所成的角为θ,当cos θ∈(0,33)时,平面α与圆锥侧面的交线为椭圆12、已知圆台1OO 上、下底面的半径分别为2和4,母线长为4.正四棱台上底面1111D C B A 的四个顶点在圆台上底面圆周上,下底面ABCD 的四个顶点在圆台下底面圆周上,则( ) A. 1AA 与底面所成的角为60° B. 二面角1A ABC 小于60°C. 正四棱台1111ABCD A B C D -的外接球的表面积为64πD. 设圆台1OO 的体积为1V ,正四棱台1111ABCD A B C D -的体积为2V ,则12V V π=三、填空题:本题共4小题,每小题5分,共20分.13、已知正四棱锥P ABCD -32,则正四棱锥P ABCD -的侧面积为14、已知圆台的一个底面周长是另一个底面周长的3倍,圆台的高为23cm ,母线与轴的夹角为30︒,则这个圆台的轴截面的面积等于 2.cm 15、已知,,,A B C D 在球O 的球面上,ABC 为等边三角形且其面积为33,AD ⊥平面,2ABC AD =,则球O 的表面积为 .16、在等腰梯形ABCD 中,22AB CD ==,3DAB CBA π∠=∠=,O 为AB 的中点.将BOC∆沿OC 折起,使点B 到达点B '的位置,则三棱锥B ADC '-外接球的表面积为 ;当3B D '=B ADC '-外接球的球心到平面B CD '的距离为 .四、解答题:本题共6小题,共 70分,解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分10分)在四棱锥P ABCD -中,//AB CD ,2CD AB =,AC 与BD 相交于点M ,点N 在线段AP 上,AN AP λ=(0λ>),且//MN 平面PCD . (I )求实数λ的值;(Ⅱ)若1AB AD DP ===,2PA PB ==,60BAD ︒∠=,求点N 到平面PCD 的距离.18.(本小题满分12分)如图,在以P ,A ,B ,C ,D 为顶点的五面体中,四边形ABCD 为等腰梯形,AB CD ∥,12AD CD AB ==,平面PAD ⊥平面PAB ,PA PB ⊥. (1)求证:平面PAD ⊥平面PBC ; (2)若二面角P AB D --的余弦值为33,求直线PD 与平面PBC 所成角的大小.19.(本小题满分12分)如图,直三棱柱111ABC A B C -的体积为4,1A BC 的面积为2. (1)求A 到平面1A BC 的距离;(2)设D 为1A C 的中点,1AA AB =,平面1A BC ⊥平面11ABB A ,求二面角A BD C --的正弦值.20.(本小题满分12分)如图,在多面体ABCDP 中,ABC 是边长为2的等边三角形,,22PA AB BD CD ===,22PC PB ==,点E 是BC 中点,平面ABC ⊥平面BCD .(1) 求证://DE 平面PAC ;(2) F 是直线BC 上的一点,若二面角F DA B --为直二面角,求BF 的长.21.(本小题满分12分)如图,在四棱锥P ABCD -中,PA ⊥底面ABCD ,AD BC ∥点M 在棱PB 上,2PM MB =点N 在棱PC 上,223PA AB AD BC ====. (1)若2CN NP =,Q 为PD 的中点,求证:A ,M ,N ,Q 四点共面; (2)求直线PA 与平面AMN 所成角的正弦的最大值.22.(本小题满分12分)如图1,在平行四边形ABCD 中,AB =2,AD =33,∠ABC =30º,AE ⊥BC ,垂足为E .以AE 为折痕把△ABE 折起,使点B 到达点P 的位置,且平面PAE 与平面AECD 所成的角为90º(如图2).(1)求证:PE ⊥CD ;(2)若点F 在线段PC 上,且二面角F -AD -C 的大小为30º,求三棱锥F -ACD 的体积.补充练习:1、如图,在直四棱柱1111ABCD A B C D -中,//AD BC ,AD AB ⊥,122AA AD BC ===,2AB E 在棱11A D 上,平面1BC E 与棱1AA 交于点F .(1)求证:1BD C F ⊥;(2)若BE 与平面ABCD 所成角的正弦值为45,试确定点F 的位置.【解答】(1)证明:在直四棱柱中1111ABCD A B C D -中,1AA ⊥平面ABCD ,BD ⊂平面ABCD ,1AA BD ∴⊥,连接AC ,2tan 2AB ADB AD ∠==,2tan 2CB CAB AB ∠==, ADB CAB ∴∠=∠,AC BD ∴⊥, 1AA ,AC ⊂平面11ACC A ,1AA AC A =,BD ∴⊥平面11ACC A ,1C F ⊂平面11ACC A ,1BD C F ∴⊥.(2)以A 为坐标原点,AD 为x 轴,AB 为y 轴,1AA 为z 轴,建立空间直角坐标系,则(0A ,0,0),(0B 20),(1C 20),1(1C 22), 平面ABCD 的法向量为(0n =,0,1),(BE x =,2-2),0x >,则242|cos ,|56BE n x =<>=+,解得12x =, 则1(2E ,0,2),1(2BE =,22),11(2C E =-,2-0),设(0F ,0,)z ,1(1C F =-,2-2)z -,则(1-,2-12)(2z m -=,2-12)(2n +-,2-0),∴11122222m n m n ⎧-=-⎪⎨⎪--=-⎩,解得12m =-,32n =,1z =,(0F ∴,0,1),F ∴为棱1AA 的中点.参考答案1、D2、B3、A4、D5、C6、D7、D8、A 8、【详解】根据题意,三棱锥A BCD -如图所示,图中点O 为线段BD 的中点,,N M 分别是线段,AO CO 上靠近点O 的三等分点, 因为2dm AB BC AD BD CD =====,所以ABD △和CBD 均为等边三角形,因为点O 为线段BD 的中点,所以,AO BD CO BD ⊥⊥, 所以AOC ∠为二面角A BD C --的平面角,所以23AOC π∠=, 因为ABD △和CBD 均为等边三角形,点O 为线段BD 的中点, 所以,AO CO 分别为ABD △和CBD 的中线,因为,N M 分别是线段,AO CO 上靠近点O 的三等分点, 所以,N M 分别为ABD △和CBD 的外心,过,N M 分别作平面ABD 和平面CBD 的垂线,EN EM ,交于点E ,则点E 为三棱锥A BCD -外接球的球心,即为足球的球心,所以线段EB 为球的半径,因为,AO BD CO BD ⊥⊥,2dm AB BC AD BD CD =====,所以6dm 2AO CO ==,则6dm 6NO MO ==, 因为,,90AO CO EO EO ENO EMO ==∠=∠=︒, 所以ENO △≌EMO △,所以123EON EMO AOC π∠=∠=∠=, 在直角EMO △中,2tan32EM OM π==,因为EM ⊥平面BCD ,BM ⊂平面BCD ,所以BM EM ⊥, 因为M 是CBD 的外心,所以63BM =,所以2276EB EM BM =+=, 所以3344774233627V EB πππ⎛⎫=⋅== ⎪ ⎪⎝⎭, 所以足球的体积为742dm 27π,故选:A9、ABD 10、ABD 11、BD 12、AC12、【详解】如图,过1A 作1A P AO ⊥,作出截面11ACC A 的平面图,易知11ACC A 为等腰梯形,且1,O O 为11,AC A C 中点,易得1114,8,4AC AC AA ===,1122AC AC AP -==,故22114223OO A P ==-=即圆台的高3h =111122,4222A B AB ====2242 选项A :易得1A AO ∠即为1AA 与底面所成角,则111cos 2AP A AO AA ∠==,故13A AO π∠=,正确;选项B :过P 作PQ AB ⊥于Q ,连接1A Q ,由1A P AB ⊥,1A P PQ P ⋂=,故AB ⊥面1A PQ ,1AQ ⊂面1A PQ ,故1AB A Q ⊥, 1A QP ∠即为二面角1A AB C 的平面角,111sin A P AQP A Q ∠=,111sin A PA AP A A∠=,又11A Q A A <,故11sin sin AQP A AP ∠>∠,即160AQP ∠>,B 错误; 选项C :设外接球半径为R ,球心到下底距离为x ,在11ACC A 的平面图中,2O 为球心, 则221,23O O x O O x ==,112,4O C OC ==,212O C O C R ==,故()2222164234R x R R x ⎧-=⎪⇒=⎨-=⎪⎩, 故表面积2464S R ππ==,正确;选项D :()2215632482333V ππ=++⨯=,()21112383216233V =++⨯=然12V V π≠,错误. 故选:AC.13、8 14、3 15、8π 16、4π313. 16、解:等腰梯形ABCD 中,22AB CD ==,3DAB CBA π∠=∠=,O 为AB 的中点,BOC ∴∆,ADO ∆,DOC ∆为等边三角形,1OA OB OC OD ====,∴三棱锥B ADC '-处接球的球心为O ,半径为1,414S ππ∴=⨯=,连接BD 与OC 交于M ,则OC MD ⊥,OC MB ⊥,OC MB ⊥',B MD ∴∠'是二面角的平面角,3BM DM B D =='=,3B MD π∴∠'=, B ∴'到平面COD 的距离为3334h π'==, 在△B CD '中,1B C '=,3B D '=1CD =,2133391()24B CDS '=-=, 设球心O 到平面B CD '的距离为h , 由O B CD B COD V V ''--=,得1133B CDCOD Sh S h '∆'⋅=⋅, ∴139133334h =,解得313h ,∴三棱锥B ADC '-外接球的球心到平面B ADC '-处接球的球心到平面B CD '的距离为31313. 故答案为:4π;31313.17、【详解】分析:解法一:(1)由平行线的性质可得13AM AC =,结合线面平行的性质定理有//MN PC .据此可得13λ=. (2) 由题意可知ABD ∆为等边三角形,则1BD AD ==,结合勾股定理可知PD BD ⊥且PD DA ⊥,由线面垂直的判断定理有PD ⊥平面ABCD ,进一步有平面PCD ⊥平面ABCD .作ME CD ⊥于E ,则ME ⊥平面PCD . ME 即为N 到平面PCD 的距离.结合比例关系计算可得N 到平面PCD 3解法二:(1)同解法一.(2)由题意可得ABD ∆为等边三角形,所以1BD AD ==,结合勾股定理可得PD BD ⊥且PD DA ⊥,则PD ⊥平面ABCD .设点N 到平面PCD 的距离为d ,利用体积关系:2233N PCD A PCD P ACD V V V ---==, 即2193ACDPCDPD Sd S ⋅=⋅.求解三角形的面积然后解方程可得N 到平面PCD 3 详解:解法一:(1)因为//AB CD ,所以1,2AM AB MC CD ==即13AM AC =. 因为//MN 平面PCD ,MN ⊂平面PAC ,平面PAC ⋂平面PCD PC =, 所以//MN PC . 所以13AN AM AP AC ==,即13λ=.(2) 因为0,60AB AD BAD =∠=,所以ABD ∆为等边三角形,所以1BD AD ==, 又因为1PD =,2PA PB ==,所以222PB PD BD =+且222PA PD AD =+,所以PD BD ⊥且PD DA ⊥,又因为DA DB D ⋂=,所以PD ABCD ⊥平面 因PD ⊂平面PCD ,所以平面PCD ⊥平面ABCD .作ME CD ⊥于E ,因为平面PCD ⋂平面=ABCD CD ,所以ME ⊥平面PCD . 又因为//MN 平面PCD ,所以ME 即为N 到平面PCD 的距离. 在△ABD 中,设AB 边上的高为h ,则3h =因为23MD MC BD AC ==,所以233ME h ==N 到平面PCD 3 解法二、(1)同解法一.(2)因为0,60AB AD BAD =∠=,所以ABD ∆为等边三角形,所以1BD AD ==, 又因为1PD =,2PA PB ==,所以222PB PD BD =+且222PA PD AD =+,所以PD BD ⊥且PD DA ⊥,又因为DA DB D ⋂=,所以PD ⊥平面ABCD . 设点N 到平面PCD 的距离为d ,由13AN AP =得23NP AP =, 所以2233N PCD A PCD P ACD V V V ---==, 即2193ACDPCDPD S d S ⋅=⋅.因为1322ACDS AD DC sin ADC =⋅⋅∠=,112PCDS PD CD =⋅=,1PD =, 所以23193d =,解得3d =N 到平面PCD 318、【1】因为平面PAD ⊥平面PAB ,平面PAD 平面PAB PA =,PA PB ⊥,PB ⊂平面PAB ,所以PB ⊥平面PAD ,又因为PB ⊂平面PBC ,所以平面PAD ⊥平面PBC . 【2】过D 作DH PA ⊥,⊥DO AB ,垂足分别为H ,O ,连接HO ,因为平面PAD ⊥平面PAB ,平面PAD 平面PAB PA =,DH PA ⊥,DH ⊂平面PAD ,所以DH ⊥平面PAB ,又AB 平面PAB ,所以DH AB ⊥,又⊥DO AB ,且DO DH D =,DO ,DH ⊂平面DHO ,所以AB ⊥平面DHO , 因为HO ⊂平面DHO ,所以AB HO ⊥,即DOH ∠即为二面角P AB D --的平面角, 不妨设4AB =,则可知2AD CD BD ===,且1AO =,3OD =因为3cos DOH ∠=1OH =,所以4BAP π∠=,过O 作OM ⊥平面PAB ,以{},,OA OH OM 为x ,y ,z 轴,建立空间直角坐标系,则()0,1,2D ,()1,2,0P -,()3,0,0B -,(2C -, 所以(1,2PD =-,()2,2,0BP =,(1,1,2CP =-,设平面PBC 的法向量为(),,m x y z =,则22020m BP x y m CP x y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩,令1x =,则1y =-,0z =,所以()1,1,0m =-,设直线PD 与平面PBC 所成角为θ,则2sin 211112m PD m PDθ⋅===+⋅++⋅, 即4πθ=.19、【1】在直三棱柱111ABC A B C -中,设点A 到平面1A BC 的距离为h , 则111111112211433333A A BC A A ABC A ABC AB BC C C B V S h h V S A A V ---=⋅===⋅==, 解得2h =所以点A 到平面1A BC 2;【2】取1A B 的中点E ,连接AE ,如图,因为1AA AB =,所以1AE A B ⊥, 又平面1A BC ⊥平面11ABB A ,平面1A BC平面111ABB A A B =,且AE ⊂平面11ABB A ,所以AE ⊥平面1A BC , 在直三棱柱111ABC A B C -中,1BB ⊥平面ABC ,由BC ⊂平面1A BC ,BC ⊂平面ABC 可得AE BC ⊥,1BB BC ⊥, 又1,AE BB ⊂平面11ABB A 且相交,所以BC ⊥平面11ABB A ,所以1,,BC BA BB 两两垂直,以B 为原点,建立空间直角坐标系,如图,由(1)得2AE =12AA AB ==,122A B =2BC =,则()()()()10,2,0,0,2,2,0,0,0,2,0,0A A B C ,所以1A C 的中点()1,1,1D , 则()1,1,1BD =,()()0,2,0,2,0,0BA BC ==,设平面ABD 的一个法向量(),,m x y z =,则020m BD x y z m BA y ⎧⋅=++=⎪⎨⋅==⎪⎩,可取()1,0,1m =-,设平面BDC 的一个法向量(),,n a b c =,则020m BD a b c m BC a ⎧⋅=++=⎪⎨⋅==⎪⎩, 可取()0,1,1n =-, 则11cos ,222m n m n m n⋅===⨯⋅,所以二面角A BD C --21312⎛⎫-= ⎪⎝⎭. 20、(1)ABC 是边长为2的等边三角形,则2PA AB AC ===,又22PC PB ==股定理知,PA AB PA AC ⊥⊥,故PA ⊥平面ABC ,BD CD =,点E 是BC 中点,则DE BC ⊥,由于平面ABC ⊥平面BCD 知DE ⊥平面ABC ,则//DE PA ,//DE 平面PAC (2) 以点E 为原点,EC 方向为x 轴,EA 方向为y 轴,ED 方向为z 轴建系 则(0,0,1),3,0),(1,0,0)D A B -,设(,0,0)F a平面FDA 内,(0,3,1),(,0,1)DA DF a =-=-,法向量(3,3)m a a = 平面BDA 内,(0,3,1),(1,0,1)DA DB =-=--,法向量(3,1,3)m =-设直二面角F DA B --的平面角θ,则37cos 0,430,,44m n a a BF θ==-===21、【1详】解:以A 为坐标原点建立如图所示空间直角坐标系,如图所示,则()0,0,0A ,()0,1,1Q ,42,0,33M ⎛⎫ ⎪⎝⎭,24,1,33N ⎛⎫ ⎪⎝⎭, 则42,0,33AM ⎛⎫= ⎪⎝⎭,()0,1,1AQ Q =,24,1,33AN ⎛⎫= ⎪⎝⎭,设AN x AM y AQ =+,则243314233x y x y ⎧=⎪⎪=⎨⎪⎪=+⎩,解得1,12x y ==,则12AN AM AQ =+,即A ,M ,N ,Q 四点共面.【2】解:由(1)中的空间直角坐标系,可得(0,0,2)P ,()2,3,0C ,()0,0,2AP =, 设PN PC =λ,(其中01λ≤≤),且(),,N x y z , 则()(),,22,3,2x y z λ-=-,解得()2,3,22N λλλ-, 可得42(,0,)33AM =()2,3,22AN λλλ=-设平面AMN 的法向量为(),,n a b c =,由4203323(22)0n AM a c n AN a b c λλλ⎧⋅=+=⎪⎨⎪⋅=++-=⎩, 取1a =,可得42,23b c λ=-=-,所以41,2,23n λ⎛⎫=-- ⎪⎝⎭设直线AP 与平面AMN 所成角为θ,则225sin 4523AP n AP nθλ⋅==≤⎛⎫+- ⎪⎝⎭,当且仅当23λ=时等号成立. 直线PA 与平面AMN 25.22、解:(1)方法1在平行四边形ABCD 中,AE ⊥BC ,所以AE ⊥PE .因为平面PAE 与平面AECD 所成的角为90º,即平面PAE ⊥平面AECD . ················· 2分 又因为平面PAE ∩平面AECD =AE ,PE ⊂平面PAE ,所以PE ⊥平面AECD .因为CD ⊂平面AECD ,所以PE ⊥CD . ············································································ 4分 方法2在平行四边形ABCD 中,AE ⊥BC ,所以AE ⊥PE ,AE ⊥CE , 所以∠PEC 为平面PAE 与平面AECD 所成角的平面角.因为平面PAE 与平面AECD 所成的角为90º,所以∠PEC =90º,即PE ⊥CE . ········· 2分 又PE ⊥AE ,AE ∩CE =E ,AE ⊂平面AECD ,CE ⊂平面AECD ,所以PE ⊥平面AECD . 因为CD ⊂平面AECD ,所以PE ⊥CD . ············································································ 4分 (2)方法1由(1)得PE ⊥平面AECD ,AE ⊥EC ,故以{EA →,EC →,EP →}为正交基底,建立空间直角坐标系.易得A (1,0,0),C (0,23,0),D (1,33,0),P (0,0,3),所以PC →=(0,23,-3),AP →=(-1,0,3),AD →=(0,33,0). ································································································· 5分 设PF →=λPC →=(0,23λ,-3λ),λ∈[0,1],则AF →=AP →+PF →=(-1,23λ,3-3λ). ······························································ 6分设平面FAD 的法向量为n =(x ,y ,z ),则⎩⎪⎨⎪⎧AD →·n =0,AF →·n =0,即⎩⎪⎨⎪⎧y =0,-x +23λy +(3-3λ)z =0,取z =1,得x =3-3λ,则平面FAD 的一个法向量为n =(3-3λ,0,1). ·················································· 8分 又因为平面AECD 的一个法向量为m =(0,0,1), 且二面角F -DA -C 的大小为30º,所以|cos <m ,n >|=|m ·n |m |·|n ||=|1(3-3λ)2+1|=32,整理得9λ2-18λ+8=0,即(3λ-2)(3λ-4)=0,解得λ=23或λ=43(舍去),故PF →=23PC →. ................................................................................ 10分因为S △ACD =12×33×1=332,所以V F -ACD =13V P -ACD =13S △ACD ×13PE =12. ............................................................................... 12分方法2在△PEC 中,过F 作FG ∥EC ,交PE 于点G .因为EC ∥AD ,所以FG ∥AD ,因此A ,D ,F ,G 共面. 在平行四边形ABCD 中,易知AD ⊥AE .由(1)得PE ⊥平面AECD , 因为AD ⊂平面AECD ,所以AD ⊥PE .又PE ∩AE =E ,AE ,PE ⊂平面PAE ,所以AD ⊥平面PAE . 因为AG ⊂平面PAE ,所以AD ⊥AG .所以∠GAE 为二面角F -AD -C 的平面角,所以∠GAE =30º. ································· 8分 在Rt △AEG 中,∠AEG =90º,∠GAE =30º,AE =1,所以EG =33. ···················· 10分 因为FG ∥AD ,FG ⊄平面AECD ,AD ⊂平面AECD ,所以FG ∥平面AECD .因此V F -ACD =V G -ACD =13×(12×33×1)×33=12.······················································ 12分。
新高考2023版高考数学一轮总复习练案45高考大题规范解答系列四__立体几何

高考大题规范解答系列(四)——立体几何1.(2022·安徽黄山质检)如图,直三棱柱ABC-A1B1C1中,D是BC的中点,且AD⊥BC,四边形ABB1A1为正方形.(1)求证:A1C∥平面AB1D;(2)若∠BAC=60°,BC=4,求点A1到平面AB1D的距离.[解析] (1)连接BA1,交AB1于点E,再连接DE,由已知得,四边形ABB1A1为正方形,E为A1B的中点,∵D是BC的中点,∴DE∥A1C,又DE⊂平面AB1D,A1C⊄平面AB1D,∴A1C∥平面AB1D.(2)∵在直三棱柱ABC-A1B1C1中,平面BCC1B1⊥平面ABC,且BC为它们的交线,又AD⊥BC,∴AD⊥平面BCC1B1,又∵B1D⊂平面BCC1B1,∴AD⊥B1D,且AD=2,B1D=2.同理可得,过D作DG⊥AB,则DG⊥面ABB1A1,且DG=.设A1到平面AB1D的距离为h,由等体积法可得:VA1-AB1D=VD-AA1B1,即··AD·DB1·h=··AA1·A1B1·DG,即2×2·h=4×4×,∴h=.即点A1到平面AB1D的距离为.(注:本题也可建立空间直角坐标系用向量法求解.)2.(2022·陕西汉中质检)如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点.(1)求证:平面PDE⊥平面APC;(2)求直线PC与平面PDE所成的角的正弦值.[解析] 如图所示,以点C为坐标原点,直线CD,CB,CP分别为x,y,z轴,建立空间直角坐标系C-xyz,则相关点的坐标为C(0,0,0),A(2,1,0),B(0,3,0),P(0,0,2),D(2,0,0),E(1,2,0).(1)由于DE=(-1,2,0),CA=(2,1,0),CP=(0,0,2),所以DE·CA=(-1,2,0)·(2,1,0)=0,DE·CP=(-1,2,0)·(0,0,2)=0,所以DE⊥CA,DE⊥CP,而CP∩CA=C,所以DE⊥平面PAC,∵DE⊂平面PDE,∴平面PDE⊥平面PAC.(2)设n=(x,y,z)是平面PDE的一个法向量,则n·DE=n·PE=0,由于DE=(-1,2,0),PE=(1,2,-2),所以有,令x=2,则y=1,z=2,即n=(2,1,2),再设直线PC与平面PDE所成的角为α,而PC=(0,0,-2),所以sin α=|cos〈n,PC〉|===,∴直线PC与平面PDE所成角的正弦值为.3.(2022·湖北百师联盟质检)斜三棱柱ABC-HDE中,平面ABC⊥平面BCD,△ABC为边长为1的等边三角形,DC⊥BC,且DC长为,设DC中点为M,F、G分别为CE、AD的中点.(1)证明:FG∥平面ABC;(2)求二面角B-AC-E的余弦值.[解析] (1)解法一:取BD中点N,连结GN,NF,易知N、M、F三点共线,由GN∥AB,且GN⊄平面ABC,AB⊂平面ABC,故GN∥平面ABC,同理可得NF∥平面ABC,因为GN∩NF=N,故平面GNF∥平面ABC.由FG⊂平面FGN,故FG∥平面ABC.解法二:取AB中点N,连结GN,NC,易知GN是△ABD的中位线,故GN∥BD,GN=BD,因为CE綊BD,F为CE的中点.所以CF綊GN.四边形FGNC是平行四边形,故FG∥CN,因为CN⊂平面ABC,FG⊄平面ABC,故FG∥平面ABC.(2)以BC中点O为坐标原点,以OC、ON、OA分别为x、y、z轴,建立空间直角坐标系O-xyz,由已知可得A,C,E,故CE=(1,,0),AC=,设m=(x,y,z)为平面ACE的法向量,则,解得m=(,-1,1),由于ON⊥平面ABC,不妨取平面ABC的法向量为n=(0,1,0).所以cos〈m,n〉==-.由图可知所求二面角为钝角,故二面角B-AC-E的余弦值为-.4.(2021·全国新高考)在四棱锥Q-ABCD中,底面ABCD是正方形,若AD=2,QD=QA=,QC=3.(1)证明:平面QAD⊥平面ABCD;(2)求二面角B-QD-A的平面角的余弦值.[解析] (1)取AD的中点为O,连接QO,CO.因为QA=QD,OA=OD,则QO⊥AD,而AD=2,QA=,故QO==2.在正方形ABCD中,因为AD=2,故DO=1,故CO=,因为QC=3,故QC2=QO2+OC2,故△QOC为直角三角形且QO⊥OC,因为OC∩AD=O,故QO⊥平面ABCD,因为QO⊂平面QAD,故平面QAD⊥平面ABCD.(2)在平面ABCD内,过O作OT∥CD,交BC于T,则OT⊥AD,结合(1)中的QO⊥平面ABCD,故可建如图所示的空间坐标系.则D(0,1,0),Q(0,0,2),B(2,-1,0),故BQ=(-2,1,2),BD=(-2,2,0).设平面QBD的法向量n=(x,y,z),则即,取x=1,则y=1,z=,故n=.而平面QAD的法向量为m=(1,0,0),故cos〈m,n〉==.二面角B-QD-A的平面角为锐角,故其余弦值为.5.(2021·安徽省淮北市一模)在直角梯形ABCD(如图1)中,∠ABC=90°,BC∥AD,AD=8,AB=BC=4,M为线段AD中点.将△ABC沿AC折起,使平面ABC⊥平面ACD,得到几何体B-ACD(如图2).(1)求证:CD⊥平面ABC;(2)求AB与平面BCM所成角θ的正弦值.[解析] (1)由题设可知AC=4,CD=4,AD=8,∴AD2=CD2+AC2,∴CD⊥AC,又∵平面ABC⊥平面ACD,平面ABC∩平面ACD=AC,∴CD⊥平面ABC.(2)解法一:等体积法取AC的中点O连接OB,由题设可知△ABC为等腰直角三角形,所以OB⊥面ACM,∵V B-ACM=V A-BCM且V B-ACM=S △ACM·BO=,而SΔBCM=4,∴A到面BCM的距离h=,所以sin θ==.解法二:向量法,取AC的中点O,连接OB,由题设可知△ABC为等腰直角三角形,所以OB⊥面ACM,连接OM,因为M、O分别为AD和AC的中点,所以OM∥CD,由(1)可知OM⊥AC,故以OM、OC、OB所在直线为x轴、y轴、z轴建立空间直角坐标系,如图所示.则A(0,-2,0),B(0,0,2),C(0,2,0),M(2,0,0),∴CB=(0,-2,2),CM=(2,-2,0),BA=(0,-2,-2),设平面BCM法向量n=(x,y,z)由得令y=1得n=(1,1,1)∴平面BCM的一个法向量n=(1,1,1),∴sin θ==.6.(2021·山东聊城三模)如图,在平面四边形ABCD中,BC=CD,BC⊥CD,AD⊥BD,以BD为折痕把△ABD折起,使点A到达点P的位置,且PC⊥BC.(1)证明:PD⊥CD;(2)若M为PB的中点,二面角P-BC-D的大小为60°,求直线PC与平面MCD所成角的正弦值.[解析] (1)证明:因为BC⊥CD,BC⊥PC,PC∩CD=C,所以BC⊥平面PCD,又因为PD⊂平面PCD,所以BC⊥PD,又因为PD⊥BD,BD∩BC=B,所以PD⊥平面BCD,又因为CD⊂平面BCD,所以PD⊥CD.(2)因为PC⊥BC,CD⊥BC,所以∠PCD是二面角P-BC-D的平面角,即∠PCD=60°,在Rt△PCD中,PD=CD tan 60°=CD,取BD的中点O,连接OM,OC,因为BC=CD,BC⊥CD,所以OC⊥BD,由(1)知,PD⊥平面BCD,OM为△PBD的中位线,所以OM⊥BD,OM⊥OC,即OM,OC,BD两两垂直,以O为原点,建立如图所示的空间直角坐标系O-xyz,设OB=1,则P(0,1,),C(1,0,0),D(0,1,0),M,CP=(-1,1,),CD=(-1,1,0),CM=,设平面MCD的一个法向量为n=(x,y,z),则由得令z=,得n=(,,),所以cos〈n,CP〉===,所以直线PC与平面MCD所成角的正弦值为.7.(开放题)(2022·云南昆明模拟)如图,在三棱锥A-BCD中,△BCD是边长为2的等边三角形,AB=AC,O是BC的中点,OA⊥CD.(1)证明:平面ABC⊥平面BCD;(2)若E是棱AC上的一点,从①CE=2EA;②二面角E-BD-C大小为60°;③A-BCD的体积为这三个论断中选取两个作为条件,证明另外一个成立.[证明] (1)因为AB=AC,O是BC的中点,所以OA⊥BC,又因为OA⊥CD,所以OA⊥平面BCD,因为OA⊂平面ABC,所以平面ABC⊥平面BCD.(2)连接OD,又因为△BCD是边长为2的等边三角形,所以DO⊥BC,由(1)知OA⊥平面BCD,所以AO,BC,DO两两互相垂直.以O为坐标原点,OA,OB,OD所在直线分别为x轴,y轴,z轴建立如图所示空间直角坐标系.设|OA|=m,则O(0,0,0),A(0,0,m),B(1,0,0),C(-1,0,0),D(0,,0),若选①②作为条件,证明③成立.因为CE=2EA,所以E,易知平面BCD的法向量为n=(0,0,1),BE=,BD=(-1,,0),设m=(x,y,z)是平面BDE的法向量,则,所以,可取m=,由二面角E-BD-C大小为60°可得cos θ===,解得m=3,所以A-BCD的体积为×2×××3=.若选①③作为条件,证明②成立.因为A-BCD的体积为,所以×2×××|OA|=,解得|OA|=3,又因为CE=2EA,所以E,易知平面BCD的法向量为n=(0,0,1),BE=,BD=,设m=(x,y,z)是平面BDE的法向量,则所以,可取m=,所以cos θ===,即二面角E-BD-C大小为60°.若选②③作为条件,证明①成立.因为A-BCD的体积为,所以×2×××|OA|=,解得|OA|=3,即A(0,0,3),AC=(-1,0,-3),不妨设AE=λAC(0≤λ≤1),所以E(-λ,0,-3λ+3),易知平面BCD的法向量为n=(0,0,1),BE=(-λ-1,0,-3λ+3),BD=(-1,,0),设m=(x,y,z)是平面BDE的法向量,取m=(3(1-λ),(1-λ),λ+1)cos θ===,解得λ=3(舍),λ=,所以CE=2EA.8.(2022·河北石家庄质检)如图,四棱锥P-ABCD中,底面ABCD为正方形,△PAB 为等边三角形,平面PAB⊥底面ABCD,E为AD的中点.(1)求证:CE⊥PD;(2)在线段BD(不包括端点)上是否存在点F,使直线AP与平面PEF所成角的正弦值为,若存在,确定点F的位置;若不存在,请说明理由.[解析] (1)证明:取AB的中点O,连结PO,OD,因为PA=PB,所以PO⊥AB,又因为平面PAB⊥平面ABCD,所以PO⊥底面ABCD,取CD的中点G,连结OG,则OB,OP,OG两两垂直,分别以OB,OG,OP所在直线为x轴,y轴,z轴建立空间直角坐标系(如图所示),设AB=2,则C(1,2,0),P(0,0,),E(-1,1,0),D(-1,2,0),所以CE=(-2,-1,0),PD=(-1,2,-),则CE·PD=2-2=0,故CE⊥PD,所以CE⊥PD.(2)由(1)可知,A(-1,0,0),B(1,0,0),所以PE=(-1,1,-),AP=(1,0,),BD=(-2,2,0),BE=(-2,1,0),设BF=λBD(0<λ<1),则BF=(-2λ,2λ,0),所以EF=BF-BE=(-2λ+2,2λ-1,0),设平面PEF的法向量为n=(x,y,z),令y=1,则x=,z=,故n=,所以|cos〈AP,n〉|===,整理可得9λ2-6λ+1=0,解得λ=,所以在BD上存在点F,使得直线AP与平面PEF所成角的正弦值为,此时点F为靠近点B的三等分点,即BF=BD.。
2023年高考数学一轮复习第七章立体几何与空间向量7向量法求空间角练习含解析

向量法求空间角考试要求 能用向量法解决异面直线、直线与平面、平面与平面的夹角问题,并能描述解决这一类问题的程序,体会向量法在研究空间角问题中的作用.知识梳理1.异面直线所成的角若异面直线l 1,l 2所成的角为θ,其方向向量分别是u ,v ,则cos θ=|cos 〈u ,v 〉|=|u·v ||u||v |.2.直线与平面所成的角如图,直线AB 与平面α相交于点B ,设直线AB 与平面α所成的角为θ,直线AB 的方向向量为u ,平面α的法向量为n ,则sin θ=|cos 〈u ,n 〉|=⎪⎪⎪⎪⎪⎪u ·n |u ||n |=|u·n||u||n|.3.平面与平面的夹角如图,平面α与平面β相交,形成四个二面角,我们把这四个二面角中不大于90°的二面角称为平面α与平面β的夹角.若平面α,β的法向量分别是n 1和n 2,则平面α与平面β的夹角即为向量n 1和n 2的夹角或其补角.设平面α与平面β的夹角为θ,则cos θ=|cos 〈n 1,n 2〉|=|n 1·n 2||n 1||n 2|.常用结论1.线面角θ的正弦值等于直线的方向向量a 与平面的法向量n 所成角的余弦值的绝对值,即sin θ=|cos 〈a ,n 〉|,不要误记为cos θ=|cos 〈a ,n 〉|.2.二面角的范围是[0,π],两个平面夹角的范围是⎣⎢⎡⎦⎥⎤0,π2.思考辨析判断下列结论是否正确(请在括号中打“√”或“×”)(1)两条异面直线所成的角与两直线的方向向量所成的角相等.( × )(2)直线l 的方向向量与平面α的法向量的夹角的余角就是直线l 与平面α所成的角.( × )(3)二面角的平面角为θ,则两个面的法向量的夹角也是θ.( × )(4)两异面直线夹角的范围是⎝ ⎛⎦⎥⎤0,π2,直线与平面所成角的范围是⎣⎢⎡⎦⎥⎤0,π2.( √ )教材改编题1.已知直线l 1的方向向量s 1=(1,0,1)与直线l 2的方向向量s 2=(-1,2,-2),则l 1和l 2夹角的余弦值为( ) A.24B.12C.22D.32答案 C解析 因为s 1=(1,0,1),s 2=(-1,2,-2),所以cos 〈s 1,s 2〉=s 1·s 2|s 1||s 2|=-1-22×3=-22.所以l 1和l 2夹角的余弦值为22. 2.已知向量m ,n 分别是直线l 的方向向量、平面α的法向量,若cos 〈m ,n 〉=-12,则l 与α所成的角为________.答案 30°解析 设直线l 与α所成角为θ, sin θ=||cos 〈m ,n 〉=12,又∵θ∈⎣⎢⎡⎦⎥⎤0,π2,∴θ=30°.3.已知两平面的法向量分别为(0,-1,3),(2,2,4),则这两个平面夹角的余弦值为______. 答案156解析|0,-1,3·2,2,4|1+9×4+4+16=156.题型一 异面直线所成的角例1 (1)(2022·大庆模拟)如图,已知棱长为2的正方体ABCD -A 1B 1C 1D 1,E ,F ,G 分别为AB ,CD 1,AD 的中点,则异面直线A 1G 与EF 所成角的余弦值为( )A .0 B.1010C.22D .1答案 A解析 如图,分别以DA ,DC ,DD 1所在的直线为x 轴,y 轴,z 轴建立空间直角坐标系,则A 1(2,0,2),G (1,0,0),E (2,1,0),F (0,1,1),所以A 1G —→=(-1,0,-2),EF →=(-2,0,1), 设异面直线A 1G 与EF 所成的角为θ, 则cos θ=|A 1G —→·EF →||A 1G —→||EF →|=|-1×-2-2×1|5×5=0.(2)(2022·杭州模拟)如图,已知圆锥CO 的截面△ABC 是正三角形,AB 是底面圆O 的直径,点D 在AB ︵上,且∠AOD =2∠BOD ,则异面直线AD 与BC 所成角的余弦值为( )A.34B.12C.14D.34答案 A解析 因为∠AOD =2∠BOD ,且∠AOD +∠BOD =π, 所以∠BOD =π3,连接CO ,则CO ⊥平面ABD ,以点O 为坐标原点,OB ,OC 所在直线分别为y 轴、z 轴建立如图所示的空间直角坐标系,设圆O 的半径为2,则A (0,-2,0),B (0,2,0),C (0,0,23),D (3,1,0), AD →=(3,3,0),BC →=(0,-2,23),设异面直线AD 与BC 所成的角为θ,则cos θ=|cos 〈AD →,BC →〉|=|AD →·BC →||AD →||BC →|=|-6|23×4=34,因此,异面直线AD 与BC 所成角的余弦值为34. 教师备选如图,在直三棱柱ABC -A 1B 1C 1中,AB =AC =AA 1=2,BC =2,点D 为BC 的中点,则异面直线AD 与A 1C 所成的角为( )A.π2B.π3C.π4D.π6 答案 B解析 以A 为坐标原点,AB ,AC ,AA 1所在直线分别为x 轴、y 轴、z 轴建立如图所示的空间直角坐标系,则A (0,0,0),A 1(0,0,2),B (2,0,0),C (0,2,0),∴D ⎝⎛⎭⎪⎫22,22,0, ∴AD →=⎝ ⎛⎭⎪⎫22,22,0,A 1C —→=(0,2,-2),∴cos〈AD →,A 1C —→〉=AD →·A 1C —→|AD →||A 1C —→|=12,∴即异面直线AD ,A 1C 所成角为π3.思维升华用向量法求异面直线所成的角的一般步骤 (1)建立空间直角坐标系;(2)用坐标表示两异面直线的方向向量; (3)利用向量的夹角公式求出向量夹角的余弦值;(4)注意两异面直线所成角的范围是⎝⎛⎦⎥⎤0,π2,即两异面直线所成角的余弦值等于两向量夹角的余弦值的绝对值.跟踪训练1 (1)如图所示,在棱长为2的正方体ABCD -A 1B 1C 1D 1中,E 是棱CC 1的中点,AF →=λAD →,若异面直线D 1E 和A 1F 所成角的余弦值为3210,则λ的值为______.答案 13解析 以D 为坐标原点,DA ,DC ,DD 1所在直线分别为x 轴、y 轴、z 轴,建立空间直角坐标系(图略),正方体的棱长为2,则A 1(2,0,2),D 1(0,0,2),E (0,2,1),A (2,0,0), ∴D 1E —→=(0,2,-1), A 1F —→=A 1A —→+AF →=A 1A —→+λAD → =(-2λ,0,-2).∴cos〈A 1F —→,D 1E —→〉=A 1F —→·D 1E —→|A 1F —→||D 1E —→|=22λ2+1×5=3210, 解得λ=13⎝⎛⎭⎪⎫λ=-13舍.(2)(2022·武汉模拟)若在三棱柱ABC -A 1B 1C 1中,∠A 1AC =∠BAC =60°,平面A 1ACC 1⊥平面ABC ,AA 1=AC =AB ,则异面直线AC 1与A 1B 所成角的余弦值为________.答案24解析 令M 为AC 的中点,连接MB ,MA 1, 由题意知△ABC 是等边三角形, 所以BM ⊥AC ,同理,A 1M ⊥AC , 因为平面A 1ACC 1⊥平面ABC , 平面A 1ACC 1∩平面ABC =AC ,BM ⊂平面ABC ,所以BM ⊥平面A 1ACC 1, 因为A 1M ⊂平面A 1ACC 1, 所以BM ⊥A 1M ,所以AC ,BM ,A 1M 两两垂直,以M 为坐标原点,MA →,MB →,MA 1—→的方向分别为x 轴、y 轴、z 轴的正方向建立如图所示的空间直角坐标系.设AA 1=AC =AB =2,则A (1,0,0),B (0,3,0),A 1(0,0,3),C 1(-2,0,3),所以AC 1—→=(-3,0,3),A 1B —→=(0,3,-3), 所以cos 〈AC 1—→,A 1B —→〉=-323×6=-24,故异面直线AC 1与A 1B 所成角的余弦值为24. 题型二 直线与平面所成的角例2 (2022·广州模拟)在边长为2的菱形ABCD 中,∠BAD =60°,点E 是边AB 的中点(如图1),将△ADE 沿DE 折起到△A 1DE 的位置,连接A 1B ,A 1C ,得到四棱锥A 1-BCDE (如图2).(1)证明:平面A 1BE ⊥平面BCDE ;(2)若A 1E ⊥BE ,连接CE ,求直线CE 与平面A 1CD 所成角的正弦值. (1)证明 连接图1中的BD ,如图所示.因为四边形ABCD 为菱形,且∠BAD =60°, 所以△ABD 为等边三角形,所以DE ⊥AB , 所以在图2中有DE ⊥BE ,DE ⊥A 1E , 因为BE ∩A 1E =E ,BE ,A 1E ⊂平面A 1BE , 所以DE ⊥平面A 1BE , 因为DE ⊂平面BCDE , 所以平面A 1BE ⊥平面BCDE .(2)解 因为平面A 1BE ⊥平面BCDE ,平面A 1BE ∩平面BCDE =BE ,A 1E ⊥BE ,A 1E ⊂平面A 1BE ,所以A 1E ⊥平面BCDE ,以E 为坐标原点建立如图所示的空间直角坐标系,所以A 1(0,0,1),C (2,3,0),D (0,3,0),E (0,0,0),所以A 1D —→=(0,3,-1),A 1C —→=(2,3,-1),EC →=(2,3,0), 设平面A 1CD 的法向量为n =(x ,y ,z ),则⎩⎪⎨⎪⎧n ·A 1D —→=3y -z =0,n ·A 1C —→=2x +3y -z =0,令y =1,则n =(0,1,3),所以cos 〈n ,EC →〉=n ·EC →|n ||EC →|=327=2114,所以直线CE 与平面A 1CD 所成角的正弦值为2114. 教师备选(2020·新高考全国Ⅰ)如图,四棱锥P -ABCD 的底面为正方形,PD ⊥底面ABCD .设平面PAD 与平面PBC 的交线为l .(1)证明:l ⊥平面PDC ;(2)已知PD =AD =1,Q 为l 上的点,求PB 与平面QCD 所成角的正弦值的最大值. (1)证明 在正方形ABCD 中,AD ∥BC , 因为AD ⊄平面PBC ,BC ⊂平面PBC , 所以AD ∥平面PBC ,又因为AD ⊂平面PAD ,平面PAD ∩平面PBC =l , 所以AD ∥l ,因为在四棱锥P -ABCD 中,底面ABCD 是正方形, 所以AD ⊥DC ,所以l ⊥DC , 因为PD ⊥平面ABCD ,所以AD ⊥PD , 所以l ⊥PD ,因为DC ∩PD =D ,PD ,DC ⊂平面PDC , 所以l ⊥平面PDC .(2)解 以D 为坐标原点,DA →的方向为x 轴正方向, 建立如图所示的空间直角坐标系,因为PD =AD =1,则有D (0,0,0),C (0,1,0),P (0,0,1),B (1,1,0), 因为平面PAD ∩平面PBC =l , 所以l 过点P ,设Q (m ,0,1),则有DC →=(0,1,0),DQ →=(m ,0,1),PB →=(1,1,-1), 设平面QCD 的一个法向量为n =(x ,y ,z ), 则⎩⎪⎨⎪⎧DC →·n =0,DQ →·n =0,即⎩⎪⎨⎪⎧y =0,mx +z =0,令x =1,则z =-m ,所以平面QCD 的一个法向量为n =(1,0,-m ), 则cos 〈n ,PB →〉=n ·PB →|n ||PB →|=1+0+m 3·m 2+1. 记PB 与平面QCD 所成的角为θ,根据直线的方向向量与平面法向量所成角的余弦值的绝对值即为直线与平面所成角的正弦值, 则sin θ=|cos 〈n ,PB →〉|=|1+m |3·m 2+1, 当m =0时,sin θ=33, 当m ≠0时,sin θ=|1+m |3·m 2+1=33·1+2m +m 2m 2+1=33·1+2mm 2+1≤33·1+2|m |m 2+1≤33·1+1=63, 当且仅当m =1时取等号,所以直线PB 与平面QCD 所成角的正弦值的最大值为63. 思维升华 利用空间向量求线面角的解题步骤跟踪训练2 (2022·全国百校联考)如图所示,在三棱锥S -BCD 中,平面SBD ⊥平面BCD ,A 是线段SD 上的点,△SBD 为等边三角形,∠BCD =30°,CD =2DB =4.(1)若SA =AD ,求证:SD ⊥CA ;(2)若直线BA 与平面SCD 所成角的正弦值为419565,求AD 的长.(1)证明 依题意,BD =2, 在△BCD 中,CD =4,∠BCD =30°, 由余弦定理求得BC =23, ∴CD 2=BD 2+BC 2,即BC ⊥BD .又平面SBD ⊥平面BCD ,平面SBD ∩平面BCD =BD ,BC ⊂平面BCD , ∴BC ⊥平面SBD .从而BC ⊥SD , 在等边△SBD 中,SA =AD ,则BA ⊥SD . 又BC ∩BA =B ,BC ,BA ⊂平面BCA , ∴SD ⊥平面BCA ,又CA ⊂平面BCA , ∴SD ⊥CA .(2)解 以B 为坐标原点,BC ,BD 所在直线分别为x 轴、y 轴,过点B 作平面BCD 的垂线为z 轴,建立如图所示的空间直角坐标系,则B (0,0,0),C (23,0,0),D (0,2,0),S (0,1,3),故CD →=(-23,2,0),SD →=(0,1,-3), 设平面SCD 的法向量为m =(x ,y ,z ), 则⎩⎪⎨⎪⎧m ·CD →=0,m ·SD →=0,即⎩⎨⎧-23x +2y =0,y -3z =0,取x =1,则y =3,z =1, ∴m =(1,3,1), 设DA →=λDS →(0≤λ≤1), 则DA →=(0,-λ,3λ),故A (0,2-λ,3λ),则BA →=(0,2-λ,3λ), 设直线BA 与平面SCD 所成角为θ, 故sin θ=||cos 〈m ,BA →〉=|m ·BA →||m ||BA →|=|23-3λ+3λ|5·2-λ2+3λ2=419565, 解得λ=14或λ=34,则AD =12或AD =32.题型三 平面与平面的夹角例3 (12分)(2021·新高考全国Ⅰ)如图,在三棱锥A -BCD 中,平面ABD ⊥平面BCD ,AB =AD ,O 为BD 的中点.(1)证明:OA ⊥CD; [切入点:线线垂直转化到线面垂直](2)若△OCD 是边长为1的等边三角形,点E 在棱AD 上,DE =2EA ,且二面角E -BC -D 的大小为45°,求三棱锥A -BCD 的体积.[关键点:建系写坐标]教师备选(2020·全国Ⅰ改编)如图,D为圆锥的顶点,O是圆锥底面的圆心,AE为底面直径,AE=AD.△ABC是底面的内接正三角形,P为DO上一点,PO=66 DO.(1)证明:PA⊥平面PBC;(2)求平面BPC与平面EPC的夹角的余弦值.(1)证明由题设,知△DAE为等边三角形,设AE=1,则DO=32,CO=BO=12AE=12,所以PO =66DO =24,PC =PO 2+OC 2=64, 同理PB =64,PA =64, 又△ABC 为等边三角形, 则BAsin60°=2OA ,所以BA =32,PA 2+PB 2=34=AB 2,则∠APB =90°,所以PA ⊥PB ,同理PA ⊥PC , 又PC ∩PB =P ,PC ,PB ⊂平面PBC , 所以PA ⊥平面PBC .(2)解 过O 作ON ∥BC 交AB 于点N ,因为PO ⊥平面ABC ,以O 为坐标原点,OA 所在直线为x 轴,ON 所在直线为y 轴,OD 所在直线为z 轴,建立如图所示的空间直角坐标系,则E ⎝ ⎛⎭⎪⎫-12,0,0,P ⎝ ⎛⎭⎪⎫0,0,24,B ⎝ ⎛⎭⎪⎫-14,34,0,C ⎝ ⎛⎭⎪⎫-14,-34,0, PC →=⎝ ⎛⎭⎪⎫-14,-34,-24, PB →=⎝ ⎛⎭⎪⎫-14,34,-24,PE →=⎝ ⎛⎭⎪⎫-12,0,-24, 设平面PCB 的一个法向量为n =(x 1,y 1,z 1), 由⎩⎪⎨⎪⎧n ·PC →=0,n ·PB →=0,得⎩⎨⎧-x 1-3y 1-2z 1=0,-x 1+3y 1-2z 1=0,令x 1=2,得z 1=-1,y 1=0, 所以n =(2,0,-1),设平面PCE 的一个法向量为m =(x 2,y 2,z 2),由⎩⎪⎨⎪⎧m ·PC →=0,m ·PE →=0,得⎩⎨⎧-x 2-3y 2-2z 2=0,-2x 2-2z 2=0,令x 2=1,得z 2=-2,y 2=33, 所以m =⎝ ⎛⎭⎪⎫1,33,-2, 故cos 〈m ,n 〉=m ·n|m ||n |=223×103=255, 所以平面BPC 与平面EPC 的夹角的余弦值为255.思维升华 利用空间向量求平面与平面夹角的解题步骤跟踪训练3 (2021·全国乙卷改编)如图,四棱锥P -ABCD 的底面是矩形,PD ⊥底面ABCD ,PD =DC =1,M 为BC 的中点,且PB ⊥AM .(1)求BC ;(2)求平面APM 与平面BPM 夹角的正弦值.解 (1)因为PD ⊥平面ABCD ,所以PD ⊥AD ,PD ⊥DC .在矩形ABCD 中,AD ⊥DC ,故以点D 为坐标原点建立空间直角坐标系如图所示,设BC =t ,则A (t ,0,0),B (t ,1,0),M ⎝ ⎛⎭⎪⎫t 2,1,0,P (0,0,1), 所以PB →=(t ,1,-1),AM →=⎝ ⎛⎭⎪⎫-t 2,1,0.因为PB ⊥AM ,所以PB →·AM →=-t 22+1=0,得t =2,所以BC = 2.(2)易知C (0,1,0),由(1)可得AP →=(-2,0,1),AM →=⎝ ⎛⎭⎪⎫-22,1,0,CB →=(2,0,0),PB →=(2,1,-1).设平面APM 的法向量为n 1=(x 1,y 1,z 1),则 ⎩⎪⎨⎪⎧ n 1·AP →=0,n 1·AM →=0,即⎩⎪⎨⎪⎧-2x 1+z 1=0,-22x 1+y 1=0,令x 1=2,则z 1=2,y 1=1,所以平面APM 的一个法向量为n 1=(2,1,2). 设平面PMB 的法向量为n 2=(x 2,y 2,z 2),则 ⎩⎪⎨⎪⎧n 2·CB →=0,n 2·PB →=0,即⎩⎨⎧2x 2=0,2x 2+y 2-z 2=0,得x 2=0,令y 2=1,则z 2=1,所以平面PMB 的一个法向量为n 2=(0,1,1). 设平面APM 与平面BPM 夹角为θ,cos θ=|cos 〈n 1,n 2〉|=|n 1·n 2||n 1||n 2|=37×2=31414,sin θ=1-cos 2θ=7014. 所以平面APM 与平面BPM 夹角的正弦值为7014.课时精练1.如图,在平行六面体ABCD -A 1B 1C 1D 1中,AA 1⊥平面ABCD ,且AB =AD =2,AA 1=3,∠BAD =120°.(1)求异面直线A 1B 与AC 1所成角的余弦值; (2)求平面A 1BD 与平面A 1AD 所成角的正弦值. 解 在平面ABCD 内,过点A 作AE ⊥AD ,交BC 于点E . 因为AA 1⊥平面ABCD , 所以AA 1⊥AE ,AA 1⊥AD .如图,以{AE →,AD →,AA 1—→}为一个正交基底,建立空间直角坐标系,因为AB =AD =2,AA 1=3,∠BAD =120°, 则A (0,0,0),B (3,-1,0),D (0,2,0),E (3,0,0),A 1(0,0,3),C 1(3,1,3).(1)A 1B —→=(3,-1,-3),AC 1—→=(3,1,3). 则cos 〈A 1B —→,AC 1—→〉=A 1B —→·AC 1—→|A 1B —→||AC 1—→|=3-1-37×7=-17.因此异面直线A 1B 与AC 1所成角的余弦值为17.(2)可知平面A 1AD 的一个法向量为 AE →=(3,0,0),设m =(x ,y ,z )为平面A 1BD 的一个法向量, 又A 1B —→=(3,-1,-3),BD →=(-3,3,0),则⎩⎪⎨⎪⎧m ·A 1B —→=0,m ·BD →=0,即⎩⎨⎧3x -y -3z =0,-3x +3y =0.不妨取x =3,则y =3,z =2.所以m =(3,3,2)为平面A 1BD 的一个法向量, 从而cos 〈AE →,m 〉=AE →·m |AE →||m|=333×4=34.设平面A 1BD 与平面A 1AD 所成的角为θ, 则cos θ=34.所以sin θ=1-cos 2θ=74. 因此平面A 1BD 与平面A 1AD 所成角的正弦值为74. 2.(2021·浙江)如图,在四棱锥P -ABCD 中,底面ABCD 是平行四边形,∠ABC =120°,AB =1,BC =4,PA =15,M ,N 分别为BC ,PC 的中点,PD ⊥DC ,PM ⊥MD .(1)证明:AB ⊥PM ;(2)求直线AN 与平面PDM 所成角的正弦值. (1)证明 因为底面ABCD 是平行四边形, ∠ABC =120°,BC =4,AB =1, 且M 为BC 的中点,所以CM =2,CD =1,∠DCM =60°, 易得CD ⊥DM .又PD ⊥DC ,且PD ∩DM =D ,PD ,DM ⊂平面PDM , 所以CD ⊥平面PDM .因为AB ∥CD ,所以AB ⊥平面PDM . 又PM ⊂平面PDM ,所以AB ⊥PM .(2)解 方法一 由(1)知AB ⊥平面PDM , 所以∠NAB 为直线AN 与平面PDM 所成角的余角. 连接AM ,因为PM ⊥MD ,PM ⊥DC ,所以PM ⊥平面ABCD ,所以PM ⊥AM . 因为∠ABC =120°,AB =1,BM =2, 所以由余弦定理得AM =7, 又PA =15,所以PM =22, 所以PB =PC =23, 连接BN ,结合余弦定理得BN =11. 连接AC ,则由余弦定理得AC =21, 在△PAC 中,结合余弦定理得PA 2+AC 2=2AN 2+2PN 2,所以AN =15.所以在△ABN 中,cos∠BAN =AB 2+AN 2-BN 22AB ·AN =1+15-11215=156.设直线AN 与平面PDM 所成的角为θ, 则sin θ=cos∠BAN =156. 方法二 因为PM ⊥MD ,PM ⊥DC , 所以PM ⊥平面ABCD . 连接AM ,则PM ⊥AM .因为∠ABC =120°,AB =1,BM =2, 所以AM =7,又PA =15,所以PM =22, 由(1)知CD ⊥DM ,过点M 作ME ∥CD 交AD 于点E , 则ME ⊥MD .故可以以M 为坐标原点,MD ,ME ,MP 所在直线分别为x ,y ,z 轴建立如图所示的空间直角坐标系,则A (-3,2,0),P (0,0,22),C (3,-1,0), 所以N ⎝⎛⎭⎪⎫32,-12,2.所以AN →=⎝ ⎛⎭⎪⎫332,-52,2.易知平面PDM 的一个法向量为n =(0,1,0). 设直线AN 与平面PDM 所成的角为θ, 则sin θ=|cos 〈AN →,n 〉|=|AN →·n ||AN →||n |=5215=156.3.(2022·汕头模拟)如图,在圆柱OO 1中,四边形ABCD 是其轴截面,EF 为⊙O 1的直径,且EF ⊥CD ,AB =2,BC =a (a >1).(1)求证:BE =BF ;(2)若直线AE 与平面BEF 所成角的正弦值为63,求平面ABE 与平面BEF 夹角的余弦值. (1)证明 如图,连接BO 1,在圆柱OO 1中,BC ⊥平面CEDF ,∵EF ⊂平面CEDF ,∴EF ⊥BC , ∵EF ⊥CD ,BC ∩CD =C ,BC ,CD ⊂平面ABCD ,∴EF ⊥平面ABCD ,又BO 1⊂平面ABCD ,∴EF ⊥BO 1,∵在△BEF 中,O 1为EF 的中点,∴BE =BF .(2)解 连接OO 1,则OO 1与该圆柱的底面垂直,以点O 为坐标原点,OB ,OO 1所在直线分别为y ,z 轴建立如图所示的空间直角坐标系,则A (0,-1,0),B (0,1,0),E (-1,0,a ),F (1,0,a ),AE →=(-1,1,a ),BE →=(-1,-1,a ),BF →=(1,-1,a ),设平面BEF 的法向量是n 1=(x 1,y 1,z 1),由⎩⎪⎨⎪⎧n 1·BE →=0,n 1·BF →=0, 得⎩⎪⎨⎪⎧-x 1-y 1+az 1=0,x 1-y 1+az 1=0, 取z 1=1,得n 1=(0,a ,1),设直线AE 与平面BEF 所成的角为θ,则sin θ=|cos 〈AE →,n 1〉| =2aa 2+2·a 2+1=63,化简得(a 2-2)(a 2-1)=0,∵a >1,解得a =2,∴n 1=(0,2,1),设平面ABE 的法向量是n 2=(x 2,y 2,z 2),AB →=(0,2,0),由⎩⎪⎨⎪⎧n 2·AB →=0,n 2·AE →=0,得⎩⎨⎧ 2y 2=0,-x 2+y 2+2z 2=0,取z 2=1,得n 2=(2,0,1),设平面ABE 与平面BEF 的夹角为α,则cos α=|cos 〈n 1,n 2〉|=|n 1·n 2||n 1||n 2|=13, ∴平面ABE 与平面BEF 夹角的余弦值为13.4.(2021·全国甲卷改编)已知直三棱柱ABC -A 1B 1C 1中,侧面AA 1B 1B 为正方形,AB =BC =2,E ,F 分别为AC 和CC 1的中点,D 为棱A 1B 1上的点,BF ⊥A 1B 1.(1)证明:BF ⊥DE ;(2)当B 1D 为何值时,平面BB 1C 1C 与平面DFE 夹角的正弦值最小?(1)证明 因为E ,F 分别是AC 和CC 1的中点,且AB =BC =2, 所以CF =1,BF = 5.如图,连接AF ,由BF ⊥A 1B 1,AB ∥A 1B 1,得BF ⊥AB ,于是AF =BF 2+AB 2=3,所以AC =AF 2-CF2=2 2.由AB 2+BC 2=AC 2,得BA ⊥BC ,故以B 为坐标原点,以BA ,BC ,BB 1所在直线分别为x ,y ,z 轴建立空间直角坐标系,则B (0,0,0),E (1,1,0),F (0,2,1),BF →=(0,2,1).设B 1D =m (0≤m ≤2),则D (m ,0,2),于是DE →=(1-m ,1,-2).所以BF →·DE →=0,所以BF ⊥DE .(2)解 易知平面BB 1C 1C 的一个法向量为n 1=(1,0,0).设平面DFE 的一个法向量为n 2=(x ,y ,z ),则⎩⎪⎨⎪⎧ DE →·n 2=0,EF →·n 2=0,又DE →=(1-m ,1,-2),EF →=(-1,1,1),所以⎩⎪⎨⎪⎧ 1-m x +y -2z =0,-x +y +z =0,令x =3,得y =m +1,z =2-m ,于是平面DFE 的一个法向量为n 2=(3,m +1,2-m ),所以cos 〈n 1,n 2〉=32⎝ ⎛⎭⎪⎫m -122+272.设平面BB 1C 1C 与平面DFE 的夹角为θ,则sin θ=1-cos 2〈n 1,n 2〉,故当m =12时,平面BB 1C 1C 与平面DFE 夹角的正弦值最小,为33,即当B 1D =12时,平面BB 1C 1C 与平面DFE 夹角的正弦值最小.。
2025届高考数学一轮复习讲义立体几何与空间向量之 空间角和空间距离

形,则在正四棱柱 ABCD - A 1 B 1 C 1 D 1中,异面直线 AK 和 LM 所成的角的大小为
(
D )
A. 30°
B. 45°
C. 60°
D. 90°
[解析] 根据题意还原正四棱柱的直观图,如图所示,取 AA 1的中点 G ,连接 KG ,
则有 KG ∥ LM ,所以∠ AKG 或其补角为异面直线 AK 和 LM 所成的角.由题知 AG =
A 1 C 1=5, BC 1=4 2 ,所以 cos
52 +52 −(4 2)2
9
1
∠ BA 1 C 1=
= < ,所以60°<
2×5×5
25
2
∠ BA 1 C 1<90°,则过点 D 1作直线 l ,与直线 A 1 B , AC 所成的角均为60°,即过一
点作直线,使之与同一平面上夹角大于60°的锐角的两边所在直线所成的角均成
2 z -1=0的交线,试写出直线 l 的一个方向向量 (2,2,1)
的余弦值为
65
9
.
,直线 l 与平面α所成角
[解析] 由平面α的方程为 x +2 y -2 z +1=0,可得平面α的一个法向量为 n =(1,
⑫ [0, ] ,二面角的
2
n1,n2>|.
范围是⑬
[0,π] .
易错警示
1. 线面角θ与向量夹角< a , n >的关系
π
2
π
2
如图1(1),θ=< a , n >- ;如图1(2),θ= -< a , n >.
图1
2. 二面角θ与两平面法向量夹角< n 1, n 2>的关系
图2(2)(4)中θ=π-< n 1, n 2>;图2(1)(3)中θ=< n 1, n 2>.
2025年高考数学一轮复习-立体几何中的动点及其轨迹问题-专项训练【含答案】

2025年高考数学一轮复习-立体几何中的动点及其轨迹问题-专项训练一、基本技能练1.如图,在正方体ABCD -A 1B 1C 1D 1中,P 是侧面BB 1C 1C 内一动点,若P 到直线BC 与到直线C 1D 1的距离相等,则动点P 的轨迹为()A.直线B.圆C.双曲线D.抛物线2.如图,正方体ABCD -A 1B 1C 1D 1中,P 为底面ABCD 上的动点.PE ⊥A 1C 于E ,且PA =PE ,则点P 的轨迹是()A.线段B.圆弧C.椭圆的一部分D.抛物线的一部分3.如图,圆锥的底面直径AB =2,母线VA =3,点C 在母线VB 上,且VC =1,有一只蚂蚁沿圆锥的侧面从点A 到达点C ,则这只蚂蚁爬行的最短距离是()A.13B.7C.433D.3324.如图所示,已知正方体ABCD -A 1B 1C 1D 1的棱长为2,长为2的线段MN 的一个端点M 在棱DD 1上运动,另一端点N 在正方形ABCD 内运动,则MN 中点轨迹的面积为()A.4πB.2πC.πD.π25.已知MN 是长方体外接球的一条直径,点P 在长方体表面上运动,长方体的棱长分别是1,1,2,则PM →·PN →的取值范围为()A.-12,0 B.-34,0C.-12,1 D.-34,16.点P 为棱长是25的正方体ABCD -A 1B 1C 1D 1的内切球O 球面上的动点,点M 为B 1C 1的中点,若满足DP ⊥BM ,则动点P 的轨迹的长度为()A.πB.2πC.4πD.25π7.已知正三棱锥P -ABC 的六条棱长均为6,S 是△ABC 及其内部的点构成的集合.设集合T ={Q ∈S |PQ ≤5},则T 表示的区域的面积为()A.3π4 B.πC.2πD.3π8.如图,三角形PAB 所在的平面α和四边形ABCD 所在的平面β垂直,且AD ⊥α,BC ⊥α,AD =4,BC =8,AB =6,∠APD =∠CPB ,则点P 在平面α内的轨迹是()A.圆的一部分B.椭圆的一部分C.双曲线的一部分D.抛物线的一部分9.已知正方体ABCD -A ′B ′C ′D ′的棱长为1,点M ,N 分别为线段AB ′,AC 上的动点,点T 在平面BCC ′B ′内,则MT +NT 的最小值是()A.2 B.233C.62 D.110.如图,长方体ABCD -A ′B ′C ′D ′中,AB =BC =2,AA ′=3,上底面A ′B ′C ′D ′的中心为O ′,当点E 在线段CC ′上从C 移动到C ′时,点O ′在平面BDE 上的射影G 的轨迹长度为()A.2π3B.3π3C.π3D.3π611.如图所示,在四棱锥P -ABCD 中,P A ⊥底面ABCD ,且底面各边都相等,M 是PC 上的一动点,当点M 满足________时,平面MBD ⊥平面PCD (只要填写一个你认为是正确的条件即可).12.如图,P 是棱长为1的正方体ABCD -A 1B 1C 1D 1表面上的动点,且AP =2,则动点P 的轨迹的长度为________.二、创新拓展练13.在棱长为3的正方体ABCD -A 1B 1C 1D 1中,E 是AA 1的中点,P 是底面ABCD 所在平面内一动点,设PD 1,PE 与底面ABCD 所成的角分别为θ1,θ2(θ1,θ2均不为0),若θ1=θ2,则三棱锥P -BB 1C 1体积的最小值是()A.92B.52C.32D.5414.(多选)如图,设正方体ABCD -A 1B 1C 1D 1的棱长为2,E 为A 1D 1的中点,F 为CC 1上的一个动点,设由点A ,E ,F 构成的平面为α,则()A.平面α截正方体的截面可能是三角形B.当点F 与点C 1重合时,平面α截正方体的截面面积为26C.当点D 到平面α的距离的最大值为263D.当F 为CC 1的中点时,平面α截正方体的截面为五边形15.已知面积为23的菱形ABCD 如图①所示,其中AC =2,E 是线段AD 的中点.现沿AC 折起,使得点D 到达点S 的位置,此时二面角S -AC -B 的大小为120°,连接SB ,得到三棱锥S -ABC 如图②所示,则三棱锥S -ABC 的体积为________;若点F 在三棱锥的表面运动,且始终保持EF ⊥AC ,则点F 的轨迹长度为________.16.如图,三棱锥S-ABC的所有棱长均为1,SH⊥底面ABC,点M,N在直线SH上,且MN=33,若动点P在底面ABC内,且△PMN的面积为212,则动点P的轨迹长度为________.参考答案与解析一、基本技能练1.答案D解析点P到直线C1D1的距离即为点P到点C1的距离,所以在平面BB1C1C中,点P到定点C1的距离与到定直线BC的距离相等,由抛物线的定义可知,动点P的轨迹为抛物线,故选D.2.答案A解析由题意知,△A1AP≌△A1EP,则点P 为在线段AE 的中垂面上运动,从而与底面ABCD 的交线为线段.3.答案B 解析在圆锥侧面的展开图中,AA ′=2π,所以∠AVA ′=AA ′︵VA =23,所以∠AVB =12∠AVA ′=π3,由余弦定理得AC 2=VA 2+VC 2-2VA ·VC ·cos ∠AVB =32+12-2×3×1×12=7,所以AC =7.所以这只蚂蚁爬行的最短距离是7,故选B.4.答案D 解析易知DD 1⊥平面ABCD ,∠MDN =90°,取线段MN 的中点P ,则DP =12MN =1,所以点P 的轨迹是以D 为球心,1为半径的18球面,故S =18×4π×12=π2.5.答案B 解析根据题意,以D 为坐标原点,DA →为x 轴正方向,DC →为y 轴正方向,DD 1→为z 轴正方向,建立空间直角坐标系,如图所示.设长方体外接球球心为O ,则DB 1为外接球的一条直径,设O 为DB 1的中点,不妨设M 与D 重合,N 与B 1重合.则外接球的直径长为12+12+(2)2=2,所以半径r =1,所以PM →·PN →=(PO →+OM →)·(PO →+ON →)=(PO →+OM →)·(PO →-OM →)=|PO →|2-|OM →|2=|PO →|2-1,由P 在长方体表面上运动,所以|PO →|∈12,1,即|PO →|2∈14,1,所以|PO →|2-1∈-34,0,即PM →·PN →∈-34,0.6.答案C 解析根据题意知,该正方体的内切球半径为r =5,如图,取BB 1的中点N ,连接CN ,则CN ⊥BM ,在正方体ABCD -A 1B 1C 1D 1中,CN 为DP 在平面B 1C 1CB 中的射影,∴点P 的轨迹为过D ,C ,N 的平面与内切球的交线,∵正方体ABCD -A 1B 1C 1D 1的棱长为25,∴O 到过D ,C ,N 的平面的距离为1,∴截面圆的半径为(5)2-1=2,∴点P 的轨迹的长度为2π×2=4π.7.答案B 解析设顶点P 在底面上的投影为O ,连接BO ,则O 为△ABC 的中心,且BO =23×6×32=23,故PO =36-12=2 6.因为PQ =5,故OQ =1,故Q 的轨迹为以O 为圆心,1为半径的圆,而△ABC 内切圆的圆心为O ,半径为2×34×363×6=3>1,故Q 的轨迹圆在△ABC 内部,故其面积为π.8.答案A 解析由条件易得AD ∥BC ,且∠APD =∠CPB ,AD =4,BC =8,可得tan ∠APD =AD PA =CB PB =tan ∠CPB ,即PB P A =CB AD=2,在平面P AB 内以AB 所在的直线为x 轴,AB 的中点O 为坐标原点,建立直角坐标系(图略),则A (-3,0),B (3,0),设P (x ,y ),则有PB PA =(x -3)2+y 2(x +3)2+y 2=2,整理可得x 2+y 2+10x +9=0(x ≠0).由于点P 不在直线AB 上,故此轨迹为圆的一部分,故答案选A.9.答案B 解析A 点关于BC 的对称点为E ,M 关于BB ′的对称点为M ′,记d 为直线EB ′与AC 之间的距离,则MT +NT =M ′T +NT ≥M ′N ≥d ,由B ′E ∥D ′C ,d 为E 到平面ACD ′的距离,因为V D ′-ACE =13×1×S △ACE =13×1×1=13,而V D ′-ACE =V E -ACD ′=13×d ×34×(2)2=36d =13,故d =233.10.答案B 解析如图,以CA ,CC ′分别为x 轴,y 轴正方向建立平面直角坐标系,则有C (0,0),O (1,0),O ′(1,3),设G (x ,y ),由O ′G ⊥OG ,可得y x -1·y -3x -1=-1,+(x -1)2=34,所以点O ′在平面BDE 上的射影G 的轨迹是以F半径为32的OG ︵.因为tan ∠GOF =O ′C ′OO ′=33,所以O ′G =O ′O ·sin ∠GOF =32,所以△O ′GF 是等边三角形,即∠GFO =2π3,所以圆弧OG 的长l =2π3×32=3π3.11.答案DM ⊥PC (或BM ⊥PC )解析连接AC ,BD ,则AC ⊥BD ,因为PA ⊥底面ABCD ,BD ⊂平面ABCD ,所以PA ⊥BD .又PA ∩AC =A ,所以BD ⊥平面PAC ,PC ⊂平面PAC ,所以BD ⊥PC ,所以当DM ⊥PC (或BM ⊥PC )时,有PC ⊥平面MBD ,PC ⊂平面PCD ,所以平面MBD ⊥平面PCD .12.答案3π2解析由已知AC =AB 1=AD 1=2,在平面BC 1,平面A 1C 1中,BP =A 1P =DP =1,所以动点P 的轨迹是在平面BC 1,平面A 1C 1,平面DC 1内分别以B ,D ,A 1为圆心,1为半径的三段圆弧,且长度相等,故轨迹长度和为π2×3=3π2.二、创新拓展练13.答案C 解析以D 为坐标原点建立如图所示空间直角坐标系,因为正方体的棱长为3,则3,0,32D 1(0,0,3),设P (x ,y ,0)(x ≥0,y ≥0),则PE →3-x ,-y ,32,PD 1→=(-x ,-y ,3).因为θ1=θ2,平面ABCD 的一个法向量z =(0,0,1),所以|PE →·z ||PE →|·|z |=|PD 1→·z ||PD 1→|·|z |,得32(3-x )2+y 2+94=3x 2+y 2+9,整理得x 2+y 2-8x +12=0,即(x -4)2+y 2=4(0≤y ≤2),则动点P 的轨迹为圆的一部分,所以点P 到平面BB 1C 1的最小距离为1,所以三棱锥P -BB 1C 1体积的最小值是13×12×3×3×1=32.14.答案BCD 解析如图,建立空间直角坐标系,延长AE 与z 轴交于点P ,连接PF 并延长与y 轴交于点M ,则平面α由平面AEF 扩展为平面APM .由此模型可知A 错误.当点F 与点C 1重合时,截面是一个边长为5的菱形,该菱形的两条对角线长度分别AC 1=22+22+22=23和22+22=22,则此时截面的面积为12×23×22=2 6.当F 为CC 1的中点时,平面α截正方体的截面为五边形,B ,D 正确.D (0,0,0),A (2,0,0),P (0,0,4),设点M 的坐标为(0,t ,0)(t ∈[2,4]),DA →=(2,0,0),AM →=(-2,t ,0),PA →=(2,0,-4),则可知点P 到直线AM 的距离为d =|P A →|2-|PA →·AM →|AM →||2=20t 2+644+t 2,S △APM =12t 2+4·d =5t 2+16.S △P AD =12×2×4=4,设点D 到平面α的距离为h ,利用等体积法V D -APM =V M -P AD ,即13·S △APM ·h =13·S △P AD ·t ,可得h =4t 5t 2+16,则h =45+16t 2,由h =45+16t 2在t ∈[2,4]上单调递增,所以当t =4时,h 取到最大值为263.故选BCD.15.答案323+32解析依题意,12AC ·BD =BD =23,点S 到平面ABC 的距离为3sin 60°=32,△ABC 的面积为12×23=3,则三棱锥S -ABC 的体积为13×3×32=32.如图,取AC 边上靠近点A 的四等分点G ,取BA 的中点为H ,连接EH ,EG ,GH ,故点F 的轨迹长度即为△EHG 的周长,又EG =GH =32,EH =12SB =32,故点F 的轨迹长度为3+32.16.答案6π12解析设P 到直线MN 的距离为d ,由题易得d =66,易知H 为△ABC 的中心,又MN ⊥平面ABC ,当点P 在平面ABC 内时,其轨迹是以H 为圆心,66.∵△ABC 内切圆的半径为36,∴圆H 的一部分位于△ABC 外,结合题意得,点P 的轨迹为圆H 位于底面△ABC 内的三段相等的圆弧(利用正三角形的性质判断出圆H 有一部分在△ABC 外,才能正确得到点P 的轨迹),如图,过点H 作HO ⊥AC ,垂足为O ,则HO =36,记圆H 与线段OC 的交点为K ,连接HK ,可得HK =66,∴cos∠OHK=OHHK=3666=22,∴∠OHK=π4,∴点P的轨迹长度为圆H周长的14(利用圆及正三角形的对称性分析求解),∴点P的轨迹长度为14×2π×66=6π12.。
2023届高考一轮复习试卷(立体几何)
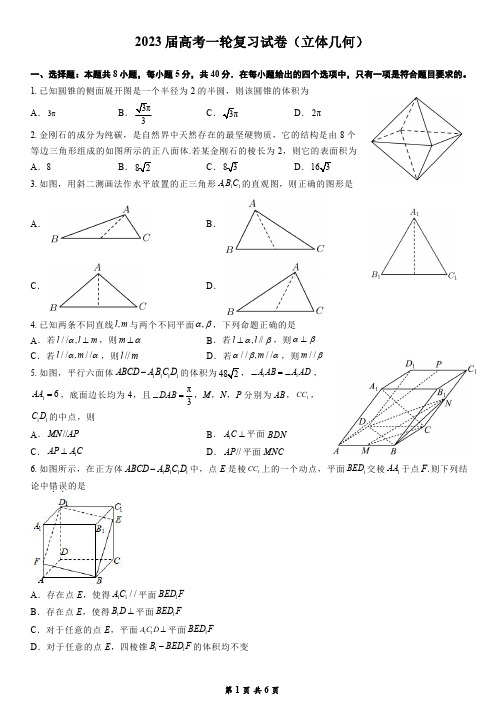
2023届高考一轮复习试卷(立体几何)一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知圆锥的侧面展开图是一个半径为2的半圆,则该圆锥的体积为A .3πB .3π3C .3πD .2π2.金刚石的成分为纯碳,是自然界中天然存在的最坚硬物质,它的结构是由8个等边三角形组成的如图所示的正八面体.若某金刚石的棱长为2,则它的表面积为A .8B .82C .83D .1633.如图,用斜二测画法作水平放置的正三角形111A B C 的直观图,则正确的图形是A .B .C .D .4.已知两条不同直线,l m 与两个不同平面,αβ,下列命题正确的是A .若//,l l m α⊥,则m α⊥B .若,//l l αβ⊥,则αβ⊥C .若//,//l m αα,则//l m D .若//,//m αβα,则//m β5.如图,平行六面体1111ABCD A B C D -的体积为482,11A AB A AD ∠=∠,16AA =,底面边长均为4,且π3DAB ∠=,M ,N ,P 分别为AB ,1CC ,11C D 的中点,则A .//MN APB .1AC ⊥平面BDN C .1AP AC ⊥D .//AP 平面MNC6.如图所示,在正方体1111ABCD A B C D -中,点E 是棱1CC 上的一个动点,平面1BED 交棱1AA 于点.F 则下列结论中错误..的是A .存在点E ,使得11//AC 平面1BED FB .存在点E ,使得1B D ⊥平面1BED FC .对于任意的点E ,平面11ACD ⊥平面1BED FD .对于任意的点E ,四棱锥11B BEDF -的体积均不变7.足球运动成为当今世界上开展最广、影响最大、最具魅力、拥有球迷数最多的体育项目之一,2022年卡塔尔世界杯是第22届世界杯足球赛.比赛于2022年11月21日至12月18日在卡塔尔境内7座城市中的12座球场举行.已知某足球的表面上有四个点A ,B ,C ,D 满足2dm AB BC AD BD CD =====,二面角A BD C --的大小为23π,则该足球的体积为A .3742dm 27πB .3352dm 27πC .314dm 27πD .3322dm 27π8.一个长方体的盒子内装有部分液体(液体未装满盒子),以不同的方向角度倾斜时液体表面会呈现出不同的变化,则下列说法中错误的个数是①当液面是三角形时,其形状可能是钝角三角形②在一定条件下,液面的形状可能是正五边形③当液面形状是三角形时,液体体积与长方体体积之比的范围是150,,166⎛⎤⎡⎫⋃ ⎪⎥⎢⎝⎦⎣⎭④当液面形状是六边形时,液体体积与长方体体积之比的范围是13,44⎛⎫ ⎪⎝⎭A .1个B .2个C .3个D .4个二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.下列关于空间向量的命题中,正确的是A .若空间向量,a b ,满足a b =r r ,则a b= B .若非零向量,,a b c ,满足,a b b c ⊥⊥ ,则有a c∥ C .若,,OA OB OC 是空间的一组基底,且111333OD OA OB OC =++ ,则,,,A B C D 四点共面D .若向量,,a b b c c a +++ 是空间的一组基底,则,,a b c 也是空间的一组基底10.如图,若正方体的棱长为1,点M 是正方体1111ABCD A B C D -的侧面11ADD A上的一个动点(含边界),P 是棱1CC 的中点,则下列结论正确的是A .沿正方体的表面从点A 到点P 的最短路程为132B .若保持2PM =,则点M 在侧面内运动路径的长度为π3C .三棱锥1B C MD -的体积最大值为16D .若M 在平面11ADD A 内运动,且111MD B B D B ∠=∠,点M 的轨迹为线段11.已知a ,b ,c 为三条不同的直线,α,β,γ为三个不同的平面,则下列说法错误的是A .若a b ∥,b α⊂,则a αP B .若a αβ⋂=,b βγ= ,c αγ⋂=,a b ∥,则b c ∥C .若b β⊂,c β⊂,a b ⊥r r ,a c ⊥,则a β⊥D .若a α⊂,b β⊂,a b ∥,则αβ∥12.如图,已知二面角l αβ--的棱l 上有A ,B 两点,C α∈,AC l ⊥,D β∈,BD l ⊥,若2AC AB BD ===,22CD =,则A .直线AB 与CD 所成角的大小为45°B .二面角l αβ--的大小为60°C .三棱锥A BCD -的体积为23D .直线CD 与平面β所成角的正弦值为64三、填空题:本题共4小题,每小题5分,共20分.13.在空间直角坐标系中,已知()3,2,1OA = ,()1,0,5OB = ,()1,2,1OC =-- ,点M 为线段AB 的中点,则CM = .14.用一个平面将圆柱切割成如图的两部分.将下半部分几何体的侧面展开,平面与圆柱侧面所形成的交线在侧面展开图中对应的函数表达式为 1.52cos y x =+.则平面与圆柱底面所形成的二面角的正弦值是.15.“云南十八怪”描述的是由云南独特的地理位置、民风民俗所产生的一些特有的现象或生活方式,是云南多元民族文化的写照.“云南十八怪”中有一怪“摘下草帽当锅盖”所指的锅盖是用秸秆或山茅草编织成的,因其形状酷似草帽而传为佳话.一种草帽锅盖呈圆锥形,其母线长为6dm ,侧面积为2183dm π,若此圆锥的顶点和底面圆都在同一个球面上,则该球体的表面积等于2dm .16.在直四棱柱1111ABCD A B C D -中,底面ABCD 为正方形,122AA AB ==.点P 在侧面11BCC B 内,满足1A C ⊥平面BDP ,设点P 到平面ABCD 的距离为1h ,到CD 的距离为2h ,则12h h +的最小值为.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.如图所示,在四棱锥P ABCD -中,底面ABCD 是边长为4的正方形,4,PA PD PB ==,点E 在线段PA 上,3,PE EA BE AD =⊥,点,F G 分别是线段,BC CD 的中点.(1)证明:PA ⊥平面ABCD ;(2)求三棱锥P EFG -的体积.18.三棱锥P ABC -中,PA PB PC BC a ====,且PB 与底面ABC 成60°角.(1)设点P 在底面ABC 的投影为H ,求BH 的长;(2)求证:ABC △是直角三角形;(3)求该三棱锥体积的最大值.19.故宫太和殿是中国形制最高的宫殿,其建筑采用了重檐庑殿顶的屋顶样式,庑殿顶是“四出水”的五脊四坡式,由一条正脊和四条垂脊组成,因此又称五脊殿.由于屋顶有四面斜坡,故又称四阿顶.如图,某几何体ABCDEF 有五个面,其形状与四阿顶相类似.已知底面ABCD 为矩形,AB =2AD =2EF =8,EF ∥底面ABCD ,EA =ED =FB =FC ,M ,N 分别为AD ,BC 的中点.(1)证明:EF ∥AB 且BC ⊥平面EFNM .(2)若二面角E AD B --为4π,求CF 与平面ABF 所成角的正弦值.20.如图,已知ABCD 和CDEF 都是直角梯形,//AB DC ,//DC EF ,5AB =,3DC =,1EF =,60BAD CDE ∠=∠=︒,二面角F DC B --的平面角为60︒.设M ,N 分别为,AE BC 的中点.(1)证明:FN AD ⊥;(2)求直线BM 与平面ADE 所成角的正弦值.21.《瀑布》(图1)是埃舍尔最为人所知的作品之一,图中的瀑布会源源不断地落下,落下的水又逆流而上,荒唐至极,但又会让你百看不腻.画面下方还有一位饶有兴致的观察者,似乎他没发现什么不对劲.此时,他既是画外的观看者,也是埃舍尔自己.画面两座高塔各有一个几何体,左塔上方是著名的“三立方体合体”由三个正方体构成,右塔上的几何体是首次出现,后称“埃舍尔多面体”(图2)埃舍尔多面体可以用两两垂直且中心重合的三个正方形构造,设边长均为2,定义正方形,1,2,3n n n n A B C D n =的顶点为“框架点”,定义两正方形交线为“极轴”,其端点为“极点”,记为,n n P Q ,将极点11,P Q ,分别与正方形2222A B C D 的顶点连线,取其中点记为,,,1,2,3,4m m E F m =,如(图3).埃舍尔多面体可视部分是由12个四棱锥构成,这些四棱锥顶点均为“框架点”,底面四边形由两个“极点”与两个“中点”构成,为了便于理解,图4我们构造了其中两个四棱锥11122A PE P E -与22131A P E P F -.(1)求异面直线12P A 与12Q B 成角余弦值(2)求平面111PA E 与平面122AE P 的夹角余弦值(3)若埃舍尔体的表面积与体积(直接写出答案)22.在长方体1111ABCD A B C D -中,(1)已知P 、Q 分别为棱AB 、1CC 的中点(如图1),做出过点1D ,P ,Q 的平面与长方体的截面.保留作图痕迹,不必说明理由;(2)如图2,已知13AB =,5AD =,112AA =,过点A 且与直线CD 平行的平面α将长方体分成两部分.现同时将两个球分别放入这两部分几何体内,则在平面α变化的过程中,求这两个球的半径之和的最大值.。
2023年高考数学一轮复习第七章立体几何与空间向量9空间动态问题突破培优课练习含解析

空间动态问题突破题型一 空间位置关系的判定例1 (1)如图,在矩形ABCD 中,BC =1,AB =x ,BD 和AC 交于点O ,将△BAD 沿直线BD 翻折,则下列说法中错误的是( )A .存在x ,在翻折过程中存在某个位置,使得AB ⊥OC B .存在x ,在翻折过程中存在某个位置,使得AC ⊥BD C .存在x ,在翻折过程中存在某个位置,使得AB ⊥平面ACD D .存在x ,在翻折过程中存在某个位置,使得AC ⊥平面ABD 答案 D解析 当AB =x =1时,此时矩形ABCD 为正方形,则AC ⊥BD , 将△BAD 沿直线BD 翻折,若使得平面ABD ⊥平面BCD 时, 由OC ⊥BD ,OC ⊂平面BCD ,平面ABD ∩平面BCD =BD ,所以OC ⊥平面ABD ,又AB ⊂平面ABD ,所以AB ⊥OC ,故A 正确; 又OC ⊥BD ,OA ⊥BD ,且OA ∩OC =O ,OA ,OC ⊂平面OAC , 所以BD ⊥平面OAC ,又AC ⊂平面OAC ,所以AC ⊥BD ,故B 正确; 在矩形ABCD 中,AB ⊥AD ,AC =1+x 2, 所以将△BAD 沿直线BD 翻折时, 总有AB ⊥AD ,取x =12,当将△BAD 沿直线BD 翻折到AC =32时,有AB 2+AC 2=BC 2,即AB ⊥AC ,且AC ∩AD =A ,AC ,AD ⊂平面ACD , 则此时满足AB ⊥平面ACD ,故C 正确;若AC ⊥平面ABD ,又AO ⊂平面ABD ,则AC ⊥AO ,所以在△AOC 中,OC 为斜边,这与OC =OA 相矛盾,故D 不正确.(2)(多选)(2022·烟台质检)如图,在正方体ABCD -A 1B 1C 1D 1中,点P 在线段BC 1上运动,则下列判断中正确的是( )A .平面PB 1D ⊥平面ACD 1 B .A 1P ∥平面ACD 1C .异面直线A 1P 与AD 1所成的角的范围是⎝⎛⎦⎥⎤0,π3D .三棱锥D 1-APC 的体积不变 答案 ABD解析 对于A ,根据正方体的性质,易证DB 1⊥平面ACD 1, 又DB 1⊂平面PB 1D ,则平面PB 1D ⊥平面ACD 1,故A 正确;对于B ,连接A 1B ,A 1C 1(图略),易证明平面BA 1C 1∥平面ACD 1, 又A 1P ⊂平面BA 1C 1,所以A 1P ∥平面ACD 1,故B 正确;对于C ,当P 与线段BC 1的两端点重合时,A 1P 与AD 1所成的角取最小值π3,当P 与线段BC 1的中点重合时,A 1P 与AD 1所成的角取最大值π2,故A 1P 与AD 1所成的角的范围是⎣⎢⎡⎦⎥⎤π3,π2,故C 错误;对于D ,11,D APC C AD P V V --=因为点C 到平面AD 1P 的距离不变,且△AD 1P 的面积不变,所以三棱锥D 1-APC 的体积不变,故D 正确. 思维升华 解决空间位置关系的动点问题 (1)应用“位置关系定理”转化. (2)建立“坐标系”计算.跟踪训练1 (多选)如图,在直三棱柱ABC -A 1B 1C 1中,△ABC 为等腰直角三角形,AB ⊥BC ,且AC =AA 1=2,E ,F 分别是AC ,A 1C 1的中点,D ,M 分别是AA 1,BB 1上的两个动点,则( )A .FM 与BD 一定是异面直线B .三棱锥D -MEF 的体积为定值13C .直线B 1C 1与BD 所成的角为π2D .若D 为AA 1的中点,则四棱锥D -BB 1FE 的外接球表面积为5π 答案 BCD解析 A 项,当M ,B 重合时,FM (即BF )与BD 是相交直线,故A 错误; B 项,由已知可得B 1F ⊥A 1C 1,又平面ABC ⊥平面CAA 1C 1, 所以B 1F ⊥平面CAA 1C 1. 在矩形AEFA 1中,△DEF 的面积S =12×EF ×A 1F =12×2×1=1.又B 1F =12A 1C 1=1,所以三棱锥D -MEF 的体积V M -DEF =13S ×B 1F =13×1×1=13,所以B 正确;C 项,由AA 1⊥平面A 1B 1C 1,得AA 1⊥B 1C 1,又B 1C 1⊥A 1B 1,A 1B 1∩AA 1=A 1,A 1B 1,AA 1⊂平面A 1B 1BA , 所以B 1C 1⊥平面A 1B 1BA , 因为BD ⊂平面A 1B 1BA , 所以B 1C 1⊥BD ,所以C 正确;D 项,由题意可得四边形BB 1FE 为矩形,连接BF (图略), 则矩形BB 1FE 外接圆的圆心为BF 的中点O 1,且O 1F =O 1B =52. 过O 1作O 1N ⊥EF ,垂足为N ,连接DN ,O 1D , 则O 1N =12,DN =1,O 1N ⊥DN ,故O 1D =52, 所以O 1是四棱锥D -BB 1FE 的外接球的球心,外接球的半径为R =52, 则外接球的表面积为S =4π×⎝ ⎛⎭⎪⎫522=5π, 所以D 正确. 题型二 轨迹问题例2 (1)(多选)(2022·日照模拟)如图,已知正方体ABCD -A 1B 1C 1D 1的棱长为4,M 为DD 1的中点,N 为ABCD 所在平面内一动点,则下列命题正确的是( )A .若MN 与平面ABCD 所成的角为π4,则点N 的轨迹为圆B .若MN =4,则MN 的中点P 的轨迹所围成图形的面积为2πC .若点N 到直线BB 1与到直线DC 的距离相等,则点N 的轨迹为抛物线D .若D 1N 与AB 所成的角为π3,则点N 的轨迹为双曲线 答案 ACD解析 如图所示,对于A ,根据正方体的性质可知,MD ⊥平面ABCD ,所以∠MND 为MN 与平面ABCD 所成的角,所以∠MND =π4,所以DN =DM =12DD 1=12×4=2,所以点N 的轨迹为以D 为圆心,2为半径的圆,故A 正确;对于B ,在Rt △MDN 中,DN =MN 2-MD 2=42-22=23,取MD 的中点E ,连接PE ,因为P 为MN 的中点,所以PE ∥DN ,且PE =12DN =3,因为DN ⊥ED ,所以PE ⊥ED ,即点P 在过点E且与DD 1垂直的平面内,又PE =3,所以点P 的轨迹为以3为半径的圆,其面积为π·(3)2=3π,故B 不正确;对于C ,连接NB ,因为BB 1⊥平面ABCD ,所以BB 1⊥NB ,所以点N 到直线BB 1的距离为NB ,所以点N 到点B 的距离等于点N 到定直线CD 的距离,又B 不在直线CD 上,所以点N 的轨迹为以B 为焦点,CD 为准线的抛物线,故C 正确;对于D ,以D 为坐标原点,DA ,DC ,DD 1所在直线分别为x ,y ,z 轴建立空间直角坐标系, 则A (4,0,0),B (4,4,0),D 1(0,0,4),设N (x ,y ,0), 则AB →=(0,4,0),D 1N —→=(x ,y ,-4), 因为D 1N 与AB 所成的角为π3,所以|cos 〈AB →,D 1N —→〉|=cos π3,所以⎪⎪⎪⎪⎪⎪4y 4x 2+y 2+16=12,整理得3y 216-x 216=1,所以点N 的轨迹为双曲线,故D 正确.(2)(2022·济南模拟)如图,已知四棱锥S -ABCD 的底面是边长为6的菱形,∠BAD =60°,AC ,BD 相交于点O ,SO ⊥平面ABCD ,SO =4,E 是BC 的中点,动点P 在该棱锥表面上运动,并且总保持PE ⊥AC ,则动点P 的轨迹的长为________.答案 8解析 如图,分别取DC ,SC 的中点G ,F ,连接GE ,GF ,FE ,∵E 是BC 的中点, ∴GE ∥DB ,FE ∥SB ,GE ⊄平面SBD ,DB ⊂平面SBD ,则GE ∥平面SBD ;FE ⊄平面SBD ,SB ⊂平面SBD ,则FE ∥平面SBD ,又GE ∩FE =E ,∴平面FEG ∥平面SBD , ∵SO ⊥平面ABCD ,∴SO ⊥AC , 又∵四边形ABCD 是菱形,∴DB ⊥AC , ∵SO ∩DB =O ,SO ,DB ⊂平面SBD , ∴AC ⊥平面SBD , 则AC ⊥平面FEG ,故只要动点P 在平面FEG 内即总保持PE ⊥AC ,又动点P 在棱锥表面上运动, ∴动点P 的轨迹的周长即为△FEG 的周长,∵四边形ABCD 是边长为6的菱形,且∠BAD =60°, ∴BD =6,则OB =OD =3, 又SO =4,∴SB =SD =5, 故FE =FG =52,GE =3,∴△FEG 的周长为8.思维升华 解决与几何体有关的动点轨迹问题的方法 (1)几何法:根据平面的性质进行判定.(2)定义法:转化为平面轨迹问题,用圆锥曲线的定义判定,或用代替法进行计算. (3)特殊值法:根据空间图形线段长度关系取特殊值或位置进行排除.跟踪训练2 (1)(2022·滨州模拟)如图,斜线段AB 与平面α所成的角为π4,B 为斜足.平面α上的动点P 满足∠PAB =π6,则点P 的轨迹为( )A .圆B .椭圆C .双曲线的一部分D .抛物线的一部分答案 B解析 建立如图所示的空间直角坐标系,设OB =OA =1,则B (0,1,0),A (0,0,1),P (x ,y ,0),则AB →=(0,1,-1), AP →=(x ,y ,-1),所以cos 〈AB →,AP →〉=y +12·x 2+y 2+1=32, 即3x 2+(y -2)2=3, 所以点P 的轨迹是椭圆.(2)(2022·宁波模拟)在棱长为22的正方体ABCD -A 1B 1C 1D 1中,E ,F 分别为棱AB ,AD 的中点,P 为线段C 1D 上的动点,则直线A 1P 与平面D 1EF 的交点Q 的轨迹长度为( ) A.2153 B.433 C.2133 D.423答案 C解析 如图,连接B 1D 1,因为E ,F 分别为棱AB ,AD 的中点,所以B 1D 1∥EF , 则B 1,D 1,E ,F 四点共面.连接A 1C 1,A 1D ,设A 1C 1∩B 1D 1=M ,A 1D ∩D 1F =N ,连接MN , 则点Q 的轨迹为线段MN , 易得A 1D =A 1D 21+DD 21=4, △A 1ND 1∽△DNF ,且A 1D 1FD=2, 所以A 1N =23A 1D =83.易知A 1C 1=C 1D =A 1D =4,所以∠C 1A 1D =60°,又A 1M =2,所以在△A 1MN 中,由余弦定理可得MN 2=A 1N 2+A 1M 2-2A 1N ·A 1M cos∠MA 1N =529,所以MN =2133,即点Q 的轨迹长度为2133.题型三 最值、范围问题例3 (1)如图所示,在正方体ABCD -A 1B 1C 1D 1中,点P 是线段B 1D 1上一动点,且AP ∥平面DBC 1,则异面直线AP 与BD 所成角的取值范围为( )A.⎣⎢⎡⎦⎥⎤π4,3π4B.⎣⎢⎡⎦⎥⎤π4,π2C.⎣⎢⎡⎦⎥⎤π3,π2 D.⎣⎢⎡⎦⎥⎤π3,2π3答案 C解析 如图,以D 为坐标原点,DA ,DC ,DD 1所在直线分别为x 轴、y 轴、z 轴建立如图所示的空间直角坐标系,设正方体棱长为1,则D (0,0,0),B (1,1,0),A (1,0,0), 设P (λ,λ,1),λ∈[0,1], ∴DB →=(1,1,0),AP →=(λ-1,λ,1), ∴DB →·AP →=2λ-1,|DB →|=2, |AP →|=2λ2-2λ+2,设异面直线AP 与BD 所成的角为θ, 则cos θ=|DB →·AP →||DB →||AP →|=|2λ-1|2λ2-λ+1 =12·2λ-12λ2-λ+1=12·4-3λ2-λ+1=12·4-3⎝ ⎛⎭⎪⎫λ-122+34,当λ=12时,cos θ取得最小值为0,当λ=0或1时,cos θ取得最大值为12,∴0≤cos θ≤12,则π3≤θ≤π2.(2)(多选)(2022·济宁模拟)如图,AC 为圆锥SO 底面圆O 的直径,点B 是圆O 上异于A ,C 的动点,SO =OC =2,则下列结论正确的是( )A .圆锥SO 的侧面积为82πB .三棱锥S -ABC 体积的最大值为83C .∠SAB 的取值范围是⎝ ⎛⎭⎪⎫π4,π3D .若AB =BC ,E 为线段AB 上的动点,则SE +CE 的最小值为2(3+1) 答案 BD解析 在Rt △SOC 中,SC =SO 2+OC 2=22,则圆锥的母线长l =22,半径r =OC =2, 对于选项A ,圆锥SO 的侧面积为πrl =42π, 故选项A 错误;对于选项B ,当OB ⊥AC 时,△ABC 的面积最大,此时S △ABC =12×4×2=4,则三棱锥S -ABC 体积的最大值为13×S △ABC ×SO =13×4×2=83,故选项B 正确;对于选项C ,当点B 与点A 重合时,∠ASB =0为最小角,当点B 与点C 重合时,∠ASB =π2,达到最大值,又因为B 与A ,C 不重合,则∠ASB ∈⎝ ⎛⎭⎪⎫0,π2,又2∠SAB +∠ASB =π,可得∠SAB ∈⎝ ⎛⎭⎪⎫π4,π2, 故选项C 不正确;对于选项D ,由AB =BC ,∠ABC =π2,AC =4,得AB =BC =22,又SA =SB =22, 则△SAB 为等边三角形, 则∠SBA =π3,将△SAB 以AB 为轴旋转到与△ABC 共面,得到△S 1AB ,则△S 1AB 为等边三角形,∠S 1BA =π3,如图所示,则(SE +CE )min =S 1C , 因为S 1B =BC =22,∠S 1BC =∠S 1BA +∠ABC =5π6,S 1C 2=S 1B 2+BC 2-2×S 1B ×BC ×cos5π6=8+8+83=(23+2)2,则(SE +CE )min =S 1C =2(3+1), 故选项D 正确.思维升华 在动态变化过程中产生的体积最大、距离最大(小)、角的范围等问题,常用的思路是(1)直观判断:在变化过程中判断点、线、面在何位置时,所求的量有相应最大、最小值,即可求解.(2)函数思想:通过建系或引入变量,把这类动态问题转化为目标函数,从而利用代数方法求目标函数的最值.跟踪训练3 (1)(2022·邢台模拟)球O 为正四面体ABCD 的内切球,AB =2,MN 是球O 的直径,点P 在正四面体ABCD 的表面运动,则PM →·PN →的最小值为______,最大值为______. 答案 0 43解析 PM →·PN →=(PO →+OM →)·(PO →+ON →)=PO →2-OM →2,如图所示:设球O 的半径为r ,由题可知正四面体ABCD 的高为h =AO 1=AD 2-O 1D 2=263,所以4×13×⎝ ⎛⎭⎪⎫34×22×r =13×⎝ ⎛⎭⎪⎫34×22×263,解得r =66.因为点P 在正四面体ABCD 的表面运动, 所以|PO →|的最大值为AO =h -r =62,最小值为r =66,又|OM →|=r =66, 所以PM →·PN →的最小值为0,最大值为43.(2)(2022·杭州检测)在长方体ABCD -A 1B 1C 1D 1中,AB =AA 1=2AD =2,E 为棱CC 1上一点,记平面BD 1E 与底面ABCD 的夹角为α,则当α取得最小值时CE 的长度为________. 答案 25解析 建立如图所示的空间直角坐标系,设CE =a ,a ∈[0,2],B (1,2,0),E (0,2,a ), D 1(0,0,2),BD 1—→=(-1,-2,2), BE →=(-1,0,a ),设平面BD 1E 的法向量为n =(x ,y ,z ), 则⎩⎪⎨⎪⎧n ·BD →1=0,n ·BE →=0,即⎩⎪⎨⎪⎧-x -2y +2z =0,-x +az =0,取x =a ,则n =⎝⎛⎭⎪⎫a ,1-a2,1, 显然平面ABCD 的一个法向量为m =(0,0,1), 即cos α=|m ·n ||m ||n |=1a 2+⎝⎛⎭⎪⎫1-a 22+1=154a 2-a +2=154⎝ ⎛⎭⎪⎫a -252+95,当α最小时,154⎝ ⎛⎭⎪⎫a -252+95取最大值,即当a =25时,cos α取最大值,α取得最小值.课时精练1.(2022·广州模拟)点P 为棱长是25的正方体ABCD -A 1B 1C 1D 1的内切球O 球面上的动点,点M 为B 1C 1的中点,若满足DP ⊥BM ,则动点P 的轨迹的长度为( ) A .πB.2πC.4πD.25π 答案 C解析 根据题意知,该正方体的内切球半径为r =5,如图.取BB 1的中点N ,连接CN ,则CN ⊥BM ,∴CN 为DP 在平面B 1C 1CB 中的射影,∴点P 的轨迹为过D ,C ,N 的平面与内切球的交线,∵正方体ABCD -A 1B 1C 1D 1的棱长为25, ∴O 到过D ,C ,N 的平面的距离为55=1,∴截面圆的半径为2,∴点P 的轨迹的长度为2π×2=4π.2.正四面体ABCD 的棱长为1,点P 是该正四面体内切球球面上的动点,当PA →·PD →取得最小值时,点P 到AD 的距离为( ) A.32-612 B.6-312 C.22-312 D.24答案 A解析 因为四面体ABCD 是棱长为1的正四面体, 所以其体积为13×12×1×1×32×63=212.设正四面体ABCD 内切球的半径为r , 则4×13×12×1×1×32×r =212,得r =612.如图,取AD 的中点E ,则PA →·PD →=(PE →+EA →)·(PE →+ED →)=PE →2+PE →·(EA →+ED →)+EA →·ED →=PE →2-14.显然,当PE 的长度最小时,PA →·PD →取得最小值. 设正四面体内切球的球心为O , 可求得OA =OD =64.因为球心O 到点E 的距离d =OA 2-AE 2=⎝ ⎛⎭⎪⎫642-⎝ ⎛⎭⎪⎫122=24, 所以球O 上的点P 到点E 的最小距离为d -r =24-612=32-612, 即当PA →·PD →取得最小值时,点P 到AD 的距离为32-612.3.如图,在正三棱柱ABC -A 1B 1C 1中,底面边长为a ,侧棱长为b ,且a ≥b ,点D 是BC 1的中点,则直线AD 与侧面ABB 1A 1所成角的正切值的最小值是( )A.13013 B.63C.33D.3913答案 D解析 如图,取A 1B 1的中点E ,连接BE ,C 1E ,则C 1E ⊥A 1B 1,由正三棱柱的性质可知,平面A 1B 1C 1⊥平面ABB 1A 1,∴C 1E ⊥平面ABB 1A 1,取BE 的中点F ,连接AF ,DF .∵D 为BC 1的中点,∴DF ∥C 1E , ∴DF ⊥平面ABB 1A 1,∴∠DAF 即为直线AD 与侧面ABB 1A 1所成的角. 在Rt △AFD 中,DF =12C 1E =34a ,AF =AD 2-DF 2=9a 2+4b24,∴tan∠DAF =DF AF=3a 9a 2+4b 2=13+4b 23a2≥13+43=3913,当且仅当a =b 时,等号成立,∴直线AD 与侧面ABB 1A 1所成角的正切值的最小值为3913. 4.(多选)(2022·长沙检测)设动点P 在正方体ABCD -A 1B 1C 1D 1上(含内部),且D 1P —→=λD 1B —→,当∠APC 为锐角时,实数λ可能的取值是( ) A.12B.13C.14D.15 答案 CD解析 设AP =x ,D 1P =t ,正方体的棱长为1, 则AC =2,在△APC 中,由余弦定理得cos∠APC =x 2+x 2-22x 2=x 2-1x 2, 若∠APC 为锐角,则x 2-1x2>0,则x 2>1,在△AD 1P 中,AD 1=2, cos∠AD 1P =22+32-12×2×3=63, 于是由余弦定理得x 2=2+t 2-2×2×t ×63, 于是2+t 2-2×2×t ×63>1, 即3t 2-43t +3>0, 解得t >3或t <33,由D 1B =3, 故λ>1(舍去)或0<λ<13.5.(多选)如图,在棱长为1的正方体ABCD -A 1B 1C 1D 1中,P ,M 分别为棱CD ,CC 1的中点.Q 为线段A 1B 上任一点,则下列说法正确的是( )A .平面APM 内存在直线与A 1D 1平行B .平面APM 截正方体ABCD -A 1B 1C 1D 1所得截面的面积为98C .直线AP 和DQ 所成的角可能为60°D .直线AP 和DQ 所成的角可能为30°答案 BC解析 对于选项A ,在正方体ABCD -A 1B 1C 1D 1中,BC ∥A 1D 1,在平面ABCD 中,直线AP ,BC 相交,所以直线BC 与平面APM 相交,故直线A 1D 1与平面APM 相交,故平面APM 内不存在直线与A 1D 1平行,所以选项A 错误;对于选项B ,如图,连接C 1D ,AB 1,因为P ,M 分别为棱CD ,CC 1的中点, 所以PM ∥C 1D ,PM =12C 1D ,在正方体ABCD -A 1B 1C 1D 1中,AB 1∥C 1D , 所以PM ∥AB 1,连接B 1M , 则梯形AB 1MP 为所求的截面, 易知AP =B 1M =1+14=52, PM =⎝ ⎛⎭⎪⎫122+⎝ ⎛⎭⎪⎫122=22,AB 1=2, 所以等腰梯形AB 1MP 的高为AP 2-⎝⎛⎭⎪⎫AB 1-PM 22=54-⎝ ⎛⎭⎪⎫242=324, 所以梯形AB 1MP 的面积为 12×⎝ ⎛⎭⎪⎫22+2×324=98, 选项B 正确;对于选项C ,D ,以D 为坐标原点,DA →,DC →,DD 1—→的方向分别为x 轴、y 轴、z 轴的正方向,建立如图所示的空间直角坐标系,则D (0,0,0),A (1,0,0),P ⎝ ⎛⎭⎪⎫0,12,0,B (1,1,0),A 1(1,0,1),A 1B —→=(0,1,-1),DA 1—→=(1,0,1),PA →=⎝⎛⎭⎪⎫1,-12,0,设A 1Q —→=λA 1B →=λ(0,1,-1)=(0,λ,-λ), 0≤λ≤1,所以DQ →=DA 1—→+A 1Q —→=(1,λ,1-λ), 所以|cos 〈PA →,DQ →〉|=⎪⎪⎪⎪⎪⎪1-12λ52×1+λ2+1-λ2=2-λ10·λ2-λ+1. 当2-λ10·λ2-λ+1=cos60°=12, 即λ2+λ-1=0时,解得λ=±5-12,其中5-12∈[0,1], 当2-λ10·λ2-λ+1=cos30°=32, 即13λ2-7λ+7=0时,方程无解.所以直线AP 和DQ 所成的角可能为60°,但不可能为30°,选项C 正确,选项D 错误. 6.(多选)在棱长为1的正方体ABCD -A 1B 1C 1D 1中,M ,N 分别为BD 1,B 1C 1的中点,点P 在正方体的表面上运动,且满足MP ⊥CN .给出的下列说法中正确的是( )A .点P 可以是棱BB 1的中点 B .线段MP 的最大值为34C .点P 的轨迹是正方形D .点P 的轨迹长度为2+ 5 答案 BD解析 在正方体ABCD -A 1B 1C 1D 1中,以D 为坐标原点,DA 为x 轴,DC 为y 轴,建立如图所示的空间直角坐标系,∵该正方体的棱长为1,M ,N 分别为BD 1,B 1C 1的中点,∴D 1(0,0,1),B (1,1,0),M ⎝ ⎛⎭⎪⎫12,12,12, N ⎝ ⎛⎭⎪⎫12,1,1,C (0,1,0),∴CN →=⎝ ⎛⎭⎪⎫12,0,1,设P (x ,y ,z ),则MP →=⎝ ⎛⎭⎪⎫x -12,y -12,z -12,∵MP ⊥CN ,∴12⎝ ⎛⎭⎪⎫x -12+z -12=0,即2x +4z -3=0,当x =1时,z =14,当x =0时,z =34,取E ⎝ ⎛⎭⎪⎫1,0,14,F ⎝ ⎛⎭⎪⎫1,1,14,G ⎝ ⎛⎭⎪⎫0,1,34, H ⎝⎛⎭⎪⎫0,0,34,连接EF ,FG ,GH ,HE , 则EF →=HG →=(0,1,0), EH →=FG →=⎝ ⎛⎭⎪⎫-1,0,12,∴四边形EFGH 为矩形, 又EF →·CN →=0,EH →·CN →=0, 即EF ⊥CN ,EH ⊥CN ,又EF 和EH 为平面EFGH 中的两条相交直线, ∴CN ⊥平面EFGH ,又EM →=⎝ ⎛⎭⎪⎫-12,12,14,MG →=⎝ ⎛⎭⎪⎫-12,12,14,∴M 为EG 的中点,则M ∈平面EFGH , 为使MP ⊥CN ,必有点P ∈平面EFGH ,又点P 在正方体表面上运动, ∴点P 的轨迹为四边形EFGH ,∴点P 不可能是棱BB 1的中点,故选项A 错误; 又EF =GH =1,EH =FG =52, ∴EF ≠EH ,则点P 的轨迹是矩形不是正方形,且矩形EFGH 的周长为2+2×52=2+5, 故选项C 错误,选项D 正确; ∵点P 的轨迹为矩形EFGH ,∴当P 点在矩形的四个端点时,MP 取得最大值,且MP 的最大值为34,故B 正确.7.(多选)如图,在棱长为1的正方体ABCD -A 1B 1C 1D 1中,M 为线段AB 1上的动点(含端点),则下列结论正确的是( )A .平面BCM ⊥平面A 1AMB .三棱锥B -MB 1C 体积的最大值为16C .当M 为AB 1的中点时,直线B 1D 与直线CM 所成的角的余弦值为23D .直线CM 与A 1D 所成的角不可能是π4答案 ABC解析 对于A ,∵BC ⊥AB ,BC ⊥BB 1,AB ∩BB 1=B ,AB ,BB 1⊂平面AA 1M , ∴BC ⊥平面AA 1M ,又BC ⊂平面BCM , ∴平面BCM ⊥平面A 1AM ,A 正确; 对于B ,1111·11,33B MBC C BB M BB M BB M V V S S BC --===△△ ∵M 为AB 1上的动点,∴当M 与A 重合时,1BB M S △取得最大值为12AB ·BB 1=12,∴1max ()B MB C V -=13×12=16,B 正确;对于C ,以D 1为坐标原点,可建立如图所示的空间直角坐标系,当M 为AB 1的中点时,M ⎝⎛⎭⎪⎫1,12,12,又B 1(1,1,0),C (0,1,1),D (0,0,1),∴B 1D —→=(-1,-1,1),CM →=⎝ ⎛⎭⎪⎫1,-12,-12,∴cos〈B 1D —→,CM →〉=B 1D —→·CM →|B 1D —→||CM →|=-13×62=-23,∴当M 为AB 1的中点时,直线B 1D 与直线CM 所成的角的余弦值为23,C 正确; 对于D ,如C 中所建立的空间直角坐标系, 设M (1,y ,z ),AM →=λAB 1—→(0≤λ≤1), 又A (1,0,1),∴AB 1—→=(0,1,-1),AM →=(0,y ,z -1), ∴(0,y ,z -1)=(0,λ,-λ), 则y =λ,z =1-λ,∴M (1,λ,1-λ), ∴CM →=(1,λ-1,-λ),又A 1D —→=(-1,0,1), ∴|cos〈CM →,A 1D —→〉|=|CM →·A 1D —→||CM →||A 1D —→|=|-1-λ|1+λ-12+λ2×2, 若直线CM 与A 1D 所成的角为π4, 则|-1-λ|1+λ-12+λ2×2=22, 解得λ=2±3,又λ∈[0,1],∴当λ=2-3,即AM →=(2-3)AB 1—→时,直线CM 与A 1D 所成的角为π4,D 错误.8.(多选)正三棱柱ABC -A 1B 1C 1(底面是正三角形,侧棱垂直底面)的各条棱长均相等,D 为AA 1的中点.M ,N 分别是BB 1,CC 1上的动点(含端点),且满足BM =C 1N .当M ,N 运动时,下列结论中正确的是( )A .平面DMN ⊥平面BCC 1B 1 B .三棱锥A 1-DMN 的体积为定值C .△DMN 可能为直角三角形D .平面DMN 与平面ABC 所成的锐二面角范围为⎝⎛⎦⎥⎤0,π4答案 ABD 解析 如图,当M ,N 分别是BB 1,CC 1上的动点(含端点),且满足BM =C 1N 时,则线段MN 一定过正方形BCC 1B 1的中心O ,而DO ⊥平面BCC 1B 1,DO ⊂平面DMN ,可得平面DMN ⊥平面BCC 1B 1,故A 正确; 当M ,N 分别是BB 1,CC 1上的动点(含端点)时,过点M 作A 1D 边上的高,其长等于AB 的长,所以△A 1DM 的面积不变,由于C 1N ∥平面A 1DM ,故点N 到平面A 1DM 的距离等于点C 1到平面A 1DM 的距离,则点N 到平面A 1DM 的距离为定值,故三棱锥A 1-DMN 的体积为定值,所以B 正确; 由BM =C 1N 可得,DN =DM ,若△DMN 为直角三角形,则一定是以∠MDN 为直角的直角三角形,但MN 的最大值为BC 1,而此时DN ,DM 的长都大于BB 1,故△DMN 不可能为直角三角形,所以C 不正确;当M ,N 分别是BB 1,CC 1的中点时,平面DMN 与平面ABC 平行,所成角为0度; 当M 与B 重合,N 与C 1重合,平面DMN 与平面ABC 所成锐二面角最大;延长C 1D 交CA 于G ,连接BG ,则平面DMN ∩平面ABC =GB ,由于D 为AA 1的中点,AA 1=CC 1,所以DA ∥CC 1,且DA =12CC 1,故在△C 1GC 中,D 为C 1G 的中点,A 为CG 的中点,在△C 1GB 中,D 为C 1G 的中点,O 为BC 1的中点,故DO ∥GB ,由于DO ⊥平面BCC 1B 1,所以GB ⊥平面BCC 1B 1,则GB ⊥BC ,GB ⊥BC 1,所以平面DMN 与平面ABC 所成锐二面角最大为∠C 1BC =π4,故D 正确.9.如图,在棱长为1的正方体ABCD -A 1B 1C 1D 1中,点M 是AD 的中点,点P 在底面ABCD 内(不包括边界)运动,若B 1P ∥平面A 1BM ,则C 1P 的长度的取值范围是____________.答案 ⎣⎢⎡⎭⎪⎫305,2 解析 如图,取BC 的中点N ,连接B 1D ,B 1N ,DN ,过C 作CO ⊥DN 于O ,连接C 1O ,由正方体的性质知DN ∥MB ,A 1M ∥B 1N ,又DN ∩B 1N =N ,MB ∩A 1M =M , ∴平面B 1DN ∥平面A 1BM ,∴点P 在底面ABCD 内的轨迹是线段DN (不含点N 和点D ). 连接C 1D ,C 1N ,在△C 1DN 中,C 1D =2,DN =C 1N =12+⎝ ⎛⎭⎪⎫122=52, ∴1C DN S △=12×2×⎝ ⎛⎭⎪⎫522-⎝ ⎛⎭⎪⎫222=64, ∵C 1C ⊥平面ABCD ,CO ⊥DN ,∴C 1O ⊥DN ,则当P 与O 重合时,C 1P 的长度取得最小值, ∴C 1P 的长度的最小值为C 1O =6412×52=305, 又C 1P <2,∴C 1P 的长度的取值范围是⎣⎢⎡⎭⎪⎫305,2. 10.在正四棱柱ABCD -A 1B 1C 1D 1中,AB =2,AA 1=4,E 为AB 的中点,点F 满足C 1F —→=3FC →,动点M 在侧面AA 1D 1D 内运动,且MB ∥平面D 1EF ,则|MD →|的取值范围是________.答案 ⎣⎢⎡⎦⎥⎤13,21095解析 因为ABCD -A 1B 1C 1D 1是正四棱柱,以点D 为坐标原点,建立如图所示的空间直角坐标系,设M (x ,0,z ),B (2,2,0),D 1(0,0,4),E (2,1,0), 因为C 1F —→=3FC →,所以F 是CC 1四等分点(靠近C ),所以F (0,2,1),所以D 1E —→=(2,1,-4),D 1F —→=(0,2,-3),设平面D 1EF 的一个法向量为n =(a ,b ,c ), 则⎩⎪⎨⎪⎧D 1E —→·n =0,D 1F —→·n =0,即⎩⎪⎨⎪⎧ 2a +b -4c =0,2b -3c =0,令c =2,则a =52,b =3,故n =⎝ ⎛⎭⎪⎫52,3,2,又MB →=(2-x ,2,-z ),MB ∥平面D 1EF ,所以MB →⊥n ,即MB →·n =0,所以52(2-x )+6-2z =0,所以z =112-54x ,故|MD →|=x 2+z 2=x 2+⎝ ⎛⎭⎪⎫112-54x 2=41x 2-220x +4844,因为0≤x ≤2,0≤z ≤4,所以112-54x ∈[0,4],故x ∈⎣⎢⎡⎦⎥⎤65,2,令y =41x 2-220x +184, 因为二次函数的对称轴为x =2202×41=11041>2,所以函数在x ∈⎣⎢⎡⎦⎥⎤65,2上单调递减,所以当x =65时,|MD →|取得最大值, 所以|MD →|的最大值为 41×⎝ ⎛⎭⎪⎫652-220×65+4844=21095,当x =2时,|MD →|取得最小值,所以|MD →|的最小值为41×22-220×2+4844=13,所以|MD →|的取值范围是⎣⎢⎡⎦⎥⎤13,21095.。
2023年新高考数学大一轮复习专题四立体几何第1讲空间几何体(含答案)

新高考数学大一轮复习专题:第1讲 空间几何体[考情分析] 几何体的结构特征是立体几何的基础,空间几何体的表面积与体积是高考题的重点与热点,多以小题的形式进行考查,属于中等难度. 考点一 表面积与体积 核心提炼1.旋转体的侧面积和表面积(1)S 圆柱侧=2πrl ,S 圆柱表=2πr (r +l )(r 为底面半径,l 为母线长). (2)S 圆锥侧=πrl ,S 圆锥表=πr (r +l )(r 为底面半径,l 为母线长). (3)S 球表=4πR 2(R 为球的半径). 2.空间几何体的体积公式V 柱=Sh (S 为底面面积,h 为高); V 锥=13Sh (S 为底面面积,h 为高); V 球=43πR 3(R 为球的半径).例1 (1)已知圆锥的顶点为S ,母线SA ,SB 所成角的余弦值为78,SA 与圆锥底面所成角为45°.若△SAB 的面积为515,则该圆锥的侧面积为________. 答案 402π解析 因为母线SA 与圆锥底面所成的角为45°, 所以圆锥的轴截面为等腰直角三角形. 设底面圆的半径为r ,则母线长l =2r . 在△SAB 中,cos∠ASB =78,所以sin∠ASB =158.因为△SAB 的面积为515,即12SA ·SB sin∠ASB=12×2r ×2r ×158=515, 所以r 2=40,故圆锥的侧面积为πrl =2πr 2=402π.(2)如图,已知正三棱柱ABC -A 1B 1C 1的各棱长均为2,点D 在棱AA 1上,则三棱锥D -BB 1C 1的体积为________.答案 233解析 如图,取BC 的中点O ,连接AO .∵正三棱柱ABC -A 1B 1C 1的各棱长均为2, ∴AC =2,OC =1,则AO = 3. ∵AA 1∥平面BCC 1B 1,∴点D 到平面BCC 1B 1的距离为 3. 又11BB C S=12×2×2=2, ∴11D BB C V =13×2×3=233.易错提醒 (1)计算表面积时,有些面的面积没有计算到(或重复计算). (2)一些不规则几何体的体积不会采用分割法或补形思想转化求解. (3)求几何体体积的最值时,不注意使用基本不等式或求导等确定最值.跟踪演练1 (1)已知圆柱的上、下底面的中心分别为O 1,O 2,过直线O 1O 2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( ) A .122π B .12π C .82π D .10π答案 B解析 设圆柱的底面半径为r ,高为h ,由题意可知2r =h =22,∴圆柱的表面积S =2πr 2+2πr ·h =4π+8π=12π.故选B.(2)如图,在Rt△ABC 中,AB =BC =1,D 和E 分别是边BC 和AC 上异于端点的点,DE ⊥BC ,将△CDE 沿DE 折起,使点C 到点P 的位置,得到四棱锥P -ABDE ,则四棱锥P -ABDE 的体积的最大值为________.答案327解析 设CD =DE =x (0<x <1),则四边形ABDE 的面积S =12(1+x )(1-x )=12(1-x 2),当平面PDE ⊥平面ABDE 时,四棱锥P -ABDE 的体积最大,此时PD ⊥平面ABDE ,且PD =CD =x ,故四棱锥P -ABDE 的体积V =13S ·PD =16(x -x 3),则V ′=16(1-3x 2).当x ∈⎝ ⎛⎭⎪⎫0,33时,V ′>0;当x ∈⎝⎛⎭⎪⎫33,1时,V ′<0. ∴当x =33时,V max =327. 考点二 多面体与球 核心提炼解决多面体与球问题的两种思路(1)利用构造长方体、正四面体等确定直径.(2)利用球心O 与截面圆的圆心O 1的连线垂直于截面圆的性质确定球心.例2 (1)已知三棱锥P -ABC 满足平面PAB ⊥平面ABC ,AC ⊥BC ,AB =4,∠APB =30°,则该三棱锥的外接球的表面积为__________. 答案 64π解析 因为AC ⊥BC ,所以△ABC 的外心为斜边AB 的中点,因为平面PAB ⊥平面ABC ,所以三棱锥P -ABC 的外接球球心在平面PAB 上, 即球心就是△PAB 的外心,根据正弦定理ABsin∠APB =2R ,解得R =4,所以外接球的表面积为4πR 2=64π.(2)(2020·全国Ⅲ)已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为________. 答案23π 解析 圆锥内半径最大的球即为圆锥的内切球,设其半径为r .作出圆锥的轴截面PAB ,如图所示,则△PAB 的内切圆为圆锥的内切球的大圆.在△PAB 中,PA =PB =3,D 为AB 的中点,AB =2,E 为切点,则PD =22,△PEO ∽△PDB , 故PO PB =OE DB ,即22-r 3=r 1,解得r =22, 故内切球的体积为43π⎝ ⎛⎭⎪⎫223=23π.规律方法 (1)长方体的外接球直径等于长方体的体对角线长.(2)三棱锥S -ABC 的外接球球心O 的确定方法:先找到△ABC 的外心O 1,然后找到过O 1的平面ABC 的垂线l ,在l 上找点O ,使OS =OA ,点O 即为三棱锥S -ABC 的外接球的球心. (3)多面体的内切球可利用等积法求半径.跟踪演练2 (1)已知A ,B 是球O 的球面上两点,∠AOB =90°,C 为该球面上的动点.若三棱锥O -ABC 体积的最大值为36,则球O 的表面积为( ) A .36πB.64πC.144πD.256π 答案 C解析 如图所示,设球O 的半径为R ,因为∠AOB =90°, 所以S △AOB =12R 2,因为V O -ABC =V C -AOB , 而△AOB 的面积为定值,当点C 位于垂直于平面AOB 的直径端点时,三棱锥O -ABC 的体积最大, 此时V O -ABC =V C -AOB =13×12R 2×R =16R 3=36,故R =6,则球O 的表面积为S =4πR 2=144π.(2)中国古代数学经典《九章算术》系统地总结了战国、秦、汉时期的数学成就,书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的三棱锥称之为鳖臑,如图为一个阳马与一个鳖臑的组合体,已知PA ⊥平面ABCE ,四边形ABCD 为正方形,AD =5,ED =3,若鳖臑P -ADE 的外接球的体积为92π,则阳马P -ABCD 的外接球的表面积为________.答案 20π解析 ∵四边形ABCD 是正方形,∴AD ⊥CD ,即AD ⊥CE ,且AD =5,ED =3, ∴△ADE 的外接圆半径为r 1=AE 2=AD 2+ED 22=2,设鳖臑P -ADE 的外接球的半径为R 1, 则43πR 31=92π,解得R 1=322. ∵PA ⊥平面ADE ,∴R 1=⎝ ⎛⎭⎪⎫PA 22+r 21,可得PA 2=R 21-r 21=102,∴PA =10.正方形ABCD 的外接圆直径为2r 2=AC =2AD =10, ∴r 2=102, ∵PA ⊥平面ABCD ,∴阳马P -ABCD 的外接球半径R 2=⎝ ⎛⎭⎪⎫PA 22+r 22=5, ∴阳马P -ABCD 的外接球的表面积为4πR 22=20π.专题强化练一、单项选择题1.水平放置的△ABC 的直观图如图,其中B ′O ′=C ′O ′=1,A ′O ′=32,那么原△ABC 是一个( )A .等边三角形B .直角三角形C .三边中只有两边相等的等腰三角形D .三边互不相等的三角形 答案 A解析 AO =2A ′O ′=2×32=3,BC =B ′O ′+C ′O ′=1+1=2.在Rt△AOB 中,AB =12+32=2,同理AC =2,所以原△ABC 是等边三角形.2.(2020·全国Ⅰ)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥.以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )A.5-14 B.5-12 C.5+14 D.5+12答案 C解析 设正四棱锥的底面正方形的边长为a ,高为h , 侧面三角形底边上的高(斜高)为h ′, 则由已知得h 2=12ah ′.如图,设O 为正四棱锥S -ABCD 底面的中心,E 为BC 的中点,则在Rt△SOE 中,h ′2=h 2+⎝ ⎛⎭⎪⎫a 22,∴h ′2=12ah ′+14a 2,∴⎝⎛⎭⎪⎫h ′a 2-12·h ′a -14=0, 解得h ′a =5+14(负值舍去). 3.已知一个圆锥的侧面积是底面积的2倍,记该圆锥的内切球的表面积为S 1,外接球的表面积为S 2,则S 1S 2等于( )A.12B.13C.14D.18答案 C解析如图,由已知圆锥侧面积是底面积的2倍,不妨设底面圆半径为r,l为底面圆周长,R为母线长,则12lR=2πr2,即12·2π·r·R=2πr2,解得R=2r,故∠ADC=30°,则△DEF为等边三角形,设B为△DEF的重心,过B作BC⊥DF,则DB为圆锥的外接球半径,BC为圆锥的内切球半径,则BCBD=12,∴r内r外=12,故S1S2=14.4.(2020·大连模拟)一件刚出土的珍贵文物要在博物馆大厅中央展出,如图,需要设计各面是玻璃平面的无底正四棱柱将其罩住,罩内充满保护文物的无色气体.已知文物近似于塔形,高1.8米,体积0.5立方米,其底部是直径为0.9米的圆形,要求文物底部与玻璃罩底边至少间隔0.3米,文物顶部与玻璃罩上底面至少间隔0.2米,气体每立方米1000元,则气体的费用最少为( )A.4500元B.4000元C.2880元D.2380元答案 B解析因为文物底部是直径为0.9米的圆形,文物底部与玻璃罩底边至少间隔0.3米,所以由正方形与圆的位置关系可知,底面正方形的边长为0.9+2×0.3=1.5米,又文物高 1.8米,文物顶部与玻璃罩上底面至少间隔0.2(米),所以正四棱柱的高为1.8+0.2=2(米),则正四棱柱的体积V=1.52×2=4.5(立方米).因为文物的体积为0.5立方米,所以罩内空气的体积为4.5-0.5=4(立方米),因为气体每立方米1000元,所以气体的费用最少为4×1000=4000(元),故选B.5.如图所示,在正方体ABCD -A 1B 1C 1D 1中,动点E 在BB 1上,动点F 在A 1C 1上,O 为底面ABCD 的中心,若BE =x ,A 1F =y ,则三棱锥O -AEF 的体积( )A .与x ,y 都有关B .与x ,y 都无关C .与x 有关,与y 无关D .与y 有关,与x 无关 答案 B解析 由已知得V 三棱锥O -AEF =V 三棱锥E -OAF =13S △AOF ·h (h 为点E 到平面AOF 的距离).连接OC ,因为BB 1∥平面ACC 1A 1,所以点E 到平面AOF 的距离为定值.又AO ∥A 1C 1,OA 为定值,点F 到直线AO 的距离也为定值,所以△AOF 的面积是定值,所以三棱锥O -AEF 的体积与x ,y 都无关.6.在梯形ABCD 中,∠ABC =π2,AD ∥BC ,BC =2AD =2AB =2.将梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体的体积为( ) A.2π3B.4π3 C.5π3D .2π 答案 C解析 如图,过点C 作CE 垂直AD 所在直线于点E ,梯形ABCD 绕AD 所在直线旋转一周而形成的旋转体是由以线段AB 的长为底面圆半径,线段BC 为母线的圆柱挖去以线段CE 的长为底面圆半径,ED 为高的圆锥,该几何体的体积为V =V 圆柱-V 圆锥=π·AB 2·BC -13·π·CE 2·DE=π×12×2-13π×12×1=5π3.7.(2020·全国Ⅰ)已知A ,B ,C 为球O 的球面上的三个点,⊙O 1为△ABC 的外接圆.若⊙O 1的面积为4π,AB =BC =AC =OO 1,则球O 的表面积为( ) A .64πB.48πC.36πD.32π 答案 A解析 如图,设圆O 1的半径为r ,球的半径为R ,正三角形ABC 的边长为a . 由πr 2=4π,得r =2, 则33a =2,a =23, OO 1=a =2 3.在Rt△OO 1A 中,由勾股定理得R 2=r 2+OO 21=22+(23)2=16,所以S 球=4πR 2=4π×16=64π.8.(2020·武汉调研)已知直三棱柱ABC -A 1B 1C 1的6个顶点都在球O 的表面上,若AB =AC =1,AA 1=23,∠BAC =2π3,则球O 的体积为( ) A.32π3B .3πC.4π3D .8π 答案 A解析 设△ABC 外接圆圆心为O 1,半径为r ,连接O 1O ,如图,易得O 1O ⊥平面ABC ,∵AB =AC =1,AA 1=23,∠BAC =2π3,∴2r =AB sin∠ACB =112=2,即O 1A =1,O 1O =12AA 1=3,∴OA =O 1O 2+O 1A 2=3+1=2,∴球O 的体积V =43π·OA 3=32π3.故选A.9.如图所示,某几何体由底面半径和高均为5的圆柱与半径为5的半球对接而成,在该封闭的几何体内部放入一个小圆柱体,且小圆柱体的上、下底面均与外层圆柱的底面平行,则小圆柱体积的最大值为( )A.2000π9B.4000π27C .81πD .128π答案 B解析 小圆柱的高分为上、下两部分,上部分的高同大圆柱的高相等,为5,下部分深入底部半球内.设小圆柱下部分的高为h (0<h <5),底面半径为r (0<r <5).由于r ,h 和球的半径构成直角三角形,即r 2+h 2=52,所以小圆柱的体积V =πr 2(h +5)=π(25-h 2)(h +5)(0<h <5),把V 看成是关于h 的函数,求导得V ′=-π(3h -5)(h +5).当0<h <53时,V ′>0,V 单调递增;当53<h <5时,V ′<0,V 单调递减.所以当h =53时,小圆柱的体积取得最大值.即V max =π⎝⎛⎭⎪⎫25-259×⎝⎛⎭⎪⎫53+5=4000π27,故选B.10.已知在三棱锥P -ABC 中,PA ,PB ,PC 两两垂直,且长度相等.若点P ,A ,B ,C 都在半径为1的球面上,则球心到平面ABC 的距离为( ) A.36B.12C.13D.32答案 C解析 ∵在三棱锥P -ABC 中,PA ,PB ,PC 两两垂直,且长度相等,∴此三棱锥的外接球即以PA ,PB ,PC 为三边的正方体的外接球O , ∵球O 的半径为1,∴正方体的边长为233,即PA =PB =PC =233,球心到截面ABC 的距离即正方体中心到截面ABC 的距离,设P 到截面ABC 的距离为h ,则正三棱锥P -ABC 的体积V =13S △ABC ×h =13S △PAB ×PC =13×12×⎝⎛⎭⎪⎫2333, ∵△ABC 为边长为263的正三角形,S △ABC =233,∴h =23, ∴球心(即正方体中心)O 到截面ABC 的距离为13.二、多项选择题11.(2020·枣庄模拟)如图,透明塑料制成的长方体容器ABCD -A 1B 1C 1D 1内灌进一些水,固定容器一边AB 于地面上,再将容器倾斜,随着倾斜度的不同,有下面几个结论,其中正确的是( )A .没有水的部分始终呈棱柱形B .水面EFGH 所在四边形的面积为定值C .随着容器倾斜度的不同,A 1C 1始终与水面所在平面平行D .当容器倾斜如图③所示时,AE ·AH 为定值 答案 AD解析 由于AB 固定,所以在倾斜的过程中,始终有CD ∥HG ∥EF ∥AB ,且平面AEHD ∥平面BFGC ,故水的部分始终呈棱柱形(三棱柱或四棱柱),且AB 为棱柱的一条侧棱,没有水的部分也始终呈棱柱形,故A 正确;因为水面EFGH 所在四边形,从图②,图③可以看出,EF ,GH 长度不变,而EH ,FG 的长度随倾斜度变化而变化,所以水面EFGH 所在四边形的面积是变化的,故B 错;假设A 1C 1与水面所在的平面始终平行,又A 1B 1与水面所在的平面始终平行,则长方体上底面A 1B 1C 1D 1与水面所在的平面始终平行,这就与倾斜时两个平面不平行矛盾,故C 错;水量不变时,棱柱AEH -BFG 的体积是定值,又该棱柱的高AB 不变,且V AEH -BFG =12·AE ·AH ·AB ,所以AE ·AH =2V AEH -BFGAB,即AE ·AH 是定值,故D 正确.12.(2020·青岛检测)已知四棱台ABCD -A 1B 1C 1D 1的上、下底面均为正方形,其中AB =22,A 1B 1=2,AA 1=BB 1=CC 1=DD 1=2,则下列叙述正确的是( )A .该四棱台的高为 3B .AA 1⊥CC 1C .该四棱台的表面积为26D .该四棱台外接球的表面积为16π 答案 AD解析 将四棱台补为如图所示的四棱锥P -ABCD ,并取E ,E 1分别为BC ,B 1C 1的中点,记四棱台上、下底面中心分别为O 1,O ,连接AC ,BD ,A 1C 1,B 1D 1,A 1O ,OE ,OP ,PE .由条件知A 1,B 1,C 1,D 1分别为四棱锥的侧棱PA ,PB ,PC ,PD 的中点,则PA =2AA 1=4,OA =2,所以OO 1=12PO =12PA 2-OA 2=3,故该四棱台的高为3,故A 正确;由PA =PC =4,AC =4,得△PAC 为正三角形,则AA 1与CC 1所成角为60°,故B 不正确;四棱台的斜高h ′=12PE =12PO 2+OE2=12×232+22=142,所以该四棱台的表面积为(22)2+(2)2+4×2+222×142=10+67,故C 不正确;易知OA 1=OB 1=OC 1=OD 1=O 1A 21+O 1O 2=2=OA =OB =OC =OD ,所以O 为四棱台外接球的球心,所以外接球的半径为2,外接球表面积为4π×22=16π,故D 正确.三、填空题13.(2020·浙江)已知圆锥的侧面积(单位:cm 2)为2π,且它的侧面展开图是一个半圆,则这个圆锥的底面半径(单位:cm)是________. 答案 1解析 如图,设圆锥的母线长为l ,底面半径为r ,则圆锥的侧面积S 侧=πrl =2π, 即r ·l =2.由于侧面展开图为半圆, 可知12πl 2=2π,可得l =2,因此r =1.14.在如图所示的斜截圆柱中,已知圆柱的底面直径为40cm ,母线长最短50cm ,最长80cm ,则斜截圆柱的侧面面积S =________cm 2.答案 2600π解析 将题图所示的相同的两个几何体对接为圆柱,则圆柱的侧面展开图为矩形.由题意得所求侧面展开图的面积S =12×(π×40)×(50+80)=2600π(cm 2).15.已知球O 与棱长为4的正四面体的各棱相切,则球O 的体积为________. 答案823π 解析 将正四面体补成正方体,则正四面体的棱为正方体面上的对角线,因为正四面体的棱长为4,所以正方体的棱长为2 2.因为球O 与正四面体的各棱都相切,所以球O 为正方体的内切球,即球O 的直径2R =22,则球O 的体积V =43πR 3=823π.16.(2020·新高考全国Ⅰ)已知直四棱柱ABCD -A 1B 1C 1D 1的棱长均为2,∠BAD =60°.以D 1为球心,5为半径的球面与侧面BCC 1B 1的交线长为________. 答案2π2解析 如图,设B 1C 1的中点为E ,球面与棱BB 1,CC 1的交点分别为P ,Q , 连接DB ,D 1B 1,D 1P ,D 1E ,EP ,EQ ,由∠BAD =60°,AB =AD ,知△ABD 为等边三角形, ∴D 1B 1=DB =2,∴△D 1B 1C 1为等边三角形, 则D 1E =3且D 1E ⊥平面BCC 1B 1,∴E 为球面截侧面BCC 1B 1所得截面圆的圆心, 设截面圆的半径为r , 则r =R 2球-D 1E 2=5-3= 2. 又由题意可得EP =EQ =2,∴球面与侧面BCC 1B 1的交线为以E 为圆心的圆弧PQ . 又D 1P =5,∴B 1P =D 1P 2-D 1B 21=1, 同理C 1Q =1,∴P ,Q 分别为BB 1,CC 1的中点, ∴∠PEQ =π2,知PQ 的长为π2×2=2π2,即交线长为2π2.。
2023年高考数学一轮复习第七章立体几何与空间向量3空间点直线平面之间的位置关系练习含解析

空间点、直线、平面之间的位置关系考试要求 1.借助长方体,在直观认识空间点、直线、平面的位置关系的基础上,抽象出空间点、直线、平面的位置关系的定义.2.了解四个基本事实和一个定理,并能应用定理解决问题.知识梳理 1.平面基本事实1:过不在一条直线上的三个点,有且只有一个平面.基本事实2:如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内. 基本事实3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.基本事实4:平行于同一条直线的两条直线平行. 2.“三个”推论推论1:经过一条直线和这条直线外一点,有且只有一个平面. 推论2:经过两条相交直线,有且只有一个平面. 推论3:经过两条平行直线,有且只有一个平面. 3.空间中直线与直线的位置关系⎩⎪⎨⎪⎧共面直线⎩⎪⎨⎪⎧相交直线,平行直线,异面直线:不同在任何一个平面内,没有 公共点.4.空间中直线与平面的位置关系直线与平面的位置关系有:直线在平面内、直线与平面相交、直线与平面平行三种情况. 5.空间中平面与平面的位置关系平面与平面的位置关系有平行、相交两种情况. 6.等角定理如果空间中两个角的两条边分别对应平行,那么这两个角相等或互补. 7.异面直线所成的角(1)定义:已知两条异面直线a ,b ,经过空间任一点O 分别作直线a ′∥a ,b ′∥b ,把直线a ′与b ′所成的角叫做异面直线a 与b 所成的角(或夹角).(2)范围:⎝⎛⎦⎥⎤0,π2.思考辨析判断下列结论是否正确(请在括号中打“√”或“×”)(1)两个平面α,β有一个公共点A ,就说α,β相交于过A 点的任意一条直线.( × ) (2)两两相交的三条直线最多可以确定三个平面.( √ ) (3)如果两个平面有三个公共点,那么这两个平面重合.( × ) (4)没有公共点的两条直线是异面直线.( × ) 教材改编题1.(多选)如图是一个正方体的展开图,如果将它还原为正方体,则下列说法正确的是( )A .AB 与CD 是异面直线 B .GH 与CD 相交C .EF ∥CD D .EF 与AB 异面 答案 ABC解析 把展开图还原成正方体,如图所示.还原后点G 与C 重合,点B 与F 重合,由图可知ABC 正确,EF 与AB 相交,故D 错. 2.如果直线a ⊂平面α,直线b ⊂平面β.且α∥β,则a 与b ( ) A .共面 B .平行 C .是异面直线D .可能平行,也可能是异面直线 答案 D解析 α∥β,说明a 与b 无公共点, ∴a 与b 可能平行也可能是异面直线.3.如图,在三棱锥A -BCD 中,E ,F ,G ,H 分别是棱AB ,BC ,CD ,DA 的中点,则(1)当AC ,BD 满足条件________时,四边形EFGH 为菱形; (2)当AC ,BD 满足条件________时,四边形EFGH 为正方形. 答案 (1)AC =BD (2)AC =BD 且AC ⊥BD 解析 (1)∵四边形EFGH 为菱形, ∴EF =EH ,∵EF 綉12AC ,EH 綉12BD ,∴AC =BD .(2)∵四边形EFGH 为正方形, ∴EF =EH 且EF ⊥EH , ∵EF 綉12AC ,EH 綉12BD ,∴AC =BD 且AC ⊥BD .题型一 基本事实应用例1 如图所示,在正方体ABCD -A 1B 1C 1D 1中,点E ,F 分别是AB ,AA 1的中点,连接D 1F ,CE .求证:(1)E ,C ,D 1,F 四点共面; (2)CE ,D 1F ,DA 三线共点.证明 (1)如图所示,连接CD 1,EF ,A 1B , ∵E ,F 分别是AB ,AA 1的中点, ∴EF ∥A 1B ,且EF =12A 1B .又∵A 1D 1∥BC ,A 1D 1=BC , ∴四边形A 1BCD 1是平行四边形, ∴A 1B ∥CD 1,∴EF ∥CD 1,∴EF 与CD 1能够确定一个平面ECD 1F , 即E ,C ,D 1,F 四点共面.(2)由(1)知EF ∥CD 1,且EF =12CD 1,∴四边形CD 1FE 是梯形, ∴CE 与D 1F 必相交,设交点为P , 则P ∈CE ,且P ∈D 1F ,∵CE ⊂平面ABCD ,D 1F ⊂平面A 1ADD 1, ∴P ∈平面ABCD ,且P ∈平面A 1ADD 1. 又∵平面ABCD ∩平面A 1ADD 1=AD , ∴P ∈AD ,∴CE ,D 1F ,DA 三线共点. 教师备选如图所示,已知在正方体ABCD -A 1B 1C 1D 1中,E ,F 分别为D 1C 1,C 1B 1的中点,AC ∩BD =P ,A 1C 1∩EF =Q .求证:(1)D ,B ,F ,E 四点共面;(2)若A 1C 交平面DBFE 于R 点,则P ,Q ,R 三点共线. 证明 (1)∵EF 是△D 1B 1C 1的中位线, ∴EF ∥B 1D 1.在正方体ABCD -A 1B 1C 1D 1中,B 1D 1∥BD , ∴EF ∥BD .∴EF ,BD 确定一个平面,即D ,B ,F ,E 四点共面. (2)在正方体ABCD -A 1B 1C 1D 1中, 设平面A 1ACC 1为α, 平面BDEF 为β. ∵Q ∈A 1C 1,∴Q ∈α.又Q∈EF,∴Q∈β,则Q是α与β的公共点,同理,P是α与β的公共点,∴α∩β=PQ.又A1C∩β=R,∴R∈A1C.∴R∈α,且R∈β,则R∈PQ,故P,Q,R三点共线.思维升华共面、共线、共点问题的证明(1)证明共面的方法:先确定一个平面,然后再证其余的线(或点)在这个平面内.(2)证明共线的方法:先由两点确定一条直线,再证其他各点都在这条直线上.(3)证明共点的方法:先证其中两条直线交于一点,再证其他直线经过该点.跟踪训练1 (1)(多选)如图是正方体或四面体,P,Q,R,S分别是所在棱的中点,则这四个点共面的图是( )答案ABC解析对于A,PS∥QR,故P,Q,R,S四点共面;同理,B,C图中四点也共面;D中四点不共面.(2)在三棱锥A-BCD的棱AB,BC,CD,DA上分别取E,F,G,H四点,如果EF∩HG=P,则点P( )A.一定在直线BD上B.一定在直线AC上C.在直线AC或BD上D.不在直线AC上,也不在直线BD上答案 B解析如图所示,因为EF⊂平面ABC,HG⊂平面ACD,EF∩HG=P,所以P∈平面ABC,P∈平面ACD.又因为平面ABC∩平面ACD=AC,所以P∈AC.题型二空间线面位置关系命题点1 空间位置关系的判断例2 (1)下列推断中,错误的是( )A.若M∈α,M∈β,α∩β=l,则M∈lB.A∈α,A∈β,B∈α,B∈β⇒α∩β=ABC.l⊄α,A∈l⇒A∉αD.A,B,C∈α,A,B,C∈β,且A,B,C不共线⇒α,β重合答案 C解析对于A,因为M∈α,M∈β,α∩β=l,由基本事实3可知M∈l,A对;对于B,A∈α,A∈β,B∈α,B∈β,故直线AB⊂α,AB⊂β,即α∩β=AB,B对;对于C,若l∩α=A,则有l⊄α,A∈l,但A∈α,C错;对于D,有三个不共线的点在平面α,β中,故α,β重合,D对.(2)已知在长方体ABCD-A1B1C1D1中,M,N分别是长方形A1B1C1D1与长方形BCC1B1的中心,则下列说法正确的是( )A.直线MN与直线A1B是异面直线B.直线MN与直线DD1相交C.直线MN与直线AC1是异面直线D.直线MN与直线A1C平行答案 C解析如图,因为M,N分别是长方形A1B1C1D1与长方形BCC1B1的中心,所以M,N分别是A1C1,BC1的中点,所以直线MN与直线A1B平行,所以A错误;因为直线MN经过平面BB1D1D内一点M,且点M不在直线DD1上,所以直线MN与直线DD1是异面直线,所以B错误;因为直线MN经过平面ABC1内一点N,且点N不在直线AC1上,所以直线MN与直线AC1是异面直线,所以C正确;因为直线MN经过平面A1CC1内一点M,且点M不在直线A1C上,所以直线MN与直线A1C是异面直线,所以D错误.命题点2 异面直线所成角例3 (1)(2021·全国乙卷)在正方体ABCD -A 1B 1C 1D 1中,P 为B 1D 1的中点,则直线PB 与AD 1所成的角为( ) A .π2B .π3C .π4D .π6答案 D解析 方法一 如图,连接C 1P ,因为ABCD -A 1B 1C 1D 1是正方体,且P 为B 1D 1的中点,所以C 1P ⊥B 1D 1,又C 1P ⊥BB 1,所以C 1P ⊥平面B 1BP .又BP ⊂平面B 1BP ,所以C 1P ⊥BP .连接BC 1,则AD 1∥BC 1,所以∠PBC 1为直线PB 与AD 1所成的角.设正方体ABCD -A 1B 1C 1D 1的棱长为2,则在Rt△C 1PB 中,C 1P =12B 1D 1=2,BC 1=22,sin∠PBC 1=PC 1BC 1=12,所以∠PBC 1=π6.方法二 如图所示,连接BC 1,A 1B ,A 1P ,PC 1,则易知AD 1∥BC 1,所以直线PB 与AD 1所成的角等于直线PB 与BC 1所成的角.根据P 为正方形A 1B 1C 1D 1的对角线B 1D 1的中点,易知A 1,P ,C 1三点共线,且P 为A 1C 1的中点.易知A 1B =BC 1=A 1C 1,所以△A 1BC 1为等边三角形,所以∠A 1BC 1=π3,又P 为A 1C 1的中点,所以可得∠PBC 1=12∠A 1BC 1=π6.(2)(2022·衡水检测)如图,在圆锥SO 中,AB ,CD 为底面圆的两条直径,AB ∩CD =O ,且AB ⊥CD ,SO =OB =3,SE =14SB ,则异面直线SC 与OE 所成角的正切值为( )A .222B .53C .1316D .113答案 D解析 如图,过点S 作SF ∥OE ,交AB 于点F ,连接CF ,则∠CSF (或其补角)为异面直线SC 与OE 所成的角.∵SE =14SB ,∴SE =13BE .又OB =3,∴OF =13OB =1.∵SO ⊥OC ,SO =OC =3, ∴SC =32.∵SO ⊥OF ,∴SF =SO 2+OF 2=10. ∵OC ⊥OF ,∴CF =10. ∴在等腰△SCF 中,tan∠CSF =102-⎝ ⎛⎭⎪⎫3222322=113. 教师备选1.(多选)设a ,b ,c 是三条不同的直线,α,β是两个不同的平面,则下列结论不正确的是( )A .若a ⊂α,b ⊂β,则a 与b 是异面直线B .若a 与b 异面,b 与c 异面,则a 与c 异面C .若a ,b 不同在平面α内,则a 与b 异面D .若a ,b 不同在任何一个平面内,则a 与b 异面 答案 ABC2.在长方体ABCDA 1B 1C 1D 1中,AB =BC =1,AA 1=3,则异面直线AD 1与DB 1所成角的余弦值为( )A .15B .56C .55D .22 答案 C解析 如图,连接BD 1,交DB 1于O ,取AB 的中点M ,连接DM ,OM .易知O 为BD 1的中点,所以AD 1∥OM ,则∠MOD 为异面直线AD 1与DB 1所成角或其补角.因为在长方体ABCD -A 1B 1C 1D 1中,AB =BC =1,AA 1=3,AD 1=AD 2+DD 21=2, DM =AD 2+⎝ ⎛⎭⎪⎫12AB 2=52, DB 1=AB 2+AD 2+BB 21=5. 所以OM =12AD 1=1,OD =12DB 1=52,于是在△DMO 中,由余弦定理,得cos∠MOD =12+⎝ ⎛⎭⎪⎫522-⎝ ⎛⎭⎪⎫5222×1×52=55,即异面直线AD 1与DB 1所成角的余弦值为55. 思维升华 (1)点、直线、平面位置关系的判定,注意构造几何体(长方体、正方体)模型来判断,常借助正方体为模型. (2)求异面直线所成的角的三个步骤一作:根据定义作平行线,作出异面直线所成的角. 二证:证明作出的角是异面直线所成的角. 三求:解三角形,求出所作的角.跟踪训练2 (1)如图所示,G ,N ,M ,H 分别是正三棱柱的顶点或所在棱的中点,则表示直线GH 与MN 是异面直线的图形有________.(填序号)答案 ②④(2)若直线l 1和l 2是异面直线,l 1在平面α内,l 2在平面β内,l 是平面α与平面β的交线,则下列结论正确的是( ) A .l 与l 1,l 2都不相交 B .l 与l 1,l 2都相交C .l 至多与l 1,l 2中的一条相交D .l 至少与l 1,l 2中的一条相交 答案 D解析 如图1,l 1与l 2是异面直线,l 1与l 平行,l 2与l 相交,故A ,B 不正确;如图2,l 1与l 2是异面直线,l 1,l 2都与l 相交,故C 不正确.图1 图2题型三 空间几何体的切割(截面)问题例4 (1)在正方体ABCD -A 1B 1C 1D 1中,M ,N 分别是棱DD 1和BB 1上的点,MD =13DD 1,NB =13BB 1,那么正方体中过M ,N ,C 1的截面图形是( ) A .三角形 B .四边形 C .五边形 D .六边形答案 C解析 先确定截面上的已知边与几何体上和其共面的边的交点,再确定截面与几何体的棱的交点.如图,设直线C 1M ,CD 相交于点P ,直线C 1N ,CB 相交于点Q ,连接PQ 交直线AD 于点E ,交直线AB 于点F ,则五边形C 1MEFN 为所求截面图形.(2)已知正方体ABCD -A 1B 1C 1D 1的棱长为2.以D 1为球心,5为半径的球面与侧面BCC 1B 1的交线长为______. 答案π2解析 以D 1为球心,5为半径的球面与侧面BCC 1B 1的交线是以C 1为圆心,1为半径的圆与正方形BCC 1B 1相交的一段弧(圆周的四分之一),其长度为14×2π×1=π2.延伸探究 将本例(2)中正方体改为直四棱柱ABCD -A 1B 1C 1D 1的棱长均为2,∠BAD =60°.以D 1为球心,5为半径的球面与侧面BCC 1B 1的交线长为________.答案2π2解析 如图,设B 1C 1的中点为E ,球面与棱BB 1,CC 1的交点分别为P ,Q ,连接DB ,D 1B 1,D 1P ,D 1E ,EP ,EQ ,由∠BAD =60°,AB =AD ,知△ABD 为等边三角形, ∴D 1B 1=DB =2,∴△D 1B 1C 1为等边三角形, 则D 1E =3且D 1E ⊥平面BCC 1B 1,∴E 为球面截侧面BCC 1B 1所得截面圆的圆心, 设截面圆的半径为r ,则r =R 2球-D 1E 2=5-3=2. 又由题意可得EP =EQ =2,∴球面与侧面BCC 1B 1的交线为以E 为圆心的圆弧PQ . 又D 1P =5,∴B 1P =D 1P 2-D 1B 21=1, 同理C 1Q =1,∴P ,Q 分别为BB 1,CC 1的中点, ∴∠PEQ =π2,知PQ ︵的长为π2×2=2π2,即交线长为2π2.教师备选如图,在正方体ABCD -A 1B 1C 1D 1中,E 是BC 的中点,平面α经过直线BD 且与直线C 1E 平行,若正方体的棱长为2,则平面α截正方体所得的多边形的面积为________.答案 92解析 如图,过点B 作BM ∥C 1E 交B 1C 1于点M ,过点M 作BD 的平行线,交C 1D 1于点N ,连接DN ,则平面BDNM 即为符合条件的平面α,由图可知M ,N 分别为B 1C 1,C 1D 1的中点, 故BD =22,MN =2, 且BM =DN =5, ∴等腰梯形MNDB 的高为h =52-⎝⎛⎭⎪⎫222=322, ∴梯形MNDB 的面积为 12×(2+22)×322=92. 思维升华 (1)作截面应遵循的三个原则:①在同一平面上的两点可引直线;②凡是相交的直线都要画出它们的交点;③凡是相交的平面都要画出它们的交线. (2)作交线的方法有如下两种:①利用基本事实3作交线;②利用线面平行及面面平行的性质定理去寻找线面平行及面面平行,然后根据性质作出交线. 跟踪训练3 (1)(多选)正方体ABCD -A 1B 1C 1D 1的棱长为2,已知平面α⊥AC 1,则关于α截此正方体所得截面的判断正确的是( ) A .截面形状可能为正三角形 B .截面形状可能为正方形 C .截面形状可能为正六边形 D .截面面积最大值为3 3 答案 ACD解析 易知A ,C 正确,B 不正确,下面说明D 正确,如图,截面为正六边形,当六边形的顶点均为棱的中点时,其面积最大,MN =22,GH =2,OE =OO ′2+O ′E 2=1+⎝⎛⎭⎪⎫222=62, 所以S =2×12×(2+22)×62=33,故D 正确.(2)(2022·兰州模拟)如图,正方体A 1C 的棱长为1,点M 在棱A 1D 1上,A 1M =2MD 1,过M 的平面α与平面A 1BC 1平行,且与正方体各面相交得到截面多边形,则该截面多边形的周长为________.答案 3 2解析 在平面A 1D 1DA 中寻找与平面A 1BC 1平行的直线时,只需要ME ∥BC 1,如图所示,因为A 1M =2MD 1,故该截面与正方体的交点位于靠近D 1,A ,C 的三等分点处,故可得截面为MIHGFE ,设正方体的棱长为3a , 则ME =22a ,MI =2a ,IH =22a ,HG =2a ,FG =22a ,EF =2a ,所以截面MIHGFE 的周长为ME +EF +FG +GH +HI +IM =92a , 又因为正方体A 1C 的棱长为1,即3a =1, 故截面多边形的周长为32.课时精练1.下列叙述错误的是( )A .若P ∈α∩β,且α∩β=l ,则P ∈lB.若直线a∩b=A,则直线a与b能确定一个平面C.三点A,B,C确定一个平面D.若A∈l,B∈l且A∈α,B∈α,则l⊂α答案 C解析选项A,点P是两平面的公共点,当然在交线上,故正确;选项B,由基本事实的推论可知,两相交直线确定一个平面,故正确;选项C,只有不共线的三点才能确定一个平面,故错误;选项D,由基本事实2,直线上有两点在一个平面内,则这条直线在平面内.2.已知m,n是两条不同的直线,α,β是两个不同的平面,则下列判断正确的是( ) A.若m⊥α,n⊥β,α⊥β,则直线m与n可能相交或异面B.若α⊥β,m⊂α,n⊂β,则直线m与n一定平行C.若m⊥α,n∥β,α⊥β,则直线m与n一定垂直D.若m∥α,n∥β,α∥β,则直线m与n一定平行答案 A解析m,n是两条不同的直线,α,β是两个不同的平面,对于A,若m⊥α,n⊥β,α⊥β,则直线m与n相交垂直或异面垂直,故A正确;对于B,若α⊥β,m⊂α,n⊂β,则直线m与n相交、平行或异面,故B错误;对于C,若m⊥α,n∥β,α⊥β,则直线m与n相交、平行或异面,故C错误;对于D,若m∥α,n∥β,α∥β,则直线m与n平行或异面,故D错误.3.(2022·营口模拟)已知空间中不过同一点的三条直线a,b,l,则“a,b,l两两相交”是“a,b,l共面”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件答案 A解析空间中不过同一点的三条直线a,b,l,若a,b,l在同一平面,则a,b,l相交或a,b,l有两个平行,另一直线与之相交,或三条直线两两平行.所以a,b,l在同一平面,则a,b,l两两相交不一定成立;而若a,b,l两两相交,则a,b,l在同一平面成立.故“a,b,l两两相交”是“a,b,l共面”的充分不必要条件.4.如图所示,在正方体ABCD-A1B1C1D1中,E是平面ADD1A1的中心,M,N,F分别是B1C1,CC1,AB的中点,则下列说法正确的是( )A .MN =12EF ,且MN 与EF 平行B .MN ≠12EF ,且MN 与EF 平行C .MN =12EF ,且MN 与EF 异面D .MN ≠12EF ,且MN 与EF 异面答案 D解析 设正方体ABCD -A 1B 1C 1D 1的棱长为2a , 则MN =MC 21+C 1N 2=⎝ ⎛⎭⎪⎫2a 22+⎝ ⎛⎭⎪⎫2a 22 =2a ,作点E 在平面ABCD 内的射影点G ,连接EG ,GF ,所以EF =EG 2+GF 2=⎝ ⎛⎭⎪⎫2a 22+2a2=3a ,所以MN ≠12EF ,故选项A ,C 错误;连接DE ,因为E 为平面ADD 1A 1的中心, 所以DE =12A 1D ,又因为M ,N 分别为B 1C 1,CC 1的中点,所以MN ∥B 1C , 又因为B 1C ∥A 1D ,所以MN ∥ED , 且DE ∩EF =E ,所以MN 与EF 异面,故选项B 错误.5.(多选)(2022·临沂模拟)如图,在正方体ABCD -A 1B 1C 1D 1中,O 是DB 的中点,直线A 1C 交平面C 1BD 于点M ,则下列结论正确的是( )A.C1,M,O三点共线B.C1,M,O,C四点共面C.C1,O,B1,B四点共面D.D1,D,O,M四点共面答案AB解析∵O∈AC,AC⊂平面ACC1A1,∴O∈平面ACC1A1.∵O∈BD,BD⊂平面C1BD,∴O∈平面C1BD,∴O是平面ACC1A1和平面C1BD的公共点,同理可得,点M和C1都是平面ACC1A1和平面C1BD的公共点,∴三点C1,M,O在平面C1BD与平面ACC1A1的交线上,即C1,M,O三点共线,故A,B正确;根据异面直线的判定定理可得BB1与C1O为异面直线,故C1,O,B1,B四点不共面,故C不正确;根据异面直线的判定定理可得DD1与MO为异面直线,故D1,D,O,M四点不共面,故D不正确.6.(多选)(2022·厦门模拟)下列说法不正确的是( )A.两组对边分别相等的四边形确定一个平面B.和同一条直线异面的两直线一定共面C.与两异面直线分别相交的两直线一定不平行D.一条直线和两平行线中的一条相交,也必定和另一条相交答案ABD解析两组对边分别相等的四边形可能是空间四边形,故A错误;如图1,直线DD1与B1C1都是直线AB的异面直线,同样DD1与B1C1也是异面直线,故B错误;如图2,设直线AB与CD是异面直线,则直线AC与BD一定不平行,否则AC∥BD,有AC与BD确定一个平面α,则AC⊂α,BD⊂α,所以A∈α,B∈α,C∈α,D∈α,所以AB⊂α,CD⊂α,这与假设矛盾,故C正确;如图1,AB∥CD,而直线AA1与AB相交,但与直线CD不相交,故D错误.图1 图27.(2022·哈尔滨模拟)已知在直三棱柱ABC -A 1B 1C 1中,∠ABC =120°,AB =2,BC =CC 1=1,则异面直线AB 1与BC 1所成角的余弦值为________. 答案105解析 如图所示,补成直四棱柱ABCD -A 1B 1C 1D 1,则所求角为∠BC 1D 或其补角,∵BC 1=2,BD =22+1-2×2×1×cos60°=3,C 1D =AB 1=5, 易得C 1D 2=BD 2+BC 21,即BC 1⊥BD , 因此cos∠BC 1D =BC 1C 1D =25=105. 8.(2022·本溪模拟)在空间中,给出下面四个命题,其中假命题为________.(填序号) ①过平面α外的两点,有且只有一个平面与平面α垂直; ②若平面β内有不共线三点到平面α的距离都相等,则α∥β; ③若直线l 与平面α内的任意一条直线垂直,则l ⊥α; ④两条异面直线在同一平面内的射影一定是两条相交直线. 答案 ①②④解析 对于①,当平面α外两点的连线与平面α垂直时,此时过两点有无数个平面与平面α垂直,所以①不正确;对于②,若平面β内有不共线三点到平面α的距离都相等,平面α与β可能平行,也可能相交,所以②不正确;对于③,直线l 与平面内的任意直线垂直时,得到l ⊥α,所以③正确;对于④,两条异面直线在同一平面内的射影可能是两条相交直线或两条平行直线或直线和直线外的一点,所以④不正确.9.(2022·上海市静安区模拟)如图所示,在棱长为2的正方体ABCD -A 1B 1C 1D 1中,E ,F 分别是AB ,CC 1的中点.(1)求异面直线A 1E 与D 1F 所成的角的余弦值; (2)求三棱锥A 1-D 1EF 的体积.解 (1)如图,设BB 1的中点为H ,连接HF ,EH ,A 1H ,因为F 是CC 1的中点,所以A 1D 1∥CB ∥HF ,A 1D 1=CB =HF , 因此四边形A 1D 1FH 是平行四边形, 所以D 1F ∥A 1H ,D 1F =A 1H ,因此∠EA 1H 是异面直线A 1E 与D 1F 所成的角或其补角, 正方体ABCD -A 1B 1C 1D 1的棱长为2,E 是AB 的中点, 所以A 1E =A 1H =22+12=5,EH =12+12=2,由余弦定理可知,cos∠EA 1H =A 1E 2+A 1H 2-EH 22A 1E ·A 1H =5+5-22×5×5=45,所以异面直线A 1E 与D 1F 所成的角的余弦值为45.(2)因为A 1D 1∥HF ,HF ⊄平面A 1D 1E ,A 1D 1⊂平面A 1D 1E , 所以HF ∥平面A 1D 1E ,因此点H ,F 到平面A 1D 1E 的距离相等, 即111111F A D E H A D E D A EH V V V ---==,11D A EH V -=13D 1A 1·1A EH S △=13×2×⎝ ⎛⎭⎪⎫22-12×2×1×2-12×1×1=1,所以三棱锥A 1-D 1EF 的体积为1.10.如图,四棱柱ABCD -A 1B 1C 1D 1的侧棱AA 1⊥底面ABCD ,四边形ABCD 为菱形,E ,F 分别为AA 1,CC 1的中点,M 为AB 上一点.(1)若D 1E 与CM 相交于点K ,求证D 1E ,CM ,DA 三条直线相交于同一点; (2)若AB =2,AA 1=4,∠BAD =π3,求点D 1到平面FBD 的距离.(1)证明 ∵D 1E 与CM 相交于点K , ∴K ∈D 1E ,K ∈CM ,而D 1E ⊂平面ADD 1A 1,CM ⊂平面ABCD , 且平面ADD 1A 1∩平面ABCD =AD , ∴K ∈AD ,∴D 1E ,CM ,DA 三条直线相交于同一点K . (2)解 ∵四边形ABCD 为菱形,AB =2, ∴BC =CD =2,而四棱柱的侧棱AA 1⊥底面ABCD , ∴CC 1⊥底面ABCD ,又∵F 是CC 1的中点,CC 1=4,∴CF =2, ∴BF =DF =22,又∵四边形ABCD 为菱形,∠BAD =π3,∴BD =AB =2, ∴S △FBD =12×2×222-1=7.设点D 1到平面FBD 的距离为h ,点B 到平面DD 1F 的距离为d , 则d =2sin π3=3,又∵11D FBD B DD F V V --=, ∴13×S △FBD ×h =13×1DD F S △×d , ∴13×7×h =13×12×4×2×3, 解得h =4217.即点D1到平面FBD的距离为421 7.11.(多选)(2022·太原模拟)如图是正四面体的平面展开图,G,H,M,N分别为DE,BE,EF,EC的中点,在这个正四面体中,下列结论正确的是( )A.GH与EF平行B.BD与MN为异面直线C.GH与MN成60°角D.DE与MN垂直答案BCD解析如图,还原成正四面体A-DEF,其中H与N重合,A,B,C三点重合,连接GM,易知GH与EF异面,BD与MN异面.又△GMH为等边三角形,∴GH与MN成60°角,易证DE⊥AF,MN∥AF,∴MN⊥DE.∴B,C,D正确.12.(多选)(2022·广州六校联考)如图,在正方体ABCD-A1B1C1D1中,M,N,P分别是C1D1,BC,A1D1的中点,下列结论正确的是( )A.AP与CM是异面直线B.AP,CM,DD1相交于一点C.MN∥BD1D.MN∥平面BB1D1D答案 BD解析 如图,连接MP ,AC ,因为MP ∥AC ,MP ≠AC ,所以AP 与CM 是相交直线,又平面A 1ADD 1∩平面C 1CDD 1=DD 1,所以AP ,CM ,DD 1相交于一点,则A 不正确,B 正确;令AC ∩BD =O ,连接OD 1,ON .因为M ,N 分别是C 1D 1,BC 的中点,所以ON ∥D 1M ∥CD ,ON =D 1M =12CD , 则四边形MNOD 1为平行四边形,所以MN ∥OD 1,因为MN ⊄平面BB 1D 1D ,OD 1⊂平面BB 1D 1D ,所以MN ∥平面BB 1D 1D ,C 不正确,D 正确.13.(2022·玉林模拟)在正方体ABCD -A 1B 1C 1D 1中,E ,F ,P ,Q 分别为A 1B ,B 1D 1,A 1D ,CD 1的中点,则直线EF 与PQ 所成角的大小是________.答案 π3解析 如图,连接A 1C 1,BC 1,则F 是A 1C 1的中点,又E 为A 1B 的中点,所以EF ∥BC 1,连接DC 1,则Q 是DC 1的中点,又P 为A 1D 的中点,所以PQ ∥A 1C 1,于是∠A 1C 1B 是直线EF 与PQ 所成的角或其补角.易知△A 1C 1B 是正三角形,所以∠A 1C 1B =π3. 14.(2022·盐城模拟)在棱长为4的正方体ABCD -A 1B 1C 1D 1中,P ,Q 分别为棱A 1D 1,CC 1的中点,过P ,Q ,A 作正方体的截面,则截面多边形的周长是________.答案 25+95+2133 解析 如图所示,过Q 作QM ∥AP 交BC 于M ,由A 1P =CQ =2,tan∠APA 1=2,则tan∠CMQ =2,CM =CQtan∠CMQ=1, 延长MQ 交B 1C 1的延长线于E 点,连接PE ,交D 1C 1于N 点,则多边形AMQNP 即为截面,根据平行线性质有C 1E =CM =1, C 1N ND 1=C 1E PD 1=12, 则C 1N =43,D 1N =83, 因此NQ =22+⎝ ⎛⎭⎪⎫432=2133, NP =22+⎝ ⎛⎭⎪⎫832=103, 又AP =42+22=25,AM =42+32=5,MQ =12+22=5,所以多边形AMQNP 的周长为AM +MQ +QN +NP +PA=5+5+2133+103+2 5 =25+95+2133.15.(2022·大连模拟)如图,直四棱柱ABCD -A 1B 1C 1D 1的底面是边长为2的正方形,AA 1=3,E ,F 分别是AB ,BC 的中点,过点D 1,E ,F 的平面记为α,则下列说法中错误的是( )A .点B 到平面α的距离与点A 1到平面α的距离之比为1∶2B .平面α截直四棱柱ABCD -A 1B 1C 1D 1所得截面的面积为732C .平面α将直四棱柱分割成的上、下两部分的体积之比为47∶25D .平面α截直四棱柱ABCD -A 1B 1C 1D 1所得截面的形状为四边形 答案 D解析 对于A ,因为平面α过线段AB 的中点E ,所以点A 到平面α的距离与点B 到平面α的距离相等.由平面α过A 1A 的三等分点M 可知,点A 1到平面α的距离是点A 到平面α的距离的2倍,因此,点A 1到平面α的距离是点B 到平面α的距离的2倍.故选项A 正确;延长DA ,DC 交直线EF 的延长线于点P ,Q ,连接D 1P ,D 1Q ,交棱A 1A ,C 1C 于点M ,N .连接ME ,NF ,可得五边形D 1MEFN ,故选项D 错误;由平行线分线段成比例可得AP =BF =1,故DP =DD 1=3,则△DD 1P 为等腰三角形.由相似三角形可知,AM =AP =1,A 1M =2,则D 1M =D 1N =22,ME =EF =FN =2.连接MN ,则MN =22,因此五边形D 1MEFN 可分为等边三角形D 1MN 和等腰梯形MEFN .等腰梯形MEFN 的高h =22-⎝ ⎛⎭⎪⎫22-222=62, 则等腰梯形MEFN 的面积为22+22×62=332.又1D MN S △=12×22×6=23,所以五边形D 1MEFN 的面积为332+23=732,故选项B 正确;记平面将直四棱柱分割成上、下两部分的体积分别为V 1,V 2,则V 2=1D DPQ V --V M -PAE -V N -CFQ=13×12×3×3×3-13×12×1×1×1-13×12×1×1×1=256, 所以V 1=1111ABCD A B C D V --V 2=12-256=476, V 1∶V 2=47∶25,故选项C 正确.16.如图1,在边长为4的正三角形ABC 中,D ,F 分别为AB ,AC 的中点,E 为AD 的中点.将△BCD 与△AEF 分别沿CD ,EF 同侧折起,使得二面角A -EF -D 与二面角B -CD -E 的大小都等于90°,得到如图2所示的多面体.图1 图2(1)在多面体中,求证:A ,B ,D ,E 四点共面;(2)求多面体的体积.(1)证明 因为二面角A -EF -D 的大小等于90°,所以平面AEF ⊥平面DEFC ,又AE ⊥EF ,AE ⊂平面AEF ,平面AEF ∩平面DEFC =EF ,所以AE ⊥平面DEFC ,同理,可得BD ⊥平面DEFC ,所以AE ∥BD ,故A ,B ,D ,E 四点共面.(2)解 因为AE ⊥平面DEFC ,BD ⊥平面DEFC ,EF ∥CD ,AE ∥BD ,DE ⊥CD ,所以AE 是四棱锥A -CDEF 的高,点A 到平面BCD 的距离等于点E 到平面BCD 的距离, 又AE =DE =1,CD =23,EF =3,BD =2,所以V =V A -CDEF +V A -BCD =13S 梯形CDEF ·AE +13S △BCD ·DE =736.。
2023年高考数学一轮复习第七章立体几何与空间向量4空间直线平面的平行练习含解析

空间直线、平面的平行考试要求 1.理解空间中直线与直线、直线与平面、平面与平面的平行关系,并加以证明.2.掌握直线与平面、平面与平面平行的判定与性质,并会简单应用.知识梳理1.线面平行的判定定理和性质定理文字语言图形语言符号语言判定定理如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行错误!⇒a∥α性质定理一条直线与一个平面平行,如果过该直线的平面与此平面相交,那么该直线与交线平行错误!⇒a∥b2.面面平行的判定定理和性质定理文字语言图形语言符号语言判定定理如果一个平面内的两条相交直线与另一个平面平行,那么这两个平面平行错误!⇒β∥α性质定理两个平面平行,如果另一个平面与这两个平面相交,那么两条交线平行错误!⇒a∥b常用结论(1)垂直于同一条直线的两个平面平行,即若a⊥α,a⊥β,则α∥β.(2)平行于同一个平面的两个平面平行,即若α∥β,β∥γ,则α∥γ.(3)垂直于同一个平面的两条直线平行,即a⊥α,b⊥α,则a∥b.(4)若α∥β,a⊂α,则a∥β.思考辨析判断下列结论是否正确(请在括号中打“√”或“×”)(1)若一条直线平行于一个平面内的一条直线,则这条直线平行于这个平面.( ×)(2)若直线a∥平面α,P∈α,则过点P且平行于直线a的直线有无数条.( ×)(3)若直线a⊂平面α,直线b⊂平面β,a∥b,则α∥β.( ×)(4)如果两个平面平行,那么分别在这两个平面内的两条直线平行或异面.( √)教材改编题1.下列说法中,与“直线a∥平面α”等价的是( )A.直线a上有无数个点不在平面α内B.直线a与平面α内的所有直线平行C.直线a与平面α内无数条直线不相交D.直线a与平面α内的任意一条直线都不相交答案 D解析因为a∥平面α,所以直线a与平面α无交点,因此a和平面α内的任意一条直线都不相交.2.已知不重合的直线a,b和平面α,则下列选项正确的是( )A.若a∥α,b⊂α,则a∥bB.若a∥α,b∥α,则a∥bC.若a∥b,b⊂α,则a∥αD.若a∥b,a⊂α,则b∥α或b⊂α答案 D解析若a∥α,b⊂α,则a∥b或异面,A错;若a∥α,b∥α,则a∥b或异面或相交,B错;若a∥b,b⊂α,则a∥α或a⊂α,C错;若a∥b,a⊂α,则b∥α或b⊂α,D对.3.如图是长方体被一平面所截得的几何体,四边形EFGH为截面,则四边形EFGH的形状为______.答案平行四边形解析∵平面ABFE∥平面DCGH,又平面EFGH∩平面ABFE=EF,平面EFGH∩平面DCGH=HG,∴EF∥HG.同理EH∥FG,∴四边形EFGH是平行四边形.题型一 直线与平面平行的判定与性质 命题点1 直线与平面平行的判定例1 如图,在四棱锥P -ABCD 中,底面ABCD 是平行四边形,E ,F 分别是BC ,PD 的中点,求证:(1)PB ∥平面ACF ;(2)EF ∥平面PAB .证明 (1)如图,连接BD 交AC 于O ,连接OF ,∵四边形ABCD 是平行四边形, ∴O 是BD 的中点,又∵F 是PD 的中点,∴OF ∥PB , 又∵OF ⊂平面ACF ,PB ⊄平面ACF , ∴PB ∥平面ACF .(2)取PA 的中点G ,连接GF ,BG . ∵F 是PD 的中点, ∴GF 是△PAD 的中位线, ∴GF 綉12AD ,∵底面ABCD 是平行四边形,E 是BC 的中点, ∴BE 綉12AD ,∴GF 綉BE ,∴四边形BEFG 是平行四边形, ∴EF ∥BG ,又∵EF ⊄平面PAB ,BG ⊂平面PAB , ∴EF ∥平面PAB .命题点2 直线与平面平行的性质例2 如图所示,在四棱锥P-ABCD中,四边形ABCD是平行四边形,M是PC的中点,在DM 上取一点G,过G和PA作平面交BD于点H.求证:PA∥GH.证明如图所示,连接AC交BD于点O,连接OM,∵四边形ABCD是平行四边形,∴O是AC的中点,又M是PC的中点,∴PA∥OM,又OM⊂平面BMD,PA⊄平面BMD,∴PA∥平面BMD,又平面PAHG∩平面BMD=GH,∴PA∥GH.教师备选如图,四边形ABCD是矩形,P∉平面ABCD,过BC作平面BCFE交AP于点E,交DP于点F,求证:四边形BCFE是梯形.证明∵四边形ABCD为矩形,∴BC∥AD.∵AD⊂平面PAD,BC⊄平面PAD,∴BC∥平面PAD.∵平面BCFE∩平面PAD=EF,BC⊂平面BCFE,∴BC∥EF.∵AD=BC,AD≠EF,∴BC≠EF,∴四边形BCFE是梯形.思维升华(1)判断或证明线面平行的常用方法①利用线面平行的定义(无公共点).②利用线面平行的判定定理(a⊄α,b⊂α,a∥b⇒a∥α).③利用面面平行的性质(α∥β,a⊂α⇒a∥β).④利用面面平行的性质(α∥β,a⊄β,a∥α⇒a∥β).(2)应用线面平行的性质定理的关键是确定交线的位置,有时需要经过已知直线作辅助平面确定交线.跟踪训练1 如图所示,已知四边形ABCD是正方形,四边形ACEF是矩形,M是线段EF的中点.(1)求证:AM∥平面BDE;(2)若平面ADM∩平面BDE=l,平面ABM∩平面BDE=m,试分析l与m的位置关系,并证明你的结论.(1)证明如图,记AC与BD的交点为O,连接OE.因为O,M分别为AC,EF的中点,四边形ACEF是矩形,所以四边形AOEM是平行四边形,所以AM∥OE.又因为OE⊂平面BDE,AM⊄平面BDE,所以AM∥平面BDE.(2)解l∥m,证明如下:由(1)知AM∥平面BDE,又AM⊂平面ADM,平面ADM∩平面BDE=l,所以l∥AM,同理,AM∥平面BDE,又AM⊂平面ABM,平面ABM∩平面BDE=m,所以m∥AM,所以l∥m.题型二平面与平面平行的判定与性质例3 如图所示,在三棱柱ABC-A1B1C1中,过BC的平面与上底面A1B1C1交于GH(GH与B1C1不重合).(1)求证:BC∥GH;(2)若E,F,G分别是AB,AC,A1B1的中点,求证:平面EFA1∥平面BCHG.证明(1)∵在三棱柱ABC-A1B1C1中,∴平面ABC∥平面A1B1C1,又∵平面BCHG∩平面ABC=BC,且平面BCHG∩平面A1B1C1=HG,∴由面面平行的性质定理得BC∥GH.(2)∵E,F分别为AB,AC的中点,∴EF∥BC,∵EF⊄平面BCHG,BC⊂平面BCHG,∴EF∥平面BCHG.又G,E分别为A1B1,AB的中点,A1B1綉AB,∴A1G綉EB,∴四边形A1EBG是平行四边形,∴A1E∥GB.∵A1E⊄平面BCHG,GB⊂平面BCHG,∴A1E∥平面BCHG.又∵A1E∩EF=E,A1E,EF⊂平面EFA1,∴平面EFA1∥平面BCHG.延伸探究在本例中,若将条件“E,F,G分别是AB,AC,A1B1的中点”变为“点D,D1分别是AC,A1C1上的点,且平面BC1D∥平面AB1D1”,试求ADDC的值.解如图,连接A1B交AB1于O,连接OD1.由平面BC 1D ∥平面AB 1D 1, 且平面A 1BC 1∩平面BC 1D =BC 1, 平面A 1BC 1∩平面AB 1D 1=D 1O , 所以BC 1∥D 1O ,则A 1D 1D 1C 1=A 1OOB=1. 又由题设A 1D 1D 1C 1=DC AD, 所以DC AD=1,即AD DC=1. 教师备选如图,在三棱柱ABC -A 1B 1C 1中,E ,F ,G 分别为B 1C 1,A 1B 1,AB 的中点.(1)求证:平面A 1C 1G ∥平面BEF ;(2)若平面A 1C 1G ∩BC =H ,求证:H 为BC 的中点. 证明 (1)∵E ,F 分别为B 1C 1,A 1B 1的中点, ∴EF ∥A 1C 1,∵A 1C 1⊂平面A 1C 1G ,EF ⊄平面A 1C 1G , ∴EF ∥平面A 1C 1G ,又F ,G 分别为A 1B 1,AB 的中点, ∴A 1F =BG , 又A 1F ∥BG ,∴四边形A 1GBF 为平行四边形, 则BF ∥A 1G ,∵A 1G ⊂平面A 1C 1G ,BF ⊄平面A 1C 1G , ∴BF ∥平面A 1C 1G ,又EF ∩BF =F ,EF ,BF ⊂平面BEF , ∴平面A 1C 1G ∥平面BEF .(2)∵平面ABC∥平面A1B1C1,平面A1C1G∩平面A1B1C1=A1C1,平面A1C1G与平面ABC有公共点G,则有经过G的直线,设交BC于点H,如图,则A1C1∥GH,得GH∥AC,∵G为AB的中点,∴H为BC的中点.思维升华证明面面平行的常用方法(1)利用面面平行的判定定理.(2)利用垂直于同一条直线的两个平面平行(l⊥α,l⊥β⇒α∥β).(3)利用面面平行的传递性,即两个平面同时平行于第三个平面,则这两个平面平行(α∥β,β∥γ⇒α∥γ).跟踪训练2 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形.(1)证明:平面A1BD∥平面CD1B1;(2)若平面ABCD∩平面CD1B1=直线l,证明:B1D1∥l.证明(1)由题设知BB1綉DD1,所以四边形BB1D1D是平行四边形,所以BD∥B1D1.又BD⊄平面CD1B1,B1D1⊂平面CD1B1,所以BD∥平面CD1B1.因为A1D1綉B1C1綉BC,所以四边形A1BCD1是平行四边形,所以A1B∥D1C.又A1B⊄平面CD1B1,D1C⊂平面CD1B1,所以A1B∥平面CD1B1.又因为BD∩A1B=B,BD,A1B⊂平面A1BD,所以平面A1BD∥平面CD1B1.(2)由(1)知平面A1BD∥平面CD1B1,又平面ABCD∩平面CD1B1=直线l,平面ABCD∩平面A1BD=直线BD,所以直线l∥直线BD,在四棱柱ABCD-A1B1C1D1中,四边形BDD1B1为平行四边形,所以B 1D 1∥BD ,所以B 1D 1∥l .题型三 平行关系的综合应用例4 如图,在正方体ABCD -A 1B 1C 1D 1中,P ,Q 分别为对角线BD ,CD 1上的点,且CQ QD 1=BP PD =23.(1)求证:PQ ∥平面A 1D 1DA ;(2)若R 是AB 上的点,AR AB的值为多少时,能使平面PQR ∥平面A 1D 1DA ?请给出证明. (1)证明 连接CP 并延长,与DA 的延长线交于M 点,如图,连接MD 1,因为四边形ABCD 为正方形, 所以BC ∥AD ,故△PBC ∽△PDM , 所以CP PM =BP PD =23,又因为CQ QD 1=BP PD =23, 所以CQ QD 1=CP PM =23, 所以PQ ∥MD 1.又MD 1⊂平面A 1D 1DA ,PQ ⊄平面A 1D 1DA , 故PQ ∥平面A 1D 1DA .(2)解 当AR AB 的值为35时,能使平面PQR ∥平面A 1D 1DA .如图,证明如下:因为AR AB =35,即BR RA =23, 故BR RA =BP PD. 所以PR ∥DA .又DA ⊂平面A 1D 1DA ,PR ⊄平面A 1D 1DA , 所以PR ∥平面A 1D 1DA ,又PQ ∥平面A 1D 1DA ,PQ ∩PR =P ,PQ ,PR ⊂平面PQR , 所以平面PQR ∥平面A 1D 1DA . 教师备选如图,四边形ABCD 与ADEF 均为平行四边形,M ,N ,G 分别是AB ,AD ,EF 的中点.求证:(1)BE ∥平面DMF ; (2)平面BDE ∥平面MNG .证明 (1)如图,连接AE ,则AE 必过DF 与GN 的交点O ,连接MO ,则MO 为△ABE 的中位线,所以BE ∥MO . 又BE ⊄平面DMF ,MO ⊂平面DMF , 所以BE ∥平面DMF .(2)因为N ,G 分别为平行四边形ADEF 的边AD ,EF 的中点,所以DE ∥GN , 又DE ⊄平面MNG ,GN ⊂平面MNG , 所以DE ∥平面MNG . 又M 为AB 的中点,所以MN 为△ABD 的中位线,所以BD ∥MN , 又MN ⊂平面MNG ,BD ⊄平面MNG , 所以BD ∥平面MNG ,又DE ,BD ⊂平面BDE ,DE ∩BD =D ,所以平面BDE ∥平面MNG .思维升华 证明平行关系的常用方法熟练掌握线线、线面、面面平行关系间的相互转化是解决线线、线面、面面平行的综合问题的关键.面面平行判定定理的推论也是证明面面平行的一种常用方法.跟踪训练3 如图所示,四边形EFGH 为空间四边形ABCD 的一个截面,若截面为平行四边形. (1)求证:AB ∥平面EFGH ;(2)若AB =4,CD =6,求四边形EFGH 周长的取值范围.(1)证明 ∵四边形EFGH 为平行四边形, ∴EF ∥HG .∵HG ⊂平面ABD ,EF ⊄平面ABD , ∴EF ∥平面ABD . 又∵EF ⊂平面ABC , 平面ABD ∩平面ABC =AB , ∴EF ∥AB ,又∵AB ⊄平面EFGH ,EF ⊂平面EFGH , ∴AB ∥平面EFGH . (2)解 设EF =x (0<x <4), 由(1)知EF ∥AB , ∴CF CB =EF AB =x4, 与(1)同理可得CD ∥FG , ∴FG CD =BF BC, 则FG 6=BF BC=BC -CF BC =1-x4, ∴FG =6-32x .∴四边形EFGH 的周长L =2⎝⎛⎭⎪⎫x +6-32x =12-x .又∵0<x <4,∴8<L <12,故四边形EFGH 周长的取值范围是(8,12).课时精练1.(2022·宁波模拟)下列命题中正确的是( )A.若a,b是两条直线,且a∥b,那么a平行于经过b的任何平面B.若直线a和平面α满足a∥α,那么a与α内的任何直线平行C.平行于同一条直线的两个平面平行D.若直线a,b和平面α满足a∥b,a⊂α,b⊄α,则b∥α答案 D解析A中,a可以在过b的平面内;B中,a与α内的直线也可能异面;C中,两平面可能相交;D中,由直线与平面平行的判定定理知b∥α,正确.2.(2022·呼和浩特模拟)设a,b是两条不同的直线,α,β是两个不同的平面,则α∥β的一个充分条件是( )A.存在一条直线a,a∥α,a∥βB.存在一条直线a,a⊂α,a∥βC.存在两条平行直线a,b,a⊂α,b⊂β,a∥β,b∥αD.存在两条异面直线a,b,a⊂α,b⊂β,a∥β,b∥α答案 D解析对于A,一条直线与两个平面都平行,两个平面不一定平行,故A不正确;对于B,一个平面中的一条直线平行于另一个平面,两个平面不一定平行,故B不正确;对于C,两个平面中的两条直线平行,不能保证两个平面平行,故C不正确;对于D,如图,在直线b上取点B,过点B和直线a确定一个平面γ,交平面β于a′,因为a∥β,所以a∥a′,又a′⊄α,a⊂α,所以a′∥α,又因为b∥α,b∩a′=B,b⊂β,a′⊂β,所以β∥α.3.(2022·广州模拟)如图,在三棱柱ABC-A1B1C1中,AM=2MA1,BN=2NB1,过MN作一平面分别交底面△ABC的边BC,AC于点E,F,则( )A.MF∥EBB.A1B1∥NEC.四边形MNEF为平行四边形D.四边形MNEF为梯形答案 D解析由于B,E,F三点共面,F∈平面BEF,M∉平面BEF,故MF,EB为异面直线,故A错误;由于B1,N,E三点共面,B1∈平面B1NE,A1∉平面B1NE,故A1B1,NE为异面直线,故B错误;∵在平行四边形AA1B1B中,AM=2MA1,BN=2NB1,∴AM∥BN,AM=BN,故四边形AMNB为平行四边形,∴MN∥AB.又MN⊄平面ABC,AB⊂平面ABC,∴MN∥平面ABC.又MN⊂平面MNEF,平面MNEF∩平面ABC=EF,∴MN∥EF,∴EF∥AB,显然在△ABC中,EF≠AB,∴EF≠MN,∴四边形MNEF为梯形,故C错误,D正确.4.(2022·杭州模拟)已知P为△ABC所在平面外一点,平面α∥平面ABC,且α交线段PA,PB,PC于点A′,B′,C′,若PA′∶AA′=2∶3,则S△A′B′C′∶S△ABC等于( )A.2∶3B.2∶5C.4∶9D.4∶25答案 D解析∵平面α∥平面ABC,∴A′C′∥AC,A′B′∥AB,B′C′∥BC,∴S△A′B′C′∶S△ABC=(PA′∶PA)2,又PA′∶AA′=2∶3,∴PA′∶PA=2∶5,∴S△A′B′C′∶S△ABC=4∶25.5.(多选)(2022·济宁模拟)如图,在下列四个正方体中,A,B为正方体的两个顶点,D,E,F为所在棱的中点,则在这四个正方体中,直线AB与平面DEF平行的是( )答案AC解析对于A,AB∥DE,AB⊄平面DEF,DE⊂平面DEF,∴直线AB与平面DEF平行,故A正确;对于B,如图,取正方体所在棱的中点G,连接FG并延长,交AB延长线于H,则AB与平面DEF相交于点H,故B错误;对于C,AB∥DF,AB⊄平面DEF,DF⊂平面DEF,∴直线AB与平面DEF平行,故C正确;对于D,AB与DF所在平面的正方形对角线有交点B,DF与该对角线平行,∴直线AB与平面DEF相交,故D错误.6.(多选)如图,透明塑料制成的长方体容器ABCD-A1B1C1D1内灌进一些水,固定容器一边AB 于地面上,再将容器倾斜,随着倾斜程度的不同,有下面几个结论,其中正确的是( )A .没有水的部分始终呈棱柱形B .水面EFGH 所在四边形的面积为定值C .随着容器倾斜程度的不同,A 1C 1始终与水面所在平面平行D .当容器倾斜如图(3)所示时,AE ·AH 为定值 答案 AD解析 根据棱柱的特征(有两个面互相平行,其余各面都是四边形,并且相邻两个四边形的公共边都互相平行),结合题中图形易知A 正确;由题图可知水面EFGH 的边EF 的长保持不变,但邻边的长却随倾斜程度而改变,可知B 错误;因为A 1C 1∥AC ,AC ⊂平面ABCD ,A 1C 1⊄平面ABCD ,所以A 1C 1∥平面ABCD ,当平面EFGH 不平行于平面ABCD 时,A 1C 1不平行于水面所在平面,故C 错误;当容器倾斜如题图(3)所示时,因为水的体积是不变的,所以棱柱AEH -BFG 的体积V 为定值,又V =S △AEH ·AB ,高AB 不变,所以S △AEH 也不变,即AE ·AH 为定值,故D 正确.7.考查①②两个命题,①⎭⎪⎬⎪⎫m ⊂αl ∥m ⇒l ∥α;②⎭⎪⎬⎪⎫l ∥m m ∥α ⇒l ∥α,它们都缺少同一个条件,补上这个条件就可以使其构成真命题(其中l ,m 为直线,α为平面),则此条件为__________. 答案 l ⊄α解析 ①由线面平行的判定定理知l ⊄α;②由线面平行的判定定理知l ⊄α.8.如图所示,在正四棱柱ABCD —A 1B 1C 1D 1中,E ,F ,G ,H 分别是棱CC 1,C 1D 1,D 1D ,DC 的中点,N 是BC 的中点,点M 在四边形EFGH 及其内部运动,则M 只需满足条件______,就有MN ∥平面B 1BDD 1.(注:请填上你认为正确的一个条件即可,不必考虑全部可能情况)答案 点M 在线段FH 上(或点M 与点H 重合) 解析 连接HN ,FH ,FN (图略), 则FH ∥DD 1,HN ∥BD ,∴平面FHN ∥平面B 1BDD 1,只需M ∈FH , 则MN ⊂平面FHN ,∴MN ∥平面B 1BDD 1.9.如图,在正方体ABCD -A 1B 1C 1D 1中,E ,F ,G ,H 分别是BC ,CC 1,C 1D 1,AA 1的中点,求证:(1)BF ∥HD 1; (2)EG ∥平面BB 1D 1D ; (3)平面BDF ∥平面B 1D 1H . 证明 如图.(1)取B 1B 的中点M ,连接HM ,MC 1,易证四边形HMC 1D 1是平行四边形, ∴HD 1∥MC 1. 又MC 1∥BF , ∴BF ∥HD 1.(2)取BD 的中点O ,连接OE ,OD 1, 则OE 綉12DC .又D 1G 綉12DC ,∴OE 綉D 1G .∴四边形OEGD 1是平行四边形, ∴EG ∥D 1O .又D 1O ⊂平面BB 1D 1D ,EG ⊄平面BB 1D 1D , ∴EG ∥平面BB 1D 1D .(3)由(1)知BF ∥HD 1,由题意易证B 1D 1∥BD .又B 1D 1,HD 1⊂平面B 1D 1H ,BF ,BD ⊂平面BDF ,且B 1D 1∩HD 1=D 1,DB ∩BF =B , ∴平面BDF ∥平面B 1D 1H .10.如图,在四棱锥P -ABCD 中,AD ∥BC ,AB =BC =12AD ,E ,F ,H 分别为线段AD ,PC ,CD 的中点,AC 与BE 交于O 点,G 是线段OF 上一点.(1)求证:AP ∥平面BEF ; (2)求证:GH ∥平面PAD . 证明 (1)如图,连接EC , 因为AD ∥BC ,BC =12AD ,所以BC ∥AE ,BC =AE ,所以四边形ABCE 是平行四边形, 所以O 为AC 的中点. 又因为F 是PC 的中点, 所以FO ∥AP , 因为FO ⊂平面BEF ,AP ⊄平面BEF ,所以AP ∥平面BEF .(2)连接FH ,OH ,因为F ,H 分别是PC ,CD 的中点, 所以FH ∥PD ,因为PD ⊂平面PAD ,FH ⊄平面PAD , 所以FH ∥平面PAD .又因为O 是BE 的中点,H 是CD 的中点, 所以OH ∥AD ,因为AD ⊂平面PAD ,OH ⊄平面PAD , 所以OH ∥平面PAD .又FH ∩OH =H ,FH ,OH ⊂平面OHF , 所以平面OHF ∥平面PAD . 又因为GH ⊂平面OHF , 所以GH ∥平面PAD .11.(多选)已知α,β是两个平面,m,n是两条直线.下列命题正确的是( )A.如果m∥n,n⊂α,那么m∥αB.如果m∥α,m⊂β,α∩β=n,那么m∥nC.如果α∥β,m⊂α,那么m∥βD.如果α⊥β,α∩β=n,m⊥n,那么m⊥β答案BC解析如果m∥n,n⊂α,那么m∥α或m⊂α,故A不正确;如果m∥α,m⊂β,α∩β=n,那么m∥n,这就是线面平行推得线线平行的性质定理,故B正确;如果α∥β,m⊂α,那么m∥β,这就是利用面面平行推线面平行的性质定理,故C正确;缺少m⊂α这个条件,故D不正确.12.(2022·福州检测)如图所示,正方体ABCD-A1B1C1D1中,点E,F,G,P,Q分别为棱AB,C1D1,D1A1,D1D,C1C的中点,则下列叙述中正确的是( )A.直线BQ∥平面EFGB.直线A1B∥平面EFGC.平面APC∥平面EFGD.平面A1BQ∥平面EFG答案 B解析过点E,F,G的截面如图所示(H,I分别为AA1,BC的中点),连接A1B,BQ,AP,PC,易知BQ与平面EFG相交于点Q,故A错误;∵A1B∥HE,A1B⊄平面EFG,HE⊂平面EFG,∴A1B∥平面EFG,故B正确;AP⊂平面ADD1A1,HG⊂平面ADD1A1,延长HG与PA必相交,故C错误;易知平面A1BQ与平面EFG有交点Q,故D错误.13.(多选)(2022·临沂模拟)如图1,在正方形ABCD 中,点E 为线段BC 上的动点(不含端点),将△ABE 沿AE 翻折,使得二面角B -AE -D 为直二面角,得到图2所示的四棱锥B -AECD ,点F 为线段BD 上的动点(不含端点),则在四棱锥B -AECD 中,下列说法正确的有( )图1 图2A .B ,E ,C ,F 四点不共面 B .存在点F ,使得CF ∥平面BAE C .三棱锥B -ADC 的体积为定值D .存在点E 使得直线BE 与直线CD 垂直 答案 AB解析 对于A ,假设直线BE 与直线CF 在同一平面上,所以E 在平面BCF 上, 又因为E 在折前线段BC 上,BC ∩平面BCF =C ,所以E 与C 重合,与E 异于C 矛盾, 所以直线BE 与直线CF 必不在同一平面上,即B ,E ,C ,F 四点不共面,故A 正确; 对于B ,如图,当点F 为线段BD 的中点,EC =12AD 时,直线CF ∥平面BAE ,证明如下:取AB 的中点G ,连接GE ,GF , 则EC ∥FG 且EC =FG ,所以四边形ECFG 为平行四边形, 所以FC ∥EG ,又因为EG ⊂平面BAE , 则直线CF 与平面BAE 平行,故B 正确;对于C ,在三棱锥B -ADC 中,因为点E 的移动会导致点B 到平面ACD 的距离发生变化,所以三棱锥B -ADC 的体积不是定值,故C 不正确;对于D ,过D 作DH ⊥AE 于H ,因为平面BAE ⊥平面AECD ,平面BAE ∩平面AECD =AE ,所以DH ⊥平面BAE ,所以DH ⊥BE ,若存在点E 使得直线BE 与直线CD 垂直,DH ⊂平面AECD ,且DC ⊂平面AECD ,DH ∩DC =D ,所以BE ⊥平面AECD ,所以BE ⊥AE ,与△ABE 是以B 为直角的三角形矛盾,所以不存在点E 使得直线BE 与直线CD 垂直,故D 不正确.14.如图,在长方体ABCD -A 1B 1C 1D 1中,AD =DD 1=1,AB =3,E ,F ,G 分别是AB ,BC ,C 1D 1的中点,点P 在平面ABCD 内,若直线D 1P ∥平面EFG ,则线段D 1P 长度的最小值是________.答案72解析 如图,连接D 1A ,AC ,D 1C .因为E ,F ,G 分别为AB ,BC ,C 1D 1的中点, 所以AC ∥EF ,又EF ⊄平面ACD 1,AC ⊂平面ACD 1, 则EF ∥平面ACD 1.同理可得EG ∥平面ACD 1,又EF ∩EG =E ,EF ,EG ⊂平面EFG ,所以平面ACD 1∥平面EFG . 因为直线D 1P ∥平面EFG , 所以点P 在直线AC 上.在△ACD 1中,易得AD 1=2,AC =2,CD 1=2, 所以1AD C S △=12×2×22-⎝⎛⎭⎪⎫222=72, 故当D 1P ⊥AC 时,线段D 1P 的长度最小,最小值为7212×2=72.15.(2022·合肥市第一中学模拟)正方体ABCD -A 1B 1C 1D 1的棱长为1,点M ,N 分别是棱BC ,CC 1的中点,动点P 在正方形BCC 1B 1(包括边界)内运动,且PA 1∥平面AMN ,则PA 1的长度范围为( )A.⎣⎢⎡⎦⎥⎤1,52B.⎣⎢⎡⎦⎥⎤324,52C.⎣⎢⎡⎦⎥⎤324,32 D.⎣⎢⎡⎦⎥⎤1,32答案 B解析 取B 1C 1的中点E ,BB 1的中点F ,连接A 1E ,A 1F ,EF , 取EF 的中点O ,连接A 1O ,如图所示,∵点M ,N 分别是棱长为1的正方体ABCD -A 1B 1C 1D 1中棱BC ,CC 1的中点, ∴AM ∥A 1E ,MN ∥EF ,∵AM ∩MN =M ,A 1E ∩EF =E ,AM ,MN ⊂平面AMN ,A 1E ,EF ⊂平面A 1EF , ∴平面AMN ∥平面A 1EF ,∵动点P 在正方形BCC 1B 1(包括边界)内运动, 且PA 1∥平面AMN ,∴点P 的轨迹是线段EF ,∵A 1E =A 1F =12+⎝ ⎛⎭⎪⎫122=52,EF =1212+12=22,∴A 1O ⊥EF ,∴当P 与O 重合时,PA 1的长度取最小值A 1O , A 1O =⎝ ⎛⎭⎪⎫522-⎝ ⎛⎭⎪⎫242=324,当P 与E (或F )重合时,PA 1的长度取最大值A 1E 或A 1F ,A 1E =A 1F =52.∴PA 1的长度范围为⎣⎢⎡⎦⎥⎤324,52.16.如图,正方体ABCD -A 1B 1C 1D 1中,棱长为a ,M ,N 分别为AB 1,A 1C 1上的点,A 1N =AM .(1)求证:MN ∥平面BB 1C 1C ;(2)求MN 的最小值.(1)证明 如图,作NE ∥A 1B 1交B 1C 1于点E ,作MF ∥AB 交BB 1于点F ,连接EF , 则NE ∥MF .∵NE ∥A 1B 1,∴NEA 1B 1=C 1NA 1C 1.又MF ∥AB ,∴MF AB =B 1MAB 1,∵A 1C 1=AB 1,A 1N =AM ,∴C 1N =B 1M .∴NE A 1B 1=MF AB,又AB =A 1B 1,∴NE =MF .∴四边形MNEF 是平行四边形,∴MN ∥EF , 又MN ⊄平面BB 1C 1C ,EF ⊂平面BB 1C 1C , ∴MN ∥平面BB 1C 1C .(2)解 设B 1E =x ,∵NE ∥A 1B 1, ∴B 1E B 1C 1=A 1NA 1C 1.又∵MF ∥AB ,∴B 1F BB 1=B 1M AB 1,∵A 1N =AM ,A 1C 1=AB 1=2a ,B 1C 1=BB 1=a ,B 1E =x ,∴B 1E B 1C 1+B 1F BB 1=A 1N A 1C 1+B 1MAB 1,∴x a +B 1F a =1,∴B 1F =a -x ,从而MN =EF =B 1E 2+B 1F 2 =x 2+a -x2 =2⎝ ⎛⎭⎪⎫x -a 22+⎝ ⎛⎭⎪⎫a 22, ∴当x =a 2时,MN 的最小值为22a .。
2023届高三数学一轮复习专题 立体几何垂直系统 讲义 (解析版)

高三数学第一轮复习专题 垂直系统专题第一部分 直线与平面垂直的判定及性质一。
线面垂直的定义:l l αα若直线与平面内的任意一条直线都垂直,则称直线与平面垂直.记作:l α⊥。
l 直线叫做α平面的垂线,α平面叫做l 直线的垂面。
(★★★)线面垂直的定义可以作为线面垂直的性质定理使用: 若l 直线与α平面垂直,则l 直线与α平面内任意一条直线都垂直。
,l a l a αα⊥⊂⇒⊥ ⇒线面垂直线线垂直二。
线面垂直的判定定理:1。
判定定理1:若一条直线和一个平面内的两条相交直线都垂直,则该直线与这个平面垂直。
(★★★)⇒线线垂直线面垂直,,,,a b a b P l a l b l ααα⊂⊂⋂=⊥⊥⇒⊥两个核心条件:,l a l b ⊥⊥2。
判定定理2:若两平行直线中的一条垂直于一个平面,则另一条也垂直于这个平面。
(★★)a ∥b ,a α⊥b α⇒⊥三。
线面垂直的性质定理:1。
性质定理1:垂直于同一平面的两直线平行。
a α⊥,b α⊥a ⇒∥bα2。
性质定理2:垂直于同一直线的两平面平行。
l α⊥,l β⊥⇒α∥β题型一:线线垂直与线面垂直的互相证明 ★★★★★判定定义线线垂直线面垂直这两个定理(定义)构成了一个很重要的小循环:⇒⇒⇒⇒⋅⋅⋅⋅⋅⋅线线垂直线面垂直线线垂直线面垂直例1。
P 为ABC 所在平面外一点,PA ABC ⊥平面,090ABC ∠=,AE PB E ⊥于,AF PC F ⊥于。
求证:PC AEF ⊥平面。
(★★)规律:常用线面垂直来证明两直线“异面垂直”。
已知的是相交垂直,要证的是异面垂直。
分析:从后往前分析。
要证()PC AF PC AEF PC AE AE PBC ⎧⊥⎪⊥⇐⎨⊥⇐⊥⎪⎩已知平面平面 α()090AE PB BC AB ABC AE BC BC PAB BC PA PA ABC ⎧⊥⎪⎪⇐⎨⎧⊥⇐∠=⎪⊥⇐⊥⇐⎨⎪⊥⇐⊥⎩⎩已知平面平面 但写证明过程时要从前往后写。
2025届新高考一轮复习特训---立体几何初步(含解析)

2025届新高考一轮复习特训 立体几何初步一、选择题1.平行六面体1111ABCD A B C D -中,底面ABCD 为正方形,11A AD A AB ∠=∠=11AA AB ==,E 为11C D 的中点,则异面直线BE 和DC 所成角的余弦值为( )2.已知正方体1111ABCD A B C D -的棱长为2,E ,F ,G 分别是AB ,1BB ,11B C 的中点,则过这三点的截面面积是( )A.3.已知平面α,β,γ,l αβ= ,则“l γ⊥”是“αγ⊥且βγ⊥”的( )A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件4.如图,某车间生产一种圆台形零件,其下底面的直径为4cm ,上底面的直径为8cm ,高为4cm ,已知点P 是上底面圆周上不与直径AB 端点重合的一点,且AP BP =,O 为上底面圆的圆心,则OP 与平面ABC 所成的角的正切值为( )5.已知长方体的一条棱长为2,体积为16,则其外接球表面积的最小值为( )A.5πB.12πC.20πD.80π6.如图,在棱长为1的正方体1111ABCD A B C D -中,E 为线段1DD 的中点,F 为线段1BB 的中点.直线1FC 到平面1AB E 的距离为( ).7.在三棱柱111ABC A B C -中,AB BC AC ==,侧棱1AA ⊥底面ABC ,若该三棱柱的所有顶点都在同一个球O 的表面上,且球O 的表面积的最小值为4π,则该三棱柱的侧面积为( )A.8.设A ,B ,C ,D 是同一个半径为4的球的球面上的四点,ABC △为等边三角形且其面积为D ABC -体积的最大值为( )A. C.二、多项选择题9.在ABC △中,AC BC ==2AB =,ABD △是有一个角是30°的直角三角形,若二面角D AB C --是直二面角,则DC 的长可以是( )10.如图,P 为矩形ABCD 所在平面外一点,矩形对角线的交点为O ,M 为PB 的中点,则下列结论成立的是( )A.//OM 平面PCDB.//OM 平面PDAC.//OM 平面PBAD.平面PBC11.如图,正方体1111ABCD A B C D -的棱长为1,动点P 在对角线1BD 上,过P 作垂直于1BD 的平面α,记平面α与正方体1111ABCD A B C D -的截面多边形(含三角形)的周长为L,面积为S ,BP x =,(x ∈,下面关于函数()L x 和()S x 的描述正确的是( )A.(S x B.()L x 在x=C.()L x 在⎛⎝上单调递增,在上单调递减;D.()S x 在⎛⎝上单调递增,在上单调递减三、填空题12.如图一个正六棱柱的茶叶盒,底面边长为10cm ,高为20cm ,则这个茶叶盒的表面积为______2cm .13.已知正三棱柱111ABC A B C-的各棱长都等于2,点E 是11A B 的中点,则异面直线AE 与1BC 所成角的余弦值为________.14.底面边长为4的正四棱锥被平行于其底面的平面所截,截去一个底面边长为2,//OM高为3的正四棱锥,所得棱台的体积为____________.四、解答题15.如图,在三棱锥A BCD -中,BCD △是边长为2的等边三角形,AB AC =,O 是BC 的中点,OA CD ⊥.(1)证明:平面ABC ⊥平面BCD .(2)若点E 是棱AC 上的一点,则从①2CE EA =,②二面角E BD C --的大小为60︒,③三棱锥A BCD -成立.16.如图,垂直于梯形ABCD 所在平面,,F 为线段PA 上一点,112ABAD CD ===,四边形为矩形.(1)若F 是PA 的中点,求证:平面DEF ;(2)求直线与平面BCP 所成角的正弦值;(3)若点F 到平面的长.17.如图,P 为圆锥的顶点,O 为圆锥底面的圆心,AC 为底面直径,ABD △为底面四O 的内接正三角形,且△PC 上,且AE =1CE =.PD 90ADC BAD ∠∠==︒PD =PDCE //AC AE(1)求证:BD AE ⊥,并求三棱锥P BDE -的体积;(2)若点M 为线段PO 上的动点,当直线DM 与平面ABE 所成角的正弦值最大时,求此时点M 到平面ABE 的距离.18.如图,在多面体ABCDEF 中,已知四边形ABCD 是菱形,AF ⊥平面ABCD .(1)证明:平面BDE ⊥平面ACF ;(2)若4AD =,6AF =,3DE =,//DE AF ,AE 与平面BDE 三棱锥F CDE -的体积.19.如图所示,已知正方形ABCD 和矩形ACEF 所在的平面互相垂直,AB =1AF =,M 是线段EF 的中点.求证:(1)//AM 平面BDE ;(2)AM ⊥平面BDF .参考答案1.答案:A解析:由题意,11π11cos 3AA AB AA AD ⋅=⋅=⨯⨯= 0AB AD ⋅= ,又DC AB = ,1111112BE AE AB AA A D D E AB AA AD AB =-=++-=+-,所以111100222BE DC AA AD AB AB ⎛⎫⋅=+-⋅=+-= ⎪⎝⎭,即有BE DC ⊥ ,故选:A.2.答案:D解析:如图所示,分别取11C D ,1DD ,AD 的中点H ,M ,N ,连接GH ,HM ,MN ,NE ,在正方体1111ABCD A B C D -中,可得//GH NE ,//HM EF ,//MN FG ,所以经过点E,F ,G 的截面为正六边形EFGHMN ,又因为正方体1111ABCDA B C D -的棱长为2,在直角BEF△中,可得EF==所以截面正六边形的面积为26=故选:D.3.答案:C解析:由于l αβ= ,所以l α⊂,l β⊂,若l γ⊥,则αγ⊥,βγ⊥,故充分性成立,若αγ⊥,βγ⊥,设m αγ= ,n βγ= ,则存在直线,a γ⊂使得a m ⊥,所以a α⊥,由于l ⊂α,故a l ⊥,同理存在直线,b γ⊂使得b n ⊥,所以b β⊥,由于l β⊂,故b l ⊥,由于a ,b 不平行,所以a ,b 是平面γ内两条相交直线,所以l γ⊥,故必要性成立,故选:C.4.答案:A解析:设O '为下底面圆的圆心,连接OO ',CO '和CO ,因为AP BP =,所以AB OP ⊥,又因为AB OO ⊥',OP OO O '= ,OP ,OO '⊂平面OO P ',所以AB ⊥平面OO P ',因为PC 是该圆台的一条母线,所以O ,O ',C ,P 四点共面,且//O C OP ',又AB ⊂平面ABC ,所以平面ABC ⊥平面POC ,又因为平面ABC 平面POC OC =,所以点P 在平面ABC 的射影在直线OC 上,则OP 与平面ABC 所成的角即为POC OCO ∠=∠',过点C 作CD OP ⊥于点D ,因为4cm OP =,2cm O C '=,所以tan tan 2OO POC OCO O C∠=''∠=='.故选:A.5.答案:C解析:设长方体的长、宽、高分别为a ,b ,2,所以长方体的体积为216V ab ==,解得:8ab =,设长方体的外接球的半径为R ,所以2R =22242420R a b ab =++≥+=,即R ≥b ==所以min R =所以其外接球表面积的最小值为24π20πS R ==.故选:C.6.答案:D解析:1//AE FC ,1FC ⊂/平面1AB E ,AE ⊂平面1AB E ,1//FC ∴平面1AB E ,因此直线1FC 到平面1AB E 的距离等于点1C 到平面1AB E 的距离,如图,以D 点为坐标原点,DA 所在的直线为x 轴,DC 所在的直线为y 轴,1DD 所在的直线为轴,建立直角坐标系.则(1,0,0)A ,1(1,1,1)B ,1(0,1,1)C ,10,0,2E ⎛⎫ ⎪⎝⎭,11,1,2F ⎛⎫ ⎪⎝⎭,,,,,设平面的法向量为,则,令,则设点到平面1AB E 的距离为d ,则1113n C B d n⋅==故直线1FC 到平面1ABE 故选:D.7.答案:B解析:如图:设三棱柱上,下底面中心分别为1O ,2O ,则12OO 的中点为O ,111,0,2FC ⎛⎫=- ⎪⎝⎭ 11,0,2AE ⎛⎫=- ⎪⎝⎭ 1(0,1,1)AB =11(1,0,0)C B = 1AB E (,,)n x y z =11020n AE x z n AB y z ⎧⋅=-+=⎪⎨⎪⋅=+=⎩2z =(1,2,2)n =- 1C设球O 的半径为R ,则OA R =,设AB BC AC a ===,1AA h =,则212OO h =,223O A AB ==,则在2Rt OO A △中,222222*********R OA OO O A h a h ==+=+≥⨯=,当且仅当h =时,等号成立,所以24π4πS R =≥球4πah =,所以ah =所以该三棱柱的侧面积为3ah =故选:B.8.答案:B解析:如图,设点O 为球心,点M 为三角形ABC 的中心,E 为AC 的中点,连接OB ,DM ,且DM 过球心O ,连接BE ,且BE 过点M ,当DM ⊥平面ABC 时,三棱锥D ABC -的体积最大.2ABC S AB == △6AB =.又 点M 为三角形ABC 的中心,23BM BE ∴==,在Rt OMB △中,2OM ==,426DM OD OM ∴=+=+=,∴三棱锥D ABC -体积的最大6=9.答案:ACD 解析:如图①,当60ADB ∠=︒且90DBA ∠=︒时,二面角D AB C --是直二面角,故平面ABD ⊥平面ABC ,且平面ABD 平面ABC AB =,DB ⊂平面ABD ,故DB ⊥平面ABC ,所以DB BC ⊥,因为tan AB DB ADB ==∠==同理可得,当30ADB ∠=︒且90DBA ∠=︒时,DB ⊥平面ABC ,所以DB BC ⊥,因为tan ABDB ADB==∠==当90ADB ∠=︒且30DAB ∠=︒时,如图②,过点D 作DE AB ⊥,垂足为E ,连接CE ,因为平面ABD ⊥平面ABC ,且平面ABD 平面ABC AB =,DE ⊂平面ABD ,故DE ⊥平面ABC ,所以DE CE ⊥,此时cos DA AB DAB =∠=,sin DE DA DAB =∠=cos AE AD DAB =∠===所以DC ==当90ADB ∠=︒且60DAB ∠=︒时,同理可得,sinDE DA DAB=∠====故选:ACD.10.答案:AB解析:矩形ABCD 的对角线AC 与BD 交于点O ,所以点O 为BD 的中点,在△PBD 中,因为点M 是PB 的中点,所以OM 是的中位线,,平面PCD ,平面PCD ,平面PCD ,故A 正确;PD ⊂平面PDA ,平面PDA ,平面PDA ,故B 正确;因为M ∈PB ,O ∉平面PBC ,O ∉平面PAB ,所以OM 与平面PAB ,平面PBC 相交,故CD 错误;故选:AB.11.答案:AD解析:当x ⎛∈⎝时,截面为等边三角形,如图:因为BP x =,所以EF =,所以:()L x =,()2S x x =,x ⎛∈ ⎝.此时()L x ,()S x 在上单调递增,且当时截面为六边形,如图:PBD △//OM PD PD ⊂OM ⊄//OM ∴OM⊄//OM ∴⎛ ⎝()L x ≤()x ≤x ∈设AE t =,则11AE AF CG CH B N B M t======所以六边形EFGHMN 的周长为:)1t +-=为定值;做1NN ⊥平面ABCD 于1N ,1MM ⊥平面ABCD 于1M .设平面EFGHMN 与平面ABCD 所成的角为α,则易求cos α=所以11cos EFDHMN FAN M CG S S α⋅=,所以()22111122EFDHMN S t t ⎡⎤=---⎢⎥⎣⎦212t t ⎫=+-⎪⎭,在10,2t ⎛⎤∈ ⎥⎝⎦上递增,在1,12t ⎡⎫∈⎪⎢⎣⎭上递减,111224⎫+-=⎪⎭=x =所以()S x 在上递增,在上递减.x =()x当x ∈时,易得:())L x x =,())2S x x=-此时()L x ,()S x 在上单调递减,()L x <()x <综上可知:AD 是正确的,BC 错误.故选:AD12.答案:300(4解析:由题设,一个底面的面积为21161010sin 602S =⨯⨯⨯⨯︒=,一个侧面矩形面积为22102020c 0m S =⨯=,所以茶叶盒的表面积为22126300(4c mS S +=+.故答案为:300(4解析:连结1A B ,交AE 于点M ,作1//MN BC ,交11A C 于点N ,连结EN ,异面直线AE 与1BC 所成的角为EMN ∠或其补角,因为1//A E AB ,且,所以1::1:2EM MA A M MB ==,所以113BC ==,EN ==中,222cos 2ME MN EN EMN ME MN +-∠==⋅14.答案:28=(44)6⨯⨯=(22)34⨯⨯=,所以棱台的体积为32428-=.112A E AB =13ME AE ==123A N =EMN △3(16428⨯++=.故答案为28.15.答案:(1)证明见解析(2)见解析解析:(1)证明:因为AB AC =,O 是BC 的中点,所以OA BC ⊥.又因为OA CD ⊥,BC CD C = ,,BC CD ⊂平面BCD ,所以OA ⊥平面BCD .因为OA ⊂平面ABC ,所以平面ABC ⊥平面BCD .(2)如图,连接OD .因为BCD △是边长为2的等边三角形,所以DO BC ⊥.由(1)知,OA ⊥平面BCD ,所以AO ,BC ,DO 两两互相垂直.以O 为坐标原点,分别以OB ,OD ,OA 所在直线为x 轴、y 轴、z 轴建立空间直角坐标系.设||(0)OA m m =>,则(0,0,0)O ,(0,0,)A m ,(1,0,0)B ,(1,0,0)C -,D .若选①②作为条件,证明③成立.因为2CE EA =,所以2CE EA = ,所以12,0,33m E ⎛⎫- ⎪⎝⎭.易知平面BCD 的一个法向量为(0,0,1)=n ,42,0,33m BE ⎛⎫=- ⎪⎝⎭,(BD =-.设(,,)x y z =m 是平面BDE 的法向量,则0,0,BE BD ⎧⋅=⎪⎨⋅=⎪⎩m m 所以420,330.m x z x ⎧-+=⎪⎨⎪-=⎩令1x =,则y =z =2m ⎛⎫= ⎪ ⎪⎝⎭.由二面角EBD C --的大小为60||60||||⋅︒===m n m n 3m =.所以三棱锥A -1232⨯=若选①③作为条件,证明②成立.因为三棱锥A -122m ⨯=3=,即(0,0,3)A .又因为2CE EA =,所以1,0,23E ⎛⎫- ⎪⎝⎭.易知平面BCD 的一个法向量为(0,0,1)=n ,4,0,23BE ⎛⎫=- ⎪⎝⎭,(BD =-.设(,,)x y z =m 是平面BDE 的法向量,则0,0,BE BD ⎧⋅=⎪⎨⋅=⎪⎩ m m 即420,30.x z x ⎧-+=⎪⎨⎪-=⎩令1x =,则y =z =23⎛⎫= ⎪ ⎪⎝⎭.设二面角E BD C --的大小为θ,则|||cos |||||θ⋅===m n m n BD C --的大小为60︒.若选②③作为条件,证明①成立.又(1,0,0)C -,所以(1,0,3)AC =--.设(,,)E x y z .不妨设(01)AE AC λλ=≤≤,则(,,3)(1,0,3)x y z λ-=--,所以(,0,33)E λλ--+.易知平面BCD 的一个法向量为(0,0,1)=n ,(1,0,33)BE λλ=---+ ,(BD =-.设(,,)x y z =m 是平面BDE 的法向量,则0,0,BE BD ⎧⋅=⎪⎨⋅=⎪⎩ m m 即(1)(33)0,0.x z x λλ--+-=⎧⎪⎨-+=⎪⎩当1λ=时,二面角E BD C --的大小为0︒,不合题意,所以01λ≤<.令1x =,则y=z =133λλ⎛⎫+= ⎪ ⎪-⎝⎭.设二面角E BD C --的大小为θ,则|||cos |||||θ⋅===m n m n 解得3λ=(舍去)或λ=所以2CE EA =.16.答案:(1)证明见解析;;解析:(1)设CP DE G = ,连接, 四边形为矩形,∴G 为中点,又F 为PA 中点,,又FG ⊂平面,AC ⊄平面,//AC ∴平面.(2)以D 为坐标原点,DA ,,DP正方向为x ,y ,z 轴,可建立如图所示空间直角坐标系,FG PDCE PC //AC FG ∴DEF DEF DEF DC则,()1,1,0B ,,(P ,()1,1,0BC ∴=-,,(1,AE =-设平面BCP 的法向量,20BC n x y CP n y ⎧⋅=-+=⎪∴⎨⋅=-+=⎪⎩,令,解得:1x=,(n = ;设直线与平面BCP 所成角为,sin cos ,AE n AE n AE n θ⋅∴===⋅则直线与平面(3)(1,0,PA =,设,[]0,1λ∈由平面的法向量(n =,点F 到平面的距离2PF n d nλ⋅===解得,13PA = 解析:(1)设AC BD F = ,连接EF ,ABD △为底面圆O 的内接正三角形,2AC ∴==,F 为BD 中点,又AF ==322CF ∴=-=312AO AF ==;()1,0,0A ()0,2,0C (0,E (0,CP =- (),,n x y z =1y =z =AE θAE (),0,PF PA λλ==BCP BCP 13λ=AE = 1=,222AE CE AC ∴+=,AE EC ∴⊥,AF AE =AEF ACE ∽△△,AFE AEC ∠∠∴=,EF AC ∴⊥,;PO ⊥ 平面ABD ,PO ⊂平面PAC ,∴平面PAC ⊥平面ABD ,平面PAC 平面ABD AC =,EF ⊂平面PAC ,EF ∴⊥平面ABD ,又BD ⊆面ABD ,EF BD ⊥,又BD AC ⊥,EF AC F = ,BD ⊥面AEC ,又AE ⊂面AEC ,所以BD AE⊥又PO ⊥平面ABD ,//EF PO ∴,PO ⊄ 平面BDE ,EF ⊂平面BDE ,//PO ∴平面BDE ;F 为BD 中点,AF BD ∴⊥,即OF BD ⊥,又EF ⊥平面ABD ,平面,,OF BD ⊂平面ABD ,EF OF ∴⊥,EF BD ⊥,EF BD F = ,,EF BD ⊂平面BDE ,OF ∴⊥平面BDE ,EF === BD ⊥,1122BDE S BD EF ∴=⋅==△又12OF AF ==//平面BDE ,11313342P BDE O BDE BDE V V S OF --∴==⋅=⨯⨯=△(2)OF CF ==F 为OC 中点,又//PO EF ,∴E 为PC 中点,2PO EF =,PO ∴=2=,以F 为坐标原点,FB ,FC ,FE正方向为x ,y ,z 轴,可建立如图所示空间直角坐标系,则30,,02A ⎛⎫-⎪⎝⎭,B ⎫⎪⎪⎭,E ⎛⎝,D ⎛⎫ ⎪ ⎪⎝⎭,10,,02O ⎛⎫- ⎪⎝⎭,10,2P ⎛-⎝,3,02AB ⎫∴=⎪⎪⎭ ,30,2AE ⎛=⎝ ,(OP =,1,02DO ⎫=-⎪⎪⎭ ,3,02DA ⎫=-⎪⎪⎭ ,设()()01OMOP λλ==≤≤,12DM DO OM ⎫∴=+=-⎪⎪⎭ ;设平面ABE 的法向量(),,n x y z =,则302ABn x y ⋅=+= 则302AE n y z ⋅=+=令1y =-,解得:x =z =n =-,设直线DM 与平面ABE 所成角为θ,sin DM n DM n θ⋅∴===⋅令32t λ=+,则[]2,5t ∈,λ∴=2222222(2)1314717431(32)33t t t t t t t λλ-++-+⎛⎫∴===-+ ⎪+⎝⎭,111,52t⎡⎤∈⎢⎥⎣⎦,∴=即λ=22min 3131449(32)4λλ+⎤+==⎥+⎦max (sin )1θ∴==,此时12DM =- ,0,1,MA DA DM ⎛∴=-=- ⎝,∴点M 到平面ABE的距离MA n d n ⋅=== 18.答案:(1)证明见解析;(2)解析:(1)如图,设AC 与BD 交于点O .因为四边形ABCD 是菱形,所以AC BD ⊥.因为AF ⊥平面ABCD ,BD ⊂平面ABCD ,所以AF BD ⊥.因为AF AC A = ,AF AC ⊂、平面ACF ,所以BD ⊥平面ACF.又因为BD ⊂平面BDE ,所以平面BDE ⊥平面ACF .(2)因为AF ⊥平面ABCD ,//DE AF ,所以DE ⊥平面ABCD ,因为AC ⊂平面ABCD ,所以DE AC ⊥.又因为AC BD ⊥,DE BD D = ,,DE BD ⊂平面BDE ,所以AC ⊥平面BDE .连接OE ,AEO ∠即为AE 与平面BDE 所成的角,所以sin AO AEO AE ∠==因为4AD =,3DE =,所以5AE =,所以2AO =,所以24AC AO ==,所以ACD △是等边三角形.因为//DE AF ,DE ⊂平面BDE ,AF ⊄平面BDE ,所以//AF 平面BDE,所以111443332F CDE A CDE E ACD ACD V V V S DE ---===⋅=⨯⨯⨯=△19.答案:(1)见解析;(2)见解析解析:(1)建立如图所示的空间直角坐标系,设AC BD N = ,连结NE .则N ⎫⎪⎪⎭,()0,0,1E ,)A,M ⎫⎪⎪⎭.∴NE ⎛⎫ ⎪ ⎪⎝=⎭,AM ⎛⎫ =⎪ ⎪⎝⎭ .∴//AM NE 且NE 与AM 不共线.∴//NE AM . NE ⊂平面BDE ,AM ⊄平面BDE ,∴//AM 平面BDE .(2)由(1)知AM ⎛⎫ =⎪⎪⎝⎭ ,)D,)F ,∴()DF = ,∴0DF AM ⋅= ,∴AM DF ⊥.同理.又,平面.AM BF ⊥DF BF F = ∴AM ⊥BDF。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高三数学文一轮复习专题突破训练立体几何一、选择、填空题1、(2016年全国I 卷)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是283π,则它的表面积是(A )17π (B )18π (C )20π (D )28π2、(2016年全国II 卷)体积为8的正方体的顶点都在同一球面上,则该球面的表面积为(A )12π (B )323π(C )8π (D )4π3、(2016年全国I 卷)平面α过正方体1111ABCD A B C D -的顶点A ,//α平面11CB D ,α平面ABCD m =,α平面11ABB A n =,则m ,n 所成角的正弦值为 (A)2(B)2 (C(D )134、(2016年全国II 卷)如图是由圆柱及圆锥组合而成的几何体的三视图,则该几何体的表面积为111(A )20π (B )24π (C )28π (D )32π5、(2016年全国III 卷)如图,网格纸上小正方形的边长为1,粗实现画出的是某多面体的三视图,则该多面体的表面积为(A )18365+ (B )54185+ (C )90 (D )81 6、(2016年全国III 卷)在封闭的直三棱柱111ABC A B C -内有一个体积为V 的球,若AB BC ⊥,6AB =,8BC =,13AA =,则V 的最大值是 (A )4π (B )92π(C )6π(D )323π7、(2015年全国I 卷)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问”积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米有()(A)14斛(B)22斛(C)36斛(D)66斛8、(2015年全国I卷)圆柱被一个平面截去一部分后及半球(半径为r)组成一个几何体,该几何体的三视图中的正视图和俯视图如图所示,若该几何体的表面积为1620π+,则r=( )(A)1(B)2(C)4(D)89、(广东省2016届高三3月适应性考试)某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,两条虚线互相垂直且相等,则该几何体的体积是()A.203 B.163C .86π- D .83π-10、(广东佛山市2016届高三二模)已知A 、B 、C 都在半径为2的球面上,且AC BC ⊥,30ABC ∠=,球心O 到平面ABC 的距离为1,点M 是线段BC 的中点,过点M 作球O 的截面,则截面面积的最小值为( ) A .34π B .34πC .3πD .3π11、(广东广州市2016届高三二模)如图, 网格纸上的小正方形的边长为1, 粗实线画出的是某几何体的三视图, 则该几何体的体积是 (A) 86+π (B) 46+π (C) 412+π (D) 812+π12、(广东深圳市2016届高三二模)设,l m 是两条不同的直线,α是一个平面,下列命题正确的是( )A .若l m ⊥,m α⊂,则l α⊥B .若l α⊥,l //m ,则m α⊥C .若m //α,m α⊂,则l //mD .若l //α,m //α,则l //m 13、(广东珠海市2016届高三二模)某几何体三视图如图所示,则该几何体的最短的棱 长度是( )A .2314、(揭阳市2016届高三上学期期末学业水平考试)已知棱长为2的正方体ABCD-A1B1C1D1的一个面A1B1C1 D1在一半球底面上,且A、B、C、D四个顶点都在此半球面上,则此半球的体积为(A) 46π (B) 26π (C) 163π (D) 86π15、(茂名市2016届高三第一次高考模拟)一个几何体的三视图如图所示,则该几何体的体积为()A、43B、23C、13D、216、(清远市2016届高三上学期期末)一个几何体的三视图如图所示,正视图为直角三角形、侧视图为等边三角形,俯视图为直角梯形,则该几何体的体积等于()A3B.3C .D.二、解答题1、(2016年全国I 卷高考)如图,已知正三棱锥P -ABC 的侧面是直角三角形,PA =6,顶点P 在平面ABC 内的正投影为点D ,D 在平面PAB 内的正投影为点E ,连结PE 并延长交AB 于点G . (I )证明:G 是AB 的中点;(II )在图中作出点E 在平面PAC 内的正投影F (说明作法及理由),并求四面体PDEF 的体积.PABD CGE2、(2016年全国II 卷高考) 如图,菱形ABCD 的对角线AC 及BD 交于点O ,点E 、F 分别在AD ,CD 上,AE CF =,EF交BD 于点H ,将DEF ∆沿EF 折到'D EF ∆的位置. (Ⅰ)证明:'AC HD ⊥;(Ⅱ)若55,6,,'4AB AC AE OD ====求五棱锥D ABCEF '-体积.3、(2016年全国III卷高考)如图,四棱锥P ABC-中,PA⊥平面ABCD,AD BC,3==,M为线段AD上一点,2PA BCAB AD AC===,4=,AM MDN为PC的中点.(I)证明MN平面PAB;(II)求四面体N BCM-的体积.4、(2015年全国I卷)如图四边形ABCD为菱形,G为AC及BD交点,⊥平面,BE ABCD(I )证明:平面AEC ⊥平面BED ;(II )若120ABC ∠=,,AE EC ⊥ 三棱锥E ACD -的体积为6的侧面积.5、(广东省2016届高三3月适应性考试)如图所示,在直三棱柱ABC DEF -中,底面ABC 的棱AB BC ⊥,且2AB BC ==.点G 、H 在侧棱CF 上,且1CH HG GF ===. (1)证明:EH ⊥平面ABG ; (2)求点C 到平面ABG 的距离.6、(广东佛山市2016届高三二模)如图,在直四棱柱1111ABCD A B C D -中,60,,BAD AB BD BC CD ∠===.(1)求证:平面11ACC A ⊥平面1A BD ;(2)若BC CD ⊥,12AB AA ==,求三棱锥11B A BD -的体积.H A CBDEF G A C D 1OMDCB A7、(广东广州市2016届高三二模) 如图,在多面体ABCDM 中,△BCD 是等边三角形,△CMD 是等腰直角三角形,90CMD ︒∠=,平面CMD ⊥平面BCD ,AB ⊥平面BCD ,点O 为CD 的中点, 连接OM .(Ⅰ) 求证:OM ∥平面ABD ;(Ⅱ) 若2AB BC ==,求三棱锥A BDM -的体积.8、(广东深圳市2016届高三二模)如图,平面ABCD ⊥平面ADEF ,四边形ABCD 为菱形,四边形ADEF 为矩形,M 、N 分别是EF 、BC 的中点,2AB AF =,60CBA ∠=. (1)求证:DM ⊥平面MNA ; (2)若三棱锥A DMN -的体积为3,求点A 到平面DMN 的距离.9、(广东珠海市2016届高三二模)B CDAEFM N图311DB如图,四棱锥P ABCD -中,四边形ABCD 是等腰梯形,其中//AB CD ,132AB CD ==,且60BCD ∠=;E 为CD 中点,4PA PB PC PD ====.⑴ 求证:AD PE ⊥. ⑵ 求四棱锥P ABCD -的体积10、(惠州市2016届高三第三次调研)如图,已知等腰梯形ABCD 中,1//,2,2AD BC AB AD BC E ===是BC 的中点,AEBD M =,将BAE ∆沿着AE 翻折成1B AE ∆.(Ⅰ)求证:CD ⊥平面1B DM ;(Ⅱ)若101=C B ,求棱锥1B CDE -的体积11、(揭阳市2016届高三上学期期末学业水平考试)如图4,在三棱柱ABC A 1B 1C 1中,底面△ABC 是边长为2(Ⅰ)求证:BC 1∥平面A 1CD ;(Ⅱ)若四边形CB B 1C 1是正方形,且15,A D求多面体11CAC BD 的体积.PABCDEABDC EM AM1B D ECG FEDCBA12、(韶关市2016届高三上学期调研)如图,四边形ABCD是矩形,GF⊥平面1,2AB AD==,E是AD的中点,BE及AC交于点F,ABCD.(Ⅰ)求证:AF⊥面BEG;(Ⅱ) 若AF FG=,求点E到平面ABG距离.13、(湛江市2016年普通高考测试(一))如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,AB1⊥平面A1CD,AC⊥BC,D为AB中点。
(I)证明:CD⊥平面AA1B1B;(II)若AA1=1,AC=2,求三棱锥C1-A1DC的体积。
14、(肇庆市2016届高三第二次统测(期末))如图3,正方形ABCD的边长为22E、F分别是DC和BC的中点,H是正方形的对角线AC及EF的交点,N是正方形两对角线的交点,现沿EF将CEF∆折起到PEF∆的位置,使得PH AH⊥,连结PA,PB,PD (如图4).(Ⅰ)求证:BD⊥AP;(Ⅱ)求三棱锥A BDP-的高.15、(珠海市2016届高三上学期期末)如图,四棱锥P ABCD-底面ABCD为平行四边形,且AC BD O=,PA PC=,PB BD⊥,平面PBD⊥平面PAC(I)求证PB⊥面ABCD(II)若PAC∆为正三角形,60BAD∠=︒,且四棱锥P ABCD-的体积为66PCD∆的面积.ODAPC第19题图参考答案一、选择、填空题 1、【答案】A得的【解析】原几何体是一个球被切掉左上角的18后所几何体(如图所示),其体积是球的体积78,即37428833r ππ⨯=,故球的半径2r =;其三视图表面积是球面面积78和三个扇形面积之和,即2271=42+32=1784S πππ⨯⨯⨯⨯,故选A .2、【答案】A【解析】因为正方体的体积为8,所以正方体的体对角线长为,所以球面的表面积为2412ππ⋅=,故选A. 3、【答案】A【解析】如图所示:∵11CB D α∥平面,若设平面11CB D 平面1ABCD m =, 则1m m ∥又∵平面ABCD ∥平面1111A B C D ,结合平面11B D C 平面111111A B C D B D = ∴111B D m ∥,故11B D m ∥ 同理可得:1CD n ∥故m 、n 的所成角的大小及11B D 、1CD 所成角的大小相等,即11CD B ∠的大小.而1111B C B D CD ==(均为面对交线),因此113CD B π∠=,即11sin CD B ∠=.故选A . 4、【答案】C【解析】因为原几何体由同底面一个圆柱和一个圆锥构成,所以其表面积为28S π=,故选C. 5、【答案】B 【解析】试题分析:由三视图该几何体是以侧视图为底面的斜四棱柱,所以该几何体的表面积2362332354S =⨯⨯+⨯⨯+⨯⨯=+B .6、【答案】B7、【答案】B 【解析】试题分析:设圆锥底面半径为r ,则12384r ⨯⨯==163r =,所以米堆的体积为211163()5433⨯⨯⨯⨯=3209,故堆放的米约为3209÷1.62≈22,故选B. 考点:本题主要考查圆锥的性质及圆锥的体积公式 8、【答案】B 【解析】试题分析:由正视图和俯视图知,该几何体是半球及半个圆柱的组合体,圆柱的半径及球的半径都为r ,圆柱的高为2r ,其表面积为22142222r r r r r r πππ⨯+⨯++⨯=2254r r π+=16 + 20π,解得r=2,故选B. 9、A10、【答案】B【解析】∵AC BC ⊥,∴90ACB ∠=,∴圆心O 在平面的射影为AB D 的中点,∴22112AB OB OD =-=,∴2AB =.∴cos303BC AC ==当线段BC 为截面圆的直径时,面积最小,∴截面面积的最小值为2334ππ⨯=.11、A 12、B13、【答案】B.A DOC B【解析】解:由三视图可知该几何体是四棱锥,利用勾股定理可求出棱长分别为2,2,5,3等,故选B 14、A 15、B16、A二、解答题 1、(II )在平面PAB 内,过点E 作PB 的平行线交PA 于点F ,F 即为E 在平面PAC 内的正投影.理由如下:由已知可得PB PA ⊥,⊥PB PC ,又//EF PB ,所以EF PA EF PC ,⊥⊥,因此EF ⊥平面PAC ,即点F 为E 在平面PAC 内的正投影. 连结CG ,因为P 在平面ABC 内的正投影为D ,所以D 是正三角形ABC 的中心.由(I )知,G 是AB 的中点,所以D 在CG 上,故2.3=CD CG由题设可得⊥PC 平面PAB ,⊥DE 平面PAB ,所以//DE PC ,因此21,.33==PE PG DE PC 由已知,正三棱锥的侧面是直角三角形且6=PA ,可得2,==DE PE 在等腰直角三角形EFP 中,可得 2.==EF PF 所以四面体PDEF 的体积114222.323=⨯⨯⨯⨯=V2、试题解析:(I )由已知得,,.⊥=AC BD AD CD又由=AE CF 得=AE CFAD CD,故//.AC EF 由此得,'⊥⊥EF HD EF HD ,所以//.'AC HD . (II )由//EF AC 得1.4==OH AE DO AD由5,6==AB AC 得 4.===DO BO 所以1, 3.'===OH D H DH于是2222219,''+=+==OD OH D H 故.'⊥OD OH 由(I )知'⊥AC HD ,又,'⊥=AC BD BD HD H , 所以⊥AC 平面,'BHD 于是.'⊥AC OD又由,'⊥=OD OH AC OH O ,所以,'⊥OD 平面.ABC 又由=EF DH AC DO 得9.2=EF 五边形ABCFE 的面积11969683.2224=⨯⨯-⨯⨯=S所以五棱锥'ABCEF D -体积169342=⨯⨯=V3、(Ⅱ)因为⊥PA 平面ABCD ,N 为PC 的中点, 所以N 到平面ABCD 的距离为PA 21. ....9分取BC 的中点E ,连结AE .由3==AC AB 得BC AE ⊥,522=-=BE AB AE . 由BC AM ∥得M 到BC 的距离为5,故525421=⨯⨯=∆BCM S . 所以四面体BCM N -的体积354231=⨯⨯=∆-PA S V BCM BCM N . .....12分 4、【答案】(I )见解析(II )3+25试题解析:(I )因为四边形ABCD 为菱形,所以AC ⊥BD ,因为BE ⊥平面ABCD ,所以AC ⊥BE ,故AC ⊥平面BED. 又AC ⊥平面AEC ,所以平面AEC ⊥平面BED(II )设AB=x ,在菱形ABCD 中,由∠ABC=120°,可得3x ,GB=GD=2x . 因为AE ⊥EC ,所以在Rt AEC 中,可得3x . 由BE ⊥平面ABCD ,知EBG 为直角三角形,可得2x . 由已知得,三棱锥E-ACD 的体积3116632EACDV AC GD BE x .故x =2从而可得AE=EC=ED=6.所以△EAC 的面积为3,EAD 的面积及ECD 的面积均为5. 故三棱锥E-ACD 的侧面积为3+25. 5、解:(Ⅰ)因为ABC DEF -是直三棱柱,所以FC ⊥平面ABC ,而 AB ⊂平面ABC ,所以,FC ⊥AB .又AB ⊥BC ,BC FC C =.∴AB ⊥平面BCFE ,又EH ⊂平面BCFE ,∴AB ⊥EH .由题设知EFH ∆及BCG △均为直角三角形,2EF FH ==,2BC CG ==,∴ 45EHF ∠=,45BGC ∠=.设BG EH P =,则90GPH ∠=,即EH ⊥BG . 又AB BG B =,∴EH ⊥平面ABG .(Ⅱ)2AB BC ==,AB BC ⊥, ∴122ABC S AB BC ∆=⨯=.CG ⊥平面ABC ,1433G ABC ABC V S CG -∆∴=⨯=.由(1)知AB BG ⊥,2CG BC ==,22222222BG BC CG =+=+=,1222ABG S AB BG ∆∴=⨯=. 设点C 到平面ABG 的距离为h ,则1242333C ABG ABG G ABC V S h h V -∆-∴=⋅====,2h ∴=.即点C 到平面ABG 的距离为2.6、【解析】(1)证明:∵,60AB BD BAD =∠=,………6分………12分HOMDBA ∴ABD ∆为正三角形,∴AB AD =. ∵CB CD =,AC 为公共边, ∴ABC ADC ∆≅∆.∴CAB CAD ∠=∠,∴AC BD ⊥.∵四棱柱1111ABCD A B C D -是直四棱柱, ∴1AA ⊥平面ABCD ,∴1AA BD ⊥.∵1AC AA A =,∴BD ⊥平面11ACC A .∵BD ⊂平面1A BD ,∴平面1A BD ⊥平面11ACC A . (2)∵1AA ∥1BB ,∴11111B A BD A BB D A BB D V V V ---==, 由(1)知AC BD ⊥.∵四棱柱1111ABCD A B C D -是直四棱柱, ∴1BB ⊥平面ABCD ,∴1BB AC ⊥.∵1BD BB B =,∴AC ⊥平面1BB D . 记AC BD O =,∴11111(22)332A BB D BB D V S AO -∆=⋅=⨯⨯⨯=, ∴三棱锥11B A BD -7、(Ⅰ)证明:∵ △CMD 是等腰直角三角形,90CMD ︒∠=,点O 为CD 的中点, ∴OM CD ⊥. (1)分∵ 平面CMD ⊥平面BCD ,平面CMD平面BCD CD =,OM ⊂平面CMD ,∴ OM ⊥平面BCD .………………………………2分 ∵ AB ⊥平面BCD ,∴ OM ∥AB .………………………………………3分 ∵ AB ⊂平面ABD ,OM ⊄平面ABD ,∴ OM ∥平面ABD .………………………………4分 (Ⅱ)解法1:由(Ⅰ)知OM ∥平面ABD ,∴ 点M 到平面ABD 的距离等于点O 到平面ABD 的距离. …………………5分过O 作OH BD ⊥,垂足为点H , ∵ AB ⊥平面BCD ,OH ⊂平面BCD , ∴OH AB ⊥. (6)分∵ AB ⊂平面ABD ,BD ⊂平面ABD ,AB BD B =, ∴OH ⊥平面ABD . ………………………………………7分∵ 2AB BC ==,△BCD 是等边三角形,∴ 2BD =,1OD =,sin 602OH OD ︒=⋅=.………………………………9分 ∴A BDM M ABD V V --= (10)分1132AB BD OH =⨯⨯⋅⋅ ………………………………………11分11223223=⨯⨯⨯⨯=. ∴ 三棱锥A BDM-的体积为3. ………………………………………12分 解法2: 由(Ⅰ)知OM ∥平面ABD ,∴ 点M 到平面ABD 的距离等于点O 到平面ABD 的距离. …………………5分∵ 2AB BC ==,△BCD 是等边三角形, ∴2BD =,1OD =. ………………………………………6分连接OB, 则OB CD⊥,sin 60OB BD ︒=⋅=……………………………7分∴A BDM M ABD O ABD A BDO V V V V ----=== ………………………………………10分1132OD OB AB =⨯⨯⋅⋅ ………………………………………11分111232=⨯⨯=. ∴ 三棱锥A BDM-的体积为………………………………………12分 8、【解析】(1)证明:连接AC ,在菱形ABCD 中,∵60CBA ∠=且AB AC =,∴ABC ∆为等边三角形. ∵N 是BC 的中点, ∴AN BC ⊥,AN BC ⊥.∵ABCD ⊥平面ADEF ,AN ⊂平面ADEF ,ABCD 平面ADEF AD =,∴AN ⊥平面ABEF .∵DM ⊂平面ADEF ,∴AN DM ⊥.∵矩形ADEF 中,2AD AF =,M 是的中点, ∴AMF ∆为等腰直角三角形,∴45AMF ∠=,同理可证45DME ∠=,∴90DAM ∠=,∴DM AM ⊥. ∵AMAN N =,AM ⊂平面MNA ,AN ⊂平面MNA ,∴DM ⊥平面MNA .(2)设AF x =,则22AB AF x ==,在Rt ABN ∆中,2AB x =,BN x =,60ABN ∠=,∴AN =.∴2122ADN S x ∆=⋅=. ∵ABCD ⊥平面ADEF ,FA AD ⊥,ABCD 平面ADEF AD =,∴FA ⊥平面ABCD .设h 为点M 到平面ADN 的距离,则h FA x ==.∴231133M ADN CDF V V h x -∆=⋅=⋅=,∵M ADN D AMNV V --==,∴1x =. 作AH MN ⊥交MN 于点H .H NMF EADCB∵DM ⊥平面MNA ,∴DM AH ⊥. ∴AH ⊥平面DMN ,即AH 为求点A 到平面DMN 的距离,∵在Rt MNA ∆中,MA =,AN =5AH =.∴点A 到平面DMN 9、【解析】 ⑴证明:连接EBABCD 为等腰梯形,E 为CD 中点, ∴BE AD BC ==,所以EBC 为等腰三角形,又60BCD ∠=,故EBC 为等边三角形. ∴BE BC =PD PC =,E 为CD 的中点,PE CD ⊥,由BE BC =,PB PC =,PE PE =,得PEB 全等于PEC ,知PE EB ⊥,BEBC B =,故PE ABCD ⊥,AD ABCD ⊂,得AD PE ⊥. …………6分⑵因为4PC =,3EC =,所以PE =,1(36)2ABCD S =+=,13P ABCD V -==…………12分10、【解析】(I ) 连接DE ,由题意可知四边形ABED 和AECD 是平行四边形,又AB=AD ,所以ABED 是菱形 (2分)故BM AE ⊥,.DM AE ⊥ 即AE M B ⊥1,.DM AE ⊥ (4分) 又因为M M B DM =⋂1,MD 、⊂M B 1平面MD B 1,所以⊥AE 平面MD B 1.(5分)D 1B 1C 1A 1DCBA由题可得AE ∥CD ,所以1CD B DM ⊥平面 (6分)(Ⅱ) 连接CM ,由(Ⅰ)得AB=AE=BE=2 ,所以1B AE ∆为等边三角形 ,31=∴M B (7分)又722=+=CD DM CM ,101=C B21221C B CM M B =+∴,即1B M MC ⊥ (9分)又AE M B ⊥1,MC AE M ⋂=,⊥∴M B 1平面CDE (10分)3322121=⨯⨯=⋅=∆DM AE S CDE (11分)1111133B CDE CDE V S B M -∆∴=⋅== (12分)11、(I)证法1:连结AC 1,设AC 1及A 1C 相交于点E ,连接DE ,则E 为AC 1中点,-------------------------------2分 ∵D 为AB 的中点,∴DE ∥BC 1,------------------4分 ∵BC 1平面A 1CD ,DE 平面A 1CD ,------------5分∴BC 1∥平面A 1CD . -----------------------------6分 【证法2:取11A B 中点1D ,连结1BD 和11C D ,-----1分 ∵BD 平行且等于11A D ∴四边形BD 11A D 为平行四边形∴11//A D BD -----------------------------------2分 ∵1A D ⊂平面1A CD ,1BD ⊄平面1A CD∴1//BD 平面1A CD ,------------------------------3分 同理可得11//C D 平面1A CD ------------------------4分∵1111BD C D D = ∴平面1A CD //平面11BD C又∵1BC ⊂平面11BD C∴BC 1∥平面A 1CD. -------------------------------6分】 (Ⅱ)222115AD +A A =A D1,A AAD -------------------------------------7分 又111,//B B BC B B A A1A ABC ,又AD BC B=1A A面ABC -------------------------------------------9分EH B 1C 1A 1DCBA(法一)∴所求多面体的体积V =1111111ABC A B C A ACD B A B C V V V ----------------------------10分111111133ABC ACD A B C AA S AA S BB S ∆∆∆=⨯-⋅⨯-⋅⨯112ABC AA S ∆=⋅⨯21122222=⋅⋅⋅⋅= 即所求多面体11CAC BD.----------------12分【(法二)过点1A 作111A H B C ⊥H ,∵平面11BB C C ⊥平面111A B C 且平面11BB C C 平面111A B C 11B C = ∴1A H ⊥平面11BB C C ,----------------------------------------------------------10分∴所求多面体的体积V =1111A ACD A A CCV V --+1111133BCD BCC S AA S A H ∆∆=⋅+⋅11114243232=⨯⨯+⨯⨯=.------------------------------------------12分】 12、证法1:∵四边形ABCD 为矩形,∴AEF ∆∽CBF ∆, ∴21===BC AE BF EF CF AF ……………1分又∵矩形ABCD 中,2,1==AD AB ,∴3,22==AC AE 在BEA Rt ∆中,2622=+=AE AB BE ∴3331==AC AF ,3632==BE BD (2)分在ABF ∆中,222221)36()33(AB BF AF ==+=+∴90=∠AFB ,即BE AC ⊥ ……………4分∵⊥GF 平面ABCD ,⊂AC 平面ABCD ∴GF AC ⊥ ……………5分又∵F GF BE = ,⊂GF BE ,平面BCE ∴⊥AF 平面BEG ……………6分证法2:(坐标法)证明1-=⋅BE AC K K ,得BE AC ⊥,往下同证法1. (2)在AGF Rt ∆中,22GF AF AG +=36)33()33(22=+= 在BGF Rt ∆中,22GF BF BG +=1)33()36(22=+= ………… ……………8分在ABG ∆中,36=AG ,1==AB BG ∴2)66(13621-⨯⨯=∆ABG S 656303621=⨯⨯=………………………………10分设点E 到平面ABG 的距离为d ,则GF S d S ABF ABG ⋅=⋅∆∆3131, ………………………………11分 ∴ABG ABF S GF S d ∆⋅=1030653312221=⨯⨯⨯= ………………………………12分13、14、(Ⅰ)证明: ∵E 、F 分别是CD 和BC 的中点, ∴EF //BD . (1分)又∵AC BD ⊥,∴AC EF ⊥, 故折起后有PH EF⊥.(2分)又PH AH ⊥,所以PH ⊥平面ABFED . (3分) 又∵BD ⊂平面ABFED ,∴PH BD ⊥, (4分) ∵AH PH H =,,AH PH ⊂平面APH ,∴BD ⊥平面APH , (5分)又AP ⊂平面APH ,∴BD ⊥AP (6分) (Ⅱ)解:∵正方形ABCD 的边长为22∴4AC BD ==,2,1AN NH PH ===,PE PF = (7分) ∴PBD ∆是等腰三角形,连结PN ,则PN BD ⊥,222PN NH PH =+= ∴PBD ∆的面积11422222PBD S BD PN ∆=⋅=⨯=(8分) 设三棱锥A BDP -的高为h ,则三棱锥A BDP -的体积为12233A BDP PBD h V S h -∆=⋅= (9分)由(Ⅰ)可知PH 是三棱锥P ABD -的高,∴三棱锥P ABD -的体积:1111141332323P ABD ABD V S PH AB AD PH -∆=⋅=⨯⋅⋅=⨯⨯= (11分)∵A BDP P ABD V V --=,43=,解得h =即三棱锥A BDP -. (12分)15、(I)证明:由于四边形ABCD 为平行四边形,所以O 为AC 的中点;连接POPA PC =∴AC PO ⊥ ———1分平面PBD ⊥平面PAC ,又平面PBD 平面=PAC PO ,AC ∈平面PAC∴AC ⊥面PBD ∴AC ⊥PB —————4分 又PB BD ⊥,且AC BD O =,AC BD ABCD ∈、面∴PB ⊥面ABCD —————6分(II)解:由(I)知AC ⊥面PBD ,所以AC ⊥BD ,可知底面设AB BC a ==,又因为60BAD ∠=︒,所以BD a =,AC=因为PAC ∆为正三角形,所以PC = —————7分 由(I)知PB BC ⊥,从而PBC ∆为直角三角形,PB ∴= —————8分211132332P ABCD ABCD V S PB a -===1a = ———9分所以PC =、1CD =、PB =PD ∴==—————10分取CD 的中点E ,连接PE ,可知PE CD ⊥2PE ==11124PCD S CD PE == —12分高考数学一轮复习专题训练立体几何1 / 1。
