九年级第三次月考
长郡双语实验中学2023-2024学年九年级上学期第三次月考数学试题(答案)

初三数学作业精选练习参考答案题号 1 2 3 4 5 6 7 8 9 10 答案 C C B B A D D A B C二.填空题(共6小题)11. 0.35 12. (﹣3,2) 13. 114. 80 15. 4 16. 9三.解答题(共8小题)17.解:√8+|√2−1|−ππ0+(12)−1=2√2+√2−1−1+2……………………4分=3√2.……………………6分18.解:原式=x2﹣4xy+4y2+x2﹣4y2﹣2x2+2xy=﹣2xy.……………………4分当xx=−38,y=4时,原式=−2×(−38)×4=3.……………………6分19.解:(1)在Rt△ABC中,∠C=90°,∠BAC=40°,∴∠ABC=50°,∵将△ABC绕着点B逆时针旋转得到△FBE,∴∠EBF=∠ABC=50°,AB=BF,∴∠BAF=∠BF A=12(180°﹣50°)=65°,故答案为:65°;……………………3分(2)∵∠C=90°,AC=8,BC=6,∴AB=10,∵将△ABC绕着点B逆时针旋转得到△FBE,∴BE=BC=6,EF=AC=8,∴AE=AB﹣BE=10﹣6=4,∴AF=√AAEE2+EEFF2=4√5.……………………6分20.解:(1)由统计图可得,这次抽样调查共抽取:16÷32%=50(人),m=50×14%=7,故答案为:50,7;……………………2分(2)由(1)知,m=7,等级为A的有:50﹣16﹣15﹣7=12(人),补充完整的条形统计图如图所示,C等所在扇形圆心角的度数为:360°×1550=108°;……………………4分(3)树状图如下所示:由上可得,一共存在12种等可能性,其中抽出的两名学生恰好是甲和丁的可能性有2种,∴抽出的两名学生恰好是甲和丁的概率为212=16.……………………8分21.解:(1)∵点A(1,4)在函数yy1=kk xx的图象上,∴k=1×4=4,∴反比例函数解析式为:y1=4xx,∵B(m,﹣2)在反比例函数图象上,∴m=4−2=−2,∴B(﹣2,﹣2),∵点A(1,4),B(﹣2,﹣2)在一次函数y2=ax+b图象上,∴�aa+bb=4−2aa+bb=−2,解得�aa=2bb=2,∴直线AB的解析式y2=2x+2.令x=0,y=2,∴D(0,2),即OD=2,∴S△AOB=S△AOD+S△BOD=12×2×2+12×2×1=3.……………………5分(2)y1>y2成立的自变量x的取值范围为:0<x<1或x<﹣2;………………8分22.解:(1)设A型与B型汽车每辆的进价分别是x万元、y万元,�2xx+3yy=1408xx+14yy=620解得�xx=25yy=30,∴A型与B型汽车每辆的进价分别是25万元、30万元;答:A型与B型汽车每辆的进价分别是25万元、30万元;……………………4分(2)设购进A型汽车a辆,则购进B型汽车(10﹣a)辆,�aa<10−aa25aa+30(10−aa)≤290,解得:2≤a<5,又a为正整数,所以a取2、3、4,∴购进A型汽车2辆,则购进B型汽车8辆;购进A型汽车3辆,则购进B型汽车7辆;购进A型汽车4辆,则购进B型汽车6辆.……………………9分23.(1)证明:如图,连接BD,∵AB是直径,∴∠ADB=90°,∵AB=BC,∴∠ABD=∠CBD,�=AAEE�,∴AAAA∴AD=DE;……………………3分(2)解:①∵AB=BC,∠ADB=90°,∴AD=CD=3,∵AD=DE,∴CD=DE=3,∴∠C=∠CED=∠BAC,∴△BAC∽△DCE,∴AAAA AAAA=AACC AACC,∴62rr=xx3,∴r=9xx;……………………6分②当x=r时,则x=r=3,连接OD,OE,则△AOD、△DOE是等边三角形,∴∠AOD=∠DOE=60°,∴∠BOE=60°,∴△BOE是等边三角形,∴阴影部分的面积为S扇形OBE﹣S△OBE=60ππ×32360−�34×32=3ππ2−9�34.…………9分24.解:(1)y =﹣x 图象上的点(x ,﹣x )和y =2x 图象上的点(x ,2x )关于(x ,x )成中心对称, ∴y =﹣x 和y =2x 是“友好函数”;y =x +3图象上的点(x ,x +3)和y =x ﹣3图象上的点(x ,x ﹣3)关于(x ,x )成中心对称, ∴y =x +3和y =x ﹣3是“友好函数”;y =x 2+1图象上的点(x ,x 2+1)和y =x 2﹣1图象上的点(x ,x 2﹣1)不关于(x ,x )成中心对称, ∴不是“友好函数”;∴互为“友好函数”的是①②,故答案为:①②; ……………………3分 (2)①根据“友好函数”的定义得:,∴,∴y 2=﹣x +4,即函数y =2x ﹣4的“友好函数”解析式为y =﹣x +4,∵反比例函数 的图象与直线y =﹣x +4在第一象限内有两个交点,∴方程有两个不相等的实数根,且两根均为正数,整理得:x 2﹣4x +m =0,∴Δ=(﹣4)2﹣4m >0且m >0,解得:0<m <4; ……………………5分 ②如图,设C ,D 的坐标分别为 ),,(2211),(y x y x ∴x 1,x 2 是方程 x 2﹣4x +m =0 的两根,∴x 1+x 2=4,x 1•x 2=m ,且44882121=−=+−=+)(x x y y244-1624)(2)(2)(2121221121221==−+=−=−+=∴∆m x x x x x x x x y y S COD )(28416==−∴m m ,故 ……………………7分(3)由=x 得:y 2=ax 2+bx +c ,∴y =﹣ax 2+(1﹣b )x ﹣c (a ≠0)的“友好函数”解析式为 y =ax 2+bx +c , ∵M (1,m ),N (3,n )在函数 y =ax 2+bx +c 的上, ∴m =a +b +c ,n =9a +3b +c , ∵m <n <c ,∴a +b +c <9a +3b +c <c , ∴a +b <9a +3b <0, ∵a >0, ∴3<﹣<4,∵点M (1.m ),P (t ,m )的纵坐标相等, ∴抛物线对称轴为直线x =,即,∴﹣=t +1, ∴3<t +1<4, 解得:2<t <3,设h =﹣t 2﹣t +2=﹣(t +2)2+3, 当t =2时,h =﹣1; 当t =3时,h =﹣;∴﹣<h <﹣1,∵2412+−−>t t w 恒成立, ∴w ≥﹣1, ……………………10分25.解:(1)∠DAC=60° ……………………3分 (2)证明:连接BG ,∵AD 为⊙O 的直径,CG ⊥AD ,∴AAAA�=AAAA �, ∴∠AGF =∠ABG , ∵∠GAF =∠BAG , ∴△AGF ∽△ABG , ∴AG :AB =AF :AG , ∴AF •AB=AG 2=25法2:证明△ACF ∽△ABC 可得AF •AB=AG 2=25 ……………………6分 (3)解:AC AG x由△ACF ∽△ABC 可得AC AF CFAB AC BC∴22,101010x x AF BF ,=10CF AC x BC AB 由△AEF ∽△ABD 得2x AF AB AD AE =×=×或:由△ACE ∽△ADC 得22x AC AD AE ==×由△ACF ∽△ABC 可得)(10102x x FB AG FG CB −=×=× 2022221197220252++−=+×+×××=∴x x BC CF AD AE FG CB y对称轴为直线=2x05x所以当=2x 时,max 2024y ……………………10分(每写出一个相似给1分)。
2024-2025学年九年级数学上学期第三次月考卷(广东省卷专用,人教版九上第21~24章)考试版

2024-2025学年九年级数学上学期第三次月考卷(广东省卷专用)(考试时间:120分钟 试卷满分:120分)注意事项:1.答卷前,考生务必将自己的姓名、准考证号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.测试范围:人教版,第21~24章。
5.难度系数:0.69。
第Ⅰ卷一、选择题:本大题共10小题,每小题3分,共30分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.第十九届亚运会于2023年9月23日至10月8日在杭州隆重举行,下列图标是亚运会上常见的运动图标,其中是轴对称图形的是( )A .B .C .D .2.如图,在O e 中,弦AB CD ∥,若40ABC Ð=°,则BOD Ð的度数是( )A .80°B .50°C .40°D .20°3.抛物线()278y x =-+-的顶点坐标是( )A .()7,8-B .()7,8-C .()7,8D .()7,8--4.把方程2470x x --=化成2()x m n -=的形式,则点(,)P m n 关于x 轴对称的点的坐标为( )A .(2,11)B .(2,11)-C .(2,11)-D .(2,11)--5.若点()10,A y ,()21,B y ,()32,C y -是抛物线22y x x c =-+上的三点,则( )A .321y y y >>B .123y y y >>C .132y y y >>D .312y y y >>6.已知12,x x 是方程2420x x -+=的两个根,则12x x +的值是( )A .4-B .2-C .4D .27.如图,PA 、PB 切⊙O 于点A 、B ,10PA =,CD 切O e 于点E ,交PA 、PB 于C 、D 两点,则PCD △的周长是( )A .10B .18C .20D .228.如图,P ,Q 分别是O e 的内接正五边形的边AB ,BC 上的点,BP CQ =,则POQ Ð=( )A .75°B .54°C .72°D .60°9.如图,在平面直角坐标系xOy 中,直线AB 经过点()6,0A 、()0,6B ,O e 的半径为2(O 为坐标原点),点P 是直线AB 上的一动点,过点P 作O e 的一条切线PQ ,Q 为切点,则切线长PQ 的最小值为( )A .7B .3C .D 10.如图,二次函数y =﹣x 2+2x +m +1的图象交x 轴于点A (a ,0)和B (b ,0),交y 轴于点C ,图象的顶点为D .下列四个命题:①当x >0时,y >0;②若a =﹣1,则b =4;③点C 关于图象对称轴的对称点为E ,点M 为x 轴上的一个动点,当m =2时,△MCE 周长的最小值为;④图象上有两点P (x 1,y 1)和Q (x 2,y 2),若x 1<1<x 2,且x 1+x 2>2,则y 1>y 2,其中真命题的个数有( )A .1个B .2个C .3个D .4个第Ⅱ卷二、填空题:本大题共5小题,每小题3分,共15分。
2023-2024学年山东省德州市九年级上学期第三次月考物理试题

2023-2024学年山东省德州市九年级上学期第三次月考物理试题1.在物理学的发展过程中,许多物理学家做出了杰出的贡献。
通过大量的实验研究最先精确地确定了电流产生的热量跟电流、电阻和通电时间的关系的科学家是()A.安培B.奥斯特C.欧姆D.焦耳2.下列实例中,通过做功的方式改变物体内能的是()A.用煤气炉给水加热,水的温度升高B.小朋友坐滑梯,臀部的温度升高C.在阳光照射下,石凳的温度升高D.把饮料放进冰箱,饮料的温度降低3.如图所示,小磁针静止在螺线管附近,闭合开关S后,下列判断正确的是( )A.通电螺线管外A点的磁场方向向右B.通电螺线管的左端为S极C.小磁针一直保持静止D.小磁针N极向左转动4.汽车发动机之一是汽油机,汽油的热值为4.6×107J/kg,王同学阅读了某汽车发动机的说明书后,将内燃机的能量流向制成如图所示,下列回答正确的是()A.该内燃机的效率为70%B.1kg的汽油燃烧一定能够释放4.6×10 7 J的能量C.利用废气的能量及减小摩擦是提高热机效率的有效途径D.汽油机压缩冲程把燃料燃烧产生的内能转化为机械能5.如图所示的四个实例中,用热传递的方式改变物体内能的是()A.取火时,不断地摩擦木头B.烧水时,用火焰给水加热C.打气时,气筒一端明显发热D.敲打铁钉时,铁钉温度升高6.分子很小,看不见摸不着,但我们可以通过一些直接感知的现象,经过合理的推测来认识分子,下列推测既合理又符合事实的是A.现象:红墨水滴入水中,整杯水变红;推测:分子在做无规则运动B.现象:注射器内的水很难压缩;推测:水分子之间没有间隙C.现象:破镜不能重圆;推测:分子之间斥力太大D.现象:磁铁上吸住了很多铁屑;推测:分子之间存在引力作用7.关于如图所示的四个情景,下列说法正确的是()A.甲图中两个底面削平的铅块紧压在一起后能吊住重物,表明分子之间只存在引力B.乙图中试管中的水沸腾后,水蒸气将软木塞推出,瓶口的白雾是水蒸气C.丙图中抽去玻璃板后,两瓶中的气体逐渐混合,说明二氧化氮的密度小D.丁图中是内燃机的做功冲程,涉及的能量转化是内能转化为机械能8.商场和超市出口处的报警器由检测天线、检测门、检测器构成。
辽宁省本溪市实验中学2023-2024学年九年级上学期第三次月考语文试题(含答案)

2023-2024年度(上)实验中学九年级阶段验收语文试卷考试时间:150分钟满分:120分注意:所有试题必须在答题卡上作答,在本试卷上作答无效。
一、积累与应用(17 分)1.下列词语中加点字的字音、字形完全正确的一项是()(2分)A.恣睢(suī)天娇(jiāo)瞥见(piě)间不容发(fà)B.冒然(mào)旁骛(wù)逞办(chéng)自吹自擂(léi)C.吹嘘(xū)杜绝(jué)筵席(yán)言不及义(yì)D.糟踏(tà)端详(xiáng)炊烟(cuī)鸠占鹊巢(què)2. 依次填入下面句子横线处的词语最恰当的一项是()(2分)你若盛开,那是______在春日枝头上的一种情怀。
盛开,是花朵潜伏已久的梦,也是它不得不______的一种职责。
盛开,总是令人欣喜的。
花朵的盛开是______,是热闹;生命的盛开是激情,是______。
A.悄然绽放履行绚丽奋进B.含苞待放施行妖艳前进C.悄然绽放施行绚丽前进D.含苞待放履行妖艳奋进3.下列各项中分析正确的一项是()(2分)①被誉为楚国“丝绸宝库”的江陵马山一号楚墓,出土了大批精美的丝绸织物。
②这些织物轻薄细密、流光溢彩、柔软如梦。
③那锦上添花的刺绣,构图既生动流畅又艳丽繁复,有龙飞凤舞的灵动造型,也有花草枝蔓的自然延伸,其作品之精美、绣工之细腻,令人赞不绝口。
④历经两千余年的沧桑,颜色仍然鲜艳如新,令人叹为观止。
A.第②句中的“轻薄细密”“流光溢彩”“柔软如梦”都是并列短语。
B.第③句是病句,“龙飞凤舞”用词不当。
C.第④句中的“历经两千余年的沧桑”是状语。
D.第③句中的“赞不绝口”和第④句中的“叹为观止”可以调换位置。
4. 文学、文化常识与名著阅读(5分)(1)下列各项中表述不正确的一项是()(2分)A.运用典故是古诗词常见的表现方法,分为事典和语典两类,《水调歌头》开头、结尾是对语典的改造运用。
2024-2025学年九年级数学上学期第三次月考卷(北京版,九上第18章-第21章)(全解全析)

2024-2025学年九年级数学上学期第三次月考卷(北京版)(考试时间:120分钟 试卷满分:100分)注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。
写在本试卷上无效。
4.测试范围:北京版九年级上册第18章15%、第19章32%、第18章20%、第21章34%。
5.难度系数:0.8。
第Ⅰ卷一、选择题:本题共8小题,每小题2分,共16分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.如图,这是一张海上日出照片,如果把太阳看作一个圆,把海平面看作一条直线,那么这个圆与这条直线的位置关系是( )A .相离B .相切C .相交D .不确定【答案】C 【详解】解:由图可知:这个圆与这条直线的位置关系是相交,故选:C .2.若2x =5y ,则下列正确的是( )A .25x y =B .52x y =C .53x y =D .35x y =【答案】B【详解】解:∵25x y =,3.将抛物线22y x =-向右平移1个单位长度,再向上平移1个单位长度所得的抛物线解析式为( )A .()221y x =-+B .()2212y x =-++C .()2212y x =--+D .()2211y x =--+【答案】D 【详解】解:Q 抛物线22y x =-向右平移1个单位长度,\平移后的解析式为()221y x =--,\再向上平移1个单位长度,\平移后的解析式为()2211y x =--+.故选:D .4.如图,AB 是O e 的直径,CD 是O e 的弦,连接AC 、AD ,若65ACD Ð=°,则BAD Ð的度数为( )度.A .15B .25C .35D .45【答案】B 【详解】解:连接BC ,∵AB 是直径,∴90ACB Ð=°,∴90ACD BCD Ð+Ð=°,∵65ACD Ð=°,∴25BCD Ð=°,∴25BAD BCD Ð=Ð=°,故选:B .5.已知点()()()3,1,5,A a B b C c -,,在反比例函数k y x =(0k <)的的图像上,下列结论正确的是( )A .a b c<<B .a c b <<C .b c a<<D .c b a <<6.小致利用测角仪和皮尺测量学校旗杆的高度,如图,小致在D 处测得顶端P 的仰角∠PDC =a ,D 到旗杆的距离CD =5米,测角仪BD 的高度为1米,则旗杆PA 的高度表示为( ).A .5tan a +1B .5sin a +1C .5cos a +1D .5tan a+1【答案】A 【详解】根据题意可知:四边形ABDC 是矩形,∴∠PCD =90°,AC =BD =1,在Rt △PCD 中,PC =CD tanα=5tanα,∴PA =PC +AC =5tanα+1.故选:A .7.如图,在等腰ABC V 中,,AB AC BD AC =^于点35D cosA =,,则sin CBD Ð的值( )A .12B .2C D8.如图,点E 在DBC 边DB 上,点A 在DBC 内部,∠DAE =∠BAC =90°,AD =AE ,AB =AC ,给出下列结论,其中正确的是( )①BD =CE ;②∠DCB ﹣∠ABD =45°;③BD ⊥CE ;④BE 2=2(AD 2+AB 2).A .①③B .②③C .②④D .①④【答案】A 【详解】解:∵∠DAE =∠BAC =90°,∴∠DAB =∠EAC .∵AD =AE ,AB =AC ,∴△DAB ≌△EAC (SAS ),∴BD =CE ,∠ABD =∠ECA ,故①正确;∵∠DCB ﹣∠DCA =∠ACB =45°,显然ABD ACD йÐ,故②错误;∵∠ABD =∠ECA∴90EBC ECB ABD ABC BCA ECA ABC BCA Ð+Ð=Ð+Ð+Ð-Ð=Ð+Ð=°∴90BEC Ð=°∴BD CE ^,故③正确;222222222222222)2()(BE BC EC AB CD DE AB CD AD AD AB CD =-=--=+--+=即22222()BE AD AB CD +=-,故④错误,故选A.第Ⅱ卷二、填空题:本题共8小题,每小题2分,共16分。
2024-2025学年九年级数学上学期第三次月考卷(沪教版,九上全部)(考试版A4)

2024-2025学年九年级数学上学期第三次月考卷(沪教版)(考试时间:100分钟 试卷满分:150分)注意事项:1.答卷前,考生务必将自己的姓名、准考证号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.测试范围:沪教版,第14章相似三角形40%、第15章锐角的三角比20%、第16章二次函数40%。
5.难度系数:0.69。
第一部分(选择题 共24分)一、选择题(本大题共6小题,每小题4分,满分24分.在每个小题给出的四个选项中,只有一项符合题目要求的)1.如果一幅地图的比例尺为1:50000,那么实际距离是3千米的两地在地图上的图距是( )A .6厘米B .15厘米C .60厘米D .150厘米2.如图,在ABC V 中,90C Ð=°,13AB =,5BC =,则sin A 的值是( )A .135B .512C .513D .12133.二次函数()221y x =-+图象的顶点坐标是( )A .()2,1B .()2,1-C .()1,2D .()12-,4.将二次函数()212y x =+-的图象向左平移2个单位长度,再向下平移3个单位长度得到的二次函数解析式是( )A .y =(x ―1)2―5B .()211y x =-+C .()231y x =++D .()2y 35x =+-5.已知2b a =-r r ,那么下列判断错误的是( )A .2b a =r rB .20a b +=r rC .b a r r ∥D .b a¹r r 6.如图,在△ABC 中,AD ⊥BC ,点D 为垂足,为了证明∠BAC =90°,以下添加的等积式中,正确的有( )222•••••AD BD CD AB CD AC AD AC BC CD AB AC BD①=②=③=④=A .1个B .2个C .3个D .4个第二部分(非选择题 共126分)二、填空题(本大题共12小题,每小题4分,满分48分)7.若()21m y m x =-+是关于x 的二次函数,则m = .8.二次函数2251y x x =+-的图像与y 轴的交点坐标为9.已知在ABC V 中,AD 是中线,G 是重心,如果3cm GD =,那么AG = cm .10.在Rt ABC △中,90C Ð=°,B a Ð=,2AB =,那么BC = .(结果用a 的锐角三角函数表示)11.如图,正五角星中包含了许多黄金三角形,许多线段之间构成了黄金比,如点C 是线段AD 的黄金分割点()AC CD >.已知1)BC =厘米,那么AC = 厘米.12.如图,已知,AD 是ABC V 的中线,E 是AD 的中点,则:AF FC = .13.如图,在ABC V 中,点D 为AB 上的点,3,5,AD AB CD ACD B ===Ð=Ð,则BC = .14.如图,E 是平行四边形ABCD 的边BA 延长线上的一点,CE 交AD 于点F ,交BD 于点G ,:1:2AE AB =,设BA a =uuu r r ,BC b uuu r r =.用向量a r 、b r 分别表示向量CG =uuu r .15.已知点A ()11x y ,和 B ()22x y ,是抛物线()2=235y x -+上的两点,如果124x x >>,那么1y 2y .(填“>”、“=”或“<”)16.如图,矩形DEFG 的一边GF 在ABC D 的边BC 上,D 、E 分别在AB 、AC 上,AH BC ^交DE 于M ,:1:2DG DE =,12BC =cm ,8AH =cm ,则DE 的长 cm .17.如图,边长分别为5,3,2的三个正方形拼接在一起,它们的底边在同一直线上,则图中阴影部分的面积为 .18.二次函数2y ax bx c =++的图象如图所示,顶点坐标(1,2),且关于x 的一元二次方程20ax bx c m ++-=没有实数根,有下列结论:①24ac b <;②0abc >;③2m >;④点(,)P m n 是抛物线上任意一点,则()+£+m am b a b ,其中,正确的结论是 .三、解答题(本大题共7小题,满分78分.解答应写出文字说明,证明过程或演算步骤)19.(10()02sin 45cos 45°+°20.(10分)如图,在ABC V 中,AC =BC =,cos A =,点D 在BC 边上,且2CD BD =,DE AB ^,垂足为E ,联结CE .(1)求线段AB 的长;(2)求CEA Ð的正切值.21.(10分)如图,在平行四边形ABCD 中,对角线AC 、BD 相交于点O ,E 为边AB 上一点,且2BE AE =.设,AB a AD b ==uuu r uuu r rr .(1)填空:用向量,a b r r 的式子表示向量DE =uuu r _____;(2)如果点F 是线段OC 的中点,那么用向量,a b r r 的线性组合表示向量EF =uuu r ______,并在图中画出向量EF uuu r 在向量AB uuu r 和AD uuu r方向上的分向量.22.(1020个,每个盈利12元,为了扩大销售,增加盈利,该小组决定采取适当的降价措施,经调查发现,如果每个书包每降价1元,平均每天可以多卖5个.(1)若每个书包降价x 元,则可多卖__________个,每个盈利__________元;(2)若该兴趣小组同学想要一天盈利300元,每个书包应降价多少元;(3)该兴趣小组同学想要一天盈利最大,应降价多少元,所得最大利润是多少元?23.(12分)已知:如图,在梯形ABCD 中,AD BC ∥,AB BC ^,点M 在边BC 上,且MDB ADB Ð=Ð,2BD AD BC =×.(1)求证:BM CM =;(2)作BE DM ^,垂足为点E ,并交CD 于点F .求证:2AD DM DF DC ×=×.24.(12分)如图,已知抛物线223y x x =--+与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C.(1)求点A、B,C的坐标;(2)抛物线的对称轴l与x轴的交点为D,连接AC,在抛物线上是否存在点E、F(点E、F关于直线l对称,△相似,若存在,求出点E的坐标,若不存在,且E在点F左侧),使得以D、E、F为顶点的三角形与AOC请说明理由.25.(14分)已知矩形ABCD 中,68AB BC ==,,P 是边AD 上一点,将ABP V 沿直线BP 翻折,使点A 落在点E 处,连接DE ,直线DE 与射线CB 交于点F .(1)如图1,当点F 在边BC 上,若PD BF =时,求AP 的长;(2)若射线AE 交BC 的延长线于点Q ,设AP x =,QC y =,求y 与x 的函数解析式,并写出x 定义域;(3)①如图2,直线DE 与边AB 交于点G ,若PDE △与BEG V 相似,求AEG Ð的正切值;②如图3,当直线DE 与BP 的延长线交于点H ,若BPE V 和DHP V 面积相等,请直接写出DH 的长.。
北师大版九年级上册数学第三次月考试题含答案详解

北师大版九年级上册数学第三次月考试卷一、选择题。
(每小题只有一个正确答案)1.若34yx=,则x yx+的值为()A.1B.47C.54D.742.下列函数中,反比例函数是()A.x(y+1)=1B.11yx=+C.21yx=D.13yx=3.若函数y=4x2+1的函数值为5,则自变量x的值应为()A.1B.-1C.±1D.32 24.在同一坐标系中,抛物线y=4x2,y=14x2,y=-14x2的共同特点是()A.关于y轴对称,开口向上B.关于y轴对称,y随x的增大而增大C.关于y轴对称,y随x的增大而减小D.关于y轴对称,顶点是原点5.已知二次函数y=a(x﹣h)2+k(a>0),其图象过点A(0,2),B(8,3),则h的值可以是()A.6B.5C.4D.36.下列各问题中,两个变量之间的关系不是反比例函数的是A.小明完成100m赛跑时,时间t(s)与跑步的平均速度v(m/s)之间的关系.B.菱形的面积为48cm2,它的两条对角线的长为y(cm)与x(cm)的关系.C.一个玻璃容器的体积为30L时,所盛液体的质量m与所盛液体的体积V之间的关系. D.压力为600N时,压强p与受力面积S之间的关系.7.如图,AB、CD相交于点O,AD∥CB,若AO=2,BO=3,CD=6,则CO等于()A.2.4B.3C.3.6D.48.如图,平面直角坐标系中,点M是直线2y=与x轴之间的一个动点,且点M是抛物线212y x bx c =++的顶点,则方程2112x bx c ++=的解的个数是()A .0或2B .0或1C .1或2D .0,1或29.如图,已知点C 是线段AB 的黄金分割点(其中AC >BC ),则下列结论正确的是()A .512BC AC -=B .512AC BC -=C .AB 2=AC 2+BC 2D .BC 2=AC•BA10.如图,已知四边形OABC 是菱形,CD ⊥x 轴,垂足为D ,函数4y x=的图象经过点C ,且与AB 交于点E .若OD=2,则△OCE 的面积为()A .2B .4C .D .二、填空题11.在比例尺为1:5000的地图上,量得甲、乙两地的距离为25cm ,则甲、乙两地间的实际距离是_____km.12.如图,圆O 的半径为2.C 1是函数y=x 2的图象,C 2是函数y=−x 2的图象,则阴影部分的面积是___.13.已知实数x ,y ,z 满足x +y +z =0,3x ﹣y ﹣2z =0,则x :y :z =_____.14.如图,在正方形ABCD 中, BPC 是等边三角形,BP ,CP 的延长线分别交AD 于点E ,F ,连接BD ,DP ,BD 与CF 相交于点H .给出以下结论:①AF =DE ;②∠ADP =15°;③13PF PC =;④PD 2=PH •PB ,其中正确的是_____.(填写正确结论的序号)三、解答题15.已知a 、b 、c 为三角形ABC 的三边长,且36a b c ++=,345a b c==,求三角形ABC 三边的长.16.已知二次函数的顶点坐标为(1,4),且其图象经过点(﹣2,﹣5),求此二次函数的解析式.17.新冠疫情暴发后,口罩的需求量增大.某口罩加工厂承揽生产1600万个口罩的任务,计划用t 天完成.(1)写出每天生产口罩w (万个)与生产时间t (天)(t >4)之间的函数表达式;(2)由于国外的疫情形势严峻,卫生管理部门要求厂家提前4天交货,那么加工厂每天要多做多少万个口罩才能完成任务?(用含t 的代数式表示)18.如图,D 、E 分别是 ABC 的边AB 、BC 上的点,DE ∥AC ,若:BDE CDE S S △△=1:3,求DOE AOC S S △△:的值.19.抛物线y =mx 2﹣4m (m >0)与x 轴交于A ,B 两点(A 点在B 点左边),与y 轴交于C 点,已知OC =2OA .求:(1)A ,B 两点的坐标;(2)抛物线的解析式.20.如图,点P是菱形ABCD的对角线AC上一点,连接DP并延长,交AB于点F,交CB的延长线于点E.求证:(1) APB≌ APD;(2)PD2=PE•PF.21.如图,在平面直角坐标系中有抛物线c:y=x2+m和直线l:y=﹣2x﹣2,直线l与x轴的交点为B,与y轴的交点为A.(1)求m取何值时,抛物线c与直线l没有公共点;(2)向下平移抛物线c,当抛物线c的顶点与点A重合时,试判断点B是否在平移后的抛物线上.22.反比例函数y=kx(k≠0,x>0)的图象与直线y=3x相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.(1)求k的值;(2)在y轴上确定一点M,使点M到A,B两点距离之和d=MA+MB最小,求点M的坐标.23.在 ABC中,∠C=90°,AC=BC,点M,N分别在AC,BC上,将 ABC沿MN折叠,顶点C恰好落在斜边的P点上.(1)如图1,若点N为BC中点时,求证:MN∥AB;(2)如图2,当MN与AB不平行时,求证:PA CM PB CN=;(3)如图3,当AC≠BC且MN与AB不平行时,(2)中的等式还成立吗?请直接写出结论.参考答案与详解1.D【详解】∵34 yx=,∴x yx+=434+=74,故选D2.D【分析】判断一个函数是否是反比例函数,首先看看两个变量是否具有反比例关系,然后根据反比例函数的意义去判断,其形式为y=kx(k为常数,k≠0)或y=kx﹣1(k为常数,k≠0).【详解】解:A、不是反比例函数,故A选项不合题意;B、不是反比例函数,故B选项不合题意;C、不是反比例函数,故C选项不合题意;D、是反比例函数,故D选项符合题意.故选:D.【点睛】此题主要考查了反比例函数的定义,解题的关键是牢记反比例函数的形式然后判断.3.C【分析】根据题意,把函数的值代入函数表达式,然后解方程即可.【详解】解:根据题意,得4x2+1=5,x2=1,解得x=-1或1.故选C.【点睛】本题考查给出二次函数的值去求函数自变量的值.代入转化为求一元二次方程的解.4.D【详解】解:因为抛物线y=4x2,y=14x2,y=-14x2都符合抛物线的最简形式y=ax2,其对称轴是y轴,顶点是原点.故选D.【点睛】本题考查二次函数的图象性质.5.D【详解】解:根据题意可得当0<x<8时,其中有一个x的值满足y=2,则对称轴所在的位置为0<h<4故选:D【点睛】本题考查二次函数的性质,利用数形结合思想解题是关键.6.C此题可先对各选项列出函数关系式,再根据反比例函数的定义进行判断.【详解】A、根据速度和时间的关系式得,t=100 v;B、因为菱形的对角线互相垂直平分,所以12xy=48,即y=96x;C、根据题意得,m=ρV;D、根据压强公式,p=600s;可见,m=ρV中,m和V不是反比例关系.故选C.【点睛】本题主要考查了反比例函数的定义,正确表示出各量之间的函数关系是解决本题的关键.7.C【分析】由平行线分线段成比例定理,得到CO BODO AO=;利用AO、BO、CD的长度,求出CO的长度,即可解决问题.【详解】如图,∵AD∥CB,∴CO BO DO AO=;∵AO=2,BO=3,CD=6,∴362COCO=-,解得:CO=3.6,故选C.【点睛】本题考查了平行线分线段成比例定理及其应用问题.掌握平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例是解题的关键..8.D【分析】分三种情况:点M的纵坐标小于1;点M的纵坐标等于1;点M的纵坐标大于1;进行讨论即可得到方程12x2+bx+c=1的解的个数.解:点M 的纵坐标小于1,方程2112x bx c ++=的解是2个不相等的实数根;点M 的纵坐标等于1,方程2112x bx c ++=的解是2个相等的实数根;点M 的纵坐标大于1,方程2112x bx c ++=的解的个数是0.故方程2112x bx c ++=的解的个数是0,1或2.故选D .【点睛】本题考查了二次函数的性质,本题涉及分类思想和方程思想的应用.9.A 【分析】根据黄金分割的定义得出512BC AC AC AB -==,从而判断各选项.【详解】解:∵点C 是线段AB 的黄金分割点,且AC >BC ,∴512BC AC AC AB -==,∴选项A 符合题意,2AC BC AB =⋅,∴选项D 不符合题意;∵12AC BC +==,∴选项B 不符合题意;∵222AB AC BC ≠+,∴选项C 不符合题意;故选:A .【点睛】本题主要考查了黄金分割,熟练掌握黄金分割的定义是解题关键.10.C如图:连接AC ,∵OD=2,CD ⊥x 轴,∴OD×CD=xy=4,解得CD=2,由勾股定理,得OC ==由菱形的性质,可知OA=OC ,∵△OCE 与△OAC 同底等高,∴S △OCE =S △OAC =12×OA×CD=12.故选C .11.1.25【分析】根据比例尺=图上距离:实际距离,列比例式直接求得甲、乙两地间的实际距离.【详解】设甲、乙两地间的实际距离为xcm ,则:1255000x=,解得:x =125000.125000cm =1.25km .故答案为:1.25.【点睛】本题考查了比例尺的概念、比例的性质;根据比例尺进行计算,注意单位的转换问题.12.2π【分析】根据圆和二次函数图象的对称性,用割补法和圆的面积公式,即可求解.把x 轴下方阴影部分关于x 轴对称后,原图形阴影部分的面积和,变为一个半圆的面积,即2222ππ⋅=【点睛】利用图形的对称性,把不规则的阴影部分,补成规则的图形,再用圆的面积公式求解.13.1:(﹣5):4【分析】通过解方程组,用x 分别表示出y 与z ,然后求x :y :z 的值.【详解】解:x +y +z =0①,3x ﹣y ﹣2z =0②,①+②得4x ﹣z =0,则z =4x ,把z =4x 代入①得x +y +4x =0,则y =﹣5x ,所以x :y :z =x :(﹣5x ):4x =1:(﹣5):4.故答案为1:(﹣5):4.【点睛】本题考查了比例的性质:熟练掌握比例的性质(内项之积等于外项之积、合比性质、分比性质、合分比性质、等比性质)是解决此类问题的关键.14.①②④【分析】先判断出BP =PC =BC ,∠PBC =∠PCB =∠BPC =60°,再判断出AB =BC =CD ,∠A =∠ADC =∠BCD =90°,进而得出∠ABE =∠DCF =30°,即可判断出△ABE ≌△DCF (ASA ),即可得出结论;由等腰三角形的性质得出∠PDC =75°,则可得出答案;证明△FPE ∽△CPB ,得出PF EF PC BC =,设PF =x ,PC =y ,则DC =y ,得出y =32(x +y ),则可求出答案;先判断出∠DPH =∠DPC ,进而判断出△DPH ∽△CPD ,即可得出结论.【详解】解:∵△BPC 是等边三角形,∴BP =PC =BC ,∠PBC =∠PCB =∠BPC =60°,在正方形ABCD 中,∵AB=BC=CD,∠A=∠ADC=∠BCD=90°,∴∠ABE=∠DCF=30°,∴△ABE≌△DCF(ASA),∴AE=DF,∴AE﹣EF=DF﹣EF,∴AF=DE;故①正确;∵PC=CD,∠PCD=30°,∴∠PDC=75°,∴∠ADP=∠ADC﹣∠PDC=90°﹣75°=15°.故②正确;∵∠FPE=∠PFE=60°,∴△FEP是等边三角形,∴△FPE∽△CPB,∴PF EF PC BC=,设PF=x,PC=y,则DC=y,∵∠FCD=30°,∴y=32(x+y),整理得:(1﹣32)y=32x,解得:2333xy=,则2333PFPC=,故③错误;∵PC=CD,∠DCF=30°,∴∠PDC=75°,∵∠BDC=45°,∴∠PDH =∠PCD =30°,∵∠DPH =∠DPC ,∴△DPH ∽△CPD ,∴PD PH PC PD=,∴PD 2=PH •CP ,∵PB =PC ,∴PD 2=PH •PB ;故④正确.故答案为:①②④.【点睛】本题考查的正方形的性质,等边三角形的性质以及相似三角形的判定和性质,解答此题的关键是熟练掌握性质和定理.15.9a =,12b =,15c =【分析】根据比例的性质,可得a 、b 、c 的关系,根据a 、b 、c 的关系,可得一元一次方程,根据解方程,可得答案.【详解】解:由345a b c ==,得35a c =,45b c =,把35a c =,45b c =代入36a b c ++=,得343655c c c ++=,解得15c =,395a c ==,4125b c ==,所以三角形ABC 三边的长为:9a =,12b =,15c =.【点睛】本题考查了比例的性质,利用了比例的性质.利用等式的性质得出35a c =,45b c =是解题关键.16.()214y x =--+【分析】设顶点式()214y a x =-+,然后把(﹣2,﹣5)代入求出a 的值即可.【详解】解:设抛物线解析式为()214y a x =-+,把(﹣2,﹣5)代入得()22145a --+=-,解得:a =﹣1,所以抛物线解析式为:()214y x =--+.【点睛】本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数解析式时,要根据题目给定的条件,选择恰当的方法设出解析式,从而代入数值求解.17.(1)w =1600t (t >4);(2)每天要多做264004t t -(t >4)万个口罩才能完成任务【分析】(1)根据每天生产口罩w (万个)、生产时间t (天)(t >4)、生产总量之间的关系可直接列出函数表达式;(2)用提前4天交货的情况下每天生产的口罩数量减去计划每天生产的口罩数量即可得到结论.【详解】解:(1)由题意可得,函数表达式为:w =1600t(t >4);(2)由题意得:()()2160016004160016006400444t t t t t tt t ---==---(万个),答:每天要多做264004t t-(t >4)万个口罩才能完成任务.【点睛】本题主要考查了列反比例函数关系式,了解每天生产口罩w (万个)、生产时间t (天)(t >4)、生产总量之间的关系是解决问题的关键.18.1:16【分析】由已知得出BE:BC=1:4;证明△DOE∽△AOC,得到14DEAC=,由相似三角形的性质即可解决问题.【详解】解:∵S△BDE:S△CDE=1:3,∴BE:EC=1:3;∴BE:BC=1:4;∵DE∥AC,∴△DOE∽△AOC,∴1=4 DE BEAC BC=,∴S△DOE:S△AOC=1:16.【点睛】本题主要考查了相似三角形的判定及其性质的应用问题;熟练掌握相似三角形的判定与性质,证出BE:BC=1:4是解决问题的关键解题的关键.19.(1)A(﹣2,0),B(2,0);(2)y=x2﹣4【分析】(1)通过解方程mx²﹣4m=0可得A、B点的坐标;(2)先利用OA=2得到OC=4,所以|﹣4m|=4,然后求出满足条件的m的值,从而得到抛物线解析式.【详解】解:(1)当y=0时,mx2﹣4m=0,即x2﹣4=0,解得x1=2,x2=﹣2,∴A(﹣2,0),B(2,0);(2)当x=0时,y=mx2﹣4m=﹣4m,∴C(0,﹣4m),∵OA=2,∴OC=2OA=4,∴|﹣4m|=4,解得m=1或m=﹣1,∵m>0,∴m =1,∴抛物线解析式为y =x 2﹣4.【点睛】本题考查了抛物线与x 轴的交点:把求二次函数y=ax 2+bx+c (a ,b ,c 是常数,a≠0)与x 轴的交点坐标问题转化为解关于x 的一元二次方程.也考查了二次函数的性质.20.(1)见解析;(2)见解析【分析】(1)由菱形的性质可得AB =AD ,∠BAC =∠DAC ,由“SAS”可证△ABP ≌△ADP ;(2)由全等三角形的性质可得PB =PD ,∠ADP =∠ABP ,通过证明△EPB ∽△BPF ,可得BP PE PF PB=,可得结论.【详解】证明:(1)∵四边形ABCD 是菱形,∴AB =AD ,∠BAC =∠DAC ,在△ABP 和△ADP 中,AD AB BAP DAP AP AP =⎧⎪∠=∠⎨⎪=⎩,∴△ABP ≌△ADP (SAS );(2)∵△ABP ≌△ADP ,∴PB =PD ,∠ADP =∠ABP ,∵AD //BC ,∴∠ADP =∠E ,∴∠E =∠ABP ,又∵∠FPB =∠EPB ,∴△EPB ∽△BPF ,∴BP PE PF PB=,∴PB 2=PE•PF ,∴PD 2=PE•PF .【点睛】本题考查了菱形的性质,三角形全等的判定与性质,三角形相似的判定与性质,解题的关键是熟练掌握三角形全等与相似的判定方法.21.(1)m>﹣1时,抛物线c与直线l没有公共点;(2)点B不在平移后的抛物线上,见解析【分析】(1)令x2+m=﹣2x﹣2,整理得x2+2x+m+2=0,根据判别式的意义得到△=22﹣4(m+2)<0,则抛物线c与直线l没有公共点;(2)先利用一次函数解析式确定A(0,﹣2),B(﹣1,0),再写顶点在A点的抛物线解析式为y=x2﹣2,然后根据二次函数图象上点的坐标特征进行判断.【详解】解:(1)根据题意得x2+m=﹣2x﹣2,整理得x2+2x+m+2=0,∵抛物线c与直线l没有公共点,∴△=22﹣4(m+2)<0,解得m>﹣1,∴m>﹣1时,抛物线c与直线l没有公共点;(2)当x=0时,y=﹣2x﹣2=﹣2,∴A(0,﹣2),当y=0时,﹣2x﹣2=0,解得x=﹣1,∴B(﹣1,0),∵抛物线c的顶点与点A重合,∴平移后的抛物线解析式为y=x2﹣2,当x=﹣1时,y=x2﹣2=﹣1,∴点B不在平移后的抛物线上.【点睛】本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x 轴的交点坐标问题转化为解关于x的一元二次方程,把抛物线与一次函数的交点问题转化为一元二次方程根的问题.也考查了二次函数的几何变换.22.(1)k=1;(2)M(0,3 2)【分析】(1)A(1,3),则AB=3,OB=1,而AB=3BD,故BD=1,则D(1,1),将D坐标代入反比例解析式得:k=1;(2)作点B(1,0)关于y轴的对称点E(﹣1,0),连接AE交y轴于点M,则点M为所求点,即可求解.【详解】解:(1)∵A(1,3),AB⊥x轴,∴AB=3,OB=1,∵AB=3BD,∴BD=1,∴D(1,1),将D坐标代入反比例解析式得:k=1;(2)作点B(1,0)关于y轴的对称点E(﹣1,0),连接AE交y轴于点M,则点M为所求点,理由:d=MA+MB=MA+ME=AE为最小,设直线AE的表达式为y=mx+b,则3m bm b=+⎧⎨=-+⎩,解得3232mb⎧=⎪⎪⎨⎪=⎪⎩,故AE的表达式为y=32x+32,当x=0时,y=3 2,故点M的坐标为(0,3 2).【点睛】本题为反比例函数的综合应用,涉及待定系数法、函数图象的交点、轴对称的性质等知识,本题考查知识点较多,综合性较强,难度适中.23.(1)见解析;(2)见解析;(3)不成立【分析】(1)根据折叠的性质得到∠CNM=∠PNM,CN=PN,得到PN=BN,根据等腰直角三角形的性质、平行线的判定定理证明结论;(2)过点M作ME⊥AB于E,过点N作NF⊥AB于F,证明△MEP∽△PFN,根据相似三角形的性质得到MPPN=MEPF=EPFN,根据等腰直角三角形的性质得到ME=AE,PN=BF,根据比例的性质计算,证明结论;(3)仿照(2)的证明方法可以判断(2)中的等式不成立.【详解】解:(1)∵∠C=90°,AC=BC,∴∠B=∠A=45°,∵点N为BC中点,∴CN=BN,由折叠的性质可知,∠CNM=∠PNM,CN=PN,∴PN=BN,∴∠NPB=∠B=45°,∴∠BNP=90°,∴∠CNM=45°,∴∠CNM=∠B,∴MN∥AB;(2)证明:如图2,过点M作ME⊥AB于E,过点N作NF⊥AB于F,由折叠的性质可知,MP=MC,NP=NC,∠MPN=∠C=90°,∴∠MPE+∠NPF=90°,∵∠PNF+∠NPF=90°,∴∠MPE=∠PNF,∵∠MEP=∠PFN=90°,∠MPE=∠PNF,∴△MEP∽△PFN,∴MPPN=MEPF=EPFN,∵ME⊥AB,NF⊥AB,∠B=∠A=45°,∴ME=AE,PN=BF,∴MPPN=MEPF=EPFN=ME PEPF FN++=AE PEPF FB++=APBP,∴MPPN=APBP;(3)解:不成立,理由如下:过点M作MG⊥AB于G,过点N作NH⊥AB于H,∵∠C=90°,AC≠BC,不妨设AC<BC,则∠A<45°,∠B>45°,∴MG<AG,NH>BH,由(2)的证明方法可知:MPPN≠APBP.【点睛】本题考查的是相似三角形的判定和性质、翻转变换的性质、比例的性质,掌握相似三角形的判定定理和性质定理是解题的关键.。
2023-2024学年湖南省长沙市师大附中教育集团九年级上学期第三次月考语文试题

2023-2024学年湖南省长沙市师大附中教育集团九年级上学期第三次月考语文试题阅读下面的文字,完成下面小题。
11月22下午,初2021级语文备课组举办了主题为“成长路上,选择和努力哪个更重要”的年级辩论赛决赛。
在最精彩的自由辩论环节中,双方辩手前仆后继....,互不相让,立足已方观点,针对对方的漏洞将辩论赛推向高潮。
辨手们在言语中碰撞思维的火花,灌溉..成长的种子,①赛后,陈婧校长对整场比赛进行了点评,可谓是抛砖引玉。
经过激烈角理,最终正方摘得本次比赛的桂冠..,②反方三辨获得最佳辨手的称号。
③辩论()一门语言的艺术。
()一门思维的艺术,④通过这次辩论比赛,使同学们对“选择”和“努力”有了更加全面的认识。
如果人生是一次远航,那么正确的选择就是duòshǒu 必经途径。
1. 下面是小语对这段文字做的字音字形及词义的梳理记录,其中有错误的一项是()A.注意词语的误用,文段中加点成语“前仆后继”使用错误。
B.注意因音近造成的误写,文段中加点词语“灌溉”不要写成“灌概”C.注意多音字的误读,文段中加点词语“桂冠”和“既加冠”的读音不一样。
D.注意积累常见的字音字形,文段中“duòshǒu”一词字形为“舵手”。
2.下面是小语对这段话的理解,其中最恰当的一项是()A.在语言表述中,要注意语言表达得体,文段中画线句子①表达得体。
B.在语言表达中,也要注意标点符号的使用,文段中画线句子②“最佳辩手”属于特定称谓,应加上双引号。
C.在语言表述中,要注意语言的连贯,文段中划线句子③括号里的关联词应该填“不是”“而是”。
D.在语言表述中,要注意语病,文段中画线句子④表述恰当,句意明确。
3. 古诗文默写人生无处不在面对着选择,有的人面对生与义的选择时义无反顾:(1)“______________,____________。
(孟子《鱼我所欲也》):有的人在面对回家和建功立业的选择时,生发出(2)“_____________,____________”的矛盾心理(范仲淹《渔家傲·秋思》)。
24-25学年九年级数学第三次月考(华东师大版)【测试范围:第23章~第24章】(全解全析)

2024-2025学年九年级数学上学期第三次月考(华东师大版)(考试时间:120分钟试卷满分:120分)注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.测试范围:华东师大版第23章图形的相似~第24章解直角三角形,第21章占比15%,第22章占比15%,第23-24章占比70%。
5.难度系数:0.68。
第一部分(选择题共30分)一、选择题:本题共10小题,每小题3分,共30分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1x的取值范围是()A.x>2024B.x=2024C.D.∴,∴,2.已知2a=3b(ab?0),则下列比例式成立的是()A.a2=3bB.a3=b2C.ab=23D.ba=323.在△ABC中,,AB=15,sin B=35,则AC等于()A.25B.12C.9D.16根据题意得:在中,∴AC=35×15=9,故选C.4.下列方程中是关于x的一元二次方程的是()A.x2+2x=x2+1B.1x2+1x―2=0C.3x+2y=5D.3(x+1)2=2x+15.如图,△ABC与是位似图形,点O是位似中心,若OA:OA′=3:1,则B′C′BC的值为( )A .13B .23C .12D .34与是位似图形,∴,6.福州白塔是福州的标志性建筑之一,也是中国现存最早的木塔之一(如图1).小明想测量白塔AB 的高度(如图2),在离白塔底端B 正前方8米的C 处,用高为1.5米的测角仪CD 测得白塔顶部A 处的仰角为,则白塔AB 的高度为( )A .(8tan a +1.5)米B .米C .(8cos a +1.5)米D .(8sin a +1.5)米【答案】A【解析】过点D 作,垂足为E ,由题意得:CD=BE=1.5米,DE=BC=8米,在中,,(米),米,白塔AB的高度为(8tan a+1.5)米.故选A.7.若关于x一元二次方程mx2+2x+1=0有实数解,则m的取值范围是()A.B.C.m≥―1且D.且∴,解得:且.8.实数a,b―|a―b|化简的结果是()A.―2b B.―2a C.2b―2a D.0故选A .9.如图,在矩形ABCD 中,AB =6cm ,BC =9cm ,点E,F 分别在边AB,BC 上,AE =2cm ,BD,EF 交于点G ,若G 是EF 的中点,则线段BG 的长度是( )A B .203cm C .103cm D 【答案】D【解析】四边形ABCD 是矩形, ,,,,,,是EF 的中点,,,,∽△DCB ,,,,,.10.如图,正方形ABCD中,AE平分∠CAB,交BC于点E,将△ABE绕点B顺时针旋转得到△CBF,延长AE交CF于点G,连BG、DG,DG交AC于点H.下列结论①BE=BF;②;③;④AE=正确的是()A.①②③④B.②③C.①③D.①②顺时针旋转得到,∴,,故正确;∴,,∴,∵,∴,∴,∴,故正确;∵,∴,∴,∴,∵,∴,∴,∴,∴,,即,∴,故正确;∵,∴,∵,∴,∵,∴,,故正确;∴正确,第二部分(非选择题共90分)二、填空题:本题共8小题,每小题3分,共24分。
安徽省涡阳县石弓学区2024-2025学年第一学期九年级第三次月考语文试题(文字版,含答案)

2024-2025学年第一学期第三次月考九年级测评・语文▶上册全部◀注意事项:1.满分为150分(其中卷面书写占5分),答题时间为150分钟;2.请将各题答案填写在答题卡上。
一、语文积累与运用(35分)1.默写。
(10分)(1)经典诗歌里有古人的巧思。
李白《行路难(其一)》中“,”,以用典手法,表达自己希望得到重用的心情;李商隐《无题》中“,”,以寻常之物设喻,巧用双关,写尽相思之苦;刘禹锡《酬乐天扬州初逢席上见赠》中“,”鼓励我们要有坚忍不拔的意志,重新投入生活。
(2)故乡往往是游子魂牵梦萦的地方。
杜甫《月夜忆舍弟》中表达诗人感物伤怀、思念家乡的诗句是“,”;温庭筠《商山早行》中将自然景物与梦境结合起来,抒发作者思乡之情的句子是“,”。
2.请运用积累的知识,完成(1)~(4)题。
(12分)【甲】郑屠道:“着人与提辖拿了,送将府里去?”鲁达道:“再要十斤寸金软骨,也要细细地剁做sào子,不要见些肉在上面。
”郑屠笑道:“却不是特地来消遣我?”鲁达听得,跳起身来,拿着那两包sào子在手,睁着眼,看着郑屠道:“洒家特地要消遣你!”把两包s ào子劈面打将去,却似下了一阵的“肉雨”郑屠大怒,两条忿.气从脚底下直冲到顶门,心头那一把无名火腾腾的按捺.不住,从肉案上抢了一把剔骨尖刀,托地跳将下来。
鲁提辖早拔步在当街上。
【乙】话休絮繁。
武松、施恩两个一处走着,但遇酒店便入去吃三碗,约莫也吃过十来处好酒肆。
施恩看武松时,不十分醉。
武松问施恩道:“此去快活林还有多少路?”施恩道:“没多了。
只在前面,远远地望见那个林子便是。
”武松道:“既是到了,你且在别处等我,我自去寻他。
”施恩道:“这话最好。
小弟自有安身去处。
望兄长在意,切不可轻敌。
”武松道:“这个却不妨。
你只要叫仆人送我,前面再有酒店时,我还要吃。
”施恩叫仆人仍旧送武松。
施恩自去了。
(1)根据拼音写出相应的汉字,给加点的字注音。
(3分)sào()子忿.()气按捺.()(2)下列短语的类型与“那个林子”相同的一项是()(3分)A.自去寻他B.跳将下来C.直冲脑门D.剔骨尖刀(3)《水浒传》采用链式结构:每回出现一个中心人物,成为一个环,同时这一环又与下一环相连,环环相扣,把小说的主要人物一个个连缀起来。
河南省许昌市2023-2024学年九年级上学期第三次月考语文试题(原卷版)

2023~2024学年上学期九年级第三次核心素养检测语文试题注意:本试卷分试题卷和答题卡两部分。
考试时间120分钟,满分120分。
考生应首先阅读答题卡上的文字信息,然后在答题卡上作答,在试题卷上作答无效,交卷时只交答题卡。
一、积累与运用(共23分)班级开展“无悔青春难忘初中生活”主题活动,以下是资料组准备的部分材料,请你帮忙完善。
【追忆美好】1. 小豫回忆自己作为志愿者参加2023年中华轩辕龙舟大赛时的感受,并分享了下面一段话。
其中有些字词他拿不准,请帮他判断。
龙舟竞渡,又称赛龙舟,每年在端午前后举行。
它是全民性特征明显的文化活动,船上操桨驾①______(驭育)的舵手多,岸上加油助威观看比赛者更多。
轩辕龙舟大赛有着广泛的群众基础,且其竞渡习俗也有着本地文化的独特烙印。
当嘹亮的哨音响起,数十条龙舟在眼前奔驶而出,竞技的热血在水面喷薄时没有人会无精打②______(彩采),因为人们只会感受到文化传承所带来的滚烫的澎湃。
(1)语段中三个加点字怎么读?请帮他作出选择()A. tuóluòbóB. tuólàobáoC. duòlàobóD. duòluòbáo(2)语段中两个横线处应分别选用哪个字?请工整书写。
2. 小文和同学们分享了鸡冠洞独特的钟乳石景观,还为同学们搜集了相关科普知识,但有几句话的顺序不小心弄乱了,请你帮忙选出衔接最恰当的一项()钟乳石是在碳酸盐岩地区的洞穴内广泛分布的一种钟乳状次生碳酸钙沉积物。
______。
______;______;______。
①石钟乳是从洞顶像时钟的钟摆一样向下垂直悬挂的部分②当自上向下的石钟乳和由下向上的石笋长到一起上下相连时,就称为石柱③这些地质形态主要分为石钟乳、石笋和石柱三种④这些沉积物在漫长地质历史中,在特定地质环境条件下形成了不同的形态⑤石笋一般位于石钟乳的正下方,像地面长出的竹笋一样A. ③④②①⑤B. ③④②⑤①C. ④③⑤①②D. ④③①⑤②【回味经典】3. 古诗文默写。
吉林省名校调研系列卷2024-2025学年九年级上学期第三次月考数学试题(含答案)
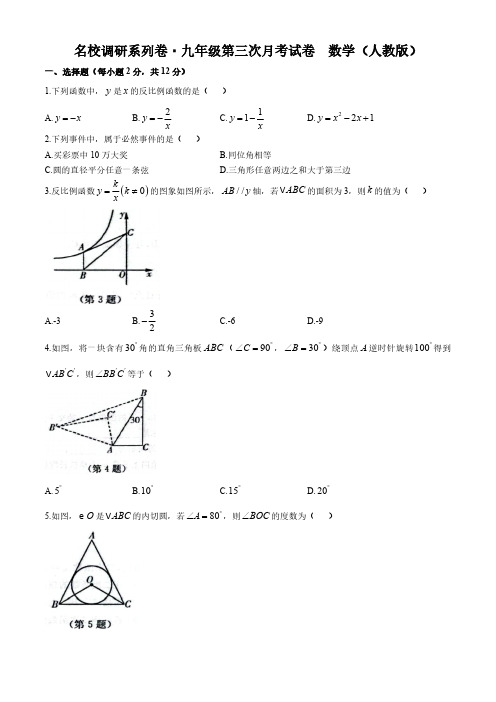
名校调研系列卷・九年级第三次月考试卷 数学(人教版)一、选择题(每小题2分,共12分)1.下列函数中,是的反比例函数的是( )A. B. C. D.2.下列事件中,属于必然事件的是( )A.买彩票中10万大奖B.同位角相等C.圆的直径平分任意一条弦D.三角形任意两边之和大于第三边3.反比例函数的图象如图所示,轴,若的面积为3,则的值为( )A.-3 B. C.-6 D.-94.如图,将一块含有角的直角三角板(,)绕顶点逆时针旋转得到,则等于( )A. B. C. D.5.如图,是的内切圆,若,则的度数为()y x y x =-2y x =-11y x =-221y x x =-+()0k y k x=≠//AB y ABC V k 32-30︒ABC 90C ︒∠=30B ︒∠=A 100︒AB C ''V BB C ''∠5︒10︒15︒20︒O e ABC V 80A ︒∠=BOC ∠A. B. C. D.6.如图是二次函数的部分图象,该函数图象的对称轴是直线,图象与轴交点的纵坐标是2,则下列结论:①;②方程一定有一个根在-2和-1之间;③方程一定有两个不相等的实数根;④,其中正确结论的个数有( )A.1个 B.2个 C.3个 D.4个二、填空题(每小题3分,共24分)7.在平面直角坐标系中,点关于原点对称的点是点,则_____.8.在一个不透明的袋中装有100个红、紫两种颜色的球,除颜色外其他都相同,通过多次摸球试验后发现,摸到紫球的频率稳定在0.45左右,则袋中紫球大约有_____个.9.如图,已知、、、四个点均在上,若,弦的长等于半径,则_____度.10.如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于点、,当时,的取值范围是_____.100︒110︒120︒130︒()20y ax bx c a =++≠1x =y 20a b +=20ax bx c ++=2302ax bx c ++-=0a b c -+>()6,0P -P 'PP '=A B C D O e 44A ︒∠=CD BOC ∠=1y kx b =+2m y x=()4,4A -(),2B n -12y y >x11.已知关于的一元二次方程有两个不相等的实数根,则的取值范围是_____.12.当灯泡两端电压恒定时,通过灯泡的电流与其电阻成反比例,关于的函数图象如图所示,当电流时,电阻的取值范围是_____.13.如图,五边形为的内接正五边形,与相切于点,则_____度.14.如图,抛物线与轴相交于点、,与轴相交于点,点在该抛物线上,坐标为,则点的坐标是_____.三、解答题(每小题5分,共20分)15.用因式分解法解方程:.x 2230x x m ++=m ()A I ()R ΩI R 0.2A I ≤R ΩABCDE O e PA O e A PAB ∠=2y ax bx c =++x A ()2,0B m +y C D (),m c A ()2324x x x -=-16.如图,在中,,,将绕点顺时针旋转得到,交于点,若,求的长.17.已知反比例函数(为常数).(1)若该反比例函数的图象位于第二、四象限,求的取值范围;(2)若、是该反比例函数图象上的点,直接写出函数值、的大小.18.如图,的直径垂直弦于点,是圆上一点,是的中点,连接交于点,连接.(1)求证:;(2)若,,求的长.四、解答题(每小题7分,共28分)19.有3张相同的卡片,正面分别写有数字-3、8、10,将卡片的背面朝上放在桌面上.(1)洗匀后,从中随机抽取1张卡片,抽到写有正数的卡片的概率为_____;(2)洗匀后,从中随机抽取2张卡片,用画树状图或列表的方法,求抽取的2张卡片上的数字之积是负数的概率.20.如图,二次函数的图象与轴交于点、、与轴交于点.ABC V 90C ︒∠=20B ︒∠=ABC V A 25︒ADE V AD BC F 3AE =AF 26a y x+=a a ()11,4,a A y =-()21,B y -1y 2y O e AB CD E F D »BFCF OB G BC GE BE =6AG =4BG =CD 243y x x =+-x A B y C(1)该二次函数的顶点坐标是_____;(2)连接、,的面积为_____,(3)若将该二次函数的图象向上平移个单位长度后恰好过点,求的值.21.已知反比例函数,点、都在该反比例函数的图象上.(1)求反比例函数的解析式;(2)当时,直接写出的取值范围;(3)若经过的直线与轴交于点,求的面积.22.如图①是一座抛物线型拱桥,小星学习二次函数后,受到该图启示设计了一建筑物造型,它的截面图是抛物线的一部分(如图②),抛物线的顶点在处,对称轴与水平线垂直,,点在抛物线上,且点到对称轴的距离,点在抛物线上,点到对称轴的距离是1.(1)求抛物线的解析式;(2)如图②,为更加稳固,小星想在上找一点,加装拉杆、,同时使拉杆的长度之和最短,请你帮小星求出点的坐标.五、解答题(每小题8分,共16分)AC BC ABC V m (2,0)-m ()0k y k x=≠()2,A a -()9,1B a +1x >y AB y C OAC V C OC OA 9OC =A A 3OA =B B OC P PA PB P23.如图,点、、在上,,,延长到点,使,连接、.(1)求证:是的切线;(2)若,求图中阴影部分的面积(结果保留根号和).24.在中,,,,将绕点逆时针旋转得到,其中点、的对应点分别为点、.【教材呈现】(1)如图①,将绕点旋转得到,则线段的长为_____;【问题解决】(2)在旋转的过程中,连接,交边于点,当时,如图②,求证:;【拓展延伸】(3)点为边的中点,在旋转的过程中,连接,当的值最大时,连接,直接写出此时的长.六、解答题(每小题10分,共20分)25.如图,在等腰直角三角形中,,,点从点出发,以的速度沿边向终点运动,过点作,交折线于点Q ,D 为的中点,以为边向右侧作正方形,设正方形与重叠部分图形的面积是,点的运动时间为.A B C O e 150AOB ︒∠=45ABC ︒∠=OB D BD OB =OC CD CD O e 12CD =πRt ABC △90ACB ︒∠=10AB =8AC =ABC V B A BC ''V A C A 'C 'ABC V B 180︒A BC ''V CC 'ABC V CC 'ABD //CC A B ''12CD AB =E AC ABC V CC 'CC 'C E 'C E 'ABC 90ACB ︒∠=4cm AB =P A 2cm/s AB B P PQ AB ⊥AC CB -PQ DQ DEFQ DEFQ ABC V ()2cm y P ()s x(1)当点在边上时,正方形的边长为_____(用含的代数式表示);(2)当点不与点重合时,求点落在边上时的值;(3)当时,求关于的函数解析式;(4)直接写出边的中点落在正方形内部时的取值范围.26.如图,在平面直角坐标系中,抛物线(为常数)经过点,且与轴交于点,点在该抛物线上,横坐标为,将该抛物线、两点之间(包括、两点)的部分记为图象.(1)求此抛物线对应的二次函数的解析式;(2)当时,二次函数的最大值是_____,最小值是_____;(3)当图象的最大值与最小值的差为3时,求的值;(4)抛物线(为常数)与轴的另一交点为,若点在抛物线上,且在轴下方,点为轴上一动点,当以、、、为顶点的四边形是平行四边形时,直接写出点的坐标.名校调研系列卷・九年级第三次月考试卷数学(人教版)参考答案一、1.B2.D3.C4.B5.D6.B二、7.12 8.45 9.28 10.或 11. 12. 13.3614.三、15.解:,.16.解:Q AC DEFQ cm x P B F BC x 02x <<y x BC DEFQ x 223y x bx =-++b ()1,0A -y B C 21m -B C B C G 23x -≤≤G m 223y x bx =-++b x D M x N x B D M N N 4x <-08x <<98m <15R ≥()2,0-11x =22x =AF =17.解:(1)的取值范围是.(2).18.(1)证明:是的中点,,,,,,,.(2)解:.四、19.解:(1).(2)画树状图如图.由树状图知共有6种等可能的结果,其中抽取的2张卡片上的数字之积是负数的结果有4种,抽取的2张卡片上的数字之积是负数的概率为.20.解:(1).(2).(3)由题意,得平移后的抛物线的解析式为,经过点(-2,0),,解得.21.解:(1)反比例函数的解析式为.(2)的取值范围是.(3)的面积为2.22.解:(1)抛物线的解析式为.(2)点的坐标为.五、23.(1)证明:,,,,,是等边三角形,,,,,,是半径,是的切线.(2)解:图中阴影部分的面积为.24.(1)解:12.a 3a <-12y y >D »BFECG ECB ∴∠=∠CD AB ⊥ 90CEG CEB ︒∴∠=∠=CGE CBE ∴∠=∠CG CB ∴=CE BG ⊥ EG EB ∴=8CD =23∴4263=()2,7--()227y x m =+-+ ()20227m ∴=-+-+7m =6y x=y 06y <<OAC V 29y x =-+P (0,6),150OA OB AOB ︒=∠= 15A OBA ︒∴∠=∠=45ABC ︒∠= 60OBC ︒∴∠=OC OB = OBC ∴V OB BC ∴=BD OB = BC BD ∴=30BCD D ︒∴∠=∠=603090OCD OCB BCD ︒︒︒∴∠=∠+∠=+=OC CD ∴O e 8π-(2)证明:将绕点逆时针旋转得到,,,,,,,,,,,,.,,,,,.(3)解:.六、25.解:(1).(2)延长交于点,由题意,得,为的中点,,,,解得.(3)分三种情况:当时,;当时,;当时,.(4)的取值范围是.26.解:(1)二次函数的解析式为.(2)4;-5.(3)图象的最大值与最小值的差为3时,分两种情况:当点在点右侧时,图象的最大值是4,图象的最大值与最小值的差为3,∴图象的最小值是1,点的纵坐标是1,∵点在该抛物线上,横坐标为,,解得,(舍去),;当点在点左侧时,图象的最大值是3,∵图象的最大值与最小值的差为3,∴图象的最小值是0,∴点的纵坐标是,点在该抛物线上,横坐标为,点与重合,,解得,的值为0.综上所述,或0.(4)点的坐标为或.ABC V B A BC ''V A A '∴∠=∠A C B ''∠90ACB ︒=∠=BC BC '=BCC BC C ''∴∠=∠//CC A B '' 180A A C C A BC C A C B '''''''︒∴∠+∠=∠+∠+∠=90A BC C ''︒∴∠+∠=90A BC C '︒∴∠+∠=90A BCC '︒∴∠+∠=90ACB BCC ACD '︒∠=∠+∠= A ACD ∴∠=∠AD CD ∴=90ACB ︒∠= 90A ABC ︒∴∠+∠=ABC ∴∠BCC '=∠CD BD ∴=BD AD AB += 12CD AB ∴=C E '=x FE AB G 2AP x =D PQ DQ x ∴=GP x =224x x x ∴++=45x =405x <≤2y x =415x <≤2232082y x x =-+-12x <<21222y x x =-+x 312x <<223y x x =-++G C B G G G ∴C C 223y x x =-++21m -()()21212213m m ∴=--+-+1m =2m =m ∴C B G G G C 0 C 223y x x =-++21m -∴C A 211m ∴-=-0m =m ∴m N ()2-()2-。
吉松原市前郭县南部学区2024~2025学年度九年级上第三次月考试卷 语文(含答案

九年 ·语文(省命题) H学校姓名考号名校调研系列卷·九年级第三次月考试卷语文(人教版)题号二三总分得分一、积累与运用(15分)阅读语段,按要求完成1-4题。
(8分)青春,如诗如画,是人生中最为璀璨的篇章。
在这最美的时光里,青春是最美的奋斗时节。
青春的奋斗,如同一幅xuàn 丽多彩的画卷在眼前徐徐展开。
【甲】青春的奋斗,是一首激昂的乐章。
在奋斗的旋律中,有挫折时的低沉,有拼搏时的高亢,更有成功时的激昂海湃。
当遇到困难时,我们不退缩、不放弃,勇敢地迎难而上。
【七。
青春的奋斗,是一场没有终点的旅程。
在这个旅程中,我们怀揣梦想,不断前行。
【丙】1.根据拼音写汉字,给加点字注音。
(2分)(1)xuàn( )丽多彩(2)高亢( )2.下列选项中与“奋斗时节”短语类型一致的是( )(2分)A.徐徐展开B.激昂澎湃C. 迎难而上D.怀揣梦想3.将下列语句依次填入文中甲、乙、丙横线处,最恰当的一项是( )(2分)①每一次的挑战都是成长的机遇,每一次的挫折都是奋斗的勋章②也许前方的道路崎岖不平,但我们坚信,只要努力奋斗,就一定能抵达成功的彼岸③那是清晨第一缕阳光洒在书本上的专注,是深夜灯火下为梦想拼搏的身影A.②①③B.③①②C.②③①D.①②③4.请提取文中画波浪线句子的主于:。
(2分)5.在下面田字格中填写古诗词名句。
(7分)赏读经典,砥砺人生。
范仲淹《渔家傲·秋思》中的(1)告诉我们戌边将士的思乡之情与报国之志;苏轼《定风波》中的“(2) 归去,也无风雨也无晴”告诉我们面对人生的“风雨”,要坚守自己的精神世界,顺境不骄,逆境不惧;辛弃疾《破阵子·为陈同甫赋壮词以寄之》中的(3)”表达了作者渴望建功立业的雄心壮志;秋瑾《满江红》中的(4)“身不得,男儿列,告诉我们词人巾帼不让须眉的豪迈气概。
语文试卷第1 页 ( 共8 页)得分评卷人(一)阅读下面材料,完成6-11题。
2024-2025学年九年级数学上学期第三次月考卷(安徽专用,九上第21~23.1章)(考试版A4)

2024-2025学年九年级数学上学期第三次月考卷(安徽专用)(考试时间:120分钟 满分:150分)注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回.4.测试范围:沪科版九上第21章二次函数与反比例函数30%+第22章相似形40%+23.1锐角三角函数30%.5.难度系数:0.60.第一部分(选择题 共40分)一、选择题:本题共10小题,每小题4分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知△ABC 与△DEF 相似,且相似比为1:3,则△ABC 与△DEF 的周长之比是( )A .1:1B .1:3C .1:6D .1:92.如图,在△ABC 中,若∠B =90°,AB =3,BC =4,则tan A =( )A .45B .35C .43D .343.反比例函数y =―10x 的图象一定经过的点是( )A .(1,10)B .(―2,5)C .(2,5)D .(2,8)5.如图,在平面直角坐标系中,△ABC 与△A ′B ′C ′是位似图形,位似中心为点O .若点A (―3,1)的对应点为A ′(―6,2),则点B (―2,4)的对应点B ′的坐标为( )A .(―4,8)B .(8,―4)C .(―8,4)D .(4,―8)6.如图,在△ABC 中,AB =AC =5,sin B =45,则BC 的长是( )A .3B .6C .8D .97.已知二次函数y =ax 2+(2a ﹣3)x +a ﹣1(x 是自变量)的图象经过第一、二、四象限,则实数a 的取值范围为( )A .1≤a <9B .0<a <3C .0<a <9D .1≤a <3A .B ...9.如图,二次函数y =ax 2+bx +c (a ≠0)的图象与x 轴交于点A (3,0),与y 轴交于点B ,对称轴为直线x=1,下列四个结论:①bc <0; ②3a +2c <0; ③ax 2+bx ≥a +b ;④若―2<c <―1,则―83<a +b +c <―43,其中正确结论的个数为( )A .1个B .2个C .3个D .4个 A .BE DE =B .CE DE +第二部分(非选择题 共110分)二、填空题:本题共4小题,每小题5分,共20分。
人教版九年级上册数学第三次月考试题带答案
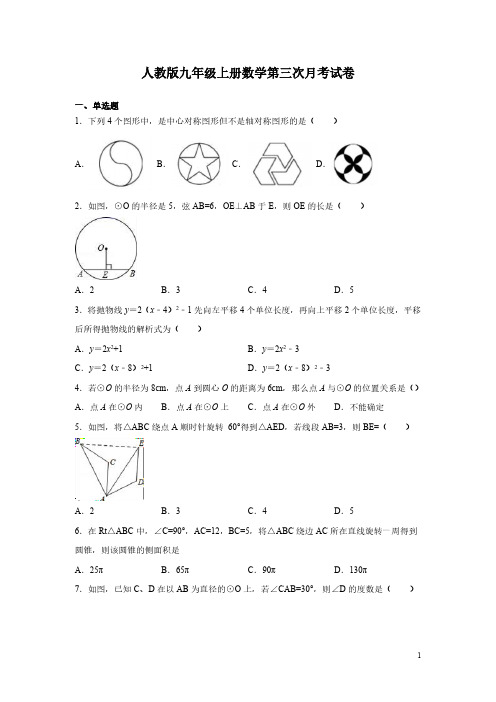
人教版九年级上册数学第三次月考试卷一、单选题1.下列4个图形中,是中心对称图形但不是轴对称图形的是()A.B.C.D.2.如图,⊙O的半径是5,弦AB=6,OE⊥AB于E,则OE的长是()A.2B.3C.4D.53.将抛物线y=2(x﹣4)2﹣1先向左平移4个单位长度,再向上平移2个单位长度,平移后所得抛物线的解析式为()A.y=2x2+1B.y=2x2﹣3C.y=2(x﹣8)2+1D.y=2(x﹣8)2﹣34.若⊙O的半径为8cm,点A到圆心O的距离为6cm,那么点A与⊙O的位置关系是()A.点A在⊙O内B.点A在⊙O上C.点A在⊙O外D.不能确定5.如图,将△ABC绕点A顺时针旋转60°得到△AED,若线段AB=3,则BE=()A.2B.3C.4D.56.在Rt△ABC中,∠C=90°,AC=12,BC=5,将△ABC绕边AC所在直线旋转一周得到圆锥,则该圆锥的侧面积是A.25πB.65πC.90πD.130π7.如图,已知C、D在以AB为直径的⊙O上,若∠CAB=30°,则∠D的度数是()A.30°B.70°C.75°D.60°8.如图,△ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,且AD=2,BC =5,则△ABC的周长为()A.16B.14C.12D.109.如图,在矩形ABCD中,AB=8,AD=12,经过A,D两点的⊙O与边BC相切于点E,则⊙O的半径为()A.4B.214C.5D.25410.如图,点C在以AB为半径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关AC对称,DF⊥DE于点D,并交EC的延长线与点F.下列结论:①CE=CF;②线段EF的最小值为3③当AD=2时,EF与半圆相切;④当点D从点A运动到点B时,线段EF扫过的面积是3.其中正确的结论()A.1个B.2个C.3个D.4个二、填空题11.若点P(a,﹣2)、Q(3,b)关于原点对称,则a﹣b=_____.12,则它的周长是______.13.已知圆锥形工件的底面直径是40cm,母线长30cm,其侧面展开图圆心角的度数为________.14.如图,⊙C过原点,且与两坐标轴分别交于点A,点B,点A的坐标为(0,3),M是第三象限内弧OB上一点,∠BMO=120°,则⊙C的半径为______.15.如图,正六边形ABCDEF的顶点B,C分别在正方形AMNP的边AM,MN上.若AB =4,则CN=_____.三、解答题16.如图,⊙O的弦AB与半径OC相交于点P,BC∥OA,∠C=50°,那么∠APC的度数为.17.解方程(1)x2﹣4x=0(2)2x2+3=7x18.如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点,△ABC的三个顶点A,B,C都在格点上.(1)画出△ABC绕点A逆时针旋转90°后得到的△AB1C1;(2)求旋转过程中动点B所经过的路径长(结果保留π).19.如图,AB是⊙O的一条弦,且AB=C,E分别在⊙O上,且OC⊥AB于点D,∠E=30°,连接OA.求OA的长.20.如图,已知四边形ABCD内接于圆O,连结BD,∠BAD=105°,∠DBC=75°.(1)求证:BD=CD;(2)若圆O的半径为3,求 BC的长.21.如图,AB为⊙O的直径,直线l经过⊙O上一点C,过点A作AD⊥l于点D,交⊙O 于点E,AC平分∠DAB.(1)求证:直线l是⊙O的切线;(2)若DC=4,DE=2,求线段AB的长.22.如图,以等边三角形ABC一边AB为直径的⊙O与边AC,BC分别交于点D,E,过点D作D F⊥BC,垂足为点F.(1)求证:D F为⊙O的切线;(2)若等边三角形ABC的边长为4,求D F的长;(3)求图中阴影部分的面积.23.如图直角坐标系中,已知A(-8,0),B(0,6),点M在线段AB上.(1)如图1,如果点M是线段AB的中点,且⊙M的半径为4,试判断直线OB与⊙M的位置关系,并说明理由;(2)如图2,⊙M与x轴、y轴都相切,切点分别是点E、F,试求出点M的坐标.24.已知抛物线的顶点坐标为M(1,4),且经过点N(2,3),与x轴交于A,B两点(点A在点B左侧),与y轴交于点C、设直线CM与x轴交于点D.(1)求抛物线的解析式.(2)在抛物线的对称轴上是否存在点P,使以点P为圆心的圆经过A、B两点,且与直线CD相切?若存在,求出P的坐标;若不存在.请说明理由.(3)设直线y=kx+2与抛物线交于Q、R两点,若原点O在以QR为直径的圆外,请直接写出k的取值范围.参考答案1.A2.C3.A4.A5.B6.B7.D8.B9.D10.C 11.-5 12.12 13.240°14.315.6-16.75°.17.(1)x1=0,x2=4;(2)x1=12,x2=318.(1)画图见解析;(2)点B所经过的路径长为5π2.19.4.20.(1)证明过程见解析;(2)π21.(1)详见解析;(2)AB=10.22.(1)证明见解析;(2(3)332 23π-.23.(1)直线OB与⊙M相切.;(2)M的坐标为(-247,247).24.(1)y=﹣x2+2x+3;(2)满足题意的点P存在,其坐标为(1,﹣);(3)213 3 -<k<213 3.。
2023-2024学年湖南师大附中高新学校九年级(上)第三次月考数学试卷及参考答案

2023-2024学年湖南师大附中高新学校九年级(上)第三次月考数学试卷一.选择题(每小题3分,10小题,共30分)1.(3分)如图交通标志是中心对称图形的为()A.B.C.D.2.(3分)下列函数中,y不是x的反比例函数的是()A.y=﹣B.C.D.3xy=23.(3分)若=,则ab=()A.6B.C.1D.4.(3分)下列说法正确的是()A.两个矩形一定相似B.两个菱形一定相似C.两个正方形一定相似D.两个直角三角形一定相似5.(3分)如表是一位同学在罚球线上投篮的试验结果,根据表中数据回答下列问题:投篮次数(n)50100150200250300500投中次数(m)286078104124153252估计这位同学投篮一次,投中的概率约是()(精确到0.1)A.0.4B.0.5C.0.55D.0.66.(3分)如图,AB是⊙O的直径,C是⊙O上一点.若∠BOC=66°,则∠A=()A.66°B.33°C.24°D.30°7.(3分)如果圆锥侧面展开图的面积是15π,母线长是5,则这个圆锥的底面半径是()A.3B.4C.5D.68.(3分)如图,正六边形ABCDEF内接于⊙O,若⊙O的周长是6π,则正六边形的边长是()A.B.3C.6D.9.(3分)如图,在平面直角坐标系中,点A在y轴上,点B的坐标为(6,0),将△ABO绕着点B顺时针旋转60°,得到△DBC,则点C的坐标是()A.(3,3)B.(3,3)C.(6,3)D.(3,6)10.(3分)如图,动点P在函数(x>0)的图象上运动,PM⊥x轴于点M,PN⊥y轴于点N,线段PM、PN分别与直线AB:y=﹣x+1交于点E、F,则AF•BE的值是()A.2B.1C.D.二.填空题(每小题3分,6小题,共18分)11.(3分)某蓄电池的电压为48V,使用此蓄电池时,电流I(单位:A)与电阻R(单位:Ω)的函数表达式为I=,当R=16Ω时,I的值为A.12.(3分)抛物线y=﹣(x+2)2+6顶点坐标是.13.(3分)一个不透明的布袋里只有6个红球和n个白球(仅有颜色不同).若从中任意摸出一个球是红球的概率为,则n=.14.(3分)若一元二次方程x2﹣4x+a=0配方后为(x﹣2)2=1,则a=.15.(3分)如图,在矩形ABCD中,AB=1,(AD>AB)在BC上取一点E,沿AE将△ABE向上折叠,使点B落在AD上的点F,若四边形EFDC与原矩形相似,则AD的长度为.16.(3分)以点P(1,2)为圆心,r为半径画圆,与坐标轴恰好有三个交点,则r=.三.解答题(9题,共72分)17.(6分)计算:3﹣2+﹣(π﹣1)0+|﹣1+|.18.(6分)如图,在平面直角坐标系xOy中,一次函数y1=﹣2x+6的图象与反比例函数的图象相交于A(a,4),B(b,2)两点.(1)求反比例函数的表达式及点B的坐标;(2)观察图象,直接写出y1>y2时x的取值范围.19.(6分)随着科技的进步,购物支付方式日益增多.为了解某社区居民支付的常用方式(A微信,B支付宝,C现金,D其他),某学习小组对红星社区部分居民进行问卷调查,根据查结果,绘制成如图统计图.根据统计图表中的信息,解答下列问题:(1)a=,b=,在扇形统计图中C种支付方式所对应的圆心角为度;(2)本次调查中用现金支付方式的居民里有2名男性,其余都是女性,现从该种支付方式中随机选2名居民参加线上支付方式培训,求恰好都是女性的概率.20.(8分)如图,在由边长为1个单位长度的小正方形组成的网格中,△ABC的顶点均为格点(网格线的交点).(1)将△ABC向上平移6个单位,再向右平移2个单位,得到△A1B1C1,请画出△A1B1C1;(2)以边AC的中点O为旋转中心,将△ABC按逆时针方向旋转180°,得到△A2B2C2,请画出△A2B2C2.21.(8分)如图,已知直线l1、l2、l3分别截直线l4于点A、B、C,截直线l5于点D、E、F,且l1∥l2∥l3.(1)如果AB=3,BC=6,DE=4,求EF的长;(2)如果DE:EF=2:3,AC=25,求AB的长.22.(9分)随着国家乡村振兴政策的推进,凤凰村农副产品越来越丰富.为增加该村村民收入,计划定价销售某土特产,他们把该土特产(每袋成本10元)进行4天试销售,日销量y(袋)和每袋售价x(元)记录如下:时间第一天第二天第三天第四天x/元15202530y/袋25201510若试销售和正常销售期间,日销量y与每袋售价x的一次函数关系相同,解决下列问题:(1)求日销量y关于每袋售价x的函数关系式;(2)请你帮村民设计,每袋售价定为多少元,才能使这种土特产每日销售的利润最大?并求出最大利润.(利润=销售额﹣成本)23.(9分)在⊙O中,半径OC垂直于弦AB,垂足为D,∠AOC=60°,E为弦AB所对的优弧上一点.(1)如图①,求∠AOB和∠CEB的大小;(2)如图②,CE与AB相交于点F,EF=EB,过点E作⊙O的切线,与CO的延长线相交于点G,若OA=3,求EG的长.24.(10分)如图,在直角坐标系中,⊙M经过原点O(0,0),点A(,0)与点B(0,﹣),点D在劣弧上,连接BD交x轴于点C,且∠COD=∠CBO.(1)求⊙M的半径;(2)求证:BD平分∠ABO;(3)在线段BD的延长线上找一点E,使得直线AE恰好为⊙M的切线,求此时点E的坐标.25.(10分)若关于x的函数y,当t﹣1≤x≤t+1时,函数y的最大值为P,最小值为Q,令函数m=P﹣Q,我们不妨把函数m称之为函数y的“至善函数”.(1)若函数y=2023x,求函数y的“至善函数”m的值;(2)若函数,求函数y的“至善函数”m的解析式;(3)对于函数y=﹣x2+tx+a,若无论实数t为何值,函数y的最大值恒大于函数y的“至善函数”m的最小值,求出a的范围.2023-2024学年湖南师大附中高新学校九年级(上)第三次月考数学试卷参考答案与试题解析一.选择题(每小题3分,10小题,共30分)1.(3分)如图交通标志是中心对称图形的为()A.B.C.D.【分析】根据中心对称图形的概念对各选项分析判断即可得解.【解答】解:选项B、C、D中的图形都不是中心对称图形,选项A中的图形是中心对称图形,故选:A.【点评】本题考查了中心对称图形的概念,解答本题的关键要明确:一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形.2.(3分)下列函数中,y不是x的反比例函数的是()A.y=﹣B.C.D.3xy=2【分析】根据反比例函数解析式判断求解.【解答】解:根据反比例函数解析式,知A.,符合定义,本选项不符合题意;B.,符合定义,本选项不符合题意;C.,不符合定义,本选项符合题意;D.3xy=2,得,符合定义,本选项不符合题意.故选:C.【点评】本题考查反比例函数的定义,理解解析式的特征是解题的关键.3.(3分)若=,则ab=()A.6B.C.1D.【分析】直接利用比例的性质,内项之积等于外项之积即可得出答案.【解答】解:∵=,∴ab=6.故选:A.【点评】此题主要考查了比例的性质,正确将原式变形是解题关键.4.(3分)下列说法正确的是()A.两个矩形一定相似B.两个菱形一定相似C.两个正方形一定相似D.两个直角三角形一定相似【分析】利用相似图形的定义分别判断后即可确定正确的选项.【解答】解:A、两个矩形满足对应角相等但不满足对应边的比相等,故不相似,不符合题意;B、两个菱形满足对应边的比相等但不满足对应角相等,故不相似,不符合题意;C、两个正方形一定相似,正确,符合题意;D、两个直角三角形不一定相似,故原命题错误,不符合题意.故选:C.【点评】本题考查了相似图形的定义,解题的关键是了解相似图形的定义,难度不大.5.(3分)如表是一位同学在罚球线上投篮的试验结果,根据表中数据回答下列问题:投篮次数(n)50100150200250300500投中次数(m)286078104124153252估计这位同学投篮一次,投中的概率约是()(精确到0.1)A.0.4B.0.5C.0.55D.0.6【分析】计算出所有投篮的次数,再计算出总的命中数,继而可估计出这名球员投篮一次,投中的概率.【解答】解:根据题意得:28÷50=0.56,60÷100=0.6,78÷150=0.52,104÷200=0.52,124÷250=0.496,153÷300=0.51,252÷500=0.504,由此,估计这位同学投篮一次,投中的概率约是0.5,故选:B.【点评】此题考查了利用频率估计概率的知识,注意这种概率的得出是在大量实验的基础上得出的,不能单纯的依靠几次决定.6.(3分)如图,AB是⊙O的直径,C是⊙O上一点.若∠BOC=66°,则∠A=()A.66°B.33°C.24°D.30°【分析】根据圆周角定理解答即可,在同圆或等圆中,同弧所对的圆周角等于这条弧所对的圆心角的一半.【解答】解:∵∠A=∠BOC,∠BOC=66°,∴∠A=33°.故选:B.【点评】本题考查了圆周角定理,圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.定理成立的条件是“同一条弧所对的”两种角,在运用定理时不要忽略了这个条件,把不同弧所对的圆周角与圆心角错当成同一条弧所对的圆周角和圆心角.7.(3分)如果圆锥侧面展开图的面积是15π,母线长是5,则这个圆锥的底面半径是()A.3B.4C.5D.6【分析】根据圆锥的侧面积=底面周长×母线长÷2即可求出答案.【解答】解:设底面半径为R,则底面周长=2πR,圆锥的侧面展开图的面积=×2πR×5=15π,∴R=3.故选:A.【点评】本题考查了圆锥的计算,利用了圆的周长公式和扇形面积公式求解,牢记公式是解答本题的关键.8.(3分)如图,正六边形ABCDEF内接于⊙O,若⊙O的周长是6π,则正六边形的边长是()A.B.3C.6D.【分析】连接OB、OC,根据⊙O的周长等于6π,可得⊙O的半径OB=OC=3,而六边形ABCDEF 是正六边形,即知∠BOC==60°,△BOC是等边三角形,即可得正六边形的边长为3.【解答】解:连接OB、OC,如图:∵⊙O的周长等于6π,∴⊙O的半径OB=OC==3,∵六边形ABCDEF是正六边形,∴∠BOC==60°,∴△BOC是等边三角形,∴BC=OB=OC=3,即正六边形的边长为3,故选:B.【点评】本题考查正多边形与圆的相关计算,解题的关键是掌握圆内接正六边形中心角等于60°,从而得到△BOC是等边三角形.9.(3分)如图,在平面直角坐标系中,点A在y轴上,点B的坐标为(6,0),将△ABO绕着点B顺时针旋转60°,得到△DBC,则点C的坐标是()A.(3,3)B.(3,3)C.(6,3)D.(3,6)【分析】作CM⊥x轴于M,再利用旋转的性质求出BC=OB=6,根据直角三角形30°角所对的直角边等于斜边的一半求出BM,利用勾股定理列式求出CM,然后求出点C的横坐标,再写出点C的坐标即可.【解答】解:作CM⊥x轴于M,∵点B的坐标为(6,0),∴BC=OB=6,∵∠OBC=60°,∴BM=,CM==3,∴OM=OB﹣BM=6﹣3=3,∴C(3,3).故选:B.【点评】本题考查了坐标与图形变化﹣旋转,解直角三角形,求出OM、CM的长度是解题的关键.10.(3分)如图,动点P在函数(x>0)的图象上运动,PM⊥x轴于点M,PN⊥y轴于点N,线段PM、PN分别与直线AB:y=﹣x+1交于点E、F,则AF•BE的值是()A.2B.1C.D.【分析】由于P的坐标为,且PN⊥OB,PM⊥OA,那么N的坐标和M点的坐标都可以a 表示,那么BN、NF的长度也可以用a表示,接着F点、E点的也可以a表示,然后利用勾股定理可以分别用a表示AF、BE,最后即可求出AF⋅BE.【解答】解:作FG⊥x轴,∵P的坐标为,且PN⊥OB,PM⊥OA,∴N的坐标为,M点的坐标为(a,0),∴,令x=0,则y=1,令y=0,则x=1,则A(1,0),B(0,1),∴OB=OA=1,则△OAB是等腰直角三角形,∴∠NBF=45°,在Rt△BNF中,∠NBF=45°,∴,∴F点的坐标为,同理可得出E点的坐标为(a,1﹣a),∴,BE2=(a)2+(﹣a)2=2a2,∴,即AF•BE=1.故选:B.【点评】本题考查了反比例函数的性质、勾股定理,解题的关键是通过反比例函数上的点P坐标,来确定E、F两点的坐标,进而通过勾股定理求出线段乘积的值.二.填空题(每小题3分,6小题,共18分)11.(3分)某蓄电池的电压为48V,使用此蓄电池时,电流I(单位:A)与电阻R(单位:Ω)的函数表达式为I=,当R=16Ω时,I的值为3A.【分析】直接将R=16代入I=中可得I的值.【解答】解:当R=16Ω时,I==3(A).故答案为:3.【点评】此题考查的是反比例函数的应用,掌握反比例函数的点的坐标是解决此题的关键.12.(3分)抛物线y=﹣(x+2)2+6顶点坐标是(﹣2,6)..【分析】根据抛物线的顶点式直接求得顶点坐标.【解答】解:抛物线y=﹣(x+2)2+6的顶点坐标是(﹣2,6),故答案为:(﹣2,6).【点评】本题考查了求二次函数的性质,熟练掌握二次函数的图象与性质是解题关键.13.(3分)一个不透明的布袋里只有6个红球和n个白球(仅有颜色不同).若从中任意摸出一个球是红球的概率为,则n=9.【分析】根据红球的概率公式,列出方程求解即可.【解答】解:根据题意,,解得n=9,经检验n=9是方程的解.∴n=9.故答案为:9.【点评】本题考查概率公式,根据公式列出方程求解则可.用到的知识点为:概率=所求情况数与总情况数之比.14.(3分)若一元二次方程x2﹣4x+a=0配方后为(x﹣2)2=1,则a=3.【分析】利用配方法求解可得a的值.【解答】解:x2﹣4x+a=0,x2﹣4x=﹣a,x2﹣4x+4=﹣a+4,(x﹣2)2=4﹣a,∴4﹣a=1,解得a=3.故答案为:3.【点评】本题主要考查解一元二次方程,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.15.(3分)如图,在矩形ABCD中,AB=1,(AD>AB)在BC上取一点E,沿AE将△ABE向上折叠,使点B落在AD上的点F,若四边形EFDC与原矩形相似,则AD的长度为.【分析】可设AD=x,由四边形EFDC与矩形ABCD相似,根据相似多边形对应边的比相等列出比例式,求解即可.【解答】解:∵AB=1,设AD=x,则FD=x﹣1,FE=1,∵四边形EFDC与矩形ABCD相似,∴=,即:,解得x1=,x2=(不合题意舍去),经检验x1=是原方程的解.故答案为:.【点评】本题考查了翻折变换(折叠问题),相似多边形的性质,本题的关键是根据四边形EFDC与矩形ABCD相似得到比例式.16.(3分)以点P(1,2)为圆心,r为半径画圆,与坐标轴恰好有三个交点,则r=2或.【分析】由以点P(1,2)为圆心,r为半径画圆,与坐标轴恰好有三个交点,可得⊙P与x轴相切或⊙P过原点,然后分别分析求解即可求得答案.【解答】解:∵以点P(1,2)为圆心,r为半径画圆,与坐标轴恰好有三个交点,∴⊙P与x轴相切(如图1)或⊙P过原点(如图2),当⊙P与x轴相切时,r=2;当⊙P过原点时,r=OP==.∴r=2或.故答案为:2或.【点评】此题考查了直线与圆的位置关系以及坐标与图形的性质.此题难度适中,注意掌握数形结合思想与分类讨论思想的应用.三.解答题(9题,共72分)17.(6分)计算:3﹣2+﹣(π﹣1)0+|﹣1+|.【分析】按照实数的运算法则依次计算,注意:3﹣2=,(π﹣1)0=1,|﹣1+|=.【解答】解:原式=+2﹣1+=2.【点评】本题需注意的知识点是:a﹣p=,任何不等于0的数的0次幂是1,负数的绝对值是正数.18.(6分)如图,在平面直角坐标系xOy中,一次函数y1=﹣2x+6的图象与反比例函数的图象相交于A(a,4),B(b,2)两点.(1)求反比例函数的表达式及点B的坐标;(2)观察图象,直接写出y1>y2时x的取值范围.【分析】(1)先根据两函数图象的交点情况确定a、b的值,进而确定A、B的坐标,然后代入反比例函数解析式即可解答;(2)直接根据函数图象即可解答.【解答】解:(1)∵一次函数y1=﹣2x+6的图象与反比例函数的图象相交于A(a,4),B(b,2)两点.∴4=﹣2a+6,2=﹣2b+6,∴a=1,b=2,∴A点坐标为(1,4)两点B点坐标为(2,2)两点.∴k=1×4=4,∴反比例函数.(2)∵一次函数y1=﹣2x+6的图象与反比例函数的图象相交于A(1,4),B(2,2)两点.∴当y1>y2时x的取值范围1<x<2.【点评】本题主要考查了反比例函数与一次函数的综合、求函数解析式、运用图象求不等式的解集的等知识点,掌握两函数图象的交点坐标必满足两函数解析式成为解题的关键.19.(6分)随着科技的进步,购物支付方式日益增多.为了解某社区居民支付的常用方式(A微信,B支付宝,C现金,D其他),某学习小组对红星社区部分居民进行问卷调查,根据查结果,绘制成如图统计图.根据统计图表中的信息,解答下列问题:(1)a=20人,b=18人,在扇形统计图中C种支付方式所对应的圆心角为36度;(2)本次调查中用现金支付方式的居民里有2名男性,其余都是女性,现从该种支付方式中随机选2名居民参加线上支付方式培训,求恰好都是女性的概率.【分析】(1)根据统计图中的信息列式计算即可;(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与恰好抽到1个男生和1个女生的情况,再利用概率公式求解即可求得答案.【解答】解:(1)a=7÷14%×40%=20(人),b=7÷14%﹣5﹣7﹣20=18(人),在扇形统计图中C 种支付方式所对应的圆心角为360°×=36°,故答案为:20人,18人,36;(2)设男生为A,女生为B,画树状图得:∵共有20种等可能的结果,恰好抽到都是女性的有6种情况,∴恰好都是女性的概率=.【点评】本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.20.(8分)如图,在由边长为1个单位长度的小正方形组成的网格中,△ABC的顶点均为格点(网格线的交点).(1)将△ABC向上平移6个单位,再向右平移2个单位,得到△A1B1C1,请画出△A1B1C1;(2)以边AC的中点O为旋转中心,将△ABC按逆时针方向旋转180°,得到△A2B2C2,请画出△A2B2C2.【分析】(1)根据平移的性质可得△A1B1C1;(2)根据旋转的性质可得△A2B2C2.【解答】解:(1)如图,△A1B1C1即为所求;(2)如图,△A2B2C2即为所求.【点评】本题主要考查了作图﹣平移变换,旋转变换,熟练掌握平移和旋转的性质是解题的关键.21.(8分)如图,已知直线l1、l2、l3分别截直线l4于点A、B、C,截直线l5于点D、E、F,且l1∥l2∥l3.(1)如果AB=3,BC=6,DE=4,求EF的长;(2)如果DE:EF=2:3,AC=25,求AB的长.【分析】(1)根据平行线分线段成比例定理得出=,再把AB=3,BC=6,DE=4代入,即可求出EF;(2)根据平行线分线段成比例定理得出=,再把DE:EF=2:3,AC=25代入,即可求出AB.【解答】解:(1)∵l1∥l2∥l3,∴=,∵AB=3,BC=6,DE=4,∴=,解得:EF=8;(2))∵l1∥l2∥l3,∴=,∵DE:EF=2:3,AC=25,∴=,解得:AB=10.【点评】本题考查了平行线分线段成比例定理,能正确根据平行线分线段成比例定理得出比例式是解此题的关键.22.(9分)随着国家乡村振兴政策的推进,凤凰村农副产品越来越丰富.为增加该村村民收入,计划定价销售某土特产,他们把该土特产(每袋成本10元)进行4天试销售,日销量y(袋)和每袋售价x(元)记录如下:时间第一天第二天第三天第四天x/元15202530y/袋25201510若试销售和正常销售期间,日销量y与每袋售价x的一次函数关系相同,解决下列问题:(1)求日销量y关于每袋售价x的函数关系式;(2)请你帮村民设计,每袋售价定为多少元,才能使这种土特产每日销售的利润最大?并求出最大利润.(利润=销售额﹣成本)【分析】(1)根据表格中的数据,利用待定系数法,即可求出日销售量y(袋)与销售价x(元)的函数关系式;(2)利用“每袋利润×日销量=总利润”列出函数解析式,进而求出二次函数最值即可.【解答】解:(1)依题意,根据表格的数据,设日销售量y(袋)与销售价x(元)的函数关系式为y =kx+b,得,解得,故日销售量y(袋)与销售价x(元)的函数关系式为:y=﹣x+40;(2)依题意,设利润为w元,得w=(x﹣10)(﹣x+40)=﹣x2+50x﹣400,配方,得w=﹣(x﹣25)2+225,∵﹣1<0∴当x=25时,w取得最大值,最大值为225,故要使这种土特产每日销售的利润最大,每袋的销售价应定为25元,每日销售的最大利润是225元.【点评】本题考查一次函数的应用,二次函数的应用,理解题意,掌握待定系数法是解题的关键.23.(9分)在⊙O中,半径OC垂直于弦AB,垂足为D,∠AOC=60°,E为弦AB所对的优弧上一点.(1)如图①,求∠AOB和∠CEB的大小;(2)如图②,CE与AB相交于点F,EF=EB,过点E作⊙O的切线,与CO的延长线相交于点G,若OA=3,求EG的长.【分析】(1)由垂径定理得到=,因此∠BOC=∠AOC=60°,得到∠AOB=∠AOC+∠BOC=120°,由圆周角定理即可求出∠CEB的度数;(2)由垂径定理,圆周角定理求出∠CEB的度数,得到∠C的度数,由三角形外角的性质求出∠EOG 的度数,由锐角的正切定义即可求出EG的长.【解答】解:(1)∵半径OC垂直于弦AB,∴=,∴∠BOC=∠AOC=60°,∴∠AOB=∠AOC+∠BOC=120°,∵∠CEB=∠BOC,∴∠CEB=30°;(2)如图,连接OE,∵半径OC⊥AB,∴=,∴∠CEB=∠AOC=30°,∵EF=EB,∴∠EFB=∠B=75°,∴∠DFC=∠EFB=75°,∵OE=OC,∴∠C=∠OEC=15°,∴∠EOG=∠C+∠OEC=30°,∵GE切圆于E,∴∠OEG=90°,∴tan∠EOG==,∵OE=OA=3,∴EG=.【点评】本题考查垂径定理,圆周角定理,切线的性质,等腰三角形的性质,直角三角形的性质,解直角三角形,三角形外角的性质,关键是由圆周角定理,等腰三角形的性质求出∠C=15°,由三角形外的性质求出∠EOG的度数,由锐角的正切定义即可求出EG的长.24.(10分)如图,在直角坐标系中,⊙M经过原点O(0,0),点A(,0)与点B(0,﹣),点D在劣弧上,连接BD交x轴于点C,且∠COD=∠CBO.(1)求⊙M的半径;(2)求证:BD平分∠ABO;(3)在线段BD的延长线上找一点E,使得直线AE恰好为⊙M的切线,求此时点E的坐标.【分析】(1)由点A(,0)与点B(0,﹣),可求得线段AB的长,然后由∠AOB=90°,可得AB是直径,继而求得⊙M的半径;(2)由圆周角定理可得:∠COD=∠ABC,又由∠COD=∠CBO,即可得BD平分∠ABO;(3)首先过点A作AE⊥AB,垂足为A,交BD的延长线于点E,过点E作EF⊥OA于点F,易得△AEC 是等边三角形,继而求得EF与AF的长,则可求得点E的坐标.【解答】解:(1)∵⊙M经过O、A、B三点,且∠AOB=90°,∴AB为直径∵点A为(,0),点B为(0,﹣),∴OA=,OB=,∴AB==2,∴⊙M的半径为:;(2)∵∠COD=∠CBO,∠COD=∠CBA,∴∠CBO=∠CBA,即BD平分∠ABO;(3)如图,过点A作AE⊥AB,垂足为A,交BD的延长线于点E,过点E作EF⊥OA于点F,即AE 是切线,∵在Rt△AOB中,tan∠OAB===,∴∠OAB=30°,∴∠ABO=90°﹣∠OAB=60°,∴∠ABC=∠OBC=∠ABO=30°,∴OC=OB•tan30°=×=,∴AC=OA﹣OC=,∴∠ACE=∠ABC+∠OAB=60°,∴∠EAC=60°,∴△ACE是等边三角形,∴AE=AC=,∴AF=AE=,EF=AE=,∴OF=OA﹣AF=,∴点E的坐标为:(,).【点评】此题属于圆的综合题,考查了勾股定理、圆周角定理、等边三角形的判定与性质以及三角函数等知识.注意准确作出辅助线是解此题的关键.25.(10分)若关于x的函数y,当t﹣1≤x≤t+1时,函数y的最大值为P,最小值为Q,令函数m=P﹣Q,我们不妨把函数m称之为函数y的“至善函数”.(1)若函数y=2023x,求函数y的“至善函数”m的值;(2)若函数,求函数y的“至善函数”m的解析式;(3)对于函数y=﹣x2+tx+a,若无论实数t为何值,函数y的最大值恒大于函数y的“至善函数”m的最小值,求出a的范围.【分析】(1)直接根据“至善函数”的定义解答即可;(2)分k>0、k<0两种情况分别运用根据“至善函数”的定义解答即可;(3)先根据二次函数的性质求得对称轴,然后分、、三种情况,分别结合题意以及二次函数的最值求解即可.【解答】解:(1)∵在y=2023x中,2023>0,∴y随x的增大而增大,∵,∴函数y的最大值为P=2023(t+1),最小值为Q=2023(t﹣1),∴函数y的“至善函数”m的值为m=2023(t+1)﹣2023(t﹣1)=4046.(2)①当k>0时,∴y随x的增大而减小,∵,∴函数y的最大值为,最小值为,∴函数y的“至善函数”m的值为;②当k<0时,∴y随x的增大而增大,∵,∴函数y的最大值为,最小值为,∴函数y的“至善函数”m的值为;综上,函数y的“至善函数”m的解析式为或.(3)∵,∴函数的对称轴为直线,y的最大值为,①当时,即t≥2时,此时,函数y的最大值为,最小值为:,∴y的“至善函数”m的值为:m=(a﹣1+t)﹣(a﹣1﹣t)=2t,∵t≥2,∴当且仅当t=2时,m的最小值为4,∵无论实数t为何值,函数y的最大值恒大于函数y的“至善函数”m的最小值,∴a﹣1﹣t>4,即a>4+1+t=5+t>7;②当时,即t≤﹣2,此时,函数y的最大值为,最小值为:,∴y的“至善函数”m的值为:m=(a﹣1﹣t)﹣(a﹣1+t)=﹣2t,∵t≤﹣2,∴当且仅当t=﹣2时,m的最小值为4,∵无论实数t为何值,函数y的最大值恒大于函数y的“至善函数”m的最小值,∴a﹣1+t>4,即a>4+1﹣t=5﹣t>7;③当,即﹣2≤t≤2时,函数y的最大值为,当时,即0≤t≤2时,此时,函数y的最小值,∴y的“至善函数”m的值为:,∴当且仅当t=0时,m的最小值为1,∴,即,∵0≤t≤2∴0<a<1;当时,即﹣2≤t≤0时,此时,函数y的最小值,∴y的“至善函数”m的值为:,∴当且仅当t=0时,m的最小值为1,∴,即,∵0≤t≤2∴0<a<1.综上,a的取值范围为0<a<1或a>7.【点评】本题主要考查了新定义函数、二次函数的性质、二次函数的最值等知识点,理解“至善函数”的概念是解题的关键.。
2024-2025学年九年级数学上学期第三次月考卷(浙江专用,浙教版九上+九下1~2章)(考试版)

2024-2025学年九年级数学上学期第三次月考卷(浙教版)(考试时间:120分钟试卷满分:120分)注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.测试范围:浙教版九年级上册全册+下册第1章,其中二次函数20%,概率11.7%,圆32.5%,相似17.5%,解三角形18.3%。
5.难度系数:0.65。
第一部分(选择题共30分)一、选择题:本题共10小题,每小题3分,共30分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知⊙O的半径为5cm,PO=3cm,则点P与⊙O的位置关系是()A.点P在圆外B.点P在圆上C.点P在圆内D.无法确定2.一个转盘白色扇形和红色扇形的圆心角分别为120°和240°,让转盘自由转动2次,一次落在白色,一次落在红色区域的概率是()A.19B.29C.13D.493.将抛物线y=(m―1)x2+mx+m+3向左平移2个单位,再向上平移3个单位后经过(―2,3),则m的值是()A.―1B.2C.―3D.04.如图,在△ABC中,ADDC =BEEC=23,△CDE与四边形ABED的面积的比是()A.23B.49C.1625D.9165.如图,在扇形OAB中,点D在OA上,点C在AB上,∠AOB=∠BCD=90°.若CD=3,BC=4,则⊙O 的半径为()D.A.4B.4.8C.6.中国体育代表团在巴黎奥运会上取得了优异的成绩,图1是2024年巴黎奥运会的一枚金牌,金牌正中间镶嵌了一块来自埃菲尔铁塔的正六边形铁块.这个正六边形铁块的示意图如图2所示,已知该正六边mm,则AD的长约为()形ABCDEF的周长约为A.mm B.mm C.mm D.mm7.如图,在平面直角坐标系中,已知点A,B的坐标分别为(―3,1),(―1,4),以点O为位似中心,在原点的另一侧按2:1的相似比将△缩小,则点A的对应点A′的坐标是()A.(―3,1)B.―3,C.(3,―1)D28.在边长相等的小正方形组成的网格中,点A,B,C都在格点上,那么sin∠ACB的值为()A B C D.139.如图,AB是⊙O的直径,AB=6,CD是⊙O的弦,连接AC,BC,OD.若∠ACD=2∠BCD,则 BD的长为()A.πB.π2C.π3D.π410.如图,AB是⊙O的直径,OC为半径,过A点作AD∥OC交⊙O于点D,连接AC,BC,CD,连接BD交OC 于点E,交AC于点F,若图中阴影部分分别用S1和S2表示,则下列结论:①∠CAD+∠OBC=90°;②若F 为AC中点,则CE=2OE;③作DP∥BC交AB于点P,则BC2=OB⋅BP;④若S1:S2=12,则∠ACO=30°;其中正确的个数为()A.4个B.3个C.2个D.1个第二部分(非选择题共90分)二、填空题:本题共6小题,每小题3分,共18分。
安徽省淮南市高新区2024_2025学年九年级上学期第三次月考数学试题(无答案)

2024~2025学年第三次作业反馈(命题范围:九上全册)数学RJ(试题卷)注意事项:1.你拿到的试卷满分为150分,考试时间为120分钟;2.试卷包括“试题卷”和“答题卷”两部分,“试题卷”共4页“答题卷”共6页;3.请务必在“答题卷”上答题,在“试题卷”上答题是无效的;4.考试结束后,请将“试题卷”和“答题卷”一并交回.一、选择题(本大题共10小题,每小题4分,满分40分)每小题都给出A ,B ,C ,D 四个选项,其中只有一个是符合题目要求的.1.剪纸艺术是最古老的中国民间艺术之一,先后入选中国国家级非物质文化遗产名录和人类非物质文化遗产代表作名录.下列剪纸图案中,是中心对称图形的是( )A .B .C .D .2.若抛物线经过A (-1,0),B (5,0),则它的对称轴为( )A .直线x =0B .直线x =1C .直线x =2D .直线x =33已知关于的一元二次方程(p 为常数)有两个不相等的实数根和,若,则p 的值是( )A .-1B .3C .-1或3D .不存在4.掷一枚质地均匀的骰子,落地后向上一面的点数为偶数的概率为( )A.B .C .D .5.如图,AB 是半圆的直径,∠BAC =35°,则∠D 的度数为( )A .110°B .115°C .120°D .125°6.已知m ,n ,s ,t 互不相等的实数,且,,则的值为( )A .-2B .0C .D .27.已知抛物线经过点中的两点,且与y 轴221(1)y ax ax c c =-++>2(0)y ax bx c a =++≠210x px -+=1x 2x 221221x x p +=+16141312()()2m s m t ++=()()2n s n t ++=mn st -12(2,2),(2,2),(2,2)A m c B c C m c -+交于点D ,则下列判断正确的是( )A .B .C .D .8.如图,在ABCD 中,AB =4,∠B =60°,BC =3,E 为AB 上一点,且BE =1,F 为BC 边上的一个动点,连接EF ,将其绕点E 逆时针30°旋转至直线EG ,使得∠EGF =120°,连接AG ,则AG 的最小值为( )AB .2CD9.如图,AB 、CD是⊙O 的两条弦, ,CD =2,AB、CD 的延长线相交于点P ,若∠P =60°,则⊙O 的半径是( )A B C D .10.如图,抛物线与y 轴交于点A ,与x 轴交于点B ,线段CD 在抛物线的对称轴上移动(点C 在点D 下方),且CD =3,当AD +BC 的值最小时,点C 的坐标是( )A .(8,6)B .(8,3)C .(4,-2)D .(4,1)二、填空题(本大题共4小题,每题5分,满分20分)11.一个不透明的盒子里有形状、大小相同的黄球2个、红球3个,从盒子里任意摸出1个球,摸到红球的概率是 .12.若关于x 的一元二次方程有两个实数根,则k 的取值范围是 .31a c +<2AOB ADB S S >V V 0a <1m >Y 1AB =+1+21462y x x =-+2210kx x ++=13.若二次函数在时的最大值为3,那么m 的值是 .14.如图,点A 在以BC 为直径的半圆上,BC =8,∠ACB =30°,点D 在线段BC 上运动,点E 与点D 关于AB 对称,点F 与点D 关于AC 对称,点G 与点D 关于点A 对称.连结DE 、EG 、GF 、FD 、EF 、GD ,则:(1)当四边形DEGF 是正方形时,BD = ;(2)当△GEF 的一边EG 与⊙O 相切时,BD 的长为 .三、(本大题共2题,每题8分,满分16分)15.解方程:.16.已知二次函数.(1)求对称轴和顶点坐标.(2)求这个二次函数图像与x 轴、y 轴的交点坐标.四、(本大题共2题,每题8分,满分16分)17如图,在8×8的正方形网格中,点A ,B ,C ,P 都在格点上,仅用无刻度的直尺在给定网格中按要求画图,画图过程用虚线表示,画图结果用实线表示.(1)将线段BC 绕点B 逆时针旋转90°得到,画出线段;(2)在AC 上画一点M ,使∠AMP =45°.18.如图,电路图上有四个开关A ,B ,C ,D 和一个小灯泡,闭合开关D 或同时闭合开关A ,B ,C 都可使小灯泡发光.(1)求任意闭合其中一个开关小灯泡发光的概率.(2)求任意闭合其中两个开关小灯泡发光的概率.2y x mx =-+12x -≤≤(2)(5)10x x --=223y x x =+-BC 'BC '五、(本大题共2题,每题10分,满分20分)19.某超市销售一种成本为每千克20元的商品,已知这种商品的月销售是y (千克)与销售单价x (元千克)之间的函数关系式为.(1)当这种商品的销售单价x 定为多少时,每月可获得最大利润?(2)如果这种商品的销售单价x 不超过32元/千克,超市想要每月通过销售这种商品获得的利润不低于2000元,那么该超市对这种商品的月投资总成本最少是多少元?(月投资总成本=商品每千克的成本×月销售量)20.如图,⊙O 为△ABC 的外接圆,C 是的中点,接OC 交AB 于点D ,延长OC 至点E ,使得AC 平分∠EAB .(1)求证:直线AE 是⊙O 的切线.(2)若⊙O 的半径为5,AB =8,求AC 的长.(3)在(2)的前提下,点F 在⊙O 上,△ACF 的内心G 在AB 边上,求BG 的长.图1 图2六、(本大题满分12分)21在菱形ABCD 中,∠ABC =60°,点E 、G 分别是边DC 、BC 上的点,AE 与BD 相交于点F ,且∠EFG =60°.(1)如图1,当点G 与点C 重合时,证明:FA =FG ;(2)如图2,当点G 与点C 不重合时,FA =FG 是否还成立,若不成立,请说明理由;若成立,请给出证明.(3)如图3,若AB =6,当CE =CG 时,直接写出DE的长;10500y x =-+»AB图1 图2 图3七、(本大题满分12分)22.如图1,正方形ABCD 中,点E 、F 为边AD 、CD 上的点,若DE =DF ,点G 为BE 中点,连接AG .(1)探索并证明AG 与BF 有怎样的位置和数量关系;(2)转动△DEF 至如图2位置时,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请说明理由.(3)若DE=AD =2,绕着点D 旋转过程中,请直接写出CG 的取值范围.图1 图2八、(本大题满分14分)23.已知抛物线与x 轴交于A ,B 两点(点B 在x 轴正半轴),与y 轴交于点C ,连接BC ,AB =4,∠BCO =45°.(1)求抛物线的解析式;(2)若点D 在点B ,C 之间的抛物线上运动(不与点B ,C 重合),连接OD 交BC 于点E ,连接CD .记△CDE ,△COE 的面积分别为,求的最大值;(3)已知抛物线的顶点的为G ,过点G 的直线l 与抛物线的另一个交点为P ,直线l 与直线:交于点F ,过点F 作的垂线,交抛物线于点Q ,过PQ 的中点M 作MN ⊥于点N .求证:MN =PQ .1223(0)y ax bx a =+->12,S S 2S l '174y =-l 'l '12。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二一四年秋九年级第三次月考语文试卷一积累运用(20分)1.下列词语中,加点字读音和字形全都正确的一项是()(3分)A.喑.(yīn)哑破绽.(zàn)断璧残垣.(yuán)不屑.(xiè)置辩B.惬.(qiè)意分泌.(bì)戛.(gá)然而止屏.(bǐng)气凝神C.戳.(chō)破蓬蒿.(hāo)脍.(kuài)炙人口恃.(shì)才放旷D.蓑.(suō)衣迸.(bèng)射苦心孤诣.(yì)万恶不赦.(shè)2.下列表述不正确的一项是:()(2分)A.“基本条件”“空气干燥”“摘下军帽”“品德高尚”这四个短语中,“空气干燥”与“品德高尚”结构相同。
B.“他的晚年,仍然精力充沛,充满创作激情,留下了许多优秀作品。
”此句是一个病句。
C.“我的那个寂静而又黑暗的世界里,根本就不会有温柔和同情”。
这个句子的主干是“世界里。
D.“最近的心情如同石灰水洗过,有点刺痛!”此句是一句正确的夸张句。
3.下列表述正确的一项是:()2分A.《水浒》是一部以北宋末年宋江起义为题材的长篇白话小说。
B. “这朦胧的橘红的光,实在照不了多远”,句中的“朦胧”“橘红”“实在”都是形容词。
C.由于长江流域连续干旱,导致洞庭湖、鄱阳湖水面大面积缩小,给人们的生产和生活带来很大影响。
”是个病句,应删掉“给”。
D.“要弄清楚蛋白质在体内为什么不可或缺?就要了解它对人体的作用。
”这个句子没有问题。
4.填入下面横线处的句子,与上下文衔接最恰当的一组是()(2分)去年暑假,爸爸带我去潜山爬山。
;山顶上,电视塔高高矗立,煞是雄伟。
A.这里的景色真美!山脚下,温泉河静静流淌,碧波粼粼。
B. 这里的景色真美!山脚下,静静流淌的温泉河,碧波粼粼C. 那儿的景色真美!山脚下,温泉河静静流淌,碧波粼粼D. 那儿的景色真美!山脚下,静静流淌的温泉河,碧波粼粼5.按课文默写古诗(4分)(1)《望江南》中表明思妇从希望到失望的心理变化产生的原因的句子是:。
(2)范仲淹在《渔家傲秋思》,揭示自己和征夫们想家却又不甘无功而返的矛盾心理的句子是:,。
(3)《武陵春》中被词论家称赞为写愁“创意出奇”的句子是:,。
(4)苏轼的《江城子密州出猎》中抒写人到中年的主人公,壮志未酬的感叹的诗句是:,,。
6.名著阅读(3分)①《傅雷家书》主要讲的是:。
②《傅雷家书》凝聚着傅雷对,对深厚的爱。
7.综合性学习(4分)1.青春是班斓绚丽的诗,欢迎参加综合性学习活动“青春随想”。
(1)描绘青春色彩。
在你的眼里,青春是什么颜色的?请写出你的看法。
(2分)青春是色的,因为青春是:。
(2)为了让青春的脚步迈得更加雄健有力,给自己写个青春座右铭吧。
(2分)二、阅读理解(50分)一只空气瓶子的温暖魏得强①星期天,一家人购物回到小区,女儿把空的纯净水瓶子顺手放到了垃圾箱旁。
13岁的女儿是进步了,以前她可是随手乱扔。
但我没有表扬她,我想,这反倒是一个很好的教育机会。
②我不动声色,走过去把空瓶子又捡了起来,随手放进了我的手提袋里。
这是我的习惯,我不会把它们扔掉的,我家里不缺几个瓶子的钱,但瓶子问题折射出来的是一个人的素养。
今天,我更是要做给女儿看的。
③我知道女儿会不屑一顾,还会说我老土。
如今的孩子,把面子看得很重要,穿名牌,吃肯德基,而且会比着谁会浪费。
不过我会用事实告诉她,即使像有钱的比尔·盖茨,在生活中也是反对浪费的。
④果然,女儿看到我的举动很吃惊,她竟然要把瓶子从我手提袋中拿出来重新给扔掉。
看女儿进入我设的圈套,我这才谆谆地教导她:“孩子,不是老爸吝啬,一只瓶子一毛钱,不值什么钱,但这也是钱,节俭是从一个空瓶子开始的。
”⑤我等待着女儿的惭愧,或者向我道歉,或者默默地从我身边走开。
不想,她趁我不备,伸手把空瓶子从我手提袋里取了出来,回过头,又重新把它放到了原处。
没等我反应过来,她又轻快地跑到我身边,拉着我的手臂撒娇:“爸,一个瓶子对咱们不算什么,但对一些人很重要。
咱小区每天都有一个捡废品的老人在这转悠,好可怜哪!把瓶子放在这里,她就可以轻松地拿走。
我知道,她不是乞讨的,她是靠劳动吃饭的……”⑥看着女儿清水般闪亮的眼眸,我忽然有些惭愧了。
那个老人我是知道的,每天靠捡一些废品养活自己,平时我见到她时,偶尔也会递上一两块硬币,想着自己的慈善,会自我陶醉上好一阵子。
我怎么没有想到女儿说的这一层意思呢?帮助一个人,更主要的是给她劳动的尊严。
⑦我没有说话,只是感激地冲女儿笑,夸她长大了。
我看到,暖暖的夕阳下,那只空瓶子稳稳地站在垃圾箱旁边,等待着一个真正需要它的人.........。
⑧它带去的,有温暖,有尊严。
(一)阅读下面文字,完成8-12题(16分)8.根据你对文章内容的理解,填写下表。
(4分)9.爸爸本想教育女儿不要浪费,教育过后,为什么“忽然有些惭愧了”?(3分)10.赏析下面句子。
(3分)她又轻快地跑到我身边,拉着我的手臂撒娇。
11.第⑦段中加点的词语“一个真正需要它的人”是指什么样的人?(3分)12.理解题目“一只空瓶子的温暖”的含义。
(3分)(二)阅读下面文字,完成13-17题(11分)飞秒激光①激光曾被视为神秘之光,但现在已被人类广泛使用。
近年来,科学家研究发现了一种更为奇特的激光一飞秒激光。
②飞秒激光是一种以脉冲形式运转的激光,持续时间非常短,只有几个飞秒,1飞秒就起10-15秒,也就是1杪的千万亿分之一,它比利用电子学方法所获得的最短脉冲要短几千倍,有效的治疗近视,是人类自前在实验条忤下所能获得的最短脉冲。
飞秒激光具有非常高的瞬时功率,可达到百万亿瓦,比目前全世界发电总功率还要多出百倍。
飞秒激光的第三个特点是,它能聚焦到比头发的直径还要小的空间区域,使电磁场的强度比原子核对其周围电子的作用力还要高数倍。
③飞秒激光的上述恃性,主要是通过四个步骤实现的:在振荡器内,利用一种特殊技术,获得飞秒激光脉冲:由展宽器将这个飞秒种子脉冲按不同波长在时间上拉开;再经放大器使这一展宽脉冲获得充分能量;压缩器挖放大后的不同成分的光谱再辽聚到一起,恢复到飞秒宽度,从而形成具有极高瞬时功率的飞秒激光脉冲。
④飞秒激光能像照相机一梓,用足够短的“快门”来捕捉分子运动和变化的瞬间行为信息。
因此,飞秒激光在物理学、生物学、化学控制反应、光通讯等领域中得到了广泛应用。
⑤物质在高强度飞秒激光的作用下会出现非常奇恃的现象:气态、液态、匡态的物质瞬倉间变成了等离子体3这种等离子体可以辐射出各种波长的射线的激光。
高功率飞秒激光与电子束碰撞能够产生硬x射线飞秒激光,产生β射线激光,产生正负电子对n⑥由于飞秒激光具有快速和高分辨率特性,它在病变早期诊断、啄学成像和生物活体检派、外科医疗及超小型卫星的制造上都有其独特的优点和不可替代的作用。
⑦高功率飞秒激光在医学、超精细微加工、高密度信息储存和记录方面都有着很好的发展前景。
高功率飞秒激光还可以将大气击穿,从而制造放电通道,实现人工引雷,避免飞机、火箭、发电厂因天然雷击而造成的灾难性破坏。
⑧飞秒激光也是未来能源的选择之一..。
利用飞秒激光能够非常有效地加速电子,使加速器的规模得到上千倍的压缩。
高功率飞秒激光与物质相互作用,能够产生足够数量的中子,实现激光受控核聚变的快速点火。
从而为人类实现新一代能源开辟一条崭新的途径。
13.根据第②段概括飞秒激光的三个特点。
(3分)14.第②段在说明飞秒激光的每个特点时运用了哪些说明方法?(1分)15.请对第③④段语言表达进行比较分析。
(2分)16.第⑧段中加点的“之一”能删去吗?为什么?(2分)17.请根据选文内容说说利用飞秒激光的未来发展。
(3分)(三)阅读下面文字,完成18-21题(10分)做人与处世①一个人活在世界上,必须处理好三个关系:第一,人与大自然的关系;第二,人与人的关系,尤其是家庭关系;第三,内心思想与外在行为的关系。
这三个关系,如果能处理很好,生活就能愉快;否则,生活就有苦恼。
②人本来也是属于大自然范畴的。
但是,人自从变成了“万物之灵”以后,就同大自然闹起独立来,有时竟成了大自然的对立面。
人类的衣食住行所有的资料都取自大自然,我们向大自然索取是不可避免的。
关键是怎样去索取?索取手段不出两途:一用和平手段,一用强制手段。
我个人认为,东西文化之分野,就在这里。
西方对待大自然的基本态度或指导思想是“征服自然”。
结果呢,从表面上看上去,西方人是胜利了,大自然真的被他们征服了。
自从西方产业革命以后,西方人屡创奇迹。
大至宇宙飞船,小至原子,无一不出自西方征服者"之手。
③然而,大自然的容忍是有限度的,它是能报复的,它是能惩罚的。
报复或惩罚的结果,人皆见之,比如环境污染,生态失衡,物种灭绝,人口爆炸,资源匮乏,新疾病产生,如此等等,不一而足。
这些弊端中哪一项不解决都能影响人类生存的前途。
④东方对待大自然的态度是“天人合一”。
宋代张载说得最简明扼要:“民吾同胞,物吾与也。
”"与" 的意思是伙伴。
我们把大自然看作伙伴。
可惜我们的行为没能跟上。
在某种程度上,也采取了“征服自然”的办法,结果也受到了大自然的报复。
⑤至于人与人的关系,我的想法是:对待一切善良的人,不管是家人,还是朋友,都应该有一个两字箴言:一曰真,二曰忍。
真者,以真情实意相待,不允许弄虚作假。
对待坏人,则另当别论。
忍者,相互容忍也。
日子久了,难免有点磕磕碰碰。
在这时候,头脑清醒的一方应该能够容忍。
如果双方都不冷静,必致因小失大,后果不堪设想。
唐朝张公艺⑴的“百忍”是历史上有名的例子。
⑥至于内心思想与外在行为的关系,则是个人修养与选择的问题。
当私心杂念占据心灵,人往往身不由己,说违心的话,做违心的事,表面上得到了利益,内心却矛盾痛苦。
解之之方,唯有消灭私心,学习诸葛亮的“淡泊以明志,宁静以致远”,听从内心的召唤,做本真的人,方能获得内心的平静,俯仰无愧于天地。
(选自《季羡林随想录(十一)做人与处世》,有删改)【注】[1]张公艺生于578年,卒于676年。
其家自北齐至唐朝九代人未曾分家,家庭和睦,世人誉称“九世同堂”。
唐高宗问他治家要诀,他书写了一百个“忍”字。
后人为其修建“百忍堂”,以示纪念。
18.全文的论证结构式,详写的内容是。
(2分)19.作者认为“一个人活在世上,应该处理好三个关系”,这三个关系应该怎样处理?(3分)20.作者在论述“人与自然”的关系时运用了哪些论证方法?作用是什么?试举一例说明。
(3分)21.在第⑤段后补写一句话,阐明张公艺的事例与观点之间的联系。
(2分)(四)文言文阅读,完成22-26题(13分)亮答曰:“自董卓已来,豪杰并起,跨州连郡者不可胜数。
曹操比于袁绍,则名微而众寡'然操遂能克绍,以弱为强者,非惟天时,抑亦人谋也。
