Sobel边缘检测算子
halcon边缘检测例子

halcon边缘检测例子Halcon是一款功能强大的机器视觉库,其边缘检测功能可以帮助我们在图像中找出物体的边缘,从而实现目标检测和分割。
下面将以Halcon边缘检测例子为题,列举一些常用的边缘检测方法和技巧。
一、Sobel算子边缘检测Sobel算子是一种常用的边缘检测算法,它通过计算图像的一阶导数来寻找边缘。
Halcon中可以使用函数SobelA来实现Sobel算子的边缘检测,可以设置不同的参数来调整检测结果的灵敏度。
二、Canny算子边缘检测Canny算子是一种经典的边缘检测算法,它结合了高斯滤波、梯度计算和非最大值抑制等步骤,可以得到更准确的边缘检测结果。
Halcon中可以使用函数EdgesSubPix来实现Canny算子的边缘检测,可以设置不同的参数来调整检测结果的质量和灵敏度。
三、Laplacian算子边缘检测Laplacian算子是一种基于二阶导数的边缘检测算法,它可以检测出图像中的高频变化,从而找到边缘。
Halcon中可以使用函数Laplace来实现Laplacian算子的边缘检测,可以设置不同的参数来调整检测结果的灵敏度。
四、Roberts算子边缘检测Roberts算子是一种简单但有效的边缘检测算法,它通过计算图像中像素点的灰度差来判断是否存在边缘。
Halcon中可以使用函数RobertsA来实现Roberts算子的边缘检测,可以设置不同的参数来调整检测结果的灵敏度。
五、Prewitt算子边缘检测Prewitt算子是一种基于一阶导数的边缘检测算法,它通过计算图像中像素点的灰度变化来寻找边缘。
Halcon中可以使用函数PrewittA来实现Prewitt算子的边缘检测,可以设置不同的参数来调整检测结果的灵敏度。
六、Scharr算子边缘检测Scharr算子是一种改进的Sobel算子,它可以更好地抵抗噪声干扰,提供更准确的边缘检测结果。
Halcon中可以使用函数ScharrA来实现Scharr算子的边缘检测,可以设置不同的参数来调整检测结果的灵敏度。
基于sobel和canny的边缘检测原理

基于sobel和canny的边缘检测原理
Sobel的原理:
Sobel 算子是图像处理中的算子之一,主要用作边缘检测。
它是一种离散性差分算子,用来运算图像亮度函数的梯度之近似值。
在图像的任何一点使用此算子,将会产生对应的梯度矢量或是其法矢量.
该算子包含两组3x3的矩阵,分别为横向及纵向,将之与图像作平面卷积,即可分别得出横向及纵向的亮度差分近似值。
以I代表原始图像,Gx及Gy分别代表经横向及纵向边缘检测的图像,其公式如下:
由于Sobel算子是滤波算子的形式,用于提取边缘,可以利用快速卷积函数,简单有效,因此应用广泛。
但是Sobel算子并没有将图像的主体与背景严格地区分开来,换言之就是Sobel算子没有基于图像灰度进行处理,由于Sobel算子没有严格地模拟人的视觉生理特征,所以提取的图像轮廓有时并不能令人满意。
在观测一幅图像的时候,我们往往首先注意的是图像与背景不同的部分,正是这个部分将主体突出显示,基于该理论,我们给出了下面阈值化轮廓提取算法,该算法已在数学上证明当像素点满足正态分布时所求解是最优的。
Canny的原理:
1、图象边缘检测必须满足两个条件:其一必须有效地抑制噪声;其次必须尽量精确确
定边缘的位置。
2、根据对信噪比与定位乘积进行测度,得到最优化逼近算子。
这就是Canny边缘检测
算子。
3、类似于LoG边缘检测方法,属于先平滑后求导数的方法。
Canny边缘检测算法可以分为四个步骤:
1)用高斯滤波器平滑图象;
2)用一阶偏导的有限差分来计算梯度的幅值和方向;3)对梯度幅值进行非极大值抑制
4)用双阈值算法检测和连接边缘。
Sobel边缘检测算子

经典边缘检测算子比较一各种经典边缘检测算子原理简介图像的边缘对人的视觉具有重要的意义,一般而言,当人们看一个有边缘的物体时,首先感觉到的便是边缘。
灰度或结构等信息的突变处称为边缘。
边缘是一个区域的结束,也是另一个区域的开始,利用该特征可以分割图像。
需要指出的是,检测出的边缘并不等同于实际目标的真实边缘。
由于图像数据时二维的,而实际物体是三维的,从三维到二维的投影必然会造成信息的丢失,再加上成像过程中的光照不均和噪声等因素的影响,使得有边缘的地方不一定能被检测出来,而检测出的边缘也不一定代表实际边缘。
图像的边缘有方向和幅度两个属性,沿边缘方向像素变化平缓,垂直于边缘方向像素变化剧烈。
边缘上的这种变化可以用微分算子检测出来,通常用一阶或两阶导数来检测边缘,如下图所以。
不同的是一阶导数认为最大值对应边缘位置,而二阶导数则以过零点对应边缘位置。
(a )图像灰度变化(b )一阶导数(c )二阶导数基于一阶导数的边缘检测算子包括Roberts 算子、Sobel 算子、Prewitt 算子等,在算法实现过程中,通过22⨯(Roberts 算子)或者33⨯模板作为核与图像中的每个像素点做卷积和运算,然后选取合适的阈值以提取边缘。
拉普拉斯边缘检测算子是基于二阶导数的边缘检测算子,该算子对噪声敏感。
一种改进方式是先对图像进行平滑处理,然后再应用二阶导数的边缘检测算子,其代表是LOG 算子。
前边介绍的边缘检测算子法是基于微分方法的,其依据是图像的边缘对应一阶导数的极大值点和二阶导数的过零点。
Canny 算子是另外一类边缘检测算子,它不是通过微分算子检测边缘,而是在满足一定约束条件下推导出的边缘检测最优化算子。
1 Roberts (罗伯特)边缘检测算子景物的边缘总是以图像中强度的突变形式出现的,所以景物边缘包含着大量的信息。
由于景物的边缘具有十分复杂的形态,因此,最常用的边缘检测方法是所谓的“梯度检测法”。
设(,)f x y 是图像灰度分布函数;(,)s x y 是图像边缘的梯度值;(,)x y ϕ是梯度的方向。
【OpenCV】边缘检测:Sobel、拉普拉斯算子 .

【OpenCV】边缘检测:Sobel、拉普拉斯算子转自:/xiaowei_cqu/article/details/7829481边缘边缘(edge)是指图像局部强度变化最显著的部分。
主要存在于目标与目标、目标与背景、区域与区域(包括不同色彩)之间,是图像分割、纹理特征和形状特征等图像分析的重要基础。
图像强度的显著变化可分为:∙阶跃变化函数,即图像强度在不连续处的两边的像素灰度值有着显著的差异;∙线条(屋顶)变化函数,即图像强度突然从一个值变化到另一个值,保持一较小行程后又回到原来的值。
图像的边缘有方向和幅度两个属性,沿边缘方向像素变化平缓,垂直于边缘方向像素变化剧烈.边缘上的这种变化可以用微分算子检测出来,通常用一阶或二阶导数来检测边缘。
(a)(b)分别是阶跃函数和屋顶函数的二维图像;(c)(d)是阶跃和屋顶函数的函数图象;(e)(f)对应一阶倒数;(g)(h)是二阶倒数。
一阶导数法:梯度算子对于左图,左侧的边是正的(由暗到亮),右侧的边是负的(由亮到暗)。
对于右图,结论相反。
常数部分为零。
用来检测边是否存在。
梯度算子 Gradient operators 函数f(x,y)在(x,y)处的梯度为一个向量:计算这个向量的大小为:近似为:梯度的方向角为:Sobel算子sobel算子的表示:梯度幅值:用卷积模板来实现:【相关代码】接口[cpp]view plaincopyprint?1.CV_EXPORTS_W void Sobel( InputArray src, OutputArray dst, int ddepth,2.int dx, int dy, int ksize=3,3.double scale=1, double delta=0,4.int borderType=BORDER_DEFAULT );使用[cpp]view plaincopyprint?1./////////////////////////// Sobe l////////////////////////////////////2./// Generate grad_x and grad_y3.Mat grad_x, grad_y;4.Mat abs_grad_x, abs_grad_y;5./// Gradient X6.//Scharr( src_gray, grad_x, ddepth, 1, 0, scale, delta, BORDER_DEFAULT );7.//Calculates the first, second, third, or mixed image derivatives using an extended Sobel operator.8.Sobel( src_gray, grad_x, ddepth, 1, 0, 3, scale, delta, BORDER_DEFAULT );9.convertScaleAbs( grad_x, abs_grad_x );10./// Gradient Y11.//Scharr( src_gray, grad_y, ddepth, 0, 1, scale, delta, BORDER_DEFAULT );12.Sobel( src_gray, grad_y, ddepth, 0, 1, 3, scale, delta, BORDER_DEFAULT );13.convertScaleAbs( grad_y, abs_grad_y );14./// Total Gradient (approximate)15.addWeighted( abs_grad_x, 0.5, abs_grad_y, 0.5, 0, grad );二阶微分法:拉普拉斯二阶微分在亮的一边是负的,在暗的一边是正的。
sobel算子计算例题

sobel算子计算例题Sobel算子是一种常用的边缘检测算法,它能够通过计算图像中像素点的梯度来找到图像中的边缘。
本文将介绍一个使用Sobel算子计算边缘的例子,并拓展讨论Sobel算子的原理和应用。
假设我们有一幅灰度图像,我们想要找到图像中的水平边缘。
首先,我们需要将图像转化为灰度图像,这可以通过常见的方法如将RGB图像的三个通道取平均值来实现。
接下来,我们需要应用Sobel算子来计算每个像素点的梯度。
Sobel算子分为水平和垂直两个方向的算子,分别用于计算像素点在水平方向和垂直方向上的梯度。
在这个例子中,我们只关注水平边缘,所以我们只需要使用水平方向的Sobel算子。
水平方向的Sobel算子如下:```-1 0 1-2 0 2-1 0 1```我们需要将该算子与图像中的每个像素进行卷积运算。
卷积运算的过程是将算子与图像的局部区域进行元素级别的乘法,并将乘积相加,最后得到一个新的像素值。
这个新的像素值表示了该位置上的梯度大小。
我们可以使用以下公式来计算每个像素点的梯度:```Gx = (P1 * -1) + (P2 * 0) + (P3 * 1) +(P4 * -2) + (P5 * 0) + (P6 * 2) +(P7 * -1) + (P8 * 0) + (P9 * 1)```其中,P1到P9表示了图像中某个像素点周围的8个像素点。
计算完所有像素点的梯度之后,我们可以将梯度值进行阈值处理,以确定哪些像素点属于边缘。
一种简单的方法是将梯度值与一个预先设定的阈值进行比较,大于阈值的像素点被认为是边缘点,小于阈值的像素点被认为是非边缘点。
除了边缘检测之外,Sobel算子还可以用于图像的模糊处理、图像增强等。
在图像模糊处理中,我们可以通过计算图像的梯度来减少图像中的高频噪声,从而实现图像的平滑效果。
在图像增强中,我们可以通过增加图像的梯度来强化图像的边缘信息,使图像更加清晰。
总结而言,Sobel算子是一种常用的边缘检测算法,它可以通过计算图像中像素点的梯度来找到图像中的边缘。
cvinvoke.sobel原理

cvinvoke.sobel原理Sobel算子是一种常用的边缘检测算法,它利用图像的空间梯度来识别不同区域之间的边界。
本文将详细介绍Sobel算子的原理及其在图像处理中的应用。
第一部分:Sobel算子的背景和原理在介绍Sobel算子之前,我们先来了解一下边缘检测的概念。
边缘通常是图像中颜色、亮度或纹理等视觉特征的突变之处。
在图像处理中,我们经常需要识别和提取出图像中的边缘信息,例如在物体检测、图像分割和特征提取等领域。
Sobel算子是一种基于梯度的边缘检测算法,它利用图像中的亮度变化来寻找边缘。
Sobel算子构建了两个卷积核,分别用于计算图像中水平和垂直方向的梯度。
这两个卷积核分别为:Gx = [-1 0 1 Gy = [-1 -2 -1-2 0 2] 0 0 0-1 0 1] 1 2 1]其中Gx和Gy分别表示水平和垂直方向的梯度运算。
Sobel算子通过将这两个卷积核与图像进行卷积操作,得到了两个梯度图像分量,即水平方向梯度图像和垂直方向梯度图像。
然后,通过对这两个梯度图像进行平方和开方运算,我们可以得到最终的边缘图像。
第二部分:Sobel算子的实现步骤接下来,我们将详细说明Sobel算子的实现步骤。
步骤一:灰度变换在使用Sobel算子进行边缘检测之前,首先需要将原始图像转换为灰度图像。
这是因为灰度图像只包含亮度信息,而不包含颜色信息,这样有助于提取边缘信息。
步骤二:图像卷积接下来,我们需要将卷积核与灰度图像进行卷积操作。
这一步骤可以通过使用卷积运算的公式来实现。
对于每个像素点,我们需要用卷积核中的数值与其周围像素点的数值相乘,并将结果相加,最后再除以一个标准化因子。
这个过程可以通过遍历整个图像来完成,对于每个像素点(i, j):1. 获取像素点(i, j)的8邻域像素值。
2. 用Gx卷积核与该像素点的8邻域进行卷积运算,得到水平方向梯度值Gx(i, j)。
3. 用Gy卷积核与该像素点的8邻域进行卷积运算,得到垂直方向梯度值Gy(i, j)。
Sobel、Prewitt、Roberts算子的边缘检测
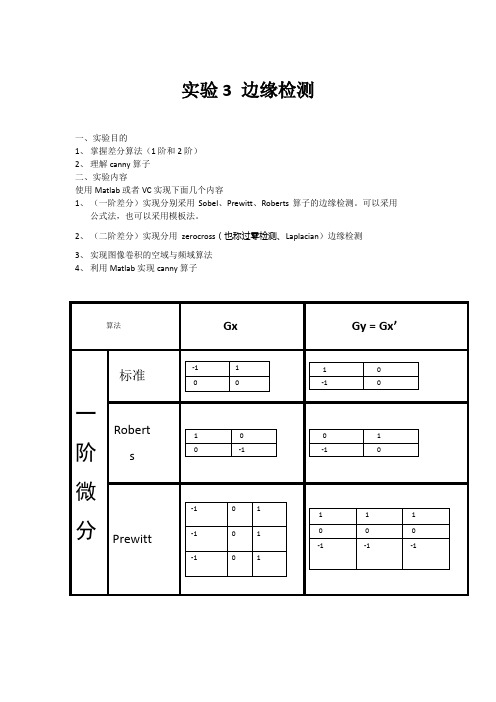
实验3 边缘检测一、实验目的1、掌握差分算法(1阶和2阶)2、理解canny算子二、实验内容使用Matlab或者VC实现下面几个内容1、(一阶差分)实现分别采用Sobel、Prewitt、Roberts算子的边缘检测。
可以采用公式法,也可以采用模板法。
2、(二阶差分)实现分用zerocross(也称过零检测、Laplacian)边缘检测3、实现图像卷积的空域与频域算法4、利用Matlab实现canny算子三、实验程序1.(一阶差分)%% Sobel算子clear;sourcePic=imread('111.jpg');%读取原图像grayPic=mat2gray(sourcePic);%实现图像矩阵的归一化操作[m,n]=size(grayPic);newGrayPic=grayPic;%为保留图像的边缘一个像素sobelNum=0;%经sobel算子计算得到的每个像素的值sobelThreshold=0.8;%设定阈值for j=2:m-1 %进行边界提取for k=2:n-1sobelNum=abs(grayPic(j-1,k+1)+2*grayPic(j,k+1)+grayPic(j+1,k+1)- ..., grayPic(j-1,k-1)-2*grayPic(j,k-1)-grayPic(j+1,k-1))+abs( ...,grayPic(j-1,k-1)+2*grayPic(j-1,k)+grayPic(j-1,k+1)-grayPic(j+1,k-1) ...,-2*grayPic(j+1,k)-grayPic(j+1,k+1));if(sobelNum > sobelThreshold)newGrayPic(j,k)=255;elsenewGrayPic(j,k)=0;endendendfigure,imshow(newGrayPic);title('Sobel算子的处理结果')%% Prewitt算子clear;sourcePic=imread('111.jpg');%读取原图像grayPic=mat2gray(sourcePic);%实现图像矩阵的归一化操作[m,n]=size(grayPic);newGrayPic=grayPic;%为保留图像的边缘一个像素PrewittNum=0;%经Prewitt算子计算得到的每个像素的值PrewittThreshold=0.5;%设定阈值for j=2:m-1 %进行边界提取for k=2:n-1PrewittNum=abs(grayPic(j-1,k+1)-grayPic(j+1,k+1)+grayPic(j-1,k) ...,-grayPic(j+1,k)+grayPic(j-1,k-1)-grayPic(j+1,k-1))+abs ...,(grayPic(j-1,k+1)+grayPic(j,k+1)+grayPic(j+1,k+1)-grayPic(j-1,k-1) ...,-grayPic(j,k-1)-grayPic(j+1,k-1));if(PrewittNum > PrewittThreshold)newGrayPic(j,k)=255;elsenewGrayPic(j,k)=0;endendendfigure,imshow(newGrayPic);title('Prewitt算子的处理结果')%% Roberts算子clear;sourcePic=imread('111.jpg'); %读取原图像grayPic=mat2gray(sourcePic); %实现图像矩阵的归一化操作[m,n]=size(grayPic);newGrayPic=grayPic;%为保留图像的边缘一个像素robertsNum=0; %经roberts算子计算得到的每个像素的值robertThreshold=0.2; %设定阈值for j=1:m-1 %进行边界提取for k=1:n-1robertsNum = abs(grayPic(j,k)-grayPic(j+1,k+1)) + abs(grayPic(j+1,k)-grayPic(j,k+1));if(robertsNum > robertThreshold)newGrayPic(j,k)=255;elsenewGrayPic(j,k)=0;endendendfigure,imshow(newGrayPic);title('roberts算子的处理结果')2.(2阶算子)I=imread('111.jpg'); %读取图像I1=im2double(I); %将彩图序列变成双精度I2=rgb2gray(I1); %将彩色图变成灰色图[thr, sorh, keepapp]=ddencmp('den','wv',I2);I3=wdencmp('gbl',I2,'sym4',2,thr,sorh,keepapp); %小波除噪I4=medfilt2(I3,[9 9]); %中值滤波I5=imresize(I4,0.8,'bicubic'); %图像大小h=fspecial('gaussian',5); %高斯滤波BW=edge(I5,'zerocross',[ ],h); %zerocross 图像边缘提取figure;imshow(BW);title('Zerocross');3.图像卷积的空域与时域算法inimg = imread('cameraman.tif');subplot(131)imshow(inimg), title('Original image')[M,N] = size(inimg); % Original image size%====================================================================h = fspecial('gaussian',25,4); % Gaussian filter%====================================================================% 空域滤波gx = imfilter(inimg,h,'same','replicate'); % 空域图像滤波subplot(132)imshow(gx,[]);title('Spatial domain filtering')%====================================================================% 频域滤波%====================================================================h_hf = floor(size(h)/2); % 空域滤波器半高/宽imgp = padarray(inimg, [h_hf(1),h_hf(2)],'replicate'); % Padding boundary with copying pixelsPQ = 2*size(imgp);Fp = fft2(double(imgp), PQ(1), PQ(2)); % 延拓图像FFTP = PQ(1); Q = PQ(2);center_h = h_hf+1; % 空域小模板h中心位置hp = zeros(P,Q); % 预分配内存,产生P×Q零矩阵hp(1:size(h,1),1:size(h,2)) = h; % h置于hp左上角hp = circshift(hp,[-(center_h(1)-1),-(center_h(2)-1)]); % 循环移位,h中心置于hp左上角%====================================================================Hp = fft2(double(hp)); % hp滤波器做FFT%====================================================================Gp = Hp.*Fp; % 频域滤波gp = real(ifft2(Gp)); % 反变换,取实部gf = gp(h_hf(1)+1:M+ h_hf(1), h_hf(2)+1:N + h_hf(2)); % 截取有效数据subplot(133)imshow(uint8(gf),[]), title('Frequency domain filtering')% 注:以上处理中,频域图像Fp与滤波器Hp均未中心化,因此,返回空域时无需反中心化。
sobel检验原理

sobel检验原理
Sobel算子是一种图像边缘检测算法,使用它可以识别图像中的边缘信息,分为水平方向和垂直方向两个方向。
此算法的原理是将图像中的每个像素点与其邻域像素点按指定的权值进行加权求和,得到一个新的像素值作为该像素点的边缘强度。
然后,将水平方向和垂直方向的结果进行平方和再开方,即可得到该像素点的最终边缘强度。
具体的,以水平方向为例,对于一个像素点的水平方向边缘强度的计算公式如下:
Gx = P(x-1,y-1)*(-1) + P(x-1,y)*(-2) + P(x-1,y+1)*(-1) + P(x+1,y-1)*(1) + P(x+1,y)*(2) + P(x+1,y+1)*(1)
其中,P(x,y)表示图像中坐标为(x,y)的像素值。
Sobel算子使用了一组预先确定的权值,将该像素点的相邻6个像素点按照权值进行加权求和,从而得到像素点的水平边缘强度。
同理,垂直方向的边缘强度计算公式如下:
然后,将Gx和Gy的平方和进行开方,得到像素点的最终边缘强度:
G = sqrt(Gx^2 + Gy^2)
这样,我们就得到了该像素点的水平和垂直方向的边缘强度,并且将其平方和再开方得到了最终的边缘强度。
Sobel算子通常用于图像的前期处理,例如边界检测、目标检测等。
其优点在于计算简单,效率高,同时能够保留边缘的结构信息。
但是,它也有一定的缺点,例如对于图像噪声比较敏感,容易受到光照变化等因素的影响,误检率较高。
因此,在实际应用中必须针对具体的场景进行参数的调整和优化,才能得到比较好的结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
经典边缘检测算子比较一 各种经典边缘检测算子原理简介图像的边缘对人的视觉具有重要的意义,一般而言,当人们看一个有边缘的物体时,首先感觉到的便是边缘。
灰度或结构等信息的突变处称为边缘。
边缘是一个区域的结束,也是另一个区域的开始,利用该特征可以分割图像。
需要指出的是,检测出的边缘并不等同于实际目标的真实边缘。
由于图像数据时二维的,而实际物体是三维的,从三维到二维的投影必然会造成信息的丢失,再加上成像过程中的光照不均和噪声等因素的影响,使得有边缘的地方不一定能被检测出来,而检测出的边缘也不一定代表实际边缘。
图像的边缘有方向和幅度两个属性,沿边缘方向像素变化平缓,垂直于边缘方向像素变化剧烈。
边缘上的这种变化可以用微分算子检测出来,通常用一阶或两阶导数来检测边缘,如下图所以。
不同的是一阶导数认为最大值对应边缘位置,而二阶导数则以过零点对应边缘位置。
(a )图像灰度变化 (b )一阶导数 (c )二阶导数基于一阶导数的边缘检测算子包括Roberts 算子、Sobel 算子、Prewitt 算子等,在算法实现过程中,通过22⨯(Roberts 算子)或者33⨯模板作为核与图像中的每个像素点做卷积和运算,然后选取合适的阈值以提取边缘。
拉普拉斯边缘检测算子是基于二阶导数的边缘检测算子,该算子对噪声敏感。
一种改进方式是先对图像进行平滑处理,然后再应用二阶导数的边缘检测算子,其代表是LOG 算子。
前边介绍的边缘检测算子法是基于微分方法的,其依据是图像的边缘对应一阶导数的极大值点和二阶导数的过零点。
Canny 算子是另外一类边缘检测算子,它不是通过微分算子检测边缘,而是在满足一定约束条件下推导出的边缘检测最优化算子。
1 Roberts (罗伯特)边缘检测算子景物的边缘总是以图像中强度的突变形式出现的,所以景物边缘包含着大量的信息。
由于景物的边缘具有十分复杂的形态,因此,最常用的边缘检测方法是所谓的“梯度检测法”。
设(,)f x y 是图像灰度分布函数;(,)s x y 是图像边缘的梯度值;(,)x y ϕ是梯度的方向。
则有 [][]{}1222(,)(,)(,)(,)(,)s x y f x n y f x y f x y n f x y =+-++- (1)(n=1,2,...) [][]{}1(,)tan (,)(,)/(,)(,)x y f x y n f x y f x n y f x y ϕ-=+-+- (2)式(1)与式(2)可以得到图像在(x,y )点处的梯度大小和梯度方向。
将式(1)改写为:{}1222(,)g x y =+ (3)(,)g x y 称为Roberts 边缘检测算子。
式中对(,)f x y 等的平方根运算使该处理类似于人类视觉系统的发生过程。
事实上Roberts 边缘检测算子是一种利用局部差分方法寻找边缘的算子,Robert 梯度算子所采用的是对角方向相邻两像素值之差,所以用差分代替一阶偏导,算子形式可表示如下:(,)(,)(1,1)(,)(1,)(,1)x y f x y f x y f x y f x y f x y f x y ∆=---⎧⎪⎨∆=---⎪⎩ (4)上述算子对应的两个22⨯模板如图(A )所示。
实际应用中,图像中的每个像素点都用这两个模板进行卷积运算,为避免出现负值,在边缘检测时常提取其绝对值。
(a ) (b )图(A )Robert 算子模板2 Sobel (索贝尔)边缘检测算子该算子是由两个卷积核1(,)g x y 与2(,)g x y 对原图像(,)f x y 进行卷积运算而得到的。
其数学表达式为:121111(,)(,)(,),(,)(,)M N M Nm n m n S x y MAX f m n g i m j n f m n g i m j n ====⎡⎤=----⎢⎥⎣⎦∑∑∑∑(5)实际上Sobel 边缘算子所采用的算法是先进行加权平均,然后进行微分运算,我们可以用差分代替一阶偏导,算子的计算方法如下:[][][][](,)(1,1)2(,1)(1,1)(1,1)2(,1)(1,1)(,)(1,1)2(1,)(1,1)(1,1)2(1,)(1,1)x y f x y f x y f x y f x y f x y f x y f x y f x y f x y f x y f x y f x y f x y f x y ⎧∆=-++++++---+-++-⎪⎨∆=--+-+-+-+-+++++⎪⎩ (6)Sobel 算子垂直方向和水平方向的模板如图(B )所示,前者可以检测出图像中的水平方向的边缘,后者则可以检测图像中垂直方向的边缘。
实际应用中,图像中的每一个像素点都用这两个卷积核进行卷积运算,取其最大值作为输出。
运算结果是一幅体现边缘幅度的图像。
(a ) (b ) 图(B )Sobel 算子模板3 Prewitt (普瑞维特)边缘检测算子Prewitt 边缘检测算子就是一种利用局部差分平均方法寻找边缘的算子,它体现了三对像素点像素值之差的平均概念,因为平均能减少或消除噪声,为此我们可以先求平均,再求差分,即利用所谓的平均差分来求梯度。
用差分代替一阶偏导可得算子形式如下:[][][][](,)(1,1)(,1)(1,1)(1,1)(,1)(1,1)(,)(1,1)(1,)(1,1)(1,1)(1,)(1,1)x y f x y f x y f x y f x y f x y f x y f x y f x y f x y f x y f x y f x y f x y f x y ⎧∆=+++++-+-+-+-+--⎪⎨∆=--+-+-+-+-+++++⎪⎩ (7) Prewitt 边缘检测算子的两个模板如图(C )所示,它的使用方法同Sobel 算子一样,图像中的每个点都用这两个核进行卷积,取得最大值作为输出。
Prewitt 算子也产生一幅边缘图像。
(a ) (b ) 图(C )Prewitt 算子模板4 Laplacian (拉普拉斯)边缘检测算子对于阶跃状边缘,其二阶导数在边缘点出现过零交叉,即边缘点两旁的二阶导数取异号,据此可以通过二阶导数来检测边缘点。
拉普拉斯边缘检测算子正是对二维函数进行二阶导数运算的标量算子,它的定义是:22222(,)(,)(,)f x y f x y f x y x y∂∂∇=+∂∂ (8)用差分代替二阶偏导时,与前述三个一阶导数算子不同,拉普拉斯算子的形式可表示如下:22(,)(1,)(1,)(,1)(,1)4(,)(,)(1,1)(,1)(1,1)(1,)(1,)(1,1)(,1)(1,1)8(,)f x y f x y f x y f x y f x y f x y f x y f x y f x y f x y f x y f x y f x y f x y f x y f x y ⎧∆=++-+++--⎪⎨∆=--+-++-+-++⎪⎩+-++++++-(9) 拉普拉斯边缘检测算子的模板如图(D )所示,模板的基本特征是中心位置的系数为正,其余位置的系数为负,且模板的系数之和为零。
它的使用方法是用图中的两个点阵之一作为卷积核,与原图像进行卷积运算即可。
拉普拉斯算子又是一个线性的移不变算子,它的传递函数在频域空间的原点为零,因此,一个经拉普拉斯滤波过的图像具有零平均灰度。
拉普拉斯检测模板的特点是各向同性,对孤立点及线端的检测效果好,但边缘方向信息丢失,对噪声敏感,整体检测效果不如梯度算子。
因此,它很少直接用于边缘检测。
但注意到与Sobel 算子相比,对图像进行处理时,拉普拉斯算子能使噪声成分得到加强,对噪声更敏感。
(a ) (b ) 图(D )Laplace 算子模板5 Marr-Hildreth (马尔)边缘检测算子实际应用中,由于噪声的影响,对噪声敏感的边缘检测点检测算法(如拉普拉斯算子法)可能会把噪声当边缘点检测出来,而真正的边缘点会被噪声淹没而未检测出。
为此Marr 和Hildreth 提出了马尔算子,因为是基于高斯算子和拉普拉斯算子的,所以也称高斯-拉普拉斯(Laplacian of Gaussian,LoG )边缘检测算子,简称LoG 算子。
该方法是先采用高斯算子对原图像进行平滑又降低了噪声,孤立的噪声点和较小的结构组织将被滤除由于平滑会导致边缘的延展,因此在边缘检测时仅考虑那些具有局部最大值的点为边缘点,这一点可以用拉普拉斯算子将边缘点转换成零交叉点,然后通过零交叉点的检测来实现边缘检测。
所谓零交叉点就是:如果一个像素处的值小于一0θ,而此像素8-连通的各个像素都是大于0θ (0θ是一个正数),那么这个像素就是零交叉点。
这样还能克服拉普拉斯算子对噪声敏感的缺点,减少了噪声的影响。
二维高斯函数为222(,)()2x y h x y exp σ+=- (10) 则连续函数(,)f x y 的LoG 边缘检测算子定义为[]2(,)(,)(,)G x y h x y f x y =-∇*2(,)*(,)h x y f x y ⎡⎤=-∇⎣⎦(,)*(,)H x y f x y = (11)222242(,)(,)exp()2r r H x y h x y σσσ-=-∇=- (12) 其中222,r x y σ=+是标准差。
算子(,)H x y 是一个轴对称函数,其横截面如图(E )所示。
由于它相当的平滑,能减少噪声的影响,所以当边缘模糊或噪声较大时,利用(,)H x y 检测过零点能提供较可靠的边缘位置。
图(E)H(x,y)的截面图LoG算子在(x,y)空间具有以原点为中心旋转的对称性,LoG滤波器具有如下三个显著特点:✧该滤波器中的高斯函数部分对图像具有平滑作用,可有效地消除尺度远小于高斯分布因子σ的噪声信号。
✧高斯函数在空域和频域都具有平滑作用。
∇可以减少计算量。
✧该滤波器采用拉普拉斯算子2马尔算子用到的卷积模板一般比较大(典型半径为8-32个像素),不过这些模板可以分⨯模板,如图(F)。
与其他边缘检测算子解为一维卷积来快速计算。
常用的LoG算子是55一样,LoG算子也是先对边缘做出假设,然后再这个假设下寻找边缘像素。
但LoG算子对边缘的假设条件最少,因此它的应用围更广。
另外,其他边缘检测算子检测得到的边缘时不连续的,不规则的,还需要连接这些边缘,而LoG算子的结果没有这个缺点。
对于LoG算子边缘检测的结果可以通过高斯函数标准偏差σ来进行调整。
即σ值越大,噪声滤波效果越好,但同时也丢失了重要的边缘信息,影响了边缘检测的性能;σ值越小,又有可能平滑不完全而留有太多的噪声。
因此,在不知道物体尺度和位置的情况下,很难准确确定滤波器的σ值。
