专题4.2.2 由视图到立体图形(课件

合集下载

4.2.2 由视图到立体图形课件 (共20张PPT)华东师大版数学七年级上册

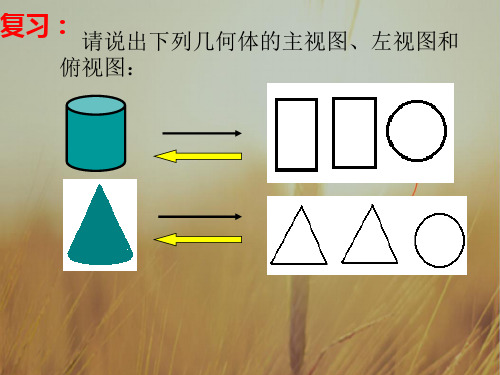
长方形、长方形、长方形
圆、圆、圆
长方体球
预习导学
2.由此可知，如果知道三视图中的一个或两个，一般不能 (填“能”或“不能”)确定该立体图形的形状. ·导学建议·
教师出示正方体、球、圆柱、圆锥等几何模型，帮助学生体会由已知视图判断立体图形的形状.
预习导学
归纳总结:常见三视图与立体图形的对应关系:三视图都是长方形的立体图形是长方体；三视图都是圆的立体图形是球；主视图和左视图都是长方形，俯视图是圆的立体图形是圆柱；主视图和左视图都是三角形，俯视图是带有圆心的圆的立体图形是圆锥.
预习导学
组合体的三视图与立体图形的关系阅读课本“试一试”的内容，体会如何由组合体的三视图确定立体图形. 1.主视图反映了立体图形正面的形状，俯视图反映了立体图形上面的形状，左视图反映了立体图形左面的形状.
预习导学
2.已知三视图确定正方体的组合体的形状，要从主视图或左视图确定层数，通过三视图确定每一层的形状. ·导学建议·
4.由若干个完全相同的小正方体组成一个立体图形，它的左
视图和俯视图如图所示，则小正方体的个数不可能是( A )
A.5
B.6
C.7
D.8
合作探究
【变式演练】一个几何体由若干个相同的正方体组成，其主视图和俯视图如图所示，则这个几何体中正方体的个数最多是( C )
A.3
B.4
C.5
D.6
合作探究
【方法归纳交流】主视图确定立体图形的长和高，左视图确定立体图形的宽和高，俯视图确定立体图形的长和宽.
第4章图形的初步认识
4.2 立体图形的视图 2.由视图到立体图形

5.由三视图到立体图形课件北师大版数学九年级上册

图
图
正五边形
俯视图
矩形且有棱
五条棱,两条被遮挡
【例2】根据下图的三种视图，你能画出与之对应的几何体吗？
主
左
视
视
图
图
俯
解：该几何体如下图所示.
视
图
随堂练习
1.由三视图想象实物形状.
主
左
视
视
图
图
俯视图
解：该几何体如下图所示.
2.两个长方体如图所示叠放，画出这个组合体的三视图.
主视图
左视图
俯视图
3.由三视图想象实物形状.
主
左解：该几何体如下图所示.
视
视
图
图
俯视图
4.由三视图想象实物形状.
主
左解：该几何体如下图所示.
视
视
图
பைடு நூலகம்
图
俯视图
课堂小结
由三视图到立体图形
画法步骤
1.由视图想象的几何体的形状； 2.由视图反应的几何体三个方向的空间特征，确定轮廓线位置； 3.根据“长对正，高平齐，宽相等”确定几何体的具体形状.
如何根据三种视图判断几何体的形状呢？
观想
根据“长对正，高平齐，宽相等”
定形确定几何体的具体形状. 判断由视图反应的几何体三个方向的空间
特征，确定轮廓线位置；由视图想象从三个方向看到的几何体的形状；
例题解析
【例1】根据下图的三种视图，你能画出与之对应的几何体吗？
主
左
视
视
解：该几何体是正五棱柱.
主视图
左视图
A
B
圆柱底面的
直径与长方
俯视图

由视图到立体图形（ppt）

新知讲解
例1 下图所示的是一些立体图形的三视图，请根据视图说出立体图形的名称。
（1）
主视
左视
图
图
俯视图
新知讲解
例1 下图所示的是一些立体图形的三视图，请根据视图说出立体图形的名称。
（2）主
左
视
视
图
图
俯视图
新知讲解
解：（1）该立体图形是长方体，如下图所示。
解：（2）该立体图形是圆锥，如下图所示。
正视图
左视图
课堂练习
解：（2）该立体图形的正视图和左视图如下图所示。
正视图
左视图
拓展提高
用小方块搭成一个几何体，使它的正视图和俯视图如图所示，它最少需要多少个小立方块，最多需要多少个小立方块?
正视图
俯视图
拓展提高
解：它最少需要10个小立方块，即最下边一层放7个，第二层放2个，最上边一层放1个，如下图所示。
新知讲解
由视图画立体图形的画法：从主视图观察，画出物体的前面。从俯视图观察，画出物体的上面。从左（右）视图观察，画出物体的左（右面）。读图时，必须综合各个视图之间的关系，从而把握整个立
体图形的形状
新知讲解
下图是一个物体的三视图，试想像该物体的形状。
主
左
视
视
图
图
俯视图
你能想出物体的形状吗？
课堂练习
2、请根据三视图画出立体图形。
主
左
视
视
图
图
俯视图
课堂练习
解：该立体图形如下图所示。
课堂练习
3、如图是几个小立方体所搭成的立体图形的俯视图，小正方形中的数字表示在该位置上小立方体的个数，请画出这个立体图形的正视图和左视图。

由三视图想象出立体图形课件

解：物体是正五棱柱形状的，如图所示.
例3 一个几何体由大小相同的小立方块搭成，从上面看到的几何体的形状如图所示，其中小正方形中的数字表示在该位置的小立方块的个数，则从正面看到几何体的形状是图中的( D )
解析：俯视图中，第一列最高有3个小立方块，第二列最高有2个小立方块，第三列最高有3个小立方块，因此，主视图从左到右可看到的小立方块个数依次为3、2、3，故选D.
由三视图想象出立体图形
知识回顾下面是哪个几何体的三视图？
主视图
左视图
俯视图
A
B
C
D
例题讲解例1 如图，分别根据三视图(1) (2)说出立体图形的名称.
(先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面，然后再综合起来考虑整体图形.
解：(1) 从三个方向看立体图形，视图都是矩形，可以想象出：整体是长方体，如图①所示；
②
①
(2) 从正面、侧面看立体图形，视图都是等腰三角形；从上面看，视图是圆；可以想象出：整体是圆锥，如图②所示.
例2 根据物体的三视图描述物体的形状.
分析：由主视图可知，物体的正面是正五边形；由俯视图可知，由上向下看到物体有两个面的视图是矩形，它们的交线是一条棱 (中间的实线表示)，可见到，另有两条棱 (虚线表示) 被遮挡；由左视图可知，物体左侧有两个面是矩形，它们的交线是一条棱 (中间的实线表示)，可见到；综合各视图可知，物体的形状是正五棱柱.
获取新知
归纳：由三视图想象立体图形时，先分别根据主视图、
俯视图和左视图想象立体图形的前面、主面和左侧面的局部形状，然后再综合起来考虑整体图形．

4、2、2由视图到立体图形

海南省洋浦中学教师教案 1
上面图圆柱和长方体只有给出的几种可能的图形，其实物图为长方形的立体图形有很多。

二、新授
上节课我们学习了从立体图形的三个不同
⑴⑵⑶
解：⑴长方体；⑵圆锥；⑶四棱锥
例2：下面是一个物体的三视图，
的形状.
例3：如图是几个小立方体所搭成的立体图形的俯视图，小正方形中的数字表示在该位置上小立方体的个数，请画出这个立体图形的正视
四、课堂小结
本节学习了由视图到立体图形，
想象能力，要充分认识到角度的转化。

五、作业。

华师版七年级初一数学 4.2.2 由视图到立体图形

2019/9/11
4
主（2）视
左视
图
图
俯
视

图
解：（2）从正面、侧面看立体图形，图象都是等腰三角形；从上面看，
图象是圆；可以想象出：整体是圆锥，如图所示.
2019/9/11
5
例2 根据物体的三视图摸索物体的形状．
主
左
视
视
图
图
俯视图
分析：由主视图可知，物体正面是正五边形；由俯视图可知，由上向下看物体是矩
主视图
左视图
俯视图
2019/9/11
13
5.下列是一个物体的三视图，请描述出它的形状.
主视图
左视图
俯视图
2019/9/11
14
课堂小结
由三视图描述几何体（或实物原型），一般步骤为： ① 想象：根据各视图想象从各个方向看到的几何体形状； ② 定形：综合确定几何体（或实物原型）的形状； ③ 定大小位置：根据三个视图“长对正，高平齐，宽相等”的关系，确定轮廓线
实物
8
根据三视图描述物体的形状．
主
左
视图
视图
俯视图
实物形状
2019/9/11
9
当堂练习
1.下面所给的三视图表示什么几何体?
2019/9/11
直四棱柱
10
2.下面所给的三视图表示什么几何体?
2019/9/11
11
3.下面所给的三视图表示什么几何体?
2019/9/11
12
4.用小立方块搭出符合下列三视图的几何体：
第4章图形的初步认识 4.2 立体图形的视图
2019/9/11
1
学习目标

4[1].2.2由视图到立体图形。ppt

从上面看
正视图
从左边看
左视图
俯视图
考考你:下面是一些立体图形的三视图，你知道它们分别是什么图形的三视图吗?
主视图
左视图主视图左视图
俯视图俯视图
四棱柱
圆锥体
二、得出定义，揭示内涵
现在我们要想做的事情是根据视图来描述物体的形状。让我们先看一些较为简单的、熟悉的物体。
主视图俯视图
学习目标
1.尽可能地搭出由小立方块组成的不同的几何体，并观察画出这个几何体的三视图. 2.能根据每个位置的小立方块的个数及其中一种视图画出另外两种视图. 3.有意识培养学生学习数学的信心和克服困难的勇气，从中体味成功的快乐
一、温故知新、引入课题
从上面看
练
（主视图）
（俯视图）
（左视图）
3.由四个小长方形搭成的物体，它的俯视图如图所示。问这个物体有几种搭法？试分别画出来。
用小方块搭成一个几何体，使它的主视图和俯视图如图所示，它最少需要多少个小立方块，最多需要多少个小立方块?
主视图
俯视图
最少十个
俯视图
主视图
最多十三个
俯视图
主视图
最多十三个
符合条件的几何体有几种？
畅谈收获
本节课里我的收获是……
体会从不同方向观察物体可能看到不同图形的基础上，识别简单的三视图，会画立方体及其简单组合体的三视图.
六、布置作业，引导预习
1.课本P134页，习题4.2 2.预习课本P135—P138
3， 4
家庭作业
正视图
左视图
俯视图
左视图
三例题示范，具体运用
例1.一个几何体的三视图如下,你能说出它是什么立体图形吗?

由视图到立体图形教学课件

THANKS.
练习1
根据给定的主视图和左视图，画出可能的三维立体图形。
练习2
根据给定的立体图形，分别画出其主视图、左视图和俯视图。
练习3
判断给定的立体图形是否可以通过旋转得到。
思考题
思考1
在三维空间中，一个物体的三个视图是否唯一确定其立体形状？
思考2
是否存在两个不同的立体图形，它们在某两个视图上完全相同，但在第三个视图上不同？
思考2解析
此题主要考察学生对三维视图的理解。学生需要思考是否存在两个不同的立体图形，它们在某两个视图上完全相同，但在第三个视图上不同。答案是肯定的，因为三维空间中的物体形状是连续变化的，有可能存在两个不同的立体图形在某两个视图上相同，但在第三个视图上不同。
思考3解析
此题主要考察学生对三维视图的理解和应用。学生需要理解如何通过三个视图来判断立体图形的质量特性，如体积、表面积等。这需要学生理解视图中面积和长度等参数与实际物体质量特性之间的关系，并能够进行相应的计算。
组合体的视图分析
组合体由两个或多个基本立体图形组合而成。通过分析组合体的三视图，可以帮助学生理解复杂立体图形的构成和特点。
斜截体的视图分析
斜截体是立体图形的一种，其特点是有一个面与水平面不平行。通过分析斜截体的三视图，可以帮助学生理解斜截体的特点和画法。
实际工程中的视图与立体图形转换
机械零件的视图分析
。
阴影的过渡
自然的阴影过渡可以使立体图形更加自然、真实，提高整体的美
感。
透视效果的营造
透视角度的选择
透视面的处理
选择合适的透视角度可以使得立体图形更加符合视觉习惯，增强立体感。

4.2.2由视图到立体图形课件

1、一个几何体的三视图如右所示，则这个几何体是（） A、正方体 B、球 C、圆柱 D、圆锥
2、如图是由一些相同的小正方体组成的几何体的三视图，则组成该几何体的小正方体的个数为（） A、4 B、5 C、6 D、7
中考题连接
1、一个几何体的三视图如图所示，那么这个几何体是（）
A、
B、
正视图
左视图
俯视图
你能搭出它的图形吗？
正视图左视图
俯视图
问题探究
【例1】如图是由几个小立方体块所搭几何体的俯视图，小正方形中的数字表示在该位置小立块的个数，请画出这个几何体的主视图和左视图。
试一试
你能根据下面的三视图来放出相应的立方体组合吗？
主视图
左视图
俯视图
1 2
俯视图
期末考试题型
主视图和俯视图长对正主视图和左视图高平齐俯视图和左视图宽相等
画出下面三视图所示的立体图形。（1）
正视图
左视图
俯视图
（3）
从正面看
从左面看
从上面看
正视图
你能根据以下立方块组合体的三个视图, 搭出组合体的形状吗?
左视图
俯视图
你能根据以下立方块组合体的三个视图, 搭出组合体的形状吗?
由视图到立体图形
就是根据视图来描述物体的形状。
例1
正视图俯 ቤተ መጻሕፍቲ ባይዱ 图
根据下面的三视图确定物体的形状
左视图正视图俯视图左视图
1.下面是某个圆锥的三视图，请根据正视图中所标出的长度，求出左视图中的线段长度和俯视图中圆的面积.
正视图左视图
35
AB

初二数学最新课件-由三视图到立体图形2 精品

·
俯视图
圆锥
这是一个立体图形的三视图，你能说出
它的名称
主视图左视图
主视图左视图
俯视图
圆柱
俯视图
四棱锥
下列是一个物体的三视图，请描述出它的形状
主视图左视图俯视图
三棱锥
下面是一个物体的三视图，试说出它的形状
主视图
下列是一个物体的三视图，请描述出它的形状
主视图左视图
俯视图
下列是一个物体的三视图，请描述出它的形状
下面所给的三视图表示什么几何体?
主视图俯视图
左视图
直四棱柱
下面所给的三视图表示什么几何体?
主视图
左视图
俯视图
直五棱柱
下面所给的三视图表示什么几何体?
主视图
左视图
俯视图
下面所给的三视图表示什么几何体?
主视图
左视图
俯视图
这是一个立体图形的三视图，你能说出
它的名称
主视图
左视图
俯视图
长方体
主视图左视图
5.一个几何体的主视图和左视图如图所示,它是什么几何体?请补画这个几何体的俯视图.
(第5题) 直三棱柱
(第6题)
6.一个直棱柱的主视图和俯视图如图所示.描述这个直棱柱的形状,并补画它的左视图.
直五棱柱,底面是五边形
探究活动
用6个相同的小方块搭成一个几何体,它的俯视图如图3-25所示.则一共有几种不同形状的搭救法(你可以用实物模型动手试一试)?你能用三视图表示你探究的结果吗?
2 41
23
主视图
左视图
下面图(1)与图(2)是几个小方块所搭几何体俯视图, 小正方形中的数字表示在该位置的小立方块的个数. 请画出这两个几何体的主视图、左视图.

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

如图是某立体图形的三视图，请根据三视图说出立体图形的名称。
正
左
视
视
图
图
俯视图
探索发现
正视图是三角形的立体图形有：圆锥、三棱锥、三棱柱等；正视图和左视图都是三角形的立体图形有：三棱锥、圆锥等；正视图、左视图是等腰三角形，俯视图是圆的立体图形有：圆锥
（1）无法根据一个视图确定其空间形状，因此必须将有关视图联系起来分析。（2）若正视图和左视图是长方形、正方形，则是柱体；若是三角形，则是锥体。
学以致用
例 4 用小方块搭成一个几何体，使它的主视图和俯视图如图所示，它最少需要多少个小立方块，最多需要多少个小立方块?
正视图
俯视图
学以致用
例 4 用小方块搭成一个几何体，使它的主视图和俯视图如图所示，它最少需要多少个小立方块，最多需要多少个小立方块?
正视图
俯视图
学以致用
例 5 由几个相同的小立方块搭成的几何体的俯视图如图所示。方格中的数字表示该位置的小方块的个数.请画出这个几何体的
探索发现
如图是某立体图形的三视图，请根据三视图说出立体图形的名称。
正
左
视
视
图
图
俯视图
探索发现
变式1：若将俯视图圆变为三角形，其余条件不变，则这个立体图形是什么？
如图是某立体图形的三视图，请根据三视图说出立体图形的名称。
正
左
视
视
图
图
俯视图
探索发现
变式2：若将俯视图三角形变为四边形，其余条件不变，则这个立体图形是什么？
三视图。
请你画出该立体图形的正视图和左
视图！
13
2
数学活动室，拓展加深
6.下面图（1）与图（2）是几个小方块所搭几何体俯视图小正方形中的数字表示在该位置的小立方块的个数.请画出这两个几何体的主视图、左视图.
经
典
2
数
41
学
23
主视图
左视图
数学活动室，拓展加深
7.下面图（1）与图（2）是几个小方块所搭几何体俯视图小正方形中的数字表示在该位置的小立方块的个数.请画出这两个几何体的主视图、左视图.
正
左
视
视
图
图
俯视图
探索发现
变式2：若将俯视图圆变为三角形，其余条件不变，则这个立体图形是什么？
如图是某立体图形的三视图，请根据三视图说出立体图形的名称。
正
左
视
视
图
图
俯视图
探索发现
正视图是长方形的立体图形有：长方体、圆柱、三棱柱等；正视图和左视图都是长方形的立体图形有：长方体、圆柱、三棱柱等；正视图、左视图和俯视图都是长方形的立体图形：长方体
温故知新
如何定义立体图形的三视图的？从这三个方向上看到的图形，叫做这个几何体的三个视图。
从上面看
从左面看
你会灵活应用吗？
从正面看到的图形，称为主视图; 从左面看到的图形，称为左视图; 从上面看到的图形，称为俯视图.
学以致用
画出如图所示圆柱的三视图：
解：圆柱的正视图和左视图都是长方形，俯视图为圆.
探索发现
现在我们要想做的事情是根据视图来描述物体的形状。让我们先看一些较为简单的、熟悉的物体。
如图是某立体图形的三视图，请根据三视图说出立体图形的名称。
正
左
视
视
图
图
俯视图
探索发现
变式1：若将俯视图正方形变为圆，其余条件不变，则这个立体图形是什么？
如图是某立体图形的三视图，请根据三视图说出立体图形的名称。
数学活动室
1.下列是一个物体的三视图，请描述出它的形状；
经
典
数
正视图
学
左视图
俯视图
数学活动室
2.下面是一个物体的三视图，试说出物体的形状。
经
典
正视图
数
学
左视图
俯视图
物体形状
和你想出的物体形状一样吗？
数学活动室
3.下列是一个物体的三视图，请描述出它的形状？
经
典
数
主视图
左视图
俯视图
学
数学活动室
4.下列是一个物体的三视图，请描述出它的形状？
经
典
数 342
节课我学到了什么？我的收获是…… 我还有……的疑惑
P 129
习题 4.2
第3、4题
一个人一天也不能没有理想，凭侥幸、怕吃苦、没有真才实学，再好的理想也不能实现不了。
正
左
视
视
图
图
注意摆放位置哟！
俯视图
三视图的位置及画图原则：长对正、高平齐、宽相等.
学以致用
将四位同学看到的视图用线连接起来：
情境激疑
通过前面学习，已知一个立体图形可以画出它的三视图已知一个立体图形的三视图，也可以得到这个立体图形
由立体图形到视图由视图到立体图形
由立体图形到视图由视图到立体图形
学以致用
例 1 你能根据下面的三视图画出立体图形吗？
正视图俯视图
左视图
从哪里入手！
学以致用
例 2 你能根据下面的三视图画出立体图形吗？
正视图俯视图
左视图
你有何体会！
【由三视图到正方体组合的方法】 1.以俯视图为基准操作: 俯视图定有几行几列； 2.正视图定每列的正方体最大层数； 3.左视图定每行的正方体最大层数。
经
典
数
主视图
左视图
俯视图
学
数学活动室，拓展加深
5.在一个仓库里堆积着正方体的货箱若干，要搬运这些箱子很困难，可是仓库管理员要落实一下箱子的数量，于是就想出一个办法：将这堆货物的三种视图画了出来，你能
经根据三视图，帮他清点一下数量吗？
典
数
学
正视图
左视图
俯视图
学以致用
例 3 由四个小长方形搭成的物体，它的俯视图如图所示。问这个物体有几种搭法？试分别画出来。