大学物理 力矩 转动定律 转动惯量
合集下载
大学物理-力矩

dF PdA [ p0 g(h y)]Ldy
h
F 0 [ p0 g(h y)]Ldy
p0Lh
1 2
gLh2
y
dA
代入数据,得
hy
dy
F 5.911010 N
O
L
x
第四章 刚体的转动
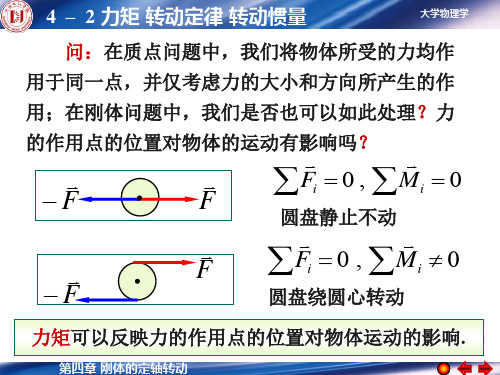
4-2 力矩 转动定律 转动惯量
dF [ p0 g(h y)]Ldy
dF对通过点Q的轴的力矩 dM ydF
第四章 刚体的转动
4-2 力矩 转动定律 转动惯量
例3 一长为 l 、质量
为 m 匀质细杆竖直放置,
其下端与一固定铰链O相 接,并可绕其转动.由于 此竖直放置的细杆处于非
m,l
θ mg
O
稳定平衡状态,当其受到微小扰动时,细
杆将在重力作用下由静止开始绕铰链O 转
动.试计算细杆转动到与竖直线成 角时
的角加速度和角速度.
z
M
Ft
F
O
r
m
Fn
第四章 刚体的转动
4-2 力矩 转动定律 转动惯量
(2)刚体
质量元受外力
内力
Fij
Fej,
Mej Mij mjrj2
外力矩 内力矩
z
O rj
Fej
m j
Fij
Mej Mij mjrj2
Байду номын сангаас
j
j
Mij M ji Mij 0
j
第四章 刚体的转动
4-2 力矩 转动定律 转动惯量
Mej ( mjrj2 )α
j
定义转动惯量
J mjrj2 J r2dm j
z
O rj
Fej
《大学物理》3.2转动定理
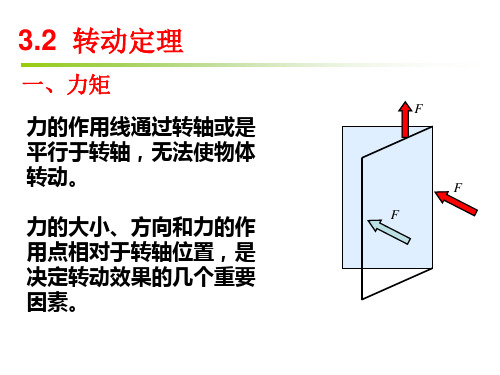
3.2 转动定理
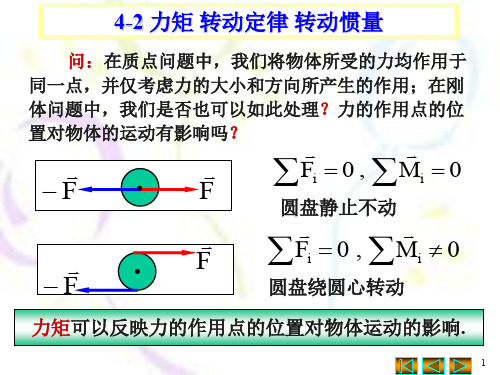
一、力矩
F
力的作用线通过转轴或是 平行于转轴,无法使物体 转动。 力的大小、方向和力的作 用点相对于转轴位置,是 决定转动效果的几个重要 因素。
F
F
1.定义:
力的大小与力臂乘积为力对转轴的力矩。用M表示
z
M
M F d Fr sin
F r P
M
z
F
1 2
1 其中滑轮转动惯量 J MR 2
2
a R
m m g a
2 1 1 2
m2 m1 g
M m1 m2 R 2
2 1
M m m 2
1 2
M m 2m g 2 T M m m 2
1 1 2
M m 2m g 2 T M m m 2
四、转动定理应用举例
例3-4如图所示,一不能伸长的轻绳跨过一轴承光滑的定 滑轮,滑轮视为圆盘,绳的两端分别悬有质量为m1和m2 的物体,且m1<m2,设滑轮的质量为M,半径为R,绳与 轮之间无相对滑动,求物体的加速度和绳中张力。
解:将三个物体隔离出来受力分析
其中 T 和 T 大小不能假定相等,但
m r 刚体内各质点相对于转轴的分布决定
M J
—— 绕定轴转动的刚体,其角加速度与它所 受合外力矩成正比,与刚体转动惯量成反比。 这一结论就是刚体定轴转动定理。
三、转动惯量
刚体的转动惯量等于刚体内各质点的质量与 其到转轴距离平方的乘积之和。
J m r J r dm
2
2
ij
j
F r f r m r
2 it i it i i i
一、力矩
F
力的作用线通过转轴或是 平行于转轴,无法使物体 转动。 力的大小、方向和力的作 用点相对于转轴位置,是 决定转动效果的几个重要 因素。
F
F
1.定义:
力的大小与力臂乘积为力对转轴的力矩。用M表示
z
M
M F d Fr sin
F r P
M
z
F
1 2
1 其中滑轮转动惯量 J MR 2
2
a R
m m g a
2 1 1 2
m2 m1 g
M m1 m2 R 2
2 1
M m m 2
1 2
M m 2m g 2 T M m m 2
1 1 2
M m 2m g 2 T M m m 2
四、转动定理应用举例
例3-4如图所示,一不能伸长的轻绳跨过一轴承光滑的定 滑轮,滑轮视为圆盘,绳的两端分别悬有质量为m1和m2 的物体,且m1<m2,设滑轮的质量为M,半径为R,绳与 轮之间无相对滑动,求物体的加速度和绳中张力。
解:将三个物体隔离出来受力分析
其中 T 和 T 大小不能假定相等,但
m r 刚体内各质点相对于转轴的分布决定
M J
—— 绕定轴转动的刚体,其角加速度与它所 受合外力矩成正比,与刚体转动惯量成反比。 这一结论就是刚体定轴转动定理。
三、转动惯量
刚体的转动惯量等于刚体内各质点的质量与 其到转轴距离平方的乘积之和。
J m r J r dm
2
2
ij
j
F r f r m r
2 it i it i i i
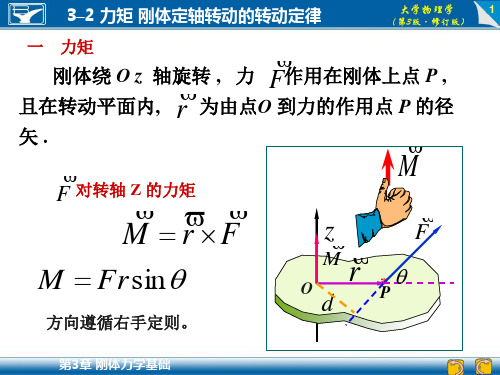
力矩 刚体定轴转动的转动定律
dJ R dm
2
第3章 刚体力学基础
3–2 力矩 刚体定轴转动的转动定律
12
考虑到所有质元到转轴的距离均为R,所以细圆环对 中心轴的转动惯量为
J dJ R dm R
2 m
2
m
dm mR
2
(2)求质量为m,半径为R的圆盘对中心轴的转动惯量
m 如图 dS 2 rdr , , dm dS 2 rdr 2 R
l 2
o
P
d d d d dt d dt d
代入初始条件积分 得
第3章 刚体力学基础
3g d sin d 2l 3g (1 cos ) l
1 2 J x dx ml 0 3
l 2
由此看出,同一均匀细棒,转轴位置不同,转动惯 量不同.
第3章 刚体力学基础
3–2 力矩 刚体定轴转动的转动定律
11
例3.2 设质量为m,半径为R的细圆环和均匀圆盘分 别绕通过各自中心并与圆面垂直的轴转动,求圆环和 圆盘的转动惯量. 解 (1) 在环上任 取一质元,其质量 为dm,距离为R, 则该质元对转轴的 转动惯量为
解 (1)转轴通过棒的中心并与棒垂直
m l
dm dx
dJ x 2dm x 2dx
第3章 刚体力学基础
3–2 力矩 刚体定轴转动的转动定律
10
整个棒对中心轴的转动惯量为
J dJ
l 2 l 2
1 x dx ml 2 12
2
(2)转轴通过棒一端并与棒垂直时,整个棒对该轴的 转动惯量为
解 (1) M k 2 ,故由转动定律有
k k J 即 J 2 1 k0 0 3 9J
4.3 力矩 转动定律

v −F v
i
v F
v ∑ Mi ≠ 0
i
∑ F = 0,
i
武汉纺织大学 物理教研室
大学物理学
第4章
刚体的定轴转动
讨论
v 不在转动平面内, (1)若力 F 不在转动平面内,把力分 )
解为平行和垂直于转轴方向的两个分量
力矩为零, 力矩为零,故 F 对转 轴的力矩
v 其中 Fz 对转轴的 v
v v v F = Fz + F⊥
大学物理学
第4章
刚体的定轴转动
4.3 力矩 刚体的转动定律 一 力矩
用来描述力对刚体 的转动作用. 的转动作用.
M = Fr sin θ = Fd d : 力臂 v F 对转轴 z 的力矩 v v v M = r ×F
z
v M
v F
O
v r
*
d
P
θ
v −F
i
v F
v ∑ Mi = 0
i
v ∑ Fi = 0,
M = I β , β 与 M 方向相同. 方向相同.
(2) 为瞬时关系. ) 为瞬时关系. (3) 转动中 M = I β 与平动中F = ma ) 地位相同. 地位相同.
武汉纺织大学 物理教研室
大学物理学
第4章
刚体的定轴转动
质量为m 的物体A 例2 质量为 A的物体 静止在光滑水 平面上,和一质量不计的绳索相连接, 平面上,和一质量不计的绳索相连接,绳 索跨过一半径为R、质量为m 索跨过一半径为 、质量为 C的圆柱形滑轮 C,并系在另一质量为 B 的物体 上,B 竖 ,并系在另一质量为m 的物体B上 直悬挂.滑轮与绳索间无滑动, 直悬挂.滑轮与绳索间无滑动, 且滑轮与 轴承间的摩擦力可略去不计. ) 轴承间的摩擦力可略去不计.(1)两物体的 线加速度为多少? 线加速度为多少? 水平和竖直两段绳索的 张力各为多少? ) 张力各为多少?(2) 物体 B 从静止落下距 其速率是多少? 离 y 时,其速率是多少?
转动定律、转动惯量讲解
Fit*ri+Fit'*ri= Δmi*(ri^2)*α
这是一个质点的规律,如果把所有的质点加起来,即∑Fit*ri+∑Fit'*ri= ∑Δmi*(ri^2)*α,因为刚体内部质点间的合力对转轴的力矩为零,即∑Fit'*ri= 0, 于是就有∑Fit*ri = ∑Δmi*(ri^2)*α,等式左边表示刚体所有质点所受外力对转轴 的力矩,也就是合力矩M;
《地球能平稳转动而不受外界干扰,全 靠转动定律与转动惯量》
上一章讲了刚体的定轴转动与角速度和角加速度的概念,如果有外力作用在刚体 上,那么刚体会发生什么变化呢?这就是本章要讲到的力矩、转动定律以及转动 惯量等概念。
首先来说力矩,在如图1所示的坐标系中,有一外力F作用在刚体内的P点,刚体 相对于原点的位置矢量为r,显然力F不经过原点O,于是把从O点到力F延长线的 垂直距离d叫做力F对转轴的力臂,其大小d=rsinθ ,而力F的大小和力臂d的乘积 Frsinθ 就叫做F对转轴的力矩,用大写字母M表示,力矩除了有小外,也有方向,
为了深刻理解转动惯量,以地球的转动惯量公式Je = (2mR^2)/5为例子,将地 球质量和半径带入式子可知,地球在转动时转动惯量非常大,根据转动定律可知, 需要非常大的力矩才能使地球加速或者减速,对于地球表面的所有物体而言,没 有哪个物体可以提供这样的力矩,这也就是地球平稳转动的原因。
讲完了转动定律,下一章《芭蕾舞演员的旋转加速秘诀-角动量守恒》将继续讲 解角动量。
而等式右边表示的量只与刚体的形状、质量、刚体的转轴有关。这个量就叫做转 动惯量,用大写字母J表示。于是等式可以表示为:M=J *α。这就是刚体的转动 定律,它的形式对应牛顿第二定律,其物理意义就是在同一力矩下,转动惯量大 的刚体,获得的角加速度就小,转动惯量小的刚体获得的角加速度就大。
这是一个质点的规律,如果把所有的质点加起来,即∑Fit*ri+∑Fit'*ri= ∑Δmi*(ri^2)*α,因为刚体内部质点间的合力对转轴的力矩为零,即∑Fit'*ri= 0, 于是就有∑Fit*ri = ∑Δmi*(ri^2)*α,等式左边表示刚体所有质点所受外力对转轴 的力矩,也就是合力矩M;
《地球能平稳转动而不受外界干扰,全 靠转动定律与转动惯量》
上一章讲了刚体的定轴转动与角速度和角加速度的概念,如果有外力作用在刚体 上,那么刚体会发生什么变化呢?这就是本章要讲到的力矩、转动定律以及转动 惯量等概念。
首先来说力矩,在如图1所示的坐标系中,有一外力F作用在刚体内的P点,刚体 相对于原点的位置矢量为r,显然力F不经过原点O,于是把从O点到力F延长线的 垂直距离d叫做力F对转轴的力臂,其大小d=rsinθ ,而力F的大小和力臂d的乘积 Frsinθ 就叫做F对转轴的力矩,用大写字母M表示,力矩除了有小外,也有方向,
为了深刻理解转动惯量,以地球的转动惯量公式Je = (2mR^2)/5为例子,将地 球质量和半径带入式子可知,地球在转动时转动惯量非常大,根据转动定律可知, 需要非常大的力矩才能使地球加速或者减速,对于地球表面的所有物体而言,没 有哪个物体可以提供这样的力矩,这也就是地球平稳转动的原因。
讲完了转动定律,下一章《芭蕾舞演员的旋转加速秘诀-角动量守恒》将继续讲 解角动量。
而等式右边表示的量只与刚体的形状、质量、刚体的转轴有关。这个量就叫做转 动惯量,用大写字母J表示。于是等式可以表示为:M=J *α。这就是刚体的转动 定律,它的形式对应牛顿第二定律,其物理意义就是在同一力矩下,转动惯量大 的刚体,获得的角加速度就小,转动惯量小的刚体获得的角加速度就大。
大学物理力矩转动惯量定轴转动定律资料

Fi sin i fi sin i mi ai mi ri
上页 下页 返回 退出
用 ri 乘以上式左右两端得
Fi ri sin i fi ri sin i mi ri 2
设刚体由N个质元构成,对每个质元可写出上述 类似方程,将这N个方程左右相加得
F r sin f r sin (m r
N i 1
刚体定轴 转动定律
2 2 r m 单位: kg· m i i
上页 下页 返回 退出
d M z J J dt
刚体定轴转动定律:刚体在合外力矩的作用下,所获 得的角加速度与合外力矩的大小成正比,与刚体的转 动惯量成反比。
说明: α ,转动惯量是转动惯性 (1)Mz 一定,J 大小的量度;例如地球的转动惯量非常巨大,因此转 动惯性也非常巨大,地球的自转角速度亘古不变!
§3-2 力矩 转动惯量 定轴转动定律
一、力矩 F对O点的力矩: M r F M rF sin
Z
M
F
M
F
MZ
转 动 平 面
A
O r
r
M 沿Z 轴分量为 F 对Z 轴的力矩 M Z
上页 下页 返回 退出
力不在转动平面内
M r F r (F1 F2 ) r F1 r F2
i i i
x
上页 下页 返回 退出
几种典型形状刚体的转动惯量
O' ω m O 圆环 J=mR2 细棒 R
l
1 J ml 2 12 ω
R2
L
R
R1
1 圆柱 J mR 2 2
1 2 圆筒 J m( R12 R2 ) 2
大学物理-力矩、转动定律、转动惯量

gh
yLdy
1 2
p0 Lh 2
1 6
gLh2
h
y
o
L
dA
x
dy
y
Q
dy
x
二、转动定律
质点的动力学问题 刚体的动力学问题
F ma
M
设刚体有n个质点组成,
先取任一质点i来研究
mi ri
外力:Fi 内力:Fi
由牛 顿第二定律得: Fi Fi miai
切线方向:Fit Fit miait
X
dV r2dZ (R2 Z 2 )dZ
其质量:dm dV (R2 Z 2 )dZ
其转动惯量:dJ 1 r 2dm 1 (R2 Z 2 )2 dZ
2
2
dJ 1 r 2dm 2
1 (R2 Z 2 )2 dZ
2
Z r dZ
O
R
Y
J dJ
X
R 1 (R2 Z 2 )2 dZ
比较
牛顿第二定律 F m a
转动定律
M J
三、转动惯量 J miri2 (4 9)
对质量连续分布的刚体 J r 2dm (4 11)
转动惯量的单位:kg m2
影响转动惯量得因素
注意:
(1)、刚体的质量(材料) (2)、刚体质量的分布
质点也有转动惯量
J mr2
(3)、转轴的位置
对质量不连续分布的刚体 J m 2
R 2
8 R5 2 mR2
m 4 R3
3
15
5
例3)求一质量为m的均匀实心球对其一条直径
为轴的转动惯量。
Z x
解:方法二 在球上取一体积元
dV
dV dxdydz
大学物理实验转动惯量

对形状简单且质量分布均匀的物体,转动惯量 可直接理论计算,如
这些物体绕其他与特定轴平行的轴转动时,转 动惯量由平行轴定理计算。
若刚体绕过质心的轴转动的转动惯量为I0,则 绕另一与之平行的轴转动的转动惯量为
I I0 mx2
x为两平行轴之间的距离。
四、弹簧扭转常数K和载 物盘转动惯量的测定
设载物盘的转动惯量为I0,转动周期可测量为 T0,另一转动惯量可理论计算的物体的转动惯 量为I1′,将该物体放在载物盘上,两轴重合, 复合摆周期T1,,则
I 2 转动周期 T K
由此可知,通过测量刚体转动的周期,再由已 知的扭转常数K,就可以计算出转动惯量I。
2
二、仪器描述
光电探头 实心球体
空心金属 圆柱体
扭摆 周期测定仪 挡光杆
塑料圆柱体
游标卡尺
夹具
滑块
金属杆
载物盘
转动轴 螺旋弹簧 水平调 节螺钉 气泡水 平仪
三、转动的平行轴定理
2 2 I0 T0 4 K
I1 K 4 2 T1 T02
2
I 0 I1 T 4 K
2 1 2
2 I T I 0 4 2 2 0 2 T1 T0
五、实验内容及步骤
计算各物体转动惯量的理论值 根据各待测物转动惯量计算公式,测量各物体 有关几何尺寸及质量,各测量三次取平均值。 扭转常数K的确定 ①调整扭摆基座底角螺丝,使扭摆水平。 ②装上载物盘,调整光电探头的位置,使挡光 杆处于缺口中央,测定周期T0。 ③将塑料圆柱体放在载物盘上,测定周期T1。 ④由T0 、T1及塑料圆柱转动惯量的理论值I1′ 计算扭转常数K和载物盘的转动惯量I0。
相关参数:
金属细杆夹具的转动惯量
这些物体绕其他与特定轴平行的轴转动时,转 动惯量由平行轴定理计算。
若刚体绕过质心的轴转动的转动惯量为I0,则 绕另一与之平行的轴转动的转动惯量为
I I0 mx2
x为两平行轴之间的距离。
四、弹簧扭转常数K和载 物盘转动惯量的测定
设载物盘的转动惯量为I0,转动周期可测量为 T0,另一转动惯量可理论计算的物体的转动惯 量为I1′,将该物体放在载物盘上,两轴重合, 复合摆周期T1,,则
I 2 转动周期 T K
由此可知,通过测量刚体转动的周期,再由已 知的扭转常数K,就可以计算出转动惯量I。
2
二、仪器描述
光电探头 实心球体
空心金属 圆柱体
扭摆 周期测定仪 挡光杆
塑料圆柱体
游标卡尺
夹具
滑块
金属杆
载物盘
转动轴 螺旋弹簧 水平调 节螺钉 气泡水 平仪
三、转动的平行轴定理
2 2 I0 T0 4 K
I1 K 4 2 T1 T02
2
I 0 I1 T 4 K
2 1 2
2 I T I 0 4 2 2 0 2 T1 T0
五、实验内容及步骤
计算各物体转动惯量的理论值 根据各待测物转动惯量计算公式,测量各物体 有关几何尺寸及质量,各测量三次取平均值。 扭转常数K的确定 ①调整扭摆基座底角螺丝,使扭摆水平。 ②装上载物盘,调整光电探头的位置,使挡光 杆处于缺口中央,测定周期T0。 ③将塑料圆柱体放在载物盘上,测定周期T1。 ④由T0 、T1及塑料圆柱转动惯量的理论值I1′ 计算扭转常数K和载物盘的转动惯量I0。
相关参数:
金属细杆夹具的转动惯量
力矩转动定律转动惯量jm汇总课件

力矩的物理意义
总结词
力矩描述了力使物体绕某点转动的趋势或转动效果。
详细描述
力矩决定了物体绕某点转动的趋势或转动效果,其方向与力和力臂的乘积方向 相同。力矩越大,物体转动的趋势或转动效果越明显。
力矩的计算方法
总结词
力矩的大小等于力和力臂的乘积,计中力臂是从转动轴(或转动中心)到力的垂 直距离。计算公式为 M=FL,其中 M 为力矩,F 为力,L 为力臂。同时,力矩的 方向与力和力臂的乘积方向相同。
转动惯量的大小决定了物体旋转运动 的加速度、角速度和角动量等参数的 变化规律,进而影响物体的运动状态 和稳定性。
转动惯量的计算方法
转动惯量的计算方法主要包括平行轴定理和垂直轴定理。
平行轴定理指出,对于一个质量分布均匀的刚体,其相对于某固定轴的转动惯量,等于该刚体的质量乘以质心到该轴的距离 的平方,再加上所有相对于此轴的离散质量的转动惯量之和。垂直轴定理则说明,一个质量分布均匀的刚体相对于任一垂直 于其对称平面的轴的转动惯量,等于该刚体的质量乘以其对称轴到质心的距离的平方。
车辆工程
在车辆工程中,力矩转动定律用于分析车辆动力学和稳定性 问题。例如,通过分析车轮的力矩,可以研究车辆的操控性 能和行驶稳定性。
力矩转动定律在科研中的应用
物理学研究
力矩转动定律是物理学中分析转 动问题的基本原理,广泛应用于 分析天体运动、刚体动力学等问 题。
生物学研究
在生物学研究中,力矩转动定律 用于分析生物体的运动和平衡机 制,如动物的行走、飞行等。
动惯量。
实验步骤
2. 将刚体安装到实验装置上 ,调整力矩计和角位移传感
器的位置和角度。
1. 准备实验器材:刚体、力 矩计、角位移传感器、数据
4-2力矩转动定律转动惯量

J r2dm
图1
图2
J1 J2
➢ 常用的转动惯量 (P110 表)
21
四 平行轴定理
质量为m 的刚体,
如果对其质心轴的转动 惯量为 JC ,则对任一与
该轴平行,相距为 d 的
转轴的转动惯量
JO JC md 2
d
C mO
J Jc
22
J Jc md2
圆盘对P 轴的转动惯量 P R O m
Fit Fit miait miri
11
➢ 质元绕Z轴转动的力矩
M i ri Fit ri Fit miri2
➢ 刚体绕Z轴转动的力矩
z
Fi内
Fi外
r O i m i 质量元
Mi riFit riFit
mi ri 2
M
r
F
M Frsin Fd
5
4、一对力偶的力矩
M Fd
F
F
o
l
F 0 M 0
M F l F l Fl
22
ro
F'
F
F 0
M 0
M Fr Fr 0
6
讨论
(1)若力 F不在转动平面内,把力分
解为平行和垂直于转轴方向的两个分量
41
➢ 常用的转动惯量公式
m质点:J r2m 圆盘(圆柱): J 1 mR2
2
杆:
Jc
1 12
mL2
J
端
1 3
mL2
R Om
O1
O1’
d=L/2
3力矩转动定律(大学物理 - 刚体部分)

F
二、转动定律
刚体作定轴转动时,合外力矩等于 刚体的转动惯量与角加速度的乘积。 M Jβ
注意几点
1. 是矢量式 2. 具有瞬时性。 3. M、J、是对同一轴而言的。
§5.力矩、转动定律 / 二、转动定律
三. 解题方法及应用举例
M Jβ
1.确定研究对象。
2.受力分析(只考虑对转动有影响的力矩)。
M J
l 1 2 mg cos ml 2 3 3 g cos 2l
习题课 / 例3
m,l
mg
3 g cos 2l
60时
0时
3 g 4l 3 g 2l
m,l
mg
习题课 / 例3
3.列方程求解(平动物体列牛顿定律方程,转 动刚体列转动定律方程和角量与线量关系)。
§5.力矩、转动定律 / 三、解题方法及应用举例
例1:如图所示,两个同心圆盘结合在一 起可绕中心轴转动,大圆盘质量为 m1、 半径为 R,小圆盘质量为 m2、半径为 r, 两圆盘都用力 F 作用,求角加速度。
解:以 m1、 m2 为研 究对象,它们有共同 的角加速度,只有 F、 F 产生力矩。 FR Fr ( J1 J 2 )
第三节
力矩 转动定律
一、力矩
力与力臂的乘积。
O d
M
r
P r M dF r sin F M rF sin 根据矢量乘积法则: A B AB sin 用矢量方法表示力矩: M r F 单位:牛顿· 米, N ·m 方向:从r沿小于角右旋到F,大拇指指向。
§5.力矩、转动定律 / 一、力矩
m2 r
R
m1
大学物理-力矩-转动定律-转动惯量
F
p
18
2 – 5 刚体的定轴转动
第二章 动力学基础
解 (1) Fr J
Fr 98 0.2 39.2 rad/s2
J 0.5
mg T ma
(2) Tr J
a r
两者区别?
rO
F T
T
J
mgr mr 2
98 0.2 0.5 10 0.22
i
J r2dm
9
2 – 5 刚体的定轴转动
第二章 动力学基础
四. J 的计算
质量连续分布刚体的转动惯量
J mjrj2 r2dm dm :质量元 j
对质量线分布的刚体: dm dl
:质量线密度
对质量面分布的刚体:
:质量面密度
对质量体分布的刚体:
在圆规迹切线方向
mk ak mk rk Fk fk
两边乘以rk,并对整个刚体求和
第二章 动力学基础
z
o
vk
mk
( mk rk2 ) Fk rk fk rk
k
k
k
5
2 – 5 刚体的定轴转动
第二章 动力学基础
( mk rk2 ) Fk rk fk rk
17
2 – 5 刚体的定轴转动
第二章 动力学基础
四、转动定律的应用举例
例1 一轻绳绕在半径 r =20 cm 的飞轮边缘, 在绳端施以F=98 N 的拉力,飞轮的转动惯量 J=0.5 kg·m2,飞轮与转轴间的摩擦不计 。
rO
求: (1) 飞轮的角加速度。
(2) 如以重量P =98 N的物体挂在 绳端,试计算飞轮的角加速度。
大学物理-第四章-力矩 转动定律 转动惯量
0
3
8
以上各例说明:
(1)刚体的转动惯量 与刚体的质量有关, 与刚体的质量分布有关, 与轴的位置有关。
(2)质量元的选取:
线分布 dm dx(或dl)
面分布 dm ds
体分布 dm dv
线分布
面分布
体分布
9
习题4-11: 质量为m1和m2 的两物体A、B 分别悬挂在图示的组合轮两端.设两轮的半 径分别为R 和r,两轮的转动惯量分别为J1 和J2 ,轮与轴承间、绳索与轮间的摩擦力 均略去不计,绳的质量也略去不计.试求两 物体的加度度和绳的张力.
解: 系统角动量守恒
J11 J22 (J1 J2 )
J11 J 22
(J1 J2 )
22
习题4-16:一质量为m′、半径为R 的均匀圆盘,通过 其中心且与盘面垂直的水平轴以角速度ω转动,若在 某时刻,一质量为m 的小碎块从盘边缘裂开,且恰好 沿垂直方向上抛,问它可能达到的高度是多少? 破裂
Lz x mv y ymv x
15
2 刚体定轴转动的角动量
L mirivi ( miri2 )
i
i
z
L J
二 刚体定轴转动的角动量定理
dL d(J) M
dt dt
O ri
v i
mi
t2 Mdt
t1
L2 L1
dL
J2
J1
非刚体定轴转动的角动量定理
20
有许多现象都可以用角 动量守恒来说明. 它是自然 界的普遍适用的规律.
花样滑冰 跳水运动员跳水
飞轮
1
2
航天器调姿
大学物理课件考研备考期末复习 角动量 角动量守恒定律

解:对M:M =T1 R=J
J= 1 MR2 2
对m : mg T1 ma a R
解 方 程 得 :a
m
m M
2
g
v 2ah 4mgh 2m M
v 1 4mgh
R R 2m M
·R 绳 v0=0
m
th
2m g
r2 R2
dr
2 3
m gR
根据转动定律,得
M
2 3
m gR
4g
J
1 m R2
3R
2
角加速度为常量,且与ω0的方向相反,
表明圆盘作匀减速转动
0 t
当圆盘停止转动时,ω=0,则得
t 0 3R0 4g
一个质量为M、半径为R 的定滑轮 上面绕有细绳,绳的一端固定在滑轮边上, 另一端挂一质量为m 的物体而下垂。忽略 定轴O 轴处摩擦,求物体m由静止下落高度h时的 速度和此时滑轮的角速度。
Mdt
L2
L1
冲量矩
t2
M
dt
t1
质点的角动量定理:对同一参考点 O ,质点所 受的冲量矩等于质点角动量的增量.
3 质点的 角动量守恒定律 M 0, L 恒矢量
质点所受对参考点 O 的合力矩为零时,质点对该 参考点 O 的角动量为一恒矢量.
例
例1 一半径为 R 的光滑圆环置于竖直平面内.一质 量为 m 的小球穿在圆环上, 并可在圆环上滑动. 小球开始 时静止于圆环上的点 A (该点在通过环心 O 的水平面上), 然后从 A 点开始下滑.设小球与圆环间的摩擦略去不计.求 小球滑到点 B 时对环心 O 的角动量和角速度.
解 小虫与细杆的碰撞视为完全非弹性碰撞,碰撞 前后系统角动量守恒
(完整版)转动定律讲解
d力臂:转轴到力作用线的垂直距离
方向: r F 的方向 单位: N m
对于定轴转动;
z
M
r
Od
F
P*
规定转动正方向,力矩使刚体绕
正方向转动, M 取正,反之取负。
第四章 刚体的定轴转动
4 – 2 力矩 转动定律 转动惯量
大学物理学
讨论 1)与转轴平行的力对转轴不产生力矩;
2)与转 轴垂直但通过转轴的力对转轴不产生力矩; 3)若力 F 不在转动平面内,把力分解为平行和垂
直于转轴方 向的两个分 量 F Fz F
其中 Fz 对转轴的力
矩为零,故 F 对转轴的
力矩
M r F
M z rF sin
4)合 力矩 等于各分力矩的矢量和
M M1 M2 M3
第四章 刚体的定轴转动
z
k
Fz
F
O r
F
定轴转动:(规定转动 正方向)
M Mi
i
4 – 2 力矩 转动定律 转动惯量
力矩可以反映力的作用点的位置对物体运动的影响.
第四章 刚体的定轴转动
4 – 2 力矩 转动定律 转动惯量
大学物理学
一 力矩
刚体绕 O z 轴旋 转 , 力 F 作用在刚体上点 P ,
r 且在转动平面内, 为由点O 到力的作用点 P 的径
矢 .
F 对转轴 Z 的力矩 M rF
M
力矩是矢量
大小: M Frsin Fd
M i Fitri (mi )atri
at ri
Mi (mi )ri2
z
Fit
O
ri
mi
M Mi (mi )ri2 (mi )ri2
➢ 转动惯量
方向: r F 的方向 单位: N m
对于定轴转动;
z
M
r
Od
F
P*
规定转动正方向,力矩使刚体绕
正方向转动, M 取正,反之取负。
第四章 刚体的定轴转动
4 – 2 力矩 转动定律 转动惯量
大学物理学
讨论 1)与转轴平行的力对转轴不产生力矩;
2)与转 轴垂直但通过转轴的力对转轴不产生力矩; 3)若力 F 不在转动平面内,把力分解为平行和垂
直于转轴方 向的两个分 量 F Fz F
其中 Fz 对转轴的力
矩为零,故 F 对转轴的
力矩
M r F
M z rF sin
4)合 力矩 等于各分力矩的矢量和
M M1 M2 M3
第四章 刚体的定轴转动
z
k
Fz
F
O r
F
定轴转动:(规定转动 正方向)
M Mi
i
4 – 2 力矩 转动定律 转动惯量
力矩可以反映力的作用点的位置对物体运动的影响.
第四章 刚体的定轴转动
4 – 2 力矩 转动定律 转动惯量
大学物理学
一 力矩
刚体绕 O z 轴旋 转 , 力 F 作用在刚体上点 P ,
r 且在转动平面内, 为由点O 到力的作用点 P 的径
矢 .
F 对转轴 Z 的力矩 M rF
M
力矩是矢量
大小: M Frsin Fd
M i Fitri (mi )atri
at ri
Mi (mi )ri2
z
Fit
O
ri
mi
M Mi (mi )ri2 (mi )ri2
➢ 转动惯量
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
m1 m2 g
m m 1 m r 1 2 2
0 t
m2 g
m1 m2 gt
21
1 m1 m2 m r 2
2 – 5 刚体的定轴转动
第二章 动力学基础
例3一根长为l、质量为 m 的均匀细直棒, 其一端有一固定的 光滑水平轴, 因而可以在竖直平面内转动。最初棒静止在竖 直位置, 由于微小扰动, 在重力作用下由 静止开始转动。
1 2 J L / 2x dx ML 12
L/2 2
z M O L
dx
x
对端点
注意 二者关系:
J 0 x dx 0
2
L
L
M 1 2 x dx ML L 3
2
J 与转轴的位置有关
1 1 2 1 2 L 2 J O+m mL mL mL J 端点 4 3 2 12
7
2 – 5 刚体的定轴转动
讨论
第二章 动力学基础
(1) 转动定律与牛顿第二定律比较:
M J 、 F ma M F , J m, a
两个定律在形式上对应, 都是反映瞬时效应的。
dv F ma m dt
d M J J dt
(2) m反映质点的平动惯性,J 则反映刚体的转动惯性。
12
2
2 – 5 刚体的定轴转动
平行轴定理
第二章 动力学基础
z'
z M L C
J z' J z ML
2
J z' 刚体绕任意轴的转动惯量;
Jz
刚体绕通过质心的轴的转动惯量; 两轴间垂直距离。
13
L
2 – 5 刚体的定轴转动
第二章 动力学基础
例3 求图所示刚体对经过棒端且与棒垂直的轴的转动惯量如何 计算?(棒长为L、圆盘半径为R)
k k k
5
2 – 5 刚体的定轴转动
2 k k
第二章 动力学基础
( m r ) Fk rk f k rk
k k k
其中
F r
k k k
k
M z 称为合外力矩 ;
内力矩之和为零;
f k rk 0
k
令
2 J z m, r k k
称为刚体对z轴的转动惯量。
J r dm
2 0
m
R dr r
m
注意
R
0
2m 3 m 2 r dr R 2 R 2
J 与质量分布有关
O
16
2 – 5 刚体的定轴转动
(2)用平行轴定理、迭加法
第二章 动力学基础
M
J = J 大– J 小 J = J 大+ J 小
o
. .
R
O
(3) 实验法
如三线扭摆法。
17
2 – 5 刚体的定轴转动
四、转动定律的应用举例
第二章 动力学基础
例1 一轻绳绕在半径 r =20 cm 的飞轮边缘, 在绳端施以F=98 N 的拉力,飞轮的转动惯量 J=0.5 kg· m2,飞轮与转轴间的摩擦不计 。
rO
求: (1) 飞轮的角加速度。
(2) 如以重量P =98 N的物体挂在 绳端,试计算飞轮的角加速度。
F
J L1
1 2 J o mo R 2
1 2 mL L 3
(棒对边缘轴) (圆盘对中心轴)
2
J L 2 J 0 m0 d
(圆盘对棒边缘轴)
1 1 2 2 2 J mL L mo R mo ( L R ) 3 2
14
2 – 5 刚体的定轴转动
例4 圆环绕中心轴旋转的转动惯量。
两边积分:
0
d
0
3g sin d 2l
角速度:
3g 1 cos l
24
1 2 J ml 3
23
2 – 5 刚体的定轴转动
棒处于θ角时: 而
第二章 动力学基础
d dt
作变换:
1 mgl sin M 3 g sin 2 1 2 J 2l ml 3
3g d d d d sin d d d 2l dt d dt d
mg
19
2 – 5 刚体的定轴转动
第二章 动力学基础
例2 一定滑轮质量为 m,半径为 r , 不能伸长的轻绳两边 分别系 m1 和 m2 的物体挂于滑轮上, m1 >m2, 绳与滑轮间 无相对滑动。设轮轴光滑无摩擦, 滑轮的初角速度为零。
求:滑轮转动角速度随时间变化的规 律。
m r
m2
m1
20
2 – 5 刚体的定轴转动
二、刚体绕定轴转动微分方程
第二章 动力学基础
作用在 mk 上的外力F ,内力 f k k dvk mk Fk f k dt
在圆规迹切线方向
z
o
vk
mk ak mk rk Fk f k
两边乘以rk,并对整个刚体求和
2 k k
mk
( m r ) Fk rk f k rk
则
J z M z
或
d Jz Mz dt
6
2 – 5 刚体的定轴转动
第二章 动力学基础
M z J z
刚体绕定轴转动时,刚体对该轴的转动惯量与角 加速度的乘积等于作用在刚体上所有外力对该轴力 矩的代数和。
刚体定轴转动的角加速度与它所受的合外力矩成 正比,与刚体的转动惯量成反比。
— 刚体绕定轴转动微分方程,或转动定律。
M ij
O
M ji
d
ri
F ji i F
ij
rj
j
Mij M ji
2 – 5 刚体的定轴转动
第二章 动力学基础
2 不在转动平面内的力对定轴力矩的矢量形式
z
F//
M Z r F
方向由右螺旋法则确定。
F
r
A
F
4
2 – 5 刚体的定轴转动
第二章 动力学基础
J 0 R dm 0 R dl
2 2
L
2 πR
R
2 3
2 πR
dl
0
dl
R
O
m
m 2 2 πR mR 2 πR
15
2 – 5 刚体的定轴转动
例5 圆盘绕中心轴旋转的转动惯量。
第二章 动力学基础
m 2mr dm ds 2 2 πrdr 2 dr πR R
第二章 动力学基础
J m r r dm
2 j j 2 j
dm
:质量元
对质量线分布的刚体:
dm dl
dm dS
dm dV
:质量线密度
对质量面分布的刚体:
:质量面密度
对质量体分布的刚体:
:质量体密度
2 – 5 刚体的定轴转动
(1)用定义式计算
第二章 动力学基础
p
18
2 – 5 刚体的定轴转动
解 (1)
第二章 动力学基础
Fr J
Fr 98 0.2 39.2 rad/s2 J 0 .5
rO
mg T ma
(2)
Tr J
两者区别?
F
T
T
a r
mgr 98 0.2 2 21.8 rad/s 2 2 J mr 0.5 10 0.2
8
2 – 5 刚体的定轴转动
三、转动惯量 刚体质量不连续分布 刚体质量连续分布 确定转动惯量的三个要素: (1) 总质量; (2) 质量分布; (3) 转轴的位置。
第二章 动力学基础
J mi ri 2
J r dm
2
i
9
2 – 5 刚体的定轴转动
四. J 的计算
质量连续分布刚体的转动惯量
求:它由此下摆角
时的
l
O
角加速度和角速度。
l /2
P
22
2 – 5 刚体的定轴转动
第二章 动力学基础
解: 棒下摆为加速过程, 外力矩为重力对O 的力矩。重力作用在棒重心, 当棒处在下 l 摆 角时, 重力矩大小为:
l /2
1 M mgl sin 2
J
O
P
重力对整个棒的合力矩与全部重力集中 作用在质心所产生的力矩一样。 因此棒绕 轴O的转动惯量为:
2 – 5 刚体的定轴转动
第二章 动力学基础
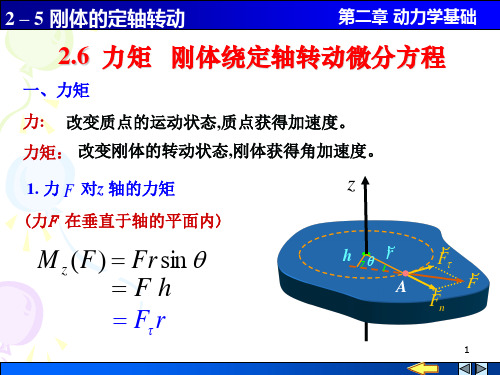
2.6 力矩 刚体绕定轴转动微分方程
一、力矩 力: 改变质点的运动状态,质点获得加速度。
力矩: 改变刚体的转动状态,刚体获得角加速度。 1. 力 F 对z 轴的力矩 (力F 在垂直于轴的平面内)
z
r
A
M z ( F ) Fr sin Fh Fτ r
解:以m1 ,m2 ,m 为研究对象,受力分析 m1:
Байду номын сангаас
第二章 动力学基础
m1 g T1 m1a1 m2: T m g m a 2 2 2 2
T2
T2 m2
m r
T1 T1
滑轮 m:
1 2 T1r T2 r J mr 2 a1 a2 a r
m1
m1 g
h θ
F Fn
F
1
2 – 5 刚体的定轴转动
第二章 动力学基础
矢量形式
M r F
z
