力矩 转动定律资料
合集下载
大学物理— 力矩 转动定律

第五版来自2.2 力矩 转动定律
j
M
ej
( m j r j )α
2
z
O
定义转动惯量
J
rj
Fej
m j
j
m jrj
2
J
r dm
2
F ij
转动定律 M J 刚体定轴转动的角加速度与它所受的合外力 矩成正比,与刚体的转动惯量成反比。
第二章 刚体的定轴转动
7
物理学
2.2 力矩 转动定律 质元受外力
M
ej
2.刚体
Fej
,内力
2 j
F ij
z
O
M ij m j r
rj
Fej
m j
外力矩
内力矩
F ij
j
M
ej
j
M
ij
j
m jrj
2
M ij M
ji
M ij 0
第二章 刚体的定轴转动
6
物理学
i
i
Mi 0
1
第二章 刚体的定轴转动
物理学
第五版
2.2 力矩 转动定律
讨论
1.若力 F 不在转动平面内,把力分解为平行和 垂直于转轴方向的两个分量 F F z F 其中 F z 对转轴的力 z 矩为零,故 F 对转轴
的力矩
M
M z k r F
2 2 2
dm
:质量元
r dV
dV
V
:体积元
第二章 刚体的定轴转动
10
j
M
ej
( m j r j )α
2
z
O
定义转动惯量
J
rj
Fej
m j
j
m jrj
2
J
r dm
2
F ij
转动定律 M J 刚体定轴转动的角加速度与它所受的合外力 矩成正比,与刚体的转动惯量成反比。
第二章 刚体的定轴转动
7
物理学
2.2 力矩 转动定律 质元受外力
M
ej
2.刚体
Fej
,内力
2 j
F ij
z
O
M ij m j r
rj
Fej
m j
外力矩
内力矩
F ij
j
M
ej
j
M
ij
j
m jrj
2
M ij M
ji
M ij 0
第二章 刚体的定轴转动
6
物理学
i
i
Mi 0
1
第二章 刚体的定轴转动
物理学
第五版
2.2 力矩 转动定律
讨论
1.若力 F 不在转动平面内,把力分解为平行和 垂直于转轴方向的两个分量 F F z F 其中 F z 对转轴的力 z 矩为零,故 F 对转轴
的力矩
M
M z k r F
2 2 2
dm
:质量元
r dV
dV
V
:体积元
第二章 刚体的定轴转动
10
力矩转动定律转动惯量解析课件

02
CATALOGUE
转动惯量基础概念
转动惯量的定义
转动惯量
描述刚体绕固定轴转动的惯性大 小的物理量。
定义公式
I = Σ(m * r^2),其中m为刚体的 质量,r为刚体上任意质点到转动 轴的距离。
转动惯量的性质
转动惯量只与刚体的质量分布 和转动轴的位置有关,与刚体 的运动状态无关。
对于同一刚体,不同的转动轴 位置,其转动惯量可能不同。
力矩转动定律转动 惯量解析课件
contents
目录
• 力矩转动定律概述 • 转动惯量基础概念 • 力矩与转动惯量的关系 • 转动惯量的计算方法 • 转动惯量的应用实例
01
CATALOGUE
力矩转动定律概述
力矩的定义
力矩是描述力的转动效果的物理量,其大小等于力和力臂的乘积。
力矩是一个向量,其大小等于力和力臂的乘积。力臂是从转动轴到力的垂直距离 。在二维平面中,力矩可以表示为M=F×r,其中F是力,r是力臂。
CATALOGUE
转动惯量的应用实例
飞轮的设计与优化
飞轮的设计
飞轮是利用转动惯量储存能量的重要 装置,其设计需要考虑转动惯量的大 小、质量分布、转速等因素。
飞轮的优化
为了提高飞轮的储能效率和稳定性, 需要对飞轮进行优化设计,如采用轻 质高强度的材料、优化飞轮的形状和 尺寸等。
陀螺仪的设计与优化
陀螺仪的设计
陀螺仪是利用角动量守恒原理工作的惯性导 航和姿态测量器件,其设计需要考虑转动轴 的稳定性、转动惯量的大小和分布等因素。
陀螺仪的优化
为了提高陀螺仪的测量精度和稳定性,需要 对陀螺仪进行优化设计,如采用高性能的轴 承材料、减小摩擦力矩等。
电机转子的设计与优化
力矩和转动定律

m σ= 2 πR ds = rdrdθ dm = σ ds = σ rdrdθ
dN = gdm = σ rgdrdθ df = dN = σ rgdrdθ dM f = rdf = σ r gdrdθ
2
M f = ∫ dM f = σ g ∫ dθ ∫ r 2 dr
0 0
2π
R
2 = mgR 3 M f = jβ 1 mR 2 2 4 g β = 3R 3R j=
三 转动惯量
J = ∑ mi ri
2
2
如果刚体连续分布
m:质点惯性的量度 : J:刚体惯性的量度 : 转动惯量是描述刚体在转动中的惯性大小的物理量 几种常见刚体的转动惯量: 有关推导详见教材 有关推导详见教材P120) 几种常见刚体的转动惯量:(有关推导详见教材 细棒 细棒
标量. 标量 J = ∫ r dm kg . m2,标量. r r 对比 F = m a M = Jβ
F2 =
r2
= j β = j dω dt cω = j dω dt dω = c dt ω j ω dω t c ∫ω0 ω =∫0 j dt
ct ω = ω0e j ct ω = ω0e j
M f = cω
练习18 练习
dθ = ω dt
t = c ln 2 j
= 1 ω0 2
jω0 c ln 2) (t = θ= j 2c θ = jω0 N= 2π 4π c
L m
1 J = mL2 + m1 L2 3
m1
质点 与刚 体组 合的 转动 惯量
R
m
r m1
1 J = mR 2 + m1 r 2 2
五,转动定律的应用 例1,一根轻绳跨过一定滑轮(滑轮 ,一根轻绳跨过一定滑轮( 视为圆盘), ),绳的两端分别 视为圆盘),绳的两端分别 悬有质量 为 m1 和 m2 的物体,m1 <m2 ,滑轮的 质量为 m ,半径为 R,所受的摩擦阻 , 绳与滑轮间无相对滑动. 力矩为 Mf ,绳与滑轮间无相对滑动. 试求:物体的加速度和绳的张力. 试求:物体的加速度和绳的张力. 已知: 已知: m1,m2 ,m, R ,Mf , 求: a , T1 , T2 解: 研究对象 m1 ,m2 ,m 建立坐标, 建立坐标,受力分析 如图 对m1 : 1 m1 g = m1a T 对m2: m 2 g T 2 = m 2 a
第四章 5力矩转动定律

第五节
力矩 转动定律
一、力矩
力与力臂的乘积。
M dF r sin F M rF sin
O d
M
r
P
F
r
根据矢量乘积法则:
A B AB sin
用矢量方法表示力矩: M r F 单位:牛顿· 米, N ·m 方向:从r沿小于角右旋到F,大拇指指向。
§5.力矩、转动定律 / 一、力矩
§5.力矩、转动定律 / 三、解题方法及应用举例
M ,R
m
h
受力分析:
以m为研究对象
mg T ma (1)
T
M ,R
以M为研究对象
TR J (2)
T
物体从静止下落时满足
h at /2
2
h
(3)
补充方程:
a R (4)
§5.力矩、转动定律 / 三、解题方法及应用举例
mg
联立方程(1)----(4)求解得:
三. 解题方法及应用举例
1.确定研究对象。 2.受力分析(只考虑对转动有影响的力矩)。 3.列方程求解(平动物体列牛顿定律方程,转 动刚体列转动定律方程和角量与线量关系)。
§5.力矩、转动定律 / 三、解题方法及应用举例
第一类问题:已知运动情况和 J ,确定运 动学和动力学的联系---- ,从而求出 M 或 F。
T1
m1
M ,R
(3)
T1
J
1 2
MR
2
§5.力矩、转动定律 / 三、解题方法及应用举例
补充方程: a R (4) 联立方程(1)---(4)求解得
a T1 T2 m1 g m1 m 2 M / 2 m1 (m 2 M / 2 ) g m1 m 2 M / 2 m 1m 2 g m1 m 2 M / 2 T1 T 2 m 1m 2 g m1 m 2
力矩 转动定律
一、力矩
力与力臂的乘积。
M dF r sin F M rF sin
O d
M
r
P
F
r
根据矢量乘积法则:
A B AB sin
用矢量方法表示力矩: M r F 单位:牛顿· 米, N ·m 方向:从r沿小于角右旋到F,大拇指指向。
§5.力矩、转动定律 / 一、力矩
§5.力矩、转动定律 / 三、解题方法及应用举例
M ,R
m
h
受力分析:
以m为研究对象
mg T ma (1)
T
M ,R
以M为研究对象
TR J (2)
T
物体从静止下落时满足
h at /2
2
h
(3)
补充方程:
a R (4)
§5.力矩、转动定律 / 三、解题方法及应用举例
mg
联立方程(1)----(4)求解得:
三. 解题方法及应用举例
1.确定研究对象。 2.受力分析(只考虑对转动有影响的力矩)。 3.列方程求解(平动物体列牛顿定律方程,转 动刚体列转动定律方程和角量与线量关系)。
§5.力矩、转动定律 / 三、解题方法及应用举例
第一类问题:已知运动情况和 J ,确定运 动学和动力学的联系---- ,从而求出 M 或 F。
T1
m1
M ,R
(3)
T1
J
1 2
MR
2
§5.力矩、转动定律 / 三、解题方法及应用举例
补充方程: a R (4) 联立方程(1)---(4)求解得
a T1 T2 m1 g m1 m 2 M / 2 m1 (m 2 M / 2 ) g m1 m 2 M / 2 m 1m 2 g m1 m 2 M / 2 T1 T 2 m 1m 2 g m1 m 2
力矩转动定律转动惯量

PB y
31
第32页/共42页
a
mB g
mA mB mC 2
解 得
FT1
mA
mAmB g mB mC
2
FT2
(mA mC 2)mB g mA mB mC 2
A mA
mC 0时: FT1 FT2
32
第33页/共42页
C mC
mB B
FT1
mA
mAmB g mB mC
2
FT2
(mA mC 2)mB g mA mB mC 2
的角加速度和角速度. M J
35
第36页/共42页
36
解: 受力分析,力矩(O)分析
重力对O点的力矩
M mgd
J
d L sin
2
有: 1 mgl sin J
2
m,l
O
θ
FN
mg
d
式中 J 1 ml2 3
得 3g sin
2l
第37页/共42页
由角加速度的定义
dω dω dθ ω dω
F
F
Fi 0 , Mi 0
M rF
M Frsin Fd
3
第4页/共42页
4、一对力偶的力矩
M Fd
F
F
ol
F 0 M 0
F'
ro
F
F 0 M 0
M F l F l Fl
22
M Fr Fr 0
4
第5页/共42页
讨论
(1)若力 F 不在转动平面内,把力分
解为平行和垂直于转轴方向的两个分量
如令 mC 0 ,可得
A mA
FT1
FT2
力矩 刚体定轴转动的转动定律
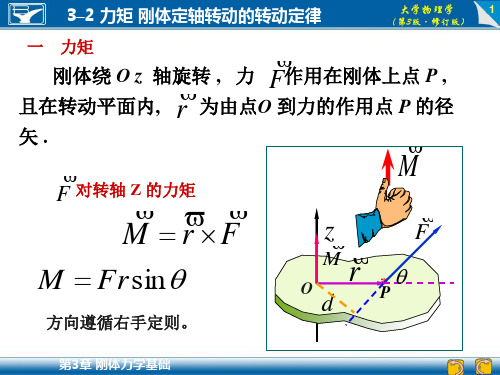
dJ R dm
2
第3章 刚体力学基础
3–2 力矩 刚体定轴转动的转动定律
12
考虑到所有质元到转轴的距离均为R,所以细圆环对 中心轴的转动惯量为
J dJ R dm R
2 m
2
m
dm mR
2
(2)求质量为m,半径为R的圆盘对中心轴的转动惯量
m 如图 dS 2 rdr , , dm dS 2 rdr 2 R
l 2
o
P
d d d d dt d dt d
代入初始条件积分 得
第3章 刚体力学基础
3g d sin d 2l 3g (1 cos ) l
1 2 J x dx ml 0 3
l 2
由此看出,同一均匀细棒,转轴位置不同,转动惯 量不同.
第3章 刚体力学基础
3–2 力矩 刚体定轴转动的转动定律
11
例3.2 设质量为m,半径为R的细圆环和均匀圆盘分 别绕通过各自中心并与圆面垂直的轴转动,求圆环和 圆盘的转动惯量. 解 (1) 在环上任 取一质元,其质量 为dm,距离为R, 则该质元对转轴的 转动惯量为
解 (1)转轴通过棒的中心并与棒垂直
m l
dm dx
dJ x 2dm x 2dx
第3章 刚体力学基础
3–2 力矩 刚体定轴转动的转动定律
10
整个棒对中心轴的转动惯量为
J dJ
l 2 l 2
1 x dx ml 2 12
2
(2)转轴通过棒一端并与棒垂直时,整个棒对该轴的 转动惯量为
解 (1) M k 2 ,故由转动定律有
k k J 即 J 2 1 k0 0 3 9J
4.3 力矩 转动定律

v −F v
i
v F
v ∑ Mi ≠ 0
i
∑ F = 0,
i
武汉纺织大学 物理教研室
大学物理学
第4章
刚体的定轴转动
讨论
v 不在转动平面内, (1)若力 F 不在转动平面内,把力分 )
解为平行和垂直于转轴方向的两个分量
力矩为零, 力矩为零,故 F 对转 轴的力矩
v 其中 Fz 对转轴的 v
v v v F = Fz + F⊥
大学物理学
第4章
刚体的定轴转动
4.3 力矩 刚体的转动定律 一 力矩
用来描述力对刚体 的转动作用. 的转动作用.
M = Fr sin θ = Fd d : 力臂 v F 对转轴 z 的力矩 v v v M = r ×F
z
v M
v F
O
v r
*
d
P
θ
v −F
i
v F
v ∑ Mi = 0
i
v ∑ Fi = 0,
M = I β , β 与 M 方向相同. 方向相同.
(2) 为瞬时关系. ) 为瞬时关系. (3) 转动中 M = I β 与平动中F = ma ) 地位相同. 地位相同.
武汉纺织大学 物理教研室
大学物理学
第4章
刚体的定轴转动
质量为m 的物体A 例2 质量为 A的物体 静止在光滑水 平面上,和一质量不计的绳索相连接, 平面上,和一质量不计的绳索相连接,绳 索跨过一半径为R、质量为m 索跨过一半径为 、质量为 C的圆柱形滑轮 C,并系在另一质量为 B 的物体 上,B 竖 ,并系在另一质量为m 的物体B上 直悬挂.滑轮与绳索间无滑动, 直悬挂.滑轮与绳索间无滑动, 且滑轮与 轴承间的摩擦力可略去不计. ) 轴承间的摩擦力可略去不计.(1)两物体的 线加速度为多少? 线加速度为多少? 水平和竖直两段绳索的 张力各为多少? ) 张力各为多少?(2) 物体 B 从静止落下距 其速率是多少? 离 y 时,其速率是多少?
刚体定轴转动的力矩转动定律转动惯量资料重点
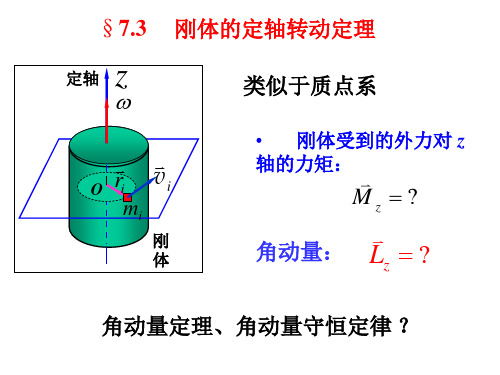
L L/ 2
12
例2、均质细圆环的转动惯量
任取线元dl , dm=dl,距离轴 r
I r2dm r2 dm mr2
例3、质量为m,半径为R 的均质圆盘的转动惯量
可看作由半径不同的圆环构成,盘面
单位面积的质量为 m R2
任取面元ds(离r 远处dr 宽细环)
R
dm 2rdr
对转动惯量的贡献为: dI r2dm 2 r3dr
5)假想将物体的质量集中在半径为 rc 的细圆环
上,而保持转动惯量不变,称这圆环半径为物体 的回转半径.
I mrc2
注意
转动惯量的大小取决于刚体的质量、形状 及转轴的位置 .
说 明:
(1)实际上只有对于形状简单、质量连续且均匀分布 的刚体,才能用积分的方法算出它们的转动惯量。
(2)对于任意刚体的转动惯量,通常是用实验的方法 测定出来的。
2、M 符号 ——使刚体向规定的转动正方向加速的力矩为正;
确定了转轴方向时, M 方向与转轴方向相同取为正;
M 方向与转轴方向相反取为负.
§ 转动惯量的计算
1、定义(对轴):
I miri2
i
(ri 为质元相对于转轴的垂直距离)
dm ➢ 物理意义:描述刚体对轴转动惯
性大小的物理量.
m
r
理论计算:
JC
J
Cdm
平行
1)对同一轴 I 具有可叠加性
I Ii
2)平行轴定理
I Ic md 2 d --两平行轴距离
2) 平行轴定理
质量为m 的刚体,如果对
其质心轴的转动惯量为 JC ,则
对任一与该轴平行,相距为 d
的转轴的转动惯量
IO IC md 2
4-3转动定律

[例2]有一均质细直杆在一个粗糙的水平 例 有一均质细直杆在一个粗糙的水平 面上可绕一条通过其一端的竖直轴旋转, 面上可绕一条通过其一端的竖直轴旋转,它 与平面之间的摩擦系数为µ 。设杆子质量为 m,长度为 l ,其初始转速为ω0 。试求当它 长度为 的转速为原来的一半时所用的时间。 的转速为原来的一半时所用的时间。 o l o´
结束
返回
4. J 和转轴有关。同一个物体对不同转 和转轴有关。 轴的转动惯量是不同的。 轴的转动惯量是不同的。 o o´ 1 ml J = 12
2
o o´ 1 ml J= 3
o 1 mr 2 J= 4 o´
o 1 mr 2 J= 2 o´
结束
返回
5*. 回转半径:假想将物体的质量集中在 回转半径: 的细圆环上, 半径为 rc 的细圆环上,而保持转动惯量不 回转半径。 称这圆环半径为物体的回转半径 变,称这圆环半径为物体的回转半径。即任 何物体的转动惯量为: 何物体的转动惯量为: J = mrc o
ห้องสมุดไป่ตู้结束
1 µ 1 ml 2 d ω mg l = dt 2 3 3µ g dt = d ω 2l 3µ g t ∫ 0 dt = 2l
∫ω dω
2 0
ω0
3µ g ω ω t= 2 2l
0
0
∴
ωl t= 3µ g
0 结束
返回
[例3]有一高为 ,宽为 ,质量为 的 例 有一高为 有一高为h,宽为b 质量为m 均质平板可绕一条通过其一端的竖直轴旋转, 均质平板可绕一条通过其一端的竖直轴旋转, 板上面元所受到的阻力和面元的大小与面元 的速度平方乘积成正比,比例系数为k 。板 的速度平方乘积成正比,比例系数为 的初始角速度为ω0 。 试求其角速度变化规律。 试求其角速度变化规律。 o b m
力矩转动定律转动惯量ppt
物理学教程 (第二版)
* 例4 如图一斜面长 l = 1.5m, 与水平面的夹角 = 5o.
有两个物体分别静止地位于斜面的顶端, 然后由顶端沿
斜面向下滚动, 一个物体是质量 m1 = 0.65kg、半径为R1 的实心圆柱体, 另一物体是质量为 m2 = 0.13 kg 、半径 R2 = R1 = R 的薄壁圆柱筒. 它们分别由斜面顶端滚到斜 面底部各经历多长时间?
直放置的细杆处于非稳定平衡状态,当其受到微小扰
动时,细杆将在重力作用下由静止开始绕铰链O 转动.
试计算细杆转动到与竖直线成 角时的角加速度和角
速度.
解 细杆受重力和
铰链对细杆的约束力
FN
作用,由转动定律得
1 mgl sin J
2
m FN
l2
l oP
第四章 刚体转动
4 – 2 力矩 转动定律 转动惯量
圆盘绕圆心转动
力矩可以反映力的作用点的位置对物体运动的影响.
第四章 刚体转动
4 – 2 力矩 转动定律 转动惯量
物理学教程 (第二版)
一 力矩
刚体绕 O z 轴旋 转 , 力 F 作用在刚体上点 P ,
且在转动平面内,
矢.
r
为由点O 到力的作用点 P 的径 M
F
对转轴Z
的力矩
M rF
M Frsin Fd
例2 有一半径为R质量为 m 匀质圆盘, 以角速度ω0绕
通过圆心垂直圆盘平面的轴转动.若有一个与圆盘大小相
同的粗糙平面(俗称刹车片)挤压此转动圆盘,故而有正压
力N 均匀地作用在盘面上, 从而使其转速逐渐变慢.设正
压力N 和刹车片与圆盘间的摩擦系数均已被实验测出.试
问经过多长时间圆盘才停止转动?
力矩转动定律转动惯量jm汇总课件

力矩的物理意义
总结词
力矩描述了力使物体绕某点转动的趋势或转动效果。
详细描述
力矩决定了物体绕某点转动的趋势或转动效果,其方向与力和力臂的乘积方向 相同。力矩越大,物体转动的趋势或转动效果越明显。
力矩的计算方法
总结词
力矩的大小等于力和力臂的乘积,计中力臂是从转动轴(或转动中心)到力的垂 直距离。计算公式为 M=FL,其中 M 为力矩,F 为力,L 为力臂。同时,力矩的 方向与力和力臂的乘积方向相同。
转动惯量的大小决定了物体旋转运动 的加速度、角速度和角动量等参数的 变化规律,进而影响物体的运动状态 和稳定性。
转动惯量的计算方法
转动惯量的计算方法主要包括平行轴定理和垂直轴定理。
平行轴定理指出,对于一个质量分布均匀的刚体,其相对于某固定轴的转动惯量,等于该刚体的质量乘以质心到该轴的距离 的平方,再加上所有相对于此轴的离散质量的转动惯量之和。垂直轴定理则说明,一个质量分布均匀的刚体相对于任一垂直 于其对称平面的轴的转动惯量,等于该刚体的质量乘以其对称轴到质心的距离的平方。
车辆工程
在车辆工程中,力矩转动定律用于分析车辆动力学和稳定性 问题。例如,通过分析车轮的力矩,可以研究车辆的操控性 能和行驶稳定性。
力矩转动定律在科研中的应用
物理学研究
力矩转动定律是物理学中分析转 动问题的基本原理,广泛应用于 分析天体运动、刚体动力学等问 题。
生物学研究
在生物学研究中,力矩转动定律 用于分析生物体的运动和平衡机 制,如动物的行走、飞行等。
动惯量。
实验步骤
2. 将刚体安装到实验装置上 ,调整力矩计和角位移传感
器的位置和角度。
1. 准备实验器材:刚体、力 矩计、角位移传感器、数据
刚体定轴转动的转动定律力矩-文档资料

讨论 (1) 合力矩的功 2 2 2 A M d ( M )d M d A i i i 1 1 1 i i i (2) 力矩的功就是力的功。
Δmk 的动能为 1 2 1 2 2 E Δ m v Δ m r k k k k k 2 2
刚体的总动能
z
O
rk
P
vk
• Δ mk
1 2 2 1 2 2 1 2 E E Δ m r Δ m r J k kk kk 2 2 2 结论 绕定轴转动刚体的动能等于刚体对转轴的转动惯量与其 角速度平方乘积的一半
r
A
(力对轴的力矩只有两个指向)
F F
2. 刚体定轴转动的转动定律 k k
rk
fk
Fk
F f m a k k k k
在上式两边同乘以 rk 对所有质元求和
F r f r m a r m r r k k k k k k k k k k
求 (1) 飞轮的角加速度 (2) 如以重量P =98 N的物体挂在绳
端,试计算飞轮的角加速 解 (1) Fr J
Fr 98 0 . 2 2 39 . 2 rad/s J 0 . 5
mgr 2 J mr
两者区别
rO
T F
T ma (2) mg
Tr J
kk kk 2 k k
F r f r ( m r )
内力矩之和为0 转动惯量 J
刚体绕定轴转动微分方程(刚体的转动定律)
M J
与牛顿第二定律比较: M F , J m , a
3. 转动惯量 定义
力矩转动定律转动惯量

有
解 (1) 用隔离法分别对各物体作受力分析,取如图所示坐标系.
A
B
C
O
O
O
O
解得:
如令 ,可得
B由静止出发作匀加速直线运动,下落的速率
稳定平衡状态,当其受到微小扰动时,细杆将在重力作用下由静止开始绕铰链O 转动.试计算细杆转动到与竖直线成 角时的角加速度和角速度.
同一刚体,转轴位置不同,J 就不相同
质量离散分布
J 的计算方法
质量连续分布
:质量元
:体积元
例.求长L,质量m均匀细棒的转动惯量. (1)O轴通过棒一端且与棒垂直;(2)O'轴通过棒中点且与棒垂直.
x
dx
O
O'
解: 取轴为坐标原点, 取长度微元如图
dm=dx,
=m/L
例3 一长为 l 、质量为 m 匀质细杆竖直放置,其下端与一固定铰链O相接,并可绕其转动.由于此竖直放置的细杆处于非
m,l
O
mg
θ
解 细杆受重力和铰链对细杆的约束力 作用,由转动定律得
式中
得
m,l
O
mg
θ
由角加速度的定义
对上式积分,利用初始条件,
m,l
O
mg
θ
解得:
dJ=r2dm
=x2dx
(1)过棒的一端O
=L3/3
=mL2/3
(2)过棒的中点O'
=x3/3
=L3/12
=mL2/12
结果表明: 同一刚体对不同位置的转轴,转动惯量并不相同。
例题 求圆盘对于通过中心并与盘面垂直的转轴的 转动惯量。设圆盘的半径为R,质量为m,密度均匀。
r
R
解 (1) 用隔离法分别对各物体作受力分析,取如图所示坐标系.
A
B
C
O
O
O
O
解得:
如令 ,可得
B由静止出发作匀加速直线运动,下落的速率
稳定平衡状态,当其受到微小扰动时,细杆将在重力作用下由静止开始绕铰链O 转动.试计算细杆转动到与竖直线成 角时的角加速度和角速度.
同一刚体,转轴位置不同,J 就不相同
质量离散分布
J 的计算方法
质量连续分布
:质量元
:体积元
例.求长L,质量m均匀细棒的转动惯量. (1)O轴通过棒一端且与棒垂直;(2)O'轴通过棒中点且与棒垂直.
x
dx
O
O'
解: 取轴为坐标原点, 取长度微元如图
dm=dx,
=m/L
例3 一长为 l 、质量为 m 匀质细杆竖直放置,其下端与一固定铰链O相接,并可绕其转动.由于此竖直放置的细杆处于非
m,l
O
mg
θ
解 细杆受重力和铰链对细杆的约束力 作用,由转动定律得
式中
得
m,l
O
mg
θ
由角加速度的定义
对上式积分,利用初始条件,
m,l
O
mg
θ
解得:
dJ=r2dm
=x2dx
(1)过棒的一端O
=L3/3
=mL2/3
(2)过棒的中点O'
=x3/3
=L3/12
=mL2/12
结果表明: 同一刚体对不同位置的转轴,转动惯量并不相同。
例题 求圆盘对于通过中心并与盘面垂直的转轴的 转动惯量。设圆盘的半径为R,质量为m,密度均匀。
r
R
2.2 力矩 转动定律 转动惯量
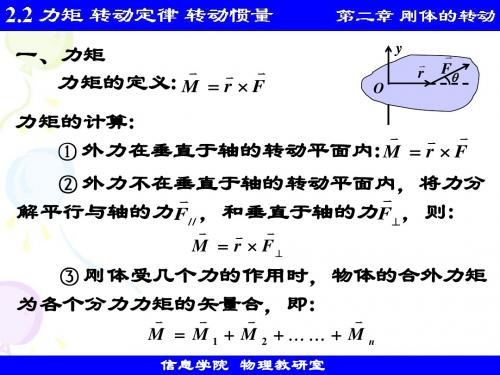
二、转动定律和转动惯量 由牛顿第二定律得: 如图,由牛顿第二定律得
Fi + f i = ∆m i a i
分解可得: 分解可得 切向: 切向 Fi sin θ i + f i sin φ i = ∆m i a it = ∆m i riα 法向: 法向 − ( Fi cos θ i + f i cos φ i ) = ∆m i a in = ∆m i riω 2 在切向表达式中的每一项都乘以r 在切向表达式中的每一项都乘以 i得:
一、力矩 力矩的定义: 力矩的定义 M = r × F
y
O
r Fθ
力矩的计算: 力矩的计算 外力在垂直于轴的转动平面内: ① 外力在垂直于轴的转动平面内 M = r × F 外力不在垂直于轴的转动平面内, ② 外力不在垂直于轴的转动平面内,将力分 解平行与轴的力 F// ,和垂直于轴的力 F⊥,则:
J = ∫ r dm
2
A L
dx
B X
=∫
1 l 2 1 − l 2
1 2 2 λx dx = ml 12
2
l 2
(2)建立图示坐标系,取为分元 ,则: 建立图示坐标系,取为分元dx,
1 2 J = ∫ r dm = ∫ λx dx = ml 0 3
信息学院 物理教研室
例题: 质量为m, 的细圆环, 例题 质量为 ,半径为R 的细圆环,转轴过环心 且垂直于环面,求转动惯量。 且垂直于环面,求转动惯量。 取图示微分元dm, 解: 取图示微分元 ,则: y
信息学院 物理教研室
转动惯量 数学表达式: 数学表达式 J = ∑ ∆mi ri2
单位: 单位 kg ⋅ m
2
物理意义---描述刚体在转动中的惯性大小的 物理意义 描述刚体在转动中的惯性大小的 量度,是维持转动状态不变的原因。 量度,是维持转动状态不变的原因。决定转动惯 量大小的因素: 量大小的因素 刚体的质量 转轴的位置 刚体的质量分布 质量、 位置、 刚体的质量、转轴的位置、刚体的质量分布 的计算: 转动惯量J 的计算 刚体质量不连续: ① 刚体质量不连续 J = ∑ m i ri2 刚体质量连续分布: ② 刚体质量连续分布 J = r 2 dm = r 2 ρdv ∫ ∫
9 力矩 转动定律

r fi
ω
i
o ri
∑r Fτ + ∑r f τ = (∑∆m r
i i i i i i
i=1
n
2
i i
)α
fiτ
∆ mi
Fiτ
τ
∴
∑r Fτ = Jα
i=1 i i
n
Mz = Jα
( 转动定律 )
1. Mz = Iα 反映了力矩 Mz与角加速度 α 间的瞬时关系。 间的瞬时关系。 瞬时关系 2. 矢量关系(但在定轴转动中力矩只有两个方向)。 矢量关系(但在定轴转动中力矩只有两个方向 只有两个方向)。 3. Mz、I、α 皆对同一轴而言。 同一轴而言 而言。 4. 综合解题时,除了考虑运用牛顿定律外, 还需考 综合解题时,除了考虑运用牛顿定律外, 虑刚体的转动定律。 虑刚体的转动定律。 转动定律
I = ∫ r 2 dm
绕细杆边缘轴的转动惯量为 m l 1 2 I = ml o 3
通过棒中心并与棒垂直的轴的转动惯量
1 I = ml 2 12
m l o
过圆盘中心轴的转动惯量为
1 2 I = mR 2
m
R
过圆环中心轴的转动惯量为
I = mR
2
m
R
平行轴定理 定理表述: 定理表述:刚体绕平行于质心轴的转动惯 量 I,等于绕质心轴的转动惯量 IC 加上刚 , 体质量与两轴间的距离平方的乘积。 体质量与两轴间的距离平方的乘积。 IC I 2 I = I C + md 刚体绕质心轴 的转动惯量最小。 的转动惯量最小。
在总质量一定的情况下, 在总质量一定的情况下, 越大。 质量分布离轴越远 I与转轴的位置有关。 与转轴的位置有关
刚体的动能
ω
i
o ri
∑r Fτ + ∑r f τ = (∑∆m r
i i i i i i
i=1
n
2
i i
)α
fiτ
∆ mi
Fiτ
τ
∴
∑r Fτ = Jα
i=1 i i
n
Mz = Jα
( 转动定律 )
1. Mz = Iα 反映了力矩 Mz与角加速度 α 间的瞬时关系。 间的瞬时关系。 瞬时关系 2. 矢量关系(但在定轴转动中力矩只有两个方向)。 矢量关系(但在定轴转动中力矩只有两个方向 只有两个方向)。 3. Mz、I、α 皆对同一轴而言。 同一轴而言 而言。 4. 综合解题时,除了考虑运用牛顿定律外, 还需考 综合解题时,除了考虑运用牛顿定律外, 虑刚体的转动定律。 虑刚体的转动定律。 转动定律
I = ∫ r 2 dm
绕细杆边缘轴的转动惯量为 m l 1 2 I = ml o 3
通过棒中心并与棒垂直的轴的转动惯量
1 I = ml 2 12
m l o
过圆盘中心轴的转动惯量为
1 2 I = mR 2
m
R
过圆环中心轴的转动惯量为
I = mR
2
m
R
平行轴定理 定理表述: 定理表述:刚体绕平行于质心轴的转动惯 量 I,等于绕质心轴的转动惯量 IC 加上刚 , 体质量与两轴间的距离平方的乘积。 体质量与两轴间的距离平方的乘积。 IC I 2 I = I C + md 刚体绕质心轴 的转动惯量最小。 的转动惯量最小。
在总质量一定的情况下, 在总质量一定的情况下, 越大。 质量分布离轴越远 I与转轴的位置有关。 与转轴的位置有关
刚体的动能
§4.3 力矩 转动定律(打印稿)

1 M = mgl cosθ 2
)θ
M = Jα = 1 ml 2 ⋅ dω⋅ dθ dθ dt 3
3g ωdω = cosθ dθ 2l
ω
l 2
θ
m、 、 l C
mg
3g 3g ∫ ωdω = ∫ 2l cosθ dθ ∴ ω= l sinθ 0 0
θ
(解毕)
10 ·
Chapter 4. 刚体的转动
i=1 i i
n
Mz = Jα
( 转动定律 )
5·
Chapter 4. 刚体的转动
§4. 3 力矩 转动定律
明确几点
1. Mz = Jα 反映了力矩 Mz与角加速度 α 间的 间的瞬时关系。 。 2. 矢量关系(但在定轴转动中力矩 (但在定轴转动中力矩只有两个方向)。 )。 3. Mz、J、α皆对同一轴而言。 而言。 4. 综合解题时,除了考虑运用牛顿定律外, 还需考 综合解题时,除了考虑运用牛顿定律外, 虑刚体的转动定律。 虑刚体的 。
m1 g −T1 = m1a
m2
T2
T2 = m2a (T −T2 )R = Jα = 1 M α R 1 2 a= Rα
2
T2 M, R T 1
a
T 1
m1
2g a= 4+ M / m
{
( 2 + M / m) T1 = mg 4+ M / m 2mg T2 = (解毕) 4+ M / m
m1 g
Chapter 4. 刚体的转动
§4. 3 力矩 转动定律
§4.3 力矩
转动定律
1·
Chapter 4. 刚体的转动
§4. 3 力矩 转动定律
一、作用在刚体上的力矩
)θ
M = Jα = 1 ml 2 ⋅ dω⋅ dθ dθ dt 3
3g ωdω = cosθ dθ 2l
ω
l 2
θ
m、 、 l C
mg
3g 3g ∫ ωdω = ∫ 2l cosθ dθ ∴ ω= l sinθ 0 0
θ
(解毕)
10 ·
Chapter 4. 刚体的转动
i=1 i i
n
Mz = Jα
( 转动定律 )
5·
Chapter 4. 刚体的转动
§4. 3 力矩 转动定律
明确几点
1. Mz = Jα 反映了力矩 Mz与角加速度 α 间的 间的瞬时关系。 。 2. 矢量关系(但在定轴转动中力矩 (但在定轴转动中力矩只有两个方向)。 )。 3. Mz、J、α皆对同一轴而言。 而言。 4. 综合解题时,除了考虑运用牛顿定律外, 还需考 综合解题时,除了考虑运用牛顿定律外, 虑刚体的转动定律。 虑刚体的 。
m1 g −T1 = m1a
m2
T2
T2 = m2a (T −T2 )R = Jα = 1 M α R 1 2 a= Rα
2
T2 M, R T 1
a
T 1
m1
2g a= 4+ M / m
{
( 2 + M / m) T1 = mg 4+ M / m 2mg T2 = (解毕) 4+ M / m
m1 g
Chapter 4. 刚体的转动
§4. 3 力矩 转动定律
§4.3 力矩
转动定律
1·
Chapter 4. 刚体的转动
§4. 3 力矩 转动定律
一、作用在刚体上的力矩
力矩刚体绕定轴转动定律

求: 到圆盘静止所需时间。
解: 取宽为dr的细圆环 其质量为
dm
σdS
π
m R2
2π
rdr
dm 摩擦力 df gdm
dr r
df
df 的力矩 dM rdf
圆盘摩擦力矩 M
R
dM
2
mgR
0
3
转动定律 M J d
dM
2 mgR 1 mR2 d
3
2 dt
dt
t
0
dt
0
0
3R d 4g
t 3R0 4g
解: (1) M J
M Fr Fr 39.2[rad / s2 ]
J
(2) mg T ma
Tr J
a r
21.8[rad / s2 ]
rO
T
F
mg
例: 均匀细直棒m 、l ,可绕轴 O 在竖直平面内转动
初始时它在水平位置
求: 它由此下摆 角时的
解: dm 质元 dm m dx l
三、 转动惯量的计算
J miri2
质量连续分布物体 J r2dm
例: 求均质细棒(L, M ),绕端点轴 z 和质心轴 z 的转
动惯量。
解:质元质量 dm M dx L
质元转动惯量 dJ z x2dm
z
z
dx
x
o
x L/2-x
Jz
dJ L x2 M dx ML2
0L
3
Jz'
J
m
dJ
0
R 0
2m R2
r 3dr
1 2
mR2
dr m
r o
R
转动惯量取决于转轴、刚体形状及质量,它反映了 质量相对转轴在空间的分布。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.3 力矩
转动定律
——寻求类似于牛顿定律、确定刚体 在外力矩作用下运动状态发生变化的 规律——转动定律。
(一)刚体定轴转动的力矩 1 .对固定点的力矩 M r F
2 .对固定转轴的力矩 (1)力垂直于转轴 这种情况相当于质点绕固定 点O 转动的情形, 可用上面公式. (2)力与转轴不垂直 可以把力分解为平行于转轴的 分量和垂直于转轴的分量. 平行于转轴的力不产生转动效 果,该力对转轴的力矩为零.
R
m dm ds 2rdr 2 R dM r dF rgdmk m rg 2 2rdrk R
(二)转动定律
要揭示转动惯量的物理意义,实际上是要找到一 个类似于牛顿定律的、确定刚体在外力矩作用下运动 状态发生变化的规律——转动定律。
质点的牛顿运动定律:
o
v
ΔLi ri Δmi vi ri Δmi ri Δmi ri ω
2
刚体的总角动量,应为组成刚体的所有质元的角 动量的矢量和。由于刚体作定轴转动时,各质点对定 轴的角动量都具有相同的方向(沿转轴方向),因此
L ΔLi ( Δmi ri ) Iω
2
i
矢量式:
i
L I
M 合 r dF
(5) 刚体内作用力和反作用力的力矩互相抵消,即 内力矩之和总是为零。
M ij
O
M ji
d
ri
F ji iF
ij
rj
j
M ij M ji , M 合内力 Mij 0
i, j
例1:一匀质细杆,长为 l 质量为 m ,在摩擦系数为 的水平桌面上转动,求摩擦力的力矩 M阻。
M阻 dM阻
l 0
大小 dM阻 dmgx
方向沿 -z 轴 1 1 2 gl mgl 2 2
细杆受的阻力矩:
gxdx
例2)现有一质量为m,半径为R的匀质薄圆盘在 平面内以角速度ω转动,求摩擦力产生的力矩。 ω
r
dr 解: 取细圆环为质元
m 2 2 M dM g 2 2r dr gmR R 3 0
解:摩擦力沿杆连续分布,杆上各质元均受摩擦力作用, 但各质元受的摩擦阻力矩不同。 z 如图建立坐标系,分割质元。
细杆的质量密度 m / l 质元的质量 dm dx 质元受摩擦阻力矩:
l dm o x m dx
y
x
r xi , dF dmg j dM阻 r dF dmgxk
例1: 一质量为 m1 的物体绕在一半径为 r 质量为 m2 的圆 盘上, 开始时静止, 求重物的加速度、绳中的张力和 t 时 刻重物下降多高? (绳的质量与轴上的磨擦力不计). 已知: m1 、m2、r N 求:a、T、h r + r T m2 T’ 解:取刚体顺时针转 T’ 动、m1 向下运动为 T m1g m2g a 正方向. m1 隔离物体,分析受力
质点系的角动量定理:
dp F dt dL M外 dt
应用于刚体 => 转动定律 问题归结为确定刚体的角动量。
1. 定轴转动刚体的角动量 (a) 质点对点的角动量 L r p r mv
作圆周运动质点的角动量 L= rmv
Z
ri
P
பைடு நூலகம்
(b) 定轴转动刚体的角动量 在以角速度ω作定轴转动的刚体内, 取 质元 mi , 则其对OZ 轴的角动量为
i i
M 合 M i=r1 F1 r2 F2 rN FN
i
(b) 以上公式中, 力都应理解为垂直于转轴的分量, 下同.
(4) 若作用在刚体各处的力是连续分布的,可将 刚体分割成很多小质元,先求作用在每个质 元上的元力矩,再对所有元力矩求和
M I
M
M
纸风车
电风扇
没事!
不敢!
怎么解释?
M I I ,
I小,速度慢,用很小 阻力矩就可以停下
I大,速度快,用很 大阻力矩才能停下
飞轮的质量为什么 大都分布于外轮缘? 飞轮是一种惯性装置,是连接在曲轴上的一个 盘状的构件,它依靠较大的转动惯性来维持发 动机的平稳转动。
由刚体转动定律
2. 转动定律
质点系的角动量定理: 应用于定轴转动刚体:
M外
dL dt
刚体的角动量:
L I
刚体的转动定律: d dL d ( I ) M外 I I dt dt dt dp 比较:质点的牛顿运动定律 F ma dt
M O r
d P
F
r
z M
o
F∥
F θ
F⊥
M r F 方向:沿转 大小:M rF sin 轴方向.
r
转动平面
转轴
(3) 若刚体受N个外力作用, F1 , F2 , , FN
ri Fi M i i i 注意: (a) M 合 ri Fi
刚体的转动定律:绕某定轴转动的刚体,所 受合外力矩等于刚体对该轴的转动惯量与角 加速度的乘积,方向沿转轴。
M I
说明: 1) 是矢量式(在定轴转动中力矩只有两个方向)
2) M , I , 应是对同一轴而言的;
3)转动定律是瞬时对应关系;
4) 刚体转动定律的地位与牛顿第二定律相当。
M I
设杆子倾斜 角,则
M 外 mgLsin L
1 2 I mL L2 3 g 1 3 sin L L
L
即:杆越长, 角加 速度越小, 状态越 不容改变 ( 惯性 大), 因而越安全.
mg
支撑点 (肩膀)
竿 子 长 些 还 是 短 些 较 安 全 ?
5)转动定律说明了I 是物体转动惯性大小的量 度。因为: M一定时I I 即I 越大的物体,保持原来转动状态的性质就 越强,转动惯性就越大;反之,I 越小,越容 易改变状态,保持原有状态的能力越弱。或者 说转动惯性越小。
如一个外径和质量相同的实心圆柱与 空心圆筒,若受力和力矩一样,谁转 动得快些呢?
转动定律
——寻求类似于牛顿定律、确定刚体 在外力矩作用下运动状态发生变化的 规律——转动定律。
(一)刚体定轴转动的力矩 1 .对固定点的力矩 M r F
2 .对固定转轴的力矩 (1)力垂直于转轴 这种情况相当于质点绕固定 点O 转动的情形, 可用上面公式. (2)力与转轴不垂直 可以把力分解为平行于转轴的 分量和垂直于转轴的分量. 平行于转轴的力不产生转动效 果,该力对转轴的力矩为零.
R
m dm ds 2rdr 2 R dM r dF rgdmk m rg 2 2rdrk R
(二)转动定律
要揭示转动惯量的物理意义,实际上是要找到一 个类似于牛顿定律的、确定刚体在外力矩作用下运动 状态发生变化的规律——转动定律。
质点的牛顿运动定律:
o
v
ΔLi ri Δmi vi ri Δmi ri Δmi ri ω
2
刚体的总角动量,应为组成刚体的所有质元的角 动量的矢量和。由于刚体作定轴转动时,各质点对定 轴的角动量都具有相同的方向(沿转轴方向),因此
L ΔLi ( Δmi ri ) Iω
2
i
矢量式:
i
L I
M 合 r dF
(5) 刚体内作用力和反作用力的力矩互相抵消,即 内力矩之和总是为零。
M ij
O
M ji
d
ri
F ji iF
ij
rj
j
M ij M ji , M 合内力 Mij 0
i, j
例1:一匀质细杆,长为 l 质量为 m ,在摩擦系数为 的水平桌面上转动,求摩擦力的力矩 M阻。
M阻 dM阻
l 0
大小 dM阻 dmgx
方向沿 -z 轴 1 1 2 gl mgl 2 2
细杆受的阻力矩:
gxdx
例2)现有一质量为m,半径为R的匀质薄圆盘在 平面内以角速度ω转动,求摩擦力产生的力矩。 ω
r
dr 解: 取细圆环为质元
m 2 2 M dM g 2 2r dr gmR R 3 0
解:摩擦力沿杆连续分布,杆上各质元均受摩擦力作用, 但各质元受的摩擦阻力矩不同。 z 如图建立坐标系,分割质元。
细杆的质量密度 m / l 质元的质量 dm dx 质元受摩擦阻力矩:
l dm o x m dx
y
x
r xi , dF dmg j dM阻 r dF dmgxk
例1: 一质量为 m1 的物体绕在一半径为 r 质量为 m2 的圆 盘上, 开始时静止, 求重物的加速度、绳中的张力和 t 时 刻重物下降多高? (绳的质量与轴上的磨擦力不计). 已知: m1 、m2、r N 求:a、T、h r + r T m2 T’ 解:取刚体顺时针转 T’ 动、m1 向下运动为 T m1g m2g a 正方向. m1 隔离物体,分析受力
质点系的角动量定理:
dp F dt dL M外 dt
应用于刚体 => 转动定律 问题归结为确定刚体的角动量。
1. 定轴转动刚体的角动量 (a) 质点对点的角动量 L r p r mv
作圆周运动质点的角动量 L= rmv
Z
ri
P
பைடு நூலகம்
(b) 定轴转动刚体的角动量 在以角速度ω作定轴转动的刚体内, 取 质元 mi , 则其对OZ 轴的角动量为
i i
M 合 M i=r1 F1 r2 F2 rN FN
i
(b) 以上公式中, 力都应理解为垂直于转轴的分量, 下同.
(4) 若作用在刚体各处的力是连续分布的,可将 刚体分割成很多小质元,先求作用在每个质 元上的元力矩,再对所有元力矩求和
M I
M
M
纸风车
电风扇
没事!
不敢!
怎么解释?
M I I ,
I小,速度慢,用很小 阻力矩就可以停下
I大,速度快,用很 大阻力矩才能停下
飞轮的质量为什么 大都分布于外轮缘? 飞轮是一种惯性装置,是连接在曲轴上的一个 盘状的构件,它依靠较大的转动惯性来维持发 动机的平稳转动。
由刚体转动定律
2. 转动定律
质点系的角动量定理: 应用于定轴转动刚体:
M外
dL dt
刚体的角动量:
L I
刚体的转动定律: d dL d ( I ) M外 I I dt dt dt dp 比较:质点的牛顿运动定律 F ma dt
M O r
d P
F
r
z M
o
F∥
F θ
F⊥
M r F 方向:沿转 大小:M rF sin 轴方向.
r
转动平面
转轴
(3) 若刚体受N个外力作用, F1 , F2 , , FN
ri Fi M i i i 注意: (a) M 合 ri Fi
刚体的转动定律:绕某定轴转动的刚体,所 受合外力矩等于刚体对该轴的转动惯量与角 加速度的乘积,方向沿转轴。
M I
说明: 1) 是矢量式(在定轴转动中力矩只有两个方向)
2) M , I , 应是对同一轴而言的;
3)转动定律是瞬时对应关系;
4) 刚体转动定律的地位与牛顿第二定律相当。
M I
设杆子倾斜 角,则
M 外 mgLsin L
1 2 I mL L2 3 g 1 3 sin L L
L
即:杆越长, 角加 速度越小, 状态越 不容改变 ( 惯性 大), 因而越安全.
mg
支撑点 (肩膀)
竿 子 长 些 还 是 短 些 较 安 全 ?
5)转动定律说明了I 是物体转动惯性大小的量 度。因为: M一定时I I 即I 越大的物体,保持原来转动状态的性质就 越强,转动惯性就越大;反之,I 越小,越容 易改变状态,保持原有状态的能力越弱。或者 说转动惯性越小。
如一个外径和质量相同的实心圆柱与 空心圆筒,若受力和力矩一样,谁转 动得快些呢?
