离散数学图论树共42页
合集下载
离散数学-图论-树
二叉树
• 定义:二元有序树称为二叉树.
– 每个顶点最多有两个子顶点,一般称为左子顶 点和右子顶点. – 类似地,称每个顶点的左子树和右子树. – 每个顶点的出度都是0或2,称为二叉正则树.
二叉树的性质
• 定理:设有二叉树T, (1)第i层最多有2i个顶点; (2)若T高度为h,则T最多有2h11个顶点，最 少有h个顶点; (3)树叶个数出度为2的顶点个数1.
1 2
Huffman树与最优编码
• 若以符号为树叶,符号概率为树叶的权,利 用通过Huffman算法得到的二叉树对符号 编码,则可以保证i pili最小. • 例:对1,1,2,3,5,6,7,8构造Huffman树.
7 3 2 1 1 5 6
8
编码：设 A, B, C, D 的频率（即权值）分别为 17％, 25％, 38％, 20％， 试设计哈夫曼编码（最佳前缀码/最优编码）。
最优编码
• 构成消息的各符号的使用频率是不一样 的,显然常用符号编码短一些,罕用符号编 码长一点,可以使传输的二进制位数最少. • 最优编码问题:给定符号集{a1,a2,...,am}, ai 的出现概率是pi,编码长度为li,要使i pili最 小.
例：如果需传送的电文为 ‘A B A C C D A’，它只用到四种字符， 用两位二进制编码便可分辨。假设 A, B, C, D 的编码分别为 00， 01，10，11，则上述电文便为 ‘00010010101100’（共 14 位）， 译码员按两位进行分组译码，便可恢复原来的电文。 数据的最小冗余编码问题 在编码过程通常要考虑两个问题 译码的惟一性问题
5 1 5 6 6
U 1
1 5 6 1 5 5 4 6 5 4 5 5
2
《离散数学》课件-第16章树
解：易见所求为该图的一棵最小生成树，如图所示 总造价为57
18
16.3 根树及其应用
19
定义（有向树）设D是有向图，如果D的基图是无向 树，则称D为有向树。
在有向树中最重要的是根树。 定义16.6（根树）一棵非平凡的有向树，如果恰有 一个顶点的入度为O，其余所有顶点的入度均为1,则称该 树为根树。 入度为0的顶点称为树根，入度为1出度为0的顶点称 为树叶，入度为1出度不为0的点称为内点，内点和树根统 称为分支点。 树根到一个顶点的有向通路的长度称为该顶点的层数。 层数最大顶点的层数称为树高。 平凡树也称为根树。
2
16.1 树及其性质
3
定义16.1（树和森林） 连通且无回路的无向图称为无向树，简称为树，常用
T表示树。 平凡图为树，称为平凡树。 非连通且每个连通分支是树的无向图称为森林。 T中度数为1的顶点（悬挂顶点）称为树叶，度数大于
1的顶点称为分支点。 称只有一个分支点，且分支点的度数为n-1的n（n≥3）
定义16.8（子树）设T为一棵根树，则其任一顶点v 及其后代导若将层数相同的顶点都 标定次序，则称T为有序树。
根据每个分支点的儿子数以及是否有序，可将根树 分成如下若干类：
定义（跟树分类）设T为一棵根树 （1）若T的每个分支点至多有r个儿子，则称T为r叉 树。又若r叉树是有序的，则称它为r叉有序树。 （2）若T的每个分支点恰好有r个儿子，则称T为r叉 正则树。又若r叉正则树是有序的，则称它为r叉正则有 序树。 （3）若T为r叉正则树，且每个树叶的层数均为树高， 则称T为r叉完全正则树。又若r叉完全正则树是有序的， 则称它为r叉完全正则有序树。
8
平均编码长度为：L = ∑ P( i )× l( i ) = 2.53bit i=1
18
16.3 根树及其应用
19
定义（有向树）设D是有向图，如果D的基图是无向 树，则称D为有向树。
在有向树中最重要的是根树。 定义16.6（根树）一棵非平凡的有向树，如果恰有 一个顶点的入度为O，其余所有顶点的入度均为1,则称该 树为根树。 入度为0的顶点称为树根，入度为1出度为0的顶点称 为树叶，入度为1出度不为0的点称为内点，内点和树根统 称为分支点。 树根到一个顶点的有向通路的长度称为该顶点的层数。 层数最大顶点的层数称为树高。 平凡树也称为根树。
2
16.1 树及其性质
3
定义16.1（树和森林） 连通且无回路的无向图称为无向树，简称为树，常用
T表示树。 平凡图为树，称为平凡树。 非连通且每个连通分支是树的无向图称为森林。 T中度数为1的顶点（悬挂顶点）称为树叶，度数大于
1的顶点称为分支点。 称只有一个分支点，且分支点的度数为n-1的n（n≥3）
定义16.8（子树）设T为一棵根树，则其任一顶点v 及其后代导若将层数相同的顶点都 标定次序，则称T为有序树。
根据每个分支点的儿子数以及是否有序，可将根树 分成如下若干类：
定义（跟树分类）设T为一棵根树 （1）若T的每个分支点至多有r个儿子，则称T为r叉 树。又若r叉树是有序的，则称它为r叉有序树。 （2）若T的每个分支点恰好有r个儿子，则称T为r叉 正则树。又若r叉正则树是有序的，则称它为r叉正则有 序树。 （3）若T为r叉正则树，且每个树叶的层数均为树高， 则称T为r叉完全正则树。又若r叉完全正则树是有序的， 则称它为r叉完全正则有序树。
8
平均编码长度为：L = ∑ P( i )× l( i ) = 2.53bit i=1
离散数学PPT课件 5树与生成树(ppt文档)
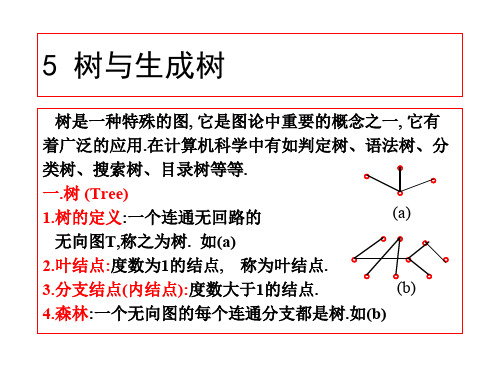
(b)
4.森林:一个无向图的每个连通分支都是树.如(b)
5.与树定义等价的几个命题
定理8-9.1给定图T,以下关于树的定义是等价的.
⑴无回路的连通图.
⑵无回路且e=v-1 其中e是T的边数,v是T的结点数.
⑶连通的且e=v-1.
⑷无回路但添加一条新边则得到一条仅有的回路.
⑸连通的,但删去任一条边,T便不连通.
v2 71
2 3 2
v3 51
v1 8 v8 7 v5 3 v4
4 2 v7 4
34 6 6 v6
Kruskal算法: 设G是有n个结点,m条边(m≥n-1)的连通图. S=Φ i=0 j=1
将所有边按照权升序排序: 43;1
⑹每对结点之间有一条且仅有一条路.
证明:⑴⑵:已知T是连通无回路图,通过不断地增加T中
的结点数,归纳证明.
当 v=2时, T如右图所示,e=1 显然e=v-1.
以后对T在保证连通又无回路的前提下每增加一个结点,
也增加一条边. 设最后T有v个结点e条边, 所以 e=v-1.
⑵⑶: 已知T是无回路的,且e=v-1.(推出T是连通的) 假设T不是连通的,设T有k个连通分支, T1,T2,...,Tk,(k≥2) 因为它的每个连通分支都是连通无回路的,所以都是树, 设Ti有结点数vi,边数ei, 所以边数 ei =vi-1 设T有v个结点,e条边. 所以
边 e78 e56 e35 e46 e67 e58 e12 e18
权4 4 5 6 6 7 7 8
v2
2 3
7 12
v3 51
v1 8 v8 7 v5 3 v4
离散数学——图论PPT课件
第19页/共93页
• 完全图：一个（n,m）图G，其n个结点中每个结点均与其它n-1个结点相邻接，记为Kn。 • 无向完全图：m=n(n-1)/2 • 有向完全图：m=n(n-1) • 举例说明以上几种图。
第20页/共93页
定义补图
• 设图G=<V,E> ， G’=<V,E’> ，若G’’=<V,E∪E’> 是完全图，且E∩E’= 空集，则称G’是G的补图。 • 事实上，G与G’互为补图。
正则图
• 所有结点均有相同次数d的图称为d次正则图。 • 如4阶的完全图是3次正则图，是对角线相连的四边形。 • 试画出两个2次正则图。
第27页/共93页
两图同构需满足的条件
• 若两个图同构，必须满足下列条件： （1）结点个数相同 （2）边数相同 （3）次数相同的结点个数相同
• 例子
第28页/共93页
• 图是人们日常生活中常见的一种信息载体，其突出的特点是直观、形象。图论，顾 名思义是运用数学手段研究图的性质的理论，但这里的图不是平面坐标系中的函数， 而是由一些点和连接这些点的线组成的结构 。
第8页/共93页
• 在图形中，只关心点与点之间是否有连线，而不关心点具体代表哪些对象，也不关 心连线的长短曲直，这就是图的概念。
定义图的子图
• 子图：设G=<V,E> ， G’=<V’,E’> ，若V’是V的子集， E’是E的子集，则 G’是G的子图。 • 真子图：若V’是V的子集，E’是E的真子集。 • 生成子图：V’=V，E’是E的子集。 • 举例说明一个图的子图。
第18页/共93页
定义（n,m）图
• (n,m)图：由n个结点，m条边组成的图。 • 零图：m=0。即（n,0）图，有n个孤立点。 • 平凡图：n=1,m=0。即只有一个孤立点。
• 完全图：一个（n,m）图G，其n个结点中每个结点均与其它n-1个结点相邻接，记为Kn。 • 无向完全图：m=n(n-1)/2 • 有向完全图：m=n(n-1) • 举例说明以上几种图。
第20页/共93页
定义补图
• 设图G=<V,E> ， G’=<V,E’> ，若G’’=<V,E∪E’> 是完全图，且E∩E’= 空集，则称G’是G的补图。 • 事实上，G与G’互为补图。
正则图
• 所有结点均有相同次数d的图称为d次正则图。 • 如4阶的完全图是3次正则图，是对角线相连的四边形。 • 试画出两个2次正则图。
第27页/共93页
两图同构需满足的条件
• 若两个图同构，必须满足下列条件： （1）结点个数相同 （2）边数相同 （3）次数相同的结点个数相同
• 例子
第28页/共93页
• 图是人们日常生活中常见的一种信息载体，其突出的特点是直观、形象。图论，顾 名思义是运用数学手段研究图的性质的理论，但这里的图不是平面坐标系中的函数， 而是由一些点和连接这些点的线组成的结构 。
第8页/共93页
• 在图形中，只关心点与点之间是否有连线，而不关心点具体代表哪些对象，也不关 心连线的长短曲直，这就是图的概念。
定义图的子图
• 子图：设G=<V,E> ， G’=<V’,E’> ，若V’是V的子集， E’是E的子集，则 G’是G的子图。 • 真子图：若V’是V的子集，E’是E的真子集。 • 生成子图：V’=V，E’是E的子集。 • 举例说明一个图的子图。
第18页/共93页
定义（n,m）图
• (n,m)图：由n个结点，m条边组成的图。 • 零图：m=0。即（n,0）图，有n个孤立点。 • 平凡图：n=1,m=0。即只有一个孤立点。
离散数学——树ppt课件
11
无向树的性质
定理16.2 设T是n阶非平凡的无向树，则T中至少有两片树叶。
证明
设T有x片树叶，由握手定理及定理16.1可知，
2(n 1) d(vi ) x 2(n x)
由上式解出x≥2。
12
例16.1
例16.1 画出6阶所有非同构的无向树。
解答 设Ti是6阶无向树。 由定理16.1可知，Ti的边数mi＝5， 由握手定理可知，∑dTi(vj)＝10，且δ(Ti)≥1，△(Ti)≤5。 于是Ti的度数列必为以下情况之一。
(1) 1，1，1，1，1，5 (2) 1，1，1，1，2，4 (3) 1，1，1，1，3，3 (4) 1，1，1，2，2，3 (5) 1，1，2，2，2，2
(4)对应两棵非同构的树， 在一棵树中两个2度顶点相邻， 在另一棵树中不相邻， 其他情况均能画出一棵非同构 的树。
13
例16.1
人们常称只有一个分支点，且分支点的度数为n-1的 n(n≥3)阶无向树为星形图，称唯一的分支点为星心。
知，G-e已不是连通图， 所以，e为桥。
9
(5)(6)
如果G是连通的且G中任何边均为桥，则G中没有回路，但在任 何两个不同的顶点之间加一条新边，在所得图中得到唯一的 一个含新边的圈。
因为G中每条边均为桥，删掉任何边，将使G变成不连通图， 所以，G中没有回路，也即G中无圈。
又由于G连通，所以G为树，由(1) (2)可知，
u,v∈V，且u≠v，则u与v之间存在唯一的路径Г，
则Г∪(u,v)（(u,v)为加的新边）为G中的圈， 显然圈是唯一的。
10
(6)(1)
如果G中没有回路，但在任何两个不同的顶点之间加一条新边， 在所得图中得到唯一的一个含新边的圈，则G是树。
无向树的性质
定理16.2 设T是n阶非平凡的无向树，则T中至少有两片树叶。
证明
设T有x片树叶，由握手定理及定理16.1可知，
2(n 1) d(vi ) x 2(n x)
由上式解出x≥2。
12
例16.1
例16.1 画出6阶所有非同构的无向树。
解答 设Ti是6阶无向树。 由定理16.1可知，Ti的边数mi＝5， 由握手定理可知，∑dTi(vj)＝10，且δ(Ti)≥1，△(Ti)≤5。 于是Ti的度数列必为以下情况之一。
(1) 1，1，1，1，1，5 (2) 1，1，1，1，2，4 (3) 1，1，1，1，3，3 (4) 1，1，1，2，2，3 (5) 1，1，2，2，2，2
(4)对应两棵非同构的树， 在一棵树中两个2度顶点相邻， 在另一棵树中不相邻， 其他情况均能画出一棵非同构 的树。
13
例16.1
人们常称只有一个分支点，且分支点的度数为n-1的 n(n≥3)阶无向树为星形图，称唯一的分支点为星心。
知，G-e已不是连通图， 所以，e为桥。
9
(5)(6)
如果G是连通的且G中任何边均为桥，则G中没有回路，但在任 何两个不同的顶点之间加一条新边，在所得图中得到唯一的 一个含新边的圈。
因为G中每条边均为桥，删掉任何边，将使G变成不连通图， 所以，G中没有回路，也即G中无圈。
又由于G连通，所以G为树，由(1) (2)可知，
u,v∈V，且u≠v，则u与v之间存在唯一的路径Г，
则Г∪(u,v)（(u,v)为加的新边）为G中的圈， 显然圈是唯一的。
10
(6)(1)
如果G中没有回路，但在任何两个不同的顶点之间加一条新边， 在所得图中得到唯一的一个含新边的圈，则G是树。
离散数学课件 第七章 树trees
第7章树trees分类§7.1 树定义1：T是集合A上一个二元关系，T称为树tree，如果存在v0∈A，任意v∈A，v≠v0，到v0都有唯一一条路径，（v0, v0） T. T叫做根树，记做（T，v0）。
A中元素称为T的顶点vertex，T中元素称为边，v0称为根root。
定理1. 设（T，v0）是树，则(a)T中没有回路。
(b)只有一个根v0。
(c)任意v∈A，v≠v0，v有入度1，v0入度是0。
证明：定义2层次levelv0的层次为0，v0的子女offspring层次为1，v0是子女的父母parent。
v i的层次为k，v i的子女offspring层次为k ＋1，v i是子女的父母parent，T的最大层次称为高度height。
无子女的顶点叫叶leaf。
v i的子女叫同胞sibling，同胞如有长幼，从左到右，老大，老二，老三等，组成线性序，T称为有序树，ordered tree定理2. 设（T，v0）是根树，则(a)T反自反。
(b)T反对称。
(c)(a,b)∈T，(b，c)∈T ⇒ (a，c)∉T。
定义3：n－树：每个顶点至多n个子女。
二叉树：2－树。
完全n－树：每个非叶顶点恰有n个子女。
定义4A rooted binary tree is a rooted tree in which every node has at most two children.A full binary tree (sometimes proper binary tree or 2-tree) is a tree in whichevery node other than the leaves has two children.A perfect binary tree is a full binary tree in which all leaves are at the same depth or same level.[1] (This is ambiguously also called a complete binary tree.)A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.[2]An infinite complete binary tree is a tree with levels, where for each level d thenumber of existing nodes at level d is equal to 2d. The cardinal number of the set of all nodes is . The cardinal number of the setof all paths is .A balanced binary tree is a tree where the depth of all the sub-trees differs by at most 1.定理3. 设（T，v0）是根树，v∈T，则T(v)是T的子树，T(v)的根是v。
离散数学ch04图论根树(课件)
04
根树的性质与算法
根树的性质
根树的定义
根树的性质1
根树的性质2
根树的性质3
根树是一种有向无环图，其中 有一个节点被指定为根节点， 其他节点按层次结构排列，从 根节点出发，每个节点恰好有 一条有向边指向其子节点。
根树的节点数等于其子树的节 点数之和加一。
根树的深度等于其最深叶子节 点的深度加一。
路径与回路
总结词
路径与回路是图论中重要的概念，路径是指一系列连续的边和顶点，回路是指起点和终点相同的路径 。
详细描述
在图论中，路径是指从起始顶点到终止顶点的一系列连续的边和顶点。每个顶点和边在路径中只出现 一次，且顺序必须一致。回路则是指起点和终点相同的路径，即路径中存在一个顶点，通过一系列的 边回到该顶点。回路在图论中具有重要意义，如在欧拉路径。
图论的重要性
图论在计算机科学、电子工程、 交通运输、生物信息学等领域有
广泛应用。
图论为复杂系统提供了统一的数 学框架，使得可以运用数学方法 和计算机技术来分析和优化这些
系统。
图论在解决实际问题中发挥了关 键作用，如路由优化、社交网络 分析、蛋白质相互作用网络等。
算法效率和复杂性的优化
在解决实际问题时，算法的效率和复杂性是关键因素。如 何优化图论和根树的算法，提高其计算效率和降低其计算 复杂性，是一个具有挑战性的问题。
THANKS
感谢观看
低运输成本。
交通控制
03
根树可以用于构建交通信号灯的控制逻辑，提高道路的通行效
率。
06
总结与展望
图论与根树的重要性和发展前景
重要应用领域
图论和根树在计算机科学、电子 工程、交通运输、生物信息学等 领域有广泛的应用，对解决实际 问题具有重要意义。
离散数学CH04_图论_根树
4.6 树
4.6 树
图中的三棵树T1，T2和T3都是带权2，2，3，3，5
的二叉树，它们的权分别是：
W(T1)=2×2＋2×2＋3×3＋5×3＋3×2=38 W(T2)=3×4＋5×4＋3×3＋2×2＋2×1=47 W(T3)=3×3＋3×3＋5×2＋2×2＋2×2=36 以上三棵树都是带权2,2,3,3,5的赋权二叉树，但不 是最优树。
【例】求图所示的二叉树产 生的前缀码。 解：在图(a)中，每一个 分枝点引出的左侧边标记0， 右侧边标记1。由根结点到 树叶的路经上各边的标记组 成的0、1序列作为对应树叶 的标记，如图 (b)所示。产 生的前缀码为： 01,11,000,0010,0011
4.6 树
定理 任意一个前缀码，都对应一个二叉树。 证明：
4.6 树
给定了一个前缀码，设h是其中最长序列的长度。画出一个高为 h的正则二叉树。按定理9.6.7中描述的办法给各边标记0或1。 每一个结点对应一个0、1序列，它是由根结点到该结点的路经 上各边的标记组成的。如果某个0、1序列是前缀码的元素，则 标记该结点。将已标记结点的所有后代和该结点的射出边全部删 除，得到了一个二叉树，再删除未加标记的树叶，就得到要求的 二叉树。
在通信中常用0、1字符串表示英文字母，即用二进制 数表示英文字母。最少用多少位二进制数就能表示26
个英文字母呢？1位二进数可以表示2=21个英文字母
，两位二进制数可以表示4=22个英文字母，……，n 位二进制数可以表示2n个英文字母。如果规定，可以 用1位二进制数表示英文字母，也可以用两位二进制数 表示英文字母。
4.6 树
定理 在完全m叉树中，其树叶数为t，分枝点数为i，则 (m1)*i=t-1。 证明：
离散数学 树共38页
谢谢
11、越是没有本领的就越加自命不凡。——邓拓 12、越是无能的人，越喜欢挑剔别人的错儿。——爱尔兰 13、知人者智，自知者明。胜人者有力，自胜者强。——老子 14、意志坚强的人能把世界放在手中像泥块一样任意揉捏。——歌德 15、最具挑战性的挑战莫过于提升自我。——迈克尔·F·斯特利
离散数学 树
51、没有哪个社会可以制订一部永远 适用的 宪法， 甚至一 条永远 适用的 法律。 ——杰 斐逊 52、法律源于人的自卫本能。——英 格索尔
53、人们通常会发现，法律就是这样 一种的 网，触 犯法律 的人， 小的可 以穿网 而过， 大的可 以破网 而出， 只有中 等的才 会坠入 网中。 ——申 斯通 54、法律就是法律它是一座雄伟的大石上。 ——高 尔斯华 绥 55、今天的法律未必明天仍是法律。 ——罗·伯顿
离散数学 第8章 树(祝清顺版)88页PPT文档
e6
e5
e3
e10
e9 e11
e6
e7 e8
e10
e11
离散数学
第八章 树
2007年8月20日
生成树的存在条件
定理3 任何无向连通图G 至少存在一棵生成树.
[证] 若连通图G中无回路, 则G为自身的生成树. 若G中包含回路, 则随意地删除回路上的一条边, 而
vVdeg(vi) =2m =2(n1). 另一方面, 设T有x片树叶, 可得
2(n1)= vVdeg(vi) ≥x+2(nx) 由上式解出x≥2.
离散数学
第八章 树
2007年8月20日
例题
例2 设T为6条边的树, 其顶点度为1, 2, 3. 如果T恰有3个 度为2的顶点，那么T有多少片树叶？并画出满足要求的 非同构的无向树. [解] 设T有x片树叶, 于是结点总数为
本章将对树进行详细的讨论，主要包括：
树的基本性质和生成树，
根树、有向树中的n元树、有序树和搜索树等。
离散数学
第八章 树
2007年8月20日
Discrete Mathematics
科学出版社
第1节 树
主讲：祝清顺 教授
树的概念
定义1 连通而无简单回路的无向图称为无向树, 简称树, 常用T表示树. 在树中度数为1的结点称为树叶, 度数大于1的结点称为分支结点.
e1
e4 e2 e7 e8
e6
e5 e3Fra biblioteke10
e9 e11
e1 e4 e2 e5
e3
e9
生成树T1
离散数学
第八章 树
离散数学课件-无向树
12
(5) (6)的证明
如果G连通且每条边均为桥，则G中任意两个结点之间存在 惟一的路径。 证明 由G是连通的可知，任意两个结点间有一条路， 若存在两点它们之间有多于一条的路， 则G中必有回路， 删去该回路上任一边， 图仍是连通的， 与G中每条边都是桥矛盾。
13
(6) (1)的证明
如果G中任意两个结点之间存在惟一的路径，则G是无回路 的连通图。 证明 因为任意两结点间有唯一条路，则图G必连通。 若G有回路， 则在回路上任意两结点间有两条路， 与已知矛盾。
6 b 5
删除边6
a
2 (c)
e
最小生成树
对无向图或有向图的每一条边e附加一个实数w(e), 称作边e 的权. 图连同附加在边上的权称作赋权图, 记作G=<V,E,W>. 设G是G的子图, G所有边的权的和称作G的权, 记作W(G).
最小生成树: 赋权图的权最小的生成树
求最小生成树的算法——避圈法 (克鲁斯卡尔/Kruskal算法) 设G=<V,E,W>, 将非环边按权从小到大排序：e1, e2, …, em. (1) 把e1加入T中 (2) 检查e2, 若e2与e1不构成回路, 则将e2加入T中, 否则弃去e2. (3) 检查e3,…, 重复进行直至得到生成树为止.
11
(4) (5)的证明
如果G中无回路, 但增加一条新边，得到一个且仅有一个包含 新边的回路，则G连通且每条边均为桥。 证明 反证法。 假设G不连通， 则存在结点ui与uj，在ui和uj之间没有路， 所以增加边(ui,uj)不会产生回路，与已知矛盾。 由于G无回路，故删掉任意条边e都使G-e为非连通， 所以G中每条边都是桥。
从连通图从连通图ggee中的某一顶点中的某一顶点uu出出发选择与它关联的具有最小权值的边发选择与它关联的具有最小权值的边uu00vv将其顶点加入到将其顶点加入到生成树的顶点集合生成树的顶点集合uu中
离散数学 第9章_树
是 v1 v5,v7,v8,v9,v10,v11
v2,v3,v4,v6
否
§9.2.1 基本概念
二、有向树的性质 设有向树T=<V,E>, |V|=n, |E|=m，则:
① T 中无回路； ② T 是连通图； ③ m = n 1； ④ 删去T中任何一条边后，所得到的图不连通。
避圈法 破圈法
求最小生成树 (方法一)
Kruskal避圈算法 (从边的角度) (1)将各条边按照权值从小到大的顺序排列； (2)依次选取权值最小并且没有造成回路的边； (3)总共选取n-1条边（n为图中的结点数）。
求最小生成树(方法二)
破圈法 (从边的角度) 每次删去回路中权最大的边。
举例
（3） 由性质②来推证性质③。 对结点数进行归纳。 当n = 2时，m = n 1 = 1，由T的连通性质，T没有回路。如果两个结点之 间增加一条边，就只能得到唯一的一个基本回路。 假设n = k时，命题成立。则当n = k + 1时，因为T是连通的并有(n1)条边 ，所以每个结点的度数都至少为1，且至少有一个结点的度数为1。否则 ，如果每个结点的度数都至少为2 ，那么必然会有结点的总度数2m 2n ，即m n。这与m = n 1相矛盾，所以，至少有一个结点v的度数为1。 删除结点v及其关联的边，得到图T*，由假设知，图T*无回路。现将结点 v及其关联的边添加到图T*，则还原成T，所以，T没有回路。 在连通图T中，任意两个结点vi和vj之间必存在一条通路，且是基本通路。 如果这条基本通路不唯一，则T中必有回路，这与已知条件矛盾。进一步 地，如果在连通图T中，增加一条边(vi, vj)，则边(vi, vj)与T中结点vi和vj之 间的一条基本通路，构成一个基本回路，且该基本回路必定是唯一的。 否则，当删除边时，T中必有回路，这与已知条分支结点各1个，其余 结点均为叶结点，求树T中叶结点的数目？ 解 设树T中叶结点的数目为x，则树T的结点数目为(x+3) 。 由树的性质知，树T中边的数目为 (x+3) 1 = x +2。 由握手定理知：2(x+2) = 41 + 31 +1 + x1 可以解出： x = 5。
离散数学——树ppt课件
4
(1)(2)
如果G是树，则G中任意两个顶点之间存在唯一的路径。
存在性。 由G的连通性及定理14.5的推论（在n阶图G中，若从顶点vi到 vj(vivj)存在通路，则vi到vj 一定存在长度小于等于n-1的初级 通路(路径)）可知，
u,v∈V，u与v之间存在路径。
唯一性（反证法）。 若路径不是唯一的，设Г1与Г2都是u到v的路径， 易知必存在由Г1和Г2上的边构成的回路， 这与G中无回路矛盾。
ij，i, j互不为前缀，则称A为前缀码。
若i(i=1,2,…,m)中只出现0与1两个符号，则称A为二元前缀码。 (2)如何产生二元前缀码？ 定理16.6 由一棵给定的2叉正则树，可以产生唯一的一个二元前缀
码。
35
方法：
将每个分支点引出的两条边分别标上0和1。
结果：
图所示树产生的前缀码为{00, 10, 11, 011, 0100, 0101}。
r叉完全正则有序树——r叉完全正则树是有序的
30
最优二叉树
定义16.9 设2叉树T有t片树叶v1, v2, …, vt，权分别为w1, w2,
t
…, wt，称 W (t) wil(vi ) 为T的权，其中l(vi)是vi的层数， i 1
在所有有t片树叶、带权w1, w2, …, wt的2叉树中，权最小的 2叉树称为最优2叉树。
1，1，1，2，2，2，3
由度数列可知，Ti中有一个3度顶点vi，vi的邻域N(vi)中有3个 顶点，这3个顶点的度数列只能为以下三种情况之一：
1,1,2
1,2,2
2,2,2
设它们对应的树分别为T1，T2，T3。此度数列只能产生这三棵 非同构的7阶无向树。
15
例16.2
(1)(2)
如果G是树，则G中任意两个顶点之间存在唯一的路径。
存在性。 由G的连通性及定理14.5的推论（在n阶图G中，若从顶点vi到 vj(vivj)存在通路，则vi到vj 一定存在长度小于等于n-1的初级 通路(路径)）可知，
u,v∈V，u与v之间存在路径。
唯一性（反证法）。 若路径不是唯一的，设Г1与Г2都是u到v的路径， 易知必存在由Г1和Г2上的边构成的回路， 这与G中无回路矛盾。
ij，i, j互不为前缀，则称A为前缀码。
若i(i=1,2,…,m)中只出现0与1两个符号，则称A为二元前缀码。 (2)如何产生二元前缀码？ 定理16.6 由一棵给定的2叉正则树，可以产生唯一的一个二元前缀
码。
35
方法：
将每个分支点引出的两条边分别标上0和1。
结果：
图所示树产生的前缀码为{00, 10, 11, 011, 0100, 0101}。
r叉完全正则有序树——r叉完全正则树是有序的
30
最优二叉树
定义16.9 设2叉树T有t片树叶v1, v2, …, vt，权分别为w1, w2,
t
…, wt，称 W (t) wil(vi ) 为T的权，其中l(vi)是vi的层数， i 1
在所有有t片树叶、带权w1, w2, …, wt的2叉树中，权最小的 2叉树称为最优2叉树。
1，1，1，2，2，2，3
由度数列可知，Ti中有一个3度顶点vi，vi的邻域N(vi)中有3个 顶点，这3个顶点的度数列只能为以下三种情况之一：
1,1,2
1,2,2
2,2,2
设它们对应的树分别为T1，T2，T3。此度数列只能产生这三棵 非同构的7阶无向树。
15
例16.2
离散数学教学图论【共58张PPT】
一 、图的基本概念
• 邻接和关联 • 无向图和有向图 • 零图和平凡图 • 简单图 • 完全图（无向完全图和有向完全图） • 有环图
一 、图的基本概念
• 有限图和无限图 设图G为< V，E，Ψ>
（l）当V和E为有限集时，称G为有限图，否则称G为无限图。 （2）当ΨG为单射时，称G为单图；当ΨG为非单射时，称G为重图，又称满足
二、生成树
1、生成树定义：
若无向图的一个生成子图T是树，则称T 为G的生 成树，T中的边称为树枝，E（G）-E（T）称为树T 的补，其中的每一边称为树T 的弦。
在任何图中，结点v的度（degree）d(v)是v所关联边的数目。
第三节 生成树、最短路径和关键路径 由结点a和它所有的后代导的子图，称为T的子树.
∴ T连通且具有m=n-1的图
{e5,e4,e8} ， {e7，e6，e5，e2，e4} 第四节 欧拉图和哈密顿图
第四节 特殊图（欧拉图和哈密顿图等）
第五节 树、二叉树和哈夫曼树
离散数学教学图论
（优选 欧拉图和哈密顿图
(3)2=>3 ∴W(T)≤W(T1) ∴W(ei+1)≥W(f) 二. 哈密顿图的由来—周游世界问题：
第二节 图的矩阵表示 第四节 欧拉图和哈密顿图
证明：若G中一个边割集和一生成 树无公共边，则表示该边割集所分离的结点不在生成树中，这导致与生成树的定义矛盾。 哈密顿图的由来—周游世界问题： c)对新图向下旋转45度。 ei之后将取f而不是ei+1
为该顶点的度,列之和一定为2. • 有向图的关联矩阵 ----- 以节点数为行,边数为列.节点与边无关系,为0,有关系,则起点为1,
终点为-1;列之和一定为0,每行绝对值之和等于该节点的度数;其 中1的个数为该节点的出度,-1的个数为对应节点的入度;所有元 素的和为0,1的个数等于-1的个数,都等于边数m.