实验——阶梯波
南京理工大学EDA1实验报告(模电部分)

南京理工大学EDA课程设计(一)实验报告专业:自动化班级:姓名:学号:指导老师:2013年10月摘要在老师的悉心指导下,通过实验学习和训练,我已经掌握基了于Multisim的电路系统设计和仿真方法。
在一周的时间内,熟悉了Multisim软件的使用,包括电路图编辑、虚拟仪器仪表的使用和掌握常见电路分析方法。
能够运用Multisim软件对模拟电路进行设计和性能分析,掌握EDA设计的基本方法和步骤。
实验一:单级放大电路的仿真及设计,设计一个分压偏置的单管电压放大电路,并进行测试与分析,主要测试最大不失真时的静态工作点以及上下限频率。
实验二:负反馈放大电路的设计与仿真,设计一个阻容耦合两级电压放大电路,给电路引入电压串联深度负反馈,,观察负反馈对电路的影响。
实验三:阶梯波发生器的设计与仿真,设计一个能产生周期性阶梯波的电路,对电路进行分段测试和调节,直至输出合适的阶梯波。
改变电路元器件参数,观察输出波形的变化,确定影响阶梯波电压范围和周期的元器件。
关键词:EDA设计及仿真multisim 放大电路反馈电路阶梯波发生器实验一:单级放大电路的仿真及设计一、实验要求1、设计一个分压偏置的单管电压放大电路,要求信号源频率5kHz(峰值10mV) ,负载电阻5.1kΩ,电压增益大于50。
2、调节电路静态工作点(调节电位计),观察电路出现饱和失真和截止失真的输出信号波形,并测试对应的静态工作点值。
3、调节电路静态工作点(调节电位计),使电路输出信号不失真,并且幅度最大。
在此状态下测试:(1)电路静态工作点值;(2)三极管的输入、输出特性曲线和 、r be 、r ce值;(3)电路的输入电阻、输出电阻和电压增益;(4)电路的频率响应曲线和f L、f H值。
二、实验步骤1、设计分压偏置的单级放大电路如图1-1所示:图1-1、单级放大电路原理图2、电路饱和失真输出电压波形图调节电位器的阻值,改变静态工作点,当电阻器的阻值为0%Rw,交流电压源为10mV时,显示饱和失真的波形图如图1-2所示:图1-2、电路饱和失真输出电压波形图饱和失真时的静态工作点:Ubeq=636。
实验四——阶梯波电路

阶梯波发生电路的设计一.实验目的1)掌握阶梯波发生器电路的结构特点。
2)掌握阶梯波发生器电路的工作原理。
3)学习复杂的集成运算放大电路的设计。
二.试验设计原理为了设计一个负阶梯波发生器,首先考虑产生一个方波,其次,经过微分电路输出得到上下都有的尖脉冲,然后经过限幅电路,只留下所需的正脉冲,再经过几分电路,实现累加二输出一个负阶梯。
对应一个尖脉冲就是一个阶梯,在没有尖脉冲时,积分器保持输出不变,在下一个尖脉冲到来时,积分器在原来的基础上进行积分,因此,积分器就起到了几分累加的作用。
当积分累加到比较器的比较电压时,比较器翻转,比较器输出正电压,使振荡控制电路起作用,方波停振。
同时,这个正电压使电子开关导通,积分电容放电,积分器输出对地短路,恢复到起始状态,完成一次阶梯波的输出。
积分器输出由负值向零跳变的过程,又使比较器发生翻转,比较器输出变为负值,这样振荡控制电路不起作用,方波输出,同时电子开关断开,积分器进行积分累加,如此循环往复,就形成了一系列阶梯波。
其原理框图如下:原理框图阶梯波发生电路原理图三.实验要求和实验步骤1.实验要求1)设计一个能产生周期性阶梯波的电路,要求阶梯波周期在18ms左右,输出电压范围10V,阶梯个数5个。
(注意:电路中均采用模拟、真实器件,不可以选用计数器、555定时器、D/A转换器等数字器件,也不可选用虚拟器件。
)2)对电路进行分段测试和调节,直至输出合适的阶梯波。
3)改变电路元器件参数,观察输出波形的变化,确定影响阶梯波电压范围和周期的元器件。
2.试验步骤1)首先设计一个方波发生器,设计电路原理图如下图所示:方波发生电路的原理图双击上图示波器得到方波发生器的输出波形如图所示:方波发生器输出波形从上图可看出方波的周期为3.103ms,幅度为10.813V,上图中锯齿波是从C1断输出得曲线。
2)在方波发生器的输出端接电阻R3和电容C2就组成了微分电路如下图所示:方波发生+微波电路原理图双击上图示波器得到输出波形为双边脉冲波形如图所示:由微分电路输出的双边脉冲波形3)设计限幅电路,将负半周的尖脉冲滤除掉。
阶梯波课程设计

阶梯波课程设计一、教学目标本课程的教学目标是使学生掌握阶梯波的基本概念、性质和应用。
通过本课程的学习,学生将能够:1.知识目标:理解阶梯波的定义、特点和分类;掌握阶梯波的求解方法和相关公式。
2.技能目标:能够运用阶梯波的知识分析和解决实际问题;能够运用数学软件或手工绘制阶梯波图形。
3.情感态度价值观目标:培养学生对数学的兴趣和好奇心,提高学生分析问题和解决问题的能力;培养学生的团队合作意识和沟通能力。
二、教学内容本课程的教学内容主要包括以下几个部分:1.阶梯波的基本概念:介绍阶梯波的定义、特点和分类,使学生能够理解和区分不同类型的阶梯波。
2.阶梯波的求解方法:讲解阶梯波的求解方法和相关公式,引导学生掌握求解阶梯波的技巧。
3.阶梯波的应用:通过实际问题引导学生运用阶梯波的知识分析和解决问题,培养学生的实际应用能力。
4.阶梯波的绘制:教授学生如何运用数学软件或手工绘制阶梯波图形,使学生能够直观地理解和表达阶梯波。
三、教学方法为了达到本课程的教学目标,将采用以下教学方法:1.讲授法:通过教师的讲解,使学生掌握阶梯波的基本概念、性质和应用。
2.讨论法:学生进行小组讨论,引导学生主动思考和探索,提高学生的分析问题和解决问题的能力。
3.案例分析法:通过分析实际问题,引导学生运用阶梯波的知识分析和解决问题,培养学生的实际应用能力。
4.实验法:引导学生运用数学软件或手工绘制阶梯波图形,使学生能够直观地理解和表达阶梯波。
四、教学资源为了支持本课程的教学内容和教学方法的实施,将准备以下教学资源:1.教材:选择合适的教材,为学生提供系统的阶梯波知识学习。
2.参考书:提供相关的参考书籍,丰富学生的学习资料。
3.多媒体资料:制作多媒体课件和教学视频,生动形象地展示阶梯波的概念和应用。
4.实验设备:准备计算机和相关软件,为学生提供实践操作的机会。
五、教学评估本课程的评估方式将包括以下几个方面,以全面、客观、公正地评价学生的学习成果:1.平时表现:通过观察学生在课堂上的参与程度、提问回答、小组讨论等表现,评估学生的学习态度和理解程度。
北京工业大学电子实验报告 压控阶梯波发生器(数字类)

北京工业大学课程设计报告学院电子信息与控制工程专业班级组号题目1、压控阶梯波发生器2、基于运放的信号发生器设计姓名学号指导老师成绩年月日压控阶梯波发生器(数字类)(一)设计任务在规定时间内设计并调试一个由电压控制的阶梯波发生器。
(二)设计要求1、输出阶梯波的频率能被输入直流电压所控制,频率控制范围为600Hz至1000Hz。
2、输出阶梯波的台阶级数为10级,且比例相等。
3、输出阶梯波的电压为1V/级。
4、输入控制电压的范围0.5V至0.6V。
5、电路结构简单,所用元器件尽量少,成本低。
(三)调试要求利用实验室设备和指定器件进行设计、组装和调试,达到设计要求,写出总结报告。
(四)方案选择在压频转换部分存在两种方案。
1、Lm358组成压频转换电路;2、NE555构成压频转换电路。
方案论证数字电路精确度较高、有较强的稳定性、可靠性和抗干扰能力强,数字系统的特性不易随使用条件变化而变化,尤其使用了大规模的继承芯片,使设备简化,进一步提高了系统的稳定性和可靠性,在计算精度方面,模拟系统是不能和数字系统相比拟的。
数字系统有算术运算能力和逻辑运算能力,电路结构简单,便于制造和大规模集成,可进行逻辑推理和逻辑判断;具有高度的规范性,对电路参数要求不严,功能强大。
为了得到更精彩的波形采用数模混合方案。
(五)实验元器件和芯片运算放大器Lm358,TTL电路74LS20、74LS161、74LS175,CMOS缓冲器CD4010,稳压管,二极管1N4148,电位器,电容,电阻。
(六)设计方案整体设计思路:压频转换→计数器→权电阻→运放=>阶梯波利用Lm358组成压频转换电路;使用CD4010缓冲,形成可被数字电路识别的矩形波信号;74LS161与74LS20组合构成十进制计数器;利用74LS175提高负载、整流信号,并组成权电阻网络;最后利用运放放大信号,并输出。
仿真电路图:详细设计: 压频转换部分:V1 2 V C11uFR1100kΩR25kΩR31kΩR4100kΩR5100kΩU174LS161NQA 14QB 13QC 12QD 11RCO 15A 3B 4C 5D 6ENP 7ENT 10~LOAD 9~CLR 1CLK2U274LS175D1D 4CLK 91Q 2~CLR 12D 53D 124D 13~1Q 3~2Q 63Q 10~3Q 112Q 74Q 15~4Q14U3A74LS20D5U4ALM358D32481U5ALM358D 32481U6ALM358D3248134U7A40106BD_5V6R6100kΩKey=A 50%GNDVDD 15V VDD 15V VEE-15VVEE -15VVEE -15VVDD15V VEE VEEVDDVDDR71kΩVCC 5V R81kΩR92kΩR104kΩR118kΩR122kΩKey=A 50%R132kΩKey=A 50%R142kΩKey=A 50%R152kΩKey=A50%1718192021222324VEE VDDR161kΩ0R17680Ω27R182kΩ26XSC1ABExt Trig++__+_1211D11N4148109830729VCCGND D21N575815251228压频转换将一定的输入电压按线性的比例关系转化成频率信号,当输入电压变化时,输出频率也相应变化。
片段采样与阶梯波测量——阶梯波研究之二

片段采样与阶梯波测量——阶梯波研究之二陆祖良;杨雁;黄璐;王磊【摘要】阶梯波是连接交流和直流的桥梁,也是连接动态和静态过程的潜在桥梁.提出了片段采样的概念,分析了这种采样下阶梯波的性质.通过实验着重讨论了阶梯波的测量方法,以克服过渡过程和吉布斯现象的影响.以1种带抗混迭滤波器的典型模数转换器为例,说明为达到准确测量目的,应该如何选择片段采样的参数.实验结果表明片段采样大幅降低了数据波动对测量结果的影响.【期刊名称】《计量学报》【年(卷),期】2019(040)001【总页数】9页(P31-39)【关键词】计量学;阶梯波测量;片段采样;交流测量;测量技术;数字模拟转换;采样;量化误差;动态测量【作者】陆祖良;杨雁;黄璐;王磊【作者单位】中国计量科学研究院,北京100029;中国计量科学研究院,北京100029;中国计量科学研究院,北京100029;中国计量科学研究院,北京100029【正文语种】中文【中图分类】TB9711 引言阶梯波是连接交流和直流的桥梁,也是连接动态和静态过程的潜在桥梁.在初步认识阶梯波的性质之后,本文讨论阶梯波的测量.从1个台阶到下1个台阶的转换过程中,由于转换时间不可能无限小,因此无论是传统的基于电子线路的数模转换器(DAC)还是量子的可编程量子电压基准,由它们生成的阶梯波总存在过渡过程(transient effect),即在台阶的两端出现起伏.如果用模数转换器(ADC)测量阶梯波,而ADC 又带有抗混迭滤波器,采样数据中将存在吉布斯现象(Gibbs phenomenon),在台阶两端的数据中出现较大的波动.它们都将使测量出现误差.鉴于采样测量的灵活性和实用性,本文以ADC作为测量仪器,讨论阶梯波的测量方法.为克服上述两种误差因素,提出片段采样(piecewise sampling)的概念;进而讨论这种概念下阶梯波的性质;具体以1 种带抗混迭滤波器的典型ADC为例,通过实验研究阶梯波的测量过程,探索了各种因素的影响.进而提出为准确测量阶梯波,应如何选择片段采样的参数.文中报告了相应的实验结果.本文在已有研究成果基础上进行深入探索[1],包括用新的观点展开讨论,对实验现象作更清晰的解释;同时增加新的内容,以期达到较为系统和完整的效果,并为后续研究奠定基础.2 测量阶梯波的几种方法在以可编程量子电压基准为参考的交流电压测量中,可编程量子电压基准产生与被测正弦波接近的阶梯波电压,将该阶梯波与被测正弦波电压做差分测量,由此建立交流电压的量子基准.在这种测量中,一般使用数字电压表[2,3],例如Agilent3458A(为叙述方便,文中提到若干仪器和器件,但并不表示实验必须由它们来完成,也不表示它们最好).通过时间控制,使数字电压表延时,在1个适当的时间点开始测量;同时通过预先设置的孔径时间(aperture),使数字电压表仅仅在1 段时间内进行测量.延时和孔径时间的预先设置,是按照被测阶梯波的参数做出的,为的是使测量在台阶中间的平坦部分进行.数字电压表对每个台阶给出1个测量结果,可视为位于台阶的中间点上,或者可认为它们位于每个台阶的相同位置上,总之它们中间的间隔相同.因此后续计算被测正弦波电压的幅值(或有效值)时将不存在问题.上述测量,仅仅针对台阶电压的平坦部分,过渡过程未包括在内;同时,即使数字电压表的测量功能单元含有抗混迭滤波器,由于台阶两端的突跳部分没有进入数字电压表的测量功能单元,因此也不会产生吉布斯现象.文献[2]报道,在差分测量中,当测量的部分占每个台阶的70%,被测正弦波电压频率为62.5 Hz时,获得的A 类不确定度为4X10-7.在对阶梯波本身的测量中,有利用带抗混迭滤波器ADC 作测量仪器的报道,例如使用NI 5922[4,5].不过为了克服过渡过程和吉布斯现象的影响,需要对采样数据进行处理:有的将台阶两端的数据用中间的数据来代替;有的删除不理想的数据,代之于剩下数据的平均值.这些方法具有一定的合理性.然而处理后的数据中,1部分是真实的,1部分是重构的,实际上是增加了某些数据的权重,其中不可避免带有人为操作的因素.此外,这些方法只适用于阶梯波本身的测量,但并不适用于阶梯波与正弦波的差分测量,因为差分信号中没有平坦部分.最近,也见有采用带抗混迭滤波器ADC 做差分采样测量的报道,例如使用NI 5922[6].其中的阶梯波含20个台阶,共10 000个采样点;每台阶500个采样点中,删除了90个点,认为它们包含了过渡过程的振荡部分.由此,在对40 Hz至1kHz的正弦波电压测量中,获得了0.62μV/V(k=1)的不确定度.本文作者认为,数字电压表方法能获得不错的结果,但1个台阶只给出1个数据,而且每个台阶中不被测量部分的占比较大;现有基于ADC 的方法能获得较多的数据,但其中重构台阶的做法具有不够客观的缺陷;相关报道中删除的数据点过多.说明这些方法对阶梯波测量中细节的了解不是十分清晰.文献[6]指出,丢弃的采样点是个数(90个)而不是比例,这个结论与本文作者的研究相吻合.文献[6]的结论源自每周期10 000个采样点的特例,缺少一般规律的研究;同时,对于如此采样点数量的要求,需要ADC提供较高的采样率,进而也限制了被测信号的频率.例如对于1kHz的被测阶梯波,对应于每周期10 000个采样点数量,需要的采样率将为10 MHz,几乎到了某些高性能ADC指标的极限;如果被测阶梯波频率进一步提高,ADC 将不能满足.因此有必要做进一步的探索.本文作者提出了用采样方法测量阶梯波的方法,其特点是保留数据较多,删除两端数据之后剩下的部分仍可进行傅里叶变换[7^9],并在此基础上进行了应用研究.2014年提出了片段采样思想,但在一个较长时期内,其中的测量方法受到质疑.作者因此转而研究阶梯波采样测量的一般性问题[10].获得的结果使作者认识到,阶梯波的测量与阶梯波的性质一样,是十分重要、必须首先搞清楚的基础性问题.3 片段采样3.1 片段采样的概念假设原始正弦信号为y=sin x,对应正弦型阶梯波含有N个等宽的台阶,每个台阶均含有M个等间隔的采样点[11].在此离散条件下,离散正弦波可表示为:yn,m=sin(nMh+mh) (1)不失一般性,假设M为偶数,每个台阶中间点的采样值为:yn=sin(nMh+0.5 Mh) (2)第2类离散阶梯波表示为:zn,m=zn=yn=sin(nMh+0.5 Mh) (3)式中:n=0,1,…,(N-1),m=0,1,…,(M-1),而h=2!/(NM) (4)在每个台阶上,只保留从m=S至m=E的采样点,参数S及E一般位于台阶中点的两侧,0<S<M/2<E<(M-1).如此,阶梯波与正弦波的交叉点将位于台阶的中点.符合这个要求的离散正弦波还可以是yn,m=sin([nMh+(m-0.5 M)h].图1刻画了这种情况的阶梯波.图中表示了片段采样,以空点和实点分别表示丢弃不用和保留的采样点.每个台阶6个采样,开始2个和最后1个(空点)丢弃不用,中间3个(实点)保留用于后续计算.图1 片段采样图示Fig.1 Piecewise sampling事实上,让阶梯波台阶值取M个采样点中某个点的值,则该点就成为阶梯波与正弦波的交叉点.式(2)取中点是1个典型的情况.片段采样的特点是每个台阶保留的采样点具有相同的个数和相同的位置,因此又称其为"规则片段采样".为了区别和叙述的方便,将原先不丢弃采样点的情况,称为"全采样".片段采样概念下的运算体现为:(1)求平均,如计算阶梯波的台阶值:计算有效值的运算也可以参照式(5).(2)傅里叶变换运算,如计算阶梯波基波的余弦系数和正弦系数:式(6)、式(7)的计算过程可以这样理解:第1步在每个台阶的相同位置各取1个采样点,获得N个等间隔的数据,对它们进行傅里叶变换.尽管从1个周期看,采样中出现了空缺,但这N个数据是等间隔的,符合Nyquist采样定理.从m=S至m=E,这样的操作一共进行(E-S+1)次,获得(E-S+1)个中间结果.第2 步取这些中间结果的平均值,即为最后的结果.这两步运算意味着将台阶两端的采样点丢弃了,那里包含了过渡过程和吉布斯现象这些误差因素,运算仍符合Nyquist采样定理.3.2 规则片段采样概念下阶梯波的性质(1)离散阶梯波的有效值片段采样概念下,如果只考虑采样点的减少,阶梯波的有效值与原始正弦波的有效值相等:式(8)成立的理由是即:从m=S至m=E阶梯波采样值平方的平均值等于从m=0至m=M-1采样值平方的平均值,后者为台阶值的平方的平均值.这个性质表明,阶梯波每个台阶上以相同方式丢弃若干采样点,有效值保持不变.式(8)是片段采样概念应用于阶梯波有效值测量的基础.(2)离散阶梯波的基波分量式(6)可具体表示为:为便于比较,这里采用第1 类正弦型离散阶梯波的概念.所得到关于幅值的结论可用于第2类,只是初相角(相应的,余弦与正弦系数之比)有所不同.由此推导得到的基波的余弦和正弦系数分别为:因而基波的幅值和初相角为:当E=M-1,S=0时,就成为全采样的情况,上述式子则改变为:这些与文献[11]第2.2节(2)中的公式一致.为估计参数的作用,式(11)可近似写为与全采样相比较,片段采样的基波幅值比全采样的稍大,增大的部分与成比例;而初相角则差不多.(3)离散阶梯波的混迭分量傅里叶变换由下式表示:当k≠tN±1,t为正整数时,ak=0,bk=0.当k=tN+1时,有:当t=0时,式(13)至式(15)与前述基波分量的公式[式(9)至式(11)]相一致;当E=M-1,S=0时,与全采样情况,即文献[11]第2.2节(3)中的公式一致.4 阶梯波的片段采样测量以下通过实验研究片段采样概念下测量阶梯波的具体方法.这里的问题是,在准确测量(例如10-6)的要求下,应该保留多少点?它们在什么位置上?即需要确定保留片段的长度和位置.4.1 主要实验设备及相关参数(1)模数转换器ADC,用于测量阶梯波信号.选用两个商用ADC卡.其中1个型号为NI 5922,带抗混迭滤波器,在文献中常见使用.在不同采样率下该ADC 卡的分辨率为24bit@500kHz至16 bit@15MHz;其内部参考电压10V,采用其中2V(峰峰值)量程.本文称该卡为卡A.另1个ADC卡的型号为NI 6289,使用它的不带抗混迭滤波器模式.它的分辨率为18bits@625 kHz;内部参考电压为10V,采用其2V(峰峰值)量程.本文简称其为卡B.(2)数模转换器DAC,用于产生阶梯波信号.选用型号为NI 6733 的商用DAC 卡,分辨率16 bit,内部参考电压10V.正弦型阶梯波是1种周期信号,与原始正弦信号有相同的频率[11].在实验中,对于选定的原始正弦信号频率fsin,阶梯波频率fstair应与fsin相同,其实现可通过设置DAC 的转换时间(或台阶宽度)T进行,即:fstair=1/(NT) (21)至于ADC采样率fs的选取,由每个台阶上安排M个采样点来确定,具体为:fs=M/T(22)4.2 抗混迭滤波器ADC不同滤波模式的选择ADC卡NI5922中的抗混迭滤波器有4 个模式,分别为"48Tap Standard","48Tap Hanning","16Tap Hanning"和"8Tap Hanning".适当的滤波窗函数具有对1个周期内非理想部分的抑制功能,因此寻找合适的滤波窗函数是研究应有的方向之一.但本文涉及的信号具有如下的特点:1个周期分成N 等份,每份的两端均存在非理想的成分;在1个周期内观察,由于前1台阶的尾部与后1台阶的首部相接,因此这些非理想部分大体上呈现N个等间隔分布的状态.对此情况,作者认为应该优先选择其"Standard"模式,因为相对于"Hanning"模式而言,"Standard"是基本的工作模式,每个采样点的权均为1.本文实验中采用"48Tap Standard"模式,其中"48"是其有限冲击响应(FIR)滤波器的系数.4.3 台阶波动程度的实验估计实验中,由DAC 卡按照原始正弦信号的离散数字值产生阶梯波,然后由ADC 卡采样.由此获得的实验结果,每个台阶上的采样数据呈现波动的形状,特别表现在台阶的两端波动比较明显.为了观察这种波动,定义以下差值为数据的波动.式中:zn,m是阶梯波的采样值;而(r)是片段采样概念下由式(5)定义的台阶值.图2以卡A 为例,显示1个周期内数据波动的实验结果.具体的参数是N=24,M=50,T=50 μs,片段采样选为(14,23,13),表示中间部分保留23个,开始和最后部分丢弃各14个和13个.相应的阶梯波频率是833.333 Hz.当N和T为整数时,按照式(21),fstair将不会总是整数,其中的参数S和E是反复尝试后确定的.图2 阶梯波1个周期内采样数据的波动情况Fig.2 Fluctuation of samples in one period of staircase waveform图2(a)的纵坐标限值为±1 000μV,能看到波动的全貌.每个台阶的两边有较大的波动,少数达±800μV;中间存在1个完整的区间,其中波动程度较小.为了看清细节,图2(b)将纵坐标限值改为±20μV,则能看到中间波动细节,大部分点在±5 μV 之内,作为1个大体上的估计,以±5μV 作为台阶中间部分波动程度的估计(下同).需要特别提出的是:中间区间内基本没有超过±5μV 幅度的采样点;中间与两端波动水平相差将近3个数量级;中间部分采样个数约占台阶采样总数的一半;整个周期内每个台阶的上述特征是相似的.这是1个非常理想的现象.由于存在3个数量级的差别,故确定参数S和E并不十分困难.引起波动的来源除了已经提到的ADC 中抗混迭滤波器的影响,DAC 的过渡过程之外,还有噪声等因素.4.4 有无抗混迭滤波器的比较一般的理解,在阶梯波测量中,由于过渡过程存在,以及滤波器产生的吉布斯现象,应该首先考虑使用不带抗混迭滤波器的ADC.但是实际情况,还需要通过实验进行比较. 实验中设置阶梯波参数为N=10,T=100μs,这样fstair=1kHz.首先选两个ADC 卡的采样率均为fs=100kHz,这样M=10.选择同样的片段采样(1,8,1).实验结果表明卡A 有明显波动,即使在台阶的中间部分,按上述提供的估计方法,波动程度约为±8 000μV.而卡B的情况,除少数点和个别台阶外,波动约为±10μV.卡A 的波动约为卡B的800倍.然后将采样率改为fs=500kHz,这样M=50.两个ADC 卡的波动情况显示于图3,参数N=10,M=50.图3(a)表示卡A 的情况,片段采样选为(12,25,13),结果表示卡A 的波动为±10μV;图3(b)表示卡B的情况,片段采样仍为(1,48,1),两端仍各丢弃1个点,因为它不需要丢弃更多的点,其波动程度仍为±10μV.图3 模数转换器中有无滤波器的比较Fig.3 Comparison between both ADCs,with and without antialiasing filter这说明,当每个台阶的采样数增加到50时,卡A 的波动达到与卡B 差不多的水平.这也说明带抗混迭滤波器的ADC是可以使用的.卡B在M=10,50两种情况下,波动均为±10 μV,这可视为DAC 的输出波动本来就在这个水平上(不考虑前述的噪声).图3(b)还显示,在n=0、5两个台阶上,卡B 在台阶中间部分的数据也出现了较大的波动(M=10类似).事实上,这两点是原始正弦信号的过零点,具有较大的导数,原始数据突跳本身较大.对此情况,卡B 有反应,而卡A 却比较平缓.实验显示了带抗混迭滤波器的ADC 对每个台阶均匀一致的优点.综合各方面的优缺点,下面着重研究带抗混迭滤波器的ADC.4.5 不同参数对台阶波动的影响(1)每台阶采样总数M的影响设置参数N=10,T=96μs,如此,fstair=1.041 6kHz.然后分别取采样率为125,250,500,625和1 000kHz,M则分别为12,24,48,60和96.在此条件下,卡A 波动程度的实验结果列于表1中.可见当M从12起增大到48,波动大幅减少,具体从±5 000μV 减少到±10μV;但从48起继续增大M值,波动则基本不变,保持在M=48 的水平上,即±10μV;同时,从M=48开始,台阶两端各丢弃的采样个数基本保持不变,均约为12个.(2)M影响的简略解释在ADC器件内部具体细节不可能获知的情况下,上述波动随M变化的规律,可以做如下简略解释.卡A 所带抗混迭滤波器属于有限冲击响应(FIR)型,对于采用的滤波模式"48Tap Standard",其滤波原理可以用下式表示:y(i)=∑b(k)x(i-k) (24)式中:x是滤波器的输入而y是其输出;b(k)是冲击响应,k=0 至(K-1),系数K=48.当K值较大时,输出中将含有较高的频率分量,或者说,其输出将较为平坦.式(24)中的输入x,即DAC给出的波形,可以从图3 显示出的卡B 的表现中得以了解,即基本上两端波动较大的点不多,中间部分的波动程度在±10μV 范围内.首先讨论M大于K的情况.不难知道,从M等于K到大于K,M的增加是通过提高采样率实现的.由于DAC给出的波形没有变,从表观上看,输入x的点的分布更密了,但所有点的包络外形不变.同时在此过程中,冲击响应b也没有改变,即对于一个输出y,还是需要那么多输入采样点(即x).由于采样点的分布加密了,因此这些点在时间轴上占据较窄的区间.既然DAC 给出的波形没有变,那么ADC 输出在台阶开始部分的表现,仍然有较大波动,但位置将会前移;这些较大波动点的整体在时间轴上占据的宽度也将变窄.考虑吉布斯现象的对称性,台阶的结束部分也有如开始部分相似的较大波动,整体波动更向两端靠拢,因而中间剩下的平坦部分将变得更宽,这种平坦度与M=K的情况相类似. 再回来看实验结果:在表1中,当M=48时,片段采样为(12,24,12),即中间有24个点的波动在±10μV 之内;当M=96时,片段采样为(12,72,12),即中间有72个点的波动同样在±10μV 之内.实验结果与分析解释相符.当M>K时,实验结果准确地给出了两端较大波动的个数总是约12个,而不是1个比例.当M<K时,对于1个输出的y值,所需要的输入采样点分布将更宽,台阶前端的y所需要的输入甚至延伸到前1个临近的台阶上,从而引起更大的波动.ADC的输出在台阶上将保持比例大体相似的数据个数的波动,因此中间平坦部分的数据个数变少,并且平坦度变差.这就是为什么M较小时,波动较大的原因.由此,M至少应设置等于K.回顾第4.4节一开始提到M=10的情况,应视为没有充分利用ADC的特性.表1 波动程度及影响随M的变化Tab.1 Variation of fluctuation and impact with parameter of MM 12 24 48 60 96片段采样 (3,6,3) (6,11,7) (12,24,12)(12,35,13) (12,72,12)波动程度波动/V 5 000 200 10 10 10波动影响基波幅值/V 5X10-5 2X10-5 2X10-7 5X10-8 5X10-8有效值/V 2X10-5 3X10-73X10-11 8X10-12 2X10-11(3)台阶总数N的影响同样的原始正弦信号,当N增大时,阶梯波相邻台阶之间的突跳将会变小,对于同样的DAC,相应的过渡过程也将会变小.按照式(24)的原理,ADC输出数据将会更平坦.因此设置较大的N是有益的,卡A 在图2和图3中的表现也证实了这个结论.在其他参数相同的条件下,在图3(a)中,N=10,波动为±10μV,在图2(b)中,N=24,波动变为±5μV.但是参数N的影响不如参数M的大,一般可设置N大于等于20.(4)阶梯波频率的影响当阶梯波频率较高时,对于同样的N值,台阶的宽度将会变窄.如此,过渡过程将影响中间的平坦部分.不同频率的波动程度实验结果如表2所示.结果表明,波动程度随频率成比例增加.这里波动程度增加的原因,有阶梯波本身高频的因素,也有与ADC 分辨率的下降有关.阶梯波频率较高时,ADC 采样率也应增大,此时分辨率会下降.阶梯波的频率为10kHz时,其所需要的片段采样为(16,22,12),这意味着台阶的开始部分需要丢弃更多的采样点,表明过渡过程(不对称)的作用已经掩盖了吉布斯现象(对称).表2 波动程度及影响随频率的变化Tab.2 Variation of fluctuation and impact with frequencyfstair/kHz 1 2 5 10T/μs 50 25 10 5fs/MHz 1 2 5 10波动程度波动/V ±5 ±10 ±20 ±40波动影响基波幅值/V 4X10-8 1X10-7 4X10-7 7X10-7有效值/V 1X10-11 4X10-11 1X10-10 5X10-104.6 片段采样参数选择关于片段采样参数S和E的选择,实验研究表明,按下述方法选择:(1)按照式(5)计算每个台阶的平均值,其中参数S和E通过观察和调节获得,以使保留部分的波动较小;(2)计算每个台阶上所有采样点与上述平均值的差,并观察这些差值的分布;(3)选择具有最小波动程度的中间部分,进一步确定参数S和E.返回到第(2)步,直至每个台阶中间部分的波动程度不能再小为止.对于其他原理的滤波器,不难通过实验获得相应的采样测量方法.文献[12]报告了使用带RC 滤波器的ADC 的测量方法,并介绍其也取得了较好的效果.5 剩余波动对阶梯波测量值的影响台阶两端各丢弃若干采样点(如上述的约12个)后,剩下的中间平坦部分还有没有更为平坦的区间?为弄清这个问题,本文作者对1kHz的阶梯波进行了N为20,M分别为100,500的实验,但没有发现更小的波动区间.相反,在M=500情况下,由于采样率升高至10MHz,使ADC的分辨率指标下降,反而波动更大.对于由可编程量子电压基准输出的阶梯波,采取必要的抗干扰措施,不排除存在波动程度更小的区间的可能性,可作为专门课题进行深入探索.不过,这里需要提出的另一个问题是,片段采样保留台阶的中间部分,仍然有较小的波动,这些剩余波动对测量值的影响有多大?5.1 剩余波动对阶梯波基波分量幅值的影响对于实验中获得的采样结果zn,m,以式(23)定义的波动δn,m为对象,对其做基波的离散傅里叶变换.获得余弦系数和正弦系数,计算它们的平方和,再开方,其结果是1个周期的δn,m在基波上的投影,具有剩余波动对基波幅值影响的意义.以图2的实验为例,在全采样概念下,这个影响为549μV,为10-4数量级;而在片段采样概念下,这个影响减小为13nV,小至10-8数量级.表1中关于波动与M关系的实验,以及表2中关于波动与频率关系的实验,均进行了剩余波动影响的分析,结果列于这些表中.实验结果表明:在M≥48及fstair不大于10kHz的条件下,剩余波动对基波幅值的影响为10-7数量级.5.2 波动对阶梯波有效值的影响上述的方法不能用于分析对有效值的影响,此时需要构建一个不含波动的新的理想离散阶梯波:式中是台阶值,是基于片段采样概念,由式(5)计算得到.然后分别计算两个离散阶梯波zn,m和一个周期内的有效值.以图2 的实验为例,全采样概念下,zn,m的有效值是0.707 082V,的有效值是0.707 152V,两者相差70μV(不考虑正负号),为10-5数量级;在片段采样概念下,zn,m的有效值是0.707 152V,的有效值仍是0.707 152V,两者相差为1X10-11 V.在表1和表2中也列出了相应结果,当M≥48,fstair为1kHz,2kHz时,剩余波动对有效值的影响仅为10-11数量级;而fstair为5kHz,10kHz时,剩余波动对有效值的影响为10-10数量级.关于剩余波动对阶梯波有效值的影响,可进一步分析如下.由式(23)和式(25)可得:对上式等号两边同时做平方运算,得到:上式等号右边第2项为交叉项,其中由于每个台阶上为常数,而δn,m在每个台阶上的和为零;在整个周期内,的和为零.因此等号右边第2项在1个周期内的平均值非常小,一般在10-17数量级,可忽略不计.上式等号右边第3项在整个周期内取平均,其含义是剩余波动的方差σ2.以上涉及求"和"与取"平均",均为片段采样概念下的运算. 假如zn,m的有效值为Z,的有效值为Z0,则Z含有波动而Z0不含波动.按照式(8)定义的片段采样概念下有效值公式,丢弃可忽略不计的交叉项,上式可以表示为。
晶体管输出特性曲线实验报告
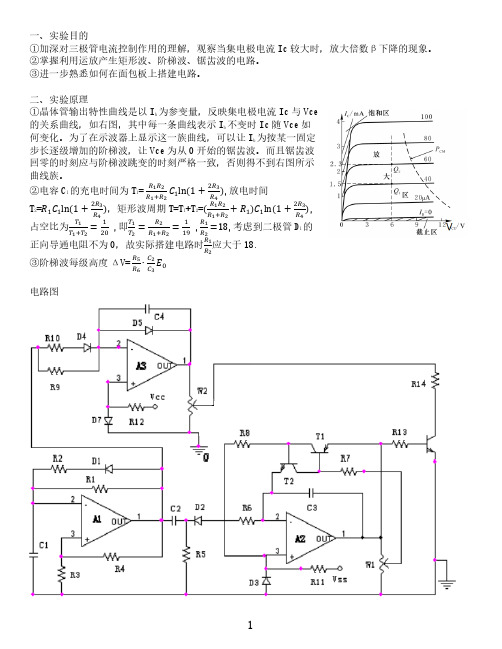
回零的时刻应与阶梯波跳变的时刻严格一致,否则得不到右图所示
曲线族。
②电容
C1
的充电时间为
T1=
������1������2 ������1+������2
������1ln(1
+
2������3),放电时间
������4
T2=������1������1ln(1
+
2������3),矩形波周期
������4
在锯齿波发生电路与电阻 R14 之间,波形为较理想的锯齿波,如图 4,但经过电阻 R14 之后,波形似 乎是两个频率之比近似为 9 的锯齿波相乘的结果,如图 5.
图4
图5
阶梯波发生电路的运放输出端不与电阻 R13 相连时,也能得到较理想的阶梯波。与电阻 R13 以及被测 三极管相连时,在运放输出端与 R13 之间的测得的阶梯波已有畸变。在较高的台阶处,本应水平的部 分向下倾斜了一定的角度,即电容 C3 通过电阻 R13 和被测三极管的 B-E 极进行缓慢放电,如图 6.而 在 R13 与被测三极管之间,阶梯波已经完全消失,如图 7.
2
1. 矩形波的设计频率为 800Hz(设计过程中,并未忽略 D1 导通时 R1 的分流作用),由于电阻、电容等 器件的不精确性,以及实际二极管的正向电阻并不为零,当矩形波发生电路不与其他任何电路相连 时,其频率 f=761Hz,占空比为 5.3%,Vopp=16V.当与阶梯波和锯齿波发生电路相连时,频率 f=910Hz,占空比变为 9%,Vopp=11.6V.
回扫线,本人尝试过将 R10 变为 0(短路)以及同时加大 R10 和 R2 两种方案。这两种方案所得回扫线的形
状与特性曲线十分相似,在屏幕上的位置相当于特性曲线向下平移了一定的距离。将 R10 变为 0 得到的
阶梯波发生器的设计与实现实验报告

阶梯波发生器的设计与实现实验报告摘要:本实验主要用了三个运算放大器来实现阶梯波的发生,其中一个作为迟滞电压比较器,一个作为窄脉冲发生器,还有一个作为积分器。
窄脉冲发生器形成方波后,通过一个二极管使积分器对其中的负脉冲部分进行积分,形成阶梯波。
阶梯波的周期由迟滞电压比较器来控制,随着积分器的输出电压不断增高,迟滞电压比较器的会从输出低电平变为输出高电平,这时积分器输出电压会下降,当输出电压值降到迟滞比较器的下门限电压时,完成一个周期。
关键词:负脉冲积分反馈设计任务要求:基本要求>= 3V, 阶数N=6;1.利用所给元器件设计一个阶梯波发生器,f >= 500HZ, Uopp2.设计该电路的电源电路(不要求实际搭建),用PROTEL软件绘制完整的电路原理图(SCH)及印制电路板图(PCB)。
提高要求1.利用基本要求里设计的阶梯波发生器设计一个三极管输出特性测试电路,在示波器上可以观测到基本电流为不同值时三极管的输出特性曲线束。
探究环节:1. 能否提供其他阶梯波发生器的设计方案?若能,请通过仿真或实验结果加以证明;2.探索其他阶梯波发生器的应用实例,给出应用方案。
设计思路:要形成阶梯波,可以用一个运算放大器对负脉冲进行积分,因此需要设计一个积分器;要发生负脉冲,还需要一个负脉冲发生器;最后,为控制阶梯波能达到的高度和阶梯波的周期,需要一个迟滞电压比较器。
总体结构框图如下。
总体结构框图下面就依次对负脉冲发生器、积分器、迟滞电压比较器的部分电路进行设计。
1.电源电路(原理图在14页PROTEL绘制的原理图中有)该实验不对电源电路进行要求,直接使用实验室已有的电源。
2.负脉冲发生器负脉冲虽然不能直接通过电路得到,但容易想到,如果在方波发生器与积分器之间加上一个二极管D4,使方波发生器与积分器之间只能导通负脉冲,那么方波发生器与二极管就形成了一个负脉冲发生器了。
方波发生器由一个LM741运算放大器U1、一个0.01u的电容C1和一个100k的电阻R1构成,如下图。
实验十九阶梯波产生电路

实验十九阶梯波产生电路(设计型)
一、实验目的
1、掌握梯形波产生的原理
2、学会数字电路与模拟电路的综合应用。
3、培养独立设计的能力。
二、实验设备及器件
1、示波器 1台
2、器件自选
三、实验内容及步骤
梯形波产生电路应由D/A转换器、可逆计数器、上下限比较器、定时器、启动复位五部分组成。
下面步骤由学生独立设计完成;
1、设计原理线路图;
2、选择元器件;
3、组装调试。
4、写出实验报告.
四、设计提示
用 4 位二进制计数器 74LS161 、 D/A 转换器 DAC0832 和集成运放组成阶梯波发生器,电路如图19-1所示。
将 f = 1000Hz 的脉冲信号加到计数器的 CP 端,用示波器观察输出的波形并记录。
图 19-1 阶梯波发生器。
阶梯波发生器原理-概念解析以及定义

阶梯波发生器原理-概述说明以及解释1.引言概述:阶梯波发生器是一种能够产生具有固定幅度和可控升降时间的方波信号的电路。
它在电子工程领域中具有重要的应用价值,可以用于数字电路的时序控制、模拟电路的测试和测量等方面。
本文将深入探讨阶梯波发生器的工作原理、实际应用及其未来发展前景,以期为相关领域提供理论支持和技术指导。
波发生器的未来发展": {}}}}请编写文章1.1 概述部分的内容1.2 文章结构文章结构部分的内容可以包括对整篇文章内容的概述和安排,以及对每个章节的简要介绍。
例如:文章结构部分旨在概述本篇文章的内容和安排,并对每个章节进行简要介绍。
本文分为引言、正文和结论三个部分。
在引言部分,我们将介绍阶梯波发生器的概念、工作原理和在实际中的应用。
在正文部分,我们将详细讨论阶梯波发生器的概念、工作原理和应用案例。
最后,在结论部分,我们将总结阶梯波发生器的重要性、阐述其优势,并展望其未来发展。
通过本篇文章的阅读,读者将能够深入了解阶梯波发生器的原理和应用,以及对其未来发展进行展望。
1.3 目的本文的目的是对阶梯波发生器进行深入剖析,以便读者对该设备的工作原理和实际应用有更清晰的理解。
通过对阶梯波发生器的概念、工作原理和实际应用进行详细介绍,旨在帮助读者掌握该设备的基本原理,并为相关领域的研究和应用提供理论支撑。
同时,通过对阶梯波发生器的重要性、优势及未来发展进行展望,旨在引导读者对该设备的前景有更深入的认识,为相关领域的领先发展提供参考建议。
通过本文的阐述,希望读者能够全面了解阶梯波发生器,并对其在工程技术领域的应用有更广泛的认识和应用。
2.正文2.1 阶梯波发生器的概念阶梯波发生器是一种能够产生稳定、周期性的阶梯状波形信号的电子设备。
它可以将输入的连续波形信号转换为一系列等幅度、等时隔的阶梯波形信号输出。
通常情况下,阶梯波发生器会采用不同的工作原理和电路设计来实现这一功能,例如利用计数器、比较器、递推电路等。
晶体管输出特性测试仪阶梯波发生电路设计

阶梯波发生器电路设计一、实验目的:(1)、学习和理解晶体管输出特性测量仪原理,并学会阶梯波发生器电路的其设计方法。
(2)、查阅有关手册,了解所用的器件性能。
二、实验原理:通用的晶体管特性图示仪的扫描信号和阶梯信号是由50H Z工频市电变换的得到的。
有下列几个缺点。
1、使用了50H Z的低扫描频率,显示的特性曲线闪烁比较严重。
2、X轴扫描为正弦波,线性度差。
3、波形变换电路复杂。
本实验旨在设计一个基于555定时器和加法计数器的阶梯波信号发生器。
通过555定时器产生同步的X轴扫描锯齿波和Y轴扫描阶梯波。
克服使用50H Z扫描频率低带来的缺点。
1.设计原理:晶体管的输出特性是指集电极电流I c在一系列一定的基极电流I b下,随集电极-发射极电压U ce变化的一簇曲线束,如图1所示。
对其中任意一条曲线而言,相当于I b为常数时,电压U ce与集电极电流I c之间的关系。
图1、晶体管输出特性曲线对于给定的I b,只能表现出其中一条曲线。
为了显示出整个曲线簇,只要使得I b(即U b)是阶梯波变化,而Uc是锯齿波变化,锯齿波的周期等于等于每一阶梯的维持时间即可,如图2所示。
因此,本设计实验如何运用数字电路知识设计产生阶梯波产生电路。
图2.阶梯波和锯齿波之间的关系2.设计要求:能够在示波器上稳定的显示出阶梯波,且阶梯波的幅度可调。
3.电路设计:(1)总框图:阶梯波产生电路由多谐振荡器(555定时器构成)、四位二进制加法器(CD4518)、数—模转换电路(R1~R4与加减运算电路构成)和反相比例运算器组成。
框图如图3所示图3.总框图(2)多谐振荡器部分:由555定时器构成的多谐振荡器如图4(a)所示,其工作波形见图4(b)图4(a)555振荡器构成(b)工作波形图接通电源后,电源V DD通过R1和R2对电容C充电,当U c<1/3V DD时,振荡器输出V o=HIGH,放电管截止。
当U c充电到≥2/3V DD后,振荡器输出V o翻转成LOW,此时放电管导通,使放电端(DIS)接地,电容C通过R2对地放电,使U c下降。
阶梯波实验报告总结

阶梯波实验报告总结1. 实验目的本次实验的目的是通过观察和研究阶梯波在传播过程中的特点,了解阶梯波在不同介质中的传播规律,并进一步探讨阶梯波的应用。
2. 实验原理阶梯波是一种特殊的波形,其波纹间存在突变。
在传播过程中,阶梯波会发生反射、折射等现象,其传播速度也会发生变化。
根据介质的不同,阶梯波的特性也会发生变化。
3. 实验装置与方法实验装置主要包括信号发生器、波形观测器、示波器等仪器。
实验方法主要是通过调节信号发生器的频率和振幅、监测观测器上的波形变化来研究和验证阶梯波的传播规律。
4. 实验过程与结果我们首先搭建好实验装置,将信号发生器与波形观测器以及示波器相连接,保证电路连接正确。
之后,我们设置信号发生器的频率和振幅,观测波形观测器上的波形变化。
在不同介质条件下,我们观测到了不同的波形变化。
当阶梯波传播到介质边界时,会发生反射和折射。
我们发现,当阶梯波从一个密度较大的介质传播到一个密度较小的介质时,反射波幅度增大,传播速度变小;相反,当阶梯波从一个密度较小的介质传播到一个密度较大的介质时,反射波幅度减小,传播速度变大。
这说明阶梯波在介质边界的传播受到了介质密度的影响。
在实验过程中,我们还改变了信号发生器的频率和振幅,观察到了阶梯波传播的不同情况。
当频率较低时,波形较为平缓;当频率较高时,波形变得更加陡峭。
通过实验,我们进一步验证了阶梯波在不同频率下的传播特点。
5. 实验分析与讨论通过本次实验,我们对阶梯波的传播规律有了更深入的了解。
阶梯波在传播过程中会发生反射、折射等现象,其传播速度也会随着介质的密度变化而变化。
此外,阶梯波的频率和振幅也会对传播过程产生影响。
阶梯波在实际中有着重要的应用价值。
例如,在地震勘探中,我们可以利用阶梯波的传播速度和频率响应来分析地下地质结构,从而获取有关地下资源的信息。
阶梯波的应用也可扩展到其他领域,如医学影像学、无线通信等。
6. 实验总结通过本次实验,我们深入了解了阶梯波的传播规律。
第一组实验指导书4.0

示波器的使用一、初级使用1. 接通电源,打开示波器上方的电源开关。
2. 连接示波器探头。
将示波器探头上的插槽对准示波器CH1上的插口插入,将另一端鳄鱼夹夹到实验箱上对应模块的GND上,将测试探头挂钩与测试点连接。
手柄上有×1、×10档可供选择,应选择×1档。
说明:选择×1档信号是未经衰减进入示波器的,选择×10档,信号是经过衰减到1/10后才进入示波器的,此时应将示波器读数扩大10倍后再读数。
当测量较大电压时,应选择×10档。
若发现示波器上显示的信号远远小于实际信号大小时,应查看示波器探头上的档位选择是否正确。
3. 示波器探头连接好后,按下示波器上的AUTO键。
转动scale键,波形逐渐显示出来。
若无波形显示,注意检查示波器探头两端是否有松动。
若波形不稳定,则转动示波器的level 键,使用触发控制功能,可以获得稳定重复波形。
说明:所谓触发,即使得示波器的扫描与被观测信号同步,从而显示稳定波形。
第一种是“自动模式(AUTO)”,在这种模式下,示波器根据采集到的信号自动选择合适的触发电平,如果信号比较复杂,auto自动设定的触发电平并不是最佳的,最好手动设定出发模式。
第二种是“正常模式/常规模式(NORM)”,这种模式与自动模式不同,在这种模式下示波器只有当触发条件满足了才进行扫描,如果没有触发,就不进行扫描。
因此在这种模式下如果没有触发的话,对于模拟示波器会看不到扫描线,屏幕上什么都没有,对于数字示波器会看不到波形更新,不了解这一点常常会以为是信号没连上或什么其他故障。
这种情况下,按下面板右边的“menu”按钮,可以选择触发模式。
其中包括边沿触发、脉宽触发、斜率触发。
然后设定触发条件,当满足触发条件时才可以触发。
如在CVSD编译码系统实验中,负极性一致脉冲信号输出波形,可以设置脉宽大于一定时间,这样只有当脉宽大于这个时间时,才会触发,从而使波形稳定下来。
阶梯波信号发生器

实验6阶梯波发生器的设计与实现课题名称:阶梯波发生器的设计与实现摘要:本报告主要由三部分组成。
第一部分为分析设计过程,囊括了本实验的设计任务与要求,以及根据实验要求所设计出的总体的实现计划。
对各个部分进行了层次分化,重点讨论了各个基础层次(包括窄脉冲发生器、积分器与迟滞电压比较器)的设计原理,详细的叙述了在设计阶段里对各个元件参数的设计思想和设计过程,并包含了在正式实验前对各个部分的Simulate的情况。
第二部分为实验记录过程,包括实际搭载的电路板所实现的功能,一些必要的测试数据以及在实验过程中的一些记录与故障问题的分析。
最后一部分是对实验的总结。
关键字:阶梯波、脉冲发生器、积分器、电压比较器一、 实验目的:1. 通过实验进一步掌握集成运放和电压比较器的应用。
2. 进一步提高工程设计和实践动手能力,建立系统概念。
二、 实验任务1. 基本要求:1) 利用所给元件设计一个阶梯波发生器,V U Hz f opp 3,500≥≥,阶数6=N ;2) 设计该电路的电源电路(不要求实际搭建)。
用Protel 软件绘制完整的电路原理图(SCH )及印制电路板图(PCB )。
2、 提高要求:利用基本要求里设计的阶梯波发生器设计一个三极管输出特性测试电路,在示波器上可以观测到基极电流为不同值时三极管的输出特性曲线束。
3、 探究环节:1) 能否提供其它阶梯波发生器的设计方案? 2) 探索其他阶梯波发生器的应用实例。
三、 实验原理基本原理图四、实验所用仪器及元器件仪器:1.函数信号发生器2.示波器3.晶体管毫伏表4.万用表5.直流稳压电源元器件:集成运算放大器uA741*3电位器(200K*1、22K*1,10K*2)二极管*2电阻(10K*2、50K*1,1000K)电容(0.01uF*2)u A741参数如下:五、 设计与制作步骤1、设计电路1)由参考公式可知])()(41ln['])(21ln['])(21ln['21221211111111112111111R m f m f P P R m f mP R m f mP U U R U R R R C R T U U R U R C R T U U R U R C R T -++=++=-+=T 为阶梯波脉冲,T ’为脉冲波周期;T1’高电平持续时间;T2’为低电平持续时间。
毕业设计76北京邮电大学电子电路综合实验-阶梯波发生器设计与实现

电子电路综合实验阶梯波发生器设计与实现阶梯波发生器设计与实现一中英文摘要及关键词:中文摘要:阶梯波是一种取值不随时间连续变化的信号,它的取值具离散性。
当今这个数字时代,在一些实际应用中,由于阶梯波信号的数字特性而被广泛使用。
本次实验是利用运算放大器组合,利用二极管单向导通特性,设计一个阶梯波发生器。
由方波-三角波发生器与迟滞电路比较器实现了一个阶梯波发生器关键词:阶梯波、运算放大器、迟滞电压比较器Abstract of ladder waveform generator design experiment:Ladder waveform is a signal whose values change almost discretely. Nowadays it’s a digital era,step signal is widely used in many practical ways,This experiment design a ladder waveform generator by diode characteristic and combinations of operation amplifiers.Key words:Ladder Waveform , Operation Amplifier , Hysteresis Voltage Comparator二实验目的:1 通过实验进一步掌握集成运放和电压比较器的应用2 进一步增强工程设计和实践动手能力,建立系统概念三设计任务要求:1基本要求:1)利用所给元器件设计一个阶梯勃发生器,f>=500Hz,Uopp>=3V,阶梯N=6. 2)设计该电路的电源电路(不要求实际搭建),用PROTEL绘制完整的电路原理图(SCH);2提高要求:1)用PROTEL绘制完整的印制电路板图(PCB);2)在接替勃发生器的基础上,设计一个三极管输出特性测试电路,在示波器上可以观测到基极电流为不同值时三极管的输出特性曲线束;3探究环节:1)提供其他阶梯波的设计方案,(通过仿真或实验结果加以证明);2)探究其他阶梯波发生器的应用实例,给出应用实例。
阶梯波发生器实验报告

电子电路综合实验设计实验名称:阶梯波发生器的设计与实现学院: 信息与通信工程学院班级: xxxxxxxxx学号: xxxxxxxxxx班内序号: xx姓名:大学霸实验报告大纲一、实验课题二、实验要求1.实验内容摘要及关键词2.实验任务及设计要求三、实验设计1.设计思路及总体结构框图2.元器件资料3.分块电路和总体电路的设计四、所实现功能说明1.基本功能2.扩展功能3.探索环节五、故障及问题分析六、实验总结和结论七、其他1.PROTEL绘制的原理图(SCH)及印制电路板(PCB)2.实验所用元器件及测试仪表清单3.参考文献一、实验课题阶梯波发生器的设计与实现二、实验要求1.实验内容摘要及关键词(1)实验内容摘要本实验的目的是设计与实现一个阶梯波发生器。
实验电路由窄脉冲-锯齿波发生器构成,通过将运算放大器的几个典型电路——方波发生器、积分器和迟滞电压比较器,以及二极管形成的控制门等主要元器件,进行合理的改进组合,设计出阶梯波发生电路。
实验用两个二极管分别作为阶梯波形成控制门和阶梯波返回控制门;通过调节相应的电位器,改变阶梯数、阶梯幅值、阶梯周期以及阶梯波周期等波形特性。
而且通过对该电路的适当改价,可以完成一个三极管输出特性测试电路。
阶梯波发生器还有多种设计方案,本实验将就其中一种进行研究。
(2)关键词阶梯波、集成运放、窄脉冲发生器、迟滞电压比较器、积分器2.实验任务及设计要求1、 基本要求:1) 利用所给元器件设计一个阶梯波发生器,500,3opp f Hz U V ≥≥,阶数6N =;2) 设计该电路的电源电路(不要求实际搭建),用PROTEL 软件绘制完整的电路原理图(SCH )及印制电路板图(PCB )。
2、 提高要求:利用基本要求里设计的阶梯波发生器设计一个三极管输出特性测试电路,在示波器上可以观测到基极电流为不同值时的三极管的输出特性曲线束。
3、 探究环节:能否提供其他阶梯波发生器的设计方案?如果能提供,请通过仿真或实验对结果加以证明;探索其他阶梯波发生器的应用实例,给出应用方案。
EDA实验设计

EDA实验设计报告实验一单极放大电路的设计与仿真目录一、实验原理图 (3)二、电路饱和、截至、放大三种情况下的波形图和静态工作点 (3)三、测量电路输入、输出阻值、电压增益并与理论值比较 (7)四、电路的幅频、相频曲线和f L和f H值 (9)五、实验结果分析 (9)一、实验原理图二、电路饱和、截至、放大三种情况下静态工作值(一)电路饱和失真1、电路饱和失真电路图2、电路饱和失真静态工作点值由原理图可知标点2/4/6分别为三极管的b/c/e点,所以Vbe=V(2)-V(6)=649.7765mVVce=V(4)-V(6)=48.78381mVIc=1.30726mA;Ib=204.58856µA因为Vce远小于稳压电压12V所以电路应处于饱和失真区3、电路饱和失真输出信号波形图(二)电路截止失真1、截止失真电路图2、截止失真静态工作点值由电路图可知标点2/4/6分别为三极管的b/c/e点,所以Vbe=V(2)-V(6)=618.12657mVVce=V(4)-V(6)=5.33305VIc=740.69955μA;Ib=5.65936µA因为Ib≈0,所以电路应处于截止失真区,而Vce由于电路交流负载线的斜率绝对值较大,所以并不能接近于Vcc。
3、截止失真输出波形图(三)电路正常放大1、正常放大电路图2、正常放大静态工作点值由电路图可知标点2/4/6分别为三极管的b/c/e点,所以Vbe=V(2)-V(6)=631.93983mVVce=V(4)-V(6)=2.61460VIc=1.03967mA;Ib=9.45763µA因为Vce>1V大小处于正常区域所以电路应处于正常放大区3、正常放大输出波形图三、测量电路输入、输出阻值、电压增益(一)求解电路输入电阻Ri由电路图所接电压表电流表所示Vi=999.962µV,Ii=401.66nA,而输入电阻Ri=Vi/Ii=999.962µV/401.66n A=2.49kΩ(二)求解输出电阻Ro由电路图所接电压表电流表所示V o=999.962µV,Io=270.417nA,而输出电阻Ro=V o/Io=999.962µV/270.417n A =3.70kΩ(三)求解电压增益Av1、求解电压增益的电路图四、电路的幅频、相频曲线和f l和f h值由上图可知fl=x2=2.9363kHZ, fh=x1=1.2750MHZ五、实验结果分析(一)以实验方法求取输入电阻Ri、输出电阻Ro和电压增益Av 以上计算可知实验测试结果:Ri =2.49kΩ;Ro =3.70kΩ;Av=-95.22;(二)以理论计算方法求解输入电阻Ri、输出电阻Ro和电压增益AvIc=1.03967mA;Ib=9.45763µA; β≈Ic/Ib=109.93; Ie≈Ic=1.03967mAR be≈rbb’+(1+β)*re =rbb’+ (1+β)*(Vt/Ieq)≈200+(1+110)*(26/1.03967)=2.97kΩ①输入电阻Ri’=R1//R2//r be=70//35//2.97 kΩ=2.63 kΩ;输入电阻相对误差ΔRi%=|Ri-Ri’|/Ri’*100%=|2.49-2.63|/2.63*100%=5.3%试验数据与理论计算值相差不大。
Multisim仿真——阶梯波信号发生器

仿真与设计报告设计课题:阶梯波信号发生器班级:学号:姓名:阶梯波发生器一、设计要求设计一个频率可调、阶数可调的阶梯波发生器,在Multisim中进行仿真分析。
实现的功能:频率可调、阶数可调的平滑的阶梯波。
性能指标:频率可调范围较大,阶数可调的阶数范围合理,输出平滑无毛刺的阶梯波。
二、设计方案1、由时钟信号发生器、计数器和D/A转换器组成电路2、时钟信号发生器的信号频率可调,采用555构成的多谐振荡器3、计数器的进制数决定阶梯波的阶数,采用有预置数功能的减法计数器,通过置数改变计数器的进制数。
4、D/A转换器将计数器的输出值转换为模拟电压。
5、利用低通滤波器使输出的波形变平滑。
三、电路框图四、电路原理图及说明总体电路如图:图中从左至右依次为:第一部分为由555构成的多谐振荡器,第二部分为有74LS161D 构成的十六进制计数器,第三部分为D/A转换器,第四部分为低通滤波器。
1、由555构成的多谐振荡器电路图(图一):图一电源接通后,Vcc通过电阻R1、R2、R3向电容C2充电。
当C2上电压达到2/3Vcc时,THR端触发,比较器翻转,输出V0变低电平,同时放电管导通,电容C2通过R2放电;当C2上电压下降到1/3Vcc时,下比较器工作,输出电压V0变高电平,C2放电终止,重新充电,周而复始,形成矩形波。
通过调节电位计R3大小,可改变矩形波频率。
图二中频率计示数为R3滑片位于中点时的频率。
输出矩形波波形如图三。
图二图三2、四位二进制计数器74LS161(图四)(74LS161是常用的四位二进制可预置的同步加法计数器,)图四电路采用74LS161十进制加法计数器构成的十六进制计数器。
采用置数端归零的方法,清零端接高电平。
通过控制单刀双掷开关将A、B、C、D与高电平或低电平相连,DCBA表示的十进制数是15-N,N为输出阶梯波的阶数,即通过单刀双掷开关控制阶梯波的阶数。
如,DCBA为0111时,即ABC接高电平,D接低电平,输出为8阶阶梯波。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
阶梯波发生电路的设计
一.实验目的
1)掌握阶梯波发生器电路的结构特点。
2)掌握阶梯波发生器电路的工作原理。
3)学习复杂的集成运算放大电路的设计。
二.试验设计原理
为了设计一个负阶梯波发生器,首先考虑产生一个方波,其次,经过微分电路输出得到上下都有的尖脉冲,然后经过限幅电路,只留下所需的正脉冲,再经过几分电路,实现累加二输出一个负阶梯。
对应一个尖脉冲就是一个阶梯,在没有尖脉冲时,积分器保持输出不变,在下一个尖脉冲到来时,积分器在原来的基础上进行积分,因此,积分器就起到了几分累加的作用。
当积分累加到比较器的比较电压时,比较器翻转,比较器输出正电压,使振荡控制电路起作用,方波停振。
同时,这个正电压使电子开关导通,积分电容放电,积分器输出对地短路,恢复到起始状态,完成一次阶梯波的输出。
积分器输出由负值向零跳变的过程,又使比较器发生翻转,比较器输出变为负值,这样振荡控制电路不起作用,方波输出,同时电子开关断开,积分器进行积分累加,如此循环往复,就形成了一系列阶梯波。
其原理框图如下:
原理框图
阶梯波发生电路原理图
三.实验要求和实验步骤
1.实验要求
1)设计一个能产生周期性阶梯波的电路,要求阶梯波周期在18ms左右,输出电压范围10V,阶梯个数5个。
(注意:电路中均采用模拟、真
实器件,不可以选用计数器、555定时器、D/A转换器等数字器件,
也不可选用虚拟器件。
)
2)对电路进行分段测试和调节,直至输出合适的阶梯波。
3)改变电路元器件参数,观察输出波形的变化,确定影响阶梯波电压范围和周期的元器件。
2.试验步骤
1)首先设计一个方波发生器,设计电路原理图如下图所示:
方波发生电路的原理图
双击上图示波器得到方波发生器的输出波形如图所示:
方波发生器输出波形
从上图可看出方波的周期为3.103ms,幅度为10.813V,上图中锯齿波是从C1断
输出得曲线。
2)在方波发生器的输出端接电阻R3和电容C2就组成了微分电路如下图所示:
方波发生+微波电路原理图
双击上图示波器得到输出波形为双边脉冲波形如图所示:
由微分电路输出的双边脉冲波形
3)设计限幅电路,将负半周的尖脉冲滤除掉。
利用二极管的单向导电性来进行
限幅,电路图如下:
方波发生器+微波+限幅电路原理图
得到单边尖脉冲如下图:
限幅电路输出的单边尖脉冲波形
通过上图可以看出波形进过二极管后下部分的波形被滤除掉了,只剩下了正半轴的波形。
4)设计积分累加电路,用集成运放组成的积分电路实现积分累加,在前面电路的基础上连接积分累加电路如图所示:
方波发生器+微波+限幅+积分累计电路原理图
打开仿真开关,得到积分累加的输出波形如下图所示:
接入积分累加电路后输出的波形
5)设计周期阶梯波,在(4)的基础上加上电压比较器和开关控制电路,就组成了完整的阶梯波发生电路,其原理图如下图所示:
阶梯波发生电路原理图
其输出波形如下图所示:
输出的阶梯波形
从上图可以看出阶梯波周期在18.029ms左右,输出电压范围10.009V,阶梯个数为5个。
6)改变电路元器件参数,观察输出波形的变化
a)研究哪些元件影响阶梯波周期
当R10=30KΩ时的阶梯波形,其周期变为了12.369ms,说明R10变小周期也变小
当C1=10nF时的阶梯波形,其周期为4.612ms,说明C1变小周期也变小
通过以上两图以及逐步分析各个电路的输出波形,发现改变R10和C1可以改变
阶梯波的周期,因为振荡周期
1
11
2
(1)
101
2ln
R
R
T R C
+
=
,所以阶梯波的周期与R10C1
成正比。
b)研究阶梯波的电压范围与那些元件有关
当C3=62nF时的阶梯波形图,其电压范围从10.009V变为9.586V,说明改变电容C3会影响电压范围,并且C3变大电压范围变小成反比。
并且阶梯波的阶梯数从5变到了9.
当R5=5.1kΩ时的阶梯波形图,其电压范围从10.009V变为9.867V,说明改变
电容R5会影响电压范围,并且R5变大电压范围变小成反比。
通过以上两图以及逐步分析各个电路的输出波形,发现改变R5和C3可以改变阶梯波的电压范围,所以得出R5C3与阶梯波的电压范围成反比。
改变R12波形图会出现如上图所示的毛刺
c)同时影响周期和幅度的量
1)改变R
7的值会改变阶梯波的周期与电压范围,若增大R
7
则周期变小,电压
范围变小
将R
7
增大到11KΩ时的阶梯波形图
2)改变R
12
的值,阶梯高度基本不变,但阶梯波电压变化范围变化,周期也会变
化,增大R
12
时,阶梯波电压变化范围变大,周期变小。
R
12
变为16.5KΩ的波形图
3) 改变R
8时,电压范围和周期也会变化,阶梯高度不变。
减小R
8
时,电压范围
和周期均变小。
R
8
变为9.09KΩ的波形图
4)改变二极管D
1和D
2
的型号对波形的影响
四. 试验分析及体会
1.误差分析
a)对阶梯波的周期的误差进行分析
本次实验中根据输出的波形图测量出阶梯波的周期为18.029ms 而实验要求阶梯波的周期为18ms ,其误差率为
100%0.16%T T E T -=⨯=真
真
产生以上误差的有很多原因,其中主要原因是:阶梯波的周期主要是由方波发生器确定的方波电路中对周期起作用的主要是电阻R 10电容C 1共同决定的并且与他们的值成正比所以调节两个的值就可以了但是软件给的电阻与电容的值都不是连续的所以产生了误差,产生的误差在误差允许的范围内。
所以在本次实验中对周期的调整蛮成功的。
b)对阶梯波的电压范围的误差进行分析
本次实验中根据输出的波形图测量出阶梯波的电压范围为10.009V 而实验要求阶梯波的电压范围为10V ,其误差率为
100%0.09%U U E U -=⨯=真
真
产生以上误差的有也有很多原因,其中主要原因是:阶梯波的电压范围主要有积分电路确定的而在积分电路中决定电压范围的是电阻R 5电容C 3决定的,并且与他们的值成反比。
其产生的主要误差与上面的差不多都是由于软件给的元器件实的值不是连续变化的所以很难调到与要求的值一样。
2.实验的体会
本次实验主要是设计一个周期阶梯波产生电路,要实现阶梯波产生电路需实现几个部分,因为阶梯波是由及部分实现的。
第一部分是方波产生电路,该部分主要是产生一系列需要的方波;第二部分是微分电路,该部分主要是对方波进行微分产生一系列的脉冲波;第三部分是限幅电路,该部分主要是把第二部分产生的双边脉冲波变成单边脉冲波形;第四部分是积分累加电路,该部分主要是产生阶梯波。
最后两部分是比较器与振荡控制电路,这两部分是让第四部分产生的阶梯波生成周期阶梯波。
了解以上几部分的功能后就一部分一部分的设计,一部分一部分的调试。
本次实验中的元器件的值都很敏感,只要稍微变一下产生的波形就会发生变化,所以本次实验的难点是选择好每个元器件的型号以及值。
并且实验中所用到的三极管和二极管的型号对实验的影响也很大。
其次还要注意阶梯波的周期和电压范围与哪些因素有关,经过试验的出阶梯波的周期与R 10C 1成正比。
电压范围与R 5C 3成反比。
波形的最后一介的毛刺主要是由电阻R 12产生的。
这次实验整体难度比前两个实验难,并且比较复杂需要一级一级的分析,哪一级出问题就会影响整体电路。
但是整体也是由局部组成的,也需要一步一步的分析,这次实验让我感受颇多,让我了解到了从局部到整体的分析方法。
