激光原理周炳琨答案
周炳坤版激光原理习题答案第七章
第七章 激光特性的控制与改善习题1.有一平凹氦氖激光器,腔长0.5m ,凹镜曲率半径为2m ,现欲用小孔光阑选出TEM 00模,试求光阑放于紧靠平面镜和紧靠凹面镜处的两种情况下小孔直径各为多少?(对于氦氖激光器,当小孔光阑的直径约等于基模半径的3.3倍时,可选出基模。
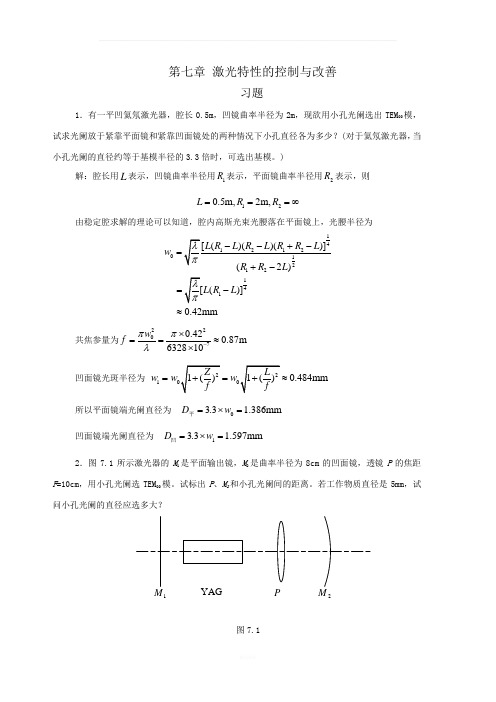
)解:腔长用L 表示,凹镜曲率半径用1R 表示,平面镜曲率半径用2R 表示,则120.5m,2m,L R R ===∞由稳定腔求解的理论可以知道,腔内高斯光束光腰落在平面镜上,光腰半径为012141 ()] 0.42mmw L R L ==-≈共焦参量为22070.420.87m 632810w f ππλ-⨯==≈⨯ 凹面镜光斑半径为10.484mm w w w ==≈ 所以平面镜端光阑直径为 03.3 1.386mm D w =⨯=平 凹面镜端光阑直径为 13.3 1.597mm D w =⨯=凹2.图7.1所示激光器的M 1是平面输出镜,M 2是曲率半径为8cm 的凹面镜,透镜P 的焦距F =10cm ,用小孔光阑选TEM 00模。
试标出P 、M 2和小孔光阑间的距离。
若工作物质直径是5mm ,试问小孔光阑的直径应选多大?图7.112解:如下图所示:12P小孔光阑的直径为:31.061010022mm 0.027mm 2.5f d a λππ-⨯⨯==⨯≈⨯其中的a 为工作物质的半径。
3.激光工作物质是钕玻璃,其荧光线宽F ν∆=24.0nm ,折射率η=1.50,能用短腔选单纵模吗?解:谐振腔纵模间隔222q q c LLνηλλη∆=∆=所以若能用短腔选单纵模,则最大腔长应该为215.6μm 2L ληλ=≈∆所以说,这个时候用短腔选单纵模是不可能的。
6.若调Q 激光器的腔长L 大于工作物质长l ,η及'η分别为工作物质及腔中其余部分的折射率,试求峰值输出功率P m 表示式。
解:列出三能级系统速率方程如下:2121 (1)2 (2)R dN l NcN n dt L d nN n dtστσυ=∆-'∆=-∆式中,()L l L l ηη''=+-,η及'η分别为工作物质及腔中其余部分的折射率,N 为工作物质中的平均光子数密度,/,/R c L c υητδ'==。
1-习题集-激光原理

解:
f
F 20 2 0 2 2.67 m , 0 '2 ( F l )2 w2 ( z ) 2 2
z 2 2 1 ( )
(1)当 1 103 rad , 0.5145 m, z 3.8 105 km 时 光腰半径为 w0
2
3.3 104 m
一、课堂作业题答案
1. ( 习 题 2.11 ) 如 图 , 已 知 :
0 3mm, 10.6um, z1 2cm, d 50cm, f1 2cm, f 2 5cm 。求: 02 和 z2 ,并
叙述聚焦原理。
解答; 方法一。复杂方法
解答二:简单方法
聚焦原理
第一个透镜, 物距等于焦距, 具有最大焦点,
F 20 2
(1) ( F l )
0
2
f 2 1.885m2
l 1.39m
(2) ( F l )
F 20 2
0
2
f 2 568.9m2
l 23.87m
3. 如图所示,假设一高斯光束垂直入射到折射率为 n 的介质块上,试问: (1)在左图情况下,出射光束发散角为多大? (2)若将介质块的位置左移,使其左端面移至
一定成立,因此,只要满足 稳定条件。 类似的分析可以知道,
凸凹腔的稳定条件是: R1 0
R2 L ,且 R1 R2 L 。
双凹腔的稳定条件是: R1 L , R2 L
激光原理周炳坤-第2章习题答案

第二章 开放式光腔与高斯光束习题(缺2.18 2.19 2.20)1. 题略证明:设入射光()11,r θ,出射光()22,r θ,由折射定理1122sin sin ηθηθ=,根据近轴传输条件,则1122sin ,sin θθθθ≈≈1122ηθηθ∴=,联立21r r =,则所以变换矩阵为 2. 题略证明:由题目1知,光线进入平面介质时的变换矩阵为:经过距离d的传播矩阵为: 光线出射平面介质时: 故3. 试利用往返矩阵证明共焦腔为稳定腔,即任意傍轴光线在其中可以往返无限多次,而且两次往返即自行闭合。
证:设光线在球面镜腔内的往返情况如下图所示:其往返矩阵为:122212111210101122110101212(1) 222222[(1)][(1)(1)]A B L L T C D R R L L L R R L L L L R R R R R R ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭ ⎪ ⎪⎝⎭⎝⎭⎛⎫-- ⎪⎪= ⎪-+----- ⎪⎝⎭212211100r r θηηθ⎛⎫⎛⎫⎛⎫= ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭21100T ηη⎛⎫= ⎪⎝⎭121100T ηη⎛⎫= ⎪⎝⎭2100d T ⎛⎫=⎪⎝⎭312100T ηη⎛⎫= ⎪⎝⎭3113213112211101010000r r r d T T T θθηηηηθ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫== ⎪ ⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭123211221101011000000d d T T T T ηηηηηη⎛⎫⎛⎫⎛⎫⎛⎫∴=== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭由于是共焦腔,有 12R R L == 往返矩阵变为若光线在腔内往返两次,有可以看出,光线在腔内往返两次的变换矩阵为单位阵,所以光线两次往返即自行闭合。
于是光线在腔内往返任意多次均不会溢出腔外,所以共焦腔为稳定腔。
4. 试求平凹、双凹、凹凸共轴球面镜腔的稳定性条件。
激光原理第四章习题解答

《激光原理》习题解答作者:周炳琨等 国防工业出版社 第五版解答人:广东海洋大学理学院光电科学系 石友彬(2008年修正版)习题解答说明:习题解答参考蓝信鉅的激光技术、陈家璧版激光原理及应用等,在此对上述作者表示敬意! 本章习题是在我系前外聘教授郭振华习题解答基础上汇总而成,在此表示衷心感谢。
1 静止氖原子的4223P S →谱线中心波长为632.8纳米,设氖原子分别以0.1C 、O.4C 、O.8C 的速度向着观察者运动,问其表观中心波长分别变为多少? 解答:根据公式(激光原理P136)ccυυνν-+=110υλν=由以上两个式子联立可得:0λυυλ⨯+-=C C代入不同速度,分别得到表观中心波长为:nm C 4.5721.0=λ,nm C 26.4144.0=λ,nm C 9.2109.0=λ解答完毕(验证过)2 设有一台麦克尔逊干涉仪,其光源波长为λ,试用多普勒原理证明,当可动反射镜移动距离L 时,接收屏上的干涉光强周期性的变化L 2次。
证明:对于迈氏干涉仪的两个臂对应两个光路,其中一个光路上的镜是不变的,因此在这个光路中不存在多普勒效应,另一个光路的镜是以速度υ移动,存在多普勒效应。
在经过两个光路返回到半透镜后,这两路光分别保持本来频率和多普勒效应后的频率被观察者观察到(从半透境到观察者两个频率都不变),观察者感受的是光强的变化,光强和振幅有关。
以上是分析内容,具体解答如下:无多普勒效应的光场:()t E E ⋅=πνν2cos 0 产生多普勒效应光场:()t E E ⋅=''02cos ''πνν在产生多普勒效应的光路中,光从半透经到动镜产生一次多普勒效应,从动镜回到半透镜又产生一次多普勒效应(是在第一次多普勒效应的基础上) 第一次多普勒效应:⎪⎭⎫⎝⎛+=c υνν1'第二次多普勒效应:⎪⎭⎫ ⎝⎛+≈⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+=c c c υνυνυνν21112'''在观察者处:()⎪⎭⎫⎝⎛⋅⋅⎪⎭⎫ ⎝⎛⋅+⋅==⎭⎬⎫⎩⎨⎧⎪⎪⎭⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛++⋅=+=t c t c t E t c t E E E E πνυπνυπνυπνπν2cos 22cos 2212cos 2cos 0021观察者感受到的光强:⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡⋅⎪⎭⎫ ⎝⎛⋅+=t c I I υνπ22cos 120 显然,光强是以频率cυν⋅2为频率周期变化的。
激光原理 第六版 周炳琨编著9章

激光器种类
典型激光器
典型激光器
典型激光器
典型激光器
固体激光器
一、光泵激励 1. 气体放电灯激励
脉冲激光器采用脉冲氙灯,连续激光器采用氪灯或碘钨灯
气体放电灯能量转换环节多,辐射光谱宽,激光效率低。
固体激光器
一、光泵激励 2. 半导体激光二极管激励
激光二极管泵浦可采用端面与侧面泵浦两种形式。
Sirah Dye Lasers
Lamda Physik XeCl及染料激光器
Lamda Physik XeCl及染料激光器
染料激光器
6.通常采用闪光灯、N2分子激光器、 准分子激光器、倍频Nd:YAG激光器 作为脉冲染料激光器泵浦源;连续 激光器使用氩或氙离子激光器。 7.泵浦光波长必须小于激光输出波 长。 8.采用光栅、棱镜、标准具、双折 射虑光片等波长选择元件进行波长 调谐。 9.在紫外(330nm)到近红外 (1.85um)连续可调谐输出。
0 0
9 . 6 m 激光。
气体激光器
三、CO2激光器
CO2通过以下三个过程激发到0001 1.直接电子碰撞 2.级联跃迁 3.共振转移
气体激光器
三、CO2激光器
激光下能级的抽空过程:
阻塞在0110能级上的CO2分子 与He原子碰撞,缩短了能级 寿命。 高气压下碰撞加宽占主导地位:
L
57
1.激发过程:
N2 X g e1
g
e
N2
C
g
3
u
e e
2.上下能级寿命分别为40ns 和10us。 3.上能级寿命比下能级寿命大 的多,在激励起始很短时间内 形成积聚数反转,超过这段时 间自行终止。 4.只能以脉冲方式运转,泵浦 放电脉冲小于40ns。 5.以火花脉冲放电方式激励。
周炳坤版激光原理习题答案第六章

第六章 激光放大特性习题1. 在增益工作物质两端设置二反射率为r 的反射镜,形成一个法布里—珀罗再生式放大器,如图6.1.1所示。
入射光频率为ν,谐振腔频率为c ν。
工作物质被均匀激励,其小信号增益系数为0g ,损耗系数为α。
试求:(1)用多光束干涉方法求再生放大器的小信号增益00()/G I l I =;(2)c νν=时再生放大器的增益0m G ; (3)再生放大器的带宽δν;(4)若无反射镜时放大器的增益为3,试作0m G —r 及δν-r 的曲线; (5)再生放大器正常工作时r 的范围。
解:(1) 若设入射光场为0E ,若忽略色散效应,则电场的传播情况如图所示,图中2k πνυ=,在输出端将各分波相加可得总的输出电场。
(这里的R 即为反射镜的反射率r )l g ikl ee E 2)(00)α--l g kli eeE R )(23300)α--这样就有:1()2()20(1)[1e ]g l ikli kl gll E R E eeR e αα----=-++其中中括号的内部是一个无穷等比数列,这样上式就可以写为:1()22()(1)1g l ikll i kl glR eeE E Re e αα-----=-放大器的小信号增益为:0000*2()0*22()()0002()()2()2()(1)12e cos 2(1) [1e ]4sin g l l l g l g l g lgl glE E I l R e G I E E R e R kl R eR Re klαααααα-------===+--=-+(2) c νν=的时候,c 2m lυνν==(m 为正整数)22sin sin 0kl m π==所以有02()0()2(1)[1]g lmg l R e G Reαα---=-(3) 2c δννν=+时,0012m G G =,比较0G 和0mG 的表达式有: 000()2()2()224sin()4sin 2[1]g lg lc gl Rel Rel Re αααπδνπδννυυ---+==-因为δν远小于/l νπ,所以22sin()l l πδνπδνυυ≈,由上式可得: 00()()12g lg l Re l Reααυδνπ---=(4) 根据题意知0()3g leα-=,可得:2023(1)(13)mR G R -=-,1323Rl Rυδνπ-=0m G -r 及δν—r 的曲线如下图所示。
周炳坤激光原理课后习题答案

《激光原理》习题解答第一章习题解答1 为了使氦氖激光器的相干长度达到1KM ,它的单色性0λ∆应为多少?解答:设相干时间为τ,则相干长度为光速与相干时间的乘积,即 c L c ⋅=τ根据相干时间和谱线宽度的关系 cL c ==∆τν1又因为 0γνλλ∆=∆,00λνc=,nm 8.6320=λ由以上各关系及数据可以得到如下形式: 单色性=0ννλλ∆=∆=cL 0λ=101210328.61018.632-⨯=⨯nmnm解答完毕。
2 如果激光器和微波激射器分别在10μm、500nm 和Z MH 3000=γ输出1瓦连续功率,问每秒钟从激光上能级向下能级跃迁的粒子数是多少。
解答:功率是单位时间内输出的能量,因此,我们设在dt 时间内输出的能量为dE ,则功率=dE/dt激光或微波激射器输出的能量就是电磁波与普朗克常数的乘积,即d νnh E =,其中n 为dt 时间内输出的光子数目,这些光子数就等于腔内处在高能级的激发粒子在dt 时间辐射跃迁到低能级的数目(能级间的频率为ν)。
由以上分析可以得到如下的形式:ννh dth dE n ⨯==功率 每秒钟发射的光子数目为:N=n/dt,带入上式,得到:()()()13410626.61--⨯⋅⨯====s s J h dt n N s J νν功率每秒钟发射的光子数 根据题中给出的数据可知:z H mms c13618111031010103⨯=⨯⨯==--λν z H mms c1591822105.110500103⨯=⨯⨯==--λνz H 63103000⨯=ν把三个数据带入,得到如下结果:19110031.5⨯=N ,182105.2⨯=N ,23310031.5⨯=N3 设一对激光能级为E1和E2(f1=f2),相应的频率为ν(波长为λ),能级上的粒子数密度分别为n2和n1,求(a)当ν=3000兆赫兹,T=300K 的时候,n2/n1=? (b)当λ=1μm ,T=300K 的时候,n2/n1=? (c)当λ=1μm ,n2/n1=0.1时,温度T=?解答:在热平衡下,能级的粒子数按波尔兹曼统计分布,即: TK E E T k h f f n n b b )(expexp 121212--=-=ν(统计权重21f f =) 其中1231038062.1--⨯=JK k b 为波尔兹曼常数,T 为热力学温度。
激光原理周炳坤-第2章习题答案

第二章 开放式光腔与高斯光束习题(缺2.18 2.19 2.20)1. 题略证明:设入射光()11,r θ,出射光()22,r θ,由折射定理1122sin sin ηθηθ=,根据近轴传输条件,则1122sin ,sin θθθθ≈≈1122ηθηθ∴=,联立21r r =,则所以变换矩阵为 2. 题略证明:由题目1知,光线进入平面介质时的变换矩阵为:经过距离d的传播矩阵为: 光线出射平面介质时: 故3. 试利用往返矩阵证明共焦腔为稳定腔,即任意傍轴光线在其中可以往返无限多次,而且两次往返即自行闭合。
证:设光线在球面镜腔内的往返情况如下图所示:其往返矩阵为:122212111210101122110101212(1) 222222[(1)][(1)(1)]A B L L T C D R R L L L R R L L L L R R R R R R ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪== ⎪ ⎪⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭⎪ ⎪⎝⎭⎝⎭⎛⎫-- ⎪⎪= ⎪-+----- ⎪⎝⎭212211100r r θηηθ⎛⎫⎛⎫⎛⎫= ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭21100T ηη⎛⎫= ⎪⎝⎭121100T ηη⎛⎫= ⎪⎝⎭2100d T ⎛⎫=⎪⎝⎭312100T ηη⎛⎫= ⎪⎝⎭3113213112211101010000r r r d T T T θθηηηηθ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫== ⎪ ⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭123211221101011000000d d T T T T ηηηηηη⎛⎫⎛⎫⎛⎫⎛⎫∴=== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭由于是共焦腔,有 12R R L == 往返矩阵变为若光线在腔内往返两次,有可以看出,光线在腔内往返两次的变换矩阵为单位阵,所以光线两次往返即自行闭合。
于是光线在腔内往返任意多次均不会溢出腔外,所以共焦腔为稳定腔。
4. 试求平凹、双凹、凹凸共轴球面镜腔的稳定性条件。
激光原理 第六版 周炳琨编著2章f

缺点:腔长太短,输出功率低。
腔内插入F-P标准具法
物理基础: F-P只能对某些特定频率的光通过。产生振荡的频率 不仅要符合谐振腔共振条件,还要对标准具有最大的透过率
腔内插入F-P标准具法
平板组合透过率是入射光波频率和平板反射率的函数
T ( ) (1 R )
2 2 2
(1 R ) 4 R sin
双凸非稳定腔的几何放大率
将从腔镜边缘外 侧逸出的球面波 作为激光器的有 用输出,非稳腔 中每一往返的平 均能量损耗率就 是其往返输出耦 合率。
双凸非稳定腔的几何放大率
球面波经M1反射到达M2的几何自 再现波型放大率: a2 l1 L m1 a2 l1
M2的几何自再现波型放大率:
纵模的选择
激光器的振荡频率范围和频谱:由工作物质增益曲线 的频率宽度来决定。P165表2-10-1给出了几种典型 激光器系统的光谱特征。
一般的谐振腔中,不同的纵模具有相同的损耗,因而进 行模式鉴别和选择时应可以利用不同纵模的不同增益。 同时,也可以引入人为的损耗差。
缩短腔的长度(短腔法)
相邻两个纵模的频率差: q q q 1 c 2L c 则当: q 2 L T 时可以实现单纵模谐振。
系统中总存在一对 轴上共轭像点p1和 P2,腔内存在一对发 散球面自再现波型, 由这一对像点发出的 球面波满足在腔内往 返一次成像的自再现 条件。
双凸腔中光线传输路径
根据球面镜成像公式,对凸面反射镜M2:
1 l1 L 1 l2 2 R2
对凸面反射镜M1:
1 l2 L
1 l1
2 R1
l2
l1 L
g 1 g 2 ( g 1 g 2 1) g 1 g 2 g 2 2g1g 2 g1 g 2 g 1 g 2 ( g 1 g 2 1) g 1 g 2 g 1 2g1g 2 g1 g 2
激光原理周炳坤-第4章习题答案

第四章 电磁场和物质的共振相互作用习题(缺7)1.解:根据多普勒效应,有ccz z /1/10υυυυ-+=则ccc c cc z z z z /1/1/1/1/0υυλυυυυλ+-=+-== 当c z 1.0=υ时,nm 4.5721≈λ 当c z 4.0=υ时,nm 3.4142≈λ 当c z 8.0=υ时,nm 9.2103≈λ2.设有一台迈克尔逊干涉仪,其光源波长为λ。
试用多普勒原理证明,当可动反射镜移动距离L 时,接收屏上的干涉光强周期地变化2/L λ次。
证明:如右图所示,光源S 发出频率为ν的光,从M 上反射的光为I ',它被1M 反射并且透过M ,由图中的I 所标记;透过M 的光记为II ',它被2M 反射后又被M 反射,此光记为II 。
由于M 和1M 均为固定镜,所以I 光的频率不变,仍为ν。
将2M 看作光接收器,由于它以速度v 运动,故它感受到的光的频率为:因为2M 反射II '光,所以它又相当于光发射器,其运动速度为v 时,发出的光的频率为:这样,I 光的频率为ν,II 光的频率为(12/)v c ν+。
在屏P 上面,I 光和II 光的广场可以分别表示为:S2M (1)v cνν'=+2(1)(1)(12)vv v c c cνννν'''=+=+≈+因而光屏P 上的总光场为:光强正比于电场振幅的平方,所以P 上面的光强为:它是t 的周期函数,单位时间内的变化次数为:由上式可得在dt 时间内屏上光强亮暗变化的次数为:(2/)mdt c dL ν=因为dt 是镜2M 移动dL 长度所花费的时间,所以mdt 也就是镜2M 移动dL 过程中屏上光强的明暗变化的次数。
对上式两边积分,即可以得到镜2M 移动L 距离时,屏上面光强周期性变化的次数S :式中1t 和2t 分别为镜2M 开始移动的时刻和停止移动的时刻;1L 和2L 为与1t 和2t 相对应的2M 镜的空间坐标,并且有21L L L -=。
激光原理周炳坤-第4章习题答案

第四章 电磁场和物质的共振相互作用习题(缺7)1.解:根据多普勒效应,有ccz z /1/10υυυυ-+=则ccc c cc z z z z /1/1/1/1/0υυλυυυυλ+-=+-== 当c z 1.0=υ时,nm 4.5721≈λ 当c z 4.0=υ时,nm 3.4142≈λ 当c z 8.0=υ时,nm 9.2103≈λ2.设有一台迈克尔逊干涉仪,其光源波长为λ。
试用多普勒原理证明,当可动反射镜移动距离L 时,接收屏上的干涉光强周期地变化2/L λ次。
证明:如右图所示,光源S 发出频率为ν的光,从M 上反射的光为I ',它被1M 反射并且透过M ,由图中的I 所标记;透过M 的光记为II ',它被2M 反射后又被M 反射,此光记为II 。
由于M 和1M 均为固定镜,所以I 光的频率不变,仍为ν。
将2M 看作光接收器,由于它以速度v 运动,故它感受到的光的频率为:因为2M 反射II '光,所以它又相当于光发射器,其运动速度为v 时,发出的光的频率为:这样,I 光的频率为ν,II 光的频率为(12/)v c ν+。
在屏P 上面,I 光和II 光的广场可以分别表示为:S2M (1)v cνν'=+2(1)(1)(12)vv v c c cνννν'''=+=+≈+因而光屏P 上的总光场为:光强正比于电场振幅的平方,所以P 上面的光强为:它是t 的周期函数,单位时间内的变化次数为:由上式可得在dt 时间内屏上光强亮暗变化的次数为:(2/)mdt c dL ν=因为dt 是镜2M 移动dL 长度所花费的时间,所以mdt 也就是镜2M 移动dL 过程中屏上光强的明暗变化的次数。
对上式两边积分,即可以得到镜2M 移动L 距离时,屏上面光强周期性变化的次数S :式中1t 和2t 分别为镜2M 开始移动的时刻和停止移动的时刻;1L 和2L 为与1t 和2t 相对应的2M 镜的空间坐标,并且有21L L L -=。
激光原理答案 周炳琨

R12(R 2 − L) L(R1− L)(R1+ R 2−
L)
4
=
λ π
1
[L(R2−L)] 4
(R → ∞) 1
=4 3 λ ≈1.7*10−3m
4π
1
ω s2 =
λL π
R 22(R1− L) L(R 2− L)(R1+ R 2−
L)
4
=
λ
(
L
R
2 2
1 4
R=∞
R
R
R=∞
该三镜环形腔的往返矩阵为:
T = 10
10 10
L1
1 -1
f
10
1 0
L 1
1 -1
f
10
1 0
L 1
=
A C
B D
A = D = 1− 3 L + L 2 f f
能级之间实现了集居数反转。
τ (1) 4 =
A43
+
1 A42
+
A41
=
1.1*10−8
s
(2) 在稳定状态时,不考虑无辐射跃迁和热驰豫过程,
E 对 : 3
A43 n4 =
n3 τ3
,
n3 n4
=
A43τ
3
=5*10−1
E E 实现 和 能级集居数反转
4
3
对
E2 : A42 n4 =
n2 τ2
,
n2 n4
(2) n=
1W *500nm 6.626*10−34 Js*3*108
ms−1
激光原理 周炳琨版课后习题答案

(b)当 ,T=300K时:
(c)当 , 时:
6.某一分子的能级 到三个较低能级 、 和 的自发跃迁几率分别是 , 和 ,试求该分子 能级的自发辐射寿命 。若 , , ,在对 连续激发并达到稳态时,试求相应能级上的粒子数比值 、 和 ,并回答这时在哪两个能级间实现了集居数反转。
8.今有一球面腔, , , 。试证明该腔为稳定腔;求出它的等价共焦腔的参数;在图上画出等价共焦腔的具体位置。
解:该球面腔的g参数为
由此, ,满足谐振腔的稳定性条件 ,因此,该腔为稳定腔。
两反射镜距离等效共焦腔中心O点的距离和等价共焦腔的焦距分别为
根据计算得到的数据,在下图中画出了等价共焦腔的具体位置。
于是光线在腔内往返任意多次均不会溢出腔外,所以共焦腔为稳定腔。
3.激光器的谐振腔由一面曲率半径为1m的凸面镜和曲率半径为2m的凹面镜组成,工作物质长0.5m,其折射率为1.52,求腔长L在什么范围内是稳定腔。
解:设两腔镜 和 的曲率半径分别为 和 ,
工作物质长 ,折射率
根据稳定条件判据:
其中
由(1)解出
激光原理
周炳琨
(长按ctrl键点击鼠标即可到相应章节)
注:考华科者如需激光原理历年真题与答案可联系
E-mail:745147608@
第一章
习题
2.如果激光器和微波激射器分别在 、 和 输出1W连续功率,问每秒从激光上能级向下能级跃迁的粒子数是多少?
解:若输出功率为P,单位时间内从上能级向下能级跃迁的粒子数为n,则:
得
10m
1m
10cm
0
2.00cm
2.08cm
2.01cm
2.00cm
