概率论与数理统计课件_第六章2
概率与统计学课件-第六章-数理统计的基本概念2-1

�总体与样本
基本概念: 总体:研究的问题所涉及的对象的全体 个体:总体中的每个成员 样本:从总体中抽取部分个体 样本容量:样本所包含的个体数量 样本观测值:
数的属性 样本的二重性 随机变量的属性
设X1,X2, …,Xn为总体X的一个容量为 n的 样本。若它满足 独立性,即X1,X2, …,Xn 相互独立; 同分布性,即每个 Xi都与总体X服从相 同的分布. 则称这样的样本为简单随机样本,简称为 样本。
�统计量
设是总体X的样本,g(X1,X2, …,Xn)是样本 的实值函数,且不包含任何未知参数,则 称g(X1,X2, …,Xn)为统计量。
例2.若X1,X2, X3是来自总体X~N(μ, σ 2)的 其中参数μ未知, σ2已知,则
X 1 X 3 − 3µ , X12 + 4 X 22 + 5µ 都不是统计量
�定理
若X1,X2, …,Xn是来自总体X的样本,设X 的分布函数为 F(x),则样本X1,X2, …,Xn的 联合分布函数为
n
∏ F (x )
i i =1
例1.若X1,X2, …,Xn是来自总体X的样本,设 X的分布函数为 F(x),则样本 X1,X2, …,Xn的联合分布函数为
⎧ n − λ xi (1 − e ), xi > 0(i = 1, 2,⋯ , n) ⎪∏ F ( x1 , x2 ,⋯ , xn ) = ⎨ i =1 ⎪ 0 , 其他 ⎩
1/8, 25 ≤ x<27 2/8, 27 ≤ x<30 3/8, 30 ≤ x<33 Fn(x)= 5/8, 33 ≤ x<35 6/8, 35 ≤ x<45 7/8, 45 ≤ x<65 1, 65 ≤ x
概率论与数理统计(06)第6章 统计量及其抽样分布

σx =
σ
n
当样本容量足够 大时( 大时(n ≥ 30) , 样本均值的抽样 分布逐渐趋于正 态分布
6 - 11
µx = µ
xቤተ መጻሕፍቲ ባይዱ
x 的分布趋 于正态分布 的过程
6 - 12
6.4 正态总体 6.3.1 χ2分布 6.3.2 t 分布 6.3.3 F 分布
6 - 13
χ2 分布
第六章 样本与统计量
6.1引言 6.1引言
数理统计学: 运用概率论的基础知识,对要研究的随机现象进行 多次观察或试验,研究如何合理地获得数据资料, 建立有效的数学方法,根据所获得的数据资料,对 所关心的问题作出估计与检验。
6-1
§6.2总体与样本 6.2总体与样本
对某一问题的研究对象全体称为总体。 组成总体的某个基本单元,称为个体。 总体可以是具体事物的集合,如一批产品。 也可以是关于事物的度量数据集合,如长度测量。 总体可以包含有限个个体,也可以包含无限个个体。 有限总体在个体相当多的情况下,可以作为无限 总体进行研究。 总体中的个体,应当有共同的可观察的特征。该 特征与研究目的有关。
6 - 16
χ2分布
(图示) 图示)
n=1 n=4 n=10
n=20
6 - 17 不同容量样本的抽样分布
χ2
t 分布
6 - 18
t 分布
1. 高 塞 特 (W.S.Gosset) 于 1908 年 在 一 篇 以 (W. “Student”(学生)为笔名的论文中首次提出 Student”(学生)
X ~ N(µ,σ ) ,则
2
χ2分布
2. 3.
z=
X −µ
Y=z
华东师范大学茆诗松《概率论与数理统计教程》第6章 参数估计.
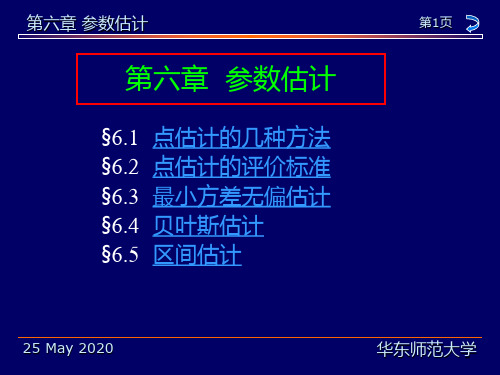
ˆ (a , , a ), j j 1 k
其中
1 n j a j xi n i1
j 1, , k ,
25 November 2018
华东师范大学
第六章 参数估计
第7页
例6.1.2 设总体服从指数分布,由于EX=1/, 即 =1/ EX,故 的矩法估计为
ˆ 1/ x
华东师范大学
第六章 参数估计
第8页
例 6.1.3 x1, x2, …, xn 是来自 (a,b) 上的均匀分布 U(a,b) 的样本, a 与 b 均是未知参数,这里 k=2 , 由于
ab EX , 2 (b a ) 2 Var( X ) , 12
不难推出
a EX 3Var( X ), b EX 3Var( X ),
L( ) ( ) [2 (1 )] [(1 ) ]
2 n1 n2 2 n3
2
n2
2 n1 n 2
(1 )
2 n3 n2
其对数似然函数为
ln L( ) (2n1 n2 ) ln (2n3 n2 ) ln(1 ) n2 ln 2
1 n n n 2 2 ln L( , ) 2 ( xi ) ln ln(2) 2 i 1 2 2
2
25 November 2018
华东师范大学
第六章 参数估计
第14页
将 lnL(, 2) 分别关于两个分量求偏导并令 其为0, 即得到似然方程组
ln L( , 2 ) 1 n 2 ( xi ) 0 i 1 ln L( , 2 ) 1 n n 2 4 ( xi ) 2 0 2 2 i 1 2
西北工业大学《概率论与数理统计》课件-第六章 参数估计

(2) 似然函数
定义6.1 设总体X的分布密度(或分布律)为 p(x; ), 其中 (1, 2, ,m )为未知参数. 又设
( x1, x2,, xn ) 为自总体X的样本(X1,X2,…,Xn) 的一 个观察值,则称样本的联合分布
n
L( ) p(x1, x2, … , xn; ) p( xi; )
2º似然估计方程组与最大似然估计之间没有必 然
从中解得 pˆ k n
参数 p的估计值
这时, 对一切 0< p <1, 均有
P{Y k; pˆ } P{Y k; p}
综上所述: 设某试验的可能结果为: A1, A2 , ···, Ai , ···
若在一次试验中,某结果 Ai 出现,则应选择参 数使Ai 出现的概率最大.
以上这种选择一个参数使得实验结果具有
(k 1,2,, m)
(4) 求最大似然估计(MLE)的步骤:
1 写出似然函数
(1, 2 , ,m )
n
L( ) L( x1, x2,, xn; ) p( xi; )
n
i 1
2 取对数 ln L( ) ln p( xi; )
i 1
3 解似然方程(组)
ln L
ln L
2
为来自总体X的简单随机样本. 矩估计法的具体步骤:
1 求出k E( X k ) (1,2,,m ), k 1,2,,m;
2 要求k Ak , k 1,2,, m
这是一个包含 m个未知参数1,2 ,,m的方程组.
3 解出其中1,2,,m , 用ˆ1,ˆ2,,ˆm表示.
4 用方程组的解ˆ1, ˆ2 , ,ˆm 分别作为 1,2 ,,m的估计量,这个估计量称为
东华大学《概率论与数理统计》课件 第6章样本与抽样分布

X
的
n
一
个
样
本的
观察
值
,
则g( x1 , x2 , xn )是统计量g( X1 , X 2 , X n )的观察值.
例1 设总体X 服从两点分布b(1, p) ,其中p 是未知参数,
X1,
,
X
是
5
来自X的简
单
随机样本.试指出
X1
X
,
2
max
1 i 5
X
i
,
X5 2 p,
( X5 X1)2
哪些是统计量,哪些不是统计量,为什么?
从国产轿车中抽5辆进行耗 油量试验
样本容量为5 抽到哪5辆是随机的
对总体X在相同条件下,进行n次重复、独立观察,其结果依次记 为 X1,X2,…,Xn.这样得到的随机变量X1,X2,…,Xn.是来自总体的一个简单 随机样本,其特点是:
1. 代表性:X1,X2,…,Xn中每一个与所考察的总体X有相同的分布. 2. 独立性:X1,X2,…,Xn相互独立.
k同分布,
E(
X
k i
)
k
k 1, 2, , n 再由辛钦大数定律可得上述结论.
再由依概率收敛性质知,可将上述性质推广为
g( A1 , A2 , , Ak ) P g(1, 2 , , k )
其中g为连续函数.
矩估计法的理论依据
2. 经验分布函数
设X1, X2,
,
X
是
n
总
体
F的
一
个Hale Waihona Puke 本,用S(
x
则称变量
t X Yn
所服从的分布为自由度为 n的 t 分布.
概率论与数理统计-第六章

这200人的年龄数据。
总体:北京市民的年龄 随机变量:年龄X
个体:张三28岁;李四5岁;
样本:{ 28;5;14;56;23;2;39;…;69} 样本容量:200
抽样:随机抽取200人进行调查的过程
6
例2:为了确定工厂生产的电池电量分布情况,在
产品中随机抽取500个,测量其电量。记录了
x
0
F n1 , n2
F分布的分位数
x
F分布的上α分位点
对于给定的 , 0 1, 称满足条件
F n1 , n2
f x; n1 , n2 dx 的点F n1 , n2
为F n1 , n2 分布的上 分位数。F n1 , n2 的值可查F 分布表
17
不易计算!
18
抽样分布 —— 任意统计量 Q = g (X1, X2, …, Xn ) 的分布函数 抽样分布的计算: 多维随机变量(独立、同分布)的函数的分布 函数的计算问题。
得到统计量 Q 的抽样分布,就可以用来解决
关于总体 X 的统计推断问题。
19
关于随机变量独立性的两个定理
解:(1)作变换 Yi
显然Y1 , Y2 ,
2 n i 1
Xi
, Yn相互独立,且Yi N 0,1 i 1, 2,
Xi
i 1, 2,
,n
,n
于是 (
) Yi 2 2 n
2 i 1
28
n
(2)
2 ( X X ) X1 X 2 ~ N (0, 2 2 ), 1 2 2 ~ 2 (1) 2
概率论与数理统计第六章样本及抽样分析

期望与方差:E(Y) = n, D(Y) = 2n
X1, X2,……, Xn 来自标准正态总体 X 的样本,那么
Y (X1 X2 )2 (X3 X4 )2 (X5 X6 )2
是否服从卡方分布?若 kY ~ χ2( n ),求 k,n
第六章 样本及抽样分析
… 19.675 2… 21.026 23.337 26.217 28.299
… 22.362 24.736 27.688 29.819
… 23.685 26.119 29.141 30.319
…
…
…
…
…
…
…
…
…
…
查表练习: 求下列各式中的 C 值
1. Y ~ 2(24), P(Y C ) 0.1 2. Y ~ 2(40), P(Y C ) 0.95
样本可看成 n 维随机变量(X1, X 2 ,, X n), 则有 P( x1, x2 ,, xn ) = P( x1)P( x2 ) P( xn )
或 f ( x1, x2 ,, xn ) = f ( x1) f ( x2 ) f ( xn )
身高总体
178.4 161.5 174.9 182.7 171.0 165.3 172.8 182.1 180.2 176.8 181.7 175.7 177.3 180.0 179.4 177.0 181.3 176.5 176.0 175.7 168.1 184.6 169.1 177.8 175.1 161.8 174.3 176.0 163.7 176.8 177.3 175.3 180.2 176.8 181.9 178.4 181.5 177.6 179.9 178.2 174.7 176.0 175.7 180.3 166.2 177.2 171.9 182.9 176.8 179.5 167.0 174.8 182.7 174.9 178.1 179.9 175.4 184.4 175.1 179.4 173.2 176.1 177.6 180.5 164.3 170.5 177.5 168.3 173.0 176.8 173.9 180.7 166.5 180.0 165.6 179.4 182.2 176.3 177.4 183.4 167.9 176.1 177.4 183.4 176.9 168.0 179.0 178.8 173.1 173.2 162.2 179.9 178.2 183.0 174.0 180.8 173.1 173.2 176.8 171.1 169.0 178.3 171.6 181.2 167.6 161.1 166.0 190.2 180.3 166.2 174.9 175.8 176.5 164.2 173.0 176.8 170.5 180.5 177.3 175.3 163.7 176.8 171.1 168.5 171.2 170.2 177.1 169.4 175.7 177.3 183.2 168.6 175.1 179.4 169.1 169.9 168.5 180.2 174.9 171.0 171.0 168.8 177.7 168.6 176.6 175.9 176.8 179.5 174.3 176.0
《概率论与数理统计》第六章

既然总体是随机变量X,自然就有其概率分布。
我们把X的分布称为总体分布。
总体的特性是由总体分布来刻画的。因此,常 把总体和总体分布视为同义语。
第六章 样本及抽样分布 ‹#›
例2
在例1中,假定物体真实长度为(未知)。一般 说来,测量值X就是总体,取 附近值的概率要大一 些,而离 越远的值被取到的概率就越小。
k=1,2,…
第六章 样本及抽样分布 ‹#›
它反映了总体k 阶矩的信息
样本k阶中心矩
Bk
1 n
n i 1
(Xi
X )k
它反映了总体k 阶 中心矩的信息
第六章 样本及抽样分布 ‹#›
统计量的观察值
1 n
x n i1 xi;
s2
1 n 1
n i1
(xi
x )2
s
1 n 1
n i1
(xi
x
)2
第六章 样本及抽样分布 ‹#›
实际上,我们真正关心的并不一定是总体或个
体本身,而真正关心的是总体或个体的某项数量指 标。
如:某电子产品的使用寿命,某天的最高气温, 加工出来的某零件的长度等数量指标。因此,有时也
将总体理解为那些研究对象的某项数量指标的全
体。
第六章 样本及抽样分布 ‹#›
为评价某种产品质量的好坏,通常的做法是: 从全部产品中随机(任意)地抽取一些样品进行观测(检
样本X1,X2,…,Xn 既被看成数值,又被看成随机变量, 这就是所谓的样本的二重性。
随机样本
例 4 (例2续) 在前面测量物体长度的例子中,如果我们 在完全相同的条件下,独立地测量了n 次,把这 n 次测 量结果,即样本记为
X1,X2,…,Xn .
概率论与数理统计基本概念及抽样分布PPT课件

~
2 (n1 ),
2 2
~
2 (n2 ), 且它们相互独立,
则
2 1
2 2
~
2 (n1
n2 )
《概率统计》
返回
下页
结束
4. 2分布的百分位点
对给定的α(0<α<1)
(1)称满足
P{ 2
2
(n)}
,即
f ( y)dy
x2 ( n)
的点为 2分布的上100α百分位点。
f(y)
(2)称满足
注:在研究中,往往关心每个个体的一个(或几个)数量指标和 该数量指标在总体中的分布情况. 这时,每个个体具有的数量 指标的全体就是总体.
或,总体:研究对象的某项数量指标的值的全体.
《概率统计》
某批 灯泡的 寿命
该批灯泡寿命的 全体就是总体
返回
下页
结束
为推断总体分布及各种特征,按一定规则从总体中抽取若 干个体进行观察试验,以获得有关总体的信息,这一抽取过程 为 “抽样”.
( x)
(1)称满足条件 P{X>Xα} =α,
α
即
( x)dx
X
的点Xα为N(0,1)分布的上100α百分位点.
X1-α
0
由于 P{X X } 1 记 -Xα= X1-α
(2)称满足条件 P {| X | X }
2
2
的点 X 为N(0,1)分布的双侧100α百分位点.
X
2
则
E(X )
E(1 n
n i 1
Xi)
1 n
n i 1
E(Xi )
1 n
n
D(X ) D(1 n
n i1
Xi)
第六章《概率论与数理统计教程》课件

1
例5. 设X服从[0,λ]区间上的均匀分布,参数
λ>0,求λ的最大似然估计. 1 解:由题意得: X ~ f ( x; )
1 L( x1 , x 2 ,..., x n ; ) n 0
0 x
0 其它 0 x1 , x 2 ,..., x n
dL n n1 0 d
其它
无解.
应用最大似然估计基本思想: L越大,样本观察值越可能出现 取 max( x1 , x 2 ,..., x n ) 此时,L取值最大, 所以,所求最大似然估计为 max( x1 , x 2 ,..., x n )
考虑L的取值,要使L取值最大,λ应最小, 0 x1 , x 2 ,..., x n
例2 设总体 X ~ N ( , 2 ) ,其中 及 2 都是未知参数,如
果取得样本观测值为 x1 ,, x n , 求 及 2 的矩估计值。
解: 因为总体X的分布中有两个未知参数,所以应考虑一、二阶 原点矩,我们有 v1 ( X ) E ( X )
v 2 ( X ) E( X 2 ) D( X ) [ E( X )]2 2 2
e
e
1 2
2
2
( x )2 2 2
e
L( x1 , x 2 ,..., x n ; , )
2
i 1
1 2
2
( xi )2
(
2
1 2
2
1 2 2
) e
n
i 1
n
( xi )2
1 n 2 n 1 n 2 2 ) 2 ( x i ) ln 2 ln L n ln( ( xi ) 2 i 1 2 2 2 n 2 2 i 1 1 ln L 1 n Xi X 2 ( xi ) 0 n i 1 i 1 1 n 2 1 n n ln L n 1 ( xi )2 ( xi X )2 2 2 4 ( x i ) 0 n i 1 n i 1 2 2 2 i 1
概率论与数理统计(王明慈第二版)第6章参数区间估计2,3节

第三节 正态总体参数的区间估计
基本内容: 一、区间估计的概念 二、正态总体均值的区间估计 三、正态总体方差的区间估计
一、区间估计的概念
定义 设总体 X 的分布中含有未知参数,对于 给定的概率 1- (0 < < 1), 若存在两个统计量 ˆ1(X1, X2, , Xn )与ˆ2(X1, X2, , Xn ), 使得
即
P
i
n 1
tα/
2
(n
-
1),
x
s n
tα/
2(n
1)
得到的95%的置信区间为
(14.92-0.138, 14.92+0.138) 即(14.782, 15.058) (mm)
三、正态总体方差 2 的区间估计
1. 已知均值= 0的正态总体 X, 求未知参数 2 1- 的置信区间
解:设总体 X ~ N( , 2), 有
k 1,2,L ,m
第三步: 解含m个参数ˆ1,ˆ2,L的,mˆ个m 方程组, 得
ˆk ˆk X1, X2, , Xn k 1,2, ,m
以ˆk作为参数 的k 估计量.
第四步:将 θˆk中的X1 , X2 , , Xn换成x1 , x2 , , xn, 便得到θk的矩估计值θˆk ( x1 , x2 , , xn ).
例3. 设X1,X2,X3是来自总体X的样本, 且
总体均值E(X)= 未知, 则下列4个关于 的
统计量中哪个更有效?( C )
A. X1 X 2 3X 3 ; 55 5
C. X1 X 2 X3 ; 333
B. X1 X 2 X 3 ; 424
D. X1 X 2 X 3 . 362
分析:利用P181的7题结论,可选C.
概率论与数理统计课件(完整)

1.3 频率与概率
某人向目标射击, 以A表示事件“命中目标”, P( A) =? 定义:(p8) 事件A在n次重复试验中出现nA次,则 比值nA/n称为事件A在n次重复试验中
(1) P(A) ≥0;
(2) P()=1;
(3) 可列可加性:设A1,A2,…, 是一列两两互不 相容的事件,即AiAj=,(ij), i , j=1, 2, …, 有 P( A1 A2 … )= P(A1) +P(A2)+…. 则称P(A)为事件A的概率。 (1.1)
2.概率的性质 P(8-9) (1) 有限可加性:设A1,A2,…An , 是n个两两互 不相容的事件,即AiAj= ,(ij), i , j=1, 2, …, n ,则有 P( A1 A2 … An)= P(A1) +P(A2)+… P(An); (2) 单调不减性:若事件AB,则 P(A)≥P(B) (3)事件差 A、B是两个事件, 则 P(A-B)=P(A)-P(AB)
种取法.
1、抽球问题
例1:设合中有3个白球,2个红球,现从合中 任抽2个球,求取到一红一白的概率。 解:设A-----取到一红一白
N () C
2 5
1 1 N ( A) C3 C2
CC 3 P( A) 2 C5 5
1 3
1 2
答:取到一红一白的概率为3/5
一般地,设盒中有N个球,其中有M个白 球,现从中任抽n个球,则这n个球中恰有
概率论与数理统计6-8

无关的样本的连续函数,则称g(X1,X2,…,Xn)为
统计量。 统计量是样本的函数,它是一个随机变量, 如果x1, x2, …, xn是样本观察值, 则g(x1, x2, …, xn)是统计量g(X1, X2, …, Xn)的一个观察值.X i ; n i 1 2 n 1 2 2. 样本方差 S (X i X ) ; n - 1 i 1 1 n k 3. 样本k阶原点矩 A k X i , k 1, 2, ; n i 1 1 n 4. 样本k阶中心矩 Bk (X i X ) k , k 2, 3, . n i 1
§7.1 点估计 一. 问题的提法:
设总体X的分布函数F ( x; θ )的形式为已知 ,
是待估参数, 1 , X 2 , , X n 是X的一个样本, X
x1, x2 , , xn 是相应的一个样本值。
点估计问题就是要构造 一个适当的统计量 ˆ ( X , X , X ),用它的观察值 ˆ( x , x , , x )
2
分布具有可加性,定义 X 1 ,X 2 , ,X n 独立 中 n 1 同服从N (0,1),所以 = X ~ ( , ) 2 2 i 1
2 2 i n
β α α-1 -x x e , x 0, 分布的概率密度为 f ( x) Γ (α ) : 0 , 其它. n 1 2 2 比较 (n)的密度可知: (n) 分布就是 , 2 2 2 的分布, 即 (n) (n / 2, 1/2).
N (0, 2 ) ,X1,X2,X3 为取自总体的一个样本, 2.设总体 X~
试求:(1)3X1-2X2+X3 的分布;(2)
2 X1 X 22 X 32
的分布。
大连理工大学《概率论与数理统计》课件-第6章

第6章数理统计的基本概念一. 统计的基本概念二. 统计量的分布三. 抽样分布,由大数定律:(3)则在 8.1,需确定估计区间()。
(2)构造2σ甲μ甲μ乙μμ−→−PX1.8=x统计工作最基本内容:1.估计电视机寿命的平均值µ,估计电视机寿命的方差2.比较两厂电视机寿命值有无差别,方差有无差别。
总体样本统计量参数点估计假设检验区间估计目的:(方差同理)方法:()··21是否一致与μμ()··2221是否一致与σσ()··0是否一致与μμ()··22是否一致与σσ().,...,21n x x x 统计工作的基本步骤1.收集资料:2.统计分析:对数据整理和分析3.统计推断:i )点估计:确定未知参数θ的估计量ii )区间估计:确定(左,右)区间(1)参数估计:(2)假设检验:i )推断两个总体均数是否一致ii )推断两个总体方差是否一致iii )推断一个总体均数有无变化iv )推断一个总体方差有无变化⎪⎪⎩⎪⎪⎨⎧-2221212σσμμσμθ一. 统计的基本概念()为样本一组观察值。
,21n x x x ⎩⎨⎧总体有限总体(观察值有限个)无限总体(观察值无穷多个)随机变量 X 总体⇔(n 为样本容量)研究对象观察值的全体(样本是从总体中抽取的部分个体)n X X X 21,个体:每个观察值。
独立同分布,则称()n X X X 21,为简单随机样本,简称为样本。
(),,21n X X XnX X X 21,(),...2,1,===i p x X P i i ()n n x X x X x X P ===,...,2211()∏===ni i x X P 1样本联合分布列:(1)代表性:保证总体中每个个体有同等机会被抽到。
(2)独立性:每次抽取独立进行,各个体值互不影响。
(1)离散型:总体X 的分布列()发生的概率x x x 样本点n 21,与总体同分布()n x x x F ,...,21()n x x x f ,...,21(2)连续型:总体X 的分布密度f (x )样本联合密度:(3)总体X 的分布函数F (x )样本联合分布函数为:()()()n x f x f x f 21=()()()n x F x F x F 21=()发生的可能性x x x 样本点n 21,n X X X ,,21n X X X ,,21()n X X X 21,设为总体X 的样本,()n X X X T T 21,=函数,且不含任何未知参数,称T 为统计量。
概率论与数理统计ppt课件

注:P( A) 0不能 A ; P( B) 1不能 B S .
2。 A1 , A2 ,...,An , Ai Aj , i j, P( P(
n n i 1
Ai ) P( Ai )
i 1
n
证:令 Ank (k 1, 2,...), Ai Aj , i j, i, j 1, 2,....
•
5.1 大数定律 5.2 中心极限定理
•
第六章 数理统计的基本概念
• • 6.1 总体和样本 6.2 常用的分布
4
第七章 参数估计
• • • 7.1 参数的点估计 7.2 估计量的评选标准 7.3 区间估计
第八章 假设检验
• • • • • • • 8.1 8.2 8.3 8.4 8.5 8.6 8.7 假设检验 正态总体均值的假设检验 正态总体方差的假设检验 置信区间与假设检验之间的关系 样本容量的选取 分布拟合检验 秩和检验
A B 2 A=B B A
B A
S
例: 记A={明天天晴},B={明天无雨} B A
记A={至少有10人候车},B={至少有5人候车} B
A
一枚硬币抛两次,A={第一次是正面},B={至少有一次正面}
BA
13
事件的运算
A与B的和事件,记为 A B
8
§1 随机试验
确定性现象
自然界与社会Βιβλιοθήκη 活中的两类现象不确定性现象
确定性现象:结果确定 不确定性现象:结果不确定
例:
向上抛出的物体会掉落到地上 ——确定 ——不确定 明天天气状况 ——不确定 买了彩票会中奖
概率论与数理统计 第六章

F-分布的概率密度为
n1 n1 1 2 2 [(n1 n2 ) / 2](n1 / n2 ) x , x 0, n1 n2 f ( x) (n1 / 2)(n2 / 2)[1 (n1 x / n2 )] 2 0, 其它.
河南理工大学精品课程
概率论与数理统计
河南理工大学精品课程
n 1 2
( x )
概率论与数理统计
f (x)
n
n 10
n 1
O
x
t-分布的概率密度性质
t-分布的概率密度为偶函数,且以标准正态概率 密度为其极限(n→∞)。
河南理工大学精品课程 概率论与数理统计 上α分位点(双侧 Nhomakorabea/2分位点)
定义 点 t (n) 为 t (n) 分布的上α 分位点
究,就是对相应的随机变量X的研究。
今后,我们称X的分布函数和数字特征分别为总体的 分布函数和数字特征,并不再区分总体与相应的随机变量
X.对总体的称呼:总体,总体X与总体F.
河南理工大学精品课程 概率论与数理统计
例如,当X~N(μ,σ2)时,称总体X为正态总体.正态 总体有以下三种类型: ①μ未知,但σ2已知; ②σ2未知,但μ已知; ③μ,σ2均未知.
P{t t (n)} (0 1).
查附表4[P.298]:
t0.025 (8) 2.3060, t0.005 (4) 4.6041.
河南理工大学精品课程
概率论与数理统计
双侧α/2分位点:
t1 / 2 (n), t / 2 (n)
f (x)
/2
t1 / 2 (n) O
河南理工大学精品课程
概率论与数理统计
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Xi 2 i 1 ~ ( n) 2 i 1 2 2 2 ( n ), ( n) 查 - 分布表,确定双侧分位数 1 2 2
2 n i
2
X
n
2
从而得2的置信水平为1-的置信区间为 n n 2 2 Xi Xi i 1 i 1 2 , 2 1 2 (n) 2 ( n)
小
假设置信水平为1-
结
总体服从正态分布的均值或方差的区间估计 (1)方差已知,对均值的区间估计 构造U-统计量,反查标准正态分布表, 确定U的双侧分位数 得EX的区间估计为
u 2
, X u 2 n
X u 2
n
小
假设置信水平为1-
结
总体服从正态分布的均值或方差的区间估计
2 (n), 2 (n)
1 2 2
n 2 Xi i 1 2 , 2 ( n)
X
i 1
n
i
( n)
2
2
1 2
小 结
总体服从正态分布的均值或方差的区间估计 假设置信水平为1- (4)均值未知,对方差的区间估计 构造2-统计量,查2-分布临界值表, 2 2 2 确定 的双侧分位数 1 2 (n 1), 2 (n 1) 得2的区间估计为
(n 1) S 2 2 , (n 1) 2
(n 1) S 2 2 1 2 (n 1)
区间估计
总体服从正态分布的对均值的区间估计 (1)方差已知,对均值的区间估计,构造U统计量
, X u 2 X u 2 n n (2)方差未知,对均值的区间估计,构造T统计量
S X t 2 (n 1) n
例3 某厂生产的一种塑料口杯的重量X被认为服从正态 分布,今随机抽取9个,测得其重量为(单位:克): 21.1,21.3,21.4,21.5,21.3,21.7,21.4,21.3, 21.6。试用95%的置信度估计全部口杯的平均重量。 解 由题设可知:口杯的重量X~N(,2) 由抽取的9个样本,可得 S 0.18
x 11.6
2 0.05 (4) 0.711
210.05 (4) 9.488
(n 1) S 2 0.4195 2 0.95 (4)
(n 1) S 2 4 0.995 5.5977 2 0.05 (4) 0.711
2的置信区间为(0.4195,5.5977)
续解 要以99%的概率满足10000户居民对该种商品的 需求,则最少要准备的量为
9.229 10000 92290 (公斤)
最多准备
10.771 10000 107710 (公斤)
正态总体均值已知,对方差的区间估计
如果总体X~N(,2),其中已知,2未知 Xi ~ N (0,1) 构造2-统计量 由
S t 2 (n 1) , X n S X t 2 (n 1) n
区间估计
总体服从正态分布的对方差的区间估计 (3)均值已知,对方差的区间估计,构造2统计量
例2 假定某地一旅游者的消费额X服从正态分布 N(,2),且标准差=12元,今要对该地旅游者的平 均消费额EX加以估计,为了能以95%的置信度相信这种 估计误差小于2元,问至少要调查多少人? 解 由题意知:消费额X~N(,122),设要调查n人。 由 1 0.95 得 0.05 查表得 即 而
练习 假设某片居民每月对某种商品的需求量X服从正态 分布,经调查100家住户,得出每户每月平均需求量为 10公斤,方差为9,如果某商店供应10000户,试就居民 对该种商品的平均需求量进行区间估计(=0.01),并 依此考虑最少要准备多少这种商品才能以99%的概率满 足需求? 解 由题设可知:平均需求量X~N(,2) S 2 9 x 10 n 100 由 0.01 查表得 t0.005 (99) u0.005 2.57 S 3 t 2 (99) 2.57 0.771 n 100 平均消费额的置信区间为(9.229,10.771)
X ~ t (n 1) S n
X 构造T-统计量 T S n
当置信水平为1-时,由 P T t 2 (n 1) 1 查t-分布表确定 t 2 (n 1) 从而得的置信水平为1-的置信区间为
S t 2 (n 1) , X n
u 2 1.96
X P 1.96 0.95 n
X 2
2
1.96
n
2
至少要调查139人
1.96 12 解得 n 138.29 2
正态总体方差未知,对均值的区间估计
如果总体X~N(,2),其中,均未知 由
X 由 P 0.95 n 查表得 1.96
X 1.96
0.95
n
X 1.96
n
置信水平、置信区间
设总体的分布中含有一个参数,对给定的,如果 由样本(X1,X2,…,Xn)确定两个统计量 1( X1,X2,…,Xn ), 2( X1,X2,…,Xn ), 使得P{1 << 2}=1- ,则称随机区间( 1 , 2 )为 参数的置信度(或置信水平)为1- 的置信区间。 1——置信下限 2——置信上限
1 EX x 14.6 15.1 14.9 14.8 15.2 15.1 14.95 6
续解 (2)由题设知X~N(,0.06) 构造U-统计量,得EX的置信区间为 , X u 2 X u 2 n n 0.06 而 x 14.95, 0.1 n 6 当=0.05时,u0.025 1.96 所以,EX的置信区间为(14.754,15.146) 当=0.01时, u0.005 2.58 所以,EX的置信区间为(14.692,15.208) 置信水平提高,置信区间扩大,估计精确度降低。
1 x 1455 1502 1370 1610 1430 1473.4 5
可以认为该种灯泡的使用寿命在1473.4个单位时间左右, 但范围有多大呢?又有多大的可能性在这“左右”呢? 如果要求有95%的把握判断在1473.4左右,则由U统计 量可知
X U ~ N 0,1 n
2
~ (n 1)
2
构造2-统计量
2
(n 1) S 2
2
(n 1) S 2 1 2 (n 1)
2
例4 设某灯泡的寿命X~N(,2), ,2未知,现 从中任取5个灯泡进行寿命试验,得数据10.5,11.0, 11.2,12.5,12.8(单位:千小时),求置信水平为 90%的2的区间估计。 解 样本方差及均值分别为 S 2 0.995 由 1 0.9 得 0.1 查表得
果树方差的置信区间为
2931 2931 , 202.84, 2363.71 14.45 1.24
正态总体均值未知,对方差的区间估计
如果总体X~N(,2),其中2未知 由
(n 1) S 2
当置信水平为1-时,由 2 (n 1) S 2 2 P 1 2 (n 1) 2 (n 1) 1 2 2 2 2 ( n 1), (n 1) 查 - 分布表,确定双侧分位数 1 2 2 从而得2的置信水平为1-的置信区间为
(2)方差未知,对均值的区间估计 构造T-统计量,查t-分布临界值表, 确定T的双侧分位数 得EX的区间估计为
t 2 (n 1)
S X t 2 (n 1) n
S t 2 (n 1) , X n
小 结
总体服从正态分布的均值或方差的区间估计 假设置信水平为1- (3)均值已知,对方差的区间估计 构造2-统计量,查2-分布临界值表, 确定2的双侧分位数 得2的区间估计为
正态总体方差已知,对均值的区间估计
如果总体X~N(,2),其中2已知, 未知, X 则取U-统计量 U ,对做区间估计。 n 对给定的置信水平1-,由 P U u 1 2 确定临界值(X的双侧分位数)得的置信区间为
, X u 2 X u 2 n n
几点说明
1、参数的置信水平为1-的置信区间( 1, 2) 表示该区间有100(1-)%的可能性包含总体参 数的真值。 2、不同的置信水平,参数的置信区间不同。 3、置信区间越小,估计越精确,但置信水平会降低; 相反,置信水平越大,估计越可靠,但精确度会降 低,置信区间会较长。一般:对于固定的样本容量, 不能同时做到精确度高(置信区间小),可靠程度也 高(1- 大)。如果不降低可靠性,而要缩小估计范 围,则必须增大样本容量,增加抽样成本。
将观测值 x1 , x2 , , xn 代入,则可得具体的区间。
例1 某车间生产滚珠,从长期实践中知道,滚珠直径X 可以认为服从正态分布,从某天的产品中随机抽取6个, 测得直径为(单位:cm) 14.6,15.1,14.9,14.8,15.2,15.1 (1)试求该天产品的平均直径EX的点估计; (2)若已知方差为0.06,试求该天平均直径EX的置信 区间:=0.05;=0.01。 解 (1)由矩法估计得EX的点估计值为
例题 已知某种果树产量服从N(218,2),随机 抽取6棵计算其产量为(单位:公斤) 221,191,202,205,256,236 试以95%的置信水平估计产量的方差。 解 计算
x
i 1 i
6
2
