高中物理竞赛_话题1:重心与质心的确定
高二物理竞赛课件:质心(center of mass) 质心运动定理

一、质点对定点的角动量
说角动量时,
t 时刻, 如图 ,
必须指明是对 哪个固定点的
定义 L r P 为质点对固定点o 的角动量
大小:L rP 方向:垂直于
sri,nP
rmv sin
组成的平面
[SI] kgm 2/s
o r
L
P
m
力对定点的力矩
说力矩时,也
t 时 刻,如图,
必须指明是对 哪个固定点的
例 已知1/4圆M, m由静止下滑,求
t1→t2 过程中M移动的距离 S。 解: 选(M+m)为体系
水平方向: 合外力=0,质心静止
t1时刻
m
t2时刻
Mபைடு நூலகம்
M
m
x -R O
体系质心
X1
MxmR Mm
x-S -S O
体系质心
X
2
M
x
M
SmS
m
质心静止 X1 X 2
M
移动的距离
S
m Mm
R
思路:与处理动量定理 动量守恒问题相同
等于质点角动量的增量。
M 和L 是对惯性系中的同一固定点的。
角动量定理 Mdt dL
t2
Mdt ΔL
t1
若 M 0 则 L 0 角动量守恒定律
讨论
1)动量守恒与角动量守恒
是相互独立的定律。 如行星运动
2)有心力—力始终指向一点
直升飞机
动量不守恒 角动量守恒
质点在有心力作用下运动时角动量守恒
M r F 0 角动量守恒
o
F
mi
ri c质心
rc
o
重心是指各质点所受重力的合力作用点。
物理重心的知识点总结

物理重心的知识点总结一、重心的概念。
1. 定义。
- 一个物体的各部分都受到重力的作用,从效果上看,我们可以认为各部分受到的重力作用集中于一点,这一点叫做物体的重心。
重心是物体所受重力的等效作用点。
2. 与质心的关系(对于质量分布均匀、形状规则的物体)- 在地球表面附近,当物体的线度远小于地球半径时,物体可视为质点系,质心与重心的位置重合。
质心是从质量分布角度定义的一个点,而重心是从重力作用角度定义的点。
二、重心的位置确定。
1. 质量分布均匀、形状规则物体的重心。
- 形状规则且质量分布均匀的物体,它的重心就在其几何中心上。
- 例如:- 均匀直棒的重心在棒的中点;- 均匀球体的重心在球心;- 均匀圆柱体的重心在轴线的中点。
2. 薄板状物体重心的实验测定 - 悬挂法。
- 原理:薄板静止时,受重力和绳子的拉力,根据二力平衡,重心一定在绳子的延长线上。
- 操作步骤:- 用细线将薄板状物体悬挂起来,画出细线的延长线;- 再换一个位置将薄板悬挂起来,画出另一条细线的延长线;- 两条细线延长线的交点就是薄板的重心。
3. 不规则物体重心的计算(高中阶段较少涉及复杂计算,简单了解)- 对于由多个质点组成的物体系统,可以根据重心坐标公式x_c=frac{∑_i =1^nm_ix_i}{∑_i = 1^nm_i},y_c=frac{∑_i = 1^nm_iy_i}{∑_i = 1^nm_i},z_c=frac{∑_i = 1^nm_iz_i}{∑_i = 1^nm_i}(m_i是第i个质点的质量,x_i,y_i,z_i是第i个质点的坐标)来计算重心位置,但在高中阶段主要以理解概念和简单确定特殊物体重心为主。
三、重心与物体平衡的关系。
1. 重心与稳度。
- 稳度是指物体的稳定程度。
- 物体的重心越低,底面积越大,物体的稳度就越高。
- 例如:- 不倒翁的底部较重,重心很低,所以它不容易倾倒;- 而一些高大的建筑物,底部面积大,也是为了增加稳度,防止倾倒。
巧用质心和质心系求解竞赛题

A巧用质心和质心系求解竞赛题应用质心和质心系解答竞赛题是一中重要的解题方法。
特别是系统所受外力为零时,质心做匀速直线运动,抓住这个特点来求解有关力学问题往往能化难为易,化繁为简。
下面举例说明。
例1、如图,一水平放置的圆环形刚性套槽固定在桌面上。
槽内嵌着三个大小相同的刚性小球,它们的质量分别为1m 、2m 、3m ,其中1322m m m ==接触,而它们之间的摩擦可以忽略不计。
开始时三球处在槽中I 、II 、III 的位置,彼此之间距离相等,2m 、3m 静止。
1m 以初速度20Rv π=沿槽运动,R 为圆环的内半径和小球半径之和。
设各球间的碰撞皆为弹性碰撞。
求此系统的运动周期T 。
分析与解答:此题的常规解法是逐一应用动量守恒,找出系统的运动规律。
从而求出周期。
该方法比较麻烦。
如果注意到三个小球在运动过程中在圆的切线方向不受力。
故可以认为系统的质心作匀速圆周运动。
系统运动一个周期,即质心运动一个圆周。
设质心的速率为c v105032101R v m m m v m v c π==++=,所以周期s v RT c202==π例2、在光滑水平面上有两个质量均为m 的物体A 和B ,B 上有一劲度系为k 的轻弹簧。
物A 以速度0v 向静止的物体B 运动,并开始压缩弹簧,求:从开始压缩弹簧到最大压缩量过程中物体B 的位移。
分析与解答:先求出弹簧的最大压缩量。
当两物体速度相等时,弹簧压缩量最大。
此时两物体速度为v 设最大压缩量为m x 。
由动量守恒和能量守恒得:mv mv 20= (1)22202122121mkx mv mv += (2) 由(1)(2)得:kmv x m 20= 在运动过程中相对于地面来说。
A 、B 两物体都做复杂的变加速运动。
现在以质心为参考系来研究A 、B 两物体的运动规律。
注意到系统不受外力,质心做匀速直线运动。
其中质心位于AB 两物体的中点处,质心速度2200v m mv v c ==。
质心物理竞赛讲义

质心物理竞赛讲义一、质心的概念及基本原理质心,又称质点的几何中心或重心,是一个物体在力学中重要的概念。
质心的位置可以简化物体受力分析,并在物体的运动中发挥重要作用。
质心的定义:质心是一个物体所有质点的平均位置,根据物体质量和质点的位置来计算。
在一个均匀分布的物体中,质心位于几何中心。
质心的基本原理:- 物体质心位于物体的对称轴上,若物体是各向同性的,则质心位于物体的中心。
- 质心是物体重心的一种特殊情况,仅在重力场中才与物体重心重合。
- 质心是物体的一个特殊点,对物体运动的描述具有重要意义。
二、质心的计算方法质心的位置可以通过物体的质量分布以及质点位置的加权平均来计算。
具体的计算方法取决于物体的几何形状和质量分布。
1. 均匀物体的质心对于均匀物体,质心的计算相对简单。
可以通过以下公式计算质心的位置:质心的x坐标:x = (m₁x₁ + m₂x₂ + … + mₙxₙ) / (m₁ + m₂ + … + mₙ)质心的y坐标:y = (m₁y₁ + m₂y₂ + … + mₙyₙ) / (m₁ + m₂ + … + mₙ)其中,m₁, m₂, ..., mₙ是物体分布的质量,x₁,x₂,…,xₙ和y₁,y₂,…,yₙ是对应质点的坐标。
2. 不规则物体的质心对于不规则形状的物体,可以通过近似方法计算质心。
常见的方法有:- 使用几何图形的质心公式,如矩形、三角形、圆形等。
- 分割不规则物体为规则形状,计算各部分的质心,最后取加权平均。
三、质心在物体运动中的应用质心在物体运动中有广泛的应用,以下是一些典型的例子:1. 系统的位移和速度质心可以作为系统的参考点,用于描述物体的位移和速度。
通过跟踪质心的运动,可以了解系统整体的运动情况。
2. 系统的动量和力质心也可以用来分析物体系统的动量和力学问题。
由于质心是物体的一个特殊点,可以简化受力分析,直接用力对质心产生的效果来计算系统的动量和力。
3. 轨迹和旋转对于旋转运动的物体,质心可以帮助我们分析物体的轨迹和旋转情况。
高中物理竞赛课件:质心平衡共33页文档

•
26、我们像鹰一样,生来就是自由的 ,但是 为了生 存,我 们不得 不为自 己编织 一个笼 子,然 后把自 己关在 里面。 ——博 莱索
•
27、法律如果不讲道理,即使延续时 间再长 ,也还 是没有 制约力 的。创造出来的。 ——马 克罗维 乌斯
23、一切节省,归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰,决心到最后会全部推倒。——莎士比亚
25、学习是劳动,是充满思想的劳动。——乌申斯基
谢谢!
•
29、在一切能够接受法律支配的人类 的状态 中,哪 里没有 法律, 那里就 没有自 由。— —洛克
•
30、风俗可以造就法律,也可以废除 法律。 ——塞·约翰逊
21、要知道对好事的称颂过于夸大,也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤,荒于嬉;行成于思,毁于随。——韩愈
高中物理竞赛关于质心的~

高中物理竞赛关于质心的~
高中物理竞赛关于质心的~ 做题用的到老师讲的质心不变不过不太敢做,因为不知道质心不变的条件,物体组质心不变的条件是什么呀
还有,关于质心的一些定理,比如质心运动定律等等,都有哪些呀(少说多说没关系~)
参考答案当一个系统受到的合外力为零时,系统的总动量守恒,由牛顿第一定律可知,系统质心的速度也将保持不变,同样系统在某一方向上受到的合外力为零,则系统在该方向上的动量守恒,系统的质心在这一方向上的速度将保持不变。
所以如果物体初始是静止满足上条件则质心不变。
大学理论力学里有讲。
至于质心运动定理其实比较好理解,但对于高中来说却不好应用。
下面就是质心运动定理:
质心运动定理是质点系动量定理的另一种形式,可由质点系动量定理直接导出。
即将P =Mvc 代入质点系动量定理 dP /dt =∑F e ,得:
M d vc/dt =∑F e
或 M ac =∑F e ——称为质心运动定理。
( ∵ac= d vc/dt )
即:质点系的质量M 与质心加速度 ac 的乘积等于作用于质点系所有外力的
矢量和(外力主矢量)。
可见:只有外力才能改变质点系质心的运动。
2、质心运动守恒定律
(1)若∑F e ≡0,则ac = 0,vc =常矢量
即当外力系主矢量等于零时,质心的加速度等于零,质心保持静止或作匀速直
线运动。
(2)若∑Fxe ≡0,则acx = 0,vcx =常量
即当外力系在某轴上投影的代数和等于零时,质心的加速度在该轴上投影为零,
质心沿该轴方向保持静止或匀速运动。
这两种情况称为质心运动守恒。
质心运动定理经常用来求约束反力。
高中物理竞赛(静力学)

力、物体的平衡补充:杠杆平衡(即力矩平衡),对任意转动点都平衡。
一、力学中常见的三种力1.重力、重心①重心的定义:++++=g m g m gx m gx m x 212211,当坐标原点移到重心上,则两边的重力矩平衡。
②重心与质心不一定重合。
如很长的、竖直放置的杆,重心和质心不重合。
如将质量均匀的细杆AC (AB =BC =1m )的BC 部分对折,求重心。
以重心为转轴,两边的重力力矩平衡(不是重力相等):(0.5-x )2G =(x +0.25)2G ,得x =0.125m (离B 点). 或以A 点为转轴:0.5⨯2G +(1+0.5)2G =Gx ', 得x '=0.875m ,离B 点x =1-x '=0.125m.2.巴普斯定理:①质量分布均匀的平面薄板:垂直平面运动扫过的体积等于面积剩平面薄板重心通过和路程。
如质量分布均匀的半圆盘的质心离圆心的距离为x , 绕直径旋转一周,2321234R x R πππ⋅=,得π34R x = ②质量分布均匀的、在同一平面内的曲线:垂直曲线所在平面运动扫过的面积等于曲线长度剩曲线的重心通过路程。
如质量分布均匀的半圆形金属丝的质心离圆心的距离为x ,绕直径旋转一周,R x R πππ⋅=242,得πR x 2= 1. (1)半径R =30cm 的均匀圆板上挖出一个半径r =15cm的内切圆板,如图a 所示,求剩下部分的重心。
(2)如图b 所示是一个均匀三角形割去一个小三角形AB 'C ',而B 'C '//BC ,且∆AB 'C '的面积为原三角形面积的41,已知BC 边中线长度为L ,求剩下部分BCC 'B '的重心。
[答案:(1) 离圆心的距离6R ;(2)离底边中点的距离92L ] 解(1)分割法:在留下部分的右边对称处再挖去同样的一个圆,则它关于圆心对称,它的重心在圆心上,要求的重心就是这两块板的合重心,设板的面密度为η,重心离圆心的距离为x .有力矩平衡: ),2()2(])2(2[222x R R x R R -=-ηπηπ得6R x ==5cm. 填补法:在没挖去的圆上填上一块受”重力”方向向上的圆,相当于挖去部分的重力被抵消,其重心与挖去后的重心相同,同理可得6R x =. 能量守恒法:原圆板的重力势能等于留下部分的重力势能和挖去部分的重力势能之和,可得6R x =. (2) ∆AB 'C '的面积为原三角形面积的1/4,质量为原三角形质量的41,中线长度应为原三角形中线长度的21。
高中物理竞赛_话题1:重心与质心的确定

话题1:重心与质心的确定一、平行力的合成与分解物体所受的几个力的作用线彼此平行,且不作用于一点,即为平行力(系)。
在平行力的合成或分解的过程中,必须同时考虑到力的平动效果和转动效果,后者要求合力和分力相对任何一个转轴的力矩都相同。
两个同向平行力的合力其方向与两个分力方向相同,其大小等于分力大小之和。
其作用线在两个分力作用点的连线上。
合力作用点到分力作用点的距离与分力的大小成反比。
例如:两个同向平行力A F 和B F ,其合力的大小A B F F F =+,合力作用点O 满足A B AO F BO F ⋅=⋅的关系。
两个反向平行力的合力其方向与较大的分力方向相同,其大小等于分力大小之差。
其作用线在两个分力作用点的连线的延长线上,且在较大的分力的外侧。
合力作用点到分力作用点的距离与分力的大小成反比。
例如:两个反向平行力A F 和B F 的合成其合力的大小B A F F F =-(假如B A F F >,则F 和B F 同向)其合力的作用点满足A B AO F BO F ⋅=⋅的关系。
一个力分解成两个平行力,是平行力合成的逆过程。
二、重心和质心重心是重力的作用点。
质心是物体(或由多个物体组成的系统)质量分布的中心。
物体的重心和质心是两个不同的概念,当物体远离地球而不受重力作用时,重心这个概念就失去意义,但质心却依然存在。
对于地球上体积不太大的物体,由于重力与质量成正比,重心与质心的位置是重合的。
但当物体的高度和地球半径比较不能忽略时,两者就不重合了,如高山的重心比质心要低一些。
在重力加速度g 为常矢量的区域,物体的重心是惟一的(我们讨论的都是这种情形),BF AF FO BA BF AF F OBA重心也就是物体各部分所受重力的合力的作用点,由于重力与质量成正比,重力合力的作用点即为质心,即重心与质心重合。
求重心,也就是求一组平行力的合力作用点。
相距L ,质量分别为12,m m 的两个质点构成的质点组,其重心在两质点的连线上,且与12,m m 相距分别为1L ,2L :1122m L m L = 12L L L +=2112m LL m m =+1212m LL m m =+均匀规则形状的物体,其重心在它的几何中心,求一般物体的重心,常用的方法是将物体分割成若干个重心容易确定的部分后,再用求同向平行力合力的方法找出其重心。
质心、刚心、重心

质心质量中心简称质心,指物质系统上被认为质量集中于此的一个假想点。
与重心不同的是,质心不一定要在有重力场的系统中。
值得注意的是,除非重力场是均匀的,否则同一物质系统的质心与重心不通常在同一假想点上。
在一个N维空间中的质量中心,坐标系计算公式为:X表示某一坐标轴mi 表示物质系统中,某i质点的质量xi 表示物质系统中,某i质点的坐标。
质点系质量分布的平均位置。
质量中心的简称。
它同作用于质点系上的力系无关。
设n个质点组成的质点系,其各质点的质量分别为m1,m2,…,mn。
若用r1 ,r2,…,rn分别表示质点系中各质点相对某固定点的矢径,rc 表示质心的矢径,则有rc=Image:质心1.jpgmiri/Image:质心1.jpgmi。
当物体具有连续分布的质量时,质心C的矢径rc=Image:质心2.jpgρrdτ/Image:质心2.jpgρdτ,式中ρ为体(或面、线)密度;dτ为相当于ρ的体(或面、线)元;积分在具有分布密度ρ的整个物质体(或面、线)上进行。
由牛顿运动定律或质点系的动量定理,可推导出质心运动定理:质心的运动和一个位于质心的质点的运动相同,该质点的质量等于质点系的总质量,而该质点上的作用力则等于作用于质点系上的所有外力平移到这一点后的矢量和。
由这个定理可推知:①质点系的内力不能影响质心的运动。
②若质点系所受外力的主矢始终为零,则其质心作匀速直线运动或保持静止状态。
③若作用于质点系上外力的主矢在某一轴上的投影始终为零,则质心在该轴上的坐标匀速变化或保持不变。
质点系的任何运动一般都可分解为质心的平动和相对于质心的运动。
质点系相对某一静止坐标系的动能等于质心的动能和质点系相对随质心作平动的参考系运动的动能之和。
质心位置在工程上有重要意义,例如要使起重机保持稳定,其质心位置应满足一定条件;飞机、轮船、车辆等的运动稳定性也与质心位置密切相关;此外,若高速转动飞轮的质心不在转动轴线上,则会引起剧烈振动而影响机器正常工作和寿命。
高二物理竞赛课件:质心和质心运动定律

例2. 求半径为R、顶角为2 的均匀圆弧的质心。
解:选择如图所示的坐标系,圆弧关于x 轴对称。
由对称性知,质心位于 x 轴上
设圆弧的线密度为 ,取线元d l = R d
质量元 dm = dl= R d 坐标为x=R cos
则圆弧质心坐标为
xC
xdm dm
R cosRd Rd
R2 cosd R d
Rsin
d
R
α θ
Oα
dl
x
x
当
2
时,xC
0.6R
当 时,xC 0
例3. 有一 厚度和密度都均匀的扇形薄板,其半径为 R, 顶角为2α,求质心位置
解:根据对称性可知 yC= 0
xdm xC dm
dm ds rddr
1.
将体系分割成许多小份n,任一小份质量
由 rC
mi ri mi
可得
rC
dnmi
对应位矢
dmi ri
i 1
n
dmi
ri
i 1
2. 为了使每一小份真正成为一个质点,可取 n →∞
n
rC
lim
n
i 1 n
ri dmi
lim
n
i 1
dmi
rdm dm
3. 上式在直角坐标系的分量式
质心和质心运动定律
一、质心
定义:n个质点组成的质点系的质心位置为
rC
m1r1
m2r2
mn rn
m1 m2 mn
n mi ri
i 1 n
mi
n mi ri
i 1
m
i 1
重心与质心

重心与质心重心与质心是物理学中两个重要概念,由于它们只有一字之差,运用中很容易混淆。
其实,“重心”和“质心”这两个概念有着不同的内涵和外延,是两个截然不同的力学概念。
首先看重心,任何物体都可以看作是由很多微粒所组成,每个微粒都受到竖直向下的重力的作用,由于地球很大,这些力可认为彼此平行。
因此,又可以说任何一个物体都受到很多的平行力——物体的各微粒所受的重力的作用。
所有这些重力的合力就等于整个物体的重力,它可以根据平行力的合成法则来求得。
这些平行力...的合力作用点就叫做物体的重心..............(如图1-18的C点)。
由此可见,重心必须依赖重力而存在。
实际上,重心反映了重力“三要素”中的“作用点”要素,因此,可以说重心是重力概念的一个派生概念。
根据重心的定义,严格地讲,在地面上方的物体有重心的充分必要条件是作用在它各部分的重力的作用线是相互平行的。
在地面上方的大物体不存在以上意义的重心1。
可见,重心概念只对地球附近处受到地球引力的一切小物体有意义。
另外,根据重心定义可以知道,重心是一个定点,与物体所在的位置和如何放置无关。
均匀物体的重心只跟物体的形状有关,规则形状的均匀物体的重心就在它的几何中心。
如均匀直棒的重心就在它的中点,均匀圆板的重心就在圆板的圆心,均匀球体的重心就在它的球心等等。
几何上之所以把三角形的二条中线的交点称为重心,就是因为此交点实为物理上的重心位置。
形状不规则、质量分布又不均匀的物体的重心位置,除与物体的形状有关外,还与物体内部质量的分布情况有关:找物体重心除用计算法外还可用实验悬挂法;用线悬挂物体(A点),平衡时,物体重心一定在悬挂线(或其延长线)上,然后把悬挂点换到物体上另一点(B点),再使之平衡,则物体的重心又一定在新的悬挂线(或其延长线)上,前后两次悬挂线的交点C就是所求物体的重心位置,如图1-19所示。
有一点必须注意,即物体的重心可以不在物体内部,关于这点,请读者自行举例。
高中物理奥林匹克竞赛专题--质心运动定律(共13张PPT)
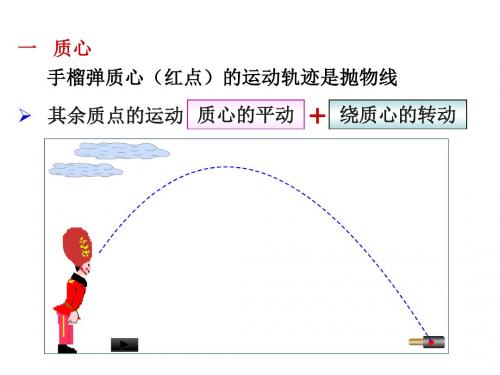
+ 其余质点的运动 质心的平动 绕质心的转动
对于N个质点组成的质点系:
m r 11 ,,r m 2,2 , ,,r im , i, r N mN Mmi
直角坐标系中
y mN
xc yc
mixi /M miyi /M
m1
对于内力 f1 2 f2 1 0 , ,fin fn i0 ,
acm ia i mmi ai i Fi
ac
Fi mi
Fi
M
Fi M ac
质心运 动定理
表明:不管物体的质量如何分布,也不管外力
作用在物体的什么位置上,质心的运动就象是物体 的质量全部都集中于此,而且所有外力也都集中作 用其上的一个质点的运动一样。
设弹丸碎片落地时质心离原点的距离为 xC
xC
m1x1 m2x2 m1 m2
x2 2xC
yH
d
C
o Od
H
52.3o
x
52.3o
解: 由于氢原子对 x 轴对称,故 yC = 0 .
n
x代C入数i1 据m m ixx iCi=6m .8×Hd 10s-12i3 mn.7 7 m H m r m O C O 0 6 m .m 8 H Hd 1s 1 i0 3m n 2.7 7 i
y a
xc
xdm
a/
2
2
x 2d x
0
2a
m
1 a2
3
O
x
x
2
dx
这个结果和熟知的三角形重心位置一致。
例 一段均匀铁丝弯成半圆形,其半径为R,求此半圆 形铁丝的质心。
高中物理奥林匹克竞赛专题--质心-质心运动定理-动量守恒定律

v 3 1 2v 1 2 v 2 2 1 232 0 32 0 2.2 m 1/s v 1和 v所3 成角由下式决定:
1800
因 tgv2 1,450,所以
根据动量守恒定理有对地面参考系而言设炮弹相对地面的速度按速度变换定理为cos动量守恒定律动量守恒定律解物体的动量原等于零炸裂时爆炸力是物体内力它远大于重力故在爆炸中可认为动量守恒
§3-4 质心 质心运动定理 动量守恒定律
1. 质心
Y
质点系(或物体) 的质量中心,简称 质心。
C
O
X
抛手榴弹的过程
质心运动反映了质点系的整体运动趋势。
m 1 x 1 m 2 x 2 m 1 x 1 m 2 x 2
m1(x1x1)m1(l d) (人相对地的移动距离)
m2(x2 x2)m2d (船相对地的移动距离)
dm1m 1m2l0.8(m)
解法二:
设人相对地的运动速度为 v
,船相对
1
地的运动速度为 v 2 , 由动量守恒
xc
m2x20 m1x10 m1 m2
动量守恒定律
例 一质量 m1 的5人0k站g在一条质量为
,m2长度20k0g
的船的l 船4头m上。开始时船静止,试求当人走到船尾时船移
动的距离。(假定水的阻力不计。)
解:
y
设 表c b示船
x1
x1
本身的质心
o x 2 x 2
c b c b d
ac
Fi mi
Fi
M
质心运
Fi M ac 动定理
物理学中的质心与系统重心研究

物理学中的质心与系统重心研究质心是物体在三维空间中的一个点,可以看作是物体的整体质量均匀分布在该点上。
而系统重心则是由多个物体构成的系统相对于参考点的平均位置。
质心和系统重心在物理学中都扮演着重要的角色,它们的研究对于理解物体的运动和相互作用具有重要意义。
一、质心的概念与应用质心是一个抽象概念,用于简化计算物体的运动和力学性质。
由于质心是物体整体质量的平均分布点,因此在计算物体的运动时,可以将其视为单个点参与运动。
质心的坐标可以通过将物体分割成小元素,然后根据质量加权求和的方法得到。
在动力学中,质心经常被用来计算物体的运动状态。
根据牛顿第二定律,质心所受到的合力等于物体的质量乘以质心加速度。
通过计算质心的运动状态,可以推导出物体的运动轨迹、速度和加速度等物理量。
除了运动学和动力学,质心还在其他物理学领域中有广泛的应用。
例如,在流体力学中,质心被用来描述液体或气体的运动和平衡状态。
在电磁学中,质心也是重要的概念之一,用于计算电荷和电流的分布情况。
二、系统重心的研究与应用系统重心是由多个物体组成的系统相对于参考点的平均位置,和质心有些相似,但是系统重心更加强调整个系统的集体性质。
在研究多体系统的运动和力学性质时,系统重心被广泛应用。
在天体物理学中,系统重心是研究星系、行星系统和天体碰撞等现象的重要概念。
通过计算系统重心的运动状态,可以推导出天体运动的规律,从而揭示宇宙的内在规律。
例如,在研究行星围绕太阳运动的过程中,系统重心的位置和速度变化可以告诉我们行星的轨道形状和周期。
除了天体物理学,系统重心还在机械力学、固体力学和流体力学等领域中得到应用。
在机械力学中,系统重心是计算刚体运动和静力学平衡的重要工具。
在固体力学中,系统重心被用来计算物体的旋转和倾斜等运动状态。
在流体力学中,系统重心被用于描述液体或气体的稳定性和平衡条件。
总结质心和系统重心是物理学中重要的概念,它们在物体的运动和相互作用研究中起到了关键性的作用。
重心物理知识点总结

重心物理知识点总结一、质心1.1 定义质心是物体或系统的质量分布所决定的一个点,通常用G表示。
对于均匀物体而言,质心可看作物体质量均匀分布时的几何中心,是物体平衡的关键点。
1.2 质心的计算对于均匀物体而言,质心的计算可以通过物体的几何形状和质量分布来求解。
一般可以利用积分的方法来计算质心的位置。
对于复杂形状的物体,可以将其分割成小块,然后分别计算各小块的质心位置,最后进行加权平均即可得到整个物体的质心位置。
1.3 重心与质心在力学中,有时会将重心与质心混用,其实两者是有区别的。
重心通常是指物体受重力作用时的作用点,而质心是物体的质量分布确定的一个点。
对于地球上的物体而言,由于重力场的影响,重心和质心大致重合,因此一般情况下可以认为它们是相同的。
二、力矩2.1 定义力矩是指力对物体产生的转动效应,通常用M表示。
力矩的大小等于力乘以力臂的长度,方向由转动的方向决定。
力矩是引起物体转动的关键因素,对于力矩的平衡和计算是静力学中的重要内容。
2.2 力矩的平衡条件当一个物体对一个轴产生的力矩为零时,物体就处于力矩平衡状态。
力矩平衡的条件是物体受到的力矩之和为零。
在实际问题中,可以利用这个条件来解决平衡问题,比如找到物体的支点位置、杠杆原理等。
2.3 力矩的计算对于给定的力,可以通过力矩的计算来求解物体的转动效应。
力矩的计算可以利用叉乘的方法进行,也可以将外力分解成平行和垂直于转轴的力,然后分别计算它们对转动的影响。
三、转动惯量3.1 定义转动惯量是物体对于自身的旋转运动的惯性度量,通常用I表示。
转动惯量的大小取决于物体的质量分布和其关于旋转轴的位置。
与质心类似,转动惯量是物体的固有属性,对于给定的物体,其转动惯量是一个固定的值。
3.2 转动惯量的计算对于简单的几何形状,可以通过积分的方法来计算物体的转动惯量。
比如对于均匀的细棒,可以将其分割成许多小块,然后分别计算每个小块的转动惯量,最后再进行加权平均。
高中物理知识延伸拓展之--重心或质心的求法
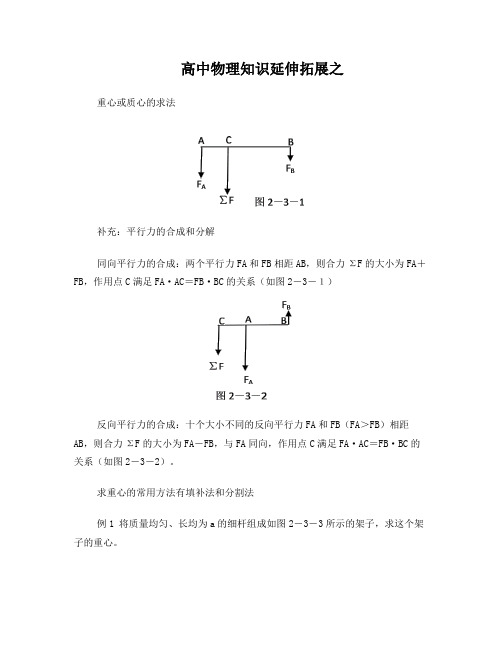
高中物理知识延伸拓展之
重心或质心的求法
补充:平行力的合成和分解
同向平行力的合成:两个平行力FA和FB相距AB,则合力ΣF的大小为FA+FB,作用点C满足FA·AC=FB·BC的关系(如图2-3-1)
反向平行力的合成:十个大小不同的反向平行力FA和FB(FA>FB)相距AB,则合力ΣF的大小为FA-FB,与FA同向,作用点C满足FA·AC=FB·BC的关系(如图2-3-2)。
求重心的常用方法有填补法和分割法
例1 将质量均匀、长均为a的细杆组成如图2-3-3所示的架子,求这个架子的重心。
解法1:“填补法”。
就是把残缺部分补全,即先补上一根同样的细杆于AD处,构成的正方形的重心在正中间O处,设原架子的重心在点O 正上方
处的O’点,每段细杆重G,根据同向平行力的合成法则有
解得
,即重心在对称轴上离横杆
处。
解法2:“分割法”。
即把整体分割成重心易求的几部分,本题中分成BC与AB和CD两部分,BC杆的重心在其正中间,AB与CD整体的中心在图中的O点,这样可得同上法一样的方程。
解法3:“坐标法”。
该法是建立在以上两种方法基础上的,它是解决由均质体组成的极为复杂的“集合体”的一种通用的方法。
如本题可取BC为χ轴正向,BA为y轴正向。
设每段细杆质量为m,这样有。
重心和质心

重心和质心一个物体如果没有重心就会很快地飘向一边,那么怎样才能使物体保持平衡呢?于是人们想到了“重心”。
“重心”就是一个物体各部分受到同一方向的作用时,距离支点最近的那一点。
用公式表示:重心坐标=重力×半径。
许多力学家都在研究质心和重心之间的关系,但是直到现在还没有人发现,除非一种物体不是球体或者其他特殊形状。
其实,在物理学中所指的“质心”并不是一般意义上所说的物体的几何中心,而是指某个物体重力的合力为零的位置。
由于物体的质量分布不均匀,各处的质量也不等,因此,重力也分布不均匀,那么重力集中在哪儿,也就是质心也就不一定落在什么地方,因此我们把物体的质心称为质量的合力为零的点,这样就更好理解些。
比如,一个人拿着锤子要往墙上砸去,要看锤子的重心放在哪儿,才知道是否能够将锤子举起来。
如果说质心就是几何中心,那就太含糊了,根本就谈不上准确。
而质心只是一个相对的位置,不同物体的质心不同,在空间中并不是固定不变的。
《新概念英语》第三册课本也讲了这样一则故事,说的是古希腊哲学家阿基米德设计一个飞行机器,为此他查阅了大量的资料,想弄清楚,飞机翅膀是否有一个固定的位置,才能保证机翼对飞机重心的合力为零。
后来经过反复实验和测量,他终于发现,飞机两翼的重心并不是在机身的同一水平面内,而是与机身有一个夹角,这个夹角的数值恰好等于飞机所受的重力与机翼的面积之比。
如果用a表示机翼的面积,那么重心就应该选择a=0。
53a,这就是机翼的质心。
有趣的是,美国发明家莱特兄弟刚开始造飞机时,也曾遇到类似的问题。
在一次试飞中,他们将飞机翻转过来,又发现飞机还是平衡的,而且从各个方向的受力情况看,飞机都是轻的,不管是前飞还是后飞,都是平衡的。
经过反复试验,终于找到了这架飞机的质心,即重心。
它们是我国唐代的两位著名诗人白居易和元稹,白居易和元稹是一对好友,也是当时著名的文学家。
他们以友情为主题,分别写了四首传世佳作,即《长恨歌》、《琵琶行》、《离思五首》和《和乐天春词五首》,其中的《长恨歌》和《琵琶行》是流传最广的叙事诗,写出了一个个感人肺腑的爱情故事。
物理竞赛-质心平衡

• 例题:长分别为l1和l2的不可伸长的轻绳悬 挂质量都是m的两个小球,如图所示,它们 处于平衡状态。突然连接两绳的中间小球 受水平向右的冲击(如另一球的碰撞), 瞬间内获得水平向右的速度V0,求这瞬间 连接m2的绳的拉力为多少?
0
l1 V0 m1
l2l2 m2
• 当m1受到冲击力后,使小球具有初速度v0,m1将 以顶点为圆心做圆周运动 ∵此时m1处于顶点正下方 ∴m1所受合力只能在竖直方向,其加速度为: a1=v02/l1 ∵m2相对于M1也做圆周运动。其相对m1的初速 度向左,大小为v0,m2相对m1的加速度为 a21=v02/l2 ∴m2所受惯性力为m2a1,方向向下。 设绳对M2的拉力为T2 则有:t2-m2g-m2a1=m2v02/l2 ∴T2=m2(g+a1+a21 )
定义:力与力臂的乘积称为力矩
M dF
通常规定:绕逆时方向转动的力矩为正。当物体受到多个力作用 时,物体所受的总力矩等于各个力产生力矩的代数和 受力与否的三个判据 条 效 特 件 果 征
3)有固定转动轴物体的平衡
有固定转轴的物体,若处于平衡状态,作用于物体上各力的 力矩的代数和为零。 M x 0
对斜面体,只看水平方向平衡就行了
P f cos N sin 4mgsin cos N cos N sin 综合以上可以得到: Fy mgcos 则:Fx 3mgsin
F Fx2 Fy2 mg 1 8 sin 2
1 t an cot Fx 3 Fy
4R x 3
推论:一条质量均匀分布的平面曲线,其上各点沿垂直 于曲线平面方向运动,在空间扫过一曲面,则此曲面的 面积等于质心在运动中所经路程和曲线长度的乘积
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
话题1:重心与质心的确定一、平行力的合成与分解物体所受的几个力的作用线彼此平行,且不作用于一点,即为平行力(系)。
在平行力的合成或分解的过程中,必须同时考虑到力的平动效果和转动效果,后者要求合力和分力相对任何一个转轴的力矩都相同。
两个同向平行力的合力其方向与两个分力方向相同,其大小等于分力大小之和。
其作用线在两个分力作用点的连线上。
合力作用点到分力作用点的距离与分力的大小成反比。
例如:两个同向平行力A F 和B F ,其合力的大小A B F F F =+,合力作用点O 满足A B AO F BO F ⋅=⋅的关系。
两个反向平行力的合力其方向与较大的分力方向相同,其大小等于分力大小之差。
其作用线在两个分力作用点的连线的延长线上,且在较大的分力的外侧。
合力作用点到分力作用点的距离与分力的大小成反比。
例如:两个反向平行力A F 和B F 的合成其合力的大小B A F F F =-(假如B A F F >,则F 和B F 同向)其合力的作用点满足A B AO F BO F ⋅=⋅的关系。
一个力分解成两个平行力,是平行力合成的逆过程。
二、重心和质心重心是重力的作用点。
质心是物体(或由多个物体组成的系统)质量分布的中心。
物体的重心和质心是两个不同的概念,当物体远离地球而不受重力作用时,重心这个概念就失去意义,但质心却依然存在。
对于地球上体积不太大的物体,由于重力与质量成正比,重心与质心的位置是重合的。
但当物体的高度和地球半径比较不能忽略时,两者就不重合了,如高山的重心比质心要低一些。
在重力加速度g v为常矢量的区域,物体的重心是惟一的(我们讨论的都是这种情形),BF AF FO BA BF AF F OBA重心也就是物体各部分所受重力的合力的作用点,由于重力与质量成正比,重力合力的作用点即为质心,即重心与质心重合。
求重心,也就是求一组平行力的合力作用点。
相距L ,质量分别为12,m m 的两个质点构成的质点组,其重心在两质点的连线上,且与12,m m 相距分别为1L ,2L :1122m L m L = 12L L L +=2112m LL m m =+1212m LL m m =+均匀规则形状的物体,其重心在它的几何中心,求一般物体的重心,常用的方法是将物体分割成若干个重心容易确定的部分后,再用求同向平行力合力的方法找出其重心。
三、物体重心(或质心)位置的求法1、定义法(坐标法)质心位置的定义表达式是一个矢量表达式,将质点组各质点参量记为i m 、i r r,质点组的质心记为C ,则 1NC i i m m ==∑C 的位置定义在坐标(,,)C C C x y z1Ni ii C Cm xx m ==∑ 1Ni ii C Cm yy m ==∑ 1Ni ii C Cm zz m ==∑其意义可以这样理解:假定由多质点组成的物体被分成许多小块,每块都有相同的质量m ,物体总质量等于块数(设为N 块)乘以每块质量m ,第一式可以改写成:1111NNC ii i i x mx x mN N ====∑∑即等于各小块的位置i x 之和除以块数N 。
因此,在假定每块质量相等时,C x 就是所有i x 的平均值。
如果其中有一块(设第i 块)的质量是其它小块质量的两倍,则在求和时,相应的ix应出现两次。
这可以设想把此两倍的质量的小块分成相等的两块即可看出。
因此,C x 是所有质量在x 方向上的平均位置,其中每小块质量所计算的次数都正比于这个质量自身。
这就是人们常说的,质心位置是以质量为权重的加权位置平均值。
根据定义式是求质心位置最普遍最基本的方法。
首先建立直角坐标,再利用直角坐标下定义式给出质心的位置。
对质量连续分布的物体,计算中通常要用到积分,对于中学生来说暂时还无力求解。
因此,此法通常用于质量离散分布或系统可以等效成离散质点情况的处理。
物体重心(或质心)位置的求法例1、 如图所示,一根竖直悬挂着的无限长细线上等距离地固定着n 个质量不等的质点小球,相邻两个小球之间的距离为a 。
已知最上端小球与悬点之间距离也为a ,它的质量为m ,其余各球的质量依次为2m 、3m 、……,一直到nm 。
求整个体系的质心位置到天花板的距离。
解、首先建立一维坐标系,以悬点为坐标原点,竖直向下为x 轴的正方向。
1(1)232NC ii m m n n m m m nm m ==+=+++⋅⋅⋅⋅⋅⋅+=∑12222233(1)2123(1)2(1)(21)(21)6(1)32Ni ii C Cm xx m m a m a m a nm nan n m n an n n n n n a an n ==⋅+⋅+⋅+⋅⋅⋅⋅⋅⋅+⋅=++++⋅⋅⋅⋅⋅⋅+=++++==+∑例2、如图,有5个外形完全一样的均匀金属棒首尾相接焊在一起,从左至右其密度分别为ρ、1.1ρ、1.2ρ、1.3ρ、1.4ρ,设每根棒长均为l ,求其质心位置,若为n 段,密度仍如上递增,质心位置又在什么地方?ρ解:设整个棒重心离最左端距离为x ,则由求质心公式有11225512535791.1 1.2 1.3 1.4222221.1 1.2 1.3 1.42.67i iim x x mm x m x m x m m m l v v l v l v l v l v v v v blρρρρρυρρρρ=+++=+++⋅+⋅+⋅+⋅+⋅=++++=∑∑L L若为n 段,按上式递推得:11 1.13 1.25 1.37(1)(21)10121 1.1 1.2 1.3(1)10n n l x n -+⨯+⨯+⨯+++-=⋅-++++++L L 将坐标原点移到第一段棒的重心上,则上式化为:11211.1 1.22 1.33(1)(1)(1)(1)2(1)(1)10101010111 1.1 1.2(1)1 1.1 1.2(1)1010n n n n x l n n --+⨯+⨯+++-+++⨯+++-==--++++++++++L L L L []222112(1)12(1)(1)(229)1013(19)1 1.1 1.2(1)10n n n n l l n n ⎡⎤+++-++++-⎣⎦-+==-++++++L L L2、力矩法利用力矩和为零的平衡条件来求物体的重心位置。
如图由重量分别为1G ,2G 的两均匀圆球和重量为3G 的均匀杆连成的系统,建立如图坐标系,原点取在A 球最左侧点,两球与杆的重心的坐标分别为123,,x x x ,系统重心在P 点,我们现在求其坐标x 。
设想在P 处给一支持力R , 令123R G G G =++达到平衡时有:1122330M G x G xG x Rx =++-=∑xO112233112233123G x G x G x G x G x G x x R G G G ++++==++这样就得出了如图所示的系统的重心坐标。
若有多个物体组成的系统,我们不难证明其重心位置为: i ii ii iiiiG x G y G z x y z GGG===∑∑∑∑∑∑一般来说,物体的质心位置与重心位置重合,由上面公式很易得到质心位置公式:i ii ii iiiim x m y m z x y z mmm===∑∑∑∑∑∑例3、如图所示,A ,B 原为两个相同的均质实心球,半径为R ,重量为G ,A ,B 球分别挖去半径为2R 和34R 的小球,均质杆重量为3564G ,长度4l R =,试求系统的重心位置。
解:将挖去部份的重力,用等值、反向的力取代,图示系统可简化为图所示平行力系;其中27,864a b G G G G ''==。
设重心位置为O ,则合力279386464G W G G G G =+--= 且()0Oi MG =∑2735(3)(3)(3(3)6448264R G R G R OC G OC R R OC G OC G R OC -+++=--+⋅++ ∴ 0.53OC R =3、实验室质量作平面分布的物体用实验法求质心位置较为简便。
在此平面物体上,选两点A 和B (设A 、B 和质心不在同一直线上),分别作为悬挂点,悬挂在垂直于平面的光滑转轴上,过悬挂点的两个铅垂线的交点即为质心位置。
4、对称法如果一个物体质量分布具有轴对称性,例如质量平面均匀分布的菱形物体,其质心必处在对角线上,两对角线的交点即为此菱形的质心位置。
这是因为垂直于对称轴方向上,轴两旁的正负坐标的质量对应相等。
5、分割法这种方法把整个物体分割成质心易求的若干部分,再把各部分看成位置在各自质心处、并具有该部分质量的质点,再依质心定义表达式求出整个物体的质心位置。
如下左图的棒锤,假设匀质球A 质量为M 、半径为R ;匀质棒B 质量为m 、长度为l ,求它的重心。
第一种方法是将它分隔成球和棒两部分,然后用同向平行力合成的方法找出其重心C 。
C 在AB 连线上,且AC M BC m ⋅=⋅(如图)。
6、负质量法容易看出,负质量法本质上是分割法的一种推论,仍然是把整个物体分割成质心易求的几个部分。
不同的是,每一部分既可以是正质量,也可以是负质量。
同样,将棒锤看成一个对称的“哑铃”和一个质量为M -的球A '的合成(如图),用反向平行力合成的方法找出其重心C ,C 在AB 连线上,且(2)BC M m A C M '⋅+=⋅.不难看出两种方法的结果都是:()2M lBC R m M =++证明方法与分割法相同。
有时,根据质心的定义,我们还可用坐标法求物体系的质心。
通常把物体分割成n 个部分,求得这n 个部分的质量分别为123,,,,n m m m m ⋅⋅⋅。
所受的重力相应为123,,,,n m g m g m g m g ⋅⋅⋅。
又求得它们的重心(质心)的坐标分别为111(,,)x y z ,222(,,)x y z ,333(,,)x y z ,⋅⋅⋅,(,,)n n n x y z 。
由于这n 个部分所受的重力i i G m g =(1,2,,)i n =⋅⋅⋅可看作是平行力,故可用类似于求同向平行力合力的方法,求得这n 个平行力合力的作用点位置(,,)C C C x y z ,得出整个物体质心(重心)的位置坐标为lR +i iiCi im x x m=∑∑;i iiCi im y y m=∑∑;i iiCi im z z m=∑∑上例中,以B 点为原点,水平向右为。
轴正方向,则,A B 的合质心的位置为:()02C lM R m x M m⋅--+⋅=+ 00C M m y M m ⋅+⋅=+ 即:()2C lM R x M m⋅+=-+ 0Cy = 负号表示质心的位置在B 点左侧(如上右图)。
