八年级数学竞赛例题专题：几何变换

合集下载

几何的变换压轴题(含答案)

图形的变换压轴题1．如图1，将两个完全相同的三角形纸片ABC 和DEC 重合放置，其中∠C =90°，∠B =∠E=30°．（1）操作发现如图2，固定△ABC ，使△DEC 绕点C 旋转．当点D 恰好落在AB 边上时，填空：①线段DE 与AC 的位置关系是；②设△BDC 的面积为1S ，△AEC 的面积为2S ，则1S 与2S 的数量关系是．（2）猜想论证当△DEC 绕点C 旋转到图3所示的位置时，小明猜想（1）中1S 与2S 的数量关系仍然成立，并尝试分别作出了△BDC 和△AEC 中BC 、CE 边上的高DM 和AN ，请你证明小明的猜想．（3）拓展探究已知∠ABC =60°，点D 是其角平分线上一点，BD =CD =4，DE ∥AB 交BC 于点E （如图4）．若在射线BA 上存在点F ，使DCF BDE S S =，请求出相应的BF 的长．【答案】（1）DE AC ①； 12S S =②．（2）证明见解析；（3）BF ．【解析】（1）DE AC ①； 12S S =②．（2）证明：90DCE ACB ∠=∠=︒， 180DCM ACE ∴∠+∠=︒．又180ACN ACE ∠+∠=︒， ACN DCM ∴∠=∠．又90CNA CMD ∠=∠=︒， AC CD =，ANC DMC ∴≌． AN DM ∴=．又CE CB =， 12S S ∴=．（3）如图，延长CD 交AB 于点P ，则有∠ABD =30°，PD =2，由BD =CD =4可得∠BCD =30°，∴∠BPD =90°，BP =同理可求DE =BE ，故BDE S =，当DCF BDE S S =时， 1423DCF S PF =⨯⨯=，∴3PF =，∴BF =，即BF ． 2．已知，正方形ABCD 的边长为4，点E 是对角线BD 延长线上一点，AE=BD ．将△ABE 绕点A 顺时针旋转α度（0°＜α＜360°）得到△AB ′E ′，点B 、E 的对应点分别为B ′、E ′．（1）如图1，当α=30°时，求证：B ′C=DE ；（2）连接B ′E 、DE ′，当B ′E=DE ′时，请用图2求α的值；（3）如图3，点P 为AB 的中点，点Q 为线段B ′E ′上任意一点，试探究，在此旋转过程中，线段PQ 长度的取值范围为．【答案】（1）证明见解析（2）45°（3） ≤PQ≤4 +2然后结合旋转图形的性质得出△ADE和△AB′C全等，从而得出答案；(2)、根据旋转图形的性质得出△AEB′和△AE′D全等，从而得出∠DAE′=∠EAB′，然后结合旋转图形的性质得出∠EAE′=∠BAB′，从而得到∠BAB′=∠DAB′，最后根据∠BAB′+∠DAB′=90°得出答案；(3)、点P作PM⊥BE，∵AB=4，点P是AB中点，根据BP=2得出PM=；在旋转过程中，△ABE在旋转到点E在BA的延长线时，点Q和点E重合，然后求出PQ的长度，从而得出取值范围.试题解析：（1）如图，连接AC，B′C，∵四边形ABCD是正方形，∴AB=AD，AC⊥BD，AC=BD=2OA，∠CAB=ADB=45°，∵AE=BD，∴AC=AE=2OA，在Rt△AOE中，∠AOE=90°，AE=2OA，∴∠E=30°，∴∠DAE=∠ADB﹣∠E=45°﹣30°=15°，由旋转有，AD=AB=AB′∠BAB′=30°∴∠DAE=15°，在△ADE和△AB′C中，，∴△ADE≌△AB′C，∴DE=B′C，（2）如图，由旋转得，AB′=AB=AD，AE′=AE，在△AEB′和△AE′D中，，∴△AEB′≌△AE′D，∴∠DAE′=∠EAB′，∴∠EAE′=∠DAB′，由旋转得，∠EAE′=∠BAB′，∴∠BAB′=∠DAB′，∵∠BAB′+∠DAB′=90°，∴α=∠BAB′=45°，（3）如图，由点到直线的距离，过点P作PM⊥BE，∵AB=4，点P是AB中点，∴BP=2，∴PM=，在旋转过程中，△ABE在旋转到点E在BA的延长线时，点Q和点E重合，∴AQ=AE=BQ=4∴P Q=AQ+AP=4+2，故答案为≤PQ≤4+2．3．如图①，C为线段BE上的一点，分别以BC和CE为边在BE的同侧作正方形ABCD和正方形CEFG，M、N（1）线段MN和GD的数量关系是，位置关系是；（2）将图①中的正方形CEFG绕点C逆时针旋转90°，其他条件不变，如图②，（1）的结论是否成立？说明理由；（3）已知BC=7，CE=3，将图①中的正方形CEFG绕点C旋转一周，其他条件不变，直接写出MN的最大值和最小值．【答案】（1） MN=12DG；MN⊥DG；（2）成立，理由见解析；（3）5，2.【解析】试题分析：（1）连接FN并延长，与AD交于点S，如图①．易证明△SDN≌△FGN，则有DS=GF，SN=FN．然后运用三角形中位线定理即可解决问题；（2）过点M作MT⊥DC于T，过点M作MR⊥BC于R，连接FC、MD、MG，如图②，根据平行线分线段成比例即可得BR=GR=12BG，DT=ET=12DE，根据梯形中位线定理可得MR=12（FG+AB），MT=12（EF+AD），从而可得MR=MT，RG=TD，由此可得△MRG≌△MTD，则有MG=MD，∠RMG=∠TMD，则有∠RMT=∠GMD，进而可证得△DMG是直角三角形，然后根据等腰三角形的性质和直角三角形斜边上的中线等于斜边的一半，即可解决问题；（3）连接GM到点P，使得PM=GM，延长GF、AD交于点Q，连接AP，DP，DM如图③，易证△APD≌△CGD，则有PD=DG，根据等腰三角形的性质可得DM⊥PG，根据直角三角形斜边上的中线等于斜边的一半可得MN=12 DG，要求MN的最大值和最小值，只需求DG的最大值和最小值，由GC=CE=3可知点G在以点C为圆心，3为半径的圆上，再由DC=BC=7，就可求出DG的最大值和最小值.试题解析：（1）连接FN并延长，与AD交于点S，如图①．∵四边形ABCD和四边形EFGC都是正方形，∴∠D=90°，AD=DC，GC=GF，AD∥BE∥GF，DSN GFN SND FNG DN GN ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△SDN≌△FGN，∴DS=GF，SN=FN ．∵AM=FM，∴MN∥AS，MN=12AS ， ∴∠MNG=∠D=90°， MN=12（AD-DS ）=12（DC-GF ）=12（DC-GC ）=12DG ．（2）（1）的结论仍然成立．理由：过点M 作MT⊥DC 于T ，过点M 作MR⊥BC 于R ，连接FC 、MD 、MG ，如图②，则A 、F 、C 共线，MR∥FG∥AB，MT∥EF∥AD．∵AM=FM， ∴BR=GR=12BG ，DT=ET=12DE ， ∴MR=12（FG+AB ），MT=12（EF+AD ）． ∵四边形ABCD 和四边形EFGC 都是正方形，∴FG=GC=EC=EF，AB=BC=DC=AD ，∴MR=MT，RG=TD ．在△MRG 和△MTD 中，MR MT MRG MTD RG TD =⎧⎪∠=∠⎨⎪=⎩，∴△MRG≌△MTD，∴MG=MD，∠RMG=∠TMD，∴∠RMT=∠GMD．∴∠RMT=90°，∴∠GMD=90°．∵MG=MD，∠GMD=90°，DN=GN ，∴MN⊥DG，MN=12DG ．（3）连接GM 到点P ，使得PM=GM ，延长GF 、AD 交于点Q ，连接AP ，DP ，DM 如图③，在△AMP 和△FMG 中，AM FMAMP FMG PM GM=⎧⎪∠=∠⎨⎪=⎩，∴△AMP≌△FMG，∴AP=FG，∠APM=∠FGM，∴AP∥GF，∴∠PAQ=∠Q，∵∠DOG=∠ODQ+∠Q=∠OGC+∠GCO，∠ODQ=∠OGC=90°，∴∠Q=∠GCO，∴∠PAQ=∠GCO．∵四边形ABCD 和四边形EFGC 都是正方形，∴DA=DC，GF=GC ，∴AP=CG．在△APD 和△CGD 中，AP CGPAD GCD AD CD=⎧⎪∠=∠⎨⎪=⎩，∴△APD≌△CGD，∵PM=GM，∴DM⊥PG．∵DN=GN，∴MN=12 DG．∵GC=CE=3，∴点G在以点C为圆心，3为半径的圆上，∵DC=BC=7，∴DG的最大值为7+3=10，最小值为7-3=4，∴MN的最大值为5，最小值为2．考点：正方形综合题.4．如图1，已知△ABC中，AB＝BC＝1，∠ABC＝90°，把一块含30°角的直角三角板DEF的直角顶点D放在AC的中点上（直角三角板的短直角边为DE，长直角边为DF），将直角三角板DEF绕D点按逆时针方向旋转．（1）在图1中，DE交AB于M，DF交BC于N．①求证:DM＝DN；②在这一旋转过程中，直角三角板DEF与△ABC的重叠部分为四边形DMBN，请说明四边形DMBN的面积是否发生变化？若发生变化，请说明是如何变化的？若不发生变化，求出其面积；（2）继续旋转至如图2的位置，延长AB交DE于M，延长BC交DF于N，DM＝DN是否仍然成立？若成立，请给出证明；若不成立，请说明理由；（3）继续旋转至如图3的位置，延长FD交BC于N，延长ED交AB于M，DM＝DN是否仍然成立？请写出结论，不用证明．【答案】（1）①证明详见解析；②四边形DMBN的面积不发生变化，理由详见解析；（2）DM=DN仍然成立，理由详见解析；（3）DM=DN．试题分析：（1）①连接DB ，根据AAS 证明△BMD ≌△CND ，所以DM=DN ；②由①知△BMD ≌△CND ，所以BMD CND S S =，所以四边形DMBN 的面积等于△ABC 的面积的一半；（2）连接DB ，依然可以证得△BMD ≌△CND ，所以DM=DN ；（3）根据（2）的思路可以得到DM=DN ．试题解析：（1）①证明：连接DB ，在Rt △ABC 中，因为AB=BC ，AD=DC ，所以DB=DC=AD ，∠BDC=90°，所以∠ABD=∠C=45°，因为∠MDB+∠BDN=∠CDN+∠BDN=90°，所以∠MDB=∠NDC ，所以△BMD ≌△CND ，所以DM=DN ．②四边形DMBN 的面积不发生变化，理由如下：由①知△BMD ≌△CND ，所以BMD CND S S =，所以=DBN DMB DMBN S S S +四边形=DBN DNC S S +=1124DBC S S ABC ==．（2）DM=DN 仍然成立，理由如下：连接DB ，在Rt △ABC 中，因为AB=BC ，AD=DC ，所以DB=DC=AD ，∠BDC=90°，所以∠DCB=∠DBC=45°，所以∠DBM=∠DCN=135°，因为∠NDC+∠CDM=∠BDM+∠CDM=90°，所以∠MDB=∠NDC ，所以△BMD ≌△CND ，所以DM=DN ．（3） DM=DN ．5．已知，正方形ABCD中，，绕点A顺时针旋转，它的两边长分别交CB、DC或它们的延长线于点MN，于点H．如图，当点A旋转到时，请你直接写出AH与AB的数量关系；如图，当绕点A旋转到时，中发现的AH与AB的数量关系还成立吗？如果不成立请写出理由，如果成立请证明．【答案】；（2）数量关系还成立．证明见解析.【解析】【分析】(1)由题意可证△ABM≌△ADN，可得AM=AN，∠BAM=∠DAN=22.5°，再证△ABM≌△AMH可得结论；(2)延长CB至E，使BE=DN，可证△ABE≌△ADN，可得AN=AE，∠BAE=∠DAN，可得∠EAM=∠MAN=45°且AM=AM，AE=AN，可证△AME≌△AMN，则结论可证．【详解】，理由如下：是正方形，且，≌，，，，，，，，，且，，≌，；，，，≌，，，，即，且，，≌，，≌，，.【点睛】本题考查了旋转的性质，正方形的性质，全等三角形的判定和性质，正确添加辅助线构建全等三角形是解题的关键.6．在ABC中，AB=AC，∠BAC=α，点P是ABC内一点，且∠PAC+∠PCA=，连接PB，试探究PA、PB、PC 满足的等量关系．（1）当α=60°时，将ABP绕点A逆时针旋转60°得到ACP′，连接PP′，如图1所示．由ABP≌△ACP′可以证得APP′是等边三角形，再由∠PAC+∠PCA=30°可得∠APC的大小为度，进而得到CPP′是直角三角形，这样可以得到PA、PB、PC满足的等量关系为；（2）如图2，当α=120°时，参考（1）中的方法，探究PA、PB、PC满足的等量关系，并给出证明；（3）PA、PB、PC满足的等量关系为．【答案】（1）150，PA2+PC2=PB2；（2）3PA2+PC2=PB2；（3）4PA2sin2+PC2=PB2试题分析：（1）根据旋转变换的性质得到△PAP′为等边三角形，得到∠P′PC=90°，根据勾股定理解答即可；（2）如图2，作将△ABP绕点A逆时针旋转120°得到△ACP′，连接PP′，作AD⊥PP′于D，根据余弦的定义得到PP′=PA，根据勾股定理解答即可；（3）与（2）类似，根据旋转变换的性质、勾股定理和余弦、正弦的关系计算即可．试题解析：（1）∵△ABP≌△ P′，∴ P= P′，由旋转变换的性质可知，∠P P′=60°，P′ =P ，∴△PAP′为等边三角形，∴∠ PP′=60°，∵∠PAC+∠PCA==30°，∴∠APC=150°，∴∠P′P =90°，∴PP′2+PC2=P′ 2，∴PA2+PC2=PB2，故答案为：150，PA2+PC2=PB2；（2）如图2，作将ABP绕点A逆时针旋转120°得到ACP′，连接PP′，作AD⊥PP′于D，由旋转变换的性质可知，∠P P′=120°，P′ =P ，∴∠ PP′=30°，∵∵∠PAC+∠PCA==60°，∴∠APC=120°，∴∠P′P =90°，∴PP′2+PC2=P′ 2，∵∠ PP′=30°，∴PD=PA，∴PP′=PA，∴3PA2+PC2=PB2；（3）如图2，与（2）的方法类似，作将ABP绕点A逆时针旋转α得到ACP′，连接PP′，作AD⊥PP′于D，由旋转变换的性质可知，∠P P′=α，P′ =P ，∴∠ PP′=90°﹣，∵∵∠PAC+∠PCA=，∴∠APC=180°﹣，∴∠P′P =（180°﹣）﹣（90°﹣）=90°，∴PP′2+PC2=P′ 2，∵∠ PP′=90°﹣，∴P =P •cos（90°﹣）=P •sin，∴PP′=2P •sin，∴4PA2sin2+PC2=PB2，故答案为：4PA2sin2+PC2=PB2．【点睛】考查的是旋转变换的性质、等边三角形的性质、勾股定理的应用，掌握等边三角形的性质、旋转变换的性质、灵活运用类比思想是解题的关键．7．（操作发现）如图①，在边长为1个单位长度的小正方形组成的网格中，△ABC的三个顶点均在格点上．（1）请按要求画图：将△ABC绕点A按逆时针方向旋转90°，点B的对应点为B′，点C的对应点为C′，连接BB′（2）在（1）所画图形中，∠AB′B=．（问题解决）如图②，在等边三角形ABC中，AC=，点P在△ABC内，且∠APC=90°，∠BPC=120°，求△APC的面积．小明同学通过观察、分析、思考，对上述问题形成了如下想法：想法一：将△APC绕点A按顺时针方向旋转60°，得到△AP′B，连接PP′，寻找线段PA、PC之间的数量关系；想法二：将△APB绕点A按逆时针方向旋转60°，得到△AP′C′，连接PP′，寻找线段PA、PC之间的数量关系；请参考小明同学的想法，完成该问题的解答过程．（求解一种方法即可）（灵活运用）如图③，在四边形ABCD中，AE⊥BC，垂足为E，∠BAE=∠ADC，BE=CE=2，CD=5，AD=kAB（k为常数），直接写出BD的长（用含k的式子表示）．【答案】【操作发现】（1）作图见解析；（2）45°；【问题解决】S△APC=；【灵活运用】BD=2 2 ．【解析】【分析】（1）根据旋转角，旋转方向画出图形即可；（2）只要证明ABB′是等腰直角三角形即可；【问题解决】如图②，将APB绕点A按逆时针方向旋转60°，得到AP′C′，证明∠PP′C=90°，利用勾股定理即可得出答案. 【灵活运用】如图③中，由AE⊥BC，BE=EC，推出AB=AC，将ABD绕点A逆时针旋转得到ACG，连接DG．则BD=CG，只要证明∠GDC=90°，可得CG=，由此即可解决问题；【详解】（1）如图所示，AB′C′即为所求；（2）连接BB′，将ABC绕点A按顺时针方向旋转90°，∴AB=AB′，∠B′AB=90°，∴∠AB′B=45°，故答案为：45°；【问题解决】如图②，∵将APB绕点A按逆时针方向旋转60°，得到AP′C′，∴△APP′是等边三角形，∠AP′C=∠APB=360°﹣90°﹣120°=150°，∴PP′=AP，∠AP′P=∠APP′=60°，∴∠PP′C=90°，∠P′PC=30°，∴PP′=PC，即AP=PC，∵∠APC=90°，∴AP2+PC2=AC2，即（PC）2+PC2=∴PC=2，∴AP=，∴S APC=AP•PC=××2=，【灵活运用】如图③中，∵AE⊥BC，BE=EC，∴AB=AC，将ABD绕点A逆时针旋转得到ACG，连接DG．则BD=CG，∵∠BAD=∠CAG，∴∠BAC=∠DAG，∵AB=AC，AD=AG，∴∠ABC=∠ACB=∠ADG=∠AGD，∴△ABC∽△ADG，∵AD=kAB，∴DG=kBC=4k，∵∠BAE+∠ABC=90°，∠BAE=∠ADC，∴∠ADG+∠ADC=90°，∴∠GDC=90°，∴CG==．∴BD=CG=．【点睛】本题考查等边三角形的判定和性质、等腰三角形的判定和性质、勾股定理、相似三角形的判定和性质等知识，学会用旋转法添加辅助线，构造全等三角形或相似三角形是解题关键.8．正方形ABCD中，点P为直线AB上一个动点不与点A，B重合，连接DP，将DP绕点P旋转得到EP，连接DE，过点E作CD的垂线，交射线DC于M，交射线AB于N．问题出现：当点P在线段AB上时，如图1，线段AD，AP，DM之间的数量关系为______；题探究：当点P在线段BA的延长线上时，如图2，线段AD，AP，DM之间的数量关系为______；当点P在线段AB的延长线上时，如图3，请写出线段AD，AP，DM之间的数量关系并证明；问题拓展：在的条件下，若 P，，则______．【答案】（1） P；（2） P； P，理由见解析；（3）或．【解析】【分析】根据正方形的性质和全等三角形的判定和性质得出≌，进而解答即可；根据正方形的性质和全等三角形的判定和性质得出≌，进而解答即可；根据正方形的性质和全等三角形的判定和性质得出≌，进而解答即可；分两种情况利用勾股定理和三角函数解答即可．【详解】解： P，理由如下：正方形ABCD，， P，将DP绕点P旋转得到EP，连接DE，过点E作CD的垂线，交射线DC于M，交射线AB于N， P P ， P ， P ，P P ， P P ，P P ，在 P与 P 中，，P≌ P ，P ， P，P P P；P，理由如下：正方形ABCD，， P，将DP绕点P旋转得到EP，连接DE，过点E作CD的垂线，交射线DC于M，交射线AB于N， P P ， P ， P ，P P ， P P ，P P ，在 P与 P 中，，P≌ P ，P ， P，P P P；P，理由如下：P P ， P P ，P P ，又 P ， P P ，P≌P ，P ，P P P；有两种情况，如图2，，如图3，；如图2：，P P ，，在P 中 P， PnP；如图3：，P P ，在P 中， P， P n，P．故答案为； P； P；或．【点睛】此题是四边形综合题，主要考查了正方形的性质,全等三角形的判定和性质，旋转的性质,锐角三角函数的知识，以及分类讨论的数学思想解决问题，判断出≌是解本题的关键．9．如图，在菱形ABC D中，，点E在对角线B D上.将线段C E绕点C顺时针旋转，得到C F，连接D F.（1）求证：B E=DF；（2）连接AC，若EB=EC，求证：.【答案】证明见解析【解析】【分析】（1）根据菱形的性质可得BC=DC，α，再根据α，从而可得，继而得=，由旋转的性质可得=，证明≌，即可证得=；（2）根据菱形的对角线的性质可得，，从而得，由 = ，可得 = ，由（1）可知，可推得，即可得，问题得证.【详解】（1）∵四边形ABCD是菱形，∴ = ，α，∵α，∴，∴ = ，∵线段由线段绕点顺时针旋转得到，∴ = ，在和中，，，，∴≌，∴ = ；（2）∵四边形ABCD是菱形，∴，，∴，∵ = ，∴ = ，由（1）可知， = ，∴，∴，∴.【点睛】本题考查了旋转的性质、菱形的性质、全等三角形的判定与性质等，熟练掌握和应用相关的性质与定理是解题的关键.10．如图1，在等边ABC中，点D，E分别在边AB，AC上，AD=AE，连接BE，CD，点M、N、P分别是BE、CD、BC的中点．（1）观察猜想：图1中，PMN的形状是；（2）探究证明：把ADE绕点A逆时针方向旋转到图2的位置，PMN的形状是否发生改变？并说明理由；（3）拓展延伸：把ADE绕点A在平面内自由旋转，若AD=1，AB=3，请直接写出PMN的周长的最大值．【答案】(1)等边三角形；(2)PMN的形状不发生改变，仍然为等边三角形,理由见解析；（3）6【解析】分析：（1）如图1，先根据等边三角形的性质得到AB=AC，∠ABC=∠ACB=60°，则BD=CE，再根据三角形中位线性质得PM∥CE，PM=CE，PN∥AD，PN=BD，从而得到PM=PN，∠MPN=60°，从而可判断△PMN为等边三角形；（2）连接CE、BD，如图2，先利用旋转的定义，把△ABD绕点A逆时针旋转60°可得到△CAE，则BD=CE，∠ABD=∠ACE，与（1）一样可得PM=PN，∠BPM=∠BCE，∠CPN=∠CBD，则计算出∠BPM+∠CPN=120°，从而得到∠MPN=60°，于是可判断△PMN为等边三角形．（3）利用AB﹣AD≤BD≤AB+AD（当且仅当点B、A、D共线时取等号）得到BD的最大值为4，则PN 的最大值为2，然后可确定△PMN的周长的最大值．详解：（1）如图1．∵△ABC为等边三角形，∴AB=AC，∠ABC=∠ACB=60°．∵AD=AE，∴BD=CE．∵点M、N、P分别是BE、CD、BC的中点，∴PM∥CE，PM=CE，PN∥AD，PN=BD，∴PM=PN，∠BPM=∠BCA=60°，∠CPN=∠CBA=60°，∴∠MPN=60°，∴△PMN为等边三角形；故答案为：等边三角形；（2）△PMN的形状不发生改变，仍然为等边三角形．理由如下：连接CE、BD，如图2．∵AB=AC，AE=AD，∠BAC=∠DAE=60°，∴把△ABD绕点A逆时针旋转60°可得到△CAE，∴BD=CE，∠ABD=∠ACE，与（1）一样可得PM∥CE，PM=CE，PN∥AD，PN=BD，∴PM=PN，∠BPM=∠BCE，∠CPN=∠CBD，∴∠BPM+∠CPN=∠CBD+∠CBD=∠ABC﹣∠ABD+∠ACB+∠ACE=60°+60°=120°，∴∠MPN=60°，∴△PMN 为等边三角形．（3）∵PN=BD，∴当BD的值最大时，PN的值最大．∵AB﹣AD≤BD≤AB+AD（当且仅当点B、A、D共线时取等号）∴BD的最大值为1+3=4，∴PN的最大值为2，∴△PMN的周长的最大值为6．点睛：本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了等边三角形的判定与性质和三角形中位线性质．11．如图1，在矩形ABCD中，AD=4，AB=2，将矩形ABCD绕点A逆时针旋转α（0＜α＜90°）得到矩形AEFG．延长CB与EF交于点H．（1）求证：BH=EH；（2）如图2，当点G落在线段BC上时，求点B经过的路径长．【答案】（1）见解析；（2）B点经过的路径长为．【解析】分析：(1)、连接AH，根据旋转图形的性质得出AB=AE，∠ABH=∠AEH=90°，根据AH为公共边得出Rt△ABH和Rt△AEH全等，从而得出答案；(2)、根据题意得出∠EAB的度数，然后根据弧长的计算公式得出答案．详解：(1)、证明：如图1中，连接AH，由旋转可得AB=AE，∠ABH=∠AEH=90°，又∵AH=AH，∴Rt△ABH≌Rt△AEH，∴BH=EH．(2)、解：由旋转可得AG=AD=4，AE=AB，∠EAG=∠BAC=90°，在Rt△ABG中，AG=4，AB=2，∴cos∠BAG=，∴∠BAG=30°，∴∠EAB=60°，∴弧BE的长为=π，即B点经过的路径长为．点睛：本题主要考查的是旋转图形的性质以及扇形的弧长计算公式，属于中等难度的题型．明白旋转图形的性质是解决这个问题的关键．12．如图1，在Rt ABC中，∠A=90°，AB=AC，点D，E分别在边AB，AC上，AD=AE，连接DC，点M，P，N 分别为DE，DC，BC的中点．（1）观察猜想图1中，线段PM与PN的数量关系是，位置关系是；（2）探究证明把ADE绕点A逆时针方向旋转到图2的位置，连接MN，BD，CE，判断PMN的形状，并说明理由；（3）拓展延伸把ADE绕点A在平面内自由旋转，若AD=4，AB=10，请直接写出PMN面积的最大值．【答案】（1）PM=PN，PM⊥PN；（2）PMN是等腰直角三角形；（3）．【解析】试题分析：（1）利用三角形的中位线得出PM=CE，PN=BD，进而判断出BD=CE，即可得出结论，再利用三角形的中位线得出PM∥CE得出∠DPM=∠DCA，最后用互余即可得出结论；（2）先判断出ABD≌△ACE，得出BD=CE，同（1）的方法得出PM=BD，PN=BD，即可得出PM=PN，同（1）的方法即可得出结论；（3）先判断出MN最大时，PMN的面积最大，进而求出AN，AM，即可得出MN最大=AM+AN，最后用面积公式即可得出结论．试题解析：（1）∵点P，N是BC，CD的中点，∴PN∥BD，PN=BD，∵点P，M是CD，DE的中点，∴PM∥CE，PM=CE，∵AB=AC，AD=AE，∴BD=CE，∴PM=PN，∵PN∥BD，∴∠DPN=∠ADC，∵PM∥CE，∴∠DPM=∠DCA，∵∠BAC=90°，∴∠ADC+∠ACD=90°，∴∠MPN=∠DPM+∠DPN=∠DCA+∠ADC=90°，∴PM⊥PN，故答案为：PM=PN，PM⊥PN，（2）由旋转知，∠BAD=∠CAE，∵AB=AC，AD=AE，∴△ABD≌△ACE（SAS），∴∠ABD=∠ACE，BD=CE，同（1）的方法，利用三角形的中位线得，PN=BD，PM=CE，∴PM=PN，∴△PMN是等腰三角形，同（1）的方法得，PM∥CE，∴∠DPM=∠DCE，同（1）的方法得，PN∥BD，∴∠PNC=∠DBC，∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC，∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC=∠BCE+∠DBC=∠ACB+∠ACE+∠DBC=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC，∵∠BAC=90°，∴∠ACB+∠ABC=90°，∴∠MPN=90°，∴△PMN是等腰直角三角形，（3）如图2，同（2）的方法得，PMN是等腰直角三角形，∴MN最大时，PMN的面积最大，∴DE∥BC且DE在顶点A上面，∴MN最大=AM+AN，连接AM，AN，在ADE中，AD=AE=4，∠DAE=90°，∴AM=2，在Rt ABC中，AB=AC=10，AN=5，∴MN最大=2+5=7，∴S PMN最大=PM2=×MN2=×（7）2=．点睛：解（1）的关键是判断出PM=CE，PN=BD，解（2）的关键是判断出ABD≌△ACE，解（3）的关键是判断出MN最大时，PMN的面积最大13．如图1：在等边ABC中，点D，E分别在边AB，AC上，AD＝AE，连结BE，CD，点M、N、P分别是BE、CD、BC的中点．(1)观察猜想图1中PMN的形状是；(2)探究证明把ADE绕点A逆时针方向旋转到图2的位置，PMN的形状是否发生改变？并说明理由．【答案】（1）等边三角形；（2）△PMN的形状不发生改变，仍为等边三角形【解析】分析：（1）由等边三角形的性质，得到AB=BC=AC，∠A=∠ABC=∠ACB=60°．由AD=AE，得到BD=EC．由中位线的性质，得到NP∥BD，BD=2NP，进而有∠NPC=∠ABC=60°，BD=2NP．同理有EC=2MP，∠MPB=∠ECB=60°，得到MP=NP，∠MPN=180°－∠MPB－∠NPC=60°，即可得到结论．（2）连接BD，CE．易证ABD≌△ACE，得到BD=CE，∠ABD=∠ACE．由PM是△BCE的中位线，得到PM=1 2CE且PM∥BD．同理可证PN=12BD且PN∥BD，得到BD=CE，∠MPB=∠ECB，∠NPC=∠DBC，进而得到∠MPN=60°，即可得到结论．详解：（1）等边三角形．理由如下：∵△ABC是等边三角形，∴AB=BC=AC，∠A=∠ABC=∠ACB=60°．∵AD=AE，∴BD=EC．∵N、P分别是DC、BC的中点，∴NP是△BCD的中位线，∴NP∥BD，BD=2NP，∴∠NPC=∠ABC=60°，BD=2NP．同理可证：EC=2MP，∠MPB=∠ECB=60°．∴MP=NP，∠MPN=180°－∠MPB－∠NPC=60°，∴△MPN是等边三角形．（2）△PMN的形状不发生改变，仍为等边三角形．理由如下：连接BD，CE．由旋转可得∠BAD=∠CAE．∵△ABC是等边三角形，∴AB=AC，∠ACB=∠ABC=60°，∴ABD≌ACE，∴BD=CE，∠ABD=∠ACE．∵M是BE的中点，P是BC的中点，∴PM是△BCE的中位线，∴PM=12CE且PM∥BD．同理可证PN=12BD且PN∥BD，∴BD =CE ，∠MPB =∠ECB ，∠NPC =∠DBC ，∴∠MPB +∠NPC =∠ECB +∠DBC =(∠ACB +∠ACE )+(∠ABC -∠ABD )= ∠ACB +∠ABC =120°，∴∠MPN =60°，∴△PMN 是等边三角形．点睛：本题考查了等边三角形的性质和判定以及三角形中位线的性质．解题的关键是熟练运用三角形中位线定理．14．问题提出()1如图1，点A 为线段BC 外一动点，且BC a AB b ==，，填空：当点A 位于______时，线段AC 的长取得最大值，且最大值为______(用含a b ，的式子表示)．问题探究()2点A 为线段BC 外一动点，且63BC AB ==，，如图2所示，分别以AB AC ，为边，作等边三角形ABD 和等边三角形ACE ，连接CD BE ，，找出图中与BE 相等的线段，请说明理由，并直接写出线段BE 长的最大值．问题解决：()3①如图3，在平面直角坐标系中，点A 的坐标为()20，，点B 的坐标为()50，，点P 为线段AB 外一动点，且290PA PM PB BPM ==∠=，，，求线段AM 长的最大值及此时点P 的坐标．②如图4，在四边形ABCD 中， 60AB AD BAD BC =∠==，，，若对角线BD CD ⊥于点D ，请直接写出对角线AC 的最大值．【答案】 CB 的延长线上； a b +【解析】分析：（1）由题意可知，当点A 在CB 的延长线上时，线段AC 的值最大，最大值为：AC=AB+BC=a+b ；（2）由已知条件易证△ABE ≌△ADC ，由此可得BE=DC ，结合（1）中结论可知，当点D 在CB 的延长线上时，BE 最长=CD 最长=BC+AB=9；（3）①如下图5，连接BM ，将△APM 绕着点P 顺时针旋转90得到 PBN ，连接AN ，则△APN 是等腰直角三角形，则由已知易得AB=3，AP=1）可知，当点N 在BA 的延长线上时，AM 最大=BN 最大=AB+AN=3+6，当点N 在BA 的延长线上时，过点P 作PE ⊥AN 于点E ，由△APN 是等腰直角三角形，AP=2，即可求得OE 和PE 的长，从而可得此时点P 的坐标；②如下图7，以BC 为边作等边三角形 BCM ，连接DM ，由已知条件易证△ABC ≌△DBM ，从而可得AC=DM ，由此可得当DM 的值最大时，AC 的值就最大，由∠BDC=90°可知点D 在以BC 为直径的O 上运动，由图可知当D 在BC 上方，且DM ⊥BC 时，DM 的值最大，最大值为：等腰直角△BDC 斜边BC 上的高+等边△BMC 的高.详解：（1）∵点A 为线段BC 外一动点，且BC a AB b ==，，∴当点A 位于CB 的延长线上时，线段AC 的长取得最大值，且最大值为BC AB a b +=+，故答案为：CB 的延长线上， a b +；()2CD BE =①，理由：∵ABD 与ACE 是等边三角形，∴60AD AB AC AE BAD CAE ==∠=∠=，，，∴BAD BAC CAE BAC ∠+∠=∠+∠，即CAD EAB ∠=∠，在CAD 与EAB 中，{ AD ABCAD EAB AC AE=∠=∠=，∴CAD ≌()EAB SAS ，∴CD BE =；②∵线段BE 长的最大值=线段CD 的最大值，∴由()1知，当线段CD 的长取得最大值时，点D 在CB 的延长线上，∴最大值为369BD BC AB BC +=+=+=；（3）①如图5，连接BM ，将APM 绕着点P 顺时针旋转90得到PBN ，连接AN ，则APN 是等腰直角三角形，∴2PN PA BN AM ===，，∵A 的坐标为()20，，点B 的坐标为()50，，∴25OA OB ==，，∴3AB =，∴线段AM 长的最大值=线段BN 长的最大值，∴当N 在线段BA 的延长线时，线段BN 取得最大值，最大值AB AN =+，∵AN ==∴最大值为3；如图6，过P 作PE x ⊥轴于E ，∵APN 是等腰直角三角形，∴PE AE ==∴532OE BO AB AE =--=-=∴(2.P如下图7，以BC 为边作等边三角形 BCM ，连接DM ，∵60ABD CBM ∠=∠=，∴ABC DBM ∠=∠，∵AB DB BC BM ==，，∴ABC ≌DBM ，∴AC MD =，∴欲求AC 的最大值，只要求出DM 的最大值即可，∵BC ==定值， 90BDC ∠=，∴点D 在以BC 为直径的O 上运动，由图象可知，当点D 在BC 上方，DM ⊥BC 时，DM 的值最大，最大值=等腰直角 BDC 斜边上的高+等边△BCM 的高，∵BC=∴DM 最大=，∴AC 最大=．点睛：这是一道涉及多种几何图形性质的几何综合题，解题时，需注意：（1）弄懂第1小题的题意和结论是解决后面问题的基础；（2）解第2小题时，“通过证 ABE ≌△ADC ，得到BE=DC ，把求BE 的最大值转变为求CD 的最大值”是解决本问的关键；（3）解第3小题时，“作出如图所示的辅助线，把问题分别转化为求线段BN 和DM 的最大值”是解决第3题中2个小问的关键.15．如图，已知 ABC 和 ADE 都是等腰直角三角形，∠ACB=∠ADE=90°，点F 为BE 的中点，连接CF ，DF ．（1）如图1，当点D在AB上，点E在AC上时①证明：BFC是等腰三角形；②请判断线段CF，DF的关系？并说明理由；（2）如图2，将图1中的ADE绕点A旋转到图2位置时，请判断（1）中②的结论是否仍然成立？并证明你的判断．【答案】（1）①证明见解析；②结论：CF=DF且CF⊥DF．理由见解析；（2）（1）中的结论仍然成立．理由见解析.【解析】分析：(1)、根据“直角三角形斜边上的中线等于斜边的一半”可知CF=BF=EF，根据∠CFD=2∠ABC，∠ACB=90°，∠ABC=45°得出∠CFD=90°，从而得出答案；(2)、延长DF至G使FG=DF，连接BG，CG，DC，首先证明△BFG和△EFD全等，然后再证明△BCG和△ACD全等，从而得出GC=DC，∠BCG=∠ACD，∠DCG=∠ACB=90°，最后根据直角三角形斜中线的性质得出答案．详解：（1）①证明：∵∠BCE=90°．EF=FB，∴CF=BF=EF，∴△BFC是等腰三角形．②解：结论：CF=DF且CF⊥DF．理由如下：∵∠ADE=90°，∴∠BDE=90°，又∵∠BCE=90°，点F是BE的中点，∴CF=DF=BE=BF，∴∠1=∠3，∠2=∠4，∴∠5=∠1+∠3=2∠1，∠6=∠2+∠4=2∠2，∴∠CFD=∠5+∠6=2（∠1+∠2）=2∠ABC，又∵△ABC是等腰直角三角形，且∠ACB=90°，∴∠ABC=45°，∴∠CFD=90°，∴CF=DF且CF⊥DF．（2）（1）中的结论仍然成立．理由如下：如图，延长DF至G使FG=DF，连接BG，CG，DC，∵F是BE的中点，∴BF=EF，又∵∠BFG=∠EFD，GF=DF，∴△BFG≌△EFD（SAS），∴∠FBG=∠FED，BG=ED，∴BG∥DE，∵△ADE和ACB都是等腰直角三角形，∴DE=DA，∠DAE=∠DEA=45°，AC=BC，∠CAB=∠CBA=45°，又∵∠CBG=∠EBG﹣∠EBA﹣∠ABC=∠DEF﹣（180°﹣∠AEB﹣∠EAB）﹣45°=∠DEF﹣180°+∠AEB+∠EAB﹣45°=（∠DEF+∠AEB）+∠EAB﹣225°=360°﹣∠DEA+∠EAB﹣225°=360°﹣45°+∠EAB﹣225°=90°+∠EAB，而∠DAC=∠DAE+∠EAB+∠CAB=45°+∠EAB+45°=90°+∠EAB，∴∠CBG=∠DAC，又∵BG=ED，DE=DA，∴BG=AD，又∵BC=AC，∴△BCG≌△ACD（SAS），∴GC=DC，∠BCG=∠ACD，∴∠DCG=∠DCB+∠BCG=∠DCB+∠ACD=∠ACB=90°，∴△DCG是等腰直角三角形，又∵F是DG的中点，∴CF⊥DF且CF=DF．点睛：主要考查了旋转的性质，等腰三角形和全等三角形的判定，及勾股定理的运用．要掌握等腰三角形和全等三角形的性质及其判定定理并会灵活应用是解题的关键．16．阅读理解：如图1，在四边形ABCD的边AB上任取一点E（点E不与点A、点B重合），分别连接ED，EC，可以把四边形ABCD分成三个三角形，如果其中有两个三角形相似，我们就把E叫做四边形ABCD的边AB上的相似点；如果这三个三角形都相似，我们就把E叫做四边形ABCD的边AB上的强相似点．解决问题：（1）如图1，∠A=∠B=∠DEC=55°，试判断点E是否是四边形ABCD的边AB上的相似点，并说明理由；（2）如图2，在矩形ABCD中，AB=5，BC=2，且A，B，C，D四点均在正方形网格（网格中每个小正方形的边长为1）的格点（即每个小正方形的顶点）上，试在图2中画出矩形ABCD的边AB上的一个强相似点E；拓展探究：（3）如图3，将矩形ABCD沿CM折叠，使点D落在AB边上的点E处．若点E恰好是四边形ABCM的边AB上的一个强相似点，试探究AB和BC的数量关系．【答案】（1）见解析；（2）见解析；（3）【解析】试题分析：(1)要证明点E是四边形ABCD的AB边上的相似点，只要证明有一组三角形相似就行，很容易证明ADE∽△BEC，所以问题得解．(2)根据两个直角三角形相似得到强相似点的两种情况即可．(3)因为点E是梯形ABCD的AB边上的一个强相似点，所以就有相似三角形出现，根据相似三角形的对应线段成比例，可以判断出AE和BE的数量关系，从而可求出解．解：（1）点E是四边形ABCD的边AB上的相似点．理由：∵∠A=55°，∴∠ADE+∠DEA=125°．∵∠DEC=55°，∴∠BEC+∠DEA=125°．∴∠ADE=∠BEC．∵∠A=∠B，∴△ADE∽△BEC．∴点E是四边形ABCD的AB边上的相似点．（2）作图如下：（3）∵点E是四边形ABCM的边AB上的一个强相似点，∴△AEM∽△BCE∽△ECM，∴∠BCE=∠ECM=∠AEM．由折叠可知：△ECM≌△DCM，∴∠ECM=∠DCM，CE=CD，∴∠BCE=∠BCD=30°，∴BE=CE=AB．在Rt△BCE中，tan∠BCE==tan30°，∴，。

八年级数学竞赛例题专题讲解26：几何变换(含答案)

专题29 几何变换阅读与思考几何变换是指把一个几何图形1F 变换成另一个几何图形2F 的方法，若仅改变图形的位置，而不改变图形的形状和大小，这种变换称为合同变换，平移、对称、旋转是常见的合同变换.l图3图2图1F 1F 2F 1F 2F 2F 1α1.平移变换如图1，如果把图形1F 上的各点都按一定方向移动一定距离得到图形2F 后，则由1F 到2F 的变换叫平移变换.平移变换前后的对应线段相等且平行，对应角的两边分别平行且方向一致. 2.对称变换如图2，将平面图形1F 变换到与它成轴对称的图形2F ，这样的几何变换就叫做关于直线l （对称轴）的对称变换.对称变换前后的对应线段相等，对应角相等，其对称轴是连结各对应点线段的垂直平分线. 3.旋转变换如图3，将平面图形1F 绕这一平面内一定点M 旋转一个定角α，得到图形2F ，这样的变换叫旋转变换，M 叫旋转中心，α叫旋转角.旋转变换前后的图形是全等的，对应点到旋转中心的距离相等，对应线段的夹角等于旋转角.例题与求解【例l 】如图，∠AOB =045，角内有点P ，PO =10，在角的两边上有两点Q ，R （均不同于O ），则△PQR 的周长的最小值为_______________. （黄冈市竞赛试题）解题思路：作P 点关于OA ，OB 的对称点，确定Q ，R 的位置，化折线为直线，求△PQR 的最小值.BAOP【例2】如图，P 是等边△ABC 的内部一点，∠APB ，∠BPC ，∠CPA 的大小之比是5:6:7，则以PA ，PB ，PC 为边的三角形的三个角的大小之比（从小到大）是（）A. 2:3:4B. 3:4:5C. 4:5:6D.不能确定（全国通讯赛试题）ABCP解题思路：解本例的关键是如何构造以PA ，PB ，PC 为边的三角形，若把△PAB ，△PBC ，△PCA 中的任一个，绕一个顶点旋转060，就可以把PA ，PB ，PC 有效地集中在一起.【例3】如图，在△ABC 中，AD ⊥BC 于D ，∠B =2∠C ，求证：AB+BD=CD.（天津市竞赛试题）解题思路：用截长法或补短法证明，实质都利用AD 翻折造全等.ACBD【例4】如图，六边形ABCDEF 中，AB ∥DE ，BC ∥FE ，CD ∥AF ，对边之差BC -FE=ED -AB=AF -CD ＞0，求证：该六边形的各角都相等.（全俄数学奥林匹克竞赛试题）解题思路：设法能将复杂的条件BC -FE=ED -AB=AF -CD ＞0，用一个基本图形表示，题设条件有平行条件，考虑实施平移变换.A FEDC B【例5】已知Rt △ABC 中，AC=BC ，∠ACB =090，∠MCN =045 （1）如图1，当M 、N 在AB 上时，求证：222MN AM BN =+（2）如图2，将∠MCN 绕C 点旋转，当M 在BA 的延长线时，上述结论是否成立？若成立，请证明；若不成立，请说明理由.（天津市中考试题）解题思路：222MN AM BN =+符合勾股定理的形式，需转化为直角三角形可将△ACM 沿直线CM 对折，得△DCM . 连DN ，只需证DN=BN ，∠MDN =090；或将△ACM (或△BCM )旋转.【例6】如图，∠DAC=012，∠DBC=024，∠CAB=036，∠ABD=048，求∠DCA 的度数.（日本算术奥林匹克试题）解题思路：已知角的度数都是12的倍数，0362460+=，这使我们想到构作正三角形.CD AB图2图1NMABC C BA MN能力训练1.在如图所示的单位正方形网格中，将△ABC 向右平移3个单位后得到△A B C '''，则BA A '∠的度数是_______.（泰安市中考试题）ABCAB CPyx BAOC(第1题) （第2题）（第3题）2.如图，P 是等边△ABC 内一点，PA =6，PB =8，PC =10，则∠APB =_________.3.如图，直线143y x =与双曲线2(0)k y k x =>交于点A ，将直线143y x =向右平移92个单位后，与双曲线2k y x =交于点B ，与x 轴交于点C . 若2AOBC=，则k =______________. （武汉市中考试题） 4.如图，△ABC 中，∠BAC =045，AD ⊥BC ，DB =3，DC =2，则△ABC 的面积是___________. 5.如图，P 为正方形内一点，若::1:2:3PA PB PC =，则∠APB 的度数是（）. A. 0120 B. 0135 C. 0145 D. 0150（第6题）（第5题）（第4题）D'OACB ABDC PABDCD A'6.如图，边长为2的正方形ABCD 的对角线交于点O ，把边BA 、CD 分别绕点B 、C 同时逆时针旋转060，得四边形A BCD '',下列结论：①四边形A BCD ''为菱形；②12ABCD A BCD S S ''=正方形四边形；③线段OD '的长为31-. 其中正确的结论有（）.A. 0个B. 1个C. 2个D. 3个7. 如图，A ，B 两个电话机离电话线l 的距离分别是3米，5米，CD =6米，若由L 上一点分别向A ，B 连电话线，最短为（）.A. 11米B. 10米C. 9米D. 8米8. 如图，在△ABC 中，∠BAC =0120，P 是△ABC 内一点，若记x PA PB PC =++，y AB AC =+，则（）.A. x y <B. x y =C. x y >D. x 与y 的大小关系不确定l第8题图第7题图CBDACBA P9. 如图，已知D 是△ABC 中BC 边的中点，过D 作DE ⊥DF ，分别交AB 于E ，交AC 于F ，求证：BE CF EF +>.（天津市竞赛试题）FDBCAE10.如图，△ABC ，△A B C '''其各边交成六边形DEFGHK ，且EF ∥KH ，GH ∥DE ，FG ∥KD ，0KH EF FG KD DE GH -=-=->. 求证：△ABC ，△A B C '''均为为正三角形.（“缙云杯”邀请赛试题）GFED H KABC C'B'A'11.如图，已知△ABC 中，AB=AC ，P ，Q 分别为AC ，AB 上的点，且AP=PQ=QB=BC ，求∠PCQ .（北京市竞赛试题）PQAB C12.如图，已知在平面直角坐标系中，A ，B 两点的坐标分别为(2,3)A -，(4,1)B -. (1) 若(,0)P x 是x 轴上的一个动点，当△PAB 的周长最短时，求x 的值；（2）若(,0),(3,0)C a D a +是x 轴上的两个动点，当四边形ABCD 的周长最短时，求a 的值；（3）设M ，N 分别为x 轴，y 轴上的动点，问：是否存在这样的点(,0)M m 和(0,)N n ，使四边形ABMN 的周长最短？若存在，求出,m n 的值；若不存在，请说明理由.（浙江省湖州市中考试题）yxOAB13.如图，梯形ABCD 中，AD ∥BC ，分别以两腰AB ，CD 为边向两边作正方形ABGE 和正方形DCHF ，设线段AD 的垂直平分线l 交线段EF 于点M ，EP ⊥l 于P ，FQ ⊥l 于Q ，求证：EP=FQ.（全国初中数学联赛试题）lM L P Q NC HFEGA DB14.如图所示，已知Rt △ABC 中，AB=BC ，在Rt △ADE 中，AD=DE ，连结EC ，取EC 中点M ，连结DM 和BM .（1）若点D 在边AC 上，点E 在边AB 上且与点B 不重合，如图1，求证：BM=DM ，且BM ⊥DM ；（2）如图2中的△ADE 绕点A 逆时针旋转小于045的角，那么（1）中的结论是否仍成立？如果不成立，请举出反例；如果成立，请给予证明.（广州市中考试题）图2图1MEMACBBCAEDD15.如图，在△ABC 中，∠BAC =045，AD ⊥BC 于D ，若BD =3，CD =2，求△ABC 的面积.（山东省竞赛试题）23BCAD。

12-2-6 全等专题-几何变换模型2021-2022学年八年级数学上册练(人教版)(解析版)

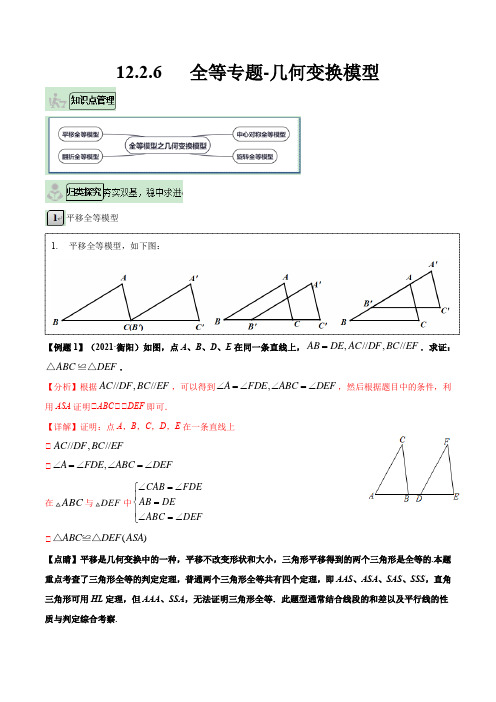
12.2.6 全等专题-几何变换模型平移全等模型【例题1】（2021·衡阳）如图，点A 、B 、D 、E 在同一条直线上，,//,//AB DE AC DF BC EF =．求证：ABC DEF △≌△．【分析】根据//,//AC DF BC EF ，可以得到,A FDE ABC DEF ∠=∠∠=∠，然后根据题目中的条件，利用ASA 证明△ABC △△DEF 即可．【详解】证明：点A ，B ，C ，D ，E 在一条直线上 △//,//AC DF BC EF△,A FDE ABC DEF ∠=∠∠=∠在ABC 与DEF 中CAB FDE AB DEABC DEF ∠=∠⎧⎪=⎨⎪∠=∠⎩△()ABC DEF ASA △≌△【点睛】平移是几何变换中的一种，平移不改变形状和大小，三角形平移得到的两个三角形是全等的.本题重点考查了三角形全等的判定定理，普通两个三角形全等共有四个定理，即AAS 、ASA 、SAS 、SSS ，直角三角形可用HL 定理，但AAA 、SSA ，无法证明三角形全等．此题型通常结合线段的和差以及平行线的性质与判定综合考察.1. 平移全等模型，如下图：变式训练【变式1-1】（2021·河南）如图，在ABC 和DEF 中，B 、E 、C 、F 在同一直线上，下面有四个条件，请你从中选三个作为题设，余下的—个作为结论，写出一个正确的命题，并加以证明． △AB DE =；△AC DF =；△ABC DEF ∠=∠；△BE CF =；解：我写的真命题是：在ABC 和DEF 中，已知：________________．求证：________________．（不能只填序号）【详解】解：将△△△作为题设，△作为结论，可写出一个正确的命题，如下：已知：如图，在ABC 和DEF 中，B 、E 、C 、F 在同一直线上，AB DE =，AC DF =，BE CF =．求证：ABC DEF ∠=∠．证明：△BE CF =， △BC EF =．在ABC 和DEF 中，AB DEAC DF BC EF =⎧⎪=⎨⎪=⎩，△()ABC DEF SSS ≌． △ABC DEF ∠=∠；将△△△作为题设，△作为结论，可写出一个正确的命题，如下：已知：如图，在ABC 和DEF 中，B 、E 、C 、F 在同一直线上，AB DE =，ABC DEF ∠=∠，BE CF =．求证：AC DF =．证明：△BE CF =， △BC EF =．在ABC 和DEF 中，AB DEABC DEF BC EF =⎧⎪∠=∠⎨⎪=⎩，△()ABC DEF SAS ≌， △AC DF =．【变式1-2】（2021·北京一模）如图，点B ，E ，C ，F 在一条直线上，//,,AB DE AB DE BE CF ==．求证：A D ∠=∠．【分析】根据平行得出B DEF ∠=∠，然后用“边角边”证明ABC DEF △≌△即可．【详解】证明：△//AB DE ， △B DEF ∠=∠． △BE CF =，△BE EC CF EC +=+． △BC EF =．在ABC 和DEF 中，,,,AB DE B DEF BC EF =⎧⎪∠=∠⎨⎪=⎩△ABC DEF △≌△． △A D ∠=∠．【变式1-3】（2021·湖北武汉市·九年级三模）已知：如图，点E 、C 在线段BF 上，BE ＝CF ，AB △DE ，AC △DF ．求证：△ABC △△DEF ．【分析】由BE ＝CF ，可推出BC ＝EF ，再由平行线的性质可推出△B ＝△DEF ，△ACB ＝△F ．即可利用“ASA”证明△ABC △△DEF ．【详解】证明：△BE ＝CF ， △BC ＝EF ，△AB △DE ，AC △DF ， △△B ＝△DEF ，△ACB ＝△F ，在△ABC 和△DEF 中，B DEFBC EF ACB F ∠∠⎧⎪⎨⎪∠∠⎩＝＝＝， △△ABC △△DEF （ASA ）．翻折全等模型【例2】（2021·全国九年级专题练习）如图，AB ＝AD ，AC ＝AE ，△BAE ＝△DAC ．求证：△C ＝△E ．【分析】根据△BAE =△DAC ，可推出△BAC =△DAE ，解题已知可证△BAC △△DAE 即可得出答案．【详解】△△BAE =△DAC ，△△BAE ＋△EAC =△DAC ＋△EAC ，即：△BAC =△DAE ．在△BAC 和△DAE 中，AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩△△BAC △△DAE ． △△C =△E ．【点睛】翻折是几何变换中的一种，翻折不改变形状和大小，其实就是一种抽对称变换.翻折的边，角都对应相等．此题型通常结合公共边、公共角、角的和差以及等量代换综合考察三角形全等. 变式训练【变式2-1】（2021·苏州一模）已知：如图，点D 在AB 上，点E 在AC 上，,AD AE BD CE ==．求证：B C ∠=∠．【分析】根据全等三角形的判定定理SAS 推出即可．【详解】证明：△AD ＝AE ，BD ＝CE ， △AB ＝AC ，翻折全等模型，如下图：在△ABE 和△ACD 中AB AC BAE CAD AE AD =⎧⎪∠=∠⎨⎪=⎩， △△ABE △△ACD （SAS ）， △△B =△C ．【变式2-2】（2021·昆明二模）如图，已知AE 平分CAD ∠，AC AD =，求证：CBE DBE ∠=∠．【分析】根据题意得出CAB DAB ∠=∠，再利用SAS 即可证明ABC ABD △≌△，然后利用全等三角形的性质得出CBA DBA ∠=∠，最后根据等角的补角相等即可证明．【详解】证明：△AE 平分CAD ∠， △CAB DAB ∠=∠．在ABC 和ABD △中，,,,AC AD CAB DAB AB AB =⎧⎪∠=∠⎨⎪=⎩△ABC ABD △≌△（SAS ）． △CBA DBA ∠=∠． △CBE DBE ∠=∠．【变式2-3】（2021·全国练习）你见过如图所示的风筝吗？开始制作时，AB CD =，AC DB =，后来为了加固，又过点O 加了一根竹棒EF ，分别交AB ，CD 于点E ，F ，且AOE DOF =∠∠，你认为OE ，OF 相等吗？请说明理由．【答案】OE OF =，理由见解析【分析】连接BC ，首先证明△ABC △△DCB 可得△A =△D ，然后再证明△ABO △△DCO 可得AO =DO ，最后证明△AEO △△DFO 可得EO =FO ．【详解】解：OE OF =；理由如下：连接BC ，如图在ABC ∆和DCB ∆中，AB DC AC BD BC BC =⎧⎪=⎨⎪=⎩， ()ABC DCB SSS ∴∆≅∆，A D ∴∠=∠，在ABO ∆和DCO ∆中，A D AOB DOC AB CD ∠=∠⎧⎪∠=∠⎨⎪=⎩， ()ABO DCO AAS ∴∆≅∆，AO DO ∴=，在AEO ∆和DFO ∆中，A D AO DOAOE DOF ∠=∠⎧⎪=⎨⎪∠=∠⎩， ()AEO DFO ASA ∴∆≅∆，EO FO ∴=．中心对称全等模型【例题3】（2020·浙江温州市·八年级期末）如图，,,AE BF AD BC DF CE===，求证：//AD CB．【分析】根据AE=BF，得到AF=BE，再利用SSS证明△ADF△△BCE，得到△A=△B，可得AD//B C．【详解】解：△AE=BF，△AE+EF=BF+EF，△AF=BE，又△AD=BC，DF=CE，△△ADF△△BCE（SSS），△△A=△B，△AD//B C．【点睛】中心对称是几何变换中的一种，中心对称不改变形状和大小，其实就是一种特殊的旋转变换（旋转180°）.中心对称的边，角都对应相等．此题型通常结合公共边、公共角、角的和差以及等量代换综合考察三角形全等.变式训练【变式3-1】（2021·辽宁大连市·九年级二模）如图，点A，F，E，D在一条直线上，AF＝DE，CF△BE，AB△CD．求证BE＝CF．中心对称全等模型，如下图：【分析】根据线段的和差关系可得AE ＝DF ，根据平行线的性质可得△D ＝△A ，△CFD ＝△BEA ，利用ASA 可证明△ABE △△DCF ，根据全等三角形的性质即可得结论．【详解】 △AF ＝DE ，△AF ＋EF ＝DE ＋EF ，即AE ＝DF ， △AB //CD ， △△D ＝△A ， △CF //BE ， △△CFD ＝△BEA ，在△ABE △△DCF 中，A D AE DF BEA CFD ∠=∠⎧⎪=⎨⎪∠=∠⎩，△△ABE △△DCF ， △BE ＝CF ．【点睛】本题考查平行线的性质及全等三角形的判定与性质，熟练掌握相关性质及判定定理是解题关键．【变式3-2】（2021·广东肇庆市·九年级一模）如图，四边形ABCD 的对角线交于点O ，点E 、F 在AC 上，//DF BE ，且DF BE =，AE CF =．求证：AB CD =，且//AB CD ．【详解】//DF BE BEO DFO ∴∠=∠AEB CFD ∴∠=∠又DF BE =∵，AE CF =ABE CDF ∴△≌△AB CD ∴=，BAE DCF ∠=∠ //AB CD ∴【变式3-3】（2021·山东济南市·七年级期末）如图，已知//AB CD ，AB CD =，BF CE =．求证：AE DF =且//AE DF ．【答案】见解析【分析】先由平行线的性质得△B =△C ，结合BF EF CE EF +=+，从而利用SAS 判定△ABE △△DCF ；根据全等三角形的性质得AE DF =且//AE DF ．【详解】证明：BF CE =，BF EF CE EF ∴+=+，即BE CF =，//AB CD ， B C ∴∠=∠，在ABE △与CDF 中，AB CD B C BE CF =⎧⎪∠=∠⎨⎪=⎩， ()ABE CDF SAS ∴△≌△，AEB DFC ∴∠=∠，AE DF =//AE DF ∴．【点睛】本题考查了全等三角形的判定与性质，属于全等基础知识的考查，难度不大，注意证明过程的规范性．简单旋转全等模型【例题4】（2021·广东广州市·九年级一模）如图，∠B ＝∠E ，∠1＝∠2，BC ＝EC ．求证：AB ＝DE ．【分析】先证出△ACB =△DCE ，再根据AAS 证明 △ABC △△DEC ，即可得出AB =DE ；【详解】证明：△△1=△2 ， △△ACB =△DCE ，在△ABC 和△DCE 中，=B E ACB DCE BC EC ⎧⎪=⎨⎪=⎩∠∠∠∠ △△ABC △△DEC (AAS )， △AB =DE ．变式训练【变式4-1】（2021·陕西中考真题）如图，//BD AC ，BD BC =，点E 在BC 上，且BE AC =．求证：D ABC ∠=∠．【分析】由题意易得EBD C ∠=∠，进而可证EDB ABC ≌△△，然后问题可求证．【详解】证明：△//BD AC ， △EBD C ∠=∠． △BD BC =，BE AC =， △()EDB ABC SAS ≌． △D ABC ∠=∠．简单旋转全等模型，如下图：【变式4-2】（2021·昆明二模）如图所示，AC BC ⊥，DC EC ⊥，垂足均为点C ，且AC BC =，EC DC =．求证：AE BD =．【分析】根据SAS 证明ACE BCD △≌△即可．【详解】证明：△AC BC ⊥，DC EC ⊥，△90ACB ECD ∠=∠=︒△ACB BCE ECD BCE ∠+∠=∠+∠即ACE BCD ∠=∠在ACE 和BCD △中AC BC ACE BCD EC DC =⎧⎪∠=∠⎨⎪=⎩△()SAS ACE BCD ≌△△ △AE BD =【变式4-3】在△ABC 中，AB =AC ，点D 是直线BC 上一点（不与B 、C 重合），以AD 为一边在AD 的右侧作△ADE ，使AD =AE ，△DAE =△BAC ，连接CE ．（1）如图1，当点D 在线段BC 上，如果△BAC =90°，则△BCE 为多少？说明理由；（2）设△BAC =α，△BCE =β．△如图2，当点D 在线段BC 上移动，则α，β之间有怎样的数量关系？请说明理由；△当点D 在直线BC 上移动，则α，β之间有怎样的数量关系？请直接写出你的结论，不需证明．【答案】（1）90°；（2）△α＋β＝180°，理由见详解；△点D 在直线BC 上移动，α＋β＝180°或α＝β．【分析】（1）由等腰直角三角形的性质可得△ABC ＝△ACB ＝45°，由“SAS”可证△BAD△△CAE ，可得△ABC ＝△ACE ＝45°，可求△BCE 的度数；（2）△由“SAS”可证△ABD△△ACE 得出△ABD ＝△ACE ，再用三角形的内角和即可得出结论；△分两种情况画出图形，由“SAS”可证△ABD△△ACE 得出△ABD ＝△ACE ，再用三角形的内角和即可得出结论．【详解】解：（1）△AB ＝AC ，△BAC ＝90°，△△ABC ＝△ACB ＝45°，△△DAE ＝△BAC ，△△BAD ＝△CAE ，且AB ＝AC ，AD ＝AE ，△△BAD△△CAE （SAS ）△△ABC ＝△ACE ＝45°，△△BCE ＝△ACB ＋△ACE ＝90°；（2）△α＋β＝180°，理由：△△BAC ＝△DAE ，△△BAC−△DAC ＝△DAE−△DAC ．即△BAD ＝△CAE ．在△ABD 与△ACE 中，AB AC BAD CAE AD AE ⎧⎪∠∠⎨⎪⎩＝＝＝，△△ABD△△ACE （SAS ），△△B ＝△ACE ．△△B ＋△ACB ＝△ACE ＋△ACB ．△△ACE ＋△ACB ＝β，△△B ＋△ACB ＝β，△α＋△B ＋△ACB ＝180°，△α＋β＝180°；△如图1：当点D 在射线BC 上时，α＋β＝180°，连接CE ，△△BAC ＝△DAE ，△△BAD ＝△CAE ，在△ABD 和△ACE 中，AB AC BAD CAE AD AE ⎧⎪∠∠⎨⎪⎩＝＝＝，△△ABD△△ACE （SAS ），△△ABD ＝△ACE ，在△ABC 中，△BAC ＋△B ＋△ACB ＝180°，△△BAC ＋△ACE ＋△ACB ＝△BAC ＋△BCE ＝180°，即：△BCE ＋△BAC ＝180°，△α＋β＝180°，如图2：当点D 在射线BC 的反向延长线上时，α＝β．连接BE ，△△BAC ＝△DAE ，△△BAD ＝△CAE ，又△AB ＝AC ，AD ＝AE ，△△ABD△△ACE（SAS），△△ABD＝△ACE，△△ABD＝△ACE＝△ACB＋△BCE，△△ABD＋△ABC＝△ACE＋△ABC＝△ACB＋△BCE＋△ABC＝180°，△△BAC＝180°−△ABC−△ACB，△△BAC＝△BCE．△α＝β；综上所述：点D在直线BC上移动，α＋β＝180°或α＝β．【点睛】此题是三角形综合题，主要考查了全等三角形的判定和性质，三角形的内角和定理，证明△ABD△△ACE是解本题的关键．。

初二数学竞赛讲义——几何变换：轴对称与平移

初二数学竞赛讲义——几何变换：轴对称与平移例1、牧童在A处放牛, 家在B处, 天色将晚，需要回家了，但牛需要喝水。

则在何处饮水，所走路程最短？lABB解：作出A关于l的对称点C,连接CB,交l于P，则P就是所求的点。

证明：在l上任意取一点Q，只要证明QA+QB>PA+PB即可。

根据轴对称性，PC=PA,QC=QA,因此PA+PB=PC+PB=BC<QC+QB=QA+QB.说明：本题也可以换成以下物理背景：(1)l是一面镜子，A处的光线要想经过镜子反射以后照亮B处的物体，应如何选择入射点？(2)在A处击台球，要想经过桌子边缘反射以后击中B处的球，应如何选择入射点？这些问题的解决和上面是一样的。

例2、A、B在直线两侧，且到直线的距离不等，要在直线上找一点P,使得P到A、B的距离之差最大。

AB解：作B关于直线的对称点B’,连接AB’交直线于点P，则P就是所求的点。

证明：在直线上另外取点Q，连接QA、QB、QB’,那么QA-QB=QA-QB’<AB’=AP-B’P=AP-BP.说明：请你比较一下例1和例2的区别。

例3、锐角∠AOB内有一点P，求作△PEF，使E在OA 上，F在OB上，且使△PEF的周长最小.MC解：如图，分别作出P关于OA、OB的对称点M、N，连接MN交OA、OB于E、F，则△PEF就是所求的三角形。

证明：在OA、OB上分别取异于E、F的点G、H，只要证明PG+GH+PH>PE+EF+PF即可。

事实上，PG+GH+PH=NG+GH+HM>NM=NE+EF+FM=PE+EF+PF.说明：(1)如果∠AOB是直角或钝角，那么图示的△PEF不复存在。

如果P看作一个锐角三角形的一边上的点，那么问题相当于求经过P点的△ABC的内接三角形，并使得周长最短。

(2)进一步的问题是：P在AC边上什么位置时，得到的内接三角形周长最短？答案是：当P 是AC边上的垂足时，内接三角形周长最短，这样的三角形叫做垂足三角形。

初二数学几何图形变换练习题

初二数学几何图形变换练习题在初中数学学习中，几何图形变换是一个重要的内容。

通过对图形进行平移、旋转、反射和放缩等操作，可以帮助我们加深对几何图形性质的理解。

下面将给出一些初二数学几何图形变换的练习题，希望能够帮助同学们巩固与拓展相关知识。

题目一：平移1. ABCD为一个平行四边形，EF是平行四边形的一条对角线。

（1）将平行四边形ABCD沿向量→→→→e向右平移3个单位得到平行四边形A1B1C1D1，连接DD1，证明A1D1∥EF。

（2）将平行四边形ABCD沿向量→→−→−→a向左平移4个单位得到平行四边形A2B2C2D2。

若A1A2的向量表示为→→−→−→b，则求向量→→−→−→b。

题目二：旋转2. 将正方形ABCD顺时针旋转90°得到正方形A1B1C1D1，连接CC1并延长，证明A1C1⊥CC1。

3. 将正方形ABCD顺时针旋转45°得到正方形A2B2C2D2，连接A2C2，若AC的长度为a，则求A2C2的长度。

题目三：反射4. 已知顶点是A(1,-3)的三角形ABC关于x轴反射得到三角形A1B1C1，连接AA1并延长，若直线AA1与x轴交于点D，求点D的坐标。

5. 直线y=x与直线y=2x关于直线y=-x反射，分别得到直线L1和L2。

若L1与L2的交点为P，则求P的坐标。

题目四：放缩6. 图中三角形ABC经过放缩得到三角形A1B1C1，若放缩比例为k，求A1B1 : BC的比值。

解答：题目一：平移1.（1）设向量→→→→AD=a，向量→→→→AC=b，由平移的性质知AA1=a+3，DD1=b+3。

根据平行四边形的性质，有AD=BC，AC=BD。

故A1D1∥EF得证。

（2）设向量→→−→−→a=〈x，y〉，则向量→→−→−→b=〈x-4，y〉。

根据平行四边形的性质，有AB=A1B1，AD=A1D1。

故向量→→−→−→a=AB-AD=〈x，y〉=A1B1-A1D1=向量→→−→−→b=〈-√2，0〉。

八年级数学几何三大变换(平移、旋转)(含答案)

学生做题前请先回答以下问题问题1：平移、旋转、轴对称统称为几何三大变换.几何三大变换都是_________，只改变图形的_________，不改变图形的_____________.问题2：平移的思考层次分别是什么？问题3：旋转的思考层次分别是什么？几何三大变换（平移、旋转）一、单选题(共9道，每道8分)1.如图，将边长为3cm的等边三角形ABC沿BC方向向右平移2cm得到△DEF，则四边形ABFD 的周长为( )cm．A.10B.11C.12D.13答案：D解题思路：试题难度：三颗星知识点：平移的性质2.如图，在梯形ABCD中，AD∥BC，AD=6cm，BC=10cm，高为7cm，若将梯形ABCD向右平移4cm得到梯形A′B′C′D′，则平移前后两梯形重叠部分的面积为( )cm2．A.28B.35C.42D.56答案：A解题思路：试题难度：三颗星知识点：平移的性质3.如图，把Rt△ABC放在平面直角坐标系内，其中∠CAB=90°，，点A，B的坐标分别为（2，0）（8，0），将△ABC沿x轴向右平移，当点C落在直线y=3x-3上时，线段BC扫过的面积为( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：平移的性质4.如图，△COD是△AOB绕点O顺时针旋转40°后得到的图形，若点C恰好落在AB上，且∠AOD的度数是90°，则∠B的度数是( )A.70°B.60°C.50°D.40°答案：B解题思路：试题难度：三颗星知识点：旋转的性质5.如图，E是正方形ABCD内一点，将△CDE绕点D按顺时针方向旋转90°后得到△ADF．若DE=3，则EF的长是( )A. B.C.3D.6答案：A解题思路：试题难度：三颗星知识点：旋转的性质6.如图，在△ABC中，∠ACB=90°，∠BAC=30°，将△ABC绕点C按逆时针方向旋转α角，得到△DEC，CD与AB交于点F，连接AD．当旋转角α的度数为( )时，△ADF是等腰三角形．A.30°或60°B.20°或40°C.25°或50°D.20°或40°或60°答案：B解题思路：试题难度：三颗星知识点：旋转的性质7.如图，已知△ABC中，∠C=90°，AC=BC=，将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置，连接C′B，则C′B的长为( )A. B.C. D.1答案：C解题思路：试题难度：三颗星知识点：旋转的性质8.如图所示直角三角板ABC，斜边AB=6，∠A=30°，现将其绕点C沿顺时针方向旋转90°至△A′B′C的位置，再沿CB向左平移使点B′落在原三角板ABC的斜边AB上．则三角板向左平移的距离为( )A.1B.C. D.答案：C解题思路：试题难度：三颗星知识点：旋转的性质9.如图，已知，将△AOB绕点O旋转150°后，得到，则此时点A的对应点的坐标为( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：作图二、填空题(共3道，每道9分)10.如图，将边长为2cm的正方形ABCD沿其对角线AC剪开，再把△ABC沿着BC平移得到△A′B′C′，若重叠部分的面积为1cm2，则平移的距离AA′=____cm．答案：1解题思路：试题难度：知识点：平移的性质11.如图，在四边形ABCD中，∠BAD=∠BCD=90°，AB=AD，如果cm，则四边形ABCD的面积为____cm2.答案：6解题思路：试题难度：知识点：作图—旋转变换12.如图，在等边三角形ABC中，点O是AC边上，且OA=3,OC=6,点P是AB上一动点，连接OP，将线段OP绕O逆时针旋转60°得到线段OD，要使点D恰好落在BC上，则AP的长是____.答案：6解题思路：试题难度：知识点：作图。

初中数学竞赛第二轮专题复习(2)几何

初中数学竞赛第二轮专题复习（2）几何证明的基本方法（1)一、常用定理梅涅劳斯定理设',','C B A 分别是ΔABC 的三边BC ，CA ，AB 或其延长线上的点，若',','C B A 三点共线，则.1''''''=⋅⋅BC AC A B CB C A BA 梅涅劳斯定理的逆定理条件同上,若.1''''''=⋅⋅BC AC A B CB C A BA 则',','C B A 三点共线。

塞瓦定理设',','C B A 分别是ΔABC 的三边BC ，CA ，AB 或其延长线上的点，若',','CC BB AA 三线平行或共点，则.1''''''=⋅⋅BC AC A B CB C A BA 塞瓦定理的逆定理设',','C B A 分别是ΔABC 的三边BC ，CA ，AB 或其延长线上的点，若.1''''''=⋅⋅BC AC A B CB C A BA 则',','CC BB AA 三线共点或互相平行。

角元形式的塞瓦定理 ',','C B A 分别是ΔABC 的三边BC ，CA ，AB 所在直线上的点，则',','CC BB AA 平行或共点的充要条件是.1'sin 'sin 'sin 'sin 'sin 'sin =∠∠⋅∠∠⋅∠∠BAB CBB CBC ACC AC A BAA 广义托勒密定理设ABCD 为任意凸四边形，则AB •CD+BC •AD ≥AC •BD,当且仅当A,B ，C ，D 四点共圆时取等号.斯特瓦特定理设P 为ΔABC 的边BC 上任意一点，P 不同于B ，C ，则有AP 2=AB 2•BC PC +AC 2•BCBP -BP •PC 。

八年级数学上册几何变换法练习试题

轧东卡州北占业市传业学校第四十讲几何变换法利用几何图形的变换解答几何题的方法叫做几何变换法。

在实际生产和生活中，几何形体往往不是以HY的形状出现，而是以比较复杂的组合图形出现，很难直接利用公式计算其面积或体积。

如果在保持图形的面积或体积不变的前提下，对图形进行适当的变换，就容易找出计算其面积或体积的方法。

〔一〕添辅助线法有些组合图形按一般的思考方法好似条件缺乏，很难解答。

如果在图形中添加适当的辅助线，就可能找到解题的途径。

辅助线一般用虚线表示。

*例1 求图40-1阴影局部的面积。

〔单位：平方米〕解：图40-1中，右边两个局部的面积分别是20平方米和30平方米，所以可如图40-2那样添上三条辅助线，把整个长方形分成5等份。

这样图中右边的五个小长方形的面积相等。

同时，左边五个小长方形的面积也相等。

左边每个小长方形的面积是：25÷2=1〔平方米〕所以，阴影局部的面积是：1×3=3〔平方米〕答略。

*例2 如图40-3，一个平行四边形被分成两个局部，它们的面积差是10平方厘米，高是5厘米。

求EC的长。

〔单位：厘米〕解：如图40-4，过E点作AB的平行线EF，那么△AEF与△ABE是等底等高的三角形。

所以，△AEF 的面积与△ABE的面积相等。

小平行四边形EFDC的面积就是10平方厘米。

因为它的高是5厘米，所以，EC=10÷5=2〔厘米〕答：EC长2厘米。

*例3 如图40-5，图中四边形两条边的长度和三个角的度数，求这个四边形的面积。

〔单位：厘米〕解：这是一个不规那么的四边形，无法直接计算它的面积。

如图40-6，把AD和BC两条线段分别延长，使它们相交于E点。

这样，四边形ABCD的面积就可以转化为△ABE的面积与△DCE的面积之差。

在△ABE中，∠A是直角，∠B=45°，所以∠E=45°，即△ABE是等腰直角三角形。

所以AB=AE=7〔厘米〕，那么△ABE的面积是：7×7÷2=2〔平方厘米〕在△DCE中，∠DCE是直角，∠E=45°，所以，∠CDE=45°，即△DCE是等腰直角三角形。

初中数学竞赛——几何变换——平移

初中数学竞赛——几何变换——平移(共9页)-本页仅作为预览文档封面，使用时请删除本页-第1讲几何变换——平移典型例题【例1】如图，在梯形ABCD 中，AD BC ∥，已知3AD BC +=，AC =，BD ABCD 的面积．【例2】如图所示，梯形ABCD 中，AB CD ∥，90A B ︒∠+∠=，AB a =，CD b =，E 、F 分别是AB 、CD 的中点，求EF 的长．【例3】求证：两中线相等的三角形都是等腰三角形．ACDB FDCBAE【例4】求证10条两两相交的直线所成的所有角中，至少有一个角不大于18︒．【例5】已知六边形ABCDEF 的三双对边分别平行并且AB ED =，求证：BC EF =，CD FA =．【例6】在六边形ABCDEF 中，AB DE BC EF CD AF ∥，∥，∥，且BC EF -=DE AB -=AF CD -0＞．求证：六边形ABCDEF 的各内角相等．【例7】如图，ABC △中，D 是BC 的中点，DE DF ⊥，试判断BE CF +与EF 的大小关系，并证明你的结论．【例8】如图，ABC △中，BD DC AC ==，E 是DC 的中点，求证：AD 平分BAE ∠．【例9】已知：ABCD 是凸四边形，且AC BD =．E 、F 分别是AD 、BC 的中点，EF 交AC 于M ；EF 交BD 于N ，AC 和BD 交于G 点．【例10】求证：GMN GNM ∠=∠．ED CABABCFEE NGDCBAM【例11】已知，如图，四边形ABCD 中AD ＝BC ，E 、F 分别是AB 、CD 的中点，延长AD 、EF和BC 的延长线分别交于M N ，两点，求证：AME BNE ∠=∠．【例12】如图，任意五边形ABCDE 中，M 、N 、P 、Q 分别为AB 、CD 、BC 、DE 的中点，K 、L 分别为MN 、PQ 的中点，求证：KL AE ∥，且14KL AE =．【例13】已知：矩形ABCD 内有定点M ，求证：存在四边形，它的四条边分别等于MA 、MB 、MC 、MD ，对角线分别等于AB 和BC ，且两条对角线互相垂直．DAMN DCBEFE DCBAL NMKQP【例14】如图，已知ABC △中，AB=AC ，D 为AB 上一点，E 为AC 延长线上一点，BD=CE ，连DE ，求证：DE BC ＞．【例15】如图，在等腰三角形ABC 的两腰AB 、AC 上分别取点E 和F ，使得AE CF =．已知2BC =，求证：1EF ≥．【例16】已知：M 是三角形ABC 内的定点，从M 点出发沿平行于边BC 的直线运动，直到和AC 边交于1B 点，然后再沿平行于AB 边的直线运动，直到和BC 边交于1A 点，然后再沿平行于AC 边的直线运动，直到和AB 边交于1C 点，…如此继续下去．求证：若干步后，M 点的轨迹将是封闭的．CB【例17】已知ABC △的三条中线长分别为3，4，5，求ABC △的面积．【例18】已知：ABCD 是梯形，A ∠、B ∠的平分线交于M 点，C ∠、D ∠的平分线交于N ．【例19】求证：2MN AB CD BC AD =+--．【例20】如图所示，在ABC △中，90C ︒∠=，点M 在BC 上，且BM AC =，N 在AC 上，且AN MC =，AM 与BN 相交于P ．求证：45BPM ︒∠=．A作业1. 如图，在梯形ABCD 中，//AB CD ，AC BD ⊥．求证：222()AC BD AB DC +=+．2. 如图，在四边形ABCD 中，AB CD ∥，AD BC =，BD DC =，AC BD ⊥于M ．求证：1()2CM AB DC =+．3. 四边形ABCD 中，AB CD ∥，2D B ∠=∠，若AD a =,AB b =，求CD 的长．AMDCB4. 叙述并证明梯形中位线的性质定理．5. 如图，等腰梯形ABCD 中，对角线AC BD ⊥，垂足为E ，DF BC ⊥于F ，MN 是梯形的中位线，求证：DF MN =．6. 在正方形ABCD 中，E 、F 、G 、H 分别AB 、BC 、CD 、DA 边上的点，且EG FH ⊥，求证：EG FH =．7. ABCD 是四边形，N 是BC 中点，M 是AD 边中点，BA 、NM 的延长线交于P ，CD 、NM 的延长线交于Q ，如果BPN NQC ∠=∠，求证：AB CD =．EFN ND CBA8. ABC △中，BE 和CD 分别是B ∠和C ∠的角平分线，P 是DE 的中点，PQ BC ⊥于Q ，PM AB ⊥于M ，PN AC ⊥于N ．求证：PQ PM PN =+．。

初中数学竞赛专题-第十八章几何变换的性质及应用

第十八章几何变换的性质及应用【基础知识】平面几何中的几何变换主要有合同（包括平移、旋轴、轴对称）、相似（包括位似）、仿射和反演变换．在平面到自身的一一变换下,如果任意线段的长和它的象的长总相等,那么这种变换叫做合同变换．合同变换具有下述基本性质：性质1在合同变换下,直线变为直线,线段变为线段,射线变为射线；两直线的平行性、垂直性,所成的角度都不变；共线点变为共线点,且保持顺序关系不变；直线上A 、B 、C 三点的简比ACBC不变．性质2在合同变换下,三角形、多边形和圆分别变为与它们全等的三角形、多边形和圆；封闭图形的面积不变．在平面到自身的一一变换下,若任意一对对应点A ,A '连结的有向线段等于定向量a ,则这种变换叫做平移,记为()T a ．a 叫平移向量,a 的方向叫做平移方向,其长度叫平移距离．在平面到自身的一一变换下,若每对对应点A ,A '所连结的线段,都被定直线l 所垂直平分,则这种变换叫做关于直线l 的轴对称或轴反射,记为()S l ．直线l 叫做对称轴或反射轴,点A '叫做点A 关于轴l 的对称点．在平面到自身的一一变换下,若任意一对对应点A ,A '与平面上一定点O 的距离总相等,且AOA '∠等于定角θ,这种变换叫做关于点O 的旋转,记为(),R O θ．点O 叫做旋转中心,θ叫做旋转角．特别地,旋转角180θ=︒的旋转变换称为中心对称变换或点反射,记为()(),180C O R O =︒．性质3在平移变换下,直线（线段）变成与它平行（或重合）的直线（线段）；在轴对称变换下,P 为对称轴l 上任一点,则一对对应点所成的角APA '∠被l 所平分；在旋转变换下,对应直线的交角总等于旋转角；在中心对称变换下,对应点连线段过对称中心且被它平分,对应线段相等且反向平行或共线,不过对称中心的直线与其对应的直线平行．在平面到自身的一一变换下,若线段A B ''是AB 的象,且A B AB k ''=∶（k 为正的常数）,则这种变换叫做相似变换,记为()H k ．常数R 叫做相似系数或相似比．特别地,若1k =,则为合同变换；1k =-,则为中心对称变换．性质4在相似变换下,直线变为直线,线段变为线段,射线变为射线；点与直线的结合关系不变,点在直线上的顺序关系不变；直线上三点的简比不变,两直线的夹焦不变,两相似多边形面积比不变且等于相似比的平方．在平面到自身的一一变换下,若对于任一对对应点A ,A '与平面上一定点O ,都有OA OA k '=∶（k 为非零常数）,则这种变换叫做位似变换,记为H （O ,k ）．点O 叫做位似中心,k 叫做位似比．特别地,当0k >时,A ,A '在点O 同侧,这种变换叫顺（或正或外）位似；0k <时,A ,A '在点O 两侧,这种变换叫逆（或反或内）位似．性质5在位似变换下,对应线段之比相等,对应角相等且转向相同；不过位似中心的对应直线平行．在平面到自身的一一变换下,若对于任一对对应点A ,A '与平面上一定点O ,都有OA OA k '=∶（k 为正的常数）,且AOA θ'∠=（θ为有向的定角）,则这种变换叫做位似旋转变换,记为(),,S O k θ．点O 叫做位似中心,k 叫做位似比,θ叫做旋转角,且()()()()(),,,,,,S O k H O k R O R O H O k θθθ=⋅=⋅；()(),0,,S O k H O k =；()(),,,S O k H O k π=-；()(),,1,S O R O θθ=．性质6在位似旋转变换下,把两个相似形中的一个变到另一个；具有共同中心的两个位似旋转变换之积仍是一位似旋转,即有()()()11221212,,,,,,S O k S O k S O k k θθθθ⋅=+⋅．在平面到自身的一一变换下,若满足任意共线三点的对应点仍共线,且其三点的简比保持不变,则称此变换为仿射变换．显然,若建立平面坐标系,仿射坐标系与直角坐标系的差别就在于两轴间的夹角及轴上单位长度不相同．若两轴夹角仍为90︒,则称为伸缩变换：()()12,,x y k x k y →,其中10k >,20k >．性质7在仿射变换下,点变成点,直线变成直线；保持点和直线的结合关系；保持直线的平行关系；保持两平行（共线）线段的长度比；任一封闭凸曲线所围成的图形的面积S 和它对应图形所围成的面积S '之比为常数．性质8在仿射变换下,任一三角形变成正三角形；梯形变为等腰梯形；任一平行四边形变成正方形；任一椭圆变为圆,相应地椭圆中心变成圆心,椭圆直径变成圆的直径,椭圆的切线变成圆的切线．设O 是平面上一定点,对于一个变换,若任一对对应点A ,A '（异于O ）,都有OA OA k ⋅=（k 为非零常数）,则称此变换为反演变换,记为I O k （，）．O 点称为反演中心,k 为反演幂．显然,0k <时,A ,A '在点O 两侧,可经以O 为中心对称变换变成0k >的情形．故只考虑0k >的情形,且令2k r =．此时,反演变换的几何意义为,满足“以O 为圆心,r 为半径的圆中直角三角形的射影定理形式：22r OP OA OA '==⋅”的图形,并称这个圆叫反演变换的基圆．性质9在反演变换下,基圆上的点仍变为自己；基圆内的点（除中心外）变为基圆外的点．反之亦然．性质10在反演变换下,过反演中心的直线是不变直线（除中心）；过反演中心的圆变为不过反演中心的直线；过反演中心的相切两圆（或一圆一直线）变为不过反演中心的两平行直线；过反演中心的两相交圆变为不过反演中心的相交直线．反之亦然．性质11在反演变换下,不过反演中心的圆变为不过反演中心的圆；以反演中心为圆心的圆变为同心圆；不过反演中心相切（交）的圆变为不过反演中心的相切（交）的圆；不共线的任意两对对应点必共圆；圆和圆、圆和直线、直线和直线的交角保持不变．【典型例题与基本方法】例1如图18-1,设A ',B ',C '分别是ABC △的边BC ,CA ,AB 的中点,1O ,2O ,3O ,1I ,2I ,3I 分别是AB C ''△,A BC ''△,A B C ''△的外心和内心．求证：123123O O O I I I △≌△．证明由三角形中位线性质,知C B B A AC ''''==,故()T AC AB C C A B '''''−−−→△△．于是()12T AC O O '−−−→,()12T AC I I −−−→,所以1212O O AC I I '==．同理,1313O O I I =,2323O O I I =．故123123O O O I I I △≌△．例2设DPQ △是锐角ABC △的垂足三角形（即D ,P ,Q 分别为三条高线的垂足）．求证：DPQ △是ABC △中周长最短的内接三角形．证明由题设,如图18-2,AD ,BP ,CQ 分别是DPQ △的内角平分线．图18-2D "D 'R"R'F EDABCRQP ST令DEF △是ABC △中以D 为一顶点的任一内接三角形,且()S ABD D '−−−→,()S ACD D ''−−−→,则D ',D ''落在直线PQ 上,且D Q DQ '=,D P D P ''=,线段D D '''之长等于DPQ △之周长．连D E ',D F '',刚折线D EFD '''之长等于DEF △之周长,显然D D D E EF FD ''''''++≤．不难计算2sin D D AD BAC '''=⋅∠．若RST △是ABC △的任一内接三角形,则用类似方法可以证得RST △的周长大于或等于2sin AR BAC ⋅∠．由于AR AD ≥,从而RST △的周长DPQ ≥△的周长,即垂足三角形DPQ △的周长最短．例3在ABC △内有一点P ,满足120APB BPC CPA ∠∠=∠=︒=．求证：P 是到三顶点距离之和最小的点（即费马点）．图18-3Q Q 'P'ABCEP证明由120CPA BPC ∠=∠=︒,故对APC △施行旋转变换(),60R C -︒,则(),60R C APC EP C -︒'−−−−→△△．由于60P PC PP C ''∠=∠=︒,则B ,P ,P ',E 共线,且 BE BP PP P E BP CP AP ''=++=++．对于ABC △内任一点Q ,令(),60R C AQC EQ C -︒'−−−−→△△,则QQ QC '=,Q E QA '=,于是QA QB QC Q E QQ QB BF BP CP AP ''++=++=++≥,故P 点是到三顶点距离之和最小的点．例4如图18-4,在ABC △中,AB AC >,A ∠的一个外角的平分线交ABC △的外接圆于点E ,过E 作EF AB ⊥,垂足为F ．求证：2AF AB AC =-．（1989年全国高中联赛题）图18-4F EDA BCT证明1902AEF BAE BAC ∠=︒∠=∠-．作A 关于F 的对称点D ,则AED CAB ∠=∠,且EA ED =．又EB EC =（因EBC EAT EAB ∠=∠=∠）,则EB EC =,且CEB CAB AED ∠∠=∠=,所以可将AEC △绕E 点旋转AED ∠到DEB △处,从而AC DB =．故2AB AC AD AF -==．例5如图18-5,ABC △和ADE △是两个不全等的等腰直角三角形,现固定ABC △,而将ADE △绕A 点在平面上旋转,试证：不论ADE △旋转到什么位置,线段EC 上必有点M 使BMD △为等腰直角三角形．（1987年全国高中联赛题）图18-5A'E 1C 1EDABCM证法1先证BMD △为等腰直角三角形,再证M 为EC 上．作A 关于BD 的对称点A ',则ADB AD B '∠∠=．由902ADE BDM ∠=︒-∠, 有|45|9045|EDM A DM A DB ADB ''∠∠=︒-∠︒-︒-∠==|．而DA DA DE '==,则A '是E 关于DM 的对称点．同理,A '也是C 关于BM 的对称点．从而EM D A M D '∠=∠,CMB A MB '∠∠=,而90BMD ∠=︒,故180CME ∠=︒,即M 在BC 上．证法2先取EC 中点M ,再证BMD △为等腰直角三角形．作AC 关于AB 的对称线段1AC ,连1BC ,1EC ,将1AC E △绕A 点顺时针方向旋转90︒到1ACE △的位置如图18-5,则11C E CE ⊥,11AC E ACE △≌△,且1190C AC EAE ∠=∠︒=,从而由1AE AE =有1ADE ADE ∠=∠,即知E ,D ,1E 三点共线且D 为1EE 中点．再由112BM C E ∥,112DM CE ∥及1C E 1CE ,即证．例6如图18-6,在锐角ABC △的BC 边上有两点E ,F ,满足BAE CAF ∠∠=,作FM AB ⊥于M ,作FN AC ⊥于N ,延长AE 交ABC △的外接圆于D ．证明：四边形AMDN 与ABC △的面积相等．图18-6LFE DABC M NK（2000年全国高中联赛题）证明作DK AB ⊥于K ,作DL AC ⊥于L ,则只需证明 FBM FCN FDM FDN S S S S +=+△△△△．利用FDM FKM S S =△△,FDN FLN S S =△△,只需证明FBM PCN FKM FLN S S S S +=+△△△△,即FM BM FN CN FM MK FN NL ⋅+⋅=⋅+⋅．因此,只需证明()()FM BM MK FN NL CN -=-,即FM BK FN CL ⋅=⋅．设BAE CAF α∠=∠=,利用BKD CLD △∽△,有 ()sin sin BK DK FNCL DL A FM αα===-．故结论成立．例7如图18-7,1O 与2O 外切于点A ,半径分别为1r 和2r ,PB ,PC 分别为1O ,2O 的切线,B ,C 为切点,且12PB PC r r =∶∶,又PA 交2O 于E 点．求证：PAB PEC △∽△．图18-7证法1（相似证法）连线1BO ,1PO ,2PO ,2EO ,2CO ．注意到1O ,A ,2O 三点共线,由12PB PC r r =∶∶有12Rt Rt PBO PCO △∽△,从而1212PO PO O A O A =∶∶．由角平分线性质定理的逆定理,知12BPO O PA ∠=∠．又22O AP O EA ∠=∠,有12O AP O EP ∠=∠,从而12O AP O EP △∽△,则12PA PE r r =∶∶,即PA PE PB PC =∶∶．而BPA CPE ∠=∠,故PAB PEC △∽△．证法2（位似证法）考虑以A 为位似中心的变换,把1O 变到2O ,PAB △变到P AC ''△,则P C ''切2O 于C '．由12PB P C r r PB PC ''==∶∶∶,知P C PC ''=．延长P C ''与PC 的延长线相交于点Q ,如图18-7,由QC QC '=,知PQP '△为等腰三角形．连2QO 并延长交AE 于F ,则QF AE ⊥,故QF 平分AE ,则AP PE '=．由此知PEC P AC PAB '△≌△∽△．例8如图18-8,设H 为ABC △的垂心,L ,M ,N 分别是BC ,CA ,AB 边的中点．D ,E ,F 分别是三条高的垂足,P ,Q ,R 分别是HA ,HB ,HC 的中心,试证：L ,M ,N ,D ,E ,F ,P ,Q ,R 九点共圆（九点圆定理）．图18-8BC证明由于P ,Q ,R 分别是HA ,HB ,HC 的中点,故以H 为位似中心,位似比为2的位似变换把PQR 变成ABC ．因此,要证L ,M ,N ,D ,E ,F 在PQR 上,只要证明这些点在上述位似变换下的象点均在ABC 上即可．作()C D H D '−−−→,()C L H L '−−−→,则D ',L '在ABC 上．同理E ,M ,F ,N 的象点也在ABC 上．再由上述位似变换之逆即证得结论成立．例9如图18-9,2AB CD ∥,1AC BD ∥,A 在12D D 上．求证：122ABC ABCD ACD S S S =⋅△△△．图18-945°45°MD 2'D 1'C 'B'A'D 2ABCD 1证明因为梯形是仿射不变形,所以题设中的两个梯形可由两个特殊梯形经仿射变换后得到,设梯形2C B A D ''''和梯形1C B D A ''''皆为直角梯形,且221C D D A MB '''''===．梯形2A D C B ''''−−−→仿射梯形2AD CB ,梯形1A C B D ''''−−−→仿射梯形1ACBD ,则112A B C S A B MC ''''''=⋅=△,11122A B D S A B A D '''''''=⋅=△,212A C D S '''=△．从而122A B C A B D A C D S S S '''''''''=⋅△△△．故122ABC ABD ACD S S S ⋅△△△=．例10在凸四边形ABCD 的边AB 和BC 上取点E 和F ,使线段DE 和DF 把AC 三等分,已知ADE △和CDF △的面积等于四边形面积的14．求证：ABCD 是平行四边形．（第16届全俄竞赛题）证明题中条件与结论均满足仿射变换不变性特性．将ABC △变换成图18-10所示直角三角形,设3AB BC ==,则()3,0A ,()0,3C ,()2,1P ,()1,2Q ．图18-10DO ABCEFP Qxy设(),D a b 为所求,则直线DE 的方程为()1122b y x a --=--．令0y =得221E ax b -=+-．于是11232221ADE D a S AE y b b -⎛⎫=⋅=--⋅ ⎪-⎝⎭△ 1321a b b b +-=⋅⋅-．同理,得1321CDF a b S a a +-=⋅⋅-△．()11333222ABD BCD ABCD S S S b a a b =+=⋅⋅+⋅⋅=+△△四边形．由已知易得()131313212142a b a b b a a b b a +-+-⋅⋅=⋅⋅=⋅+--．解得3a b ==．即33D （，）,故ABCD 为平行四边形．例11如图18-11,H 是ABC △的垂心,P 是ABC △内任一点,由H 分别向PA ,PB ,PC 引垂线HL ,HM ,HN 与BC ,CA ,v 的延长线相交于X ,Y ,Z ,其中L ,M ,N 为垂足．求证：X ,Y ,Z 三点共线．图18-11PXYZ L DH AC EF MN证明由于H 是一特殊点,将其作为反演中心,则只须证X ,Y ,Z 的象点（或反点）与H 共圆．设ABC △的高线分别交BC ,CA ,AB 的垂足为D ,E ,F ,则HA HD HB HE HC HF ⋅=⋅=⋅．又A ,D ,L ,X 共圆,有HL HX HA HD ⋅=⋅．同理,H M H Y H B H E ⋅=⋅,HN HZ HC HF ⋅=⋅．以H 为反演中心,则L 与X ,N 与Z ,M 与Y 均为反点．又L ,P ,N ,H 共圆,L ,P ,M ,H 共圆,有L ,N ,M ,H 共圆,故X ,Z ,Y 三点共直线．例12如图18-12,四边形ABCD 内接于圆O ,对角线AC 与BD 相交于P ．设三角形ABP ,BCP ,CDP 和DAP 的外接圆心分别是1O ,2O ,3O ,4O ．求证：OP ,13O O ,24O O 三直线共点．图18-12（1990年全国高中联赛题）证明由于本题涉及的圆很多,于是可考虑反演变换．取P 为反演中心,P 关于圆O 的幂为反演基圆半径,则圆O 反演为本身,()1,2,3,4i O i =反演为四边形ABCD 各边所在直线,过点P 的直线也反演为本身．由直线2PO 与2O 正交,可知它们的反形也正交,即2PO AD ⊥．又易知4O O AD ⊥,所以24PO O O ∥．同理,42PO O O ∥．所以24PO OO 为平行四边形,PO ,24O O 互相平分．同理,PO ,13O O 也互相平分,命题得证．【解题思维策略分析】1．注意同一类变换的多次运用例13如图18-13,凸四边形ABCD 的边是位于形外的、两两相似的等腰APB △、BQC △,CRD △、DSA △的底边．已知PQRS 是矩形,且PQ QR ≠．证明：ABCD 是菱形．图18-13FSPQRD OABCE（第15届全俄第三阶段赛题）证明设这些相似的等腰三角形的顶角为θ（90≠︒）．考虑一系列的旋转变换：点A 绕点P 转θ角到点B ,点B 绕点Q 转θ角到点C ,合成为点A 绕点E 转2θ角到点C ．同理点C 绕点F 转2θ角到点A ,其中12EPQ PQE FRS RSF θ∠=∠=∠=∠=．从而EA EC =,FA FC =,2180AEC AFC θ∠=∠=≠︒．于是AEC AFC △≌△,AECF 是菱形．又由于PQ SR =,则PEQ SFR △≌△．因此,E ,F 在矩形PQRS 的中位线上,从而AC 被该中位线垂直平分于矩形中心O 点．同理BD 也被矩形PQRS 的另一中位线垂直平分于矩形中心O 点．故ABCD 是菱形．若90θ=︒,则E ,F 都与矩形PQRS 的中心O 重合,且90POQ ROS ∠=∠=︒,从而知PQRS 是正方形,矛盾．所以90θ≠︒．例14设ABCDEF 是凸六边形,AB BC CD ==,DE EF FA ==,60BCD EFA ∠=∠=︒,G ,H 是六边形内两点,使120AGB DHE ∠=∠=︒．求证：AG GB GH DH HE CF ++++≥．（IMO -36试题）证明如图18-14,分别以AB ,DE 为边向六边形外作正ABM △和DEN △,将AGB △绕A 逆时针方向旋转60︒到AG M '△,则AGG '△为正三角形．故AG GG '=,GB G M '=．图18-14FCH 'ENH DG 'MABG同样,将EHD △绕E 点顺时针方向旋转60︒到EH N '△,则EHH '△为正三角形,于是EH HH '=,HD H N '=．连MN ,则多边形AMBCDEF 关于轴BE 对称,MN CF =．另一方面,由“两点间线段最短”有 AG GB GH DH HE MG G G GH HH H N MN CF '''''++++=+++=+≥． 2．注意几类变换的配合运用例15平面上有两个直角三角形,其斜边上的中线互相平行,证明：一个三角形的一条直角边与另一个三角形的某条直角边之间的（小于直角的）夹角小于两条斜边之间的夹角．（第19届全俄竞赛题）证明平行移动两个给定的Rt ABC △和Rt A B C '''△中的一个,使两三角形的直角顶点C 与C '重合,并以点C 为中心,作位似变换,使得两三角形的中线重合,如图18-15．那么以E 为圆心,CE 为半径的圆将外接这两个三角形,并且它们斜边之间的夹角是圆心角,而它是相应的圆周角的两倍,这圆周角是直角边之间（小于直角）的夹角（图中2AEA ACA ''∠=∠）,注意到上述的平移及位似变换均不改变直线间的夹角,于是结论获证．图18-15A BC =C 'EB'A'例16如图18-16,ABC LMN △∽△,且AC BC =,LN MN =,顶点按逆时针顺序排列,并在同一平面内,而且AL BM =．证明：CN 平行于AB 和LM 中点的连线．图18-16N LM（第19届全俄第3阶段竞赛题）证明平移线段AB 到QM ,因AL BM =,BM AQ =,则AL AQ =,即ALQ △为等腰三角形．若F 为LQ 的中点,则AF LQ ⊥．设E 为LM 的中点,D 为AB 的中点,则FE 是QLM △的中位线,1122FE QM AB AD ===及FE QM AD ∥∥,因此AFED 是平行四边形,即AF DE ∥,AF DE =．又AF LQ ⊥,故DE LQ ⊥．平移ABC △,使A 点重合于F 点,D 点重合于E 点,则C 点移到G 点,ADC FEG △≌△,AF CG DE ∥∥及CG DE =．由ADC LEN △∽△,得FEG LEN △∽△且FE CELE NE=．又因90GEF NEL ∠=∠=︒,故GEN LEF ∠=∠,进而FEL ∠可由GEN ∠绕E 点逆时针旋转90︒并经位似变换而得到．由此得GN LF ⊥,即GN LQ ⊥．又GC LQ ⊥,即G ,C ,N 都在垂直于LQ 的一条直线上,因此,CN AF ∥,亦即CN DE ∥,原命题得证．【模拟实战】习题A1．给定以O 为圆心,AB 为直径的半圆周,在其上取点K 和M ,在直径上取点C ,使得KCA MCB ∠=∠．证明：K ,C ,O ,M 四点共圆．（第18届全俄竞赛题）2．在ABC △中,AB AC =．任意延长CA 到P ,再延长AB 到Q ,使AP BQ =．求证：ABC △的外心O 与A ,P ,Q 四点共圆．（1994年全国初中联赛题） 3．在半径为1的圆周上给定弦AB ,不与圆相交的直线l 与弦AB 成45︒．用圆规和直尺在直线l 上作出点C ,使得线段DE 与AB 垂直（C ,E 分别是CA ,CB 与圆的交点）．（第16届全俄竞赛题） 4．ABC △中,2AB AC ==,BC 边—上有100个不同的点1P ,2P ,…,100P ,记2(1,2,,10)i i i i m AP BP PC i =+⋅=,求12100m m m +++的值．（1990年全国初中联赛题）5．从以AD 为直径的半圆周上的点B ,C 分别作BE ,CF 垂直于AD 于E ,F ．线段AC 与BD 相交于P ,线段BF 与CE 相交于Q ．求证：直线PQ AD ⊥．（第17届全俄第3阶段竞赛题）6．设两个等圆相交,由其对称中心引出两条射线,它们交圆周于不在同一直线上的四点．证明：这四点共圆．（第19届全俄竞赛题） 7．在矩形ABCD 的边AB ,BC ,CD ,DA 上分别取异于顶点的点K ,L ,M ,N ．已知KL MN ∥,KM NL ⊥于O ．证明：KM 和LN 的交点在矩形的对角线BD 上．（第25届全苏竞赛题）8．ABC △的中线AE ,BF 和CD 相交于M ．已知E ,C ,F 和M 共圆,且CD n =．求线段AB 的长度．（第18届全俄竟赛题）9．等边ABC △和KMN △（顶点按逆时针顺序）在同一平面内,且AK NB =．证明：线段CM 和AN 互相垂直,且CMAN=（第19届全俄竞赛题） 10．运用位似旋转变换证明例5． 11．四边形ABCD 中,以一对对边的比AB CD ∶内分另一对对边AD ,BC 于E ,F ,延长BA ,CD 与EF 的延长线分别相交于G ,Q ．试证：BGF FQC ∠=∠． 12．四边形ABCD 的对边AD ,BC 延长交于E ,AB ,CD 延长交于F ．O 为其对角线交点,过O 作AB 的平行线OQ 交EF 于Q ．求证：OG GQ =．习题B1．已知平面上三个半径相等的圆1O ,2O ,3O 两两相交于A ,B ,C ,D ,E ,F ,如图18-17．证明：弧AB ,CD ,EF 的和等于180︒．图18-172．如图18-18,111A B C △,在ABC △内,且111ABC A B C △∽△．作1B D AC ⊥于D ,1C E AB ⊥于E ,1A F BC ⊥于F ．求证：1112ABC A F BC B D AC C E AB S ⋅+⋅+⋅=△．图18-18D A BCE C 1B 1A 13．设D 是锐角ABC △内部的一点,使得90ADB ACB ∠∠+︒=,并有AC BD AD BC ⋅=⋅．（1）计算比值AB CDAC BD⋅⋅；（2）求证：ACD △的外接圆和BCD △的外接圆在C 点的切线互相垂直．（IMO34-2试题）4．BK 是锐角ABC △的高,以BK 为直径作圆分别交AB ,BC 于E ,F ．过E ,F 分别引所作圆的切线．证明：两切线的交点在过顶点B 的ABC △的中线所在的直线上．（第21届俄罗斯竞赛题）5．在梯形ABCD 中,腰AB CD =．将ABC △绕点C 转过一个角度,而得到A B C ''△．证明：线段A D ',BC 和B C '的中点共线．（第23届全苏竞赛题） 6．111A B C △是不等边锐角ABC △的垂足三角形,2A ,2B ,2C 是111A B C △的内切圆分别切11B C ,11C A ,11A B 的切点．证明：222A B C △与ABC △的欧拉线重合．（第7届巴尔干地区竞赛题）7．在钝角ABC △（C ∠为钝角）的BC 边上选取点D （异于B ,C 点）．过线段BC （异于D ）的内点M 引直线AM ,交ABC △的外接圆S 于点N ．经过点M ,D 和N 作圆,交圆S 于N 及另一点P ,问点M 在何位置时,线段MP 的长度最短？（第22届全苏竞赛题）8．ABCD 是一个四边形,且BC AD ∥,M 是CD 的中点,P 是MA 的中点,Q 是MB 的中点,直线DP ,CQ 交于点N ．求证：点N 不在ABM △外部的充要条件是上下底边长之比在1,33⎡⎤⎢⎥⎣⎦上．（IMO -35预选题）9．在ABC △中,12AB =,16AC =,M 是BC 的中点,E ,F 分别在AB ,AC 上,EF 交AM 于G ,且2AE AF =．求比值EFGF．（IMO -29预选题） 10．三个全等的圆有一个公共点Q ,并且都在一个已知三角形内,每一个圆与三角形的两条边相切,求证：三角形的内心I ,外心O 与已知点Q 共线．（IMO -22试题） 11．123A A A △是一个非等腰三角形,它的边长分别为1a ,2a ,3a ,其中i a 是i A 的对边（123i =，，）,i M 是边i a 的中点,123A A A △的内切圆I 切边i a 于i T 点,i S 是i T 关于i A ∠的平分线的对称点．求证：11M S ,22M S ,33M S 三直线共点．（IMO -23试题）12．设A 是两个不相等的,分别以1O 与2O 为圆心而共面的圆1C 与2C 的两个不同交点之一,一条外公切线切1C 于1P ,切2C 于2P ；另一条公切线切1C 于1Q ,切2C 于2Q ．设1M 是11PQ 的中点,2M 是22P Q 的中点．证明：1212O AO M AM ∠∠=．（IMO -24试题）13．已知两相切圆1C ,2C ,点P 在根轴上,即与两圆连必线垂直的公切线上．试用圆规和直尺作所有的圆C ,使得C 与1C ,2C 相切,且过P 点．（1991年亚太地区竞赛题）14．给定两个圆,其中一个圆在另一个内部,且两圆相切于点N ．外圆的弦BA 和BC 分别与内圆相切于点K 和M ．外圆的弦BA 和BC 分别与内圆相切于点K 和M ．设不包含点N 的弧AB 和BC 的中点分别是Q 和P ．BQK △和BPM △的外接圆的第二个交点为1B ．证明：1BPB Q 为平行四边形．（第26届俄罗斯竞赛题）15．四边形ABCD 外切于圆ω,边AB 和CD 所在的直线相交于点O ．圆1ω与边BC 相切于点K ,且与边AB 和CD 所在的直线都相切；圆2ω与边AD 相切于点L ,且亦与边AB 和CD 作在的直线都相切,现知点O ,K ,L 共线,证明：边BC 和AD 的中点以及圆ω的圆心三点共线．（第26届俄罗斯竞赛题）第十八章几何变换的性质及应用习题A1．若C 与O 重合,则结论显然成立．今设C 与O 不重合,将半圆以直径为轴,对称变换成整圆,设K ',M '为K ,M 关于AB 的对称点,则K ',C ,M 共线,K ,C ,M '也共线．1(2M KCM KM ∠=+)K M KOM ''=∠．故K ,C ,O ,M 共圆．2．等腰ABC △的外心O 在顶角平分线上,而顶角平分线又是ABC △的对称轴,以AO 为轴作AOQ △的对称AOR △,则,OQA ORA AQ AR ∠=∠=．由AB AC =,有CR AR AC AQ AB BQ AP =-=-==．连OC ,OP ,设OM 是等腰OAC △的对称轴,则OM 垂直平分AC （M 为垂足）．于是MR MC CR MA AP MP =+=+=,从而OMR △与OMP △关于OM 为轴对称,所以OPA ORA ∠=∠．又已证ORA OQA ∠=∠,所以OPA OQA ∠=∠,故O ,A ,P ,Q 四点共圆．3．设直线AB 与l 的交点为P ,过P 作直线m AB ⊥,分别作出A ,B 关于l 的对称点1A ,1B ,则1A ,1B 在m 上．连1AB 交l 于C ,则C 点为所求．设CB ,CA 与圆的交点为E ,D ．由对称性,知11A B C ABC ∠=∠．又CDE ABC ∠=∠,所以,11A B C CDE ∠=∠,DC m ∥,从而DE AB ⊥．4．将i ABP △绕A 点逆时针旋转i ACP '△处,使AB 重合于AC ．因180i i APC APC '∠+∠=︒,故A ,i P ,C ,i P '共圆．设AC ,i i PP '交于D 点．由i APD △∽i ACP △∽i PCD '△,知2i AP AD AC =⋅,i i PCPC '⋅= DC AC ⋅,于是22()4i i i i m AP BP PC AD DC AC AC =+⋅=+⋅==,故12100400m m m +++=．5．易知90ABD ACD ∠=∠=︒．分别过P ,Q 引KL ,MN 垂直于BE 交BE 于K ,N ,交CF 于L ,M ．显然,它们也垂直于,CF MN KL =．由BKP △∽AEB △,KP BP BE AB =；ABP △∽DCP △,BP CPAB DC=；PCL △∽CDF △,CP PL DC CF =．于是KP PL BE CF =,即KP BEPL CF=．又BQE △∽FQC △,有BE MQ CF QN =（相似三角形对应高的比等于相似比）,于是KP MQ PL QN =,故11KP MQ PL QN +=+,即KL MNPL QN =,故PL QN =．因此PQ AD ⊥．注：此题中,若P 为直线AB 与DC 的交点,可类似证明,得到PQ AD ⊥．6．设这两个等圆的对称中心为O ．从O 引出的两条射线分别交圆周于1A ,2A 及1B ,2B ,如图所示．又3A ,3B 及4B 分别是2B ,1A 及2A 关于O 点的对称点,由对称性知2313B B A A =,从而321312A A A B B B ∠=∠,即122211A A B B B A ∠=∠,所以1A ,1B ,2A ,2B 四点共圆．对于右图情形,有1323A A B B =,从而321213A A A B B B ∠=∠．而122321180A A B A A A ∠=︒-∠,因此,312B B B ∠122180A A B +∠=︒,故1A ,1B ,2B ,2A 四点共圆．7．由MN KL ∥,有MNO OLK ∠=∠,NMO LKO ∠=∠,从而ONM △∽OLK △,即有MO NOOK OL=．又OMD OKB ∠=∠,OND OLB ∠=∠,因此OMDN 和OKBL 关于O 点为中心位似,所以点D ,O ,B 在一直线上．结论证毕．注：题中条件KM NL ⊥可省略；当ABCD 为平行四边形时结论亦成立．8．以C 为位似中心,2为位似比作位似变换,则E B →,F A →．四边形ECFM 的外接圆变为ABC △的外接圆,并且点M 变为点G 在ABC △的外接圆上．由CM ∶2MD =∶1,CM MG =,知MD DG ==3n ．由相交弦定理及BD DA =,有BD DA CD DG ⋅=⋅,即23n BD n =⋅,即BD =亦即AB =． 9．由AK NB =知ANBK 是平行四边形．因此,等边三角形的边AB ,NK 互相平分于点P ,从而CP PA ⊥,CD 及PM NP ⊥,PM =．今以P 点为中心,先作按顺时针方向旋转90︒的变换,再作位似比为的位似变换,于是A 点变为C点,N 点变为M 点,从而线段AN 变为线段CM ．因此AN CM ⊥且CM ．10．设ADE △在旋转过程中的任一位置如图195-．考虑这样两个位似旋转变换：(,45,S E ︒和(,45,S C ︒．在前一个变换下,点D 变到A ,EC 的中点M 变到M '．在第二个变换下,点A 变到点B ,点M '变到M ．因此M 是两个变换的复合的不变点．由于(,45,(,45,S E S C ︒⋅︒= (,90,1)S M ︒．在这个复合变换下点D 变到B ,所以90DMB ∠=︒．又DM BM =,由此即证得命题成立．11．由于要证明的两角在两个三角形中,且题设中有线段的比内分不在一条直线上两线段,条件较分散,须作辅助线将条件集中．不妨连BD ,则(,)(,),CDCDH B H D AB CDAB CDC F A E ++−−−−−→−−−−−−→．假设(,)ABH B AB CDD P +−−−−−→,则,BP AB DP CD BD AB CD DB AB CD==++．（*）故(,)CDH D AB CDB P +−−−−−−→．因为在位似变换下,直线变成与它平行的直线,则,PF CD PE AB ∥∥,从而PEF BGF ∠=∠,PFE ∠=FQC ∠．又,BF BP PF DE DP PE BC BD CD DA DB AB ====,由此两式相除,得AB PF BP CD PE DP ⋅=．又BP AE ABPD ED CD==,则1PFPE=,从而PEF PFE ∠=∠．故BGF FQC ∠=∠． 12．设直线QGO 交AD 于R ,交EB 于P ,作位似变换：(,),,,,ER H E EAA B F R P Q −−−−→；(,),,COH C CAA B F O −−−−→,,P G ；(,),,,,DB H D DAA B F R O G −−−−→,则RQ RP AF AB =,RO RG AB AF =,OP OGAB AF=．由GO RQ RG RQ RG RP RO OP OGAF AF AF AF AB AB AB AF -==-=-==,故OG GQ =．习题B 1．连1AO ,2AO ,1BO ,2CO ,2DO ,3EO ,3FO ,易知21AO DO 为平行四边形,即21O D AO ∥．同理,有31O E BO ∥,32O F CO ∥．于是,分别将2O ,3O 平移使之与1O 重合．设21()O O CD C D ''−−−−→平移,31()O O EF E F ''−−−−→平移,则1,,A O D '共线,1,,B O E '共线,1,,C O F ''共线,由此即知12AO B CO D ∠+∠3111180EO F AO B C O D E O F ''''+∠=∠+∠+∠=︒．即证．2．将111A B C △绕1A 点旋转α角到1A B C ''△的位置,使1AC AB '∥,则111sin C E C E AC α''=+⋅,1B D = 11sin B D A B α''-,于是11111111(sin )(A F BC B D AC C E AB A F BC B D A B AC C E AC α''''⋅+⋅+⋅=⋅+-⋅++⋅ 111111sin ()sin AB A F BC B D AC C E AB AC AB A B AC αα'''')⋅=⋅+⋅+⋅+⋅-⋅⋅．由ABC △∽111A B C △,有1111AB ACA B A C =,即11110AC AB A B AC ⋅-⋅=．又因为1B D A D ''''=,1E C A E ''''=,从而11A F BC B D AC ⋅+⋅+ 11112ABC C E AB A F BC A D AC A E AB S ''''⋅=⋅+⋅+⋅=△（其中C E AB ''⊥于E ',1A E AB ''⊥于E '',1A D AC''⊥于D '',B D AC ''⊥于D '）．3．（1）由ADB ACB CAD CBD ∠=∠+∠+∠,知90CAD CBD ∠+∠=︒．将D 、B 旋转90︒到E ,则由ADB CAD CBD ACB ∠=∠+∠+∠及已知90ADB ACB ∠=∠+︒知CBE ∠= 90CBD CAD ︒-∠=∠．又BC BC AC BE BD AD ==（因AC BD AD BC ⋅=⋅）,知BCE △∽ACD △,从而ACBC=CD CE ,ACD BCE ∠=∠,则ACB DCE ∠=∠,于是又有ABC △∽DEC △,即有AB ACDE CD =,而2BE BD =,则2AB CD AC BD ⋅=⋅,故2AB CDAC BD⋅=⋅．（2）ACD △的外接圆在C 点的切线与CD 夹角等于CAD ∠（弦切角与圆周角）,BCD △的外接圆在C 点的切线与CD 夹角等于CBD ∠,且两切线在CD 不同侧,故它们的夹角等于90CAD CBD ∠+∠=︒,即两切线互相垂直．4．若证踢类似结论：对于以B力位似中心,与以BK 为直径的圆位似的圆也有类似的性质,则原命题的结论即可成立．设ABC △的三条高AM ,BK ,CL 相交于点H ,则以BH 为直径的O 与以BK 为直径的圆位似,且O 过点M ,L ．由OM OM =,有90OMB OBM ACB ∠=∠=︒-∠．设N 为AC 的中点,连MN ,则90AMN MAN ACB ∠=∠=︒-∠,从而AMN OMB ∠=∠．于是OMN ∠= 90OMA AMN OMA OMB AMB ∠+∠=∠+∠=∠=︒,所以MN 是O 的切线．同理可证LN 也是O 的切线．由位似图形性质的对称性,以BK 为直径的圆也有同样的性质．5．将BCB '△沿DC 平移至EFG △,那么以D 为中心,位似比为2,将BC ,B C '和A D '的中点变到E ,G 到A '．由图形的对称性可知,EC CA ECB CAD BCA =∠=∠=∠,所以BC EA ⊥,从而EA EF ⊥．1(1802)2AEG FEG ∠=︒-∠（因EA EF ⊥）12EFG =∠（因EF BC B C GF '===）1122BCB ACA ''=∠=∠（因BCB B CA ACA B CA ''''∠+∠=∠+∠）AEA '=∠（因E ,A ,A '在以C 为圆心的同一圆上）．所以E ,G ,A '共线,因而在上述位似变换下,它们的原象：BC 的中点,B C '的中点,DA '的中点也共线． 6．设H 为ABC △的垂心,由11190BA H BC H CB H ∠=∠=∠=︒,知1A ,B ,1C ,H 和1A ,C ,1B ,H 分别四点共圆,因此,111111BAC BHC B HC B AC ∠=∠=∠=∠,从而1111119090C A H BAC B AC ∠=︒-∠=-∠= 11B A H ∠,即1A H 平分111B AC ∠．同理,11,B H C H 也平分111111,A B C AC B ∠∠,故H 是111A B C △的内心（此可由垂心性质直接得H 为其内心）．从而H 也是222A B C △的外心．由1212,A B AC 分别是111A B C △内切圆的切线,22,B H C H 分别是内切圆的半径,所以1212A B AC =,2B H 2C H =,从而122A H B C ⊥,但1A H BC ⊥,从而22B C BC ∥．同理,22A B AB ∥,22A C AC ∥．由于ABC △与222A B C △的边对应平行,因此它们是位似形．于是这两个三角形的欧拉线（对应的线）或者平行或者重合．由于ABC △的垂心即222A B C △的外心,而这一点分别在这两个三角形的欧拉线上,所以这两个三角形的欧拉线重合．7．过点A 引AK CB ∥,交圆S 于点K ,延长KD ,交圆S 于点0P ．现证明：对每一个符合条件的点M ,点P 和0P 重合．（i ）当点0N P ≠时,设点N 在00()P B CP 内,由A ,K ,N ,0P 共圆,知0ANP ∠与0AKP ∠相等（相补）,由CB AK ∥,有00MDP AKP ∠=∠,则0MNP ∠与0MDP ∠相筹（相补）,因此,M ,D ,N ,0P 共圆,0P P =．（ii ）当点0N P =时,以点0P 为位似中心,将点K 变为点D ,直线0AP 变换为自身．由CB AK ∥,所以线段AK 变换为线段MD ,即点A 变换为点M ,于是圆S 就变换为三角形NMD 的外接圆,因为0P 为位似中心,所以这两圆只有一个公共点,0P P =．所以,所要求的点M 的位置应是点0P 在BC 的射影．因为A ∠是锐角,所以该射影在线段BC 内．又因为KDC KBC ACB ∠>∠=∠,所以KDC ∠为钝角,故点0P 在BC 上的射影不会与点D 重合．8．题中条件及结论均满足伸缩变换的不变特性．设AB 中点为R ,将AMR △变换为以R 为直角顶点的等腰直角三角形,建立仿射坐标系,(0,0)M ．可设(2,2)A ,(2,0)R ,(2,2)B -,(,2)C a --,(,2)D a ,则(1,1),(1,1)P Q -．由直线DP ：211(1)1y x a --=--和CQ ：2(1)1(1)1y x a ---+=---的方程联立,解得2(2,)N a a --,点N 在ABM △之外的充要条件是：。

八年级数学尖子生培优竞赛专题辅导专题07 四边形中的图形变换

专题07 四边形中的图形变换专题解读】几何变换一般是指图形的平移，翻折，旋转，在四边形的背景下的图形的几何变换问题，需抓住几何变换的本质，变化中的不变量，变换后的图形的新生成，几何变换的性质等，建立相关的模型，运用勾股定理，方程思想解决问题，从思维视角看，转化为常见的模型是解决问题的一般思路。

思维索引例1.在平面直角坐标系中，已知线段AB ，且A （1，－2），B （3，0），如图1所示，平移线段AB 到线段CD ，使点A 的对应点为D ，点B 的对应点为C.（1）若点C 的坐标为（－2，4），求点D 的坐标；（2）若点C 在y 轴的正半轴上，点D 在第二象限内，连接BC ，BD ，如图2所示，且7BCD S ∆=（BCDS ∆表示三角形BCD 的面积），求点C 、D 的坐标。

（3）在（2）的条件下，在y 轴上是否存在一点P ，使23PCD BCD S S ∆∆=（PCD S ∆表示三角形PCD 的面积），若存在，求出点P 的坐标；若不存在，请说明理由.图2图1例2.（1）如图，Rt △ABC 中，∠ACB ＝90°，AC ＝3，BC ＝4，将边AC 沿CE 翻折，使点A 落在AB 上的点D 处；再将边BC 沿CF 翻折，使点B 落在CD 的延长线上的点'B 处，两条折痕与斜边AB 分别交于点E 、F ，求线段'B F 的长.（2）如图，△AOC 和△BOD 均为等腰直角三角形，∠AOC ＝∠B 0D ＝90°，若△BOC 的面积为1，试求以AD ，BC ，OB ＋OD 的长度为三边长的三角形的面积.ODCBA例题2第(2)题图例题2第(1)题图ABCDEFB'素养提升1.如图，将平行四边形ABCD 沿对角线BD 折叠，使点A 落在点E 处，交BC 于点F ，若∠ABD ＝48°，∠CFD ＝40°，则∠E 为（）A.102°B.112°C.122°D.92°第1题图ABCDE F∠°第2题图ABCD E FC'B'第3题图AB CDA'D'C'2.将矩形纸片ABCD 按如图所示的方式折叠，AE 、EF 为折痕，∠BAE ＝30°，AB ，折叠后，点C 落在AD 边上的'C 处，并且点B 落在EC 边上的'B 处，则BC 的长为（）B.2C.3D.3.如图，将矩形ABCD 沿对角线AC 剪开,再把△ACD 沿CA 方向平移得到'''A C D ∆,连结'AD 、B C.若∠ACB ＝30°,AB ＝1,'CC ＝x ,△ACD 与'''A C D ∆重叠部分的面积为S ,则下列结论：①△A ′AD ′≌△CC ′B ；②当x ＝1时,四边形ABC ′D 是菱形；③当x ＝2时,△BDD ′为等边三角形.其中正确的是（）A.①②B.①③C.②③D.①②③4.如图，△ABC 是等腰直角三角形，DE 是过点C 的直线，BD ⊥DE ，AE ⊥DE ，则△BDC 与△ACE 通过下列变换：①绕点C 旋转后重合；②沿AB 的中垂线翻折后重合；③沿ED 方向平移△CEA 后与△BDC 重合；④将△ACE 绕中点M 逆时针旋转90度后与△BDC 重合；⑤先将△CEA 先沿ED 方向平移，使点E 与点D 重合后，再将平移后的三角形绕点D 逆时针旋转90度后与△BDC 重合。

八年级数学竞赛讲座图形的平移与旋转附答案

第二十九讲图形的平移与旋转前苏联数学家亚格龙将几何学定义为：几何学是研究几何图形在运动中不变的那些性质的学科．几何变换是指把一个几何图形F l变换成另一个几何图形F2的方法，若仅改变图形的位置，而不改变图形的形状和大小，这种变换称为合同变换，平移、旋转是常见的合同变换．如图1，若把平面图形F l上的各点按一定方向移动一定距离得到图形F2后，则由的变换叫平移变换．平移前后的图形全等，对应线段平行且相等，对应角相等．如图2，若把平面图F l绕一定点旋转一个角度得到图形F2，则由F l到F2的变换叫旋转变换，其中定点叫旋转中心，定角叫旋转角．旋转前后的图形全等，对应线段相等，对应角相等，对应点到旋转中心的距离相等．通过平移或旋转，把部分图形搬到新的位置，使问题的条件相对集中，从而使条件与待求结论之间的关系明朗化，促使问题的解决．注合同变换、等积变换、相似变换是基本的几何变换．等积变换，只是图形在保持面积不变情况下的形变'而相似变换，只保留线段间的比例关系，而线段本身的大小要改变．例题求解【例1】如图，P为正方形ABCD内一点，PA：PB：PC＝1：2：3，则∠APD= ．思路点拨通过旋转，把PA、PB、PC或关联的线段集中到同一个三角形．【例2】如图，在等腰Rt△ABC的斜边AB上取两点M，N，使∠MCN=45°，记AM＝m，MN= x，DN=n，则以线段x、m、n为边长的三角形的形状是( )A．锐角三角形 B．直角三角形C．钝角三角形 D．随x、m、n的变化而改变思路点拨把△ACN绕C点顺时针旋转45°，得△CBD，这样∠ACM+∠BCN=45°就集中成一个与∠MCN 相等的角，在一条直线上的m、x、n 集中为△DNB，只需判定△DNB的形状即可．注下列情形，常实施旋转变换：(1)图形中出现等边三角形或正方形，把旋转角分别定为60°、90°；(2)图形中有线段的中点，将图形绕中点旋转180°，构造中心对称全等三角形；(3)图形中出现有公共端点的线段，将含有相等线段的图形绕公共端点，旋转两相等线段的夹角后与另一相等线段重合．【例3】如图，六边形ADCDEF中，AN∥DE，BC∥EF，CD∥AF，对边之差BC－EF＝ED—AB＝AF—CD>0，求证：该六边形的各角相等．(全俄数学奥林匹克竞赛题)思路点拨设法将复杂的条件BC—FF=ED—AB=AF—CD>0用一个基本图形表示，题设中有平行条件，可考虑实施平移变换．注平移变换常与平行线相关，往往要用到平行四边形的性质，平移变换可将角，线段移到适当的位置，使分散的条件相对集中，促使问题的解决．【例4】如图，在等腰△ABC的两腰AB、AC上分别取点E和F，使AE=CF．已知BC=2，求证：EF≥1． (西安市竞赛题)思路点拨本例实际上就是证明2EF≥BC，不便直接证明，通过平移把BC与EF集中到同一个三角形中．注三角形中的不等关系，涉及到以下基本知识： (1)两点间线段最短，垂线段最短；(2)三角形两边之和大于第三边，两边之差小于第三边；(3)同一个三角形中大边对大角(大角对大边)，三角形的一个外角大于任何一个和它不相邻的内角．【例5】如图，等边△ABC 的边长为31225+=a ，点P 是△ABC 内的一点，且PA 2+PB 2＝PC 2，若PC=5，求PA 、PB 的长． (“希望杯”邀请赛试题)思路点拨题设条件满足勾股关系PA 2+PB 2＝PC 2的三边PA 、PB 、PC 不构成三角形，不能直接应用，通过旋转变换使其集中到一个三角形中，这是解本例的关键．学历训练1．如图，P 是正方形ABCD 内一点，现将△ABP 绕点B 顾时针方向旋转能与△CBP ′重合，若PB=3，则PP ′= ．2．如图，P 是等边△ABC 内一点，PA ＝6，PB=8，PC ＝10，则∠APB ．3．如图，四边形ABC D 中，AB ∥CD ，∠D=2∠B ，若AD=a ，AB=b ，则CD 的长为．4．如图，把△ABC 沿AB 边平移到△A'B'C'的位置，它们的重叠部分(即图中阴影部分)的面积是△ABC 的面积的一半，若AB=2，则此三角形移动的距离AA'是( ) A ．12- B ．22C ．lD ．21 (2002年荆州市中考题)5．如图，已知△ABC 中，AB=AC ，∠BAC=90°，直角EPF 的顶点P 是BC 中点，两边PE 、PF 分别交AB 、AC 于点C 、F ，给出以下四个结论：①AE=CF ；②△EPF 是等腰直角三角形；③S 四边形AEPF =21S △ABC ；④EF=AP ．当∠EPF 在△ABC 内绕顶点P 旋转时(点E 不与A 、B 重合)，上述结论中始终正确的有( ) A ．1个 B ．2个 C ．3个 D ．4个 (2003年江苏省苏州市中考题)6．如图，在四边形ABCD中，AB＝BC，∠ABC=∠CDA=90°，BE⊥AD于E， S四边形ABCD d=8，则BE的长为( ) A．2 B．3 C．3 D．22 (2004年武汉市选拔赛试题)7．如图，正方形ABCD和正方形EFGH的边长分别为22和2，对角线BD、FH都在直线l上，O1、O2分别为正方形的中心，线段O1O2的长叫做两个正方形的中心距，当中心O2在直线l上平移时，正方形EFGH也随之平移，在平移时正方形EFGH的形状、大小没有变化．(1)计算：O1D= ，O2F= ；(2)当中心O2在直线l上平移到两个正方形只有一个公共点时，中心距O1O2= ；(3)随着中心O2在直线l上平移，两个正方形的公共点的个数还有哪些变化?并求出相对应的中心距的值或取值范围(不必写出计算过程)． (徐州市中考题)8．图形的操做过程（本题中四个矩形的水平方向的边长均为a，竖直方向的边长均为b）：在图a中，将线段A1A2向右平移1个单位到B1B2,得到封闭图形A1A2B1B2（即阴影部分）；在图b中，将折线A1A2A3向右平移1个单位到B1B2B3，得到封闭图形A1A2A3B1B2B3（即阴影部分）；（1）在图c中,请你类似地画一条有两个折点的折线,同样向右平移1个单位,从而得到一个封闭图形,并用斜线画出阴影；（2）请你分别写出上述三个图形中除去阴影部分后剩余部分的面积：S1= ，,S2= ，S3= ；（3）联想与探索：如图d，在一块矩形草地上,有一条弯曲的柏油小路（小路任何地方的水平宽度都是1个单位），请你猜想空白部分表示的草地面积是多少？并说明你的猜想是正确的．(2002年河北省中考题)9．如图，已知点C为线段AB上一点，△ACM、△CBN是等边三角形，求证：AN＝BM．说明及要求：本题是《几何》第二册几15中第13题，现要求：(1)将△ACM绕C点按逆时针方向旋转180°，使A点落在CB上，请对照原题图在图中画出符合要求的图形(不写作法，保留作图痕迹)．(2)在①所得的图形中，结论“AN＝BM”是否还成立?若成立，请证明；若不成立，请说明理由．(3)在①得到的图形中，设MA的延长线与BN相交于D点，请你判断△ABD与四边形MDNC的形状，并证明你的结论．10．如图，在Rt△ABC中，∠A＝90°，AB＝3cm，AC=4cm，以斜边BC上距离B点3cm的点P为中心，把这个三角形按逆时针方向旋转90°至△DEF，则旋转前后两个直角三角形重叠部分的面积是 cm2．11．如图，在梯形ABCD中，AD∥BC，∠D=90°，BC=CD=12，∠ABE=45°，点E在DC上，AE、BC的延长线交于点F，若AE=10，则S△ADE+S△CEF的值是．(绍兴市中考题)12．如图，在△ABC中，∠BAC=120°，P是△ABC内一点，则PA+PB+PC与AB+AC的大小关系是( )A．PA+PB+PC>AB+AC B．PA+PB+PC<AD+ACC． PA+PB+PC＝AB+AC D．无法确定13．如图，设P到等边三角形ABC两顶点A、B的距离分别为2、3，则PC所能达到的最大值为( )A ．5B ．13C ．5D ．6 (2004年武汉市选拔赛试题)14．如图，已知△ABC 中，AB=AC ，D 为AB 上一点，E 为AC 延长线上一点，BD=CE ，连DE ，求证：DE>DC ． 15．如图，P 为等边△ABC 内一点，PA 、PB 、PC 的长为正整数，且PA 2+PB 2=PC 2，设PA=m ，n 为大于5的实数，满456593022++≤++mn m n m n m ，求△ABC 的面积．16．如图，五羊大学建立分校，校本部与分校隔着两条平行的小河，1l ∥2l 表示小河甲，3l ∥4l 表示小河乙，A 为校本部大门，B 为分校大门，为方便人员来往，要在两条小河上各建一座桥，桥面垂直于河岸．图中的尺寸是：甲河宽8米，乙河宽10米，A 到甲河垂直距离为40米，B 到乙河垂直距离为20米，两河距离100米，A 、B 两点水平距离(与小河平行方向)120米，为使A 、B 两点间来往路程最短，两座桥都按这个目标而建，那么，此时A 、D 两点间来往的路程是多少米? (“五羊杯”竞赛题)17．如图，△ABC 是等腰直角三角形，∠C=90°，O 是△ABC 内一点，点O 到△ABC 各边的距离都等于1，将△ABC 绕点O 顺时针旋转45°，得△A 1B l C 1，两三角形公共部分为多边形KLMNPQ ． (1)证明：△AKL 、△BMN 、△CPQ 都是等腰直角三角形； (2)求△ABC 与△A 1B l C 1公共部分的面积． (山东省竞赛题)18．(1)操作与证明：如图1，O是边长为a的正方形ACBD的中心，将一块半径足够长，圆心角为直角的扇形纸板的圆心放在O点处，并将纸板绕O点旋转，求证：正方形ABCD的边被纸板覆盖部分的总长度为定值．(2)尝试与思考：如图2，将一块半径足够长的扇形纸板的圆心放在边长为a的正三角形或正五边形的中心O点处，并将纸板绕O点旋转，当扇形纸板的圆心角为时，正三角形的边被纸板覆盖部分的总长度为定值a；当扇形纸板的圆心角为时，正五边形的边被纸板覆盖部分的总长度也为定值a．(3)探究与引申：一般地，将一块半径足够长的扇形纸板的圆心放在边长为a的正n边形的中心O点处，并将纸板绕O点旋转．当扇形纸板的圆心角为时，正n边形的边被纸板覆盖部分的总长度为定值a；这时正n边形被纸板覆盖部分的面积是否也为定值?若为定值，写出它与正n边形面积S之间的关系；若不是定值，请说明理由．(江苏省连云港市中考题)。

初中数学竞赛中考讲义之几何三大变换之旋转

第32讲几何三大变换之旋转旋转的性质【例题讲解】例题1．如图所示，将一副三角板的直角顶点重合摆放在桌面上，若145AOD ∠=︒，则BOC ∠=度．【解答】解：由图145AOD ∠=︒ ，1459055AOC AOD COD ∴∠=∠-∠=︒-︒=︒，则905535BOC ∠=︒-︒=度．故答案为：35．例题2．如图，ABC ∆中，90ACB ∠=︒，30A ∠=︒，将ABC ∆绕C 点按逆时针方向旋转α角(090)α︒<<︒得到DEC ∆，设CD 交AB 于F ，连接AD ，当旋转角α度数为，ADF ∆是等腰三角形．旋转中心：O旋转角：∠AOA'=∠BOB'=∠COC'性质：OA=OA'、OB=OB'、OC=OC'旋转中心：B旋转角：∠ABA'=∠CBC'性质：AB=A'B 、CB=C'B 连接AA'、CC'△ABA'∽△CBC'，且均为等腰三角形【解答】解：ABC ∆ 绕C 点按逆时针方向旋转α角(090)α︒<<︒得到DEC ∆，DCA α∴∠=，CD CA =，11(180)9022CDA CAD αα∴∠=∠=︒-=︒-，ADF ∆ 是等腰三角形，30DFA α∠=︒+，①CD CA =，则CDA CAD ∠=∠，当FD FA =，则FDA FAD ∠=∠，这不合题意舍去，②当AF AD =，ADF AFD ∴∠=∠，190302αα∴︒-=︒+，解得40α=︒；③当DF DA =，DFA DAF ∴∠=∠，13090302αα∴︒+=︒--︒，解得20α=︒．故答案为40︒或20︒．【旋转60°】得等边例题3.如图，在直角坐标系中，点A 在y 轴上，△AOE 是等边三角形，点P 为x 轴正半轴上任意一点，连接AP ，将线段AP 绕点A 逆时针60°得到线段AQ ，连接QE 并延长交x 轴于点F .（1）问∠QFP 角度是否发生变化，若不变，请说明理由；（2）若AO =，OP =x ，请表示出点Q 的坐标（用含x 的代数式表示）【解答】（1）不变（2）【旋转90°】构造全等例题4．如图，在平面直角坐标系中，点(,)A a b 为第一象限内一点，且a b <．连结OA ，并以点A 为旋转中心把OA 逆时针转90︒后得线段BA ．若点A 、B 恰好都在同一反比例函数的图象上，则b a的值等于多少？【解答】解：过A 作AE x ⊥轴，过B 作BD AE ⊥，90OAB ∠=︒ ，90OAE BAD ∴∠+∠=︒，90AOE OAE ∠+∠=︒ ，BAD AOE ∴∠=∠，在AOE ∆和BAD ∆中，90AOE BAD AEO BDA AO BA ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩，()AOE BAD AAS ∴∆≅∆，AE BD b ∴==，OE AD a ==，DE AE AD b a ∴=-=-，OE BD a b +=+，则(,)B a b b a +-；A 与B 都在反比例图象上，得到()()ab a b b a =+-，整理得：22b a ab -=，即2(10b b a a--=， △145=+=，∴152b a ±=，点(,)A a b 为第一象限内一点，0a ∴>，0b >，则152b a +=．故答案为152+．【旋转180°】由中心对称得平行四边形例题5．如图所示，抛物线2:(0,0)m y ax b a b =+<>与x 轴于点A 、B （点A 在点B 的左侧），与y 轴交于点C ．将抛物线m 绕点B 旋转180︒，得到新的抛物线n ，它的顶点为1C ，与x 轴的另一个交点为1A ．（1）四边形11AC A C 是什么特殊四边形，请写出结果并说明理由；（2）若四边形11AC A C 为矩形，请求出a ，b 应满足的关系式．【解答】解：（1）当1a =-，1b =时，抛物线m 的解析式为：21y x =-+．令0x =，得：1y =．(0,1)C ∴．令0y =，得：1x =±．(1,0)A ∴-，(1,0)B ，C 与1C 关于点B 中心对称，∴抛物线n 的解析式为：22(2)143y x x x =--=-+；四边形11AC A C 是平行四边形．理由：连接AC ，1AC ，11A C ，C 与1C 、A 与1A 都关于点B 中心对称，1AB BA ∴=，1BC BC =，∴四边形11AC A C 是平行四边形．（2）令0x =，得：y b =．(0,)C b ∴．令0y =，得：20ax b +=，∴x =∴(A B ，∴AB BC ===．要使平行四边形11AC A C 是矩形，必须满足AB BC =，∴=，∴24(b b b a a⨯-=-，3ab ∴=-．a ∴，b 应满足关系式3ab =-．例题6．如图1，抛物线23y ax ax b =-+经过(1,0)A -，(3,2)C 两点，与y 轴交于点D ，与x 轴交于另一点B ．（1）求此抛物线的解析式；（2）如图2，过点(1,1)E -作EF x ⊥轴于点F ，将AEF ∆绕平面内某点旋转180︒后得MNQ ∆（点M ，N ，Q 分别与点A ，E ，F 对应），使点M ，N 在抛物线上，求点M ，N 的坐标．【解答】解：（1）抛物线23y ax ax b =-+过(1,0)A -、(3,2)C ，03a a b ∴=++，299a a b =-+．解得12a =-，2b =，∴抛物线解析式213222y x x =-++．（2）如图2，由题意知，AEF ∆ 绕平面内某点旋转180︒后得MNQ ∆，∴设绕点I 旋转，联结AI ，NI ，MI ，EI ，AI MI = ，NI EI =，∴四边形AEMN 为平行四边形，//AN EM ∴且AN EM =．(1,1)E - 、(1,0)A -，∴设(,)M m n ，则(2,1)N m n -+M 、N 在抛物线上，213222n m m ∴=-++，2131(2)(2)222n m m +=--+-+，解得3m =，2n =．(3,2)M ∴，(1,3)N ．【旋转过后落点问题】例题7．如图，Rt ABC ∆中，已知90C ∠=︒，48B ∠=︒，点D 在边BC 上，2BD CD =，把Rt ABC ∆绕点D 逆时针旋转(0180)m m ︒<<︒度后，如果点B 恰好落在初始Rt ABC ∆的边上，那么m =．【解答】解：当旋转后点B 的对应点B '落在AB 边上，如图1，Rt ABC ∆ 绕点D 逆时针旋转(0180)m m ︒<<︒度得到Rt △A B C '''，DB DB ∴'=，B DB m ∠'=，48DB B B ∴∠'=∠=︒，18084B DB DB B B ∴∠'=︒-∠'-∠=︒，即84m =︒；当点B 的对应点B '落在AB 边上，如图2，Rt ABC ∆ 绕点D 逆时针旋转(0180)m m ︒<<︒度得到Rt △A B C '''，DB DB ∴'=，B DB m ∠'=，2BD CD = ，2DB CD ∴'=，90C ∠=︒ ，30CB D ∴∠'=︒，60CDB ∴∠'=︒，18060120B DB ∴∠'=︒-︒=︒，即120m =︒，综上所述，m 的值为84︒或120︒．故答案为84︒或120︒．例题8．如图，在Rt ACB ∆中，90ACB ∠=︒，点O 在AB 上，且6CA CO ==，1cos 3CAB ∠=，若将ACB ∆绕点A 顺时针旋转得到Rt △AC B ''，且C '落在CO 的延长线上，连接BB '交CO 的延长线于点F ，则BF =．【解答】解：过C 作CD AB ⊥于点D ，CA CO = ，AD DO ∴=，在Rt ACB ∆中，16cos 3AC CAB AB AB∠===，318AB AC ∴==，在Rt ADC ∆中：1cos 3AD CAB AC ∠==，123AD AC ∴==，24AO AD ∴==，18414BO AB AO ∴=-=-=，△AC B ''是由ACB ∆旋转得到，AC AC ∴='，AB AB ='，CAC BAB ∠'=∠'，1(180)2ACC CAC ∠'=︒-∠' ，1(180)2ABB BAB ∠'=︒-∠'，ABB ACC ∴∠'=∠'，∴在CAO ∆和BFO ∆中，BFO CAO ∠=∠，CA CO = ，COA CAO ∴∠=∠，又COA BOF ∠=∠ （对顶角相等），BOF BFO ∴∠=∠，14BF BO ∴==．故答案为：14．例题9．在平面直角坐标系xOy 中，抛物线26(0)y mx mx n m =++>与x 轴交于A ，B 两点（点A 在点B 左侧），顶点为C ，抛物线与y 轴交于点D ，直线BC 交y 轴于E ，且ABC ∆与AEC ∆这两个三角形的面积之比为2:3．（1）求点A 的坐标；（2）将ACO ∆绕点C 顺时针旋转一定角度后，点A 与B 重合，此时点O 的对应点O '恰好也在y 轴上，求抛物线的解析式．【解答】解：（1）如图1，抛物线26(0)y mx mx n m =++>∴对称轴3x =-，当:2:3ABC AEC S S ∆∆=时，:2:1ABC AEB S S ∆∆∴=，过点C 作CF x ⊥轴于F ，:2:1CF OE ∴=易知，BFC BOE ∆∆∽，::2:1BF OB CF OE ∴==，1OB ∴=，2BF =，5OA ∴=，(5,0)A ∴-，(1,0)B -；（2）(1,0)B - ，06m m n ∴=-+，5n m ∴=，(3,4)C m ∴--，如图2，作CF AB ⊥于F ，CP OD ⊥于P ，则四边形CFOP 是矩形，4OP CF m ∴==，3CP OF ==，OP O P '=，28OO OP m'∴==由旋转知，5OA BO '==，在Rt BOO '∆中，1OB =，根据勾股定理得，2285126m =-=，64m ∴=263656424y x x ∴=++【旋转+“恰好”问题】例题10．如图，在直角坐标系中，直线4y =+分别与x 轴、y 轴交于点M 、N ，点A 、B 分别在y 轴、x 轴上，且30B ∠=︒，4AB =，将ABO ∆绕原点O 顺时针转动一周，当AB 与直线MN 平行时点A 的坐标．【另外再可思考，当“AB 所在直线与MN 垂直时点A 的坐标”】【解答】解：①4AB = ，30ABO ∠=︒，122OA AB ∴==，903060BAO ∠=︒-︒=︒，120OAD ∴∠=︒，直线MN 的解析式为43y x =-+，30NMO ∴∠=︒，//AB MN ，30ADO NMD ∴∠=∠=︒，30AOC ∴∠=︒，112AC OA ∴==，OC ∴==∴点A 的坐标为，1)；② 图②中的点A 与图①中的点A 关于原点对称，∴点A 的坐标为：(，1)-，故答案为：，1)、(1)-．例题11．在平面直角坐标系中，已知O 为坐标原点，点(3,0)A ，(0,4)B ，以点A 为旋转中心，把ABO ∆顺时针旋转，得ACD ∆．记旋转角为α．ABO ∠为β．（Ⅰ）如图①，当旋转后点D 恰好落在AB 边上时，求点D 的坐标；（Ⅱ）如图②，当旋转后满足//BC x 轴时，求α与β之间的数量关系：（Ⅲ）当旋转后满足AOD β∠=时，求直线CD 的解析式（直接写出结果即可）．【解答】解：（1）点(3,0)A ，(0,4)B ，得3OA =，4OB =，∴在Rt AOB ∆中，由勾股定理，得225AB OA OB =+=，根据题意，有3DA OA ==．如图①，过点D 作DM x ⊥轴于点M ，则//MD OB ，ADM ABO ∴∆∆∽．有AD AM DM AB AO BO==，得39355AD AM AO AB ==⨯= ，65OM ∴=，∴125MD =，∴点D 的坐标为6(5，12)5．（2）如图②，由已知，得CAB α∠=，AC AB =，ABC ACB ∴∠=∠，∴在ABC ∆中，1802ABC α∴=︒-∠，//BC x 轴，得90OBC ∠=︒，9090ABC ABO β∴∠=︒-∠=︒-，2αβ∴=；（3）若顺时针旋转，如图，过点D 作DE OA ⊥于E ，过点C 作CF OA ⊥于F ，AOD ABO β∠=∠= ，3tan 4DE AOD OE ∴∠==，设3DE x =，4OE x =，则43AE x =-，在Rt ADE ∆中，222AD AE DE =+，2299(43)x x ∴=+-，2425x ∴=，96(25D ∴，72)25，∴直线AD 的解析式为：247277y x =-，直线CD 与直线AD 垂直，且过点D ，∴设724y x b =-+，把96(25D ，72)25代入得，72796252425b =-⨯+，解得4b =，互相垂直的两条直线的斜率的积等于1-，∴直线CD 的解析式为7424y x =-+．同理可得直线CD的另一个解析式为7424y x=-．【巩固练习】1．如图，在等边ABC ∆中，D 是边AC 上一点，连接BD ．将BCD ∆绕点B 逆时针旋转60︒得到BAE ∆，连接ED ．若10BC =，9BD =，则AED ∆的周长是．2.如图一段抛物线：(3)(03)y x x x =--，记为1C ，它与x 轴交于点O 和1A ；将1C 绕1A 旋转180︒得到2C ，交x 轴于2A ；将2C 绕2A 旋转180︒得到3C ，交x 轴于3A ，如此进行下去，直至得到10C ，若点(28,)P m 在第10段抛物线10C 上，则m 的值为.3．如图，Rt ABC ∆中，90C ∠=︒，30ABC ∠=︒，2AC =，ABC ∆绕点C 顺时针旋转得△11A B C ，当1A 落在AB 边上时，连接1B B ，取1BB 的中点D ，连接1A D ，则1A D 的长度是．4．如图，AOB ∆中，90AOB ∠=︒，3AO =，6BO =，AOB ∆绕点O 逆时针旋转到△A OB ''处，此时线段A B ''与BO 的交点E 为BO 的中点，求线段B E '的值．5．如图，在直角坐标系中，直线14:83l y x =+与y 轴交于点A ，与x 轴交于点B ，将直线1l 绕着点A 顺时针旋转45︒得到2l ．求2l 的函数表达式．6．如图，四边形ABCO 是平行四边形，2OA =，6AB =，点C 在x 轴的负半轴上，将ABCO 绕点A 逆时针旋转得到ADEF ，AD 经过点O ，点F 恰好落在x 轴的正半轴上，若点D 在反比例函数(0)k y x x =<的图象上，则k 的值为．7.在平面直角坐标系中，O 为坐标原点，点A 的坐标为(8,0)-，直线BC 经过点(8,6)B -，(0,6)C ，将四边形OABC 绕点O 按顺时针方向旋转a 度得到四边形OA B C '''，此时直线OA '、直线B C ''分别与直线BC 相交于点P 、Q ．在四边形OABC 旋转过程中，若使12BP BQ =？则点P 的坐标为．8．如图，在BDE ∆中，90BDE ∠=︒，BD =，点D 的坐标为(5,0)，15BDO ∠=︒，将BDE∆旋转到ABC ∆的位置，点C 在BD 上，则旋转中心的坐标为．9．已知正方形ABCD 的边长为5，E 在BC 边上运动，DE 的中点G ，EG 绕E 顺时针旋转90︒得EF ，问CE =时，A 、C 、F 在一条直线上．10．如图，一次函数1(0)2y x m m =-+>的图象与x 轴、y 轴分别交于点A 、B ，点C 在线段OA 上，点C 的横坐标为n ，点D 在线段AB 上，且2AD BD =，将ACD ∆绕点D 旋转180︒后得到△11A C D ．（1）若点1C 恰好落在y 轴上，试求n m的值；（2）当4n =时，若△11A C D 被y 轴分得两部分图形的面积比为3:5，求该一次函数的解析式．11．在ABC ∆中，5AB AC ==，3cos 5ABC ∠=，将ABC ∆绕点C 顺时针旋转，得到△11A B C ．（1）如图①，当点1B 在线段BA 延长线上时．①求证：11//BB CA ；②求△1AB C 的面积；（2）如图②，点E 是BC 边的中点，点F 为线段AB 上的动点，在ABC 绕点C 顺时针旋转过程中，点F 的对应点是1F ，求线段1EF 长度的最大值与最小值的差．12．如图（1），在ABC=，动点P在线段AC上以5/cm s的速度从=，3BC cmAB cmC∆中，90∠=︒，5点A运动到点C，过点P作PD AB'，设点P的⊥于点D，将APD∆绕PD的中点旋转180︒得到△A DP 运动时间为()x s．（1）当点A'落在边BC上时，求x的值；（2）在动点P从点A运动到点C过程中，当x为何值时，△A BC'是以A B'为腰的等腰三角形；（3）如图（2），另有一动点Q与点P同时出发，在线段BC上以5/cm s的速度从点B运动到点C，过点Q 作QE AB⊥于点E，将BQE'，连结A B''，当直线A B''与ABC∆绕QE的中点旋转180︒得到△B EQ∆的一边垂直时，求线段A B''的长．13．如图，(0,2)A ，(1,0)B ，点C 为线段AB 的中点，将线段BA 绕点B 按顺时针方向旋转90︒得到线段BD ，抛物线2(0)y ax bx c a =++≠经过点D ．（1）若该抛物线经过原点O ，且13a =-，求该抛物线的解析式；（2）在（1）的条件下，点(,)P m n 在抛物线上，且POB ∠锐角，满足90POB BCD ∠+∠<︒，求m 的取值范围．14．如图1，抛物线210y ax ax c =-+经过ABC ∆的三个顶点，已知//BC x 轴，点A 在x 轴上，点C 在y 轴上35OA BC =，且AC BC =．（1）求抛物线的解析式；（2）如图2，将AOC ∆沿x 轴对折得到1AOC ∆，再将1AOC ∆绕平面内某点旋转180︒后得△112(A O C A ，O ，1C 分别与点1A ，1O ，2C 对应）使点1A 、2C 在抛物线_P 上，求点1A 、2C 的坐标；15．点P为图①中抛物线22m>上任一点，将抛物线绕顶点G逆时针旋转90︒=-+为常数，0)y x mx m m2(后得到的新图象与y轴交于A、B两点（点A在点B的上方），点Q为点P旋转后的对应点．（1）若点Q的坐标为(-，求该抛物线的函数关系式；（2）如图②，若原抛物线恰好也经过A点，点Q在第一象限内，是否存在这样的点P使得AGQ∆是以AG 为底的等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由．参考答案1.【解答】解：ABC ∆ 是等边三角形，10AC AB BC ∴===，BAE ∆ 由BCD ∆逆时针旋旋转60︒得出，AE CD ∴=，BD BE =，60EBD ∠=︒，10AE AD AD CD AC ∴+=+==，60EBD ∠=︒ ，BE BD =，BDE ∴∆是等边三角形，9DE BD ∴==，AED ∴∆的周长19AE AD DE AC BD =++=+=．故答案为：19．2.【解答】解：令0y =，则(3)0x x --=，解得10x =，23x =，1(3,0)A ∴，由图可知，抛物线10C 在x 轴下方，相当于抛物线1C 向右平移3927⨯=个单位，再沿x 轴翻折得到，∴抛物线10C 的解析式为(27)(273)(27)(30)y x x x x =---=--，(28,)P m 在第10段抛物线10C 上，(2827)(2830)2m ∴=--=-．3.【解答】解：90ACB ∠=︒ ，30ABC ∠=︒，2AC =，9060A ABC ∴∠=︒-∠=︒，4AB =，BC =，1CA CA = ，1ACA ∴∆是等边三角形，112AA AC BA ===，1160BCB ACA ∴∠=∠=︒，1CB CB = ，1BCB ∴∆是等边三角形，1BB ∴=，12BA =，1190A BB ∠=︒，1BD DB ∴==，1A D ∴==，．4.【解答】解：90AOB ∠=︒ ，3AO =，6BO =，AB ∴==AOB ∆ 绕顶点O 逆时针旋转到△A OB ''处，3AO A O ∴='=，A B AB ''==，点E 为BO 的中点，116322OE BO ∴==⨯=，OE A O ∴='，过点O 作OF A B ⊥''于F ，1362A OB S OF ''=⨯=⨯⨯ ，解得655OF =，在Rt EOF ∆中，5EF ==，OE A O =' ，OF A B ⊥''，22A E EF ∴'==（等腰三角形三线合一），B E A B A E ∴'=''-'=5.【解答】解：直线483y x =+与y 轴交于点A ，与x 轴交于点B ，(0,8)A ∴、(6,0)B -，如图2，过点B 做BC AB ⊥交直线2l 于点C ，过点C 作CD x ⊥轴，在BDC ∆和AOB ∆中，CBD BAO CDB AOB BC BA ∠=∠⎧⎪∠=∠⎨⎪=⎩()BDC AOB AAS ∴∆≅∆，6CD BO ∴==，8BD AO ==，6814OD OB BD ∴=+=+=，C ∴点坐标为(14,6)-，设2l 的解析式为y kx b =+，将A ，C 点坐标代入，得1468k b b -+=⎧⎨=⎩，解得178k b ⎧=⎪⎨⎪=⎩，2l ∴的函数表达式为187y x =+；6.【解答】解：如图所示：过点D 作DM x ⊥轴于点M ，由题意可得：BAO OAF ∠=∠，AO AF =，//AB OC ，则BAO AOF AFO OAF ∠=∠=∠=∠，故60AOF DOM ∠=︒=∠，624OD AD OA AB OA =-=-=-= ，2MO ∴=，MD =，(2,D ∴--，2(k ∴=-⨯-=．故答案为：．7.【解答】解：存在这样的点P 和点Q ，使12BP BQ =．理由如下：过点Q 画QH OA ⊥'于H ，连接OQ ，则QH OC OC ='=，12POQ S PQ OC ∆= ，12POQ S OP QH ∆= ，PQ OP ∴=．设BP x =，12BP BQ =，2BQ x ∴=，如图4，当点P 在点B 左侧时，3OP PQ BQ BP x ==+=，在Rt PCO ∆中，222(8)6(3)x x ++=，解得13612x =+，23612x =-，（不符实际，舍去）．3692PC BC BP ∴=+=+，1(92P ∴--，6)，如图5，当点P 在点B 右侧时，OP PQ BQ BP x ∴==-=，8PC x =-．在Rt PCO ∆中，222(8)6x x -+=，解得254x =，257844PC BC BP ∴=-=-=，27(4P ∴-，6)，综上可知，存在点136(92P --，6)，27(4P -，6)使12BP BQ =．8.【解答】解：如图，AB 与BD 的垂直平分线的交点即为旋转中心P ，连接PD ，过P 作PF x ⊥轴于F ．点C 在BD 上，∴点P 到AB 、BD 的距离相等，都是12BD ，即12⨯=45PDB ∴∠=︒，4PD ==，15BDO ∠=︒ ，451560PDO ∴∠=︒+︒=︒，30DPF ∴∠=︒，114222DF PD ∴==⨯=，点D 的坐标是(5,0)，523OF OD DF ∴=-=-=，由勾股定理得，PF ===∴旋转中心的坐标为(3，．故答案为：(3，．9.【解答】解：过F 作FN BC ⊥，交BC 延长线于N 点，连接AC ，90DCE ENF ∠=∠=︒ ，90DEC NEF ∠+∠=︒，90NEF EFN ∠+∠=︒，DEC EFN ∴∠=∠，Rt FNE Rt ECD ∴∆∆∽，DE 的中点G ，EG 绕E 顺时针旋转90︒得EF ，:2:1DE EF ∴=，:::2:1CE FN DE EF DC NE ∴===，2CE NF ∴=，1522NE CD ==．45ACB ∠=︒ ，∴当45NCF ∠=︒时，A 、C 、F 在一条直线上．则CNF ∆是等腰直角三角形，CN NF ∴=，2CE CN ∴=，22553323CE NE ∴==⨯=．53CE ∴=时，A 、C 、F 在一条直线上．故答案为：53．10.【解答】解：（1）由题意，得(0,)B m ，(2,0)A m ，如图，过点D 作x 轴的垂线，交x 轴于点E ，交直线11A C 于点F ，易知：23DE m =，2(3D m ，2)3m ，14(3C m n -，4)3m ，∴403m n -=，∴43n m =；（2）由（1）得，当3m >时，点1C 在y 轴右侧；当23m <<时，点1C 在y 轴左侧．①当3m >时，设11A C 与y 轴交于点P ，连接1C B ，由△11A C D 被y 轴分得两部分图形的面积比为3:5，S ∴△1:BA P S △13:1BC P =，11:3A P C P ∴=，∴，185m ∴=，11825y x ∴=-+；②当23m <<时，同理可得：11827y x =-+；综上所述，11827y x =-+或11825y x =-+．11.【解答】解：（1）①证明：AB AC = ，1B C BC =，1AB C B ∴∠=∠，B ACB ∠=∠，1AB C ACB ∠=∠ （旋转角相等），111B CA AB C ∴∠=∠，11//BB CA ∴；②过A 作AF BC ⊥于F ，过C 作CE AB ⊥于E ，如图①：AB AC = ，AF BC ⊥，BF CF ∴=，3cos 5ABC ∠=，5AB =，3BF ∴=，6BC ∴=，16B C BC ∴==，1318655BE B E ∴==⨯=，1365BB ∴=，424655CE =⨯=，13611555AB ∴=-=，∴△1AB C 的面积为：1112413225525⨯⨯=；（2）如图2，过C 作CF AB ⊥于F ，以C 为圆心CF 为半径画圆交BC 于1F ，1EF 有最小值，此时在Rt BFC ∆中，245CF =，1245CF ∴=，1EF ∴的最小值为249355-=；如图，以C 为圆心BC 为半径画圆交BC 的延长线于1F ，1EF 有最大值；此时11369EF EC CF =+=+=，∴线段1EF 的最大值与最小值的差为936955-=．12.【解答】解：（1）如图1，在ABC ∆中，90C ∠=︒，5AB cm =，3BC cm =，4AC cm ∴=，当点A '落在边BC 上时，由题意得，四边形APA D '为平行四边形，PD AB ⊥ ，90ADP C ∴∠=∠=︒，APD ABC ∴∆∆∽，5AP x = ，4A P AD x ∴'==，45PC x =-，A PD ADP ∠'=∠ ，//A P AB ∴'，∴△A PC ABC '∆∽，∴PC A P AC AB '=，即45445x x -=，解得：2041x =，∴当点A '落在边BC 上时，2041x =；（2）当A B BC '=时，222(58)(3)3x x -+=，解得：4012373x ±=．45x ，∴4073x -=；当A B A C '='时，58x =．（3）Ⅰ、当A B AB ''⊥时，如图6，DH PA AD '∴==，HE B Q EB ='=，2224235AB AD EB x x =+=⨯+⨯= ，514x ∴=，514A B QE PD x ∴''=-==；Ⅱ、当A B BC ''⊥时，如图7，5B E x ∴'=，57DE x =-，53cos 575x B x ∴==-，1546x ∴=，2523A B B D A D ∴''='-'=；Ⅲ、当A B AC ''⊥时，如图8，由（1）有，2041x =，12sin 41A B PA A ∴''='=；当A B AB ''⊥时，514x =，514A B ''=；当A B BC ''⊥时，1546x =，2546A B ''=；当A B AC ''⊥时，2053x =，2553A B ''=．13.【解答】解：（1）过点D 作DF x ⊥轴，垂足为F ．90ABD ∠=︒ ，90DBF ABO ∴∠+∠=︒．又90OAB ABO ∠+∠=︒ ，DBF OAB ∴∠=∠．由旋转的性质可知AB BD =．在AOB ∆和BFD ∆中DBF OAB AOB BFD AB BD ∠=∠⎧⎪∠=∠⎨⎪=⎩，AOB BFD ∴∆≅∆．1DF OB ∴==，2AO BF ==．(3,1)D ∴．把点D 和点O 的坐标代入213y x bx c =-++得：1300b c c -++=⎧⎨=⎩，解得：43b =，0c =．∴抛物线的解析式为21433y x x =-+．（2）如图2所示：点(0,2)A ，(1,0)B ，C 为线段AB 的中点，1(2C ∴，1)．C 、D 两点的纵坐标为1，//CD x ∴轴．BCD ABD ∴∠=∠．∴当POB BAO ∠=∠时，恰好90POB BCD ∠+∠=︒．设点P 的坐标为214(,)33m m m -+．当点P 在x 轴上且POB BAO ∠=∠时，则1tan tan 2POB BAO ∠=∠=，即2141332m m m -+=，解得：52m =或0m =（舍去）．当点P 位于x 轴的下方，点P '处时，且POB BAO ∠=∠时，则1tan tan 2POB BAO ∠=∠=，即2141332m m m -=，解得：112m =或0m =（舍去）．POB ∠ 为锐角，4m ∴≠．由图形可知：当点P 在抛物线上P 与P '之间移动时，90POB BCD ∠+∠<︒．m ∴的取值范围是：51122m <<且4m ≠．14.【解答】解：（1）35OA BC = ，AC BC =∴设3OA k =，5(0)AC BC k k ==>4OC k∴= 当0x =时，210y ax ax c c=-+=(0,)C c ∴，即4OC c k==4c k ∴=3(4c A ∴-，50)(4c B ，)c 抛物线经过点A 、B ∴2233()10()04455(1044c c a a c c c a a c c ⎧---+=⎪⎪⎨⎪-+=⎪⎩解得：1128a c ⎧=-⎪⎨⎪=⎩∴抛物线解析式为：2158126y x x =-++（2）如图1，1AOC ∆旋转后得到△112A O C 的位置如图所示116O A OA ∴==，128O C OC ==，11//O A x 轴，12O C x ⊥轴设2C 坐标为215(,8)126t t t -++，则2115(6,)126A t t t +-+221515(6)(6)8126126t t t t ∴-++++=-+解得：10t =1A ∴坐标为(16,0)，2C 坐标为(10,8)．15.【解答】解：（1）对于222y x mx m =-+，当0y =时，x m =，OG m ∴=，点Q 为点P 绕顶点G 逆时针旋转90︒后的对应点，P m ∴，2)m +，把P m +，2)m +代入222y x mx m =-+中，得222)2)m m m m m +=-+，4m ∴=，∴该抛物线的函数关系式为；2816y x x =-+；（2）存在，点Q 在第一象限内，AQ GQ =，如图2中，由题意可知OA OG =，∴m =，1m ∴=，∴点(0,1)A ，点A 的对应点(2,1)C ，(1,0)G ，∴直线CG 解析式为1y x =-，线段CG 的中垂线MN 解析式为2y x =-+，由2221y x y x x =-+⎧⎨=-+⎩解得15232x y ⎧=⎪⎪⎨⎪=⎪⎩或15232x y ⎧=⎪⎪⎨⎪=⎪⎩，点P 在第一象限，∴点P坐标1(2+，32-．。

初中数学竞赛中考讲义之几何三大变换之翻折

第30讲几何三大变换之翻折翻折的性质（轴对称的性质）如图，将△ABC 沿着DE 翻折，使得点A 落在BC 的点F 处结论有：①ADE FDE ∆≅∆（即AD =DF ，AE =EF ，∠A =∠DFE ，∠ADE =∠FDE ，∠AED =∠FED ）②DE 垂直平分AF函数的对称变换①一次函数y kx b=+关于x 轴对称后的解析式：y kx b=--关于y 轴对称后的解析式：y kx b=-+②二次函数2y ax bx c=++关于x 轴对称后的解析式：2y ax bx c=---关于y 轴对称后的解析式：2y ax bx c=-+【例题讲解】例题1.如图，ABC ∆中，AB AC =，54BAC ∠=︒，BAC ∠的平分线与AB 的垂直平分线交于点O ，将C ∠沿(EF E 在BC 上，F 在AC 上）折叠，点C 与点O 恰好重合，则OEC ∠的度数是______解：如图，连接OB 、OC ，54BAC ∠=︒ ，AO 为BAC ∠的平分线，11542722BAO BAC ∴∠=∠=⨯︒=︒，又AB AC = ，11(180)(18054)6322ABC BAC ∴∠=︒-∠=︒-︒=︒，DO 是AB 的垂直平分线，OA OB ∴=，27ABO BAO ∴∠=∠=︒，632736OBC ABC ABO ∴∠=∠-∠=︒-︒=︒，AO 为BAC ∠的平分线，AB AC =，()AOB AOC SAS ∴∆≅∆，OB OC ∴=，∴点O 在BC 的垂直平分线上，又DO 是AB 的垂直平分线，∴点O 是ABC ∆的外心，36OCB OBC ∴∠=∠=︒，将C ∠沿(EF E 在BC 上，F 在AC 上）折叠，点C 与点O 恰好重合，OE CE ∴=，36COE OCB ∴∠=∠=︒，在OCE ∆中，1801803636108OEC COE OCB ∠=︒-∠-∠=︒-︒-︒=︒，故选：B ．例题2.如图，将边长为6cm 的正方形ABCD 折叠，使点D 落在AB 边的中点E 处，折痕为与边AD 、BC 交于点F 、H ，点C 落在Q 处，EQ 与BC 交于点G .（1）尺规作图作出折痕FH ；（2）求折痕FH 的长；（3）求△EBG 的周长；（4）若将题目中的“点E 为AB 中点”改为“点E 为AB 上任意一点”，其它条件不变，则△EBG 的周长是否发生变化，若不变，请求出该值，若发生变化，请说明理由.例题3、如图，矩形ABCD 中，8AB =，6BC =，P 为AD 上一点，将ABP ∆沿BP 翻折至EBP ∆，PE 与CD 相交于点O ，且OE OD =，则AP 的长为．解：四边形ABCD 是矩形，90D A C ∴∠=∠=∠=︒，6AD BC ==，8CD AB ==，由折叠的性质可知ABP EBP ∆≅∆，EP AP ∴=，90E A ∠=∠=︒，8BE AB ==，在ODP ∆和OEG ∆中，DOP EOG OD OE D E ∠=∠⎧⎪=⎨⎪∠=∠⎩，()ODP OEG ASA ∴∆≅∆，OP OG ∴=，PD GE =，DG EP ∴=，设AP EP x ==，则6PD GE x ==-，DG x =，8CG x ∴=-，8(6)2BG x x =--=+，根据勾股定理得：222BC CG BG +=，即2226(8)(2)x x +-=+，解得： 4.8x =，4.8AP ∴=，故答案为：4.8．例题4.如图1，在矩形纸片ABCD 中，AB =，10AD =，点E 是CD 中点，将这张纸片依次折叠两次；第一次折叠纸片使点A 与点E 重合，如图2，折痕为MN ，连接ME 、NE ；第二次折叠纸片使点N 与点E 重合，如图3，点B 落到B '处，折痕为HG ，连接HE ，则tan EHG ∠=________．解：如图2中，作NF CD ⊥于F ．设DM x =，则10AM EM x ==-，DE EC = ，AB CD ==，12DE CD ∴==在RT DEM ∆中，222DM DE EM += ，222(10)x x ∴+=-，解得 2.6x =，2.6DM ∴=，7.4AM EM ==，90DEM NEF ∠+∠=︒ ，90NEF ENF ∠+∠=︒，DEM ENF ∴∠=∠，90D EFN ∠=∠=︒ ，DME FEN ∴∆∆∽，∴DE EM FN EN =，∴7.4EN=，EN ∴=AN EN ∴==tanAN AMN AM ∴∠==如图3中，ME EN ⊥ ，HG EN ⊥，//EM GH ∴，NME NHG ∴∠=∠，NME AMN ∠=∠ ，EHG NHG ∠=∠，AMN EHG ∴∠=∠，tan tanEHG AMN ∴∠=∠=方法二，tan tan EN BC EHG EMN EM DE ∠=∠==．故答案为例5.如图，已知ABCD 的三个顶点(,0)A n 、(,0)B m 、(0D ，2)(0)n m n >>，作ABCD 关于直线AD 的对称图形11AB C D（1）若3m =，试求四边形11CC B B 面积S 的最大值；（2）若点1B 恰好落在y 轴上，试求n m 的值．解：（1）如图1，ABCD 与四边形11AB C D 关于直线AD 对称，∴四边形11AB C D 是平行四边形，1CC EF ⊥，1BB EF ⊥，11////BC AD B C ∴，11//CC BB ，∴四边形BCEF 、11B C EF 是平行四边形，1111BCEF BCDA B C DA B C EF S S S S ∴=== ，112BCC B BCDA S S ∴= ．(,0)A n 、(,0)B m 、(0,2)D n 、3m =，3AB m n n ∴=-=-，2OD n =，()()223932232(22BCDA S AB OD n n n n n ∴=⋅=-⋅=--=--+ ，211324(92BCC B BCDA S S n ∴==--+ ．40-< ，∴当32n =时，11BCC B S 最大值为9；（2）当点1B 恰好落在y 轴上，如图2，1DF BB ⊥ ，1DB OB ⊥，1190B DF DB F ∴∠+∠=︒，1190B BO OB B ∠+∠=︒，11B DF OBB ∴∠=∠．190DOA BOB ∠=∠=︒ ，AOD ∴∆∽△1B OB ，∴1OB OA OD OB =，∴12OB n n m=，12m OB ∴=．由轴对称的性质可得1AB AB m n ==-．在1Rt AOB ∆中，222(()2m n m n +=-，整理得2380m mn -=．0m > ，380m n ∴-=，∴38n m =．例题6.如图，在平面直角坐标系xOy 中，矩形OABC 的边OA 、OC 分别在y 轴和x 轴的正半轴上，D 为边AB 的中点，一抛物线22(0)y x mx m m =-++>经过点A 、D（1）求点A 、D 的坐标（用含m 的式子表示）；（2）把OAD ∆沿直线OD 折叠后点A 落在点A '处，连接OA '并延长与线段BC 的延长线交于点E ，①若抛物线经过点E ，求抛物线的解析式；②若抛物线与线段CE 相交，直接写出抛物线的顶点P 到达最高位置时的坐标：解：（1）当0x =时，y m =，(0,)A m ∴，当y m =时，0x =或2m(2,)D m m ∴；（2）①如图，设A D '与x 轴交于点Q ，过点A '作A N x '⊥轴于点N ．把OAD ∆沿直线OD 折叠后点A 落在点A '处，OAD ∴∆≅△OA D '，OA OA m ='=，2AD A D m ='=，90OAD OA D ∠=∠'=︒，ADO A DO ∠=∠'，矩形OABC 中，//AD OC ，ADO DOQ ∴∠=∠，A DO DOQ ∴∠'=∠，DQ OQ ∴=．设DQ OQ x ==，则2A Q m x '=-，在Rt △OA Q '中，222OA A Q OQ '+'= ，222(2)m m x x ∴+-=，解得54x m =， 1122OA Q S OQ A N OA A Q '='='' ，334554m m A N m m ∴'==，45ON m ∴==，A ∴'点坐标为4(5m ，3)5m -，易求直线OA '的解析式为34y x =-，当4x m =时，3434y m m =-⨯=-，E ∴点坐标为(4,3)m m -．代入22(0)y x mx m m =-++>得0m =（舍)，12m =，∴抛物线的解析式为：212y x x =-++．②当4x m =时，2222(4)248x mx m m m m m m m -++=-++=-+ ，即抛物线l 与直线CE 的交点为2(4,8)m m m -+，抛物线l 与线段CE 相交，2380m m m ∴--+，0m > ，3810m ∴--+解得：1182m ，2222()y x mx m x m m m =-++=--++ ，∴当x m =时，y 有最大值2m m +，又2211()24m m m +=+- ，∴当1182m 时，2m m +随m 的增大而增大，∴当12m =时，顶点P 到达最高位置，22113(224m m +=+=，∴抛物线顶点P 到达最高位置时的坐标为1(2，3)4．【巩固练习】1、如图，在矩形ABCD 中，点E 为边CD 上一点，沿AE 折叠，点D 恰好落在BC 边上的F 点处，若3AB =，5BC =，则tan EFC ∠的值为________.2.如图，先将一平行四边形纸片ABCD 沿AE ，EF 折叠，使点E ，B '，C '在同一直线上，再将折叠的纸片沿EG 折叠，使AE 落在EF 上，则AEG ∠=度．3、点E、F 分别在一张长方形纸条ABCD 的边AD 、BC 上，将这张纸条沿着直线EF 对折后如图，BF 与DE 交于点G ，长方形纸条的宽AB=2cm ，那么这张纸条对折后的重叠部分的面积的GEF S ∆最小值为_____________。

初二奥数之几何变换

2020年数学竞赛初二奥数之几何变换专题29 几何变换阅读与思考几何变换是指把一个几何图形1F 变换成另一个几何图形2F 的方法，若仅改变图形的位置，而不改变图形的形状和大小，这种变换称为合同变换，平移、对称、旋转是常见的合同变换.1.平移变换如图1，如果把图形1F 上的各点都按一定方向移动一定距离得到图形2F 后，则由1F 到2F 的变换叫平移变换.平移变换前后的对应线段相等且平行，对应角的两边分别平行且方向一致. 2.对称变换如图2，将平面图形1F 变换到与它成轴对称的图形2F ，这样的几何变换就叫做关于直线l （对称轴）的对称变换.对称变换前后的对应线段相等，对应角相等，其对称轴是连结各对应点线段的垂直平分线. 3.旋转变换如图3，将平面图形1F 绕这一平面内一定点M 旋转一个定角α，得到图形2F ，这样的变换叫旋转变换，M 叫旋转中心，α叫旋转角.旋转变换前后的图形是全等的，对应点到旋转中心的距离相等，对应线段的夹角等于旋转角.例题与求解【例l 】如图，∠AOB =045，角内有点P ，PO =10，在角的两边上有两点Q ，R （均不同于O ），则△PQR 的周长的最小值为_______________. （黄冈市竞赛试题）解题思路：作P 点关于OA ，OB 的对称点，确定Q ，R 的位置，化折线为直线，求△PQR 的最小值.l图3图2图1F 1F 2O【例2】如图，P 是等边△ABC 的内部一点，∠APB ，∠BPC ，∠CP A 的大小之比是5:6:7，则以P A ，PB ，PC 为边的三角形的三个角的大小之比（从小到大）是（）A. 2:3:4B. 3:4:5C. 4:5:6D.不能确定（全国通讯赛试题）解题思路：解本例的关键是如何构造以P A ，PB ，PC 为边的三角形，若把△P AB ，△PBC ，△PCA 中的任一个，绕一个顶点旋转060，就可以把P A ，PB ，PC 有效地集中在一起.【例3】如图，在△ABC 中，AD ⊥BC 于D ，∠B =2∠C ，求证：AB+BD=CD.（天津市竞赛试题）解题思路：用截长法或补短法证明，实质都利用AD 翻折造全等.【例4】如图，六边形ABCDEF 中，AB ∥DE ，BC ∥FE ，CD ∥AF ，对边之差BC -FE=ED -AB=AF -CD ＞0，求证：该六边形的各角都相等.（全俄数学奥林匹克竞赛试题）解题思路：设法能将复杂的条件BC -FE=ED -AB=AF -CD ＞0，用一个基本图形表示，题设条件有平行条件，考虑实施平移变换.BCC【例5】已知Rt △ABC 中，AC=BC ，∠ACB =090，∠MCN =045 （1）如图1，当M 、N 在AB 上时，求证：222MN AM BN =+（2）如图2，将∠MCN 绕C 点旋转，当M 在BA 的延长线时，上述结论是否成立？若成立，请证明；若不成立，请说明理由.（天津市中考试题）解题思路：222MN AM BN =+符合勾股定理的形式，需转化为直角三角形可将△ACM 沿直线CM 对折，得△DCM . 连DN ，只需证DN=BN ，∠MDN =090；或将△ACM (或△BCM )旋转.【例6】如图，∠DAC=012，∠DBC=024，∠CAB=036，∠ABD=048，求∠DCA 的度数.（日本算术奥林匹克试题）解题思路：已知角的度数都是12的倍数，0362460+=，这使我们想到构作正三角形.A图2图1MA B B能力训练1.在如图所示的单位正方形网格中，将△ABC 向右平移3个单位后得到△A B C '''，则BA A '∠的度数是_______.（泰安市中考试题）(第1题) （第2题）（第3题）2.如图，P 是等边△ABC 内一点，P A =6，PB =8，PC =10，则∠APB =_________.3.如图，直线143y x =与双曲线2(0)k y k x =>交于点A ，将直线143y x =向右平移92个单位后，与双曲线2k y x =交于点B ，与x 轴交于点C . 若2AOBC=，则k =______________. （武汉市中考试题） 4.如图，△ABC 中，∠BAC =045，AD ⊥BC ，DB =3，DC =2，则△ABC 的面积是___________. 5.如图，P 为正方形内一点，若::1:2:3PA PB PC =，则∠APB 的度数是（）. A. 0120 B. 0135 C. 0145 D. 01506.如图，边长为2的正方形ABCD 的对角线交于点O ，把边BA 、CD 分别绕点B 、C 同时逆时针旋转060，得四边形A BCD '',下列结论：①四边形A BCD ''为菱形；②12ABCD A BCD S S ''=正方形四边形；③线段OD '的长1. 其中正确的结论有（）.A. 0个B. 1个C. 2个D. 3个B（第6题）（第5题）（第4题）ACB ABDADA'7. 如图，A ，B 两个电话机离电话线l 的距离分别是3米，5米，CD =6米，若由L 上一点分别向A ，B 连电话线，最短为（）.A. 11米B. 10米C. 9米D. 8米8. 如图，在△ABC 中，∠BAC =0120，P 是△ABC 内一点，若记x PA PB PC =++，y AB AC =+，则（）.A. x y <B. x y =C. x y >D. x 与y 的大小关系不确定9. 如图，已知D 是△ABC 中BC 边的中点，过D 作DE ⊥DF ，分别交AB 于E ，交AC 于F ，求证：BE CF EF +>.（天津市竞赛试题）10.如图，△ABC ，△A B C '''其各边交成六边形DEFGHK ，且EF ∥KH ，GH ∥DE ，FG ∥KD ，0KH EF FG KD DE GH -=-=->. 求证：△ABC ，△A B C '''均为为正三角形.（“缙云杯”邀请赛试题）l第8题图第7题图CBBA B C A'11.如图，已知△ABC 中，AB=AC ，P ，Q 分别为AC ，AB 上的点，且AP=PQ=QB=BC ，求∠PCQ .（北京市竞赛试题）12.如图，已知在平面直角坐标系中，A ，B 两点的坐标分别为(2,3)A -，(4,1)B -. (1) 若(,0)P x 是x 轴上的一个动点，当△P AB 的周长最短时，求x 的值；（2）若(,0),(3,0)C a D a +是x 轴上的两个动点，当四边形ABCD 的周长最短时，求a 的值；（3）设M ，N 分别为x 轴，y 轴上的动点，问：是否存在这样的点(,0)M m 和(0,)N n ，使四边形ABMN 的周长最短？若存在，求出,m n 的值；若不存在，请说明理由.（浙江省湖州市中考试题）13.如图，梯形ABCD 中，AD ∥BC ，分别以两腰AB ，CD 为边向两边作正方形ABGE 和正方形DCHF ，设线段AD 的垂直平分线l 交线段EF 于点M ，EP ⊥l 于P ，FQ ⊥l 于Q ，求证：EP=FQ.（全国初中数学联赛试题）B14.如图所示，已知Rt △ABC 中，AB=BC ，在Rt △ADE 中，AD=DE ，连结EC ，取EC 中点M ，连结DM 和BM .（1）若点D 在边AC 上，点E 在边AB 上且与点B 不重合，如图1，求证：BM=DM ，且BM ⊥DM ；（2）如图2中的△ADE 绕点A 逆时针旋转小于045的角，那么（1）中的结论是否仍成立？如果不成立，请举出反例；如果成立，请给予证明.（广州市中考试题）15.如图，在△ABC 中，∠BAC =045，AD ⊥BC 于D ，若BD =3，CD =2，求△ABC 的面积.（山东省竞赛试题）图2图1ACBBCAB专题29 几何变换例1 210例2 A 提示：将ABP ∆绕B 点顺时针旋转︒60得CBD ∆，则ABP ∆≌CBD ∆，BPD ∆为等边三角形. 例3 提示:延长BD 至E ,使AB BE =,连接AE ,E ABC ∠=∠2.例4 提示:过E 作ER ∥,CD 过C 作CP ∥AB ,过A 作AQ ∥EF ,则PQR ∆为等边三角形.例5 (1)如图a ，由DCM ∆≌ACM ∆则AM DM AC DC ==,,,ACM DCM ∠=∠A CDM ∠=∠.又由CB CA =，得CB CD =.由DCM DCN ∠-︒=∠45,得BCN DCN ∠=∠,又CN CN =,则DCN ∆≌BCN ∆,有BN DN =,B CDN ∠=∠, ∴︒=∠+∠=∠+∠=∠90B A CDN CDM MDN ∴222DN MD MN +=即222BN AM MN +=(2)关系式: 222BN AM MN +=仍成立,方法同上,如图b 例6 如图,作ACD ∆关于AD 所在直线的轴对称图形,APD 则,12,60,APD ACD PAD CAD PAB AP AB AC ∠=∠∠=∠=∠===，连接PB ，则PAB 为正三角，得12PBD ∠=.123648,,,DAB DBA AD BD PAD PBD ∠=+==∠∴=∴≅故30.30APD BPD ACD APD ∠=∠=∴∠=∠=能力训练1. 452. 1503. 12 提示: 如图, 设4(,)3A a a 过A 作AD x ⊥轴, 交于点D , 过B 作BE x ⊥轴, 交于点E由,2AO AD OD AOD BCE BC BE CE ∴===, 则2912,,(,)23223a CE BE a B a a ==+ ,A B 都在双曲线上, 4291()3322a a a a ∴=+, 解得 123,0a a ==(舍去) 3412k ∴=⨯=4. 15 提示: 分别以,AB AC 为对称轴作D 点的对称点,E F , 连接,FC EB 相交于G , 证明四边形AFGE 为正方形5. B6. C7. B8. D9. 提示: 延长FD 至G , 使DG FD =, 连接EG10. 提示: 作//,//,//EQ FG PG KH KR DE ，交成等边三角形PQR11. 提示: 作//CD BQ , 连,PD CD ，∴四边形QBCD 为菱形, DQ QB = , 由,AP QB CD AQ PC === ,A PCD ∠=∠ 得,,DCP PAQ PD PQ QB QD ≅=== Q P D ∴为等边三角形, 又,CDP A PQA ∠=∠=∠2,QPC A ∠=∠360QPD A ∠=∠= 20,A ∴∠=80B ACB ∠=∠=又,QB BC = 50QCB ∴∠= 30PCQ ∠=12. 提示: (1) 作(4,1)B -关于x 轴对称点'(4,1)B ,连','AB AB 交x 轴于P ,PAB 周长最短, (3.5,0)P ∴ (2) 将点(4,1)B -向左平移3个单位得1(1,1)B -，再作1B 关于x 的对称点2(1,1)B ，连2AB 交x 轴于C ，再将C 向右平移3个单位得点D ，(1.25,0), 1.25C a ∴=(3) 作点A 关于y 轴对称点'(2,3)A --,作点B 关于x 轴的对称点'(4,1)B ,连''A B 交x 轴于M , 交y 轴于N 5(2.5,0),(0,)3M N ∴-13. 提示: 过N 作'//NQ DF ,作'//,NP AE 作//,//.NS DC NR AB 由','PP N LNR RN AB AE P N ∠=∠=== 则''Rt PP N Rt LNR PP LN ≅∴= 同理可证: ''PP QQ =又 '//,'//EP AN FQ ND , 又''AN ND EP FP =∴= 从而'',''PE PP P E FQ FQ QQ =+=+则 PE FQ =14. 提示:(1)11,,BM EC DM EC BM DM ==∴= 由2BME BCM ∠=∠ 2,DME DCM ∠=∠2()90BMD BME DME BCM DCM ∴∠=∠+∠=∠+∠= B M D M ∴⊥(2) 延长DM 至点F ,使DM FM =,连,,BD BF FC . 可证:EMD CMF ≅,ED AD CF DEM FCN ∴==∠=∠ //ED CF延长AD ,交BC 于T ,交CF 延长线于S 90EDS CST ∠=∠= 又BTA CTS ∠=∠BAD BCF ∠=∠ ,,,AB CB ABD CBF BD BF ABD CBF =∴≅∴=∠=∠, 又90ABD DBC CBF DBC ∠+∠=∠+∠=, BDF ∴为等腰三角形, ,BM DM BM DM ∴=⊥15. 如图, 以AB 为对称轴作ADB 的对称AGB ,以AC 为对称轴作ADC 的对称AFC ,并延长,GB FC 交于点E ,则易知四边形AGEF 是正方形, 不妨设AD h =,则2,3,BE h CE h =-=-由2222222(2)(3)5560BC BE CE h h h h =+⇒-+-=⇒--=116561522ABC h SBC AD ⇒=⇒==⨯⨯=。

(试卷)奥赛经典-奥林匹克数学中的几何问题---第十八章几何变换的性质及应用

第十八章几何变换的性质及应用【基础知识】平面几何中的几何变换主要有合同（包括平移、旋轴、轴对称）、相似（包括位似）、仿射和反演变换．在平面到自身的一一变换下，如果任意线段的长和它的象的长总相等，那么这种变换叫做合同变换．合同变换具有下述基本性质：性质1在合同变换下，直线变为直线，线段变为线段，射线变为射线；两直线的平行性、垂直性，所成的角度都不变；共线点变为共线点，且保持顺序关系不变；直线上A 、B 、C 三点的简比ACBC不变．性质2在合同变换下，三角形、多边形和圆分别变为与它们全等的三角形、多边形和圆；封闭图形的面积不变．在平面到自身的一一变换下，若任意一对对应点A ，A '连结的有向线段等于定向量a r，则这种变换叫做平移，记为()T a u u u r ．a r 叫平移向量，a r的方向叫做平移方向，其长度叫平移距离．在平面到自身的一一变换下，若每对对应点A ，A '所连结的线段，都被定直线l 所垂直平分，则这种变换叫做关于直线l 的轴对称或轴反射，记为()S l ．直线l 叫做对称轴或反射轴，点A '叫做点A 关于轴l 的对称点．在平面到自身的一一变换下，若任意一对对应点A ，A '与平面上一定点O 的距离总相等，且AOA '∠等于定角θ，这种变换叫做关于点O 的旋转，记为(),R O θ．点O 叫做旋转中心，θ叫做旋转角．特别地，旋转角180θ=︒的旋转变换称为中心对称变换或点反射，记为()(),180C O R O =︒．性质3在平移变换下，直线（线段）变成与它平行（或重合）的直线（线段）；在轴对称变换下，P 为对称轴l 上任一点，则一对对应点所成的角APA '∠被l 所平分；在旋转变换下，对应直线的交角总等于旋转角；在中心对称变换下，对应点连线段过对称中心且被它平分，对应线段相等且反向平行或共线，不过对称中心的直线与其对应的直线平行．在平面到自身的一一变换下，若线段A B ''是AB 的象，且A B AB k ''=∶（k 为正的常数），则这种变换叫做相似变换，记为()H k ．常数R 叫做相似系数或相似比．特别地，若1k =，则为合同变换；1k =-，则为中心对称变换．性质4在相似变换下，直线变为直线，线段变为线段，射线变为射线；点与直线的结合关系不变，点在直线上的顺序关系不变；直线上三点的简比不变，两直线的夹焦不变，两相似多边形面积比不变且等于相似比的平方．在平面到自身的一一变换下，若对于任一对对应点A ，A '与平面上一定点O ，都有OA OA k '=∶（k 为非零常数），则这种变换叫做位似变换，记为H （O ，k ）．点O 叫做位似中心，k 叫做位似比．特别地，当0k >时，A ，A '在点O 同侧，这种变换叫顺（或正或外）位似；0k <时，A ，A '在点O 两侧，这种变换叫逆（或反或内）位似．性质5在位似变换下，对应线段之比相等，对应角相等且转向相同；不过位似中心的对应直线平行．在平面到自身的一一变换下，若对于任一对对应点A ，A '与平面上一定点O ，都有OA OA k '=∶（k 为正的常数），且AOA θ'∠=（θ为有向的定角），则这种变换叫做位似旋转变换，记为(),,S O k θ．点O 叫做位似中心，k 叫做位似比，θ叫做旋转角，且()()()()(),,,,,,S O k H O k R O R O H O k θθθ=⋅=⋅；()(),0,,S O k H O k =；()(),,,S O k H O k π=-；()(),,1,S O R O θθ=．性质6在位似旋转变换下，把两个相似形中的一个变到另一个；具有共同中心的两个位似旋转变换之积仍是一位似旋转，即有()()()11221212,,,,,,S O k S O k S O k k θθθθ⋅=+⋅．在平面到自身的一一变换下，若满足任意共线三点的对应点仍共线，且其三点的简比保持不变，则称此变换为仿射变换．显然，若建立平面坐标系，仿射坐标系与直角坐标系的差别就在于两轴间的夹角及轴上单位长度不相同．若两轴夹角仍为90︒，则称为伸缩变换：()()12,,x y k x k y →，其中10k >，20k >．性质7在仿射变换下，点变成点，直线变成直线；保持点和直线的结合关系；保持直线的平行关系；保持两平行（共线）线段的长度比；任一封闭凸曲线所围成的图形的面积S 和它对应图形所围成的面积S '之比为常数．性质8在仿射变换下，任一三角形变成正三角形；梯形变为等腰梯形；任一平行四边形变成正方形；任一椭圆变为圆，相应地椭圆中心变成圆心，椭圆直径变成圆的直径，椭圆的切线变成圆的切线．设O 是平面上一定点，对于一个变换，若任一对对应点A ，A '（异于O ），都有OA OA k ⋅=u u u r u u u r（k 为非零常数），则称此变换为反演变换，记为I O k （，）．O 点称为反演中心，k 为反演幂．显然，0k <时，A ，A '在点O 两侧，可经以O 为中心对称变换变成0k >的情形．故只考虑0k >的情形，且令2k r =．此时，反演变换的几何意义为，满足“以O 为圆心，r 为半径的圆中直角三角形的射影定理形式：22r OP OA OA '==⋅”的图形，并称这个圆叫反演变换的基圆．性质9在反演变换下，基圆上的点仍变为自己；基圆内的点（除中心外）变为基圆外的点．反之亦然．性质10在反演变换下，过反演中心的直线是不变直线（除中心）；过反演中心的圆变为不过反演中心的直线；过反演中心的相切两圆（或一圆一直线）变为不过反演中心的两平行直线；过反演中心的两相交圆变为不过反演中心的相交直线．反之亦然．性质11在反演变换下，不过反演中心的圆变为不过反演中心的圆；以反演中心为圆心的圆变为同心圆；不过反演中心相切（交）的圆变为不过反演中心的相切（交）的圆；不共线的任意两对对应点必共圆；圆和圆、圆和直线、直线和直线的交角保持不变．【典型例题与基本方法】例1如图18-1，设A '，B '，C '分别是ABC △的边BC ，CA ，AB 的中点，1O ，2O ，3O ，1I ，2I ，3I 分别是AB C ''△，A BC ''△，A B C ''△的外心和内心．求证：123123O O O I I I △≌△．证明由三角形中位线性质，知C B B A AC ''''==u u u r u u u u r u u u u r，故图18-1I1I 2I 3O 1O 2O 3C 'B'A'A BC()T AC AB C C A B '''''−−−→△△u u u u u u u r ．于是()12T AC O O '−−−→u u u u u u u r，()12T AC I I −−−→u u u u u u r ，所以1212O O AC I I '==u u u u u r u u u u r u u u r ．同理，1313O O I I =u u u u u r u u u r，2323O O I I =u u u u u r u u u u r ．故123123O O O I I I △≌△．例2设DPQ △是锐角ABC △的垂足三角形（即D ，P ，Q 分别为三条高线的垂足）．求证：DPQ △是ABC △中周长最短的内接三角形．证明由题设，如图18-2，AD ，BP ，CQ 分别是DPQ △的内角平分线．令DEF △是ABC △中以D 为一顶点的任一内接三角形，且()S ABD D '−−−→，()S ACD D ''−−−→，则D '，D ''落在直线PQ 上，且D Q DQ '=，D P DP ''=，线段D D '''之长等于DPQ △之周长．连DE '，DF ''，刚折线D EFD '''之长等于DEF △之周长，显然D D D E EF FD ''''''++≤．不难计算2sin D D AD BAC '''==⋅∠．若RST △是ABC △的任一内接三角形，则用类似方法可以证得RST △的周长大于或等于2sin AR BAC ⋅∠．由于AR AD ≥，从而RST △的周长DPQ ≥△的周长，即垂足三角形DPQ △的周长最短．例3在ABC △内有一点P ，满足120APB BPC CPA ∠∠=∠=︒=．求证：P 是到三顶点距离之和最小的点（即费马点）．证明由120CPA BPC ∠=∠=︒，故对APC △施行旋转变换(),60R C -︒，则(),60R C APC EP C -︒'−−−−→△△．图18-2D "D 'R"R'F EDABCRQP ST图18-3Q Q 'P'ABCEP由于60P PC PP C ''∠=∠=︒，则B ，P ，P '，E 共线，且 BE BP PP P E BP CP AP ''=++=++．对于ABC △内任一点Q ，令(),60R C AQC EQ C -︒'−−−−→△△，则QQ QC '=，Q E QA '=，于是 QA QB QC Q E QQ QB BF BP CP AP ''++=++=++≥，故P 点是到三顶点距离之和最小的点．例4如图18-4，在ABC △中，AB AC >，A ∠的一个外角的平分线交ABC △的外接圆于点E ，过E 作EF AB ⊥，垂足为F ．求证：2AF AB AC =-．（1989年全国高中联赛题）证明1902AEF BAE BAC ∠=︒∠=∠-．作A 关于F 的对称点D ，则AED CAB ∠=∠，且EA ED =．又»»EB EC =（因EBC EAT EAB ∠=∠=∠），则EB EC =，且CEB CAB AED ∠∠=∠=，所以可将AEC△绕E 点旋转AED ∠到DEB △处，从而AC DB =．故2AB AC AD AF -==．例5如图18-5，ABC △和ADE △是两个不全等的等腰直角三角形，现固定ABC △，而将ADE △绕A 点在平面上旋转，试证：不论ADE △旋转到什么位置，线段EC 上必有点M 使BMD △为等腰直角三角形．（1987年全国高中联赛题）证法1先证BMD △为等腰直角三角形，再证M 为EC 上．作A 关于BD 的对称点A '，则A DB ADB '∠∠=．由902ADE BDM ∠=︒-∠，有|45|9045|EDM A DM A DB ADB ''∠∠=︒-∠︒-︒-∠==|．而DA DA DE '==，则A '是E 关于DM 的对称点．图18-4F EDA BCT图18-5A'E 1C 1EDABCM同理，A '也是C 关于BM 的对称点．从而EMD A MD '∠=∠，CMB A MB '∠∠=，而90BMD ∠=︒，故180CME ∠=︒，即M 在BC 上．证法2先取EC 中点M ，再证BMD △为等腰直角三角形．作AC 关于AB 的对称线段1AC ，连1BC ，1EC ，将1AC E △绕A 点顺时针方向旋转90︒到1ACE △的位置如图18-5，则11C E CE ⊥，11AC E ACE △≌△，且1190C AC EAE ∠=∠︒=，从而由1AE AE =有1ADE ADE ∠=∠，即知E ，D ，1E 三点共线且D 为1EE 中点．再由112BM C E ∥，112DM CE ∥及1C E 1CE ，即证．例6如图18-6，在锐角ABC △的BC 边上有两点E ，F ，满足BAE CAF ∠∠=，作FM AB ⊥于M ，作FN AC ⊥于N ，延长AE 交ABC △的外接圆于D ．证明：四边形AMDN 与ABC △的面积相等．（2000年全国高中联赛题）证明作DK AB ⊥于K ，作DL AC ⊥于L ，则只需证明 FBM FCN FDM FDN S S S S +=+△△△△．利用FDM FKM S S =△△，FDN FLN S S =△△，只需证明FBM PCN FKM FLN S S S S +=+△△△△，即FM BM FN CN FM MK FN NL ⋅+⋅=⋅+⋅．因此，只需证明()()FM BM MK FN NL CN -=-，即FM BK FN CL ⋅=⋅．设BAE CAF α∠=∠=，利用BKD CLD △∽△，有 ()sin sin BK DK FNCL DL A FMαα===-．故结论成立．例7如图18-7，1O e 与2O e 外切于点A ，半径分别为1r 和2r ，PB ，PC 分别为1O e ，2O e 的切线，B ，C 为切点，且12PB PC r r =∶∶，又PA 交2O e 于E 点．求证：PAB PEC △∽△．图18-6LFE DABC M NK证法1（相似证法）连线1BO ，1PO ，2PO ，2EO ，2CO ．注意到1O ，A ，2O 三点共线，由12PB PC r r =∶∶有12Rt Rt PBO PCO △∽△，从而1212PO PO O A O A =∶∶．由角平分线性质定理的逆定理，知12BPO O PA ∠=∠．又22O AP O EA ∠=∠，有12O AP O EP ∠=∠，从而12O AP O EP △∽△，则12PA PE r r =∶∶，即PA PE PB PC =∶∶．而BPA CPE ∠=∠，故PAB PEC △∽△．证法2（位似证法）考虑以A 为位似中心的变换，把1O e 变到2O e ，PAB △变到P AC ''△，则P C ''切2O e 于C '．由12PB P C r r PB PC ''==∶∶∶，知P C PC ''=．延长P C ''与PC 的延长线相交于点Q ，如图18-7，由QC QC '=，知PQP '△为等腰三角形．连2QO 并延长交AE 于F ，则QF AE ⊥，故QF 平分AE ，则AP PE '=．由此知PEC P AC PAB '△≌△∽△．例8如图18-8，设H 为ABC △的垂心，L ，M ，N 分别是BC ，CA ，AB 边的中点．D ，E ，F 分别是三条高的垂足，P ，Q ，R 分别是HA ，HB ，HC 的中心，试证：L ，M ，N ，D ，E ，F ，P ，Q ，R 九点共圆（九点圆定理）．证明由于P ，Q ，R 分别是HA ，HB ，HC 的中点，故以H 为位似中心，位似比为2的位似变换把PQR e 变成ABC e ．因此，要证L ，M ，N ，D ，E ，F 在PQR e 上，只要证明这些点在上述位似变换下的象点均在ABC e 上即可．图18-7图18-8BC作()C D H D '−−−→，()C L H L '−−−→，则D '，L '在ABC e 上．同理E ，M ，F ，N 的象点也在ABC e 上．再由上述位似变换之逆即证得结论成立．例9如图18-9，2AB CD ∥，1AC BD ∥，A 在12D D 上．求证：122ABC ABCD ACD S S S =⋅△△△．证明因为梯形是仿射不变形，所以题设中的两个梯形可由两个特殊梯形经仿射变换后得到，设梯形2C B A D ''''和梯形1C B D A ''''皆为直角梯形，且221C D D A MB '''''===．梯形2A D CB ''''−−−→仿射梯形2AD CB ，梯形1A C B D ''''−−−→仿射梯形1ACBD ，则112A B C S A B MC ''''''=⋅=△，11122A B D S A B A D '''''''=⋅=△，212A C D S '''=△．从而122A B C A B D A C D S S S '''''''''=⋅△△△．故122ABC ABD ACD S S S ⋅△△△=．例10在凸四边形ABCD 的边AB 和BC 上取点E 和F ，使线段DE 和DF 把AC 三等分，已知ADE △和CDF △的面积等于四边形面积的14．求证：ABCD 是平行四边形．（第16届全俄竞赛题）证明题中条件与结论均满足仿射变换不变性特性．将ABC △变换成图18-10所示直角三角形，设3AB BC ==，则()3,0A ，()0,3C ，()2,1P ，()1,2Q ．图18-945°45°MD 2'D 1'C 'B'A'D 2ABCD1图18-10设(),D a b 为所求，则直线DE 的方程为 ()1122b y x a --=--．令0y =得221E ax b -=+-．于是11232221ADE D a S AE y b b -⎛⎫=⋅=--⋅ ⎪-⎝⎭△1321a b b b +-=⋅⋅-．同理，得1321CDF a b S a a +-=⋅⋅-△．()11333222ABD BCD ABCD S S S b a a b =+=⋅⋅+⋅⋅=+△△四边形．由已知易得()131313212142a b a b b a a b b a +-+-⋅⋅=⋅⋅=⋅+--．解得3a b ==．即33D （，），故ABCD 为平行四边形．例11如图18-11，H 是ABC △的垂心，P 是ABC △内任一点，由H 分别向PA ，PB ，PC 引垂线HL ，HM ，HN 与BC ，CA ，v 的延长线相交于X ，Y ，Z ，其中L ，M ，N 为垂足．求证：X ，Y ，Z 三点共线．证明由于H 是一特殊点，将其作为反演中心，则只须证X ，Y ，Z 的象点（或反点）与H 共圆．设ABC △的高线分别交BC ，CA ，AB 的垂足为D ，E ，F ，则HA HD HB HE HC HF ⋅=⋅=⋅．又A ，D ，L ，X 共圆，有HL HX HA HD ⋅=⋅．同理，HM HY HB HE ⋅=⋅，HN HZ HC HF ⋅=⋅．以H 为反演中心，则L 与X ，N 与Z ，M 与Y 均为反点．又L ，P ，N ，H 共圆，L ，P ，M ，H 共圆，有L ，N ，M ，H 共圆，故X ，Z ，Y 三点共直线．例12如图18-12，四边形ABCD 内接于圆O ，对角线AC 与BD 相交于P ．设三角形ABP ，BCP ，CDP 和DAP 的外接圆心分别是1O ，2O ，3O ，4O ．求证：OP ，13O O ，24O O 三直线共点．图18-11PXYZ L DH AC EF MN（1990年全国高中联赛题）证明由于本题涉及的圆很多，于是可考虑反演变换．取P 为反演中心，P 关于圆O 的幂为反演基圆半径，则圆O 反演为本身，()1,2,3,4i O i =e 反演为四边形ABCD 各边所在直线，过点P 的直线也反演为本身．由直线2PO 与2O e 正交，可知它们的反形也正交，即2PO AD ⊥．又易知4O O AD ⊥，所以24PO O O ∥．同理，42PO O O ∥．所以24PO OO 为平行四边形，PO ，24O O 互相平分．同理，PO ，13O O 也互相平分，命题得证．【解题思维策略分析】1．注意同一类变换的多次运用例13如图18-13，凸四边形ABCD 的边是位于形外的、两两相似的等腰APB △、BQC △，CRD △、DSA △的底边．已知PQRS 是矩形，且PQ QR ≠．证明：ABCD 是菱形．（第15届全俄第三阶段赛题）证明设这些相似的等腰三角形的顶角为θ（90≠︒）．考虑一系列的旋转变换：点A 绕点P 转θ角到点B ，点B 绕点Q 转θ角到点C ，合成为点A 绕点E 转2θ角到点C ．同理点C 绕点F 转2θ角到点A ，其中12EPQ PQE FRS RSF θ∠=∠=∠=∠=．从而EA EC =，FA FC =，2180AEC AFC θ∠=∠=≠︒．于是AEC AFC △≌△，AECF 是菱形．又由于PQ SR =，则PEQ SFR △≌△．因此，E ，F 在矩形PQRS 的中位线上，从而AC 被该中位线垂直平分于矩形中心O 点．同理BD 也被矩形PQRS 的另一中位线垂直平分于矩形中心O 点．故ABCD 是菱形．若90θ=︒，则E ，F 都与矩形PQRS 的中心O 重合，且90POQ ROS ∠=∠=︒，从而知PQRS 是正方形，矛盾．所以90θ≠︒．图18-12图18-13FSPQRD OABCE例14设ABCDEF 是凸六边形，AB BC CD ==，DE EF FA ==，60BCD EFA ∠=∠=︒，G ，H 是六边形内两点，使120AGB DHE ∠=∠=︒．求证：AG GB GH DH HE CF ++++≥．（IMO -36试题）证明如图18-14，分别以AB ，DE 为边向六边形外作正ABM △和DEN △，将AGB △绕A 逆时针方向旋转60︒到AG M '△，则AGG '△为正三角形．故AG GG '=，GB G M '=．同样，将EHD △绕E 点顺时针方向旋转60︒到EH N '△，则EHH '△为正三角形，于是EH HH '=，HD H N '=．连MN ，则多边形AMBCDEF 关于轴BE 对称，MN CF =．另一方面，由“两点间线段最短”有 AG GB GH DH HE MG G G GH HH H N MN CF '''''++++=+++=+≥． 2．注意几类变换的配合运用例15平面上有两个直角三角形，其斜边上的中线互相平行，证明：一个三角形的一条直角边与另一个三角形的某条直角边之间的（小于直角的）夹角小于两条斜边之间的夹角．（第19届全俄竞赛题）证明平行移动两个给定的Rt ABC △和Rt A B C '''△中的一个，使两三角形的直角顶点C 与C '重合，并以点C 为中心，作位似变换，使得两三角形的中线重合，如图18-15．那么以E 为圆心，CE 为半径的圆将外接这两个三角形，并且它们斜边之间的夹角是圆心角，而它是相应的圆周角的两倍，这圆周角是直角边之间（小于直角）的夹角（图中2AEA ACA ''∠=∠），注意到上述的平移及位似变换均不改变直线间的夹角，于是结论获证．例16如图18-16，ABC LMN △∽△，且AC BC =，LN MN =，顶点按逆时针顺序排列，并在同一平面内，而且AL BM =．证明：CN 平行于AB 和LM 中点的连线．图18-14FCH 'EH DG 'MABG图18-15A BC =C 'EB'A'（第19届全俄第3阶段竞赛题）证明平移线段AB 到QM ，因AL BM =，BM AQ =，则AL AQ =，即ALQ △为等腰三角形．若F 为LQ 的中点，则AF LQ ⊥．设E 为LM 的中点，D 为AB 的中点，则FE 是QLM △的中位线，1122FE QM AB AD ===及FE QM AD ∥∥，因此AFED 是平行四边形，即AF DE ∥，AF DE =．又AF LQ ⊥，故DE LQ ⊥．平移ABC △，使A 点重合于F 点，D 点重合于E 点，则C 点移到G 点，ADC FEG △≌△，AF CG DE ∥∥及CG DE =．由ADC LEN △∽△，得FEG LEN △∽△且FE CELE NE=．又因90GEF NEL ∠=∠=︒，故GEN LEF ∠=∠，进而FEL ∠可由GEN ∠绕E 点逆时针旋转90︒并经位似变换而得到．由此得GN LF ⊥，即GN LQ ⊥．又GC LQ ⊥，即G ，C ，N 都在垂直于LQ 的一条直线上，因此，CN AF ∥，亦即CN DE ∥，原命题得证．【模拟实战】习题A1．给定以O 为圆心，AB 为直径的半圆周，在其上取点K 和M ，在直径上取点C ，使得KCA MCB ∠=∠．证明：K ，C ，O ，M 四点共圆．（第18届全俄竞赛题） 2．在ABC △中，AB AC =．任意延长CA 到P ，再延长AB 到Q ，使AP BQ =．求证：ABC △的外心O 与A ，P ，Q 四点共圆．（1994年全国初中联赛题） 3．在半径为1的圆周上给定弦AB ，不与圆相交的直线l 与弦AB 成45︒．用圆规和直尺在直线l 上作出点C ，使得线段DE 与AB 垂直（C ，E 分别是CA ，CB 与圆的交点）．（第16届全俄竞赛题） 4．ABC △中，2AB AC ==，BC 边—上有100个不同的点1P ，2P ，…，100P ，记2(1,2,,10)i i i i m AP BP PC i =+⋅=L ，求12100m m m +++L 的值．（1990年全国初中联赛题） 5．从以AD 为直径的半圆周上的点B ，C 分别作BE ，CF 垂直于AD 于E ，F ．线段AC 与BD 相交于P ，线段BF 与CE 相交于Q ．求证：直线PQ AD ⊥．（第17届全俄第3阶段竞赛题）6．设两个等圆相交，由其对称中心引出两条射线，它们交圆周于不在同一直线上的四点．证明：这四点共圆．（第19届全俄竞赛题） 7．在矩形ABCD 的边AB ，BC ，CD ，DA 上分别取异于顶点的点K ，L ，M ，N ．已知KL MN ∥，KM NL ⊥于O ．证明：KM 和LN 的交点在矩形的对角线BD 上．（第25届全苏竞赛题） 8．ABC △的中线AE ，BF 和CD 相交于M ．已知E ，C ，F 和M 共圆，且CD n =．求线段AB的长图18-16N LM度．（第18届全俄竟赛题） 9．等边ABC △和KMN △（顶点按逆时针顺序）在同一平面内，且AK NB =u u u r u u u r．证明：线段CM 和AN互相垂直，且CMAN=（第19届全俄竞赛题） 10．运用位似旋转变换证明例5．11．四边形ABCD 中，以一对对边的比AB CD ∶内分另一对对边AD ，BC 于E ，F ，延长BA ，CD 与EF 的延长线分别相交于G ，Q ．试证：BGF FQC ∠=∠．12．四边形ABCD 的对边AD ，BC 延长交于E ，AB ，CD 延长交于F ．O 为其对角线交点，过O 作AB 的平行线OQ 交EF 于Q ．求证：OG GQ =．习题B1．已知平面上三个半径相等的圆1O e ，2O e ，3O e 两两相交于A ，B ，C ，D ，E ，F ，如图18-17．证明：弧»AB ，»CD，»EF 的和等于180︒．2．如图18-18，111A B C △，在ABC △内，且111ABC A B C △∽△．作1B D AC ⊥于D ，1C E AB ⊥于E ，1A F BC ⊥于F ．求证：1112ABC A F BC B D AC C E AB S ⋅+⋅+⋅=△．3．设D 是锐角ABC △内部的一点，使得90ADB ACB ∠∠+︒=，并有AC BD AD BC ⋅=⋅．（1）计算比值AB CDAC BD⋅⋅；（2）求证：ACD △的外接圆和BCD △的外接圆在C 点的切线互相垂直．（IMO34-2试题）4．BK 是锐角ABC △的高，以BK 为直径作圆分别交AB ，BC 于E ，F ．过E ，F 分别引所作圆的切线．证明：两切线的交点在过顶点B 的ABC △的中线所在的直线上．（第21届俄罗斯竞赛题）5．在梯形ABCD 中，腰AB CD =．将ABC △绕点C 转过一个角度，而得到A B C ''△．证明：线段A D '，BC 和B C '的中点共线．（第23届全苏竞赛题） 6．111A B C △是不等边锐角ABC △的垂足三角形，2A ，2B ，2C 是111A B C △的内切圆分别切11B C ，11C A ，图18-17图18-18D A CE C 1B 1A 111A B 的切点．证明：222A B C △与ABC △的欧拉线重合．（第7届巴尔干地区竞赛题）7．在钝角ABC △（C ∠为钝角）的BC 边上选取点D （异于B ，C 点）．过线段BC （异于D ）的内点M 引直线AM ，交ABC △的外接圆S 于点N ．经过点M ，D 和N 作圆，交圆S 于N 及另一点P ，问点M 在何位置时，线段MP 的长度最短？（第22届全苏竞赛题） 8．ABCD 是一个四边形，且BC AD ∥，M 是CD 的中点，P 是MA 的中点，Q 是MB 的中点，直线DP ，CQ 交于点N ．求证：点N 不在ABM △外部的充要条件是上下底边长之比在1,33⎡⎤⎢⎥⎣⎦上．（IMO -35预选题）9．在ABC △中，12AB =，16AC =，M 是BC 的中点，E ，F 分别在AB ，AC 上，EF 交AM 于G ，且2AE AF =．求比值EFGF．（IMO -29预选题） 10．三个全等的圆有一个公共点Q ，并且都在一个已知三角形内，每一个圆与三角形的两条边相切，求证：三角形的内心I ，外心O 与已知点Q 共线．（IMO --22试题）11．123A A A △是一个非等腰三角形，它的边长分别为1a ，2a ，3a ，其中i a 是i A 的对边（123i =，，），i M 是边i a 的中点，123A A A △的内切圆I e 切边i a 于i T 点，i S 是i T 关于i A ∠的平分线的对称点．求证：11M S ，22M S ，33M S 三直线共点．（IMO -23试题）12．设A 是两个不相等的，分别以1O 与2O 为圆心而共面的圆1C 与2C 的两个不同交点之一，一条外公切线切1C 于1P ，切2C 于2P ；另一条公切线切1C 于1Q ，切2C 于2Q ．设1M 是11PQ 的中点，2M 是22P Q 的中点．证明：1212O AO M AM ∠∠=．（IMO --24试题）13．已知两相切圆1C ，2C ，点P 在根轴上，即与两圆连必线垂直的公切线上．试用圆规和直尺作所有的圆C ，使得C 与1C ，2C 相切，且过P 点．（1991年亚太地区竞赛题）14．给定两个圆，其中一个圆在另一个内部，且两圆相切于点N ．外圆的弦BA 和BC 分别与内圆相切于点K 和M ．外圆的弦BA 和BC 分别与内圆相切于点K 和M ．设不包含点N 的弧»AB 和»BC的中点分别是Q 和P ．BQK △和BPM △的外接圆的第二个交点为1B ．证明：1BPB Q 为平行四边形．（第26届俄罗斯竞赛题）15．四边形ABCD 外切于圆ω，边AB 和CD 所在的直线相交于点O ．圆1ω与边BC 相切于点K ，且与边AB 和CD 所在的直线都相切；圆2ω与边AD 相切于点L ，且亦与边AB 和CD 作在的直线都相切，现知点O ，K ，L 共线，证明：边BC 和AD 的中点以及圆ω的圆心三点共线．（第26届俄罗斯竞赛题）。