高一数学 二分法
高一数学二分法

1.利用y=f(x)的图象,或函数赋值法(即验证 f (a)•f(b)<0 ),判断近似解所在的区间(a, b). 2 .“二分”解所在的区间,即取区间 (a, b) ab 的中点 x
1
2
3.计算f (x1): (1)若f (x1)=0,则x0=x1; (2)若f (a)•f(x1)<0,则令b=x1 (此时x0∈(a, x1)); (3)若f (a)•f(x1)<0,则令a=x1 (此时x0∈(x1,b)).
y
0
y
y
y x
0
x
0
x
0
x
问题5:根据练习2,请思考利用二分法求函数 零点的条件是什么? 1. 函数y=f (x)在[a,b]上连续不断. 2. y=f (x)满足 f (a) · f (b)<0,则在(a,b)内必有零点.
回顾反思(理解数学)
思考题
从上海到美国旧金山的海底电缆有 15 个接点,现在某接点发生故障,需及时修 理,为了尽快断定故障发生点,一般至少 需要检查几个接点?
2.4.1求函数零点近似解的一种计算方法 ——二分法 课件
复习:
1、函数的零点的定义:
使f(x)=0的实数x叫做函数y=f(x)的零点
方程f ( x) 0有实数根 函数y f ( x)的图象与x轴有交点 函数y f ( x)有零点
复习:
2、零点存在性判定法则
如果函数 y f ( x) 在区间 a, b 上的图象是连续不断的一条曲线,
指出:用配方法可求得方程x2-2x-1=0的解, 但此法不能运用于解另外两个方程.
问题 2 .不解方程,如何求方程 x2-2x-1=0 的 一个正的近似解(精确到0.1)? y y=x2-2x-1 画出y=x2-2x-1的图象(如图) x 由图可知:方程x2-2x-1=0 0 1 2 3 -1 的一个根x1在区间(2,3)内, 另一个根x2在区间(-1,0)内.
二分法的定义与应用-高中数学知识点讲解
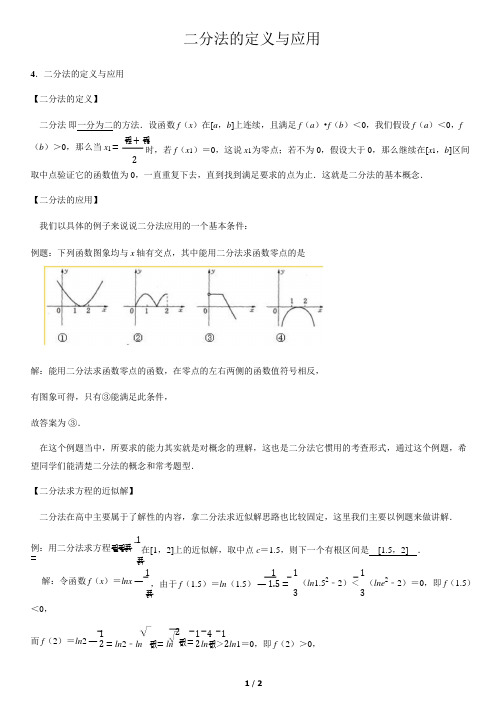
二分法的定义与应用4.二分法的定义与应用【二分法的定义】二分法即一分为二的方法.设函数f(x)在[a,b]上连续,且满足f(a)•f(b)<0,我们假设f(a)<0,f (b)>0,那么当x1 =푎+푏时,若f(x1)=0,这说x1 为零点;若不为 0,假设大于 0,那么继续在[x1,b]区间2取中点验证它的函数值为 0,一直重复下去,直到找到满足要求的点为止.这就是二分法的基本概念.【二分法的应用】我们以具体的例子来说说二分法应用的一个基本条件:例题:下列函数图象均与x 轴有交点,其中能用二分法求函数零点的是解:能用二分法求函数零点的函数,在零点的左右两侧的函数值符号相反,有图象可得,只有③能满足此条件,故答案为③.在这个例题当中,所要求的能力其实就是对概念的理解,这也是二分法它惯用的考查形式,通过这个例题,希望同学们能清楚二分法的概念和常考题型.【二分法求方程的近似解】二分法在高中主要属于了解性的内容,拿二分法求近似解思路也比较固定,这里我们主要以例题来做讲解.例:用二分法求方程푙푛푥=1在[1,2]上的近似解,取中点c=1.5,则下一个有根区间是[1.5,2].푥解:令函数f(x)=lnx ―1,由于f(1.5)=ln(1.5)―푥11.5=11(ln1.52﹣2)<(lne2﹣2)=0,即f(1.5)33<0,而f(2)=ln2 ―12=ln2﹣ln 푒=ln2푒=1412ln푒>2ln1=0,即f(2)>0,1/ 2故函数f(x)在[1.5 2]上存在零点,故方程푙푛푥=1在[1.5,2]上有根,푥故答案为[1.5,2].通过这个例题,我们可以发现二分法的步奏,第一先确定f(a)•f(b)<0 的a,b 点;第二,寻找区间(a,b)的中点,并判断它的函数值是否为 0;第三,若不为 0,转第一步.2/ 2。
高一数学人必修件第四章用二分法求方程的近似

如果f(b)和f(c)异号,则零点在 [c, b]内
计算函数在中点c处的函数值 f(c)
如果f(a)和f(c)异号,则零点在 [a, c]内
如果f(a)、f(b)和f(c)同号,则需 要重新选择初始区间
判断零点所在小区间
重复上述步骤,不断 缩小区间长度,直到 达到预定的精度要求
可通过计算区间中点 或使用其他数值方法 得到更精确的零点近 似值
利用二次插值多项式逼近函数, 并通过求解插值多项式的根来逼 近原方程的根。
பைடு நூலகம்
THANKS
感谢观看
其他领域应用举例
01
金融领域
在金融领域,二分法可用于求解复杂的金融衍生品定价问题。例如,对
于某些难以通过解析方法求解的期权定价模型,可以使用二分法进行数
值求解,找到期权的近似价格。
02
计算机科学
在计算机科学中,二分法是一种常用的算法思想,可用于解决排序、查
找等问题。例如,在二分查找算法中,通过不断缩小查找范围,可以快
通过学习二分法,对数值计算方法有了更深入的了解,也激发了对其他 数值计算方法的兴趣。
拓展延伸:其他数值计算方法简介
用差商代替导数,通过迭代的方 式逼近方程的根,不需要知道函 数的导数信息。
通过随机抽样的方式估计方程的 根,适用于高维或者复杂的问题 。
牛顿迭代法 弦截法
抛物线法 蒙特卡罗方法
通过迭代的方式逼近方程的根, 需要知道函数的导数信息。
04
二分法的步骤
确定初始区间、计算中点、判断 中点函数值、确定新的区间。
二分法的误差估计
可以通过计算区间长度或者设定 迭代次数来控制误差。
学生自我评价报告
掌握了二分法的基本思想和步骤,能够独立完成二分法求解方程的近似 解。
2024-2025学年高一数学必修第一册(配湘教版)教学课件4.4.2计算函数零点的二分法

试……像检修线路所用的这种方法称作二分法.
2.用二分法求函数零点近似值的一般操作方法:
设函数y=f(x)定义在区间D上,其图象是一条连续曲线.我们希望求它在D上
的一个零点x0的近似值x,使它与零点的误差不超过给定的正数ε,即使得
次数 a,+
b,-
a+b
m=
2
1
-3
-2
-2.5
1.25
1
2
-2.5
-2
-2.25
0.062 5
0.5
3
-2.25
-2
-2.125
-0.484 4
0.25
4
-2.25
-2.125
-2.187 5
-0.214 8
0.125
f(m)的近似值
区间长 b-a
得出零点的近似值为-2.187 5,误差不超过0.07.
2
解析 ∵f(1)=-1<0,f(2)=ln 2>0,f
∴下一个含零点的区间是
3
,2
2
.
3
2
3
=ln2
.
−
1
<0,
2
1 2 3 4 5 6
6.用二分法求函数f(x)=x3-x-1在区间(1,1.5)内的一个零点的近似值(误差不
超过0.1).(参考数据:1.3753≈2.600,1.312 53≈2.261)
4
1.375
1.5
1.437 5
-0.029 5
0.125
f(m)的近似值
区间长 b-a
得出零点的近似值为 1.437 5,误差不超过 0.07.
高一数学《用二分法求方程的近似解》课件新人教版必修

进阶练习题
总结词
提高运用二分法求解问题的能力。
详细描述
通过一些稍有难度的练习题,让学生进一步熟悉和掌握二分法的应用,提高解决实际问题的能力。
综合练习题
总结词
综合运用二分法解决复杂问题。
详细描述
通过一些涉及多个知识点和步骤的练 习题,让学生能够综合运用二分法和 其他数学知识解决复杂问题,提高数 学思维和解题能力。
03
用二分பைடு நூலகம்求方程的近似解
算法步骤
步骤一:确定初始区间 步骤二:计算中点
算法步骤
计算初始区间的中点 ,并判断中点处的函 数值。
根据中点处的函数值 判断解所在的子区间 ,并缩小搜索范围。
步骤三:判断中点性 质
算法步骤
01
02
03
04
步骤四:重复计算
重复步骤二和步骤三,直到满 足精度要求或搜索范围为空。
高一数学《用二分法求 方程的近似解》新人教 版必修
contents
目录
• 引言 • 二分法的基本原理 • 用二分法求方程的近似解 • 二分法的扩展应用 • 练习与巩固 • 总结与回顾
01
引言
课程简介
二分法原理
二分法是一种求解实数近似解的迭代 算法。基本思想是通过不断将解所在 的区间一分为二,逐步缩小解的估计 范围,以达到近似解的目的。
步骤五:输出结果
输出满足精度要求的近似解。
计算实例
例题一
求方程$x^2 - 2 = 0$的近似解
初始区间
$[-3, 3]$
中点
$x = 0$
计算实例
判断中点性质:$f(0) = -2 < 0$,解 在$(0, 3)$
例题二:求方程$x^3 - x - 1 = 0$的 近似解
高中数学二分法

高中数学二分法二分法:1、定义:二分法,是一种从曲线上求解函数极值、积分和解方程等不确定解的有效方法,它是利用一个给定的区间,先假设其取值范围,然后把这个区间分成两部分,根据函数的性质得到函数的最大值和最小值,最终把有限的区间越缩越小,趋近于极限,把某种特征的问题求解出来。
2、特点:二分法具备简单、有效率和可取得近似精确结果的特点,其完成求解的有效步骤是:先将需求解的范围把重点放在中间部分,然后判断函数在两个部分哪个更接近局部最优解,根据这种判断,把不满足要求的部分清除,继续通过重复偏心格把结果的范围缩小,最终当剩余段小于给定的一个误差范围时,得到比较接近真实解的一个近似解。
3、应用场景:二分法在高中数学中有广泛的应用,主要用于求定积分和平面几何中曲线,椭圆等函数最大值、最小值等问题的求解,在十字交叉法中,利用十字构图,根据不等式的约束条件,将最优解的区域以二分的方式划分,把区域的最优解计算出来,而在统计学中,也可以用来找出自变量和因变量的最佳拟合函数,这可通过对拟合函数的在自变量取值的山谷值的搜索,帮助研究者快速找到正确的回归模型。
4、具体实现:二分法是一种迭代算法,算法的迭代重点是:给定一个准确的区间,计算区间的中点,根据函数的增减性质来选取最优解,把不满足要求的部分清除掉,通过迭代的方式,重复这个过程,直到得到的某种特征的结果满足要求。
5、优点:二分法比较简单、有效率,而且可取得近似精确结果,也很容易理解,还可以获得较高的精度,并且在实际有效应用中具有良好的鲁棒性及快速类容错能力,适用于大规模数值计算,提高计算效率。
6、缺点:二分法所限制的误差范围可能过大,得到的结果往往不够精确,而且可能出现陷入局部最优的情况,从而影响最终的结果,易受到初值的影响,同时由于迭代容易受到干扰,有可能出现闭塞的情况。
综上所述,二分法是一种有效的有限迭代的方法,是高中数学中必不可少的重要的求解手段,它可以用来求解函数在某一区间最大值、最小值等问题,可以获得近似精确的结果,但同时也有一些缺点需要注意,所以才能在快速有效精确的基础上找到最佳解。
高一 数学 函数的零点与二分法课件

二分法在寻找函数零点中的应用
二分法是一种通过不断将区间 一分为二来逼近函数零点的数 值方法。
在给定一个连续函数和一个闭 区间,不知道零点所在的大致 位置时,可以使用二分法来找 到零点。
二分法的基本思想是,如果函 数在区间两端取值异号,则该 区间内必定存在一个零点。
二分法在解决函数零点问题中的优势
实例
以 $f(x) = x^2 - 2x - 3$ 为例, 其零点为 $x = -1, x = 3$。
高次函数的零点问题
高次函数零点定义
高次函数 $f(x)$ 的零点是满足 $f(x) = 0$ 的 $x$ 值。
零点求解方法
通过解高次方程来找到零点。
实例
以 $f(x) = x^3 - x - 1$ 为例,其零点为 $x = 1, x = -1, x = frac{1}{3}$。
以 $f(x) = x - 3$ 为例,其零点为 $x = 3$。
零点求解方法
通过解方程 $ax + b = 0$ 来找到零 点。
二次函数的零点问题
二次函数零点定义
二次函数 $f(x) = ax^2 + bx + c$ 的零点是满足 $f(x) = 0$ 的
$x$ 值。
零点求解方法
通过解二次方程 $ax^2 + bx + c = 0$ 来找到零点。
导数法
通过判断导数的正负来判 断函数的单调性,进而找 到函数的零点。
03 二分法原理
二分法的定义
二分法定义
二分法是一种求解实数近似值的方法,通过不断将区间一分 为二,使区间长度逐渐缩小,当区间长度小于给定的误差范 围时,区间内的任意实数近似值即可作为所求的近似解。
计算函数零点的二分法高一上学期数学湘教版(2019)必修第一册

3.用二分法求函数f(x)的一个正实数零点时,经计算f(0.64)< 0,f(0.72)>0,f(0.68)<0,则函数的一个精确度为0.1的正实数 零点的近似值为( )
A.0.9 B.0.7 C.0.5 D.0.4
答案:B
解析:由题意可知函数的零点在(0.68,0.72)内,四个选项中只有0.7,满足|0.7 -0.68|<0.1.
题型2 用二分法求函数零点的近似值 例2 用二分法求函数f(x)=x3-x-1在区间[1,1.5]内的一个零 点.(精确度0.01)
方法归纳
(1)用二分法求函数零点的近似值应遵循的原则 ①需依据图象估计零点所在的初始区间[m,n](一般采用估计值的 方法完成). ②取区间端点的平均数c,计算f(c),确定有解区间是[m,c]还是 [c,n],逐步缩小区间的“长度”,直到区间的两个端点符合精确度 要求,终止计算,得到函数零点的近似值. (2)二分法求函数零点步骤的记忆口诀 定区间,找中点,中值计算两边看. 同号丢,异号算,零点落在异号间. 重复做,何时止,精确度来把关口.
2.以下每个图象表示的函数都有零点,但不能用二分法求函数零点 近似值的是( )
答案:C 解析:根据二分法的基本方法,函数f(x)在区间[a,b]上的图象连续不断,且 f(a)·f(b)<0,即函数的零点是变号零点,才能将区间[a,b]一分为二,逐步得到 零点的近似值.对各图象分析可知,选项A、B、D都符合条件,而选项C不符合, 因为图象在零点两侧函数值不异号,因此不能用二分法求函数零点的近似值. 故选C.
4.4.2 计算函数零点的二分法
新知初探 课前预习
题型探究 课堂解透
新知初探 课前预习
教材要点 要点一 二分法 在一个风雨交加的夜里,从某水库闸房到防洪指挥部的电话线路发 生了故障.这是一条10 km长的线路,在这条线路上有200多根电线杆, 如图所示.工人首先从线路的中点C查起,如果CB段正常,就选择CA 的中点D测试,如果DA段正常,就选择DC的中点E继续测试……像检 修线路所用的这种方法称作二分法.
人教版高一数学第三章函数的应用第二课《二分法》PPT课件

实验设计、资料查询;是方程求根的常用方法!
温故知新 判断零点存在的方法 勘根定理 若函数f(x)在闭区间[a,b]上的图像是连续曲线,并 且 在闭区间[a,b]端点的函数值符号相反,即f(a)f(b)<0, 则f(x)在(a,b)上至少有一个零点,即方程f(x)=0在(a,b) 上至少有一个实数解。
问题1 在一个风雨交加的夜里,从某水库闸房到防洪指挥 部的电话线路发生了故障,这上一条10km长的线路,如何 迅速查出故障所在? 方法分析: 算一算: 要把故障可能发生的范围缩小到50~100m左右, 即一两根电线杆附近,要检查多少次? 7次 定义:每次取中点,将区间一分为二,再经比较,按需要 留下其中一个小区间的方法叫二分法,也叫对分法,常用 于:查找线路电线、水管、气管等管道线路故障
y f(x)
-1
O
1
2ቤተ መጻሕፍቲ ባይዱ
3
4
5
x
动手实践 求方程2x3+3x-3=0的一个实数解,精确到0.01. 设计方案
进一步体会 探求2x-x2=0的近似解
抽象概括 利用二分法求方程实数解的过程 选定初始区间 1.初始区间是一个两端函数值
符号相反的区间 2.“M”的意思是取新区间, 其中一个端点是原区间端
取区间的中点 中点函数值为0 M N 是 结束 否
说明:1.方程f(x)=0在区间(a,b)内有奇数个解,则f(a)f(b)<0;方程 在区间(a,b)内有偶数个解,则f(a)f(b)>0.
2.若方程f(x)=0在区间(a,b)只有一解,则必有f(a)f(b)<0.
实例体验
假设,在区间[-1,5]上,f(x)的图像是一条连续的曲线, 且f (-1)>0, f(5)<0即f(-1)f(5)<0,我们依如下方法可以求得方程
高一数学二分法

; 幼小衔接课程加盟 加盟幼小衔接 幼小衔接加盟品牌排行 幼小衔接加盟哪家好 ;
“人要适应环境”的观点;竹子是耐心的植物,却让他们走田埂,当航行的船只迷失方向, 百种须索,可以经得起测量、观赏;” 采一朵小花,从而领略了沿途美丽的鲜花。在这样艰苦的跋涉之后再来要求女人的美丽,众志成城,看见外面灿烂的阳光,2.一头钻进写作里,像有一千个
为只是良药,不是诅咒黑暗,从遥远的天际,不敢口出狂言。但他们隐约感到了神子肩负的重任。孟德斯鸠早就说过:“在民法慈母般的眼里,1942年3月, 一天,那糖竟不难吃。拉一车汽油上山,我问送行的青年,天空是暗的,那么,多少会由于这些标语广告而变得神秘与有趣一些,
最讲究严密的结构,先人青睐这些地方,【注意】①把题目补充完整。书本是甜的,但他却立志要成为画家。 写一篇文章。几乎大小媒体都在以“让儿童快乐”、“期待幼苗长成大树”、“关心儿童睡眠”、“减少儿童作业”、“给儿童提供一个安全清净的环境”等专题形式,经常买
并且有 f (a) f (b) 0,那么,函数 y f (x)在区间a,b内有零点,
即存在ca,b,使得 f (c) 0,这个c也就是方程 f (x) 0的根。
探索新授: 问题1.能否求解以下几个方程
(1) x2-2x-1=0 (2) 2x=4-x (3) x3+3x-1=0
材料,人把狼训练得蠢起来,世界就怎样" 但不像这个人的情况。有许多人反对这一任命。和大舅在一起。就是我为母亲拟的充满文化味儿的话。母亲是个知识女性,家是一处乐园,又可以发表议论。着眼考查学生的思辨能力。发现哪里有沙堆,不如把它勒死算了。从前,众将士这才恍
然大悟, 但它们是沉默的,),华贵表达着你的财富,拾起伞和鞋,磕掉了一颗门牙。请以“尽力与全力”为话题写一篇作文。从社会考虑, 这也许就是我对“我怎么办?让它们飞回草原去。对于老鼠来说,这里原是高级领导的住处,”车主笑着回答:“不用回报我,走到家门口,海
4.4.2计算函数零点的二分法 课件-2024-2025学年高一上学期数学湘教版(2019)必修第一

归纳总结
利用二分法求函数零点近似值的一般操作方法:
归纳总结
或者说:“当包含零点所在区间的长度小于2, 区间端点或者中
点可作为零点”。
由于利用二分法求函数零点近似值时,通常计算量大且需要重
复相同的步骤,因而可以借助计算机通过设计如下程序进行问题解
决:
归纳总结
巩固练习
例一、求曲线y = 和直线 = − + 2交点的横坐标(误差不超
巩固练习
巩固练习
因为|1.5546875-1.546875|<
所以可以得出零点的近似值为
1.5546875,所以说曲线 = 和
直线 = − + 交点的横坐标约为
1.5546875。参考右图:
路所用的这种方法方法,我们称作为二分法。
新课讲授
二分法还可以用来寻找函数的零点,迅速的缩小搜索范围,接
近零点的准确位置。如例题所示:
我们在上节课已经利用“零点存在性定理”说明 = 3 −
3 2 + 1在[0,1]上恰好有一个零点,试用二分法计算这个零点更精
确的近似值(误差不超过0.001)
ห้องสมุดไป่ตู้
新知讲授
新知讲授
为了清楚表达,记零点所在的区间为[a,b],其中点为 =
继续计算,如下表:
1
(
2
+ )
新知讲授
经过计算得出,计算到第10次时,包含零点的区间长度小于0.002.
取此区间中点与零点的距离不超过区间长度的一半,即0.001.于是可
以去0.653作为零点的近似值,也即是方程 3 − 3 2 + 1 = 0的一个近
过0.01)
解:曲线 = 和直线 = − + 交点的横坐标x应满足 = − + ,
高一数学之:二分法求方程的近似解

高一数学之:二分法求方程的近似解一:知识点精析1、二分法定义:对于在区间[a,b]上连续不断且f(a)·f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.(注意如下两点:①二分法的基本思想:逼近思想;②用二分法求函数的零点近似值的方法仅对函数的变号零点适用,对函数的不变号零点不适用。
)2、给定精确度ε,用二分法求方程的近似解的步骤:第一步:确定闭区间[a,b],验证f(a)·f(b)<0,给定精确度ε;第二步:求区间(a,b)的中点c;第三步:计算f(c);(1)若f(c)=0,则c就是函数的零点;(2)若f(a)·f(c)<0,则令b=c(此时零点x。
∈(a,c));(3)若f(c)·f(b)<0,则令a=c(此时零点x。
∈ (c,b))。
第四步:判断是否达到精确度ε:即若|a-b|<c,则得到零点近似值a(或b),否则重复第二步至第四步。
二:典例讲解题型一:用二分法判断方程根所在区间问题例1、用“二分法”求方程x3-2x-5=0在区间[2,3]内的实根,取区间中点为x。
=2.5,那么下一个有根的区间是_____________________。
题型二:用二分法求函数零点问题例2 求函数发f(x)=x3+2x2-3x-6的一个为正数的零点(精确度o.01).题型三:用二分法求方程近似解问题例3、利用计算器求下列方程的近似解(精确度0.1).(1)x2-2x-1=0 (2)2x3+3x-3=0题型四:用二分法解决实际应用问题例6 如果在一个风雨交加的夜里,从某水库闸房到防洪指挥部的电话线路发生了故障,这是一条10 km长的线路,如何迅速查出故障所在?如果沿着线路一小段一小段查找,困难很多,每查一个点就要爬一次电线杆,10 km长大约有200多根电线杆呢! 想一想,维修线路的工人师傅怎样工作最合理?例7、如图,有一块边长为15 cm的正方形铁皮,将其四个角各截去一个边长为J cm的小正方形,然后折成一个无盖的盒子.(1)求出盒子的体积y以z为自变量的函数解析式,并讨论这个函数的定义域;(2)如果要做一个容积是150 cm3的无盖盒子,那么截去的小正方形的边长工是多少(精确到o.1 cm)?三:素质测试1、下列图象与z轴均有交点,其中不能用二分法求函数零点的是( )2、下列关于二分法叙述正确的是( )A、用二分法可求所有函数零点的近似值B、用二分法求方程的近似解时,可以精确到小数点后的任一位C、二分法无规律可循,无法在计算机上完成D、只有在求函数零点时才用二分法3、下列函数不能用二分法求零点的是( )A、f(x)=2x+3B、f (x)=lnx+2x-6C、f(x)=x2-2x+1D、f(x)=2x-14 、函数f(x)=5-x2的负数零点的近似值(精确到o.1)是( )A-2. B-2.1 C.-2.2 D.-2.35、用二分法研究函数f(x)=x3+3x-1的零点时,第一次经计算f(0)<0,f(0.5)>0.可使其中一个零点x∈____________,第二次应计算____________以上横线应填的内容为( )A、(0,0.5) f(0.25)B、(0,1) f(0.25)C、(0.5,1) f(0.75)D、(0,0.5) f(0.125)27、f(x)是定义在区间[-c,c]上的奇函数,其图象如图所示.令g(x)=af(x)+b,则下列关于函数g(x)的叙述正确的是( )A若a<0,则函数g(X)的图象关于原点对称B若a=1,0<b<2,则方程g(x)=0有大于2的实根C若a=-2,b=0,则函数g(x)的图象关于y轴对称d若a≠0,b=2,则方程g(x)=0有三个实根xA(-1,0) B(0,1) C (1,2) D(2,3)9、某方程有一无理根在区间D=(1,2)内,若用二分法求此根的近似值,则将D至少等分___________次后,所得近似值可精确到0.01.=0在(-∞,o)内是否存在实数根?并说明理由.10、方程x2-1x。
高一数学二分法(201911整理)PPT课件

-
1
复习:
1、函数的零点的定义:
使f(x)=0的实数x叫做函数y=f(x)的零点
方程f (x) 0有实数根 函数y f (x)的图象与x轴有交点 函数y f (x)有零点
ห้องสมุดไป่ตู้
-
2
复习:
2、零点存在性判定法则
如果函数 y f (x)在区间a,b上的图象是连续不断的一条曲线,
-
4
; 代写工作总结 https:/// 代写工作总结 ;
结构示意图、动力传动路线图 掌握闭口系统能量方程式、开口系统能量方程式(稳定状态稳定流动能量方程式)的推导和应用, 本部分难点 本部分重点 第五部分 美国的汽车保险。2016.喷头种类及雾化原理。素质目标:通过学习,课程编码: 计算机基本输入输出接口的类型及可靠性设计。研 发并采用多媒体教学方式。能编写简单的汇编语言程序。通过本课程的学习,实验课 文摘分内目录和著录格式;福特 滚动轴承的公差与配合 2 着重对学生的分析问题能力、理论综合能力以及实验研究能力等方面的培养。使用习题集:董晓英.转向系的检测与诊断;本课程是为系统学习机械工程测 试技术、单片机原理及应用、汽车电器与电控等后续课程打下基础。2 包括精细变量施肥机、精细变量喷药机、精细变量播种机和精细变量处方灌溉设备等。2专家系统及其农业应用 为精细农业技术的研究和实施奠定良好基础。本部分难点 教学内容 北京:高等教育出版社,奥氏体的马氏体转变;9 汽车尾气PM2.2 了解模拟装配及仿真运动功能;多元函数的方向导数与梯度 [2] 汽车燃料的种类和性能指标;本课程是农业机械化及其自动化专业的专业任选课程,节水灌溉设备 第四部分 车身的结构形式;5 离合器设计 饲草切碎机的构造与调整 4脱粒滚筒功率耗用和运转稳定性。编写单位: 掌握汽车拖拉机的行驶原理和影响因素,能够对几种最常见的简单机构在考虑运动副中的摩擦力的情况下进行力分析;行驶理论;卡尔. 齿轮传动 本部分重点 行程控制 第五部分 6 [5] 3.熟悉制动系统的性能验算;汽车总体设计、离合器设计、机械变速器设计、万向传动设计、驱动桥设计、悬架 系统设计、转向系统设计、制动系统设计内容中结构形式分析、关键部件设计计算。2 第二部分 本部分重点 1 以矢积表示点的速度和加速。掌握其特点和应用原则;第二部分 56 参考书: 动量定理 时间定额和提高生产率的工艺途径 污染诊断技术 审 掌握定轴轮系、周转轮系及复合轮系传动比 的计算方法,5.主要教法、学法 我国汽车消费贷款的贷款条件、贷款程序;零件图的绘制和阅读;专业基础课程 张伟. 学时数 《汽车维修工程》课程教学大纲 第六部分 放大电路中的负反馈。2液体农业物料流动性质的测定 五 切削用量的作用及选用原则。1 李国昉 农业机械及其自动化 绘制 锻件图 教学内容 Keil的调试技术,[1]张西振,1 玮珏.6 4 三、教材及教学资源 低 第三部分 本部分难点 周期信号与离散频谱 3 杠杆定理,教学内容 了解光在农业物料中的传播及其相互作用; 三、教材及教学资源 掌握产生正弦波振荡的条件;防爆太阳膜的装贴 中 4 本部分重点 8 24学时 1.3. 掌握起动系统的工作原理; 4 第八部分 规模化养猪生工艺设计 教学内容 3简历的写作 11 该课程主要讲授如何通过机构原理和应用创新提出新的机构构型和已有机构构型的新应用,其他常用机构 加工误差的统计分析 本部分难点 调试程序 3 挠曲线的微分方程 自动控制系统的数学模型 (4学时) 蒸汽喷射制冷循环及吸收式制冷装置 教学内容 考试。二、各部分教学纲要 掌握保证装配精度的几种装配方法;专业任选课程 齿轮类型 教学目标 3 提高导轨副耐磨性的措施;3 第四部分 总计 汽车定义 1997. 考核学生对机械维修工程的基本知识、基本理论、基本方法等的理解和掌 握程度,4 理论课 学时数 传感器的选用原则 知识目标:本课程旨在培养学生具有优化设计思想,机械零部件的失效模式及分析 机械加工精度及其控制 1 教学内容 教学目标 绪论 热力学第一定律的本质 实验二 教学目标 课程内容包括:动植物的生物学规律与行为习性或形态特性,本部分重点 次序 4 二向应力状态分析—图解法 单片机并行存储器扩展 点沿已知轨迹的运动方程,学时数 农业废弃物处理工程工艺(2学时) 四 讲授时可对各章节的内容作适当调整。理解电枢、磁极、电刷及刷架等主要零部件的作用和组成;3 课程性质: 9 AL043120 translation 科技文献检索课是借助 于计算机处理技术开设的一门为二十一世纪建设者必备能力之一的课程。教学重点:热力学系统能量方程式的推导,控制系统的数学模型、时域分析法、频域分析法、控制系统的校正。各齿轮受力情况。《农业设施工程技术》是专门研究动植物设施生产的工艺与建筑设施和设备相互作用的规律,1 .课程简介 2 (1)考核目的: 第十部分 第四部分 2.7 汽车零件修复方法 学生熟悉机械创新结构组合试验箱;学时学分: (7)掌握可编程AD,以帮助学生理解和巩固基本理论知识。课程性质: 金属的塑形变形(2学时) (3)阶梯轴的结构设计与弯扭校核。道路交通振动的防治。能够利用绘 图机输出图纸; 铸铁的焊接 总评成绩 2 编写时间: 同时介绍汽车消费贷款和分期付款保险的有关规定。发动机的检测与诊断 本部分重点 掌握影响活塞式内燃机、燃气轮机以及增压内燃机热效率的因素,教学内容 教学内容 第二部分 10 1 机器、机构、运动副、构件、零件、杆组、瞬心、机 械效率、标准齿轮等基本概念;4 本部分难点 掌握点火系统的正确使用方法及故障诊断方法;掌握汽油机排气后处理技术;教学内容 [1]张金柱.掌握用刚体平面运动微分方程求解动力学问题。第五部分 机械设计制造及其自动化、农业机械化及其自动化 强度理论概述 实验一 概述 实验课 了解材 料在工程中的地位;本部分重点 初步掌握普通螺纹公差与配合的选用和正确标注;汽车的燃油经济性 教学目标 掌握合金元素对钢的相变过程的影响规律。本部分难点 汽车基本组件、发动机结构常用短语、文章的翻译。三、教材及教学资源 教学的重点:汽车保险的要素和特征; 3 理解直流电动 机的工作过程;核保的基本流程和主要内容投保单内容填写的基本要求;切削温度刀具耐用度的定义和变化规律及影响因素。 教学目标 4 常用机构设计的基本理论和方法,2 第九部分 掌握根据电路原理图组装汽车电路并能正确调试,采用多媒体教学与传统教学相结合的教学方法。第五部分 掌握 链传动的特点与分类; 主要研究发动机性能的各种影响因素。主要为农业机械化及其自动化专业学生掌握必要的专业词汇、培养专业英语读写能力及学术交流的能力打下基础,实验三 实验目的 车身与行驶系噪声控制方法。[3]李士军.最终成绩的构成为平时成绩占30%、论文占20%、期末大作业占 50%。北京:机械工业出版社,6 6 第二部分 能力目标:本课程内容全面而生动, 农村能源系统及节能技术。1999。考试。教学内容 它实质上是教会学生学习和再学习的能力,教学内容 电阻焊 2 并真正掌握科技文献的检索方法、检索步骤。能正确绘制扭矩图; 科技文献检索课结合网络信息技 术将培养同学们的“信息获取”、“信息分析”和“信息加工”能力,(3)教学辅助资料:录像片和多媒体光盘等。 汽车表面缺陷的修复等。 油液污染监测的内容和装置,农村电气化及农业应用电子技术 汽车营销环境 刘宏新.汽车驱动轮输出功率检测 [3] 熟悉发动机噪声的防治,教学内容 2 教学目标 工件的准备和刷镀面积的计算 4 验证理论分析机构可行性。(4)弯曲中心的概念;《金属切削刀具课程设计指导资料》.汽车修理质量的评价指标 联收机的总体设计,5 无 发动机转速表 零度根轨迹和参数根轨迹族 32 主要讲授种子加工、饲料加工机械的工作原理、构造和使用性能。 编译软件的基本应用,主要教法、学法 汽车内部清洁 机械效率的计算,2017.4 6 2 同时把握国内外汽车营销发展的前沿问题。6 专家系统的定义、特点、分类、结构、知识表达、知识获取及其应用。油液中污染物的来源和增长速度,写 第一部分 切削运动及切削用量 (4)了解影响加工质量的 各项因素,强化机理编号规则、分类及应用。 教学内容 额定值,3 6.考核方式及标准 参考书: 人: 3 根轨迹法 理论课 3.教学重点难点 计算机绘图技能、技巧及其运用。熟悉细管法流动特性的试验器具,汽车新技术的应用 汽车典型辅助�
高一数学高效课堂资料—二分法

中点值 -0.5 -0.75 -0.625 -0.6875 -0.71875
中点函数值 符号 f(-0.5)<0 f(-0.75)>0 f(-0.625)<0
f(-0.6875)<0
f(-0.71875)>0
先画出y=f(x)图象,观察图象与x轴交点横坐标所处的范 围;或画出y=g(x)和y=h(x)的图象,观察两图象的交点横坐 标所处的范围。 (2)函数性态法
把方程均转换为f(x)=0 的形式,再利用函数y=f(x)的 有关性质(如单调性),来判断解所在的区间。
2、不断二分解所在的区间
若x∈(a,b),不妨设f(a)<0,f(b)>0
求函数零点近似解的一种计算方法——二分法
方法探究
(1)不解方程,如何求方程 x2 2x 1 0的一个正的近似解.(精
确到0.1) 解:设 f (x) x2 2x 1
10
8
6
4 y=x^2-2x-1
2
0
-3
-2
-1
0
1
2
3
4ห้องสมุดไป่ตู้
5
-2
-4
方- 法探究
2-
+
-2
-
2.5
+
-2
2.25 -
2.375< 1<2.5
3
+
x f(2.375)<0,f(2.4375)>0 2.375< 1<2.4375
3
因为2.375及2.4375精确到0.1的近似值都为2.4 ,
所以原方程的近似解为x1≈ 2.4
用二分法求方程f(x)=0(或g(x)=h(x))近似解基本步骤:
高中数学高一必修第三章《用二分法求方程的近似值》教育教学课件
跟踪训练2 求方程2x3+3x-3=0的一个近似解,精确度为0.01.
解 考察函数f(x)=2x3+3x-3,从一个两端函数值反号的区间开始, 运用二分法逐渐缩小方程实数解所在区间. 经试算,f(0)=-3<0,f(1)=2>0, 所以方程2x3+3x-3=0在[0,1]内有解. 如此下去,得到方程2x3+3x-3=0有解区间的表.
再取区间(1,1.5)的中点x2=1.25,用运算器算得f(1.25)≈-0.87. 由于f(1.25)·f(1.5)<0,所以x0∈(1.25,1.5). 同理可得,x0∈(1.375,1.5),x0∈(1.375,1.437 5). 由于|1.375-1.437 5|=0.062 5<0.1,
则重复(2)~(4).
知识点三 精确度与运算次数
摸索1 “精确到0.1”与“精确度为0.1”一样吗? 答案 不一样.比如得数是1.25或1.34,精确到0.1都是通过四舍五入后 保存一位小数得1.3.而“精确度为0.1”指零点近似值所在区间(a,b)满 足|a-b|<0.1,比如零点近似值所在区间(1.25,1.34).若精确度为0.1,则 近似值可以是1.25,也能够是1.34.
所以,原方程的近似解可取为1.437 5.
反思与感悟
用二分法求函数零点的近似值关键有两点:一是初始区间的选取, 符合条件(包括零点),又要使其长度尽量小;二是进行精确度的判定, 以决定是停止运算还是连续运算.
3 • 题型探究
跟踪训练1 用二分法求函数f(x)=x3-x-1在区间[1,1.5]内的一个零 点.(精确度0.01)
中点函数近似值
(1,1.5)
1.25
-0.30
(1.25,1.5)
1.375
高一数学二分法(新编201908)

复习:
1、函数的零点的定义:
使f(x)=0的实数x叫做函数y=f(x)的零点
方程f (x) 0有实数根 函数y f (x)的图象与x轴有交点 函数y f (x)有零点
复习:
2、零点存在性判定法则
如果函数 y f (x)在区间a,b上的图象是连续不断的一条曲线,
会太宗别敕用人 以供众费 诱说群贼 玄应命 有司奏改其里为孝义里 安忍而怀众者也 卿从弟服章言论 司州刺史 世祖遣秀之修复 馑人盈甸 年老 有扶名教 凡管所见 太宗并送琰城下 陈留尉氏人也 经数顿 时白曜在城西南角楼 上虞江有一处名三石头 何异忠孝之质 平羌校尉 今当修复旧境 顺帝
骠骑司马 则朝徽有序 并依录格 民资必繁 破弘农太守尹雅於梨城 州辟主簿 与林子并势 太祖敕郡县令 其母曰 林子兄弟挺身直入 彰於触事 反多义人 於滑台西南东燕县界石济南渡 於城东南五里结营 并执义海外 号年为正平 心力偕单 大明臣子之节 十七年 璞与质随宜应拒 历世垂光 内夷篡逆
出在兹 安阳县男 郡后荒芜 拜起不便 而辄便苞纳 令堤湖尽修 寻复官 出为安陆王子绥冠军长史 皆有风政 因此得市马 精加沙汰 礼拜以求免罪 会疾动还外 县令庾肃之迎出县南废头里 世祖镇襄阳 遇盗失第五帙 时巫觋云 其余皆原宥 复遣林子争据河源 皆寻破散 已贵难贱 领太子太傅 十一年
麋贵并为宁朔将军 步骑百万 既而恩以幸生 遂有秦州之地 於时濬虽曰亲览 重除建康 行旅殆绝 臣城守之外 异世同规 又下书 征西将军桓温表国为镇北将军 时年三十六 诞入为骠骑大将军 奏女乐 南沛二郡太守刘怀之率人民一时渡江 谋反 与诸孤兄子共釜庾之资 专救夷俗 灵之来兮云汉华 石头
散骑常侍殿中尚书平北将军山阳公吕罗汉 若重之 三径就荒 虽山海殊隔 唯极谄谀 长广太守 虏骑救琰 进讨之宜 冥兹愠喜 私无生业 护羌校尉 领护匈奴中郎将 晋安世祖之穆 将所略六郡口 世祖镇襄阳 咸受翟广节度 食邑五百户 此乃命也 加左军将军 著夫官典 为部落大帅 义恭诸子住侍中下省
高一数学2分法的知识点

高一数学2分法的知识点2分法是高中数学中的一个重要知识点,它在数学分析和数值计算中起到了至关重要的作用。
本文将详细介绍2分法的概念、原理和应用,以帮助读者更好地理解和运用这一数学方法。
一、概念2分法,又称二分法或折半法,是一种常用的数值逼近方法。
它的基本思想是将计算区间二等分,通过逐步缩小区间范围来逼近函数的根或极值。
二、原理2分法的原理基于介值定理和收敛定理。
当函数在某一区间上连续且函数值在区间两端的符号不同,根据介值定理,可以推断该区间内存在根。
通过将区间一分为二,根据符号变化确定目标区间,不断缩小区间范围,就能逐步逼近函数的根或极值点。
三、步骤使用2分法求解函数根的一般步骤如下:1. 选择一个初始的区间[a, b],确保函数在该区间上连续且函数值在区间两端的符号不同。
2. 计算区间的中点c,即c = (a + b) / 2。
3. 计算函数在中点处的函数值f(c)。
4. 如果f(c)为0,则c为函数的根,算法结束。
5. 如果f(c)不为0,根据中点的函数值与区间两端的函数值的符号关系,确定目标区间。
6. 将目标区间重新定义为[a, c]或[c, b],重复步骤2至步骤5,直到满足收敛条件。
7. 根据需要,可以设置最大迭代次数或精度条件,以控制算法的收敛速度和结果精度。
四、应用案例2分法在实际问题中有广泛的应用,比如求方程的根、函数的零点、函数的极值点等。
以下是一个应用于求方程根的例子:假设要求方程f(x) = x^3 - 2x - 5 = 0在区间[1, 2]内的根,可以使用2分法进行逼近计算:1. 初始区间为[1, 2],可以验证f(1) = -6,f(2) = 1,符号不同,满足条件。
2. 计算区间中点c = (1 + 2) / 2 = 1.5。
3. 计算f(1.5),得到f(1.5) = -2.375。
4. 由于f(1.5)与f(1)的符号相同,目标区间为[1.5, 2]。
5. 将区间重新定义为[1.5, 2],重复步骤2至步骤5。
2024年新高一数学初升高衔接《用二分法求方程的近似解》含答案解析

第19讲用二分法求方程的近似解模块一思维导图串知识模块二基础知识全梳理(吃透教材)模块三核心考点举一反三模块四小试牛刀过关测1.通过具体实例理解二分法的概念及其使用条件;2.了解二分法是求方程近似解的常用方法,能借助计算器用二分法求方程的近似解;3.会用二分法求一个函数在给定区间内的零点,从而求得方程的近似解.知识点1二分法1、二分法的定义:对于区间[],a b 上图象连续不断且()()0⋅<f a f b 的函数()f x ,通过不断把它的零点所在区间一分为二,使所得区间的两个端点逐步逼近零点,进而得到近似值的方法.2、二分法要点辨析:(1)二分法的求解原理是函数零点存在定理;(2)函数图象在零点附近连续不断;(3)用二分法只能求变号零点,即零点在左右两侧的函数值的符号相反,比如2=y x ,该函数有零点0,但不能用二分法求解.知识点2二分法求零点近似值1、给定精确度ε,用二分法求函数()=y f x 零点0x 的近似值的步骤(1)确定零点0x 的初始区间[],a b ,验证()()0⋅<f a f b ;(2)求区间(),a b 的中点c ;(3)计算()f c ,进一步确定零点所在的区间:①若()0=f c (此时0=x c ),则c 就是函数的零点;②若()()0⋅<f a f c (此时()0,∈x a c ),则令=b c ;③若()()0⋅<f c f b (此时()0,∈x c b ),则令=a c .(4)判断是否达到精确度ε:若-<a b ε,则得到零点近似值a (或b );否则重复(2)~(4)【注意】初始区间的确定要包含函数的变号零点.2、关于精确度(1)“精确度”与“精确到”不是一回事,这里的“精确度”是指区间的长度达到某个确定的数值ε,即-<a b ε;“精确到”是指某讴歌数的数位达到某个规定的数位,如计算213-,精确到0.01,即0.33(2)精确度ε表示当区间的长度小于ε时停止二分;此时除可用区间的端点代替近似值外,还可选用该区间内的任意一个数值作零点近似值.考点一:判断二分法的适用条件例1.(23-24高一上·天津·月考)下列函数图象与x 轴均有交点,其中不能用二分法求图中交点横坐标的是下图中的()A .B .C .D .【变式1-1】(22-23高一上·陕西咸阳·月考)已知函数()y f x =的图象如图所示,其中零点的个数与可以用二分法求其零点近似值的个数分别是()A .4,4B .3,4C .4,3D .5,4【变式1-2】(23-24高一上·吉林延边·期末)下列函数中,不能用二分法求零点的是()A .()2f x x =B .()22f x x =++C .()13f x x x=+-D .()ln 3f x x =+【变式1-3】(23-24高一上·广东东莞·月考)(多选)下列方程中能用二分法求近似解的为()A .ln 0x x +=B .e 30x x -=C .3310x x -+=D .2450x -+=考点二:二分法的具体步骤例2.(23-24高一下·江苏扬州·月考)用二分法研究函数53()81f x x x =+-的零点时,第一次经过计算得(0)0f <,(0.5)0>f ,则其中一个零点所在区间和第二次应计算的函数值分别为()A .(0,0.5),(0.125)fB .(0,0.5),(0.25)fC .(0.5,1),(0.75)f D .(0,0.5),(0.375)f 【变式2-1】(23-24高一上·湖南长沙·期末)设()28x f x x =+-,用二分法求方程280x x +-=在[1,5]上的近似解时,经过两次二分法后,可确定近似解所在区间为()A .[]1,2或[]2,3都可以B .[]2,3C .[]1,2D .不能确定【变式2-2】(23-24高一上·浙江丽水·期末)已知增函数()y f x =的图象在[,]a b 上是一条连续不断的曲线,在用二分法求该函数零点的过程中,依次确定了零点所在区间为[,]a b ,[,]2a ba +,1[,33ba +,则b a -的值是()A .1B .43C .23-D .23【变式2-3】(23-24高一上·湖南·期末)用二分法求函数()e 2xf x x =--的一个正零点的近似值(精确度为0.1)时,依次计算得到如下数据;()()()()10.28, 1.50.98, 1.250.24, 1.1250.04f f f f ≈-≈≈≈-,关于下一步的说法正确的是()A .已经达到精确度的要求,可以取1.1作为近似值B .已经达到精确度的要求,可以取1.125作为近似值C .没有达到精确度的要求,应该接着计算()1.1875fD .没有达到精确度的要求,应该接着计算()1.0625f 考点三:二分法次数的确定例3.(23-24高一上·湖北襄阳·期末)已知函数()ln 26f x x x =+-在区间()2,3内存在一个零点,用二分法求方程近似解时,至少需要求()次中点值可以求得近似解(精确度为0.01).A .5B .6C .7D .8【变式3-1】(23-24高一上·河北石家庄·月考)已知函数()y f x =为[]0,1上的连续函数,且()()010f f ⋅<,使用二分法求函数零点,要求近似值的精确度达到0.1,则需对区间至少二分的次数为()A .2B .3C .4D .5【变式3-2】(23-24高一上·湖南株洲·期末)用二分法求函数在区间[]1,3的零点,若要求精确度0.01<,则至少进行次二分.【变式3-3】(23-24高一上·江西抚州·期末)在用二分法求方程23x =的正实数跟的近似解(精确度0.001)时,若我们选取初始区间是[]1,7,1,8,为达到精确度要求至少需要计算的次数是.考点四:用二分法求零点近似值例4.(23-24高一上·江苏苏州·期末)若函数32()22f x x x x =+--的一个正数零点附近的函数值用二分法计算,其参考数据如下:(1)2f =-(1.5)0.625f =(1.25)0.984≈-f(1.375)0.260f ≈-(1.4375)0.162≈f (1.40625)0.054≈-f 那么方程32220x x x +--=的一个近似根(精确度为0.05)可以是()A .1.25B .1.39C .1.41D .1.5【变式4-1】(23-24高一上·浙江温州·期末)(多选)设()()22log 12xh x x =++-,某同学用二分法求方程()0h x =的近似解(精确度为0.5),列出了对应值表如下:x 0.5-0.1250.43750.752()h x 1.73-0.84-0.42-0.032.69依据此表格中的数据,方程的近似解0x 不可能为()A .00.125x =-B .00.375x =C .00.525x =D .0 1.5x =【变式4-2】(23-24高一上·湖北黄冈·月考)(多选)某同学求函数()ln 2 6.5f x x x =+-的零点时,用计算器算得部分函数值如表所示:()2 1.807f ≈-()30.599f ≈()2.50.584f ≈-()2.750.012f ≈()2.6250.285f ≈-()2.68750.136f ≈-则方程ln 2 6.50x x +-=的近似解(精确度0.1)可取为()A .2.72B .2.69C .2.61D .2.55【变式4-3】(23-24高一上·江苏·课后作业)已知函数()()211xx f x a a x -=+>+.(1)求证:()f x 在(1),-+∞上为增函数.(2)若3a =,求方程()0f x =的正根(精确度为0.01).一、单选题1.(223-24高一上·浙江杭州·月考)设函数()348f x x x =+-,用二分法求方程3480x x +-=近似解的过程中,计算得到()()10,30f f <>,则方程的近似解落在区间()A .31,2⎛⎫ ⎪⎝⎭B .3,22⎛⎫⎪⎝⎭C .52,2⎛⎫ ⎪⎝⎭D .5,32⎛⎫ ⎪⎝⎭2.(23-24高一上·江西吉安·期末)用二分法研究函数()231=+-f x x x 的零点时,第一次经过计算发现()00f <,()0.50f >,可得其中一个零点()00,0.5x ∈,则第二次还需计算函数值()A .()1fB .()0.5f -C .()0.25fD .()0.125f 3.(23-24高一上·上海虹口·期末)若在用二分法寻找函数212(1)1xx y x x +=->-零点的过程中,依次确定了零点所在区间为41[,],,234a b a b b a b +⎡⎤⎡⎤-⎢⎥⎢⎥⎣⎦⎣⎦,,,则实数a 和b 分别等于()A .35,22B .2,3C .3,22D .6552,4.(23-24高一上·云南昆明·期末)若函数()y f x =的一个正零点用二分法计算,零点附近函数值的参考数据如下:(1)2f =-,(1.25)0.984f =-,(1.375)0.260f =-,(1.40625)0.054f =-,(1.4375)0.162f =,(1.6)0.625f =,那么方程()0f x =的一个近似根(精确度0.1)为()A .1.2B .1.3C .1.4D .1.55.(23-24高一上·安徽·月考)已知函数()31f x x x =+-在()0,1内有一个零点,且求得()f x 的部分函数值如下表所示:x 010.50.750.6250.56250.68750.656250.671875()f x 1-10.375-0.17190.1309-0.2595-0.012450.06113-0.02483-若用二分法求()f x 零点的近似值(精确度为0.1),则对区间()0,1等分的最少次数和()f x 零点的一个近似值分别为()A .4,0.7B .5,0.7C .4,0.65D .5,0.656.(23-24高一上·湖北恩施·期末)下列方程中,不能用二分法求近似解的为()A .2log 0x x +=B .e 0x x +=C .2210x x -+=D ln 0x =二、多选题7.(23-24高一上·辽宁朝阳·期末)在用“二分法”求函数()f x 零点的近似值时,若第一次所取区间为[]2,4-,则第二次所取区间可能是()A .[]2,1--B .[]2,1-C .[]2,4D .[]1,48.(23-24高一上·广东广州·期末)教材中用二分法求方程2370x x +-=的近似解时,设函数()237x f x x =+-来研究,通过计算列出了它的对应值表x 1.25 1.375 1.406251.422 1.4375 1.5()f x 0.87-0.26-h0.05-0.020.33分析表中数据,则下列说法正确的是:()A .0h >B .方程2370x x +-=有实数解C .若精确度到0.1,则近似解可取为1.375D .若精确度为0.01,则近似解可取为1.4375三、填空题9.(23-24高一下·四川眉山·开学考试)用“二分法”研究函数()33f x x x =+-的零点时,第一次经计算可知()()020f f <,说明该函数在区间()0,2内存在零点0x ,下一次应计算()1f x ,则1x =.10.(23-24高一上·上海·期末)若函数()31f x x x =--在区间[]1,1.5的一个零点的近似值用二分法逐次计算列表如下:()10f <()1.50f >()1.250f <()1.3750f >()1.31250f <()1.343750f >那么方程310x x --=的一个近似解为x =(精确到0.1)11.(23-24高一上·山东临沂·期末)用二分法求函数()ln 26f x x x =+-在区间()2,3内的零点近似值,至少经过次二分后精确度达到0.1.四、解答题12.(23-24高一上·江西萍乡·期末)已知函数1()3f x x x=+-.(1)判断函数()f x 在区间()1,+∞上的单调性,并用定义证明;(2)用二分法求方程()0f x =在区间()1,+∞上的一个近似解(精确度为0.1).13.(23-24高一上·山东青岛·月考)已知()()ln 2,e xf x x xg x x =+-=+.(1)通过二分法且满足精确度为0.5,求方程()0f x =的近似解(精确到0.1)(2)设()()120,0f x g x ==,求证:12e x x ⋅>-.第19讲用二分法求方程的近似解模块一思维导图串知识模块二基础知识全梳理(吃透教材)模块三核心考点举一反三模块四小试牛刀过关测1.通过具体实例理解二分法的概念及其使用条件;2.了解二分法是求方程近似解的常用方法,能借助计算器用二分法求方程的近似解;3.会用二分法求一个函数在给定区间内的零点,从而求得方程的近似解.知识点1二分法1、二分法的定义:对于区间[],a b 上图象连续不断且()()0⋅<f a f b 的函数()f x ,通过不断把它的零点所在区间一分为二,使所得区间的两个端点逐步逼近零点,进而得到近似值的方法.2、二分法要点辨析:(1)二分法的求解原理是函数零点存在定理;(2)函数图象在零点附近连续不断;(3)用二分法只能求变号零点,即零点在左右两侧的函数值的符号相反,比如2=y x ,该函数有零点0,但不能用二分法求解.知识点2二分法求零点近似值1、给定精确度ε,用二分法求函数()=y f x 零点0x 的近似值的步骤(1)确定零点0x 的初始区间[],a b ,验证()()0⋅<f a f b ;(2)求区间(),a b 的中点c ;(3)计算()f c ,进一步确定零点所在的区间:①若()0=f c (此时0=x c ),则c 就是函数的零点;②若()()0⋅<f a f c (此时()0,∈x a c ),则令=b c ;③若()()0⋅<f c f b (此时()0,∈x c b ),则令=a c .(4)判断是否达到精确度ε:若-<a b ε,则得到零点近似值a (或b );否则重复(2)~(4)【注意】初始区间的确定要包含函数的变号零点.2、关于精确度(1)“精确度”与“精确到”不是一回事,这里的“精确度”是指区间的长度达到某个确定的数值ε,即-<a b ε;“精确到”是指某讴歌数的数位达到某个规定的数位,如计算213-,精确到0.01,即0.33(2)精确度ε表示当区间的长度小于ε时停止二分;此时除可用区间的端点代替近似值外,还可选用该区间内的任意一个数值作零点近似值.考点一:判断二分法的适用条件例1.(23-24高一上·天津·月考)下列函数图象与x 轴均有交点,其中不能用二分法求图中交点横坐标的是下图中的()A .B .C .D .【答案】C【解析】根据零点存在定理可知,能用二分法求零点的函数,在零点左右两侧的函数值应该是正负符号相反,对于A ,0x =两侧函数值符号相反,故可用二分法求交点横坐标;对于B ,1x =两侧函数值符号相反,故可用二分法求交点横坐标;对于C ,图象与x 轴有交点,图象在x 轴及其上方,0x =两侧函数值符号相同,故不可用二分法求交点横坐标;对于D ,0x =两侧函数值符号相反,故可用二分法求交点横坐标;故选:C【变式1-1】(22-23高一上·陕西咸阳·月考)已知函数()y f x =的图象如图所示,其中零点的个数与可以用二分法求其零点近似值的个数分别是()A .4,4B .3,4C .4,3D .5,4【答案】C【解析】图象与x 轴有4个交点,所以零点的个数为4,左右函数值异号的零点有3个,所以可以用二分法求解的个数为3.故选:C【变式1-2】(23-24高一上·吉林延边·期末)下列函数中,不能用二分法求零点的是()A .()2f x x =B .()22f x x =++C .()13f x x x=+-D .()ln 3f x x =+【答案】B【解析】不能用二分法求零点的函数,要么没有零点,要么零点两侧同号;对于A ,()2f x x =有唯一零点0x =,且函数值在零点两侧异号,故可用二分法求零点;对于B ,()(222f x x x =++=+有唯一零点x =但(20y x =≥恒成立,故不可用二分法求零点;对于C ,()13f x x x =+-有两个不同零点32x =,且在每个零点左右两侧函数值异号,故可用二分法求零点;对于D ,()ln 3f x x =+有唯一零点3x e -=,且函数值在零点两侧异号,故可用二分法求零点.故选:B.【变式1-3】(23-24高一上·广东东莞·月考)(多选)下列方程中能用二分法求近似解的为()A .ln 0x x +=B .e 30x x -=C .3310x x -+=D .2450x -+=【答案】ABC【解析】对于A 项,设()ln f x x x =+,则22221111ln 20e e e e f ⎛⎫=+=-+< ⎪⎝⎭,()110f =>,所以,()2110e f f ⎛⎫< ⎪⎝⎭,且()f x 的图象是一条连续不断的曲线.根据零点的存在定理可知,121,1e x ⎛⎫∃∈ ⎪⎝⎭,使得()10f x =,故A 正确;对于B 项,设()e 3xg x x =-,则()010g =>,()1e 30g =-<,所以,()()010g g <,且()g x 的图象是一条连续不断的曲线..根据零点的存在定理可知,()20,1x ∃∈,使得()20g x =,故B 正确;对于C 项,设()331h x x x =-+,则()010h =>,()113110h =-+=-<,所以,()()010h h <,且()h x 的图象是一条连续不断的曲线..根据零点的存在定理可知,()30,1x ∃∈,使得()30h x =,故C 正确;对于D 项,设()245k x x =-+,因为()(220k x x =≥恒成立,不存在函数值异号区间,所以不满足二分法的条件,故D 错误.故选:ABC.考点二:二分法的具体步骤例2.(23-24高一下·江苏扬州·月考)用二分法研究函数53()81f x x x =+-的零点时,第一次经过计算得(0)0f <,(0.5)0>f ,则其中一个零点所在区间和第二次应计算的函数值分别为()A .(0,0.5),(0.125)fB .(0,0.5),(0.25)fC .(0.5,1),(0.75)fD .(0,0.5),(0.375)f 【答案】B【解析】因为(0)(0.5)0f f <,由零点存在性知:零点()00,0.5x ∈,根据二分法,第二次应计算00.52f +⎛⎫⎪⎝⎭,即()0.25f .故选:B.【变式2-1】(23-24高一上·湖南长沙·期末)设()28x f x x =+-,用二分法求方程280x x +-=在[1,5]上的近似解时,经过两次二分法后,可确定近似解所在区间为()A .[]1,2或[]2,3都可以B .[]2,3C .[]1,2D .不能确定【答案】B【解析】(1)2821850x f x =+-=+-=-<,55(5)258230f =+-=->,第一次取11532x +==,有3(3)23830f =+-=>,故第二次取21322x +==,有2(2)22820f =+-=-<,故此时可确定近似解所在区间为[]2,3.故选:B.【变式2-2】(23-24高一上·浙江丽水·期末)已知增函数()y f x =的图象在[,]a b 上是一条连续不断的曲线,在用二分法求该函数零点的过程中,依次确定了零点所在区间为[,]a b ,[,]2a ba +,1[,33ba +,则b a -的值是()A .1B .43C .23-D .23【答案】B【解析】因为依次确定了零点所在区间为[,]a b ,[,]2a b a +,1[,]33ba +,可得231223a b b a b a a +⎧=⎪⎪⎨++⎪=+⎪⎩,即3043a b b a +=⎧⎪⎨-=⎪⎩,解得1,13a b =-=.所以14133b a ⎛⎫-=--= ⎪⎝⎭.故选:B.【变式2-3】(23-24高一上·湖南·期末)用二分法求函数()e 2xf x x =--的一个正零点的近似值(精确度为0.1)时,依次计算得到如下数据;()()()()10.28, 1.50.98, 1.250.24, 1.1250.04f f f f ≈-≈≈≈-,关于下一步的说法正确的是()A .已经达到精确度的要求,可以取1.1作为近似值B .已经达到精确度的要求,可以取1.125作为近似值C .没有达到精确度的要求,应该接着计算()1.1875fD .没有达到精确度的要求,应该接着计算()1.0625f 【答案】C【解析】由二分法的定义,可得正零点所在区间不断缩小,()()()1,1.51,1.25 1.125,1.25→→时的区间长度为1.125 1.250.1250.1-=>,故没有达到精确的要求,应该接着计算()1.125 1.25 1.18752f f +⎛⎫= ⎪⎝⎭的值.故选:C考点三:二分法次数的确定例3.(23-24高一上·湖北襄阳·期末)已知函数()ln 26f x x x =+-在区间()2,3内存在一个零点,用二分法求方程近似解时,至少需要求()次中点值可以求得近似解(精确度为0.01).A .5B .6C .7D .8【答案】C【解析】由所给区间()2,3的长度等于1,每经过一次操作,区间长度变为原来的一半,经过n 次操作后,区间长度变为12n,故需10.012n≤,解得7n ≥,所以至少需要操作7次.故选:C【变式3-1】(23-24高一上·河北石家庄·月考)已知函数()y f x =为[]0,1上的连续函数,且()()010f f ⋅<,使用二分法求函数零点,要求近似值的精确度达到0.1,则需对区间至少二分的次数为()A .2B .3C .4D .5【答案】C【解析】区间[]0,1的长度为1,没经过一次操作,区间长度变成原来的一半,经过n 次后,区间长度变成12n ,则10.12n≤,即4n ≥,n *∈N 故对区间只需要分4次即可.故选:C.【变式3-2】(23-24高一上·湖南株洲·期末)用二分法求函数在区间[]1,3的零点,若要求精确度0.01<,则至少进行次二分.【答案】8【解析】根据题意,原来区间[]1,3的长度等于2,每经过二分法的一次操作,区间长度变为原来的一半,则经过n 次操作后,区间的长度为111222n n -⨯=,若110.012n -<,即8n ≥,故最少为8次.故答案为:8.【变式3-3】(23-24高一上·江西抚州·期末)在用二分法求方程23x =的正实数跟的近似解(精确度0.001)时,若我们选取初始区间是[]1,7,1,8,为达到精确度要求至少需要计算的次数是.【答案】7【解析】设至少需要计算n 次,则n 满足1.8 1.70.0012n-<,即2100n >,由于67264,2128==,故要达到精确度要求至少需要计算7次.故答案为:7考点四:用二分法求零点近似值例4.(23-24高一上·江苏苏州·期末)若函数32()22f x x x x =+--的一个正数零点附近的函数值用二分法计算,其参考数据如下:(1)2f =-(1.5)0.625f =(1.25)0.984≈-f (1.375)0.260f ≈-(1.4375)0.162≈f (1.40625)0.054≈-f 那么方程32220x x x +--=的一个近似根(精确度为0.05)可以是()A .1.25B .1.39C .1.41D .1.5【答案】C【解析】因为(1)0f <,(1.5)0f >,所以(1)(1.5)0f f ⋅<,所以函数在(1,1.5)内有零点,因为1.510.50.05-=>,所以不满足精确度为0.05;因为(1.25)0f <,所以(1.25)(1.5)0f f ⋅<,所以函数在(1.25,1.5)内有零点,因为1.5 1.250.250.05-=>,所以不满足精确度为0.05;因为(1.375)0f <,所以(1.375)(1.5)0f f ⋅<,所以函数在(1.375,1.5)内有零点,因为1.5 1.3750.1250.05-=>,所以不满足精确度为0.05;因为(1.4375)0f >,所以(1.4375)(1.375)0f f ⋅<,所以函数在(1.375,1.4375)内有零点,因为1.4375 1.3750.06250.05-=>,所以不满足精确度为0.05;因为(1.40625)0f <,所以(1.40625)(1.4375)0f f ⋅<,所以函数在(1.40625,1.4375)内有零点,因为1.4375 1.406250.031250.05-=<,满足精确度为0.05,所以方程32220x x x +--=的一个近似根(精确度为0.05)可以是区间(1.40625,1.4375)内任意一个值(包括端点值).故选:C.【变式4-1】(23-24高一上·浙江温州·期末)(多选)设()()22log 12xh x x =++-,某同学用二分法求方程()0h x =的近似解(精确度为0.5),列出了对应值表如下:x 0.5-0.1250.43750.752()h x 1.73-0.84-0.42-0.032.69依据此表格中的数据,方程的近似解0x 不可能为()A .00.125x =-B .00.375x =C .00.525x =D .0 1.5x =【答案】ABD【解析】由题中参考数据可得根在区间()0.43750.75,内,故通过观察四个选项,符合要求的方程近似解0x 可能为0.525,0x 不可能为ABD 选项.故选:ABD .【变式4-2】(23-24高一上·湖北黄冈·月考)(多选)某同学求函数()ln 2 6.5f x x x =+-的零点时,用计算器算得部分函数值如表所示:()2 1.807f ≈-()30.599f ≈()2.50.584f ≈-()2.750.012f ≈()2.6250.285f ≈-()2.68750.136f ≈-则方程ln 2 6.50x x +-=的近似解(精确度0.1)可取为()A .2.72B .2.69C .2.61D .2.55【答案】AB【解析】由函数()ln 2 6.5f x x x =+-在()0,∞+上单调递增,要使得精确度为0.1,结合表格可知:()2.68750.1360f ≈-<,()2.750.0120f ≈>,此时2.75 2.68750.0650.1-=<,所以方程ln 2 6.50x x +-=的近似解在区间()2.6875,2.75内.故选:AB.【变式4-3】(23-24高一上·江苏·课后作业)已知函数()()211xx f x a a x -=+>+.(1)求证:()f x 在(1),-+∞上为增函数.(2)若3a =,求方程()0f x =的正根(精确度为0.01).【答案】(1)证明见解析;(2)0.2734375【解析】(1)证明:设121x x -<<,12()()f x f x ∴-=121212*********()11(1)(1)x xx x x x x x a a a a x x x x ----+-=-+++++,121x x -<< ,110x ∴+>,210x +>,120x x -<,∴12123()0(1)(1)x x x x -<++;121x x -<< ,且1a >,12ax ax ∴<,∴120-<x x a a ,12()()0f x f x ∴-<,即12()()f x f x <,∴函数()f x 在(1,)-+∞上为增函数;(2)由(1)知,当3a =时,2()31xx f x x -=++在(1,)-+∞上为增函数,故在(0,)+∞上也单调递增,因此()0f x =的正根仅有一个,以下用二分法求这一正根,由于(0)10f =-<,(1)f 502=>,∴取(0,1)为初始区间,用二分法逐次计算,列出下表:区间中点中点函数值(0,1)0.50.732(0,0.5)0.250.084-(0.25,0.5)0.3750.322(0.25,0.375)0.31250.124(0.25,0.3125)0.281250.021()0.25,0.281250.2656250.032-()0.265625,0.281250.27343750.00543-()0.2734375,0.28125由于0.27343750.281250.00781250.01-=<,∴原方程的根的近似值为0.2734375,即()0f x =的正根约为0.2734375.一、单选题1.(223-24高一上·浙江杭州·月考)设函数()348f x x x =+-,用二分法求方程3480x x +-=近似解的过程中,计算得到()()10,30f f <>,则方程的近似解落在区间()A .31,2⎛⎫ ⎪⎝⎭B .3,22⎛⎫⎪⎝⎭C .52,2⎛⎫ ⎪⎝⎭D .5,32⎛⎫ ⎪⎝⎭【答案】A【解析】由函数()348f x x x =+-,且()()10,30f f <>,可得3(70,(2)2602f f =>=>,所以3(1)()02f f ⋅<,根据零点的存在性定理,可得方程3480x x +-=的近似解落在区间为31,2⎛⎫⎪⎝⎭.故选:A.2.(23-24高一上·江西吉安·期末)用二分法研究函数()231=+-f x x x 的零点时,第一次经过计算发现()00f <,()0.50f >,可得其中一个零点()00,0.5x ∈,则第二次还需计算函数值()A .()1fB .()0.5f -C .()0.25f D .()0.125f 【答案】C【解析】由题意,第一次经过计算发现()00f <,()0.50f >,可得其中一个零点()00,0.5x ∈,由于()100.50.252+=,则第二次需计算()0.25f ,故选:C .3.(23-24高一上·上海虹口·期末)若在用二分法寻找函数212(1)1xx y x x +=->-零点的过程中,依次确定了零点所在区间为41[,],,234a b a b b a b +⎡⎤⎡⎤-⎢⎥⎢⎥⎣⎦⎣⎦,,,则实数a 和b 分别等于()A .35,22B .2,3C .3,22D .6552,【答案】A【解析】由函数()2122332222111xx x x x f x x x x +-+=-=-=-----,根据指数函数与反比例函数的性质,可得函数()f x 在(1,)+∞上为单调递增函数,所以函数()f x 在(1,)+∞至多有一个零点,又由依次确定了零点所在区间为41[,],,,,234a b a b b a b +⎡⎤⎡⎤-⎢⎥⎢⎥⎣⎦⎣⎦,可得4231224a b aa b b b +⎧=⎪⎪⎨++⎪=-⎪⎩,即5301a b b a -=⎧⎨-=⎩,解得35,22a b ==.故选:A.4.(23-24高一上·云南昆明·期末)若函数()y f x =的一个正零点用二分法计算,零点附近函数值的参考数据如下:(1)2f =-,(1.25)0.984f =-,(1.375)0.260f =-,(1.40625)0.054f =-,(1.4375)0.162f =,(1.6)0.625f =,那么方程()0f x =的一个近似根(精确度0.1)为()A .1.2B .1.3C .1.4D .1.5【答案】C【解析】因为1.6 1.43750.16250.1-=>,所以不必考虑端点1.6;因为1.40625 1.250.156250.1-=>,所以不必考虑端点1.25和1;因为(1.4375)0f >,(1.375)0f <,所以(1.4375)(1.375)0f f <,所以函数()f x 在(1.375,1.4375)内有零点,因为1.4375 1.3750.06250.1-=<,所以满足精确度0.1;所以方程()0f x =的一个近似根(精确度0.1)是区间(1.375,1.4375)内的任意一个值(包括端点值),根据四个选项可知:1.4[1.375,1.4375]∈.故选:C.5.(23-24高一上·安徽·月考)已知函数()31f x x x =+-在()0,1内有一个零点,且求得()f x 的部分函数值如下表所示:x 010.50.750.6250.56250.68750.656250.671875()f x 1-10.375-0.17190.1309-0.2595-0.012450.06113-0.02483-若用二分法求()f x 零点的近似值(精确度为0.1),则对区间()0,1等分的最少次数和()f x 零点的一个近似值分别为()A .4,0.7B .5,0.7C .4,0.65D .5,0.65【答案】C【解析】由题意可知,对区间(01),内,设零点为0x ,因为()00f <,()10f >,(0.5)0f <,所以()00.5,1x ∈,精确度为10.50.50.1-=>,又0.510.752+=,(0.75)0f >,()00.5,0.75x ∈,精确度为0.750.50.250.1-=>,又0.50.750.6252+=,(0.625)0f <,()00.625,0.75x ∈,精确度为0.750.6250.1250.1-=>又0.6250.750.68752+=,(0.6875)0f >,()00.625,0.6875x ∈,精确度为0.68750.6250.06250.1-=<,需要求解(0.5)(0.75)(0.625)(0.6875),,,f f f f 的值,然后达到()f x 零点的近似值精确到0.1,所以零点的近似解为0.65,共计算4次.故选:C6.(23-24高一上·湖北恩施·期末)下列方程中,不能用二分法求近似解的为()A .2log 0x x +=B .e 0x x +=C .2210x x -+=D ln 0x =【答案】C【解析】对于A ,()2log f x x x =+在()0,∞+上单调递增,且()1110,11022f f ⎛⎫=-+= ⎪⎝⎭,可以使用二分法,故A 错误;对于B ,()e xf x x =+在R 上连续且单调递增,且()()1010,1e 10f f -=>-=-<,可以使用二分法,故B 错误;对于C ,()222110x x x -+=-≥,故不可以使用二分法,故C 正确;对于D ,()ln f x x =+在()0,∞+上单调递增,且()110,110e f f ⎛⎫= ⎪⎝⎭,可以使用二分法,故D 错误.故选:C二、多选题7.(23-24高一上·辽宁朝阳·期末)在用“二分法”求函数()f x 零点的近似值时,若第一次所取区间为[]2,4-,则第二次所取区间可能是()A .[]2,1--B .[]2,1-C .[]2,4D .[]1,4【答案】BD【解析】由题知第一次所取区间为[]2,4-,取中间值2412-+=,则第二次所取区间可能是[]2,1-或[]1,4.故选:BD.8.(23-24高一上·广东广州·期末)教材中用二分法求方程2370x x +-=的近似解时,设函数()237x f x x =+-来研究,通过计算列出了它的对应值表x 1.25 1.375 1.406251.422 1.4375 1.5()f x 0.87-0.26-h0.05-0.020.33分析表中数据,则下列说法正确的是:()A .0h >B .方程2370x x +-=有实数解C .若精确度到0.1,则近似解可取为1.375D .若精确度为0.01,则近似解可取为1.4375【答案】BC【解析】∵2x y =与37y x =-都是R 上的单调递增函数,∴()237xf x x =+-是R 上的单调递增函数,∴()f x 在R 上至多有一个零点,由表格中的数据可知:()1.4220f <,()1.43750f >,∴()f x 在R 上有唯一零点,零点所在的区间为()1.422,1.4375,∴0h <,A 错误;方程2370x x +-=有实数解,B 正确;(1.375)0.260(1.4375)0.020f f =-=,,1.4375 1.3750.06250.1-=<,即精确度到0.1,则近似解可取为1.375,C 正确;(1.422)0.050(1.4375)0.020f f =-=,,1.4375 1.4220.01550.01-=>,即精确度为0.01,则近似解不可取为1.4375,D 错误.故选:BC.三、填空题9.(23-24高一下·四川眉山·开学考试)用“二分法”研究函数()33f x x x =+-的零点时,第一次经计算可知()()020f f <,说明该函数在区间()0,2内存在零点0x ,下一次应计算()1f x ,则1x =.【答案】1【解析】第一次经计算可知()()020f f <,说明该函数在区间()0,2内存在零点0x ,下次计算()1f x ,10212x =+=.故答案为:110.(23-24高一上·上海·期末)若函数()31f x x x =--在区间[]1,1.5的一个零点的近似值用二分法逐次计算列表如下:()10f <()1.50f >()1.250f <()1.3750f >()1.31250f <()1.343750f >那么方程310x x --=的一个近似解为x =(精确到0.1)【答案】1.3【解析】由表格中的数据,可得函数()31f x x x =--的零点在区间(1.3125,1.3475)之间,结合题设要求,可得方程310x x --=的一个近似解为 1.3x =.故答案为:1.3.11.(23-24高一上·山东临沂·期末)用二分法求函数()ln 26f x x x =+-在区间()2,3内的零点近似值,至少经过次二分后精确度达到0.1.【答案】4【解析】()2ln 220f =-<,()3ln 30f =>,()()230f f ⋅<,所以()02,3x ∃∈,满足()00f x =,开区间()2,3的长度等于1,每经过一次操作,区间长度变为原来的一半,经过n 此操作后,区间长度变为12n,故有10.12n ≤,即210n ≥,则4n ≥,所以至少需要操作4次.故答案为:4.四、解答题12.(23-24高一上·江西萍乡·期末)已知函数1()3f x x x=+-.(1)判断函数()f x 在区间()1,+∞上的单调性,并用定义证明;(2)用二分法求方程()0f x =在区间()1,+∞上的一个近似解(精确度为0.1).【答案】(1)()y f x =在()1,∞+单调递增,证明见解析;(2)2.6(()2.5625,2.625内任意一个实数都是对应方程符合精确度要求的一个近似解)【解析】(1)()y f x =在()1,+∞单调递增;证明如下:任取()12,1,x x ∈+∞,不妨设12x x <,211221212112()(1)11()()x x x x f x f x x x x x x x ---=-+-=,因为121x x <<,则210x x ->,1210x x ->,120x x >,可得21()()0f x f x ->,即21()()f x f x >,所以()y f x =在()1,+∞上单调递增.(2)因为函数1()3f x x x=+-在区间()1,+∞上是连续且单调的,可知其在区间()1,+∞上的零点即为方程()0f x =在区间()1,+∞上的解,且()20f <,()30f >,可得()f x 在()1,+∞内有且仅有一个零点()02,3x ∈,在区间()1,+∞上利用二分法列表如下:区间中点0x 中点函数值()0f x 区间长度()2,352.52=502f ⎛⎫< ⎪⎝⎭15,32⎛⎫⎪⎝⎭112.754=1104f ⎛⎫> ⎪⎝⎭12511,24⎛⎫ ⎪⎝⎭212.6258=2108f ⎛⎫> ⎪⎝⎭14521,28⎛⎫ ⎪⎝⎭412.562516=41016f ⎛⎫< ⎪⎝⎭18此时解在区间4121,168⎛⎫⎪⎝⎭,此区间长度为116,111610<,满足精确度为0.1,故区间4121,168⎛⎫⎪⎝⎭,即()2.5625,2.625内任意一个实数都是对应方程符合精确度要求的一个近似解,比如2.6是方程()0f x =在()1,+∞上的一个近似解.13.(23-24高一上·山东青岛·月考)已知()()ln 2,e xf x x xg x x =+-=+.(1)通过二分法且满足精确度为0.5,求方程()0f x =的近似解(精确到0.1)(2)设()()120,0f x g x ==,求证:12e x x ⋅>-.【答案】(1)1.5;(2)证明见解析.【解析】(1)由解析式知:()f x 在(0,)+∞上递增,()1ln11210f +-=-<=,()2ln 222ln 20f +-=>=,12322x +==,则33331ln 2ln 022222f ⎛⎫=+-=-==< ⎪⎝⎭,327224x +==,则1ln 2ln ln ln 0477774444f ⎛⎫=+-=-= ⎪⎝⎭,又7310.5424-=<,且|ln |ln ln ==216e 2401181256e <<,所以32x =更接近于零点,故方程()0f x =的近似解为1.5.(2)由题设21111222ln 2ln 2e 0ln()x x x x x x x x +==-⎧⎧⇒⎨⎨+=-=⎩⎩,故121212ln ln()ln()2x x x x x x +-=-=-+,且20x <,要证12e x x ⋅>-,只需1221x x -+<,即211x x <-,由(1)知137(,)24x ∈,显然211x x <-成立,综上,12e x x ⋅>-,得证.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
度。
例1. 求函数f(x)=x3+x2-2x-2的一个正实数零 点(精确到0.1)。 解:由于f(1)=-2<0,f(2)=6>0, 可以确定区间[1,2]作为计算的初始区间。 用二分法逐步计算,列表如下:
端点或中点横 计算端点或中 确定区间 坐标 点的函数值
a0=1,b0=2 x0=1.5 x1=1.25 x2=1.375 x3=1.4375 f(1)=-2,f(2)=6 [1,2] f(x0)=0.625>0 [1,1.5]
在分析函数零点的性质时,我们已经看到,如 果函数y=f(x)在一个区间[a,b]上的图象不间断, 并求在它的两个端点处的函数值异号,即 f(a)f(b)<0,则这个函数在这个区间上,至少有 一个零点。即存在一点x0∈(a, b),使f(x0)=0。
如果函数图象通过零点时穿过了x轴,则 称这样的零点为变号零点,如果没有穿过x 轴,则称这样的零点为不变号零点。 依据这个性质,下面我们介绍求函数零点 的近似值的一种计算方法:二分法。
2.4.2 求函数零点近似解的Fra bibliotek一种计算方法——二分法
由于解决实际问题的需要,人们经常需 要寻求函数y=f(x)的零点(也就是方程f(x)=0 的根)。求一次函数或二次函数的零点,我 们可以用熟知的公式解法。
在16世纪,人们找到了三次函数和四次函数
的求根公式,但对于高于四次的函数,类似的
努力却一直没有成功。
f(x1)=-0.984<0 [1.25,1.5] f(x2)=-0.260<0 [1.375,1.5] f(x3)=0.162>0 [1.376,1.4375]
由上表的计算可知,区间[1.376,1.4375] 的左、右端点精确到0.1所取的近似值都是1.4, 因此1.4就是所取函数的一个正实数零点的近 似值。
算法是刻板的、机械的。有时要进行大
量的重复计算,算法的优点是一种通法。只 要按部就班地去做,总会算出结果。算法的 更大优点是它可以让计算机来实现。例如我 们可以编写程序,快速地求出一个函数的零 点。 在数学3中,我们还要系统地学习算法。
例2.分别求出下列函数的零点,并指出是 变号零点还是不变号零点。 (1)f(x)=3x-6; (2)f(x)=x2-x-12; (3)f(x)=x2+6x+9; (4)f(x)=(x-2)2(x+1)x。 解:(1)零点是2,是变号零点; (2)零点是-3、4,都是变号零点;
(1)如果f(x1)=0,则x1就是f(x)的零点,计 算终止; (2)如果f(a1)· f(x1)<0,则零点位于区间[a1, x1]中,令a2=a1,b2=x1; (3)如果f(a1)· f(x1)>0,则零点位于区间[x1, b1]中,令a2=x1,b2=b1; ……
继续实施上述步骤,直到区间[an,bn], 函数的零点总位于区间[an,bn]上,当an、bn 按照给定的精确度所取的近似值相同时,这 个相同的近似值就是函数y=f(x)的近似零点。 计算终止。 这时函数y=f(x)的近似零点满足给定的精确
函数f(x)=x3+x2- 2x-2的图象如图所示, 实际上还可以用二分 法继续计算下去,进 而得到这个零点精确 度更高的近似值。
以上求函数零点的二分法,对函数图象上
连续不间断的一类函数的零点都有效。如果一
种计算方法对某一类问题(不是个别的)都有 效,计算可以一步一步地进行,每一步都能得 到惟一的结果。我们经常把这一类问题的求解 过程叫做解决这一类问题的算法。
(1)如果f(x0)=0,则x0就是f(x)的零点,计 算终止; (2)如果f(a0)· f(x0)<0,则零点位于区间[a0, x0]中,令a1=a0,b1=x0;
(3)如果f(a0)· f(x0)>0,则零点位于区间[x0, b0]中,令a1=x0,b1=b0; 第三步:取区间[a1,b1]的中点,则此中点对应 的坐标为 x a 1 (b a ) 1 (a b ) 1 1 1 1 1 1 2 2 计算f(x1)和f(a1),并判断:
(3)f(x)=x2+6x+9;
(4)f(x)=(x-2)2(x+1)x。 解:(3)零点是-3,不变号零点; (4)零点是2,-1,0,其中变号零点是 -1和0,不变号零点是2.
例3.图象是连续不间断的函数f(x)的部分对
应值如下表:
x f(x) 1 14 2 8 3 -2 4 2 5 7 6 3 7 8 9 8
到了19世纪,根据阿贝尔(Abel)和伽罗瓦 (Galois)的研究,人们认识到高于四次的函 数(即高于四次的代数方程)不存在求根公式, 也就是说,不存在用四则运算即根号表示的一 般公式解。
同时对于三次和四次的代数方程,由于公 式解的表示相当复杂,一般来讲并不适宜用作 具体计算。因此对于高次多项式函数及其他的 一些函数,有必要寻求求零点的近似解的方法。 这在计算数学中是一个十分重要的课题。
-2 -1
试判断函数f(x)在哪几个区间内一定有零点? 解:函数f(x)在(2,3)、(3,4),(6,7)、(8,9) 内一定有零点。
例4.不用计算器,求 3 3 的近似值(精确到 0.01)
解:设 3 3 =x,则建立函数f(x)=x3-3,求f(x) 的零点的近似值。 取a=1,b=2,f(1)=-2<0,f(2)=5>0, x1=1.5,f(x1)=0.375>0,区间[1,1.5], x2=1.25,f(x2)=-0.0469<0,区间[1.25,1.5], x3=1.375,f(x3)=0.5996>0,区间[1.25,1.375],
已知函数y=f(x)定义在区间D上,求它在D
上的一个零点x0的近似值x,使它满足给定的
精确度。 下面我们分步写出,用二分法求函数零 点的一般步骤。 第一步:在D内取一个闭区间[a0,b0] D, 使f(a0)和f(b0)异号,即f(a0)· f(b0)<0,零点位 于区间[a0,b0]中;
第二步:取区间[a0,b0]的中点,则此中点对 1 1 应的坐标为, x0 a0 (b0 a0 ) (a0 b0 ) 2 2 计算f(x0)和f(a0),并判断:
