贵州省绥阳县绥阳中学2020-2021学年高一数学月考试题【含答案】
2021-2022学年贵州省遵义市绥阳县绥阳中学高一数学理月考试题含解析

2021-2022学年贵州省遵义市绥阳县绥阳中学高一数学理月考试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1.如图在中,,,若,.则( )A. B.C. D.参考答案:2. 有下列4个命题:(1)“若,则互为相反数”的否命题(2)“若,则”的逆否命题(3)“若,则”的否命题(4)“若,则有实数根”的逆命题其中真命题的个数是()A.1 B.2 C.3 D.4 参考答案:A3. 在△ABC中,内角A,B,C所对应的边分别为a,b,c,若c2=(a﹣b)2+6,C=,则△ABC的面积()A.3 B.C.D.3参考答案:C【考点】HR:余弦定理.【分析】根据条件进行化简,结合三角形的面积公式进行求解即可.【解答】解:∵c2=(a﹣b)2+6,∴c2=a2﹣2ab+b2+6,即a2+b2﹣c2=2ab﹣6,∵C=,∴cos===,解得ab=6,则三角形的面积S=absinC==,故选:C4. 函数是()A.最小正周期为的奇函数B.最小正周期为的奇函数C.最小正周期为的偶函数D.最小正周期为的偶函数参考答案:B略5. 已知角的终边经过点(-3,-4),则的值为()A. B. C. D.参考答案:C试题分析:由题意得=5,由三角函数定义可得sin=,= -sin=.考点:三角函数公式 .6. 某个几何体的三视图如图所示(单位:m),则该几何体的表面积(结果保留π)为A.B.C.D.参考答案:C球的半径为1,故半球的表面积的公式为,半球下底面表面积为π长方体的表面积为24,所以几何体的表面积为。
7. 函数f(x)=(A>0,ω>0,|φ|<)的部分图象如图所示,则=()A.B.C.D.参考答案:D【考点】函数的图象.【分析】根据图象,求出A,ω,φ,再求出相应的函数值.【解答】解:由题意,可得A=2,T=π,∴ω=2,∵=2,=﹣2,∴φ=,∴f(x)=.∴==﹣2,故选D.8. 某厂生产总值连续两年持续增加,第一年的增长率为a,第二年的增长率为b,则该厂这两年生产总值的年平均增长率为()A.B.C.D.参考答案:C【考点】函数的值.【分析】设前两年的平均增长率为x,由已知列出方程,能求出该厂这两年生产总值的年平均增长率.【解答】解:设前两年的平均增长率为x,∵第一年的增长率为a,第二年的增长率为b,∴(1+x)2=(1+a)(1+b),解得x=﹣1.故选:C.9. 下列各函数中,与y= x表示同一个函数的是()A. B. C. D.参考答案:D10. 设一随机试验的结果只有A和,且A发生的概率为m,令随机变量,则()A.1B.C.D.参考答案:C二、填空题:本大题共7小题,每小题4分,共28分11. 某种饮料每箱装5听,其中有3听合格,2听不合格,现质检人员从中随机抽取2听进行检测,则检测出至少有一听不合格饮料的概率是_________.参考答案:0.7略12. 设数列满足:,则为2006项的最大公约数为________________ .参考答案:313. 圆心在直线2x-y-7=0上的圆C与y轴交于两点A(0,-4)、B(0,-2),则圆C的方程为____________参考答案:14. 已知集合中只有一个元素,则的值为.参考答案:略15. 如图,在长方体ABCD—A1B1C1D1中,棱锥A1——ABCD的体积与长方体的体积之比为_______________.参考答案:略16. 在空间直角坐标系中,若点A(1,2,﹣1),B(﹣3,﹣1,4).则|AB|=_________.参考答案:17. 已知f(x)=x2+ax+b,满足f(1)=0,f(2)=0,则f(-1)=_ ___.参考答案:6三、解答题:本大题共5小题,共72分。
贵州省绥阳县绥阳中学2020_2021学年高一物理月考试题

贵州省绥阳县绥阳中学2020—2021学年高一物理月考试题时间:120分钟,满分:100分一、选择题(本题共15小题,共50分;1-10小题为单项选择题,每题3分,共30分,在每小题给出的四个选项中,只有一个选项正确;11-15小题为多项选择题,每题4分,共20分,在所给出的四个选项中,有多个选项符合题目要求,全选对的得4分,选对但不全的得2分,选错或不答的得0分)1.下列关于质点的说法正确的是()A.质点是客观存在的一种物体,其体积比分子还小B.若物体的形状和大小对所研究的问题无影响,即可把物体看作质点C.给正在参加吊环比赛的陈一冰打分时,裁判们可以把陈一冰看作质点D.很长的火车一定不可以看作质点2.下列正确的是()A.参考系一定要选静止的物体B.研究地球上物体的运动,只能以地球为参考系C.加速度、速度变化、位移都属于矢量D.某地出租车的收费标准“2。
00元/公里”,其公里数应是指按位移计算3.做直线运动的物体,在下面所说的运动情况中,不可能...出现的是()A.物体在某时刻运动速度很大,而加速度为零B.物体在某时刻运动速度很小,而加速度很大C.运动的物体在某时刻速度为零,而其加速度不为零D.加速度方向与运动方向相同,当物体加速度减小时,它的速度也减小4.如图所示,直线a和曲线b分别是在平直公路上行驶的汽车a和b的位移—时间图像,由图可知()A.在t1时刻,a、b两车的运动方向相同B.在t2时刻,a、b两车的运动方向相反C.在t1到t3这段时间内,a 、b两车的平均速度大小相等D.在t1到t3这段时间内,a 、b两车的平均速率相等5.“一带一路”战略带动我国汽车走向全世界,具有自主知识产权的汽车越来越多。
现有两辆不同型号的汽车a、b,在0时刻汽车a和b沿两条平直的平行车道以相同速度同时经过同一地点,图中的直线a和曲线b分别是这两车行驶的v—t图线,由图可知()A.在t1时刻两车运动方向相反B.在t1时刻,两车再次相遇C.在0-t1这段时间内,b车先正向加速后反向减速D.在0—t1这段时间内,b车的平均速度大于6.一个朝着某方向做直线运动的物体,在时间t内的平均速度是v,紧接着内的平均速度是,则物体在这段时间内的平均速度为()A.B.C.D.7.某质点做直线运动时位移x与时间t的关系为x=5+3t+t2(各物理量均采用国际单位),则该质点()A.在第1s内发生的位移为9mB.任意1s内的速度增量的大小都是3m/sC.前3s内的平均速度的大小是6m/sD.任意相邻的ls内位移之差都是1m8.如图所示,一小球(可视为质点)沿斜面匀加速下滑,依次经过A、B、C三点。
贵州省遵义市绥阳县绥阳中学2019-2020学年高一第二次联考数学试卷 Word版含答案

数 学本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,共150分,考试用时120分钟。
第I 卷(选择题 共60分)一、选择题(本大题共12小题,每小题5分,共60分,在每小题四个选项中,只有一项符合要求)1. 若集合2},8N {=<∈=a x x A ,则下列结论中正确的是A.A a ⊆}{B.A a ⊆C.A a ∈D.A a ∉ 2. 已知52)1(2++=+x x x f ,则=)1(fA.1B.3C.5D.83. 已知22.02.02.022log ===c b a ,,,则A.c b a >>B.a c b >>C.a b c >>D.c a b >>4. 若0tan <α,则下列结论一定正确是A.0sin <αB.02sin <αC.0cos <αD.02cos <α5. 若等差数列}{n a 的前7项之和为35,则=4aA.5B.10C.15D.35 6. 已知两非零向量b a ,b a b a +=,则b a >b a = C.b a ⊥ D.b a // 7. 针对柱、锥、台、球,给出下列命题,其中正确的是①如果一个几何体的三视图是完全相同的,则这个几何体是正方体; ②如果一个几何体的正视图和俯视图都是矩形,则这个几何体是长方体; ③如果一个几何体的三视图都是矩形,则这个几何体是长方体;④如果一个几何体的正视图和侧视图都是等腰梯形,则这个几何体是圆台.A.①②B.③C.③④D.①③ 8. 已知平面α和α外的一条直线l ,下列说法不正确的是 A.若l 垂直于α内的两条平行线,则α⊥l B.若l 平行于α内的一条直线,则α//l C.若l 垂直于α内的两条相交直线,则α⊥l D.若l 平行于α内的无数条直线,则α//l9. 某几何体的三视图如图所示,该几何体的表面积为 A.610+ B.620+ C.6210+ D.6220+10. 在直三棱柱111C B A ABC -中,底面ABC 是等腰直角三角形,1==BC AB ,D 为侧棱1BB 上的动点,若1ADC ∆的周长的最小值为53+,则三棱锥ABC C -1的外接球的体积为 A.43πB.π3C.23πD.43π11. 关于函数x x x f cos cos )(+=,下列说法中正确的个数是 ①)(x f 是偶函数;②)(x f 在)2,0(π上单调递增;③)(x f 在]2,0[π上有两个零点;④)(x f 的最小值为2-.A.1个B.2个C.3个D.4个12. 已知函数21112)22(4)(a a ex f x x x -+-=---有唯一的零点,则负实数a 的值为A.1-B.2-C.2-D.4-第II 卷(非选择题 共90分)二、填空题(本大题共4个小题,每小题5分,共20分,请将正确答案填写在答题卡相应位置)13. 在等比数列}{n a 中,16,151==a a ,则=3a . 14.在△ABC 中,6,5,4===c b a ,则=BAsin 2sin . 15. 圆锥的轴截面是边长为2的正三角形,则该圆锥的表面积为 .16. 魏晋时期数学家刘徽在为《九章算术》作注时,提出利用“牟合方盖”解决球体体积,“牟合方盖”由完全相同的四个曲面构成,相对的两个曲面在同一圆柱的侧面上,正视图和侧视图都是圆,每一个水平截面都是正方形,好似两个扣合 (牟合)在一起的方形伞(方盖).二百多年后,南北朝时期数学家祖暅在前人研究的基础上提出了《祖暅原理》:“幂势既同,则积不容异”.意思是:两等高立方体,若在每一等高处的截面积都相等,则两立方体体积相等.如图有一牟合方盖,其正视图与侧视图都是半径为1的圆,正边形ABCD 是为体现其直观性所作的辅助线,根据祖暅原理,该牟合方盖体积为 .三、解答题(本大题共6个小题,共70分,解答应写出必要的文字说明,证明过程或演算步骤)17. (本题满分10分)已知函数x x x x f 2cos 3sin cos )(-=.(I )求)(x f 的最小正周期和最大值; (II )求)(x f 在]32,6[ππ上的值域.第16题18. (本题满分12分)△ABC 的内角C B A ,,所对的边分别为c b a ,,,且B c C b a sin cos =-. (I )求角B ;(II )若2=b ,求△ABC 面积的最大值.19. (本题满分12分)记数列}{n a 的前n 项和为,*∈+=N ,2n n n S n .(I )求数列}{n a 的通项公式; (II )数列}32{nna ⨯的前n 项和n T .20. (本题满分12分) 如图,在直三棱柱111C B A ABC -中,D 是AB 的中点,AC BC AC AB AC AA 3,2,21====.(I )证明://1BC 平面CD A 1; (II )证明:⊥1BC C A 1.21. (本题满分12分)如图,BC 是半圆O 的直径,平面ABCD 与半圆O 所在的平面垂直, CD AB //,90=∠ABC ,141==CD AB ,E 是半圆O 上不同于C B ,的点,四边形FECD 是矩形. (I )若3=BE ,证明:⊥FA 平面AEC ; (II )若2=BC ,求三棱锥AEC D -体积的最大值.22. (本题满分12分)已知函数)0(1)1(log )(4>++=x x x x f 的图象上有一点列)N (),(*∈n y x P n n n ,点n P 在x 轴上的射影是)0,(n n x Q 且3),N ,2(3411=∈≥+=*-x n n x x n n .(I )求数列}{n x 的通项公式;(II )对任意的正整数n ,当]1,1[-∈m 时,不等式n y mt t >+-41332恒成立,求实数t 的取值范围;(III )设四边形11++n n n n P Q Q P 的面积是n S ,求证:38121121<+++n nS S S .答案一、选择题二、填空题三、解答题 17. (I )23)32sin(232cos 232sin 21212cos 3sin cos )(--=--=+⋅-=πx x x x x x x f ...........3分ππ==∴22T ,)(x f 的最大值为231-........................................................................................................7分 (II )当]32,6[ππ∈x 时,],0[32ππ∈-x ,]231,23[)(--∈∴x f .......................................................10分 18. (I )在△ABC 中,根据正弦定理知B C C B A sin sin cos sin sin =-................................................2分B C B C B C C B C B sin sin cos sin ,sin sin cos sin )sin(=∴=-+∴4,cos sin ,0sin ),,0(ππ=∴=∴≠∴∈B B B C C .......................................................6分(II )根据余弦定理知,ac ac c a B ac c a b )22(24,cos 222222-≥-+=∴-+=224224+=-≤ac .................................................................................................9分12sin 21+≤=∴∆B ac S ABC .............................................................................................12分19. (I )①当1=n 时,211==S a ;②当2≥n 时,n S S a n n n 21=-=-,)N (2*∈=∴n n a n ..........5分(II )由(I )知,nnn n a )31(32⨯=⨯,n n n n n T )31()31()1()31(3)31(2)31(11321⨯+⨯-++⨯+⨯+⨯=-1432)31()31()1()31(3)31(2)31(131+⨯+⨯-++⨯+⨯+⨯=n n n n n T 两式相减得1112)31())31(1(21)31(311))31(1(31)31()31()31(3132+++⨯--=⨯---=⨯-+++=n n n n n n n n n n T n n n n T )31(2)31(41431⨯-⨯-=∴-............................................................................................................................12分20. (I )连接,1AC 记O C A AC =11 ,在△1ABC 中,D O ,分别是AB AC ,1的中点,1//BC DO ∴....2分⊄1BC 平面CD A 1,⊂DO 平面CD A 1,1//BC DO ,∴//1BC 平面CD A 1..............................................5分(II )1BC 和C A 1为异面直线,由(I )知11,//BC DO BC ∴与C A 1所成角即DO 与C A 1所成角.............8分在△DO A 1中,121,221,3211111=====+=C A O A BC OD D A ∴=∠∴=+,90,121221 OD A D A OD O A 异面直线1BC 与C A 1所成角为 90,⊥1BC C A 1.....................12分22.(I ))1(413411+=+∴+=--n n n n x x x x ,又}1{31+∴=n x x 是以4为首项4为公比的等比数列)N (14,41*∈-=∴=+∴n x x n n n n .......................................................................................................................3分 (II )n n n n x f y nn41144log )(4=+-==, 不等式n y mt t >+-41332对正整数n 恒成立,max 2)(4133n y mt t >+-∴ 而131411<++=+=+n n n n n y y n n ,}{n y ∴是一个减数列,41)(1max ==y y n (或用作差等方法判断单调性).....5分0332>-∴mt t 对]1,1[-∈m 恒成立,解得1>t 或1-<t ..................................................................................7分(III ))15(83)44)(414(21))((21)(211111111+=-++=-+=⨯+=+++++++n n n x x y y Q Q Q P Q P S n n n n n n n n n n n n n n n)111(38)55151(340)15151(340)15(51340)15(381+-=+-<+-=+⨯=+=∴n n n n n n n n n n nS n .....................10分38)111(38)1113121211(38121121<+-=+-++-+-<+++∴n n n nS S S n ..................................................12分。
贵州省遵义市绥阳县绥阳中学2020-2021学年高一数学理月考试题含解析

贵州省遵义市绥阳县绥阳中学2020-2021学年高一数学理月考试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. ,,,是第三象限角,则()A、 B、 C、 D、参考答案:A2. 化简的结果是( )A B C cos80° D参考答案:C略3. 在等比数列{a n}中,已知,公比,则()A. 27B. 81C. 243D. 192参考答案:B【分析】首先求出数列中的首项,再利用数列的通项公式即可求解.【详解】是等比数列,且,,所以,所以,所以,故选:B【点睛】本题考查了等比数列的通项公式,熟记公式是关键,属于基础题.4. ﹣=()A.2lg5 B.0 C.﹣1 D.﹣2lg5参考答案:B【考点】对数的运算性质.【分析】利用对数性质、运算法则求解.【解答】解:﹣=lg50﹣1﹣(1﹣lg2)=lg5﹣1+lg2=0.故选:B.5. 已知函数f(x)是定义在R上的增函数,则函数y=f(|x﹣1|)﹣1的图象可能是()A.B.C.D.参考答案:B考点:函数的图象.专题:函数的性质及应用.分析:去掉y=f(|x﹣1|)﹣1中的绝对值,讨论复合函数y的增减性.解答:解:∵y=f(|x﹣1|)﹣1=,且f(x)是R上的增函数;∴当x≥1时,y=f(x﹣1)﹣1是增函数,当x<1时,y=f(﹣x+1)﹣1是减函数;∴函数y=f(|x﹣1|)﹣1的图象可能是第二个;故选:B.点评:本题考查了复合函数的增减性问题,判定f(g(x))的单调性,当f(x)、g(x)单调性相同时,f(g(x))是增函数;当f(x)、g(x)单调性相反时,f(g(x))是减函数6. 在R上定义运算?:x?y=x(1﹣y),若不等式(x﹣a)?(x﹣b)>0的解集是(2,3),则a+b的值为( )A.1B.2C.4D.8参考答案:C考点:一元二次不等式的解法.专题:新定义.分析:根据定义,利用一元二次不等式的解法求不等式的解集.解答:解:∵x?y=x(1﹣y),∴(x﹣a)?(x﹣b)>0得(x﹣a)>0,即(x﹣a)(x﹣b﹣1)<0,∵不等式(x﹣a)?(x﹣b)>0的解集是(2,3),∴x=2,和x=3是方程(x﹣a)(x﹣b﹣1)=0的根,即x1=a或x2=1+b,∴x1+x2=a+b+1=2+3,∴a+b=4,故选:C.点评:本题主要考查一元二次不等式的解法,利用新定义列出不等式是解决本题的关键.7. 满足,下列不等式中正确的是()A.B.C.D.参考答案:C因为,而函数单调递增,所以.8. 已知,函数在上单调递减,则的取值范围是( )A.B. C. D.(0,2]参考答案:A9. 设S n表示等差数列{a n}的前n项和,已知,那么等于()A.B.C.D.参考答案:B【考点】8F:等差数列的性质;85:等差数列的前n项和.【分析】先根据等差数列的前n项和公式由可得a1与d的关系,再代入到即可求得答案.【解答】解:根据等差数列的前n项和公式得到=∴a1=3d==故选B.【点评】本题主要考查等差数列的前n项和公式.属基础题.10. 已知角终边上一点,那么()A. B. C. D.参考答案:A略二、填空题:本大题共7小题,每小题4分,共28分11. 如图,在正方体ABCD﹣A1B1C1D1中,点P在面对角线AC上运动,给出下列四个命题:①D1P∥平面A1BC1;②D1P⊥BD;③平面PDB1⊥平面A1BC1;④三棱锥A1﹣BPC1的体积不变.则其中所有正确的命题的序号是.参考答案:①③④【考点】命题的真假判断与应用.【分析】①根据线面平行的判断定理进行判断D 1P∥平面A 1BC 1; ②D 利用特殊值法即可判断D 1P⊥BD 不成立;③根据面面垂直的判断条件即可判断平面PDB 1⊥平面A 1BC 1;④将三棱锥的体积进行等价转化,即可判断三棱锥A 1﹣BPC 1的体积不变. 【解答】解:①∵在正方体中,D 1A∥BC 1,D 1C∥BA 1,且D 1A∩DC 1=D 1, ∴平面D 1AC∥平面A 1BC 1; ∵P 在面对角线AC 上运动, ∴D 1P∥平面A 1BC 1;∴①正确.②当P 位于AC 的中点时,D 1P⊥BD 不成立,∴②错误; ③∵A 1C 1⊥平面BDD 1B 1;∴A 1C 1⊥B 1D , 同理A 1B⊥B 1D , ∴B 1D⊥平面A 1BC 1, ∴平面BDD 1B⊥面ACD 1, ∴平面PDB 1⊥平面A 1BC 1; ∴③正确.④三棱锥A 1﹣BPC 1的体积等于三棱锥B ﹣A 1PC 1的体积. △A 1PC 1的面积为定值,B 到平面A 1PC 1的高为BP 为定值,∴三棱锥A 1﹣BPC 1的体积不变,∴④正确. 故答案为:①③④.12. 若函数f(x)=x 2+(a─2)x+1为偶函数,为奇函数,则的大小关系是______________.参考答案:13. 若函数,且,则。
贵州省遵义市绥阳县黄杨中学2020年高一数学文测试题含解析

贵州省遵义市绥阳县黄杨中学2020年高一数学文测试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 下列三个命题,其中正确的有 ( )①用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台;②两个底面平行且相似,其余各面都是梯形的多面体是棱台;③有两个面互相平行,其余各面都是等腰梯形的六面体是棱台.A.0个 B.1个 C.2个 D.3个参考答案:A2. 若a,b,c∈R,且a>b,则下列不等式一定成立的是().D>0B3. 函数,那么的奇偶性是()A.奇函数 B.既不是奇函数也不是偶函数C.偶函数 D.既是奇函数也是偶函数参考答案:略4. 在各项均为正数的等比数列{a n}中,若,则()A.B.C. 4D.参考答案:B略5. 同时满足下列条件:(1)是奇函数,(2)在定义域内是增函数的是()A. B. C. D.参考答案:B略6. 直角梯形OABC中AB∥OC、AB=1、OC=BC=2,直线l:x=t截该梯形所得位于l左边图形面积为S,则函数S=f(t)的图象大致为()A.B.C.D.参考答案:C【考点】函数的图象与图象变化;函数模型的选择与应用.【分析】本题考查的是函数的图象和分段函数的综合类问题.在解答的过程当中,首先应该直线l的运动位置分析面积的表达形式,进而得到分段函数:然后分情况即可获得问题的解答.【解答】解:由题意可知:当0<t≤1时,,当1<t≤2 时,;所以.结合不同段上函数的性质,可知选项C符合.故选C.7. 把函数y=sin(2x﹣)的图象向右平移个单位得到的函数解析式为()A. y=sin(2x﹣)B. y=sin(2x+)C. y=cos2xD. y=﹣sin2x参考答案:D试题分析:三角函数的平移原则为左加右减上加下减.直接求出平移后的函数解析式即可.解:把函数y=sin(2x﹣)的图象向右平移个单位,所得到的图象的函数解析式为:y=sin[2(x﹣)﹣]=sin(2x﹣π)=﹣sin2x.故选D.考点:函数y=Asin(ωx+φ)的图象变换.8. 已知log0.3(m+1)<log0.3(2m﹣1),则m的取值范围是()A.(﹣∞,2)B.C.(2,+∞)D.(﹣1,2)参考答案:B【考点】指、对数不等式的解法.【专题】计算题;函数思想;转化思想;数学模型法;不等式的解法及应用.【分析】直接利用对数函数的性质化对数不等式为一元一次不等式组得答案.【解答】解:由log0.3(m+1)<log0.3(2m﹣1),得,解得.∴m的取值范围是.故选:B.【点评】本题考查指数不等式和对数不等式的解法,考查了对数函数的性质,是基础题.9. 过原点且倾斜角为60°的直线被圆x2+y2-4y=0所截得的弦长为(A)(B)2 (C)(D)2参考答案:D10. 若奇函数在上为增函数,且有最小值0,则它在上A.是减函数,有最小值0B.是增函数,有最小值0C.是减函数,有最大值0D.是增函数,有最大值0参考答案:D二、填空题:本大题共7小题,每小题4分,共28分11. ∠ACB=90°,平面ABC外有一点P,PC=4cm,点P到角的两边AC、BC的距离都等于2 cm,那么PC与平面ABC所成角的大小为.参考答案:【考点】直线与平面所成的角.【分析】设P点在ABC平面投影点为O,过P点作BC边的垂线垂足为D,连接OP,OC,OD,根据,∠ACB=90°,平面ABC外一点P满足PC=4,P到两边AC,BC的距离都是2 cm,我们分别求出CD,OD,OP的长,进而解出∠PCO的大小,即可得到PC与平面ABC所成角的大小.【解答】解:设P点在ABC平面投影点为O,过P点作BC边的垂线垂足为D,连接OP,OC,OD,如图所示:则∠PCO即为PC与平面ABC所成角的平面角∵P到两边AC,BC的距离都是2cm,故O点在∠ACB的角平分线上,即∠OCD=45°由于PC为4cm,PD为2cm,则CD为2cm.则△PCD在底面上的投影△OCD为等腰直角三角形.则OD=CD=2,然后得CO=2cm,根据勾股定理得PO=2cm=CO,∴∠PCO=45°.故答案为:45°.12. 函数的定义域是_________ ;参考答案:(13. 已知α为第二象限角,sinα=,则tan2α= .参考答案:【考点】GL:三角函数中的恒等变换应用.【分析】由已知求出cosα,进一步得到tanα,代入二倍角公式得答案.【解答】解:∵α为第二象限角,且sinα=,∴cosα=,则tanα=.∴tan2α===.故答案为:.14. (5分)已知函数f(x)=log a(x+1)(a>0,a≠1)在上的值域是,若函数g(x)=a x﹣m﹣4的图象不过第二象限,则m的取值范围是参考答案:m≥﹣2考点:对数函数的图像与性质.专题:函数的性质及应用.分析:对a分类讨论:利用对数函数的单调性可得a=2.由于函数g(x)=2x﹣m﹣4的图象不过第二象限,可得g(0)≤0,解出即可.解答:当a>1时,函数f(x)在上单调递增,∴log a1=0,log a2=1,解得a=2.当0<a<1时,函数f(x)在上单调递减,∴log a1=1,log a2=0,舍去.故a=2.∵函数g(x)=2x﹣m﹣4的图象不过第二象限,∴g(0)=2﹣m﹣4≤0,∴﹣m≤2,解得m≥﹣2.点评:本题考查了指数函数与对数函数的单调性,考查了数形结合的思想方法、推理能力与计算能力,属于中档题.15. 下列命题中所有正确的序号是.(1)函数的图象一定过定点P;(2)函数的定义域是,则函数的定义域为;(3)已知函数在区间是单调增函数,则实数;(4)已知,且,则实数.参考答案:16. 用列举法表示集合:= 。
贵州省绥阳县绥阳中学2020-2021学年高一月考历史试卷Word版含答案

历史试题考前须知:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折叠、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
6.考试时间:150分钟;历史政治地理同堂分卷考试,每科100分,共300分第I卷选择题〔60分〕一、单项选择题〔每题4分,共15个小题,共60分〕1.西周分封制在中国历史上影响深远。
以下省级行政区的简称源自西周封国国名的是〔〕A.河南〔豫〕、河北〔冀〕B.湖南〔湘〕、湖北〔鄂〕C.山东〔鲁〕、山西〔晋〕D.广东〔粤〕、广西〔桂〕2.走进孙中山故居,就会看到先生题写的“天下为公〞四个大字,彰显了先生的伟大胸襟。
在历史上,也曾存在“天下为公〞局面,后被“家天下〞的局面所取代。
这一局面被改变始于A.禹B.启C.商D.汤3.典故“指鹿为马〞出自?史记·秦始皇本纪?:“赵高欲为乱,恐群臣不听,乃先设验,持鹿献于二世,曰:‘马也。
’二世笑曰:‘丞相误邪?谓鹿为马。
’问左右,左右或默,或言马以阿顺赵高。
〞该典故反映的本质问题是A.司马迁挖苦秦二世无能B.实行丞相制度不合时宜C.丞相位高权重威胁了皇权D.秦朝面临着被灭亡的危险4.中国古代通常用分割或削弱相权的方法来加强皇权,以下表述不正确的选项是〔〕A、汉武帝重用侍从、秘书为近臣以削弱相权B、唐朝实行三省六部制度把相权一分为三C、宋代设三司使分割宰相财权D、清代设军机处消除了皇权与相权之间的矛盾5.家谱是记载某个姓氏家族子孙世系传承之书,具有区分家族成员血缘关系亲疏远近的作用。
中国古代与此相关的制度是A.禅让制B.宗法制C.礼乐制D.郡县制6.1848年,威廉姆斯在?中央王国?一书中说:“……中国政府的高官阶层中的不少官员都怀有让人极为敬佩的才能和知识……。
贵州省绥阳县绥阳中学2020-2021学年高二第一学期第一次月考语文试卷Word版含答案

2021—2021学年上学期第一次月考高二语文试题说明:全卷总分值150分。
考试用时150分钟考前须知:考生在答题前请认真阅读本考前须知及各题答题要求。
1.答题前,请务必将自己的姓名、准考证号或IS号用书写黑色字迹0.5毫米签字笔填写在答题卡和答题纸上。
2.作答非选择题必须用书写黑色字迹的0.5毫米签字笔写在答题纸上的指定位置,在其它位置作答一律无效。
作答选择题必须用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,请用橡擦干净后,再选涂其它答案,请保持卡面清洁和答题纸清洁,不折叠、不破损。
3.考试结束后,请将答题纸交回。
一、现代文阅读(36分)〔一〕论述类文本阅读〔此题共 3 题,共9分〕阅读下面的文字,完成 1—3 题。
“天下〞是中国传统文化对世界秩序的一种原初想象,“天下主义〞是以“天下〞理念为核心,由具有普遍性和开放性的世界秩序、价值标准与理想人格构成的思想体系。
在当今全球化语境之下,中国文化理念和文化战略的自觉自信表达的正是“天下主义〞的精神内核。
文化自信首先是一种“以天下观天下〞的世界观的自信。
?道德经?有云:“修之于天下,其德乃普。
故以身观身,以家观家,以乡观乡,以国观国,以天下观天下。
〞“天下〞是中国文化特有的思维尺度,是一个最宏大、最完备的分析单位,具有最广阔的容纳力。
面对差异性的多元文化格局,西方文化多以民族国家为根本单位,文化视域限于国家、民族内部,虽然也有关于世界的思考,比方斯多葛学派的“世界主义〞等,但其思考方式是“以国家观世界〞,与中国文化的立足点和尺度不同。
中国文化的“天下〞蕴含了“天下无外〞的理想,各个民族的历史文化在世界内部是平等共存的;中国文化依循“修身、齐家、治国、平天下〞的进路,从“身-家-国〞逻辑同构的角度,最终到达“天下大同〞的境界。
与西方文化相较,“天下〞的世界观更具有开放性和包容性。
文化自信的核心是“以天下为一家〞的价值观的自信。
中国文化是以儒家文化为代表的伦理型文化,梁漱溟认为“中国伦理始于家庭而不止于家庭〞,中国文化重视家庭生活,整个社会关系是依照家庭关系推广发挥的。
贵州省绥阳中学2020届2018-2019学年第一学期第一次月考数学试卷(无答案)
绥阳中学2020届2018-2019学年第一学期第一次月考数学试卷试卷分为两卷,第一卷80分,第二卷70分,共计150分考试时间:120分钟 (所有试题均在答题卡上作答!)班级: 姓名:第一卷一、选择题:(本大题共12小题,每小题5分,共60分)1. 已知集合U ={1,2,3,4,5,6,7,8,9},集合B={})5ln(x y N x -=∈*则B C U=( )A .{1,3}B .{5,6,7,8,9}C .{3,5,9}D .{3,9}2.︒210cos = ( ) A.21 B. 23 C. 21-D. 23-3.若球的体积与表面积相等,则球的半径是 ( )A .1B .2C .3D .44.在等差数列{}n a 中,1910,a a +=则5a 的值是 ( )A .5B .6C .8D .10 5.某程序框图如图所示,若该程序中的a 为4,运行后输出的值是( ) A.59B.5C. 6D.76.若a b >且c R ∈,则下列不等式中一定成立的是 ( )A .22a b >B .ac bc >C .22ac bc > D .a c b c +>+(第5题图)7.要得到82sin )(π-=x x f 的图象,只需把x x f 2sin )(=的图象 ( )A. 向右平移8π个单位B. 向右平移16π个单位C. 向左平移8π个单位 D. 向左平移4π个单位8.由若干个小正方体组成的几何图形的三视图如图所示,则组成这个组合体的小正方体的个数是 ( )A.3B. 4C.5D.69.已知函数)(,)31(3)(x f x f x x 则-= ( )A.是偶函数,且在R 上为增函数B. 是奇函数,且在R 上为减函数C.是偶函数,且在R 上为减函数D.是奇函数,且在R 上为增函数10.已知向量、满足2||,1||,0===⋅,则=-|2| ( ) A. 0B. 22C. 4D. 811.若函数()⎪⎭⎫⎝⎛<≤+=20sin 3cos πx x x x f ,则()x f 的最小值是 ( ) A. 1B. -1C. 2D. -212.中秋佳节,绥阳中学校园的树上挂了两串彩灯,这两串彩灯的第一次闪亮相互独立,若接通电后的4秒内任一时刻等可能发生,然后每串彩灯在内4秒为间隔闪亮,那么这两串彩灯同时通电后,它们第一次闪亮的时刻相差不超过2秒的概率是( ) A.14 B.12 C.78 D.34二、填空题(本大题共4小题,每小题5分,共20分)13.设变量x 、y 满足条件⎪⎩⎪⎨⎧-≥≥+≤632x y y x x y ,则目标函数y x z +=2的最小值为 .14.已知不等式250ax x b -+>的解集为{|32}x x -<<,则a b +的值是 .15.若0,0x y >>1x y +=,则41x y+的最小值为 . 16.如图在底面为正方形,侧棱垂直于底面的四棱柱ABCD A 1B 1C 1D 1中,AA 1=2,AB =2,则异面直线A 1B 与AD 1所成角的余弦值为 .第二卷17.(本小题满分10分)在ABC ∆中,角A 、B 、C 的对边分别为a 、b 、c ,且A 、B 、C 成等差数列. (Ⅰ)角B 的大小;(Ⅱ)若2,a =ABC ∆的面积2S =求b 、c 的长及ABC ∆外接圆半径.18.(本小题满分12分)已知{}n a 是公差不为零的等差数列,11a =,且139,,a a a 成等比数列. (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)求数列11n n a a +⎧⎫⎨⎬⋅⎩⎭的前n 项和n S .19. (本小题满分12分)如图所示,在四边形ABCD 中,∠DAB =90°,∠ADC =135°,AB =5,CD =22,AD =2,求四边形ABCD 绕AD 旋转一周所成几何体的表面积及体积.20.(本小题满分12分)已知:A 、B 、C 三点坐标分别为)0,3(A 、)3,0(B 、)sin ,(cos ααC ,⎪⎭⎫ ⎝⎛∈23,2ππα。
贵州省绥阳县绥阳中学2020-2021学年高一9月月考历史试卷含答案 (1)

高一历史试卷注意事项:1.答题前考生务必将自己的姓名,准考证号填涂在答题卡上。
2.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
3.回答非选择题时,将答案写在答题卡上,在试卷上作答无效。
4.考试结束后,将答题卡交回。
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共100分,考试用时90分钟。
第I卷(选择题共50分)一、选择题(本大题共25小题,每小题2分,共50分,在每小题给出的四个选项中,只有一项是最符合题目要求的。
)1.下图为夏朝世系示意图。
读图可知,夏王朝实行()A.禅让制B.王位世袭制C.分封制D.嫡长子继承制2.夏朝设秩宗,商朝卜、巫、史,西周设太史、太祝、太卜、太士等,他们既是神权的掌握者,又是国家的重要执政官,权位显赫。
由此可见夏、商、周政治制度()A.分封制与宗法制互为表里B.政权和神权相结合C.血缘纽带与政治权力相结合D.统治集团实现高度集权3.西周时期,分封的齐、鲁、燕、楚、秦等国,基本都是地广人稀、土地尚未开发的地区;到春秋时期,这些地区的农业和手工业发展水平在某些方面至超过了周王室附近地区。
这表明西周分封制()A.有助于王室对地方管理B.推动边远地区经济发展C.容易形成地方割据势力D.扩大周王朝的统治区域4.大槐树位于山西省洪洞县大槐树寻根祭祖园内,虽然该园内没有宏伟的建筑,但是不论严冬酷暑,祭拜人员都络绎不绝到此仰望古槐,以抒发“饮水思源”之幽情。
这种“寻根”现象()A.说明传统宗法观念影响深远B.得到了全体国人的一致认同C.维护了社会的安定和团结D.导致了封建迷信思想的复活5.每年的春节是农历一月初一。
一月古时本来又叫“政月”,到了秦朝为了避皇帝嬴政的讳,就把“政月”改为“正月”,“正”字的读音也为“征”了。
这说明皇帝制度的主要特征是()A.神权与王权相结合 B.中央权力高度集中C.皇权至上,皇帝独尊D.独断性和随意性6.秦朝中央官职设三公九卿。
贵州高一高中数学月考试卷带答案解析

贵州高一高中数学月考试卷班级:___________ 姓名:___________ 分数:___________一、选择题1.下列所给的对象能构成集合的是()A.2019届的优秀学生B.高一数学必修一课本上的所有难题C.遵义四中高一年级的所有男生D.比较接近1的全体正数2.下列关系正确的个数是()①;②;③;④A.1B.2C.3D.43.已知集合,,则()A.B.C.D.4.设集合,,则集合与的关系是()A.B.C.D.与关系不确定5.集合,,若,则的值为()A.2B.4C.-2D.-46.若全集,则集合的补集为()A.B.C.D.7.下列各组函数表示同一函数的是()A.B.C.D.8.如图,有四个平面图形分别是三角形、平行四边形、直角梯形、圆,垂直于轴的直线经过原点向右平行移动,在移动过程中扫过平面图形的面积为(图中阴影部分),若函数的大致图像如图,那么平面图形的形状不可能是()9.已知函数的对应关系如下表,函数的图象是如图的曲线,其中,,,则的值为()A.3B.2C.1D.010.已知,则的值等于()A.-2B.4C.2D.-411.已知偶函数在区间上是增函数,则与的大小关系是()A.B.C.D.12.已知函数与的图象上存在关于轴对称的点,则实数的取值范围是()A.B.C.D.二、填空题1.若是偶函数,则函数的增区间是 .2.已知全集,,,则 .3.设是定义在上的偶函数,若在上是增函数,且,则不等式的解集为 .4.函数,给出函数下列性质:(1)函数的定义域和值域均为;(2)函数的图像关于原点成中心对称;(3)函数在定义域上单调递增;(4)为函数图象上任意不同两点,则.请写出所有关于函数性质正确描述的序号 .三、解答题1.已知全集,集合,,求,,.2.设全集是实数集,集合,.(1)当时,求;(2)若,求实数的取值范围.3.已知函数.(1)证明函数在区间上为减函数;(2)求函数在区间上的最值.4.函数在闭区间上的最小值记为.(1)求的解析式;(2)求的最大值.5.设是定义在上的减函数,且满足,.(1)求,,的值;(2)若,求的取值范围.6.已知函数.(1)讨论函数的奇偶性,并说明理由;(2)若函数在上为增函数,求的取值范围.贵州高一高中数学月考试卷答案及解析一、选择题1.下列所给的对象能构成集合的是()A.2019届的优秀学生B.高一数学必修一课本上的所有难题C.遵义四中高一年级的所有男生D.比较接近1的全体正数【答案】C【解析】对于A、B、D来说,分别含有“所有”、“优秀”、“接近”字眼,它们的含义是模糊的、不明确的,所以不能构成集合.【考点】集合的元素性质.2.下列关系正确的个数是()①;②;③;④A.1B.2C.3D.4【答案】C【解析】显然,,,故①、②、③正确;而,故④不正确.【考点】元素与集合的关系.3.已知集合,,则()A.B.C.D.【答案】D【解析】不难发现中元素均在集合中,且中元素不在中,故.【考点】集合与集合间的关系.4.设集合,,则集合与的关系是()A.B.C.D.与关系不确定【答案】B【解析】=,,显然表示所有的整数,而表示所有的奇数,显然,集合中的元素均在中,故.【考点】1、集合表示方法中的描述法;2、集合的包含关系判断及应用.5.集合,,若,则的值为()A.2B.4C.-2D.-4【答案】B【解析】由题易知=,所以,故.【考点】集合的并集运算.6.若全集,则集合的补集为()A.B.C.D.【答案】C【解析】因为全集,,所以=.【考点】集合的补集运算.7.下列各组函数表示同一函数的是()A.B.C.D.【答案】B【解析】选项A,定义域不同,不是同一函数;选项B,定义域、对应法则都一样,是同一函数;选项C,定义域不同,不是同一函数;选项D,对应法则不同,导致值域不同,不是同一函数.【考点】同一函数概念.8.如图,有四个平面图形分别是三角形、平行四边形、直角梯形、圆,垂直于轴的直线经过原点向右平行移动,在移动过程中扫过平面图形的面积为(图中阴影部分),若函数的大致图像如图,那么平面图形的形状不可能是()【答案】C【解析】由函数的图象可知,几何体具有对称性,选项A,B,D,在移动过程中扫过平面图形的面积为,在中线位置前,都是先慢后快,然后相反.选项C,后面是直线增加,不满足题意.【考点】函数的图象与图形面积的变换关系.9.已知函数的对应关系如下表,函数的图象是如图的曲线,其中,,,则的值为()A.3B.2C.1D.0【答案】B【解析】由图象可知,由表格可知,,故选:B.【考点】函数的对应法则.10.已知,则的值等于()A.-2B.4C.2D.-4【答案】B【解析】,.【考点】分段函数.【方法点睛】本题主要考查了分段函数的应用.在高中,除了基本初等函数,还加入了分段函数和复合函数,从而函数大家庭变得更加丰富多彩.分段函数的本质就是按规则办事,每一段有每一段的对应规则,大于零走第一段,小于等于零走第二段,本题第二段又加入了抽象函数,对学生有一定的考验,理解好法则是做好题目的关键.11.已知偶函数在区间上是增函数,则与的大小关系是()A.B.C.D.【答案】D【解析】偶函数在区间上是增函数,可得:.故选:D.【考点】函数的单调性与奇偶性.【思路点晴】本题综合考查了函数的单调性与奇偶性,常规并且典型.比较大小最常用的方法就是确定函数的单调性,把所给的两个自变量想办法请到同一个单调区间上.奇函数在对称区间上单调性一致,而偶函数在对称区间上单调性正好相反,通过奇偶性不仅能转化单调性,同时能很好的处理符号的变化,特别是奇函数,如果外面有负号可以放到里面来.12.已知函数与的图象上存在关于轴对称的点,则实数的取值范围是()A.B.C.D.【答案】C【解析】若函数与的图象上存在关于轴对称的点,则方程在区间上有解,令,由的图象是开口朝上,且以直线为对称轴的抛物线,故当时,取最小值,当时,函数取最大值,故,故选:C.【考点】构造函数法求方程的解及参数范围.【方法点晴】本题是一道综合性较强的试题.切入点是对称性的转化,把“形”的问题转化为“数”的问题.数与形的完美结合,是处理好函数问题的关键所在.方程的有解问题往往通过变量分离转化为函数的值域问题.不等式的有解问题往往通过变量分离转化为函数的最值问题.二次函数的最值不一定在端点取到,要结合图象进行高低的判断,来进行最值得取舍.二、填空题1.若是偶函数,则函数的增区间是 .【答案】【解析】因为函数是偶函数,所以,所以,其图象是开口方向朝下,以轴为对称轴的抛物线,故的增区间.【考点】奇偶性与单调性的综合.2.已知全集,,,则 .【答案】【解析】∵全集,,,,即,解得:,当时,,,,不合题意,舍去,则.故答案为:.【考点】补集及其运算.【易错点睛】本题主要考查了集合的补集运算.本题的易错之处就是忽略了所得字母的取值要使得题设条件成立,也就是等价性.集合中有很多陷阱值得同学们总结,比如,,同学们在分析时,容易丢掉一种特殊情况,即是空集;还有在求得字母取值时,要注意两方面:一要满足互异性,二要满足题设条件是成立的.3.设是定义在上的偶函数,若在上是增函数,且,则不等式的解集为 .【答案】【解析】由题意,,解得,故答案为:.【考点】单调性与奇偶性的应用.4.函数,给出函数下列性质:(1)函数的定义域和值域均为;(2)函数的图像关于原点成中心对称;(3)函数在定义域上单调递增;(4)为函数图象上任意不同两点,则.请写出所有关于函数性质正确描述的序号 .【答案】(2)【解析】因为函数,∴,解得且,∴函数的定义域为,(1)错误;∵,作出函数图象,如图所示,由图象知函数的图象关于原点成中心对称,(2)正确;由图象知函数在上为单调增函数,在上也是单调增函数,但在定义域上不是增函数,如,故(3)错误;由图象知图象为两个四分之一个圆弧构成,且半径为,最大为连线且过原点,最大值为,最小为是,但取不到,即,故(4)错误.综上,正确的命题是(2).【考点】1、分段函数的图象与性质的应用问题;2、函数的定义域和值域的应用问题.【方法点晴】处理函数问题要优先考虑定义域.判断奇偶性定义域必须关于原点对称,否则,其为非奇非偶函数;判断函数的单调性,单调区间一定是定义域的子集;求函数的最值,要在定义域上来考虑,特别是在取最值时,一定要考虑一下相应的在不在定义域上,否则,取不到最值;在画函数的图象时,一定要注意端点处到底是实点还是空点.三、解答题1.已知全集,集合,,求,,.【答案】,,.【解析】全集,集合,,求出,由此能求出,,.画数轴是最直观的方法.试题解析:∵,,∴,∴,,.【考点】集合的交并补的运算.2.设全集是实数集,集合,.(1)当时,求;(2)若,求实数的取值范围.【答案】(1),;(2).【解析】(1)当时,求出集合,即可求和;(2)若,则,根据集合关系即可求实数的取值范围.试题解析:解:(1)∵,当时,,∴,.(2)当时,当时,即时,满足;当时,即时,要使,只需,解得.综上所述,实数的取值范围是.【考点】集合的基本运算.3.已知函数.(1)证明函数在区间上为减函数;(2)求函数在区间上的最值.【答案】(1)证明见解析,(2)最大值为,最小值为.【解析】(1)运用单调性的定义证明,注意取值、作差、变形、定符号和下结论几个步骤;(2)运用(1)的结论,即可得到最值.试题解析:(1)证明:任取,且,则由于,则,,,则,即,所以函数在区间上为减函数(2)由(1)可知,在区间上递减,则最大,最大值为2,最小,最小值为.【考点】1、函数的单调性的证明和运用;2、函数的最值.4.函数在闭区间上的最小值记为.(1)求的解析式;(2)求的最大值.【答案】(1),(2)的最大值.【解析】(1)根据函数的图象的对称轴在所给区间的左侧、中间、右侧三种情况,分别求得,综合可得结论;(2)根据函数的解析式,画出函数的图象,数形结合求得函数取得最大值.试题解析:解:(1)由,对称轴为,当时,为减区间,最小值为,当时,最小值为,当时,为减区间,最小值为综上可得:.(2)由(1),可得,可分三种情况分析:当时,函数取得最大值为.【考点】二次函数在闭区间上的最值.5.设是定义在上的减函数,且满足,.(1)求,,的值;(2)若,求的取值范围.【答案】(1) ,,;(2).【解析】(1)利用赋值法即可求,,的值;(2)结合函数单调性以及抽象函数的关系将不等式进行转化即可.试题解析:(1)令,则,所以.令,则,所以.故,.(2)因为,所以由是定义在上的减函数,得解得,即 .故的取值范围为.【考点】抽象函数的应用.【思路点睛】本题主要考查抽象函数的应用,利用赋值法是解决抽象函数的基本方法,综合考查函数的性质是应用.常考模型:(1),特殊模型:;(2),特殊模型:;(3),特殊模型:,(4) ,特殊模型:.6.已知函数.(1)讨论函数的奇偶性,并说明理由;(2)若函数在上为增函数,求的取值范围.【答案】(1)当时,为偶函数,当时,为非奇非偶函数;(2).【解析】(1)为偶函数,欲判函数的奇偶性,只需判定的奇偶性,讨论判定就可;(2)处理函数的单调性问题通常采用定义法好用.试题解析:(1)当时对任意,∴为偶函数.当时,取,得,即.∴函数非奇非偶.(2)设,则有.要使函数在上为增函数,则需恒成立.∵,所以恒成立又因为,所以,故的取值范围为.【考点】函数的单调性与奇偶性.【思路点睛】本题主要考查了单调性与奇偶性的综合应用,属于中等题.含参函数的奇偶性判断是学生的一个难点,很多同学忽视了参数的特殊性,是可以取到零这个特值的.利用定义法判断函数的单调性也是学生非常棘手的题型,注意基本步骤:(1)取值(在定义域范围内任取两个变量,并规定出大小);(2)做差(即,并且到“积”时停止);(3)判号(判“积”的符号);(4)结论(回归题目).。
贵州高三高中数学月考试卷带答案解析

贵州高三高中数学月考试卷班级:___________ 姓名:___________ 分数:___________一、选择题1.复数的虚部为()A. B C. D.2.条件,条件,则是的()A.充分非必要条件B.必要不充分条件C.充要条件D.既不充分也不必要的条件3.若满足约束条件,则的最大值是()A.B.C.D.4.已知公比为的等比数列中,,则的值为( )A.B.C.D.5.已知函数,则的值是()A.-2B.-3C.1D.36.已知向量的夹角为()A.30°B.45°C.60°D.90°7.若直线与曲线有两个不同的交点,则实数的取值范围为()A.B.C.D.8.顶点都在一个球面上的正四棱柱中,,,则两点间的球面距离为()A.B.C.1D.9.已知双曲线的两条渐近线的夹角为,则双曲线的离心率为A.2B.C.D.表示等差数列的前n项和,且()10.已知SnA.B.C.D.11.设F 1,F 2是椭圆的两个焦点,P 是椭圆上的点,且,则的面积为( )A .4B .C .D .612.把函数的图象沿向量a=(-m ,m)(m >0)的方向平移后,所得的图象关于y 轴对称,则m 的最小值是 ( )二、填空题1.展开式中的系数为10,则实数a 等于2.曲线在点处的切线与坐标轴所围成的三角形面积为________3.某工厂生产A、B、C三种不同型号的产品,产品数量之比为3:4:7,现用分层抽样的方法抽取容量为的样本,样本中A型号产品有15件,那么样本容量为________4.若函数对任意实数满足:,且,则下列结论正确的是____________ ①是周期函数;②是奇函数;③关于点对称;④关于直线对称.三、解答题1.设锐角三角形的内角的对边分别为,。
(1)求的大小; (2)若,求2.某大学举办“我爱记歌词”校园歌手大赛,经过层层选拔,有5人进入决赛,决赛办法如下:选手参加“千首电脑选歌”演唱测试,测试过关者即被授予“校园歌手”称号,否则参加“百首电脑选歌”演唱测试。
贵州省遵义市绥阳中学高一数学下学期第二次月考试卷(含解析)

2014-2015学年贵州省遵义市绥阳中学高一(下)第二次月考数学试卷一、选择题:(本大题共12小题,每题5分,共计50分,在每题给出的四个选项中,只有一个是正确的).1.A={1,2,3},B={﹣1,2,﹣3},A∩B=()A. {2} B. 2 C. {﹣3,﹣1,1,2,3} D.φ2.sin(﹣60°)的值为()A.B.C.D.3.下列函数中既是偶函数又在(0,+∞)上是增函数的是()A. y=x3B. y=|x|﹣3 C. y=x2﹣2x+1 D. y=2﹣|x| 4.若θ是△ABC的一个内角,且sinθcosθ=,则sinθ+cosθ=()A.B.C.D.5.若,则tanα=()A. 1 B.﹣1 C.D.6.已知α为第二象限角,,则cos2α=()A.B.C.D.7.在等差数列{a n}中,若a4=4,则a2+a6等于()A. 4 B. 8 C. 16 D. 328.函数y=Asin(ωx+φ)在一个周期内的图象如图,此函数的解析式为()A. y=2sin(2x+) B. y=2sin(2x+)C. y=2sin(﹣)D. y=2sin(2x﹣)9.已知数列{a n}的通项公式为,则a1=()A.B.C.D. 210.等差数列{a n}中,首项a1=1,a5=9,则数列的前10项之和是()A. 90 B. 100 C. 145 D. 19011.已知△ABC的角A、B、C所对边的边为a,b,c,acosA=bcosB,则该三角形现状为()A.直角三角形B.等腰三角形C.等腰直角三角形D.直角三角形或等腰三角形12.在平行四边形ABCD中,AC与BD交于O,F是线段DC的三等分点,AF与CD交于点E,若,=,则等于()A.+B.+C.+D.+二、填空题(本题共4道小题,每小题5分,共20分)13.sin10°cos20°+sin80°sin20°=.14.数列{a n}为等差数列,且log3(a3+a5)=4,则a4= .15.求和+++…+= .16.已知S n,T n分别为等差数列{a n},{b n}的前n项和且=,则= .三、解答题(本题共6道小题共70分)17.已知等差数列{a n},a1=2,a4=7.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)求数列{a n}的前n项和S n.18.已知函数f(x)=2cos2x﹣2(Ⅰ)求f(x)的最小正周期及最值;(Ⅱ)若x∈[,],f(x)的范围.19.已知数列{a n},其前n项和为(Ⅰ)求a1,a2,a3;(Ⅱ)求{a n}的通项公式a n.20.在△ABC中,A,B,C所对的边分别为a,b,c,有acosC﹣csinA=0.(Ⅰ)求角C的大小;(Ⅱ)若,S△ABC=3,求b,c的值.21.已知非常数数列{a n}的前项n和为S n,且有a n>0,(Ⅰ)求数列{a n}的通项公式;(Ⅱ)令,求数列{b n}的前项n和T n.22.在边长为1的正方形ABCD中,E,F分别为AD,AB边上的点,△AEF的周长为2;(Ⅰ)设∠BCF=α,∠ECD=β,,求tanα,tanβ.(Ⅱ)求∠ECF的度数.2014-2015学年贵州省遵义市绥阳中学高一(下)第二次月考数学试卷参考答案与试题解析一、选择题:(本大题共12小题,每题5分,共计50分,在每题给出的四个选项中,只有一个是正确的).1.A={1,2,3},B={﹣1,2,﹣3},A∩B=()A. {2} B. 2 C. {﹣3,﹣1,1,2,3} D.φ考点:交集及其运算.专题:集合.分析:由A与B,求出两集合的交集即可.解答:解:∵A={1,2,3},B={﹣1,2,﹣3},∴A∩B={2},故选:A.点评:此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.2.sin(﹣60°)的值为()A.B.C.D.考点:运用诱导公式化简求值.专题:三角函数的求值.分析:由条件利用诱导公式进行化简所给的式子,可得结果.解答:解:sin(﹣60°)=﹣sin60°=﹣,故选:C.点评:本题主要考查利用诱导公式进行化简求值,属于基础题.3.下列函数中既是偶函数又在(0,+∞)上是增函数的是()A. y=x3B. y=|x|﹣3 C. y=x2﹣2x+1 D. y=2﹣|x|考点:函数单调性的判断与证明;函数奇偶性的判断.专题:函数的性质及应用.分析:根据偶函数、奇函数的定义,一次函数、指数函数的单调性即可找出符合条件的选项.解答:解:A.y=x3是奇函数;B.y=|x|﹣3是偶函数,显然在(0,+∞)上为增函数,∴该选项正确;C.根据二次函数y=x2﹣2x+1的图象便知该函数非奇非偶;D.y=2﹣|x|,x>0时该函数变成y=,该函数在(0,+∞)上为减函数.故选:B.点评:考查偶函数、奇函数的定义,偶函数图象的对称性,一次函数及指数函数的单调性.4.若θ是△ABC的一个内角,且sinθcosθ=,则sinθ+cosθ=()A.B.C.D.考点:同角三角函数基本关系的运用.专题:三角函数的求值.分析:利用完全平方公式及同角三角函数间基本关系化简得到(sinθ+cosθ)2=1+2sinθcosθ,把已知等式代入,开方即可求出值.解答:解:∵θ是△ABC的一个内角,且sinθcosθ=>0,∴sinθ>0,cosθ>0,即sinθ+cosθ>0,∵(sinθ+cosθ)2=1+2sinθcosθ=,∴sinθ+cosθ=,故选:C.点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.5.若,则tanα=()A. 1 B.﹣1 C.D.考点:同角三角函数基本关系的运用.专题:计算题.分析:已知等式的左边分子分母同时除以cosα,利用同角三角函数间的基本关系弦化切后,得到关于tanα的方程,求出方程的解即可得到tanα的值.解答:解:∵==2,即tanα+1=4tanα﹣2,解得:tanα=1.故选A点评:此题考查了同角三角函数间的基本关系的运用,涉及的关系式为tanα=,熟练掌握基本关系是解本题的关键.6.已知α为第二象限角,,则cos2α=()A.B.C.D.考点:二倍角的余弦.专题:计算题;三角函数的求值.分析:利用二倍角的正弦与同角三角函数间的关系可求得sinα﹣cosα=,再利用二倍角的余弦即可求得cos2α.解答:解:∵sinα+cosα=,∴两边平方得:1+2sinαcosα=,∴2sinαcosα=﹣<0,∵α为第二象限角,∴sinα>0,cosα<0,sinα﹣cosα>0.∴sinα﹣cosα===,∴cos2α=cos2α﹣sin2α=(cosα﹣sinα)(cosα+sinα)=(﹣)×=﹣.故选:D.点评:本题考查二倍角的正弦、余弦与同角三角函数间的关系,属于中档题7.在等差数列{a n}中,若a4=4,则a2+a6等于()A. 4 B. 8 C. 16 D. 32考点:等差数列的性质.专题:计算题.分析:先根据等差中项的性质知a2+a6=2a4求得答案.解答:解:∵{a n}是等差数列,∴a2+a6=2a4=8.故选B.点评:本题主要考查了等差数列的性质.属基础题.8.函数y=Asin(ωx+φ)在一个周期内的图象如图,此函数的解析式为()A. y=2sin(2x+) B. y=2sin(2x+)C. y=2sin(﹣)D. y=2sin (2x﹣)考点:由y=Asin(ωx+φ)的部分图象确定其解析式.分析:根据已知中函数y=Asin(ωx+ϕ)在一个周期内的图象经过(﹣,2)和(﹣,2),我们易分析出函数的最大值、最小值、周期,然后可以求出A,ω,φ值后,即可得到函数y=Asin(ωx+ϕ)的解析式.解答:解:由已知可得函数y=Asin(ωx+ϕ)的图象经过(﹣,2)点和(﹣,2)则A=2,T=π即ω=2则函数的解析式可化为y=2sin(2x+ϕ),将(﹣,2)代入得﹣+ϕ=+2kπ,k∈Z,即φ=+2kπ,k∈Z,当k=0时,φ=此时故选A点评:本题考查的知识点是由函数y=Asin(ωx+ϕ)的部分图象确定其解析式,其中A=|最大值﹣最小值|,|ω|=,φ=L•ω(L是函数图象在一个周期内的第一点的向左平移量).9.已知数列{a n}的通项公式为,则a1=()A.B.C.D. 2考点:数列的概念及简单表示法.专题:点列、递归数列与数学归纳法.分析:根据数列的通项公式直接进行求解即可.解答:解:∵,∴a1==,故选:C点评:本题主要考查数列通项公式的应用,比较基础.10.等差数列{a n}中,首项a1=1,a5=9,则数列的前10项之和是()A. 90 B. 100 C. 145 D. 190考点:等差数列的前n项和.专题:等差数列与等比数列.分析:利用公差d=及求和公式计算即可.解答:解:∵a1=1,a5=9,∴公差d===2,∴S10=10a1+d=10×1+×2=100,故选:B.点评:本题考查等差数列的简单性质,注意解题方法的积累,属于基础题.11.已知△ABC的角A、B、C所对边的边为a,b,c,acosA=bcosB,则该三角形现状为()A.直角三角形B.等腰三角形C.等腰直角三角形D.直角三角形或等腰三角形考点:正弦定理.专题:解三角形.分析:a cosA=bcosB,利用正弦定理可得sinAcosA=sinBcosB,利用倍角公式可得sin2A=sin2B,可得2A=2B或2A+2B=π,即可得出.解答:解:∵acosA=bcosB,由正弦定理可得sinAcosA=sinBcosB,∴sin2A=sin2B,∴2A=2B或2A+2B=π,化为A=B或A+B+.∴哎三角形为直角三角形或等腰三角形.故选:D.点评:本题考查了正弦定理、倍角公式、正弦函数的单调性,属于基础题.12.在平行四边形ABCD中,AC与BD交于O,F是线段DC的三等分点,AF与CD交于点E,若,=,则等于()A.+B.+C.+D.+考点:向量的线性运算性质及几何意义.专题:平面向量及应用.分析:根据两个三角形相似对应边成比例,得到E是BD的四等分点,进而可得=+=+=+(﹣),进而得到答案.解答:解:在平行四边形ABCD中,AB∥CD,∴△ABE∽△FDE,∵F是线段DC的三等分点,∴DF:CD=DF:AB=DE:BE=1:3,即E是BD的四等分点,∴=+=+=+(﹣)=+,∵,=,∴=故选:A点评:向量是数形结合的典型例子,向量的加减运算是用向量解决问题的基础,要学好运算,才能用向量解决立体几何问题,三角函数问题,好多问题都是以向量为载体的.二、填空题(本题共4道小题,每小题5分,共20分)13.sin10°cos20°+sin80°sin20°=.考点:两角和与差的正弦函数;运用诱导公式化简求值.专题:三角函数的求值.分析:由条件利用诱导公式、两角和的正弦公式求得所给式子的值.解答:解:sin10°cos20°+sin80°sin20°=sin10°cos20°+cos10°sin20°=sin30°=,故答案为:.点评:本题主要考查两角和的正弦公式,诱导公式的应用,属于基础题.14.数列{a n}为等差数列,且log3(a3+a5)=4,则a4= .考点:等差数列的通项公式.专题:等差数列与等比数列.分析:由对数的运算法则求得a3+a5,然后结合等差数列的性质得答案.解答:解:由log3(a3+a5)=4,得a3+a5=34=81,∵数列{a n}为等差数列,则2a4=a3+a5=81,∴.故答案为:.点评:本题考查等差数列的性质,考查了对数的运算法则,是基础的计算题.15.求和+++…+= .考点:数列的求和.专题:计算题;等差数列与等比数列.分析:结合数列的通项的特点,考虑利用裂项求和解答:解:∵+++…+===故答案为:点评:本题主要考查了数列的裂项求和方法的应用,属于基础试题16.已知S n,T n分别为等差数列{a n},{b n}的前n项和且=,则= .考点:等差数列的前n项和.专题:等差数列与等比数列.分析:利用等差中项即得=,计算即得结论.解答:解:∵数列{a n}、{b n}均为等差数列,∴S9==9a5,T9==9b5,又∵=,∴===,故答案为:.点评:本题考查等差数列的简单性质,利用等差中项是解决本题的关键,注意解题方法的积累,属于中档题.三、解答题(本题共6道小题共70分)17.已知等差数列{a n},a1=2,a4=7.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)求数列{a n}的前n项和S n.考点:等差数列的前n项和;等差数列的通项公式.专题:等差数列与等比数列.分析:(Ⅰ)利用公差d=,进而计算即得结论;(Ⅱ)利用公式S n=计算即得结论.解答:解:(Ⅰ)∵a1=2,a4=7,∴公差d===,∴数列{a n}的通项a n=a1+(n﹣1)d=2+(n﹣1)=n+;(Ⅱ)∵a n=n+,a1=2,∴数列{a n}的前n项和S n==.点评:本题考查等差数列的通项及求和,注意解题方法的积累,属于基础题.18.已知函数f(x)=2cos2x﹣2(Ⅰ)求f(x)的最小正周期及最值;(Ⅱ)若x∈[,],f(x)的范围.考点:余弦函数的图象;三角函数的化简求值;三角函数的周期性及其求法.专题:三角函数的图像与性质.分析:(Ⅰ)由条件利用二倍角的余弦公式化简函数的解析式,再利用余弦函数的周期性、定义域和值域求得f(x)的最小正周期及最值.(Ⅱ)根据x∈[,],利用余弦函数的定义域和值域求得f(x)的范围.解答:解:(Ⅰ)对于函数f(x)=2cos2x﹣2=cos2x﹣1,它的最小正周期为=π,它的最大值为0,最小值为﹣2.(Ⅱ)若x∈[,],则2x∈[,π],∴cos2x∈[﹣1,],∴f(x)=cos2x﹣1的范围为[﹣2,﹣].点评:本题主要考查二倍角的余弦公式、余弦函数的周期性、定义域和值域,属于基础题.19.已知数列{a n},其前n项和为(Ⅰ)求a1,a2,a3;(Ⅱ)求{a n}的通项公式a n.考点:数列递推式.专题:等差数列与等比数列.分析:通过与S n+1=(n+1)2+(n+1)作差、计算即得结论.解答:解:(Ⅰ)∵,∴S n+1=(n+1)2+(n+1),两式相减得:a n+1=S n+1﹣S n=(n+1)2+(n+1)﹣(n2+n)=2(n+1),又∵a1=12+1=2满足上式,∴a n=2n,∴a1=2,a2=4,a3=6;(Ⅱ)由(I)知数列{a n}的通项公式a n=2n.点评:本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.20.在△ABC中,A,B,C所对的边分别为a,b,c,有acosC﹣csinA=0.(Ⅰ)求角C的大小;(Ⅱ)若,S△ABC=3,求b,c的值.考点:余弦定理;正弦定理.专题:计算题;解三角形.分析:(Ⅰ)由正弦定理得:sinAcosC﹣sinCsinA=0,即可解得tanC=,从而求得C的值;(Ⅱ)由面积公式可得S△ABC=absinC=3,从而求得得b的值,由余弦定理即可求c的值.解答:解:(Ⅰ)在△ABC中,由正弦定理得:sinAcosC﹣sinCsinA=0.…(2分)因为0<A<π,所以sinA>0,从而cosC=sinC,又cosC≠0,…(4分)所以tanC=,所以C=.…(6分)(Ⅱ)在△ABC中,S△ABC=absinC==3,得b=,…(9分)由余弦定理得:c2=2+()2﹣2×××cos=,所以c=.…(12分)点评:本小题主要考查正弦定理、余弦定理、三角形的面积公式、同角三角函数的基本关系式等基础知识,考查运算求解能力,考查化归与转化思想,属于中档题.21.已知非常数数列{a n}的前项n和为S n,且有a n>0,(Ⅰ)求数列{a n}的通项公式;(Ⅱ)令,求数列{b n}的前项n和T n.考点:数列的求和;数列递推式.专题:等差数列与等比数列.分析:(I)利用递推式可得a n+a n﹣1=2或a n﹣a n﹣1=2,通过分类讨论即可得出;(II)利用“裂项求和”即可得出.解答:解:(I)∵a n>0,,∴当n=1时,a1=,解得a1=1或3.当n≥2时,a n=S n﹣S n﹣1=﹣,化为(a n+a n﹣1﹣2)(a n﹣a n﹣1﹣2)=0,∴a n+a n﹣1=2或a n﹣a n﹣1=2,①若a n+a n﹣1=2,当a1=1时,可得a n=1,(n∈N*),数列{a n}为常数数列,舍去;当a1=3时,可得a2=﹣1,与a n>0矛盾,舍去;②若a n﹣a n﹣1=2,当a1=1时,可得a n=2n﹣1,(n∈N*),满足题意.当a1=3时,可得a n=2n+1,(n∈N*),满足题意.综上可得:a n=2n±1,(n∈N*).(II)当a n=2n﹣1,==,则数列{b n}的前项n和T n=++…+=1﹣=.同理可得:当a n=2n+1,=,则数列{b n}的前项n和T n=1﹣=.点评:本题考查了递推式的应用、等差数列的通项公式、分类讨论方法、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.22.在边长为1的正方形ABCD中,E,F分别为AD,AB边上的点,△AEF的周长为2;(Ⅰ)设∠BCF=α,∠ECD=β,,求tanα,tanβ.(Ⅱ)求∠ECF的度数.考点:两角和与差的正切函数.专题:解三角形.分析:(Ⅰ)根据AE、AF的值求出DE和BF,在RT△CBF和RT△CDE中求出tanα,tanβ;(Ⅱ)利用两角和的正切函数求出tan(α+β)的值,由α、β的范围求出α+β的值,再求出∠ECF的度数.解答:解:(Ⅰ)∵,∴DE=BF=,在RT△CBF中,tanα==,在RT△CDE中,tanβ==;(Ⅱ)由(Ⅰ)得,tan(α+β)====1,∵α+β∈(0,),∴α+β=,则∠ECF=﹣(α+β)=.点评:本题考查两角和的正切函数,以及正切函数的定义,注意角的范围和正切函数的符号,属于中档题.。
贵州省绥阳县绥阳中学2020_2021学年高一语文月考试题

贵州省绥阳县绥阳中学2020—2021学年高一语文月考试题一、现代文阅读(36分)(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成1-3题.现代诗派,是对三十年代到抗战前新崛起的有大致相似的创作风格的年轻的都市诗人的统称。
现代诗派因《现代》杂志而得名,其兴起的标志,即是1932年在上海创刊的由施蛰存、杜衡主编的《现代》杂志.戴望舒是现代派诗歌领袖,重要的诗人还有卞之琳、何其芳、李广田、施蛰存、金克木、废名等,他们都以各自意象新颍、想象独特的诗作,推进现代派诗歌的发展.在20世纪30年代阶级对垒的社会历史背景下,现代派诗人们大多是游离于政党与政治派别之外的边缘人;同时,许多人来自乡土在都市中感受着传统与现代双重文明的挤压,又成为乡土和都市夹缝中的边缘人。
他们深受法国象征派诗人的影响,濡染了波德莱尔式的对现代都市的疏离感和陌生感及魏尔伦式的世纪末颓废情绪。
而五四运动的退潮和大革命的失败,更摧毁了年青诗人的纯真信念,辽远的国士由此成为一代诗人的精神寄托.戴望舒的《雨巷》典型地表达了一代青年普遍的理想幻灭的忧郁情绪.作为理想象征的“丁香一样的姑娘”,像梦飘过一样,在面前一闪,转瞬即逝了。
就这样用暗示象征的手法,表达了追求美好理想而不得的那种孤苦心情。
这点深受法国象征派诗人魏尔伦的影响.在诗艺上,现代派诗人注重暗示的技巧,很少直接呈示主观感受,而是采用意象隐喻、通感、象征来间接传达情调和意绪,这使得现代派诗歌大多含蓄、朦胧,既避免了狂叫、直说,又纠正了初期象征派晦涩难懂的弊病,创造性地转化了波德莱尔、魏尔伦的象征主义诗艺.现代派诗人重视向内在的心灵世界和平凡的日常生活开掘诗的题材,运用象征的意象与曲折隐藏的方法,表达其忧伤之思情,追求“象征派的形式、古典派的内容”的统一.现代派诗歌的现代诗形体体现在表层形式上,它有以象征主义为主、兼有浪漫主义、古典主义、意象派的艺术特点;而在审美趣味和文化心理取向上则显示出鲜明的古典主义特征,呈现出朦胧而又明朗、单纯而又丰富的东方民族审美特色,成为真正意义上的东方民族现代诗.正是现代派诗人们这样孜孜不倦,兼收并蓄,不断地进行着“化古化欧的创造性的转化工作”,使中国新诗既民族化又现代化,从而构建起真正的东方民族现代诗。
贵州省绥阳县绥阳中学2020-20201学年高一月考英语试卷含答案

英语试题注意事项:1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
第一部分听力(共两节,满分30分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1.What troubles the man?A.The phone rings.B.The poor service.C.The TV noise.2.What is Jack’s house like?A.It is small.B.It is messy.C.It is clean.3.Which shirt will the man probably wear?A.The blue one.B.The orange one.C.The white one.4.What does the woman suggest the man do?A.Rest at home.B.Go outdoors.C.Watch a football match.5.What does the woman mean?A.She will take a boat tour.B.She will work on the ship.C.She will be busy this summer.第二节(共15小题;每题1.5分,满分22.5分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
解析贵州省遵义市绥阳中学2020┄2021学年高一下学期第一次月考物理试卷

贵州省遵义市绥阳中学2020┄2021学年高一下学期第一次月考物理试卷一、选择题(每题6分,1-5为单选;6-8为不定项选择,全对得6分,不全对得3分,有错不得分,共48分)1.(6分)宋代诗人陈与义乘着小船在风和日丽的春日出游时曾写下了一首诗,在这首诗中,诗人艺术性地描述了他对运动的相对性的理解.下列说法正确的是()A.ﻩ第三句选择的参考系为大地ﻩB.第四句选择的参考系为云C.ﻩ第四句选择的参考系为“我”D. 第三句选择的参考系为“我”2.(6分)以下各物理量属于矢量的是()ﻩA.质量ﻩB.时间ﻩC.摩擦力D.ﻩ动摩擦因数3.(6分)一辆汽车从车站从静止做匀加速直线运动,开出一段时间之后,司机发现一乘客未上车,便紧急刹车做匀减速运动.从启运到停止一共经历t=20s,前进了30m,在此过程中,汽车的最大速度为()A.ﻩ1.5m/s B.ﻩ4m/s C. 3m/sD.无法确定4.(6分)如图,关于速度﹣时间图的理解,说法正确的是()ﻩA.ﻩ反映的是物体运动的实际轨迹B.ﻩ由图知物体先向正方向运动,后向负方向运动ﻩC.其斜率表示速度ﻩD. 其斜率表示加速度5.(6分)一物体受大小分别为100N、20N、150N的三个力作用,这三个力的合力最小值是()A.30N B.ﻩ0ﻩC.70NﻩD.ﻩ无法确定6.(6分)下列关于速度和加速度的说法中,正确的是()ﻩA.ﻩ速度很大的物体时,其加速度也一定很大ﻩB.物体的速度变化越快,加速度越大ﻩC.ﻩ物体的速度变化量越大,加速度越大ﻩD.ﻩ当物体的加速度减小时,其速度可能在增加7.(6分)如图所示,x轴在水平地面内,y轴沿竖直方向.图中画出了从y轴上沿x轴正向抛出的三个小球a、b和c的运动轨迹,其中b和c是从同一点抛出的.不计空气阻力,则()ﻩA. b和c的飞行时间相同B.a的飞行时间比b的长C.b的初速度比c的大ﻩD.a的水平速度比b的小二、填空题(共16分),把答案填在题中的横线上.8.(8分)在“研究平抛物体运动”的实验中,可以描绘平抛物体运动轨迹和求物体的平抛初速度.实验简要步骤如下:A.让小球多次从位置上滚下,记下小球穿过卡片孔的一系列位置;B.测出曲线上某点的坐标x、y,用v0=算出该小球的平抛初速度,实验需要对多个点求v0的值,然后求它们的平均值.C.安装好器材,注意斜槽末端水平和平板竖直,记下斜槽末端O点和过O点的竖直线,检测斜槽末端水平的方法是.D.取下白纸,以O为原点,以竖直线为轴建立坐标系,用平滑曲线画平抛轨迹.上述实验步骤的合理顺序是(只排列序号即可).9.(8分)某次实验用打点计时器交流电的频率为50Hz,纸带的记录如图所示,图中O点为纸带的第一个点,接下来的前几个点模糊,因此从A点开始每打五个点取一个计数点,推测纸带的运动是(加速、减速),在打出A、F这两点的时间间隔中,纸带运动的平均速度是,B点的瞬时速度为.二、本题共3小题,共36分.按题目要求作答.解答题应写出必要的文字说明、方程和重要演算步骤.只写出最后答案的不能得分.有数值计算的题,答案中必须明确写出数值和单位.10.(10分)水平抛出的一个石子,经过0.4s落到地面,落地时的速度方向跟水平方向的夹角是53°(sin53°=0.8;cos53°=0.6,g取10m/s2).不计阻力,试求:(1)石子的抛出点距地面的高度;(2)石子抛出的水平初速度.11.(11分)如图所示,电灯的质量m=0.1kg,绳与顶板间的夹角为45°度,灯泡处于静止状态,绳OB水平,则绳OA所受的拉力F1是多少?绳OB所受的拉力F2是多少?(g取10m/s2)12.(15分)一静止在水平面质量为5kg的滑块在F=15N的水平拉力作用下,由静止开始做匀加速直线运动,若滑块与水平面间的动摩擦因素是0.2,g取10m/s2,问:(1)滑块运动的加速度是多大?(2)滑块在力F作用下经5s,通过的位移是多大?(3)如果力F作用8s后撤去,则滑块在撤去F后还能滑行多远?贵州省遵义市绥阳中学2020┄2021学年高一下学期第一次月考物理试卷参考答案与试题解析一、选择题(每题6分,1-5为单选;6-8为不定项选择,全对得6分,不全对得3分,有错不得分,共48分)1.(6分)宋代诗人陈与义乘着小船在风和日丽的春日出游时曾写下了一首诗,在这首诗中,诗人艺术性地描述了他对运动的相对性的理解.下列说法正确的是()ﻩA.第三句选择的参考系为大地ﻩB.ﻩ第四句选择的参考系为云ﻩC.第四句选择的参考系为“我”ﻩD. 第三句选择的参考系为“我”考点:ﻩ参考系和坐标系.专题:ﻩ常规题型.分析:参考系是为了研究问题方便而假定静止不动的物体.故只要研究对象与参考系的相对位置不发生变化,则观察到的结果是物体静止不动.卧看满天云不动”是指“云与我”保持相对静止即以相同的速度相对于地球向东运动.解答:ﻩ解:A、参考系是为了研究问题方便而假定静止不动的物体.故只要研究对象与参考系的相对位置不发生变化,则观察到的结果是物体静止不动.在本题中船是向东高速行驶,而“卧看满天云不动”是指“云与我”保持相对静止,故参考系是我或我所所在的小船;故A错误,D正确;B、“云与我俱东”所选择的参考系是地球和地球上相对于地球保持静止不动的物体,故BC 错误.故选:D.点评:ﻩ真正理解了参考系的概念即可顺利解决此类题目,而要理解这一概念就必需多看课本,多认真处理此类题目.2.(6分)以下各物理量属于矢量的是()A.ﻩ质量B.ﻩ时间ﻩC.摩擦力D.动摩擦因数考点:矢量和标量.专题:常规题型.分析:ﻩ矢量是既有大小,又有方向的物理量,而标量是只有大小,没有方向的物理量,根据有没有方向区分是标量还是矢量.解答:ﻩ解:A、B、D、质量、时间、动摩擦因数都是只有大小,没有方向的标量.故ABD 错误.C、摩擦力既有大小,又有方向,是矢量.故C正确.故选C.点评:对于物理量的矢标性与物理量的定义、物理意义、单位、公式等要一起学习,是物理概念内涵的一部分.3.(6分)一辆汽车从车站从静止做匀加速直线运动,开出一段时间之后,司机发现一乘客未上车,便紧急刹车做匀减速运动.从启运到停止一共经历t=20s,前进了30m,在此过程中,汽车的最大速度为()A. 1.5m/s B.4m/sﻩC.ﻩ3m/sﻩD.无法确定考点:ﻩ匀变速直线运动规律的综合运用.专题:ﻩ直线运动规律专题.分析:ﻩ设汽车的最大速度为v,分别用平均速度表示匀加速运动和匀减速运动汽车的位移,根据位移之和求解该过程中汽车前进的距离.解答:解:设最大速度为v,则根据平均速度公式,汽车加速过程和减速过程的平均速度均为:,则有:解得:v===3m/s.所以选项C正确.故选:C点评:ﻩ本题是两个过程问题,寻找两个过程的关系是解题的关键.也可以通过作速度图象求解.4.(6分)如图,关于速度﹣时间图的理解,说法正确的是()A. 反映的是物体运动的实际轨迹B.由图知物体先向正方向运动,后向负方向运动C. 其斜率表示速度D.其斜率表示加速度考点: 匀变速直线运动的图像;匀变速直线运动的速度与时间的关系.专题:ﻩ运动学中的图像专题.分析:速度时间图线反映的是速度随时间的变化规律,图线不是运动的轨迹.图线的斜率表示加速度.解答:解:A、图线的斜率在变化,知加速度是变化的.故A错误.B、物体的速度始终为正值,知物体始终向正方向运动,即速度的方向不变.故B错误.C、速度时间图线的斜率表示加速度.故C错误,D正确.故选:D.点评:解决本题的关键知道速度时间图线表示的物理意义,知道图线的斜率表示加速度,速度的正负值表示运动的方向.5.(6分)一物体受大小分别为100N、20N、150N的三个力作用,这三个力的合力最小值是()A.30N B.ﻩ0ﻩ C. 70NﻩD.ﻩ无法确定考点:ﻩ合力的大小与分力间夹角的关系.专题:ﻩ平行四边形法则图解法专题.分析:ﻩ当这三个力作用在同一物体上,并且作用在同一直线上,方向相同,三个力的合力最大.如果三个力不在同一直线上,夹角可以变化,当两个较小力的合力大小等于第三个力,方向相反时,此时三个力的合力的最小.解答:解:当三个力作用在一个物体上,不在一条直线,并且夹角可以改变,150N不在100N与20N最大与最小之间,故此时三个力的合力的最小值为150﹣120=30N.故A正确,BCD错误;故选:A.点评:当多个力合成时,它们作用在同一直线上、同方向时,合力最大;求最小合力时,先考虑合力为零的情况.6.(6分)下列关于速度和加速度的说法中,正确的是()A. 速度很大的物体时,其加速度也一定很大B.物体的速度变化越快,加速度越大ﻩC.物体的速度变化量越大,加速度越大ﻩD.当物体的加速度减小时,其速度可能在增加考点:ﻩ加速度;匀变速直线运动的速度与时间的关系.专题:ﻩ直线运动规律专题.分析:ﻩ根据加速度的定义式a=可知物体的加速度等于物体的速度的变化率,加速度的方向就是物体速度变化量的方向,与物体速度无关,即物体的速度变化越快物体的加速度越大.解答:解:A、速度很大的物体时,其加速度可能为零,例如匀速直线运动,故A错误; B、加速度的物理意义是表示物体速度变化的快慢,则知速度变化越快,加速度一定越大.故B正确;C、根据a=可知加速度a由速度的变化量△v和速度发生改变所需要的时间△t共同决定,虽然△v大,但△t更大时,a可以很小.故C错误;D、当物体的加速度减小时,如果加速度方向与速度方向相同,其速度在增加,故D正确;故选:BD.点评:本题的解题关键是抓住速度与加速度无关的特点和加速度的物理意义,来理解加速度与速度的关系.7.(6分)如图所示,x轴在水平地面内,y轴沿竖直方向.图中画出了从y轴上沿x轴正向抛出的三个小球a、b和c的运动轨迹,其中b和c是从同一点抛出的.不计空气阻力,则()A.ﻩb和c的飞行时间相同ﻩB. a的飞行时间比b的长ﻩC.ﻩb的初速度比c的大D.a的水平速度比b的小考点:ﻩ平抛运动.专题:ﻩ平抛运动专题.分析:平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据高度比较运动的时间,结合水平位移和时间比较初速度.解答:解:A、根据t=知,b、c的高度相同,则b和c的飞行时间相同,a的高度小于b的高度,则a的飞行时间小于b的飞行时间,故A正确,B错误.C、b、c的运动时间相等,b的水平位移大,根据x=vt知,b的初速度大,故C正确.D、a的飞行时间短,根据x=vt知,a的水平位移大,则a的水平速度大于b的水平速度,故D错误.故选:AC.点评:ﻩ解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,知道运动的时间由高度决定,初速度和时间共同决定水平位移.二、填空题(共16分),把答案填在题中的横线上.8.(8分)在“研究平抛物体运动”的实验中,可以描绘平抛物体运动轨迹和求物体的平抛初速度.实验简要步骤如下:A.让小球多次从同一位置上滚下,记下小球穿过卡片孔的一系列位置;B.测出曲线上某点的坐标x、y,用v0=x算出该小球的平抛初速度,实验需要对多个点求v0的值,然后求它们的平均值.C.安装好器材,注意斜槽末端水平和平板竖直,记下斜槽末端O点和过O点的竖直线,检测斜槽末端水平的方法是将小球放在水平槽中若能静止则可认为水平.D.取下白纸,以O为原点,以竖直线为轴建立坐标系,用平滑曲线画平抛轨迹.上述实验步骤的合理顺序是CADB(只排列序号即可).考点: 研究平抛物体的运动.专题:实验题.分析:让小球多次从同一位置上静止滚下,目的是保证小球多次做平抛运动的初速度相等,这样目的是为了保证轨迹相同;保证小球做平抛运动,所以斜槽末端保持水平;平抛运动分解为:水平方向的匀速直线运动,竖直方向的自由落体运动,根据平抛运动的特点即可求解初速度大小;实验步骤的合理顺序的排列要明确实验的正确安排顺序.解答:ﻩ解:A、在“研究平抛物体运动”的实验中,要保证小球从斜槽末端飞出时的速度是相同的,因此,要让小球多次从斜槽上的同一位置滚下.B、平抛运动分解为:水平方向的匀速直线运动,竖直方向的自由落体运动,水平方向有:x=v0t竖直方向有:h=gt2;联立求出初速度:v0=xC、在画竖直线时要利用重垂线进行,检验斜槽末端水平的方法有多种,如用水平仪或者将小球放在斜槽末端看其是否滚动,若不滚动,则斜槽末端水平.根据,安装器材,进行试验,数据处理的思路,可知实验步骤合理顺序是:CADB.故答案为:同一;x;将小球放在水平槽中若能静止则可认为水平;CADB.点评:关于平抛运动实验要掌握实验的注意事项、实验步骤、实验原理.平抛运动分解为:水平方向的匀速直线运动,竖直方向的自由落体运动,尤其是注意应用匀变速直线运动规律解决平抛运动问题.9.(8分)某次实验用打点计时器交流电的频率为50Hz,纸带的记录如图所示,图中O点为纸带的第一个点,接下来的前几个点模糊,因此从A点开始每打五个点取一个计数点,推测纸带的运动是加速(加速、减速),在打出A、F这两点的时间间隔中,纸带运动的平均速度是0.365m/s,B点的瞬时速度为0.252m/s.考点:ﻩ探究小车速度随时间变化的规律.专题:ﻩ实验题.分析:ﻩ知道相邻的计数点之间的时间间隔相等.根据纸带上相邻点的距离间隔判断小车的运动情况.根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出打纸带上B时小车的瞬时速度大小.解答:ﻩ解:相邻的计数点之间的时间间隔相等,根据纸带上数据得出相邻的计数点距离逐渐增大,所以纸带做加速运动.按打点先后顺序每5个点取1个计数点,所以相邻的计数点之间的时间间隔为0.1s.打出A、F这两点的时间间隔中,纸带运动的平均速度==0.365m/s,根据匀变速直线运动中时间中点的速度等于该过程中的平均速度得v B==0.252m/s故答案为:加速;0.365m/s;0.252m/s.点评:ﻩ要提高应用匀变速直线的规律以及推论解答实验问题的能力,在平时练习中要加强基础知识的理解与应用.二、本题共3小题,共36分.按题目要求作答.解答题应写出必要的文字说明、方程和重要演算步骤.只写出最后答案的不能得分.有数值计算的题,答案中必须明确写出数值和单位.10.(10分)水平抛出的一个石子,经过0.4s落到地面,落地时的速度方向跟水平方向的夹角是53°(sin53°=0.8;cos53°=0.6,g取10m/s2).不计阻力,试求:(1)石子的抛出点距地面的高度;(2)石子抛出的水平初速度.考点: 平抛运动.专题:ﻩ平抛运动专题.分析:ﻩ平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据时间求出石子的抛出点距离地面的高度.根据时间求出落地时竖直分速度,结合平行四边形定则求出石子抛出的初速度.解答:ﻩ解:(1)根据h=得,h==0.8m.(2)石子落地时竖直分速度v y=gt=4m/s,根据tan53°=,解得v0=3m/s.答:(1)石子抛出点距离地面的高度为0.8m;(2)石子抛出的水平初速度为3m/s.点评:解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解.11.(11分)如图所示,电灯的质量m=0.1kg,绳与顶板间的夹角为45°度,灯泡处于静止状态,绳OB水平,则绳OA所受的拉力F1是多少?绳OB所受的拉力F2是多少?(g取10m/s2)考点:共点力平衡的条件及其应用;物体的弹性和弹力.专题: 共点力作用下物体平衡专题.分析:ﻩ将电灯对O点的拉力分解为沿AO方向的分力和沿BO方向的分力,作出力图,由几何知识求解.解答:解:将电灯对O点的拉力沿两个绳子方向进行分解,如图.由几何知识得,F2=G=10N答:AO绳所受的拉力F1是10N,BO绳所受的拉力F2是10N.点评:ﻩ本题也可以以结点O为研究对象,采用正交分解法或合成法求解,难度不大,属于基础题.12.(15分)一静止在水平面质量为5kg的滑块在F=15N的水平拉力作用下,由静止开始做匀加速直线运动,若滑块与水平面间的动摩擦因素是0.2,g取10m/s2,问:(1)滑块运动的加速度是多大?(2)滑块在力F作用下经5s,通过的位移是多大?(3)如果力F作用8s后撤去,则滑块在撤去F后还能滑行多远?考点:匀变速直线运动的位移与时间的关系.专题: 直线运动规律专题.分析:根据牛顿第二定律求出滑块的加速度.根据位移时间公式求出滑块的位移.根据牛顿第二定律求出撤去F后的加速度,结合速度位移公式求出还能滑行的距离.解答:ﻩ解:(1)根据牛顿第二定律得,滑块运动的加速度为:a=.(2)滑块的位移为:x=.(3)撤去F后,滑块的加速度大小为:a′=μg=2m/s2,撤去F时的速度为:v=at=1×8m/s=8m/s,则还能滑行的距离为:.答:(1)滑块运动的加速度为1m/s2;(2)滑块通过的位移为12.5m;(3)滑块在撤去F后还能滑行的距离为16m.点评:ﻩ本题考查了牛顿第二定律和运动学公式的基本运用,知道加速度是联系力学和运动学的桥梁,注意撤去F前后的加速度大小不等.。
贵州省绥阳县绥阳中学2018-2019学年高一上学期第一次月考物理试题 含解析
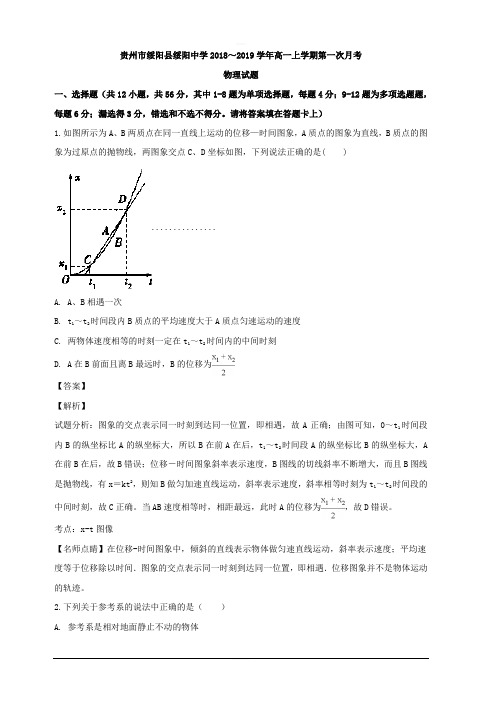
贵州市绥阳县绥阳中学2018~2019学年高一上学期第一次月考物理试题一、选择题(共12小题,共56分,其中1-8题为单项选择题,每题4分;9-12题为多项选题题,每题6分;漏选得3分,错选和不选不得分。
请将答案填在答题卡上)1.如图所示为A、B两质点在同一直线上运动的位移—时间图象,A质点的图象为直线,B质点的图象为过原点的抛物线,两图象交点C、D坐标如图,下列说法正确的是( )...............A. A、B相遇一次B. t1~t2时间段内B质点的平均速度大于A质点匀速运动的速度C. 两物体速度相等的时刻一定在t1~t2时间内的中间时刻D. A在B前面且离B最远时,B的位移为【答案】【解析】试题分析:图象的交点表示同一时刻到达同一位置,即相遇,故A正确;由图可知,0~t1时间段内B的纵坐标比A的纵坐标大,所以B在前A在后,t1~t2时间段A的纵坐标比B的纵坐标大,A 在前B在后,故B错误;位移-时间图象斜率表示速度,B图线的切线斜率不断增大,而且B图线是抛物线,有x=kt2,则知B做匀加速直线运动,斜率表示速度,斜率相等时刻为t1~t2时间段的中间时刻,故C正确。
当AB速度相等时,相距最远,此时A的位移为,故D错误。
考点:x-t图像【名师点睛】在位移-时间图象中,倾斜的直线表示物体做匀速直线运动,斜率表示速度;平均速度等于位移除以时间.图象的交点表示同一时刻到达同一位置,即相遇.位移图象并不是物体运动的轨迹。
2.下列关于参考系的说法中正确的是()A. 参考系是相对地面静止不动的物体B. “小小竹排江中游,巍巍青山两岸走”,其中“青山两岸走”作者所选取的参考系是岸C. 研究同一物体的运动时,选取不同的参考系所得出的关于物体运动的结论可能是不同的D. 坐在高速行驶列车里的乘客,看到桌上的水杯静止不动是以地面为参考系【答案】【解析】【分析】描述一个物体的运动时,参考系可以任意选取,选取参考系时要考虑研究问题的方便,使之对运动的描述尽可能的简单.选取不同的参考系,物体的运动情况不一定相同,在不说明参考系的情况下,通常取地面为参考系的.【详解】参考系是在描述物体的运动时,被选定做为参考、假定为不动的其他物体。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
贵州省绥阳县绥阳中学2020-2021学年高一数学月考试题一、单择题(本大题共12小题,每小题5分,共60分) 1.已知集合M ={x ∈N |x 2-1=0},则有( ) A .{}1M ∈B .1M -∈C .{}1,1M -⊆D .{1,-0,{}1}1M ⋂= 【答案】D{}{})的真子集个数是(,则集合,且,,,,已知集合A A C M M 354321.2== A .15 B .8C .7D .16【答案】A)21.()13.()12.()31.(,3,4,,2,2,.3,,,,))是(),则(的作用下对应点是()在映射若点()的作用下对应点是()在映射已知点(D C B A b a f b a y x y x f y x -+【答案】B【解析】.1,2,32,42===-=+b a b a b a 解得依题意:4.已知集合{}20,,32A m m m =-+,且2A ∈,则实数m 的值为 ( ) A .2 B .3或0 C .3 D .2或0 【答案】C5.下列各组函数中,()f x 与()g x 相等的是( ) A .()2f x x =-,()2g x x =-B .()2f x x =()33g x x =C .()22x f x x=+,()2g x x =+D .()2x x f x x -=,()21x g x x=-【答案】D6.已知111f x x ⎛⎫= ⎪+⎝⎭,则()f x 的解析式为( ) A .()11f x x =+ B .()1xf x x+=C .()1f x x x=+ D .()1f x x =+【答案】C7.已知全集U =R ,集合{}202,{0}A x x B x x x =≤≤=->,则图中的阴影部分表示的集合为( )A .(1](2,)-∞⋃+∞,B .(0)(12)-∞⋃,,C .[1)2,D .(12], 【答案】A【解析】B={x|x 2﹣x >0}={x|x >1或x <0},由题意可知阴影部分对应的集合为∁U (A∩B)∩(A∪B), ∴A∩B={x|1<x≤2},A∪B=R,即∁U (A∩B)={x|x≤1或x >2},∴∁U (A∩B)∩(A∪B)={x|x≤1或x >2},即(﹣∞,1]U (2,+∞)故选:A8.某工厂6年来生产某种产品的情况是:前3年年产量的增长速度越来越快,后3年年产量保持不变,则该厂6年来这种产品的总产量C 与时间t (年)的函数关系图象正确的是( )A .B .C .D .【答案】A9.若函数y =f (x )是定义在R 上的偶函数,在(-∞,0]上是减函数,且f (2)=0,则使函数值y <0的x 的取值范围为( )A .(-∞,2)B .(2,+∞)C .(-∞,-2)∪(2,+∞)D .(-2,2)解析:由于f (x )是偶函数,且f (2)=0,故f (-2)=0,根据已知条件,可画出函数y =f (x )的示意图,图象关于y 轴对称,由图象可知,使函数值y <0的x 的取值范围为(-2,2).故选D.答案:D10.某班共50人,参加A 项比赛的共有28人,参加B 项比赛的共有33人,且A ,B 两项都不参加的人数比A ,B 都参加的人数的13多1人,则只参加A 项不参加B 项的有()人.A .7B .8C .10D .无法计算【答案】C解析:如图所示,设A ,B 两项都参加的有x 人,则仅参加A 项的共(28-x )人,仅参加B项的共(33-x )人,A ,B 两项都不参加的共⎝ ⎛⎭⎪⎫13x +1人,根据题意得x +(28-x )+(33-x )+⎝ ⎛⎭⎪⎫13x +1=50,解得x =18,所以只参加A 项不参加B 项共有28-18=10,故选C11.若函数234y x x =-+的定义域为[]0,m ,值域为7,44⎡⎤⎢⎥⎣⎦,则m 的取值范围是( )A .3,32⎡⎤⎢⎥⎣⎦B .3,42⎡⎤⎢⎥⎣⎦C .(]0,4D .3,2⎡⎫+∞⎪⎢⎣⎭【答案】A【解析】由题意得函数223734=()24y x x x =-+-+, 所以函数图象的对称轴3=2x ,在3,2⎛⎫-∞ ⎪⎝⎭单调递减,在3,+2⎛⎫∞ ⎪⎝⎭单调递增,所以最小值为74,[]0,x m ∈时值域为7,44⎡⎤⎢⎥⎣⎦,∴ 32x =必在定义域内,即32m ≥; 又有=0x 或=3x 时=4y ∴ 3m ≤,综上可得3,32m ⎡⎤⎢⎥⎣⎦的取值范围为.故选A . 12.设函数22,()6,x x x af x ax x a⎧--≥⎪=⎨-<⎪⎩是定义在R 上的增函数,则实数a 取值范围( )A .[)2,+∞B .[]0,3C .[]2,3D .[]2,4 【答案】D【解析】画出函数22y x x =--的图象如下图所示,结合图象可得,要使函数()22,,6,,x x x a x ax x a ⎧--≥⎪=⎨-<⎪⎩是R 上的增函数,需满足22226a a a a ≥⎧⎨--≥-⎩,解得24x ≤≤.所以实数a 取值范围是[]2,4.故选D . 二.填空题:本大题共4小题,每小题5分,共20分。
_____))9((,.0,2,0,)(.1321=⎪⎩⎪⎨⎧≤>-=f f x x x x f x 则已知函数【答案】8114.函数()21f x x =-在[]2,0-上的最大值与最小值的和为_______. 【答案】83-15.已知函数()1f x +的定义域为[]2,1-,则函数()()122g x f x x =+--的定义域为 ————————【答案】[)(]1,22,4【详解】()1f x +定义域为[]2,1- 112x ∴-≤+≤,即()f x 定义域为[]1,2-由题意得:20122x x -≠⎧⎨-≤-≤⎩,解得:12x ≤<或24x <≤()g x ∴定义域为:[)(]1,22,416.若一系列函数的解析式和值域相同,但定义域不同,则称这些函数为“同族函数”,例如函数2yx ,[]1,2x ∈与函数2y x ,[]2,1x ∈--就是“同族函数”.下列有四个函数:①2xy =;②12y x =;③2yxx ;④1y x =;可用来构造同族函数的有__________【答案】①③【解析】2x y =是偶函数,可构造“同族函数”,如函数2,[0,1]xy x =∈与函数2,[1,0]xy x =∈-是“同族函数”;12y x =在定义域[0,)+∞上单调递增,不可构造“同族函数”;2yx x 的对称轴是12x =,可构造“同族函数”,如函数21,[,1]2y x x x =-∈与函数21,[0,]2y x x x =-∈是“同族函数”;1y x=在(0,)+∞上递减且0y >,在(,0)-∞上也递减且0y <,不可构造“同族函数”;故答案为:①③.三.解答题(第17题10分,其余每题12分,共70分)215303125.03225064.01.17+-⎪⎭⎫⎝⎛-+-)计算:((2)已知13x x -+=,求44x x --的值. 【答案】4-; ()5212±. 【解析】45.0815.25.0214.0121253531-3-=+-+=+-+=⨯⨯⎪⎭⎫ ⎝⎛⨯)()原式((2)由13x x -+=,得227x x -+=∴4447x x -=+∴()22244245x x x x ---=-+=即2235x x --=±()()521442222±=-=-+∴---x x x x x x{}{}312|,2,1|.18+≤≤-=>-<=p x p x B x x x A 或已知集合();,211B A p 求若=()的取值范围。
求实数若p B B A ,2=【详解】(1)当时,B={x |0≤x ≤}, ∴A∩B={x |2<x ≤};(2)当A∩B=B 时,可得B ⊆A ;当时,令2p -1>p +3,解得p >4,满足题意;当时,应满足解得; 即综上,实数p 的取值范围.19.已知函数()bf x ax x=+的图象经过点A (1,1),21B -(,). (1)求函数()f x 的解析式;(2)判断函数()f x 在(0,+∞)上的单调性并用定义证明; 【答案】(1)()()20f x x x x=-+≠.(2)见解析. 【解析】(1)由 f(x)的图象过A 、B ,则,解得.∴()()20f x x x x=-+≠. (2)证明:设任意x 1,x 2∈0(,)+∞,且x 1<x 2.∴.由x 1,x 2∈0(,)+∞,得x 1x 2>0,x 1x 2+2>0. 由x 1<x 2,得.∴,即.∴函数()f x 在0(,)+∞上为减函数. .2)(0)(.202x x x f x R x f +-=>时,上的奇函数,当是定义在已知函数内的解析式;在)求函数(R x f )(1 []的取值范围。
上是单调函数,求实数,在区间)若函数(a a x f 11-)(2-【答案】解:错误!未找到引用源。
设错误!未找到引用源。
,则错误!未找到引用源。
,错误!未找到引用源。
又错误!未找到引用源。
为奇函数,所以错误!未找到引用源。
于是错误!未找到引用源。
时 又f(0)=0 所以 .⎪⎩⎪⎨⎧<+≥+-=)0(,2)0(,2)(22x x x x x x x f错误!未找到引用源。
由题意,错误!未找到引用源。
在[]11--a ,上单调递增, 则⎩⎨⎧≤-->-1111a a 所以 20≤<a 故实数a 的取值范围是(]2,0.).1(52)(.212>+-=a ax x x f 已知[]的值;求实数,的定义域和值域均为)若函数(a a x f ,1)(1 (][].,4|)()(|,1,12,)(221,2,1的取值范围求实数总有的上是减函数,且对任意在区间)若(a x f x f a x x x f ≤-+∈∞-[][](][][].32231,4)5(26,4)()(,4|)()(|,1,1,.5)()(,26)1()(,11,1,1.22,)()2(.2.152)(,521)1(11)(),0(5)()(132)2(;212min max 21212min max 222≤≤∴≥≤≤-≤---≤-∴≤-+∈-==-==∴-≤-++∈=≥∴∞-=⎩⎨⎧=+-==+-=∴∴>-+-=≤≤=a a a a a x f x f x f x f a x x a a f x f a f x f a a a a a x a x f a a a a f a a f a a x f a a a x x f a a ,又解得)即(总有对任意的)且(又上是减函数,在区间解得,,和值域均为上是减函数,又定义域,在)(解析:)答案:(22.已知定义域为()(),00,I =-∞+∞的函数()f x 满足对任意()()12,,00,x x ∈-∞+∞,都有()()()1212f x x f x f x =+. (1)求证:()f x 是偶函数; (2)设1x >时()0f x <,①求证:()f x 在()0,∞+上是减函数; ②求不等式()()12f x f x ->的解集. 【答案】(1)证明见解析(2)①证明见解析, ②1|1113x x x x ⎧⎫<-<<>⎨⎬⎩⎭或或 【解析】(1)取121x x ==得()()()1111f f f ⨯=+,即()10f =, 取121x x ==-得()()()1110f f f =-+-=,即()10f -=,取1x x =,21x =-得()()()()1f x f x f f x -=+-=,即()f x 是偶函数.(2)①设120x x >>,则121x x >, 由1x >时,()0f x <得120x f x ⎛⎫<⎪⎝⎭, 则()()()11122222x x f x f x f x f f x x x ⎛⎫⎛⎫=⋅=+< ⎪ ⎪⎝⎭⎝⎭, 即()f x 在()0,∞+上为减函数,②由()f x 是偶函数且在()0,∞+上是减函数, 则不等式()()12f x f x ->等价为()()12fx f x ->,即102012x x x x ⎧-≠⎪≠⎨⎪-<⎩得()()221012x x x x ⎧≠⎪⎪≠⎨⎪-<⎪⎩,得2013210x x x x ≠≠⎧⎨+->⎩且得01113x x x x ≠≠⎧⎪⎨><-⎪⎩且或, 即1x <-或113x <<或1x >,即不等式的解集为1|1113x x x x ⎧⎫<-<<>⎨⎬⎩⎭或或。
