大数的阶乘(求末尾有几个0)
阶乘的应用题

阶乘的应用题阶乘是数学中一个重要的概念,常常在组合数学和概率论中被广泛应用。
它不仅用于解决数学问题,还可以在实际生活和科学领域中发挥作用。
本文将介绍阶乘的概念及其在实际问题中的应用。
一、阶乘的概念阶乘通常用符号"!"表示,表示一个正整数乘以比它小的所有正整数的积。
例如,4的阶乘表示为4!,计算方法为4×3×2×1=24。
一般地,n 的阶乘可表示为n!,计算方法为n×(n-1)×(n-2)× (1)二、排列组合问题中的应用阶乘在组合数学中经常被用于解决排列组合问题。
当需要计算从n 个元素中选取r个元素进行排列时,可以使用排列公式nPr = n!/(n-r)!。
例如,从6个人中选取3个人进行排列的方式数为6P3 = 6!/(6-3)! =6×5×4 = 120。
排列问题的应用广泛,比如在考试中的座位安排、球队成员的选择等场景中都有其影子。
三、概率问题中的应用阶乘在概率论中也有重要的应用。
当计算从n个元素中选取r个元素的组合数时,可以使用组合公式nCr = n!/(r!(n-r)!)。
例如,从8个人中选取4个人的组合数为8C4 = 8!/(4!4!) = 70。
组合问题的应用包括抽奖、赌博、实验设计等方面,能够帮助我们计算事件发生的可能性。
四、计算问题中的应用阶乘在计算问题中也经常发挥重要作用。
当计算一个较大数的阶乘时,通常需要借助计算机或计算器进行计算。
而随着阶乘数增加,计算结果会变得非常庞大。
例如,20的阶乘为2,432,902,008,176,640,000。
这种计算问题常常涉及到计算器算法的优化和大数运算的技术。
五、实际生活中的应用除了上述数学问题中的应用,阶乘在实际生活中也有其应用价值。
例如,在排队问题中,当需要计算n个人的排列方式时,可以利用n的阶乘来求解。
此外,阶乘还可以用于计算一些复杂的组合方式,比如洗牌、安排座位等。
10000的阶乘的算法(大数的阶乘)

10000的阶乘的算法(⼤数的阶乘)很多天没有更新⾃⼰的Blog了,前⼏天拿到⼀个题⽬.就是写⼀段程序计算10000的阶乘.当时我还以为这题⽬⾮常简单,没想到还是需要动点⼤脑的.花了将近半个⼩时才搞定,拿出来分享⼀下.为什么不能⽤普通的⽅法来写呢,⽐如说递归?在我的教科书上可是⽤的是递归呀?不知道你注意没有,如果是100的阶乘的话,其结果肯定是⾮常⼤的,以我们现有语⾔的数据类型肯定是没法使⽤的,就拿C来说,long型能存的下100的阶乘吗?未必.所以我就使⽤数组来存储结果的每⼀位,然后输出每⼀位不就是结果吗.那么具体怎样去做?⾸先确定结果的位数?如何确定呢?请看下⾯.2!=1*2<=10*103!=1*2*3<=10*10*10.......所以我们可以得出⼀个结论n!<=10n所以n!的位数可以这样计算:两边取对数,即log10n!<=log1010n两边n>=Log101+Log102+Log10 3+....Log10 n这样n!的位数肯定等于⼩于Log101+Log102+Log10 3+....Log10 n.以上是错误的正确的推断如下:可以将n!表⽰成10的次幂,即n!=10^M(10的M次⽅)则不⼩于M的最⼩整数就是 n!的位数,对该式两边取对数,有 =log10^n!即:M = log10^1+log10^2+log10^3...+log10^n循环求和,就能算得M值,该M是n!的精确位数。
位数的确定解决之后,就看看如何计算了.看看如下代码:1int index=0;2long carrier=0;3double bitCount = 1;4int begin = 0;56for(index=2; index<=n; ++index)7 {8long multiValue = 0;9 bitCount += log10((long double)index);10if(arrValue[begin] == 0)11 begin++;1213for(int j=begin; j<int(bitCount); ++j)14 {15 multiValue += (index*arrValue[j]);16 arrValue[j] = char(multiValue % 10);17 multiValue /= 10;18 }19 }这⾥就是计算的关键了.注意⼀下进位问题即可.所有代码如下:12//////////////////////////////////////////////////////////////////////////3// Date created: 2005/07/124// Author: Confach Zhang5// Purpose: 计算n!的值6//////////////////////////////////////////////////////////////////////////789using namespace std;10#include "StdAfx.h"11#include <iostream.h>12#include <conio.h>13#include <stdlib.h>14#include <math.h>15#include <stdio.h>16#include <iomanip.h>1718int GetNumber(); //输⼊ n19int GetBitLength(int n); //求n!的位数20char* Initialize(int); //初始化存储结果的值21void PrintValue(char *a,int size); //打印值到屏幕22void PrintValue(char *a,int size,char* fileName); //打印值到⽂件 23char* GetValue(int val); //计算24char* SubGetValue(char* ,int);252627int main()28{29int value=GetNumber();30char fileName[16];31int size=GetBitLength(value);32char *pa = Initialize(size);3334//pa=GetValue();35 pa=GetValue(value);3637 PrintValue(pa,size);3839//sprintf(fileName,"%s","10000!.txt");40 sprintf(fileName,"%d!.txt",value);4142 PrintValue(pa,size,fileName);43 delete []pa; //note:44return 1;45}46//函数GetValue47// 求得计算结果48//返回结果49//History:50//1)char* GetValue()51//2)GetValue(int val)52// 参数:val 计算阶乘的值53char* GetValue(int val)54{55//定义⼀个数组存储阶乘的值56 //⾸先得到10000!阶乘的位数57int VALUE=val;58int length=GetBitLength(VALUE);59char *arrValue = new char[length];60if(!arrValue) {61 cout <<"申请内存失败!" << endl;62 exit(1);63 }64 arrValue[0] = 1;65for(int i=1; i<length; i++)66 arrValue[i] = 0;67 arrValue=SubGetValue(arrValue,VALUE);68return arrValue;69}7071char* SubGetValue(char* arrValue,int n)72{73int index=0;74long carrier=0;75double bitCount = 1;76int begin = 0;7778for(index=2; index<=n; ++index)79 {80long multiValue = 0;81 bitCount += log10((long double)index);82if(arrValue[begin] == 0)83 begin++;8485for(int j=begin; j<int(bitCount); ++j)86 {87 multiValue += (index*arrValue[j]);88 arrValue[j] = char(multiValue % 10);89 multiValue /= 10;90 }91 }92return arrValue;93}9495//得到计算阶乘的值,此函数为新增96int GetNumber()97{98int n;99 cout << "请输⼊要计算阶乘的n值: ";100 cin >> n;101while(n < 0) {102 cout << "输⼊错误,请重新输⼊: ";103 cin >> n;104 }105if(n == 0)106 exit(1);107return n;108}109110//函数GetBitLength111// 求得计算结果的位数,本函数为新增加112//参数113// n 需要计算的阶乘的数114//返回结果的位数115int GetBitLength(int n)116{117double sum = 1.0;118for(int i=1; i<=n; i++)119 sum += log10((long double)i);120return int(sum);121}122//-----------123//函数:Initialize124// 初始化存储结果的数组125//参数:126// size 数组的长度127//返回值128// 初始化后的数组129//-------------130char * Initialize(int size)131{132char *arrValue = new char[size];133if(!arrValue) {134 cout << size<<"太⼤,申请内存失败!" << endl; 135 exit(1);136 }137 arrValue[0] = 1;138for(int i=1; i<size; i++)139 arrValue[i] = 0;140return arrValue;141}142143//-----------144//函数:PrintValue145// 将结果输⼊到屏幕上146//参数:147// buff 存储结果的数组148// buffLen 数组的长度149// fileName ⽂件名150//-------------151void PrintValue(char *buff, int buffLen)152{153int bit = 0;154int nCol=0;155for(int i=buffLen-1; i>=0; i--) {156if(bit % 10 == 0)157 {158 cout << " " ;159 nCol++;160if(nCol==10)cout<<endl;161 }162 cout << int (buff[i]);163 bit++;164 }165 cout << endl;166167}168//-----------169//函数:PrintValue170// 将结果输⼊到⼀个⽂件中171//参数:172// buff 存储结果的数组173// buffLen 数组的长度174// fileName ⽂件名175//-------------176177void PrintValue(char *buff,int buffLen,char *fileName) 178{179int bit = 0;180int nCol=0;181182 FILE *fp=NULL;183//-----------------------------184185if (fileName==NULL) return ;186 fp=fopen(fileName,"wt");187if (fp==NULL)188 {189 printf("不能创建⽂件%s",fileName);190return ;191 }192193for(int i=buffLen-1; i>=0; i--)194 {195 fprintf(fp,"%d",int(buff[i]));196197if(bit % 9 == 0)198 {199 fprintf(fp,"%s"," ");200 nCol++;201if(nCol==8)202 {203 fprintf(fp,"%s","\n");204 nCol=0;205 }206 }207 bit++;208209 }210 fprintf(fp,"\n");211 fclose(fp);212}213好了,不说了.Last Updated: 2005年7⽉14⽇12:43:07 感谢的建议Last Updated: 2005年7⽉15⽇ 8:48:20 感谢的精彩建议posted on 2005-07-14 12:17 阅读(1260) 所属分类:re: 10000的阶乘 2005-07-14 12:34@Milestone能写多点⽂字吗?⽐如说说,⽤普通的递归会出现什么问题和不⾜你的这种新⽅法的原理是什么,关键的技术点⼜在哪?这样⼀堆代码,我真的看不懂,可能我技术太菜了;)*¥—#**re: 10000的阶乘 2005-07-14 12:36@kwklover谢谢你的提议,有空我写上.re: 10000的阶乘 2005-07-14 13:13普通的递归不⾏猜想原因是C的标准数据类型有可能不能保存结果那么⼤的数值。
1×2×3×4×.×40的末尾有几个零?奥数题目,求简算,急!悬赏20分

1×2×3×4×.×40的末尾有几个零?奥数题目,求简算,急!悬赏20分1×2×3×4×.×40的末尾有几个零?奥数题目,求简算,急!悬赏20分从1到10,连续10个整数相乘:1×2×3×4×5×6×7×8×9×10。
连乘积的末尾有几个0?答案是两个0。
其中,从因数10得到1个0,从因数2和5相乘又得到1个0,共计两个。
刚好两个0?会不会再多几个呢?如果不相信,可以把乘积计算出来,结果得到原式=3628800。
你看,乘积的末尾刚好两个0,想多1个也没有。
那么,如果扩大规模,拉长队伍呢?譬如说,从1乘到20:1×2×3×4×…×19×20。
这时乘积的末尾共有几个0呢?现在答案变成4个0。
其中,从因数10得到1个0,从20得到1个0,从5和2相乘得到1个0,从15和4相乘又得到1个0,共计4个0。
刚好4个0?会不会再多几个?请放心,多不了。
要想在乘积末尾得到一个0,就要有一个质因数5和一个质因数2配对相乘。
在乘积的质因数里,2多、5少。
有一个质因数5,乘积末尾才有一个0。
从1乘到20,只有5、10、15、20里面各有一个质因数5,乘积末尾只可能有4个0,再也多不出来了。
把规模再扩大一点,从1乘到30:1×2×3×4×…×29×30。
现在乘积的末尾共有几个0?很明显,至少有6个0。
你看,从1到30,这里面的5、10、15、20、25和30都是5的倍数。
从它们每个数可以得到1个0;它们共有6个数,可以得到6个0。
刚好6个0?会不会再多一些呢?能多不能多,全看质因数5的个数。
25是5的平方,含有两个质因数5,这里多出1个5来。
大数阶乘和大指数整数幂的计算

若 直接计 算 , 由于计算 组合 数 C( , ) n 忌 时可能会 出现 计算 溢 出 , 计算 P 或 ( 一 p r 1 ) 时可 能会 出现将 接 近 于零 的小数 视 为零 , 而得不 到 需要 的结果. 从 当然
可 以采用 大数 和小 数 相 乘 的策 略 , 一 定 程度 上 避 能
能 、 优 化 方 法研 究 . mal pu 2 0 @y h o cr.n 最 E i jn 03 a o .o c . l n
可 以通 过定 义高 有 效 位 数值 的类 , 定 义该 数 并 值 的乘 、 除运算 , 而定 义 阶乘 和整数 次幂 运算来 计 进 算上 面这 些 问题[ , 2 算法 通 用性好 , 实现 高精度 计 ] 可
Gn ag
Ab t a t I hi a r we gi e a x mpl o pr s n a i r l m o i t t r sr c : n t s p pe v n e a e t e e ta b sc p ob e f r fnie ne wo ks: wh t e t i s i e o tf r a i t t e h r i spo sbl r no o ny fniene wor fd v c s t ha k o e i e o c nge iss a u r t t t s fom he i iil t n ta s a u t l is de ie e ng i “co e s a e t h i a t t s wih a lis d v c s b i g i t t s wih a l t v c s b i n l s ” t t o t e fn l s a u t l t e ie e n n
免 上述 问题. 即使 相 乘 的 顺 序 用一 些 复 杂 的组 合 方 式 , 于充分 大 的 , 不 同的 k 仍 存在 溢 出或 得到 对 对 ,
阶乘函数 (2)

阶乘函数阶乘函数是数学中常见的函数之一,用于计算非负整数的阶乘。
在数学中,阶乘表示为n!,其中n是一个非负整数。
定义如下:n! = n * (n-1) * (n-2) * … * 3 * 2 * 1在本文档中,我们将讨论阶乘函数的计算方法、应用场景以及相关注意事项。
阶乘函数的计算方法阶乘函数可以通过多种方法进行计算。
以下是两种常见的计算方法:递归方法递归方法是一种将问题分解为较小子问题的解决方法。
通过不断地调用自身来实现计算阶乘函数。
以下是使用递归方法计算阶乘函数的示例代码:def factorial_recursive(n):if n ==0:return1else:return n * factorial_recursive(n-1)上述代码中,首先判断n是否为0,如果是,则返回1(0的阶乘为1)。
否则,计算n与n-1的阶乘的乘积,并返回。
使用递归方法计算阶乘函数时,需要注意避免堆栈溢出。
当计算的数值较大时,递归方法可能会导致堆栈溢出的问题。
迭代方法迭代方法是一种使用循环结构来计算阶乘函数的方法。
通过不断迭代更新一个变量的值来实现计算阶乘。
以下是使用迭代方法计算阶乘函数的示例代码:def factorial_iterative(n):result =1for i in range(1, n+1):result *= ireturn result上述代码中,使用一个变量result来保存计算结果,并通过循环结构不断更新result的值,最终得到阶乘函数的结果。
迭代方法相对于递归方法来说,不会存在堆栈溢出的问题,适用于计算较大数值的阶乘。
阶乘函数的应用场景阶乘函数在数学和计算机科学中有广泛的应用场景。
以下是一些常见的应用场景:排列组合在排列组合中,阶乘函数用于计算不同元素的排列或组合数量。
例如,计算从n个元素中取出k个元素进行排列的数量可以使用阶乘函数。
概率统计在概率统计中,阶乘函数用于计算事件的可能性。
0的阶乘等于什么

0的阶乘等于什么0的阶乘等于什么?很好理解,0的一个阶乘除等于1,另有一个除法:即0的阶乘等于0,也就是这个数是0阶,即乘以它自身的阶;这就是“零”了。
还有一个“不”之说呢?你看下面这张图:上面所写到的符号“?”其实我们已经把这部分内容删除了,所以后面不再展示。
那么问题来了,0和1相比有什么区别呢?其实只要对数概念了解一些,就可以知道了。
现在再讲这个内容,因为它比较抽象而且复杂。
所以我来给大家讲解一下它的原理。
下面我们再具体说一说。
1、数的单位化为什么把0分成阶乘呢?其实是为了方便对数字的书写,在我们平时理解的时候,0会变成0或者1的倍数,那么0就是它实际存在的数值:也就是说,它是有阶乘产生的:0阶乘以1。
这就是0的阶乘的含义。
比如我们常见的50,实际上是这样,它其实很小很容易被理解为50个大数、小数单位,所以50也被称为小数点后45位,所以从“小”到“大”会形成这一阶乘或除法,但它的“阶乘”没有定义。
因为在一般情况下要用其他符号表示才可以。
下面具体介绍:我们把“乘”定义为,当两个元素相乘时;当一个变量变成另一个变量时,另一个变量可以用这种方式表示。
例如0比1大……所以在这里要用到乘法;所以0阶又被称为“大数”,简称“零”。
还有我们熟悉的“1”,也都是单位化后出现“4”开头的数字;也就是现在我们使用的“1”和“4”;所以它的阶乘=1=(4-1)×2=4 (*2)。
所以0是一个常数。
所以就构成了1、2、3、4、5、7、8、9……等等。
如果上面4个都是一个“零”那么我们就知道他是0阶乘了。
接下来我们来看一下为什么0对“1”来说是没有阶乘呢?2、最小实数的不变性当我们要计算一个最小实数时,也是需要考虑它的不变性的。
不变性就是任何一个数只满足在0到无穷大、所以无穷多这个范围。
如果我们不需要计算无穷大,可以忽略任何单位,或者只是取最小值。
在自然数和实数集中往往有很多不同的例子。
比如说:我们想知道一组数集合里只有1和3这样简单的数时,如果把它们集合起来可以得到一个1/3或者2大小号和0都是一样的数字或者只是小数字,那这个数在集合里的意义就非常大了(有0).这就是我们常说的最小实数。
讲两道常考的阶乘算法题

讲两道常考的阶乘算法题读完本⽂,你可以去⼒扣拿下如下题⽬:-----------笔试题中经常看到阶乘相关的题⽬,今天说两个最常见的题⽬:1、输⼊⼀个⾮负整数n,请你计算阶乘n!的结果末尾有⼏个 0。
⽐如说输⼊n = 5,算法返回 1,因为5! = 120,末尾有⼀个 0。
函数签名如下:int trailingZeroes(int n);2、输⼊⼀个⾮负整数K,请你计算有多少个n,满⾜n!的结果末尾恰好有K个 0。
⽐如说输⼊K = 1,算法返回 5,因为5!,6!,7!,8!,9!这 5 个阶乘的结果最后只有⼀个 0,即有 5 个n满⾜条件。
函数签名如下:int preimageSizeFZF(int K);我把这两个题放在⼀起,肯定是因为它们有共性,下⾯我们来逐⼀分析。
题⽬⼀肯定不可能真去把n!的结果算出来,阶乘增长可是⽐指数增长都恐怖,趁早死了这条⼼吧。
那么,结果的末尾的 0 从哪⾥来的?我们有没有投机取巧的⽅法计算出来?⾸先,两个数相乘结果末尾有 0,⼀定是因为两个数中有因⼦ 2 和 5,因为 10 = 2 x 5。
也就是说,问题转化为:n!最多可以分解出多少个因⼦ 2 和 5?⽐如说n = 25,那么25!最多可以分解出⼏个 2 和 5 相乘?这个主要取决于能分解出⼏个因⼦ 5,因为每个偶数都能分解出因⼦ 2,因⼦ 2 肯定⽐因⼦ 5 多得多。
25!中 5 可以提供⼀个,10 可以提供⼀个,15 可以提供⼀个,20 可以提供⼀个,25 可以提供两个,总共有 6 个因⼦ 5,所以25!的结果末尾就有 6 个 0。
PS:我认真写了 100 多篇原创,⼿把⼿刷 200 道⼒扣题⽬,全部发布在,持续更新。
建议收藏,按照我的⽂章顺序刷题,掌握各种算法套路后投再⼊题海就如鱼得⽔了。
现在,问题转化为:n!最多可以分解出多少个因⼦ 5?难点在于像 25,50,125 这样的数,可以提供不⽌⼀个因⼦ 5,怎么才能不漏掉呢?这样,我们假设n = 125,来算⼀算125!的结果末尾有⼏个 0:⾸先,125 / 5 = 25,这⼀步就是计算有多少个像 5,15,20,25 这些 5 的倍数,它们⼀定可以提供⼀个因⼦ 5。
大数的认识奥数题

大数的认识奥数题导语在奥数竞赛中,大数问题常常是让学生们感到头疼的一类题目。
这些问题涉及到了对大数的认识和运算技巧。
本文将解析几个经典的大数题目,帮助读者更好地理解和应对这类题目。
一、问题一:最大的n位数问题描述:给定一个正整数n,要求输出由n个9组成的最大的整数。
解析:这道题目很简单,只需要将n个9连接起来即可得到最大的n位数。
解答:假设n=3,最大的3位数就是999;假设n=5,最大的5位数就是99999。
可以用一个循环来实现这个问题。
二、问题二:大整数相加问题描述:给定两个正整数a和b,要求计算它们的和。
解析:这道题目考察了大整数的相加运算,需要注意的是两个整数的位数可能不相等。
解答:可以使用数组来存储大整数,并且从末位开始逐位相加,将结果保存在另一个数组中。
需要注意的是,如果相加的结果超过了9,就需要进位。
具体步骤如下:1. 将两个大整数拆分成数组,并对齐使其位数相等,不足位的用0填充。
2. 从最后一位开始相加,将结果保存在结果数组中,并判断是否需要进位。
3. 将结果数组转化为字符串即为最终答案。
三、问题三:大整数相乘问题描述:给定两个非负整数a和b,求其乘积。
解析:这道题目是大数运算中比较经典的问题,需要注意的是乘法的进位问题。
解答:同样可以使用数组来存储大整数,在计算过程中进行逐位相乘,并将结果保存在结果数组中。
需要注意的是,乘法的进位规律。
具体步骤如下:1. 将两个大整数分解成数组,并定义一个结果数组,数组长度为a的位数+b的位数。
2. 从后向前遍历乘法计算,每次计算两个位上的乘积,并将结果保存在对应的位置上。
3. 遍历结果数组,将每个位置上的数字都进行进位处理。
4. 将结果数组转化为字符串即为最终答案。
四、问题四:大数的阶乘问题描述:给定一个正整数n,求n的阶乘。
解析:阶乘的计算涉及到大数的乘法运算,需要考虑进位问题。
解答:可以通过逐位乘法来计算阶乘。
将每个乘积的结果保存在数组中,并在遍历过程中将进位处理。
10000的阶乘是几位数?附C语言程序计算程序,计算结果

10000的阶乘是⼏位数?附C语⾔程序计算程序,计算结果10000的阶乘是⼏位数?我们知道,阶乘的结果随着N的增长速度⾮常快,在C语⾔中,由于数值范围原因,普通乘法运算⽆法计算⼤数字的阶乘,那么如果想要计算100,1000,10000或更⼤的数的阶乘,C语⾔能处理吗?答案⾃然是没问题。
下⾯给出C语⾔实现⼤数的阶乘算法程序:void factorial(short n){int i, j, m;int top = 0;short f[10000];if (n > 10000){printf("少来,1万还不够!⾃⼰写\n");return;}memset(f, 0, sizeof(f));// 循环计算阶乘for (i=1; i<=n; i++){short carry = 0; // 进位数值for (j=0; j<top; j++){m = f[j]*i + carry;f[j] = m%10000;carry = m/10000;}// 进位if (carry > 0){f[j] = carry;top++;}// 初始化if (top == 0){f[0] = 1;top = 1;}}// 输出结果printf("Result of (%d)! is:\n", n);FILE *fp = fopen("result.txt", "wb");fprintf(fp, "top: (%d)\n", top);fprintf(fp, "Result of (%d)! is:\n", n);for (i=top-1; i>=0; i--){printf("%04d, ", f[i]);fprintf(fp, "%04d, ", f[i]);}fclose(fp);}10000的阶乘是⼏位数?答案是35660位。
阶乘数最右边一个非零数字如何求?

求阶乘数最右边一个非零数字的通用解法在数竞书上碰到了这样一个问题:求98!(十进制数)的最右边一个非零数字。
更一般地,把98换为任意正整数n,如何解决此问题?解决这个问题之前,先看一个很多人都知道的东西:求n!的末尾有多少个连续的零,n为正整数。
换句话说,找一个10的整数幂,使其为n!的约数,问这个指数最大是多少?这个问题的经典解法是看n!的质因数分解中2和5的次幂(因为2×5=10),然后2和5配对,能配成多少对就有多少个末尾0。
也就是说,要在两者中取较小值。
2和5的次幂数是如何算的?先对2进行分析:前n个正整数中有多少个2的倍数?显然有[n/2]个(这里[ ]为高斯函数,表示不超过给定实数的最大整数)。
如果把2换为4,8,16,...对于2k,则有[n/2k]个被2k整除的数。
接下来,把这些整数加起来,就是我们要的n!中2的次幂数。
容易看出,这个总和中2的倍数算了1次,4的倍数算了2次([n/2]和[n/4]中都有),8的倍数算了3次,等等。
恰好就是最后的结果。
对5进行同样分析,写出下面两个公式:注意到,我们可以把这两个和写成无穷项相加的形式,但是总是从某一项开始,所有项全部为0,因此也可以看做有限项相加。
对T2和T5进行比较,就可以得到较小值。
直觉上肯定是T5较小,事实上很容易证明T2>=T5:依次查看两数列对应的每两项,如果把中括号去掉,肯定是上边大于下边;加上中括号之后,下边也不会超过上边项(这个很容易说明,较小数向下取整后得到的整数肯定小于较大数)。
于是就有上边的和大于等于下边的和。
这样所求的较小值就是T5了。
于是计算T5的公式就可以作为计算末尾连续零个数的公式。
还有一点值得注意:对于n>1,总有T2>T5。
事实上这也是很容易证的:当n>1时,第一项相比,一定有[n/2]严格大于[n/5]。
(n=2,3 时,这个结论成立;n>=4时,n/2-n/5>1,这样n/2和n/5中间至少夹着一个整数,显然取整后就大于了)。
阶乘公式 (3)

阶乘公式什么是阶乘?在数学中,阶乘是一个非常常见的运算,用于计算正整数的乘积。
阶乘由一个正整数 n 表示,记作 n!,其定义如下:n! = n × (n-1) × (n-2) × … × 3 × 2 × 1例如,5! = 5 × 4 × 3 × 2 × 1 = 120。
阶乘的计算方法阶乘的计算可以使用循环或递归两种方法。
下面分别介绍这两种方法。
使用循环计算阶乘使用循环计算阶乘的方法很简单,只需要从 1 开始不断乘以后续的数字,直到乘到 n 为止。
下面是一个使用循环计算阶乘的示例代码:def factorial(n):result =1for i in range(1, n +1):result *= ireturn result以上代码首先初始化result为 1,然后使用for循环从 1 到 n,不断将result与循环变量 i 相乘,并将结果重新赋值给result。
最后返回result即为 n 的阶乘。
使用递归计算阶乘使用递归计算阶乘的方法稍微复杂一些。
递归是一种自己调用自己的方法。
计算阶乘时,可以将问题划分为两部分,即当前数和其余数字的阶乘之积。
下面是一个使用递归计算阶乘的示例代码:def factorial(n):if n ==0:return1else:return n * factorial(n-1)以上代码首先判断 n 是否等于 0,若是,则直接返回 1,表示 0 的阶乘为 1。
否则,计算 n 与factorial(n-1)相乘的结果,并将其作为函数的返回值。
使用递归计算阶乘的方法更加简洁,但在计算大数的阶乘时可能会导致栈溢出的问题。
因此,在实际应用中需要根据具体需求选择合适的计算方法。
阶乘的性质阶乘具有以下几个重要的性质:1.0 的阶乘为 1,即 0! = 1。
2. 1 的阶乘也为 1,即 1! = 1。
积末尾零的个数的判断方法_概述及解释说明

积末尾零的个数的判断方法概述及解释说明1. 引言1.1 概述在数学和计算机科学中,我们经常需要判断一个数字的末尾零的个数。
尾部零的个数对于一些问题解决方法的选择以及算法效率的估算非常重要。
因此,本文将探讨三种判断方法来确定一个数字末尾零的个数。
1.2 文章结构本文以引言为开端,接下来将介绍每种判断方法,并提供相应示例和算法分析。
最后,我们将进行结果比较与讨论,并展望这些判断方法在不同应用场景中的潜在价值。
1.3 目的本文旨在深入探究积末尾零个数判断方法,并就其算法复杂度、准确性和使用场景等方面进行评估和讨论。
通过对这些方法的研究,旨在提供给读者们选择适合自己问题的最佳解决方案时有所帮助。
同时,本文也希望能够促进更多关于数字处理领域的技术交流和思考。
以上是“1. 引言”部分内容,请注意使用普通文本格式回答,不包含网址信息。
2. 判断方法一2.1 方法介绍判断一个数的末尾有几个零是通过计算这个数可以被多少个10整除来实现的。
我们知道,一个数被10整除就意味着它的末尾有一个零,被100整除意味着末尾有两个零,以此类推。
因此,判断一个数末尾有几个零的方法一是通过计算这个数能够被多少个10整除。
2.2 示例说明以数字120为例来说明方法一的使用。
我们需要判断数字120的末尾有几个零。
首先,我们可以观察到数字120可以被10整除两次(即120 / 10 = 12),因此它的末尾有两个零。
2.3 算法分析基于上面的示例说明,我们可以总结出判断方法一的具体步骤:步骤1:找出待判断数可以被多少个10整除;步骤2:将得到的结果作为末尾零的数量。
这种方法较为简单直接,但是需要注意对0进行特殊处理。
当待判断数为0时,无法执行步骤1中的操作。
因此,在实际应用中要注意处理这种情况。
通过以上分析和示例,我们已经详细介绍了判断方法一的内容,接下来将会继续探讨判断方法二。
3. 判断方法二3.1 方法介绍判断方法二是一种基于数学原理的方法,用于确定一个数字中末尾零的个数。
自然数阶乘 非零尾数

自然数阶乘非零尾数
自然数的阶乘指的是从1乘到这个自然数本身的连乘积。
简单来说,就是一个自然数与小于它的所有自然数相乘的结果。
当计算自然数的阶乘时,我们可以观察到一个有趣的现象,即阶乘的结果的末尾通常会有很多零。
但是,有一些特殊的自然数的阶乘结果却没有零,我们把这样的阶乘结果称为非零尾数。
非零尾数的阶乘在数学上是非常重要的,它们具有一些特殊的性质和应用。
例如,在组合数学中,非零尾数的阶乘可以用来计算排列和组合的数量。
此外,在概率论和统计学中,非零尾数的阶乘也被广泛应用于计算可能性和概率。
要计算一个自然数的阶乘,可以使用循环或递归的方法。
无论使用哪种方法,都需要注意处理大数运算和溢出的问题。
有时候,我们可以利用数学性质来简化计算,例如,计算阶乘时可以先判断这个数是否为偶数,从而减少乘法的次数。
总之,非零尾数的阶乘是自然数阶乘中的一类特殊结果,具有重要的数学应用。
计算阶乘时需要注意运算溢出和大数运算的问题,并可以利用数学性质来简化计算过程。
大数阶乘算法

*************************************(1)************************************ ****************假如需要计算n+16的阶乘,n+16接近10000,已经求得n!(共有m个单元),(每个单元用一个long数表示,表示1-100000000)第一种算法(传统算法)计算(n+1)! 需要m次乘法,m次加法(加法速度较快,可以不予考虑,下同),m次求余(求本位),m次除法(求进位),结果为m+1的单元计算(n+2)! 需要m+1次乘法,m+1次求余,m+1次除法, 结果为m+1个单元计算(n+3)! 需要m+1次乘法,m+1次求余,m+1次除法,结果为m+2个单元计算(n+4)! 需要m+2次乘法,m+2次求余,m+2次除法,结果为m+2个单元计算(n+5)! 需要m+2次乘法,m+2次求余,m+2次除法,结果为m+3个单元计算(n+6)! ...计算(n+7)! ...计算(n+8)! ...计算(n+9)! ...计算(n+10)! ...计算(n+11)! ...计算(n+12)! ...计算(n+13)! ...计算(n+14)! 需要m+7次乘法,m+7次求余,m+7次除法,结果为m+7个单元计算(n+15)! 需要m+7次乘法,m+7次求余,m+7次除法,结果为m+8个单元计算(n+16)! 需要m+8次乘法,m+8次求余,m+8次除法,结果为m+8个单元该算法的复杂度:共需:m+(m+8)+(m+1+m+7)*7=16m+64次乘法,16m+64次求余,16m+64次除法第二种算法:1.将n+1 与n+2 相乘,将n+3 与n+4 相乘,将n+5 与n+6...n+15与n+16,得到8个数,仍然叫做n1,n2,n3,n4,n5,n6,n7,n82. n1 与n2相乘,结果叫做p2,结果为2个单元,需要1次乘法。
c语言大数加法、阶乘和乘法

c语⾔⼤数加法、阶乘和乘法⼀.⼤数加法定义两个⾜够⼤的数字,其数值远超过long的取值范围,设该⼤数的位数有两百位,求其相加所得⼤数加法的核⼼思想详见此链接,内有详细的动画演⽰,这⾥不再赘述直接上代码:#include<string.h>#include<stdio.h>#define N 10//定义当前⼀个⾜够⼤的数字为10位,可任意更改void print_num(int a[],int n){int i=n-1;//从逆序数组的最后⼀项开始查找,进⾏反逆序while(a[i]==0)//由于规定的数组⽐真实计算的数字⼤,所以数组最后⼏位必定存在0的情况--i;//这种情况下⼀定要将0舍去,否则会抬⾼数组的位数for(;i>=0;i--)//找到⾮零的数组,进⾏反逆序输出printf("%d",a[i]);}void plus(int num1[],int num2[],int n){//尤其注意!由于数组是逆序的,所以num[0]是个位,num[1]是⼗位,num[2]是百位for(int i=0,up=0;i<n;i++)//算法参考⼩学加法,这⾥定义⼀个up进位标记{int temp=num1[i]+num2[i]+up;//up最开始设为0,因为在个位⽆法获取进位num1[i]=temp%10;//若产⽣进位⾏为,则选取个位部分赋给num1up=temp/10;//在个位上,若个位相加产⽣进位,则⽤temp/10取整加到下⼀次的⼗位上}print_num(num1, n);}int main(){char buffer1[]="123456";//缓冲数组,将当前数组倒序写⼊num1中char buffer2[]="78951234";//同上,写⼊num2中int num1[N]={0};//将num1,2全部置为0,⽤来将缓冲数组写⼊到num数组当中int num2[N]={0};int n=N;//定义上述两个数组的长度为10for(int i=0,temp=(int)strlen(buffer1)-1;temp>=0;temp--)num1[i++]=buffer1[temp]-'0';//⽤倒序的⽅式将缓冲数组写⼊num中,意味着num的第⼀位是个位,第⼆位是⼗位,三是百位...for(int i=0,temp=(int)strlen(buffer2)-1;temp>=0;temp--)num2[i++]=buffer2[temp]-'0';plus(num1, num2, n);//将两数字相加printf("\n");}⼆.⼤数阶乘⼤数阶乘的中⼼思想参考上述视频和⼀篇博客,博客详情:但是,这⾥需要说明⼀个点:1*2=2,将2存到a[0]中,接下来是⽤a[0]*3;2*3=6,将6储存在a[0]中,接下来是⽤a[0]*4;6*4=24,是两位数,那么24%10==4存到a[0]中,24/10==2存到a[1]中,接下来是⽤a[0]*5;a[1]*5+num(如果前⼀位相乘结果位数是两位数,那么num就等于⼗位上的那个数字;如果是⼀位数,num==0)24*5=120,是三位数,那么120%10==0存到a[0]中,120/10%10==2存到a[1]中,120/100==1存到a[2]中由于上述博客存在某些地⽅没有说清楚的情况,这⾥解释⼀下关于上述博客的Q&A:1.这⾥的num指的是什么?答:这⾥的num指的是前⾯两数值相乘后进位数位多少:例如6*4得24,这⾥的num值的是24/10=2,进位数为2,num=22.下⾯代码为什么要充i=2开始?答:如果这⾥看懂了代码其实理解2不是很难,但是没有看懂是真的难懂:⾸先明确⼀点:5的阶乘是1*2*3*4*5,我定义的value数组的第⼀位为1,⽽我的i是从2起的,这样以来不就直接凑出了1*2了吗?当我的i⾃增到3,我直接在value数组中找出1*2的值,拿他们去和3相乘,也就凑成了1*2*3了3.如何在代码当中表现出进位的思想?答:我们以5!为例,当计算到1*2*3*4的时候,value当中的表现形式是42000000,从左到右依次是个位,⼗位,百位,千位...etc(value表⽰的是24这个数字)我们在关于j的循环当中拿i=5去和value数组求乘积:5先和位于个位的4求积得20:20%10得0,0放⼊个位中;20/10得2,进位为2,up=2。
0的阶乘等于多少计算方法是什么

0的阶乘等于多少计算方法是什么
阶乘是指一个数连乘它自身和比它小的所有正整数的乘积,并且通常被表示为n。
形式上来讲,阶乘的定义是这样的:
n!=n*(n-1)*(n-2)*…*2*1
当n=0时,0的阶乘定义为1,即n!=1、这是一个比较特殊的定义,因为当n等于任何正整数时,n!的定义都是有意义的,而n=0时,只有将0的阶乘定义为1,才使得n!在n=0时同样有意义。
阶乘算法是用来计算阶乘的算法,即在计算机语言中,用其中一种语句结构实现的阶乘计算函数。
阶乘算法可以有多种实现方式,这里介绍一种递归法:
递归法:
输入:一个正整数n
输出:n!
算法步骤如下:
Step 1:如果 n = 0 ,那么 n! = 1
Step 2:否则,n! = n * (n-1)!
Step 3:递归调用, n-1! 的值将由递归调用的过程给出,直到
n=0为止
根据上述算法,当n=0时,由Step 1得到n!=1,因此0的阶乘等于1。
100阶乘末尾有多少个0

100阶乘末尾有多少个01×2×3.。
×1001 每隔5个,会产生一个0,比如 5, 10 ,15,20.。
2 每隔 5×5 个会多产生出一个0,比如 25,50,75,1003 每隔 5×5×5 会多出一个0,比如125.。
所以 100的末尾0的个数为100/5 + 100/25 = 20+4 = 24个对于其它的数字,同样可以这样计算。
1024! 末尾有多少个0?Posted on October 9th, 2011 by gemini1024的阶乘末尾有多少个0,这个问题只要理清思想就很好解了。
有多少个0取决于有多少个10相乘,即1024拆成小单元后有多少个10。
由于10不是素数,所以直接用10进行计算的话会有很多问题,于是将10分解。
10可以分解成2*5,2和5都是素数,由于每2个相邻的数中一定包含2,所以只要计算出有多少个5就可以了(2会在5之后及时出现)。
于是解法如下:是5的倍数的数有: 1024 / 5 = 204个是25的倍数的数有:1024 / 25 = 40个是125的倍数的数有:1024 / 125 = 8个是625的倍数的数有:1024 / 625 = 1个所以1024! 中总共有204+40+8+1=253个因子5。
即1024!后有253个0算题思想:(1)先找出有1个5的数(2)然后找出有两个5的,2个5的数虽然在第一步算过了,但是两个中剩下的那个5还可以形成0(3)之后就是找出有3个5的,4个5的,直到n个5(5的n次方小于阶乘的数)求N! 末尾有多少个0求N的阶乘的末尾有多少个0.因为任何数都可以表示为所有素数n 次幂的乘积, 所以N! = 2^x * 3^y * 5^z * 7^m + …所以求N! 末尾有多少个0也就是求min{x, z}.另外, Z 是一定大于x 的, 这是因为N! = 1 * 2 * 3 * 4 *5 * 6 *…也就是说在每个 5 的倍数之前至少有 2 个数是 2 的倍数, 碰到整十整百的时候, 2 和 5 的倍数又同时增加. 所以说, Z 是一定大于x 的.所以, 求N! 末尾有多少个0 的问题也就转换为求z 的值了, 也就是求1~N 之间有多少个数字是 5 的倍数.如计算2009! 的末尾有多少个0:2009/5 = 401 1~2009之间有401 个数是5 的倍数(余数省略).401/5 = 80 1~2009 之间有80 个数是25 的倍数.80/5 = 16 1~2009 之间有16 个数是125 的倍数.16/5 = 3 1~2009 之间有3个数是625 的倍数.3/5 = 0 1~2009 之间有0 个数是3125 的倍数.所以, 2009! 的末尾有401 + 80 + 16 + 3 = 500 个0.。
100的阶乘[最新]
![100的阶乘[最新]](https://img.taocdn.com/s3/m/f96bef3e905f804d2b160b4e767f5acfa1c78391.png)
其实从数学的角度来看,这个算法是完全正确的,但是现实世界比数学世界要复杂的多。
这样的算法无疑会导致数据溢出。
(说到底“溢出”是“黑客”们吃饭的本钱,关于溢出的话题这里不做过多讨论,不懂得可以自己去google,简单说就是100的阶乘这个结果太大了,以至于C语言内置的任何一中变量都盛不下)根据我一个印度朋友的实验,用MatLab可以不考虑溢出而顺利的得出结果。
C 语言是以简洁著称的,标准库里没有提供处理大数的方案。
不过这也不是什么缺点,刚好给了我们一个自己动手来探索在其他语言内部大数乘法实现方法的机会。
废话说道这里。
问题的核心在于,C并没还有给我们提供一个储存大数的方法,更毋提数学运算了。
所以首先我们需要一个储存大数的方法。
这里采用一个最简单的解决方案:数组。
我们用一个整数数组来代表一个大数,数组中的每一个元素储存大数中的一位数。
数组下标从小到大分别表示大数的低位到高位。
举个例子:个位数由下标为0的元素来表示。
有了储存的方法,下面我们考虑一下怎样来让两个储存在数组里的大数相乘。
其实现在我们更接近原始的数学运算。
由于数组的运用,我们重新“获得”了数位的概念。
拿出纸和笔,回想一下用竖式演算的过程。
这里以456*123为例:4 5 6X 1 2 3-----------1 3 6 89 1 24 5 6-----------5 6 0 8 8呵呵,没算错吧?不难看出,这个笔算的过程可以总结成这样:用第二个大数的每一位和第一个大数的每一位相乘,把每一次乘完得到的结果按照相应位数累加起来,就得到了结果。
这里有几个关键的细节,我们不妨给每一个数位都标上对应的数组下标:4 5 6X 1 2 3-----------1 3 6 89 1 24 5 6-----------5 6 0 8 84 3 2 1 0 <===数组下标经过观察,可以发现,当第一个大数下标为x的数字和第二个大数下标为y的数字相乘的时候,所得结果的最低位的下标是x+y。
求大数阶乘(10000以内)
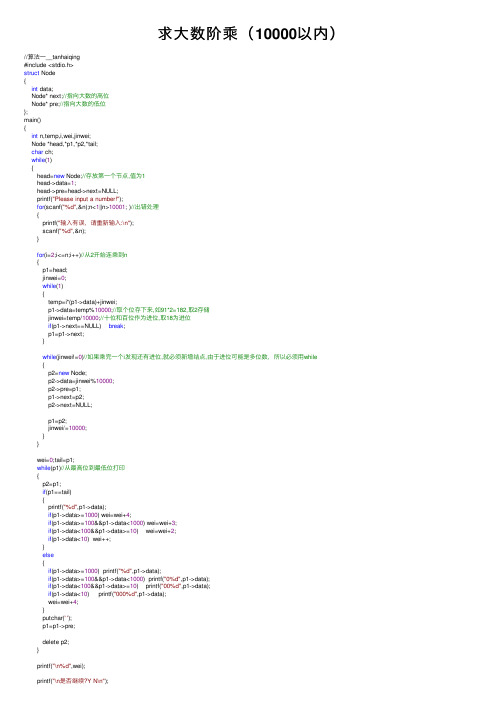
求⼤数阶乘(10000以内)//算法⼀__tanhaiqing#include <stdio.h>struct Node{int data;Node* next;//指向⼤数的⾼位Node* pre;//指向⼤数的低位};main(){int n,temp,i,wei,jinwei;Node *head,*p1,*p2,*tail;char ch;while(1){head=new Node;//存放第⼀个节点,值为1head->data=1;head->pre=head->next=NULL;printf("Please input a number!");for(scanf("%d",&n);n<1||n>10001; )//出错处理{printf("输⼊有误,请重新输⼊:\n");scanf("%d",&n);}for(i=2;i<=n;i++)//从2开始连乘到n{p1=head;jinwei=0;while(1){temp=i*(p1->data)+jinwei;p1->data=temp%10000;//取个位存下来,如91*2=182,取2存储jinwei=temp/10000;//⼗位和百位作为进位,取18为进位if(p1->next==NULL) break;p1=p1->next;}while(jinwei!=0)//如果乘完⼀个i发现还有进位,就必须新增结点,由于进位可能是多位数,所以必须⽤while{p2=new Node;p2->data=jinwei%10000;p2->pre=p1;p1->next=p2;p2->next=NULL;p1=p2;jinwei/=10000;}}wei=0;tail=p1;while(p1)//从最⾼位到最低位打印{p2=p1;if(p1==tail){printf("%d",p1->data);if(p1->data>=1000) wei=wei+4;if(p1->data>=100&&p1->data<1000) wei=wei+3;if(p1->data<100&&p1->data>=10) wei=wei+2;if(p1->data<10) wei++;}else{if(p1->data>=1000) printf("%d",p1->data);if(p1->data>=100&&p1->data<1000) printf("0%d",p1->data);if(p1->data<100&&p1->data>=10) printf("00%d",p1->data);if(p1->data<10) printf("000%d",p1->data);wei=wei+4;}putchar('');p1=p1->pre;delete p2;}printf("\n%d",wei);printf("\n是否继续?Y N\n");getchar();ch=getchar();if(ch!='Y'&&ch!='y') break;};return0;}//算法⼆__⾬中飞燕#include<stdio.h>#define N 1000 //要计算的Nlong s[N]={1,1},n=N,t=2,a=1,b=0;int main(){for(; a<=*s||(++t<=n?(b=0,a=1):0); (*s==a++&&b)?(*s)++:0)s[a]=(b+=s[a]*t)%10000,b/=10000;for(printf("%d",s[*s]); --*s>0; )printf(" %04d",s[*s]);return0;}或#include<stdio.h>#define N 1000 //要计算的Nlong s[N]={1},n=10000,t=2,a,b,m;main(){for( ;a<=m||++t<=N&&(a=b=0,1); m==a++&&b&&m++)s[a]=(b+=s[a]*t)%n,b/=n;for(printf("%d",s[m]);m--;)printf(" %04d",s[m]);}运算结果实例:Please input a number!10004023 8726 0077 0937 7354 3702 4339 2300 3985 7193 7486 4210 7146 3254 3799 9104 2993 8512 3986 2902 0592 0442 0848 6969 4048 0047 9988 6101 9719 6058 6316 6687 2994 8085 5890 1323 8296 6994 4590 9974 2450 4087 0737 5991 8823 6277 2718 8732 5197 7950 5950 9952 7612 0874 9754 6249 7043 6014 1827 8094 6464 9629 1056 3938 8743 7886 4873 3711 9181 0458 2578 3647 8499 7701 2476 6328 8983 5955 7354 3251 3185 3239 5846 3075 5574 0911 4262 4174 7434 9347 5534 2864 6576 6116 6779 7396 6688 2029 1207 3791 4385 3719 5882 4980 8126 8678 3837 4559 7317 4613 6085 3795 3452 4221 5865 9320 1928 0908 7829 7308 4313 9284 4403 2812 3155 8611 0369 7680 1357 3042 1616 8747 6096 7587 1348 3120 2547 8589 3207 6716 9132 4484 2623 6131 4125 0878 0208 0002 6168 3151 0273 4182 7977 7047 8463 5868 1701 6436 5024 1536 9139 8281 2648 1021 3092 7612 4489 6359 9287 0511 4964 9754 1990 9342 2215 6683 2572 0808 2133 3186 1168 1155 3615 8365 4698 4046 7089 7560 2900 9505 3761 6475 8477 2842 1889 6796 4624 4945 1607 6535 3408 1989 0138 5442 4879 8495 9953 3191 0172 3355 5566 0213 9450 3997 3628 0750 1378 3761 5307 1277 6192 6849 0343 5262 5200 0158 8853 5147 3316 1170 2103 9681 7592 1510 9077 8801 9393 1781 1419 4545 2572 2386 5541 4610 6289 2187 9602 2383 8971 4760 8850 6276 8629 6714 6674 6975 6291 1234 0824 3920 8160 1537 8088 9893 9645 1826 3243 6716 1676 2179 1689 0977 9911 9037 5403 1274 6222 8998 8005 1954 4441 4282 0121 8736 1745 9926 4295 6581 7466 2830 2955 5702 9902 4324 1531 8161 7210 4658 3203 6786 9061 1726 0158 7835 2075 1516 2842 2554 0265 1704 8330 4226 1439 7428 6933 0616 9089 7968 4825 9012 5458 3271 6822 6458 0665 2676 9958 6526 8227 2807 0757 8139 1858 1788 8965 2208 1643 4834 4825 9932 6604 3367 6601 7699 9612 8318 6078 8386 1502 7946 5955 1311 5655 2036 0939 8818 0612 1385 5860 0301 4356 9452 7224 2063 4463 1797 4605 9468 2573 1037 9008 4024 4324 3846 5657 2450 1440 2821 8852 5247 0935 1906 2092 9023 1364 9327 3497 5655 1395 8720 5596 5422 8749 7740 1141 3346 9627 1542 2845 8623 7738 7538 2304 8386 5688 9764 6192 7383 8149 0014 0767 3104 4664 0259 8994 9022 2221 7659 0433 9901 8860 1856 6526 4850 6179 9702 3561 9389 7017 8600 4081 1889 7299 1831 1021 1712 2984 5901 6419 2106 8884 3871 2185 5646 1249 6079 8722 9085 1929 6819 3723 8864 2614 8396 5738 2291 1231 2502 4186 6493 5314 3970 1374 2853 1926 6498 7533 7218 9406 9428 1434 1185 2015 8014 1233 4482 8015 0513 9969 4290 1534 8307 7644 5690 9907 3152 4332 7828 8269 8646 0278 9864 3211 3908 3506 2170 9500 2597 3898 6355 4277 1967 4282 2248 7575 8676 5752 3442 2020 7573 6305 6949 8825 0879 6892 8162 7538 4886 3396 9099 5982 6280 9561 2145 0994 8717 0124 4516 4612 6037 9029 3091 2088 9086 9420 2851 0640 1821 5439 9457 1568 0594 1872 7489 9809 4254 7421 7358 2401 0636 7740 4595 7417 8516 0829 2301 3535 8081 8400 96996372 5242 3056 0855 9037 0062 4271 2434 1690 9004 1536 9010 5933 9838 3577 7939 4109 7002 7753 4720 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 00002568是否继续?Y N。
阶乘学习计算阶乘的方法

阶乘学习计算阶乘的方法阶乘是数学中一个重要的概念,用于表示一个正整数与小于它的所有正整数的乘积。
在数学和计算机科学中,阶乘经常被用于统计和排列组合等问题。
本文将介绍不同的方法来计算阶乘。
一、迭代法迭代法是计算阶乘的一种基本方法。
它通过不断相乘来计算阶乘的结果。
具体步骤如下:1.设定一个初始值,通常将阶乘的结果设置为1。
2.设置一个循环,从1开始,一直迭代到需求的阶乘数。
3.在每次迭代中,将当前的数与阶乘的结果相乘,并将结果存储。
4.当循环结束时,所得到的结果就是所求的阶乘。
下面是一个示例代码展示了如何使用迭代法计算阶乘:```pythondef factorial_iterative(n):result = 1for i in range(1, n+1):result *= ireturn resultnum = 5print("5的阶乘是:", factorial_iterative(num))```二、递归法递归法是另一种计算阶乘的常用方法。
它通过将问题不断分解为更小的子问题,并通过递归的方式计算子问题来得到最终结果。
具体步骤如下:1.判断所需求的阶乘数是否为1,若为1,则直接返回1。
2.若不为1,则将问题分解为计算n-1的阶乘,并乘以n。
下面是一个示例代码展示了如何使用递归法计算阶乘:```pythondef factorial_recursive(n):if n == 1:return 1else:return n * factorial_recursive(n-1)num = 5print("5的阶乘是:", factorial_recursive(num))```三、数学方法除了迭代法和递归法外,还有一些数学方法可以用来计算阶乘。
1. 斯特林公式:斯特林公式是一种近似计算阶乘的方法,在n趋近于无穷大时,具有较高的精度。
斯特林公式的表达式如下:n! ≈ √(2πn) * (n/e)^n其中,π是圆周率,e是自然对数的底数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
}
c[len] = '\0';
int i = 0, j = len - 1;
for(;i < j; i++, j--)
{
char temp = c[i];
c[i] = c[j];
c[j] = temp;
}
return c;
}
cout<<"input a number:";
cin>>num;
//cout<<convert(num)<<endl;
char ch[10000] = "1";
for(i = 2; i <= num; i++)
{
strcpy(ch, multi(ch, convert(i)));//乘出后的结果赋给ch数组
a[j + 1] = a[j];
a[0] = 0;
len++;
}
}
//求出结果后。满10向前进一位
for(i = len - 1; i > 0; i--)
{
a[i - 1] += a[i] /10;
a[i] %= 10;
}
if(a[0] > 10)//当第一位数大于10的时候说明位数不够
a[0] = temp % 10;
temp /= 10;
len++;
}
}
//将整形数组转换乘字符数组
char *c = new char[10000];
for(i = 0; i < len; i++)
{
c[i] = a[i] + '0';
max = p;
}
else
{
min = p;
max = q;
}
int len = strlen(max);
for(i = strlen(min) - 1; i >= 0; i--)//乘法----是长的字符串依次乘以短的字符串
{
for(j = 0; j < strlen(max); j++)
{
a[j] += (min[i] - '0') * (max[j] - '0');//将乘出来的结果保存在整形数组a中
}
if(i > 0)//当短的字符串没有遍历完时,数据要向后移动一位,仔细想想乘法口诀表,很好理解的(个位数成完后,十位数写在个位数前面)
{
for(j = len - 1; j >= 0; j--)
}
char *multi(char *p, char *q)
{
char *min, *max;//max存放长度长的字符串,min存放长度短的字符串
int a[10000] = {0}, i, j;
if(strlen(p) > strlen(q))
{
min = q;
{
int temp = a[0];
a[0] = temp % 10;
temp /= 10;
while(temp)//将位数补齐
{
for(i = len - 1; i >= 0; i--)
{
a[i + 1] = a[i];
}
}
c[i] = '\0';
return c;
}
char *convert(int n)//这个就不用解释了吧...
{
char *c = new char[10000];
int len = 0;
while(n) 10 + '0';
}
int totalNum = 0;
//从后往前搜索,出现ch[i] != '0'的时候跳出循环
for(i = strlen(ch) - 1; i >= 0; i--)
{
if(ch[i] != '0')
break;
totalNum++;
}
cout<<totalNum<<endl;
#include<iostream>
#include<string.h>
using namespace std;
char *multi(char *p, char *q);//大乘法
char *convert(int n);//将整形转换成字符串
void main()
{
int num, i;
