极值的概念与费马定理
高考数学讲义微专题17函数的极值(含详细解析)

微专题17 函数的极值一、基础知识: 1、函数极值的概念:(1)极大值:一般地,设函数()f x 在点0x 及其附近有定义,如果对0x 附近的所有的点都有()()0f x f x <,就说()0f x 是函数()f x 的一个极大值,记作()0y f x =极大值,其中0x 是极大值点(2)极小值:一般地,设函数()f x 在点0x 及其附近有定义,如果对0x 附近的所有的点都有()()0f x f x >,就说()0f x 是函数()f x 的一个极小值,记作()0y f x =极小值,其中0x 是极小值点极大值与极小值统称为极值2、在定义中,取得极值的点称为极值点,极值点是自变量的值,极值指的是函数值。
请注意以下几点:(1)极值是一个局部概念:由定义,极值只是某个点的函数值与它附近点的函数值比较是最大或最小并不意味着它在函数的整个的定义域内最大或最小(2)函数的极值不是唯一的即一个函数在某区间上或定义域内极大值或极小值可以不止一个(3)极大值与极小值之间无确定的大小关系即一个函数的极大值未必大于极小值(4)函数的极值点一定出现在区间的内部,区间的端点不能成为极值点 3、极值点的作用:(1)极值点为单调区间的分界点 (2)极值点是函数最值点的候选点4、费马引理:()f x 在0x x =处可导,那么0x x =为()f x 的一个极值点⇒()0'0f x = 说明:①前提条件:()f x 在0x x =处可导②单向箭头:在可导的前提下,极值点⇒导数0=,但是导数0=不能推出0x x =为()f x 的一个极值点,例如:3y x =在()0,0处导数值为0,但0x =不是极值点③费马引理告诉我们,判断极值点可以通过导数来进行,但是极值点的定义与导数无关(例如:y x =在()0,0处不可导,但是0x =为函数的极小值点) 5、求极值点的步骤: (1)筛选: 令()'0fx =求出()'f x 的零点(此时求出的点有可能是极值点)(2)精选:判断函数通过()'f x 的零点时,其单调性是否发生变化,若发生变化,则该点为极值点,否则不是极值点(3)定性: 通过函数单调性判断出是极大值点还是极小值点:先增后减→极大值点,先减后增→极小值点6、在综合题分析一个函数时,可致力于求出函数的单调区间,当求出单调区间时,极值点作为单调区间的分界点也自然体现出来,并且可根据单调性判断是极大值点还是极小指点,换言之,求极值的过程实质就是求函数单调区间的过程。
考研数学必考的定理证明整理

考研数学必考的定理证明整理在考研数学中,有一些定理是非常重要且必考的,掌握了这些定理的证明方法,可以在考试中帮助我们更好地理解和解答数学问题。
下面整理了一些考研数学中必考的定理证明,希望对大家复习有所帮助。
1.逆序数定理:逆序数是指在一个排列中,如果一个数之前有比它大的数,则称这个数是逆序的。
逆序数定理指出,对于任意的排列,其逆序数的奇偶性与该排列的逆序数的个数是相同的。
即如果逆序数的个数是偶数,则排列的逆序数是偶数;如果逆序数的个数是奇数,则排列的逆序数是奇数。
证明思路:利用归纳法进行证明,首先证明初始情况成立,然后假设逆序数的定理对于所有小于n的情况成立,再证明对于n的情况也成立。
2.幂级数:幂级数在数学中是一个重要的概念,特别是在微积分和函数论中应用广泛。
幂级数的收敛半径和收敛域是幂级数的重要性质。
幂级数的收敛半径可以通过柯西-阿达玛公式求得,而收敛域的边界上收敛性需要通过级数的边界性分析得到。
证明思路:根据幂级数的定义,首先确定幂级数的通项项、幂级数求和函数的定义域和收敛半径。
然后通过柯西-阿达玛公式计算幂级数的收敛半径。
最后通过比较判断幂级数的收敛性。
3.极值定理:极值定理也是考研中的一个重要定理,它指出一个连续函数在闭区间上必有最大值和最小值。
极值定理有两个重要的推论,即费马定理和魏尔斯特拉斯定理。
费马定理指出,如果函数在一点处取得极值,则该点处的导数为0。
魏尔斯特拉斯定理指出,一个函数在闭区间上连续,则它在该区间上必有最大值和最小值。
证明思路:根据连续函数的定义和闭区间的定义,利用极值定理的条件和结论,通过反证法进行证明。
首先假设函数在闭区间上没有取得最大值或最小值,然后通过构造序列和利用辅助函数等方法逐步推导出矛盾,从而证明极值定理成立。
以上是一些考研数学中必考的定理证明,这些定理在数学理论和应用中都有着重要的地位,掌握了它们的证明方法可以提高我们对数学知识的理解和应用能力。
在备考过程中,除了熟悉定理的证明过程,还要注意练习相关的例题和应用题,加强对定理的理解和掌握,提高解题的能力。
费马定理极值必要条件

费马定理极值必要条件1.引言1.1 概述费马定理是数学中的一个重要定理,它关于极值问题给出了一个必要条件。
极值问题是数学中研究函数在一定区间上取得最大值或最小值的问题,它在经济学、物理学、工程学等领域中都有着广泛的应用。
费马定理通过对函数的导数进行分析,给出了一个在极值点附近的特殊性质。
本文将首先介绍费马定理的背景和相关概念,然后从数学推导的角度解释极值必要条件,并最终利用费马定理推导出极值必要条件的表达式。
通过本文的阐述,读者将能够更加深入地理解极值问题以及费马定理的作用。
1.2 文章结构本文主要分为引言、正文和结论三个部分。
引言部分包括概述、文章结构和目的三个小节。
概述部分将简要介绍费马定理的极值问题及其重要性。
文章结构部分将详细说明本文按照怎样的顺序和方式来讨论费马定理的极值必要条件。
目的部分将阐明本文的写作目的,即通过对费马定理的极值必要条件的推导和讨论,帮助读者更好地理解和运用该定理。
正文部分主要分为费马定理的介绍与极值问题的背景两个小节。
费马定理的介绍将回顾费马定理的基本定义和主要内容,介绍其在求解极值问题中的重要作用。
极值问题的背景将探讨极值问题的起源和应用领域,并举例说明极值问题在实际生活和科学研究中的重要性。
结论部分主要包括极值必要条件的推导和费马定理的极值必要条件两个小节。
极值必要条件的推导将详细推导出费马定理的极值必要条件,通过对导数的分析和运用,解释为什么该定理能够有效地帮助我们找到极值点。
费马定理的极值必要条件将阐述该定理在实际问题中的应用,并列举一些实例进行说明。
综上所述,本文将通过分析费马定理的极值必要条件,帮助读者更好地理解和运用该定理,并展示该定理在求解极值问题中的重要性和应用价值。
1.3 目的本文旨在探讨费马定理在极值问题中的应用,并推导出极值条件的必要性。
通过深入研究费马定理的原理和极值问题的背景,我们将阐述费马定理的极值必要条件,帮助读者更好地理解极值问题的求解过程。
费马最后定理数学概念

费马最后定理数学概念
费马原理最早由法国科学家皮埃尔·德·费马在1660年提出,又名“最短光时”原理.费马原理:光沿着所需时间为平稳的路径传播.(所谓的平稳是数学上的变分概念,可以简单理解为一阶导数为零,它可以是极大值、极小值甚至是拐点.多数情况是极小值.宇宙学中指的时空透镜就是极大值,椭圆状镜面的表面则是拐点.)光程s=n l(n 为光所在介质的折射率,l为几何路程) 又因为 n=c/v 和 l=vt 所以得到 s=ct.由此可见,光在某种介质中的光程等于同一时间内光在真空中所走的几何路程.费马原理指出,光从一点传播到另一点,其间无论经过多少次折射和反射,光程为极值.也就是说,光是沿着光程为极值(极大值、极小值或常量)的路径传播的.。
微分中值定理

四 柯西(cauchy)中值定理 1 定理: 设f ( x), g ( x)在[a, b]上连续, 在(a, b)内可导, 且g ′( x) ≠ 0, x ∈ (a, b)
f ′(ξ ) f (b) − f (a ) 则∃ξ ∈ (a, b), 使得 = g ′(ξ ) g (b) − g (a )
b−a
② 令θ = ξ − a ,
Q ξ ∈ ( a, b)
∴θ ∈ (0,1), ξ = a + θ (b − a )
∴ f (b) − f (a ) = f ′(a + θ (b − a))(b − a), θ ∈ (0,1)
③
再令b = a + h, 则有f (a + h) − f (a ) = f ′(a + θ h)h,
则F ( x)在[a, b]上满足Rolle定理的条件,∴ ∃ξ ∈ (a, b), 使F ′(ξ ) = 0
f ′(ξ ) f (b) − f (a ) f (b) − f (a ) 即f ′(ξ ) − g ′(ξ ), g ′(ξ ) ≠ 0, ∴ = g (b) − g (a ) g ′(ξ ) g (b) − g (a )
∴依x1 , x2的任意性知, f ( x)在[a, b]上严格单增
类似地有
若f ′( x) < 0, 则f ( x)在[a, b]上严格递减
【4-1-16】
例6 证明不等式
x < ln(1 + x) < x, x > 0 1+ x
证明: 证明: Q f ( x) = ln(1 + x)在[0, +∞)连续可导,
第四章 §4.1
趣谈极值问题

趣谈极值问题1 引言在我们生活中经常遇到各种各样的数学问题,应用不同的数学理论来解决相应的问题,会起到意想不到的效果,使我们的生活简单化,并且在日常生活中不断发现数学的美.极值理论是数学分析中一个很重要的知识点,而且在我们现实生活中也有很强的应用价值.希望通过讨论函数极值问题,使我们对相关的定理理解更深刻,也提高解决实际问题的能力,从而加深对函数性质的认识,同时提高自己的数学修养.2 一元函数极值2.1 一元函数极值的概念与求法 定义2.1)92](1[P 若函数)(x f 在点0x 的某邻域)(0x U 内对一切∈x )(0x U 有)(0x f ≥)(x f )((0x f ≤))(x f则称函数)(x f 在点0x 取得极大(小)值,称点0x 为极大(小)值点.极大值、极小值统称为极值,极大值点、极小值点统称为极值点.显然,极值是一个局部概念,与其定义中的邻域究竟有多大无关紧要. 定义2.2)93](1[P 若0)(0='x f ,则点0x 称为函数)(x f 的驻点或稳定点.定理2.1(费马定理))93](1[P 若函数)(x f 在点0x 的邻域),(00δδ+-x x 内有定义,且在点0x 可导.若点0x 为)(x f 的极值点,则0)(0='x f .也就是说,可微函数的极值点必定是驻点.费马定理的几何意义是:若函数)(x f 在点0x 处达到极值,且)(0x f '存在,则曲线=y )(x f 在点))(,(000x f x M 处有水平切线.费马定理给出了可导函数取极值的必要条件,但其逆不真.也就是说导数为零的点不一定是极值点,例)(x f 3x =在0=x 处0)0(='f ,但0=x 不是极值点.求极值的方法步骤:(1)求可疑点.可疑点包括:1)稳定点(亦称为驻点,指一阶导数等于零的点);2)导数不存在的点;3)区间端点.(2)对可疑点进行判断.基本方法是: 1)用定义判断; 2)用实际背景进行判断;3)查看一阶导数的符号,当x 从左向右穿越可疑点0x ,若)(x f '的符号由“正”变为“负”,则)(0x f 为极大值由,“负”变为“正”,则)(0x f 为极小值,不变号,则)(0x f 不是极值.4)若0)(0='x f ,则(1)当0)(0<''x f 时,)(0x f 为极大值(2)当0)(0>''x f 时,)(0x f 为极小值.5)0)(0)(=x f k )1,,2,1(-=n k Λ,0)(0)(≠x f n ,若n 为偶数,则)(0x f 为极值且当0)(0)(<x fn 时)(0x f 为极大值,当0)(0)(>x f n 时)(0x f 为极小值.若n 为奇数,则)(0x f 不是极值.例1 设函数)(x y y =由方程1222223=-+-x xy y y 确定的,求)(x y y =的驻点,并判断其 驻点是否为极值点?解 将1222223=-+-x xy y y 两边对x 求导,有0222462=-'++'-'x y x y y y y y ,得 xy y yx y +--='232. 令0='y ,得x y =,将x y =代入原方程,得12222223=-+-x x x x ,即 0)12)(1(2=++-x x x , 得驻点1=x ,从而y =1=x .将0222462=-'++'-'x y x y y y y y ,两边再对x 求导得022224)(46)(12222=-''+'+'+''-'-''+'y x y y y y y y y y y ,将 y =1=x ,0)1(='y 代入上式,得 021)1(>=''y . 所以)(x y y =在1=x 处取得极小值.例2 设)(x f 在x 0=的某邻域内连续,且0)0(=f ,2cos 1)(lim 0=-→xx f x ,问)(x f 在x 0=处有无极值,是极大值还是极小值?解 由02cos 1)(lim0>=-→xx f x 及极限的保号性定理知,在0=x 的某一去心邻域内恒有0cos 1)(>-xx f ,而0cos 1>-x ,所以0)(>x f =)0(f ,说明)(x f 在0=x 处取极值,且为极小值.2.2 利用极值证明相关问题例3 设函数)(x f 在),(+∞-∞内二阶可导且满足xe xf x x f x --='+''1)]([3)(2,又)(x f 在0x )0(0≠x 处取得极值,证明:)(0x f 是)(x f 的极小值.证明 因为)(x f 在0x 处取得极值,且)(0x f '存在,所以0)(0='x f . 代入已知等式得:0x ='')(0x f 01x e --,则='')(0x f 01x e x --.当00<x 时 10>-x e⇒0)(0>''x f ;当00>x 时 10<-x e ⇒0)(0>''x f .所以当0x 0≠时,)(0x f 是)(x f 的极小值.2.3 极值的应用问题所谓最值,指最大值、最小值.它要求极值定义里的不等式在整个定义域里统统成立.也可以 说最值是整体极值.显然内部最值必为极值,反之未必.求最值时,有时为了省事,在求出可疑点之后,不判断极大、极小,可将所有可疑点的值拿来比较,其中最大、最小者就是整体最大、最小值.求函数最值的两种常用情况:(1)单峰函数:若)(x f 在连续的开区间),(b a 内仅有一个极值点0x ,且)(0x f 是极大(小)值时,则)(0x f 必是函数在闭区间],[b a 上的最大(小)值,求解极值应用问题大多属于此种情况.(2)单调函数:若)(x f 在连续的闭区间],[b a 上是单调增加(减少)的,则最值必在区间端点取得.例4)293](5[P 已知小球半径为r ,求其外切圆锥的最小体积.解法一 如图1,记圆锥底圆半径为R ,圆锥高为h ,圆锥中轴线与母线夹角为θ,则rhh r r r h r h R 2)(tan 222-=--==θ,r h h r R 222-= 故圆锥体积 r h h r h R V 2331222-⋅==ππ.令0)2()4()2(22=--='-r h r h h r h h h ,得0=h ,r 4. 因为0=h 不合题意,故r h 4=.⋅='32r V π2)2()4(r h r h h --在r h 4=邻域里从左到右由负变为正,故 38423322minr r h r h h r V ππ==-⋅=.图1解法二 r r r h ⋅+=+=θθθsin sin 1sin ,θtan ⋅=h R h h V ⋅=2)tan (31θπ)1()1(31cos sin )1(sin 3123233x x x r r-+=+=πθθθπ(其中令x =θsin ), 令0)1()1(2='⎪⎪⎭⎫ ⎝⎛-+x x x ,得311=x ,12-=x (舍去),实际背景有最小值,只有一个可疑点. 故 383minr V π= (这时31sin =θ).例5 一房地产公司有50套公寓要出租,当月租金为1000元时,公寓会全部租出去,当月租金每增加50元时,就会多一套公寓租不出去,而租出去的公寓每月需花费100元的维修费,试问房租定为多少可获得最大收入?解 设房租定为x 元时可获得的收入为)(x f ,则租出去的公寓数目为50350050100050xx -=--由题意知5035003600)100(503500)(2-+-=--=x x x x x f令 05036002)(=+-='x x f , 得=x 1800.Rrhθ又因为0251)(<-=''x f ,所以当=x 1800时,)(x f 取得极大值即最大值. 故房租定为1800时,可获得最大收入.注 求实际问题的极值时要注意:(1)要明确目标函数;(2)必须选择恰当的自变量,使之能最简捷地表达目标函数.3 多元函数极值多元函数极值是多元函数微分学的重要应用,这里我们以二元函数为例进行讨论. 3.1 自由极值 定义3.1)136](2[P 设函数f 在点),(000y x P 的某邻域)(0P U 内有定义,若对于任何点)(),(0P U y x P ∈,恒有)()(0P f P f ≤ (或)()(0P f P f ≥)则称函数f 在点0P 取得极大(或极小)值,点0P 称为f 的极大(或极小)值点.极大值、极小值统称为极值,极大值点、极小值点统称为极值点.定理3.1(极值的必要条件))136](2[P 若函数f 在点),(000y x P 存在偏导数,且在0P 取得极值,则有 0),(00=y x f x ,0),(00=y x f y .定义3.2)136](2[P 若函数f 在点0P 满足0),(00=y x f x ,0),(00=y x f y ,则称点0P 为函数f 的稳定点.注 若f 存在偏导数,则其极值点必是稳定点,但稳定点并不都是极值点.如xy y x z =),(,原点为其稳定点,但它在原点并不取得极值.求自由极值的方法步骤:(1)求可疑点,可疑点包括:1)稳定点(即一阶偏导数同时等于零的点);2)使至少某一阶偏导数不存在的点.(2)对可疑点进行判断.基本方法是: 1)用定义判断; 2)用实际背景进行判断;3)利用二阶导数:若),(00y x f x '=0),(00='y x f y ,记=A 2xy yy xxf f f ''-''''),(00y x ,则当0>A ,且xxf ''0),(00>y x 时,f 在),(00y x 处取(严格)极小值;当0>A ,且xxf ''0),(00<y x 时,f 在),(00y x 处取(严格)极大值;当0<A ,f 在),(00y x 处无极值.多元函数极值有一个观念值得澄清:一元函数的极大值与极小值总是交替地出现,多元函数谈不上交替,甚至只有一种极值(无穷多个),如例6 )689](5[P 证明函数z =),(y x f =yyye x e -+cos )1(有无穷多个极大值,但无极小值.证明 ='x f )1(ye +)sin (x -,yf 'y e y x )1(cos --=,令x f '=0,y f '=0,解方程,可得无穷多个稳定点)1cos ,(),(-=ππn n y x n n ),3,2,1,0(Λ±±±=n .当n 为偶数时,在),(n n y x 上,=A 022>=''-''''xy yy xxf f f ,02<-=''xx f . 故f 在)0,2(πk 上取极大值),3,2,1,0(Λ±±±=k .当n 为奇数时,在),(n n y x 上,0)1(222<+-=''-''''--e e f f f xy yy xx. 此处无极值,总之,f 有无穷多个极大值而无极小值.3.2 条件极值函数满足若干条件(约束方程)的极值称为条件极值. 求条件极值的方法:(1)化为无条件极值,例如求z =),(y x f 在条件0),(=y x ϕ下的极值,若可由0),(=y x ϕ解出)(x y y =代入z =),(y x f 便化为无条件极值.(2)拉格朗日数乘法,如求z =),(y x f 在条件0),(=y x ϕ下的极值,作辅助函数),(),(),,(y x y x f y x L λϕλ+=⎪⎩⎪⎨⎧=='+'='+'0),(0),(),(0),(),(y x y x y x f y x y x f y y x x ϕϕλϕλ 解此方程组,求出),,(λy x L 的驻点),,(000λy x ,),(00y x 是z =),(y x f 在条件0),(=y x ϕ下可能的极值点.例7 设生产某种产品的数量与所用原料A 、B 的数量x 、y 间有关系式y x y x P 2005.0),(=,欲用150元购料,已知A 、B 两种原料的单价分别为1元、2元,问购进两种原料各多少,可使生产的数量最多?解 该题是函数y x y x P 2005.0),(=在1502=+y x 条件下的最大值问题,令)1502(005.0),(2-++=y x y x y x F λ由 ⎪⎩⎪⎨⎧=-+=+='=+='0150202005.0001.02y x x F xy F y x λλ得 ⎩⎨⎧==25100y x当购进A 、B 两种原料的数量分别为100和25时,生产的数量最多,为125件.3.3 求函数在闭区域上的最大值、最小值一般方法:先求函数在区域内部的极大极小值,以及边界上的(条件)极大极小值,然后进行比较.或者,直接将全部可疑点的值进行比较,最大者为最大值,最小者为最小值.例8 确定),(y x f 224y xy x ++=在圆域122≤+y x 上的最大值和最小值.解 因为04),(2>+='y y x f x ,所以在圆内无极值,最大值、最小值均在圆周122=+y x 上取得,这时 )(514),(3222x x x x y xy x y x f ϕ≡--+=++=, 令 0)1)(35(325)(2=-+=--='x x x x x ϕ,根据)(x ϕ'的符号,可知)(x ϕ在]1,1[-上,1-=x 处取最小值,1=x 处取最大值. 从而4)0,1(max ==f f ,4)0,1(min -=-=f f .3.4 利用极值证明不等式 例9)695](5[P 求证:1)1(),(-<-=e x yx y x f y ,10<<x ,+∞<<y 0.证明 ),(y x f 在区域10<<x ,+∞<<y 0的边界上恒为0,而区域内部0),(>y x f .故),(y x f 的最大值只能在内部取得.)()1(),(112x xy y yx yx x x y y x f y y y x --=--='--.x x yx x x y x f y y y ln )1()1(),(-+-=')ln 1)(1(x y x x y +-=.令0),(),(='='y x f y x f y x ,在10<<x ,+∞<<y 0内求稳定点, 得 0=--x xy y 即x x y =-)1( (1) 及 0ln 1=+x y 即1-=e x y (2)这表明),(y x f 在10<<x ,+∞<<y 0内最大值点应满足方程(1)、(2).然而在(1)、(2)所确定的点上 11)1(),(--<=-=e x e x yx y x f y,所以1)1(),(-<-=e x yx y x f y (10<<x ,+∞<<y 0).3.5 极值的应用问题例10 某公司通过电台及报纸做商品的销售广告,据统计销售收入R (万元)与电台广告费1x 万元及报纸广告费2x 万元的函数关系为22212121211028321415),(x x x x x x x x R ---++=,求:(1)在不限广告费时的最优广告费策略.(2)在仅用5.1万元做广告费时的最优广告费策略.解 (1)最优广告策略,即用于电台和报纸的广告费为多少时,可使商品的利润),(21x x L 最大,故目标函数为利润函数,这是一个二元函数的无条件极值问题.记电台和报纸的广告费之和为),(21x x C ,则2121),(x x x x C +=,于是=),(21x x L -),(21x x R =),(21x x C 222121211028311315x x x x x x ---++ )0,0(21>>x x , 令 ⎪⎩⎪⎨⎧=--='=--='02083104813211221x x L x x L x x, 解得⎩⎨⎧==25.175.021x x .所以在不限广告费时的最优广告费策略是用于电台和报纸的广告费各为75.0万元和25.1万元.(2)这是一个条件极值问题,约束条件为5.121=+x x ,一般地从这一约束条件中解出215.1x x -=,代入利润函数得22222222210)5.1(2)5.1(831)5.1(1315)(x x x x x x x L -----+-+=22241230x x -+= )5.10(2≤≤x ,于是将条件极值问题转化为一元函数的普通极值问题.由于08122≥-='x L )5.10(2≤≤x ,这表明L 关于变量2x 是单调增加的,从而L 在5.12=x 时取得极大值.因此,在仅有5.1万元做广告费的条件下,相应的最优广告费策略是将其全部用于报纸广告费用,而不做电台广告.。
费马引理

费马引理费马(Fermat)引理是实分析中的一个定理,以皮埃尔·德·费马命名。
通过证明函数的每一个极值都是驻点(函数的导数在该点为零),该定理给出了一个求出可微函数的最大值和最小值的方法。
因此,利用费马引理,求函数的极值的问题便化为解方程的问题。
需要注意的是,费马引理仅仅给出了函数在某个点为极值的必要条件。
也就是说,有些驻点不是极值,它们是拐点。
要想知道一个驻点是不是极值,并进一步区分最大值和最小值,我们需要分析二阶导数(如果它存在)。
当该点的二阶导数大于零时,该点为极小值点;当该点的二阶导数小于零时,该点为极大值点。
若二阶导数为零,则无法用该法判断,需列表判断。
费马引理的内容:函数f(x)在点x0的某邻域U(x0)内有定义,并且在x0处可导,如果对于任意的x∈U(x0),都有f(x)≤f(x0)(或f(x)≥f(x0)),那f'(x0)=0。
费马引理费马引理说的是怎么个破事呢:函数一极小区间内部的一点是这个极小区间上的最值点(之前已经说过,不是严格的最值点,旁边点的值可以跟这点的值相等),并且这点可导,则这点的导数为0。
为什么说是引理,因为这是证明罗尔定理时要用到的重要条件:
罗尔定理的三个条件是
1)闭区间连续;
2)开区间可导;
3)端点值相等。
所以证明罗尔定理变为用这三个条件证明函数在这个区间上有极值点(不严格的),加上已知的在这点可导,借用费马引理,得到跟费马引理相同的结论,这点的导数为0。
关
于费马引理证明:
1)抽象函数,用导数定义;导数存在,左右导数存在并且相等;
2)极限的保号性(保的是什么,保的是函数的符号为极限的符号)。
极值的定理

极值的定理极值定理,又称费马定理,是微分学中的一个重要定理。
它在数学计算中有着广泛的应用和意义。
极值定理是指在区间[a,b]上连续的函数f(x)要么在内点取得最大值,要么在端点取得最大值。
下面将介绍极值定理的具体内容和应用。
极值定理的核心思想是通过函数的导数来判断函数的极值。
首先,我们需要了解什么是导数。
在数学中,导数表示了函数在某一点的瞬时变化率,也可以理解为函数曲线在该点的切线的斜率。
对于可导函数,如果导数大于零,则函数在该点是递增的;如果导数小于零,则函数在该点是递减的;而导数等于零的点则可能是函数的极值点。
对于区间[a,b]上的函数f(x),如果在内点x0处取得最大值,则必须满足f'(x0)=0。
这是因为如果在x0处导数大于零,则说明函数在x0的右侧是递增的,不可能取得最大值;同样地,如果导数小于零,则说明函数在x0的右侧是递减的,也不可能取得最大值。
因此,导数等于零是函数取得极值的必要条件。
接下来,我们需要判断导数等于零的点是否真的是函数的极值点。
这里引入了极值定理的关键内容:函数的全局性质。
全局性质包括函数的连续性和定义域的闭区间[a,b]。
如果函数f(x)在闭区间[a,b]上连续,并在开区间(a,b)上可导,那么函数必定在[a,b]上有极值。
具体来说,如果在内点x0处导数为零,而在x0的邻域内函数值由正变负,则说明函数在x0处取得最大值;如果在x0的邻域内函数值由负变正,则说明函数在x0处取得最小值。
极值定理的应用非常广泛。
它可以用于求解最大值和最小值问题,例如在经济学中,通过对成本函数或利润函数求导,可以确定最大化利润的产量或价格;在物理学中,通过对物体运动的位移、速度和加速度函数求导,可以确定最大或最小的速度和加速度值;在工程学中,通过对能量函数或材料强度函数求导,可以确定最佳的设计参数等等。
极值定理还可以用于对凸函数和凹函数的判断,凸函数的导数单调递增,凹函数的导数单调递减。
最优解与极值点定理证明

最优解与极值点定理证明那咱就来说说最优解与极值点定理的证明哈。
一、啥是最优解和极值点呢?二、证明极值点定理(以一元函数为例哈)1. 费马定理(这可是基础哦)费马定理说的是,如果函数y = f(x)在点x_0处可导,并且在x_0这个点取得极值(不管是极大值还是极小值),那么f^′(x_0)=0。
咱这么想哈,假如你在山上的一个点是极值点,就像在山顶或者山谷底。
你要是从这个点往旁边稍微走一点点,因为它是极值点嘛,所以高度不会突然增加或者减少得很厉害。
如果函数可导,那就意味着有切线,那这个切线肯定是水平的呀,因为要是切线不水平,那你朝某个方向就会有很明显的上升或者下降,那就不是极值点了。
所以f^′(x_0) = 0。
2. 第一充分条件(判断是极大值还是极小值)设函数y = f(x)在x_0的某个邻域内连续,在去心邻域内可导。
如果当x∈(x_0 δ,x_0)时,f^′(x)>0,而当x∈(x_0,x_0+δ)时,f^′(x)<0,那就说明在x_0的左边函数是上升的,到了x_0右边函数是下降的,那x_0这个点就是极大值点。
就好比你爬山,从左边走过来是上坡,到了这个点后往右边走就是下坡了,这个点就是山顶(极大值点)。
反过来,如果当x∈(x_0 δ,x_0)时,f^′(x)<0,而当x∈(x_0,x_0+δ)时,f^′(x)>0,那就说明x_0是极小值点。
就像走到了山谷底,从左边来是下坡,到了这再往右边走就是上坡啦。
3. 第二充分条件(这个比较简单直接)如果函数y = f(x)在点x_0处二阶可导,且f^′(x_0)=0,f^′′(x_0)<0,那么x_0就是极大值点;如果f^′′(x_0)>0,那么x_0就是极小值点。
你可以这么想,f^′(x_0) = 0说明这个点可能是极值点(就像前面费马定理说的)。
那f^′′(x_0)呢?如果f^′′(x_0)<0,就好比函数的“弯曲方向”是向下的,那这个点就是个山顶(极大值点);要是f^′′(x_0)>0,函数的“弯曲方向”是向上的,那这个点就是山谷底(极小值点)。
高等数学:函数费马引理
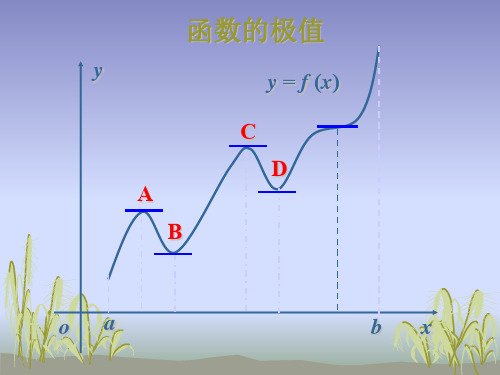
o
(2)若 x U (x0, ) 时, f (x) 的符号保持不变,
则点 x0 不是 f (x) 的极值点.
y
f (x0)=0
f (x)>0
f (x)<0
O
x0
x
x0 是极大值点
f(x0) 是极大值
y
f (x)<0
f (x)>0
注 1:本定理可利用极限的保号性加以证明;
注 2:当 f (x0 ) 0 时,本定理失效!
例如,函数 f (x) x3 时,本定理失效!
因此,遇到一阶导数不存在的点,或驻 点的二阶导数为零,只能用极值判定的第一 充分条件来判断。
例4 求函数y 1 x4 1 x3 x2的极值
y C
A D
B
oa
bx
注1:可导函数 f ( x) 的极值点必定是它的驻点, 但函数的驻点却不一定是极值点.
例如, y x3 , y x0 0, 但x 0不是极值点.
y y x3
Ox
பைடு நூலகம்
注2:极值点有可能是导数不存在的点
例如, f (x) | x | ,x=0 是极值点
又如, y y 3 x2
43
例4 求函数y 1 x4 1 x3 x2的极值
43
y x3 x2 2x x(x 2)(x 1)
求得驻点为 x 1, x 0, x 2
y 3x2 2x 2
y (3x2 2x 2) 3 0
x1
x1
y (3x2 2x 2) 2 0
f
(
x)
费马定理 极值

费马定理极值
费马定理,也被称为费马最后定理,是法国数学家皮埃尔·德·费马在1637年提出的一个著名数学问题。
它的具体内容是:对于任何大于2的整数n,不存在任何非零整数a、b、c,使得a^n + b^n = c^n成立。
关于这个定理的极值,并没有特别明确的定义。
但是,我们可以从这个定理本身来找一些相关的极值。
例如,如果n是一个质数(大于2的整数,且只能被1和它自身整除的数),那么费马定理的左式a^n + b^n就构成了一个数域上的多项式。
在这个情况下,如果费马定理不成立,那么根据阿贝尔不等式(或称算术-几何不等式),我们就得到了一个关于a和b的极值:a^n + b^n至多为c^n,当且仅当a=b时等号成立。
这就是说,如果费马定理不成立,那么a^n + b^n的最大值就是c^n,而且这个最大值只能由a=b时达到。
另一个可能的极值是关于a^n + b^n和c^n的距离。
如果费马定理不成立,那么就一定存在非零整数a、b、c,使得a^n + b^n = c^n 成立。
因此,a^n + b^n和c^n的距离最小值为0。
这也是一种极值。
总的来说,费马定理的极值主要体现在它给出了一些关于多项式的界和关于距离的极值。
fermat极值的显式表示

fermat极值的显式表示
Fermats最优极值解法是数学分析中一种非常有用的解决最优化问题的
方法,这种方法来源于法国数学家费马。
1. Fermats极值定理:如果一个函数可以在拐点处、其中就是处处可导
的点,在拐点处拥有极大值或极小值,则这一函数的导数等于零。
2.最优化原理:当一个函数的取值趋近于极值,与此同时其导数等于零,那么这时候,这个函数即达到了其取值的极值。
3.Fermats极值求解步骤:
(1)设定目标函数,并求得关于未知变量的极值点。
(2)计算极值点所对应的函数值,然后选取函数取值最大/最小值,从而得到最优解。
(3)若极值点处的函数值不是函数取值的最大/最小值,则说明极值点不是最优的解,应搜索更多的极值点进行分析,最终得到最优解。
4. Fermats极值求解的优点:
(1)方便快捷:可以很快的找到最优解,减少搜索的时间;
(2)精准度高:通过解析法求解出的最优解,精确性和有效性都较高;(3)易于理解: Fermats极值求解过程简单,理解起来比较容易。
同时,Fermats极值求解技术也有一定的局限性,临界点只能存在于单
自变量函数中,对于多自变量函数,比如二次型函数,就无法采用Fermats极值求解方法。
因此,要小心地确定求解的方面,才能获得最
佳的求解效果。
2020高考数学100个必考知识点详解17 函数的极值

第17 函数的极值一、基础知识: 1、函数极值的概念:(1)极大值:一般地,设函数()f x 在点0x 及其附近有定义,如果对0x 附近的所有的点都有()()0f x f x <,就说()0f x 是函数()f x 的一个极大值,记作()0y f x =极大值,其中0x 是极大值点(2)极小值:一般地,设函数()f x 在点0x 及其附近有定义,如果对0x 附近的所有的点都有()()0f x f x >,就说()0f x 是函数()f x 的一个极小值,记作()0y f x =极小值,其中0x 是极小值点 极大值与极小值统称为极值2、在定义中,取得极值的点称为极值点,极值点是自变量的值,极值指的是函数值。
请注意以下几点:(1)极值是一个局部概念:由定义,极值只是某个点的函数值与它附近点的函数值比较是最大或最小并不意味着它在函数的整个的定义域内最大或最小(2)函数的极值不是唯一的即一个函数在某区间上或定义域内极大值或极小值可以不止一个(3)极大值与极小值之间无确定的大小关系即一个函数的极大值未必大于极小值(4)函数的极值点一定出现在区间的内部,区间的端点不能成为极值点3、极值点的作用:(1)极值点为单调区间的分界点 (2)极值点是函数最值点的候选点4、费马引理:()f x 在0x x =处可导,那么0x x =为()f x 的一个极值点⇒()0'0f x = 说明:①前提条件:()f x 在0x x =处可导②单向箭头:在可导的前提下,极值点⇒导数0=,但是导数0=不能推出0x x =为()f x 的一个极值点,例如:3y x =在()0,0处导数值为0,但0x =不是极值点③费马引理告诉我们,判断极值点可以通过导数来进行,但是极值点的定义与导数无关(例如:y x =在()0,0处不可导,但是0x =为函数的极小值点) 5、求极值点的步骤: (1)筛选: 令()'0fx =求出()'f x 的零点(此时求出的点有可能是极值点)(2)精选:判断函数通过()'fx 的零点时,其单调性是否发生变化,若发生变化,则该点为极值点,否则不是极值点(3)定性: 通过函数单调性判断出是极大值点还是极小值点:先增后减→极大值点,先减后增→极小值点6、在综合题分析一个函数时,可致力于求出函数的单调区间,当求出单调区间时,极值点作为单调区间的分界点也自然体现出来,并且可根据单调性判断是极大值点还是极小指点,换言之,求极值的过程实质就是求函数单调区间的过程。
极值、最值和凹凸性
注:凹也叫上凹或下凸;凸也叫下凹或上凸。
2、凹向的判定办法
定理:如果 y f (x) 在 (a,b) 内有二阶导数:
(1)若 f (x) 0 , 则曲线 y f (x) 是凹的;
(2)若f (x) 0 , 则曲线 y f (x) 是凸的;
例:判断曲线 y x3 的凹向。
5
2. 求 y (x 2)3 的凹向与拐点。 3.求 y xex的单调性、极值、凹向与拐点。
x4
x5 x6 x7 b x 极值点极 极小 大值 值点 点
注:1.极值是指函数值,极值点是指自变量的值。 2.极值是一个局部性概念,最值则是整体概念。 3. 极值只能在区间内部取得,不能在区间端点处取 得。 4.容易看出,极值点是单调区间的分界点。
y
y=f(x)
x3
O a x1 x2
x4
可能的 不可导点 极值点驻点(可导)
x5 x6 x7 b x
二、极值的必要条件 费马定理:如果f(x) 在x0处可导,且在x0处取得极值, 则 f ' (x0) . 注:1.可导函数的极值点必定是它的驻点,反之不然。 如: f(x)= x3. 2.不可导点也可能是极值点。如: f(x)=| x |.
y
f (x)>0
f (x)<0
例:求y=x4–2x2+5在[–2,3]上的最值。
练习:求y=ln(x2+1) 在[–1,2] 上的最值。 答案:ymax ln 5 ymin 0 二、两种特殊情形下函数的最值 1.函数f(x)在[a,b]上是单调的,显然它在区间端点 取得最大值和最小值;
2.可导函数的唯一极值 f(x0)一定是最值。 例:证明:当x≠0时,有ex >1+x . 注:利用最大(小)值办法证明不等式的方法:将 不等式写成是f(x)≥0,然后证明f(x)的最小值非负。
费马定理

定理及其证明费马定理:设)(f x 在c 的某邻域)(δδ+-c c ,内有定义,而且在这个领域上有)()(c f x f ≤(其中)c (f 为局部最大值)或者)()(c f x f ≥(其中)c (f 为局部最小值),当)(f x 在c 处可导时,则有0)c ('=f .证明:因为假设)c ('f 存在,由定义可得左导数)('-x f 和右导数)(f 'c +均存在且满足:)(f )()('''-c c f c f ==+当c x <时,0)()(≥--c x c f x f ,所以0)(f )(lim )(f '≥--=-→c x c x f c c x当c >x 时,0)()(≤--c x c f x f ,所以0)(f )(lim)(f '≤--=+→c x c x f c cx 所以0)c ('=f以上是对于)()(c f x f ≤这种情况进行的证明,同理也可证明)()(c f x f ≥这种情形 罗尔定理:设)(f x 在[]b ,a 上连续,在()b ,a 上可导,若)()a (b f f =,则必有一点()b a ,c ∈使得0)c ('=f .证明:分两种情况,若)(f x 为常值,结论显然成立.若)(f x 不为常值,根据最大、最小值定理(有界闭区间[]b ,a 上的连续函数)(f x 具有最大值和最小值)可知,)(f x 必在()b ,a 内某一点c 处达到最大值或最小值,再有费马定理可得,0)c ('=f .拉格朗日中值定理:设)(f x 在[]b ,a 上连续,在()b ,a 上可导,则一定有一点()b ,a ∈ξ使ab a f --=)(f )b ()(f 'ξ.证明:分两种情况,若)(f x 恒为常数,则0)x ('=f 在()b ,a 上处处成立,则定理结论明显成立.若)(f x 在[]b ,a 不恒为常数时,由于)(f x 在[]b ,a 上连续,由闭区间连续函数的性质,)(f x 必在[]b ,a 上达到其最大值M 和最小值m ,有一种特殊情况)()a (b f f =时,定理成立,这就是上面所证明过的罗尔定理.考虑一般情形,)()a (b f f ≠.做辅助函数x )(f )b ()(f )x (ab a f x ---=ϕ.由连续函数的性质及导数运算法则,可得)x (ϕ在[]b ,a 上连续,在()b ,a 上可导,且()a ab b a bf ϕϕ=--=)(f )a ()b (,这就是说)x (ϕ满足刚刚的特殊情况,因此在()b ,a 内至少有一点ξ,使得()0)(f )b (f )(''=---=ab a f ξξϕ.即()ab a f --=)(f )b (f 'ξ.定理得证. 柯西中值定理:若)(f x 和)(g x 在[]b ,a 上连续,在()b ,a 上可导,且0)x (g '≠,则一定存在()b ,a ∈ξ使()()()()ξξ''g )(f )b (g f a g b a f =--. 证明:首先能肯定)()a (g b g ≠,因为如果)()a (g b g =,那么由拉格朗日中值定理,)x (g '在()b ,a 内存在零点,因此与假设矛盾. 还是做辅助函数()()()()()a g a g b a f x F ----=x g g )(f )b ()(f )x (.由()()b F F =a ,再由拉格朗日中值定理,可以证明定理成立.泰勒中值定理:若)(f x 在0x =点的某个邻域内有直到1n +阶连续导数,那么在此邻域内有()()()()()()()x R x n f x f f f x n nn +++++=!0...!20x 00f 2'''.其中()()()()11n x !1+++=n n n f x R ξ.ξ是介于0与x 之间的某个值.证明:做辅助函数()()()()()()()()()()n n t x n t f t x t f t x t f t f x f -------+=!...!2t 2'''ϕ.由假设容易看出()t ϕ在[]x ,0或[]0,x 上连续,且()()x R n 0=ϕ,()0x =ϕ,()()()()()[]()()()()()()()()()()()()()()()⎥⎦⎤⎢⎣⎡-----------⎥⎦⎤⎢⎣⎡------=-+11n 2'''''2''''''''!1!...!2...f -!2-f n n n t x n t f t x n t f t x t f t x t f t x t t x t f t f t x t f t t ϕ化简后有()()()()n 1n '!-t x n t f t -=+ϕ.在引进一个辅助函数()()1t +-=n t x ψ.对函数()t ϕ和()t ψ利用柯西中值定理得到()()()()()()ξψξϕψψϕϕ''00x =--x ,ξ是介于0与x 之间的某个值,此时有()()x R n 0=ϕ,()0x =ϕ,()()()()n x n f ξξξϕ-=+!-1n ',()1n x 0+=ψ,()0x =ψ,()()()nx ξξψ-+=1n -',代入上式,即得()()()()11n x !1+++=n n n f x R ξ.定理证明完毕.这是函数()x f 在0x =点的泰勒公式,同理推导可得()x f 在0x x =点附近的泰勒公式()()()()()()()()()()x R x x n x f x x x f x x x f x f x n n o n +-++-+-+=0200''00'0!...!2f .其中()()()()()101n !1++-+=n n x x n f x R ξ.ξ是介于0x 与x 之间的某个值.定理间关系:罗尔定理,拉格朗日定理,柯西定理以及泰勒公式是微分学的基本定理。
函数的极值与最大[小]值
![函数的极值与最大[小]值](https://img.taocdn.com/s3/m/50f69effce2f0066f433221e.png)
2 求开区间上函数的最值稍复杂些, 因为开区间上的连续 函数甚至可以没有最值,常需要利用导函数f 的符号,即f 的 单调性,以及自变量趋于区间端点时函数的极限,对f 的全局性 态作大致的分析,进而确定函数的最值, 但有一个特殊情况下, 可确定开区间上函数的极值必是最值:
如果 (1) 目标函数 f ( x )在所讨论的区间 I(开或闭,有限或无限) 内处处可微; (2) f ( x ) 在区间 I 内部只有一个驻点 x 0 ,则在驻点 x 0 取 得极值 f ( x 0 ) ; (3)若 f ( x 0 )是极大值,这极大值就是其最大值;若 f ( x 0源自) 是极 小值,这极小值就是其最小值.
8 6 4 f( 6 ) = ( 2 + 3) 6 > 0 x = 6= x
依定理6.11, x = 6 为
f
的极小值点,极小值
f (6)=108.
定理6.12 (极值的第三充分条件) 设 f 在 x 0 的某邻域内存 ( k ) 在直到n-1阶导函数,在 x 0 处n阶可导且 f ( x ) = 0 ( k = 1 , 2 , … , n 1 ) , 0 f n x0 0, 则 (ⅰ)当n为偶数时, f 在 x 0 处取得极值,且当 f (n)(x0) 0 时 取极大值,f (n)(x0) 0 时取极小值. (ⅱ)当n为奇数时, f 在 x 0 处不取极值. 该定理的证明类似于定理6.11,我们将它留给读者.
4 4 0 ) f( 1 ) 0 及 f( ) 0 , 由此得 f ( 所以 f ( x )在x 时取得极小 7 7
值.求三阶导数 3 2 fx ( )6 x ( 3 5 x 6 0 x 3 04 x ) ( 0 ) 0 , f ( 1 ) 0 . 由于 n = 3 为奇数,由定理6.12知 有 f 在 x 1不取极值.再求四阶导数
极值的概念与费马定律

第4章微分中值定理和导数的应用【第4章导语】我们学习了导数与微分的概念,并掌握了初等函数与某些特殊函数的求导运算.本章主要介绍导数在研究函数性态和解决有关实际问题中的应用,给出利用导数解决一些具体问题的一般方法.由于导数只是反映了函数在一点的性质,为了将其与函数在某个范围上的性态联系起来,就需要寻找它们之间的一座桥梁,微分中值定理就承担了桥梁的作用,它是导数应用的理论基础.§4.1 极值与极值点【导语】【正文】一、极值与极值点概念定义1 设函数()f x 在0x x =的某个邻域0(,)U x δ中有定义.如果对任意0(,)x U x δ∈,都有()()0f x f x ≥成立,则称0x 是函数()f x 的一个极小值点,0()f x 称为函数()f x 的一个极小值;如果对任意0(,)x U x δ∈,都有()()0f x f x ≤成立,则称0x 是函数()f x 的一个极大值点,0()f x 称为函数()f x 的一个极大值.极大值与极小值统称为极值,极大值点与极小值点统称为极值点.函数定义区间的端点不会是函数的极值点.函数的极值是一个局部性的概念,它的大小只是与极值点0x 附近其他点的函数值作比较,函数的极大值不一定大于其极小值.如图,1()f x 和3()f x 是函数()y f x =的极大值,2()f x 和4()f x 是函数()y f x =的极小值,而1()f x <4()f x .二、费马(Fermat )定理在图中,假设连续曲线()y f x =除了端点外,处处都有切线.从图中可以看出在局部最高点11(,())x f x 和33(,())x f x ,以及在局部最低点22(,())x f x 和44(,())x f x ,曲线的切线都是水平的.定理1 如果函数)(x f 在0x 处可导,且在0x 处取得极值,那么函数)(x f 在0x 处的导数为零,即0)(0=′x f .证不妨假设0()f x 是极大值.因为函数()f x 在点0x 处可导,所以0()f x −′与+0()f x ′均存在,且00+0()()()f x f x f x −′′′==.当0x x −→时,因为0()()0f x f x −≤,00x x −<,所以根据极限的局部保号性,可知0000()()()lim 0x x f x f x f x x x −−→−′=−≥.当0x x +→时,因为0()()0f x f x −≤,00x x −>,所以根据极限的局部保号性,可知0000()()()lim 0x x f x f x f x x x ++→−′=−≤.综上可知0()0f x ′=.导数等于零的点称为函数的驻点或临界点.费马定理说明,函数的可导极值点一定是驻点.驻点是否一定是极值点呢?函数3()f x x =在0x =处的导数为零,但0x =却不是它的极值点!导数不存在的点是否可以是极值点?函数()||f x x =在0x =处的导数不存在,但0 x=却是它的极小值点!函数)(x f 的极值点在()0f x ′=或()f x ′不存在的点中.例1 求函数32()215241f x x x x =−++的驻点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第4章 微分中值定理和导数的应用
【第4章导语】
我们学习了导数与微分的概念,并掌握了初等函数与某些特殊函数的求导运算.本章主要介绍导数在研究函数性态和解决有关实际问题中的应用,给出利用导数解决一些具体问题的一般方法.由于导数只是反映了函数在一点的性质,为了将其与函数在某个范围上的性态联系起来,就需要寻找它们之间的一座桥梁,微分中值定理就承担了桥梁的作用,它是导数应用的理论基础.
§4.1 极值与极值点
【导语】
【正文】
一、极值与极值点概念
定义1 设函数()f x 在0x x =的某个邻域0(,)U x δ中有定义. 如果对任意0(,)x U x δ∈,都有()()0f x f x ≥成立,则称0x 是函数()f x 的一个极小值点,0()f x 称为函数()f x 的一个极小值;
如果对任意0(,)x U x δ∈,都有()()0f x f x ≤成立,则称0x 是函数()f x 的一个极大值点,0()f x 称为函数()f x 的一个极大值.
极大值与极小值统称为极值,极大值点与极小值点统称为极值点.
函数定义区间的端点不会是函数的极值点.
函数的极值是一个局部性的概念,它的大小只是与极值点0x 附近其他点的函数值作比较,函数的极大值不一定大于其极小值.
如图,
1()f x 和3()f x 是函数()y f x =的极大值,2()
f x 和4()f x 是函数()y f x =的极小值,而1()f x <4()f x .
二、费马(Fermat )定理
在图中,假设连续曲线()y f x =除了端点外,处处都有
切线.从图中可以看出在局部最高点11(,())x f x 和33(,())x f x ,
以及在局部最低点22(,())x f x 和44(,())x f x ,曲线的切线都是水平的.
定理1 如果函数)(x f 在0x 处可导,且在0x 处取得极值,那么函数)(x f 在0x 处的导数为零,即0)(0=′x f .
证 不妨假设0()f x 是极大值.
因为函数()f x 在点0x 处可导,所以0()f x −′与+0()f x ′均存在,且
00+0()()()f x f x f x −
′′′==. 当0x x −→时,因为
0()()0f x f x −≤,00x x −<,
所以根据极限的局部保号性,可知
0000
()()()lim 0x x f x f x f x x x −−→−′=−≥. 当0x x +→时,因为
0()()0f x f x −≤,00x x −>,
所以根据极限的局部保号性,可知
0000
()()()lim 0x x f x f x f x x x ++→−′=−≤.
综上可知 0()0f x ′=.
导数等于零的点称为函数的驻点或临界点. 费马定理说明,函数的可导极值点一定是驻点.驻点是否一定是极值点呢?
函数3()f x x =在0x =处的导数为零,但0x =却不是它的极值点!
导数不存在的点是否可以是极值点?函数()||f x x =在0x =处的导数不存在,但0
x
=
却是它的极小值点!
函数)(x f 的极值点在()0f x ′=或()f x ′不存在的点中.
例1 求函数32()215241f x x x x =−++的驻点。
解 由32()215241f x x x x =−++,得
2()630246(1)(4)f x x x x x ′=−+=−−。
令 ()0f x ′=得驻点1x =和4x =。
例2 求函数21()sin cos 2f x x x x x =−−
的驻点。
解 由21()sin cos 2
f x x x x x =−−,得 ()cos cos sin (sin 1)f x x x x x x x x ′=−+−=−。
令 ()0f x ′=得驻点0x =和π2π2
x n =
+(n 是整数)。
例3 设函数()f x 在[,]a b 内可导.若()()f a f b ′′≠,则对于任意的介于()f a ′与()f b ′之间的µ,总存在(,)a b ξ∈,使得()f ξµ′=.
分析 ()()0[(x)]0f f f x ξξµξµµ′′′=⇔−=⇔−=。
证 令()()F x f x x µ=
−,则()()0F a F b ′′<.不妨设()0F a ′>,()0F b ′<.
由于()0F a ′>,所以存在1(,)x a b ∈,使得1()()F x F a >;
又因为()0F b ′<,所以存在21(,)x x b ∈,使得2()()F x F b >. 因为()[,]F x C a b ∈,所以()F x 在区间[,]a b 取得最大值()F ξ,且最大值点ξ在开区间(,)a b 内取到.
根据Fermat 定理可知()()0F f ξξµ′′=−=,即()f ξµ′=.
【本讲总结与下讲预告】。
